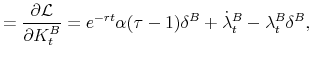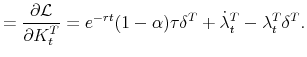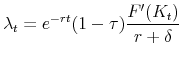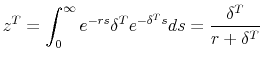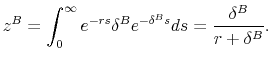Investment, Accounting, and the Salience of the Corporate Income Tax
Keywords: Investment, taxes, bonus depreciation, expensing, accounting, salience.
Abstract:
JEL Codes: H25, H32, G31, M41.
1 Introduction
The effects of taxation on capital formation have inspired a great deal of economic research and frequent tax policy changes. Striking results from Chamley (1986) and Judd (1985) indicate that the socially optimal tax system involves no distortion to capital investment decisions, which is often interpreted as a zero tax rate on capital income. However, Hall and Jorgenson (1967) and, more recently, Abel (2007), have stressed that the size of any distortion from capital income taxation does not depend solely on the statutory tax rate, but also on the timing of deductions from taxable income that firms may take to account for depreciation. Under "expensing," when all investment spending is fully deductible in the year of purchase, investment decisions may not be distorted at all.1
The U.S. government has used accelerated depreciation provisions to encourage capital expenditures for more than 50 years.2 Recently, so-called "bonus depreciation"--a large, temporary acceleration of depreciation deductions--was among the major policy responses to the recessions of 2001 and 2008. Full expensing of all equipment investment was recently enacted for 2011, and a permanent switch to expensing is often discussed as a component of possible corporate tax reforms.3
This paper studies how the accounting system may affect the perception of the timing of these depreciation deductions and may thus affect the impact of tax policy on firm investment decisions. Evidence suggests that shareholders, managers, and observers of publicly-traded firms focus a great deal of attention on one particular measure of firm performance among the vast amount of data available on public firms. This measure is the bottom line of a firm's income statement when prepared under Generally Accepted Accounting Principles (GAAP), the set of rules that govern financial reporting in the United States.4 This measure is commonly referred to as "net income," or "earnings," and I will hereafter refer to it as "book earnings."
Equity analysts and the business press devote a great deal of attention to book earnings. Commonly reported and forecasted metrics like earnings growth, earnings per share, and the price-to-earnings ratio are all based on this measure. The literature on the "accrual anomaly" further supports the notion that investors focus attention on earnings. Sloan (1996) writes that "stock prices are found to act as if investors `fixate' on earnings, failing to reflect fully information contained in the accrual and cash-flow components of current earnings." This "fixation" is consistent with boundedly-rational investors attempting to make decisions based on only a subset of the information potentially available to them.
If investors fixate on book earnings, managers may rationally devote their energy to improving them. Indeed, incentive payments are often explicitly tied to earnings and other accounting metrics.5 In their survey of corporate Chief Financial Officers, Graham, Harvey, and Rajgopal (2005) find that, "CFOs believe that earnings, not cash flows, are the key metric considered by outsiders." Beyond this survey evidence, accounting researchers have documented myriad empirical examples where managers sacrifice actual cash flows or alter real decisions in order to improve book earnings. For example, Erickson, Hanlon, and Maydew (2004) report that their sample of 27 firms paid a total of $320 million dollars of real cash taxes on earnings that were later alleged to be fraudulent. Baber, Fairfield, and Haggard (1991) and others suggest that firms may reduce their real spending on activities like research and development in order to avoid reporting a loss for accounting purposes, in an example of what is known as "real earning management." Shackelford, Slemrod, and Sallee (2007) survey related literature and call for more research into its implications for tax policy.
This paper develops, formalizes, and tests the hypothesis that GAAP accounting rules obscure the timing of tax payments in a way that can mitigate the impact of tax policy on investment decisions. A key tenet of GAAP is the "matching principle," or the notion that revenues and expenses associated with the same activity should affect earnings at the same time. For example, expenses associated with future repairs to goods sold under warranty are recorded when the goods are sold, even though the repairs have not yet been made. Application of the matching principle to depreciation of investment goods requires that tax savings from depreciation deductions be recognized at the same time that depreciation is recognized. Although the timing of cash tax payments is affected by accelerated depreciation in the tax code, the income tax expense reported in GAAP earnings is not.
The effects of this matching on the impact of tax policy on investment can be understood through a comparison to expensing. The key feature of expensing that makes it nondistortionary is the matching in time of expenditure on investment and the tax deductions associated with that investment. Under expensing, firms are not required to make immediate expenditures on investment and recoup their associated tax deductions only in the future--instead they realize the tax savings immediately as well. It is this feature of expensing that makes it nondistortionary.
A key insight of the paper is that the book earnings numbers reported under GAAP enforce a similar matching in time of expenditures and tax savings. The "cost" of an investment under GAAP--the depreciation expense--occurs at the same time as the associated benefit in the form of tax savings. When managers focus more heavily on book earnings, their decisions will thus more closely resemble the undistorted decisions they would make under expensing. As a result, the long-run effective tax burden on corporate capital may be lower than it otherwise would be, but, in the short run, accelerated depreciation provisions are less effective than they otherwise would be.
I develop a formal model of a firm that chooses its investment policy in order to maximize a weighted average of book earnings and cash flows. I show how the cost of capital and the impact of tax incentives for investment depend on the weight placed on book earnings. I also show that, in principle, this weight can be estimated by comparing the impact of accelerated depreciation--which does not affect book earnings--and the investment tax credit (ITC)--which does--on firm investment decisions. I estimate this weight using data from the Compustat panel of firms and historical changes in the depreciation and ITC rules. There is considerable variation across specifications, but baseline estimates suggest that accelerated depreciation has been about half as effective as the ITC in influencing firm investment decisions.
There are reasons to be concerned, however, that accelerated depreciation may be less effective than the ITC for reasons other than its accounting treatment. First, measuring the present value of future depreciation deductions requires assumptions about appropriate discount rates. If these discount rates are improperly measured, estimates of the effect of accelerated depreciation could be improperly attenuated or otherwise biased. Second, if changes in accelerated depreciation rules take the form of shifting tax deductions from a distant future year to a less distant future year, then these changes have no impact on firm cash flows in the year of investment. The ITC, of course, does affect firm cash flows in the year of invesment. If cash flows affect investment decisions, we might expect the ITC to have more impact on investment through this cash flow channel alone.
Fortunately, it is possible to isolate the depreciation deductions that are available to the firm in the year it makes an investment. These deductions need not be discounted and have the same cash flow implications as the ITC. I find little evidence that these first-year depreciation deductions have any more impact than discounted future depreciation deductions, so results do not appear to be driven by these obvious discounting or cash flow channels. I discuss a number of other factors that one might suggest as reasons that accelerated depreciation could be less effective than the ITC, but none seem clearly compelling. I thus conclude that results are at least consistent with a role for the accounting system in determining investment responses to tax policy, although I suspect that many readers will wish to see more evidence before drawing definitive conclusions.
In the next section of the paper, I briefly discuss related literature, provide additional intuition on why a tax system with expensing does not distort investment decisions, and discuss accounting rules related to depreciation deductions in more detail. Section 3 models a firm that chooses its investment policy to maximize a weighted average of cash flows and book earnings. In section 4, I discuss the data used to estimate this weight. Section 5 presents results, and Section 6 concludes.
2.1 Related literature
I consider this paper part of the literature in behavioral corporate finance. Baker, Ruback, and Wurgler (2007) distinguish two types of behavioral corporate finance--one where managers themselves may be irrational (or boundedly-rational), and a second where managers respond rationally to the irrationality of others. In my view, this paper falls in the second category--I test the hypothesis that boundedly-rational investors focus their attention on earnings, leading rational managers to focus on them as well.6 Note that even if one was not interested in the effects of tax policy for their own sake, one could motivate this paper with the question "Does the accounting system affect real investment decisions?" This paper provides a tax-based test of this hypothesis.
I also consider this paper part of a recent strand of public finance literature that has emphasized the importance of the salience of taxation in understanding its effects on behavior. This literature develops the insight--perhaps obvious to non-economists--that less noticeable taxes may have smaller effects on the behavior of boundedly-rational agents. Chetty, Looney, and Kroft (2009) find that sales taxes have larger effects on consumer purchases when these taxes are more salient, and Chetty and Saez (2009) find that providing detailed information on the structure of the earned income tax credit increases its effects on labor supply. This paper argues that salience may also be important for understanding the impact of taxation on business investment decisions, although through a more nuanced channel. In this case, it is investors and other firm outsiders for whom book earnings are claimed to be particularly salient. Given this fixation on earnings, perfectly rational managers would have the incentive to act as if they did not find taxes salient, even if they actually understand the tax code very well.
Note that in a well-known paper by Stein (1989), a rational market still induces managers to forsake positive NPV investments in order to boost current earnings. However, Stein's use of the term "earnings" does not comport with the accounting definition used in this paper. In fact, in the model presented in this paper, a focus on current accounting earnings would tend to encourage overinvestment, because the upfront cash cost of investment does not appear on the earnings statement immediately--rather it appears only in depreciation charges in future quarters. Rogerson (1997) formalizes the well-known notion that focusing attention (and compensation) on appropriately-calculated alternative performance measures like economic value added can restore appropriate investment incentives.
Finally, this paper joins recent literature that brings insights from the study of the separation of ownership and control in corporate finance to bear on our understanding of the effects of taxation. Examples include Desai, Dyck, and Zingales (2007), Chetty and Saez (2010), Edgerton (2010), and Keuschnigg and Ribi (2010). Beyond the previously-cited Shackelford, Slemrod, and Sallee (2007), however, few papers have yet studied the potential implications for tax policy of the much-discussed fixation on earnings. Neubig (2006) and Poterba, Rao, and Seidman (2011) discuss implications for the political economy of corporate tax reform. Graham, Hanlon, and Shevlin (2010) report survey evidence suggesting that the accounting treatment of taxation is quite important for multinational firms deciding where to locate their operations and when to repatriate earnings. Perhaps the paper most similar to this one is Robinson and Sansing (2008), who study a model where both cash flows and accounting profits enter the objective function of a manager choosing a mix of tangible and intangible investments. Their key insight is that an accounting system that fails to distinguish between operating expenses and intangibles investment could tend to discourage intangibles investment. This issue is distinct from the ones studied in this paper.
2.2 Why expensing does not distort investment decisions
The result that a tax system with expensing need not distort investment decisions dates at least to Hall and Jorgenson (1967). To make clear the parallel between expensing and the accounting treatment of depreciation, I revisit this result in a simple model of an
equity-financed firm evaluating an investment project using the net present value criterion.7 The firm considers an investment project that requires an
expenditure ![]() today that will produce expected cash flows
today that will produce expected cash flows ![]() in year
in year
![]() . Students in an introductory corporate finance course would be taught to calculate the net present value of this project by discounting the future cash flows at an appropriate risk-adjusted
rate
. Students in an introductory corporate finance course would be taught to calculate the net present value of this project by discounting the future cash flows at an appropriate risk-adjusted
rate ![]() , with,
, with,
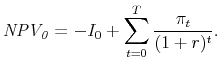
Now introduce a tax on the project's future cash flows at a rate ![]() , and also allow the firm to expense its initial investment, that is, to realize tax
savings of
, and also allow the firm to expense its initial investment, that is, to realize tax
savings of ![]() in the year of investment. Throughout the paper, I will assume that a firm's taxable income is always large enough for the firm to fully utilize any tax deductions or
credits. See Edgerton (2010) for a detailed treatment of the effects of investment incentives on loss-making firms. With this tax system in place, the project now has an after-tax NPV of
in the year of investment. Throughout the paper, I will assume that a firm's taxable income is always large enough for the firm to fully utilize any tax deductions or
credits. See Edgerton (2010) for a detailed treatment of the effects of investment incentives on loss-making firms. With this tax system in place, the project now has an after-tax NPV of
![]() , with,
, with,
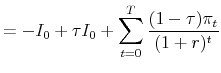 |
||
Thus, under expensing, the government simply captures a fraction
This tax system does not alter investment decisions due to the fact that the cost of investment and the tax savings from the investment are realized at the same time. It is easy to see that if the tax savings ![]() in the model above were realized in future years and were thus discounted, there could indeed be projects that would have a positive NPV with no taxation, but a negative NPV with taxation. Under the current U.S. tax system, for example, the tax savings from
investment are not realized at the same time as investment expenditures; rather they are realized in future years in accordance with the depreciation schedules required by the tax code. As a result, few would disagree that the current tax code discourages some investments that would be made in the
absence of taxation.
in the model above were realized in future years and were thus discounted, there could indeed be projects that would have a positive NPV with no taxation, but a negative NPV with taxation. Under the current U.S. tax system, for example, the tax savings from
investment are not realized at the same time as investment expenditures; rather they are realized in future years in accordance with the depreciation schedules required by the tax code. As a result, few would disagree that the current tax code discourages some investments that would be made in the
absence of taxation.
2.3 Accounting for investment and depreciation
When firms make an investment in physical capital, this spending appears as a capital expenditure on the cash flow statement, but it does not appear immediately on the earnings statement. The "cost" of an investment appears on the earnings statement only as depreciation is deducted over the life of the investment, typically in a straight-line pattern. As noted earlier, application of GAAP's matching principle to depreciation of investment goods requires that tax savings from depreciation deductions be recognized at the same time that the depreciation itself is recognized. That is, GAAP requires that recognition of tax savings from depreciation deductions follow the same straight-line pattern as the recognition of depreciation, regardless of the timing of the tax savings that policymakers put into the tax code. This discrepancy between the timing of the accounting recognition of expenses for tax and financial reporting purposes creates what is known as a "temporary book-tax difference."9
The difference is only temporary because the total amount of depreciation deductions available for book and tax purposes is the same, but the time at which deductions are taken differs. Tax depreciation typically exceeds book depreciation in the year an investment is made, but, at some point in the future, book depreciation for the investment will exceed tax depreciation. GAAP views any tax savings in excess of book depreciation early on as a "deferred tax liability" that will have to be "paid back" by the end of the life of the investment. Eventually, the investment will have been fully depreciated for both tax and book purposes, and the deferred tax liability will be zero.
Table 1 presents a simple numerical example to illustrate these accounting concepts. It depicts a firm that is considering buying a machine for $900 in year 1. The machine produces net sales of $500 in each of years 1 and 2, and it depreciates completely by the end of
year 2, so that it can produce nothing and has no salvage value. The firm is taxed on its profits at a rate
![]() , and it makes no interest payments.
, and it makes no interest payments.
The "Straight-line" columns depict the firm's income and cash flows when book and tax depreciation are both equal to straight-line depreciation of $450 per year. The firm's earnings in both years for both book and tax purposes are Sales ($500) - Depreciation ($450) - Current Taxes ($25) = $25. In year 1, the firm's cash flows are Sales ($500) - Current Taxes ($25) - Capital Expenditure ($900) = -$425. In year 2, cash flows are just Sales ($500) - Current Taxes ($25) = $475.
The "Expensing" columns depict the same firm making the same investment when it may expense the investment for tax purposes--that is, when it may deduct the entire purchase price of the machine in the year it is puchased. We see that this treatment shifts $225 worth of tax liability from year 1 into year 2, and thus that $225 of cash flow is shifted forward from year 2 to year 1. With any positive discount rate, expensing thus makes the project more attractive. The memo line shows that with a discount rate of 20%, the project has a negative NPV under straight-line depreciation, but a positive NPV under expensing. Thus, if the firm evaluates projects based on the NPV of their cash flows, a switch to expensing would encourage this firm to make an investment that it otherwise would not make.
Note, however, that expensing does not change the timing of book earnings. Because the firm will still record $450 of book depreciation in both year 1 and year 2, the matching principle dictates that it still book $225 of tax savings from depreciation deductions in each year. Expensing has saved the firm $225 in cash in year 1, which it will instead pay in year 2. GAAP treats this saving as "Deferred Taxes," which will need to be "paid back" in year 2, and thus still deducts the $25 in income tax expense from earnings in year 1.
The key point, of course, is that expensing affects only the cash flow line and not the earnings line. If a firm considers the cash flow line when evaluating whether to undertake the investment, then expensing makes the net present value of making the investment larger. The more focus that the firm places on the earnings line when evaluating the project, however, the smaller are the benefits of a switch to expensing.
Note that with the tax rate of 0.5, earnings in each of year of the project are $25, while with no taxes at all, earnings in each year would be $50. Thus the NPV of the earnings from the project with taxes is exactly ![]() times the earnings of the project with no taxes. This observation highlights a key insight of the paper: the matching principle of GAAP enforces the same matching in time of the costs and tax savings from investment that is the hallmark of expensing. If one
were evaluating an investment project based on the NPV of its book earnings, one could always write the after-tax NPV of the project as
times the earnings of the project with no taxes. This observation highlights a key insight of the paper: the matching principle of GAAP enforces the same matching in time of the costs and tax savings from investment that is the hallmark of expensing. If one
were evaluating an investment project based on the NPV of its book earnings, one could always write the after-tax NPV of the project as ![]() times the NPV with no taxes, just as we could
in the expensing example in the previous section. Thus every project has a positive NPV after taxes if and only if it has a positive NPV with no taxes at all. To summarize, if firms evaluate projects based on the NPV of the projects' book earnings, the tax rate will not affect
which investments are made.10
times the NPV with no taxes, just as we could
in the expensing example in the previous section. Thus every project has a positive NPV after taxes if and only if it has a positive NPV with no taxes at all. To summarize, if firms evaluate projects based on the NPV of the projects' book earnings, the tax rate will not affect
which investments are made.10
Note that one might well question the premise of this statement, that is, that NPV is the function of earnings upon which investors and firms are focused. Indeed, some accounts of the earnings fixation would suggest that firms are most concerned with smoothing the volatility of earnings or with minimizing any shortfall in earnings relative to their or outsiders' stated expectations. If these views are the correct ones, then the conclusion of the italicized statement need not hold.
I would draw a distinction, however, between this conclusion and the earlier conclusion that a focus on book earnings will mitigate the impact of a move towards expensing. The latter conclusion is more robust to changes in the form of the earnings fixation. For example, suppose a firm is considering a new investment, but decides against the investment because it would push their earnings for the year below analysts' expectations. In this case, a sudden switch to expensing might make little difference in the decision, because expensing does not matter for the effect of the investment on the firm's earnings.
Although studying the implications of a focus on other functions of the earnings stream may well prove fruitful at some point, modeling a firm as concerned with the NPV of both its cash flows and its earnings seems a very natural place to start. The next section of the paper embeds such an assumption into a canonical investment model that can then easily be taken to the data.
3.1 Terminology and Setup
Firms will maximize a discounted weighted average of their streams of after-tax cash flows (
![]() ) and their book earnings (
) and their book earnings (
![]() ). Define after-tax cash flows as,
). Define after-tax cash flows as,
where
The depreciation deductions permitted for tax purposes are determined by the stock of the firm's past capital expenditures that have not yet been used as a deduction from taxable income. I denote this quantity by ![]() , and I will hereafter refer to it as "tax capital." Deductions are allowed in the amount
, and I will hereafter refer to it as "tax capital." Deductions are allowed in the amount
![]() , so that tax capital evolves according to:
, so that tax capital evolves according to:
Next define the firm's accounting profits, or book earnings, as,
Note that revenues
These terms should be familiar to anyone acquainted with the reconciliation of earnings and cash flows that appears in firms' Statement of Cash Flows under GAAP. Beginning with book earnings, one adds back the noncash charges for depreciation
![]() and deferred taxes
and deferred taxes
![]() to reach Cash Flow from Operating Activities. To Cash Flow from Operating Activities, we add Cash Flow from Investing Activities (
to reach Cash Flow from Operating Activities. To Cash Flow from Operating Activities, we add Cash Flow from Investing Activities (![]() ), and Cash Flow from Financing Activities (
), and Cash Flow from Financing Activities (![]() ), to reach total Net Cash Flow. Tables
2 and 3 present the income and cash flow statements that would appear in SEC filings or annual reports presented under US GAAP for the firm in the model.
), to reach total Net Cash Flow. Tables
2 and 3 present the income and cash flow statements that would appear in SEC filings or annual reports presented under US GAAP for the firm in the model.
3.2 Investment Policy
I assume that the firm places a weight ![]() on book earnings and a weight
on book earnings and a weight
![]() on after-tax cash flows when choosing its investment. The firm solves,
on after-tax cash flows when choosing its investment. The firm solves,
![\displaystyle \max_{\{I_{t}, B_t\}} \int^{\infty}_0 e^{-rt} \left[ \alpha \mathit{BE}_t + (1-\alpha) \mathit{CF}_t \right] dt](img98.gif)
The final constraint crudely prevents the firm from choosing to be fully debt financed, which would otherwise be optimal.12 This problem is very similar to a standard investment problem, with two important differences. First, it is traditionally assumed that
From this model, with no adjustment costs (![]() ), I derive the user cost of capital,
), I derive the user cost of capital,
where
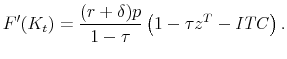
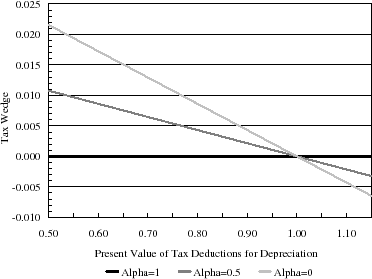
Define the tax wedge as the distortion to the return on a marginal dollar of investment that is induced by the tax system:
![\displaystyle F'(\tilde{K}_{SS})/p - F'(K_{SS})/p = \left[ (1-\alpha) \tau (1-z^T) - \mathit{ITC} \right] \frac{r+\delta}{1-\tau},](img118.gif)
As ![]() falls below 1, the tax wedge rises less quickly when
falls below 1, the tax wedge rises less quickly when ![]() than
when
than
when ![]() . The departure from expensing induces less distortion when
. The departure from expensing induces less distortion when ![]() because it affects only cash flows and not book earnings. These results suggest that the distortion to the capital stock created by the corporate income tax is smaller than we would calculate if we assumed that firms did not include book earnings in their objective
function. Likewise, a policy change that moves towards expensing would have smaller effects than we might otherwise anticipate. For example, under current law, most business investments in structures are depreciated over 39 years. The present discounted value of the depreciation deductions
associated with $1 of investment in business structures is not far from $0.55. If
because it affects only cash flows and not book earnings. These results suggest that the distortion to the capital stock created by the corporate income tax is smaller than we would calculate if we assumed that firms did not include book earnings in their objective
function. Likewise, a policy change that moves towards expensing would have smaller effects than we might otherwise anticipate. For example, under current law, most business investments in structures are depreciated over 39 years. The present discounted value of the depreciation deductions
associated with $1 of investment in business structures is not far from $0.55. If
![]() , then Figure 1 suggests that the tax wedge on equity-financed business structures is about 2 percentage points (on a base around 5%, for a rate of 40%).
A switch to expensing would drastically reduce the tax wedge from 2% to zero. If, however,
, then Figure 1 suggests that the tax wedge on equity-financed business structures is about 2 percentage points (on a base around 5%, for a rate of 40%).
A switch to expensing would drastically reduce the tax wedge from 2% to zero. If, however,
![]() , then the tax wedge on structures is only 1 percentage point, and a switch to expensing would produce only half as large a reduction in the tax burden.
, then the tax wedge on structures is only 1 percentage point, and a switch to expensing would produce only half as large a reduction in the tax burden.
3.3 Estimating 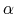
With adjustment costs nonzero, I solve for the derivative of the adjustment cost function,
where
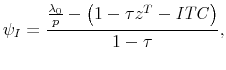
In particular, with ![]() , we find new implications for the effects of the tax policy variables. First, note that changes to the investment tax credit,
, we find new implications for the effects of the tax policy variables. First, note that changes to the investment tax credit,
![]() , are no longer equivalent to changes to depreciation allowances,
, are no longer equivalent to changes to depreciation allowances, ![]() . That is,
. That is,
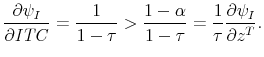
In principle, ![]() can be estimated quite easily. Under the familiar assumption of quadratic adjustment costs,
can be estimated quite easily. Under the familiar assumption of quadratic adjustment costs,
![\displaystyle \psi (I_t, K_{t}) = \frac{1}{2c} \left[ \frac{I_t}{K_{t}} - a \right]^2 K_{t},](img135.gif)
In theory, the same coefficient
Desai and Goolsbee (2004) take a particularly simple and transparent approach to dealing with this measurement error for the purpose of isolating the effects of the tax variables. They observe that,
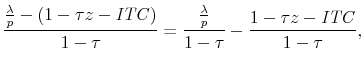
![\displaystyle \frac{I_{it}}{K_{i,t-1}} = \beta_1 \left[ \frac{ \frac{\lambda_{ti}}{p_t} } {1 - \tau_t } \right] + \beta_2 \left[ \frac{ 1 - \tau_t z_{tj} - \mathit{ITC}_{tj} }{1 - \tau_t } \right],](img139.gif)
I take a very similar approach by simply noting that the expression in (3) above can be written,
That is, the ITC and accelerated depreciation terms can also be separated. If I run the simple linear regression,
then the ratio
Note that (4) suggests that other coefficients might also be of use in estimating ![]() . However, I would not expect the coefficient on the Q term to
provide useful information due to the well-known attenuation problems discussed above. The penultimate term will be absorbed by year fixed effects. The last term involving
. However, I would not expect the coefficient on the Q term to
provide useful information due to the well-known attenuation problems discussed above. The penultimate term will be absorbed by year fixed effects. The last term involving ![]() , the present
value of depreciation deductions for book purposes, would likely largely be absorbed by firm fixed effects, although one could also think it might change slowly over time as each firm's investment mix evolves.16 Although one could consider constructing a time-varying measure of
, the present
value of depreciation deductions for book purposes, would likely largely be absorbed by firm fixed effects, although one could also think it might change slowly over time as each firm's investment mix evolves.16 Although one could consider constructing a time-varying measure of ![]() from the information on book depreciation charges
in Compustat, this exercise strikes me as unlikely to produce much more than noise. I will thus include no controls for
from the information on book depreciation charges
in Compustat, this exercise strikes me as unlikely to produce much more than noise. I will thus include no controls for ![]() beyond firm fixed effects. Some readers could then worry that the
omission of
beyond firm fixed effects. Some readers could then worry that the
omission of ![]() from the equation above will bias empirical estimates. Note, however, that for this concern to be valid, one would need to assume that
from the equation above will bias empirical estimates. Note, however, that for this concern to be valid, one would need to assume that
![]() and thus that the null hypothesis to be tested can already be rejected.
and thus that the null hypothesis to be tested can already be rejected.
The model just presented provides an explicit theoretical foundation for the equation to be estimated, but this specification is also intuitively appealing. Results will take the form of simple, transparent OLS regressions of investment ratios on tax variables, controlling for variables like Q (and cash flows) that are known to affect investment decisions. These results are also straightforward modifications of specifications that have a long history in the literature on taxes and investment, and thus should be familiar to readers of this literature. Finally, the key result is a simple, intuitive comparison of two coefficients. The hypothesis developed in the paper thus far suggests that tax incentives for investment that affect both book earnings and cash flows should have more impact than those that affect only cash flows. A simple comparison of the coefficients on the ITC and accelerated depreciation provides an intuitively appealing test of this hypothesis.
4 Data
Following many prior papers in the literature, I use firm-level financial statement data from Compustat to construct measures of investment, Q, cash flows, and earnings management indicators. I also construct tax variables that reflect repeated changes in corporate tax laws in the United States over the last several decades. Legislation changed corporate tax rates in 1964, 1968, 1970, 1979, and 1987. There were important changes to depreciation rules in 1962, 1971, 1981, and 1987. Bonus depreciation was in place from 2002 to 2004 (and again from 2008 to 2010). The investment tax credit was introduced in 1962, repealed in 1969, reinstated in 1971, increased in 1975, and repealed in 1986.17 These changes have often differentially affected investments in different assets in rather arbitrary ways. As one example, the Tax Reform Act of 1986 changed the investment tax credit available for trucks from 10% to 0%, while it changed the ITC available for cars from 6% to 0%.18
I follow Cummins, Hassett, and Hubbard (1994), Desai and Goolsbee (2004), and others in using this variation in the tax treatment of different kinds of assets to identify the impact of tax variables on investment. I thank Dale Jorgenson for providing data on investment tax credits and the present value of depreciation deductions available in each year for each asset type. I collected additional information on the depreciation deduction available in the year of investment from IRS publications. These variables are matched to the 1997 Capital Flows table from the Bureau of Economic Analysis, which records the amount of investment made by each industry in each asset category.19 I construct depreciation deduction values and investment tax credit rates at the industry level by taking a weighted average across the assets purchased by each industry, with the weights equal to the percentage of the industry's spending accounted for by each asset. I then construct the tax term components of tax-adjusted Q,
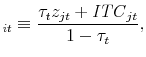
Tax terms constructed in this manner depend only on statutory variables like the corporate tax rate, depreciation schedules, and investment tax credit parameters.20 These variables are averaged at the industry level using a set of weights that are fixed over time and do not vary with any (possibly tax-induced) changes in the mix of assets employed by a given industry. Thus, there is no mechanical relation between the decisions of firms in Compustat and changes in the tax variables that are included in regression results. Further, I present specification that include year fixed effects to deflect concerns about policy endogeneity that would arise, for example, when investment incentives become more generous exactly when investment is low. With year fixed effects included, identification of the effects of tax variables comes only from differences across industries in changes in the tax treatment of the assets that they purchase (with the bundle of assets held fixed) and not from time series variation in the generosity of tax incentives. I present results from the sample period 1962 to 2005.21
5 Results
Columns 1 and 2 of Table 4 present regressions of the form,
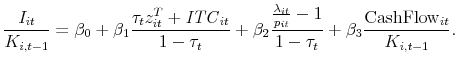
The results in column 2 are quite similar to those of Desai and Goolsbee (2004) in that the coefficient on the "Tax Term",
![]() , is economically important. When clustering standard errors at the firm level, Desai and Goolsbee (2004) find it to be
statistically significant as well. However, in this setting where the annual variation in the tax variables occurs only at the industry level, it is appropriate to cluster standard errors at the industry level. Column 2 shows that the Desai and Goolsbee (2004) result is no
longer statistically significant at conventional levels when clustering by industry, although it is significant at the 21% level. Note again, however, that we should expect a downward bias on the tax term coefficient in column 1, where year dummies are not included. Thus
the coefficient in this column still provides evidence of an economically important effect of the tax variables on investment that is also robustly statistically significant.
, is economically important. When clustering standard errors at the firm level, Desai and Goolsbee (2004) find it to be
statistically significant as well. However, in this setting where the annual variation in the tax variables occurs only at the industry level, it is appropriate to cluster standard errors at the industry level. Column 2 shows that the Desai and Goolsbee (2004) result is no
longer statistically significant at conventional levels when clustering by industry, although it is significant at the 21% level. Note again, however, that we should expect a downward bias on the tax term coefficient in column 1, where year dummies are not included. Thus
the coefficient in this column still provides evidence of an economically important effect of the tax variables on investment that is also robustly statistically significant.
Columns 1 and 2 present regressions of the form, 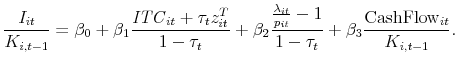 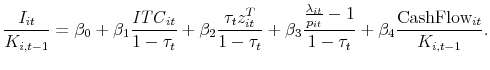 *** indicates statistical significance at the 1% level, ** at 5%, and * at 10%. |
In columns 3 through 8 of Table 4, the terms on the right-hand side are rearranged as in Equation 5 above. The equipment tax term is split into two parts--one for the present value of depreciation deductions ![]() , and the other for the ITC. The even-numbered columns include year fixed effects; the odd-numbered columns do not. The distribution of investment is highly skewed towards the largest firms, so it is useful to test
whether results hold in samples consisting of large firms only. The sample in columns 3 and 4 include all Compustat firms, columns 5 and 6 include only the largest 3000 firms when ranked by assets in the previous year, and columns 7 and 8 include only the largest 500 firms each year.
, and the other for the ITC. The even-numbered columns include year fixed effects; the odd-numbered columns do not. The distribution of investment is highly skewed towards the largest firms, so it is useful to test
whether results hold in samples consisting of large firms only. The sample in columns 3 and 4 include all Compustat firms, columns 5 and 6 include only the largest 3000 firms when ranked by assets in the previous year, and columns 7 and 8 include only the largest 500 firms each year.
Results show clearly that the effect of the Tax Term in columns 1 and 2 is driven more by the investment tax credit than by accelerated depreciation. That is, the coefficient on the ITC is larger in magnitude than that on the depreciation term in every column. The bottom row of estimates
presents the value of
![]() , the estimate of
, the estimate of ![]() . The next row presents the
p-value from the linear hypothesis test that the coefficients on the ITC and
. The next row presents the
p-value from the linear hypothesis test that the coefficients on the ITC and ![]() are equal, which would imply
are equal, which would imply ![]() .
.
Estimates of ![]() range from .169 in column 8 to 0.814 in column 6, with the other four estimates all close to 0.5. The equality of the
range from .169 in column 8 to 0.814 in column 6, with the other four estimates all close to 0.5. The equality of the ![]() and ITC coefficients can be rejected with 95% confidence in columns 3, 5 and 7, and with 90% confidence in column 4. The p-value in the test of the null hypothesis of coefficient equality in column 6 is 0.138. Only in column 8,
which includes year dummies and limits the sample to the largest 500 firms in each year, is the difference between coefficients not close to statistical significance. It is worth noting also that the estimated magnitude of the overall effect of the tax variables tends to decline as the sample is
limited to larger and larger firms. As the larger firms have a far larger impact on aggregate investment, this suggests that the baseline results from Desai and Goolsbee (2004) would tend to overstate the magnitude of the effect of tax variables on aggregate investment
because they weight the small firms equally.
and ITC coefficients can be rejected with 95% confidence in columns 3, 5 and 7, and with 90% confidence in column 4. The p-value in the test of the null hypothesis of coefficient equality in column 6 is 0.138. Only in column 8,
which includes year dummies and limits the sample to the largest 500 firms in each year, is the difference between coefficients not close to statistical significance. It is worth noting also that the estimated magnitude of the overall effect of the tax variables tends to decline as the sample is
limited to larger and larger firms. As the larger firms have a far larger impact on aggregate investment, this suggests that the baseline results from Desai and Goolsbee (2004) would tend to overstate the magnitude of the effect of tax variables on aggregate investment
because they weight the small firms equally.
Table 5 presents results to address the concern that ![]() may mismeasure the value of depreciation deductions relative to investment tax credits. As
calculated,
may mismeasure the value of depreciation deductions relative to investment tax credits. As
calculated, ![]() reflects assumptions about the discount rate applied to future depreciation deductions. If these assumptions are incorrect, estimated coefficients could be attenuated by
classical measurement error or otherwise biased. Further, the investment tax credit may provide additional cash flows in the year of investment, making it more effective than accelerating depreciation deductions from one future year to another. Table 5 addresses these
concerns by estimating a separate coefficient for depreciation deductions available in the year an investment is made. These deductions need not be discounted and have the same cash flow benefits as the ITC.
reflects assumptions about the discount rate applied to future depreciation deductions. If these assumptions are incorrect, estimated coefficients could be attenuated by
classical measurement error or otherwise biased. Further, the investment tax credit may provide additional cash flows in the year of investment, making it more effective than accelerating depreciation deductions from one future year to another. Table 5 addresses these
concerns by estimating a separate coefficient for depreciation deductions available in the year an investment is made. These deductions need not be discounted and have the same cash flow benefits as the ITC.
All specifications include firm fixed effects. Standard errors in parentheses are clustered at the industry level. |
Table 5 provides little reason to worry that the observed lack of responsiveness to accelerated depreciation is driven by discounting or cash flows. The estimates of ![]() coming from a comparison of the coefficient on the ITC and on the first-year depreciation deduction are a bit lower than those in Table 4 in the even-numbered specifications which include year dummies, but are actually higher in the specifications
without year dummies. In fact, the estimated coefficient on the first-year depreciation deduction is actually slightly negative in the odd-numbered columns without year dummies. Again this is consistent with policy endogeneity in the form of depreciation being accelerated into the first year during
downturns in investment. In columns with year dummies, there is little difference between the coefficients on the first-year depreciation deduction and those on the discounted, future deductions. Thus it seems that there is little reason to believe that the results in Table 4 are driven by discounting or cash flows.
coming from a comparison of the coefficient on the ITC and on the first-year depreciation deduction are a bit lower than those in Table 4 in the even-numbered specifications which include year dummies, but are actually higher in the specifications
without year dummies. In fact, the estimated coefficient on the first-year depreciation deduction is actually slightly negative in the odd-numbered columns without year dummies. Again this is consistent with policy endogeneity in the form of depreciation being accelerated into the first year during
downturns in investment. In columns with year dummies, there is little difference between the coefficients on the first-year depreciation deduction and those on the discounted, future deductions. Thus it seems that there is little reason to believe that the results in Table 4 are driven by discounting or cash flows.
5.1 Discussion
Some might also worry that an exercise comparing two coefficients like this one is easily confounded by measurement error.22 One could worry here that depreciation deductions--even in the first year, when they need not be discounted--are measured less accurately than the investment tax credit, inappropriately producing more attenuated coefficients on depreciation deductions than on the ITC. I myself gathered the maximum available first-year deduction amounts from IRS publications, however, and I see no reason why this process would be particularly error-prone. Selecting the right depreciation schedule appears no more difficult to me than choosing the correct ITC amount. In fact, the ITC amounts are determined based on the same equipment categories as the depreciation schedules.
There is, however, one important sense in which the statutory maximum depreciation deduction available in the first year that I include in Table 5 mismeasures the depreciation deductions that firms actually used. Namely, firms often did not claim the most accelerated depreciation schedule that was available to them. Congress explicitly authorized the use of double declining balance depreciation in 1954 (Brazell, Dworin, and Walsh (1989)), but Jorgenson and Sullivan (1981) report that a substantial fraction of investment was still depreciated using straight line methods up until the mandatory adoption of the Accelerated Cost Recovery System in 1981. A similar lack of take-up has been reported for recent bonus depreciation incentives by Knittel (2007). I would not consider this discrepancy between statutory maximum deductions and the deductions actually taken by firms to be measurement error--rather, I would consider it a reflection of the phenomenon under study. Firms do not appear to value accelerated depreciation as much as economists think they should.
Still, one must wonder if this apparent undervaluation of depreciation deductions results not from the accounting channel which I study in this paper, but from other facets of accelerated depreciation. A prime candidate would be the complexity of the depreciation rules. Firms may have simply preferred to stick with straight line depreciation after double declining balance was available because the calculations were simpler. Firms may opt to continue claiming depreciation under the Modified Accelerated Cost Recovery System rather than claiming bonus depreciation because they are already familiar with the MACRS rules or because state-level tax laws did not always change to allow bonus depreciation. It is hard, however, to square this story with the economist's typical view of firms--particularly the large publicly-traded firms in Compustat--as coldly calculating profit-maximizers with teams of accountants and lawyers ready to wring savings from the tax code. Particularly in recent years, tax accounting software should make it essentially costless for firms to maximize their depreciation deductions.
One could also wonder if there are other aspects of the tax code that might make depreciation deductions less attractive than ITCs. One might ask, for example, if firms in a loss position benefit more from ITCs than from accelerated depreciation. I see little reason, however, why this should be the case. It was true from 1964 to 1976 that an ITC could be carried forward for 7 years and a loss for only 5, but this could make only a trivial difference for their relative values. One could also wonder if the timing of investment during the year might affect the two kinds of incentives differently. It is true that the depreciation deductions available from an investment can sometimes depend on the month during the year when an investment is placed in service. If a large portion of investments were placed in service during the last quarter of the year and thus qualified for less than the standard first-year deduction, the variables used in regressions here could overstate the true value of depreciation deductions to many firms. However, data from the Census Bureau indicate that seasonality in equipment investment is relatively muted.23 Thus, it again seems that any impact on the true value of depreciation deductions must be trivial.
In summary, the most obvious alternative explanations for the weaker impact of accelerated depreciation do not receive much support from the data. I (and many other knowledgeable commentators) have been unable to come up with other alternatives that remain compelling when subjected to scrutiny. Nonetheless, I find it hard to shake the suspicion that something other than the accounting system could drive the results in Tables 4 and 5. I thus view them as more suggestive than conclusive.
6 Conclusions
A large literature and a great deal of survey and anecdotal evidence suggests that both investors and managers are quite focused on firms' accounting profits as a primary measure of their performance. This paper has developed and tested the implications of this claim for the impact of tax policy on firm investment decisions. I modeled a firm that places some weight on both its cash flows and its accounting profits when making investment decisions, and I showed how this assumption translates into simple modifications of canonical results from Hall and Jorgenson (1967) and Summers (1981). I estimated the weight placed on accounting profits using an equation derived from the model that is also a straightforward extension of specifications that have featured prominently in the tax and investment literature, particularly in Desai and Goolsbee (2004). Results would suggest that firms do indeed place a significant weight on accounting profits when making investment decisions. As a result, the long-run effective tax burden on corporate capital may be lower than it otherwise would be, but, in the short run, accelerated depreciation provisions may be less effective.
In truth, I view these results as a "first pass" at the question of whether the accounting system could affect firms' real investment responses to taxation. It seems hard to overstate how often accountants, businesspeople, and various other commentators repeat the claim that firms care deeply about their accounting profits. This claim has clear implications for the effectiveness of tax incentives for investment--incentives that affect accounting profits should have more impact than incentives that affect only cash flows. This paper's empirical work could be seen as the simplest possible test of whether the data on investment might be consistent with this oft-repeated claim. And, in fact, it seems that they are. In straightforward investment regressions with a long pedigree in the tax literature, it is indeed the case that accelerated depreciation has smaller effects on investment than does the investment tax credit, just as this story would predict.
I find it unlikely, however, that anyone with a healthy skepticism toward empirical work would be unwaveringly convinced that the accounting system is driving these results. Although I have been unable to identify any clearly compelling alternative explanations, it is hard not to harbor some suspicion that other factors might be at work. Further research attempting to measure any impact of the accounting system on investment responses to tax policy would be most welcome.
7 Appendix 1: Descriptive statistics
|
This table contains descriptive statistics for the full sample of 128,023 observations on 12,457 unique firms that is used in regressions presented in the text. The sample is truncated at the 99th percentile of the investment, Q, and cashflow variables and at the 1st percentile of the cash flow variable. I follow prior literature in constructing these variables. The dependent variable in all regressions is the investment to capital stock ratio easily observed in Compustat,
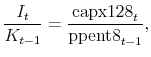
I follow Kaplan and Zingales (1997) in constructing a measure of Q, which is intended to proxy for the increase in the value of the firm's cash flows created by a marginal dollar of capital, or
![]() . Desai and Goolsbee (2004) show that this "corporate finance Q" performs better in investment regressions than the "public finance Q" constructed
a bit differently by Cummins, Hassett, and Hubbard (1994). I construct,
. Desai and Goolsbee (2004) show that this "corporate finance Q" performs better in investment regressions than the "public finance Q" constructed
a bit differently by Cummins, Hassett, and Hubbard (1994). I construct,
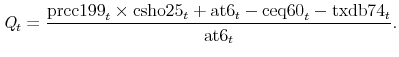
I again follow Kaplan and Zingales (1997) in constructing a cash flow measure,
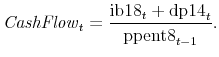
8 Appendix 2: Model derivation
Here I derive the user cost and tax-adjusted Q expressions that appear in the text. The firm solves,
![\displaystyle \max_{\{I_{t}\}} \int^{\infty}_0 e^{-rt} \left[ \alpha \mathit{BE}_t + (1-\alpha) \mathit{CF}_t \right] dt](img167.gif)
Form the Lagrangian,
![\displaystyle \int^{\infty}_0 e^{-rt} \left[ \right. \alpha \left[(1-\tau)[F(K_t) - p \psi (I_t, K_t) - \delta^B K^B_t - rD_t] + p I_t \mathit{ITC} \right]](img169.gif) |
||
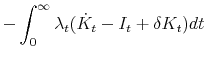 |
||
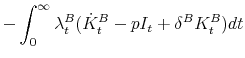 |
||
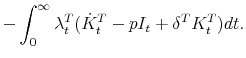 |
Note that,
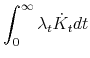 |
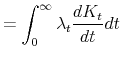 |
|
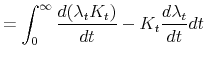 |
||
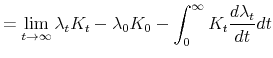 |
||
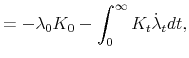 |
where the second line follows from integration by parts and the last line from the transversality assumption,
![\displaystyle \int^{\infty}_0 e^{-rt} \left[ \right. \alpha \left[(1-\tau)[F(K_t) - p \psi (I_t, K_t) - \delta^B K^B_t - rD_t] + p I_t \mathit{ITC} \right]](img169.gif) |
||
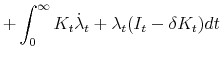 |
||
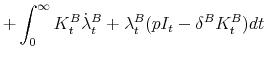 |
||
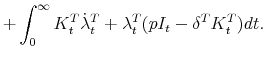 |
The first-order conditions are,
Define
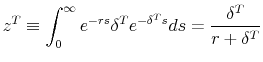
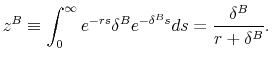
are solutions to the ordinary differential equations in (8) and (9).
First consider the case with no adjustment costs, that is, where ![]() . Equations (10) and (6) together imply that
. Equations (10) and (6) together imply that
![]() for some constant
for some constant ![]() . Equation (7)
then implies
. Equation (7)
then implies ![]() constant, and,
constant, and,
is a solution to (7). Plugging (11) and (10) into (6) produces the user cost equation (1) in the text. When
Office of Tax Analysis Papers, 98, 2007.
Footnotes
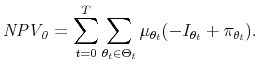
Regarding the potential for a focus on book earnings to distort investment upwards, it is important to remember that other features of the separation of ownership and control, namely investors' uncertainty that managers will pay out the returns to their investments, would tend to distort aggregate investment downwards. Most commentators seem to think that aggregate savings and investment rates are "too low" in some sense, so I find it most natural to think about taxation exacerbating this downward distortion rather than correcting an upward distortion. Return to Text
![\displaystyle F'(K_t) = \frac{(r+\delta)p}{1-\tau} \left( 1 - \alpha + \alpha z^B - \tau [(1-\alpha)z^T + \alpha z^B] - \mathit{ITC} \right),](img112.gif)
![\displaystyle \psi_I = \frac{ \frac{\lambda_0}{p_0} - \left( 1 - \alpha + \alpha z^B - \tau [(1-\alpha)z^T + \alpha z^B] - \mathit{ITC}\right) }{ 1 - \tau },](img129.gif)
![\displaystyle \frac{I_0}{K_0} = a + c\frac{ \frac{\lambda_0}{p_0} - \left( 1 - \alpha + \alpha z^B - \tau [(1-\alpha)z^T + \alpha z^B] - \mathit{ITC}\right) }{ 1 - \tau }.](img136.gif)
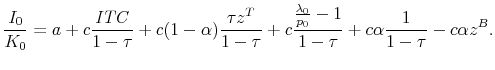
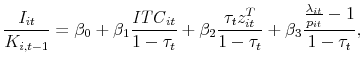
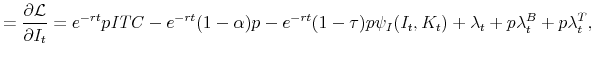
![\displaystyle =\frac{\partial \mathcal{L}}{\partial K_t} = e^{-rt}(1-\tau) [F'(K_t) - p \psi_K(I_t, K_t)] +\dot{\lambda}_t- \lambda_t \delta,](img189.gif)