Plant-Level Responses to Antidumping Duties: Evidence from U.S. Manufacturers1
Keywords: Antidumping; temporary protection; heterogeneous firms; productivity
Abstract:
This paper describes the effects of a temporary increase in tariffs on the performance and behavior of U.S. manufacturers. Using a dataset that includes the full population of U.S. manufacturing plants, I show that an apparent positive correlation between antidumping duties and traditional revenue productivity is likely misleading. For the subset of plants reporting quantity-based output data, increases in prices and markups artificially inflate the effect of antidumping duties on revenue productivity, while physical productivity actually falls. Moreover, antidumping duties allow low-productivity plants to continue producing protected products, slowing the reallocation of resources from less productive to more productive uses.
Section 1: Introduction
While temporary trade policies like antidumping duties have become one of the primary forms of trade protection worldwide, the empirical evidence needed to evaluate these policies has been lacking. This paper provides the first micro-level evidence on the effects of antidumping duties in the United States with a dataset that includes the full population of U.S. manufacturing plants. Using output data measured in units of quantity, I show that apparent increases in traditional revenue productivity associated with antidumping protection are most likely misleading. For the subset of plants reporting output data measured in units of quantity, increases in revenue productivity are driven primarily by increases in prices and markups, while physical productivity actually falls at protected plants. In addition, I show that antidumping duties allow for continued production by low-productivity plants that would have otherwise stopped production, slowing the reallocation of resources toward more productive uses.
The ability of antidumping duties to alter or halt trade flows is unparalleled and their effects can be used to examine broader aspects of international trade. When aluminum sulfate from Venezuela was assigned a 259 percent antidumping duty in December 1989, annual U.S. imports from Venezuela fell 98 percent. The use of antidumping duties is also widespread in the U.S. economy-sixteen of nineteen manufacturing sectors contain products that petitioned for antidumping protection.3 Moreover, the imposition of antidumping duties provides a rare opportunity to study how firms in a developed country respond to a major tariff shock. But despite the importance and ubiquity of antidumping duties, there is disagreement about some of their most fundamental implications, including their effect on firm and plant-level productivity.
Theoretical evidence regarding the effect of unilateral changes in tariffs on productivity is limited and mixed. Melitz and Ottaviano (2008), show that a unilateral increase in tariffs lowers industry productivity in the short run by allowing for continued operation by low-productivity firms, although productivity rises in the long run due to increased entry. Bernard, Redding and Schott (2011) show that symmetric trade liberalization can yield within-firm productivity gains by inducing firms to reallocate resources to their most productive products, but this result has not been extended to a setting with unilateral liberalization. In contrast, Matsuyama (1990) shows that temporary protection can speed up the time of technology adoption-and hence increase productivity-by increasing the incentive to invest in new technology, while noting that the government's threat to remove protection if the domestic firm fails to invest is not credible. Similarly, Miyagiwa and Ohno (1995) show that protection can induce investment in a fixed-cost technology by increasing the market share of domestic firms. Nocke and Yeaple (2008) show that a unilateral increase in tariffs induces high-capability firms to add products, while low-capability firms drop products, but their results do not have a firm-product-level productivity component.
In the empirical literature, many papers including Pavcnik (2002) and Fernandes (2007) (for developing countries) and Bernard, Jensen and Schott (2006) (for the U.S.) find that tariff rates and plant or firm-level productivity are negatively correlated. There is, however, evidence that tariff protection-especially temporary protection-may increase productivity along the lines discussed by Matsuyama (1990) and Miyagiwa and Ohno (1995). In particular, Konings and Vandenbussche (2008), find that antidumping duties are associated with a mean increase in revenue productivity at E.U. manufacturers.4 As noted in that paper, however, increases in revenue productivity can be caused not only by increases in physical productivity, but also by increases in prices and mark-ups.
I examine these issues by comparing the behavior of a treatment group of plants that receive protection to a control group of plants in similar industries that do not receive protection. As described below, this control group is constructed in a manner that controls for two potential sources of bias described in Konings and Vandenbussche (2008): a self-selection bias that exists if industries that apply for protection differ from those that do not apply and a "government-selection bias" that arises if the government bases its decision of whether to provide protection on variables that are correlated with productivity. I employ a difference-in-difference estimator to estimate the effect of antidumping protection, which nets out time-invariant differences between the treatment and control groups, as well as macro-level shocks affecting the treatment and control groups identically.
I find that the effect of antidumping duties on plant-level productivity depends crucially on whether output is measured in revenue or physical units of quantity. While antidumping protection is associated with increases in revenue productivity, these increases are driven primarily by increases in prices and mark-ups. Antidumping duties are associated with lower physical productivity among the set of protected plants reporting output data in units of quantity. These results underscore the importance of differentiating between revenue and physical productivity-a distinction described in Foster, Haltiwanger and Syverson (2008) and Syverson (2004) and recently discussed in the trade literature by Eslava, Haltiwanger, Kugler and Kugler (2004), De Loecker (2010) and Katayama, Lu and Tybout (2008). This distinction is particularly important when considering the case of antidumping duties, since increases in prices and markups would likely be taking place at the same time as any changes in physical productivity.
It is important to note that output data measured in units of quantity are only available for a subset of products and hence results for physical productivity, prices and markups are not available for all plants. This data limitation raises the possibility of an additional selection bias if plants reporting quantity data are different than those that do not report quantity data and are selected through non-random sampling. To address this concern, I calculate the probability that a plant reports quantity data and use the inverse of this predicted probability as a regression weight, to generate results that are more representative of the sample as a whole. Importantly, the main results of the paper are robust to this adjustment for potential section bias.
I also describe a potential reason for the decline in physical productivity associated with antidumping protection. I show that in the unprotected control group, low-productivity plants are forced to stop production through product-dropping or exit. In contrast, low-productivity plants in the protected treatment group are able to continue producing. This continued production by low-productivity plants in the treatment group leads to a productivity decline relative to the control group.
The remainder of the paper is organized as follows. Section 2 describes the data. Section 3 provides a brief discussion of the antidumping investigation process in the United States, as well as a description of the products typically involved in antidumping investigations. Section 4 defines the treatment and control groups and describes the productivity measures employed in this paper. Section 5 describes the empirical strategy and reports results. Section 6 concludes.
Section 2: Data
This analysis uses data from the U.S. Census Bureau's Census of Manufactures (CM) for the years 1987, 1992 and 1997.5 The CM is conducted every five years, in years ending in two and seven and all U.S. manufacturers, regardless of size, are required by law to respond.6 The CM contains plant-level data on the value of shipments, as well as input data including the number of production and non-production employees, raw material usage and book value of capital, which can be used to calculate total factor productivity. In addition, the CM includes plant-product-level output data measured in revenue for every product and in physical units of quantity for some products.
An important benefit of the CM is the availability of output data measured in units of quantity for certain products. The availability of quantity-based output data allows for the calculation of physical productivity-described in detail below-as well as average unit prices and price-cost mark-ups. Indeed, these quantity-based output data have been used in recent studies examining differences between revenue and physical productivity, including Foster, Haltiwanger and Syverson (2008). This information is especially important when studying antidumping duties, since changes in physical productivity are likely accompanied by changes in prices and mark-ups. Below, I discuss steps that control for a potential selection bias that can arise if plants that report output data in units of quantity differ from those that do not.
It is important to define a number of terms that will be used throughout this paper. The term plant refers to a manufacturing establishment, which is a production facility located at a single physical location. Products and industries are 5-digit and 4-digit categories of the SIC, respectively.7 A sub-industry is the set of plants producing a particular product. Lastly, an investigated product is a product that was involved in an antidumping investigation, regardless of the outcome of the investigation.
The use of plant-level data is an important innovation of this paper and provides many advantages over more aggregated data, even including firm-level data. Many firms involved in petitioning for antidumping protection are large multi-product manufacturers. In fact, some firms participated as petitioners in multiple antidumping investigations involving multiple products. Individual plants on the other hand, tend to produce a much narrower set of products than firms as a whole. The use of plant-level data, therefore allows for more accurate matching between the products named in antidumping investigations and the facilities that actually produce those products.
In addition, I am able to greatly refine the identification of plants that did and did not receive antidumping protection through the use of plant-product-level data contained in the CM. These data report the full list of products manufactured at each plant, as well as the value, and sometimes quantity, of shipments attributable to each product. The availability of this plant-product-level data represents an additional level of disaggregation beyond the "major industry" codes generally used to identify plants and firms in micro-level datasets.
The list of products involved in antidumping investigations in the United States is from version 3.0 of Chad Bown's Global Antidumping Database (2010). Products subject to antidumping investigations are identified using the Harmonized Tariff System (HTS) and products may be defined from the 4-digit level to the 10-digit level. In addition to a description of the products involved in each investigation, the antidumping database provides the dates and outcomes of each phase of the investigation-e.g. preliminary and final injury and dumping determinations-along with the final remedy. The HTS product codes in the Bown dataset are mapped to the SIC5 product codes in the CM using an official U.S. Census Bureau concordance that is described in detail in Pierce and Schott (2011). This concordance, which links HTS codes to SIC5 codes via an eight-character "base code" results in a median of 12 ten-digit HTS codes being matched to each SIC5.
The analysis in this paper considers the effects of antidumping investigations that were completed during the period from 1988 to 1996. This setup ensures that I am able to observe plant-level outcomes both before and after the imposition of protection for every product group.8 Lastly, because successful antidumping investigations in the United States almost always result in ad-valorem tariffs-rather than price undertakings or suspension agreements-I am able to study the effect of variation in the antidumping duty rate on productivity.
Section 3: Antidumping Duties in the United States
Under GATT Article VI and the WTO's Antidumping Agreement, WTO members are permitted to impose discriminatory tariffs on goods sold by foreign producers at prices that are deemed to be less than fair value (LTFV), if these sales result in material injury to the domestic industry. In the United States, sales are considered to be made at LTFV-i.e. dumped-when a foreign firm sells a good in the United States at a price that is below that offered on comparable sales in its home market, or below a constructed value similar to average total cost (ATC).
Antidumping investigations in the United States are initiated by individual firms, groups of firms or sometimes labor unions, which are referred to in antidumping investigations as petitioners. The foreign firms selling allegedly dumped merchandise are referred to as respondents. Petitioners apply for antidumping protection by submitting a petition to the Import Administration of the Department of Commerce (DOC) and the International Trade Commission (ITC). The DOC determines whether sales made by foreign firms in the U.S. are being made at LTFV. The ITC determines whether the U.S. industry has been injured as a result of the dumping.
If the DOC finds that sales have been made at LTFV and the ITC concludes that these sales have injured U.S. producers, an ad-valorem tariff is placed on imports of goods from the respondents' home countries.9 This ad-valorem tariff, which is known as an antidumping duty is equal to the percentage difference between the U.S. price and the home-market price or ATC. I refer to the magnitude of the antidumping duty as the antidumping duty rate. Because the antidumping duty is applied to all dumped goods, it benefits the petitioners, as well-as non-participating producers of the investigated product.
Table 1 reports the types of products involved in antidumping investigations that were completed from 1988 to 1996, showing the number of antidumping duty investigations by 2-digit HTS Chapter. The most frequent seekers of antidumping duties were producers of "Iron and Steel" (Chapter 72) and "Articles of Iron and Steel" (Chapter 73). Other active applicants for antidumping protection included producers of machinery and parts (Chapters 84 and 85) and inorganic and organic chemicals (Chapters 28 and 29).
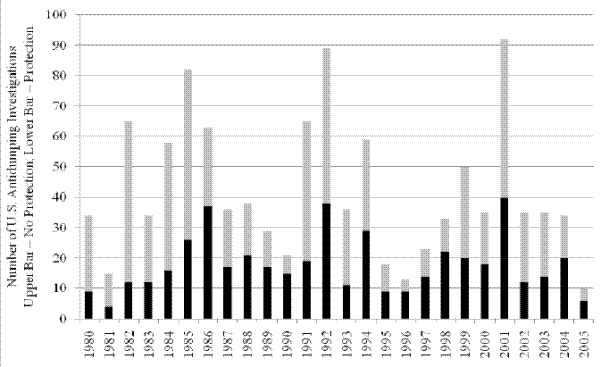
Figure 1 shows the number of antidumping investigations completed, by outcome for the years 1980 to 2005. As described in Knetter and Prusa (2003), the number of antidumping investigations tends to increase during and immediately following periods of recession, and we see that this phenomenon did, in fact, occur following the recession of 1990-1991, when the number of new investigations spiked in 1991 and 1992. Aside from this countercyclical trend in new investigations, the period from 1988 to 1996 was typical in terms of the number of investigations initiated.10
Section 4: Pre-Estimation Definitions
A. Definition of Treatment and Control Groups
I conduct this analysis by comparing the behavior of plants in a treatment group receiving antidumping protection to plants in a control group that do not. The treatment group consists of plants in sub-industries that applied for and received antidumping protection. Each plant in the treatment group is assigned a date of treatment and an ad-valorem duty rate, which comes from the results of the antidumping investigation associated with the product it produces. If a plant produces more than one product that receives protection, the treatment date and duty are those associated with the product that accounts for the highest share of its shipments. These products are also the basis of the product-level fixed effects used in this analysis.
In defining an appropriate control group, I will control for two potential sources of bias described in Konings and Vandenbussche (2008). The first is a self-selection bias, which arises if the types of sub-industries that apply for antidumping protection are different from those that do not. This is almost certainly the case. For example, antidumping applicants produce goods that are subject to import competition, perceive themselves as being injured by imports and operate in sub-industries capable of cooperating to file a case. Moreover, antidumping petitions are concentrated in particular sectors, especially metals, chemicals and basic mechanical goods.
The second source of bias, which I will refer to as the "government selection bias," arises if the government bases its decision of whether or not to approve protection for petitioners based on variables that are correlated with productivity or other dependent variables I will examine. The variables considered by the ITC when determining the injury portion of an antidumping investigation are publicly disclosed and include, among others, import penetration and employment. Because these variables are likely correlated with productivity, it will be necessary to address this government selection bias.
I control for these potential sources of bias in two steps. First, to control for the self-selection bias, I limit the control group to plants in sub-industries that applied for protection, but whose petitions were rejected by the government. I refer to these sub-industries whose petitions were rejected as "terminated sub-industries." As with the treated (protected) sub-industries, terminated sub-industries face import competition, perceive themselves as being injured by those imports and are able to collaborate to file an antidumping petition. Moreover, as shown in Table 2, both the treated and terminated sub-industries are concentrated in the sectors that are most frequently involved in antidumping investigations, namely primary and fabricated metals, chemical products and industrial equipment.
The government selection bias arises if the treatment and control group differ in terms of the variables considered by the government when deciding whether to provide protection. I control for this bias with a second step that limits the control group to the set of terminated sub-industries that are most similar to the treated sub-industries in terms of variables considered by the ITC in its determinations. This procedure, therefore, controls for selection based on observable variables.11
To determine which of the terminated sub-industries are most "similar" to the treated sub-industries, I estimate a probability of protection with the following logistic regression:
 |
(1) |
where the binary dependent variable
takes a value of 1 if a product in industry i received protection and a value of zero if it did not and where 
is lagged import penetration, 
is the log of lagged employment, 
is the GDP growth rate between period 
and period t, 
is the growth rate of industry-level prices from period to period t and 
is the log of labor productivity.12 After calculating the probability of protection using the fitted values from this regression, the control group is limited to terminated sub-industries that were in the top 75
percentile in terms of their predicted probability of receiving protection.13
Results of the logit regression described above are reported in Table 5.
14 Estimated coefficients take the expected sign and are consistent with results in Blonigen and Park (2004) and Konings and Vandenbussche (2008). Specifically, the probability of receiving antidumping protection increases with
higher levels of import penetration and labor productivity and increases with negative price growth.
Through these two steps, the control group has the attractive property of being composed of plants in industries that applied for protection-thus controlling for potential self-selection bias-while also being highly similar to the treated industries, in terms of the variables considered by the ITC, therefore controlling for the government selection bias. In addition, as described in Table 3, plants in the treatment and control groups are comparable in terms of their mean value of shipments, mean number of employees and mean capital to labor ratios.15 As discussed below, the results are robust to consideration of two alternate control groups.
B. Calculation of Productivity
1. Revenue Versus Physical Productivity
As discussed above, the observed effects of trade protection on productivity may differ based on whether productivity is calculated as revenue or physical productivity. To examine these differences I calculate TFP and labor productivity using both revenue and physical units of quantity as measures of output. Throughout this paper, the term revenue productivity refers to productivity measures where output is measured as revenue, or price multiplied by quantity. The term physical productivity refers to productivity measures that use physical units of quantity as a measure of output. Revenue is deflated by constructing a plant-specific deflator that is a value-weighted average of industry-level price indexes for industries in which the plant operates. Importantly, even with this relatively sophisticated deflation strategy, I find that antidumping protection on revenue productivity is drastically different from the effect on physical productivity.
2. The Quantity Sample
Manufacturing establishments may produce more than one product, and they may report output data in physical units of quantity for some products, but not others. Following Foster, Haltiwanger and Syverson (2008), I restrict calculation of physical productivity measures to those plants that earn at least 50 percent of the value of their shipments from products for which physical output data are reported. Naturally, in my analysis, these products must also be in the set of products included in the treatment and control groups defined above.16
I also make adjustments to the sample to eliminate plants with imputed quantity data. Specifically, I exclude plants from the quantity sample if the price associated with a particular product is equal to the average price at the 4-digit, 5-digit or 7-digit SIC level. This eliminates imputations based on industry or product averages. In addition, I exclude products defined by "balancing product codes," which are used by Census to ensure that the sum of a plant's product-level shipments is equal to that plant's total shipments. These exclusions based on average price imputations and balancing codes do not affect the results qualitatively.
Lastly, I exclude certain outlier observations from the baseline quantity sample. Specifically, plants reporting product-level prices that were outside three standard deviations of the mean price at the 5-digit SIC level were excluded from the quantity sample. I note that the main results are robust to a number of alternative outlier restrictions including no dropping of outliers, the exclusion of plants reporting prices that were ten times the product-level median and the exclusion of plants reporting prices that were ten times the plant-level median.17
3. Methods of Calculating Productivity
I first calculate revenue and physical TFP using the standard index number employed by Foster, Haltiwanger and Syverson (2008) (referred to as FHS TFP, hereafter) in their study of differences between revenue and physical productivity.18 This technique employs a Cobb Douglas production function with an implicit assumption of constant returns to scale19 and measures TFP as follows:
 |
(2) |
Here, lower-case letters represent the logarithms of TFP, output, capital, labor and raw materials (including energy), respectively at plant p at time t. Output, 
, is measured as the logarithm of deflated revenue (for revenue productivity) or physical units of quantity (for physical productivity). Capital is measured as the real book value of capital, labor is the total number of employees and materials are the real
value of material expenditures. Nominal values for revenue, capital and raw materials are deflated using the industry-level price indices in the NBER-CES manufacturing industry database from Bartelsman, Becker and Gray (2005).
The factor elasticities,
(j={k,l,m}) are measured as the average cost share for each input at the industry level. The numerators of the cost shares are calculated using the real value of wages and
salaries for labor and the real value of materials expenditures for materials. The equivalent term for the capital share is calculated by multiplying the real book value of capital by the rental rate of capital at the two-digit SIC level, using rental rates from the Bureau of Labor Statistics. The
denominator of the cost shares is the real total value of shipments. Note that results discussed below based on FHS TFP measures are also robust to calculation of TFP with the index number technique presented in Caves, Christensen and Diewert (1982).
As a robustness check, I also report results with a simple, single-factor labor productivity, defined as output per employee:
 |
(3) |
where 
is output, measured in either real revenue or physical units of quantity and TE
is the total number of employees at plant p at time t.20
C. Effective Antidumping Duty Rates
A single antidumping investigation can be filed against imports from multiple countries and if the case ends with a determination by the DOC and ITC to offer protection, each country may be assigned a different ad-valorem antidumping duty. Naturally, imports from certain countries account for larger shares of U.S. imports of a good than others. In order to account for the true importance of an antidumping duty on U.S. trade, therefore, I calculate an effective antidumping duty rate for each product that is assigned an ad-valorem antidumping duty. The effective antidumping rate is calculated as follows:
 |
(4) |
where
is country c's share of U.S. imports of product g in time t-1 and
is the ad-valorem duty applied to imports of product g from country c at time t. More
specifically,
is the "all others" rate assigned to country c, which is the weighted average of the duty rates assigned to each foreign respondent firm in the
investigation. A country's share is calculated based on imports in time t-1, rather than time t, because antidumping duties often lead to significant reductions in imports from pre-protection levels. Using a pre-protection share, therefore,
provides a more accurate representation of a country's importance to U.S. trade.
Section 5: Empirical Strategy and Results
A. The Effect of Temporary Tariffs on Plant-Level Productivity
1. Empirical Strategy
I examine the effect of temporary protection on plant-level productivity, prices and mark-ups using a difference-in-difference approach. As discussed above, the treatment group is composed of plants producing products that receive antidumping protection. The control group is composed of plants producing products that applied for protection and are similar to those in the treatment group, but did not receive antidumping protection. The difference-in-difference estimator is attractive because it isolates the effect of the treatment-antidumping protection-by eliminating time-invariant differences between the treatment and control group, as well as time-specific effects common to both treatment and control. The difference-in-difference estimator, therefore, measures not simply the change in the dependent variable that occurs following antidumping protection, but rather the difference between the changes in the treatment group and the changes in the control group.
Let T be the set of products that receive antidumping protection and let C be the set of products in the control group. Further, define I
to be the treatment year for product g.21 I measure the difference-in-difference
effect by estimating Equation (5):
 where |
(5) |
 and  |
 and 0 otherwise22 |
Here,
is the outcome variable of interest-such as productivity, prices or mark-ups-at plant p, which produces product g at time
t. Year fixed effects capture any macro-level shocks affecting plants in T and C equally. Similarly, product fixed effects,
, capture time-invariant differences between products. Note that Equation (5) contains product-level fixed effects, rather than a more general Treatment dummy used in the most basic difference-in-difference expressions. This specification captures time-invariant differences between producers of different products within T and C. This is likely important when dealing
with a diverse set of manufacturers from different sectors and industries. Finally, the coefficient
on the interaction term is the coefficient of interest and measures the difference-in-difference effect of antidumping protection on the plant-level outcomes discussed below.
Equation (5) defines protection with a binary variable-any plant that receives any antidumping protection is considered to be equally protected. It seems reasonable to expect, however, that plants' reactions to protection could depend not only on this simple binary classification, but also on the level of protection they receive. That is, plants producing products that receive high ad-valorem duty rates-such as the 259.17 percent antidumping duty rate on Aluminum Sulfate from Venezuela-may respond differently than those producing products that receive low antidumping duty rates, such as the 4.18 percent rate on Corrosion Resistant Carbon Steel Sheet from Germany. As these two examples indicate, the variation in duty rates among cases that receive protection is large: the mean duty rate is 51 percent and the standard deviation is 49 percent at the product-country-level.
I measure the effects of heterogeneity in antidumping rates by augmenting Equation (5) with an additional interaction term:
 |
(6) |
Here, Rate
is the ad-valorem effective antidumping duty rate on product g at time t. By
interacting Rate with the Post dummy, I am able to separate the effect of varying rates of protection from the mean response of all plants receiving antidumping protection.
I will also employ the difference-in-difference framework in Equations (5) and (6)-with the same treatment and control groups-to examine the effect of antidumping duties on plant-product-level prices, as well as mark-ups over average variable cost. These measures of prices and mark-ups are calculated with plant-product-level data from the CM, where products are defined at the five-digit SIC level. Specifically, prices are defined as follows:
 |
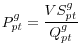(7) |
where VS is the value of shipments of good g by plant p at time t and Q is the associated quantity of units shipped. Plant-level mark-ups over average variable cost are defined as:
 |
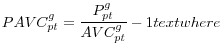(8) |
 |
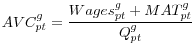(9) |
Results showing the effect of AD on AVC are preserved when markups are calculated over average total cost. Reported results for revenue productivity, physical productivity, prices and mark-ups all include robust standard errors that have been adjusted for clustering at the product-level.
2. Results
a. Plant-Level Productivity
I find that antidumping protection is associated with increases in revenue productivity of 3 to 7 percent. Table 6 reports the results for Equations (5) and (6) for both the TFP and LP revenue productivity measures in columns 1 and 2. I continue to find a positive relationship between antidumping protection and revenue productivity when the effective duty rate is included in the specification, in columns 3 and 4, although the effect is not significant when using FHS TFP. The results indicate that antidumping protection is associated with an increase in measured revenue productivity.
As can be seen in columns 1-4 of Table 7, however, the effect of AD on physical productivity is starkly different from that for revenue productivity. In columns 1 and 2 of Table 7, antidumping duties are actually associated with a decrease in physical productivity among the set of plants reporting quantity data. In fact, physical productivity actually falls by a greater amount as the effective duty rate protecting the plant increases, as shown in columns 3 and 4 of Table 7. These results highlight substantial differences between the effects of AD on physical, as opposed to revenue productivity.
A word of warning in terms of interpreting these results is necessary here. It would be inappropriate based on these results to claim that antidumping duties, in general, decrease plant-level physical productivity. It is true that antidumping duties are associated with a relative decline in productivity among the set of plants reporting output data in units of quantity. However, this group is subject to a potential selection bias if plants that report output data in units of quantity differ from those that do not. Indeed, when I examine the effect of antidumping protection on the revenue productivity of the subset of plants reporting output in units of quantity in columns 5-8 of Table 6, I find that, on average, revenue productivity was unaffected by antidumping protection.23 I will directly address this potential selection bias below and demonstrate that it is not driving the results.
b. Prices and Mark-Ups
The disparity between results showing the effect of antidumping protection on revenue versus physical productivity suggests that increases in prices and mark-ups are playing a role in the apparent increase in revenue productivity. I use the same difference-in-difference specifications and treatment and control groups from the productivity analysis to examine the effects of antidumping duties on the measures of prices and mark-ups over average variable cost defined above. In these estimates, prices are plant-product-level prices from the CM, which are calculated as in Equation (7) and then measured in logs. Markups are measured in percentages, as defined in Equation (8).
As reported in columns 5-8 of Table 7, I find that increases in the effective duty rate are associated with increases in both prices and mark-ups, while the relationship between the binary protection measure and prices and mark-ups is weaker. On average, each 1 percentage point increase in the
effective duty rate is associated with a price increase of 3 percent at protected plants. Similarly, I find that for each 1 percentage point increase in the effective duty rate, mark-ups over average variable cost increase by 0.3 percentage points.24 These results illustrate the reason that the results for revenue and physical
productivity differ so sharply-the effect of AD on revenue productivity is inflated by increases in prices and markups.
D. Robustness Checks
i. Examination of Sample Selection Bias
As mentioned above, results for physical productivity, prices and markups could only be calculated for the sub-sample of plants that reported output data in units of quantity. This data limitation, however, gives rise to a potential selection bias if plants that report output data in units of quantity differ from those that do not. I now examine the representativeness of results based on the quantity sample by describing characteristics of the quantity sample and re-estimating the main results using weights based on the probability of being in the quantity sample.
In its CM questionnaires, the Census Bureau only asks plants to report output data in units of quantity for certain products. The Census Bureau's primary considerations in determining whether to request quantity data for a particular product are whether the product is homogeneous enough for quantity data to be meaningful and the extent to which asking for quantity data imposes a burden on survey respondents. The Census Bureau's preference for homogeneous products can be seen in Table 2, where sectors with the highest share of quantity data include food, primary metals and textile mill products. In contrast, sectors dominated by differentiated products including industrial and electronic machinery generally do not contain much quantity data.
These criteria likely mean that products for which quantity data are reported-and hence the plants producing them-differ from those for which quantity data are not collected.25 However, the criteria also provide variables that can be used to construct weighted regression results that provide information on the population of plants in the treatment and control groups. As described in Cameron and Trivedi (2005), it is possible to control for non-random sampling by calculating the probability of inclusion in the sample-i.e. the probability that a plant reports output data in units of quantity-and using the inverse probability as a weight in the regression of interest.
I follow this approach by estimating the probability that a plant reports quantity data (QTY) in a logit regression framework. My explanatory variables are selected to replicate the criteria considered by the Census Bureau when determining whether to request quantity data from respondents. To measure product homogeneity, I calculate a SIC5-level version of the Rauch (1999) classifications, which classify goods into three categories: exchange-traded (homogeneous) goods, reference-priced goods and differentiated products. These categories are included through dummy variables that equal one if plant p produces a product that is reference-priced and zero otherwise (REF) and a dummy variable that equals one if plant p produces a product that is differentiated and zero otherwise (DIFF) The primary measure of respondent burden considered by the Census Bureau is the number of plants that would have to respond to a question and hence I include the number of plants producing each product (denoted by g) as a measure of burden (NUMPLANT). In addition, since large plants generally respond to the CM at higher rates than smaller plants, I include total employment as a measure of plant size (TE). Lastly, I include a set of dummy variables,
for the SIC2 sectors and estimate the following equation:
 |
(10) |
Coefficient results and standard errors are reported in the body of Equation (10), which yielded a pseudo-R
of 0.31. I find that producers of differentiated-products are less likely
to report quantity data than those producing homogeneous goods, as expected, although producers of reference-priced goods were actually the most likely to report quantity data. Sub-industries with more plants are less likely to report quantity data, reflecting the higher burden associated with
requesting quantity data in those sub-industries. Larger plants are more likely to report quantity data than their smaller counterparts.
Having estimated a probability of reporting quantity data for each plant in the full sample, I re-estimate the paper's main results, using the inverse predicted probability of inclusion in the quantity sample as a weight, as described in Cameron and Trivedi (2005). This strategy assigns a higher weight to plants that reported quantity data, but were similar to the plants excluded from the quantity sample. The resulting estimates then provide an indication of whether results estimated for the quantity sample are applicable for the sample as a whole.
As reported in Table 8, the results generated by this weighted regression are consistent with the main results reported in Tables 6 and 7. The effect of antidumping duties on revenue productivity is still found to be overstated due to increases in prices and markups, with physical productivity falling for protected plants, relative to unprotected plants. In sum, the results indicate that the potential selection bias associated with non-random sampling of plants in the quantity sample is not driving the results.
ii. Alternate Control Groups
I also consider two alternate control groups employed in Konings and Vandenbussche (2008). The first alternative control group, AC1, consists of all plants in sub-industries that applied for protection, but whose petitions were rejected by the government.26 The second alternative control group, AC2, consists of industries that did not receive protection, but had a high probability of receiving protection based on a multinomial logit model of antidumping protection described in Blonigen and Park (2004) and Konings and Vandenbussche (2008).27 The primary conceptual difference between AC2 and the control group used in this paper is that AC2 includes industries that never applied for protection, but were similar to those industries that did apply and receive protection.28
Results using the two alternate control groups are broadly consistent with those in the preferred control group. In particular, I find that antidumping duties were associated with an increase in revenue productivity in both alternate control groups, as they were with the preferred control group. I also continue to find that physical productivity falls, the higher the effective duty rate, as was the case in the preferred control group.29 Lastly, I continue to find that both prices and mark-ups increase as the effective duty rate increases, as they did using the preferred control group. In sum, the results presented above are robust to calculation with different control groups, even with substantial differences in the composition of plants in each group.30
iii. Additional Robustness Checks
In addition to the robustness checks described in detail above, the results are also robust to a number of other controls. First, the results are robust to inclusion of a variable measuring the duration of protection, as well as examination of subsets of investigations that took place in the years 1991-1993, 1990-1994 and 1989-1995. These robustness checks are important since the availability of CM data in 5 year intervals means that I observe plants for different amounts of time before and after antidumping investigations depending on the year in which the investigation takes place. Second, I obtain qualitatively similar results when estimating results using plant fixed effects, in place of product fixed effects.31 These results provide evidence that AD lowers physical productivity within plants over time.32 Lastly, the results are robust to exclusion of products and industries that end in 9 (which are often "miscellaneous" categories) and consideration of only those products with at least 25 establishment observations per year.
B. Antidumping Duties Allow for Continued Production of Protected Products by Low-Productivity Plants
I now examine whether antidumping protection allows for the continued operation of low-productivity plants that would have otherwise stopped production, as a potential explanation for why relative physical productivity declines in the treatment group. The analysis takes places in two steps. First, I estimate whether antidumping protection makes plants less likely to stop producing a protected product and, second, I examine whether plants that stop production are lower-productivity than plants that continue production. A novel aspect of this analysis is that I am able to define "production-stopping" based on a plant's decision to exit or to drop a product. This allows me to account for multi-product plants that remain in operation but drop a treatment product and, more generally, allows for simultaneous examination of multi-product and single-product plants.
For the first step, I estimate the effect of antidumping protection on the probability of production-stopping using the following conditional logit specification with product and year fixed effects:
 |
(11) |
As mentioned above, Stop is a binary variable that takes the value 1 if a plant stops producing a treatment or control product, either by dropping the
product or exiting.
and
are the primary coefficients of interest and measure the effect of antidumping protection and the effective duty rate on the probability that a plant stops production. X is a matrix of plant-level variables including log number of employees, plant age, log of capital-labor ratio, log of average wage and indicators for whether the plant is a multi-product plant, or a part of a multi-unit firm. As reported in Table 9, I do find that antidumping
protection makes plants between 10 and 15 percent less likely to stop producing a particular product.
For the second step, I examine whether the reduction in production-stopping associated with antidumping protection allows low-productivity plants to continue producing. To estimate the relative productivity of production-stoppers , I regress plant-level productivity, Prod, on a binary variable Stop that equals one in time t if plant p stopped producing an investigated product between time t and time t+5 and zero otherwise, with year and product fixed effects:
 |
(12) |
I find that production-stoppers are 15 percent less productive in terms of revenue TFP and 10 percent less productive in terms of physical TFP, with both estimates statistically significant at the 5 percent level.
Combining the results from these two steps, I find that antidumping protection allows more plants to continue production of protected products than would be the case without protection, which leaves low productivity plants active in the industry. This continued operation by low-productivity plants, therefore, contributes to the relative decline in physical productivity found in the treatment group.
Section 6: Conclusions
Antidumping duties have become one of the primary forms of trade protection worldwide, and the large magnitudes of the duties imposed can dramatically alter trade flows. Yet despite the growing importance of antidumping duties to international trade, there is little understanding of their effects at the micro level. In addition to increasing our understanding of an important trade policy, the study of antidumping duties can also provide new insights into the responses of firms in a developed country to a major tariff shock.
Using a difference-in-difference framework, I compare outcomes at plants in a treatment group that receives protection to those in a control group that did not. I find that apparent increases in revenue productivity associated with antidumping protection are driven primarily by increases in prices and mark-ups. Physical productivity actually falls among the protected plants reporting output data in units of quantity. Because antidumping protection allows for the continued operation of low-productivity plants that would have otherwise stopped producing the protected product, antidumping duties also prevent the reallocation of resources to their most productive uses.
The results have several implications. First, for empirical researchers, the results underscore the importance of differentiating between changes in revenue productivity-which may be driven by increases in prices and mark-ups-and changes in physical productivity. Separating these two effects is particularly important in situations where changes in productivity may be taking place concomitantly with changes in prices, as is the case with antidumping duties. Second, for theoretical researchers, the results provide stylized facts regarding the responses of plants in a large developed economy to a unilateral change in tariffs. More generally, the results suggest that antidumping protection is more likely to lead to higher prices than higher productivity.
Bibliography
Bailey, M. N., Hulten, C. and Cambell, D., 1992. Productivity Dynamics in Manufacturing Plants. Brookings Papers on Economic Activity: Microeconomics, 187-249.
Bartelsman, E., Becker, R. and Gray, W., 2005. NBER-CES Manufacturing Industry Database. NBER Technical Working Paper 205.
Bernard, A., Jensen, J. B., and Schott, P., 2006. Trade Costs, Firms and Productivity. Journal of Monetary Economics 53, 917-37.
Bernard, A., Redding, S. and Schott, P., 2010. Multi-Product Firms and Product-Switching. American Economic Review 100, 70-97.
Bernard, A., Redding, S. and Schott, P., 2011. Multi-Product Firms and Trade Liberalization. Quarterly Journal of Economics, forthcoming.
Blonigen, B. and Park, J., 2004. Dynamic Pricing in the Presence of Antidumping Policy: Theory and Evidence, American Economic Review 94, 134-154.
Bown, C. and Crowley, M., 2007. Trade Deflection and Trade Depression. Journal of International Economics 72, 176-201.
Bown, C., 2010. Global Antidumping Database. Available at http://econ.worldbank.org/ttbd/gad/.
Cameron, A. C. and Trivedi, P.K., 2005. Microeconometrics: Methods and Applications, Cambridge University Press, Cambridge, pp. 813-821.
Caves, D. W., Christensen, L. and Diewert, W.E. 1982. Multilateral Comparisons of Output, Input, and Productivity Using Superlative Index Numbers. The Economic Journal 92, 73-86.
Crowley, M., 2006. Do Antidumping Duties and Safeguard Tariffs Open or Close Technology Gaps? Journal of International Economics 68, 469-484.
De Loecker, J., 2010. Product Differentiation, Multi-Product Firms and Estimating the Impact of Trade Liberalization on Productivity, Econometrica, forthcoming.
Eslava, M., Haltiwanger, J., Kugler, A. and Kugler, M., 2004. The Effects of Structural Reforms on Productivity and Profitability Enhancing Reallocation: Evidence from Colombia. Journal of Development Economics 75, 333-371.
Fernandes, A., 2007. Trade Policy, Trade Volumes and Plant-Level Productivity in Colombian Manufacturing Industries. Journal of International Economics 71, 52-71.
Foster, L., Haltiwanger, J. and Syverson, C., 2008. Reallocation, Firm Turnover and Efficiency: Selection on Productivity or Profitability. American Economic Review 98, 394-425.
Katayama, H., Lu, S. and Tybout, J., 2008. Firm-Level Productivity Studies: Illusions and a Solution. International Journal of Industrial Organization 27, 403-413.
Hortacsu, A. and Syverson, C., 2007. Cementing Relationships: Vertical Integration, Foreclosure, Productivity and Prices. Journal of Political Economy 115, 250-301.
Konings, J. and Vandenbussche, H., 2008. Heterogeneous Responses of Firms to Trade Protection. Journal of International Economics 76, 371-83.
Konings, J. and Vandenbussche, H., 2005. Antidumping Protection and Markups of Domestic Firms: Evidence from Firm Level Data. Journal of International Economics 65, 151-65.
Levinsohn, J. and Petrin, A., 2003.Estimating Production Functions Using Intermediates to Control for Unobservables. Review of Economic Studies 70, 317-341.
Matsuyama, K., 1990. Perfect Equilibria in a Trade Liberalization Game. American Economic Review 80, 480-492.
Melitz, M. and Ottaviano, G., 2008. Market Size, Trade and Productivity. Review of Economic Studies 75, 295-316.
Miyagiwa, K. and Ohno, Y., 1995. Closing the Technology Gap Under Protection. American Economic Review 85, 755-770.
Nocke, V. and Yeaple S., 2008. Globalization and the Size Distribution of Multiproduct Firms, mimeo.
Olley, S. and Pakes, A., 1996. The Dynamics of Productivity in the Telecommunications Equipment Industry. Econometrica 64, 1263-1298.
Pavcnik, N., 2002. Trade Liberalization, Exit and Productivity Improvements: Evidence from Chilean Plants. Review of Economic Studies 69, 245-276.
Pierce, J. and Schott, P., 2011a. Concording U.S. Harmonized System Categories Over Time, 1989-2006. Journal of Official Statistics, forthcoming.
Pierce, J. and Schott, P., 2011b. A Concordance Between U.S. Harmonized System Codes and SIC/NAICS Product Classes and Industries. NBER Working Paper 15548.
Prusa, T., 2001. On the Spread and Impact of Antidumping. Canadian Journal of Economics 34, 591-611.
Prusa, T. and Knetter M., 2003. Macroeconomic Factors and Antidumping Filings, Journal of International Economics 61, 1-18.
Syverson, C., 2004. Market Structure and Productivity: A Concrete Example. Journal of Political Economy 112, 1181-1222.
Rauch, J., 1999. Networks versus Markets in International Trade, Journal of International Economics, 48 7-35.
United States International Trade Commission, 2006. Import Injury Investigations: Case Statistics: FY 1980-2005.
Vandenbussche, H. and Zanardi, M., 2010. The Global Chilling Effect of Antidumping Proliferation. European Economic Review 54, 760-777.
Van Biesebroeck, J., 2004. Robustness of Productivity Estimates. NBER Working Paper 10303.
| Description | (1) AD Investigations with No Protection | (2) AD Investigations with Protection | (3) Total AD Investigations | |
| HTS2 73 | Articles of Iron and Steel | 12 | 15 | 27 |
| HTS2 72 | Iron and Steel | 6 | 12 | 18 |
| HTS2 84 | Machinery | 6 | 9 | 15 |
| HTS2 28 | Inorganic Chemicals | 6 | 6 | 12 |
| HTS2 29 | Organic Chemicals | 4 | 8 | 12 |
| HTS2 85 | Electrical Machinery | 5 | 7 | 12 |
| HTS2 87 | Transportation Vehicles and Parts | 8 | 2 | 10 |
| HTS2 90 | Precision Instruments and Apparatus | 3 | 4 | 7 |
| HTS2 25 | Plastering, Lime and Cement | 3 | 3 | 6 |
| HTS2 39 | Plastics and articles thereof | 1 | 5 | 6 |
| HTS2 40 | Rubber and articles thereof | 1 | 3 | 4 |
| HTS2 56 | Certain Textiles | 3 | 1 | 4 |
| HTS2 20 | Preparations of Vegetables or Fruits | 1 | 2 | 3 |
| Other | 18 | 25 | 43 | |
| Total | 77 | 102 | 179 |
| SIC2 Description | Total Observations: SIC2 | Total Observations: Control | Total Observations: Treatment | Total Observations: Total | Observations With Quantity: Control | Observations With Quantity: Treatment | Observations With Quantity: Total | Share of Obs. with Quantity: Control | Share of Obs. with Quantity: Treatment | Share of Obs. with Quantity: Total |
| Food and Kindred Spirits | 20 | 0 | 1,546 | 1,546 | 0 | 1,084 | 1,084 | N/A | 70% | 70% |
| Textile Mill Products | 22 | 1,062 | 969 | 2,031 | 741 | 402 | 1,143 | 70% | 41% | 56% |
| Apparel and Other Textiles | 23 | 5,355 | 1,753 | 7,108 | 220 | 525 | 745 | 4% | 30% | 10% |
| Furniture and Fixtures | 25 | 1,741 | 0 | 1,741 | 54 | 0 | 54 | 3% | N/A | 3% |
| Paper and Allied Products | 26 | 2,646 | 0 | 2,646 | 1,063 | 0 | 1,063 | 40% | N/A | 40% |
| Chemical Products | 28 | 880 | 3,703 | 4,583 | 67 | 635 | 702 | 8% | 17% | 15% |
| Rubber Products | 30 | 12,177 | 4,009 | 16,186 | 143 | 74 | 217 | 1% | 2% | 1% |
| Leather Products | 32 | 2,077 | 650 | 2,727 | 425 | 398 | 823 | 20% | 61% | 30% |
| Primary Metals | 33 | 0 | 3,326 | 3,326 | 0 | 1,923 | 1,923 | N/A | 58% | 58% |
| Fabricated Metals | 34 | 11,834 | 4,394 | 16,228 | 965 | 486 | 1,451 | 8% | 11% | 9% |
| Industrial Machinery | 35 | 4,084 | 16,294 | 20,378 | 84 | 278 | 362 | 2% | 2% | 2% |
| Electronic Machinery | 36 | 488 | 7,950 | 8,438 | 87 | 32 | 119 | 18% | 0% | 1% |
| Transportation Equipment | 37 | 2,469 | 886 | 3,355 | * | * | * | * | * | * |
| Measuring Instruments | 38 | 611 | 7,647 | 8,258 | * | * | * | * | * | * |
| Year | Treatment | (1) Mean TVS ('000$) | (2) Mean No. Employees | (3) Mean Capital Intensity | (4) No. Plants | (5) Qty. Share | (6) Treatment Share | (7) Effective AD Rate | (8) Mean FHS TFP (Rev.) | (9) Mean LP (Rev.) | (10) Mean FHS TFP (Phys.) | (11) Mean LP (Phys.) |
| 1987 | 0 | 25,844 | 151 | 42 | 12,934 | 93% | 71% | 4.09 | 4.70 | 3.96 | 4.85 | |
| 1987 | 1 | 23,402 | 165 | 52 | 16,372 | 93% | 71% | 17% | 4.42 | 4.64 | 4.77 | 5.18 |
| 1992 | 0 | 27,783 | 125 | 46 | 15,563 | 93% | 71% | 3.98 | 4.70 | 3.79 | 4.95 | |
| 1992 | 1 | 28,267 | 149 | 55 | 17,851 | 91% | 70% | 17% | 4.37 | 4.73 | 4.64 | 5.31 |
| 1997 | 0 | 34,498 | 119 | 52 | 16,927 | 94% | 73% | 4.01 | 4.78 | 4.26 | 5.49 | |
| 1997 | 1 | 36,833 | 146 | 70 | 18,904 | 92% | 70% | 16% | 4.46 | 4.89 | 4.73 | 5.41 |
| Year | Treatment | (1) Mean TVS ('000$) | (2) Mean No. Employees | (3) Mean Capital Intensity | (4) No. Plants | (5) Qty. Share | (6) Treatment Share | (7) Effective AD Rate | (8) Mean FHS TFP (Rev.) | (9) Mean LP (Rev.) | (10) Mean FHS TFP (Phys.) | (11) Mean LP (Phys.) |
| 1987 | 0 | 22,564 | 46 | 157 | 24,670 | 67% | 17% | 4.30 | 0.70 | 4.63 | 1.03 | |
| 1987 | 1 | 34,678 | 58 | 171 | 4,636 | 93% | 91% | 17% | 4.16 | 4.47 | 4.85 | 5.11 |
| 1992 | 0 | 22,876 | 46 | 128 | 30,079 | 68% | 16% | 4.21 | 1.41 | 4.69 | 2.26 | |
| 1992 | 1 | 74,630 | 97 | 231 | 3,335 | 92% | 93% | 17% | 4.05 | 4.32 | 5.00 | 5.20 |
| 1997 | 0 | 34,819 | 56 | 128 | 33,383 | 70% | 18% | 4.25 | 1.37 | 4.82 | 2.23 | |
| 1997 | 1 | 48,155 | 141 | 199 | 2,448 | 93% | 93% | 19% | 4.20 | 4.63 | 5.12 | 5.50 |
| Probability of Protection | |
| Lagged Import Penetration | 0.453** |
| Lagged Import Penetration Standard Error | 0.181 |
| ln(Lagged Employment) | -0.016 |
| ln(Lagged Employment) Standard Error | 0.086 |
| ln(Labor Productivity) | 0.550*** |
| ln(Labor Productivity) Standard Error | 0.151 |
| Real GDP Growth | 0.001 |
| Real GDP Growth Standard Error | 0.061 |
| Price Growth | -0.045*** |
| Price Growth Standard Error | 0.017 |
| Number of Observations | 694 |
| Pseudo-R Squared | 0.03 |
| Estimation Technique | Logit |
| (1) Full Sample: FHS TFP (Rev.) | (2) Full Sample: LP (Rev.) | (3) Full Sample: FHS TFP (Rev.) | (4) Full Sample: LP (Rev.) | (5) Quantity Sample: FHS TFP (Rev.) | (6) Quantity Sample: LP (Rev.) | (7) Quantity Sample: FHS TFP (Rev.) | (8) Quantity Sample: LP (Rev.) | |
| Treatment*Post | 0.0278* | 0.0644*** | 0.0203 | 0.0701*** | 0.0005 | -0.0093 | 0.0096 | 0.0411 |
| Treatment*Post Standard Errors | 0.0167 | 0.0186 | 0.0208 | 0.0249 | 0.0221 | 0.0299 | 0.0243 | 0.0288 |
| Post*Rate | 0.0005 | -0.0003 | -0.0005 | |||||
| Post*Rate Standard Errors | 0.001 | 0.0015 | 0.0007 | 0.0013 | ||||
| R-Squared | 0.5255 | 0.2978 | 0.5255 | 0.2978 | 0.6505 | 0.415 | 0.6505 | 0.4153 |
| Observations | 98,551 | 98,551 | 98,551 | 98,551 | 10,419 | 10,419 | 10,419 | 10,419 |
| (1) Physical Productivity Measures: FHS TFP (Phys.) | (2) Physical Productivity Measures: LP (Phys.) | (3) Physical Productivity Measures: FHS TFP (Phys.) | (4) Physical Productivity Measures: LP (Phys.) | (5) Price and Markups: Price | (6) Price and Markups: P/AVC | (7) Price and Markups: Price | (8) Price and Markups: P/AVC | |
| Treatment*Post | -0.3867* | -0.3878* | 0.1926 | 0.214 | 0.4022* | 0.0065 | -0.197 | -0.0467 |
| Treatment*Post Standard Errors | 0.2045 | 0.2073 | 0.1534 | 0.1583 | 0.2102 | 0.0354 | 0.1567 | 0.0365 |
| Post*Rate | -0.0312*** | -0.0325*** | 0.0323*** | 0.0029** | ||||
| Post*Rate Standard Errors | 0.004 | 0.0044 | 0.004 | 0.0012 | ||||
| R-Squared | 0.6284 | 0.6178 | 0.6324 | 0.622 | 0.6406 | 0.0829 | 0.6451 | 0.0831 |
| Observations | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 |
| (1) FHS TFP (Rev.) | (2) LP (Rev.) | (3) FHS TFP (Phys.) | (4) LP (Phys.) | (5) Price | (6) P/AVC | |
| Treatment*Post | 0.032 | -0.019 | -0.670* | -0.669* | 0.744* | 0.078* |
| Treatment*Post Standard Errors | 0.041 | 0.044 | 0.380 | 0.401 | 0.386 | 0.043 |
| Observations | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 |
| R-Squared | 0.653 | 0.335 | 0.432 | 0.443 | 0.471 | 0.074 |
| (7) FHS TFP (Rev.) | (8) LP (Rev.) | (9) FHS TFP (Phys.) | (10) LP (Phys.) | (11) Price | (12) P/AVC | |
| Treatment*Post | 0.018 | 0.040 | 0.261 | 0.349 | -0.227 | 0.018 |
| Treatment*Post Standard Errors | 0.054 | 0.062 | 0.447 | 0.465 | 0.442 | 0.068 |
| Post*Rate | 0.001 | -0.002 | -0.037*** | -0.040*** | 0.038*** | 0.002 |
| Post*Rate Standard Errors | 0.002 | 0.002 | 0.010 | 0.010 | 0.010 | 0.002 |
| Observations | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 | 10,419 |
| R-Squared | 0.653 | 0.336 | 0.435 | 0.447 | 0.475 | 0.074 |
| Stop | Stop | Stop | Stop | |
| Treatment*Post | -0.149*** | -0.114*** | -0.132*** | -0.106*** |
| Treatment*Post Standard Errors | 0.016 | 0.017 | 0.022 | 0.023 |
| Post*Rate | -0.001 | -0.0004 | ||
| Post*Rate Standard Errors | 0.001 | 0.001 | ||
| No. Employees | -0.346*** | -0.346*** | ||
| No. Employees Standard Errors | 0.008 | 0.008 | ||
| Plant Age | -0.014*** | -0.014*** | ||
| Plant Age Standard Errors | 0.001 | 0.001 | ||
| Capital Intensity | -0.118*** | -0.118*** | ||
| Capital Intensity Standard Errors | 0.009 | 0.009 | ||
| Avg. Wage | -0.332*** | -0.332*** | ||
| Avg. Wage Standard Errors | 0.023 | 0.023 | ||
| Multi-Unit | 0.237*** | 0.237*** | ||
| Multi-Unit Standard Errors | 0.020 | 0.020 | ||
| Multi-Product | 0.699*** | 0.699*** | ||
| Multi-Product Standard Errors | 0.019 | 0.019 | ||
| Year FE | Yes | Yes | Yes | Yes |
| Product FE | Yes | Yes | Yes | Yes |
| Observations | 62,671 | 62,671 | 62,671 | 62,671 |
Footnotes
takes the value zero in years when antidumping protection has
already ended. Return to Text