
Risk, Uncertainty, and Expected Returns1
Keywords: Risk, uncertainty, expected returns, ICAPM, time-series and cross-sectional stock returns, variance risk premium, consumption-based asset pricing model.
Abstract:
A consumption-based asset pricing model with risk and uncertainty implies that the time-varying exposures of equity portfolios to the market and uncertainty factors carry positive risk premiums. The empirical results from the size, book-to-market, and industry portfolios as well as individual stocks indicate that the conditional covariances of equity portfolios (individual stocks) with market and uncertainty predict the time-series and cross-sectional variation in stock returns. We find that equity portfolios that are highly correlated with economic uncertainty proxied by the variance risk premium (VRP) carry a significant premium relative to portfolios that are uncorrelated or lowly correlated with VRP. The insignificant alpha estimates indicate that the conditional asset pricing model proposed in the paper also explains the industry, size, and value premiums.
1 Introduction
This paper investigates whether the market price of risk and the market price of uncertainty are significantly positive and whether they predict the time-series and cross-sectional variation in stock returns. Although the literature has so far shown how uncertainty impacts optimal allocation decisions and asset prices, the results have been provided based on a theoretical model.4 Earlier studies do not pay much attention to empirical testing of whether the exposures of equity portfolios and individual stocks to market and uncertainty factors predict their future returns. Extending on the original consumption-based CAPM, we show that in the presence of volatility uncertainty, the traditional risk-return regression needs to be augmented because both market risk and volatility uncertainty carry a positive premium. We introduce a conditional asset pricing model in which the consumption growth and its volatility follow the joint dynamics. According to our model with time-varying volatility of the consumption growth and the volatility uncertainty in the consumption growth process, the premium on equity is composed of two separate terms; the first term compensates for the classic consumption risk in a standard consumption-based CAPM and the second term represents a true premium for variance risk. The model's parameter restrictions imply that the variance risk premium embedded in the equity risk premium is always positive.
Following Britten-Jones and Neuberger (2000), Jiang and Tian (2005), and Carr and Wu (2009), we define the variance risk premium (VRP) as the difference between expected variance under the risk-neutral measure and expected variance under the objective measure.5 We generate several proxies for financial and economic uncertainty and then compute the correlations between uncertainty variables and VRP. The first set of measures can be viewed as macroeconomic uncertainty proxied by the conditional variance of the US output growth and the conditional variance of the Chicago Fed National Activity Index (CFNAI). The second set of uncertainty measures is based on the extreme downside risk of financial institutions obtained from the left tail of the time-series and cross-sectional distribution of financial firms' returns. The third uncertainty variable is related to the health of the financial sector proxied by the credit default swap (CDS) index. The last uncertainty variable is based on the aggregate measure of investors' disagreement about individual stocks trading at NYSE, AMEX, and NASDAQ. We find that the variance risk premium is strongly and positively correlated with all measures of uncertainty considered in the paper. Our results indicate that VRP can be viewed as a sound proxy for financial and economic uncertainty.6
Anderson, Ghysels, and Juergens (2009) introduce a model in which the volatility, skewness and higher order moments of all returns are known exactly, whereas there is uncertainty about mean returns. In other words, asset returns are uncertain only because mean returns are not known. In their model, investors' uncertainty in mean returns is defined as the dispersion of predictions of mean market returns obtained from the forecasts of aggregate corporate profits. They find that the price of uncertainty is significantly positive and explains the cross-sectional variation in stock returns. Bekaert, Engstrom, and Xing (2009) investigate the relative importance of economic uncertainty and changes in risk aversion in the determination of equity prices. Different from Knightian uncertainty or uncertainty originated from disagreement of professional forecasters, Bekaert, Engstrom, and Xing (2009) focus on economic uncertainty proxied by the conditional volatility of dividend growth, and find that both the conditional volatility of cash flow growth and time-varying risk aversion are important determinants of equity returns.
Different from the aforementioned studies, we propose a model in which volatility uncertainty (proxied by VRP) plays a significant role along with the standard consumption risk. After introducing a two-factor model with risk and uncertainty, we investigate the significance of risk-return and uncertainty-return coefficients using the time-series and cross-sectional data. Our empirical analyses are based on the size, book-to-market, and industry portfolios as well as individual stocks. We first use the dynamic conditional correlation (DCC) model of Engle (2002) to estimate equity portfolios' (individual stocks') conditional covariances with the market portfolio and then test whether the conditional covariances predict future returns on equity portfolios (individual stocks). We find the risk-return coefficients to be positive and highly significant, implying a strongly positive link between expected return and market risk. Similarly, we use the DCC model to estimate equity portfolios' (individual stocks') conditional covariances with the variance risk premia and then test whether the conditional covariances with VRP predict future returns on equity portfolios (individual stocks). The results indicate a significantly positive market price of uncertainty. Equity portfolios (individual stocks) that are highly correlated with uncertainty (proxied by VRP) carry a significant premium relative to portfolios (stocks) that are uncorrelated or lowly correlated with VRP. Such a positive relationship between return and uncertainty is also consistent with our model's implication that the intertemporal elasticity of substitution or IES is larger than one--i.e., agents prefer an earlier resolution of uncertainty, hence uncertainty (proxied by VRP) carries a positive premium.
We also examine the empirical validity of the conditional asset pricing model by testing the hypothesis that the conditional alphas on the size, book-to-market, and industry portfolios are jointly zero. The test statistics fail to reject the null hypothesis, indicating that the two-factor model explains the time-series and cross-sectional variation in equity portfolios. Finally, we investigate whether the model explains the return spreads between the high-return (long) and low-return (short) equity portfolios (Small-Big for the size portfolios; Value-Growth for the book-to-market portfolios; and HiTec-Telcm for the industry portfolios). The results from testing the equality of conditional alphas for high-return and low-return portfolios provide no evidence for a significant alpha for "Small-Big", "Value-Growth", and "HiTec-Telcm" arbitrage portfolios, indicating that the two-factor model proposed in the paper provides both statistical and economic success in explaining stock market anomalies. Overall, the DCC-based conditional covariances capture the time-series and cross-sectional variation in returns on size, book-to-market, and industry portfolios because the essential tests of the model are passed: (i) significantly positive risk-return and uncertainty-return tradeoffs; (ii) the conditional alphas are jointly zero; and (iii) the conditional alphas for high-return and low-return portfolios are not statistically different from each other.7 These results are robust to using an alternative specification of the time-varying conditional covariances with an asymmetric GARCH model, using a larger cross-section of equity portfolios in asset pricing tests, and after controlling for a wide variety of macroeconomic variables.
The rest of the paper is organized as follows. Section 2 defines the variance risk premium and provides its empirical measurement. Section 3 presents the consumption-based asset pricing model with risk and uncertainty. Section 4 describes the data. Section 5 outlines the estimation methodology. Section 6 presents the empirical results. Section 7 provides a battery of robustness checks. Section 8 concludes the paper.
2 Variance Risk Premium and Empirical Measurement
The central empirical variable of this paper, as a proxy for economic uncertainty, is the market variance risk premium (VRP)--which is not directly observable but can be estimated from the difference between model-free option-implied variance and the conditional expectation of realized variance (Zhou, 2010). There are emerging evidences that VRP can forecast stock market returns (Bollerslev, Tauchen, and Zhou, 2009; Drechsler and Yaron, 2011), Treasury returns (Zhou, 2010; Mueller, Vedolin, and Zhou, 2011), credit spreads (Wang, Zhou, and Zhou, 2011; Buraschi, Trojani, and Vedolin, 2009), and international stock market returns (Londono, 2010; Bollerslev, Marrone, Xu, and Zhou, 2011). Here we are going to use the covariance of asset returns with the variance risk premium to help explain the time-series and cross-section of stock portfolio and individual stock returns.
2.1 Variance Risk Premium: Definition and Measurement
In order to define the model-free implied variance, let ![]() denote the price of a European call option maturing at time
denote the price of a European call option maturing at time ![]() with strike price
with strike price ![]() , and
, and ![]() denote the price of a time
denote the price of a time ![]() zero-coupon bond maturing at time
zero-coupon bond maturing at time ![]() . As shown by Carr and Madan (1998) and Britten-Jones and Neuberger (2000), among others, the market's risk-neutral
. As shown by Carr and Madan (1998) and Britten-Jones and Neuberger (2000), among others, the market's risk-neutral ![]() expectation of the return variance
expectation of the return variance ![]() conditional on the information set
conditional on the information set ![]() , or the implied variance
, or the implied variance ![]() , can be expressed in a "model-free" fashion as a portfolio of European calls,
, can be expressed in a "model-free" fashion as a portfolio of European calls,
which relies on an ever increasing number of calls with strikes spanning from zero to infinity.8 This equation follows directly from the classical result in Breeden and Litzenberger (1978), that the second derivative of the option call price with respect to strike equals the risk-neutral density, such that all risk neutral moments payoff can be replicated by the basic option prices (Bakshi and Madan, 2000).
In order to define the actual return variance, let ![]() denote the logarithmic price of the asset. The realized variance over the discrete
denote the logarithmic price of the asset. The realized variance over the discrete ![]() to
to ![]() time interval can be measured in a "model-free" fashion by
time interval can be measured in a "model-free" fashion by
where the convergence relies on
Variance risk premium (VRP) at time ![]() is defined as the difference between the ex-ante risk-neutral expectation and the objective or statistical expectation of the return variance over the
is defined as the difference between the ex-ante risk-neutral expectation and the objective or statistical expectation of the return variance over the
![]() time interval,
time interval,
which is not directly observable in practice.9 To construct an empirical proxy for such a VRP concept, one needs to estimate various reduced-form counterparts of the risk neutral and physical expectations. In practice, the risk-neutral expectation
To estimate the objective expectation,
![]() , we use a linear forecast of future realized variance as
, we use a linear forecast of future realized variance as
![]() , with current implied and realized variances. The model-free implied variance from options market is an
informationally more efficient forecast for future realized variance than the past realized variance (see, e.g., Jiang and Tian, 2005, among others), while realized variance based on high-frequency data also provides additional power in forecasting future realized variance
(Andersen, Bollerslev, Diebold, and Labys, 2003). Therefore, a joint forecast model with one lag of implied variance and one lag of realized variance seems to capture the most forecasting power based on time-
, with current implied and realized variances. The model-free implied variance from options market is an
informationally more efficient forecast for future realized variance than the past realized variance (see, e.g., Jiang and Tian, 2005, among others), while realized variance based on high-frequency data also provides additional power in forecasting future realized variance
(Andersen, Bollerslev, Diebold, and Labys, 2003). Therefore, a joint forecast model with one lag of implied variance and one lag of realized variance seems to capture the most forecasting power based on time-![]() available information (Drechsler and Yaron, 2011).
available information (Drechsler and Yaron, 2011).
3 Conditional ICAPM and Economic Uncertainty
The time-varying conditional version of the Sharpe (1964) and Lintner (1965) capital asset pricing model (CAPM) relates the conditionally expected excess returns on risky assets to the conditionally expected excess return on the market portfolio:
where
In equation (4), the ratio of
cov![]() to
var
to
var![]() is the asset's time-
is the asset's time-![]() expected conditional
beta
expected conditional
beta
![]() , and the ratio
, and the ratio
![]() is known as the reward-to-risk ratio that represents the compensation the investor must receive for
a unit increase in the conditional variance of the market. As pointed out by Merton (1980), the reward-to-risk ratio can also be interpreted as the relative risk aversion coefficient.
is known as the reward-to-risk ratio that represents the compensation the investor must receive for
a unit increase in the conditional variance of the market. As pointed out by Merton (1980), the reward-to-risk ratio can also be interpreted as the relative risk aversion coefficient.
Merton (1973) intertemporal capital asset pricing model (ICAPM) implies the following equilibrium relation between expected return and risk for any risky asset ![]() :
:
where
In this paper, we provide a time-series and cross-sectional investigation of the conditional ICAPM:
where
In this section, we first rely on a consumption-based asset pricing model to derive the equivalence between the investment opportunity set ![]() and variance risk premium
and variance risk premium ![]() ; then we use the nonlinear relationship between the slope coefficients
; then we use the nonlinear relationship between the slope coefficients ![]() and
and
![]() and underlying structural parameters to impose the sign restrictions. After deriving the intertemporal relation between expected return and risk and uncertainty based on the
consumption-based asset pricing model, we test whether the market price of risk and the market price of uncertainty are significantly positive and whether they help explain returns in a panel data setting:
and underlying structural parameters to impose the sign restrictions. After deriving the intertemporal relation between expected return and risk and uncertainty based on the
consumption-based asset pricing model, we test whether the market price of risk and the market price of uncertainty are significantly positive and whether they help explain returns in a panel data setting:
where the time-varying exposure of asset
To guide our economic interpretation of these empirical exercises, we rely on a structural model with recursive preference and consumption uncertainty (Bollerslev, Tauchen, and Zhou, 2009). One can show that the model-implied market compensations for risk and uncertainty are both positive, under reasonable parameter settings that agents are more risk averse than the log utility and that agents prefer an early resolution of economic uncertainty. In essence, the two risk factors--market return and variance risk premium--span all systematic variations in any risky assets.
3.1 An Economic Model of Return-Uncertainty Tradeoff
The representative agent in the economy is endowed with Epstein-Zin-Weil recursive preferences, and has the value function ![]() of her life-time utility as
of her life-time utility as
where
Suppose that log consumption growth and its volatility follow the joint dynamics
where
Let ![]() denote the logarithm of the price-dividend or wealth-consumption ratio, of the asset that pays the consumption endowment,
denote the logarithm of the price-dividend or wealth-consumption ratio, of the asset that pays the consumption endowment,
![]() ; and conjecture a solution for
; and conjecture a solution for ![]() as an affine function
of the state variables,
as an affine function
of the state variables,
![]() and
and ![]() ,
,
One can solve for the coefficients
Given the solution of price-dividend ratio, and assume that dividend equals consumption, the model-implied premium of the market portfolio can be shown as
The premium is composed of two separate terms. The first term,
The conditional variance of the time ![]() to
to ![]() market return,
market return,
![]() Var
Var![]() , can be shown as
, can be shown as
![]() The variance risk premium can be defined as the difference between risk-neutral and
objective expectations of the return variance,11
The variance risk premium can be defined as the difference between risk-neutral and
objective expectations of the return variance,11
Moreover, provided that
However, due to the measurement difficulty in consumption data and its volatility, we will use market return volatility and variance risk premium to substitute fundamental risk and uncertainty that are harder to pin down accurately,
Therefore the risk-return trade-off identified by
3.2 Calibrating Uncertainty-Return Tradeoff
To give some empirical guidance on how such a modeling framework with two risk drivers--consumption risk and volatility uncertainty--can play out in empirically testing the time-series and cross-sectional stock returns, we provide some calibration evidence based on the model parameter settings
used by Bollerslev, Tauchen, and Zhou (2009, or BTZ2009 for short) focusing on equity return predictability and Zhou (2010) also considering bond return and credit spread predictability. As shown in Table 1, consistent
with the analytical characterization above, the risk-return trade-off coefficient or ![]() should be equal to the risk-aversion coefficient, which is 10 or 2 under the two model parameter
choices. On the other hand, the uncertainty-return coefficient or
should be equal to the risk-aversion coefficient, which is 10 or 2 under the two model parameter
choices. On the other hand, the uncertainty-return coefficient or ![]() should be equal to 10.24 or 0.08, which is a highly non-linear function of both the underlying preference and structural
parameters. The model implied uncertainty-return trade-off is positive.
should be equal to 10.24 or 0.08, which is a highly non-linear function of both the underlying preference and structural
parameters. The model implied uncertainty-return trade-off is positive.
More importantly, the positive relationship between variance risk premium and excess market return is fairly robust. There are two key preference parameters--intertemporal elasticity of substitution (IES) and risk aversion coefficient that may materially affect the sign and magnitude of the
return-uncertainty trade-off. However, as shown in the top two panels of Figure 1, as long as IES--![]() is larger than one and risk aversion--
is larger than one and risk aversion--![]() is larger than one, the model-implied linkage between return and uncertainty should remain positive. In contrast, when agents prefer a late resolution of uncertainty or
is larger than one, the model-implied linkage between return and uncertainty should remain positive. In contrast, when agents prefer a late resolution of uncertainty or ![]() (bottom left panel), the model implied return-uncertainty trade-off swings between positive and negative values with a bifurcation towards infinities near
(bottom left panel), the model implied return-uncertainty trade-off swings between positive and negative values with a bifurcation towards infinities near ![]() . Similarly, if agents are less risk averse than log investor or
. Similarly, if agents are less risk averse than log investor or
![]() (bottom right panel), the uncertainty-return trade-off also swings between large positive and negative values near
(bottom right panel), the uncertainty-return trade-off also swings between large positive and negative values near
![]() . The empirical implication is rather sharp--if we find that the exposures to variance risk premium are positively priced in stock returns, it would be consistent with our
modeling framework that both IES and risk aversion are larger than one.
. The empirical implication is rather sharp--if we find that the exposures to variance risk premium are positively priced in stock returns, it would be consistent with our
modeling framework that both IES and risk aversion are larger than one.
There is a long debate in literature whether the intertemporal elasticity of substitution or IES is larger than one. As emphasized by Beeler and Campbell (2009), IES bigger than one--around 1.5--is key to the success of long-run risks model (Bansal and Yaron, 2004). Although earlier time series evidence by Hall (1988) and Campbell (1999) tend to suggest that IES is small and close to zero, their argument is typically based on measuring the slope coefficient from regressing consumption growth on the real rate, which can be downward biased if consumption volatility is time-varying (Bansal, Kiku, and Yaron, 2007). On the other hand, financial market evidence on IES being less than one are also found by examining market return predictability in both long term and short term (Kandel and Stambaugh, 1991) and by relating the momentum and contrarian profits of individual stocks or portfolios to macroeconomic fundamentals (Liu, Zhang, and Fan, 2011).
Our empirical approach on estimating the risk-return and uncertainty-return trade-off from time-series and cross-section stock returns provides an alternative reduced-form angle to judge whether IES is bigger than one. Such an angle needs not to specify the underlying preference structure or fundamental endowment dynamics. Our sharp finding of a positive uncertainty-return trade-off is consistent with an IES larger than one but without any parametric restriction, not even relying on the Euler equations or GMM estimation as in Bansal, Kiku, and Yaron (2009) and Chen, Favilukis, and Ludvigson (2011).12
4.1 Variance Risk Premia and Economic Uncertainty Measures
For the option-implied variance of the S&P500 market return, we use the end-of-month Chicago Board of Options Exchange (CBOE) volatility index on a monthly basis (VIX![]() /12). Following
earlier studies, the monthly realized variance for the S&P500 index is calculated as the summation of the 78 intra-day five-minute squared log returns from 9:30am to 4:00pm including the close-to-open interval. As shown in equation (3), variance risk premium (VRP) at time
/12). Following
earlier studies, the monthly realized variance for the S&P500 index is calculated as the summation of the 78 intra-day five-minute squared log returns from 9:30am to 4:00pm including the close-to-open interval. As shown in equation (3), variance risk premium (VRP) at time
![]() is defined as the difference between the ex-ante risk-neutral expectation and the objective or statistical expectation of the return variance over the
is defined as the difference between the ex-ante risk-neutral expectation and the objective or statistical expectation of the return variance over the
![]() time interval. The monthly VRP data are available from January 1990 to December 2010.
time interval. The monthly VRP data are available from January 1990 to December 2010.
To give a visual illustration, Figure 2 plots the monthly time series of variance risk premium (VRP), implied variance, and expected variance. The VRP proxy is moderately high around the 1990 and 2001 economic recessions but much higher during the 2008 financial crisis and to a lessor degree around 1997-1998 Asia-Russia-LTCM crisis. The variance spike during October 2008 already surpasses the initial shock of the Great Depression in October 1929. The huge run-up of VRP in the fourth quarter of 2008 leads the equity market bottom reached in March 2009. The sample mean of VRP is 18.75 (in percentages squared, monthly basis), with a standard deviation of 22.15. Notice that the extraordinary skewness (3.81) and kurtosis (27.46) signal a highly non-Gaussian process for VRP.
According to our model in Section 3, VRP can be viewed as a proxy for uncertainty. To test whether VRP is in fact associated with alternative measures of uncertainty, we generate some proxies for financial and economic uncertainty. We obtain monthly values of the US industrial production index from G.17 database of the Federal Reserve Board and monthly values of the Chicago Fed National Activity Index (CFNAI) from the Federal Reserve Bank of Chicago for the period January 1990 - December 2010.13 We use a GARCH(1,1) model of Bollerslev (1986) to estimate the conditional variance of the growth rate of industrial production and the conditional variance of the CFNAI index. These two measures can be viewed as macroeconomic uncertainty. The sample correlation between VRP and economic uncertainty variables is positive and significant; sample correlation is 33.20% with the variance of output growth and 31.82% with the variance of CFNAI index.
Our second set of uncertainty measures is based on the downside risk of financial institutions obtained from the left tail of the time-series and cross-sectional distribution of financial firms' returns. Specifically, we obtain monthly returns for financial firms (6000 ![]() SIC code
SIC code ![]() 6999) for the sample period January 1990 to December 2010. Then, the 1%
nonparametric Value-at-Risk (VaR) measure in a given month is measured as the cut-off point for the lower one percentile of the monthly returns on financial firms.14 For each month, we determine the one percentile of the cross-section of returns on financial firms, and obtain an aggregate 1% VaR measure of the financial system for the period 1990-2010. In addition to the cross-sectional distribution, we use the time-series daily
return distribution to estimate 1% VaR of the financial system. For each month from January 1990 to December 2010, we first determine the lowest daily returns on financial institutions over the past 1 to 12 months. The catastrophic risk of financial institutions is then computed by taking the
average of these lowest daily returns obtained from alternative measurement windows. The estimation windows are fixed at 1 to 12 months, and each fixed estimation window is updated on a monthly basis. These two downside risk measures can be viewed as a proxy for uncertainty in the financial sector.
The sample correlations between VRP and financial uncertainty variables are positive and significant: 47.37% with the cross-sectional VaR measure and 37.01% with the time-series VaR measure.
6999) for the sample period January 1990 to December 2010. Then, the 1%
nonparametric Value-at-Risk (VaR) measure in a given month is measured as the cut-off point for the lower one percentile of the monthly returns on financial firms.14 For each month, we determine the one percentile of the cross-section of returns on financial firms, and obtain an aggregate 1% VaR measure of the financial system for the period 1990-2010. In addition to the cross-sectional distribution, we use the time-series daily
return distribution to estimate 1% VaR of the financial system. For each month from January 1990 to December 2010, we first determine the lowest daily returns on financial institutions over the past 1 to 12 months. The catastrophic risk of financial institutions is then computed by taking the
average of these lowest daily returns obtained from alternative measurement windows. The estimation windows are fixed at 1 to 12 months, and each fixed estimation window is updated on a monthly basis. These two downside risk measures can be viewed as a proxy for uncertainty in the financial sector.
The sample correlations between VRP and financial uncertainty variables are positive and significant: 47.37% with the cross-sectional VaR measure and 37.01% with the time-series VaR measure.
The third uncertainty variable is related to the health of the financial sector proxied by the credit default swap (CDS) index. We download the monthly CDS data from Bloomberg. For the sample period January 2004 - December 2010, we obtain monthly CDS data for Bank of America (BOA), Citigroup (CICN), Goldman Sachs (GS), JP Morgan (JPM), Morgan Stanley (MS), Wells Fargo (WFC), and American Express (AXP). Then, we standardized all CDS data to have zero mean and unit standard deviation. Finally, we formed the standardized CDS index (EWCDS) based on the equal-weighted average of standardized CDS values for the 7 major financial firms. For the common sample period 2004-2010, the correlation between VRP and EWCDS is positive, 42.99%, and highly significant.
The last uncertainty variable is based on the aggregate measure of investors' disagreement about individual stocks trading at NYSE, AMEX, and NASDAQ. Following Diether, Malloy, and Scherbina (2002), we use dispersion in analysts' earnings forecasts as a proxy for divergence of opinion. It is likely that investors partly form their expectations about a particular stock based on the analysts' earnings forecasts. If all analysts are in agreement about expected returns, uncertainty is likely to be low. However, if analysts provide very different estimates, investors are likely to be unclear about future returns, and uncertainty is high. The sample correlation between VRP and the aggregate measure of dispersion is about 14.92%. Overall, these results indicate that the variance risk premia is strongly and positively correlated with all measures of uncertainty considered here. Hence, VRP can be viewed as a sound proxy for financial and economic uncertainty.
4.2 Equity Portfolios
We use the monthly excess returns on the value-weighted aggregate market portfolio and the monthly excess returns on the 10 value-weighted size, book-to-market, and industry portfolios. The aggregate market portfolio is represented by the value-weighted NYSE-AMEX-NASDAQ index. Excess returns on portfolios are obtained by subtracting the returns on the one-month Treasury bill from the raw returns on equity portfolios. The data are obtained from Kenneth French's online data library. We use the longest common sample period available, from January 1990 to December 2010, yielding a total of 252 monthly observations.
As described in Fama and French (1993), the size portfolios are constructed at the end of each June using the June market equity (ME) and NYSE breakpoints. The portfolios for July of year ![]() to June of
to June of ![]() include all NYSE, AMEX, and NASDAQ stocks for which we have market equity data for June of
include all NYSE, AMEX, and NASDAQ stocks for which we have market equity data for June of ![]() . The book-to-market portfolios are formed based on the ratio of book value equity (BE) to market value of equity (ME), BE/ME, at the end of each June using NYSE breakpoints. The BE used in June of year
. The book-to-market portfolios are formed based on the ratio of book value equity (BE) to market value of equity (ME), BE/ME, at the end of each June using NYSE breakpoints. The BE used in June of year ![]() is the book equity for the last fiscal year end in
is the book equity for the last fiscal year end in ![]() . ME is price times shares outstanding at the end of December
of
. ME is price times shares outstanding at the end of December
of ![]() . The book-to-market portfolios include all NYSE, AMEX, and NASDAQ stocks for which we have ME for December of
. The book-to-market portfolios include all NYSE, AMEX, and NASDAQ stocks for which we have ME for December of ![]() and June of
and June of ![]() , and BE for
, and BE for ![]() . The
breakpoints and portfolios include Compustat firms plus the firms hand-collected from the Moody's Industrial, Utilities, Transportation, and Financial Manuals. In addition to the size and book-to-market portfolios, we use the 10 value-weighted industry portfolios of Kenneth French. Fama and French (1997) assign each NYSE, AMEX, and NASDAQ stock to an industry portfolio at the end of June of year
. The
breakpoints and portfolios include Compustat firms plus the firms hand-collected from the Moody's Industrial, Utilities, Transportation, and Financial Manuals. In addition to the size and book-to-market portfolios, we use the 10 value-weighted industry portfolios of Kenneth French. Fama and French (1997) assign each NYSE, AMEX, and NASDAQ stock to an industry portfolio at the end of June of year ![]() based on its four-digit SIC code at that time. They use
Compustat SIC codes for the fiscal year ending in calendar year
based on its four-digit SIC code at that time. They use
Compustat SIC codes for the fiscal year ending in calendar year ![]() . Whenever Compustat SIC codes are not available, they use CRSP SIC codes for June of year
. Whenever Compustat SIC codes are not available, they use CRSP SIC codes for June of year ![]() . They then compute returns from July of
. They then compute returns from July of ![]() to June of
to June of ![]() .
.
Table 4 presents the monthly raw return and CAPM Alpha differences between high-return (long) and low-return (short) equity portfolios. The results are reported for the size, book-to-market (BM), and industry portfolios for the period January 1990 - December
2010.15 The OLS ![]() -statistics are reported in
parentheses. The Newey-West
-statistics are reported in
parentheses. The Newey-West ![]() -statistics are given in square brackets.
-statistics are given in square brackets.
For the ten size portfolios, "Small" (Decile 1) is the portfolio of stocks with the smallest market capitalization and "Big" (Decile 10) is the portfolio of stocks with the biggest market capitalization. For the 1990-2010 period, the average return difference between the Small and Big
portfolios is 0.40% per month with the OLS ![]() -statistic of 1.22 and the Newey-West (1987)
-statistic of 1.22 and the Newey-West (1987) ![]() -statistic of 1.13, implying that small stocks on average do not generate higher returns than big stocks. In addition to the average raw returns, Table 4 presents the intercept (CAPM alpha) from the regression of Small-Big portfolio return difference on a
constant and the excess market return. The CAPM Alpha (or abnormal return) for the long-short size portfolio is 0.35% per month with the OLS
-statistic of 1.13, implying that small stocks on average do not generate higher returns than big stocks. In addition to the average raw returns, Table 4 presents the intercept (CAPM alpha) from the regression of Small-Big portfolio return difference on a
constant and the excess market return. The CAPM Alpha (or abnormal return) for the long-short size portfolio is 0.35% per month with the OLS ![]() -statistic of 1.06 and the Newey-West
-statistic of 1.06 and the Newey-West ![]() -statistic of 0.98. This economically and statistically insignificant Alpha indicates that the static CAPM does explain the size effect for the 1990-2010 period.
-statistic of 0.98. This economically and statistically insignificant Alpha indicates that the static CAPM does explain the size effect for the 1990-2010 period.
For the ten book-to-market portfolios, "Growth" is the portfolio of stocks with the lowest book-to-market ratios and "Value" is the portfolio of stocks with the highest book-to-market ratios. For the sample period January 1990 - December 2010, the average return difference between the Value
and Growth portfolios is economically and statistically insignificant; 0.29% per month with the OLS ![]() -statistic of 0.92 and the Newey-West
-statistic of 0.92 and the Newey-West ![]() -statistic of 0.79, implying that value stocks on average do not generate higher returns than growth stocks. Similar to our findings for the size portfolios, the unconditional CAPM can explain the value premium for the 1990-2010 period; the
CAPM Alpha (or abnormal return) for the long-short book-to-market portfolio is only 0.28% per month with the OLS
-statistic of 0.79, implying that value stocks on average do not generate higher returns than growth stocks. Similar to our findings for the size portfolios, the unconditional CAPM can explain the value premium for the 1990-2010 period; the
CAPM Alpha (or abnormal return) for the long-short book-to-market portfolio is only 0.28% per month with the OLS ![]() -statistic of 0.86 and the Newey-West
-statistic of 0.86 and the Newey-West ![]() -statistic of 0.71.16
-statistic of 0.71.16
Interestingly, industry effects in the US equity market are economically and statistically strong over the past two decades although size and value premiums are not. The average raw and risk-adjusted return differences between the high-return and low-return industry portfolios are significant for the sample period 1990-2010. The high-return and low-return portfolios of 48 and 49 industries generate highly significant return differences, 30 and 38 industry portfolios generate marginally significant return differences, whereas the average return differences and Alphas for the high-return and low-return portfolios of 10 and 17 industries are insignificant. Specifically, for 30-, 48- and 49-industry portfolios of Kenneth French, "Coal" industry has the highest average monthly return, whereas "Other" industry has the lowest return, yielding an average raw and risk-adjusted return differences of 1.54% to 1.79% per month and statistically significant. The static CAPM cannot explain these economically and statistically strong industry effects either.
Earlier studies starting with Fama and French (1992,1993) provide evidence for the significant size and value premiums for the post-1963 period. Some readers may find the insignificant size and value premiums for the 1990-2010 period controversial. Hence, in Appendix A, we examine the significance of size and book-to-market effects for the longest sample period July 1926 - December 2010 and the subsample period July 1963 - December 2010. The results indicate significant raw return difference between the Value and Growth portfolios for both sample periods and significant risk-adjusted return difference (Alpha) only for the post-1963 period. Consistent with the findings of earlier studies, we find significant raw return difference between the Small and Big stock portfolios for the 1926-2010 period, which becomes very weak for the post-1963 period. The CAPM Alpha (or abnormal return) for the long-short size portfolio is economically and statistically insignificant for both sample periods.
5 Estimation Methodology
Following Bali (2008) and Bali and Engle (2010), our estimation approach proceeds in steps.
- 1)
- We take out any autoregressive elements in returns and VRP and estimate univariate GARCH models for all returns and VRP.
- 2)
- We construct standardized returns and compute bivariate DCC estimates of the correlations between each portfolio and the market and between each portfolio and VRP using the bivariate likelihood function.
- 3)
- We estimate the expected return equation as a panel with the conditional covariances as regressors. The error covariance matrix specified as seemingly unrelated regression (SUR). The panel estimation methodology with SUR takes into account heteroskedasticity and autocorrelation as well as contemporaneous cross-correlations in the error terms.
5.1 Estimating Time-Varying Conditional Covariances
We estimate the conditional covariance between excess returns on equity portfolio ![]() and the market portfolio
and the market portfolio ![]() based on the mean-reverting dynamic conditional correlation (DCC) model:
based on the mean-reverting dynamic conditional correlation (DCC) model:
| (19) |
| (20) |
where
We estimate the conditional covariance between each equity portfolio ![]() and the variance risk premia
and the variance risk premia ![]() ,
,
![]() , using an analogous DCC model:
, using an analogous DCC model:
| (21) |
| (25) |
where
We estimate the conditional covariances of each equity portfolio with the market portfolio and with ![]() using the maximum likelihood method described in Appendix B. Then, as discussed in
the following section, we estimate the time-series and cross-sectional relation between expected return and risk and uncertainty as a panel with the conditional covariances as regressors.
using the maximum likelihood method described in Appendix B. Then, as discussed in
the following section, we estimate the time-series and cross-sectional relation between expected return and risk and uncertainty as a panel with the conditional covariances as regressors.
5.2 Estimating Risk-Uncertainty-Return Tradeoff
Given the conditional covariances, we estimate the portfolio-specific intercepts and the common slope estimates from the following panel regression:
where
We estimate the system of equations in (26)-(27) using a weighted least square method that allows us to place constraints on coefficients across equations. We compute the ![]() -statistics of the parameter estimates accounting for heteroskedasticity and autocorrelation as well as contemporaneous cross-correlations in the errors from different equations. The estimation methodology can be regarded as an extension of the seemingly unrelated
regression (SUR) method, the details of which are in Appendix C.
-statistics of the parameter estimates accounting for heteroskedasticity and autocorrelation as well as contemporaneous cross-correlations in the errors from different equations. The estimation methodology can be regarded as an extension of the seemingly unrelated
regression (SUR) method, the details of which are in Appendix C.
6 Empirical Results
In this section we first present results from the 10 decile portfolios of size, book-to-market, and industry. Second, we discuss the economic significance of risk and uncertainty compensations and the underlying economic intuition. Third, we compare the relative performances of conditional CAPM and ICAPM with both risk and uncertainty.
6.1 Ten Decile Portfolios of Size, Book-to-Market, and Industry
The common slopes and the intercepts are estimated using the monthly excess returns on the 10 value-weighted size, book-to-market, and industry portfolios for the sample period January 1990 to December 2010. The aggregate stock market portfolio is measured by the value-weighted CRSP index. Table
5 reports the common slope estimates (![]() ), the abnormal returns or conditional alphas for each equity portfolio (
), the abnormal returns or conditional alphas for each equity portfolio (![]() ) and the market portfolio (
) and the market portfolio (![]() ), and the
), and the ![]() -statistics of the parameter estimates. The last two rows, respectively, show the Wald statistics; Wald
-statistics of the parameter estimates. The last two rows, respectively, show the Wald statistics; Wald![]() from testing the joint hypothesis
from testing the joint hypothesis
![]() , and Wald
, and Wald![]() from testing the equality
of conditional alphas for high-return and low-return portfolios (Small vs. Big; Value vs. Growth; and HiTec vs. Telcm). The
from testing the equality
of conditional alphas for high-return and low-return portfolios (Small vs. Big; Value vs. Growth; and HiTec vs. Telcm). The ![]() -values of Wald
-values of Wald![]() and Wald
and Wald![]() statistics are given in square brackets.
statistics are given in square brackets.
The risk aversion coefficient is estimated to be positive and highly significant for all equity portfolios: ![]() with the
with the ![]() -statistic of 3.12 for the size portfolios,
-statistic of 3.12 for the size portfolios, ![]() with the
with the ![]() -statistic of 2.53 for the book-to-market portfolios, and
-statistic of 2.53 for the book-to-market portfolios, and ![]() with the
with the ![]() -statistic of 2.35 for the industry portfolios.18 These results imply a positive and significant relation between expected
return and market risk.19 Consistent with our theoretical model in equation (14), the uncertainty aversion coefficient is also
estimated to be positive and highly significant for all equity portfolios:
-statistic of 2.35 for the industry portfolios.18 These results imply a positive and significant relation between expected
return and market risk.19 Consistent with our theoretical model in equation (14), the uncertainty aversion coefficient is also
estimated to be positive and highly significant for all equity portfolios: ![]() with the
with the ![]() -statistic of 2.97 for the size portfolios,
-statistic of 2.97 for the size portfolios, ![]() with the
with the ![]() -statistic of 2.27 for the book-to-market portfolios, and
-statistic of 2.27 for the book-to-market portfolios, and ![]() with the
with the ![]() -statistic of 2.78 for the industry portfolios. These results indicate a significantly positive market price of uncertainty in the aggregate stock market. Equity portfolios with higher sensitivity to increases in the variance risk premia are expected to generate higher returns next
period.
-statistic of 2.78 for the industry portfolios. These results indicate a significantly positive market price of uncertainty in the aggregate stock market. Equity portfolios with higher sensitivity to increases in the variance risk premia are expected to generate higher returns next
period.
One implication of the conditional asset pricing model in equation (14) is that the intercepts (![]() ,
, ![]() ) are not jointly different from zero assuming that the conditional covariances of equity portfolios with the market portfolio and the variance risk premia have enough predictive power for expected future returns. To examine the
empirical validity of the conditional asset pricing model, we test the joint hypothesis
) are not jointly different from zero assuming that the conditional covariances of equity portfolios with the market portfolio and the variance risk premia have enough predictive power for expected future returns. To examine the
empirical validity of the conditional asset pricing model, we test the joint hypothesis
![]() . As presented in Table 5, the Wald
. As presented in Table 5, the Wald![]() statistics for the size, book-to-market, and industry portfolios are, respectively, 16.74, 8.88, and 14.35 with the corresponding
statistics for the size, book-to-market, and industry portfolios are, respectively, 16.74, 8.88, and 14.35 with the corresponding ![]() -values of 0.12, 0.63,
and 0.21. The significantly positive risk and uncertainty aversion coefficients and the insignificant Wald
-values of 0.12, 0.63,
and 0.21. The significantly positive risk and uncertainty aversion coefficients and the insignificant Wald![]() statistics indicate that the two-factor model proposed in the paper is
empirically sound.
statistics indicate that the two-factor model proposed in the paper is
empirically sound.
We also investigate whether the model explains the return spreads between Small and Big; Value and Growth; and HiTec and Telcm portfolios. The last row in Table 5 reports Wald![]() statistics from testing the equality of conditional alphas for high-return and low-return portfolios (
statistics from testing the equality of conditional alphas for high-return and low-return portfolios (
![]() ). These intercepts capture the monthly abnormal returns on each portfolio that cannot be explained by the conditional covariances with the market portfolio and the
variance risk premia.
). These intercepts capture the monthly abnormal returns on each portfolio that cannot be explained by the conditional covariances with the market portfolio and the
variance risk premia.
The first column of Table 5 shows that the abnormal return on the small-stock portfolio is
![]() per month with a
per month with a ![]() -statistic of 0.94, whereas the abnormal return
on the big-stock portfolio is
-statistic of 0.94, whereas the abnormal return
on the big-stock portfolio is
![]() per month with a
per month with a ![]() -statistic of 0.01. The Wald
-statistic of 0.01. The Wald![]() statistic from testing the equality of alphas on the Small and Big portfolios is 1.56 with a
statistic from testing the equality of alphas on the Small and Big portfolios is 1.56 with a ![]() -value of 0.21, indicating that there is no significant risk-adjusted return difference between the small-stock and big-stock portfolios. The second column provides the conditional alphas on the Value and Growth portfolios:
-value of 0.21, indicating that there is no significant risk-adjusted return difference between the small-stock and big-stock portfolios. The second column provides the conditional alphas on the Value and Growth portfolios:
![]() per month with a
per month with a ![]() -statistic of 0.90, and
-statistic of 0.90, and
![]() per month with a
per month with a ![]() -statistic of 1.90. The Wald
-statistic of 1.90. The Wald![]() statistic from testing
statistic from testing
![]() is 1.79 with a
is 1.79 with a ![]() -value of 0.18, implying that the
conditional asset pricing model explains the value premium, i.e., the risk-adjusted return difference between value and growth stocks is statistically insignificant. The last column shows that the conditional alphas on HiTec and Telcm portfolios are, respectively, 0.26% and -0.05% per month,
generating a risk-adjusted return spread of 31 basis points per month. As reported in the last row, the Wald
-value of 0.18, implying that the
conditional asset pricing model explains the value premium, i.e., the risk-adjusted return difference between value and growth stocks is statistically insignificant. The last column shows that the conditional alphas on HiTec and Telcm portfolios are, respectively, 0.26% and -0.05% per month,
generating a risk-adjusted return spread of 31 basis points per month. As reported in the last row, the Wald![]() statistic from testing the significance of this return spread is 0.40 with a
statistic from testing the significance of this return spread is 0.40 with a
![]() -value of 0.53, yielding insignificant industry effect over the sample period 1990-2010.
-value of 0.53, yielding insignificant industry effect over the sample period 1990-2010.
The differences in conditional alphas are both economically and statistically insignificant, indicating that the two-factor model proposed in the paper provides both statistical and economic success in explaining stock market anomalies. Overall, the DCC-based conditional covariances capture the time-series and cross-sectional variation in returns on size, book-to-market, and industry portfolios because the essential tests of the conditional CAPM are passed: (i) significantly positive risk-return and uncertainty-return tradeoffs; (ii) the conditional alphas are jointly zero; and (iii) the conditional alphas for high-return and low-return portfolios are not statistically different from each other.
6.2 Economic Significance of Uncertainty-Return Tradeoff
In this section, we test whether the risk-return (![]() ) and uncertainty-return (
) and uncertainty-return (![]() )
coefficients are sensible and whether the uncertainty measure is associated with macroeconomic state variables.
)
coefficients are sensible and whether the uncertainty measure is associated with macroeconomic state variables.
Specifically, we rely on equation (27) and compute the expected excess return on the market portfolio based on the estimated prices of risk and uncertainty as well as the sample averages of the conditional covariance measures:
| (28) |
where
To evaluate the performance of our model with risk and uncertainty, we calculate the sample average of excess returns on the market portfolio, which is a standard benchmark for the market risk premium. The sample average of ![]() is found to be 0.52% per month for the period January 1990 - December 2010, indicating that the estimated market risk premiums of 0.51% - 0.54% are very close to the benchmark. This again shows outstanding performance of the two-factor model introduced
in the paper.
is found to be 0.52% per month for the period January 1990 - December 2010, indicating that the estimated market risk premiums of 0.51% - 0.54% are very close to the benchmark. This again shows outstanding performance of the two-factor model introduced
in the paper.
To further appreciate the economics behind the apparent connection between the variance risk premium (VRP) and the time-series and cross-sectional variations in expected stock returns, Figure 3 plots the VRP together with the quarterly growth rate in GDP. As seen from the figure, there is a tendency for VRP to rise in the quarter before a decline in GDP, while it typically narrows ahead of an increase in GDP. Indeed, the sample correlation equals -0.17 between lag VRP and current GDP (as first reported in Bollerslev and Zhou, 2007). In other words, VRP as a proxy for economic uncertainty does seem to negatively relate to future macroeconomic performance.
Thus, not only the difference between the implied and realized variances positively covaries with stock returns, it also covaries negatively with future growth rates in GDP. Intuitively, when VRP is high (low), it generally signals a high (low) degree of aggregate economic uncertainty. Consequently agents tend to simultaneously cut (increase) their consumption and investment expenditures and shift their portfolios from more (less) to less (more) risky assets. This in turn results in a rise (decrease) in expected excess returns for stock portfolios that covaries more (less) with the macroeconomic uncertainty, as proxied by VRP. In essence, our finding of a positive significant relation between economic uncertainty measure and stock expected returns, is consistent with our model's setting when agents prefer an earlier resolution of uncertainty. Therefore economic uncertainty carries a positive premium, and heightened VRP does signal a worsening of macroeconomic fundamentals.
6.3 Relative Performance of Conditional ICAPM with Uncertainty
We now assess the relative performance of the newly proposed model in predicting the cross-section of expected returns on equity portfolios. Specifically, we test whether the conditional ICAPM with the market and uncertainty factors outperforms the conditional CAPM with the market factor in terms of statistical fit. The goodness of fit of an asset pricing model describes how well it fits a set of realized return observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Hence, we focus on the cross-section of realized average returns on equity portfolios (as a benchmark) and the portfolios' expected returns implied by the two competing models.
Using equation (26), we compute the expected excess return on equity portfolios based on the estimated prices of risk and uncertainty (![]() ) and the sample averages
of the conditional covariance measures,
) and the sample averages
of the conditional covariance measures,
![]() and
and
![]() :
:
Table 8 presents the realized monthly average excess returns on the size, book-to-market, and industry portfolios and the cross-section of expected excess returns generated by the Conditional CAPM and the Conditional ICAPM models. Clearly the newly proposed model with risk and uncertainty provides much more accurate estimates of expected returns on the size, book-to-market, and industry portfolios. Especially for the size and industry portfolios, expected returns implied by the Conditional ICAPM with the market and VRP factors are almost identical to the realized average returns. The last row in Table 8 reports the Mean Absolute Percentage Errors (MAPE) for the two competing models:
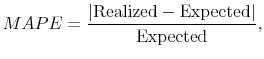 |
(30) |
where "Realized" is the realized monthly average excess return on each equity portfolio and "Expected" is the expected excess return implied by equation (29). For the conditional CAPM with the market factor, MAPE equals 5.20% for the size portfolios, 5.37% for the book-to-market portfolios, and 6.32% for the industry portfolios. Accounting for the variance risk premium improves the cross-sectional fitting significantly: MAPE reduces to 0.61% for the size portfolios, 1.66% for the book-to-market portfolios, and 0.55% for the industry portfolios.
Figure 4 provides a visual depiction of the realized and expected returns for the size, book-to-market, and industry portfolios. It is clear that our conditional ICAPM with uncertainty nails down the realized returns of the size, book-to-market, and industrial portfolios, while the conditional CAPM systematically over-predicts these portfolio returns. In other words, if there were size premium and value premium puzzles, our ICAPM model with market and VRP factors would have resolved these puzzles, which is indeed the case for the industry portfolios. Overall, the results indicate superior performance of the conditional asset pricing model introduced in the paper.
7 Robustness Check
In this section we first test whether using an alternative specification of the DCC-based conditional covariances with an asymmetric GARCH model influences our main findings. Second, we examine whether the model's performance changes when we use a larger cross-section of equity portfolios. Third, we provide robustness analysis when controlling for popular macroeconomic and financial variables. Finally, we provide results from individual stocks.
7.1 DCC with Asymmetric GARCH
Because the conditional variance and covariance of stock market returns are not observable, different approaches and specifications used in estimating the conditional variance and covariance could lead to different conclusions. We have so far used the bivariate GARCH(1,1) model of Bollerslev (1986) in equations (17)-(18) and (23)-(24) to obtain conditional variance and covariance estimates. In this section, we investigate whether changing these specifications influences our main findings.
The current volatility in the GARCH(1,1) model is defined as a symmetric, linear function of the last period's unexpected news and the last period's volatility. Since, in a symmetric GARCH process, positive and negative information shocks of the same magnitude produce the same amount of volatility, the symmetric GARCH model cannot cope with the skewness of stock return distribution. If a negative return shock causes more volatility than a positive return shock of the same size, the symmetric GARCH model underpredicts the amount of volatility following negative shocks and overpredicts the amount of volatility following positive shocks. Furthermore, if large return shocks cause more volatility than a quadratic function allows, then the symmetric GARCH model underpredicts volatility after a large return shock and overpredicts volatility after a small return shock.
In this section we use an asymmetric GARCH model of Glosten, Jagannathan, and Runkle (1993) that explicitly takes account of skewed distributions and allows good news and bad news to have different impacts on the conditional volatility forecasts. To test whether such variations in the variance forecasting specification alter our conclusion, we re-estimate the DCC-based conditional covariances using the following alternative specification:
 |
(31) |
where
A notable point in Table 9 is that the main findings from an asymmetric GARCH specification of the conditional covariances are very similar to those reported in Table 5. Specifically, the risk aversion coefficients are estimated to be positive
and highly significant for all equity portfolios; ![]() is in the range of 2.53 to 3.54 with the
is in the range of 2.53 to 3.54 with the ![]() -statistics ranging from 2.58 to 3.11, implying a significantly positive link between expected return and risk. Similar to our results from GARCH(1,1) specification, asymmetric GARCH model of Glosten et al. (1993) yields positive and significant
coefficient estimates on the covariance between equity portfolios and the variance risk premia. Specifically, the uncertainty aversion coefficients (B) are in the range of 0.0054 to 0.0075 with the
-statistics ranging from 2.58 to 3.11, implying a significantly positive link between expected return and risk. Similar to our results from GARCH(1,1) specification, asymmetric GARCH model of Glosten et al. (1993) yields positive and significant
coefficient estimates on the covariance between equity portfolios and the variance risk premia. Specifically, the uncertainty aversion coefficients (B) are in the range of 0.0054 to 0.0075 with the ![]() -statistics between 2.68 and 3.30. These results show that equity portfolios that are highly correlated with uncertainty (proxied by VRP) carry a significant premium relative to portfolios that are uncorrelated or lowly correlated with VRP.
-statistics between 2.68 and 3.30. These results show that equity portfolios that are highly correlated with uncertainty (proxied by VRP) carry a significant premium relative to portfolios that are uncorrelated or lowly correlated with VRP.
With this alternative covariance specification, we also examine the empirical validity of the conditional asset pricing model by testing the joint hypothesis. As shown in Table 9, the Wald![]() statistics for the size, book-to-market, and industry portfolios are, respectively, 16.91, 7.89, and 14.41 with the corresponding
statistics for the size, book-to-market, and industry portfolios are, respectively, 16.91, 7.89, and 14.41 with the corresponding ![]() -values of 0.11, 0.72,
and 0.21. The significantly positive risk and uncertainty aversion coefficients and the insignificant Wald
-values of 0.11, 0.72,
and 0.21. The significantly positive risk and uncertainty aversion coefficients and the insignificant Wald![]() statistics indicate that the two-factor model explains the time-series and
cross-sectional variation in equity portfolios. Finally, we investigate whether the model with asymmetric GARCH specification explains the return spreads between Small and Big; Value and Growth; and HiTec and Telcm portfolios. The last row in Table 9 reports
Wald
statistics indicate that the two-factor model explains the time-series and
cross-sectional variation in equity portfolios. Finally, we investigate whether the model with asymmetric GARCH specification explains the return spreads between Small and Big; Value and Growth; and HiTec and Telcm portfolios. The last row in Table 9 reports
Wald![]() statistics from testing the equality of conditional alphas for high-return and low-return portfolios (
statistics from testing the equality of conditional alphas for high-return and low-return portfolios (
![]() ). For the size, book-to-market, and industry portfolios, the Wald
). For the size, book-to-market, and industry portfolios, the Wald![]() statistics provide no evidence for a significant conditional alpha for "Small-Big", "Value-Growth", and "HiTec-Telcm" arbitrage portfolios. Overall, the DCC-based conditional covariances from the asymmetric GARCH model captures the time-series and cross-sectional variation
in returns on size, book-to-market, and industry portfolios and generates significantly positive risk-return and uncertainty-return tradeoffs.20
statistics provide no evidence for a significant conditional alpha for "Small-Big", "Value-Growth", and "HiTec-Telcm" arbitrage portfolios. Overall, the DCC-based conditional covariances from the asymmetric GARCH model captures the time-series and cross-sectional variation
in returns on size, book-to-market, and industry portfolios and generates significantly positive risk-return and uncertainty-return tradeoffs.20
7.2 Results from Larger Cross-Section of Industry Portfolios
Given the positive risk-return and positive uncertainty-return coefficient estimates from the three data sets and the success of the conditional asset pricing model in explaining the industry, size, and value premia, we now examine how the model performs when we use a larger cross-section of equity portfolios.
The robustness of our findings is investigated using the monthly excess returns on the value-weighted 17-, 30-, 38-, 48-, and 49-industry portfolios for the sample period January 1990 - December 2010. Table 12 reports the common slope estimates (![]() ,
, ![]() ), their
), their ![]() -statistics in parentheses, and the Wald
-statistics in parentheses, and the Wald![]() and Wald
and Wald![]() statistics along with their
statistics along with their ![]() -values in square brackets. For the industry portfolios, the risk aversion coefficients (
-values in square brackets. For the industry portfolios, the risk aversion coefficients (![]() ) are estimated to be positive, in the range of 2.20 to 2.78, and highly significant with the
) are estimated to be positive, in the range of 2.20 to 2.78, and highly significant with the ![]() -statistics ranging from 2.31 to 3.34.
Consistent with our earlier findings from the 10 size, 10 book-to-market, and 10 industry portfolios, the results from the larger cross-section of industry portfolios (17 to 49) imply a positive and significant relation between expected return and market risk. Again similar to our findings from 10
decile portfolios, the uncertainty aversion coefficients are estimated to be positive, in the range of 0.0036 to 0.0041, and highly significant with the
-statistics ranging from 2.31 to 3.34.
Consistent with our earlier findings from the 10 size, 10 book-to-market, and 10 industry portfolios, the results from the larger cross-section of industry portfolios (17 to 49) imply a positive and significant relation between expected return and market risk. Again similar to our findings from 10
decile portfolios, the uncertainty aversion coefficients are estimated to be positive, in the range of 0.0036 to 0.0041, and highly significant with the ![]() -statistics ranging from 2.44 to 4.21.
These results provide evidence for a significantly positive market price of uncertainty and show that assets with higher correlation with the variance risk premia generate higher returns next month.
-statistics ranging from 2.44 to 4.21.
These results provide evidence for a significantly positive market price of uncertainty and show that assets with higher correlation with the variance risk premia generate higher returns next month.
Not surprisingly, the Wald![]() statistics for all industry portfolios have
statistics for all industry portfolios have ![]() -values in the range of 0.20 to 0.75, indicating that the two-factor asset pricing model can explain the time-series and cross-sectional variation in larger number of equity portfolios. The last row shows that the Wald
-values in the range of 0.20 to 0.75, indicating that the two-factor asset pricing model can explain the time-series and cross-sectional variation in larger number of equity portfolios. The last row shows that the Wald![]() statistics from testing the equality of conditional alphas on the high-return and low-return industry portfolios have
statistics from testing the equality of conditional alphas on the high-return and low-return industry portfolios have ![]() -values ranging from
0.44 to 0.80, implying that there is no significant risk-adjusted return difference between the extreme portfolios of 17, 30, 38, 48, and 49 industries. The differences in conditional alphas are both economically and statistically insignificant, showing that the two-factor model introduced in the
paper provides success in explaining industry effects.
-values ranging from
0.44 to 0.80, implying that there is no significant risk-adjusted return difference between the extreme portfolios of 17, 30, 38, 48, and 49 industries. The differences in conditional alphas are both economically and statistically insignificant, showing that the two-factor model introduced in the
paper provides success in explaining industry effects.
7.3 Controlling for Macroeconomic Variables
A series of papers argue that the stock market can be predicted by financial and/or macroeconomic variables associated with business cycle fluctuations. The commonly chosen variables include default spread (DEF), term spread (TERM), dividend price ratio (DIV), and the de-trended riskless rate or the relative T-bill rate (RREL).21 We define DEF as the difference between the yields on BAA- and AAA-rated corporate bonds, and TERM as the difference between the yields on the 10-year Treasury bond and the 3-month Treasury bill. RREL is defined as the difference between 3-month T-bill rate and its 12-month backward moving average.22 We obtain the aggregate dividend yield using the CRSP value-weighted index return with and without dividends based on the formula given in Fama and French (1988). In addition to these financial variables, we use some fundamental variables affecting the state of the US economy: Monthly inflation rate based on the US Consumer Price Index (INF); Monthly growth rate of the US industrial production (IP) obtained from the G.17 database of the Federal Reserve Board; and Monthly US unemployment rate (UNEMP) obtained from the Bureau of Labor Statistics.
According to Merton's (1973) ICAPM, state variables that are correlated with changes in consumption and investment opportunities are priced in capital markets in the sense that an asset's covariance with those state variables affects its expected returns. Merton (1973) also indicates that securities affected by such state variables (or systematic risk factors) should earn risk premia in a risk-averse economy. Macroeconomic variables used in the literature are excellent candidates for these systematic risk factors because innovations in macroeconomic variables can generate global impact on firm's fundamentals, such as their cash flows, risk-adjusted discount factors and/or investment opportunities. Following the existing literature, we use the aforementioned financial and macroeconomic variables as a proxy for state variables capturing shifts in the investment opportunity set.
We now investigate whether incorporating these variables into the predictive regressions affects the significance of the market prices of risk and uncertainty. Specifically, we estimate the portfolio-specific intercepts and the common slope coefficients from the following panel
regression:
where
As presented in Table 17, after controlling for a wide variety of financial and macroeconomic variables, our main findings remain intact for all equity portfolios. The common slope estimates on the conditional covariances of equity portfolios with the market factor
(![]() ) remain positive and highly significant, indicating a positive and significant relation between expected return and market risk. Similar to our earlier findings, the common slopes on the
conditional covariances of equity portfolios with the uncertainty factor (
) remain positive and highly significant, indicating a positive and significant relation between expected return and market risk. Similar to our earlier findings, the common slopes on the
conditional covariances of equity portfolios with the uncertainty factor (![]() ) remain significantly positive as well, showing that assets with higher correlation with the variance risk premium
generate higher returns next month. Among the control variables, the growth rate of industrial production is the only variable predicting future returns on equity portfolios;
) remain significantly positive as well, showing that assets with higher correlation with the variance risk premium
generate higher returns next month. Among the control variables, the growth rate of industrial production is the only variable predicting future returns on equity portfolios;
![]() turns out to be positive and significant--especially for the industry portfolios. The positive relation between expected stock returns and innovations in output makes economic
sense. Increases in real economic activity (proxied by the growth rate of industrial production) increase investors' expectations of future growth. Overall, the results in Table 17 indicate that after controlling for variables associated with business conditions, the
time-varying exposures of equity portfolios to the market and uncertainty factors carry positive risk premiums.23
turns out to be positive and significant--especially for the industry portfolios. The positive relation between expected stock returns and innovations in output makes economic
sense. Increases in real economic activity (proxied by the growth rate of industrial production) increase investors' expectations of future growth. Overall, the results in Table 17 indicate that after controlling for variables associated with business conditions, the
time-varying exposures of equity portfolios to the market and uncertainty factors carry positive risk premiums.23
7.4 Results from Individual Stocks
We have so far investigated the significance of risk, uncertainty, and return tradeoffs using equity portfolios. In this section, we replicate our analyses using individual stocks trading at NYSE, AMEX, and NASDAQ. First, we generate a dataset for the largest 500 common stocks (share code = 10 or 11) traded at NYSE/AMEX/NASDAQ. Following Shumway (1997), we adjust for stock de-listing to avoid survivorship bias.24 Firms with missing observations on beginning-of-month market cap or monthly returns over the period January 1990 - December 2010 are eliminated. Due to the fact that the list of 500 firms changes over time as a result of changes in firms' market capitalizations, we obtain more than 500 firms over the period 1990-2010. Specifically, the largest 500 firms are determined based on their end-of-month market cap as of the end of each month from January 1990 to December 2010. There are 738 unique firms in our first dataset. In our second dataset, the largest 500 firms are determined based on their market cap at the end of December 2010. Our last dataset contains stocks in the S&P 500 index. Since the stock composition of the S&P 500 index changes through time, we rely on the most recent sample (as of December 2010). We also restrict our S&P 500 sample to 318 stocks with non-missing monthly return observations for the period January 1990 - December 2010.
Table 18 presents the common slope estimates (![]() ,
, ![]() ) and
their
) and
their ![]() -statistics for the individual stocks in the aforementioned data sets. The risk aversion coefficient is estimated to be positive and highly significant for all stock samples considered
in the paper:
-statistics for the individual stocks in the aforementioned data sets. The risk aversion coefficient is estimated to be positive and highly significant for all stock samples considered
in the paper: ![]() with the
with the ![]() -statistic of 8.04 for the first dataset containing
738 stocks (largest 500 stocks as of the end of each month from January 1990 to December 2010);
-statistic of 8.04 for the first dataset containing
738 stocks (largest 500 stocks as of the end of each month from January 1990 to December 2010); ![]() with the
with the ![]() -statistic of 8.70 for the second dataset containing largest 500 stocks as of the end of December 2010; and
-statistic of 8.70 for the second dataset containing largest 500 stocks as of the end of December 2010; and ![]() with the
with the ![]() -statistic of 6.79 for the last dataset containing 318 stocks with non-missing monthly return observations for the period 1990-2010. Confirming our findings from equity portfolios, the results from individual stocks imply a
positive and significant relation between expected return and market risk. Similarly, consistent with our earlier findings from equity portfolios, the uncertainty aversion coefficient is also estimated to be positive and highly significant for all data sets:
-statistic of 6.79 for the last dataset containing 318 stocks with non-missing monthly return observations for the period 1990-2010. Confirming our findings from equity portfolios, the results from individual stocks imply a
positive and significant relation between expected return and market risk. Similarly, consistent with our earlier findings from equity portfolios, the uncertainty aversion coefficient is also estimated to be positive and highly significant for all data sets: ![]() with the
with the ![]() -statistic of 3.61 for the first dataset,
-statistic of 3.61 for the first dataset, ![]() with the
with the ![]() -statistic of 3.67 for the second dataset, and
-statistic of 3.67 for the second dataset, and ![]() with the
with the ![]() -statistic of 3.52 for the last dataset. These results indicate a significantly positive market price of uncertainty for large stocks
trading in the U.S. stock market.
-statistic of 3.52 for the last dataset. These results indicate a significantly positive market price of uncertainty for large stocks
trading in the U.S. stock market.
8 Conclusion
Although uncertainty is more common in decision-making process than risk, relatively little attention is paid to the phenomenon of uncertainty in asset pricing literature. This paper focuses on economic uncertainty and augments the original consumption-based CAPM to incorporate the time-varying volatility of the consumption growth and the volatility uncertainty in the consumption growth process. According to the augmented asset pricing model, the premium on equity is composed of two separate terms; the first term compensating for the standard consumption risk and the second term representing a true premium for variance risk. We find that in the presence of volatility uncertainty, both market risk and volatility uncertainty carry a positive premium, which is consistent with an economy where the intertemporal elasticity of substitution (IES) is larger than one.
Since information about consumption volatility uncertainty is too imprecise to measure with available data, we have to come up with a proxy for volatility uncertainty that should be consistent with our underlying economic model. Following Zhou (2010), we measure volatility uncertainty with the variance risk premium (VRP) of the aggregate stock market portfolio. Different from earlier studies, we provide empirical evidence that VRP is indeed closely related to economic and financial market uncertainty. Specifically, we generate several proxies for uncertainty based on the macroeconomic variables, return distributions of financial firms, credit default swap market, and investors' disagreement about individual stocks. We show that VRP is highly correlated with all measures of uncertainty.
Based on the two-factor asset pricing model, we investigate whether the market prices of risk and uncertainty are economically and statistically significant in the US equity market. Using the dynamic conditional correlation (DCC) model of Engle (2002), we estimate equity portfolios' conditional covariances with the market portfolio and VRP factors and then test whether these dynamic conditional covariances predict future returns on equity portfolios. The empirical results from the size, book-to-market, and industry portfolios indicate that the DCC-based conditional covariances of equity portfolios with the market and VRP factors predict the time-series and cross-sectional variation in stock returns. We find the risk-return coefficients to be positive and highly significant, implying a strongly positive link between expected return and market risk. Similarly, the results indicate a significantly positive market price of uncertainty. That is, equity portfolios that are highly correlated with uncertainty (proxied by VRP) carry a significant premium relative to portfolios that are uncorrelated or lowly correlated with VRP. In addition to the size, book-to-market, and industry portfolios, we investigate the significance of risk, uncertainty, and return tradeoffs using the largest 500 stocks trading at NYSE, AMEX, and NASDAQ as well as stocks in the S&P 500 index. Consistent with our findings from equity portfolios, we find significantly positive market prices of risk and uncertainty for large stocks trading in the US equity market.
We also examine whether the conditional asset pricing model proposed in the paper can provide risk-uncertainty based explanation of stock market anomalies. We test whether the conditional alphas on the size, book-to-market, and industry portfolios are zero. The test statistics indicate that the conditional alphas are jointly zero, implying economically and statistically insignificant abnormal returns on equity portfolios. Finally, we investigate whether the model explains the return spreads between the high-return (long) and low-return (short) equity portfolios (Small-Big for the size portfolios; Value-Growth for the book-to-market portfolios; and HiTec-Telcm for the industry portfolios). The results from testing the equality of conditional alphas for high-return and low-return portfolios provide no evidence for a significant alpha for "Small-Big", "Value-Growth", and "HiTec-Telcm" arbitrage portfolios, indicating that the newly proposed model with risk and uncertainty provides both statistical and economic success in explaining well-known stock market anomalies.
This table reports the calibration parameter values for the stochastic volatility-of-volatility model used in this paper. BTZ2009 refers to the calibration setting of Bollerslev, Tauchen, and Zhou (2009), with an emphasis on equity risk premium and its short-run predictability, while the setting of Zhou (2010) also considers bond risk premium and credit spread and their forecastability from variance risk premium. The Campbell-Shiller linearization constants are ![]() and
and ![]() .
.
| Calibration Parameters | BTZ2009 | Zhou (2010) |
| Preference Parameters: |
|
|
| Preference Parameters: | ||
| Preference Parameters: | ||
| Endowment Parameters: |
|
|
| Endowment Parameters: |
|
|
| Endowment Parameters: |
|
|
| Endowment Parameters: |
|
|
| Endowment Parameters: |
|
|
| Endowment Parameters: |
|
|
| Risk-Return Trade-off ( |
10 | 2 |
| Uncertainty-Return Trade-off ( |
10.24 | 0.08 |
This table presents the monthly raw return and CAPM Alpha differences between high-return (long) and low-return (short) equity portfolios. The results are reported for the size, book-to-market (BM), and industry portfolios for the sample periods July 1926 - December 2010. The OLS ![]() -statistics are reported in parentheses. The Newey-West
-statistics are reported in parentheses. The Newey-West ![]() -statistics are given in square
brackets.
-statistics are given in square
brackets.
| Portfolio | Long-Short | Return Diff. | Alpha |
| 10 Size | Small-Big | 0.60% | 0.27% |
| 10 Size OLS t-statistics | Small-Big OLS t-statistics | (2.49) | (1.22) |
| 10 Size Newey-West t-statistics | Small-Big Newey-West t-statistics | [2.36] | [1.38] |
| 10 BM | Value-Growth | 0.53% | 0.24% |
| 10 BM OLS t-statistics | Value-Growth OLS t-statistics | (2.52) | (1.25) |
| 10 BM Newey-West t-statistics | Value-Growth Newey-West t-statistics | [2.46] | [1.26] |
| 10 Industry | Durbl-Telcm | 0.27% | -0.09% |
| 10 Industry OLS t-statistics | Durbl-Telcm OLS t-statistics | (1.44) | (-0.56) |
| 10 Industry Newey-West t-statistics | Durbl-Telcm Newey-West t-statistics | [1.31] | [-0.54] |
| 17 Industry | Cars-Other | 0.28% | 0.07% |
| 17 Industry OLS t-statistics | Cars-Other OLS t-statistics | (1.65) | (0.44) |
| 17 Industry Newey-West t-statistics | Cars-Other Newey-West t-statistics | [1.55] | [0.44] |
| 30 Industry | Coal-Other | 0.51% | 0.65% |
| 30 Industry OLS t-statistics | Coal-Other OLS t-statistics | (1.79) | (2.26) |
| 30 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistic | [1.71] | [2.28] |
| 38 Industry | Oil-Whlsl | 0.42% | 0.49% |
| 38 Industry OLS t-statistics | Oil-Whlsl OLS t-statistics | (1.90) | (2.18) |
| 38 Industry Newey-West t-statistics | Oil-Whlsl Newey-West t-statistics | [1.85] | [2.06] |
| 48 Industry | Aero-Other | 0.66% | 0.50% |
| 48 Industry OLS t-statistics | Aero-Other OLS t-statistics | (2.66) | (2.02) |
| 48 Industry Newey-West t-statistics | Aero-Other Newey-West t-statistics | [2.55] | [2.04] |
| 49 Industry | Aero-Other | 0.66% | 0.50% |
| 49 Industry OLS t-statistics | Aero-Other OLS t-statistics | (2.66) | (2.02) |
| 49 Industry Newey-West t-statistics | Aero-Other Newey-West t-statistics | [2.55] | [2.04] |
This table presents the monthly raw return and CAPM Alpha differences between high-return (long) and low-return (short) equity portfolios. The results are reported for the size, book-to-market (BM), and industry portfolios for the sample period July 1963 - December 2010. The OLS ![]() -statistics are reported in parentheses. The Newey-West
-statistics are reported in parentheses. The Newey-West ![]() -statistics are given in square
brackets.
-statistics are given in square
brackets.
| Portfolio | Long-Short | Return Diff. | Alpha |
| 10 Size | Small-Big | 0.38% | 0.29% |
| 10 Size OLS t-statistics | Small-Big OLS t-statistics | (1.58) | (1.41) |
| 10 Size Newey-West t-statistics | Small-Big Newey-West t-statistics | [1.81] | [1.26] |
| 10 BM | Value-Growth | 0.55% | 0.55% |
| 10 BM OLS t-statistics | Value-Growth OLS t-statistics | (2.77) | (2.76) |
| 10 BM Newey-West t-statistics | Value-Growth Newey-West t-statistics | [2.48] | [2.40] |
| 10 Industry | Utils-Enrgy | 0.28% | 0.17% |
| 10 Industry OLS t-statistics | Utils-Enrgy OLS t-statistics | (1.50) | (0.93) |
| 10 Industry Newey-West t-statistics | Utils-Enrgy Newey-West t-statistics | [1.50] | [0.91] |
| 17 Industry | Mines-Durbl | 0.43% | 0.45% |
| 17 Industry OLS t-statistics | Mines-Durbl OLS t-statistics | (1.54) | (1.58) |
| 17 Industry Newey-West t-statistics | Mines-Durbl Newey-West t-statistics | [1.48] | [1.51] |
| 30 Industry | Coal-Other | 0.82% | 0.79% |
| 30 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.14) | (2.05) |
| 30 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [1.95] | [1.84] |
| 38 Industry | Smoke-Govt | 1.06% | 1.07% |
| 38 Industry OLS t-statistics | Smoke-Govt OLS t-statistics | (2.38) | (2.40) |
| 38 Industry Newey-West t-statistics | Smoke-Govt Newey-West t-statistics | [2.61] | [2.69] |
| 48 Industry | Coal-Other | 0.92% | 0.92% |
| 48 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.24) | (2.25) |
| 48 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [2.06] | [2.04] |
| 49 Industry | Coal-Other | 0.92% | 0.92% |
| 49 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.24) | (2.25) |
| 49 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [2.06] | [2.04] |
This table presents the monthly raw return and CAPM Alpha differences between high-return (long) and low-return (short) equity portfolios. The results are reported for the size, book-to-market (BM), and industry portfolios for the sample period January 1990 - December 2010. The OLS ![]() -statistics are reported in parentheses. The Newey-West
-statistics are reported in parentheses. The Newey-West ![]() -statistics are given in square
brackets.
-statistics are given in square
brackets.
| Portfolio | Long-Short | Return Diff. | Alpha |
| 10 Size | Small-Big | 0.40% | 0.35% |
| 10 Size OLS t-statistics | Small-Big OLS t-statistics | (1.22) | (1.06) |
| 10 Size Newey-West t-statistics | Small-Big Newey-West t-statistics | [1.13] | [0.98] |
| 10 BM | Value-Growth | 0.29% | 0.28% |
| 10 BM OLS t-statistics | Value-Growth OLS t-statistics | (0.92) | (0.86) |
| 10 BM Newey-West t-statistics | Value-Growth Newey-West t-statistics | [0.79] | [0.71] |
| 10 Industry | HiTech-Telcm | 0.56% | 0.31% |
| 10 Industry OLS t-statistics | HiTech-Telcm OLS t-statistics | (1.55) | (0.92) |
| 10 Industry Newey-West t-statistics | HiTech-Telcm Newey-West t-statistics | [1.64] | [0.95] |
| 17 Industry | Mines-Durbl | 0.56% | 0.61% |
| 17 Industry OLS t-statistics | Mines-Durbl OLS t-statistics | (1.15) | (1.23) |
| 17 Industry Newey-West t-statistics | Mines-Durbl Newey-West t-statistics | [1.16] | [1.22] |
| 30 Industry | Coal-Other | 1.66% | 1.54% |
| 30 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.25) | (2.08) |
| 30 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [2.12] | [1.90] |
| 38 Industry | Mines-Govt | 1.34% | 1.45% |
| 38 Industry OLS t-statistics | Mines-Govt OLS t-statistics | (1.48) | (1.59) |
| 38 Industry Newey-West t-statistics | Mines-Govt Newey-West t-statistics | [1.75] | [1.90] |
| 48 Industry | Coal-Other | 1.79% | 1.71% |
| 48 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.38) | (2.26) |
| 48 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [2.33] | [2.13] |
| 49 Industry | Coal-Other | 1.79% | 1.71% |
| 49 Industry OLS t-statistics | Coal-Other OLS t-statistics | (2.38) | (2.26) |
| 49 Industry Newey-West t-statistics | Coal-Other Newey-West t-statistics | [2.33] | [2.13] |
This table reports the portfolio-specific intercepts and the common slope estimates from the following panel regression:
where
|
|
|
| Small | 0.0041 |
| Small t-statistic | (0.94) |
| 2 | 0.0022 |
| 2 t-statistic | (0.48) |
| 3 | 0.0025 |
| 3 t-statistic | (0.58) |
| 4 | 0.0015 |
| 4 t-statistic | (0.35) |
| 5 | 0.0023 |
| 5 t-statistic | (0.54) |
| 6 | 0.0023 |
| 6 t-statistic | (0.61) |
| 7 | 0.0028 |
| 7 t-statistic | (0.76) |
| 8 | 0.0020 |
| 8 t-statistic | (0.53) |
| 9 | 0.0023 |
| 9 t-statistic | (0.67) |
| Big | 0.0001 |
| Big t-statistic | (0.01) |
| Market | 0.0008 |
| Market t-statistic | (0.17) |
| 3.9562 | |
| (3.12) | |
| 0.0058 | |
| (2.97) | |
| Wald |
16.74 |
| Wald |
[0.12] |
| Wald |
1.56 |
| Wald |
[0.21] |
|
|
|
| Growth | 0.0036 |
| Growth t-statistic | (0.90) |
| 2 | 0.0048 |
| 2 t-statistic | (1.38) |
| 3 | 0.0053 |
| 3 t-statistic | (1.58) |
| 4 | 0.0065 |
| 4 t-statistic | (1.88) |
| 5 | 0.0057 |
| 5 t-statistic | (1.74) |
| 6 | 0.0051 |
| 6 t-statistic | (1.51) |
| 7 | 0.0058 |
| 7 t-statistic | (1.78) |
| 8 | 0.0059 |
| 8 t-statistic | (1.76) |
| 9 | 0.0067 |
| 9 t-statistic | (1.94) |
| Value | 0.0082 |
| Value t-statistic | (1.90) |
| Market | 0.0032 |
| Market t-statistic | (1.23) |
| 2.5101 | |
| (2.53) | |
| 0.0050 | |
| (2.27) | |
| Wald |
8.88 |
| Wald |
[0.63] |
| Wald |
1.79 |
| Wald |
[0.18] |
|
|
|
| NoDur | 0.0043 |
| NoDur t-statistic | (1.53) |
| Durbl | 0.0019 |
| Durbl t-statistic | (0.37) |
| Manuf | 0.0046 |
| Manuf t-statistic | (1.26) |
| Enrgy | 0.0059 |
| Enrgy t-statistic | (1.88) |
| HiTec | 0.0026 |
| HiTec t-statistic | (0.45) |
| Telcm | -0.0005 |
| Telcm t-statistic | (-0.13) |
| Shops | 0.0028 |
| Shops t-statistic | (0.80) |
| Hlth | 0.0036 |
| Hlth t-statistic | (1.13) |
| Utils | 0.0038 |
| Utils t-statistic | (1.39) |
| Other | 0.0018 |
| Other t-statistic | (0.47) |
| Market | 0.0019 |
| Market t-statistic | (0.55) |
| 3.4055 | |
| (2.35) | |
| 0.0060 | |
| (2.78) | |
| Wald |
14.35 |
| Wald |
[0.21] |
| Wald |
0.40 |
| Wald |
[0.53] |
This table presents the realized monthly average excess returns on the size, book-to-market, and industry portfolios and the cross-section of expected excess returns generated by the Conditional CAPM with the market factor and the Conditional ICAPM with the market and VRP factors. The last row reports the Mean Absolute Percentage Errors (MAPE) for the two competing models.
| Realized Return Benchmark: Average Excess Returns | Conditional ICAPM with VRP: Expected Excess Returns | Conditional CAPM: Expected Excess Returns | |
| Size: Small | 0.8464% | 0.8461% | 0.8742% |
| Size: 2 | 0.7737% | 0.7677% | 0.8110% |
| Size: 3 | 0.7690% | 0.7647% | 0.8093% |
| Size: 4 | 0.6632% | 0.6637% | 0.7032% |
| Size: 5 | 0.7525% | 0.7550% | 0.7943% |
| Size: 6 | 0.7055% | 0.7025% | 0.7406% |
| Size: 7 | 0.7409% | 0.7379% | 0.7749% |
| Size: 8 | 0.6837% | 0.6810% | 0.7221% |
| Size: 9 | 0.6670% | 0.6643% | 0.7000% |
| Size: Big | 0.4479% | 0.4598% | 0.4789% |
| Size: MAPE | 0.61% | 5.20% | |
| Book-to-Market: Growth | 0.5286% | 0.5327% | 0.5645% |
| Book-to-Market: 2 | 0.5614% | 0.5658% | 0.5961% |
| Book-to-Market: 3 | 0.6140% | 0.6039% | 0.6488% |
| Book-to-Market: 4 | 0.6752% | 0.6559% | 0.6960% |
| Book-to-Market: 5 | 0.6119% | 0.6017% | 0.6423% |
| Book-to-Market: 6 | 0.5439% | 0.5547% | 0.5803% |
| Book-to-Market: 7 | 0.6014% | 0.5979% | 0.6360% |
| Book-to-Market: 8 | 0.5885% | 0.5956% | 0.6233% |
| Book-to-Market: 9 | 0.6827% | 0.6666% | 0.7133% |
| Book-to-Market: Value | 0.8221% | 0.7994% | 0.8564% |
| Book-to-Market: MAPE | 1.66% | 5.37% | |
| Industry: Telcm | 0.2727% | 0.2747% | 0.3280% |
| Industry: Utils | 0.4712% | 0.4727% | 0.4965% |
| Industry: Other | 0.4965% | 0.4910% | 0.5366% |
| Industry: Durbl | 0.5313% | 0.5315% | 0.5513% |
| Industry: Shops | 0.5954% | 0.5912% | 0.6247% |
| Industry: Hlth | 0.6138% | 0.6088% | 0.6478% |
| Industry: NoDur | 0.6110% | 0.6152% | 0.6534% |
| Industry: Manuf | 0.7172% | 0.7206% | 0.7474% |
| Industry: Enrgy | 0.7606% | 0.7643% | 0.7824% |
| Industry: HiTec | 0.8358% | 0.8350% | 0.8466% |
| Industry: MAPE | 0.55% | 6.32% |
This table reports the portfolio-specific intercepts and the common slope estimates from the following panel regression:
where the conditional variance and covariances are estimated using the asymmetric GARCH model of Glosten, Jagannathan, and Runkle (1993). The parameters and their
| Size |
|
| Small | 0.0052 |
| Small t-statistics | (1.23) |
| 2 | 0.0037 |
| 2 t-statistics | (0.85) |
| 3 | 0.0040 |
| 3 t-statistics | (0.99) |
| 4 | 0.0030 |
| 4 t-statistics | (0.75) |
| 5 | 0.0038 |
| 5 t-statistics | (0.97) |
| 6 | 0.0037 |
| 6 t-statistics | (1.05) |
| 7 | 0.0041 |
| 7 t-statistics | (1.19) |
| 8 | 0.0034 |
| 8 t-statistics | (0.97) |
| 9 | 0.0036 |
| 9 t-statistics | (1.11) |
| Big | 0.0012 |
| Big t-statistics | (0.38) |
| Market | 0.0018 |
| Market t-statistics | (0.57) |
| 3.2927 | |
| (3.11) | |
| 0.0054 | |
| (3.12) | |
| Wald |
16.91 |
| Wald |
[0.11] |
| Wald |
1.48 |
| Wald |
[0.22] |
|
|
|
| Growth | 0.0035 |
| Growth t-statistics | (0.87) |
| 2 | 0.0047 |
| 2 t-statistics | (1.35) |
| 3 | 0.0052 |
| 3 t-statistics | (1.55) |
| 4 | 0.0064 |
| 4 t-statistics | (1.85) |
| 5 | 0.0056 |
| 5 t-statistics | (1.71) |
| 6 | 0.0050 |
| 6 t-statistics | (1.48) |
| 7 | 0.0057 |
| 7 t-statistics | (1.76) |
| 8 | 0.0058 |
| 8 t-statistics | (1.74) |
| 9 | 0.0066 |
| 9 t-statistics | (1.92) |
| Value | 0.0081 |
| Value t-statistics | (1.88) |
| Market | 0.0033 |
| Market t-statistics | (1.20) |
| 2.5303 | |
| (2.62) | |
| 0.0060 | |
| (2.68) | |
| Wald |
7.89 |
| Wald |
[0.72] |
| Wald |
1.99 |
| Wald |
[0.16] |
|
|
|
| NoDur | 0.0051 |
| NoDur t-statistics | (1.94) |
| Durbl | 0.0028 |
| Durbl t-statistics | (0.57) |
| Manuf | 0.0055 |
| Manuf t-statistics | (1.61) |
| Enrgy | 0.0064 |
| Enrgy t-statistics | (1.85) |
| HiTec | 0.0029 |
| HiTec t-statistics | (0.52) |
| Telcm | 0.0004 |
| Telcm t-statistics | (0.11) |
| Shops | 0.0036 |
| Shops t-statistics | (1.04) |
| Hlth | 0.0043 |
| Hlth t-statistics | (1.37) |
| Utils | 0.0042 |
| Utils t-statistics | (1.58) |
| Other | 0.0030 |
| Other t-statistics | (0.81) |
| Market | 0.0028 |
| Market t-statistics | (0.82) |
| 3.5369 | |
| (2.58) | |
| 0.0075 | |
| (3.30) | |
| Wald |
14.41 |
| Wald |
[0.21] |
| Wald |
0.46 |
| Wald |
[0.50] |
This table presents the common slope estimates (![]() ,
, ![]() ) from the following panel
regression:
) from the following panel
regression:
where
This table presents the common slope estimates from the following panel regression:
where
| Size | Book-to-Market | Industry | |
| 4.2630 | 2.5763 | 4.0421 | |
| (3.32) | (2.40) | (2.74) | |
| 0.0057 | 0.0051 | 0.0066 | |
| (2.85) | (2.25) | (2.96) | |
|
|
-0.3804 | -0.0739 | 0.6243 |
|
|
(-0.50) | (-0.09) | (1.02) |
|
|
-0.1964 | -0.5366 | -0.5405 |
|
|
(-0.64) | (-1.69) | (-2.17) |
|
|
0.2330 | 0.1834 | 0.0104 |
|
|
(0.68) | (0.52) | (0.04) |
|
|
0.0489 | 0.0228 | 0.0314 |
|
|
(1.33) | (0.60) | (1.05) |
|
|
0.0270 | 0.7158 | -0.1862 |
|
|
(0.04) | (0.93) | (-0.31) |
|
|
0.7433 | 0.8689 | 1.1941 |
|
|
(1.77) | (2.01) | (3.51) |
|
|
0.0031 | 0.0047 | 0.0026 |
|
|
(1.13) | (1.61) | (1.15) |
| Wald |
16.96 | 7.97 | 14.78 |
| Wald |
[0.11] | [0.72] | [0.19] |
| Wald |
1.46 | 1.63 | 0.67 |
| Wald |
[0.23] | [0.20] | [0.41] |
This table presents the common slope estimates (![]() ,
, ![]() ) from the following panel
regression:
) from the following panel
regression:
where
Bibliography
"The Distribution of Realized Stock Return Volatility," Journal of Financial Economics, vol. 61, 43-76.Appendix A Equity Portfolios
In addition to the 1990-2010 period, Table 4 presents the monthly raw return and CAPM Alpha differences between high-return (long) and low-return (short) equity portfolios (size, book-to-market, and industry) for the sample periods 1926-2010 and 1963-2010. For the
sample period July 1926 - December 2010, the average return difference between the Small and Big portfolios is 0.60% per month with the OLS ![]() -statistic of 2.49 and the Newey-West (1987)
-statistic of 2.49 and the Newey-West (1987)
![]() -statistic of 2.36, implying that small stocks on average generate higher returns than big stocks. The CAPM Alpha (or abnormal return) for the long-short size portfolio is 0.27% per month
with the OLS
-statistic of 2.36, implying that small stocks on average generate higher returns than big stocks. The CAPM Alpha (or abnormal return) for the long-short size portfolio is 0.27% per month
with the OLS ![]() -statistic of 1.22 and the Newey-West
-statistic of 1.22 and the Newey-West ![]() -statistic of 1.38. This
economically and statistically insignificant Alpha indicates that the static CAPM does explain the size effect for the 1926-2010 period.
-statistic of 1.38. This
economically and statistically insignificant Alpha indicates that the static CAPM does explain the size effect for the 1926-2010 period.
For the ten book-to-market portfolios, the average return difference between the Value and Growth portfolios is 0.53% per month with the OLS ![]() -statistic of 2.52 and the Newey-West
-statistic of 2.52 and the Newey-West
![]() -statistic of 2.46, implying that value stocks on average generate higher returns than growth stocks (the so-called value premium). Similar to our findings for the size portfolios, the
unconditional CAPM can explain the value premium for the 1926-2010 period; the CAPM Alpha (or abnormal return) for the long-short book-to-market portfolio is only 0.24% per month with the OLS
-statistic of 2.46, implying that value stocks on average generate higher returns than growth stocks (the so-called value premium). Similar to our findings for the size portfolios, the
unconditional CAPM can explain the value premium for the 1926-2010 period; the CAPM Alpha (or abnormal return) for the long-short book-to-market portfolio is only 0.24% per month with the OLS ![]() -statistic of 1.25 and the Newey-West
-statistic of 1.25 and the Newey-West ![]() -statistic of 1.26.
-statistic of 1.26.
The last six rows in Table 4 report average return differences and CAPM Alphas for the industry portfolios (10-, 17-, 30-, 38-, 48-, and 49-industry portfolios). For the long sample period of 1926-2010, only the extreme portfolios of 48 and 49 industries generate
significant return differences, whereas the average return differences for the high-return and low-return portfolios of 10, 17, 30, and 38 industries are either statistically insignificant or marginally significant. For 48- and 49-industry portfolios of Kenneth French, "Aero" industry has the
highest average monthly return, whereas "Other" industry has the lowest return, yielding an average monthly return difference of 66 basis points with the Newey-West ![]() -statistic of
2.55.25 More importantly, the static CAPM cannot explain the industry effect; the CAPM alpha (or abnormal return) for the "Aero-Other" arbitrage
portfolio is 0.50% per month and statistically significant with the
-statistic of
2.55.25 More importantly, the static CAPM cannot explain the industry effect; the CAPM alpha (or abnormal return) for the "Aero-Other" arbitrage
portfolio is 0.50% per month and statistically significant with the ![]() -statistic of 2.04. Although the average return differences between high-return and low-return portfolios of 30 and 38
industries are marginally significant, the CAPM Alphas are found to be significant. For 30-industry portfolios, the average return difference between "Coal" and "Other" industries is 0.51% per month and marginally significant with the
-statistic of 2.04. Although the average return differences between high-return and low-return portfolios of 30 and 38
industries are marginally significant, the CAPM Alphas are found to be significant. For 30-industry portfolios, the average return difference between "Coal" and "Other" industries is 0.51% per month and marginally significant with the ![]() -statistic of 1.71.26 However, the CAPM Alpha for the "Coal-Other" arbitrage portfolio is 0.65%
per month with the
-statistic of 1.71.26 However, the CAPM Alpha for the "Coal-Other" arbitrage portfolio is 0.65%
per month with the ![]() -statistic of 2.28. For 38-industry portfolios, the average return difference between "Oil" and "Whlsl" industries is 0.42% per month and marginally significant with
the
-statistic of 2.28. For 38-industry portfolios, the average return difference between "Oil" and "Whlsl" industries is 0.42% per month and marginally significant with
the ![]() -statistic of 1.85.27 However, the CAPM
Alpha for the "Oil-Whlsl" arbitrage portfolio is 0.49% per month with the
-statistic of 1.85.27 However, the CAPM
Alpha for the "Oil-Whlsl" arbitrage portfolio is 0.49% per month with the ![]() -statistic of 2.06.
-statistic of 2.06.
Fama and French (1992) identify economically and statistically significant value premium for the post-1963 period. Moreover, Fama and French (1992) find that the post-1963 value premium is not explained by the CAPM. However, Ang and Chen (2007) provide evidence that the value premium is captured by the CAPM for the sample period of 1926-1963. They also show that the conditional CAPM with stochastic betas can explain the return differences between value and growth portfolios even for the post-1963 period. Fama and French (2006) indicate that the performance of the CAPM with regard to the book-to-market effect varies across subperiods. We investigate the significance of size, book-to-market, and industry effects for the sample that generated heated debate on value premium. We compute the average return differences and Alphas for the subsample period of July 1963 - December 2010.
As presented in Table 4, the average return difference between the Small and Big portfolios as well as the CAPM Alpha for "Small-Big" arbitrage portfolio are positive, but they are economically and statistically insignificant, indicating that the size effect disappears for the post-1963 period. Similar to the findings of Ang and Chen (2007) and Fama and French (2006), value premium remains economically and statistically significant for the sample period July 1963 - December 2010; the average raw and risk-adjusted return differences between the Value and Growth portfolios is 0.55% per month and statistically significant, implying that value stocks on average generate higher returns than growth stocks and this value premium cannot be explained by the static CAPM.
The results for the industry portfolios are similar for the post-1963 period. The high-return and low-return portfolios of 30 and 38 industries generate marginally significant, 48 and 49 industries generate significant return differences, whereas the average return differences for the
high-return and low-return portfolios of 10 and 17 industries are insignificant. Specifically, for 30-, 48- and 49-industry portfolios of Kenneth French, "Coal" industry has the highest average monthly return, whereas "Other" industry has the lowest return, yielding an average raw and
risk-adjusted return differences of 79 to 92 basis points per month and statistically significant. The unconditional CAPM cannot explain these industry effects either. For 38-industry portfolios, the average return and Alpha differences between "Smoke" and "Govt" industries are about 1.06% and
1.07% per month and significant with the Newey-West ![]() -statistics of 2.61 and 2.69, respectively.28
-statistics of 2.61 and 2.69, respectively.28
Appendix B DCC Model of Engle (2002)
We estimate the conditional covariances of each equity portfolio with the market portfolio and ![]() (
(
![]() ,
,
![]() ) based on the mean-reverting DCC model of Engle (2002). Engle defines the conditional correlation between two random variables
) based on the mean-reverting DCC model of Engle (2002). Engle defines the conditional correlation between two random variables ![]() and
and ![]() that each has zero mean as
that each has zero mean as
where the returns are defined as the conditional standard deviation times the standardized disturbance:
where
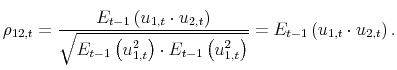 |
(A3) |
The conditional covariance matrix of returns is defined as
 |
(A4) |
where
| (A5) |
Engle (2002) introduces a mean-reverting DCC model:
| (A6) |
where
Engle (2002) assumes that each asset follows a univariate GARCH process and writes the log likelihood function as:
As shown in Engle (2002), letting the parameters in
| (A9) |
The volatility term is
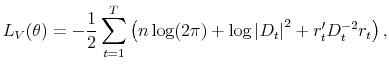 |
(A10) |
and the correlation component is
 |
(A11) |
The volatility part of the likelihood is the sum of individual GARCH likelihoods:
 |
(A12) |
which is jointly maximized by separately maximizing each term. The second part of the likelihood is used to estimate the correlation parameters. The two-step approach to maximizing the likelihood is to find
| (A13) |
and then take this value as given in the second stage:
| (A14) |
Appendix K System of Regression Equations
Consider a system of ![]() equations, of which the typical
equations, of which the typical ![]() th equation is
th equation is
where
where
| (A17) |
Equation (A15) can then be written as
| (A18) |
with
Under this setup, Parks (1967) presents a consistent and asymptotically efficient three-step estimation technique for the regression coefficients. The first step uses single equation regressions to estimate the parameters of autoregressive model. The second step uses single equation regressions on transformed equations to estimate the contemporaneous covariances. Finally, the Aitken estimator is formed using the estimated covariance,
| (A20) |
where
![\displaystyle IV_{t,t+1} \ \equiv \ \operatorname{E}^Q \left[\sigma^2_{t+1}\vert\Omega_t\right] \ = \ 2 \int_{0}^{\infty}{C_t\left(t+1,\frac{K}{B(t,t+1)}\right) - C_t\left(t,{K}\right) \over K^2}\,dK,](img10.gif)
![\displaystyle RV_{t,t+1} \equiv \sum_{j=1}^{n}\left[p_{t+\frac{j}{n}} - p_{t+\frac{j-1}{n}}\right]^2 \longrightarrow\sigma^2_{t+1},](img13.gif)
![\displaystyle E\left[R_{i,t+1}\vert\Omega_t\right]=\frac{E\left[R_{m,t+1}\vert\Omega_t\right]}{\mbox{var}\left[R_{m,t+1}\vert\Omega_t\right]}\cdot \mbox{cov}\left[R_{i,t+1},R_{m,t+1}\vert\Omega_t\right],](img22.gif)
![\displaystyle V_t ~ = ~ \left[\left(1-\delta\right)C_t^{\frac{1-\gamma}{\theta}} +\delta\left(E_t\left[V_{t+1}^{1-\gamma}\right]\right)^{\frac{1}{\theta}}\right]^{\frac{\theta}{1-\gamma}},](img55.gif)
![\displaystyle E\left[R_{m,t+1}\vert\Omega_t\right] ~ =~ \gamma \sigma^2_{m,t} \, + \, \frac{(1-\theta-\gamma)\kappa_1^2( A_{\sigma}^2 + A_q^2 \varphi_q^2)} {(\theta-1)\kappa_1\left[ A_{\sigma} + A_q \kappa_1^2 \left( A_{\sigma}^2 + A_q^2 \varphi_q^2 \right) \varphi_q^2\right]}VRP_{t} \, .](img99.gif)
![The figure shows the model-implied relationship between market excess return and variance risk premium (VRP), or the return-uncertainty trade-off coefficient (B) as implied by the model. The top panels show how the value of B changes with respect to the intertemporal elasticity of substitution (IES) ψ=[1,10] (left) and the risk aversion coefficient γ=[1,2] (right), and the lower two panels with respect to ψ=[0,1] (left) and γ=[0,1] (right). The benchmark calibration setting is based on Zhou (2010) and specified in Table 1.](img215.gif)
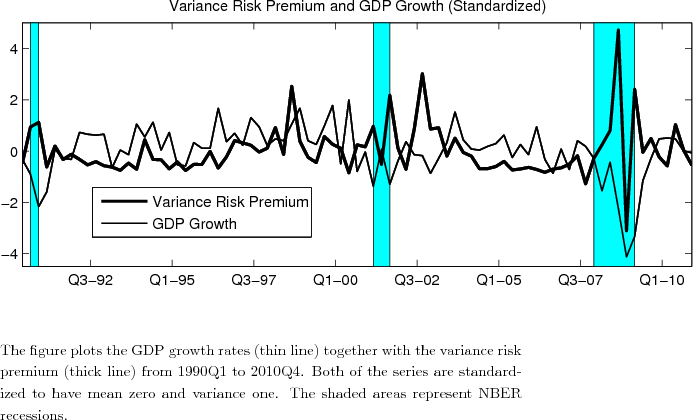
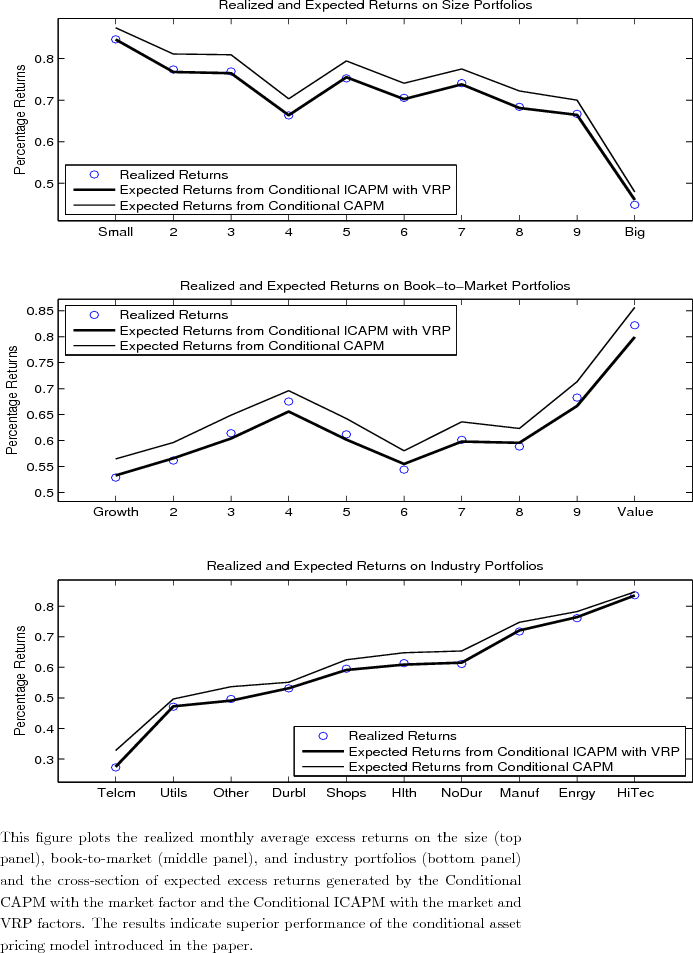
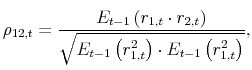
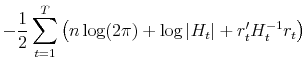
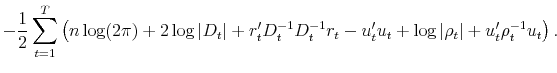
![\displaystyle P_i = \left[ \begin{array}{lllll} \left(1-\rho_i^2\right)^{-1/2} & 0 & 0 & ... & 0\\ \rho_i\left(1-\rho_i^2\right)^{-1/2} & 1 & 0 & ... & 0\\ \rho_i^2\left(1-\rho_i^2\right)^{-1/2} & \rho & 1 & ... & 0\\ .\\ .\\ .\\ \rho_i^{N-1}\left(1-\rho_i^2\right)^{-1/2} & \rho^{N-2} & \rho^{N-3} & ... & 1 \end{array} \right] \ .](img265.gif)