Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-46 Screen Reader version ^♣

From Many Series, One Cycle: Improved Estimates of the Business Cycle from a Multivariate Unobserved Components Model *

Charles A. Fleischman John M. Roberts

Board of Governors of the Federal Reserve System

October 2011

Keywords: Business cycles, output gap, potential output, state-space model, Kalman filter, NAIRU, measurement error.

Abstract:

We construct new estimates of potential output and the output gap using a multivariate approach that allows for an explicit role for measurement errors in the decomposition of real output. Because we include data on hours, output, employment, and the labor force, we are able to decompose our estimate of potential output into separate trends in labor productivity, labor-force participation, weekly hours, and the NAIRU. We find that labor-market variables-especially the unemployment rate-are the most informative individual indicators of the state of the business cycle. Conditional on including these measures, inflation is also very informative. Among measures of output, we find that although they add little to the identification for the cycle, the income-side measures of output are about as informative as the traditional product-side measures about the level of structural productivity and potential output. We also find that the output gap resulting from the recent financial crisis was very large, reaching -7 percent of output in the second half of 2009.

JEL Classification: E32, O40, E24, C32.

Introduction

Potential output-the productive capacity of the aggregate economy-is a key input into monetary policy decisions at central banks around the world, and the output gap-the difference between actual output and potential output-can be an important gauge of inflationary pressures. Crucial as it is, however, potential output cannot be observed. Economists have applied a variety of statistical methods to decompose movements in real output into cyclical and trend components, and then identify the output gap as the cyclical component and potential output as the trend component from these decompositions.

We construct new estimates of potential output and the output gap using a multivariate approach that allows for an explicit role for measurement errors in the decomposition of real output. There are a number of advantages of our multivariate approach. First, as Stock and Watson (1989) and Basistha and Startz (2008) have emphasized, a multivariate approach improves the precision of cycle estimates. Second, by including many of the major macroeconomic indicators in a single system, we are able to assess the trade-offs among competing signals from these indicators in an integrated, coherent fashion. Third, because we use a growth-accounting framework similar to that used by the Congressional Budget Office (CBO) (and numerous central banks) and include data on hours, output, employment, and the labor force, we are able to decompose our estimate of potential output into separate trends in labor productivity, labor-force participation, and weekly hours, as well as the NAIRU. Fourth, because we assume that cyclical fluctuations in output affect inflation, we can give our trend estimates a "natural rate" interpretation as in Friedman (1968) and Phelps (1968). Finally, because we include both income- and product-side measures of output, we are able to obtain meaningful estimates of measurement error in output, which should improve our estimates of the underlying trends and cycle.

Our trend and cycle estimates exploit a number of identifying assumptions that have been used in the literature. Our multivariate approach means that we can rely on comovement in important indicators of output and the labor market to identify the business cycle. The idea that the business cycle is marked by comovement goes back at least to the early work of Burns and Mitchell (1946). It also lies behind the factor-model approach to estimating the underlying forces driving the business cycle (Stock and Watson, 2002; Giannone, Reichlin, and Small, 2005). Another assumption we make is that trends are permanent and cycles are transitory. This idea is behind many of the early state-space decompositions of output into trend and cycle, such as Clark (1987) and Watson (1986). A third idea we incorporate is that cyclical fluctuations ought to affect inflation. A version of this idea can already be found in Burns and Mitchell (1946), who noted that inflation tended to fall in recessions and rise in booms. It has been used in a time-series context by Kuttner (1994) and Staiger, Stock, and Watson (1997).

Our identifying assumptions have been combined in various ways in past research. Kuttner (1994), for example, combines the permanent trend/transitory cycle identification with the natural rate identification. Blanchard and Quah (1989) is an early example of combining the permanent/transitory identification with the comovement identification. The paper that comes closest to our approach is Basistha and Startz (2008), who combine all three elements. However, because we use more variables and we base our model of potential output on the growth-accounting framework, we are able to give a more structural interpretation of our results. In particular, we are able to identify the trend in labor productivity-which, given its important role in a wide variety of macroeonomic models, is of independent interest beyond its contribution to our estimate of potential output.

In all, we use nine series in our model: real GDP (gross domestic product); real GDI (gross domestic income-that is, overall output measured on the income side of the accounts); the unemployment rate; the labor-force participation rate; aggregate hours for the nonfarm business (NFB) sector of the economy; a corresponding measure of NFB employment; NFB-sector output, measured both on the product side and on the income side; and inflation as measured by the CPI excluding food and energy. Our choice of series has several motivations. First, it allows us to present a conventional decomposition of trends. Thus, for example, productivity is typically measured for the NFB sector, and so we wanted to include measures of NFB output and hours. Trends in unemployment, labor force participation, and the workweek are of important independent interest, and so we wanted to include all of these broad measures of labor market activity. Second, including both income- and product-side measures of output should sharpen our estimates of both trends and the cycle (see Nalewaik, 2010, for a full discussion of the properties of GDP and GDI). On the other hand, state-space techniques are more computationally intensive (and sensitive to excessive parameterization) than rival techniques based, for example, on principal components. We thus use far fewer series than are included in principal-component-based measures, such as the Chicago Fed's National Activity Index. We feel that we have nonetheless included a fairly broad range of data; indeed, our results suggest that we are already achieving diminishing returns from additional data-at least among the series we examine here.

We have four key findings: First, labor-market indicators-such as the unemployment rate and NFB employment-are better cyclical indicators than either GDP or GDI, in the sense that the model chooses to put larger weight on the labor-market indicators in deriving its estimates of the cycle. Second, we also find that, despite evidence of instabilities in the Phillips curve, inflation is also very helpful in identifying the cycle. Third, we find that our model yields estimates of the output gap with a considerably higher signal-to-noise ratio than the univariate approaches explored by Orphanides and van Norden (2002). Finally, we find that although they add little to the identification for the cycle, the income-side measures of output are about as informative as the traditional product-side measures about the level of structural productivity.

Model

1.1-General specification

In our model, we break each of the measures of real output and labor-market activity into the sum of a cyclical component, a trend, and an idiosyncratic residual:

X ${}_{it}$ = $\lambda$ ${}_{i}$ (L) cyc ${}_{t}$ ${}_{ }$ + X ${}_{it}$ ${}^{*}$ + u ${}_{it}$ . (1)

The cyclical component cyc is common across all the series.¹ By introducing a lag polynominal $\lambda$ ${}_{i}$ (L), we allow for the possibility that the cyclical component may have both contemporaneous and lagged effects that can differ across the variables x ${}_{i}$ . The trend is X ${}_{i}$ ${}^{*}$ and the residual is u ${}_{i}$ .

For the cycle, we assume an AR(2) specification:

cyc ${}_{t}$ = $\rho$ ${}_{1}$ cyc ${}_{t}$ ${}_{-1}$ + $\rho$ ${}_{2}$ cyc ${}_{t}$ ${}_{-2}$ + $\eta$ ${}_{t}$ (2)

Typically, $\rho$ ${}_{1}$ 1 and $\rho$ ${}_{2}$ 0, so that the cycle has a "hump-shaped" response to a shock to $\eta$ , with the initial shocks magnified over suseqent periods. Also, $\rho$ ${}_{1}$ + $\rho$ ${}_{2}$ is typically large, but less than one-meaning that the business cycle is highly persistent, but stationary.

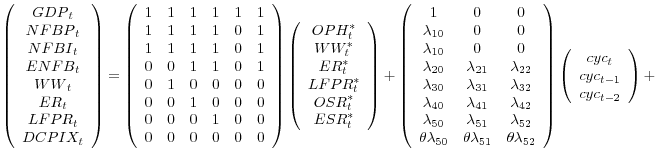
Our system includes eight labor-market and output variables: the log of real Gross Domestic Product (GDP); the log of real Gross Domestic Income (GDI); the log of real NFB output measured on the product side (NFBP); the log of real NFB output measured on the income side (NFBI); the log of NFB sector (all persons) employment (ENFB); the log of the NFB-sector (all persons) workweek (WW); the log of the labor-force participation rate (LP); and the log of the employment rate: ER = log[1 - (UR/100)], where UR is the civilian unemployment rate. The log of the civilian working-age population is subtracted from each of GDP, GDI, NFBP, NFBI, and ENFB, as population is a readily identifiable common trend. We also include inflation as measured by the CPI excluding food and energy (DCPIX) in our baseline model.

1.2-Output variables

The specific versions of the observation equation 1 for the four output variables are:

GDP ${}_{t}$ = cyc ${}_{t}$ ${}_{ }$ + GDO ${}_{t}$ ${}^{*}$ + u ${}_{1}$ ${}_{t}$ (3)

GDI ${}_{t}$ = cyc ${}_{t}$ ${}_{ }$ + GDO ${}_{t}$ ${}^{*}$ + u ${}_{2}$ ${}_{t}$ (4)

NFBP ${}_{t}$ = $\lambda$ ${}_{10}$ cyc ${}_{t}$ ${}_{ }$ + NFBO ${}_{t}$ ${}^{*}$ + u ${}_{3}$ ${}_{t}$ (5)

NFBI ${}_{t}$ = $\lambda$ ${}_{10}$ cyc ${}_{t}$ ${}_{ }$ + NFBO ${}_{t}$ ${}^{*}$ + u ${}_{4}$ ${}_{t}$ (6)

In equations 3 through 6, we exploit the fact that output measured on the income and product sides are alternative measures of the same concept. Thus, GDP and GDI should have the same trend and cycle and differ only by measurement error, and similarly for NFBP and NFBI. We give the label GDO-for gross domestic output-to the common component of GDP and GDI, and the label NFBO to the common component of NFBP and NFBI. We make the identifying assumption that the effect of the cycle on GDP and GDI is contemporaneous with a coefficient of one.² Making the effect of the cycle on GDP and GDI contemporaneous reflects the common assumption that overall output is the best contemporaneous business-cycle indicator. Restricting the coefficient to be one is a normalization that has the effect of making the units of cyc the same as those of an output gap. In equations 5 and 6, we again restrict the effect of the cycle on NFB output to be contemporaneous and the same across the income and product measures, but allow the coefficient on the cycle to be freely estimated; we would expect it to be greater than one because the non-NFB portions of GDP (such as government) are not very cyclical.

1.3-Labor market variables

In the equations for labor-market variables, we allow for lags between movements in the cycle and changes in the signal variable:

ENFB ${}_{t}$ = $\lambda$ ${}_{20}$ cyc ${}_{t}$ ${}_{ }$ + $\lambda$ ${}_{21}$ cyc ${}_{t}$ ${}_{-1}$ ${}_{ }$ + $\lambda$ ${}_{22}$ cyc ${}_{t}$ ${}_{-2}$ ${}_{ }$ + ENFB ${}_{t}$ ${}^{*}$ + u ${}_{5}$ ${}_{t}$ . (7)

WW ${}_{t}$ = $\lambda$ ${}_{30}$ cyc ${}_{t}$ ${}_{ }$ + $\lambda$ ${}_{31}$ cyc ${}_{t}$ ${}_{-1}$ ${}_{ }$ + $\lambda$ ${}_{32}$ cyc ${}_{t}$ ${}_{-2}$ ${}_{ }$ + WW ${}_{t}$ ${}^{*}$ ${}_{ }$ + u ${}_{6}$ ${}_{t}$ . (8)

ER ${}_{t}$ = $\lambda$ ${}_{40}$ cyc ${}_{t}$ ${}_{ }$ + $\lambda$ ${}_{41}$ cyc ${}_{t}$ ${}_{-1}$ ${}_{ }$ + $\lambda$ ${}_{42}$ cyc ${}_{t}$ ${}_{-2}$ ${}_{ }$ + ER ${}_{t}$ ${}^{*}$ ${}_{ }$ + $\alpha$ EEB ${}_{t}$ + u ${}_{7}$ ${}_{t}$ . (9)

LP ${}_{t}$ = $\lambda$ ${}_{50}$ cyc ${}_{t}$ ${}_{ }$ + $\lambda$ ${}_{51}$ cyc ${}_{t}$ ${}_{-1}$ ${}_{ }$ + $\lambda$ ${}_{52}$ cyc ${}_{t}$ ${}_{-2}$ ${}_{ }$ + LP ${}_{t}$ ${}^{*}$ - $\alpha$ EEB ${}_{t}$ + u ${}_{8}$ ${}_{t}$ . (10)

This assumption reflects the view that, perhaps owing to adjustment costs, firms do not adjust employment and hours immediately in response to cyclical shocks. It is also consistent with the conventional view that the unemployment rate is a lagging indicator of the business cycle. The lags in the effect of the cycle on NFB employment in equation 7 may seem at odds with the conventional view that payroll employment is a coincident indicator. We treat this as an empirical question and allow for the possibility that employment is a coincident indicator, but do not impose this restriction.³

To account for the influence of federal and state emergency and extended benefits (EEB) programs on the unemployment rate and labor force participation, we included a measure of the size of the EEB programs in equations 9 and 10.⁴ There are several reasons why the availability of EEB can lead to an increase in the unemployment rate (equivalently a decrease in the employment rate) that is unrelated to our estimate of the cycle. First, EEB programs are typically enacted on an ad hoc basis and so bear a less-systematic relationship to the business cycle than do the regular state-level unemployment insurance programs. Second, because eligibility for EEB is largely contingent on continued job search, the availability of EEB can induce some individuals who otherwise would have ended their job search and left the labor force to report active job search. Finally, these benefits may induce some workers to become more selective in their job search, thus extending their period of unemployment. On the other hand, the EEB programs typically are available only during periods of unusual weakness in labor demand. As a result, we hypothesize that while the EEB programs may have a first-order effect on the unemployment rate, they are less likely to significantly curtail employment. Thus, in our model, we impose the restriction that EEB programs do not affect employment by including the EEB variable in equations 9 and 10 with coefficients that are equal but of opposite sign.

1.4-Inflation

As in other time-series decompositions of the trend and cyclical components of output and labor market variables (Kuttner, 1994; Staiger, Stock, and Watson, 1997; Gordon, 1997, 1998; Laubach and Williams, 2003; Basistha and Startz, 2008), we include a model of inflation in our baseline analysis. Including inflation gives our estimates of trends a "natural rate" interpretation, as in Friedman (1968) and Phelps (1968). Our Phillips curve uses the current-methods CPI excluding food and energy-which we will refer to as core inflation, and indicate as DCPIX-as its dependent variable. Another commonly used measure of core inflation is change in the price index for personal consumption expenditures (PCE) other than food and energy. We use core CPI prices rather than core PCE prices because the latter include nonmarket prices which can be very volatile. Core inflation is related to lags of core price inflation, relative changes in consumer energy prices, drpe, relative changes in the prices of imported goods drpi, and the employment rate gap, purged of measurement error and the EEB effect, ER ${}_{t}$ - (ER ${}_{t}$ ${}^{*}$ + $\alpha$ EEB ${}_{t}$ + u ${}_{7}$ ${}_{t}$ ):

DCPIX ${}_{t}$ = A(L)DCPIX ${}_{t}$ ${}_{-1}$ + β ${}_{11}$ (L)drpe ${}_{t}$ ${}_{-1}$ + β ${}_{12}$ (L)x d85 ${}_{t}$ x drpe ${}_{t}$ ${}_{-1}$

+ β ${}_{2}$ (L)drpi ${}_{t}$ + θ (ER ${}_{t}$ - [ER ${}_{t}$ ${}^{*}$ ${}_{ }$ + $\alpha$ EEB ${}_{t}$ + u ${}_{7}$ ${}_{t}$ ${}_{ }$ ]) + u ${}_{9}$ ${}_{t}$ (11)

Using equation 9, we have:

DCPIX ${}_{t}$ = A(L)DCPIX ${}_{t}$ ${}_{-1}$ + β ${}_{11}$ (L)drpe ${}_{t}$ ${}_{-1}$ + β ${}_{12}$ (L)x d85 ${}_{t}$ x drpe ${}_{t}$ ${}_{-1}$

+ β ${}_{2}$ (L)drpi ${}_{t}$ + θ ( $\lambda$ ${}_{50}$ cyc ${}_{t}$ ${}_{ }$ + $\lambda$ ${}_{51}$ cyc ${}_{t}$ ${}_{-1}$ ${}_{ }$ + $\lambda$ ${}_{52}$ cyc ${}_{t}$ ${}_{-2}$ ) + u ${}_{9}$ ${}_{t}$ ${}_{ }$ (12)

We include ten lags of core inflation. The sum of the coefficients on lagged inflation is constrained to equal one, with the coefficient on the first lag freely estimated and the coefficients on lags two through ten constrained to be the same. The relative price of energy enters with a six-quarter moving average.

An important issue with regard to reduced-form Phillips curve of the sort we include here is the possibility that its parameters have changed over time (Hooker, 1996; Roberts, 2006; Williams, 2006). Among the possible parameter changes that have been conjectured are a reduction in the effects of relative energy prices; an increase in the effects of relative import prices; and a decline in the effect of economic slack. Our own empirical work suggests that the strongest evidence for a shift is in the energy-price relationship. Since the 1970s, the share of energy in consumer spending has declined sharply and the ratio of imports to consumer spending has risen substantially, so one modification we make to address concerns about changing effects of energy and import prices is to weight them by their nominal expenditure shares. While the share adjustment proved to be adequate for accounting for the changes in the relationship between core inflation and import prices, such was not the case for energy prices. We therefore introduce a break in the coefficient on relative energy prices in 1985, captured by the dummy variable d85.

We did not find as strong evidence of instability in other coefficients in the Phillips curve and therefore did not make an adjustment in our baseline estimates.⁵ In our sensitivity analysis in Section 4, we revisit this issue and address concerns about the stability of the Phillips curve in two ways, in one case leaving the Phillips curve out of the model and in another, re-estimating the model with a shorter sample period.

1.5-Potential output and its components

We impose structural relationships among the trend components in equations 5 through 10 based on a decomposition of NFB-sector potential output, NFBO ${}_{t}$ ${}^{*}$ , into the trends in nonfarm business sector hours, HNFB ${}^{*}$ , and productivity, OPH ${}^{*}$ :

NFBO ${}_{t}$ ${}^{*}$ = HNFB ${}_{t}$ ${}^{*}$ + OPH ${}_{t}$ ${}^{*}$ (13)

The trend in NFB sector hours is the sum of trend NFB employment, ENFB ${}^{*}$ , and trend NFB workweek, WW ${}^{*}$ :

HNFB ${}_{t}$ ${}^{*}$ = ENFB ${}_{t}$ ${}^{*}$ + WW ${}_{t}$ ${}^{*}$ . (14)

Implicit in our analysis are multiple measures of aggregate employment: In addition to (per capita) nonfarm business sector employment (ENFB), the employment rate and labor-force participation rate (ER and LP) implicitly define (per capita) aggregate employment as measured in the Current Population survey (CPS):

ECPS ${}_{t}$ = ER ${}_{t}$ + LP ${}_{t}$ (15)

These two employment measures differ in both sectoral coverage and concept: CPS employment covers the whole economy, including the government, nonprofit, and farm sectors, which are excluded from ENFB. Also, because ECPS focuses on the employment status of the individual whereas ENFB focuses on jobs, changes over time in the degree of multiple jobholding can drive a wedge between these trends. We refer to the difference in employment trends the employment sector ratio (ESR ${}^{*}$ ):

ENFB ${}_{t}$ ${}^{*}$ = ECPS ${}_{t}$ ${}^{*}$ + ESR ${}_{t}$ ${}^{*}$ . (16)

The trend in CPS employment, ECPS ${}^{*}$ , is related to the trend in the employment rate, ER ${}^{*}$ , and the trend in the labor force participation rate, LP ${}^{*}$ , according to:

ECPS ${}_{t}$ ${}^{*}$ = ER ${}_{t}$ ${}^{*}$ + LP ${}_{t}$ ${}^{*}$ , (17)

Note that ER ${}^{*}$ is the trend employment rate and is thus a transformation of the NAIRU:

NAIRU ${}_{t}$ = 100 [1 - exp(ER ${}_{t}$ ${}^{*}$ )] (18)

We define potential output in the aggregate economy as potential gross domestic output (GDO ${}_{t}$ ${}^{*}$ ):

GDO ${}_{t}$ ${}^{*}$ = NFBO ${}_{t}$ ${}^{*}$ + OSR ${}_{t}$ ${}^{*}$ , (19)

where OSR ${}^{*}$ is the output sector ratio-the trend in the ratio of GDO to NFBO.

As can be seen in equations 13, 14, 16, 17, and 19, the set of six trends-LP ${}^{*}$ , ER ${}^{*}$ , WW ${}^{*}$ , OPH ${}_{t}$ ${}^{*}$ , and the output and employment sector ratios, OSR ${}^{*}$ and ESR ${}^{*}$ -are the blocks upon which the other trends are built. These basic trend components are assumed to follow a random walk with drift; the drift terms are assumed to follow a random walk without drift:

Z ${}_{t}$ ${}^{*}$ = Z ${}_{t}$ ${}_{-1}$ ${}^{*}$ ${}_{ }$ + $\gamma$ ${}_{Zt}$ + $\varepsilon$ ${}_{Z}$ ${}_{t}$ (20)

$\displaystyle \gamma Zt = \gamma Zt-1 + \nu Zt (21)$

One exception is the trend employment rate, ER ${}^{*}$ , which is assumed to follow a random walk without drift-that is, $\gamma$ ${}_{ER}$ ${}_{t}$ = 0 for all t.

1.6-Idiosyncratic errors

We turn next to the idiosyncratic errors-the u ${}_{i}$ 's in equations 3 through 10, plus 12. The errors for the labor market and inflation (u ${}_{5}$ , u ${}_{6}$ , u ${}_{7}$ , u ${}_{8}$ , and u ${}_{9}$ ) are straightforward: We assume that they follow IID processes. Note that we are agnostic as to the interpretation of these idiosyncratic errors. Among the possible interpretations are measurement error and (IID) structural shocks.

For the output measures in equations 3 through 6, the interrelationships among the idiosyncratic errors are more complex. We model the idiosyncratic errors for the NFB sector, u ${}_{3}$ and u ${}_{4}$ , as composed of two components, one that is common to the two and another that is measure-specific:

u ${}_{3}$ ${}_{t}$ = v ${}_{3}$ ${}_{t}$ + $\varepsilon$ ${}_{3}$ ${}_{t}$ (22)

u ${}_{4}$ ${}_{t}$ = v ${}_{4}$ ${}_{t}$ + $\varepsilon$ ${}_{3}$ ${}_{t}$ (23)

The common component, $\varepsilon$ ${}_{3}$ , is assumed to be IID. It is thus specified in the same way as the idiosyncratic components of the labor and inflation residuals. There is one key difference, however: Because we have both product- and income-side measures of output, we can hope to distinguish a structural component ( $\varepsilon$ ${}_{3}$ ) from measurement error (v ${}_{3}$ and v ${}_{4}$ ).

We assume the following relationship between the idiosyncratic errors for GDP and NFBP and for GDI and NFBI:

u ${}_{1}$ ${}_{t}$ = $\sigma$ u ${}_{3}$ ${}_{t}$ + $\xi$ ${}_{1}$ ${}_{t}$ (24)

u ${}_{2}$ ${}_{t}$ = $\sigma$ u ${}_{4}$ ${}_{t}$ + $\xi$ ${}_{1}$ ${}_{t}$ (25)

where $\sigma$ = (1/ $\lambda$ ${}_{10}$ ). Equations 24 and 25 reflect the accounting identity that GDP is the sum of product-side NFB output plus the (log) ratio of GDP to NFBP, while GDI is the sum of income-side NFB output plus the (log) ratio of GDI to NFBI. Thus, the idiosyncratic errors for NFBP and NFBI (u ${}_{3}$ ${}_{ }$ and u ${}_{4}$ , respectively) affect the errors for GDP and GDI. We have included only one idiosyncratic error for both GDP and GDI- $\xi$ ${}_{1}$ . That's because in the national accounts data, the discrepancy between nonfarm business output and overall output-that is output in the farm, households and institutions, and general government sectors-is measured only on the income side. As a consequence, nominal GDP minus nominal NFB output measured on the product side is equal to nominal GDI minus NFB output measured on the income side.⁶

We can summarize equations 22 through 25 as:

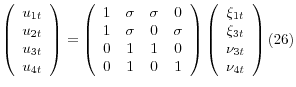
$\displaystyle \left( \begin{array}{c} u_{1t} \ u_{2t} \ u_{3t} \ u_{4t} \end{array}\right)=\left( \begin{array}{cccc} 1 & \sigma & \sigma & 0 \ 1 & \sigma & 0 & \sigma \ 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 1 \end{array}\right) \left( \begin{array}{c} {\xi }_{1t} \ {\xi }_{3t} \ {\nu }_{3t} \ {\nu }_{4t} \end{array}\right) (26)$

There are only three independent rows in equation 26, which implies that any three output variables contain the same information as the full set of four variables. In the empirical work that follows, we report results for the model excluding GDI.

To gain some insight into the statistical properties of the measurement error components, $\nu$ ${}_{3t}$ and $\nu$ ${}_{4t}$ , we can exploit the fact that the difference between them corresponds to the statistical discrepancy (in log ratio form), and thus is directly observable:

stat ${}_{t}$ = u ${}_{3}$ ${}_{t}$ - u ${}_{4}$ ${}_{t}$ = v ${}_{3}$ ${}_{t}$ - v ${}_{4}$ ${}_{t}$ (27)

We conducted some preliminary statistical analysis to help guide our specifications of $\nu$ ${}_{3}$ and $\nu$ ${}_{4}$ . We found that the statistical discrepancy is well represented by an AR(1) process and thus we allow the measurement errors in NFBP and NFBI to follow an AR(1) process:

v ${}_{3}$ ${}_{t}$ = $\psi$ v ${}_{3}$ ${}_{t}$ ${}_{-1}$ + $\upsilon$ ${}_{3}$ ${}_{t}$ (28)

v ${}_{4}$ ${}_{t}$ = $\psi$ v ${}_{4}$ ${}_{t}$ ${}_{-1}$ + $\upsilon$ ${}_{4}$ ${}_{t}$ (29)

We impose the restriction that the two processes for NFB output measurement error have the same degree of persistence, $\psi$ .⁷

1.7-Model summary

After excluding the equation for GDI and imposing the relationships between the residuals for GDP, NFBP, and NFBI, the eight observation equations can be summarized as:

$\displaystyle \left( \begin{array}{c} {GDP}_t \ {NFBP}_t \ {NFBI}_t \ {EN... ...t( \begin{array}{c} {cyc}_t \ {cyc}_{t-1} \ {cyc}_{t-2} \end{array}\right)+$

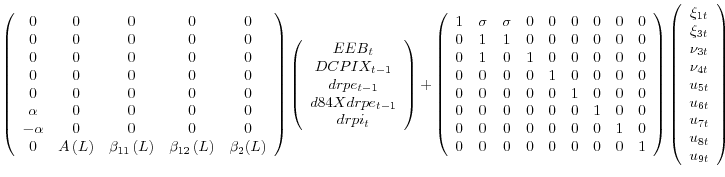
$\displaystyle \left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 &... ..._{4t} \ u_{5t} \ u_{6t} \ u_{7t} \ u_{8t} \ u_{9t} \end{array}\right)$

A few notes on our estimation approach: We estimated the model with quarterly data over the 1963:Q2-to-2011:Q1 period. Except where explicitly modeled (as in equations 22 and 23), we assume that all of the shocks are orthogonal. We estimate the model using standard maximum likelihood techniques for state-space models.⁸ In such techniques, the Kalman filter is used to find the mapping between the coefficients to be estimated and model's predictions of the fitted values of the observable data, and numerical methods are used to search over the coefficients to make the fitted values as close as possible to observed data.

Results-Baseline model

We present the estimates of the parameters in the observation equations in Table 1a and the parameters of the state equations in Table 1b. However, to keep the discussion of the results manageable (and interesting), we have organized our results around four themes:

What is the model's estimate of the business cycle?
How do the labor market and inflation respond to the cycle in the model?
What are the model's estimates of output measurement error and how do they affect our assessment the cycle in the recent period?
What are the model's implications for movements in trends?

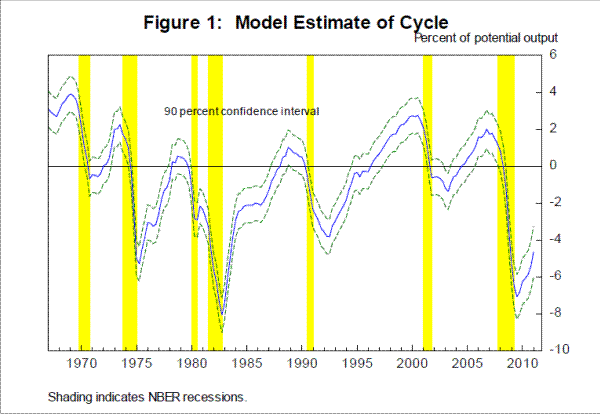
2.1-Model estimate of the cycle

Figure 1 presents the (two-sided) estimate of the cycle along with a 90 percent confidence interval and recession shading. As we discussed above, we have normalized the model so that the cycle variable has the same interpretation as a conventional output gap. Our estimate of the output gap typically falls sharply during NBER-dated recessions, after topping out within a couple of quarters of the NBER-dated peak. Consistent with the conventional view, the recessions of the mid-1970s and early 1980s were particularly deep, while the 1990-91 and 2001 recessions were relatively shallow, with the cyclical component dropping by only a few percent below its long-run value of zero. In the recent crisis, this gap estimate moved down sharply from 1 percent at the NBER peak in 2007:Q4 to -7 percent in 2009:Q3. The degree of slack at the trough was somewhat less than at the trough of the 1981-82 recession (-7¾ percent in 1982:Q4) and surpassed that of the 1973-75 recession (-5¼ percent in 1975:Q2).

By 2011:Q1, we estimate that the output gap had narrowed 2¼ percentage points to -4¾ percent. Following the deep 1974-75 and 1981-82 recessions, the cyclical component rebounded more sharply. In contrast, the cyclical component continued to drift downward after the 1990-91 and 2001 recessions, consistent with the notion that these were generally sluggish-and "jobless"-recoveries.

Figure 1: Model Estimate of Cycle. See link below for data.

Figure 1 Data

The main parameters responsible for the cyclical properties of the model are $\rho$ ${}_{1~}$ and $\rho$ ${}_{2}$ and the standard error of the shock to the cycle, shown in the top portion of Table 1b. Our estimate of the cycle is highly persistent; the modulus of the pair of complex roots is 0.81. Furthermore, the point estimates of $\rho$ ${}_{1}$ and $\rho$ ${}_{2}$ imply that largest effect of a cyclical shock is about twice as large as the impact effect and occurs about three quarters after the initial shock. The estimate of $\lambda$ ${}_{10}$ indicates that the amplitude of the cycle in NFB output is significantly larger than for GDO, consistent with the view that the business cycle is concentrated in the private sector; a shock that increases GDO by 1 percent will increase NFBO by 1.4 percent.

2.2-Reaction of the labor market and inflation to the cycle

The parameters linking the labor-market variables to the cycle are presented in lines 4 through 7 of Table 1a. The estimates of the NFB employment and workweek equations indicate that employment initially rises about 0.5 percent and the workweek about 0.3 percent in response to a cyclical movement that increases GDO by 1 percent. Taking account of the greater cyclicality of NFB output implies that a shock that raises NFBO by 1 percent increases NFB employment by about 0.4 percent and the workweek by about 0.2 percent. ${}^{ }$ Thus, a shock that increases NFB output by 1 percent will raise NFB hours contemporaneously by about 0.6 percent and NFB productivity by about 0.4 percent. By the end of three quarters, NFB output and hours will have both increased by about 2 percent; thus, the response of labor productivity to a cyclical shock dies off quickly, and is essentially gone after three quarters.

Table 1a : Parameter Estimates Observation Equations Baseline Model

Observation Equation	cyclet (λX0)	cyclet-1 (λX1)	cyclet-2 (λX2)	Extend. & Emerg. UI	Std. Err. Resid
GDP	1.00
GDP (Standard Error)	---
NFBP (x=1)	1.41
NFBP (x=1) (Standard Error)	(-0.04)
NFBI (x=1)	1.41
NFBI (x=1) (Standard Error)	(-0.04)
NFB Employment (x=2)	0.53	0.33	0.26		0.05
NFB Employment (x=2) (Standard Error)	(-0.07)	(-0.07)	(-0.06)		(-0.03)
NFB Workweek (x=3)	0.28	0.06	-0.10		0.11
NFB Workweek (x=3) (Standard Error)	(-0.07)	(-0.09)	(-0.06)		(-0.02)
Employment Rate (x=4)	0.35	0.19	0.03	-0.07	0.06
Employment Rate (x=4) (Standard Error)	(-0.04)	(-0.05)	(-0.04)	(-0.02)	(-0.01)
Labor Force Part. Rate (x=5)	-0.05	0.11	0.08	0.07	0.17
Labor Force Part. Rate (x=5) (Standard Error)	(-0.05)	(-0.08)	(-0.05)	(-0.02)	(-0.01)

State or Exogenous Variable

Observation Equation	CPIXt-1	ER Gap (Θ)	Energy (β11) Relative Price	Energy (T>1984) (β12) Relative Price	Importst (β21) Relative Price	Importst-1 (β22) Relative Price	Std. Err. Resid
Core CPI	0.37	0.30	0.06	-0.04	0.08	-0.04	0.71
Core CPI (Standard Error)	(-0.07)	(-0.06)	(-0.01)	(-0.02)	(-0.02)	(-0.02)	(-0.04)

Note: Estimation period is 1963:Q2 to 2011:Q1.

As can be seen by comparing the coefficients in lines 4 and 6, cyclical movements in the employment rate are more muted than for NFB employment. There are three main reasons for this: (1) The CPS measure of employment-the numerator of the employment rate-includes government-sector workers, whose employment is likely less cyclical than private-sector employment. (2) The CPS measures employment at any job, whereas NFB employment measures the number of jobs. Thus, if a person with multiple jobs loses one, NFB employment falls but CPS employment does not; such multiple jobholding is likely to be strongly procyclical. (3) Finally, as can be seen in the next part of the table, the labor-force participation rate (LP) is somewhat cyclical and that cyclicality helps mitigate some of the impact of employment fluctuations on the employment rate. Put another way, some job losers and discouraged job seekers choose to leave the labor force and are thus not counted as unemployed.

Note that the employment rate equation can be interpreted as a kind of "Okun's law." The point estimates suggest that after three quarters, a 1-percentage-point cyclical movement in GDO leads to a 0.57 percentage point increase in the employment rate, similar to other estimates of Okun's law.

Table 1a also includes estimates of the standard error of labor-market-related idiosyncratic errors. For the NFB workweek, the employment rate, and labor-force participation, the idiosyncratic errors are estimated to be statistically significant; for NFB employment, the error variance was small and only marginally significant.

The lower portion of Table 1a reports the estimates of the parameters of the Phillips curve. We include the employment rate gap (ER gap) in the Phillips curve to represent economic slack, where the employment gap is defined as the cyclical component of the employment rate. The slope of the Phillips curve is estimated to be 0.30; the point estimate is very precise, with a t-ratio of 5. Our Phillips curve includes ten lags of core CPI inflation, with the coefficient on the first lag freely estimated and the coefficients on the remaining lags constrained to be the same; the sum of the coefficients on all ten lags is constrained to sum to 1. The coefficient on CPIX ${}_{t-1 }$ is 0.37, which, combined with the restrictions on the remaining coefficients on lagged inflationimplies that the mean inflation lag is about one year and the sacrifice ratio is about 3½. Terms for relative energy and import prices are strongly statistically significant, as is the coefficient for a shift in the effect of energy prices beginning in 1985. This finding is consistent with Hooker's (1996) results indicating a falling effect of energy prices. ${}^{ }$ ⁹

Table 1b: Parameter Estimates State Equations Baseline Model

Cyclical parameters	Coefficient	Std. Error
Ρ1	1.62	(0.06)
Ρ2	-0.66	(0.06)
Std. error ε1	0.47	(0.05)

Trend parameters	Level Shocks Std deviation	Level Shocks Std. error	Drift Shocks Std deviation	Drift Shocks Std. error
Labor productivity	0.33	(0.06)	0.19	(0.08)
NFB workweek	0.23	(0.03)	0.03	(0.03)
Employment rate	0.11	(0.02)
Labor force part. rate	0.10	(0.03)	0.10	(0.03)
Employment discrepancy	0.19	(0.03)	0.07	(0.03)
Output discrepancy	0.15	(0.01)	0.02

Measurement error parameters	Coefficient	Std. Error
ψ1	0.88	(0.04)
Std. error of v3	0.36	(0.03)
Std. error of v4	0.29	(0.03)

Note: & Drift ratios estimated using median unbiased method; see text for details.

2.3-Measurement error and recent movements in GDI and GDP

The main parameters affecting output measurement error are shown at the bottom of Table 1b. The point estimate of $\psi$ ${}_{1}$ indicates that measurement error for NFB output has considerable serial persistence; as noted in equations 25 and 26, this measurement error persistence is inherited by GDI and GDP. The standard deviation of the innovation to the NFB product-side measurement error ( $\upsilon$ ${}_{3}$ ${}_{t}$ )is about 25 percent greater than income-side measurement error ( $\upsilon$ ${}_{4}$ ${}_{t}$ ), which is broadly consistent with Nalewaik's (2010) finding that GDI is a better measure of underlying real activity than is GDP.¹⁰

Figure 2 presents recent estimates of the cycle from our model along with two "gap" measures: the deviations of GDP and GDI from potential GDO. Recalling equations 2 and 3, these gaps will differ from the cycle owing to measurement error. As can be seen, movements in the cycle are somewhat closer to the GDI gapthan to the GDP gap, consistent with the results in Table 1 indicating that the variance of GDP measurement error was somewhat larger than the variance of GDI measurement error.

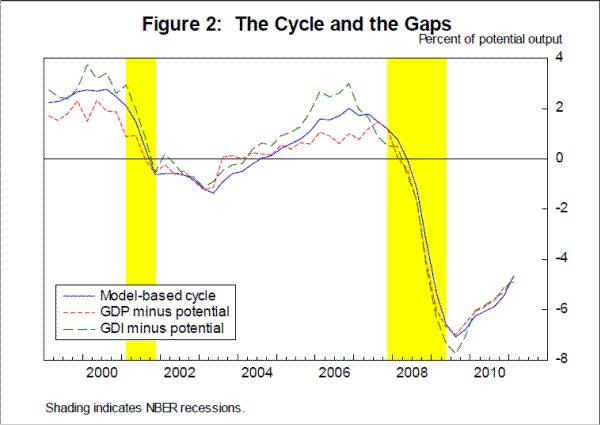
Figure 2: The Cycle and the Gaps. See link below for data.

Figure 2 Data

Table 2 presents detail on the model's decomposition of recent movements in GDP and GDI. In 2007, GDI was notably weaker than GDP, following two years in which GDI increased somewhat more than GDP. Since 2007, however, the movements in GDP and GDI have been similar. The table indicates that over the 2007 to 2009 period, potential output rose at an average annual rate of about 2 percent, for a total increase of nearly 6 percent. By contrast, the cyclical component of output fell a total of 8¾ percentage points. Thus, according to this model, the weakness in GDO over this period was overwhelmingly the consequence of the cycle.

Table 2: Decomposition of Recent Movements in GDP and GDI Q4/Q4 percent change

	2005	2006	2007	2008	2009	2010
Actual real GDP	2.8	2.4	2.2	-3.4	-0.5	3.1
Actual real GDI	3.7	3.0	-0.5	-2.9	-0.9	3.4
Common components Potential output	2.3	1.9	2.0	2.0	1.8	1.7
Common components Cycle	1.0	0.9	-0.8	-4.5	-3.4	1.4
Measurement errors GDP	-0.6	-0.6	1.1	-0.7	0.9	0.0
Measurement errors GDI	0.3	0.1	-1.4	-0.3	0.6	0.4

2.4-Model estimates of trends

The model parameters most directly related to trend estimates are found in the middle part of Table 1b. The standard errors of the trend level shocks-the I(1) components-are highly statistically significant. For productivity and labor-force participation, the estimates of the standard errors of the drift terms-the I(2) components-are also large and statistically significant. The estimates of the standard errors of the I(2) components for the workweek and employment discrepancy were smaller and marginally significant; in contrast, the initial FIML estimates of the standard error of the output discrepancy was quite small, raising the possibility of downward bias owing to the pile-up problem. In this case, estimates of the ratio of the I(2) standard error to the I(1) standard error were obtained in a preliminary step, and these ratios were imposed in the FIML estimation.¹¹

Table 3 presents recent movements in the model's trend components, while Table 4 shows the decomposition over a longer period. As can be seen in Table 3, potential output growth decelerated slightly from 2007 to 2010, as an acceleration in trend productivity was more than offset by a deceleration in trend labor input, especially in 2009. Of particular note, the model estimates that the level of the trend labor force participation rate fell 2 percent from 2007 to 2010, accounting for most of the 2¾ percent decline in the actual participation rate; this contrasts with the remaining variables in our decomposition, where the downturn over the past few years largely reflected cyclical developments.

Table 3: Decomposition of Potential Output 2005-2010 Q4/Q4 percent change

	2005	2006	2007	2008	2009	2010
Potential output	2.3	1.9	2.0	2.0	1.8	1.7
Total hours	1.0	1.2	0.6	1.1	-0.1	0.7
Population	1.2	1.1	1.1	1.1	1.0	0.9
LFPR	0.0	0.0	-0.2	-0.2	-0.7	-0.9
Employment rate	0.0	0.0	0.0	-0.1	-0.2	-0.3
Workweek	-0.1	0.0	-0.3	0.2	-0.2	1.0
NFB labor productivity	2.1	1.4	1.4	1.5	2.5	2.1
Sector Ratios GDO to NFBO	-0.2	-0.3	0.1	0.0	-0.7	-0.5
Sector Ratios NFB to total employment	-0.5	-0.4	-0.1	-0.6	0.1	-0.6

The longer-run decomposition of potential output shown in Table 4 is largely conventional: Gains in trend productivity were sluggish in the 1973-1995 period, but picked up starting in the late 1990s. Working-age population decelerated after the 1970s; labor-force participation increased rapidly in the 1970s but has been stagnant since 1990. Overall output has grown less rapidly than output in the nonfarm business sector, as government has grown less rapidly than the rest of the economy.

Table 4: Decomposition of Changes in Potential Output 1973-2010

	1973:Q4- 1980:Q1	1980:Q1- 1990:Q2	1990:Q2- 1995:Q2	1995:Q2- 2000:Q4	2000:Q4- 2010:Q4
Potential output	3.1	3.0	2.5	3.7	2.2
Total hours	2.0	1.5	1.1	1.0	0.6
Population	1.9	1.2	1.1	1.2	1.1
LFPR	0.7	0.4	-0.1	0.0	-0.3
Employment rate	0.0	0.0	0.0	0.0	-0.1
Workweek	-0.6	-0.2	0.0	-0.2	0.0
NFB labor productivity	1.2	1.5	1.5	2.9	2.3
Sector Ratios GDO to NFBO	-0.4	-0.1	-0.3	-0.4	-0.3
Sector Ratios NFB to total employment	0.4	0.1	0.2	0.2	-0.4

Figure 3 shows the smoothed (two-sided) estimates of the drift terms in the model. The broad historical patterns are similar to those shown in Table 4.

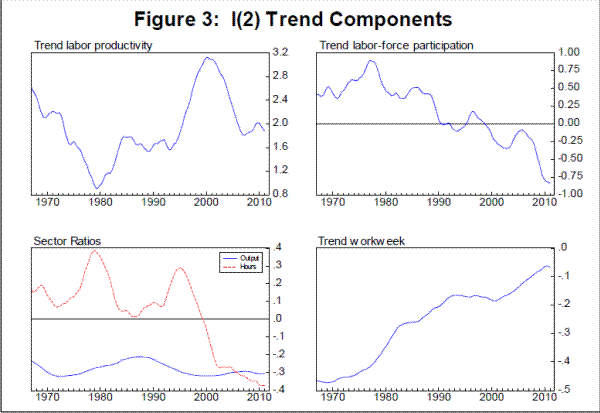
Figure 3: Trend Components. See link below for data.

Figure 3 Data

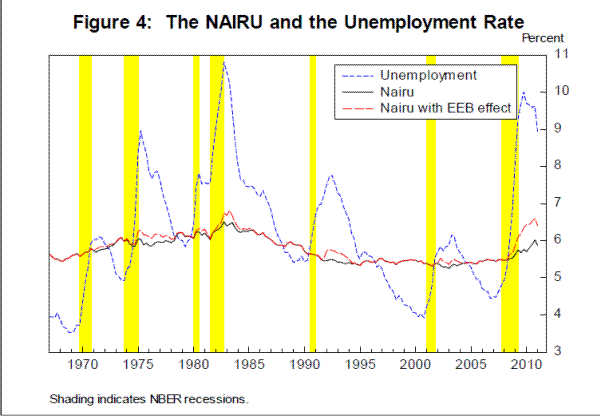
Figure 4 presents the model's estimate of the NAIRU along with the unemployment rate and a second variant of the NAIRU that includes the model's estimate of the effects of extended and emergency unemployment benefits (EEB). The basic NAIRU estimate varies somewhat over time, but the variation is fairly modest, and the NAIRU mostly remains in a range of 5¼ to 6½ percent, with the peak occurring in the early 1980s. Between 2005 and 2010, this estimate of the NAIRU moved up about ½ percentage point to around 6 percent as of the end of our sample. Taking account of the effects of EEB leads to more variation in the NAIRU, pushing the early 1980s peak somewhat higher and implying an estimate of about 6½ percent at the end of our sample. We will return to the issue of the variability of the NAIRU in Section 4.

Figure 4: The NAIRU and the Unemployment Rate. See link below for data.

Figure 4 Data

How informative are various data for estimates of trends and cycles?

Our model can be used assess which macroeconomic indicators are most informative for gauging the state of the business cycle, the NAIRU, and gains in trend productivity. In Table 5, we begin by examining the simple correlations between the signal variable residuals and the innovations to the selected state variables-the one-sided estimate of the state variable in period t less its expectation as of period t-1. In the table, the rows ordered by the absolute magnitude of the correlations with the cycle innovation. As shown in the first column, by this metric, the employment rate residual is most closely related to the innovation in the cycle ( $\rho$ = 0.91), followed by the NFB employment residual ( $\rho$ = .79) and the NFBI and NFBP residuals ( $\rho$ = .75 and $\rho$ = .67). These four variables are strongly procyclical, and it is not surprising that the "news" in these variables is highly correlated with the innovation to the cycle. Because most GDP is produced in the NFB sector, the GDP residual (equation 1) and the NFBP residual (equation 3) are highly correlated ( $\rho$ = .97). We therefore we focus on the difference between the GDP and NFBP residuals, which for convenience we label the output ratio. Because NFB output is more procyclical than GDO, the output ratio is negatively correlated with the cycle, as is its residual ( $\rho$ = -.64). The correlations of the innovation of the cycle with the residuals of the remaining signal variables (core inflation, the participation rate, and the workweek) are all less than 0.4.

Table 5: Correlations of Signal-Variable Residuals with State-Variable Innovations

Signal Residual	Cycle	ER*	Prod* (growth)
Employment rate	0.91	0.64	-0.01
NFB employment	0.79	0.36	-0.21
NFB output (income)	0.75	0.32	0.42
NFB output (product)	0.67	0.31	0.42
Output ratio	-0.64	-0.25	-0.20
NFB workweek	0.34	0.15	-0.34
Core CPI	0.28	-0.79	0.06
LFPR	-0.16	0.03	-0.06

The second column reports the correlations of the signal residuals with the innovations to the trend employment rate. Only the employment rate and core CPI residuals show large correlations with trend-employment innovations. Not surprisingly, the correlation with the core CPI residual is negative, as an upward surprise in inflation would, everything else equal, be consistent with a lower trend employment rate (higher NAIRU). Column 3 reports the correlations of the growth rate of trend productivity with the signal residuals. In this case, no variable has a correlation coefficient greater than 0.45, which suggests that no single variable is especially informative for the productivity trend. As expected, the residuals in the NFB output variables are positively correlated with the innovations to trend productivity, while the residuals in NFB employment and the NFB workweek are negatively correlated.

Table 5 presented the correlation of individual signal innovations with the states. To take account of the interrelationships among the variables, Table 6 reports the Kalman gains for one-standard-deviation surprise movements in the model variables. The gains are estimated by regressing the innovation to the state variable on the residuals from the signal equations, where the signal residuals are normalized to have a unit variance. (We report the standard deviation of the actual residuals in the last column.) Because the estimates of the state variables are simply manifestations of the information in the observable series, the R ${}^{2}$ statistics from these regressions are one.

Consistent with the finding that the employment rate residual is the most tightly correlated with the cycle innovation, its Kalman gain coefficient is also the largest: A one-standard-deviation innovation in the employment rate (0.23 percentage point) implies an upward revision in the estimate of the cycle of 0.30 percent (or 0.67 standard deviation). Table 5 indicated that, by itself, inflation was a poor indicator of aggregate demand. However, in this multivariate setting, it is the second-most informative variable for the cycle, with a Kalman gain coefficient of 0.16. Inflation is relatively more informative in this context because the innovations to the employment rate, employment, and output variables are highly correlated with each other, the inflation innovation is nearly orthogonal to them.

The innovation to the cycle is nearly fully explained by just the employment rate and inflation residuals; the R ${}^{2}$ of a regression of the innovation on these two residuals is 0.93. The incremental information in any of the other cyclical variables is small and the Kalman gain coefficients are less than or equal to 0.1; adding any one of stocktickerNFB employment, stocktickerNFB output (product and income measures), and the output sector ratio to the regression with the employment rate and the core stocktickerCPI residuals raises the R ${}^{2}$ to between 0.95 (stocktickerNFB output measured on the product side) to 0.97 (the output sector ratio). The workweek residual and the LFPR residual contain almost no incremental information for the cycle on top of the employment rate and inflation.

Table 6: Correlations of Signal-Variable Residuals with State-Variable Innovations

Signal Risdual	Cycle	ER*	Prod* (Growth)	Std. Dev. Signal Residual
Employment rate	0.30	0.07	-0.03	0.23
Core CPI	0.16	-0.09	0.00	0.62
NFB employment	0.09	-0.01	-0.15	0.36
NFB output (income)	0.07	0.001	0.16	0.90
NFB output (product)	-0.07	0.02	0.22	0.87
NFB workweek	0.04	-0.01	-0.11	0.29
LFPR	-0.02	0.00	0.00	0.23
Output Ratio	-0.10	0.02	0.10	0.27
Std. Dev. State Innovation	0.45	0.10	0.18

The important role for the employment rate in the estimation of the cycle may be surprising, given the traditional view that the unemployment rate is a lagging indicator. Our model is consistent with the view that the employment rate lags the cycle (see Table 1), but nonetheless finds that it is highly informative about the current state of the economy. One reason the output measures are relatively uninformative is that shocks to trends are more important for productivity than for the employment rate. This finding is consistent with other work that finds that shocks to trend productivity are much larger than shocks to trend hours (Roberts, 2001). Another reason is that, according to this model, output measures are more strongly affected by measurement error.

Column 2 reports the Kalman gain coefficients for the trend employment rate. In this case, a one standard deviation surprise in the employment rate (0.23 percentage point) raises the trend employment rate by 0.07 percentage point-or about one-third of the total surprise. Core CPI is also informative for the model's estimates of the trend employment rate; the Kalman gain coefficient on the core CPI residual is -0.09, indicating that a one standard deviation surprise in core CPI reduces the trend employment rate by 0.09 percentage point. This is about 90 percent of the 0.1 percentage point standard deviation in the trend employment rate innovation (shown in the last row of Table 6). Taken together, the employment rate and core CPI residuals explain 98 percent of the variation in the trend employment rate.

Column 3 shows the regression results for trend productivity. The gain coefficients on the normalized errors suggest that both income- and product-side measures of output are informative for the productivity trend, with a slight edge to the product-side measure. Not surprisingly, the components of NFB hours-NFB employment and the workweek-enter with the opposite sign as output and are also very informative. In this context, the employment rate is not as informative as NFB employment; the four variables just mentioned (NFBI, NFBP, ENFB, and WW) together account for 94 percent of the variability in innovations to trend productivity.

Sensitivity analysis

In this section, we examine the robustness of our results. We first consider a version of our model that uses fewer variables. We next turn to the question of the stability of the parameters of the Phillips curve, which we address by dropping the Phillips curve-and thus inflation-from the model. Finally, we allow for the possibility that the NAIRU may be more variable than we have assumed.

4.1-Smaller models

Many other studies have looked at smaller models than we examine here. Kuttner (1994), for example, looks at only output and inflation, while Basistha and Startz (2008) add the unemployment rate. To explore the effect our larger dataset may be having on our results, we consider models more on the scale of those used in earlier work. We first consider a model using only GDP, GDI, unemployment, and inflation. To consider the effects of including GDI, we then look at a model with only GDP, unemployment, and inflation.

The observation equations for our four-variable model are equations 3, 4, 9, and 12 from Section 2. The cycle is, as before, a simple second-order autoregression (equation 10). The model of the NAIRU is also as before: ER* is assumed to follow a random walk with no drift.¹² We now model potential output-GDO*-directly, assuming that GDO* follows a random walk with time-varying drift, as in equations 20 and 21. In the four-variable version, we also include AR(1) measurement errors for GDP and GDI, as in equation 25; as discussed below, in the three-variable version, we drop AR(1) measurement error and allow only for a white-noise idiosyncratic error.

Table 7 presents results from our four-variable model. Many of the estimated coefficients are similar to those in the larger model that is presented in Table 1. In particular, estimates of the employment rate equation show the same "Okun's law" relationship between the cycle and the unemployment rate as in the baseline model, with the sum of the coefficients on the cycle and its lags equal to 0.57. Estimates of the persistence and cyclicality of the cycle are also very similar to the earlier estimates. And, as shown by the relative standard errors of their measurement error components, GDI continues to be estimated to be a somewhat less noisy indicator of underlying output than does GDP.

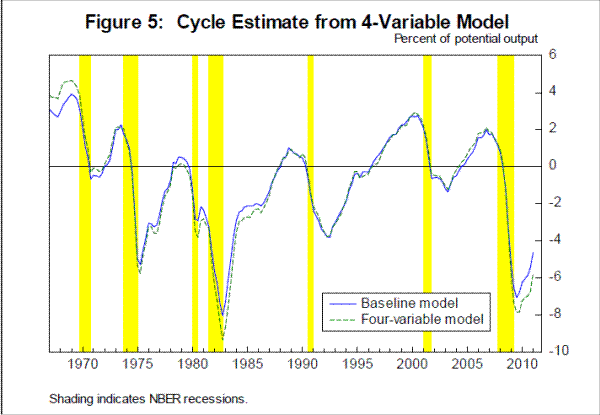
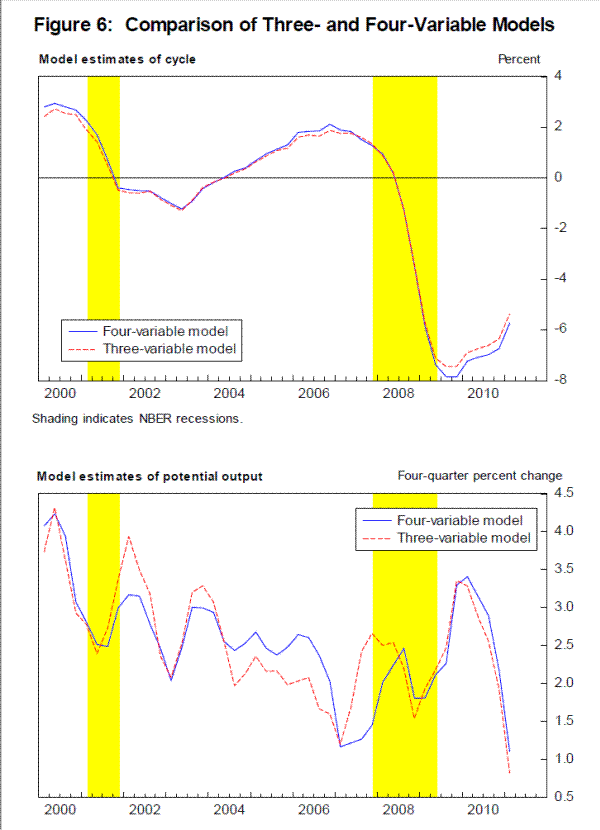
Figure 5 compares the estimate of the cycle from the smaller model with that from the larger baseline model. The estimates are broadly similar, although the four-variable model has somewhat greater cyclical variability than does the baseline model. The estimate of the standard error of the cycle at the end of the estimation sample (not shown) is somewhat larger in the four-variable version of the model: 1.0 percentage point, versus 0.8 percentage point in the larger model.

Table 7: Parameter Estimates: Baseline Three- and Four-Variable Models

	Baseline Model Coeff	Baseline Model (SE)	Four-Variable Model Coeff	Four-Variable Model (SE)	Three-Variable Model Coeff	Three-Variable Model (SE)
Cyclical parameters Ρ1	1.62	(0.06)	1.62	(0.05)	1.61	(0.07)
Cyclical parameters Ρ2	-0.66	(0.06)	-0.66	(0.06)	-0.65	(0.07)
Cyclical parameters Std. error ε1	0.46	(0.05)	0.51	(0.04)	0.51	(0.05)
Trend Parameters Potential Output Level	--	--	0.41	(0.04)	0.49	(0.07)
Trend Parameters Potential Output Drift	--	--	0.06	&	0.06	&
Trend employment rate	0.11	(0.03)	0.10	(0.03)	0.11	(0.02)
Measurement error parameters ψ1	0.88	(0.04)	0.89	(0.04)	--	--
Measurement error parameters Std. error ∨1	0.36	(0.03)	0.35	(0.05)	--	--
Measurement error parameters Std. error ∨2	0.29	(0.03)	0.24	(0.04)	--	--
Okun's law parameters Cyclet (λ40)	0.35	(0.05)	0.38	(0.05)	0.37	(0.06)
Okun's law parameters Cyclet-1 (λ41)	0.21	(0.05)	0.13	(0.04)	0.12	(0.04)
Okun's law parameters Cyclet-2 (λ42)	0.02	(0.04)	0.06	(0.03)	0.09	(0.03)
Phillips curve parameters CPIXt-1	0.37	(0.07)	0.36	(0.06)	0.36	(0.06)
Phillips curve parameters Employment rate gap (θ)	0.30	(0.06)	0.27	(0.04)	0.27	(0.04)
Idiosyncratic errors (std. dev.) GDP and GDI	0.12	(0.05)	0.10	(0.04)	0.18	(0.08)
Idiosyncratic errors (std. dev.) Employment rate	0.06	(0.01)	0.06	#	0.06	#
Idiosyncratic errors (std. dev.) Core CPI inflation	0.71	(0.04)	0.71	(0.04)	0.71	(0.04)

& Drift ratios estimated using median unbiased method; see text for details.
# Variance of the employment rate residual was estimated to be zero with a large standard error. We imposed the parameter value estimated from the baseline model.

Note: Models estimated from 1963:Q2 to 2011:Q1

Figure 5: Cycle Estimate from 4-variable Model. See link below for data.

Figure 5 Data

The last two columns of Table 7 present estimates from the three-variable model, which drops GDI. This version is of interest because it is most comparable to earlier work with multivariate state-space models, such as Kuttner (1994), Basistha and Startz (2008), and Laubach and Williams (2005), who do not include GDI. Without GDI, it is no longer possible to identify a serially correlated measurement-error component, and so measurement error is specified as a simple white-noise process.

There are some notable differences between the estimates of the three-variable model and the four-variable model. In particular, the estimate of the idiosyncratic error of GDP in the three-variable model (0.18) is notably smaller than the combined contributions of measurement and idiosyncratic error in the four-variable model (0.84).

Some sense of the consequences of dropping GDI from the model for recent estimates of the trend and cycle can be gleaned from Figure 6. Recall from Table 2 that GDP growth outstripped GDI growth by 2¾ percentage point in 2007. The bottom panel shows the implications for potential output: The four-variable model-informed by sluggish GDI gains-views potential output as having risen less than 1½ percent in 2007. By contrast, the three-variable model puts more weight on the GDP data, and thus infers that potential output rose about 2¾ percent in 2007. On the other hand, as shown in the top panel of Figure 6, the estimates of the cycle for the past few years are quite similar.

Figure 6: Comparison of Three- and Four- Variable Models. See link below for data.

Figure 6 Data

4.2-Model without a Phillips curve

The results of the Section 3 suggest that the Phillips curve makes a substantial contribution to the estimation of the cycle. Nonetheless, the well-know instabilities associated with the Phillips curve may raise concerns that including it may lead to misleading signals and biased results. We therefore consider results from a model that does not include a Phillips curve.

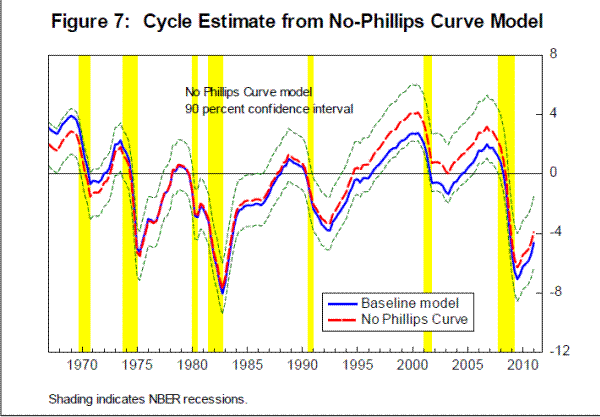
Figure 7: Cycle Estimate from No-Phillips Curve Model. See link below for data.

Figure 7 Data

The parameter point estimates from the no-Phillips-curve (NPC) model are very similar to those for the baseline model and therefore not shown. This model does, however, have different implications for the estimates of the latent variables. Figure 7 presents the estimate of the cycle from the no-Phillips-curve (NPC) model along with a 90 percent confidence interval and the baseline-model estimate. The confidence interval around the NPC estimate is 87 percent wider than that around the baseline model, consistent with the earlier finding that the Phillips curve is quite helpful in identifying the cycle. The NPC cycle is broadly similar to the baselineestimate. There are, nonetheless, some notable differences, especially in the latter part of the sample. In particular, since the mid-1990s, the average level of the cycle has been notably higher in the model without the Phillips curve. Thus, the two most-recent peaks-in the late 1990s and around 2007-are both higher in the NPC model; the estimated cyclical component never dropped below zero in the trough between those dates; and the 2011:Q1 estimate of the cyclical component of output is around -5 percent, compared with -5¾ percent in the baseline model.

While the no-Phillips-curve estimates present some risk that the current level of economic slack may be smaller than in our baseline estimates, we feel that the baseline estimates should be preferred. First of all, as discussed in Section 3, inflation adds valuable information to the estimation of the cycle, and, as a consequence, the estimates of the state of the business cycle from the baseline model are more precise, as evidenced in the tighter confidence intervals. Second, it is noteworthy that early in the sample, the estimates of the cycle from the two models are very similar. That suggests that the additional information from the Phillips curve is actually most helpful in the latter period.

4.3-A more-variable NAIRU

In our baseline estimates, the variability of the NAIRU is fairly modest: The standard error of the shock to NAIRU is 0.1 percentage point and, as we saw in Figure 4, the version of the NAIRU with the EEB adjustment stays within a fairly narrow range of 5¼ to 6¾ percent.¹³It is possible, however, that the NAIRU has varied more over time. For example, Basistha and Startz (2008) estimate the standard error of the NAIRU shock to be closer to 0.2 percentage point.

To explore the implications of a more-variable NAIRU, in Figure 8, we present estimates of the NAIRU from a version of the model in which the NAIRU standard error is imposed to be 0.2 percentage point, in line with the Basistha and Startz (2008) estimate. As can be seen, the movements in the NAIRU are larger than before. Notably, the NAIRU reaches as high as 7¼ percent in the early 1980s. As in the baseline estimate, this estimate of the NAIRU falls from the early 80s through the 00's, dropping close to 5 percent in mid-decade.

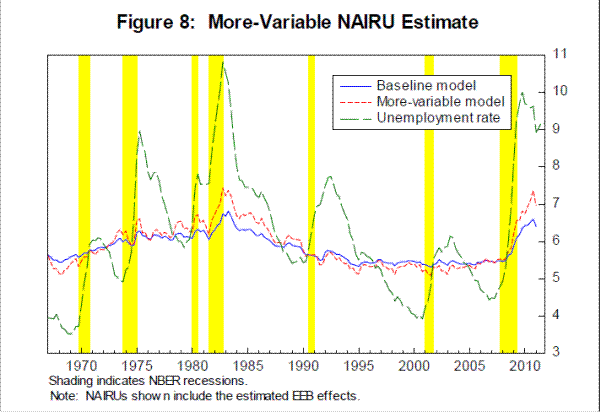
Figure 8: More- Variable NAIRU Estimate. See link below for data.

Figure 8 Data

Recently, the more-variable estimate of the NAIRU has moved up considerably, to more than 7 percent as of 2011:Q1. Consistent with the higher NAIRU estimate, the corresponding estimate of the output gap (not shown) also suggests less slack recently, with a gap of -4½ percent at the end of the sample, compared with -5¾ percent in the baseline. The standard error around the estimate of the output gap in this model is somewhat larger than for the baseline model, at 1.0 percent.

Revisions to the estimates of the cycle

Orhpanides and Van Norden (2002) have criticized output gap estimates derived using econometric methods on the grounds that the revisions implied by these methods are so large as to make the resulting gap estimates suspect if not useless. Orphanides and Van Norden (OVN) examined a number of filtering methods, including Kalman-filter-based methods similar to the ones we use here. OVN, however, focus mostly on univariate models of real GDP (with the exception of one case, where they also add inflation). It is of interest, therefore, to see whether our multivariate method performs better. In particular, none of the models OVN examined included the unemployment rate, which, as we note in Section 3, is particularly informative about the state of the business cycle.

To evaluate the potential size of revisions using our multivariate methods, we performed a "quasi-real-time" (QRT) assessment¹⁴ using current vintage data. ${}^{ }$ ¹⁵ Specifically, we backed up to 1988, re-estimated our model for each subsequent quarter through the end of 2008, and generated estimates of the output gap for each period. We performed this exercise using our preferred nine-variable model, as well for the three- and four-variable models that we found worked about as well for estimating the cycle. For comparison with OVN, we also consider two univariate real GDP models and one bivariate output-inflation model that are similar to those analyzed by OVN. As in our larger models, the cycle is assumed to follow an AR(2) process (as in Equation 2) and the trend in real GDP is assumed to follow a random walk with drift (as in Equation 20). The first univariate model, which is based on Watson (1986), assumes that the drift is constant. The second univariate model, which is based on Clark (1987), assumes that the drift is a random walk process. The bivariate model, which is similar to that described by Kuttner (1994), adds to the Watson model our CPIX Phillips curve (differing from Equation 12 in that the cycle enters only contemporaneously).

Table 8 reports a variety of summary statistics from this quasi-real-time estimation exercise for each of the six models, as well as, in the first column, an estimate of the standard deviation of the final, end-of-sample two-sided estimate of the cycle, which we take as the "true" estimate with which we compare the QRT estimates. ${}^{ }$ ¹⁶ As can be seen in the third column, the root-mean-squared revision error of the cycle estimates is about 1 percent for our large model as well as for the three- and four-variable models; it is also around 1 percent for the bivariate Kuttner-type model. By contrast, the two univariate models yield RMSEs that are more than twice as large as for the multivariate models.

Table 8: Cycle Revisions

Model	Final Cycle Std. dev	QRT Revision Std. dev.	QRT Revision RMSE	Revision Ratios NS	Revision Ratios NSR	QRT vs Final Corr	QRT vs Final OPS
Baseline	1.73	0.98	0.98	0.56	0.56	0.83	0.20
CPIX, ER, GDP, GDI	1.61	1.05	1.06	0.65	0.66	0.78	0.26
CPIX, ER, GDP	1.77	1.13	1.14	0.64	0.65	0.78	0.25
Kuttner (CPIX, GDP)	1.39	1.01	1.01	0.73	0.73	0.76	0.27
Watson (GDP)	2.03	1.48	2.16	0.73	1.07	0.75	0.14
Clark (GDP)	2.23	2.04	2.38	0.92	1.07	0.42	0.37

Note: Final cycle is the 2-sided estimate using the full 1963:Q2 to 2011:Q1 sample period; QRT estimates from extending ending date from 1988:Q1 to 2008:Q4; QRT revisions are finalt - QRTt; NS is the ratio of the standard deviation of the QRT revision to the standard deviation of the final cycle estimate; NSR is the ratio of the RMSE of the QRT revision to the standard deviation of the final cycle estimate; Corr is the simple correlation of the QRT and final estimates; OPS is the percent of the sample period where the QRT and final estimates of the cycle have different signs.

One of OVN's critiques of time-series estimates of output gaps is that the revisions were large relative to the variation in the gaps. Table 8 reports in column 5 the ratio of the RMSE of the revisions to the standard deviation of the final estimate of the output gap. For the univariate models, the revision RMSE is larger than the standard deviation of the cycle (shown in column 1). These ratios are similar to those OVN criticized as implying that the models are not very informative. By contrast, the signal-to-noise ratios are much higher for the multivariate models: In our large model, the revision RMSE is only 56 percent the size of the variation in the cycle, and the ratios for the three- and four-variable models are only slightly higher. Measuring the signal-to-noise ratio as the ratio of the squared signal standard deviation to the squared noise RMSE, our preferred model sports a ratio above three; the smaller models have somewhat smaller s/n ratios, but they are still considerably higher than for the univariate models that were the main focus of Orphanides and Van Norden.

Conclusions

Our most striking findings concern which variables are the most informative about the state of the business cycle: Despite its traditional characterization as a lagging indicator, the unemployment rate is the most informative variable about the state of the business cycle, by a wide margin. And despite concerns about the instability of the Phillips curve, inflation turns out to be the second-most informative variable. Conditional on unemployment and inflation, measures of real output add little to the identification of the business cycle. We also find that including the unemployment rate and inflation greatly improves the "real-time" reliability of the estimates of the output gap.

While measures of output are not very informative about the business cycle, we find that they are quite informative about the levels and growth rates of trend productivity and potential output. We include both product- and income-side measures in the model and are thus able to decompose real GDP (and real GDI) into trend, cycle, and measurement error components. We find that both GDP and GDI are informative, with a slight edge to GDI, based on the model's estimates of measurement error. In contrast, the traditional approach-which includes only real GDP-allows only for a bivariate decomposition that necessarily lumps measurement errors into either or both of the trend and cyclical components. Comparisons of the estimates of the cycle and potential output from our three- and four-variable models-which differ only in that the three-variable model excludes GDI-suggest that measurement errors have a larger effect on estimates of potential output than on estimates of the cycle.

References

Basistha, Arabinda and Richard Startz (2008)
"Measuring the NAIRU with Reduced Uncertainty: A Multiple-Indicator Common-Cycle Approach," Review of Economics and Statistics 90, 805-11.

Blanchard, Olivier Jean, and Danny Quah (1989)
"The Dynamic Effects of Aggregate Demand and Supply Disturbances," American Economic Review 79, 655-73.

Burns, Arthur F., and Wesley C. Mitchell (1946)
Measuring Business Cycles. New York: NBER.

Chicago Fed (2011)
"The Chicago Fed National Activity Index," http://www.chicagofed.org/webpages/research/data/cfnai/data_series.cfm.

Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson (2003).
"What Happens after a Technology Shock?" NBER Working Paper no. 9819 (July).

Clark, Peter K. (1987)
"The Cyclical Component of U.S. Economic Activity," Quarterly Journal of Economics 102, 797-814.

Friedman, Milton (1968)
"The Role of Monetary Policy," American Economic Review 58, 1-17.

Fujita, Shigeru (2011)
"Effects of Extended Unemployment Insurance Benefits: Evidence from the Monthly CPS," Federal Reserve Bank of Philadelphia working paper no. 10-35/R.

Gali, Jordi (1999)
"Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations?" American Economic Review 89, 249-71.

Giannone, Domenico, Lucrezia Reichlin, and David Small (2005)
"Nowcasting GDP and Inflation: The Real-Time Informational Content of Macoreconomic Data Releases," FEDS working paper no. 2005-42.

Gordon, Robert J. (1982)
"Price Inertia and Policy Ineffectiveness in the United States," Journal of Political Economy 90, 1087-1117.

Gordon, Robert J. (1997)
"The Time-Varying NAIRU and Its Implications for Economic Policy," Journal of Economic Perspectives 11, 11-32.

Gordon, Robert J. (1998)
"Foundations of the Goldilocks Economy: Supply Shocks and the Time-Varying NAIRU," Brookings Papers on Economic Activity 1998:2, 297-346.

Hooker, Mark A. (2006)
"What Happened to the Oil-Price Macroeconomy Relationship?" Journal of Monetary Economics 38, 195-213.

Kuttner, Kenneth N. (1994)
"Estimating Potential Output as a Latent Variable," Journal of Business and Economic Statistics 12, 361-8.

Laubach, Thomas (2001)
"Measuring the NAIRU: Evidence from Seven Economies," Review of Economics and Statistics 83, 218-31.

Laubach, Thomas and John C. Williams (2003)
"Measuring the Natural Rate of Interest," Review of Economics and Statistics 85, 1063-70.

Nalewaik, Jeremy J. (2007)
"Estimating Probabilities of Recession in Real Time Using GDP and GDI," Board of Governors of the Federal Reserve System FEDS working paper no. 2007-7 (January).

Nalewaik, Jeremy J. (2010)
"The Income- and Product-Side Estimates of U.S. Output Growth," Brookings Paper on Economic Activity 2010:1, 71-106.

NBER (2008)
"Determination of the December 2007 Peak in Economic Activity," http://www.nber.org/dec2008.pdf (December).

Orphanides, Athanasios and Simon van Norden (2002)
"The Unreliability of Output-Gap Estimates in Real Time," The Review of Economics and Statistics 84, 569-583.

Phelps, Edmund S. (1968)
"Money-Wage Dynamics and Labor-Market Equilibrium," Journal of Political Economy 76, 678-711.

Quantitative Micro Software (QMS, 2010)
Eviews 7 User's Guide and Command Reference Irvine, California: QMS.

Roberts, John M. (2001)
"Estimates of the Productivity Trend Using Time-Varying Parameter Techniques," Contributions to Macroeconomics 1(1), article 3.

Roberts, John M. (2006)
"Monetary Policy and Inflation Dynamics,"' International Journal of Central Banking 2, 193-230.

Staiger, Douglas, James H. Stock, and Mark W. Watson (1997)
"The NAIRU, Unemployment, and Monetary Policy," Journal of Economic Perspectives 11, 33-49.

Stock, James H., and Mark W. Watson (1989)
"New Indices of Coincident and Leading Economic Indicators," NBER Macroeconomics Annual 1989, Olivier Blanchard and Stanley Fischer, eds., 351-394.

Stock, James H., and Mark W. Watson (1998)
"Median Unbiased Estimation of Coefficient Variance in a Time-Varying Parameter Model," Journal of the American Statistical Association 93, 349-58.

Stock, James H., and Mark W. Watson (2002)
"Macroeconomic Forecasting Using Diffusion Indices," Journal of Business and Economic Statistics 20, 147-62.

Valletta, Rob and Katherine Kuang (2010)
"Extended Unemployment and UI benefits," FRBSF Economic Letter 2010-12.

Watson, Mark W. (1986)
"Univariate Detrending Methods with Stochastic Trends," Journal of Monetary Economics 18, 49-75.

Weidner, Justin, and John C. Williams (2009)
"How Big Is the Output Gap?" Federal Reserve Bank of San Francisco Economic Letter (June 12).

Williams, John C. (2006)
"The Phillips Curve in an Era of Well-Anchored Inflation Expectations," unpublished working paper, Federal Reserve Bank of San Francisco (September).

Footnotes

* The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the research staff or the Board of Governors. We are grateful to Candace Adelberg and Dane Vrabac for able research assistance, and to Bruce Fallick, Mike Kiley, David Lebow, Dan Sichel and Thomas Trimbur for helpful comments and suggestions. Earlier drafts of this paper were distributed with the title, "A Multivariate Estimate of Trends and Cycles." Return to Text

1. Some business-cycle theories include macroeconomic shocks that drive output and labor input in opposite directions, contrary to our common-cycle assumption. Gali (1999) presents evidence that such shocks may be empirically important. However, the results of Christiano, Eichenbaum, and Vigfusson (2003) suggest that this finding is sensitive to the details of the specification. In the context of a state-space model, Roberts (2001) tests for effects of permanent productivity shocks on hours and finds little effect. And Basistha and Startz (2008) allow for the possibility of separate cycles for unemployment and output and find that the data strongly prefer a single cycle, which is the assumption we make in this paper. Return to Text

2. Nalewaik (2007, 2010) has argued that in recent years, GDP has systematically understated the cyclicality of the business cycle relative to GDI. However, Nalewaik emphasizes the importance of this phenomenon the period since the mid-1980s, and we focus on a longer estimation period here. We leave exploration of time-variation in the cyclicality of GDP and GDI to future research. Return to Text

3. Also, our definition of employment is broader than the measure used in the coincident indicators. Return to Text

4. Specifically, we include the ratio of total quarterly payments of federal and state emergency and extended benefits programs to the backward-looking four-quarter average of total private wages and salaries. We are grateful to our colleague, Stephanie Aaronson, who suggested this measure to us; of course, all responsibility for its inclusion is ours. For other approaches, see Valletta and Kuang (2010) and Fujita (2011). Return to Text

5. When we allow the slope of the Phillips curve to be a time-varying parameter, the variance of the shock driving changes in the slope was not statistically significant. Return to Text

6. For convenience, we replace the national accounts definition of the statistical discrepancy with the log difference of the product-side and income-side measures of real NFB output. Return to Text

7. When this restriction was relaxed, the relative degrees of persistence proved very sensitive to details of the specification; however, the main results of interest are little affected by this restriction. Return to Text

8. In particular, we used the SSpace command in Eviews 7 (QMS, 2010). Return to Text

9. Relative energy prices are weighted by the nominal share of personal consumption expenditures (PCE) on energy goods and services. Given the decline in the expenditure share of energy, the estimated effect of energy prices on core inflation would be smaller now than in the 1970s even if there was no evidence of a break in the coefficient. Return to Text

10. Over our sample period, the average level of real NFBP is about 0.6 percent higher than the average level of real NFBI; we account for this difference by including a constant in the NFBP and NFBI equations that we constrain to be of equal and opposite signs. Return to Text

11. Specifically, we applied the Stock-Watson (1998) median-unbiased estimator to estimates of the constant term in a regression of the growth rates of the relevant variables on a constant. Return to Text

12. We drop our measure of the effects of extended and emergency unemployment benefits (EEB) from the three- and four-variable models. Return to Text

13. EEB = emergency and extended unemployment benefits. Return to Text

14. Orphanides and Van Norden (2002) also examine the impact of real-time data on output gap estimates. We do not, for two reasons. First, although OVN find that data revisions make some contribution to the unreliability of output gap estimates, OVN find that the contribution of the econometric methods is much larger. Second, the two variables that we find to be most important for the estimate of the output gap-the unemployment rate and CPI inflation-don't revise, reducing the likelihood that data revisions will have an important impact on our estimates. Return to Text

15. We use data from 1963:Q2 to 2011:Q1 as they were available in August 2011. Return to Text

16. Specifically, the two-sided estimate of the cycle from each model estimated over the full 1963:Q2 to 2011:Q1 sample period. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Last update: April 4, 2012