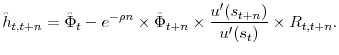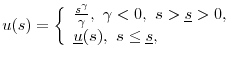An Empirical Investigation of Consumption-based Asset Pricing Models with Stochastic Habit Formation*
Keywords: Asset pricing, consumption-based asset pricing models, habit formation, stochastic internal habit, aggregate equity, bond returns.
Abstract:
1 Introduction
Consumption-based capital asset pricing models (CCAPMs) with time non-separable preferences including habit formation have received considerable attention recently as a potential mechanism for explaining the equity premium puzzle (see, e.g., Sundaresan (1989), Abel (1990), Constantinides (1990), and Campbell & Cochrane (1999)). The joint behavior of stock and bond returns within the context of consumption-based models has been understood much less. In this paper we present a structural model with stochastic internal habits that helps resolve the dichotomy between the autocorrelation properties of the stochastic discount factors and those of bond returns.1 Our formulation nests many of the previously studied specifications along one or both of the following two dimensions. First, by adopting the GMM approach (Hansen, 1982), we are completely agnostic about the dynamics of the aggregate endowment or technology imposed in other papers, such as, e.g., Campbell & Cochrane (1999), Wachter (2006), and Bekaert, et al. (2010). This means that our model implicitly nests any parametric specifications of the aggregate endowment process. Second, we adopt a general parametric specification of the consumption habit process that nests many of the previous habit specifications. Specifically, we start with a standard geometric distributed lag specification, and then introduce a stochastic shock to the weights in the distributed lag. The timing of the new shock is such that it can be literally interpreted as an unexpected shock to the habit stock itself.2
Using the same econometric method, Dunn & Singleton (1986, DS) and Ferson & Constantinides (1991, FC) test the over-identifying restrictions implied by the stochastic Euler equations derived from such models, while
being agnostic about the endowment specification and the nature of the temporal dependence of consumption. Heaton (1995), on the other hand, uses the simulated method of moments to estimate a model that incorporates both a parametric form of consumption durability and
habit.3![]() 4 These studies find that there is empirical evidence for both consumption habit and local substitution. However, which effect dominates may depend on the decision interval, the instruments used
in estimating the model, and the investment horizon. The overall goodness-of-fit test econometrically rejects all of the models. The econometric rejection of existing CCAPMs with time separable and time nonseparable utility is largely due to the notorious failure of these models to explain bond
returns. Singleton (1993) and Heaton (1995) explore in depth such models' inability to explain the autocorrelation properties of bond returns. This problem arises because a stochastic discount factor (SDF henceforth) in the time separable models
and some of the time nonseparable models is a simple function of the nearly i.i.d consumption growth process, and this makes it difficult for models to explain persistent properties of
long-term bond returns.
4 These studies find that there is empirical evidence for both consumption habit and local substitution. However, which effect dominates may depend on the decision interval, the instruments used
in estimating the model, and the investment horizon. The overall goodness-of-fit test econometrically rejects all of the models. The econometric rejection of existing CCAPMs with time separable and time nonseparable utility is largely due to the notorious failure of these models to explain bond
returns. Singleton (1993) and Heaton (1995) explore in depth such models' inability to explain the autocorrelation properties of bond returns. This problem arises because a stochastic discount factor (SDF henceforth) in the time separable models
and some of the time nonseparable models is a simple function of the nearly i.i.d consumption growth process, and this makes it difficult for models to explain persistent properties of
long-term bond returns.
The failure of earlier asset pricing models with time non-separable preferences to explain time-varying bond returns arises because both types of models, either external or internal habits, (Constantinides (1990) and Campbell & Cochrane (1999, CC), respectively) side-step the issue of term structure dynamics by imposing restrictions so that the real term structure is constant and flat. Several papers extend the CC model in order to accommodate stochastic interest rates. Campbell & Cochrane (1999) show how to extend their model by relaxing a parametric restriction on the specification of the surplus consumption ratio. However, in their model, interest rates and bond risk premium are perfectly correlated with consumption shock, which is counter-factual. Wachter (2006) relaxes the assumption of the CC model of an i.i.d. consumption growth rate and shows that interest rates and the risk premium have properties broadly consistent with observed bond return predictability in her model. Buraschi & Jiltsov (2007) develop a continuous term structure model in the context of the CC model and show that habit persistence can help reproduce various properties of the term structure. Bekaert, et al. (2009) also consider a generalized version of the CC model where a surplus consumption ratio is stochastic, which allows them to obtain some non-trivial implications for the term structure of interest rates. All of these extensions share the common feature that the external habit process is no longer locally deterministic.
There has been much less work done extending deterministic internal habit process to accommodate preference shocks. However, this venue is important in view of two recent empirical papers by Chen & Ludvigson (2009) and Grishchenko (2010), who investigate the properties of habit persistence at the aggregate level and conclude that aggregate data are more consistent with internal rather than external habit formation preferences. The reason is that internal habit generates the necessary autocorrelations in the stochastic discount factor via a non-trivial impact of current consumption on future marginal utility. This channel is absent in the external habit models where current consumption affects only the surplus consumption ratio, but the functional form of the marginal utility stays unaltered (compared to marginal utility in the time separable preferences). Dai (2003) is the first who introduces the stochastic internal habit model. He relaxes Constantinides' assumption of a constant investment opportunity set by allowing the instantaneous short rate to be driven by the level of the habit stock, and shows that the time-varying risk premium implied by the model is capable of explaining the violation of the Campbell & Shiller (1991) expectations hypothesis puzzle. In our work, the deterministic internal habit formation models of Sundaresan (1989) and Constantinides (1990), and the stochastic internal habit formation model of Dai (2003) are nested special cases in the continuous-time limit.
The presence of the habit shock in the economy - in addition to the consumption shock - breaks the tight linkage between asset returns and consumption growth rates in the standard CCAPM or its extension with deterministic habit. Economically, the habit shock can be broadly interpreted as a taste shock. Its high realization occurs in the bad state of the world, associated with the low dividend payoff and the low level of consumption. In this state, the additional dollar of return becomes even more valuable because marginal utility depends positively on this shock.
To our knowledge, this work is the first empirical investigation of stochastic internal habit models. It relates to prior and rather limited work on the impact of preference shocks on asset prices. Among the first, Campbell (1986) includes random shocks in the CRRA utility to examine the conjecture of Modigliani & Sutch (1966) that investor preferences might cause negative term premiums on long-term bonds. He argues that randomness in preferences (interpreted as taste shocks) generates predictable excess returns even when agents are risk-neutral. Normandin & St-Amour (1998) include taste shocks in the preference specification of Epstein & Zin (1989) to study their effect on the equity premium. They argue that taste shocks help alleviate the emphasis on the consumption risk in explaining the historical equity premium. More recently, Brandt & Wang (2003) allow for a preference shock in the CC model to be correlated with business-cycle factors. In a similar spirit, Bekaert, et al. (2010) allow for a latent preference shock in the CC model to be imperfectly correlated with consumption growth and interpret it as unexpected change in the "moodiness" of the investor behavior.5
In contrast to previous studies (with the exception of Bekaert, et al. (2009) and Bekaert et al. (2010)), we study the implications of introducing the preference shock to the habit stock to simultaneously explain time series properties of equity and bond returns.6 Our modeling and econometric framework allows us to address, among others, two important empirical questions.
- Q1:
- Do stochastic habit formation models explain long-term bond returns better than their deterministic counterparts?
- Q2:
- Do internal habit (IH) formation models and their external counterparts (EH) perform equally well when they are confronted by both equity and bond returns?
The answer to Q1 is an emphatic "yes!" We find that when the habit process is deterministic, the model is incapable of explaining quarterly holding-period returns of long-term bonds, regardless of whether the consumption habit is external or internal. When the consumption habit is internal and stochastic, the model better explains both equity and bond returns simultaneously. This suggests the joint importance of internal habit and taste shock in preferences, absent in models discussed above.
The answer to Q2 is negative. Based on Euler equations derived from the level of the three-month Treasury bill rate, the quarterly return of a 10-year long-term Treasury bond, and the quarterly return of the broad equity market index, the parameter estimates of IH models are all very reasonable. The point estimates of the coefficient of the relative risk aversion in the IH model (either deterministic or stochastic) are around 2, while they are roughly 8 for the deterministic EH models. In contrast, the parameter estimates of the stochastic EH models are such that either the relative risk aversion parameter or the subjective discount rate is in the wrong region when they are unconstrained. When the relative risk aversion parameter and the subjective discount rate are constrained to be positive, we find a corner solution in minimizing the GMM objective function under the optimal weighting matrix. This result suggests that EH models, whether deterministic or stochastic, cannot reconcile various moments of bond returns. Our results are complementary to the results in Dai, et al. (2010). The authors specify the dynamics of state variables (in contrast to our agnostic approach) and construct the maximum likelihood estimates of a nonlinear discrete time dynamic term structure model with CC-type external habit preferences in which bond prices are known in closed form. Consequently, Dai et al. show that such models do not match the key features of the conditional distribution of bond yields.
The data seems to favor internal relative to external habit formation for a reason. Introducing a stochastic shock to an external habits does not affect the the autocorrelation structure of the marginal rate of substitution because its functional form remains the same. In contrast, a stochastic habit shock materially impacts the performance of an internal habit formation model because it induces an additional term in the marginal rate of substitution that makes it more persistent. Our results are consistent with Ljungqvist & Uhlig (2000), who argue that when agents are "catching up with the Joneses", the social welfare in a competitive equilibrium is reduced relative to the socially optimal allocation that takes into account the negative externality of habit formation. Agents consume too much when productivity is high and too little when productivity is low. Government intervention (through income transfer) can induce competitive agents with external habit formation to achieve socially optimal consumption behavior. Thus, aggregate consumption behavior and asset prices seem to be more consistent with internal habit even though agents may exhibit external habit formation at individual levels. Overall, this evidence suggests that stochastic internal habit models should be preferred to their external counterparts when studying the joint behavior of the aggregate stock and bond returns.
The rest of the paper is organized as follows. In Section 2 we set forth a model specification and derive Euler equations. In Section 3 we discuss methodological issues related to our empirical study. In Section 4 we present empirical results for deterministic/stochastic external and internal habit models, discuss miscellaneous estimation issues and also report some robustness checks. We conclude in Section 5.
2 A CCAPM with stochastic habit formation
We assume that there exists a representative agent with a time non-separable expected utility:
where
where, conditional on
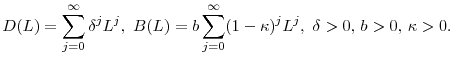
2.1 Stochastic Euler Equations
Following Dunn & Singleton (1986), Ferson & Constantinides (1991), and Heaton (1995), we can derive the stochastic Euler equation for the model specified by equations (1) -
(3). In Appendix 6, we show that, for any security with the price-dividend pair
![]() , the following pricing equation holds:
, the following pricing equation holds:
where
Here MUC
(By convention we set
For an internal habit formation model,
![]() for
for ![]() , which means that the individual agent accounts for
the consumption externality induced by her own consumption choice. Given a particular model parametrization with internal habit formation, the corresponding model with external habit formation is obtained by setting
, which means that the individual agent accounts for
the consumption externality induced by her own consumption choice. Given a particular model parametrization with internal habit formation, the corresponding model with external habit formation is obtained by setting
![]() for all
for all ![]() .
.
Equation (4) can be extended to deal with returns on investment strategies with multiple holding periods. Let ![]() be the return on an investment strategy held
for
be the return on an investment strategy held
for ![]() periods, then the same reasoning behind the derivation of (4) implies
periods, then the same reasoning behind the derivation of (4) implies
2.2 Determinants of MUC and MRS: intuition
To develop some intuition on the relative importance of various ingredients of the model, let us consider a first-order approximation of
MUC![]() when
when ![]() is small.8 First, note that when
is small.8 First, note that when ![]() is small, the approximation of
is small, the approximation of ![]() is given by
is given by
![\displaystyle a_{t, j} = \delta^j - b_j ( 1 + \beta v_{t+1} ), \,\,\,\, b_j = b\, (1-\kappa)^{j-1}\, \left[ \frac{1 - \left(\frac{\delta}{1-\kappa} \right)^j}{1 - \frac{\delta}{1-\kappa}} \right], \,\,\,\, \textup{for} \,\,\,\, \forall j \geq 1.](img51.gif)
where
![\displaystyle \Psi_t^{(\delta)} = E_t \left[ \sum_{j=1}^\infty e^{-\rho j} \delta^j \frac{u'(s_{t+j})}{u'(s_t)} \right] \propto \delta,](img55.gif) |
![\displaystyle \Psi_t^{(b)} = - E_t \left[ \sum_{j=1}^\infty e^{-\rho j} \, b_j \, \frac{u'(s_{t+j})}{u'(s_t)} \right] \propto b,](img56.gif) |
||
represent the expected future marginal utility or dis-utility (depending on the sign), from future service flow and consumption habit. In
Note that
![]() when
when
![]() (the time-separable case), and
(the time-separable case), and
![]() whenever
whenever ![]() (no habit). When
(no habit). When
![]() , the relative magnitude of
, the relative magnitude of
![]() and
and
![]() depends on, in large part, the relative magnitude of
depends on, in large part, the relative magnitude of ![]() , and
, and
![]() . The magnitude of
. The magnitude of
![]() relative to
relative to
![]() is also controlled by the parameter
is also controlled by the parameter ![]() , or more precisely the
"leverage ratio"
, or more precisely the
"leverage ratio"
![]() , which is the long-run mean of
, which is the long-run mean of
![]() .
.
The decomposition (10) provides clear intuition for how model parameters are identified: given the preference parameters ![]() ,
, ![]() , and the persistence parameter
, and the persistence parameter ![]() , the parameters
, the parameters ![]() ,
, ![]() , and
, and ![]() are
identified, respectively, from
are
identified, respectively, from
![]() ,
,
![]() , and
, and
![]() . This intuition is helpful in guiding the choice of asset returns and instruments that help achieve identification and efficiency.
. This intuition is helpful in guiding the choice of asset returns and instruments that help achieve identification and efficiency.
2.3 Discussion
Let
![]() be the shock to aggregate consumption growth rate. Our model implies that the pricing kernel is a function of the history of both the consumption shock
be the shock to aggregate consumption growth rate. Our model implies that the pricing kernel is a function of the history of both the consumption shock
![]() and the habit shock
and the habit shock ![]() . That is, for any
. That is, for any ![]() ,
,
In general, the identity of the shocks that appear in the MRS (which means that they are priced risk factors) and the functional form of the MRS are part of the model specification. In this paper, however, we interpret the stochastic habit formation model as some "reduced-form" specification of an underlying structural model based on micro-economic foundations. In particular, we interpret the shock to the habit level as taste shock, that proxies some economy-wide shock different from the shock to the consumption growth rate. In this way, the aggregate asset returns are driven by two shocks, the endowment shock and the taste shock. Campbell (1986) and Normandin & St-Amour (1998) undertake similar interpretation of the random shocks in the preferences. They study different questions however. Campbell studies the effect of the taste shocks on bond premia, while Normandin & St-Amour study the impact of taste shocks on equity premia. In both papers, multiplicative shocks are added to the utility specifications, albeit to different ones: Campbell considers standard CRRA utility function, while Normandin & St-Amour consider Epstein-Zin preferences. More recently, Bekaert, et al. (2010) develop an extension to the external habit CC model by modeling a stochastic surplus consumption ratio where a preference shock to it is interpreted as an unexpected change in the "moodiness" of the investor behavior. Bekaert, et al. (2009) use this model to study the relative importance of the economic uncertainty (conditional variance of fundamentals) and change in the risk aversion.
Our preference specification (including the habit specification) allows us to derive a specific functional form for MRS. In order to make the model empirically testable, we choose an empirical proxy for the taste shock based on an educated guess of which macro variables may be the most relevant to asset pricing. Consequently, we will be testing the joint hypothesis that the model is correctly specified and the stochastic habit shock is correctly identified. This is important for a proper interpretation of our results.
3 Methodological and econometric issues
In this section, we discuss several methodological and econometric issues related to the estimation and testing of the model. Before we proceed, let us give a brief description of the GMM procedure to establish some notations.
In the most general form with pure habit (
![]() ), our model has five parameters, collected in the vector
), our model has five parameters, collected in the vector
![]() . Let
. Let
![]() be a
be a
![]() vector of asset returns, and
vector of asset returns, and
![]() be a
be a
![]() vector of instruments. Then under the null, the following
vector of instruments. Then under the null, the following ![]() orthogonality conditions must hold:
orthogonality conditions must hold:
Let
Under the null, the GMM objective function
![]() has an asymptotic
has an asymptotic ![]() distribution with degrees of
freedom equal to
distribution with degrees of
freedom equal to
![]() dim
dim![]() . This provides an overall goodness-of-fit test.
. This provides an overall goodness-of-fit test.
3.1 Evaluation of the Euler equations
A well-known issue associated with the econometric estimation and test of internal habit formation models is that the "marginal utility of consumption",
MUC![]() , is defined in terms of the conditional expectation of future marginal utilities (see equation (6)). Two distinct approaches have been adopted to deal with this
issue. Dunn & Singleton (1986), Ferson & Constantinides (1991), Ferson & Harvey (1992), etc., adopted the first approach, which avoids the evaluation of the conditional expectations
altogether. Specifically, rewriting equation (9) as
, is defined in terms of the conditional expectation of future marginal utilities (see equation (6)). Two distinct approaches have been adopted to deal with this
issue. Dunn & Singleton (1986), Ferson & Constantinides (1991), Ferson & Harvey (1992), etc., adopted the first approach, which avoids the evaluation of the conditional expectations
altogether. Specifically, rewriting equation (9) as
and removing the conditional expectation operator by appealing to the law of iterated expectations, we obtain
Note that the "disturbance"
In principle, we can follow Heaton's approach to estimate our model. An added benefit of adopting Heaton's approach is that there is no requirement that the stochastic habit shock be observed. Our concerns about potential mis-specification errors associated with the VAR specification of the
state vector and potential numerical errors in computing
MUC![]() , however, lead us to develop a new approach. The idea is to rewrite the Euler equation (13) as
, however, lead us to develop a new approach. The idea is to rewrite the Euler equation (13) as
where
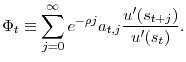
First, we construct an information set
![]() that includes all the instruments we will use for estimating the model as well as
that includes all the instruments we will use for estimating the model as well as
![]() and an appropriate number of its lags. Second, we condition the Euler equation (15) down to the
information set
and an appropriate number of its lags. Second, we condition the Euler equation (15) down to the
information set ![]() :
:
Finally, we compute the linear projection of
where
Equations (17) and (18) are the "projected" Euler equations that we actually use in our econometric analysis. Under the null, the vector of projected disturbances
The projection procedure does not affect consistency of the GMM estimators. However, it does affect inference. To obtain standard errors and test statistics properly, we need to (a) compute standard errors with the projection fixed at the converged parameter estimates; and (b) account for sampling noise in the first-stage linear projection when we compute the standard errors and test statistics in the second (GMM) stage.9
3.2 Empirical proxy for a stochastic habit (taste) shock
Implicit in our model is the assumption that economic agents observe both consumption and habit shocks, conditional on which consumption and portfolio demands are formed. As a consequence, the Euler disturbances
![]() or their projected versions
or their projected versions
![]() can not be constructed using consumption and return data alone, because they also depend on the realizations of the habit shock
can not be constructed using consumption and return data alone, because they also depend on the realizations of the habit shock
![]() . If the habit(taste) shocks are not observed by the econometrician, they must be integrated out in the Euler equations. Our new approach assumes that the
econometrician also observes the habit shock, and identifies it with the shock to one of the observed macro-economic variables. Thus, our model should be treated as a semi-structural model (based on a particular parametric specification of the habit process and a particular assumption on the
identity of the habit shocks). While we do not provide a formal justification for our semi-structural specification, we motivate our choice by the following intuition.
. If the habit(taste) shocks are not observed by the econometrician, they must be integrated out in the Euler equations. Our new approach assumes that the
econometrician also observes the habit shock, and identifies it with the shock to one of the observed macro-economic variables. Thus, our model should be treated as a semi-structural model (based on a particular parametric specification of the habit process and a particular assumption on the
identity of the habit shocks). While we do not provide a formal justification for our semi-structural specification, we motivate our choice by the following intuition.
There are several reasons why the aggregate labor income shock may be a sensible empirical proxy for the stochastic habit shock. First, a growing body of work in asset pricing literature (see, e.g., Jagannathan & Wang (1996) and Lettau & Ludvigson (2001a)) suggests that aggregate labor income risk is a relevant source of risk factor in explaining equity returns. Second, a growing body of work in macroeconomics literature (see, e.g., Calvo (1983) and Christiano, et al. (2005)) suggests that both real marginal cost, which is closely related to the aggregate labor share, and wage rigidity are important in driving inflation and channeling the propagation of monetary shocks through the real economy. Both strands of literature suggest that labor income risk may play a non-trivial role in explaining asset returns, through either the cash flows (dividend and inflation risks) or the discount rates (pricing kernel). Since we take asset returns and endowment processes as given, the only place that the labor income risk can play a role is through the utility specification. In our framework, it can only enter the model through the shock to the habit stock. We directly estimate the sensitivity of the habit shock to the labor income shock (as the volatility of the habit shock) from the Euler equations.10
3.3 Miscellaneous issues
A practical issue that arises in estimating internal habit formation models is that the ex post realization of the marginal utility of consumption, namely (see equation (6)),
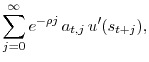
We base our estimation and testing procedure on the assumption that the null is correctly specified. This means that we need to impose restrictions on the admissible parameter region so that the ex post MUC stays positive. Such restrictions are also helpful in practice in making the GMM objective function more robust and the GMM estimation easier to converge. Finally, we check that the ex post MUC is strictly positive at the converged parameter estimates and the parametric restrictions that ensure MUC positivity are not binding.
Another practical issue is that based on the observed data, there is no guarantee that the surplus consumption
![]() is strictly positive, because a large realization of the habit shock can send
is strictly positive, because a large realization of the habit shock can send ![]() above
above ![]() under at least some parameter configurations. Fortunately, under realistic parameter values, this occurs only infrequently. Since this situation occurs at the
tail end of the steady-state distribution, and most interesting economic behavior takes place at or near the long-run mean of the steady-state distribution, we can deal with this issue by designing a utility function
under at least some parameter configurations. Fortunately, under realistic parameter values, this occurs only infrequently. Since this situation occurs at the
tail end of the steady-state distribution, and most interesting economic behavior takes place at or near the long-run mean of the steady-state distribution, we can deal with this issue by designing a utility function ![]() that coincides with a standard CRRA specification when s is sufficiently far away from 0, and is still well-behaved when
that coincides with a standard CRRA specification when s is sufficiently far away from 0, and is still well-behaved when ![]() is close to zero or slightly
negative.11
is close to zero or slightly
negative.11
This is not an unknown issue that arises with additive habit models. It has been addressed in the literature in the different context. Detemple & Zapatero (1991) impose a nonlinear parameter restriction to insure the nonnegativity of marginal utility. In addition, Chapman (1998) constructs an example of an endowment economy with linear internal habit formation such that implies negative marginal utility of with probability one. His calibration exercise assumes a specific endowment process (lognormal diffusion, Eq. (6), pg. 1225), which we are agnostic about. He finds that marginal utility is negative for a CRRA utility function when relative risk aversion is set to a specific range of values and other endowment process parameters match the sample moments of standard aggregate consumption and returns data. Yogo (2008) solves this issue by proposing a power reference-dependent utility function in which the representative household has power gain-loss utility in the spirit of Tversky & Kahneman (1992). In this set up, the marginal utility is always positive even when consumption falls below its subsistence (reference) level, by virtue of imposing the absolute value function on the difference between consumption and its subsistence level. For us, it is more a practical than modeling issue as we abstract from the specific form of the endowment process in the economy.
Finally, in a finite sample, it is not possible to construct the ex post realization of MUC as an infinite sum. All of our estimation results are based on truncating the infinite sum to 50 terms, which corresponds to the assumption that a habit shock dies out before twelve and half years.
This represents a sufficiently long period for the MUC to be affected by habit shock so long as the mean reversion parameter ![]() for the habit shock is not too small.
for the habit shock is not too small.
4 Empirical results
In this section, we report key empirical findings. We begin by describing the data. We then report estimation results and address the questions Q1 and Q2 raised in the introduction.
4.1 Data
Summary statistics of the macro variables and asset returns are reported in Table 1.
- Consumption:
- We use quarterly consumption data to estimate our model because it contains less measurement errors than monthly consumption data.12 Quarterly decision
interval also allows us to focus on pure habit effect, as Heaton (1995) shows that local substitution is important only for decision intervals much shorter than a quarter. Consequently, we set
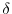 = 0 throughout our empirical estimations. Our sample period is from the fourth quarter of 1951 to the fourth quarter of 2002.
= 0 throughout our empirical estimations. Our sample period is from the fourth quarter of 1951 to the fourth quarter of 2002.
We measure aggregate consumption as expenditures on non-durables and services excluding shoes and clothing.13 In order to distinguish between long-term habit persistence and short-term seasonality, we use seasonally adjusted data at annual rates, in billions of chain-weighted 2000 dollars.14 We define aggregate labor income as wages and salaries plus transfer payments plus other labor income minus personal contributions for social insurance minus taxes. Real aggregate labor income is obtained by deflating nominal aggregate labor income by the implicit chain-type price deflator (2000=100).
Real per capita consumption and labor income is obtained by dividing real aggregates by a measure of U.S. population. The latter is obtained by dividing real total disposable income by real per capita disposable income. Consumption, labor income, price deflator, and measure of population are obtained from NIPA (National Income and Product Account) tables.15
- Asset returns:
- Nominal quarterly U.S. broad value-weighted equity index returns as well as three-month and 10-year Treasury Bond Portfolio returns are obtained from CRSP (Center for Research in Security Prices). Real asset returns are deflated by the implicit chain-type price deflator (2000=100).
- Instruments:
- We use two sets of instruments. The first one is the standard set of lagged consumption growth and asset returns used in the previous studies to estimate the parameters and test the Euler equation model. One of the potential problems with consumption data is time aggregation, which means that
consumption decisions are made more frequently than the observation interval, and thus, measured consumption is the sum of the expenditures of the interval. Ferson & Constantinides (1991) argue that time aggregation can induce a spurious correlation
between the error terms and information set, thereby increasing the order of the MA process followed by
 . Variables in the information set at time
. Variables in the information set at time  , which were not in the information set at
, which were not in the information set at 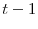 , may not be valid instruments for testing over-identifying
restrictions (12). We nevertheless estimate our model using this set of instruments for comparative purposes. Another set of variables is described in Section 4.7.
, may not be valid instruments for testing over-identifying
restrictions (12). We nevertheless estimate our model using this set of instruments for comparative purposes. Another set of variables is described in Section 4.7.
Next, we need to obtain the habit shock ![]() . We proxy
. We proxy ![]() as the aggregate labor
income shock obtained from the following bivariate process with 4 lags for
as the aggregate labor
income shock obtained from the following bivariate process with 4 lags for
![]() :
:
where
To get a sense of what the habit stock looks like under reasonable parameterizations of the model, Figure 2 plots real consumption, habit stock, and surplus consumption based on the following baseline parameterization:
![]() . These parameters correspond roughly to those calibrated by Dai (2003), so they
are broadly consistent with some key moments of equity and bond returns.
. These parameters correspond roughly to those calibrated by Dai (2003), so they
are broadly consistent with some key moments of equity and bond returns.
4.2 Deterministic habit: risk premium
We begin by estimating the risk-aversion parameter ![]() for three models with no habit (NH), deterministic external habit (DEH), and deterministic internal habit (DIH).16 For the model with no habit,
for three models with no habit (NH), deterministic external habit (DEH), and deterministic internal habit (DIH).16 For the model with no habit,
![]() . For habit models, we fix
. For habit models, we fix ![]() and
and
![]() , which correspond to a pair of values for
, which correspond to a pair of values for
![]() and
and ![]() used by Constantinides (1990).
Grishchenko (2010) estimates these parameters in the deterministic habit model set up and finds that they are broadly consistent with Constantinides (1990) values.17 For all three models, we fix
used by Constantinides (1990).
Grishchenko (2010) estimates these parameters in the deterministic habit model set up and finds that they are broadly consistent with Constantinides (1990) values.17 For all three models, we fix
![]() . The instruments used for the estimation include two lags of consumption growth rates and two lags of equity returns. Estimation results are reported in Table 2. There are two panels in the table. The top panel reports results when the excess return on the value-weighted NYSE index is used to identify the risk aversion parameter. For NH model, the estimate for the relative risk aversion
. The instruments used for the estimation include two lags of consumption growth rates and two lags of equity returns. Estimation results are reported in Table 2. There are two panels in the table. The top panel reports results when the excess return on the value-weighted NYSE index is used to identify the risk aversion parameter. For NH model, the estimate for the relative risk aversion ![]() is 85.9148. Thus, we recover the equity premium puzzle. For DEH model, the coefficient
is 85.9148. Thus, we recover the equity premium puzzle. For DEH model, the coefficient ![]() drops down to
drops down to ![]() , indicating that the presence of consumption habit helps resolve the equity premium puzzle. For DIH model, the coefficient
, indicating that the presence of consumption habit helps resolve the equity premium puzzle. For DIH model, the coefficient ![]() reduces further to 2.90. For all three models, the parameter
reduces further to 2.90. For all three models, the parameter ![]() is sharply identified, and the over-identifying restrictions implied by the
equity premium, alone, are not rejected.18 At this point, the data favor the DIH, with much lower
is sharply identified, and the over-identifying restrictions implied by the
equity premium, alone, are not rejected.18 At this point, the data favor the DIH, with much lower ![]() than either NH or DEH. The bottom panel reports estimation results when both the equity premium and the risk premium on a long-term 10-year Treasury bond are used under the same model specifications and same
parameterization.19 The coefficients of the relative risk aversion decline as we proceed from NH to DEH, and then to DIH, and have a similar magnitude to
Panel A's estimates of RRA. Including a long-term bond represents an additional challenge for the models. Indeed, the
than either NH or DEH. The bottom panel reports estimation results when both the equity premium and the risk premium on a long-term 10-year Treasury bond are used under the same model specifications and same
parameterization.19 The coefficients of the relative risk aversion decline as we proceed from NH to DEH, and then to DIH, and have a similar magnitude to
Panel A's estimates of RRA. Including a long-term bond represents an additional challenge for the models. Indeed, the ![]() -values for the overall goodness-of-fit test decline for all three
models. So, we reject all three models when a long-term bond is included in the estimation.20
-values for the overall goodness-of-fit test decline for all three
models. So, we reject all three models when a long-term bond is included in the estimation.20
The results reported in Table 2 confirm some well-known facts about the standard CCAPM and deterministic habit formation models. First, the equity premium can be fit easily if there is no constraint on the curvature of the utility function, namely, ![]() . The equity premium puzzle arises because the relative risk aversion parameter required to fit the equity premium is too large relative to what is required to explain individual behavior (in
terms of portfolio holdings and life-cycle patterns). Second, these models do not explain long-term bond risk premium. Adding long-term bond risk premium leads to the deterioration of the model fit. Intuitively, the real interest rate risk and the consumption growth rate are very weakly correlated
in the data (about -0.025), and have the opposite sign (negative) from what a standard consumption-based model would predict (positive). Since deterministic habit merely amplifies the risk premium, and does not affect the sign of the risk premium, all three models (NH, DEH, and DIH) would predict
the wrong sign for bond risk premium when
. The equity premium puzzle arises because the relative risk aversion parameter required to fit the equity premium is too large relative to what is required to explain individual behavior (in
terms of portfolio holdings and life-cycle patterns). Second, these models do not explain long-term bond risk premium. Adding long-term bond risk premium leads to the deterioration of the model fit. Intuitively, the real interest rate risk and the consumption growth rate are very weakly correlated
in the data (about -0.025), and have the opposite sign (negative) from what a standard consumption-based model would predict (positive). Since deterministic habit merely amplifies the risk premium, and does not affect the sign of the risk premium, all three models (NH, DEH, and DIH) would predict
the wrong sign for bond risk premium when ![]() is positive. This basic tension in CCAPM and deterministic habit formation models is even more apparent when the models are forced to
explain short-term interest rate as well. We will now consider this case.
is positive. This basic tension in CCAPM and deterministic habit formation models is even more apparent when the models are forced to
explain short-term interest rate as well. We will now consider this case.
4.3 Deterministic habit: risk-free rate and risk premium
In Table 3, we free up the subjective discount rate ![]() in our three basic models (NH, DEH, DIH), and use the risk-free rate (3-month T-bill rate) to generate
additional moment conditions to identify
in our three basic models (NH, DEH, DIH), and use the risk-free rate (3-month T-bill rate) to generate
additional moment conditions to identify ![]() . The models are still required to fit both the equity premium,
. The models are still required to fit both the equity premium,
![]() , and the 10-year bond risk premium,
, and the 10-year bond risk premium,
![]() , (so that the risk aversion parameter
, (so that the risk aversion parameter ![]() is
identified). Two panels in Table 3 correspond exactly to the panels in Table 2, except that in the former, the risk-free rate also enters the Euler equation, and two lags of the risk-free rate serve as additional instruments.
is
identified). Two panels in Table 3 correspond exactly to the panels in Table 2, except that in the former, the risk-free rate also enters the Euler equation, and two lags of the risk-free rate serve as additional instruments.
The top panel shows that DIH is able to explain both the risk-free rate and the equity premium at reasonable values of ![]() and
and ![]() :
:
![]() and
and
![]() . In contrast, NH and DEH models are rejected based on the conventional levels of
. In contrast, NH and DEH models are rejected based on the conventional levels of ![]() values. In addition, the parameter values have the wrong signs. A priori, we expect
values. In addition, the parameter values have the wrong signs. A priori, we expect ![]() (agents are impatient) and
(agents are impatient) and
![]() (agents are more risk averse than log-utility). When
(agents are more risk averse than log-utility). When ![]() is
constrained to be non-positive in the estimation, GMM finds the corner solution
is
constrained to be non-positive in the estimation, GMM finds the corner solution
![]() . The bottom panel shows that including the 10-year bond return leads to substantial deterioration of all three models. The point estimates are qualitatively similar to those in
the top panel, indicating that the long-term bond return does not have much bite in the context of these models.
. The bottom panel shows that including the 10-year bond return leads to substantial deterioration of all three models. The point estimates are qualitatively similar to those in
the top panel, indicating that the long-term bond return does not have much bite in the context of these models.
To understand this behavior, note that there are two basic forces that pull the risk aversion parameter in two different directions in these models. First, the negative correlation between the real consumption growth rate and the real risk-free rate can be explained only if ![]() is negative. Second, the high equity premium can be explained only if
is negative. Second, the high equity premium can be explained only if ![]() is
positive and large. Both NH and DEH give up explaining the equity premium in order to reconcile with the negative correlation between the consumption growth and risk-free rate.
is
positive and large. Both NH and DEH give up explaining the equity premium in order to reconcile with the negative correlation between the consumption growth and risk-free rate.
Since
![]() , the level of the risk-free rate can be fit only if the subjective discount rate is negative. To see this, note that, in NH, the unconditional mean of the Euler
equation for the risk-free rate implies approximately (under the assumption that the consumption growth rate is i.i.d.) that
, the level of the risk-free rate can be fit only if the subjective discount rate is negative. To see this, note that, in NH, the unconditional mean of the Euler
equation for the risk-free rate implies approximately (under the assumption that the consumption growth rate is i.i.d.) that
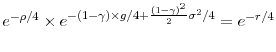 , or
, or
![]() . where
. where
![]() is the average consumption growth rate (consumption plus service),
is the average consumption growth rate (consumption plus service),
![]() is the volatility of the consumption growth rate, and
is the volatility of the consumption growth rate, and ![]() is the average risk-free rate (see Table 1 for the sample moments). For
is the average risk-free rate (see Table 1 for the sample moments). For
![]() ,
,
![]() . For DEH, the risk-free rate is priced by the growth rate of the surplus consumption ratio, which has the same mean growth rate of
. For DEH, the risk-free rate is priced by the growth rate of the surplus consumption ratio, which has the same mean growth rate of ![]() , but a higher volatility:
, but a higher volatility:
![]() . This implies
. This implies
![]() . Alternatively, the estimated value of
. Alternatively, the estimated value of ![]() implies that
implies that
![]() for NH and
for NH and
![]() for DEH.
for DEH.
4.5 Stochastic habit: risk-free rate and risk premium
Next, we free up the subjective discount factor ![]() in addition to
in addition to ![]() and
and
![]() parameters. Table 5 reports the estimation results when
parameters. Table 5 reports the estimation results when ![]() ,
, ![]() , and
, and ![]() are jointly estimated, using the risk-free
rate, the value-weighted NYSE index return, and the 10-year Treasury bond return. Comparing these results to those reported in Panel B of Table 3, we see a larger improvement for the goodness-of-fit for SIH than for SEH. For internal habit specifications we have:
are jointly estimated, using the risk-free
rate, the value-weighted NYSE index return, and the 10-year Treasury bond return. Comparing these results to those reported in Panel B of Table 3, we see a larger improvement for the goodness-of-fit for SIH than for SEH. For internal habit specifications we have:
![]() vs.
vs.
![]() . However, for external habit specifications we have:
. However, for external habit specifications we have:
![]() vs.
vs.
![]() . These differences are also reflected in the fact that the parameter
. These differences are also reflected in the fact that the parameter ![]() is not sharply identified in SEH, whereas it is sharply identified in SIH:
is not sharply identified in SEH, whereas it is sharply identified in SIH:
![]() with the standard error of 0.2340,
with the standard error of 0.2340,
![]() with the standard error of 0.0040. In addition, SEH model does not seem to have an ability to identify the subjective discount rate:
with the standard error of 0.0040. In addition, SEH model does not seem to have an ability to identify the subjective discount rate:
![]() with the standard error of 0.0127. However, the point estimate of the subjective discount rate in the SIH model is well identified, albeit low.
with the standard error of 0.0127. However, the point estimate of the subjective discount rate in the SIH model is well identified, albeit low.
4.6 Discussion
The reported empirical results help answer the two questions raised in the introduction. Our results show that introducing a shock to the consumption habit allows the model to explain long-term bond returns better than deterministic habit formation models. Furthermore, the beneficial effect of a habit shock is much more evident in internal rather than in external habit formation models. To understand these results, we note that the habit shock may help explain asset returns because it can potentially modify the autocorrelation property of the marginal rate of substitution. In an external habit formation model, the habit shock affects the marginal rate of substitution' autocorrelation property only through the surplus consumption ratio dynamics. The reason is that the functional form of the MRS,
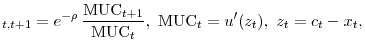
4.7 Additional tests and robustness checks
- Standard errors. Standard errors reported above are based on two-stage estimation (linear projection and GMM as separate stages). This two-step procedure might affect inference. The results from one-stage estimation (linear projection and GMM in one step) indicate that while all standard errors are larger due to sampling noises in the linear projection coefficients, they do not qualitatively change the conclusions. In particular, parameter estimates in internal habit formation models are different from zero at the conventional levels of statistical significance.
- Instrumental variables. We have also used other instruments to check the robustness of our results: unit vector, lagged values of consumption growth, a proxy for the log consumption-wealth ratio
 ,21 "relative T-bill rate" (
,21 "relative T-bill rate" (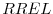 , which is measured as the three-month T-bill rate minus its four-quarter moving average) and the lagged value of the excess return on the Standard&Poor 500 (SP&500) stock market index (
, which is measured as the three-month T-bill rate minus its four-quarter moving average) and the lagged value of the excess return on the Standard&Poor 500 (SP&500) stock market index (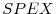 ) over the three-month T-bill rate. Lettau & Ludvigson (2001a) find that
) over the three-month T-bill rate. Lettau & Ludvigson (2001a) find that 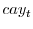 has a strong predictive power for stock returns
over one quarter to several year horizons. In their subsequent (2001b) paper they show that this variable forecasts portfolio returns too. Campbell (1991), Hodrick (1992), and Lettau & Ludvigson
(2001a) find that
has a strong predictive power for stock returns
over one quarter to several year horizons. In their subsequent (2001b) paper they show that this variable forecasts portfolio returns too. Campbell (1991), Hodrick (1992), and Lettau & Ludvigson
(2001a) find that 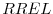 has a forecasting power for excess returns at a quarterly frequency.22 One of the problems associated with nonlinear GMM is the weak instruments problem, or the weak identification problem of the model parameter vector
has a forecasting power for excess returns at a quarterly frequency.22 One of the problems associated with nonlinear GMM is the weak instruments problem, or the weak identification problem of the model parameter vector 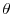 . While this issue can be identified more easily in the linear instrumental variables models, it is more difficult to deal with it in the present set up. Stock, et al. (2002) provide an excellent survey of this
issue.23 They argue that one of the informal detection of the weak identification in the GMM setting can be done through addition or change of instrumental
variables. Our results show that the choice of instruments does not affect results qualitatively, and therefore, it is unlikely that our results are driven by the presence of weak instruments in our set up.
. While this issue can be identified more easily in the linear instrumental variables models, it is more difficult to deal with it in the present set up. Stock, et al. (2002) provide an excellent survey of this
issue.23 They argue that one of the informal detection of the weak identification in the GMM setting can be done through addition or change of instrumental
variables. Our results show that the choice of instruments does not affect results qualitatively, and therefore, it is unlikely that our results are driven by the presence of weak instruments in our set up.
5 Conclusion
In this paper, we econometrically estimate and test a consumption-based asset pricing model with stochastic habit formation using generalized method of moments. The key contribution to the asset pricing literature on habit formation is the study of the novel preference specification, namely, stochastic internal habit formation. The model departs from existing models with deterministic internal habit (e.g., Dunn & Singleton (1986), Ferson & Constantinides (1991), and Heaton (1995)), by introducing shocks to the coefficients in the distributed lag specification of consumption habit and consequently an additional shock to the marginal rate of substitution. Stochastic shocks to the consumption habit are persistent and provide an additional source of time-variation in expected returns. Economically, we interpret shocks as taste shocks in the economy. Empirically, we proxy these unobserved shocks by aggregate labor income shocks. We show that stochastic internal habit formation models resolve the dichotomy between the autocorrelation properties of stochastic discount factor and those of expected returns, providing a better explanation of time-variation in expected equity and long-term bond returns than models with either deterministic or stochastic external habit. This evidence suggests that stochastic internal habit models should be preferred to external habit counterparts when studying the joint behavior of the aggregate stock and bond returns.
Appendix
6 Derivation of the stochastic Euler equation
Consider an arbitrary security with price-dividend pair
![]() . Suppose that, at
. Suppose that, at ![]() , the representative agent buys
, the representative agent buys ![]() share of the security and holds it for one period, she gives up
share of the security and holds it for one period, she gives up
![]() of consumption at
of consumption at ![]() , but receives additional consumption
, but receives additional consumption
![]() . Since no-trade is optimal for the representative agent,
. Since no-trade is optimal for the representative agent,
![]() is the solution to
is the solution to
![\displaystyle V_t = \max_{\alpha} \, E\left[ \left. u(\tilde{s}_t) + E\left[ \left. \sum_{j=1}^\infty e^{-\rho j} u(\tilde{s}_{t+j}) \right\vert c_{t+1} + \alpha (p_{t+1}+d_{t+1}), \tilde{x}_{t+1} \right] \right\vert c_t - \alpha p_t, x_t \right],](img191.gif)
The first order condition with respect to
![\displaystyle p_t \, \frac{\partial V_t^*}{\partial c_t} = E_t \left[ e^{-\rho} \, (p_{t+1} + d_{t+1}) \, \frac{\partial V_{t+1}^*}{\partial c_{t+1}} \right],](img202.gif)
Evaluating the derivative of ![]() with respect to
with respect to ![]() explicitly:
explicitly:
MUC![\displaystyle _t = \mathbb{E}_t\left[\sum_{j=0}^{\infty}e^{- \rho j}\, u'(s_{t+j}) \, a_{t,j} \right],](img205.gif) |
(21) |
where
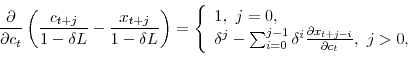
|
|||
![\displaystyle \left\{ \begin{array}{l} b (1 + \beta v_{t+1}), \,\, j = 1, \ \frac{\partial x_{t+1}}{\partial c_t}\prod_{i=1}^{j-1} \left[1-\kappa-b (1 + \beta v_{t+i+1}) \right], \,\, j > 1. \end{array} \right.](img210.gif) |
7 Distributed lag with arbitrary weights
Suppose that
![]() , and
, and
![]() , then
, then
![]() ,
,
![]() ,
,
![]() for
for ![]() . The
time-varying coefficients
. The
time-varying coefficients
![]() capture an extra unit of current consumption's marginal effect on future habit levels, and can be computed through the following recursion:
capture an extra unit of current consumption's marginal effect on future habit levels, and can be computed through the following recursion:
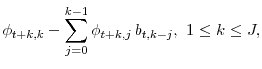 |
|||
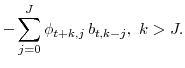 |
where
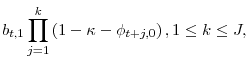 |
|||
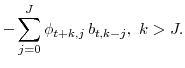 |
If
Bibliography
American Economic Review Papers and Proceedings 80:38-42.
Journal of Empirical Finance 17:867-894.
Journal of Financial Economics 91(1):59-82.
Brookings Papers on Economic Activity 1985(2):465-521.
Journal of Monetary Economics 50(7):1457-1498.
Journal of Finance 62(6):3009-3063.
Journal of Monetary Economics 12(3):383-396.
Journal of Political Economy 107(2):205-251.
The Quarterly Journal of Economics 101(4):785-804.
Economic Journal 101(405):157-179.
Review of Economic Studies 58:495-514.
Econometrica 66(5):1223-1230.
Journal of Applied Econometrics 24(7):1057-1093.
Journal of Political economy 113(1):1-45.
Journal of Political Economy 98(3):519-543.
Mimeo, NYU.
Review of Financial Studies 23(5).
Econometrica 59(6):1633-1657.
Econometrica 61:929-952.
Journal of Finance 36:769-799.
Journal of Financial Economics 17:27-55.
Econometrica 57:937-969.
Journal of Financial Economics 29:199-240.
Journal of Finance 47(2):511-552.
Econometric Theory 12:657-681.
Journal of Applied Econometrics 8:S85-S118.
Journal of Economics and Business 62:176-194.
Econometrica 50:1029-1286.
Econometrica 63(3):681-717.
Working paper, London Business School.
Review of Financial Studies 5:357-386.
Journal of Finance 51(1):3-53.
Journal of Finance 56(3):815-849.
Journal of Political Economy 109(6):1238-1287.
The American Economic Review 90(3):356-366.
Econometrica 46:1429-1445.
Journal of Monetary Economics 15:145-161.
The American Economic Review 56(1/2):178-197.
Journal of Applied Econometrics 13(3):265-281.
Journal of Financial Economics 98(2):385-413.
In J. J. Laffont & C. A. Sims (eds.), Advances in Econometrics, Sixth World Congress. Cambridge University Press.
Econometrica 68:1055-1096.
Journal of Business and Economic Statistics 20(4).
Review of Financial Studies 2:73-88.
Journal of Risk and Uncertainty 5:297-323.
SSRN eLibrary, http://ssrn.com/paper=1101456.
Journal of Financial Economics 79(2):365-399.
Journal of Business and Economic Statistics 26(2).
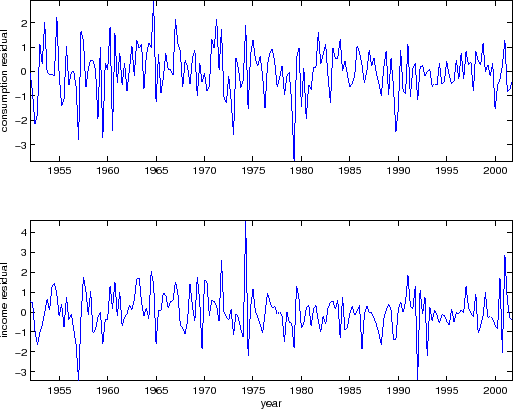 This figure presents residuals from the estimated Vector Auto Regression Model (20). Consumption and labor income data are measured as log real per capita consumption growth and log real labor income growth. The sample period is from 1952:Q1 to 2002:Q4, quarterly frequency. |
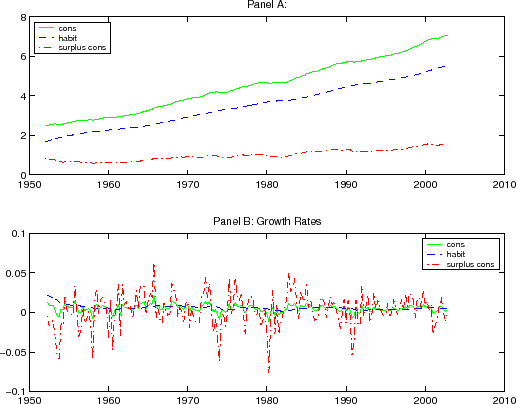 Panel A represents consumption, habit stock, and surplus consumption level time series for model parameters
|
This table reports means, standard deviations and the first five autocorrelations of the data. Panel A reports the statistics of aggregate seasonally-adjusted (SA) real quarterly consumption series and aggregate labor income. NDS refers to nondurable consumption plus services. Panel B reports the statistics of the real quarterly returns on value-weighted portfolios on NYSE, NYSE and AMEX, and NYSE, AMEX, and NASDAQ exchanges. Panel C reports the statistics of the real quarterly returns on Treasury bond indices. Nominal returns are converted into real returns by dividing them by one plus the growth rate of the seasonally unadjusted Consumer Price Index. The sample period is from 1947:Q1 to 2002:Q4, quarterly frequency.
Panel A: Macroeconomic variables statistics
| Mean | Std. Dev. | ||||||
| Nondurables plus services, SA | 0.0315 | 0.0128 | 0.3125 | 0.2017 | 0.2057 | 0.0717 | 0.0269 |
| Nondurables, SA | 0.0195 | 0.0166 | 0.1234 | 0.2140 | 0.1038 | 0.0068 | 0.0747 |
| Services, SA | 0.0428 | 0.0148 | 0.4344 | 0.2835 | 0.3426 | 0.1293 | 0.0446 |
| Real labor income growth | 0.0333 | 0.0254 | 0.0786 | 0.0449 | 0.0090 |
Panel B: Equity index returns
| Mean | Std. Dev. | ||||||
| VWR - NYSE | |||||||
| VWR - NYSE/AMEX | |||||||
| VWR - NYSE/AMEX/NASDAQ |
Panel C: Treasury bond returns
| Mean | Std. Dev. | ||||||
| 3-month T-bill | 0.0140 | 0.0180 | 0.4646 | 0.3904 | 0.4388 | 0.3756 | 0.1937 |
| 10-year T-bond | 0.0183 | 0.0819 | 0.0719 | 0.0335 | 0.1296 | 0.0744 | -0.2176 |
This table reports GMM estimated coefficients of the preference parameter
Panel A: No long-term T-Bond included, DF = 4
| Model |
|
s.e.
|
||
| NH | -84.9148 | 2.3126 | 7.9656 | 0.0928 |
| DEH | -7.9498 | 1.0908 | 8.7061 | 0.0689 |
| DIH | -1.8994 | 0.0438 | 4.9215 | 0.2954 |
Panel B: 10-year T-Bond included, DF = 13
| Model |
|
s.e.
|
||
| NH | -139.7899 | 1.1919 | 23.7577 | 0.0334 |
| DEH | -7.8087 | 0.8355 | 32.6927 | 0.0019 |
| DIH | -2.0438 | 0.0353 | 28.3454 | 0.0081 |
This table reports GMM estimated coefficients of the preference parameters
Panel A:
![]()
| Model |
|
s.e.
|
|
s.e.
|
p-value | |
| NH | ||||||
| DEH | ||||||
| DIH |
Panel B:
![]()
| Model |
|
s.e.
|
|
s.e.
|
p-value | |
| NH | 0.0054 | 0.1534 | 0.1344 | 46.7029 | 0.0053 | |
| DEH | 0.0059 | 0.6467 | 0.0839 | 51.0445 | 0.0016 | |
| DIH | 0.0534 | 0.0393 | 0.3535 | 50.2571 | 0.0020 |
This table reports GMM estimated coefficients of the preference parameter
Panel A: Value-weighted NYSE index
| Model |
|
s.e.
|
|
s.e.
|
p-value | |
| SEH | 6.7888 | 0.0047 | 0.0496 | 31.6562 | 0.0016 | |
| SIH | 0.4839 | 0.0116 | 23.9664 | 0.0206 |
Panel B: Value-weighted NYSE/AMEX index
| Model |
|
s.e.
|
|
s.e.
|
p-value | |
| SEH | 6.7537 | 0.0036 | 0.0503 | 31.7751 | 0.0015 | |
| SIH | 0.4528 | 0.0112 | 23.4363 | 0.0242 |
Panel C: Value-weighted NYSE/AMEX/NASDAQ index
| Model |
|
s.e.
|
|
s.e.
|
p-value | |
| SEH | 6.6915 | 0.0044 | 0.0500 | 31.3037 | 0.0018 | |
| SIH | 0.2015 | 0.0075 | 17.9489 | 0.1173 |
This table reports GMM estimated coefficients of the preference parameters
Footnotes
where
![\displaystyle V_0 = E \left[ \left. \sum_{t=0}^\infty\, e^{-\rho t} \, u(s_t) \right\vert I_0 \right],](img6.gif)
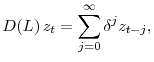
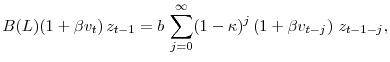
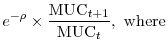
![\displaystyle E_t\left[\sum_{j=0}^{\infty} e^{- \rho j}\times a_{t,j}\times u'(s_{t+j}) \right].](img37.gif)
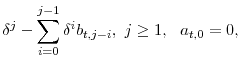 where
where![\begin{displaymath}\left\{ \begin{array}{ll} \left[(1-\kappa)\prod_{i=1}^{j-1} - \prod_{i=0}^{j-1}\right][1 - \kappa - b(1 + \beta v_{t+i+1})], & \mbox{(internal),} \ 0, & \mbox{(external).} \end{array} \right.\end{displaymath}](img42.gif)
![\displaystyle E_t \left[ \frac{\mbox{MUC}_{t+n}}{\mbox{MUC}_t} \times R_{t, t+n} \right]= 1.](img49.gif)
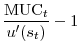
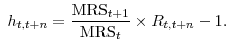
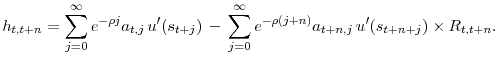
![\displaystyle E \left[ \left. \Phi_t - e^{-\rho n} \times \Phi_{t+n} \times \frac{u'(s_{t+n})}{u'(s_t)} \times R_{t, t+n} \right\vert I_t \right] = 0,](img103.gif)
![\displaystyle E \left[ \left. \Phi_t - e^{-\rho n} \times \Phi_{t+n} \times \frac{u'(s_{t+n})}{u'(s_t)} \times R_{t, t+n} \right\vert J_t \right] = 0.](img109.gif)