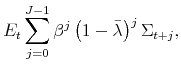Optimal Monetary Policy with State-Dependent Pricing*
Keywords: Monetary policy, state-dependent pricing, monopolistic competition
Abstract:
1 Introduction
A key normative question in monetary economics is the design of optimal monetary policy. An extensive amount of literature studies this question under the assumption that the timing of price changes is given exogenously, typically using the Calvo (1983) model with a constant adjustment rate. 1 Useful as it is as a first approximation, this literature nevertheless is subject to the Lucas (1976) critique: In principle, the frequency of price changes should not be treated as a parameter which is independent of policy. Many economists, therefore, have argued against the use of the Calvo model, claiming that it provides a poor approximation to more elaborate models of price adjustment. For example, Golosov and Lucas (2007) show that the behavior of firms in the Calvo model is very different from that in a " menu cost" model, when firms are subject to idiosyncratic productivity shocks as well as aggregate money growth shocks.
This paper studies optimal monetary policy in a model of state-dependent pricing by monopolistically competitive firms. In models of this sort the frequency of adjustment is a statistic determined in equilibrium, not an exogenous parameter. In particular, we will work with a model in which individual prices are sticky because firms are subject to random idiosyncratic lump-sum costs of adjustment à la Dotsey, King, and Wolman (1999). Each firm would change its price only if the increase in the firm's value due to adjustment exceeds the " menu cost." As a result, the probability with which firms reoptimize prices depends on the gains from adjustment. This framework is very flexible because it nests a variety of pricing specifications, including the Calvo model and the fixed menu cost model as extreme limiting cases (Costain and Nakov, 2011).
Aside from pricing being state-dependent, our setup follows closely the standard New Keynesian model with Calvo pricing (for example, Benigno and Woodford, 2005). In particular, the monetary authority is assumed to set the nominal interest rate, with money's role being only that of a unit of account. An important distinction with Clarida, Galí, and Gertler (1999), Woodford (2002), and Yun (2005), is that we assume no production subsidy to offset the markup distortion due to monopolistic competition. This implies that the steady state level of output is inefficiently low. Hence, the central bank has a constant temptation to inflate the economy so as to bring output closer to its efficient level.
We derive the optimal plan from the timeless perspective, as in Woodford (2003).2 We demonstrate analytically that, if preferences are isoelastic and there is no government spending, it is optimal to commit to zero inflation both in the long run and in reaction to shocks. Importantly, this result holds for a general specification of the menu cost distribution. In the optimal allocation, price markups are positive but constant, output is at its natural (flexible-price) level, and price dispersion is minimized. Perhaps surprisingly, this prescription coincides with the one obtained under Calvo pricing (Benigno and Woodford, 2005).
The reason why zero inflation is optimal in our model of state-dependent pricing is the following. Relative to Calvo pricing, our stochastic menu costs model implies two additional welfare effects of inflation. First, firms must spend real resources (menu costs) on adjusting nominal prices. This distortion is minimized at zero inflation because under such a policy all firms are at their optimal price. The second effect is somewhat more subtle. The main difference between exogenous-timing and state-dependent pricing models is that price adjustment frequencies are endogenous in the latter. A priori, the monetary authority could have an incentive to use inflation so as to affect the rate at which firms change their prices. If firms adjusted their prices faster in reaction to shocks, in principle one would expect that to have beneficial welfare effects. However, the fact that adjusting firms set optimally their prices implies that, in the timeless perspective regime with zero inflation, a marginal increase in the rate of inflation has no effect on firms' profits, and therefore it has no effect on the rate of adjustment. This envelope property implies that the monetary authority has no incentive to deviate from zero inflation in order to affect the speed of adjustment.
We also show that the same reasons for which zero inflation is optimal under Calvo pricing continue to hold under state-dependent pricing. First, inefficient price dispersion is minimized at zero inflation. Second, in the timeless perspective regime with zero inflation, the marginal welfare gain from raising output toward its socially efficient level (i.e. a movement along the Phillips curve) exactly cancels out with the marginal welfare loss from committing to and generating expectations of future inflation (i.e., an upward shift of the Phillips curve). This finding echoes Kydland and Prescott's " rules versus discretion" . However, we find that it is independent of whether pricing is time- or state-dependent.
Our results thus lend support to more informal statements about the suitability of the Calvo model for studying optimal monetary policy despite its apparent conflict with the Lucas (1976) critique. In particular, we provide sufficient conditions under which, even though pricing is state-dependent and so the adjustment frequency is endogenously determined, it turns out that the probability of adjustment remains constant under the optimal policy. When these conditions are satisfied, which is what the literature usually assumes, the distinction between time-dependent and state-dependent pricing frameworks vanishes, provided that monetary policy is set optimally.3
The following section lays out the model and derives the conditions for equilibrium. Section 3 sets up the optimal monetary policy problem and obtains the main result regarding the optimality of zero inflation from the timeless perspective; it also formalizes the main intuition with a simplified version of the model (with the full proof in the Appendix). Section 4 analyzes numerically the case with positive government expenditure; for a plausible calibration of the model, we find that the optimal deviations from strict price stability in response both to productivity and to government spending shocks are indistinguishable from zero.4 Section 5 concludes with a discussion of a possible extension.
2 Model
There are three types of agents: households, firms, and a monetary authority. We begin by describing the behavior of households and firms.
2.1 Households
A representative household maximizes the expected flow of period utility
![]() , discounted by
, discounted by ![]() , subject
to
, subject
to
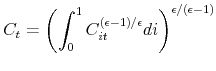 |
and
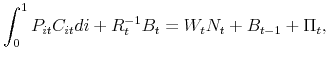 |
where
The first order conditions are
where
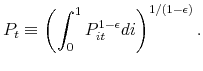 |
2.2 Firms
There is a continuum of firms on the unit interval. Firm ![]() 's production function is
's production function is
where
Following Dotsey et al. (1999), we assume that firms face random lump sum costs of adjusting prices (" menu costs" ), distributed i.i.d. across firms and over time. Let
![]() and
and
![]() denote the cumulative distribution function and the probability density function, respectively, of the stochastic menu cost
denote the cumulative distribution function and the probability density function, respectively, of the stochastic menu cost
![]() . We assume that a positive random fraction of firms draw a zero menu cost, so that
. We assume that a positive random fraction of firms draw a zero menu cost, so that
![]() .6 Assuming that
.6 Assuming that ![]() is measured in units of labor time, the total cost paid by a firm changing its price is
is measured in units of labor time, the total cost paid by a firm changing its price is
![]() .7
.7
Let ![]() denote the value of a firm that adjusts its price in period
denote the value of a firm that adjusts its price in period ![]() before
subtracting the menu cost. Let
before
subtracting the menu cost. Let
![]() denote the value of a firm that has kept its nominal price unchanged at the level
denote the value of a firm that has kept its nominal price unchanged at the level ![]() in the last
in the last ![]() periods. This firm will change its nominal price only if the value of adjustment,
periods. This firm will change its nominal price only if the value of adjustment,
![]() , exceeds the value of continuing with the current price,
, exceeds the value of continuing with the current price,
![]() . Therefore, from the set of firms that last reoptimized
. Therefore, from the set of firms that last reoptimized ![]() periods ago (which we henceforth refer to as " vintage-
periods ago (which we henceforth refer to as " vintage-![]() firms" ), only those with a menu cost draw
firms" ), only those with a menu cost draw
![]() will choose to change their price. The real value of an adjusting firm is given by
will choose to change their price. The real value of an adjusting firm is given by
![\displaystyle \max_{P}\left\{ \Pi _{t}\left( P\right) +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ G\left( \frac{v_{0,t+1}-v_{1,t+1}\left( P\right) }{w_{t+1}}\right) v_{0,t+1}-\Xi _{1,t+1}\left( P\right) \right] \right.](img42.gif) |
|||
![\displaystyle \left. +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ 1-G\left( \frac{v_{0,t+1}-v_{1,t+1}\left( P\right) }{w_{t+1}}\right) \right] v_{1,t+1}\left( P\right) \right\} ,](img43.gif) |
where
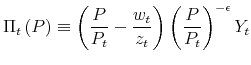 |
is the firm's real profit as a function of its nominal price
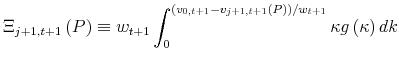 |
is next period's expected adjustment cost for a firm currently in vintage
![\displaystyle \Pi _{t}\left( P\right) +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ G\left( \frac{v_{0,t+1}-v_{j+1,t+1}\left( P\right) }{w_{t+1}}\right) v_{0,t+1}-\Xi _{j+1,t+1}\left( P\right) \right]](img49.gif) |
|||
![\displaystyle +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ 1-G\left( \frac{v_{0,t+1}-v_{j+1,t+1}\left( P\right) }{% w_{t+1}}\right) \right] v_{j+1,t+1}\left( P\right) .](img50.gif) |
(3) |
We assume that
The optimal price setting decision is given by
where
![\displaystyle \Pi _{t}^{\prime }\left( P\right) =\left[ \epsilon \frac{w_{t}}{z_{t}}% -\left( \epsilon -1\right) \frac{P}{P_{t}}\right] \left( P\right) ^{-\epsilon -1}P_{t}^{\epsilon }Y_{t}.](img57.gif) |
Iterating (5) forward, and using the implications of (3) and (4) for the terms
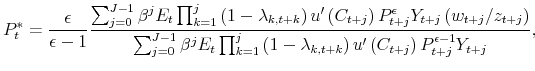
|
where
denotes the period-
where
2.3 Market clearing
Labor input is required both for the production of goods and for changing prices. Labor demand for production by firm ![]() is
is
![]() . Thus, total labor demand for production purposes equals
. Thus, total labor demand for production purposes equals
![]() , where
, where
![]() denotes relative price dispersion. At the same time, the total amount of labor used by vintage-
denotes relative price dispersion. At the same time, the total amount of labor used by vintage-![]() firms for pricing purposes equals
firms for pricing purposes equals
![]() , where
, where
![]() is the mass of firms in vintage
is the mass of firms in vintage ![]() . Equilibrium in the labor market
therefore implies
. Equilibrium in the labor market
therefore implies
Also, equilibrium in the goods market requires that
where
2.4 Inflation, price dispersion, and price distribution dynamics
All firms adjusting at time ![]() choose the same nominal price,
choose the same nominal price,
![]() . Given that no nominal price survives for longer than
. Given that no nominal price survives for longer than ![]() periods by
assumption, the finite set of beginning-of-period prices at any time
periods by
assumption, the finite set of beginning-of-period prices at any time ![]() is
is
![]() . Let
. Let
![]() denote the time-
denote the time-![]() fraction of firms with beginning-of-period nominal
price
fraction of firms with beginning-of-period nominal
price
![]() , for
, for
![]() , with
, with
![]() . The price level evolves according to
. The price level evolves according to
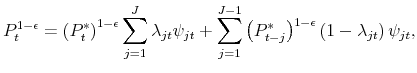 |
where adjustment probabilities
This equation determines the inflation rate
where again
for
2.5 Equilibrium
There are
![]() stationary endogenous variables:
stationary endogenous variables: ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() . The equilibrium conditions are (1), (2), the
. The equilibrium conditions are (1), (2), the ![]() equations (6), equations (7) to (11), the
equations (6), equations (7) to (11), the ![]() laws of motion (12) and (13), the value functions
laws of motion (12) and (13), the value functions
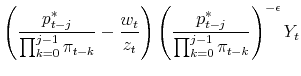 |
|||
![\displaystyle +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ \lambda _{j+1,t+1}v_{0,t+1}+\left( 1-\lambda _{j+1,t+1}\right) v_{j+1,t+1}-w_{t+1}\int\nolimits_{0}^{\left( v_{0,t+1}-v_{j+1,t+1}\right) /w_{t+1}}\kappa dG\left( \kappa \right) \right]](img109.gif) |
for
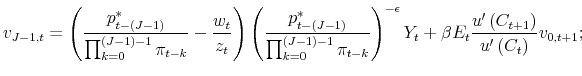
|
plus a specification of monetary policy. If we were to close the model with a Taylor rule, this would give us a total of
2.5.1 Flexible-price equilibrium
It is instructive to derive the flexible-price equilibrium in this framework. In such an equilibrium, menu costs are zero and all firms choose the same nominal price
![]() in each period
in each period ![]() . All relative prices are one:
. All relative prices are one:
![]() . The equilibrium conditions simplify to
. The equilibrium conditions simplify to
and so we obtain the classical decoupling of real and nominal variables. The flexible-price output
3.1 The general problem
For the purpose of deriving the optimality conditions of the Ramsey plan, it is useful to define
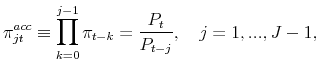 |
that is, the accumulated inflation between periods
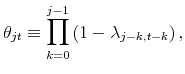 |
that is, the probability that a price chosen at
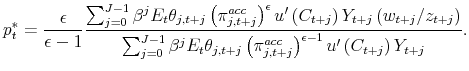
|
Similarly, we replace
where the recursions start with
Since the nominal interest rate only appears in the consumption Euler equation, the latter is excluded from the set of constraints on the Ramsey problem. Instead, this equation is used residually to back out the nominal interest rate path consistent with the optimal allocation. The first-order conditions of the above problem are derived in the Appendix.
Our object of interest is optimal monetary policy from a " timeless perspective." As explained by Woodford (2003), this type of policy does not exploit the private sector's expectations that formed prior to the particular date on which the plan was implemented. Instead, the central bank commits itself to behave, from date 0, in a way consistent with the way it would have chosen to behave had it committed to the optimal policy in the infinite past. The interest is thus in optimality in the long run, once the economy has converged to its ergodic distribution.
The Appendix proves the following result:
There are two important aspects of the above proposition. The first is that optimal trend inflation is zero. Therefore, the presence of monopolistic distortions does not justify a positive rate of trend inflation, and the optimal policy involves a commitment to eventually eliminating any inefficient price dispersion due to staggered price setting. This normative prescription is the same as the one implied by the standard New Keynesian model with Calvo price setting, as shown by Benigno and Woodford (2005).9 The main insight of the Calvo framework, about the desirability of zero long-run inflation, thus continues to hold in a general model of state-dependent pricing. The key difference between exogenous-timing models of price adjustment such as Calvo's and state-dependent pricing models is the endogeneity of the timing of price adjustment in the latter. A priori, the central bank could have an incentive to use trend inflation to influence the speed at which firms change prices, if such a policy were to have beneficial effects on society. The above result implies that the endogeneity of price adjustment frequencies does not affect the optimality of zero trend inflation.
To understand the intuition for this result, let us consider the different channels through which trend inflation affects welfare. Two of these channels are common to exogenous-timing models such as Calvo or Taylor. One is that, in the presence of staggered prices, inflation increases the extent of price dispersion, distorting the economy's pricing system. This leads to inefficient allocation of resources across product lines, and increases the total amount of (labor) resources needed to produce a given consumption basket; hence, it lowers welfare. Notice that inefficient price dispersion attains a global minimum at zero inflation because, under such a policy, all relative prices end up being equal.
The other common channel, through which trend inflation affects welfare, works through its two opposing effects on the inflation-output tradeoff: On the one hand, holding constant inflation expectations, a rise in current inflation allows the central bank to raise output toward its socially efficient level, thus reducing the monopolistic distortion and improving welfare; intuitively, the economy moves along the New Keynesian Phillips curve (NKPC).10 On the other hand, choosing higher inflation raises the inflation expectations of price-setters; the latter produces an upward shift of the NKPC, thus worsening the short-run tradeoff between inflation and output. As it turns out, at zero inflation, the marginal welfare cost of raising inflation expectations exactly offsets the marginal welfare benefit of exploiting the short-run inflation-output tradeoff.
While the former two welfare effects of trend inflation are common to exogenous-timing models, our framework with idiosyncratic menu cost shocks includes two additional channels through which trend inflation affects welfare. One is that inflation forces firms to spend real resources (menu costs)
on adjusting their nominal prices; this distortion is minimized at zero inflation, because eventually all firms end up being at their optimal price. The other extra channel is more subtle; Namely, in the stochastic menu costs model, adjustment frequencies are endogenous. In particular, trend
inflation affects the relative prices of different cohorts of firms (
![]() ,
,
![]() ), which has an effect on their profits, on their value functions, and ultimately on the gains from adjustment. A priori, the central bank may be tempted to use trend inflation
to influence the speed of price adjustment, so as to shift the NKPC in a way that improves the inflation-output tradeoff. However, the fact that adjusting firms choose their prices in an optimal way implies that, at zero inflation, a marginal increase in the inflation
rate has no effect on firms' profits, and therefore it has no effect on adjustment probabilities. This envelope property implies that the monetary authority has no incentive to create trend inflation to influence the speed with which firms change their prices.
), which has an effect on their profits, on their value functions, and ultimately on the gains from adjustment. A priori, the central bank may be tempted to use trend inflation
to influence the speed of price adjustment, so as to shift the NKPC in a way that improves the inflation-output tradeoff. However, the fact that adjusting firms choose their prices in an optimal way implies that, at zero inflation, a marginal increase in the inflation
rate has no effect on firms' profits, and therefore it has no effect on adjustment probabilities. This envelope property implies that the monetary authority has no incentive to create trend inflation to influence the speed with which firms change their prices.
The second important aspect of proposition 1 is that the optimal deviations from zero inflation in response to technology or preference shocks are zero as well. Therefore, the occurrence of these exogenous disturbances to preferences or technology does not justify temporary departures from strict price stability.11 The intuition for this result is as follows. There are four potential inefficiencies in the present model, related to: (1) the level and volatility of price dispersion; (2) the volatility of the average markup; (3) the waste of resources due to menu costs; and (4) the level of the average markup due to monopolistic competition. Distortions (1) through (3) are directly related to the friction in price setting, and-absent idiosyncratic shocks to desired prices-a policy of strict price stability eliminates all three. It does so by replicating the flexible-price equilibrium and eliminating the incentives for price adjustment. Inefficiency (4) is a static markup distortion due to monopolistic competition. As we have just seen, the optimal plan does not involve a correction of this inefficiency because it is outweighed by the gains of committing to zero inflation and achieving the minimum possible price dispersion in the long run, independently of the price-setting policies followed by firms. The aforementioned envelope property, by which a marginal increase in inflation leaves price adjustment frequencies unaffected, continues to hold as the economy is hit by aggregate shocks.
3.2 An illustration with two cohorts
While the appendix provides the proof of the optimality of zero inflation in the full-blown model, it is illustrative to formalize the above intuitions with a simplified version of the model. In particular, we consider the case of ![]() cohorts, such that firms that adjust their nominal price today may or may not adjust in the following period, but adjust with certainty two periods after the last price change. To further simplify, we assume functional forms
cohorts, such that firms that adjust their nominal price today may or may not adjust in the following period, but adjust with certainty two periods after the last price change. To further simplify, we assume functional forms
![]() and
and
![]() , such that the real wage is
, such that the real wage is
![]() . As in proposition 1, we also assume away government spending,
. As in proposition 1, we also assume away government spending, ![]() , such that
, such that
![]() . To simplify the notation, let
. To simplify the notation, let
![]() and
and
![]() denote the measure and adjustment probability of firms in vintage 1. The measure of firms in vintage 2 is then
denote the measure and adjustment probability of firms in vintage 1. The measure of firms in vintage 2 is then
![]() , and the law of motion of
, and the law of motion of ![]() is simply
is simply
![]() . Let also
. Let also ![]()
![]() denote the value of firms in vintage 1. Finally, we define
denote the value of firms in vintage 1. Finally, we define
![]() and
and
![]() , such that
, such that
![]() . Taking all these elements, the central bank maximizes the following Lagrangian:
. Taking all these elements, the central bank maximizes the following Lagrangian:
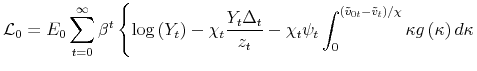 |
|||
![\displaystyle +\phi _{t}^{p^{\ast }}\left[ p_{t}^{\ast }\left( 1+\beta \left( 1-\lambda _{t+1}\right) \pi _{t+1}^{\epsilon -1}\right) -\frac{\epsilon }{\epsilon -1}% \left( \frac{\chi _{t}Y_{t}}{z_{t}}+\beta \left( 1-\lambda _{t+1}\right) \pi _{t+1}^{\epsilon }\frac{\chi _{t}Y_{t+1}}{z_{t+1}}\right) \right]](img175.gif)
|
|||
![\displaystyle +\phi _{t}^{\pi }\left[ \left( p_{t}^{\ast }\right) ^{1-\epsilon }\left( \lambda _{t}\psi _{t}+1-\psi _{t}\right) +\left( \frac{p_{t-1}^{\ast }}{\pi _{t}}\right) ^{1-\epsilon }\left( 1-\lambda _{t}\right) \psi _{t}-1\right]](img176.gif) |
|||
![\displaystyle +\phi _{t}^{\Delta }\left[ \left( p_{t}^{\ast }\right) ^{-\epsilon }\left( \lambda _{t}\psi _{t}+1-\psi _{t}\right) +\left( \frac{p_{t-1}^{\ast }}{\pi _{t}}\right) ^{-\epsilon }\left( 1-\lambda _{t}\right) \psi _{t}-\Delta _{t}% \right]](img177.gif) |
|||
![\displaystyle +\phi _{t}^{\lambda }\left[ \lambda _{t}-G\left( \frac{\tilde{v}_{0t}-% \tilde{v}_{t}}{\chi _{t}}\right) \right] +\phi _{t}^{\psi }\left[ \psi _{t}+\left( 1-\lambda _{t-1}\right) \psi _{t-1}\right]](img178.gif) |
|||
![\displaystyle +\phi _{t}^{v_{0}}\left[ \left( p_{t}^{\ast }-\frac{\chi _{t}Y_{t}}{z_{t}}% \right) \left( p_{t}^{\ast }\right) ^{-\epsilon }-\tilde{v}_{0t}+\beta \left( \lambda _{t+1}\tilde{v}_{0,t+1}+\left( 1-\lambda _{t+1}\right) \tilde{% v}_{t+1}-\chi _{t}\int\nolimits_{0}^{\left( \tilde{v}_{0,t+1}-\tilde{v}% _{t+1}\right) \ /\chi }\kappa g\left( \kappa \right) d\kappa \right) \right]](img179.gif)
|
|||
![\displaystyle \left. +\phi _{t}^{v}\left[ \left( \frac{p_{t-1}^{\ast }}{\pi _{t}}-\frac{% \chi _{t}Y_{t}}{z_{t}}\right) \left( \frac{p_{t-1}^{\ast }}{\pi _{t}}\right) ^{-\epsilon }-\tilde{v}_{t}+\beta \tilde{v}_{0,t+1}\right] \right\} .](img180.gif) |
For the present analysis, it suffices to differentiate the Lagrangian with respect to inflation and the optimal relative price for a particular state at time
respectively.12 We now conjecture that the central bank commits to follow a policy of zero net inflation, or
Imposing the latter conjecture in expressions (15) and (16), we obtain
where we have also used the fact that
In equation (17), the term involving
![]() captures the marginal welfare effect from an increase in time (
captures the marginal welfare effect from an increase in time (![]() ) expectations of inflation at time
) expectations of inflation at time ![]() , whereas the term involving
, whereas the term involving
![]() in equation (18) reflects the marginal
welfare effect from an increase in the optimal relative price (and thus in inflation) at time
in equation (18) reflects the marginal
welfare effect from an increase in the optimal relative price (and thus in inflation) at time ![]() . We show in the Appendix that, in the full-blown model, the multiplier
. We show in the Appendix that, in the full-blown model, the multiplier
![]() converges to a constant value
converges to a constant value
![]() in the timeless perspective regime, which is also true in this simplified version. Using this in (18), setting the resulting expression equal to zero (as required by the first-order optimality condition), and solving for
in the timeless perspective regime, which is also true in this simplified version. Using this in (18), setting the resulting expression equal to zero (as required by the first-order optimality condition), and solving for
![]() , we obtain
, we obtain
Using this to substitute for
Therefore, once the economy has converged to the timeless perspective regime with zero inflation, the central bank has no incentive to create positive or negative inflation at the margin, because the potential welfare costs cancel out the potential gains. The term involving
The specific example above is intended to formalize the main intuition; more generally, the optimality of zero inflation from the timeless perspective holds for any number of cohorts and for standard (isoelastic) preferences, as shown in the Appendix.
4 Optimal policy with positive government expenditure
The previous section derived the optimal policy under the assumption that government expenditure is zero. We now briefly analyze the more general case with positive government expenditure. In this case, we no longer have a closed-form analytical solution, so we illustrate the results by simulation. We show the optimal dynamic responses of several key variables to two types of shocks: aggregate productivity and government consumption. Our main finding is that, under a first- or second-order approximation to the general equilibrium dynamics of the model, the optimal deviations of inflation from zero are negligible. Thus, the optimal stabilization policy is basically equivalent to strict inflation targeting, and all real variables follow closely their flexible-price counterparts. We also find that the responses are virtually identical to the ones obtained in the Calvo model.
4.1 Calibration
To produce impulse responses, we must first choose functional forms and assign values to the model's parameters. We take most of the parameters from Golosov and Lucas (2007). In particular,
![]() with
with
![]() and
and
![]() with
with ![]() and
and
![]() The discount factor is
The discount factor is
![]() and the elasticity of substitution among product varieties is
and the elasticity of substitution among product varieties is
![]() .
.
We further assume that the cumulative distribution function of menu costs takes the form
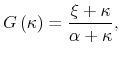 |
where both
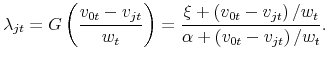 |
As in Costain and Nakov (2011), this function is increasing in the gain from adjustment
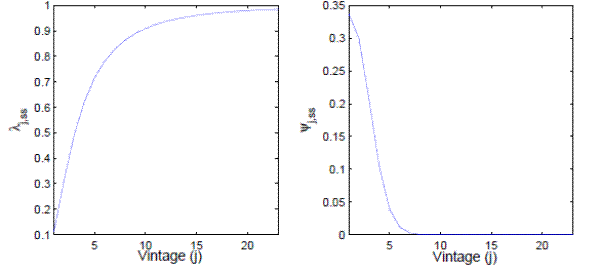
Figure 1 shows the adjustment hazard function and the distribution of firms by price vintage with 2% trend inflation. In the left panel, the adjustment probability increases rapidly with price age, reaching 90% after 10 quarters. As shown in the right panel, this implies that virtually no price survives more than eight quarters.
We focus on two types of shocks. One is an aggregate productivity shock with persistence
![]() and the other is a government expenditure shock with persistence
and the other is a government expenditure shock with persistence
![]() Government expenditure is calibrated so that it accounts for roughly 17% of GDP in steady state, consistent with U.S. postwar experience.
Government expenditure is calibrated so that it accounts for roughly 17% of GDP in steady state, consistent with U.S. postwar experience.
4.2 Impulse responses under the optimal policy
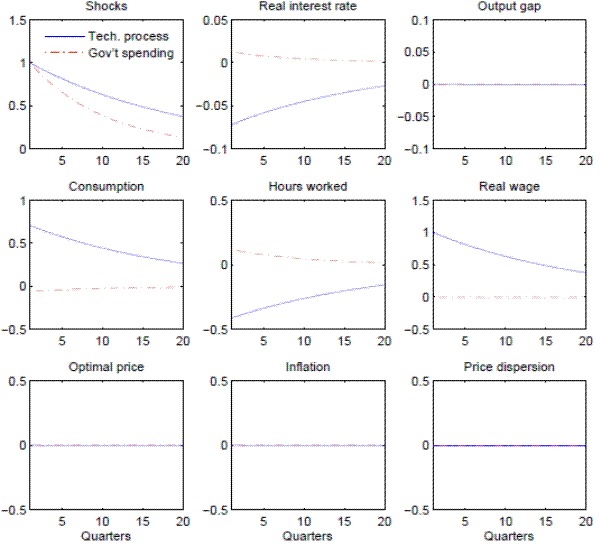
We use a first-order Taylor expansion to approximate the equilibrium dynamics of our model. Figure 2 plots the responses of several variables of interest to two independent shocks: a 1% improvement in aggregate productivity, and a 1% increase in the level of government spending. Characteristically, four variables - the optimal reset price, inflation, price dispersion (shown in the last row of the figure), and the output gap, defined as the ratio between actual output and its flexible price counterpart (and shown in the third panel on the top row), remain constant in response to each of the shocks. This is precisely what happens in response to the same shocks in the Calvo model (not shown due to the overlap, but available upon request). Moreover, the responses of the interest rate, consumption, hours worked, and wages, all coincide with their counterparts in the Calvo model. Hence, the central bank's incentives to deviate from zero inflation to reduce monopolistic distortions are virtually nonexistent in response to the two real shocks.
In passing, we note that a second-order accurate solution of the model yields virtually identical impulse responses, both under Calvo and under stochastic menu costs, at least for small aggregate shocks.13 We thus find that the simple linear Calvo framework offers a very good approximation to the behavior of a cashless state-dependent pricing economy under the optimal monetary policy from the timeless perspective, even though the two economies behave quite differently under suboptimal policies.
5 Conclusion
We have shown that the main lessons for optimal monetary policy derived in the canonical Calvo model carry over to a more general setup in which firms' likelihood of adjusting prices depends on the state of the economy. In particular, the optimal long-run rate of inflation is zero, and the optimal dynamic policy is strict inflation targeting. This finding means that the central bank should not use inflation to try to offset the static distortion arising from monopolistic competition.
We show that, under conditions typically assumed in the literature, the probability of adjustment remains constant even if pricing is state-dependent, provided that monetary policy is set optimally. Thus, when the sufficient conditions are met, any difference between time-dependent and state-dependent pricing vanishes under the optimal policy. These results lend support to more informal statements about the suitability of the Calvo model for studying optimal monetary policy despite its apparent conflict with the Lucas (1976) critique.
Our analysis is a step toward a fuller model that would include firm-level shocks not only to the price adjustment costs, but also to desired prices, for example, due to idiosyncratic productivity shocks.14 In this extended model, monetary policy would not be able to replicate the flexible-price equilibrium " for free," because firms with different productivities would want to set different prices. Instead, deviations from price stability would affect the balance between price increases and price decreases, with potential welfare gains coming from this rebalancing. The magnitude of such a welfare effect of inflation is an intriguing question, which we leave for future research.
Appendix
In this appendix, we obtain the solution to the optimal monetary policy problem from the timeless perspective. The central bank maximizes the Lagrangian given by expression (14) in the main text. The first-order conditions are as follows (all expressions are equal to
zero):
![\displaystyle u^{\prime }\left( C_{t}\right) +\sum_{j=0}^{J-1}\phi _{t-j}^{p^{\ast }}\left[ \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\left[ u^{\prime }\left( C_{t}\right) +Y_{t}u^{\prime \prime }\left( C_{t}\right) \right] -\frac{\epsilon }{\epsilon -1}\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}}\right] \theta _{jt}(\pi _{jt}^{acc})^{\epsilon }-\phi _{t}^{N}\frac{\Delta _{t}}{z_{t}}](img233.gif)
|
|||
![\displaystyle +\sum_{j=0}^{J-1}\phi _{t}^{v_{j}}\left[ \frac{p_{t-j}^{\ast }}{% \pi _{jt}^{acc}}\left[ u^{\prime }\left( C_{t}\right) +u^{\prime \prime }\left( C_{t}\right) Y_{t}\right] -\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}}\right] \left( \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}} \right) ^{-\epsilon }, \hspace{6cm} \TCItag{($Y_{t}$)}](img234.gif)
|
![\displaystyle \phi _{t}^{p^{\ast }}E_{t}\sum_{j=0}^{J-1}\beta ^{j}\theta _{j,t+j}(\pi _{j,t+j}^{acc})^{\epsilon -1}Y_{t+j}u^{\prime }\left( C_{t+j}\right) -\left[ \phi _{t}^{\pi }\left( \epsilon -1\right) p_{t}^{\ast }+\phi _{t}^{\Delta }\epsilon \right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}\sum_{j=1}^{J}\lambda _{jt}\psi _{jt}](img235.gif)
|
|||
![\displaystyle -E_{t}\sum_{j=1}^{J-1}\beta ^{j}\left[ \phi _{t+j}^{\pi }\left( \epsilon -1\right) \frac{p_{t}^{\ast }}{\pi _{j,t+j}^{acc}}+\phi _{t+j}^{\Delta }\epsilon \right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}(\pi _{j,t+j}^{acc})^{\epsilon }\left( 1-\lambda _{j,t+j}\right) \psi _{j,t+j}](img236.gif)
|
|||
![\displaystyle +E_{t}\sum_{j=0}^{J-1}\beta ^{j}\phi _{t+j}^{v_{j}}\left[ \epsilon \frac{x^{\prime }\left( N_{t+j};\chi _{t+j}\right) }{z_{t+j}u^{\prime }\left( C_{t+j}\right) }-\left( \epsilon -1\right) \frac{p_{t}^{\ast }}{\pi _{j,t+j}^{acc}}\right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}(\pi _{j,t+j}^{acc})^{\epsilon }Y_{t+j}u^{\prime }\left( C_{t+j}\right) , \hspace{2cm} \TCItag{($p_{t}^{\ast }$)}](img237.gif)
|
![\displaystyle \phi _{t-j}^{p^{\ast }}\left[ \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}% \left( \epsilon -1\right) -\frac{\epsilon }{\epsilon -1}\epsilon \frac{% x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}u^{\prime }\left( C_{t}\right) }\right] \theta _{jt}(\pi _{jt}^{acc})^{\epsilon -1}Y_{t}u^{\prime }\left( C_{t}\right)](img238.gif)
|
|||
![\displaystyle +\left[ \phi _{t}^{\pi }\frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\left( \epsilon -1\right) +\phi _{t}^{\Delta }\epsilon \right] (p_{t-j}^{\ast })^{-\epsilon }(\pi _{jt}^{acc})^{\epsilon -1}\left( 1-\lambda _{jt}\right) \psi _{jt}](img239.gif) |
|||
![\displaystyle +\phi _{t}^{v_{j}}\left[ \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\left( \epsilon -1\right) -\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{% z_{t}u^{\prime }\left( C_{t}\right) }\epsilon \right] (p_{t-j}^{\ast })^{-\epsilon }(\pi _{jt}^{acc})^{\epsilon -1}Y_{t}u^{\prime }\left( C_{t}\right)](img240.gif)
|
|||
![\displaystyle \phi _{t-\left( J-1\right) }^{p^{\ast }}\left[ \frac{p_{t-\left( J-1\right) }^{\ast }}{\pi _{J-1,t}^{acc}}\left( \epsilon -1\right) -\frac{% \epsilon }{\epsilon -1}\epsilon \frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}u^{\prime }\left( C_{t}\right) }\right] \theta _{J-1,t}(\pi _{J-1,t}^{acc})^{\epsilon -1}Y_{t}u^{\prime }\left( C_{t}\right)](img242.gif)
|
|||
![\displaystyle +\left[ \phi _{t}^{\pi }\frac{p_{t-\left( J-1\right) }^{\ast }}{\pi _{J-1,t}^{acc}}\left( \epsilon -1\right) +\phi _{t}^{\Delta }\epsilon \right] (p_{t-\left( J-1\right) }^{\ast })^{-\epsilon }(\pi _{J-1,t}^{acc})^{\epsilon -1}\left( 1-\lambda _{J-1,t}\right) \psi _{J-1,t}](img243.gif) |
|||
![\displaystyle +\phi _{t}^{v_{j}}\left[ \frac{p_{t-\left( J-1\right) }^{\ast }}{\pi _{J-1,t}^{acc}}\left( \epsilon -1\right) -\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}u^{\prime }\left( C_{t}\right) }\epsilon \right] (p_{t-\left( J-1\right) }^{\ast })^{-\epsilon }\left( \pi _{J-1,t}^{acc}\right) ^{\epsilon -1}Y_{t}u^{\prime }\left( C_{t}\right) +\phi _{t}^{\pi _{J-1}^{acc}}, \hspace{2cm} \TCItag{($\pi _{J-1,\text{ }t}^{acc}$)}](img244.gif)
|
![\displaystyle \phi _{t-j}^{p^{\ast }}\left[ \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}-\frac{% \epsilon }{\epsilon -1}\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{% z_{t}u^{\prime }\left( C_{t}\right) }\right] (\pi _{jt}^{acc})^{\epsilon }Y_{t}u^{\prime }\left( C_{t}\right) +\phi _{t}^{\theta _{j}}-\beta E_{t}\phi _{t+1}^{\theta _{j+1}}\left( 1-\lambda _{j+1,t+1}\right), \hspace{2.2cm} \nonumber](img246.gif)
|
(
|
![\displaystyle \phi _{t-\left( J-1\right) }^{p^{\ast }}\left[ \frac{p_{t-\left( J-1\right) }^{\ast }}{\pi _{J-1,t}^{acc}}-\frac{\epsilon }{\epsilon -1}\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}u^{\prime }\left( C_{t}\right) }\right] (\pi _{J-1,t}^{acc})^{\epsilon }Y_{t}u^{\prime }\left( C_{t}\right) +\phi _{t}^{\theta _{J-1}}, \hspace{4cm} \nonumber](img248.gif)
|
(
|
![\displaystyle \phi _{t}^{\pi }\left[ \left( p_{t}^{\ast }\right) ^{1-\epsilon }-\left( \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\right) ^{1-\epsilon }\right] \psi _{jt}+\phi _{t}^{\Delta }\left[ \left( p_{t}^{\ast }\right) ^{-\epsilon }-\left( \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\right) ^{-\epsilon }\right] \psi _{jt}](img249.gif)
|
|||
![\displaystyle -\phi _{t}^{N}\int_{0}^{\left( \tilde{v}_{0t}-\tilde{v}% _{1t}\right) /x^{\prime }\left( N_{t};\chi _{t}\right) }\kappa g\left( \kappa \right) d\kappa +\phi _{t}^{\pi }\left[ \left( p_{t}^{\ast }\right) ^{1-\epsilon }\lambda _{1t}+\left( \frac{p_{t-1}^{\ast }}{\pi _{1t}^{acc}}% \right) ^{1-\epsilon }\left( 1-\lambda _{1t}\right) \right]](img251.gif)
|
|||
![\displaystyle +\phi _{t}^{\Delta }\left[ \left( p_{t}^{\ast }\right) ^{-\epsilon }\lambda _{1t}+\left( \frac{p_{t-1}^{\ast }}{\pi _{1t}^{acc}}\right) ^{-\epsilon }\left( 1-\lambda _{1t}\right) \right] -\beta E_{t}\phi _{t+1}^{\psi _{2}}\left( 1-\lambda _{1t}\right) +\phi _{t}^{\psi _{1}}, \hspace{4cm} \TCItag{($\psi _{1,t}$)}](img252.gif)
|
![\displaystyle -\phi _{t}^{N}\int_{0}^{\left( \tilde{v}_{0t}-\tilde{v}% _{jt}\right) /x^{\prime }\left( N_{t};\chi _{t}\right) }\kappa g\left( \kappa \right) d\kappa +\phi _{t}^{\pi }\left[ \left( p_{t}^{\ast }\right) ^{1-\epsilon }\lambda _{jt}+\left( \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}% \right) ^{1-\epsilon }\left( 1-\lambda _{jt}\right) \right]](img253.gif)
|
|||
![\displaystyle +\phi _{t}^{\Delta }\left[ \left( p_{t}^{\ast }\right) ^{-\epsilon }\lambda _{jt}+\left( \frac{p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\right) ^{-\epsilon }\left( 1-\lambda _{jt}\right) \right] \hspace{8cm}\TCItag{($\psi_{j=2,...,J-1,\text{ }t}$)}](img254.gif) |
|||
| (
|
![\displaystyle -\phi _{t}^{N}\sum_{j=1}^{J-1}\frac{\psi _{jt}}{x^{\prime }\left( N_{t};\chi _{t}\right) }L_{jt}g\left( L_{jt}\right) -\sum_{j=1}^{J-1}\phi _{t}^{\lambda _{j}}g\left( L_{jt}\right) \frac{% 1}{x^{\prime }\left( N_{t};\chi _{t}\right) }-\phi _{t}^{v_{0}}+\sum_{j=0}^{J-2}\phi _{t-1}^{v_{j}}\left[ \lambda _{j{\small +}1,t}-L_{j+1,t}g\left( L_{j+1,t}\right) \right] +\phi _{t-1}^{v_{J-1}},](img259.gif)
|
(
|
![\displaystyle \phi _{t}^{N}\psi _{jt}\frac{1}{x^{\prime }\left( N_{t};\chi _{t}\right) }% L_{jt}g\left( L_{jt}\right) +\phi _{t}^{\lambda _{j}}g\left( L_{jt}\right) \frac{1}{x^{\prime }\left( N_{t};\chi _{t}\right) }-\phi _{t}^{v_{j}}+\phi _{t-1}^{v_{j-1}}\left[ 1-\lambda _{jt}+L_{jt}g\left( L_{jt}\right) \right] , \hspace{2cm}](img261.gif)
|
(
|
![\displaystyle -x^{\prime }\left( N_{t};\chi _{t}\right) -\sum_{j=0}^{J-1}\phi _{t-j}^{p^{\ast }}\frac{\epsilon }{\epsilon -1}\theta _{jt}(\pi _{jt}^{acc})^{\epsilon }Y_{t}\frac{x^{\prime \prime }\left( N_{t};\chi _{t}\right) }{z_{t}}+\phi _{t}^{N}\left[ 1+\sum_{j=1}^{J-1}\psi _{jt}% \frac{x^{\prime \prime }\left( N_{t};\chi _{t}\right) }{x^{\prime }\left( N_{t};\chi _{t}\right) }\left( L_{jt}\right) ^{2}g\left( L_{jt}\right) % \right]](img262.gif)
|
|||
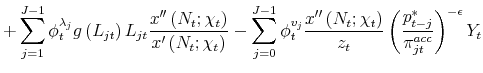
|
|||
![\displaystyle +\sum_{j=0}^{J-2}\phi _{t-1}^{v_{j}}x^{\prime \prime }\left( N_{t};\chi _{t}\right) \left[ \left( L_{j+1,t}\right) ^{2}g\left( L_{j+1,t}\right) -\int_{0}^{L_{j+1,t}}\kappa g\left( \kappa \right) d\kappa \right] , \hspace{6cm} \TCItag{($N_{t}$)}](img264.gif) |
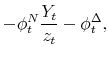 |
(
|
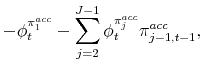 |
( |
where we have defined the adjustment gain
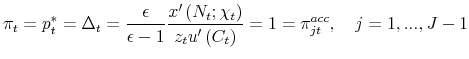 |
|
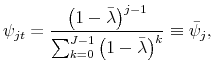 |
|
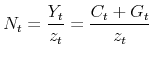 |
for all
We now use equations (20) to (33) to solve for the Lagrange multipliers. From (25) and (24), it follows immediately that
Equations (27) to (29) allow us to solve for the
Using (35) and (36) in equations (26), we obtain
| (37) |
Using the latter, equations (30) and (31) can be expressed compactly as

|
The matrix
![\displaystyle \phi _{t}^{N}=x^{\prime }\left( N_{t};\chi _{t}\right) \left[ 1+\frac{% \epsilon }{\epsilon -1}\frac{N_{t}x^{\prime \prime }\left( N_{t};\chi _{t}\right) }{x^{\prime }\left( N_{t};\chi _{t}\right) }\tsum \limits_{j=0}^{J-1}\left( 1-\bar{\lambda}\right) ^{j}\phi _{t-j}^{p^{\ast }}+% \frac{x^{\prime \prime }\left( N_{t};\chi _{t}\right) N_{t}}{x^{\prime }\left( N_{t};\chi _{t}\right) }\sum_{j=0}^{J-1}\bar{\phi}^{v_{j}}% \right] .](img311.gif)
|
Using the latter in (20), we obtain
![\displaystyle \left[ \frac{Y_{t}u^{\prime \prime }\left( C_{t}\right) }{\left( ... ...ime }\left( N_{t};\chi _{t}\right) }\right] \sum_{j=0}^{J-1}\bar{\phi}^{v_{j}},](img312.gif) |
where we have used the fact that, under our conjecture,
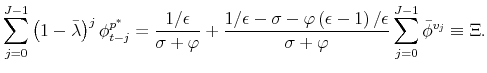 |
It can be shown that all
where we have defined
which pins down the multiplier
Equation (23) can be solved for
![]() , obtaining
, obtaining
where we have used
It only remains to verify that equation (34) holds given the solution of the Lagrange multipliers. This is obvious, as we have already shown that
![]() for
for
![]() .
.
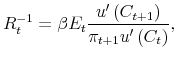
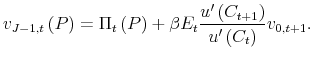
![\displaystyle 0=\Pi _{t}^{\prime }\left( P_{t}^{\ast }\right) +\beta E_{t}\frac{u^{\prime }\left( C_{t+1}\right) }{u^{\prime }\left( C_{t}\right) }\left[ 1-G\left( \frac{v_{0,t+1}-v_{1,t+1}(P_{t}^{\ast })}{w_{t+1}}\right) \right] v_{1,t+1}^{\prime }\left( P_{t}^{\ast }\right) ,](img56.gif)
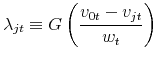
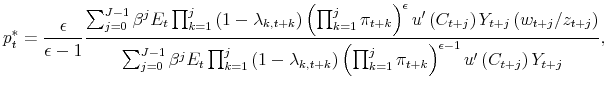
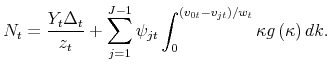
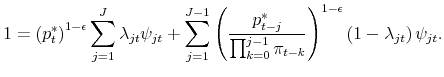
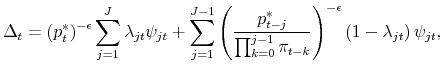
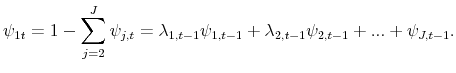
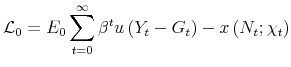
![\displaystyle +\phi _{t}^{p^{\ast }}\left[ p_{t}^{\ast }\sum_{j=0}^{J-1}\beta ^{j}\theta _{j,t+j}(\pi _{j,t+j}^{acc})^{\epsilon -1}Y_{t+j}u^{\prime }\left( Y_{t+j}-G_{t+j}\right) -\frac{\epsilon }{\epsilon -1}% \sum_{j=0}^{J-1}\beta ^{j}\theta _{j,t+j}(\pi _{j,t+j}^{acc})^{\epsilon }Y_{t+j}\frac{x^{\prime }\left( N_{t+j};\chi _{t+j}\right) }{z_{t+j}}\right]](img144.gif)
![\displaystyle +\phi _{t}^{N}\left[ N_{t}-Y_{t}\Delta _{t}/z_{t}-\sum_{j=1}^{J-1}\psi _{jt}\int_{0}^{\left( \tilde{v}_{0t}-\tilde{v}_{jt}\right) /x^{\prime }\left( N_{t};\chi _{t}\right) }\kappa g\left( \kappa \right) d\kappa \right]](img145.gif)
![\displaystyle +\phi _{t}^{\pi }\left[ \left( p_{t}^{\ast }\right) ^{1-\epsilon }\sum_{j=1}^{J}\lambda _{jt}\psi _{jt}+\sum_{j=1}^{J-1}\left( p_{t-j}^{\ast }/\pi _{jt}^{acc}\right) ^{1-\epsilon }\left( 1-\lambda _{jt}\right) \psi _{jt}% \right]](img146.gif)
![\displaystyle +\phi _{t}^{\Delta }\left[ \left( p_{t}^{\ast }\right) ^{-\epsilon }\sum_{j=1}^{J}\lambda _{jt}\psi _{jt}+\sum_{j=1}^{J-1}\left( p_{t-j}^{\ast }/\pi _{jt}^{acc}\right) ^{-\epsilon }\left( 1-\lambda _{jt}\right) \psi _{jt}-\Delta _{t}\right]](img147.gif)
![\displaystyle +\sum_{j=1}^{J-1}\phi _{t}^{\lambda _{j}}\left[ \lambda _{jt}-G\left( \frac{\tilde{v}_{0t}-\tilde{v}_{jt}}{x^{\prime }\left( N_{t};\chi _{t}\right) }\right) \right] +\sum_{j=2}^{J}\phi _{t}^{\psi _{j}}\left[ \psi _{j,t}-\left( 1-\lambda _{j-1,t-1}\right) \psi _{j-1,t-1}\right] +\phi _{t}^{\psi _{1}}\left[ \psi _{1t}+\sum_{j=2}^{J}\psi _{j,t}\right]](img148.gif)
![\displaystyle +\sum_{j=0}^{J-2}\phi _{t}^{v_{j}}\left[ \left( \frac{% p_{t-j}^{\ast }}{\pi _{jt}^{acc}}u^{\prime }\left( Y_{t}-G_{t}\right) -\frac{% x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}}\right) \left( \frac{% p_{t-j}^{\ast }}{\pi _{jt}^{acc}}\right) ^{-\epsilon }Y_{t}-\tilde{v}_{jt}% \right]](img149.gif)
![\displaystyle +\sum_{j=0}^{J-2}\phi _{t}^{v_{j}}\beta \left[ \lambda _{j{\small +% }1,t{\small +}1}\tilde{v}_{0,t{\small +}1}+\left( 1-\lambda _{j{\small +}1,t{\small +}1}\right) \tilde{v}_{j{\small +}1,t{\small +}1}-x^{\prime }\left( N_{t+1};\chi _{t+1}\right) \int_{0}^{\left( \tilde{v}_{0t+1}-% \tilde{v}_{j+1,t+1}\right) /x^{\prime }\left( N_{t+1};\chi _{t+1}\right) }\kappa g\left( \kappa \right) d\kappa \right]](img150.gif)
![\displaystyle +\phi _{t}^{v_{J-1}}\left[ \left( \frac{p_{t-\left( J-1\right) }^{\ast }}{% \pi _{J-1,t}^{acc}}u^{\prime }\left( Y_{t}-G_{t}\right) -\frac{x^{\prime }\left( N_{t};\chi _{t}\right) }{z_{t}}\right) \left( \frac{p_{t-\left( J-1\right) }^{\ast }}{\pi _{J-1,t}^{acc}}\right) ^{-\epsilon }Y_{t}-\tilde{v}% _{J-1,t}+\beta \tilde{v}_{0,t+1}\right]](img151.gif)
![\displaystyle +\phi _{t}^{\pi _{1}^{acc}}\left[ \pi _{1t}^{acc}-\pi _{t}\right] +\sum_{j=2}^{J-1}\phi _{t}^{\pi _{j}^{acc}}\left[ \pi _{jt}^{acc}-\pi _{t}\pi _{j-1,t-1}^{acc}\right]](img152.gif)
![\displaystyle +\phi _{t}^{\theta _{1}}\left[ \theta _{1t}-\left( 1-\lambda _{1t}\right) % \right] +\sum_{j=2}^{J-1}\phi _{t}^{\theta _{j}}\left[ \theta _{jt}-\left( 1-\lambda _{jt}\right) \theta _{j-1,t-1}\right].](img153.gif)
![\displaystyle \phi _{t-1}^{p^{\ast }}\left[ \frac{p_{t-1}^{\ast }}{\pi _{t}}\left( \epsilon -1\right) -\frac{% \epsilon }{\epsilon -1}\frac{\chi _{t}Y_{t}}{z_{t}}\epsilon \right] \pi _{t}^{\epsilon -1}\left( 1-\lambda _{t}\right)](img185.gif)
![\displaystyle +\left[ \phi _{t}^{\pi }\left( \epsilon -1\right) \frac{p_{t-1}^{\ast }}{% \pi _{t}}+\phi _{t}^{\Delta }\epsilon \right] \left( p_{t-1}^{\ast }\right) ^{-\epsilon }\pi _{t}^{\epsilon -1}\left( 1-\lambda _{t}\right) \psi _{t}](img186.gif)
![\displaystyle +\phi _{t}^{v}\left[ \left( \epsilon -1\right) \frac{p_{t-1}^{\ast }}{\pi _{t}}-\epsilon \frac{\chi _{t}Y_{t}}{z_{t}}\right] \left( p_{t-1}^{\ast }\right) ^{-\epsilon }\pi _{t}^{\epsilon -1},](img187.gif)
![\displaystyle -\beta E_{t}\left[ \phi _{t+1}^{\pi }\left( \epsilon -1\right) \frac{% p_{t}^{\ast }}{\pi _{t+1}}+\phi _{t+1}^{\Delta }\epsilon \right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}\pi _{t+1}^{\epsilon }\left( 1-\lambda _{t+1}\right) \psi _{t+1}](img190.gif)
![\displaystyle +\phi _{t}^{v_{0}}\left[ \epsilon \frac{\chi _{t}Y_{t}}{z_{t}}-\left( \epsilon -1\right) p_{t}^{\ast }\right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}+\beta E_{t}\phi _{t+1}^{v}\left[ \epsilon \frac{\chi _{t}Y_{t+1}}{z_{t+1}}-\left( \epsilon -1\right) \frac{p_{t}^{\ast }}{\pi _{t+1}}\right] \left( p_{t}^{\ast }\right) ^{-\epsilon -1}\pi _{t+1}^{\epsilon },](img191.gif)
![\displaystyle \frac{\partial \mathcal{L} _{0}}{\partial \pi _{t}}=-\phi _{t-1}^{p^{\ast }}\left( 1-\bar{\lambda}\right) +\left[ \phi _{t}^{\pi }\left( \epsilon -1\right) +\phi _{t}^{\Delta }\epsilon \right] \left( 1-\bar{\lambda}\right) \bar{\psi},](img198.gif)
![\displaystyle \frac{\partial \mathcal{L} _{0}}{\partial p_{t}^{\ast }}=\phi _{t}^{p^{\ast }}\left[ 1+\beta \left( 1-\bar{\lambda}\right) \right] -\left[ \phi _{t}^{\pi }\left( \epsilon -1\right) +\phi _{t}^{\Delta }\epsilon \right] \bar{\psi}-\beta \left( 1-\bar{\lambda}\right) E_{t}\left[ \phi _{t+1}^{\pi }\left( \epsilon -1\right) +\phi _{t+1}^{\Delta }\epsilon \right] \bar{\psi},](img199.gif)
![\displaystyle 0=1+\frac{Y_{t}u^{\prime \prime }\left( C_{t}\right) }{u^{\prime }\left( C_{t}\right) }\sum_{j=0}^{J-1}\phi _{t-j}^{p^{\ast }}\left( 1-\bar{% \lambda}\right) ^{j}-\frac{\phi _{t}^{N}}{z_{t}u^{\prime }\left( C_{t}\right) }+\sum_{j=0}^{J-1}\phi _{t}^{v_{j}}\left[ 1+\frac{% u^{\prime \prime }\left( C_{t}\right) Y_{t}}{u^{\prime }\left( C_{t}\right) }% -\frac{\epsilon -1}{\epsilon }\right] ,](img276.gif)
![\displaystyle \phi _{t}^{p^{\ast }}E_{t}\sum_{j=0}^{J-1}\beta ^{j}\left( 1-% \bar{\lambda}\right) ^{j}Y_{t+j}u^{\prime }\left( C_{t+j}\right) -\left[ \phi _{t}^{\pi }\left( \epsilon -1\right) +\phi _{t}^{\Delta }\epsilon % \right] \left( \bar{\lambda}\sum_{j=1}^{J-1}\bar{\psi}_{j}+\bar{\psi}% _{J}\right)](img277.gif)
![\displaystyle -E_{t}\sum_{j=1}^{J-1}\beta ^{j}\left[ \phi _{t+j}^{\pi }\left( \epsilon -1\right) +\phi _{t+j}^{\Delta }\epsilon \right] \left( 1-\bar{% \lambda}\right) \bar{\psi}_{j},](img278.gif)
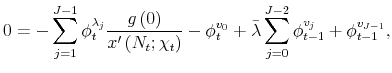
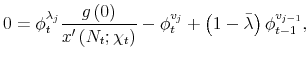
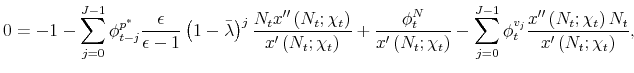
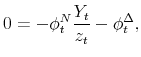
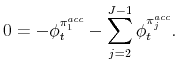
![\displaystyle E_{t}\sum_{j=0}^{J-1}\beta ^{j}\left( 1-\bar{\lambda}\right) ^{j}\left\{ \bar{\phi}^{p^{\ast }}Y_{t+j}u^{\prime }\left( C_{t+j}\right) -% \left[ \phi _{t+j}^{\pi }\left( \epsilon -1\right) +\phi _{t+j}^{\Delta }\epsilon \right] \bar{\psi}_{1}\right\}](img323.gif)