Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-09 Screen Reader version ^♣

What Does Financial Volatility Tell Us About Macroeconomic Fluctuations? *

Marcelle Chauvet¹

Zeynep Senyuz²

Emre Yoldas³

February 6, 2012

Keywords: Realized volatility, business cycles, forecasting, probit model, dynamic factor model, markov switching.

Abstract:

This paper provides an extensive analysis of the predictive ability of financial volatility measures for economic activity. We construct monthly measures of aggregated and industry-level stock volatility, and bond market volatility from daily returns. We model log financial volatility as composed of a long-run component that is common across all series, and a short-run component. If volatility has components, volatility proxies are characterized by large measurement error, which veils analysis of their fundamental information and relationship with the economy. We find that there are substantial gains from using the long term component of the volatility measures for linearly projecting future economic activity, as well as for forecasting business cycle turning points. When we allow for asymmetry in the long-run volatility component, we find that it provides early signals of upcoming recessions. In a real-time out-of-sample analysis of the last recession, we find that these signals are concomitant with the first signs of distress in the financial markets due to problems in the housing sector around mid-2007 and the implied chronology is consistent with the crisis timeline.

JEL Classification: C32, E32, E44.

1 Introduction

The cyclical nature of the systematic movements in the first two moments of financial asset returns and economic activity has been widely documented in the literature. Bear markets, which correspond to periods of generally decreasing asset prices, usually lead economic recessions by a few months and end before the trough, anticipating the economic recovery. These periods are characterized by negative returns and high volatility, whereas bull markets, during which market prices generally increase, are associated with positive returns and lower volatility.⁴

In particular, the empirical regularity that stock market volatility is time-varying has led to a vast literature on modeling and forecasting its dynamics. At the business cycle frequency, the empirical literature in this area has mostly focused on whether macroeconomic variables that behave differently over expansion and recession phases can help predict stock volatility, see Schwert (1989b), Hamilton and Lin (1996), Engle and Rangel (2008), and David and Veronesi (2009), among others.

On the other hand, there is only a small and incipient literature that uses stock market volatility to forecast economic activity. Measures of return volatility may also be useful to predict the future path of the economy as they proxy for the uncertainty surrounding future cash flows and discount rates. In general, this view is supported by the standard present value model of stock prices (e.g., Schwert 1989a, 1989b). Recently, Mele (2007) provides an explicit theoretical analysis of this relation in a continuous time rational valuation framework, using the fact that risk premia are counter-cyclical, i.e. investors require higher returns during relatively bad times. However, the mechanism that leads to counter-cyclical volatility is that changes in risk premia are larger in magnitude in bad times. This can be caused by habit formation in consumption as in Campbell and Cochrane (1999), and by restricted stock market participation as in Basak and Cuoco (1998). Further theoretical underpinnings of the counter-cyclical character of asset return volatility can be found in the financial accelerator framework of Bernanke, Gertler and Gilchrist (1999) and more recently in Bloom (2009), who investigates the impact of shocks to economic uncertainty under stochastically evolving business conditions. Andreou, Osborn, and Sensier (2000) consider interest rate volatility while use option implied volatility as a predictor of economic activity.

A closely related paper is Fornari and Mele (2009) who study whether aggregate stock market volatility impacts investment decisions, and has marginal predictive ability to economic activity. The paper considers exclusively monthly stock market volatility and focuses on the aggregate market portfolio using linear regressions and probit models with financial volatility and other commonly used financial indicators.

In this paper, we analyze the predictive value of various volatility measures for future economic activity. We consider not just the aggregate stock market volatility, but also stock volatility at the industry level as well as bond market volatility. Realized volatility offers a natural framework to match the quarterly or monthly frequency of macro series, by aggregating financial data available at higher frequencies.⁵ We use daily data to construct realized monthly volatility, which allows us to treat volatility as an observable variable. We then use a variety of linear and nonlinear methods to assess the predictive power of financial volatility measures and their relation with the real activity.

Ex-post sample variances that are computed from higher frequency return data as lower frequency volatility measures have been extensively used in empirical finance, see for example the early work of Poterba and Summers (1986), French, Schwert and Stambaugh (1987), Schwert (1989a, 1989b).⁶ More recently, Andersen, Bollerslev, Diebold, and Labys (2001), and Andersen, Bollerslev, Diebold, and Ebens (2001) show the empirical success of realized volatility for measuring and modeling underlying return variability. Barndorff-Nielsen and Shephard (2002a, 2002b) provide the theoretical foundation of using realized volatility as a proxy for the true underlying variability in returns based on the theory of quadratic variation. Subsequently, Andersen, Bollerslev, Diebold and Labys (2003) advance theoretical underpinnings linking the conditional covariance matrix and realized volatility. Realized volatility has clear advantages over alternatives since it incorporates information from higher frequency, it is a fully nonparametric method, and any measurement errors due to limitations on sampling frequency within a finite horizon are uncorrelated over time, as discussed in Andersen, Bollerslev, Diebold and Labys (2001, 2003).

In this paper, we model log realized volatility as composed of a long-run component that is common across all series, and a short-run, sectoral component. We find that there are substantial advantages in extracting volatility components. If volatility indeed has components, volatility proxies are characterized by large measurement error, which veils analysis of their fundamental information and relationship with the economy. For example, although Schwert (1989b) finds that stock market volatility is associated with the business cycle, there is little evidence of links between asset volatility and volatility of real economic activity when aggregating daily data into monthly realized volatilities, whereas there is a growing literature that models volatility as composed of multiple factors that finds substantial evidence of their linkages, see Ding and Granger (1996), Gallant, Hsu, and Tauchen (1999), Engle and Lee (1999), Alizadeh, Brandt, and Diebold (2002), Bollerslev and Zhou (2002), Chernov, Gallant, Ghysels, and Tauchen (2003), Chacko and Viceira (2003), Adrian and Rosenberg (2008), Engle, Ghysels, and Sohn (2008). In particular, Adrian and Rosenberg (2008) develop a three-factor ICAPM where factors are the total stock market volatility and its long-term and transitory components. They show that this approach is successful in modeling the cross sectional variation of expected returns and that the long-term component of volatility is strongly related with economic fundamentals.

This paper provides an extensive analysis of the predictive ability to economic activity of several measures of asset volatility, at the aggregate and industry-level stock market, and from the bond market. We provide analysis of the gains obtained from using the long term component of the volatility measures for linearly projecting future economic activity, as well as for forecasting business cycle turning points. The analysis is implemented both in-sample and out-of-sample. We find that volatility of asset returns helps predict future economic activity. We first analyze the predictive power of constructed volatility measures using linear predictive regressions for monthly industrial production growth and an economic factor extracted from four coincident macroeconomic series. We extract the long-run component of volatility that is common across all series, motivated by the ICAPM of Adrian and Rosenberg (2008). Combining information in the realized volatility series proves to be very useful in predicting both growth of industrial production and the economic factor as well as turning points of business cycles via nonlinear dynamic factor models. When we allow for nonlinear dynamics in the common factor of volatility and in the common factor of coincident macro variables, we observe that the estimated factors as well as their implied regime classifications are highly correlated with each other.

We also provide an out-of-sample real time analysis of the last five years of the sample using the nonlinear dynamic factor model of volatility. Given the unexpected severity of the recent 2007-2009 recession, this period offers an ideal environment to evaluate ex-ante predictive performance. The nonlinear long run component of volatility gives early signals of the upcoming recession, simultaneously with the first signs of distress in financial markets due to problems in the housing market, which made headlines in mid-2007. In addition, the model implied chronology is consistent with the crisis timeline in the subsequent period.

The rest of the paper is organized as follows. Next section explains construction of the volatility measures in detail. Section 3 describes the data sets used and provides an analysis of the macroeconomic and asset volatility relations in the context of dynamic factor models. Section 4 contains a comprehensive analysis of the predictive power of various volatility measures for economic activity using linear regressions, probit models, and Markov-switching dynamic factor models in-sample and out-of-sample. Section 5 concludes.

2 Volatility Measures

We construct three measures of realized volatility series: aggregate stock market volatility, aggregated industry level volatility, and bond market volatility. Let $r_{ms}$ denote the daily excess return over the risk free rate for the value-weighted market portfolio, where s denotes the trading days in a given month, indexed by . Then, the monthly realized market volatility, $R{VM}_t$ , is defined as follows

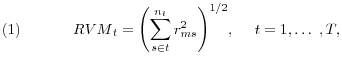
$\displaystyle \left(1\right)\ \ \ \ \ \ \ \ \ \ R{VM}_t={\left(\sum^{n_t}_{s\in t}{r^2_{ms}}\right)}^{1/2},\ \ \ \ t=1,\dots \ ,T,$

where denotes the number of trading days in month , and denotes the total number of months in the sample.⁷

Following Campbell, Lettau, Malkiel, and Xu (2001), we also consider a measure of industry level realized volatility, constructed from the difference between industry returns and the market return. Let $r_{is}$ denote the daily value-weighted return of all firms in industry . Defining $e_{is}=r_{is}-r_{ms}$ and aggregating across industries, we obtain the monthly industry realized volatility measure, :

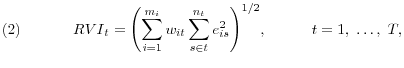
$\displaystyle \left(2\right)\ \ \ \ \ \ \ \ \ \ R{VI}_t={\left(\sum^{m_i}_{i=1}{w_{it}\sum^{n_t}_{s\in t}{e^2_{is}}}\right)}^{1/2},\ \ \ \ \ \ \ \ \ t=1,\ \dots ,\ T,$

where $w_{it}$ is the weight of industry in the market portfolio with respect to market capitalization, and denotes the total number of industries. This definition of volatility stands between the systemic volatility as measured by the volatility of the market portfolio, and the idiosyncratic firm level volatility. Campbell, Lettau, Malkiel, and Xu (2001) document strong correlation between this measure and GDP growth.

Finally, the third volatility measure is obtained from the Treasury bond market. Let denote the continuously compounded yield of the 10-year zero coupon T-bond. The daily bond return is given by $r_{bs}=10(y_{s-1}-y_s)$ . We then construct the bond market realized volatility measure, $R{VB}_t$ based on this daily return as follows

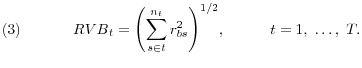
$\displaystyle \left(3\right)\ \ \ \ \ \ \ \ \ \ R{VB}_t={\left(\sum^{n_t}_{s\in t}{r^2_{bs}}\right)}^{1/2},\ \ \ \ \ \ \ \ \ t=1,\ \dots ,\ T.$

The realized volatility approach provides directly observable return volatility measures, which are fully nonparametric and incorporate the inherent information in the higher-frequency data. We use these properties to understand the extent of the relation between financial return volatility and aggregate economic activity.

3 Volatility and the Business Cycle

We use daily stock market and industry returns to calculate monthly realized volatilities, retrieved from Kenneth French's online Data Library. We consider 48 industries in our data set. The bond dataset is obtained from Gurkaynak, Sack, and Wright (2007). ⁸ The sample is from September 1971 to September 2009, mainly determined by the availability of the daily bond yield data. Our first goal is to understand the relation between economic activity and these realized volatility measures, which contain information on systematic movements in the stock and bond markets. We then explore whether these realized volatility series forecast economic activity in the following sections.

Figure 1 plots the natural logarithm of the three realized volatility measures as described in Section 2, with shaded areas representing recessions as dated by the NBER. The volatilities are individually very noisy. However, a slightly similar pattern can be observed, volatilities are generally higher during recessions and lower during expansions. The aggregated industry level stock volatility moves closely with the market volatility. Notice that both series increased considerably from mid-1990s to early 2000s, reflecting the great uncertainty surrounding the stock market boom and subsequent crash during this period. Interestingly, a very low volatility period followed, which lasted until the beginning of the recent financial crisis in 2007-2008. Bond market volatility generally coincides with the dynamics of the stock market volatility, with some exceptions. In terms of its level, the bond market volatility is lower in the 1970s, compared to the last three decades. Second, contrarily to the stock market, bond market volatility remained relatively low from the mid-1990 to the early 2000s.

The differences in the dynamics of the volatility measures suggest that a combination of the series could contain additional information on their relationship with the economy. However, we face two potential problems in this analysis. First, as observed in Figure 1, the volatility series are very noisy, which veils to some extent their relationship with the economy. Second, the volatility series are highly correlated with each other in the entire sample, and even more so when the sample is divided into recession or expansion phases. These two features make it difficult to study how the various volatility series are related to the economy. Therefore, to reduce noise and to aggregate information across volatility series in a formal way, we propose a common factor specification. A dynamic factor model is a signal-noise extractor that filters out idiosyncratic noise inherent to each series from common cyclical movement. Thus, this framework enables analysis of the common variation in the three realized volatility series. The proposed model is related to Adrian and Rosenberg's (2008) ICAPM, which decomposes return volatility into a relatively persistent long-term component and a transitory short-term component.

Let $Y_{it}$ denote the log of the $i^{{\rm th}}$ realized volatility series where for , for , and for . The dynamic factor model of volatility dynamics can be represented as follows:

$\displaystyle \left(4\right)\ \ \ \ \ \ \ \ \ Y_{it}={\lambda }_iVF_t+u_{it},\ \ \ \ \ u_{it}\ \sim \ NID\left(0,{\sigma }^2_{u_i}\right),$

$\displaystyle \left(5\right)\ \ \ \ \ \ \ \ \ VF_t=\alpha +{\phi}VF_{t-1}+{\epsilon}^v_t,\ \ \ \ \ \ \ {\epsilon}^v_t\ \sim \ NID\left(0,{\sigma }^2_v\right),$

where is the common volatility factor, $u_{it}$ denotes the idiosyncratic component and ${\lambda }_i$ denotes the factor loading for the $i^{{\rm th}}$ series. The factor loadings show to what extent each realized volatility series is affected by the common factor. The common factor is extracted as a single volatility measure from all three realized volatility series and is assumed to be uncorrelated with idiosyncratic terms at all leads and lags to ensure identification. The model is estimated using the Kalman filter, and the maximum likelihood estimates are reported in Table 1. The extracted volatility factor is highly persistent with an autoregressive coefficient estimate of around 0.92. All factor loadings are positive indicating positive correlation between the realized volatility measures and the extracted factor.

Figure 2 plots the extracted common volatility factor along with the NBER recessions. Notice how the dynamic factor model filters out the noise and yields a smooth variable that summarizes information common to all three realized volatility measures. This feature is important in relating financial volatility to macroeconomic dynamics. The common cyclical volatility in the aggregate and industry-level stock market and in the bond market shows a striking business cycle pattern and is closely related to NBER recessions: it starts rising in the middle of economic expansions, reaching a peak around recessions, subsequently falling during the first stages of economy recoveries. It then reaches a trough around the middle of expansions. The low volatility in the bond market in the early 1970s and in the late 1990s, when combined with the information of high uncertainty in the stock market, yields a common volatility factor that is more closely related to business cycle phases and more robust to outliers. The volatility factor still exhibits some spikes in two other periods that were not followed by recessions. The highest such increase takes place during the 1987 stock market crash. There is also an increase in volatility around 1998-1999 during which the U.S. economy experienced a mild slowdown associated with the effects of the 1997 Asian crisis, the 1998 Russian crisis, and the 1999 Brazilian and Argentinean currency crises. The common volatility in the stock and bond markets rose in 1998 and remained high during the 2001 recession and jobless recovery that lasted until 2003, signaling the high uncertainty surrounding this period.

Next, we compare the relationship of the volatility factor with a comprehensive measure of aggregate economic activity at the monthly frequency. We estimate a dynamic economic factor that summarizes information common to four coincident economic variables, as in Chauvet (1998). The macro variables used are 100 times the log first differences of seasonally adjusted monthly U.S. industrial production index (IP), real personal income less transfer payments (PILTP), real manufacturing and trade sales (MTS), and employees on non-agricultural payroll (PAYROLL). ⁹ These are the same four coincident series used in Chauvet (1998) and Chauvet and Piger (2008). These variables are used by the Conference Board to build its coincident indicator and by the NBER Business Cycle Dating Committee to date recessions.

Let $Z_{kt}$ be 100 times the log first difference of the observable macroeconomic variables where for IP, for PILTP, for MTS, and for PAYROLL. Then, the measurement equation, which links the observables variables and the unobservable factor, and the transition equation are given by:

$\displaystyle \left(6\right)\ \ \ \ \ \ \ \ \ Z_{kt}={\lambda }_kEF_t+u_{kt},$

$\displaystyle \left(7\right)\ \ \ \ \ \ \ \ \ EF_t=\alpha +{\phi}EF_{t-1}+{\epsilon}^e_t,\ \ \ \ \ \ \ {\epsilon}^e_t\ \sim \ NID\left(0,{\sigma }^2_e\right),$

$\displaystyle \left(8\right)\ \ \ \ \ \ \ \ \ u_{kt}={\psi }_ku_{k,t-1}+{\omega }_{kt},\ \ \ \ \ \ \ {\omega }_{kt}\ \sim \ NID\left(0,{\sigma }^2_{{\omega }_k}\right),$

where is the scalar common economic factor and $u_{kt}$ denotes the idiosyncratic component for the $k^{{\rm th}}$ series of the economic factor model.

Table 2 presents the maximum likelihood estimates of the macroeconomic model. The extracted economic factor is much less persistent, with an autoregressive parameter estimate of 0.57. The underlying economic series are positively correlated with the factor. Parameters estimates of all idiosyncratic components indicate significant idiosyncratic variation in each of the macroeconomic series.

Figure 3 plots the extracted economic factor and the volatility factor obtained from the dynamic factor models described above. The strong association between the two factors is striking. There is a negative relationship between the two series, with the volatility factor tending to rise when the economic factor falls, especially around NBER recessions. This suggests that the extracted factors that combine information in the individual series may provide useful information to the predictive relationship between financial volatility dynamics and the economy.

4 Predicting Economic Activity Using Financial Volatility

We now investigate whether the individual realized volatility series and the extracted factor representing common variation in the stock and bond markets contain useful information to forecast macroeconomic activity at the monthly frequency. First, we examine the marginal predictive content of the individual volatility series and of the volatility factor in predicting industrial production growth and the coincident indicator of the economy. Second, we use probability based models to determine if they anticipate the peaks and troughs of NBER-dated recessions. We first estimate probit models for each volatility series and for the dynamic volatility factor. We then estimate a Markov switching version of the factor model of realized volatilities. The estimated probabilities of high or low states are used in the analysis of the lead-lag relationship with NBER recessions.

The analysis is implemented for both full sample and out of sample prediction. The full sample runs from September 1971 to September 2009. The out-of-sample analysis is conducted by estimating all models from September 1971 to September 1999, and then recursively re-estimating each of them for the remaining 10 years.¹⁰ The forecasting performance is evaluated with respect to symmetric mean squared error (MSE) loss. To assess statistical significance of out-of-sample loss differences, we use Hansen's (2005) Superior Predictive Ability (SPA) test. In this framework, a number of alternative models are jointly compared to a benchmark where the null simply states that the best alternative is not better than the benchmark with respect to the selected loss function.

4.1 Evaluation of Point Forecasts

We first check whether the volatility measures help improve the predictions of a benchmark AR(1) model in the context of Granger causality tests. We consider cumulative forecast horizons of 1, 3, 6, and 12 months. In order to smooth out the raw realized volatility measures we take simple averages corresponding to the cumulative forecast horizon. No such averaging is implemented for the factor as it is a smooth measure by construction. Table 3 presents the results. In the case of IP growth the factor-based model dominates the benchmark model and leads to loss reductions of approximately 5% for the shortest and 7% for the longest horizon considered. The p-values from the Granger causality test indicate that these reductions in MSE when we consider the volatility factor as a predictor are highly statistically significant. In the case of EF we observe similar results. The factor model-based volatility measure is the best among the alternatives considered. The benchmark AR(1) model is rejected at 1% with the relative loss ranging from 95.6% ( to 93.1% . Notably, the other models that use plain realized volatility measures also have lower MSE relative to the AR(1) model, which is typically significant.

We now turn to an out-of sample evaluation of various predictive models. We consider benchmark specifications that use the first lag of a financial variable, known to predict economic activity, in addition to the lag of the predicted variable. The financial variables used are the 10 year minus 3-month Treasury yield spread (TERM), default premium given by Moody's seasoned Corporate Bond Yield (DEF), and return on the value weighted market portfolio (MKTR). Our alternative models include the first lag of a volatility measure. The models can be summarized as follows:

$\displaystyle \left(9\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M_1:\ \ \ \ \ \ \ \ \ g^h_t={\beta }^1_0+{\beta }^1_1g^h_{t-h}\ +{\gamma }^1x_{t-h}{+\varepsilon }^h_{1t},$

$\displaystyle \left(10\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M_i:\ \ \ \ \ \ \ \ \ g^h_t={\beta }^i_0+{\beta }^i_1g^h_{t-h}+{\gamma }^iY^h_{i-1,t-h}+{\varepsilon }^h_{it},\ \ \ \ \ i\in \left\{2,3,4\right\},$

$\displaystyle \left(11\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M_5:\ \ \ \ \ \ \ \ \ g^h_t={\beta }^5_0+{\beta }^5_jg^h_{t-h}+{\gamma }^5VF_{t-h}+{\varepsilon }^h_{5t},\$

where is the h-period cumulative growth in IP or EF from to , $x_t\in \{TERM,\ DEF,\ MKTR\}$ , $Y^h_{i,t}$ is the arithmetic average of the log of the $i^{{\rm th}}$ realized volatility series over the same forecasting period, and $h\in \{1,\ 3,\ 6,\ 12\}$ . The lag structure is set to ensure that there is no information overlap in the cumulative growth rates and averages.

Table 4 reports the out-of sample forecast comparison results for IP. When the benchmark model uses yield spread, the common factor based model, , stands out as the best performing model with statistically significant loss reductions for horizons up to 6 months as indicated by the SPA p-values. The out-of-sample loss associated with relative to the benchmark ranges from 88.6% () to 71.8 % (). When the benchmark model uses default premium, that includes information from the volatility factor leads to significant loss reductions for all horizons except for the shortest. On the other hand, when we use a benchmark that includes market return, we have a statistically significant loss reduction of 9.5% only at the one-month horizon. This result suggests that the volatility factor is most useful at the shortest horizon compared to the market return and performs equally well at longer horizons.

The economic factor provides more comprehensive information about the state of the economy at the monthly frequency by summarizing dynamics of the four coincident macro series as explained above. Table 5 reports the out-of sample forecast comparison results for this measure of economic activity. The factor based model, proves to be the best model with substantial loss reductions at all considered horizons with respect to the benchmarks using TERM and DEF. These reductions are significant at the 10% level for horizons up to 6 months when TERM is used in the benchmark model, whereas it is the case for horizons greater than or equal to three months under DEF. The benchmark that seems to be harder to beat is the one that incorporates information from market return. We obtain significant loss reductions only at the shortest one month horizon, as in the case of predicting IP growth.

To sum up, our results from both in-sample and out-of-sample forecasting analysis indicate that the lagged volatility factor helps predict economic growth with statistically significant gains over the benchmark models that utilize various popular financial indicators. Even though the individual volatility series can be helpful for predicting growth rate of real activity, the results strongly points out to the importance of combining information across individual volatility series.

4.2 Event Timing Analysis

In this sub-section we study the performance of the constructed realized volatility measures and the extracted volatility factor in event timing predictions. The recent financial crisis and economic recession have revived widespread interest in predicting business cycle turning points rather than just focusing on linear point forecasts. We conduct event timing analysis to predict business cycle phases by estimating both probit models and nonlinear Markov switching dynamic factor models. The probit models use as the dependent variable the NBER reference cycle that takes the value 0 for expansions and 1 for recessions. The Markov-switching models produce probabilities of recessions that can be used for regime classification. We compare their ability to predict NBER business cycle turning points. By comparing the frequencies of correctly identified business cycle phases, we assess the usefulness of the information provided by the realized volatility measures. The models are estimated in-sample and out-of-sample. The out-of-sample here also goes from October 1999 to September 2009.

4.2.1 Probit-based Predictions of Recessions

We consider various volatility measures and the alternative financial indicators as predictors in the context of a probit model. The recession probability predictions are generated as follows:

$\displaystyle (12)\ \ \ \ \ \ \ \ \ \ \ P{\rm (}{NBER}_t{\rm =1}\vert I_{t-h}{\rm\ )=}\Phi {\rm (}\beta {\rm '\ }X_{t-h}{\rm\ ),}$

where is the 0/1 dummy that equals to one (zero) during NBER recessions (expansions), $I_{t-h}$ denotes the information set available at time , $X_{t-h}$ is the vector composed of a constant and a lagged predictive variable, ${\rm\ }$ $\beta {\rm\ }$ is the vector of regression coefficients, $\Phi (.)$ is the Gaussian cumulative distribution function, and $h\in \{3,\ 6,\ 12,\ 18\}$ . Note that since we are predicting a categorical variable, the forecasts are simply -step ahead instead of being cumulative -period predictions.

Table 6 presents the sensitivity of the models, that is, the proportion of correct recession prediction for the full sample. We first convert model probabilities into binary series by using a cut-off equal to the sample mean. We then calculate the percentage of correctly identified recession phases with respect to the NBER classification. For the shortest horizon of 3 months, the volatility factor (VF) exhibits the highest percentage of correctly identified NBER recessions with 86%. For the 6 month horizon the market return (MKTR) is the variable that yields the most accurate recession predictions while it is the term premium (TERM) for longer horizons. The predictive power of the yield spread for recessions for longer forecast horizons has been widely documented in the literature, see Estrella and Hardouvelis (1991), and Estrella and Mishkin (1998) among others.

Table 7 reports the out-of-sample sensitivity for the different models. Once again, we find that the model using the volatility factor dominates for shorter horizons, achieving the highest proportion of correct recession predictions across the models, with an impressive rate of 93% for 3 months ahead. The model with the term premium (TERM) performs best for the longer horizons also out-of-sample.

4.2.2 Nonlinear Dynamic Factor Model-Based Predictions of Recessions

This sub-section considers nonlinear versions of the common dynamic factor models specified for financial volatility and economic activity described in section 4.1. In the factor volatility model, we allow for both the drift and variance of the common factor to switch across different regimes according to an unobservable Markov process. This characterization allows for potential time-varying and countercyclical volatility dynamics. We let the drift and variance switch between phases, without imposing any a priori assumption to restrict their values. The transition equation for the factor volatility (5) is now replaced with:

$\displaystyle \left(5'\right)\ \ \ \ \ \ \ \ \ VF_t={\alpha }_{S^v_t}+{\phi}VF_{t-1}+{\epsilon}^v_t,\ \ \ \ \ \ \ {\epsilon}^v_t\ \sim \ NID\left(0,{\sigma }^2_{S^v_t}\right),$

where ${\alpha }_{S^v_t}={\alpha }_0(1-S^v_t)+{\alpha }_1S^v_t$ and ${\sigma }^2_{S^v_t}={\sigma }^2_0(1-S^v_t)+{\sigma }^2_1S^v_t$ . is the state variable that governs the regimes for the volatility factor. This state variable takes values 0 or 1, according to a first order two-state Markov process, with transition probabilities given by $p^v_{ij}={\rm Pr}[S^v_t=j\vert S^v_{t-1}=i]$ where $i,j=0,\ 1$ . States 0 and 1 represent low and high volatility periods, respectively. The nonlinear dynamic factor model of the volatility measures is composed of equations (4) and (5´).

Similarly, in the context of the economic factor model, we allow the drift of the common factor to switch between recessions and expansions. The transition equation for the economic factor (7) is replaced with:

$\displaystyle \left(7'\right)\ \ \ \ \ \ \ \ \ EF_t={\alpha }_{S^e_t}+{\phi}EF_{t-1}+{\epsilon}^e_t,\ \ \ \ \ \ \ {\epsilon}^e_t\ \sim \ NID\left(0,{\sigma }^2_e\right),$

where ${\alpha }_{S^e_t}={\alpha }_0(1-S^e_t)+{\alpha }_1S^e_t$ , and is the state variable that drives dynamics of the economic factor with transition probabilities $p^e_{ij}={\rm Pr}[S^e_t=j\vert S^e_{t-1}=i]$ . States 0 and 1 are associated with low and high values of the economic factor, respectively. The dynamic factor economic model is now composed of the equations (6), (7´), and (8).

The models are estimated by numerical optimization. We first cast them in state space form and then combine a nonlinear discrete version of the Kalman filter with Hamilton's (1989) filter using Kim's (1994) approximate maximum likelihood method. This allows the estimation of the unobserved state vector and the Markov state probabilities using the observable data. A nonlinear optimization procedure is used to maximize the likelihood function, which is based on the probabilities of the Markov states. Predictions of the factors and the Markov probabilities are obtained from the filter.

Table 8 presents the maximum-likelihood estimates of the nonlinear common factor model of realized volatilities. The model distinguishes between two different levels of volatility, producing a classification of high versus low volatility regimes. All regime switching parameters are highly statistically significant. The intercept estimate for the level of volatility is around 0.24 in the high volatility regime, whereas it is around 0.15 in the low volatility regime. The standard deviation of the factor in the high volatility regime is around 0.2, whereas it is close to 0.07 in the low volatility regime. This indicates that the volatility of volatility is positively correlated with the level of volatility. Transition probability estimates reveal that the low volatility regime is more persistent than the high volatility regime, which is in line with the documented dynamics of financial volatility, e.g. Andersen, Bollerslev, Diebold, and Labys (2003). The factor loading of market realized volatility is normalized to one to provide a scale for the common factor. Note that this has no effect on the time series properties of the extracted factor. The other two realized volatility series are positively correlated with the common factor with statistically significant factor loadings.

Table 9 presents the maximum likelihood estimates of parameters and standard deviations of Markov-switching dynamic factor models of the real economy. The intercept of the economic factor during recessions is estimated to be around -1.27, whereas the one for expansions is around 0.82. Both parameters are statistically significant, supporting the presence of asymmetry in the mean behavior of the common economic factor. Expansions, characterized by positive growth, are more persistent than recessions, which are shorter and more abrupt. Factor loadings for all series are significant and positive indicating positive correlation with the factor. The autoregressive coefficients in the idiosyncratic components and error variances are also statistically significant for all series, indicating persistent sectoral dynamics.

Given that we are interested in predicting the beginning and end of recessions as depicted by the estimated probabilities, we need a decision rule to convert the probabilities produced by the nonlinear dynamic factor model into turning point dates. One approach, used by Hamilton (1989) among others, is to classify a turning point as occurring when the probabilities move from below 50% to above 50% or vice versa. This has an intuitive appeal as it separates times when an expansion state is more likely from those when a recession state is more likely. We apply the same rule to distinguish economic expansions and recessions as well as high volatility versus low volatility states. We then compare the chronology obtained from the volatility factor with that of the economic factor and with the NBER reference dates to analyze the lead-lag relationship between the economic states and the volatility states.

The smoothed probabilities from the economic and volatility models are plotted in Figure 4. The probabilities of recessions from the economic factor closely match the NBER business cycle classification, rising above 50% during recessions, and reaching values close to zero during expansions. Noticeably, the high volatility states obtained from the volatility factor are strongly correlated with NBER recessions and the economic model predictions. Each high volatility period is associated with economic recessions, with the exception of 1987 stock market crash. The volatility factor moves ahead of the economic factor and of most NBER recessions, giving early warning signals.

Table 10 reports the peak signals from the economic and realized volatility factors and the reference business cycle chronology from the NBER Business Cycle Committee.¹¹ The economic factor is on average coincident with recessions. On the other hand, the volatility factor leads all economic recessions. Notice that before the severe double-dip recession (1980-1981 to 1982), the probabilities of high volatility state increase, signaling the recession that started in January 1980 with a four month lead. Before the 1981-1982 recession, the probabilities of high volatility regime rise again ten months before the next peak, signaling the vulnerable state of the economy. Noticeably, starting from early 1998, the probabilities of high volatility regime rise above 50% and remain high until after the official ending of the 2001 recession. The increase in volatility is associated with the uncertainty surrounding the 1997 Asian crisis, the 1998 Russian crisis, and the 1999 Brazilian and the 1999-2001 Argentinean currency crises. Interestingly, the probabilities of high volatility regime also remained above 50% even after the 2001 recession had ended, reflecting the great uncertainty during the jobless recovery between 2002-2003. In fact, the weak economic activity during this period led most to believe that the recession had not ended. This was reflected on the NBER Business Cycle Dating Committee's decision to delay announcement that the recession had ended in 2001 until mid-2003. The results indicate that the common realized volatility factor has information about future economic activity and is therefore useful in anticipating beginnings of recessions. The nonlinear factor anticipates the beginning of the last recession with a five-month lead.

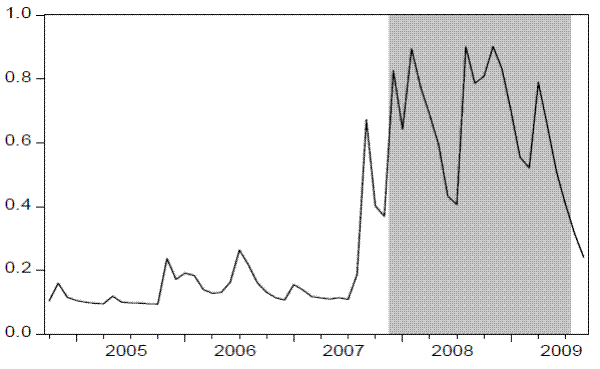
We also provide an out-of-sample real time analysis of the last five years of the sample using the nonlinear dynamic factor model of volatility and the nonlinear economic dynamic factor model. Given the unexpected severity of the recent 2007-2009 recession, this period offers an ideal environment to evaluate the performance of the extracted common volatility factor model in signaling the downturn. Figure 5 plots the out-of-sample probabilities of high volatility state from 2004:10 to 2009:9. Around mid-2007 there is a steep increase in the probabilities. This is when first signs of distress in the financial market due to housing market problems made headlines. The probabilities remained high until the end of the sample and their behavior closely match periods of financial turmoil during 2008.

5 Conclusion

We analyze the predictive value of various volatility measures for economic activity by considering stock and bond market dynamics. Inspired by recent developments in the financial volatility literature, we construct measures of realized volatility from the market portfolio and industry portfolios from the stock market and from the bond market. Monthly measures of realized volatility are obtained by aggregating information in the daily series. This method provides observable asset return volatility series, which allows assessment of their predictive power and relationship with the economy.

We model log realized volatility as composed of a long-run component that is common across all series and transitory sectoral components. The dynamic factor framework extracts a long-run component that represents common information in the realized volatility series as a single smoothed factor, and separates out measurement errors inherent to each series. We find that there are substantial advantages in extracting volatility components. The realized volatilities - especially its long run component - help predict industrial production growth and a coincident indicator of the business cycle. This measure performs remarkably well compared to other popular financial variables, especially over short horizons.

The recent financial crisis and economic recession have revived widespread interest in predicting business cycle turning points. We conduct event timing analysis to predict business cycle phases by estimating both probit models and nonlinear Markov switching dynamic factor models. When we allow for asymmetric behavior of the long run component of realized volatility series, the volatility factor consistently enters into a high volatility state prior to all economic recessions. The in-sample and out of sample turning point analyses reveal that the volatility factor consistently leads business cycle peaks and performs remarkably well in anticipating the recent 2007-2009 recession.

References

Adrian, T. and J. Rosenberg, 2008, "Stock Returns and Volatility: Pricing the Long-Run and Short-Run Components of Market Risk," The Journal of Finance, 63, 2997-3030.

Alizadeh, S., M.W. Brandt, and F.X. Diebold, 2002, "Range-Based Estimation of Stochastic Volatility Models," The Journal of Finance, 57, 1047-1091.

Andersen, T.G., T. Bollerslev, F.X. Diebold and H. Ebens, 2001, "The Distribution of Realized Stock Return Volatility," Journal of Financial Economics, 61, 43-76.

Andersen, T.G., T. Bollerslev, F.X. Diebold and P. Labys, 2001, "The Distribution of Realized Exchange Rate Volatility," Journal of the American Statistical Association, 96, 42-55.

Andersen, T. G., T. Bollerslev, F.X. Diebold and P. Labys, 2003, "Modeling and Forecasting Realized Volatility," Econometrica, 71, 579-625.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and J. Wu, 2005, "A Framework for Exploring the Macroeconomic Determinants of Systematic Risk," American Economic Review, 95, 398-404.

Andreou, E., E. Ghysels, and A. Kourtellos, 2010, "Should Macroeconomic Forecasters Use Daily Financial Data and How?" Working Paper, Duke University.

Andreou, E., D.R. Osborn, and M. Sensier, 2000, "A Comparison of the Statistical Properties of Financial Variables in the USA, UK and Germany over the Business Cycle," The Manchester School, 68, 396-418.

Basak, S. and D. Cuoco, 1998, "An Equilibrium Model with Restricted Stock Market Participation," Review of Financial Studies, 11, 309-341.

Barndorff-Nielsen, O.E. and N. Shephard, 2002a, "Econometric Analysis of Realised Volatility and its Use in Estimating Stochastic Volatility Models", Journal of the Royal Statistical Society, Series B, 64, 253-280.

Barndorff-Nielsen, O.E. and N. Shephard, 2002b, "Estimating Quadratic Variation Using Realised Variance", Journal of Applied Econometrics, 17, 457-477.

Bernanke, B.S., M. Gertler, and S. Gilchrist, 1999, "The Financial Accelerator in a Quantitative Business Cycle Framework," in J.B. Taylor and M. Woodford (Eds.): Handbook of Macroeconomics, Vol. 1C, 1341-1393. Elsevier.

Bloom, N., 2009, "The Impact of Uncertainty Shocks," Econometrica, 77, 623-685.

Bollerslev, T., and H. Zhou, 2002, "Estimating Stochastic Volatility Diffusion using Conditional Moments of Integrated Volatility," Journal of Econometrics, 109, 33-65.

Campbell., J., M. Lettau, B.G. Malkiel, and Y. Xu, 2001, "Have Individual Stocks Become More Volatile? An Empirical Exploration of Idiosyncratic Risk," The Journal of Finance, 56, 1-44.

Campbell, J.Y. and J. Cochrane, 1999, "By Force of Habit: A Consumption-based Explanation of Aggregate Stock Market behavior," Journal of Political Economy, 107, 205-251.

Chacko, G., and L. Viceira, 2003, "Spectral GMM estimation of Continuous-Time Processes," Journal of Econometrics 116, 259-292.

Chauvet, M. 1998, "An Econometric Characterization of Business Cycle Dynamics with Factor Structure and Regime Switching," International Economic Review 39, 969-996.

Chauvet, M., 1998/1999, "Stock Market Fluctuations and the Business Cycle," Journal of Economic and Social Measurement, 25, 235-258.

Chauvet, M. and S. Potter, 2000, "Coincident and Leading Indicators of the Stock Market," Journal of Empirical Finance, 7, 87-111.

Chauvet, M. and S. Potter, 2001, "Nonlinear Risk," Macroeconomic Dynamics, 5, 621-646.

Chauvet, M. and J. Piger, 2008, "A Comparison of the Real-Time Performance of Business Cycle Dating Methods," Journal of Business Economics and Statistics, 26, 42-49.

Chernov, M., A.R. Gallant, E. Ghysels, and G. Tauchen, 2003, Alternative Models for Stock Price Dynamics, Journal of Econometrics, 116, 225-257.

David, A., and P. Veronesi, 2009, Inflation and Earnings Uncertainty and Volatility Forecasts, Working Paper.

Ding, Z. and C.W. Granger, 1996, Volatility Persistence of Speculative Returns: A new approach, Journal of Econometrics, 73, 185-215.

Engle, R.F., E. Ghysels, and B. Sohn, 2008, "On the Economic Sources of Stock Market Volatility," mimeo, New York University.

Engle, R.F. and J.G. Rangel, 2008, "The Spline GARCH Model for Low Frequency Volatility and its Macroeconomic Causes," Review of Financial Studies, 21, 1187-1222.

Engle, R.F. and G.G.J. Lee, 1999, "A Permanent and Transitory Component Model of Stock Return Volatility," in R.F. Engle and H. White (eds.), Cointegration, Causality, and Forecasting: A Festschrift in Honor of Clive W.J. Granger, 475-497. Oxford, UK: Oxford University Press.

Estrella, A. and G. Hardouvelis, 1991, "The Term Structure as a Predictor of Real Economic Activity," The Journal of Finance, 46, 555-576.

Estrella, A. and F.S. Mishkin, 1998, "Predicting U.S. recessions: Financial Variables as Leading Indicators," The Review of Economics and Statistics, 80, 45-61.

Fama, E.F. and K.R. French, 1989, "Business Conditions and Expected Returns on Stock and Bonds," Journal of Financial Economics, 25, 23-49.

Ferson, W.E. and C.R. Harvey, 1991, The Variation of Economic Risk Premiums, Journal of Political Economy, 99, 385-415.

Fornari, F. and A. Mele, 2009, "Financial Volatility and Economic Activity," mimeo, London School of Economics.

French, K.R., G.W. Schwert, and R.F. Stambaugh, 1987, "Expected Stock Returns and Volatility," Journal of Financial Economics, 19, 3-29.

Gallant, R. C.-T. Hsu, and G. Tauchen, 1999, "Using Daily Range Data to Calibrate Volatility Diffusions and Extract the Forward Integrated Variance," Review of Economics and Statistics, 81, 617-631.

Gurkaynak, R.S., B. Sack, and J.H. Wright, 2007, "The U.S. Treasury Yield Curve: 1961 to the Present," Journal of Monetary Economics, 24, 2291-2304.

Hamilton, J.D., 1989, "A New Approach to the Economic Analysis of Nonstationary Time Series and Business Cycles," Econometrica, 57, 357-384.

Hamilton, J.D., and G. Lin, 1996, "Stock Market Volatility and the Business Cycle," Journal of Applied Econometrics, 11, 574-593.

Hansen, P.R., 2005, "A Test for Superior Predictive Ability," Journal of Business and Economic Statistics, 23(4), 365-380.

Kim, C.-J., 1994, "Dynamic Linear Models with Markov-Switching," Journal of Econometrics, 60, 1-22.

Maheu, J.M. and T.H. McCurdy, 2000, "Identifying Bull and Bear Markets in Stock Returns," Journal of Business and Economic Statistics, 18, 100-112.

Mele, A., 2007, "Asymmetric Stock Market Volatility and the Cyclical Behavior of Expected Returns," Journal of Financial Economics, 86, 446-478.

Officer, R.R., 1973, "The Variability of the Market Factor of the NYSE," Journal of Business, 46(3), 434-453.

Perez-Quiros, G., Timmermann A., 1995, "Variations in the Mean and Volatility of Stock Returns around Turning Points of the Business Cycle," In: Forecasting Volatility in the Financial Markets, Knight J., Satchell S. (eds.). Butterworth-Heinemann: Oxford.

Poterba, J.M. and L. Summers, 1986, "The Persistence of Volatility and Stock Market Fluctuations," The American Economic Review, 76, 1142-1151.

Senyuz, Z., 2011, "Factor Analysis of Permanent and Transitory Components of U.S. Economy and the Stock Market," Journal of Applied Econometrics, 26, 975-998.

Schwert, G.W., 1989a, "Business Cycles, Financial Crises and Stock Volatility," Carnegie-Rochester Conference Series on Public Policy, 31, 83-125.

Schwert, G.W., 1989b, "Why Does Stock Market Volatility Change Over Time?", The Journal of Finance, 44, 1115-1153.

Whitelaw, R., 1994, "Time Variations and Covariations in the Expectation and Volatility of Stock Market Return," The Journal of Finance, 49, 515-541.

Table 1: Maximum Likelihood Estimates of the Dynamic Volatility Factor Model

Parameter	Estimate	(Standard Error)
$\alpha$	0.909	0.19
$\phi$	0.917	0.02
${\lambda }_{{\rm 1}}$	0.127	0.01
${\lambda }_{{\rm 2}}$	0.118	0.01
${\lambda }_{{\rm 3}}$	0.082	0.01
${\sigma }_{u_1}$	0.337	0.01
${\sigma }_{u_2}$	0.144	0.01
${\sigma }_{u_3}$	0.488	0.02
Log-L	832.01

The monthly sample runs from September 1971 to September 2009. Asymptotic standard errors in parentheses correspond to the diagonal elements of the inverse hessian obtained through numerical calculation. The variance of the common factor ( ${\sigma }^2_v$ ) is set to one for identification.

Table 2: Maximum Likelihood Estimates of the Dynamic Economic Factor Model

Parameter	Estimate	Parameter	Estimate
$\alpha$	0.224	${\psi }_2$	-0.166
$\alpha$ SE	(0.06)	${\psi }_2$ SE	(0.05)
$\phi$	0.574	${\psi }_3$	-0.320
$\phi$ SE	(0.06)	${\psi }_3$ SE	(0.05)
${\lambda }_1$	0.449	${\psi }_4$	0.915
${\lambda }_1$ SE	(0.03)	${\psi }_4$ SE	(0.05)
${\lambda }_2$	0.237	${\sigma }_{{\omega }_1}$	0.519
${\lambda }_2$ SE	(0.02)	${\sigma }_{{\omega }_1}$ SE	(0.02)
${\lambda }_3$	0.425	${\sigma }_{{\omega }_2}$	0.561
${\lambda }_3$ SE	(0.03)	${\sigma }_{{\omega }_2}$ SE	(0.02)
${\lambda }_4$	0.152	${\sigma }_{{\omega }_3}$	0.839
${\lambda }_4$ SE	(0.01)	${\sigma }_{{\omega }_3}$ SE	(0.03)
${\psi }_1$	-0.194	${\sigma }_{{\omega }_4}$	0.519
${\psi }_1$ SE	(0.06)	${\sigma }_{{\omega }_4}$ SE	(0.01)
Log-L	495.89

The monthly sample runs from September 1971 to September 2009. Asymptotic standard errors in parentheses correspond to the diagonal elements of the inverse hessian obtained through numerical calculation. The variance of the common economic factor ( ${\sigma }^2_e$ ) is set to one for identification in each model.

Table 3: Full Sample Evaluation of the Predictive Ability of Volatility Measures for Industrial Production

	IP Growth: Best Predictor	IP Growth: Relative Loss	IP Growth: GC p-value	EF: Best Predictor	EF: Relative Loss	EF: GC p-value
1	VF	94.9%	1.4E-06	VF	95.6%	7.4-E06
3	VF	93.1%	2.5E-08	VF	94.0%	2.0E-07
6	VF	92.3%	5.3E-09	VF	93.0%	2.2E-08
12	VF	92.9%	2.9-E08	VF	93.1%	5.3E-08

The monthly sample runs from September 1971 to September 2009. denotes cumulative forecast horizon in months. Log realized volatilities of stock market (RVM), aggregated industry portfolios (RVI), and bond market (RVB) and their common factor (VF) are the set of predictors augmenting the AR(1) models for Industrial Production (IP) growth and Economic Factor (EF). GC p-value is the asymptotic p-value from the Granger causality test.

Table 4: Out of Sample Forecast Evaluation of Predictive Regressions for Industrial Production
	TERM: Best Model	TERM: Relative Loss	TERM: SPA p-value	DEF: Best Model	DEF: Relative Loss	DEF: SPA p-value	MKTR: Best Model	MKTR: Relative Loss	MKTR: SPA p-value
1		88.6%	0.078		97.4%	0.358		90.5%	0.080
3		78.5%	0.098		84.5%	0.074		100.0%	0.570
6		71.8%	0.072		79.0%	0.058		99.1%	0.572
12		85.6%	0.248		87.7%	0.088		96.6%	0.526

The estimation period is from September 1971 to September 1999. The out of sample period consists of the remaining 10 years in the sample, from October 1999 to September 2009. denotes cumulative forecast horizon in months. $M_{{\rm 1}}$ denotes the benchmark predictive regression that use the first lag of term spread (TERM), default premium (DEF) or market return (MKTR) in addition to the first lag of IP growth. Models $M_{{\rm 2}}-M_5$ include the first lag of the realized volatility-based predictors in addition to lagged IP growth. Relative minimum loss and Hansen's superior predictive ability (stocktickerSPA) p-values are reported under MSE loss.

Table 5: Out of Sample Forecast Evaluation of Predictive Regressions for the Economic Factor
	TERM: Best Model	TERM: Relative Loss	TERM: SPA p-value	DEF: Best Model	DEF: Relative Loss	DEF: SPA p-value	MKTR: Best Model	MKTR: Relative Loss	MKTR: SPA p-value
1		76.9%	0.056		90.3%	0.310		85.9%	0.076
3		72.3%	0.058		81.6%	0.066		100%	0.560
6		69.6%	0.042		78.0%	0.046		100%	0.632
12		85.9%	0.250		89.5%	0.082		99.3%	0.484

Table 6: Full Sample Evaluation of Probit Predictions for NBER Recessions

Predictor
RVM	69.23	67.95	55.13	69.57
RVI	79.49	65.38	56.41	71.01
RVB	62.82	52.56	55.13	52.17
VF	82.05	70.51	56.41	44.93
MKTR	69.23	76.92	41.03	53.62
TERM	64.10	74.36	84.62	85.51
DEF	52.56	42.31	44.87	52.17

This table reports the percentage of correctly identified NBER recessions. The sample is from September 1971 to September 2009. We assess predictive power by comparing probit probabilities with NBER recessions. denotes forecast horizon in months. The predictors we use are realized volatilities of stock market (RVM), aggregated industry portfolios (RVI), and bond market (RVB), common long-run component of volatility (VF), market return (MKTR), term spread (TERM), and default premium (DEF).

Table 7: Out-of-Sample Evaluation of Probit Predictions for NBER Recessions

Predictor
RVM	82.14	78.57	35.71	0.00
RVI	89.29	75.00	0.00	39.29
RVB	71.43	39.29	0.00	46.43
VF	92.86	82.14	57.14	32.14
MKTR	75.00	82.14	7.14	0.00
TERM	28.57	46.43	75.00	82.14
DEF	53.57	39.29	0.00	0.00

This table reports the percentage of correctly identified NBER recessions. The estimation period is from September 1971 to September 1999. The out of sample evaluation period consists of the remaining 10 years in the sample. We assess predictive power by comparing probit probabilities with NBER recessions. denotes forecast horizon in months. The predictors we use are realized volatilities of stock market (RVM), aggregated industry portfolios (RVI), and bond market (RVB), common long-run component of volatility (VF), market return (MKTR), term spread (TERM), and default premium (DEF).

Table 8: Maximum Likelihood Estimates of the Nonlinear Dynamic Factor Volatility Model

Parameter	Estimate	Parameter	Estimate
${\alpha }_1$	0.239	${\sigma }_1$	0.191
${\alpha }_1$ SE	(0.06)	${\sigma }_1$ SE	(0.03)
${\alpha }_0$	0.146	${\sigma }_0$	0.072
${\alpha }_0$ SE	(0.04)	${\sigma }_0$ SE	(0.01)
$p_{11}$	0.915	${\sigma }_{u_1}$	0.332
$p_{11}$ SE	(0.04)	${\sigma }_{u_1}$ SE	(0.01)
$p_{00}$	0.965	${\sigma }_{u_2}$	0.145
$p_{00}$ SE	(0.02)	${\sigma }_{u_2}$ SE	(0.01)
$\phi$	0.874	${\sigma }_{u_3}$	0.489
$\phi$ SE	(0.03)	${\sigma }_{u_3}$ SE	(0.02)
${\lambda }_2$	0.925
${\lambda }_2$ SE	(0.01)
${\lambda }_3$	0.642
${\lambda }_3$ SE	(0.02)
Log-L	851.36

The monthly sample runs from September 1971 to September 2009. Asymptotic standard errors in parentheses correspond to the diagonal elements of the inverse hessian obtained through numerical calculation. The factor loading of aggregate stock market volatility ( ${\lambda }_1$ ) is normalized to one for identification.

Table 9: Maximum Likelihood Estimates of the Nonlinear Dynamic Economic Factor Model

Parameter	Estimate	Parameter	Estimate
${\alpha }_1$	-1.273	${\psi }_1$	-0.160
${\alpha }_1$ SE	0..32	${\psi }_1$ SE	(0.06)
${\alpha }_0$	0.815	${\psi }_2$	-0.168
${\alpha }_0$ SE	0.14	${\psi }_2$ SE	0.05
$p_{11}$	0.895	${\psi }_3$	-0.300
$p_{11}$ SE	0.05	${\psi }_3$ SE	0.05
$p_{00}$	0.981	${\psi }_4$	0.949
$p_{00}$ SE	(0.01)	${\psi }_4$ SE	(0.02)
$\phi$	0.189	${\sigma }_{{\omega }_1}$	0.539
$\phi$ SE	0.07	${\sigma }_{{\omega }_1}$ SE	(0.02)
${\lambda }_1$	0.389	${\sigma }_{{\omega }_2}$	0.564
${\lambda }_1$ SE	(0.03)	${\sigma }_{{\omega }_2}$ SE	(0.02)
${\lambda }_2$	0.209	${\sigma }_{{\omega }_3}$	0.855
${\lambda }_2$ SE	(0.02)	${\sigma }_{{\omega }_3}$ SE	(0.03)
${\lambda }_3$	0.370	${\sigma }_{{\omega }_4}$	(0.03)8
${\lambda }_3$ SE	(0.03)	${\sigma }_{{\omega }_4}$ SE	(0.01)
${\lambda }_4$	0.130
${\lambda }_4$ SE	(0.01)
Log-L	517.26

The sample runs from 1971:9 to 2009:9. Asymptotic standard errors in parentheses correspond to the diagonal elements of the inverse hessian obtained through numerical calculation. The variance of the common factor ( ${\sigma }^2_e$ ) is set to one for identification in each model.

Table 10: Cycle Turning Point Signals of the Volatility Factor

NBER peaks	${\rm VF}$	${\rm EF}$ peaks	${\rm VF}$
1973:11	-2 -52	1974:04	-7
1980:01	-4 -17	1980:03	-6
1981:07	-10	1981:09	-12
1990:07	0	1990:07	0
2001:03	-35	2001:01	-33
2007:12	-5	2008:02	-8

The minus sign refers to the lead in which the extracted volatility factor (VF) anticipates the recession dates. EF refers to the economic factor.

Figure 1: Logarithm of Realized Volatility Measures and NBER dated Recessions

Figure 1: Logarithm of Realized Volatility Measures and NBER dated Recessions. See link below for figure data.

Figure 1 Data

Figure 2: Common Linear Realized Volatility Factor and NBER Recessions

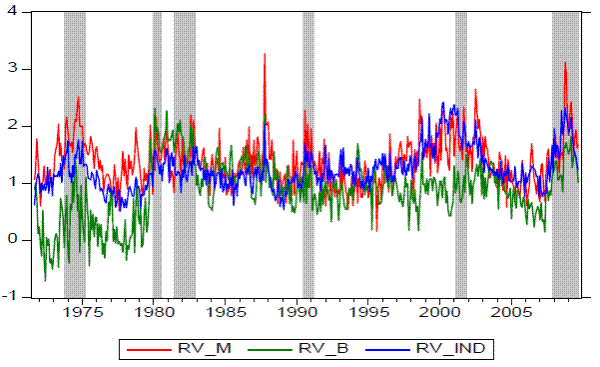
Figure 2: Common Linear Realized Volatility Factor and NBER Recessions. See link below for figure data.

Figure 2 Data

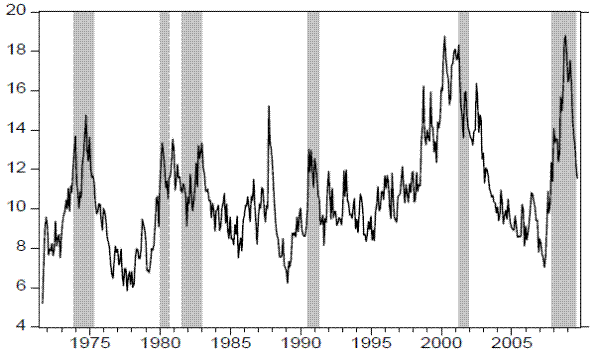
Figure 3: Common Volatility Factor, Economic Factor, and NBER Recessions

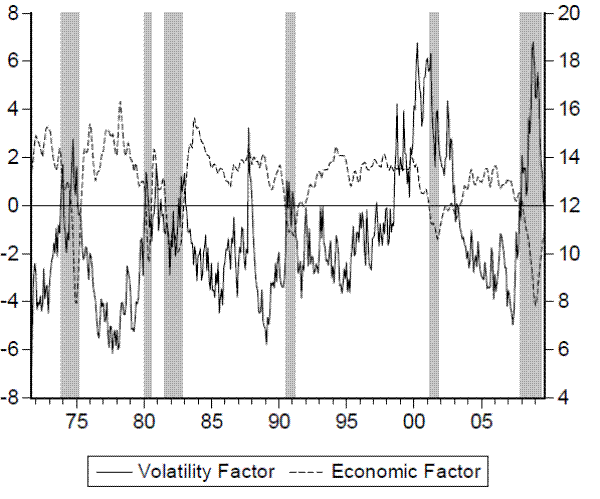
Figure 3: Common Volatility Factor, Economic Factor, and NBER Recessions. See link below for figure data.

Figure 3 Data

Figure 4: Smoothed Probabilities of the Volatility Factor (--) and of the Economic Factor (), and NBER Recessions (Shaded Areas)

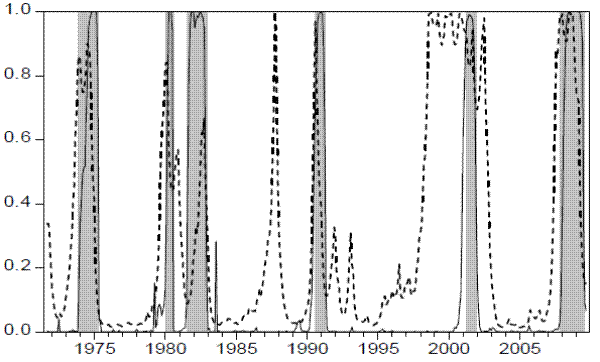
Figure 4: Smoothed Probabilities of the Volatility Factor (--) and of the Economic Factor (--), and NBER Recessions (Shaded Areas). See link below for figure data.

Figure 4 Data

Figure 5: Out of sample Recursive Predictive Probabilities of High Volatility State

Figure 5: Out of sample Recursive Predictive Probabilities of High Volatility State. See link below for figure data.

Figure 5 Data

Footnotes

* We would like to thank participants of the Applied Time Series Workshop at the Federal Reserve Bank of St. Louis 2011, European Central Bank Workshop on the Role of Nonlinear Methods in Empirical Macroeconomics and Forecasting 2011, 19th Annual Symposium of the Society for Nonlinear Dynamics and Econometrics, Conference on Real-Time Data Analysis at the Federal Reserve Bank of Philadelphia/CIRANO 2010, International Symposium on Forecasting 2010, Joint Statistical Meetings 2010, and seminar participants at the Federal Reserve Board, Cornerstone Research, Indiana University, and The University of Queensland for useful comments. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, its staff or any other person associated with the Federal Reserve System. Return to Text

1. Department of Economics, University of California, Riverside. E-mail: [email protected] Return to Text

2. Federal Reserve Board, Division of Monetary Affairs. E-mail: [email protected]. Return to Text

3. Federal Reserve Board, Division of Monetary Affairs, 20th and C Streets NW, Washington, DC 20551, Phone: +1 202 973 7302 E-mail: [email protected] (Corresponding author). Return to Text

4. See for example Officer (1973), Fama and French (1989), Schwert (1989b), Ferson and Harvey (1991), Whitelaw (1994), Perez-Quiros and Timmermann (1995), Hamilton and Lin (1996), Chauvet (1998/1999), Chauvet and Potter (2000, 2001), Maheu and McCurdy (2000), and Senyuz (2011). Return to Text

5. An alternative approach is to handle various sampling frequencies using the MIDAS regressions as in Andreou, Ghysels, and Kourtellos (2010), who focus on the information content of mostly the first moment of financial return series to predict inflation and real economic activity. Return to Text

6. See survey by Andersen, Bollerslev, Diebold, and Wu (2005). Return to Text

7. A realized volatility measure taking into account the first order autocorrelation in daily returns can be calculated similarly. We consider this alternative in our calculations and find that the results obtained are qualitatively similar across these measures. Return to Text

8. For a complete list of the industries and classification procedures refer to Kennett French's data library http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html. Gurkaynak, Sack, and Wright (2007) dataset can be downloaded from the Board of Governors of the Federal Reserve System at http://www.federalreserve.gov/pubs/feds/2006/index.html. Return to Text

9. PILTP and MTS are obtained from the Bureau of Economic Analysis, and PAYROLL from the Bureau of Labor Statistics. Return to Text

10. We have also implemented fixed and rolling schemes as well, and the results are qualitatively similar. Return to Text

11. Note that these signals are based on the smoothed probabilities of recession obtained from a sample that excludes recessions in the late 1950s and in 1960s. This explains some differences in the peak dates compared to Chauvet and Hamilton (2006) and in Chauvet and Piger (2008). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text