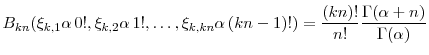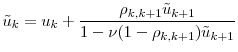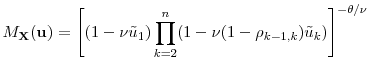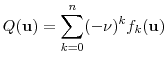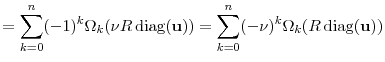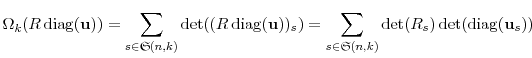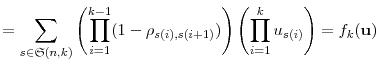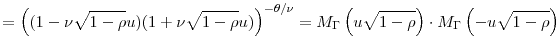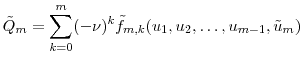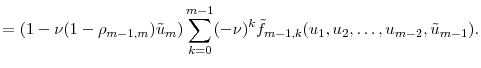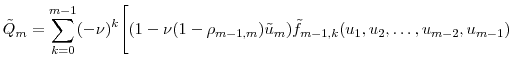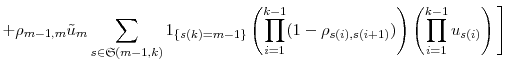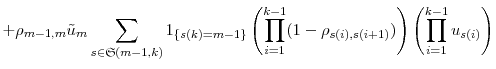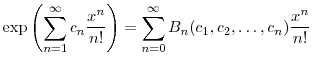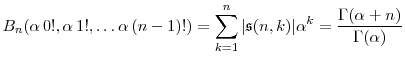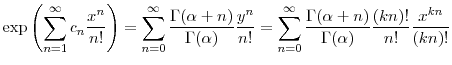Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-12 Screen Reader version ^♣

On the Distribution of a Discrete Sample Path of a Square-root Diffusion*

Michael B. Gordy

Federal Reserve Board

March 1, 2012

Keywords: Square-root diffusion, CIR process, multivariate gamma distribution, difference of gamma variates, Krishnamoorthy-Parthasarathy distribution, Kibble-Moran distribution, Bell polynomials

Abstract:

We derive the multivariate moment generating function for the stationary distribution of a discrete sample path of

observations of a square-root diffusion (CIR) process,

. The form of the mgf establishes that the stationary joint distribution of $(X(t_1),\ldots,X(t_n))$ for any fixed vector of observation times $t_1,\ldots,t_n$ is a Krishnamoorthy-Parthasarathy multivariate gamma distribution. As a corollary, we obtain the mgf for the increment $X(t+\delta)-X(t)$ , and show that the increment is equivalent in distribution to a scaled difference of two independent draws from a gamma distribution. Simple closed-form solutions for the moments of the increments are given.

JEL Classification: C46, C58

Let follow the Feller (1951) square-root diffusion process with stochastic differential equation

$\displaystyle dX_t = \kappa(\theta-X_t)dt + \sigma\sqrt{X_t}dW_t$

(1)

where

is a Brownian motion. We assume that $\kappa>0$ , $\theta>0$ and $\sigma>0$ . This process is widely used in economics and finance, especially in modeling interest rates and corporate credit risk, where it is usually known as the CIR process after Cox, Ingersoll and Ross (1985). In this paper, we derive the moment generating function for the stationary multivariate distribution of a discrete sample path of this process.

Let $\ensuremath{\mathbf{X}}\equiv (X(t_1),\ldots,X(t_n))$ be a discrete sample path for a given vector of ordered observation times $t_1< t_2< \ldots < t_n$ . Let $\ensuremath{\mathbf{u}}$ denote the vector of auxilliary variables $u_1,\ldots,u_n$ and let $\ensuremath{\operatorname{diag}(\ensuremath{\mathbf{u}})}$ be the diagonal matrix with diagonal entries $u_1,\ldots,u_n$ . Let be the symmetric $n\times n$ matrix with elements $R[i,j]=\exp(-(\kappa/2)\vert t_i-t_j\vert)$ . $\ensuremath{{\cal I}_n}$ is the $n\times n$ identity matrix. Define the scale parameter $\ensuremath{\nu}=\sigma^2/(2\kappa)$ . The central result of this paper is

Theorem 1
The mgf of $(X(t_1),\ldots,X(t_n))$ under stationarity is

$\displaystyle M_\ensuremath{\mathbf{X}}(\ensuremath{\mathbf{u}})=\ensuremath{{\operatorname E}\left\lbrack \exp(\ensuremath{\langle{\ensuremath{\mathbf{u}},\ensuremath{\mathbf{X}}}\rangle})\right\rbrack} =\det(\ensuremath{{\cal I}_n}-\ensuremath{\nu}R\ensuremath{\operatorname{diag}(\ensuremath{\mathbf{u}})})^{-\theta/\ensuremath{\nu}}$

The proof is set out in Section 1.

The distribution of $\ensuremath{\mathbf{X}}$ is a special case of the broader class of Krishnamoorthy and Parthasarathy (1951) multivariate gamma distributions with mgf of the form $\det(\ensuremath{{\cal I}_n}- R\ensuremath{\operatorname{diag}(\ensuremath{\mathbf{u}})})^{-\alpha}$ for nonsingular and $\alpha>0$ (see also Kotz et al., 2000, §48.3.3). Series solutions for the density and cumulative distribution functions are given by Royen (1994) for the case in which the inverse of is tridiagonal (see also Kotz et al., 2000, §48.3.6), which applies for our matrix . These series solutions are computationally practical only for low dimension .

The stationary square-root process has exponential decay in the autocorrelation function (Cont and Tankov, 2004, §15.1.2), so for pairs in $\{1,\ldots,n\}^2$ , the correlation $% latex2html id marker 2752 $ \operatorname{corr}(X(t_i),X(t_j))$$ is given by

$\displaystyle \rho_{i,j}=\exp(-\kappa\vert t_i-t_j\vert) =R[i,j]^2.$

From this relationship, the matrix

is known as the accompanying correlation matrix.

In the bivariate case, the mgf has a simple form

Corollary 1
The mgf of $(X(t),X(t+\delta))$ under stationarity is

$\displaystyle M_\ensuremath{\mathbf{X}}(u_1,u_2)=\ensuremath{{\operatorname E}\left\lbrack \exp(u_1X(t)+u_2X(t+\delta))\right\rbrack} =((1-\ensuremath{\nu}u_1)(1-\ensuremath{\nu}u_2) -\rho u_1u_2)^{-\theta/\ensuremath{\nu}}$

where $\rho=\exp(-\kappa\delta)$ .

This is the Kibble-Moran bivariate gamma distribution (see Kotz et al., 2000, §48.2.3). In Section 2, we use this corollary to study the stationary distribution of the increment $X(t+\delta)-X(t)$ for fixed time-step $\delta$ . We show that this increment is equivalent in distribution to a scaled difference between two independent gamma variates, and provide a simple closed-form solution for the moments of this distribution. Applications are discussed in the concluding section.

1 Moment generating function

It is well known that the transition distribution for $X(t+\delta)$ given is noncentral chi-squared.¹ Letting denote the conditional mgf for $X(t+\delta)$ given , we have

$\displaystyle M_c(u;\delta,x)$	$\displaystyle =\ensuremath{{\operatorname E}\left\lbrack \exp(uX(t+\delta))\vert X(t)=x\right\rbrack}$	(2)
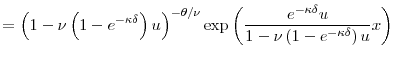	$\displaystyle = \left(1-\ensuremath{\nu}\left(1-e^{-\kappa\delta}\right)u\right)^{-\theta/\ensuremath{\nu}} \exp\left(\frac{e^{-\kappa\delta}u} {1-\ensuremath{\nu}\left(1-e^{-\kappa\delta}\right)u}x\right)$

As the square-root diffusion is a Markov process, we have

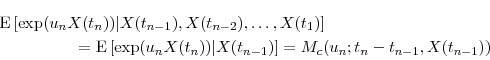
$\begin{multline*} \ensuremath{{\operatorname E}\left\lbrack \exp(u_nX(t_n))\vert X(t_{n-1}),X(t_{n-2}),\ldots,X(t_1)\right\rbrack}\ = \ensuremath{{\operatorname E}\left\lbrack \exp(u_nX(t_n))\vert X(t_{n-1})\right\rbrack} =M_c(u_n;t_n-t_{n-1},X(t_{n-1})) \end{multline*}$

To exploit the conditional mgf, we write $M_\ensuremath{\mathbf{X}}$ in nested form:

$\displaystyle M_\ensuremath{\mathbf{X}}(\ensuremath{\mathbf{u}}) = \ensuremath{{\operatorname E}\left\lbrack \exp(u_1X(t_1)+\ldots+ u_{n-1}X(t_{n-1})) M_c(u_n;t_n-t_{n-1},X(t_{n-1}))\right\rbrack}$
$\displaystyle = (1-\ensuremath{\nu}(1-\rho_{n-1,n})u_n)^{-\theta/\ensuremath{\nu}}\cdot$
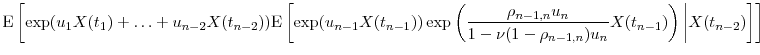
$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \exp(u_1X(t_1)+\ldots+u_{n-2}X(t_{n-2})) \ensuremath{{\operatorname E}\left\lbrack \exp(u_{n-1}X(t_{n-1})) \exp\left(\frac{\rho_{n-1,n}u_n} {1-\ensuremath{\nu}(1-\rho_{n-1,n})u_n}X(t_{n-1})\right)\bigg\vert X(t_{n-2})\right\rbrack}\right\rbrack}$
$\displaystyle = (1-\ensuremath{\nu}(1-\rho_{n-1,n})u_n)^{-\theta/\ensuremath{\nu}}\cdot$
$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \exp(u_1X(t_1)+\ldots+ u_{n-2}X(t_{n-2})) M_c(\tilde{u}_{n-1};t_{n-1}-t_{n-2},X(t_{n-2}))\right\rbrack}$	(3)

where

$\displaystyle \tilde{u}_{n-1} = u_{n-1} + \frac{\rho_{n-1,n}u_n} {1-\ensuremath{\nu}(1-\rho_{n-1,n})u_n}$

Repeating this process

times in total, we get

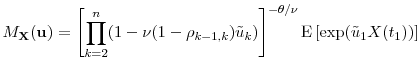
$\displaystyle M_\ensuremath{\mathbf{X}}(\ensuremath{\mathbf{u}}) = \left\lbrack \prod_{k=2}^n (1-\ensuremath{\nu}(1-\rho_{k-1,k})\tilde{u}_k)\right\rbrack^{-\theta/\ensuremath{\nu}} \ensuremath{{\operatorname E}\left\lbrack \exp(\tilde{u}_1X(t_1))\right\rbrack}$

where the modified auxilliary variables have the forward recursive relationship

$\displaystyle \tilde{u}_k = u_k + \frac{\rho_{k,k+1}\tilde{u}_{k+1}} {1-\ensuremath{\nu}(1-\rho_{k,k+1})\tilde{u}_{k+1}}$

(4)

for $k=1,\ldots,n$ and where we fix $\tilde{u}_{n+1}=0$ (so $\tilde{u}_n=u_n$ ). The stationary distribution of

is gamma with shape parameter $\theta/\ensuremath{\nu}$ and scale parameter $\ensuremath{\nu}$ , which has mgf

$\displaystyle M_\Gamma(u)=(1-\ensuremath{\nu}u)^{-\theta/\ensuremath{\nu}}$

(5)

so we arrive at

$\displaystyle M_\ensuremath{\mathbf{X}}(\ensuremath{\mathbf{u}}) = \left\lbrack (1-\ensuremath{\nu}\tilde{u}_1) \prod_{k=2}^n (1-\ensuremath{\nu}(1-\rho_{k-1,k})\tilde{u}_k)\right\rbrack^{-\theta/\ensuremath{\nu}}$

(6)

Equation (6) is computationally convenient but analytically cumbersome. Let $\ensuremath{Q}(\ensuremath{\mathbf{u}})$ be the expression inside the brackets, so that $M_\ensuremath{\mathbf{X}}(\ensuremath{\mathbf{u}})=\ensuremath{Q}(\ensuremath{\mathbf{u}})^{-\theta/\ensuremath{\nu}}$ . We now simplify $\ensuremath{Q}(\ensuremath{\mathbf{u}})$ by writing it as a finite series in powers of $\ensuremath{\nu}$ .

Let $\ensuremath{\mathfrak{S}}(n,k)$ be the set of subsequences of length from the sequence $1,\ldots,n$ , so that if $s\in\ensuremath{\mathfrak{S}}(n,k)$ , then

$\displaystyle 1\leq s(1) < s(2) < \ldots < s(k) \leq n.$

For $k=1,\ldots,n$ , define the functions

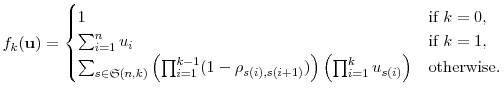
$\displaystyle f_k(\ensuremath{\mathbf{u}})= \begin{cases}1 & \text{if $k=0$}, \\ \sum_{i=1}^n u_i & \text{if $k=1$}, \\ \sum_{s\in\ensuremath{\mathfrak{S}}(n,k)} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^ku_{s(i)}\right) & \text{otherwise.} \end{cases}$

(7)

In Appendix A, we prove

Proposition 1

$\displaystyle \ensuremath{Q}(\ensuremath{\mathbf{u}}) = \sum_{k=0}^n (-\ensuremath{\nu})^k f_k(\ensuremath{\mathbf{u}})$

To prove Theorem 1, we need to prove that $\det(\ensuremath{{\cal I}_n}-\ensuremath{\nu}R\ensuremath{\operatorname{diag}(\ensuremath{\mathbf{u}})})$ has the same expansion as in Proposition 1. Recall that the characteristic polynomial of a square $n\times n$ matrix is defined as $\det(\lambda \ensuremath{{\cal I}_n}-A)$ . For a subsequence $s\in\ensuremath{\mathfrak{S}}(n,k)$ , let denote the $k^{\text th}$ order diagonal minor of with elements and let $\Omega_k(A)$ for $1\leq k\leq n$ be defined as

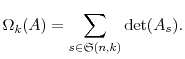
$\displaystyle \Omega_k(A) = \sum_{s\in \ensuremath{\mathfrak{S}}(n,k)} \det(A_s).$

For notional convenience, we define $\Omega_0(A)=1=f_0(\ensuremath{\mathbf{u}})$ . Then the characteristic polynomial of

has the expansion (Gantmacher, 1959, §III.7)

$\displaystyle \det(\lambda\ensuremath{{\cal I}_n}-A) = \lambda^n - \Omega_1(A)\lambda^{n-1} + \Omega_2(A)\lambda^{n-2} - \ldots + (-1)^n\Omega_n(A)$

(8)

Substituting $\lambda=1$ and $A=\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})$ in (8), we have

$\displaystyle \det(\ensuremath{{\cal I}_n}-\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) = 1 - \Omega_1(\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) + \Omega_2(\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) - \ldots + (-1)^n\Omega_n(\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}))$

$\displaystyle = \sum_{k=0}^n (-1)^k \Omega_k(\ensuremath{\nu}R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) = \sum_{k=0}^n (-\ensuremath{\nu})^k \Omega_k(R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}))$

(9)

Since $\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})$ is a diagonal matrix, the diagonal minor $(R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}))_s$ is equal to the product $R_s\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}_s)$ . Thus, we have

$\displaystyle \Omega_k(R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) = \sum_{s\in \ensuremath{\mathfrak{S}}(n,k)} \det((R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}))_s) = \sum_{s\in\ensuremath{\mathfrak{S}}(n,k)} \det(R_s)\det(\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}_s))$

(10)

For the case of , $\det(R_s)=1$ for all $s\in \ensuremath{\mathfrak{S}}(n,1)$ , so

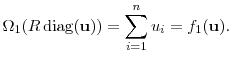
$\displaystyle \Omega_1(R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) = \sum_{i=1}^n u_i = f_1(\ensuremath{\mathbf{u}}).$

For the case of $2\leq k\leq n$ , we make use of this lemma:²

Lemma 1
Let be an $m\times m$ matrix with elements $A[i,j]=\exp(-(c/2)\vert t_i-t_j\vert)$ for some constant $c\geq0$ and vector of nonnegative $t_1,\ldots,t_m$ . Then $\det(A)=\prod_{i=1}^{m-1} (1-\exp(-c\vert t_{i+i}-t_{i}\vert))$ .

Proof. Let

be an $m\times m$ matrix with diagonal elements

for $i=1,\ldots,m-1$ and

on each element of the superdiagonal, and zero elsewhere. It is easily verified that the matrix

is lower triangular with diagonal entries

$\displaystyle C[i,i]=1/A[i,i+1]-A[i,i+1]=\left(1/A[i,i+1]\right)\cdot\left(1-A[i,i+1]^2\right)$

for $i=1,\ldots,m-1$ and

. Thus,

$\displaystyle \det(A)=\frac{\det(C)}{\det(B)} = \frac{\prod_{i=1}^{m} C[i,i]}{\prod_{i=1}^{m} B[i,i]} = \prod_{i=1}^{m-1} (1-A[i,i+1]^2)$

$\qedsymbol$

The diagonal minor takes on the same form as , i.e., there is a vector $t'=(t_{s(1)},\ldots,t_{s(k)})$ such that has elements $R_s[i,j]=\exp(-(\kappa/2)\vert t'_i-t'_j\vert)$ . Applying Lemma 1, for any $2\leq k\leq n$ and $s\in\ensuremath{\mathfrak{S}}(n,k)$ we have

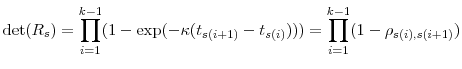
$\displaystyle \det(R_s)=\prod_{i=1}^{k-1} (1-\exp(-\kappa(t_{s(i+1)}-t_{s(i)}))) =\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})$

Since $\det(\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}_s))=\prod_{i=1}^k u_{s(i)}$ , we have

$\displaystyle \Omega_k(R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}})) = \sum_{s\in \ensuremath{\mathfrak{S}}(n,k)} \det((R\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}))_s) = \sum_{s\in\ensuremath{\mathfrak{S}}(n,k)} \det(R_s)\det(\ensuremath{\operatorname{diag}}(\ensuremath{\mathbf{u}}_s))$
$\displaystyle = \sum_{s\in \ensuremath{\mathfrak{S}}(n,k)} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^ku_{s(i)}\right) = f_k(\ensuremath{\mathbf{u}})$	(11)

We substitute equation (11) into equation (9) and arrive at the same expansion as in Proposition 1. This completes the proof of Theorem 1.

2 Moments of the increments

Under stationarity, $X_{t+\delta}-X_t \overset{d}{=} X_{\delta}-X_0$ for all , so without loss of generality we examine the stationary distribution of $\Delta_\delta=X_\delta-X_0$ . From Corollary 1,

$\displaystyle M_\Delta(u;\delta) = M_\ensuremath{\mathbf{X}}(-u,u) =(1-\ensuremath{\nu}^2(1-\rho) u^2)^{-\theta/\ensuremath{\nu}}$
$\displaystyle =\left((1-\ensuremath{\nu}\sqrt{1-\rho} u)(1+\ensuremath{\nu}\sqrt{1-\rho} u) \right)^{-\theta/\ensuremath{\nu}} =M_\Gamma\left(u\sqrt{1-\rho}\right)\cdot M_\Gamma\left(-u\sqrt{1-\rho}\right)$	(12)

where $\rho=\exp(-\kappa\delta)$ and $M_\Gamma$ is the univariate mgf for

. An immediate implication of (12) is that $\Delta_\delta$ is equivalent in distribution to $(1-\rho)^{1/2}$ times $\Delta_\infty$ . Furthermore, $\Delta_\infty$ is equivalent in distribution to the difference between two independent draws from the stationary distribution of

. This gives a very simple method for sampling from the stationary distribution of $\Delta_\delta$ .

Consider the general problem of the moments of the difference between two independent and identically distributed (iid) gamma variates. Let $Z_1,Z_2 \overset{iid}{\sim} Ga(\alpha,\ensuremath{\nu})$ for shape parameter $\alpha>0$ and scale parameter $\ensuremath{\nu}>0$ , and define $\ensuremath{Y}=Z_1-Z_2$ . The $n^{\rm th}$ cumulant of $\ensuremath{Y}$ is

$\displaystyle \ensuremath{\psi}_n =\left(1+(-1)^n\right)(n-1)!\alpha\ensuremath{\nu}^n.$

Central moments are obtained from the cumulants via the complete Bell polynomials, i.e.,

$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^n\right\rbrack} = \ensuremath{B}_{n}(\ensuremath{\psi}_1,\ensuremath{\psi}_2,\ldots,\ensuremath{\psi}_n).$

For any sequence $c_1,c_2,\ldots$ , the Bell polynomials satisfy

$\displaystyle \ensuremath{B}_{n}(\ensuremath{\nu}c_1, \ensuremath{\nu}^2 c_2,\ldots, \ensuremath{\nu}^n c_n) = \ensuremath{\nu}^n\ensuremath{B}_{n}(c_1,c_2,\ldots,c_n)$

$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^n\right\rbrack} = \ensuremath{\nu}^n \ensuremath{B}_{n}(0,2\alpha\, 1!,0,2\alpha\, 3!,0,2\alpha\, 5!,\ldots).$

(13)

Furthermore, since the distribution is symmetric around zero, we know that the odd moments $\ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^{2n+1}\right\rbrack}$ are zero.

In Appendix B, we prove a general identity on the complete Bell polynomials:

Lemma 2
Let be a positive integer and let $\ensuremath{\xi}_{k,1},\ensuremath{\xi}_{k,2},\ldots$ be the sequence of integers defined by

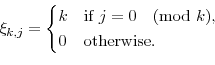
$\begin{displaymath} \ensuremath{\xi}_{k,j} = \begin{cases} k & \text{if } j=0 \pmod{k}, \ 0 & \text{otherwise.} \end{cases}\end{displaymath}$

Then for any scalar $\alpha\in\Re^+$ ,

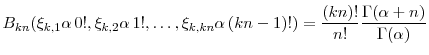
$\displaystyle \ensuremath{B}_{kn}(\ensuremath{\xi}_{k,1}\alpha\, 0!,\ensuremath{\xi}_{k,2}\alpha\, 1!,\ldots, \ensuremath{\xi}_{k,kn}\alpha\, (kn-1)!) = \frac{(kn)!}{n!}\frac{\Gamma(\alpha+n)}{\Gamma(\alpha)}$

where $\Gamma(\cdot)$ is the Gamma function. For any positive integer not divisible by ,

$\displaystyle \ensuremath{B}_m(\ensuremath{\xi}_{k,1}\alpha\, 0!,\ensuremath{\xi}_{k,2}\alpha\, 1!,\ldots, \ensuremath{\xi}_{k,m}\alpha\, (m-1)!)=0.$

It follows immediately that the even central moments of $\ensuremath{Y}$ are

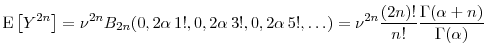$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^{2n}\right\rbrack}=\ensuremath{\nu}^{2n} \ensuremath{B}_{2n}(0,2\alpha\, 1!,0,2\alpha\, 3!,0,2\alpha\, 5!,\ldots) = \ensuremath{\nu}^{2n}\frac{(2n)!}{n!} \frac{\Gamma(\alpha+n)}{\Gamma(\alpha)}$

(14)

and the odd central moments are zero. As kurtosis is often of particular interest, we note

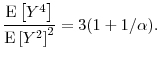$\displaystyle \frac{\ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^4\right\rbrack}}{\ensuremath{{\operatorname E}\left\lbrack \ensuremath{Y}^2\right\rbrack}^2} = 3(1+1/\alpha).$

Application to the moments of $\Delta_\delta$ is direct. We substitute $\alpha=\theta/\ensuremath{\nu}$ and get even moments

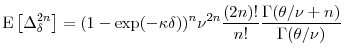$\displaystyle \ensuremath{{\operatorname E}\left\lbrack \Delta_\delta^{2n}\right\rbrack} = (1-\exp(-\kappa\delta))^n \ensuremath{\nu}^{2n}\frac{(2n)!}{n!} \frac{\Gamma(\theta/\ensuremath{\nu}+n)}{\Gamma(\theta/\ensuremath{\nu})}$

(15)

The kurtosis of $\Delta_\delta$ is $3(1+\ensuremath{\nu}/\theta)$ , which is invariant with respect to the time increment $\delta$ .

3 Conclusion

Our main result is a simple closed-form expression for the moment generating function of the stationary multivariate distribution of a discrete sample path of a square-root diffusion process. We establish that the distribution is within the Krishnamoorthy-Parthasarathy class, and thereby draw a connection between a stochastic process and a multivariate distribution that each first appeared in the literature in 1951.

Our result has application to estimation of parameters of the continuous-time square-root process from a discrete sample. It gives a simple and computationally efficient way to generate moment conditions for the generalized method of moments estimator of Chan et al. (1992). The empirical characteristic function approach of Jiang and Knight (2002) can also be easily implemented. Indeed, Jiang and Knight consider the example of a square-root diffusion, but their solution to the characteristic function corresponds roughly to our intermediate equation (6), rather than to the simple form in our Theorem 1.

Three of our auxilliary results may have application elsewhere. First, Lemma 1 provides a simple solution to the determinant of the autocorrelation matrix for a discrete sample of any process with exponential decay in autocorrelation. This decay rate holds in a large class of stationary Markov processes, including Gaussian and non-Gaussian Ornstein-Uhlenbeck processes as well as the square-root process (Cont and Tankov, 2004, §15.1.2, §15.3.1). Second, our Bell polynomial identity in Lemma 2 generalizes a known relationship between Bell polynomials and the Gamma function (i.e., for the case of in our lemma). Finally, we provide a simple formula for the moments of the difference of two iid gamma variates. It complements existing results that allow the variates to differ in scale parameter (Johnson et al., 1994, §12.4.4), but which lead to more complicated expressions for the moments.

A. Proof of Proposition 1

Let us define $\tilde{\ensuremath{Q}}_1=1-\ensuremath{\nu}\tilde{u}_1$ and, for $2\leq m\leq n$ , recursively define

$\displaystyle \tilde{\ensuremath{Q}}_m = (1-\ensuremath{\nu}(1-\rho_{m-1,m})\tilde{u}_m) \tilde{\ensuremath{Q}}_{m-1}$

Since $\tilde{u}_{n+1}=0$ , we have $\tilde{\ensuremath{Q}}_n=\ensuremath{Q}(\ensuremath{\mathbf{u}})$ . We similarly generalize the

functions as

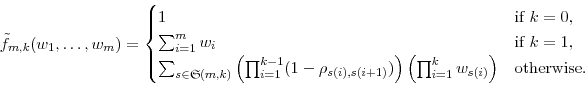
$\begin{displaymath} \tilde{f}_{m,k}(w_1,\ldots,w_m) = \begin{cases} 1 & \text{if $k=0$}, \ \sum_{i=1}^{m} w_i & \text{if $k=1$}, \ \sum_{s\in\ensuremath{\mathfrak{S}}(m,k)} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^kw_{s(i)}\right) & \text{otherwise.} \end{cases}\end{displaymath}$

Observe that the set $\ensuremath{\mathfrak{S}}(m,k)$ can be expressed as the union of two disjoint subsets

$\displaystyle \ensuremath{\mathfrak{S}}(m,k) = \ensuremath{\mathfrak{S}}(m-1,k) \cup \{(s,m)\vert s\in\ensuremath{\mathfrak{S}}(m-1,k-1)\}.$

The latter set is equivalent to the subset of $\ensuremath{\mathfrak{S}}(m,k)$ for which

. This implies that the $\tilde{f}$ functions have the recurrence relation

$\displaystyle \tilde{f}_{m,k}(w_1,w_2,\ldots,w_m) = \tilde{f}_{m-1,k}(w_1,w_2,\ldots,w_{m-1})$
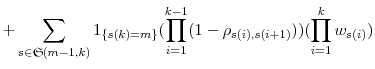$\displaystyle + \sum_{s\in\ensuremath{\mathfrak{S}}(m-1,k)}\ensuremath{1_{\{s(k)=m\}}}(\prod_{i=1}^{k-1}(1-\rho_{s(i),s(i+1)}))(\prod_{i=1}^{k}w_{s(i)})$	(16)

We now demonstrate

$\displaystyle \tilde{\ensuremath{Q}}_m = \sum_{k=0}^m (-\ensuremath{\nu})^k \tilde{f}_{m,k}(u_1,u_2,\ldots,u_{m-1},\tilde{u}_m)$

(17)

by induction. For the case

$\displaystyle \tilde{\ensuremath{Q}}_1=1-\ensuremath{\nu}\tilde{u}_1 = \tilde{f}_{1,0}(\tilde{u}_1)-\ensuremath{\nu}\tilde{f}_{1,1}(\tilde{u}_1)$

which satisfies equation (17). For $2\leq m\leq n$ , let us assume that (17) is satisfied for $\tilde{\ensuremath{Q}}_1,\tilde{\ensuremath{Q}}_2, \ldots,\tilde{\ensuremath{Q}}_{m-1}$ . Then

$\displaystyle \tilde{\ensuremath{Q}}_m = (1-\ensuremath{\nu}(1-\rho_{m-1,m})\tilde{u}_m) \tilde{\ensuremath{Q}}_{m-1}$
$\displaystyle = (1-\ensuremath{\nu}(1-\rho_{m-1,m})\tilde{u}_m)\sum_{k=0}^{m-1} (-\ensuremath{\nu})^k \tilde{f}_{m-1,k}(u_1,u_2,\ldots,u_{m-2},\tilde{u}_{m-1}).$	(18)

Since $\tilde{f}_{m-1,k}$ is linear in each argument,

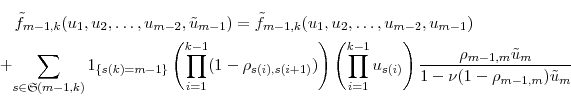
$\begin{multline*} \tilde{f}_{m-1,k}(u_1,u_2,\ldots,u_{m-2},\tilde{u}_{m-1}) = \tilde{f}_{m-1,k}(u_1,u_2,\ldots,u_{m-2},u_{m-1})\ + \sum_{s\in\ensuremath{\mathfrak{S}}(m-1,k)}\ensuremath{1_{\{s(k)=m-1\}}} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1}u_{s(i)}\right) \frac{\rho_{m-1,m}\tilde{u}_{m}} {1-\ensuremath{\nu}(1-\rho_{m-1,m})\tilde{u}_{m}} \end{multline*}$

Substituting into (18), we get

$\displaystyle \tilde{\ensuremath{Q}}_m = \sum_{k=0}^{m-1} (-\ensuremath{\nu})^k \Bigg\lbrack (1-\ensuremath{\nu}(1-\rho_{m-1,m})\tilde{u}_m) \tilde{f}_{m-1,k}(u_1,u_2,\ldots,u_{m-2},u_{m-1})$
$\displaystyle + \rho_{m-1,m}\tilde{u}_{m}\sum_{s\in\ensuremath{\mathfrak{S}}(m-1,k)}\ensuremath{1_{\{s(k)=m-1\}}} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1}u_{s(i)}\right) \Bigg\rbrack$	(19)

Collecting terms on $(-\ensuremath{\nu})^k$ , we can write

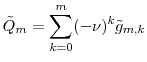
$\displaystyle \tilde{\ensuremath{Q}}_m = \sum_{k=0}^{m} (-\ensuremath{\nu})^k \tilde{g}_{m,k}$

where

$\displaystyle \tilde{g}_{m,0} = \tilde{f}_{m-1,0}(u_1,\ldots,u_{m-1}) = 1 = \tilde{f}_{m,0}(u_1,\ldots,u_{m-1},\tilde{u}_m),$

and

$\displaystyle \tilde{g}_{m,m} = (1-\rho_{m-1,m})\tilde{u}_m\tilde{f}_{m-1,m-1}(u_1,\ldots,u_{m-1}) = \tilde{f}_{m,m}(u_1,\ldots,u_{m-1},\tilde{u}_m)$

and, for $1\leq k< m$ ,

$\displaystyle \tilde{g}_{m,k} = \tilde{f}_{m-1,k}(u_1,\ldots,u_{m-1})+ (1-\rho_{m-1,m})\tilde{u}_m\tilde{f}_{m-1,k-1}(u_1,\ldots,u_{m-1})$
$\displaystyle + \rho_{m-1,m}\tilde{u}_{m}\sum_{s\in\ensuremath{\mathfrak{S}}(m-1,k)}\ensuremath{1_{\{s(k)=m-1\}}} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1}u_{s(i)}\right)$	(20)

The last term is

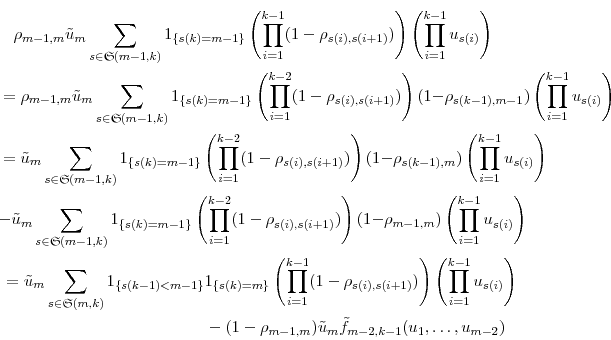
$\begin{multline*} \rho_{m-1,m}\tilde{u}_{m}\sum_{s\in\ensuremath{\mathfrak{S}}(... ...rho_{m-1,m})\tilde{u}_{m}\tilde{f}_{m-2,k-1}(u_1,\ldots,u_{m-2}) \end{multline*}$

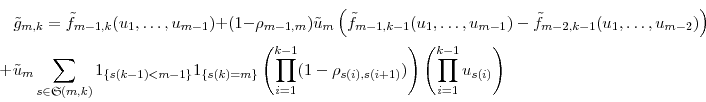
$\begin{multline*} \tilde{g}_{m,k} = \tilde{f}_{m-1,k}(u_1,\ldots,u_{m-1})+ (1-\rho_{m-1,m})\tilde{u}_{m}\left(\tilde{f}_{m-1,k-1}(u_1,\ldots,u_{m-1}) -\tilde{f}_{m-2,k-1}(u_1,\ldots,u_{m-2})\right) \\ + \tilde{u}_{m}\sum_{s\in\ensuremath{\mathfrak{S}}(m,k)}\ensuremath{1_{\{s(k-1)<m-1\}}}\ensuremath{1_{\{s(k)=m\}}} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1}u_{s(i)}\right) \end{multline*}$

By equation (A),

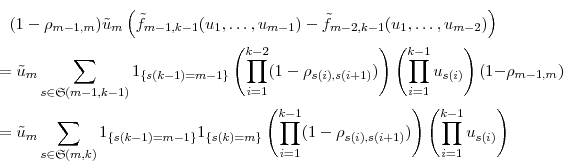
$\begin{multline*} (1-\rho_{m-1,m})\tilde{u}_{m}\left(\tilde{f}_{m-1,k-1}(u_1,\ldots,u_{m-1}) -\tilde{f}_{m-2,k-1}(u_1,\ldots,u_{m-2})\right)\ = \tilde{u}_m\sum_{s\in\ensuremath{\mathfrak{S}}(m-1,k-1)} \ensuremath{1_{\{s(k-1)=m-1\}}} \left(\prod_{i=1}^{k-2} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1} u_{s(i)}\right)(1-\rho_{m-1,m})\ = \tilde{u}_m\sum_{s\in\ensuremath{\mathfrak{S}}(m,k)} \ensuremath{1_{\{s(k-1)=m-1\}}}\ensuremath{1_{\{s(k)=m\}}} \left(\prod_{i=1}^{k-1} (1-\rho_{s(i),s(i+1)})\right) \left(\prod_{i=1}^{k-1} u_{s(i)}\right) \end{multline*}$

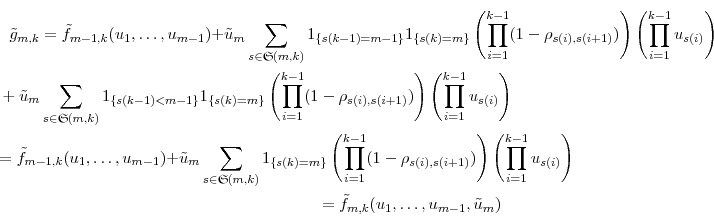
$\begin{multline*} \tilde{g}_{m,k} = \tilde{f}_{m-1,k}(u_1,\ldots,u_{m-1})+ \ti... ...i)}\right)\ = \tilde{f}_{m,k}(u_1,\ldots,u_{m-1},\tilde{u}_m) \end{multline*}$

where the last equality is by equation (A). Thus, $\tilde{g}_{m,k}= \tilde{f}_{m,k}(u_1,\ldots,u_{m-1},\tilde{u}_m)$ for $k=0,\ldots,m$ , so equation 17 is proved. Substituting

and $\tilde{u}_n=u_n$ , we arrive at Proposition 1.

B. Proof of the Bell polynomial identity

For any sequence of scalars $c_1,c_2,\ldots$ , the generating function of the complete Bell polynomials is

$\displaystyle \exp\left(\sum_{n=1}^\infty c_n\frac{x^n}{n!}\right) = \sum_{n=0}^\infty \ensuremath{B}_n(c_1,c_2,\ldots,c_n)\frac{x^n}{n!}$

(21)

where we fix $\ensuremath{B}_0=1$ . When $c_j=\ensuremath{\xi}_{k,j}\alpha (j-1)!$ , we have

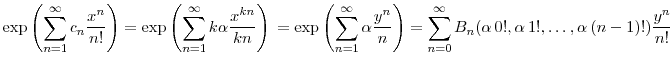
$\displaystyle \exp\left(\sum_{n=1}^\infty c_n\frac{x^n}{n!}\right) =\exp\left(\sum_{n=1}^\infty k\alpha \frac{x^{kn}}{kn}\right)\ = \exp\left(\sum_{n=1}^\infty \alpha \frac{y^{n}}{n}\right) =\sum_{n=0}^\infty \ensuremath{B}_n(\alpha\, 0!,\alpha\, 1!,\ldots, \alpha\, (n-1)!) \frac{y^n}{n!}$

where we introduce the change of variable

Using identities from Comtet (1974, pp. 135, 136) and DLMF (2010, §26.8.7), we have

$\displaystyle \ensuremath{B}_{n}(\alpha\, 0!,\alpha\, 1!,\ldots \alpha\, (n-1)!) = \sum_{k=1}^n \vert\ensuremath{\mathfrak{s}(n,k)}\vert \alpha^k = \frac{\Gamma(\alpha+n)}{\Gamma(\alpha)}$

where $\ensuremath{\mathfrak{s}(n,k)}$ denotes the Stirling number of the first kind. Restoring the original variable

, we have

$\displaystyle \exp\left(\sum_{n=1}^\infty c_n\frac{x^n}{n!}\right) = \sum_{n=0}^\infty \frac{\Gamma(\alpha+n)}{\Gamma(\alpha)} \frac{y^n}{n!} = \sum_{n=0}^\infty \frac{\Gamma(\alpha+n)}{\Gamma(\alpha)} \frac{(kn)!}{n!} \frac{x^{kn}}{(kn)!}$

(22)

Matching terms to the right hand side of (21) with the same power of

, we have

Whenever

is not a multiple of

, the coefficient on

in the right hand side of (22) is zero, so

$\displaystyle \ensuremath{B}_m(\ensuremath{\xi}_{k,1}\alpha\, 0!,\ensuremath{\xi}_{k,2}\alpha\, 1!,\ldots, \ensuremath{\xi}_{k,m}\alpha\, (m-1)!)=0.$

Bibliography

Alfonsi, Aurélien

"Cox-Ingersoll-Ross (CIR) Model," in Rama Cont, ed., Encyclopedia of Quantitative Finance, John Wiley & Sons, 2010.