Gamblers as Personal Finance Activists
Keywords: Gambling, consumption, household balance sheet, insurance, charitable giving, unobserved heterogeneity.
Abstract:
1 Introduction
Despite the fact that more than 50% of all consumers have gambled in a given year, little is known about how gambling costs fit in household budgets and the relationship of these costs to other expenditures, how gamblers' balance sheets compare with those of other consumers, and how gamblers manage risks. There is not even much consensus regarding why people gamble at all. This paper fills some of this important void in the literature. We present, to the best of our knowledge, the first comprehensive study of gamblers' consumption and personal finances. On balance, the facts presented in this paper suggest that, except for a small fraction of problematic gamblers, most gamblers perceive gambling as a form of pastime, the spending of which is budgeted as a part of their entire expenditure basket. Further, we argue that gambling is a type of pastime in which only consumers with certain traits will engage. We interpret such traits as a "personal finance activism" that makes a consumer more actively participate in a variety of service and financial markets. Because such traits are conceivably difficult to observe directly in data, we argue that gambling behavior can serve as an informative indicator for important household heterogeneities.
Indeed, gamblers represent one of the most intriguing subjects of research on consumer behaviors. To the extent that most gambling games have negative expected payoffs, the fact that some people gamble reveals certain aspects of their preferences that are potentially at odds with the assumptions made in canonical consumption and saving models. Gamblers' investment and consumption behaviors therefore can be different from those of consumers who do not gamble. For example, if the risk-loving (e.g., Quandt 1986) or skewness-loving (e.g. Golec and Tamarkin 1998) type of preferences make consumers willing to play unfair games with expected returns below break-even, such a preference may also make gamblers take a more risky and aggressive position on their balance sheets in general.
Conversely, studying certain behaviors of gamblers, such as how they insure against risks (financial and nonfinancial) they encounter helps advance our understanding of their preferences over risky alternatives. For example, motivated by anecdotal evidence that some people buy both lotteries and insurance at the same time, Friedman and Savage (1948) propose a utility function with both a concave and a convex segment.1 Establishing that many people simultaneously engage in gambling activities and buy non-mandatory insurance has the potential to boost our confidence in Friedman and Savage's characterization of preferences and its contemporary applicability.
Furthermore, research on gamblers' consumption and balance sheets in a broad context sheds light on gambling's welfare effects, of which previous studies have examined certain aspects but not in a systematic way using a comprehensive data source. Notably, there has been longstanding interest in whether gamblers cut other spending to pay for gambling costs. Kearney (2005) shows that household non-gambling expenditures decline appreciably after state lotteries are introduced to the state in which the household lives. In her study, the identity of gamblers is not observable. The identification of the "crowding-out" effect therefore relies on the average expenditure changes among all consumers--gamblers and nongamblers--before and after the introduction of a state lottery, an exogenous change to household budgets. Our paper complements to Kearney (2005) by focusing on how other expenditures of gamblers change when their gambling costs vary for endogenous reasons.
In addition, an extensive literature has examined the health and economic consequences of gambling (e.g., National Gambling Impact Study Commission (1999), Treasury (1999) and National Opinion Research Center (2006)). These studies typically focus on gambling's effects on the so-called pathological gamblers, who represent only 1% of all gamblers in a given year. Moreover, most of these studies lack information on household expenditures and balance sheets that is critical to evaluate gambling's economic consequences.
This paper also contributes to a growing literature exploring how gambling propensity is related to investment strategies. Using individual account data from a discount brokerage house, Kumar (2009) presents evidence that investors with a higher gambling propensity are also more likely to invest in lottery-like stocks. However, his data do not speak to whether gamblers are more likely to participate in the stock market in the first place. Moreover, whether an investor is a gambler is not observable in the discount brokerage data and one has to estimate the likelihood of being a gambler using investors' demographic and socioeconomic characteristics, which may be fairly inaccurate.
This paper uses Consumer Expenditure Survey (CE) data collected in the 2000s. Relative to previously used data sources, the CE data present a unique combination of detailed household expenditure data, including gambling costs, with extensive information on household balance sheets and demographic characteristics of a nationwide representative sample. Unlike Kearney (2005), Kumar (2009) and Kumar, Page, and Spalt (forthcoming), the CE data allow us to observe directly who the gamblers are and how much they spend on gambling. Thus, our study also provides a complement to Kumar (2009) by presenting direct evidence on gamblers' balance sheets. One limitation of the CE data, however, is that the information on gambling costs is collected with substantial measurement errors. Later in the paper, we will discuss in detail the statistical implications of such measurement errors.
Our key findings are summarized as follows: gambling costs appear to be complementary to other expenditures in the sense that households who spend more on gambling also tend to have higher expenditures in a wide array of other categories. This result holds in both expenditure level and quarterly growth analysis. Then, how do consumers finance their gambling? We find that the income of gambler households is significantly higher than its long run "normal" level predicted by observed demographic and socioeconomic characteristics. Accordingly, despite positive gambling costs and higher other expenditures, total-expenditure-to-income ratio is on average lower for gamblers than for nongamblers.
Moveover, we explore whether some consumers buy lotteries, at least partly, as they perceive state lotteries as substitutes for donation to charities, given that the net revenue of state lotteries is used for financing public projects. Consistent with this hypothesis, we present evidence that charitable donors are more likely to be gamblers than nondonors (and vice versa), and that among donors, gamblers on average make smaller amount of contributions than nongamblers. Interestingly, gambling behaviors do not appear to be correlated with religious donations.
Regarding gamblers' balance sheets, we find that, relative to nongamblers with similar observable characteristics, gamblers are more active participants both as borrowers and as investors in household finance markets. As borrowers, they are more likely to have credit card debt, mortgages, and car loans, and they also manage their liabilities more actively: for example, a greater share of the mortgages owed by gamblers have been refinanced previously. As investors, they are more likely to invest in financial security markets and to own a second home. Nevertheless, gamblers' net worth is not necessarily higher than nongamblers', consistent with the hypothesis that gamblers are "personal finance activists" who have stronger aspirations for wealth and are more willing to participated in a wide range of financial markets, but may not on average have better investment and debt management skills.
Finally, we document that gamblers have a higher propensity to engage in behaviors risky to one's heath, such as heavy drinking and smoking. That said, noticeably, consistent with the assertion of Friedman and Savage (1948) that people buy both lotteries and insurance, we find gamblers are more likely to pay out-of-pocket for non-mandatory, such as health, life, and home, insurance than nongamblers. Further, we present evidence that gamblers who smoke and drink appear to be more informed regarding the health risks associated with these behaviors and are more likely to purchase health and life insurance than comparable nongambling smokers and drinkers and than other comparable consumers in general.
One prominent explanation for the differences between gamblers and nongamblers documented in this paper is that some consumers report more complete answers to the survey, including their gambling expenditures. Should this be true, it is then not surprising that gamblers observed in data also appear to be more active in many other aspects of their personal finances. We present extensive evidence, at the end of the paper, that careless reporting is not likely the main factor responsible for our findings.
2.1 Overview of the Gambling Cost Data in the Consumer Expenditure Survey
Before 2001, nationwide survey data that explicitly identify gamblers while collecting detailed household expenditure and balance sheet information were lacking. An addition to the questions asked by the Consumer Expenditure Survey (CE) has expanded the scope of possible research on gamblers' consumption and financial behaviors to a great extent. The CE is a nationwide representative survey conducted by the Bureau of Labor Statistics.2 Although the primary purpose of the CE is for updating the estimate of the consumer expenditure basket to facilitate the construction of the Consumer Price Index, the micro level data of the CE have been used extensively in research because the survey collects rich and detailed information on household expenditures, demographic characteristics, income, and household assets and liabilities. The CE interviews each participating household quarterly four times, collecting detailed data on the consumption expenditures incurred during the three months prior to the interview. The first and the last interviews collect data on income earned during the respective twelve months prior to that interview. The last interview also collects information about household financial assets. After the last interview, existing households leave the sample and new households are selected to replenish the sample. Consequently, the CE provides, for each household completing all interviews, a short panel of four quarters, a useful structure that we will exploit in this paper.
Beginning in the second quarter of the 2001, CE added a question about gambling costs--"in the last 3 months have you (or any members of your CU) had expenses for lotteries and games of chance"(section 19-A in the CE questionnaire).3 Each spending category is assigned a Universal Classification Code (UCC) in the CE data and UCC 620926 is assigned to gambling costs.4 Hence, the CE allows us to identify the consumers who gambled in a given quarter and how much they spent on gambling. We define gamblers as households that reported positive costs on lotteries or other games of chance during the survey year. To categorize gamblers by their gambling intensity, we define occasional gamblers as those who reported positive gambling costs in only one of the four quarterly interviews, and frequent gamblers as those who reported positive gambling costs in all four interviews and had annual gambling costs above $40.
Table 1 presents the summary statistics of the share of gamblers and gambling costs among the CE sample households that were surveyed after 2001:Q2, have participated in all four interviews, and have reported valid income data in both the first and the last interview. For this table, our sample includes only the households whose heads were between 20 and 80 years old at the time of the survey. We focus on the households that participated in all four interviews to study the prevalence of gambling within a year and the annual gambling costs. Of note, our summary statistics include older consumers (older than 65). We subsequently exclude older consumers when we study household consumption and balance sheet because most of the older consumers are retired and likely to have different objectives and budget constraints than younger consumers. We deflate all expenditure amounts to year 2000 dollars. As the top line of the table shows, 29% of the households in our sample gambled during the year they were surveyed by the CE. Moreover, 11% of the sample households (40% of all gamblers) are occasional gamblers, while 5.6% of the sample households (about 20% of all gamblers) are frequent gamblers. Among gamblers, the mean and median annual gambling costs are $201 and $57, respectively.5 The mean and median gambling-cost-to-income ratios are 0.35% and 0.13%, respectively. Moreover, the CE allows participants to note in which months the costs occurred if they did not occur in all three months of the reference quarter. Using this information, we find that nearly half of the occasional gamblers only played in one of the three months prior to the interview. Thus, 20% of gamblers only gambled in one month during a year.
2.2 Measurement Errors
A prominent observation that stands out from Table 1 is that, relative to other surveys, the CE may understate the prevalence of gambling at both the extensive and the intensive margins. For example, the Gambling Impact and Behavior Study (National Opinion Research Center (NORC) 1999) report that 63% of survey participants gambled in the previous year, more than double the share in the CE sample. Using the same survey, Kearney (2005) reports the average annual spending on lotteries alone was more than $100 per adult, or more than $200 per gambler, in 1998. Given that what is spent on state lotteries is only a fraction of total gambling cost and most households have more than one adult, the CE estimates of prevalence rate and annual gambling costs are significantly below those derived from the NORC survey. More recently, NORC conducted the 2006 California Problem Gambling Prevalence Survey (CPGPS). The survey reveals that 58% of the surveyed California residents gambled in 2005, losing an average of nearly $300. Again, the CE underestimates relative to the CPGPS.
Several factors may have contributed to the gaps. Most importantly, unlike the NORC 1998 and 2006 survey that focused on people's gambling behavior, the CE is a general purpose survey that collects information on all aspects of household expenditures. Consequently, the survey time spent on teasing out accurate gambling-related information is considerably less than the more focused surveys. Relatedly, the CE asks only one question on the total costs for all gambling activities. Respondents may find it more difficult to provide an estimate of total gambling cost than cost per activity, as gambling-focused surveys are designed. Lack of detailed information on what types of gambling activities households participated in also imposes another data limitation because people who gamble in casinos may be different from people who buy lotteries. For example, it is possible that people who buy state lotteries perceive lotteries as a form of donation to public projects, while people gamble in casinos mainly for fun or monetary gains. Finally, the CE surveys one respondent from each household. Should the household member responding to the survey not be aware of the gambling costs of other family members, gambling prevalence and costs will be underreported at the household level. We see some suggestive evidence of such a potential bias. Arguably, we expect the likelihood that at least one spouse in a married couple gambles is higher than the likelihood that a single individual gambles, and consequently we expect that gambling costs per couple will be higher than per individual. However, as shown in table 1, about 30% of households with married couples reported positive annual gambling costs that average $199. Both statistics are close to those for single males and only moderately higher than single females.
Despite the significant underreporting in the CE data, we argue that the CE data remain a useful, and possibly unique, source for studying gamblers' consumption and balance sheet for the following three reasons. First, a key advantage of the CE is that the data show who the gamblers are. The CE's tendency of under-estimating gambling prevalence suggests that many gamblers did not truthfully report their gambling cost. However, it is hard to imagine that people who did not gamble mistakenly or deliberately reported positive gambling costs. Therefore, the measurement errors on gamblers' identity tend to be one-sided and likely bias statistical inference in a predictable direction. Second, it is possible that the gamblers under-report their gambling costs. But it is less likely that they under-report to various extents in the four quarterly interviews they participate in. We will exploit the panel structure to further examine the effects of gambling costs on other expenditure categories. Third, as we will discuss below in Section 2.3, cross-state variations in gambling prevalence and average costs observed in the CE data are consistent with the presence of state lotteries, offering further reassurance of the information merit of the data.
To characterize how the measurement errors may affect our estimates, we assume the following relationship between the true gambling costs, ![]() and the reported gambling costs,
and the reported gambling costs, ![]() .
.
| (1) |
where
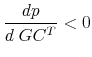 . Basically, we assume that the reported gambling costs are a constant fraction of the true gambling costs if the household chooses to report a
positive number. The likelihood of reporting a positive number is assumed to be increasing with the true gambling costs. Thus, when we estimate the relationship between gambling costs and other household expenditures, our point estimate can potentially be biased away from zero due to
. Basically, we assume that the reported gambling costs are a constant fraction of the true gambling costs if the household chooses to report a
positive number. The likelihood of reporting a positive number is assumed to be increasing with the true gambling costs. Thus, when we estimate the relationship between gambling costs and other household expenditures, our point estimate can potentially be biased away from zero due to
2.3 Gambling Prevalence by Demographic and Socioeconomic Characteristics
Table 1 also shows how gambling prevalence varies across demographic and socioeconomic status. Because the CE is a household, instead of individual, survey, we take the household head's demographic and socioeconomic characteristics as those for the household. Consistent with earlier findings using surveys focusing on gambling behaviors (e.g. Clotfelter et al. (1999) and Kearney (2005)), the CE data indicate that people between 45 and 65 years old and those who have high school diploma but no college degree are most likely to have gambled in a given year. About 33% of such households in the CE data gambled in a given year. They are also more likely to be frequent gamblers. As discussed above, married households in the CE sample have about the same propensity to gamble as single males, perhaps reflecting the possibility that the responding household member is overlooking other members' gambling activities. Moreover, 30% of non-Hispanic white are gamblers, a share significantly higher than Hispanic and black households. Though gambling prevalence is somewhat lower among black households and high school dropouts, for such consumers who gamble, their average gambling costs are higher than those of white consumers and those with higher educational attainment. Retired households are more likely to be frequent gamblers than those who are working. They also have the highest average gambling costs, both in dollar values ($266) and as a ratio to income (0.75%).
Throughout our sample period (2001-2010), several states did not have state lotteries.7 As shown in the lower part of table 1, we find that gambling prevalence is significantly lower in these states (13%) than in other states (30%). Noticeably, conditional on being a gambler, the average gambling costs are similar regardless of whether the household lived in a state with or without state lotteries, suggesting that access to state lotteries affects prevalence but has little effect on the intensity of gambling. Furthermore, several states introduced state lotteries between 2001 and 2010 (South Carolina 2002, Tennessee 2004, North Carolina 2004, and Arkansas 2009). We find that the gambling prevalence in these states increased significantly following the introduction of state lotteries, from 19% to 25%, reinforcing the information content of the CE gambling-related data.8 Finally, we find that gambling prevalence declined somewhat during the Great Recession years. Average gambling prevalence was 29% between 2001 and 2007 and declined to 26% after 2008.
3 Do Gambling Costs Crowd out Other Household Expenditures?
Researchers have long been interested in how households finance their gambling costs. When gambling costs rise, do households cut other spending or reduce saving during the same period? Kearney (2005) exploits differences in the timing in which each state introduced its state lottery. In her experiment, gambling costs vary due to exogenous reasons--the introduction of state lotteries. Conceivably, residents of the states that recently introduced a state lottery are likely to experience a surge in gambling costs because such gambling vehicles had not been available to them previously. She finds that on average household non-gambling expenditures declined by nearly $140 during the quarter after state lotteries were introduced and concludes that lottery spending is financed by a reduction in non-gambling expenditures.
Besides regulatory changes, gambling costs may also change endogenously as households choose to vary how much to spend on gambling when their financial situations and budgets change. For example, a household receiving a bonus may choose to take a cruise trip, on which gambling is part of the fun. Therefore, variations in gambling costs that are due to different reasons can have different implications on other expenditures. The CE data we use are collected after 2001. Unlike the sample period that Kearney (2005) focuses on, only a handful of states introduced state lotteries during our sample period; changes to gambling costs in our sample are most likely due to endogenous reasons. Thus, the statistical correlations between gambling and nongambling expenditures that we are presenting below do not necessarily speak to any causal relationship between the expenditures. Rather, these results illuminate that spending on gambling is more likely to vary as a part of the household total expenditure basket.
3.1 Expenditure Levels Analysis
We first study the cross-sectional correlation between annual gambling costs and other household expenditures. Although the CE collects gambling costs and other expenditure information quarterly, we use the annual aggregation in the baseline analysis because first, many households only incurred gambling costs in one quarter and second, the timing of some non-gambling expenditures can be fairly random and lumpy within a year. In a robustness analysis, we estimate the relationship between gambling costs and other expenditures at a quarterly frequency. Our baseline results are all qualitatively preserved.
The permanent income hypothesis postulates that consumption is largely determined by a household's permanent income. We augment the canonical consumption function with a term for gambling costs. Specifically, we estimate the following model
In the above equation,
Because the observed income ![]() is at best a noisy indicator of a household's permanent income
is at best a noisy indicator of a household's permanent income
![]() , we impute the logarithm of permanent income,
, we impute the logarithm of permanent income,
![]() , using the following equation:
, using the following equation:
where
As mentioned above, our sample for estimating the model includes only households younger than 65. Moreover, because the estimation of a consumption equation in the form of eq.(2) using household survey data is often heavily influenced by outliers, in our baseline analysis we
trim the top 1% of the distribution of ![]() when we estimate the model for expenditure category
when we estimate the model for expenditure category ![]() .12 To further assure that our results are not driven by tail observations, in a robustness analysis, we re-estimate the model, trimming
the top 5% of the expenditure level distributions. The results (not shown) are qualitatively the same as the baseline results.
.12 To further assure that our results are not driven by tail observations, in a robustness analysis, we re-estimate the model, trimming
the top 5% of the expenditure level distributions. The results (not shown) are qualitatively the same as the baseline results.
The upper panel of table 2 shows the estimated ![]() coefficients for total expenditure (net of gambling costs) and expenditure subcategories. The coefficients
reported in column (1) are estimated with nongamblers being included as the control group. The most striking observation from the results is that nearly all estimated
coefficients for total expenditure (net of gambling costs) and expenditure subcategories. The coefficients
reported in column (1) are estimated with nongamblers being included as the control group. The most striking observation from the results is that nearly all estimated ![]() coefficients are
coefficients are
![]() and are highly statistically significant for total expenditure and for most expenditure subcategory. For example, as shown in the top row,
and are highly statistically significant for total expenditure and for most expenditure subcategory. For example, as shown in the top row,
![]() for total expenditure, suggesting that one more dollar spent on gambling is associated with 3 more dollars of other expenditures. Recall that the reported gambling costs in the
CE are likely only a fraction of the true gambling costs, so the estimated
for total expenditure, suggesting that one more dollar spent on gambling is associated with 3 more dollars of other expenditures. Recall that the reported gambling costs in the
CE are likely only a fraction of the true gambling costs, so the estimated ![]() is potentially upward biased. However, at a minimum, the results present no evidence that other household
expenditures are crowded out by higher spending on gambling.
is potentially upward biased. However, at a minimum, the results present no evidence that other household
expenditures are crowded out by higher spending on gambling.
The increase in nongambling expenditures does not appear to be concentrated in any expenditure subcategory. Essentially all expenditures, from food to reading materials, increase by margins that are both economically and statistically significant (in the perspective of each expenditure category's typical budget share). For example, when spending on gambling is 1 dollar higher, food expenditure is almost 40 cents higher while housing and transportation expenditures are 60 cents higher.13 Moreover, alcoholic beverages, tobacco, and entertainment expenditures are all higher and the margin is appreciable given their small shares in total expenditure for typical consumers.14 Relatedly, gamblers' expenditure shares on alcoholic beverage, tobacco, and entertainment are noticeably higher than nongamblers.15 By contrast, expenditures on health care and education do not appear to be affected by variations in gambling costs. Accordingly, gamblers' expenditure shares on health care and education are lower than nongamblers. The differences in other expenditures as a share of total expenditure between gamblers and nongamblers, though statistically significant, are not pronounced in a proportional sense.
It is possible that gamblers on average have higher expenditures on everything than non-gamblers. If so, the positive coefficients in column (1) reflect this difference between gamblers and nongamblers and do not necessarily speak to how nongambling expenditures vary with gambling costs. To address this caveat, we re-estimate eq.(2) using only the gambler sample, without including nongamblers as the control group. Apart from the point estimates being somewhat smaller and some coefficients becoming less statistically significant, the results--reported in column (2)--are largely similar to those in column (1). Our estimates continue to suggest that most categories of household expenditure are positively correlated with gambling costs. For example, among all consumers who gambled in a given year, their total expenditure in that year net of gambling costs will be 1.8 dollars higher if their annual spending on gambling is 1 dollar higher. The increase also tends to be broadly distributed across expenditure categories, in particular, on food, alcoholic beverage, tobacco, apparel, housing, transportation, and entertainment.16
We are also interested in the potential heterogeneities between the occasional and the frequent gamblers. We re-estimate eq.(2) using the subsamples that include only the occasional and the frequent gamblers, respectively. The results are reported in column (3) and (4). Strikingly, the estimated expenditure responses to gambling cost variations are much more pronounced for occasional gamblers--those who gambled in only one quarter during the year they were in the sample. In contrast, coefficients estimated for frequent gamblers--those who gambled in all four quarters--are broadly similar to those reported in column (2). The large point estimates derived from the occasional gamblers subsample is consistent with the aforementioned hypothesis that, for some consumers, gambling activities were triggered by positive changes to their financial conditions. They chose to increase spending on a wide range of goods and services and at the same time entertain themselves with some occasional gambling fun of a small budget.
3.2 Expenditure Growth Analysis
Even focusing on the subsample of gamblers, the positive coefficients in columns (2), (3) and (4) may still be accounted for by the possible scenario where more aggressive gamblers also spend more on other things (i.e, the gambler fixed effects). To further assess how other household expenditures change with variations in gambling costs, we exploit the short panel design of the CE and estimate the following expenditure growth model
where
The results are shown in the lower panel of table 2. When nongamblers are included as the control group, the estimation results of eq.(4) are similar to those for eq.(2), with the only differences being somewhat smaller point
estimates and several coefficients, in particular housing and transportation expenditure coefficients, becoming statistically insignificant. For example, the change in total expenditure (net of gambling costs) from one quarter to the next will be 2.7 dollars greater if gambling costs increase one dollar between these two quarters. Not surprisingly, the coefficients are essentially unchanged when eq.(4) was estimated using the subsample of gamblers because for
nongamblers
![]() .
.
Furthermore, the coefficients estimated using the subsample of occasional gamblers remain statistically significant for total expenditure and most expenditure subcategories. Also, relative to the expenditure levels analysis reported in the top panel, the occasional gambler sample point estimates are closer to those in column (2). One potential factor accounting for this difference is that although occasional gamblers had higher expenditures on many goods and services, these additional expenditures did not necessarily occur in the same quarter as they engaged in gambling activities. Should this be the case, nongambling expenditures will appear to be more sensitive to gambling expenditures in the annual expenditure level regressions than in the quarterly expenditure growth regressions.
The positive correlation between gambling and nongambling expenditures becomes somewhat less pronounced when we estimate eq.(4) using the frequent gamblers subsample. Unlike occasional gamblers, all three quarterly expenditure growth observations corresponding to each
frequent gambler have nonzero ![]() , providing more identification power. First, we find that, when gambling costs are higher than the previous quarter, food, alcoholic beverage, apparel,
and personal care expenditures are also higher than the previous quarter and the increases are statistically and economically significant. Second, total expenditures and expenditures on most other categories also tend to be higher when gambling costs are higher but not in a statistically
significant manner.
, providing more identification power. First, we find that, when gambling costs are higher than the previous quarter, food, alcoholic beverage, apparel,
and personal care expenditures are also higher than the previous quarter and the increases are statistically and economically significant. Second, total expenditures and expenditures on most other categories also tend to be higher when gambling costs are higher but not in a statistically
significant manner.
In sum, our analysis above presents essentially no evidence that any expenditure was materially reduced in a quarter when gambling costs are higher.
3.3 Higher Expenditure or Higher Income?
If those with higher spending on gambling have higher other expenditures at the same time, a question that arises is how do they finance everything? Since other expenditures are not squeezed, are gamblers saving less relative to other consumers? Table 3 contrasts the average propensity to consume (APC) of gamblers to that of nongamblers. APC is defined as the ratio between total expenditures (including gambling costs) and total income. We compute both the APC out of the imputed permanent income and the observed current income as observed in the last interview. Because, as table 2 shows, gamblers have higher other expenditures, it is perhaps not surprising that gamblers have higher APC out of their permanent income than nongamblers--98% versus 89%--with the average APC for frequent gamblers being the highest, topping 100%. However, it is interesting to notice that the order is reversed for APC out of current observed income. Gamblers have lower APC (93%) than nongamblers (96%). Furthermore, frequent gamblers have even lower APC out of current income at 91%.
The differences between APC calculated with different income metrics suggest that the gap between current income and the imputed permanent income for gamblers, especially the frequent gamblers, is very different than that for nongamblers. Indeed, examining the residuals of the permanent income imputation equation, we find gamblers' current income is significant higher than their permanent income predicted by the model. As the memo line of table 3 suggests, gamblers' current income as observed in the survey is on average more than 7 percent higher than their imputed permanent income. The gap for frequent gamblers is even wider at nearly 10 percent. By contrast, nongamblers' observed current income is on average 3% lower than their imputed permanent income.
How do we interpret these results? On balance, our results suggest that gambling tends to occur when household income in a given year is higher than normal income in the long run as predicted by eq.(3), i.e., when ![]() is larger. In such a scenario, households tend to increase expenditures broadly, with gambling being one part of it. To see this, we estimate the following logistic model:
is larger. In such a scenario, households tend to increase expenditures broadly, with gambling being one part of it. To see this, we estimate the following logistic model:
and the indicator variable,
| (6) |
The logistic model correlates the likelihood of being a gambler in a given year with
We find that a one-standard-deviation increase in the current-permanent income gap, ![]() , is associated with a nearly 40% higher likelihood of being a gambler, whereas the imputed logarithm
of permanent income,
, is associated with a nearly 40% higher likelihood of being a gambler, whereas the imputed logarithm
of permanent income,
![]() does not affect the likelihood of being a gambler.18 In addition, we examine how gambling intensity (the dollar amount of gambling costs) varies with
does not affect the likelihood of being a gambler.18 In addition, we examine how gambling intensity (the dollar amount of gambling costs) varies with
![]() , the level of imputed permanent income, and
, the level of imputed permanent income, and
![]() , with the same set of control variables. In this regression, we only use the gambler sample. We find that gambling costs are also positively correlated with
, with the same set of control variables. In this regression, we only use the gambler sample. We find that gambling costs are also positively correlated with
![]() but are negatively correlated with
but are negatively correlated with
![]() . Not surprisingly, in light of this result, gambling expenditure's share in total expenditure consistently declines with income (both imputed permanent and current income). As
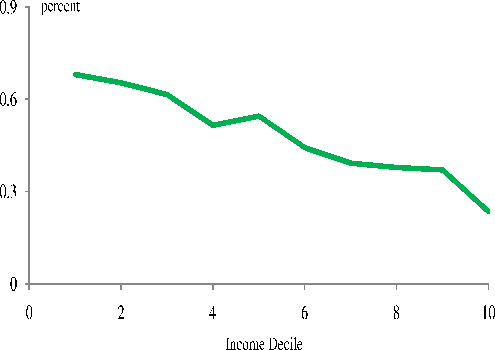
shown in figure 1, the average share of gambling costs in total expenditures for consumers in the lowest income decile is about 0.7%. The share declines to 0.2% for the highest income decile consumers.
. Not surprisingly, in light of this result, gambling expenditure's share in total expenditure consistently declines with income (both imputed permanent and current income). As
shown in figure 1, the average share of gambling costs in total expenditures for consumers in the lowest income decile is about 0.7%. The share declines to 0.2% for the highest income decile consumers.
3.4 Reconciling with Kearney (2005)
Our findings above are in stark contrast to those presented in Kearney (2005). Kearney finds that the introduction of state lotteries crowded out other consumer expenditures, whereas our analysis suggests that higher gambling costs are associated with higher other consumption expenditures, likely attributable to the higher-than-normal realized income in the survey year. Part of the reason why our findings are different from hers is that Kearney exploits exogenous changes in gambling costs due to the introduction of state lotteries, which are not frequently observed in our sample period. Indeed, in our data only four states (Arkansas, North Carolina, South Carolina, and Tennessee) introduced state lotteries. To examine whether the introduction of state lotteries also caused nongambling expenditure to decline during our sample period, we estimate a model similar to Kearney (2005) using data from these four states. Our point estimates suggest that both total and nondurable expenditures of residents in these states indeed declined after state lotteries were introduced, though some of the estimates are not statistically significant. Because none of these states is very populous or has many observations in the CE sample, the statistical power of replicating Kearney's analysis using our sample can be limited.
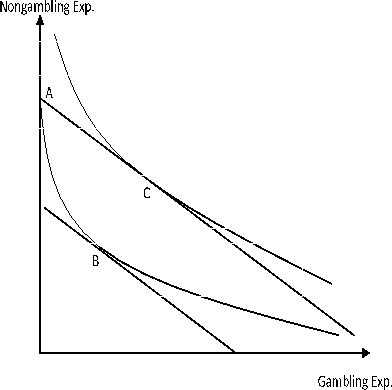
Figure 2 illustrates why regulatory changes cause gambling costs to crowd out other expenditures whereas absent such regulatory changes higher gambling costs tend to be associated with higher other expenditures. The figure plots two indifference curves regarding
consumption bundles of gambling and nongambling expenditures. Between the two indifference curves, the one farther away from the origin corresponds to a higher utility level and is achieved with a higher budget constraint--line ![]() . The pivotal factor that accounts for the difference is that in Kearney (2005), assuming there are no other forms of gambling except state lotteries, consumers are moving from point A (no gambling is allowed) to point C (gambling is allowed due to the
introduction of state lotteries), causing gambling expenditure to increase from zero to positive but nongambling expenditure, on net, to decline. By contrast, in our analysis, consumers are moving from point B to point C. Gambling expenditure increases (likely) because of a higher budget
constraint. Accordingly, nongambling expenditures also go up.
. The pivotal factor that accounts for the difference is that in Kearney (2005), assuming there are no other forms of gambling except state lotteries, consumers are moving from point A (no gambling is allowed) to point C (gambling is allowed due to the
introduction of state lotteries), causing gambling expenditure to increase from zero to positive but nongambling expenditure, on net, to decline. By contrast, in our analysis, consumers are moving from point B to point C. Gambling expenditure increases (likely) because of a higher budget
constraint. Accordingly, nongambling expenditures also go up.
3.5 Charitable Giving? Other Potential Motivations for Gambling
In addition to entertainment values, could there be alternative motivations for gambling, in particular, for buying lotteries?19 Many commercials advertise state lotteries as, instead of a form of gambling, a way of giving on the basis that the net revenue of state lottery programs will be used for financing public projects.20 State lotteries, interpreted as a substitute for donations to public projects, are more expensive than other direct donations because the costs on state lotteries are not tax deductible. That said, should such public relation campaigns be effective and the attached entertainment value of state lotteries offset some of their tax-related disadvantages, it is possible that some consumers buy lotteries out of charitable giving motivations.
If state lotteries are perceived by consumers as (imperfect) substitutes for charitable giving, there should be two testable hypothesis. Other factors held constant, first, charitable donors are more likely to buy state lottery tickets, and second, among charitable donors, gamblers' donations to charities are smaller in dollar amount because a portion of such donations is substituted for lottery expenses. The CE data record four types of donations--charitable, religious, political, and educational.21 We combine charitable and educational donations and refer to them as charitable donations.22 Table 4 presents the summary statistics of the share of households making a certain type of donation and, among the subsample of households making such a donation, the average donation value. In the CE sample, slightly more than 40% of nongamblers made charitable donations in a given year, while this share is much higher, 57%, among gamblers. By contrast, the share of households making religious donations in a given year looks remarkably similar between gamblers and nongamblers (near 45%). Finally, the share of households making a political donation is much smaller in general and is slightly higher among gamblers (5.5% versus 4.5%).23 Notably, the share of gamblers making donations does not appear to vary much with gambling intensities. Looking at the dollar amount of such donations, consistent with the second testable hypothesis, gamblers, though more likely to make a charitable donation, have a much lower value of annual donations than nongamblers ($296 versus $417). Similarly, the average amount of religious and political donations among donors is much lower among gamblers.
Table 5 reports results of logistic and OLS regressions, controlling for observable characteristics. Specifically, we estimate the following logistic model:
where
| (8) |
In addition, we estimate eq.(7) with the
To summarize, we find some suggestive and preliminary evidence that some consumers appear to take state lotteries as a substitute for charitable donations, despite their tax disadvantages. The relationship between state lottery and charitable giving thus presents a promising topic for future research.
4 Gamblers' Balance Sheets
We argue that a key insight from our analysis of gamblers' expenditure is that gambling, to most households who gamble, is a form of pastime and entertainment, and is budgeted along with other household expenditures. That said, given that only a fraction of consumers gambled in a given year and some consumers have not gambled over their entire lives, gambling is likely a type of pastime or entertainment that only individuals with certain traits will engage in. The subsequent analysis that contrasts balance sheets and attitudes towards risks (financial and nonfinancial) between gamblers and nongamblers suggests that such traits can be understood as a "personal finance activism."
4.1 Asset Holdings
Table 6 presents summary statistics of key liability and asset holdings indicators. Johnson and Li (2010) document that the CE liability data compare favorably with their counterparts in the Survey of Consumer Finances (SCF), which is widely regarded as the most comprehensive and accurate data source of household balance sheet for U.S. households. The CE financial assets data, however, have many fewer details and potentially greater measurement errors. Therefore, results related to the levels of financial asset should be interpreted with a grain of salt. For this reason, we focus more on indicators of whether a household owns a particular type of asset, such as securities, instead of asset holding levels.
On balance, the table shows that gamblers tend to be more active than nongamblers on both sides of the household balance sheet in the sense that they are more likely to have various types of debt while at the same time are more likely to own various types of assets, financial and nonfinancial. Looking at the top of table 6, nongamblers on average hold about $13,000 (in year 2000 dollars) liquid financial assets (balances in checking and saving accounts), while gamblers on average hold more than $16,000, or more than 20% higher. Comparing holdings between occasional and frequent gamblers, we find the variations in liquid financial asset levels are relatively small as measured by the intensity of gambling. More interestingly, gamblers are more likely to hold financial securities, including stocks.26 More than 21% of gamblers hold financial securities, in contrast to a 14% financial security ownership among nongamblers.27
Looking at ownership of real assets, we find that gamblers are somewhat more likely to be homeowners than nongamblers (75.5% versus 71.8%). Similarly, gamblers are slightly more likely to own a car. Among gamblers, home and car ownerships do not appear to vary much by gambling intensity. Perhaps more notably, gamblers are more likely to own a second home. Specifically, 6.5% of nongamblers own a "second home, vacation home, or recreational property," while 7.7% (20% higher) of gamblers own such properties.28 In a similar spirit, another intriguing observation from table 6 is that, among car owners, gamblers are more likely to concurrently lease a car (5.7%) than nongamblers (4.4%). We interpret these findings as suggestive evidence that gamblers are more willing to enter various markets of services and products.
4.2 Liabilities
We now turn to the liability side of the household balance sheet. First, gamblers and nongamblers, conditional on owning a home, have essentially the same probability of having a mortgage. That said, gamblers appear to manage their mortgage in a more active fashion. More than 38% of gamblers with a mortgage reported that they have refinanced their mortgages before, in contrast to only 31% of nongambler mortgagors. In particular, frequent gamblers are also frequent refinancers, with 40% of their mortgages having been refinanced previously.
Looking at debt with shorter maturities, we find that, despite a significantly higher liquid financial asset holding, gamblers are at the same time more likely to owe debt that typically carries substantial interests and financial charges. 38% of gambler car owners have car loans, compared with 33% of nongambler car owners. More strikingly, 47% of gamblers owe credit card debt, with the share among frequent gamblers being even higher (51%), while only 35% of nongamblers owe credit card debt. Furthermore, gamblers, and in particular frequent gamblers, are more likely to accumulate net credit card debt over the year they participated in the CE survey.
Gamblers not only are more likely to have various types of asset and debt on their balance sheets, they are also more likely to own certain assets and owe certain debts at the same time. For example, about 9% of nongamblers owe significant credit card debt (greater than $1,000) and simultaneously have a substantial amount of liquid financial assets (at least 50% of their credit card debt balance).29 By contrast, this share is almost 50% higher among gamblers. Such a concurrent holding of low-yield liquid assets and high-cost credit card debt is often viewed as a puzzle--the so-called "credit card debt puzzle" (Wright and Telyukova (2008) and Telyukova (2011)). Presumably, a household would be better off paying off the expensive credit card debt using their checking account balances. Potentially speaking to this puzzle, we also find that (not shown) gamblers are appreciably more likely to concurrently owe credit card debt or car loans and invest in financial securities, such as stocks. Because the checking account balances reported to the CE include balances on brokerage accounts, it is possible that security investors choose to hold a certain level of liquidity and simultaneously borrow expensive credit card debt. Amromin, Huang, and Sialm (2007) show that many households have a debt aversion, i.e., they do not want to participated in financial markets, both as a borrower or as a lender. Our analysis suggests that gamblers' attitudes towards financial markets are markedly different: They do not shy away from indebtedness while at the same time appear to keep their assets in fairly active portfolios.
4.3 Logistic Analysis
The statistics presented in table 6 are unconditional. Gamblers and nongamblers are different in many ways apart from whether they gamble. Such differences may also lead them to have different balance sheets. To control for the differences in observable characteristics between gamblers and nongamblers, we estimate a series of logistic regressions, one for each asset and liability ownership indicator, to answer the question of whether a gambler is more likely to owe a given type of debt or to own a given type of asset than a nongambler who otherwise has similar demographic and socioeconomic characteristics.
Specifically, we estimate the logisitic models defined as in eq.(7), with dependent variables being replaced with indicators of debt and asset ownership. Table 7 presents the coefficients, standard errors, and odds ratios estimated from the logistic
regressions. The odds ratios are evaluated by switching the ![]() dummy from zero to one. For brevity, we only report regression results of a subset of asset and debt ownership
indicators.
dummy from zero to one. For brevity, we only report regression results of a subset of asset and debt ownership
indicators.
Consistent with table 6, logistic regression results indicate that first, gamblers, controlling for other observable characteristics, are 60% more likely to invest in financial securities than nongamblers and the margin is essentially the same for both occasional and frequent gamblers. Second, gamblers are 17% more likely to own a second home or vacation property, almost entirely due to the higher ownership of such properties among occasional gamblers. Third, gamblers are nearly 60% more likely to concurrently have credit card debt and liquid financial assets (the "credit card puzzle"). The difference in odds ratio between occasional and frequent gamblers is small and statistically insignificant. Fourth, gamblers are 27% more likely to have had their mortgage refinanced before, with the odds ratio for frequent gamblers significantly higher than that for occasional gamblers. Finally, both occasional and frequent gamblers are 30% more likely to own a car and lease a car at the same time. Results for other ownership indicators (not shown) are all consistent with the statistics reported in table 6 and are all statistically significant.
4.4 Does the Activism Pay Off?
Having documented extensive evidence that gamblers tend to more actively participate in a wide range of household finance markets, we are interested in whether such active investment and borrowing behaviors help improve their net financial positions. We compare the net worth of gamblers and
nongamblers, taking into account their potential income differences. Because the CE does not collect comprehensive information on household balance sheets, our measure is only a part of the household total net worth. In particular, we do not observe the value of owned vehicles. Moreover, we do not
use the CE data on some liabilities, such as home equity loans, because they are substantially different from the SCF counterparts. Accordingly, we construct the partial net worth (![]() )
as
)
as
![]()
We argue that the constructed ![]() is informative regarding understanding the total net worth because the SCF counterpart of our partial net worth measure accounts for about 80% of the SCF
comprehensive measure of net worth and the SCF partial and comprehensive measures of net worth are highly correlated, with a correlation coefficient equal to 0.8.
is informative regarding understanding the total net worth because the SCF counterpart of our partial net worth measure accounts for about 80% of the SCF
comprehensive measure of net worth and the SCF partial and comprehensive measures of net worth are highly correlated, with a correlation coefficient equal to 0.8.
We find that, notwithstanding active management of their portfolios, gamblers and nongamblers have remarkably similar levels of net worth. After all, simultaneously holding debt and assets per se does not necessarily improve the bottom line of the balance sheet. In many scenarios, a household would be better off had they paid off more expensive debt using liquid assets with lower yields (see, for example, Li and Smith (2010)). As shown in the lower part of table 6, both gamblers and nongamblers have a net worth somewhat higher than $160,000. Because gamblers have, on average, higher current income, the net worth to income ratio is lower for gamblers. As discussed in Section 3, gamblers' higher current income likely reflects (potentially transitory) deviations from their long-run normal levels (the permanent income). Accordingly, we also present the mean of the logarithm of permanent income imputed with eq.(3). The mean statistics are calculated within each subsample, respectively.30 As shown in the data, gamblers' imputed permanent income, though higher than nongamblers, is much more similar to that of nongamblers. The difference in current income is 15 log points, while the difference in imputed permanent income is only 5 log points. On balance, net worth relative to long-run normal income appears to be fairly similar between gamblers and nongamblers.31
5 Risky Behaviors and Non-mandatory Insurance
Most gambling games feature huge variances in payoffs, presenting substantial financial risks to players. Gamblers' willingness to bear the risks despite such games' typical negative expected payoffs, besides entertainment motivation, may also reflect these consumers' more tolerant and accommodative attitudes towards financial risks. Indeed, balance sheet analysis reveals that gamblers are more likely to assume more aggressive positions when managing their own finances. In this section, we study whether such a bold attitude also applies to nonfinancial risks, in particular, health risks. Our findings suggest that gamblers do have a higher propensity to engage in activities risky to one's health, prompting us to also examine whether gamblers understand such risks and choose to insure themselves against them. In this regard, our analysis shows that gamblers are more willing to pay out-of-pocket to purchase non-mandatory insurance policies, such as health, home, and life insurance.
We consider two types of activities that are potentially risky for one's health--(excessive) drinking and smoking. We define a household as a drinker and a smoker if within a given year it has positive spending on alcoholic beverages and tobacco products, respectively. Because moderate drinking may not be harmful, we further define someone as a heavy drinker if the household spent more than 2.5 percent of its annual income on alcoholic beverages and spent more than $100 in each of the four quarters.
Table 8 presents summary statistics of engaging in drinking and smoking and purchasing home, life and health insurance. Gamblers, especially the frequent gamblers, are more likely to drink alcohol, both moderately and heavily, and to smoke. For example, 5% of nongamblers behaved like heavy drinkers, in contrast to nearly 10% of gamblers. The heavy drinker share among frequent gamblers is even higher (11%). In addition, about 30% of nongamblers smoke, compared with 43% of gamblers.
We then explore the opposite side of engaging in risky behaviors, namely, what share of gamblers buy insurance. Documenting gamblers' purchases of insurance potentially sheds light on the preferences of such consumers. A famous assertion due to Friedman and Savage (1948) claims that people buy lotteries and auto insurance at the same time, a seemingly violation of the global concavity of preferences. More than six decades later, concurrent purchases of lotteries and auto insurance likely no longer speak to consumers' preferences because auto insurance has largely become mandatory. We therefore focus on optional insurance. Besides life and health insurance, home insurance is essentially optional if there is no outstanding mortgage attached. Finally, we count a household as having purchased such non-mandatory insurance only when there are some out-of-pocket expenses incurred, thus excluding insurance provided entirely by employers.
Despite the higher likelihood of engaging in activities potentially harmful for one's health, a large share of gamblers pay out-of-pocket costs to buy home, life, and health insurance.32 The statistics show that, while about 45% of nongamblers buy life insurance and health insurance, the shares for gamblers who buy these insurance are somewhat higher at 57% and 50%, respectively. In addition, two thirds of gamblers who own a home without having a mortgage continue to buy home insurance, a share almost 10 percentage points higher than nongamblers.33 Finally, we point out, in the memo line of table 8, that although gamblers are more willing to buy non-mandatory insurance, conditional on buying insurance, gamblers appear to spend a similar amount of money on this insurance.34
If people are rational and properly informed about the health-related risk of smoking and drinking but choose to engage in these activities due to non-risk-aversion related idiosyncratic preferences, we would expect heavy drinkers and smokers to be more likely to buy life and health insurance. Accordingly, we further examine the simultaneity of risky behaviors and insurance purchases--are heavy drinkers and smokers the same individuals who buy life and health insurance? The answer appears to be "no" on an unconditional basis and "yes" among gamblers after controlling for observables. As shown in table 8, the share of consumers who buy life or health insurance, conditional on behaviors of smoking and heavy drinking, are not dramatically different from shares computed without conditioning on such behaviors. The similarity largely holds for both gamblers and nongamblers.
The regression results, with the same controls as in eq.(7), are presented in Table 9. Essentially all of the unconditional differences in the propensity of drinking, smoking, and purchasing insurance are preserved in the coefficients estimated from the models. In all regressions the estimated gambler dummy coefficient is positive and statistically significant at a 99% level or higher. The estimated odds ratios suggest that the differences between gamblers and nongamblers in the propensity of heavy drinking and smoking are substantial. Specifically, gamblers are 100% and 80% more likely to be heavy drinkers and smokers than nongamblers.35
Turning to the purchase of insurance, the results are essentially the same. Controlling for observable characteristics, gamblers are about 20% more likely to buy health insurance, almost 50% more for life insurance, and 30% more for home insurance. That said, apart from life insurance, occasional gamblers do not appear to have a higher propensity to buy insurance than nongamblers, at least in a statistically significant manner, while the differences between frequent gamblers and nongamblers hold and are somewhat more pronounced.
The lower panel of the table presents a tentative test of the hypothesis that people rationally insure themselves when they choose to engage in risky behaviors, conditional on observable characteristics. We run logistic regressions with health and life insurance dummies on the left hand side. On
the right hand side, in addition to the same control variables in eq.(7), we include a risky behavior dummy (smoking or heavy drinking) and a term of this dummy interacting with the gambler dummy. The estimation results largely reject the hypothesis in the general population.
Except that heavy drinkers appear to be more likely to buy health insurance regardless whether they gamble (column 3), estimated smoker and heavy drinker coefficients are either negative and statistically significant (columns 1 and 2) or being a insignificant small positive number (column 4). By
contrast, the coefficients on the smoker-gambler interaction terms are positive and significant and outweigh the negative smoker dummies in both life and health insurance regressions.36 Thus, though smokers in general are less likely to buy life and health insurance, gambling smokers are more likely to do so. The gambling heavy drinker coefficient in the health insurance regression is positive and, though not
statistically significant at the 90% level, has a Wald ![]() = 2.4 (p-value 0.12). Finally, in contrast to the small and insignificant coefficient for the heavy drinker dummy, the
coefficient of the gambling heavy drinker dummy is positive and both statistically and economically significant in the life insurance regression. To summarize, our analysis indicates that it is not generically true that smokers and drinkers are more willing to buy insurances. Rather, only those
smokers and drinkers who also gamble appear to be more willing to buy insurance, relative to other consumers with similar observable characteristics.37 We
interpret these results as broadly consistent with the notion that gamblers are more active in taking on and managing risks, similar to their attitudes and strategies taken with respect to financial risks.
= 2.4 (p-value 0.12). Finally, in contrast to the small and insignificant coefficient for the heavy drinker dummy, the
coefficient of the gambling heavy drinker dummy is positive and both statistically and economically significant in the life insurance regression. To summarize, our analysis indicates that it is not generically true that smokers and drinkers are more willing to buy insurances. Rather, only those
smokers and drinkers who also gamble appear to be more willing to buy insurance, relative to other consumers with similar observable characteristics.37 We
interpret these results as broadly consistent with the notion that gamblers are more active in taking on and managing risks, similar to their attitudes and strategies taken with respect to financial risks.
6 Personal Finance Activists or Careful Survey Participants?
We argue that the expenditure, charitable donations, balance sheets, and risk management patterns among gamblers reflect such consumers' unique traits, which we refer to as a "personal finance activism." One prominent alternative explanation is that gamblers recorded in the CE data are simply careful survey participants. They answer questions related to expenditures and balance sheet more carefully and it is not surprising that they are more likely to report positive gambling expenditures and, for the same reason, more activities such as making donations, investing in financial securities, owning a second home, smoking, buying health insurance, etc. We argue that this is not likely the main factor responsible for differences between gamblers and nongamblers.
First, previous studies have shown that though the CE data on average underestimate total household expenditures relative to the Personal Consumption Expenditure statistics compiled by the Bureau of Economic Activities (see, for example, Branch (1994) and Gieseman (1987)), there is little evidence that certain households systematically underreport their expenditures to a greater extent. Second, we have shown that consumers are more likely to gamble when their income is (potentially temporarily) higher than its long run normal level. Could this be due to nongamblers, in addition to underreporting their expenditures, also underreporting their income? Research on income underreporting to household surveys is scarce, with a recent exception of Hurst, Li, and Pugsley (2012), who have documented that the self-employed are likely to underreport their income to household surveys partly because of the complexity of their income. Nevertheless, we find that in the CE sample, gamblers and nongamblers have very similar share of self-employed (10% and 11% respectively). Furthermore, looking at the detailed composition of total income, 85% of total income of both gamblers and nongamblers is salary income.38 Earlier research by Bound et al. (1994) has found that households typically report salary income fairly accurately. Therefore, the income difference between gamblers and nongamblers is likely real.
Are the lower expenditures and narrower range of asset and liability ownership due to careless responses to the survey? Although we cannot reject such a hypothesis outright, we will present extensive evidence that suggests otherwise. First, we make use of the paradata that CE released for the 2005 - 2010 surveys. These paradata include information recorded by interviewers regarding whether respondents used records, such as receipts and bank statements, while answering questions and total interview time. We find that the fraction of households not referring to records while answering survey questions in any quarterly interviews (the most careless survey participants) is only slightly higher among nongamblers (15.6%) than among gamblers (13.5%). The fraction of consumers who referred to records in all four quarterly interviews (the most careful survey participants) are essentially the same for gamblers and nongamblers, both are 46%.
Comparing the total survey time aggregating all four interviews, we find that the total time spent with nongamblers on average are 1,800 seconds shorter, or 7.5 minutes shorter per interview, than gamblers.39 This is not surprising if nongamblers genuinely have fewer expenditures to report. However, the total time difference may also be due to some consumers deliberately skipping certain questions. To see whether the survey time gaps account for the differences between nongamblers and gamblers, we remove consumers whose total interview time is shorter than 10,000 seconds from the sample, or about 20% of the entire 2005-2010 sample. Gamblers and nongamblers in the restricted sample have very similar mean of total interview time. Essentially all the gambler-nongambler differences documented before are preserved in the restricted sample.
Finally, we take advantage of the fine details of the CE expenditure data and use the UCC-level information to compare expenditure reporting patterns of gamblers and nongamblers. Specifically, if careless reporting and question-skipping causes some gamblers being categorized as nongamblers and frequent gamblers as occasional gamblers, we will see that gamblers report positive expenditures for more UCCs than nongamblers, and that frequent gamblers report positive expenditures for more UCCs than occasional gamblers. Over the entire four interviews, gamblers on average report positive expenditures on 88 UCCs, 16 more than nongamblers. However, the average number of UCCs reported by frequent and occasional gamblers are almost identical. Unless true frequent gamblers underreport themselves as occasional gamblers to a much lesser extent than true gamblers in general underreport themselves as nongamblers, the lack of difference in the number of UCCs reported between frequent and occasional gamblers appears to suggest that careless reporting and questions skipping is not the main factor that explains the documented behavior differences between gamblers and nongamblers.
We then calculate, for each UCC, the share of gamblers and nongamblers (and of occasional and frequent gamblers) who reported positive expenditure. The ratio, ![]() , of the two shares
measures the relative propensity of reporting positive expenditures on a particular UCC. Eliminating the UCCs rarely reported by all consumers, we find that
, of the two shares
measures the relative propensity of reporting positive expenditures on a particular UCC. Eliminating the UCCs rarely reported by all consumers, we find that ![]() calculated between
occasional and frequent gamblers has a mean and median both very close to one, suggesting that there are about equal number of UCCs that are more likely being reported by occasional gamblers and UCCs that are more likely being reported by frequent gamblers.
calculated between
occasional and frequent gamblers has a mean and median both very close to one, suggesting that there are about equal number of UCCs that are more likely being reported by occasional gamblers and UCCs that are more likely being reported by frequent gamblers. ![]() calculated between nongamblers and gamblers has a mean and median equal to 0.8, suggesting that a positive expenditure on the same UCC is 20% less likely to be reported by nongamblers than gamblers. Although we cannot
rule out careless reporting as an explanation for
calculated between nongamblers and gamblers has a mean and median equal to 0.8, suggesting that a positive expenditure on the same UCC is 20% less likely to be reported by nongamblers than gamblers. Although we cannot
rule out careless reporting as an explanation for
![]() , examining the
, examining the ![]() that has the lowest value--the UCCs
that are least likely to be reported by nongamblers relative to the reporting propensity of gamblers on the same UCCs--we find that most of these UCCs correspond to either expenses directly speaking to gamblers's more active balance sheets (for example, membership fees for credit cards) or expenses
that are not likely to be overlooked or skipped during the survey (for example, newspaper and magazine subscriptions).40
that has the lowest value--the UCCs
that are least likely to be reported by nongamblers relative to the reporting propensity of gamblers on the same UCCs--we find that most of these UCCs correspond to either expenses directly speaking to gamblers's more active balance sheets (for example, membership fees for credit cards) or expenses
that are not likely to be overlooked or skipped during the survey (for example, newspaper and magazine subscriptions).40
7 Concluding Remarks
Why do people gamble? Are gamblers intrinsically different from other consumers? What else can we learn from observing people's gambling behaviors? Little consensus has been reached regarding answers to these questions. Our paper takes a first step in answering these questions. We show that most gamblers appear to perceive gambling as a form of pastime, the spending on which is budgeted along with other household spending and does not necessarily crowd out nongambling expenditures. If consumers engage in gambling merely for its entertainment value instead of as an investment vehicle or a way of generating revenue, important caveats should apply regarding the extent to which preference parameters teased out from gambling betting strategies can be generalized to the broad context of household financial decision making. That said, our analysis also reveals significant merit in using gambling behavior as an indicator for important household heterogeneities that are difficult to observe directly in data.
Indeed, classical household consumption and saving models were developed in a homogeneous representative agent framework. These models, though insightful and elegant, often fall short in explaining empirical regularities. Extending these models to allow for heterogeneous agents has been on the research agenda of the students of consumer behavior and financial markets for a long time. However, in addition to the daunting computational costs of solving these models, it is also difficult to establish a mapping between such heterogeneous agent models and data because what these models attempt to address involves differences in household preferences, perceptions, the information they possess, and other personal traits and characteristics, which are infamously hard to observe.
Data regarding such heterogeneity can rarely be collected directly in surveys. For example, it is unlikely that an econometrician will get useful answers if she asks the survey respondents "are you a rule-of-thumb consumer or a PIH consumer?" Or, "what is your subjective discounting factor and risk aversion coefficient?" Instead, the identification of household heterogeneity in these regards often relies on inference made by comparing observed state variables or individual behaviors. For example, Hurst (2006) labels consumers as "grasshoppers" (spenders) and "ants" (savers) by their pre-retirement level of wealth. He finds that the consumers who have low pre-retirement wealth would have consistently deviated from the permanent income hypothesis over their life cycles. Similarly, Ameriks, Caplin, and Leahy (2003) find that "planners," who spend more time on developing financial plans, are more likely to have higher wealth. More recently, Cadena and Keys (2011) infer time discounting factors of young adults using information about whether they were patient while participating in a survey.
We show that the observed gambling activities, even those that are infrequent and in fairly small dollar amounts, potentially speak to important household characteristics such as tolerance to risks, attitude towards financial markets, and confidence over own financial sophistication, which all play pivotal roles in determining household consumption, saving, and portfolio choices. We argue that differences in these characteristics potentially lead certain households to more actively participate in a wide range of financial markets. In particular, gamblers tend to be both active borrowers and investors, markedly different from households reluctant to be either a lender or a borrower (Amromin, Huang, and Sialm (2007)).
Understanding the intensity of households' participation in financial markets, how it varies across households, and how it influences financial well-being, besides being an interesting subject of research, has important policy implications. For example, many government-sponsored programs designed for strengthening household financial well-being, such as improved access to credit and subsidized loans, are market-based. These policy instruments would have little effects on those who have only limited participation in personal finance markets. Moreover, it is well documented that stock market participation rates are fairly low in the population as a whole, and that for stock investors their stock holdings are moderate relative to their entire asset portfolio (Mankiw and Zeldes (1991), Vissing-Jorgesen (2002), and Gomes and Michaelides (2005), among others). Identifying certain "traits" of active stock investors potentially could help promote more efficient investment strategies among those "passive" investors.
| Characteristics | % Gamblers | % Occasional | % Frequent | (Among gamblers) Gambling costs ($) | (Among gamblers) Gambling costs ($) [Median] | (Among gamblers) Ratio to income (%) | (Among gamblers) Ratio to income (%) [Median] |
| All | 29.3 | 11.3 | 5.6 | 201 | [57] | 0.35 | [0.13] |
| Age <30 | 22.3 | 11.4 | 1.7 | 89 | [35] | 0.20 | [0.10] |
| Age 30 - 44 | 27.7 | 12.0 | 4.4 | 147 | [47] | 0.23 | [0.09] |
| Age 45 - 64 | 33.2 | 11.7 | 7.1 | 225 | [64] | 0.37 | [0.13] |
| Age >65 | 27.1 | 9.7 | 6.3 | 269 | [79] | 0.70 | [0.26] |
| Married | 30.6 | 11.7 | 6.0 | 199 | [59] | 0.29 | [0.11] |
| Divorced/widowed | 27.7 | 10.5 | 5.4 | 215 | [52] | 0.57 | [0.18] |
| Single male | 29.9 | 12.0 | 5.9 | 223 | [67] | 0.53 | [0.19] |
| Single female | 24.4 | 10.6 | 3.6 | 141 | [43] | 0.36 | [0.15] |
| Non-Hispanic white | 30.0 | 11.6 | 5.7 | 194 | [56] | 0.33 | [0.12] |
| Hispanic | 26.3 | 10.7 | 4.7 | 151 | [50] | 0.34 | [0.15] |
| Black | 25.5 | 9.8 | 4.9 | 229 | [65] | 0.53 | [0.22] |
| Below high school | 23.4 | 8.7 | 4.8 | 227 | [60] | 0.68 | [0.23] |
| High school | 32.8 | 12.3 | 6.7 | 222 | [64] | 0.45 | [0.16] |
| Some college | 32.8 | 12.7 | 6.5 | 190 | [58] | 0.35 | [0.13] |
| College degree | 27.3 | 11.1 | 4.4 | 147 | [44] | 0.19 | [0.07] |
| Above college | 23.2 | 10.0 | 3.7 | 177 | [42] | 0.20 | [0.06] |
| Retired | 27.9 | 9.8 | 6.5 | 266 | [81] | 0.75 | [0.28] |
| Unemployed | 22.7 | 9.4 | 3.4 | 136 | [47] | 0.47 | [0.17] |
| Self-employed | 27.4 | 11.1 | 4.9 | 216 | [51] | 0.30 | [0.10] |
| State lottery | 29.9 | 11.5 | 5.8 | 201 | [58] | 0.35 | [0.13] |
| No State lottery | 12.8 | 7.9 | 0.6 | 229 | [40] | 0.42 | [0.10] |
| Pre-Great Recession | 29.1 | 11.7 | 5.3 | 190 | [56] | 0.33 | [0.13] |
| Great Recession | 26.2 | 10.3 | 4.4 | 204 | [60] | 0.37 | [0.14] |
- Note: The sample includes the households that were surveyed after the second quarter of 2001 through the first quarter of 2011 and have participated all four interviews and reported valid income data in both the first and the last interview. The sample includes the households whose head was between 20 and 80 at the time of the survey. Gamblers are defined as the households that had positive gambling expenditure in the survey year. Occasional gamblers refer to the households that reported positive gambling costs in only one of the four interviews, frequent gamblers refer to those reported positive gambling costs in all four interviews and had annual gambling costs above $40. Gambling costs and ratio to income are estimated among the gamblers sample. The median is reported in the bracket.
| Exp. Category | (1) All Households | All Households (Standard Deviation) | (2) All Gamblers | All Gamblers (Standard Deviation) | (3) Occasional Gamblers | Occasional Gamblers (Standard Error) | (4) Frequent Gamblers | Frequent Gambles (Standard Deviation) |
| Total expenditure | 3.02*** | (0.35) | 1.78*** | (0.37) | 7.20*** | (2.13) | 1.72*** | (0.54) |
| Food | 0.37*** | (0.04) | 0.28*** | (0.04) | 0.87*** | (0.26) | 0.30*** | (0.06) |
| Alcohol | 0.10*** | (0.01) | 0.07*** | (0.01) | 0.34*** | (0.05) | 0.03** | (0.01) |
| Tobacco | 0.11*** | (0.01) | 0.07*** | (0.01) | 0.20*** | (0.06) | 0.05*** | (0.02) |
| Apparel | 0.18*** | (0.02) | 0.11*** | (0.02) | 0.34*** | (0.11) | 0.10*** | (0.03) |
| Housing | 0.60*** | (0.13) | 0.38*** | (0.13) | 1.85* | (0.78) | 0.46*** | (0.18) |
| Transportation | 0.61*** | (0.14) | 0.24* | (0.15) | 1.57* | (0.84) | 0.11 | (0.22) |
| Health care | -0.00 | (0.02) | -0.02 | (0.02) | -0.15 | (0.10) | -0.04 | (0.03) |
| Entertainment | 0.29*** | (0.03) | 0.15*** | (0.03) | 1.04*** | (0.20) | 0.18*** | (0.05) |
| Personal care | 0.03*** | (0.00) | 0.01*** | (0.00) | 0.03 | (0.03) | 0.01 | (0.01) |
| Reading | 0.01*** | (0.00) | 0.00 | (0.00) | 0.03** | (0.01) | 0.00 | (0.00) |
| Education | -0.01 | (0.03) | -0.01 | (0.03) | -0.24 | (0.19) | 0.01 | (0.05) |
| Exp. Category | (1) All Households | All Households (Standard Deviation) | (2) All Gamblers | All Gamblers (Standard Deviation) | (3) Occasional Gamblers | Occasional Gamblers (Standard Error) | (4) Frequent Gamblers | Frequent Gambles (Standard Deviation) |
| Total expenditure | 2.71*** | (0.56) | 2.68*** | (0.60) | 4.30*** | (1.23) | 1.44 | (1.27) |
| Food | 0.37*** | (0.07) | 0.37*** | (0.07) | 0.71*** | (0.14) | 0.45*** | (0.14) |
| Alcohol | 0.08*** | (0.01) | 0.08*** | (0.01) | 0.06*** | (0.02) | 0.11*** | (0.02) |
| Tobacco | 0.02*** | (0.01) | 0.02* | (0.01) | 0.01 | (0.02) | 0.03 | (0.02) |
| Apparel | 0.23*** | (0.04) | 0.23*** | (0.04) | 0.15** | (0.08) | 0.16** | (0.08) |
| Housing | 0.21 | (0.14) | 0.20 | (0.14) | 0.66** | (0.29) | 0.14 | (0.29) |
| Transportation | 0.47 | (0.42) | 0.46 | (0.46) | 0.60 | (0.91) | 0.26 | (1.01) |
| Health care | 0.09* | (0.05) | 0.09* | (0.05) | 0.18* | (0.11) | 0.09 | (0.10) |
| Entertainment | 0.25*** | (0.06) | 0.25*** | (0.06) | 0.28** | (0.12) | 0.15 | (0.11) |
| Personal Care | 0.04*** | (0.01) | 0.04*** | (0.01) | 0.05*** | (0.01) | 0.03** | (0.01) |
| Reading | 0.01*** | (0.00) | 0.01*** | (0.00) | 0.03*** | (0.01) | 0.01 | (0.01) |
| Education | 0.05 | (0.05) | 0.05 | (0.05) | 0.13 | (0.10) | -0.02 | (0.10) |
- Note: *, **, *** indicate statistical significance of 90, 95 and 99 percent, respectively. The upper panel reports
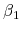 coefficients in eq.(2) estimated for
various expenditure categories. Control variables include imputed permanent income interacted with its decile dummy, demographic characteristics, and year dummies. The lower panel reports
coefficients in eq.(2) estimated for
various expenditure categories. Control variables include imputed permanent income interacted with its decile dummy, demographic characteristics, and year dummies. The lower panel reports 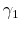 coefficients in eq.(4) estimated for various expenditure categories. Control variables include an age polynomial, family size changes, and year and month dummies. The samples used for the estimation include only households whose heads were younger than
65. In the level regression, the top 1% of the corresponding expenditure level distribution is excluded. In the growth regression, the top and bottom 1% of the corresponding expenditure growth distribution is excluded. Standard errors are reported in parentheses.
coefficients in eq.(4) estimated for various expenditure categories. Control variables include an age polynomial, family size changes, and year and month dummies. The samples used for the estimation include only households whose heads were younger than
65. In the level regression, the top 1% of the corresponding expenditure level distribution is excluded. In the growth regression, the top and bottom 1% of the corresponding expenditure growth distribution is excluded. Standard errors are reported in parentheses.
| Nongamblers | Gamblers | Occasional Gamblers | Frequent Gamblers | |
| Relative to imputed permanent income | 88.6% | 98.2% | 96.8% | 100.3% |
| Relative to observe current income | 96.4% | 93.0% | 93.7% | 90.6% |
| Memo:
|
-0.033 | 0.077 | 0.067 | 0.098 |
| Memo:
|
(0.004) | (0.003) | (0.004) | (0.003) |
- Note: Average propensity to consume is calculated as the ratio between total expenditure (including gambling costs) and the observed current income and the imputed permanent income. We impute the logarithm of permanent income,
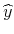 , and the level of permanent income is calculated as
, and the level of permanent income is calculated as
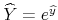 . Standard errors of the mean of imputation residuals are reported in parentheses.
. Standard errors of the mean of imputation residuals are reported in parentheses.
| Nongamblers | All Gamblers | Occasional Gamblers | Frequent Gambler | |
| Charitable donations [Share of households that made a donation (%)] | 41.0 | 56.7 | 55.2 | 57.4 |
| Religious donations [Share of households that made a donation (%)] | 43.8 | 45.4 | 44.5 | 45.5 |
| Political donation [Share of households that made a donation (%)] | 4.5 | 5.5 | 5.3 | 5.2 |
| Charitable donations [Donation amount (subsample of donors 2000$)] | 417 | 296 | 291 | 300 |
| Religious donations [Donation amount (subsample of donors 2000$)] | 1614 | 981 | 1036 | 962 |
| Political donation [Donation amount (subsample of donors 2000$)] | 295 | 162 | 123 | 199 |
- Note: Charitable donations include donations made to educational entities. Donation amounts refer to annual donations and their means are calculated within the subsample of consumers who made such donations.
| Logistic regression: Probability of making a donation (Charitable) | Logistic regression: Probability of making a donation (Religious) | Logistic regression: Probability of making a donation (Political) | OLS regression (subsample of donors): Value of donations (Charitable) | OLS regression (subsample of donors): Value of donations (Religious) | OLS regression (subsample of donors): Value of donations (Political) | |
| Gambler | 0.62*** | 0.02 | 0.13** | -97.3*** | -616.2*** | -121.9 |
| Gambler (Standard Error) | (0.03) | (0.03) | (0.06) | (30.3) | (48.2) | (80.1) |
| Gambler [Odds Ratio] | [1.85] | [1.02] | [1.13] | |||
| Occasional gambler | 0.58*** | 0.01 | 0.13 | -80.6* | -448.5*** | -145.2 |
| Occasional gambler (Standard Error) | (0.04) | (0.04) | (0.09) | (41.7) | (68.9) | (112.8) |
| Occasional gambler [Odds Ratio] | [1.78] | [1.01] | [1.14] | |||
| Frequent gambler | 0.59*** | -0.04 | -0.01 | -72.4 | -519.1*** | -40.5 |
| Frequent gambler (Standard Error) | (0.06) | (0.05) | (0.12) | (57.1) | (95.5) | (160.1) |
| Frequent gambler [Odds Ratio] | [1.81] | [0.98] | [0.99] |
- Note: *, **, *** indicate statistical significance of 90, 95 and 99 percent, respectively. The logistic regressions use the entire sample whose heads were younger than 65. The control variables include a vector of dummies indicating imputed permanent income deciles, a vector of demographic variables as used in eq.(2), and a vector of year dummies. The OLS regressions use the subsample of households who made a certain type of donation, with the same set of control variables as in the logistic analysis. Standard errors are reported in parentheses and odds ratios estimated from logistic regressions are reported in brackets.
| Nongamblers | All gamblers | Occasional gamblers | Frequent gamblers | |
| Assets ownership: Liquid financial assets | 12,942 | 16,104 | 16,146 | 15,63 |
| Assets ownership: Securities ownership(%) | 14.0 | 21.6 | 20.7 | 23.0 |
| Assets ownership: Home ownership (%) | 71.8 | 75.5 | 74.5 | 77.3 |
| Assets ownership: Homeowners with a second home (%) | 6.5 | 7.7 | 8.0 | 7.2 |
| Assets ownership: Own a car (%) | 91.8 | 94.3 | 94.5 | 94.1 |
| Assets ownership: Car owners leasing a car (%) | 4.4 | 5.7 | 5.8 | 5.3 |
| Household Debt: Homeowners having a mortgage (%) | 75.4 | 76.4 | 77.6 | 73.5 |
| Household Debt: Homeowners having refinanced (%) | 31.3 | 37.9 | 36.1 | 40.1 |
| Household Debt: Car owners with a loan (%) | 33.3 | 37.9 | 37.4 | 38.2 |
| Household Debt: Have credit card debt (%) | 35.4 | 47.2 | 44.9 | 51.3 |
| Household Debt: Have added credit card debt (%) | 21.9 | 27.8 | 25.9 | 29.9 |
| Household Debt: "Credit card puzzle" (%) | 8.9 | 13.5 | 13.0 | 13.6 |
| Household Debt: Partial net worth |
163,005 | 164,399 | 164,516 | 169,449 |
| memo: Annual income | 57,392 | 62,527 | 63,193 | 62,356 |
| memo: Log(annual income) | 10.65 | 10.80 | 10.79 | 10.82 |
| memo: Imputed log(permanent income) | 10.69 | 10.74 | 10.74 | 10.73 |
- Note: All dollar values are in 2000$.
 Partial net worth is calculated as the sum of financial assets and home value net of mortgage and credit card debt balances. Have added credit
card debt refers to the households who reported higher credit card debt balances in the last interview than in the first one. Liquid financial assets refer to balances in checking and saving accounts, including discount brokerage account. Securities include stocks, mutual funds, private bonds,
government bonds or Treasury notes. Second home includes second home, vacation home, and recreational property. "Credit card puzzle" refers to the households who concurrently have more than $1,000 credit card debt while holding liquid financial assets greater than 50% of their credit card debt
balances. Annual income refers to the observed annual income reported in the last interview. Imputed log(permanent income) is imputed from eq.(3).
Partial net worth is calculated as the sum of financial assets and home value net of mortgage and credit card debt balances. Have added credit
card debt refers to the households who reported higher credit card debt balances in the last interview than in the first one. Liquid financial assets refer to balances in checking and saving accounts, including discount brokerage account. Securities include stocks, mutual funds, private bonds,
government bonds or Treasury notes. Second home includes second home, vacation home, and recreational property. "Credit card puzzle" refers to the households who concurrently have more than $1,000 credit card debt while holding liquid financial assets greater than 50% of their credit card debt
balances. Annual income refers to the observed annual income reported in the last interview. Imputed log(permanent income) is imputed from eq.(3).
| Investing in financial securities | Second home ownership | Credit card puzzle | Have refinanced mortgage before | Car Owner and leaser | |
| Gambler | 0.48*** | 0.15** | 0.46*** | 0.24** | 0.27*** |
| Gambler (Standard Error) | (0.04) | (0.06) | (0.04) | (0.05) | (0.06) |
| Gambler [Odds ratio] | [1.61] | [1.17] | [1.59] | [1.27] | [1.31] |
| Occasional gambler | 0.47*** | 0.22** | 0.43*** | 0.16*** | 0.25*** |
| Occasional gambler (Standard Error) | (0.05) | (0.08) | (0.06) | (0.06) | (0.09) |
| Occasional gambler [Odds ratio] | [1.60] | [1.24] | [1.54] | [1.18] | [1.29] |
| Frequent gambler | 0.45*** | 0.04 | 0.46*** | 0.34*** | 0.27*** |
| Frequent gambler (Standard Error) | (0.07) | (0.12) | (0.08) | (0.09) | (0.12) |
| Frequent gambler [Odds ratio] | [1.56] | [1.04] | [1.59] | [1.41] | [1.30] |
| memo: fraction among nongamblers | 14.0% | 6.5% | 8.9% | 31.3% | 4.4% |
- Note: *, **, *** indicate statistical significance of 90, 95 and 99 percent, respectively. The logistic regressions use the entire sample whose heads were younger than 65. The control variables include a vector of dummies indicating imputed permanent income deciles, a vector of demographic variables as used in eq.(2), and a vector of year dummies. Standard errors are reported in parentheses. Odds ratios are reported in brackets.
| Nongamblers | All gamblers | Occasional gamblers | Frequent gamblers | |
| Alcohol Drinker (%) | 62.1 | 78.8 | 78.0 | 79.8 |
| Heavy drinker (%) | 4.9 | 9.6 | 8.2 | 11.2 |
| Tobacco smoker (%) | 29.5 | 43.2 | 39.1 | 47.6 |
| Purchase life insurance (%) | 45.4 | 56.7 | 54.0 | 62.0 |
| Purchase health insurance (%) | 44.7 | 49.3 | 47.7 | 50.7 |
| Purchase home insurance (%) | 57.8 | 66.3 | 62.7 | 70.6 |
| Heavy drinkers who buy life insurance (%) | 42.8 | 50.1 | 48.1 | 57.6 |
| Heavy drinkers who buy health insurance (%) | 50.0 | 53.1 | 50.0 | 55.4 |
| Smokers who buy life insurance (%) | 42.5 | 52.8 | 50.0 | 59.4 |
| Smokers who buy health insurance (%) | 42.5 | 48.3 | 46.2 | 49.0 |
| Memo: Total out-of-pocket expenditure for life, home, and health insurance (2000$) | 1,669 | 1,755 | 1,670 | 1,833 |
- Heavy drinkers refer to those who spent more than 2.5% of annual income on alcoholic beverages and spent more than $100 in each quarter. Purchases of insurances refer to households pay out-of-pocket on insurances. Life insurance includes life, endowment, annuities, and other insurance policies providing death benefits. The share of households purchased home insurance is estimated using the sample of homeowners who do not have outstanding mortgages.
| Risky Behavior: Heavy drinker | Risky Behavior Smoker | Health Insurance | Life Insurance | Home Insurance | |
| Gambler | 0.72*** | 0.58*** | 0.17*** | 0.39*** | 0.27*** |
| Gambler (Standard Error) | (0.05) | (0.03) | (0.03) | (0.03) | (0.07) |
| Gambler [Odds ratio] | [2.06] | [1.79] | [1.19] | [1.47] | [1.31] |
| Occasional gambler | 0.52*** | 0.43*** | 0.10 | 0.31*** | 0.16 |
| Occasional gambler (Standard Error) | (0.07) | (0.04) | (0.04) | (0.04) | (0.10) |
| Occasional gambler [Odds ratio] | [1.68] | [1.54] | [1.11] | [1.37] | [1.36] |
| Frequent gambler | 0.95*** | 0.74*** | 0.24*** | 0.54*** | 0.42*** |
| Frequent gambler (Standard Error) | (0.09) | (0.06) | (0.05) | (0.06) | (0.14) |
| Frequent gambler [Odds ratio] | [2.59] | [2.09] | [1.27] | [1.72] | [1.53] |
| Statistically different? | Yes | Yes | Yes | Yes | Yes |
| Memo: propensity among nongamblers (%) | 4.9 | 29.5 | 44.7 | 45.4 | 57.8 |
| Concurrent behavior | Health insurance (1) | Life insurance (2) | Health insurance (3) | Life insurance (4) |
| Smoker | -0.09*** | -0.19*** | ||
| Smoker (Standard Error) | (0.03) | (0.03) | ||
| Smoker [Odds Ratio] | [0.91] | [0.83] | ||
| Smoker |
0.19*** | 0.29*** | ||
| Smoker |
(0.04) | (0.05) | ||
| Smoker |
[1.21] | [1.34] | ||
| Heavy drinker | 0.16** | 0.06 | ||
| Heavy drinker (Standard Error) | (0.07) | (0.07) | ||
| Heavy drinker [Odds Ratio] | [1.17] | [1.07] | ||
| Heavy drinker |
0.15 | 0.18* | ||
| Heavy drinker |
(0.10) | (0.07) | ||
| Heavy drinker |
[1.16] | [1.19] |
- Note: *, **, *** indicate statistical significance of 90, 95 and 99 percent, respectively. The logistic regressions use the entire sample whose heads were younger than 65. The control variables include a vector of dummies indicating imputed permanent income deciles, a vector of demographic variables as used in eq.(2), and a vector of year dummies. Standard errors are reported in parentheses. Smoker gambler is defined as the smoke dummy interacting with gambler dummy. Heavy drinker gambler is defined as the heavy drinker dummy interacting with gambler dummy. Standard errors are reported in parentheses. Odds ratios are reported in brackets.