Arbitrage, liquidity and exit: The repo and federal funds markets before, during, and emerging from the financial crisis
Keywords: Repurchase agreement, federal funds, financial crisis, monetary policy implementation, exit strategy
Abstract:
1 Introduction
How does monetary policy implementation work? The first step is for the Federal Open Market Committee (FOMC) to set a price for reserves. This price is called the target federal funds rate, or the desired level for the interest rate at which institutions lend balances at the Federal Reserve to "banks" overnight.1 For many years, open market operations-purchases and sales of U.S. Treasury and federal agency securities using repurchase agreements (repos)-were the Federal Reserve's most often used tool for changing the level of reserves and thus implementing monetary policy.
After the Federal Reserve initiates the monetary policy transmission process, the most immediate next step is for the federal funds rate to influence the behavior of other short-term interest rates. In order for monetary policy transmission to be effective, these other rates should move with the federal funds rate. As the participants in the federal funds market and other short-term markets frequently overlap, controlling for risk, collateral, and other frictions, all rate differences should be arbitraged away. Consequently, it seems plausible that all short-term interest rates should move in tandem with the federal funds rate. In particular, it seems likely that the rate on repurchase agreements - the repo rate - and the federal funds rate would be very likely to move together, as both markets are involved in the earliest stages of the monetary policy transmission process.
But do they? While there are long periods when the repo rate and the federal funds rate move together, there are also notable times when they do not. For example, figure 1 displays the federal funds rate and the Treasury general collateral (GC) repo rate, or the rate charged on secured overnight lending against Treasury-issued collateral. Although for much of the sample, there appear to be only small differences between these two rates, there are spells when the spread widens considerably and the rate movements seem decoupled. One might question whether the monetary policy transmission mechanism is effective during these spells.
In order to provide perspective on the comovement of the two rates, this paper characterizes the relationship between the Treasury GC repo rate and the federal funds rate during three periods: a period of relative calm in financial markets, from 2002 to 2007, the early stages of the financial crisis, from August 2007 to December 2008, and post-December 2008, after the FOMC set a target range for the federal funds rate of 0 to 25 basis points.2 We are able to use our analysis to investigate three key issues in the federal funds market and the repo market. The first is the description of the monetary policy transmission process. We characterize this by the length of time it takes for a disequilibrium between the two rates to dissipate, or, in other words, how quickly movements in one rate affect movements in the other. Our model suggests that the magnitude of the liquidity effect changed dramatically during the early crisis period, consistent with a change in slope of the demand curve for liquidity.
Using these key results, we conduct simulation exercises using key selected coefficients to illustrate the possible effect of reserve draining operations by the Federal Reserve on the federal funds rate and the repo rate. After the failure of Lehman Brothers, the Federal Reserve markedly expanded its balance sheet. As a result, the level of reserve balances rose, and currently is well over $1.5 trillion. In June 2010, when reserve balances were around $1 trillion, U.S. commercial banks held about 6 percent of their assets in these balances. If the Federal Reserve engages in either asset sales or large-scale reverse repurchase agreements, not only would reserve balances decrease, but it is likely that the federal funds rate and the repo rate would rise as a result. Overall, our estimates imply that, holding both the interest on excess reserves rate and the target rate constant, the federal funds rate would move up if reserve balances were drained; our outside estimates suggest that the funds rate would rise more than 40 basis points above its starting level if balances were drained to a level in line with required operating balances, or the amount of reserve balances needed to comply with both reserve and clearing balance requirements.
One of the major contributions of this paper is a careful analysis of the interplay between two key rates for monetary policy implementation. To the best of our knowledge, there are few works using relatively modern econometric techniques that evaluate this relationship fully.3 Given the increased focus on these markets and on their functioning during the financial crisis, it is important to uncover the factors that make them work together. In particular, there is a long literature evaluating the monetary policy transmission mechanism. But much of this previous work examines lower-frequency changes in interest rates, and then traces these changes through to real output and the rest of the economy. Often ignored - or assumed to work seamlessly - is the first step in this transmission, which is the link across short-term funding markets, where the federal funds rate should be somewhat of an anchor. Because the federal funds market and the repo market have many of the same participants, are both liquid, and have the same term, the rates should move together. Furthermore, monetary policy implementation - past and present - often relies on both of these markets simultaneously, making it important from a policy perspective to understand fully the interaction between these markets. As we demonstrate in this paper, emerging from the crisis, the two markets seem not to move together in the same way as before the crisis, making it important to understand how things changed and how tools proposed to drain balances and push up the federal funds rate may function in the future. Importantly, these results, which look at the interplay of these markets, offer some guidance to policy makers as to how to interpret federal funds rates in an environment with elevated reserve balances and in the early stage of an exit. It gives some idea as to whether the federal funds rate can be used to signal actions in broader money markets, and also, whether policy makers can use the federal funds rate for monetary policy transmission in an exit strategy.
The paper proceeds as follows. Section 2 provides background on key overnight funding markets, both secured and unsecured. Section 3 describes the empirical framework for the results reported in section 4. With these results in hand, section 5 provides information on changes in the speed of adjustment to market equilibrium during the crisis, evidence of changes in the probability of default in lending markets, and possible effects of reserve draining measures on the federal funds and repo rates using dynamic liquidity effects. Section 6 concludes.
2 Background
This section reviews basic facts on the repo market and the federal funds market, the two markets that are the focus of this paper, as well as discusses monetary policy implementation.
2.1 The markets
Both the repo market and the federal funds market are money markets. However, they differ in important ways, as will be described below.
The repo market
A repurchase agreement is a sale of a security coupled with an agreement to repurchase the security at a specified price at a later date.4 It is economically similar to a collateralized loan, where the lender of cash receives securities as collateral, and the borrower pays the lender interest on the overnight loan the following day. From the perspective of the borrower of cash, the transaction is called a "repo," and from the perspective of the lender of cash, it is a "reverse repo."5 Participation in the repo market is broad; selected types of participants include depository institutions, the U.S. government and its agencies, institutional investment funds, primary dealers, and money market mutual funds. If the rate on a repurchase agreement is low relative to other market rates, it indicates that the underlying collateral is in demand and relatively dear, and as a result, the borrower does not have to pay much interest for using the funds overnight. In contrast, if the rate on a repurchase agreement is relatively high, it signals a relative abundance of collateral, and the borrower has to pay a higher interest rate in order to obtain funds.
There are two main methods of clearing and settling repos: direct (delivery versus payment) and triparty.6 In a direct repo transaction, the holder of the securities initiates the transaction and the cash payment moves automatically as a result of the securities movement. Many of these transactions use the Fedwire Securities Settlement system for clearing and settlement, or they use the infrastructure provided by the Fixed Income Clearing Corporation (FICC). In a triparty repo transaction, both the borrower and the lender of securities must hold accounts at a clearing bank (either JPMorgan Chase or Bank of New York Mellon). Clearing and settlement work much the same way as in a direct repo transaction, with a few exceptions. First, there are some operational costs savings, as the parties to the transactions do not have to have their own infrastructure in order to participate in the market. Second, should the borrower of cash incur a daylight overdraft when the collateral is returned, the clearing bank generally extends a daylight overdraft to the borrower; within the delivery-versus-payment world, this function would be provided by the Federal Reserve if Fedwire were used.7 And third, triparty repo platforms generally offer services to customers that minimize transactions costs, including efficient collateral allocation. For these reasons, triparty repo has gained in popularity in recent years.
Data on aggregate repo market activity is not generally available.8 However, there are a few sources of information on repo market volume that can help to characterize its size. One source is statistics compiled by the Federal Reserve Bank of New York (FRBNY) on repurchase agreements conducted by the primary dealers, which are the banks and broker-dealers that trade directly with the Open Market Desk (the "Desk") at FRBNY for the purposes of open market operations. As shown in figure 2, within the primary dealer community, total repurchase agreement market volume in Treasury securities averaged about $52 billion in 1994, and then started to climb steadily through the 2000s, peaking at a little below $200 billion. Interestingly, the volume of repos brokers executed outside of the primary dealer community more than quadrupled in 10 years, while the volume within the community only doubled. At the onset of the crisis, repo market volume climbed even higher, but then backed down to pre-crisis levels near the end of 2009 and the start of 2010.
The broker-dealer volume reported above includes both direct trades and triparty trades. The main difference between the two types of trades is whether there is a bank acting as the custodial agent in the transaction. The triparty market grew substantially over the past decade, and according to data gathered by FRBNY in April 2010, there was about $474 billion in U.S. Treasury triparty repo volume.9 Overall, then, the data from the primary dealers likely represents a significant fraction of total repo market activity, but not necessarily all.
The repo market experienced significant strains during the financial crisis. For example, one of the reasons cited for the failure and takeover of Bear Stearns was its inability to access funding in the repo market.10 Even in Treasury GC repo among dealers, as shown in the figure, volumes declined more than $200 billion, although rebounded once the early part of the crisis was over.
The federal funds market
Federal funds are a liability of a depository institution that is issued or undertaken and held for the account of an office located in the United States of another depository institution, foreign bank, Edge or Agreement Corporation, the U.S. government or agency thereof, a Federal Home Loan Bank, or selected other institutions.11 Anecdotal reports suggest that in the current environment, most funds are sold by Federal Home Loan Banks and other government-sponsored enterprises (GSEs), while most funds are bought by banks. The rate at which these transactions occur is called the federal funds rate and the market in which these transactions occur is the federal funds market. In many ways, the federal funds market is similar to the repo market, in that they are both used as short-term funding markets, have overlapping participants to a notable extent, and are generally very liquid. But, there are important differences. Traditionally, the federal funds market was used by banks to buy funds in order to satisfy reserve requirements, or to sell funds in excess of those requirements, as well as to fund payments settling in banks' accounts at the Federal Reserve. Banks satisfy reserve requirements on the basis of average balances held over a 14 day period, and previous research shows that funds rate behavior differed according to the day of the maintenance period.12 Moreover, this research also provided evidence of a short-term "liquidity effect," or a price response to changes in the level of reserve balances. In addition, partly because of federal funds' unique ability to be used to satisfy reserve requirements, the federal funds market is more restricted than the repo market in its participants, which are limited to banks, government-sponsored enterprises (GSEs) and selected other entities. This has the important implication that while many types of institutions (both financial and nonfinancial) are theoretically able to participate in the repo market, the federal funds market is limited only to selected institution types, which could restrict possible opportunities for arbitrage across markets.
Even though the federal funds market has traditionally been very important for monetary policy implementation, the market is quite small and by many measures, federal funds market volume is much lower than repo market volume. For example, figure 3 plots federal funds transactions identified in the Fedwire data.13 According to this series, federal funds market volume ranges from around $100 billion in daily volume in 1998 to a peak above $400 billion in 2008, before falling closer to $300 billion in 2010. The decline in federal funds volume could be associated with the large volume of reserves outstanding emerging from the early part of the crisis, diminishing the possibility that institutions would be short on reserves. In addition, the introduction of interest on reserves might also dampen the need for institutions to lend excess cash, as these institutions would still earn interest on excess balances left at the Federal Reserve.
Comparing the two
These observations regarding the size of the federal funds market relative to the size of the repo market are consistent with data from the Call reports, which suggest that commercial bank federal funds market volume is only a small fraction of total repo market volume, and that commercial banks' federal funds market activity is smaller than the repo market activity. As shown in figure 4, federal funds sold peaked at around $250 billion near the start of the financial crisis, and then dropped to less than half that volume by March 2010. As a percentage of assets, federal funds peaked much earlier, in 2003. Notably, federal funds purchased generally exceeds federal funds sold, indicating that commercial banks are net buyers of funds.14 Moreover, while federal funds sold stayed relatively steady from 2002 to 2007, securities purchased to resell, or reverse repos, rose at a moderate pace, and then began to rise rapidly through the end of 2008. Repos, or securities sold to be repurchased, peaked noticeably earlier than reverse repos, and at a higher level. Still, for a majority of the sample period, commercial banks had more of their balance sheets in repos than in federal funds, and consequently, were a more prominent share of the portfolio.
Information on combined federal funds and repo activity for commercial banks is also available. As shown in figure 5, compared to the quantity outstanding for the dealers, commercial bank participation in overnight funding markets constitutes only a small fraction. For both federal funds and repo combined, the amount outstanding for repos with banks and nonbanks reaches a maximum of only about $750 billion, near the height of the crisis. Moreover, as a share of total assets, federal funds and repo are only about 10 percent. One exception is the spike that occurs on September 12, 2001, immediately following the terrorist attacks on the World Trade Center.15
Even though the volumes in these markets are quite different and there is imperfect overlap between the two markets, over much of the past decade or so, these rates have moved together quite closely. Figure 7 plots the spread between the federal funds rate and the repo rate from 2002 to 2010. As is evident from the figure, these rates were similar up until 2007. Because federal funds transactions are unsecured while repo transactions are secured, the repo rate is usually a bit below federal funds. Spreads started to widen in the beginning of the financial crisis, from August 2007 onward, and then skyrocketed during the early crisis as investors flocked to the relative safety of secured overnight lending in repo.
2.2 Monetary policy implementation
There is a special connection between the federal funds market and the repo market for Federal Reserve monetary policy implementation. In the textbook version of monetary policy implementation, the Federal Reserve buys securities from dealers in the repo market, which gives the dealers cash which they deposit in their bank's accounts, and the banks then proceed to sell the funds in the federal funds market. By sizing this "open market operation" appropriately, the Federal Reserve could ensure that the federal funds rate - the policy rate - was close to the target set by the FOMC.
This operating procedure and target interest rate worked for many years. Repo rates and federal funds rates traded in line with each other, and longer-term interest rates moved up and down with the federal funds rate. According to Simmons (1954), repurchase agreements were used as part of the Federal Reserve System's operations since 1917. In addition, as documented by Friedman and Schwartz (1963), as early as the 1920s, open market operations were the Federal Reserve's preferred operating procedure. Furthermore, before the FOMC started announcing an explicit target federal funds rate, market participants would determine the new target federal funds rate by observing the sizes of the open market operations immediately following an FOMC meeting. Although market participants arguably stopped looking to repos for a signal regarding the stance of policy once target announcements began, open market operations remained an important tool: The Desk used repos almost daily to adjust the level of reserves so that federal funds would trade close to the target federal funds rate.
Monetary policy implementation changed with the recent financial crisis, although not all at once. At the start of the crisis in August 2007, the Federal Reserve relied on larger-than-normal repo operations to inject liquidity into the federal funds market. Later, in the fall of 2008, the Federal Reserve conducted reverse repos in order to drain reserves from the system as well as to add some collateral back to the market. However, because reserve balances were elevated, the effective federal funds rate traded well below the target rate. In addition to the reverse repos, the Federal Reserve also conducted 28-day single-tranche repos, where the collateral pledged was agency MBS. The repos provided dealers with financing for agency MBS when the spread between one month agency MBS repo and one-month Treasury GC repo was particularly wide.16 Although regular repo activity by the Desk ceased in the early part of 2009, in 2010 and 2011, the Desk conducted a series of small-value reverse repurchase agreements with a broad set of counterparties as part of its operational readiness program for tools to use in the future to drain reserve balances.
In sum, although the repo market's role in monetary policy implementation has certainly changed in recent years, overall, it is likely to be a tool used for monetary policy implementation in the future.
3 Empirical preliminaries and framework
This section first performs some preliminary data analysis to provide justification for the statistical strategy used in this paper. It then describes the primary estimating equation of interest and reviews its ability to capture the three aspects of the market on which this paper focuses.
3.1 Preliminary statistical analysis
The primary data used in this study are daily observations on the effective federal funds rate and the overnight Treasury GC repo rate from January 2, 2002 to June 16, 2010.17 The daily effective federal funds rate is a volume-weighted average of rates on trades arranged by major brokers calculated and published by the Federal Reserve Bank of New York. The Treasury GC repo rate is a collateral-weighted average of a survey of all primary dealers conducted daily between 8:00 a.m. and 9:00 a.m.18 Because a large fraction of federal funds market activity takes place in the late afternoon, the federal funds rate implicitly measures late-day funding activity, while the repo rate we use necessarily focuses on trading earlier in the day. Nevertheless, both measure activity when the respective markets are most active.19
The spread and correlations between federal funds and repo reviewed in section 2 suggest that there could be a cointegrating relationship between these two series. To test for this possibility, table 1 presents augmented Dickey-Fuller tests to determine whether these series have unit roots.20 We perform the tests over three subsamples: from January 2, 2002 to August 8, 2007; from August 9, 2007 to December 15, 2008; and from September 1, 2008 to June 2010. While the null of a unit root is accepted for the first two periods, the null of a unit root is rejected for the year-and-a-half sample for the last period with very high balances.21
Given that these series have unit roots over some sample periods, we next use the Johansen test to determine whether the series are cointegrated. As shown in table 2, the series are cointegrated in both the relatively stable period before the August 2007 start of the crisis, and in the window between the start of the crisis and the failure of Lehman Brothers. However, after the failure of Lehman Brothers and the concomitant rise in reserve balances, the cointegrating relationship breaks down.
Taken together, these results suggests the existence of distinct regimes for the relationship between the federal funds rate and the repo rate. As a result, portions of our analysis will divide the period up into these separate regimes and report statistics separately.
3.2 Empirical framework
The empirical framework we use elucidates the three results we outlined earlier, namely that (1) the speed of monetary policy transmission slowed over the financial crisis; (2) the implied probabilities of default climbed in the crisis; and (3) the dynamics of the liquidity effect changed over time.
Our primary tool for evaluating these claims is a vector error correction model (VEC). We posit that the federal funds rate and the repo rate have the following relationship:
where
The ![]() are autoregressive coefficients to be estimated. We use three lags of all interest rates in the specification as suggested by the Schwarz Information Criterion (SIC)
test.22 Furthermore, significance of all coefficients is reported with respect to Bollerslev-Wooldridge robust standard errors.
are autoregressive coefficients to be estimated. We use three lags of all interest rates in the specification as suggested by the Schwarz Information Criterion (SIC)
test.22 Furthermore, significance of all coefficients is reported with respect to Bollerslev-Wooldridge robust standard errors.
In addition to the lagged values of the repo rate and the effective rate, the other variables included are factors that likely shift the effective rate and the repo rate on a daily basis. These are captured in the
![]() vector, with coefficients to be estimated,
vector, with coefficients to be estimated, ![]() . We specify
. We specify
![]() as
as
| (2) |
where the four terms represent groups of variables that are used to evaluate the liquidity effect, proxy for financial market risk measures (a few are similar to those used in Collin-Dufrense et al (2002)), plus some factors that are specific controls for the funds market and for the repo market, and a vector of calendar effects.
To start reviewing each group individually, the first group of factors is used to identify the liquidity effect in each market, and in both markets simultaneously. In a basic money demand framework, there is a demand curve for some type of money that depends negatively on an interest rate. The liquidity effect is related to the slope of this demand curve. Many researchers have investigated the liquidity effect; methodologies for evaluating and evidence for its existence are mixed. In lower frequency data, there is often a lack of correlation between monetary aggregates and interest rates. In contrast, in high frequency data, Hamilton (1997) and others find a significant liquidity effect at a daily frequency. One of Hamilton's innovations in estimating a daily liquidity effect was the identification of an exogenous shift to reserve balances that could be used to identify the liquidity effect. This shift was the forecast miss in reserve balances. His estimating equation, and the starting point for subsequent research on this topic, had the form
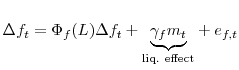 |
(3) |
where
An important omission is that there are limited dynamic demand adjustments. More specifically, there are no cross effects between the federal funds and repo markets. A step forward would be to include the repo rate in the specification, and to evaluate a system of equations. With these factors
in mind, we can rewrite the vector error correction model specification in equation (1) to evaluate a dynamic liquidity effect. Emphasizing the parameters of interest, the model is
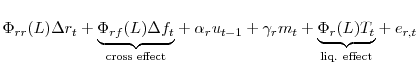 |
|||
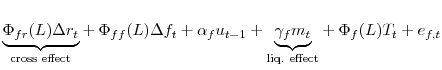 |
where
Choosing the "right" exogenous shocks to the supply curve takes some care. When balances were low, the forecast miss allowed the researcher to trace out the demand curve and determine the liquidity effect without incurring problems of simultaneity. However, once reserve balances climbed to high levels, the level of the miss was miniscule relative to total balances, and in general, was not the most important factor adding unexpected reserve balances. In addition, exogenous changes in the supply of reserve balances should not have an effect on the repo rate, and therefore will not be an appropriate instrument for tracing out the demand curve for repos.
To address these issues, we use a number of different instruments. One of the instruments we use is changes in the Treasury's General Account (TGA) at the Federal Reserve. As shown in the top panel of figure 8, before the fall of 2008, the Treasury targeted an account balance at the Federal Reserve at a relatively constant level, typically $5 billion. Excess cash was invested in depository institution accounts through the Treasury Tax and Loan (TT&L) account system; the rate of return was typically the effective federal funds rate less 25 basis points. A relatively constant TGA balance contributed to the smooth implementation of monetary policy. After the effective rate fell and reserve balances rose, the return that the Treasury received on TT&L investments was negligible, and the Desk ceased conducting open market operations on a daily basis to target a specific level of reserve balances. As a result of these policy changes, as shown in the bottom panel of figure 8, the TGA level varied widely. Changes in the level of the TGA represent exogenous changes in the supply of reserve balances, and so are useful to trace out the demand curve in the federal funds market.
For the last subsample, we use another one of the Treasury's accounts to identify the liquidity effect in the funds market. Starting in September 2008, at the request of the Federal Reserve, the Treasury announced a series of bill auctions separate from its primary borrowing program and deposited the proceeds of these auctions in an account at the Federal Reserve. Just like the TGA, this account drains reserves, and therefore, changes in the level of this account can help to trace out the liquidity effect.
Another instrument we use for identifying the liquidity effect in the repo market is net Treasury securities issuance. These represent exogenous, known supply shocks, and the repo rate tends to increase after issuance dates, as the market absorbs the collateral. As a result, we can use this issuance to estimate the liquidity effect in the repo market.
Our final instrument is related to Federal Reserve open market operations. Beginning in November 2008 and continuing through to March 2010, the Federal Reserve conducted a series of securities purchases with the intent of lowering longer-term interest rates. There were more than $1.7 trillion in "Large Scale Asset Purchases" (LSAPs) of Treasury securities, agency debt securities and agency mortgage-backed securities, which had the effect of adding a staggering amount of reserves to the Federal Reserve's balance sheet. The amounts to be settled were known in advance and largely independent of general reserves conditions. As a result, we can use the increment in the LSAPs each day as an instrumental variable in our estimation equations. The effects of the LSAP, however, are less clear cut than some of our other instruments. LSAPs both add balances, thereby affecting the funds rate, and remove collateral, thereby affecting the repo rate. Consequently, this instrument likely affects both the funds and repo rates simultaneously, rather than one individually. Still, LSAPs are exogenous changes in these supplies, and thus allow us to trace out the demand curve.
Beyond the rates and the liquidity effects, we also include other factors that likely affect these rates. The next group controls for overall indications of financial risk. Over the estimation period, market sentiment changed dramatically with the advent of the financial crisis. As a result, indicators such as the Libor-OIS spread, the aggregate of U.S. commercial bank capital ratios, and the monetary policy outlook - as captured by the slope of the yield curve (the 10-year Treasury rate less the 2-year Treasury rate) - generally reflected more negative sentiment about the financial markets and the economy towards the second half of the sample.
The next group of controls includes factors specifically related to the repo market or the federal funds market. On the repo side, included is a measure of how heavily weighted primary dealers' books are towards trades with other dealers versus with non-dealers.23 This gives some idea of market concentration in the Treasury market. To address market functioning, fails in Treasury securities are included as an independent variable; these are reported by primary dealers to FRBNY on a weekly basis. In addition, actions on the SOMA Treasury portfolio are added as controls, including the level of Treasury securities lent through the SOMA securities lending programs. Again, securities lending tends to increase during times of market stress and for a particular security that are considered to be trading on "special" in the market.24
On the federal funds side, we use a number of controls for the size of and participation in the federal funds market, including federal funds market volume, the number of sellers, and specifically, the quantity sold by the government sponsored enterprises (GSEs). In addition, we control for days when there is movement in the target federal funds rate; this variable equals the change in the target rate on days of FOMC announcements, but equals zero on all other days.
The final group of controls is ![]() , a vector of maintenance period and other calendar effects. Previous work, including Hamilton (1996) and others, showed that these are significantly
correlated with changes in the federal funds rate. Repo rates also move with calendar effects, as illustrated by Happ (1984) and Fleming, Hrung and Keane (2010). Reasons for these patterns include elevated payment flows on beginning- mid-, and end-month dates, as well as Treasury coupon securities
issuance on the dates. Moreover, some research indicates that repo rate tend to exhibit maintenance period patterns as well, suggesting that there is some comovement in the federal funds and repo rates that derives from the maintenance period construct (for example, Griffiths and Winters
(1997)).
, a vector of maintenance period and other calendar effects. Previous work, including Hamilton (1996) and others, showed that these are significantly
correlated with changes in the federal funds rate. Repo rates also move with calendar effects, as illustrated by Happ (1984) and Fleming, Hrung and Keane (2010). Reasons for these patterns include elevated payment flows on beginning- mid-, and end-month dates, as well as Treasury coupon securities
issuance on the dates. Moreover, some research indicates that repo rate tend to exhibit maintenance period patterns as well, suggesting that there is some comovement in the federal funds and repo rates that derives from the maintenance period construct (for example, Griffiths and Winters
(1997)).
Preliminary estimation results, as well as some signs of volatility clustering in figure 7, suggest that there exists heteroskedasticity of the residuals.25 As a result, in conjunction with the mean equation described above, we also estimate variance and covariance processes with GARCH and TARCH components:
| (4) | |||
| (5) |
where
Because we are interested in the linkages between these two rates over different time periods, we run the model over multiple samples. While our baseline methodology is a VEC model with GARCH errors, in the last sample period, as discussed in section 3.1, the rates do not have unit roots and are therefore are not cointegrated. As a result, we specify a VAR model and evaluate
which generally uses the same control variables as the vector error correction model. Similar to the cointegrated case, we use a GARCH specification for the second moment equation and report results with Bollerslev-Wooldridge robust standard errors.
To highlight identification of the dynamic liquidity effect, we can rewrite the VAR model emphasizing the parameters of interest,
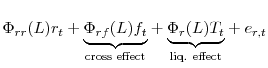 |
|||
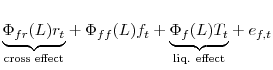 |
|||
Operationally, we use a two-stage estimation procedure similar to Engle and Granger (1987). In the first stage, we test for cointegration of the repo rate and the federal funds rate. After establishing this, we construct the cointegrating term using ordinary least squares. This constructed term is included as an independent variable in our system GARCH estimation. Although it is possible that some efficiency is lost using this procedure, it allows us to use a GARCH specification relatively easily in the second stage estimation.
4 Results
This section reviews the results over the three sample periods. Overall, the results suggest that the repo rate and the federal funds rate were cointegrated during normal times and during the first stages of the financial crisis. However, transmission of policy from the federal funds market to the repo market slowed, and this relationship broke down after the introduction of the 0-25 basis point target range for the federal funds rate in late December 2008. In addition, the spread between the two rates widened over time, consistent with a possible perceived higher probability of default in the federal funds market. Finally, the effect of changes in balances on the federal funds rate and in the amount of collateral on the repo rate shifted over time, suggesting some nonlinearities in the demand for these.
The following subsections explain these results in more detail.
4.1 Normal times: 2002-2007
Table 4 provides results for the early part of the sample, a time of relative calm in financial markets. As shown by the constant term within the cointegrating relationship, the stationary series that is formed by the difference between the federal funds rate and the repo
rate has a mean of about 2 basis points. This can be interpreted as the steady-state risk premium of federal funds over repo. In addition, over the early sample, the cointegrating equation coefficients (the ![]() s) suggest a relationship between federal funds and repo that is close to 1-to-1.
s) suggest a relationship between federal funds and repo that is close to 1-to-1.
With the cointegrating term in hand, the remainder of table 4 reports results from estimating the second stage VEC model with GARCH errors. The first set of columns report results for the repo equation; the second set report results for the federal funds equation. As
indicated by the ![]() , or cointegrating term, coefficients, the repo rate appears to move from disequilibrium, as the
, or cointegrating term, coefficients, the repo rate appears to move from disequilibrium, as the ![]() coefficient is statistically significant, but the federal funds rate does not. Moreover, we interpret statistically significant
coefficient is statistically significant, but the federal funds rate does not. Moreover, we interpret statistically significant ![]() terms as
consistent with the existence of overnight arbitrage; that is, traders are willing to exploit pricing anomalies and trade until the differences between the two rates are minimized. Importantly, this arbitrage is consistent with effective monetary policy transmission.
terms as
consistent with the existence of overnight arbitrage; that is, traders are willing to exploit pricing anomalies and trade until the differences between the two rates are minimized. Importantly, this arbitrage is consistent with effective monetary policy transmission.
There are three possible reasons why the federal funds rate does not appear to adjust to deviations from the cointegration relationship. First, over this sample period, the Desk was actively manipulating the federal funds market in order to achieve an effective rate near the target federal funds rate. As a result, the ability for the federal funds rate to adjust to movements in the repo rate may have been hindered. Second, the markets have different kinds of participants. As an example, as shown in figure 6, Call report data indicate that both on the asset and liability sides of the balance sheet, repo holdings are concentrated in larger banks, while federal funds holdings tend to be more spread out. The charts suggest that the top 10 banks account for over 80 percent of commercial bank holdings of repo assets in some years, while the share of federal funds liabilities remains below 50 percent for nearly all of the sample, and medium-sized banks comprise a much larger share. If one assumes that larger, more sophisticated institutions are more likely to arbitrage differences, and that nonbank participants in the repo market also tend to be larger, more sophisticated institutions, then repo could potentially move back to equilibrium more readily than federal funds. And third, because repo transactions are secured, participants may be more willing to exploit pricing anomalies than they would if transactions were unsecured, as in the federal funds market.
The next six rows display the effects of past changes in rates on current ones. Own lags of the variables are statistically significant out to the third lag, consistent with some persistence in these series. The results for cross-market effects, when taken together, suggest limited causality from the repo market to the federal funds market, and no causality from the federal funds market to the repo market. As displayed in table 3, Granger causality tests indicate that the repo market is more likely to drive the federal funds market than vice versa. Although it appears from these short-run dynamics that the repo market may have been "ground zero" for monetary policy implementation, the fact that the two series are cointegrated in the long run suggest that these movements are transitory in nature and are not necessarily significant for long-run monetary policy transmission.
Turning to the liquidity variables, the next few lines in the table indicate that supply effects exist in both markets, and in general, a short-term liquidity effect existed. The coefficient on the " miss" term for the federal funds equation suggests that for a $10 billion miss that adds balances, the effective federal funds rate declines by 3 basis points. This liquidity effect is a little bit smaller than that estimated by Judson and Klee (2010), which could be a result of both the richer specification and different sample period used here. Note that the regression coefficient considered on its own is just a back-of-the-envelope approximation to the "dynamic" liquidity effect, as it does not take into account the propagation mechanism of changes in supply of reserve balances captured by the structure of the entire VEC model. The effect of the miss is not significantly different from zero in the repo equation, as expected. In contrast, net Treasury issuance tends to push up the repo rate, but has no discernible effect on the federal funds rate. The effect of net Treasury issuance on the repo rate tends to dissipate after the first day, implying that markets quickly return to their long-run relationship during this period. Still, according to the estimated coefficients, for a $10 billion increase in Treasury issuance, the change in the repo rate increases by about 0.4 basis point.
Turning to the risk variables, the estimated coefficients on the factors that control for overall indications of financial risk are broadly in line with intuition. During this period of relative calm, movements in the Libor-OIS spread were likely idiosyncratic, and therefore, did not have much connection to repo rates or to federal funds rates. Changes in the overall capital ratio of U.S. commercial banks were positively associated with repo rates, but not associated with material movements in federal funds rates. In contrast to these other indicators, the change in the slope of the yield curve is associated with a more negative change in federal funds rates (at the 10 percent level); that is, as the difference between the ten-year rate and the two-year rate increases, changes in the federal funds rate become more negative. Interestingly, the repo rate is unaffected by changes in the slope of the yield curve.
Not surprisingly, there are different effects on the repo rate and on the funds rate of our various market-specific controls. Turning to those for the repo rate, as shown in the next line, the composition of dealers' books appears to have little impact on either the repo market or the federal funds market in this period. In addition, occasions with large amounts of fails in the Treasury market were also relatively sporadic over this period, and as such, changes in fails had little bearing on movements in the repo or federal funds rate. Consistently, securities lending was also not correlated with changes in either rate.
For those variables included specifically to address conditions in the federal funds market, a positive change in federal funds market volume is associated with a movement up in both the federal funds and repo rates, reflecting demand for cash in both markets. More federal funds sellers pushes repo rates up and federal funds rates down, consistent with heightened cash supply. Supply of funds by GSEs works slightly differently, in that increases in GSE loan amounts tend to push both rates down; the point estimates suggest that this effect is a touch stronger for the repo rate than for the federal funds rate. This could be capturing a supply effect: If the GSEs have excess cash to invest, rates in both markets trade lower.
The final set of coefficients displays controls for calendar effects. Day-of-maintenance period factors are not significantly different from the first day of the maintenance period for repo on any day, while for federal funds, only the penultimate day of the maintenance period is significant. Day-of-month factors are also important. Both federal funds and repo tend to rise on mid-month and end-of-days, while repo also rises on the 25th of the month, when Fannie Mae makes principal and interest payments on their securities. Rates fall in the repo market on quarter-end but rise in the funds market, and both rates fall on the last business day of the year.
Table 7 summarizes the estimation results for the variance equation. The ARCH and GARCH components suggest that there the residuals are both autoregressive and persistent. 26 The positive coefficients on the end of the quarter and the 15th of the month suggest systematic volatility on these days, consistent with large rate swings often seen on these days of the month.
4.2 Early crisis: August 2007 to December 2008
On August 9, 2007, BNP Paribas stopped redemptions on three investment funds and the financial crisis began. Over the next year-and-a-half, the Federal Reserve used a variety of unconventional policy measures to combat the financial crisis. During this period, the Federal Reserve cut the target federal funds rate nearly 5 percentage points and provided the federal funds market with reserve balances in order to provide ample liquidity.
Despite these changes, the federal funds rate and the repo rate stayed together. Table 5 presents results for the crisis, from August 2007 through December 2008. Although December 2008 was likely not the end of the financial crisis, it marks the period before the funds rate fell to 25 basis points. As shown in the top panel, the mean of the stationary series that is formed by the difference between the federal funds rate and the repo rate jumped to 18 basis points, consistent with a perceived higher counterparty default probability. Moreover, repo market adjustment to arbitrage opportunities between the funds market and the repo market slowed considerably, and significant adjustment in federal funds continued to be absent. There are a few reasons why the speed of adjustment may have changed. First, credit concerns in the unsecured federal funds market may have been greater than those in the secured repo market, creating conditions where investors were willing to leave arbitrage opportunities unexploited.27 Second, some federal funds market investors may have experienced capital limitations, and were unwilling to expand their balance sheets in order to take advantage of arbitrage opportunities, similar to the phenomenon described by Brunnermeier and Pedersen (2009). Finally, the federal funds market was likely changing to some degree at this point in time, both in terms of participants and in the composition of reserve balances. For example, some banks may have dropped out of the market as a result of the abundance of funds from the term auction facility (TAF) and other credit and liquidity programs.
The cross-correlation terms, shown in the next few lines of the table, provide further evidence of the comovement of these rates. The funds market appears to lead changes in the repo market, and vice versa, although interestingly, own market correlations are a bit more muted than previously.
The next few lines display the results associated with the liquidity effect. The level of the "factors miss," or the forecast miss for the supply of reserve balances at the Federal Reserve, is not correlated with changes in either the repo rate or the funds rate over the period. This result is likely highly influenced by the inclusion of the very high balances period from October to December 2008 in the sample; in results not reported, the factors miss is significant and negatively correlated with changes in the federal funds rate for a shorter sample period. The coefficient on the factors miss is insignificant, as balances climbed towards the end of the sample, and similarly, the coefficient on the TGA is also insignificant, as it was allowed to float only towards the end of the sample. However, raising the level of significance to 15 percent, the coefficient on TGA balances appears to suggest a liquidity effect an order of the magnitude smaller than that estimated for the normal period: a decrease of $100 billion in reserve balances would push the federal funds rate up by just 3 basis points. Increases in net Treasury issuance are associated with higher repo rates; the effect lingers for an extra day as the market absorbs the higher quantity of collateral. The effect of net Treasury issuance on the funds market is limited during this period, however. The Supplementary Financing Account (SFA) balance does not significantly affect either rate.
Turning to the risk variables, positive changes in the Libor-OIS spread push federal funds rate up and repo rates down, while positive changes in the slope of the yield curve are associated with decreases in the federal funds rate. Changes in risk-weighted capital ratios has significant effects on both the repo and the funds rate, although in opposite directions, as repos move up and funds move down.
The next few lines show the correlations of the market-specific factors with the repo and federal funds rates. Composition effects of dealers' books appear to have a strong influence on the repo rate during this period. As the share of transactions with entities other than dealers grew, the sensitivity of movements also became more pronounced. For a 1 percentage point change in this ratio, the repo rate increases by about 6 basis points. Changes in the amount of securities lending curiously affect changes in the funds rate; it may be the case that the federal funds market experiences strains as well when repo markets tighten up. Specific factors affecting the funds market have similar coefficients to the normal period, suggesting that the market still had some semblance of normal functioning. One key difference is that while movements in the repo rate were one-to-one with the target rate, movements in the funds rate were not.
Finally, maintenance-period frequency calendar effects are less relevant in the early crisis period, particularly those at the end of the maintenance period. In contrast, the month-end, quarter-end, and year-end effects are magnified, with changes in funds and repo rates exceeding 25 and 45 basis points, respectively. Window-dressing pressures for balance sheet reporting periods may have intensified during the early crisis period.
4.3 "Extended period": December 2008 to June 2010
On December 16, 2008, amid weak economic conditions, elevated reserve balances and a very low effective federal funds rate, the FOMC lowered its target rate to a range of 0 to 25 basis points.28 Even though the interest rate paid on reserve balances was 25 basis points, the federal funds rate consistently traded below that level. Perhaps in part due to these factors, table 1 shows that during this period, the repo rate and the funds rate fail to exhibit unit roots, and as a result, the two rates are no longer cointegrated. Consequently, we use the specification in equation 6.
Table 6 displays the results. Turning first to the lagged effects of the two rates, the results suggest that both own lags and cross-lags affect the repo rate, but only own lags of the federal funds rate significantly influence movements in that rate. This offers further evidence of some, but not complete, decoupling of the two rates. The fact that the coefficients are positive is consistent with some persistence in changes in rates that was less evident in earlier periods; that is, rates were more likely to revert to long-run averages during calmer markets.
The next four lines show that, despite high balances and ample Treasury issuance, there was still a liquidity effect in both markets. For the repo market, most of the liquidity effect was through net Treasury issuance; a $100 billion increase in Treasury net issuance pushed up the repo rate by about 4 basis points. Interestingly, this effect is similar to that before the crisis. For the federal funds market, the liquidity effect is evident primarily through LSAPs, net Treasury issuance, and the Supplementary Financing Account (SFA) balance. Note that each of these has a different effect on reserve balances. LSAPs add balances, which would cause the funds rate to fall. In contrast, net Treasury issuance increases the level of the TGA and therefore drains balances, supporting the federal funds rate. Finally, the SFA works similarly to the TGA and increases in this account drain balances, which also pushes up the federal funds rate. Hence, the LSAP effect is in the opposite direction to the other two effects.
Interestingly, the absolute values of the liquidity effects identified through LSAPs, net Treasury issuance, and SFA balances are in a narrow range, between 0.007 and 0.01. Hence, our results suggest that a $100 billion decrease in supply of reserve balances through any one of these channels would lead to a less than 1 basis point increase in the federal funds rate. However, it is important to note that the regression coefficient considered on its own does not capture the complete, dynamic liquidity effect. The coefficient on its own does not take into account the propagation mechanism of changes in supply of reserve balances captured by the structure of the entire VAR model. This point will become evident later in the paper.
Turning to the risk controls, although movements in the Libor-OIS spread had little effect on the funds market, they did have an effect on the repo market: for a 10 basis point change in this spread, the repo rate falls by about 2 basis points. Conversely, increases in capital ratios were associated with increases in the repo rate, but not correlated with the federal funds rate. Positive increases in capital ratios are associated with higher federal funds and repo rates. This is consistent with arbitrage in these markets, that is, amid higher capital ratios, banks are able to expand balance sheets and take advantage of the rate differential between federal funds and the interest on excess reserves rate. Unlike earlier periods, the slope of the yield curve exhibits little correlation with movements in either of these rates. Because policy was likely seen as being on hold for "an extended period," it is possible that other factors that might cause movements in this slope would not be associated with rate movements in very short-term funding markets.
For the specific market controls, fails were associated with larger changes in the federal funds and repo rates. During periods of high repo demand, fails increase and rates fall considerably, pushing these changes higher. Somewhat counterintuitively, as activity in the funds market increased, as indicated by the change in federal funds market volume, rates in both markets fell. However, the coefficients are fairly small and thus these changes were likely not economically meaningful during this period. Finally, increases in the number of funds sellers - an indicator of supply - is associated with higher federal funds rates, but changes in the quantity of funds sold by the GSEs was not significantly correlated with changes in these rates.
5 Policy experiments and implications of results
The next few subsections use the parameters estimated above to perform a series of policy experiments. The first experiment examines the monetary policy transmission mechanism, the second explores the probability of default in the federal funds market, and the third performs simulations of the possible effects on the funds rate and the repo rate of engaging in large-scale reverse repurchase agreements to drain reserves balances.
5.1 The effect of the crisis on monetary policy transmission
Our first exercise evaluates the effectiveness of the monetary policy transmission mechanism over the different sample periods. The ![]() terms estimated above give some clue as to the
ability of changes in the funds rate to transmit to other financial markets. Overall, the results suggest that if markets were in disequilibrium, the speed-of-adjustment slowed over the financial crisis.
terms estimated above give some clue as to the
ability of changes in the funds rate to transmit to other financial markets. Overall, the results suggest that if markets were in disequilibrium, the speed-of-adjustment slowed over the financial crisis.
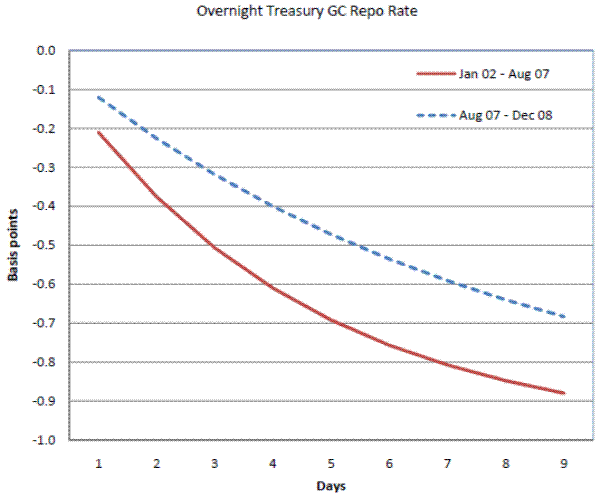
This result is clearly reflected in figure 9. It plots the implied speed of adjustment for the repo rate in days for a one basis point change in the long-run relationship between the repo rate and the federal funds rate. We can evaluate the "half-life" of the shock by looking at the number of days until the repo rate moves halfway back into its equilibrium relationship with the funds rate; that is, until it moves to the 0.5 basis point line. In the pre-crisis period, the average length of time it took for the repo rate to adjust halfway back to its longer-run average relationship with the federal funds market was about three days. Notably, the crisis slowed down the speeds of adjustment, as shown by the early crisis line. The adjustment speed during the crisis was between five and six days, almost twice as long as before the crisis.
As evidenced by the statistically insignificant long run relationship between the federal funds and repo rates, we know that only the repo rate would be able to adjust to the longer-run equilibrium. The funds rate was continuously managed by the Desk in order to stay close to the target federal funds rate. As a result, the repo rate was the only rate that adjusted to disequilibria. In this sense, the funds rate influenced the repo rate, offering evidence that the daily transmission of monetary policy was functioning. Moreover, it also suggests rate differences were arbitraged faster in the repo market than in the funds market, perhaps because it is collateralized and has larger participants. In the later periods, adjustments to disequilibria slowed considerably. However, because adjustments were still evident, there was at least some continuing arbitrage in the repo market.
5.2 The effect of the crisis on the probability of default
The next set of exercises uses the parameter estimates to investigate changes in the implied probability of default over the sample period. In order to fix ideas, we present a simple framework for the relationship between secured and unsecured lending. Following Barro (1976), we assume that a
loan of amount ![]() is made from lender to a borrower today and the full principal and interest comes due tomorrow. We assume that there are two types of loan contracts in the money markets-an
unsecured contract and a secured contract-each for an overnight loan of $1. Borrowers renege on both the principal and interest payment with probability
is made from lender to a borrower today and the full principal and interest comes due tomorrow. We assume that there are two types of loan contracts in the money markets-an
unsecured contract and a secured contract-each for an overnight loan of $1. Borrowers renege on both the principal and interest payment with probability ![]() and
and ![]() under the unsecured and secured contracts respectively, possibly reflecting differences in borrower characteristics. For simplicity, we assume that if the unsecured borrower defaults, the lender
gets nothing. Although the secured loans are backed by collateral, secured lending is not risk free: if the borrower defaults, the collateral might not be recovered fully or it might be not sufficient ex post to cover the principal, if there were a drop in the market
value of that collateral. The parameter
under the unsecured and secured contracts respectively, possibly reflecting differences in borrower characteristics. For simplicity, we assume that if the unsecured borrower defaults, the lender
gets nothing. Although the secured loans are backed by collateral, secured lending is not risk free: if the borrower defaults, the collateral might not be recovered fully or it might be not sufficient ex post to cover the principal, if there were a drop in the market
value of that collateral. The parameter
![]() captures the recovery rate of the loan principal.29
captures the recovery rate of the loan principal.29
Lenders are assumed to be risk neutral and, hence, arbitrage should, all else equal, ensure that the lender's expected return from secured lending be the same as that from unsecured lending. Suppose the unsecured loan contract specifies an interest rate of ![]() , whereas the secured loan contract specifies an interest rate of
, whereas the secured loan contract specifies an interest rate of ![]() . The expected returns of a lender in the
unsecured and secured markets-
. The expected returns of a lender in the
unsecured and secured markets-![]() and
and ![]() , respectively-are given by
, respectively-are given by
| (7) |
and
| (8) |
Assuming no impediments to arbitrage, in equilibrium, the two returns should be equal, that is,
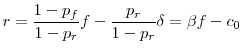 |
(9) |
where
| (10) |
implying that the spread between the unsecured and secured rates increases with either an increase in the recovery rate,
Obviously, the same value of the spread between the federal funds and repo rates is consistent with a continuum of combinations of recovery rates and default probabilities. To trace all these combinations, we construct a default probability-recover rate isocurve, a ![]() isocurve for short, for each value of the estimated
isocurve for short, for each value of the estimated ![]() . The isocurve for period
. The isocurve for period ![]() is given by
is given by
| (11) |
where
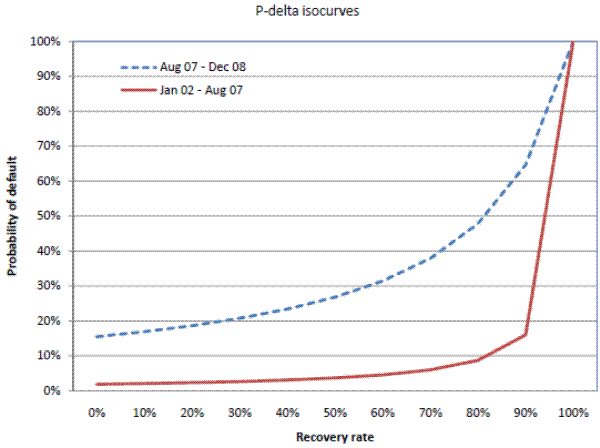
The isocurves corresponding to a ![]() of about 0.02 estimated for the January 2002 - August 2007 period and a
of about 0.02 estimated for the January 2002 - August 2007 period and a ![]() of about 0.18 estimated for the August 2007 - December 2008 are shown in figure 10. The January 2002 - August 2007 isocurve is much lower than the August 2007 - December 2008 curve, suggesting that at any recovery rate, the implied
probability of default is much higher in the later period than that in the earlier period. While the early period might be characterized as the period with high recovery rates (that is, stable collateral market values), the later period might be characterized as the period with low recovery rates,
even though both rates reflect Treasury securities collateral. Nevertheless, the implied probabilities of default in the later period are much higher than that for the earlier period. For example, at the recovery rate of 80 percent the implied probability of default for the later period is about 50
percent, while that for the earlier period is about 10 percent.
of about 0.18 estimated for the August 2007 - December 2008 are shown in figure 10. The January 2002 - August 2007 isocurve is much lower than the August 2007 - December 2008 curve, suggesting that at any recovery rate, the implied
probability of default is much higher in the later period than that in the earlier period. While the early period might be characterized as the period with high recovery rates (that is, stable collateral market values), the later period might be characterized as the period with low recovery rates,
even though both rates reflect Treasury securities collateral. Nevertheless, the implied probabilities of default in the later period are much higher than that for the earlier period. For example, at the recovery rate of 80 percent the implied probability of default for the later period is about 50
percent, while that for the earlier period is about 10 percent.
Of course, this is a simple model and the probabilities here should be taken more as illustrative, rather than as canonical parameters of an underlying true default function. However, we can conclude that despite a possible decline in the recovery rate, the probability of default jumped notably in the later period.
5.3 The dynamic liquidity effect and implications for the exit strategy
Our final exercise is an investigation of the dynamic liquidity effect and the implications for draining reserve balances using reverse repurchase agreements.
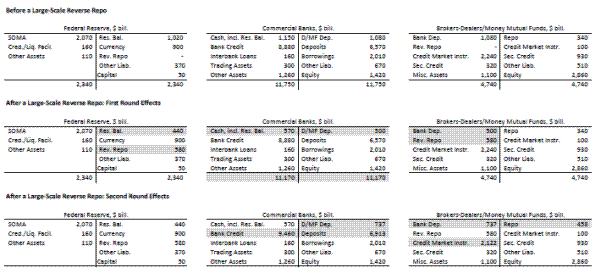
One of the measures currently undergoing operational tests for draining reserves are reverse repurchase agreements with a wide set of counterparties; that is, a counterparty list that includes primary dealers as well as other entities.31 Our results allow us to evaluate how this program might affect money market interest rates. But, how does a reverse repurchase agreement with the Federal Reserve work? In order to explain this, we present a stylized exercise, shown in figure 11, of a reverse repo between the Federal Reserve and a set of extended counterparties, which includes broker-dealers and money mutual funds. Banks act as intermediaries-for these institutions, reserve balances are an asset, and deposits due to broker-dealers and money mutual funds are a liability. This repo affects the balance sheet of these actors differently. The top panel shows the starting point, where all values are roughly in line with actual levels for the institution types.32 Dealers' and mutual funds' balance sheets have been combined into one: since dealers are typically cash borrowers and funds are cash lenders, it is simpler to present a "netted" balance for these two types of institutions.
The figure illustrates both the first and second round effects of a reverse repo. The first round effects cover immediate changes in the balance sheets, while the second round effects show possible balance sheet adjustments in the aftermath of the operation. In this exercise, the Federal Reserve conducts a $500 billion reverse repo, the immediate effect of which is to drain $500 billion in reserve balances, to reduce dealer-mutual funds deposits at depository institutions by $500 billion, and to bias the composition of assets of dealers-mutual funds towards repos, as illustrated in the middle panel of the figure. Clearly, banks' balance sheets shrink with the outflow of deposits due to dealers-mutual funds and the corresponding reduction in reserve balances. In contrast, the sizes of the balance sheets of the Federal Reserve and dealers-mutual funds remain constant. Because of the reverse repo, dealers-mutual funds are short on cash and long on collateral. This bias pushes up the repo rate in the short run. The higher repo rate boosts the federal funds rate, which was already propped up by the reduction in supply of reserve balances. Over time, as shown by the bottom panel second-round effects, dealers-mutual funds adjust their balance sheet by selling their outright holdings or doing repos to increase their holdings of cash. The shift of their balance sheet composition towards cash puts some downward pressure on the repo rate. Because of leverage constraints, dealers cannot adjust their balance sheet fully, so the repo rate in the long run remains above the repo rate before the large-scale reverse repo. The reduction in the size of the balance sheet of depository institutions, assuming no change in their capital, implies a lower leverage ratio. In addition, it is possible that the "excess" room for leverage gives these institutions an opportunity to raise more deposits and increase lending or bank credit more broadly. However, depository institutions might prefer to keep leverage ratios high amid the current regulatory environment.33
With this example in mind, we use the estimated VEC and VAR models to simulate the effects of a large-scale reverse repurchase agreement (draining operations) on the federal funds and repo rates.34 In light of the model setup, we make four key assumptions.
First, we assume that through movements in net Treasury issuance and LSAPs (both affecting supply of liquidity), the models can trace out the dynamic liquidity effect. In particular, a reverse repurchase agreement with the Federal Reserve would increase the amount of collateral and reduce the amount of cash in the repo market (analogous to an increase in net Treasury issuance) and would reduce the level of reserve balances (similar to a change in the level of the LSAP holdings). As a result, we can use the net Treasury issuance and LSAP coefficient estimates to evaluate the draining effects.
Second, we assume that the parameter estimates for one period are applicable to a different one, despite the possibility of fundamental changes in these markets. Inarguably, financial markets in general and the federal funds market in particular have changed notably since 2007, and could very well change again in the future. Consequently, the parameters we estimate on pre- or post-crisis data may not be completely applicable to the regime that could be in place in the future. We find some comfort, though, in the fact that some of our results are fairly consistent across sample periods. For example, our results suggest that the effect of net Treasury issuance on repo rates is roughly unchanged, on net, over the entire sample.
Third, we assume that, before liquidity draining, reserve balances are at $1,020 billion, while the federal funds rate and the repo rate are at 19 and 20 basis points respectively -in line with that observed in mid-June 2010. For completeness, we choose a wide range of possible sizes for draining operations: $320 billion, $520 billion, $720 billion, $920 billion and $980 billion.35
And fourth, we use different parameter estimates to evaulate the effects of draining that depend on the amount drained. In particular, to evaluate the effects of the draining operations of $920 billion or less, we apply parameter estimates from the December 2008 to June 2010 sample period. To illustrate the effects of the draining operation of $980 billion, which would reduce the level of reserve balances to that occasionally seen before the crisis, we explicitly recognize that the demand for balances is nonlinear. Hence, we use the parameter estimates from the December 2008 to June 2010 period to evaluate the draining effects of the first $920 billion and then we switch to the parameter estimates from the January 2002 to August 2007 period to evaluate the draining effects of the remaining $60 billion, to a level of $40 billion. We chose $40 billion for the final level of reserve balances as it roughly corresponds to the top of the range of the average level of required operating balances, or the amount of balances that banks are required to hold in order to satisfy reserve requirements as well as clearing needs.
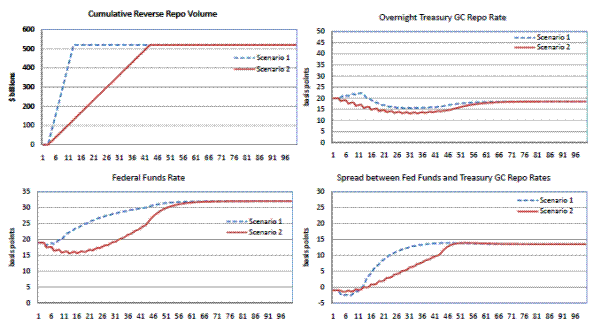
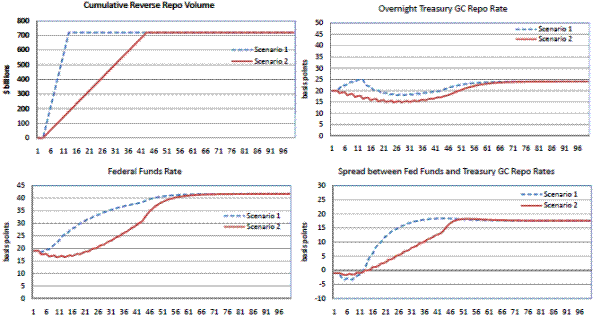
Overall, the results suggest that large-scale draining of reserve balances might exert weak upward pressure on the federal funds and repo rates at high levels of balances, but should exert strong upward pressure at lower levels. To illustrate this phenomenon, figures 12, 13, and 14 show the simulated effects of draining a range of levels of reserve balances. As shown in the top two panels of figures 12, 13, and 14, we assume two different patterns for draining operations. The first, depicted by the blue dashed line in the top left panel, is a fast approach, where the draining occurs over 10 days. The second, shown by the red line, is a more gradual approach, where the same amount is drained over 30 days. The former strategy requires individual repo operations to be larger, while the latter relaxes this requirement. In both scenarios, however, the cumulative effect on reserve balances is the same. The top right and bottom left panels in figures 12, 13, and 14 show the effect of draining on rates. As shown in figure 12, with a simulated draining of $520 billion through reverse repo operations, even though the funds rate eventually firms a considerable amount of 12 basis points, the impact on the repo rate is fairly minimal. At the end of the projection, the equilibrium repo rate is actually at a lower level than the starting point. Within the context of the discussion above regarding the adjustment of the size of the dealers-mutual funds balance sheets, it could be the case that with smaller-sized repos, balance sheets would be able to adjust fully and there might actually be downward pressure on the repo rate in equilibrium. Because the equilibrium repo rate and funds rates move in opposite directions from their initial positions, the spread widens, as shown in the bottom right panel.
However, this pattern does not apply exactly to the other sizes of draining operations, as our model implies some nonlinearities in draining effects. As shown in the top right panel of figure 13, repo rates initially climb about 5 basis points, before falling for a bit and retracing back to that level at the end of the projection. In contrast, under scenario 2, rates dip down at the outset and then reach the same level as under scenario 1 in the end. These patterns show that the dynamics of reaching the steady state equilibrium can change depending on the pace of the operation, which are a result of the lagged effects of operations in the model and perhaps the estimated effects of changes in issuance on rate dynamics as the market absorbs collateral. The path of the federal funds rate, shown in the bottom left panel, is smoother and shows a steady climb to the equilibrium outcome, which is a tightening of about 20 basis points from its initial level. The bottom right panel shows that the spread between the two rates, initially set to zero, widens to about 17 basis points in equilibrium. The reason for this spread could be that only selected institutions can participate in the federal funds market, limiting the ability of investors to fully arbitrage away differences in the rates.
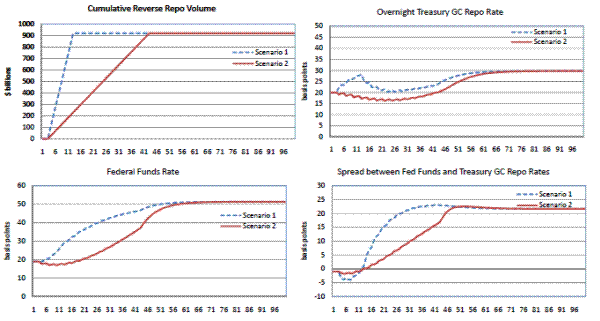
Figure 14 shows similar patterns to draining operations of $720 billion. As shown in the top right panel, the repo rate under scenario 1 initially pops up, and then settles down at a level that is about 10 basis points above baseline. The funds rate evolution is smooth, with about 30 basis points of tightening. The change in the spread replicates the movement of both of these, with the spread landing at a little above 20 basis points in long-run equilibrium.
Table 8 summarizes these results. As discussed above, draining $520 billion in balances raises the funds rate 12 basis points in the long run; higher amounts of balances drained implies higher federal funds rates and higher repo rates, as well. We also include two other levels of repo operations for comparison, namely draining $320 billion and $980 billion in balances. Interestingly, as reported in the top line of the table, while draining only $320 billion in reserve balances firms the federal funds rate, on net, the repo rate falls somewhat. By contrast to the stylized example above, the balance sheets of the repo participants may adjust fully to the repo operation, and rather than the repo rate rising in the long run, it is more than compensated for. The final simulation, as reported in the last line of the table, drains balances down to levels seen before the crisis started. To drain $980 billion in balances total, we apply the parameter estimates from the third sample to simulate draining the first $920 billion and for the remaining $60 billion, we use the parameter estimates for the first sample. The dynamics for draining this final $60 billion are different from that for the first stage: most of the action is in the repo rate, and less occurs in the federal funds rate. As shown in the table, in the second stage, the repo rate rises about 30 basis points, while the federal funds rate edges up 10 basis points. The net effect of these dynamics is to cause a narrowing of the spread between the two rates. One interpretation of this simulation is that once dealers-mutual funds have saturated their balance sheets with reverse repos from the Federal Reserve, the marginal effects of a repo are much larger. Along these lines, once reserve balances have reached relatively low levels, a small drain can result in a relatively large bump-up in the federal funds rate.
Overall, the experiments above give some characterization of the model's suggestions regarding the evolution of the federal funds and repo rates. A couple of caveats are necessary. To start, these are model-based and do not necessarily reflect market participants' appetite for collateral; some values of draining operations may be unrealistic or operationally infeasible. In addition, these model-driven results is that they depend on the assumption that the relevant parameters of the demand function will not change substantially from those that are estimated on past data. Given the introduction of interest on reserves in the fall of 2008, there is some chance that demand for reserve balances fundamentally changed since the early part of our sample - for example, since 2002. Still, we see scope for the relevance of this theoretical exercise, as it at least attempts to characterize the dynamics that still exist, as well as the possibility of differences in demand for balances as the level of balances approaches that of required operating balances. 36
6 Conclusion
Financial markets experienced remarkable changes over the crisis, and money markets were no exception. This paper attempts to characterize the changes in these markets and to use these characterizations to address situations that could occur should operations one day return to "normal." Along the way, we showed how the speed of monetary policy transmission changed during the crisis; how banks were compensated for the possibility of default in the federal funds market; and how the demand curve for reserve balances morphed over time.
In sum, our results suggest that monetary policy transmission still functioned through a good part of the crisis. The link changed somewhat as reserve balances rose and short-term interest rates dropped to the zero lower bound. Still, our results suggest that draining balances should help restore the relationship between the federal funds and repo rates. Extensions to the analysis could include explicit modeling of interest on excess reserves; however, draining balances down to near requirements should put markets on the downward sloping part of the demand curve for balances, and consequently, our results should likely still hold.
Bibliography
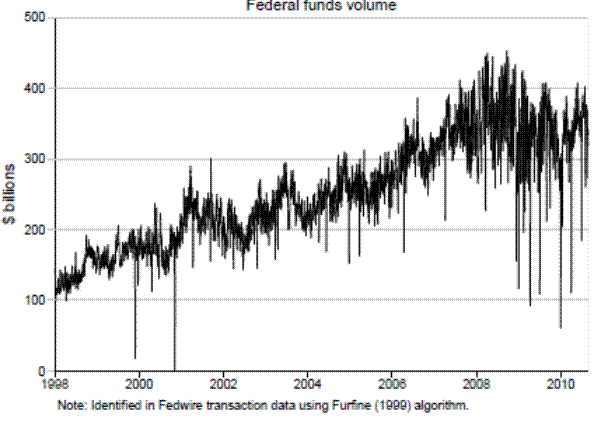 Note. Identified in Fedwire transaction data using Furfine (1999) algorithm.
Note. Identified in Fedwire transaction data using Furfine (1999) algorithm.| Federal funds | Repo | N | |
| January 2002 - August 2007 | 1.054 | 1.068 | 1399 |
| January 2002 - August 2007 Lag Length | 10 | 6 | |
| August 2007 - December 2008 | -0.769 | 2.345 | 331 |
| August 2007 - December 2008 Lag Length | 3 | 1 | |
| December 2008 - June 2010 | -6.513 ** | -5.076 ** | 385 |
| December 2008 - June 2010 Lag Length | 2 | 1 | |
| confidence level. |
Lag length below test statistic. ** Reject hypothesis of a unit root at the 5 percent
| Series/No. of eq. | Eigenvalue | Trace stat. | C | Prob |
| January 2002 - August 2007: None | 0.083 | 123.102 | 15.495 | 0.000 |
|---|---|---|---|---|
| January 2002 - August 2007: At most 1 | 0.001 | 0.775 | 3.841 | 0.379 |
| August 2007 - December 2008: None | 0.101 | 34.134 | 20.262 | 0.000 |
| August 2007 - December 2008: At most 1 | 0.021 | 5.690 | 9.165 | 0.216 |
| Excluded rate | DF | Prob. | |
| Repo rate (January 2002 - August 2007) | 9.07 | 3 | 0.03 |
| Federal funds rate (January 2002 - August 2007) | 2.68 | 3 | 0.44 |
| Repo rate (August 2007 - December 2008) | 9.98 | 3 | 0.02 |
| Federal funds rate (August 2007 - December 2008) | 29.40 | 3 | 0.00 |
| Repo rate (December 2008 - June 2010) | 2.79 | 3 | 0.43 |
| Federal funds rate (December 2008 - June 2010) | 51.40 | 3 | 0.000 |
| D(Repo rate) Coeff. | D(Repo rate) Std. Error | D(Repo rate) z-Stat. | D(Repo rate) Prob. | D(Repo rate) Coeff. | D(Repo rate) Std. Error | D(Repo rate) z-Stat. | D(Repo rate) Prob. | |
|---|---|---|---|---|---|---|---|---|
| Speed of adjustment | -0.21 | 0.04 | -5.30 | 0.00 | -0.01 | 0.04 | -0.19 | 0.85 |
| D(Repo rate(-1)) | -0.28 | 0.05 | -5.52 | 0.00 | -0.05 | 0.06 | -0.83 | 0.41 |
| D(Repo rate(-2)) | -0.18 | 0.04 | -4.63 | 0.00 | -0.08 | 0.03 | -2.76 | 0.01 |
| D(Repo rate(-3)) | -0.08 | 0.02 | -3.37 | 0.00 | -0.04 | 0.03 | -1.62 | 0.10 |
| D(Federal funds rate(-1)) | 0.03 | 0.05 | 0.53 | 0.59 | -0.38 | 0.06 | -6.13 | 0.00 |
| D(Federal funds rate(-2)) | 0.06 | 0.05 | 1.34 | 0.18 | -0.22 | 0.04 | -5.87 | 0.00 |
| D(Federal funds rate(-3)) | 0.04 | 0.03 | 1.34 | 0.18 | -0.15 | 0.03 | -5.38 | 0.00 |
| Factor miss | 0.05 | 0.10 | 0.51 | 0.61 | -0.34 | 0.12 | -2.72 | 0.01 |
| Net Treasury sec. issuance | 0.04 | 0.01 | 3.07 | 0.00 | 0.00 | 0.01 | 0.09 | 0.93 |
| Net Treasury sec. issuance(-1) | 0.02 | 0.01 | 1.81 | 0.07 | -0.00 | 0.01 | -0.08 | 0.93 |
| D(Libor-OIS spread) | 0.11 | 0.09 | 1.13 | 0.26 | -0.03 | 0.08 | -0.36 | 0.72 |
| D(Capital ratios) | 19.55 | 10.15 | 1.93 | 0.05 | 21.42 | 19.36 | 1.11 | 0.27 |
| D(Treasury yield curve slope) | 0.06 | 0.04 | 1.47 | 0.14 | -0.07 | 0.04 | -1.88 | 0.06 |
| D(Repo market composition) | 0.03 | 0.17 | 0.18 | 0.86 | 0.06 | 0.17 | 0.34 | 0.73 |
| D(Treasury sec. delivery fails) | -0.01 | 0.01 | -0.80 | 0.43 | -0.00 | 0.01 | -0.01 | 0.99 |
| D(Securities lending) | -0.00 | 0.05 | -0.02 | 0.98 | 0.07 | 0.08 | 0.78 | 0.43 |
| D(Federal funds volume) | 0.05 | 0.01 | 4.64 | 0.00 | 0.11 | 0.01 | 8.27 | 0.00 |
| D(Number of funds sellers) | 0.00 | 0.00 | 1.97 | 0.05 | -0.01 | 0.00 | -2.70 | 0.01 |
| D(Fed funds sold by GSEs) | -0.10 | 0.02 | -5.96 | 0.00 | -0.13 | 0.02 | -7.39 | 0.00 |
| D(Federal funds target rate) | 0.16 | 0.12 | 1.29 | 0.20 | 0.15 | 0.10 | 1.51 | 0.13 |
| MP day 1 | -1.81 | 1.44 | -1.26 | 0.21 | -2.05 | 1.03 | -1.98 | 0.05 |
| MP day 2 | -4.53 | 1.42 | -3.18 | 0.00 | -5.17 | 1.00 | -5.18 | 0.00 |
| MP day 5 | -1.76 | 1.43 | -1.23 | 0.22 | -2.05 | 1.03 | -1.99 | 0.05 |
| MP day 6 | -2.92 | 1.46 | -2.00 | 0.05 | -3.93 | 1.06 | -3.71 | 0.00 |
| MP day 7 | -2.84 | 1.42 | -2.00 | 0.05 | -3.86 | 1.00 | -3.86 | 0.00 |
| MP day 8 | -1.90 | 1.42 | -1.33 | 0.18 | -2.08 | 1.03 | -2.03 | 0.04 |
| MP day 9 | -3.16 | 1.42 | -2.23 | 0.03 | -4.29 | 1.02 | -4.22 | 0.00 |
| MP day 12 | -1.54 | 1.42 | -1.09 | 0.28 | -2.46 | 1.00 | -2.45 | 0.01 |
| MP day 13 | -2.84 | 1.47 | -1.94 | 0.05 | -5.35 | 1.05 | -5.10 | 0.00 |
| MP day 14 | -3.32 | 1.43 | -2.33 | 0.02 | -3.66 | 1.07 | -3.41 | 0.00 |
| 15th of the month | 4.34 | 0.56 | 7.79 | 0.00 | 4.21 | 0.47 | 8.90 | 0.00 |
| End of the month | 2.45 | 0.52 | 4.68 | 0.00 | 3.66 | 0.51 | 7.13 | 0.00 |
| 25th of the month | 0.51 | 0.40 | 1.27 | 0.20 | 3.64 | 0.43 | 8.44 | 0.00 |
| End of the quarter | -7.69 | 3.08 | -2.50 | 0.01 | 6.22 | 2.41 | 2.59 | 0.01 |
| End of the year | -12.36 | 6.80 | -1.82 | 0.07 | -17.18 | 4.73 | -3.63 | 0.00 |
| Adjusted R-squared | 0.40 | 0.36 | ||||||
| Durbin-Watson statistic | 1.94 | 1.74 |
| D(Repo rate) Coeff. | D(Repo rate) Std. Error | D(Repo rate) z-Stat. | D(Repo rate) Prob. | D(Federal funds rate) Coeff. | D(Federal funds rate) Std. Error | D(Federal funds rate) z-Stat. | D(Federal funds rate) Prob. | |
|---|---|---|---|---|---|---|---|---|
| Speed of adjustment | -0.12 | 0.02 | -5.59 | 0.00 | 0.01 | 0.01 | 0.34 | 0.73 |
| D(Repo rate(-1)) | -0.02 | 0.04 | -0.53 | 0.60 | -0.08 | 0.03 | -2.62 | 0.01 |
| D(Repo rate(-2)) | -0.04 | 0.04 | -1.17 | 0.24 | 0.03 | 0.01 | 1.79 | 0.07 |
| D(Repo rate(-3)) | -0.04 | 0.03 | -1.32 | 0.19 | 0.01 | 0.01 | 0.58 | 0.56 |
| D(Federal funds rate(-1)) | 0.22 | 0.05 | 4.65 | 0.00 | -0.03 | 0.05 | -0.76 | 0.45 |
| D(Federal funds rate(-2)) | 0.18 | 0.07 | 2.67 | 0.01 | -0.14 | 0.04 | -3.33 | 0.00 |
| D(Federal funds rate(-3)) | 0.06 | 0.04 | 1.34 | 0.18 | -0.10 | 0.03 | -3.58 | 0.00 |
| Factor miss | -0.02 | 0.08 | -0.22 | 0.82 | 0.05 | 0.05 | 1.01 | 0.31 |
| Treasury General Acct. bal. | -0.09 | 0.02 | -3.81 | 0.00 | 0.03 | 0.02 | 1.49 | 0.14 |
| Net Treasury sec. issuance | 0.17 | 0.04 | 4.87 | 0.00 | 0.04 | 0.04 | 1.20 | 0.23 |
| Net Treasury sec. issuance(-1) | 0.14 | 0.03 | 4.82 | 0.00 | 0.03 | 0.02 | 1.17 | 0.24 |
| D(Supplement. Fin. Acct. bal.) | -0.08 | 0.12 | -0.67 | 0.50 | 0.03 | 0.07 | 0.37 | 0.71 |
| D(Libor-OIS spread) | -0.49 | 0.10 | -5.08 | 0.00 | 0.12 | 0.06 | 1.89 | 0.06 |
| D(Capital ratios) | 221.78 | 89.88 | 2.47 | 0.01 | -210.95 | 28.99 | -7.28 | 0.00 |
| D(Treasury yield curve slope) | -0.07 | 0.10 | -0.71 | 0.47 | -0.14 | 0.07 | -2.01 | 0.04 |
| D(Repo market composition) | 5.62 | 1.55 | 3.63 | 0.00 | 0.33 | 0.58 | 0.57 | 0.57 |
| D(Treasury sec. delivery fails) | -0.00 | 0.02 | -0.12 | 0.90 | 0.01 | 0.01 | 1.06 | 0.29 |
| D(Securities lending) | 0.23 | 0.16 | 1.46 | 0.14 | 0.36 | 0.13 | 2.69 | 0.01 |
| D(Federal funds volume) | -0.01 | 0.04 | -0.23 | 0.82 | 0.12 | 0.04 | 3.18 | 0.00 |
| D(Number of funds sellers) | 0.10 | 0.03 | 2.93 | 0.00 | -0.06 | 0.03 | -2.29 | 0.02 |
| D(Fed funds sold by GSEs) | -0.01 | 0.06 | -0.23 | 0.81 | 0.04 | 0.06 | 0.60 | 0.55 |
| D(Federal funds target rate) | 1.00 | 0.11 | 9.50 | 0.00 | 0.56 | 0.08 | 7.38 | 0.00 |
| MP day 1 | -140.49 | 87.08 | -1.61 | 0.11 | -108.69 | 40.85 | -2.66 | 0.01 |
| MP day 2 | -143.03 | 87.06 | -1.64 | 0.10 | -116.99 | 40.84 | -2.86 | 0.00 |
| MP day 5 | -142.25 | 87.03 | -1.63 | 0.10 | -111.92 | 40.92 | -2.74 | 0.01 |
| MP day 6 | -144.76 | 87.07 | -1.66 | 0.10 | -112.80 | 40.87 | -2.76 | 0.01 |
| MP day 7 | -145.06 | 87.07 | -1.67 | 0.10 | -110.84 | 40.86 | -2.71 | 0.01 |
| MP day 8 | -140.57 | 87.07 | -1.61 | 0.11 | -110.32 | 40.85 | -2.70 | 0.01 |
| MP day 9 | -146.22 | 87.10 | -1.68 | 0.09 | -116.51 | 40.84 | -2.85 | 0.00 |
| MP day 12 | -139.91 | 87.09 | -1.61 | 0.11 | -111.14 | 40.81 | -2.72 | 0.01 |
| MP day 13 | -146.60 | 87.06 | -1.68 | 0.09 | -114.72 | 40.79 | -2.81 | 0.00 |
| MP day 14 | -146.48 | 87.05 | -1.68 | 0.09 | -110.56 | 40.82 | -2.71 | 0.01 |
| 15th of the month | -1.59 | 2.17 | -0.73 | 0.46 | -1.55 | 1.93 | -0.80 | 0.42 |
| End of the month | -8.41 | 2.90 | -2.90 | 0.00 | 1.23 | 2.57 | 0.48 | 0.63 |
| 25th of the month | -3.85 | 2.36 | -1.63 | 0.10 | 7.79 | 1.97 | 3.95 | 0.00 |
| End of the quarter | -47.10 | 7.55 | -6.24 | 0.00 | 27.30 | 7.20 | 3.79 | 0.00 |
| End of the year | -92.18 | 60.80 | -1.52 | 0.13 | -83.76 | 28.74 | -2.91 | 0.00 |
| Adjusted R-squared | 0.25 | 0.14 | ||||||
| Durbin-Watson statistic | 1.87 | 2.02 |
| Coeff. (Repo rate) | Std. Error (Repo rate) | z-Stat. (Repo rate) | Prob. (Repo rate) | Coeff. (Federal funds rate) | Std. Error (Federal funds rate) | z-Stat. (Federal funds rate) | Prob. (Federal funds rate) | |
|---|---|---|---|---|---|---|---|---|
| Speed of adjustment | NA | NA | NA | NA | NA | NA | NA | NA |
| Repo rate(-1) | 0.666 | 0.053 | 12.534 | 0.000 | 0.045 | 0.026 | 1.704 | 0.088 |
| Repo rate(-2) | 0.023 | 0.058 | 0.400 | 0.690 | -0.035 | 0.032 | -1.109 | 0.267 |
| Repo rate(-3) | 0.120 | 0.052 | 2.320 | 0.020 | 0.005 | 0.023 | 0.236 | 0.814 |
| Federal funds rate(-1) | 0.416 | 0.073 | 5.682 | 0.000 | 0.855 | 0.056 | 15.151 | 0.000 |
| Federal funds rate(-2) | 0.065 | 0.102 | 0.633 | 0.527 | 0.063 | 0.068 | 0.918 | 0.359 |
| Federal funds rate(-3) | -0.292 | 0.079 | -3.682 | 0.000 | 0.013 | 0.048 | 0.261 | 0.794 |
| Treasury General Acct. bal. | -0.004 | 0.003 | -1.373 | 0.170 | -0.001 | 0.001 | -0.807 | 0.420 |
| LSAP | -0.003 | 0.009 | -0.281 | 0.779 | -0.007 | 0.003 | -1.927 | 0.054 |
| Net Treasury sec. issuance | 0.044 | 0.004 | 10.269 | 0.000 | 0.011 | 0.002 | 4.592 | 0.000 |
| Net Treasury sec. issuance(-1) | 0.012 | 0.005 | 2.612 | 0.009 | 0.002 | 0.002 | 0.925 | 0.355 |
| D(Supplement. Fin. Acct. bal.) | 0.008 | 0.012 | 0.661 | 0.509 | 0.011 | 0.006 | 1.773 | 0.076 |
| D(Libor-OIS spread) | -0.192 | 0.074 | -2.612 | 0.009 | 0.005 | 0.042 | 0.111 | 0.912 |
| D(Capital ratios) | 31.704 | 3.590 | 8.831 | 0.000 | 11.088 | 4.069 | 2.725 | 0.006 |
| D(Treasury yield curve slope) | 0.011 | 0.023 | 0.462 | 0.644 | 0.003 | 0.011 | 0.303 | 0.762 |
| D(Repo market composition) | -0.003 | 0.189 | -0.017 | 0.986 | -0.087 | 0.099 | -0.882 | 0.378 |
| D(Treasury sec. delivery fails) | 0.062 | 0.025 | 2.439 | 0.015 | 0.037 | 0.012 | 3.146 | 0.002 |
| D(Securities lending) | 0.018 | 0.071 | 0.261 | 0.794 | 0.000 | 0.026 | 0.002 | 0.998 |
| D(Federal funds volume) | -0.050 | 0.018 | -2.758 | 0.006 | -0.008 | 0.009 | -0.966 | 0.334 |
| D(Number of funds sellers) | 0.016 | 0.015 | 1.112 | 0.266 | 0.019 | 0.008 | 2.282 | 0.023 |
| D(Fed funds sold by GSEs) | 0.001 | 0.011 | 0.068 | 0.946 | 0.001 | 0.005 | 0.272 | 0.786 |
| Constant | 0.504 | 0.588 | 0.858 | 0.391 | 1.075 | 0.290 | 3.711 | 0.000 |
| MP day 2 | -0.681 | 0.405 | -1.683 | 0.092 | -0.468 | 0.206 | -2.273 | 0.023 |
| MP day 5 | -0.297 | 0.399 | -0.744 | 0.457 | 0.136 | 0.208 | 0.656 | 0.512 |
| MP day 6 | -1.857 | 0.371 | -5.012 | 0.000 | -0.274 | 0.213 | -1.286 | 0.199 |
| MP day 7 | -1.530 | 0.409 | -3.737 | 0.000 | -0.374 | 0.195 | -1.914 | 0.056 |
| MP day 8 | -0.157 | 0.454 | -0.346 | 0.729 | -0.212 | 0.189 | -1.125 | 0.261 |
| MP day 9 | -0.539 | 0.402 | -1.341 | 0.180 | -0.342 | 0.195 | -1.751 | 0.080 |
| MP day 12 | -0.750 | 0.375 | -2.002 | 0.045 | -0.266 | 0.213 | -1.248 | 0.212 |
| MP day 13 | -1.851 | 0.366 | -5.051 | 0.000 | -0.343 | 0.205 | -1.668 | 0.095 |
| MP day 14 | -1.422 | 0.398 | -3.572 | 0.000 | -0.250 | 0.215 | -1.162 | 0.245 |
| 15th of the month | 2.344 | 0.446 | 5.251 | 0.000 | 1.224 | 0.285 | 4.297 | 0.000 |
| End of the month | -0.256 | 0.495 | -0.518 | 0.605 | 0.202 | 0.248 | 0.813 | 0.416 |
| 25th of the month | 0.090 | 0.447 | 0.201 | 0.841 | -0.092 | 0.205 | -0.451 | 0.652 |
| End of the quarter | -9.010 | 3.287 | -2.741 | 0.006 | -2.842 | 2.207 | -1.288 | 0.198 |
| End of the year | -0.454 | 3.547 | -0.128 | 0.898 | -1.609 | 4.402 | -0.365 | 0.715 |
| Adjusted R-squared | 0.85 | 0.81 | ||||||
| Durbin-Watson statistic | 2.13 | 1.78 |
| Repo rate Jan. 2002 --Aug. 2007 | Repo rate Aug. 2007 --Dec. 2008 | Repo rate Dec. 2008 --Jun. 2010 | Federal funds rate Jan. 2002 --Aug. 2007 | Federal funds rate Aug. 2007 --Dec. 2008 | Federal funds rate Dec. 2008 --Jun. 2010 | |
|---|---|---|---|---|---|---|
| Constant | 19.8 | 48.6 | NS | 4.2 | 236.8 | 0.17 |
| ARCH(1) coefficient | 0.5 | 0.4 | NS | 0.2 | 1.4 | 0.19 |
| TARCH(1) coefficient | NA | 2.1 | NS | NA | NS | NS |
| GARCH(1) coefficient | 0.2 | 0.3 | 1.0 | 0.7 | 0.1 | 0.63 |
| End of the quarter | 328.7 | 167.0 | NS | 65.8 | 1110.0 | NS |
| 15th of the month | 15.8 | NA | NA | NS | NA | NA |
| Correlation coefficient | 0.4 | 0.2 | 0.4 |
| Amount of reserve balances drained $ billions * | Change in Federal funds rate basis points | Change in Treasury GC repo rate basis points |
|---|---|---|
| 320 ** | 3 | -7 |
| 520 | 12 | -1 |
| 720 | 23 | 4 |
| 920 | 32 | 10 |
| 980 *** | 42 | 38 |
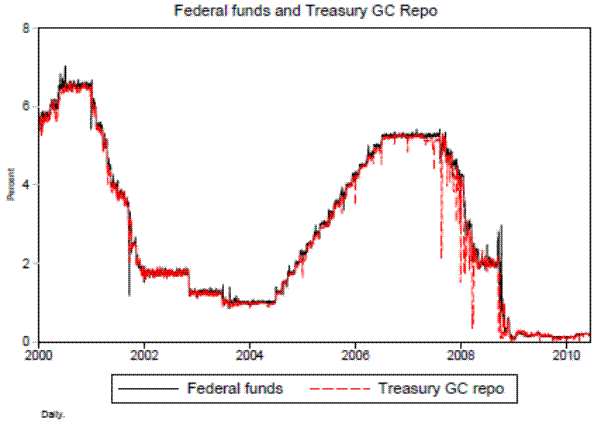 Daily.
Daily.
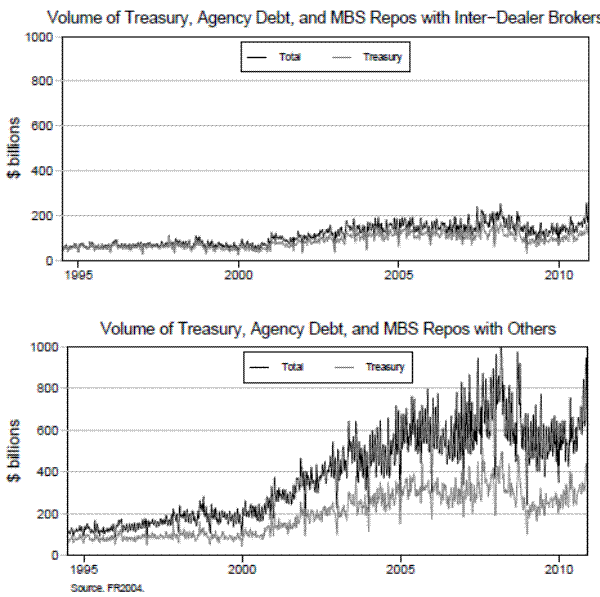 Source. FR2004.
Source. FR2004.
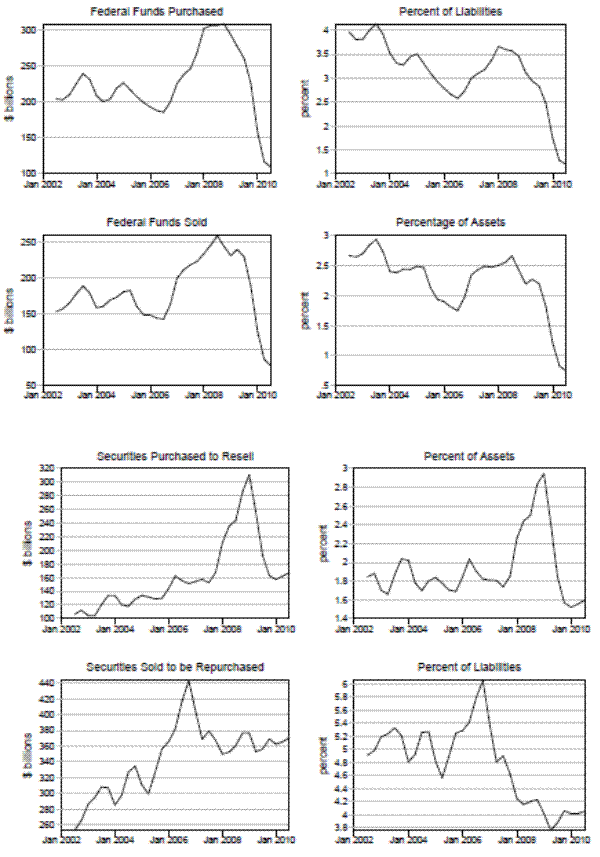
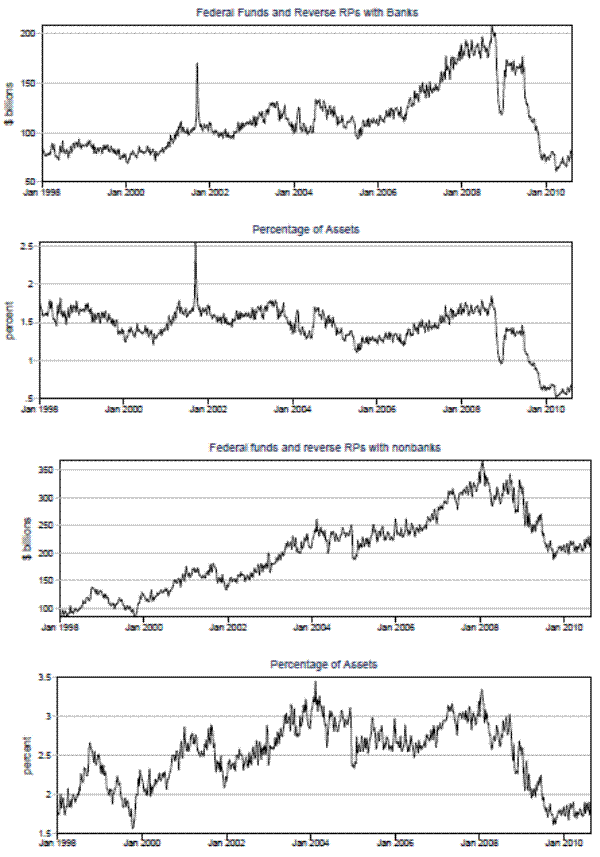
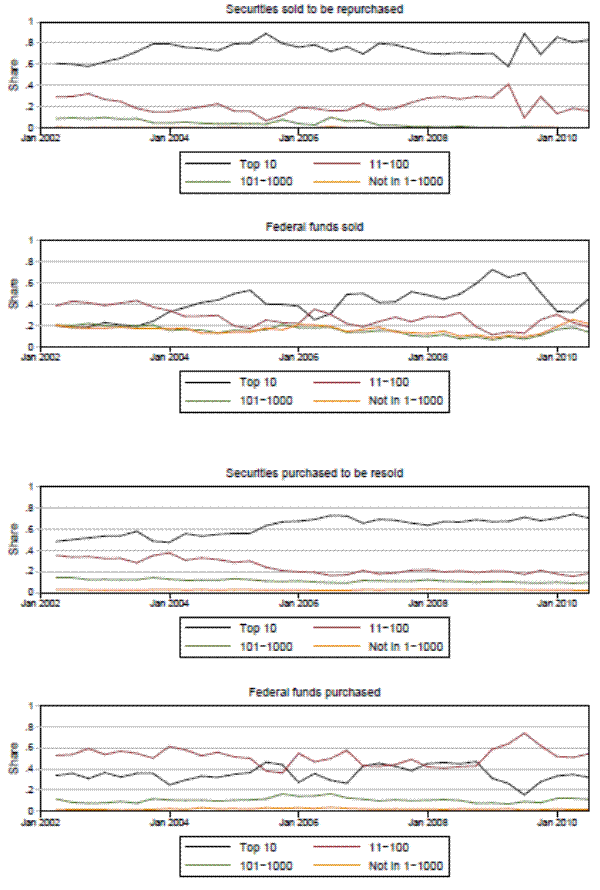
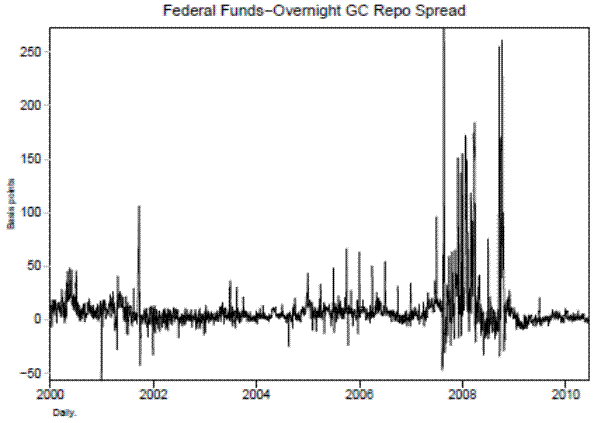 Daily.
Daily.
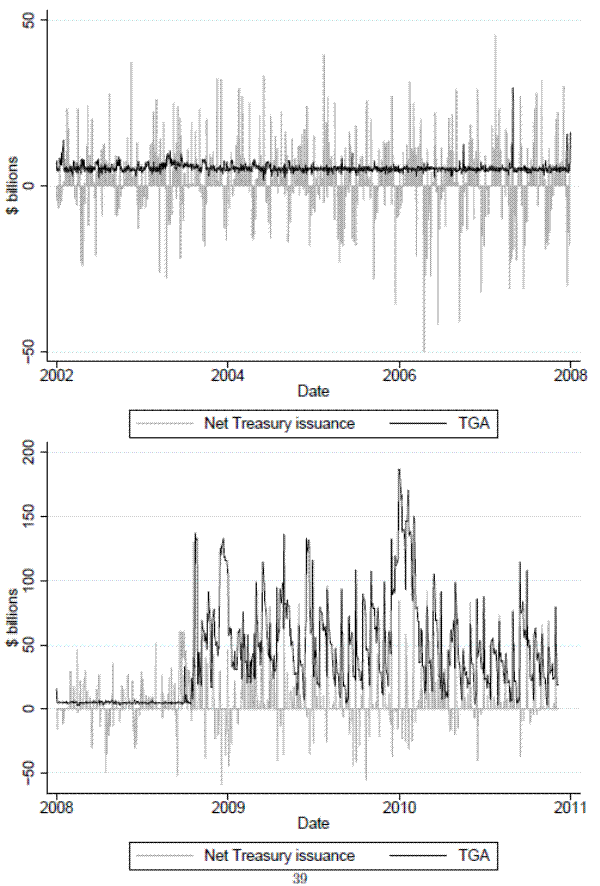 Daily.
Daily.