Interest Rate Risk and Bank Equity Valuations*
Keywords: FOMC announcements, interest rate surprises, maturity transformation, bank profitability
Abstract:
JEL Classification: G21, G32
1 Introduction
Conventional wisdom holds that banks benefit from a steep yield curve because they intermediate funds across maturities by borrowing "short" and lending "long." However, a steepening of the yield curve caused by rising long-term interest rates will also result in immediate capital losses on longer-term assets, which may offset part of any benefits of higher net interest margins. Given the centrality of interest rates to banks' business model, banking practitioners and regulators devote considerable effort to the management and monitoring of interest rate risk at financial institutions. The current economic landscape--with short-term rates constrained by the zero lower bound and longer-term rates at historically low levels--presents banks with an especially challenging environment for managing interest rate risk, a challenge that is likely to become even greater when the Federal Open Market Committee (FOMC) begins the process of monetary policy normalization (Kohn (2010)).
While interest rate risk is intrinsic to the process of maturity transformation, banks may hedge such exposure through the use of interest rate derivatives or limit its effects on interest income by making longer-term loans at floating rates. Moreover, the effect of interest rate changes on interest margins may be offset by changes in the noninterest components of revenues or expenses, such as income from fees or credit losses, or changes in the size and composition of bank balance sheets. These latter effects may be especially important because fluctuations in interest rates are, in general, correlated with cyclical changes in economic conditions that can exert their own influence on the different components of bank profitability.4 Indeed, as discussed below, the existing literature offers little consensus regarding the effects of changes in interest rates on the profits of financial institutions.
In this paper, we employ a novel approach to examine the link between bank equity values and changes in interest rates. Specifically, we use intraday stock price data to estimate the effects of unanticipated changes in interest rates prompted by FOMC announcements on the stock returns of U.S. bank holding companies (BHCs).5 Our contribution is three-fold. First, the high-frequency interest rate surprises induced by monetary policy actions are uncorrelated with other economic news or developments elsewhere in the economy. As a result, these interest rate shocks allow us to identify more cleanly the response of bank stock prices to interest rate changes by circumventing the difficult issues of endogeneity and simultaneity that plague the common practice of using the observed interest rate changes, which are correlated with other news about economic conditions; see Bernanke & Kuttner (2005) for a thorough discussion.6 Motivated by the conventional notion of banks as maturity transformers, we analyze the response of bank-level stock returns to unexpected shifts in the slope of the yield curve associated with monetary policy actions, as well as to surprise changes to the general level of interest rates.
Second, we examine how the reaction of stock returns to these interest rate surprises varies with key bank characteristics: the degree to which the bank is engaged in maturity transformation; the extent to which the bank relies on core deposits to fund its assets; the bank's use of interest rate derivatives; and the bank's size. To measure the degree of maturity transformation at an individual bank level--empirically a difficult problem--we employ Call Report data to construct a new, more refined measure of the mismatch between the repricing time or maturity of bank assets and liabilities than previously used in the literature. And lastly, to gain a better insight into the potential mechanisms behind the magnitude and cross-sectional patterns of the estimated reaction of bank equity valuations to interest rate surprises, we also analyze how changes in interest rates affect accounting measures of bank profitability, as well as the size and composition of bank balance sheets.
Our results indicate that unanticipated changes in both the level and slope of the yield curve associated with FOMC announcements have large effects on bank equity prices. A parallel upward shift in the yield curve prompted by an unexpected increase in the target federal funds rate of 25 basis points is estimated to lower the average bank's stock market value between 2.0 and 2.5 percent; a shock that steepens the yield curve by the same amount causes the average bank's stock price to drop by a bit more than 1.0 percent. Thus, FOMC communication that leads to higher expected future short-term interest rates causes bank equity values to fall. This reaction likely reflects some combination of capital losses on longer-term assets, higher discount rates on future earnings, and reduced expectations of future profits, as monetary policy actions affect not only net interest margins, but also future economic growth and thereby loan demand and asset quality.7
The negative reaction of bank stock prices to positive slope surprises, however, is significantly attenuated for banks with assets whose repricing time or maturity exceed that of their liabilities--that is, institutions that engage more heavily in maturity transformation. This result partially confirms the conventional wisdom, which claims that banks benefit from a steeper yield curve due to their role as maturity transformers. We stress only partially because a large repricing/maturity gap only damps the negative reaction of bank stock returns to slope surprises.
Other characteristics that significantly influence the sign and magnitude of the cross-sectional response of bank stock returns to interest rate shocks include bank size and the extent to which the bank relies on core deposits to fund its interest-earning assets. In particular, larger banks react more strongly to unanticipated changes in the general level of interest rates, whereas banks that rely heavily on core deposits exhibit significantly greater sensitivity to both types of interest rate shocks. Lastly, a very high intensity of interest rate derivatives use appears to mitigate the negative reaction of stock returns to a positive slope surprise, though this effect is estimated relatively imprecisely.
To provide a context for the above results, we then examine how changes in interest rates affect accounting measures of bank profitability, as well as the size and composition of bank balance sheets. Using a panel of more than 4,500 U.S. commercial banks, we estimate the impact of changes in interest rates on the main components of banks' return on assets (ROA). Our results indicate that movements in interest rates affect bank profitability primarily through their impact on net interest margins. An increase in short-term interest rates significantly boosts banks' net interest margins because most institutions fund some of their interest-earning assets with noninterest-bearing liabilities--an effect that we dub the "Samuelson effect" after Samuelson (1945). As expected, a steepening of the yield curve is also associated with significantly higher net interest margins, with the size of the effect increasing in the degree of mismatch between the maturity or repricing intervals of bank assets and those of bank liabilities, a finding consistent with the conventional wisdom.
Although the improvement in banks' net interest margins as a result of a higher level or slope of the yield curve is reflected in a higher ROA, these changes in the configuration of interest rates are also associated with significantly slower growth of the size of bank balance sheets. The slowdown in the growth of bank assets in the wake of rising short-term interest rates and a steeper yield curve appears to reflect primarily an outflow of core deposits (savings, demand, and transaction deposits), an inexpensive source of funding relative to market alternatives. This outflow is consistent with standard monetary theory, according to which an increase in market interest rates raises the opportunity cost of investing in low-yielding savings and transaction deposits. We find that this so-called deposit disintermediation is especially pronounced for large banks and institutions that rely heavily on demand and transaction deposits to fund their activities, a result consistent with the more pronounced negative reaction of stock returns of such banks to interest rate shocks associated with FOMC announcements.
On the asset side of the balance sheet, the outflow in core deposits is reflected in a sharp runoff in (gross) federal funds sold and reverse repurchase agreements, a small but highly liquid component of banks' balance sheets that appears to represent the first margin of balance-sheet adjustment to changes in interest rates. In combination with the fact that rising long-term interest rates lead to immediate capital losses on longer-term assets, these balance sheet dynamics highlight the importance of adjustments in quantities, as well as interest margins, for understanding the reaction of bank stock prices to movements in interest rates.
The remainder of the paper is organized as follows. In the next section, we review the empirical literature on the effects of interest rate changes on bank profitability. Section 3 introduces our measure of interest rate shocks and presents the baseline results concerning the average reaction of bank stock returns to unexpected changes in the level and slope of the yield curve induced by monetary policy actions. In Section 4, we analyze how this reaction varies in the cross section with key bank characteristics; at the end of this section, we also place our results in the context of a standard empirical asset pricing model. Section 5 further examines the mechanism(s) behind the size and cross-sectional patterns of the reaction of bank equity values to interest rate shocks by analyzing the effect of interest rates changes on accounting measures of bank profitability. Section 6 concludes.
2 Existing Literature
The link between fluctuations in interest rates and stock returns of commercial banks--or financial institutions more generally--has been an active area of research for some time. In their seminal contribution, Flannery & James (1984) (F-J hereafter) found that bank stock prices react negatively to increases in the general level of interest rates, and that this reaction is stronger for institutions for which the maturity of their assets significantly exceeds that of their liabilities--that is, banks with a large "maturity gap." As argued by the authors, these results support the conventional wisdom that financial intermediaries are exposed the interest rate risk because they engage in maturity transformation.
Since then, many papers on this issue have, to a greater or lesser extent, employed an empirical methodology similar to that of F-J, so it is worth summarizing their approach in a bit more detail. Specifically, F-J used a two-stage approach to examine the impact of interest rate changes on bank equity values. In the first stage, they regressed the bank's stock return on the market return and an interest rate risk factor, the innovation in the holding period return on short- and longer-term risk free bonds.8 Thus, in the first stage F-J obtained bank-specific "interest rate betas" (as well as market betas), which yielded their first main result: Stock returns of most banks react negatively to positive innovations in interest rates.9
In the second stage, F-J estimated a cross-sectional regression of the bank-specific interest rate betas on an (inverse) measure of the bank's maturity gap--namely, the normalized difference between the average amount of "short assets" and "short liabilities," where "short" is defined as having a maturity of one year or less. Their second main finding was that banks with fewer short-term assets relative to short-term liabilities--that is, banks that perform more maturity transformation in the traditional sense--are more exposed to interest rate risk, in that their share prices decline more when interest rates rise.
Following in their footsteps, Aharony et al. (1986), Saunders & Yourougou (1990), Yourougou (1990), Bae (1990), Kwan (1991), Akella & Greenbaum (1992), Lumpkin & O'Brien (1997), and Choi & Elyasiani (1997) all confirmed the gist of the F-J results concerning the average effect of interest rate changes on banks' equity valuations. Among these studies, Bae (1990), Kwan (1991), Akella & Greenbaum (1992), and Lumpkin & O'Brien (1997) also analyzed how the reaction of bank stock returns to interest rate changes varies with the extent to which banks engage in maturity transformation. Although using a variety of different measures of maturity transformation, the general conclusion reached is that a greater asset-liability mismatch is associated with a greater sensitivity of bank stock returns to interest rate changes.
Following a different tack, Schuermann & Stiroh (2006) examined the cross-section of bank stock returns by adding changes in the short-term rate, the term spread, various credit spreads, and changes in liquidity and volatility measures to the standard Fama-French 3-factor model of returns. According to their results, the inclusion of these additional risk factors--which, according to Demsetz & Strahan (1997) and Stiroh (2006), are thought to be particularly relevant for banks--yields a negligible improvement in the fit of the model, suggesting that the Fama-French 3-factor model is not missing an obvious bank-specific risk factor.
While the econometric techniques used in the aforementioned literature differ in important respects, a common thread running though these papers is that they do not concern themselves with the underlying cause(s) of interest rate changes. In particular, they treat all changes in interest rates in the same way, making no attempt to control for economic news that might be causing interest rates to move. Such news, however, may well have its own direct effect on bank stock prices. Thus, it would be incorrect to interpret the results of these papers as measuring the effect of exogenous interest rate changes on bank equity values.
Now, it is possible that the market return, which is included as an explanatory variable in many specifications, controls to some extent for the direct effect of other economic news on bank stock prices. The inclusion of the market return, however, does not imply that the coefficient on the interest rate risk factor captures the direct effect of interest rate changes on bank equity values. The reason is that changes in interest rates prompted by FOMC announcements will simultaneously affect the market return (see Bernanke & Kuttner (2005)) and, in our context, bank stock returns. Thus including the market return as an explanatory variable in our return regressions would, in a sense, amount to controlling for changes in interest rates twice. This is especially true in our framework because in the narrow window we consider, the FOMC announcement is by far the most important factor driving stock prices.10
A complementary literature on this topic employs income and balance sheet data to examine the effect of interest rates on accounting measures of bank profitability. Somewhat surprisingly, the results here are much less supportive of the notion that bank profits are especially sensitive to movements in interest rates. Studies that looked at the relationship between banks' net interest margins (net interest income as a percentage of interest-earnings assets) and interest rates have generally found little evidence that net interest margins respond to changes in short-term rates or the slope of the yield curve; see, for example, English (2002), Hanweck & Ryu (2005) and references therein. Looking at net operating income--a broader measure of bank profitability--Flannery (1981,1983) reached a similar conclusion. In contrast, Memmel (2011), using data from German banks' internal models, found that maturity transformation contributes importantly to bank income and exposes banks to interest rate risk, which varies systematically with the slope of the yield curve.
Another exception in this strand of literature--and one that is somewhat more closely related to our paper--is den Haan (2007), who found that increases in short-term interest rates lead to substantial declines in the book value of aggregate bank equity, a result consistent with a reduction in earnings for the sector as a whole. Unlike the previous studies, however, den Haan (2007) are concerned with the underlying cause of interest rate changes and rely on an identified vector autoregression to isolate changes in interest rates that are uncorrelated with current and lagged macroeconomic conditions. Under their identification assumptions, these interest rate innovations can be interpreted as "exogenous" monetary policy shocks, though this interpretation is not without controversy.11 In our paper, by contrast, we employ high-frequency financial market data to measure directly the unanticipated changes in interest rates induced by monetary policy actions, an approach that allows us to skirt the difficult issues surrounding the identification of monetary policy shocks at lower frequencies.
3 Interest Rate Surprises and Bank Stock Returns
In this section, we present the baseline results concerning the reaction of bank stock returns to unexpected changes in interest rates induced by monetary policy actions. We begin by describing the measurement of the two interest rate surprises used in the analysis--the "level" and "slope" surprises. Our baseline regressions provide us with the estimate of the average effect of these two interest rate surprises on bank stock returns. In the next section, we analyze how this reaction varies across banks, focusing especially on the degree to which banks engage in maturity transformation, a fundamental source of interest rate risk for the banking sector.
3.1 Data Sources and Methods
The sample period underlying our analysis covers all FOMC announcements between July 2, 1997, and June 28, 2007. As is customary in this kind of analysis, we exclude the September 17, 2001, announcement, which was made when the major stock exchanges re-opened after their closure following the 9/11 terrorist attacks. Nearly all of the 84 announcements during our sample period followed regularly scheduled FOMC meetings; only three were associated with intermeeting policy moves.12
The start of the sample is the earliest FOMC meeting for which the detailed Call Report data on the maturity or repricing times of assets and liabilities used to construct our measure of the repricing/maturity gap are available. We end the sample before the onset of the 2007-09 financial crisis because of the presence of unusual government support for the financial system during that period. In particular, the references in FOMC statements during that period to the stability and functioning of financial markets may have altered investors' views of the likelihood and extent of government support for the banking sector during the crisis. The inclusion of the recent financial crisis in the analysis might thus bias our results because the estimates would reflect not only the effects of unanticipated interest rate changes induced by monetary policy actions on bank stock prices, but potentially also the effects of changing perceptions regarding the likelihood of extraordinary Federal Reserve actions to support the financial system during this period of financial turmoil.
For each FOMC announcement during our sample period, we decompose the observed change in the target federal funds rate--denoted by
![]() --into two components:
--into two components:
where
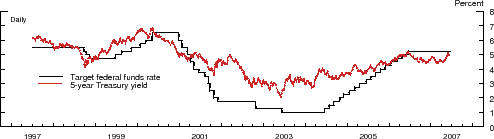 (a) Selected Interest Rates 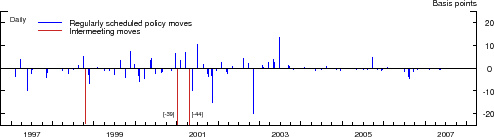 (b) Level Surprise 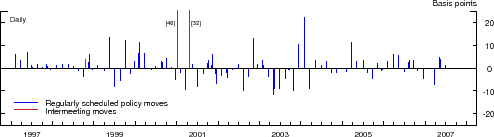 (c) 5-year Slope Surprise |
Motivated by the conventional wisdom of banks "riding the yield curve," we also construct a slope surprise, defined as the unexpected change in the slope of the yield curve following each FOMC announcement. We measure the slope of the yield curve by the difference
between a medium or longer-term Treasury yield and the federal funds rate; we use, alternatively, the 2-, 5-, and 10-year Treasury yields and calculate changes in those yields over the same 30-minute window around each FOMC announcement. Reasonable bounds on expected
changes in bond yields over the course of 30 minutes are on the order of less than one-tenth of a basis point, so we simply use the actual change in the yield to measure its corresponding unanticipated component.14 The slope surprise of maturity ![]() is then measured as the actual change in the
is then measured as the actual change in the ![]() -year Treasury yield less the level surprise and is denoted by
-year Treasury yield less the level surprise and is denoted by
![]() , where
, where
![]() denotes the change in the
denotes the change in the ![]() -year Treasury yield over the same
30-minute window used to compute the level surprise.
-year Treasury yield over the same
30-minute window used to compute the level surprise.
The three panels of Figure 1 depict the path of the target federal funds rate, the 5-year Treasury yield, along with the corresponding level and slope surprise, over our sample period. According to the top panel, this period was marked by substantial variation in both the short- and longer-term interest rates. Moreover, our sample period contains several distinct stages of U.S. monetary policy, including the tightening phase that preceded the bursting of the "tech bubble" in early 2001; the subsequent aggressive easing of policy in response to a rapid slowdown in economic activity and the emergence of substantial disinflationary pressures; the 2003-04 period of very low interest rates; and the gradual removal of monetary accommodation that commenced in the spring of 2004. As indicated by the red spikes in the middle panel, the largest (absolute) level surprises over this period are associated with the intermeeting policy actions, a pattern that also characterizes the corresponding slope surprises (bottom panel).15
To examine the reaction of bank stock prices to the two interest rate surprises, we rely on the Trade and Quote (TAQ) intraday stock price data collected and published by the New York Stock Exchange (NYSE). Specifically, for U.S. publicly-traded BHCs in the NYSE/TAQ data set, we use the average of the recorded bid and ask prices to construct a simple intraday stock return over a 2-hour window around each FOMC announcement in our sample period. Compared with daily stock returns, the use of intraday data limits the possibility that other news occurring during the day of an FOMC announcement would influence bank share prices. While it seems highly unlikely that any such news would be correlated with our interest rate surprises, which are constructed over a narrow 30-minute window, eliminating this type of "noise" from stock returns is likely to result in more precise estimates. The use of a 2-hour window (15 minutes before and 1 hour and 45 minutes after the FOMC announcement) allows for some time for price discovery to occur, a process that may be especially important when considering stock prices of smaller institutions.16 (The exact timing of the protocol used to construct the intraday returns is described in Appendix A.)
To ensure that our results are not driven by a small number of extreme observations, we eliminated all observations with an absolute 2-hour return in excess of 10 percent. We matched the resulting panel of banks with the quarterly income and balance sheet data reported on their Call Reports. In the match, each FOMC date is associated with the most recent, but strictly prior Call Report. After screening out extreme observations, we were left with an unbalanced panel of 355 BHCs, for a total of 11,026 observations. (Appendix B contains the detailed description of the filters used to eliminate extreme observations). In terms of assets, our panel accounts, on average, for about three-quarters of banking industry assets over the sample period, an indication that it is fairly representative of the U.S. commercial banking sector as a whole.
3.2 Baseline Results
To estimate the average reaction of banks' stock returns to our two interest rate surprises, we use the following regression specification:
where
We estimate equation (1) by OLS. Because our data consist of irregularly-spaced, non-adjacent intraday stock returns, the error term
![]() is almost certainly serially uncorrelated. However, given that we focus on a set of very specific common shocks to bank stock returns, disturbances in equation (1) are likely to exhibit a complex pattern of cross-sectional dependence. As shown recently by Petersen (2009) in the context of typical panel data models used in finance applications, erroneously ignoring possible correlation of regression
disturbances between subjects (and over time) can seriously bias statistical inference. To ensure that our inference is robust to the presence of arbitrary cross-sectional dependence in the error term
is almost certainly serially uncorrelated. However, given that we focus on a set of very specific common shocks to bank stock returns, disturbances in equation (1) are likely to exhibit a complex pattern of cross-sectional dependence. As shown recently by Petersen (2009) in the context of typical panel data models used in finance applications, erroneously ignoring possible correlation of regression
disturbances between subjects (and over time) can seriously bias statistical inference. To ensure that our inference is robust to the presence of arbitrary cross-sectional dependence in the error term
![]() , we compute the covariance matrix of the regression coefficients using a nonparametric covariance matrix estimator proposed by Driscoll &
Kraay (1998), which produces heteroscedasticity-consistent standard errors that are robust to very general forms of cross-sectional and/or temporal dependence.
, we compute the covariance matrix of the regression coefficients using a nonparametric covariance matrix estimator proposed by Driscoll &
Kraay (1998), which produces heteroscedasticity-consistent standard errors that are robust to very general forms of cross-sectional and/or temporal dependence.
| Explanatory Variable | |||
| Expected change:
|
0.617 | 0.560 | 0.525 |
| (Standard Error) | (0.478) | (0.422) | (0.426) |
| Level surprise:
|
-8.166*** | -8.627*** | -10.20*** |
| Level surprise:
|
(1.458) | (1.584) | (1.962) |
| Slope surprise:
|
-4.913*** | -4.819*** | -5.807*** |
| Slope surprise:
|
(1.694) | (1.446) | (1.854) |
| Constant | 0.065 | 0.085 | 0.078 |
| Constant (Standard Error) | (0.080) | (0.082) | (0.083) |
| Adj. |
0.103 | 0.102 | 0.099 |
- NOTE: Sample period: 84 policy actions between 7/2/1997 and 6/28/2007 (excludes 9/17/2001); No. of banks = 355; Obs. = 11,026. Dependent variable in each regression is
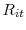 , the stock return of bank
, the stock return of bank 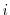 during the 2-hour window bracketing the FOMC announcement on day
during the 2-hour window bracketing the FOMC announcement on day 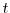 . Entries in the table denote OLS estimates of the coefficients associated with explanatory variables:
. Entries in the table denote OLS estimates of the coefficients associated with explanatory variables:
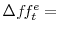 expected change in the target federal funds rate;
expected change in the target federal funds rate;
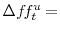 level surprise; and
level surprise; and
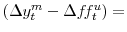
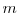 -year slope surprise. Robust standard
errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively.
-year slope surprise. Robust standard
errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively.
Table 1 contains our baseline results. As evidenced by the entries in the table, the expected change in the federal funds rate is never statistically or economically significant, a result consistent with the efficient market hypothesis. In contrast, level
surprises have an economically large and negative effect on banks' equity valuations. An unanticipated increase in the federal funds rate of 25 basis points--with no surprise change in the slope of the yield curve--is estimated to lower, on average, bank share prices between 2.0 and
2.5 percent, depending on the value of ![]() . Because the slope surprise enters the regression as a separate explanatory variable, a positive surprise to the federal funds target rate
in our specification represents a parallel upward shift of the yield curve, hence the term "level surprise."17
. Because the slope surprise enters the regression as a separate explanatory variable, a positive surprise to the federal funds target rate
in our specification represents a parallel upward shift of the yield curve, hence the term "level surprise."17
In our context, a slope surprise can arise because an unexpected change in the federal funds rate target of a given magnitude was associated with a smaller move in the longer rate, or because FOMC communication about the likely future course of policy caused a shift in longer-term yields in the
absence of a surprise to the short rate. According to our estimates, such a slope surprise of 25 basis points lowers, on average, bank stock prices between 1.2 and 1.5 percent, with the effect again depending on the maturity segment of the yield curve (that is, the value
of ![]() ). Thus, FOMC communication that leads to higher expected future short-term interest rates--and therefore to a steeper yield curve--causes bank equity values to fall. At first
glance, this result may seem at odds with the conventional wisdom that banks benefit from a steep yield curve. However, as noted earlier, the negative reaction of bank stock returns to such a slope surprise likely reflects some combination of capital losses on longer-term assets, higher discount
rates on future earnings, and reduced expectations of future profits, factors that appear to outweigh the implied improvement in net interest margins.
). Thus, FOMC communication that leads to higher expected future short-term interest rates--and therefore to a steeper yield curve--causes bank equity values to fall. At first
glance, this result may seem at odds with the conventional wisdom that banks benefit from a steep yield curve. However, as noted earlier, the negative reaction of bank stock returns to such a slope surprise likely reflects some combination of capital losses on longer-term assets, higher discount
rates on future earnings, and reduced expectations of future profits, factors that appear to outweigh the implied improvement in net interest margins.
In addition to being economically large, the reaction of bank stock returns to both types of interest rate surprises is highly statistically significant, and these unanticipated changes in the level and slope of the term structure explain about 10 percent of the variation in intraday returns on the days of FOMC announcements. It is worth noting that all the results in Table 1 (and those reported subsequently) are robust to excluding the three intermeeting policy moves from the sample.
4 Bank-Specific Determinants of Interest Rate Risk
In this section, we examine how the reaction of bank stock returns to policy-induced interest rate shocks varies across banks, according to key banks characteristics that a priori can be expected to influence that reaction. We construct these variables using data on individual bank's balance sheet and income statements, which we obtain from regulatory filings by the bank holding companies and their commercial bank subsidiaries. Specifically, these data come from the quarterly Call Reports filed by banks regulated by the Federal Reserve System, Federal Deposit Insurance Corporation, and the Comptroller of the Currency (almost all U.S. commercial banks), as well as from the FR Y-9C forms filed quarterly by bank holding companies.
While the holding company was the natural unit to match to the NYSE/TAQ stock price data, some of the most crucial bank characteristics used in our analysis are only collected at the bank subsidiary level. For those variables, we added up the relevant quantities of all bank subsidiaries of each
holding company to the holding company level.18 In terms of timing, we matched the bank stock returns around the FOMC announcement made on
day ![]() to bank-specific characteristics taken from the most recent Call Report (or the Y-9C form) dated strictly before day
to bank-specific characteristics taken from the most recent Call Report (or the Y-9C form) dated strictly before day ![]() . (To avoid cumbersome notation, we use the subscript
. (To avoid cumbersome notation, we use the subscript ![]() when indexing the predetermined bank-specific variables.)
when indexing the predetermined bank-specific variables.)
4.1.1 Repricing/Maturity Gap
One of the key bank characteristics used in our analysis is the mismatch between the maturity or repricing time of bank assets and that of their liabilities--the so-called repricing/maturity gap. As discussed in Section 2, a significant portion of the literature on this topic relies on the difference between assets and liabilities with a maturity of one year or less to measure the degree to which a bank engages in maturity transformation. To better approximate the extent of maturity transformation performed by a bank, we, on the other hand, utilize considerably more granular and comprehensive information on the maturity and repricing time of assets and liabilities that became available on the Call Reports starting in 1997:Q2.
Specifically, the average repricing/maturity gap between bank ![]() 's assets and liabilities at the end of quarter
's assets and liabilities at the end of quarter ![]() --denoted by
--denoted by
![]() --is defined as
--is defined as
where
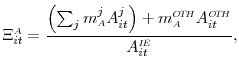 |
where
The 26 asset categories with repricing/maturity information together account, on average, for more than 90 percent of interest-earning assets. We will refer to the remainder, for which we have no maturity or repricing information, as "other assets" and denote it by
![]() . That is,
. That is,
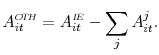 |
These interest-earning assets have an unknown average repricing/maturity period, denoted by
In a similar fashion, we calculate the weighted-average repricing/maturity period of bank liabilities according to
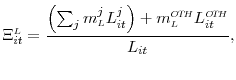 |
where
Analogous to the asset side of the balance sheet,
![]() denotes the dollar amount of "other" liabilities--that is, liabilities for which no explicit repricing information is available:
denotes the dollar amount of "other" liabilities--that is, liabilities for which no explicit repricing information is available:
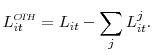 |
As before, we let
The measured or observed component of the average maturity gap for bank ![]() in quarter
in quarter ![]() --the component that excludes the asset and liability categories for which repricing/maturity information is not available--is thus given by
--the component that excludes the asset and liability categories for which repricing/maturity information is not available--is thus given by
whereas the "true" gap in equation (2) is equal to
Although improving substantially on the indicators used in the previous literature, the repricing/maturity gap
![]() , like any measure of term transformation, does not capture two potentially important aspects of the bank's full exposure to interest rate risk. First, it does not incorporate
off-balance-sheet items, such as interest rate derivatives, which can be used to take on or hedge interest rate risk; for this reason, some of our specifications will include controls measuring the bank's usage of interest rate derivatives. Second, some products in banks' portfolios have embedded
options, the values of which can change significantly in response to movements in interest rates, which can result in additional complex exposures to interest rate risk.
, like any measure of term transformation, does not capture two potentially important aspects of the bank's full exposure to interest rate risk. First, it does not incorporate
off-balance-sheet items, such as interest rate derivatives, which can be used to take on or hedge interest rate risk; for this reason, some of our specifications will include controls measuring the bank's usage of interest rate derivatives. Second, some products in banks' portfolios have embedded
options, the values of which can change significantly in response to movements in interest rates, which can result in additional complex exposures to interest rate risk.
4.1.2 Treatment of Core Deposits
Notwithstanding the zero contractual maturity of consumer demand and savings deposits, there is substantial empirical evidence that such deposits are quite sticky and, in many cases, the rates paid on these deposits respond very sluggishly to changes in market interest rates; see, for example, Hannan & Berger (1991) and Neumark & Sharpe (1992). Moreover, interest rates on these special bank liabilities are often substantially below market rates; demand deposits, for example, yield no interest at all, obviously a very low and sticky rate.22 Although banks incur noninterest costs while servicing such deposits, funding interest-earning assets with these special liabilities is likely to boost bank profits in an environment of rising short-term interest rates, a point made long ago by Samuelson (1945). Accordingly, we will include demand, transaction, and savings deposits as separate explanatory variables in our regressions.
An alternative approach would involve estimating their effective maturity, in a way that is similar to the treatment of other liabilities discussed above. Other than raising an issue of how to interpret the results, this alternative approach would make very little difference to the fit of our empirical model. That said, Hutchison & Pennacchi (1996) show, both theoretically and empirically, that it is possible for even "sticky" retail deposits to have negative duration, implying that the present value of such a liability increases as market interest rates rise. This counterintuitive result occurs when a rise in market rates lowers the current or future volume of deposits to such a degree that the present value of the rents associated with those deposits falls. We also illustrate this point with a simple example in Appendix C. Reflecting the special nature of bank core deposits, we thus believe that it is more straightforward to use their contractual maturity and offer an interpretation of our results in terms of changing rents from deposit-finance in response to fluctuations in interest rates.
4.1.3 Descriptive Statistics
Table 2 presents summary statistics for the key bank-specific variables used in the analysis. The average repricing time or maturity of assets in our sample is about 4.5 years, with a standard deviation of almost 2 years. In contrast, the average repricing time or maturity of liabilities is less than 5 months--with a standard deviation of only about 2.5 months--which highlights the fact than an average bank is exposed to interest rate risk in the traditional sense of being "liability sensitive." According to the conventional wisdom, the profitability of a liability-sensitive bank is expected to be positively affected by the steepening of the yield curve. Note also that Call Report information on the repricing or maturity time of assets and liabilities covers a significant portion of banks' balance sheets. For example, assets for which no repricing or maturity information is available account, on average, for only 9 percent of interest-earning assets; on the liability side of the balance sheet, the coverage is somewhat less comprehensive as such items account, on average, for 17 percent of total liabilities.23
| Variable | Mean | StdDev | Min | Median | Max |
| Repricing/maturity - assetsa | 4.46 | 1.86 | 0.73 | 4.12 | 17.2 |
| Repricing/maturity - liabilitiesb | 0.41 | 0.22 | 0.01 | 0.38 | 2.25 |
| Assets without repricing informationc | 0.09 | 0.07 | 0.00 | 0.07 | 0.68 |
| Liabilities without repricing informationd | 0.17 | 0.12 | 0.00 | 0.14 | 0.86 |
| Savings depositsd | 0.33 | 0.13 | 0.00 | 0.31 | 0.90 |
| Demand and transaction depositsd | 0.16 | 0.09 | 0.00 | 0.15 | 0.55 |
| Total assetse | 27.6 | 133.3 | 0.14 | 1.93 | 2,324 |
- Note: Sample period: 1997:Q2-2007:Q2; No. of banks = 355; Obs. = 9,855. Sample statistics are based on trimmed data.
- The weighted average reported repricing/maturity time of assets (in years).
- The weighted average reported repricing/maturity time of liabilities (in years). Savings, demand, and transaction deposits are included at their contractual (that is, zero) maturity.
- As a share of interest-earning assets.
- As a share of total liabilities.
- In billions of chain-weighted dollars
 .
.
Banks in our sample tend to rely quite heavily on core deposits to fund their activities: For an average bank, savings deposits account for one-third of liabilities, with demand and transaction deposits accounting for an additional 16 percent of total liabilities. In terms of size, as measured by total assets, the sample covers a wide spectrum of the industry's size distribution, with the range running from about $140 million to more than $2.3 trillion. Note that with the median observation of about $1.9 billion, the sample includes many smaller banks.
Figure 2 shows the evolution of the cross-sectional distribution of the repricing/maturity gap over time. The solid line is the (asset-weighted) median maturity gap for the 355 banks in our sample, while the shaded band represents the corresponding (asset-weighted) inter-quartile range; for comparison, the dotted line shows the (asset-weighted) median repricing maturity gap for the entire U.S. commercial banking sector. Although generally trending higher over time, the median repricing/maturity gap in the sample has, nonetheless, fluctuated in a relatively narrow range of 3 to 5 years. More important for our purposes, however, is the considerable degree of variation in the asset-liability mismatches across banks at each point in time--it is this cross-sectional variation that will help us identify the role that maturity transformation plays in determining how banks' equity valuations react to unanticipated movements in interest rates.
(By Repricing/Maturity Gap Quintile)
| Variable | Qntl. 1 | Qntl. 2 | Qntl. 3 | Qntl. 4 | Qntl. 5 |
| Total loansa | 0.71 | 0.69 | 0.69 | 0.67 | 0.61 |
| Commercial & industrial loansb | 0.20 | 0.19 | 0.18 | 0.14 | 0.13 |
| Commercial real estate loansb | 0.42 | 0.36 | 0.34 | 0.31 | 0.30 |
| Residential real estate loansb | 0.17 | 0.25 | 0.26 | 0.32 | 0.37 |
| Consumer loansb | 0.05 | 0.07 | 0.10 | 0.10 | 0.09 |
| Interest-bearing liabilitiesc | 0.83 | 0.83 | 0.85 | 0.86 | 0.86 |
| Savings depositsd | 0.29 | 0.31 | 0.33 | 0.31 | 0.33 |
| Demand and transaction depositsd | 0.17 | 0.15 | 0.16 | 0.13 | 0.13 |
| Total assetse | 1.43 | 1.54 | 2.26 | 2.45 | 1.98 |
- Note: Sample period: 1997:Q2-2007:Q2; No. of banks = 355; Obs. = 9,855. Entries in the table denote the sample median of each variables across the five quintiles (Qntl. 1-5) of the repricing/maturity gap distribution. The 355 banks are sorted into the five quintiles based on their average value of the repricing/maturity gap (see text for details).
- As a share of total assets.
- As a share of total loans.
- As a share of interest-earning assets.
- As a share of total liabilities.
- In billions of chain-weighted dollars
 .
.
An obvious question that emerges at this point concerns the extent to which banks that, according to our metric, perform more maturity transformation also differ systematically in other dimensions. To get at this question, we sort our sample of banks into quintiles based on their average repricing/maturity gap over the sample period and then compute medians of selected bank characteristics for each quintile. The results of this exercise are shown in Table 3.
In general, there appears to be only modest correlation between the banks' repricing/maturity gaps and the composition of their loan portfolios. As expected, banks with large holdings of residential real estate loans--and correspondingly fewer business loans--tend to have somewhat greater
asset-liability mismatches, a finding that is not at all surprising given the fact that residential mortgage loans typically have long maturities and fixed rates. There is also little evidence that either the extent to which banks fund their interest-earning assets with interest-bearing liabilities
or their reliance on core deposits are systematically related to the repricing/maturity gap. Indeed, a simple pooled OLS regression of the repricing/maturity gap on all the bank characteristics listed in Table 3 (total assets are, of course, in
logarithms), yields an ![]() of only 0.25, indicating that our measure of banks' asset-liability mismatch contains substantial independent variation.
of only 0.25, indicating that our measure of banks' asset-liability mismatch contains substantial independent variation.
4.2 Interest Rate Risk in the Cross Section of Banks
This section examines how the reaction of bank stock returns to interest rate surprises varies with individual bank characteristics, especially the degree to which banks engage in maturity transformation. To do so, we consider a variant of our baseline regression (1), in which the two policy-induced interest rate shocks are interacted with bank-specific variables, according to
This interactive specification exploits the cross-sectional aspect of the data by allowing the reaction of bank stock returns to both the level and slope surprises to depend linearly on the repricing/maturity gap
In light of the discussion in Section 4.1, the vector of bank-specific control variables
![]() includes the following variables:
includes the following variables:
![]() = "other" assets (as a share of interest-earning assets);
= "other" assets (as a share of interest-earning assets);
![]() = "other" liabilities (as a share of total liabilities);
= "other" liabilities (as a share of total liabilities); ![]() = savings deposits (as a share of total liabilities);
= savings deposits (as a share of total liabilities); ![]() = demand and transaction deposits (as a share of total liabilities). In addition, we control for the extent
to which a bank engages in lending--a traditional banking activity--by including the ratio of total loans to total assets (
= demand and transaction deposits (as a share of total liabilities). In addition, we control for the extent
to which a bank engages in lending--a traditional banking activity--by including the ratio of total loans to total assets (![]() ) in the vector
) in the vector
![]() , as well as for bank size measured by the log of (real) total assets (
, as well as for bank size measured by the log of (real) total assets (![]() ).
).
Recall that "other" assets (
![]() ) and "other" liabilities (
) and "other" liabilities (
![]() ) represent portions of the bank's balance sheet for which we have no repricing or maturity information. Abusing our notation slightly (see
equation (4)), the actual repricing/maturity gap is equal to
) represent portions of the bank's balance sheet for which we have no repricing or maturity information. Abusing our notation slightly (see
equation (4)), the actual repricing/maturity gap is equal to
![]() . In our empirical framework, therefore, the maturities of these
other assets and liabilities can be implicitly estimated as
. In our empirical framework, therefore, the maturities of these
other assets and liabilities can be implicitly estimated as
![]() and
and
![]() , where
, where
![]() and
and
![]() denote the estimated coefficients associated with the interaction terms (
denote the estimated coefficients associated with the interaction terms (
![]() ) and (
) and (
![]() ) in equation (5), respectively, and
) in equation (5), respectively, and
![]() is the estimated coefficient on the interaction term
is the estimated coefficient on the interaction term
![]() .
.
Alternatively, these implied maturities can be estimated using the analogous coefficients associated with the slope surprises:
![]() and
and
![]() . A testable implication of our empirical framework is that the
implied maturities
. A testable implication of our empirical framework is that the
implied maturities
![]() and
and
![]() , whether estimated using coefficients associated with the level surprise or slope surprise, should be the same. It turns out
that we cannot reject the equality of the estimates based on the level and slope surprises. Both methods, however, yield rather imprecise estimates of the repricing/maturity time of other assets and other liabilities, a finding that may reflect differences in the composition of these balance sheet
items across banks.
, whether estimated using coefficients associated with the level surprise or slope surprise, should be the same. It turns out
that we cannot reject the equality of the estimates based on the level and slope surprises. Both methods, however, yield rather imprecise estimates of the repricing/maturity time of other assets and other liabilities, a finding that may reflect differences in the composition of these balance sheet
items across banks.
| Variable |
|||
| Maturity gap:
|
0.500** | 0.453* | 0.598** |
|
|
(0.238) | (0.237) | (0.256) |
|
|
0.553** | 0.426** | 0.521** |
|
|
(0.244) | (0.217) | (0.246) |
| Other assets:
|
7.527 | 7.929 | 9.583 |
|
|
(6.815) | (6.965) | (8.134) |
|
|
8.307 | 7.529 | 8.418 |
|
|
(5.459) | (4.768) | (6.191) |
| Other liabilities:
|
-7.356* | -9.672** | -11.01** |
|
|
(3.903) | (4.230) | (5.269) |
|
|
-6.875 | -9.128** | -9.322* |
|
|
(4.987) | (4.393) | (5.394) |
| Savings deposits:
|
-7.793* | -8.750 | -7.937 |
|
|
(4.637) | (5.467) | (6.309) |
|
|
-11.02** | -11.32** | -9.004* |
|
|
(4.437) | (4.401) | (5.366) |
| Demand deposits:a
|
-14.27** | -17.80*** | -18.58*** |
|
|
(5.644) | (5.522) | (6.928) |
|
|
-4.516 | -8.046 | -8.002 |
|
|
(6.349) | (5.882) | (6.863) |
| Loans/assets:
|
0.994 | 1.666 | 2.439 |
|
|
(2.863) | (3.166) | (3.931) |
|
|
-0.218 | 0.636 | 1.478 |
|
|
(3.026) | (3.089) | (3.657) |
| Bank size:
|
-1.714*** | -1.766*** | -2.035*** |
|
|
(0.340) | (0.347) | (0.460) |
|
|
-0.111 | -0.123 | -0.394 |
|
|
(0.429) | (0.390) | (0.447) |
| Level surprise:b
|
-7.270*** | -7.588*** | -8.902*** |
|
|
(1.410) | (1.516) | (1.879) |
| Slope surprise:c
|
-4.268** | -4.111*** | -4.929*** |
|
|
(1.720) | (1.461) | (1.821) |
| 0.126 | 0.127 | 0.123 |
- Note: Sample period: 84 policy actions between 7/2/1997 and 6/28/2007 (excludes 9/17/2001); No. of banks = 355; Obs. = 11,026. Dependent variable is
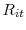 , the stock
return of bank
, the stock
return of bank 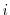 during the 2-hour window bracketing the FOMC announcement on day
during the 2-hour window bracketing the FOMC announcement on day 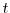 .. Entries in the table denote OLS estimates of the coefficients associated with the interaction of bank-specific variables with
.. Entries in the table denote OLS estimates of the coefficients associated with the interaction of bank-specific variables with
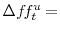 level surprise and
level surprise and
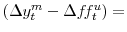
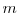 -year slope surprise (see text for
details). All specifications include bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively.
-year slope surprise (see text for
details). All specifications include bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively. - Includes transaction deposits.
- The marginal effect of
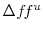 evaluated at the median of all bank-specific variables.
evaluated at the median of all bank-specific variables. - The marginal effect of
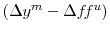 evaluated at the median of all bank-specific variables.
evaluated at the median of all bank-specific variables.
The results from estimating equation (5) are summarized in Table 4. For a bank with median characteristics, the effects of the level and slope surprises on its stock returns are shown at the bottom of the table. According to
these estimates, an unexpected increase in the federal funds rate of 25 basis points--with no surprise change in the slope of the yield curve--causes the median bank's share price to drop between 1.75 and 2.25 percent; a shock to the slope of the yield curve of the same magnitude is
estimated to lower the bank's equity value between 1.0 and 1.25 percent. Note that in both economic and statistical terms, the estimates of these two effects--for all three values of ![]() --are very similar to those from our baseline specification reported in Table 1.
--are very similar to those from our baseline specification reported in Table 1.
In the cross section, however, several important findings emerge. First, as indicated by the positive coefficient on the interaction term
![]() , a large repricing/maturity gap significantly attenuates the negative reaction of bank stock prices to an
unanticipated steepening of the yield curve. This result provides some support for the notion that banks in their role as maturity transformers benefit from a steeper yield curve. However, banks with large mismatches between the repricing time (or maturity) of assets and that of liabilities benefit
only in a relative sense because the overall effect of a slope surprise on bank stock prices--which reflects a combination of immediate capital losses on longer-term assets and the effect of a higher discount rate, as well as potential effects of a higher term spread on lending volumes, deposit
flows, and asset quality--is overwhelmingly negative. In addition to mitigating the negative effects of slope surprises, a larger repricing/maturity gap also significantly damps the response of bank share prices to an unexpected increase in the general level of interest rates.
, a large repricing/maturity gap significantly attenuates the negative reaction of bank stock prices to an
unanticipated steepening of the yield curve. This result provides some support for the notion that banks in their role as maturity transformers benefit from a steeper yield curve. However, banks with large mismatches between the repricing time (or maturity) of assets and that of liabilities benefit
only in a relative sense because the overall effect of a slope surprise on bank stock prices--which reflects a combination of immediate capital losses on longer-term assets and the effect of a higher discount rate, as well as potential effects of a higher term spread on lending volumes, deposit
flows, and asset quality--is overwhelmingly negative. In addition to mitigating the negative effects of slope surprises, a larger repricing/maturity gap also significantly damps the response of bank share prices to an unexpected increase in the general level of interest rates.
Second, equity values of banks that rely extensively on savings deposits to finance their activities appear to be particularly adversely affected by slope surprises; in contrast, a heavy reliance on demand and transaction deposits seems to expose banks to level surprises. In general, stock returns of banks whose liabilities include a large share of core deposits are substantially more sensitive to interest rate fluctuations induced by monetary policy actions. A priori, this is a somewhat surprising result and suggests that the rents on deposit-finance decline--potentially due to adjustments in the quantities of those deposits--when interest rates unexpectedly rise and that this effect is anticipated by the stock market.
Lastly, larger banks exhibit a significantly more pronounced reaction to an unanticipated change in the general level of interest rates, as evidenced by the large negative coefficient on the interaction between bank size and the level surprise
![]() . For example, in response to a positive level surprise of 25 basis points, a bank with $500 billion in (real) assets--and keeping all other bank
characteristics at their median values--will see its stock price drop 3.8 percent, compared with a decline of 1.8 percent for the median bank.
. For example, in response to a positive level surprise of 25 basis points, a bank with $500 billion in (real) assets--and keeping all other bank
characteristics at their median values--will see its stock price drop 3.8 percent, compared with a decline of 1.8 percent for the median bank.
4.3 The Usage of Interest Rate Derivatives
As emphasized, for example, by Gorton & Rosen (1995), Choi & Elyasiani (1997) and Purnanandam (2007), banks can, and in many cases do, actively use derivatives to alter their interest rate risk profile. Banks may choose do so for the purpose of hedging interest rate risk in their loan portfolios or in order to take specific positions on future interest rate movements.
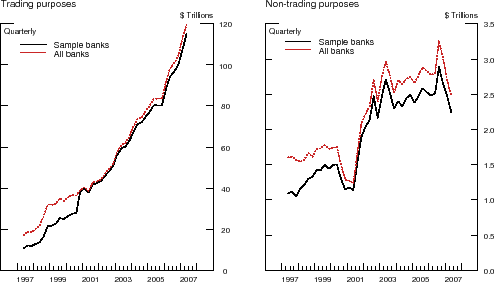
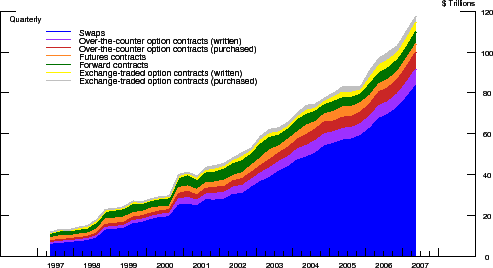
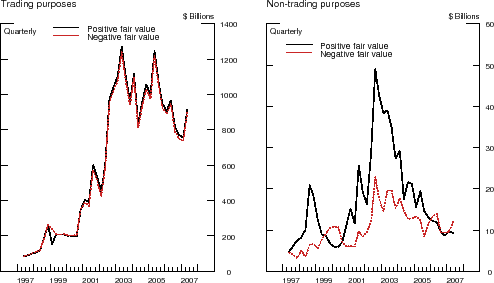
According to the Call Report data, the notional value of interest rate derivative contracts involving U.S. commercial banks has risen dramatically since the mid-1990s, reaching about $120 trillion by the end of our sample period. The vast bulk of this amount is held for trading purposes, with only about $2.5 trillion of that amount categorized for non-trading (that is, hedging) purposes. For interest rate derivatives used for trading purposes, contracts with positive fair (that is, market) values almost exactly offset those with negative values, a pattern consistent with the banking sector serving primarily as an intermediary in the process of allocating interest rate risk, while, in the aggregate, avoiding large net exposures.24 It is worth noting that our sample of 355 BHCs accounts for almost all of the notional positions in both the trading and non-trading categories (see Appendix D).
For our purposes, the most important fact about banks' usage of interest rate derivatives is the extent to which these off-balance-sheet positions are concentrated among a few very large institutions. As shown in Appendix D, even in the top quintile of the bank size distribution, typical usage of interest rate derivatives is scant. The fact that in the aggregate, the notional value of interest rate derivative contracts outstanding exceeds the amount of banking industry assets by something like a factor of 100 is due to a small group of very large institutions that play the key intermediary role in the transfer of interest rate risk in the derivatives markets.
To examine the extent to which the reaction of bank stock returns to interest rate shocks is influenced by the usage of interest rate derivatives, we expand the set of control variables--the vector
![]() in equation (5)--to include a battery of controls for the banks' usage of interest rate derivatives. Specifically, we control for all the
bank-level information that is reported on Call Reports by contract type, which includes the notional amounts outstanding of interest rate swaps, futures, forwards, and the following interest rate options: over-the-counter (OTC) options written/purchased; and exchange-traded (ET) options
written/purchased.25 The notional amount for each type of contract is normalized by the bank's total assets. Because of the extreme skewness of these
exposures, we use the transformation
in equation (5)--to include a battery of controls for the banks' usage of interest rate derivatives. Specifically, we control for all the
bank-level information that is reported on Call Reports by contract type, which includes the notional amounts outstanding of interest rate swaps, futures, forwards, and the following interest rate options: over-the-counter (OTC) options written/purchased; and exchange-traded (ET) options
written/purchased.25 The notional amount for each type of contract is normalized by the bank's total assets. Because of the extreme skewness of these
exposures, we use the transformation
![]() notional value/total assets
notional value/total assets![]() when interacting interest rate derivative positions with the level
and slope surprise.
when interacting interest rate derivative positions with the level
and slope surprise.
| Variable |
Interest Rate Surprise Level | Interest Rate Surprise Slope |
| Swaps | 0.212 | 0.956 |
| Swaps (Standard Error) | (2.083) | (1.393) |
| OTC options (written) | -4.379 | -1.227 |
| OTC options (written) (Standard Error) | (5.945) | (5.213) |
| OTC options (purchased) | -12.76*** | -10.30** |
| OTC options (purchased) (Standard Error) | (4.736) | (5.016) |
| ET options (written) | 32.68*** | 22.77** |
| ET options (written) (Standard Error) | (9.747) | (10.23) |
| ET options (purchased) | -22.46*** | -15.77** |
| ET options (purchased) (Standard Error) | (7.310) | (6.249) |
| Futures | -1.701 | -3.997 |
| Futures (Standard Error) | (2.292) | (3.166) |
| Forwards | 12.56*** | -8.174** |
| Forwards (Standard Error) | (3.642) | (3.696) |
| Maturity gap:
|
0.514** | 0.597** |
| Maturity gap:
|
(0.241) | (0.248) |
| Other assets:
|
9.398 | 9.716* |
| Other assets:
|
(6.850) | (5.154) |
| Other liabilities:
|
-8.002** | -7.326 |
| Other liabilities:
|
(3.655) | (4.510) |
| Savings deposits: |
-7.193* | -10.77** |
| Savings deposits: |
(4.538) | (4.352) |
| Demand deposits:a
|
-13.18** | -3.862 |
| Demand deposits:a
|
(5.713) | (6.454) |
| Loans/Assets: |
1.304 | 0.955 |
| Loans/Assets: |
(2.869) | (3.095) |
| Size: |
-1.621*** | -0.098 |
| Size: |
(0.361) | (0.450) |
| Exclusion test: derivativesb | 0.000 | 0.005 |
- Note:
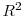 (within) = 0.130. Sample period: 84 policy actions between 7/2/1997 and 6/28/2007 (excludes 9/17/2001); No. of banks = 355; Obs. = 11,026. Dependent variable is
(within) = 0.130. Sample period: 84 policy actions between 7/2/1997 and 6/28/2007 (excludes 9/17/2001); No. of banks = 355; Obs. = 11,026. Dependent variable is
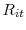 , the stock return of bank
, the stock return of bank 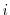 during the 2-hour window bracketing the
FOMC announcement on day
during the 2-hour window bracketing the
FOMC announcement on day 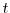 . Entries in the table denote OLS estimates of the coefficients associated with the interaction of bank-specific variables with
. Entries in the table denote OLS estimates of the coefficients associated with the interaction of bank-specific variables with
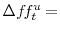 level surprise and
level surprise and
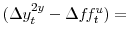 2-year slope surprise. The specification includes bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote
statistical significance at the 10-, 5-, and 1-percent level, respectively.
2-year slope surprise. The specification includes bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote
statistical significance at the 10-, 5-, and 1-percent level, respectively. - Includes transaction deposits.
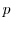 -value for the Wald test of the null hypothesis that the coefficients on the derivative variables interacted with each interest rate surprise are jointly equal to zero.
-value for the Wald test of the null hypothesis that the coefficients on the derivative variables interacted with each interest rate surprise are jointly equal to zero.
We use notional values because fair values are not available by contract type. In addition, it is not clear a priori whether fair values would be more informative about the hedging of interest rate risk. For example, interest rate swaps are typically created so that their market price is equal to zero initially, but they still mitigate the bank's exposure to interest rate risk. As a robustness check, we re-did the analysis using the available fair value information on interest rate derivatives and found that it had no effect on our main results. Regardless of the notional vs. fair value distinction, the key limitation of the Call Report data is that they do not provide any information on whether the bank's derivatives positions are "long" or "short" on the future direction of interest rates.
Table 5 contains the results of this exercise. To economize on space, we focus on the slope surprises associated with the two-year segment of the yield curve (that is, ![]() ), though the results using the 5- and 10-year yields to construct the slope surprises were essentially identical. Several of the interest rate derivative positions--most notably the OTC and ET options and forwards--significantly affect the reaction of bank stock returns to
interest rate surprises. As expected, coefficients on the written and purchased options tend to have opposite signs: Purchased interest rate options exacerbate the negative reaction of stock returns to both the level and slope surprises, while written options tend to have the opposite effect (or
are statistically insignificant). Somewhat surprisingly, swap exposures--by far the most important category of interest rate derivatives--are not a statistically significant determinant of the bank's reaction to interest rate shocks. This result, however, may reflect the inherent limitation of the
data because we do know not if a bank is predominantly on the buy or the sell side of, say, its fixed-for-floating swap arrangements.
), though the results using the 5- and 10-year yields to construct the slope surprises were essentially identical. Several of the interest rate derivative positions--most notably the OTC and ET options and forwards--significantly affect the reaction of bank stock returns to
interest rate surprises. As expected, coefficients on the written and purchased options tend to have opposite signs: Purchased interest rate options exacerbate the negative reaction of stock returns to both the level and slope surprises, while written options tend to have the opposite effect (or
are statistically insignificant). Somewhat surprisingly, swap exposures--by far the most important category of interest rate derivatives--are not a statistically significant determinant of the bank's reaction to interest rate shocks. This result, however, may reflect the inherent limitation of the
data because we do know not if a bank is predominantly on the buy or the sell side of, say, its fixed-for-floating swap arrangements.
Most importantly, the estimated effects of all the other bank characteristics remain, without exception, very similar to those reported in Table 4. In some sense, this result should not be surprising in light of the fact that the vast majority of banks appears to have negligible off-balance-sheet exposure in terms of interest rate derivatives. In particular, the results reported in Table 4 continue to indicate that the bank's repricing/maturity gap, its reliance on core deposits, and size, are the most important determinants of the reaction of the bank's stock returns to unanticipated movements in interest rates induced by monetary policy actions.
| Median Bank | Interest Rate Surprise Level | Interest Rate Surprise Slope |
| With median interest rate derivatives position | -7.234*** | -4.279** |
| With median interest rate derivatives position (Standard Error) | (1.407) | (1.717) |
| With large interest rate derivatives position | -6.278** | -2.480 |
| With large interest rate derivatives position (Standard Error) | (3.169) | (3.518) |
- Note: Entries in the table denote estimates of the effects associated with the level and slope (2-year) interest rate surprises, based on the specification in Table 5. The effect of each interest rate surprise for the median bank is evaluated at the median of all bank-specific variables; the effect of each interest rate surprise for the median bank with large derivative position is evaluated at 99th percentile of each derivative variable, while the remaining bank-specific variables are kept at their respective median values. Robust standard errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively.
At the same time, the economic and statistical significance of the coefficients on some of the derivative variables reported in Table 5 suggests that these positions may matter for banks that are intense users of such instruments. To get a sense of the overall impact of the various types of interest rate derivatives, Table 6 summarizes the estimated stock price reactions to level and slope surprises for a hypothetical bank that has--relative to its assets--very large interest rate derivative positions of all types. To calculate these effects, we set the values of all interest rate derivative variables in the interaction terms at their respective 99th percentiles, while keeping all other bank-specific variables at their median values. For comparison, the table also shows the reaction of stock returns to both surprises for the median bank, which implies zero usage of interest rate derivatives. As shown in the table, the estimated effect of level surprises is economically and statistically the same across these two hypothetical institutions. In contrast, a very heavy usage of interest rate derivatives appears to attenuate the reaction of stock returns to slope surprises, though the size of this effect is subject to a fair amount of uncertainty.
4.4 Bank Characteristics as Determinants of Market Betas
It is well known that interest rate surprises induced by monetary policy actions have economically large effects on the aggregate stock market (see Bernanke & Kuttner (2005)). Accordingly, a natural question to consider is whether our results thus far represent a departure from standard empirical asset pricing models. In other words, is the reaction of bank stock returns to interest rate surprises associated with the FOMC announcements in line with their usual comovement with the market return (or other risk factors), or does this reaction point to a possible asset pricing anomaly?
Uncovering such anomalies is not the primary focus of this paper.26 Nevertheless, we now present some evidence suggesting that our results are actually consistent with commonly-used asset pricing models. In fact, we find that the same bank characteristics that help explain the magnitude and direction of the response of bank stock returns to the two interest rate shocks also help to account for banks' exposure to systematic risk. In particular, fundamental bank characteristics such as the maturity mismatch of bank assets and liabilities and reliance on core deposits are important determinants of banks' (time-varying) market betas, a result in the spirit of Gomes et al. (2009), who relate--both empirically and theoretically--the durability of output produced by nonfinancial firms to their expected stock returns.
The first part of our empirical strategy uses daily data from the Center for Research in Security Prices (CRSP) database to estimate a dynamic version of the capital asset pricing model (CAPM) for all the banks in the sample:
where
Using the time-varying estimates of
![]() and
and
![]() , we then calculate an idiosyncratic 2-hour return for each FOMC announcement day
, we then calculate an idiosyncratic 2-hour return for each FOMC announcement day ![]() , according to
, according to
![]() , where
, where ![]() ,
,
![]() , and
, and ![]() are all measured over a 2-hour window
surrounding the FOMC announcement, and the constant
are all measured over a 2-hour window
surrounding the FOMC announcement, and the constant
![]() reflects the conversion from a trading day to a 2-hour window.28 When we use idiosyncratic returns instead of actual returns as the dependent variable in equation (1), the coefficients on both the level and slope surprises are statistically indistinguishable
from zero for all values of
reflects the conversion from a trading day to a 2-hour window.28 When we use idiosyncratic returns instead of actual returns as the dependent variable in equation (1), the coefficients on both the level and slope surprises are statistically indistinguishable
from zero for all values of ![]() . This result implies that the reaction of bank stock returns to changes in interest rates induced by monetary policy actions is in line with their usual
co-movement with the market return, provided that one uses a dynamic version of the CAPM.
. This result implies that the reaction of bank stock returns to changes in interest rates induced by monetary policy actions is in line with their usual
co-movement with the market return, provided that one uses a dynamic version of the CAPM.
| Explanatory Variable | Coef. | S.E. |
| Maturity gap:
|
-0.067*** | 0.012 |
| Other assets:
|
-0.589*** | 0.208 |
| Other liabilities:
|
1.242*** | 0.310 |
| Savings deposits: |
2.090*** | 0.408 |
| Demand deposits:a
|
1.930*** | 0.410 |
| Loans/Assets: |
-0.014 | 0.177 |
| Size: |
0.561*** | 0.052 |
| Swaps | -0.752*** | 0.090 |
| OTC options (written) | -0.295* | 0.163 |
| OTC options (purchased) | 0.207 | 0.133 |
| ET options (written) | 0.217 | 0.178 |
| ET options (purchased) | -0.123 | 0.147 |
| Futures | 0.027 | 0.099 |
| Forwards | 0.168** | 0.073 |
- Note: Memo:
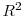 (within) = 0.175. Sample period: 1997:Q2-2007:Q2; No. of banks = 355; Obs. = 9,456. Dependent variable is the market beta
(within) = 0.175. Sample period: 1997:Q2-2007:Q2; No. of banks = 355; Obs. = 9,456. Dependent variable is the market beta
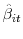 , an estimate of the coefficient (for bank
, an estimate of the coefficient (for bank 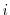 in
quarter
in
quarter 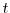 ) on the excess market return in the dynamic CAPM (see text for details). Entries in the column "Coef." are the OLS estimates of the coefficients
associated with the specified bank-specific explanatory variables, while entries in the column "S.E." are the corresponding robust standard errors; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively, The specification includes
bank fixed effects.
) on the excess market return in the dynamic CAPM (see text for details). Entries in the column "Coef." are the OLS estimates of the coefficients
associated with the specified bank-specific explanatory variables, while entries in the column "S.E." are the corresponding robust standard errors; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively, The specification includes
bank fixed effects. - Includes transaction deposits.
In combination with our cross-sectional results that employ actual returns, this finding also implies that the same bank-specific characteristics that govern the magnitude and direction of the reaction of bank stock returns to the policy-induced interest rate surprises ought to be correlated with the market beta. We test this hypothesis by estimating the following regression:
where, in a slight abuse of time index notation,
As shown in Table 7, a large repricing/maturity gap is associated with a smaller market beta, a result consistent with our finding that share prices of banks that perform more maturity transformation are significantly less sensitive to both types of interest rate shocks. In addition to being statistically highly significant, this effect is also economically meaningful; for example, a bank with a market beta of 1.0 would see its beta fall to 0.89, were its repricing/maturity gap to increase by one standard deviation (1.7 years).
In contrast, greater dependence on savings or demand and transaction deposits is associated with a bigger market beta, implying a greater comovement with the market. Similarly, large banks appear to be significantly more exposed to systematic risk. Again, these effects--which are economically important--are consistent with our findings that stock prices of large banks and institutions that rely heavily on core deposits to fund their activities exhibit a more pronounced reaction to policy-induced interest rate surprises.
Viewed through the lens of a conditional CAPM, our results have a natural interpretation. Suppose that a particular bank's business model implies a large exposure to interest rate risk. A change in market interest rates will then have a large effect on its stock price--at the same time, changes
in interest rates are known to be associated with movements in the aggregate stock market. All else equal, the high exposure to interest rate risk will thus mechanically result in this bank having a larger beta. Of course, for this effect to be noticeable, it must be the case that fluctuations in
interest rates contribute importantly to the volatility of the market return. As evidenced by the (within) ![]() of almost 0.18, bank characteristics that help account for the exposure
to interest rate risk also explain a nontrivial portion of the heterogeneity in banks' market betas, suggesting that this may indeed be the case.
of almost 0.18, bank characteristics that help account for the exposure
to interest rate risk also explain a nontrivial portion of the heterogeneity in banks' market betas, suggesting that this may indeed be the case.
5 Interest Rates and Accounting Measures of Bank Profitability
To deepen our understanding of the economic mechanisms behind the reaction of bank stock returns to fluctuations in interest rates, we now turn to income and balance sheet data. Specifically, we analyze the response of banks' interest and noninterest income to changes in interest rates, as well as the associated dynamics of their balance sheets. To that end, we used Call Reports to construct an unbalanced panel of 4,776 U.S. commercial banks from 1997:Q2 to 2007:Q2, the same sample period as before.29
Letting ![]() denote a measure of the profitability of bank
denote a measure of the profitability of bank ![]() in
quarter
in
quarter ![]() , we estimate the following dynamic fixed effects regression:
, we estimate the following dynamic fixed effects regression:
where
An obvious limitation of accounting data is the fact that we cannot employ the same high-frequency event study methodology that was used in the case of stock returns. As a result, we simply use the 3-month Treasury yield and the 10y/3m term spread to examine the effect of interest rate changes
on various accounting measures of bank profitability. To mitigate potential endogeneity problems arising from such an approach, we include a number of macroeconomic and financial indicators--denoted by the vector
![]() --in the regression in order to control for the cyclical changes in macroeconomic conditions that are likely influencing the behavior of interest rates.30 We estimate equation (7) by OLS, allowing for fourth-order serial correlation and arbitrary cross-sectional dependence in the
error term
--in the regression in order to control for the cyclical changes in macroeconomic conditions that are likely influencing the behavior of interest rates.30 We estimate equation (7) by OLS, allowing for fourth-order serial correlation and arbitrary cross-sectional dependence in the
error term
![]() when calculating the Driscoll-Kraay standard errors.31
when calculating the Driscoll-Kraay standard errors.31
| Variable |
|
|||
| Maturity gap:
|
-0.001 | 0.000 | -0.000 | 0.105* |
| Maturity gap:
|
(0.002) | (0.001) | (0.002) | (0.060) |
|
|
0.007*** | -0.001 | 0.007*** | 0.291*** |
|
|
(0.002) | (0.002) | (0.002) | (0.059) |
| Other assets:
|
0.082 | -0.033 | 0.049 | -2.051 |
|
|
(0.079) | (0.028) | (0.076) | (1.660) |
|
|
0.000 | 0.009 | -0.037 | -2.975 |
|
|
(0.090) | (0.032) | (0.092) | (2.967) |
| Other liabilities:
|
-0.027 | -0.054 | -0.034 | 1.926 |
|
|
(0.064) | (0.033) | (0.051) | (2.172) |
|
|
-0.066 | -0.071 | -0.030 | 4.043 |
|
|
(0.079) | (0.044) | (0.064) | (2.649) |
| Saving deposits:
|
0.057 | -0.099*** | 0.002 | 0.411 |
|
|
(0.037) | (0.018) | (0.034) | (0.585) |
|
|
-0.018 | -0.077*** | -0.046 | 2.646*** |
|
|
(0.048) | (0.023) | (0.044) | (0.688) |
| Demand deposits:a
|
0.110*** | -0.144*** | 0.015 | -2.883*** |
|
|
(0.035) | (0.024) | (0.022) | (0.920) |
|
|
-0.020 | -0.126*** | -0.106*** | -2.670** |
|
|
(0.045) | (0.032) | (0.030) | (1.365) |
| Loans/assets:
|
-0.078*** | -0.023 | -0.122*** | 1.008 |
|
|
(0.019) | (0.026) | (0.031) | (2.090) |
|
|
-0.114*** | -0.000 | -0.170*** | 0.653 |
|
|
(0.029) | (0.023) | (0.042) | (2.480) |
| Bank size:
|
0.005** | -0.003* | 0.001 | -0.410*** |
|
|
(0.002) | (0.002) | (0.002) | (0.151) |
|
|
0.003 | -0.003 | -0.004 | -0.583*** |
|
|
(0.003) | (0.002) | (0.002) | (0.207) |
| Level effect:b
|
0.088*** | -0.015 | 0.051*** | -2.139** |
|
|
(0.014) | (0.011) | (0.010) | (0.879) |
| Slope effect:c
|
0.071*** | -0.005 | 0.037*** | -1.830*** |
|
|
(0.011) | (0.008) | (0.008) | (0.618) |
| 0.690 | 0.321 | 0.258 | 0.104 |
- Note: Sample period: 1997:Q2-2007:Q2; No. of banks = 4,776; Obs. = 149,509. Dependent variables:
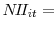 net interest income as a percent of assets;
net interest income as a percent of assets;
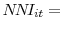 net noninterest income as a percent of assets;
net noninterest income as a percent of assets;
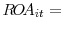 return on assets; and
return on assets; and
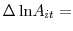 log-difference of assets. All dependent variables are expressed in annualized percent. Entries in the table denote OLS estimates of the coefficients associated with
the interaction of bank-specific variables with
log-difference of assets. All dependent variables are expressed in annualized percent. Entries in the table denote OLS estimates of the coefficients associated with
the interaction of bank-specific variables with
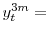 3-month Treasury yield and
3-month Treasury yield and
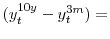 10y/3m slope of the yield curve. All specifications include bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote
statistical significance at the 10-, 5-, and 1-percent level, respectively.
10y/3m slope of the yield curve. All specifications include bank fixed effects. Robust standard errors are reported in parentheses; *, **, *** denote
statistical significance at the 10-, 5-, and 1-percent level, respectively. - Includes transaction deposits.
- The short-run marginal effect of
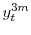 evaluated at the median of all bank-specific variables.
evaluated at the median of all bank-specific variables. - The short-run marginal effect of
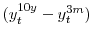 evaluated at the median of all bank-specific variables.
evaluated at the median of all bank-specific variables.
The first three columns of Table 8 present the estimation results for the main accounting measures of bank profitability: Net interest income (NII); net noninterest income (NNI); and (after-tax) return on
assets (ROA).32 The last column uses the same approach to estimate the effect of interest rate changes on the size of bank
balance sheets by replacing the dependent variable in equation (7) with the growth of bank total assets (
![]() ).
).
The results in columns 1-3 indicate that changes in interest rates affect bank profitability primarily through their impact on net interest income. A 100 basis point increase in the general level of interest rates in quarter ![]() is estimated to boost the median bank's net interest income relative to assets almost 9 basis points in that quarter.33Because net interest income is quite persistent (the sum of
is estimated to boost the median bank's net interest income relative to assets almost 9 basis points in that quarter.33Because net interest income is quite persistent (the sum of ![]() coefficients in equation (7) is 0.716), such a transitory
parallel upward shift in the yield curve ultimately results in an increase of about 30 basis points in this component of bank profitability. A steepening of the yield curve by the same amount has a similar effect, providing an immediate boost to the median bank's net interest income of about
7 basis points and 25 basis points in the long run. While these magnitudes may appear small at first glance, the within standard deviation of net interest income as a percent of assets is only about 35 basis points, around a sample average of almost 4 percent.
coefficients in equation (7) is 0.716), such a transitory
parallel upward shift in the yield curve ultimately results in an increase of about 30 basis points in this component of bank profitability. A steepening of the yield curve by the same amount has a similar effect, providing an immediate boost to the median bank's net interest income of about
7 basis points and 25 basis points in the long run. While these magnitudes may appear small at first glance, the within standard deviation of net interest income as a percent of assets is only about 35 basis points, around a sample average of almost 4 percent.
As evidenced by the statistically significant coefficient on the interaction term
![]() , the size of the estimated level effect depends positively on the extent to which a bank relies on demand and transaction deposits to fund its activities. The sign of
this effect is consistent with the hypothesis advanced by Samuelson (1945), who argued that an increase in market interest rates will, all else equal, boost bank profits because banks fund a portion of their interest-earning assets with noninterest bearing
liabilities, primarily demand and transaction deposits.34 This effect should be stronger for banks that rely more on such funding sources, so a parallel
upward shift of the yield curve should boost net interest income of those institutions by a greater amount, a prediction borne out by the positive coefficient on the interaction term
, the size of the estimated level effect depends positively on the extent to which a bank relies on demand and transaction deposits to fund its activities. The sign of
this effect is consistent with the hypothesis advanced by Samuelson (1945), who argued that an increase in market interest rates will, all else equal, boost bank profits because banks fund a portion of their interest-earning assets with noninterest bearing
liabilities, primarily demand and transaction deposits.34 This effect should be stronger for banks that rely more on such funding sources, so a parallel
upward shift of the yield curve should boost net interest income of those institutions by a greater amount, a prediction borne out by the positive coefficient on the interaction term
![]() .
.
In economic terms, the estimate of the "Samuelson effect" implies that by increasing its reliance on demand and transaction deposits by 10 percentage points of its liabilities (about one standard deviation), an average bank will register--in response to a 100 basis point increase in the general level of interest rates--an increase in the ratio of net interest income to assets of about one basis point in the subsequent quarter; though seemingly small, this effect is equivalent to more than one-tenth of the overall level effect.
The positive and statistically significant coefficient on the interaction term
![]() is consistent with the conventional wisdom, which claims that a steep yield curve environment is beneficial for bank profits.
According to our estimates, an average bank, by increasing the repricing/maturity gap between its assets and liabilities by one standard deviation (1.7 years), will see--in response to a 100 basis point increase in the 10y/3m term spread--its net interest income rise about one basis point
relative to assets in the subsequent quarter, again a nontrivial portion of the overall slope effect.
is consistent with the conventional wisdom, which claims that a steep yield curve environment is beneficial for bank profits.
According to our estimates, an average bank, by increasing the repricing/maturity gap between its assets and liabilities by one standard deviation (1.7 years), will see--in response to a 100 basis point increase in the 10y/3m term spread--its net interest income rise about one basis point
relative to assets in the subsequent quarter, again a nontrivial portion of the overall slope effect.
In contrast to their impact on banks' net interest income, changes in the level of interest rates or in the slope of the yield curve have no discernible effect on net noninterest income--the estimates of both the level and slope effect are statistically indistinguishable from zero. However, as shown in column 3, both the increase in the general level of interest rates and the steepening of the yield curve are reflected in a higher ROA--a broader accounting measure of bank profitability--an effect that is primarily due to the response of net interest income to changes in interest rates.35
The improvement in the ROA, however, is accompanied by a significant slowdown in the growth of bank assets. As shown in column 4, an increase in the general level of interest rates of 100 basis points in quarter ![]() shaves off more than 2.0 percentage points from the median bank's (annualized) growth of assets in that quarter, while a steepening of the yield curve of the same magnitude lowers asset growth about 1.75 percentage points. In the cross section,
banks with more demand and transactions deposits and larger banks exhibit a more pronounced deceleration in their balance sheets in response to such changes in interest rates.
shaves off more than 2.0 percentage points from the median bank's (annualized) growth of assets in that quarter, while a steepening of the yield curve of the same magnitude lowers asset growth about 1.75 percentage points. In the cross section,
banks with more demand and transactions deposits and larger banks exhibit a more pronounced deceleration in their balance sheets in response to such changes in interest rates.
An interesting question, of course, concerns the net effect of these two opposing forces--higher ROA and the stepdown in asset growth--on the level of net income across banks. In order to get at this question, we use the estimates in columns 3 and 4 of Table 8 to simulate the dynamics of ROA and asset growth in response two shocks: (1) a "level surprise," a parallel shift in the yield curve of 100 basis points (lasting one quarter); and (2) a "slope surprise," a one-time steepening of the yield curve caused by a
100 basis point increase in the 10-year Treasury yield (again lasting only one quarter). For each of these transitory interest rate moves, we trace out the impulse responses of ROA and bank assets, which are then used to calculate the response of net income (
![]() ). We explore the implications of the level shock for net income by considering differences in the extent to which banks rely on demand and transaction deposits to fund their
assets, while letting the response of net income to the slope shock vary with the repricing/maturity gap; in both cases, all other bank characteristics are kept at their respective median values.
). We explore the implications of the level shock for net income by considering differences in the extent to which banks rely on demand and transaction deposits to fund their
assets, while letting the response of net income to the slope shock vary with the repricing/maturity gap; in both cases, all other bank characteristics are kept at their respective median values.
(By Type of Shock and Selected Bank Characteristics)
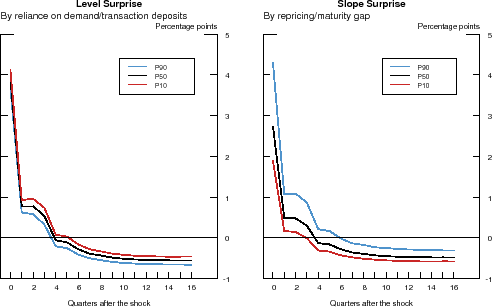 |
As shown in the left panel of Figure 3, a temporary increase in the general level of interest rates significantly boosts bank profits in the near term. For the median bank (P50), for example, quarterly net income jumps more than 3.5 percentage points upon impact, though it is back to the baseline within one year after the shock. More importantly, this temporary parallel shift in the yield curve leads to a persistently lower level of net income of about 0.5 percentage point relative to the baseline, a deterioration in the long-term profitability outlook that is due entirely to a contraction in bank assets. It is also worth noting that this negative effect appears to be somewhat stronger for banks that rely more on demand and transaction deposits, though the difference is relatively small.
A temporary steepening of the yield curve caused by rising long-term interest rates has a similar effect. According to the right panel, a steeper yield curve environment leads to an immediate increase in net income, with the median bank (P50) recording a gain of about 3.75 percentage points relative to the baseline. Moreover, this response differs considerably with the extent to which a bank engages in maturity transformation--for a bank with the repricing/maturity gap at the 90th percentile of the distribution, the boost to net income from the steeper yield curve is more than twice as large as that of a bank whose repricing/maturity gap is at the 10th percentile. Regardless of the degree of maturity transformation performed, however, the associated contraction in bank assets ultimately causes net income to fall below baseline, again indicating a deterioration in the longer-term profitability outlook.
| Dependent Variable - Growth Contribution of Selected Assets | Interest Rate Effect Level | Interest Rate Effect Slope | Share | |
|
|
0.973* | -0.836** | 0.116 | 0.637 |
|
|
(0.514) | (0.384) | - | - |
|
|
0.823 | 0.464 | 0.110 | 0.234 |
|
|
(1.267) | (0.899) | - | - |
|
|
-3.646*** | -3.540*** | 0.215 | 0.033 |
|
|
(1.019) | (0.560) | - | - |
|
|
-0.556*** | -0.499*** | 0.118 | 0.012 |
|
|
(0.149) | (0.099) | - | - |
| Dependent Variable - Growth Contribution of Selected Liabilities | Interest Rate Effect Level | Interest Rate Effect Slope | Sharea | |
|
|
-2.152** | -0.729 | 0.116 | 0.432 |
|
|
(1.045) | (0.748) | - | - |
|
|
0.037 | -0.721*** | 0.121 | 0.281 |
|
|
(0.321) | (0.192) | - | - |
|
|
0.465 | 0.447* | 0.085 | 0.167 |
|
|
(0.366) | (1.717) | - | - |
- Note: Sample period: 1997:Q2-2007:Q2; No. of banks = 4,773; Obs. = 149,509. Dependent variable is the change in the selected balances sheet component in quarter
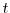 ,
normalized by the assets
,
normalized by the assets  at the beginning of quarter
at the beginning of quarter 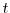 ; all variables are
expressed in annualized percent. Asset components:
; all variables are
expressed in annualized percent. Asset components:
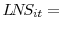 total loans & leases;
total loans & leases;
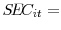 total securities;
total securities;
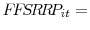 gross federal funds sold and reverse repos; and
gross federal funds sold and reverse repos; and
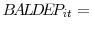 balances at DIs. Liability components:
balances at DIs. Liability components:
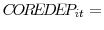 core deposits (that is, savings, demand, and transaction deposits);
core deposits (that is, savings, demand, and transaction deposits);
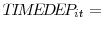 small time deposits; and
small time deposits; and
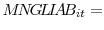 managed liabilities. Entries under the heading "Level" denote estimates of the short-run marginal effect of
managed liabilities. Entries under the heading "Level" denote estimates of the short-run marginal effect of
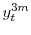 , the 3-month Treasury yield, while entries under the heading "Slope" denote estimates of the short-run marginal effect of
, the 3-month Treasury yield, while entries under the heading "Slope" denote estimates of the short-run marginal effect of
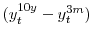 , the 10y/3m slope of the yield curve; both interest rate effects are evaluated at the median of all bank-specific variables. All specifications include bank fixed
effects. Robust standard errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively.
, the 10y/3m slope of the yield curve; both interest rate effects are evaluated at the median of all bank-specific variables. All specifications include bank fixed
effects. Robust standard errors are reported in parentheses; *, **, *** denote statistical significance at the 10-, 5-, and 1-percent level, respectively. - Median share of the specified balance sheet component relative to assets.
In an effort to better understand these balance sheet dynamics, we use the empirical framework in equation (7) to decompose the change in the size of banks' balance sheets in response to movements in interest rates into contributions of the key asset and liability
items. The results of this exercise are presented in Table 9. Turning first to the liability side of the balance sheet, our estimates indicate that an increase in the general level of interest rates is associated with a sizable runoff in core deposits for the
median bank, a finding consistent with classic monetary theory. A steepening of the yield curve, on the other hand, leads to a contraction in (small) time deposits, which for the median bank is partially offset by increased reliance on managed liabilities. According to the estimates in
column 4 of Table 8, the effect of deposit disintermediation on bank balance sheets in the wake of a general increase in interest rates appears to be especially pronounced for institutions that rely heavily on demand and transaction deposits to fund their
activities (the negative coefficient on the
![]() term).
term).
On the asset side of the balance sheet, the outflow in core deposits in response to higher interest rates is offset by a sharp runoff in (gross) federal funds sold and reverse repurchase agreements. In fact, fed funds sold and reverse repos also shrinks considerably in reaction to the steepening of the yield curve. These two results suggests that this small but highly liquid component of banks' balance sheets represents the first margin of balance-sheet adjustment to changes in interest rates, a finding consistent with that of Adrian & Shin (2010), who document that broker-dealers primarily use repos to adjust the size of their balance sheets in response to fluctuations in asset prices.
Taken together, the results in Tables 8-9 and Figure 3 help explain the negative reaction of bank stock prices to positive level and slope surprises induced by monetary policy actions. Although an increase in the general level of interest rates and a steepening of the yield curve lead to a higher ROA for the banking industry in the near term, such changes in interest rates are also associated with a significant deceleration in the size of banks' balance sheets over time. The latter effect reflects primarily an outflow of core deposits, a relatively inexpensive source of funding compared with market alternatives. And in spite of an improved near-term profitability outlook, the stock market appears to view slower growth of assets going forward, along with the associated changes in the composition of bank balance sheets, as weighing on future net income. In combination with the fact that rising interest rates imply higher discount factors and that increases in long-term interest rates lead to immediate capital losses on longer-term assets, the expected reduction in future net income can help account for the negative reaction of bank stock prices to interest rate surprises.
The above argument applies not only to the average reaction of bank stock returns to interest rate surprises associated with FOMC announcements, but also to the differences in that response across banks. Recall that our results showed that banks with more core deposits or larger balance sheets experience a greater decline in equity values when the yield curve shifts up or steepens (Table 4). This finding is consistent with our result that such banks undergo a greater reduction in asset growth and a larger decline in future net income in response to such changes in the configuration of interest rates (Table 8). Similarly, we found that the negative reaction of bank stock prices to a positive slope surprise is significantly attenuated for institutions with a large repricing/maturity gap, evidence that is in line with the result that such banks register a greater improvement in net interest margins--and, consequently, a smaller decline in future net income--in response to a steepening of the yield curve.
6 Conclusion
In this paper, we used unexpected changes in interest rates prompted by FOMC announcements to examine the link between bank equity valuations and interest rates. The results indicate that policy-induced shocks to both the level and slope of the yield curve have large negative effects on bank stock prices. In the cross section, share prices of banks that engage more heavily in maturity transformation have a significantly less negative reaction to an unanticipated steepening of the yield curve, a result that partially confirms the conventional wisdom that banks benefit from a steeper yield curve due to their role as maturity transformers. In contrast, banks with liabilities that include a greater fraction of demand and transaction deposits exhibit a more negative reaction to both types of interest rate shocks, a finding at odds with Samuelson's 1945 conjecture that a rise in market rates should boost bank profitability because banks fund a portion of their interest-earning assets with noninterest bearing liabilities.
The results using accounting data indicate that changes in interest rates affect bank profit margins primarily through their impact on net interest income. An increase in the general level of interest rates results in significantly higher interest margins, a finding that supports Samuelson's conjecture. The steepening of the yield curve is also associated with higher interest margins, with the size of the effect increasing in the degree of mismatch between the maturity or repricing intervals of bank assets and those of bank liabilities, a result consistent with the conventional wisdom.
At the same time, such changes in the configuration of interest rates also reduce the size of bank balance sheets over time, primarily as a result of an outflow of core deposits, an inexpensive source of funding relative to market alternatives. In combination with the fact that the steepening of the yield curve caused by rising long-term interest rates will lead to immediate capital losses on longer-term assets and that higher rates lower the discounted value of future profits, these balance sheet dynamics highlight the importance of adjustments in quantities, as well as interest margins, for understanding the reaction of bank stock prices to changes in interest rates.
Bibliography
Journal of Money, Credit, and Banking 1:27-42.
Journal of Money, Credit, and Banking 42:179-198.
Oxford University Press, Oxford, UK.
Review of Financial Studies 19:1001-1040.
Journal of Financial Research 1:71-79.
Journal of Finance 60:1221-1257.
Journal of Financial Services Research 12:267-286.
Journal of Money, Credit, and Banking 29:300-313.
Journal of Monetary Economics 54:904-924.
Journal of Financial Intermediation 10:54-84.
Review of Economics and Statistics 80:549-560.
Journal of Money, Credit, and Banking 36:719-737.
BIS Quarterly Review December:67-82.
Federal Reserve Bulletin 84:391-419.
Journal of Finance 5:1085-1101.
Journal of Money, Credit, and Banking 15:355-362.
Journal of Finance 4:1141-1153.
Working Paper, UCLA-Andersen School of Management.
Journal of Political Economy 117:941-986.
Journal of Political Economy 111:693-732.
In B. S. Bernanke & J. J. Rotemberg (eds.), NBER Macroeconomics Annual, pp. 299-349. The MIT Press, Cambridge.
International Journal of Central Banking 1:55-93.
Journal of Money, Credit, and Banking 17:189-202.
American Economic Review 81:938-945.
Econometrica 55:587-613.
Working Paper No.5-03, Federal Deposit Insurance Corporation.
Journal of Financial and Quantitative Analysis 31:399-417.
Journal of Finance 51:3-53.
Journal of Banking and Finance 19:79-95.
Journal of Financial Economics 40:213-237.
Speech at the Federal Deposit Insurance Corporation's Symposium on Interest Rate Risk Management, Arlington VA, January 29, 2010. http://www.federalreserve.gov/newsevents/speech/kohn20100129a.htm.
Journal of Monetary Economics 47:523-544.
Journal of Financial Services Research 5:61-76.
Journal of Monetary Economics 39:341-357.
Journal of Banking and Finance 35:282-289.
Bank of England Quarterly Bulletin Summer:172-182.
Quarterly Journal of Economics 107:657-680.
Review of Financial Studies 22:435-480.
Journal of Monetary Economics 55:677-691.
Journal of Monetary Economics 54:1769-1808.
Journal of Monetary Economics 51:1553-1575.
International Economic Review 39:907-931.
American Economic Review 35:16-27.
Journal of Economics and Business 42:171-182.
Federal Reserve Bank of New York Staff Report No.52.
Journal of Money, Credit, and Banking 36:853-882.
Journal of Money, Credit, and Banking 38:1351-1361.
Journal of Finance 52:635-654.
Journal of Banking and Finance 14:803-820.
Appendices
A. The Protocol for Constructing the Intraday Returns
We used the Trade and Quote (TAQ) data provided by the NYSE to construct bank stock returns over the two-hour window surrounding each FOMC announcement in our sample period.36 Specifically, let
![]() denote the average of the recorded bid and ask prices (that is, "the price") at time hh:mm:ss on the day of an FOMC announcement. For
regularly-scheduled FOMC announcements--which take place at 14:15:00 (Eastern Standard Time)--we calculated a simple two-hour stock return according to
denote the average of the recorded bid and ask prices (that is, "the price") at time hh:mm:ss on the day of an FOMC announcement. For
regularly-scheduled FOMC announcements--which take place at 14:15:00 (Eastern Standard Time)--we calculated a simple two-hour stock return according to
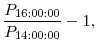 |
using the following protocol:
- If
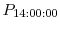 was not available, we used the last available price before 14:00:00, but after 09:30:00.
was not available, we used the last available price before 14:00:00, but after 09:30:00. - If
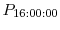 was not available, we used the last price after 16:00:00, but before 16:30:00.
was not available, we used the last price after 16:00:00, but before 16:30:00. - In case we observed no bid or ask prices between 9:30:00 and 14:00:00 or between 16:00:00 and 16:30:00, the return was set to missing.
For the FOMC announcements associated with the intermeeting policy moves, let ![]() denote the announcement time (e.g., 15:15:00 for the intermeeting announcement on October 15,
1998). In that case, the return was calculated as
denote the announcement time (e.g., 15:15:00 for the intermeeting announcement on October 15,
1998). In that case, the return was calculated as
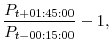 |
using the following protocol:
- If
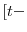 00:15:00
00:15:00![] <](img171.gif) 09:30:00, we used the last price on or before 16:30:00--but
after 15:00:00--of the previous day.
09:30:00, we used the last price on or before 16:30:00--but
after 15:00:00--of the previous day. - If
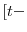 00:15:00
00:15:00![] >](img172.gif) 16:30:00, we used the last price on or before 16:30:00--but
after 15:00:00--of the same day.
16:30:00, we used the last price on or before 16:30:00--but
after 15:00:00--of the same day. - If
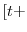 01:45:00
01:45:00![] <](img171.gif) 09:30:00, we used the first price on or after 09:30:00, but
before 11:30:00.
09:30:00, we used the first price on or after 09:30:00, but
before 11:30:00. - If
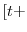 01:45:00
01:45:00![] >](img172.gif) 16:30:00, we used the last price on or after 16:30:00 on the
same day, but after
16:30:00, we used the last price on or after 16:30:00 on the
same day, but after
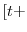 00:30:00
00:30:00![]](img174.gif) ; if
; if
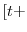 00:30:00
00:30:00![] >](img172.gif) 16:30:00, we used the first available price on the following
day.
16:30:00, we used the first available price on the following
day. - In case the above criteria were not met, the return was set to missing.
In all cases, we checked that no stock went ex-dividend during the time interval used to compute the intraday returns. To ensure that our results were not driven by a small number of extreme observations, we eliminated from our sample all absolute returns greater than 10 percent, implying cutoffs that correspond roughly to the 99th and 0.5th percentiles of the distribution of bank stock returns on the days of FOMC announcements.
B. Sample Selection Criteria
This appendix describes the filters used to eliminate extreme observations from our bank-level data sets. The following selection criteria were used in Section 4:
- All BHC/quarter observations with zero total loans and leases were eliminated.
- We eliminated all BHC/quarter observations with a repricing/maturity gap (
 ) above the 99th percentile and below the 1st percentile of its distribution over the 1997:Q2-2007:Q2 period.
) above the 99th percentile and below the 1st percentile of its distribution over the 1997:Q2-2007:Q2 period.
In Section 5, the following filters were used to screen for the extreme observations:
- We eliminated all bank/quarter observations with absolute asset growth in excess of 20 percent. Although our bank-level data are adjusted for bank-to-bank mergers, it is still the case that banks frequently acquire assets outside the banking industry--for example, by purchasing a thrift or a mortgage servicing company, etc. This filter ensured that such activity did not unduly influence our results.
- We eliminated from our sample all banks whose total loans and leases accounted for less than 25 percent of their total assets, on average. This filter eliminated institutions that do not engage primarily in traditional banking activity--namely lending to businesses and households.
- To mitigate the effects of outliers on our regression results, we trimmed the following variables above the 99th percentile and below the 1st percentile of their respective distribution over the 1997:Q2-2007:Q2 period: (1) repricing/maturity gap (
 ); (2) net interest income as a percent of assets (
); (2) net interest income as a percent of assets (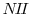 ); (3) net noninterest income as a percent of assets (
); (3) net noninterest income as a percent of assets ( ); and (4) return on assets (
); and (4) return on assets (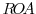 ).
). - We eliminated all banks with less than 24 continuous quarters of data during our sample period.
It is well known, that the time-series variation in the accounting measures of bank profitability and asset growth can be influenced significantly by seasonal fluctuations. To abstract from these effects, we used the additive X11 filter to seasonally adjusted bank-specific measures of accounting profitability, asset growth, and the associated growth contributions used in our regressions.37
C. Deposits with Negative Duration: A Simple Example
This appendix provides a simple example, illustrating how zero-interest retail deposits can be simultaneously "sticky" and have low or even negative duration. As discussed in the main text (Subsection 4.1.2), negative duration of retail deposits also arises as a possible case in the model of Hutchison & Pennacchi (1996); in fact, they estimate significant rents and negative durations for certain types of retail deposits at a sizable portion of banks in their sample.
Suppose a bank has initially ![]() in deposits on which it pays no interest. Assume further that these deposits are withdrawn at the rate of
in deposits on which it pays no interest. Assume further that these deposits are withdrawn at the rate of
![]() per period, where
per period, where ![]() denotes the short-term market
interest rate. Because
denotes the short-term market
interest rate. Because ![]() represent the opportunity cost for savers of holding their wealth in this deposit, it is natural to assume that
represent the opportunity cost for savers of holding their wealth in this deposit, it is natural to assume that ![]() is an increasing function of
is an increasing function of ![]() --a depositor is more likely to transfer to a higher-yielding investment when market interest rates
are higher. Assuming no change in market rates, the amount of the initial deposits
--a depositor is more likely to transfer to a higher-yielding investment when market interest rates
are higher. Assuming no change in market rates, the amount of the initial deposits ![]() remaining in period
remaining in period ![]() is
is
![]() , and withdrawals in that period are equal to
, and withdrawals in that period are equal to
![]() . The value of the initial deposit liability--denoted by
. The value of the initial deposit liability--denoted by
![]() --is equal to the present discounted value of this stream of withdrawals:
--is equal to the present discounted value of this stream of withdrawals:
![\displaystyle V_{\scriptscriptstyle D}(r) = \sum_{t=0}^{\infty} \left[ \frac{1 - w (r)}{1 + r} \right]^{t} w (r) D = w (r) D \left[ \frac{1 + r}{r + w (r)} \right].](img185.gif) |
With
Differentiating the above equation with respect to ![]() yields, after some rearranging of terms and suppressing the dependence of
yields, after some rearranging of terms and suppressing the dependence of ![]() on
on ![]() ,
,
![\displaystyle \frac{dV_{\scriptscriptstyle D}}{dr} = \left[ \left(\frac{r}{w}\right) \frac{d w}{d r} - \frac{1 - w}{1 + r} \right] \left[ \frac{1}{r + w} \right] V_{\scriptscriptstyle D}.](img188.gif) |
Hence, the present discounted value of the deposit liability increases with interest rates if and only if
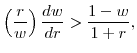 |
where the left-hand side of the above inequality represents the elasticity of withdrawals with respect to market interest rates. Thus, if withdrawals are sufficiently interest-elastic, the value of this deposit liability increases with the interest rate, which would imply a negative duration. This can happen even if the withdrawal rate
D. Interest Rate Derivatives at U.S. Commercial Banks
This appendix presents several stylized facts about banks' usage of interest rate derivatives, facts that guided our econometric strategy and highlight some of the limitations inherent in the available data. The solid lines in the two panels of Figure D-1 show that, according to the Call Report data, the notional value of interest rate derivative contracts involving U.S. commercial banks has risen dramatically since the mid-1990s. The increase has been especially pronounced for interest rate derivatives used for trading purposes (left panel), a category in which the notional amount of outstanding derivatives increased (in real terms) from less than $20 trillion in 1997 to almost $120 trillion by the end of 2007.
The increase in the notional amount of interest rate derivatives used for non-trading (that is, hedging) purposes over that period (right panel) has been less dramatic, though still substantial--note that the notional amount of interest rate derivatives used for hedging pales in comparison with the corresponding trading positions. As indicated by the dotted lines, our sample of publicly-traded BHCs accounts for almost all of the notional positions in both categories.
In addition to the notional amounts by type of purpose, Call Reports contain a breakdown of all interest rate derivatives--used either for trading or other purposes--by contract type, which for our sample of banks is shown in Figure D-2. According to these data, interest rate swaps account for the vast bulk of the notional amount of interest rate derivative contracts. Interest rate options, both exchange traded (ET) and those that trade over-the-counter (OTC), represent the next most important category, with futures and forwards accounting for the remainder.
The final breakdown of interest rate derivatives reported on the Call Reports is in terms of their "fair" (that is, market) values. It is important to note that when an up-to-date market price for the derivative is not readily available, banks may use a "mark-to-model" approach to determine its fair value. Banks report these exposures only as totals of all interest rate derivatives by type of purpose--that is, trading vs. non-trading--and by their sign, that is, contracts with positive or negative fair values.
As shown in the left panel of Figure D-3, the absolute market value of interest rate derivatives used for trading purposes peaked in 2003 at about $2.5 trillion, before falling to less that $2 trillion by the end of our sample period. In that category, contracts with positive fair values almost exactly offset those with negative values, a pattern consistent with the banking sector serving primarily as an intermediary in the process of allocating interest rate risk, while, in the aggregate, avoiding large net exposures. In contrast, fair values of such derivatives held for non-trading purposes (right panel) appear to be less well matched over time, though their absolute market values are orders of magnitude smaller than the corresponding trading exposure.
Table D-1 documents the extent to which these off-balance-sheet positions are concentrated among a few very large institutions. Specifically, it shows how interest rate derivatives--in both notional and net fair-value terms and measured as a percent of bank assets--vary across the size distribution of banks in our sample. Note that in all but the largest size quintile, the median net fair value of all interest rate derivative contracts amounts to literally zero percent of total assets. In general, this pattern holds true even for the notional amounts. The only minor exception is the fourth size quintile, a size category in which the median notional amount of interest rate derivatives used for non-trading purposes equals a negligible 0.21 percent of bank assets.
Average notional positions tend to be somewhat higher, though net fair values still average to zero in all but the largest bank-size category. Even in the top quintile, a size category that includes about 70 of the largest publicly-traded BHCs, typical usage of interest rate derivatives appears scant; of course, the average notional exposures in that size category are noticeably higher, reflecting the extreme skewness of the distribution.
(By Size Quintile)
| Valuation | Qntl. 1 | Qntl. 2 | Qntl. 3 | Qntl. 4 | Qntl. 5 |
| Notional Value: Mean | 0.09 | 0.01 | 0.06 | 0.32 | 133.1 |
| Notional Value: Median | 0.00 | 0.00 | 0.00 | 0.00 | 1.37 |
| Notional Value: Max | 72.2 | 14.8 | 10.5 | 29.6 | 4608 |
| Net Fair Value: Mean | -0.00 | 0.00 | 0.00 | 0.00 | 0.03 |
| Net Fair Value: Min | -0.05 | -0.03 | -0.07 | -0.05 | -21.6 |
| Net Fair Value: Median | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Net Fair Value: Max | 0.08 | 0.03 | 0.70 | 0.09 | 2.00 |
(By Size Quintile)
| Valuation | Qntl. 1 | Qntl. 2 | Qntl. 3 | Qntl. 4 | Qntl. 5 |
| Notional Value: Mean | 1.87 | 0.79 | 2.11 | 6.53 | 19.8 |
| Notional Value: Median | 0.00 | 0.00 | 0.00 | 0.21 | 8.54 |
| Notional Value: Max | 146.8 | 20.1 | 94.8 | 760.9 | 430.2 |
| Net Fair Value: Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.07 |
| Net Fair Value: Min | -0.66 | -0.63 | -1.14 | -0.94 | -1.22 |
| Net Fair Value: Median | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 |
| Net Fair Value: Max | 2.46 | 0.53 | 0.99 | 1.23 | 2.69 |
- Note: Sample period: 1997:Q2-2007:Q2; No. of banks = 355; Obs. = 9,855. The five size quintiles (Qntl. 1-5) are based on the period-specific quintiles of the distribution of total assets. Net Fair Value = market value of all interest rate derivative contracts with positive value less absolute market value of all contracts with negative value.
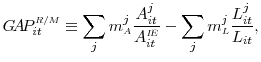
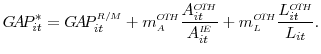
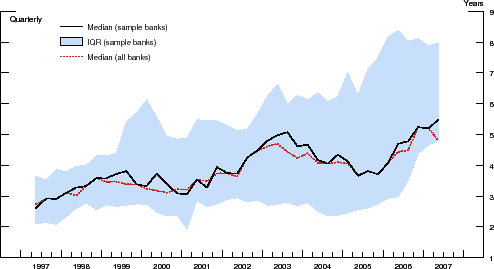
![\begin{displaymath}\begin{split}R_{it} = & \; \beta_{1} \Delta f\!f_{t}^{u} + \b... ...a f\!f_{t}^{u}) \right] + \eta_{i} + \epsilon_{it}. \end{split}\end{displaymath}](img52.gif)