Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-28 Screen Reader version ^♣

An Extensive Look at Taxes: How does endogenous retirement affect optimal taxation?

William B Peterman

Federal Reserve Board of Governors¹

Keywords: Optimal taxation, capital taxation, endogenous retirement

Abstract:

This paper considers the impact on optimal tax policy of including endogenously determined retirement in a life cycle model. Allowing individuals to determine when they retire causes the optimal tax on capital to increase by 75% because of two implicit changes in the aggregate labor supply elasticity. First, including endogenous retirement causes an increase in the overall aggregate labor supply elasticity since agents can change their labor supply on both the intensive and extensive margins. In response, the government limits the distortions from the tax policy by lowering the tax on labor and increases the tax on capital. Second, given that the choice to retire is more relevant for older individuals, endogenous retirement disproportionately increases older agent's elasticity compared to younger individuals. Ideally, the government would decrease the relative labor income tax on individuals when they are older and supply labor more elastically. However, in the absence of age-dependent taxes, the government mimics such a tax policy by further increasing the tax on capital. I find that the welfare lost from not accounting for endogenous retirement when solving for the optimal tax policy is equivalent to approximately one percent of lifetime consumption.

JEL Classification: E24, E62, H21.

1 Introduction

Previous work demonstrates that in a life cycle model the optimal tax on capital is directly related to the representative cohort's Frisch labor supply elasticity (see Garriga (2001), Atkeson et al. (1999), Erosa and Gervais (2002), Conesa et al. (2009), and Peterman (2011)). This elasticity is governed by decisions on both the intensive and extensive margins. However, previous studies that determine the optimal tax on capital in a life cycle model typically only allow individuals to make labor supply decisions on the intensive margin and assume agents are completely inelastic on the extensive margin. The aim of this paper is to determine the effect on optimal tax policy of relaxing this assumption by including endogenously determined retirement.

In order to assess the quantitative effect of this assumption I solve computationally for the optimal tax policy in two similar life cycle models where the government is required to raise a fixed amount of revenue. In the first model, individuals are forced to retire at an exogenously set age. In the second model, agents endogenously determine when they retire. Both models includes a reduced form social security program that is in a similar spirit to the program in the United States. In the exogenous model agents are forced to retire at the normal retirement age and then receive a social security benefit. Similar to the U.S. social security program, the reduced form social security program is set up in the endogenous model such that if agents choose to retire anytime within a nine year window, centered around the normal retirement age, then they receive an actuarially equivalent amount of benefits from social security. I find that the optimal tax on capital is seventy five percent larger in the model with endogenously determined retirement compared to the exogenous model. These results indicate that this modelling assumption is of first order importance when determining the optimal tax policy.

Including retirement endogenously increases the optimal tax on capital because it alters the implied agent's aggregate Frisch labor supply elasticity in two ways.² First, by removing the restrictions on labor participation, the agent now has two margins (intensive and extensive) by which they can alter their labor supply. Therefore, the aggregate Frisch elasticity is larger than in the exogenous model where the agent can only alter their labor supply on the intensive margin. Accordingly, the government would prefer to rely less on a labor tax and more heavily on a capital tax in order to minimize the distortions imposed by the tax code.³ Second, since the choice to retire is more relevant for older individuals, endogenous retirement disproportionately increases the elasticity when an agent is old compared to when they are young. The government would like to respond by decreasing the relative tax on the labor income when agents are old and more responsive. When the government cannot use age-dependent taxes, it will use a larger tax on capital in order to mimic such a tax policy.

Examine the effect of this exogenous retirement decision is relevant because other studies indicate that decisions on the extensive margin have a large impact on both the level of the aggregate Frisch elasticity and the slope of the lifetime Frisch elasticity profile. Importantly, the lifetime Frisch labor supply elasticity profile from a simulated model tends to be more consistent with the data if endogenous retirement is included. Using simulated data from a simple model, Rogerson and Wallenius (2009) demonstrate that ignoring the extensive margin could significantly lower estimates of the aggregate Frisch elasticity. Erosa et al. (2011) calibrate a life cycle model of labor markets which incorporates choices on both the intensive and extensive margin. They find that the extensive margin accounts for approximately half of the aggregate labor supply response to a temporary wage change. Finally, Chetty et al. (2011), Peterman (2012), and Fiorito and Zanella (2008) find that incorporating fluctuations on the extensive margin causes estimates of the Frisch elasticity to increase substantially. These larger estimates are more consistent with the parameters used in macro models that are calibrated such that the model's fluctuations in aggregate hours over the business cycle match the data. Additionally, there is some empirical evidence that older individuals have a relatively higher Frisch elasticity compared to younger individuals. French (2005) estimate a life cycle model in which he allows for a break point in the in Frisch elasticity parameter at the age of forty. The author finds that the Frisch elasticity is over three times larger for the older individuals compared to younger individuals.⁴ A model that includes endogenously determined retirement is more consistent with the larger estimates of the Frisch labor supply elasticity for older individuals.

I choose to focus on endogenously determined retirement, as opposed to examining both the entry and exit from the labor force, since the empirical evidence is consistent with the extensive margin having a larger impact on the labor supply elasticity of older individuals.⁵ Moreover, Jacobs and Bovenberg (2009) demonstrate that including the decision of when to stop education and enter the workforce could further enhance the motive for a positive tax on capital. The authors analyze the trade off between a labor and capital tax in a life cycle model with pre-work education. They find that in a two-period model where agents acquire education in the first period and work in the second period the optimal tax on capital is generally positive if educational investment is not verifiable. The tax on capital reduces the tax on labor income, which in turn reduces the distortions on the benefit to education. Therefore, including an endogenous entry decision may further increase the optimal tax on capital.

This paper is organized as follows: Section 2 introduces the computational model, and presents the competitive equilibrium. Section 3 describes the functional forms and calibration parameters. Section 4 sets up the computational experiment and section 5 reports the results of the computational experiment. Section 5 concludes.

2 Computational Model

In this section, I describe the computational model and present the definition of a stationary competitive equilibrium which is used to determine the effect of endogenous retirement on optimal tax policy.

2.1 Demographics

In the model, time is assumed to be discrete and there are J overlapping generations. $\Psi_{j}$ is the probability of an agent living to age conditional on being alive at age . All agents who live to an age of die the next period. If an agent dies with assets, the assets are confiscated by the government and distributed equally to all the living agents as transfers ( $Tr_{t}$ ).

An agent retires at the age $j_{r}$ . Once they retire they receive a social security benefit and can no longer work. In the exogenous model, agents are forced to retire at the age $j_{\text{exog}}$ ( $j_{r}=j_{\text{exog}}$ ). In the endogenous model agents choose $j_{r}$ and $j_{\text{exog}}$ is considered the "normal retirement age". Agents can choose to retire up to four years before or after the normal retirement age ( $j_{r}\in (j_{\text{exog}}-4,j_{\text{exog}}+4)$ ) and receive an actuarially equivalent social security benefit.⁶

In each period a continuum of new agents is born. The population of new agents born each period grows at rate . Given the population growth rate and conditional survival probabilities, the time invariant cohort shares, $\{\mu_{j}\}_{j=1}^{J}$ , are given by

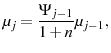$\displaystyle \mu_{j}=\frac{\Psi_{j-1}}{1+n}\mu_{j-1},$ for $\displaystyle i = 2, ...., J,$

(1)

where $\mu_{1}$ is normalized such that

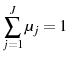$\displaystyle \sum_{j=1}^{J}\mu_{j}=1$

(2)

2.2 Individual

An individual is endowed with one unit of productive time per period which he splits between providing labor services and leisure prior to his retirement. After retirement he uses all his time for leisure. An agent maximize his lifetime utility

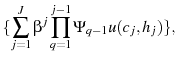$\displaystyle \{\sum_{j=1}^{J}\beta^{j}\prod_{q=1}^{j-1}\Psi_{q-1}u(c_{j},h_{j})\},$

(3)

where $c_{j}$ is the consumption of an agent at age

and $h_{j}$ is the hours spent providing labor services. The agent faces a fixed utility cost to working which implies the disutility from working discontinuously increases when an agent goes from zero to positive hours worked.⁷ The discount factor conditional on surviving is $\beta$ .

An agent receives labor income of $h_{j}\epsilon_{j}w_{t}$ where $\epsilon_{j}$ is the agent's age-specific human capital. This labor income is split between consumption and saving using a risk free asset. An agent's stock of assets are denoted by $a_{j}$ and he receives a pre-tax net return of $r_{t}$ on the assets per period.

2.3 Firm

Firms are perfectly competitive with constant returns to scale production technology. Aggregate technology is represented by a Cobb-Douglas production function. The aggregate resource constraint is,

$\displaystyle C_{t} + K_{t+1}-(1-\delta)K_{t}+G_{t}\leq K_{t}^{\alpha}N_{t}^{1-\alpha},$

(4)

where $K_{t}$ , $C_{t}$ , $N_{t}$ , $G_{t}$ , $\alpha$ , and $\delta$ represent the aggregate capital stock, aggregate consumption, aggregate labor (measured in efficiency units), government consumption, the capital share, and the depreciation rate for physical capital, respectively.

2.4 Government Policy

The government is exogenously forced to consume in an unproductive sector. The government uses two fiscal instruments to finance their consumption, $G_{t}$ , in an unproductive sector.⁸ First, the government taxes capital income, $y_{k}\equiv r_{t}(a+Tr_{t})$ , according to a capital income tax schedule $T^{K}[y_{k}]$ . Second, the government taxes part of each individual's labor income. Part of the pre-tax labor income is accounted for by the employer's contributions to social security, which is not taxable under current U.S. tax law. Therefore, the taxable labor income is $y_{l}\equiv w_{t}\epsilon_{j}h_{j}(1-.5\tau_{ss})$ , which is taxed according to a labor income tax schedule $T^{l}[y_{l}]$ . I impose three restrictions on the labor and capital income tax policies. First, I assume anonymity of the tax code so the rates cannot be personalized, nor can they be age-dependent. Second, both of the taxes are functions only of the individual's relevant taxable income in the current period. Finally, as is typical in a Ramsey problem, I assume the government cannot use lump sum taxation.

The government also runs a pay-as-you-go social security system. I include a reduced form social security program because Peterman (2011) demonstrates that in a model with retirement, a social security program is necessary to produce realistic life cycle profiles. In the reduced form program included in the model, the government pays an annual benefit, $SS_{t}$ , to all individuals that are retired. These benefits are set such that retired agents receive an exogenously determined fraction, $b_{t}$ , of the average income of all working individuals. An agent's social security benefits are proportional to their lifetime earnings.⁹ However, in the endogenous model, if an agent chooses to retire earlier than $j_{\text{exog}}$ then they are charged a lump sum penalty at the time of retirement which is the equivalent of the net present value of the actuarially fair amount of extra benefit he will receive in the years prior to $j_{\text{exog}}$ . Alternatively, if he chooses to retire later than $j_{\text{exog}}$ then he receives an actuarially fair rebate. This formulation mimics the spirit of the US social security program.¹⁰

Social security is financed by taxing labor income at a flat rate, $\tau_{ss,t}$ . The payroll tax rate $\tau_{ss,t}$ is set to ensure the social security system has a balanced budget each period. The social security system is not considered part of the tax policy that the government optimizes.

2.5 Definition of Stationary Competitive Equilibrium

In this section I define the competitive equilibria for the computational model. Given a social security replacement rate , government expenditures , and a sequence of population shares $\{\mu_{j}\}_{j=1}^{J}$ , a stationary competitive equilibrium is a sequence of agent allocations, $\{c_{j},a_{j+1},h_{j},j_{r}\}$ , a production plan for the firm , a government labor tax function $T^{l}:\mathbb{R}_{+}\rightarrow\mathbb{R}_{+}$ , a government capital tax function $T^{k}:\mathbb{R}_{+}\rightarrow\mathbb{R}_{+}$ , a social security tax rate $\tau_{ss}$ , a utility function $U:\mathbb{R}_{+} \times \mathbb{R}_{+} \rightarrow\mathbb{R}_{+}$ , social security benefits , prices , and transfers such that:

Given prices, policies, transfers, and benefits the agent maximizes the following

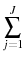$\displaystyle \sum_{j=1}^{J}$ Max $\displaystyle _{c_{j},h_{j},a_{j+1},j_{r}}\beta^{j-1}[\prod_{q=0}^{j-1}\Psi_{q}]u(c_{j},h_{j})$

subject to

$\displaystyle c_{j}+a_{j+1}=w\epsilon_{j}h_{j}-\tau_{ss}ws_{j}h_{j},+(1+r)(a_{j}+Tr)-T^{l}[w\epsilon_{j}h_{j}(1-.5\tau_{ss})] -T^{k}[r(a_{j}+Tr)]$ for $j<j_{r}$ ,

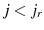$\displaystyle c_{j}+a_{j+1}=SS+(1+r)(a_{j}+Tr)-T^{k}[r(a_{j}+Tr_{t})],$ for $j> j_{r}$

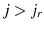
$\displaystyle c_{j}+a_{j+1}=SS+(1+r)(a_{j}+Tr)-T^{k}[r(a_{j}+Tr_{t})]-SS\sum_{s=j}^{j_{\text{exog}}}[\prod_{q=j+1}^{s}\Psi_{q}(1+r)^{j-s}] \text{ for $j=j_{r}$}$

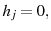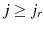
$\displaystyle h_{j}=0,$ for $j\geq j_{r}$

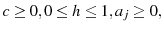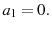
$\displaystyle c\geq0,0\leq h\leq1,a_{j} \geq 0,$ and $\displaystyle a_{1}=0.$
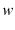Prices and 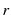satisfy:

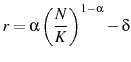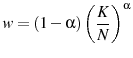
$\displaystyle r=\alpha\left(\frac{N}{K}\right)^{1-\alpha}-\delta$ and $\displaystyle w=(1-\alpha)\left(\frac{K}{N}\right)^{\alpha}$
The social security policies satisfy:

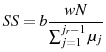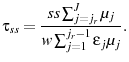
$\displaystyle SS=b\frac{wN}{\sum_{j=1}^{j_{r}-1}\mu_{j}}$ and $\displaystyle \tau_{ss}=\frac{ss\sum_{j=j_{r}}^{J}\mu_{j}}{w\sum_{j=1}^{j_{r}-1}\epsilon_{j}\mu_{j}}.$
Transfers are given by:

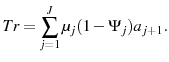
$\displaystyle Tr=\sum_{j=1}^{J}\mu_{j}(1-\Psi_{j})a_{j+1}.$
Government budget balance:

$\displaystyle G=\sum_{j=1}^{J}\mu_{j} T^{k}[r(a_{j}+Tr)] + \sum_{j=1}^{j_{r}-1} \mu_{j}T^{l}[w\epsilon_{j}h_{j}(1-.5\tau_{ss})].$
Market clearing:

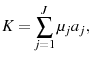
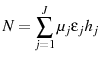$\displaystyle K=\sum_{j=1}^{J}\mu_{j} a_{j},$ $\displaystyle N=\sum_{j=1}^{J} \mu_{j}\epsilon_{j}h_{j}$ and

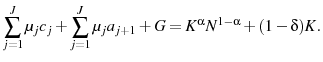
$\displaystyle \sum_{j=1}^{J} \mu_{j}c_{j} + \sum_{j=1}^{J}\mu_{j} a_{j+1}+ G= K^{\alpha}N^{1-\alpha}+(1-\delta)K.$

3 Calibration and Functional Forms

To determine the optimal tax policy it is necessary to choose functional forms and calibrate the model's parameters. I base my life cycle model on Conesa et al. (2009) and Peterman (2011). Calibrating the model involves a two-step process. The first step is choosing parameter values for which there are direct estimates in the data. Second, the remaining parameters are determined so that under the baseline-fitted U.S. tax policy certain targets in the model match the values observed in the U.S. economy.¹¹ I calibrate all of the second group of parameters in a model with endogenously determined retirement which implies that the parameter values are the same in both models. The parameter values are listed in table 3.

Table 1: **Calibration Parameters**
Parameter	Value	Source
Demographics: Normal Retirement Age: $j_{\text{exog}}$	65	By Assumption
Demographics: Max Age:	100	By Assumption
Demographics: Surv. Prob: $\Psi_{j}$		Bell and Miller (2002)
Demographics: Pop. Growth:	$1.1\%$	Data
Firm Parameters: $\alpha$	.36	Data
Firm Parameters: $\delta$	8.33%	$\frac{I}{Y}=25.5\%$
Firm Parameters: A	1	Normalization
Calibration Parameters: Conditional Discount: $\beta$	0.995	$\frac{K}{Y}=2.7$
Calibration Parameters: Risk aversion: $\sigma_{1}$	2	Conesa et al. (2009)
Calibration Parameters: Frisch Elasticity: $\sigma_{2}$	0.5	Intensive Frisch $=\frac{1}{2}$
Calibration Parameters: Disutility to Labor: $\chi_{1}$	60.9	Avg. $h_{j}$ = 1/3
Calibration Parameters: Fixed Cost to Working: $\chi_{2}$	0.5	Normal Retirement = 65
Government Parameters: $\Upsilon_{0}$	.258	Gouveia and Strauss (1994)
Government Parameters: $\Upsilon_{1}$	.768	Gouveia and Strauss (1994)
Government Parameters: G	0.137	17% of Y
Government Parameters: b	0.5	Conesa et al. (2009)

3.1 Demographics

In the model, agents are born at a real world age of 20 that corresponds to a model age of 1. The current population in the U.S. faced a normal retirement age of between 65 and 66.¹² Since I am calibrating the model to the current U.S. economy, I choose the normal retirement age to be 65 which implies that in the exogenous model agents are forced to retire at a real world age of 65. In the endogenous model, there is a fixed cost to working ( $\chi_{2}$ ), which is calibrated such that individuals choose to retire at age 65.¹³ If an individual survives until the age of 100, he dies the next period. I set the conditional survival probabilities in accordance with the estimates in Bell and Miller (2002). I assume a population growth rate of 1.1 percent.

3.2 Preferences

Agents have time-separable preferences over consumption and labor services, and conditional on survival, they discount their future utility by $\beta$ . I use a utility function that is separable and homothetic in both consumption and labor. I choose to use this type of utility function since both Garriga (2001) and Peterman (2011) demonstrate that violating these assumptions will lead to a large optimal tax on capital and I do not want this motive to be confounded with a motive from endogenous retirement. 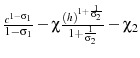The utility function I use is $\frac{c^{1-\sigma_{1}}}{1-\sigma_{1}}-\chi\frac{(h)^{1+\frac{1}{\sigma_{2}}}}{1+\frac{1}{\sigma_{2}}}-\chi_{2}$ . I determine $\beta$ such that the capital-to-output ratio matches U.S. data of 2.7.¹⁴ I determine $\chi_{1}$ such that under the baseline-fitted U.S. tax policy, agents work on average one third of their time endowment prior to retiring.¹⁵ As mentioned, I determine $\chi_{2}$ such that under the baseline-fitted U.S. tax policy individuals choose to retire at the normal retirement age (65) in the endogenous model. Following Conesa et al. (2009), I set $\sigma_{1} = 2$ , which controls the relative risk aversion.¹⁶

The parameter $\sigma_{2}$ controls the Frisch elasticity on the intensive margin (intensive Frisch elasticity). The intensive Frisch elasticity is different from the aggregate Frisch elasticity in that it only incorporates changes in hours on the intensive margin while the aggregate Frisch elasticity incorporates changes in hours on both the intensive and extensive margins. Unlike the intensive Frisch elasticity, which is determined by $\sigma_{2}$ , the aggregate Frisch elasticity does not equal a calibration parameter but instead is implicitly determined within the model. Past micro-econometric studies estimate that the intensive Frisch elasticity is between 0 and 0.5.¹⁷ However, more recent research has shown that these estimates may be biased downward. Reasons for this bias include: utilizing weak instruments; not accounting for borrowing constraints; disregarding the life cycle effect of endogenous-age specific human capital; omitting correlated variables such as wage uncertainty; and not accounting for labor market frictions.¹⁸ Therefore, I set $\sigma_{2}$ such that the intensive Frisch elasticity is at the upper bound of the range ( 0.5).¹⁹ I use the values for $\{\epsilon_{j}\}_{j=0}^{j_{r}-1}$ from Conesa et al. (2009) which are a smoothed version of the relative hourly earnings estimated by age in Hansen (1993).²⁰

3.3 Firm

I assume the aggregate production function is Cobb-Douglas. The capital share parameter, $\alpha$ , is set at .36. The depreciation rate is set to target the observed investment output ratio of 25.5 percent.

3.4 Government Policies and Tax Functions

In order to calibrate the second set of parameters that imply the targets in the models match the values in the data, it is necessary to include a baseline tax function in the model that mimics the U.S. tax code. I use Gouveia and Strauss (1994) estimates of the U.S. tax code, which I refer to as the baseline-fitted U.S. tax policy. The authors match the U.S. tax code to the data using a three parameter functional form,

$\displaystyle T(y;\Upsilon_{0},\Upsilon_{1},\Upsilon_{2})=\Upsilon_{0}(y-(y^{-\Upsilon_{1}}+\Upsilon_{2})^{-\frac{1}{\Upsilon_{1}}}),$

(5)

where

represents labor or capital income. The average tax rate is principally controlled by $\Upsilon_{0}$ , and $\Upsilon_{1}$ governs the progressivity of the tax policy. The third parameter, $\Upsilon_{2}$ , is set so that taxes satisfy the budget constraint. Gouveia and Strauss (1994) estimate that $\Upsilon_{0}=.258$ and $\Upsilon_{1}=.768$ . The authors do not fit separate tax functions for labor and capital income. Accordingly, I use the same parameter values on both sources of income for the baseline-fitted U.S. tax policy. I calibrate government consumption,

, so that it equals 17 percent of output under the baseline-fitted U.S. tax policy, as observed in the U.S. data.²¹ More specifically, $\Upsilon_{2}$ is determined as the value that causes taxes to be equal to 17 percent of GDP. When searching for the optimal tax policy, I restrict my attention to flat taxes on capital and labor that induce revenue neutral changes.²² These policies imply that government consumption is equal under the baseline-fitted U.S. tax policy and the optimal tax policy.

In addition to consuming, the government runs a balanced-budget social security program. Social security benefits are set so that the replacement rate, , is 50 percent.²³ In the endogenous model, an agent can choose to retire at any age within four years of the normal retirement age. Once an agent retires they receive the annual social security benefit. If an agent chooses to retire prior to the normal retirement age then they must pay a fixed amount when they retire which is actuarially equivalent to the expected benefits they will receive before the normal retirement age. If they choose to retire after the normal age of retirement then they receive an actuarially equivalent transfer. The payroll tax, $\tau_{ss}$ , is determined so that the social security system is balanced each period.

4 Computational Experiment

The computational experiment is designed to determine the tax policy that maximizes a given social welfare function. I choose a social welfare function (SWF) that corresponds to a Rawlsian veil of ignorance (Rawls (1971)). Since living agents face no earnings uncertainty, the social welfare is equivalent to maximizing the expected lifetime utility of a newborn,

$\displaystyle SWF(\tau_{h}, \tau_{k})=\sum_{j=1}^{J}\beta^{j-1}[\prod_{q=0}^{j-1}\Psi_{q}]u(c_{j},h_{j}),$

(6)

where $\tau_{h}$ is the flat tax rate on labor income and $\tau_{k}$ is the flat tax rate on capital income.²⁴

When I determine the optimal tax policy, I search over a grid of values of the tax on labor income ( $\tau_{h}$ ) and determine the corresponding values for the tax on capital ( $\tau_{k}$ ) which implies a revenue neutral change. Therefore, the experiment is to find $\tau_{h}$ that satisfies

$\displaystyle \max_{\tau_{h}} SWF(\tau_{h}, \tau_{k})$

(7)

subject to,

$\displaystyle G=\sum_{j=1}^{J}\mu_{j} \tau_{k}r(a_{j}+Tr)] + \sum_{j=1}^{j_{r}-1} \mu_{j}\tau_{h}[ws_{j}h_{j}(1-.5\tau_{ss})].$

(8)

5 Results

Table 5 describes the optimal tax policies in both models. The optimal tax policy in the exogenous model is an 18.2 percent tax on capital income ( $\tau_{k}=18.2\%)$ and a 23.7 percent tax on labor income ( $\tau_{h}=23.7\%)$ . Including endogenously determined retirement has a large impact on the optimal tax policy. The optimal tax on capital increased by almost seventy five percent to 31.8 percent ( $\tau_{k}= 31.8\%$ and $\tau_{h}=20.6\%$ ) when endogenous retirement is included. Using the endogenous model, I find that the welfare is reduced by an amount equivalent to one percent of total lifetime consumption if the planner adopts the tax system that is optimal for the exogenous model.

Table 2: Optimal Tax Policies

Tax Rate	Exogenous	Endogenous
$\tau_k$	$18.2\%$	$31.8\%$
$\tau_h$	$23.7\%$	$20.6\%$
$\frac{\tau_k}{\tau_{h}}$	0.77	1.54

The differences in the optimal tax policy are primarily driven by two key changes in the aggregate Frisch labor supply elasticity. Note that the aggregate Frisch elasticity is determined within the model and incorporates labor changes on both the intensive and extensive margin. In contrast, the intensive Frisch elasticity only incorporates changes in hours on the intensive margin and is equal to $\sigma_{2}$ . First, introducing a retirement decision in the model provides the agents with an additional margin on which to change their labor supply. The result is an overall increase in the level of the aggregate Frisch labor supply elasticity. In order to minimize the distortion that the tax policy induces, the government relies more heavily on a capital income tax as opposed to a labor income tax. Second, since the choice to retire is more relevant for individuals when they are older, endogenous retirement disproportionately increases the elasticity when agents are older compared to when they are younger. This change in the slope of the aggregate Frisch elasticity profile causes the government to want to reduce the relative tax rate on the labor income from when agents are older. Since the government cannot condition labor income taxes on age, they increase the tax on capital in order to mimic this type of age-dependent tax policy.

Next, I quantify the relative impact of the change in the level and the slope of the aggregate Frisch elasticity profile. I determine the effect of the increase in the aggregate Frisch elasticity on the optimal tax policy by solving for the optimal tax policy in the exogenous model using an alternative value for the intensive Frisch elasticity which equals the aggregate Frisch elasticity in the endogenous model. I estimate that the aggregate Frisch elasticity in the endogenous model is 2.18.²⁵ This larger aggregate Frisch elasticity in the endogenous model is in line with estimates of the aggregate Frisch elasticity in Peterman (2012). In the altered exogenous model, where the Frisch elasticity parameter matches the aggregate Frisch elasticity in the endogenous model, I find that the optimal tax on capital is $25.8\%$ .²⁶ This result indicates that, by itself, the larger aggregate Frisch elasticity is responsible for roughly half of the increase in the optimal tax on capital income in the endogenous model.

Table 3: **Aggregate Economic Variables**
	Exogenous Baseline	Exogenous Optimal	% Change from Baseline to Optimal (Exogenous)	Endogenous Baseline	Endogenous Optimal	% Change from Baseline to Optimal (Endogenous)
Aggregate: Y	0.81	0.82	1.2%	0.81	0.81	0.1%
Aggregate: K	2.17	2.25	3.5%	2.17	2.12	-2.5%
Aggregate: N	0.46	0.46	0%	0.46	0.47	1.5%
Aggregate: Avg Hours	0.33	0.34	0.9%	0.33	0.33	-0.1%
Aggregate: w	1.12	1.13	1.3%	1.12	1.1	-1.5%
Aggregate: r	0.05	0.047	-5.9%	0.05	0.054	7%
Aggregate: tr	0.026	0.027	3.7%	0.026	0.026	-0.1%
Aggregate: Value	-160.2	-159.9	0.2%	-160.2	-158.3	1.2%
Aggregate: CEV			0.3%			1.8%
Average Tax Rate: Capital	15.6%	17.6%		15.6%	31.8%
Average Tax Rate: Labor	23.7%	24.1%		23.7%	20.6%
Average Tax Rate: Ratio	0.66	0.73		0.66	1.54
Marginal Tax Rate: Capital	19.4%	17.6%		19.4%	31.8%
Marginal Tax Rate: Labor	25.5%	24.1%		25.5%	20.6%
Marginal Tax Rate: Ratio	0.76	0.73		0.76	1.54

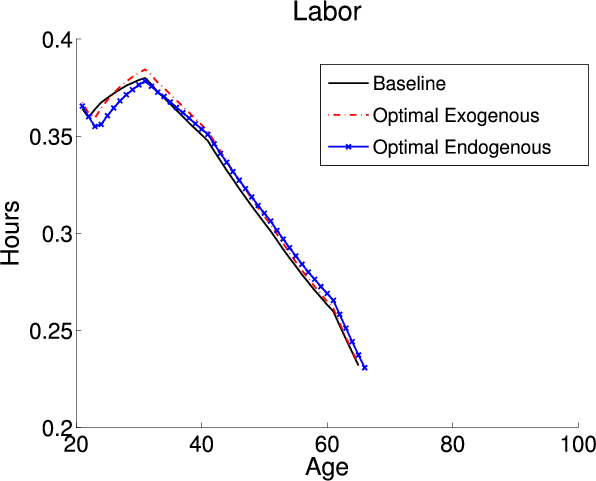
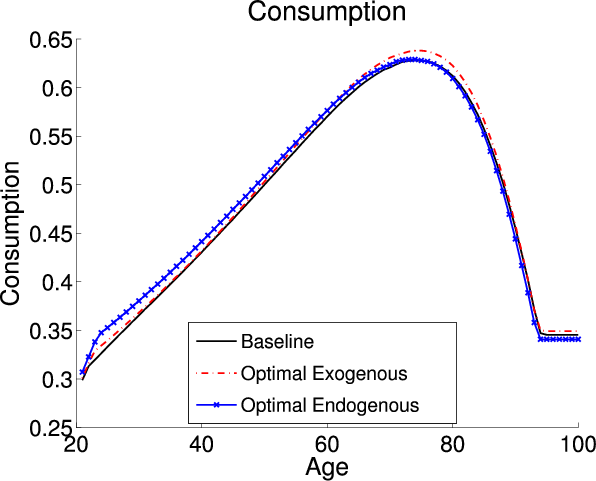
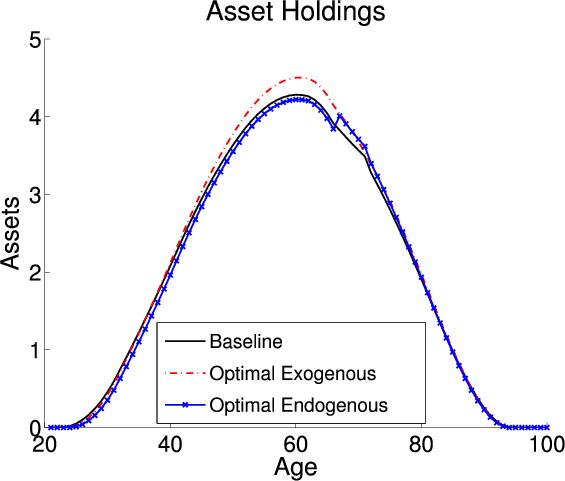
Finally, I focus on the differences in the underlying economies with and without endogenous retirement. Table 5 details the aggregate economic variables; the first, second and third columns describe the model with exogenous retirement and the fourth, fifth, and sixth columns detail the model with endogenous retirement. The first and fourth columns describe the aggregates under the baseline-fitted US tax policy. Since the two models have the same calibration parameters and targets they are identical under the baseline-fitted US tax policy. The second and fifth columns describe the exogenous and endogenous models when I impose each models optimal tax policies, respectively. Finally, the third and sixth columns describe the percent change in the aggregates that occurs when I switch from the baseline-fitted US tax policy to the optimal tax policies. Figure 1 plots the life cycle profiles for labor, consumption, and savings. The black lines are the profiles under the baseline-fitted US tax policy. As previously mentioned, by construction the endogenous and exogenous models are identical under the baseline-fitted US tax policy. The red lines are the profiles in the exogenous model under the optimal tax policy. The blue lines are the profiles in the endogenous model under the optimal tax policy.

In the exogenous model adopting the optimal tax policy causes the average marginal tax rate on both capital and labor fall.²⁷ In response to changing from the baseline to optimal tax policy, capital increases and labor stays relatively constant. The changes in aggregate labor and capital cause output to increase, the pre-tax wage rate to increase, and the pre-tax return to capital to fall. In order to assess the impact on welfare I calculate the consumption equivalent variation (CEV) which is the uniform percentage increase in consumption required to make an individual indifferent between the baseline and optimal two tax policies in the exogenous model. I find the CEV is small in the exogenous model ( $0.3\%$ ).

Figure 1: Life Cycle Profiles

Note: These plots are life cycle profiles in both models under the baseline-fitted U.S. tax policy and the optimal tax policies. Since the calibration parameters and targets are the same the economies in both models are identical under the baseline-fitted US tax policy.

In the endogenous model adopting the optimal tax policy causes a large increase in the tax on capital income and a decrease in the tax on labor income. In response to changing from the baseline-fitted US tax policy to the optimal tax policy, aggregate capital falls two and a half percent and aggregate labor increases one and a half percent. The changes in capital and labor offset each other and overall output stays approximately constant. The drop in aggregate capital and rise in aggregate labor leads to an increase in the pre-tax return to capital and decrease in the pre-tax wage. Overall, I find that the welfare gains from adopting the optimal tax policy is more than six times larger in the endogenous model compared to the exogenous model ( $1.8\%$ ).

Figure 1 plots the life cycle profiles for the exogenous model under the baseline-fitted US tax policy and the optimal tax policy. Adopting the optimal tax policy in the exogenous model causes a decrease in the tax on capital which decreases the implicit tax on younger labor income. The decrease translates into younger agents working more under the optimal tax policy. The changes in the consumption and savings profiles are governed by the change in the after tax return to capital. Adopting the optimal tax policy has two counteracting effects on the after tax return to capital. First, the pre-tax return to capital decreases. Second, the tax on capital returns decreases which increases the after-tax return. The first effect is consistent for all individuals. Since the baseline-fitted US tax policy is progressive and the optimal tax policy is flat the second effect is larger for individuals with higher income. Overall, the second effect dominates for most individuals and their after-tax return to capital increases causing the consumption profile to be steeper. The change in the consumption profile is more pronounced for middle-aged individuals with higher incomes since they experience the largest decrease in the tax on capital. Additionally, these higher income individuals respond to the larger drop in the tax on capital by holding more assets.

Since adopting the optimal tax policy in the endogenous model increases the tax on capital the changes in the life cycle profiles are different compared to the changes in the exogenous model. The larger tax on capital implicitly taxes young labor income at a higher rate. Therefore, in response to adopting the optimal tax policy in the endogenous model individuals shifts hours worked from earlier to later years. In the endogenous model adopting the optimal tax policy causes agents to change their labor supply not only on the intensive margin but also to choose to retire one year later. The higher tax on capital translates into a lower after-tax return to capital which causes a flattening of the consumption profile. Prior to retirement, agents choose to hold less savings under the optimal tax policy since the tax on capital is larger. However, since they choose to postpone retirement until after the normal retirement age they receive a lump sum benefit equal to the missed social security payment. This lump sum transfer results in a higher level of post-retirement savings under the optimal tax policy.

6 Conclusion

In this paper I computationally solve for the optimal capital and labor tax rates in separate life cycle models with exogenously and endogenously determined retirement. I find that including endogenous retirement causes a large increase in the optimal tax on capital. In the model with exogenous retirement the optimal tax policy includes a $24.1\%$ tax on labor income and a $17.6\%$ tax on capital. In the model with endogenous retirement the optimal tax policy includes a $20.6\%$ tax on labor income and a $31.8\%$ tax on capital income. Relaxing the simplifying assumption that retirement is exogenously determined causes a seventy five percent increase in the optimal tax on capital. Furthermore, I find that the welfare cost of adopting the lower optimal tax on capital from the exogenous model in the model with endogenous retirement, which calls for a higher tax on capital, is equivalent to one percent of total lifetime consumption. These result indicates that this simplifying assumption of exogenously determined retirement has large consequences when solving for optimal tax policy.

Including endogenously determined retirement causes the optimal tax on capital to increase because it affects the aggregate Frisch elasticity in two ways. First, it increases the aggregate responsiveness of hours to changes in the return to labor. Therefore, the government would prefer to rely more heavily on a capital tax as opposed to a labor tax in order to minimize the distortions induced by the tax policy. Second, including a retirement decision causes individuals to be relatively more responsive to changes in the after-tax wage when they are old. The government would like to condition labor income taxes on age to tax agents when they are older and more responsive at a relatively lower rate. Since age-dependent labor income taxes are unavailable, the government uses a higher tax on capital to mimic such a tax policy.

Economists are constantly trying to balance realism and tractability when they model the economy. In this paper I demonstrate that the simplifying assumption of exogenously determined retirement has a sizable impact on optimal tax policy. Therefore, future work that examines optimal taxation in a life cycle model should incorporate endogenous retirement. Additionally, most of the previous work analyzing optimal taxation assumes that the social security program is outside of the control of the government. Given the large impacts of endogenous retirement on optimal tax policy it seems that there maybe welfare gains from optimizing both the tax policy and social security program together as opposed to optimizing them in isolation. I leave this exercise for future research.

Bibliography

Altonji, Joseph G.

"Intertemporal Substitution in Labor Supply: Evidence from Micro Data," The Journal of Political Economy, 1986, 94 (3), S176-S215.