A Dynamic Factor Model of the Yield Curve as a Predictor of the Economy*
Keywords: Forecasting, business cycles, dynamic factor models, markov switching.
Abstract:
In this paper, we propose an econometric model of the joint dynamic relationship between the yield curve and the economy to predict business cycles. We examine the predictive value of the yield curve to forecast future economic growth as well as the beginning and end of economic recessions at the monthly frequency. The proposed nonlinear multivariate dynamic factor model takes into account not only the popular term spread but also information extracted from the level and curvature of the yield curve and from macroeconomic variables. The nonlinear model is used to investigate the interrelationship between the phases of the bond market and of the business cycle. The results indicate a strong interrelation between these two sectors. The proposed factor model of the yield curve exhibits substantial incremental predictive value compared to several alternative specifications. This result holds in-sample and out-of-sample, using revised or real time unrevised data.
JEL Classification: C32, E32, E44
1 Introduction
The yield curve has become one of the most popular leading indicators of economic activity, as there is substantial evidence of systematic association between changes in its slope and the future state of the economy. Under the liquidity preference theory, investors require a premium for acquiring long maturity bonds rather than the risk-free, short-term rate. Thus, the yield curve is generally upward sloping. This is especially the case in the end of recessions and at the early stages of economic expansions, when short term interest rates are at relatively low levels. On the other hand, the slope of the curve tends to flatten out or become inverted towards the middle and end of expansions. In addition, according to the expectation theory, long-term rates reflect market expectation for future short-term rates. Hence, a flat or inverted curve may indicate that the market expects a fall in future interest rates given the prospect of future weak economic activity.
There is a large literature that investigates prediction of future economic activity using the term structure of interest rates. See, for example, Harvey (1988, 1989), Stock and Watson (1989), Estrella and Hardouvelis (1991), Estrella and Mishkin (1998), Chauvet and Potter (2002, 2005), Hamilton and Kim (2002), Wright (2006), and Ang, Piazzesi and Wei (2006), among many others, or Stock and Watson (2003) for an extensive survey of this literature. In general, linear regression models are used to forecast the growth rate of economic activity and discrete choice models such as probit or logit specifications to predict the probability of a recession. While the term structure is predominantly used in these models, recent work by Ang, Piazzesi, and Wei (2006) show that the information across the entire yield curve can result in more efficient and accurate forecasts of real economic growth.
This paper proposes an econometric model of the joint dynamic relationship between the yield curve and the economy to predict business cycles. In contrast with previous literature, we examine the predictive value of the yield curve to forecast future economic growth as well as the beginning and end of economic recessions at the monthly frequency. In addition, the proposed dynamic latent bi-factor model takes into account not only the term spread but also the information extracted from other components of the yield curve and from real economic activity. In particular, we use empirical time series proxies of the level, slope, and curvature of the yield curve, from which we extract a latent factor to predict the economy.3 We also consider a second latent factor constructed using monthly industrial production, which is the most commonly used measure of economic activity at the monthly frequency, to represent the real sector. These two factors are then simultaneously estimated from the observable variables and from their relationship with each other. Since some changes in the yield curve are cyclical and potentially related to future economic expansions and recessions, we allow the latent factors to follow different two-state Markov switching processes.4 The resulting cyclical phases of the bond market and the economy are linked through the dependence structure of the factors in the transition equations.5
The proposed framework has several advantages over previous literature on forecasting recessions using the yield curve. First, our framework parsimoniously incorporates comprehensive information from the components of the yield curve and from the economy in a parsimonious setting. An important feature of this model is that the nonlinear combination of several variables mitigates the instability of each individual series.
Second, the methodology takes into consideration the interrelationship between the yield curve and economic activity through the dynamic factors and the Markov processes. In particular, the Markov probabilities allow analysis of the interactions between the yield curve and the phases of the business cycle. Since bond market phases anticipate the phases of business cycles with a variable lead, rather than pre-imposing a structure to their linkages, the proposed flexible framework enables us to study their specific lead-lag relation over each one of the expansions and recessions that occurred in the US in the last 40 years. As the results show, this information turns out to be very important in predicting the onset of business cycle phases.
Finally, the nonlinearities in the form of switching states can capture changes in the stochastic structure of the economy such as the possibility of recurrent breaks. Several recent papers have shown that the predictive content of the yield curve is not stable over time. In general, linear regression models that use output growth as the dependent variable indicate that the forecasting ability of the term spread has reduced since mid 1980s.6 Although the results from binary models of recession are less unambiguous, Chauvet and Potter (2002, 2005) find overwhelming evidence of breaks in the relationship between the yield curve and economic activity using Bayesian techniques to estimate probit models, and show that not taking them into account affect real time forecasts.7 Our models include the possibility of abrupt changes in the underlying series, based on the results of endogenous breakpoint tests.
We investigate the in-sample and out-of-sample forecasting performance of our extracted yield factor to future economic activity both in form of linear projections, as well as in terms of event timing - the beginning and end of business cycle phases. The analysis is performed using revised data and real time unrevised data. In addition to the proposed joint model of the yield curve and the economy, we also estimate for comparison a multivariate model in which only the information on the yield components are used to extract a single yield factor, linear models of the yield curve components, and probit models.
Our results point out to a strong correlation between the real economy and the bonds market. The yield factor extracted from the interrelationship between both sectors displays a better performance in anticipating economic recessions compared to alternative frameworks. In particular, the yield-economy factor predicts the beginning and end of all recessions (including the 2007-2009) in the sample studied with no false peaks or troughs and no missed turns - a perfect forecast score. An important feature of the model is its usefulness to predict not only the beginning but also the end of recessions. For example, the yield-economy factor model predicts in real time the end of the 2007-2009 recession as occurring in June 2009 with a lead of 18 months.8 We also evaluate the in-sample and out-of-sample forecasting performance of the proposed models and univariate alternatives in terms of calibration, resolution, and skill score. The yield-economy factor model is well calibrated and is the only one with positive skill score (i.e. it forecasts better than the benchmark constant forecast). In addition, the model displays the highest discrimination power, the lowest conditional and unconditional biases, and a better balance between accuracy and resolution, leading to a substantially smaller mean squared error compared to other models.
Finally, the forecasting performance of alternative models for future values of industrial production growth is also examined. The joint bi-factor model of the yield curve and the economy outperforms the alternative specifications. The model reduces the dimensionality of the information on the yield curve down to one state variable that leads to better predictions compared to a specification that uses the term spread or all three components of the yield curve in probit models or linear regressions.9 This result holds in-sample and out-of-sample, using both revised and real time data.
In summary, we find that the components of the yield curve have useful information to forecast recessions and expansions and future projections of industrial production growth. Although the popular term spread model and the probit model have a reasonable forecasting performance, the proposed factor model that use information of the components of the yield curve and the interrelationship between the bonds market and the economy exhibits better predictability of the beginning and end of recessions.
The paper is organized as follows. Section 2 introduces the data and the construction of the components of the yield curve. Section 3 discusses univariate Markov switching models and the multivariate dynamic factor models for the yield curve components. The proposed joint bifactor model of the bond market and the economy that allows for their interrelation is presented in Section 4. The estimation results are discussed in Section 5. Sections 6 and 7 present, respectively, the turning point forecasting evaluation and the projection predictive performance of the proposed model compared to alternative specifications. Section 8 concludes.
2 The Data
The series on U.S. Treasury yields with maturities of 3 months, 2 years, and 10 years are used to construct the three components of the yield curve. We use data compiled and made publicly accessible by Gurkaynak, Sack, and Wright (2007). Monthly yields are obtained by taking the average of daily
yields. The data are available from 1971:08 to 2007:12. The empirical proxies used to represent the level, the slope, and the curvature of the yield curve are then constructed as follows: the level factor (![]() ) is computed as the arithmetic average of the 3-month, 2-year, and 10-year bond yields; the curvature (
) is computed as the arithmetic average of the 3-month, 2-year, and 10-year bond yields; the curvature (![]() )is
measured as two times the 2-year bond yield minus the sum of the 3-month and 10-year bond yields; and the slope of the yield curve (
)is
measured as two times the 2-year bond yield minus the sum of the 3-month and 10-year bond yields; and the slope of the yield curve (![]() ) corresponds to the
difference between the 10-year bond rate and the 3-month T-bill rate. These empirical proxies are highly correlated with estimated latent factors from models of the entire yield curve as shown in Ang and Piazzesi (2003), Diebold and Li (2006), and Diebold, Rudebusch, and Aruoba (2006).
) corresponds to the
difference between the 10-year bond rate and the 3-month T-bill rate. These empirical proxies are highly correlated with estimated latent factors from models of the entire yield curve as shown in Ang and Piazzesi (2003), Diebold and Li (2006), and Diebold, Rudebusch, and Aruoba (2006).
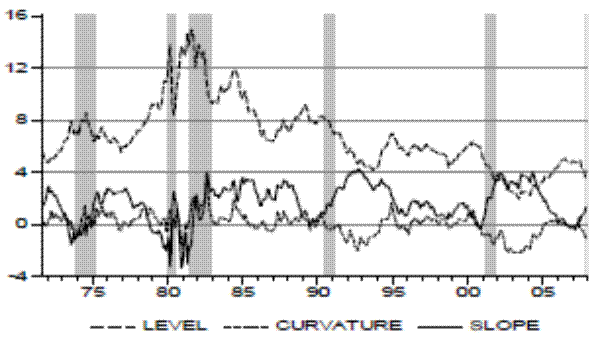
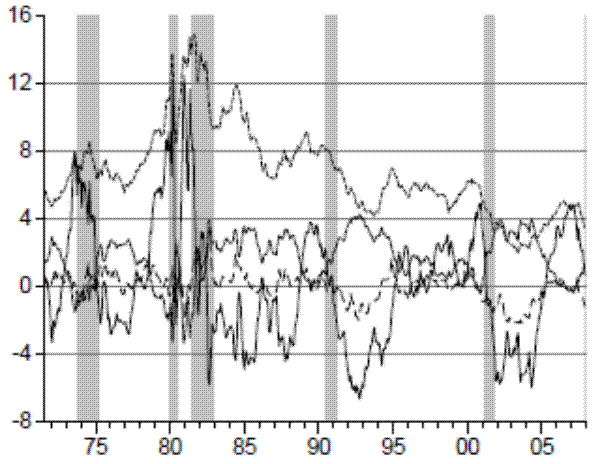
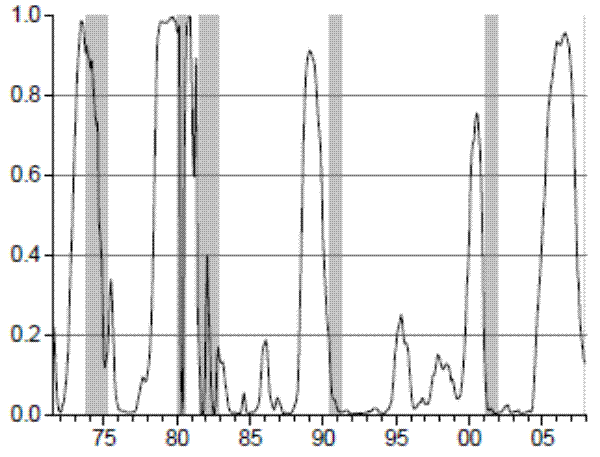
Figure 1 plots the level, curvature, and slope of the yield curve with the shaded regions indicating the recession periods as dated by the National Bureau of Economic Research (NBER). The level is highly persistent and it is often interpreted as the long run component of the yield curve. The curvature and the slope are considered the medium run and the short run components, respectively. Diebold and Li (2006) and Diebold, Rudebusch and Aruoba (2006) show that the level is closely associated with inflation expectations, while the slope is related to future economic activity. The curvature is not generally associated with any specific macroeconomic variable. However, notice that the curvature displays correlation with the NBER-dated recessions, although weaker than the term spread (slope).
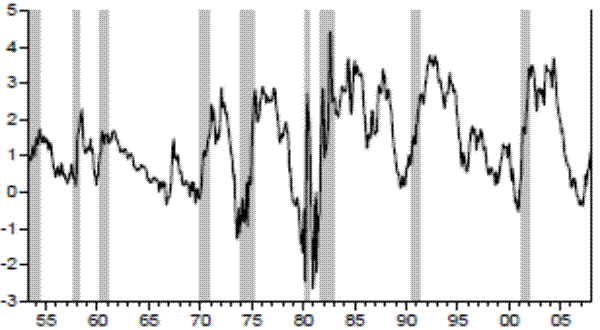
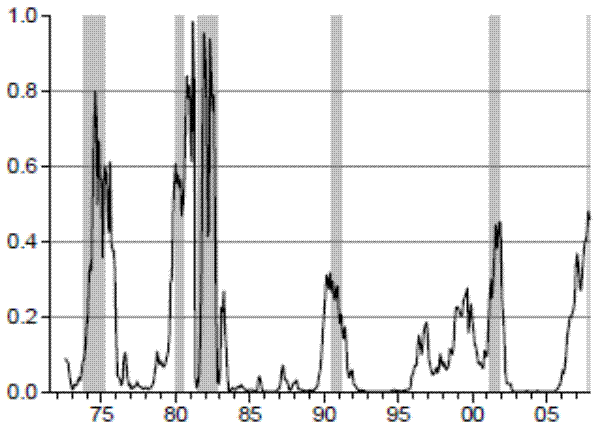
The slope of the curve is considered the best predictor of recessions among the yield curve components. As it can be observed, the yield curve has inverted before five out of six recessions in the sample as dated by the NBER. However, as found by several other authors, the slope did not turn negative before the 1990 recession. It is interesting to investigate the power of the slope in predicting previous recessions as well. Although data for the other series are not available before 1971, the slope series goes back to 1953:01 (Figure 2). During the period between 1953 and 1971 there were four recessions as dated by the NBER.10 The term spread had a much less clear-cut relationship with business cycles during this time. In particular, the slope only inverted before the 1969-1970 recession and did not become negative before the 1957-1958 and the 1960-1961 recessions. In addition, the slope inverted in 1966-1967 and no recession followed. It is important to keep this performance in mind, as it illustrates the instability of the term spread in predicting recessions over time. We further investigate this for our period in the next section.
Rather than relying on only one variable, we use the empirical proxies of level, curvature, and slope of the yield curve to extract the yield factor. The economic factor is built from the monthly industrial production index, obtained from the FRED system of the Federal Reserve Bank of St. Louis.
The series is transformed by taking log growth from t-12 to t expressed at the monthly frequency, i.e.
![]() . For consistency, we use the same sample as available for the yield curve data.
. For consistency, we use the same sample as available for the yield curve data.
3 Univariate and Multivariate Nonlinear Single-Factor Models of the Yield Curve
We first specify univariate Markov switching models for each of the components of the yield curve, and a multivariate unobserved dynamic factor model of the yield curve that summarizes the information content of its level, curvature, and slope into a single factor. These models of the yield curve without linkage to the real economy are going to be used for comparison with our joint model of the yield curve that includes an economic factor as well.
3.1 Univariate Nonlinear Models of the Yield Curve
Before October 1979, the Federal Reserve (Fed) used to target bank reserves in the financial system. A measure of the tightness of monetary policy was the changes in the federal funds rate. In October 1979, the Federal Reserve Bank adopted new operating procedures shifting their emphasis from targeting the federal funds rate to the quantity of non-borrowed bank reserves in order to achieve the desired rates of growth in the monetary aggregates. As a consequence, there was a widening of the range of the federal funds rate. The funds rate rose drastically from 11.4% in September to 13.8% by the end of 1979, and peaked at 19.1% in June 1982. By the end of 1982, the funds rate had then decreased to 8.9%. The wide fluctuations in the average federal funds rate between 1979 and 1982 were associated with a double dip recession and also a sharp fall in inflation. The policy actions by the FOMC not only corresponded to a change in the way monetary policy was conducted, but also engendered potential structural breaks in interest rate dynamics and in its relationship with the real economy.
We test for potential breaks in each component of the yield curve series and in the growth rate of industrial production using the asymptotically optimal tests developed by Andrews (1993), Andrews and Ploberger (1994), and the sequential procedure of Bai (1997b) and Bai and Perron (1998) for multiple breaks. Since we examine the dynamics of each of its components, the tests allow us to investigate the source of the potential breaks in the yield curve. We consider two separate hypotheses. First, we test for the possibility of a break in the variance of the series assuming that the mean has remained constant. However, the results of this test would be unreliable if there was a break in the parameters of the underlying model. In this case, evidence of a break in the volatility from this test could be due to neglected structural change in the conditional mean of the series. In order to account for this, we also test for a break in the conditional mean of the series, allowing for changing variance.11
The tests indicate strong evidence of several breaks in the components of the yield curve. First, all three series display a break in volatility between 1980:05 and 1981:08. In the case of the term spread, there is also strong evidence of a break in its mean in this period. Several papers have found instability in the predictive power of the yield curve, particularly with respect to the 1990-1991 recession.12 We find significant structural breaks in the mean of both the curvature and the level series around 1990:06 and 1990:12. In addition, the variance of the level also displays a break in 1990:11. On the other hand, the tests applied to the growth rate of industrial production find a break in its volatility in 1983:12. These results are summarized in Table 1.
Based on this evidence, we specify a variant of CityplaceHamilton's univariate Markov switching model that takes into account changes in the mean and variance before and after the breakpoints in addition to the switching in the parameters related to cyclical changes in the components of the yield curve or industrial production.
Let
![]() represent each of the components of the yield curve, which is modeled as the sum of two integrated components: a Markov trend term,
represent each of the components of the yield curve, which is modeled as the sum of two integrated components: a Markov trend term,
![]() , and a Gaussian component,
, and a Gaussian component,
![]() , as in CityplaceHamilton (1989):
, as in CityplaceHamilton (1989):
| (1) |
The Markov trend is given by,
| (2) |
where S
| (3) |
where e
| (4) |
for
| (5) |
| (6) |
| (7) |
where the state variables,
The models produce probabilities of low and high states, which will be used to evaluate the ability of the models to anticipate business cycle turning points in section 6. Notice, however, that CityplaceHamilton's model decomposes
![]() into the sum of two unit roots processes that are not identifiable from each other. Thus, in the presence of structural breaks, both terms confound low and high phases with the
breaks themselves.
into the sum of two unit roots processes that are not identifiable from each other. Thus, in the presence of structural breaks, both terms confound low and high phases with the
breaks themselves.
There are different ways to handle the problem of structural breaks in Markov switching models. The venue that we pursue is to augment the model by allowing
![]() to follow two independent two-state Markov processes: one that captures recurrent switches between low and high values of the series and the other that captures permanent
structural breaks. The Markov process for detecting structural break has a switching drift and variance:
to follow two independent two-state Markov processes: one that captures recurrent switches between low and high values of the series and the other that captures permanent
structural breaks. The Markov process for detecting structural break has a switching drift and variance:
3.2 The Multivariate Nonlinear Single-Factor Model of the Yield Curve
We combine the information from each one of the components of the yield curve in a single factor, using a dynamic factor model with regime switching. Let ![]() be the
be the ![]() vector of observable variables, which consists of the empirical proxies of the level (
vector of observable variables, which consists of the empirical proxies of the level (![]() ), slope (
), slope (![]() ) and the curvature (
) and the curvature (![]() ) of the yield curve. The measurement equations are given by,
) of the yield curve. The measurement equations are given by,
| (8) |
where,
unobservable yield factor can be written as:
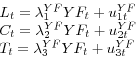 |
(9) |
where
We assume that the dynamics of the common yield curve factor can be represented by an autoregressive process whose intercept is subject to discrete changes depending on the state of the bond market cycle:
| (10) |
where
In order to account for the potential remaining variation in the three yield curve factors not shared by all of them simultaneously, we model the idiosyncratic components as the following autoregressive processes:
| (11) | ||
4 The Multivariate Joint Bi-Factor Model of the Yield curve and the Economy
We propose a unified model of bond market cycles and economic cycles that takes into account their dynamic interrelationships. The state space model is now augmented to include two unobserved factors, representing the yield curve and the economy. The latent yield curve factor,
![]() , is extracted from the empirical proxies for the level, the slope, and the curvature of the yield curve, as before. The industrial production series is used to construct the
latent economic factor at the monthly frequency,
, is extracted from the empirical proxies for the level, the slope, and the curvature of the yield curve, as before. The industrial production series is used to construct the
latent economic factor at the monthly frequency,
![]() .
.
The model is cast in state-space, which allows us to simultaneously estimate the two unobservable factors as well as their intertemporal relationship. The interactions are investigated by specifying the factors as following a vector autoregressive system. The measurement equations still take the following form:
| (12) |
but now
| (13) |
where
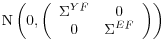 ,
,
Each factor follows an unobservable autoregressive process whose intercept is a function of two distinct Markov variables,
![]() for the yield factor and
for the yield factor and
![]() for the economic factor. By allowing for potentially independent Markov processes for the two factors, we do not restrict the latent variables representing bond markets and the
real economy to switch between phases at the same time, which would be an unreasonable assumption given that the yield curve anticipates the business cycle. The transition equations are:
for the economic factor. By allowing for potentially independent Markov processes for the two factors, we do not restrict the latent variables representing bond markets and the
real economy to switch between phases at the same time, which would be an unreasonable assumption given that the yield curve anticipates the business cycle. The transition equations are:
| (14) |
The coefficients of the 2x2 transition matrix,
![\Phi =\left[\begin{array}{cc} {\phi ^{YF} } & {\theta ^{YF} } \\ {\theta ^{EF} } & {\phi ^{EF} } \end{array}\right]](img76.gif) , capture the lead-lag relationship between the yield factor and
the economic factor, and we also assume that the variance covariance matrix of the common shocks to each factor,
, capture the lead-lag relationship between the yield factor and
the economic factor, and we also assume that the variance covariance matrix of the common shocks to each factor,
![\alpha _{S_{t} } =\left[\begin{array}{c} {\alpha _{0}^{YF} (1-S_{t}^{YF} )+\alpha _{1}^{YF} S_{t}^{YF} } \\ {\alpha _{0}^{EF} (1-S_{t}^{YF} )+\alpha _{1}^{EF} S_{t}^{EF} } \end{array}\right]](img78.gif) , switch between states, governed by the transition probabilities of the first order two-state
Markov processes,
, switch between states, governed by the transition probabilities of the first order two-state
Markov processes,
We estimate all parameters and factors simultaneously in one step. The joint modeling and estimation has the advantage that it does not carry out parameter estimation uncertainty associated with extracting the factors to the VAR model that specifies the dynamic relation between the factors, compared to two-step procedures. We first cast the models in state space form and then combine a nonlinear discrete version of the Kalman filter with placeCityHamilton's (1989) algorithm. The increasing number of Markov cases is truncated at each iteration using an approximation suggested by Kim (1994). The nonlinear Kalman filter is initialized using the unconditional mean and unconditional covariance matrix of the state vector. A nonlinear optimization procedure is used to maximize the likelihood function, which is obtained as a by-product of the probabilities of the Markov states. The predictions of the unobserved factors and of the probabilities of the Markov states are obtained as final pass of the nonlinear filter based on the maximum likelihood estimates.
5 Estimation Results
We estimate our proposed dynamic single factor and bi-factor models (models 5 and 6) and four alternative specifications for comparison (models 1 to 4), in addition to the benchmark model that produces the forecast object for the turning point analysis. The models are:15
Benchmark Model - univariate Markov switching model for industrial production.
Model 1 - univariate Markov switching model for the level of the yield curve.
Model 2 - univariate Markov switching model for the curvature of the yield curve.
Model 3 - univariate Markov switching model for the slope of the yield curve.
Model 4 - probit model of the level, curvature, and slope of the yield curve.
Model 5 - multivariate Markov switching single-factor model for the level, curvature, and slope of the yield curve.
Model 6 - multivariate Markov switching bifactor model for the level, curvature, and slope of the yield curve, and for the economy.
5.1 Benchmark Univariate Model of the Economy
A two-state Markov switching model as described in section 3.1 is fitted to changes in the log of industrial production,
![]() :
:
| (15) |
where the state variable
The estimated probability of a recession (regime 0) at time t conditional on the full sample information ![]() , denoted
, denoted
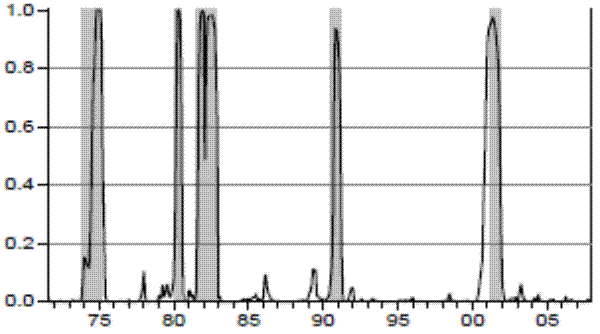
![]() , is plotted in Figure 3 along with recessions as dated by the NBER (shaded area). The estimated probability of recession captures the NBER chronology very closely.
During periods in which the NBER classifies as expansions the probability of a recession is close to zero. At around the time where the NBER recession starts, the probability of a recession rises substantially and remains high until around the end of the recession period.
, is plotted in Figure 3 along with recessions as dated by the NBER (shaded area). The estimated probability of recession captures the NBER chronology very closely.
During periods in which the NBER classifies as expansions the probability of a recession is close to zero. At around the time where the NBER recession starts, the probability of a recession rises substantially and remains high until around the end of the recession period.
Since we are interested in dating turning points, we need to use a rule to convert the recession probabilities into a 0/1 variable that defines whether the economy is in an expansion or recession regime at time t. In particular, we assume that a business cycle peak
occurs in month ![]() if the economy was in an expansion in month t,
if the economy was in an expansion in month t,
![]() , and it entered a recession in
, and it entered a recession in ![]() ,
,
![]() . A business cycle trough occurs in month
. A business cycle trough occurs in month ![]() if the economy was in a recession in month t,
if the economy was in a recession in month t,
![]() , and it entered an expansion in month
, and it entered an expansion in month![]() ,
,
![]() .
.
This simple rule produces a monthly business cycle dating that closely matches the NBER dating. The phases of
![]() captures each of the NBER business cycle peaks and troughs in the sample with no false peaks and no missed signals. The average divergence between the six peaks from the NBER
and from the switching model applied to industrial production growth is approximately 1.5 months with a standard deviation of 2.9 months. Generally, the model tends to determine peaks at or after the ones established by the NBER with a discrepancy of one or two months. The only exception is for the
1973-1975 recession peak, for which the switching model dates the peak eight months after the NBER date. The troughs from the NBER and from the model applied to industrial production are dated even closer. Four out of the five recession troughs as dated by the model coincide with the troughs as
dated by the NBER. There is only one discrepancy of one month in the 1982 recession trough.
captures each of the NBER business cycle peaks and troughs in the sample with no false peaks and no missed signals. The average divergence between the six peaks from the NBER
and from the switching model applied to industrial production growth is approximately 1.5 months with a standard deviation of 2.9 months. Generally, the model tends to determine peaks at or after the ones established by the NBER with a discrepancy of one or two months. The only exception is for the
1973-1975 recession peak, for which the switching model dates the peak eight months after the NBER date. The troughs from the NBER and from the model applied to industrial production are dated even closer. Four out of the five recession troughs as dated by the model coincide with the troughs as
dated by the NBER. There is only one discrepancy of one month in the 1982 recession trough.
The phases of
![]() closely match the NBER business cycle phases, but the proposing dating has the advantage that it is readily available and can be estimated in real time, whereas the NBER dating
is generally available ex-post and with long delays. Since our main goal is to forecast business cycle turning points in real time, we use both the monthly business cycle dating from industrial production and the NBER dating as benchmarks for evaluation of the real time forecasting performance of
the models.
closely match the NBER business cycle phases, but the proposing dating has the advantage that it is readily available and can be estimated in real time, whereas the NBER dating
is generally available ex-post and with long delays. Since our main goal is to forecast business cycle turning points in real time, we use both the monthly business cycle dating from industrial production and the NBER dating as benchmarks for evaluation of the real time forecasting performance of
the models.
5.2 Univariate and Multivariate Single-Factor Yield Models
Table 3 shows the maximum likelihood estimates of the univariate Markov switching models and the multivariate nonlinear dynamic single factor model of the yield curve. The coefficients of the Markov states are statistically significant in all models.
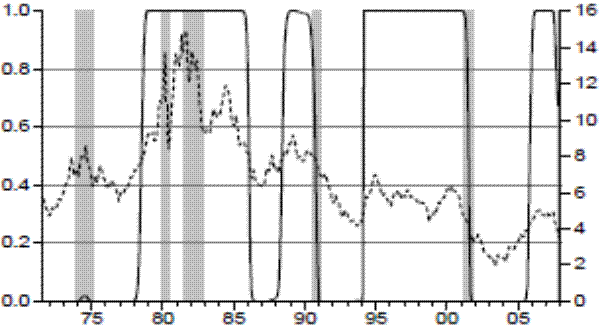
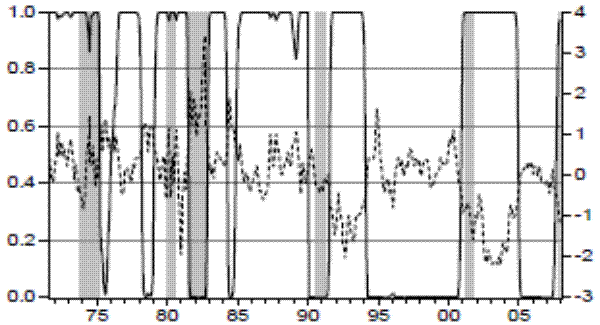
The level, curvature, and slope of the yield curve switch between low and high values but these values are not stable over time. In particular, the level of the yield curve shows striking changes pre and post 1990. The high mean value was 10.1% whereas the one for the low mean state was 5.5% before 1990. After 1990, the mean in both states decreases substantially, with the high mean equal to 5.4% and the low mean equal to 3%. This can be visualized in Figure 4, which plots the level of the yield curve and the smoothed probabilities of the high level state. Notice that the high level state is the one that predicts future recessions - the probabilities indicate that this state generally occurs from the middle of an expansion until a couple of months before the beginning of recessions. The exception is during the period of the Great Inflation between 1978 and 1985, in which the probabilities remain high even during recessions. The estimated probabilities of the Markov states for the level are consistent with the dynamics of inflation expectations over the business cycle.
The curvature of the yield curve also shows changes before and after 1990. Before 1990, the high and low values were around 1.3% and 0.2%, respectively. After this point, the high mean decreases to 0.3%, whereas the low mean of the curvature becomes negative, decreasing to -1.3%. Figure 5 shows the probabilities of low mean state and the curvature series. In contrast with the level, it is the low mean state of the curvature that is associated with economic recessions. In particular, the probabilities of low mean increase (as the curvature decreases or becomes negative) right before or during recessions. Notice that after 1990-1991 and the 2001 recessions, the probabilities remain high even after the recessions were over and until the middle of the subsequent expansions. This and other features of the curvature make it a less reliable leading indicator of recessions, as discussed in section 6.
The dynamics of the slope of the yield curve - the term spread - has also changed significantly over time. The break date for this series is earlier than for the other two components, occurring in 1980-1981. We find that both the mean and variance of the slope display a break around this period. Prior to this date, the high mean state was around 2% and the low mean state was negative, at -1%. Differently from the other two components, both the high and low state mean values have increased after the break: the high mean to 3%, and the low mean became positive at 0.9% in the posterior period. That is, since 1980-1981 a flat curve -rather than an inversion of the curve - signals recession. This can be seen in Figure 6, which plots the smoothed probabilities of the low (flat or inverted) slope state with the extracted slope series. The term spread displays a distinct business cycle pattern - the probabilities of flat or inverted slope generally rise to around 100% towards the middle to the end of economic expansions and fall to values around 0% during recessions. The fact that the low mean state has turned positive since 1980-1981 illustrates the uncertainty on inferring subsequent recessions from changes in the term spread. For example, there were some instances - such as in 1995 or in 1998, in which the slope became flat but no recession followed. This will be discussed in more detail in section 6.
There is a large body of literature documenting changes in the volatility of the placecountry-regionU.S. economy. In particular, McConnell and Perez-Quiros (2000) find evidence of a break towards more stability in the economy since 1984. We find that the level and slope of the yield curve also display an increased stability. The variance of the level fell to ¼ of its value after 1990, while the variance of the slope decreased to half its value after 1982. On the other hand, we do not find a significant change in the volatility of the curvature.
The last column of Table 3 shows the estimated coefficients from the multivariate dynamic single factor model of the yield curve. The model extracts an indicator from the common information underlying the level, curvature, and slope of the yield curve. An important feature of this model is that the nonlinear combination of several variables mitigates the instability of each individual series. The resulting yield factor does not display structural breaks. The high mean state is 0.6 and the low mean state is negative, -0.4. Notice that the low mean state is lengthier than the high mean state, as implied by the larger transition probability of the former. The factor loadings measure the sensitivity of the series to the extracted yield curve factor. The loadings are negative for the curvature and the slope and positive for the level. This implies that high values of the yield factor are associated with future recessions.
Figure 7 plots the smoothed probabilities of high state for the yield factor. The probabilities consistently rise above 50% a couple of years before economic recessions - in the middle of expansions - and remain high until the beginning of recessions. Notice that the probabilities were noisy in the period between 1994 and 2001 as did the probabilities of the individual yield components described above. In fact, it would have been difficult to interpret movements of the yield curve factor at that time since it signaled the possibility of future recessions around 1995 and 1998 (probabilities increased above 80%) but no recession followed these high values of the yield curve factor. During this period, the level of the yield curve increased and the slope became flat.16 Thus, this model is still not able to extract unambiguous future recession signals when the movements in the components of the yield curve are subtle.
5.3 Multivariate Joint Bi-Factor Model of the Yield Curve and the Economy
We propose a bi-factor model that takes into account the dynamic interrelationship between the bonds market and the real economy. This model uses the components of the yield curve to extract the yield factor as before, but now it is estimated conditional on its relationship with the economic factor - which is extracted using information from the growth rate of industrial production.
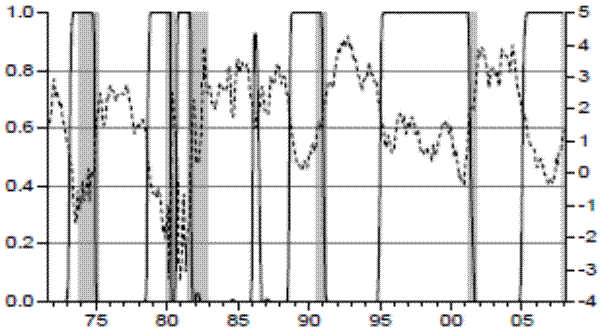
Table 4 shows the maximum likelihood estimates.17 The yield factor extracted from this framework shares some similarities with the single yield factor that uses information on the yield curve only. Most parameters are close in value. In particular, the factor loadings have the same signs - positive for the level and negative for the curvature and slope, implying that the high state of the yield-economy factor is associated with future economic recessions. Figure 8 plots the extracted yield-economy factor and its components along with the NBER-dated recessions. The yield-economy factor, which is a nonlinear combination of the yield components, is found to be stationary and with more pronounced cyclical fluctuations than its individual components. These features substantially increase the ability of the factor to signal future recessions, as will be discussed in more detail in the next section. Notice that the yield-economy factor rises substantially around two years before the beginning of recessions. This can also be observed in the dynamics of the smoothed probabilities of high value for the yield-economy factor, as shown in Figure 9. Each one of the six recessions in-sample and out-of-sample - including the most recent one that started in 2007:12 - is preceded by a rise in the probabilities of high yield factor above 50%. At around the onset of recessions the forward-looking probabilities - and the yield factor - fall indicating the future end of the recessions.
The main difference between the yield-economy factor extracted from the joint model of the yield curve components and economic information and the factor extracted only from the yield components is that the smoothed probabilities of high state from the yield-only factor remain high and display two false signals during the mid-1990s, while the ones from the yield-economy factor do not give any false signals during this period and only increase before the 2001 recession. Thus, by including the relationship between the bonds market and the real economy, we obtain a factor that more accurately anticipates economic recessions.
The last column of Table 4 reports the parameter estimates for the economic factor. The Markov switching coefficients are highly significant. The two states for the economic factor share very similar patterns to the phases of growth in industrial production (Table 2), with a negative mean growth rate in state 0 and a positive one in state 1. However, the two states do not have a symmetric duration, with expansions lasting longer than recessions.
The relationship between the yield factor and the economic factor is represented by the coefficients of the vector autoregression in the transition equations (14), ![]() =
=
![\left[\begin{array}{cc} {\phi ^{YF} } & {\theta ^{YF} } \\ {\theta ^{EF} } & {\phi ^{EF} } \end{array}\right]](img96.gif) . The signs of the coefficients are as expected. The lagged yield factor
is negatively correlated with the current economic factor (
. The signs of the coefficients are as expected. The lagged yield factor
is negatively correlated with the current economic factor (
![]() ). That is, high values of the lagged yield factor are associated with low future values of the economic factor. On the other hand, the economic factor is positively
associated with future values of the yield factor (
). That is, high values of the lagged yield factor are associated with low future values of the economic factor. On the other hand, the economic factor is positively
associated with future values of the yield factor (
![]() ). Notice that these coefficients reflect the average relationship over the states. The lead-lag dynamics of the bonds market and the real economy is better depicted by
studying the linkages between their phases. This can be directly examined within our proposed nonlinear framework that allows for two distinct (but potentially dependent) Markov processes to represent the yield curve cycle and the business cycle.
). Notice that these coefficients reflect the average relationship over the states. The lead-lag dynamics of the bonds market and the real economy is better depicted by
studying the linkages between their phases. This can be directly examined within our proposed nonlinear framework that allows for two distinct (but potentially dependent) Markov processes to represent the yield curve cycle and the business cycle.
6 Event Timing Forecast - Turning Point Analysis
The proposed Markov switching models serve as important tools for event timing analysis, which is examined in this section. The forecast objects are turning points of business cycles - the beginning (peaks) and end (troughs) of economic recessions. Once the economy enters a recession (or in an expansion) its end is certain, but not the timing in which it will occur.
Tables 5 and 6 report turning point signals and errors of our proposed models and the univariate alternatives in signaling recessions, as dated by the benchmark model of industrial production (section 5.1) and by the NBER dating. The turning points for all models are determined according to the simple rule based on the full sample probabilities of the Markov states as described in section 5.1.
In addition to in-sample turning point forecasts, we also test the ability of the models to forecast the last two recessions out-of-sample using unrevised real time data. In particular, we estimate the models up to 1999:01 and recursively re-estimate them out-of-sample until 2007:12. The results are shown in Tables 5, 6, 7, and 10.
The level of the yield curve (Model 1) misses 3 out of 5 peaks and 3 out of 4 troughs in-sample, while the curvature of the yield curve (Model 2) misses 2 peaks and 3 troughs in-sample. Note that the probabilities of a recession from the level series remained above 50% from 1994 to 2001, giving very mixed signals of a recession since the early stages of the longest expansion in the country-regionplaceU.S. history. This is related to the fact that the level series decreased substantially in the last two decades, which contributes to confound the low and high state phases compared to previous decades. The worst performance is from model 2. In addition to missing many turning points, the curvature also signals 2 false peaks and 2 false troughs. As it can be seen in Figure 5, these false signals took place in 1976-1978 and in 1984-1989. The forecasting performance of Models 1 and 2 is also poor out-of-sample, with the level missing 1 out of 2 peaks and the curvature missing 1 out of 1 recession trough.
As it is found in the literature, the term spread does well in forecasting business cycle turning points (Model 3), signaling all troughs and peaks in-sample. However, its performance is not as good out-of-sample, missing 1 out of 2 peaks and 1 out of 1 trough. In addition, it falsely signals a peak and trough in-sample, in 1985-1986, and gives very mixed signals for the 2001 recession. As for the model for the level, the smoothed probabilities of recession from the term spread rose above 50% since 1995 and remained high until the beginning of the recession in 2001, six years later. The reason for this uncertainty can be visualized in Figure 6. The slope of the curve became flat from 1995 to 1999, but it only inverted in 2000. If this model were to be used to forecast recession at that time, there would certainly be large uncertainty on whether and when the economy would be heading to a recession during these six years, since prior to this period the spread identified recessions with an average lead of two years.
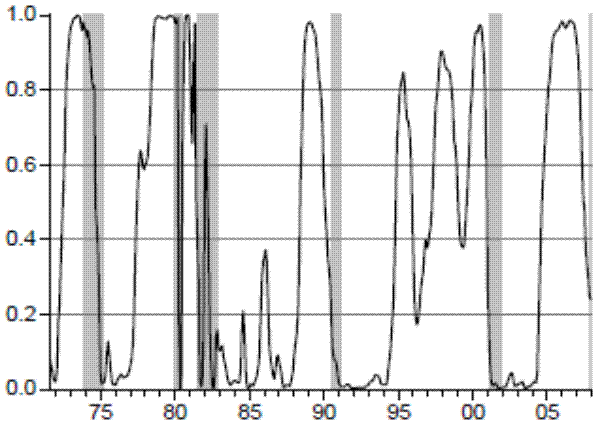
The probit model of the yield slope is a popular framework to forecast recessions. Recent literature has shown, however, the predictive power of the yield curve has decreased over time. Chauvet and Potter (2002, 2005) relate this evidence to the presence of structural breaks in the relationship between the yield curve and the economy. Figure 10 plots the probabilities of recessions from the probit specification (Model 4). As it can be seen in Figure 10 and Tables 5 and 6, the probit specification signals all peaks and troughs before the 1990 recession, but misses all business cycle turning points afterwards, in-sample and out-of-sample. The probabilities of recession do not rise above the 50% threshold before or during the last three recessions.
As shown in Tables 5 and 6, Models 5 (single yield factor) and 6 (yield-economy factor) signal all peaks and troughs in-sample and out-of-sample. The advantage of our proposed models is that it combines information from the level, curvature, and slope of the yield curve and filter out idiosyncratic movements in these components that are not common to all. The resulting factors are improved leading indicators of the economy - especially the one obtained from Model 6, which in addition to the yield components uses information on the lead-lag relationship between the yield curve and the real economy.
Model 5 correctly signals out-of-sample the 2001 recession with a lead of 15 months. However, the in-sample probabilities of recession increase above 50% in 1995-1996 and again in 1997-1998 (Figure 8). Thus, as Models 1 and 3, the single factor model that uses information from the three yield components still does not correctly filter the information from the flat yield curve from 1994 on.
On the other hand, Model 6 has a striking performance, with a perfect forecast score (i.e, zero turning point errors, Table 6). It anticipates all peaks and troughs in-sample and out-of-sample. The average lead for detecting peaks is 18 months and for troughs is 16 months, respectively. In addition, it does not give any false signals, even when the yield curve turns flat and no recession follows as in the mid-1990s. Finally, Model 6 (and Model 5) not only signals the beginning of the 2007 recession out-of-sample, it has already identified its end (probabilities of recession fell below 50%), which none of the alternative models have.18
Tables 7, 8, and 9 compare the forecasting performance of the alternative models in predicting business cycle turning points using different measures. Generally, the accuracy (or calibration) of probability to forecast the occurrence of a binary event is evaluated by the match between forecasts and realizations. Resolution (or discrimination) is another important measure of probability forecast performance, which refers to the ability of forecasts to discriminate states with relatively high conditional probabilities of the event from states with relatively low conditional probabilities. Finally, a popular test is the forecast skill, which refers to the accuracy of forecasts relative to a benchmark forecast. There are a number of different measures of accuracy, resolution, and skill, but most are based on a probability counterpart of the mean squared error. We evaluate the probability forecasts using the Quadratic Probability Score (QPS) (Brier and Allen 1951), which was popularized by the seminal work of Diebold and Rudebusch (1989), the Yates (1982) Decomposition, and the Murphy (1988) Skill Score.
The QPS is the most used probabilistic evaluation test. It measures the closeness of the probability forecasts from the realization of the event:
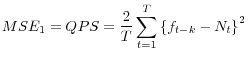 |
(16) |
where
Resolution or discrimination is not measured by the QPS, which also does not allow for evaluation of the probability of occurrence against non-occurrence. We use a test proposed by Yates (1982), which decomposes the covariance of the Mean Squared Error into calibration and resolution as:
| (17) |
Finally, we also use two measures of the skill score as proposed in Murphy (1988). First, the skill score based on the mean-squared-error measure of accuracy
![]() compares the accuracy of the forecast with the constant forecast of the mean of
compares the accuracy of the forecast with the constant forecast of the mean of ![]() :
:
| (18) |
where
| (19) |
where
Table 7 compares the accuracy of different models in predicting the NBER-dated recessions, using the Quadratic Probability Score. The tests were calculated for all horizons from 0 to 36 months. For conciseness, the table shows the forecast horizons in which the models perform best in-sample and out-of-sample.19 The level (Model 1) and the slope (Model 3) of the yield curve produce the most accurate forecasts at the 15-month horizon, the probit model (Model 4) at the 12-month horizon, while the curvature (Model 2), the yield factor (Model 5), and the yield-economic factor (Model 6) do best at the 22-month forecast horizon. The joint dynamic factor model of the yield and the economy (Model 6) displays the best accuracy in-sample and out-of-sample. With the exception of the probit model, the QPS value from Model 6 is less than half of the non-factor models. The probit model (Model 4) displays the second best performance. Models 6 and 5 have their lowest out-of-sample QPS at the 22-month horizon (QPS = 0.263 and QPS = 0.395, respectively), while the term spread (Model 3) has its lowest out-of-sample QPS=0.873 at the 15-month horizon, and the probit model (Model 4) at the 12-month forecast horizon (QPS=0.273). The worst accuracy is again for the curvature (Model 2) and for the level (Model 1).
Table 7 also shows the benchmark forecast,![]() , which is the constant forecast of the mean of the observed event. With the exception of Model 6, the other models do not display
forecast advantage at any horizon relatively to the benchmark forecast. This poor performance is not conveyed by the QPS values, which show a fair accuracy for the models.
, which is the constant forecast of the mean of the observed event. With the exception of Model 6, the other models do not display
forecast advantage at any horizon relatively to the benchmark forecast. This poor performance is not conveyed by the QPS values, which show a fair accuracy for the models.
The source of the forecast inaccuracy can be examined using Murphy's decomposition of the skill score in-sample (Table 8) and out-of-sample (Table 10). Model 6 is the only one that displays a positive skill score (from horizon 14 to 24). The main contributor of this performance is its larger correlation with the business cycle dating, although the biases are also very small. The other models have negative skill at any horizon. The forecasts from the level and curvature of the yield curve (Models 1 and 2) have large conditional bias and very low resolution. The term spread (Model 3) and the yield-only factor (Model 5) models have high resolution at the 15 and 22-month horizons, but this advantage is offset by their high conditional and unconditional biases. In particular, the popular term spread model (Model 3) shows a reasonable degree of resolution (Table 8 column 4). The tests indicate that the main weakness of the spread model is the high variability of its forecasts, in addition to a relative large unconditional bias, which together imply a high degree of miscalibration. The probit model (Model 4) displays negative skill score, but very close to zero - this result is mainly due to the fact that the unconditional bias is small and the squared correlation is high.
The in-sample and out-of-sample forecasting performance in terms of resolution can be examined in more detail in Tables 9 and 10, respectively, which show the ![]() . Model 6 displays
the lowest mean squared error for any horizon compared to the other models. The decomposition shows that this performance is achieved due to the small unconditional bias of this model,
. Model 6 displays
the lowest mean squared error for any horizon compared to the other models. The decomposition shows that this performance is achieved due to the small unconditional bias of this model,
![]() and the low excess variability of the forecast,
and the low excess variability of the forecast,
![]() . In addition, the conditional minimum value of forecast variance, which reflects forecast discrimination with respect to times of occurrence and non-occurrence of the
event, is also the smallest for Model 6. The lowest
. In addition, the conditional minimum value of forecast variance, which reflects forecast discrimination with respect to times of occurrence and non-occurrence of the
event, is also the smallest for Model 6. The lowest ![]() for Model 6 is achieved at horizon 22, with a value less than half of the
for Model 6 is achieved at horizon 22, with a value less than half of the ![]() for all the univariate models at any horizon. Model 5 also displays a good forecasting performance, especially at longer horizons, achieving a good balance between resolution and calibration.
for all the univariate models at any horizon. Model 5 also displays a good forecasting performance, especially at longer horizons, achieving a good balance between resolution and calibration.
Overall, the tests suggest that all models of the yield curve perform best at leads of at least 12 months. Although the QPS shows that the models generally have reasonable forecasting accuracy, most of them have negative skill score. Model 6 is well calibrated and has positive skill score (forecasts better than the benchmark constant forecast). In addition, the probabilities from Model 6 have effective information with respect to the event occurrence, showing high discrimination power compared to the other models (the highest resolution and the lowest conditional and unconditional biases). In addition, it has a good balance between accuracy and resolution, leading to the smallest MSE compared to the alternatives.
In summary, we find that the components of the yield curve have useful information to forecast recession and expansions. Although the term spread model (Model 3) and the probit model (Model 4) have a reasonable forecasting performance, the proposed factor models that use information on the components of yield curve and of the economy exhibit better predictive value to anticipate the beginning and end of recessions. Using information from the yield curve only as in Model 5 leads to a reasonable forecast performance overall, but the results of Model 6 shows that a substantial incremental predictive value is achieved when the interrelationship between the bonds market and the economy are considered.
7 Out-of-Sample Forecasting Analysis
The out-of-sample forecasting performance of alternative models for future values of the industrial production growth is examined in this section. In addition to revised data, we also use real-time data for Industrial Production obtained from the Federal Reserve Bank of CityplacePhiladelphia. These are the unrevised series as available at any given date in the past instead of the revised data currently available. Industrial production has been substantially revised over the period considered.
We consider three models to examine the usefulness of the information of the components of the yield curve in predicting the growth rate of Industrial Production. Model 7 uses lags of the slope and lags of Industrial Production itself. Model 8 uses lags of the level, curvature, and slope of the yield curve in addition to lags of Industrial Production. Finally, we estimate a model that includes lags of the yield curve factor extracted from the Markov-switching dynamic bifactor yield-economy model in addition to lags of Industrial Production (Model 9). The lags for each model are selected using Akaike, Schwarz and Hannan-Quinn criteria. The best specifications for the autoregressive model of the growth of Industrial Production are the following:
Model 7:
![]()
Model 8:
![]()
Model 9:
![]()
Variables that exhibit high power in explaining the linear long-run variance of output may be less important in specific situations. In fact, the largest errors in predicting output occur around business cycle turning points. Thus, we choose to investigate the period before, during, and after the 2001 recession, which will allow analysis of the ability of the models in predicting in an out-of-sample real time exercise the substantial fall and recovery in the rate of growth of industrial production during this phase.20
The models are first estimated using data from 1971:08 to 1999:12 and then recursively re-estimated for each month for the period starting in 2000:1 and ending in 2003:12. We use the in-sample estimates to generate h-step ahead forecasts in real time, using only
collected real time realizations of industrial production as first released at each month for this analysis. We consider forecast horizons from 1 to 10 months,
![]() . The loss functions are evaluated using h-step ahead forecast errors obtained through a recursive forecasting scheme. We consider three loss
functions: the root mean squared error (RMSE), Theil inequality coefficient (THEIL) and the LINLIN asymmetric loss function of Granger (1969):
. The loss functions are evaluated using h-step ahead forecast errors obtained through a recursive forecasting scheme. We consider three loss
functions: the root mean squared error (RMSE), Theil inequality coefficient (THEIL) and the LINLIN asymmetric loss function of Granger (1969):
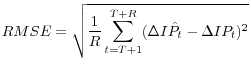

![\displaystyle LINLIN=\frac{1}{R} \sum _{t=T+1}^{T+R}I(\Delta I\hat{P}_{t} -\Delta IP_{t} )a\vert\Delta I\hat{P}_{t} -\Delta IP_{t} \vert+[1-I(\Delta I\hat{P}_{t} -\Delta IP_{t} )]b\vert\Delta I\hat{P}_{t} -\Delta IP_{t} \vert](img129.gif)
Table 11 summarizes the results of the out-of sample forecast performance of the models in real time. For all considered forecast horizons, the model that includes lags of the extracted yield-economy factor (Model 9) does better than the other models with respect to each loss function, and its advantage increases for longer horizons. Model 9 also performs relatively better when we consider the asymmetric loss function that penalizes negative errors more than the positive ones.
We repeat the same exercise using the revised Industrial Production series in order to evaluate the models forecasting performance in terms of what actually happened to the economy rather than in real time. The results are reported in Table 12. Once again, for all horizons considered, Model 9 outperforms the alternative ones. This is especially the case for horizons longer than six, for which the predictive ability of Model 9 increases further. For example, the asymmetric loss function LINLIN at h= 10 for Model 9 is 55% the value for Model 8 and 61% the value for Model 7.
8 Conclusion
We propose a new econometric framework that uses information from the entire curve and models the joint dynamic interrelationship of the the economy and the yield curve to predict business cycles. The multivariate bi-factor model follows two separate Markov processes, each representing phases of the bond market and of the business cycle. The framework allows direct analysis of the lead-lag relationship between the cyclical phases of these two sectors. We use the model to forecast in-sample and out-of-sample the beginning and end of recessions and future projections of industrial production growth at the monthly frequency.
The results show a strong correlation between the real economy and the bond market. The yield factor extracted from the joint model of the economy and the yield curve has a better ability to anticipate economic recessions compared to alternative frameworks. In particular, it predicts the beginning and end of all recessions in the sample studied with no false peaks or troughs and no missed turns. In addition, the yield-economy factor model is well calibrated and exhibits a high discrimination power. This model's balance between accuracy and resolution yields a small mean squared error compared to alternative models. The proposed model also outperforms alternative specifications in terms of linear time series forecasting.
In summary, we find that the components of the yield curve - especially the term spread specification - have useful information to forecast recessions and expansions, and linear projections of industrial production growth. However, the proposed nonlinear model reduces the dimensionality of the information on the yield curve down to one state variable that exhibits substantial incremental predictive value compared to each of the components of the yield curve individually or even all the components combined in linear or nonlinear regressions, especially when the extracted yield factor is combined with information on the economic activity.
We conclude that several attributes lead to the better predictive performance of the model: the use of combined information from the components of the yield curve in a latent factor, the extraction of the yield factor based on the interrelationship of the yield curve with the real economic activity, and the flexibility of the model, which allows for nonlinearities and asymmetries in the cyclical phases of the bond markets and of the business cycle, as represented by the Markov processes.
References
Andrews, D.W.K., 1993, "Tests for Parameter Instability and Structural Change with Unknown Change Point," Econometrica, July, 61:4, 821-56.
Andrews, D.W.K. and W. Ploberger, 1994, "Optimal Tests When a Nuisance Parameter is Present Only under the Alternative." Econometrica, 62:6, pp. 1383-414.
Ang, A., Piazzesi, M., 2003, "A No-Arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables," Journal of Monetary Economics, 50, 745-787.
Ang, A., Piazzesi, M., Wei, M., 2006, "What Does the Yield Curve Tell us About GDP Growth?" Journal of Econometrics, 127, 359-403.
Bai, J., 1997, "Estimating Multiple Breaks One at a Time," Econometric Theory, 13, 315-352.
Bai, J. and P. Perron, 1998, "Estimating and Testing Linear Models with Multiple Structural Changes, Econometrica, 66, 47-78.
Bernadell, C., J. Coche, and K. Nyholm, 2005, "Yield Curve Prediction for the Strategic Investor," European Central Bank Working Paper 472.
Brier, G.W. and R.A. Allen, 1951, "Verification of Weather Forecasts;" in: T.F. Malone (ed.) Compendium of Meteorology; American Meteorology. Soc. 841-848.
Camacho, M. and G.P. Quiros, (2007), "Jump and Rest Effects in the U.S. Business Cycle," Studies in Nonlinear Dynamics and Econometrics, 11, 4, 3, 1-37.
Chauvet, M., 1998/1999, "Stock Market Fluctuations and the Business Cycle," Journal of Economic and Social Measurement, 25, 235-258.
Chauvet, M. and S. Potter, 2002, "Predicting Recessions: Evidence from the Yield Curve in the Presence of Structural Breaks," Economics Letters, 77, 2, 245-253.
Chauvet, M. and S. Potter, 2005, "Forecasting Recessions Using the Yield Curve," Journal of Forecasting, 24, 2, 77-103.
Chib, S., 1998, "Estimation and Comparison of Multiple Change-Point Models," Journal of Econometrics, 86, 22, 1998, 221-241.
Dickey, D.A. and W.A. Fuller, 1979, "Distribution of the Estimators for Autoregressive Time Series with a Unit Root," Journal of the American Statistical Association, 74, 366, 427-431.
Diebold, F.X. and G.D. Rudebusch, 1989, "Scoring the Leading Indicators," Journal of Business, 62, 3, 369-91.
Diebold, F.X. and C. Li, 2006, "Forecasting the Term Structure of Government Bond Yields," Journal of Econometrics, 130, 337-364.
Diebold, F.X., G.D. Rudebusch, and B. Aruoba, 2006, "The Macroeconomy and the Yield Curve," Journal of Econometrics, 131, 309-338.
Dotsey, M., 1998, "The Predictive Content of the Interest Rate Term Spread for Future Economic Growth," Federal Reserve Bank of CityplaceRichmond, Economic Quarterly, 84, 31-51.
Duffie, D., StateplaceKan, R., 1996, "A Yield-Factor Model of Interest Rates, Mathematical Finance, 6, 379-406.
Estrella, A. and G. Hardouvelis, 1991, "The Term Structure as a Predictor of Real Economic Activity," Journal of Finance, 46, 2, 555-576.
Estrella, A. and F.S. Mishkin, 1998, "Predicting country-regionplaceU.S. recessions: Financial Variables as Leading Indicators," The Review of Economics and Statistics, 80, 45-61.
Estrella, A., A.P. Rodrigues, and S. Schich, 2003, "How Stable is the Predictive Power of the Yield Curve? Review of Economics and Statistics, 85, 3, 629-644.
Friedman, B.M. and K.N. Kuttner, 1998, "Indicator Properties of the Paper-Bill Spread: Lessons from Recent Experience," The Review of Economics and Statistics, 80, 34-44.
Giacomini, R. and B. Rossi, 2006, "How Stable is the Forecasting Performance of the Yield Curve for Output Growth?" Oxford Bulletin of Economics and Statistics 68(s1), December, 783-795.
Granger, C.W.J., 1969, "Prediction with a Generalized Cost of Error Function," Operational Research Quarterly, 20, 199-207.
Gurkaynak, R.S., B. Sack, and J.H. Wright, 2007, "The country-regionplaceU.S. Treasury Yield Curve: 1961 to the Present." Journal of Monetary Economics, 24, 8, 2291-2304.
Hamilton, J.D., 1989, "A New Approach to the Economic Analysis of Nonstationary Time Series and Business Cycles," Econometrica ,57, 357-384.
Hamilton, J.D. and D.H. Kim, 2002, "A Re-Examination of the Predictability of Economic Activity Using the Yield Spread," Journal of Money, Credit and Banking, 34, 340-344.
Harvey, C., 1988, "The Real Term Structure and Consumption Growth," Journal of Financial Economics 22, 305-334.
Harvey, C., 1989, "Forecasting Economic Growth with the Bond and Stock Markets," Financial Analysts Journal, 38-45.
Haubrich, J.G. and A.M. Dombrosky, 1996, "Predicting Real Growth Using the Yield Curve," Federal Reserve Bank of Cleveland Economic Review, 32, 1, 26-34.
Kim, C.-J., 1994, "Dynamic Linear Models with Markov-Switching," Journal of Econometrics, 60, 1-22.
McConnell, M. and G. Perez-Quiros, 2000, "Output Fluctuations in the country-regionplaceUnited States: What Has Changed Since the Early 1980s?", American Economic Review, 90, 1464-1476.
Murphy, A. 1988, "Skill Scores based on the Mean Square Error and their Relationships to the Correlation Coefficient," Monthly Weather Review, 116, 2417-2424.
Nelson, C.R. and A.F. Siegel, 1987, "Parsimonious Modeling of Yield Curves," Journal of Business, 60, 473-489.
Nyholm, K., 2007, "A New Approach to Predicting Recessions," Economic Notes, 36, 27-42.
Phillips, P. and P. Perron, 1988, "Testing for a Unit Root in Time Series Regression," Biometrika, 75, 2, 335-346.
Perron, P., 1989, "The Great Crash, the Oil Shock and the Unit Root Hypothesis," Econometrica, 57, 1361-1401.
Senyuz, Z. (2008) "Essays on Nonlinear Modeling of Real and Financial Markets with Applications to country-regionplaceU.S. and International Data", UCR Ph.D. Dissertation.
Stock, J.H. and M.W. Watson, 2003, "Forecasting Output and Inflation: The Role of Asset Prices," Journal of Economic Literature, 41, 3, 788-829.Journal of Monetary Economics 24(8), November 2007, 2291-230
Stock, J. and M. Watson, 1989, "New Indices of Coincident and Leading Indicators," In O. Blanchard and S. Fischer ed. NBER Macroeconomic Annual, CityplaceCambridge, MIT Press
Wright, J., 2006, "The Yield Curve and Predicting Recessions," Federal Reserve Board, Washington, Working Paper no. 2006-7.
Yates, J.F. (1982), "External Correspondence: Decompositions of the Mean Probability Score," Organizational Behavior and Human Performance, 30,132-156.
| Level Mean | Level Variance | Curvature Mean | Curvature Variance | Slope Mean | Slope Variance | Industrial Production Mean | Industrial Production Variance |
| - | 1980:05 |
- | 1980:08 |
1982:01 |
1980:06 |
- | 1983:12 |
| - | - | - | - | - | 1981:02 |
- | - |
| - | - | - | - | - | 1981:08 |
- | - |
| 1990:11 |
- | 1990:6 |
- | - | - | - | - |
![]()
![]()
![]() significant at the 10% level,
significant at the 10% level, ![]()
![]() significant at the 5% level,
significant at the 5% level, ![]()
![]() significant at the
1% level.
significant at the
1% level.
Table 2: Maximum Likelihood Estimates for the Univariate Markov Switching (MS) Model for DIP
| Parameter | Estimates |
|---|---|
|
|
4.13 |
|
|
(0.16) |
|
|
-4.24 |
|
|
(0.42) |
| 0.99 | |
| (0.01) | |
| 0.93 | |
| (0.03) | |
|
|
8.28 |
|
|
(0.57) |
| LogL | -395.12 |
| Parameters | Univariate Models Level | Univariate Models Curvature | Univariate Models Slope | Multivariate Yield Factor Model |
|---|---|---|---|---|
|
|
10.12 | 1.27 | 1.99 | 0.59 |
|
|
(0.17) | (0.67) | (0.08) | (0.162) |
|
|
5.48 | 0.190 | -0.96 | -0.42 |
|
|
(0.10) | (0.05) | (0.12) | (0.15) |
|
|
5.44 | 0.327 | 3.04 | - |
|
|
(0.06) | (0.03) | (0.06) | - |
|
|
3.03 | -1.27 | 0.89 | - |
|
|
(0.12) | (0.07) | (0.06) | - |
|
|
2.60 | 0.25 | 0.63 | - |
|
|
(0.18) | (0.02) | (0.07) | - |
|
|
0.54 | 0.32 | 0.37 | - |
|
|
(0.05) | (0.03) | (0.03) | - |
| 0.98 | 0.94 | 0.97 | 0.93 | |
| (0.01) | (0.03) | (0.02) | (0.04) | |
| 0.99 | 0.97 | 0.96 | 0.96 | |
| (0.01) | (0.01) | (0.01) | (0.02) | |
| - | - | - | 0.89 | |
| - | - | - | (0.03) | |
|
|
- | - | - | 0.015 |
|
|
- | - | - | (0.00) |
|
|
- | - | - | -0.10 |
|
|
- | - | - | (0.02) |
|
|
- | - | - | -0.27 |
|
|
- | - | - | (0.01) |
| - | - | - | 0.99 | |
| - | - | - | (0.00) | |
|
|
- | - | - | 0.95 |
|
|
- | - | - | (0.02) |
| - | - | - | -0.91 | |
| - | - | - | (0.04) | |
|
|
- | - | - | 0.04 |
|
|
- | - | - | (0.00) |
|
|
- | - | - | 0.37 |
|
|
- | - | - | (0.01) |
|
|
- | - | - | 0.01 |
|
|
- | - | - | (0.00) |
| LogL | -395.12 | 25.23 | -91.89 | 1680.66 |
Asymptotic standard errors in parentheses correspond to the diagonal elements of the inverse hessian obtained through numerical calculation. The variance of the single factor is set to one for normalization.
| Parameters | Yield Factor | Economic Factor |
|---|---|---|
|
|
0.596 | 0.802 |
|
|
(0.184) | (0.068) |
|
|
-0.374 | -0.934 |
|
|
(0.136) | (0.100) |
| 0.930 | 0.962 | |
| (0.041) | (0.017) | |
| 0.971 | 0.877 | |
| (0.021) | (0.045) | |
|
|
1 | 0.856 |
|
|
(0.029) | |
| 0.883 | 0.885 | |
| (0.011) | (0.017) | |
|
|
- | 1 |
|
|
0.015 | - |
|
|
(0.002) | - |
|
|
-0.274 | - |
|
|
(0.009) | - |
|
|
-0.102 | - |
|
|
(0.015) | - |
|
|
0.043 | - |
|
|
(0.001) | - |
|
|
0.371 | - |
|
|
(0.010) | - |
|
|
0.002 | - |
|
|
(0.582) | - |
| 0.038 | -0.116 | |
| (0.018) | (0.009) | |
|
|
0.946 | - |
|
|
(0.014) | - |
| Log L | 367.212 |
Asymptotic standard errors in parentheses. Note: given that the estimate of ![]() was not statistically significant at any level, the final selected
specification above does not include this parameter.
was not statistically significant at any level, the final selected
specification above does not include this parameter.
| Model 1 Level | Model 2 Curvature | Model 3 Slope | Model 4 Probit | Model 5 Yield-only | Model 6 Yield-Economy | |
|---|---|---|---|---|---|---|
| In-sample 1973:11 | - | -26 | -6 | -1 | -9 | -9 -22 |
| In-sample 1980:01 | -19 | -12 | -17 | -13 | -29 | -20 -17 |
| In-sample 1981:07 | - | - | -10 | -8 | -13 | -13 |
| In-sample 1990:07 | -28 | - | -24 | - | -24 | -26 |
| Out-of-Sample 2001:03 | - | 3 | - | - | -16 | -14 |
| Out-of-Sample 2007:12 | -25 | -4 | -32 | - | -29 | -28 |
| Model 1 Level | Model 2 Curvature | Model 3 Slope | Model 4 Probit | Model 5 Yield-only | Model 6 Yield-Economy | |
|---|---|---|---|---|---|---|
| In-Sample 1975:03 | - | -9 | -12 | -10 | -4 | -16 |
| In-Sample 1980:07 | - | - | -11 | -3 | -13 | -13 |
| In-Sample 1982:11 | - | - | -18 | -13 | -17 | -23 |
| In-Sample 1991:03 | -6 | - | -2 | - | -16 | -16 |
| Out-of-Sample 2001:11 | -3 | - | -7 | - | -15 | -12 |
| Out-of-Sample Not available* | - | - | - | - | Yes | Yes |
The criterion adopted to determine turning points in cols. (2)-(5) is if the smoothed probability of state 0 is equal or greater than 0.5: P(
![]() )
) ![]() 0.5. The minus sign refers to the lead in which
the models anticipate the recession dates. The last two rows of both tables refer to the models recursively estimated using real time data from 1999:01 to 2007:12. (*) The trough of the 2007-? recession had not been announced at the time the paper was written, and the coincident probabilities of
recession from industrial production had not reached a trough.
0.5. The minus sign refers to the lead in which
the models anticipate the recession dates. The last two rows of both tables refer to the models recursively estimated using real time data from 1999:01 to 2007:12. (*) The trough of the 2007-? recession had not been announced at the time the paper was written, and the coincident probabilities of
recession from industrial production had not reached a trough.
| Turning Point Evaluation | Model 1 Level | Model 2 Curvature | Model 3 Slope | Model 4 Probit | Model 5 Yield-only | Model 6 Yield-Economy |
|---|---|---|---|---|---|---|
| Correct TP | 3 | 4 | 5 | 3 | 6 | 6 |
| Missed TP | 3 | 2 | 1 | 3 | 0 | 0 |
| False TP | 0 | 2 | 2 | 0 | 2 | 0 |
| TP Error | 3 | 4 | 3 | 3 | 2 | 0 |
| Turning Point Evaluation | Model 1 Level | Model 2 Curvature | Model 3 Slope | Model 4 Probit | Model 5 Yield-only | Model 6 Yield-Economy |
|---|---|---|---|---|---|---|
| Correct TP | 2 | 1 | 4 | 3 | 5 | 5 |
| Missed TP | 3 | 4 | 1 | 3 | 0 | 0 |
| False TP | 0 | 2 | 1 | 0 | 2 | 0 |
| TP Error | 3 | 6 | 2 | 3 | 2 | 0 |
(*) It does not include the trough for the current recession (2007-), which Models 5 and 6 have already signaled. Correct TP refers to prediction of a turning point when one does occur. Missed TP refers to prediction of no turning point when one does occur. False TP refers to prediction of a turning point when one does not occur. TP error refers to the total of Missed and False TP. A perfect forecast is when TP error is zero.
Table 7: Evaluation of Turning Point Forecasts of the Reference Cycle (NBER) Using the Quadratic Probability Score (![]() ) In-Sample and Out-of-Sample
) In-Sample and Out-of-Sample
In-Sample
| Forecast Horizon | |||||||
|---|---|---|---|---|---|---|---|
| 12-month | 0.285 | 0.807 | 1.091 | 0.556 | 0.291 | 0.482 | 0.278 |
| 15-month | 0.286 | 0.805 | 1.092 | 0.549 | 0.363 | 0.436 | 0.259 |
| 22-month | 0.290 | 0.808 | 1.088 | 0.604 | 0.497 | 0.362 | 0.209 |
Out-of-Sample Real Time
| Forecast Horizon | |||||||
|---|---|---|---|---|---|---|---|
| 12-month | 0.252 | 0.723 | 1.082 | 0.881 | 0.273 | 0.699 | 0.381 |
| 15-month | 0.253 | 0.718 | 1.076 | 0.873 | 0.379 | 0.634 | 0.362 |
| 22-month | 0.281 | 0.792 | 0.978 | 0.941 | 0.547 | 0.395 | 0.263 |
Forecast horizons from 1 to 36 months were computed. They are not shown here due to space considerations. The ![]() values for each model reach a minimum in the horizon in bold.
values for each model reach a minimum in the horizon in bold.
| Models | Forecast Horizon | Total Score | Squared Correlation | Conditional Bias | Uncond. Bias |
|---|---|---|---|---|---|
| Model 1 | 3 | -2.502 | 0.003 | 1.561 | 0.944 |
| Model 1 (cont'd) | 15 | -1.888 | 0.070 | 1.081 | 0.876 |
| Model 1 (cont'd) | 22 | -1.777 | 0.058 | 1.073 | 0.761 |
| Model 2 | 3 | -2.967 | 0.001 | 1.689 | 1.280 |
| Model 2(cont'd) | 15 | -2.951 | 0.000 | 1.582 | 1.369 |
| Model 2(cont'd) | 22 | -2.771 | 0.000 | 1.449 | 1.322 |
| Model 3 | 3 | -2.281 | 0.000 | 1.712 | 0.569 |
| Model 3(cont'd) | 15 | -0.972 | 0.219 | 0.683 | 0.507 |
| Model 3(cont'd) | 22 | -1.067 | 0.141 | 0.787 | 0.422 |
| Model 4 | 3 | -0.623 | 0.292 | 0.832 | 0.083 |
| Model 4 (cont'd) | 12 | -0.040 | 0.150 | 0.117 | 0.073 |
| Model 4(cont'd) | 22 | -0.124 | -0.024 | 0.054 | 0.046 |
| Model 5 | 3 | -1.835 | 0.026 | 1.436 | 0.425 |
| Model 5 (cont'd) | 15 | -0.555 | 0.195 | 0.355 | 0.396 |
| Model 5 (cont'd) | 22 | -0.233 | 0.299 | 0.210 | 0.322 |
| Model 6 | 3 | -0.982 | 0.001 | 0.904 | 0.079 |
| Model 6 (cont'd) | 15 | 0.094 | 0.299 | 0.139 | 0.065 |
| Model 6 (cont'd) | 22 | 0.295 | 0.396 | 0.062 | 0.039 |
Forecast horizons from 1 to 36 months were computed. They are not shown here due to space considerations. The ![]() values for each model reach a maximum in the horizon in bold.
values for each model reach a maximum in the horizon in bold.
Table 9 : Evaluation of Turning Point Forecasts of the Reference Cycle (NBER) Using Yates' Decomposition (MSE![]() )
)
| Models | Forecast Horizon | Var( |
DVar( |
MinVar ( |
|
2cov( |
|
|---|---|---|---|---|---|---|---|
| Model 1 | 3 | 0.488 | 0.139 | 0.236 | 0.001 | 0.132 | 0.019 |
| Model 1 (cont'd) | 15 | 0.401 | 0.139 | 0.230 | 0.007 | 0.122 | 0.098 |
| Model 1 (cont'd) | 22 | 0.403 | 0.145 | 0.234 | 0.003 | 0.111 | 0.090 |
| Model 2 | 3 | 0.553 | 0.139 | 0.221 | 0.000 | 0.179 | -0.014 |
| Model 2 (cont'd) | 15 | 0.551 | 0.139 | 0.217 | 0.003 | 0.191 | -0.001 |
| Model 2 (cont'd) | 22 | 0.548 | 0.145 | 0.215 | 0.002 | 0.192 | 0.006 |
| Model 3 | 3 | 0.458 | 0.139 | 0.236 | 0.000 | 0.079 | -0.003 |
| Model 3 (cont'd) | 15 | 0.272 | 0.139 | 0.209 | 0.024 | 0.071 | 0.172 |
| Model 3 (cont'd) | 22 | 0.300 | 0.145 | 0.229 | 0.003 | 0.061 | 0.139 |
| Model 4 | 3 | 0.502 | 0.139 | 0.163 | 0.009 | 0.0629 | 0.1281 |
| Model 4 (cont'd) | 12 | 0.181 | 0.139 | 0.076 | 0.023 | 0.045 | -0.102 |
| Model 4 (cont'd) | 22 | 0.284 | 0.145 | 0.151 | 0.062 | 0.059 | -0.133 |
| Model 5 | 3 | 0.396 | 0.139 | 0.143 | 0.007 | 0.059 | -0.047 |
| Model 5 (cont'd) | 15 | 0.215 | 0.139 | 0.087 | 0.063 | 0.055 | 0.130 |
| Model 5 (cont'd) | 22 | 0.179 | 0.145 | 0.121 | 0.025 | 0.047 | 0.160 |
| Model 6 | 3 | 0.276 | 0.139 | 0.120 | 0.000 | 0.011 | -0.006 |
| Model 6 (cont'd) | 15 | 0.124 | 0.139 | 0.079 | 0.039 | 0.009 | 0.143 |
| Model 6 (cont'd) | 22 | 0.102 | 0.145 | 0.093 | 0.019 | 0.006 | 0.161 |
![]() is the 0/1 dummy that takes the value 0 if the probability of state 0 for DIP is equal to or greater than 50% Yates' decomposition is:
is the 0/1 dummy that takes the value 0 if the probability of state 0 for DIP is equal to or greater than 50% Yates' decomposition is: ![]() = Var (
= Var (![]() )+
)+ ![]() Var (
Var (![]() ) + Min Var(
) + Min Var(![]() )+ (
)+ (
![]() - 2Cov (
- 2Cov (![]() ,
, ![]() ).
).
Table 10: Yates' ![]() and Murphy's Skill Score
and Murphy's Skill Score ![]() Out-of-Sample Real time
Out-of-Sample Real time
| Models | Forecast Horizon | ||
|---|---|---|---|
| Model 1 | 3 | -2.732 | 0.491 |
| Model 1 (cont'd) | 15 | -1.925 | 0.427 |
| Model 1 (cont'd) | 22 | -1.802 | 0.415 |
| Model 2 | 3 | -3.012 | 0.591 |
| Model 2 (cont'd) | 15 | -2.999 | 0.568 |
| Model 2 (cont'd) | 22 | -2.851 | 0.551 |
| Model 3 | 3 | -2.302 | 0.499 |
| Model 3 (cont'd) | 15 | -0.998 | 0.281 |
| Model 3 (cont'd) | 22 | -1.110 | 0.368 |
| Model 4 | 3 | -0.691 | 0.581 |
| Model 4 (cont'd) | 12 | -0.100 | 0.211 |
| Model 4 (cont'd) | 22 | -0.151 | 0.294 |
| Model 5 | 3 | -1.911 | 0.403 |
| Model 5 (cont'd) | 15 | -0.601 | 0.225 |
| Model 5 (cont'd) | 22 | -0.281 | 0.181 |
| Model 6 | 3 | -1.022 | 0.294 |
| Model 6 (cont'd) | 15 | 0.101 | 0.144 |
| Model 6 (cont'd) | 22 | 0.313 | 0.111 |
Forecast horizons from 1 to 36 months were computed. The ![]() and
and ![]() values for each model reach a maximum and minimum, respectively, in the horizon in bold.
values for each model reach a maximum and minimum, respectively, in the horizon in bold.
| h = 1 M7 | h = 1 M8 | h = 1 M9 | h = 2 M7 | h = 2 M8 | h = 2 M9 | h = 3 M7 | h = 3 M8 | h = 3 M9 | |
|---|---|---|---|---|---|---|---|---|---|
| RMSE | 0.615 | 0.670 | 0.598 | 0.966 | 1.121 | 0.909 | 1.384 | 1.645 | 1.270 |
| THEIL | 0.092 | 0.101 | 0.090 | 0.144 | 0.166 | 0.135 | 0.206 | 0.241 | 0.188 |
| LINLIN | 1.112 | 1.294 | 1.062 | 2.048 | 2.498 | 1.939 | 3.097 | 3.780 | 2.833 |
| h = 4 M7 | h = 4 M8 | h = 4 M9 | h = 5 M7 | h = 5 M8 | h = 5 M9 | h = 6 M7 | h = 6 M8 | h = 6 M9 | |
|---|---|---|---|---|---|---|---|---|---|
| RMSE | 1.872 | 2.236 | 1.693 | 2.314 | 2.781 | 2.085 | 2.726 | 3.314 | 2.476 |
| THEIL | 0.278 | 0.323 | 0.250 | 0.341 | 0.393 | 0.307 | 0.396 | 0.452 | 0.361 |
| LINLIN | 4.393 | 5.292 | 4.022 | 5.493 | 6.753 | 5.072 | 6.650 | 8.164 | 6.141 |
| h = 7 M7 | h = 7 M8 | h = 7 M9 | h = 8 M7 | h = 8 M8 | h = 8 M9 | h = 9 M7 | h = 9 M8 | h = 9 M9 | h = 10 M7 | h = 10 M8 | h = 10 M9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 3.120 | 3.800 | 2.845 | 3.453 | 4.210 | 3.169 | 3.733 | 4.555 | 3.450 | 3.943 | 4.824 | 3.673 |
| THEIL | 0.447 | 0.502 | 0.412 | 0.487 | 0.540 | 0.456 | 0.519 | 0.568 | 0.493 | 0.543 | 0.589 | 0.524 |
| LINLIN | 7.662 | 9.455 | 7.046 | 8.666 | 10.648 | 7.925 | 9.440 | 11.666 | 8.599 | 10.056 | 12.461 | 9.192 |
The data on ![]() is released in the middle of the month with information for the previous month. We use real time data on
is released in the middle of the month with information for the previous month. We use real time data on ![]() starting with the vintage 1971:9, which includes the value for 1971:8 and ending with the vintage 2004:1, which includes the value for 2003:12. Estimation Period: 1971:M8-1999:12. Forecast Period: 2000:1-2003:12. Numbers in bold
indicate the smallest loss among all models for the particular forecast horizon.
starting with the vintage 1971:9, which includes the value for 1971:8 and ending with the vintage 2004:1, which includes the value for 2003:12. Estimation Period: 1971:M8-1999:12. Forecast Period: 2000:1-2003:12. Numbers in bold
indicate the smallest loss among all models for the particular forecast horizon.
| h = 1 M7 | h = 1 M8 | h = 1 M9 | h = 2 M7 | h = 2 M8 | h = 2 M9 | h = 3 M7 | h = 3 M8 | h = 3 M9 | |
|---|---|---|---|---|---|---|---|---|---|
| RMSE RMSE | 0.615 | 0.670 | 0.598 | 0.966 | 1.121 | 0.909 | 1.384 | 1.645 | 1.270 |
| THEIL | 0.092 | 0.101 | 0.090 | 0.144 | 0.166 | 0.135 | 0.206 | 0.241 | 0.188 |
| LINLIN | 1.209 | 1.244 | 1.133 | 1.764 | 1.763 | 1.560 | 2.121 | 2.225 | 1.874 |
| h = 4 M7 | h = 4 M8 | h = 4 M9 | h = 5 M7 | h = 5 M8 | h = 5 M9 | h = 6 M7 | h = 6 M8 | h = 6 M9 | |
|---|---|---|---|---|---|---|---|---|---|
| RMSE | 1.872 | 2.236 | 1.693 | 2.314 | 2.781 | 2.085 | 2.726 | 3.314 | 2.476 |
| THEIL | 0.278 | 0.323 | 0.250 | 0.341 | 0.393 | 0.307 | 0.396 | 0.452 | 0.361 |
| LINLIN | 2.467 | 2.671 | 1.929 | 2.833 | 2.996 | 1.941 | 3.410 | 3.638 | 2.363 |
| h = 7 M7 | h = 7 M8 | h = 7 M9 | h = 8 M7 | h = 8 M8 | h = 8 M9 | h = 9 M7 | h = 9 M8 | h = 9 M9 | h = 10 M7 | h = 10 M8 | h = 10 M9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 3.120 | 3.800 | 2.845 | 3.453 | 4.210 | 3.169 | 3.733 | 4.555 | 3.450 | 3.943 | 4.824 | 3.673 |
| THEIL | 0.447 | 0.502 | 0.412 | 0.487 | 0.540 | 0.456 | 0.519 | 0.568 | 0.493 | 0.543 | 0.589 | 0.524 |
| LINLIN | 3.776 | 4.121 | 2.522 | 4.077 | 4.487 | 2.565 | 4.486 | 4.877 | 2.750 | 4.859 | 5.332 | 2.940 |
Revised data on ![]() is used from 1971:8 to 2003:12. Recursive forecasting scheme is used. Estimation Period: 1971:08-1999:01. Forecast Period: 2000:01-2003:12. Numbers in bold
indicate the smallest loss among all models for the particular forecast horizon.
is used from 1971:8 to 2003:12. Recursive forecasting scheme is used. Estimation Period: 1971:08-1999:01. Forecast Period: 2000:01-2003:12. Numbers in bold
indicate the smallest loss among all models for the particular forecast horizon.
Figure 1: Empirical Proxies for the Level, Slope, and Curvature of the Yield Curve and NBER-Dated Recessions
Figure 2: The Term Spread and NBER-Dated Recessions
Figure 3: Probability of Recession from Growth Rate of Industrial Production and NBER-Dated Recessions
Figure 4: Level, Probability of High Level State, and NBER-Dated Recessions (Shaded Area)
Figure 5: Curvature, Probability of Low Curvature State, and NBER-Dated Recessions (Shaded Area)
Figure 6: Slope and Probability of Flat or Inverted Slope State and NBER-Dated Recessions (Shaded Area)
Figure 7: Probability of High State for the Yield Curve Single Factor, NBER-Dated Recessions (Shaded Area)
Figure 8: Yield Curve Factor from Joint Bi-factor Model of the Yield Curve and the Economy and its Components. Shaded Areas are NBER-Dated Recessions
Figure 9: Probability of High State for the Yield Curve Factor from the Joint Model of the Yield Curve and the Economy. Shaded Areas are NBER-Dated Recessions
Figure 10: Probabilities of Recessions from the Probit Model, NBER-Dated Recessions (Shaded Area)