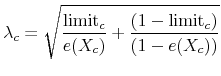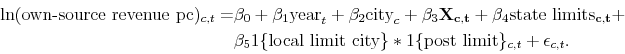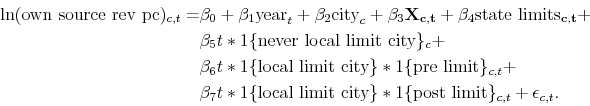Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-52 Screen Reader version ^♣

Spending within Limits: Evidence from Municipal Fiscal Restraints *

Leah Brooks

Division of Research and Statistics

Federal Reserve Board of Governors

Yosh Halberstam

Department of Economics

University of Toronto

Justin Phillips

Department of Political Science

Columbia University

April 2012

Keywords: Tax and expenditure limits, cities

Abstract:

This paper studies the role of a constitutional rule new to the literature: a limit placed by a city on its own ability to tax or spend. We find that such a limit exists in at least 1 in 8 cities, and that limits are not adopted in response to high levels of or variability in taxation. After limit adoption, municipal revenue growth declines by 16 to 22 percent. Our results suggest that institutional constraints may be effective when representative government falls short of the median voter ideal.

JEL Classification: H4, H7, P16

Political economists have long debated the extent to which majority rule limits the behavior of elected officials. Black (1958) and Downs (1957) suggest that policy outcomes are limited to the median voter's preference. In contrast, Buchanan & Tullock (1962), Niskanen (1971) and Romer & Rosenthal (1979,1978) argue that the ballot box provides little, if any, constraint. They contend either that government is fundamentally a Leviathan (a government that maximizes revenue) or that agency problems in political representation are severe; thus, societies must turn to constitutional rules to constrain government.¹

In this paper, we ask when representative government falls short in limiting government and whether constitutional rules that act to constrain representative government are effective. Specifically, we study rules at the municipal level that constrain a city's ability to tax or spend. To do this, we identify a hitherto unclassified type of constitutional limit: a fiscal limit placed by a city on its own ability to tax or spend, which we call a locally- or municipally-imposed tax or expenditure limit. We find that these constitutional limits are effective in curbing the growth of municipal spending.

There are several reasons that a self-imposed local limit is unlikely. Under Dillon's Rule, the legal precedent for state preeminence over local government affairs, state legislatures already have near complete control over local governments and therefore provide a de facto constitutional constraint on local government power (City of Clinton v. Cedar Rapids and Missouri River Railroad Company, 24 Iowa 455 (1868)). In addition, many cities already face stringent limits imposed by states, many adopted after the 1970s, that further restrict municipal revenue-gathering. Further, the Tiebout hypothesis argues that voter mobility constrains the ability of governments to diverge significantly from voter preferences Tiebout (1956). Specifically, dissatisfied municipal residents and businesses are able to restrict Leviathan governments by credibly threatening to move to nearby jurisdictions.

Although a large literature has analyzed fiscal limits that states place on cities, such as California's Proposition 13, limits that cities place on themselves are, to the best of our knowledge, unanalyzed in the academic literature. While state-imposed limits on cities can be rationalized as the desire of voters in some cities to control the fiscal behavior of those in other cities (as in Vigdor (2004)), municipally-imposed limits cannot be explained in this way.² Thus, the existence of municipal self-imposed local limits poses a direct challenge to the idea that the size of government is sufficiently constrained by electoral institutions.

To examine whether self-imposed limits exist at the municipal level, we conducted a survey of 347 municipalities. We find that at least 1 in 8 municipalities has a limit. This partial pattern of adoption paints a mixed picture. In some cases, voters turn to constitutional constraints, while in other cases either elections or an institutional substitute suffice.

We combine these survey data with numerous other data sources to examine patterns of limit adoption. We find that cities with higher median incomes are less likely to adopt a limit. In addition, local limits are less likely where certain institutional substitutes exist. The first such institutional substitute is general law status. "General law" cities have tighter state restrictions on behavior than cities operating under "home rule," the other possible legal status for cities. The second institutional substitute more likely to exist when a limit is absent is the presence of a relatively large number of jurisdictions in the metropolitan area. Following the Tiebout hypothesis, more alternative jurisdictions may provide a check on politicians' behavior. Conversely, fewer alternative jurisdictions may require other mechanisms to limit a politician's range of actions. Surprisingly, we do not find evidence that limits are a response to current or previous high levels of taxation.

Guided by these patterns in the data, we propose a model to understand the correlates and consequences of limit adoption. Our model has two types of voters that vary in their tastes for public goods, motivated by the finding that adoption differs by municipal median income. A politician is elected from one of the two groups of voters. When the group with a low taste for public goods is the majority, uncertainty about both the politician's type and the costs of public goods yields majority support for fiscal limits. Notably, we posit a rationale for limits without assuming Leviathan-like behavior; this is consistent with our empirical finding that limit adoption is not responsive to changes in tax revenues. The model also motivates why limits are most likely to be adopted when institutional substitutes for limits do not exist. Finally, the model suggests that a limit may constrain politicians and bind spending. That said, a limit is a welfare improvement only for certain distributions of the two types in the population, possibly explaining why support for limits varies across cities.

Consistent with the theory, we use panel data to show that, on average, after the passage of a limit, the average rate of revenue growth declines by 16 to 22 percent relative to either the pre-limit period or to never-limited cities. This finding is in contrast to the sparse literature on self-imposed limits at the state level. This literature generally finds that such limits do not affect revenues Kousser et al. (2008). Since limit adoption is likely to be endogenous, this result may be driven by other underlying trends in the jurisdiction correlated with limit passage. To address this concern, we use matching techniques to suggest that observed revenue declines may be causally affected by limits. We also use graphical and statistical methods to show that our findings are unlikely to be driven by changes in tastes that precede limit adoption.

Our paper is related to two literatures. The first is the political economy debate on whether electoral institutions can restrict political behavior. The pioneering work of Black (1958) and Downs (1957) has spawned many empirical tests; early contributors include Inman (1978); Holcombe (1980); McEachern (1978) and Munley (1984). In contrast, other researchers argue that government is naturally expansionary and cannot be checked by the ballot box: constitutional rules are thus necessary to limit government growth. Brennan & Buchanan (1979) and Brennan & Buchanan (1980) discuss the tax revolt of the 1970s as an example of such constitutional rules.³ Tabellini & Alesina (1990) discuss when constitutional balanced budget limits are adoptable and Besley & Smart (2007) motivate the importance of term limits when political agency problems exist.⁴

This paper also contributes to a literature focused directly on tax and expenditure limits. To date, this literature has discussed limits imposed by states on cities, and limits imposed by states on themselves. Mullins & Wallins (2004) and Advisory Commission on Intergovernmental Relations (1995) document the presence and extent of these limits, while other researchers study why these limits are imposed Ladd & Wilson (1982); Temple (1996); Stein et al. (1983); Cutler et al. (1999); Vigdor (2004); Anderson & Pape (2010); Ladd & Wilson (1983); Alm & Skidmore (1999). Further work examines their effect on expenditures and fiscal structure Mullins & Joyce (1996); Mullins (2004); Joyce & Mullins (1991); Figlio & O'Sullivan (2001); Shadbegian (1996) and their effect on the distribution of taxation Chernick & Reschovsky (1982). Another branch of the literature examines the effect of these limits on service quality Downes et al. (1998); Dye & McGuire (1997); Downes & Figlio (1999); Figlio & Rueben (2001).

We proceed by describing our survey and findings on the existence of self-imposed limits and exploring patterns of limit adoption. In section 2, we propose a model, consistent with the survey findings, that provides an explanation for limit adoption and investigates its consequences for revenues and welfare . Section 3 empirically analyzes the revenue consequences of limit adoption and Section 4 concludes.

1 The Existence of Local Limits

1.1 Survey and Supplemental Data

To explore the existence of self-imposed municipal expenditure limits, we undertook a survey of large and mid-sized American cities. Our survey sample consists of all 247 cities with populations of 100,000 or more, and a random sample of 100 cities with populations between 25,000 and 100,000.⁵ Our sampled cities account for 26 percent of the total U.S. population. While the principal purpose of the survey is to identify cities that adopted a local limit, we also use it to collect data on the features of the limits, such as their date of adoption and override provisions, and the perceptions of local officials about the effects of limits.⁶

We conducted the survey in 2007 primarily by telephone.⁷ For each city in our sample, we collected contact information from municipal websites for the City Manager, Budget Director, and Finance Director and attempted to contact each of the 736 officials for whom we had information.⁸ In total, we spoke with 412 officials, and received responses from 320 unique cities, generating a 92 percent response rate. While none of the questions asked were of a sensitive nature, we assured all participants that their identities would remain anonymous.⁹

We define a self-imposed local tax and expenditure limit as a law (appearing in the municipal code or charter) that explicitly caps total municipal revenues or outlays, that caps the overall rate or total revenue generated from a given tax or fee, or that requires a referendum to raise an existing tax or fee. Importantly, we require that this limit be adopted by the city itself and not by the state government.¹⁰

Finally, when a city reported having a locally-imposed limit, we verified its existence by looking in the municipal code or charter for the limit. If we could not find it, we re-contacted the city to verify the survey response. This lead to the exclusion of a handful of false positives, including some state-imposed limits that respondents mistook for locally-imposed limits. We did not conduct a similar exclusion for false negatives - cities that do have a limit, but which mistakenly reported that they do not. For this reason, we interpret our results as a firm lower bound on the presence of local limits. We believe the true extent of local limits to be larger than our estimate indicates.¹¹

1.2 Existence and Types of Limits

Forty of our 320 respondent cities, or 12.5 percent, have at least one self-imposed limit. In total, the 40 limited municipalities have 56 individual limits. Because these limits are entirely new to the literature, we begin with a description of the limits, and then discuss basic covariates of limit adoption.

As shown by the top panel of Table 1, self-imposed limits overwhelmingly target the property tax - historically the largest source of revenue for local governments Sokolow (1998). Property tax rate limits and levy limits, at 39 and 16 percent respectively, make up the majority of the limits we observe. To help make these limits clear, Table 2 gives an example of each type of limit. A rate limit sets a ceiling on the city's property tax rate. For example, the city of Eastpointe, Michigan, has a rate limit that caps its property tax rate at 1.5 percent. A levy limit constrains the total amount of money that can be generated from the property tax, independent of the overall rate. Lincoln, Nebraska, limits the total property tax levy (i.e., total property tax revenues raised) to no more than a seven percent annual increase from a 1966 baseline. The third type of property tax restriction we observe is an assessment limit (7 percent of all local limits). Assessment limits are intended to restrict a city's ability to "automatically" garner increased revenues from rising property values or through administrative reassessment of value. These limits are usually expressed as an allowable annual percentage increase in assessed value. Baltimore, Maryland, limits the annual growth in property assessments to no more than four percent.

The most comprehensive and restrictive type of local limit, existing in two cities (comprising three separate legal limits), is a general revenue or expenditure limit. Such a limit caps either the total amount of own-source revenue or total own-source expenditures, and is typically expressed as an annual allowable percentage increase. Anchorage, Alaska limits tax revenue growth to inflation and population growth.

The remaining tax and expenditure limits either apply to the sales tax or are categorized as "other." Sales tax limits, consisting of nearly 11 percent of local limits, typically cap the overall rate that can be charged or restrict the items that can be taxed. Tucson, Arizona, limits the municipal sales tax to two percent. Limits that fall into the "other" category, just over 21 percent, target a wide range of municipal revenue sources, including entertainment, business, and income taxes as well as certain user fees. For example, Columbus, Ohio, caps the municipal income tax rate at one percent.

Our survey finds that most self-imposed local limits are constitutional, in the Buchanan & Tullock (1962) sense of setting the constitutional rules that govern the game. As shown in the middle of Table 1, over two-thirds of limits are written into municipal charters, making their repeal more difficult and politically costly than a similar limit in the municipal code. A charter is the municipal correlate of a constitution; the code is parallel to statutory regulation. Although most limits have an override provision, overrides typically require a majority or supermajority vote of the electorate. Only 15 percent of limits can be circumvented through city council action alone, and nearly one-third of these require a council supermajority for override.

Local limits exist in all census regions, though cities in the Northeast are least likely to adopt a limit. While cities in the Northeast constitute 18 percent of respondent municipalities, they account for only 7 percent of the limits identified by our survey. Midwestern and Southern cities, however, constitute 15 and 28 percent of respondent cities (respectively), but account for 35 and 33 percent of all limits. Western cities are 38 percent of respondents, and account for 25 percent of all local limits.

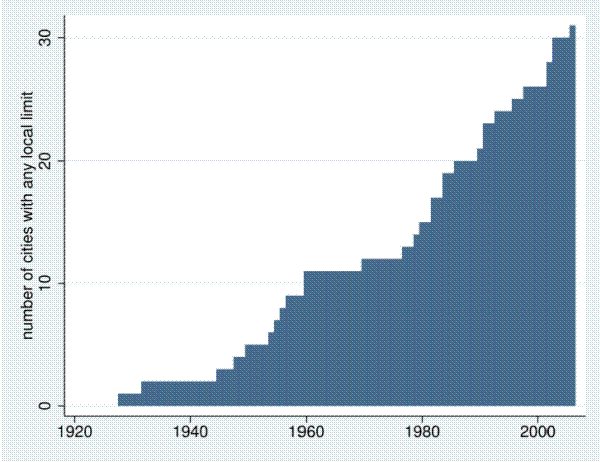
Through the survey and subsequent research efforts we have obtained the date of adoption for over half of the limits identified by our survey and, in some instances, the method of adoption as well.¹² Local limits generally come into existence through one of two mechanisms: city council action or a ballot measure proposed by a citizen or interest group. The earliest limit among our sampled cities was enacted in 1928 - a property tax rate limit in the city of Eastpointe, Michigan - and the median year of limit adoption is 1980. As Figure 1 demonstrates, there is no distinct period of local limit adoption. Unlike many of the stringent state-imposed limits, local limits do not appear to be closely connected to the tax revolt of the late 1970s and early 1980s, and are thus unlikely to be caused by the forces identified in Anderson & Pape (2010). Importantly, many of the local limits we identify are more restrictive than the limit imposed by the state government (if one exists), apply to different revenue sources than the state limit, or pre-date many of the most rigorous state restrictions.

1.3 Correlates of Limit Adoption

We now aim to generate stylized facts about the correlates of local limits. We first consider basic descriptive statistics on limit adoption and then move to regressions that investigate the causes of limit adoption.

To this end, we combine the results of our cross-sectional survey data and information on the year of limit adoption with a wealth of data on municipalities.¹³ To describe cities' fiscal condition, we use the Census Bureau's Annual Survey of Government Finances, 1970-2004. This survey is a census in years ending in two and seven. In all other years, the Census of Governments collect fiscal information from all larger cities and from a random sample of smaller cities. To describe the demographic features of cities, including the metropolitan area in which each city is located, we use the Census's Summary Tape File 3, combining information from the decennial censuses of 1970, 1980, 1990, and 2000.¹⁴ We linearly interpolate all decennial census data between sample years. Data on city political structure comes from the 1987 Census of Government Organization and from the Legal Landscape Database which describes direct democracy provisions in the thousand largest American cities.¹⁵ Information on state-mandated tax and expenditure limits come from Mullins & Wallins (2004) and Advisory Commission on Intergovernmental Relations (1995). We use the urban consumer price index to convert all of our fiscal and economic data into 2006 dollars.

This merging yields an unbalanced panel of 10,135 city-year observations. All but one respondent city is present for at least one year in the panel data.¹⁶ Seventy-seven percent of cities are present in all 35 years of the panel, and 89 percent are present for at least 25 years.

We begin with basic descriptive statistics using the 2002 cross-section, the most complete year of data in our sample, presented in Table 3. The table's top panel shows demographic covariates. The lone demographic characteristic that differs statistically between limited and unlimited cities is median household income. In 2002, the median family income in limited cities (in 2006 dollars) was $55,000 whereas in unlimited cities it was $62,000. In contrast, limited cities are more populous, but not statistically significantly more populous, than unlimited cities. As well, racial shares do not differ by limit status, suggesting that the heterogeneous demand for public goods that motivates limits does not follow strict racial lines.

We examine whether locally-imposed limits are more likely to appear in the presence of a variety of municipal institutions in the second panel of Table 3. We consider five types of institutions that may plausibility limit politicians' revenue decisions: home rule, initiative power, form of government (mayor-council or other), the number of cities in the metropolitan area, and the presence of a binding state limit.¹⁷

Cities in the US have two types of authorizing legal status: general law or home rule. General law cities have only the powers given to them by the state. Any powers not expressly given are the province of the state Krane et al. (2000). Most U.S. cities are general law cities. In contrast, home rule cities have the power to act more independently and design their own institutional structures. In some states, the power of home rule extends to taxation. For example, California home rule cities have broader assessment powers than general law cities, and are able to collect a tax when property is sold, which general law cities cannot League of California Cities (2011). Panel 2 of Table 3 shows that cities with a limit are 25 percent more likely to be home rule.

Panel 2 of Table 3 also shows that jurisdictions in which voters have access to the citizen initiative, which is the ability to initiate legislation via referendum, are weakly more likely to adopt a fiscal limit. The type of municipal government, either mayor-council or other, is unrelated to limit status.

The jurisdictional structure of the metropolitan area may also constrain politicians' behavior. As in Tiebout (1956), the presence of neighboring cities may introduce option value for voters. Thus, an unsatisfied voter might consider migrating to an alternative city that better meets her needs. It is easier to find a city that is a match for a voter's optimal public good and tax package when there are more cities in a metropolitan area. Consistent with this line of reasoning, limit adopters tend to be in metropolitan areas with fewer cities - 19 on average - compared to non-adopters, which are in metropolitan areas with an average of 41 cities.¹⁸

Interestingly, there appears to be little direct relationship between the existence of state-imposed municipal limits and the adoption of local limits. While 80 percent of limit-adopting cities also face a potentially-binding state-mandated limit, 70 percent of non-adopting cities do as well. We also find no evidence that local limit adoption is related to the strength of the state-mandated limit (i.e., whether the state limit is constitutional or merely statutory).

The final panel of Table 3 examines the relationship between limit adoption and local tax revenue. We do not believe that this relationship is well-described using cross-sectional data, and we present summary statistics here for descriptive purposes only. We find no statistically significant difference in total revenue, total own-source revenue, or total property tax revenue between limited and un-limited cities. A panel analysis, to which we turn in Section 3, is better suited for examining whether the fiscal time path differs between limited and unlimited cities.

To explore whether the characteristics present in the summary statistics are associated with limit adoption in a multivariate context, we turn to regression analysis. To examine the role of city features that are very slowly changing, such as political institutions, we use cross-sectional data and a probit model. Such features would be either entirely or substantially collinear in a city fixed-effects model. For city features that exhibit greater variation over time, such as revenues, we rely on a hazard model, where the dependent variable is time to limit adoption.

We begin with the cross-sectional analysis, for which we estimate the probit model in Equation 1. The dependent variable, ${local limit}_{c}$ , is 1 if the city ever has a local limit and 0 otherwise. The covariates of interest, $\mathbf{V_{c}}$ , are median income, and the two institutional variables - home rule status and the number of jurisdictions in the city's metropolitan area - that differed significantly between limited and unlimited cities in the summary statistics.¹⁹ We assess whether these variables are still associated with limit adoption, controlling for region and other demographic and institutional covariates.

local limit $\displaystyle _{c}=\Phi(\beta_{0}+\beta_{1}\mathbf{V_{c}}+\beta_{2}$ region $\displaystyle _{c}+\beta_{3}$ institutions $\displaystyle _{c}+\beta_{4}$ demographics $\displaystyle _{c}+\epsilon_{c})$

(1)

We present estimated coefficients from Equation 1, evaluated at the dependent variable means, in Table 4.²⁰ The first four columns present results using only regional dummies as covariates. The first column presents the coefficient on median family income in $1,000s. As in the summary statistics, this measure is significantly associated with limit adoption. A one standard deviation increase in median income is associated with a 25 percent lower likelihood of limit adoption. In the second column, the coefficient suggests that a switch from general law status to home rule status is associated with a 65 percent greater likelihood of adopting a local limit. In the third column, cities in metropolitan areas with more cities are insignificantly less likely to adopt a local limit.

Column 4 includes all three variables together with the regional dummies. Median income and home rule both remain statistically significant. Column 5 adds controls for institutional covariates (see table notes for the complete list of covariates), and the pattern persists. Column 6 adds demographic covariates, including population and log of population. Home rule remains a significant predictor of local limit status, and the number of cities in the MSA becomes significantly associated with limit adoption. A ten percent increase in the number of cities in a MSA (roughly four additional cities) yields a five percent decrease in the likelihood of adopting a limit. In this specification, the coefficient on median income is now statistically indistinguishable from zero, likely because this variable is substantially correlated with other demographic covariates. The institutional findings are consistent with the hypothesis that a local limit acts as a substitute for other institutions and with the moderating role of Tiebout competition on partisanship found in Ferreira & Gyourko (2009).

While the probit model is appropriate for examining the correlation between slow-changing municipal features and limit adoption, it is not well-suited to examining how time-varying features may determine local limit adoption. For example, local limits could be adopted in response to high levels of taxation, or to variability in taxation. To assess whether limit adoption is related to fiscal behavior before the limit, we estimate hazard models, where the dependent variable is the time to adoption of a limit.²¹ We use both the Cox proportional hazard and the exponential hazard models. Specifically, we estimate

$\displaystyle h(t) = h_0(t) \exp(\beta_1$ real own-source revenue pc $\displaystyle _{c,t} + \beta_2 \mathbf{I_c} + \beta_3 \mathbf{V_{c,t}})$ ,

(2)

where

is the baseline hazard function. We use this equation to estimate whether the likelihood a city adopts a local limit is responsive to the city's own-source revenues at time

(own source revenues are those raised from local taxation, and not received from other governments, such as the state). We control for variables $\mathbf{I_c}$ , which are time invariant city characteristics and include home rule status, the number of cities in the metropolitan area and others (see table notes for full list). Additional controls $\mathbf{V_{c,t}}$ are time varying and include population, log of population, and median family income (see table notes for the complete list). When we estimate the exponential hazard model, we include year dummies.²²

We present the results of these specifications in Table 5. The table highlights the key variable of interest, real own-source revenues per capita, and the three variables of interest from the cross-sectional analysis: home rule status, the number of cities in the metropolitan area, and the real median family income. Regardless of specification and covariates, own-source revenue is not statistically significantly related to limit adoption. Thus, we find no obvious evidence that limits are driven by high levels of taxation.

One might believe, however, that limits are driven not by high total levels of taxation, but by particular types of taxation, or by variance in taxation, as suggested in Anderson & Pape (2010). If this is the case, we should look at both specific tax sources and variance in tax revenue. Table 6 repeats the analysis in equation 2, using total own-source revenue, total revenue (from all sources), total tax revenue, and property tax revenue as the independent variable of interest. In addition, we also examine variation in each of these series, by estimating separate regressions with the three-year moving average, and the three-year coefficient of variation for each revenue sources.

Table 6 shows the results from these twelve models (corresponding to four revenue sources by three measures of variation). In this table, each coefficient comes from a separate regression. In only one of the twelve specifications is the coefficient on the taxation variable statistically significant. A ten percent increase in the three-year moving average of property taxes is associated with a eighteen percent greater likelihood of limit adoption. While this is a substantial increase, we are reluctant to draw too much from it for two reasons. First, it is the only significant coefficient in the table. Second, the coefficient on the three-year coefficient of variation in property taxes, which should be similarly correlated with limit adoption if variability in tax revenues drive adoption, has the opposite sign. Overall, we take these estimates as providing no strong evidence that levels or variance in taxation drive limit adoption.

Finally, to complement the quantitative evidence on limit adoption, and to explore other avenues for limit adoption, we read newspaper articles detailing the adoption of local limits. We were able to find newspaper accounts for 17 of the 40 limited cities. After reading the articles, we classified them by reported cause of the limit. Our qualitative work finds three primary causes of limits: (a) that taxes are too high, (b) that a politician wants to raise tax X and in return promises to limit tax Y and (c) that an entrepreneurial politician wishes to build a reputation by leading the passage of a limit. Douglas Bruce, who spearheaded Colorado Springs' stringent limit, which in turn led to the adoption of a statewide limit is the best example of this case: Bruce subsequently gained statewide office.

2 Theory

Guided by the stylized facts we obtained in the previous section, we motivate why a self-imposed tax or expenditure limit might exist and explore its possible effects. Most of the existing literature on fiscal restraints explains them as a consequence of electoral institutions that fall short of implementing the median voter's preferences. When the median voter's preferred policy is not implemented, institutional substitutes, such as direct democracy (i.e., ballot initiative), may alleviate welfare losses. We use a similar approach and evaluate a self-imposed fiscal limit as a possible remedy to institutional failure.

The theory highlights agency problems inherent in representative government. For example, voter uncertainty about a politician's actions combined with a desire to hold her accountable may create incentives for voters to constrain her behavior Besley & Smart (2007). Alternatively, an incentive to limit government may arise when voter preferences conflict over the optimal amount of public good provision and when the type of politician elected to office is unobserved by voters Coate & Knight (2011). We employ a variant of this latter framework.²³ We assume that groups in the population differ in their demand for public goods, and that voters are uncertain about both the cost of public goods and the type of politician elected for office. Although there is real option value in spending more on public goods when costs are low, preference heterogeneity in the population and uncertainty may create an incentive for voters with a low taste for public goods to limit spending. This idea that divisiveness, driven by heterogeneous tastes, limits public spending is in the spirit of Alesina & Easterly (1999).²⁴

In our model, we evaluate when a limit is likely to pass in a referendum, characterize the optimal limit, and discuss how a limit may arise in the absence of institutional substitutes. We then consider the limit's impact on municipal revenues and conclude with the welfare consequences of limit adoption.

2.1 Citizens

Let there be two types of voters $j\in\left\{ 1,2\right\}$ , where the proportion of type 1 in the population is $\pi$ . Both types have preferences over the provision of a public good G. The cost of the public good is determined by an unobservable state variable $\theta>0$ , which is a measure of how much public goods cost. For example, the cost of snow removal depends at least partially on a currently unobservable state variable - the weather. We assume that $\theta$ is distributed uniformly between $\underline{\theta}$ and $\bar{\theta}$ , where $\bar{\theta}>2\underline{\theta}>1/2$ .²⁵

Let the utility of type j be $u_{j}\left(G,\theta\right)=\sqrt{jG}-\theta G$ , where $\theta G$ is the cost of public good G in state $\theta$ and j is a preference parameter. Given this utility specification, the optimal provision of public good G for each type is $G_{j}^{*}\left(\theta\right)=\frac{j}{4\theta^{2}}$ and the cost is $\theta G_{j}^{*}\left(\theta\right)=\frac{j}{4\theta}$ . Thus, in any given state $\theta$ , a type 1 voter always desires less spending on public goods than does a type 2 voter.

2.2 The Political Process

Two candidates for office run for election, and the winner is determined by majority rule. For simplicity, we assume that the winner governs by herself. In our empirical application, cities are governed either by a city council or a mayor in concert with the council. Our results are unaffected if we modify the model to have officeholders, and require a majority for legislative decisions.²⁶

We assume that while candidates compete on different policy platforms before the election, voters are uncertain about the politicians' preferences over public good provision and subsequent spending choices.²⁷ The degree of uncertainty that voters have about the politician type does not play a crucial role in our analysis. For simplicity, we assume that candidates are independent random draws from the underlying distribution of types, and that the preference type, j, of each candidate is unobservable to voters. This means that each candidate is type 1 with probability $\pi$ , and the probability that a type 1 holds office is also $\pi$ . If we let candidates signal their type to voters, our key results remain qualitatively unchanged; however, the proportion of type 1 to type 2 office holders changes.²⁸ Finally, we assume that once in office, each type implements her optimal policy.²⁹

2.3 A Limit on Spending

Because cities face strict balanced budget requirements, we assume that a limit on tax revenues is equivalent to a limit on public good spending. We denote a limit on public good expenditures, $\theta G$ , by , such that $\theta G\leq x$ must hold. For simplicity, if a limit is supported by the majority of the population in a referendum, then it is subsequently adopted in the city code or charter ("adopted").³⁰ Further, we assume that if a limit is proposed in a referendum it solves voter 's utility maximization problem. Formally, voter j maximizes her expected utility given a limit, j, and the share of type 1 voters, $\pi$ , in the population:

$\displaystyle x^*\in$ argmax $\displaystyle _{x\in\left[\frac{1}{4\bar{\theta}},\frac{1}{2\underline{\theta}}\right]}E_{\theta}\left(u_{j}\vert x,\pi\right),$

(3)

where the optimal limit,

, is chosen from the interval of possible expenditures given any state of the world and politician type (see Subsection 2.1).

2.4 Results

Consider the costs and benefits of adopting a fiscal limit. If the entire population is the type 1 low-demanding group, there is no benefit to a limit, and no limit is adopted.³¹ If type 1 is a minority, or $\pi<1/2$ , the benefit of the limit accrues only to a minority, which cannot sustain a limit in a referendum.³² Thus, a limit is viable only when the minority prefers more public goods than the majority. In this case, type 1 voters wish to restrain the behavior of a type 2 politician were she elected. However, limiting spending comes at the cost of potentially restraining a type 1 politician from implementing her preferred policy. For example, suppose there is a strict limit on expenditures, that a type 1 politician is in office and that there is a technological innovation that lowers the cost of street lighting. The resulting higher benefit relative to cost may induce even type 1s to prefer more street lighting. However, the existence of a limit means that the type 1 politician cannot respond to the change in costs $\theta$ by increasing spending on street lights. Thus, the optimal limit is less restrictive when the proportion of type 1 in the population is high and the likelihood that a type 2 politician is elected is low. We summarize this result in the following proposition.

PROPOSITION 1: For any $\pi>1/2$ , there exists an optimal expenditure limit that wins the support of a majority in a referendum. Furthermore, the value of the optimal revenue limit, $x^{*}$ , increases in $\pi$ . PROOF: See Appendix.

The existence of a limit is implied when type 1 voters are a majority in the population.³³ This explanation is consistent with our empirical finding that limit adoption is more likely in less wealthy municipalities. Many researchers have argued that income can be a relatively good proxy for preference types. Both across and within countries, demand for public goods increases in income (seminal contributions in this literature are Borcherding & Deacon (1972) and Bergstrom & Goodman (1973); a recent contribution is Hokby & Soderqvist (2003), and Lindauer (1988) provides cross-country evidence). Thus, $\pi$ may reflect the proportion of lower income citizens in a given city. If income is a good proxy for preference type, wealthier cities may be less likely to adopt expenditure limits.

The need for an expenditure limit can also arise in the absence of institutions that act as substitutes for limits. We do not formally model these substitutes, but offer a sketch of how such institutions can impact the prevalence of limits. We conceive of institutions, such as the restrictions inherent in municipal incorporation (e.g., a restriction on allowable tax bases), as a de facto constraint on revenue, say $\bar{x}$ . If the city sets a limit $x^{*}$ , and $x^{*}>\bar{x}$ , then the optimal limit never binds and is immaterial. Therefore, we expect cities with sufficiently restrictive institutions to be less likely to adopt additional fiscal constraints. This explanation provides a motivation for our finding that limit adoption is more likely in home rule cities and in cities with relatively more municipal jurisdictions.

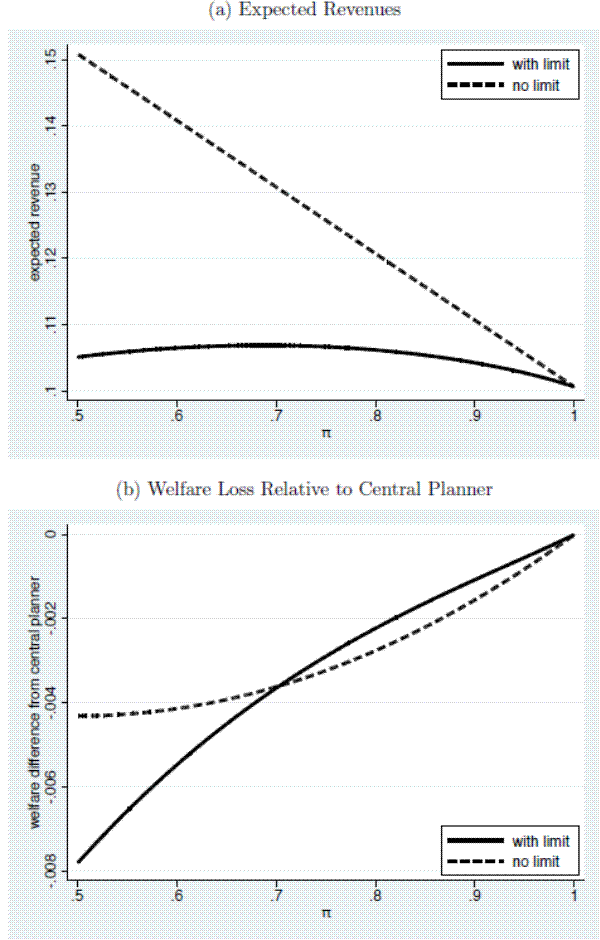
Having analyzed why limits are adopted and what an optimal limit is, we now turn to how adopting the optimal limit impacts spending on public goods. We derive the expected municipal revenues (equal to expenditures) given the optimal limit, $E_{\theta}\left[R\vert x^{*},\pi\right]$ , as a function of the share of type 1 voters. In Figure 2, we plot expected municipal revenues for a given city as a function of $\pi$ . The figure shows that expected revenues when the city does not have a limit - the dashed line - are higher than when the city adopts the optimal limit - the solid line - for any $\pi < 1$ . However, expected revenues in limited cities do not necessarily decline in $\pi$ . Rather, the relationship between expected revenues and $\pi$ (in the limited cities) may depend non-monotonically on preferences and the degree of uncertainty (about $\theta$ and politician type) in the population. We summarize this result in the proposition below.

PROPOSITION 2: For any given $\pi$ , expected revenues are lower in a city when the optimal limit is adopted. In the absence of a limit, expected revenues are strictly decreasing in $\pi$ ; when the optimal limit is adopted, the relationship between revenues and $\pi$ is ambiguous.

PROOF: See Appendix.

Finally, we ask whether adoption of a fiscal limit improves welfare, and whether welfare depends on $\pi$ . To explore this question, we compare a weighted sum of utilities for type 1 and 2 when the optimal limit is adopted, $W(\pi)=\pi E_{\theta}\left[u_{1}\vert x^{*}\right]+\left(1-\pi\right)E_{\theta}\left[u_{2}\vert x^{*}\right]$ , to the no-limit benchmark, $W_{n}\left(\pi\right)=\pi E_{\theta}\left[u_{1}\right]+\left(1-\pi\right)E_{\theta}\left[u_{2}\right]$ . In Figure 2, we plot the differences of $W(\pi)$ and $W_{n}\left(\pi\right)$ from the welfare generated by a central planner who maximizes the total welfare of the city:

$\displaystyle W_{c}\left(\pi\right)=\max_{G}E_{\theta}\left[\pi u_{1}+\left(1-\pi\right)u_{2}\right].$

(4)

Neither the limited nor unlimited regime is welfare dominant for all values of $\pi$ . Furthermore, neither regime is ever able to generate welfare levels equal to those created by the social planner. Figure 2 depicts welfare losses, relative to the centrally planned regime, by limit status (values closer to zero indicate lower welfare losses, or higher welfare). Which regime generates lower losses depends on the share of type 1 voters in the population. Limited cities - shown with the solid line - are preferred for values of $\pi$ that are greater than approximately 0.7. For lower values of $\pi$ , unlimited cities, shown with the dashed line, are preferred. Intuitively, welfare gains from limit adoption accrue only to type 1 voters and these gains are therefore largest when type 1 voters are a substantial share of the population. Thus, if the welfare gain from limit adoption ( $W(\pi)$ - $W_{n}\left(\pi\right)$ ) is positive for some $\pi^{*}$ , it must be positive for any $\pi>\pi^{*}$ . This suggests that a fiscal limit may generate welfare gains relative to the unlimited case if the procedure to adopt a limit (e.g., referendum) is designed in a manner that reflects the preferences of the underlying electorate, the extent of electoral uncertainty, and the social value public goods generate.³⁴

In sum, our model motivates the need for a fiscal limit without using the obvious assumption of a Leviathan government; an assumption that appears to be without empirical merit in our case. We find that a limit is likely when the share of the population that prefers lower levels of public goods is a majority. Limits are also more likely when institutional substitutes to restrain political behavior are absent, suggesting that the power of the ballot box alone may not curb spending in line with the desires of the median voter. If a limit is adopted, municipal revenues are lower. However, welfare is not necessarily higher, relative to the no-limit benchmark, for all potential distributions of preference types in the population.

3 Fiscal Consequences of Limit Adoption

3.1 Empirical Strategy

With this theoretical framework in hand, we now turn to analyzing the fiscal consequences of limit adoption. In the model, revenues decline (in expectation) when an optimal limit exists because the limit sometimes binds politicians from implementing their preferred level of public good provision. We now examine the empirical support for this contention. Some of the limits we observe are likely to be strictly binding, such as those on overall revenues. Other limits, however, such as a limit on property assessment increases without a similar limit on the property tax rate, may have no strict ability to limit revenues; they may limit behavior only through the set of revenue choices to which a politician has access. For example, a politician can circumvent the assessment limit to raise the desired amount of revenue simply by increasing the property tax rate.

However, even if a limit never directly binds politicians' fiscal behavior, there are at least two additional reasons why revenues and limits can change concurrently. First, a limit might be adopted simultaneously with a change in population characteristics. For example, the limit is adopted, and at the same time the share of type 1 voters in the population increases. In this case, the limit may never bind, but the level of revenues declines. We show empirically that this case is unlikely to be the exclusive explanation for our findings.

To explore the second reason limits may dampen revenues, suppose there is a cost of running for office. In this case, imposing a limit affects the pool of candidates. In particular, type 2 candidates have less to gain from the prospect of holding office, since their optimal revenue choice is likely to be unfeasible. Consequently, municipal revenues again decline without having the limit bind.³⁵ However, we are comfortable calling this type of result an "effect" of the limit in the causal sense, as the limit generates different political patterns and therefore changes revenues.

We begin a simple test of the model's contention that limit adoption decreases expected revenues after the limit relative to unlimited cities. To estimate whether own source revenues decline after limit adoption, we estimate

$\begin{displaymath}\begin{split}\ln(\mbox{own-source revenue pc})_{c,t}= & \beta_{0}+\beta_{1}\mbox{year}_{t}+\beta_{2}\mbox{city}_{c}+\beta_{3}\mathbf{X_{c,t}}+\beta_{4}\mathbf{\mbox{state limits}_{c,t}}+\\ & \beta_{5} 1\{\mbox{local limit city}\}*1\{\mbox{post limit}\}_{c,t}+ \epsilon_{c,t}.\end{split}\end{displaymath}$

(5)

The dependent variable is logged municipal own-source revenue per capita, $\ln($ own source rev pc $)_{c,t}$ , where

denotes city, and

denotes years 1970 through 2004. $\mathbf{\text{{\it X}}_{c,t}}$ is a matrix of time-varying city characteristics, including population, log of population, median family income, racial composition and other variables (see table notes for complete list). The vector $\mathbf{\mbox{\it {state limits}}_{c,t}}$ contains two dummy variables: the first equal to one if the state has a self-imposed limit (state limit on itself), and the second equal to one if the state has a limit on cities.³⁶

We employ year fixed effects, year $_{t}$ , to account for macroeconomic and political factors affecting all cities in a given year. We include adopting and non-adopting cities in this regression to identify the year effects primarily from non-adopting cities, which allows us to separate post-limit effects from overall macroeconomic conditions.

We also use city fixed effects, city $_{c}$ . These fixed effects capture unchanging or slowly changing institutional, demographic, and cultural characteristics of cities as well as any fixed component of state-level restrictions. With the exception of state-imposed and local limits, we observe municipal institutional data only at a single point in time. These features are therefore captured in the city fixed effects and do not enter directly.³⁷

The variable of interest in this model is $1\{$ local limit city $\}*1\{$ post limit $\}_{c,t}$ , which takes on the value one when the observation is a limited city after the limit. The coefficient on this variable, $\beta_5$ , measures the percent change in own sources revenues after limit adoption, relative to non-adopting cities and adopting cities before the limit.³⁸ If limit adoption decreases revenue, we expect $\beta_5<0$ .

While the specification in Equation 5 is consistent with our model, there are strong reasons to believe that it does not correspond well with the institutional details. The literature on state limits on cities recognizes limits on total revenue or expenditures as being the most stringent type. Our sample has two cities with such limits: Colorado Springs, Colorado and Anchorage, Alaska. Even these most restrictive limits do not attempt to lower total revenue levels. Instead, these limits restrict future increases in revenues to population plus inflation. In the specification above, if all cities had limits like these two cities, this would imply no change in revenues after limit adoption, or $\beta_5 = 0$ , since our specification uses real per capita dollars. However, these very stringent limits do attempt to decrease the growth rate of revenues, in the extreme to zero. Other less stringent limits have similar flavors. For example, limits on assessments generally restrict the growth of assessed values to percent per year. Such a limit should slow the growth of revenues rather than to cause an absolute decline. For these reasons, we focus on the effect of limit adoption on revenue growth.

To this end, we estimate Equation 6 below. Equation 6 modifies Equation 5 by replacing the "post limit" dummy with an interaction of "post limit" and a time trend. Equation 6 also includes linear trends for revenue growth in non-adopting cities, and in adopting cities before the limit (to include all these trends, we drop an additional year dummy). Specifically, we use a linear trend variable, (we omit the subscript), interacted with three indicator terms for limit status. The trend variable increments by one for each year of the sample and yields a coefficient that reports the average linear trend, net of covariates. The first of the three variables for limit status is the indicator $1\{$ never local limit city $\}_{c}$ , equal to one for cities that never adopt a local limit. The indicator $1\{$ local limit city $\}*1\{$ pre limit $\}_{c,t}$ is one for limit-adopting cities before adoption, and the indicator $1\{$ local limit city $\}*1\{$ post limit $\}_{c,t}$ is one for limit-adopting cities after adoption. The three interaction terms are mutually exclusive. Each observation has a non-zero value for one of the three trend variables in each year.

$\begin{displaymath}\begin{split}\ln(\mbox{own source rev pc})_{c,t}= & \beta_{0}+\beta_{1}\mbox{year}_{t}+\beta_{2}\mbox{city}_{c}+\beta_{3}\mathbf{X_{c,t}}+\beta_{4}\mathbf{\mbox{state limits}_{c,t}}+\\ & \beta_{5}t*1\{\mbox{never local limit city}\}_{c}+\\ & \beta_{6}t*1\{\mbox{local limit city}\}*1\{\mbox{pre limit}\}_{c,t}+\\ & \beta_{7}t*1\{\mbox{local limit city}\}*1\{\mbox{post limit}\}_{c,t} +\epsilon_{c,t}.\end{split}\end{displaymath}$

(6)

We interpret the coefficients on the trend interaction terms as annual percent changes in real own-source revenue per capita associated with the group designated by the indicator variable.

This specification generates two potential counterfactuals for revenue growth after the limit ( $\beta_{7}$ ): revenue growth for non-limited cities ( $\beta_{5}$ ) and revenue growth for cities with limits before the limit was adopted ( $\beta_{6}$ ). Post-limit growth versus pre-limit growth ( $\beta_{7}$ versus $\beta_{6}$ ) is likely the cleaner empirical test, because both the treatment and control groups, by construction, possess the same time-invariant component of municipal selection into limit adoption (for which we control via the city fixed effect). However, post-limit growth versus never-limited growth ( $\beta_{6}$ versus $\beta_{5}$ ) is probably closest to the model's motivation. Never-limited cities are only a good counterfactual if their growth is similar to limited cities pre-limit, which we will show is true empirically.

To claim that the differences between limited and unlimited cities are causal, limits must be randomly assigned across cities and time. As we have motivated above, limits are clearly not adopted randomly. However, the covariates we have identified as being associated with limit adoption - income distribution, home rule status and the number of cities in the metropolitan area - change either slowly or not at all. Thus, these characteristics are well-captured by city fixed effects. In addition, our time series investigation into the causes of limit adoption (see the end of Subsection 1.3) finds no time-varying correlates of limit adoption. If there are no time-varying observed components correlated with limit adoption, and if the same holds for time-varying unobserved components, the fixed effects approach suffices to identify a causal effect.

Of course, it is possible that unobserved features of cities, such as the political tastes of citizens, do co-vary in time with limit adoption in a way we have not been able to capture with our data. Further, it is possible that our comparison of revenue growth before limit adoption ( $\beta_{6}$ ) with revenue growth after the limit ( $\beta_{7}$ ) or revenue growth in non-adopting cities ( $\beta_{5}$ ) picks up the difference in these time-varying unobservables rather than (or in addition to) the impact of the local limit. In the event that these unobservables are quite important, we use three additional procedures to estimate a cleaner causal effect. We first use matching to better pair adopting cities with non-adopting cities. Second, we use graphical evidence to show that our findings are unlikely to be driven by pre-existing trends in revenue. Third, we statistically investigate whether revenues decline in advance of limit adoption, in order to rule out that our findings are driven by anticipatory effects of limit passage.

3.2 Results

We begin with evidence on whether the adoption of a local limit is associated with an absolute decline in own-source revenues. The left panel of Table 7 shows estimates of $\beta_5$ from Equation 5 for all cities. In this panel, there are 279 non-adopting cities, 18 cities that adopt a limit at some point during the period, and 13 cities that adopt a limit either before or after our sample period (we omit the 9 limited cities for which we do not observe a date of adoption). The right panel presents the same specification, dropping the 13 limited cities that never change limit status. In the left panel, the first column reports coefficients from a specification with only city and year fixed effects. The second column adds demographic controls, and the third column adds the two types of state limits.

Regardless of specification, we find that limits have an insignificant negative effect, in the range of five to seven percentage points, on local revenues. This is not an insubstantial decline, but it is never statistically significantly different from zero at the five percent level. Further, this finding is consistent with the design of limits, which generally try to restrict revenue growth, rather than cause declines in revenue levels.

Therefore, we believe that the institutional details more closely motivate the specification in Equation 6. Results from this estimation are presented in Table 8. This table uses the same format as the previous one, with all cities in the left panel, and only non-adopting and adopters after 1970 on the right. The pattern of covariates we employ is identical. Regardless of specification, the results are consistent. After limit passage, column 3 reports that cities with a limit have revenue growth of 1.4 percent per year ( $\beta_7 = 0.014$ ). We test whether this rate of growth is greater than 1.8 percent pre-limit revenue growth for limited cities ( $\beta_6=0.018$ ). We can reject this hypothesis with a p value of 0.02 (row 4). We can reject equality of the coefficients with a p value of 0.04 (row 3). Put simply, revenue growth declines by 22 percent after limit adoption relative to the pre-limit baseline.

We also compare the post limit growth rate of 1.4 percent in column 3 to the 1.7 percent growth rate of never-limited cities ( $\beta_5 = 0.017$ ). Such a comparison makes sense only if revenues in never-limited cities grow at the same rate as revenues in limited cities, before the limit. Our hazard models in Section 1.3 suggested this finding, and this table provides additional supportive evidence. Row 1 reports the p value for a test that the pre-limit and never-limit trends are equal ( $H_0: \beta_5 = \beta_6$ ). Regardless of specification, this p value is never lower than 0.6. In words, we can never reject that the pre-limit and never-limit growth trends are equal. This suggests that never-limited cities provide a good counterfactual for limited cities.

Having ascertained that never-limited cities are a plausible control group, we now compare the growth rate in never-limited cities to that in limited cities, post limit. Row 6 reports the result of the test that revenue growth post-limit exceeds revenue growth in never-limited cities ( $\beta_7 > \beta_5$ ). We can reject this hypothesis with a p value of 0.075. A stricter test of equality (row 5) has a p value of 0.15. Converting the estimated coefficients into dollars, this estimation suggests that after ten years, unlimited cities have $70 higher per capita revenue than limited cities. This is roughly 4 percent more total own-source revenues (all of these numbers are calculated from the 2002 average per capita own-source revenue of $1,579). This evidence is consistent with limits weakly constraining politician behavior.³⁹

The right hand set of columns in Table 8 drops the 13 cities with limits outside of our sample period and tells a very similar story. This empirical strategy is arguably cleaner, since we now use only cities that enact a limit during the period of time included in our analysis. This specification also shows that after limit adoption, limited cities ( $\beta_7 = 0.016$ ) have a decline in the rate of revenue growth relative to both limited cities pre-limit ( $\beta_6 = 0.019$ ) and never limited cities ( $\beta_5 = 0.018$ ). We reject that post-limit growth exceeds pre-limit growth in the final specification (column 6) at the 5 percent level (row 4) and that never-limited growth exceeds post-limit growth at the higher 18.5 percent level (row 6). Comparing pre-limit to post-limit growth, we find a 16 percent decrease in the rate of revenue growth. Thus, regardless of which sample (left or right panel) or which counterfactual (never-limited cities, or pre-limit cities), limit adoption is associated with a decline in municipal revenue growth.

The estimates in Table 8 do not distinguish among limits on different revenue sources (i.e., property taxes versus sales taxes) or between limits that target a single revenue instrument but work through slightly different mechanisms (i.e., a property tax rate limit versus a property tax levy limit). Unfortunately, our sample is not large enough to distinguish between these fine-grained categorizations. If we only include in our analysis the most rigorous limits--those that restrict the property tax and those that restrict total tax revenues or expenditures--our results remain unchanged, and the difference between the coefficients widens (see Online Appendix Table 6). Our results also remain unchanged if we use total revenues as our dependent variable instead of total own-source revenues (see Online Appendix Table 7). This indicates that local limit adopters do not compensate for lost local revenue by obtaining increased intergovernmental transfers from either the state or federal government. Similarly, we do not observe an increase in the state-government share of total revenues following limit adoption.

The estimated coefficients show a substantive relationship between local limits and relative declines in revenue growth, but require strong assumptions to yield causal relationships. Our data offer no natural experiment or obvious instrument. Thus, to provide further causal evidence, we use three strategies: propensity score matching, and both visual and regression tests for the presence of anticipatory revenue behavior before limit adoption.

We begin with propensity score matching, which weights non-adopting cities with covariates similar to adopting cities more heavily than the estimation of Equation 6 by OLS. To provide a causal estimate, a matching procedure must meet two criteria. First, treated and untreated observations must have at least some common support; in this case, this means that there must be limited cities with propensity scores similar to unlimited cities. The second requirement for matching to yield a causal estimate is that, once observable criteria are controlled for via the match, limit status is "as good as random." This second requirement is inherently unobservable, like the exclusion restriction in an instrumental variables framework.

If these assumptions are satisfied, this empirical strategy yields causal estimates of limits' effect on fiscal behavior. We generate propensity scores in two ways--using cross-sectional data and time-series data. For the cross-section, the propensity score uses all cities in the sample for which we observe data in 1970. With this sample, we estimate a probit for local limit adoption as a function of all the demographic and institutional data employed above. For the time-series matching, we use a probit model for local limit adoption in a given year as a function of the same covariates. The predicted values from these regressions are used to create weights which are employed in new estimations of Equation 1.⁴⁰ Both types of propensity scores have some common support for limited and unlimited cities. Using propensity scores from cross-sectional information, the 10th-90th percentile range for unlimited cities is [0.001,0.268], while the range for limited cities is [0.059,0.867]. Using time series information, the 10th-90th percentile range for unlimited cities is [0.000,0.180], and for limited cities [0.050,0.631].

The matching results in Table 9 affirm that, even relative to cities that are more like adopters, revenue growth in limited cities declines after local limit adoption. The coefficients on revenue growth pre- and post-adoption using matching techniques are quite similar to those generated in our original estimations (Table 8). Tests of equality show that differences in pre- and post-limit revenue growth remain statistically significant, at either the 5 or 10 percent level, regardless of the propensity score or the sample. While we do lose precision in our ability to distinguish revenue growth post-limit from never-limited growth, the point estimates tell a broadly similar story to that of Table 8.

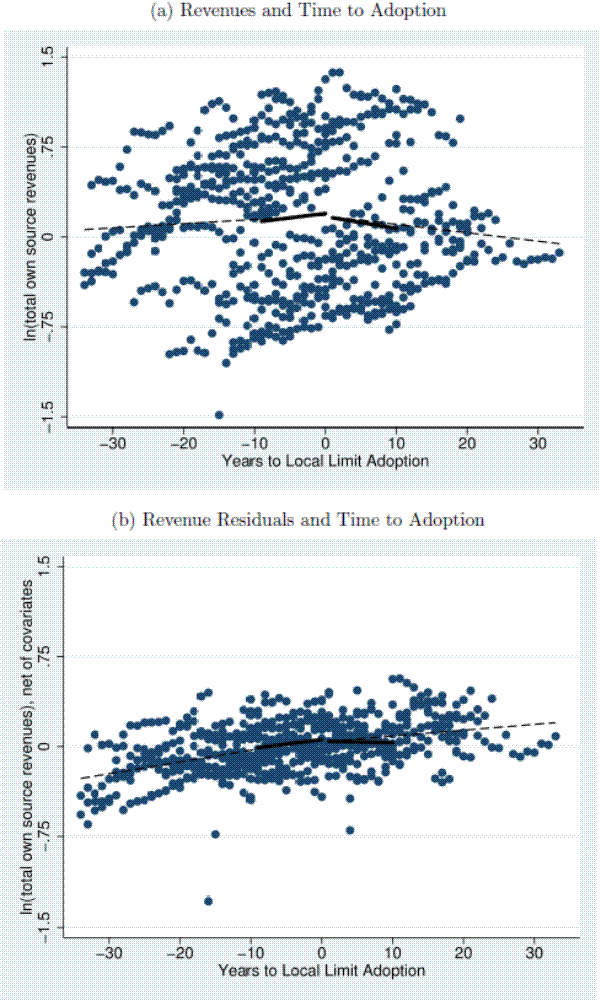
The remaining challenge to the claim that limits causally affect revenue growth, in our opinion, is the possibility that public sentiment about the size of government changes concurrently with limit adoption. We evaluate this possibility graphically and then statistically. Figure 3 shows the log of total own-source revenue per capita as a function of the time to limit adoption, where the limit begins in year 1. Figure 3 shows the raw data, with separate best fit lines for the pre- and post-limit years drawn with a dashed line. In addition, the figure shows two additional best fit lines for the ten years preceding and following the limit with solid lines. Suppose that public sentiment changes slowly, but that limit status changes discretely, as seems very empirically likely. In this case, if public sentiment drove the results we observe, the growth rate of revenues should begin to change before the limit is adopted. This figure shows that the data do not support this hypothesis. Visually, even when restricting our scrutiny to years close to limit adoption, there is no evidence of an decrease in revenue growth before limit adoption. After limit adoption, in both the near- and farther-term, the rate of revenue growth decreases.

Of course, this analysis is subject to concerns about which cities are likely to be early or late limit adopters, and the prevailing macroeconomic conditions at the time of adoption. For this reason, we use city and time fixed effects in the regression. Figure 3 reports the residuals from a regression of log own-source per capital real revenues on city fixed effects, year fixed effects, and a linear trend for non-adopting cities (specifically, the residuals from Equation 6, omitting the $\beta_3, \beta_4, \beta_6$ , and $\beta_7$ terms). Again, even when we consider a relatively short horizon before limit adoption, there is no visual evidence that the pre-limit trend in revenues has changed.

We test this argument more concretely by dividing the pre-limit trend term in Equation 6, $\beta_{6}t*1\{$ local limit city $\}*1\{$ pre limit $\}_{c,t}$ into two parts, one to measure the revenue trend far from limit adoption, and another to measure the trend close to adoption. Close and far are defined as being years away from limit adoption. These terms are therefore $\beta_{6a}t*1\{$ local limit city $\}*1\{$ pre limit $\}*1\{t\leq$ adoption year $-j\}_{c,t}+\beta_{6b}t*1\{$ local limit city $\}*1\{$ pre limit $\}*1\{t>$ adoption year $-j\}_{c,t}$ . Using $j\in\{1,2,3,4,5\}$ , we find that $\beta_{6b}$ , the rate of revenue growth pre-limit near the limit, is almost always statistically significantly greater than the rate of revenue growth after the limit, $\beta_{7}$ . Put differently, the timing of the discrete break at the limit is important, and the trend in revenues pre-limit does not begin to change shortly before limit adoption.

In sum, we find that limited cities decrease revenue growth after the adoption of a local limit. This is true even when we use matching to compare limited cities more closely to cities with the same observed characteristics. Other evidence suggests it is unlikely that our result is driven by preference changes that occur at a similar time as the adoption of the limit. That said, our paper is clearly only a first step in this analysis: our sample is not large, and limits may have very heterogeneous effects.

4 Conclusion

We document that at least 1 in 8 cities has a self-imposed restriction on its ability to tax or spend. To the best of our knowledge, this type of self-imposed municipal limit is new to the literature. We use these limits to explore when the power of the median voter suffices to limit government, and when institutional constraints are instead required to curb representative government. Since limit adoption is prevalent, we show that the median voter is surely not sufficient in all cases.

Limit adoption is less likely in higher income cities and in cities in metropolitan areas with a larger number of jurisdictions. Limit adoption is also substantially more likely in home rule jurisdictions. Surprisingly, we find no evidence that limit adoption is a function of tax receipts.

Our model of limit adoption builds on these stylized facts to motivate why limits are adopted, explain the likely consequences and consider the welfare implications of limit adoption. We find that the welfare consequences of limits differ depending on the underlying distribution of tastes in the population. This uneven pattern of welfare benefits may explain the partial pattern of local limit adoption.

Finally, our evidence suggests that limits have fiscal consequences. After the adoption of a limit, municipal revenue growth in the average limited city declines by 16 to 22 percent.

Bibliography

Advisory Commission on Intergovernmental Relations (1995).

Tax and Expenditure Limits on Local Government.
Washington, D.C.

A. Alesina, et al. (2004).

`Political Jurisdictions in Heterogeneous Communities'.
Journal of Political Economy 112(2):348-396.

A. Alesina & W. Easterly (1999).

`Public Goods and Ethnic Divisions'.
Quarterly Journal of Economics 114(4):1243-1284.

J. Alm & M. Skidmore (1999).

`Why do Tax and Expenditure Limitations Pass in State Elections?'.
Public Finance Review 27(5):481-510.

N. B. Anderson & A. D. Pape (2010).

`A Reassessment of the 1970s Property Tax Revolt'.
Working Paper, University of Illinois at Chicago.

R. Baqir (2002).

`Districting and Government Overspending'.
Journal of Political Economy 110(6):1318-1354.

T. C. Bergstrom & R. P. Goodman (1973).

`Private Demands for Public Goods'.
American Economic Review 63:380-296.

T. Besley & M. Smart (2007).

`Fiscal Restraints and Voter Welfare'.
Journal of Public Economics 91:755-773.

D. Black (1958).

The Theory of Committees and Elections.
Cambridge University Press, Cambridge, UK.

T. E. Borcherding & R. T. Deacon (1972).

`The Demand for Services of Non-Federal Governments'.
American Economic Review 62:891-901.

G. Brennan & J. Buchanan (1979).

`The Logic of Tax Limits: Alternative Constitutional Constraints on the Power to Tax'.
National Tax Journal 32:149-170.

G. Brennan & J. M. Buchanan (1980).

The Power to Tax: Analytical Foundations of a Fiscal Constitution.
Cambridge University Press, Cambridge, MA.

L. Brooks & J. H. Phillips (2010).

`An Institutional Explanation for the Stickiness of Federal Grants'.
Journal of Law, Economics and Organization 26:1-21.

J. M. Buchanan & G. Tullock (1962).

The Calculus of Consent: Logical Foundations of Constitutional Democracy.
University of Michigan Press, Ann Arbor, MI.

H. Chernick & A. Reschovsky (1982).

`The Distributional Impact of Proposition 13: A Microsimulation Approach'.
National Tax Journal 35:149-170.

S. Coate & B. Knight (2011).

`Government Form and Public Spending: Theory and Evidence from US Municipalities'.
American Economic Journal: Economic Policy 3(3):82-112.

D. M. Cutler, et al. (1999).

`Restraining the Leviathan: Property Tax Limitation in Massachusetts'.
Journal of Public Economics 71(3):313-334.

T. A. Downes, et al. (1998).

`Do Limits Matter? Evidence on the Effects of Tax Limitations on Student Performace'.
Journal of Urban Economics 43:401-417.

T. A. Downes & D. N. Figlio (1999).

`Do Tax and Expenditure Limits Provide a Free Lunch? Evidence on the Link Between Limits and Public Sector Quality'.
National Tax Journal 52(1):113-128.

A. Downs (1957).

An Economic Theory of Democracy.
Harper, New York, NY.

R. F. Dye & T. J. McGuire (1997).

`The Effect of Property Tax Limitation Measures on Local Government Fiscal Behavior'.
Journal of Public Economics 66(3):469-487.

F. Ferreira & J. Gyourko (2009).

`Do Political Parties Matter? Evidence from U.S. Cities'.
Quarterly Journal of Economics 124(1):349-397.

D. N. Figlio & A. O'Sullivan (2001).

`The Local Response to Tax Limitation Measures: Do Local Governments Manipulate Voters to Increase Revenues?'.
Journal of Law and Economics XLIV:233-257.

D. N. Figlio & K. S. Rueben (2001).

`Tax Limits and the Qualification of New Teachers'.
Journal of Public Economics 80:49-71.

T. Hobbes (2003).

Leviathan.
Thoemmes Continuum, Bristol.

S. Hokby & T. Soderqvist (2003).

`Elasticities of Demand and Willingness to Pay for Environmental Services in Sweden'.
Environmental and Resource Economics 26(3):361-383.

R. Holcombe (1980).

`An empirical test of the median voter model'.
Economic Inquiry 18(2):260-274.

D. J. Hopkins (2009).

`The Diversity Discount: When Increasing Ethnic and Racial Diversity Prevents Tax Increases'.
Journal of Politics 71(1):160-177.

ICMA (2006).

Municipal Form of Government, 2006: Trends in Structure, Responsibility, and Composition.
International City/County Management Association, Washington, D.C.

G. W. Imbens (2004).

`Nonparametric Estimation of Average Treatment Effects Under Exogeneity: A Review.'.
The Review of Economics and Statistics 86(1):4-29.

R. Inman (1978).

`Testing Political Economy's `as if' assumption: is the median income voter really decisive?'.
Public Choice 33(4):45-65.

P. G. Joyce & D. R. Mullins (1991).

`The Changing Fiscal Structure of the State and Local Public Sector: The Impact of Tax and Expenditure Limits'.
Public Administration Review 51(3):240-253.

T. Kousser, et al. (2008).

`For Whom the TEL Tolls: Can State Tax and Expenditure Limits Effectively Reduce Spending?'.
State Politics and Policy Quarterly 8(4):331-362.

D. Krane, et al. (2000).

Home Rule in America.
Congressional Quarterly Press, Washington, D.C.

H. F. Ladd & J. B. Wilson (1982).

`Why Voters Support Tax Limitations: Evidence from Massachusetts' Proposition 2 1/2'.
National Tax Journal 35:121-147.

H. F. Ladd & J. B. Wilson (1983).

`Who Supports Tax Limitations: Evidence from Massachusetts' Proposition 2 1/2'.
Journal of Policy Analysis and Management 2:256-279.

League of California Cities (2011).

`General Law vs. Charter City'.
http://www.cacities.org/resource_files/29142.Chart_General

D. L. Lindauer (1988).

`The Size and Growth of Government Spending'.
Tech. rep., World Bank Working Paper.

W. A. McEachern (1978).

`Collective Decision Rules and local debt choice: A test of the median voter hypothesis'.
National Tax Journal 31(2):129-136.

D. R. Mullins (2004).

`Tax and Expenditure Limitations and the Fiscal Response of Local Government: Asymmetric Intra-Local Fiscal Effects'.
Public Budgeting and Finance winter:111-147.

D. R. Mullins & P. G. Joyce (1996).

`Tax and Expenditure Limitations and State and Local Fiscal Structure: An Empirical Assessment'.
Public Budgeting and Finance 16:75-101.

D. R. Mullins & B. A. Wallins (2004).

`Tax and Expenditure Limits: Introduction and Overview'.
Public Budgeting and Finance 24(2):2-15.

V. Munley (1984).

`Has the median voter found a ballot box he can control?'.
Economic Inquiry 22(3):323-336.

W. Niskanen (1971).

Bureaucracy and Representative Government.
Aldine-Atherton, Chicago, IL.

M. J. Osborne & M. Turner (2010).

`Cost benefit analysis versus referenda'.
Journal of Political Economy 118(1):156-187.

T. Persson & G. Tabellini (1996a).

`Federal Fiscal Constitutions: Risk Sharing and Moral Hazard'.
Econometrica 64(3):623-646.

T. Persson & G. Tabellini (1996b).

`Federal Fiscal Constitutions: Risk Sharing and Redistribution'.
Journal of Political Economy 104(5):979-1009.

T. A. Romer & H. Rosenthal (1978).

`Political Resource Allocation, Controlled Agendas, and the Status Quo'.
Public Choice 33:27-43.

T. A. Romer & H. Rosenthal (1979).

`Bureaucrats Versus Voters: On the Political Economy of Resource Allocation by Direct Democracy'.
Quarterly Journal of Ecnomics 93:563-587.

R. J. Shadbegian (1996).

`Do Tax and Expenditure Limitations Affect the Size and Growth of State Government?'.
Contemporary Economic Policy 14:22-35.

A. D. Sokolow (1998).

`The Changing Property Tax and State-Local Relations'.
Publius: The Journal of Federalism 28:165-187.

R. M. Stein, et al. (1983).

`An Analysis of Support for tax and Expenditure Limitation Referenda'.
Public Choice 40:187-194.

G. Tabellini & A. Alesina (1990).

`Voting on the Budget Deficit'.
American Economic Review 80(1):37-49.

J. Temple (1996).

`County Composition and Voter Support for Tax Limitations: Evidence from Home Rule Elections'.
Southern Economic Journal 62:1002-1016.

C. Tiebout (1956).

`A Pure Theory of Local Expenditures'.
Journal of Political Economy 64:416-424.

J. L. Vigdor (2004).

`Other People's Taxes: Nonresident Voters and Statewide Limitation of Local Government'.
Journal of Law and Economics 47:453-476.

Figure 1: Limit Adoption Over Time

Source: Authors' survey.
Notes: This chart presents the total number of surveyed cities reporting any local limit by year. We do not observe a year of adoption for all limited cities, so the total in this picture does not equal the total number of cities with limits in Table 1.

Figure 2: Predicted Effects of Limits on Revenue and Welfare $Figure 2: Predicted Effects of Limits on Revenue and Welfare. Figure 2 reports expected revenues (E(R|\pi)) for unlimited and limited cities, with the share of type 1 voters on the x axis, ranging from 0.5 to 1. The figure shows that revenues are always lower in limited cities when \pi<1. Figure 2b compares welfare losses relative to a centrally planned regime for limited and unlimited cities (formally, W - W_c and W_n - W_c), with the share of type 1 voters on the x axis, ranging from 0.5 to 1. Limited cities are preferred for \pi approximately greater than 0.7. Below this, unlimited cities generate smaller welfare losses.$

Notes: These figures assume $\bar{\theta}=5$ and $\underline{\theta}=1$ . Figure 2 reports expected revenues ( $E(R\vert\pi)$ ) for unlimited and limited cities, showing that revenues are always lower in limited cities for $\pi < 1$ . Figure 2 compares welfare losses relative to a centrally planned regime for limited and unlimited cities (formally,

and

). Limited cities, shown with the solid line, are preferred for $\pi$ approximately greater than 0.7. Below this, unlimited cities (dashed line) generate smaller welfare losses.

Figure 3: Fiscal Consequences of Limit Adoption

Notes: The top panel presents the log of real per capita municipal own source revenues for limited cities (each point is a city-year observation), where year one is normalized to be the year of limit adoption. The bottom panel presents the same cities, but where revenues are now net of city fixed effects, year fixed effects, and a linear trend for cities that do not adopt limits. In both figures, dashed lines separate the best fit lines for the pre- and post-limit periods. The solid lines are similar best fit lines when the sample is restricted to ten years before or after limit adoption.

**Table 1: Description of Local Limits**
	(1) Number	(2) Share
Number of Cities with Limits	40	12.5
By Type of Limit: Assessment Limit	4	7.1
By Type of Limit: Property Tax Rate Limit	22	39.3
By Type of Limit: Other	12	21.4
By Type of Limit: Property Tax Levy Limit	9	16.1
By Type of Limit: Revenues or Expenditure Limit	3	5.4
By Type of Limit: Sales Tax Limit	6	10.7
By Type of Limit: Total	56	100
By where is the Limit adopted?: In municipal charter	38	67.9
By where is the Limit adopted?: In municipal code	13	23.2
By where is the Limit adopted?: No valid response	5	8.9
By whether an override possible?: No valid response	5	8.9
By whether an override possible?: No	2	3.6
By whether an override possible?: Yes- Majority vote of the city council	6	10.7
By whether an override possible?: Yes- Majority vote of the electorate	36	64.3
By whether an override possible?: Yes- Super majority of the city council	3	5.4
By whether an override possible?: Yes- Super majority of the electorate	4	7.1
Has Your City Reached the Legislated Limit?
No valid response	3	7.4
No, but close	3	7.4
No, not close	16	39.3
Yes	19	45.9

Source: Authors' survey.

**Table 2: Local Limit Examples**
City	Limit Type	Description	Override
Eastpointe, MI	Property Tax Rate	Property tax rate is capped at 1.5%	Majority of Voters
Lincoln, NE	Property Tax Levy	The total property tax levy may not increase annually by more than seven percent from the 1966 baseline	Majority of Voters
Baltimore, MD	Assessment	Assessments on property cannot increase by more than 4%	Majority of City Council
Anchorage, AK	Revenue or Expenditure	Total tax revenue cannot increase by more than the rate of inflation plus population growth	Majority of Voters
Tucson, AZ	Sales Tax	The city cannot levy a sales tax that exceeds 2%	Majority of Voters
Columbus, OH	Other	The city income tax is capped at 1%	Majority of Voters

Source: Authors' survey.

Notes: This table presents an example of each type of local limit about which our survey asked. While the state of Ohio does have a state-level limit on municipalities' income tax rate, the Columbus limit preceded this state-level limit.

**Table 3: Comparison of Cities with and without Limits**
	Local Limit Status : Yes (1)	Local Limit Status :No (2)	t-test, yes=no (3)
Demographic Variables: Population	349,289	227,844	1.34
Demographic Variables: Population (Standard Error)	(535,612)	(561,357)
Demographic Variables: Median Family Income ($1,000s)	55.3	62.4	3.11
Demographic Variables: Median Family Income ($1,000s) (Standard Error)	(12.1)	(20.9)
Demographic Variables: Share African American	0.15	0.15	0.01
Demographic Variables: Share African American (Standard Error)	(0.17)	(0.17)
Demographic Variables: Share Latino	0.20	0.18	0.43
Demographic Variables: Share Latino (Standard Error)	(0.19)	(0.19)
Political & Institutional Variables: Home Rule (1 if yes; 0 otherwise)	0.79	0.55	3.42
Political & Institutional Variables: Home Rule (1 if yes; 0 otherwise)	(0.41)	(0.50)
Political & Institutional Variables: Citizen Initiative (1 if city has; 0 otherwise)	0.94	0.84	2.22
Political & Institutional Variables: Citizen Initiative (1 if city has; 0 otherwise)	(0.23)	(0.36)
Political & Institutional Variables: Mayor-Council Form of Government (1 if yes; 0 otherwise)	0.48	0.34	1.57
Political & Institutional Variables: Mayor-Council Form of Government (1 if yes; 0 otherwise)	(0.51)	(0.48)
Political & Institutional Variables: Number of Cities in the MSA	19.3	41.0	3.98
Political & Institutional Variables: Number of Cities in the MSA	(28.51)	(49.05)
Political & Institutional Variables: 1 if State Has a Binding Limit	0.80	0.70	1.44
Political & Institutional Variables: 1 if State Has a Binding Limit	(0.41)	(0.46)
Fiscal Variables: Total Revenue ($1,000s, per capita)	2.03	2.07	0.15
Fiscal Variables: Total Revenue ($1,000s, per capita) (Standard Error)	(1.96)	(1.44)
Fiscal Variables: Total Own Source Revenue ($1,000s, per capita)	1.47	1.60	0.62
Fiscal Variables: Total Own Source Revenue ($1,000s, per capita) (Standard Error)	(1.20)	(1.11)
Fiscal Variables: Total Property Tax Revenue ($1,000s, per capita)	0.37	0.42	0.70
Fiscal Variables: Total Property Tax Revenue ($1,000s, per capita) (Standard Error)	(0.40)	(0.46)

Sources: Decennial census data, Census of Governments political and fiscal data.

Notes: We report means of the named variables; standard deviations are below the means in parentheses. These data are from the 2002 cross-section. We do not observe all variables for all respondent cities. In Panel 1, all "yes" and "no" figures are calculated from 40 and 269 observations, respectively. The same figures of Panel 2 are 40 and 274. For Panel 3 we observe between 36 and 40 "yes" observations for each calculation and between 238 and 274 "no" observations.

**Table 4: Cross-sectional Evidence on Limit Adoption**
	(1)	(2)	(3)	(4)	(5)	(6)
Median Income, $1,000s	-0.013**			-0.012**	-0.014**	-0.034
Median Income, $1,000s (Standard Error)	(0.006)			(0.006)	(0.007)	(0.037)
1 if Home Rule, 0 Otherwise		0.648***		0.653***	0.654***	0.933**
1 if Home Rule, 0 Otherwise (Standard Error)		(0.232)		(0.232)	(0.252)	(0.366)
Number of Cities in MSA / 100			-0.484	-0.35	-0.283	-1.368**
Number of Cities in MSA / 100 (Standard Error)			(0.316)	(0.328)	(0.338)	(0.562)
Regional Dummies	x	x	x	x	x	x
Other Institutional Covariates					x	x
Demographic Covariates						x
Observations	254	254	254	254	254	254

Sources: Please see data appendix.

Notes: *** Significant at the 1% level; ** significant at the 5% level; * significant at the 10% level. The dependent variable in this regression is a dummy variable equal to one if a city has a local limit. These probit regressions are performed on the 2002 cross-section, and we report coefficients evaluated at the variable means (Stata's dprobit). Estimates are for the largest sample that contains information on all variables. The dependent variable is 1 if the city ever has a local limit, a 0 otherwise. Regional dummies are Midwest, South and West; Northeast is the omitted category. Demographic covariates are population, log of population, share of persons 25 and older with 4 years of college, share of persons 25 and older with at least a high school education, number of housing units, real median family income, share black, share Hispanic, share employed in government, share of housing units built since last census, housing units built before 1940, share manufacturing employment, share service employment by industry, unemployment rate, share of persons less than 18, share of persons greater than 64 years, share of population of foreign origin, vacancy rate, poverty rate, housing units per person and a Herfindahl index for income. Institutional variables are dummy for council-manager cities, total number of elected officials, dummy if the mayor is directly elected, and share of representatives elected at large.

**Table 5: Local Limit Adoption and Tax Revenues**
	(1) Cox Proportional Hazard	(2) Cox Proportional Hazard	(3) Exponential Survivor Model	(4) Exponential Survivor Model
Real Own-Source Revenue, per capita	0.140	0.147	0.142	0.130
Real Own-Source Revenue, per capita (Standard Error)	(0.176)	(0.200)	(0.174)	(0.204)
Key Covariates: 1 if Home Rule, 0 otherwise	1.197	1.144	1.195	1.149
Key Covariates: 1 if Home Rule, 0 otherwise (Standard Error)	(0.775)	(0.857)	(0.773)	(0.858)
Key Covariates: Number of Cities in MSA	-2.533	-2.437*	-2.549	-2.533*
Key Covariates: Number of Cities in MSA (Standard Error)	(1.863)	(1.436)	(1.876)	(1.425)
Key Covariates: Real Median Family Income, $1000s	0.013	0.038**	0.013	0.049**
Key Covariates: Real Median Family Income, $1000s (Standard Error)	(0.015)	(0.018)	(0.016)	(0.024)
Key Covariates: Region Dummies (Northeast omitted)	x	x	x	x
Key Covariates: Time Varying Covariates I	x	x	x	x
Key Covariates: Time Varying Covariates II		x		x
Key Covariates: Time Invariant Covariates I	x	x	x	x
Key Covariates: Time Invariant Covariates II		x		x
Key Covariates: Year Fixed Effects			x	x
Key Covariates: Observations	6,741	6,741	6,741	6,741

Sources: Please see data appendix.

Notes: This table reports results from a hazard model that considers the likelihood a city adopts a local limit at time t, given that it has not adopted a limit at time t-1. Time Varying Covariates I are population, log of population, and real median family income in $1,000s. Time Invariant Covariates I are region dummies, home rule status, and the number of cities in the metropolitan area. Time Varying Covariates II are a dummy for state binding limits on cities, the share African-American, the share Hispanic, and a Herfindahl index for income. Time Invariant Covariates II are a dummy for initiative power, and a dummy for being the mayor-council form of government. We use the largest sample for which all variables are available. Standard errors are clustered at the city level.

**Table 6: Local Limit Adoption and Volatility in Revenues**
	(1) Real per Capita Dollars	(2) Real per capita dollars relative to 3-year moving average	(3) 3-Year coefficient of variation
Own-Source Revenue	0.128	0.857	-1.145
Own-Source Revenue (Standard Error)	(0.205)	(0.872)	(2.213)
Total Revenue	0.175	0.521	1.767
Total Revenue (Standard Error)	(0.137)	(1.381)	(1.907)
Total Tax Revenue	0.349	0.782	-9.939
Total Tax Revenue (Standard Error)	(0.225)	(0.517)	(10.329)
Property Tax Revenue	0.826	1.661***	-3.037
Property Tax Revenue (Standard Error)	(0.761)	(0.601)	(3.925)

Sources: Please see data appendix.

Notes: Each cell in this table reports the coefficient and standard error from a separate Cox proportional hazard model that considers the likelihood a city adopts a local limit at time t, given that it has not adopted a limit at time t-1. The first coefficient in this table is the same specification as the first coefficient in Table 5, but with a sample of 6.549 observations. This is the largest sample available for all the estimates in this table, and all coefficients in this table come from models estimated with this sample. All models in this table use the full set of covariates from Table 5.

**Table 7: Local Limit Adoption and Own-Source Revenues Per Capita** Non-Adoptrs, and Adopters, Before 1970
	(1) Including Adoption	(2) Including Adoption	(3) Including Adoption	(4) Excluding Adopters	(5) Excluding Adopters	(6) Excluding Adopters
1{Limit Adopting City}	-0.073*	-0.054	-0.053	-0.075*	-0.057	-0.055
*1{After Limit Adoption}	(0.038)	(0.052)	(0.052)	(0.038)	(0.052)	(0.053)
Year Fixed Effects	x	x	x	x	x	x
City Fixed Effects	x	x	x	x	x	x
Demographic Controls		x	x		x	x
State Limits, on Cities & States			x			x
Observations	9,348	9,348	9,348	8,972	8,972	8,972
Number of Unique Cities	310	310	310	297	297	297

Sources: Please see data appendix.

Notes: *** Significant at the 1% level; ** significant at the 5% level; * significant at the 10% level. Dependent variable is per capita own-source revenue, and standard errors are clustered at the city level. Each column is a separate regression, and we report the coefficient $\beta$ ${}_{5}$ from Equation 5. 18 cities with local limits report a year of limit adoption over the period observed (1970-2004); 13 cities report dates of adoption outside of our sample period. Standard errors are clustered at the city level. Demographic control variables are population, share of persons 25 and over with a college degree, share of persons 25 and over with a high school degree or more, number of families, number of housing units, number of occupied housing units, civilian labor force 16 and over, real median per capita income, persons below the poverty level, share black, share hispanic, share employed in government, share of housing units built since last census, housing units built before 1940, share manufacturing employment, number of occupied housing units with more than 1.01 persons per room, share service employment (by industry), share wholesale/retail employment, unemployment rate, share of persons less than 18, share of persons greater than 65, share of population of foreign origin, number of vacant housing units, log of population. "State Limits, on Cities and States" refers to two variables: one is a dummy equal to one if the state has a potentially binding limit on municipalities (defined as either a property tax levy limit, a general revenue or expenditure limit, or a property tax rate limit combined with an assessment limit) in that state in a given year, and the other is a dummy equal to one if the state has a limit on state spending in that year.

**Table 8: Local Limit Adoption and Trend in Own-Source Revenues Per Capita**
	(1) Including Adoption	(2) Including Adoption	(3) Including Adoption	(4) Excluding Adopters	(5) Excluding Adopters	(6) Excluding Adopters
Linear Time Trend *: 1{Never Local Limit City} ${}^{ [\beta5]}$	0.0218***	0.0171***	0.0171***	0.0218***	0.0179***	0.0179***
Linear Time Trend *: 1{Never Local Limit City} ${}^{ [\beta5]}$ (Standard Error)	(0.001)	(0.005)	(0.005)	(0.001)	(0.005)	(0.005)
Linear Time Trend *: 1{Local Limit City, Pre-Limit} ${}^{[\beta6]}$	0.0215***	0.0181***	0.0181***	0.0202***	0.0187***	0.0186***
Linear Time Trend *: 1{Local Limit City, Pre-Limit} ${}^{[\beta6]}$ (Standard Error)	(0.003)	(0.005)	(0.005)	(0.003)	(0.006)	(0.006)
Linear Time Trend *: 1{Local Limit City, Post-Limit} ${}^{[\beta7]}$	0.0181***	0.0142***	0.0143***	0.0181***	0.0156***	0.0156***
Linear Time Trend *: 1{Local Limit City, Post-Limit} ${}^{[\beta7]}$ (Standard Error)	(0.002)	(0.005)	(0.005)	(0.002)	(0.006)	(0.006)
Year Fixed Effects	x	x	x	x	x	x
City Fixed Effects	x	x	x	x	x	x
Demographic Controls		x	x		x	x
State Limits, on Cities & States			x			x
Observations	9,348	9,348	9,348	8,972	8,972	8,972
Number of Cities	310	310	310	297	297	297
p-value, test [ $\beta_{5}$ ] = [ $\beta_{6}$ ]	0.923	0.687	0.683	0.634	0.794	0.806
p-value, test [ $\beta_{5}$ ] [ $\beta_{6}$ ]	0.462	0.343	0.342	0.317	0.397	0.403
p-value, test [ $\beta_{7}$ ] = [ $\beta_{6}$ ]	0.122	0.030	0.037	0.301	0.083	0.100
p-value, test [ $\beta_{7}$ ] [ $\beta_{6}$ ]	0.061	0.015	0.018	0.150	0.042	0.050
p-value, test [ $\beta_{7}$ ] = [ $\beta_{5}$ ]	0.032	0.138	0.150	0.074	0.359	0.370
p-value, test [ $\beta_{7}$ ] [ $\beta_{5}$ ]	0.016	0.069	0.075	0.037	0.179	0.185

Notes: *** Significant at the 1% level; ** significant at the 5% level; * significant at the 10% level. This table presents estimates for $\beta_{5}$ , $\beta_{6}$ and $\beta_{7}$ from Equation 6. Dependent variable is per capita own-source revenue, and standard errors are clustered at the city level. 18 cities with local limits report a year of limit adoption over the period observed (1970-2004); 13 cities report dates of adoption outside of our sample period. Standard errors are clustered at the city level. Control variables are population, share of persons 25 and over with a college degree, share of persons 25 and over with a high school degree or more, number of families, number of housing units, number of occupied housing units, civilian labor force 16 and over, real median per capita income, persons below the poverty level, share black, share hispanic, share employed in government, share of housing units built since last census, housing units built before 1940, share manufacturing employment, number of occupied housing units with more than 1.01 persons per room, share service employment (by industry), share wholesale/retail employment, unemployment rate, share of persons less than 18, share of persons greater than 65, share of population of foreign origin, number of vacant housing units, log of population. "State Limits, on Cities and States" refers to two variables: one is a dummy equal to one if the state has a potentially binding limit on municipalities (defined as either a property tax levy limit, a general revenue or expenditure limit, or a property tax rate limit combined with an assessment limit) in that state in a given year, and the other is a dummy equal to one if the state has a limit on state spending in that year.

**Table 9: Using Matching to Test Results**
	(1) Propensity Score Based on Cross-Section Including Adoption	(2) Propensity Score Based on Time Series Including Adoption	(3) Propensity Score Based on Cross-Section Excluding Adopters	(4) Propensity Score Based on Time Series Excluding Adopters
Linear Time Trend *: 1{Never Local Limit City} ${}^{ [\beta5]}$	0.0144***	0.0152***	0.0163***	0.0167***
Linear Time Trend *: 1{Never Local Limit City} ${}^{ [\beta5]}$ (Standard Error)	(0.006)	(0.005)	(0.006)	(0.005)
Linear Time Trend *: 1{Local Limit City, Pre-Limit} ${}^{[\beta6]}$	0.0141**	0.0148**	0.0176**	0.0179***
Linear Time Trend *: 1{Local Limit City, Pre-Limit} ${}^{[\beta6]}$ (Standard Error)	(0.007)	(0.006)	(0.007)	(0.007)
Linear Time Trend *: 1{Local Limit City, Post-Limit} ${}^{[\beta7]}$	0.0110*	0.0115**	0.0147**	0.0146**
Linear Time Trend *: 1{Local Limit City, Pre-Limit} ${}^{[\beta6]}$ (Standard Error)	(0.006)	(0.006)	(0.007)	(0.006)
Year Fixed Effects	x	x	x	x
City Fixed Effects	x	x	x	x
Demographic Controls	x	x	x	x
State Limits, on Cities & States	x	x	x	x
Observations	7,029	8,030	6,612	7,654
Number of Cities	310	310	297	297
p-value, test [ $\beta_{5}$ ] = [ $\beta_{6}$ ]	0.909	0.890	0.639	0.690
p-value, test [ $\beta_{5}$ ] [ $\beta_{6}$ ]	0.454	0.445	0.319	0.345
p-value, test [ $\beta_{7}$ ] = [ $\beta_{6}$ ]	0.082	0.053	0.133	0.089
p-value, test [ $\beta_{7}$ ] [ $\beta_{6}$ ]	0.041	0.027	0.067	0.045
p-value, test [ $\beta_{7}$ ] = [ $\beta_{5}$ ]	0.117	0.066	0.543	0.439
p-value, test [ $\beta_{7}$ ] [ $\beta_{5}$ ]	0.059	0.033	0.271	0.219

Sources: Authors' survey & U.S. Census Bureau; see Section 3in text for complete details.

Notes: *** Significant at the 1% level; ** significant at the 5% level; * significant at the 10% level. This table repeats columns the estimation in columns 3 and 6 of the previous table, using propensity score weights. Standard errors are clustered at the city level. For the cross-section, the propensity score estimation uses cities in the sample for which we observe data in 1970. With this sample, we estimate a probit for local limit adoption ever as a function of population, share of persons 25 and over with a college degree, share of persons 25 and over with a high school degree or more, number of families, number of housing units, number of occupied housing units, civilian labor force 16 and over, real median per capita income, persons below the poverty level, real median gross rent, share black, share hispanic, share employed in government, share of housing units built since last census, housing units built before 1940, share manufacturing employment, number of occupied housing units with more than 1.01 persons per room, share service employment (by industry), share wholesale/retail employment, unemployment rate, share of persons less than 18, share of persons greater than 65, share of population of foreign origin, number of vacant housing units, log of population and census division dummy variables (9 divisions). For the time-series matching, we estimate a probit for local limit adoption in a given year as a function of the same covariates.

Mathematical Appendix

PROOF OF PROPOSITION 1: We obtain the optimal limit by solving a type 1 voter's utility maximization problem. Because only type 1 voters have an incentive to limit revenues, if they comprise a majority of the electorate, the optimal limit will have sufficient support to be adopted. We posit that for type 1 voters the optimal limit dominates any alternative limit; thus, if a limit is proposed in a referendum, it will be the one that maximizes their utility.

To find the optimal fiscal limit, $x^{*}$ , we derive the expected utility of a type 1 voter, given limit x and proportion $\pi$ as follows:

$\displaystyle E_{\theta}\left[u_{1}\vert x,\pi\right]$	$\displaystyle = \pi\left\{ E_{\theta}\left[u_{1}\vert x>\theta G_{1}^{}\left(\theta\right)\right]+E_{\theta}\left[u_{1}\vert x\leq\theta G_{1}^{}\left(\theta\right)\right]\right\} +$
	$\displaystyle \left(1-\pi\right)\left\{ E_{\theta}\left[u_{1}\vert x>\theta G_{2}^{}\left(\theta\right)\right]+E_{\theta}\left[u_{1}\vert x\leq\theta G_{2}^{}\left(\theta\right)\right]\right\} .$

Notice that $u_{j}\left(G_{j}^{*}\left(\theta\right),\theta\right)=\frac{j}{4\theta}$ and that a limit, x, is binding for type j if and only if $\theta\leq\frac{j}{4x}$ . Because we assume that $\bar{\theta}/\underline{\theta}>2$ , we decompose the constraint set into two regions, $\left[\frac{1}{4\bar{\theta}}\frac{1}{2\bar{\theta}}\right]$ and $\left[\frac{1}{2\bar{\theta}},\frac{1}{4\underline{\theta}}\right]$ : in the first, the limit binds a type 2 politician in all states but only in some states does it bind a type 1 politician. In the second, the limit is only sometimes binding for either type. Given the specifications of our model, we rewrite the expected utility for a type 1 voter explicitly: $E_{\theta}\left[u_{1}\vert x,\pi\right]=$

$\begin{align*}\begin{cases}\frac{\pi}{b}\left(\int_{\frac{1}{4x}}^{\bar{\theta}}... ...ac{1}{2\bar{\theta}}\frac{1}{4\underline{\theta}}\right] \end{cases}\end{align*}$

where $u_{1}\left(G_{2}^{*}\left(\theta\right),\theta\right)=\frac{\sqrt{2}-1}{2\theta}$ and $u_{1}\left(\frac{x}{\theta},\theta\right)=\sqrt{\frac{x}{\theta}}-x$ .

Solving for the optimal limit, we obtain $x^{*}\equiv a\left(\pi\right)\frac{1}{4\underline{\theta}}$ where the coefficient on $\frac{1}{4\underline{\theta}}$ is

$\displaystyle a\left(\pi\right)=\begin{cases} \left(\frac{\pi}{1-\left(1-\pi\right)\sqrt{\bar{\theta}/\underline{\theta}}+\sqrt{1-\pi}\left(\sqrt{\bar{\theta}/\underline{\theta}}-1\right)}\right)^{2} & x^{*}\in\left[\frac{1}{4\bar{\theta}},\frac{1}{2\bar{\theta}}\right]\ \left(\frac{\pi+\left(1-\pi\right)2\left(\sqrt{2}-1\right)}{1+\sqrt{\left(1-\pi\right)\left(1-2\left(\sqrt{2}-1\right)\right)}}\right)^{2} & x^{*}\in\left[\frac{1}{2\bar{\theta}},\frac{1}{4\underline{\theta}}\right] \end{cases}$

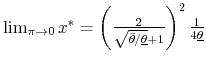Since $\bar{\theta}/\underline{\theta}>2$ , when $x^{*}=\frac{1}{2\bar{\theta}}$ we move from the former case to the latter. When $\bar{\theta}/\underline{\theta}\in\left(2,3+2\sqrt{2}\right)$ , both cases are relevant; if $\bar{\theta}/\underline{\theta}>3+2\sqrt{2}$ , then only the latter case is relevant and $x^{*}$ is interior for any $\pi$ . For the former case $\lim_{\pi\rightarrow0}x^{*}=\left(\frac{2}{\sqrt{\bar{\theta}/\underline{\theta}}+1}\right)^{2}\frac{1}{4\underline{\theta}}$ , so $x^{*}$ is interior for any $\pi$ only if $\underline{\theta}>1/4$ . For simplicity we assume that $\underline{\theta}>1/4$ and $\bar{\theta}/\underline{\theta}\in\left(2,3+2\sqrt{2}\right)$ . Finally since $a\left(\pi\right)$ is increasing in $\pi$ , so is the optimal limit. $\square$

PROOF OF PROPOSITION 2: In a city without a limit

$\displaystyle E_{\theta}\left[R\vert\pi\right]=\pi E_{\theta}\left[\theta G_{1}^{*}\left(\theta\right)\right]+\left(1-\pi\right)E_{\theta}\left[\theta G_{2}^{*}\left(\theta\right)\right],$

where $E_{\theta}\left[\theta G_{1}^{*}\left(\theta\right)\right]=\int_{\underline{\theta}}^{\bar{\theta}}\frac{1}{4\theta b}$ and $E_{\theta}\left[\theta G_{2}^{*}\left(\theta\right)\right]=\int_{\underline{\theta}}^{\bar{\theta}}\frac{1}{2\theta b}$ . We obtain $E_{\theta}\left[R\vert\pi\right]=\frac{2-\pi}{4b}\ln\bar{\theta}/\underline{\theta}$ , which is strictly decreasing in $\pi$ . A city that faces a limit may be forced to lower its revenues. Thus, for any $\pi$ , we must have $E_{\theta}\left[R\vert x^{*},\pi\right]\leq E_{\theta}\left[R\vert\pi\right]$ .

Finally, in a city with a limit, we have:

$\displaystyle E_{\theta}\left[R\vert x^{*},\pi\right]$	$\displaystyle = \pi\left\{ E_{\theta}\left[\theta G\vert x^{}>\theta G_{1}^{}\left(\theta\right)\right]\Pr\left(x^{}>\theta G_{1}^{}\left(\theta\right)\right)+x^{}\Pr\left(x^{}<\theta G_{1}^{*}\left(\theta\right)\right)\right\}$
	$\displaystyle +\left(1-\pi\right)\left\{ E_{\theta}\left[\theta G\vert x^{}>\theta G_{2}^{}\left(\theta\right)\right]\Pr\left(x^{}>\theta G_{2}^{}\left(\theta\right)\right)+x^{}\Pr\left(x^{}<\theta G_{2}^{*}\left(\theta\right)\right)\right\} .$

As before, there are two cases to consider. We can rewrite the expected revenue explicitly as follows:

$\displaystyle E_{\theta}\left[R\vert x^{*},\pi\right]=\begin{cases} \pi\left(\frac{1}{b}\left(\frac{1}{4}-\underline{\theta}x^{*}+\frac{1}{4}\ln4\bar{\theta}x^{*}\right)\right)+\left(1-\pi\right)x^{*} & x^{*}\in\left[\frac{1}{4\bar{\theta}},\frac{1}{2\bar{\theta}}\right]\ \frac{\pi}{b}\left(\frac{1}{4}-\underline{\theta}x^{*}+\frac{1}{4}\ln4\bar{\theta}x^{*}\right)+\frac{\left(1-\pi\right)}{b}\left(\frac{1}{2}-\underline{\theta}x^{*}+\frac{1}{2}\ln2\bar{\theta}x^{*}\right) & x^{*}\in\left[\frac{1}{2\bar{\theta}},\frac{1}{4\underline{\theta}}\right] \end{cases}$

To prove that the relationship between $E_{\theta}\left[R\vert x^{*},\pi\right]$ and $\pi$ is ambiguous we show that for some values of $\bar{\theta}/\underline{\theta}$ expected revenue is non-monotone. First, we show that as $\pi$ goes to zero expected revenue is increasing for $\bar{\theta}/\underline{\theta}>2$ . Second, we show that as $\pi$ goes to one expected revenue is increasing only if $\bar{\theta}/\underline{\theta}<4\exp\left(5-4\sqrt{2}\right)\thickapprox2.074$ .

We can write $\frac{\partial E_{\theta}\left[R\vert x^{*},\pi\right]}{\partial\pi}$ as

$\displaystyle \left\{ \pi\frac{\partial E_{\theta}\left[R_{1}\vert x^{*},\pi\right]}{\partial\pi}+\left(1-\pi\right)\frac{\partial E_{\theta}\left[R_{2}\vert x^{*},\pi\right]}{\partial\pi}\right\} \frac{\partial x^{*}}{\partial\pi}-\left[E_{\theta}\left[R_{2}\vert x^{*},\pi\right]-E_{\theta}\left[R_{1}\vert x^{*},\pi\right]\right].$

Setting $\bar{\theta}/\underline{\theta}$ to m, we have that for $x^{*}\in\left[\frac{1}{4\bar{\theta}},\frac{1}{2\bar{\theta}}\right]$

$\displaystyle \lim_{\pi\rightarrow0}\frac{\partial E_{\theta}\left[R\vert x^{*},\pi\right]}{\partial\pi}=-\frac{1}{2}\left\{ \frac{1}{\left(m+1\right)^{2}}+\frac{1}{\left(m+1\right)^{3}}\right\} +\frac{1}{m^{2}-1}\left\{ \frac{1}{2}+\frac{1}{\left(m+1\right)^{2}}+\frac{1}{2}\ln\frac{2m}{m+1}\right\} ,$

which is strictly positive for . On the other hand, $\lim_{\pi\rightarrow1}x^{*}=\frac{1}{4\underline{\theta}}$ ; we obtain that $\lim_{\pi\rightarrow1}\frac{\partial E_{\theta}\left[R\vert x^{*},\pi\right]}{\partial\pi}$ is positive only if $\bar{\theta}/\underline{\theta}\lessapprox2.074$ . $\square$

Appendix

Data Sources

This note lists the data sources we combine with our survey information.

Demographic Data

Decennial Censuses
1. 1970 Census, ICPSR 8109, 8129
2. 1980 Census Summary File 3A, ICPSR 8071
3. 1990 Census Summary File 3A, ICPSR 9782, save CA which is damaged; used file from UCLA ATS
4. 2000 Census Summary File 3, ICPSR 13324-13392

Fiscal Data

Annual Survey of Government Finances, Census of Government Finances
1. 1970-2006, municipal data only
Consumer Price Index
1. Bureau of Labor Statistics, 1970-2006
2. Series is Seasonally Adjusted, All Urban Consumers (CUSR0000SA0)

Institutional Data

Home Rule status, Mayor-Council status, elected officials, & other municipal institutional characteristics:
1. 1987 Census of Governments, Organization File, Municipal Level
Municipal Initiative Information
1. Legal Landscape Database, USC Initiative and Referendum Institute
Tax and Expenditure Limits by States on Cities
1. Advisory Commission on Intergovernmental Relations, 1995. Tax and Expenditure Limits on Local Government, placeCityWashington, StateDC.
2. Mullins, Daniel R. and Wallins, Bruce A., 2004. "Tax and Expenditure Limits: Introduction and Overview." Public Budgeting and Finance 24(2): 2-15.
Tax and Expenditure Limits by States on States
1. Waisanen, Bert. "State Tax and Expenditure Limits - 2008." National Conference of State Legislatures, 2008. http://www.ncsl.org/default.aspx?tabid=12633
Additional information on Home Rule
1. Krane, Dale, Platon N. Rigos, and Melvin B. Hill, 2000. Home Rule in country-regionAmerica, placeCityWashington, StateD.C.: Congressional Quarterly Press.

Case Study Data

We relied on the sources below, supplemented by searches on municipal websites. Please contact us for specific citation on any particular limit.

www.newsbank.com, with coverage of many local daily newspapers, primarily starting in the late 1990s or early 2000s
Lexis/Nexis, with coverage of additional local daily newspapers
for placeCityPueblo, StateColorado, Researcher Carol Edwards undertook primary source investigation

Appendix

Survey Instrument

This instrument reports the questions we used. However, the vast majority of our responses were by phone.

Hello -

I am conducting a Columbia University/McGill University survey on city-level restrictions on taxes and expenditures, and am writing to ask for your help in completing the survey.

In particular, our research team is interested in whether your city imposes limits on taxes and expenditures in addition to those limits imposed by state statutory or constitutional law. More information on the team and the survey is available at www.municipaltaxandexpenditurelimits.org.

To complete the survey, fill in this writeable pdf file. If you have Acrobat Writer, you may save the form and return it to us as an attachment by email ([email protected]). If you don't have Acrobat Writer or if you prefer to print and mail or fax the form, our fax number is 212-222-0598, and address is Justin Phillips/Columbia University/Mail Code 3320/420 W. 118th St./CityplaceNew York, StateNY PostalCode10027.

We greatly appreciate your completing our survey. If you have questions, please feel free to call me at 347-404-5590. If you would like a copy of the completed survey, please check here:

Many thanks,

Kieran Shah

Research Assistant, Municipal Tax and Expenditure Limit Project

City Name: State:

Position: Name (optional):

This is a graphic of the survey which has multiple questions about tax and expenditures of cities, and if there were any limits on them.

If you have any additional notes or comments about municipally imposed tax and expenditures limits, we are eager to hear them. Please write in the box below.

We thank you again for your participation in this survey.

**Appendix Table 1: Comparison of Sampled and Non-Sample Cities**
	(1) Sampled with Certainty	(2) Cities Between 25,000 & 100,0000 people In Sample	(3) Cities Between 25,000 & 100,0000 people Out of Sample	(4) t test: (2) vs (3)
Fiscal Covariates: Total Revenues mean($1,000s per capita)	2.131	1.874	1.608	2.26
Fiscal Covariates: Total Revenues sd($1,000s per capita)	1.612	1.076	1.010
Fiscal Covariates: Total Revenues count($1,000s per capita)	246	90	908
Fiscal Covariates: Own-Source Revenues mean($1,000s per capita)	1.609	1.445	1.285	1.79
Fiscal Covariates: Own-Source Revenues sd($1,000s per capita)	1.188	0.810	0.835
Fiscal Covariates: Own-Source Revenues count($1,000s per capita)	246	90	908
Fiscal Covariates: Property Tax Revenues mean($1,000s per capita)	0.374	0.522	0.413	1.65
Fiscal Covariates: Property Tax Revenues sd($1,000s per capita)	0.364	0.609	0.486
Fiscal Covariates: Property Tax Revenues count($1,000s per capita)	246	90	905
Demographic Covariates: Population mean	318,763	47,605	47,851	0.13
Demographic Covariates: Population sd	625,360	18,168	19,569
Demographic Covariates: Population count	246	95	963
Demographic Covariates: Real Median Family Income ($1,000s) mean	58.3	67.1	65.3	0.65
Demographic Covariates: Real Median Family Income ($1,000s) sd	16.4	25.5	22.5
Demographic Covariates: Real Median Family Income ($1,000s) count	246	95	963
Demographic Covariates: Share African American mean	0.18	0.11	0.10	0.20
Demographic Covariates: Share African American sd	0.18	0.16	0.15
Demographic Covariates: Share African American count	246	95	960
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) mean	0.62	0.51	0.48	0.38
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) sd	0.49	0.50	0.50
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) count	227	77	790
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) mean	0.39	0.33	0.36	0.65
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) sd	0.49	0.47	0.48
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) count	246	95	963
Institutional Covariates: Citizen Initiative (1 if city has, 0 otherwise) mean	0.87	0.82	0.83	0.26
Institutional Covariates: Citizen Initiative (1 if city has, 0 otherwise) sd	0.34	0.39	0.37
Institutional Covariates: Citizen Initiative (1 if city has, 0 otherwise) count	230	67	692

Notes: This table uses data from the 2002 cross-section, the most complete and recent year of data. Column one includes cities with a population greater than 100,000 in 2002; columns 2 and 3 compare sampled and unsampled cities between 25,000 and 100,000 people.

**Appendix Table 2: Respondent vs. Non-Respondent Cities**
	(1) All Cities	(2) Respondents	(3) Non-Respondents	(4) t-test: (2) vs (3)
Fiscal Covariates: Total Revenues ($1,000s, per capita) mean	2.062	2.067	2.005	0.25
Fiscal Covariates: Total Revenues ($1,000s, per capita) sd	1.490	1.512	1.229
Fiscal Covariates: Total Revenues ($1,000s, per capita) count	336	309	27
Fiscal Covariates: Own-Source Revenues ($1,000s, per capita) mean	1.565	1.579	1.401	1.12
Fiscal Covariates: Own-Source Revenues ($1,000s, per capita) sd	1.101	1.125	0.766
Fiscal Covariates: Own-Source Revenues ($1,000s, per capita) count	336	309	27
Fiscal Covariates: Property Tax Revenues ($1,000s, per capita) mean	0.413	0.411	0.444	0.41
Fiscal Covariates: Property Tax Revenues ($1,000s, per capita) sd	0.447	0.451	0.413
Fiscal Covariates: Property Tax Revenues ($1,000s, per capita) count	336	309	27
Demographic Covariates: Population mean	243,220	243,315	242,121	0.02
Demographic Covariates: Population sd	544,716	558,785	348,188
Demographic Covariates: Population count	341	314	27
Demographic Covariates: Real Median Family Income ($1,000s) mean	60.8	61.5	52.4	3.47
Demographic Covariates: Real Median Family Income ($1,000s) sd	19.7	20.1	12.5
Demographic Covariates: Real Median Family Income ($1,000s) count	341	314	27
Demographic Covariates: Share African American mean	0.16	0.15	0.21	1.42
Demographic Covariates: Share African American sd	0.18	0.17	0.22
Demographic Covariates: Share African American count	341	314	27
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) mean	0.59	0.58	0.67	0.84
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) sd	0.49	0.49	0.48
Institutional Covariates: Home Rule Status (1 if yes, 0 otherwise) count	304	280	24
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) mean	0.37	0.36	0.48	1.22
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) sd	0.48	0.48	0.51
Institutional Covariates: Mayor-Council Form of Government (1 if yes, 0 otherwise) count	341	314	27
Institutional Covariates: Citizen Initiative (1 if yes, 0 otherwise) mean	0.86	0.86	0.83	0.39
Institutional Covariates: Citizen Initiative (1 if yes, 0 otherwise) sd	0.35	0.35	0.39
Institutional Covariates: Citizen Initiative (1 if yes, 0 otherwise) count	297	274	23

Notes: This table uses data from the 2002 cross-section, the most complete and recent year of data. "All Cities" is all sampled cities.

**Appendix Table 3: Share of Cities with Local Limit by Type of State Limit**
Local Limit	State Limit on City Property Tax Rate	State Limit on City Property Tax Levy	State Limit on City Assessment	State Limit on City Revenue or Expenditure	Any State Limit on Cities
Any Local Limit	0.83	0.75	0.33	0.25	0.65
Property Tax Rate	0.91	0.91	0.36	0.18	0.77
Property Tax Levy	0.89	0.89	0.11	0.33	0.56
Assessment	0.25	0.25	0.25	0.00	0.25
Revenue or Expenditure	1.00	1.00	0.00	0.50	0.50

Sources: Local limit information from authors' survey. State limit data from ACIR (1995) and Mullins and Wallins (2004).

Notes: This table presents the share of cities with a local limit that have that named limit at the state level.

Appendix Table 4: Additional Covariates for Limit Adoption

(a) Additional Covariates, Table 3, Column 6

	(1)
Share 18 Years Old	-17.964*
Share 18 Years Old (Standard Error)	(10780)
Share = 65 Years Old	-25.884***
Share = 65 Years Old (Standard Error)	(8068)
Poverty Rate	-8.039
Poverty Rate (Standard Error)	(6824)
Herfindahl Index, Income	-14.875
Herfindahl Index, Income (Standard Error)	(22667)

(b) Coefficient for Each Covariate, Added Separately, to Specification in Table 3, Column 6

Covariates, Entered Singly	(1)
Share, Bottom Income Category	-8.801*
Share, Bottom Income Category (Standard Error)	(4721)
Share, Bottom Two Income Categories	-7.505**
Share, Bottom Two Income Categories (Standard Error)	(3422)
Share, Bottom to Middle Income Categories	-4.283*
Share, Bottom to Middle Income Categories (Standard Error)	(2550)
Share, Middle Income, Narrow Definition	3.172
Share, Middle Income, Narrow Definition (Standard Error)	(2615)
Share, Middle Income, Broad Definition	2.351*
Share, Middle Income, Broad Definition (Standard Error)	(1386)
Share, Top Income Category	-10.317
Share, Top Income Category (Standard Error)	(6895)
Share, Top Two Income Categories	-6.315
Share, Top Two Income Categories (Standard Error)	(3980)
Share, Top to Middle Income Categories	-3.803
Share, Top to Middle Income Categories (Standard Error)	(2672)
Share 2*poverty line	-1.603
Share 2*poverty line (Standard Error)	(1879)
Share, Non-Owner Occupants	-3.611
Share, Non-Owner Occupants (Standard Error)	(3525)
Ratio, Share 65+ / Share 18 or under	-0.985
Ratio, Share 65+ / Share 18 or under (Standard Error)	(0956)
Ratio, Share Top Income Category/ Share Bottom Income Category	-0.324
Ratio, Share Top Income Category/ Share Bottom Income Category (Standard Error)	(0223)
Herfindahl Index, Race	-0.138
Herfindahl Index, Race (Standard Error)	(0682)
Herfindahl Index, Age	-3.817
Herfindahl Index, Age (Standard Error)	(2984)
Cities in MSA*1{Income Average Income}	0.000
Cities in MSA*1{Income Average Income} (Standard Error)	(0010)
Local Government Employment Share	-12.515**
Local Government Employment Share (Standard Error)	(5147)

Notes: All regressions include 254 observations. The top panel shows coefficients for variables included, but not presented, in Table 3, Column 6 (Equation 1). The bottom panel repeats the regression from Table 3, Column 6, but adds each listed covariate separately; each cells reports results from a separate regression. Note that all coefficients in panel (b) are conditional on median family income, which is included in the specification in Table 3 column 6. For additional table notes, please see Table 3.

**Appendix Table 5: Has the Limit Affected Practices in Your City?**
	(1) Number	(2) Share
Affects long term projects only	1	1.6
No valid response	9	14.1
No clear effect	22	34.4
Other	9	14.1
We have increased borrowing	1	1.6
We have new revenue sources	11	17.2
We have reduced service provision	11	17.2

Source: Local limit survey. Responses at the official level weighted to correspond to one answer per city.

**Appendix Table 6: Local Limit Adoption and Own-Source Revenues, Strong Limits Only** (Non-adopters, and Adopters Before 1970)
	(1) Including Adoption	(2) Including Adoption	(3) Including Adoption	(4) Excluding Adopters	(5) Excluding Adopters	(6) Excluding Adopters
1{Never Local Limit City} ${}^{ [A]}$	0.0218***	0.0172***	0.0171***	0.0218***	0.0180***	0.0179***
1{Never Local Limit City} ${}^{ [A]}$ (Standard Error)	(0001)	(0005)	(0005)	(0001)	(0005)	(0005)
1{Local Limit City, Pre-Limit} ${}^{[B]}$	0.0220***	0.0187***	0.0187***	0.0209***	0.0197***	0.0196***
1{Local Limit City, Pre-Limit} ${}^{[B]}$ (Standard Error)	(0003)	(0006)	(0006)	(0004)	(0006)	(0006)
1{Local Limit City, Post-Limit} ${}^{[C]}$	0.0185***	0.0144***	0.0145***	0.0188***	0.0165***	0.0165***
1{Local Limit City, Post-Limit} ${}^{[C]}$ (Standard Error)	(0002)	(0005)	(0005)	(0002)	(0006)	(0006)
Year Fixed Effects	x	x	x	x	x	x
City Fixed Effects	x	x	x	x	x	x
Demographic Controls		x	x		x	x
State Limits, on Cities & States			x			x
Observations	9,176	9,176	9,176	8,867	8,867	8,867
Number of Cities	305	305	305	294	294	294
1. p-value, test [A] = [B]	0.962	0.577	0.566	0.806	0.581	0.585
2. p-value, test [A] [B]	0.481	0.288	0.283	0.403	0.290	0.292
3. p-value, test [B] = [C]	0.156	0.031	0.038	0.383	0.105	0.124
4. p-value, test [B] [C]	0.078	0.016	0.019	0.191	0.053	0.062
5. p-value, test [C] = [A]	0.075	0.175	0.193	0.197	0.568	0.588
6. p-value, test [C] [A]	0.038	0.088	0.096	0.098	0.284	0.294

Notes: Notes from Table 3 from the paper apply. This table has fewer unique cities than Table 3 in the paper; we drop cities that adopt local limits, but which do not adopt strong limits.

**Appendix Table 7: Effects of Local Limits on Alternative Dependent Variables**
	(1) Log of Total Revenue per capita (Including Adoption)	(2) Log of Share of Revenue from State (Including Adoption)	(3) Log of Total Revenue per capita (Excluding Adopters)	(4) Log of Share of Revenue from State (Excluding Adopters)
1{Never Local Limit City} ${}^{ [A]}$	0.0189***	-0.0189	0.0200***	-0.0188
1{Never Local Limit City} ${}^{ [A]}$ (Standard Error)	(0004)	(0012)	(0004)	(0012)
1{Local Limit City, Pre-Limit} ${}^{[B]}$	0.0211***	-0.0096	0.0226***	-0.0055
1{Local Limit City, Pre-Limit} ${}^{[B]}$ (Standard Error)	(0005)	(0017)	(0005)	(0019)
1{Local Limit City, Post-Limit} ${}^{[C]}$	0.0167***	-0.0164	0.0192***	-0.0114
1{Local Limit City, Post-Limit} ${}^{[C]}$ (Standard Error)	(0004)	(0014)	(0005)	(0016)
Year Fixed Effects	x	x	x	x
City Fixed Effects	x	x	x	x
Demographic Controls	x	x	x	x
State Limits, on Cities & States	x	x	x	x
Observations	9,176	9,112	8,867	8,840
Number of Cities	305	305	294	294
1. p-value, test [A] = [B]	0.387	0.419	0.401	0.300
2. p-value, test [A] [B]	0.194	0.209	0.200	0.150
3. p-value, test [B] = [C]	0.013	0.420	0.053	0.461
4. p-value, test [B] [C]	0.007	0.210	0.026	0.230
5. p-value, test [C] = [A]	0.245	0.681	0.747	0.366
6. p-value, test [C] [A]	0.123	0.340	0.373	0.183

Notes: Notes from Table 3 apply here.

Footnotes

* We are very appreciative of the many academics with whom we corresponded who confirmed that no systematic knowledge about locally-imposed tax and expenditure limits existed. We are particularly grateful to Michael Pagano, who offered helpful advice on how to conduct our survey of municipal officials, and to the Lincoln Institute for providing the funding without which this project would not have been realized (Brooks received funding for this project before arriving at the Federal Reserve Board). We also thank Nate Anderson, Elliot Anenberg, Chris Cunningham, John Curry, John Huber, Jenny Hunt, Melissa Marschall, Emily Satterthwaite, and Daniel Wilson; attendees at the fall 2009 National Tax Association meetings, the University of Waterloo and the NYU Wagner School; and colleagues at the University of Toronto (with particular thanks to Michael Smart and Colin Stewart). Literally hundreds of municipal officials were extremely generous with their time in answering the questions in this survey, and we are very appreciative. This survey would not have been possible without a number of marvelous research assistants from McGill University. Kasia Dworakowski set up the initial Access database and provided technical support along the way; Raissa Fabregas-Gil helped with final data clean-up. Our final and most appreciative thanks are to our surveyors, Emily Gaus, Kieran Shah, and Michelle Segal, who almost never took no for an answer. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by the Board of Governors of the Federal Reserve. Return to Text

1. This concept of the Leviathan comes from Hobbes (2003), and Brennan & Buchanan (1980) comment further. Return to Text

2. However, one might conceive of a self-imposed limit as a useful tool to attract residents from other cities. We consider this empirically. Return to Text

3. In the 1970s, many states passed limits on cities and themselves, most famous among them California's 1978 Proposition 13. Return to Text

4. Persson & Tabellini (1996a) and Persson & Tabellini (1996b) discuss the role of a fiscal constitution in funding a federation. Return to Text

5. We use the Census of Governments 2002 Governments Integrated Directory as our sample frame. We kept only cities with the following political descriptions: Charter Township, City, City and Borough, City and County, City-Parish, Consolidated Government, Municipality, Town, and Village. We refer to all of these entities throughout as either cities or municipalities. Summary statistics comparing our randomly sampled cities (those with populations between 25,000 and 100,000) to all non-sampled cities show few differences; see Appendix Table 1 for the formal test. Return to Text

6. We use the universe of larger cities and a sample of smaller cities for three key reasons. First, by sampling larger cities with certainty, we have a sample that represents a substantially larger proportion of the U.S. population, making our findings more policy-relevant. Second, when choosing where in the distribution to sample, we prefer to sample the "thicker" part of the population distribution (smaller cities) rather than the "thinner" part (larger cities). Relative to the thin part of the distribution, the thick part of the distribution has more similar cities, and any sampled city is more likely to be representative of non-sampled cities. Third, the Annual Survey of Government Finances data uses a population weighted sampling scheme, so that larger cities are more likely to have finance data. Return to Text

7. Before conducting the full survey, we made a preliminary effort to determine whether locally-imposed limits exist. During the summer of 2006, we selected a sample of 60 cities and searched their municipal charters or code for evidence of limits. We also called local officials from each sampled city to ask whether their city had adopted such limits. The results led us to conclude that a larger survey was warranted. It also revealed that reading municipal documents is a very poor mechanism for identifying limits absent interviews. Return to Text

8. Not all municipalities have all three of these offices; we collected contact information for all available types. Return to Text

9. The survey instrument is included in the appendix. Though the survey is presented as a form which respondents could return, the vast majority of responses were by telephone. Return to Text

10. We are confident in the reliability of our survey results for several reasons. First, respondents were well qualified to answer the questions we posed. We surveyed only individuals in formal positions in municipal budgeting. Because survey responses were primarily by phone, we know that the questions were answered by the targeted individuals or by someone similarly qualified. Second, our survey results do not appear to suffer from non-response bias. Appendix Table 2 contrasts respondent and non-respondent cities across several key fiscal, demographic, and institutional characteristics, showing that there are very few statistically significant differences (only income varies across response status). This absence of selection into respondent status suggests that our results are representative of the sampled population. Return to Text

11. The citation, and wording of the locally-adopted limits identified by our survey and located in municipal charters or code, are available upon request. Return to Text

12. We did not collect information on the method of limit adoption in our survey. Return to Text

13. For complete details on data sources, please see the Appendix. Return to Text

14. Census municipal codes change from 1980 to 1990, and we construct a cross-walk to merge across years. Full information on all data sources is in the appendix. Return to Text

15. This means we observe most institutions at only one point in time. However, institutional features change quite slowly; see Baqir (2002) pages 1324-5 on the size of the city council. Return to Text

16. The unmatched city is Centennial, Colorado which was created though a merger of many census designated places in 2001. Return to Text

17. Potentially binding limits include revenue or expenditure limits, property tax levy limits, or the combination of a property tax rate limit and a limit on assessment increases. For more discussion of what constitutes a potentially-binding state-imposed limit as well as their effects on local budgeting see Brooks & Phillips (2010) and Mullins & Wallins (2004). For a complete correlation table between the types of locally-imposed and state-imposed limits, please see Appendix Table 3. Return to Text

18. Data on the number of municipalities in a metropolitan area come from decennial censuses. For each year in the sample, we count the number of cities with more than 25,000 people per metropolitan statistical area (MSA). We find the maximum and the minimum for each MSA over all years. We report the maximum here; no results are affected by using the minimum. Return to Text

19. One obvious covariate, suggested by the literature on heterogeneity and public goods, is a Herfindahl index for racial or income heterogeneity. We find no association between racial heterogeneity and limit adoption, and a very weak association between income heterogeneity and limit adoption. Return to Text

20. When we estimate using OLS, there are no appreciable qualitative differences. Return to Text

21. We observe date of limit adoption within our sample range for 18 of the 40 limit-adopting cities. This raises the concern that our estimates may be biased by use of a selected sample of limit adopters. To evaluate this, we compare the 18 in-sample and 22 out-of-sample cities using means of the regression covariates. We find statistically significant differences for only 6 of 28 covariates. While this is above the 1.5 covariates we would expect to have a significant difference due to random chance (at the 5 percent level), it signals that differences between in-sample and out-of-sample adopters are insubstantial. Return to Text

22. Formally, a properly specified Cox proportional hazard model does not require year dummies, as they should be captured in the

term. In practice, our model fails to converge with their inclusion. Return to Text

23. Another explanation entails intertemporal uncertainty, whereby the median voter's desire to limit government stems from uncertainty about whether the preferences of the median voter in the future will differ from her own Tabellini & Alesina (1990); Anderson & Pape (2010). Return to Text

24. For two conflicting interpretations of empirical evidence see Alesina et al. (2004) and Hopkins (2009). Return to Text

25. The latter assumption simplifies our analysis and is without loss of generality with respect to our key results. Return to Text

26. Results are similarly unaffected if we conceived of $\pi$ as the share of the council that is type 1. Thus, for simplicity we continue with the model with the single politician. Return to Text

27. For a similar approach, see Coate & Knight (2011). Return to Text

28. If signals are perfectly informative, a type 1 candidate wins office with probability 1, when $\pi>\frac{1}{2}$ . Alternatively, if signals are perfectly uninformative, then a type 1 candidate wins with probability $\pi$ , which is what we assume. Given majority rule, signal precision has a similar effect to increasing $\pi$ - it increases the cleavage between type 1 and type 2 office holders. For example, let $\sigma\in\left\{ 1,2\right\}$ be a signal of candidate type and $\Pr\left(j=1\vert\sigma=1\right)=\Pr\left(j=2\vert\sigma=2\right)=q\in\left(\frac{1}{2},1\right)$ . Then only when both candidates signal different types will electoral outcomes differ from those generated in our model. In this case, the probability that a type 1 wins office is $\frac{q\pi}{q\pi+\left(1-q\right)\left(1-\pi\right)}>\pi$ - the win probability when

. Return to Text

29. In the context of municipalities, politicians are likely to follow their policy preferences since the benefits of holding office are not large (see Coate & Knight (2011) for more discussion). Return to Text

30. If we allow a politician to limit expenditures and the electorate to subsequently reverse the limit (we do observe many limits that are reversible via referenda or supermajority vote; see Table 1), the predictions of our model are similar. Return to Text

31. Technically, a type 1 voter would be indifferent between adopting a limit $x=\frac{1}{4\underline{\theta}}$ and not adopting a limit at all. But for any positive cost of holding a referendum or subsequent implementation, limiting expenditures is not optimal. Return to Text

32. This does raise the interesting question of whether the model should include a floor on public goods provision, and not just a limit. To the best of our knowledge, no such explicit spending floors exist. However, legal mandates to provide services may act as de facto floors. We leave this question to future research. Return to Text

33. For example, type 1 voters prefer a limit of $x=\underline{\theta}G_{1}^{*}\left(\underline{\theta}\right)$ , a type 1 voter's ideal spending in the "best" state of the world, to no limit at all. Because $x^{*}$ weakly dominates any other x - as it is the solution to type 1's utility maximization problem - any alternative to $x^{*}$ would not garner sufficient support in a referendum. Return to Text

34. See Osborne & Turner (2010) for a relevant theoretical evaluation of cost-benefit analysis versus referenda in environments of preference heterogeneity. Return to Text

35. The behavior of candidates in our model is consistent with an environment without prospects for reelection. Alternatively, the model is consistent with an environment in which the gains for a politician from implementing her preferred policy trump any benefits from compromising her position in return for greater payoffs in the future (either from holding office or from implementing a preferred policy; see Coate & Knight (2011) for more discussion). One could imagine that while type 1 office holders will remain non-strategic independent of reelection considerations, a type 2 politician might moderate her position if it would result in a greater likelihood of pooling type 1 and type 2 politicians by voters. One (possibly naive) way to do that is never spend up to the limit Return to Text

36. For state limits on cities, we only use limits or combinations of limits that are considered to be "potentially binding," which are those the literature suggests affect municipal budgets. Return to Text

37. An alternative source for institutional data is the International City/County Management Association (ICMA) which conducts a survey of municipal forms of government every five years. The survey's response rate, however, is under fifty percent and responses come disproportionately from cities that are professionally managed ICMA (2006). The Census of Governments remains the most complete source of data on local institutions. Return to Text

38. It is standard, when including an interaction term to separately include both parts of the interaction. In this case, the "post limit" period exists only for limit adopters, so a "post limit" dummy is effectively the same as our variable of interest. In addition, a "local limit city" dummy would be collinear with our city fixed effects, which more flexibly control for any type of variation that is constant within a city over time. Return to Text

39. A different estimation method concurs with this finding. Our survey asked whether the official thought the local limit had an effect. Roughly half of cities (responses from officials weighted to correspond to one answer per city) suggested that the limit had some effect; see Appendix Table 8 for details. Return to Text

40. The approach we use here is that of Imbens (2004). The weights are calculated as below, where the propensity score is $e(X_{c})$ (the fitted value from the matching estimation) and limit $_{c}$ is coded one for cities that have a locally-adopted tax and expenditure limitation and zero otherwise. When we use time series data in the matching process, the equation has a

subscript in addition to the

subscript.

$\displaystyle \lambda_{c}=\sqrt{\frac{\mbox{limit}_{c}}{e(X_{c})}+\frac{(1-\mbox{limit}_{c})}{(1-e(X_{c}))}}$

Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text