Estimating Changes in Supervisory Standards
and Their Economic Effects
Keywords: CAMELS ratings, bank supervision and regulation, financial frictions.
Abstract:
The disappointingly slow recovery in the U.S. from the recent recession and financial crisis has once again focused attention on the relationship between financial frictions and economic growth. With bank loans having only recently started growing and still sluggish, some bankers and borrowers have suggested that unnecessarily tight supervisory policies have been a constraint on new lending that is hindering recovery. This paper explores one specific aspect of supervisory policy: whether the standards used to assign commercial bank CAMELS ratings have changed materially over time (1991-2011). We show that models incorporating time-varying parameters or economy-wide variables suggest that standards used in the assignment of CAMELS ratings in recent years generally have been in line with historical experience. Indeed, each of the models used in this analysis suggests that the variation in those standards has been relatively small in absolute terms over most of the sample period. However, we show that when this particular aspect of supervisory stringency becomes elevated, it has a noticeable dampening effect on lending activity in subsequent quarters.
1 Introduction
The financial crisis that began in mid 2007 and continued well into 2009 has sparked renewed interest in the channels through which changes in the cost and availability of credit are linked to economic performance, as well as the magnitudes of the effects generated by such financial frictions. Particular attention regularly focuses on the unique role of commercial banks in the financial system, in large part because they are often viewed as the most efficient or sometimes the sole providers of credit to many households and small businesses.2 For instance, Lown and Morgan (2006) showed that changes in bank lending standards have important macroeconomic effects, and Bassett, Chosak, Driscoll, and Zakrajsek (2010) document the large contractionary shock to lending standards during the recent financial crisis and its material effects on lending and GDP.
The excesses of the mid-2000s that contributed importantly to the crisis left many commercial banks in a significantly weakened state that resulted in downgrades of their supervisory ratings over the 2007 to 2009 period. The share of banks that supervisors consider "weak" remains elevated to this day, and the pace of decline in the share of weak banks has lagged significantly behind the pace seen following the banking crisis of the early 1990s, despite noticeable improvements in banking conditions since the height of the financial crisis. Moreover, as in the recession and slow recovery in the early 1990s, weak banks have contributed disproportionately to the contraction in loans over the past several years (exhibit 1). In addition, Peek, Rosengren, and Tootell (2003b) identify loan supply shocks by the fraction of banks that receive the worst supervisory risk rating, and find that this measure is important in explaining inventory movements, the component of GDP most dependent on bank lending, from 1978 to 1998. Two earlier papers by the same authors argue that exploiting such confidential supervisory information generates important synergies in the Federal Reserve's monetary policymaking process by allowing the FOMC to account for potential swings in credit supply in setting interest rates (Peek, Rosengren, and Tootell (1999) and Peek, Rosengren, and Tootell (2003a)). Therefore, if CAMELS ratings are currently unduly stringent, then supervisors could be a source of headwinds in the economy.
To be sure, banks continue to face ongoing, heightened scrutiny of their risk management practices by both supervisors and market participants as they also adjust to a host of new regulations. Among the vast array of financial regulatory reforms required under the Dodd-Frank Act and Basel III, one important goal is to provide a framework for enhanced macroprudential supervision of financial institutions. As part of that goal, regulators are more closely considering the potential feedback loops between bank supervision and the broader economy. For instance, a common refrain is that the worst performing loans are made during the late stages of economic expansions, in part because banks and regulators have become less attuned to risks (Berger and Udell (2004)).3 A corollary might be that many good loans are not made during and shortly after the end of economic downturns because risk aversion lingers too long.
Note: Strong banks have CAMELS ratings of 1 or 2; weak banks have CAMELS ratings of 3, 4, or 5. Shaded lines represent recessions as identified by the NBER.
Source. Call Reports, FFIEC.
Recognizing these parallel risks, the new regulations seek to ensure that banks retain adequate capital and liquidity cushions to support lending. In particular, they include provisions directing supervisors to implement a countercyclical capital buffer that will lean against additional lending during a boom and support lending during a downturn. But, capital standards and other quantitive measures of bank health are importantly complemented by direct supervisory oversight of institutions and their practices. While good arguments exist against regulatory forbearance to stimulate lending during downturns, macroprudential goals might at least seek to ensure that supervisors are consistently applying these more-subjective standards through time.
Many bankers and some borrowers, particularly small businesses, have suggested that that regulators have maintained an excessive level of scrutiny of bank lending practices in recent years. Further, they note that this scruitiny is contributing to the weakness in bank lending and by extension the sluggish recovery.4 In response to those concerns, the federal bank regulatory agencies issued joint guidance to their examination teams and reviewed their performance to ensure that examination standards are not unduly affecting the flow of credit.5 In addition, the Federal Reserve has engaged in extensive community outreach and discussions with various stakeholders to identify policies and strategies that would help ensure that creditworthy borrowers have access to appropriate financing sources.6
This paper considers the extent to which variation in supervisory stringency is evident in composite CAMELS ratings, the overall supervisory assessment of the conditions of banks, between the third quarter of 1991 to the second quarter of 2011.7 That sample period spans two eras often referred to as "credit crunch" periods--the first in the early 1990s and the most recent since the end of 2008. Importantly, such ratings are supposed to be invariant to business cycle fluctuations, instead conveying an absolute assessment of a bank's condition and risk of failure at any given point in time.
Because of the various peculiarities of the process used to assign CAMELS ratings and the relatively short time series dimension of our dataset, standard econometric models for panel data are somewhat imperfect for the task. Likely in part for that reason, most of a small existing literature attempted to model stringency using time-period fixed effects estimated from pooled cross-sectional data, and generally concluded that supervisors were more stringent in the early 1990s than during other periods. In this study, we expand upon the existing literature in three ways. First, we extend the sample used in previous studies to include the most recent financial crisis. Second, we incorporate an improved measure of local economic conditions facing the bank as well as various macroeconomic indicators and financial market variables (hereafter, "economy-wide variables") in several alternative statistical models to capture supervisory reactions not only to the bank's observed condition but also to the economic environment it faces. Third, in hopes of mitigating concerns about the potential shortcomings of any particular model, we use a variety of different panel-based econometric specifications for comparison, as well as a series of repeated cross-sectional regressions. The latter methodology has not been fully explored in the existing literature and provides greater flexibility in modeling the time variation of both the thresholds associated with a given CAMELS rating and the coefficients on the explanatory variables.
Our analysis results in three fairly robust conclusions. First, supervisory standards used in the assignment of CAMELS ratings appear to have been reasonably constant across the sample period, with some evidence that they were somewhat tighter than average during the early-1990s and in 2008. Second, the extent of stringency estimated from CAMELS ratings is somewhat model-dependent: our use of economy-wide variables instead of time fixed effects (which were used in much of the existing literature) to control for macroeconomic conditions reduces the extent of supervisory stringency commonly observed in the early 1990s and also suggests that much less stringency existed during the recent financial crisis. Third, the degree of supervisory stringency identified by our model is associated with statistically significant changes in lending standards and with changes in bank lending. Although the effects are relatively small, these results provide support for an active bank lending channel in the transmission of monetary policy.
The next section of the paper places our analysis in the context of the existing literature. The following section describes the data and specific variable definitions used in the analysis. Section 4 describes the tradeoffs involved in the methodologies used to estimate the relationship between CAMELS ratings and observed data. Section 5 describes the results of that estimation and the calculation of aggregate supervisory stringency. Section 6 explores the relationship between aggregate supervisory stringency, lending, and economic growth. Section 7 concludes.
2 Review of Existing Literature
A small number of authors have studied the extent to which bank supervisors change their standards and policies over the economic and financial cycle, with some extending the analysis to how such changes affect lending behavior (and, by extension, broader economic performance). Previous work at the commercial bank level, such as Berger, Kyle, and Scalise (2001), concluded that supervisors indeed were "tougher" during the credit crunch in the early 1990s than they were in the mid-1990s. Curry, Fissel, and Hanweck (2008) and Krainer and Lopez (2009) examine bank-holding company supervisory ratings - BOPEC ratings - over the 1987 to 2004 period and arrive at similar conclusions. Controlling for some bank balance sheet and aggregate macroeconomic variables, Bizer (1993) finds stricter supervisory standards in the 1989 to 1992 period relative to 1988 as well as an economically significant association between CAMELS ratings and loan growth. Curry, Fissel, and Ramirez (2008) also provide some evidence that bank lending was sensitive to ratings between 1985 and 1993, but then show that ratings and lending were not as intertwined in subsequent years. Finally, though they do not model supervisory ratings per se, Kiser, Prager, and Scott (2012) examine the extent to which changes in banks' CAMELS ratings are associated with changes in the rate of growth of their lending to small businesses, and find that small banks that experienced ratings downgrades between 2007 and 2010 exhibited significantly lower rates of growth in small business loans outstanding compared with banks that maintained their ratings at healthy levels during the same period.
The standard approach in most of those papers has been to model the discrete CAMELS ratings distribution within a pooled cross section using an ordered limited-dependent variable framework. The controls generally included a range of bank-specific characteristics and a set of regional indicator variables or state-level variables for local economic conditions. With the exception of Bizer (1993), who estimated bank CAMEL ratings for limited time periods separately, all of the studies incorporate time-period fixed effects, and interpret the series of coefficients on those indicator variables as the relative degree of "tightness" applied by bank supervisors over time.
However, the results of our study suggest that this approach has two critical weaknesses. First, the time fixed effects could also be picking up the response of regulators to conditions in broader financial markets or the macroeconomic environment that are not accounted for by regional or state-level control variables. If we define supervisory stringency as stricter supervisory standards than what can be explained by identifiable factors, economy-wide variables may explain an important portion of supervisory standards that were deemed "stricter" in the previous literature.8 Second, by construction, the time fixed effects shift each of the cutoff points simultaneously and by equal amounts across different rating categories. Therefore, the approach does not allow for standards to change differentially across the various CAMEL rating categories. For example, regulators may become stricter in assigning ratings for only the weakest set of banks. Therefore, we also devise a methodology that allows the thresholds to vary through time separately for each rating, while still incorporating economy-wide variables.
3 Data
The paper combines confidential supervisory data on CAMELS ratings with bank-specific balance sheet and income items from the commercial bank Call Report. In addition, we use the annual Summary of Deposits survey data to identify the location of the branches in which banks book their deposits, and combine that information with state-level economic indicators to generate bank-specific economic conditions variables. Finally, we obtain macroeconomic and financial sector variables from a variety of commonly referenced sources. The sample begins in the third quarter of 1991, which is the first period in which we have enough quarters of data on regulatory capital ratios, a key determant of CAMELS over the past two-plus decades, to estimate all of our specifications. It ends in the second quarter of 2011, because data on CAMELS ratings sometimes enters the database with a significant lag, at times making very recent quarters unrepresentative.
3.1 CAMELS Ratings
For our dependent variable that describes the conditions of a bank, we use composite CAMELS ratings taken from a confidential supervisory database maintained by federal bank regulatory agencies that includes key information about the timing and scope of the exams. Banks with composite ratings of 1 or 2 are considered "strong," while banks with ratings of 3, 4, 5 are considered "weak" and subjected to increasing levels of regulatory scrutiny as they progress down the scale.9 So called "full-scope" exams, in which an on-site team of examiners assesses the full range of bank operations, are mandated every 12 to 18 months for strong banks (depending on a threshold of total assets), and every 6 months for weak banks.10
We begin by including all commercial bank examination data that led to a designation by bank regulators (the Federal Reserve, the OCC, the FDIC, and the state agencies) of CAMELS ratings between the third quarter of 1991 and the second quarter of 2011. Sometimes a bank may have more than one exam registered in a given quarter; in those cases, the exam closest to quarter-end was used.11
As shown in the second exhibit, the number of exams for a given bank in our 20 year sample varies considerably. This variation is accounted for by new commercial banks, the staggered exam schedule that depends on both the size of the bank and the previous CAMELS rating, and exits from the sample due to mergers, aquisitions and failures. The average bank in the sample has been examined about 14 times, but even when examination data for banks with fewer than five exams over the sample period are removed, about 35 percent of the banks in our sample have been examined no more than ten times.
Exhibit 3 shows the average CAMELS rating of banks examined during each quarter over the full sample period that is used in the panel data models. In addition, in order to construct relevant and large samples for our repeated cross-section analysis, we use a rolling two-year window of exams and consider only the most recent exam for each bank within that window. The average CAMELS rating for this two-year grouped data is also displayed in the top panel in the first exhibit. Each point on that line is centered two quarters from the end of the two-year window, reflecting the average date of the exams conducted during the typical subsample. The two CAMELS averages are highly correlated. Bank ratings were significantly worse than average during the credit crunch of the early 1990s and they worsened quickly and substantially during the most recent financial crisis. This pattern in the average rating reflects changes in the number of banks rated in each of the five CAMELS rating categories, as shown in the middle and bottom panels in the third exhibit.
* Strong banks are those with a CAMELS rating of 1 or 2.
** Weak banks are those with a CAMELS rating of 3, 4, or 5.
Source. Call Reports, FFIEC.
Large banks are usually reviewed in a much different manner than their smaller counterparts, including by a team of resident examiners that are in consistent contact with bank management. Further, large banks have much broader scope and complexity of their operations, much of which cannot be adequately assessed with the limited number of Call Report items that could be included in an econometric model. Therefore, we excluded from our sample any banks that are subsidiaries of the 25 largest bank holding companies in any given quarter. However, this still accounts for about 40 percent of industry loans, on average, over our sample period.12
Bank Balance Sheet and Income Items
The majority of the explanatory variables are constructed from bank balance sheet and income data from the Call Reports. Those variables are are detailed in Table 1. In choosing explanatory variables, we used those bank balance sheet and income items that are closely related to the components of the CAMELS ratings.13
- Capital adequacy: Total risk-based capital ratio, the leverage ratio as defined in FDICIA, and the ratio of delinquencies to loan loss reserves
- Asset quality: Noncurrent loan ratio, and the ratio of private security holdings (which excludes Treasuries, agency securities, and agency MBS) to total assets, the ratio of loans secured by commercial real estate (CRE) to total assets, the ratio of loans secured by residential real estate (RRE) to total assets, and the ratio of other loans (not secured by real-estate) to total assets
- Management quality: Noninterest expense to revenue (net interest income plus noninterest income)
- Earnings: Return on assets (ROA) and the net interest margin (NIM)
- Liquidity: The ratio of core deposits to total assets and the "volatile liability dependence ratio," which measures the extent to which a bank is funding long-term investments with short-term liabilities.14
- Sensitivity to market risk: Return on risky assets defined as noninterest income net of deposit fees and fiduciary income divided by average total assets
As in the literature, we also include the log of total assets to account for factors such as the degree of portfolio diversification and potential to exploit scale economies, in addition to possible differences in supervisory treatment of larger institutions. For all of the balance sheet items, we use the average value of the four quarters preceding the exam, while for the income and flow items, we use four-quarter cumulative amounts scaled by relevant balance sheet or income items when necessary. All the financial ratios based on flow items are normalized by Schedule K balance sheet items (i.e., reflect the average outstandings in that item during the quarter or year, as appropriate). The financial ratios based solely on balance sheet items are based on end-of-period values with the exception of the volatile liability dependence ratio, which is more subject to quarter-end window dressing and therefore based on Schedule-K values. We use data only if it would be available to examiners at the time of the exam. If the exam began on the last day of the quarter, we assume that the examiners were able to use the data for that quarter and consider the exam to have been conducted in the following quarter.
| Variable | Average | Deviation | Acronym |
| Leverage Ratio | 9.007 | 2.629 | LEV |
| Total Capital Ratio | 14.905 | 6.617 | TCR |
| Non-Interest Expense Ratio | 257.41 | 51.739 | NIE |
| Noncurrent Loan Ratio | 2.291 | 2.130 | NON |
| Delinquent Loans to Reserves Ratio | 163.92 | 138.966 | D2R |
| Return-on-Assets | 4.465 | 2.577 | ROA |
| Net Interest Margin | 17.364 | 3.132 | NIM |
| Core Deposits Ratio | 75.443 | 9.157 | CORE |
| Volatile Liability Ratio | 10.163 | 10.524 | VOL |
| Return on Risky Assets | 0.889 | 1.685 | RISK |
| Security Holdings Ratio | 4.805 | 5.340 | SEC |
| Commercial Real Estate Loan Ratio | 11.801 | 12.516 | CRE |
| Loans Secured by Real Estate (Non-CRE) Ratio | 19.799 | 10.257 | RE |
| Other Loans Ratio | 22.693 | 11.213 | OTH |
| Log of Total Assets | 11.317 | 1.181 | TA |
Other Items
We include several variables to control for the structure of the bank and the agency performing the exam. They are composed of indicators for whether a bank is part of a Bank Holding Company (BHC), and also for which of the federal or state regulatory agencies was the lead agency in the bank examination. All else equal, banks that are part of a larger bank holding company may be stronger because they can be supported by the financial strength of the parent. Whereas state chartered member banks are supervised jointly by state regulators and the Federal Reserve, non-member banks are supervised jointly by state regulators and the FDIC. Moreover, national banks are subject to the regulation of the OCC. Because the Federal Reserve has the authority to examine bank holding companies, those banks that are part of a BHC but regulated by the OCC or FDIC effectively have two federal supervisors, an arrangement that may improve the oversight of such entities. In addition, systematic differences in the manner in which banks are reviewed by their lead regulators may exist as in Agarwal, Lucca, Seru, and Trebbi (2012). A dummy variable for whether the bank changed its charter since the previous exam is included as Rezende (2011) finds evidence of more favorable ratings for banks that changed charters. We also control for mergers, because many mergers involve a stronger bank acquiring a weakened bank, and balance sheet and income statement data may not be sufficient to control for conditions of banks when they go through structural changes.
|
|
|
|
|
|
|
|
|
85.01% | 14.42% | 0.54% | 0.03% | 0.00% |
|
|
10.25% | 84.51% | 4.68% | 0.53% | 0.03% |
|
|
0.19% | 35.35% | 58.60% | 5.56% | 0.30% |
|
|
0.00% | 4.88% | 33.11% | 57.76% | 4.25% |
|
|
0.00% | 3.16% | 4.21% | 38.95% | 53.68% |
| Number of banks | 41,834 | 69,076 | 10,270 | 2,069 | 95 |
A set of indicator variables for the previous CAMELS ratings accounts both for sample selection, in that banks with poorer ratings are reviewed more frequently, and for the "stickiness" in the ratings found in the literature such as in Berger, Kyle, and Scalise (2001). Table 2 describes the transition matrix from one CAMELS rating category to another for the banks in our sample in percentage terms and by count, respectively. For example, 85 percent of the banks that enter an exam with an existing CAMELS rating of 1 or 2, exit the exam with the rating unchanged. For banks rated a three, four, or five, they are also more likely than not to retain the same rating in the next exam. In addition, about 17 percent of banks maintained their CAMELS rating throughout the whole sample, while 21 percent of banks had just one switch.15 We also include indicator variables for the quarter in which the exam was performed. Banks tend to be examined more frequently in quarters 1 and 3 (mostly using financial statements from December and June, respectively), than in quarters 2 and 4 of each year.
In addition, we include several dummies and weighted indexes to allow for bank assessments based on the broader economic environment. First, following the lead of existing literature, we include dummies for each of the census divisions in which a particular bank is headquartered. This is to control for the differences in economic performance in the various regions of the United States. Nonetheless, because these variables are identified by the location of the headquarters, they do not capture the full exposure to local conditions that banks face throughout their branch networks. Therefore, we also include bank-level series for the unemployment rate and annual growth in house prices. Those are constructed by weighting state-level economic data by the share of total deposits held in branches of the bank operating in that state.
Finally, we use a set of financial and macro indicators to control for national economic conditions, which have been underutilized in the literature to date. The variables included are the BBB spread over the 10-year Treasury rate, the four-quarter growth rate of the CoreLogic house price index, the four-quarter growth rate of GDP, the effective federal funds rate, the national unemployment rate, and the four-quarter total retun on the S&P 500.
4.1 Panel Analysis
We first consider econometric specifications based on the analysis of time fixed effects used in most of the previous studies of this and related topics.16 Because the ratings are ordered discrete responses and due to the likelihood of significant unobserved heterogeneity across banks, the preferred approach would be to use limited dependent variable models that are consistent for estimating bank-specific fixed effects in panel data. However, the existing literature mainly uses pooled cross-sections rather than bank-level fixed- or random-effects, presumably in part because the time series dimensions of the panels were insufficient to thoroughly mitigate the well-known biases owing to the estimation of dynamic panels or nonlinear models with incidental parameters. Although some methods have been developed to address those issues, they have only been proven to be consistent estimators for balanced panels. Unfortunately, supervisory exams are infrequent and irregularly timed, making it difficult ot construct a representative balanced panel. Therefore, we take the approach of comparing several imperfect models, and find that they reach similar conclusions in the face of their shortcomings and competing biases.
Specifically, we start by ignoring the categorical nature of CAMELS ratings and use the linear bank-fixed effects model. Although the standard errors may be inefficient, this model provides consistent estimates even on our unbalanced panel (whereas the nonlinear fixed effects model is biased, particularly for small T) and is preferred to a random effects model if, as is likely, the bank specific factors are correlated with the other regressors.
Therefore, we begin with this simple alternative to the pooled cross-section probit models used in previous studies as our benchmark,
where ![]() is a quantitative variable that is descriptive of the conditions of bank
is a quantitative variable that is descriptive of the conditions of bank ![]() in quarter
in quarter ![]() obtained by a linear transformation - in order to provide a more intuitive relationship between the sign of the coefficients and bank conditions, we designate
obtained by a linear transformation - in order to provide a more intuitive relationship between the sign of the coefficients and bank conditions, we designate
![]() to be equal to 6 minus the
to be equal to 6 minus the ![]() rating for bank
rating for bank ![]() in period
in period ![]() so that higher values are associated with better conditions for the bank;
so that higher values are associated with better conditions for the bank; ![]() is a vector that contains indicators of a bank's previous supervisory assessment, which
includes indicators for having a previous rating of a 1, 2, 3, 4, 5, or no rating at all;
is a vector that contains indicators of a bank's previous supervisory assessment, which
includes indicators for having a previous rating of a 1, 2, 3, 4, 5, or no rating at all; ![]() is a vector that contains the time-varying variables from bank-specific balance sheet and
income items;
is a vector that contains the time-varying variables from bank-specific balance sheet and
income items; ![]() is a vector that contains variables that relate to bank structural characteristics which may, but usually do not, change over time;
is a vector that contains variables that relate to bank structural characteristics which may, but usually do not, change over time; ![]() is a vector that contains variables that describe the local and regional economic conditions of a particular bank;
is a vector that contains variables that describe the local and regional economic conditions of a particular bank; ![]() is a vector of time fixed effects or variables that describe the national economic environment, but not both; and
is a vector of time fixed effects or variables that describe the national economic environment, but not both; and ![]() denotes the bank-specific effects for bank
denotes the bank-specific effects for bank
![]() ; and
; and ![]() are disturbances that are independent across banks and across
time.
are disturbances that are independent across banks and across
time.
However, CAMELS ratings change very infrequently, and the bank-fixed effects fully capture the bank's average rating. Therefore, the explanatory variables compete to explain only the limited movements in the ratings across time. In order to test whether this feature of the data drives the
results of the fixed-effects model, we also consider a second specification based on Mundlak (1978), which modifies a random-effects framework to account for likely correlation between the random effect and the control variables by employing an additional functional form assumption.
If valid, that assumption removes the correlation between the bank-specific effects, ![]() in equation 1 and banks' financial ratios. This is accomplished by assuming
that the correlation can be modeled as a function of both the average values of the bank specific variables and the deviations from those averages. In effect, we explicitly model the expected value of the bank-specific disturbance term as a linear combination of time-averages of the time-varying
financial ratios derived from a bank's balance sheet and income items,
in equation 1 and banks' financial ratios. This is accomplished by assuming
that the correlation can be modeled as a function of both the average values of the bank specific variables and the deviations from those averages. In effect, we explicitly model the expected value of the bank-specific disturbance term as a linear combination of time-averages of the time-varying
financial ratios derived from a bank's balance sheet and income items,
![]() , or
, or
Then plugging in
![]() , where
, where ![]() is not correlated with
is not correlated with
![]() , we get
, we get
where ![]() is a disturbance term not correlated with the explanatory variables. One added benefit of this framework is that the coefficients on the deviations from the average financial
ratios can be interpreted as short-run effects on a bank's rating and condition, while the coefficients on the average values can be considered the long-run effects of that ratio as in Afonso, Gomes, and Rother (2011).
is a disturbance term not correlated with the explanatory variables. One added benefit of this framework is that the coefficients on the deviations from the average financial
ratios can be interpreted as short-run effects on a bank's rating and condition, while the coefficients on the average values can be considered the long-run effects of that ratio as in Afonso, Gomes, and Rother (2011).
However, both the linear fixed-effects and linear random-effects model assume that the numerical CAMELS ratings have cardinal (as opposed to ordinal) meaning. Therefore, the third specification tested is a modified random-effects ordered probit model, which is a more natural approach for
modeling categorical variables such as CAMELS ratings. Here, we interpret the unobserved latent variable in the probit specification, ![]() , as a continuous measure of a bank's underlying
condition. The framework is a nonlinear generalization of the Mundlak (1978) specification, and it is described in Wooldridge (2010).
, as a continuous measure of a bank's underlying
condition. The framework is a nonlinear generalization of the Mundlak (1978) specification, and it is described in Wooldridge (2010).
and
The parameters of equation 3 and 4, and the cut-off points ![]() to
to ![]() are estimated using maximum likelihood, assuming that
are estimated using maximum likelihood, assuming that ![]() and
and ![]() are normally distributed.
are normally distributed.
Although a nonlinear fixed effects regression also might be considered, given the large cross-sectional sample and a comparatively limited time series, that model would likely be hampered by the well known "incidental parameters problem." The estimation procedure outlined above overcomes this limitation (if one accepts the assumption required to model the correlation between the random effects and independent variables) and, as noted, correctly models the ordinal nature of the ratings. However, to our knowledge, these estimates have not been proven to be consistent when applied to unbalanced panel datasets (as our data is based on exams being conducted at different intervals for different banks). A greater challenge arises when we consider accounting for the persistent and dynamic nature of the designation of CAMELS ratings by including lagged CAMELS ratings in the specification despite the relatively short panel available for many banks in the sample. Wooldridge (2005)'s framework to deal with such unobserved heterogeneity from serial correlation in nonlinear panel models has only been shown to produce consistent estimates in balanced panel data, or at the very least, an unbalanced panel dataset that uses specified sample selection mechanisms, which we do not have, to create an adequate balanced subset that spans the entire sample period.
Separately, in our robustness checks we incorporate a first-stage probit model for the probability of being examined within a given quarter within a selection equation system to account for sample selection that may arise in the timing and frequency of exams. The identification assumption is that, controlling for the general risk profile of a bank and it's previous rating (whether it was a strong or weak bank), the number of quarters since the last exam should only affect whether a bank is examined or not, not its rating.17 Within that framework, standard statistical tests also indicate that the number of quarters since the previous exam is a valid instrument.
4.2 Repeated Cross-Section Analysis
In our fourth approach, we estimate a series of ordered probit models using repeated cross sections.18 This approach generates time-varying coefficients and thresholds that, under certain assumptions, imply that the evolution of the coefficients on the explanatory variables and the changes in the estimated thresholds for each rating category partly reflect changes in supervisory standards. Of course, this approach is not optimal either, as it has the disadvantage of discarding the information that can be gleaned from the panel structure of the data.
Specifically, for each time period, ![]() , we assume a latent variable,
, we assume a latent variable, ![]() ,
that proxies for the condition of bank
,
that proxies for the condition of bank ![]() at time
at time ![]() 19 :
19 :
where ![]() , is a vector of of bank-specific variables,
, is a vector of of bank-specific variables, ![]() is a vector of
corresponding coefficients, and
is a vector of
corresponding coefficients, and
![]() is a normally distributed random variable. We can then track the evolution of the cutoffs in an ordered probit framework by assuming that CAMELS rating
is a normally distributed random variable. We can then track the evolution of the cutoffs in an ordered probit framework by assuming that CAMELS rating
![]() is designated based on the relationship between
is designated based on the relationship between ![]() and cutoff,
and cutoff,
![]() , where the cutoff point is defined as the threshold value of
, where the cutoff point is defined as the threshold value of ![]() needed to achieve a CAMELS rating of
needed to achieve a CAMELS rating of ![]() , a value that varies through time
, a value that varies through time ![]() . More
specifically,
. More
specifically,
Thus, we are able to estimate the supervisory assessment of aggregate bank conditions,
![]() , at time
, at time ![]() , by taking the average of the
, by taking the average of the
![]() across all banks
across all banks ![]() in a given sample, where
in a given sample, where
![]() is the estimated
is the estimated ![]() . Then, due to the properties of the probit
framework, the average CAMELS rating,
. Then, due to the properties of the probit
framework, the average CAMELS rating,
![]() , can also be expressed by the following equation,
, can also be expressed by the following equation,
![\displaystyle \overline{CAMELS}_t=\frac{1}{N_t}\sum_{i=1}^{N_t}E[CAMELS_{i,t}]](img43.gif) |
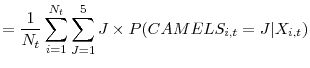 |
(7) |
![\displaystyle =\frac{1}{N_t}\sum_{i=1}^{N_t}[1+\sum_{J=1}^4\{\Phi(c_{t,J}- X_{it} \hat{\beta}_t)\}].](img45.gif) |
(8) |
4.2.1 Decomposing changes in aggregate bank conditions
Our measures of aggregate bank conditions at any point in time,
![]() , can be decomposed into the "composition" component and "risk" component based on the Blinder-Oaxaca decomposition method (Blinder (1973) and Oaxaca (1973)). Algebraically,
, can be decomposed into the "composition" component and "risk" component based on the Blinder-Oaxaca decomposition method (Blinder (1973) and Oaxaca (1973)). Algebraically,
The first term on the right hand side is the compositional component at time ![]() and the second term is the risk component. The portion of the change in
and the second term is the risk component. The portion of the change in
![]() assigned to the composition component reflects improvement or deterioration in bank profitability, bank balance sheets, or regional economic conditions holding supervisory
assessments of the importance of those factors constant. Meanwhile, the portion of the change in
assigned to the composition component reflects improvement or deterioration in bank profitability, bank balance sheets, or regional economic conditions holding supervisory
assessments of the importance of those factors constant. Meanwhile, the portion of the change in
![]() assigned to the risk component reflects changes in the coefficients over time, holding constant the condition of the banks and the factors affecting them. We define this as
the risk component because changes in the coefficients can be interpreted as reflecting changes in the supervisory assessment of the risks inherent in each of the bank-specific factors and regional or state-level economic indicators. The estimated portion of the change in
assigned to the risk component reflects changes in the coefficients over time, holding constant the condition of the banks and the factors affecting them. We define this as
the risk component because changes in the coefficients can be interpreted as reflecting changes in the supervisory assessment of the risks inherent in each of the bank-specific factors and regional or state-level economic indicators. The estimated portion of the change in ![]() assigned to each component across adjacent time periods is then chained to construct a time series of the compositional effects and risk assessments for the whole sample.
assigned to each component across adjacent time periods is then chained to construct a time series of the compositional effects and risk assessments for the whole sample.
Because low values of the latent variable are associated with poor bank conditions, lower values of risk assessment index indicate that supervisors see larger risks facing the banking industry, ceteris paribus. Algebraically, this can be illustrated as follows, with
![]() denoting the aggregate change in risk tolerance:
denoting the aggregate change in risk tolerance:
However, that measure of the supervisory risk assessment includes not only changes in the "true" risks associated with a particular factor, such as might be expected from a reassessment of the riskiness of residential mortgage lending in light of the large, sustained nationwide declines in home prices over the past five years, but also with any changes in supervisory attitudes toward various factors that are not strictly based on economic fundamentals. We assume that the portion of the aggregate risk component that can be explained by changes in economy-wide variables represents an endogenous change in the aggregate risk tolerance of supervisors, while the portion that is not captured by those variables is more closely associated with an exogenous change in the tolerance for risk of supervisors. The exogenous changes are most closely related to what we consider "supervisory stringency."
Therefore, in order to better identify the portion of the risk component that is attributable to supervisory stringency, we regress the time series of that component, ![]() , on the vector of
time series for economy-wide variables,
, on the vector of
time series for economy-wide variables, ![]() .20
More formally,
.20
More formally,
where
![]() is the vector of coefficients corresponding to the economy-wide variables and
is the vector of coefficients corresponding to the economy-wide variables and ![]() is the residual. Holding composition constant, higher values of the
is the residual. Holding composition constant, higher values of the ![]() 's (explained by macro fundamentals) imply better overall banking conditions and thus less risk in
the sector. Therefore, a higher value of
's (explained by macro fundamentals) imply better overall banking conditions and thus less risk in
the sector. Therefore, a higher value of ![]() , in the aggregate, means that examiners are showing greater tolerance for risk. As a result, a negative residual,
, in the aggregate, means that examiners are showing greater tolerance for risk. As a result, a negative residual,
![]() , in the equation for
, in the equation for ![]() means economic factors suggest supervisors
should be less strict than they are and represents supervisory stringency in terms of "perceived" risk.
means economic factors suggest supervisors
should be less strict than they are and represents supervisory stringency in terms of "perceived" risk.
4.2.2 Decomposing changes in rating thresholds
Under the strong assumption that all changes in the true riskiness of the banking sector are captured by changes in the ![]() 's or changes in the explanatory variables, then absent
changes in supervisory standards, the thresholds, or
's or changes in the explanatory variables, then absent
changes in supervisory standards, the thresholds, or ![]() 's, should be constant. Therefore, any changes in the
's, should be constant. Therefore, any changes in the ![]() 's could be interpreted as changes in supervisory standards. However, as shown above, it is likely that changes in the overall riskiness of the economy (for instance, if the financial crisis led to a reassessment of the likelihood of large shocks) would be
reflected in both the
's could be interpreted as changes in supervisory standards. However, as shown above, it is likely that changes in the overall riskiness of the economy (for instance, if the financial crisis led to a reassessment of the likelihood of large shocks) would be
reflected in both the ![]() 's and the
's and the ![]() 's. Therefore, we also attempt to
parse the thresholds into a component related to the "true" change in riskiness and changes in how supervisors perceive those risks. Hence, we separately regress the thresholds for each rating category on the economy-wide variables according to the following equation:
's. Therefore, we also attempt to
parse the thresholds into a component related to the "true" change in riskiness and changes in how supervisors perceive those risks. Hence, we separately regress the thresholds for each rating category on the economy-wide variables according to the following equation:
Then the estimated residual from those regressions,
![]() is a better estimate of the supervisory stringency present in the application of the threshold values for each rating
is a better estimate of the supervisory stringency present in the application of the threshold values for each rating ![]() than the just the raw changes in the estimates of the cut-off points themselves.
than the just the raw changes in the estimates of the cut-off points themselves.
In order to calculate adjusted CAMELS ratings for individual banks, we use the residuals from equations 11 and 12. The residuals from equation 11, ![]() , representing the changes in aggregate perceived risk, are applied uniformly across all banks within the given two-year subsample. Then, the adjusted bank conditions for individual banks are:
, representing the changes in aggregate perceived risk, are applied uniformly across all banks within the given two-year subsample. Then, the adjusted bank conditions for individual banks are:
The adjusted CAMELS ratings,
![]() , are then based on both
, are then based on both
![]() and the adjusted cutoffs for the different thresholds, i.e., the components of the cutoff values that are explained by macro fundamentals. These are represented by the predicted
value from equation 12.
and the adjusted cutoffs for the different thresholds, i.e., the components of the cutoff values that are explained by macro fundamentals. These are represented by the predicted
value from equation 12.
In other words, the adjusted latent variables,
![]() , and adjusted thresholds,
, and adjusted thresholds,
![]() map to adjusted CAMELS,
map to adjusted CAMELS,
![]() :
:
Then the adjusted average CAMELS rating for the banking system as a whole, denoted
![]() , can be written as follows:
, can be written as follows:
In the last step, we compute the difference between the actual CAMELS rating (which reflects supervisory stringency in perceived risk and the thresholds) and the counterfactual (which does not), or
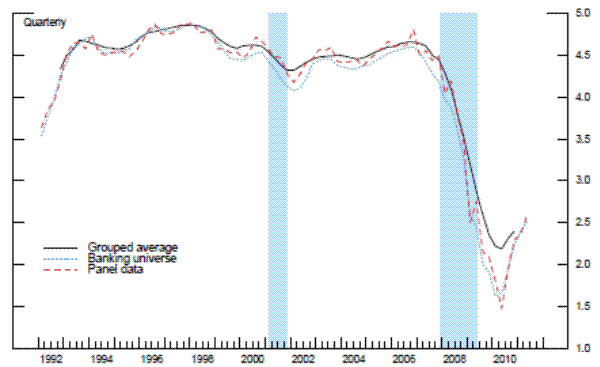
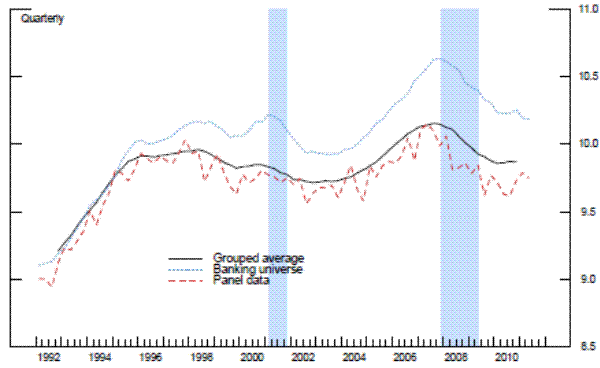
We interpret this difference as a measure that reflects overall supervisory stringency. In our opinion, this difference is a more accurate depiction of supervisory stringency than what can be found with the period fixed effects traditionally used in the literature.21 Not only do we gain flexibilty of the time-vaying parameters, this method also appears to reduce the selection bias in the resulting sample. As can be seen in the fourth exhibit, the grouped data for the repeated cross-section analysis is a better representation of the universe of banks (not in the top 25 BHCs) than the samples in the panel datasets; this is true whether you look at profitability measures, such as ROA, or balance sheet measures, such as the regulatory leverage ratio.22
Source. Call Reports.
5.1 Panel Regression Results
Selected results for the panel regressions are shown in Table 3. It compares three models: the linear model with bank fixed effects, the linear model with bank random effects, and the ordered probit model with bank random effects. These specifications include economy-wide variables in lieu of time-fixed effects. Positive coefficients are associated with a better assessment of banks (i.e. lower CAMELS ratings). Below we discuss the interpretation of the residuals.
5.1.1 Discussion of Control Variables
Across the three models, the same variables are typically statistically significant, suggesting that the overall results may in fact be robust to the various potential specification errors discussed above. Moreover, where experience confers a prior expectation about the direction of the effect of a bank-specific variable, the coefficients have the anticipated sign. Banks with stronger capital ratios, fewer nonperforming assets, greater shares of stable funding, and higher earnings than their peers tend to be rated better by supervisors.
Most of the broader economic variables also enter each of the specifications significantly with the expected sign. For example, increases in both the bank-specific regional home price index and the national home price index are associated with better CAMELS ratings, as is stronger GDP growth. A high unemployment rate at the national level is associated with worse CAMELS ratings, and the magnitude of the coefficient on the national unemployment rate dominates the estimated effect at the regional level. Indeed, the coefficients on the bank-specific unemployment rate are economically small and at times also statistically insignificant. In addition, supervisory ratings are negatively related to the spread on BBB-rated corporate bonds, suggesting that high risk aversion in financial markets is internalized by examiners. Finally the growth in returns on the S&P 500 are also associated with better CAMELS ratings, but for the random-effects models, these effects are statistically insignificant.
The response of ratings to interest rates is also of note. High federal funds target rates are associated with lower CAMELS ratings, ceteris paribus, suggesting that examiners are somewhat forward looking in their ratings assignments. Increases (decreases) in the funds rate are likely to cool (strengthen) an economy that is growing quickly (weakly), and that slowdown in activity could be expected to negatively affect loan performance and hence the condition of the bank. In addition, if the federal funds rate is considered a proxy for the level of short-term interest rates in general, supervisors may also be attuned to higher funding costs faced by banks which may lead to reduced expectations of future profits as noted in English, Van den Heuvel, and Zakrajsek (2011). A steeper slope in the yield curve, despite studies such as Stock and Watson (1989) that have shown it to be a predictor of economic expansion, is associated with a worse CAMELS rating. However, English, Van den Heuvel, and Zakrajsek (2011) have also noted that while the slope of the yield curve may be associated with higher interest margins at banks, total profitability depends on both the margin and volume, which may decline when margins are high. In addition, conditional on short-term interest rates, higher long-term interest rates may result in capital losses on long-term assets that banks typically hold.
In order to compare the relative magnitudes of the marginal effects across the three specifications, we report the change in the average CAMELS rating implied by a one standard deviation move in the listed variables. For marginal effects from the modified random effects model reported in Panel B, we look at the impact of changes in particular variables on the CAMELS rating of a bank with the median characteristics of a bank rated a three. Because lower values of CAMELS ratings are better ratings, negative impacts on CAMELS ratings implies positive impacts on supervisory assessment of banks. As shown in Panel A and the last column of Panel B of Table 4, in general, return on assets has the largest marginal effect on CAMELS ratings, followed by the noncurrent assets ratio and the ratio of CRE loans to total assets.
Some economy-wide variables, such as the national unemployment rate and the Fed Funds target rate, also are among the more economically important factors in determining CAMELS ratings. Based on linear econometric specifications, a one standard deviation decrease in the national unemployment rate leads to about 5 percent of banks being rated one notch better, on average, than otherwise. A one standard deviation decrease in the federal funds rate leads to 3 to 5 percent of banks being rated one notch better, on average. The marginal effect of that change in the aggregate unemployment rate in the random-effects ordered probit specification, setting all other explanatory values at their median levels, leads to a slightly larger effect on the average CAMELS rating, of about 8 percent. That effect is accounted for by an increase in the probabilities of the bank being rated a three or a four and a lower probability of it being rated a four, as described in Panel B of Table 4
| Explanatory Variable | Specification (I) Level | Specification (II) Dev. | Specification (II) Avg. | Specification (III) Dev. | Specification (III) Avg. |
|
|
|
|
|
|
|
| (.0016) | (.0018) | (.0019) | (.0075) | (.0082) | |
|
|
.0000 |
|
|
||
| (.0007) | (.0009) | (.0008) | (.0038) | (.0038) | |
|
|
|
.0001 |
|
.0000 | |
| (.0000) | (.0001) | (.0001) | (.0002) | (.0003) | |
|
|
|
|
|
|
|
| (.0012) | (.0014) | (.0018) | (.0052) | (.0069) | |
|
|
|
|
|
.0000 | |
| (.0000) | (.0000) | (.0000) | (.0001) | (.0001) | |
|
|
|
|
|
|
|
| (.0009) | (.0009) | (.0018) | (.0036) | (.0074) | |
| .0052*** |
|
-.0006 |
|
.0005 | |
| (.0008) | (.0009) | (.0009) | (.0035) | (.0022) | |
| .0017*** |
|
.0005 |
|
-.0006 | |
| (.0005) | (.0005) | (.0006) | (.0022) | (.0026) | |
|
|
|
|
|
|
|
| (.0004) | (.0004) | (.0006) | (.0017) | (.0023) | |
|
|
|
|
|
-.0034 | |
| (.0010) | (.0015) | (.0014) | (.0059) | (.0055) | |
| .0005 | .0004 |
|
|
|
|
| (.0004) | (.0004) | (.0005) | (.0018) | (.0019) | |
|
|
|
|
|
|
|
| (.0003) | (.0003) | (.0003) | (.0014) | (.0014) | |
|
|
|
|
|
|
|
| (.0003) | (.0003) | (.0003) | (.0013) | (.0011) | |
|
|
|
|
|
|
|
| (.0003) | (.0004) | (.0003) | (.0014) | (.0014) | |
|
|
|
|
|
|
|
| (.0044) | (.0051) | (.0021) | (.0205) | (.0084) | |
|
|
.0010 | .0075 | |||
| (.0019) | (.0016) | (.0063) | |||
|
|
|
|
|||
| (.0004) | (.0004) | (.0016) | |||
|
|
|
|
|||
| (.0022) | (.0022) | (.0093) | |||
|
|
|
|
|||
| (.0017) | (.0017) | (.0067) | |||
|
|
|
|
|||
| (.0022) | (.0022) | (.0088) | |||
|
|
|
|
|||
| (.0003) | (.0003) | (.0012) | |||
|
|
|
|
|||
| (.0009) | (.0009) | (.0038) | |||
|
|
|
|
|||
| (.0021) | (.0021) | (.0082) | |||
| .0099 | .0407 | ||||
| (.0062) | (.0062) | (.0255) |
| Explanatory Variable | Fixed Effects | Random Effects Avg. | Random Effects Dev. |
| Return on assets | -0.14 | -0.11 | -0.09 |
| Leverage ratio | -0.06 | -0.03 | -0.02 |
| Noncurrent ratio | 0.09 | 0.05 | 0.09 |
| CRE loans ratio | 0.09 | 0.07 | 0.03 |
| RRE loans ratio | 0.02 | 0.03 | 0.01 |
| Non-real-estate loans ratio | 0.07 | 0.04 | 0.03 |
| Term premium | 0.02 | 0.01 | - |
| Fed Funds effective rate | 0.05 | 0.03 | - |
| Aggregate unemployment rate | 0.05 | 0.04 | - |
| R-squared | 0.752 | 0.730 | - |
| Number of banks | 9,038 | 9,120 | - |
| Number of observations | 123,344 | 116,921 | - |
| Explanatory Variables | ||||
| Return on assets (avg.) | 0.122 | -0.090 | -0.033 | -0.156 |
| Return on assets (dev.) | 0.126 | -0.093 | -0.034 | -0.160 |
| Leverage ratio (avg.) | 0.022 | -0.016 | -0.006 | -0.028 |
| Leverage ratio (dev.) | 0.019 | -0.014 | -0.005 | -0.024 |
| Noncurrent ratio (avg.) | -0.120 | 0.088 | 0.032 | 0.153 |
| Noncurrent ratio (dev.) | -0.065 | 0.048 | 0.017 | 0.083 |
| CRE loans ratio (avg.) | -0.074 | 0.054 | 0.020 | 0.094 |
| CRE loans ratio (dev.) | -0.040 | 0.029 | 0.011 | 0.051 |
| RRE loans ratio (avg.) | -0.029 | 0.021 | 0.008 | 0.037 |
| RRE loans ratio (dev.) | -0.034 | 0.025 | 0.009 | 0.043 |
| Non-real-estate loans ratio (avg.) | -0.045 | 0.033 | 0.012 | 0.058 |
| Non-real-estate loans ratio (dev.) | -0.040 | 0.029 | 0.011 | 0.051 |
| Volatile liability ratio (avg.) | -0.005 | 0.004 | 0.001 | 0.006 |
| Volatile liability ratio (dev.) | -0.015 | 0.011 | 0.004 | 0.019 |
| Log of total assets (avg.) | 0.042 | -0.031 | -0.011 | -0.054 |
| Aggregate unemployment rate | -0.061 | 0.045 | 0.016 | 0.077 |
| Fed Funds effective rate | -0.049 | 0.036 | 0.013 | 0.062 |
| Term premium | -0.019 | 0.014 | 0.005 | 0.025 |
NOTE: Impact is from one standard deviation increase in selected variables in models with economy-wide variables (rather than time-fixed effects) on a bank with a previous CAMELS rating of 3 with the median characteristics of all banks with CAMELS ratings of 3. Because lower values of CAMELS ratings are better ratings, negative impacts on CAMELS ratings implies positive impacts on supervisory assessment of banks. All listed variables are significant at the 1% level. Avg. is the average over the bank's time in the sample for bank-specific variables or the level for economy-wide variable. Dev. is difference between the the value in the current period and the average. The impact on P(CAMELS=1) and P(CAMELS=5) is negligible.
| Estimation procedure | Obs. | Prediction error (notches) -2 | Prediction error (notches) -1 | Prediction error (notches) 0 | Prediction error (notches) 1 | Prediction error (notches) 2 | Prediction error (notches) 3 | % Correctly predicted | % Within 1 notch |
| Time-fixed effects | 116,921 | 41 | 8,494 | 96,850 | 11,090 | 421 | 25 | 82.83 | 99.58 |
| Macro variables | 116,921 | 44 | 8,651 | 97,053 | 10,787 | 362 | 24 | 83.01 | 99.63 |
| Baseline | 116,921 | 48 | 8,625 | 96,974 | 10,872 | 379 | 23 | 82.94 | 99.62 |
NOTE: Negative numbers represent the prediction of a better CAMELS rating than assigned.
Goodness of fit measures are shown in Table 5. The R-squareds for the bank-fixed effects and random effects linear models in the specifications with macro variables are 0.74 and 0.73, respectively. When we look at the ordered-probit models, regardless of whether we use macro variables or not, about 83 percent of actual CAMELS ratings match the rating that the model predicts is most likely. With only a few exceptions, the rest of the ratings are predicted to be different by only one notch. The strong fit of the models presages the conclusions about changes in supervisory stringency over time, as CAMELS seem to be well explained by observable characteristics of the bank and the macroeconomic environment.
5.1.2 Relative Supervisory Stringency Implied by Panel Data Models
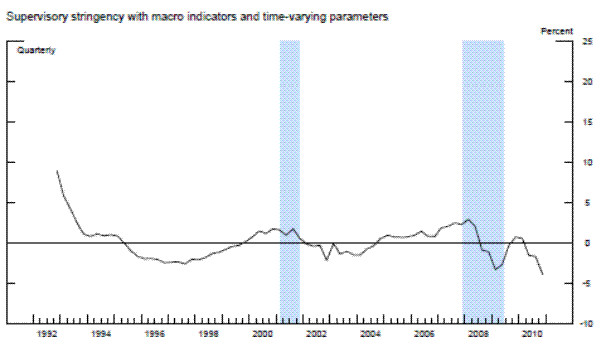
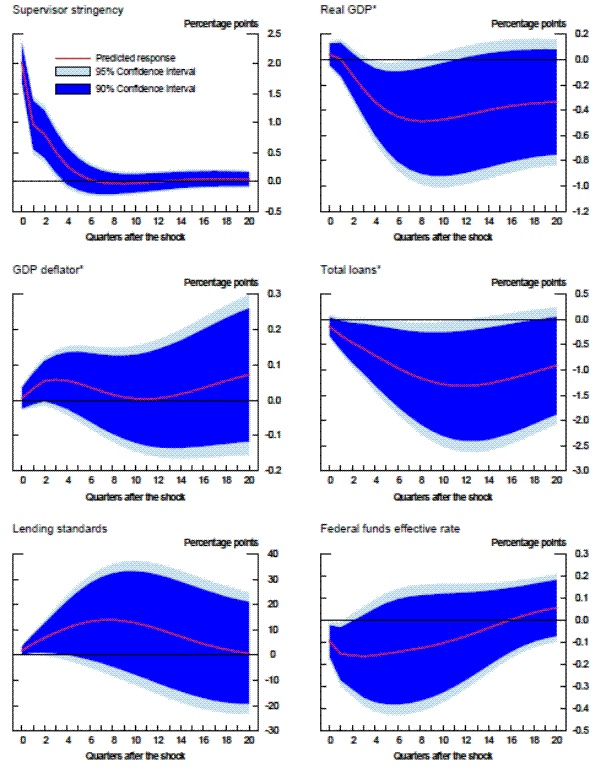
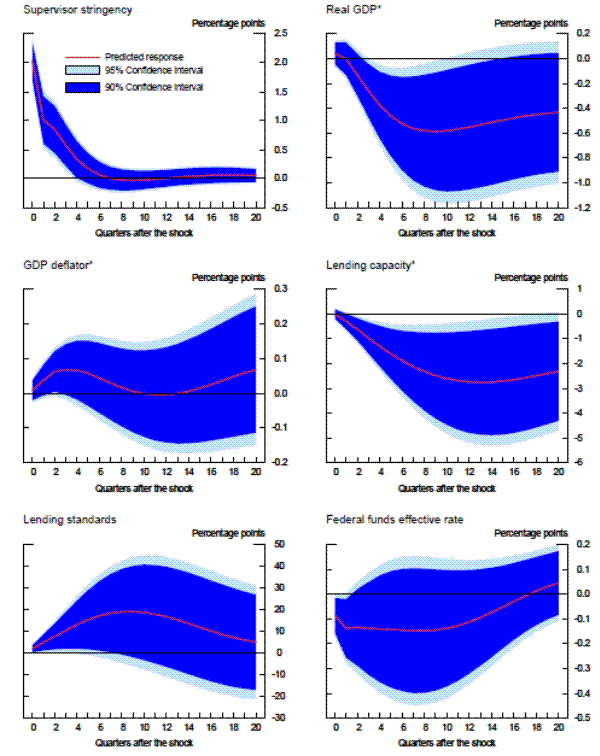
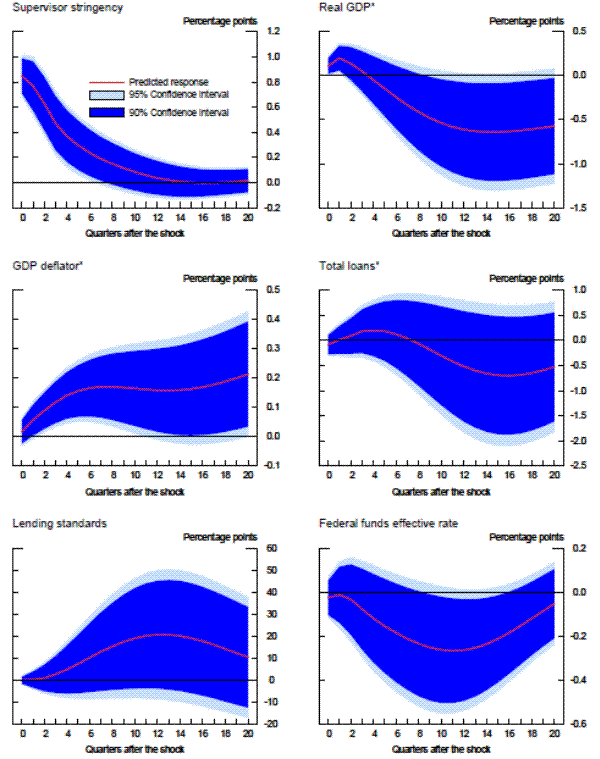
We now turn to an analysis of the residuals from the three panel data models, i.e., the difference between the actual and the model-implied aggregate CAMELS ratings. These residuals are what we will define as the aggregate degree of "supervisory stringency," and are shown by the black lines in the three panels of exhibit 5. In practice, the vertical scale of those panels can be interpreted as the percentage of banks that would have been upgraded one notch-when the line is in the positive region-or downgraded one notch-when the line is in the negative region-during a given period had supervisory standards been at the average level that prevailed over the sample period.23 Importantly, therefore, we are measuring the degree of stringency relative to the average, not the absolute level of stringency over time.
Exhibit 5a: Measures of Supervisory Stringency
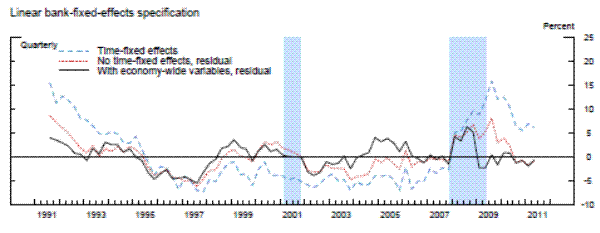
Linear bank-fixed-effects specification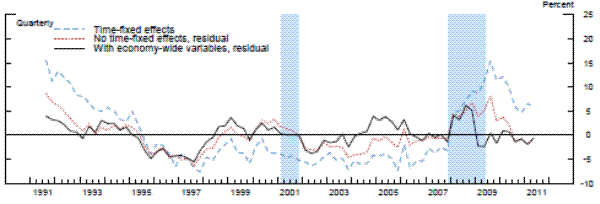 Figure 5a Data
Figure 5a Data
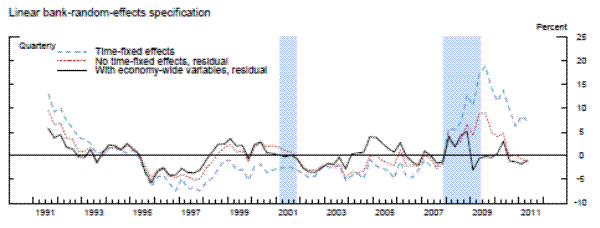
Exhibit 5b: Measures of Supervisory Stringency
Linear bank-random-effects specification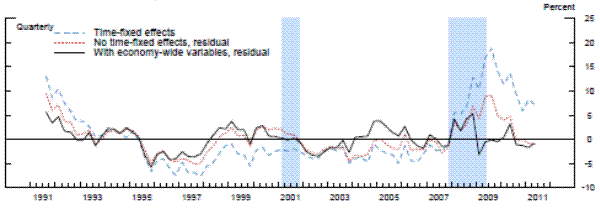 Figure 5b Data
Figure 5b Data
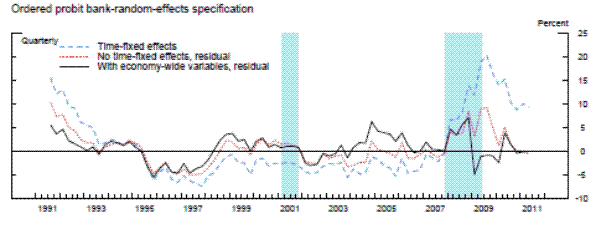
Exhibit 5c: Measures of Supervisory Stringency
Ordered probit bank-random-effects specification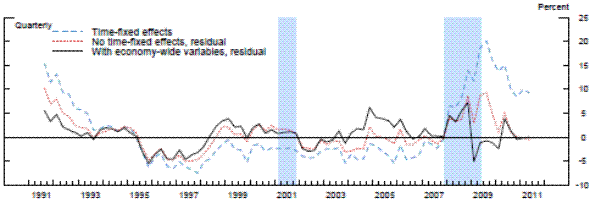 Figure 5c Data
Figure 5c Data
Note. Supervisory stringency is an index that can be interpreted as the percent of banks, on average, that deserve to be upgraded to the next rating according to each model's benchmark standards.
The results are striking in two important aspects: 1) supervisory standards exhibit, in absolute terms, little variation across time, and 2) the three models suggest both quantitatively and quantitatively similar results. In the beginning of the sample, which was the second half of 1991, each of the three models with economy-wide variables indicated that about 5 percent of banks, on average, would have been rated one notch better under the average supervisory standards, whereas the mid-1990s was a period of relatively less stringent supervision. This measure of supervisory stringency peaked early in the 2007-2009 recession and then dropped off as the crisis came to a head in late 2008 and early 2009. Indeed, for most of the period from the first quarter of 2009 to the second quarter of 2011, panel data models that account for the macroeconomic environment show little deviation in CAMELS ratings from the model predictions. In addition, although 2008 can be seen as a period where supervisors were relatively stringent conditional on bank-specific, regional, and national economic factors, only about 5 percent of the banks, on average, can be interpreted as being rated worse compared to the benchmark period than what the model predicts, roughly the same fraction as in the less severe downturn of the early 1990s.
Next, we re-estimated the panel data models without the macroeconomic control variables (and with no time fixed effects). As shown by the red lines in the exhibit, the failure to account for those macroeconomic factors materially alters the conclusions. The fraction of banks that appear to warrant a rating upgrade increases about two-fold in the early 1990s. Likewise, without the macroeconomic controls, we would have concluded that there had been no leveling off of supervisory stringency until most recently. However, note that even this specification suggests that the degree of stringency in the 2007 to 2009 recession was similar to the degree seen as the country exited the 1990s recession.
To compare our results with the previous literature, we next run the panel regression models with the same bank-specific and structural variables as in the previous two exercises, but with time fixed effects.24 For each model with the time-fixed effects, we index the level of supervisory stringency to the average of the fixed effects over whole sample period in order to place it on the same scale as the residuals. Once again, whether we used a fixed-effects linear model, a random-effects linear model with an identifying assumption to mitigate the problem of correlation between the random effect and the regressors, or the analogous modified random-effects ordered-probit model, the estimates of the time fixed effects are very similar to each other-mainly, supervisory standards were strict in the early 1990s and became strict again in the beginning of 2008. However, the magnitude of the fixed effects estimates in the early 1990s and from 2008 to present are much larger than the estimates of supervisory stringency inferred instead from the residuals in models that include economy-wide variables. The coefficients on the time fixed effects across the different specifications peak at 15 to 20 percent in the middle of 2009, before retreating some in more recent quarters, though to levels that remain still elevated as compared to supervisory stringency prior to 2008. In addition, across all three specifications with time fixed effects, supervisory stringency, as of the middle of 2011, was still between 5 percent and 10 percent.
However, recall that time fixed effects control for all factors that are invariant across banks in a given time period, including both economy-wide conditions and exogenous shifts in supervisory attitudes. Thus, those much larger effects include both the change in the supervisory assessment that is related to the change in the macroeconomic environment and the exogenous change in supervisory stringency. Therefore, the difference between actual average CAMELS ratings with the average model-implied ratings when time fixed effects are removed and when they are replaced with economy-wide variables, likely represents a cleaner estimate of supervisory stringency.25
5.2 Repeated Cross-Section Results
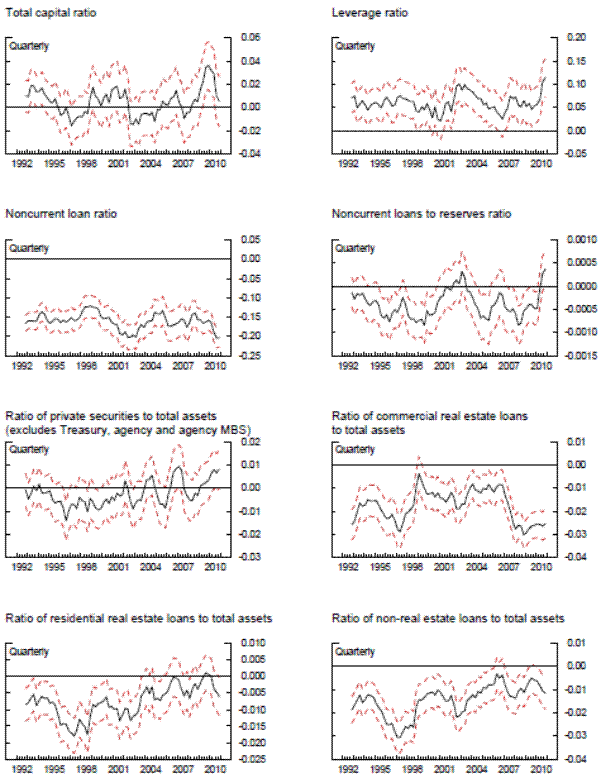
The results from the cross-section analysis are qualitatively similar to results of the panel regressions. Exhibit 6 includes various charts that plot the time-varying estimates of the coefficients and standard errors for various capital adequacy, asset quality, and asset composition indicators. Some of the more consistently statistically significant estimates of coefficients include those on the leverage ratio, the noncurrent loan ratio, the ratio of commercial real estate loans to total assets, and the ratio of non-real estate loans to total assets, results that are broadly consistent with the qualitative results in the panel regressions.
5.2.1 Time-Varying Coefficient Estimates
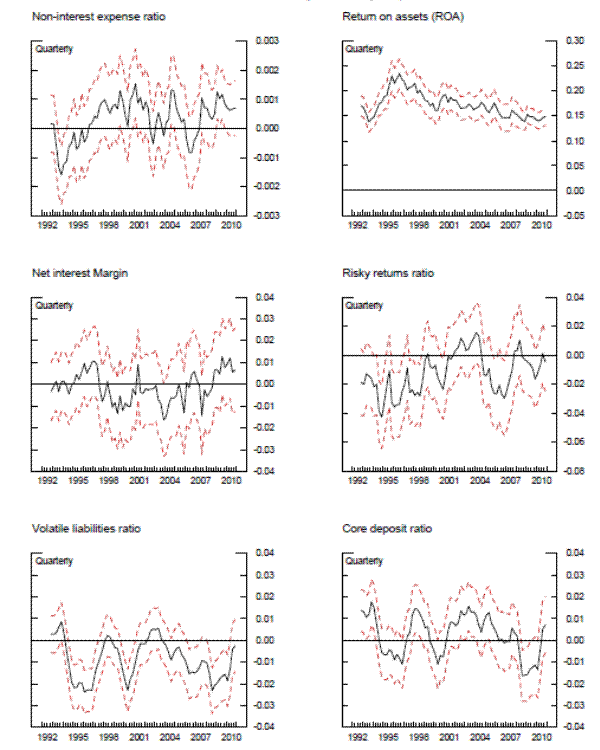
Exhibit 7 includes charts that plot the coefficients for various profitability and liability composition measures, which show the consistent prominence of return on assets in the results and the general significance of the volatile liabilities ratio. The latter becomes more negative and significant during and after the recent financial crisis, a change in emphasis that might be expected given the increased focus on short-term funding implied by the adoption of the Liquidity Coverage Ratio and Net Stable Funding Ratio under Basel III. That coefficient also became fairly deeply negative in the period after the failure of Long-Term Capital Management in 1998 and associated Emerging Market crisis. This pattern underlines the importance of considering time variation in the weights that supervisors place on certain bank conditions rather than assuming that they remain constant.
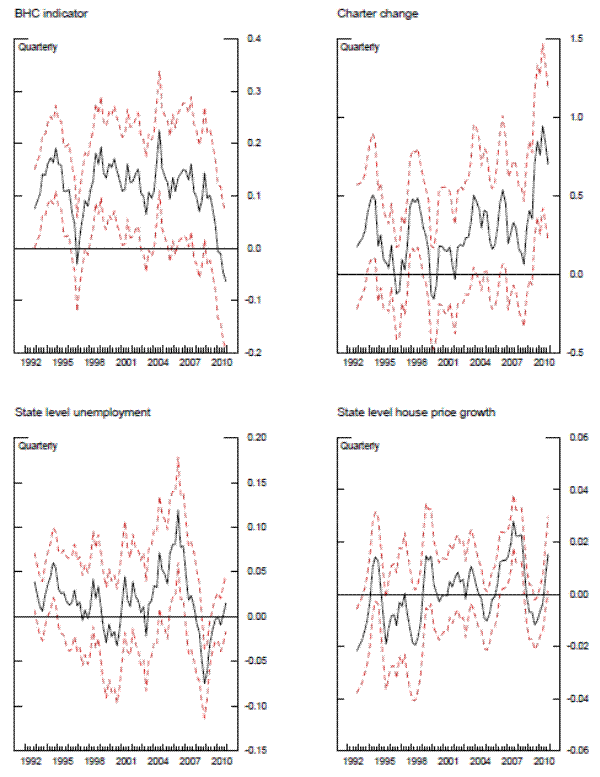
The top panels of exhibit 8 plot the coefficients for two structure variables, which show significant variation across time, with the BHC indicator fluctuating between periods in which it is statistically significant and those that are not. The bottom of exhibit 8 shows the coefficients on local economic indicators. The unemployment rate was generally not significant in the cross section, probably because much of the variation was captured by indicator variables for the census region. However, examiners appear to have been slightly more tuned into the local unemployment rate by the end of 2008. House prices in regions where the bank had branches were generally not significant, though the weight on house prices became significant and positive as the home price bubble burst in 2007 and 2008, as banks in regions not as exposed to the bubble likely outperformed.
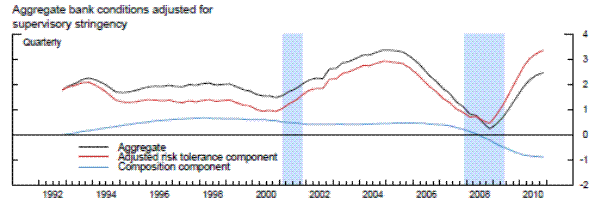
Exhibit 9 describes the key results from the repeated cross-section analysis. The black line in the top panel plots the estimated aggregate bank conditions,
![]() . The line indicates that the supervisory assessment of bank conditions was fairly constant through the 1990s, before strengthening noticeably between 2000 and 2006. That
improvement corresponds to a period in which almost all banks retained CAMELS ratings of 1 or 2 despite a recession and episodes of considerable geopolitical uncertainty. However, overall bank conditions drop precipitiously well before the onset of the crisis, reaching a nadir near the end of the
recession and recovering somewhat by the end of 2010.26
. The line indicates that the supervisory assessment of bank conditions was fairly constant through the 1990s, before strengthening noticeably between 2000 and 2006. That
improvement corresponds to a period in which almost all banks retained CAMELS ratings of 1 or 2 despite a recession and episodes of considerable geopolitical uncertainty. However, overall bank conditions drop precipitiously well before the onset of the crisis, reaching a nadir near the end of the
recession and recovering somewhat by the end of 2010.26
5.2.2 Decomposition of Changes in Aggregate Bank Conditions Index
A breakdown of the aggregate supervisory assessment of bank conditions into the risk tolerance component (adjusted for macroeconomic conditions, denoted ![]() in equation 11) and the composition component reveals that for most of the period aggregate conditions largely paralleled risk tolerance rather than composition. The composition portion (based on actual changes in bank balance sheets and economic indicators, etc.) started out fairly low in the
early 1990s and recovered steadily through the mid 1990s. It then remained roughly at that same level until early 2007, except for a small dip though the recession of 2001. However, with the troubles in subprime mortgage industry emerging in early 2007 and the onset of the recession at the end of
that year, bank health and economic performance worsened, and the intensification of the financial crisis and deepening recession drove the composition factor into increasingly negative territory in 2009. Moreover, this factor had shown no improvement through the end of 2010.
in equation 11) and the composition component reveals that for most of the period aggregate conditions largely paralleled risk tolerance rather than composition. The composition portion (based on actual changes in bank balance sheets and economic indicators, etc.) started out fairly low in the
early 1990s and recovered steadily through the mid 1990s. It then remained roughly at that same level until early 2007, except for a small dip though the recession of 2001. However, with the troubles in subprime mortgage industry emerging in early 2007 and the onset of the recession at the end of
that year, bank health and economic performance worsened, and the intensification of the financial crisis and deepening recession drove the composition factor into increasingly negative territory in 2009. Moreover, this factor had shown no improvement through the end of 2010.
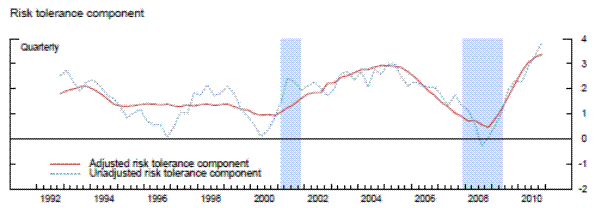
In contrast, adjusted supervisory risk tolerance swung quite widely over the sample period. Risk tolerance was about average in the early 1990s even as overall sentiment and the composition component were low, suggesting that supervisors were not unduly penalizing banks through that channel in the assignment of CAMELS ratings. Risk tolerance rose through the recession of 2001, likely resulting in fewer downgrades than if supervisory attitudes toward risk had remained constant or tightened. Although supervisory risk tolerance reached a local peak in the mid-2000s, it is notable that risk tolerance declined precipitously well before the onset of the crisis and even before the observable factors captured in the composition component began to signal deterioration. Since reaching its lowest point during the sample period at the height of the financial crisis, the risk index has eased considerably. At the end of 2010, it was near the at its peak. However, because the composition component of bank conditions remains extraordinarily weak, the aggregate supervisory assessment of the condition of the banking industry in the fourth quarter of 2010 has, according to the model, improved only to levels last seen in the middle of 2006.
For reference, the dotted line in the middle panel of exhibit 9 plots the risk component prior to adjustment with economy-wide variables. The contour of the unadjusted series is qualitatively similar to the adjusted series, suggesting that while the adjustments are material they act appropriately to smooth the series rather than drive the results. The dip in risk tolerance at the height of the financial crisis is significantly attenuated by controlling for the macroeconomic factors, as is a smaller decline just before the recession of 2001. The attenuation is exactly consistent with our decomposition of changes in examiners' risk tolerance into an endogenous portion that is related to the deterioriation in economic conditions and a portion that is exogenous or described as a change in the tastes or preferences of the examiners toward risk.
Note. Aggregate bank conditions are aggregated predicted latent values (excluding thresholds) of bank conditions with macro indicators and is the sum of the risk tolerance and composition components. The risk component is adjusted with economy-wide variables.
Note. The unadjusted risk tolerance component is the risk tolerance component prior to adjustment with economy-wide variables.
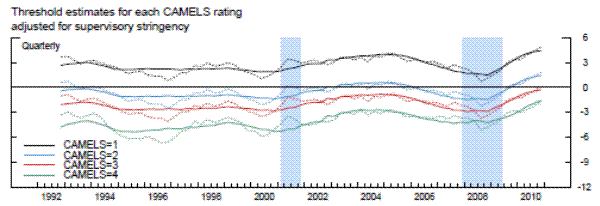
Note. Banks must exceed the threshold to be acheive the particular rating. No banks were rated 5 in 1995:Q4, the threshold for that quarter is interpolated. Dotted lines represent the threshold estimates prior to adjustment with economy-wide variables.
5.2.3 Decomposition of Changes in Threshold Estimates
The bottom panel in exhibit 9 plots the time series of the estimates for each of the thresholds to achieve the next rating.27 The threshold estimates
prior to adjusting for economy-wide variables are plotted in dotted lines. The solid lines are the adjusted threshold values, i.e., the predicted values of ![]() from equation 12, and are the values that would maintain if supervisory stringency in this aspect of ratings remained constant over time. Nonetheless, important distinctions are evident over time in the adjusted thresholds. For instance, the threshold to achieve a rating of a 4 rather than a
rating of 5 began to increase slightly earlier in the most recent financial crisis than those for other ratings. Moreover, even as the financial crisis has receded, each of the thresholds has risen further, indicating that a bank must have a better conditions score during the post crisis period to
achieve the same CAMELS rating as before the crisis.
from equation 12, and are the values that would maintain if supervisory stringency in this aspect of ratings remained constant over time. Nonetheless, important distinctions are evident over time in the adjusted thresholds. For instance, the threshold to achieve a rating of a 4 rather than a
rating of 5 began to increase slightly earlier in the most recent financial crisis than those for other ratings. Moreover, even as the financial crisis has receded, each of the thresholds has risen further, indicating that a bank must have a better conditions score during the post crisis period to
achieve the same CAMELS rating as before the crisis.
| Explanatory Variable | Specification Risk Component | Specification Threshold 1 | Specification Threshold 2 | Specification Threshold 3 | Specification Threshold 4 |
|
|
|
-.1909 | -.2081 | -.2858 | |
| (.1609) | (.1681) | (.1775) | (.1967) | (.2263) | |
|
|
|
|
|
-.0119 | |
| (.0146) | (.0153) | (.0161) | (.0170) | (.0206) | |
| -.0126 | -.0191 | .0676 | 0.0510 | ||
| (.0893) | (.0933) | (.0985) | (.1036) | (.1256) | |
|
|
|
|
.1296 | ||
| (.1014) | (.1060) | (.1119) | (.1177) | (.1427) | |
|
|
|
|
|
|
|
| (.0939) | (.0982) | (.1037) | (.1090) | (.1322) | |
|
|
|
|
|
|
|
| (.1224) | (.1279) | (.1351) | (.1421) | (.1722) | |
| -1.178 | -1.358 | -1.762 | -1.955 | -2.637 | |
| (2.078) | (2.171) | (2.293) | (2.412) | (2.924) | |
|
|
|
-.5920 | -1.279 | -.0434 | |
| (.9493) | (1.081) | (1.142) | (1.201) | (1.456) |
Table 6 describes how the various economy-wide factors are related to risk tolerance and the various thresholds to achieve a higher CAMELS ratings. First, it is important that aggregate risk tolerance and thresholds are highly positively correlated, so if one financial or macro factor is positively associated with risk tolerance, it is usually the case that it is also positively associated with the level of a given threshold. Therefore, the best way to interpret the effects of a change in a specific macroeconomic variable on stringency is to consider its effect on risk tolerance in combination with its effect on the various thresholds.
For instance, the coefficient estimates in this set of regressions suggest that an increase in the BBB spread will reduce the risk component, a result suggesting that examiners are attuned to changes in risk tolerance by market participants. However, somewhat counterintuitively, this change also induces a reduction in the four thresholds for achieving a certain CAMELS rating. But, the changes in the thresholds for achieving a CAMELS rating of 2, 3, or 4 are smaller in absolute value than the change in risk tolerance, and insignificantly different from zero. Thus, an increase in the BBB spread generally results in worse CAMELS ratings, ceteris paribus.
Most other macroeconomic variables also have combined marginal effects that move CAMELS in the expected direction. An increase in the federal funds target rate pushes down risk tolerance, but reduces the estimates of all four threshold values by a greater extent, resulting, on balance, in better CAMELS ratings as the Federal Reserve is tightening monetary policy. A steep term structure, a predictor of expected improvement in economic performance, is associated with less risk tolerance, but far lower thresholds, i.e., a higher probability of better CAMELS ratings. The effect of growth in house prices on risk tolerance and the thresholds has only a small net effect on CAMELS ratings of 1, 2 and 3, but does make it more likely that bank will avoid being rated a 5. GDP is generally insignificant in the regressions for risk tolerance and the thresholds, while the unemployment rate generally enters with the wrong absolute and net effects-it is associated with increased risk tolerance that is about equal to or greater than the effect on the thresholds-thus, the model implies that an increase in the unemployment rate generally results in improved CAMELS ratings, all else equal. The growth in returns of the S&P 500 is intuitive, with higher growth rates associated with lower thresholds, but are statistically insigificant in all the regressions.
5.2.4 Combining the Adjusted Conditions Index and Adjusted Thresholds
In sum, as changes in thresholds have been positively correlated with changes in the risk component, the combined effect of changes in those two measures on the assignment of CAMELS is ambiguous without further analysis. Therefore, we next construct a combined index of stringency based on movements in both measures. Exhibit 10 shows the difference between the average actual CAMELS rating and the average CAMELS rating based on the adjusted thresholds and adjusted risk component, which is the measure of supervisory stringency. The difference in these ratings was about 9 percent in the fourth quarter of 1992, but fell rapidly in subsequent quarters. The average actual ratings were also somewhat worse than what the adjusted model suggests prior to the 2001 recession, largely driven by a decrease in risk tolerance. Supervisory standards apparently tightened gradually between 2004 and 2008, and peaked in the first half of 2008, near the beginning of the financial crisis, this time largely driven by an increase in overall thresholds. However, that peak value was just slightly higher than the level that was reached around the prior recession, and the highest levels reached in both of those more recent recessionary periods were less than half the peak level seen at the beginning of the sample period. Moreover, the estimate of stringency began declining at the end of 2008, and by the end of 2010 our measure suggests that about 4 percent of banks, on average, could be downgraded one notch. Thus, the analysis provides little evidence that CAMELS ratings are currently, on balance, too stringent given the condition of banks and the state of the economy and financial markets.
Note. Supervisory stringency is an index that can be interpreted as the percent of banks, on average, that deserve to be upgraded to the next rating according to each model's benchmark standards.
5.3 Robustness
Each of our estimates, whether based on panel data with economy-wide control variables or repeated cross sectional regressions subsequently adjusted for macroeconomic conditions, supervisory stringency is high in the beginning of the 1990s and at the beginning of the recent crisis. Moreover, all of those specifications suggest that stringency in the assingment of CAMELS ratings dissipated recently. The models differ slightly in the degree of stringency apparent in the early 1990s, with the measure for the repeated cross-section somewhat higher than the equivalent measure in the ordered-probit panel regression. Moreover, the repeated-cross-section methodology indicates that supervisory stringency was much worse during the early 1990s than it was at the height of the recent crisis, whereas the panel data models suggest that the degree of stringency was about equal across all three of the extented periods where it was evident. Nonetheless, the broad agreement in the qualitative path of stringency over the past two-plus decades across all four specifications adds to the confidence in the results in the face of the potential for specification errors discussed earlier.
We also perform several additional robustness checks on our results. First, instead of using all exam information that resulted in a designation or confirmation of CAMELS ratings, we exclude any examinations that were not full-scope. Our results are robust to this omission, though the standard errors become larger due to the decrease in the number of observations. We try a specification that includes the changes in balance sheet and income measures of all the explanatory variables in addition to the levels. Again, our results carry through, and many of the coefficients on the additional variables are not significant. As we are concerned that we do not have a good proxy for the quality of management, we also include a dummy for whether the category-specific rating of the bank's management (i.e., the M in CAMELS) was worse than the composite CAMELS rating in the previous exam. Although the coefficient on this "bad management" variable comes in statistically signficant, it does not alter our results. Our results are also robust to the inclusion of different sets of macroeconomic and financial indicators.
In addition, we construct alternative indexes of supervisory stringency by weighting the the stringency estimates for each bank by the amount of loans on its balance sheet. Although the degree of stringency is somewhat more variable, our main results hold qualitatively-in particular, including macro variables explains much of stringency that appeared to be prevalent after 2008.
Finally, we also run each of the panel specifications in a two-stage framework to account for sample selection in the banks examined each period. The first stage regression uses the identification assumption that the date since the last exam and the date since the last exam interacted with an indicator variable of whether the bank was a weak bank should be related only to whether a bank is examined and not necessarily to the current condition of the bank. The coefficient on the mills ratio in the second stage turns out to be significant in only the random-effects linear model, but its inclusion does not change our results as seen in exhibit 11. Therefore, although this can be interpreted to mean that there is selection bias, it is apparently of limited economic magnitude. This may be due to the tension between the fact that worse-off banks are both more likely to be examined and more likely to fail or be acquired by another bank. In addition, larger banks, though maybe of higher quality, are examined more frequently due to their size.
Note. Supervisory stringency is an index that can be interpreted as the percent of banks, on average, that deserve to be upgraded to the next rating according to each model's benchmark standards.
6 Macroeconomic Effects
Banks with poor CAMELS ratings are less likely to be significant providers of new credit as they focus on repairing their balance sheets or addressing other shortcomings that led to the poor rating. Thus, the misclassification of CAMELS ratings, particularly if it were widespread, could potentially affect macroeconomic outcomes. Thus, the conclusions of this study, showing the relatively muted degree to which CAMELS ratings appear to have been misclassified over time are somewhat reassuring. Nonetheless, even small distortions in markets can have widespread effects, and periods in which examiners are marginally more stringent in assigning CAMELS ratings may also be periods in which they exert other pressures on banks that affect lending volumes. Therefore, small deviations in our index may have large effects on other variables of interest. Therefore, we next turn to whether these estimates of supervisory stringency are associated with changes in lending or in overall output.
For this analysis, we turn to a fairly standard vector autoregression (VAR) model that incorporates the time series of supervisory stringency produced by the modified random-effects ordered probit specification. Because this series is constructed to be orthogonal in the current period to a number of macroeconomic variables, including GDP and the effective federal funds rate, we choose to order it first.28 The other variables in the model, as they are ordered, are growth of nominal GDP, inflation as measured by the GDP deflator, the growth of total loans, the aggregate change in bank lending standards to households and businesses as constructed from the Federal Reserve's Senior Loan Officer Opinion Survey29 , and the effective federal funds rate. We also run a second VAR in which we substitute total lending capacity for total loans to narrow in on the supply restraints.30
Exhibit 12 displays the impulse response functions for the level of each variable generated by the VAR for a one standard deviation (about 2 percentage point) increase in supervisory stringency as measured by the modified random-effects ordered probit regression with economy-wide variables for the specification with total loans. The shock generates a statistically significant and long-lasting decline in total loans that peaks at between 1 to 1.5 percent below trend, and remains less than 1 percent below trend 20 quarters after the shock. The propagation mechanism could be a tightening of lending standards, shown in the bottom left, as banks respond to increased scrutiny by rationing available loans to their highest quality borrowers. However, the degree of tightening is marginally statistically significant for only a few quarters. The model also suggests that the dip in lending is potentially detrimental to broader economic performance, cumulating to about a 0.5 percentage point decline in nominal GDP about 6 quarters after the shock, after which the effect begins to unwind and becomes statistically insignificant.
The specification with lending capacity instead of total loans is described by Exhibit 13. This model shows a relatively greater effect of the shock on lending-lending capacity drops by more than 2 percentage points-though the other effects remain similar in magnitude. However, it is important to note that lending capacity over the recent financial crisis fell more than 20 percent, whereas total loans fell by more than 10 percent since the beginning of the most recent recession. Compared with the estimated effects of supervisory stringency on trend growth in both loans and lending capacity, those drops were far larger in magnitude.
We also conduct a similar exercise with the stringency estimates based on the repeated cross section analysis and find similar results. As shown in exhibit 14 and 15, a one-standard deviation in stringency estimates has similar or smaller effects on nominal GDP, loan growth, and lending capacity. One important difference, however, is that the positive impact on lending standards becomes statistically insignificant over the medium term.
* Cumulative impulse response.
* Cumulative impulse response.
* Cumulative impulse response.
Exhibit 15: Implications of Supervisory Stringency on Lending Capacity - Repeated Cross-Section
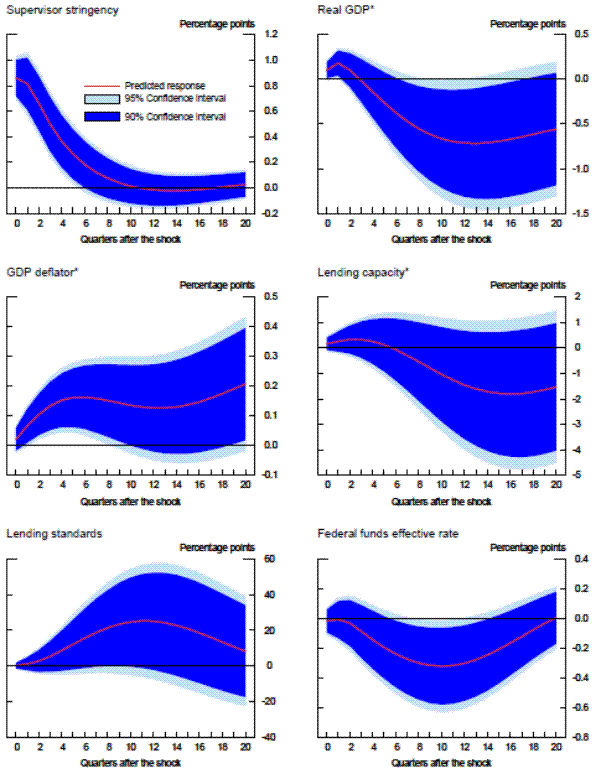 Figure 15 Data
Figure 15 Data
* Cumulative impulse response.
7 Conclusion
This paper investigates several alternative statistical models that could help explain the assignment of bank CAMELS ratings over the period 1991 to 2011. Despite the potential shortcomings of any particular model choice (given the limitations inherent in the irregular frequency and timing of CAMELS data and private information available only to examiners), the key results are highly consistent across the different specifications used in this paper. In general, we find that swings in supervisory stringency are quite modest, implying quite little misclassification in CAMELS ratings at most points over the past two plus decades. Nonetheless, as in earlier studies by other authors using a different empirical strategy, we find that supervisory standards appeared to be somewhat tighter than average in the early 1990s. In addition, we show that supervisory standards likely tightened noticeably at the beginning of the recent financial crisis. However, we find little evidence that supervisors continued to be unusually stringent in the assignment of CAMELS ratings after the end of the recent recession.
Despite the relatively small disrepancies between the model implied and actual CAMELS ratings over time, those changes appear to be related to swings in the lending cycle. A standard VAR model suggests that a one-standard-deviation shock to a measure of supervisory stringency is associated with a statisically significant decline in total loans and lending capacity from their trends, and that the effect persists for several years. Moreover, that decline in lending may also be concommitant with a tightening of lending standards and a dip in the level of real GDP below trend of about 0.4 to 0.6 percent after a year or two.
In comparing our results with those of earlier researchers, we show that the estimated degree of stringency can be influenced importantly by the choice of conditioning variables and to a lesser extent the econometric framework. Whereas most earlier researchers had interpreted the coefficients on time fixed effects in a pooled cross-sectional regression as the degree of stringency, in this paper, we use frameworks that control directly for the overall macroeconomic environment at the time of the exam. Specifically, we use economy-wide real and financial variables rather than time fixed effects in three panel data models, and separately we use those variables to adjust the time-varying parameter estimates from repeated cross-sectional regressions.
Our approaches generally produce smaller estimates of stringency in both the early 1990s and throughout the period of 2007 to 2011 than the strategy used by previous researchers of interpreting the coefficients on time fixed effects. Although one may question whether supervisory standards should reflect assessments of both the local and the national economic environment, this is a normative critique. Both on average and in the aggregate, banks lend to firms, for example, that operate in markets other than the market where the banks or firms are headquarted (or where banks hold most of their deposits). Also, the macroeconomic and financial environment may be good indicators of expected changes in bank conditions over the next several quarters and broader risks facing banks. Therefore, the the national economic environment and financial conditions may well be an important factor in determining aggregate supervisory standards.
We conclude by noting a few caveats and further investigation necessary in these types of analyses.
- The assignment of CAMELS ratings is only one way in which supervisors can apply pressure on the risk management practices of banks. This paper does not examine changes in supervisory standards for loan classifications, memorada of understanding, or in the other interactions between bank management and supervisors.
- Our analysis was based on a sample of banks that were not a part of the top 25 BHCs, an important set of institutions that may have been subject to more or less stringent supervisory standards. If so, these institutions would disproportionately affect a weighted estimate for the entire banking industry.
- We acknowledge that our proxies for management quality and sensitivity to market risk may be inadequate. Changes in the supervisory assessments of these components may be related to the financial cycle in ways that bias the results toward finding unusually stringent standards during recessions (that is, good times can mask a lot of deficiencies in risk management from both markets and regulators). In terms of management quality, this is also reflected in the various loan shares that we use as explanatory variables. As for sensitivity to market risk, because we exclude the largest BHCs in our sample, we believe that we are starting off with a sample that has minimal exposure to market risk as measured by the exposures in the trading book.
- Though we tried various specifications and included not only levels but also changes in bank balance sheet variables in robustness checks, we may have omitted other variables that are related to the financial cycle.
- Bank exams are not randomly timed through the cycle. Though we also estimated a selection model for whether a bank was examined in a given quarter as a robustness test, we still note that any selection bias in determining the banks that are examined during a given quarter may affect the results for the panel regressions.
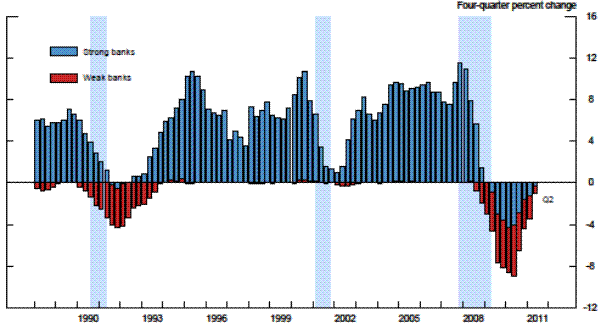
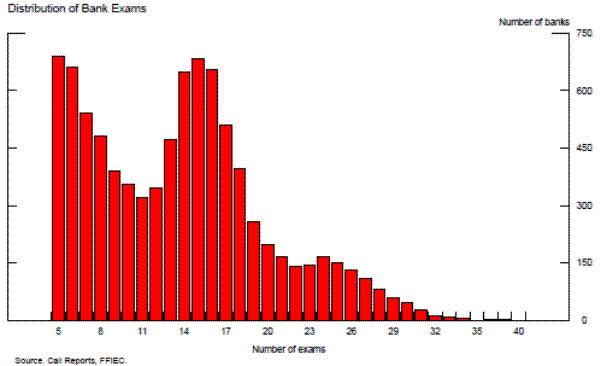
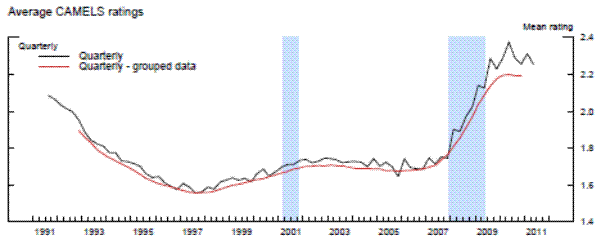
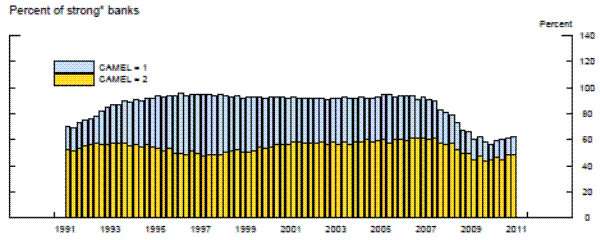
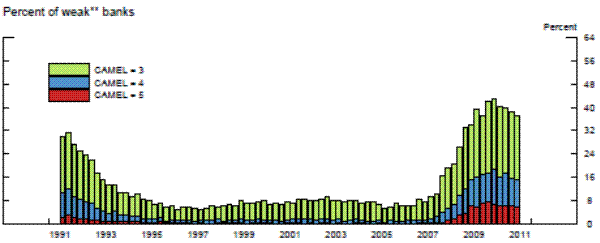
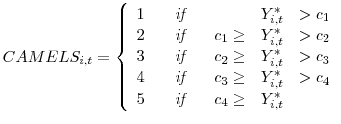
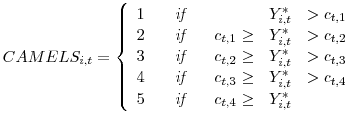
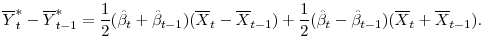
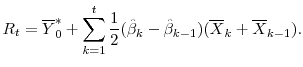
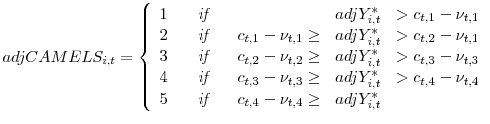
![\displaystyle \overline{adjCAMELS}_t=\frac{1}{N_t}\sum_{i=1}^{N_t}[1+\sum_{J=1}^4\{\Phi(c_{t,J}-\hat{\nu}_{t,J}-\hat{\beta}_t X_{it}+\hat{\mu}_t)\}],](img63.gif)