Profitability and the Lifecycle of Firms
Keywords: Firm lifecycles, profitability, product development
Abstract:
Using data on listed and unlisted firms in the U.K., this study documents that average profitability changes systematically with age. In their early years, firms realize substantial profitability increases, while mature firms face slow declines in profitability. A model of endogenous profitability changes arising from product development captures this pattern. Investment in product development generates profitability increases for young firms while competitive pressures from new entrants lead to profitability declines for mature firms. In addition, the model predicts that young firms realize profitability jumps more frequently and that the effect of age on firms' policies would be stronger for young firms. Empirical tests support these predictions. Taken together, these findings show that changes in profitability influences the lifecycle of firms.
1 Introduction
Firms are born, live, and die. The extant literature on firm lifecycles focuses on the role of financing frictions, either in the form of costly external finance (see Cooley & Quadrini (2001) and Cabral & Mata (2003)) or in the form of agency costs (see DeAngelo et al. (2006) and DeAngelo et al. (2010)). However, Angelini & Generale (2008) document that costly external finance explains only a small portion of the effect of firm age on firm size. Moreover, data from the Small Business Economic Trends survey carried out by the National Federation of Independent Businesses indicate that since 1986, 13.2% of firms declare sales to be their most pressing problem while only 4.3% of firms declare financing and interest rates to be their most pressing problem.1 These observations suggest that operating factors may also influence the observed lifecycle patterns of firm financing and growth.
This study begins by presenting a new finding obtained from data on listed and unlisted U.K. firms: profitability, measured as operating income before depreciation scaled by lagged total assets, changes systematically with firm age. Up to 5 years of age, on average, firms realize statistically significant profitability increases that cumulate to more than 0.03, a substantial increase given that average profitability equals 0.11.2 In contrast, firms above 10 years of age realize small profitability declines, on average. Standard models based on financial frictions cannot explain this pattern as they take profitability as exogenously given.
In order to better understand the observed age profile of profitability changes, this study presents a dynamic model of firm growth based on the quality ladder literature. The following key assumptions underpin the model. New entrants have low product quality, which limit the demand for the firm's product and the price it can charge. However, firms can expend resources on product development that, if successful, generate an outward shift in the downward-sloping demand curve for the firm's product.3 In addition, new entrants have higher output productivity than incumbents, ensuring that all firms eventually exit as they become less competitive over time.4
In contrast to standard models based on financial frictions, the product development mechanism enables the model to generate the observed age profile of profitability changes. Analysis of a simulated data set obtained by calibrating the model shows that the model can generate a cumulative average profitability increase of about 0.03 from birth to 10 years of age, similar to that observed in the data. These profitability increases arise from successful product development. Further, due to competitive pressures from new entrants with higher output productivity, the model generates the slow decline in average profitability for mature firms observed in the data.
The product development mechanism also influences firms' financing and growth decisions. Young firms, who typically have low quality levels and low cash flows, spend significant resources on product development as they face large gains in firm value from successful quality increases. This leads young firms to require substantial external funds. They also grow rapidly, as the higher demand for their products arising from successful product development leads them to invest in their physical capital to boost output. In contrast, mature firms typically have high quality levels and cash flows, and they invest less in product development. Thus, mature firms have slower growth and they return their surplus cash flows to shareholder through dividend payouts.5As such, the model's ability to generate the observed age profile of profitability changes does not come at the cost of the well known lifecycle patterns of financing and growth.
The analysis of the simulated data also reveals two other predictions of interest that would not necessarily arise in models based on financial frictions. First, the model predicts that young firms would realize profitability jumps more frequently, reflecting their higher rate of successful product development. Second, the model predicts that the effect of age on firms' policies would be much stronger for young firms than mature firms. While the first prediction follows directly from the model, the second prediction is less obvious. The age effects for young firms arise mainly from the quality improvement channel, and since quality indices vary quickly with age for the youngest firms, changes in age have a bigger impact on these firms. In comparison, age effects arise for mature firms less due to changes in quality indices and more due to changes in their competitive position, which changes slowly, leading to a smaller effect of age on the policies of mature firms.
Testing the first prediction using data on listed and unlisted U.K. firms, a logit regression of a profitability jump dummy on firm age and controls reveals that young firms generate profitability jumps more frequently than mature firms. A firm is considered to have had a profitability jump if its current profitability level is higher than its lagged 3-year moving average by 0.10 or more. This finding remains robust to different definitions of profitability jumps. In addition, the effect of age on profitability jumps is stronger for younger firms, as predicted by the model.
Testing the second prediction, an examination of whether the age coefficients in firm financing and growth regressions differ across young and mature firms reveals a stronger age effect for young firms, as predicted by the model. The differences in age effects are statistically and economically significant. This finding remains robust to changing the criteria for distinguishing young and mature firms and suggests that studies such as DeAngelo et al. (2006) and DeAngelo et al. (2010) may understate the effect of age, as their data mostly consist of mature public corporations.
Taken together, these findings further challenge the view that financial frictions are sufficient to understand firm lifecycles. Instead, it suggests a more complex view of firm lifecycles: one in which, product development also plays a vital role, in addition to the financial frictions emphasized in the literature. In terms of policy prescriptions, this view suggest that policies that help small firms develop their products may prove helpful in encouraging entrepreneurship and firm growth.
Finally, it is worth highlighting the noteworthy features of the data set employed in the study as, to the best of my knowledge, it has not yet been used to study firm lifecycle dynamics. The data set is obtained from the Bureau van Dijk Amadeus data set, which provides balance sheet and income statement data on listed and unlisted firms in the U.K. The underlying source for the data are compulsory filings at the Companies House in the U.K. One benefit of the data set is that it has much better coverage of small and young firms than data sets with mostly public firms such as Compustat. In addition, the data set also includes the year of incorporation, enabling a fairly precise measure of firm age.
Other related studies on entrepreneurship and firm dynamics include Albuquerque & Hopenhayn (2004), who study firm dynamics in a model with optimal debt contracts. Bitler et al. (2005) find that higher entrepreneurial ownership stakes lead to increased effort and performance. Cagetti & De Nardi (2006) demonstrate that a model of entrepreneurship in the presence of borrowing constraints can generate the observed wealth distribution in the U.S. economy. The internal governance model of Acharya et al. (2009) generates a lifecycle for dividend payments. However, their lifecycle begins from the IPO of the firm, whereas this study generates a firm lifecycle from the birth of the firm. Haltiwanger et al. (2010) examine the effect of firm age and size on growth, and argue in favor of further research on how productivity and earnings of firms vary with age. Huynh & Petrunia (2010a, 2010b) study how financial conditions affect firm growth and survival. And Chen et al. (2010) examine the effect of entrepreneurial non-diversifiable risk on the financing and investment decisions of firms.
This study is organized as follows. Section 2 discusses the Amadeus data set used in the study. Section 3 documents the age profile of profitability changes observed in the data. Section 4 presents the model. Section 5 uses simulation methods to derive further implications from the model. Section 6 examines these implications using the Amadeus data and Section 7 concludes.
2 Data
The data set used in the study is obtained from the Amadeus database maintained by Bureau van Dijk. This data set provides balance sheet and income statements for listed and unlisted firms in many European countries. The analysis uses data on firms from the U.K. to avoid any cross country differences. Focusing only on U.K. firms helps mitigate any cohort effects that may arise from the introduction of the euro in continental Europe. Further, the accounting regulations in the U.K. require all firms to file annual accounts at the Companies House. These legally required filings provide the source data for the Amadeus data set.6 One limitation of the data set is that it does not include information on dividends or product development expenses such as research and development and advertising.
The data set includes the year of incorporation of the firm. This enables a more accurate measure of firm age in the data than compared to what could be obtained using data sets such as Compustat, where age is typically measured from the date of the initial public offering. In addition, the data set includes observations of firms in their earliest years, enabling a more detailed analysis of lifecycle effects than would be possible using data sets of mostly public firms. The Longitudinal Business Database maintained by the Census Bureau also provides accurate measures of firm birth and includes the early years of firms, but does not include accounting data on profitability or financing measures.
2.1 Sample
The sample period extends from 1997 to 2007, as the data set contains few observations in the years prior to 1997. Firms with missing values for total assets, year of incorporation, or revenue are excluded from the sample. Firms with less than 5 employees are also excluded, partly to eliminate self-employed individuals that have chosen to incorporate as a firm. The sample excludes any firms with total assets less than 100,000 pounds. The sample also excludes observations of firms that are either inactive or in bankruptcy proceedings, observations with accounting periods other than one year, and observations of financial firms, as identified by 2-digit SIC codes. All observations are rescaled to take into account different units of observations for different firms in the data set.7
The study uses the following variable definitions. Firm size equals the log of total assets. Sales growth is defined as the growth rate of operating revenues. Profitability equals operating profits before interest and depreciation divided by lagged total assets. This measure captures the operational strength of the firm. Physical investment is constructed as fixed assets plus depreciation minus lagged fixed assets divided by lagged fixed assets, where fixed assets are reported net of depreciation. All variables except firm age and size are Winsorized at the 1 percent level to reduce the impact of outliers.
One key variable in the subsequent analysis is a profitability jump dummy that attempts to capture when a firm realizes large profitability increases. The profitability jump dummy equals 1 if the difference between the current period profitability level and the average profitability over the past three years is greater than 0.1. Computing the difference using the average over the past three years helps mitigate misclassification errors arising from a one-period decrease in profitability that reverses in the next period. Section 6.3 examines the robustness of the results to different definitions of the profitability jump dummy.
One limitation of the data is that it does not provide direct measures of whether the firm obtains external finance. As such, this study constructs two measures of financing using balance sheet data. The equity issue dummy variable equals one if the firm's contributed capital was greater than last period's contributed capital plus 2 percent. The external financing dummy variable equals one if the sum of the firms contributed capital, debt, and bank loans was greater than the corresponding last period value plus 2 percent.
2.2 Summary statistics
Table 1 presents the summary statistics for the data used in the regression analysis. Panel A presents the summary statistics for the entire sample. Panels B and C present the summary statistics for the young and mature firm subsamples, respectively. Young firms comprise those with age less than or equal to its sample median value of 16, while mature firms comprise those with age greater than its median value.
The summary statistics reveal that firms realize profitability increases of more than .10 about once every 9 years. However, young firms realize profitability jumps at a substantially higher rate than mature firms. This suggests that the average profitability increases of young firms subsequently documented in Section 3 arises from the higher rate of profitability jumps realized by young firms.
The other summary statistics also demonstrate a marked effect of age on firms' policies. On average, young firms have higher sales growth, profitability, and investment rates than mature firms. Young firms also obtain external financing at a higher frequency than mature firms. This difference is particularly notable for equity issues. The differences in the mean values across the young and mature firm subsamples are statistically significant at the 5 percent level. These findings suggest that age has a marked effect on the growth and financing decisions of the firm, as noted in the literature.
3 Profitability over the lifecycle
The existing literature on lifecycle models considers firms' profitability as exogenously determined. As such, this literature has not examined the age profile of profitability. However, many young firms have considerable difficulty generating sufficient earnings to be viable. Young firms also invest heavily in product development and marketing in order to increase market share and profit margins. These factors suggest that firms profitability may vary systematically with age.
3.1 Profitability levels
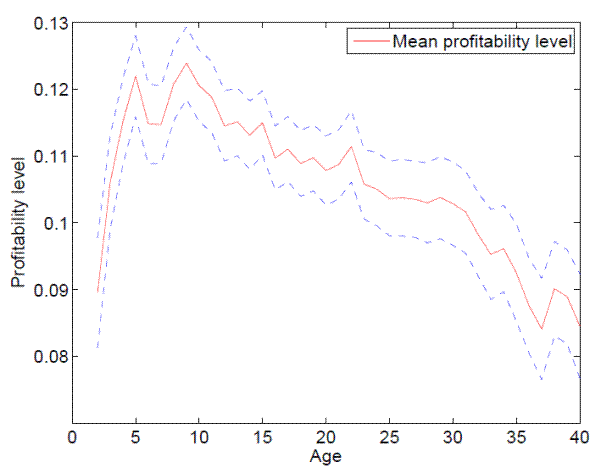
Figure 1 plots mean profitability as a function of age.8 The dashed (blue) lines represent the 95 percent confidence interval around the estimated sample means. The figure demonstrates that average profitability increases up to age 5, remains at about this level until age 10, and declines slowly thereafter. In statistical terms, firms between ages 5 and 10 have higher profitability levels than new firms or firms older than 25 years.
The above figure helps inform whether firms with widely different ages have different profitability levels. Examining mean changes in profitability levels provides a sharper test of whether firms of a given age realize profitability increases or decreases, on average.
3.2 Profitability changes
Figure 2 plots the mean change in firms' profitability from age ![]() to
to ![]() as a function of age,
as a function of age, ![]() . The dashed (blue) lines represent the 95 percent confidence interval around the estimated sample means. The figure demonstrates that firms with age
less than or equal to 5 years generate profitability increases, on average. These profitability increases are statistically and economically significant, with a cumulative profitability increase of more than 0.03 over this period. In comparison, the average profitability level of all firms reported
in Table 1 equals 0.106. Average profitability changes become negative, though for the most part not significant, after firms become more than 10 years old. These findings indicate that, in addition to the age profiles of growth and financing documented in the literature,
the underlying profitability of firms also varies with age.
. The dashed (blue) lines represent the 95 percent confidence interval around the estimated sample means. The figure demonstrates that firms with age
less than or equal to 5 years generate profitability increases, on average. These profitability increases are statistically and economically significant, with a cumulative profitability increase of more than 0.03 over this period. In comparison, the average profitability level of all firms reported
in Table 1 equals 0.106. Average profitability changes become negative, though for the most part not significant, after firms become more than 10 years old. These findings indicate that, in addition to the age profiles of growth and financing documented in the literature,
the underlying profitability of firms also varies with age.
One possibility is that the profitability increases of young firms reflects a survival bias. The above analysis includes observations of profitability changes for exiting firms prior to the year of exit. However, it does not include observations for the year of exit, as that data is not observable. One method of examining the possible impact of survival biases is to examine the rates of exit. The exit rate for firms of age 1 to 5 equals 15.26%, statistically indistinguishable from the exit rate for firms of age 6 to 10, which equals 15.30%. This indicates that any survival effects should equally impact firms of ages 1 to 10, and would not be able to explain the positive profitability increases for firms of ages 1 to 5. In addition, although the exit rate for firms of age 1 to 5 is statistically significantly higher than the exit rate for all firms with age above 5, the difference in exit rates is only 0.58%, an economically small magnitude.
The age profile of profitability changes remains robust to changing the Winsorization threshold to 5 percent and to computing profitability using current assets versus lagged assets. It also remains basically unchanged when the firm-year observations are weighted by their log assets. Adjusting for year fixed effects on profitability changes has no effect on the age profile of profitability changes. However, median profitability changes are about zero for all ages, indicating that the average profitability increases realized by young firms reflect profitability increases by some, but not all, firms.
3.3 Selected major industries
The previous figure examined profitability changes after lumping together firms from all industries. Figure 3 plots the age profile of profitability changes for the manufacturing, service, and trade major industry groups. The manufacturing sector comprises firms with SIC codes between 20 and 39; The service sector comprises firms with SIC codes above 70 and between 40 and 49; The trade sector comprises firms with SIC codes between 50 and 59. The dashed (blue) lines represent the 95 percent confidence interval around the estimated sample means.
The figures demonstrate that young firms realize economically significant profitability increases in all three industry groups. These increases are largest for the service industry, where they are also statistically significant.9This could potentially reflect the greater importance of product development in service sectors such as computer software and business services.
3.4 Regression analysis
Non-linear regressions provide another method to study the effect of age on profitability changes. Table 2 presents the results of estimating the following non-linear regression of profitability changes on age:
| (1) |
where
The table reports results for all firms and for firms in each major industry group. The standard errors are heteroskedasticity robust. The overall predictive power of the regression is quite low, reflecting the high variability of profitability changes in the data.
The results for all firms confirm the age profile of profitability changes documented in Figure 2. The age of a firm has a significant impact on profitability change, with profitability changes slowly decaying with age. Further, predicted profitability changes are positive for the youngest firms. The estimates imply that average profitability changes become negative between ages 7 and 8. Finally, as firms mature, profitability changes become significantly negative. These findings further indicate that profitability changes systematically with age.
The regression findings for the major industry groups broadly reflect the patterns observed in Figure 3. As with all firms, service sector firms have significant positive profitability changes at birth that slowly become negative with age. Manufacturing firms follow a
similar pattern, though the ![]() coefficient that indicates whether profitability decays or increases with age is not significant. Retail and wholesale trade firms have no significant effect of
age on profitability changes. However, these firms also have a negative asymptotic value for profitability change as a function of age. In order to better understand this finding, the next section presents a model that endogenously generates an age profile of profitability changes.
coefficient that indicates whether profitability decays or increases with age is not significant. Retail and wholesale trade firms have no significant effect of
age on profitability changes. However, these firms also have a negative asymptotic value for profitability change as a function of age. In order to better understand this finding, the next section presents a model that endogenously generates an age profile of profitability changes.
4 Model
The model economy consists of a large number of heterogenous firms, each of whom produces a differentiated product. The quantity produced by a firm varies with its productivity, capital stock and labor input. The price of its product depends on the product quality, with higher quality products earning a higher price. Firms invest resources on physical investment and quality improvements in order to maximize the present value of dividends over their lifetimes.
One important distinction this study makes is to differentiate between output productivity and product quality. In the model, productivity measures the quantity of goods that can be produced by a unit of inputs and quality measures the relative importance of that good in the consumption aggregator. The profitability of a firm depends on both its productivity, which enables a firm to produce more, and its quality, which increases the demand for its good. The commonly used revenue-based measure of productivity in the literature measures the combination of output productivity and product quality. Other studies that make this distinction include Foster et al. (2008) and Fasil (2009).
4.1 Output, demand, and profits
Each firm uses capital, ![]() , and labor,
, and labor, ![]() , to produce a single product using a
Cobb-Douglas production function. The average productivity of an existing firm of age
, to produce a single product using a
Cobb-Douglas production function. The average productivity of an existing firm of age ![]() at time
at time ![]() ,
, ![]() , is assumed to be fixed by its vintage
, is assumed to be fixed by its vintage ![]() .10 Firms with a later vintage have a higher average productivity level, reflecting the higher productivity of entrants documented by Foster
et al. (2008). The output of a firm of age
.10 Firms with a later vintage have a higher average productivity level, reflecting the higher productivity of entrants documented by Foster
et al. (2008). The output of a firm of age ![]() at time
at time ![]() is given by
is given by
where
The output of all firms are combined into a consumption aggregate, ![]() , using a quality-weighted Dixit-Stiglitz aggregator with constant elasticity of substitution.
, using a quality-weighted Dixit-Stiglitz aggregator with constant elasticity of substitution.
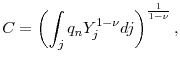
where the mark-up
Let ![]() denote the wage level. The gross profit of a firm of quality index
denote the wage level. The gross profit of a firm of quality index ![]() is given by
is given by
where the price,
where
The above profit function trends with the consumption aggregator, ![]() , and the wage level,
, and the wage level, ![]() . In order to solve for the value function and simulate the economy, one needs to detrend the profit function as in Eberly et al. (2008). The appropriate detrending variable,
. In order to solve for the value function and simulate the economy, one needs to detrend the profit function as in Eberly et al. (2008). The appropriate detrending variable, ![]() , is given by:
, is given by:
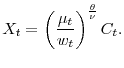 |
Detrending by
where
4.2 Endogenous product quality
The above discussion examines the effect of firm age on profitability while treating product quality, ![]() , as given. However, firms spend significant resources on product development.
These include not only research and development expenditures, but also expenditures such as advertising that can potentially increase the demand for a good. Foster et al. (2010) find that variation in the size of plants mainly reflects demand-side fundamentals, and
argue in favor of a demand accumulation process at the plant level. In addition to demand increases, firms may also face exogenous shocks that lower the demand for their good.
, as given. However, firms spend significant resources on product development.
These include not only research and development expenditures, but also expenditures such as advertising that can potentially increase the demand for a good. Foster et al. (2010) find that variation in the size of plants mainly reflects demand-side fundamentals, and
argue in favor of a demand accumulation process at the plant level. In addition to demand increases, firms may also face exogenous shocks that lower the demand for their good.
In the model, firms have product quality levels ![]() indexed by
indexed by ![]() . New firms
enter the economy with a product quality index of 1. Each period, a firm spends resources on product development, denoted by
. New firms
enter the economy with a product quality index of 1. Each period, a firm spends resources on product development, denoted by ![]() . If the firm's product development was successful it realizes an
increase in product quality, with probability of success increasing in
. If the firm's product development was successful it realizes an
increase in product quality, with probability of success increasing in ![]() .11 At the same time, independent of their product development, firms also face the possibility of an exogenous shock that lowers their quality level. The probability of a negative quality shock,
.11 At the same time, independent of their product development, firms also face the possibility of an exogenous shock that lowers their quality level. The probability of a negative quality shock, ![]() , is assumed to be fixed. The next period quality level depends both on the success of the product development process and on whether the firm faces an exogenous negative quality shock. Formally, the evolution of product quality is given by the following
equation:
, is assumed to be fixed. The next period quality level depends both on the success of the product development process and on whether the firm faces an exogenous negative quality shock. Formally, the evolution of product quality is given by the following
equation:
| (7) | ||
where
The quality indices are parameterized such that, ceteris paribus, increases (or decreases) in the quality index have the same effect on profits regardless of the current quality level. Formally, this requires that
The success probability of generating a quality increase is parameterized as follows:
where
The scaling of the success probability with the capital stock, ![]() , implies that a larger firm would need to spend proportionally more resources to obtain the same probability of a quality
increase. This captures the idea that the product development efforts required to obtain a firm-wide increase in product quality would be much larger for a large firm than a small firm. For example, one could compare the resources spent by Microsoft on developing the latest Windows products with
those spent by a small software company on developing their latest product.
, implies that a larger firm would need to spend proportionally more resources to obtain the same probability of a quality
increase. This captures the idea that the product development efforts required to obtain a firm-wide increase in product quality would be much larger for a large firm than a small firm. For example, one could compare the resources spent by Microsoft on developing the latest Windows products with
those spent by a small software company on developing their latest product.
4.3 Discussion of lifecycle mechanics
Although notationally complex, the economics underlying the model are quite simple. The evolution of profitability with firm age drives the lifecycle in the model. Profitability varies with age as both the firm's quality level and its output productivity relative to other firms changes with age.
Equations (7) and (8) specify how product quality evolves over time while the
![]() term in Equation (6) presents the effect of firm age on productivity due to competition from new entrants.
term in Equation (6) presents the effect of firm age on productivity due to competition from new entrants.
The higher output productivity of new firms implies that the competitiveness of existing firms slowly deteriorates over time. However, this effect is offset by increases in product quality, which translate into higher demand for the product.12 Young firms enter the economy with quality index 1. These firms can realize a large jump in firm value through a quality increase, leading them to expend significant resources on product development. Firms increase physical investment following a quality increase as the increased demand for the good raises the optimal capital stock. At the beginning, the increases in product quality will overcome the effect of relative productivity declines, resulting in profitability rising with age. As quality increases and firms grow, they reduce spending on product development, and the effect of competitive pressures on productivity dominates the effect of quality changes. These changes in profitability with firm age generate the lifecycle features of the model.
The key mechanism driving the age profile of profitability in the model is that, proportional to their capital, young firms spend more resources on product development, resulting in more quality increases. What drives this higher investment in product development in the model? First, young firms have a higher expected lifespan, resulting in a greater increase in firm value from a quality increase. Second, due to the decreasing returns in the profit function, the increase in the optimal capital stock from a quality increase lessens as the quality index increases, even though increases in quality have the same effect on profit levels. This lowers the benefit that firms with higher quality - who are typically older - obtain from a quality increase. Last, young firms with low quality indices face an additional benefit from product development in that it lowers the possibility of quality decreasing to 0, which would force them to exit.
4.4 Other firm policies
The investment, entry and exit, and taxation in the model follow standard assumptions. The model abstracts from financial frictions in order to focus on the impact of the product development mechanism.
4.4.1 Investment
Each period, firms can invest in new capital. Denote new investment by ![]() . The detrended next period capital of a firm is given by
. The detrended next period capital of a firm is given by
4.4.2 Entry and exit
A fixed cost of operating each period, ![]() , implies that firms will exit if their value falls below a certain threshold. Firms exit each period after they realize their idiosyncratic shock
, implies that firms will exit if their value falls below a certain threshold. Firms exit each period after they realize their idiosyncratic shock
![]() . Exiting firms sell their capital at a discounted price
. Exiting firms sell their capital at a discounted price ![]() . Firms decide
to exit optimally if their continuation value is lower than the value they would obtain by selling their capital. In addition to this, firms also have to exit if their quality index declines to 0.
. Firms decide
to exit optimally if their continuation value is lower than the value they would obtain by selling their capital. In addition to this, firms also have to exit if their quality index declines to 0.
New firms enter the economy with quality index 1. They have an initial capital stock of ![]() and begin operations immediately. In the steady state simulations, the rate of entry is assumed to equal the rate of exit.
and begin operations immediately. In the steady state simulations, the rate of entry is assumed to equal the rate of exit.
4.4.3 Taxation
The model incorporates a simplified tax structure. Firms pay linear taxes on operating profits net of fixed costs, depreciation, and product development expenses. The last term reflects the tax deductibility of research and development and advertising expenses. Denote the tax rate by
![]() . The tax payable by a firm is given by
. The tax payable by a firm is given by
4.5 Firm value
Firm value and optimal policies can be derived from a sequence of Bellman equations indexed by the quality index, ![]() . The value function,
. The value function,
![]() , for quality level
, for quality level ![]() is given by:
is given by:
| (9) | ||
| with |
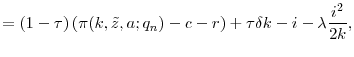 |
where
In economic terms, the above Bellman equation states that the value of a firm in a given quality stage equals the dividend payment plus the expected future value of the firm. Negative dividend values correspond to equity issuance. The expected future value of the firm takes into account that the
firm may realize an increase in the quality index with probability
![]() , or that the firm may realize an decrease in the quality index with probability
, or that the firm may realize an decrease in the quality index with probability
![]() , or stay at the same quality level. The discount rate remains unchanged over the lifecycle, reflecting the finding of Moskowitz & Vissing-Jorgensen
(2002) that private firms generate similar returns as public firms. Each firm chooses its physical investment and product development expense to maximize value. The optimal policies of a firm can be derived from the above
, or stay at the same quality level. The discount rate remains unchanged over the lifecycle, reflecting the finding of Moskowitz & Vissing-Jorgensen
(2002) that private firms generate similar returns as public firms. Each firm chooses its physical investment and product development expense to maximize value. The optimal policies of a firm can be derived from the above
4.6 Optimal product development expenses
Firms trade off the cost of product development expenses with the higher probability of an increase in the quality index (and the lower probability of a decrease in the quality index). The firm value increase with the quality index reflects both the ability of the firm to sell current output at a higher price, and the ability of the firm to invest and increase production in the future to take advantage of the shift in the demand curve.
The following proposition establishes the optimality condition for product development expenses:
The first order condition for product development implies that
| marginal cost of funds | ||
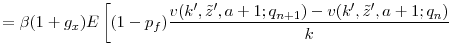 |
||
![\displaystyle \left. \hspace{1cm} + p_f\frac{v(k', \tilde{z}', a+1;q_{n}) - v(k', \tilde{z}', a+1;q_{n-1})}{k} \right] b (1-p(r)).](img83.gif) |
Proof: See Appendix A.
The marginal benefit from product development expenses increases with the expected increase in firm value from a quality increase per unit of current capital. This expression averages over the possibility that, with probability ![]() , firms may face an exogenous decrease in their quality levels. The
, firms may face an exogenous decrease in their quality levels. The ![]() term implies that an increase in the success probability
term implies that an increase in the success probability
![]() lowers the marginal benefit, thereby ensuring an interior solution for product development expenses. The marginal cost of funds in the above expression equals
lowers the marginal benefit, thereby ensuring an interior solution for product development expenses. The marginal cost of funds in the above expression equals ![]() , reflecting the tax deductibility of product development expenses.
, reflecting the tax deductibility of product development expenses.
5 Model simulation and analysis
The model links age to firms' policies through the evolution of profitability over the lifecycle. The stochastic nature of the lifecycle and the complexity of the model makes it difficult to generate explicit propositions relating age to the firm policies. As such, this section investigates the lifecycle effects in the model using regression analysis of data obtained from simulating a calibrated version of the model, where the calibration attempts to match the observed age profile of profitability changes. The regression specification exactly matches that used with the actual data. Whited (2006), Bloom et al. (2007), and Warusawitharana (2008), among others, use the same approach of comparing regression results from a simulated model with the results from actual data.
5.1 Calibration
The calibration of the model parameters employs values either estimated or commonly used in the literature where possible. The quality level parameters are calibrated to match the observed age profile of profitability changes.
The following parameters are set to values commonly used in the literature. The capital share of output, ![]() , equals 0.33. The price markup parameter
, equals 0.33. The price markup parameter ![]() equals 0.10. These imply that
equals 0.10. These imply that
![]() . The depreciation rate is set at an annual rate of 10 percent. The discount rate
. The depreciation rate is set at an annual rate of 10 percent. The discount rate
![]() , corresponding to an annual real return to capital (equity) of 6.5 percent.
, corresponding to an annual real return to capital (equity) of 6.5 percent.
The corporate tax rate is set at 20 percent. This follows the marginal tax rate applicable for small companies (defined as those with profits less than 300,000 pounds) in the U.K., which ranged from 19 to 21 percent over the sample period.14
The adjustment cost parameter ![]() equals 2. This value is slightly higher than the estimates obtained by Cooper & Haltiwanger (2006). However, their
model includes a range of other adjustment costs as well, while the model in this study has only a quadratic term. The resale value of capital is set at 0.8, in between the estimate of 0.6 obtained by Hennessy & Whited (2005) and the estimate of 0.95 obtained by
Cooper & Haltiwanger (2006). The success rate parameter for quality improvements,
equals 2. This value is slightly higher than the estimates obtained by Cooper & Haltiwanger (2006). However, their
model includes a range of other adjustment costs as well, while the model in this study has only a quadratic term. The resale value of capital is set at 0.8, in between the estimate of 0.6 obtained by Hennessy & Whited (2005) and the estimate of 0.95 obtained by
Cooper & Haltiwanger (2006). The success rate parameter for quality improvements, ![]() , is set to 2.0. Warusawitharana (2011) estimates this
parameter using research and development expenses by public firms and obtains estimates between 2 and 5. The autocorrelation and standard deviation of productivity shocks are set to 0.75 and 0.10, respectively. The exogenous probability of a decline in quality levels,
, is set to 2.0. Warusawitharana (2011) estimates this
parameter using research and development expenses by public firms and obtains estimates between 2 and 5. The autocorrelation and standard deviation of productivity shocks are set to 0.75 and 0.10, respectively. The exogenous probability of a decline in quality levels,
![]() . The fixed costs generate an exit rate of about 2.8%.15
. The fixed costs generate an exit rate of about 2.8%.15
The quality index parameters are calibrated to generate the observed age profile of profitability changes. The parameter for the increase in quality from successful product development,
![]() ; a higher value generates a greater increase in average profitability for young firms in the simulated data. The simulations limit the maximum quality index to 10; using a
higher value increases the age at which average profitability changes become negative.
; a higher value generates a greater increase in average profitability for young firms in the simulated data. The simulations limit the maximum quality index to 10; using a
higher value increases the age at which average profitability changes become negative.
5.2 Model solution and simulation
The sequence of value functions given in equation (9) can be solved iteratively. First, given solutions to the value functions for quality indices ![]() and
and
![]() , one can solve for the value function at quality index
, one can solve for the value function at quality index ![]() . This process iterates
until the sequence of value functions converge. The solution employs the optimal product development policy given in Proposition 4.6.
. This process iterates
until the sequence of value functions converge. The solution employs the optimal product development policy given in Proposition 4.6.
The simulated data set is obtained by simulating the model economy with 1000 firms over a period of 400 years. Observations in the first 300 years are discarded as a burn-in sample. An examination of the cross-sectional distributions indicate that the simulations reach their steady state well before 300 years. The simulation uses the optimal policies derived from solving the sequence of value functions. Each period, exiting firms are replaced by new entrants. This simulated sample provides a steady state cross-section of firms that can be employed to investigate firm policies in the model. Appendix B provides further detail on the numerical solution of the model and the construction of the simulated sample.
5.3 Lifecycle profile of profitability changes
Figure 4 presents average profitability changes as a function of age from the simulated data set. The underlying data excludes the first and last years of a firm's life. Profitability is derived from equation (6) as
The figure demonstrates a strong lifecycle effect on profitability changes for firms. Young firms obtain sharp profitability increases, reflecting quality increases from successful product development. As firms age, they realize fewer endogenous quality increases. Beyond a point, the competitive pressures from the productivity advantage of new entrants dominates the effect of quality increases. This leads to negative average profitability changes. Overall, the figure demonstrates that the model captures a strong effect of age on average profitability changes of firms.
In comparison with the age profiles of profitability changes shown in Figures 2 and 3, the model generates positive profitability changes for longer than the data. However, these profitability changes are smaller on average than those observed in the data. Thus, the cumulative profitability change observed by young firms before their profitability begins to decline is roughly similar in the simulated and actual data.
5.4 Regression analysis of simulated data
This section reports the results of various regressions of firms' policies on age and other controls using the simulated data set. These regressions shed light on the impact of firm age on policies of interest in the model and motivate the subsequent analysis using data on U.K. firms.
Table 3 presents the results of regressions of various firm policies on firm age and controls. Panel A presents linear panel regressions for sales growth, investment, and dividends. Panel B presents logit regressions on whether the firm obtained a quality increase and on whether it obtained external financing. The availability of actual data constrain the controls used in the regressions.17 All the regressors are statistically significant at the 5 percent level, reflecting the importance of the regressors in the model.
The results demonstrate that younger firms generate quality increases at a much higher rate than older firms, reflecting the higher product development expenses of young firms. The higher rate of quality increases translates to a higher sales growth rate. Further, firms respond to the quality increases by increasing investment, as seen by the higher investment rates of younger firms. Increased product development expenses and high investment rates imply that young firms require external financing more often. In contrast, mature successful firms become self-financing and pay dividends as they generate higher cash flows and have lower investment rates and product development expenses.18 Taken together, these findings demonstrate that the model captures a clear lifecycle effect on firms' policies.
The analysis demonstrates a linear effect of age on the firm's policies. However, the impact of age may differ over the firm's lifecycle. Young firms will obtain quality increases at a higher rate than mature firms who, for the most part, will have already achieved a high quality level. Thus, changes in age translate to bigger changes in product quality and profitability for young firms. This implies that firm age will have a greater effect on the policies of young firms than mature firms. This hypothesis can be tested by replicating the lifecycle regressions after separating the simulated sample into young and mature firms.
Table 4 present the results of replicating the analysis in Table 3 on firms with age less than or equal to 24, its median value in the simulated data set. As before, Panel A presents linear panel regressions for sales growth, investment, and dividends; Panel B presents logit regressions on whether the firm obtained a quality increase and on whether it obtained external financing.
The results indicate a stronger effect of age on firms' policies for firms with age below its median value. In this subsample, a firm that is one year younger will have higher product development expenses, resulting in more frequent quality increases. These quality increases lead to higher investment rates. The lower cash flows and higher expenditures imply that younger firms obtain external finance more frequently and that they pay less dividends. Further, the effect of age is economically larger for this sample for all the regressions.
In unreported results, replicating the regressions on firms with age above the median in the simulated data set yields age effects that, although significant, are much smaller than those for young firms. A full interaction specification reveals that the differences in age effects between young and mature firms are statistically significant.
The results obtained from the analysis of the simulated data set remain robust to changes in the calibrated parameter values. Although the estimated coefficients change, the main findings remain. Young firms obtain more frequent quality increases, which result in higher sales growth and investment rates. High product development expenses and physical investment lead young firms to obtain external finance more frequently. Further, the effect of firm age on these policies is more pronounced for younger firms.
6 Additional findings from U.K. firms
This section presents the findings from estimating the lifecycle regressions on data on U.K firms. Comparison of these regression results with those obtained using simulated data in Section 5.4 informs whether the model captures the lifecycle features observed in the actual data. In addition, we can test the further implications of the model. Namely, that young firms realize profitability jumps more frequently, and that age effects are stronger for young firms. The section also presents some additional robustness checks. Unfortunately, the data set does not include information on product development expenses such as research and development or advertising. As such, it is not possible to test this prediction directly.
6.1 Full sample analysis
Table 5 presents the results of the lifecycle regressions on U.K. firms. Panel A presents the panel regressions with sales growth and investment as dependent variables. Panel B presents the logit regressions with the profitability jump dummy and two measures of external financing as dependent variables. The regressions include year dummies and industry dummies constructed at the 2-digit SIC level. The reported standard errors are heteroskedasticity robust and adjust for clustering at the firm level. These results mimic the analysis of the simulated sample reported in Table 3 with the exception of the dividend regression.19
Young firms realize profitability jumps - defined as a profitability increase of more than 0.1 from its lagged 3-year moving average - at a higher rate than older firms. In economic terms, the results translate to about a 0.9 percent increase in the probability of obtaining a profitability jump for a firm that is one year younger. This compares with an overall probability of obtaining profitability jumps of 13.6 percent. This finding supports the mechanism highlighted in the model, where higher product development expenses generate more frequent quality increases for young firms.
The analysis also reveals that the lifecycle stage of the firm strongly affects sales growth and investment. Young firms exhibit higher sales growth and investment rates, even after accounting for their smaller size. These differences are statistically and economically significant. A firm that is one year younger will have, on average, a 0.63 percent and 0.20 percent higher sales growth and investment rates, respectively.
The logit regressions reveal that younger firms obtain external financing more frequently.20 This effect is particularly striking for the equity issue dummy. A firm that is one year younger obtains equity financing at a 0.13 percent higher rate, compared to an overall rate of equity financing of 5.7 percent. Defining external financing using book values of debt and equity generates a statistically significant - albeit economically weaker - effect of firm age.
Comparison of the estimates for the control variables provides another gauge of the model. The sales growth and profitability coefficients obtained using the actual data have the same sign and significance as those obtained with the simulated data. This indicates that the ability of the model to capture the lifecycle effect does not come at the expense of the effects of profitability and sales growth on firms' policies.
6.2 Split sample analysis
The model predicts that lifecycle effects will be much stronger for young firms than mature firms, as shown by the analysis of the simulated data. This section examines this prediction using the data on U.K. firms.
Table 6 reports the results of replicating the lifecycle regressions reported in the previous section on firms with age less than or equal to 16, its median value in the data set. The regressions include year and industry dummies at the 2-digit SIC code level, and the standard errors are heteroskedasticity robust and adjust for clustering at the firm level. Table 4 presents the corresponding results with the simulated data.
The results indicate a much stronger effect of age for young firms. Within this subsample, a firm that is one year younger has about a 3.6 percent higher probability of obtaining profitability jumps. Both in absolute terms and relative to the subsample average, this is much higher than the corresponding age effect on profitability jumps for the entire sample. This matches the age effect observed in the model, where quality increases from product development mainly affects young firms.
The analysis also reveals a much stronger age effect on sales growth and investment. In economic terms, a firm that is one year younger will have a 5.7 percent higher sales growth rate and a investment rate that is about 0.9 percent higher in this subsample. The logit regressions reported in Panel B also demonstrate a stronger effect of firm age on equity issues for young firms; measuring external financing using the book values of debt plus equity yields a similar result.
In comparison, Table 7 presents the results of the lifecycle regressions on firms with age greater than its median value. The regressions include year and industry dummies at the 2-digit SIC code level, and the standard errors are heteroskedasticity robust and adjust for clustering at the firm level.
The results reveal that the effect of age on firms is much weaker for this subsample. The age coefficients for all the regressions are significantly less negative than those obtained with young firms in Table 6. Also, the effect of age on equity issue becomes insignificant in this subsample. These findings demonstrate that the effect of age weakens substantially when one focuses on more mature firms. This reflects the pattern observed in the model, where changes in product quality has little effect on mature firms. Instead, lifecycle effects arise in mature firms due to the slow decline in profitability arising from the output productivity advantage of new entrants.
Furthermore, the mature firm subsample results have mostly lower adjusted and pseudo R-squared values than the young firm subsample. This indicates that the predictors in the regression have lower overall explanatory power, consistent with a smaller role for the firm's lifecycle stage. As before, the profitability and sales growth coefficients for the mature firm subsample have similar qualitative properties in the actual and simulated data sets.
Repeating the analysis on the entire data set with a set of interaction terms for young firms confirms the finding that age has a greater effect on firms decisions for young firms than mature firms. This difference is statistically significant for all the regression equations. This finding indicates that data sets consisting of mostly mature public firms may understate firm lifecycle effects.21
6.3 Robustness and additional findings
One key finding from the Amadeus data set is that younger firms realize profitability jumps more frequently. Table 8 examines the robustness of this result to changing the definition of profitability jumps to require profitability increases relative to the lagged 3-year moving average of 0.05, 0.15, and 0.2, respectively. Changing the cutoff value for the profitability jump dummy has little effect on the result other than to increase the point estimate with the cutoff value. As before, younger firms realize more profitability jumps, with the effect of age being stronger for the young firm subsample. Further, in unreported results, defining profitability jumps using the increase in profitability from the last period value leads to similar results.
One additional concern is that these jump regressions are capturing a volatility effect. Including a measure of firm level profitability volatility in the logit regressions does not change the basic results.22 As before, younger firms realize more profitability jumps than older firms and the effect of age on the likelihood of profitability jumps strengthens when the sample is limited to firms with age below the median.
The model emphasizes the role of product development in understanding profitability changes of young firms. One additional test of the model would be to examine whether the effect of age on firms' policies would be stronger in R&D intensive industries. Table 9 presents the results of estimating the model only on firms in selected R&D intensive industries. As the Amadeus data does not include R&D investment, industry R&D intensity is measured using data on U.S. firms from Compustat. This follows the research design of Rajan & Zingales (1998), who measure industry financial dependence using data on U.S. firms. The R&D intensive industries comprise of those with 2-digit SIC codes 28, 35, 36, 38, 73, and 87. This list includes R&D intensive manufacturing industries such as pharmaceuticals and electronics as well as service industries such as engineering and research and computer software.
The findings indicate that age has a bigger impact on firms' policies in this subsample, compared to the results obtained with all firms in Table 5. Using a full set of interactions, the age coefficients are statistically different from those for the non-R&D intensive industries for the sales growth, investment, and equity issue regressions. The profitability jump regression coefficients become statistically different when profitability jumps are measured using higher threshold values of 0.15 and 0.2. That said, age remains significant for firms in the industries that are not R&D intensive, indicating that product development may influence lifecycle behavior in these industries as well. In unreported results, the effect of age on firms' policies remains stronger for young firms in the R&D intensive industries.
The empirical results obtained using the Amadeus data set remain robust to the following changes. Increasing the Winsorization cutoff to 5 percent results in somewhat higher adjusted ![]() values and lower point estimates for the control variables. Using a higher value for the firm size cutoff in the sample leads to similar results. Changing the definition of the equity issue and external financing dummies, respectively, to require growth in contributed capital and contributed
capital plus debt of either 0.1 or 5 percent generates similar findings.23 Changing the cutoff values used in identifying young and mature firms to the 40th
and 60th percentiles also leads to similar results.
values and lower point estimates for the control variables. Using a higher value for the firm size cutoff in the sample leads to similar results. Changing the definition of the equity issue and external financing dummies, respectively, to require growth in contributed capital and contributed
capital plus debt of either 0.1 or 5 percent generates similar findings.23 Changing the cutoff values used in identifying young and mature firms to the 40th
and 60th percentiles also leads to similar results.
The estimated age effects become insignificant when the regression specification is changed to a standard fixed effects estimator. This arises due to the fact that the sample spans only 10 years, and eliminating firm fixed effects takes out much of the interesting variation in firm age, which ranges from 1 to 151 years in the sample. Effectively, a fixed effects specification absorbs the difference in behavior between a firm with an average age of 5 years and a firm with an average age of 30 years into the fixed effect, thereby ignoring this variation. Replicating the analysis using a quasi-fixed-effects approach that demeans all variables except age using firm specific means - effectively imposing fixed effects for all variables except age - generates similar results to those reports in Tables 5 to 9.
7 Conclusion
This study documents that firms' average profitability changes systematically with age. On average, firms realize profitability increases in their early years, followed by a slow decline after 10 years of age. Standard models based on financial frictions cannot explain this finding as they take profitability as exogenously determined. Instead, a model based on quality increases through product development endogenously generates this age profile of profitability changes. The model also generates the lifecycle properties of firm growth and financing observed in the data. Empirical tests provide support for two additional predictions that help differentiate the model: specifically, that young firms realize profitability jumps more frequently, and that age has a more pronounced effect on firms' decisions for younger firms. Taken together, these findings indicate that, in addition to the financing constraints highlighted in the literature, product development concerns also play a vital role in understanding firm lifecycles.
More generally, the model highlights the importance of endogenous profitability changes on firm dynamics. The existing literature on financial policies of firms typically considers cash flows as entirely exogenously determined (for instance, see Miao (2005), Gamba & Triantis (2008) and Bolton et al. (2009)). Further research into understanding the effect of endogenous profitability changes on firms' decisions may prove fruitful.
In terms of policy discussions, the findings highlight the importance of operating conditions for small, young firms. Much of the recent policy discussions on small firms have focused on providing financial support by encouraging lending. The results in this study suggest, however, that providing operating assistance, through policies such as payroll tax holidays and investment tax credits, may have an equal impact on small firms.
A Proofs
Proposition 1 The first order condition for product development implies that
marginal cost of funds = marginal benefit of product development expenses
![\Rightarrow \hspace{2cm} 1-\tau & = \beta (1+g_x) E\left[(1-p_f)\frac{v(k', \tilde{z}', a+1;q_{n+1}) - v(k', \tilde{z}', a+1;q_{n})}{k}\right. \ & \left. \hspace{1cm} + p_f\frac{v(k', \tilde{z}', a+1;q_{n}) - v(k', \tilde{z}', a+1;q_{n-1})}{k} \right] b (1-p(r)). \end{align*}\end{proposition}](img98.gif)
Taking first order conditions from the above Bellman equation, one obtains that,
| R.H.S. | 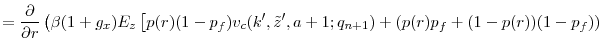 |
|
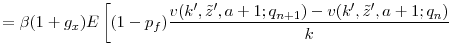 |
||
![\displaystyle \left. \hspace{1cm} + p_f\frac{v(k', \tilde{z}', a+1;q_{n}) - v(k', \tilde{z}', a+1;q_{n-1})}{k} \right]\frac{\partial{E[j]}}{\partial{r}}.](img103.gif) |
Some algebra yields that
![\displaystyle \frac{\partial{E[j]}}{\partial{r}} = \frac{\partial{p(r)}}{\partial{r}} = \frac{b}{k}(1-p(r)).](img104.gif)
B Model solution and simulation
The optimal policies of the firm are obtained using value function iteration to solve for the sequence of Bellman equations indexed by quality level given in equation (9). Since the value for the quality index ![]() depends on the value functions for quality indices
depends on the value functions for quality indices ![]() and
and ![]() , not only does each value function needs to converge by itself, but the entire sequence of value functions also need to converge. This is ensured by first solving for the value function for quality index
, not only does each value function needs to converge by itself, but the entire sequence of value functions also need to converge. This is ensured by first solving for the value function for quality index ![]() given a guess for quality indices
given a guess for quality indices ![]() and
and ![]() , and then repeatedly iterating on the entire sequence of value functions. This process employs the optimal product development expense given in Proposition 1. At each step, the solution for investment is carried out numerically over a grid of values
for capital.
, and then repeatedly iterating on the entire sequence of value functions. This process employs the optimal product development expense given in Proposition 1. At each step, the solution for investment is carried out numerically over a grid of values
for capital.
The simulation sample is constructed using the value function solutions over 10 different product quality values. The numerical solution is carried using the following grid sizes: a profitability shock grid with 5 values, a capital grid with 120 values, and an age grid of 1 to 60. Only a very small fraction of firms reach the maximum age level in the simulation. The construction of the simulated sample follows fairly trivially from the numerical solution.
Firms exit endogenously in the simulation when their exit value exceeds the continuation value. Firms also exit when their quality index reaches 0, but this happens infrequently as most firms realize quality increases in their early years. Each firm that exits is replaced with a new firm of age 1 with capital stock level at the lowest grid value. New entrants are assigned a random profitability shock level and are discarded from the simulated data set to ensure that the assumptions on entering firms have no direct effect on the results.
Bibliography
Working paper, New York University.
Review of Economic Studies 71:285-315.
Journal of Financial Economics 61:43-76.
American Economic Review 98:426-438.
Journal of Finance 60:539-576.
Review of Economic Studies 74:391-415.
NBER working paper #14845.
Journal of Finance 64:263-308.
American Economic Review 93:1075-1090.
Journal of Political Economy 114:835-870.
Review of Financial Studies 23:4348-4388.
American Economic Review 91:1286-1310.
Review of Economic Studies 73:611-633.
NBER Macroeconomics Annual 21:107-180.
Foundations and Trends in Finance 3:95-287.
Journal of Financial Economics 81:293-315.
Forthcoming, Journal of Financial Economics.
NBER working paper #13866.
Working paper, European University Institute.
American Economic Review 98:394-425.
Working paper, University of Chicago.
Journal of Finance 63:2263-2296.
Quarterly Journal of Economics 106:557-586.
Review of Economic Studies 58:43-61.
NBER working paper #16300.
Econometrica 50:213-224.
Journal of Finance 60:1129-1165.
Journal of Economic Dynamics & Control 34:1003-1013.
Working paper.
Econometrica 50:649-670.
American Economic Review 86:562-583.
Journal of Political Economy 112:986-1018.
Pearson Education, Upper Saddle River, 10th edn.
Econometrica 76:1317-1373.
Bell Journal of Economics 9:508-523.
Journal of Finance 60:2621-2660.
American Economic Review 92:745-778.
American Economic Review 88:559-586.
Quarterly Journal of Economics 80:190-207.
Journal of Financial Economics 87:471-497.
Working paper.
Journal of Financial Economics 81:467-502.
The table presents summary statistics for variables of interest from the Amadeus data set. Panels A, B, and C report values for all firms, firms with age less than or equal to its median, and firms with age greater than its median, respectively. Section 2 details the construction of the sample. Firm age is measured from the date of incorporation. Sales growth equals the annual growth rate of revenue. Investment equals the growth rate of fixed assets adjusted for depreciation. Profitability jump dummy equals 1 if the firms profitability was more than 0.10 higher than its average value over the past three years. Equity issuance equals 1 if the firms contributed equity is greater than the corresponding value for the previous year plus 2 percent. External financing equals 1 if the sum of book debt and contributed equity is greater than the corresponding sum for the previous year plus 2 percent. All continuous variables (except firm age) are Winsorized at the 99th percentile to reduce the impact of outliers.
| Age | Sales growth | Profitability | Investment | Prof. jump | Equity issue | Ext. financing | |
| Mean | 23.3 | 0.197 | 0.106 | 0.163 | 0.136 | 0.057 | 0.470 |
| Median | 16.2 | 0.064 | 0.094 | 0.138 | - | - | - |
| St. dev. | 21.3 | 0.708 | 0.248 | 0.899 | 0.343 | 0.231 | 0.499 |
| Obs. (1000s) | 269 | 269 | 269 | 259 | 123 | 236 | 178 |
Panel B: Young firms
| Age | Sales growth | Profitability | Investment | Prof. jump | Equity issue | Ext. financing | |
| Mean | 8.7 | 0.300 | 0.114 | 0.220 | 0.176 | 0.076 | 0.482 |
| Median | 8.4 | 0.093 | 0.105 | 0.160 | - | - | - |
| St. dev. | 4.0 | 0.881 | 0.304 | 1.033 | 0.380 | 0.266 | 0.500 |
| Obs. (1000s) | 133 | 133 | 133 | 125 | 48 | 111 | 83 |
Panel C: Mature firms
| Age | Sales growth | Profitability | Investment | Prof. jump | Equity issue | Ext. financing | |
| Mean | 37.4 | 0.096 | 0.098 | 0.110 | 0.111 | 0.038 | 0.459 |
| Median | 30.0 | 0.045 | 0.086 | 0.123 | - | - | - |
| St. dev. | 21.9 | 0.461 | 0.177 | 0.748 | 0.314 | 0.192 | 0.498 |
| Obs. (1000s) | 136 | 136 | 136 | 134 | 76 | 125 | 95 |
The table reports the results obtained from estimating the following nonlinear regression on the Amadeus data set:
whereand
denote profitability and age, respectively. Section 2 details the construction of the sample and the variable definitions. The major industry classification groups are based on 2-digit SIC codes. Standard errors are heteroskedasticity robust.
and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively.
| All firms | Manufacturing | Service | Trade | |
| -0.0036** | -0.0036** | -0.0042** | -0.0039** | |
| (0.0004) | (0.0008) | (0.0009) | (0.0007) | |
| 0.108* | 0.037 | 0.146* | 0.135 | |
| (0.050) | (0.024) | (0.070) | (0.191) | |
| 0.467** | 0.232** | 0.446** | 0.602 | |
| (0.107) | (0.112) | (0.112) | (0.363) | |
| Observations | 209577 | 51299 | 81412 | 44434 |
The table reports the results obtained from estimating the lifecycle equations on all observations from the simulated data set. Table 5 presents the corresponding results obtained from the Amadeus data set. Panel A presents the panel regressions on sales growth, investment, and dividends. Panel B presents logit regressions on quality jumps, and external financing. Section 5.2 details the construction of the simulated data set. The simulation sample excludes new entrants. The standard errors are heteroskedasticity robust.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, investment, and dividends are reported in percentage terms.
| Sales growth | Investment | Dividends | |
| Age | -0.840** | -0.200** | 0.880** |
| Age (Standard Error) | (0.010) | (0.000) | (0.010) |
| Size | -15.82** | -15.30** | 48.09** |
| Size (Standard Error) | (0.19) | (0.11) | (0.35) |
| Profitability | 0.09** | 0.33** | |
| Profitability (Standard Error) | (0.00) | (0.00) | |
| Sales growth | 0.13** | 0.30** | |
| Sales growth (Standard Error) | (0.00) | (0.00) | |
| Observations | 97177 | 97177 | 97177 |
| Adjusted R-squared | 0.15 | 0.63 | 0.78 |
Panel B: Logit regressions
| Quality jump | External financing | |
| Age | -0.062** | -0.062** |
| Age (Standard Error) | (0.001) | (0.001) |
| Size | -1.02** | -2.81** |
| Size (Standard Error) | (0.02) | (0.07) |
| Profitability | -2.65** | |
| Profitability (Standard Error) | (0.03) | |
| Sales growth | 0.35** | |
| Sales growth (Standard Error) | (0.06) | |
| Observations | 97177 | 97177 |
| Pseudo R-squared | 0.13 | 0.57 |
The table reports the results obtained from estimating the lifecycle equations on observations with firm age less than or equal to its median value in the simulated data set. Table 6 presents the corresponding results obtained from the Amadeus data set. Panel A presents the panel regressions on sales growth, investment, and dividends. Panel B presents logit regressions on quality jumps, and external financing. Section 5.2 details the construction of the simulated data set. The simulation sample excludes new entrants. The standard errors are heteroskedasticity robust.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, investment, and dividends are reported in percentage terms.
| Sales growth | Investment | Dividends | |
| Age | -1.820** | -0.550** | 1.060** |
| Age (Standard Error) | (0.020) | (0.010) | (0.030) |
| Size | -6.62** | -12.83** | 53.64** |
| Size (Standard Error) | (0.24) | (0.11) | (0.41) |
| Profitability | 0.11** | 0.23** | |
| Profitability (Standard Erro) | (0.00) | (0.00) | |
| Sales growth | 0.12** | 0.29** | |
| Sales growth (Standard Error) | (0.00) | (0.00) | |
| Observations | 50704 | 50704 | 50704 |
| Adjusted R-squared | 0.14 | 0.68 | 0.78 |
Panel B: Logit regressions
| Quality jump | External financing | |
| Age | -0.090** | -0.134** |
| Age (Standard Error) | (0.002) | (0.003) |
| Size | -0.87** | -2.48** |
| Size (Standard Error) | (0.03) | (0.07) |
| Profitability | -2.28** | |
| Profitability (Standard Error) | (0.04) | |
| Sales growth | -0.08 | |
| Sales growth (Standard Error) | (0.07) | |
| Observations | 50704 | 50704 |
| Pseudo R-squared | 0.12 | 0.63 |
The table reports the results obtained from estimating the lifecycle equations on the Amadeus data set. Panel A presents the panel regressions on sales growth and investment. Panel B presents logit regressions on profitability jumps, equity issuance, and external financing. Section 2 details the construction of the sample and the variable definitions. All regressions include year and 2-digit SIC code industry dummies. Standard errors are heteroskedasticity robust and clustered at the firm level.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, and investment are reported in percentage terms.
| Sales growth | Investment | |
| Age | -0.630** | -0.300** |
| Age (Standard Error) | (0.010) | (0.010) |
| Size | 1.91** | 0.91** |
| Size (Standard Error) | (0.17) | (0.15) |
| Profitability | 0.19** | |
| Profitability (Standard Error) | (0.02) | |
| Sales growth | 0.20** | |
| Sales growth (Standard Error) | (0.01) | |
| Observations | 269029 | 258676 |
| Adjusted R-squared | 0.02 | 0.04 |
Panel B: Logit regressions
| Profitability jump | Equity issue | External financing | |
| Age | -0.009** | -0.013** | -0.003** |
| Age (Standard Error) | (0.001) | (0.001) | (0.000) |
| Size | -0.22** | 0.19** | 0.07** |
| Size (Standard Error) | (0.01) | (0.01) | (0.00) |
| Profitability | -1.24** | -0.92** | |
| Profitability (Standard Error) | (0.04) | (0.03) | |
| Sales growth | 0.30** | 0.27** | |
| Sales growth (Standard Error) | (0.01) | (0.01) | |
| Observations | 122765 | 236157 | 178211 |
| Pseudo R-squared | 0.05 | 0.07 | 0.02 |
The table reports the results obtained from estimating the lifecycle equations on the Amadeus data set for observations with age less than or equal to its median value, 16. Panel A presents the panel regressions on sales growth and investment. Panel B presents logit regressions on profitability jumps, equity issuance, and external financing. Section 2 details the construction of the sample and the variable definitions. All regressions include year and 2-digit SIC code industry dummies. Standard errors are heteroskedasticity robust and clustered at the firm level.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, and investment are reported in percentage terms.
| Sales growth | Investment | |
| Age | -5.670** | -0.930** |
| Age (Standard Error) | (0.090) | (0.090) |
| Size | 1.71** | -0.13 |
| Size (Standard Error) | (0.23) | (0.22) |
| Profitability | 0.15** | |
| Profitability (Standard Error) | (0.02) | |
| Sales growth | 0.20** | |
| Sales growth (Standard Error) | (0.01) | |
| Observations | 132821 | 125115 |
| Adjusted R-squared | 0.06 | 0.04 |
Panel B: Logit regressions
| Profitability jump | Equity issue | External financing | |
| Age | -0.036** | -0.077** | -0.007** |
| Age (Standard Error) | (0.005) | (0.004) | (0.002) |
| Size | -0.21** | 0.18** | 0.05** |
| Size (Standard Error) | (0.01) | (0.01) | (0.00) |
| Profitability | -1.11** | -0.97** | |
| Profitability (Standard Error) | (0.04) | (0.03) | |
| Sales growth | 0.22** | 0.25** | |
| Sales growth (Standard Error) | (0.01) | (0.01) | |
| Observations | 48099 | 111178 | 83073 |
| Pseudo R-squared | 0.04 | 0.08 | 0.02 |
The table reports the results obtained from estimating the lifecycle equations on the Amadeus data set for observations with age greater than its median value, 16. Panel A presents the panel regressions on sales growth, and investment. Panel B presents logit regressions on profitability jumps, equity issuance, and external financing. Section 2 details the construction of the sample and the variable definitions. All regressions include year and 2-digit SIC code industry dummies. Standard errors are heteroskedasticity robust and clustered at the firm level.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, and investment are reported in percentage terms.
| Sales growth | Investment | |
| Age | -0.090** | -0.160** |
| Age (Standard Error) | (0.010) | (0.010) |
| Size | 1.68** | 1.13** |
| Size (Standard Error) | (0.12) | (0.17) |
| Profitability | 0.27** | |
| Profitability (Standard Error) | (0.03) | |
| Sales growth | 0.19** | |
| Sales growth (Standard Error) | (0.01) | |
| Observations | 136208 | 133561 |
| Adjusted R-squared | 0.01 | 0.03 |
Panel B: Logit regressions
| Profitability jump | Equity issue | External financing | |
| Age | -0.005** | -0.000 | -0.003** |
| Age (Standard Error) | (0.001) | (0.001) | (0.000) |
| Size | -0.23** | 0.24** | 0.10** |
| Size (Standard Error) | (0.01) | (0.01) | (0.00) |
| Profitability | -1.49** | -0.84** | |
| Profitability (Standard Error) | (0.09) | (0.05) | |
| Sales growth | 0.30** | 0.31** | |
| Sales growth (Standard Error) | (0.02) | (0.02) | |
| Observations | 74635 | 124912 | 95138 |
| Pseudo R-squared | 0.05 | 0.05 | 0.01 |
The table reports the results obtained from estimating the logit regression for profitability jumps, defined using different cutoff values, on the Amadeus data set. Panels A, B, and C present the results for all firms, firms with age less than or equal to its median value, and firms with age above its median value, respectively. The profitability jump dummy equals 1 in each column if profitability increased by more than 0.05, 0.15, and 0.2 from the average value over the past three years. Section 2 details the construction of the sample and the variable definitions. All regressions include year and 2-digit SIC code industry dummies. Standard errors are heteroskedasticity robust and clustered at the firm level.and
denote statistical significance at the 5 and 1 percent confidence levels, respectively.
| > 0.05 | > 0.15 | > 0.20 | |
| Age | -0.005** | -0.012** | -0.017** |
| Age (Standard Error) | (0.000) | (0.001) | (0.001) |
| Size | -0.15** | -0.25** | -0.27** |
| Size (Standard Error) | (0.01) | (0.01) | (0.01) |
| Observations | 122765 | 122738 | 122738 |
| Pseudo R-squared | 0.03 | 0.07 | 0.08 |
Panel B: Young firms
| > 0.05 | > 0.15 | > 0.20 | |
| Age | -0.024** | -0.046** | -0.057** |
| Age (Standard Error) | (0.004) | (0.005) | (0.006) |
| Size | -0.14** | -0.24** | -0.25** |
| Size (Standard Error) | (0.01) | (0.01) | (0.01) |
| Observations | 48111 | 48056 | 48056 |
| Pseudo R-squared | 0.03 | 0.06 | 0.06 |
Panel C: Mature firms
| > 0.05 | > 0.15 | > 0.20 | |
| Age | -0.003* | -0.006** | -0.008** |
| Age (Standard Error) | (0.001) | (0.001) | (0.001) |
| Size | -0.16** | -0.27** | -0.30** |
| Size (Standard Error) | (0.01) | (0.01) | (0.02) |
| Observations | 74645 | 74614 | 74512 |
| Pseudo R-squared | 0.03 | 0.06 | 0.07 |
The table reports the results obtained from estimating the lifecycle equations on firms in selected R&D intensive industry. Industry R&D intensity is measured using data on R&D investment by U.S. firms, obtained from Compustat. R&D intensive industries comprise of those with 2-digit SIC codes 28, 35, 36, 38, 73, and 87. Panel A presents the panel regressions on sales growth and investment. Panel B presents logit regressions on profitability jumps, equity issuance, and external financing. Section 2 details the variable definitions. All regressions include year and 2-digit SIC code industry dummies. Standard errors are heteroskedasticity robust and clustered at the firm level.and ** denote statistical significance at the 5 and 1 percent confidence levels, respectively. Sales growth, profitability, and investment are reported in percentage terms.
| Sales growth | Investment | |
| Age | -0.920** | -0.270** |
| Age (Standard Error) | (0.030) | (0.020) |
| Size | 2.39** | 4.86** |
| Size (Standard Error) | (0.36) | (0.30) |
| Profitability | 0.07** | |
| Profitability (Standard Error) | (0.02) | |
| Sales growth | 0.22** | |
| Sales growth (Standard Error) | (0.01) | |
| Observations | 70052 | 66534 |
| Adjusted R-squared | 0.03 | 0.04 |
Panel B: Logit regressions
| Profitability jump | Equity issue | External financing | |
| Age | -0.011** | -0.019** | -0.003** |
| Age (Standard Error) | (0.002) | (0.002) | (0.001) |
| Size | -0.18** | 0.21** | 0.07** |
| Size (Standard Error) | (0.01) | (0.01) | (0.01) |
| Profitability | -1.19** | -0.94** | |
| Profitability (Standard Error) | (0.06) | (0.04) | |
| Sales growth | 0.28** | 0.29** | |
| Sales growth (Standard Error) | (0.01) | (0.02) | |
| Observations | 31066 | 61014 | 42087 |
| Pseudo R-squared | 0.03 | 0.07 | 0.02 |
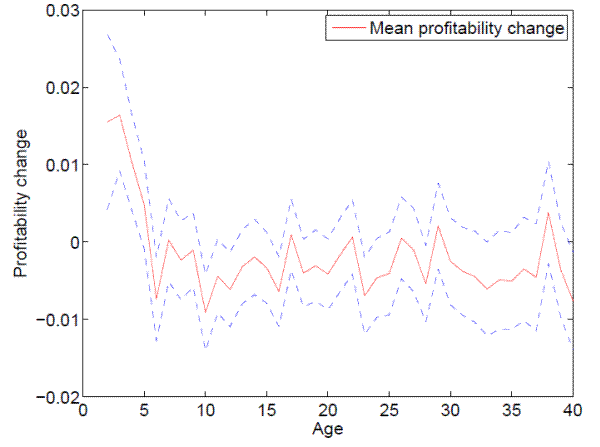 The figure plots the mean change in profitability from age
The figure plots the mean change in profitability from age 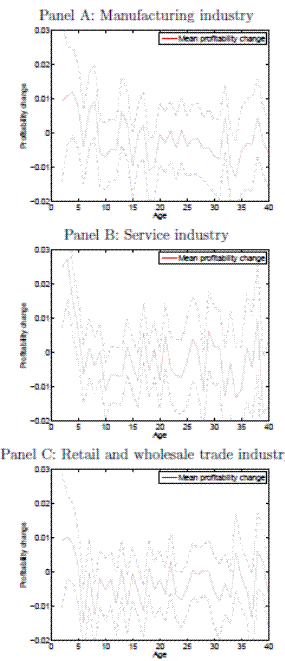 Panels A, B, and C plot the mean change in profitability from age
Panels A, B, and C plot the mean change in profitability from age 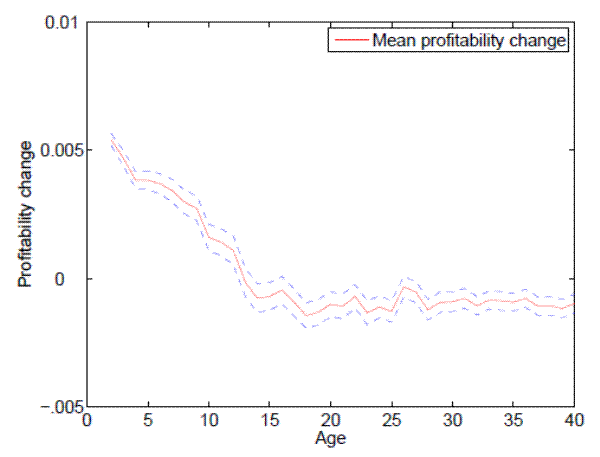 Using the simulated data set, the figure plots the mean change in profitability from age
Using the simulated data set, the figure plots the mean change in profitability from age ![\displaystyle \Pi_t(K, \tilde{z}, a; q_n) = (1-\theta) \left(\frac{\theta}{w_t}\right)^{\frac{\theta}{1-\theta}} \left[q_n C_t^{\nu} (\mu_{z,t-a}\tilde{z})^{1-\nu} K^{\alpha (1-\nu)} \right]^{\frac{1}{1-\theta}},](img27.gif)
![\displaystyle \pi(k, \tilde{z}, a; q_n) = (1-\theta) (\theta)^{\frac{\theta}{1-\theta}} \left[q_n (1+g_{\mu})^{-a}\tilde{z}^{1-\nu} k^{\alpha (1-\nu)} \right]^{\frac{1}{1-\theta}},](img34.gif)