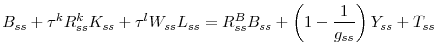Financial Intermediation, Investment Dynamics and
Business Cycle Fluctuations*
Keywords: DSGE model, financial frictions, financial shocks, Bayesian estimation, capital expenditure financing
Abstract:
Is the financial sector an important source of business cycle fluctuations? My model analysis suggests that the answer is `yes'. I find that financial sector shocks account for 35% and 60% of output and investment volatility, respectively. These are the implications of a dynamic model estimated using the past 20 years of data for the United States.
A key input into the analysis is a characterization of how important financial markets are for physical investment. To this end, I analyze the cash flow statements of all the U.S. public non-financial companies available in Compustat. I find that 35% of the capital expenditures of these firms is funded using financial markets. Of this funding, around 75% is raised by issuing debt and equity and 25% by liquidating existing assets. My analysis at quarterly frequencies suggests that the financial system is crucial in reconciling imbalances between the positive operating cash flows and capital expenditures.
Shocks that affect the degree of efficiency of the financial system in allocating private savings to productive needs can have large effects on capital accumulation and aggregate activity. To quantify the effects of such disturbances on the business cycle, I build a dynamic general equilibrium model with financial frictions in which entrepreneurs, like firms in the Compustat dataset, issue and trade financial claims to fund their investments. The model builds on (Kiyotaki & Moore, 2008), henceforth KM. In my theoretical framework, trading of financial assets occurs through banks and exogenous shocks can affect the financial intermediation technology. Differently from KM, I assume that prices and wages are sticky and show that this feature of the model is key for the financial shock to generate procyclical movements in labor inputs, consumption and investment.
In my model, entrepreneurs are endowed with random heterogeneous technologies to accumulate physical capital. Those entrepreneurs who receive better technologies issue financial claims to increase their investment capacity. Entrepreneurs with worse investment opportunities instead prefer to buy financial claims and lend to more efficient entrepreneurs, expecting higher rates of return than those granted by their own technologies.
I introduce stylized financial intermediaries (banks) that bear a cost to transfer resources from entrepreneurs with poor capital accumulation technologies to investors with efficient capital production skills. Banks buy financial claims from investors and sell them to other entrepreneurs. In doing so, perfectly competitive banks charge an intermediation spread to cover their costs ((Chari et al., 1995), (Goodfriend & McCallum, 2007) and (Cúrdia & Woodford, 2010a)). I assume that these intermediation costs vary exogenously over time and interpret these disturbances as financial shocks. When the intermediation costs are higher, the demand for financial assets drops and so does their price. Consequently the cost of borrowing for investing entrepreneurs rises. As a result, aggregate investment and output plunge.
I use Bayesian methods, as in (Smets & Wouters, 2007) and (An & Schorfheide, 2007) to estimate a log-linearized version of the model buffeted by a series of random disturbances, including the financial intermediation shock, on a sample of US macroeconomic time series that spans from 1989 to 2010. I include high-yield corporate bond spreads as one of the observables series to identify the financial shock ((Gilchrist & Zakrajsek, 2011)). I choose priors for financial parameters so that the model estimation can be consistent with Compustat evidence on corporate investment financing during the same sample period. The estimation results show that approximately 35% of the variance of output and 60% of the variance of investment can be explained by financial intermediation shocks. The shock is also able to explain the dynamics of the real variables that shaped the last recession, as well as the 1991 recession and the boom of the 2000s.
Why is the financial shock able to explain such a large fraction of business cycle dynamics? The reason for this lies in the ability of my neo-Keynesian model to generate both booms and recessions of a plausible magnitude and a positive co-movement among all of the real variables, including consumption and investment, following a financial intermediation shock. I find that nominal rigidities and in particular sticky wages ((Erceg et al., 2000)) are the key element in delivering this desirable feature of the model. In a model with flexible wages aggregate consumption and investment move in opposite directions in response to a financial intermediation shock: the shock acts as an intertemporal wedge ((Chari et al., 2007) and (Christiano & Davis, 2006)) that affects investment, substituting present with future consumption.
In my model with sticky wages instead there are two classes of agents: entrepreneurs who optimize their intertemporal consumption profile by trading assets on financial markets and building capital, and workers who consume their labor income in every period. On the intertemporal margin, increased financial intermediation costs lower the real rate of return on financial assets, discourage savings and investment and induce entrepreneurs to consume more in the current period. Additionally, the shock induces a drop in aggregate demand that translates into a downward shift in the demand for labor inputs. When workers cannot re-optimize their wages freely, the decrease in labor demand translates into a large drop in the equilibrium amount of hours worked. As a result, the wage bill falls and so does workers' consumption. The drop in workers' consumption dominates over the rise in entrepreneurs' consumption and the reduction in hours amplifies the negative effect of the shock on aggregate output.
To verify the importance of wage rigidities, I re-estimate the model under flexible wages and find that financial disturbances are in fact able to explain only 9.5% and 49% of output growth and investment growth variance at business cycle frequencies, compared to 35% and 60% in the benchmark sticky-wage case.
The estimation also allows me to quantify the role of the different structural shocks to output dynamics during the Great Recession. Running counterfactual experiments on the estimated model using the series of smoothed shocks, I find that total factor productivity has increased during the recession, in line with evidence from (Fernald, 2009). The positive shocks to TFP helped reduce the drop in output by 0.5% at the deepest point of the recession and increase the speed of the recovery. Similarly, I find that positive innovations in government spending reduced the size of the recession by 1% of GDP at the trough. Public sector deficits are beneficial in the model, in the spirit of policy experiments in (Kiyotaki & Moore, 2008): when conditions on financial markets worsen, credit constrained entrepreneurs benefit from holding an increasing stock of government bonds (i.e. liquid assets) that help them self-insure against idiosyncratic risk.
Related Literature
This paper is related to the literature that explores and quantifies the relations between financial imperfections and macroeconomic dynamics. A large part of the literature has focused on the ability of financial market frictions to amplify aggregate fluctuations. In this tradition (Kiyotaki & Moore, 1997) first analyzed the macroeconomic implications of the interaction of agency costs in credit contracts and endogenous fluctuations in the value of collateralizable assets, followed by (Carlstrom & Fuerst, 1997) and (Bernanke et al., 1999) who first introduced similar frictions in dynamic general equilibrium models.
My model explores the role of shocks that originate on financial markets as possible drivers of cyclical fluctuations. In this tradition, (Christiano et al., 2010) estimate a general equilibrium model of the US and Euro Area economies, in which a financial shock can hit in the form of unexpected changes in the distribution of entrepreneurial net worth and riskiness of credit contracts. They find that this `risk' shock can account for approximately 30% of fluctuations in aggregate output.2
My model is close in its set-up to (Kiyotaki & Moore, 2008) (KM). They focus on financial market transactions and on the aggregate implications of a shock to the degree of liquidity of private assets. The liquidity shock takes the form of a drop in the fraction of assets that can be liquidated to finance new investment projects. Their model, in which prices and wages are perfectly flexible, has two unappealing features.
First of all, while, the KM liquidity shock does lead to a reduction in investment, consumption instead rises on impact, and the negative effect on output is limited. As mentioned above, I find that introducing nominal rigidities and in particular sticky wages can correct this feature of the model. (Jermann & Quadrini, 2011) also underline the importance of labor markets in the transmission of financial shocks by calibrating and then estimating a dynamic general equilibrium model where firms issue debt and equity to finance both their investment and their working capital needs. In their set-up, a financial shock corresponds to a tightening of firms' borrowing constraints. If raising equity financing in substitution of debt is costly, reduced borrowing capacity translates into weaker labor demand that can generate sizable recessions.
A second unappealing feature of KM is that the primary impact of their liquidity shock on the price of equity operates through a supply channel, under plausible calibrations of the model parameters. By restricting the supply of financial claims on the market, a negative liquidity shock results in a rise in their price. (Shi, 2011) documents this finding extensively, questioning the ability of liquidity shocks to generate meaningful business cycle dynamics. To obtain a positive co-movement of asset prices and output, I instead introduce random disturbances in the financial intermediation technology.
My modeling of these financial intermediation shocks is inspired by (Kurlat, 2010)'s work on the role of adverse selection on asset markets in the amplification of aggregate shocks. He shows that an adverse selection friction in a model with heterogeneous assets maps into a tax-wedge on financial transactions in a framework with homogeneous securities similar to KM. In my work, I translate this tax wedge into a financial intermediation cost in the spirit of (Chari et al., 1995), (Goodfriend & McCallum, 2007) and (Cúrdia & Woodford, 2010a). Moreover I assume the cost to be time-varying and subject to exogenous independent shocks over time.
More recently, (Bigio, 2011) builds and calibrates a model with limited enforcement in contractual agreements and asymmetric information on the quality of capital. In his framework, negative shocks to the dispersion of the quality of capital generate endogenous fluctuations in the degree of liquidity of assets. These shocks also tighten firms' constraints on working capital financing and reduce labor demand as in (Jermann & Quadrini, 2011), delivering positive co-movement between consumption and investment.
To conclude, I briefly compare my analysis with that of (Del Negro et al., 2010). They work with a liquidity shock modeled as in KM. An advantage of my intermediation shock is that it corresponds closely to an observed variable, namely, the interest rate spread. In addition, (Del Negro et al., 2010) focus is on the period of the recent financial turmoil and the associated monetary policy challenges. I study the past 20 years of data using Bayesian estimation and model evaluation methods. In relation to (Del Negro et al., 2010), my analysis confirms that financial shocks were the driving force in the recent recession. However, I also find that these shocks have been important in the past 20 years.
The paper is structured so to offer an empirical description of corporate investment financing from the Compustat quarterly data in section 1. Section 2 describes the features of the model. Section 3 discusses the estimation strategy, the prior selection on the model parameters and significant moments. Section 4 presents the model estimation results and section 5 concludes.
1 Empirical Evidence on Investment Financing: the Compustat Cash-Flow Data
This section of the paper is devoted to an empirical analysis of the degree of dependence of firms' capital expenditures on financial markets. My objective is to quantify the fraction of quarterly corporate investment in physical capital that firms fund by accessing financial markets as opposed to using current operative cash flows. Here I also distinguish between the role of primary markets (debt or equity financing) and secondary markets (sales of old assets with different degrees of liquidity) as sources of funds for capital expenditures and assess their relative importance at a quarterly level.
For this purpose, I analyze cash flow data of U.S. firms. The Flow of Funds table for corporations (table F.102) reports a measure of financial dependence of the corporate sector on transfer of resources from other actors in the economy (e.g. households) defined as the Financing Gap. This
variable is computed as the difference between internal funds generated by business operations in the U.S. for the aggregate of firms, US Internal Funds![]() ,3and total investment (or expenditure) on physical capital, CAPX
,3and total investment (or expenditure) on physical capital, CAPX![]() 4
4
In a given quarter FG![]() is positive when the aggregate of U.S. corporations generate cash flows from their business operations large enough to cover their capital expenditures and lend
resources to the rest of the economy. On the other hand, in a quarter when FG
is positive when the aggregate of U.S. corporations generate cash flows from their business operations large enough to cover their capital expenditures and lend
resources to the rest of the economy. On the other hand, in a quarter when FG![]() is negative, the firms draw resources from the rest of the economy to finance a fraction of their capital
expenditures. This aggregate measure however is not informative of the degree of dependence of single corporations on financial markets. Firms in deficit are aggregated with firms in surplus and positive values for the aggregate financing gap can coexist with corporations with large deficits at the
micro-level.5
is negative, the firms draw resources from the rest of the economy to finance a fraction of their capital
expenditures. This aggregate measure however is not informative of the degree of dependence of single corporations on financial markets. Firms in deficit are aggregated with firms in surplus and positive values for the aggregate financing gap can coexist with corporations with large deficits at the
micro-level.5
To avoid this aggregation problem and obtain a more accurate statistics on the degree of financial dependence of corporations, I build on work from (Chari & Kehoe, 2009) and rely on micro evidence from Compustat.6 Compustat contains cash flow statement data both at annual and at quarterly frequency for the universe of publicly traded North American companies. Quarterly data are available from 1984, while a consistent break-down into their components is available since 1989.
I concentrate on the sample period that goes from 1989Q1 to 2010Q4. I focus on companies based in the U.S. excluding Canadian corporations from the analysis.7 I focus on Compustat quarterly cash flow data to quantify the extent of short-term cash-flow imbalances of the companies that are not visible at annual frequencies. I start my analysis from the basic cash flow equality for a generic firm ![]() , within a quarter
, within a quarter ![]() :
:
that states that the variation of liquid assets on the balance sheet of the firm (
If ![]() > 0, then firm
> 0, then firm ![]() reports a financing surplus in period
reports a financing surplus in period ![]() : it is able to self-finance its investment in physical capital and its dividend pay-outs,
: it is able to self-finance its investment in physical capital and its dividend pay-outs,
![]() , and can use the additional resources to buy back shares and/or pay back its debt obligations (
, and can use the additional resources to buy back shares and/or pay back its debt obligations (
![]() +
+
![]()
![]() 0). In addition, the firm could use its surplus to increase the
stock of financial assets on its balance sheet and/or its cash reserves (
0). In addition, the firm could use its surplus to increase the
stock of financial assets on its balance sheet and/or its cash reserves (![]() +
+ ![]()
![]()
![]() 0).
0).
If instead ![]() < 0, the negative financing gap in period
< 0, the negative financing gap in period ![]() can be funded by relying on external investors to subscribe new debt and/or equity securities (
can be funded by relying on external investors to subscribe new debt and/or equity securities (
![]() +
+
![]()
![]() 0), by liquidating assets (
0), by liquidating assets (![]()
![]() 0) and/or depleting deposits and cash-reserves (
0) and/or depleting deposits and cash-reserves (![]()
![]()
![]() 0).
0).
In each quarter, I compute ![]() for all firms in the dataset and identify those that show a negative financing gap. I then add the absolute value of these deficits across the firms, to
find a measure of the total financing gap in each quarter
for all firms in the dataset and identify those that show a negative financing gap. I then add the absolute value of these deficits across the firms, to
find a measure of the total financing gap in each quarter ![]() for the aggregate of Compustat firms:
for the aggregate of Compustat firms:
I also recognize that a fraction of firms that report a negative financing gap do so because they occasionally post negative quarterly operating cash flows: firms that report
Table 2 in the appendix shows that from 1989Q1 and 2010Q1, the average of the financing gap share,
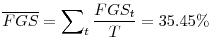 |
The share of capital expenditures that relies on funding from either primary or secondary markets is substantial. Persistent shocks to the operating conditions on financial markets can disrupt the accumulation of aggregate capital and potentially affect the dynamics of output growth and contribute to business cycle fluctuations.
Figure 4 shows the evolution of the seasonally adjusted Financing Gap Share defined in (5) (black solid line in panel A) and its trend (black solid line in panel B) along the sample period 1989Q1 and 2010Q1.10
Panel B shows that reliance of capital expenditures on financial markets features increasing trends along the two economic expansions of the 1990s and in the 2000s. Moreover all three recessions start with a sudden drop in the Financing Gap Share and loosely mark the beginning of prolonged
periods of decline in the variable that last well into the initial phase of following economic expansion. The right-hand side of equation 3 suggests how corporations fund their Financing Gap. I use data in Compustat to determine what fraction of the Financing Gap is funded using
resources coming from equity and/or debt holders,
![]() and
and
![]() , and what fraction is instead financed by liquidation of assets on firms' balance sheets and/or depletion of cash reserves,
, and what fraction is instead financed by liquidation of assets on firms' balance sheets and/or depletion of cash reserves, ![]() +
+![]()
![]() . In each quarter
. In each quarter ![]() , debt and equity intakes account for a fraction,
, debt and equity intakes account for a fraction,
![]() , of the total financing gap defined in equation 3:
, of the total financing gap defined in equation 3:
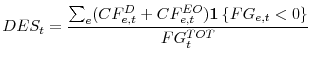 |
(6) |
On average, along the sample period debt and equity fund 75.67% of the total financing gap (standard deviation 22.45%):
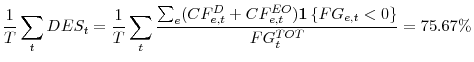 |
while the remaining 24.43% is covered by portfolio liquidations and changes in cash reserves, as summarized in table 2.11
Figure 7 plots the share of the total financing gap that is covered by portfolio liquidations and variation in cash reserves, ![]() , with
, with ![]() = 1 -
= 1 - ![]() :
:
The graph suggests that the relative importance of asset liquidations versus debt and equity intakes is increasing in recessions. Recessions seem to be characterized mostly by a reduced inflow of external sources of finance per unit of investment undertaken (Figure 7) and a shift towards asset liquidation for the aggregate of U.S. corporations.
The data in Figure 7 shows some important features. Positive realizations of the series represent quarters when firms liquidate assets or deplete cash reserves. Negative realizations instead represent episodes in which firms are able to borrow from the market not only to cover their financing gap, but also to acquire new financial assets on secondary markets. This phenomenon is particularly pronounced before the burst of the dotcom bubble at the end of the 90s, when the share of corporate mergers and acquisitions had risen to 15% of US GDP in 1999 alone, compared to an average of 4% during the 1980s, ((Weston & Weaver, 2004)). Another important characteristic of the data series is the difference in the relevance of portfolio liquidations in the 2000s, compared to the 1990s. The average fraction of financing gap covered through asset liquidations is lower along the expansion of the 1990s (average contribution amounts to 19.74% of Financing Gap from 1991 to 2001), and higher in the boom of the 2000s (34.27% from 2002 to 2008).
2 The Model
In this section I describe a model that can capture the features of firms' investment financing in the Compustat quarterly data. In the model described in this section entrepreneurs: 1) produce enough aggregate resources to fund total investment, 2) singularly issue and trade financial claims through a competitive banking sector, to raise funds to finance their capital expenditures and, 3) trade and hold liquid assets as precautionary savings against idiosyncratic investment opportunity, in line with firm-level data in Compustat.
The economy described below consists of a unit measure of entrepreneurs and a unit measure of households, perfectly competitive financial intermediaries (banks),competitive producers of a homogeneous consumption good, intermediate goods producers who act in regime of imperfect competition, capital producers who transform final goods into ready-to-install capital goods, households that supply differentiated labor inputs combined in homogeneous work hours by employment agencies. The government is composed of a monetary authority and a fiscal authority.
2.1 Entrepreneurs
Entrepreneurs are indexed by e. They own the capital stock of the economy, ![]() . In each period they receive an idiosyncratic technological shock to install new
capital. After observing their technology level, they can decide to increase their capital stock if they receive a good technology draw. To increase their investment capacity and take advantage of their technology, they can borrow resources by issuing and selling equity claims (
. In each period they receive an idiosyncratic technological shock to install new
capital. After observing their technology level, they can decide to increase their capital stock if they receive a good technology draw. To increase their investment capacity and take advantage of their technology, they can borrow resources by issuing and selling equity claims (![]() ) on their physical assets (
) on their physical assets (![]() ) to financial intermediaries. Alternatively, if
their technology is inefficient, they can decide to forgo investment opportunities that are not remunerative and instead lend resources to more efficient entrepreneurs in exchange for the rate of return on the new capital produced. Entrepreneurs can also accumulate liquid assets in the form of
government bonds (
) to financial intermediaries. Alternatively, if
their technology is inefficient, they can decide to forgo investment opportunities that are not remunerative and instead lend resources to more efficient entrepreneurs in exchange for the rate of return on the new capital produced. Entrepreneurs can also accumulate liquid assets in the form of
government bonds (![]() ).
).
At the beginning of the period a snapshot of each entrepreneur's balance sheet will include his capital stock, ![]() , the equity claims on other entrepreneurs' capital stock,
, the equity claims on other entrepreneurs' capital stock,
![]() and interest bearing government bond holdings,
and interest bearing government bond holdings,
![]() on the assets side. On the liability side, entrepreneurs sell claims on their capital stock to others, so that part of their
on the assets side. On the liability side, entrepreneurs sell claims on their capital stock to others, so that part of their ![]() is backed by
is backed by
![]() :
:
| A | L |
|
|
|
|
|
|
|
|
Net Worth |
Entrepreneur ![]() maximizes his life-time utility of consumption:
maximizes his life-time utility of consumption:
subject to a flow of funds constraint:
The entrepreneur receives after-tax income from his assets at the beginning of the period (the right-hand side of (9)) and uses it to purchase consumption goods,
An entrepreneur can increase his equity stock by purchasing and installing capital goods ![]() by means of the technology
by means of the technology ![]() , where
, where
![]() .13
He can also increase his assets by purchasing new equity claims from financial markets
.13
He can also increase his assets by purchasing new equity claims from financial markets
![]() , or decrease them by selling equity claims,
, or decrease them by selling equity claims,
![]() . The law of motion of the equity stock for entrepreneur e will be:
. The law of motion of the equity stock for entrepreneur e will be:
Entrepreneurs are constrained in the amount of financial claims that they can issue and sell on the market, as in KM. Those who decide to purchase and install capital goods can write claims just on a fraction
so they do not exceed the sum of the external finance limit,
Note finally that entrepreneurs' discount factor in (8),
![]() , is subject to an intertemporal preference exogenous shock that follows the AR(1) process:
, is subject to an intertemporal preference exogenous shock that follows the AR(1) process:
where
To sum up, entrepreneurs maximize (8), subject to (9), (10) and (11) and under the non-negativity constraints:
The problem can be solved at time
New capital and old equity units share the same resale and purchase prices, ![]() and
and ![]() , and return profile in the future,
, and return profile in the future,
![]() for i =
for i =
![]() . Entrepreneurs will then always treat them as perfect substitutes. Following (Kurlat, 2010), at the beginning of the period an entrepreneur observes
the price at which he can sell financial claims to a bank,
. Entrepreneurs will then always treat them as perfect substitutes. Following (Kurlat, 2010), at the beginning of the period an entrepreneur observes
the price at which he can sell financial claims to a bank,
![]() , the one at which he can buy financial claims from the bank
, the one at which he can buy financial claims from the bank
![]() , and the level of his installation technology,
, and the level of his installation technology, ![]() . Entrepreneurs
compare their own relative price of capital goods,
. Entrepreneurs
compare their own relative price of capital goods,
![]() , with the resale and purchase prices of equity claims,
, with the resale and purchase prices of equity claims, ![]()
![]()
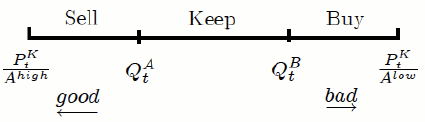
![]() (Figure 8). Depending on his random technology
draw, an entrepreneur can becomes a Seller and optimally decide to buy capital goods at price
(Figure 8). Depending on his random technology
draw, an entrepreneur can becomes a Seller and optimally decide to buy capital goods at price ![]() and install them by means of his technology
and install them by means of his technology ![]() , while selling claims to financial intermediaries at price
, while selling claims to financial intermediaries at price ![]() . Alternatively, he can become a Keeper and install
capital goods using his own technology and income, or become a Buyer, forgoing installation of capital goods and buying claims on the capital stock of other entrepreneurs paying
. Alternatively, he can become a Keeper and install
capital goods using his own technology and income, or become a Buyer, forgoing installation of capital goods and buying claims on the capital stock of other entrepreneurs paying ![]() for
each financial claim.
for
each financial claim.
Figure 8 shows the partition into the three subsets: Sellers, Keepers and Buyers, depending on the random draw of installation technology for the period. In particular:
- SELLERS (index
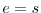 ):
):
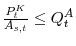
Sellers can take advantage of good technology draws. Their relative price of a unit of installed capital,
![]() , is lower than the real price at which the entrepreneur can issue new equity claims or sell old ones,
, is lower than the real price at which the entrepreneur can issue new equity claims or sell old ones, ![]() , and lower than the price at which he can buy financial claims on other people's capital stock,
, and lower than the price at which he can buy financial claims on other people's capital stock, ![]() . The entrepreneur can then
profit from building new physical assets at a relative price
. The entrepreneur can then
profit from building new physical assets at a relative price
![]() and selling equity claims to the financial intermediaries at price
and selling equity claims to the financial intermediaries at price ![]() . The optimal decision then implies that the entrepreneur sells the intermediaries the highest amount of equity claims possible, from 11:
. The optimal decision then implies that the entrepreneur sells the intermediaries the highest amount of equity claims possible, from 11:
and avoids buying assets from the market, so that
with:
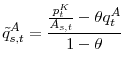 |
and real asset prices and rates of return defined as
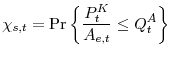 |
- KEEPERS (index
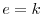 ):
):
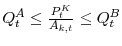
nor will they buy financial assets:
so that their budget constraint (9) in real terms becomes:
The measure of keepers in the economy is:
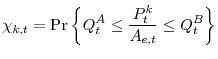 |
- BUYERS (index
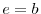 ):
):
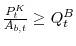
Buyers receive poor investment technology draws. The relative price of a unit of installed capital,
![]() , is higher than both the market price of equity
, is higher than both the market price of equity ![]() and of the amount obtained from market makers for each units of equity sold or issued,
and of the amount obtained from market makers for each units of equity sold or issued, ![]() . These entrepreneurs will decide not to install new physical capital.
They will instead acquire financial claims at their market price
. These entrepreneurs will decide not to install new physical capital.
They will instead acquire financial claims at their market price ![]() . Similarly to KM, Buyers will accumulate government bonds,
. Similarly to KM, Buyers will accumulate government bonds, ![]() in non-arbitrage with equity claims. They acquire these liquid assets to self-insure against the arrival of good technology draws in the future, so to overcome their binding borrowing and liquidity constraints. Their budget constraint
in real terms will then become:
in non-arbitrage with equity claims. They acquire these liquid assets to self-insure against the arrival of good technology draws in the future, so to overcome their binding borrowing and liquidity constraints. Their budget constraint
in real terms will then become:
where:
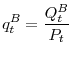 |
Finally, the fraction of buyers in the economy will be:
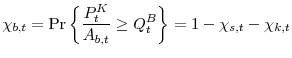 |
The three budget constraints (14), (15), (16) now display entrepreneurs' net worth on their right-hand side. By properties of the log-utility function, optimal consumption in period ![]() is a fixed fraction
is a fixed fraction
![]() of the entrepreneur's net worth. 15
of the entrepreneur's net worth. 15
2.2 Financial Intermediaries
Financial intermediaries (or banks) manage the transfer of resources between Sellers and Buyers of financial claims.
In each period, a multitude of intermediaries indexed by i compete to acquire equity claims,
![]() , at price
, at price ![]() and sell the quantity
and sell the quantity
![]() to Buyers at a price
to Buyers at a price ![]() . To do this, they bear an
intermediation cost equal to
. To do this, they bear an
intermediation cost equal to
![]() for each financial claim they process. Banks maximize their nominal profits:
for each financial claim they process. Banks maximize their nominal profits:
subject to the constraint that the number of claims they buy is the same as the one they sell:
Perfect competition among intermediaries implies that profits are maximized when:
The real `bid' price, q
Sellers and Buyers share the incidence of the intermediation cost. An increase in the cost reduces the expected return on savings to the Buyers. At the same time, it lowers the amount of resources that are transferred to investing entrepreneurs for each unit of equity sold. The price of equity
claims sold by investing entrepreneurs, ![]() , falls and their cost of borrowing rises. The immediate result of the negative shock on
, falls and their cost of borrowing rises. The immediate result of the negative shock on
![]() is that investment drops with potential effects on output and consumption dynamics, discussed at length in section 4.
is that investment drops with potential effects on output and consumption dynamics, discussed at length in section 4.
In the literature, see (Chari et al., 1995), (Goodfriend & McCallum, 2007) and (Cúrdia & Woodford, 2010b) introduce wedges similar to the one proposed here to model financial market imperfections and the evolution of credit spreads. Work by (Kurlat, 2010) shows that an adverse selection friction in a model with lemon and non-lemon assets is isomorphic to a model with homogeneous equity claims in which financial transactions are hit by a tax wedge, as discussed in this paper. In his formulation, the wedge is a reduced form representation of the share of lemon claims over total claims traded on the market.16
In Kurlat's model, this wedge evolves endogenously and depends positively on the share of lemons traded in every period and the proceeds from the tax are rebated to the government. The wedge generates a spread between the expected cost of borrowing perceived by Sellers and the expected return on savings perceived by Buyers.
In my model, I assume that this tax wedge maps into a cost that financial intermediaries bear for each unit of financial claims that they transfer from Sellers to Buyers. The total amount of resources that banks spend to purchase a unit of financial claims from Sellers is then equal to
![]() . To evaluate the role of financial disturbances as potential drivers of business cycles that are orthogonal to other sources of business fluctuation, I
assume that the intermediation costs
. To evaluate the role of financial disturbances as potential drivers of business cycles that are orthogonal to other sources of business fluctuation, I
assume that the intermediation costs ![]() follow an exogenous process of the kind:
follow an exogenous process of the kind:
where
2.3 Final Good Producers
At each time ![]() , competitive firms operate to produce a homogeneous consumption good,
, competitive firms operate to produce a homogeneous consumption good, ![]() , as a combination of differentiated intermediate good,
, as a combination of differentiated intermediate good, ![]() , through the technology:
, through the technology:
![\displaystyle Y_{t}=\left[ \int_{0}^{1}Y_{t}\left( i\right) ^{\frac{1}{1+\lambda _{p,t}}}di \right] ^{1+\lambda _{p,t}}](img178.gif) |
(19) |
where
with
Standard profit maximization of the final good producers and their zero profit condition determine the price of the final good, ![]() , as a CES aggregator of the prices of the intermediate
goods,
, as a CES aggregator of the prices of the intermediate
goods,
![]() :
:
![\displaystyle P_{t}=\left[ \int_{0}^{1}P_{t}\left( i\right) ^{\frac{1}{\lambda _{p,t}}}di\right] ^{\lambda _{p,t}}](img183.gif) |
and the demand for intermediate good
2.4 Intermediate Goods Producers
Firms in regime of monopoly use capital and labor inputs,
![]() and
and ![]() , to produce differentiated intermediate goods,
, to produce differentiated intermediate goods,
![]() , using the following technology:
, using the following technology:
where
Firms employ homogeneous labor inputs,
![]() , from households at a nominal wage rate
, from households at a nominal wage rate ![]() and rent the
capital stock,
and rent the
capital stock,
![]() , from entrepreneurs at a competitive rate
, from entrepreneurs at a competitive rate ![]() .
Firms minimize their costs and maximize their monopolistic profits, knowing that in period
.
Firms minimize their costs and maximize their monopolistic profits, knowing that in period ![]() they will only be able to re-optimize their prices with probability
they will only be able to re-optimize their prices with probability
![]() . The remaining fraction of firms that do not re-optimize,
. The remaining fraction of firms that do not re-optimize, ![]() ,
are assumed to update their prices according to the indexation rule:
,
are assumed to update their prices according to the indexation rule:
where
Those firms who can choose their price level will then set
![]() optimally by maximizing the present discounted value of their flow of profits:
optimally by maximizing the present discounted value of their flow of profits:
subject to the demand function for good
2.5 Capital Goods Producers
Capital goods producers operate in regime of perfect competition and on a national market. Producers purchase consumption goods from the final goods market, ![]() at a price
at a price
![]() , transforms them into investment goods,
, transforms them into investment goods, ![]() , by means of a linear
technology:
, by means of a linear
technology:
Producers then have access to a capital production technology to produce
![\displaystyle i_{t}=\left[ 1-S\left( \frac{I_{t}}{I_{t-1}}\right) \right] I_{t}](img211.gif) |
where
s.t.
I assume that the households own stocks in the capital producers, so that the stream of their future profits is weighted by their marginal utility of consumption,
![]() . Free entry on the capital goods producing sector requires profits to be zero in equilibrium, so that the value of capital goods sold in every period
. Free entry on the capital goods producing sector requires profits to be zero in equilibrium, so that the value of capital goods sold in every period ![]() across all capital producers has to be equal to the nominal value of aggregate investment:
across all capital producers has to be equal to the nominal value of aggregate investment:
2.6 Employment Agencies
The economy is populated by a unit measure of households, indexed by ![]() , who consume and supply a differentiated labor force to employment agencies. A large number of such agencies
combines the differentiated labor into a homogeneous labor input
, who consume and supply a differentiated labor force to employment agencies. A large number of such agencies
combines the differentiated labor into a homogeneous labor input ![]() , by means of the Dixit-Stiglitz technology:
, by means of the Dixit-Stiglitz technology:
![\displaystyle L_{t}=\left[ \int_{0}^{1}L_{w,t}{}^{\frac{1}{1+\lambda _{w,t}}}dw\right] ^{1+\lambda _{w,t}}](img224.gif) |
where
| (27) |
with
Agencies hire specialized labor, ![]() at monopolistic wages,
at monopolistic wages, ![]() , and
provide homogeneous work hours,
, and
provide homogeneous work hours, ![]() , to the intermediate producers, in exchange for a nominal wage,
, to the intermediate producers, in exchange for a nominal wage, ![]() . Similarly to the good production technology, profit maximization delivers a conditional demand for labor input for each employment agency equal to:
. Similarly to the good production technology, profit maximization delivers a conditional demand for labor input for each employment agency equal to:
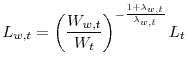 |
The nominal wage paid by the intermediate firms to the employment agencies is an aggregate of the different specialized salaries
![\displaystyle W_{t}=\left[ \int_{0}^{1}W_{w,t}^{\frac{1}{\lambda_{w,t}}}dz\right] ^{\lambda _{w,t}}](img231.gif) |
2.7 Households
Households maximize their lifetime utility of consumption, ![]() :
:
subject to their nominal budget constraint:
and to limited participation constraints on financial markets:
In every period only a fraction
![]() of workers re-optimizes the nominal wage. To make aggregation simple, I assume that workers are able to insure themselves against negative realizations of their
labor income that occur in each period
of workers re-optimizes the nominal wage. To make aggregation simple, I assume that workers are able to insure themselves against negative realizations of their
labor income that occur in each period ![]() , by trading claims
, by trading claims ![]() with other
workers before they are called to re-optimize
with other
workers before they are called to re-optimize ![]() .
.
The wage is set monopolistically by each household as in (Erceg et al., 2000): a fraction
![]() of workers supplies labor monopolistically and sets
of workers supplies labor monopolistically and sets ![]() by maximizing:
by maximizing:
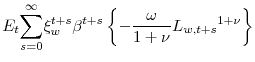
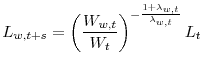 |
The remaining fraction
that describe their evolution as a geometric average of past and steady-state values of inflation and labor productivity.
2.8 Monetary Authority
The central bank sets the level of the nominal interest rate, ![]() , according to a Taylor-type rule of the kind:
, according to a Taylor-type rule of the kind:
where the nominal risk free rate depends on its lagged realization and responds to deviations of a 4-period trailing inflation index
where
2.9 Fiscal Authority
The fiscal authority issues debt, ![]() and collects distortionary taxes on labor income and capital rents,
and collects distortionary taxes on labor income and capital rents,
![]() and
and
![]() to finance a stream of public expenditures,
to finance a stream of public expenditures, ![]() , lump-sum
transfers to households,
, lump-sum
transfers to households, ![]() , and interest payments on the stock of debt that has come to maturity,
, and interest payments on the stock of debt that has come to maturity,
![]() :
:
Following the DSGE empirical literature, the share of government spending over total output follows an exogenous process:
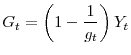 |
where:
and
My model requires an empirically plausible description of the dynamics of the supply of liquid assets that originates from the public authority. I then follow (Leeper et al., 2010) in their empirical work on the dynamics of fiscal financing in a DSGE model of the US
economy.18 To obtain a fiscal rule that resembles the one in the de-trended model in (Leeper et al., 2010) as closely as possible,
I assume the share of transfers over total output,
![]() , to depart from its steady-state value,
, to depart from its steady-state value, ![]() , in response to
deviations of the average growth rate of output in the past quarter from the stable growth path as well as to deviations of the debt to output ratio
, in response to
deviations of the average growth rate of output in the past quarter from the stable growth path as well as to deviations of the debt to output ratio
![]() from a specific target,
from a specific target, ![]() :19
:19
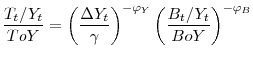 |
Transfers then increase when output growth falls below its steady-state value. On the other hand, transfers fall when
Notice also that the description of the public provision of liquid assets in the form of government bonds assumes a key role in this model. Fiscal policy is non-Ricardian (as in (Woodford, 1990)): different agents accumulate government bonds than those who bear the burden of taxation. Workers do not save, so that they are not able to smooth out the impact of their fiscal contribution and entitlements along time. Entrepreneurs, on the other hand, do not save for tax-smoothing purposes. They instead accumulate government bonds to self-insure against the arrival of good investments in the future and overcome their borrowing and liquidity constraints described in section 2.1.
2.10 Aggregation, Market Clearing and Model Solution
Aggregation across entrepreneurs is made easy by the log-preferences assumption and by the independence of the realizations of installation technology idiosyncratic shocks, ![]() , with
the amount of capital and financial assets that agents enter the period with,
, with
the amount of capital and financial assets that agents enter the period with, ![]() and
and ![]() . Log-utility implies linearity of their consumption, investment and portfolio decisions with respect to the state variables,
. Log-utility implies linearity of their consumption, investment and portfolio decisions with respect to the state variables, ![]() and
and ![]() . Summing over the individual flow of funds constraints, output at time
. Summing over the individual flow of funds constraints, output at time ![]() ,
, ![]() , is absorbed by consumption of sellers (S), keepers (K), buyers (B) and workers (W), by investment and government spending and financial intermediation costs:
, is absorbed by consumption of sellers (S), keepers (K), buyers (B) and workers (W), by investment and government spending and financial intermediation costs:
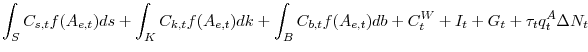 |
||
where GDP is instead defined as:
To solve the model, I first rewrite its equilibrium conditions in stationary terms, rescaling such variables as output and GDP,
3 Estimation
In this section I describe the estimation of the model in section 2 on U.S. data using Bayesian methods. I start with a description of the data and of the choice of prior distributions for the model parameters and for certain moments, based on previous work in the DSGE estimation literature and on the micro-data evidence from Compustat reported in section 1. I here discuss the estimates and the features of the impulse response functions to the financial intermediation shock, the model fit and the variance decomposition of the observables in the fundamental shocks implied by the estimation. I finally present the historical decomposition of the observables into the smoothed fundamental shocks and perform some counterfactual exercises on the last 3 years of GDP growth to identify the driving forces of the Great Recession.
3.1 Data and Prior Selection
I estimate the model by Bayesian methods on sample that spans from 1989Q1 to 2010Q1. To estimate the model parameters I use the following vector of eight observable time series, obtained from Haver Analytics:
![\displaystyle \left[ \Delta \log X_{t},\text{ }\Delta \log I_{t},\text{ }\Delta \log C_{t}, \text{ }R_{t}^{B},\text{ }\pi _{t},\text{ }Sp_{t},\text{ }\log \left( L_{t}\right) ,\text{ }\Delta \log \frac{W_{t}}{P_{t}}\right] \text{.}](img289.gif) |
The dataset is composed of the log growth rate of real per-capita GDP,
![\displaystyle Sp_{t}=E_{t}\left[ \log \left( \frac{R_{t+1}^{K}+\left( 1-\delta \right) Q_{t+1}^{A}}{Q_{t}^{A}}\right) -R_{t}^{B}\right] +\eta_{t}^{Sp}](img293.gif) |
The choice of this particular series of spreads uniforms to the literature that finds high-yield spreads to have a significant predictive content for economic activity ((Gertler & Lown, 1999)). In particular these spreads are the mid-credit-quality-spectrum spreads that (Gilchrist et al., 2009) find to be good predictors of unemployment and investment dynamics. The measurement error is intended to account for the differences in the federal funds rate and the AAA corporate bond yield, used as reference points to compute the spread in the model and the data respectively. The measurement error is also intended to correct for the imperfect mapping of rates of return on equity in the model onto yields on state-non-contingent bonds in the data.
Estimates for the parameters are obtained by maximizing the posterior distribution of the model ((An & Schorfheide, 2007)) over the vector of observables. The posterior function combines the model likelihood function with prior distributions imposed on model parameters and on theoretical moments of specific variables of interest.
The choice of the priors for most parameters of the model is rather standard in the literature ((Del Negro et al., 2007), (Justiniano et al., 2010)) and is reported in table 3.
A few words are necessary to discuss the priors selection on parameters that influence entrepreneurs' investment financing decisions and the efficiency of financial intermediation in the model. I set a Gamma prior on the steady-state quarterly intermediation cost,
![]() , with mean equal to 62.5 basis points and standard deviation equal
to 15, compatible with an annual intermediation costs of 250 basis points chosen by (Cúrdia & Woodford, 2010a) to match the median spread between the Federal
Reserve Board index of commercial and industrial loan rates and the federal funds rate, over the period 1986-2007. I use my analysis of quarterly Compustat cash flow data to set the prior mean and standard deviation on the steady-state level of the financing gap share,
, with mean equal to 62.5 basis points and standard deviation equal
to 15, compatible with an annual intermediation costs of 250 basis points chosen by (Cúrdia & Woodford, 2010a) to match the median spread between the Federal
Reserve Board index of commercial and industrial loan rates and the federal funds rate, over the period 1986-2007. I use my analysis of quarterly Compustat cash flow data to set the prior mean and standard deviation on the steady-state level of the financing gap share, ![]() .
.
The aggregate of entrepreneurs in the model can easily represent the universe of corporations in Compustat: they earn operating cash flows from their capital stock and use them to finance new capital expenditures. They also access financial markets to either raise external financing or to liquidate part of their assets.
Starting from the accounting cash flow identity (3) in section 1, I can map its components to the flow of funds constraint of an entrepreneur that is willing to buy and install new capital goods in my model in section 2:
The returns on the equity holdings,
From (31), it is easy to derive the model equivalent of the Financing Gap Share defined in (5). Entrepreneurs with the best technology to install capital goods (sellers) are willing to borrow resources and to utilize their liquid assets to carry on their
investment. The aggregate financing gap over the
![]() measure of sellers, S, can be written as:
measure of sellers, S, can be written as:
![\displaystyle \int_{S}\left[\underbrace{R_{t}^{K}N_{s,t-1}}_{CF_{s,t}^{O}}- \underbrace{PC_{s,t}}_{DIV_{s,t}}-\underbrace{P_{t}^{K}i_{s,t}}_{CAPX_{s,t}}\right]f(A_{s,t})ds](img309.gif) |
||
![\displaystyle \int_{S} \left[\underbrace{Q_{t}^{A}\phi \left( 1-\delta\right) N_{s,t-1}} _{NFI_{s,t}}+\underbrace{\left(R_{t-1}^{B}B_{s,t-1}-B_{s,t}\right) } _{\Delta CASH_{s,t}}-\underbrace{\theta Q_{t}^{A}A_{s,t}i_{s,t}}_{\left( CF_{s,t}^{D}+CF_{s,t}^{EO}\right) }\right]f(A_{s,t})ds](img310.gif) |
||
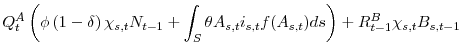 . . |
so that the average financing gap share is equal to the mean ratio of the market value of the resources raised by external finance,
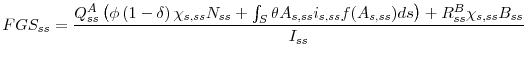 . . |
I set a Beta prior on the distribution of
Similarly, I use Compustat evidence to choose a prior on the steady-state share of the financing gap that is covered by portfolio liquidations of equity claims,
![]() (
( ![]() (1-
(1-![]() )
)
![]()
![]() ), and government bonds,
), and government bonds,
![]()
![]()
![]() :
:
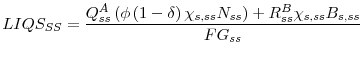 . . |
I choose a prior the average share of the Financing Gap covered by portfolio liquidations, ![]() , to be a Beta distribution with mean equal to .25 and a standard deviation of .10.
, to be a Beta distribution with mean equal to .25 and a standard deviation of .10.
I also help the identification of ![]() by calibrating the share of government liquidity held by entrepreneurs over GDP,
by calibrating the share of government liquidity held by entrepreneurs over GDP,
![]() . I choose to calibrate the amount of liquid assets in circulation in the economy by referring to the Flow of funds data on corporate asset levels (table L.102). There, I
identify a broad set of government-backed liquid assets held by firms that include Treasuries, Currency, Checking and Saving deposits, Municipal Bonds, and GSE and Agency-backed private bonds. Along the sample considered, corporate holdings of government-backed liquid assets amounts to a share of
around 5% of GDP. I therefore fix
. I choose to calibrate the amount of liquid assets in circulation in the economy by referring to the Flow of funds data on corporate asset levels (table L.102). There, I
identify a broad set of government-backed liquid assets held by firms that include Treasuries, Currency, Checking and Saving deposits, Municipal Bonds, and GSE and Agency-backed private bonds. Along the sample considered, corporate holdings of government-backed liquid assets amounts to a share of
around 5% of GDP. I therefore fix ![]() . This is clearly an understatement of the extent of the average amount of government-backed liquidity over GDP present in the US economy, for which
the public debt share of GDP alone over the same period amounts to an average of around 60%. I make this choice because aggregate Flow of funds data suggest that firms are not the primary holders of government bonds and because the primary goal of this work is to offer a realistic picture of the
balance sheet and cash flow statements of US corporations to study the interaction between financial market conditions and investment decisions.
. This is clearly an understatement of the extent of the average amount of government-backed liquidity over GDP present in the US economy, for which
the public debt share of GDP alone over the same period amounts to an average of around 60%. I make this choice because aggregate Flow of funds data suggest that firms are not the primary holders of government bonds and because the primary goal of this work is to offer a realistic picture of the
balance sheet and cash flow statements of US corporations to study the interaction between financial market conditions and investment decisions.
This brings the discussion to the calibration of fiscal parameters that govern the government budget constraint in steady state:
To calibrate the tax rates on capital and labor income,
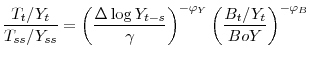 |
where I calibrate
A few more choices of priors require a brief discussion. In particular, the parameters governing the distribution of idiosyncratic technology of entrepreneurs
![]() . I set priors on
. I set priors on ![]() and on the
difference
and on the
difference
![]() , so that combined with prior mean values for the financial parameters, I can approximately match the steady-state share of Sellers in the model with the average share of
Compustat firms that rely on financial markets in every quarter,
, so that combined with prior mean values for the financial parameters, I can approximately match the steady-state share of Sellers in the model with the average share of
Compustat firms that rely on financial markets in every quarter, ![]() . Finally, I calibrate the quarterly rate of capital depreciation to 0.025, a standard value in the RBC and DSGE literature.
. Finally, I calibrate the quarterly rate of capital depreciation to 0.025, a standard value in the RBC and DSGE literature.
The model is buffeted by i.i.d. random innovations:
that respectively hit seven exogenous processes: the growth rate of total factor productivity,
To conclude, the priors on the persistence parameters for the exogenous processes are all Beta distributions. All have mean equal to 0.6 and standard deviation 0.2, except for the persistence of the neutral technology process, ![]() . The monetary policy shock is assumed to be i.i.d., because the Taylor rule already allows for autocorrelation in the determination of the risk-free rate. The priors on the standard deviations of the innovations expressed in percentage deviations
are inverse Gammas with mean 0.5 and standard deviation equal to 1, excluding the shock to the monetary policy rule,
. The monetary policy shock is assumed to be i.i.d., because the Taylor rule already allows for autocorrelation in the determination of the risk-free rate. The priors on the standard deviations of the innovations expressed in percentage deviations
are inverse Gammas with mean 0.5 and standard deviation equal to 1, excluding the shock to the monetary policy rule,
![]() , to the price and wage mark-ups,
, to the price and wage mark-ups,
![]() and
and
![]() , and to the discount factor, where the prior has a mean of 0.10 and a standard deviation of 1. I set a prior on the standard deviation of the measurement error on the
spread that wants to be conservative with a mean of 15 basis points and a standard deviation of 5.
, and to the discount factor, where the prior has a mean of 0.10 and a standard deviation of 1. I set a prior on the standard deviation of the measurement error on the
spread that wants to be conservative with a mean of 15 basis points and a standard deviation of 5.
I complement this set of calibrated parameters and exogenous priors, with prior information on the second moments of the observed variables computed over a pre-sample that spans from 1954Q3 to 1988Q4. Pre-sample data is available for all the series, excluding the spread, ![]() . In particular, I follow (Christiano et al., 2011a) and set prior distributions on the variance of the observable variables using the asymptotic Normal distribution of
their GMM estimator computed over the pre-sample. This helps the identification of the model parameters by directing the estimation procedure toward regions of the parameter space that can generate business cycle fluctuations of plausible magnitude. Table 5 reports the mean and
standard deviations of the moment priors.
. In particular, I follow (Christiano et al., 2011a) and set prior distributions on the variance of the observable variables using the asymptotic Normal distribution of
their GMM estimator computed over the pre-sample. This helps the identification of the model parameters by directing the estimation procedure toward regions of the parameter space that can generate business cycle fluctuations of plausible magnitude. Table 5 reports the mean and
standard deviations of the moment priors.
4 Results
This section reports the results of the Bayesian estimation of the model parameters, devolving particular attention to the coefficients that govern the financial structure of the model. I then discuss the model fit and describe the impulse responses of key variables to a financial intermediation shock. I present the variance decomposition of the observable variables and their historical decomposition during the Great Recession. I conclude the section with evidence that wage rigidities are the key element that allows the financial intermediation shock to play a fundamental role in driving the business cycle in the past 20 years of data.
4.1 Parameter Estimates
Table 3 reports the median and 90% confidence intervals for the set of model parameters, while table 6 reports the same quantiles for model-implied moments of the key financial variables introduced in section 1 and compares them with their empirical counterparts. I compute the confidence interval by running a Markov chain Monte Carlo exploration of the posterior distribution.
Estimates of conventional parameters such as those governing price and wage rigidities, the investment adjustment cost friction as well as the degree of persistence and magnitudes of traditional shocks are in line with previous findings in the literature. The estimated steady-state annualized
spread, 400![]() , ranges between 1 and 36 basis points, despite its prior distribution mean matching a quarterly risk spread equal to 250 basis points ((Cúrdia & Woodford, 2010b)). The estimation favors steady-state equilibria in which financial intermediation costs are low and attributes the observed cyclical fluctuations in the spread to large realizations of the financial shock (see 7 where the
model-implied volatility of the spread is higher than in the data).
, ranges between 1 and 36 basis points, despite its prior distribution mean matching a quarterly risk spread equal to 250 basis points ((Cúrdia & Woodford, 2010b)). The estimation favors steady-state equilibria in which financial intermediation costs are low and attributes the observed cyclical fluctuations in the spread to large realizations of the financial shock (see 7 where the
model-implied volatility of the spread is higher than in the data).
Table 6 shows that the estimated steady-state value of the financing gap share assumes values that are consistent with Compustat evidence. The 90% confidence interval for the model-implied moment ranges between
![]()
![]() , compatible with the
, compatible with the ![]() fraction of total investment funded using financial markets found in Compustat data in section 1. The estimated steady-state share of the financing gap that is covered by liquidation of assets
ranges between
fraction of total investment funded using financial markets found in Compustat data in section 1. The estimated steady-state share of the financing gap that is covered by liquidation of assets
ranges between
![]() , compatible with the
, compatible with the ![]() average over the whole sample
period available in Compustat.
average over the whole sample
period available in Compustat.
Finally, the table shows the average over time of the fraction of firms that record a negative Financing Gap in Compustat in each quarter and compares its model equivalent,
![]() =
=
![]() . The model estimation does not match this moment perfectly, although the 90% confidence interval (
. The model estimation does not match this moment perfectly, although the 90% confidence interval (
![]() ) contains values that are far from the sample realization observed in Compustat (
) contains values that are far from the sample realization observed in Compustat (![]() ).
).
4.2 Model Fit
Table 7 reports confidence intervals for the standard deviations of the variables relative to output volatility and compares them to the sample data standard deviations. The table also includes the standard deviations implied by the endogenous priors on the second moments of the observables introduced in section 3.1.
The model is able to match the absolute volatility of investment, as well as the standard deviation of the risk-free-rate observed in the data. The estimation also delivers standard deviations that are compatible with pre-sample evidence for inflation and hours worked and tries to balance the differences in the volatility of the growth rate of real wages across the two periods. The model however comes short when trying to match the standard deviations of output and consumption. As discussed in section 2.7, workers in the model earn and consume a large fraction of total GDP, with no access to financial market that can help smooth out the effect of aggregate shocks on labor earnings over time. The increased volatility in households' consumption translates in higher volatility of total output and prevents the model from delivering a successful matching of the relative volatility of the observables (Table 7).
Table 8 reports the autocorrelation coefficients of order one of the observable variables, compared to their data counterparts. The model is able to reproduce significant positive autocorrelations for all the observables, except for consumption growth. The model matches the autocorrelations coefficients for the nominal interest rate, the spread, the level of hours worked and for the rate of growth of real wages (computed excluding the last recession, see note in table 8) at a 90% confidence level. It fails to generate a sufficient level of persistence for output, investment and consumption, while it overstates the autocorrelation of inflation.
4.3 Impulse Responses to a Financial Intermediation Shock
Figure 9 reports the impulse responses to a one-standard-deviation financial shock, evaluated at the estimated parameter mode.
The plots are intuitive and show a recession of plausible magnitude, in which the negative response of output, consumption and investment on impact is significant at a ![]() confidence
level.
confidence
level.
When the financial intermediation cost rises, the spread between the cost of raising external resources of entrepreneurs and the risk free rate rises by 150 basis points on an annual
basis. Investment drops by ![]() on impact, while consumption growth is reduced by
on impact, while consumption growth is reduced by ![]() . Accordingly, the growth rate of output falls by
. Accordingly, the growth rate of output falls by ![]() .
.
A remarkable feature of the impulse responses is that a negative financial shock in the model delivers a large drop in the price of equity, driving it 4% below its steady-state level on impact. Hence, the financial intermediation shock generates intuitive and highly volatile cyclical movements in asset prices. This finding contrasts with the rise in equity price that follows a liquidity shock in the original KM model as carefully characterized by (Shi, 2011). 20
The high degree of persistence of the impulse responses is attributable partly to the high autocorrelation coefficient of the exogenous process for the intermediation cost,
![]() , that tries to match the features of the observed high-yield spread in the data (Figure 10). In addition, the slow convergence of the economy to its steady
state after a financial intermediation shock is also due to the path followed by equilibrium real wages and aggregate consumption. As discussed in section 2.7, households do not trade on financial markets and consequently are only able to smooth out their consumption
through wage re-optimization. Modeling entrepreneurs and workers as members of a single representative household, as in (Shi, 2011), can eliminate barriers to intertemporal consumption smoothing and allow for a less persistent response of real wages and workers' consumption path.
21
, that tries to match the features of the observed high-yield spread in the data (Figure 10). In addition, the slow convergence of the economy to its steady
state after a financial intermediation shock is also due to the path followed by equilibrium real wages and aggregate consumption. As discussed in section 2.7, households do not trade on financial markets and consequently are only able to smooth out their consumption
through wage re-optimization. Modeling entrepreneurs and workers as members of a single representative household, as in (Shi, 2011), can eliminate barriers to intertemporal consumption smoothing and allow for a less persistent response of real wages and workers' consumption path.
21
One additional source of persistence originates from the endogenous effect that a financial shock has on the average investment technology adopted in the economy. A negative financial shock increase the cost of borrowing for the most productive entrepreneurs (with a high level of investment technology). The financial shock also reduces the rate of return to savings on financial assets. This induces some of the less efficient entrepreneurs to start using their capital accumulation technology instead of trading assets on financial markets. Referring to Figure 8, higher financial intermediation costs lower the amount of external resources available to the most efficient entrepreneurs and at the same increase the fraction of Keepers, so that as a result the average relative price of investment in the economy goes up. In a model with heterogenous capital accumulation technologies, a negative financial shock induces a contemporaneous adverse investment-specific technology shock (ISTSs), as pointed out in (Buera & Moll, 2011). Empirical work by (Justiniano et al., 2010) shows that ISTSs can account for large fractions of business cycle variation in output and suggest that these disturbances could originate on financial markets. (Kahn & Thomas, 2011) also study the effects of credit market shocks on the allocation of capital across firms with heterogeneous productivity. They find that credit shocks are amplified and propagated through large negative endogenous technology shocks, generated by disruptions to the distribution of capital away from the most productive firms. In my model a financial shock is paired endogenously with a negative ISTS.22
4.4 Variance Decomposition
This section quantifies the relative importance of the fundamental shocks in the model in driving business cycle fluctuations. Table 9 reports the contribution of each shock to the volatility of the observable variables in periodic cycles that range between 6 to 32 quarters in length, as in (Stock & Watson, 1999).
The sixth column suggests that the financial intermediation shock is the most important source of business cycle fluctuations, explaining around ![]() of the unconditional variance of GDP
growth and around
of the unconditional variance of GDP
growth and around ![]() of the volatility of investment. The shock is also able to explain around
of the volatility of investment. The shock is also able to explain around ![]() of cyclical movements in inflation and the vast majority of the variance of the nominal risk-free rate. This result suggests an active role of monetary policy through the Taylor rule in response to changes in output and prices induced by financial disturbances.23
of cyclical movements in inflation and the vast majority of the variance of the nominal risk-free rate. This result suggests an active role of monetary policy through the Taylor rule in response to changes in output and prices induced by financial disturbances.23
The financial intermediation wedge,
![]() , maps closely to the observed high-yield spread series. The estimation procedure naturally attributes around
, maps closely to the observed high-yield spread series. The estimation procedure naturally attributes around ![]() of cyclical fluctuations of the observed spread to the financial shock. This result is a product of the log-linearization of the model's equilibrium conditions that does not allow pricing of other sources of aggregate risk.24
of cyclical fluctuations of the observed spread to the financial shock. This result is a product of the log-linearization of the model's equilibrium conditions that does not allow pricing of other sources of aggregate risk.24
Column 1 in table 9 shows how, according to the model estimates, neutral technology shocks only explain a small fraction of the variance of GDP growth in the last 20 years. The 90% confidence inverval for the share of GDP growth variance explained by TFP shocks ranges from 9% to 20%. This result confirms the conclusions of previous work in the empirical macro literature that attributes the cause of economic fluctuations in the past 20 years predominantly to demand shocks.25
4.5 Smoothed Shocks and Historical Decomposition of the Great Recession
In this section I present the historical contribution of the financial shock to the dynamics of output growth along the sample and run some counterfactual exercises to study the contribution of aggregate shocks to the dynamics of the Great Recession.
Figure 11 provides a time series representation of the evolution of quarterly output growth conditional on the presence of financial shocks alone (red dotted line) and compares it to the observed data series (black solid line). The two lines show remarkably similar features and the financial shock seems to drive output growth variations alone in the boom of the 2000s. The shock is also identified as the main cause of the recessions in 1990-1991, when the junk bond market and the Savings and Loans industry collapsed, as well as in 2008-2010, marked by the upheaval on the subprime mortgage market.
Figure 12 offers a closer look at the contribution of shocks in the model to the evolution of output growth during the last recession. I concentrate on the role of financial shocks,
![]() , as well as of the neutral technology shocks,
, as well as of the neutral technology shocks,
![]() , and the two policy disturbances: the monetary policy shocks,
, and the two policy disturbances: the monetary policy shocks,
![]() , modeled as random deviations from the Taylor rule, and the government spending shock,
, modeled as random deviations from the Taylor rule, and the government spending shock,
![]() . I compute the counterfactual smoothed series for output growth at the posterior mode. This exercise shows how output growth dynamics would have differed from the path
observed historically when excluding the smoothed realizations of each type of shock one at a time.
. I compute the counterfactual smoothed series for output growth at the posterior mode. This exercise shows how output growth dynamics would have differed from the path
observed historically when excluding the smoothed realizations of each type of shock one at a time.
For example, the top left panel in Figure 12 shows what output growth would have been in absence of the financial shock (red dashed line) compared to the data (blue solid line) from 2007Q1 to 2010Q1. The estimation suggests that a series of negative financial shocks raised intermediation costs and slowed down output growth starting in 2007Q3. In absence of the negative financial shocks, the contraction in output growth observed in the data would have been isolated to the second half of 2008 and would have been more limited in magnitude.
A second interesting finding comes from the analysis of the role of innovations to total factor productivity. The top right panel suggests that the past recession was characterized by an increase in TFP, in line with recent findings by (Fernald, 2009) and (Shimer, 2010). As evidenced by the red dashed line, in absence of positive technology shocks, output would have contracted by an additional ![]() at the trough and the recovery
would have been slower.
at the trough and the recovery
would have been slower.
The bottom left panel also suggests that government spending shocks played an important role in reducing the impact on output of the recession. In absence of positive government spending shocks, the red dashed line shows that output would have fallen by an additional ![]() at the trough. Public sector deficits are beneficial in the model, as financially constrained entrepreneurs demand government bonds as a form of precautionary savings to insure against the future
arrival of investment opportunities, in the spirit of policy experiments in (Kiyotaki & Moore, 2008) and (Guerrieri & Lorenzoni, 2011).
at the trough. Public sector deficits are beneficial in the model, as financially constrained entrepreneurs demand government bonds as a form of precautionary savings to insure against the future
arrival of investment opportunities, in the spirit of policy experiments in (Kiyotaki & Moore, 2008) and (Guerrieri & Lorenzoni, 2011).
On the other hand, the bottom right panel and the smoothed series of monetary policy shocks in Figure 13 seem to suggest that, although the reduction in the federal funds rate helped sustain economic growth at the onset of the recession, monetary policy interventions became ineffective and that the zero-lower bound on the nominal interest rate became binding in the second half of 2008. The series of positive monetary policy shocks in Figure 13 suggest that the nominal interest rate has been consistently higher than the value implied by the estimated Taylor-type rule.26
4.6 Why are Financial Shocks Important?
Any general equilibrium model that aims to identify the role of non-TFP shocks as possible drivers of business cycle fluctuations has to be able to generate the positive co-movement between consumption and investment observed in the data at business cycle frequencies. In an influential article, (Barro & King, 1984) show how, in a general equilibrium model with flexible prices and wages in the Real Business Cycle tradition, it is hard to detect sources of business cycle fluctuations different from changes in total factor productivity, that can trigger positive co-movement of hours worked, consumption and investment. In fact, any shock that increases the equilibrium quantity of hours worked on impact must induce a contemporaneous drop in consumption to maintain the equilibrium equality between the marginal product of labor and the marginal rate of substitution between consumption and hours worked (see (Justiniano et al., 2010) for further details).
In this section I explore the reason why the posterior maximization favors the financial shock as the main driver of business cycle fluctuations. I find that nominal rigidities, and in particular sticky wages are the key element in driving aggregate consumption, investment and hours worked in the same direction on impact after a financial intermediation shock.
4.6.1 Sticky Wages and Positive Co-movement of Investment and Consumption
In this section I discuss the importance of the assumption of nominal and real wage rigidities in generating a recession in which aggregate output, consumption and investment drop simultaneously on impact after the shock. To establish the importance of the frictions, I first discuss the impulse responses in the benchmark model estimated under the assumption that wages are sticky. I then re-estimate the model under flexible wages and compare the impulse responses to the benchmark. I finally analyze the variance decomposition of the model under flexible wages and note how the new assumption significantly reduces the importance of the financial intermediation shock in explaining business cycle fluctuations.
In my model there are two classes of agents: entrepreneurs and households. Entrepreneurs optimize their stream of consumption through time and save by accumulating equity claims as well as government bonds. They do not supply hours worked on the labor market. Households, on the other hand, have no access to financial markets and consume the realization of their income in every period. This feature of the model allows me to describe intuitively the intertemporal and the intratemporal transmission channels of an intermediation shock, by studying the effects on each of the two sets of agents separately.
Figure 10 shows the impulse responses for aggregate output, investment and consumption growth to a one-standard deviation financial shock, together with the breakdown of aggregate consumption into entrepreneurs' and households' shares, ![]() and
and ![]() respectively. The Figure also shows the dynamics of hours worked. The impulse response in the black
dashed lines are computed at the posterior mode parameters in table 3 for the benchmark model with price and wage rigidities.
respectively. The Figure also shows the dynamics of hours worked. The impulse response in the black
dashed lines are computed at the posterior mode parameters in table 3 for the benchmark model with price and wage rigidities.
On the intertemporal margin, If the intermediation spread,
![]() , rises and intermediation of financial claims becomes more expensive, entrepreneurs with a good investment opportunity perceive an increase in their cost of borrowing: the price
of equity claims drops and entrepreneurs can rely on a reduced amount of external resources to install new capital. As a consequence investment,
, rises and intermediation of financial claims becomes more expensive, entrepreneurs with a good investment opportunity perceive an increase in their cost of borrowing: the price
of equity claims drops and entrepreneurs can rely on a reduced amount of external resources to install new capital. As a consequence investment, ![]() , plunges. On the other side of the
financial market, entrepreneurs with inefficient technologies expect lower real returns on financial assets and consequently reduce their savings and increase their consumption. In aggregate, investment and savings drop, while consumption of entrepreneurs,
, plunges. On the other side of the
financial market, entrepreneurs with inefficient technologies expect lower real returns on financial assets and consequently reduce their savings and increase their consumption. In aggregate, investment and savings drop, while consumption of entrepreneurs, ![]() , rises.27
, rises.27
On the intratemporal margin, instead, the model is able to make households' consumption drop on impact thanks to sticky wages. The drop in aggregate demand translates into a downward shift in the demand for labor inputs. If workers cannot re-optimize their wages freely, the decrease in labor
demand translates into a large drop in the equilibrium amount of hours worked, ![]() . The drop in hours amplifies the negative effect of the shock on aggregate production and GDP, and
contemporaneously reduces the wage bill,
. The drop in hours amplifies the negative effect of the shock on aggregate production and GDP, and
contemporaneously reduces the wage bill, ![]()
![]() . In equilibrium the drop in the
wage bill pushes down households' and aggregate consumption,
. In equilibrium the drop in the
wage bill pushes down households' and aggregate consumption, ![]() and
and ![]() ,
and generates the right positive co-movement between investment and consumption on impact. The shock has also a secondary effect: the fall in aggregate demand reduces the marginal costs of intermediate monopolists and increases the price mark-up and firms' monopolistic profits. Households own the
intermediate firms and the rise in profits levels helps them sustain their consumption after the shock hits. The secondary effect however is not strong enough to dominate the drop in households' consumption generated by the decrease in the aggregate wage bill.28
,
and generates the right positive co-movement between investment and consumption on impact. The shock has also a secondary effect: the fall in aggregate demand reduces the marginal costs of intermediate monopolists and increases the price mark-up and firms' monopolistic profits. Households own the
intermediate firms and the rise in profits levels helps them sustain their consumption after the shock hits. The secondary effect however is not strong enough to dominate the drop in households' consumption generated by the decrease in the aggregate wage bill.28
To confirm this intuition, Figure 10 also shows the impulse response functions for the same variables at the posterior mode, when the model is re-estimated under the assumption that wages are perfectly flexible (blue solid lines).29 As in the case of sticky wages, the reduction in labor demand translates into lower equilibrium wages and hours worked. Simultaneously, lower real wages translate into higher mark-ups for the monopolistic firms and the increase in firms' profits. This generates a positive income effect for households that allows them to reduce their labor supply. The equilibrium outcome shows a larger negative adjustment in the wage rate relative to the benchmark sticky wages model, while hours worked drop by a lower amount. Households' wage bill falls, but they are able to keep a smoother consumption profile with respect to the sticky wages case by relying on both a sustained equilibrium level of hours worked and higher profits from the monopolistic firms. As a consequence, the drop in households' consumption is not large enough to drive aggregate consumption down in response to a financial intermediation shock. Consumption and investment move in opposite direction in the short run and the financial shock loses its ability to generate an empirically plausible recession.
This intuition is confirmed by comparing the variance decomposition exercises for the model estimated under the assumption of sticky and flexible wages. I report results for the two cases respectively in tables 9 and 10.30 The estimation of the model under flexible wages shows that the importance of the financial intermediation shock in explaining business cycle fluctuations in output, investment and consumption growth drops significantly with respect to the sticky wages model. The shock is able to explain 9.5% of GDP growth variance and 49% of aggregate investment growth variance compared to 35% and 60% under sticky wages. The financial shock in the benchmark model is able to explain 7% of business cycle volatility in aggregate consumption, while under flexible wages it can account for a mere 1%.
This result is in line with the intuition discussed for the impulse responses in Figure 10: financial intermediation shocks are not able to generate the right co-movement between investment and consumption and hence meaningful booms and recessions. Consequently, under flexible
wages, TFP shocks gain importance in explaining business cycle fluctuations as in the traditional RBC literature (from 13% to 30% of GDP growth volatility explained at business cycle frequencies). Similarly, exogenous shocks to wage mark-ups, ![]() , increase their relevance in explaining aggregate cycles. As noted in (Justiniano et al., 2010), sticky wages create an endogenous wedge between the real wage and the marginal rate of substitution between
consumption and hours worked in the intratemporal Euler equation of the households. Under flexible wages, exogenous shocks to the wage mark-up substitute the endogenous change in equilibrium mark-ups induced by the other structural shocks (including financial intermediation shocks) in the
sticky-wage case. As a result, exogenous wage mark-up shocks go from explaining 12% of GDP growth variance under sticky wages to 25% under flexible wages.31
, increase their relevance in explaining aggregate cycles. As noted in (Justiniano et al., 2010), sticky wages create an endogenous wedge between the real wage and the marginal rate of substitution between
consumption and hours worked in the intratemporal Euler equation of the households. Under flexible wages, exogenous shocks to the wage mark-up substitute the endogenous change in equilibrium mark-ups induced by the other structural shocks (including financial intermediation shocks) in the
sticky-wage case. As a result, exogenous wage mark-up shocks go from explaining 12% of GDP growth variance under sticky wages to 25% under flexible wages.31
5 Conclusions
In this paper I have addressed the question of how important are shocks to the ability of the financial sector in driving the business cycle. The main finding of this research is that the contribution of financial shocks to cyclical fluctuations is very large and accounts for around 35% of output and 60% of investment volatility, when estimated on the last 20 years of US macro data.
In obtaining this result, I have estimated a dynamic general equilibrium model with nominal rigidities and financial frictions in which entrepreneurs rely on external finance and trading of financial claims to fund their investments. The model features stylized financial intermediaries (banks) that bear a cost to transfer resources from savers to investors.
Shocks to the financial intermediation costs intuitively map into movements of the interest rate spreads and are able to explain the dynamics of the real variables that shaped the last recession, as well as the 1990-1991 downturn and the boom of the 2000s. I find that nominal rigidities play an important role in the transmission of the financial shocks. In particular wage rigidities allow the shock to generate the positive co-movement of investment and consumption that is observed in the data along the business cycles. Assuming flexible wages and re-estimating the model on the same data series along the same sample period delivers very different results: the financial intermediation shock is only able to explain around 9.5% of output growth and 49% of investment growth volatilities.
Bibliography
The Quarterly Journal of Economics 84(3):488-500.
Econometric Reviews 26(2):113-172.
The Quarterly Journal of Economics pp. 817-839.
Handbook of Macroeconomics, edited by J. B. Taylor and M. Woodford 1:1341-1393.
Manuscript, New York University .
Working Paper .
Journal of Monetary Economics 12(3):383-398.
The American Economic Review 87(5):893-910.
Econometrica 75(3):781-836.
Journal of Money, Credit and Banking 27(4):1354-86.
Presentation (mimeo) .
NBER Working Paper (12647).
Handbook of Monetary Economics, Vol 3A, chapter 7, edited by B.M. Friedman and M. Woodford pp. 285-367.
Journal of Economic Dynamics and Control p. forthcoming.
Journal of Political Economy 113(1):1-45.
Working Paper Series, European Central Bank (1192).
Working Paper, Northwestern University .
Federal Reserve Bank of St. Louis 92(4):229-264.
Journal of Money, Credit and Banking 42:3-35.
Federal Reserve Bank of New York .
Journal of Business and Economic Statistics 25(2):123-143.
Journal of Monetary Economics 53(3):369-399.
Journal of Monetary Economics 46(2):281-313.
Journal of the American Statistical Association 63(324):1132-1161.
Manuscript, Federal Reserve Bank of San Francisco .
Norges Bank Working Paper N.2010/30 .
Oxford Review of Economic Policy 15(3):132.
Journal of Monetary Economics 56(4).
American Economic Review p. forthcoming.
Journal of Monetary Economics 1954(5):1480-1507.
Econometrica 70(1):47-89.
NBER Working Paper (17583).
The Quarterly Journal of Economics 109(4):841-879.
Journal of Public Economics 91:1273 - 1297.
The American Economic Review p. forthcoming.
Journal of Monetary Economics 57(2):132-145.
Working Paper .
Journal of Political Economy 105(2):211Ð248.
International Economic Review 46:317 - 349.
Unpublished manuscript, Princeton University and Edinburgh University .
Job Market Paper pp. 1-70.
Review of Financial Studies .
Journal of Econometrics 156(2):304-321.
The American Economic Review 46(2):97-113.
Job Market Paper .
In T. Cooley (ed.), Frontiers of Business Cycle Research. Princeton University Press.
University of Toronto Department of Economics, Working Papers Series (434).
Working Paper, University of Chicago .
Journal of Applied Econometrics 20(2):161-183.
American Economic Review 97(3):586-606.
In J. B. Taylor & M. Woodford (eds.), Handbook of Macroeconomics, vol. 1 of Handbook of Macroeconomics, chap. 1, pp. 3-64. Elsevier.
McGraw-Hill Professional.
American Economic Review 80(2):382-388.
Princeton University Press.
Tables and Figures
| Moment |
|
||
| E[
|
1 | 73.11% | 35.64% |
| E[
|
0.96% | 1.03% | 0.81% |
| 100 Stdev[
|
4.9% | 2.7% | 3.6% |
| Corr[
|
1 | 0.63 | 0.30 |
Variables V
Source: Compustat and Flow of Funds Tables. Sample Period 1989Q1 - 2010Q1.
| Variable |
Mean( |
StdDev( |
| FGS |
35.45% | 4.74% |
| FGS |
18.74% | 5.17% |
| FGS |
39.12% | 6.75% |
| WKS |
32.05% | 4.34% |
| DIVS |
25.87% | 7.02% |
| DES |
75.67% | 22.45% |
| LIQS |
24.33% | 22.45% |
| CASHS |
20.74% | 14.49% |
Mean and standard deviations of variables across sample Period 1989Q1 - 2010Q1, if not otherwise specified. Source: Compustat. 1. Financing Gap Share of Capital Expenditure defined in equation 5, total of U.S. corporations. 2. Financing Gap Share, Chari and Kehoe's method, total of North American corporations (U.S. and Canada). Sample period: 1971 - 2009. 3. Financing Gap Share, Chari and Kehoe's method, total of North American corporations. 4. Share of Total Financing Gap due to working capital needs. U.S. corporations. 5. Weight of Dividend payouts on Total Financing Gap. U.S. corporations. 6. Share of Financing Gap funded by external sources (debt and/or equity). U.S. corporations. 7. Share of Financing Gap funded by portfolio liquidations. U.S. corporations 8. Share of Financing Gap funded by variations in cash reserves. U.S. corporations
Parameters Estimates - Sticky Wages
| Parameter | Explanation | Prior |
Mode | [5% |
| Entrepreneurs's tech distribution (level) | N(0.90,.010) | 0.879 | [ 0.787 - 1.065 ] | |
| Entrepreneurs's tech distribution (width) | IG(0.025,0.05) | 0.023 | [0.019 - 0.033 ] | |
|
|
Discount factor | Calibrated | 0.900 | [ - - - ] |
| Habit | Calibrated | 0.900 | [ - - - ] | |
|
|
Labor Supply | N(2,0.50) | 1.779 | [ 1.027 - 2.604 ] |
| Inverse Frisch | G(2,0.50) | 1.295 | [ 0.862 - 1.961 ] | |
| Borrowing Constraint | B(0.30,0.10) | 0.271 | [ 0.257 - 0.297 ] | |
|
|
Liquidity Constraint | G(0.50,0.10) | 0.074 | [ 0.027 - 0.102 ] |
| Liquidity over GDP | Calibrated | 0.025 | [ - - -] | |
|
|
Fiscal Rule - Debt | Calibrated | 0.500 | [ - - - ] |
|
|
Fiscal Rule - Output | Calibrated | 0.130 | [ - - - ] |
| Capital Tax Rate | Calibrated | 0.184 | [- - - ] | |
| Labor Tax Rate | Calibrated | 0.223 | [- - - ] | |
| Share of Capital | B(0.30,0.10) | 0.287 | [ 0.266 - 0.315 ] | |
| Investment Adj. Costs | G(2,0.50) | 1.276 | [ 0.965 - 2.060 ] | |
|
|
Price Mark up | IG(0.15,0.05) | 0.061 | [ 0.047 - 0.079 ] |
| Calvo prices | B(0.70,0.10) | 0.799 | [ 0.722 - 0.835 ] | |
|
|
Indexation Prices | B(0.50,0.15) | 0.125 | [ 0.058 - 0.236 ] |
|
|
Wage Mark up | IG(0.15,0.05) | 0.124 | [ 0.090 - 0.226 ] |
| Calvo wages | B(0.70,0.10) | 0.729 | [ 0.654 - 0.781 ] | |
|
|
Indexation Wages | B(0.50,0.15) | 0.201 | [ 0.118 - 0.378 ] |
|
|
Taylor rule - Inflation | N(1.7,0.30) | 1.900 | [ 1.716 - 2.091] |
| Taylor rule - Output | N(0.125,0.05) | 0.269 | [ 0.2400 - 0.300 ] | |
| Taylor rule - Persistence | B(0.60,0.20) | 0.847 | [ 0.815 - 0.870] | |
| SS Inflation | N(0.50,0.10) | 0.758 | [ 0.584 - 0.849 ] | |
| SS Output Growth | N(0.30,0.05) | 0.326 | [ 0.254 - 0.395 ] | |
| SS Spread | G(0.625,0.15) | 0.018 | [ 0.003 - 0.090 ] | |
|
|
MA(1) Price Mark up | B(0.50,0.10) | 0.820 | [ 0.653 - 0.853 ] |
|
|
MA(1) Wage Mark up | B(0.50,0.10) | 0.660 | [ 0.416 - 0.751 ] |
| AR(1) TFP shock | B(0.40,0.20) | 0.412 | [ 0.301 - 0.487 ] | |
| AR(1) Gov't spending | B(0.60,0.20) | 0.982 | [ 0.960 - 0.991 ] | |
| AR(1) Price Mark up | B(0.60,0.20) | 0.933 | [ 0.880 - 0.968 ] | |
| AR(1) Wage Mark up | B(0.60,0.20) | 0.890 | [ 0.784 - 0.914 ] | |
|
|
AR(1) Financial Spread | B(0.60,0.20) | 0.981 | [ 0.972 - 0.984 ] |
| AR(1) Intertemporal pref. | B(0.40,0.20) | 0.973 | [ 0.947 - 0.990] | |
|
|
Stdev TFP Shock | IG(0.50,1) | 0.482 | [ 0.431 - 0.515 ] |
|
|
Stdev MP Shock | IG(0.50,1) | 0.119 | [ 0.107 - 0.140 ] |
|
|
Stdev Gov't Shock | IG(0.50,1) | 0.326 | [ 0.296 - 0.376] |
|
|
Stdev Pr. Mark up Shock | IG(0.50,1) | 0.151 | [ 0.127 - 0.187 ] |
|
|
Stdev Wage Mark up Shock | IG(0.50,1) | 0.298 | [ 0.264 - 0.368] |
|
|
Stdev Financial Shock | IG(0.50,1) | 4.870 | [ 4.212 - 5.603 ] |
|
|
Stdev Preference Shock | IG(0.50,1) | 0.027 | [ 0.025 - 0.030 ] |
|
|
Stdev Meas Error Spread | IG(0.25,1) | 0.475 | [ 0.482 - 0.565] |
Standard deviations of the shocks are scaled by 100 for the estimation with respect to the model. 1 N stands for Normal, B Beta, G Gamma and IG Inverse-Gamma1 distribution.
2 Posterior percentiles from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm Acceptance rate 31%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
Parameters Estimates - Flexible Wages
| Parameter | Explanation | Prior1 | Mode | [5%2 - 95%2] |
| Entrepreneurs's tech distribution (level) | N(0.90,.010) | 0.909 | [ 0.798 - 1.060] | |
| Entrepreneurs's tech distribution (width) | IG(0.025,0.05) | 0.023 | [0.018 - 0.028] | |
|
|
Discount factor | Calibrated | 0.900 | [ - - - ] |
| Habit | Calibrated | 0.900 | [ - - - ] | |
|
|
Labor Supply | N(2,0.50) | 1.855 | [ 1.179 - 2.542 ] |
| Inverse Frisch | G(2,0.50) | 0.438 | [ 0.291 - 0.589 ] | |
| Borrowing Constraint | B(0.30,0.10) | 0.268 | [ 0.252 - 0.285 ] | |
|
|
Liquidity Constraint | G(0.50,0.10) | 0.072 | [ 0.048 - 0.096 ] |
| Liquidity over GDP | Calibrated | 0.025 | [ - - - ] | |
|
|
Fiscal Rule - Debt | Calibrated | 0.500 | [ - - - ] |
|
|
Fiscal Rule - Output | Calibrated | 0.130 | [ - - - ] |
| Capital Tax Rate | Calibrated | 0.184 | [ - - - ] | |
| Labor Tax Rate | Calibrated | 0.223 | [ - - - ] | |
| Share of Capital | B(0.30,0.10) | 0.272 | [ 0.253 - 0.291 ] | |
| Investment Adj. Costs | G(2,0.50) | 2.470 | [ 1.842 - 3.339 ] | |
|
|
Price Mark up | IG(0.15,0.05) | 0.053 | [ 0.042 - 0.066 ] |
| Calvo prices | B(0.70,0.10) | 0.603 | [ 0.533 - 0.659 ] | |
| Indexation Prices | B(0.50,0.15) | 0.109 | [ 0.049 - 0.247 ] | |
|
|
Labor Pref | IG(0.15,0.05) | 0.161 | [ 0.098 - 0.261 ] |
|
|
Taylor rule - Inflation | N(1.7,0.30) | 1.764 | [ 1.582 - 1.914 ] |
| Taylor rule - Output | N(0.125,0.05) | 0.209 | [ 0.182 - 0.237 ] | |
| Taylor rule - Persistence | B(0.60,0.20) | 0.790 | [ 0.757 - 0.817 ] | |
| SS Inflation | N(0.50,0.10) | 0.786 | [ 0.685 - 0.884 ] | |
| SS Output Growth | N(0.30,0.05) | 0.343 | [ 0.276 - 0.400 ] | |
| SS Spread | G(0.625,0.15) | 0.013 | [ 0.001 - 0.028 ] | |
|
|
MA(1) Price Mark up | B(0.50,0.10) | 0.444 | [ 0.145 - 0.741 ] |
|
|
MA(1) Laboor Pref | B(0.50,0.10) | 0.297 | [ 0.171 - 0.406 ] |
| AR(1) TFP shock | B(0.40,0.20) | 0.153 | [ 0.080 - 0.244 ] | |
| AR(1) Gov't spending | B(0.60,0.20) | 0.983 | [ 0.963 - 0.992 ] | |
| AR(1) Price Mark up | B(0.60,0.20) | 0.981 | [ 0.970 - 0.988 ] | |
| AR(1) Labor Pref | B(0.60,0.20) | 0.672 | [ 0.326 - 0.928 ] | |
|
|
AR(1) Financial Spread | B(0.60,0.20) | 0.981 | [ 0.975 - 0.986 ] |
| AR(1) Intertemporal pref. | B(0.40,0.20) | 0.954 | [ 0.922 - 0.981 ] | |
|
|
Stdev TFP Shock | IG(0.50,1) | 0.450 | [ 0.417 - 0.483 ] |
|
|
Stdev MP Shock | IG(0.50,1) | 0.129 | [ 0.113 - 0.15 ] |
|
|
Stdev Gov't . Shock | IG(0.50,1) | 0.320 | [ 0.287 - 0.362 ] |
|
|
Stdev Pr. Mark up Shock | IG(0.50,1) | 0.225 | [ 0.169 - 0.314 ] |
|
|
Stdev Labor Pref Shock | IG(0.50,1) | 44.162 | [ 41.651 - 46.787 ] |
|
|
Stdev Financial Shock | IG(0.50,1) | 4.50 | [ 3.89 - 5.158 ] |
|
|
Stdev Preference Shock | IG(0.50,1) | 0.031 | [ 0.029 - 0.034 ] |
|
|
Stdev Meas Error Spread | IG(0.25,1) | 0.435 | [ 0.373 - 0.503 ] |
Standard deviations of the shocks are scaled by 100 for the estimation with respect to the model. 1. N stands for Normal, B Beta, G Gamma and IG Inverse-Gamma distribution
2. Posterior percentiles from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm. Acceptance rate 29%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
| Moment | Prior Type | Prior Mean | Prior Std |
| Var(
|
N | 1.15 | 0.18 |
| Var(
|
N | 16.35 | 2.63 |
| Var(
|
N | 0.29 | 0.04 |
| Var( |
N | 0.84 | 0.23 |
| Var( |
N | 0.43 | 0.10 |
| Var( |
N | 10.74 | 2.36 |
| Var( |
- | - | - |
| Var(
|
N | 0.20 | 0.03 |
| E[ |
B | 0.30 | 0.05 |
| E[ |
B | 0.25 | 0.10 |
Prior distributions on the variances of observables are the Normal asymptotic distributions of the GMM variance estimators, computed on a pre-sample that spans from 1954:Q3 to 1988:Q4. Source: Haver Analytics. Prior distributions on steady-state level of financing gap share (FGS
| Data | Model Median | [ 5% - 95% ] | |
| 0.355 | 0.364 | [ 0.349 - 0.378 ] | |
| 0.243 | 0.267 | [ 0.236 - 0.296 ] | |
|
|
0.49 | 0.610 | [ 0.586 - 0.630 ] |
Estimated steady-state level of financing gap share (FGS
| Observables | Data | Model Median | [ 5% - 95% ] | Prior Mean |
| Stdev
|
0.63 | 0.80 | [ 0.69 - 0.93 ] | 1.07 |
| Stdev
|
2.58 | 2.41 | [ 2.03 - 2.84 ] | 4.04 |
| Stdev
|
0.50 | 0.68 | [ 0.59 - 0.78 ] | 0.54 |
| Stdev
|
0.58 | 0.72 | [ 0.42 - 1.24] | 0.92 |
| Stdev
|
0.27 | 0.54 | [ 0.40 - 0.77] | 0.66 |
| Stdev
|
4.75 | 2.77 | [ 1.75 - 4.39] | 3.28 |
| Stdev |
0.52 | 1.11 | [ 0.75 - 1.84] | - |
| Stdev
|
0.75 | 0.58 | [0.49 - 0.67] | 0.45 |
Standard deviations of observable variables. Model implied vs. Data and implied prior distribution mean from Table 5. Source: Haver Analytics. Sample period: 1989Q1 - 2010Q1. Pre-sample for priors: 1954Q3 - 1988Q4. Posterior percentiles from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm. Acceptance rate 31%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
| Observables | Data | Model Median | [ 5% - 95% ] |
| Corr
|
0.47 | 0.194 | [ 0.003 - 0.382 ] |
| Corr
|
0.60 | 0.239 | [ 0.050 - 0.412 ] |
| Corr
|
0.51 | 0.140 | [ -0.050 - 0.326 ] |
| Corr
|
0.93 | 0.956 | [ 0.902 - 0.981 ] |
| Corr
|
0.52 | 0.782 | [ 0.621 - 0.889 ] |
| Corr
|
0.93 | 0.927 | [ 0.845 - 0.968 ] |
| Corr
|
0.81 | 0.742 | [ 0.455 - 0.899 ] |
| Corr
|
0.035 * | 0.312 | [ 0.112 - 0.492 ] |
Autocorrelation of Order 1 of Observable Variables. Model implied vs. Data Data source: Haver Analytics, Sample period 1989Q1 - 2010Q1. Posterior percentiles from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm. Acceptance rate 31%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
* The autocorrelation of real wages computed over a sample that ends in 2007:Q4 and excludes the last recession is 0.15.
| TFP | MP | Gov't | Price Mark up | Wage Mark up | Financial | Preference | Meas. Error | |
|---|---|---|---|---|---|---|---|---|
|
|
13.7 | 7.7 | 2.6 | 18.9 | 15.2 | 34.8 | 5.4 | 0.0 |
|
|
[8.6 - 20.1] | [4.9 - 11.1] | [1.6 - 4.4] | [13.3 - 25.8] | [8.7 - 24.6] | [25.4 - 45.5] | [4.1 - 7.0] | [0.0 - 0.0] |
|
|
5.8 | 3.5 | 0.5 | 19.9 | 4.3 | 60.80 | 4.6 | 0.0 |
|
|
[4.1 - 8.1] | [2.5 - 5.6] | [0.4 - 0.9] | [15.1 - 31.1] | [3.1 - 6.0] | [53.1 - 68.4] | [3.1 - 7.1] | [0.0 - 0.0] |
|
|
22.7 | 6.7 | 8.95 | 7.0 | 26.7 | 4.7 | 22.0 | 0.0 |
|
|
[15.9 - 30.3] | [3.7 - 10.0] | [5.8 - 13.3] | [3.6 - 11.1] | [18.2 - 37.3] | [1.9 - 8.9] | [17.3 - 26.5] | [0.0 - 0.0] |
| 0.7 | 2.8 | 0.9 | 3.4 | 1.9 | 85.9 | 4.0 | 0.0 | |
| [0.3 - 1.9] | [2.0 - 3.9] | [0.5 - 1.7] | [2.2 - 5.2] | [0.9 - 3.4] | [88.9 - 90.2] | [2.9 - 5.3] | [0.0 - 0.0] | |
| 18.1 | 4.8 | 0.3 | 16.0 | 14.0 | 43.6 | 2.6 | 0.0 | |
| [12.8 - 24.3] | [3.5 - 6.5] | [0.2 - 0.6] | [10.8 - 22.9] | [9.2 - 19.8] | [34.7 - 52.0] | [1.9 - 3.8] | [0.0 - 0.0] | |
|
|
8.0 | 8.4 | 3.5 | 28.5 | 29.3 | 16.1 | 4.1 | 0.0 |
|
|
[3.0 - 16.2] | [5.1 - 11.7] | [1.8 - 6.2] | [20.4 - 37.6] | [16.6 - 46.1] | [9.8 - 23.9] | [2.9 - 5.6] | [0.0 - 0.0] |
| 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 99.9 | 0.0 | 0.0 | |
| [0.0 - 0.0] | [0.0 - 0.0] | [0.0 - 0.1] | [0.0 - 0.1] | [0.0 - 0.0] | [99.8 - 99.9] | [0.0 - 0.0] | [0.0 - 0.20] | |
|
|
16.7 | 1.9 | 2.7 | 37.1 | 35.1 | 1.8 | 1.8 | 0.0 |
|
|
[12.5 - 26.1] | [1.0 - 3.1] | [1.7 - 3.9] | [27.8 - 46.3] | [25.6 - 45.5] | [0.6 - 3.8] | [1.0 - 3.0] | [0.0 - 0.0] |
Variance Decomposition of the observables, periodic component with cycles between 6 and 32 quarters. Median values and 90% confidence intervals reported. Posterior percentiles obtained from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm. Acceptance rate 31%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
Values are percentages. Rows may not sum up to 100% due to rounding error.
Computed used parameter estimates in table 3.
| TFP | MP | Gov't | Price Mark up | Labor Preference | Financial | Preference | Meas. Error | |
|---|---|---|---|---|---|---|---|---|
|
|
31.2 | 0.4 | 17.5 | 12.3 | 27.2 | 9.5 | 1.3 | 0.0 |
|
|
[27.3 - 35.2] | [0.3 - 0.7] | [14.5 - 21.5] | [9.7 - 15.7] | [23.8 - 30.7] | [7.6 - 12.4] | [1 - 1.9] | [0.0 - 0.0] |
|
|
5.1 | 1.0 | 2.1 | 22.4 | 3.0 | 49.1 | 16.7 | 0.0 |
|
|
[4.2 - 6.3] | [0.7 - 1.5] | [1.6 - 2.9] | [18.4 - 28.2] | [2.3 - 3.8] | [42.9 - 55.5] | [12.8 - 20.7] | [0.0 - 0.0] |
|
|
42.4 | 0.0 | 1.0 | 2.2 | 40.7 | 0.8 | 12.8 | 0.0 |
|
|
[38.0 - 46.6] | [0.0 - 0.1] | [0.7 - 1.4] | [1.6 - 3.0] | [36.6 - 44.6] | [0.5 - 1.1] | [10.7 - 15.5] | [0.0 - 0.0] |
| 0.5 | 4.1 | 2.1 | 3.2 | 1.1 | 82.5 | 6.1 | 0.0 | |
| [0.4 - 0.8] | [3.1 - 5.6] | [1.5 - 3.1] | [2.5 - 4.3] | [0.7 - 1.7] | [78.9 - 85.7] | [4.7 - 7.8] | [0.0 - 0.0] | |
| 9.1 | 6.5 | 1.9 | 10.2 | 5.5 | 58.4 | 7.5 | 0.0 | |
| [7.0 - 12.4] | [5.1 - 8.5] | [1.3 - 2.9] | [7.8 - 13.3] | [4.1 - 7.1] | [51.9 - 65.3] | [6.1 - 9.3] | [0.0 - 0.0] | |
|
|
2.1 | 0.4 | 30.0 | 22.7 | 42.8 | 0.7 | 0.7 | 0.0 |
|
|
[1.7 - 2.8] | [0.2 - 0.7] | [25.1 - 365.7] | [17.8 - 28.9] | [37.9 - 48.1] | [0.4 - 1.1] | [0.4 - 1.1] | [0.0 - 0.0] |
| 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 99.9 | 0.0 | 0.0 | |
| [0.0 - 0.0] | [0.0 - 0.0] | [0.0 - 0.2] | [0.0 - 0.1] | [0.0 - 0.0] | [99.8 - 99.9] | [0.0 - 0.0] | [0.0 - 0.0] | |
|
|
16.8 | 3.4 | 5.7 | 48.6 | 15.7 | 1.2 | 8.1 | 0.0 |
|
|
[13.0 - 21.1] | [2.5 - 4.7] | [4.4 - 7.8] | [43.8 - 53.3] | [13.0 - 18.8] | [0.6 - 2.1] | [6.2 - 10.3] | [0.0 - 0.0] |
Variance Decomposition of the observables, periodic component with cycles between 6 and 32 quarters. Median values and 90% confidence intervals reported. Posterior percentiles obtained from 3 chains of 100,000 draws generated using a Random Walk Metropolis algorithm. Acceptance rate 29%. Burning period: initial 20,000 draws. Observations retained: one in every 10 draws.
Values are percentages. Rows may not sum up to 100% due to rounding error.
Computed used parameter estimates in table 4.
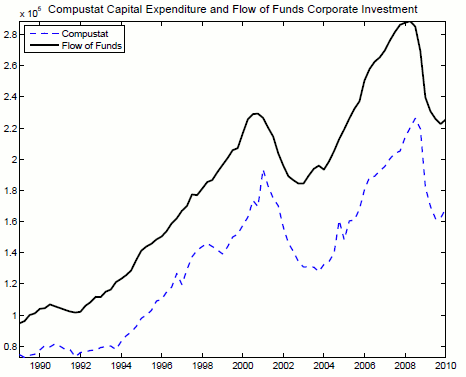
Figure 1 Data
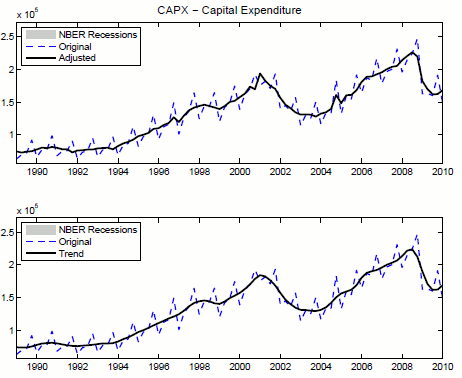
Figure 2 Data
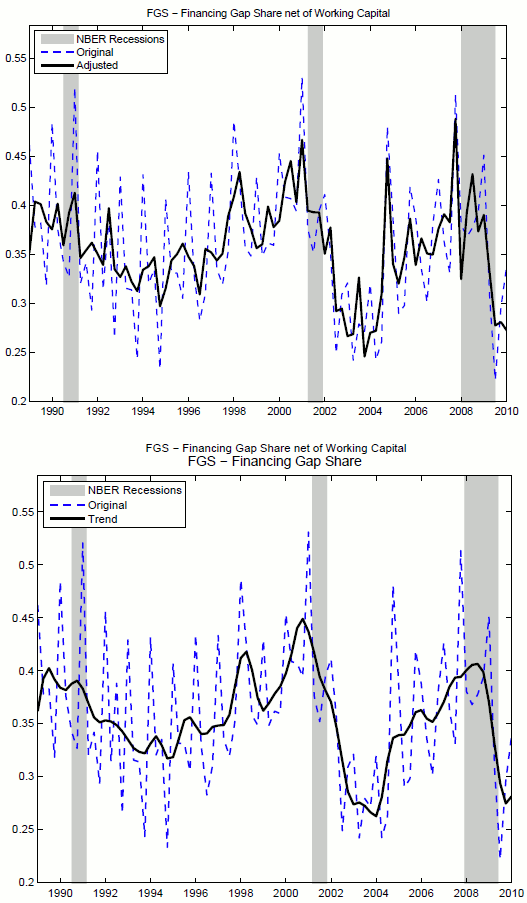
Figure 3 Data
Figure 4: WKS
Figure 4 Data
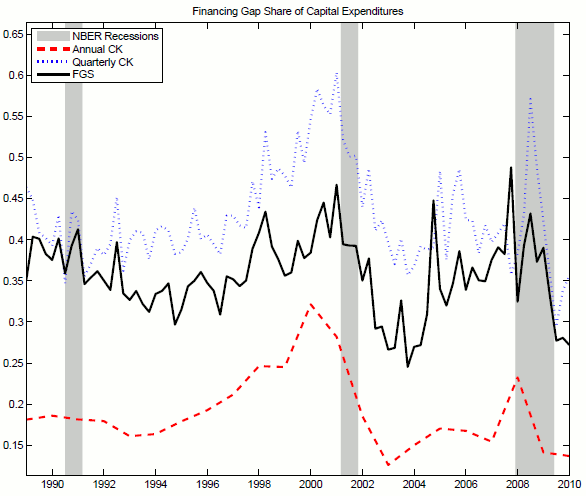
Figure 5 Data
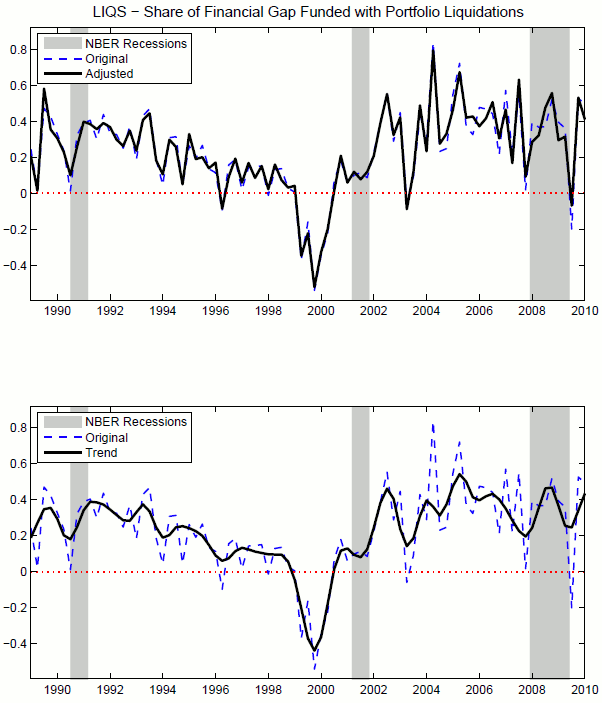
Figure 6 Data
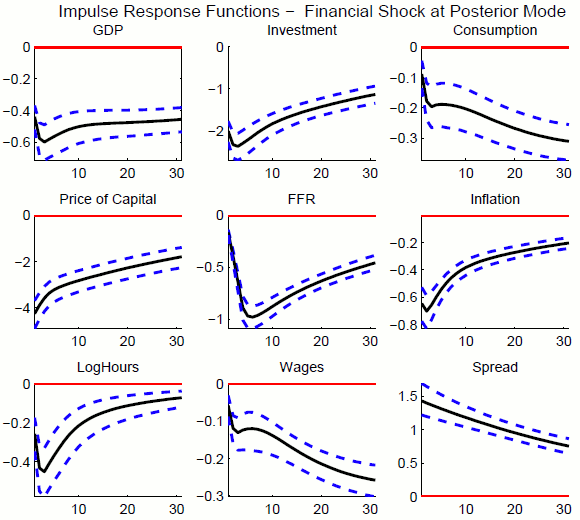
Figure 8 Data
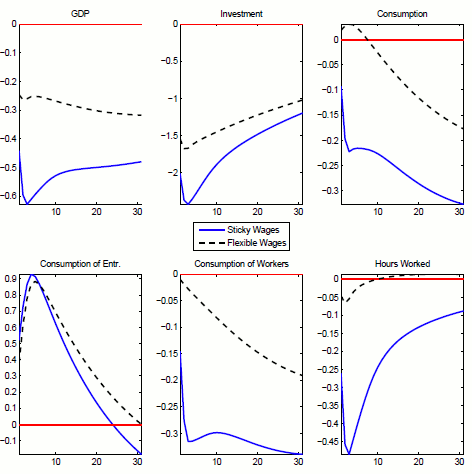
Figure 9 Data
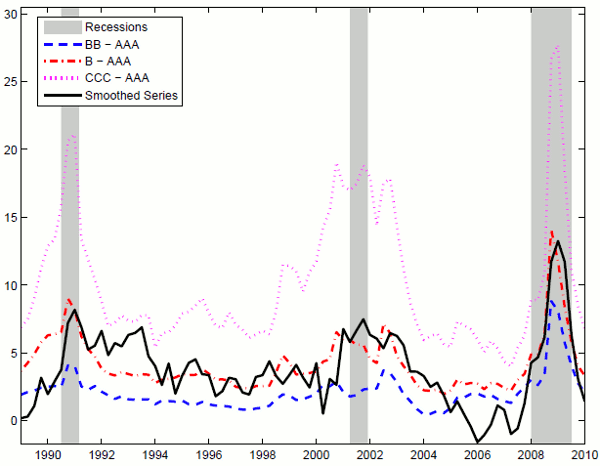
Figure 10 Data
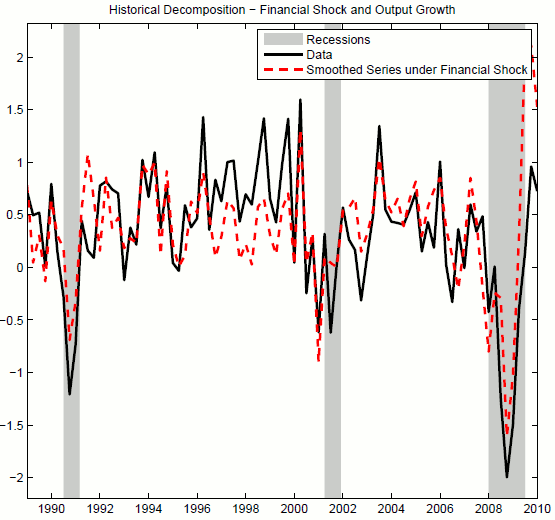
Figure 11 Data
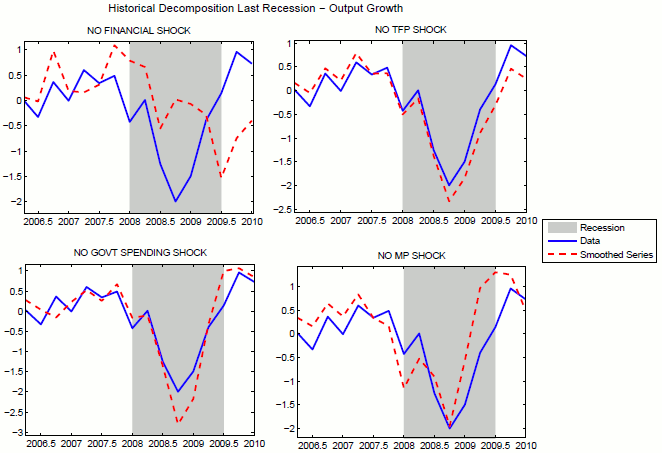
Figure 12 Data
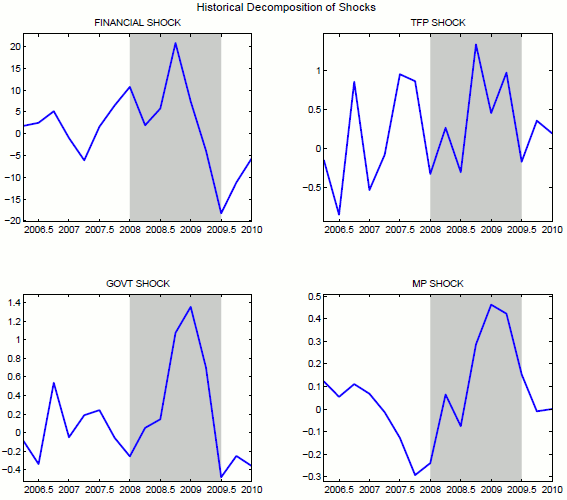
Figure 13 Data
Footnotes
| US Internal Funds |
Return to Text
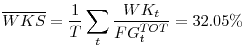 |
and find that around 32% of firms' total financial dependence is connected to funding operating expenses.
Moreover, I report the Financing Gap Share statistics computed over annual and quarterly data using CK's definition of financing gap in (3). By direct comparison of their methodology with mine, I can compute and report the share of total financing gap that arises by treating
dividends as an unavoidable commitment rather than disposable resources. I find that dividend payouts amount to around ![]() of the total financing gap in (4). Return to Text
of the total financing gap in (4). Return to Text
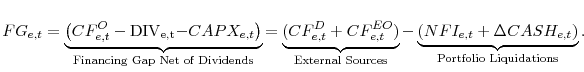
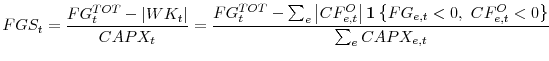
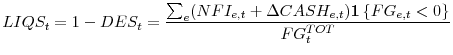
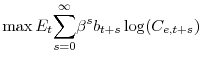
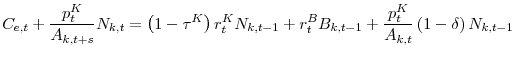
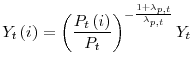
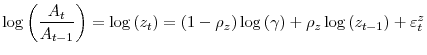
![\displaystyle E_{t} {\displaystyle\sum\limits_{s=0}^{\infty}} \xi_{p}^{s}\beta^{s}\Lambda_{t+s}^{w}\left\{ \left[ P_{t}\left( i\right) \left( {\displaystyle\prod\limits_{j=0}^{s}} \pi_{t-1+j}^{\iota_{p}}\pi^{1-\iota_{p}}\right) \right] Y_{t+s}\left( i\right) -\left[ W_{t}L_{t}\left( i\right) +R_{t}^{k}K_{t}\left(i\right) \right] \right\}](img204.gif)
![\displaystyle \max_{I_{t+s}} E_{t} \sum_{s=0}^{\infty }\beta ^{s}E_{t+s}\left\{\Lambda _{t+s}^{w} \left[ P_{t+s}^{k}i_{t+s}-P_{t+s}I_{t+s} \right] \right\}](img218.gif)
![\displaystyle i_{t+s}=\left[ 1-S\left( \frac{I_{t+s}}{I_{t+s-1}}\right) \right]I_{t+s}](img219.gif) .
.![\displaystyle {\displaystyle\sum\limits_{s=0}^{\infty}} \beta^{s}\left[\log\left( C_{w,t+s}-hC_{w,t+s-1}\right) -\omega\frac{L_{w,t+s}{}^{1+v}}{1+v}\right]](img233.gif)
![\displaystyle \frac{R_{t}^{B}}{R^{B}}=\left( \frac{R_{t-1}^{B}}{R^{B}}\right) ^{\rho _{R}} \left[ \left( \frac{\bar{\pi}_{t}}{\pi }\right) ^{\phi _{\pi }}\right] ^{1-\rho _{R}}\left( \frac{\Delta \overline{X}_{t-s}}{\gamma }\right) ^{\phi _{Y}}\eta _{mp,t}](img251.gif)
![\displaystyle \underbrace{PC_{e,t}}_{DIV_{e,t}}+\underbrace{P_{t}^{K}i_{e,t}}_{CAPX_{e,t}}- \left[ \underbrace{Q_{t}^{A}\phi \left( 1-\delta \right) N_{e,t-1}} _{NFI_{e,t}}+\underbrace{\left( R_{t-1}^{B}B_{e,t-1}-B_{e,t}\right) } _{\Delta CASH_{e,t}}\right] -\underbrace{\theta Q_{t}^{A}A_{e,t}i_{e,t}} _{\left(CF_{e,t}^{D}+CF_{e,t}^{EO}\right)}=\underbrace{R_{t}^{K}N_{e,t-1}} _{CF_{e,t}^{O}}](img298.gif)