
Financing Constraints, Firm Dynamics, and International Trade1
Keywords: Private information, long-term financial contracts, exporter dynamics, international trade, financial intermediation
Abstract:
There is growing empirical support for the conjecture that access to credit is an important determinant of firms' export decisions. We study a multi-country general equilibrium economy in which entrepreneurs and lenders engage in long-term credit relationships. Financial constraints arise in consequence of financials contracts that are optimal under private information. Consistent with empirical regularities, as firm age and size increase, the model implies decreasing mean and variance of firm growth and increasing firm survival. Exporters are larger, their survival in international markets increases with the time spent exporting, and the sales of older exporters are larger and more stable.
1 Introduction
Empirical studies of firms and industries across countries reveal that most exports are produced by a small number of very large firms. In the United States, for example, less than 5 percent of all firms exported some of their production in 2010. More than 97 percent of these exporters were small- and medium-sized firms (500 employees or less), which only accounted for about 34 percent of total exports4 In contrast to large exporters, there is substantial year-to-year transition in and out of export markets for smaller firms. Furthermore, new exporters are typically small relative to the average exporter and frequently stop exporting after one year. Continuing exporters are more likely to expand rapidly in export markets (Bernard & Jensen, 2004).
Does access to credit affect a firm's decision to export? How does the nature of the credit relationship between banks and firms shape the growth of new exporters? Small- and medium-sized firms tend to be more reliant on external financing to operate, which is mostly debt as equity is typically owned by proprietors. There is substantial empirical evidence that the financial conditions faced by small and young firms play an important role in shaping their growth, which is widely interpreted as indirect evidence of frictional financial markets.5 Hysteresis in export markets suggests the presence of a fixed cost of entry (e.g.,(Das et al., 2007), (Paravisini et al., 2011)), thereby suggesting that participating in international trade requires a greater access to working capital financing. This in turn could imply that the export decisions of small and medium-sized firm to export is sensitive to the availability of credit.(Minetti & Zhu, 2011) finds evidence supporting this hypothesis by showing that the probability of exporting and the intensity of export is significantly lower for credit rationed firms in Italy.6
Economic theory posits that small and young firms are generally more opaque to external scrutiny. This opaqueness creates an informational asymmetry between lenders and entrepreneurs leading to adverse selection and moral hazard problems. As a result, competitive banks may ration the supply of credit to young and small firms instead of increasing the price of credit to clear the market (e.g., (Stiglitz & Weiss, 1981)). Banks may also find it profitable to reduce the private information through repeated interaction and monitoring of firms. For example, banks may offer self-enforcing contracts that facilitate insurance, such as continued extension of credit during bad times (Allen & Gale, 1999). Such contracts could also induce young entrepreneurs to establish their trustworthiness and the viability of their business by servicing their loans over time (e.g., (Diamond, 1984,1991), and (Rajan, 1992)).7 In line with the above argument, (Clementi & Hopenhayn, 2006) show that long-term financial contracts that are optimal given such informational asymmetry can help account for some of the empirical regularities firm dynamics - firm entry and exit, and the mean and variance of firm growth.
Economic theory is relatively uninformative regarding how private information and long-term credit relationships may affect firms' export decisions and shape their growth in international markets. We propose to fill this gap by studying a general equilibrium multi-country model economy in which entrepreneurs and lenders enter into multi-period credit relationships subject to an informational asymmetry. In the model, atomistic entrepreneurs are born with a blueprint to start a long-lived firm that produces an intermediate input. Starting and operating a firm requires paying an initial fixed cost, which is sunk, and working resources each period. Once started, a firm may ship some of its production overseas by paying additional fixed and variable trade costs. We assume that new entrepreneurs do not have any wealth with which to fund their firm, and must seek financing from competitive financial intermediaries. Financial frictions arise because financial intermediaries cannot directly observe the revenue generated by the firms they are financing, and must instead rely on the reports from creditor entrepreneurs.
With limited liability, entrepreneurs have an incentive to under-report the revenues generated by their firm to avoid repaying their debt. Financial intermediaries mitigate this moral hazard by offering new entrepreneurs a long-term financial contract designed to induce truthful reporting. The contractual arrangement in our model is closely related to that in (Clementi & Hopenhayn, 2006), and a financing constraint emerges as an outcome of the optimal contract. New firms operate below their efficient level, and the financing constraint is relaxed as the entrepreneur's claim to future cash-flows increases. Well-performing firms - those which service their debt for a sufficiently long time - gain access to sufficient credit to pay the export costs. New exporters are less financially constrained than domestic firms, but their growth continues to depend on their performance each period until they become fully unconstrained.
We show that there exists a stationary equilibrium in which firms differ by their capital structure. Even if the aggregate quantities are constant in the steady state, the life cycle of individual firms is not. Each period, new firms are funded, and incumbent firms grow, shrink, begin or stop exporting or exit permanently. Consistent with empirical regularities on firms dynamics (e.g, (Cooley & Quadrini, 2001)), we show that the mean and variance of firm growth and the likelihood of exit are negatively related to firm age and size. We also show that smaller and younger firms pay fewer dividends, borrow and invest more, and that the investment of small firms is more sensitive to cash flows, even after controlling for their future profitability. Furthermore, in line with empirical studies on firm export dynamics (e.g., (Eaton et al., 2007), and (Ruhl & Willis, 2008)), we show that new exporters account only for a small share of total exports, and that a large fraction of new exporters does not continue to export in the following year. Continuing exporters, on the other hand, are less likely to exit export markets as the number of years exporting increases, have larger and more stable sales, and generally reach their efficient size in a few years.
This paper contributes to the theoretical literature exploring the dynamics of firm export decisions. Research in this direction has modeled firm export dynamics as the outcome of learning as in (Eaton et al., 2012), investment in risky R&D as in (Atkeson & Burstein, 2010), and stochastic shocks to productivity as in (Ruhl & Willis, 2008), (Arkolakis, 2011) and (Alessandria & Choi, 2011). Our paper is closest in focus to (Kohn et al., 2011) in which firms face stochastic shocks to productivity and a borrowing constraint arises because of one-period contracts that are optimal under limited enforcement. A key difference with (Kohn et al., 2011) is that the stochastic process underlying firm dynamics in our model is an outcome of the long term financial contract, and not persistent productivity shocks. That is, an entrepreneur's financing constraint binds less as its claim to future cash flows increases, and not because she becomes more productive. Furthermore, we conduct our analysis in general equilibrium. In the model, financial intermediaries actively engage in maturity and risk transformation in a competitive financial market using workers' and entrepreneurs' short-term deposits to fund a portfolio of long-term risky projects. The general equilibrium provides a link between the dynamics of firm balance sheets, aggregate conditions, and the balance sheets of the lenders, thereby relating financial intermediation to international trade.
Our paper is also related to research on the impact of financing constraints on the welfare gains of international trade. Financing constraints in these models arise because of exogenous collateral requirement (e.g., (Chaney, 2005), (Manova, 2008)), one-period contracts that are optimal under private information (Feenstra et al., 2011), or long-term contracts that are optimal under limited enforcement (Wang, 2010), (Brooks & Dovis, 2011). Last, our paper is related to studies of the efficient allocations in dynamic economies with private information such as (Atkeson & Lucas, 1992), (Smith & Wang, 2006) and (Verani, 2011).
The rest of the paper is organized as follows: Section 2 presents the model and Section 3 describes the financial arrangement between investors and entrepreneurs and derives the properties of the optimal contract. Section 4 defines the general equilibrium, and section 5.1 analyzes the model numerically. Concluding comments are contained in Section 6; proofs of propositions and derivations are relegated to the Appendix.
2.1 Workers
Workers are born without wealth, survive into the next period with exogenous probability
![]() , and are instantly replaced by new ones when deceased. Workers discount the future at rate
, and are instantly replaced by new ones when deceased. Workers discount the future at rate
![]() and are endowed with one unit of time each period that they allocate between labor
and are endowed with one unit of time each period that they allocate between labor ![]() and leisure. Labor is paid at wage
and leisure. Labor is paid at wage ![]() , and workers use their income to either buy the numéraire consumption good
, and workers use their income to either buy the numéraire consumption good ![]() , or to purchase contingent claims
, or to purchase contingent claims ![]() at price
at price ![]() that pay
that pay ![]() units of consumption in the next period if the agent is alive, and zero otherwise. Agents do not value bequests, and will thus
place all their savings in these claims. Workers assess their consumption-leisure decision according to
units of consumption in the next period if the agent is alive, and zero otherwise. Agents do not value bequests, and will thus
place all their savings in these claims. Workers assess their consumption-leisure decision according to
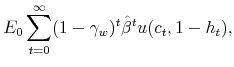 |
(1) |
which they maximize subject to a budget constraint
| (2) |
and the no-Ponzi condition
2.2 Entrepreneurs
New entrepreneurs are born with a blueprint to produce an intermediate good
![]() . Entrepreneurs, like workers, are born without wealth, survive into the next period with probability
. Entrepreneurs, like workers, are born without wealth, survive into the next period with probability
![]() , and are instantly replaced upon death. Entrepreneurs are risk-neutral, and discount the future at the rate
, and are instantly replaced upon death. Entrepreneurs are risk-neutral, and discount the future at the rate
![]() . We assume entrepreneurs do not make labor-leisure decisions, and instead devote a fixed fraction of their time to supervise their firm. Entrepreneurs assess their
consumption decision according to
. We assume entrepreneurs do not make labor-leisure decisions, and instead devote a fixed fraction of their time to supervise their firm. Entrepreneurs assess their
consumption decision according to
where
2.3 Financial intermediaries
Financial intermediaries are risk-neutral and discounts the future at the same rate as entrepreneurs. They raise short-term deposits from workers via the annuity market, and can offer long-term financing to the entrepreneurs. The assumptions on worker characteristics imply stationary
demographics of workers so that annuities can be offered without risk. Deposits from workers and entreprenuers in period ![]() are used to fund entrepreneurs' risky projects in period
are used to fund entrepreneurs' risky projects in period
![]() . Repayments from entrepreneurs to the intermediary are used to repay the deposits with interest. Perfect competition in the financial market implies that we can focus on a representative
financial intermediary.
. Repayments from entrepreneurs to the intermediary are used to repay the deposits with interest. Perfect competition in the financial market implies that we can focus on a representative
financial intermediary.
2.4 Final good firms
The final good is assembled by a large number of firms using domestically produced and imported intermediate goods and a constant elasticity of substitution aggregator. Intermediate goods are imperfect substitutes, and final good producers maximize their profit
by choosing quantities
2.5 Intermediate goods firms
Producing an intermediate good
![]() requires an initial investment
requires an initial investment ![]() that is sunk,
and per period working resources
that is sunk,
and per period working resources ![]() to hire labor and to be used as capital. The
to hire labor and to be used as capital. The ![]() -th firm produces the
-th firm produces the ![]() -th good according to a neo-classical production function
-th good according to a neo-classical production function
![]() , where
, where ![]() is capital input and
is capital input and ![]() is labor input. We assume that the capital used in production is fully depreciated at the end of the period. An entrepreneur wishing to export must pay a fixed export cost
is labor input. We assume that the capital used in production is fully depreciated at the end of the period. An entrepreneur wishing to export must pay a fixed export cost ![]() before production begins, and chooses the quantity
before production begins, and chooses the quantity ![]() and
and
![]() of goods to sell domestically and abroad, respectively.9 It follows that the allocation of period working resources
of goods to sell domestically and abroad, respectively.9 It follows that the allocation of period working resources ![]() must satisfy:
must satisfy:
| (5) |
where
| (6) |
The ![]() -th firm is a monopolist for its differentiated product, but takes the inverse demand function for its product
-th firm is a monopolist for its differentiated product, but takes the inverse demand function for its product ![]() - price as a function of quantity - as given. Project returns of all firms
- price as a function of quantity - as given. Project returns of all firms
![]() are subject to a sequence of independent and identically distributed idiosyncratic revenue shocks
are subject to a sequence of independent and identically distributed idiosyncratic revenue shocks
![]() , where
, where
![]() High
High![]() Low
Low![]() . Firm status is indexed by
. Firm status is indexed by
![]() , where
, where ![]() and
and ![]() indicate that a firm sells to the domestic market only, or to both the domestic and export market, respectively. The maximum revenue a firm can generate with resources
indicate that a firm sells to the domestic market only, or to both the domestic and export market, respectively. The maximum revenue a firm can generate with resources ![]() is:10
is:10
| (7) | ||
| s.t. | ||
A firm is terminated when the entrepreneur dies.11
3 Information and long-term credit relationship
Revenues are only observed by entrepreneurs, so lenders can only learn about the firm's performance and the realizations of the revenue shocks ![]() through entrepreneurs' reports,
through entrepreneurs' reports,
![]() . We denote the history of reports up to period
. We denote the history of reports up to period ![]() by
by
![]() . A contract is a set of decision rules
. A contract is a set of decision rules
![]()
![]() . Conditional on surviving, a firm is either liquidated,
. Conditional on surviving, a firm is either liquidated,
![]() , in which case the entrepreneur receives
, in which case the entrepreneur receives
![]() and the financial intermediary receives
and the financial intermediary receives
![]() , where
, where
![]() is the salvage value, or it remains in operation. If a firm is kept in operation, the contract specifies whether or not the firm exports,
is the salvage value, or it remains in operation. If a firm is kept in operation, the contract specifies whether or not the firm exports,
![]() , and the size of the loan,
, and the size of the loan,
![]() . After production takes place and revenues are realized, an entrepreneur makes a repayment
. After production takes place and revenues are realized, an entrepreneur makes a repayment
![]() to the financial intermediary conditional on his ex-post report
to the financial intermediary conditional on his ex-post report
![]() . Figure (1) summarizes the timing of events within one period.
. Figure (1) summarizes the timing of events within one period.
3.1 The optimal financial contract
A reporting strategy for an entrepreneur is a sequence of reports
![]() , where
, where
![]() is the true history of realizations of revenue shocks. After every history
is the true history of realizations of revenue shocks. After every history ![]() , the pair
, the pair
![]() implies an expected discounted cash flow
implies an expected discounted cash flow
![]() and
and
![]() for the entrepreneur and the financial intermediary, respectively. A feasible and incentive compatible contract is optimal if it maximizes
for the entrepreneur and the financial intermediary, respectively. A feasible and incentive compatible contract is optimal if it maximizes
![]() for every possible
for every possible ![]() . Following (Clementi & Hopenhayn, 2006), we refer to
. Following (Clementi & Hopenhayn, 2006), we refer to ![]() and
and ![]() as equity and debt, respectively, so that the joint surplus
as equity and debt, respectively, so that the joint surplus
![]() is the value of the firm.
is the value of the firm.
Using the method of (Abreu et al., 1990), the optimal contract can be written recursively by using ![]() as a state variable and by defining
as a state variable and by defining ![]() and
and ![]() as promised continuation values. It follows that equity must satisfy
the following accounting identity:
as promised continuation values. It follows that equity must satisfy
the following accounting identity:
which states that current period equity is equal to the expected net cash flow this period plus the discounted expected equity next period. In order to induce truthful reporting, incentive compatibility constraints are required. Since entrepreneurs who receive a low shock do not have an incentive to report a high shock, there is only one binding such constraint:
Limited liability requires entrepreneurs' dividends to be non-negative,12 so that
Conditional on surviving, the value of an
| (11) | ||
| s.t. | (8), (9), and (10) | |
There exists a region ![]() within which a greater value of the joint surplus can be reached by allowing for a lottery on the export decision:13
within which a greater value of the joint surplus can be reached by allowing for a lottery on the export decision:13
where ![]() is the probability of becoming an exporter and
is the probability of becoming an exporter and ![]() and
and
![]() are the respective continuation values (within the same period) if the firm sells purely domestically or also exports.14 Furthermore,
are the respective continuation values (within the same period) if the firm sells purely domestically or also exports.14 Furthermore, ![]() takes into account the option of liquidating the firm
takes into account the option of liquidating the firm
| (13) | ||
| s.t. | ||
where
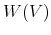 is linear for
is linear for
![V \in [0,V_r] \cup [V_D,V_E]](img125.gif) , equal to
, equal to
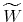 when
when
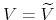 and strictly increasing when
and strictly increasing when
![V \in [V_r,V_D] \cup [V_E,\widetilde{V})](img128.gif)
- The firm is liquidated with probability
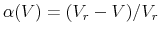 if
if
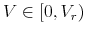
- The firm exports with probability one when
![V \in [V_E,\widetilde{V}]](img131.gif) , with probability
, with probability
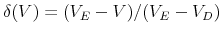 when
when
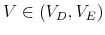 , and zero otherwise
, and zero otherwise
3.2 Properties of the financial contract
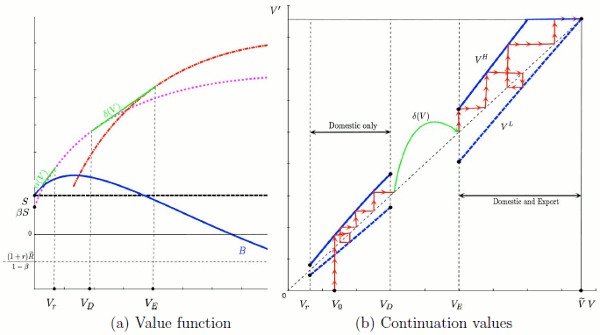
Panel (a) of Figure 2 plots the optimal value of the firm, ![]() , and the value to the intermediary,
, and the value to the intermediary, ![]() , as a function of equity,
, as a function of equity, ![]() . A firm faces a binding borrowing constraint whenever its equity is below
. A firm faces a binding borrowing constraint whenever its equity is below
![]() , where
, where
![]() is the unconstrained level of resources. That is,
is the unconstrained level of resources. That is,
![]() is the level of resources that solves the static profit maximization of the firm such that
is the level of resources that solves the static profit maximization of the firm such that
![]() argmax
argmax![]() . New firms start at
. New firms start at
![]() , so that expected profits of the intermediary
, so that expected profits of the intermediary ![]() cover
the cost of the initial investment
cover
the cost of the initial investment ![]() . Smaller firms take on more debt than larger firms, and firms with equity less than
. Smaller firms take on more debt than larger firms, and firms with equity less than ![]() cannot borrow enough to pay the trade costs.
cannot borrow enough to pay the trade costs.
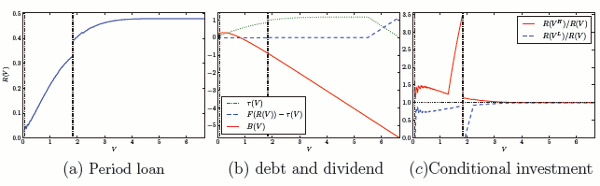
Firms' access to credit and growth are determined by the evolution of their capital structure. Using constraints (8), (9) and (10), and solving for next period's equity conditional on the revenue report yields the following law of motion for equity:
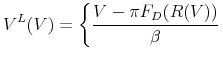 |
if |
(14) |
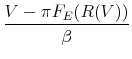 |
if |
and
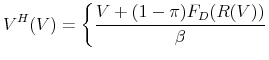 |
if |
(15) |
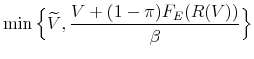 |
if |
Panel (b) of Figure 2 summarizes the evolution of firm equity following a particular sequence of revenue shocks. Small domestic firm may start exporting after receiving a finite sequence of positive revenue shocks. New exporters are less financially constrained than domestic firms, but their growth continues to be shaped by the optimal contract and the revenue shocks as long as
Figure 3 plots the decision rules for loans, repayments, and dividends as a function of equity. Due to risk-neutrality, joint surplus is maximized when equity grows fastest, so dividends to the entrepreneur are optimally zero until the firm can no longer grow faster by postponing dividends,
which is when
![]() . This implies that it is optimal for the financial intermediary to set the entrepreneur's repayments to
. This implies that it is optimal for the financial intermediary to set the entrepreneur's repayments to
![]() for
for ![]() whenever
whenever
![]() as it allows for the fastest accumulation of equity toward the unconstrained level. Furthermore, the optimization problem takes place on the convex set
as it allows for the fastest accumulation of equity toward the unconstrained level. Furthermore, the optimization problem takes place on the convex set
![]() , which implies
, which implies
![]() whenever
whenever
![]() . From constraints (8) and (9):
. From constraints (8) and (9):
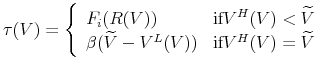 |
(16) |
which implies that conditional on a high revenue shock, resource advancement
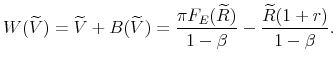 |
(17) |
Therefore, a firm is financially unconstrained when its entrepreneur has accumulated enough capital through its repayments to the financial intermediary to finance the firm operation at full scale in every period and under all contingencies at the current interest rate.
Panel (c) of Figure 3 plots the investment rate conditional on receiving a high and low revenue shock as a function of equity. Investment by constrained firms is always positive after receiving a high shock, and always negative after recieving a low shock for constrained firms. The investment of small firm, and therefore cashflow, is also more sensitive to revenue shocks than that of larger firms. Furhermore, there is a large increase in investment once the firm becomes an exporter, with subsequent very high possible disinvestment should the firm receive a low shock and exit export markets.
4 General equilibrium
Perfect competition in the financial sector implies that annuities are priced at the workers' survival rate
![]() .16 The assumptions on worker
characteristics ensure that there exists a stationary demographic with constant aggregate deposits and labor supply. Let
.16 The assumptions on worker
characteristics ensure that there exists a stationary demographic with constant aggregate deposits and labor supply. Let ![]() and
and ![]() be the deposits and hours worked of a
be the deposits and hours worked of a ![]() -period old worker. Setting the mass of workers to one, it follows that aggregate
deposits by workers each period are given by
-period old worker. Setting the mass of workers to one, it follows that aggregate
deposits by workers each period are given by
Similarly, the aggregate labor supply in each period is
Perfect competition in the financial sector also implies that financial intermediaries break even on new contracts with entrepreneurs, or that
![]() in equilibrium. As discussed in the previous section, firm equity evolves according to the conditional continuation values specified in the contract,
in equilibrium. As discussed in the previous section, firm equity evolves according to the conditional continuation values specified in the contract,
![]() and
and ![]() , and the sequence of revenue shocks. Let
, and the sequence of revenue shocks. Let
![]() be the state space for firm equity so that
be the state space for firm equity so that
![]() ,
,
![]() be the Borel
be the Borel ![]() algebra generated by
algebra generated by
![]() , and
, and ![]() the measure defined over
the measure defined over
![]() . Proposition 4.1 follows:
. Proposition 4.1 follows:
Proposition 4.1 There exists a unique stationary distribution of firms that is ergodic.
The intermediary uses the capital it has accumulated through entreprenuers' repayment, ![]() , and workers' deposits,
, and workers' deposits, ![]() , to finance the initial set-up cost and the wage and capital expenditures of all firms before production takes place. It follows that the capital market clears when
, to finance the initial set-up cost and the wage and capital expenditures of all firms before production takes place. It follows that the capital market clears when
where
Furthermore, the intermediary's budget must be balanced each period. That is, the intermediary's receipts from entrepreneurs plus the scrap value from liquidating poorly performing firms and the return on their own equity must be large enough to finance the cost of borrowing funds on the capital
market. A stationary distribution of firms implies that
![]() in equilibrium, and it follows that:
in equilibrium, and it follows that:
Equation 21 shows that the interest earned on bank capital is equal to the difference between aggregate receipts from, and disbursements to, entrepreneurs in the financial intermediary's portfolio.
Labor market clearing requires that the labor supply from workers is equal to the demand for labor by firms, so that:
Clearing of the intermediate goods markets requires that the demand from the final good producer is equal to the supply of intermediate goods:
where
The final good market clears when total production equals aggregate consumption of workers and entrepreneurs plus investment.21 That is,
| (25) |
where total capital expenditure
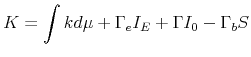 |
(26) |
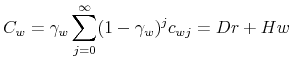 |
(27) |
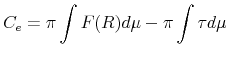 . . |
(28) |
The definition of the worldwide stationary equilibrium follows:
Definition 4.2 (Worldwide Stationary Equilibrium) A stationary equilibrium consists of decision rules for labor supply ![]() , consumption
, consumption
![]() , and deposits
, and deposits
![]() for workers in each country; a contract policy in each country, consisting of: promised values
for workers in each country; a contract policy in each country, consisting of: promised values ![]() and
and ![]() , period resource advancements
, period resource advancements ![]() , liquidation lottery
, liquidation lottery ![]() , export lottery
, export lottery ![]() , and
repayments
, and
repayments ![]() ; an initial contract state
; an initial contract state ![]() in each country; wages
in each country; wages
![]() and interest rates
and interest rates ![]() ; prices
; prices
![]() and
and
![]() for intermediate goods; and an exchange rate
for intermediate goods; and an exchange rate ![]() ,
such that
,
such that
- the labor and consumption function maximize the workers' value function
 in each country
in each country - the contract policy maximizes the value of the firm
 in each country
in each country - the initial state
 is such that the intermediary in each country breaks even on a new contract - i.e.
is such that the intermediary in each country breaks even on a new contract - i.e.
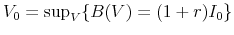
- the intermediary's budget in each country is balanced every perio
- the labor and capital markets clear in each country
- the domestic and imported intermediary goods market clear in each country
- trade between the two countries is balanced
Proposition 4.3 There exists a worldwide stationary equilibrium.
5 Numerical analysis
The contract needs to be solved numerically.22 Once the value of the firm ![]() and the decision rule for loan size
and the decision rule for loan size ![]() are known, the remaining decision rules can be expressed in closed form as functions of
are known, the remaining decision rules can be expressed in closed form as functions of ![]() . Given the initial firm size
. Given the initial firm size ![]() and the law of motion for
and the law of motion for ![]() , we can simulate the life-cycle of a large number of firms to estimate the stationary distribution of firms.23
, we can simulate the life-cycle of a large number of firms to estimate the stationary distribution of firms.23
5.1 Parametrization and parameter values
Let the instantaneous utility function for the workers be
![]() .24 We
simplify the analysis by considering the case of symmetric countries and a constant returns to scale Cobb-Douglas production technology for intermediate goods:
.24 We
simplify the analysis by considering the case of symmetric countries and a constant returns to scale Cobb-Douglas production technology for intermediate goods:
![]() , with
, with
![]() . The final good is produced according to a constant elasticity of substituion (CES) production function with constant returns to scale.
. The final good is produced according to a constant elasticity of substituion (CES) production function with constant returns to scale.
A period in the model is 1 year. We begin by fixing five parameters: The worker death rate
![]() is chosen so that the average life of workers is 50 years. The iceberg cost of exporting is set to 40 percent, which is in line with previous studies such as (Anderson & van Wincoop, 2004). The probability of a high revenue shock
is chosen so that the average life of workers is 50 years. The iceberg cost of exporting is set to 40 percent, which is in line with previous studies such as (Anderson & van Wincoop, 2004). The probability of a high revenue shock ![]() is 0.5, which produces investment volatility roughly in line with studies of firm such
as (Cooper & Haltiwanger, 2006); and the salvage value
is 0.5, which produces investment volatility roughly in line with studies of firm such
as (Cooper & Haltiwanger, 2006); and the salvage value ![]() is set to 80 percent of the set-up cost
is set to 80 percent of the set-up cost ![]() . We set the elasticity of substitution between intermediates to
. We set the elasticity of substitution between intermediates to
![]() , which is consistent with (Broda & Weinstein, 2006).25
, which is consistent with (Broda & Weinstein, 2006).25
|
Given the above, the six remaining parameters are jointly chosen to match the following six moments:26 a labor income share of 60 percent, an average
working time of 35 percent, an interest rate of 4 percent, an exit and entry rate of 6.3 percent (in line with (Lee & Mukoyama, 2008)), a share of exporters of 27 percent in line with (Bernard et al., 2007), and we require that new
firms start at a size that is 15 percent of the unconstrained firm size.27 Table (1) summarizes the calibration. After solving the model, we simulate the
life of ![]() firms from which we compute the statistics reported in Table (2) and the figures discussed in the next sub-section.
firms from which we compute the statistics reported in Table (2) and the figures discussed in the next sub-section.
|
Table 2 shows that, in the aggregate, the consumption-to-output and investment-to-output ratios are roughly in line with data, which principally follows from targeting the labor income share and labor hours. The export-to-output ratio is 8.7 percent, which is in line with the US over the last four decades.28
5.2 Firm export dynamics
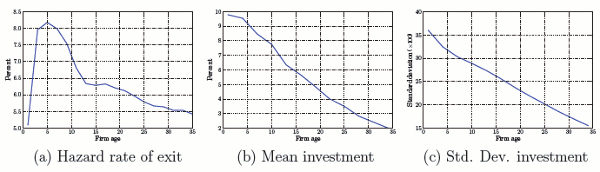
Our results on firm dynamics are consistent with the empirical regularities reported in (Cooley & Quadrini, 2001) and similar to those in (Clementi & Hopenhayn, 2006). Panel (a) of Figure 4 shows that the hazard rate of exit first increases for new firms and then decreases with firm age. On average, 1.2 percent of all firms are liquidated every period, which accounts for about 20 percent of all exiting firms. Panels (b) and (c) of Figure 4 plots the mean and standard deviation for firms of a given age, respectively, and show that younger firms experience a faster albeit more volatile growth than older ones.29
Comparing exporters to domestic firms, Table 2 shows that the average exporter is four times larger (in terms of labor and capital) than the average domestic firm. On one hand, the contract requires that the entrepreneur have sufficient stake into the firm (by accumulating equity) to obtain a loan that is sufficiently large to pay the export costs and generate the additional revenue. On the other hand, the financial position of a firm improves and its access to credit increases after it begins exporting (Figure 3). Thus, while less financially constrained firms are able to export, the financial health of exporters is substantially higher than that of domestic firms because of their activities. This observation highlights the great difficulty of disentangling these two effects in the data.
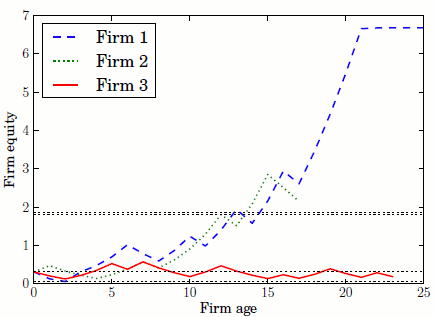
Let us begin our discussion of exporter dynamics with an example. Panel (a) of Figure 5 plots the life-cycle of three firms taken from our sample of simulated firms. It takes 13 years for Firm 1 to accumulate enough equity to beginning exporting, but it exits export markets after its first year. Firm 1 gains access again to export markets at age 15, from which time it continues to grow until it reaches its efficient size at age 21 and finally exits at age 25. Firm 2 reaches the export lottery region after 12 years but initially fails to secure funding to export. Firm 2 successfully become an exporter 2 years later and continue to export until it exits at age 17. Firm 3 is the least successful of our three firms, and was never able to grow nearly large enough to export, and was liquidated by the bank at age 23.30
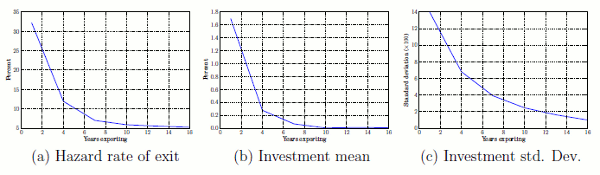
The long-term financial contract plays an important role in shaping both the extensive as well as the intensive margin of trade. New exporters face a high probability of exit from export markets during their first year. Panel (a) of Figure 6 plots the hazard rate of exit from export markets. A third of new exporters exit after their first year. Continuing exporters become less likely to exit as their export spells increase, until they only face the exogenous exit rate of 5 percent. To see this, note that new exporters start out with equity that is close to the export lottery region, so that a low shock leads to exit from export markets if the firm loses the lottery. But since firms grow on average, older exporters, who have more equity, are further away from the export lottery region; and unconstrained exporters only cease to export when the entrepreneur dies.
Young exporters grow faster than established ones, but their growth is more volatile. Panels (b) and (c) of of Figure 6 plot the mean and standard deviation of investment of exporter conditional on the length of their export spell. The average growth rate of a two year old exporter is 1.2 percent, and is close to 0 after ten years. The standard deviation of investment, however, is about five times higher for a two year old exporter than a ten year old one.
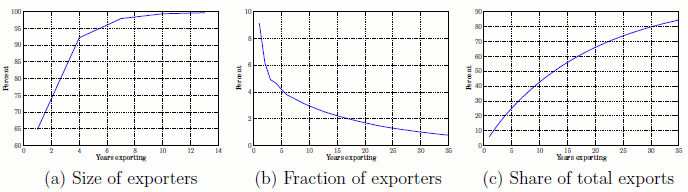
Few firms start exporting every year, and continuing exporters expand rapidly. Panel (a) of Figure 7 shows that new exporters start with about two thirds of the resources used by an unconstrained firm, and operate close to their unconstrained size (95 percent) after exporting for five years (on average).
New exporters are small, and most exports are produced by very large firms. Only 3.3 percent of domestic firms start exporting every period, and this cohort accounts for about 9 percent of all exporters (panel (b) of Figure 7). Exporters that have been exporting for up to five years account only for approximately 25 percent of all exports (panel (c) of Figure 7). Therefore, the model predicts that the bulk of all exports is produced by established firms that have been exporting for five years or more.
6 Conclusion
There is widespread empirical evidence that financial fictions play an important role in shaping the growth of small and young firms. There is also growing empirical evidence that the export decisions of firms are sensitive to the availability of credit. This paper investigated how private information and long-term credit relationships may affect firms' export decisions and shape their growth in international markets. We proposed and analyzed a general equilibrium multi-country model economy in which entrepreneurs and lenders enter into multi-period credit relationships subject to an informational asymmetry.
We showed that the model is consistent with empirical regularities on firms dynamics from the industrial organization literature, and with the models proposed to account for them. Furthermore, in line with recent empirical studies on firm export dynamics, our model predicts that new exporters account only for a small share of total exports, and that a large fraction of new exporters does not continue to export in the following year. Continuing exporters, are less likely to exit export markets as the export spell increases, experience faster and more volatile growth, and generally reach their efficient size in a few years.
Bibliography
Econometrica 58(5):1041-63.
Working Papers 11-19, Federal Reserve Bank of Philadelphia.
Management Science 45(9):1239-1253.
Journal of Economic Literature 42(3):691-751.
NBER Working Papers 17553, National Bureau of Economic Research, Inc.
Journal of Political Economy 118(3):433-484.
Review of Economic Studies 59(3):427-53.
The World Economy 33(3):347-373.
Tech. rep.
The Review of Economics and Statistics 86(2):561-569.
Journal of Economic Perspectives 21(3):105-130.
The Quarterly Journal of Economics 121(2):541-585.
NBER Working Papers 16174, National Bureau of Economic Research, Inc.
The Quarterly Journal of Economics 121(1):229-265.
Journal of Political Economy 112(4):817-847.
American Economic Review 91(5):1286-1310.
Review of Economic Studies 73(3):611-633.
Econometrica 75(3):837-873.
Review of Economic Studies 51(3):393-414.
Journal of Political Economy 99(4):689-721.
Borradores de Economia 003957, Banco de la República.
NBER Working Papers 16940, National Bureau of Economic Research, Inc.
Review of World Economics 143(3):416-432.
Journal of Economic Literature 36(1):193-225.
Working Paper 0718, Federal Reserve Bank of Cleveland.
Economic Theory 33(2):333-348.
NBER Working Papers 14531, National Bureau of Economic Research, Inc.
Journal of International Economics 83(2):109-125.
Working Paper 16975, National Bureau of Economic Research.
Journal of Finance 49(1):3-37.
Journal of Finance 47(4):1367-400.
Tech. rep.
Journal of Monetary Economics 53(4):847-877.
The MIT Press.
In G. Constantinides, M. Harris, & R. M. Stulz (eds.), Handbook of the Economics of Finance, vol. 1 of Handbook of the Economics of Finance, chap. 2, pp. 111-165. Elsevier.
American Economic Review 71(3):393-410.
Harvard University Press.
A. Demand for intermediate goods
The first-order condition for the maximization of equation (4) with respect to variety
![]() yields
yields
| (29) |
Dividing by the equivalent expression of another variety
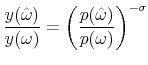 |
(30) |
and similarly for imported goods to
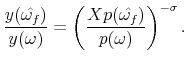 |
(31) |
Multiplying by
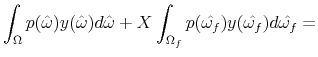 |
(32) |
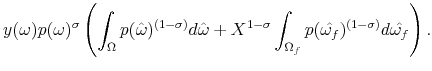 |
Since the final goods producer generates zero profits, the left-hand side is simply equal to total output
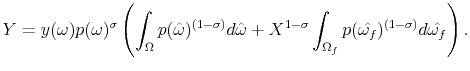 |
(33) |
Let
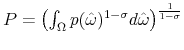 be the price index of domestic intermediate goods, and
be the price index of domestic intermediate goods, and and equivalently
These inverse demand functions are used in the intermediate goods producers' maximization problems. Since each entrepreneur is atomistic, he cannot affect the demand functions and thus takes them as given. Note that
B. Optimal revenue function for intermediate good producers
Let us redefine the inverse demand functions as
![]() and similarly
and similarly
![]() , where
, where
| (36) | ||
| (37) |
Our analysis thus far has made no assumption on the form of the production function, and the results of this paper are robust to a wide choice of production technology. Consider now the case of a Cobb-Douglas production function such that
| (38) |
where
![\displaystyle \widetilde{R}_D = \left[ \pi \frac{A x^{(1-1/\sigma)} \nu (1-1/\sigma)}{1+r} \right]^{\frac{1}{1-\nu(1-1/\sigma)}}](img266.gif) . . |
(39) |
From the underlying first-order condition one can deduce that
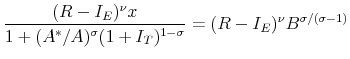 , and , and |
(40) | |
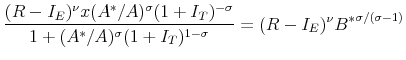 .
. |
(41) |
where
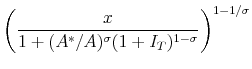 , and , and |
(42) | |
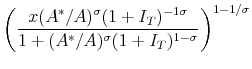 . . |
(43) |
The quantity sold domestically depends positively on the (endogenous) domestic demand parameter
![\displaystyle \widetilde{R}_E = \left[\pi \frac{(AB + A^*B^*) \nu (1-1/\sigma)}{1+r} \right]^\frac{1}{1-\nu(1-1/\sigma)} + I_E](img278.gif) . . |
(44) |
In this case, the markup is constant, as is common in the literature with monopolistic competition. Finally, we can infer the amount of resources above which it pays off to incur the fixed export cost, i.e. the
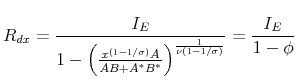 ,
, |
(45) |
where
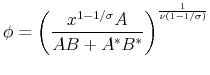 . . |
(46) |
It follows that the necessary condition for exports to be profitable is
C. Workers' decision rules
The workers problem can be written recursively as
We assume that the instantaneous utility function for workers is
| (48) |
where
![\displaystyle = \frac{w[(1+r)\hat{\beta}-1]}{(1+r)-(1-\gamma_w)} + (1+r)\hat{\beta}d](img288.gif) |
(49) | |
![\displaystyle = \frac{(1+r) + \lambda (1-\gamma_w) \hat{\beta} (1+r) - (1-\gamma_w) (1+\lambda)}{(1+\lambda)[(1+r) - (1-\gamma_w)]}](img290.gif) |
(50) | |
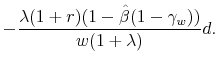 |
It follows that workers' deposits increase with age as long as the interest rate plus the principal is greater than the inverse of the workers' discount factor (i.e.,
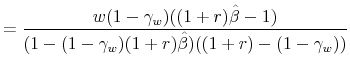 |
(51) | |
![\displaystyle = \frac{(1+r) + \lambda (1-\gamma_w) \hat{\beta} (1+r) - (1-\gamma_w) (1+\lambda)}{(1+\lambda)[(1+r) - (1-\gamma_w)]}](img290.gif) |
(52) | |
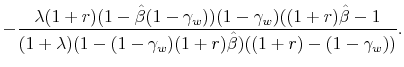 |
D. Final good market clearing
To show this condition holds, we start from the zero profit condition for final goods producers and invoke the market clearing condition for intermediate goods (Equation 23):
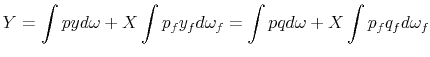 |
(53) |
where we omit the argument
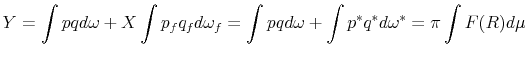 . . |
(54) |
Using the definition of entrepreneurial consumption,
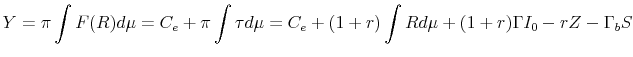 . . |
(55) |
The clearing of the capital market (Equation 20) allows to substitute for
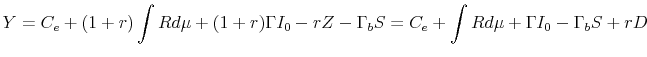 .
. |
(56) |
Plugging in for the use of resource advancements yields
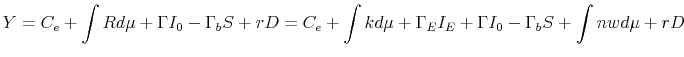 .
. |
(57) |
The definition of total capital expenditures allows us to rewrite this as
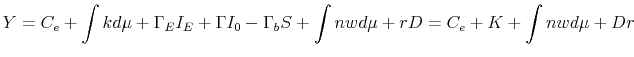 . . |
(58) |
Finally, the labor market clearing condition (Equation 22), and the aggregate budget constraint for workers
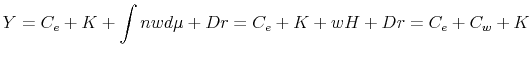 . . |
(59) |
E. Other proofs
Proposition E.1 There exists a point ![]() such that
such that
![]() for all
for all
![]() , and
, and
![]() for all
for all
![]() .
.
Proof It is optimal to reach the unconstrained value
![]() in the shortest time possible because the joint surplus is maximized there and both the entrepreneur and the financial intermediary are risk-neutral and share the same discount
factor. Hence, repayments should be set equal to revenues
in the shortest time possible because the joint surplus is maximized there and both the entrepreneur and the financial intermediary are risk-neutral and share the same discount
factor. Hence, repayments should be set equal to revenues
![]() as long as
as long as
![]() . This follows the argument set forth in (Clementi & Hopenhayn, 2006). Let us thus rewrite the value of a firm with a given export
status
. This follows the argument set forth in (Clementi & Hopenhayn, 2006). Let us thus rewrite the value of a firm with a given export
status
![]() as
as
Since
When the equity of a domestic firm goes to zero, its value goes to ![]() : the first constraint, together with the fact that continuation values have to be non-negative, forces
continuation values to go to zero, as equity
: the first constraint, together with the fact that continuation values have to be non-negative, forces
continuation values to go to zero, as equity ![]() approaches zero. It follows that the spread between
approaches zero. It follows that the spread between ![]() and
and ![]() goes to zero, so
goes to zero, so ![]() has to go to zero to
maintain incentive compatibility. Therefore, the optimal resource advancement of a domestic firm will approach zero and thus its value
has to go to zero to
maintain incentive compatibility. Therefore, the optimal resource advancement of a domestic firm will approach zero and thus its value
![]() will go to the discounted scrap value. In the case of an exporting firm, the logic is very similar, except that the resource advancement approaches the fixed cost of
exporting
will go to the discounted scrap value. In the case of an exporting firm, the logic is very similar, except that the resource advancement approaches the fixed cost of
exporting ![]() , which cannot be seized by the entrepreneur. The value of an exporting firm with equity zero will hence be the discounted scrap value minus the cost of paying the export
cost,
, which cannot be seized by the entrepreneur. The value of an exporting firm with equity zero will hence be the discounted scrap value minus the cost of paying the export
cost,
![]() . As both firm value functions are increasing and concave, and strictly so for
. As both firm value functions are increasing and concave, and strictly so for
![]() , the fact that
, the fact that
![]() and
and
![]() implies a unique crossing.
implies a unique crossing.
Proposition E.2 The function
![]() contains an interval
contains an interval
![]() on which it is not concave. This implies together with risk neutrality that it is optimal to use an export lottery.
on which it is not concave. This implies together with risk neutrality that it is optimal to use an export lottery.
Proof As shown in the previous proposition, there exists a unique equity value ![]() where the two value functions cross. For any given
where the two value functions cross. For any given
![]() , the slope of the exporting firm's value function is steeper than the slope of the non-exporting firm, i.e.
, the slope of the exporting firm's value function is steeper than the slope of the non-exporting firm, i.e.
![]() . This follows from the fact that the same is true for the underlying revenue functions. Therefore, by continuity of the value
functions,
. This follows from the fact that the same is true for the underlying revenue functions. Therefore, by continuity of the value
functions,
![]() . This implies that the function
. This implies that the function
![]() is not concave on some interval
is not concave on some interval ![]() .
Since the marginal profit of an extra unit of resources goes to infinity as
.
Since the marginal profit of an extra unit of resources goes to infinity as ![]() approaches zero,
approaches zero, ![]() , and as the slope of the exporting value function is zero at the unconstrained level,
, and as the slope of the exporting value function is zero at the unconstrained level,
![]() .
.
Proof of Proposition 3.1 As outlined above,
![]() is increasing and concave for
is increasing and concave for
![]() , so any convex combination of the two functions and
, so any convex combination of the two functions and ![]() is too. Since
is too. Since
![]() and
and
![]() for some
for some
![]() (otherwise it would not pay to finance firms at all),
(otherwise it would not pay to finance firms at all), ![]() and by assumption,
and by assumption, ![]() . We know that
. We know that
![]() , so by concavity of the functions
, so by concavity of the functions
![]() , it follows that
, it follows that ![]() . Finally, because
. Finally, because
![]() , it has to be that
, it has to be that
![]() .
.
The first point follows immediately from the fact that the expected value of the liquidation lottery is equal to the equity with which an entrepreneur enters it, thus pinning down the probabilities of liquidation and survival. To prove the second point, we have to show that
![]() . From the above, it follows that the interval is non-empty. By definition,
. From the above, it follows that the interval is non-empty. By definition,
![]() , which implies together with concavity that
, which implies together with concavity that
![]() . This means that no company with
. This means that no company with
![]() finds it profitable to export, and all companies with
finds it profitable to export, and all companies with
![]() do. A company with equity
do. A company with equity
![]() is offered a lottery with expected value equal to the equity the entrepreneur had before. The probabilities of getting
is offered a lottery with expected value equal to the equity the entrepreneur had before. The probabilities of getting ![]() and
and ![]() are determined thereby. An entrepreneur wins the lottery with probability
are determined thereby. An entrepreneur wins the lottery with probability ![]() , receiving
, receiving ![]() and thus exporting; with probability
and thus exporting; with probability
![]() , he gets
, he gets ![]() and will hence not export.
and will hence not export.
Concerning the third point, it is clear that ![]() is linear in the two lottery regions. When
is linear in the two lottery regions. When
![]() , the value of the firm does not change anymore, so it will stay constant at
, the value of the firm does not change anymore, so it will stay constant at
![]() . The functions
. The functions
![]() are strictly increasing as long as
are strictly increasing as long as
![]() , since
, since
![]() is strictly increasing in that region. Therefore the firm value function
is strictly increasing in that region. Therefore the firm value function ![]() is strictly increasing for all
is strictly increasing for all
![]() .
.
Proof of Proposition 3.2 Partition the domain of the contract
![]() in five parts
in five parts
![]() . From the above
. From the above
![]() when
when
![]() and when
and when
![]() .32 When
.32 When
![]() , the firm is unconstrained and there is no need to provide any incentives to report the truth (as all revenues will go to the entrepreneur), and hence
, the firm is unconstrained and there is no need to provide any incentives to report the truth (as all revenues will go to the entrepreneur), and hence
![]() , so
, so
![]() . Whenever
. Whenever
![]() or
or
![]() , the firm enters a lottery and will either end up with
, the firm enters a lottery and will either end up with ![]() or
or ![]() , with the expected value of the lottery being exactly equal to the promised value
, with the expected value of the lottery being exactly equal to the promised value ![]() or
or ![]() . The expected next period equity for each of these is
. The expected next period equity for each of these is ![]() and
and ![]() , so that
, so that
![]() . Similarly, when
. Similarly, when
![]() , the lottery for liquidation yields the expected payoff
, the lottery for liquidation yields the expected payoff ![]() ,
and the expected equity for next period is then just
,
and the expected equity for next period is then just ![]() .
.
F. Stationary equilibrium
In the stationary steady state, given interest rate ![]() and wage
and wage ![]() , perfect
competition in the financial market implies financial intermediaries earn zero-profit on a new contract. This implies new entrepreneurs receive an initial equity
, perfect
competition in the financial market implies financial intermediaries earn zero-profit on a new contract. This implies new entrepreneurs receive an initial equity
![]() , for which the lender earns just enough to break even. The initial equity
, for which the lender earns just enough to break even. The initial equity ![]() is endogenous in the general equilibrium.
is endogenous in the general equilibrium.
Consider the sequence
![]() of equity levels from a single firm indefinitely replaced by a new one when it dies. It is clear
of equity levels from a single firm indefinitely replaced by a new one when it dies. It is clear
![]() is a sequence of random variables, and its evolution depends on the properties of the contracts and on the sequence of shocks - productivity, death, export, and
liquidation. In what follows, we show that
is a sequence of random variables, and its evolution depends on the properties of the contracts and on the sequence of shocks - productivity, death, export, and
liquidation. In what follows, we show that
![]() is a time-homogeneous Markov chain such that
is a time-homogeneous Markov chain such that
| (61) |
where
Proposition F.1
![]() is a time-homogeneous Markov chain on a general state space and is globally stable.
is a time-homogeneous Markov chain on a general state space and is globally stable.
Equip the state space ![]() with a boundedly compact, separable, metrizable topology
with a boundedly compact, separable, metrizable topology
![]() . Let
. Let
![]() be the measure space for the shocks. Let
be the measure space for the shocks. Let ![]() be any subset of
be any subset of
![]() . It follows for any
. It follows for any
![]() and
and ![]()
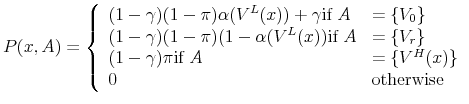 |
(62) |
For any
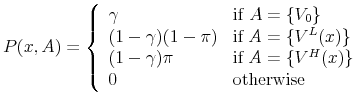 |
(63) |
For any
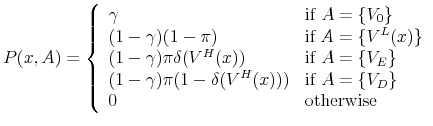
|
(64) |
For any
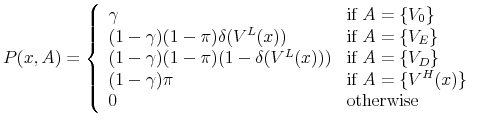
|
(65) |
For any
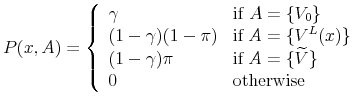 |
(66) |
And for
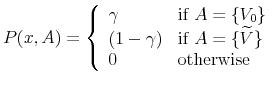 |
(67) |
For each
![]() ,
,
![]() is a non-negative function on
is a non-negative function on
![]() , and for each
, and for each ![]() ,
,
![]() is a probability measure on
is a probability measure on
![]() . Therefore, for any initial distribution
. Therefore, for any initial distribution ![]() , the stochastic
process
, the stochastic
process
![]() defined on
defined on
![]() is a time-homogeneous Markov chain. Let
is a time-homogeneous Markov chain. Let
![]() denote the corresponding Markov operator, and let
denote the corresponding Markov operator, and let
![]() denote the collection of firms distribution generated by
denote the collection of firms distribution generated by
![]() for a given initial distribution.33
for a given initial distribution.33
Write the stochastic kernel ![]() with the density representation
with the density representation ![]() so that
so that
![]() for all
for all ![]() . The Dobrushin coefficient
. The Dobrushin coefficient ![]() of a stochastic kernel
of a stochastic kernel ![]() is defined by
is defined by
![\displaystyle \alpha(p) := \min \left \{ \int p(x,y) \wedge p(x^{\prime},y)dy : (x,x^{\prime})\in S \times S \right \}%\]](img416.gif) |
(68) |
| (69) |
Equation (11.15) and Exercise (11.2.24) in (Stachurski, 2009) yield
| (70) |
for every pair
Proposition F.2 (Existence of a stationary equilibrium) The unique and ergodic invariant distribution of
![]() is continuous in prices.
is continuous in prices.
The result follows if the conditions of (LeVan & Stachurski, 2007) (Proposition 2) are satisfied and the proof is similar to the one in (Verani, 2011).
G. A higher elasticity of substitution
We investigate the effect of the elasticity of substitution between intermediate goods firms on firm dynamics and the aggregate by considering another world economy with
![]() . To help with the comparison, we calibrate the economy with
. To help with the comparison, we calibrate the economy with
![]() to the same moments as the economy with
to the same moments as the economy with
![]() . Table 3 summarizes the value of the parameters used for each economy.
. Table 3 summarizes the value of the parameters used for each economy.
|
|
|
|
|
|
0.959 | 0.959 |
| 2.300 | 2.304 | |
|
|
0.02 | 0.02 |
| 0.137 | 0.2 | |
| 0.452 | 0.26 | |
| 0.8 |
0.8 |
|
| 0.4 | 0.4 | |
| 0.033 | 0.012 | |
| 0.5 | 0.5 | |
|
|
0.047 | 0.05 |
Table 4 reports the results for the two economies. Given the calibration, the wage rate, aggregate output, consumption and investment are roughly the same in the two model economies so that, from a macroeconomic point of view, the two world economies are comparable. However, a higher
![]() reduces the market power of intermediate goods producers at home and abroad. This translates into lower prices for all goods, with a comparatively greater decrease in the price of
internationally traded goods. Furthermore, a decrease in firms' market power leads to a substantial reduction of the export share of aggregate output. A greater fraction of domestic firms begins exporting every period, and the hazard rate of exit for new exporters after one year is also higher.
Last, a reduction in market power also increases the size differential between domestic and exporting firms, while the share of unconstrained firms becomes smaller.
reduces the market power of intermediate goods producers at home and abroad. This translates into lower prices for all goods, with a comparatively greater decrease in the price of
internationally traded goods. Furthermore, a decrease in firms' market power leads to a substantial reduction of the export share of aggregate output. A greater fraction of domestic firms begins exporting every period, and the hazard rate of exit for new exporters after one year is also higher.
Last, a reduction in market power also increases the size differential between domestic and exporting firms, while the share of unconstrained firms becomes smaller.
|
|
|
|
| Targeted: Interest rate | 0.040 | 0.040 |
|---|---|---|
| Targeted: Hours worked | 0.350 | 0.349 |
| Targeted: Labor income share | 0.597 | 0.602 |
| Targeted: Entry/exit rate | 0.066 | 0.063 |
| Targeted: Relative size of entrants | 0.158 | 0.153 |
| Targeted: Share of exporters | 0.273 | 0.269 |
| Not targeted: Wage rate | 0.493 | 0.501 |
| Not targeted: Domestic goods price index | 3.272 | 3.079 |
| Not targeted: Imported goods price index | 6.033 | 4.925 |
| Not targeted: Output | 0.289 | 0.291 |
| Not targeted: Consumption/Output | 0.796 | 0.792 |
| Not targeted: Investment/Output | 0.204 | 0.208 |
| Not targeted: Export/Output | 0.138 | 0.087 |
| Not targeted: Entry rate in export market | 0.028 | 0.033 |
| Not targeted: Exit rate from export market after 1 year | 0.256 | 0.320 |
| Not targeted: New firm size relative to incumbents | 0.321 | 0.335 |
| Not targeted: Domestic firm size relative to exporters | 0.269 | 0.242 |
| Not targeted: Share of unconstrained firms | 0.177 | 0.148 |
The results for exports are driven by how the calibration for the economy with
![]() affects the fixed and variable trade costs,
affects the fixed and variable trade costs, ![]() and
and ![]() . We keep the variable trade costs
. We keep the variable trade costs ![]() constant across the two economies, which
implies that the ratio of exports to domestic sales decreases as market power decreases for each exporter.34 It follows that the fixed cost of exporting
must be lower in an economy with a higher
constant across the two economies, which
implies that the ratio of exports to domestic sales decreases as market power decreases for each exporter.34 It follows that the fixed cost of exporting
must be lower in an economy with a higher ![]() to keep the number exporters constant. This implies that the export lottery region is smaller making it easier for firms to enter and exit
export markets.
to keep the number exporters constant. This implies that the export lottery region is smaller making it easier for firms to enter and exit
export markets.
Furthermore, unconstrained firms with lower market power use more resources and sell higher quantities of goods. Since large firms are always exporters, the relative size of exporters is also higher. A lower market power implies that firm profit is also lower, thereby reducing the speed of firm
growth and leading to a smaller fraction of unconstrained firms.35 To see this, note that the incentive compatibility constraint binds for constrained
firms, which implies that
![]() . It follows that smaller revenue implies that the spread between the continuation values is smaller too; and the number of steps needed to reach the unconstrained
level is higher.
. It follows that smaller revenue implies that the spread between the continuation values is smaller too; and the number of steps needed to reach the unconstrained
level is higher.
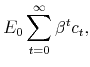
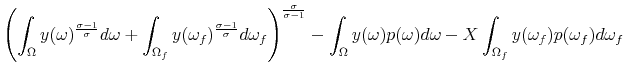
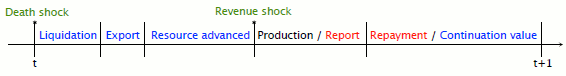
![\begin{displaymath}\begin{array}{rl} \widehat{W}(V) = \displaystyle \max_{\delta\in[0,1],V_{D},V_{E}} & \delta \widehat{W}_{E}(V_{E}) + (1 - \delta) \widehat{W}_{D}(V_{D})\\ \mbox{s.t.} & \delta V_{E} + (1 - \delta)V_{D} = V\\ & V_{D},V_{E} \geq 0 \end{array}\end{displaymath}](img99.gif)
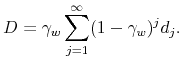
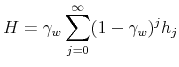 .
.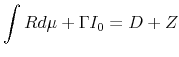 ,
,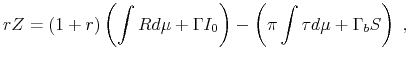
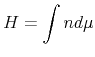 .
.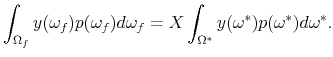
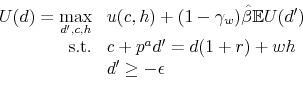
![\begin{displaymath}\begin{array}{ll} \widehat{W}_{i}(V) = & \max_{R,V^{H},V^{L}} \{ \pi F_{i}(R) - R (1+r) + \beta [\pi W(V^{H}) + (1-\pi) W(V^{L})]\} \\ \mbox{s.t. } & V = \beta(\pi V_H + (1-\pi) V_L) \\ & F_{i}(R) \leq \beta (V^{H} - V^{L}) \\ & V^{H},V^{L} \geq 0 \\ & R_{E} \geq I_{X}. \end{array}\end{displaymath}](img319.gif)