Practical Tools for Policy Analysis in DSGE Models with Missing Channels*
Keywords: Misspecification, DSGE Models, policy analysis.
Abstract:
1 Introduction
Over the past decade, there has been a marked increase in the use of dynamic stochastic general equilibrium (DSGE) models in policy institutions. The seminal work of (Smets & Wouters, 2007,2003) is regarded by many as a proof of concept that medium-scale DSGE models can be useful tools for policy analysis (Sims, 2008). (Smets & Wouters, 2007), SW henceforth, showed that models of this type could deliver reasonable forecast performance as well as the story-telling capabilities that flow from explicit assumptions about the optimization decisions of economic agents. Indeed, a number of central banks have recently developed operational policy models based on this blueprint.4
Though DSGE models in use at central banks follow the approach pioneered by SW, they dwarf them in scale. While the SW model is estimated on seven data series, operational models are designed to explain the behavior of two to three times as many data series. One reason why operational central bank models are larger than their academic counterparts surely stems from policymakers' desire to have detailed and comprehensive discussions about a large number of shocks and transmission channels.
But all models, regardless of size, are misspecified. For example, DSGE models in use at central banks typically contain only basic modelling of financial frictions, banking, and the labor market. This is not to say that models with such features do not exist. Indeed, research on these issues is currently a very fertile area, and one response to the observation that operational models exclude some channels and mechanisms of interest is to expand them accordingly. Naturally, there are some difficulties associated with this approach: if the model is to be estimated, then computational considerations place a (practical) upper bound on the number of observable variables; and larger models are inherently harder to understand and explain to busy policymakers. But even if this strategy is a desirable long-term objective, in the short run it is possible that the economic issues relevant for policy discussions develop more quickly than the operational models used to support those discussions. For instance, during the financial crisis policy-makers were interested in the effects of financial shocks and the interaction between the financial sector, the macro-economy, and the conduct of monetary and fiscal policy. Re-designing the policy models from scratch to inform policy-makers would have been too costly, and more importantly, too slow.
In this paper, we describe a practical approach for modelling the propagation of shocks originating in sectors that are not included in a baseline estimated DSGE model (henceforth the policy model) used for forecasting and policy analysis. As an example, suppose that policy-makers want to know how an increase in house prices due to unexpectedly strong demand for housing might affect GDP growth and inflation. Unfortunately, their policy model does not contain a housing sector. Our procedure works as follows.5
First, we identify a shock to the housing sector and the associated impulse response functions (IRFs) using an auxiliary model. In our example, we identify a shock in house prices using a structural vector autoregression (SVAR) as in (Iacoviello, 2005). More generally, we select a suitable auxiliary model that is able to capture the dynamic response of a (sub)set of variables that have a clear counterpart in the policy model. Auxiliary models could be smaller DSGE models, SVARs, or forecasting models already in use within the central bank. Impulse responses do not necessarily have to come from a formal model. For instance, they might reflect institutional knowledge, including the policy-makers' views, or findings documented in memos and policy reports written within the organization.
Second, we introduce the missing housing sector in the policy model through some observable variables and, if necessary, a small set of unobserved factors, which we model as a reduced-form VAR. We allow both the observable variables and the factors to feed into the exogenous processes of the policy model to create correlated disturbances. The unobserved factors capture propagation mechanisms that are specific to the housing sector and are not present in the policy model.
Third, we estimate the additional parameters in the augmented policy model by matching its impulse responses to those generated by the auxiliary model. We do not re-estimate the deep parameters of the policy model because re-estimation of the entire model could create identification problems and would make the method inapplicable in a short time frame. Impulse responses from the auxiliary model capture the likely propagation of the shock of interest, summarizing moments in the data that are affected by the additional parameters.
We use our methodology to study the propagation of two missing shocks in a three-equation New Keynesian (NK) model (Clarida et al., 1999). We consider two examples in which data used in the estimation exercise are simulated from larger DSGE models. In the first example, the data generating process (DGP) is the oil model of (Nakov & Pescatori, 2010b). In the second example, the DGP is the housing model of (Iacoviello, 2005).
We find that oil shocks are propagated as correlated disturbances to technology and price mark-up, without relying on unobserved factors. Instead, the NK model does a poor job at propagating house demand shocks without relying on unobserved factors. The reason is that this simple model misses the financial accelerator mechanism present in (Iacoviello, 2005), which provides hump-shaped and persistent dynamic responses. We are able to capture such mechanisms through two unobserved factors, loading either on the technology or the mark-up process. We show that the policy implications derived from the augmented policy model are similar to those derived from the DGP.
We also provide an empirical application, estimating the effects of housing shocks in the SW model using U.S. data. We find impulse responses to housing shocks in line with the existing theoretical and empirical literature. Furthermore, our results suggest that the richer the structure of the policy model, the less reliant the augmented policy model may be on unobserved factors to propagate the missing shock. Since operational DSGE models in use at central banks are large-scale models, policy experiments conducted in augmented versions of such models might only moderately rely on unobserved factors, which reduces the reliance on nonstructural dynamics.
We think that augmenting the policy model to study the effects of missing shocks, as opposed to directly using different models, is sensible for at least three reasons. First, the policy model provides a careful micro-foundation of the main transmission channels of monetary policy, which we would like to preserve in the analysis of the alternative scenarios involving missing sectors. Second, the augmented policy model can be used to conduct policy experiments, assuming that the modelling of the missing sector is policy invariant. Third, communications between staff and policy-makers often rely on the policy model.
We emphasize that the approach presented in this paper is not an ideal approach to deal with misspecification. The only correct approach is to develop models with a careful articulation of the sector of interest, and the interaction of that sector with the rest of the economy. Our methodology provides a compromise between the use of reduced-form models and fully structural models, preserving the structural dimensions of the policy model that best fit the data. This argument is also the corner stone of the DSGE-VAR approach discussed in (Del Negro & Schorfheide, 2009). Although we design our modelling and estimation approaches to be of practical use in policy institutions, these tools can be of broader applicability, for instance by macroeconomists who want to evaluate the ability of a DSGE model to propagate shocks of interest.
One paper that is related to ours is (Cúrdia & Reis, 2010), which estimate DSGE models with correlated disturbances, and use these models to account for empirical regularities in the US business cycle. We differ from their study because we generate correlated disturbances through a specific channel, which we identify using information from auxiliary models.
The remainder of the paper is structured as follows. In Section 2, we provide a description of the methodology. In Sections 3 and 4 we illustrate the approach using simple examples with a known data generating process. In Section 5, we turn to an empirical example using the DSGE model of (Smets & Wouters, 2007) to track the effects of house price shocks. Section 6 concludes the paper.
2 Methodology
The baseline model - the policy model - has the following form:6
where
The exogenous processes are modeled as a VAR:
where matrices
The endogenous variables ![]() can be partitioned into predetermined endogenous variables,
can be partitioned into predetermined endogenous variables, ![]() , and non-predetermined endogenous variables,
, and non-predetermined endogenous variables, ![]() :
:
![\displaystyle X_{t} \equiv \left[\begin{array}{c} z_{t}\\ Z_{t} \end{array} \right]](img17.gif) |
so that the state space representation of the rational expectations equilibrium can be written as:
where
Here, ![]() is the state vector collecting together the
is the state vector collecting together the
![]() vector of exogenous processes
vector of exogenous processes ![]() , and the predetermined endogenous
variables,
, and the predetermined endogenous
variables, ![]() .7
.7
In the VAR model for the exogenous processes, (2), ![]() and
and ![]() are usually assumed to be diagonal. The assumptions that
are usually assumed to be diagonal. The assumptions that ![]() is diagonal and that the shocks
is diagonal and that the shocks
![]() are orthogonal have two key advantages. First, these assumptions reduce the number of parameters in the model. Second, they add to the ability of the model to tell coherent
stories. Because the structural shocks are given an economic interpretation, it is important that innovations to them are orthogonal. Orthogonality makes it easier to trace through the effects of an exogenous impulse through the structural shock processes and onto the endogenous variables in the
model.
are orthogonal have two key advantages. First, these assumptions reduce the number of parameters in the model. Second, they add to the ability of the model to tell coherent
stories. Because the structural shocks are given an economic interpretation, it is important that innovations to them are orthogonal. Orthogonality makes it easier to trace through the effects of an exogenous impulse through the structural shock processes and onto the endogenous variables in the
model.
We model the variables that proxy the effects of the missing channel, assuming that the model is now driven by a new vector of exogenous processes
![]() :
:
The process
![]() is defined as follows:
is defined as follows:
This means that the state vector
![]() of the model becomes:
of the model becomes:
and that the rational expectations solution is given by:
where
We refer to the model described by equations (7)-(11) and (12)-(14) as the augmented policy model.8
The vector
![]() that enters in the augmented policy model is the sum of two components. The first component
that enters in the augmented policy model is the sum of two components. The first component ![]() is the vector of traditional DSGE exogenous processes. Innovations to this component can be traced through the model and the story of how that shock affects the endogenous variables can be constructed as usual. The second component
is the vector of traditional DSGE exogenous processes. Innovations to this component can be traced through the model and the story of how that shock affects the endogenous variables can be constructed as usual. The second component ![]() is a
is a
![]() vector of exogenous processes, which consists of weighted-averages of unobserved factors
vector of exogenous processes, which consists of weighted-averages of unobserved factors ![]() , and observable variables
, and observable variables ![]() . The factors are driven by an exogenous disturbance
. The factors are driven by an exogenous disturbance ![]() , which captures the missing shock.
, which captures the missing shock. ![]() is an
is an
![]() vector of observable variables that summarizes the evolution of the missing sector.9 For instance, in the housing model
vector of observable variables that summarizes the evolution of the missing sector.9 For instance, in the housing model ![]() contains data on house prices.
contains data on house prices. ![]() and
and ![]() are coefficient matrices that capture the dynamics of the factors and the proxy for the missing
sector.10 The matrices
are coefficient matrices that capture the dynamics of the factors and the proxy for the missing
sector.10 The matrices ![]() and
and ![]() control how the shock
control how the shock ![]() affects the factors and missing channel proxy variables.
affects the factors and missing channel proxy variables.
In the exercises presented in the paper, we consider two different specifications of equation (9). In the first specification , we set all elements of
![]() to zero, i.e. we drop the unobserved factors
to zero, i.e. we drop the unobserved factors ![]() . The missing shock
. The missing shock
![]() propagates in the augmented policy model through the transmission mechanisms already embedded in the model, and through the law of motion (11).11 This assumption implies that the structure of the policy model is sufficiently rich to propagate the missing shock. In the second specification, we set all
elements of
propagates in the augmented policy model through the transmission mechanisms already embedded in the model, and through the law of motion (11).11 This assumption implies that the structure of the policy model is sufficiently rich to propagate the missing shock. In the second specification, we set all
elements of
![]() to zero. The missing shock
to zero. The missing shock ![]() propagates in the augmented policy
model through the transmission mechanisms already embedded in the model, and through the law of motion of the unobserved factors (10). We assume that there are two unobserved factors,
propagates in the augmented policy
model through the transmission mechanisms already embedded in the model, and through the law of motion of the unobserved factors (10). We assume that there are two unobserved factors, ![]() and
and ![]() , which follow a
, which follow a ![]() process. We find that
this parsimonious specification is sufficient to generate impulse responses with hump shapes and persistence similar to those produced by large-scale DSGE models. To identify the factors, we restrict the top
process. We find that
this parsimonious specification is sufficient to generate impulse responses with hump shapes and persistence similar to those produced by large-scale DSGE models. To identify the factors, we restrict the top
![]() block of
block of
![]() to be an identity matrix. This normalization solves the rotational indeterminacy problem ruling out linear combinations that lead to observationally equivalent models ((Bernanke et al., 2005) and (Baumeister et al., 2010)). It would be possible to consider specifications where both
to be an identity matrix. This normalization solves the rotational indeterminacy problem ruling out linear combinations that lead to observationally equivalent models ((Bernanke et al., 2005) and (Baumeister et al., 2010)). It would be possible to consider specifications where both
![]() and
and
![]() are different from zero, but we leave that for future research.
are different from zero, but we leave that for future research.
We assume that the unobserved factors can either load on all exogenous processes or on a subset, imposing zero restrictions in one or more rows of matrices ![]() or
or ![]() . If and where to impose zero restrictions depends on two considerations. First, in operational models with 20 or more exogenous processes, estimating a full matrix
. If and where to impose zero restrictions depends on two considerations. First, in operational models with 20 or more exogenous processes, estimating a full matrix ![]() or
or ![]() could create identification problems and would require a non-trivial
amount of time.12 Second, the choice of zero restrictions depends on the type of propagation (and story) we believe is plausible. For instance, if we judge
that the missing shock mostly affects aggregate demand, we could impose zero restrictions on the coefficients loading on processes that predominantly affect the model through their effect on potential supply (eg the TFP process). We would narrow down the channels through which the shock propagates
(and rule out potentially counterfactual behavior of variables that are not targeted in the estimation), and simplify the interpretation of the results. For these considerations, we think that the judgment of the economist is a central part of the process, and cannot be replaced by purely
statistical tools.
could create identification problems and would require a non-trivial
amount of time.12 Second, the choice of zero restrictions depends on the type of propagation (and story) we believe is plausible. For instance, if we judge
that the missing shock mostly affects aggregate demand, we could impose zero restrictions on the coefficients loading on processes that predominantly affect the model through their effect on potential supply (eg the TFP process). We would narrow down the channels through which the shock propagates
(and rule out potentially counterfactual behavior of variables that are not targeted in the estimation), and simplify the interpretation of the results. For these considerations, we think that the judgment of the economist is a central part of the process, and cannot be replaced by purely
statistical tools.
One feature of our approach is that the modelling of the missing sector does not affect the transmission of shocks already present in the policy model. While this dimension might be of interest, allowing for feedback between existing shocks and the missing sector would complicate substantially the estimation exercise, making the procedure less practical to use in short periods of time. In particular, to use the impulse-response matching procedure we would need to rely on auxiliary models to estimate impulse responses to more shocks in the presence of the missing sector. In a companion paper (Caldara et al., 2012), we use likelihood-based Bayesian techniques to estimate the effects of missing shocks, allowing for feedback between the missing sector and the remaining model structure. A key advantage of a full information approach is that it does not require the use of an auxiliary model, which can be useful when the economist has little knowledge about the effects of the missing shocks.13
2.1 Estimation
Our methodology involves the estimation of three different models. First we estimate the parameters of the policy model,
![]() . In central banks, these estimates are already available to the economist. In our exposition, we estimate
. In central banks, these estimates are already available to the economist. In our exposition, we estimate
![]() using likelihood-based Bayesian estimation, as it is common practice in many central banks.14 We denote by
using likelihood-based Bayesian estimation, as it is common practice in many central banks.14 We denote by
![]() the mean of the posterior distributions.
the mean of the posterior distributions.
Second, we estimate the auxiliary model. We summarize inference from auxiliary models by impulse responses of selected variables to the shock of interest, which we denote by
![]() .15
.15
Third, we estimate the augmented policy model. We partition the parameters in two groups. The first group is composed of all the parameters of the baseline policy model
![]() . The second group includes all parameters of the augmented block:
. The second group includes all parameters of the augmented block:
We estimate the parameters
![]() to minimize a measure of the distance between the impulse responses generated by the augmented policy model, denoted by
to minimize a measure of the distance between the impulse responses generated by the augmented policy model, denoted by
![]() , and those from the auxiliary model
, and those from the auxiliary model
![]() . We estimate
. We estimate
![]() , fixing the parameters of the baseline policy model to their posterior mean
, fixing the parameters of the baseline policy model to their posterior mean
![]() . This choice is dictated by practical considerations, as the analysis needs to be conducted in a short period of time. Furthermore, impulse responses to the missing shock
might have little information on the deep parameters of the baseline policy model. Our estimator of
. This choice is dictated by practical considerations, as the analysis needs to be conducted in a short period of time. Furthermore, impulse responses to the missing shock
might have little information on the deep parameters of the baseline policy model. Our estimator of
![]() is the solution to:
is the solution to:
where
To perform the minimization of the loss function, we use the version of the CMA-ES evolutionary algorithm developed by (Andreasen, 2010). This algorithm performs well in finding global optima of ill-behaved objective functions such as the likelihood functions of DSGE models. In our experience, this algorithm is more reliable and robust than gradient based search methods.
2.2 Evaluation
We validate the augmented policy model by studying the IRFs of variables that are not targets in the estimation.17 The idea is to check whether the dynamics of such variables behave reasonably. For instance, in Section 5 we validate the SW model augmented with a housing sector studying the (unrestricted) IRFs of private consumption, investment, real wages, and hours worked to a housing demand shock. If we think the behavior of some of these variables is in contrast with the likely effects of a housing demand shock, we either re-estimate the model modifying the target variables, or we re-estimate the model imposing additional restrictions in the augmented (housing) block.
This procedure is well suited to validate the model, given that our main objective is to have an augmented policy model capable of explaining the propagation of missing shocks and that is useful for policy analysis. We do not use root mean square errors or likelihood-based criteria because a good forecasting model might not necessarily be a good model for policy analysis.
3 The Effects of Oil Price Shocks
In this section, we investigate how to augment a policy model to track the effects of oil price shocks. We first describe a DSGE model with a micro-founded oil sector. We use this model as the data generating process in the estimation exercise. We then describe and estimate a policy model that does not contain the oil sector. Finally, we augment the policy model as described in Section 2 to track the effects of oil shocks.
3.1 The Data Generating Process
We take the oil model described by (Nakov & Pescatori, 2010b,a) as the data generating process (DGP). In this model, the oil sector has two players: a dominant producer, representing the OPEC cartel, which has monopoly power, and a set of atomistic producers, who act under perfect competition and restrain the market power of the cartel. These assumptions imply that the oil price and the oil supply are endogenous variables, that react to all shocks in the economy and to the conduct of monetary policy. For convenience, we report the log-linear equilibrium conditions of the model in the Appendix.
We describe the calibration of the model in Table 1, which relies on the estimates for the great moderation period documented in (Nakov & Pescatori, 2010a).18 We use the DGP to produce 500 observations for output growth, inflation, interest rate, and the growth rate of oil prices.
3.2 The Policy Model
The policymaker has access to a smaller model, which does not contain the oil sector. The log-linear equilibrium conditions are:
There are three exogenous processes: a technology shock ![]() , a mark-up shock
, a mark-up shock ![]() and monetary policy shock
and monetary policy shock ![]() . The exogenous processes evolve as:
. The exogenous processes evolve as:
where
We estimate the policy model using Bayesian maximum likelihood on data simulated from the model in section 3.1, which includes the oil sector.19 Thus, relative to the true DGP, the estimated policy model is misspecified. The observed variables are output growth, inflation, and the nominal interest rate. Estimation results are reported in Table 2. The mean estimate for nearly all parameters is close to the true value. The only coefficient for which the true value does not lie within one standard deviation is ![]() . This bias is largely due to the misspecification of the policy model.20 Yet, misspecification seems to be
mostly captured by the exogenous processes. In particular, the correlation between the smoothed series for the technology and the mark-up processes is 0.51. Hence the assumption that the
processes are uncorrelated is clearly violated.
. This bias is largely due to the misspecification of the policy model.20 Yet, misspecification seems to be
mostly captured by the exogenous processes. In particular, the correlation between the smoothed series for the technology and the mark-up processes is 0.51. Hence the assumption that the
processes are uncorrelated is clearly violated.
3.3 The Augmented Policy Model
We now assume that an economist wants to estimate the effects of a 10% increase in oil prices on output, inflation, and the interest rate, without having access to the data generating process described in Section 3.1.
The policy model described in the previous section is similar to the DGP. The main difference is that in the policy model, the mark up process is exogenous. This misspecification means that the economist cannot identify correctly the sources of fluctuations in the mark-up and in the efficient
real interest rate. Yet, the transmission mechanisms embedded in the two models are nearly identical. For this reason, we augment the policy model without relying on unobserved factors (that is, assuming that
![]() in the context of equation 9):
in the context of equation 9):
We assume that oil prices ![]() follow an
follow an ![]() process, and they only
react to an exogenous oil price shock
process, and they only
react to an exogenous oil price shock ![]() . We allow the oil price process to affect all of the existing exogenous processes, i.e. we do not restrict any element of
. We allow the oil price process to affect all of the existing exogenous processes, i.e. we do not restrict any element of ![]() to zero.
to zero.
We fix all parameters of the policy model to the posterior means reported in Table 2. We estimate the loading factors ![]() and the persistence parameter for the oil process
and the persistence parameter for the oil process ![]() matching impulse responses to an oil shock produced by an
auxiliary model, which in this exercise is the DGP described in Section 3.1. The reason is that in this controlled experiment we want to test whether our method is able to match the true IRFs. In real life applications, when the DGP is unknown, the auxiliary model can be
a SVAR.21 We report in Table 3 the
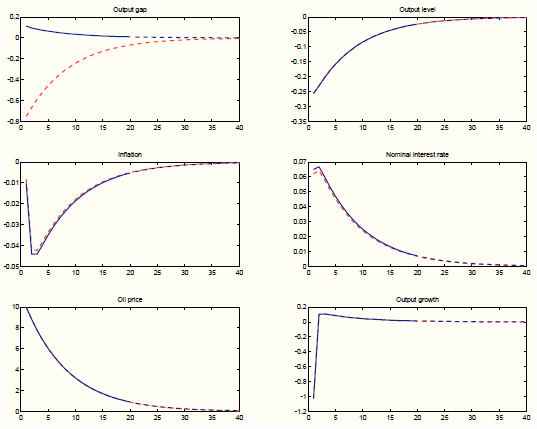
parameter estimates. We plot in Figure 1 the target impulse responses (blue line), and the impulse responses from the augmented model (red dashed). The estimation targets
the first 20 periods only (in the figure, periods 21 to 40 are not targeted).
matching impulse responses to an oil shock produced by an
auxiliary model, which in this exercise is the DGP described in Section 3.1. The reason is that in this controlled experiment we want to test whether our method is able to match the true IRFs. In real life applications, when the DGP is unknown, the auxiliary model can be
a SVAR.21 We report in Table 3 the
parameter estimates. We plot in Figure 1 the target impulse responses (blue line), and the impulse responses from the augmented model (red dashed). The estimation targets
the first 20 periods only (in the figure, periods 21 to 40 are not targeted).
We target the impulse responses of inflation, interest rate, oil prices, and output growth. The augmented model is able to match these responses almost perfectly, loading the process for oil prices on the technology and mark-up processes. These loadings are consistent with how the oil technology shock enters in the true model, where it affects both the mark up and the real efficient rate. The figure also shows the response of the output level which, not surprisingly, perfectly resembles the response in the DGP. However, the response of the output gap between the two models is very different. In the augmented model, the oil shock loads mostly on the mark-up shock, which does not affect potential output. As a result, the output gap in the augmented model closely follows the dynamics of the output level.
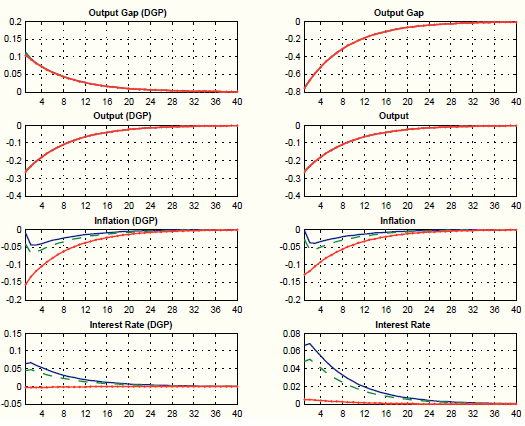
Figure 2 plots impulse responses from the DGP (left column) and from the augmented policy model (right column) to a 10% increase in oil prices for different values of the Taylor rule coefficient on inflation. The augmented policy model is able to correctly identify changes in the responses of output, inflation, and the interest rate generated by a less aggressive stance of monetary policy on inflation. The small quantitative errors are due to the fact that in the augmented policy model, we neglect the feedback effect of the change in monetary policy on oil prices, which in the DGP happens via the output gap in the oil mark-up determination. The augmented policy model does a poor job in tracking the effects of the policy change on the output gap (for the same reasons explained in the previous paragraph).
4 The Effects of House Price Shocks
In this section, we consider a model where the missing channel is more deeply embedded within the endogenous structure of the economy. Specifically, we assume that the data generating process is a model where there is an important role for house prices in determining consumption. We follow the same steps as in Section 3. First, we specify the data generating process; then we specify and estimate the policymaker's (misspecified) model; we finally augment the policymaker's model to try to account for the missing channel.
4.1 The Data Generating Process
We use the model of (Iacoviello, 2005). Here, we provide a general description of the model, the structural equations of the model can be found on page 745 in (Iacoviello, 2005). The model is a variant of the (Bernanke et al., 1999) New Keynesian model where endogenous changes in the balance sheets of firms create a financial accelerator effect. The model also includes collateral constraints tied to the value of housing property for firms which is used as one of the factors of production. These features create a financial accelerator where demand shocks are amplified. When demand rises, asset prices rise, which in turn increases the borrowing capacity of debtors (i.e firms). This boosts consumption spending and investment. As consumer prices rise, the real value of debtors' outstanding obligations falls and real net worth rises. Because borrowers have a higher propensity to spend than lenders, there are further increases in demand.
As noted, the main innovations of the model are related to the behavior of demand. The remainder of the model is standard. Calvo price setting leads to a conventional New Keynesian Phillips curve relating inflation to marginal costs. The monetary policymaker is assumed to operate a reaction
function for the nominal interest rate, which has a (Taylor, 1993) formulation adjusted to include interest rate smoothing. The model is driven by four shocks: to technology (![]() ), to the Phillips curve (
), to the Phillips curve (![]() ), to monetary policy (
), to monetary policy (![]() ),
and to housing preferences (
),
and to housing preferences (![]() ). The housing preference shock is a stochastic variation in the relative weight on housing in consumers' utility functions. We refer to this shock as a
house price shock (following (Iacoviello, 2005)) in what follows.
). The housing preference shock is a stochastic variation in the relative weight on housing in consumers' utility functions. We refer to this shock as a
house price shock (following (Iacoviello, 2005)) in what follows.
(Iacoviello, 2005) sets the parameters of the model using a minimum distance estimator that matches the impulse responses of the model to those in an identified VAR estimated on US data. For our data generating process, we largely rely on Iacoviello's reported parameter estimates, and the calibration is reported in Table 4. We use the DGP to produce 500 observations for output growth, inflation, interest rate, and house prices.
4.2 The Policy Model
We assume that the policy model is the same three-equation New Keynesian model described in Section 3.2. The only exception is that, following (Iacoviello, 2005), we write the model in terms of output growth instead of the output gap and the Taylor rule is assumed to respond to the output level rather than the output gap.
We estimate the parameters of the policy model using Bayesian Maximum likelihood. The central bank observes data on output growth, inflation, and the nominal interest rate.
Estimation results are reported in Table 5. The policy model lacks mechanisms capable of generating persistence in the effects of exogenous shocks embedded in the true model. For this reason, the degree of price stickiness and the autocorrelation coefficient for the technology process display a marked upward bias. Furthermore, part of the volatility in the data generated by the house preference shock, is accounted by the estimated volatility of the mark-up shock, which is also substantially larger than the true volatility of this shock in the data generating process.
4.3 The Augmented Policy Model
To incorporate the effect of house prices in the policy model, we consider two alternative augmented policy models. In both exercises house prices, the proxy variable, follow an AR(1) process:
| (15) |
For the first exercise, we check how a shock to house prices ![]() propagates in the augmented policy model without relying on unobserved factors (
propagates in the augmented policy model without relying on unobserved factors (
![]() ). In the estimation exercise, we keep all parameters of the policy model fixed to the posterior means reported in Table 5.
). In the estimation exercise, we keep all parameters of the policy model fixed to the posterior means reported in Table 5.
We estimate the loading factors ![]() and the persistence parameter for the housing process
and the persistence parameter for the housing process ![]() matching the responses for output, inflation, the interest rate, and house prices to a housing shock obtained from the DGP. We report in Table 6
the estimated parameters. House prices load mostly on the technology process
matching the responses for output, inflation, the interest rate, and house prices to a housing shock obtained from the DGP. We report in Table 6
the estimated parameters. House prices load mostly on the technology process ![]() .
.
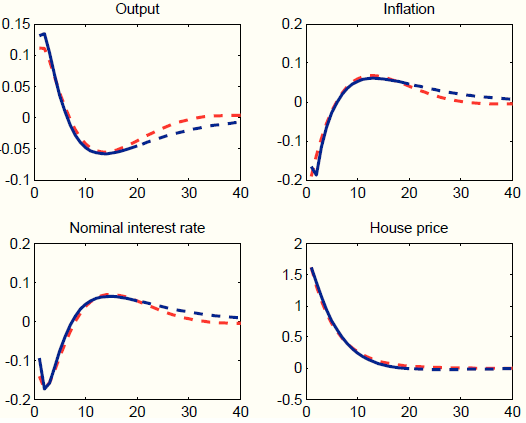
We plot in Figure 3 the target impulse responses (blue line), and the impulse responses from the augmented model (red dashed). The estimation targets the first 20 periods (solid line), while we leave periods 21 to 40 unrestricted. The augmented model captures well the dynamics of house prices, but does a fairly poor job at mimicking the dynamics of the remaining variables. The reason is simple: the propagation mechanisms embedded in the policy model are not capable of generating the hump-shaped and persistent response due to the financial accelerator in the DGP.
To mimic such dynamics, without altering the propagation of other shocks, we augment the policy model introducing two unobserved factors as described in equations (7)-(11). The loading factor matrix ![]() is:
is:
![\displaystyle \Lambda_1 = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \lambda_{r,1} & \lambda_{r,2} \\ \end{array} \right],](img117.gif) |
and we set
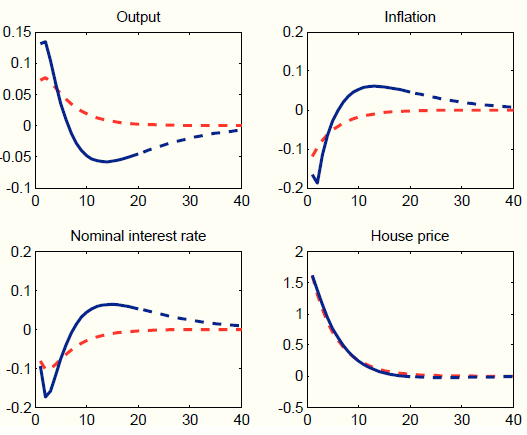
Figure 4 plots the target responses (blue line) and the responses generated by the augmented policy model (red dashed line). The augmented policy model does a very good
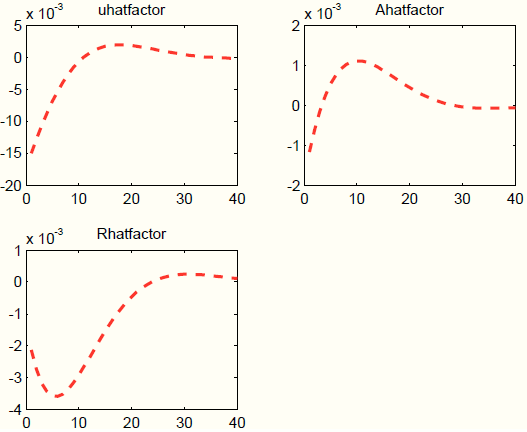
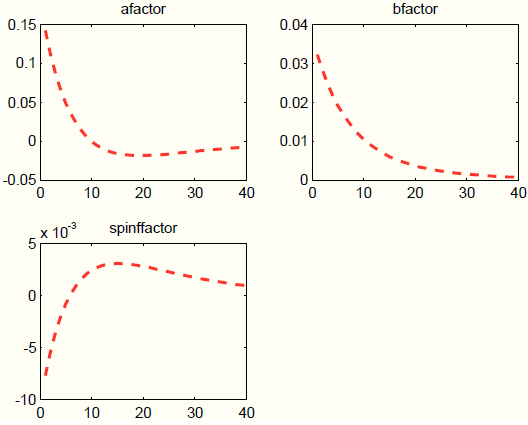
job at tracking the true impulse responses, although it slightly underestimates the persistence at longer (untargeted) horizons. Instead of reporting the estimates for the loading coefficients ![]() , which are hard to interpret, Figure 5 plots
, which are hard to interpret, Figure 5 plots ![]() , the process-specific factors.
, the process-specific factors.
The mark-up factor
![]() is 1 order of magnitude larger than the factors loading on the technology and monetary processes. In fact, setting
is 1 order of magnitude larger than the factors loading on the technology and monetary processes. In fact, setting
![]() ,
,
![]() , and
, and
![]() to zero, the impulse responses from the augmented policy model are nearly unchanged. These results are not surprising, given that the housing shock in the (Iacoviello, 2005) model induces negative correlation between output and inflation, which can be also generated by a mark-up shock. Since the Taylor rules in the policy model and the DGP are similar, the policy response in both models is also very close. The technology process
is also capable of generating negative correlation between output and inflation. In a separate exercise (not reported), we re-estimate the augmented policy model restricting all elements of
to zero, the impulse responses from the augmented policy model are nearly unchanged. These results are not surprising, given that the housing shock in the (Iacoviello, 2005) model induces negative correlation between output and inflation, which can be also generated by a mark-up shock. Since the Taylor rules in the policy model and the DGP are similar, the policy response in both models is also very close. The technology process
is also capable of generating negative correlation between output and inflation. In a separate exercise (not reported), we re-estimate the augmented policy model restricting all elements of ![]() to zero, except for the loading factors on the technology process. This restricted version of the model is capable of generating impulse responses that are nearly identical to the responses reported in Figure 4.
to zero, except for the loading factors on the technology process. This restricted version of the model is capable of generating impulse responses that are nearly identical to the responses reported in Figure 4.
Figure 6 plots impulse responses from the data generating process (left column) and from the augmented policy model (right column) to an increase in house prices for different values of the Taylor rule coefficient on inflation. The augmented policy model is able to correctly identify the qualitative changes in the responses of output, inflation, and the interest rate generated by a less aggressive response of monetary policy to inflation. The augmented policy model also does a good job capturing the quantitative response of output, while it underestimates the stronger response of inflation and the interest rate when monetary policy responds less aggressively to inflation. The reason is that the augmented policy model lacks sufficient endogenous persistence to generate changes in the inflation response, generating such persistence through the (policy invariant) unobserved factors. Notice that differences in quantitative results are not due to the lack of endogenous response in house prices, which in the data generating process and in the augmented policy model are nearly identical.22
5 Housing in the Smets and Wouters (2007) Model
In Sections 3 and 4 we estimated the policy and augmented policy models on simulated data. Results suggest that the specification of the augmented policy model is flexible enough to generate responses in line with the data generating process and that are easy to interpret. In this section, we apply our methodology in a more realistic environment. In particular, we use the (Smets & Wouters, 2007) (henceforth SW) model as the policy model. We augment the SW model to study the implications of alternative assumptions about the future path of house prices for the variables in the model. Although the SW model includes a wide range of frictions and transmission channels, it does not include the housing market. Therefore, we use a small VAR to help us adjust the baseline DSGE model projections in the light of alternative house price scenarios. We conduct estimation exercises using US data.
We proceed as follows. In Section 5.1, we briefly describe the SW model and the US data set that we assume to be available for the forecaster. In Section 5.2, we describe the VAR that is used to identify the effects of house price shocks on a small number of key macroeconomic variables. In Section 5.3 we incorporate shocks to house prices into the DSGE model. This is done along the lines discussed in Section 4 for the (Iacoviello, 2005) model.
5.1 The Smets and Wouters (2007) Model
We use the medium-scale DSGE model of (Smets & Wouters, 2007). As noted in the Introduction, this model has been used as a blueprint for the operational DSGE models developed at a number of central banks. It is also an important benchmark model in the literature. Given that the model is very well known, we only provide a sketch of its structure.
The model includes a wide variety of nominal and real frictions. Households maximize utility subject to habit formation in their consumption choices. They accumulate capital (which they rent to firms) subject to costs of adjusting the rates of investment and utilization. Households (via unions) also supply differentiated labor to firms and set the nominal wage according to a Calvo scheme. Wages that are not re-optimized are increased in line with a weighted average of trend nominal wage growth and lagged inflation.
Firms rent capital services and labor from households which are used to produce output. Output is used for consumption, government purchases, and investment. Retailers set prices according to a Calvo mechanism, with a partial indexation of prices that are not re-optimized that is analogous to the scheme for nominal wages described above. Monetary policy is conducted through a reaction function for the nominal interest rate. The reaction function specifies that nominal interest rates respond to deviations of inflation from the target, the output gap, and the change of the output gap. The output gap is defined using a flexible-price specification of the model.
The model is driven by seven shocks: to the level of TFP; to the investment adjustment cost function; to household preferences; to government spending; to price and wage mark-ups; and to the monetary policy reaction function. Government spending and TFP shocks are assumed to be correlated with each other. These shocks are designed to explain the movements of seven data series: GDP growth; consumption growth; investment growth; inflation (GDP deflator); the Fed funds rate; real wage growth; and hours worked.
As in (Smets & Wouters, 2007), we estimate the parameters of the model using Bayesian techniques. We estimate the model for the period 1984-2004 using the same dataset and prior distributions as (Smets & Wouters, 2007). Estimation results are reported in Tables 7 and 8.
5.2 The VAR Model
We construct a small VAR along the lines of that estimated by (Iacoviello, 2005). We use the output, inflation and interest rate data from the (Smets & Wouters, 2007) data set. For house prices, we use the OFHEO house price index (all transactions). We apply the X12 seasonal adjustment process to seasonally adjust the data. We measure the house price relative to the GDP deflator, which is the price series used to define the inflation measure in (Smets & Wouters, 2007). The house price series starts in 1984Q1 and the Smets-Wouters data set ends in 2004Q4. So this defines our sample.
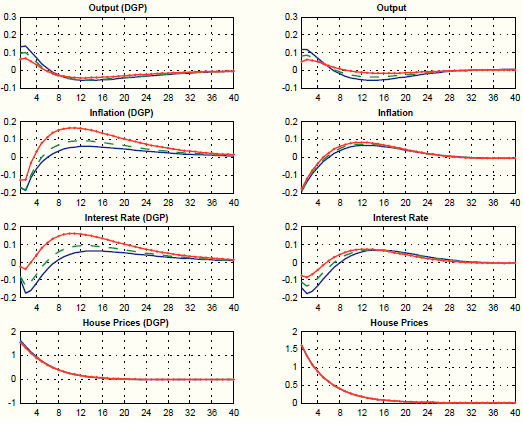
We estimate a VAR(2) and identify a house price shock using a Cholesky decomposition with the following ordering: nominal interest rate, inflation, house prices and output. This ordering follows (Iacoviello, 2005). We report the impulse responses to a shock to house prices in Figure 7 (blue lines).
5.3 Incorporating House Price Effects into the DSGE Model
We explore two options to introduce shocks to house prices in the SW model. Both options rely on two unobserved factors ![]() , as the SW lacks a financial accelerator mechanism.
Furthermore, we assume that house prices follow an exogenous
, as the SW lacks a financial accelerator mechanism.
Furthermore, we assume that house prices follow an exogenous ![]() process:
process:
where
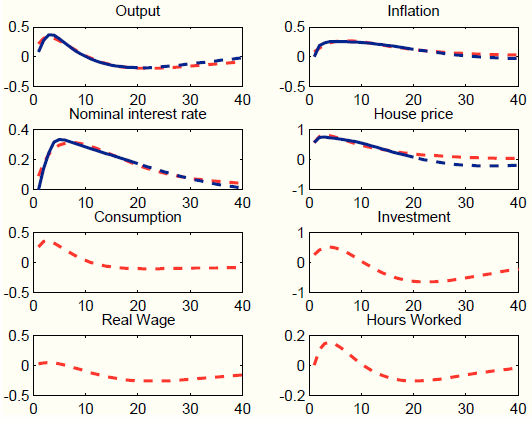
We first assume that the unobserved factors ![]() load on all seven exogenous processes. Results are presented in Figure 7. This approach does a very good job at matching the target impulse responses (for output, inflation, house prices and the nominal interest rate). This is of little surprise, since loading the unobserved factors on seven exogenous processes
grants much flexibility. The model does also a good job at capturing the persistent response of output, inflation, and the interest rate from quarter 21 to 40 (untargeted). The four bottom panels of Figure 7 plot the response of variables that are not targets, namely consumption, investment, the real wage, and hours worked. These variables are key in providing a coherent story for policy-makers. The response of consumption, investment, and hours
worked is negative, while the response the real wage is very strongly positive. These responses are not in line with most evidence on the effects of housing demand shocks. For instance, (Iacoviello & Neri, 2010) document an increase in both private consumption and
investment.
load on all seven exogenous processes. Results are presented in Figure 7. This approach does a very good job at matching the target impulse responses (for output, inflation, house prices and the nominal interest rate). This is of little surprise, since loading the unobserved factors on seven exogenous processes
grants much flexibility. The model does also a good job at capturing the persistent response of output, inflation, and the interest rate from quarter 21 to 40 (untargeted). The four bottom panels of Figure 7 plot the response of variables that are not targets, namely consumption, investment, the real wage, and hours worked. These variables are key in providing a coherent story for policy-makers. The response of consumption, investment, and hours
worked is negative, while the response the real wage is very strongly positive. These responses are not in line with most evidence on the effects of housing demand shocks. For instance, (Iacoviello & Neri, 2010) document an increase in both private consumption and
investment.
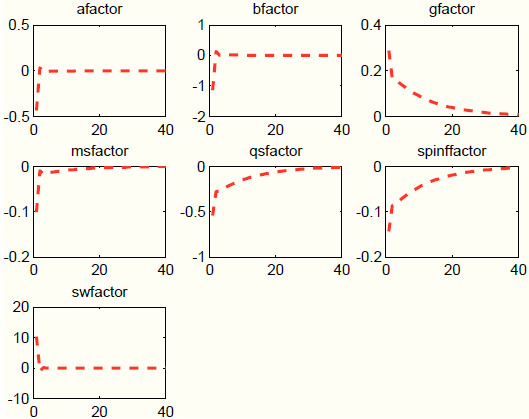
Figure 7 provides an explanation for this finding. The dynamic responses are predominantly driven by three shocks: investment-specific technology, government spending, and price mark-up shocks. The decline in private consumption is due to the increase in government spending, which increases output (target variable), but in the SW model crowds out private demand. The decline in investment is due to the negative response in investment specific technology. Finally, the decline in hours worked and the sharp rise in real wages is due to a large but short-lived increase in the wage mark-up.
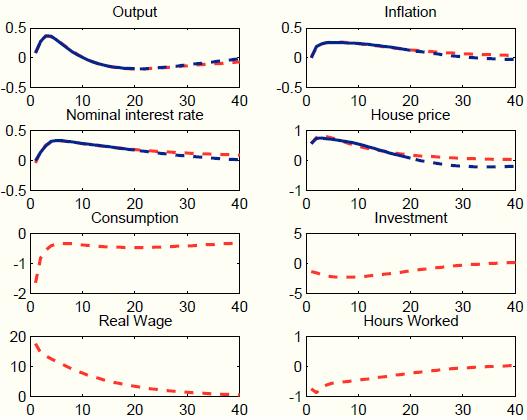
Guided by the counter-factual responses of private demand and labor market variables, in the second experiment, we load the unobserved factors only on three processes: general technology, risk premium, and price mark-up. We load on general technology because we want to generate an expansion in real activity. We load on the risk premium because we want to induce an increase in the interest rate faced by households and introduce a wedge between such interest rate and the one controlled by the central bank. Finally, we load on the price mark-up process because it helps to fine-tune the response of inflation. Figure 9 shows that, despite loading on only three processes instead of seven, our procedure still does well in terms of matching the target responses, both in the short-medium run (targeted) and in the long run (not targeted). In addition, the short-run responses of private demand and labor market variables are all positive. The negative response at long horizons mimics the negative response of output to the housing demand shock.23
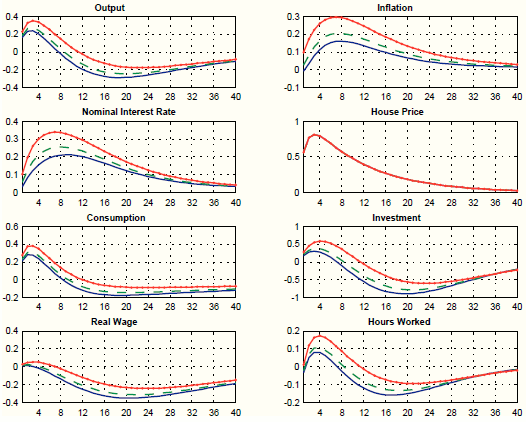
Figure 11 plots impulse responses to an increase in house prices for different values of the Taylor rule coefficient on inflation. As we can see, in contrast to the augmented policy model in Section 4, the augmented SW model is able to generate differences in the response of inflation associated with different parameterizations of the monetary policy rule. One possible explanation for this result may be the richer structure of the SW model, which may allow the augmented policy model not to rely much on the (policy invariant) unobserved factors.
Finally, we consider an alternative specification of the house price equation (16). In particular, we use in the augmented policy model the house price equation estimated in the auxiliary VAR model. The advantage of this specification is that we allow house prices to depend
on variables included in the policy model, so that we can produce a model-consistent baseline forecast for ![]() . We use the equation from the auxiliary model because it provides a
reasonable reduced-form description of the evolution of house prices. The specification of the augmented policy model with the VAR equation for house prices generates IRFs and policy implications in line with those reported for the benchmark model.24 The main reason is that the evolution of output, inflation, and the interest rate described by the policy model does not explain much volatility in house prices. Yet, we believe that this
generalization can be useful when the proxy variable is endogenous to the variables modelled in the policy model.
. We use the equation from the auxiliary model because it provides a
reasonable reduced-form description of the evolution of house prices. The specification of the augmented policy model with the VAR equation for house prices generates IRFs and policy implications in line with those reported for the benchmark model.24 The main reason is that the evolution of output, inflation, and the interest rate described by the policy model does not explain much volatility in house prices. Yet, we believe that this
generalization can be useful when the proxy variable is endogenous to the variables modelled in the policy model.
6 Conclusions
In this paper, we consider the problem of how to analyze the effects of shocks that do not appear explicitly within a DSGE model that is used to inform policy and forecast discussions. To this end, we augmented a baseline DSGE model with an exogenous block that is intended to capture the effects of shocks in the un-modelled sector. We estimated the parameters of the additional block by matching impulse responses to the shock of interest from an auxiliary model. We believe that our approach has broad applicability, and provides a practical way to address an important problem.
We used our method to study the effects of oil price shocks and house price shocks in a three-equation New Keynesian model. We showed that the impulse response functions produced by the augmented DSGE models are similar to those produced by richer models with micro-founded oil and housing sectors. Furthermore, policy experiments conducted in with the augmented DSGE models and the micro-founded models delivered very similar conclusions. We then discussed an empirical application, studying the effects of house price shocks in the United States using the (Smets & Wouters, 2007) model.
Bibliography
Journal of International Economics 72(2):481-511.
Computational Economics 35(2):127-154.
Bank of England working papers 401, Bank of England.
The Quarterly Journal of Economics 120(1):387-422.
Handbook of Macroeconomics 1:1341-1393.
NBER Technical Working Papers 0332, National Bureau of Economic Research, Inc.
Norges Bank Staff Memo 2006/6 .
SERIEs 1(1):175-243.
Mimeo, Board of Governors of the Federal Reserve System.
Journal of Political Economy 113(1):1-45.
Working Paper Series 944, European Central Bank.
Journal of Economic Literature 37(4):1661-1707.
Working Paper 15774, National Bureau of Economic Research.
American Economic Review 99(4):1415-50.
SERIEs 1(1):3-49.
American Economic Review 95(3):739-764.
American Economic Journal: Macroeconomics 2(2):125-64.
Journal of Economic Dynamics and Control 28(6):1205-1226.
Working Paper Series 1289, European Central Bank.
Journal of Money, Credit and Banking 42(1):1-32.
Economic Journal 120(543):131-56.
NBER Working Papers 16781, National Bureau of Economic Research, Inc.
Journal of Economic Dynamics and Control 32(8):2460-2475.
Journal of the European Economic Association 1(5):1123-1175.
American Economic Review 97(3):586-606.
Carnegie-Rochester Conference Series on Public Policy 39(1):195-214.
A. The Nakov-Pescatori (2010a,b) Model.
We provide a parsimonious description of the model. We refer to the original papers for details.
The IS equation is:
where
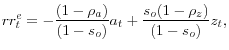 |
where
where
The Phillips curve is:
where
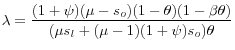 |
is the slope of the Phillips curve.
The mark up is a function of the technology process in the oil importing economy ![]() , the oil technology shock
, the oil technology shock ![]() , and the output gap in the oil importing economy
, and the output gap in the oil importing economy ![]() . The coefficients
. The coefficients ![]() ,
, ![]() , and
, and ![]() are functions
of various steady state ratios.
are functions
of various steady state ratios.
Finally, we close the model with the following Taylor rule:
where
Table 1: Calibration of structural parameters for the (Nakov & Pescatori, 2010b) oil model used as data generating process and described in Section 3.1.
| Name | Value |
| Policy Rule:
|
3.00 |
| Policy Rule: |
0.54 |
| Policy Rule: |
0.69 |
| Other Deep Parameters: |
0.48 |
| Other Deep Parameters: |
1.00 |
| Other Deep Parameters: |
0.9926 |
| Other Deep Parameters: |
0.64 |
| Other Deep Parameters: |
0.33 |
| Other Deep Parameters: |
0.03 |
| Other Deep Parameters: |
15% |
| Other Deep Parameters: |
0 |
| Shock Autocorrelations: |
0.98 |
| Shock Autocorrelations: |
0.96 |
| Shock Autocorrelations: |
0.88 |
| Shock Standard Deviations:
|
0.82 |
| Shock Standard Deviations:
|
0.21 |
| Shock Standard Deviations:
|
0.00 |
| Shock Standard Deviations:
|
15.18 |
Table 2: Prior and posterior moments - Policy model used in the oil price example described in Section 3.2. Column (1) reports the parameters of the prior distributions. Column (2) reports posterior means and standard deviations (in
parenthesis). See Section 3.3 for details.
| Name | Prior Mean | Prior (Standard Deviation) | Posterior Mean | Posterior (Standard Deviation) |
| Policy Rule:
|
2.00 | 0.50 | 2.84 | (0.33) |
| Policy Rule: |
0.40 | 0.10 | 0.36 | (0.10) |
| Policy Rule: |
0.50 | 0.20 | 0.70 | (0.06) |
| Other Deep Parameters: |
0.50 | 0.20 | 0.59 | (0.04) |
| Other Deep Parameters: |
1.00 | 0.25 | 1.00 | (0.24) |
| Shock Autocorrelations: |
0.50 | 0.20 | 0.98 | (0.00) |
| Shock Autocorrelations:
|
0.50 | 0.20 | 0.92 | (0.02) |
| Shock Standard Deviations:
|
0.50 | 4.00 | 0.86 | (0.03) |
| Shock Standard Deviations:
|
0.50 | 4.00 | 0.21 | (0.03) |
| Shock Standard Deviations:
|
0.50 | 4.00 | 0.33 | (0.07) |
Table 3: Estimates of parameters in the augmented policy model, where the targets in the estimation are impulse response from the DGP. See Section 3.3 for details.
|
|
|
|
|
| 0.0495 | 0.0756 | 0.0100 | 0.8814 |
Table 4: Calibration of structural parameters for the (Iacoviello, 2005) housing model used as data generating process and described in Section 4.1.
| Name | Value |
| Policy Rule:
|
3.00 |
| Policy Rule: |
0.50 |
| Policy Rule: |
0.60 |
| Other Deep Parameters: |
0.75 |
| Other Deep Parameters: |
1.01 |
| Other Deep Parameters: |
0.99 |
| Other Deep Parameters: |
0.98 |
| Other Deep Parameters: j | 0.1 |
| Other Deep Parameters: |
0.03 |
| Other Deep Parameters: m | 0.89 |
| Other Deep Parameters: X | 1.05 |
| Shock Autocorrelations: |
0.50 |
| Shock Autocorrelations: |
0.85 |
| Shock Autocorrelations: |
0.59 |
| Shock Standard Deviations:
|
2.740 |
| Shock Standard Deviations:
|
24.89 |
| Shock Standard Deviations:
|
0.150 |
| Shock Standard Deviations:
|
0.290 |
Table 5: Prior and posterior moments - Policy model used in the house price example described in Section 4.2. Column (1) reports the parameters of the prior distributions. Column (2) reports posterior means and standard deviations (in
parenthesis).
| Name | Prior Mean | Prior (Standard Deviation) | Posterior Mean | Posterior (Standard Deviation) |
| Policy Rule:
|
3.00 | 0.20 | 2.93 | (0.10) |
| Policy Rule: |
0.40 | 0.20 | 0.46 | (0.06) |
| Policy Rule: |
0.50 | 0.10 | 0.63 | (0.02) |
| Other Deep Parameters: |
0.50 | 0.20 | 0.90 | (0.03) |
| Shock Autocorrelations: |
0.50 | 0.20 | 0.80 | (0.02) |
| Shock Autocorrelations: |
0.50 | 0.20 | 0.44 | (0.01) |
| Shock Standard Deviations:
|
0.50 | 2.00 | 2.92 | (0.10) |
| Shock Standard Deviations:
|
0.50 | 2.00 | 0.25 | (0.01) |
| Shock Standard Deviations:
|
0.50 | 2.00 | 0.28 | (0.01) |
Table 6: Estimates of parameters in the augmented policy model, where the targets in the estimation are impulse response from a SVAR.
|
|
|
|
|
| 0.6447 | 0.00351 | 0.00015 | 0.8142 |
Table 7: Prior and posterior moments - (Smets & Wouters, 2007) model used in Section 5.3.Column (1) reports the parameters of the prior distributions. Column (2) reports posterior means and standard deviations
(in parenthesis).
| Name | Prior Mean | Prior (Standard Deviation) | Posterior Mean | Posterior (Standard Deviation) |
| 4.00 | 1.50 | 5.80 | (1.11) | |
|
|
1.50 | 0.37 | 1.03 | (0.12) |
| 0.70 | 0.10 | 0.56 | (0.04) | |
| 0.50 | 0.10 | 0.78 | (0.08) | |
| 0.50 | 0.10 | 0.80 | (0.04) | |
| 0.50 | 0.15 | 0.45 | (0.16) | |
| 0.50 | 0.15 | 0.30 | (0.09) | |
| 0.50 | 0.15 | 0.62 | (0.11) | |
| 1.25 | 0.12 | 1.48 | (0.09) | |
| 1.50 | 0.25 | 1.68 | (0.22) | |
| 0.75 | 0.10 | 0.86 | (0.02) | |
| 0.12 | 0.05 | 0.14 | (0.04) | |
|
|
0.12 | 0.05 | 0.17 | (0.03) |
|
|
0.63 | 0.10 | 0.61 | (0.07) |
|
|
0.25 | 0.10 | 0.18 | (0.04) |
|
|
0.00 | 2.00 | 0.60 | (0.58) |
|
|
0.40 | 0.10 | 0.50 | (0.02) |
| 0.30 | 0.05 | 0.18 | (0.02) |
Table 8: Prior and posterior moments - (Smets & Wouters, 2007) model used in Section 5.3.Column (1) reports the parameters of the prior distributions. Column (2) reports posterior means and standard deviations
(in parenthesis).
| Name | Prior Mean | Prior (Standard Deviation) | Posterior Mean | Posterior (Standard Deviation) |
|
|
0.10 | 2.00 | 0.38 | (0.03) |
|
|
0.10 | 2.00 | 0.09 | (0.02) |
|
|
0.10 | 2.00 | 0.40 | (0.03) |
|
|
0.10 | 2.00 | 0.40 | (0.05) |
|
|
0.10 | 2.00 | 0.12 | (0.01) |
|
|
0.10 | 2.00 | 0.13 | (0.02) |
|
|
0.10 | 2.00 | 0.23 | (0.03) |
| 0.50 | 0.20 | 0.92 | (0.03) | |
| 0.50 | 0.20 | 0.82 | (0.08) | |
| 0.50 | 0.20 | 0.97 | (0.01) | |
| 0.50 | 0.20 | 0.61 | (0.07) | |
| 0.50 | 0.20 | 0.28 | (0.06) | |
| 0.50 | 0.20 | 0.43 | (0.16) | |
| 0.50 | 0.20 | 0.67 | (0.15) | |
| 0.50 | 0.20 | 0.34 | (0.20) | |
| 0.50 | 0.20 | 0.44 | (0.20) | |
| 0.50 | 0.20 | 0.42 | (0.11) |
![\displaystyle S_{t}\equiv\left[\begin{array}{c} Z_{t}\\ s_{t}\end{array}\right],](img22.gif)
![\displaystyle \widetilde S_{t}\equiv\left[\begin{array}{c} Z_{t}\\ s_{t}\\ F_{t}\\ m_{t}\end{array}\right],](img42.gif)