Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-75 Screen Reader version ^♣

Reconciling Micro and Macro Estimates of the Frisch Labor Supply Elasticity

William B Peterman¹

Federal Reserve Board of Governors

Keywords: Frisch labor supply elasticity; intensive margin; extensive margin; calibration.

Abstract:

There are large differences between the microeconometeric estimates of the Frisch labor supply elasticity (0-0.5) and the values used by macroeconomists to calibrate general equilibrium models (2-4). The microeconometric estimates of the Frisch are typically estimated by regressing changes in hours on changes in wages conditional on the individual being a married male head of household, working some minimum number of hours and being of prime working age. In contrast macroeconomic calibration values are typically set such that fluctuations in a general equilibrium model match the observed changes in the aggregate hours and wages from the whole population over time. This paper aims to explain the gap by estimating an aggregate Frisch elasticity which is consistent with the concept of macro calibration values using the microeconometric techniques. In order to estimate the Frisch consistent with the macro concept, this paper alters the typical microeconometric approach in order to incorporate fluctuations on the extensive margin and also broadens the scope of the sample to include single males, females, secondary earners, young individuals, and old individuals. This paper finds that estimates of the aggregate macro Frisch elasticity are in the middle of the range of macroeconomic calibration values (around 3.0). Furthermore, it finds that the key to explaining the difference are the fluctuations on the extensive margin of single males, females, secondary earners, older individuals, and younger individuals.

JEL Classification: E24, and J22

1 Introduction

The Frisch labor supply elasticity is a key economic variable for economists. It is central for the design and assessments of government policies that affect labor supply and for analyzing the macroeconomy. Despite the importance of the Frisch elasticity, there are large differences between microeconometric estimates of this parameter and the values that are included in macroeconomic models. The original microeconometric estimates of the Frisch elasticity are between 0 - 0.54 (see (MaCurdy, 1981) and (Altonji, 1986)). These estimates are determined by regressing changes in the natural log of an individual's labor supply on wages over his life cycle accounting for possible endogeneity of wages. In contrast, economists calibrate the Frisch elasticity in macroeconomic models in the range of 2 - 4.² These parameter values are calibrated by matching the volatility of hours in a macroeconomic model and the aggregate volatility observed in the data over the business cycle. It is not surprising that there is a gap between these values since there are fundamental differences in the concepts they are trying to capture. The microeconometric estimates evaluate the Frisch elasticity conditional on the individual being employed, married, prime-aged, and the head of the household. I refer to the Frisch elasticity consistent with this definition as the micro Frisch elasticity. In contrast, the calibration values represent the aggregate Frisch elasticity considering all the observed data. Specifically, these values incorporate aggregate changes in hours from all individuals and the observed aggregate changes in wages from workers. I refer to the Frisch elasticity consistent with this definition as the macro Frisch elasticity. This paper determines whether the gap between the microeconometric estimates and the calibration values used in macroeconomic models can be explained by two key differences due to their alternate definitions.³ First, the original micro econometric estimates are restricted to males who are married, primary earners, and between the ages 26 to 60.⁴ In contrast, the aggregate volatility used for calibration includes observed fluctuations from the whole population. Second, the microeconometric estimates include only fluctuations on the intensive margin, while the calibration values used in macroeconomic models incorporate fluctuations in hours on both the intensive and extensive margin. The goal of this paper is to determine whether estimates of the macro Frisch elasticity determined using the original microeconometric techniques in (Altonji, 1986) and (MaCurdy, 1981) are consistent with values used to calibrate macroeconomic models. In order to estimate the macro Frisch elasticity, I alter their estimation procedure in two ways. First, I broaden the composition by including non-married individuals, females, secondary earners, younger individuals, and older individuals.⁵ Second, I incorporate fluctuations in hours on the extensive margin and use a pseudo panel instead of a traditional panel to estimate the macro Frisch. A pseudo panel is a panel data set that constructs estimates of a cohort's average over times from repeated cross sections. This approach implies that instead of estimating the parameter values directly from changes in an individual's values over time, the estimates are determined from changes in the cohort's average. This approach offers a natural framework for estimating the macro Frisch elasticity since it estimates the aggregate value for the representative cohort.⁶ Moreover, since the natural log of hours is undefined if an individual works zero hours, but the cohorts average is still defined if non-workers are included, using a pseudo panel allows me to incorporate individuals who do not work. I estimate in a traditional micro panel that the micro Frisch elasticity which is conditional on being a male, employed, married, a head of household, and between the ages of twenty-six to sixty is approximately 0.2. In contrast, when I change the composition to be more inclusive and incorporate fluctuations on the extensive margin, I estimate using a pseudo panel that the macro Frisch elasticity is between 2.9 and 3.1. Therefore, the effect of these two differences arising from alternative concepts of the Frisch elasticity can explain the gap between the microeconometric estimates of the Frisch elasticity and the calibration values used in macroeconomic models. Next, I individually determine the effect of adopting these changes on the micro estimates of the Frisch elasticity. I find that when I include a broader composition, but only incorporate fluctuations on the intensive margin, the estimates of the Frisch elasticity increase from 0.2 to 0.9. Alternatively, I find that the estimates of the Frisch elasticity increases to between 0.8 and 0.9 when I incorporate fluctuations on the extensive margin but only examine males who are employed, head of their household, of prime age, and married. Comparing the increases from incorporating each of these changes independently indicates that both explanations play a similar role in reconciling the gap between the microeconometric estimates and macro-calibration values. Furthermore, since the sum of the changes from independently accounting for these differences is not large enough to explain the gap, it is clear that the interaction of these two differences is important for explaining the gap. Specifically, fluctuations on the extensive margin of single males, females, secondary earners, older individuals, and younger individuals are critical to explaining the differences between the microeconometric estimates of the Frisch elasticity and the values used to calibrate macroeconomic models. Although the goal of this paper is not to evaluate the original microeconometric approach to estimating the Frisch elasticity, I test the sensitivity of the results with respect to the functional forms of the instruments used to account for endogeneity bias to determine the robustness of the results. I find that when I change the estimation procedure to use a more flexible set of polynomials of the instruments, the difference between my estimates of the micro and macro estimates are still large enough to explain the gap. Additionally, I estimate both the micro and macro Frish elasticity for different age ranges in order to determine the importance of older individuals in both estimates. When estimating the micro Frisch elasticity, I find that the estimates are fairly stable regardless of the range of ages included in the estimating sample. With regards to the macro Frisch elasticity, I find that excluding individuals between the ages of fifty-six to sixty-five causes the estimates to drop by almost half. These results indicate that the fluctuations in aggregate hours of older individuals are responsible for the large values calibrate the Macro Frisch elasticity are driven in large part by . This work builds on previous literature that examines whether either of these differences can explain the gap. However, prior studies tend to examine each explanation in isolation and find that neither can fully explain the gap on its own. Examples of previous work which demonstrates that the sample's composition can affect estimates of the Frisch elasticity include: (Rìos-Rull et al., 2012), (Mulligan, 1995), (Heckman and Macurdy, 1980), (Blau and Kahn, 2007), (Fiorito and Zanella, 2012), and (Kimmel and Kniesner, 1998). These works tend to indicate that married men have a lower Frisch elasticity than females, single males, and younger or older individuals.⁷ Although these studies find that broadening the sample to include more than just married men who are the head of their household increases the estimated Frisch elasticity, the authors do not incorporate fluctuations on the extensive margin and therefore do not find that their estimates of the Frisch elasticity are as large as the calibration values used in macroeconomic models. (Rogerson and Wallenius, 2009) point out that because of different treatment of fluctuations on the extensive margin "micro and macro elasticities need not be the same, and ... macro elasticities can be significantly larger."⁸ Using simulated data from a calibrated life cycle model they find that including or excluding fluctuations on the extensive margin could cause large enough differences in the estimates of the Frisch elasticity to explain the gap. In order to estimate the effect of the extensive margin, (Chetty et al., 2011) independently determine the parts of the macro Frisch elasticity from the intensive and extensive margins using a meta analysis of separate quasi-experimental studies. They use the estimates of the participation rate elasticity to determine the portion of the macro Frisch elasticity that comes from the extensive margin. These estimates, centered around 0.9, are not as large as the difference between the microeconometric estimates and the macro-calibration values. However, using the participation rate elasticity to incorporate fluctuations on the extensive margin requires the strong assumption that the average hours worked are the same for new and incumbent workers (see appendix A for more details). Instead of relying on this assumption, I use a pseudo panel which allows me to estimate the whole macro Frisch elasticity directly from the data, as opposed to separately estimating the parts of the macro Frisch elasticity. Three exceptions in which the authors examine both differences in tandem are (Mulligan, 1999), (Faberman, 2010), and (Fiorito and Zanella, 2012). The three studies estimate a Frisch elasticity consistent with the micro definition in the range of 0.1 to 0.7. Additionally, the authors' estimates of the Frisch elasticity increase to a range of 0.6 to 1.4 when they include a larger composition and incorporate fluctuations in hours on the extensive margin. In contrast to this paper, the difference between these ranges are not large enough to explain the gap between the original microeconometric estimates and the macro calibration values. The inability of these studies to show that the alternate definition explain the gap is because they use alternate approaches to estimate the Frisch elasticity in relation to this paper and the original microeconometric studies. Similar to (Altonji, 1986) and (MaCurdy, 1981), I account account for the possible endogeneity of wages by using age and education as an instrument. This approach implies that the Frisch elasticity is identified off of predicted changes in wages over the lifetime. In contrast, (Faberman, 2010), and (Mulligan, 1999) do not account for the possible bias when estimating the Frisch elasticity in a pseudo panel. Since the authors do not instrument wages, they implicitly assume that the evolution of the cohort's average wage as the cohort ages is not correlated with unexpected changes in marginal utility. If any of the unpredicted changes in wages is correlated with unexpected changes in marginal utility, then the authors' estimates will be biased, and this bias could possibly lead to the authors' lower estimates of the macro Frisch elasticity. Although, similar to this paper, (Fiorito and Zanella, 2012) accounts for the possible endogeneity of wages, there are two differences in their estimation procedure. First, the authors just regress the changes in aggregate hours on aggregate wages in a time series as opposed to a panel. This approach ignores the panel dimension of the data and instead each observation in their data set is the average of all individuals at a given point in time. Second, the authors use lagged wages as instruments to account for the possible endogeneity bias. Their approach identifies the Frisch elasticity from persistent changes in aggregate wages. One concern is that if individuals cannot parse the transitory, persistent, and permanent part of shocks to wages, then lag wages will still be correlated with unexpected changes to marginal utility. Moreover, not using the panel dimension of the data could lead to a less efficient estimate. I decompose the effects of ignoring the panel structure and using lagged wages as instruments. I find that both of these alterations to the original microeconometric techniques cause lower estimates of the macro Frisch elasticity, especially using the alternative wage. Therefore, if these alternative instruments are more susceptible to being endogenous, then the studies using these as instruments to determine the macro Frisch elasticity might underestimate the impact of the definitional differences. Although the aim of this paper is not evaluate the various estimation strategies, it is important to distinguish the implicit assumptions from these different estimation strategies since the differences are the primary cause for this paper finding different results than (Fiorito and Zanella, 2012). The rest of the paper is organized as follows: Section 2 derives the estimation equations from a simple labor supply model. Section 3 describes the data and discusses how I construct the pseudo panel. Section 4 presents the estimates of the micro and macro Frisch elasticity, while section 5 examines the robustness of the estimates. Section 6 concludes.

2 Labor Supply Model

In this section, I introduce the typical maximization problem for an individual. Next, I solve for the first order conditions and manipulate them to create two different specifications that can be used to estimate the Frisch elasticity in a reduced form setting. I demonstrate why estimates based from these specifications may be susceptible to omitted variable bias. Finally, I introduce the specific estimation strategies used in (Altonji, 1986) which are designed to account for these omitted variables and describe why I focus on just one to estimate the Frisch.⁹

2.1 Individual's Decisions

Employing a typical utility function that is homothetic and separable in consumption and labor, an individual at age solves the following problem,

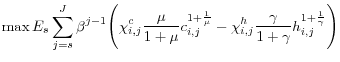$\displaystyle \max E_{s} \sum_{j=s}^{J} \beta^{j-1} \Bigg(\chi_{i,j}^{c} \frac{\mu}{1+\mu}c_{i,j}^{1+\frac{1}{\mu}}- \chi_{i,j}^{h} \frac{\gamma}{1+\gamma}h_{i,j}^{1+\frac{1}{\gamma}}\Bigg)$

(1)

subject to

$\displaystyle c_{i,j} + a_{i,j+1} = w_{i,j} h_{i,j} + (1 + r_{t}) a_{i,j},$

(2)

where $E_{s}$ represents the expectation operator at age

is the age of death, $c_{i,j}$ is consumption of individual

at age

is hours worked, $\chi_{i,j}^{c}$ is a parameter that controls the taste for consumption, $\chi_{i,j}^{h}$ is a parameter that controls the taste for work, $\beta$ is the discount rate, $a_{j}$ is savings, and $r_{t}$ is the after tax return to savings. The first order conditions for the individual are

$\displaystyle \lambda_{j}=\chi^{c}_{i,j}c_{i,j}^{\frac{1}{\mu}}$

(3)

$\displaystyle \lambda_{j}w_{j}=\chi^{h}_{i,j}h_{i,j}^{\frac{1}{\gamma}}$

(4)

$\displaystyle \lambda_{j}=E_{j}\beta\Psi_{j,j+1}(1+r)\lambda_{j+1}\footnote{This is the intertemporal Euler equation for an individual at the age $j$. If the individual is solving at a different age then the expectation operator should adjusted accordingly.}$

(5)

where $\lambda$ is the marginal utility of consumption. The parameter of interest, $\gamma$ , is the Frisch labor supply elasticity. I derive two different specifications which have been used to determine $\gamma$ . By taking the logs and combining equations 3 and 4, I derive the first specification which relates hours to consumption, tastes, and wages

$\displaystyle \ln h_{i,j} = \gamma [\frac{1}{\mu}\ln c_{i,j} + \ln \chi^{c}_{i,j} - \ln \chi^{h}_{i,j} + \ln w_{i,j}].$

(6)

I derive the second specification by taking the difference between two ages of the log of equation 4,

$\displaystyle \Delta \ln h_{i,j+1} = \gamma[\Delta \ln \lambda_{i,j+1} + \Delta \ln w_{i,j+1} -\Delta \ln \chi^{h}_{i,j+1}]$

(7)

where $\Delta$ represents the change over one year. Defining $\xi_{i,j+1}\equiv\lambda_{i,j+1}-E\lambda_{i,j+1}$ , the unexpected changes to marginal utility, and combining equations 5 and 7 the second specification used to determine $\gamma$ can be written as

$\displaystyle \Delta \ln h_{i,j+1} = \gamma[-\ln \beta -\ln(1+r_{t}) + \xi_{i,j+1} + \Delta \ln w_{i,j+1} -\Delta \ln \chi^{h}_{i,j+1}].$

(8)

This second specification relates the change in hours to the change in wages and preference parameters. I refer to equation 6 as the level specification and equation 8 as the change specification. The original estimates of the Frisch elasticity, such as those by (Altonji, 1986) and (MaCurdy, 1981), came from estimating equations based on equations 6 and 8. When estimating the Frisch elasticity with these equations, there is a general concern about omitted variables because taste parameters and the unexpected changes to marginal utility can be correlated with wages. When estimating these equations, it is important to either use instruments for wages or control for these unobserved variables. There is an additional concern about measurement error. Most individuals are not paid hourly. Therefore, to determine an hourly wage, typically economists divide an individual's total income by the total hours he works in a given period. This procedure leads to the possibility that the hours and wage estimates contain correlated measurement error. This measurement error is an additional reason why instruments are typically used for wages. The original estimates of the Frisch elasticity were done using a specification based on equations 6 and 8. The estimation equations used are

$\displaystyle \ln h_{i,j} = \gamma \ln w_{i,j} + \beta \ln c_{i,j} + \zeta$ TS $\displaystyle _{i,j} + e_{i,j}$

(9)

$\displaystyle \Delta \ln h_{i,j+1} = \gamma \Delta \ln w_{i,j+1} + \delta + \zeta \Delta$ TS $\displaystyle _{i,j} + \epsilon_{i,j},$

(10)

where $h_{i,j}$ is hours worked for the individual

at the age

, TS is a vector of variables controlling for tastes, and $\delta$ is a set of annual dummies.¹⁰ (Altonji, 1986) estimates the Frisch elasticity with three different versions of the two specifications. The first two estimates (table one and two in (Altonji, 1986)) are based off of the change specification. His third estimate (table four in (Altonji, 1986)) is based off of the level specification. I implement the specification from table 2 of (Altonji, 1986) because the other estimation strategies (table 1 and table 4) in (Altonji, 1986)) can only be estimated on a small subset of the entire population.¹¹ In this specification, the author uses age, education, education squared, interactions between age and the polynomials of education, the education of the parents, and the parents' economic status as instruments for wages.¹² These instruments are used to account for both measurement error and unexpected changes to marginal utility.¹³ Since these variables are known prior to going into a period, one would not expect them to be correlated with unexpected shocks to marginal utility. In other words, by using these instruments, the economist is identifying the responsiveness of hours to expected changes in wages over the life cycle. One concern is that age could be correlated with changes in tastes. Therefore, I add some additional controls to the regression in order to control for these possible changes.¹⁴ When estimating the macro Frisch elasticity, one complication is how to incorporate individuals who work zero hours since the natural log of zero is undefined. I choose to estimate the Frisch elasticity which incorporates individuals who do not work using a pseudo panel. Using a pseudo panel implies that I treat the cohort's average at each age as an observation.¹⁵ A pseudo panel is a natural setting in which to estimate the macro Frisch elasticity because it identifies the elasticity from the aggregate response of the cohort's average hours worked. Using a pseudo panel does not come without disadvantages. Ideally, one would use the true average of the whole cohort when creating the pseudo panel. However, I am limited to forming the cohort's averages from the sample that is observed in the data set.¹⁶ When using a pseudo panel, the economist is implicitly treating the averages from the synthetic cohort as approximations of the true cohort's average. Treating a pseudo panel as a genuine panel can cause bias due to measurement error introduced by not observing the true average. However, (Verbeek et al., 1992) demonstrates that with a sufficient number of individuals a pseudo panel can be treated as a genuine panel without introducing an economically significant amount of bias.¹⁷

3 Data

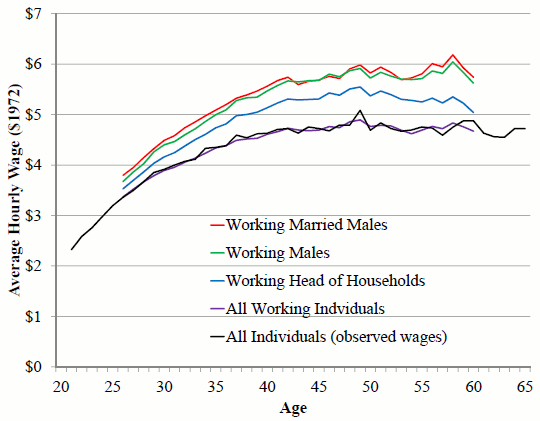
Similar to (Altonji, 1986), I use the Michigan Panel Study of Income Dynamics (PSID). I utilize the waves from 1968 until 1997.¹⁸ I use similar procedures to clean the data as employed in (Altonji, 1986). The PSID only reports hourly wages for individuals who are paid on an hourly basis. Therefore, I create a real hourly wage variable for everyone by taking the labor earnings divided by the product of annual hours working for pay and consumption price index for urban individuals. Following (Altonji, 1986), observations which exhibited a 250 percent increase or 60 percent decrease in wages or consumption were treated as missing. Furthermore, observations with swings of more than $13 or wages less than $0.40 in 1972 dollars were treated as missing.¹⁹ I do not observe the wealth of the parents for secondary earners. Therefore, I exclude these variables as instruments for changes in wages. I found that making these alterations did not affect the results on the group of individuals for which I have complete coverage. Finally, I adjusted the age variable when an individual reported no change in their age between the annual surveys or reported a change of larger than one year. Figure 1 plots the average annual hours by age for five different groups of people.²⁰ These plots are constructed by taking the traditional panel (pseudo panel) and averaging across all individuals (cohorts) by age. The black line is the average annual hours for all individuals. Compared to the other four lines, which are plots of the average hours for the subset of the sample that is working, the profile for all individuals decreases much more rapidly towards the end of the working life. This rapid decent indicates that many older aged individuals stop working. Figure 2 plots the average wage profiles for various groups of individuals by age. The wage profiles tend to be upward sloping over a majority of the lifetime for all the different groups. The black line plots the average of all the observed wages which is used to estimate the macro Frisch elasticity.

Figure 1: Hours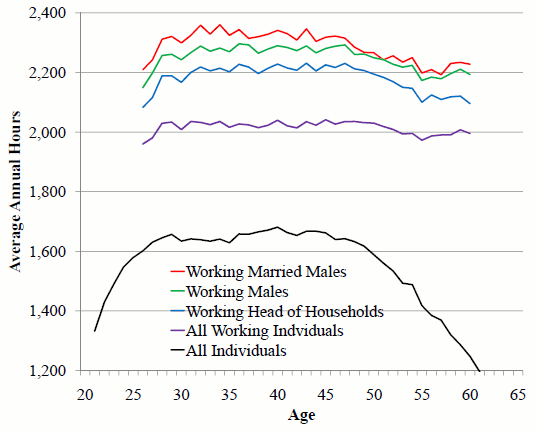

Figure 1 (line graph): Hours. The graph compares the average annual hours worked for five different groups of people: all individuals, working married males, working males, working heads of household, and working individuals. The X axis displays ages from 20 to 65; the Y axis displays average annual hours ranging from 1,200 to 2,400. Hours worked for all individuals starts around 1,325 annual hours worked for 20 year olds, increases steadily to about 1,650 for 30 year olds, then fluctuates around 1,650 hours until age 50. The average hours worked subsequently steadily declines until it reaches an average of 1,200 around age 61. The average hours worked for all individuals declines much more quickly than do average hours for the different demographic cohorts, indicating that the number of individuals working is declining. The lines for the four other cohorts have the same trends. Working married males work the greatest average number of hours per year, starting around 2,200 at age 25 and then fluctuating around 2,300 until age 45, where they decline to around 2,200. The other three demographic cohorts follow the same trend: increasing from ages 25 to 27, then fluctuating until age 45, where they subsequently decline slowly until age 61. Working males have the second highest average; they start around 2,150 hours, increase to around 2,275 hours, and then decline to slightly less than 2,200 hours. Working heads of household have an initial average of 2,100 hours at age 25, increase to 2,225 through age 45, then decline to 2,100. Working individuals start at 1,950 hours, increase to 2,025 hours, then decline to 2,000 hours.

Figure 2: Wages

4 Estimates of Micro and Macro Frisch Elasticity

I start by replicating the estimates in (Altonji, 1986) from column I and III of his table 2. The specification used to produce these estimates is a version of equation 10. Similar to (Altonji, 1986), I estimate the Frisch elasticity by regressing the change in the natural log of hours on the change in wages using age, education, education squared, interactions between education and age, mother's education, and father's education as instruments for wages. These estimates are consistent with the definition of the micro Frisch elasticity. Table 1 presents my benchmark estimates of the micro Frisch elasticity. Columns I-IV present regression results when I do not include annual dummy variables, and columns V-VIII are the results when I include annual dummies. Consistent with the definition of the micro Frisch elasticity, these estimates are from a sample which only includes males who are the head of their household, are married throughout the sample, are working throughout the whole sample, and are between the ages of 26 and 60.²¹ Column I and IV presents the estimates when I restrict the sample to the same period that is used in (Altonji, 1986) (1968-1981). The estimates (0.34 & 0.52) are close to those originally presented in (Altonji, 1986) (0.28 & 0.48).²² I find that the F-statistic for the excluded instruments in the first stage is 13.6 and 5.4 when I do not and do use annual dummies, respectively. The lower value for the specification that includes annual dummies indicates that there is some concern that the instruments are not relevant when annual dummies are included.²³ The P-value on the Hansen J-statistic for overidentification of the instruments is larger for the specification that includes annual dummies which indicates that including annual dummies leaves less unexplained variation in the second stage. The P-values are large enough in both specifications so as to not raise concerns that the instruments are invalid. Column II and VI of table 1 present estimates of the micro Frisch elasticity when I extend the sample to include the years through 1997. Extending the data set to include more years causes the two estimates of the Frisch elasticity to converge to approximately 0.20. I proceed by using all these years of the PSID in the rest of the regressions. One concern about the original estimation strategy is that there may be an omitted variable bias because age could be correlated with changes in tastes. Therefore, I include indicator variables for whether the individual lives in a big city, the number of children in the household, and the number of kids under the age of six in the household, each of which should be correlated with omitted changes in tastes. The estimates that include these controls for changes in tastes are in columns III and VII. I find that controlling for tastes causes the point estimates of the Frisch to increase slightly. Although the changes are not statistically significant, the increase indicates that omitting changes in tastes could cause a downward bias. Therefore, I include these controls for changes in tastes in all subsequent regressions. Finally, columns IV and VIII are estimates when I no longer require the panel to be balanced. Specifically, if individuals stop working prior to age 60, their observations when they are working are still included. By allowing the panel to be unbalanced, I increase the number of observations by over ten percent; however, the estimates are nearly identical. Since this change does not alter the point estimates, but increases the number of observations, I relax this restriction in all subsequent regressions. I treat columns IV and VIII as my benchmark results for the micro Frisch elasticity which I use for comparison in order to determine the effect of broadening the scope of the sample and including fluctuations on the extensive margin. One concern about these estimates is that the Hansen J-stat for overidentification of the instruments is low for all of the specifications that use the larger time period. The low J-stat is a persistent problem in all my analysis. Despite concerns about validity, I continue because the goal of this paper is to determine whether estimates of the macro Frisch using the microeconometric techniques are consistent with the values used to calibrate macroeconomic models. However, because of this concern about validity, the point estimates should be interpreted with caution.

Table 1: **Micro Benchmark Results**
Variables	Orig. I	+ Yrs. II	$\Delta$ Tastes III	Unbalanced IV	Orig. V	+ Yrs. VI	$\Delta$ Tastes VII	Unbalanced VIII
$\Delta$ W	0.34	0.2	0.23	0.23	0.52	0.2	0.23	0.22
$\Delta$ W (s.e.)	(0.11)	(0.09)	(0.1)	(0.09)	(0.16)	(0.09)	(0.1)	(0.09)
$\Delta$ kids			-0.01	-0.01			-0.01	-0.01
$\Delta$ kids (s.e.)			(0.01)	(0.01)			(0.01)	(0.01)
$\Delta$ kidsunder6			0.01	0.01			0.01	0.01
$\Delta$ kidsunder6 (s.e.)			(0.01)	(0.01)			(0.01)	(0.01)
$\Delta$ bigcity			0	0			0	0
$\Delta$ bigcity (s.e.)			(0.02)	(0.01)			(0.02)	(0.01)
Observations	9,985	24,380	24,380	27,88	9,985	24,380	24,380	27,880
Annual Dummies	No	No	No	No	Yes	Yes	Yes	Yes
Years	68-81	68-97	68-97	68-97	68-81	68-97	68-97	68-97
1st Stage: F-stat (Excl. Inst.)	13.59	21.34	18.83	23.18	5.36	17.34	14.59	16.96
1st Stage: F-stat (P-value)	0.01	0.03	0.24	0.2	0	0	0	0
1st Stage: Hansen J-Stat	6.78	17.9	19.1	19.39	5.17	17.98	19.15	19.5
1st Stage: J-Stat (P-value)	0.34	0.01	0	0	0.52	0.01	0	0

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

Next, I estimate the macro Frisch elasticity. These estimates use a pseudo panel which includes the hours fluctuations from the extensive margin. Additionally, I broaden the scope of the sample to include all individuals between the ages of twenty and sixty-five (the additional groups included are females, secondary earners, younger individuals, older individuals, and single individuals). The estimates of the macro Frisch elasticities are presented in table 2. The estimates range from 2.88 to 3.1 depending on whether annual dummies are included. I find that these estimates of the macro Frisch elasticity are statistically different from the benchmark estimates of the micro Frisch elasticity. Furthermore, the estimates of the macro Frisch elasticity are in the middle of the range of the values used to calibrate macroeconomic models. Therefore, these results indicate that the different treatment of fluctuations on the extensive margin and the different levels of inclusion of individuals in the sample implied by the different definitions can reconcile the gap between the microeconometric estimates and the macro-calibration values of the Frisch elasticity. Additionally, when estimating the macro Frisch elasticity, the first stage passes the Hansen J-test indicating that there is less concern with the instruments being endogenous.

Table 2: **Aggregate "Macro" Estimates**
Variables	Micro I	Macro II	Micro III	Macro IV
$\Delta$ W	0.23	3.1	0.22	2.88
$\Delta$ W (s.e.)	(0.09)	(0.68)	(0.09)	(0.67)
$\Delta$ kids	-0.01	-0.28	-0.01	-0.28
$\Delta$ kids (s.e.)	(0.01)	(0.11)	(0.01)	(0.11)
$\Delta$ kidsunder6	0.01	-0.21	0.01	-0.15
$\Delta$ kidsunder6 (s.e.)	(0.01)	(0.14)	(0.01)	(0.12)
$\Delta$ bigcity	0	1.09	0	0.18
$\Delta$ bigcity (s.e.)	(0.01)	(0.51)	(0.01)	(0.31)
Observations	27,880	1,288	27,880	1,288
Yr. Dummies	No	No	Yes	Yes
Years	68-97	68-97	68-97	68-97
Ages	26-60	20-65	26-60	20-65
1st Stage: F-stat (Excl. Inst.)	23.18	3.6	16.96	3
1st Stage: F-stat (P-value)	0.2	0.01	0	0
1st Stage: Hansen J-Stat	19.39	6.38	19.5	10.81
1st Stage: J-Stat (P-value)	0	0.38	0	0.09

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

In order to determine the relative importance of each demographic difference in reconciling the gap, I independently estimate the impact of adding each demongraphic. Table 3 presents estimates that determine the effect on the estimates of the Frisch elasticity of gradually expanding the sample from prime-aged, married males who are the head of the household to include all workers. Since I am not trying to incorporate fluctuations on the extensive margin, all of the estimates in table 3 use a traditional panel of working individuals. Columns I-V present regression results when I do not include annual dummy variables, and columns V-X are the results when I include dummy variables for each year. In order to determine the impact of each group, I start with the benchmark sample and successively relax restrictions on the sample. Columns II and VI are the estimates where I relax the restriction that the individual is married. Relaxing this restriction implies that I now include prime age single males who are the head of the household.²⁴ Columns III and VIII are estimates when I also relax the restriction that the individuals are male. Columns IV and IX are the estimates when I also relax the restriction that individuals are the head of the household. Finally, columns V and X are the estimates when I relax all the restrictions and also extend the age range so that all working individuals between 20 and 65 are included. I find that relaxing the marriage restriction causes an increase in the Frisch elasticity; however, since the increase is not statistically significant it is only suggestive that single males may have a higher Frisch. When I include females in columns III and VIII, the point estimates of the Frisch elasticity decrease, but a statistically insignificant amount. The sign of the change is not surprising since the group that is being added, females who are the head of the household, are likely less responsive to temporary changes in their wages. I find that when I include secondary earners in my sample the Frisch elasticity approximately doubles (columns IV and IX). I find that these estimates which include secondary earners in the data are statistically different from both the benchmark estimates (columns I and VI) and the prior estimates which exclude secondary earners in the data set (columns III and VIII). Finally, when I include younger and older individuals in the sample the estimates double again, a statistically significant increase. Comparing columns V and X to their respective benchmarks (columns I and V), indicates that relaxing all these restrictions causes the Frisch elasticity to increase by approximately 0.7, also a statistically significant increase.

Table 3: **Composition Effects**
Variables	Micro I	+Single II	+Female III	+2nd Earn IV	+Age V	Micro VI	+Single VII	+Female VIII	+2nd Earn IX	+Age X
$\Delta$ W	0.23	0.35	0.29	0.55	0.93	0.22	0.32	0.26	0.55	0.91
$\Delta$ W (s.e.)	(0.09)	(0.08)	(0.08)	(0.15)	(0.11)	(0.09)	(0.08)	(0.09)	(0.14)	(0.1)
$\Delta$ kids	-0.01	0	-0.01	-0.02	-0.02	-0.01	0	-0.01	-0.01	-0.02
$\Delta$ kids (s.e.)	(0.01)	(0)	(0)	(0)	(0)	(0.01)	(0)	(0)	(0)	(0)
$\Delta$ kidsunder6	0.01	0.01	0.01	-0.03	-0.03	0.01	0.01	0	-0.03	-0.04
$\Delta$ kidsunder6 (s.e.)	(0.01)	(0)	(0.01)	(0.01)	(0.01)	(0.01)	(0)	(0.01)	(0.01)	(0.01)
$\Delta$ bigcity	0	0.02	0.02	0.02	0.02	0	0.02	0.01	0.02	0.02
$\Delta$ bigcity (s.e.)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)
Observations	27,880	49,178	64,259	87,910	104,348	27,880	49,178	64,259	87,910	104,348
Yr. Dummies	No	No	No	No	No	Yes	Yes	Yes	Yes	Yes
Years	68-97	68-97	68-97	68-97	68-97	68-97	68-97	68-97	68-97	68-97
Restrictions: Married	Yes					Yes
Restrictions: Male	Yes	Yes				Yes	Yes
Restrictions: Primary Earner	Yes	Yes	Yes			Yes	Yes	Yes
Restrictions: Age 25 - 60	Yes	Yes	Yes	Yes		Yes	Yes	Yes	Yes
Restrictions: Age 20 - 65					Yes					Yes
1st Stage: F-stat (Excl. Inst.)	23.18	23.86	23.11	21.22	34.07	16.96	23.92	27.89	25.11	36.41
1st Stage: F-stat (P-value)	0.2	0	0	0	0	0	0	0	0	0
1st Stage: Hansen J-Stat	19.39	16.36	23.73	30.57	23.87	19.5	18.55	25.79	30.34	23.53
1st Stage: J-Stat (P-value)	0	0.01	0	0	0	0	0	0	0	0

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

Table 4 tests the impact on the estimates of the Frisch elasticity of including fluctuations on the extensive margin in the more restricted subset of the data that only include married males who are the head of their household. In order to estimate the Frisch elasticity which includes fluctuation on the extensive margin I use a pseudo panel.²⁵ Since I am focusing on the impact of the fluctuations on the extensive margin, I still limit my sample to married males who are the head of their household. I find that the estimates of the Frisch elasticity increases to a similar level, between 0.84 and 0.88, when I include fluctuations on the extensive margin as they did when I broadened the sample. These increases are statistically significant. Individually estimating the impact of both differences arising from the alternative definition, I find that broadening the scope of the sample increases the estimates of the Frisch elasticity by approximately 0.7. Moreover, I find that including fluctuations on the extensive margin increases the Frisch elasticity by between 0.61 and 0.66. The increase from individually accounting for each of these differences indicates that both explanations play an important role in reconciling the gap between the microeconometric estimates and macro-calibration values. The sum of these changes is not large enough to explain the difference between the micro and macro values. These results indicate that the interaction between broadening the scope of the sample and incorporating fluctuations on the extensive margin is important to explain the gap. Specifically, the fluctuations on the extensive margin of single males, females, secondary earners, young individuals, and old individuals are critical for explaining the gap.

Table 4: **Extensive Margin Effects**
Variables	Micro I	+ Extensive II	Micro III	+ Extensive IV
$\Delta$ W	0.23	0.84	0.22	0.88
$\Delta$ W (s.e.)	(0.09)	(0.17)	(0.09)	(0.19)
$\Delta$ kids	-0.01	-0.04	-0.01	-0.03
$\Delta$ kids (s.e.)	(0.01)	(0.02)	(0.01)	(0.02)
$\Delta$ kidsunder6	0.01	0.06	0.01	0.06
$\Delta$ kidsunder6 (s.e.)	(0.01)	(0.04)	(0.01)	(0.04)
$\Delta$ bigcity	0	-0.08	0	-0.12
$\Delta$ bigcity (s.e.)	(0.01)	(0.11)	(0.01)	(0.14)
Observations	27,880	980	27,880	980
Yr. Dummies	No	No	Yes	Yes
Years	68-97	68-97	68-97	68-97
Ages	26-60	26-60	26-60	26-60
1st Stage: F-stat (Excl. Inst.)	23.18	6.7	16.96	6.49
1st Stage: F-stat (P-value)	0.2	0	0	0
1st Stage: Hansen J-Stat	19.39	10.45	19.5	10.4
1st Stage: J-Stat (P-value)	0	0.11	0	0.11

Notes: The estimate are for prime age married males who are the head of the household. The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

5 Robustness of Estimates

In this section I estimate the sensitivity of the results with regards to age, the parametric assumptions used for the instruments, the effect of using the alternative estimation strategy in (Fiorito and Zanella, 2012), and the exclusion of wage information from non-working individuals.

5.1 Estimates by age

In this section I explore how the estimates of the Frisch elasticity change when I focus on different age ranges. Table 5 and table 6 provide the estimates of the macro and micro Frisch elasticity for different age ranges, respectively.²⁶ When I exclude individuals that are between sixty-one and sixty-five, the estimate of the macro Frisch drops from 2.88 to 1.8. The estimate drops further to 0.8 when I exclude individuals between fifty-one and sixty-five. These significant drops indicate that the macro Frisch elasticities are not consistent over all ages and that the large estimates are primarily driven by older individuals. Examining the black lines in the plots of the average wage and hours profiles in figures 1 and 2, it is clear that the average hours start dropping rapidly at the age of fifty. However, during the same age range the cohort's average wages stay fairly steady, dropping only a small amount. Conversely, for younger individuals, the changes in the hours profile are relatively small compared to the change in the wage profile. Therefore, if older individuals are included, a large Frisch elasticity is needed to explain the relatively larger movements in the hours profile than the wage profile. However, if older individuals are excluded, the estimates of the Frisch elasticity are much smaller since the size of the relative movements in hours to wages is smaller. One interpretation of these results is that the macro Frisch elasticity changes over the life cycle. However, current research points to a possible alternate explanation. The original microeconometric estimation strategy assumes that any predicted changes in the wages are due to market forces and exogenous to the decision with regards to how many hours to work. Additionally, the estimation strategy implicitly assumes that the causal relationship is such that any changes in hours are a result of the changes in wages. However, some recent research has documented that these changes in wages may not be exogenous from the hours decisions. (Casanova, 2012) examines whether hours and wage dynamics for older people can be explained by partial retirement. The author demonstrates that when one controls for partial retirement, the wage profile for older individuals no longer falls but is upward sloping throughout the whole working lifetime. Further, she argues that the transition out of full time work to either partial or full retirement is a choice for most workers and the subsequent drop in the wage is endogenously determined. Specifically, the author states that "while standard labor supply models would rationalize the reduction in hours worked upon partial retirement as a response to an exogenously declining wage trajectory, the evidence presented in the paper indicates instead that workers choose to trade more leisure for a lower hourly wage in a context in which a better paid, full-time job is available." In other words, individuals preferences for leisure increase as they age causing them to choose to work less hours (partially retire) and receive a lower hourly wage. The results in table 5, coupled with the finding in (Casanova, 2012), indicate that incorporating older individuals in estimates of the macro Frisch elasticity, which includes fluctuations on the extensive margin, may cause an upward bias. Specifically, if the changes in older individuals hours are not a result of decreases in potential wages but instead older agents are jointly choosing lower wages and hours in response to a increase in the desire for leisure, then a correctly specified estimate of the Frisch elasticity would be lower. Since younger individuals are less likely to be affected by partial retirement, it is likely that the estimates of the macro Frisch which only include these younger individuals are less susceptible to bias from partial retirement. Therefore, individuals may not be as responsive to changes in their wages as the macro Frisch elasticity estimates imply, but instead this may be an artifact of not totally controlling for changes in preferences. Overall, determining which value to use in a calibrated model depends crucially on which question the economist is examining and how the model is specified. For example, if the model being calibrated includes both a partial retirement decision and assumes the preferences for leisure increase with age, then a lower value in line with the value estimated when only inlcuding younger individuals should be used. Alternatively, if the model being calibrated is more parsimonious and does not include either partial retirement or changes in preferences for leisure over the life cycle, then in order for the model to replicate the observed wage and hours profiles, it will need to include a larger macro Frisch value in line with the estimates which incorporate older individuals. Furthermore, if the decision of when to retire is not relevant to the question being examined then the relevant value for calibration is the estimate of the Frisch elasticity for younger individuals, as opposed to the larger value estimated for all individuals. Conversely, if the total aggregate fluctuations in labor including retirement are relevant to the question being examined, then the larger Frisch elasticity estimated for the bigger age range is the more relevant estimate.

Table 5: **Macro Estimate by Age**
Variables	Age Range: 20-65 (I)	Age Range: 20-60 (II)	Age Range: 20-55 (III)	Age Range: 20-50 (IV)	Age Range: 20-45 (V)
$\Delta$ W	2.88	1.75	1.5	0.81	0.51
$\Delta$ W (s.e.)	(0.67)	(0.35)	(0.360)	(0.25)	(0.17)
$\Delta$ kids	-0.28	-0.11	-0.1	-0.03	-0.04
$\Delta$ kids (s.e.)	(0.11)	(0.05)	(0.05)	(0.03)	(0.03)
$\Delta$ kidsunder6	-0.15	-0.04	-0.01	0.09	0.16
$\Delta$ kidsunder6 (s.e.)	(0.12)	(0.08)	(0.07)	(0.05)	(0.05)
$\Delta$ bigcity	0.18	0.15	0.17	0.17	0.08
$\Delta$ bigcity (s.e.)	(0.31)	(0.27)	(0.25)	(0.2)	(0.19)
Observations	1,288	1,148	1,008	868	728
Yr. Dummies	Yes	Yes	Yes	Yes	Yes
Years	68-97	68-97	68-97	68-97	68-97
1st Stage: F-stat (Excl. Inst.)	3	4.85	8.39	3	6.17
1st Stage: F-stat (P-value)	0	0	0	0	0
1st Stage: Hansen J-Stat	10.81	20.21	9.09	10.81	18.73
1st Stage: J-Stat (P-value)	0.09	0	0.17	0.09	0

Notes: The estimates are from a pseudo panel which includes all individuals. The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

Table 6 presents the results when I estimate the micro Frisch for different ages. Unlike the estimates of the macro Frisch, the decrease in the estimates are small when I exclude older individuals. One explanation for the smaller changes is that the micro Frisch is estimated only on individuals who are working and focuses on younger individuals who are less likely to be partially retired.²⁷ Therefore, one needs to be less concerned about changes in the values over the life cycle when choosing calibration values for the Frisch elasticity only on the intensive margin.

Table 6: **Micro Estimate by Age**
Variables	Age Range: 25-60 (I)	Age Range: 25-55 (II)	Age Range: 25-50 (III)	Age Range: 25-45 (IV)
$\Delta$ W	0.22	0.17	0.07	0.05
$\Delta$ W (s.e.)	(0.09)	(0.11)	(0.12)	(0.12)
$\Delta$ kids	-0.01	0	0	0
$\Delta$ kids (s.e.)	(0.01)	(0.01)	(0.01)	(0.01)
$\Delta$ kidsunder6	0.01	0.01	0	0
$\Delta$ kidsunder6 (s.e.)	(0.01)	(0.01)	(0.01)	(0.01)
$\Delta$ bigcity	0	-0.01	-0.01	-0.01
$\Delta$ bigcity (s.e.)	(0.01)	(0.01)	(0.01)	(0.02)
Observations	27,880	25,459	21,939	17,774
Yr. Dummies	Yes	Yes	Yes	Yes
Years	68-97	68-97	68-97	68-97
1st Stage: F-stat (Excl. Inst.)	16.96	16.96	10.65	9.07
1st Stage: F-stat (P-value)	0	0	0	0
1st Stage: Hansen J-Stat	19.5	19.5	18.48	12.45
1st Stage: J-Stat (P-value)	0	0	0.01	0.05

Notes: The estimates are from a traditional panel which includes only prime age married males who are the head of the household. The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

5.2 Alternative Parametric Assumptions

The previous results demonstrate that the estimates of the macro Frisch elasticity decrease when older generations are excluded. Additionally, since the large macro Frisch is particularly driven by the fluctuations in wages predicted by the polynomials of the instruments from older individuals, it is important to see if using predicted wages from a more flexible set of polynomials affects the estimates of the macro Frisch. Therefore, in this section I explore the sensitivity of the results when I use a more flexible set of polynomials of age and education as instruments. Specifically, I use up to a third order Chebychev polynomial of age, second order Chebychev polynomial of education, and the interaction of all the polynomials. Chebychev polynomials are a sequence of orthogonal recursive polynomials. Using these orthogonal polynomials as instruments, as opposed to using the quadratic polynomials, allows for more flexibility in the relationship between wages and the instruments. Table 7 presents the results when I use these alternative polynomials.

Table 7: **Affect of Alternative Parametric Form**
Variables	Micro Bench. I	Micro Alt. II	Macro Bench. III	Macro Alt. IV
$\Delta$ W	0.22	0.2	2.88	2.28
$\Delta$ W (s.e.)	(0.09)	(0.1)	(0.67)	(0.48)
$\Delta$ kids	-0.01	-0.01	-0.28	-0.19
$\Delta$ kids (s.e.)	(0.01)	(0.01)	(0.11)	(0.09)
$\Delta$ kidsunder6	0.01	0	-0.15	-0.12
$\Delta$ kidsunder6 (s.e.)	(0.01)	(0.01)	(0.12)	(0.11)
$\Delta$ bigcity	0	0	0.18	0.83
$\Delta$ bigcity (s.e.)	(0.01)	(0.01)	(0.31)	(0.38)
Observations	27,880	27,880	1,288	1,288
Yr. Dummies	Yes	Yes	Yes	Yes
Years	68-97	68-97	68-97	68-97
Ages	26-60	26-60	20-65	20-65
Instruments	Quadratics	Chevycheb	Quadratics	Chevycheb
1st Stage: F-stat (Excl. Inst.)	16.96	11.83	16.96	5.2
1st Stage: F-stat (P-value)	0	0	0	0
1st Stage: Hansen J-Stat	19.5	21.5	19.5	17.17
1st Stage: J-Stat (P-value)	0	0.04	0	0.1

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

The first and third columns of table 7 are the benchmark estimates of the micro and macro Frisch elasticity using the quadratic polynomials of the instruments, respectively. The second and fourth columns are the estimates of the micro and macro Frisch elasticity using the Chebyshev polynomials of the instruments, respectively. Comparing column I and II, it is clear that the estimates of the micro Frisch elasticity are not sensitive to the different polynomials. Although the estimate of the macro Frisch elasticity is somewhat smaller when I use the more flexible polynomials, the decrease is not statistically significant. Furthermore, the estimate of the macro Frisch elasticity with the alternative polynomials is still large enough to explain the gap between the original microeconometric estimates of the Frisch and the values used to calibrate macroeconomic models. Therefore, these results further indicate that the different treatment of fluctuations on the extensive margin and the different composition of the samples can can explain the gap.

5.3 Comparison with (Fiorito and Zanella, 2012) Estimation Strategy

Similar to this exercise, (Fiorito and Zanella, 2012) also tries to determine if these differences in definition could explain the large gap between microeconometric estimates of the Frisch and calibration values used in macroeconomic models. Despite estimating a similar micro Frisch elasticity, the authors estimate a macro Frisch elasticity that is much smaller than this study (0.6). The authors use a different estimation strategy than the strategy used in this paper. As previously mentioned, when estimating the macro Frisch, this paper tries to use a strategy that is close the (Altonji, 1986). Specifically, it estimates the macro Frisch in a pseudo pane using age and education as instruments for wage. In contrast, (Fiorito and Zanella, 2012) use an alternative approach in which they just use the change in the whole population's averages over time as opposed to the changes in the different cohort's averages over time and use lagged wages as instruments for current wages. Furthermore, the authors do not address the possible bias from not observing changes in tastes for working. Identifying the Frisch elasticity using lagged wages as instruments in a time series, as opposed to age and education in a pseudo panel, implies that the estimates in (Fiorito and Zanella, 2012) are being identified off of different types of fluctuations in wages. In particular, in this study the Frisch is identified off of changes in a cohort's wages over their life cycle that can be predicted by age and education. In contrast, (Fiorito and Zanella, 2012) uses the variation in average wage across the whole economy that can be predicted from changes in the previous periods. Therefore, this paper identifies the Frisch elasticity by focusing on the life cycle changes in wages while (Fiorito and Zanella, 2012) identifies the Frisch elasticity by focusing on the persistent portion of shocks to aggregate wages. One concern is that if there is some uncertainty about how much of a shock to aggregate wages is persistent versus transitory, then lag wages could still be an endogenous instrument because they will be correlated with unexpected shocks to marginal utility. Furthermore, by not exploiting the panel structure nor distinguishing cohorts, the procedure in (Fiorito and Zanella, 2012) will produce estimates that are weakly less efficient and may be affected by changes in composition. Table 8 explores the effect of these differences in the estimation strategy. The first column of the table reproduces the benchmark estimates of the macro Frisch in a pseudo panel using the adapted microeconometric strategy described in this paper. The second column provides estimates of the macro Frisch using the same pseudo panel but switching to lagged wages as the instrument for current wages as opposed to using age and education.²⁸ I find that the estimates drop significantly when I use these alternative wages in a pseudo panel to estimate the Frisch elasticity. The large differences in the estimates indicate that lag wages could still be endogenous with current wages. Furthermore, when I estimate the Frisch elasticity using lagged wages in a time series, as opposed to a pseudo panel, the estimates (column III) fall even more.²⁹ These results indicate that by using this alternative strategy to estimate the Frisch elasticity, (Fiorito and Zanella, 2012) may have underestimated the macro Frisch and consequently understated the ability of fluctuations on the extensive margin and the different compositions to explain the gap between the macro and micro Frisch elasticity.

Table 8: **Affect of Specification in (Fiorito and Zanella, 2012)**
Variables	Benchmark I	Alt. Inst. II	No Panel & Alt. Inst. III
$\Delta$ W	2.88	0.64	0.42
$\Delta$ W (s.e.)	(0.67)	(0.23)	(0.26)
$\Delta$ kids	-0.28
$\Delta$ kids (s.e.)	(0.11)
$\Delta$ kidsunder6	-0.15
$\Delta$ kidsunder6 (s.e.)	(0.12)
$\Delta$ bigcity	0.18
$\Delta$ bigcity (s.e.)	(0.31)
Observations	1,288	1,008	18
Yr. Dummies	Yes	Yes	No
Years	68-97	68-97	68-91
Ages	20-65	20-65	20-65
Instruments	Age & Educ	Lag Wage	Lag Wage
Type of Data	Pseudo Panel	Pseudo Panel	Time Series
1st Stage: F-stat (Excl. Inst.)	3	23.31	1.5
1st Stage: F-stat (P-value)	0	0	0.15
1st Stage: Hansen J-Stat	10.81	6.38	4.5
1st Stage: J-Stat (P-value)	0.09	0.09	0.21

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

5.4 Unconditional Frisch Elasticity

This paper focuses on estimates of the aggregate Frisch elasticity consistent with the macro defintion. These estimates are consistent with the calibration values used in macroeconomic models. The macro Frisch elasticity is estimated from a pseudo panel which includes unconditional changes in hours and the observed changes in wage which exclude the potential wages for non-working (no-work) individuals.³⁰ However, the estimates of the macro Frisch elasticity (table 2) are not estimates of the unconditional aggregate Frisch elasticity because they do not include fluctuations in potential wages from non-working individuals. Since it might be of interest, I also estimate the unconditional value which accounts for possible selection bias from non-working individuals. In order to account for selection bias, I follow the procedure in (Fiorito and Zanella, 2012) in which the authors predict the wages for non-working individuals using a Heckman-type correction for selection bias.³¹ Selected results from these regressions are in appendix B. (Fiorito and Zanella, 2012) note that (Blundell et al., 2003) shows empirically that when they create an aggregate wage which includes a similar selection corrected predicted wage for non-workers, most of the aggregation bias is removed from their aggregate wage series. Table 9 presents the estimates of the unconditional aggregate Frisch elasticity. In order to account for this possible selection bias when estimating the unconditional aggregate Frisch elasticity, I use a Heckman-style correction and predict wages for non-working individuals similar to (Fiorito and Zanella, 2012). One complication is that some individuals who indicate they retired or work less than 250 hours still report labor income. Therefore, I estimate the Frisch elasticity with two different wage series for each cohort. First, I incorporate predicted wages for individuals who do not report any income and observed wages for others in the cohort's average (predict missing). Second, I incorporate predicted wages for individuals who report that they are retired or work less than 250 hours and use the observed wages for others in the cohort's average (predict non-working). The estimates of the unconditional aggregate Frisch elasticity range from 1.68 to 2.64. I find that when I control for selection bias by predicting wages for those who do not report wage information, the estimates of the Frisch elasticity are significant compared to the estimates of the macro Frisch elasticity. However, when I only control for selection by predicting wages for all of those who report not working the change in the estimates is statistically significant. These results indicate that incorporating the wage information reported for individuals who also report not working causes the estimate of the Frisch elasticity to be much lower.

Table 9: **Aggregate Unconditional Frisch**
Variables	Macro I	Unconditional II	Unconditional III	Macro IV	Unconditional V	Unconditional VI
$\Delta$ W(observed)	3.1			2.88
$\Delta$ W(observed) (s.e.)	(0.68)			(0.67)
$\Delta$ W (predict missing)		1.68			1.78
$\Delta$ W (predict missing) (s.e.)		(0.45)			(0.43)
$\Delta$ W (predict no-work)			2.41			2.64
$\Delta$ W (predict no-work) (s.e.)			(0.36)			(0.44)
$\Delta$ kids	-0.28	-0.16	-0.23	-0.28	-0.16	-0.21
$\Delta$ kids (s.e.)	(0.11)	(0.07)	(0.06)	(0.11)	(0.06)	(0.07)
$\Delta$ kidsunder6	-0.21	-0.02	-0.15	-0.15	-0.06	-0.23
$\Delta$ kidsunder6 (s.e.)	(0.14)	(0.08)	(0.07)	(0.12)	(0.08)	(0.08)
$\Delta$ bigcity	1.09	0.18	0.12	0.18	0.63	0.41
$\Delta$ bigcity (s.e.)	(0.51)	(0.17)	(0.18)	(0.31)	(0.27)	(0.29)
Observations	1,288	1,288	1,288	1,288	1,288	1,288
Yr. Dummies	No	No	No	Yes	Yes	Yes
Years	68-97	68-97	68-97	68-97	68-97	68-97
Ages	20-65	20-65	20-65	20-65	20-65	20-65
1st Stage: F-stat (Excl. Inst.)	3.6	4.85	8.39	3	6.17	8.22
1st Stage: F-stat (P-value)	0.01	0	0	0	0	0
1st Stage: Hansen J-Stat	6.38	20.21	9.09	10.81	18.73	7.73
1st Stage: J-Stat (P-value)	0.38	0	0.17	0.09	0	0.26

Notes: The F-stat for excluded instruments is for the wage regressions. Consistent with previous studies, the standard errors are clustered on cohort.

6 Conclusion

This paper evaluates two explanations for the gap between the original microeconometric estimates and the calibration values used in macroeconomic models of the Frisch labor supply elasticity. The first explanation is that the original microeconometric estimates only include married working males of prime ages who are the head of household in their sample while calibration values utilize the aggregate fluctuations from the entire population. The second difference is that the microeconometric estimates tend to focus only on labor supply changes on the intensive margin while the macroeconomic calibration values are determined to match fluctuations in hours from both changes on the intensive and extensive margin. The goal of this paper is to determine whether estimates of the macro Frisch elasticity using the microeconometric techniques are consistent with the values used to calibrate macroeconomic models. Similar to previous studies, I find that accounting for either of these differences in isolation cannot explain the whole gap. However, I estimate the macro Frisch elasticity which incorporates both differences is between 2.9 - 3.1. Since this estimate of the Frisch is in the range of typical macroeconomic calibration values, I conclude that the impact of accounting for both differences in tandem is large enough to explain the gap. This result highlights that the fluctuations on the extensive margin and inclusion of individuals other than married males, particularly older individuals, are both important explanations for the previously unexplained gap. These results are in contrast to (Fiorito and Zanella, 2012) which estimates a much lower macro Frisch elasticity. I demonstrate that two differences in their methodology contribute to the lower estimates. First, the authors use lag wags as opposed to age and education as instruments for current wages. Second, the authors do not incorporate the panel structure of the data into the estimates of the macro Frisch elasticity. Furthermore, the finding that the difference in composition and whether fluctuations on the extensive margin are included can explain the gap is robust to using an alternative set of polynomials as instruments. I find that estimates of the macro Frisch fall dramatically when older individuals are not included. Other research, such as (Casanova, 2012), points out that estimates of the Frisch elasticity that include these older individuals may be biased by people choosing to take a decrease in their wage in order to partially retire. Therefore, if a macroeconomist wants a calibration value for the Frisch elasticity in a parsimonious model that does not include partial retirement that will reconcile fluctuations in hours and wages over the business cycle, then the large values consistent with the baseline macro estimates in this paper are necessary. However, the estimates in this study may be upwardly biased estimates of the actual responsiveness of hours to changes in wages in a fully specified model that includes the decision to partially retire and changes in tastes for leisure. Therefore, future work should aim to disentangle the strength of this bias.

A. Implications of using participation rate elasticity

In order to calculate the macro elasticity, (Chetty et al., 2011) adds the micro (intensive margin elasticity) and the extensive margin elasticity. The authors value for the extensive margin comes from a meta analysis that focuses on studies that primarily estimate the labor force participation elasticity. The sum of the intensive margin elasticity and the labor force participation elasticity need not be the same as calculating the aggregate Frisch elasticity from variations on both the intensive and extensive margin. Let us consider an economy over two periods which experiences a temporary change in the after tax wage. Let there be three populations. The first group is individuals who work in both periods which I denote with . The second group is made up of individuals who do not work in either period, which I denote with . The third group contains individuals who only work in the second period, who I denote as . In the first period, let $h_{i}$ denote the hours worked on average by group and $P_{i}$ be the size of group . Let $h_{i}'$ and $P_{i}'$ represent the hours worked by group and the size of group in the second period, respectively. The aggregate Frisch elasticity is the percent change in hours divided by the percent change in wages. The percent change in hours can be written as $\frac{P_{e}h_{e}'+P_{n}'h_{n}'-P_{e}h_{e}}{P_{e}h_{e}}$ , which simplifies to, $\frac{P_{n}'h_{n}'}{P_{e}h_{e}}+\frac{h_{e}'-h_{e}}{h_{e}}$ . The first part of the expression represents the percent change in hours from the new workers (fluctuations on the extensive margin). The second part of the expression represents the percent change in hours from the increase in hours worked from individuals who work in both periods (fluctuations on the intensive margin). (Chetty et al., 2011) uses the change in the participation rate elasticity as the contribution of new workers to the aggregate Frisch elasticity and therefore calculates the percentage change in hours as $\frac{P_{n}'}{P_{e}}+\frac{h_{e}'-h_{e}}{h_{e}}$ . These two expressions are only equivalent if new workers work on average the same number of hours as existing workers did in the first period ( $h_{e}=h_{n}'$ ). If these new workers who enter after the wage increase tend to work more hours than the old workers worked prior to the wage increase, then the estimates in (Chetty et al., 2011) will be biased downward.

B. Heckman-type Selection Correction

Table 10: **Significance Tests for Selection Correction Regressions**
Var.	Participation Equation: 1968	Participation Equation: 1970	Participation Equation: 1975	Participation Equation: 1980	Participation Equation: 1985	Participation Equation: 1990	Participation Equation: 1995	Participation Equation: 1997	Wage Eq. All Yrs.
Married	0.216	0.00749	0.822	0.430	9.120	15.80	10.79	24.88	1.910
Married (s.e.)	(0.642)	(0.931)	(0.365)	(0.512)	(0.00253)	(7.04e-05)	(0.00102)	(6.11e-07)	(0.167)
Kids	18.35	20.92	27.44	42.88	34.44	18.11	17.72	43.10	21.04
Kids (s.e.)	(1.84e-05)	(4.78e-06)	(1.62e-07)	(5.82e-11)	(4.38e-09)	(2.09e-05)	(2.56e-05)	(5.21e-11)	(4.50e-06)
Sex	1484	1180	1143	925.5	514.8	751.4	355.8	459.8	450.1
Sex (s.e.)	(0)	(0)	(0)	(0)	(0)	(0)	(0)	(0)	(0)
Age polys	0.0227	3.010	3.636	1.785	8.009	2.871	4.234	6.194	0.777
Age polys (s.e.)	(0.989)	(0.390)	(0.162)	(0.618)	(0.0458)	(0.0468)	(0.0358)	(0.0414)	(0)
Educ. Polys	12.72	4.034	1.792	0.557	5.562	7.962	6.662	6.371	19.38
Educ. Polys (s.e.)	(0.00528)	(0.133)	(0.617)	(0.757)	(0.0620)	(0.238)	(0.237)	(0.103)	(0.460)
Age x Educ.	13.40	8.377	4.364	3.679	12.35	11.29	14.34	26.37	14.34
Age x Educ. (s.e.)	(0.0199)	(0.137)	(0.498)	(0.596)	(0.0303)	(0.0459)	(0.0136)	(7.58e-05)	(0)
Inverse Mills									9.454
Inverse Mills (s.e.)									(0)
All Variables	2949	2905	3808	4647	4890	6928	6379	4360	304.9
All Variables (s.e.)	(0)	(0)	(0)	(0)	(0)	(0)	(0)	(0)	(0)
Obs	7,806	7,430	9,172	10,336	10,987	14,436	15,146	9,978	226,822

Notes: The participation regression is done on an annual basis. Only selected years of the participation regression are included. The test statistic for the participation equation is a $\chi^{2}$ . The test statistic for the wage equation is an F-test. P-values for each test are included in the parenthesis. The age polys. included are age, age $^{2}$ , and age³. The education polys. included are education, education $^{2}$ , and education³. The test statistics for age, education, and interactions are joint tests of significance. Both the wage and participation regressions are done with mean values included for all variables. The significance of the mean values is not included in the table.

Bibliography

Altonji, Joseph G.

"Intertemporal Substitution in Labor Supply: Evidence from Micro Data," The Journal of Political Economy, 1986, 94 (3), S176-S215.

Blau, Francine D. and Lawrence M. Kahn

"Changes in the Labor Supply Behavior of Married Women: 1980 - 2000," Journal of Labor Economics, July 2007, 25 (3), pp. 393-438.

Blundell, Richard, Howard Reed, and Thomas M. Stoker

"Interpreting Aggregate Wage Growth: The Role of Labor Market Participation," The American Economic Review, 2003, 93 (4), pp. 1114-1131.

Casanova, María

"Wage and Earnings Profiles at Older Ages," Working Paper January 2012.

Chang, Yongsung

"Interpreting Labor Supply Regressions in a Model of Full- and Part-Time Work," American Economic Review, May 2011, 101 (3), 476-81.

Chetty, Raj

"Bounds on Elasticities with Optimization Fricitions: A Synthesis of Micro and Macro Evidence on Labor Supply," Working Paper 15616, NBER December 2009.

Chetty, Ray, Adam Guren, Day Manoli, and Andrea Weber

"Does Indivisible Labor Explain the Difference between micro and Macro Elasticityes? A Meta-Analysis of Extensive Margin Elasticities," Working Paper, Harvard January 2011.

Contreras, Juan and Sven Sinclair

"Labor supply response in macroeconomic models: Assessing the empirical validity of the intertemporal labor supply response from a stochastic overlapping generations model with incomplete markets," MPRA Paper 10533, University Library of Munich, Germany September 2008.

Deaton, Angus

"Panel Data From Time Series of Cross-sections," Journal of Econometrics, 1985, 30, 109 - 126.

Domeij, David and Martin Floden

"The labor-supply elasticity and borrowing constraints: Why estimates are biased," Review of Economic Dynamics, 2006, 9 (2), 242 - 262.

Faberman, Jason

"Revisiting the role of home production in life-cycle labor supply," Working Papers 10-3, Federal Reserve Bank of Philadelphia 2010.

Fiorito, Riccardo and Giulio Zanella

"The anatomy of the aggregate labor supply elasticity," Review of Economic Dynamics, 2012, 15 (2), 171 - 187.

Heckman, James J. and Thomas E. Macurdy

"A Life Cycle Model of Female Labour Supply," The Review of Economic Studies, 1980, 47 (1), pp. 47-74.

Imai, Susumu and Michael Keane

"Intertemporal Labor Supply and Human Capital Accumulation," International Economic Review, May 2004, 45 (2), 601-641.

Keane, Michael

"Micro and Macro Labor Supply Elasticities: A Reassessment of Conventional Wisdom," Journal of Economic Literature, June 2012, 50 (2), 464-76.

Kimmel, Jean and Thomas J. Kniesner

"New evidence on labor supply: Employment versus hours elasticities by sex and marital status," Journal of Monetary Economics, 1998, 42 (2), 289 - 301.

MaCurdy, Thomas E.

"An Empirical Model of Labor Supply in a Life-Cycle Setting," The Journal of Political Economy, 1981, 89 (6), 1059-1085.

Mulligan, Casey

"The Intertemporal Substitution of Work-What Does the Evidence Say?," University of Chicago - Population Research Center, Chicago - Population Research Center June 1995.

Mulligan, Casey

"Substition over Time: Another Look at Life-Cycle Labor Supply," NBER Macroeconomics Annual 1998, January 1999, 13.

Pistaferri, Luigi

"Anticipated and Unanticipated Wage Changes, Wage Risk, and Intertemporal Labor Supply," Journal of Labor Economics, 2003, 21 (3), 729-754.

Rìos-Rull, Josè-Vìctor, Sebastian Dyrda, and Greg Kaplan

"Business Cycles and Household Formation: The Micro vs the Macro Labor Elasticity," Working Papers 2012.

Rogerson, Richard and Johanna Wallenius

"Micro and macro elasticities in a life cycle model with taxes," Journal of Economic Theory, 2009, 144 (6), 2277 - 2292.
Dynamic General Equilibrium.

Verbeek, M., , and T. Nijman

"Can Cohort Data be Treated as Genuine Panel Data?," Empirical Economics, 1992, 17, 9-23.

Wooldridge, Jeffrey M.

"Selection corrections for panel data models under conditional mean independence assumptions," Journal of Econometrics, 1995, 68 (1), 115 - 132.

Footnotes

1. E-mail: [email protected]. Views expressed in this paper are my own and do not reflect the view of the Federal Reserve System or its staff. For extensive discussions and helpful comments, I thank Glenn Follette, Leah Brooks, Roger Gordon, Julie Cullen and Gordon Dahl, as well as seminar participants at the Federal Reserve Board of Governors, 2012 System Applied Micro Conference, University of California at San Diego, and the Federal Reserve Board of Governors. I am extremely grateful to Michael Barnett for excellent research assistance. Return to Text

2. See (Chetty et al., 2011) for a discussion of the values used to calibrate models. Return to Text

3. Some alternative explanations include: utilizing weak instruments; disregarding the life cycle effect of endogenous-age specific human capital; omitting correlated variables such as wage uncertainty; and not accounting for labor market frictions such as liquidity constraints (see (Imai and Keane, 2004), (Pistaferri, 2003), (Chetty, 2009), (Domeij and Floden, 2006), and (Contreras and Sinclair, 2008)). (Keane, 2012) summarize the individual effect of some of these explanations on the estimates of the Frisch elasticity along with the effect of the extewnsive margin. These alternative explanations are not explored in this paper. Return to Text

4. Some of the original estimates are from an even narrower age range. Return to Text

5. When estimating the macro Frisch elasticity I focus on individuals between the ages of twenty and sixty-five. Ideally, I would include all individuals who were of working age, however because of data constraints I am forced to limit the sample. Return to Text

6. (Verbeek et al., 1992) demonstrates that if the size of the panel is large enough, coefficients estimated from a pseudo panel will be unbiased estimates of the coefficients from a traditional panel. Return to Text

7. Some of these works focus on compensated elasticities as opposed to the Frisch elasticity. For example, (Kimmel and Kniesner, 1998) demonstrates that married and single individuals have different compensated elasticities. Although Frisch elasticities and compensated elasticities can be different, the variation in the compensated elasticity between the various groups indicates that there will also tend to be variation in the Frisch labor supply elasticity from the various groups. Return to Text

8. (Chang, 2011) show that estimates of the micro elasticity from aggregate data that includes a decision on the extensive margin will include large biases. Return to Text

9. Since the estimation strategy in (MaCurdy, 1981) is replicated in (Altonji, 1986), the estimation strategies in (Altonji, 1986) serve as a complete set. Therefore, for notational convenience, I only cite (Altonji, 1986) when discussing the estimation strategies. Return to Text

10. $\delta$ is included in the change specification to control for annual changes in the after tax return to capital. Return to Text

11. In both alternative estimates the author uses a second wage series in the data that exists only for hourly employees. Return to Text

12. The variable indicating economic status for the parents is not available for secondary workers. Therefore, I do not present results using this instrument. However, in the sample that contained parental economic status, I found that excluding this instrument did not impact the results. Return to Text

13. I focus on the specifications in columns one and three that include age as an instrument but not as a control. Return to Text

14. The variables I include to control for tastes are whether an individual lives in a city with a population larger than 500,000, the number of children, and the number of children under six. Return to Text

15. In order to estimate equation 8, I use the natural log of the average value of the cohort as opposed to the using the average natural log of the cohort's value. Using the natural log of the average value corresponds to determining the parameter value that governs the representative cohort. Return to Text

16. This approach was originally proposed by (Deaton, 1985) to transform cross sectional data into panel data. Return to Text

17. One difference from (Verbeek et al., 1992) is that since my data set is a traditional panel, generally the cohort contains the same individuals over time, while their data set is from repeated cross-sections. A consequence of their data is that there is more change in which individuals are observed. You would expect that a pseudo panel built from a traditional panel with a more consistent set of individuals to be less susceptible to this bias. However, the size of the data set employed in this study is on the lower end of the requirements discussed in (Verbeek et al., 1992) so the estimates of the coefficients might be attenuated. Return to Text

18. After 1997 the PSID became bi-annual and therefore, I do not include these surveys. Return to Text

19. Observations from non-working individuals are not subjected to this requirement. Return to Text

20. These plots are not the pseudo panels. Return to Text

21. Individuals who are not actively working, students, retired or work less than 250 hours a year, are considered to not be working and excluded from his data set. Formally, I consider individuals to not be working in a specific year if they report working less than or equal to 250 hours. As opposed to considering any individual who works less than 250 hours non-working, (Altonji, 1986) uses a cutoff of zero hours. I choose to use a higher threshold because I am not able to utilize all of the variables that contain reported information about retirement since the variables do not exist for secondary earners. Return to Text

22. There are a few reason for slight differences in the estimates. First, I use the weights in the PSID. Second, I was unable to replicate his restrictions for undetermined reasons. Third, I use the Consumer Price Index to deflate wages as opposed to the GDP deflator. Return to Text

23. The F-statistic is lower when annual dummies are included because there are less degrees of freedom. Return to Text

24. The estimates in columns II and VI are not an estimate of the Frisch elasticity of the single, prime age males who are the head of the household but instead a weighted average of the married and single prime age males who are head of households. Return to Text

25. These estimates of the impact of the extensive margin are consistent with the macro Frisch elasticity in the sense that they do not account for the fluctuations in potential wages of non-working individuals. Return to Text

26. I do not display the estimates when the annual dummies are not included; however, the results are similar. Return to Text

27. Since individuals are required to work a minimum number of hours in order to be included in the sample used to estimate the micro Frisch, many individuals who are partially retired may be excluded. Return to Text

28. Similar to in my benchmark macro estimates, the first stage regression is run on the cohort level as opposed to the individual level. Return to Text

29. I choose to not use annual dummies due to a lack of degrees of freedom. Furthermore, I limit the sample period when running the time series regression because (Fiorito and Zanella, 2012) point out that the wage variable may have fundamentally changed after 1992. Return to Text

30. In this estimate of aggregate wage, if an individual reports not working but still reports a wage that information is included in the pseudo panel. Return to Text

31. See section 3 of (Fiorito and Zanella, 2012) and (Wooldridge, 1995) for more details on the correction procedure. The variables used to predict employment at the first stage are gender, race, marital status, number of kids and a set of polynomials and interactions between age and education. One difference between (Fiorito and Zanella, 2012) and this study is that the level, as opposed to the natural log, of wages is predicted. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text