Stock Prices, News, and Economic Fluctuations: Comment*
Keywords: Vector Error Correction Model, long-run restrictions, news shocks
Abstract:
1 Introduction
In a highly influential paper, Beaudry and Portier (2006) estimate Vector Error Correction Models (VECMs) on U.S. data and find that shocks generating a stock market boom but no contemporaneous movement in Total Factor Productivity (![]() ) -- henceforth called "
) -- henceforth called "![]() news" -- are closely related to shocks driving long-run variations in
news" -- are closely related to shocks driving long-run variations in ![]() . Moreover, these
. Moreover, these ![]() news cause increases in consumption, investment, output and hours on impact and constitute an
important source of business cycle fluctuations. These results run counter to basic dynamic stochastic general equilibrium (DSGE) models and have sparked a new literature attempting to generate news-driven positive comovement among macroeconomic aggregates.1
news cause increases in consumption, investment, output and hours on impact and constitute an
important source of business cycle fluctuations. These results run counter to basic dynamic stochastic general equilibrium (DSGE) models and have sparked a new literature attempting to generate news-driven positive comovement among macroeconomic aggregates.1
This comment shows that in the VECMs with more than two variables estimated by Beaudry and Portier (2006), their identification scheme fails to determine ![]() news. Yet, these
higher-dimension systems are crucial to quantify the business cycle effects of
news. Yet, these
higher-dimension systems are crucial to quantify the business cycle effects of ![]() news.2 The identification problem arises from the interplay of two assumptions. First, the Beaudry-Portier identification scheme requires that one of the non-news shocks has no permanent impact on either
news.2 The identification problem arises from the interplay of two assumptions. First, the Beaudry-Portier identification scheme requires that one of the non-news shocks has no permanent impact on either ![]() or consumption. Second, the VECMs estimated by Beaudry and Portier (2006) impose that
or consumption. Second, the VECMs estimated by Beaudry and Portier (2006) impose that ![]() and consumption are
cointegrated. This means that
and consumption are
cointegrated. This means that ![]() and consumption have the same permanent component, which makes one of the two long-run restrictions redundant and leaves an infinity of candidate solutions
with very different implications for the business cycle. The results reported in Beaudry and Portier (2006) represent just one arbitrary choice among these solutions.3
and consumption have the same permanent component, which makes one of the two long-run restrictions redundant and leaves an infinity of candidate solutions
with very different implications for the business cycle. The results reported in Beaudry and Portier (2006) represent just one arbitrary choice among these solutions.3
A potential way to address the identification problem is to drop the cointegration restriction between ![]() and consumption. We do so by applying Beaudry and Portier's (2006) restrictions,
called the "BP restrictions" from hereon, on a vector autoregressive (VAR) system in levels that does not require any a priori assumptions about cointegration. The point estimates of the BP news shock responses in the level VAR resemble closely the results reported by Beaudry and Portier (2006)
for their VECM systems. However, this identification is surrounded by a tremendous degree of uncertainty because the VAR estimates imply about a 50% chance that
and consumption. We do so by applying Beaudry and Portier's (2006) restrictions,
called the "BP restrictions" from hereon, on a vector autoregressive (VAR) system in levels that does not require any a priori assumptions about cointegration. The point estimates of the BP news shock responses in the level VAR resemble closely the results reported by Beaudry and Portier (2006)
for their VECM systems. However, this identification is surrounded by a tremendous degree of uncertainty because the VAR estimates imply about a 50% chance that ![]() and consumption are
cointegrated, in which case the BP restrictions fail to identify
and consumption are
cointegrated, in which case the BP restrictions fail to identify ![]() news. One can therefore not have any reasonable degree of confidence about the results obtained from the VAR in levels.
news. One can therefore not have any reasonable degree of confidence about the results obtained from the VAR in levels.
We also apply the BP restrictions to an alternative VAR system that, consistent with a large class of DSGE models, imposes absence of cointegration between ![]() and consumption. In this
case, the identification problem disappears but the shock implied by the BP restrictions is largely unrelated to
and consumption. In this
case, the identification problem disappears but the shock implied by the BP restrictions is largely unrelated to ![]() . In sum, dropping the cointegration restriction between
. In sum, dropping the cointegration restriction between ![]() and consumption fails to solve the identification problem or generates results that are difficult to interpret as news about future productivity.
and consumption fails to solve the identification problem or generates results that are difficult to interpret as news about future productivity.
The remainder of the comment proceeds as follows. Section 2 explains the identification problem arising with the BP restrictions. Section 3 applies the BP restrictions to VAR-based systems that do not impose cointegration between ![]() and consumption. Section 4 evaluates the BP restrictions in VAR systems with alternative cointegration assumptions. Section 5 concludes by briefly describing alternative identification strategies of
and consumption. Section 4 evaluates the BP restrictions in VAR systems with alternative cointegration assumptions. Section 5 concludes by briefly describing alternative identification strategies of ![]() news that do not depend on cointegration restrictions between
news that do not depend on cointegration restrictions between ![]() and
and ![]() .
.
2 The identification problem
Beaudry and Portier (2006) estimate bivariate, three-variable and four-variable VECMs in ![]() , a real stock market price (
, a real stock market price (![]() ), consumption (
), consumption (![]() ), hours (
), hours (![]() ) and
investment (
) and
investment (![]() ). These VECMs can be expressed in vector moving average form as
). These VECMs can be expressed in vector moving average form as
where
Crucially, the VECM imposes a set of cointegration restrictions
![]() , where
, where
![]() denotes the matrix of cointegrating vectors. As discussed by King, Plosser, Stock and Watson (1991) and Hamilton (1994), cointegration imposes restrictions on
denotes the matrix of cointegrating vectors. As discussed by King, Plosser, Stock and Watson (1991) and Hamilton (1994), cointegration imposes restrictions on
![]() . In particular, since
. In particular, since
![]() is stationary,
is stationary,
![]() and thus,
and thus,
![]() is singular. This constrains the set of linearly independent restrictions that can be imposed on the VECM to identify structural shocks. The identification problem arising with the
BP restrictions stems from these constraints.
is singular. This constrains the set of linearly independent restrictions that can be imposed on the VECM to identify structural shocks. The identification problem arising with the
BP restrictions stems from these constraints.
Identification maps
![]() to structural shocks
to structural shocks
![]() by
by
![]() , with
, with
![]() and thus
and thus
![]() . Impulse responses to the structural shocks are then given by
. Impulse responses to the structural shocks are then given by
![]() . Beaudry and Portier's (2006) original idea is that news about future
. Beaudry and Portier's (2006) original idea is that news about future ![]() do not have a contemporaneous effect on measured
do not have a contemporaneous effect on measured ![]() ; i.e. if the
; i.e. if the ![]() news innovation is the second element of
news innovation is the second element of
![]() , that the
, that the ![]() element of
element of
![]() is zero. For the bivariate systems that Beaudry and Portier (2006) use as their baseline case, this restriction together with
is zero. For the bivariate systems that Beaudry and Portier (2006) use as their baseline case, this restriction together with
![]() uniquely identifies
uniquely identifies ![]() news.
news.
The identification problem arises in the three- and four-variate systems where one zero restriction is no longer sufficient to identify structural shocks. Beaudry and Portier's (2006) strategy consists of adding zero restrictions until identification is achieved. In the trivariate case, these
additional restrictions are that one of the non-news shocks has no permanent effect on ![]() and
and ![]() ; so when this non-news shock is the third element of
; so when this non-news shock is the third element of
![]() , the
, the ![]() and
and ![]() elements of the long-run impact matrix
elements of the long-run impact matrix
![]() are zero. In the four-variable case, the additional restrictions consist of the same two long-run restrictions plus the assumption that one
of the other non-news shocks can only have a contemporaneous effect on
are zero. In the four-variable case, the additional restrictions consist of the same two long-run restrictions plus the assumption that one
of the other non-news shocks can only have a contemporaneous effect on ![]() , respectively
, respectively ![]() ; so when this other non-news shock is the fourth element of
; so when this other non-news shock is the fourth element of
![]() , the
, the ![]() ,
, ![]() and
and ![]() elements of
elements of
![]() are zero.
are zero.
In a typical VAR, the additional zero restrictions, together with the zero impact restriction on ![]() and
and
![]() , would be sufficient to uniquely identify all elements of
, would be sufficient to uniquely identify all elements of
![]() and thus
and thus ![]() news. Here, this is unfortunately not the case
because the three- and four-variable VECMs estimated by Beaudry and Portier (2006) are subject to two, respectively three cointegration restrictions; i.e.
news. Here, this is unfortunately not the case
because the three- and four-variable VECMs estimated by Beaudry and Portier (2006) are subject to two, respectively three cointegration restrictions; i.e.
![]() is a
is a
![]() matrix, respectively a
matrix, respectively a
![]() matrix of linearly independent rows.5
Since
matrix of linearly independent rows.5
Since
![]() , the rows of
, the rows of
![]() and
and
![]() are linearly dependent of each other. In fact, given the number of cointegrating relationships,
are linearly dependent of each other. In fact, given the number of cointegrating relationships,
![]() and
and
![]() are just of rank 1, and only one linearly independent restriction
can be imposed on
are just of rank 1, and only one linearly independent restriction
can be imposed on
![]() . One of the two long-run zero restrictions is therefore redundant, leaving
. One of the two long-run zero restrictions is therefore redundant, leaving
![]() and the shock that is supposed to capture
and the shock that is supposed to capture ![]() news
under-identified.6
news
under-identified.6
Another, perhaps more intuitive way to understand the identification problem is to realize that the imposed cointegration relationships imply for ![]() and
and ![]() to share a common trend. But then, when a particular shock, the third element of
to share a common trend. But then, when a particular shock, the third element of
![]() in this case, is restricted to have zero long-run effect on
in this case, is restricted to have zero long-run effect on ![]() , it automatically also has zero long run effect on
, it automatically also has zero long run effect on ![]() .
.
The identification problem implies that there exists an infinity of solutions consistent with the BP restrictions. The results reported in Beaudry and Portier (2006) represent one particular solution but there is no economic justification for why this solution should be preferred over any of the
other solutions. As we show in the Web-Appendix, some of these solutions are not correlated with the shock driving long-run movements in ![]() and generate very different impulse responses. In
the context of the three- and four-variable VECMs estimated by Beaudry and Portier (2006), it is therefore impossible to draw any conclusions about
and generate very different impulse responses. In
the context of the three- and four-variable VECMs estimated by Beaudry and Portier (2006), it is therefore impossible to draw any conclusions about ![]() news based on the BP restrictions.
news based on the BP restrictions.
3 Dropping the cointegration restriction
A seemingly natural way to address the identification problem while keeping with the BP restrictions is to drop the cointegration restriction between ![]() and
and ![]() . Indeed, as Beaudry and Portier (2006) note themselves, the econometric evidence in favor of two versus one cointegration relationship between
. Indeed, as Beaudry and Portier (2006) note themselves, the econometric evidence in favor of two versus one cointegration relationship between ![]() ,
, ![]() and
and ![]() is not clear-cut,
which leaves open the door that
is not clear-cut,
which leaves open the door that ![]() and
and ![]() do not share a common trend. Beaudry and
Portier (2006) entertain this possibility in the NBER working paper version of their paper where they report results for one of their baseline bivariate systems estimated as a VAR in levels; i.e. with no cointegration restrictions imposed. However, they do not report any results for level VARs with
more than two variables.
do not share a common trend. Beaudry and
Portier (2006) entertain this possibility in the NBER working paper version of their paper where they report results for one of their baseline bivariate systems estimated as a VAR in levels; i.e. with no cointegration restrictions imposed. However, they do not report any results for level VARs with
more than two variables.
One important challenge with implementing the BP restrictions in a VAR in levels is that for the type of non-stationary variables involved in the estimation, there is no finite-valued solution for the long-run impact matrix of the different shocks. Hence, the long-run zero restrictions on which
Beaudry and Portier's (2006) identification scheme relies cannot be imposed exactly.7 We resolve this issue by first computing the linear combination of VAR
residuals that account for most of the forecast error variance (FEV) of ![]() , respectively
, respectively ![]() , at a long but finite horizon of 400 quarters; and then using a projection-based procedure to implement the BP restrictions.8
, at a long but finite horizon of 400 quarters; and then using a projection-based procedure to implement the BP restrictions.8
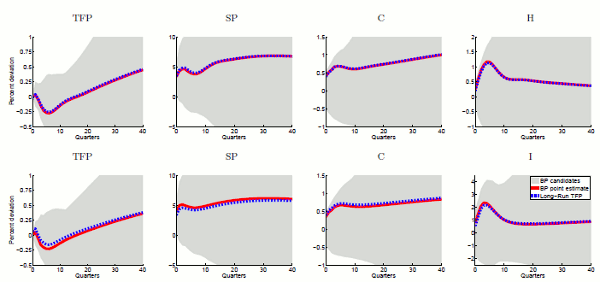
We estimate the three- and four-variable level VAR equivalents of Beaudry and Portier's (2006) VECMs using their original data with the number of lags set to four based on traditional information criteria and Portmanteau tests.9 The first row of Figure 1 reports the results for the four-variable level VAR in (
![]() ); the second row reports the results for the level VAR in (
); the second row reports the results for the level VAR in (
![]() ). Very similar results obtain for the three-variable case and are therefore not reported. The red solid lines and the blue dashed lines display, respectively, the impulse
responses -- generated by the point estimates -- to the shock identified by the BP restrictions and the shock driving long-run variations in
). Very similar results obtain for the three-variable case and are therefore not reported. The red solid lines and the blue dashed lines display, respectively, the impulse
responses -- generated by the point estimates -- to the shock identified by the BP restrictions and the shock driving long-run variations in ![]() . The grey intervals represent a measure of
uncertainty about the identification implied by the BP restrictions, which will be discussed further below.
. The grey intervals represent a measure of
uncertainty about the identification implied by the BP restrictions, which will be discussed further below.
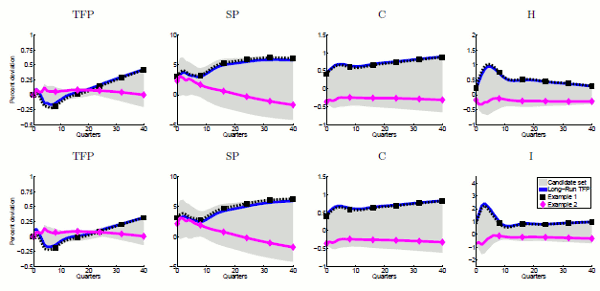
| Figure 1 about here |
The impulse responses derived from the point estimates of both level VARs come surprisingly close to the results reported in Beaudry and Portier (2006) for their VECM systems.10 In particular, the shocks identified from the BP restrictions and the long-run ![]() shock lead to almost identical impulse responses and account for a large
fraction of movements in
shock lead to almost identical impulse responses and account for a large
fraction of movements in ![]() at longer-run frequencies and
at longer-run frequencies and ![]() ,
, ![]() and
and ![]() at business cycle frequencies.
at business cycle frequencies.
At first sight, one could thus be led to conclude that dropping the cointegration assumption by estimating VARs in levels addresses the identification problem and resurrects the results reported in Beaudry and Portier (2006). However, the reported impulse responses reflect just the point
estimates of the level VARs. The problem is that when sampling confidence sets from the estimated level VARs, about 50% of all draws imply that ![]() and
and ![]() share a common trend.11 But then, as described in the previous section, the BP
restrictions do not identify
share a common trend.11 But then, as described in the previous section, the BP
restrictions do not identify ![]() news and one is left instead with an infinity of candidate solutions.
news and one is left instead with an infinity of candidate solutions.
To illustrate this uncertainty about the BP identification, we take each draw that implies a common trend between ![]() and
and ![]() and compute all candidate solutions that are consistent with the BP restrictions and generate a positive impact response of
and compute all candidate solutions that are consistent with the BP restrictions and generate a positive impact response of ![]() .12 The grey envelopes in Figure 1 show the resulting range of impulse responses. Clearly, the range is very wide, encompassing the zero line for all variables and
frequently extending far beyond the displayed scale. Hence, one cannot have any confidence in the impulse responses generated from the BP restrictions when evaluating the level VARs at their point estimates.
.12 The grey envelopes in Figure 1 show the resulting range of impulse responses. Clearly, the range is very wide, encompassing the zero line for all variables and
frequently extending far beyond the displayed scale. Hence, one cannot have any confidence in the impulse responses generated from the BP restrictions when evaluating the level VARs at their point estimates.
In principle, the lack of identification found in the VECMs could be addressed by estimating level systems, that do not impose the common trend assumption on ![]() and
and ![]() . For example, the point estimates of the level VARs generate a unique solution. But draws generated from the level VARs place sufficient odds in favor of the common trend assumption, such that this
approach does not successfully address the identification problem.
. For example, the point estimates of the level VARs generate a unique solution. But draws generated from the level VARs place sufficient odds in favor of the common trend assumption, such that this
approach does not successfully address the identification problem.
4 Alternative cointegrating restrictions
Alternatively, the identification can be addressed by estimating systems which impose that ![]() and
and ![]() have separate trends. Fisher (2010), for example, notes that DSGE models with neutral and investment-specific technology shocks imply that
have separate trends. Fisher (2010), for example, notes that DSGE models with neutral and investment-specific technology shocks imply that ![]() is not cointegrated with
is not cointegrated with
![]() , while sharing a common trend with
, while sharing a common trend with ![]() and
and ![]() .13 These balanced growth assumptions are straightforward to implement by estimating
a stationary VAR in
.13 These balanced growth assumptions are straightforward to implement by estimating
a stationary VAR in
![]() ,
, ![]() ,
, ![]() and
and ![]() , respectively
, respectively ![]() .14 Since
.14 Since ![]() is no longer cointegrated with
is no longer cointegrated with ![]() , the BP restrictions imply a unique identification across all draws.
, the BP restrictions imply a unique identification across all draws.
| Figure 2 about here |
We estimate this stationary VAR specification with Beaudry and Portier's (2006) data and apply the BP restrictions. As shown in Figure 2, the resulting point estimates are very different from the ones reported in Beaudry and Portier (2006). In particular, the identified shock generates a
drop in ![]() that lasts for 10 years or more and accounts for only a very small fraction of future movements in
that lasts for 10 years or more and accounts for only a very small fraction of future movements in ![]() . This makes it difficult to interpret the identified shock as news about future productivity.
. This makes it difficult to interpret the identified shock as news about future productivity.
5 Conclusion
This comment shows that the results reported in Beaudry and Portier (2006) are subject to an important identification problem. The problem arises from the interplay of long-run restrictions and cointegration assumptions that Beaudry and Portier (2006) impose with respect to ![]() and
and ![]() . Dropping the cointegration restriction between
. Dropping the cointegration restriction between ![]() and
and ![]() by estimating a VAR in levels fails to address the identification problem because there is about a 50%
probability that
by estimating a VAR in levels fails to address the identification problem because there is about a 50%
probability that ![]() and
and ![]() share a common trend. Alternatively, imposing that
share a common trend. Alternatively, imposing that
![]() and
and ![]() are not cointegrated by estimating a stationary VAR generate dynamics for
are not cointegrated by estimating a stationary VAR generate dynamics for
![]() that look very different from the ones reported in Beaudry-Portier (2006) and are difficult to interpret as news about future productivity.
that look very different from the ones reported in Beaudry-Portier (2006) and are difficult to interpret as news about future productivity.
The results raise the important question of how to identify ![]() news in alternative ways. One example is Beaudry and Lucke (2010) who invoke short- and long-run zero restrictions for
non-news shocks that do not depend on cointegration between
news in alternative ways. One example is Beaudry and Lucke (2010) who invoke short- and long-run zero restrictions for
non-news shocks that do not depend on cointegration between ![]() and
and ![]() . As Fisher
(2010) shows, however, the implications for
. As Fisher
(2010) shows, however, the implications for ![]() news coming out of this identification crucially depend on the number of cointegration relationships imposed.
news coming out of this identification crucially depend on the number of cointegration relationships imposed.
Another strategy, recently proposed by Barsky and Sims (2011), is to identify ![]() news as the shock orthogonal to contemporaneous
news as the shock orthogonal to contemporaneous ![]() movements that accounts for the maximum share of unpredictable future movements in
movements that accounts for the maximum share of unpredictable future movements in ![]() . This strategy, which is consistent with
Beaudry and Portier's (2006) original idea that
. This strategy, which is consistent with
Beaudry and Portier's (2006) original idea that ![]() is driven by a contemporaneous component and a slowly diffusing news component, has the advantage that it does not rely on additional zero
restrictions about other non-news shocks. As a result, it is robust to different assumptions about cointegration and can be applied to arbitrary vector moving-average systems. Interestingly, Barsky and Sims (2011) find that the
is driven by a contemporaneous component and a slowly diffusing news component, has the advantage that it does not rely on additional zero
restrictions about other non-news shocks. As a result, it is robust to different assumptions about cointegration and can be applied to arbitrary vector moving-average systems. Interestingly, Barsky and Sims (2011) find that the ![]() news resulting from their identification accounts for a substantial share of
news resulting from their identification accounts for a substantial share of ![]() and macroeconomic aggregates at medium- and long-run horizons.
However, their
and macroeconomic aggregates at medium- and long-run horizons.
However, their ![]() news shock does not generate the type of joint increase in real macroeconomic aggregates on impact that Beaudry and Portier (2006) report and that generated a lot of
interest in the literature.
news shock does not generate the type of joint increase in real macroeconomic aggregates on impact that Beaudry and Portier (2006) report and that generated a lot of
interest in the literature.
News shocks and business cycles.
Journal of Monetary Economics 58(3), 273-289.
Are technology improvements contractionary?
American Economic Review 96(5), 1418
Do mood swings drive business cycles and is it rational?
NBER Working Papers, 1765
Stock prices, news and economic fluctuations.
NBER Working Papers, 10548, National Bureau of Economic Research, Inc.
Stock prices, news, and economic fluctuations.
The American Economic Review 96(4), 1293-1307.
When can changes in expectations cause business cycle fluctuations in neo-classical settings?
Journal of Economic Theory 135(1), 458-477.
Shocks.
Carnegie-Rochester Conference Series on Public Policy 41(1), 295-364.
Anticipated growth and business cycles in matching models.
Journal of Monetary Economics 56(3), 309-327.
When do long-run identifying restrictions give reliable results?
Journal of Business & Economic Statistics 15(3), 345-53.
A quarterly, utilization-adjusted series on total factor productivity.
Working Paper Series, 2012-19, Federal Reserve Bank of San Francisco.
The dynamic effects of neutral and investment specific technology shocks.
The Journal of Political Economy 114(3), 413-451.
A flexible finite-horizon alternative to long-run restrictions with an application to technology shocks.
Working Papers, 2005-024, Federal Reserve Bank of St. Louis.
Princeton, NJ: Princeton University Press.
Can news about the future drive the business cycle?
The American Economic Review 99(4), 1097-1118.
Small-sample confidence intervals for impulse response functions.
The Review of Economics and Statistics 80(2), 218-230.
The American Economic Review 81(4), 819-40.
Econometrica 80(6), 2733-2764.
Appendix
A. The VECM's VMA representation
This appendix derives the vector-moving average (VMA) representation for the VECM systems and shows that the matrix of (non-structural) long-run coefficients,
![]() , in equation (2) of the main paper, is singular when derived from the VECM systems estimated by Beaudry and Portier (2006). This relationship holds not only in population but
also for any set of sample estimates of the underlying VECM coefficients. Moreover,
, in equation (2) of the main paper, is singular when derived from the VECM systems estimated by Beaudry and Portier (2006). This relationship holds not only in population but
also for any set of sample estimates of the underlying VECM coefficients. Moreover,
![]() has only rank 1, implying that only one (independent) long-run
restriction can be imposed on
has only rank 1, implying that only one (independent) long-run
restriction can be imposed on
![]() . Since
. Since
![]() is assumed to be non-singular, the same properties hold for the sum of the structural VMA coefficients
is assumed to be non-singular, the same properties hold for the sum of the structural VMA coefficients
![]() .
.
Let ![]() be a vector of non-stationary
be a vector of non-stationary ![]() variables, which are
cointegrated such that
variables, which are
cointegrated such that
![]() for some matrix of cointegrating vectors
for some matrix of cointegrating vectors
![]() . There is then a VECM representation
. There is then a VECM representation
For the sake of brevity it is assumed that there is only a first-order lag dependence in the VECM, which can be easily generalized to higher order cases. In addition, the notation abstracts from constants and other deterministic components of the data. (Our estimated VECM systems include a constant.)
The associated state-space representation is:
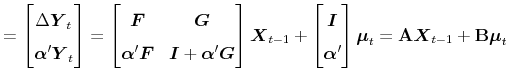
|
(3) |
And it follows the VMA representation:
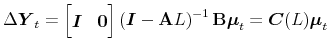 |
A..1
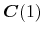 has rank 1
has rank 1
As will be shown below, the matrix of long-run coefficients
![]() is singular because of the assumed cointegrating relationships. In particular we have
is singular because of the assumed cointegrating relationships. In particular we have
![]() , since
, since
![]() measures the long-run effect of a shock on the cointegrating vectors, which are stationary and thus their long-run responses are zero (Hamilton, 1994). In the
VECM systems used by Beaudry and Portier (2006), there are
measures the long-run effect of a shock on the cointegrating vectors, which are stationary and thus their long-run responses are zero (Hamilton, 1994). In the
VECM systems used by Beaudry and Portier (2006), there are ![]() cointegrating relationships, and
cointegrating relationships, and
![]() has
has ![]() columns, when the VECM has
columns, when the VECM has ![]() variables. Thus,
variables. Thus,
![]() has only rank 1.
has only rank 1.
The same holds also in sample, for any point estimates of
![]() ,
,
![]() and
and
![]() -- provided that
-- provided that
![]() is stable. This can be verified by computing the partitioned inverse of
is stable. This can be verified by computing the partitioned inverse of
![]() :
:
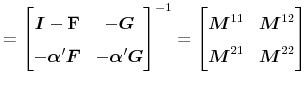 |
(4) |
The standard formulas for the inverse of a partitioned matrix imply in this case
| (5) | ||
And Sylvester's determinant theorem yields: |
||
| (6) | ||
Furthermore, it is straightforward to show that
![]() for any point estimates of
for any point estimates of
![]() ,
, ![]() and
and ![]() . To see this, notice that
. To see this, notice that
When
![]() has
has ![]() columns and
columns and
![]() is a
is a
![]() matrix, it follows that
matrix, it follows that
![]() has rank 1.
has rank 1.
A..2 Long-run shocks to TFP in the VECM
This section shows how to implement the identification of long-run shocks to ![]() in the VECM systems. Throughout, a one-to-one mapping is assumed between forecast errors
in the VECM systems. Throughout, a one-to-one mapping is assumed between forecast errors ![]() and structural shocks
and structural shocks
![]() ,
,
![]() which must obviously satisfy
which must obviously satisfy
![]() .
.
For the VECMs considered by Beaudry and Portier (2006), there is a single common trend driving the permanent component of all variables, since there are ![]() cointegrating relationships
when the system has
cointegrating relationships
when the system has ![]() variables. For the sake of convenience, the shock driving this trend will be referred to as long-run shocks to
variables. For the sake of convenience, the shock driving this trend will be referred to as long-run shocks to ![]() , while it should be understood that the same shock also accounts for all long-run movements in
, while it should be understood that the same shock also accounts for all long-run movements in ![]() ,
, ![]() and potential other variables, denoted
and potential other variables, denoted ![]() . This section describes how to construct these long-run shocks from the
reduced form parameters of the VECM.
. This section describes how to construct these long-run shocks from the
reduced form parameters of the VECM.
Consider the matrix of structural long-run responses
![]() , and let the first column of
, and let the first column of
![]() be the responses of forecast errors to the long-run shock. Since no other shock is issued to have a permanent effect on any of the VECM's variables, it follows that
be the responses of forecast errors to the long-run shock. Since no other shock is issued to have a permanent effect on any of the VECM's variables, it follows that
where
A singular-value decomposition of
![]() yields
yields
where
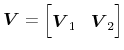 and
and
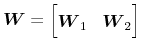 are conformably partitioned, unitary matrices,
are conformably partitioned, unitary matrices,
Without loss of generality,
![]() can be written as the product of
can be written as the product of ![]() and another matrix
and another matrix
![]() . As will be seen next, the long-run restriction requires that
. As will be seen next, the long-run restriction requires that
![]() is (block-) triangular:
is (block-) triangular:
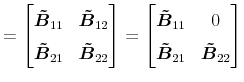 |
(9) |
The restriction
![]() follows from (7) and (8), since it ensures that
follows from (7) and (8), since it ensures that
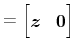 |
(10) |
where
![]() factorizes
factorizes
![]() . A factorization of
. A factorization of
![]() that satisfies the long-run restriction (7) is the Choleski factorization. The first column of
that satisfies the long-run restriction (7) is the Choleski factorization. The first column of
![]() -- the column associated with the long-run shock -- is then given by the first column of
-- the column associated with the long-run shock -- is then given by the first column of
| (11) |
and the long-run shocks are the first element of
| (12) |
where the remaining column of
B. Multiple BP shock candidates
The BP scheme for identifying news shocks hinges on two long-restrictions, namely that one of the non-news shocks has zero effect on ![]() and
and ![]() in the long-run. But as shown above, the matrix of long-run responses in the VECM's VMA representation is singular, with a rank of 1, and one of these long-run restrictions is superfluous, and news shocks are not uniquely identified by the BP scheme. This section describes how to compute the set of candidate shocks in the VECM systems, that are all consistent with the BP restrictions.
in the long-run. But as shown above, the matrix of long-run responses in the VECM's VMA representation is singular, with a rank of 1, and one of these long-run restrictions is superfluous, and news shocks are not uniquely identified by the BP scheme. This section describes how to compute the set of candidate shocks in the VECM systems, that are all consistent with the BP restrictions.
As an illustration, we reestimate Beaudry and Portier's (2006) four-variable VECMs with their original data and apply the procedure described here to obtain all possible impulse vectors that respect the BP restrictions and generate a positive impact response of the stock market. The results are reported in Section B.2 below.
B..1 The entire set of solutions the BP scheme
To recap, the BP restrictions for the four-variable case are
- There is a measurement error shock, which affects only the fourth variable in
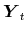 on impact; depending on the VECM specification this variable is either
on impact; depending on the VECM specification this variable is either 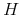 or
or 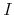 . The shock is denoted
. The shock is denoted
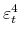 .
. - The "news shock", denoted
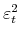 is orthogonal to
is orthogonal to 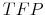 on impact.
on impact. - There is a pure demand shock, denoted
 , which has no permanent effect on
, which has no permanent effect on 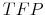 and
and 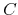 . (As argued above, this shock has thus no permanent effect on any of the VECM variables.)
. (As argued above, this shock has thus no permanent effect on any of the VECM variables.)
A candidate vector of structural shocks can simply be constructed by applying a series of projections using the forecast errors ![]() and long-run shocks
and long-run shocks
![]() (see Appendix A.2) as follows:
(see Appendix A.2) as follows:
-
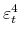 is the standardized residual in a regression of the fourth VECM residual,
is the standardized residual in a regression of the fourth VECM residual, 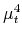 onto the other three residuals.
onto the other three residuals. - A "news shock" candidate can then be constructed as any linear combination of the VECM residuals, which is orthogonal to the forecast error for
 ,
, 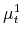 , and the measurement error shocks
, and the measurement error shocks
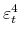 . As will be shown below, it is then always possible to construct
. As will be shown below, it is then always possible to construct
 with the desired properties. Because of the two orthogonality restrictions, only linear combinations in
with the desired properties. Because of the two orthogonality restrictions, only linear combinations in 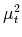 and
and 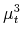 need to be considered when constructing the news shock candidate. Specifically, we use a Givens rotation to construct
need to be considered when constructing the news shock candidate. Specifically, we use a Givens rotation to construct
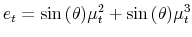 and compute the news shock candidate as the standardized residual in regressing
and compute the news shock candidate as the standardized residual in regressing 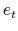 onto
onto 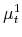 and
and
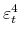 . Different news shock candidates are thus indexed by the angle
. Different news shock candidates are thus indexed by the angle
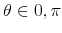 , denoted
, denoted
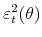 (Only the half circle is considered, since the sign of the shock is determined by the restriction that it generates a positive stock market response on impact.)
(Only the half circle is considered, since the sign of the shock is determined by the restriction that it generates a positive stock market response on impact.) - For a given
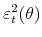 it is straightforward to compute a demand shock candidate,
it is straightforward to compute a demand shock candidate,
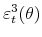 , which has no permanent effect on the VECM variables. To ensure this long-run restriction, the demand shock must be orthogonal to
, which has no permanent effect on the VECM variables. To ensure this long-run restriction, the demand shock must be orthogonal to
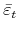 , as constructed in Appendix A.2, since
, as constructed in Appendix A.2, since
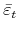 is the sole driver of the permanent component in
is the sole driver of the permanent component in 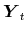 . In
addition, the demand shock has to be orthogonal to
. In
addition, the demand shock has to be orthogonal to
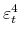 and
and
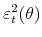 . In sum, the demand shock candidate can be constructed as any linear combination of the VECM residuals which is orthogonal to
. In sum, the demand shock candidate can be constructed as any linear combination of the VECM residuals which is orthogonal to
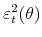 ,
,
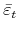 and
and
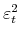 . Since there are only four VECM residuals and there are three orthogonality constraints, any linear combination of the VECM residuals yields the same projection residual (up
to scale and sign) -- unless this linear combination should lie in the span of the three orthogonality restrictions, which is easy to check.
. Since there are only four VECM residuals and there are three orthogonality constraints, any linear combination of the VECM residuals yields the same projection residual (up
to scale and sign) -- unless this linear combination should lie in the span of the three orthogonality restrictions, which is easy to check.
For a given candidate vector of shocks
![]() the corresponding candidate matrix
the corresponding candidate matrix
![]() is equal to the covariance matrix
is equal to the covariance matrix
![]() , which satisfies the BP restrictions by construction. All these computations hold both for population and sample moments.
, which satisfies the BP restrictions by construction. All these computations hold both for population and sample moments.
For the trivariate VECMs, the procedure is identical, except for the absence of
![]() . The set of BP candidate shocks is then described by any linear combination of the VECM residuals that is orthogonal to
. The set of BP candidate shocks is then described by any linear combination of the VECM residuals that is orthogonal to ![]() on impact. Again, up to scale and sign, candidate shocks can be computed by projecting of any linear combination of the residuals of
on impact. Again, up to scale and sign, candidate shocks can be computed by projecting of any linear combination of the residuals of ![]() and
and ![]() , denoted
, denoted ![]() and
and ![]() , off
, off ![]() .
.
B..2 Application to the BP-VECMs
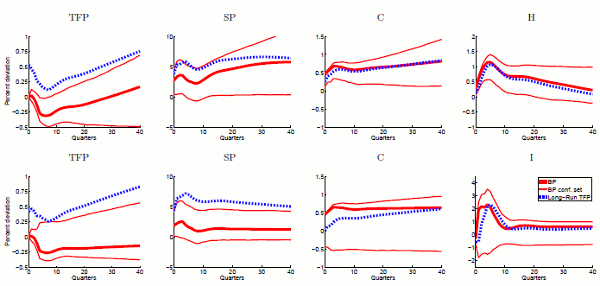
The first row of Figure 1 reports the results for Beaudry and Portier's (2006) four-variable VECM in (
![]() ).15 The second row of
Figure 1 reports equivalent results for the four-variable VECM in
).15 The second row of
Figure 1 reports equivalent results for the four-variable VECM in
(
![]() ). Results for the trivariate VECM in (
). Results for the trivariate VECM in (
![]() ) are very similar and are available upon request. The blue solid lines replicate impulse responses for the long-run
) are very similar and are available upon request. The blue solid lines replicate impulse responses for the long-run ![]() shock reported in Figure 8 of Beaudry and Portier (2006). The grey intervals show the range of candidate solutions consistent with the BP restrictions. Finally, Example 1 (dash-dotted black lines) and Example 2 (dotted red lines) display the impulse
responses for two particular solutions. Example 1 corresponds to the solution that fits the impulse response of
shock reported in Figure 8 of Beaudry and Portier (2006). The grey intervals show the range of candidate solutions consistent with the BP restrictions. Finally, Example 1 (dash-dotted black lines) and Example 2 (dotted red lines) display the impulse
responses for two particular solutions. Example 1 corresponds to the solution that fits the impulse response of ![]() to the long-run shock best in a least square sense; Example 2 corresponds to
the solution that generates a near-zero response of
to the long-run shock best in a least square sense; Example 2 corresponds to
the solution that generates a near-zero response of ![]() at the 40 quarter forecast horizon.
at the 40 quarter forecast horizon.
Consistent with the BP restrictions, none of the candidate solutions affect TFP on impact. Likewise but not shown here, none of the corresponding non-news shocks in the third position of
![]() have a permanent effect on either
have a permanent effect on either ![]() or
or ![]() ; and none of the corresponding non-news shocks in the fourth position of
; and none of the corresponding non-news shocks in the fourth position of
![]() have a contemporaneous effect on
have a contemporaneous effect on ![]() ,
, ![]() and
and ![]() . This confirms numerically that there is an infinity of candidate solutions satisfying
the BP restrictions.
. This confirms numerically that there is an infinity of candidate solutions satisfying
the BP restrictions.
The grey intervals and the two examples show that the candidate solutions have very different implications. As Example 1 shows, there exists a solution that appears very close to the impulse responses reported in Figure 8 of Beaudry and Portier (2006). By contrast, as Example 2 shows, another
solution that is equally consistent with the BP restrictions generates almost no reaction in ![]() but a persistent drop in consumption and hours, respectively investment.
but a persistent drop in consumption and hours, respectively investment.
Given the very different results across rotations, it should not come as a surprise that the range of correlation coefficients between the shocks satisfying the BP restrictions and the long-run ![]() shock is wide for both VECMs, ranging from about -0.50 to 0.99. Likewise, as Table 1 shows, the forecast error variance (FEV) shares of the different variables attributable to shocks consistent with the BP restrictions extends from basically 0% to
above 80% for certain forecast horizons.
shock is wide for both VECMs, ranging from about -0.50 to 0.99. Likewise, as Table 1 shows, the forecast error variance (FEV) shares of the different variables attributable to shocks consistent with the BP restrictions extends from basically 0% to
above 80% for certain forecast horizons.
| 1 | 4 | 8 | 16 | 40 | 120 | |
| VECM with |
0.00 - 0.00 | 0.78 - 1.56 | 0.94 - 9.09 | 1.47 - 9.03 | 2.04 - 28.04 | 2.53 - 84.41 |
| VECM with |
0.00 - 95.28 | 0.12 - 88.05 | 0.10 - 83.00 | 1.90 - 86.52 | 5.45 - 89.77 | 12.50 - 81.08 |
| VECM with |
0.00 - 95.43 | 1.50 - 88.29 | 1.73 - 83.25 | 0.94 - 82.65 | 0.46 - 88.02 | 0.34 - 95.64 |
| VECM with |
0.00 - 17.01 | 1.05 - 54.30 | 1.26 - 71.22 | 1.22 - 77.12 | 2.38 - 80.04 | 6.51 - 75.81 |
| VECM with |
0.00 - 0.00 | 0.82 - 1.24 | 0.91 - 8.84 | 1.29 - 8.78 | 2.87 - 18.38 | 2.41 - 81.92 |
| VECM with |
0.00 - 94.66 | 0.06 - 85.92 | 0.05 - 82.25 | 1.51 - 86.33 | 6.42 - 88.54 | 12.67 - 80.48 |
| VECM with |
0.00 - 94.52 | 1.54 - 84.44 | 1.76 - 79.27 | 0.97 - 80.10 | 0.41 - 87.31 | 0.32 - 95.69 |
| VECM with |
0.00 - 15.66 | 0.83 - 38.15 | 1.05 - 36.71 | 0.95 - 36.39 | 0.78 - 47.15 | 1.30 - 72.98 |
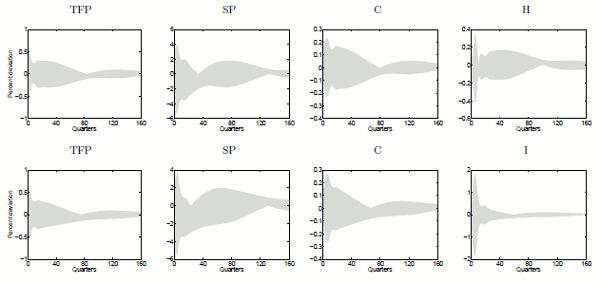
Each of these candidate solutions also implies different responses to the "demand shock",
![]() . As required, all of these solutions have zero effect on
. As required, all of these solutions have zero effect on ![]() and
and
![]() , and -- by virtue of the assumed common trend in all variables -- neither on
, and -- by virtue of the assumed common trend in all variables -- neither on ![]() and
and
![]() . This is illustrated in Figure 2, which depicts the set of impulse responses the demand shock in each VECM at very long horizons. These results
provide a computational consistency check, that the BP restrictions indeed hold for the entire range of shock responses shown in Figure 1.
. This is illustrated in Figure 2, which depicts the set of impulse responses the demand shock in each VECM at very long horizons. These results
provide a computational consistency check, that the BP restrictions indeed hold for the entire range of shock responses shown in Figure 1.
C. BP restrictions in the stationary VAR
This section describes the identification of BP shocks in the stationary VAR. The implementation is fairly similar to the VECM case described in Appendix B above. The major difference is that there is now a unique solution for the BP identification,
since the stationary VAR allows for distinct trends in ![]() and
and ![]() .
.
The BP news shock is constructed by projecting a linear combination of
![]() off the measurement error shock
off the measurement error shock
![]() , the demand shock
, the demand shock
![]() and the forecast error in
and the forecast error in ![]()
![]() . As before,
. As before,
![]() is given by projecting
is given by projecting ![]() off
off
![]() . (The construction of the demand shock will be described further below.) Let these three innovations be stacked in a vector
. (The construction of the demand shock will be described further below.) Let these three innovations be stacked in a vector
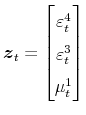
What remains to be shown is the construction of the demand shock
![]() , which in turn will depend on constructing two shocks, that drive the permanent components of
, which in turn will depend on constructing two shocks, that drive the permanent components of ![]() and
and ![]() ; denoted
; denoted
![]() and
and
![]() . These two shocks can be constructed using the conventional procedure of Blanchard and Quah (1989) for long-run identification. Notice that these two shocks have no
structural interpretation in this context, they are merely sufficient statistics for implementing the long-run restrictions on the demand shock. Specifically, the long-run restrictions amount to require that
. These two shocks can be constructed using the conventional procedure of Blanchard and Quah (1989) for long-run identification. Notice that these two shocks have no
structural interpretation in this context, they are merely sufficient statistics for implementing the long-run restrictions on the demand shock. Specifically, the long-run restrictions amount to require that
![]() is orthogonal to
is orthogonal to
![]() and
and
![]() .
.
The long-run "innovations"
![]() and
and
![]() , are constructed by factorizing the long-run variance of
, are constructed by factorizing the long-run variance of
![]() , denoted
, denoted ![]() as follows:
as follows:
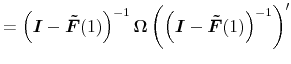 |
||
 |
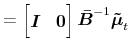 |
In this implementation,
Given
![]() ,
,
![]() and
and
![]() , the demand shock can be constructed as the standardized residual from projecting any linear combination of
, the demand shock can be constructed as the standardized residual from projecting any linear combination of
![]() onto
onto
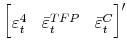 . Using similar reasoning as before, any linear combination yields the same
standardized residuals (except for the degenerate cases where the linear combination is completely spanned and the residuals are all zero).
. Using similar reasoning as before, any linear combination yields the same
standardized residuals (except for the degenerate cases where the linear combination is completely spanned and the residuals are all zero).
As before, the matrix of impact coefficients
![]() is identical to the matrix of covariances between VAR residuals and structural shocks, and these relationships hold in population as well as for sample moments.
is identical to the matrix of covariances between VAR residuals and structural shocks, and these relationships hold in population as well as for sample moments.
D. BP restrictions in the level VAR
Our implementation of the BP restrictions in the level VAR is very similar to the procedure for the stationary VAR outlined in Appendix C. For given shocks
![]() ,
,
![]() and
and
![]() , the news shock can be estimated as the projection residual between any linear combination of the VAR's forecast errors,
, the news shock can be estimated as the projection residual between any linear combination of the VAR's forecast errors,
![]() , and the above-mentioned three shocks. As before, the measurement error shock
, and the above-mentioned three shocks. As before, the measurement error shock
![]() , can be obtained by projecting the fourth VAR residual off the other three VAR residuals.
, can be obtained by projecting the fourth VAR residual off the other three VAR residuals.
The only special feature of our implementation for the level VAR, is the identification of the long-run shocks. Since point estimates of the level VAR typically imply explosive behavior, the sum of the estimated VMA coefficients does not converge to a finite number, and long-run shocks cannot be constructed as in Blanchard and Quah (1989) by factorizing the long-run variance (see also Appendix D).
We follow Francis et al. (2012) and identify the long-run shocks based on their explanatory power for variations in ![]() and
and ![]() at long but finite horizons. Specifically, we construct
at long but finite horizons. Specifically, we construct
![]() , to explain as much as possible of the forecast-error variance of
, to explain as much as possible of the forecast-error variance of ![]() at
at ![]() lags, and similarly for
lags, and similarly for
![]() and
and ![]() .
.
For this method it is convenient to express the identification in terms of an orthonormal matrix ![]() (
(
![]() ). and not in terms of the matrix of impact coefficients
). and not in terms of the matrix of impact coefficients
![]() , where both are assumed to be related via the Cholesky decomposition of the VAR's forecast error variance,
, where both are assumed to be related via the Cholesky decomposition of the VAR's forecast error variance,
![]() chol
chol![]() .
.
We seek the column of ![]() , associated with a long-run shock to
, associated with a long-run shock to ![]() . Denoting
this column
. Denoting
this column ![]() , it solves the following variance maximization problem
, it solves the following variance maximization problem
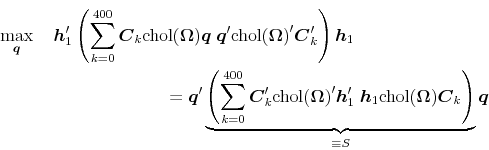
| subject to |
where
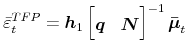
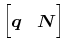 is orthonormal.
is orthonormal.
The procedure is analogous for
![]() , using instead of
, using instead of ![]() a vector
a vector ![]() , which selects
, which selects ![]() from the vector of VAR variables.
from the vector of VAR variables.
A similar procedures is also used to identify news shocks as defined by Barsky and Sims (2011) and Beaudry et al. (2011). There are just two differences: First, both procedures uses different forecast horizons. Beaudry et al. consider forecast horizons of of 40, 80 or 120 leads; and our paper
reports results for 120 leads. Barsky and Sims average over the forecast error variances at leads one to 40. Second, both approaches impose the additional requirement that the maximizing shock vector ![]() is orthogonal to a vector which selects
is orthogonal to a vector which selects ![]() from the set of VAR variables; in the present context, this requirement amounts to the first element of
from the set of VAR variables; in the present context, this requirement amounts to the first element of ![]() being zero.
being zero.
D..1 Lack of identification when long-term shocks are collinear
As a necessary condition,
![]() and
and
![]() must not be perfectly correlated, to obtain a unique solution to the projection-based procedure described in Appendix C. When both long-run shocks are perfectly correlated, the orthogonal complement to the space spanned by
must not be perfectly correlated, to obtain a unique solution to the projection-based procedure described in Appendix C. When both long-run shocks are perfectly correlated, the orthogonal complement to the space spanned by
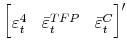 is not anymore one-dimensional. (A similar issue would arise, if one of the two
long-run shocks were perfectly correlated with
is not anymore one-dimensional. (A similar issue would arise, if one of the two
long-run shocks were perfectly correlated with
![]() , the measurement error shock to the fourth variable.)
, the measurement error shock to the fourth variable.)
When simulating confidence sets for the level VARs, we found that for about 50% of the draws,
![]() and
and
![]() are so highly collinear, that their variance covariance matrix is ill-conditioned. As a consequence, the variance-covariance matrix of
are so highly collinear, that their variance covariance matrix is ill-conditioned. As a consequence, the variance-covariance matrix of
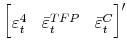 is ill-conditioned. In these cases, we treat
is ill-conditioned. In these cases, we treat
![]() and
and
![]() as perfectly correlated, such that
as perfectly correlated, such that ![]() and
and ![]() share the same common trend. The news shocks are then underidentified, and an infinite number of solutions can be traced out, using a procedure analagously to what is described in Appendix B.
share the same common trend. The news shocks are then underidentified, and an infinite number of solutions can be traced out, using a procedure analagously to what is described in Appendix B.
E. Additional Results
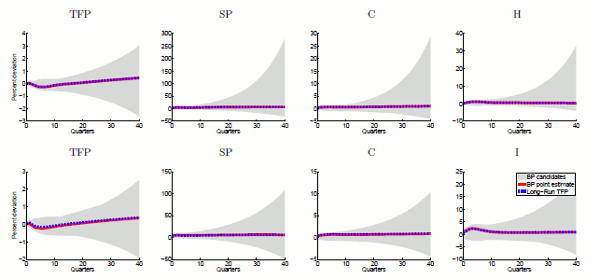
This appendix provides the following supplemental results: Figure 3 reports impulse-responses to the BP shocks in the level VARs. The results are identical to those shown in Figure 1 of the paper, except that Figure 3 displays the results at full scale. Table 2 reports the shares of forecast error variances explained by the BP shocks at different horizons in the level VARs, and Table 3 reports the analogous results for the stationary VARs.
Note: The results shown in this figure are identical to Figure 1 of the main paper, except for the scale of each plot. The top row depicts estimates generated by the VAR in| 1 | 4 | 8 | 16 | 40 | 120 | |
| VAR with |
0.00 | 0.29 | 4.85 | 8.63 | 2.89 | 76.25 |
| VAR with |
(0.00 - 99.08) | (0.02 - 97.58) | (0.13 - 98.47) | (0.06 - 98.44) | (0.06 - 99.16) | (0.22 - 99.99) |
| VAR with |
70.24 | 82.35 | 85.37 | 84.95 | 88.53 | 96.46 |
| VAR with |
(0.00 - 99.28) | (0.06 - 98.69) | (0.02 - 98.53) | (0.05 - 98.70) | (0.16 - 99.18) | (0.51 - 100.00) |
| VAR with |
43.39 | 43.23 | 44.26 | 51.92 | 73.33 | 91.08 |
| VAR with |
(0.00 - 99.76) | (0.01 - 99.75) | (0.06 - 99.29) | (0.03 - 99.62) | (0.07 - 99.93) | (0.42 - 100.00) |
| VAR with |
14.64 | 46.76 | 68.85 | 82.18 | 90.07 | 94.28 |
| VAR with |
(0.00 - 86.73) | (0.16 - 84.87) | (0.18 - 94.73) | (0.12 - 98.96) | (0.14 - 99.91) | (0.10 - 100.00) |
| VAR with |
0.00 | 0.24 | 3.39 | 6.29 | 1.99 | 63.44 |
| VAR with |
(0.00 - 99.55) | (0.01 - 99.21) | (0.01 - 96.75) | (0.01 - 96.54) | (0.11 - 98.86) | (0.43 - 99.96) |
| VAR with |
53.26 | 67.86 | 72.42 | 74.24 | 79.47 | 89.43 |
| VAR with |
(0.00 - 95.56) | (0.04 - 96.82) | (0.09 - 97.51) | (0.03 - 98.78) | (0.11 - 99.52) | (0.31 - 100.00) |
| VAR with |
59.11 | 53.94 | 54.37 | 60.25 | 78.62 | 94.74 |
| VAR with |
(0.00 - 99.90) | (0.01 - 99.38) | (0.02 - 99.80) | (0.05 - 99.97) | (0.09 - 100.00) | (0.24 - 100.00) |
| VAR with |
10.02 | 31.71 | 42.06 | 48.08 | 61.17 | 86.73 |
| VAR with |
(0.00 - 74.91) | (0.01 - 80.80) | (0.00 - 90.66) | (0.01 - 95.07) | (0.05 - 98.75) | (1.18 - 100.00) |
Note: Shares of forecast error variances explained by shocks identified from the Beaudry-Portier restrictions in the level VARs at different forecast horizons. Results are generated from VARs with 4 lags. Since the restrictions leave the solution underidentified in about 50% of the bootstraps, the entire range of potential solutions is reported in parentheses.
| 1 | 4 | 8 | 16 | 40 | 120 | |
| TFP |
0.00 | 1.15 | 11.34 | 12.21 | 5.15 | 24.64 |
| TFP |
(0.00 - 0.00) | (0.52 - 6.94) | (3.98 - 27.20) | (4.52 - 36.54) | (3.79 - 40.14) | (5.93 - 66.27) |
| C |
81.81 | 87.63 | 83.20 | 79.69 | 75.86 | 76.25 |
| C |
(50.99 - 97.66) | (64.76 - 95.13) | (60.10 - 92.69) | (56.00 - 91.38) | (49.39 - 92.08) | (45.03 - 92.74) |
| SP |
28.34 | 26.25 | 21.60 | 25.94 | 45.08 | 57.35 |
| SP |
(3.89 - 90.18) | (4.40 - 81.52) | (3.71 - 71.62) | (4.53 - 69.78) | (12.08 - 79.89) | (24.61 - 84.33) |
| H |
15.76 | 51.14 | 63.22 | 64.94 | 64.51 | 60.38 |
| H |
(7.67 - 27.50) | (33.15 - 66.25) | (39.68 - 79.52) | (41.03 - 83.46) | (40.11 - 84.32) | (33.53 - 83.12) |
| TFP |
0.00 | 0.67 | 8.31 | 10.41 | 6.63 | 1.25 |
| TFP |
(0.00 - 0.00) | (0.41 - 5.98) | (2.31 - 22.82) | (2.85 - 30.85) | (2.51 - 35.91) | (1.69 - 47.34) |
| C |
89.55 | 85.04 | 78.64 | 74.27 | 63.75 | 43.72 |
| C |
(50.50 - 96.63) | (48.97 - 91.64) | (43.31 - 89.72) | (42.58 - 89.78) | (37.11 - 90.05) | (25.49 - 91.50) |
| SP |
13.49 | 11.48 | 8.20 | 6.29 | 5.60 | 6.17 |
| SP |
(1.72 - 88.66) | (1.97 - 82.49) | (2.29 - 70.79) | (2.41 - 67.68) | (2.09 - 67.15) | (3.16 - 66.81) |
| I |
0.47 | 15.07 | 18.05 | 18.03 | 21.62 | 27.97 |
| I |
(0.04 - 4.57) | (4.98 - 32.61) | (4.70 - 44.22) | (5.61 - 45.39) | (9.08 - 49.15) | (15.63 - 61.45) |
Note: Shares of forecast error variances at different horizons explained by the shocks identified by BP restrictions in the stationary VAR. Results are generated from VARs with 4 lags. 80 percent confidence sets reported in parentheses below the point estimates.
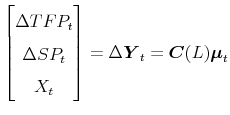 ,
,