
The Nature of Countercyclical Income Risk*
Keywords:
Abstract:
JEL classification: E24, E32, J21, J31.
1 Introduction
From 2007 to 2009, U.S. male workers experienced an average decline in their annual labor earnings of 6.5 percent.1 While this figure represents the sharpest decline of any postwar recession, it is dwarfed by the dispersion of earnings growth rates across workers during the same recession: for example, a quarter of workers saw their labor earnings rise by 16 percent or more, one in ten saw a rise of 50 (log) percent or more, whereas another one in ten saw a fall of 60 (log) percent or more. Moreover, despite the 6.5 percent mean decline just noted, the worker with median earnings change actually experienced a slight rise--of 0.1 percent--during these two years.
The goal of this paper is to understand how this dispersion of fortunes varies over the business cycle. More specifically, we ask two questions. First, how does the distribution of idiosyncratic earnings shocks change over the business cycle? Second, are there any observable characteristics of a worker that can help us predict his fortunes during a business cycle episode? To answer these questions, we decompose earnings growth over the business cycle into a component that can be predicted based on the observable characteristics of individuals (prior to the episode) and a separate "residual" component that represents purely idiosyncratic shocks that affect individuals that are ex ante very similar. The first one represents the "between-group" (systematic) component of business cycle risk, whereas the second can be thought of as the "within-group" (idiosyncratic) component.
An important advantage of our analysis is the very rich dataset that we employ. Basically, our main panel dataset is a 10 percent random sample of all U.S. males with a Social Security number between the ages of 25 and 60 from 1978 to 2010. This dataset has three important advantages. First, earnings records in our dataset are uncapped (no top-coding), allowing us to study individuals with very high earnings.2 Second, the substantial sample size allows us to employ flexible nonparametric methods and still obtain extremely precise estimates.3 Third, thanks to their records-based nature, the data contain very little measurement error, which is a serious issue with survey-based micro datasets. One drawback is possible under-reporting (e.g., cash earnings), which can be a particular concern in the lower portion of the earnings distribution.
The panel aspect of our dataset allows us to use individuals' labor earnings and employment histories to construct observable characteristics as of the beginning of a business cycle episode. For example, we can ask whether individuals that entered a recession with high average earnings are affected differently during the recession relative to those that entered with low average earnings. How about individuals who were rising stars (i.e., had fast earnings growth rate) versus those whose careers were stagnant when the recession hit? And, how does age factor into any of these patterns? To answer these questions systematically, we group individuals along three observable dimensions at the time a business cycle episode begins: (i) age, (ii) pre-episode average earnings, and (iii) pre-episode earnings growth rate.
|
Our main findings can be summarized as follows. First, we study the cyclical nature of idiosyncratic shocks, once observable factors are accounted for. Contrary to past research, we find that earnings shock variances are not countercyclical. However, uncertainty does have a significant countercyclical component, but it comes from the left-skewness increasing during recessions. That is, during recessions, the upper end of the earnings growth distribution collapses--large upward earnings movements become less likely--whereas the bottom end expands--large downward movements become more likely. The two possibilities--countercyclical variance versus left-skewness--are shown in Figure 1. Relative to the earlier literature that argued for increasing variance--which results in some individuals receiving larger positive shocks during recessions--our results are even more pessimistic: Downward risk tends to increase in recessions without an increasing chance of upward movements.
We then turn to the systematic component of business cycle risk. We find substantial between-group variation across individuals who differ in pre-episode average earnings. For example, when we sort prime-age (35-54) male workers based on their 2002-06 average earnings, those in the 10th percentile of this distribution experienced a drop in earnings during the Great Recession (2007-10) that was about 18 percent larger than that experienced by at the 90th percentile. In fact, the average percentage of earnings lost during this recession was almost a linear (upward-sloping) function of pre-recession average earnings all the way up to the 95th percentile (Figure 13). Interestingly, this good fortune of high-income workers did not extend to the very top: those in the top 1 percent, based on their 2002-2006 average earnings, experienced an average loss that was 21 percent worse than that of workers in the 90th percentile. Although these magnitudes are largest for the Great Recession, the same general patterns emerged in the other recessions too. For example, the 1980-83 double-dip recession is very similar to the Great Recession for all but the top 5 percentiles. But the large earnings loss for the top 1 percent was not observed during that recession at all. In fact, this appears to be a more recent phenomenon: The worst episode for the top 1 percent was the otherwise mild 2000-02 recession, when their average earnings loss exceeded that of those in the 90th percentile by almost 30 log points.
Our results on the business cycle behavior of top incomes complement and extend the findings in Piketty and Saez (2003) and, especially, in Parker and Vissing-Jørgensen (2010). In particular, these papers used repeated cross sections to construct synthetic groups of individuals based on their earnings level. They then documented the strong cyclicality of high earnings groups over the business cycle. With panel data, we are able to track the same individuals over time, which allows us to control for compositional change and measure how persistent the effects of such fluctuations are. Our results confirm the higher cyclicality of top earners and reveal the very high persistence of these fluctuations. For example, individuals who were in the 99.9th percentile as of 1999 experienced a 5-year average earnings loss between 2000 and 2005 that exceeded 50 log points. Similarly large persistent losses are found for the top income earners during the 5-year periods covering the Great Recession (2005-10) as well as the 1990-95 period.
The analysis in this paper is deliberately nonparametric, made possible by the large sample size. This approach allows us to present our main findings in the form of figures and easy-to-interpret statistics, which makes the results transparent. An alternative approach would impose a stylized stochastic process on labor earnings and parametrize it in a way to allow variation over the business cycle. In light of our current findings, that approach has an important drawback. Basically, earnings growth rates exhibit significant deviations from normality, in the form of very strong left-skewness and substantial leptokurtosis. Hence, to capture those features (let alone the variation in them over time and across individuals), the estimated earnings process would have to be very complicated, which would take away from the clarity afforded by the current approach.4 Our approach is similar to that of Dynarski and Gruber (1997), Moffitt and Gottschalk (2002), and Solon and Shin (2011), who focused on simple statistics for studying earnings dynamics.
1.0.0.1 Literature Discussion.
The cyclical patterns of idiosyncratic labor earnings risk have received attention from both macro and financial economists. In an infinite-horizon model with permanent shocks, Constantinides and Duffie (1996) showed that one can generate a high equity premium if idiosyncratic shocks have countercyclical variance. Storesletten et al. (2004) used a clever empirical identification scheme to estimate the cyclicality of shock variances.5 Using the Panel Study of Income Dynamics (PSID), they estimated the variance of AR(1) innovations to be three times higher during recessions. Probably due to the small sample size, they did not, however, investigate the cyclicality of the skewness of shocks, nor did they allow for a factor structure as we do here. Moreover, note that the question of interest is "the cyclical changes in the dispersion of earnings growth rates," which involves triple-differencing. Answering such a question without a very large and clean dataset is extremely challenging. Our findings are more consistent with Mankiw (1986), who showed that one can resolve the equity premium puzzle if idiosyncratic shocks have countercyclical left-skewness--as found in the current paper.
The spirit of our analysis is similar to the literature that decomposed wage inequality trends into between-group and within-group components (among many others, Juhn et al. (1993), Lemieux (2006), and Autor et al. (2008)). But there are several notable differences. First, our focus is on growth rates rather than levels, which is feasible with the panel dimension of our dataset. Second, we focus on business cycle variation, whereas that literature examined secular trends. Third, relying on repeated cross sections, that literature had to confine itself to observable characteristics that were available in the cross section, such as gender, age, education, and, sometimes, industry. With longitudinal data, we are able to define groups of individuals based on their history, such as individuals with high versus low past average earnings and/or earnings growth rates.
There is also an interesting parallel between the conclusions of this paper and an early debate in the business cycle literature. In a provocative paper, Lilien (1982) showed that the dispersion of employment growth across sectors was countercyclical. He interpreted this finding as evidence that sectoral shifts caused the cyclical fluctuations in the unemployment rate. Abraham and Katz (1986) challenged this conclusion by showing that a factor structure in which different sectors loaded differently onto an aggregate factor could generate the same correlation between dispersion and unemployment, even though the driving force was an aggregate shock. In a similar vein, our results show that the well-documented countercyclicality of earnings inequality does not have to stem from the countercyclical variance of idiosyncratic shocks, but rather is due to a factor structure that expands inequality during recessions and contracts during expansions.
Finally, in a different strand of literature, Bloom et al. (2011) fit an AR(1) process to firm-level total factor productivity (TFP) time series and allow a fixed aggregate shock and fixed firm effect. They find that the residual of the AR(1) has a larger cross-sectional dispersion during recessions. While skewness also appears to be more negative, the difference is not statistically significant. In contrast to that paper, we do allow for a factor structure (loading factor on their aggregate shock) and allow the loading factor to vary with observables. Of course, we study individual labor earnings, whereas they focus on firm-level TFP, so the two sets of results are not necessarily inconsistent with each other.
2 The Data
We employ a unique, confidential, and very large panel dataset on earnings histories from the U.S. Social Security Administration records. For our baseline analysis, we draw a 10 percent random sample of U.S. males--covering 1978 to 2010--directly from the Master Earnings File (MEF) of Social Security records.6
2.0.0.1 The Master Earnings File.
The MEF is the main source of earnings data for the Social Security Administration and grows every year with the addition of new earnings information received directly from employers (Form W-2 for wage and salary workers).7 The MEF includes data for every individual in the United States who has a Social Security number. The dataset contains basic demographic characteristics, such as date of birth, sex, race, type of work (farm or non-farm, employment or self-employment), self-employment taxable earnings, and several other variables. Earnings data are uncapped (no top-coding) and include wages and salaries, bonuses, and exercised stock options as reported on the W-2 form (Box 1).8 For more information, see Panis et al. (2000) and Olsen and Hudson (2009). Finally, all nominal variables were converted into real ones using the Personal Consumption Expenditure (PCE) deflator with 2005 taken as the base year.
2.0.0.2 Creating the 10 Percent Sample.
To construct a nationally representative panel of males, we proceed as follows. For 1978, a sample of 10 percent of U.S. males are selected based on a fixed subset of digits of (a transformation of) the Social Security Number (SSN). Because these digits of the SSN are randomly assigned, this procedure easily allows randomization. For each subsequent year, new individuals are added to account for the newly issued SSNs in the United States; those individuals who are deceased are removed (from that year forward). This process yields a representative sample of 10 percent of U.S. males every year.
For a statistic computed using data for (not necessarily consecutive) years
![]() , an individual observation is included if the following three conditions are satisfied for all these years: the individual (i) is between the ages of 25 and 60, (ii)
has annual wage/salary earnings that exceed a time-varying minimum threshold, and (iii) is not self-employed (i.e., has self-employment earnings less than the same minimum threshold). This minimum, denoted
, an individual observation is included if the following three conditions are satisfied for all these years: the individual (i) is between the ages of 25 and 60, (ii)
has annual wage/salary earnings that exceed a time-varying minimum threshold, and (iii) is not self-employed (i.e., has self-employment earnings less than the same minimum threshold). This minimum, denoted
![]() , is equal to one-half of the legal minimum wage times 520 hours (13 weeks at 40 hours per week), which amounts to an annual earnings of approximately $1,300 in 2005. This
condition allows us to focus on workers with a reasonably strong labor market attachment and avoids issues with taking the logarithm of very low earnings levels. It also makes our results more comparable to the income dynamics literature where this condition is standard (see, among others, Abowd and Card (1989), Meghir and Pistaferri (2004), Storesletten et al. (2004), as well as Juhn et al. (1993) and
Autor et al. (2008) on wage inequality). Finally, the MEF contains a small number of extremely high earnings observations each year. To avoid potential problems with outliers, we cap (winsorize) observations above the 99.999th percentile.
, is equal to one-half of the legal minimum wage times 520 hours (13 weeks at 40 hours per week), which amounts to an annual earnings of approximately $1,300 in 2005. This
condition allows us to focus on workers with a reasonably strong labor market attachment and avoids issues with taking the logarithm of very low earnings levels. It also makes our results more comparable to the income dynamics literature where this condition is standard (see, among others, Abowd and Card (1989), Meghir and Pistaferri (2004), Storesletten et al. (2004), as well as Juhn et al. (1993) and
Autor et al. (2008) on wage inequality). Finally, the MEF contains a small number of extremely high earnings observations each year. To avoid potential problems with outliers, we cap (winsorize) observations above the 99.999th percentile.
Figure 2 displays the number of individuals that satisfy these selection criteria, as well as the total number of individuals in each year. The sample starts with about 3.7 million individuals in 1978 and grows to about 5.4 million individuals by the mid-2000s. Notice that the number of individuals in the sample does not follow population growth one-for-one (black line marked with diamonds), because inclusion in the base sample also requires participating in the labor market in a given year (hence the slowdown in sample growth in the 2000s and the fall during the Great Recession).9
Further, Table A.1 in Appendix A reports key summary statistics for our sample. Similarly, Figure A.1 plots the levels of labor earnings that correspond to selected percentiles of the earnings distribution in each year. The lowest earnings that qualifies a male worker in the top 10 percent (e.g., above the 90th percentile) has been steady at approximately $98,000 since year 2000. In 2011, a worker must be making more than $297,000 to be in the top 1 percent. This threshold was highest in 2007 when it reached $318,000.
2.0.0.3 Recessionary vs. Expansionary Episodes.
The start date of a recession is determined as follows. If the National Bureau of Economic Research (NBER) peak of the previous expansion takes place in the first half of a given year, that year is classified as the first year of the new recession. If the peak is in the second half, the recession starts in the subsequent year.10 The ending date of a recession is a bit more open to interpretation for our purposes, because the NBER "troughs" are often not followed by a rapid fall in unemployment rates and a rise in individual wages. This can be seen in Figure 3. For example, whereas the NBER announced the start date of the expansion as March of 1991, the unemployment rate peaked in the summer of 1992. Similarly, while the NBER trough was November 2001, the unemployment rate remained high until mid-2003. With these considerations in mind, we settled on the following dates for the last three recessions: 1991-92, 2001-02, and 2008-10. We opt to treat the 1980-1983 period as a single recession, given the extremely short duration of the intervening expansion, the anemic growth it brought, and the lack of a significant fall in the unemployment rate (Figure 3). Based on this classification, there are three expansions and four recessions during our sample period.
As a complementary approach, in Section 6.3 we study business cycle variation by analyzing the co-movement of the earnings growth distribution with cyclical variables, such as the male unemployment rate, GDP per capita, and S&P500 returns.
3 Earnings Risk over the Business Cycle: First Look
Before delving into the full-blown panel data analysis in the next section, we begin by providing a bird's-eye view of the business cycle patterns in earnings risk. Specifically, we exploit the panel dimension of the MEF dataset to document how the dispersion and skewness of the earnings growth
distribution vary over the business cycle.11![]() 12
12
It will be useful to distinguish between earnings growth over short and long horizons. To this end, in much of the following analysis, we examine 1-year and 5-year earnings growth rates and think of these as roughly corresponding to "transitory" and "persistent" earnings shocks. A more rigorous justification for this interpretation will be provided below.
The left panel of Figure 4 plots the evolution of the log differential between the 90th and 50th percentiles of (
![]() ) distribution (hereafter L90-50), as well as the log differential between the 50th and 10th percentiles (L50-10). The first important observation is that the top and bottom ends
of the shock distributions clearly move in opposite directions over the business cycle. In particular, L50-10 rises strongly during recessions, implying that there is an increased chance of larger downward movements during recessions. In contrast, the top end (L90-50)
dips consistently in every recession, implying a smaller chance of upward movements during recessions. In other words, relative to the median growth rate, the top end compresses, whereas the bottom end expands during recessions. Similarly, the right panel of Figure 4 plots the corresponding graph for persistent (5-year) shocks. The striking co-movement of the L90-50 and L50-10 is clearly seen here (the correlation of the two series is -0.67), even more strongly than in the transitory shocks.
) distribution (hereafter L90-50), as well as the log differential between the 50th and 10th percentiles (L50-10). The first important observation is that the top and bottom ends
of the shock distributions clearly move in opposite directions over the business cycle. In particular, L50-10 rises strongly during recessions, implying that there is an increased chance of larger downward movements during recessions. In contrast, the top end (L90-50)
dips consistently in every recession, implying a smaller chance of upward movements during recessions. In other words, relative to the median growth rate, the top end compresses, whereas the bottom end expands during recessions. Similarly, the right panel of Figure 4 plots the corresponding graph for persistent (5-year) shocks. The striking co-movement of the L90-50 and L50-10 is clearly seen here (the correlation of the two series is -0.67), even more strongly than in the transitory shocks.
A couple of remarks are in order. First, the fact that L90-50 and L50-10 move in opposite directions implies that L90-10 (which is a measure of overall dispersion of shocks) changes little over the business cycle, because the fall in L90-50 (partially) cancels out the rise in L50-10. An alternative measure of shock dispersion--the standard deviation--is plotted in Figure 5 for both persistent and transitory shocks, which shows that dispersion does not increase much during recessions (notice the very small variation on the y-axis). Perhaps the only exception is the 2001-02 recession, during which time the transitory shock variance increases. In the coming sections, this point will be examined further and will be made more rigorously. This observation will provide one of the key conclusions of this paper, given how clearly it contradicts the commonly held belief that idiosyncratic earnings shock variances are strongly countercyclical (e.g., Storesletten et al. (2004)).
3.0.0.0.1 Trends in Volatility: A Brief Digression.
Second, looking at transitory shocks, L90-50 displays a clear downward trend during this time period. A fitted linear trend implies a drop of 11 log points from 1979 to 2010. The interpretation is that the likelihood of large upward movements has become smaller during this period. We see a similar, but less pronounced, trend in the L50-10, which indicates that the likelihood of large falls has also become somewhat smaller. Overall though, both the L90-10 and the standard deviation of earnings growth (Figure 5) display a clear downward trend. Notice that this conclusion is in contrast to the conventional wisdom since the 1990s that earnings shock variances have generally risen since the 1980s (Moffitt and Gottschalk (1995)). However, it is consistent with a number of recent papers that use administrative data (e.g., Sabelhaus and Song (2010) and others).13 In this paper, we will not dwell much on this trend, except when it is relevant for our analysis of the cyclical changes in earnings risk.
We now return to the discussion of cyclical facts. The finding described above--that the top end of the shock distribution compresses during recessions, while at the same time the bottom end expands--suggests that one important cyclical change could be found in the skewness of shocks. Indeed, as seen in Figure 6, both the 1- and 5-year earnings growth distributions become more left-skewed (negative skewness increases) during recessions and the magnitude of change is large. Below, we return to this point and sharpen it by conditioning earnings changes on narrowly defined groups of individuals.
4 Panel Analysis
The analysis so far provided a general look at how earnings shocks vary over the business cycle. However, one can imagine that the properties of earnings shocks vary systematically with individual characteristics and heterogeneity: for example, young and old workers can face different earnings shock distributions than prime-age workers with more stable jobs. Similarly, workers at different parts of the earnings distribution could experience different types of earnings risks. The large sample size allows us to account for such variation without making any strong parametric assumptions.
4.1 A Framework for Empirical Analysis
Although in this paper, we will not commit to any particular parametric specification for the income process, it is useful to outline a general framework to fix ideas and define some notation. To this end, let
![]() denote individual
denote individual ![]() 's log labor earnings in year
's log labor earnings in year ![]() , and let
, and let
![]() denote a vector of (possibly time-varying) individual characteristics that will be used to group individuals as of period
denote a vector of (possibly time-varying) individual characteristics that will be used to group individuals as of period ![]() Consider the following representation:
Consider the following representation:
where
Now define log labor earnings net of systematic lifecycle effects:
![]() To study between- and within-group variation over the business cycle, we difference earnings in equation (1) for periods
To study between- and within-group variation over the business cycle, we difference earnings in equation (1) for periods ![]() and
and ![]() , and modify it to
introduce a factor structure:
, and modify it to
introduce a factor structure:
The specification in (2) allows for two different types of business cycle effects. First, the factor structure--captured by the introduction of the function ![]() --allows the conditional mean of earnings growth to vary systematically with the business cycle across different groups of workers. Second, both types of shocks have variances that can potentially vary with the business cycle in a way that is also
different across groups of workers (as captured by
--allows the conditional mean of earnings growth to vary systematically with the business cycle across different groups of workers. Second, both types of shocks have variances that can potentially vary with the business cycle in a way that is also
different across groups of workers (as captured by ![]() and
and ![]() ). In our implementation,
we will consider a vector
). In our implementation,
we will consider a vector
![]() that includes three time-varying observable individual characteristics: age, past average earnings, and past earnings growth rate as of period
that includes three time-varying observable individual characteristics: age, past average earnings, and past earnings growth rate as of period ![]() . An assumption that will be maintained in the analysis is that these characteristics vary slowly with time, so that
. An assumption that will be maintained in the analysis is that these characteristics vary slowly with time, so that
![]() for small
for small ![]() .
.
This formulation allows the effects of aggregate shocks to be transmitted differently to groups that differ in their labor market characteristics at the time a recession hits or an expansion gets under way. Of course, even individuals within these finely defined groups will likely experience different earnings growth rates during recessions and expansions, which will be captured by the permanent and transitory shocks above. These capture the within-group variation in shocks, and we will also quantify the cyclical nature of such shocks. In the coming sections, we shall use this framework to interpret our findings.
4.2 Grouping Individuals into
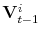
Let ![]() denote the generic time period that marks the beginning of a business cycle episode. We now describe how we group individuals based on their characteristics at time
denote the generic time period that marks the beginning of a business cycle episode. We now describe how we group individuals based on their characteristics at time ![]() . Each individual is identified by three characteristics that can be used to form groups. Not every characteristic will be used in the formation of groups in every experiment.14
. Each individual is identified by three characteristics that can be used to form groups. Not every characteristic will be used in the formation of groups in every experiment.14
4.2.0.1 1. Age.
Individuals are divided into seven age groups. The first six groups are five-year wide (25-29, 30-34,..., 50-54) and the last one covers six years: 55-60.
4.2.0.2 2. Pre-episode Average Earnings.
A second dimension individuals differ along is their average earnings (and especially where they rank relative to others). For a given year ![]() , we consider all individuals who were in the
base sample (i) in year
, we consider all individuals who were in the
base sample (i) in year ![]() and (ii) in at least two more years between
and (ii) in at least two more years between ![]() to
to
![]() . For example, an individual who is 23 years old in
. For example, an individual who is 23 years old in ![]() (and hence is not in the
base sample that year) will be included in the final sample for year
(and hence is not in the
base sample that year) will be included in the final sample for year ![]() if he has earnings exceeding
if he has earnings exceeding ![]() in every year between
in every year between ![]() and
and ![]() .
.
Furthermore, as noted above, we are interested in average earnings to see how a worker ranks relative to his peers. But even within the narrow age groups defined above, age variation can skew the rankings in favor of older workers. For example, between ages 25 and 29, average earnings grows by 35.4 percent in our sample, and between 30 and 34, it grows by 18.3 percent. So, unless this lifecycle component is accounted for, a 29-year-old worker in the first age group would appear in a higher earnings percentile than the same worker when he was 25. This variation would confound age and earnings differences.
To correct for this, we proceed as follows. First, using all earnings observations from our base sample from 1978 to 2010, we run a pooled regression of log raw earnings (
![]() ) on age and cohort dummies (without a constant) to characterize the age profile of log earnings. We then scale the age dummies (denoted with
) on age and cohort dummies (without a constant) to characterize the age profile of log earnings. We then scale the age dummies (denoted with ![]() ) so as to match the average log earnings of 25-year-old individuals used in the regression. Using these age dummies, we compute the average earnings between years
) so as to match the average log earnings of 25-year-old individuals used in the regression. Using these age dummies, we compute the average earnings between years ![]() and
and ![]() for the average worker of age
for the average worker of age ![]() in year
in year ![]() . Then for a given worker
. Then for a given worker ![]() of age
of age ![]() in year
in year ![]() , we first average his earnings from
, we first average his earnings from
![]() to
to ![]() (and set earnings below
(and set earnings below
![]() equal to the threshold) and then normalize it by the population average computed using the age dummies. This 5-year average (normalized) earnings is denoted with
equal to the threshold) and then normalize it by the population average computed using the age dummies. This 5-year average (normalized) earnings is denoted with
![]() .15
.15
4.2.0.3 3. Pre-episode Earnings Growth.
A third dimension is (recent) earnings growth. This could be an indicator of individuals whose careers are on the rise, as opposed to being stagnant, even after controlling for average earnings as done above. For this purpose, we compute
![]() where
where ![]() is the
earliest year after
is the
earliest year after ![]() in which the individual has earnings above the threshold.16
in which the individual has earnings above the threshold.16
5 Within-Group (Idiosyncratic) Shocks
One focus of this analysis will be on simple measures of earnings shock volatility, conditional on individual characteristics. That is, fix a group of workers that have the same vector
![]() at time
at time ![]() . Computing the within-group variance, we get
. Computing the within-group variance, we get
| var |
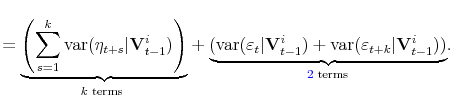
|
5.0.0.1 Transitory vs. Persistent Earnings Changes.
Two points can be observed from this formula. First, as we consider longer time differences (larger ![]() ), the variance reflects more of the permanent shocks, as seen by the addition of the
), the variance reflects more of the permanent shocks, as seen by the addition of the
![]() innovation variances and given that there are always two variances from the transitory component regardless of
innovation variances and given that there are always two variances from the transitory component regardless of ![]() For example, computing this variance over a five-year period that spans a recession (say, 1979-84 or 1989-94) would allow us to measure how the variance of permanent shocks changes during recessions. It will also contain transitory variances, but for two years that
are not part of a recession (1979 and 1984, for example). Second, looking at short-term variance, say,
For example, computing this variance over a five-year period that spans a recession (say, 1979-84 or 1989-94) would allow us to measure how the variance of permanent shocks changes during recessions. It will also contain transitory variances, but for two years that
are not part of a recession (1979 and 1984, for example). Second, looking at short-term variance, say, ![]() yields a formula that contains only one permanent shock variance and two transitory
shock variances. So, as we increase the length of the period over which the variance is computed, the statistic shifts from being informative about transitory shock variances toward more persistent variation.
yields a formula that contains only one permanent shock variance and two transitory
shock variances. So, as we increase the length of the period over which the variance is computed, the statistic shifts from being informative about transitory shock variances toward more persistent variation.
In the analysis below, we consider ![]() and
and ![]() The choice of
The choice of ![]() --as opposed to a longer or a shorter period--is motivated by the fact that recessions last 2 to 3 years, so that by year
--as opposed to a longer or a shorter period--is motivated by the fact that recessions last 2 to 3 years, so that by year ![]() the unemployment rate will have declined from its peak and will, in most cases, be close to the pre-recession level (in year
the unemployment rate will have declined from its peak and will, in most cases, be close to the pre-recession level (in year ![]() ). This feature will
facilitate the interpretation of our findings, as we discuss later. Below, we compute various group-specific statistics, including variances, to examine the nature of such variation.
). This feature will
facilitate the interpretation of our findings, as we discuss later. Below, we compute various group-specific statistics, including variances, to examine the nature of such variation.
|
We begin with the cyclicality of idiosyncratic shocks, as measured by within-group variation in earnings growth rates. An important question is whether or not idiosyncratic shocks have countercyclical variances. To answer this question, we make use of the following graphical construct. In its
most general form, we plot the quantiles of
![]() for a given age group on the x-axis against the entire distribution of future earnings growth rates for that
quantile on the y-axis:
for a given age group on the x-axis against the entire distribution of future earnings growth rates for that
quantile on the y-axis:
![]() .
.
|
Figure 7 is the first use of this graphical construct and contains a lot of information that will be referred to in the rest of this section. The top panel displays P90, P50 (median), and P10 of the distribution of long-run changes,
![]() , (on the y-axis) for each percentile of
, (on the y-axis) for each percentile of
![]() (on the x-axis). To compare recessions and expansions, we averaged each one of these percentiles separately over the four recessions (lines
marked with "circles") and three expansions (solid blue lines) during our sample period.17 Similarly, because these figures look similar across age
groups, to save space we also averaged across the age groups.
(on the x-axis). To compare recessions and expansions, we averaged each one of these percentiles separately over the four recessions (lines
marked with "circles") and three expansions (solid blue lines) during our sample period.17 Similarly, because these figures look similar across age
groups, to save space we also averaged across the age groups.
First, notice the variation in these percentiles as we move to the right along the x-axis. Interestingly, the following pattern holds in both recessions and expansions: At any point in time, individuals with the lowest levels of past average earnings face the largest dispersion of earnings
shocks (
![]() ) looking forward. That is, L90-10 is widest for these individuals and falls in a very smooth fashion moving to the right. Indeed, workers who are between the 70th and 90th
percentiles of the
) looking forward. That is, L90-10 is widest for these individuals and falls in a very smooth fashion moving to the right. Indeed, workers who are between the 70th and 90th
percentiles of the
![]() distribution face the smallest dispersion of shocks looking ahead. As we continue moving to the right (into the top 10 percent), the shock distribution widens again.
Notice that the P10 and P90 of the
distribution face the smallest dispersion of shocks looking ahead. As we continue moving to the right (into the top 10 percent), the shock distribution widens again.
Notice that the P10 and P90 of the
![]() distribution look like the mirror image of each other relative to the median, so the variation in L90-10 as we move to the right is driven by similar variations in P90
and P10 individually.
distribution look like the mirror image of each other relative to the median, so the variation in L90-10 as we move to the right is driven by similar variations in P90
and P10 individually.
Turning to the bottom panel, the same graph is plotted now for
![]() (transitory shocks).18 Precisely,
the same qualitative features are seen here, with low- and high-income individuals facing a wider dispersion of persistent shocks than those in the "safer" zones--between the 70th and 90th percentiles. Of course, the scales of both graphs are different: the overall dispersion of persistent shocks
is much larger than that of transitory shocks, which is to be expected. To summarize, both graphs reveal very strong and systematic variation in the dispersion of persistent and transitory earnings shocks across individuals with different past earnings levels.19
(transitory shocks).18 Precisely,
the same qualitative features are seen here, with low- and high-income individuals facing a wider dispersion of persistent shocks than those in the "safer" zones--between the 70th and 90th percentiles. Of course, the scales of both graphs are different: the overall dispersion of persistent shocks
is much larger than that of transitory shocks, which is to be expected. To summarize, both graphs reveal very strong and systematic variation in the dispersion of persistent and transitory earnings shocks across individuals with different past earnings levels.19
Now we turn to two key questions of interest. First, what happens to idiosyncratic shocks in recessions? For example, are shock variances countercyclical? And second, how does any potential change in the distribution of idiosyncratic shocks vary across earnings levels (i.e., the cross-partial derivative)? In other words, do we see the shock distribution of individuals in different earnings levels being affected differently by recessions?
5.0.0.2 Are Shock Variances Countercyclical?
The existing literature has largely focused on the cyclicality of persistent shocks, so this is where we also start (top panel of Figure 7). First, note that both P90 and P10 shift downward by similar amounts from expansion to recession. (As can be anticipated
from this, the L90-10 gap changes by very little over the business cycle, as we shall see momentarily.) Furthermore, following the same steps as the one used to construct these graphs, one can also compute the standard deviation of
![]() conditional on
conditional on
![]() during recessions and expansions, which is plotted in the
left panel of Figure 8. The two graphs (for expansions and recessions) virtually overlap, over the entire range of pre-episode earnings levels. For transitory shocks (bottom panel), there is more of a gap, but the two lines are
still quite close to each other.
during recessions and expansions, which is plotted in the
left panel of Figure 8. The two graphs (for expansions and recessions) virtually overlap, over the entire range of pre-episode earnings levels. For transitory shocks (bottom panel), there is more of a gap, but the two lines are
still quite close to each other.
To make the measurement of countercyclicality more precise, Figure 9 plots the ratios of (i) standard deviations and (ii) L90-10s for recessions over expansions. For persistent shocks (lines marked with circles and squares), both the standard deviation and L90-10 measures are only about 2 percent higher in recessions than in expansions. In other words, while we find some evidence of countercyclicality, the magnitude is minuscule. For comparison, Storesletten et al. (2004) used indirect methods to estimate a standard deviation of 0.13 for innovations into a persistent AR(1) process during expansions and 0.21 for recessions. The ratio is 1.75 (marked on the figure for comparison) compared with the 1.02 we find in this paper. The figure also plots the same two ratios (L90-10 and standard deviations) for transitory shocks. Here we see a bit more movement relative to persistent shocks: the standard deviation is higher by about 4 percent (averaged across the x-axis) and L90-10 is higher by about 6 percent. These findings suggest that to the extent that recessions involve a larger dispersion of shocks, these are to be found in short-term shocks without much long-term effects. Having said that, these numbers are still very small compared with the values typically used in the literature.
A second question that was raised above was whether recessions affect the distribution of shocks differently in different parts of the earnings distribution. It is probably evident by now that the answer is, perhaps surprisingly, "no." This is seen in the three figures just discussed, but is most apparent in Figure 9, where the ratios are quite flat, especially for persistent shocks. Therefore, we conclude that when it comes to the variance of persistent shocks, different earnings groups are affected similarly by business cycle fluctuations.
5.1 Countercyclical (Left-)Skewness: A Tale of Two Tails
The obvious question now is: Do recessions have any effect on earnings shocks? The answer is yes, which could already be anticipated from Figure 7, by noting that while P90 and P10 move down together during recessions, P50 (the median
of the shock distribution) remains extremely stable and moves down by only a little. This has important implications: L90-50 gets compressed during recessions, whereas L50-10 expands. In other words, for every earnings level
![]() , when individuals look ahead during a recession, they see a much smaller chance of upward movements (relative to an expansion), but a much higher chance of large
downward movements. In fact, this result is not specific to using P90 or P10, but is pervasive across the entire distribution of future earnings growth rates. This can be seen in Figure 10, which plots the change in selected percentiles above (and including) the median
from an expansion to a recession (top panel). The bottom panel shows selected percentiles below the median. Starting from the top, and focusing on the middle part of the x-axis, we see that P99 falls by about 30 log points from an expansion to a recession, whereas P95 falls by 20, P90 falls by 15,
P75 falls by 6, and P50 falls by 5 log points, respectively. As a result, the entire upper half of the shock distribution gets squeezed toward the median. In other words, the half of the population who experience earnings change above the median now experience ever smaller upward moves during
recessions. Turning to the bottom panel, we see the opposite pattern: P50 falls by 5 log points, whereas P25 falls by 9, and P10 falls by 20 log points, respectively. Consequently, the bottom half of the shock distribution now expands, with "bad luck" meaning even "worse luck" during
recessions.
, when individuals look ahead during a recession, they see a much smaller chance of upward movements (relative to an expansion), but a much higher chance of large
downward movements. In fact, this result is not specific to using P90 or P10, but is pervasive across the entire distribution of future earnings growth rates. This can be seen in Figure 10, which plots the change in selected percentiles above (and including) the median
from an expansion to a recession (top panel). The bottom panel shows selected percentiles below the median. Starting from the top, and focusing on the middle part of the x-axis, we see that P99 falls by about 30 log points from an expansion to a recession, whereas P95 falls by 20, P90 falls by 15,
P75 falls by 6, and P50 falls by 5 log points, respectively. As a result, the entire upper half of the shock distribution gets squeezed toward the median. In other words, the half of the population who experience earnings change above the median now experience ever smaller upward moves during
recessions. Turning to the bottom panel, we see the opposite pattern: P50 falls by 5 log points, whereas P25 falls by 9, and P10 falls by 20 log points, respectively. Consequently, the bottom half of the shock distribution now expands, with "bad luck" meaning even "worse luck" during
recessions.
From this analysis, a couple of conclusions can be drawn. First, idiosyncratic risk is countercyclical. However, this does not happen by a widening of the entire distribution (e.g., variance rising), but rather a shift toward a more left-skewed shock distribution. Although this is evident from the top end compressing and bottom end expanding, one can compute measures of skewness to document this. With higher order moments, one has to be careful about extreme observations. These are not likely to be outliers as with survey data, but even if they are genuine observations, we may want to be careful that a few observations do not affect the overall skewness measure. For this purpose, we use "Kelley's measure" of skewness, which relies on the quantiles of the distribution and is robust to extreme observations (Figure 11 ). It is also very straightforward to interpret, as we shall see in a moment. It is computed as the relative difference between the upper and lower tail inequalities: (L90-50 - L50-10)/L90-10. A negative number indicates that the lower tail is larger than the upper tail, and vice versa for a positive number.
Turning to Figure 11, first, notice that individuals in higher earnings percentiles face a more negatively skewed shock distribution, consistent with the idea that the higher an individual's earnings is, the more it has room to fall.
Second, and more importantly, this negative skewness increases during recessions for both transitory and persistent shocks. For example, for individuals at the median of the
![]() distribution, Kelley's measure for persistent shocks averages -0.14 during expansions. This number has a simple interpretation. It says that the dispersion of shocks above
P50 accounts for 43 percent of overall L90-10 dispersion. Similarly, dispersion below P50 accounts for the remaining 57 percent (hence
distribution, Kelley's measure for persistent shocks averages -0.14 during expansions. This number has a simple interpretation. It says that the dispersion of shocks above
P50 accounts for 43 percent of overall L90-10 dispersion. Similarly, dispersion below P50 accounts for the remaining 57 percent (hence
![]() ) of L90-10. In recessions, however, this figure falls to -0.30, indicating that L90-50 accounts for 35 percent of L90-10 and the remaining 65 percent is due to
L50-10. This is a substantial shift in the shape of the persistent shock distribution over the business cycle. The change in the skewness of transitory shocks is similar, if somewhat less pronounced. It goes from -0.14 down to -0.25 at the median. As seen in Figure 11, the increased left-skewness during recessions is pervasive--it takes place across the entire earnings distribution with similar magnitudes (with the exception of very low-income individuals).
) of L90-10. In recessions, however, this figure falls to -0.30, indicating that L90-50 accounts for 35 percent of L90-10 and the remaining 65 percent is due to
L50-10. This is a substantial shift in the shape of the persistent shock distribution over the business cycle. The change in the skewness of transitory shocks is similar, if somewhat less pronounced. It goes from -0.14 down to -0.25 at the median. As seen in Figure 11, the increased left-skewness during recessions is pervasive--it takes place across the entire earnings distribution with similar magnitudes (with the exception of very low-income individuals).
|
To understand how different this conclusion is from a simple countercyclical variance formulation, recall Figure 1, which plots the densities of two Normal random variables: one with zero mean and a standard deviation of 0.13 (expansion) and a second one with a mean of -0.03 and a standard deviation of 0.21 (recession; both numbers from Storesletten et al. (2004)). As seen here, the substantial increase in variance and small fall in the mean imply that many individuals will receive larger positive shocks in recessions than in expansions under this formulation. For comparison, the left panel of Figure 12 plots the empirical densities of earnings growth from the U.S. data, comparing the 1995-96 period to the worst year of the Great Recession (2008-09). To highlight how the density changes, the right panel plots the difference between the two densities. As seen here, the probability mass on the right side shifts from large positive shocks to more modest ones; on the left side, it shifts from small negative shocks to even larger negative ones. Thus, recessions are times when it becomes less likely for anybody to experience large upward earnings changes, whereas the risk of falling off the income ladder becomes significantly higher.
Interestingly, in one of the earliest papers on cyclical changes in earnings risk, Mankiw (1986) postulated that in recessions, a fraction ![]() of individuals
all draw the same negative shock, which adds up to
of individuals
all draw the same negative shock, which adds up to ![]() . So, ex ante, each person views a recession as a state where, with probability
. So, ex ante, each person views a recession as a state where, with probability ![]() , their individual earnings will drop by
, their individual earnings will drop by
![]() . Thus, negative shocks are concentrated among a subset of individuals in recessions. This structure induces a left-skewness of the same sort discovered in our analysis here,
unlike the countercyclical variance structure proposed by Constantinides and Duffie (1996) and others.20
. Thus, negative shocks are concentrated among a subset of individuals in recessions. This structure induces a left-skewness of the same sort discovered in our analysis here,
unlike the countercyclical variance structure proposed by Constantinides and Duffie (1996) and others.20
5.1.0.1 An Alternative Parametric Approach.
The approach in this paper has been non-parametric, which was made feasible with the very large sample size. However, an alternative approach that has been used in the literature relies on fitting a separate AR(1) process to each individual's time series of earnings (see, e.g., Bloom et al. (2011)). We have implemented different versions of this method as well. In the most general case, we first ran the following regression:
to account for a factor structure (first term; where
5.2 What Role Does Unemployment Play?
How much of the countercyclicality of left-skewness is due to the fact that unemployment rises in recessions, so more individuals experience large negative earnings changes, because they are part-year unemployed? In this section, we address this question.
Recall that the MEF dataset does not contain information on labor hours or unemployment. However, providing an upper bound on the potential effects of unemployment is still possible. To begin with, notice that unemployment (or non-employment) can affect our results through two separate channels.
First, workers that are full-year non-employed are excluded from the sample in that year. This creates a truncation at the bottom end of the earnings growth distribution, whose severity varies over the business cycle. Second, many individuals who are unemployed part of the year are still included
in our sample as long as their full-year earnings remains above
![]() Incidentally, both of these assumptions are precisely the same ones made in the bulk of existing literature on income risk. But it is useful to discuss whether and, if so, how
they might be affecting our results, especially the findings on skewness.
Incidentally, both of these assumptions are precisely the same ones made in the bulk of existing literature on income risk. But it is useful to discuss whether and, if so, how
they might be affecting our results, especially the findings on skewness.
5.2.0.1 The Effect of Part-Year Unemployment.
First, a key observation that repeatedly came up in the previous discussion is that the countercyclicality of left-skewness is due to equal parts of (i) the compression of positive earnings growth changes toward the median and (ii) the expansion of negative earnings growth rates toward the bottom end (clearly seen in figures 4, 7, 10, and 12). The compression at the top is
unlikely to be related to unemployment. So even if the bottom half were to remain unchanged, skewness would be more negative during recessions due to the compression at the top alone.21
| CPS data Year: | CPS data x>0 (wks) | CPS data x>13 | CPS data x>26 |
| 1979 | 10.5 | 4.4 | 1.5 |
| 1984 | 11.4 | 6.3 | 2.8 |
| 1989 | 10.0 | 4.7 | 1.8 |
| 1994 | 9.5 | 5.2 | 2.3 |
| 1999 | 6.0 | 3.0 | 1.1 |
| 2004 | 6.5 | 3.6 | 1.4 |
| 2005 | 6.7 | 3.6 | 1.4 |
| 2010 | 10.4 | 6.6 | 3.2 |
| avg. |
8.3 | 3.9 | 1.5 |
| avg. |
9.4 | 5.4 | 2.4 |
| SSA data Period: | SSA data
|
SSA data
|
| 1979-83 | 5.1 | 4.4 |
| 1983-90 | 4.1 | 3.8 |
| 1990-92 | 3.8 | 2.7 |
| 1992-00 | 3.1 | 2.8 |
| 2000-02 | 3.7 | 2.3 |
| 2002-07 | 3.2 | 2.7 |
| 2007-10 | 4.5 | 2.3 |
| Expansion | 3.5 | 3.1 |
| Recession | 4.3 | 2.9 |
Second, the countercyclicality of left-skewness is very apparent in 5-year earnings changes. Because the duration of recessions is less than five years, (the incidence of) unemployment is only slightly higher in ![]() than in
than in ![]() . For example, using data from the Current Population Survey (Integrated Public Use Microdata Series--IPUMS), we compute the fraction of 35-54
year-old males that experiences an unemployment spell longer than
. For example, using data from the Current Population Survey (Integrated Public Use Microdata Series--IPUMS), we compute the fraction of 35-54
year-old males that experiences an unemployment spell longer than ![]() weeks in a given year, for
weeks in a given year, for ![]() and 26 weeks. The left panel of Table I reports the results for key years in our analysis.
and 26 weeks. The left panel of Table I reports the results for key years in our analysis.
Consider spells longer than 13 weeks (third column). Only 5.4 percent of prime-age males are in this group in year ![]() (averaging over 1984, 1994, 2004, and 2010). Now let us assume that
(i) none of these individuals spent any time in unemployment in year
(averaging over 1984, 1994, 2004, and 2010). Now let us assume that
(i) none of these individuals spent any time in unemployment in year ![]() and (ii) their actual wages and hours remained the same in
and (ii) their actual wages and hours remained the same in ![]() and
and ![]() while they were employed. Then, for these individuals unemployment reduces their annual earnings by at least 25 log points between
while they were employed. Then, for these individuals unemployment reduces their annual earnings by at least 25 log points between
![]() and
and ![]() . So this would appear as a negative earnings shock of 25+ log points.
Similarly, the average incidence in year
. So this would appear as a negative earnings shock of 25+ log points.
Similarly, the average incidence in year ![]() is 3.9 percent, so by the same computation, these individuals will appear as having received a positive shock of 25+ log points between
is 3.9 percent, so by the same computation, these individuals will appear as having received a positive shock of 25+ log points between ![]() and
and ![]() So the net effect on skewness depends on the gap:
So the net effect on skewness depends on the gap:
![]() percent of individuals who get more negative shocks than positive in year
percent of individuals who get more negative shocks than positive in year ![]() . If we assume for the moment that these individuals are evenly spread across the
. If we assume for the moment that these individuals are evenly spread across the
![]() distribution, it would amount to a 1.5 percent net change of the sample within each quantile. This is a very small number considering that the entire bottom half of the
shock distribution is expanding during recessions (and, of course, the entire upper end is compressing). The same computation can be repeated for
distribution, it would amount to a 1.5 percent net change of the sample within each quantile. This is a very small number considering that the entire bottom half of the
shock distribution is expanding during recessions (and, of course, the entire upper end is compressing). The same computation can be repeated for ![]() or
or ![]() weeks, with very similar results.22
weeks, with very similar results.22
As an alternative way to investigate the sensitivity of our results, we repeat the computation of skewness, but this time using
![]() and 2000 and excluding the Great Recession. With this timing, year
and 2000 and excluding the Great Recession. With this timing, year
![]() is well into the expansion, so the incidence of unemployment of 13 weeks or longer is only 0.4 percent higher in
is well into the expansion, so the incidence of unemployment of 13 weeks or longer is only 0.4 percent higher in ![]() compared with
compared with ![]() Figure 11 (line marked with stars) plots Kelley's skewness averaged over these
three recessions. Even with the Great Recession excluded and unemployment almost unchanged, skewness becomes significantly more negative during these three recessions.
Figure 11 (line marked with stars) plots Kelley's skewness averaged over these
three recessions. Even with the Great Recession excluded and unemployment almost unchanged, skewness becomes significantly more negative during these three recessions.
Overall, this analysis suggests that the direct effect of unemployment is likely to be small for the results on skewness.23 The cyclical changes in unemployment for prime-age males is simply too small to account for the countercyclicality of skewness, which is observed across the entire range of past earnings levels and earnings growth rates.
5.2.0.2 Excluding Zeros (Full-Year Non-employed).
A second and separate issue relates to our exclusion of full-year non-employed individuals. If anything, this assumption is truncating the actual downside risk in recessions and is understating the countercyclicality of skewness. This can be seen as follows. Using our sample, we compute the
fraction of individuals that are in the sample in year ![]() but not in
but not in ![]() for every
year of the sample. Then for each business cycle episode, we report the average figure in the right panel of Table I. Not surprisingly, we are dropping more individuals from the sample in each recession (given that the likelihood of full-year
non-employment rises). On average we are dropping 4.3 percent of individuals from our sample in year
for every
year of the sample. Then for each business cycle episode, we report the average figure in the right panel of Table I. Not surprisingly, we are dropping more individuals from the sample in each recession (given that the likelihood of full-year
non-employment rises). On average we are dropping 4.3 percent of individuals from our sample in year ![]() during recessions and 3.5 percent during expansions. If these excluded individuals
were included (for example, by assigning them a nominal earnings level, say, $100 in that year), this would register as a large earnings drop in recessions and increase the left-skewness in recessions. At the same time, because the change over the business cycle is
small, the effect would also be small.
during recessions and 3.5 percent during expansions. If these excluded individuals
were included (for example, by assigning them a nominal earnings level, say, $100 in that year), this would register as a large earnings drop in recessions and increase the left-skewness in recessions. At the same time, because the change over the business cycle is
small, the effect would also be small.
6 Between-Group (Systematic) Business Cycle Risk
We now turn to the factor structure, or between-group, component of earnings risk. The goal here is to understand the extent to which earnings growth during a business cycle episode can be predicted by available observable characteristics prior to the episode.
It is useful to begin with equation (2) to compute the mean log earnings change conditional on characteristics as of ![]() :
:
Taking the means within each group eliminates both permanent and transitory shocks (since they average zero by assumption), yielding
Equation (5) provides a simple expression for between-group variation in earnings growth. Between any two periods ![]() and
and ![]() , each group has a different loading factor
, each group has a different loading factor
![]() on the aggregate shock
on the aggregate shock
![]() . The key object of interest is
. The key object of interest is ![]() , whose shape will
tell us about the factor structure of earnings changes over the business cycle.24
, whose shape will
tell us about the factor structure of earnings changes over the business cycle.24
6.0.0.1 Caution: Mean Reversion Ahead.
The derivation of equation (5) relies on the assumption that earnings changes do not exhibit mean reversion. However, if ![]() is in fact a
mean-reverting process and
is in fact a
mean-reverting process and
![]() is one of the conditioning variables,
is one of the conditioning variables, ![]() will be a
decreasing function of
will be a
decreasing function of
![]() in the absence of any factor structure, simply because of mean reversion.25 So if the estimated
in the absence of any factor structure, simply because of mean reversion.25 So if the estimated ![]() shows any sign of upward slope (overcoming this potential downward bias), this would be a strong
indication of a factor structure.
shows any sign of upward slope (overcoming this potential downward bias), this would be a strong
indication of a factor structure.
6.0.0.2 An Alternative Measure of Factor Structure: Incorporating Zeros.
One drawback of the ![]() measure is that the left-hand side of equation (5) can only be computed using individuals whose earnings are positive in
year
measure is that the left-hand side of equation (5) can only be computed using individuals whose earnings are positive in
year ![]() and
and ![]() (so that log earnings is finite). As noted above, the fraction of
individuals that are excluded varies over the business cycle. Although the average number of such individuals is not very large, it varies systematically with
(so that log earnings is finite). As noted above, the fraction of
individuals that are excluded varies over the business cycle. Although the average number of such individuals is not very large, it varies systematically with
![]() , which could be important to take into account. Thus, we also construct a modified measure for the left-hand side of (5): We use
all individuals that belong to
, which could be important to take into account. Thus, we also construct a modified measure for the left-hand side of (5): We use
all individuals that belong to
![]() to compute the average earnings in
to compute the average earnings in ![]() and in
and in ![]() and then take the logs of these averages to compute
and then take the logs of these averages to compute
This measure now includes both the intensive margin and the extensive margin of earnings changes between two periods.26 It will be our preferred measure
in this section. In Appendix B, we also compare it with the results with ![]() and discuss the differences between the two measures more fully.
and discuss the differences between the two measures more fully.
6.1 Variation Between
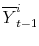 Groups
Groups
We estimate
![]() for each recession and expansion and separately for each of the six age groups defined above. As we show in Appendix B, the four age groups between ages 35 and 54 behave very similarly to each other over the business cycle. Motivated by this finding, from this point on we combine these individuals into one group and refer to them as "prime-age males." We also combine the
first two age groups into one and refer to them as "young workers" (ages 25 to 34). For brevity, we focus on prime-age males in this paper and present the results for young workers in Appendix B.
for each recession and expansion and separately for each of the six age groups defined above. As we show in Appendix B, the four age groups between ages 35 and 54 behave very similarly to each other over the business cycle. Motivated by this finding, from this point on we combine these individuals into one group and refer to them as "prime-age males." We also combine the
first two age groups into one and refer to them as "young workers" (ages 25 to 34). For brevity, we focus on prime-age males in this paper and present the results for young workers in Appendix B.
6.1.1 Recessions
Figure 13 plots the ![]() function for prime-age males for the four recessions during our sample period. For the Great Recession (black line
with squares),
function for prime-age males for the four recessions during our sample period. For the Great Recession (black line
with squares), ![]() is upward sloping in an almost linear fashion and rises by about 17 log points between the 10th and 90th percentiles. So, workers with pre-recession average earnings in
the 10th percentile saw their earnings decline by about 25 log points during the recession, compared with a decline of only 8 log points for workers in the 90th percentile.27 Clearly, this factor structure leads to a significant widening of earnings inequality over much of the distribution. However, this good fortune of high-income individuals does not extend to the very top:
is upward sloping in an almost linear fashion and rises by about 17 log points between the 10th and 90th percentiles. So, workers with pre-recession average earnings in
the 10th percentile saw their earnings decline by about 25 log points during the recession, compared with a decline of only 8 log points for workers in the 90th percentile.27 Clearly, this factor structure leads to a significant widening of earnings inequality over much of the distribution. However, this good fortune of high-income individuals does not extend to the very top: ![]() first flattens beyond the 90th percentile and then for the top 1 percent, it actually falls very steeply. Specifically, those in the top 1 percent experienced an average loss of 27 log points compared with 12.5 log points for those in the second
highest percentile. One conclusion we draw is that individuals near the 90th percentile of the average earnings distribution (about $100,000 per year) as of 2006 have suffered the smallest loss of any earnings group.
first flattens beyond the 90th percentile and then for the top 1 percent, it actually falls very steeply. Specifically, those in the top 1 percent experienced an average loss of 27 log points compared with 12.5 log points for those in the second
highest percentile. One conclusion we draw is that individuals near the 90th percentile of the average earnings distribution (about $100,000 per year) as of 2006 have suffered the smallest loss of any earnings group.
Turning to the other major recession in our sample--the 1979-83 episode--![]() looks very similar to the Great Recession period between the 10th percentile and about the 95th percentile,
with the same linear shape and a slightly smaller slope. However, for individuals with very low average earnings (below the 10th percentile), the graph is downward sloping, indicating some mean reversion during the recession.28 Also, and perhaps surprisingly, there is no steep fall in earnings for the top 1 percent during this recession--in fact, these individuals experienced the highest earnings growth of all income groups during this recession.
Overall, however, for the majority of workers, the 1979-83 recession was very similar to--slightly milder than--the Great Recession, in terms of both its between-group implications and its average effect. Of course, the former contains two actual recessions and lasts one extra year, which shows the
severity of the latter.
looks very similar to the Great Recession period between the 10th percentile and about the 95th percentile,
with the same linear shape and a slightly smaller slope. However, for individuals with very low average earnings (below the 10th percentile), the graph is downward sloping, indicating some mean reversion during the recession.28 Also, and perhaps surprisingly, there is no steep fall in earnings for the top 1 percent during this recession--in fact, these individuals experienced the highest earnings growth of all income groups during this recession.
Overall, however, for the majority of workers, the 1979-83 recession was very similar to--slightly milder than--the Great Recession, in terms of both its between-group implications and its average effect. Of course, the former contains two actual recessions and lasts one extra year, which shows the
severity of the latter.
As for the other two recessions during this period, both of them feature modest falls in average earnings--about 3 log points for the median individual in these graphs. The 1990-92 recession also features mild but clear between-group differences, with ![]() rising linearly by about 7 log points between the 10th and 90th percentiles.29 The
2000-02 recession overlaps remarkably well with the former up to about the 70th percentile and then starts to diverge downward. In particular, there is a sharp drop after the 90th percentile. In fact, for the top 1 percent, this recession turns out to have the worst outcomes of all recessions--an
average drop of 33 log points in two years!
rising linearly by about 7 log points between the 10th and 90th percentiles.29 The
2000-02 recession overlaps remarkably well with the former up to about the 70th percentile and then starts to diverge downward. In particular, there is a sharp drop after the 90th percentile. In fact, for the top 1 percent, this recession turns out to have the worst outcomes of all recessions--an
average drop of 33 log points in two years!
Inspecting the behavior of ![]() above the 90th percentile reveals an interesting pattern. For the first two recessions in our sample period, very high-income individuals fared better
than anybody else in the population, whereas for the latest two recessions, there has been a remarkable reversal of these fortunes and the highest-income workers suffered the most.
above the 90th percentile reveals an interesting pattern. For the first two recessions in our sample period, very high-income individuals fared better
than anybody else in the population, whereas for the latest two recessions, there has been a remarkable reversal of these fortunes and the highest-income workers suffered the most.
To sum up our findings for prime-age males, there is a very clear systematic pattern to average earnings growth during recessions. For the substantial majority of individuals below the 90th percentile, earnings loss during a recession varies (specifically, decreases) almost linearly with the pre-recession average earnings level. The slope of this relationship also varies with the severity of the recession: the severe recessions of 1979-83 and 2007-10 saw a gap between the 90th and 10th percentiles in the range of 15 log points, whereas the milder recessions of 1990-92 and 2000-02 saw a gap of 4-7 log points. Second, the fortunes of very high-income individuals require a different classification, one that varies over time: more recent recessions have seen substantial earnings losses for high-income individuals, unlike anything seen in previous ones. Below we will further explore the behavior of the top 1 percent over the business cycle.
6.1.2 Expansions
Figure 14 plots the counterpart of the ![]() function during expansions. Broadly speaking, during expansions
function during expansions. Broadly speaking, during expansions ![]() displays either a U-shape or a hockey stick shape, which is in stark contrast to the pervasive upward-sloping figure that emerges during recessions.
displays either a U-shape or a hockey stick shape, which is in stark contrast to the pervasive upward-sloping figure that emerges during recessions.
For prime-age males, there is a clear pattern for workers that enter an expansion with average earnings above roughly the 70th percentile: the ![]() function is upward sloping, indicating
further spreading out of the earnings distribution at the top during expansions. For workers below the median, income behavior has varied across expansions. The 1990s expansion has been the most favorable, with a strong mean reversion raising the incomes of workers at the lower end relative to the
median. The other two expansions show little factor structure in favor of low-income workers--the function is quite flat, indicating that earnings changes have been relatively unrelated to past earnings.
function is upward sloping, indicating
further spreading out of the earnings distribution at the top during expansions. For workers below the median, income behavior has varied across expansions. The 1990s expansion has been the most favorable, with a strong mean reversion raising the incomes of workers at the lower end relative to the
median. The other two expansions show little factor structure in favor of low-income workers--the function is quite flat, indicating that earnings changes have been relatively unrelated to past earnings.
The pronounced U-shape pattern in the 1990s can be viewed as a stronger version of what Autor et al. (2006) called "wage polarization" during this period. Basically, these authors compared the percentiles of the wage distribution at different points in time and concluded that the lower and higher percentiles grew more during the 1990s than the middle percentiles. Figure 14 goes one step further by following the same individuals over time and showing that it is precisely those individuals whose pre-1990s earnings were lowest and highest that experienced fastest growth during the 1990s.
6.1.3 Putting Recessions and Expansions Together
To summarize these patterns, Figure 15 aggregates ![]() across all age groups and combines separate recessions and
expansions. As seen here, a U-shape emerges during expansions--indicating a compression of the earnings distribution at the bottom and expansion at the top. In contrast, recessions reveal an upward-sloping figure, indicating a widening of the entire distribution except at the very top (above the
95th percentile). Thus, the main cyclical impact of business cycles is felt below the median, which expands during recessions and compresses during expansions. The same pattern also emerges at the top--inside the top 10 percent of the earnings distribution.
across all age groups and combines separate recessions and
expansions. As seen here, a U-shape emerges during expansions--indicating a compression of the earnings distribution at the bottom and expansion at the top. In contrast, recessions reveal an upward-sloping figure, indicating a widening of the entire distribution except at the very top (above the
95th percentile). Thus, the main cyclical impact of business cycles is felt below the median, which expands during recessions and compresses during expansions. The same pattern also emerges at the top--inside the top 10 percent of the earnings distribution.
Put together, these factor structures seen in Figure 15 explain how the earnings distribution expands in recessions and contracts in expansions (resulting in countercyclical earnings inequality) without within-group (idiosyncratic) shocks having countercyclical variances.
6.2 Rising Stars versus Stagnant Careers
We now control for three characteristics simultaneously: age,
![]() , and
, and
![]() . Because the 1979-83 period does not allow us to construct the pre-episode growth rate, we drop it from the analysis of this section.
. Because the 1979-83 period does not allow us to construct the pre-episode growth rate, we drop it from the analysis of this section.
We first sort individuals within an age group according to their
![]() and
and
![]() (independently in each dimension) and compute 50- and 40-quantile thresholds, respectively. We use these thresholds to assign each individual into groups formed by
the intersection of age, pre-episode average earnings (indexed by
(independently in each dimension) and compute 50- and 40-quantile thresholds, respectively. We use these thresholds to assign each individual into groups formed by
the intersection of age, pre-episode average earnings (indexed by ![]() ), and earnings growth (indexed by
), and earnings growth (indexed by ![]() ) categories. To give an idea about the bounds of a typical group, for the analysis of the Great Recession, one such group will consist of individuals who (i) were between the ages of 35 and 39 in year 2006, (iii) earned average annual earnings (
) categories. To give an idea about the bounds of a typical group, for the analysis of the Great Recession, one such group will consist of individuals who (i) were between the ages of 35 and 39 in year 2006, (iii) earned average annual earnings (
![]() ) between $32,033 and $33,455 from 2002 to 2006, and (iii) experienced an annual earnings growth rate between 1.30 percent and 1.49 percent per year from 2002 to 2006.
Clearly, this is a very finely defined group of individuals. For each of these 2000 cells, we compute the average labor earnings:
) between $32,033 and $33,455 from 2002 to 2006, and (iii) experienced an annual earnings growth rate between 1.30 percent and 1.49 percent per year from 2002 to 2006.
Clearly, this is a very finely defined group of individuals. For each of these 2000 cells, we compute the average labor earnings:
![]() and
and
![]() .30 We then regress
.30 We then regress
where
First, in Appendix B, we show that the additional control for
![]() has virtually no effect on the results of the previous section when we only conditioned on
has virtually no effect on the results of the previous section when we only conditioned on
![]() (see Figure A.8). Second, the main finding is that pre-episode earnings growth has a significant effect on future growth.
This is shown in Figure 16, which plots average earnings growth during expansions (blue line with circle markers) and recessions (red line with square markers). While mean reversion is apparent in both cases, the gap between the two graphs is smallest in the middle
and expands at both ends. This is clearly seen in the right panel, which plots the annualized gap between expansions and recessions. The implication is that workers with the highest and lowest earnings growth rates prior to an episode do better during expansions than recessions. This is related to
the fact documented earlier that the top of the earnings shock distribution collapses during recessions. Consequently, the earnings growth rate of those individuals whose earnings would have grown faster during expansions actually slows down during a recession.31
(see Figure A.8). Second, the main finding is that pre-episode earnings growth has a significant effect on future growth.
This is shown in Figure 16, which plots average earnings growth during expansions (blue line with circle markers) and recessions (red line with square markers). While mean reversion is apparent in both cases, the gap between the two graphs is smallest in the middle
and expands at both ends. This is clearly seen in the right panel, which plots the annualized gap between expansions and recessions. The implication is that workers with the highest and lowest earnings growth rates prior to an episode do better during expansions than recessions. This is related to
the fact documented earlier that the top of the earnings shock distribution collapses during recessions. Consequently, the earnings growth rate of those individuals whose earnings would have grown faster during expansions actually slows down during a recession.31
6.3 Broadening the Definition of Business Cycles
So far in the analysis, we have viewed business cycles as consisting of recessionary and expansionary episodes. But some important macroeconomic variables do not perfectly synchronize with these episodes. For example, as also mentioned earlier, unemployment peaked in 1993 and 2003--two years that are part of expansions. Similarly, the stock market experienced a significant drop in 1987, again during an expansion. With these considerations in mind, this section explores the robustness of our results to alternative indicators of business cycles.
|
|
|||
| 3.07 | 0.43 | -4.76 | |
| 1.45 | 0.20 | -2.42 | |
| 1.48 | 0.06 | -1.17 | |
| 0.75 | 0.06 | -1.22 | |
| 1.04 | 0.09 | -1.77 | |
| 1.63 | 0.14 | -2.80 | |
| 1.85 | 0.17 | -3.22 | |
| std. dev.(x) | 2.10 | 16.80 | 1.23 |
|
|
|||
| 4.55 | 0.46 | -6.87 | |
| 2.09 | 0.22 | -3.34 | |
| 1.70 | 0.06 | -1.21 | |
| 0.75 | 0.05 | -1.13 | |
| 1.09 | 0.08 | -1.74 | |
| 1.78 | 0.14 | -2.86 | |
| 2.06 | 0.16 | -3.34 | |
| std. dev.(x) | 1.81 | 17.78 | 1.10 |
For a given quantile ![]() of
of
![]() , we regress the change between
, we regress the change between ![]() and
and ![]() in log average earnings (
in log average earnings (![]() ) on alternative measures of business cycles, denoted
with
) on alternative measures of business cycles, denoted
with ![]() :
:
We consider three choices for ![]() (log) growth rate in GDP per capita, the annual return on the U.S. stock market (as measured by the S&P500 index), and the annual change in the male
unemployment rate (denoted
(log) growth rate in GDP per capita, the annual return on the U.S. stock market (as measured by the S&P500 index), and the annual change in the male
unemployment rate (denoted ![]() ). Table III displays the estimated
). Table III displays the estimated ![]() s for several key quantiles and for two time periods: the full sample (1978 to 2009) and one that excludes the double-dip recession (1985 to 2009).
s for several key quantiles and for two time periods: the full sample (1978 to 2009) and one that excludes the double-dip recession (1985 to 2009).
Several observations are worth noting. First, cyclicality is U-shaped across earnings quantiles, regardless of the business cycle variable chosen. This is consistent with the conclusion of Section 6.1 above, summarized in Figure 15. It is also consistent with Parker and Vissing-Jørgensen (2010)'s analysis using repeated cross sections and synthetic earnings groups. Second, cyclicality increases post-1985, especially at the very top of the earnings distribution and especially when business cycles are measured by GDP growth or the unemployment rate. Cyclicality is pretty flat in the middle of the earnings distribution (e.g., between P25 and P75) and increases slightly at the bottom end. Third, the co-movement of the earnings growth of top earners with GDP growth and stock returns is quite striking. For example, post-1985 a 1 percentage point rise in the male unemployment rate has been accompanied with an average earnings decline of 6.87 percent for individuals that were in P99.9 before the shock. Similarly, a 1 percentage point slowdown in GDP/capita growth implies a 4.55 percent decline in the earnings of the same individuals.32 For comparison, the corresponding numbers for individuals with median earnings is 1.08 and -1.77.
6.4 The Top 1 Percent
|
We now take a closer look at top earners. To understand the differences and similarities within the top 1 percent, we divide this group into 10 quantiles and focus on the 1st, 5th, 8th, and 10th quantiles. We refer to each quantile by the middle point: P99.05, P99.45, P99.75, and P99.95 (the top 0.1 percent).
The top panel of Figure 17 plots the annual change using the ![]() measure for each of these quantiles. First, notice that the four
groups move quite closely to each other until the late 1980s, after which point a clear ranking emerges: higher quantiles become more cyclical than lower ones. In particular, individuals in higher quantiles have seen their earnings plummet in recessions relative to lower quantiles, but did not see
their earnings bounce back more in the subsequent expansion, which would have allowed them to catch up. In fact, during expansions, the average earnings in each group grew by similar amounts.
measure for each of these quantiles. First, notice that the four
groups move quite closely to each other until the late 1980s, after which point a clear ranking emerges: higher quantiles become more cyclical than lower ones. In particular, individuals in higher quantiles have seen their earnings plummet in recessions relative to lower quantiles, but did not see
their earnings bounce back more in the subsequent expansion, which would have allowed them to catch up. In fact, during expansions, the average earnings in each group grew by similar amounts.
The implication is that these "differential losses" during recessions across earnings quantiles are also very persistent (bottom panel of Figure 17): individuals who were in P99.95 as of 1999 saw their earnings fall by an average of 50 log points between 2000 and 2005! Similarly large losses were experienced by the same quantile as of 1988 (from 1989 to 1994) and 2003 (from 2004 to 2009). By comparison, the 5-year loss for individuals in P99.05 ranges from 10 to 20 log points in the same three recessions. Thus, cyclicality increases strongly with the level of earnings. This conclusion is consistent with the findings in Parker and Vissing-Jørgensen (2010), who used repeated cross sections to study the same question. That paper also found that the differential cyclicality of earnings at the top has increased after the mid-1980s, as we find in this paper.33
7 Conclusions
This paper has studied between- and within-group variation in earnings changes over the business cycle. Using a very large panel dataset with little measurement error, it has documented three sets of empirical facts.
Our first set of findings concerns the cyclical nature of idiosyncratic shocks. During recessions, the upper end of the shock distribution collapses--that is, large upward wage movements become much less likely--whereas the bottom end expands--i.e., large drops in earnings become much more frequent. Moreover, the center of the shock distribution (i.e., the median) is very stable and moves very little compared with either tail.34 What does change (more significantly) is the behavior of the tails, which swing back and forth in the same direction over the business cycle. These swings in the tails, therefore, lead to cyclical changes in the skewness, but not so much in overall dispersion. We conclude that recessions are best viewed as a small negative shock to the median and a large negative shock to the skewness of the idiosyncratic earnings shock distribution, with little change in the variance.
Second, we examined the systematic component of business cycle risk. Pre-episode average earnings turns out to be an excellent predictor of a worker's earnings growth during business cycle episodes. We find that during recessions earnings growth is a monotonically increasing function of past earnings. In other words, workers who entered recessions with lower average past earnings experienced larger losses on average compared to workers with higher average past earnings. Clearly, this factor structure leads to a significant widening of earnings inequality over much of the distribution. As for the expansions, earnings growth is a U-shaped function of past earnings. Put together, these factor structures explain how earnings inequality is countercyclical without within-group (idiosyncratic) shocks having countercyclical variances. (Of course, the countercyclical left-skewness also contributes to countercyclical earnings inequality.)
Third, the one deviation we find from these simple patterns is a remarkable non-linearity for individuals who enter a recession with extremely high earnings--those in the top 1 percent of the earnings distribution. During the last two recessions, these individuals have experienced enormous and persistent earnings losses (about 30 log points), which dwarfs the losses of individuals even with slightly lower earnings. In fact, individuals who entered the last three recessions in the top 99.9th percentile of the earnings distribution had earnings levels five years later that were at least 50 log points lower than their pre-recession levels.
Overall, these empirical findings have important implications for how we think about earnings risk over the business cycle. The traditional approach to modeling recession risk consists of a (negative) aggregate shock and a positive shock to the variance of idiosyncratic shocks. Our results suggest that this simple view is seriously inadequate. Instead, they turn our focus to the countercyclical variation in the third moment (skewness) of idiosyncratic shocks as central to understanding how the fortunes of ex ante similar individuals fare during recessions. Even the change in mean earnings (which we think of as an aggregate shock) is seriously affected and driven by the change in skewness. In addition, the factor structure results imply that business cycle risk is not entirely a surprise or a shock, but it has a component that can be predicted based on information available to both individuals and economists at the beginning of business cycle episodes.
1.0
Bibliography
1.25
A. Data Appendix
| Year | Median earnings (in constant 2005 dollars) | Mean earnings (in constant 2005 dollars) | Change in log average earnings per person x100 | Change in log earnings, averaged over workers x100 | Average age | Number of observations |
| 1978 | 39,488 | 47,938 | -- | -- | 39.4 | 3,640,877 |
| 1979 | 38,971 | 46,207 | -0.94 | 1.10 | 39.3 | 3,797,417 |
| 1980 | 37,571 | 44,636 | -1.69 | -3.11 | 39.2 | 3,901,959 |
| 1981 | 37,908 | 44,785 | 0.08 | 2.00 | 39.2 | 4,011,200 |
| 1982 | 36,644 | 44,160 | -2.13 | -3.26 | 39.1 | 3,977,428 |
| 1983 | 36,431 | 44,276 | -0.35 | 0.58 | 39.1 | 4,020,508 |
| 1984 | 36,847 | 45,760 | 1.21 | 6.53 | 38.9 | 4,090,461 |
| 1985 | 37,009 | 46,772 | 1.55 | 4.40 | 38.9 | 4,243,207 |
| 1986 | 37,100 | 48,062 | 1.06 | 3.68 | 38.9 | 4,311,235 |
| 1987 | 36,788 | 47,661 | -0.09 | 1.78 | 38.9 | 4,423,615 |
| 1988 | 36,329 | 48,480 | 1.14 | 3.85 | 38.9 | 4,552,623 |
| 1989 | 35,614 | 46,572 | -1.50 | 0.62 | 39.0 | 4,670,531 |
| 1990 | 35,207 | 46,262 | -0.66 | 1.06 | 39.2 | 4,723,153 |
| 1991 | 34,451 | 45,766 | -0.78 | -1.30 | 39.3 | 4,768,475 |
| 1992 | 34,688 | 47,193 | 0.78 | 2.98 | 39.5 | 4,772,714 |
| 1993 | 34,660 | 47,471 | 0.11 | 3.33 | 39.7 | 4,829,933 |
| 1994 | 34,230 | 44,816 | -2.44 | 2.00 | 39.8 | 4,904,776 |
| 1995 | 34,281 | 45,645 | 1.08 | 3.85 | 40.0 | 5,000,660 |
| 1996 | 34,863 | 46,730 | 0.94 | 3.88 | 40.2 | 5,045,831 |
| 1997 | 35,874 | 48,898 | 2.19 | 6.38 | 40.5 | 5,134,125 |
| 1998 | 37,351 | 51,348 | 2.20 | 7.06 | 40.7 | 5,198,954 |
| 1999 | 37,900 | 52,846 | 1.58 | 4.43 | 40.9 | 5,284,142 |
| 2000 | 38,525 | 55,030 | 2.06 | 4.35 | 41.1 | 5,366,942 |
| 2001 | 39,011 | 55,283 | -0.09 | 1.93 | 41.3 | 5,376,439 |
| 2002 | 38,412 | 52,894 | -2.61 | -2.36 | 41.4 | 5,316,402 |
| 2003 | 38,187 | 53,145 | 0.01 | 0.55 | 41.6 | 5,303,052 |
| 2004 | 38,372 | 53,366 | 0.16 | 2.16 | 41.7 | 5,329,934 |
| 2005 | 38,196 | 53,586 | 0.23 | 2.12 | 41.8 | 5,359,877 |
| 2006 | 38,456 | 54,536 | 0.93 | 3.30 | 41.9 | 5,390,061 |
| 2007 | 38,526 | 55,322 | 0.67 | 2.44 | 41.9 | 5,405,122 |
| 2008 | 37,930 | 53,889 | -1.67 | -1.03 | 42.0 | 5,400,167 |
| 2009 | 36,984 | 51,946 | -3.86 | -6.64 | 42.1 | 5,238,303 |
| 2010 | 36,934 | 52,567 | -0.04 | 1.25 | 42.1 | 5,161,313 |
| Year | Mean (log) | Std. Dev. (log) | Skewness (log) | Max. Earnings |
| 1978 | 10.431 | 0.861 | -0.762 | 5,629,944 |
| 1979 | 10.420 | 0.834 | -0.798 | 3,043,686 |
| 1980 | 10.378 | 0.843 | -0.785 | 3,900,245 |
| 1981 | 10.386 | 0.850 | -0.832 | 3,191,016 |
| 1982 | 10.353 | 0.869 | -0.756 | 3,164,862 |
| 1983 | 10.337 | 0.891 | -0.747 | 3,350,164 |
| 1984 | 10.354 | 0.899 | -0.709 | 5,649,401 |
| 1985 | 10.363 | 0.907 | -0.677 | 5,997,900 |
| 1986 | 10.368 | 0.929 | -0.630 | 5,518,408 |
| 1987 | 10.355 | 0.922 | -0.644 | 8,836,576 |
| 1988 | 10.352 | 0.937 | -0.599 | 10,323,465 |
| 1989 | 10.328 | 0.929 | -0.647 | 7,963,985 |
| 1990 | 10.316 | 0.939 | -0.659 | 8,436,263 |
| 1991 | 10.303 | 0.941 | -0.585 | 7,671,863 |
| 1992 | 10.322 | 0.943 | -0.513 | 11,382,868 |
| 1993 | 10.328 | 0.951 | -0.507 | 9,824,403 |
| 1994 | 10.317 | 0.934 | -0.566 | 7,380,117 |
| 1995 | 10.326 | 0.939 | -0.536 | 7,761,374 |
| 1996 | 10.344 | 0.941 | -0.532 | 10,145,898 |
| 1997 | 10.384 | 0.934 | -0.465 | 11,928,487 |
| 1998 | 10.433 | 0.925 | -0.434 | 14,686,511 |
| 1999 | 10.450 | 0.929 | -0.420 | 18,190,317 |
| 2000 | 10.468 | 0.936 | -0.400 | 32,008,754 |
| 2001 | 10.479 | 0.951 | -0.429 | 17,144,706 |
| 2002 | 10.449 | 0.956 | -0.504 | 13,885,282 |
| 2003 | 10.443 | 0.968 | -0.499 | 14,023,289 |
| 2004 | 10.443 | 0.965 | -0.502 | 15,811,530 |
| 2005 | 10.442 | 0.967 | -0.492 | 16,138,366 |
| 2006 | 10.452 | 0.972 | -0.484 | 18,897,685 |
| 2007 | 10.455 | 0.982 | -0.476 | 20,177,930 |
| 2008 | 10.443 | 0.973 | -0.452 | 16,907,029 |
| 2009 | 10.407 | 0.979 | -0.460 | 12,541,077 |
| 2010 | 10.414 | 0.974 | -0.384 | 13,983,100 |
Tables A.1 and A.2 report some key summary statistics for the base sample used in the paper. Figure A.1 plots selected percentiles of the earnings distribution over the sample period. Panis et al. (2000) and Olsen and Hudson (2009) contain more detailed descriptions of the MEF dataset.
A..1 Comparison to CPS Data
Figure A.2 plots the log differential between the 90th and 50th percentiles of the labor earnings distribution, as well as the log differential between the 50th and 10th percentiles (hereafter abbreviated as L90-50 and L50-10, respectively). A couple of remarks are in order. First, it is useful to compare this figure to the Current Population Survey (CPS) data, which has been used extensively in the previous literature to document wage inequality trends. An important point to keep in mind is that studies that used the CPS have typically focused on hourly wage inequality, whereas our dataset only contains information on annual (wage and labor) earnings. With this difference in mind, note that Autor et al. (2008, Figure 3) report a level of L90-50 of 55 log points in 1978, which rises by about 30 log points until 2005. In this paper, the level of L90-50 is 72 log points (most likely higher because of the dispersion in labor supply) and rises by about 28 log points until 2005, a result very similar to Autor et al. (2008)'s numbers. In both datasets, the rise in L90-50 is secular and is remarkably stable over three decades.35 Thus, even though the difference between hourly wage and annual earnings matters for the levels, it has little effect on the secular trend during this period.
Second, turning to the bottom end, the CPS data show slightly different patterns, depending on whether one uses CPS March weekly wages or May/ORG hourly data. But the general pattern is a rapidly widening L50-10 gap from 1978 to 1987, which then stays flat or declines, depending on the dataset. In our case, the rise in L50-10 happens between 1979 and 1983, and then it stays relatively flat until 2000, after which time it starts rising again. It seems safe to conjecture that labor supply heterogeneity could be more important at the bottom end and could account for some of the gap between the two datasets. Another source of the difference could be the under-reporting of earnings in our administrative dataset or over-reporting in the CPS. Some papers on measurement error adopt this latter interpretation (e.g., Gottschalk and Huynh (2010)). Notice also that the level of L50-10 is much higher in our sample--about 125 log points in 1978 compared with 65 log points in the CPS, which again can be explained by a combination of labor supply heterogeneity and under- or over-reporting.36 Overall, the two datasets reveal the same pattern at the top end, while having similar but slightly different behavior at the bottom.
A..2 Evolution of Inequality: Cross-Sectional Data
In this section we document some facts about the evolution of cross-sectional inequality. In particular, inequality is clearly countercyclical, and this is due to an expansion of inequality at both the top end and bottom end. This analysis does not require the panel dimension; it is presented here for completeness and comparison to the existing work.
It is useful to distinguish between the changes in top and bottom end inequality. To this end, we plot the 1-year change in L90-50 and L50-10 in Figure ![]() . To reduce short-term mean reversion in inequality, the solid lines plot the 2-year difference in each inequality measure (divided by two), which is smoother. This differencing eliminates the secular trend and allows us to focus on the cyclical
change in inequality.
. To reduce short-term mean reversion in inequality, the solid lines plot the 2-year difference in each inequality measure (divided by two), which is smoother. This differencing eliminates the secular trend and allows us to focus on the cyclical
change in inequality.
First, notice the cyclical movement in the bottom-end inequality, rising in every one of the four recessions and falling (into the negative territory) subsequently. The increases in the 1980-83 and 2001-02 recessions are especially pronounced, as is the fall during the 1990s. The change in the top-end inequality is also cyclical, rising during the 1980-83 and 1991-92 recessions. Compared with the bottom-end inequality, though, L90-50 rises virtually throughout the period. Overall, the combination of these two pieces shows that overall inequality (L90-10) itself is countercyclical.
B..3 An Alternative Measure of Factor Structure: 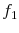
We now construct the alternative measure of average earnings growth, ![]() described in the main text (Section 6). Recall that
described in the main text (Section 6). Recall that ![]() differs from
differs from ![]() in two important ways. First,
in two important ways. First, ![]() excludes individuals with zero earnings in either year
excludes individuals with zero earnings in either year ![]() or year
or year ![]() . Because the probability of full-year non-employment rises in recessions most strongly for low-income individuals, dropping them will tend to increase
. Because the probability of full-year non-employment rises in recessions most strongly for low-income individuals, dropping them will tend to increase ![]() below the median relative to
below the median relative to ![]() . Second, because
. Second, because ![]() is based on the average of log earnings, whereas
is based on the average of log earnings, whereas ![]() is based on the log of average earnings, the latter will
tend to be higher within quantiles that have a wider dispersion of earnings growth rates (due to Jensen's inequality). So, we would expect this force to raise
is based on the log of average earnings, the latter will
tend to be higher within quantiles that have a wider dispersion of earnings growth rates (due to Jensen's inequality). So, we would expect this force to raise ![]() relative to
relative to ![]() below the median level of
below the median level of
![]() where the variance of shocks is higher, as well as at the very top end for the same reason.
where the variance of shocks is higher, as well as at the very top end for the same reason.
Figure A.7 plots ![]() for each of the four recessions. A quick comparison to Figure 13
shows that the two measures reveal the same qualitative patterns. The clear upward-sloping factor structure is there for all recessions. Quantitatively, the slope is somewhat smaller--a difference of 10 log points between the 90th and 10th percentiles during the Great Recession versus 17 log points
under
for each of the four recessions. A quick comparison to Figure 13
shows that the two measures reveal the same qualitative patterns. The clear upward-sloping factor structure is there for all recessions. Quantitatively, the slope is somewhat smaller--a difference of 10 log points between the 90th and 10th percentiles during the Great Recession versus 17 log points
under ![]() . Inspecting the two graphs shows that the difference mainly comes from the steeper drop in
. Inspecting the two graphs shows that the difference mainly comes from the steeper drop in ![]() between the 20th and 1st percentiles, probably due to the increased chance of unemployment in this range mentioned above. Between the 20th and 90th percentiles, the two graphs look very similar. The other recessions show slopes that are also slightly lower than
before. Another difference to note is that under
between the 20th and 1st percentiles, probably due to the increased chance of unemployment in this range mentioned above. Between the 20th and 90th percentiles, the two graphs look very similar. The other recessions show slopes that are also slightly lower than
before. Another difference to note is that under ![]() , the 1980-83 recession looks less favorable to individuals in the top 10 percent--their earnings growth pattern resembles the recent
recessions more closely. This suggests that the strong performance of this group revealed by
, the 1980-83 recession looks less favorable to individuals in the top 10 percent--their earnings growth pattern resembles the recent
recessions more closely. This suggests that the strong performance of this group revealed by ![]() was affected by some large gains at the right tail, which dominated the mean earnings
measure for these groups in 1983.
was affected by some large gains at the right tail, which dominated the mean earnings
measure for these groups in 1983.
Overall, the two measures are quite comparable. In the main text, we focus on ![]() so as to capture the total earnings risk, which includes the risk of long-term unemployment rising
during recessions.
so as to capture the total earnings risk, which includes the risk of long-term unemployment rising
during recessions.
B..5 Cyclicality of Top 1 Percent Using 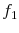
Figure A.9 plots the counterpart of Figure 17 using a different measure of earnings growth (![]() ). The
same pattern discussed in Section 6.4 is visible here with an even larger 5-year loss for all individuals in the top 1 percent.
). The
same pattern discussed in Section 6.4 is visible here with an even larger 5-year loss for all individuals in the top 1 percent.
C. A Fully Parametric Approach
In this section, we use an alternative approach to quantify the cyclicality of idiosyncratic shocks. We begin by running the following regression:
where
The advantage of the specification in (8) is that by making the factor
![]() observable and the loading term fixed over time, it allows us to estimate this regression separately for each individual using a time series of his earnings. To ensure a
sufficiently large number of observations for each individual regression, we focus on a subsample of cohorts that are between the ages of 25 to 28 in 1978. These individuals have exactly 33 yearly observations between the ages of 25 and 60 during our sample period (which may involve years with zero
annual earnings). In addition, to ensure at least a moderately strong labor market attachment, we require an individual to have earnings above the minimum threshold during at least 2/3 of the sample period--22 years. From this pool, we select a random subsample of 100,000 individuals to conduct the
analysis in this section (hence there are as many regressions).
observable and the loading term fixed over time, it allows us to estimate this regression separately for each individual using a time series of his earnings. To ensure a
sufficiently large number of observations for each individual regression, we focus on a subsample of cohorts that are between the ages of 25 to 28 in 1978. These individuals have exactly 33 yearly observations between the ages of 25 and 60 during our sample period (which may involve years with zero
annual earnings). In addition, to ensure at least a moderately strong labor market attachment, we require an individual to have earnings above the minimum threshold during at least 2/3 of the sample period--22 years. From this pool, we select a random subsample of 100,000 individuals to conduct the
analysis in this section (hence there are as many regressions).
So, how is equation (8) estimated? We include observations with zero earnings into this regression by setting them equal to
![]() . Consequently, the distribution of
. Consequently, the distribution of ![]() is very
non-symmetric due to occasionally large drops to
is very
non-symmetric due to occasionally large drops to
![]() . We conducted a Monte Carlo study, which suggested that a quantile regression for the median was more robust and yielded much less bias for the estimated
parameters.38 Therefore, we estimated equation (8) via a quantile regression for the median.
. We conducted a Monte Carlo study, which suggested that a quantile regression for the median was more robust and yielded much less bias for the estimated
parameters.38 Therefore, we estimated equation (8) via a quantile regression for the median.
Figure A.10 plots the (cross-sectional) standard deviation and skewness of the estimated innovations over time. A potentially important confounding factor in this analysis is the following. Because the sample is balanced and contains four cohorts with very similar ages, the figures over time can be alternatively interpreted as evolutions over the life cycle. With this in mind, it seems more appropriate to focus on high frequency changes in these moments and de-emphasize the longer-term patterns (such as the U-shape in the standard deviation).
With this caveat noted, we turn to Figure A.10, which plots the skewness of the
![]() distribution. There are three large dips--in 1990, 2002, and 2009--coinciding with the last three recessions. This is very similar to what we found before (cf. Figure 6).39 There is no dip for the 1980-83 recession, although skewness continuously falls during that period. As noted earlier,
however, because the sample is younger during that recession, life cycle factors could be dominating the business cycle variation in those years.
distribution. There are three large dips--in 1990, 2002, and 2009--coinciding with the last three recessions. This is very similar to what we found before (cf. Figure 6).39 There is no dip for the 1980-83 recession, although skewness continuously falls during that period. As noted earlier,
however, because the sample is younger during that recession, life cycle factors could be dominating the business cycle variation in those years.
One drawback of this analysis is that we can track only a handful of cohorts with very similar ages over time (since we need to run the regression in (3) with a sufficiently long time series). Thus, age effects are confounded with time effects, which makes us less comfortable about drawing strong conclusions. Partly due to this concern and for sake of brevity, we did not include these results in the paper.
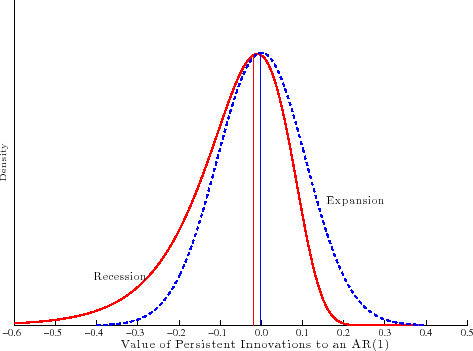
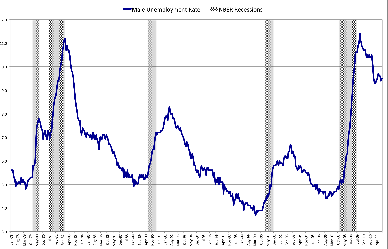
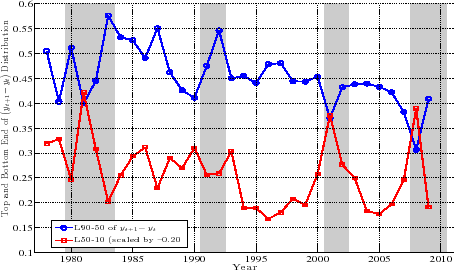
![\includegraphics[width=0.92\columnwidth,height=0.29\textheight]{AFIG_Males_P9050_P5010_OF_5YR_CHANGE_IN_LOG_WAGE_FINAL}](img20.gif)
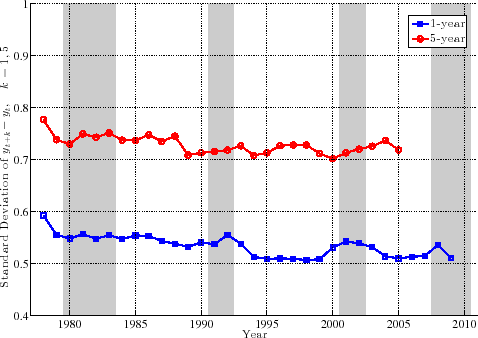
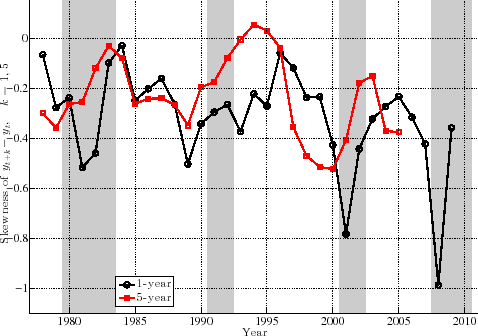
![\displaystyle =\underset{{\color{blue}\text{factor structure}}}{\underbrace{f_{1}(\mathbf{V}_{t-1}^{i})(\lambda_{t+k}-\lambda_{t})}}+\underset{{\color{blue}\text{stochastic component}}}{\underbrace{\left[(\eta_{t+k}+\eta_{t+k-1}+...+\eta_{t+1})\right]+(\varepsilon_{t+k}^{i}-\varepsilon_{t}^{i}).}}](img39.gif)
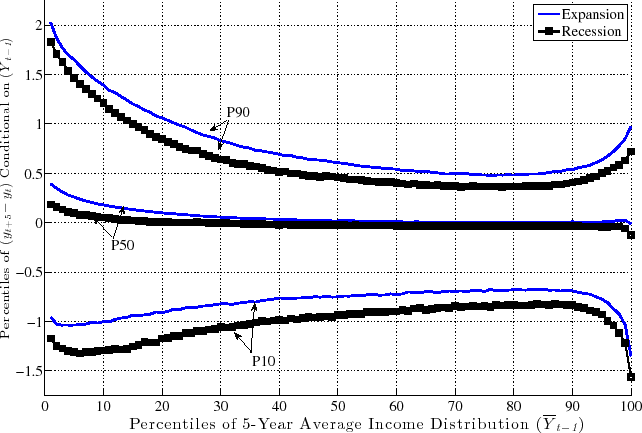
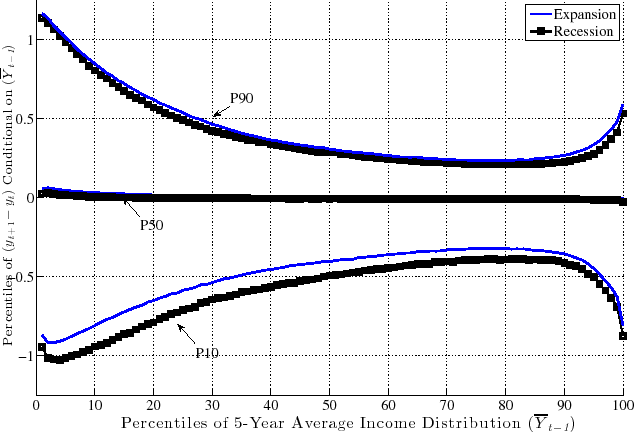
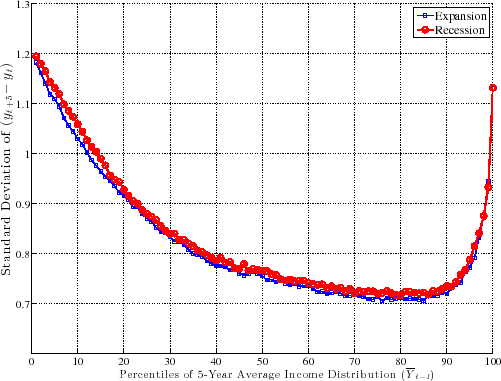
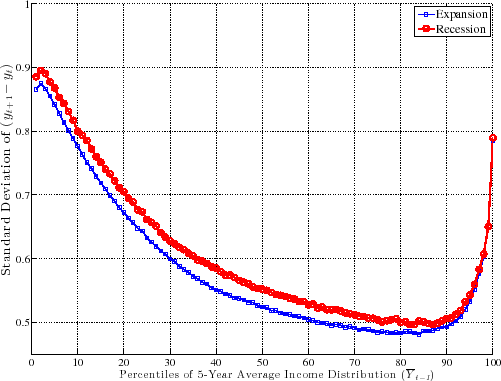
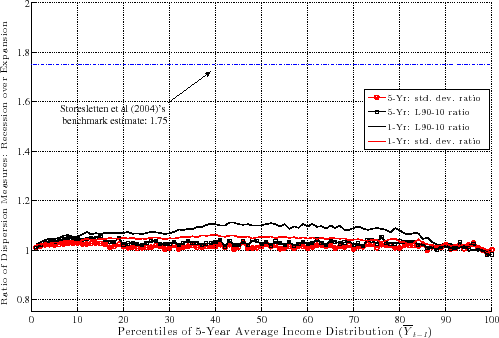
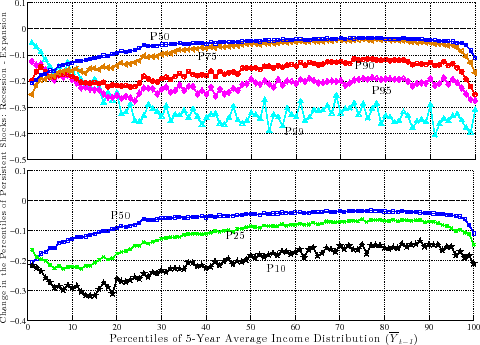
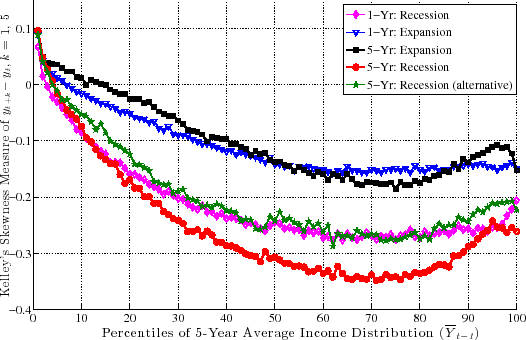
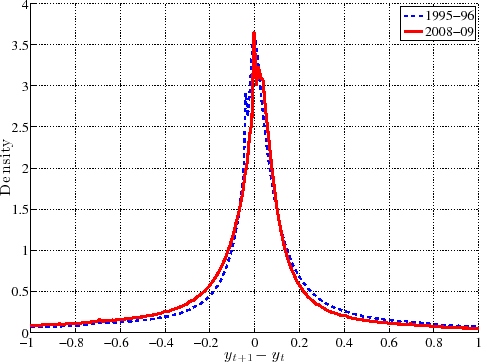
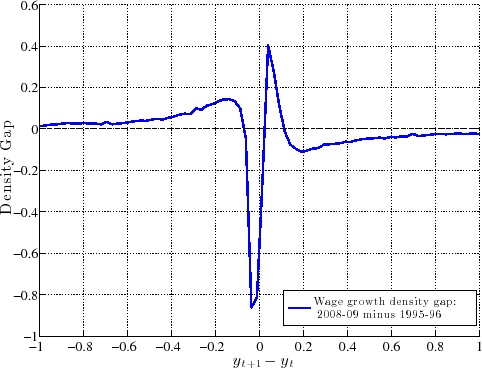


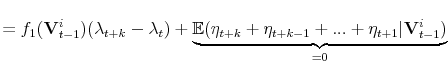
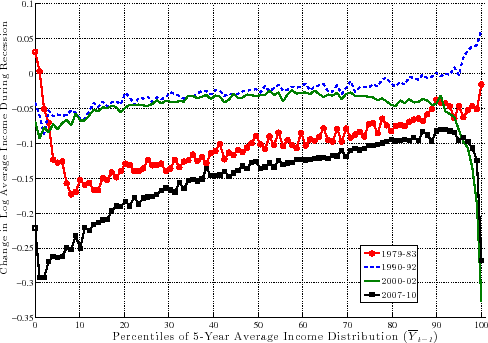
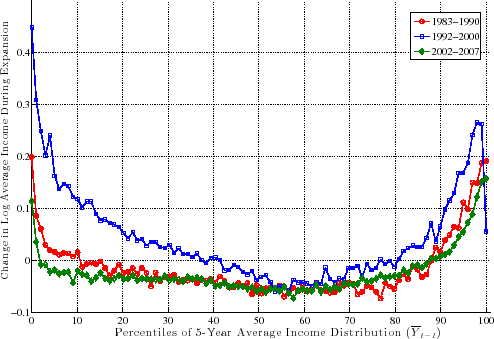
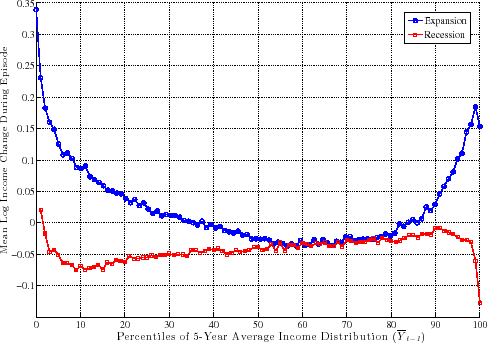
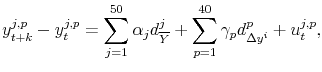
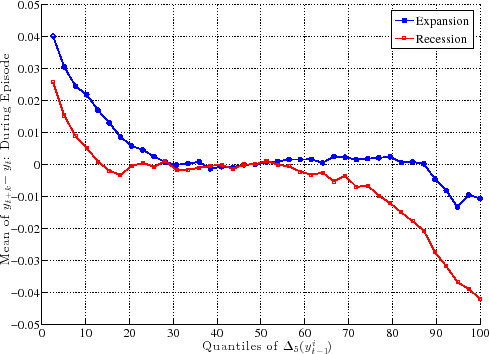
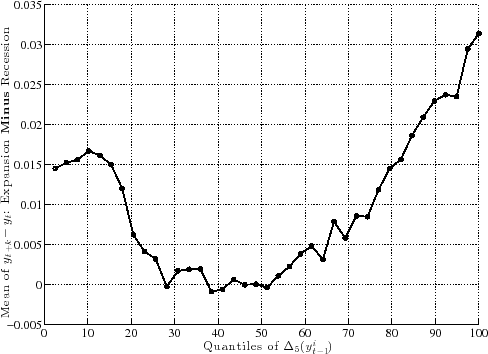
![\includegraphics[height=0.36\textheight]{AFIG_Males_PERCENTILES_WAGE_FINAL}](img147.gif)
![\includegraphics[height=0.4\textheight]{AFIG_Males_P9050_P5010_LaborIncome_10pct}](img148.gif)
![\includegraphics[height=0.36\textheight]{AFIG_Males_CHANGE_IN_P9050_P5010_WAGE_FINAL}](img149.gif)
![\includegraphics[height=0.36\textheight]{FIG_dJMP_WAGES_REPAGENT_2007RECESSIONS_AGE_GROUPS_DETAIL}](img150.gif)
![\includegraphics[height=0.36\textheight]{FIG_dJMP_WAGES_REPAGENT_4RECESSIONS_YOUNG_MALES}](img151.gif)
![\includegraphics[height=0.36\textheight]{FIG_dJMP_WAGES_REPAGENT_3EXPANSIONS_YOUNG_MALES}](img152.gif)
![\includegraphics[height=0.36\textheight]{FIG_dJMP_WAGES_NOZEROS_4RECESSIONS_PRIME_AGED_MALES}](img153.gif)
![\includegraphics[height=0.35\textheight]{FIG_dJMP_WAGES_REPAGENT_4RECESSIONS_PRIME_AGED_MALES_CONTROLLING_FOR_DELTA}](img155.gif)
![\includegraphics[height=0.4\textheight]{FIG_1YR_MEAN_CHANGE_IN_LOG_INCOME_P99X_NEW}](img156.gif)
![\includegraphics[height=0.4\textheight]{FIG_5YR_MEAN_CHANGE_IN_LOG_INCOME_P99X_NEW}](img157.gif)
![\includegraphics[height=0.4\textheight]{FIG_TIMESERIES_SKEWNESS}](img166.gif)