The Effectiveness of the Non-Standard Policy Measures during the Financial Crises: The Experiences of the Federal Reserve and the European Central Bank 1
Abstract
A growing number of studies have sought to measure the effects of non-standard policy on bank funding markets. The purpose of this paper is to carry those estimates a step further by looking at the effects of bank funding market stress on the volume of bank lending, using a simultaneous equation approach. By separately modeling loan supply and demand, we determine how non-standard central bank measures affected bank lending by reducing stress in bank funding markets. We focus on the Federal Reserve and the European Central Bank. Our results suggest that non-standard policy measures lowered bank funding volatility. Lower bank funding volatility in turn increased loan supply in both regions, contributing to sustain lending activity. We consider this as strong evidence for a "bank liquidity risk channel", operative in crisis environments, which complements the usual channels of transmission of monetary policy.
Keywords: Bank lending, non-standard policy, bank funding volatility
JEL Code: E58, G32, G21
- Introduction
In response to the financial crisis that began in the summer of 2007, central banks around the world have increasingly resorted to non-standard policy measures. The non-standard policies have taken many forms, but all have tried to ease credit and liquidity constraints that ultimately might disrupt the flow of credit to the real economy. The Federal Reserve implemented a range of new lending facilities, often with a wider set of counterparties than before. The ECB changed the maturity profile of its already relatively large financing operations. It started to provide unlimited amounts of reserves in its auctions, and it began to purchase securities outright. Given the plethora of new tools to address the challenges of the financial crisis, it is natural to ask whether and how these tools worked.
In this paper, we analyze the effectiveness of non-standard policy measures in affecting bank loans by reducing bank liquidity risk. Liquidity risk was a central concern among market participants and central banks during the crisis, reaching unprecedented levels, and much of the response of central banks can be seen as, at least in part, an effort to reduce this risk. Any such measurement is difficult. We proceed in two steps. We first measure the response of bank loans to liquidity risk, with a measure of liquidity risk that we will discuss later. We then measure the effectiveness of policy measures in reducing banks' liquidity risk, using the same metric. Combining these two steps allows us to measure the impact of central bank measures on bank loans by easing liquidity risk. We call this mechanism "bank liquidity risk channel". It can be perceived as an additional channel of monetary transmission mechanism that works through stimulating bank loans by reducing liquidity strains in the bank funding market during times of elevated stress levels.
There are a growing number of studies concerned with the assessment of non-standard measures in both the US (see e.g. McAndrews et al., 2008, Taylor and Williams, 2009, Wu, 2008) and the euro area (see e.g. Lenza et al., 2010, and Fahr et al., 2011, Gambacorta and Marques-Ibanez, 2011). Most of these studies, however, have focused more narrowly on the effects of non-standard measures on interest rate spreads, or they adopted a reduced form approach by directly relating proxies for non-standard measures with economic outcomes such as bank lending volumes. A third branch of literature investigates how the non-standard measures affected the risk exposure of banks (e.g. Black and Hazelwood, 2012, and Puddu and Waelchli, 2012). Puddu and Waelchli find that the Term Auction Facility (TAF) program in the US reduced the liquidity risk of the borrower banks. Our approach provides a natural link between the findings of Puddu and Waelchli and the effects of the non-standard measures on bank loans. Our findings suggest that non-standard measures may have stimulated bank loans in part by reducing the liquidity risk.
In order to separate fiscal from monetary policy, we distinguish between direct capital injections provided by national governments and non-standard measures (e.g. specific lending facilities) provided by central banks. Capital injections are expected to have a direct impact on bank lending. Central bank non-standard measures, on the other hand, are expected to affect bank lending either directly through the additional funds provided through these measures and incorporated into bank liabilities, or indirectly through their impact on bank liquidity risk. We thereby contribute to the growing literature on the assessment of non-standard measures by outlining and testing the specific channels through which the measures are thought to have been effective.
The link between the policy measures and any measure of bank credit or liquidity risk is important because both types of risk matter for the transmission of monetary policy through their influence on loan volumes and prices. We provide ample evidence of this latter claim for both the euro area and the US. We find that most non-standard measures were successful in reducing bank liquidity risk and in doing so have significantly contributed to safeguard the transmission of monetary policy to the respective economies. A striking finding of our paper is that non-standard measures adopted by the Federal Reserve appear to have had a substantially higher impact on loan growth than the measures taken in the euro area. One plausible reason for this finding is the difference in monetary policy implementation frameworks at the start of the crisis in August 2007. The Federal Reserve started the TAF in December 2007, extending loans against illiquid collateral to banking institutions. In the euro area, by contrast, operations with largely similar features were already part of the standard policy framework. Another candidate explanation for the large difference is the pace of recapitalization of banks. While this process in the US was considered by and large complete at the end of 2009, the recapitalization of euro area banks was still underway.
The paper is organized as follows. The first section provides a generic overview on the non-standard policy measures adopted in the US and the euro area. The empirical analysis that establishes the link between market and bank liquidity risk and bank loans is contained in the first part of the following section. To show this link, we model the demand and supply of bank loans jointly and subject our findings to a variety of robustness checks. One gap in the literature that investigates the impact of non-standard measures on bank loans is that the demand for bank loans is usually not fully modeled. As a result, it is hard to distinguish whether the observed pattern of bank loans is driven by supply or demand factors. We fill this gap by modeling the supply and demand for bank loans in a simultaneous equations framework. We then proceed to estimate the impact of the non-standard policy measures on different measures of bank liquidity risk. Finally, we obtain numerical estimates of the effects of the non-standard measures on bank loan volumes by reducing bank liquidity risk. These estimates allow us to conduct a simulation exercise to construct the dynamic path of bank loans in response to a change in the bank liquidity risk.
2. Non-Standard Policy Measures in the US and the Euro Area
Central banks around the world have responded to the unfolding financial crisis with standard interest rate policy as well as with so-called non-standard measures. Since the beginning of the financial crisis, the Federal Reserve and the ECB have both decreased their respective key policy rates to unprecedented low levels. Additionally, both central banks have adopted a whole range of policy measures aimed at providing support to the transmission mechanism of monetary policy, taking into account the specificities of this transmission in the US and the euro area.2
Non-standard measures can be broadly divided into those that are mainly bank based and those that aim to support specific financial market segments important for the transmission of monetary policy. Bank based non-standard measures typically aim at enhancing the liquidity support to the banking system, stabilizing the refinancing of banks' business, thereby positively impacting on loan supply. In this paper, we focus on bank based measures and disregard other programs that were mainly aimed at supporting markets.3
2.1 Bank based non-standard measures adopted in the US
The two main bank based measures adopted by the Federal Reserve are the Term Auction Facility (TAF) and the Troubled Asset Relief Program (TARP). TAF was introduced by the Federal Reserve in December 2007. It provided term discount window credit to depository institutions through an auction mechanism. The auction mechanism and the lag between the auction and the receipt of the funds were intended to mitigate the perceived stigma associated with borrowing directly from the discount window. When bank funding markets began to normalize in early 2009, the Fed ended the TAF program (March 2010) and the remaining outstanding loans were allowed to run off as scheduled.
Beginning in the fourth quarter of 2008, the Treasury used the capital purchase program (CPP) using funds from the Troubled Asset Relief Program (TARP) to purchase preferred stock and warrants in financial institutions. With the completion of the first stress tests of the largest financial institutions in May 2009, the largest banks began to redeem the CPP injections. Most of the largest banks have ended their participation in the program, but the US-Treasury continues to hold investments in a few hundred smaller institutions.
2.2 Bank based non-standard measures adopted in the euro area
There are three types of bank-oriented non-standard measures adopted by the ECB which we consider. In the first phase of the financial crisis, from August 2007 to September 2008, the ECB changed the maturity profile of its repo operations, by offering less short-term repo loans and significantly more longer-term repo loans, while keeping the overall supply of repo loans unchanged. Later on, the ECB changed the profile of its liquidity provision in August 2007 by providing more reserves in the first weeks of the maintenance period and less during the last weeks of the maintenance period. Finally, starting in October 2008, the ECB started to provide unlimited liquidity at the policy rate (and against eligible collateral) in all operations. As a consequence of the so-called fixed-rate tender with full allotment (FRFA) procedure, the aggregate amount of central bank reserves outstanding at any moment ceased to be under the control of the ECB. Banks themselves now determined the aggregate supply of central bank reserves provided to the system. As in the US, there were also measures aimed at providing capital support to euro area banks, not involving the ECB.
3. Effects of Liquidity Risk on Bank Loans
3.1 Empirical strategy
We are interested in the link between non-standard measures and bank lending activity. To be able to measure the effects of non-standard measures with the best possible degree of accuracy, we follow a two-step approach to quantify the effects of non-standard measures on bank loans. First, we take a risk-management perspective and analyze how elevated risk factors affected the demand for and supply of bank loans. We control for any non-standard measures that are not already incorporated in reservable and non-reservable liabilities such as TAF in the US or capital injections adopted in both regions. Next, we look at the effectiveness of the non-standard measures in containing bank liquidity risk. Combining these two steps allows us to derive the effects of non-standard measures on bank loans by reducing market risks affecting banks' balance sheets.
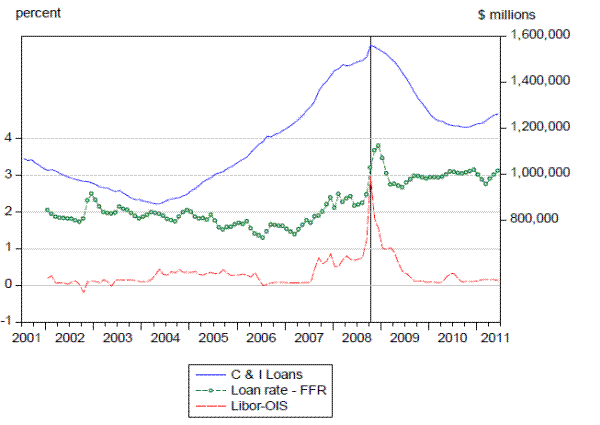
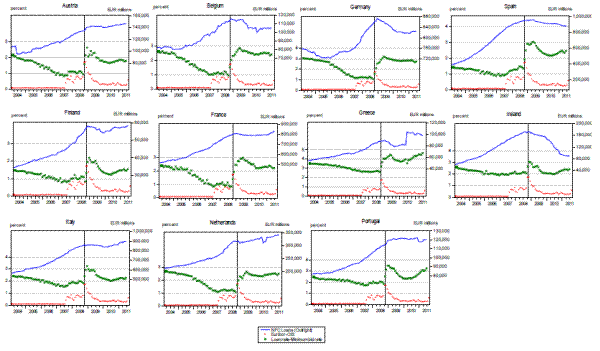
One of the most closely watched barometers of the financial crisis has been the Libor-OIS or Euribor-OIS spread. We will refer to both of these spreads as the "Ibor-OIS spread" in the remainder of this paper unless we need to refer to a specific one. A majority of the researchers attributed the increase in this spread to the elevated levels of market and/or liquidity risk (see e.g. Taylor and Williams, 2010, McAndrews et al., 2008, Eisenschmidt and Tapking, 2009, Wu, 2008, Carpenter et al., 2012). Hence, the crisis can be roughly represented by the Ibor-OIS spread and the effects of the crisis on bank loans can be analyzed by investigating the impact of the spread on bank loans. In this paper we focus on C&I loans for the US and loans to non-financial corporations (NFCs) in the euro area (EA). Both types of loans are outstanding loans.4
3.2 The relationship between market risk measures and bank loans
The Ibor-OIS spread is expected to affect the loan supply and loan demand in opposite ways. To the extent that an elevated spread reflects heightened liquidity and credit risks in the economy as a whole, banks would respond to a higher spread by restricting their supply of loans. A casual look
at the behavior of C&I loans in the US (Figure 1, solid line), as well as the NFC loans in the euro area (Figure 2, solid line) together with the spread (dashed line) supports this line of reasoning.5 Bank loans in both regions declined sharply following the peak of the crisis in October 2008 as indicated by the vertical line. The figures also plot the spread between the loan rate and the policy rate (the dotted line). The
policy rate is represented by the federal funds rate in the US and the minimum bid rate in the euro area.6![]() 7
7![]()
![]() The peak in bank loans around the same time as the peak in the Ibor-OIS spread suggests that the increase in bank loans was demand driven during that period, in
response to elevated risk factors. The subsequent peak in loan rates in the following months, however, suggests that the supply of loans declined in response to the elevated risk factors. All three series decline in the first half of 2009 suggesting that as the market risks stabilized demand for
bank loans tapered off. Further tightenings of the loan rate in 2010, long after the rate spread has stabilized, might be attributed to strengthening demand conditions both in the US and the euro area. Our estimation results are largely consistent with these arguments.
The peak in bank loans around the same time as the peak in the Ibor-OIS spread suggests that the increase in bank loans was demand driven during that period, in
response to elevated risk factors. The subsequent peak in loan rates in the following months, however, suggests that the supply of loans declined in response to the elevated risk factors. All three series decline in the first half of 2009 suggesting that as the market risks stabilized demand for
bank loans tapered off. Further tightenings of the loan rate in 2010, long after the rate spread has stabilized, might be attributed to strengthening demand conditions both in the US and the euro area. Our estimation results are largely consistent with these arguments.
3.3 Identifying demand and supply schedules for bank loans
The discussion above suggests a particular speed of adjustment of bank loans in response to shocks to measures of market risk. Note that following the height of the crisis in October 2008, the demand for loans reached its peak right away, while the contraction in loan suplly (as observed from the decline in loans as well as the increase in loan rates) took some time. We believe that this observed pattern reflects the nature of loan contracts. It is fairly easy for borrowers to tap their credit lines and receive funding immediately. Banks, on the other hand, consider their overall customer relationships and may need to redraft loan documents to make changes to lines of credit. Bernanke and Blinder (1992) note that loans are quasi-contractual commitments whose stock is difficult to change quickly. Hancock et al. (1995) also mention that banks adjust their portfolios with pronounced lags because of information imperfections and because of the costs of adjusting holdings of loans. As a result, borrowers would appear to be able to react more quickly than lenders to changes in the financial landscape, particularly in the case of committed lines of credit. Bernanke and Gertler (1995) state that an increase in C&I loans in the beginning of a slowdown is consistent with the bank lending channel so long as the demand for C&I loans increases more than the reduction in supply. Demand may increase as firms need to finance their inventory build-up when sales slow down unexpectedly. This is consistent with the claim that demand for loans adjusts quicker than supply for loans because otherwise banks would cut their lines in the beginning of the slowdown before they were drawn. In light of these arguments, in the empirical specification, we model loan supply to respond to the elevated risks with a lag while we model loan demand to respond contemporaneously, consistent with the observed behavior of bank loans during the crisis period.8 Note that we do not suggest that the real side of the economy tends to adjust more quickly than the financial side. Rather, in the narrow question of bank lending, especially lines of credit, we are assuming that borrowers can react more quickly than lenders because of the contractual framework.
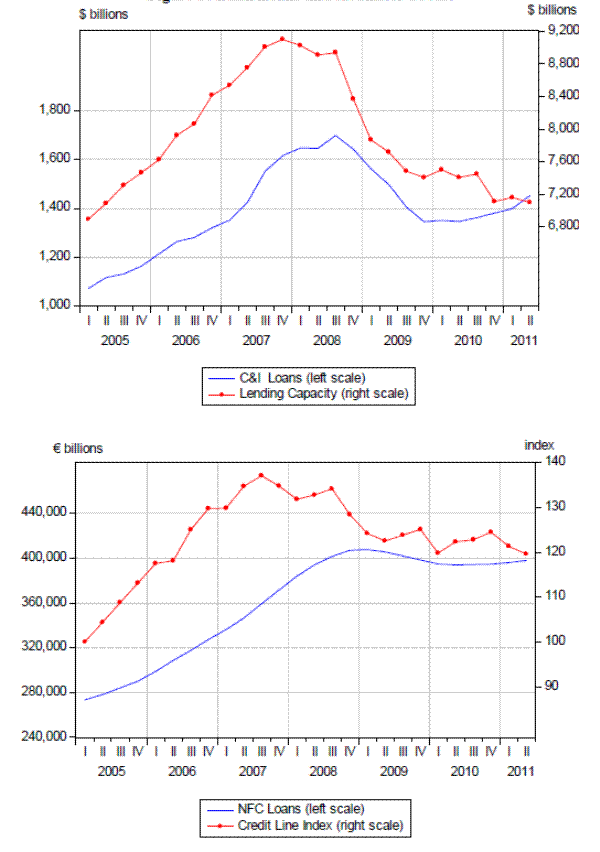
In order to support these claims, we plot total bank loans against total available credit for the US and the euro area in Figure 3.9 Total available credit is captured by the sum of total loans plus unused loan commitments in the US, denoted as the "lending capacity" in the upper panel. For the euro area, we use an aggregate index that reflects the available credit lines, as shown in the lower panel. Both of these measures are available at the quarterly frequency. In both regions, the peak in credit availability takes place around the third quarter of 2007. This suggests that banks started tightening their lines of credit right at the onset of the crisis. However, because of their loan commitments, they were not able to reduce their outstanding loans immediately, as total bank loans continued to increase while credit lines declined in the first three quarters of 2008. This figure is supportive of our speed of adjustment assumption that the supply of bank loans adjusts slower than the demand for bank loans.
3.4 Factors affecting the supply of bank loans
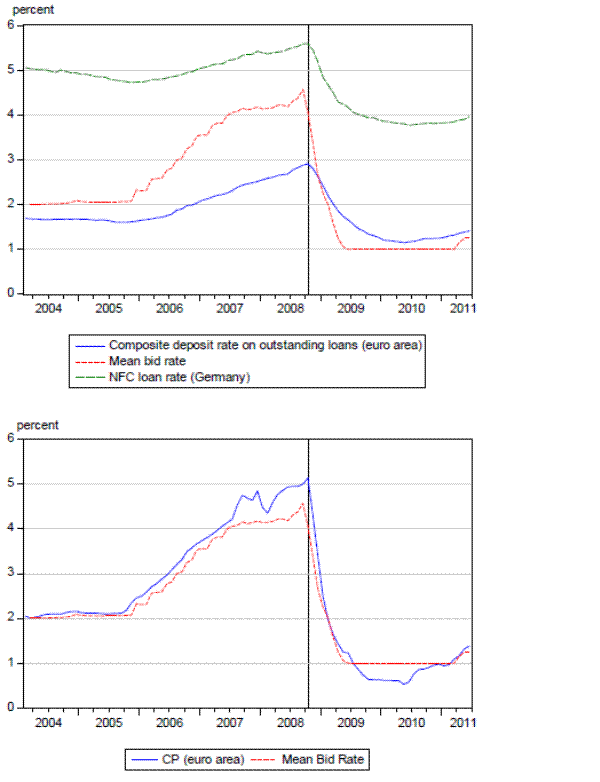
The spread between the loan rate and the policy rate that are plotted in Figures 1 and 2 can be loosely defined as the relative cost of bank lending. From the perspective of supply, the loan rate spread represents the net profit margin of bank loans after adjusting for the funding costs. Banks fund the bulk of their loans through managed liabilities (which do not have a reserve requirement) in the US and through reservable liabilities in the euro area. While the costs of bank funding in the US tracks the policy rate rather closely, the cost of bank funding in the euro area does not follow the policy rate as tightly. In order to illustrate this point, the upper panel in Figure 4 plots the rate on six-month CDs, which is a proxy for the cost of managed liabilities in the US, together with the federal funds rate and the rate on C&I loans. The CD rate and the federal funds rate likely move so closely together because both are marginal sources of funding for US banks. The fact that banks could shift from one to the other likely explains the very tight connection. An analogous figure for the euro area is provided in the upper panel of Figure 5 that shows the composite deposit rate on outstanding loans, which captures the cost of reservable liabilities, together with the mean bid rate, and the loan rate on outstanding NFC loans.10
Figure 4 shows that the CD rate follows the policy rate rather tightly. During the peak of the crisis, however, we observe a sharp upwards deviation in the CD rate from the funds rate. A milder yet more persistent increase in the deposit rate over the policy rate is also observed for the euro area after October 2008 in Figure 5. This divergence reflects the banks' difficulties in raising funds, and it can at least partly explain the elevated levels of the loan rates relative to the policy rates in the months following Lehman's bankruptcy.
Based on Figures 4 and 5, we use the loan rate spread over the federal funds rate in the US and the spread over the deposit rate in the euro area in our supply specification. The loan rate seems to follow the policy rate even better than the CD rate in the US, which justifies our choice. The differential treatment seems appropriate given the different banking systems. US banks rely on wholesale funding as a marginal source of funding whereas reservable deposits are more important in the euro area.
In this paper, we are interested in tracing the impact of various risk factors that affected bank loans during the crisis period. We expect the supply of bank loans to be a decreasing function of the borrowers' credit risk as well as the bank's liquidity risk. Furthermore, the credit risk of the lenders may also play a role by determining the ability of the banks in raising funds (see Acharya and Skeie, 2011, or Altunbas et al., 2009). Nevertheless, because the credit risk generally increases simultaneously for all parties during times of stress, it is very difficult to separate and empirically identify the credit risk of the borrowers from those of the lenders at the aggregate level. Rate spread can be used as a proxy for such risks although it has its shortcomings. In addition to not being the best measure to capture the borrowers' credit risk, there might be issues related to the potential endogeneity of the spread in the loan demand specification. We address these problems later on.
3.5 Factors affecting demand for bank loans
Turning to the demand side, it is reasonable to model the demand for bank loans as a function of the loan rate spread over the policy rate as well. A priori, one can expect the loan rate to hover around the policy rate due to competition between banks. Furthermore, one can view the policy rate to capture the costs of alternative funding of potential borrowers. Even in the euro area where the alternatives to bank funding are more limited, the loan rate spread can still be viewed as a measure of the relative cost of bank funding. For example, suppose that the policy rate declines but the loan rate remains constant. Even if the borrowers may have no alternative but to borrow from banks, the opportunity cost of getting a bank loan increases when the rest of market interest rates decline. Hence, demand will be negatively related to the loan rate spread even when the loan rate itself does not change. Another interpretation would be to think of the policy rate as a proxy for the interest income in the borrowers' portfolios. A decrease in policy rates, in the absence of a parallel decline in the loan rate reflects higher cost associated with bank loans now that the borrowers earn less from their own investments but need to pay a relatively higher rate on their debt. The lower panel in Figure 4 plots the rate of one such alternative form of borrowing, 3-month non-financial commercial paper rate in the US together with the funds rate. Similarly, the lower panel in Figure 5 shows the 3-month commercial paper rate in the euro area together with the minimum bid rate. The close resemblance between the CP rate and the policy rate in both regions supports our claim that the policy rate is a good proxy for alternative costs of borrowing.
We expect the demand for bank loans to respond to the rate spread in a positive way, in contrast to loan supply. Demand for bank loans should be a function of the liquidity risk of the borrowers as well as the liquidity risk of the lenders. Faced with elevated liquidity problems, borrowers are more likely to tap on previously established credit lines with their banks. Furthermore, as noted by Huang (2009), provision of credit through committed lines of credit is sensitive to the banks' own financial conditions. Huang argues that one reason why many borrowers tapped their credit lines after October 2008 could be because they were not sure that they could get these loans later. Based on this argument, we hypothesize that the banks' own liquidity risk should also be a relevant determinant of the demand for bank loans.
3.6 The econometric model
We specify the following model for bank loans:
Supply:11
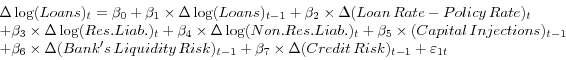
|
(1) |
Demand:
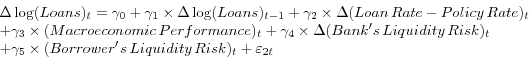
|
(2) |
where ? stands for the difference operator such that the dependent variable is the growth rate of bank loans, and t tracks the monthly observations.
In equation (1), reservable and non-reservable liabilities are aimed to capture the sources of funds for bank loans. According to the bank lending channel, reservable liabilities are the primary determinant of bank loans and should be positively related to loan supply. Carpenter and Demiralp
(2011) show that in the period after 1990, reservable liabilities are no longer a sufficient source to fund bank loans and non-reservable liabilities became the marginal source of funding bank loans in the US. We use the sum of managed liabilities and borrowings from TAF for the non-reservable
deposits in the US.12 Managed liabilities refer to deposits that can be increased or decreased at will, such as large, or wholesale, time deposits,
Eurodollar and other Eurocurrency borrowings, repos, and federal funds purchased to meet a bank's needs for funds to pay off maturing deposits and to fund new loans. For the US, we do not expect
![]() to be positive and significant but should be significant. In contrast, given the predominantly bank based intermediation on the euro area, is expected to be positive and
significant in this region.13
to be positive and significant but should be significant. In contrast, given the predominantly bank based intermediation on the euro area, is expected to be positive and
significant in this region.13
We also control for the effects of capital injections during the crisis period. These injections were provided through TARP in the US and through state capital injections in the euro area.14 With the ultimate goal of stimulating bank lending, these capital injections raised the capital-to-asset ratios in the banking system. We lag the amount of injections by one month because it is the level of the capital-to-asset ratio at the time of the origination of the loan that has to meet regulatory standards. The lagged structure also addresses the potential endogeneity between bank loans and capital injections. Bernanke and Lown (1990) note that changes in the capital-to-asset ratio might reflect anticipated changes in future activity. In that respect, capital injections might affect the loan supply in two ways. The theoretical literature is divided on the impact of bank capital on bank loans. On the one hand, a capital injection accelerates loan supply by strengthening the banks' capital positions on their balance sheets. Higher capital improves the bank's ability to absorb risk and hence higher capital ratios allow banks to create more liquidity (see e.g. Coval and Thakor, 2005). On the other hand, if an increase in bank capital signals a worse future economic environment, it may prompt banks to extend less loans. Bank capital might also impede liquidity creation because it makes the bank's capital structure less fragile (see e.g. Diamond and Rajan, 2000). The net impact of these two potential effects is indeterminate.
Studies that investigate the effectiveness of capital injections on loan issuance during the crisis periods are rare. Berrospide and Edge (2010) interpret the modest effect of capital on loan growth to be driven by weaker demand conditions that offset the impact of capital injected through
government actions. Alternatively, they note that conventional measures of capital might fail to assess banks' capital positions. Gambacorta and Marques-Ibanez (2011) reach a similar conclusion using the capital-to-asset ratio for the euro area. They note that the capital-to-asset ratio might not
properly capture the capital adequacy of banks or that accounting practices might have blurred the information content of the capital-to-asset ratio. When they use the Tier 1 ratio, they obtain significant results. Based on this discussion,
![]() can be either positive, or negative, or insignificant. Meanwhile we expect the measures of liquidity and credit risk ( and
can be either positive, or negative, or insignificant. Meanwhile we expect the measures of liquidity and credit risk ( and
![]() ) to be negative.
) to be negative.
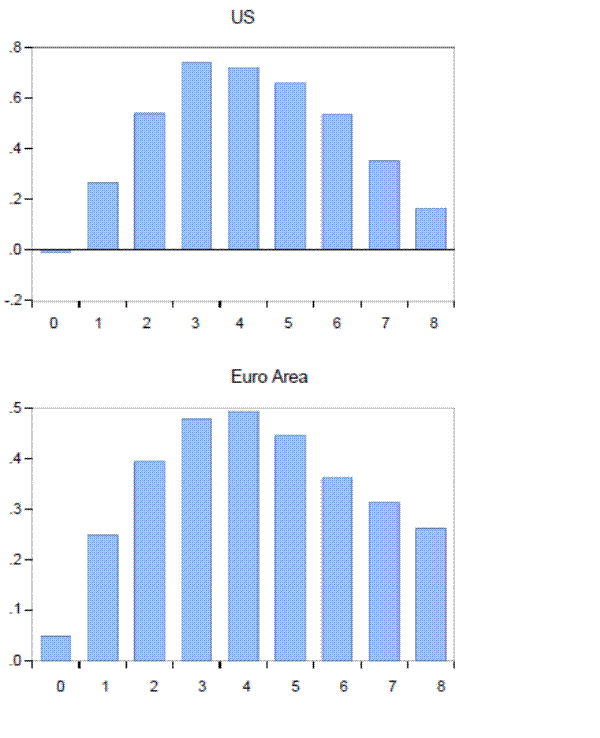
Turning to the demand side, we need to control for the impact of macroeconomic conditions on loan demand. The lagging pattern of NFC loans to business cycles is established as a stylized fact for the euro area (ECB, 2009). It is noted that the maximum correlation between loan growth and GDP growth is established when GDP growth lags loan growth by three quarters for the sample from 1980 to 2008. We replicate this analysis for both regions for our sample period, using industrial production index (IP) instead of GDP. Figure 6 shows the quarterly cross correlations between the growth rate of bank loans and growth rate of IP for the US and euro area respectively. The correlations are plotted for the contemporaneous value of IP growth as well as its eight lags as shown on the horizontal axis. Overall, the figure confirms the stylized facts highlighted in ECB (2009). The maximum correlation between bank loans and IP is established in the third quarter for the US and fourth quarter for the euro area. Based on this analysis, we construct the quarterly growth rate of IP and use a three-quarter lag (which corresponds to lag 9 at the monthly frequency) for the US and a four-quarter lag (which corresponds to lag 12 at the monthly frequency) for the euro area in the loan demand equation.
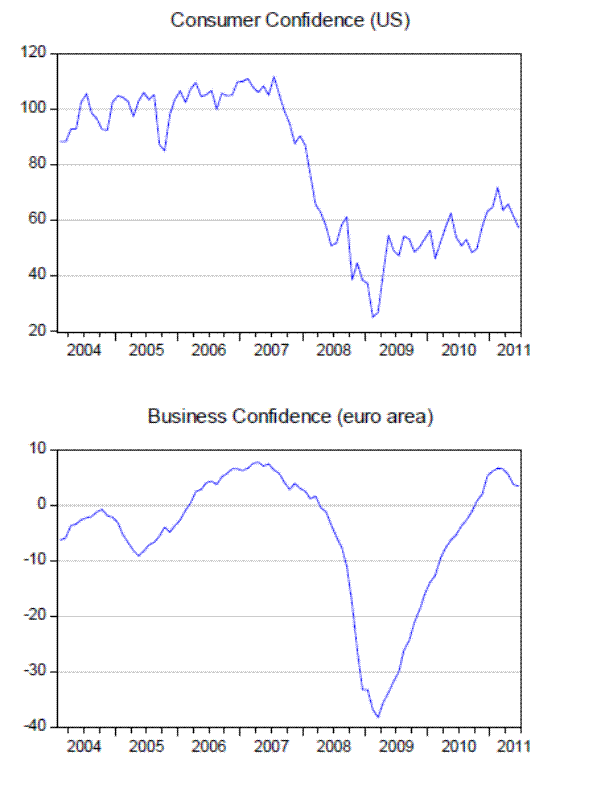
In addition to lagged IP growth, we add the changes in business confidence to the demand specification to capture any forward-looking changes in the economic outlook. Because the business confidence series is only available at the quarterly frequency for the US, we use the consumer confidence
index instead.15 Figure 7 shows the two confidence indexes for the two regions. The two indexes move surprisingly close to each other in the months prior to
the crisis and leading to Lehman's bankruptcy. While the euro area index recovers at a quicker rate, consumer confidence in US does not register a similar recovery. We expect the macroeconomic performance to affect loan demand positively (
![]()
![]() 0). In principle, the lender's and the borrower's liquidity risk
should also affect the loan demand positively (
0). In principle, the lender's and the borrower's liquidity risk
should also affect the loan demand positively (
![]()
![]() 0 and
0 and
![]()
![]() 0). Note, however, that these two types of liquidity risk can be
highly correlated and hence they may not both yield significant coefficient estimates when they are included in the regression simultaneously.
0). Note, however, that these two types of liquidity risk can be
highly correlated and hence they may not both yield significant coefficient estimates when they are included in the regression simultaneously.
3.7 Estimation results
3.7.1 Supply of bank loans
Our sample period spans from February 2004 through May 2011. Due to the endogenous nature of the loan rate, the model is estimated via TSLS. Tables 1a and 1b show the results from the supply and demand equations for the C&I loans in the US respectively. We follow the same structure for the euro area in Table 2 which shows the estimation results for loans to non-financial corporations. Because of the cross-sectional nature of the euro area data, we estimate a panel regression with fixed effects for this region. We have a long panel with over 80 observations and only ten countries, which does not justify the use of an Arellano and Bond (1991) type of estimator to address the dynamic structure.
Balance sheet variables are measured in millions of the respective currency. Growth rates are multiplied by 100 such that a 1-unit change corresponds to 1 percentage point. Interest rates, liquidity and credit risk measures are expressed in percentage points as well.
The first column in Table 1a shows the estimates from the loan supply equation in the US where the liquidity and the credit risks are captured by the Libor-OIS spread. Newey-West heteroskedasticity and autocorrelation consistent standard errors are reported. For the euro area, the first column in Table 2a uses the Euribor-OIS spread instead. Because of the small number of cross-sections, we do not cluster the errors around countries because cluster-robust estimators might be incorrect and misleading in that case. Instead, the reported standard errors control for White period heteroscedasticity and allow for a different residual variance for each period.
There is positive persistence in the growth rate of C&I loans as captured by the lagged dependent variable (Table 1a, column 1).16 The persistence is lower for the euro area (Table 2a, column 1). The price elasticity of loan supply is not significant for the US but it is significant for the euro area. Reservable liabilities are insignificant in the US consistent with Carpenter and Demiralp (2011).17 In order to control for the impact of TAF on bank loans, we add borrowings from TAF to managed liabilities in the loan supply equation. Managed liabilities are positive and significant, supporting the intuition in Carpenter and Demiralp (2011) that these liabilities constitute the marginal source of funding in the US. Turning to the euro area, reservable liabilities are positive and highly significant as expected. Indeed, the coefficient estimates of reservable liabilities for the euro area are comparable to coefficient estimates of managed liabilities in the US. Non-reservable liabilities are also marginally significant but the coefficient estimates are about half of those obtained by reservable liabilities. This is an anticipated finding which is an outcome of the differences in financial structures of the US and the euro area. The predominantly bank based intermediation in the euro area renders reservable liabilities of banks an important source of funding, as alternative funding markets play a relatively less important role than in the US.
For the US, capital injections through the TARP facility affect the supply of bank loans negatively, although the coefficient estimate is not economically significant. Specifically, an increase in TARP funding by $1 million, leads to a decline in C&I loans by much less than 1 percent. This finding suggests that TARP injections did not have the intended expansionary impact on bank loans, consistent with the findings in Bassett and Demiralp (2012) or the predictions of Diamond and Rajan (2000). Different from the US, capital injections are positive and highly significant across alternative specifications for the euro area, consistent with Coval and Thakor, 2005. Specifically, a €1 billion injection of capital leads to an approximately 0.02 percent increase in NFC loans. Consequently, our results suggest that total capital injections of approximately € 325 billion for our sample of euro area countries have boosted loan growth by a cumulative 6.5 percent.
The liquidity and credit risks as captured by the Ibor spread are not significant in either region. As it was noted earlier, the credit risk component of the Ibor-OIS spread only captures the credit risk of the lenders and not the borrowers. The second column considers a more direct measure of the borrower's credit risk and adds the median EDF of non-financial corporations to the specification. This variable is not statistically significant either. Collinearity between the Ibor-OIS spread and capital injections could be a plausible explanation for why the risk variables are not significant.18 In fact, when we remove capital injections from the specification, both the Libor-OIS spread as well as the median EDF become negative and significant (not shown). As a robustness check, we considered another credit risk measure based on the median 5-year CDS spreads of non-financial corporations. The credit risk measure was again not significant.19
Although the results that are reported in columns 1-2 are helpful and intuitive, they do not allow us to observe the individual effects of credit risk and liquidity risk on loan supply because the Ibor-OIS spread contains the liquidity as well as the credit risks of the lender. In order to disentangle these two types of risks and focus only on the liquidity risk rather than the credit risk of the lenders, we consider replacing the Ibor-OIS spread with alternative measures of liquidity risk for the banking system. To capture the liquidity risk in the bank funding market we use the daily volatility in overnight markets. In principle, bank funding volatility could be correlated with liquidity as well as credit risks in the money markets. It is plausible to think of the level of credit risk to increase with the dispersion of borrowing rates across participants in the money market which would in turn be correlated with volatility. In addition, volatility can be associated with large banks dumping reserves in the market at the end of the day. Carpenter, Demiralp, and Senyuz (2012) show that bank funding volatility is much closely correlated with alternative measures of liquidity risk relative to credit risk. In light of their findings, we use the average bank funding volatility in the previous 30 days for the US. For the euro area, we construct a similar measure based on intraday volatility in the bank funding market. "Offer volatility" is the standard deviation of the offered Eonia rate by all banks included in the panel on a given day. We take the average of this volatility over the previous 30 days to capture any persistence in risk. After controlling for the credit risk in the regression specification, the coefficient associated with volatility can be interpreted as the impact of liquidity risk in the loan supply equation.
Column three shows the results with the inclusion of bank funding volatility as a measure of liquidity risk. Liquidity risk is negative and highly significant. An increase in intraday volatility by one percent leads to a decline in bank loans by 3 ¾ percent in the US and by more than 2 ½ percent in the euro area. The finding of a negative and significant relationship between the supply of bank loans and bank liquidity risk in the euro area is consistent with the findings of Hempell and Sorensen (2010). Using the information in the bank lending survey for the euro area to identify supply and demand, Hempell and Sorensen (2010) document a significant negative impact of the bank's own liquidity conditions on loan growth during the crisis period.
The specification in column 3 does not control for the borrower's and the lender's credit risk individually because of the high correlation between these credit measures. While we only show the results using a measure for the credit risk of the borrowers, the results are almost identical if we use a measure for the lender's credit risk instead.20 Note also that price elasticity of supply is significant and positive in this specification for both regions, consistent with the theory. A one percent increase in the loan rate over the policy rate increases the supply of bank loans by more than 1 ½ percent in the US and by more than 4 percent in the euro area. An additional robustness check (displayed in Table 1a, column 4), that uses the loan rate in the euro area as an instrument for the loan rate in the US, is discussed in the appendix.
In Table 2a, column 4, we use the US Dollar/Euro swap spread as an additional measure of liquidity risk in the euro area. The swap spread can capture the Dollar funding needs of the European banks during the financial crisis. Nevertheless, the coefficient estimate is not statistically significant.
The last two rows in Tables 1a and 2a provide information on the instruments and their performance. Because of the endogeneity between bank loans and loan rates, we instrument for the loan rate in our estimation. Specifically, we need an instrument that captures changes in loan demand in the supply equation. As shown in the last row, the contemporaneous value of the Ibor-OIS spread is used as an instrument to capture changes in demand. The assumption is that the contemporaneous value of the Ibor-OIS spread affects the loan rate that is not due to changes in loan supply, consistent with the earlier discussion. We assume that loan supply conditions with respect to money market spreads are largely predetermined at the frequency that we examine. The instrument is highly significant in both regions in the first stage regression (not shown) and we reject the null hypothesis that the excluded instrument is not relevant, as indicated by the F-test. Because the specifications are just-identified, the validity of the instrument cannot be tested.
It should be noted that even though the results from any instrumental variable approach are subject to weak instruments problem, the endogeneity bias is only an issue for the coefficient of the loan rate, which is not our main focus in this paper. The remainder of the coefficient estimates are still reliable even if we do not have the perfect instruments. Indeed, if we estimate our supply specification via OLS (not shown), the significance and the magnitudes of the coefficient estimates associated with the exogenous variables are preserved, highlighting the validity of our economic inference, particularly for volatility in bank funding rates, which is our main variable of interest.
Overall, these findings grant support that our model of loan supply is plausible and robust to alternative specifications. The results underline the argument that bank loans are negatively related to liquidity risk. Therefore, to the extent that the non-standard measures are able to reduce the liquidity risk, they should stimulate loan supply.
3.7.2 Demand for bank loans
We now turn our attention to the demand specification. Recall that we hypothesized the demand for bank loans to be a function of the borrower's and the lender's liquidity risk. Furthermore, we argued that loan demand should respond to these risk measures contemporaneously. In column 1 in Tables 1b and 2b, the Ibor-OIS spread enters as an explanatory variable to capture such risks. The slope of the demand curve is negative and significant as expected.21
As we look at the variables that measure macroeconomic performance, the growth rate of lagged industrial production is positive and significant in both regions. If the industrial production index grows by one percent, the growth rate of bank loans increases by 10 basis points in the US and 4 basis points in the euro area over the course of the next year.
Changes in consumer confidence or business confidence are negatively related to bank loans. The negative coefficients associated with the confidence indexes in both regions is most likely driven by the dip in the fourth quarter of 2008 which is accompanied by the peak in bank loans (Figure 7).
Turning to the Ibor-OIS spread, the positive and significant coefficient suggests that demand for bank loans increases with increasing risk.22 This finding is consistent with the draw-downs of loan commitments that were observed around Lehman Brothers' bankruptcy. When faced with elevated liquidity pressures, borrowers are more likely to tap their credit lines to keep their balance sheets liquid.
In a specification where liquidity risk enters the loan equation contemporaneously, there might be an endogeneity bias because the liquidity risk of the lender bank might be affected from the amount of loans granted by the bank. This was not an issue in our supply specification because liquidity risk entered with a lag. In the demand specification, however, we need to be more cautious. One might argue that the liquidity risk of a bank might increase as that bank issues more loans. The greater the loans issued, the greater could be the likelihood and severity of losses associated with having to dispose illiquid assets to meet customers' liquidity demands (Allen and Santomero, 1998, Allen and Gale, 2004). We do not believe that this argument is strong enough to defeat the validity of the results that we have shown so far. Banks choose the maturity structure of both assets and liabilities. In the absence of active risk management, liquidity risk ultimately increases as a bank extends more and more long-term loans. This seems to be a rather strong assumption. Nevertheless we need to be aware of the consequences of a potential endogeneity problem and address it properly. In order to address this concern, we replace the Ibor-OIS spread with bank funding volatility measures in the second column as an instrument for the general liquidity risk of the lenders. Liquidity risk in the overnight market works as an instrument for the general liquidity risk. It is expected to be highly correlated with the general rollover risk faced by the bank but it is not likely to be affected from the bank's loan volume.23 Hence, it works as a good instrument in the demand specification. An increase in liquidity risk by one percent increases the demand for C&I loans by more than 6 ½ percent for the US and NFC loans by up to 1 percent in the euro area.24 For perspective, 1 percent increase in the level of C&I loans in the US corresponds to approximately $12 billion in loans, and a 1 percent increase in the level of outstanding loans in, say, Germany, corresponds to about € 8 billion in loans.
In order to control for the liquidity risk of the borrowers we use a measure for market tightness that is put forth by Gatev and Strahan (2006) as the spread between three-month commercial paper and the Treasury bill rate. For the euro area we use the difference between the three-month commercial paper rate and the composite government bond rate. As mentioned earlier, however, the lender's liquidity risk might be highly correlated with the borrower's liquidity risk, which may cause estimation problems. Indeed the simple correlation coefficient between the two measures is 0.84. When we include both types of liquidity risk in the specification, intraday volatility is significant whereas commercial paper spread is not (not shown). In order to deal with the collinearity problem, we enter the borrowers' liquidity risk measure separately in column 3. The measure of market liquidity is significant but smaller in size relative to bank's liquidity risk in the US, suggesting that it is the lender's liquidity risk rather than the borrower's liquidity risk that is the primary factor in determining the demand for bank loans. For the euro area, however, the coefficient associated with market liquidity risk is significantly higher than the lender's liquidity risk.
In order to address the endogeneity between loan demand and loan rates, this time we need an instrument to capture changes in loan supply. As shown by the last two rows of Tables 1b and 2b, the lagged value of bank funding volatility is used as an instrument to capture supply factors and it is highly relevant in both regions. This is consistent with column 3 in Tables 1a and 2a where lagged volatility is very significant in the supply equation. The F-tests confirm that the instrument is relevant. Once again, the specifications are just-identified. As in the case of loan supply, when we estimate the demand specification via OLS, the coefficient estimates of the exogenous variables remain intact, strengthening the validity of our conclusions even in the presence of weak instruments (not shown).
Before we conclude this section, we briefly discuss two remaining issues. First, our results are not immune from the Lucas (1976) critique. In particular, it could be the case that the changes to the framework for monetary policy implementation caused a change in market participants' behavior. That is to say, that our parameters of interest may not have remained stable over our sample period if economic agents internalized central bank policy. Although the relevance of this caveat may be limited in the beginning of the financial crisis and especially around the time of the collapse of Lehman Brothers, given the size of the shock and the novelty of policy response, over time agents may have learned and have adopted their behavior accordingly. In other words, our results are likely to be biased. While it is impossible to quantify this bias, we can at least try to check whether it matters qualitatively, i.e. whether it will change the sign of our coefficients. To this end, we estimated a reduced sample until April 2009, i.e. until the point in time the financial system started to recover and the worst fall-out from the Lehman collapse appeared to be over. We note that our results regarding the impact of (bank) liquidity risk on bank loans do not change in terms of either their signs or their significance. We consider this is as additional evidence for the robustness of our findings, although clearly the test is not definitive.
The second issue is regarding our treatment of the loan market as an equilibrium model. The simultaneous equations framework of the supply and demand for bank loans assumes market clearing whereas it is reasonable to think about the recent financial crisis to be associated with periods of market disequilibrium due to credit rationing or weak demand. Nevertheless, to the extent that the market is in equilibrium on average for the majority of the sample period, our equilibrium model would be justified. In order to check the reliability of this assumption, we estimated a disequilibrium model for bank loans for the two regions (see e.g. Fair and Jaffee, 1972; Maddala, 1986, Chen and Wang, 2008). The disequilibrium model assumes different distributions for supply and demand equations and produces coefficient estimates as well as excess demand probabilities as its output. When we plot these excess demand probabilities for the two regions, we observe that even though there are occasions where excess demand probabilities approached the upper bound, the majority of probabilities remain slightly below 50 percent, suggesting that the market clearing assumption that we have exploited is realistic for the most of the sample (not shown).25
4. Effects of Non-Standard Measures on Bank Loans
In the previous section, we illustrated the negative empirical link between bank liquidity risk and the supply of bank loans. Bank funding volatility worked as a good proxy for liquidity risk and yielded economically and statistically significant results. In this section we look into the effectiveness of the policy measures in reducing liquidity risk, and bank funding volatility in particular. There is a growing literature on the impacts of the policy measures in reducing bank liquidity risk. Connecting our work with the rest of the literature allows us to quantify the effects of the non-standard measures on bank loans.
4.1 Results for the US
Using the Libor-OIS spread as a proxy for the risk measures, Taylor and Williams (2009) detected no impact of the TAF in reducing the spread. They focused on the day of a TAF auction as well as the four subsequent days and controlled for the credit risk with the CDS spread of the Libor participating banks along with alternative credit risk measures such as the Libor-Tibor or Libor-Repo spreads. McAndrews et al. (2008) focused on the days of announcements as well as the operations of TAF auctions. Furthermore, they used the first difference of the Libor-OIS spread due to the non-stationary nature of the spread. Based on their findings, on the day of a TAF announcement or operation, the spread declined by 2 basis points. This gave a cumulative effect of 57 basis points. Wu (2008) proposed yet another specification to measure TAF effects. He argued that TAF would permanently reduce the liquidity risk affecting bank funding markets and specified a step function for the period after December 2007. He found that the TAF reduced the spread about 35 to 40 basis points on average but the TSLF was not effective.
Most of the studies cited above focused on the impact of non-standard measures at the daily frequency and used the Libor-OIS spread as a measure of risk. Because we conduct our analysis at the monthly frequency and because our focus is on the impact of non-standard measures on bank funding volatility, we make several adjustments. We take the specification in Taylor and Williams (2009) as our starting point. Because monthly frequency does not allow us detect the impact of each individual TAF announcement or operation, we use a dummy variable for the period in which TAF or TARP were effective. As the sample periods for TAF and TARP overlap for more than two-thirds of the period in which TAF was operational, we end up using one dummy variable for the TARP period to avoid collinearity. As a result, the TARP dummy summarizes any policy measure that contributed to lower rate spreads in the period after October 2008. This leaves us with equation (3):
|
|
(3) |
In equation 3, the Libor-OIS spread as well as the CDS spreads are measured in percentage points. The first column in Table 3 shows the estimation results of equation 3 for the full sample whereas the second column considers a narrower interval from 2007 through 2009. We estimate this shorter sample for both regions because the low volatility in the Ibor-OIS spread in the beginning and the end of our sample might cloud the true impact of non-standard measures on the spread. The results suggest that the Libor-OIS spread declined 59 basis points on average during the period from 2007 to 2009. This finding is very close to previous findings by McAndrews et al. (2008) or Wu (2008).
Our results in the previous section suggested that bank funding volatility works as a better proxy for bank liquidity risk in the loan supply equation. For this reason, our main focus in this section is the impact of non-standard measures on bank funding volatility. In columns 3 and 4, we replace the dependent variable in equation (3) with bank funding volatility, measured in percentage points. When we focus on the 2007-2009 sample, we observe that bank funding volatility is 17 basis points lower on average during this period. When we combine this finding with the results from the previous section, we reach the following conclusion: During the period from 2007 to 2009, non-standard policies in the US lowered bank funding volatility by 17 basis points per month, which corresponds to a cumulative decline of 6 ¼ percent over the course of 36 months relative to where the spread could have been in the absence of non-standard measures. Because a one percent decrease in volatility boosts the growth rate of bank loans by 3 ¾ percent (table 1b, column 3), our results suggest that the six percent decline in volatility due to non-standard measures increased bank loans by up to 23 percent (or $276 billion). We should note that this estimate is potentially an upper bound and the standard error bands around this estimation make it plausible to contemplate a more modest increase in bank loans due to the decline in volatility. Nevertheless, if we consider the sharp 22 percent decline in C&I loans from its peak in October 2008 to its through in October 2010 (see Figure 1), our estimated impact of non-standard measures look rather plausible and suggest that bank loans would have declined another 23 percentage points in the absence of policy measures.
4.2 Results for the euro area
The two studies that we have identified for the euro area both look at the interactions of the ECB and Fed policies in reducing the Libor-OIS and Euribor-OIS spreads. Frank and Hesse (2009) use a bivariate VAR model. In order to control for the non-standard measures, they use the days of TAF announcements and auctions for the US, and the dates of LTROs for the euro area. They find that on the day of the announcement the LTRO reduces the Euribor spread by 2.5 basis points. The cumulative effect of this finding on the spread can be calculated by multiplying the daily effect with the number of LTRO announcements in their sample, which gives 55 basis points (=2.522). Meanwhile, Kamps (2009) uses the ratio of the volume of recourse to the deposit facility over the sum of the required reserves and autonomous factors as the non-standard policy measure. In a cointegration framework, she finds that the non-standard measures reduce the Euribor spread permanently by 2.5 basis points and Libor spread by 3.4 basis points.
The studies that evaluate the effects of the non-standard measures on the Euribor-OIS spread do not incorporate the full set of bank based non-standard measures that was discussed in section 2. In particular, we include the deviation of reserve provision beyond benchmark or the switch to fixed-rate full allotment (FRFA) auctions in October 2008. In order to investigate the effectiveness of such measures we estimated the following specification for the euro area:
|
|
(4) |
In equation (4), the Euribor-OIS spread as well as the CDS spreads are measured in percentage points. We incorporate three non-standard measures in this specification. ![]() is the share
of long-term refinancing operations in total refinancing operations. Specifically, we define this ratio as (LTROs+SLTROs)/(LTROs+SLTROs+MRO) where LTRO refers to Long-Term Refinancing Operations (3-month maturity), SLTRO refers to Supplementary LTROs (maturities of 3 and 6 months), and MRO refers
to Main Refinancing Operations (1-week maturity). We can use this ratio as a legitimate instrument because the overall liquidity provision remained constant between August 2007 and September 2008.
is the share
of long-term refinancing operations in total refinancing operations. Specifically, we define this ratio as (LTROs+SLTROs)/(LTROs+SLTROs+MRO) where LTRO refers to Long-Term Refinancing Operations (3-month maturity), SLTRO refers to Supplementary LTROs (maturities of 3 and 6 months), and MRO refers
to Main Refinancing Operations (1-week maturity). We can use this ratio as a legitimate instrument because the overall liquidity provision remained constant between August 2007 and September 2008.
The remaining non-standard measures captured with equation (3) are
![]() , which is the amount of liquidity provision above benchmark (i.e. the strict needs of the banking system) in the first two weeks of the maintenance period (measured in €
billions) and
, which is the amount of liquidity provision above benchmark (i.e. the strict needs of the banking system) in the first two weeks of the maintenance period (measured in €
billions) and
![]() , which is a dummy variable that captures the FRFA period. Note that we measure the impact of the LTRO ratio and above benchmark liquidity provision only for the period before
October 2008 while they reflected the policy choices. With the switch to fixed rate full allotment policies in October 2008, the provision of liquidity was driven by demand and hence these two measures lost their meaning as policy controlled variables.
, which is a dummy variable that captures the FRFA period. Note that we measure the impact of the LTRO ratio and above benchmark liquidity provision only for the period before
October 2008 while they reflected the policy choices. With the switch to fixed rate full allotment policies in October 2008, the provision of liquidity was driven by demand and hence these two measures lost their meaning as policy controlled variables.
Equation (4) is estimated as a time series specification because most of the variables do not vary across countries, except for the LTRO ratio. For this variable, we construct the average LTRO ratio across the ten euro area countries included in our sample. The results from this specification
are provided in Table 4.26 The first column shows the estimation results for the full sample whereas the second column shows the results for the 2007-2009
sample. By focusing on the 2007-2009 interval, we may be better able to identify the impact of FRFA on the Euribor-OIS spread because the tranquil periods under FRFA regime in the post-2010 era are now removed from the analysis. Turning to the results from the later sample in column 2, the
estimation results suggest that LTRO ratio and the FRFA stand out as the significant policy measures through which the Euribor-OIS spread was reduced. Specifically, an increase in the LTRO ratio by one unit lowers the spread by 83 basis points. The LTRO ratio increased about 43 basis points from
0.27 in December 2006 to 0.7 in September 2008, prior to the switch to the FRFA regime. Combining this cumulative change with our coefficient estimate suggests a 35 basis points decline in the Euribor-OIS spread (=83![]() 0.43) which is in the ballpark of the estimate obtained by Frank and Hesse (2009). Meanwhile the FRFA period keeps the spread 59 basis point lower on average per month.
0.43) which is in the ballpark of the estimate obtained by Frank and Hesse (2009). Meanwhile the FRFA period keeps the spread 59 basis point lower on average per month.
Columns 3 and 4 show the impact of non-standard measures on offer volatility, which is our primary focus. Overall, it is observed that the impact of policy measures on bank funding volatility is much lower than their impact on the Euribor-OIS spread. This could be because of the pre-existing auction mechanism through which relatively large open market operations accessible to a wide set of counterparties and against a broad range of collateral were implemented in the euro area. Unlike in the US, many euro area banks obtain significant parts of their liquidity needs directly from the ECB, a feature which arguably has kept a lid on liquidity stress in a pre-emptive manner. Indeed, the design of the TAF resembles what was already in place in the euro area from the very start. For that reason, the need and the impact of non-standard policy measures, at least in the period immediately following the collapse of Lehman Brothers until the start of the sovereign debt crisis in May 2010 were noticeably lower in the euro area.
Our findings in Table 4 (column 4) suggest that an increase in the LTRO ratio by 1 unit leads to a 12 basis points decline in offer volatility. This suggests that the cumulative 43 basis points increase in the LTRO ratio led to a decline in bank funding volatility by about 5 basis points. As we
turn to the impact of FRFA, we observe that bank funding volatility is 5 basis points lower on average during the 2007-2009 period. This implies a cumulative decline of 1.65 percent over the 36 months from 2007-2009 (=0.05![]() 36). If we combine these results with the previous section, where a 1 percent increase in offer volatility is associated with an increase in the loan supply by 2 ½ percent, we conclude that non-standard measures in the euro area boosted the growth rate of
bank loans by up to 4 percent (=1.70
36). If we combine these results with the previous section, where a 1 percent increase in offer volatility is associated with an increase in the loan supply by 2 ½ percent, we conclude that non-standard measures in the euro area boosted the growth rate of
bank loans by up to 4 percent (=1.70![]() 2.35). This finding is somewhat higher than that obtained by Lenza et al. (2010) who found that non-standard measures adopted in the FRFA period
increased the growth rate of NFC loans by up to 2 ½ percent over the course of two years.
2.35). This finding is somewhat higher than that obtained by Lenza et al. (2010) who found that non-standard measures adopted in the FRFA period
increased the growth rate of NFC loans by up to 2 ½ percent over the course of two years.
5. Simulation Analysis
In this section, we calculate the dynamic implications of non-standard measures on bank loans using the model of supply and demand that was estimated in the previous section. We re-visit the supply and demand model from the previous section and simplify it as:
Supply:
|
|
(1)' |
Demand:
|
|
(2)' |
Setting supply equal to demand gives the following reduced form equation for bank loans:
|
|
where
![]() ,
,
![]() ,
,
![]() , and
, and
![]()
As we set the parameter estimates to those obtained in the previous section, we obtain the dynamic path for bank loans in response to changes in liquidity risk attributable to non-standard measures. For the simulations we use the results from the specification that uses bank funding volatility as a measure of bank liquidity risk.27 Table 5 shows the coefficient estimates for the reduced form. Note that the increase in loan demand due to higher volatility is higher than the decrease in loan supply in both regions, suggesting that the net initial impact of a decline in volatility should be contractionary for bank loans.
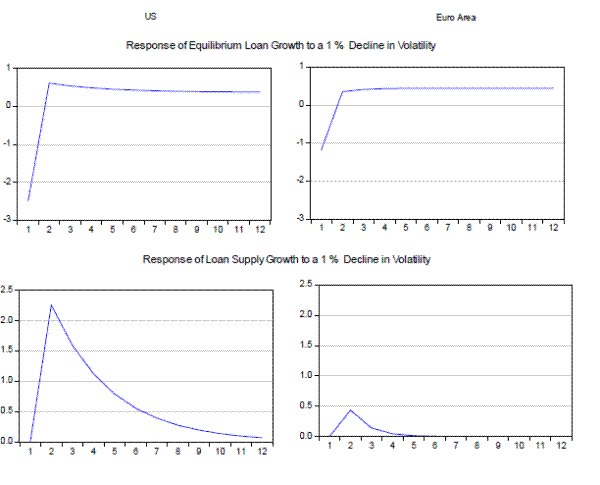
Figure 8 shows the results from the simulation exercise. The upper panels show the response of bank loans to a one percent decline in volatility for the US and euro area respectively. Consistent with our discussion of Table 5, we observe an initial decline in bank loans in both regions due to lower demand for bank loans which dominates the offsetting supply effect that kicks in in the second period. In the long run, there is a net positive impact on bank loans in both regions where the growth rate of bank loans is about 1/3 of a percentage point higher by the end of one year.
The lower panels in Figure 8 show the impact of a volatility shock on the supply of bank loans that is implicit in the upper panels. We observe that the decline in bank liquidity risk, as captured by one percent decline in bank funding volatility in the first period, leads to an increase in bank
loans through lagged volatility channel by up to 2 ½ percent in the US and ½ percent in the euro area in the second period. The estimated supply effect is lower for the euro area primarily because demand elasticity is lower in this region, which results in a lower coefficient
associated with lagged volatility (![]() ) in the reduced form as displayed in Table 5.
) in the reduced form as displayed in Table 5.
When the non-standard measures were introduced, they led to a decline in volatility. The simulation exercise suggests that the decline in volatility increased supply but also reduced demand for bank credit because the panic subdued and other sources of credit besides bank loans became available. Therefore, looking at the immediate decline in bank loans and concluding that bank loans declined due to non-standard policy would be the wrong conclusion which overlooks the impact of non-standard measures in calming the demand for liquidity driven by "animal spirits". Over time, the decline in volatility resulted in an increase in bank loans in both regions.
6. Conclusions
In response to the 2007 financial crisis, central banks around the world resorted to a variety of standard and non-standard measures. A growing number of studies assessed the effects of these measures, particularly focusing on the impact on the money markets. It remains difficult to know definitively how to identify the policy actions on market rates, in part because the counterfactual is impossible to know. Nevertheless, this paper attempts to further the discussion by focusing on the bank liquidity risk. Understanding the effect that the facilities had on money markets is not the complete story. Given the macroeconomic mandate of central banks, it is important to understand if the facilities, by easing conditions in money markets, resulted in greater extension of credit to the real side of the economy. Studying that linkage is the main contribution of this paper.
We attempt to contribute to the literature by providing a comparative analysis of the experiences of the Fed and the ECB. In particular, we are interested in what effects the bank based non-standard measures had on bank lending in their respective regions. In order to answer this question we take a two-step approach. First, we investigate the relationship between bank liquidity risk and bank loans using a simultaneous equation framework, controlling for bank recapitalization measures, allowing us to separately model loan demand and supply. Second, we estimate the effects of bank based non-standard measures on bank liquidity risk. We find strong evidence that the bank based non-standard measures adopted by Fed and ECB eased conditions in money markets and that those easier conditions resulted in an increase in business lending by banks. The results appear to hold in both the US and the euro area. The estimated impact of non-standard measures on bank loans is substantially larger in the US. Without the TARP and any other measures adopted during that period, C&I loans would have been lower by 23 percent, while without the FRFA and the increased LTRO share in the euro area, NFC loans would be 4 percent less. As we discussed earlier in the paper, the Federal Reserve made a relatively large change to its operational framework with the introduction of the TAF, whereas the changes that the ECB made in the overall framework may be seen as relatively minor in the early stages of the crisis. In addition, the more comprehensive recapitalization of US banks may also play a role in explaining the significant difference in the effectiveness of the non-standard measures of either side of the Atlantic.
References
Acharya, V., and Skeie, D., 2011. A Model of Liquidity Hoarding and Term Premia in Inter-bank Markets, Journal of Monetary Economics 58, 436-447.
Allen, F., and Gale. D., 2004. Financial Intermediaries and Markets. Econometrica 72, 1023 -61.
Allen, F., and Santomero, A. M., 1998. The Theory of Financial Intermediation. Journal of Banking and Finance 21, 1461-85.
Altunbas, Y., Gambacorta, L., and Marquez-Ibanez, D., 2009. Bank Risk and Monetary Policy, European Central Bank Working Paper Series No: 1075.
Arellano, M., and Bond, S., 1991. Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations, Review of Economic Studies 58, 277-97.
Bassett, W., and Demiralp, S., 2012. Did Government Support of Banks Boost Lending, Board of Governors of the Federal Reserve System, unpublished manuscript.
Bernanke, B., and Blinder, A., 1992. The Federal Funds Rate and the Channels of Monetary Transmission. American Economic Review 82(4): 901-921.
Bernanke, B., and Gertler, M., 1995. Inside the Black Box: The Credit Channel of Monetary Policy Transmission, Journal of Economic Perspectives 9(4), 27-48.
Bernanke, B., and Lown, C., 1991. The Credit Crunch, Brookings Papers on Economic Activity, 205-247.
Berrospide, J., and Edge, R., 2010. The Effects of Bank Capital on Lending: What do We Know, and What Does It Mean?, International Journal of Central Banking 6(4): 5-54.
Black, L., and Hazelwood, L, 2012. The Effect of TARP on Bank Risk-Taking, Board of Governors of the Federal Reserve System, International Finance Discussion Paper 1043.
Carpenter S., and Demiralp, S., 2008. The Liquidity Effect at the Federal Funds Market: Evidence at the Monthly Frequency, Journal of Money, Credit, and Banking, 40: 1-24.
Carpenter, S., and Demiralp, S., 2011. Money, Reserves, and the Transmission of Monetary Policy: Does the Money Multiplier Exist?, Journal of Macroeconomics, forthcoming.
Carpenter, S., Demiralp, S., Senyuz, Z., 2012. Money Market Dynamics and the Role of Federal Funds Rate Volatility during the 2007-2009 Financial Crisis, unpublished manuscript, Federal Reserve Board.
Chen, N.K., and Wang, H.J., 2008. Identifying the Demand and Supply Effects of Financial Crises on Bank Credit--Evidence from Taiwan, Southern Economic Journal 75, 26-49.
Coval, J. and Thakor, A., 2005. Financial Intermediation as a Beliefs-bridge between Optimists and Pessimists, Journal of Financial Economics 75, 535-569.
Diamond, D. and Rajan, R., 2000. A Theory of Bank Capital, Journal of Finance 55, 2431-2465.
European Central Bank Monthly Bulletin, October 2009.
Eisenschimdt, J., and Tapking,J., 2009. Liquidity Risk Premia in Unsecured Interbank Money Markets, European Central Bank Working Paper No: 1025.
Fahr, S., Motto, R., Rostagno, M., Smets, F., and Tristani, O., 2011. A Monetary Policy Strategy in Good and Bad Times: Lessons from the Recent Past, European Central Bank Working Paper No: 1336.
Fair, R.C., and Jaffee., D.M., 1972, Methods of Estimation for Markets in Disequilibrium, Econometrica 40, 497-514.
Frank, N., and Hesse, H., 2009. The Effectiveness of Central Bank Interventions During the First Phase of the Subprime Crisis, IMF Working Paper No: 206.
Gambacorta, L., and Marquez-Ibanez, D., 2011. The Bank Lending Channel: Lessons from the Crisis, European Central Bank Working Paper No: 1335.
Gatev, E., and Strahan, P., 2006. Banks' Advantage in Hedging Liquidity Risk: Theory and Evidence from the Commercial Paper Market, Journal of Finance 61,867-892.
Gerali, A., Neri, S., Sessa, L., and Signoretti, F., 2010. Credit and Banking in a DSGE Model for the Euro Area, Bank of Italy Working Paper No: 740.
Hancock, D., Laing, A., and Wilcox, J., 1995. Bank Capital Shocks: Dynamic
Effects on Securities, Loans, and Capital, Journal of Banking and Finance, 19: 661-677.
Hempbell, H.S., and Sorensen, C.K., 2010. The Impact of Supply Constraints on Bank Lending in the Euro Area: Crisis Induced Crunching?, European Central Bank Working Paper Series No: 1262.
Huang, R., 2009. How Committed Are Bank Lines of Credit? Evidence from the Subprime Mortgage Crisis, Federal Reserve Bank of Philadelphia, unpublished manuscript.
Kamps, A., 2009. What Drives International Money Market Rates? Lessons from a Cointegration VAR Approach, European Central Bank, unpublished manuscript.
Lenza, M., Pill, H., and Reichlin, L., 2010. Orthodox and Heterodox Monetary Policies, Economic Policy, 296-339.
Lucas, R.E. (1976). Econometric policy evaluation: A critique, in Brunner, K., Meltzer, A., The Phillips Curve and Labor Markets, Carnegie-Rochester Series on Public Policy, 1, 19-46.
Maddala, G.S., 1986, Limited dependent and Qualitative Variables in Econometrics, New York: Cambridge University Press.
McAndrews, J., Sarkar, A., and Wang, Z., 2008. The Effect of the Term Auction Facility on the London Inter-Bank Offered Rate, Federal Reserve Bank of New York Staff report, no.335
Neven, D., and Roller, L., 1997. An Aggregate Structural Model of Competition in the European Banking Industry, unpublished manuscript.
Puddu, S., and Waelchli, A., 2012. TAF Effect on Liquidity Risk Exposure, University of Lausanne, unpublished manuscript.
Taylor, J., and Williams,J., 2009. A Black Swan in the Money Market, American Economic Journal: Macroeconomics 1(1), 58-83.
Wu, T., 2008. On the Effectiveness of the Federal Reserve's New Liquidity Facilities, Federal Reserve Bank of Dallas Working Paper 0808.
The vertical line corresponds to October 2008.
The vertical line corresponds to October 2008.
The vertical line corresponds to October 2008.
The vertical line corresponds to October 2008.
The vertical line corresponds to October 2008.
The deposit rate is a weighted average of the deposits rates on outstanding amounts placed by NFCs. The deposit shares are from BSI statistic.
Correlations for lags 2-7 are statistically significant for the US while correlations for lags 3-5 are significant for the euro area at 95 percent level of confidence.
Table 1a: Supply of C&I Loans in the US (2004.02-2011.05) Dependent variable:Dlog(Loans)tNumber of observations: 88
| I | II | III | IV | |
|---|---|---|---|---|
| 1. Variable Constant | 0.09 | 0.09 | 0.08 | 0.07 |
| Variable Constant standard error | -1.25 | -1.18 | -1.16 | 1.18 |
| 2. variable Dlog(Loans)t-1 | 0.67** | 0.67** | 0.70** | 0.68** |
| variable Dlog(Loans)t-1 standard error | -8.07 | -7.7 | -8.2 | 9.83 |
| 3.variable D(Loan rate t-FFRt) | 1.49 | 1.73* | 1.65* | -0.07 |
| variable D(Loan rate t-FFRt) | -1.58 | -1.67 | -1.64 | -0.23 |
| 4. variable Dlog (Res.Liab.)t | -0.04 | -0.05 | -0.05 | -0.02 |
| variable Dlog (Res.Liab.)tstandard error | (-0.88) | (-0.97) | (-1.16) | -0.54 |
| 5. variable Dlog(Managed Liab.+TAF)t | 0.17** | 0.17** | 0.17** | 0.21** |
| variable Dlog(Managed Liab.+TAF)t standard error | -3.55 | -3.41 | -3.53 | 5.96 |
| 6. variable (Capital Injections)t-1 | -2.5×E-05** | -2.3×E-05** | -2.6×E-05** | -2.2×E-05** |
| variable (Capital Injections)t-1 standard error | (-3.72) | (-3.13) | (-3.62) | -4.5 |
| 7. variable D(Spread)t-1 | -0.6 | -0.66 | -- | -- |
| variable D(Spread)t-1 standard error | (-1.43) | (-1.43) | ||
| 8. variable D(IntradayVolatility)t-1 | -- | -- | -3.73** | -2.42** |
| 9. variable D(EDF_NFC)t-1 | -- | -10.09 | -12.62 | -5.34 |
| variable D(EDF_NFC)t-1 standard error | (-1.10) | (-1.39) | -0.69 | |
| 10. variable F-test of excluded instruments (p-value) | 16.07 | 16.34 | 17.52 | -- |
| variable F-test of excluded instruments (p-value) standard error | 0 | 0 | 0 | |
| 11. variable Instrument Used | -- |
The loan rate is the rate on outstanding C&I loans (obtained from STBL) in the TSLS specifications (columns 1-5), and the rate on outstanding NFC loans in Germany in the last column. t-statistics based on Newey-West heteroskedasticity-and au tocorrelation consistent standard errors are provided under the coefficient estimates. **/* indicates signifi cance at 95/90 percent level of confidence respectively. The model is just-identified.
Table 1b: Demand for C&I Loans in the US (2004.02-2011.05) Dependent variable: Dlog(Loans)t Number of observations:88
| I | II | III | |
|---|---|---|---|
| 1. Constant | 0.15** | 0.16** | 0.15** |
| variable Constant standard error | -2.97 | -2.62 | -2.07 |
| 2. variable Dlog(Loans)t-1 | 0.71** | 0.72** | 0.67** |
| variable Dlog(Loans)t-1 standard error | -9.18 | -8.37 | -7.32 |
| 3. variable D(Loan ratet-FFRt) | -1.64** | -2.54** | -2.39 |
| variable D(Loan ratet-FFRt) standard error | (-2.57) | (-2.73) | (-1.51) |
| 4. variable Dlog(IP)t-9 | 0.11** | 0.12** | 0.15** |
| variable Dlog(IP)t-9 standard error | -2.49 | -2.41 | -2.79 |
| 5. variable D(Consumer Conf.)t | -0.01 | -0.02* | -0.03 |
| variable D(Consumer Conf.)t standard error | (-0.95) | (-1.88) | (-1.40) |
| 6.variable D(Spread)t | 1.78** | -- | -- |
| variable D(Spread)t standard error | -7.11 | ||
| 7. variable D(IntradayVolatility)t | -- | 6.61** | -- |
| variable D(IntradayVolatility)t standard error | -5.52 | ||
| 8. variable D(CPnf-TBill)t | -- | -- | 1.44** |
| variable variable D(CPnf-TBill)t standard error | -2 | ||
| 9. variable F-test of excluded instruments (p-value) | 10.95 | 11.72 | 12.4 |
| variable F-test of excluded instruments (p-value) standard error | 0.00 | 0.00 | 0.00 |
| 10. variable Instrument Used | D(IntradayVolatility)t-1 |
The loan rate is the rate on outsta nding C&I loans (obtained from STBL). t-statistics based on Newey-West heteroskedasticity-and au tocorrelation consistent standard errors are provided under the coefficient estimates. **/* indicates signifi cance at 95/90 percent level of confidence respectively. The model is just-identified.
Table 2a: Supply of NFC Loans in the Euro Area (2004.02-2011.05) Dependent variable: Dlog(Loans)tNumber of periods: 86 Number of cross sections: 9 Fixed-Effects Model
| I | II | III | IV | IV | |
|---|---|---|---|---|---|
| 1. variable Constant | 0.21** | 0.21** | 0.22** | 0.21** | 0.21** |
| variable constant standard error | -3.74 | -3.72 | -3.83 | -3.63 | -3.63 |
| 2. variable Dlog(Loans)t-1 | 0.29** | 0.29** | 0.29** | 0.29** | 0.29** |
| variable Dlog(Loans)t-1 standard error | -2.07 | -2.06 | -2.06 | -2.08 | -2.08 |
| 3. variable D(Loanratet-Dep.ratet) | 3.85** | 3.85** | 4.37** | 4.22** | 4.22** |
| variable D(Loanratet-Dep.ratet) standard error | -4.02 | -4.05 | -4.66 | -2.39 | -2.39 |
| 4. variable Dlog(Res.Liab.)t | 0.16** | 0.16** | 0.17** | 0.16** | 0.16** |
| variable Dlog(Res.Liab.)t standard error | -3.68 | -3.69 | -3.87 | -3.74 | -3.74 |
| 5. variable Dlog(NonRes.Liab.)t | 0.08* | 0.08* | 0.08* | 0.08* | 0.08* |
| variable Dlog(NonRes.Liab.)t standard error | -1.85 | -1.85 | -1.79 | -1.82 | -1.82 |
| 6. variable (CapitalInjections)t-1 | 0.02** | 0.02** | 0.02** | 0.02** | 0.02** |
| variable (CapitalInjections)t-1 standard error | -3.63 | -3.88 | -2.96 | -2.48 | -2.48 |
| 7. variable D(Spread)t-1 | 0.19 | 0.17 | -- | -- | -- |
| variable D(Spread)t-1 standard error | -0.85 | -0.66 | |||
| 8.variable D(OfferVolatility)t-1 | -- | -- | -2.35* | -- | -- |
| variable D(OfferVolatility)t-1 standard error | (-1.69) | ||||
| 9. variable D(Swap Spread)t-1 | -- | -- | -- | -0.05 | -0.05 |
| variable D(Swap Spread)t-1 standard error | -0.09 | -0.09 | |||
| 10. variable D(EDF_NFC)t-1 | -- | 0.11 | 0.28 | 0.22 | 0.22 |
| variable variable D(EDF_NFC)t-1standard error | -0.25 | -0.63 | 0.41 | 0.41 | |
| 11.variable F-test of excluded instruments p value | 27.35 | 29.42 | 34 | 15.11 | 15.11 |
| variable F-test of excluded instruments p value standard error | 0 | 0 | 0 | 0 | 0 |
| 12. variable Instrument Used |
t-statistics based on White period standard errors are pr ovided under the coefficien t estimates. **/* indicates significance at 95/90 percent level of confidence respectively. The model is just-identified
Table 2b: Demand for NFC Loans in the Euro Area (2004.02-2011.05) Dependent variable: Dlog(Loans)tNumber of periods: 86 Number of cross sections: 9 Fixed-Effects Model
| I | II | III | |
|---|---|---|---|
| 1. variable Constant | 0.32** | 0.32** | 0.32** |
| variable standard error | -3.86 | -3.84 | -3.81 |
| 2. variable Dlog(Loans)t-1 | 0.33* | 0.33** | 0.33** |
| variable Dlog(Loans)t-1 standard error | -1.92 | -1.94 | -1.95 |
| 3. variable D(Loanratet-MinBid.t) | -1.14** | -0.99** | -0.67 |
| variable D(Loanratet-MinBid.t) standard error | (-2.33) | (-1.94) | (-1.44) |
| 4. variable Dlog(IP)t-12 | 0.04** | 0.04* | 0.04* |
| variable Dlog(IP)t-12 standard error | -1.94 | -1.69 | -1.88 |
| 5. variable D(BusinessConf.)t | -0.07** | -0.07** | -0.06* |
| variable D(BusinessConf.)t standard error | (-2.14) | (-2.44) | (-1.86) |
| 6. variable D(Spread)t | 0.93** | -- | -- |
| variable D(Spread)t standard error | -3.09 | ||
| 7. variable D(Offer Volatility)t | -- | 1.81 | -- |
| variable D(Offer Volatility)t standard error | -1.05 | ||
| 8. variable D(CPt-Gov.Bondt) | -- | -- | 0.46** |
| variable D(CPt-Gov.Bondt) standard error | -2.93 | ||
| 9. variable F-test of excluded instruments (p-value) | 179.2 | 167.19 | 182.47 |
| variable F-test of excluded instruments (p-value) standard error | 0 | 0 | 0 |
| 10. variable Instrument Used | D(OfferVolatility)t-1 |
t-statistics based on White period standard errors are pr ovided under the coefficien t estimates. **/* indicates significance at 95/90 percent level of confidence respectively. The model is just-identified.
Table 3: Policy Effectiveness in the US
| I .(spread)t 2004.02-2011.05 | II. (spread)t 2007.01-2009.12 | III. (Intraday Volatility)t 2004.02-2011.05 | IV. (Intraday Volatility)t2007.01-2009.12 | |
|---|---|---|---|---|
| 1.variable Constant | 0.04 | -0.01 | 0.02** | 0.05** |
| variable standard error | -1.41 | (-0.13) | -3.1 | -2.19 |
| 2. variable (Spread)t-1 | 0.63** | 0.62** | 0.58** | 0.53** |
| variable (Spread)t-1 standard error | -15.24 | -12.2 | -8.99 | -12.12 |
| 3. variable (CDS)t | 0.53** | 0.61** | 0.12** | 0.12** |
| variable (CDS)t standard error | -2.43 | -2.34 | -2.36 | -2.13 |
| 6. variable Dt-1TARP | -0.53** | -0.59** | -0.14** | -0.17** |
| variable Dt-1TARP standard error | (-2.49) | (-2.26) | (-2.79) | (-3.19) |
| 7. R2 | 0.79 | 0.75 | 0.74 | 0.67 |
| 8. Number of observations | 88 | 36 | 88 | 36 |
t-statistics based on Newey-West heteroskedasticity-and autoco rrelation consistent standard errors under coefficient estimates.**/* indicates significance at 95/90 percent level of confidence respectively.
Table 4: Policy Effectiveness in the Euro Area
| Variable | I. (Spread)t2004.02-2011.05 | II. (Spread)t2007.01-2009.12 | III. (OfferVolatility)t2004.02-2011.05 | IV. (OfferVolatility)t2007.01-2009.12 |
|---|---|---|---|---|
| 1.variable Constant | 0.09 | 0.25* | 0.02** | 0.04** |
| variable standard error | -0.84 | -1.93 | -2.17 | -3.33 |
| 2. variable (Spread)t-1 | 0.94** | 0.64** | 0.81** | 0.62** |
| variable (Spread)t-1 standard error | -12.08 | -4.52 | -6.44 | -3.89 |
| 3. variable (CDS)t | 0.002* | 0.01** | 0 | 0.0003** |
| variable (CDS)t standard error | -1.87 | -3.02 | -1.39 | -2.61 |
| 4. variable (AboveBM)t-1×(1-DtFRFA | 0 | 0 | 0.0003* | 0 |
| variable (AboveBM)t-1×(1-DtFRFA standard error | (-1.13) | (-0.63) | -1.9 | -1.53 |
| 5. variable (LTRO/TRO)t-1×(1-DtFRFA) | -0.37 | -0.83** | -0.07* | -0.12** |
| variable (LTRO/TRO)t-1×(1-DtFRFA) standard error | (-0.80) | (-2.18) | (-1.77) | (-4.07) |
| 6. variable Dt-1FRFA | -0.41 | -0.59** | -0.03 | -0.05** |
| variable Dt-1FRFA standard error | (-1.46) | (-3.22) | (-1.02) | (-2.47) |
| 7. R2 | 0.9 | 0.89 | 0.87 | 0.79 |
| 8. variable Number of observations | 86 | 36 | 86 | 36 |
t-statistics based on Newey-West heteroskedasticity-and autoco rrelation consistent standard errors under coefficient estimates.**/* indicates significance at 95/90 percent level of confidence respectively.
Table 5: Reduced Form Estimates
| US | Euro Area | |
|---|---|---|
| φ0 | 0.11 | 0.3 |
| φ1 | 0.7 | 0.32 |
| φ2 | 2.6 | 1.48 |
| φ3 | -2.26 | -0.43 |
Appendix: Further Robustness Checks
The model for bank loans that we have described with equations (1) and (2) is a simultaneous equations model. The main econometric problem with this model is the endogenous nature of the loan rate. In order to address this problem we used the pre-determined and exogenous variables in the supply equation as instruments in the demand equation and vice versa. An alternative way to estimate this model might be to exploit the cross-sectional dimension of our study. In particular, one might argue that the supply of bank loans exceeds national boundaries due to the existence of large banks with world-wide presence while the demand for bank loans is more local. As a result, one can use the loan rates in euro area as an instrument for the endogenous loan rate in the US (and vice versa). The two loan rates are expected to be correlated from the perspective of supply but likely exogenous for demand.28
Because we are primarily interested in how the new instruments affect the supply specification, we only report the results for loan supply. The last column in Table 1a shows the results from the least squares estimation where the loan rate in Germany is used as an instrument for the C&I loan rate. While the interest rate itself is not significant, the results regarding the negative impact of the liquidity risk on the loan supply is robust to this alternative specification. A similar exercise for the euro area does not yield significant results (not shown).