Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-35 Screen Reader version ^♣

Duration Risk versus Local Supply Channel in Treasury Yields: Evidence from the Federal Reserve's Asset Purchase Announcements

Michael E. Cahill, Stefania D'Amico, Canlin Li and John S. Sears^a

First draft November 9, 2012; This draft April 23, 2013

ABSTRACT

The FOMC's announcements of Treasury purchase programs and the subsequent or contemporaneous statements by the New York Fed about the programs' operational details provide a sequence of natural experiments with the potential to shed light on the relative importance of the duration risk channel versus the local supply channel for the transmission of supply effects to the term structure of interest rates. Using intraday security-level data on Treasury securities, we conduct five event studies to document the presence of local supply effects and duration risk effects. Further, using our new measures of local supply surprise and duration risk surprise we quantify the average impact of these two supply channels on nominal Treasury yields for each of the five events. Finally, we also try to determine how the importance of these factors has changed over time and relative to the first Large Scale Asset Purchase program in 2008-09. We find that: first, once the pre-announcement market expectations are carefully controlled for, the duration risk and local supply channels together are responsible for a decline in yields averaging about 9 basis points per $100 billion over the course of these announcements; second, these two channels are almost equally important for the transmission mechanism of purchases, as on average each of these channels accounts for about half of the yields decline; third, the efficacy of these two channels does not seem to have declined over time; and fourth, the purchase and sale price reactions to the announcements are quite similar, a result potentially relevant for the unwinding of these programs.

Keywords: Yield curve, quantitative easing, LSAP, preferred habitat, limits of arbitrage

JEL Codes: E43, E52, E58, E65, G12, G14

Introduction

In the most recent literature on the different channels through which central banks' Treasury purchase programs affect interest rates (see for example, Krishnamurthy and Vissing-Jorgensen (2011), D'Amico, English, Lopez-Salido and Nelson (2012), Benerjee, Latto, McLaren and Daros (2012), and Li and Wei (2013)), two channels emerge as most likely: duration risk and local supply/scarcity effects.¹ It is important to identify the channels through which the Federal Reserve's balance sheet policy accommodation works, as well as understand the factors that drive these channels, for two reasons. First, it is crucial for the calibration of these policies and their eventual unwinding. A better understanding of the channels can allow the Fed to maximize or minimize the impact of purchases and/or sales on Treasury yields, depending on the stance of monetary policy. Second, determining the relative importance of these supply channels across multiple purchase programs over time sheds light on whether these channels are always operating or are exceptional mechanisms prompted by the disruption of normal market functioning, and therefore it is instrumental to comprehend how their efficacy has evolved over time.

Using a new dataset and a new identification procedure, we first attempt, for each purchase program, to disentangle the local supply effect from the duration risk effect and show that the location of the supply shocks matters on top of the total duration risk removed from the market. Next, we quantify the relative importance of these two channels for the transmission mechanism of this monetary policy tool. Finally, we show how the local supply and duration risk channels have continued to drive the impact of the Fed asset purchase programs on Treasury yields over time, during periods characterized by market conditions and risk sentiment very different from those prevailing at the time of the first program in 2008-2009.

In particular, the new dataset consists of intraday price quotes on all outstanding U.S. Treasury nominal securities from 2008 to 2012. On average, we have high-frequency information for about 200 CUSIPs at each point in time over a sample of almost 4 years. The identification procedure exploits not only the prices' reactions to the FOMC announcement regarding the total size of the asset purchase program, but also the reaction to the New York Fed Open Market Trading Desk (the Desk) releases of the program's operational details, which provided the intended distribution of purchases and sales across maturity sectors.

For each asset purchase program, we attempt to carefully control for the pre-announcement market expectations in order to estimate both the total stock surprise, that is, the unexpected component of the total size of the announced program, and the maturity distribution surprise, that is, the unexpected component of the purchases' allocation (weight) to each maturity sector. The availability of these two surprises allows us to measure the supply `shock' local to each maturity sector and consequently the `shock' to the aggregate duration risk measured by the unexpected change in ten-year equivalents. Clearly, the quality of these shocks' measurement depends on the ability to control for market participants' expectations about the size and maturity distribution of each asset purchase program. To this purpose, we use the Desk Primary Dealer Survey (PDS) results compiled by the New York Fed before each FOMC announcement, supplemented by market commentaries from the same primary dealers.

While a number of studies have previously examined the effects of Large Scale Asset Purchase (LSAP) announcements on a few constant maturity U.S. Treasury yields (Gagnon, Raskin, Remache, and Sack (2011), Krishnamurthy and Vissing-Jorgensen (2012), Swanson (2011) and Neely (2010)), none has employed data at the individual security level and none has exploited the Desk releases of the operational details about the program purchases.² Observing how the price reactions to these announcements differ across duration/maturity and liquidity characteristics of the Treasury securities is essential to the identification of the channels. Even more crucial to the identification of the channels is the use of new information not only about the total size of the program, which is released during each FOMC announcement, but about the distribution of these purchases across maturity sectors, which is released by the Desk either soon after or, more recently, contemporaneously to the FOMC announcement. The only paper that uses disaggregated five minute interval data on individual securities to analyze quantitative easing (QE) announcements is Joyce and Tong (2012), which examines the Bank of England's asset purchases. However, this paper does not focus on the reaction to the operational details and therefore cannot separately identify the unexpected component of the total size and maturity distribution of each QE program.

With the exception of the case study in D'Amico, English, Lopez-Salido and Nelson (2012), none of the previous event-study analyses focused on the reaction to surprises in the maturity distribution of purchases. However, while these authors focused on a single event and a few securities, we analyze the price reactions across all outstanding nominal securities to multiple events over a period of about four years, which is essential to extrapolate how the price reaction has evolved over time and allows a more precise identification. In addition, as these announcements span a period characterized by different market conditions and risk sentiment, the results of the event studies allow us to determine how the efficacy of this policy tool was affected by market disruption. The closest relation to our study is the concurrent paper by Benerjee, Latto, McLaren and Daros (2012), which studies how the announced operational changes to the Bank of England QE program affected gilt yields.

Our empirical results suggest that the local supply and duration risk `shocks' together can explain most of the variation in the reaction of Treasury yields to the Fed purchase program announcements and each separately has about 25 to 50 percent explanatory power. In terms of impact on the 10-year nominal Treasury yield, we find that the average duration risk effect across all five events is about -5 basis points per $100 billion of purchases, and the average local supply effect across the same events is about -4 basis points per $100 billion of purchases. This suggests that the duration risk and local supply channels have similar importance in the transmission mechanism of Fed asset purchase programs to the term-structure of Treasury yields. Finally, we find that, once the pre-announcement market expectations are carefully controlled for, there does not appear to be evidence that the effects of these two channels have declined over time, suggesting that they may be key factors in the determination of Treasury securities prices rather than exceptional mechanisms triggered by market disruption or extremely high risk aversion.

The following section of the paper discusses in detail each announcement employed in the event studies. Section 3 gives an overview of our data and describes the intraday security-level yield reaction to each of the announcement. Section 4 details the computation of the local supply surprise and the duration risk surprise. Section 5 develops our empirical specification to disentangle the risk duration and local supply effects and presents our results. Section 6 introduces some robustness exercises. Section 7 concludes.

Description of the announcements employed in the event studies

In this section we outline the sequence of events that we employ in our empirical analysis. For each event we provide a description of the timing and content of the FOMC balance sheet announcement and accompanying Desk technical note detailing the program operations.

On March 18, 2009 at 2:15 p.m. the FOMC announced its decision to bring its maximum purchases of agency MBS to $1.25 trillion as well as of agency debt to $200 billion; and to purchase up to $300 billion of longer-term Treasury securities over the subsequent six months. According to market commentaries, those policy actions were more aggressive than expected both in size and scope. In particular, the Treasury purchases were largely unexpected.³ Without prior notice, the Desk announced at 2:44 p.m. that the Treasury purchases would be concentrated in the 2- to 10-year sector of the nominal Treasury curve, and that it would purchase both nominal and inflation-indexed Treasury securities. Changes over this half-hour interval (between 2:15 and 2:44 p.m.) in market expectations about the maturity distribution of purchases could have affected the Treasury yields' behavior in a way that can be revealing about the respective roles of the local-supply and duration channels. This is because, based on the 2:15 p.m. announcement, all the securities with longer-term maturities (that is, usually with maturities beyond two years) may have been perceived as equally likely candidates for purchases by the Federal Reserve. However, following the 2:44 p.m. Desk statement, investors should have assigned much smaller probability to the purchase of securities with remaining maturities above 10 years. This unexpected change in the maturity distribution of purchases would affect both the expected average duration of future purchases and the future supply available to private investors in each maturity bucket. That is, because of its concentration in the 2- to 10-year maturity sector, the assets purchased will have a smaller average duration than purchases more heavily weighted towards the 10- to 30-year sector, and the securities in the excluded sector relative to those in the 2- to 10-year sector (as a percentage of the outstanding stock of Treasuries) will become relatively less scarce, and thus cheaper. Therefore, following the Desk announcement, while in the 10- to 30-year sector the smaller-than-expected scarcity effect moves prices in the same direction as the smaller-then-expected duration effect, that is, both should drive prices down and yields up; in the 2- to 10-year sector, the larger-than-expected scarcity effect should move prices in the opposite direction of the smaller-than-expected duration effect, that is, it will drive prices up because securities become scarcer than expected, potentially balancing the decline in prices induced by the smaller average duration of future purchases. This implies that if both channels are operating and have similar importance, the second announcement by the Desk should have no material impact on the prices of Treasury securities included in the purchase sector (2- to 10-year maturities), but should exert a potentially sizable negative impact on the prices of securities outside the purchase sector (with maturities beyond ten years). This will be clearly illustrated in Figure 1 in the next section.

On August 10, 2010, at 2:15 p.m., the FOMC announced that it would keep the face value of its System Open Market Account (SOMA) holdings constant by reinvesting principal payments from agency debt and agency MBS in longer-term Treasury securities. This time, the announcement contained a footnote indicating that the Desk would issue shortly thereafter a technical note containing operational details on the announced transactions. At 2:45 p.m., the Desk indicated that it would again concentrate purchases in the 2- to 10-year sector of the nominal Treasury curve, and would refrain from purchasing securities for which there was a heightened demand or for which the SOMA already held large concentrations. According to market commentaries, only some market participants had anticipated an announcement regarding the reinvestment of principal payments and among those only a few expected this reinvestment to be in Treasuries rather than in other securities.⁴ Therefore, similar to the March 2009 episode, the announcement of the reinvestment program came mainly as a surprise, and the potential for a price reversal elicited by the Desk's announcement could again throw considerable light on the impact of Treasury operations and their channels. Further, the price reversal in some securities could have been exacerbated by the new part of the statement indicating that the Desk would refrain from purchasing securities that were already held in the SOMA portfolio in high concentration, indicating that those securities potentially had a lower probability of being bought. Figure 2 shows the yield changes during these events.

On November 3, 2010 at 2:15 p.m., the FOMC announced its decision to expand its holding of longer-term Treasury securities by $600 billion by the end of the second quarter of 2011, and, differently from the previous two announcements, simultaneously the Desk released its operating policy detailing the intended distribution of purchases for the nominal securities across seven maturity sectors. From the release of the operational details, market participants learned that the 10- to 30-year maturity sector would have received only 6 percent of purchases, compared with an allocation of about 15 percent in the two previous programs. It is plausible to assume that based on past experience, they would have expected a larger weight on the 10- to 30-year sector, and therefore the announced distribution of purchases was more heavily weighted towards short- and medium-term securities than some market participants had expected. This in turn would have implied a smaller-than-expected reduction in the average duration, driven both by a smaller-than-expected reduction in the available supply of the 10- to 30-year sector and a larger-than-expected reduction in the available supply of the 2- to 10-year sector. Since the FOMC and the Desk's announcements were done simultaneously, differently from the previous two episodes, we will not be able to observe the price behavior in between the two announcements; but, if the local supply channel is operating, we should observe prices moving in opposite directions below and above the 10-year maturity threshold to reflect the negative purchase surprise in the 10- to 30-year sector and the positive purchase surprise in the 2- to 10-year sector. This type of response is evident in Figure 3.

On September 21, 2011, at 2:23 p.m. the FOMC announced its intention to extend the average maturity of its holdings of securities by purchasing $400 billion of Treasury securities with remaining maturity between 6 and 30 years and selling an equal amount of Treasury securities with remaining maturity of 3 years or less, which is known as the Maturity Extension Program (MEP). Once again, the Desk simultaneously released the intended distribution of purchases across five rather than seven maturity sectors, to reflect the fact that purchases were going to occur only in the medium- and long-term sections of the yield curve. Most likely, based on previous purchase operations where the 10- to 30-year sector of the yield curve received at most 15 percent of the purchases, this time market participants could have been surprised by the large portion of 29 percent of the purchases allocated to the 20- to 30-year maturity range. Therefore, differently from past experience, in this program the announced distribution of purchases was more heavily weighted towards longer-term securities than expected. This would imply a larger-than-expected removal of duration risk from the market, driven by a larger-than-expected reduction of the available supply to private investors in the 20- to 30-year sector (i.e. a positive surprise). This combined with sales at the front end of the curve, which translate into an increased availability of securities with maturity of 3 years or less (i.e. a negative surprise), would suggest that if there is a local supply effect we should observe yields increasing at the front-end of the curve in response to the negative surprise and yields decreasing at the long-end of the curve in response to the positive surprise. Again, this pattern can be observed in Figure 4.

On June 20, 2012, at 12:30 p.m. the FOMC announced its decision to extend the MEP through the end of 2012 at its current pace resulting in the purchase as well as the sale of $267 billion of Treasury securities. Contemporaneously, the Desk released the operational details indicating that the maturity buckets and the weights associated to each bucket were the same as in the initial MEP. However, it also stated the suspension, for the duration of this program, of rolling over maturing Treasury securities into new issues at auction, as redeeming maturing Treasury securities has a nearly identical effect on the SOMA portfolio as selling securities that are approaching maturities. This new component of the announcement could have potentially surprised the market participants, as the decision to redeem securities maturing in the second half of 2012 allowed the Fed to increase the total size of future purchases beyond the amount of securities with maturity of 3 years or less already held in SOMA (which during the MEP were sold to finance the purchases). Therefore, it is conceivable that market participants used this amount to guide their expectations about future purchases, underestimating the size of the MEP extension. This implies that the announced size and duration of purchases could have exceeded expectations, because through the securities redemptions the Fed was going to purchase a larger-than-expected amount in the 6- to 30-year sector and implicitly sell or redeem a larger-than-expected amount in the 3 years or less maturity sector, which should lead Treasury yields to increase in this sector and to decrease in the in the 6- to 30-year sector. Figure 5 illustrates how the shape of the reaction to the MEP extension is very similar to that one of the initial MEP, except for the magnitude of the changes that was smaller because the size of the surprise was smaller.

Preliminary data analysis: Security-level event studies

Our dataset consists of intra-day CUSIP-level prices for each Treasury security outstanding over the period from 2008 to 2012, obtained from the Thomson Reuters Tick History database at minutely frequency. The availability of detailed high-frequency information on the price of each security allows us to examine the price reaction to each FOMC and Desk announcement separately within the same day, and in particular, allows us to measure the price movements between announcements or post-announcement, which is crucial to the identification of the two channels. In addition, the direction and magnitude of the high-frequency price reaction across all the outstanding CUSIPs makes it possible to analyze how the price response varies across the entire duration/maturity spectrum, which is also crucial to the identification of the channels.

In Figure 1, the red dots show the yield changes of all outstanding nominal Treasury securities from 2:00 to 2:30 p.m. as a function of their modified duration on March 18, 2009. Since this time-window includes only the reaction to the FOMC announcement about the total size of the program, we would in general expect those yield changes to be monotonically decreasing in duration, as bonds with longer duration generally bear larger exposure to interest rate risk and as such can experience a larger change in their risk premiums.⁵ The yield change reaction is indeed convex in duration but with a few important exceptions. The discontinuity around the 5-year duration sector is caused by the fact that newly issued 5- and 7-year notes reacted less strongly than the deeply off-the-run 30-year bonds. The importance of the local supply effects becomes clear following the second announcement by the Desk. The blue dots in Figure 1 show the yield changes from 2:00 to 3 p.m., about 15 minutes after the Desk announcement, and again at 4 p.m., shown in green. All securities excluded from the purchase range (i.e. outside of the 2-10-year maturity bucket, which in our sample corresponds to about 1.9-7.8 years of duration) reversed a large part of their initial yield declines after the Desk announcement, while those included in the purchase range largely maintained (or amplified) their earlier responses, even though, in the aggregate, a smaller amount of dollar duration was going to be taken out of the market. This would suggest that in the 2-10-year maturity sector, the local supply effect (elicited by a larger-than expected reduction in the supply of these securities relative to those in the 10-30-year sector) counterbalanced the smaller-than-expected total duration effect, leaving yields unchanged or lower following the second announcement. Further, we find it extremely striking that the turning point is around the 7.8 years duration, which being the average duration of 10-year Treasury securities represents the threshold between the maturity ranges included and excluded from the Fed purchase program.

Figure 2 shows that following the FOMC announcement of the reinvestment program on August 10, 2010, the initial yield reaction was quite similar in shape to the one prevailing after Desk's announcement on March 18, 2009, reflecting learning by market participants about the maturity distribution from the first round of purchases. In other words, it seems reasonable that based on the previous experience with LSAP purchases, market participants expected the maturity distribution of the Fed purchases under the reinvestment program to reflect the actual distribution of the first LSAP's purchases. However, following the second announcement by the Desk, securities with maturities beyond the purchase range more than reversed their initial yield declines, reflecting in part the relatively large concentration of 10- to 30-year Treasury securities in the SOMA holdings.⁶ In contrast, yields of securities included in the purchase range continued to decrease later in the day. This pattern suggests once more the likely existence of local supply effects, as the surprise in the maturity distribution of purchases had significant effects on yields that were not monotonic in their durations.

Differently from the previous two pictures, Figure 3 shows the yield responses only in one time-window (that is, from 2:00 to 4:00 p.m.) around the FOMC announcement of the second LSAP, because in this case, as explained in the previous section, the Desk's announcement was contemporaneous to that of the FOMC. It can be seen that the yields of short- and intermediate-term securities decreased, while the yields of securities with duration beyond 8 years increased after the announcement, most likely reflecting a larger-than-expected reduction of the available supply in the 2- to 10-year sector and a smaller-than-expected reduction of the available supply in the 10- to 30-year sector. In other words, these two wide humps elicited by yields moving in opposite directions below and above the 7-year duration threshold (at that time the duration of the 10-year benchmark was 8.5 years) cannot be explained by a supply effect mainly driven by the duration risk channel, suggesting once again that the local supply channel may be at work.

Figure 4 illustrates the yield response in the same time window (that is, from 2:00 to 4:00 p.m.) to the FOMC and Desk announcement about the MEP. In this case, the yields in the short- and medium-term sectors of the yield curve increased a little, while yields beyond the 4-year duration decreased, with the largest decline being observed at the 20- to 30-year maturity range. This would be consistent with larger-than-expected sales of securities at shorter maturities (that is, a negative surprise) and larger-than-expected purchases at longer maturities (that is, a positive surprise), suggesting again a combination of local supply and duration risk effects.

Figure 5 exhibits the yield responses to our fifth and final announcement, that is, the extension of the MEP. This time the shape of the reaction is extremely similar to the reaction to the MEP, as most likely, also in this case, larger-than-expected sales (that is, a negative surprise) pushed yields up at shorter maturities and larger-than-expected purchases (that is, a positive surprise) drove yields down at longer maturities, implying the same transmission mechanism of the impact of this program to the term structure of interest rates as during the first MEP.

Overall, our first look at the shape and magnitude of the reactions to the various Federal Reserve asset purchase programs across all nominal CUSIPs outstanding points to the existences of both a local supply effect as well as a duration risk effect. However, to formally test these conjectures we first make our best attempt at measuring the individual local supply and duration risk shocks and second estimate their effects on nominal Treasury yields.

Computations of the individual local supply and duration risk shocks

Financial markets are inherently forward looking and react only to the new information contained in any announcement. Therefore, a rigorous event-study analysis requires a careful specification of both the expected and the surprise components of the announcement. Given this study's focus on local supply and duration risk shocks, this calls for the estimation of market participants' expectations about three main variables: the probability of the announcement to occur, P, the total size of the program E(Q), and the weight E(w ${}_{k}$ ) associated to each of the k maturity buckets across which the purchases are distributed. We obtain a measure of each of these variables from the Primary Dealer Survey (PDS) conducted by the New York Fed one week before each FOMC announcement, supplemented with the available information from market commentaries published before each FOMC.

4.1 Measuring the local supply shock

Our first step is to measure the program size surprise for each maturity bucket, that is, the maturity distribution of the supply shock. Its final specification at security-level is mainly motivated by the evidence about the importance of local supply shocks shown in D'Amico and King (2013). For each FOMC program announcement, we first estimate investors' prevailing expectations of both its probability to occur, P, and its total size E(Q|the program occurs) from the PDS and/or market commentaries. Next, the associated vector of maturity bucket weights E(W ${}_{k}$ ) is calculated as follows.⁷ For LSAP1, given the novelty of the Treasury purchase program, we assume that investors expected such purchases to be spread across all maturity sectors proportional to the percentage amount outstanding in each sector.⁸ For LSAP2, we use pre-announcement weights similar to those observed for purchases under LSAP1, as those maturity allocations were cited by market observers as likely weights to be used in LSAP2 given the similarity in the broader macroeconomic motivations of the two programs. For all other announcements, we set the pre-announcement maturity weights to be identical to those observed for purchases under the immediately preceding program. One exception is the MEP due to the expectations formation about purchase and sale sectors. For the purchase sectors, we take the weights associated with purchases allotted to the 6- to 30-year sector under the LSAP2 (the immediately preceding program) and renormalize them to sum up to one.⁹ For the sale sectors, under both the MEP and the MEP extension, sales were assumed to be concentrated in the 0- to 3-year bucket as indicated in the PDS responses. Finally, the expected maturity distribution of purchases/sales, E(Q ${}_{k}$ ), is given by:

$\displaystyle E\left(Q_k\right)=P*E\left(Q\vert the\ program\ occurs\right)*E\left(w_k\right).$

Next, the FOMC announces the actual size of the program Q and the Desk releases the actual intended weights for the distribution of purchases across K maturity buckets, W ${}_{k}$ , with k=1,..,K. The purchase/sale par amount surprise for each maturity bucket, ${\ SQ}_k$ , is then computed as the difference between the actual maturity distribution and the expected maturity distribution of the purchase amount: ${SQ}_k=Q*W_k-E\left(Q_k\right).$

Therefore, a positive surprise implies larger-than-expected purchases and a negative surprise implies smaller-than-expected purchases (or larger-than-expected sales in the case of MEPs) in the maturity bucket k. We next estimate a measure of each individual security's purchase/sale surprise and related local supply shock, where these two measures are identical only when we ignore the substitution effects across securities. We first assume that within a bucket the purchase or sale surprise is allocated to each security i proportionally to its private or SOMA holdings, h ${}_{i}$ or g ${}_{i}$ , respectively:

$\displaystyle s_i=\frac{{SQ}_k*h_i}{H_k}\ for\ purchases,$

$\displaystyle s_i=\frac{{SQ}_k*g_i}{G_k}\ for\ sales,$

where $H_k=\sum^{N_k}_{j=1}{h_j}$ and $G_k=\sum^{N_k}_{j=1}{g_j}$ are the total private holdings and SOMA holdings, respectively, in the maturity bucket k containing N ${}_{k}$ ${}_{ }$ ${}_{ }$ total securities. This is because it is reasonable to assume that within a maturity bucket the amount of each security available for purchase depends on the amount left in the hands of the private investors, while the amount available for sale depends on the amount left in the SOMA portfolio.

To capture the substitution effect among nearby securities, for each security i, we define its local supply shock (ls ${}_{i}$ ) as the weighted sum of its own supply shocks and the supply shocks of J securities having remaining maturities ( ${\tau }_{{\rm j}}$ ) within a certain distance of security i's maturity, and normalized by the weighted sum of the corresponding private holdings of those securities. We chose this specification because, as shown in D'Amico and King (2013), the price of each Treasury security reacts to its own purchases and those of nearby securities. In particular:

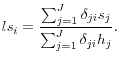
$\displaystyle {ls}_i=\frac{\sum^J_{j=1}{{\delta }_{ji}s_j}}{\sum^J_{j=1}{{\delta }_{ji}h_j}}.$

The weights ( $\delta$ ${}_{j}$ ${}_{i}$ ) are a decreasing function of the maturity distance, which is defined over a variable window size, and are specified as follows:

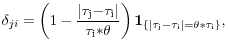
$\displaystyle {\delta }_{ji}=\left(1-\frac{\left\vert{\tau }_{{\rm j}}{\rm -}{\tau }_{{\rm i}}\right\vert}{{\tau }_{{\rm i}}{\rm *}\theta }\right){{\mathbf 1}}_{\left\{\left\vert{\tau }_{{\rm j}}{\rm -}{\tau }_{{\rm i}}\right\vert=\theta {\rm *}{\tau }_{{\rm i}}\right\}},$

with ${{\mathbf 1}}_{\left\{.\right\}}$ being an indicator function, and the weight ${\delta }_{ji}$ equal 1 only for security i, symmetric, and approaching 0 as the maturity distance approaches $\theta {\rm *}{\tau }_{{\rm i}}$ . In our baseline we set $\theta$ equal to 0.5 to consider all securities within a maturity distance of 50 percent of security i's maturity. This triangular kernel characterized by a variable window size should minimize biases due to the fact that the number of substitutes decreases as the maturity of a security increases. In other words, as we move toward the long end of the yield curve it is important to increase the window size because the number of available securities becomes smaller. However, in the robustness section, we show the sensitivity of our results to the choice of the window size and run an optimization routine to derive the best fitting value for $\theta$ .

Figures 6 to 10 show a bar graph of the maturity bucket purchase/sale surprises for each announcement, where purchases are represented as positive numbers and sales are represented as negative numbers measured in billions of dollars. In particular, the yellow shaded portion of each bar measures the expected amount of purchases/sales and the blue shaded portion of each bar measures the unexpected amount of purchases/sales within each maturity bucket. In addition, Figure 11 illustrates an example of the computation of the local supply shocks for the MEP. Maturity bucket surprises, denoted by the bars, are normalized by the amount outstanding in each bucket and the related local supply shocks are calculated for each security in the bucket, denoted by the red dots, as described in the formula above. Because there are very few substitutes for securities at maturities beyond ten years, the local supply shocks at those maturities become very similar to the normalized bucket supply surprises. Appendices A and B detail the computation of these shocks for each of the five Federal Reserve asset purchase announcements.

4.2 Measuring the duration risk shock

The construction of our empirical proxy for the security-level duration risk shock is motivated by the building blocks of the risk premium in traditional and preferred-habitat models of the term structure of interest rates. In the Vasicek (1977) model, and in particular, in the discrete-time version of a homoskedastic single-factor model, the bond risk premium can be obtained as the product of the quantity of short rate volatility or risk $\sigma$ , the market price of risk $\lambda$ , and an increasing concave function of the bond's duration, f(d ${}_{i}$ )¹⁰:

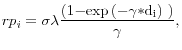
$\displaystyle {rp}_i=\sigma \lambda \frac{\left({\rm 1-}{\exp \left({\rm -}\gamma {\rm *}{{\rm d}}_{{\rm i}}\right)\ }\right)}{\gamma },$

where $f{\rm (}d_i)=\frac{\left({\rm 1-}{\exp \left({\rm -}\gamma {\rm *}{{\rm d}}_{{\rm i}}\right)\ }\right)}{\gamma }$ . Further, it is possible to show that in the one-factor version of the Vayanos and Vila (2009) model the risk premium has the same components, but the market price of risk has an economic interpretation-- it depends on the dollar value of the duration of the portfolio held by the arbitrageurs and their risk aversion. This implies that the risk premium in the discrete-time version of the Vayanos and Vila (2009) model is defined as:

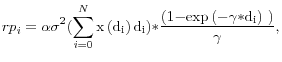
$\displaystyle {rp}_i=\alpha {\sigma }^2(\sum^N_{i=0}{{\rm x}\left({{\rm d}}_{{\rm i}}\right){{\rm d}}_{{\rm i}}{\rm )*}\frac{\left({\rm 1-}{\exp \left({\rm -}\gamma {\rm *}{{\rm d}}_{{\rm i}}\right)\ }\right)}{\gamma }},$

where now $\lambda {\rm =}\ \alpha \sigma \sum^N_{i=1}{{\rm x}\left({{\rm d}}_{{\rm i}}\right){{\rm d}}_{{\rm i}}}$ , with $\alpha$ being the coefficient of risk aversion, ${\rm x}\left({{\rm d}}_{{\rm i}}\right)$ the dollar value of the security's share in the aggregate portfolio composed of N securities, and ${{\rm d}}_{{\rm i}}$ the security i's duration.

Since in these models $\alpha \ {\rm and}\ \sigma$ are just constant across securities, in measuring the individual duration risk shocks we focus only on the dollar value of the aggregate duration, $\sum^N_{i=1}{{\rm x}\left({{\rm d}}_{{\rm i}}\right){{\rm d}}_{{\rm i}}},\$ and the concave transformation of the bond's duration, ${\rm f}\left(d_i\right)$ . In particular, we approximate the dollar value of the arbitrageurs' portfolio's aggregate duration with the amount of ten-year equivalents in billions of dollars left in the hands of private investors, and in our empirical specification the unexpected change in this variable denotes the surprise in the total duration risk (SDR). It is the availability of the maturity distribution of the supply shocks that allows the measurement of the unexpected change in the amount of ten-year equivalents, which is nothing more than the weighted sum of the individual purchase/sale surprises, where the weights are defined as the ratio between the individual security's duration and the duration of the 10-year benchmark ${(d}_{BM})$ :

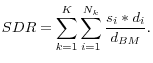
$\displaystyle SDR=\sum^K_{k=1}{\sum^{N_k}_{i=1}{\frac{s_i*d_i}{d_{BM}}}}.$

This implies that when the surprise in the total duration risk is positive, the Federal Reserve is removing from the market a larger-than-expected amount of ten-year equivalents. What determines the security-level duration risk shock is the exposure of every single security to SDR, and since the exposure to interest rate risk or duration risk is determined by the security's duration, the individual duration risk in our empirical specification is defined as follows:

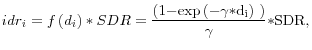
$\displaystyle {idr}_i=f\left(d_i\right)*SDR=\frac{\left({\rm 1-}{\exp \left({\rm -}\gamma {\rm *}{{\rm d}}_{{\rm i}}\right)\ }\right)}{\gamma }{\rm *}{\rm SDR,}$

where $\gamma$ , which controls the steepness of the concave function, is set equal to 0.2 based on the estimates from Li and Wei (2013). In the robustness section we show the sensitivity of our results to the value of this parameter and run an optimization routine to derive the best fitting value for $\gamma$ . Figure 12 provides an example of the computation of the individual duration risk, denoted by the yellow dots, as function of duration in years. By construction it has a concave shape.

Our next five charts, Figures 13 to 17, plot the yield reaction for each nominal Treasury security in the two-day interval measured from 15 minutes before the FOMC announcement to 4:00 p.m. of the next day (the green triangles), as well as the security's individual duration risk (the red squares) and local supply shocks (the blue circles) for each of the program as a function of duration. The plotted patterns show a strong relationship between a bond's yield response and its local supply shock from the announcement, that is, the yields change the most at maturities where local supply shocks are the largest. They also suggest a strong relationship between the yield response and its duration risk shock, that is, the yield changes are amplified at maturities where the exposure to duration risks are higher, which is typically at medium and long maturities. For example, in the case of the first Treasury LSAP announcement, the largest local supply shocks were at durations close to 3-6 years, possibly due to the Desk's announcement that Treasury purchases would be concentrated in the 2- to 10-year maturity sector. But the biggest yield drops occurred at durations around 7.5 years, possibly because the combined effects of local supply shocks and duration shocks were largest around the 10-year maturity. In the case of the MEP announcement, the largest yield drops occurred at maturities close to 30 years (15-18-year duration sector) possibly because both the local supply shocks and the duration shocks were largest at these maturities.

Estimated impact of local supply and duration risk effects

To formally test these conjectures and estimate the effects of the two channels, we run a cross-section regression of yield changes on duration risk shocks and local supply shocks for each program announcement separately, and in addition we also consider all the five announcements together and estimate a pooled data regression as in this case the estimates should be more efficient. The regression specification is the following¹¹:

$\displaystyle \triangle y_i={\beta }_0+{\beta }_1*{ls}_i+{\beta }_2*{idr}_i+u_i,$

where the yield changes are measured from 15 minutes before the FOMC announcement to 4:00 p.m. of the next day, and the number of securities used in the regression ranged from 163 in the first Treasury LSAP (LSAP1) to 245 in the MEP Extension (MEP2).

Table 1: Yield change regression results with variable window size, θ=0.5 and γ=0.2

	LSAP1(Two-day yield change regression)	Reinvestment(Two-day yield change regression)	LSAP2 (Two-day yield change regression)	MEP (Two-day yield change regression)	MEP2 (Two-day yield change regression)	Pooled (Two-day yield change regression)
Constant	0.466	-1.078	-2.982	3.169	0.367	0.629
Constant t-statistics	-0.52	(-2.45)	(-4.65)	-3.32	-0.91	-1.92
Duration risk shock	-3	-1.28	-0.952	-2.189	-0.399	-1.803
Duration risk shock t-statistics	(-22.07)	(-3.11)	(-1.97)	(-11.75)	(-3.60)	(-21.36)
Local supply shock	-0.385	-1.632	-1.21	-1.481	-0.48	-0.807
local supply shock t-statistics	(-12.51)	(-5.76)	(-25.16)	(-19.16)	(-12.00)	(-31.58)
R-squared	0.84	0.69	0.76	0.91	0.76	0.72
Observations	163	200	208	232	245	1048

Note: t-statistics in parenthesis.

As shown in Table 1, for each program announcement, the estimated coefficients on both the individual duration risk shock and the local supply shock are statistically significant and have the expected negative sign, except for the duration risk coefficient in the second LSAP (LSAP2) regression that is only marginally significant. As denoted by the R-squared, the total variation in yields explained by the two shocks is in the range of 75 to 90 percent across the various programs. In principle, the magnitude of the coefficients can vary across the different programs for a number of reasons, for example: the size of the shocks, Treasury market functioning, and investors' risk aversion. In the next two tables we will try to investigate a bit more the source of the difference in impacts across the five programs. The last column of Table 1 shows the results for the pooled data regressions, which confirms that also in this case both coefficients are negative as well as statistically significant, and that, as expected, the magnitude of each estimated coefficient is very close to the average of the estimates across the five events. The explained variation is 72 percent.

To provide an economic interpretation of these coefficients and to illustrate how the efficacy of this policy tool evolved over time, for each program, we compute the implied effects on the on-the-run ten-year yield in basis points from a totally unexpected $100 billion purchase announcement, which are reported in Table 2. This is done using the coefficient estimates from each program and by assuming that the $100-billion surprise is distributed across the maturity buckets as in the actual announced program.

Table 2: Implied effect on the 10-year yield from an unexpected $ 100B program

	LSAP1 ( Impact in basis points using individual regression’s coefficients)	Reinvestment ( Impact in basis points using individual regression’s coefficients)	LSAP2 ( Impact in basis points using individual regression’s coefficients)	MEP ( Impact in basis points using individual regression’s coefficients)	MEP2 ( Impact in basis points using individual regression’s coefficients)	Average (Impact in basis points using individual regression’s coefficients)
Total*	-8.9	-9.4	-9.2	-13.1	-3.7	-8.9
of which bond duration	-7.6	-3.4	-2.5	-8.5	-1.5	-4.7
of which local supply	-1.8	-5	-3.8	-7.8	-2.6	-4.2

*Includes the estimated constant term.

As shown in the fourth column of Table 2, the MEP is characterized by the largest impact on the 10-year yield, with a reduction of 13 basis points almost evenly split between the two channels. Further, LSAP1, the Reinvestment program, and LSAP2 have a very similar estimated effect of about 9 basis points, although in each program the relative importance of the two channels is quite different. Finally, the MEP extension is estimated to have reduced the same yield by about 4 basis points, of which 2.5 basis points are due to the local supply effect. On average, as indicated in the last column, using the individual coefficients, we find that a $100 billion purchase surprise translates in a 9-basis-point reduction in the 10-year yield, with each channel accounting for about half of the decline.

In addition, to try to isolate the impact of the programs' design rather than the change in sensitivity to supply shocks over the sample period, we repeat the same exercise using the pooled regression coefficients instead of the individual program coefficients. The reason why this should allow us to isolate the impact of the program operational characteristics is that we keep fixed the estimated coefficients across the different programs but we employ the program's actual distribution of the supply shocks, which depends on the operational details released on the day of the announcement. The results of this exercise for a $100-billion surprise are reported in Table 3.

Table 3: Implied effect on the 10-year yield from an unexpected $100B program

	LSAP1 (Impact in basis points using pooled regression’s coefficients)	Reinvestment (Impact in basis points using pooled regression’s coefficients)	LSAP2 (Impact in basis points using pooled regression’s coefficients)	MEP (Impact in basis points using pooled regression’s coefficients)	MEP2 (Impact in basis points using pooled regression’s coefficients)	Average (Impact in basis points using pooled regression’s coefficients)
Total*	-7.7	-6.6	-6.5	-10.6	-10.6	-8.4
of which bond duration	-4.6	-4.8	-4.7	-7	-6.9	-5.6
of which local supply	-3.8	-2.4	-2.5	-4.3	-4.3	-3.5

In this case, with the exception of MEP2, the total impact on the 10-year yield from each program is slightly smaller in magnitude than those reported in Table 2. However, it is very interesting to note the difference in impact between purchase programs focused on the removal of quantities and purchase/sale programs focused on the removal of duration. In particular, while the first type of programs, that is, LSAP1, the Reinvestment, and LSAP2, have a similar impact around 7 basis points, the second type of programs, that is, MEP and MEP2, have a larger impact of about 10.5 basis points, which is identical across the two programs as they have the same identical design. Considered together, the results in Table 2 and 3 seem to indicate first, that the efficacy of this policy tool, measured by the effect on Treasury yields, has not been diminishing since the announcement of the first LSAP and second, that the design of the program can be as relevant as its size. In other words, asset purchases that remove both quantity and duration from the market, shifting the composition of the Federal Reserve balance sheet toward longer-term maturities, seem more effective than those programs concentrating a larger amount of purchases in the 2-10-year maturity sector.

In addition, to better understand the relative importance of the two channels, in Table 4 we show the contribution of each channel to the total variation in yields. As pointed out earlier, the total variation explained by the two shocks is in the range of 75 to 90 percent across the various programs and for ease of comparison the individual total R-squared values are reported in the top row. The last two rows show the variation explained by each shock. Specifically, with the exception of LSAP2 where the local supply shock accounts for almost the entire explained variation, this channel explains between 25 to 50 percent of the yields reaction; while, the duration risk shock, although almost irrelevant for LSAP2, on average, accounts for about 30 to 60 percent of the yield variation in the other four programs. Overall, in the pooled results, the two shocks seem to have similar importance in explaining the Treasury yield responses to the program announcements, as the local supply shock explains about 40 percent and the duration risk shock explains about 30 percent of the total variation.

Table 4: Relative importance of the duration channel and the local-supply channel

	LSAP1 (Two-Day Yield Change Regression)	Reinvestment (Two-Day Yield Change Regression)	LSAP2 (Two-Day Yield Change Regression)	MEP (Two-Day Yield Change Regression)	MEP2 (Two-Day Yield Change Regression)	Pooled (Two-Day Yield Change Regression)
Total variation explained (R-squared)	0.84	0.69	0.76	0.91	0.76	0.72
of which bond duration	0.58	0.33	0.01	0.41	0.32	0.29
of which local supply	0.26	0.36	0.75	0.5	0.44	0.43

Finally, to provide an illustration of the goodness-of-fit of our regressions, Figures 18 to 22 plot the predicted yield reactions, denoted by the black squares, versus the observed yield reactions, denoted by the green triangles. It is quite striking how these two shocks can capture quite well these highly nonlinear price reactions, replicating patterns very similar to those simulated in the paper of Vayanos and Vila (2009). This should not be surprising as our measures of local supply and duration risk surprises are trying to approximate the shocks to their theoretical unobserved factors in the two-factor model and therefore should capture in observed data the same type of humps that their factors generate in simulated data. However, it is easy to note that the fitting errors tend to be larger for securities with higher durations. In the robustness section, we will show that a different choice of the parameters $\theta$ and $\gamma$ can improve the fitting at the long-end of the yield curve. This improvement has an intuitive explanation: when optimally chosen, the values of the parameters tend to increase the contribution of the local supply effect, which in turn is very important in explaining the size and shape of the yield reaction at very long maturities. In other words, a larger estimated coefficient for the local supply channel allows capturing these wide humps at longer maturities because, most likely, the scarcity of substitutes for securities with duration beyond 10 years magnifies the impact of a supply shock localized in these sectors. This explanation is consistent with one of the theoretical result in Gromb and Vayanos (2010), where they show, using a simple model of cross-asset arbitrage, that assets with higher idiosyncratic risk and fewer substitutes are more sensitive to demand shocks.

Overall, based on the reported estimates, there does not seem to be an obvious pattern where the price impact of asset purchase announcements has been a decreasing function either of time or of accumulated purchases since the first LSAP announcement. This result suggests that most likely these two channels are always operating and are not exceptional mechanisms elicited by the disruption of normal market functioning or the deterioration of market sentiment. Our results also indicate that, for each program, it is not only the unexpected component of the total size but also the unexpected component of the purchases' allocation to each maturity sector that matters, signifying the importance of the purchase program's design and the accompanying communication strategy. However, like all event studies, our results depend on the assumption that Treasury yields responded only to the purchase announcement and not to other events in the 2-day interval we analyzed and do not provide a satisfactory explanation on the persistency of the impact of these shocks. For example, our estimates may have also captured some effects from other factors such as the interest rate signaling channel that arises from perceived new information about the expected path of short-term rates that FOMC statements might contain. However, by restricting our sample only to securities with remaining maturity longer than 2-years, where the interest rate signaling effect should be small, we found qualitatively similar results (not shown), suggesting that our results likely captured effects of the two channels we studied.

5.1 Purchase versus sale price elasticity

In the next table, we try to address the following question: can we extrapolate our results to evaluate the potential impact of the `exit strategy', that is, possible future sales of securities held in the SOMA portfolio for the purpose of tightening monetary policy? One possible way of addressing this question, admittedly a bit less ambitious than the original question, is to test if the price elasticity in the case of purchases and sales is symmetric. In particular, exploiting the features of the MEP, during which both purchases and sales took place, we estimate different coefficients for the securities included in the purchase and sale sector, respectively. And since there is no particular reason to think that the duration risk coefficient should differ across these two sectors, we continue to run the regression for the entire full sample and simply use interactive dummies to estimate separate local-supply coefficients for securities included in the sale sector and those included in the purchase sector. Further, in accounting for the substitution effect, we choose the 5-year maturity as the threshold that divides the two sectors, rather than limiting it to 3 years as indicated in the program operational details.¹²

Table 5: Regression results with different local-supply coefficient for sales and purchases

	MEP	LSAP2	Pooled
Constant	3.6707	-3.1313	-2.0322
constant t-statistics	-2.58	(-5.10)	(-5.917)
Duration risk shock	-2.2719	-0.6038	-1.3817
duration risk shock t-statistics	(-9.77)	(-1.20)	(-14.80)
Local supply shock ≤5 years	-1.3964		-2.0869
MEP sales	(-7.23)		(-22.56)
Local supply shock > 5 years	-1.4844		-1.6162
MEP purchase	(-19.00)		(-22.79)
Local supply shock ≤ 5 years		-2.006	-2.0128
LSAP2 purchases		(-10.80)	(-10.34)
Local supply shock ≤ 5 years		-1.1531	-1.1708
LSAP2 purchases		(-24.06)	(-23.56)
R-squared	0.91	0.78	0.88

Looking at the numbers in bold in the first column, it is quite striking how similar the estimated price elasticities for sales and purchases are. The only problem is that a 1% local supply shock in the universe of outstanding Treasury securities with less than 5 years to maturity can be quite different in magnitude from a 1% shock in the universe of outstanding securities with more than 5 years to maturity. Therefore for robustness we repeat the same experiment for the LSAP2 announcement, which, being the immediately preceding program, should not be characterized by significantly different amounts outstanding in the two sectors. Because LSAP2 included only purchase operations, the comparison of the local-supply coefficients across the two programs within the same maturity sector should provide an idea of the stability of these estimates. As shown by the numbers in bold in the last column, the estimated local supply coefficient in the less-than-five-year sector is very similar across the two programs, suggesting sales and purchases have similar local supply effect.

Robustness

6.1 Robustness to LSAP1 pre- and post-announcement maturity bucket weights

Considering the novelty of the first LSAP, that is, at the time there was not any empirical evidence on the maturity distribution of previous purchases, necessarily the choice of the pre-announcement maturity bucket weights has to be somewhat arbitrary. However, since in this instance the FOMC (2:15 p.m.) and the Desk (2:44 p.m.) announcements took place at two different times, we can use changes over this half-hour interval (between 2:15 and 2:44 p.m.) in market expectations about the maturity distribution of purchases to identify the local-supply and duration risk effects, without relying on any measure of the shocks.

In particular, given the pattern of the price reversal, shown in Figure 1, it seems safe to assume that most of the yield increase that took place between 2:44 p.m. and 3:00 or 4:00 p.m. was due to the local-supply effect, as it took place only in the maturity sector that was excluded from the purchase program and seemed largely independent of the security's duration, judging from the parallel shift across different durations. Therefore, for each security in the excluded maturity sector we compute the yield increase between 2:44 and 4:00 p.m., and we find that these securities on average experienced a reversal of about 40 percent of the yield decline that had come soon after the FOMC announcement (i.e. from 2:15 to 2:44 p.m.), which in contrast should be driven by both channels. This implies that most likely about 40 percent of the total yield change was due to the local supply effect, which is larger than the variation explained by the local supply shock for LSAP1 in our baseline regression shown in Table 4.

In the second robustness exercise, also related to the choice of weights for the first program, we recomputed the surprise for each maturity bucket and consequently for each individual security according to the following assumption: the market participants form expectations only about the total size of the program and are totally agnostic about the weights, then given the actual amount we derive the total size shock and its distribution across the different maturity sectors based on the announced weights, which implies using only the post-announcement weights. The regression results of this experiment are shown in the first column of Table 6, and since the new assumptions affect also the pooled regression results, the numbers reported in the last column are different from those shown in Table 1.

Table 6: Yield change regression results using alternative weights for LSAP1

	LSAP1 (Two day yield change regression)	Reinvestment (Two day yield change regression)	LSAP2 (Two day yield change regression)	MEP (Two day yield change regression)	MEP2 (Two day yield change regression)	Pooled (Two day yield change regression)
Constant	0.5594	-1.078	-2.982	3.169	0.367	-1.269
constant t-statistics	-0.683	(-2.45)	(-4.65)	-3.32	-0.91	(-4.52)
Duration risk shock	-1.8041	-1.28	-0.952	-2.189	-0.399	-0.9901
Duration risk shock t-statistics	(-13.14)	(-3.11)	(-1.97)	(-11.75)	(-3.60)	(-13.12)
Local supply shock	-0.8031	-1.632	-1.21	-1.481	-0.48	-1.1183
local supply shock t-statistics	(-14.63)	(-5.76)	(-25.16)	(-19.16)	(-12.00)	(-40.20)
Observations	163	200	208	232	245	1048

Note: t-statistics in parenthesis

Table 7: Relative importance of the duration risk and local-supply channels using alternative weights for LSAP1

	LSAP1 (Two-Day Yield Change Regression)	Reinvestment (Two-Day Yield Change Regression)	LSAP2 (Two-Day Yield Change Regression)	MEP (Two-Day Yield Change Regression)	MEP2 (Two-Day Yield Change Regression)	All (Two-Day Yield Change Regression)
Total variation explained (R-squared)	0.87	0.69	0.76	0.91	0.76	0.79
of which bond duration	0.42	0.33	0.01	0.41	0.32	0.25
of which local supply	0.45	0.36	0.75	0.5	0.44	0.54

With this weight specification, the R-squared for both LSAP1 and the pooled regressions improved slightly relative to our baseline regressions, and as shown in Table 7, the variation explained by the local supply shock is closer to the one obtained by exploiting only the price reversal as described above, which indicated that about 40 percent of the yield variation was due to the local supply effect.

6.2 Robustness to the choice of the parameters ${\mathbf \theta }$ and ${\mathbf \gamma }$

This section considers the robustness of our results to the choice of the parameter $\theta {\rm ,}$ which controls the window size in the computation of the individual local supply shocks illustrated in Section 4.1, and to the choice of $\gamma$ , which controls the steepness of the curve in the computation of the individual duration risk shocks illustrated in Section 4.2. We compute optimal values for each parameter by jointly minimizing with respect to $\theta$ and $\gamma$ the sum of squared residuals (or alternatively by maximizing the R-squared) in the pooled regression. Our results indicate that the optimal values of $\theta$ and $\gamma$ are 0.769 and 0.095, respectively. This would suggest that if we use a broader concept of substitutability, that is, if the variable window size is extended to include all securities within a maturity distance of about 77 percent of security i's maturity, and if we choose a steeper concave function to measure the individual exposure to the aggregate duration risk, then we should be able to fit the yield reactions better. The regression results obtained using the optimal values for these parameters are reported in Table 8. The optimization surface is shown in Figure 23, where it is possible to see that given the optimal value for $\theta$ , the R-squared is not very sensitive to the changes in γ

Table 8: Yield change regression results with variable window size, θ=0.769 and γ=0.095

	LSAP1 (Two-day yield change regression)	Reinvestment (Two-day yield change regression)	LSAP2 (Two-day yield change regression)	MEP (Two-day yield change regression)	MEP2 (Two-day yield change regression)	Pooled (Two-day yield change regression)
Constant	-2.551	-1.399	-3.177	1.847	0.196	-0.624
t-statistics	(-3.31)	(-4.27)	(-14.52)	-1.91	-0.61	(-2.44)
Duration risk shock	-1.375	1.638	0.065	-1.571	-0.314	-0.992
t-statistics	(-17.37)	-6.97	-0.56	(-12.08)	(-5.01)	(-20.81)
Local supply shock	-0.68	-4.746	-2.003	-1.542	-0.539	-1.043
local supply shock t-statistics	(-18.61)	(-15.49)	(-68.93)	(-13.35)	(-11.69)	(-40.58)
R-squared	0.85	0.76	0.96	0.94	0.87	0.79
Observations	163	200	208	232	245	1048

Note: t-statistics in parenthesis.

Table 9: Relative importance of the duration risk and local-supply channels, θ=0.769 and γ=0.095

	LSAP1 ( Two-Day Yield Change Regression)	Reinvestment ( Two-Day Yield Change Regression)	LSAP2 ( Two-Day Yield Change Regression)	MEP ( Two-Day Yield Change Regression)	MEP2 ( Two-Day Yield Change Regression)	Pooled ( Two-Day Yield Change Regression)
Total variation explained (R-squared)	0.85	0.76	0.96	0.94	0.87	0.79
of which bond duration	0.4	0.26	0.04	0.47	0.41	0.27
of which local supply	0.48	0.49	0.92	0.48	0.46	0.52

As reported in Tables 8 and 9, when we use the optimized parameters, all the adjusted R-squared, for the individual programs and the pooled regression, increase somewhat, and the variation explained by the local supply channel becomes notably larger for LSAP1, LSAP2 and the Reinvestment program, as well as in the pooled specification. On the other hand, the variation explained by the duration risk channel increases for the MEP and MEP2, which intuitively makes sense considering that these programs were designed to remove a significant amount of duration risk from the market and therefore should be characterized by a larger duration risk effect on Treasury yields. In addition, using these parameters' values, as shown in Table 8, the estimated duration risk coefficient becomes positive and significant in the case of the Reinvestment program and positive but not statistically significant for LSAP2. In contrast, all the coefficients for the local supply effect stay negative and significant, which seems to suggest that these estimates are more stable and less sensitive to the parameters' choice.

As shown in figures 24 to 28, which plot the predicted yield reactions, denoted by the black squares, versus the observed yield reaction, denoted by the green triangles, using the optimized parameters, the fitting errors for securities characterized by very large durations are substantially smaller. This implies that, while the local supply effect is very important in capturing these price reactions during the first three announcements, the duration risk effect is crucial in approximating better the price reaction to the MEP and MEP2 announcements.

Further, in table 10, we report the implied effect on the 10-year yield in basis points from a totally unexpected $100 billion purchase announcement, obtained using the new estimated coefficients with optimized values of $\theta$ and $\gamma$ for the individual programs. Under this parameters' choice, the average impact of the local supply channel is somewhat larger, although the overall impact of a $100-billion surprise remains about unchanged. Finally, similarly to the baseline regressions, we repeat the same exercise using the pooled specification coefficients, and the resulting effects on the 10-year yield are reported in Table 11. Also in this case, the total impacts are quite close to those implied by the baseline regressions and reported in Table 3. However, the total variation explained by the local supply effect becomes relatively larger in the first three programs, and on average, each channel accounts for about half of the total yield decline.

Table 10: Implied effect on 10-year yield from an unexpected $100B program, θ=0.769 and γ=0.095

	LSAP1 ( Impact in basis points using individual coefficients)	Reinvestment ( Impact in basis points using individual coefficients)	LSAP2 ( Impact in basis points using individual coefficients)	MEP ( Impact in basis points using individual coefficients)	MEP2 ( Impact in basis points using individual coefficients)	Average ( Impact in basis points using individual coefficients)
Total*	-10.8	-10.2	-9	-12.3	-3.3	-9.1
of which bond duration	-5	6.2	0.2	-8.8	-1.7	-1.8
of which local supply	-3.2	-15	-6	-5.4	-1.8	-6.3

*Includes the estimated constant term.

Table 11: Implied effect on 10-year yield from an unexpected $100B program, θ = 0.769 and γ= 0.095

	LSAP1(Impact in basis points using pooled regression coefficients)	Reinvestment (Impact in basis points using pooled regression coefficients	LSAP2 (Impact in basis points using pooled regression coefficients)	MEP (Impact in basis points using pooled regression coefficients)	MEP2 (Impact in basis points using pooled regression coefficients)	Average (Impact in basis points using pooled regression coefficients)
Total*	-9.1	-7.7	-7.4	-9.8	-9.6	-8.7
of which bond duration	-3.6	-3.7	-3.7	-5.6	-5.5	-4.4
of which local supply	-4.9	-3.3	-3.1	-3.6	-3.4	-3.7

*Includes the estimated constant term.

Compared to previous studies, our total estimated effect on the 10-year Treasury yield in most specifications is quite similar to that obtained by Li and Wei (2013), as their results imply an average impact of about 7 basis points per $100 billion of 10-year equivalents; and considering that they do not explicitly account for the local supply channel, it is not surprising that in some specifications our estimates can be a bit larger in magnitude. On the other hand, our estimates of the local supply effect in some specifications are just slightly smaller than those reported in D'Amico and King (2013), which imply that in the 10-year sector the total impact of the first LSAP is about 15 basis points for the total $300 billion of purchases, that is, about 5 basis points per $100 billion of purchases. However, in that study, the authors estimate the total stock effect from the day before the announcement of the first LSAP to the day of the last purchase; therefore, they do not capture exclusively the announcement effect as is the case in this study.

Conclusions

In summary, we found that, once the pre-announcement market expectations are carefully controlled for, both duration risk channel and local supply channel are always operating and are about equally important in explaining yield reactions of nominal Treasury securities to the Federal Reserve asset purchase announcements. This result suggests that it is not only the total size of the program but also its design that matters, where the latter is mainly determined by the maturity composition of purchases/sales. It also signifies the importance of the Committee's communication strategy, as it can strongly influence all three components--the size, the total dollar duration, and the location--of the supply shocks and the resulting Treasury yield responses.

APPENDIX A: Computation of the Expected Total Size

The first LSAP (LSAP1) announcement in March 2009: In the PDS before the meeting, respondents indicated that they attached 49 percent probability to the Federal Reserve announcing purchases of long-term Treasury securities, 62 percent probability to an expansion of agency debt purchases, and 69 percent probability to an expansion of agency MBS purchases. The survey did not ask the sizes of the programs; we therefore examined the primary dealers' written comments to each answer for clues about the expected size of the purchases. Among the few who provided forecasts for the combined size of the program, none cited a number above $600 billion, which is far below the $1.15 trillion that was announced. A conservative measure of the surprise can therefore be calculated by multiplying the actual announced purchases of Treasury securities, agency debt, and agency MBS by the corresponding probability and sum up. This calculation implicitly treats all three types of securities as perfect substitutes.

Reinvestment policy announcement in August 2010: In the PDS, the respondents assigned 43 percent probability to the Fed starting to reinvest the principal payments from agency securities. Determining the expected size of the program requires us to choose a value for the expected cumulative agency MBS principal paydowns. For this we relied on the average across various projections available in market commentaries at the time, which estimated that roughly $200 billion would have been paid down over the next 6 months.

The second LSAP (LSAP2) announcement in November 2010: Primary Dealers assigned an average probability of 88 percent to the FOMC announcing at the upcoming meeting an expansion of its portfolio through additional asset purchases. They also on average indicated that the total size of the program would have been about $1 trillion over a 12-month horizon. We rescale the expected amount by the actual length of the announced program of about 7 months, assuming a constant monthly pace.

MEP announcement in September 2011: In the PDS, respondents assigned 73 percent probability to the FOMC announcing an increase in the average duration of SOMA holdings as an easing tool within 1 year. They also indicated that the program was expected to be about $376 billion over an almost 7-month horizon, with purchases occurring in the 7- to 30-year maturity sector and sales in the 0- to 3-year maturity sector. Given this detailed information, we are able to compute the surprise without relying on any strong assumption. In the statement from that meeting, the FOMC also announced it would begin reinvesting principal payments from its holdings of agency debt and agency MBS in agency MBS instead of Treasuries, which reportedly came as a surprise to the market. The effect of this surprise was likely to be small and we ignore it in the current analysis.

MEP extension announcement in June 2012: Primary dealers assigned about 54 percent probability to the FOMC easing at the upcoming meeting utilizing the size or composition of its portfolio. To estimate the size of the extension, investors appeared to look at the amount of Treasury securities in SOMA holdings with maturities that were expected to fall below 3 years over the next few months, which over a 6-month period totaled about $205 billion at the time. It is therefore safe to conjecture that, had they expected the MEP to be extended in its original form for 6 months, the expected size of the program was likely $205 billion, compared to the actual announced amount of $267 billion. Also in this case, we do not need to rely on strong assumptions and simply calculate the expected size of the program by multiplying the perceived probability of an MEP extension by the expected size of the extension conditional on the program being announced.

APPENDIX B: Computation of the Maturity Distribution of Purchases

The post-announcement maturity weights are calculated as follows. The Desk's technical notes following the LSAP1 and the reinvestment program announcements were very similar and specified only that the purchases would be concentrated in the 2- to 10-year sector. For LSAP1, we therefore assume that investors recalibrated their post-announcements weights in the following way: they understood the language to mean about 80% of purchases would occur in the 2- to 10-year sector, and weighted securities in this sector proportionally to their amounts outstanding as a fraction of the total outstanding in the 2- to 10-year sector only. Similarly, we assign the remaining 20% to the securities outside the eligible maturity sector proportionally to the amounts outstanding in the excluded maturity ranges. For the reinvestment program announcement, we assume that, based on their previous experience with purchases allocation under LSAP1, they continued to assign weights identical to those associated with the actual LSAP1 purchases; which implies that the pre- and post-announcements weights are identical for this announcement. Starting with LSAP2, the Desk would release statements simultaneously with the FOMC announcements outlining the intended weights for each of the maturity buckets, which are used as the post-announcement weights for those programs. The following tables show the pre- and post-announcements weights for each program.

LSAP1

	1.5-2.5 years	2.5-4 years	4-5.5 years	5.5-7 years	7-10 years	10-17 years	17-30 years
LSAP1 expected*	17.40%	20%	18%	8.50%	17.80%	8%	10.30%
LSAP1 announced**	9.70%	25%	22.30%	10.60%	22.10%	4.50%	5.80%

*The expected weights are assumed to be proportional to the percentage of the amount outstanding in each bucket. ** The actual weights have been recalibrated to reflect the Desk announcement specifying that purchases were going to be concentrated in the 2- to 10 year sector

Reinvestment Program

	1.5-2.5 years	2.5-4 years	4-5.5 years	5.5-7 years	7-10 years	10-17 years	17-30 years
Reinvestment expected*	8.90%	24.50%	19.70%	20.30%	11.60%	8.20%	6.20%
Reinvestment announced**	8.90%	24.50%	19.70%	20.30%	11.60%	8.20%	6.20%

* The expected weights are assumed to be equal to the actual purchases maturity distribution observed for LSAP1. ** As at that time there was no announcement about the weights, the announced weights are assumed to be equal to the expected, as following both LSAP1 and Reinvestment program announcements the Desk specified that purchases were going to be concentrated in the 2-to 10-year sector.

LSAP2

LSAP2	1.5-2.5 years	2.5-4years	4-5.5 years	5.5-7 years	7-10 years	10-17 years	17-30 years
LSAP2 expected	9%	24%	20%	20%	11%	9%	7%
LSAP2 announced	5%	20%	20%	23%	23%	2%	4%

Notes: The expected LSAP2 maturity distribution is equal to the LSAP1 actual maturity distribution of the final purchases except for rounding.

MEP

	6-8 years	8-10 years	10-20 years	20-30 years
MEP expected	44.20%	44.20%	3.80%	7.70%
MEP announced	32%	32%	4%	29%

Notes: The expected weights for the MEP have been obtained by redistributing the percentage amount previously purchased (and as such observed by the market) in the 1.5- to 6- year sector over the 6- to 30 year sector proportionally to the percentage of the sector.

MEP Extension

	6-8 years	8-10 years	10-20 years	20-30 years
MEP extension expected	32%	32%	4%	29%
MEP extension announced	32%	32%	4%	29%

Note: the maturity distribution expected for the MEP extension is assumed to be equal to that one announced for the original MEP.

References

Amihud, Y., Mendelson, H., 1991. Liquidity, maturity, and the yields on US Treasury securities. Journal of Finance 46, 1411-1425.

Andres, J., Lopez-Salido, J. D., Nelson, E., 2004. Tobin's imperfect asset substitution in optimizing general equilibrium. Journal of Money, Credit and Banking 36, 665-690.

Banerjee, R., Daros, S., Latto, D., McLaren, N., 2012. Using changes in auction maturity sectors to help identify the impact of QE on gilt yields. Quarterly Bulletin 2012 Q2, Bank of England.

Bauer, M. D., Rudebusch G.D., 2012. The signaling channel for Federal Reserve Bond Purchases. FRBSF working paper 2011-21. August.

Bernanke, B. S., Reinhart, V. R., Sack, B. P., 2004. Monetary policy alternatives at the zero bound: an empirical assessment. Brookings Papers on Economic Activity 2, 1-78.

Brandt, M.W., Kavajecz, K. A., 2004. Price discovery in the US Treasury market: the impact of order flow and liquidity on the yield curve. Journal of Finance 59, 2623-2654.

Cochrane, J. H., 2008. Comments on `Bond supply and excess bond returns' by Robin Greenwood and Dimitri Vayanos. May 12, presentation at the Initiative in Global Financial Markets Beyond Liquidity Conference, University of Chicago.

Cox, J. C., Ingersoll, J. E., Ross, S. A., 1985. A theory of the term structure of interest rates. Econometrica 53, 385-407.

Culbertson, J. M., 1957. The term structure of interest rates. Quarterly Journal of Economics 71, 485-517.

D'Amico, S., English, W., López-Salido, D., Nelson, E., 2012. The Federal Reserve's Large-Scale Asset Purchase Programs: Rationale and Effects. Economic Journal, vol.122, November, 415-446.

D'Amico, S., King, T.B., 2013. Flow and Stock Effects of Large-Scale Treasury Purchases: Evidence on the Importance of Local Supply. Journal of Financial Economics (forthcoming).

Duffie, D., 1996. Special repo rates. Journal of Finance 51, 493-526.

Engen, E., Hubbard, R. G., 2005. Federal government debt and interest rates. In: Gertler. M., Rogoff, K. (Eds.), NBER Macroeconomics Annual 2004. MIT Press, Cambridge, MA, pp. 83-160.

Gabaix, X., Krishnamurthy, A., Vigneron, O., 2007. Limits of arbitrage: theory and evidence from the mortgage-backed securities market. Journal of Finance 62, 557-595.

Gagnon, J., Raskin, M., Remache, J., Sack, B., 2011. Large-scale asset purchases by the Federal Reserve: did they work? International Journal of Central Banking 7 (1): 3-43.

Garleanu, N., Pedersen, L. H., Poteshman, A. M., 2009. Demand-based option pricing. Review of Financial Studies 22, 4259-4299.

Georges, P., 2003. The Vasicek and CIR models and the expectation hypothesis of the interest rate term structure. Department of Finance, Canada, Working Paper 2003-17.

Greenwood, R., 2005. Short- and long-term demand curves for stocks: theory and evidence on the dynamics of arbitrage. Journal of Financial Economics 75, 607-649.

Greenwood, R., Vayanos, D., 2010a. Price pressure in the government bond market. American Economic Review 100, 585-590.

Greenwood, R., Vayanos, D., 2010b. Bond supply and excess bond returns. NBER Working Paper 13806.

Gromb, D., Vayanos, D., 2010. Limits of arbitrage: the state of the theory. Annual Review of Financial Economics 2, 251-275.

Gurkaynak, R., Wright, J., 2012. Macroeconomics and the term structure. Journal of Economic Literature 50, 331-367.

Hamilton, J., Wu, J., 2012. The effectiveness of alternative monetary policy tools in a zero lower bound environment. Journal of Money, Credit and Banking 44, 3-46.

Han, B., Longstaff, F. A., Merrill, C., 2007. The US Treasury buyback auctions: the cost of retiring illiquid bonds. Journal of Finance 62, 2673-2693.

Holland, T. E., 1969. `Operation Twist' and the movement of interest rates and related economic time series. International Economic Review 10, 260-265.

Hu, X., Pan, J., J., Wang., 2012. Noise as information for illiquidity. NBER Working Paper 16468.

Jordan, B. D., Jordan, S. D., 1997. Special repo rates: an empirical analysis. Journal of Finance 52, 2051-2072.

Joyce, M. A. S., Tong, M., 2012. QE and the Gilt market: a disaggregated Analysis. Economic Journal, vol.122, November, 348-384.

Kaminska, I., Vayanos, D., Zinna, G., 2011. Preferred-habitat investors and the US term structure of real rates. Bank of England Working Paper 435.

Krishnamurthy, A., 2002. The bond/old-bond spread. Journal of Financial Economics 66, 463-506.

Krishnamurthy, A.,Vissing-Jorgensen, A., 2011. The effects of quantitative easing on interest rates: channels and implications for policy. Brookings Papers on Economic Activity, vol. 2, 215-87.

Krishnamurthy, A.,Vissing-Jorgensen, A., 2012. The aggregate demand for Treasury debt. Journal of Political Economy, vol. 120 (1), 233-67.

Kuttner, K., 2006. Can central banks target bond prices? NBER Working Paper 12454.

Li, C., Wei, M., 2012. Term Structure Modelling with Supply Factors and the Federal Reserve's Large Scale Asset Purchase Programs. International Journal of Central Banking, March 2013 .

Longstaff, F. A., 2004. The flight-to-liquidity premium in US Treasury bond prices. Journal of Business 77, 511-526.

Lou, D., Yan, H., Zhang, J., 2010. Anticipated and repeated shocks in liquid markets. Unpublished working paper. London School of Economics and Yale University.

Meaning, J., Zhu, F., 2011. The impact of recent central bank asset purchase programs. BIS Quarterly Review, December, 73-83.

Modigliani, F., Sutch, R., 1966. Innovations in interest rate policy. American Economic Review 56, 178-197.

Musto, D., Nini, G., Schwarz, K., 2011. Notes on bonds: liquidity at all costs in the great recession. Unpublished working paper, University of Pennsylvania.

Ross, M., 1966. `Operation Twist': a mistaken policy? Journal of Political Economy 74, 195-199.

Svensson, L. E. O., 1994. Estimating and interpreting forward interest rates: Sweden 1992-1994. NBER Working Paper 4871.

Swanson, E. T., 2011. Let's twist again: a high-frequency event-study analysis of Operation Twist and its implications for QE2. Brookings Papers on Economic Activity 42, 151-188.

Vayanos, D., Vila, J-L., 2009. A preferred-habitat model of the term structure of interest rates. NBER Working Paper 15487.

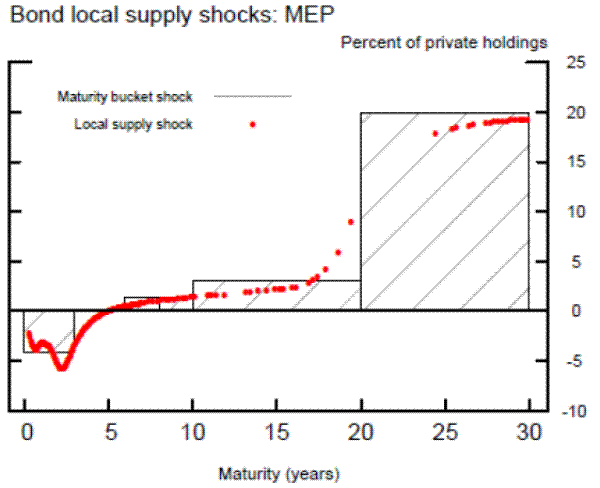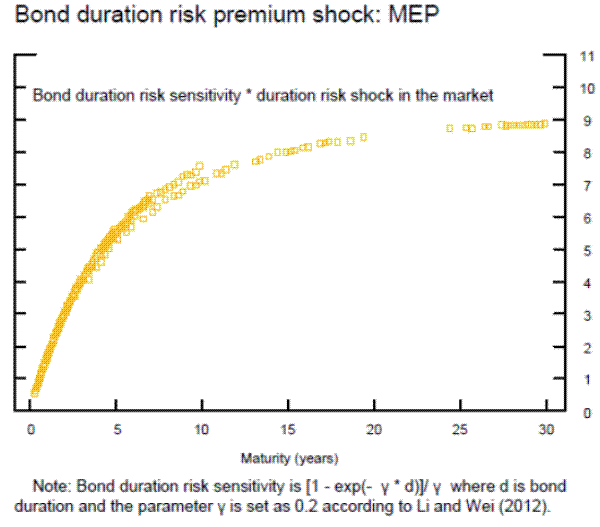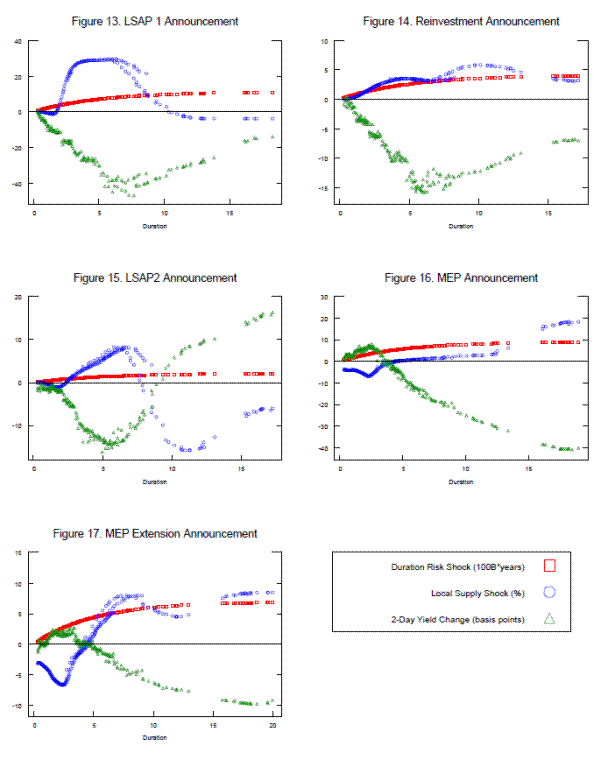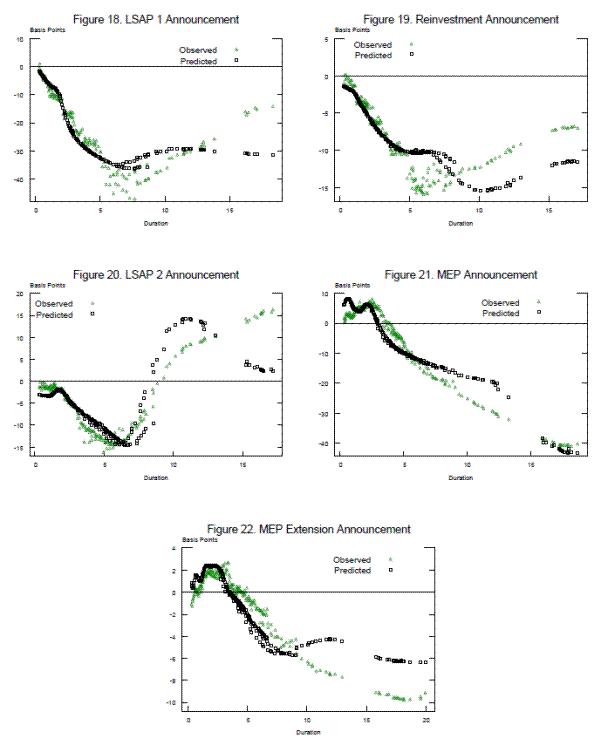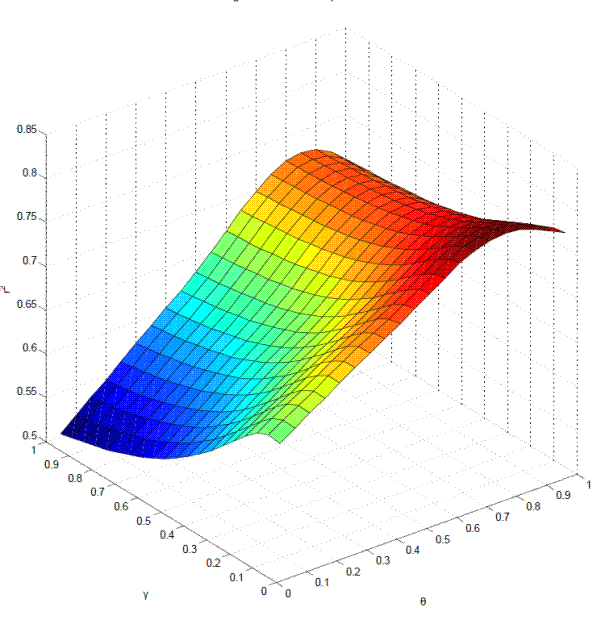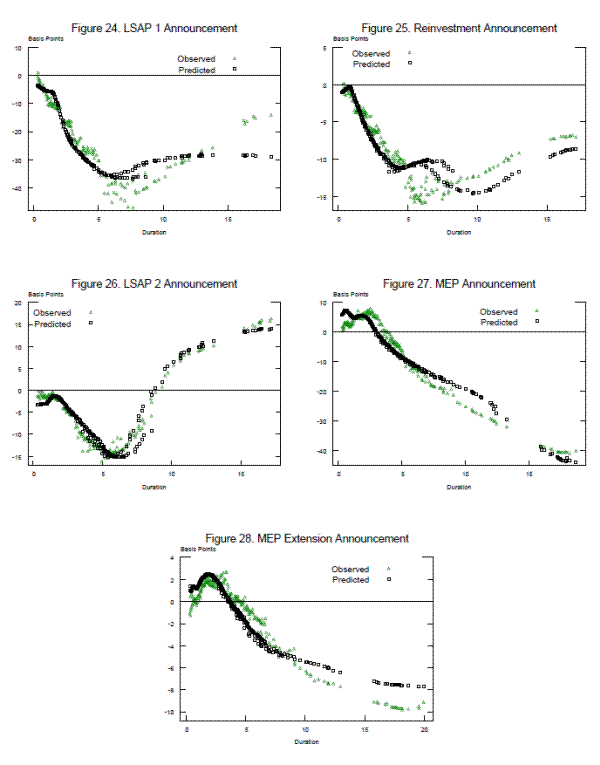**From Figure 1 to Figure 5 :**

**From Figure 6 to Figure 10 :**

**Figure 11**

**Figure 12**

**Figure 13-17**

**Figure 18-22**

**Figure 23**

Figure 23 Data

**Figure 24-28**

Footnotes

^a Division of Monetary Affairs, Federal Reserve Board, 20^th and C Streets NW Washington, DC 20551 USA.Corespondence to: Canlin Li,[email protected];202-452-2227.For helpful discussions and comments we thank other members of the Staff at the Federal Reserve Board and the Federal Reserve Bank of New York,and inparticular Jim Clouse, Thomas King, Matthew Raskin and Min Wei,as well as Greg Duffee and Jonathan Wright.The views expressed in this paper are those of the authors alone and do not necessarily reflect the views of the Board of Governors of the Federal Reserve System or its staff.Return to Text

1. Bauer and Rudebusch (2012) stress the importance of a third channel: the signaling channel; but it is not found to be a relevant driver of the impact of these policies across the above mentioned studies. Return to Text

2. D'Amico and King (2013) is the first study to use CUSIP-level data to identify the local supply effects, but the empirical analysis is not based on intraday changes around FOMC announcements and is focused only on the first Treasury asset purchase program. Return to Text

3. The March Primary Dealer Survey conducted by the Desk indicated that the average probability associated to the Treasury purchase program being announced was 49 percent and not necessarily at the upcoming March FOMC meeting. Return to Text

4. Similarly to market commentaries, the August Primary Dealer Survey indicated that the average probability of agency MBS reinvestments to be in Treasury securities was 19 percent. Return to Text

5. This is generally true in standard term structure models where the supply factor is mainly related to the level factor. Return to Text

6. The Federal Reserve's System Open Market Account (SOMA) held at the time of the announcement 18.5 percent of the outstanding amount in the 10-30-year maturity sector, 13 percent of the 7-10-year maturity sector and 14 percent of the 5.5-7-year maturity sector. Return to Text

7. A detailed description of our computations for each of these variables is provided in Appendix A and B. Return to Text

8. Because of this somewhat arbitrary choice, in the robustness section we show an estimation of the local supply effect that is independent of the shock's measurement. Return to Text

9. Most PDS respondents and market observers cited the 6- to 30-year sector as the most likely for purchases. Return to Text

10. For a detailed derivation see Georges (2003). Return to Text

11. It can be estimated by OLS due to the availability of a measure for the exogenous supply `shocks.' Return to Text

12. In plotting yield responses against maturities following the MEP announcement, 5-year maturity is where yields responses change from positive to negative values. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text