Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-42 Screen Reader version ^♣

Economic Volatility and Financial Markets: The Case of Mortgage-Backed Securities*

Gaetano Antinolfi†

Celso Brunetti‡

Abstract:

The volatility of aggregate economic activity in the United States decreased markedly in the mid eighties. The decrease involved several components of GDP and has been linked to a more stable economic environment, identified by smaller shocks and more effective policy, and a diverse set of innovations related to inventory management as well as financial markets. We document a negative relation between the volatility of GDP and some of its components and one such financial development: the emergence of mortgage-backed securities. We also document that this relationship changed sign, from negative to positive, in the early 2000's.

1 Introduction

The volatility of aggregate economic activity in the United States decreased in the mid eighties. The consensus date for a significant decrease, termed The Great Moderation by Stock and Watson (2003), is the last quarter of 1984. Three broad reasons have been suggested to explain this phenomenon: a structural change in the economy, an improvement in the implementation of economic policy, especially monetary policy, and a lucky draw in the sequence of random shocks that affect the economy. These explanations are not mutually exclusive, and can well interact with one another. A challenge has been to identify more precisely which channels of transmission from shocks to economic activity have been affected and how. Among the channels that have received much attention are monetary policy, technological change and especially inventory management, financial markets development, and international integration. Again, focusing on one aspect is dictated by convenience at some level; the idea that the decrease in volatility is diffuse across several components and therefore is not likely to be completely explained by one event is clearly expressed by Kim, Nelson and Piger (2004) and Stock and Watson (2003), among others.

We establish a link between a particular form of financial market development, the process of securitization of mortgage debt, and real economic activity. There are several reasons to focus on such an aspect of the evolution of financial markets over the last thirty to forty years. First, mortgage backed securities (MBS) markets were small as a fraction of GDP in the late seventies, but have become enormous in present days, and the timing of the market development is consistent with the timing of the Great Moderation. By the early 2000's, about sixty percent of household mortgages had been securitized. Because household mortgage debt is almost the size of GDP, the mortgage-backed securities market grew from a relatively small fraction to over half of GDP in about twenty years. It is therefore an interesting question to document whether real effects are detectable in aggregate real variables. Second, mortgage backed securities have a direct link to an important household decision, the purchase of a house, and lenders' decisions to finance the purchase. Thus, the evidence that we document points (indirectly) to the possibility that the availability of risk diversification through mortgage pools generated a smoother allocation of credit and thereby acted as a coordination mechanism for the supply side as well. This channel of transmission does not rely on or require that financial innovation be related to the quantity of credit available or to the relaxation of credit constraints. Third, mortgage backed securities allow for the diversification of different kinds of risks, in particular interest rate risk and credit risk. The credit risk or counterparty risk inherent in mortgage loans has been historically relatively low, in part because of the collateral and the fractional support of the house purchase, in part because the amount of counterparty risk is to a large extent under the control of the lender. Interest rate risk, on the other hand, is largely aggregate in nature, and not easily diversifiable by the lender. Diversification of prepayment risk is, initially, the main purpose of the creation of pools. The idea that both credit risk and interest rate risk are pooled in mortgage backed securities is important, because when one considers the potential effects of introducing a market for financial derivatives that create risk-diversification possibilities that were previously unavailable, there are at least two effects to consider. The diversification of prepayment risk could increase the resilience of intermediaries to shocks, but also increase the amount of counterparty risk that they are willing to undertake. Indeed, one of the hypothesis that we consider is that in the aggregate mortgage backed securities were associated with a decrease in aggregate volatility until about 2000, but that in the last part of the sample the relation changed sign and higher volatility is related to the growth of mortgage securities markets. A corollary of this hypothesis is that even if financial market developments contributed to the Great Moderation, their contribution could have been temporary, to the point of not only fading away over time but change direction. In light of the recent history, focusing on a transmission mechanism that highlights the potential temporary nature of changes in volatility seems particularly relevant. Finally, the structure of the mortgage pools market, which was completely dominated by agency and government sponsored enterprises until the early to mid nineties, allows us to test whether pools issued by government sponsored enterprises and private intermediaries were linked in different ways to aggregate economic activity.

We study the empirical relation between the volatility of economic activity and MBS markets between 1976 and 2011 using quarterly observations on GDP and some of its components and quarterly observations on MBS issued by government sponsored enterprises (GSE's) and private intermediaries. In particular, we construct various measures of volatility for the growth rates of real GDP, consumption, housing consumption, residential investment, and investment in single housing, and then examine the empirical relation between real and financial variables with two statistical models: a linear autoregressive model first and non-linear, Markov switching model next. Empirical evidence is supportive of a negative relationship between issuance of mortgage-backed securities and the volatility of real activity in the first part of the sample, between the mid seventies and roughly 2000; in the second part of the sample the relationship is to some extent reversed, and volatility in real economy growth is positively related to volumes in MBS markets.

2 Related Literature

The Great Moderation was identified by a set of papers by Kim and Nelson (1999), McConnell and Perez-Quiros (2000), and Blanchard and Simon (2001); Stock and Watson (2003) provide a comprehensive review of this large literature and analysis of the phenomenon.¹ These papers document a break in volatility in the mid eighties, and attribute it to smaller shocks, better implementation of monetary policy, and structural changes in the economy, especially related to technology and financial-market innovation. A particular aspect, for example stressed by Blanchard and Simon (2001), and Bernanke (2004), is the role played by a decrease in the variability of inflation during the Great Moderation, thus establishing a strong link between aggregate volatility monetary policy implementation. Financial-market development is discussed by Dynan, Elmendorf, and Sichel (2005); although they do not consider a specific form of financial innovation, they conclude that financial market developments played an important role in the Great Moderation. A type of analysis closer in spirit to ours, in the sense that it attempts to link the Moderation mainly to a single economic factor, is Kahn, McConnell and Perez-Quiros (2002). They analyze the role of inventories, and point to the technological innovations that allowed for a structural change in inventory management. Blanchard and Simon (2001) already note a reversion in the correlation between inventories and sales in the nineties; Kahn et al. (2002) go on to notice that much of the Great Moderation can be explained by a reduction in the variability in the production of durable goods, and that this reduction is not accompanied by a reduction in the volatility of sales of durable goods. A follow-up paper, Ramey and Vine (2003), however, points out that for the case of the auto industry, the explanation of the decrease in industry-output volatility is due to a structural change of the sale process rather than technical changes in inventory or production management. These ideas are in a way similar to and consistent with our approach: there is a structural change in the way a market works that leads to decreased volatility, and this change can be traced to more than one factor; we just use financial markets instead of durable goods markets.

There are two recent papers that are directly linked to our analysis. The first is Den Haan and Sterk (2010) which looks at a specific consequence of financial innovation, the reduction in credit constraints. Although they conclude that the alleviation of credit constraints does not seem to be correlated with reduction in volatility of real economic activity, Den Haan and Sterk (2010) find that the shift in who holds the economy's mortgage debt, from banks to other institutions, does seem to play an important role. Of course, the shift was a consequence of the securitization process of mortgages. The second paper is Bezemer and Grydaki (2012) who show with a multivariate GARCH approach that mortgage lending played an important role in the Great Moderation. Finally, two papers analyze the role of investment. Justiniano and Primiceri (2008) point to investment as the main variable whose change can explain the moderation in the volatility of aggregate output. Peek and Wilcox (2006), with a different methodology, consider residential investment and mortgage pools and find that securitization played an important role in the reduction of the volatility of residential investment. The important message that emerges from these papers is that to see reduction in the volatility of output it is also essential to see reduction in the volatility of investment, not surprisingly, and that this reduction can be brought about indirectly, and not necessarily through direct shocks. The change in volatility, in other words, is diffuse and systemic.

3 Descriptive Statistics

We use five series from the National Income and Product Accounts (NIPA) to measure the change in volatility of economic activity. These are quarterly observations on the seasonal adjusted annual growth rates of real gross domestic product, real personal consumption, real consumption of housing services, real residential investment, and real single family residential investment. The full sample under consideration goes from the first quarter of 1974 to the second quarter of 2011.² We employ personal housing consumption and investment in single-family homes in addition to aggregate variables because these variables correspond more closely to the financial derivatives that we consider. Specifically, we consider mortgage-backed securities issued by government-sponsored enterprises and over the full sample period, and mortgage-backed securities issued by private conduits from the fourth quarter of 1984 to the end of our sample. Observations about mortgage pools come from the Flow of Funds of the United States.

We consider only mortgage pools composed of single-family mortgages. This is by far the biggest component in the mortgage pools, much larger than multifamily and commercial pools (which are of course not held by government-sponsored enterprises) and is the aggregate for which most consistent observations are available throughout the sample.

Figure 1:Mortgage Securitization as a Fraction of Single Family Mortgages.

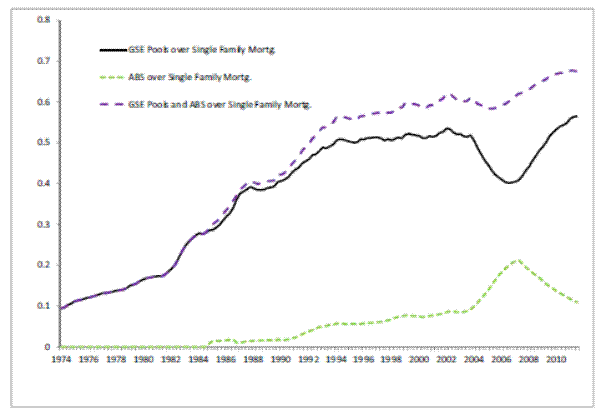
$Figure 1: Mortgage Securitization as a Fraction of Single Family Mortgages. The figure consists of three line graphs which represent the proportion of mortgage securitization as a fraction of single family mortgages. The black solid line plots the time series of the fraction of GSE (government-sponsored enterprises) out of total single family mortgages. The green dashed line plots the fraction of ABS (asset backed securities) out of total single family mortgages. The purple dashed line represents the sum of GSE and ABS securitized mortgages as a fraction of total single family mortgages over time. The horizontal axis represents time starting from year 1974 to year 2011. The vertical axis denotes the fraction of mortgage securitization and ranges from 0 to 0.8. All three plots generally increase gradually over time. The green dashed line, fraction of ABS, remains at 0 until the end of 1984, and then increases gradually to peak at 0.2 in the year of 2007. After achieving the local maximum, the fraction of ABS decays to 0.1 between 2007 and 2011. The black solid line, fraction of GSE issued mortgages, begins at 0.1 and gradually increases to 0.5 within the time interval between 1974 and 2003. The fraction then decreases to 0.4 to achieve a local minimum in 2007, and goes back up to 0.55 in 2011. In the year of 2007, the occurrence of local minimum of GSE fraction is almost synchronized with the occurrence of local maximum of the ABS fraction. The blue dashed line, which represents the fraction of GSE and ABS of single family mortgages, shows gradual growth from 0.1 to 0.65 with some minor fluctuations throughout the entire time horizon.$

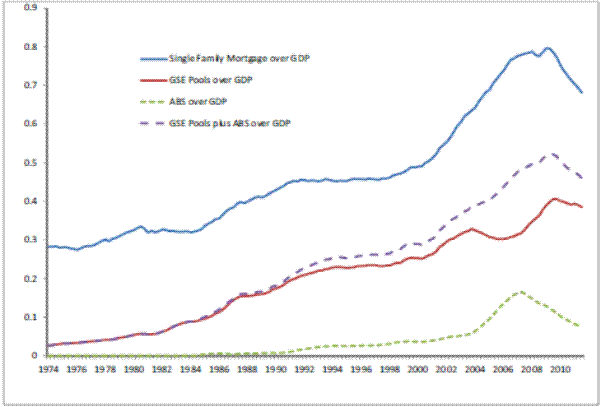
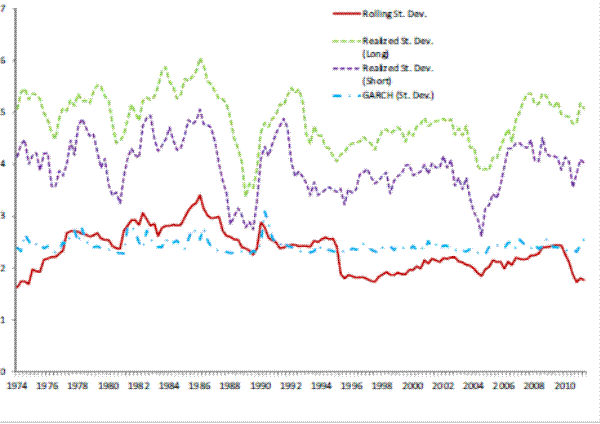
Mortgage debt, as a fraction of GDP, was about 28 percent in 1974, and it has increased to about 68 percent in 2011 after a peak of about 78 percent in 2009. The total increase in the weight of mortgage debt over GDP is mirrored by the emergence of mortgage pools. The fraction of mortgages pooled in mortgage-backed derivatives by government-sponsored enterprises (GSE's) out the total amount of (single-family) mortgage debt outstanding was slightly below 10 percent in 1974, to reach 56 percent in 2011. Mortgage pools issued by other financial institutions (i.e. not GSE's) constituted about 1 percent of all single-family mortgages in 1988, and the size of the market was negligible before then. By the end of the sample period this share had increased to 11 percent. Thus, the size of all mortgage-backed securities market went from practically negligible in the early seventies to well over two thirds of single-family mortgages in about thirty years. Figures 1 and 2 give a graphic overview of the evolution of these markets.

The main differences between mortgages in GSE's pools versus other pools concern size of the underlying loans and quality of the borrowers. GSE's are limited by regulation to create pools only with smaller mortgages (the current upper limit is $417,000 per mortgage loan) and to borrowers with high credit scores. Other institutions do not face these limits. Their pools, which we will refer to as asset backed securities (ABS) pool, are composed by mortgage loans that are characterized as jumbo, sub-prime, or alt-A. The first label refer to the size of the loan,

Figure 2: Mortgage Lending and Securitization as a Fraction of GDP.

$Figure 2: Mortgage Lending and Securitization as a Fraction of GDP. The figure illustrates growing mortgage securitization with four line graphs which represent the fraction of mortgage respect to GDP. The blue solid line plots the time series of total single family mortgages over GDP, the red solid line plots the fraction of GSE (government-sponsored enterprises) securitized mortgages over GDP. The green dotted line plots ABS (asset backed securities) pools over GDP, and the purple dashed line shows the proportion of sum of GSE and ABS over GDP. The horizontal axis represents time starting from year 1974 to 2011. The vertical axis represents the fraction of mortgage securitization and ranges from 0 to 0.9. All four plots generally increase gradually over time. The blue solid line, single family mortgages over GDP, begins around 0.28 in 1974 and increases steadily to achieve a peak at 0.8 around the year of 2009. The fraction then decreases to 0.7 from 2009 to 2011. The green dashed line, fraction of ABS over GDP, remains at 0 until the end of 1984, and then increases gradually to peak at 0.15 around 2007. After achieving the local maximum, the fraction of ABS decreases to 0.1 between 2007 and 2011. The red solid line, the fraction of GSE mortgages over GDP, begins around 0.04 and gradually increases to 0.4 over the entire horizontal axis with some fluctuations. The purple dashed line, fraction of total GSE and ABS of GDP, also shows gradual growth from 0.1 to 0.5 within the interval from 1974 to 2009. The level then decreases slightly to 0.45 in 2011.$

the second to the quality of the borrower and the third to loans that could in principle qualify for purchase by a GSE but because of some limitations not directly imputable to size and credit score, were not held by GSE's. Thus, at the level of the aggregate economy, the main difference between GSE's and non-GSE's mortgage pools is that the latter are designed to pool a potentially larger amount of credit risk. Both financial instruments pool interest rate risk.

Because of the explosive growth of MBS markets, we normalize its size and perform several stationarity tests on the resulting series. In particular, we normalize mortgage-backed securities pools, which are denominated in nominal terms in the Flow of Funds observations, in two ways: first, we express each series as a fraction of the total single-family mortgage debt outstanding (Figure 1); second, we use the average house price as a normalizing variables. We obtain average single-family house prices from the Census Bureau. Essentially, the normalization of outstanding mortgage-backed securities with average house prices supplies a (rough) measure of the average number of houses for which the "insurance coverage" is provided by mortgage pooling.

For both GSE and ABS pools we use both normalizations, by mortgage pools and house prices, throughout the analysis.

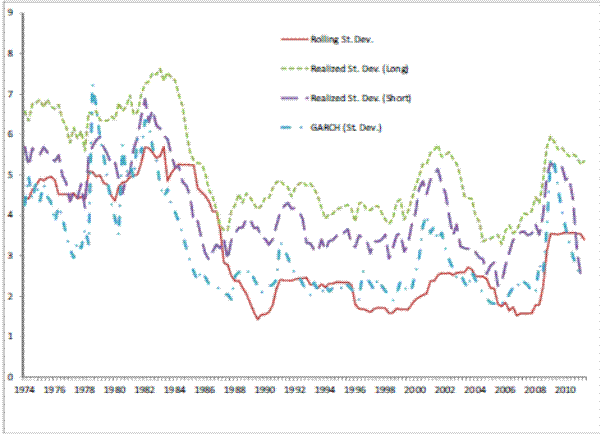
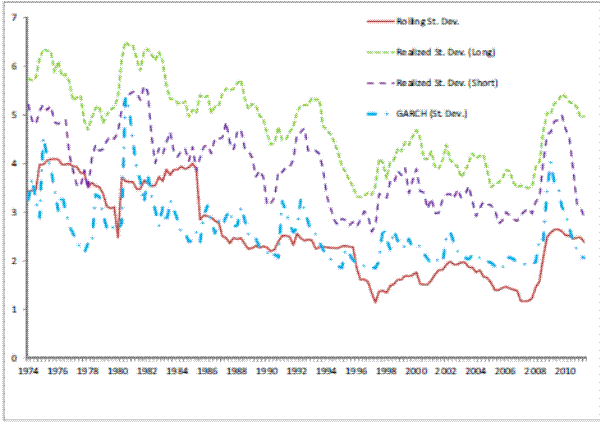
For each of the five NIPA variables (real growth of GDP, personal consumption, consumption of housing services, residential investment, single-family residential investment) we construct four measures of volatility. One is commonly used in the literature and consists of the rolling standard deviation of a series using a twenty-quarter window ( $SD{}_{y,t}$ ). This is the measure used, for example, by Blanchard and Simon (2001) and Stock and Watson (2003). We then compute two realized volatility measures. Denote $g_{y,t}$ the growth rate of variable , we first run the following regression

$\begin{displaymath} g_{y,t}=\alpha_{0,y}+\alpha_{1,y}g_{y,t-1}+\eta_{y,t} \end{displaymath}$

(1)

and then consider the absolute value of the residuals to compute realized volatilities

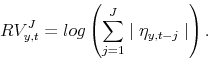$\begin{displaymath} RV_{y,t}^{J}=log\left(\sum_{j=1}^{J}\mid\eta_{y,t-j}\mid\right). \end{displaymath}$

(2)

Here

indicates the number of lags of absolute residuals that are used in the computation of realized volatility;³ we compute two measures of realized volatility for

and

The final measure of volatility that we use is an AR(1)-GARCH(1,1) specification⁴:

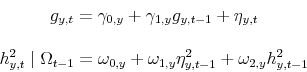$\begin{displaymath} \begin{array}{c} g_{y,t}=\gamma_{0,y}+\gamma_{1,y}g_{y,t-1}+\eta_{y,t}\ \ h_{y,t}^{2}\mid\Omega_{t-1}=\omega_{0,y}+\omega_{1,y}\eta_{y,t-1}^{2}+\omega_{2,y}h_{y,t-1}^{2} \end{array}\end{displaymath}$

(3)

where $\Omega_{t-1}$ represents the information available at time

and $\eta_{y,t}=h_{y,t}\epsilon_{y,t}$ where $\epsilon_{y,t}\sim N\left(0,1\right)$ . The first three volatility measures ( $SD{}_{y,t}$ , $RV_{y,t}^{10}$ and $RV_{y,t}^{20}$ ) are non-parametric while the fourth measure ( $h_{y,t}^{2}$ ) is parametric.

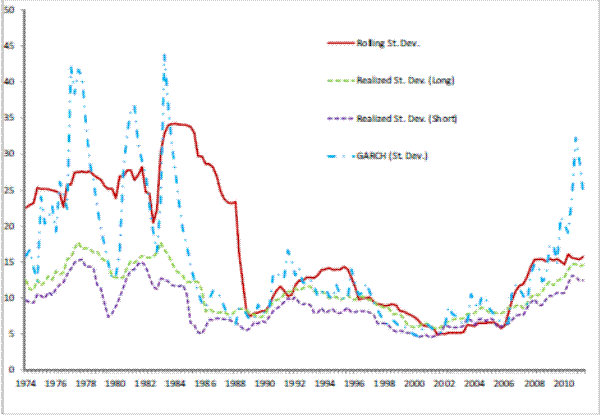
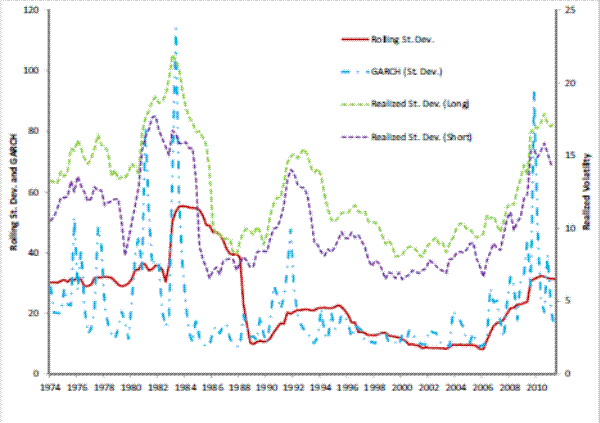
Figures 3 to 7 give a visual representation of the different volatility measures for each of the variables in the NIPA accounts used in the paper: the deseasonalized real growth rates GDP, consumption, consumption of housing services, residential investment, and investment in single housing. The graphs are similar to others in this literature (see for example Blanchard and Simon, 2001), and it is clearly visible a drop in volatility of GDP growth starting in 1984. It is also noticeable that volatility picks up, though at a reduced rate from a historic point of view, after 2000. Note that the pattern of GDP is repeated by the two residential investment measures employed, whereas consumption measure are historically much more stable, and show correspondingly a lower change in volatility both in 1984 and 2000 relative to GDP. It is also interesting to note the different magnitudes and variabilities of the volatility estimates. GDP volatility ranges between 1.4 and 7.2 percent across the different

Figure 3: GDP Growth Volatility (%)

measures⁵; consumption volatility, for both consumption and consumption of housing services, is lower and ranges between 1.1 and 5.4 percent. Real residential investment and real investment in single housing exhibit a much higher variability (between 3 and 114 percent) indicating that the volatility of these variables is itself very volatile.

The next step that we perform is to formally investigate the empirical relationships between the volatility of real variables and mortgage-backed securities.

4 Empirical Analysis and Results

We analyze the relationship between the volatility of real variables and mortgage-backed securities with two empirical approaches. First, we estimate a linear model where we regress the different volatility measures of real variables described above, on mortgage-backed security variables (MBS and ABS). Here we assume that the sample period is divided in two sub-periods. For GSE securities, the first sub-sample runs from 1974-Q1 to 2003-Q4 and the second from 1999-Q1 to 2011-Q2. For ABS, the first sub-sample starts in 1984-Q4, and before that the size of the market is negligible. The two sub-samples correspond to a decline

Figure 4: Real Consumption Growth Volatility (%).

This figure consists of four line graphs depicting volatility measures of real consumption growth rates. Each line represents different measures of standard deviation of real consumption growth. The red solid line represents rolling standard deviations, the green dashed line shows realized standard deviation (Long) and the purple dashed line plots realized standard deviation (Short). The cyan line is the GARCH (Generalized Autoregressive Conditional Heteroskedasticity) model estimated standard deviation. The horizontal axis represents time starting from year 1974 to 2011. The vertical axis represents volatility in percentages and ranges from 0 to 7. Overall, all four plots have some fluctuations and generally move together throughout the entire period. Generally, the green line dominates other lines, and the purple line dominates the cyan and red lines. The four lines generally begin around 5% and show a gradual linear decrease to 3% until 2007. There is a sudden jump from 3% level to 4.5% level in 2008; however the lines generally come back down to 3% level in 2011.

Figure 5: Real Consumption of Housing Services Growth Volatility (%).

Figure 6: Real Residential Investment Growth Volatility (%)

Figure 7: Real Investment in Single Housing Growth Volatility (%)

and to an increase in the volatility of the macro variables considered.⁶ In the first sub-period we expect to find a negative relationship between real variables and mortgage-backed securities - i.e. MBS should reduce the volatility of real variables; in the second sub-period we expect mortgage-backed securities to increase volatility levels of real variables.

For the linear approach, we need to make sure that our variables are stationary.⁷ We, therefore, perform four stationarity tests, the generalized least squares Dickey-Fuller (DF) test proposed by Elliott, Rothenberg, and Stock (1996), the Augmented Dickey-Fuller (ADF) test, the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test, and the Phillips-Perron (PP) test, for each variable and each sub-sample. The results are displayed in Table 11 in the Appendix. Stationarity is often a philosophical issue more than a substantive one and it strongly depends on the selected sample. We consider a variable to be stationary - i.e. I(0) - if at least two out of the four tests indicate that the variable is stationary (either by rejecting the null of non-stationarity, as for the DF, ADF and PP tests, or by failing to reject the null of stationarity, as in the KPSS test). Our data run over a relatively short time period (GSE emerged in the second half of the '80s). Therefore, we are generous with our critical values which we set at twenty percent level.

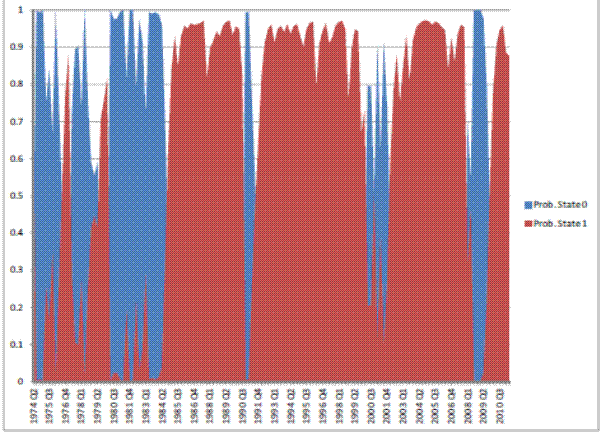
In a second approach, we postulate a non-linear relationship and estimate a Markov-switching model in which we assume that there are two possible regimes: one in which real variables are characterized by high volatility and one in which real variables are characterized by low volatility. We first estimate transition probabilities assuming that they are constant. Then, we estimate the model allowing the transition probabilities to be time varying as function of mortgage-backed securities. Stabilizing effects consist of increasing the probability of transitioning in the low-volatility state and/or decreasing the probability of leaving it. A change in transition probabilities with different sign would denote a destabilizing effect. In what follows we describe the linear and non-linear model and discuss the estimation results.

4.1 Linear Model

We estimate the following equation for each variable that survives the stationarity tests:

$\begin{displaymath} Vol{}_{y,t}=\beta_{0}+\beta_{1}Vol_{y,t-1}+\beta_{2}x_{r,t-n}+\epsilon_{t}, \end{displaymath}$

(4)

where $Vol_{y,t}$ represents one of the volatilities: $SD_{y,t}$ (rolling standard deviation), $RV_{y,t}^{10}$ (realized volatility with ten lags), $RV_{y,t}^{20}$ (realized volatility with 20 lags), and $h_{y,t}^{2}$ (GARCH volatility);⁸

refers to the real variables: GDP, consumption, consumption of housing services, residential investment and investment in single housing; and $x_{r,t-n}$ represents the nth-lag of the first difference of a measure of mortgage-backed securities outstanding, either issued by GSE's or private conduits (ABS). We normalize GSE and ABS alternatively by the total single-family mortgage debt outstanding (GSEM and ABSM) and by the average house price (GSEH and ABSH).⁹ We let the lag of the explanatory variable, measured in quarters, to be determined by best fit, so potentially this is different across different combinations of variables.¹⁰

Tables 1 - 5 display the results (missing estimated parameters indicate that at least one of the variable is not stationary).¹¹ Table 1 shows that, in the first sub-period (1974-2003), GSE is reducing the volatility of GDP. ABS, in the second sub-period (1984 - 2003) also reduces GDP volatility levels. In the third sub-period, both GSE and ABS increase GDP volatility.These results are confirmed by Table 2, which refers to the volatility of real consumption. In Tables 1 and 2, the estimated parameters are strongly significant and have negative signs in the first two sub-periods and positive signs in the last sub-period. We interpret the difference in lag-length as a statistical artifact. In fact, we report results for the optimal lag. Our main findings, however, hold for a range of lag-lengths. Table 3 reports the results for the volatility of Real Consumption of Housing Services. In sub-periods one and two, GSE and ABS reduce volatility levels. In the third sub-period, however, ABS is increasing volatility, as expected, while GSE is decreasing volatility. Although this result may seem counter intuitive, it can be explained by the behavior of housing consumption. In fact, how we shall see in the next sub-section, low activity in the housing market is concentrated during recessions and, consequently, the volatility of housing consumption behaves inversely with respect to the volatility of the other real variables we consider. Table 4 shows estimation results for the volatility of Real Residential Investment. GSE always reduces volatility, while ABS is only marginally significant. Finally, Table 5 shows estimation results for the volatility of Single-Housing Investment. GSE and ABS reduce volatility in the first two sub-periods and increase volatility in the last sub-period. Overall, our linear estimates confirm that MBS reduce volatility of real variables in the first two sub-periods and increased the same volatility in the latest period when the recent sub-prime crisis hit the economy.¹²

Table 1: Linear regression results.

Dependent variable: Volatility of Real GDP. ***, **, * refer to 5%, 10%, and 20% significance level, respectively. $RV^{20},$ $RV^{10}$ and $h^{2}$ indicate rolling standard deviation, realized volatility with lags 20 and 10 and GARCH volatility. GSEH and GSEM denote mortgage-backed securities issued by government sponsored enterprises normalized by house prices and mortgage lending. ABSH and ABSM denote the same variables issued by private conduits.

Volatility	Indep. Var.	Coeff.	St.Err.	Lag
: Sub-Period 1: 1974 - 2003	GSEH	-0.242^**	0.130	-2	0.825
: Sub-Period 1: 1974 - 2003	GSEM	-2.816^*	2.137	-2	0.822
SD:Sub-Period 2: 1984 - 2003	ABSH	0.305^***	0.153	-1	0.970
$RV^{20}$ : Sub-Period 2: 1984 - 2003	ABSH	-0.140^*	0.092	-6	0.841
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSH	-0.340^***	0.149	-2	0.735
:Sub-Period 2: 1984 - 2003	ABSH	-0.450^**	0.243	-1	0.718
SD:Sub-Period 2: 1984 - 2003	ABSM	5.671	4.631	-1	0.970
$RV^{20}$ : Sub-Period 2: 1984 - 2003	ABSM	-4.704^***	1.993	-5	0.847
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSM	-5.543^*	3.453	-1	0.724
: Sub-Period 2: 1984 - 2003	ABSM	-10.46^***	5.165	-3	0.718
$RV^{10}$ :Sub-Period 3: 1999 - 2011	GSEH	0.056^*	0.036	-3	0.817
: Sub-Period 3: 1999 - 2011	GSEH	0.162^**	0.085	-1	0.809
$RV^{10}$ : Sub-Period 3: 1999 - 2011	GSEM	0.858	1.554	-1	0.806
: Sub-Period 3: 1999 - 2011	GSEM	4.016^*	2.917	-1	0.784
$RV^{10}$ :Sub-Period 3: 1999 - 2011	ABSH	0.103^***	0.044	-6	0.827
: Sub-Period 3: 1999 - 2011	ABSH	0.245^**	0.140	-10	0.802
$RV^{10}$ : Sub-Period 3: 1999 - 2011	ABSM	5.219^***	1.787	-10	0.846
: Sub-Period 3: 1999 - 2011	ABSM	7.653	4.104	-10	0.799

Table 2: Linear regression results.

Dependent variable: Volatility of Real Consumption. ***, **, * refer to 5%, 10%, and 20% significance level, respectively. $RV^{20},$ $RV^{10}$ and $h^{2}$ indicate rolling standard deviation, realized volatility with lags 20 and 10 and GARCH volatility. GSEH and GSEM denote mortgage-backed securities issued by government sponsored enterprises normalized by house prices and mortgage lending. ABSH and ABSM denote the same variables issued by private conduits.

Volatility	Indep. Var.	Coeff.	St.Err.	Lag
: Sub-Period 1: 1974 - 2003	GSEH	-0.221^***	0.094	-10	0.653
: Sub-Period 1: 1974 - 2003	GSEM	0.727	1.386	-5	0.676
SD: Sub-Period 2: 1984 - 2003	ABSH	-0.124	0.101	-8	0.925
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSH	-0.417^***	0.135	-8	0.838
: Sub-Period 2: 1984 - 2003	ABSH	-0.454^***	0.206	-8	0.596
SD: Sub-Period 2: 1984 - 2003	ABSM	-2.392	2.590	-8	0.925
$RV^{10}$ :Sub-Period 2: 1984 - 2003	ABSM	-7.307^***	2.937	-8	0.831
:Sub-Period 2: 1984 - 2003	ABSM	-9.095^**	5.072	-6	0.595
SD:Sub-Period 3: 1999 - 2011	GSEH	0.077^***	0.018	-2	0.953
$RV^{10}$ : Sub-Period 3: 1999 - 2011	GSEH	0.096^***	0.015	-2	0.870
: Sub-Period 3: 1999 - 2011	GSEH	0.128^***	0.044	-1	0.826
SD: Sub-Period 3: 1999 - 2011	GSEM	3.029^***	0.799	-1	0.946
$RV^{10}$ : Sub-Period 3: 1999 - 2011	GSEM	2.260^***	0.915	-1	0.812
: Sub-Period 3: 1999 - 2011	GSEM	3.454^**	1.849	-1	0.785
SD: Sub-Period 3: 1999 - 2011	ABSH	0.095^***	0.039	-9	0.934
$RV^{10}$ :Sub-Period 3: 1999 - 2011	ABSH	0.120^***	0.034	-10	0.840
:Sub-Period 3: 1999 - 2011	ABSH	0.173^***	0.079	-10	0.804
SD: Sub-Period 3: 1999 - 2011	ABSM	3.127^***	1.399	-10	0.932
$RV^{10}$ : Sub-Period 3: 1999 - 2011	ABSM	4.122^***	1.050	-10	0.844
: Sub-Period 3: 1999 - 2011	ABSM	5.158^***	2.376	-10	0.797

Table 3: Linear regression results.

Dependent variable: Volatility of Real Consumption of Housing Services. ***, **, * refer to 5%, 10%, and 20% significance level, respectively. $RV^{20}$ , $RV^{10}$ and $h^{2}$ indicate rolling standard deviation, realized volatility with lags 20 and 10 and GARCH volatility. GSEH and GSEM denote mortgage-backed securities issued by government sponsored enterprises normalized by house prices and mortgage lending. ABSH and ABSM denote the same variables issued by private conduits.

Volatility	Indep. Var.	Coeff.	St.Err.	Lag
$RV^{20}$ : Sub-Period 1: 1974 - 2003	GSEH	-0.072^***	0.027	-9	0.838
$RV^{10}$	GSEH	-0.092^***	0.035	-7	0.772
	GSEH	-0.048^***	0.022	-4	0.387
$RV^{20}$	GSEM	-1.527^***	0.616	-5	0.835
$RV^{10}$	GSEM	-1.830^**	0.936	-4	0.765
	GSEM	-0.461	0.450	-3	0.375
$RV^{20}$ : Sub-Period 2: 1984 - 2003	ABSH	-0.167^**	0.100	-10	0.831
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSH	-0.189^**	0.112	-6	0.783
: Sub-Period 2: 1984 - 2003	ABSH	-0.127^*	0.083	-7	0.431
$RV^{20}$ : Sub-Period 2: 1984 - 2003	ABSM	-3.855^***	1.819	-10	0.833
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSM	-3.946^**	2.201	-6	0.782
: Sub-Period 2: 1984 - 2003	ABSM	-2.682^*	1.633	-7	0.430
$RV^{20}$ :Sub-Period 3: 1999 - 2011	GSEH	-0.034^***	0.011	-9	0.821
$RV^{20}$ :Sub-Period 3: 1999 - 2011	GSEH	-0.014^*	0.009	-5	0.811
$RV^{10}$ :Sub-Period 3: 1999 - 2011	GSEH	-0.024^**	0.014	-5	0.701
:Sub-Period 3: 1999 - 2011	GSEH	-0.013^**	0.007	-6	0.154
SD: :Sub-Period 3: 1999 - 2011	GSEM	-1.670^***	0.487	-9	0.830
$RV^{20}$ :Sub-Period 3: 1999 - 2011	GSEM	-0.711^*	0.458	-9	0.815
$RV^{10}$ :Sub-Period 3: 1999 - 2011	GSEM	-0.951^*	0.596	-7	0.699
:Sub-Period 3: 1999 - 2011	GSEM	-0.538	0.554	-9	0.138
SD:Sub-Period 3: 1999 - 2011	ABSH	0.084^***	0.021	-9	0.835
$RV^{20}$ :Sub-Period 3: 1999 - 2011	ABSH	0.024^*	0.016	-6	0.813
$RV^{10}$ :Sub-Period 3: 1999 - 2011	ABSH	0.037^**	0.019	-2	0.703
:Sub-Period 3: 1999 - 2011	ABSH	0.016	0.014	-3	0.134
SD :Sub-Period 3: 1999 - 2011	ABSM	3.169^***	0.673	-10	0.846
$RV^{20}$ :Sub-Period 3: 1999 - 2011	ABSM	0.849^*	0.536	-4	0 .814
$RV^{10}$ :Sub-Period 3: 1999 - 2011	ABSM	1.074^*	0.651	-4	0.696
:Sub-Period 3: 1999 - 2011	ABSM	0.622	0.571	-6	0.134

Table 4: Linear regression results.

Dependent variable: Volatility of Real Residential Investment. ***, **, * refer to 5%, 10%, and 20% significance level, respectively. $RV^{20},$ $RV^{10}$ and $h^{2}$ indicate rolling standard deviation, realized volatility with lags 20 and 10 and GARCH volatility. GSEH and GSEM denote mortgage-backed securities issued by government sponsored enterprises normalized by house prices and mortgage lending. ABSH and ABSM denote the same variables issued by private conduits.

Volatility	Indep. Var.	Coeff.	St.Err.	Lag
: Sub-Period 1: 1974 - 2003	GSEH	-1.779^***	0.797	-7	0.859
:Sub-Period 1: 1974 - 2003	GSEM	-28.64^***	12.61	-6	0.857
SD: Sub-Period 2: 1984 - 2003	ABSH	2.714^*	1.373	-5	0.979
$RV^{10}$ Sub-Period 2: 1984 - 2003	ABSH	0.011	0.126	-1	0.847
: Sub-Period 2: 1984 - 2003	ABSH	-0.658	1.206	-1	0.781
$\begin{displaymath}SD\end{displaymath}$ : Sub-Period 2: 1984 - 2003	ABSM	78.50^***	36.03	-5	0.980
$RV^{10}$ : Sub-Period 2: 1984 - 2003	ABSM	5.658^*	3.506	-4	0.852
: Sub-Period 2: 1984 - 2003	ABSM	13.79	29.23	-2	1.388

4.2 Non-Linear Model

We now take a different approach, and instead of postulating the presence of different sub-periods we estimate a regime-switching model over the entire sample. The assumption in this case is that the process described by the dependent variable can shift between two regimes, one of high and one of low volatility, and that the process followed by the two regimes evolves according to a two-state first-order Markov process. The advantage of this approach is that, unlike the previous case, we need not be concerned with stationarity issues and do not have to partition exogenously the whole sample period in sub-samples. The disadvantage is that we have to estimate a much larger number of parameters. The specific equation that we estimate is given by

$\begin{displaymath} g_{y,t}=\mu_{i,y}+\epsilon_{y,t}. \end{displaymath}$

Here $\epsilon_{yt}\thicksim N\left(0,\sigma_{i,y}\right)$ where

represent the state $s(i)_{t}$ . We assume that transition probabilities evolve according to a probit model

$\begin{displaymath} p\left(s_{t}=i\mid s_{t-1}=j\right)=\Phi\left(z_{t}\right) \end{displaymath}$

where $\Phi$ is the standard normal distribution. Here $z_{t}=a+bx_{r,t-n}+\delta_{t}$ where the error term $\delta_{t}$ is normally distributed and orthogonal to $\epsilon_{y,t}.$ The meaning of the explanatory variable $x_{r,t-n}$ is the same discussed in the previous section: it represents the nth-lag of a measure of mortgage-backed securities outstanding, either issued by GSE's or private conduits (GSEM, GSEH, ABSM and ABSH), and the lag is determined optimally by best fit. Estimation is by maximum likelihood using the EM algorithm by Hamilton (1994). Tables 6-10 show the results. The first column of each table reports estimation results for the model with constant transition probabilities. Table 6 refers to GDP estimates. The high-volatility state $\left(\sigma_{0}=5.022\right)$ is characterized by a low growth rate, whereas the low-volatility state $\left(\sigma_{1}=1.683\right)$ is characterized by a higher growth rate. The low-volatility regime is more persistent than the high-volatility regime. ¹³ The graphs of the transition probabilities are reported in the Appendix. When we introduce explanatory variables in the transition probabilities we allow those probabilities to change over time. GSE's securities, both as a fraction of total mortgage lending and normalized by house prices, has a significant negative coefficient in the $p\left(s_{t}=0\mid s_{t-1}=0\right)$ , i.e. the probability of remaining in the high-volatility state decreases with the introduction of securitized mortgages. The opposite result holds for ABS normalized by mortgage debt outstanding. As expected, Log-likelihood values improve when we introduce an additional explanatory variable in the transition probabilities. Table 7 reports results for real consumption. In this case the low-volatility state is much more persistent (see Figure 9). The probability of remaining in the low-volatility state increases with GSE's securities, and decreases with ABS. Similarly to the GDP results, GSE's are stabilizing whereas ABS are destabilizing. Table 8 refers to consumption of housing services. Contrary to the other models, the high-volatility regime $\left(\sigma_{0}=2.445\right)$ is characterized by high growth $\left(\mu_{0}=2.926\right)$ , whereas the low-volatility regime $\left(\sigma_{1}=1.278\right)$ is accompanied by a low growth rate $\left(\mu_{1}=0.754\right)$ . A possible reason is that low activity in the housing market is concentrated during recessions (see Figure 10 in the Appendix). GSE's increase the probability of staying in the state with high growth while ABS reduce that probability. Interestingly, GSE's also increase the probability of remaining in the low-volatility state. Tables 9 and 10 concern respectively residential investment and investment in single housing, which are among of the most volatile aggregate in the National Income Accounts. For both aggregates results are consistent: the introduction of mortgage backed securities issued by GSE's tends to decrease the probability of remaining in the high-volatility state and increase the probability of leaving the high volatility state, whereas the opposite is true for securities issued by private conduits. An important remark refers to the combined evidence from the linear and non-linear models. As the sign change the coefficient relating mortgage backed securities and real variables tends to be positive in the second sub-sample for all issuing institutions, it is likely that the different sign in the non-linear model between GSE's and private conduits is due to different samples: all signs tend to be positive over the period 1999-2011 in the linear model and private conduits become a relevant fraction of the market only in the 90's. The same phenomenon could be behind the different levels of statistical significance between GSE securities and private issuers.

As in the case of the linear model, estimates are broadly consistent across models. (Time lags are also in line between the linear and non-linear specifications.) Moreover, again like in the linear model, estimates pertaining to ABS markets tend to be statistically weaker due to the smaller sample.

Table 5: Linear regression results.

Volatility	Indep. Var.	Coeff.	St.Err.	Lag
$RV^{20},$ : Sub-Period 1: 1974- 2003	GSEH	-0.060^***	0.030	-9	0.956
$RV^{10}$ : Sub-Period 1: 1974- 2003	GSEH	-0.087^***	0.042	-7	0.930
: Sub-Period 1: 1974- 2003	GSEH	-5.436^***	2.604	-8	0.472
$RV^{20},$ : Sub-Period 1: 1974- 2003	GSEM	-1.700^***	0.989	-10	0.956
$RV^{10}$ :Sub-Period 1: 1974- 2003	GSEM	-1.700^**	0.989	-10	0.956
:Sub-Period 1: 1974- 2003	GSEM	0.461	0.450	-3
: Sub-Period 2: 1984 - 2003	ABSH	4.503^**	2.727	-5	0.975
$RV^{20},$ :Sub-Period 2: 1984 - 2003	ABSH	-0.187^**	0.095	-4	0.918
$RV^{10}$ :Sub-Period 2: 1984 - 2003	ABSH	0.119^*	0.119	-10	0.855
:Sub-Period 2: 1984 - 2003	ABSM	-4.697^*	3.587	-4	0.444
:Sub-Period 2: 1984 - 2003	ABSM	133.6^*	70.58	-5	0.976
$RV^{20},$ :Sub-Period 2: 1984 - 2003	ABSM	-7.324^***	2.787	-4	0.923
$RV^{10}$ :Sub-Period 2: 1984 - 2003	GSEH	-4.277^*	3.152	-1	0.856
:Sub-Period 2: 1984 - 2003	GSEH	-114.1^*	87.71	-4	0.445
:Sub-Period 3: 1999 - 2011	GSEH	5.796^**	3.355	-3	0.435
:Sub-Period 3: 1999 - 2011	GSEH	160.3^***	74.00	-1	0.361
:Sub-Period 3: 1999 - 2011	GSEH	3.803^*	2.276	-7	0.308
:Sub-Period 3: 1999 - 2011	GSEH	-177.3^*	105.8	-1	0.337

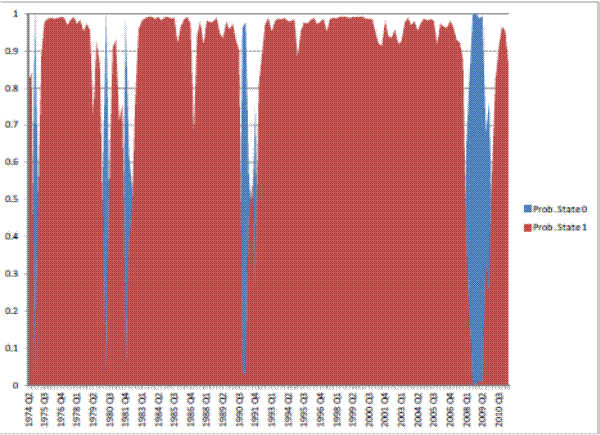
Table 6: Estimation results: regime-switching model, Real GDP.

		GSEH (2)	GSEM (4)	ABSH (4)	ABSM (5)
$\mu_{0}$	1.910^***	2.066^***	2.142^***	2.240^***	2.361^***
$\mu_{0}$ : Standard Deviation	(0.689)	(0.679)	(0.759)	(0.734)	(0.696)
$\mu_{1}$	3.217^***	3.209^***	3.197^***	3.179^***	3.217^***
$\mu_{1}$ : Standard Deviation	(0.209)	(0.213)	(0.228)	(0.212)	(0.204)
$\sigma_{0}$	5.022^***	5.000^***	5.134^***	5.117^***	4.962^***
$\sigma_{0}$ : Standard Deviation	(0.556)	(0.544)	(0.566)	(0.624)	(0.555)
$\sigma_{1}$	1.683^***	1.693^***	1.889^***	1.721^***	1.666^***
$\sigma_{1}$ : Standard Deviation	(0.185)	(0.233)	(0.197)	(0.219)	(0.168)
TVP0 constant	1.269^***	1.490^***	2.143^***	1.550^***	1.633^***
TVP0 constant: Standard Deviation	(0.305)	(0.324)	(0.769)	(0.507)	(0.440)
TVP0 expl. var.		-0.307^*	-1.042^**	0.823	0.803^*
TVP0 expl. var.: Standard Deviations		(0.210)	(0.611)	(0.787)	(0.576)
TVP1 constant	1.669^***	1.876^***	2.137^***	1.787^***	1.766^***
TVP1 constant: Standard Deviation	(0.292)	(0.402)	(0.439)	(0.388)	(0.352)
TVP1 expl. var.		-0.378	0.175	-0.143	-0.15
TVP1 expl. var.: Standard Deviation		(0.339)	(0.322)	(0.245)	(0.247)
Log-likelihood	-2.469	-2.453	-2.444	-2.447	-2.434

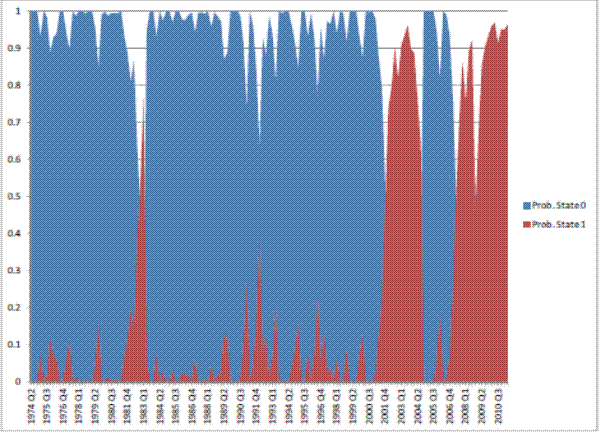
Table 7: Estimation results: regime-switching model, Real Consumption.

		GSEH (8)	GSEM (8)	ABSH (8)	ABSM (8)
$\mu_{0}$	-0.522	0.472	0.405	0.261	0.167
$\mu_{0}$ : Standard Deviation	(1.079)	(0.698)	(0.763)	(0.742)	(0.790)
$\mu_{1}$	3.727^***	3.781^***	3.735^***	3.754^***	3.737^***
$\mu_{1}$ : standard deviation	(0.210)	(0.199)	(0.203)	(0.205)	(0.206)
$\sigma_{0}$	3.085^***	3.039^***	3.172^***	3.032^***	3.069^***
$\sigma_{0}$ : standard deviation	(0.475)	(0.435)	(0.514)	(0.459)	(0.490)
$\sigma_{1}$	1.955^***	1.929^***	1.924^***	1.940^***	1.937^***
$\sigma_{1}$ :standard deviation	(0.134)	(0.136)	(0.136)	(0.136)	(0.135)
TVP0 constant	0.804^**	1.333^***	1.197^***	1.781^*	1.457^**
TVP0 constant: standard deviation	(0.418)	(0.439)	(0.647)	(1.176)	(0.829)
TVP0 expl. var.		-0.539	-1.945	1.541	1.023
TVP0 expl. var.: standard deviation		(0.477)	(2.097)	(2.192)	(1.324)
TVP1 constant	1.799^***	2.159^***	1.914^***	1.822^***	1.843^***
TVP1 constant: standard deviation	(0.252)	(0.443)	(0.352)	(0.284)	(0.291)
TVP1 expl. var.		0.937^*	0.445^*	-0.411^*	-0.358
TVP1 expl. var.: standard deviation		(0.600)	(0.322)	(0.292)	(0.293)
Log-likelihood	-2.273	-2.241	-2.238	-2.244	-2.244

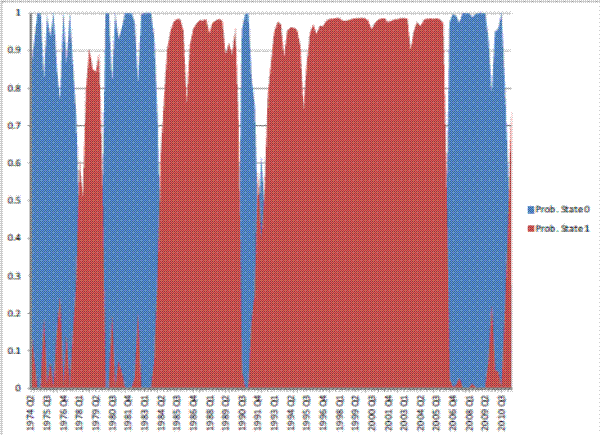
Table 8: Estimation results: regime-switching model, Real Consumption of Housing Services.

		GSEH (4)	GSEM (4)	ABSH (1)	ABSM (1)
$\mu_{0}$	2.926^***	2.950^***	2.887^***	2.947^***	2.948^***
$\mu_{0}$ : standard deviation	(0.240)	(0.252)	(0.231)	(0.235)	(0.235)
$\mu_{1}$	0.754^***	0.756^***	0.727^***	0.786^***	0.829^***
$\mu_{1}$ : standard deviation	(0.255)	(0.252)	(0.238)	(0.255)	(0.245)
$\sigma_{0}$	2.445^***	2.425^***	2.425^***	2.460^***	2.470^***
$\sigma_{0}$ : standard deviation	(0.161)	(0.169)	(0.162)	(0.163)	(0.164)
$\sigma_{1}$	1.278^***	1.301^***	1.270^***	1.294^***	1.294^***
$\sigma_{1}$ : standard deviation	(0.178)	(0.174)	(0.165)	(0.170)	(0.166)
TVP0 constant	1.970^***	2.407^***	2.697^***	2.300^***	2.262^***
TVP0 constant: standard deviation	(0.290)	(0.593)	(0.611)	(0.413)	(0.389)
TVP0 expl. var.		1.142^**	1.053^***	-0.694^***	-0.624^***
TVP0 expl. var.: standard deviation		(0.612)	(0.402)	(0.287)	(0.286)
TVP1 constant	1.878^***	1.370^***	2.264^***	2.124^***	2.523^**
TVP1 constant: standard deviation	(0.584)	(0.565)	(0.838)	(0.749)	(1.407)
TVP1 expl. var.		0.910^*	0.689^*	-0.539^*	-0.898
TVP1 expl. var.: standard deviation		(0.690)	(0.455)	(0.397)	(0.755)
Log-likelihood	-2.246	-2.218	-2.208	-2.232	-2.234

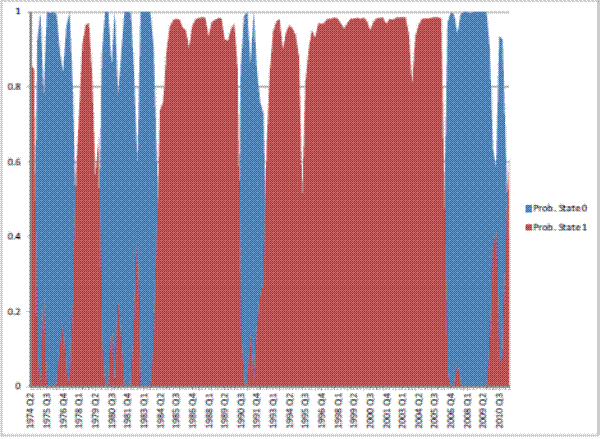
Table 9: Estimation results: regime-switching model, Real Residential Investment.

		GSEH (6)	GSEM (5)	ABSH (3)	ABSM (4)
$\mu_{0}$	-2.819	-1.107	-0.554	-2.057	-1.301
$\mu_{0}$ : standard deviation	(3.634)	(4.081)	(3.015)	(3.759)	(3.703)
$\mu_{1}$	4.744^***	4.647^***	4.754^***	4.769^***	4.816^***
$\mu_{1}$ : standard deviation	(0.961)	(0.924)	(0.909)	(0.963)	(0.983)
$\sigma_{0}$	27.97^***	28.85^***	27.45^***	28.44^***	27.92^***
$\sigma_{0}$ : standard deviation	(2.810)	(3.066)	(2.619)	(3.008)	(2.995)
$\sigma_{1}$	7.81^***	7.819^***	7.637^***	7.774^***	7.752^***
$\sigma_{1}$ : standard deviation	(0.641)	(0.628)	(0.626)	(0.644)	(0.649)
TVP0 constant	1.505^***	1.458^***	2.103^***	1.650^***	1.567^***
TVP0 constant: standard deviation	(0.292)	(0.301)	(0.607)	(0.383)	(0.344)
TVP0 expl. var.		-0.139	-0.935^**	0.358	0.169
TVP0 expl. var.: standard deviation		(0.185)	(0.524)	(0.290)	(0.251)
TVP1 constant	1.872^***	2.363^***	2.424^***	2.038^***	2.067^***
TVP1 constant: standard deviation	(0.290)	(0.485)	(0.548)	(0.376)	(0.406)
TVP1 expl. var.		1.164^***	0.691^**	-0.434^*	-0.444^*
TVP1 expl. var.: standard deviation		(0.573)	(0.381)	(0.313)	(0.336)
Log-likelihood	-4.098	-4.043	-4.047	-4.076	-4.072

Table 10: Estimation results: regime-switching model, Real Single-Housing Investment.

		GSEH (7)	GSEM (7)	ABSH (4)	ABSM (5)
$\mu_{0}$	0.043	0.702	0.706	1.387	2.008
$\mu_{0}$ : standard deviation	(0.774)	(4.209)	(4.241)	(6.062)	(6.716)
$\mu_{1}$	4.987^***	4.746^***	4.584^***	4.846^***	4.788^***
$\mu_{1}$ : standard deviation	(1.289)	(1.254)	(1.280)	(1.274)	(1.295)
$\sigma_{0}$	43.24^***	47.03^***	46.86^***	44.86^***	45.44^***
$\sigma_{0}$ : standard deviation	(4.193)	(5.006)	(5.149)	(4.559)	(4.865)
$\sigma_{1}$	10.75^***	11.40^***	11.45^***	10.86^***	11.03^***
$\sigma_{1}$ : standard deviation	(0.954)	(0.879)	(0.884)	(0.967)	(1.035)
TVP0 constant	1.479^***	1.317^***	1.748^***	1.515^***	1.461^***
TVP0 constant: standard deviation	(0.275)	(0.298)	(0.539)	(0.315)	(0.293)
TVP0 expl. var.		-0.538^*	-2.144^**	0.328	0.223
TVP0 expl. var.: standard deviation		(0.346)	(1.197)	(0.298)	(0.288)
TVP1 constant	1.821^***	2.494^***	2.180^***	1.918^***	1.926^***
TVP1 constant: standard deviation	(0.276)	(0.589)	(0.484)	(0.302)	(0.313)
TVP1 expl. var.		1.605^***	0.853^**	-0.423^*	-0.406
TVP1 expl. var.: standard deviation		(0.817)	(0.503)	(0.322)	(0.325)
Log-likelihood	-4.475	-4.416	-4.410	-4.451	-4.450

5 Conclusions

We have shown evidence of a strong and persistent statistical link between the volatility of certain real economic aggregates and financial products that ought to be directly linked to the decision process that leads to the determination of those same variables. The intent of the approach was to "let the data speak" as much as possible. The next step is to attempt to establish a closer link between mortgage backed securities and real variables. This can be done in several ways, but two seem particularly important. One is to look at empirical evidence in a different way, and use loan-level observations in mortgage pools to understand more precisely what risks mortgage pools insured and the extent to which different risks had different emphasis over time. The other is theoretical and would attempt to measure the phenomena discussed in this paper in a general equilibrium model. With regards to the housing market, our results indicate pretty explicitly that it is important to model the housing market and housing finance together to understand the aggregate behavior of the economy. In particular, it is important to model explicitly the behavior of financial institutions with some precision in terms of the risks that financial derivatives are meant to capture and the incentives that financial institutions face. With respect to the more general question of the joint behavior of real and financial variables, our analysis points to a direction of analysis that explores financial products and the risk transfer that they operate jointly with the real variables on which they are written.

References

Bezemer, D., and M. Grydaki, "Mortgage Lending and the Great Moderation: A Multivariate Garch Approach, Working Paper, January 2012.
Blanchard, O., and J. Simon, "The Long and Large Decline in U.S. Output Volatility," Brookings Papers on Economic Activity, Vol. 2001, No. 1, 135-164.
Davis, S. J., and J. A. Kahn, "Interpreting the Great Moderation: Changes in the Volatility of Economic Activity at the Macro and Micro Levels," Journal of Economic Perspectives, Vol. 22, No. 4, Fall 2008, 155-180.
Den Haan, W. J., and V. Sterk, "The Myth of Financial Innovation and the Great Moderation," The Economic Journal, 2010, Vol. 121, 107-139.
Dynan, K., D. Elmendorf, and D. Sichel, "Can Financial Innovation Help to Explain the Reduced Volatility of Economic Activity," Journal of Monetary Economics, 2006, 53, 123-150.
Kahn, J., M. McConnell, and G. Perez-Quiros, "On the Causes of the Increased Stability of the U.S. Economy," Federal Reserve Bank of New York Economic Policy Review, 2002, 8, 183-202.
Kim, C., and C. Nelson, "Has The U.S. Become More Stable? A Bayesian Approach Based on a Markov-Switching Model of the Business Cycle," Review of Economics and Statistics, 1999, 81, 8-16.
M. McConnell, and G. Perez-Quiros, "Output Fluctuations in the United States: What Has Changed since the Early 1980s?" American Economic Review, 2000, Vol. 90 No. 5, 1464-76.
Peek, J., and J. A. Wilcox, "Housing, Credit Constraints, and Macro Stability: The Secondary Mortgage Market and Reduced Cyclicality of Residential Investment," American Economic Review, Vol. 96 No. 2, May 2006, 135-140.
Ramey, V. A., and D. J. Vine, "Tracking the Source of the Decline in GDP Volatility: An Analysis of the Automotive Industry," Working Paper, 2004.
Stock, J., and M. Watson, "Has the Business Cycle Changed and Why?" National Bureau of Economic Research, Working Paper 9127, August 2002.
Yang, W., " Business Cycles and Regime-Shift Risk," mimeo 2012.

Appendix

This appendix presents tables with summary statistics, the results of the stationarity tests, and the graphs of the (exogenous) transition probabilities estimates from the Markov switching model.

Table 11: Summary Statistics: 1974-2003 Sub-sample (120 observations).

	Mean	Median	Max	Min	Std. Dev.	Skew	Kurt.
GDP	3.063	3.150	16.700	-7.900	3.451	-0.081	5.143
SD (GDP)	3.330	2.578	5.697	1.424	1.408	0.229	1.374
$RV^{20}$ (GDP)	3.301	3.210	4.064	2.574	0.427	0.195	1.656
$RV^{10}$ (GDP)	2.862	2.781	3.860	2.130	0.466	0.288	1.761
(GDP)	3.257	2.650	7.250	1.896	1.254	1.085	3.317
CONSUMPTION	3.322	3.550	8.800	-8.800	2.735	-1.067	6.113
SD (CONS)	2.706	2.464	4.092	1.142	0.871	0.156	1.667
$RV^{20}$ (CONS)	3.172	3.252	3.745	2.395	0.345	-0.391	2.378
$RV^{10}$ (CONS)	2.745	2.817	3.446	1.908	0.382	-0.259	2.226
(CONS)	2.673	2.575	5.373	1.849	0.653	1.530	6.220
HOUS CONS	2.708	2.750	8.000	-4.500	2.435	-0.255	2.930
SD(HOUS CONS)	2.400	2.424	3.411	1.631	0.409	0.071	2.166
$RV^{20}$ (HOUS CONS)	3.168	3.167	3.600	2.432	0.213	-0.607	3.703
$RV^{10}$ (HOUS CONS)	2.744	2.741	3.242	2.021	0.267	-0.353	2.869
(HOUS CONS)	2.433	2.392	3.095	2.276	0.143	1.840	6.915
RESID INV	4.142	3.200	87.700	-55.900	19.316	0.869	6.768
SD (RESID INV)	17.863	14.089	34.211	4.888	9.380	0.157	1.531
$RV^{20}$ (RESID INV)	4.681	4.699	5.750	3.464	0.621	-0.074	1.957
$RV^{10}$ (RESID INV)	4.233	4.193	5.465	3.009	0.665	0.095	2.016
(RESID INV)	15.095	11.880	43.761	4.668	9.623	1.281	3.804
SING HOUS INV	6.546	4.950	153.600	-65.200	28.218	1.495	9.119
SD (SING HOUS INV)	25.822	22.082	55.336	8.301	13.723	0.570	2.392
$RV^{20}$ (SING HOUS INV)	5.022	5.079	6.177	4.165	0.542	0.147	1.893
$RV^{10}$ (SING HOUS INV)	4.581	4.467	5.749	3.745	0.582	0.357	1.863
(SING HOUS INV)	20.626	15.109	114.006	8.930	15.391	3.032	15.287
$\Delta$ GSEH	0.456	0.371	1.487	-0.212	0.376	0.735	2.866
$\Delta$ GSEM	0.014	0.012	0.057	-0.018	0.016	0.800	3.702
$\Delta$ ABSH	0.083	0.034	0.351	-0.088	0.115	0.945	2.631
$\Delta$ ABSM	0.003	0.001	0.015	-0.006	0.005	0.964	3.278

Table 12: Summary Statistics: 1984-2003 Sub-sample (77 observations).

	Mean	Median	Max	Min	Std. Dev.	Skew	Kurt.
GDP	3.177	3.300	8.000	-3.500	2.157	-0.290	3.629
SD (GDP)	2.452	2.336	5.255	1.424	0.918	1.714	5.363
$RV^{20}$ (GDP)	3.023	2.981	3.602	2.574	0.237	0.408	2.454
$RV^{10}$ (GDP)	2.574	2.503	3.278	2.130	0.278	0.782	2.832
(GDP)	2.489	2.346	4.012	1.896	0.466	1.394	4.458
CONSUMPTION	3.490	3.600	7.800	-3.100	2.113	-0.237	3.229
SD (CONS)	2.167	2.262	3.996	1.142	0.557	0.978	4.968
$RV^{20}$ (CONS)	3.004	3.005	3.487	2.395	0.297	-0.309	2.128
$RV^{10}$ (CONS)	2.575	2.589	3.161	1.908	0.334	-0.143	1.950
(CONS)	2.384	2.378	3.277	1.849	0.372	0.516	2.379
HOUS CONS	2.545	2.500	7.000	-4.500	2.228	-0.322	3.145
SD(CONS)	2.344	2.380	3.411	1.738	0.416	0.520	2.518
$RV^{20}$ (HOUS CONS)	3.106	3.094	3.600	2.432	0.225	-0.242	3.593
$RV^{10}$ (HOUS CONS)	2.677	2.666	3.242	2.021	0.276	-0.079	2.910
(HOUS CONS)	2.409	2.366	3.095	2.276	0.138	2.655	11.433
RESID INV	3.691	3.400	24.100	-21.800	9.601	-0.345	3.418
SD (RESID INV)	12.879	10.154	34.005	4.888	7.809	1.357	3.760
$RV^{20}$ (RESID INV)	4.310	4.276	5.018	3.464	0.421	-0.173	2.045
$RV^{10}$ (RESID INV)	3.843	3.840	4.691	3.009	0.435	-0.070	2.078
(RESID INV)	9.346	9.078	17.216	4.668	2.965	0.480	2.552
SING HOUS INV	4.857	5.400	55.700	-34.900	14.496	-0.010	4.491
SD (SING HOUS INV)	20.407	16.500	54.622	8.301	13.072	1.331	3.559
$RV^{20}$ (SING HOUS INV)	4.733	4.636	5.628	4.165	0.416	0.652	2.278
$RV^{10}$ (SING HOUS INV)	4.257	4.131	5.284	3.745	0.400	1.051	3.313
(SING HOUS INV)	14.803	13.345	47.642	8.930	6.396	2.489	11.488
$\Delta$ GSEH	0.576	0.573	1.487	-0.212	0.399	0.258	2.461
$\Delta$ GSEM	0.013	0.012	0.057	-0.018	0.016	0.597	3.139
$\Delta$ ABSH	0.129	0.103	0.351	-0.088	0.121	0.242	1.959
$\Delta$ ABSM	0.005	0.003	0.015	-0.006	0.005	0.239	2.446

Table 13: Summary Statistics: 1999-2011 Sub-sample (50 observations).

	Mean	Median	Max	Min	Std. Dev.	Skew	Kurt.
GDP	1.924	2.350	8.000	-8.900	2.963	-1.278	6.444
SD (GDP)	2.412	2.404	3.577	1.521	0.684	0.507	2.040
$RV^{20}$ (GDP)	3.047	3.048	3.569	2.378	0.371	-0.288	1.654
$RV^{10}$ (GDP)	2.600	2.538	3.339	1.625	0.474	-0.036	1.995
(GDP)	2.782	2.512	5.418	1.815	0.866	1.324	4.332
CONSUMPTION	2.384	2.400	6.400	-5.100	2.324	-0.907	4.596
SD (CONS)	1.827	1.738	2.647	1.164	0.434	0.544	2.226
$RV^{20}$ (CONS)	2.877	2.819	3.383	2.502	0.269	0.421	2.038
$RV^{10}$ (CONS)	2.450	2.367	3.217	2.031	0.324	1.050	3.078
(CONS)	2.296	2.109	4.029	1.820	0.488	1.932	6.231
HOUS CONS	1.802	1.250	6.700	-1.500	2.139	0.532	2.346
(HOUS CONS)	2.108	2.121	2.443	1.729	0.177	0.030	2.634
$RV^{20}$ (HOUS CONS)	3.107	3.133	3.363	2.714	0.171	-0.700	2.961
$RV^{10}$ (HOUS CONS)	2.697	2.747	3.016	1.925	0.225	-1.274	4.713
(HOUS CONS)	2.399	2.400	2.563	2.267	0.070	0.467	2.898
RESID INV	-3.164	2.300	22.800	-35.400	14.450	-0.543	2.490
(RESID INV)	9.512	7.456	16.075	4.888	4.218	0.487	1.482
$RV^{20}$ (RESID INV)	4.300	4.174	5.376	3.464	0.564	0.483	2.149
$RV^{10}$ (RESID INV)	3.940	3.871	5.152	3.009	0.624	0.389	2.041
(RESID INV)	10.987	8.649	32.299	4.668	6.553	1.513	4.730
SING HOUS INV	-4.700	1.600	72.800	-64.700	24.218	-0.050	4.160
(SING HOUS INV)	15.620	11.279	32.384	8.177	8.431	0.954	2.405
$RV^{20}$ (SING HOUS INV)	4.736	4.576	5.768	4.165	0.497	0.934	2.565
$RV^{10}$ (SING HOUS INV)	4.382	4.235	5.527	3.745	0.559	0.878	2.451
(SING HOUS INV)	19.394	14.209	93.045	9.055	14.372	3.056	15.118
$\Delta$ GSEH	0.796	0.571	3.992	-1.435	1.231	0.814	3.435
$\Delta$ GSEM	0.004	0.005	0.050	-0.061	0.031	-0.283	2.331
$\Delta$ ABSH	0.241	0.213	1.865	-1.664	0.851	0.101	2.482
$\Delta$ ABSM	0.004	0.003	0.046	-0.031	0.023	0.263	2.077

Table 14: Stationarity Results.

For DF, ADF and PP we report the value of the test for the null that the variable is integrated of order one - I(1). DF refers to the Dickey-Fuller test proposed by Elliott, Rothenberg, and Stock (1996). ADF refers to the Augmented Dickey-Fuller test. PP refers to the Phillips-Perron test. KPSS refers to the Kwiatkowski-Phillips-Schmidt-Shin test. For the KPSS the null is that the variable is stationary - I(0). $\dag$ means rejection of the I(1) null for DF, ADF and PP at least at the 20% level, and failure to reject the null of I(0) for KPSS at least at the 1% level.

Full Sample: DF

Full Sample:ADF

Full Sample:PP

Full Sample:KPSS

1974-2003: DF

1974-2003:ADF

1974-2003:PP

1974-2003:KPSS

1984-2003:DF

1984-2003:ADF

1984-2003:PP

1984-2003:KPSS

1999-2011:DF

1999-2011:ADF

1999-2011:PP

1999-2011:KPSS

GDP

-2.87†

-8.09†

0.17 †

-2.62†

-7.99†

0.06†

-2.16†

-3.87†

-7.12†

0.08†

-2.42†

-4.25†

-4.17†

0.29†

SD(GDP)

-0.92

-1.35

-1.47

0.90

-0.41

-0.89

-1.10

0.98

-0.54

-3.16†

-3.14†

0.47†

-1.10

1.45

-1.21

0.31†

$RV^{20}$ (GDP)

-1.02

-1.65

-2.00

0.73†

-0.68

-1.36

-1.58

0.78

-0.95

-3.51†

-3.36†

0.15†

-0.94

-0.97

-1.38

0.16 †

$RV^{10}$ (GDP)

-0.94

-2.00

-2.45†

0.75

-0.96

-1.85

-2.10

0.75

-1.43†

-2.84†

-3.07†

0.11†

-2.06†

-2.09

-1.77

0.12 †

(GDP)

-2.15 †

-2.73 †

-2.76 †

0.71†

-2.02 †

-2.43 †

-2.36 †

0.76 †

-1.53 †

-3.04 †

-3.24 †

0.19 †

-2.27 †

-2.60 †

-2.24 †

0.14 †

CONSUMPTION

-1.45†

-4.06†

-9.28†

0.17†

-1.27

-8.90 †

-9.13 †

0.10 †

-2.90 †

-2.88 †

-7.89 †

0.13 †

-1.77 †

-2.37 †

-3.37†

0.48 †

SD (CONS)

-0.94

-1.49

-1.50

1.14

-0.72

-1.18

1.15

-0.31

-3.05 †

-3.12 †

0.92

-1.61 †

-1.70

-1.34

0.30 †

$RV^{20}$ (CONS)

-1.50 †

-2.07

-2.09

0.92

-0.96

-1.49

-1.74

0.99

-1.07

-1.56

-1.64

0.74

-1.04

-0.97

-1.30

0.28 †

$RV^{10}$ (CONS)

-1.06

-2.26 †

-2.65 †

0.93 †

-1.16

-2.19

-2.27 †

0.91

-1.55 †

-2.00

-2.01

0.59†

-1.39†

-1.57

-2.04

0.19†

(CONS)

-2.94†

-3.76†

-3.77†

0.84

-2.97†

-3.57†

-3.52†

0.94

-2.98†

-3.12†

-3.04†

0.57†

-1.75†

-2.25†

-2.19

0.24†

HOUS CONS

-5.29†

-5.44†

-12.18†

0.69†

-12.15†

-12.13†

0.28†

-10.67†

-10.79†

0.24†

-4.36†

-4.91†

-4.99†

0.40†

(HOUS CONS)

-1.07

-1.96

-2.13

0.62†

-0.98

-2.05

-2.12

0.47†

-0.79

-1.38

0.89

-2.46†

-3.10†

-1.90

0.17†

$RV^{20}$ (HOUS CONS)

-2.95†

-3.14†

-3.08†

0.39†

-2.71†

-2.85†

-2.61†

0.51†

-1.51†

-1.91

-2.35†

0.23†

-1.48†

-1.48

-1.52

0.27†

$RV^{10}$ (HOUS CONS)

-2.73†

-3.09†

-3.62†

0.26†

-2.34†

-2.60†

-3.11†

0.35†

-1.80†

-2.12†

-2.42†

0.11†

-2.04†

-2.08

-2.05

0.19†

(HOUS CONS)

-5.94†

-6.05†

-6.08†

0.42†

-5.25†

-5.39†

-5.42†

0.42†

-3.46†

-3.98†

-4.02†

0.24†

-4.15†

-4.28†

-4.30†

0.18†

RESID INV

-4.15†

-6.57†

-6.55†

0.21†

-3.74†

-6.04†

-5.71†

0.04†

-4.14†

-4.59†

-4.64†

0.15†

-1.49†

-2.50†

-3.87†

0.40†

SD(RESID INV)

-1.15

-1.42

-1.26

0.98

-0.71

-0.94

-0.49

1.02

-0.23

-2.62†

-2.70†

0.81

-0.30

-0.17

-0.04

0.73†

$RV^{20}$ (RESID INV)

-1.22

-1.19

-1.40

0.61†

-0.85

-1.05

-1.16

0.89

-0.78

-2.07

-2.03

0.48†

0.13

0.21

0.61

0.86

$RV^{10}$ (RESID INV)

-2.00†

-2.05

-1.91

0.54†

-1.84†

-1.97

-1.83

0.83

-1.29

-3.02†

-2.94†

0.36†

0.56

0.09

0.15

0.86

(RESID INV)

-2.62†

-2.61†

-2.58†

0.69†

-2.39†

-2.38†

-2.36†

0.89

-1.00

-3.41†

-3.43†

0.48†

2.07

2.31

0.02

0.77

SING HOUS INV

-4.18†

-5.73†

-5.42†

0.25†

-3.58†

-5.76†

-4.40†

0.04†

-0.86

-4.68†

-4.78†

0.07†

-3.46†

-3.71†

-3.72†

0.31†

(SING HOUS INV)

-1.63†

-1.71

-1.53

0.68†

-1.30

-1.38

-1.11

0.76

-0.33

-2.52†

-2.48†

0.76

0.26

0.45

0.78

0.71†

$RV^{20}$ (SING HOUS INV)

-1.68†

-1.66

-1.61

0.48†

-1.54†

-1.60

-1.44

0.73†

-1.02

-2.59†

-2.34†

0.40†

0.67

0.41

0.68

0.81

$RV^{10}$ (SING HOUS INV)

-2.15†

-2.14

-2.04

0.41†

-1.99†

-2.03

-1.93

0.69†

-1.14

-3.44†

-3.33†

0.30†

0.27

-0.31

-0.07

0.80

(SING HOUS INV)

-5.48†

-5.82†

0.32†

-4.49†

-4.81†

-4.69†

0.68†

-3.50†

-3.81†

-3.73†

0.25†

-3.67†

-3.73†

-3.61†

0.60†

$\Delta$ GSEH

-3.07†

-4.13†

-3.26†

0.26†

-1.27

-2.23†

-3.87†

0.40†

-2.54†

-2.52†

-3.62†

0.10†

-2.71†

-2.69†

-2.13

0.24†

$\Delta$ GSEM

-2.46†

-2.48†

-2.75†

0.24†

-2.22†

-2.35†

-2.11

0.45†

-0.70

-2.02

-2.36†

0.69†

-2.20†

-2.29†

-1.36

0.30†

$\Delta$ ABSH

-2.88†

- 3.20†

-2.09

0.12†

-2.19†

-2.68†

-2.60†

0.80

-2.17†

-3.01†

0.23†

-1.80†

-1.97

-1.13

0.25†

$\Delta$ ABSM

-3.20†

-3.24†

-2.55†

0.09†

-3.43†

-3.82†

-3.27†

0.41†

-3.10†

-3.62†

-3.16†

0.07†

-2.40†

-2.39†

-1.35

0.27†

Figure 8: Transition Probabilities: GDP.

This figure displays the probability of remaining in the high-volatility state as a blue area, and the probability of remaining in the low-volatility state in red. The horizontal axis represents time, from the second quarter of 1974 to the third quarter of 2010. The vertical axis represents probabilities and ranges between zero and one. Most of the area up to 1984 is blue, indicating the high-volatility state. The remaining portion of the figure shows mostly a red area, indicating the low-volatility state. The exceptions are the years of 1990, 2000-2001, and the end of 2008.

Figure 9: Transition Probabilities: Personal Consumption.

Figure 10: Transition Probabilities: Housing Consumption.

Figure 11: Transition Probabilities: Residential Investment.

Figure 12: Transition Probabilities: Investment in Single Housing.

Footnotes

* We wish to thank without implicating Sean Campbell, Steve Fazzari, Michael Gordy, James Kennedy, James Morley, Bruce Petersen, Jeremy Piger, Todd Prono, Frank Schorfheide, Tara Sinclair, and seminar participants at the Board of Governors and Midwest Macroeconomics Meetings for constructive comments. We also would like to thank Leah Brooks and Jane Dokko for their help with data. Katherine Hamilton, Matt Hayward, Bobak Moallemi, Waldo Ojeda, and Ran Tao provided excellent research assistance. All errors are our own. Any views are of the authors alone and do not represent the views of the Board of Governors of the Federal Reserve System. Return to Text

† Board of Governors of the Federal Reserve System and Washington University in Saint Louis, [email protected] Return to Text

‡ Board of Governors of the Federal Reserve System, [email protected] Return to Text

1. There is an earlier literature documenting the lower volatility of economic activity after second world war that is not the focus of our analysis - see for example Diebold and Rudebusch (1992). Return to Text

2. Note that because volatility measures have been constructed with lags between 10 and 20 quarters, the actual sample starts in 1969, first quarter. Return to Text

3. See Bansal, Khatchatrian and Yaron (2002) for details. Return to Text

4. See Bansal, Khatchatrian and Yaron (2002) for details. Return to Text

5. Detailed summary statistics are reported in Table 7 in the Appendix. Return to Text

6. We also consider different sub-sample definitions. Our main results are not affected by the definition of the sub-samples. Return to Text

7. Standard tests for cointegration indicate that there is no evidence of cointegrating relationships between the volatility of real variables and mortgage-backed security variables. Return to Text

8. Alternatively, when we add $x_{r,t-n}$ directly in the conditional variance equation of the GARCH model, the results are qualitatively similar to those reported below. Return to Text

9. We also control for the effect of interest rate but it is never significant. Return to Text

10. An alternative approach to deal with stationarity issues is to use filtering procedures (e.g., Hodrick-Prescott). All dependent variables in equation (4) are estimates of second moments and the use of filtering techniques for higher moments might be challenging. Return to Text

11. Given the persistency of the observations, we bootstrap standard errors. As a robustness check, we also computed robust standard errors, and the results hold. Return to Text

12. We also performed the same estimates using the real mortgage interest rate as a control variable, and found that it was never statistically significant. Return to Text

13. These results are in line with the literature, see for example Yang (2012). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text