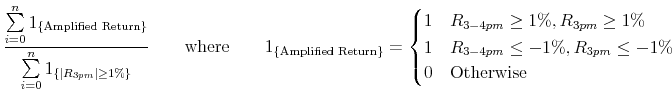Are Leveraged and Inverse ETFs the New Portfolio Insurers?
Abstract:
1 Introduction
The complex structure and behavior of Leveraged and Inverse Exchange Traded Funds (LETFs) have raised important questions about their implications for financial stability. LETFs are exchange-traded products that typically promise multiples of daily index returns. Generating multiples of daily index returns gives rise to two important characteristics of LETFs that are similar to the portfolio insurance strategies that are thought to have contibuted to the stock market crash of October 19, 1987 (, ). (1) LETFs rebalance their portfolios daily by trading in the same direction as the changes in the underlying index, buying when the index increases and selling when the index decreases. (2) This rebalancing requirement of LETFs is predictable and may attract anticipatory trading. Portfolio insurance strategies were commonly used by asset managers in the 1980s and their use reportedly declined after the stock market crash of 1987. Portfolio insurance is a dynamic trading strategy, which synthetically replicates options to protect investor portfolios. Synthetic replication of options requires buying in a rising market and selling in a declining market. Rather than buying and selling stocks as the market moves, portfolio insurers generally traded index futures. The Brady Report (1988) suggests that portfolio insurance related selling accounted for a significant fraction of the selling volume on October 19, 1987. The report also notes that "aggressive-oriented institutions" sold in anticipation of the portfolio insurance trades. This selling, in turn, stimulated further reactive selling by portfolio insurers. Price-insensitive and predictable trading of portfolio insurers contributed to the price decline of 29% in S&P 500 futures through a selling "cascade".
This paper studies the impact of equity LETFs on various stock categories while emphasizing their implications for financial stability and similarities with portfolio insurance strategies. Promising a certain multiple of daily index return induces LETFs to rebalance their portfolios daily to maintain their target stock-to-cash ratios. Rebalancing demand of a LETF can be derived from a simple formula, which dictates the LETF to buy when its target index goes up and sell when its target index goes down. Although their rebalancing formulas are more complex, portfolio insurers also trade in the same direction as the market to maintain their stock-to-cash ratios constant. Anectodal evidence suggests that LETFs commonly use swaps and futures contracts to rebalance their portfolios. Swap counterparties of LETFs are likely to hedge their positions in equity spot or futures markets. If LETFs use index futures, index arbitraguers transfer the price pressure from the futures market to the stock market. If the LETFs account for a significant fraction of trading, their rebalancing activity should leave its imprint on the stock indexes they follow.
The size of LETF rebalancing demand varies with their net assets and the multiples of daily index return they promise. Based on total net asset value of $20.14 billion as of December 15, 2011, when broad stock-market indexes change by 1%, LETFs rebalancing demand totals $1.04 billion worth of stock. This is roughly 0.84% of daily stock-market volume (excluding the volume of the ETFs and the Depository Receipts) in the United States. Kyle and Obizhaeva (2012) calculate that the portfolio insurers in 1987 would sell $4 billion (4% of stock-plus-derivatives volume) in response to a 4% price decline in the Dow Jones Industrial Average. Although LETFs are not as large as the portfolio insurers were in 1987, LETF rebalancing in response to a large market move, especially in periods of high volatility, could still pose risks. For example, the Flash Crash of May 6, 2010 was triggered by a $4.1 billion (75,000 contracts of E-Mini S&P 500 Futures) sell order, which is equivalent to only 3% of the E-Mini S&P 500 Futures daily volume (CFTC-SEC Report, 2010). With a large market move, such as 4%, the total rebalancing flows of LETFs would be equivalent to this "Flash Crash" order. Rebalancing in the last hour of trading could, in fact, reduce the possibility of a significant price dislocation since the market close could serve as a prolonged circuit breaker. On the other hand, executing orders within a short period of time, such as the last hour of trading, may cause disproportionate price changes. A significant price dislocation at the market close may also impair investor confidence. If the market closes with depressed prices, the stock market could experience large investor outflows overnight.
Naturally, LETFs follow different stock-market indexes and the size of their rebalancing differs across stock categories. LETF rebalancing is an important fraction of daily volume, especially in financial and small stocks. For instance, if the Russell 1000 Financial Services Index increases by 1%, the rebalancing demand of LETFs totals roughly 2% of the daily volume for an average financial stock. Furthermore, academic studies (Cheng and Madhavan, 2009; Bai et al., 2012) and anectodal reports1,2 suggest that LETFs rebalance their portfolio in the last hour of trading. Therefore, a large market move could make these stocks vulnerable near the market close, or even before to the extent that opportunistic traders react in anticipation of subsequent LETF rebalancing.
Although LETF activity is relatively small in some stock categories, LETF rebalancing in the last hour of trading leads to price reaction and extra volatility in all stock categories. For instance, if the S&P 500 index goes up by 1%, LETF rebalancing demand results in a 6.9 basis-point increase in price and a 22.7 basis-point increase in daily volatility in an average large-cap stock.
The size of the price reaction of LETF Flows inferred from empirical specifications could be an underestimate if prices at 3:00 pm already reflect to some extent investors' anticipation of subsequent LETF rebalancing. By directly implementing Kyle and Obizhaeva (2011a,b) measure of price impact, I show that the implied price impact of LETF rebalancing on financial markets was notable especially during the financial crisis of 2008-2009 and at the height of the European sovereign debt crisis. If LETF rebalancing exerts significant price pressure, this price pressure could amplify the market movements. Although LETFs have not been proven to disrupt stock markets, it is plausible that during periods of high volatility, their impact in response to a large market move could reach a tipping point for a"cascade" reaction.
2 Literature Review
In the United States, Exchange Traded Funds (ETFs3) have grown rapidly and hold nearly $1.3 trillion in net assets as of September 2012. The growing size of the ETF industry has prompted researchers to analyze recent trends. Agapova (2012) and Huang and Guedj (2009) suggest that ETFs are close but not perfect substitutes for index mutual funds. Poterba and Shoven (2002) show that the largest ETF (the SPDR trust) offers similar pre-tax and after-tax returns as the largest index fund (the Vanguard Index 500). Buetow and Henderson (2012) argue that, on average, ETFs closely track their target indexes. Commodity ETFs typically roll contacts in the futures markets as they expire. Bessembinder et al. (2012) estimate the transaction costs of these ETF "roll" trades in the crude oil futures market and cannot find compelling evidence for predatory trading. Another line of literature studies the arbitrage relationship between ETFs and their underlying stocks. Ben-David et al. (2012)argue that ETFs propogate liquidity shocks to the securities in their baskets. Analyzing the "Flash Crash" of May 6, 2010, Madhavan (2011) argues that ETFs are vulnerable in market disruptions because pricing of individual component securities becomes more difficult. Several other academics have studied the complex return structure of LETFs. Cheng and Madhavan (2009), Jarrow (2010), Avellanda and Zhang (2009) show that LETF returns could be significantly different than their multiple of target index returns for holding periods longer than one day. The long-horizon return structure of LETFs that rebalance daily is alone not suitable for the investment horizons of many investors4.
The daily rebalancing of LETFs has also stimulated academic research. Trainor (2010) cannot find evidence that suggests Leveraged ETFs increase volatility. Focusing on the S&P 500 index returns and aggregate LETF rebalancing demands,Cheng and Madhavan (2009) argue that aggregate LETF rebalancing demand has price pressure on the end-of-day S&P 500 index returns. Similarly, Bai et al. (2012) examine the impact of 6 LETFs on 63 real estate sector stocks and find evidence for both end-of-day LETF price pressure and extra volatility. My study contributes to this literature by quantifying the implied price effects of LETF rebalancing through examining the impact of all US-listed equity LETFs on several stock categories.
Several papers studied the role of portfolio insurers in the 1987 stock market crash. Contrary to the Brady Report (1988), Brennan and Shwartz (1989) suggest that the effect of portfolio insurance strategies is too small to explain the 1987 crash. Gennotte and Leland (1990) argue that informational changes, rather than the selling by portfolio insurers, are needed to explain the 1987 crash. They argue that if mistaken by informed trading, portfolio insurance strategies could have a much greater price impact-an impact of magnitute similar to what was observed in 1987. With the "Flash Crash" of May 6, 2010, the focus on market disruptions and large orders has been renewed. CFTC-SEC Report (2010) concludes that rapid execution of a large sell order triggered the "Flash Crash"5. Kyle and Obizhaeva (2012) examine the five stock market crashes, including the 1987 crash, with documented large sells during those events. They show that price declines in those events are similar in magnitude to price impact of large sales suggested by market microstructure invariance (Kyle and Obizhaeva, 2011a,b). My study extends their work by computing the price impact estimates of LETFs implied by market microstructure invariance.
3 LETF Rebalancing
LETFs typically promise a certain multiple of a daily index return. Producing multiples of daily returns forces LETFs to rebalance their portfolios in response to price movements. Daily rebalancing ensures that LETFs maintain their stock-to-cash ratios at market close. The mechanics of LETF rebalancing can be illustrated in a simple asset allocation setting.6
An asset allocation problem can be written in the following way:
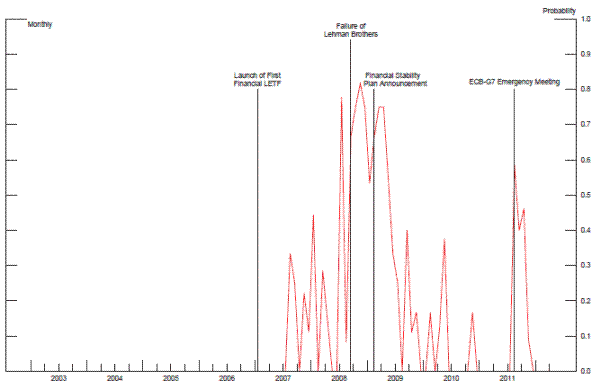
Asset managers generally invest a certain fraction, 
, of their net assets, 
, into the risky asset (underlying equity index), 
and the rest,(1- ) into the bond market.
LETFs choose consistent with their prospectuses. For example, Leveraged ETFs have 
2 or 3 while Inverse ETFs have -1,-2 or -3. Assuming interest rate is zero, if the underlying index changes by 
, then the investment on the index becomes
and this change is reflected in the size of total portfolio.
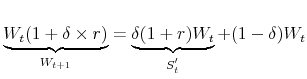
Since the LETF is promising over the daily return on the index,
should be invested on the index to maintain a constant stock-to-cash ratio.
The rebalancing amount in response to the size of change in the index can be calculated as
It is important to note that when 
[0,1], the rebalancing amount
has the same sign as , suggesting that both Inverse and Leveraged ETFs rebalance in the same direction as their target indexes and their rebalancing do not cancel each other out.
Furthermore, this formula is a function of only the target index change, not its level, making LETF rebalancing insensitive to the price level.
In practice, LETFs do not have to directly trade in the stock market to rebalance their portfolios. The use of derivatives, especially futures and swaps, is believed to be common among LETFs (Cheng and Madhavan, 2009). If they trade futures contracts, index arbitraguers will transfer this effect from the futures market to the stock market. If they enter into a swap aggrement, their counterparty is likely to hedge its exposure and trade in either the futures or the spot market. As a result, regardless of the contracts LETFs trade, their portfolio rebalancing should leave an imprint on the stock indexes they target. Brady Report (1988) notes that portfolio insurers commonly used futures contracts and index arbitraguers propagated these shocks to the stock market, suggesting that the markets for stocks and stock index futures behave as a single integrated market. More recently, Kirilenko et al. (2011) explain that although the "Flash Crash" of May 6, 2010 was triggered in the futures market, index arbitraguers quickly transmitted this price shock to the stock market.
4 Data
Data for this study is collected from multiple sources. LETF information is obtained from Morningstar Direct, which provides total net assets, net asset value, shares outstanding and category type for ETFs. After I identify an ETF as a LETF, I check its prospectus to identify both its target index and the multiple it promises. Only US-listed equity LETFs promising multiples of daily index returns are included in the sample. I also use the daily index return series (S&P 500 Index, Russell 1000 Financial Services, Russell 2000, Russell Mid Cap, Nasdaq 100) from Morningstar Direct. Volume and return variables for the stocks are calculated from the NYSE Trades and Quotes (TAQ) dataset. Membership history, monthly index weights and float factors are courteously provided by Russell Indexes for Russell 1000 Financial Services, Russell 2000 and Russell MidCap Indexes7 . Membership history of S&P500 is obtained from the Center for Research in Security Prices (CRSP). Membership history of NASDAQ 100 is obtained from Bloomberg and index weights are calculated with CRSP market capitalization information. The sample goes from June 19, 2006, when the first equity LETF was offered in the US, to December 31, 2011.
5 LETFs and Target Stock-Market Indexes
Table 1 summarizes the distribution of LETFs over stock-market index categories as of December 15, 2011. Total net assets, number of LETFs, target stock index and LETF rebalancing flows in response to a 1% change in the target index are reported. The biggest LETF category is the large stock LETFs and the majority of them follow the S&P 500. In this category, there are 19 LETFs with $8.7 billion in net assets. A 1% increase in large stock indexes generates roughly $400 million of rebalancing flow from these LETFs. The net assets of 5 LETFs, which follow financial stock indexes, total $3.5 billion and their rebalancing flow is $ 226.8 million in response to a 1% increase in financial stock indexes. 14 LETFs exist in the small stock category with $3 billion in net assets. A 1% increase in small stock indexes induces these LETFs to demand $193 million worth of stocks. The mid-cap stock category is the smallest in size with roughly $ 299 million net assets in total managed by 11 LETFs. Their rebalancing flow is only $ 13 million when there is a 1% increase in mid cap stock indexes. There are 9 LETFs with $2.2 billion in net assets following technology stock indexes and their rebalancing flow totals $ 100 million if technology stock indexes go up by 1%. In total, there are 108 equity LETFs in the US with roughly $ 20 billion in net assets. These LETFs originate $ 1.04 billion in rebalancing flows if the broad stock-market indexes go up by 1%. Daily volume of the stock market (excluding ETFs and Depository Receipts) averaged $131 billion in December 2011. Hence, LETF rebalancing flows in response to a 1% increase in stock prices are equivalent to 0.79% of stock-market volume. Because LETFs also use swap and futures contracts, LETF rebalancing is less than 0.79% of the total volume of the stock, futures and swaps markets combined. Although their size appears to be smaller than portfolio insurers of 1987, it is essential to explore the relative size and effect of LETF rebalacing in various stock categories.
5.1 LETF Performance and Rebalancing
LETFs are forced to rebalance daily to avoid tracking errors by maintaining constant stock-to-cash ratios. Low tracking errors can be interpreted as successful portfolio rebalancing. Because LETFs promise certain multiples of daily target index returns, I assess their performance at daily frequency by using the following regression.
 |
(1) |
The S&P 500, Russell 1000 Financial Services, Russell 2000, Russell MidCap and NASDAQ 100 are used as target indexes for the respective LETF categories defined in Table 1. 
is the multiple LETF 
promises. The variables are winsorized at the 1% and 99% levels to remove the effect of outliers. The regression is run for each LETF
individually and Table 2 reports the summary statistics of the regression coefficients and Adj-
's computed within each category. The asset-weighted and
equally-weighted means and medians of 
are all close to zero. In absolute value, equally-weighted mean of range from 0.01 basis points for the large category to 3.2 basis points for the financial category. Asset-weighted means of are lower in absolute
value and range from 0.01 for the large category to 1.6 basis points for the small category. Asset-weighted means of 
are close to 1 and range from 0.9 for the technology category to
1.03 for the mid-cap category. Similarly, asset-weighted means of are quite high. These results suggest that LETFs, especially the ones with large net assets, rebalance regularly since
they are, on average, successful in delivering multiples of their target indexes at daily frequency.
5.2 LETF Rebalancing Flows and Underlying Stocks
LETF categories defined in Table 1 are collapsed into one target stock index in each category. For simplicity, I assume that the LETFs following large stock indexes aim to target the S&P 500. The Russell 1000 Financial Services and NASDAQ 100 indexes are chosen for financial and technology categories. Small and mid-cap LETFs are assumed to follow the Russell 2000 and Russell Mid-Cap Stock Indexes, respectively.
Panel A of Table 3 reports the summary statistics for various stock categories from June 2006 to December 2011. The financial category includes the members of the Russell 1000 Financial Services Index. Float-adjusted and unadjusted market capitalizations of an average financial stock are $10.1 and $ 10.9 billion, respectively. Daily volatility- the standard deviation of the previous 20 days' returns- of an average financial stock is 2.9%. There are 279 different stocks in this category with $125 million in average daily volume. The large stock category, which consists of the members of the S&P 500 index, has $21.3 and $22.3 billion in float-unadjusted and -adjusted market capitalizations, respectively. There are 647 different stocks in the large stock category with an average daily volatility of 2.3% and volume of $203 million. Going from the mid-cap stock category (Russell Mid-Cap) to small stock category (Russell 2000), market capitalizations and daily volume decrease. The daily volume of an average mid-cap stock and small stock are $ 60 million and $7 million, respectively. For an average small stock, float-adjusted market capitalization, $ 550.3 milion, is considerably different then unadjusted market capitalization, $ 652.4 million. Technology stocks, which are the members of the NASDAQ 100 index, have $ 22 billion in average market capitalization, roughly equal to that of large stocks8. Yet, the daily volume of an average technology stock ($303 million) is higher, suggesting that they are traded more actively. Panel B and Panel C of Table 3 report the same variables for 2006-2009 and 2010-2011 periods. Higher volatility in all stock categories, especially among financials, is notable in the earlier sample period due to the 2008-2009 financial crisis. Daily volatility of an average financial stock is 3.5% during 2006-2009 period and 2.0% during 2010-2011 period. Other stock categories have 70 to 80 basis points higher daily volatility in the earlier sample period.
5.2.1 Size of Hypothetical LETF Rebalancing Flows
Figure 1 presents the share of total hypothetical rebalancing flows of LETFs for an average stock as a fraction of its daily volume for each category. Aggregate hypothetical LETF flows are calculated as the sum of all LETF flows in that category in response to a 1% increase in the target index and allocated to stocks based on their weights in the target index. For each stock, its share of hypothetical LETF rebalancing flows is scaled by its average daily volume. Hypothetical LETF rebalancing flows start in June 2009, when the first equity LETF was introduced in the US. These flows are less than 1% of daily volume for an average stock in large, mid-cap and technology categories. Hypothetical LETF rebalacing flows are considerable for an average stock in financial and small stock categories. In the beginning of 2009, hypothetical LETF rebalancing flows become larger than 1% of daily volume in an average financial stock and fluctuate around 2% of daily volume starting in mid 2009. Hypothetical LETF rebalancing flows become larger than 2% of daily volume in an average small stock in 2009 and reaches levels as high as 6% of daily volume in 2011. Many studies, such as Cheng and Madhavan (2009); Bai et al. (2012), and news articles mention that LETFs carry out their rebalancing in the last hour of trading. Figure 2 shows the aggregate hypothetical rebalancing flows of LETFs as a fraction of volume in the last hour of trading. These flows are 2-3% of volume in the last hour for average stocks in large, mid-cap and technology categories. For an average small stock, these flows can be as large as 18% of volume in the closing hour. Similarly, the ratio of hypothetical LETF flows to the last hour's volume is significant for an average financial stock. Hypothetical LETF rebalancing flows for an average financial stock fluctuate between 4 and 8% after 2008 and are equivalent to roughly 6% of volume in the last hour in December 2011.
5.3.1 Price Reaction of Underlying Stocks
To identify pressure points across stock categories, it is crucial to understand the impact of LETF rebalancing flows on underlying stocks. LETF rebalancing could result in end-of-day price reaction and extra volatility in those stocks. Other market participants could trade in anticipation of LETF flows, making it impossible to estimate the isolated price impact of LETF flows. However, the end-of-day net price reaction to LETF rebalancing and anticipatory trades can be estimated.
To estimate the net price reaction to LETF flows, I implement the regression specification of Obizhaeva (2009) and allow for control variables.
 |
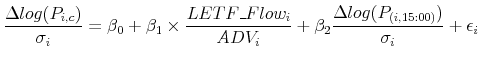(2) |
The left hand side of the regression is constructed as a ratio of two variables.
is the return on a stock 
between 15:00pm(ET) and 16:00pm (ET)
and
is the daily volatility. Explanatory variables are also contructed as ratios of two variables.
, is the share of stock i from the estimated total LETF rebalancing flow-calculated as a function of the target index return between the previous day's close and 15:00pm-implied
by its index weight9.
is scaled by 
, which is the past 20-day average dollar volume
of stock i. The variables used in this regression are winsorized at the 1% and 99% levels to remove the effect of outliers. Panel A of Table 4 reports the results of the regression for different categories from 2006 to 2011. The standard errors are clustered
daily. For all categories, the coefficients on LETF flows are positive and statistically significant, ranging from 0.83 for small stocks to 4.16 for mid cap stocks. The coefficient estimates and regression 's are little changed when the stock return between the previous day's close and 15:00pm,
, is controlled. Regression 's in this
specification range from 0.76% for the technology category to 6.33% for the financial category. Panel B of Table 4 reports the results of the regression for two subperiods, 2006-2009 and 2010-2011. The coefficients on LETF Flows and 's are higher for most of the categories in the earlier sample period. The coefficients on LETF Flows go from 0.78 for small stocks to 4.85 for mid-cap stocks for 2006-2009 and they go from 0.88 for
small stocks to 2.74 for financial stocks in the post-financial crisis period.
The coefficients on LETF Flows can be interpreted as a change in price as a percent of daily volatility in response to LETF flows equivalent to 1% of the volume. For example, LETF flows equivalent to 1% of stock volume, increases the price of a financial stock by 3.09% of its daily volatility.
As of December 2011, when the financial indexes increase by 1%, the share of LETF rebalancing flows is equivalent to 2.1% of volume in an average financial stock with 2% daily volatility. If the financial stock indexes increase by 1%, price reaction of an average financial stock in response to LETF
rebalancing is 13 basis points (3.09 
2.1% 2%). With the LETF flows in
response to a 1% change in the target indexes and the volatility of average stocks in December 2011, the same calculation can be done for other categories. The end-of-day price reaction is 6.9 basis points (4.32 0.8% 2%) in an average large stock, 5.5 basis points (4.28 0.6% 2%) in an average mid cap stock, 12.7 basis points (0.86 5% 2.9%) in an average small stock and 6.3 basis points (3.83 0.75% 2.2%) in an average technology stock. Although the largest price reactions to LETF flows occur in financial and small stock categories, all other categories
show price reactions to LETF portfolio rebalancing, suggesting that LETFs and anticipatory traders in the same direction are stronger than the traders on the opposite side. Without the traders taking the other side of the LETF rebalancing activity, the end-of-day effect of the LETF rebalancing
could be destabilizing.
Rebalancing in the last hour could also amplify the effect of LETFs since executing orders within a short period of time may move the prices disproportionately. In contrast, rebalancing in the last hour has the advantage of limiting the possibility of a price dislocation because the market close may serve as a prolonged circuit breaker. Yet, if there are enough traders following the LETF rebalancing, they may start trading well before the market close and produce similar consequences.
Table 5 reports the results of the same regression for Market Ups (Positive LETF Flows) and Market Downs (Negative LETF Flows) seperately. The standard errors are clustered daily. Coefficients of positive LETF flows range from 0.63 for small stocks to 4.66 for technology stocks and coefficients of negative LETF flows range from 0.80 for small stocks to 3.60 for large stocks. The coefficient on the LETF Flows in Market Ups are higher than Market Downs for all but small stocks, indicating that market response to positive LETF flows is slightly stronger. One explanation for this could be the short-sale constraints. Market participants who trade in anticipation of LETF flows could be constrained by short-selling and cannot implement their strategy in Market Downs as well as in Market Ups.
5.3.2 Price Reversals
In resilient markets, prices revert back after an order is executed especially if the order does not carry information about the fundamental value. The resilence of the market could counteract the late-day price reaction of the LETF rebalancing flows and other anticipatory trades. I implement the following regression to test if prices revert back the next day after the portfolio rebalancing of LETFs.
 |
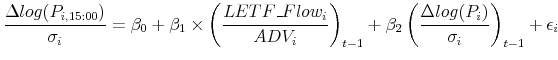(3) |
The next day's return of stock is defined as the return from today's market close to 15:00 next day, scaled by its daily volaility. Explanatory variables are LETF rebalancing flows and the previous day's returns. Panel A of Table 6 reports the results of this regression for the full sample period. The standard errors are clustered daily. The coefficients on LETF Flow are negative and significant for all stock categories, ranging from -0.35 for small stocks to -4.24 for technology stocks. Compared with the results from Table 4, these coefficients are similar in magnitude, suggesting that prices revert back the next day after LETF rebalancing. Panel B and Panel C of Table 6 present the results of the regression for 2006-2009 and 2010-2011 seperately. The coefficients for LETF rebalancing flows are negative for all categories in both sample periods. They range from -0.49 for small stocks to -4.77 for large stocks in the earlier period and go from -0.31 for small stocks to -5.23 for large stocks in the later period.
5.3.3 End-of-Day Volatility and LETF Rebalancing
LETF rebalancing and trades in anticipation of LETF rebalancing may affect the stock volatility in the last hour of trading. To estimate the volatility effects of LETF rebalancing, I use the following regression specification.
![\displaystyle \left[\frac{\Delta log(P_{i,c})}{\sigma_{i}}\right]^2=\beta_0+\beta_1\times \left\vert\frac{LETF\_Flow_i}{ADV_i}\right\vert+\beta_2\left[\frac{\Delta log(P_{i,(15:00)})}{\sigma_i}\right]^2+\epsilon_i](img30.gif) |
(4) |
The left hand side,
![\left[\frac{\Delta log(P_{i,c})}{\sigma_{i}}\right]^2](img31.gif)
, is the square of the return at the close scaled by daily return variance.
is the absolute value of LETF Flows scaled by the average daily volume and
![\left[\frac{\Delta log(P_{i,(16:00-15:00)})}{\sigma}\right]^2](img33.gif)
is the square of daily return until 15:00pm scaled by daily return variance. The variables used in this regression are
winsorized at the 1% and 99% levels to remove the effect of outliers. Panel A of Table 7 reports the results of this regression for the entire sample period. The standard errors are clustered daily. When introduced into the regression,
has a positive coefficient and increases the adjusted for all categories, indicating that high intraday volatility persists through end-of-day. The LETF Flow variable is positive and significant in all stock categories and ranges from 0.59 for small stocks to 2.57 for technology stocks. The coefficient on the
LETF Flow variable can be interpreted as the change in return variance as a percent of daily variance in response to LETF Flows equivalent to 1% of volume. For example, LETF Flows of 1% of the daily volume increases the return variance,
, by 1.30 % of the return variance, 
, in a
financial stock. Point estimates can be computed for average stocks in each category with December 2011 volume and volatility averages. The end-of-day extra return volatility in response to 1% change in stock indexes is 31.1 basis points (
) in an average financial stock, 22.7 basis points (
in an average large stock, 23 basis points (
) in an average mid-cap stock, 50.5 basis points (
) in an average small stock and 30.73 basis points (
)) in an average technology stock. These results suggest that LETF rebalancing and possible anticipatory trades of other market participants account
for extra end-of-day volatility for all stock categories. Panel B of 7 reports the results for two sample periods, 2006-2009 and 2010-2011. The coefficient on the LETF Flow is positive and significant for all categories in both sample periods. It ranges from 0.64 for
small stocks to 5.35 for technology stocks for 2006-2009. In the post-crisis period, the coefficient is smaller and goes from 0.71 for small stocks to 1.34 for mid-cap stocks.
5.3.4 Intraday Lead-Lag Relations: A Robustness Check
Lo and Mackinlay (1990) document lead-lag patterns in stocks returns. More specifically, they show that large stock returns lead small stock returns. To control for possible intraday lead-lag patterns accross and within stock categories, the S&P 500 index and underlying index returns are included in the end-of-day price reaction and volatility regressions. As mentioned previously, the underlying index is the Russell 1000 Financial Services Index for financial stocks, the S&P 500 index for large stocks, the Russell MidCap Index for midcap stocks, the Russell 2000 for small stocks and the Nasdaq 100 for technology stocks.10 Panel A of Table 8 reports the results for end-of-day price reaction. The coefficient for the LETF flow is only slighly lower than the previous regressions in Table 4 and it continues to be positive and statistically significant for all stock categories. The coefficient ranges from 0.545 for the small stock category to 3.9 for the midcap stock category. Panel B of Table 8 reports the results of the regression of end-of-day volatility. As in Table 7, the coefficient for the absolute value of LETF Flow continues to be positive and significant after controlling for the intraday volatility of the underlying index and S&P 500 index returns. These results suggest that the effect of LETF rebalancing on the end-of-day price and volatility is not driven by the intra-day lead-lag relationship between small and large stocks.
6 LETFs and Integrated Markets
The size of the price reaction of LETF Flows inferred from empirical specifications could be an underestimate if prices at 3:00 pm already reflect to some extent investors' anticipation of subsequent LETF rebalancing. A more direct way to quantify the price impact of LETF rebalancing flows is to implement the implied price impact measure developed and calibrated by Kyle and Obizhaeva (2011b,a). Kyle and Obizhava (2012) use this measure to estimate the size of five crash events implied by market microstructure invariance and conclude that estimates are close to the observed price declines.
Aggregate stock-market segments rather than individual stocks may provide more accurate price impact estimates if the markets for individual stocks are integrated. Integration of markets may result from various factors. For instance, arbitraguers operate in multiple markets and exploit arbitrage opportunities by taking opposite positions in these markets. Hence, they transmit shocks from one market to another. As a result, market integration leads to faster and more effective transmission of shocks. Moreover, price shocks to individual stocks can be transmitted to other stocks through leveraged investor portfolios. Initial losses could lead to margin calls whereby speculators are forced to deleverage by selling assets in their portfolios, hence leading broader asset price declines (Brunnermeier and Pedersen, 2009).
The expected price impact of LETF rebalancing flows in a stock-market index with daily dollar trading volume, ADV, and daily volatility, 
, is given by
 |
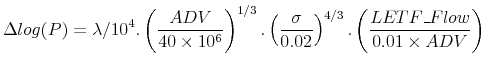(5) |
Kyle and Obizhaeva (2011a) estimate their price impact formula in portfolio transitions data and find 
equal to 5.78. This formula is implemented for 5 different
stock-market indexes; Large, Mid-Cap, Small, Financial and Technology Stock indexes. As in the previous sections, I use S&P 500 firms for the large category, Russell 2000 firms for the small category, Russell Mid Cap firms for the mid-cap category, Russell 1000 Financial Services Index firms
for the financial category and NASDAQ 100 index stocks for the technology category. ADV is calculated as the total daily volume of member stocks averaged over the previous 20 days. Volatility is estimated as the standard deviation of the daily index returns in the past 20 days. Finally, LETF Flow
is the dollar amount of LETF rebalancing in response to a 1% change in the target stock-market index. Measuring the LETF Flows in response to a constant change in the target index (such as 1%) allows for historical comparison of the impact of LETF rebalancing and critical assessment for their
current size.
Table 9 reports the averages of the variables used, and the implied price impact estimates for 5 stock-market indexes from 2007 to 2011. In 2008 and 2009, volatility is higher for each category due to the financial crisis. Not suprisingly, the financial stock index experiences the highest daily volatility, 3.7% in 2008 and 3.4% in 2009. The growth in net assets of financial LETFs increases the scaled LETF rebalancing flow from 0.4% in 2008 to 1.02% in 2009. Higher volatility and the growth in financial LETFs leads to an average implied price impact of 0.97 % in 2009.
If total LETF rebalancing leads to a price impact equal to or greater than the change in the target index level, it could significantly amplify the target index moves and force LETFs to carry out further rebalancing. As a result, the implied price impact of 1% can be considered a critical level for this analysis. Figure 3 plots the implied price impact of LETF rebalancing in response to a 1% change in the target stock index for five categories from June 19, 2006 to December 31, 2011. The implied price impact for the financial category goes above the 1% level in the summer of 2008 and reaches a level of 1.5% due to over 5% daily volatility after the collapse of Lehman Brothers. The implied price impacts for large, small and technology stock categories also rise and approach to the 1% level in late 2008. Markets reacted negatively to events following the Financial Stability Plan announcement on Feb 10, 2009 and the S&P 500 reached a record low level on March 9, 2009. The implied price impacts for the financial category skyrockets and almost reaches to the 2.5% level in the first half of 2009 because of over 5% daily volatility and the growth in financial LETFs. After the first half of 2009, all implied price impacts of LETFs remain below the 1% level until August 2011 when the daily volatility for the financial category increases to 4% due to the concerns about European soveriegn debt11. The implied price impact estimates for the small and the financial categories stay above the 1% level through late August and early September 2011.
Kyle and Obizhaeva (2012) compute the implied price impact of portfolio insurers in October 1987 and find that it ranges from 11.13% to 15.75% over the four days surrounding the stock-market crash of October 19. Although the implied price impact estimates of LETFs are not as high as that of portfolio insurers of the 1980s, the implied price impact of LETFs becomes substantial when daily volatility surges.
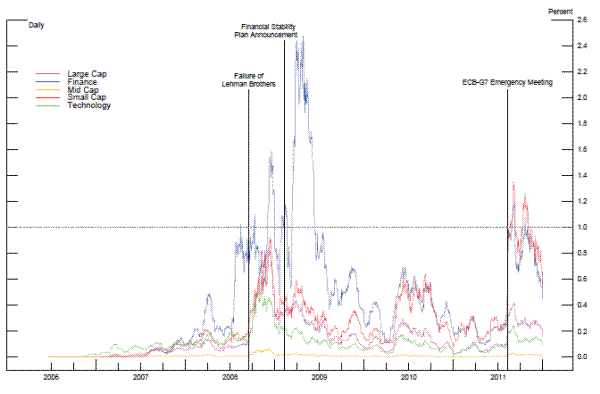
Implied price impact results indicate that the imprint of LETF rebalancing left on the financial stock index should be visible during the 2008-2009 financial crisis and again in 2011 when the European sovereign debt crisis came to the forefront. Figure 4 plots the frequency of a 1% price move of the financial stock index in the last hour of trading given that the index has already moved 1% in the same direction by 3:00pm. This frequency is calculated from a month's trading days in which the financial stock index moved by 1% by 3:00pm 12. The frequency of a large price move in the last hour of trading is zero until 2007 when the first financial LETF is launched. Consistent with the implied price impact results, the frequency of a large price move is elevated when the price volatility is high, reaching 0.8 in the 2008-2009 financial crisis and 0.6 in the second half of 2011. These results, combined with the implied price impact estimates, suggest that LETF rebalancing contributed to the stock market volatility in the 2008-2009 financial crisis and in the second half of 2011. Although LETF rebalancing has not been proven to disrupt stock market activity, their large and concentrated trading could pose risks. The rebalancing of LETFs in the last hour could amplify their impact since executing orders within a short period of time may move prices disproportionately and trigger a "cascade" reaction. In contrast, rebalancing in the last hour has the advantage of limiting the possibility of a price dislocation because the market close may serve as a prolonged circuit breaker. However, if there are enough traders following the LETF rebalancing, they may start trading well before the market close and produce similar consequences.
7 Conclusion
Contrary to plain vanilla ETFs, LETFs typically rebalance their portfolios daily to maintain their stock-to-cash ratios. Maintaining constant stock-to-cash ratios forces LETFs to rebalance in the same direction as target index moves, selling in a declining market and buying in a rising market. Similar to portfolio insurance strategies, mechanical rebalancing of LETFs is predictable and could attract opportunistic traders, who may originate orders in anticipation of LETF flows. Although the LETFs are not as large as portfolio insurance strategies of the 1980s in terms of size and impact, daily LETF rebalancing leaves its imprint on all stock categories.
The implied price impact estimates of LETFs on broad stock-market indexes become significant during periods of high volatility, especially for the stocks of financial firms. LETF rebalancing in response to a large market move could amplify the move and force them to further rebalance which may trigger a "cascade" reaction. Rebalancing in the last hour of trading could, in fact, reduce the possibility of a price dislocation since the market close could serve as a prolonged circuit breaker. On the other hand, executing orders within a short period of time, such as the last hour of trading, may cause disproportionate price changes. A significant price reduction at market close may also impair investor confidence. If the market closes with depressed prices, the stock market could experience large investor outflows overnight.
Although the long-horizon return structure of LETFs that rebalance daily is alone not suitable for the investment horizons of many investors, LETFs delivering multiples of daily index returns are greater in size and number than the ones delivering multiples of monthly and quarterly index returns13. Further research is needed to better understand the drivers of the demand for LETFs delivering multiples of daily index returns.
References
Agapova, A. (2012). Conventional mutual index funds versus ex change traded funds. Journal of Financial Markets, 14(2):323-343.
Avellanda, M. and Zhang, S. J. (2009). Path-dependence of leveraged etf returns. Working Paper.
Bai, Q., Bond, S. A., and Hatch, B. (2012). The impact of leveraged and inverse etfs on underlying stock returns. University of Cincinnati Working Paper.
Ben-David, I., Franzoni, F. A., and Moussawi, R. (2012). Etfs, arb itrage, and shock propagation. Working Paper.
Bessembinder, H., Carrion, A., Venkataraman, K., and Tuttle, L. A. (2012). Predatory or sunshine trading? evidence from crude oil etf rolls. Working Paper.
Brady Report (1988). Report of the presidential task force on market mechanisms.
Brennan, M. J. and Schwartz, E. S. (1989). Portfolio insurance and financial market equilibrium. The Journal of Business, 62(4):455-472.
Brunnermeier, M. K. and Pedersen, L. H. (2009). Market liquidity and funding liquidity. The Review of Financial Studies , 22(6):2201-2238.
Buetow, G. and Henderson, B. (2012). An empirical analysis of exchange traded funds. Journal of Portfolio Management.
CFTC-SEC Report (2010). Findings regarding the market events of may 6, 2010.
Cheng, M. and Madhavan, A. (2009). Dynamics of leveraged and inverse exchange-traded funds. Journal of Investment Management.
Gennotte, G. and Leland, H. (1990). Market liquidity, hedging, and crashes. The American Economic Review , 80(5):999-1021.
Hill, J. and Teller, S. (2010). Hedging with inverse etfs. Journal of Indexes .
Huang, J. C. and Guedj, I. (2009). Are etfs replacing index mutual funds? Working Paper.
Jarrow, R. A. (2010). Understanding the risk of leveraged etfs. Finance Research Letters, 7:135-139.
Kirilenko, A., Kyle, A. S., Samadi, M., and Tuzun, T. (2011). The flash c rash: The impact of high frequency trading on an electronic market. Working Paper
Kyle, A. S. and Obizhaeva, A. (2011a). Market microstructure inv ariants: Empirical evidence from portfolio transitions. University of Maryland Working Paper.
Kyle, A. S. and Obizhaeva, A. (2011b). Market microstructure invariants: Theory and implications of calibration. University of Maryland Working Paper.
Kyle, A. S. and Obizhaeva, A. (2012). Large bets and stock market crashes. University of Maryland Working Paper.
Lo, A. W. and Mackinlay, A. C. (1990). When are contrarian profits due to stock market underreaction? The Review of Financial Studies, 3(2):175-205.
Madhavan, A. (2011). Exchange-traded funds, market structure and the flash crash.Working Paper.
Obizhaeva, A. (2009). Portfolio transitions and stock price dynamics. University of Maryland Working Paper.
Poterba, J. M. and Shoven, J. B. (2002). Exchange traded funds: A new investment option for taxable investors. MIT Department of Economics Working Paper.
Trainor, W. J. (2010). Do leveraged etfs increase volatility? Technology and Investment.
Appendix: Investor Flows into LETFs
Since the inception of the first LETF on June 19, 2006, equity LETFs have gained popularity among investors and currently have $20B in net assets in the US. Because the size and growth of LETFs could be important from a financial stability point of view, examining the drivers of the LETF inflows could explain the intent of their use. There are several hypotheses which explain the purpose of investing in LETFs. One explanation is that LETFs provide an easy access to leverage and short-selling. LETFs can be used by retail investors to easily short stocks or build leverage. Yet, this hypothesis cannot explain why LETFs are promising a certain multiple of daily stock index returns. Generating a multiple of daily index return requires LETFs to sell when the market is down and buy when the market is up, resulting in transaction costs. Several studies (Jarrow (2010); Cheng and Madhavan (2009); Huang and Guedj (2009)) show that returns of LETFs could be significantly different that their multiple of target index returns for holding periods longer than one day. The investment horizon of a retail trader is typically longer than a day, suggesting that LETFs may not be suitable for many retail investors. Although there are 7 LETFs which target to deliver multiples of monthly index returns, their total size is very small ($ 184.1 million). Another explanation is that LETFs are used for hedging or portfolio insurance purposes. By adding a LETF into his portfolio, an investor may aim to reduce his overall risk exposure. Hill and Teller (2010) explain that Inverse ETFs could be used by investors for hedging purposes. Hedging a position involves rebalancing the hedge amount to maintain the desired risk exposure. To explore the hedging hypothesis for LETF usage among investors, I examine the drivers of investor inflows into the LETFs. The dollar amount of investor flow is calculated as the daily change in LETF shares outstanding multiplied by its net asset value. The variable of interest, Investor Flow, is defined as the dollar amount of investor flow into an LETF scaled by lagged total net assets. Explanatory variables considered for this variable are daily lagged Investor Flows, daily lagged LETF returns and daily changes in VIX. Lagged LETF returns are included to explore the dynamic hedging hypothesis. If an investor is using a LETF for hedging purposes, he dynamically adjusts his hedge position, by selling his shares when his LETF position grows and by buying new shares when his LETF position shrinks. As a result, investors should redeem their shares when LETFs are generating positive returns and buy new shares when LETFs are giving negative returns. Yet, there are other explanations such as the disposition effect for negative feedback investments. The disposition effect is the tendency of investors to sell assets whose prices have appreciated while keeping assets whose prices have declined. Table X reports the results of the regression for Investor Flows.14. The standard errors are adjusted for heteroskedasticity. When only the lagged Investor Flows are used as explanatory variables,Adj R2 is 3.23%. The coefficients on lagged Investor Flows.range from 0.10 to 0.004 and all but one are statistically significant. When the lagged LETF returns are added, Adj R2 increases to 4.66%. The coefficients on the lagged LETF returns are negative, statistically and economically significant. For instance, if a LETF delivers a 1% return, it experiences outflows equivalent to 0.07% (0.07x1%) of its net assets the next day and 0.04% of its net assets on the following day. When the lagged changes of VIX are introduced in the regression, Adj R2 increases slightly and becomes 4.72%. The disposition effect implies that LETFs should have outflows when they deliver positive returns. Hence, outflows should be more sensitive to recent returns than inflows. Table X includes the regression results for Inflows and Outflows. Inflows and Outflows respond differently to lagged Investor Flows and lagged changes in VIX. The coefficients on Investor Flows are positive for Inflows whereas the y are generally negative for Outflows, suggesting that Inflows are persistent. More interestingly, changes in VIX have positive coefficients for Inflows and negative coefficients for Outflows. Compared to Inflows, Outflows respond strongly to past LETF returns as the disposition effect suggests. Although these results are consistent with the hedging hypothesis, disposition effect cannot be ruled out.| # of LETFs | Total Net Assets ($) | Rebalancing Flow (r=1%) | |
| Large Cap Stock Indexes: S&P 500 TR | 12 | 7,251,240,249 | 316,399,014 |
| Large Cap Stock Indexes:DJ Industrial Average TR USD | 5 | 1,042,571,338 | 45,075,716 |
| Large Cap Stock Indexes:Russell 1000 TR USD | 2 | 453,400,000 | 37,704,000 |
| Total | 19 | 8,747,211,587 | 399,178,730 |
| Financial Stock Indexes: DJ US Financial TR USD | 3 | 1,223,900,000 | 39,438,000 |
| Financial Stock Indexes: Russell 1000/Financial Services TR USD | 2 | 2,287,500,000 | 187,380,000 |
| Total | 5 | 3,511,400,000 | 226,818,000 |
| Small Stock Indexes: Russell 2000 TR USD | 7 | 2,875,507,378 | 188,800,885 |
| Small Stock Indexes:Russell 2000 Growth TR USD | 2 | 35,733,226 | 1,471,907 |
| Small Stock Indexes:Russell 2000 Value TR USD | 2 | 18,493,210 | 619,596 |
| Small Stock Indexes:S&P SmallCap 600 TR | 3 | 84,805,694 | 2,483,508 |
| Total | 14 | 3,014,539,508 | 193,375,896 |
| Mid Cap Stock Indexes: Russell Mid Cap TR USD | 2 | 69,633,676 | 5,296,984 |
| Mid Cap Stock Indexes: Russell Mid Cap Growth TR USD | 2 | 14,624,142 | 405,294 |
| Mid Cap Stock Indexes:Russell Mid Cap Value TR USD | 2 | 8,669,870 | 252,112 |
| S&P MidCap 400 TR | 5 | 206,730,479 | 7,204,583 |
| Total | 11 | 299,658,167 | 13,158,973 |
| Technology Stock Indexes: NASDAQ 100 TR USD | 5 | 1,939,900,000 | 83,582,000 |
| Technology Stock Indexes:DJ US Technology TR USD | 2 | 99,360,379 | 2,545,379 |
| Technology Stock Indexes:Russell 1000/Technology TR USD | 2 | 203,460,169 | 14,257,220 |
| Total | 9 | 2,242,720,548 | 100,384,599 |
| Other Stock Indexes: Alerian MLP Infrastructure TR USD | 1 | 10,835,796 | 216,716 |
| Other Stock Indexes:DJ US Basic Materials TR USD | 3 | 287,603,995 | 8,557,523 |
| Other Stock Indexes:DJ US Consumer Goods TR USD | 2 | 16,075,166 | 521,042 |
| Other Stock Indexes:DJ US Consumer Svcs TR USD | 2 | 20,273,116 | 917,055 |
| Other Stock Indexes:DJ US Health Care TR USD | 2 | 37,383,013 | 881,799 |
| Other Stock Indexes:DJ US Industrials TR USD | 2 | 30,662,049 | 919,148 |
| Other Stock Indexes:DJ US Oil&Gas TR USD | 3 | 352,738,685 | 11,362,774 |
| Other Stock Indexes:DJ US Real Estate TR USD | 3 | 534,686,005 | 16,733,720 |
| Other Stock Indexes:DJ US Select Telecom TR USD | 1 | 2,777,478 | 166,649 |
| Other Stock Indexes:DJ US Semiconductors TR USD | 2 | 56,446,452 | 1,790,918 |
| DJ US Telecom TR USD | 1 | 3,070,287 | 61,406 |
| Other Stock Indexes:DJ US Utilities TR USD | 2 | 22,803,601 | 592,072 |
| Other Stock Indexes:ISE Revere Natural Gas PR USD | 2 | 12,099,179 | 931,071 |
| Other Stock Indexes:KBW Regional Banking TR USD | 2 | 14,480,240 | 289,605 |
| Other Stock Indexes:MSCI US REIT GR USD | 2 | 141,508,860 | 10,357,063 |
| Other Stock Indexes:NASDAQ Biotechnology TR USD | 2 | 14,441,624 | 361,157 |
| Other Stock Indexes:NYSE Arca Gold Miners Index | 2 | 89,170,194 | 5,744,884 |
| Other Stock Indexes:PHLX Semiconductor | 2 | 116,726,382 | 8,189,627 |
| Other Stock Indexes:Russell 1000 Growth TR USD | 2 | 20,007,416 | 637,600 |
| Other Stock Indexes:Russell 1000 Value TR USD | 2 | 7,927,918 | 250,571 |
| Other Stock Indexes:Russell 1000/Energy TR USD | 2 | 487,500,000 | 36,072,000 |
| Other Stock Indexes:Russell 1000/Retail TR USD | 2 | 7,702,681 | 585,902 |
| Other Stock Indexes:Russell 3000 TR USD | 2 | 8,917,945 | 263,524 |
| Other Stock Indexes:S&P Healthcare Select Sector | 2 | 6,608,294 | 603,729 |
| S&P Materials Select Sector | 2 | 7,878,608 | 705,510 |
| Total | 50 | 2,310,324,984 | 107,713,064 |
| Aggregate Total | 108 | 20,125,854,794 | 1,040,629,262 |
|---|
This table presents the descriptive variables of equity LETFs across different stock index categories. Total net assets are in dollars. Rebalancing flow is the rebalancing amount in dollars if the target index changes by 1%.
| LETF Category | # of LETFs | Statistics | Mean | Weighted Mean | Median | Min | Max | Std |
| Financial | 5 | σ | 0.028% | 0.108% | 0.099% | |||
| Financial | 5 | β | 1.001 | 1.005 | 1.001 | 0.975 | 1.014 | 0.015 |
| Financial | 5 | 0.986 | 0.995 | 0.996 | 0.947 | 0.998 | 0.022 | |
| Large Cap | 19 | σ | -0.002% | 0.0004% | 0.002% | -0.074% | 0.041% | 0.029% |
| Large Cap | 19 | β | 0.993 | 0.985 | 0.993 | 0.885 | 1.382 | 0.124 |
| Large Cap | 19 | Adj − R2 | 0.967 | 0.991 | 0.993 | 0.730 | 1.000 | 0.062 |
| MidCap | 11 | σ | -0.004% | 0.013% | -0.012% | -0.049% | 0.033% | 0.031% |
| MidCap | 11 | β | 1.052 | 1.055 | 0.999 | 0.977 | 1.561 | 0.170 |
| MidCap | 11 | Adj − R2 | 0.981 | 0.978 | 0.975 | 0.967 | 1.000 | 0.011 |
| Small | 14 | σ | -0.006% | -0.008% | -0.020% | -0.086% | 0.064% | 0.049% |
| Small | 14 | β | 0.985 | 0.993 | 0.995 | 0.945 | 1.035 | 0.030 |
| Small | 14 | Adj −2 | 0.989 | 0.996 | 0.989 | 0.978 | 1.000 | 0.008 |
| Technology | 9 | σ | -0.004% | 0.002% | -0.009% | -0.054% | 0.034% | 0.028% |
| Technology | 9 | β | 0.951 | 0.950 | 0.947 | 0.926 | 0.997 | 0.027 |
| Technology | 9 | Adj − R2 | 0.891 | 0.900 | 0.902 | 0.788 | 0.999 | 0.076 |
This table presents the descriptive statistics of the following regression run individually for each LETF.
is the multiple of the daily target index return LETF promises to deliver.
is the daily return of LETF j on day t and 
is the daily target index return on day t. The Russell 1000 Financial Services index is used for the financial LETFs, the S&P 500 index is used for the large LETFs, the Russell Mid-Cap is used for mid-cap LETFs, the Russell 2000 is used for the small LETFs and the Nasdaq 100 is used for the technology LETFs. Asset-weighted means are calculated by weighting the regression statistics with the LETF net assets.
| Financials | Large | MidCap | Small | Technology | |
| Panel A: All : Market Cap | $10,910,080,286 | $22,337,193,312 | $4,897,070,865 | $652,436,240 | $22,027,084,145 |
| Panel A: All :Float-Adjusted Market Cap | $10,120,855,466 | $21,234,404,621 | $4,502,949,167 | $550,360,313 | - |
| Panel A: All :ADV | $125,745,187 | $203,309,377 | $60,552,960 | $7,312,225 | $303,993,868 |
| Panel A: All :Daily Volatility | 0.029 | 0.023 | 0.026 | 0.034 | 0.024 |
| Panel A: All :Number of Different Stocks | 279 | 647 | 1098 | 2876 | 142 |
| Panel B: 2006-2009: Market Cap | $11,010,250,462 | $22,106,336,850 | $4,803,095,818 | $647,800,903 | $20,608,669,582 |
| Panel B: 2006-2009:Float-Adjusted Market Cap | $10,278,857,828 | $21,281,551,450 | $4,404,055,011 | $546,768,728 | - |
| Panel B: 2006-2009:ADV | $137,302,091 | $203,798,955 | $59,599,684 | $7,794,372 | $295,870,892 |
| Panel B: 2006-2009:Daily Volatility | 0.035 | 0.026 | 0.028 | 0.038 | 0.027 |
| Panel B: 2006-2009:Number of Different Stocks | 263 | 612 | 989 | 2489 | 129 |
| Panel C: 2010-2011: Market Cap | $10,751,588,913 | $22,069,126,399 | $5,058,046,367 | $658,682,773 | $24,421,343,488 |
| Panel C: 2010-2011:Float-Adjusted Market Cap | $9,870,860,785 | $21,144,825,291 | $4,671,959,829 | $555,203,498 | - |
| Panel C: 2010-2011:ADV | $107,459,608 | $202,610,171 | $62,185,885 | $6,662,489 | $317,705,312 |
| Panel C: 2010-2011:Daily Volatility | 0.020 | 0.019 | 0.021 | 0.030 | 0.020 |
| Panel C: 2010-2011:Number of Different Stocks | 212 | 527 | 876 | 2382 | 112 |
This table presents the mean variables of the stocks in the sample. Sample runs from June 19, 2006 to December 31, 2011. Market Capitalization is calculated as the product of the number of shares outstanding and the stock price. Float-adjusted market capitalization is the product of shares available for investment and the stock price. ADV is the 20 day average dollar volume of the stock. Daily volatility is calculated as the the standard deviation of the previous 20 day returns. Financials are the members of the Russell 1000 Financial Services Index. Large Stocks are the members of the S&P 500 index. Mid-cap stocks are the members of the Russell Mid Cap stock index. Small stocks are the members of the Russell 2000. Technology stocks are the members of the Nasdaq 100.
| Financials | Large Cap | Mid Cap | Small Cap | Technology | Financials | Large Cap | Mid Cap | Small Cap | Technology | |
| Panel A All: Intercept | 0.009 | 0.005 | 0.008 | 0.008 | 0.005 | 0.009 | 0.005 | 0.008 | 0.008 | 0.005 |
| Panel A All: Intercept (standard errors) | 0.007 | 0.006 | 0.006 | 0.007 | 0.006 | 0.007 | 0.006 | 0.006 | 0.007 | 0.006 |
| Panel A All: LETF_ Flow/ADV | 3.13 | 3.80 | 4.16 | 0.83 | 2.72 | 3.09 | 4.32 | 4.28 | 0.86 | 3.83 |
| Panel A All: LETF_ Flow/ADV (standard errors) | 0.25 | 0.64 | 0.42 | 0.08 | 0.86 | 0.23 | 0.57 | 0.36 | 0.08 | 0.83 |
Panel A All:
 |
0.002 | -0.011 | -0.004 | -0.006 | -0.018 | |||||
| Panel A All:
(standard errors) |
0.006 | 0.003 | 0.004 | 0.005 | 0.003 | |||||
| Panel A All: # of Obs. | 250,367 | 684,869 | 1,025,127 | 2,220,771 | 129,800 | 250,366 | 684,869 | 1,025,127 | 2,220,771 | 129,800 |
Panel A All: |
6.32% | 1.26% | 1.76% | 2.12% | 0.52% | 6.33% | 1.36% | 1.78% | 2.14% | 0.76% |
| Financials | Large Cap | Mid Cap | Small Cap | Technology | Financials (2010-2011) | Large Cap (2010-2011) | Mid Cap (2010-2011) | Small Cap (2010-2011) | Technology (2010-2011) | |
| Panel B 2006-2009: Intercept | 0.013 | 0.005 | 0.011 | 0.007 | 0.006 | 0.004 | 0.005 | 0.004 | 0.008 | 0.003 |
| Panel B 2006-2009: Intercept (standard errors) | 0.010 | 0.008 | 0.007 | 0.009 | 0.008 | 0.010 | 0.010 | 0.009 | 0.011 | 0.009 |
| Panel B 2006-2009:LETF_ Flow/ADV | 3.39 | 4.76 | 4.85 | 0.78 | 4.02 | 2.74 | 3.78 | 3.57 | 0.88 | 3.48 |
| Panel B 2006-2009:LETF_ Flow/ADV (standard error) | 0.32 | 0.85 | 0.54 | 0.13 | 1.14 | 0.31 | 0.69 | 0.42 | 0.09 | 1.08 |
| Panel B 2006-2009:
|
0.010 | -0.010 | -0.006 | -0.009 | -0.017 | -0.008 | -0.013 | -0.001 | -0.001 | -0.018 |
| Panel B 2006-2009:
(standard errors) |
0.008 | 0.004 | 0.005 | 0.006 | 0.003 | 0.006 | 0.005 | 0.006 | 0.006 | 0.004 |
| # of Obs. | 153,409 | 437,059 | 646,198 | 1,274,792 | 81,511 | 96,957 | 247,810 | 378,929 | 945,979 | 48,289 |
|
7.04% | 1.43% | 1.88% | 0.82% | 0.82% | 5.48% | 1.30% | 1.71% | 4.09% | 0.66% |
This table presents the results of the following regression.
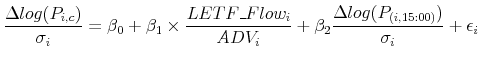
is the return of stock i between 15:00pm(ET) and 16:00pm(ET) scaled by its daily volatility, 
- the standard deviation of previous 20 days' returns.
is the share of stock i from the total LETF rebalancing flow calculated as a function of the target index return between the previous day's close and 15:00pm. is the past 20 day average dollar trading volume of stock i.
is the return of stock i from the previous day's close to 15:00pm scaled by its daily volatility. Standard errors are clustered daily and reported
below the coefficient estimates.
| Financials | Large Cap | Mid Cap | Small Cap | Technology | |
| Panel A: Market Up: Intercept | 0.021 | 0.009 | 0.020 | 0.041 | 0.001 |
| Panel A: Market Up: Intercept (standard errors) | 0.011 | 0.007 | 0.006 | 0.009 | 0.008 |
| Panel A: Market Up: LETF_ Flow/ADV | 3.06 | 4.46 | 4.36 | 0.63 | 4.66 |
| Panel A: Market Up: LETF_ Flow/ADV (standard errors) | 0.34 | 0.67 | 0.40 | 0.08 | 1.18 |
| Panel A: Market Up:
|
-0.005 | -0.014 | -0.010 | -0.019 | -0.018 |
| Panel A: Market Up:
(standard errors) |
0.006 | 0.003 | 0.003 | 0.004 | 0.003 |
| # of Obs. | 124,625 | 364,725 | 543,413 | 1,123,013 | 69,825 |
|
4.36% | 1.33% | 1.74% | 1.20% | 0.92% |
| Panel B: Market Down: Intercept | -0.009 | -0.003 | -0.008 | -0.018 | -0.001 |
| Panel B: Market Down: Intercept (standard errors) | 0.012 | 0.010 | 0.008 | 0.011 | 0.011 |
| Panel B: Market Down: LETF_ Flow/ADV | 2.60 | 3.60 | 3.36 | 0.80 | 2.93 |
| Panel B: Market Down: LETF_ Flow/ADV (standard errors) | 0.44 | 0.96 | 0.52 | 0.14 | 1.49 |
| Panel B: Market Down:
|
0.001 | -0.011 | -0.009 | -0.012 | -0.017 |
| Panel B: Market Down:
(standard errors) |
0.008 | 0.006 | 0.006 | 0.008 | 0.005 |
| # of Obs. | 125,741 | 320,144 | 481,051 | 1,097,758 | 59,975 |
|
2.54% | 0.69% | 0.87% | 1.43% | 0.37% |
This table presents the results of the following regression for Market Ups and Market Downs.
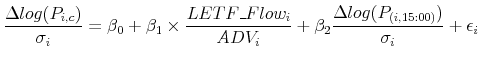
is the return of stock i between 15:00pm(ET) and 16:00pm(ET) scaled by its daily volatility, - the standard deviation of previous 20 days' returns.
is the share of stock i from the total LETF rebalancing flow calculated as a function of the target index return between the previous day's close and 15:00pm. is the past 20 day average dollar trading volume of stock i.
is the return of stock i from the previous day's close to 15:00pm scaled by its daily volatility.. Standard errors are clustered daily and reported
below the coefficient estimates.
| Financials | Large Cap | Mid Cap | Small Cap | Technology | |
| Panel A: All Intercept | -0.024 | 0.007 | 0.003 | -0.012 | 0.008 |
| Panel A: All Intercept (standard errors) | 0.018 | 0.016 | 0.015 | 0.015 | 0.016 |
Panel A: All:
 |
-1.74 | -3.52 | -2.52 | -0.35 | -4.24 |
| Panel A: All:
(standard errors) |
0.43 | 1.08 | 0.68 | 0.10 | 1.65 |
Panel A: All:
 |
0.006 | 0.009 | 0.019 | -0.015 | 0.001 |
| Panel A: All:
(standard errors) |
0.011 | 0.008 | 0.008 | 0.007 | 0.008 |
| Panel A: All:# of Obs. | 250,088 | 684,233 | 999,363 | 2,217,895 | 129,658 |
| Panel A: All: |
0.25% | 0.09% | 0.08% | 0.13% | 0.12% |
| Panel B: 2006-2009: Intercept | -0.046 | -0.003 | -0.005 | -0.021 | 0.004 |
| Panel B: 2006-2009: Intercept (standard errors) | 0.022 | 0.019 | 0.018 | 0.019 | 0.019 |
| Panel B: 2006-2009:
|
-2.00 | -4.77 | -2.66 | -0.49 | -4.62 |
| Panel B: 2006-2009:
(standard errors) |
0.54 | 3.89 | 0.94 | 0.19 | 2.09 |
| Panel B: 2006-2009:
|
0.012 | 0.008 | 0.023 | -0.019 | 0.008 |
| Panel B: 2006-2009:
(standard errors) |
0.015 | 0.009 | 0.009 | 0.010 | 0.009 |
| Panel B: 2006-2009:# of Obs. | 153,342 | 436,987 | 631,468 | 1,274,298 | 81,481 |
| Panel B: 2006-2009: |
0.30% | 0.03% | 0.09% | 0.13% | 0.12% |
| Panel C: 2010-2011:Intercept | 0.011 | 0.013 | 0.015 | -0.001 | 0.016 |
| Panel C: 2010-2011:Intercept (standard errors) | 0.028 | 0.029 | 0.028 | 0.025 | 0.029 |
| Panel C: 2010-2011:
|
-1.28 | -5.23 | -2.31 | -0.31 | -3.33 |
| Panel C: 2010-2011:
(standard errors) |
0.70 | 4.66 | 0.96 | 0.11 | 2.65 |
| Panel C: 2010-2011:
|
-0.008 | -0.001 | 0.013 | -0.010 | -0.014 |
| Panel C: 2010-2011:
(standard errors) |
0.016 | 0.013 | 0.014 | 0.012 | 0.014 |
| Panel C: 2010-2011:# of Obs. | 96,746 | 247,296 | 367,895 | 943,597 | 48,177 |
| Panel C: 2010-2011: |
0.21% | 0.06% | 0.06% | 0.14% | 0.13% |
This table presents the results of the following regression.
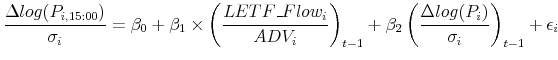
is the return of stock i between the previous day's close and 15:00pm scaled by its daily volatility, - the standard deviation of its previous 20 days' returns.
is the one-day lagged share of stock i from the total LETF rebalancing flow calculated as a function of the target index return between the previous day's close and
15:00pm.
is the one-day lagged past 20 day average dollar trading volume of stock i.
is one-day lagged return of stock i scaled by its daily volatility. Standard errors are clustered daily and reported below the
coefficient estimates.
Table VII: End-of-day Volatility and LETF Rebalancing
| Panel A All: Financials | Panel A All:Large Cap | Panel A All:Mid Cap | Panel A All:Small Cap | Panel A All:Technology | Panel A All:Financials | Panel A All:Large Cap | Panel A All:Mid Cap | Panel A All:Small Cap | Panel A All:Technology | |
| Intercept | 0.109 | 0.093 | 0.097 | 0.157 | 0.079 | 0.089 | 0.075 | 0.076 | 0.114 | 0.067 |
| Intercept (standard errors) | 0.005 | 0.003 | 0.003 | 0.011 | 0.003 | 0.005 | 0.003 | 0.003 | 0.034 | 0.004 |
|
|
1.58 | 2.33 | 2.22 | 0.73 | 3.49 | 1.30 | 1.72 | 1.96 | 0.59 | 2.57 |
|
(standard errors) |
0.21 | 0.38 | 0.22 | 0.21 | 0.63 | 0.20 | 0.34 | 0.21 | 0.24 | 0.60 |
![\left[\frac{\Delta log(P_{i,(15:00)})}{\sigma}\right]^2](img59.gif) |
0.028 | 0.021 | 0.022 | 0.045 | 0.016 | |||||
|
(standard errors) |
0.002 | 0.001 | 0.001 | 0.038 | 0.001 | |||||
| # of Obs. | 250,367 | 684,869 | 1,025,127 | 2,220,771 | 129,800 | 250,366 | 684,869 | 1,025,127 | 2,220,771 | 129,800 |
Adj- R |
2.14% | 0.98% | 1.22% | 0.26% | 1.43% | 5.11% | 4.15% | 4.86% | 8.63% | 3.90% |
| Panel B 2006-2009: Financials | Panel B 2006-2009:Large Cap | Panel B 2006-2009:Mid Cap | Panel B 2006-2009:Small Cap | Panel B 2006-2009:Technology | Panel B 2010-2011:Financials | Panel B 2010-2011:Large Cap | Panel B 2010-2011:Mid Cap | Panel B 2010-2011:Small Cap | Panel B 2010-2011:Technology | |
| Intercept | 0.095 | 0.078 | 0.079 | 0.045 | 0.077 | 0.077 | 0.069 | 0.070 | 0.136 | 0.064 |
| Intercept (standard errors) | 0.006 | 0.004 | 0.003 | 0.060 | 0.005 | 0.008 | 0.005 | 0.005 | 0.020 | 0.006 |
|
|
1.58 | 2.46 | 2.54 | 0.64 | 5.35 | 1.03 | 1.00 | 1.34 | 0.71 | 0.86 |
|
(standard errors) |
0.27 | 0.51 | 0.31 | 0.25 | 1.60 | 0.24 | 0.39 | 0.24 | 0.29 | 0.71 |
|
|
0.032 | 0.023 | 0.024 | 0.122 | 0.022 | 0.022 | 0.017 | 0.019 | 0.003 | 0.014 |
|
(standard errors) |
0.002 | 0.002 | 0.002 | 0.064 | 0.002 | 0.004 | 0.002 | 0.003 | 0.002 | 0.001 |
| # of Obs. | 153,409 | 437,059 | 646,198 | 1,274,792 | 81,511 | 96,957 | 247,810 | 378,929 | 945,979 | 48,289 |
| Adj- R |
6.03% | 4.72% | 5.45% | 26.05% | 4.67% | 4.11% | 3.57% | 4.16% | 1.14% | 3.07% |
This table presents the results of the following regression.
![\displaystyle \left[\frac{\Delta log(P_{i,c})}{\sigma_{i}}\right]^2=\beta_0+\beta_1\times \left\vert\frac{LETF\_Flow_i}{ADV_i}\right\vert+\beta_2\left[\frac{\Delta log(P_{i,(15:00)})}{\sigma}\right]^2+\epsilon_i](img61.gif)
is the return of stock i between 15:00pm(ET) and 16:00pm(ET) scaled by its daily volatility, -the standard deviation of previous 20 days' returns.
is the absolute value of the share of stock i from the total LETF rebalancing flow calculated as a function of the target index return between the previous day's
close and 15:00pm. is the past 20 day average dollar trading volume of stock i.
is the return of stock i from the previous day's close to 15:00pm. Standard errors are clustered daily and reported below the coefficient
estimates.
| Financials | Large | MidCap | Small | Technology | |
| Panel A: End-of-Day Return: Intercept | 0.009 | 0.005 | 0.008 | 0.008 | 0.005 |
| Panel A: End-of-Day Return: Intercept(standard errors) | 0.007 | 0.006 | 0.006 | 0.007 | 0.006 |
| Panel A: End-of-Day Return:LETF_ Flow/ADV | 2.528 | 3.356 | 3.909 | 0.545 | 3.564 |
| Panel A: End-of-Day Return:LETF_ Flow/ADV (standard errors) | 0.329 | 0.598 | 0.371 | 0.069 | 1.075 |
Panel A: End-of-Day Return:
 |
-0.008 | -0.018 | -0.016 | -0.028 | -0.019 |
| Panel A: End-of-Day Return:
(standard errors) |
0.006 | 0.002 | 0.002 | 0.003 | 0.002 |
Panel A: End-of-Day Return:
 |
0.003 | 0.015 | -0.015 | -0.024 | 0.022 |
| Panel A: End-of-Day Return:
(standard errors) |
0.015 | 0.005 | 0.015 | 0.016 | 0.011 |
 |
0.021 | 0.034 | 0.072 | -0.019 | |
| Panel A: End-of-Day Return:
(standard errors) |
0.020 | 0.016 | 0.018 | 0.011 | |
| Panel A: End-of-Day Return:# of Obs. | 250,365 | 684,868 | 1,025,122 | 2,220,766 | 129,799 |
| Panel A: End-of-Day Return: |
6.61% | 1.54% | 2.11% | 3.11% | 0.93% [b] |
| Panel B: End-of-Day Volatility: Intercept | 0.089 | 0.075 | 0.073 | 0.112 | 0.068 |
| Panel B: End-of-Day Volatility: Intercept (standard errors) | 0.005 | 0.004 | 0.003 | 0.028 | 0.004 |
Panel B: End-of-Day Volatility:
 |
1.303 | 1.670 | 2.037 | 0.561 | 2.999 |
| Panel B: End-of-Day Volatility:
(standard errors) |
0.197 | 0.338 | 0.217 | 0.156 | 0.641 |
Panel B: End-of-Day Volatility:
![\left[\frac{\Delta log(P_{15:00})}{\sigma}\right]^2](img68.gif) |
0.028 | 0.020 | 0.021 | 0.045 | 0.016 |
| Panel B: End-of-Day Volatility:
(standard errors) |
0.002 | 0.001 | 0.001 | 0.038 | 0.001 |
Panel B: End-of-Day Volatility:
![\left[\frac{\Delta log(P^{Index}_{15:00})}{\sigma_{Index}}\right]^2](img69.gif) |
0.0004 | 0.001 | -0.003 | 0.005 | 0.002 |
| Panel B: End-of-Day Volatility:
(standard errors) |
0.001 | 0.001 | 0.001 | 0.005 | 0.002 |
Panel B: End-of-Day Volatility:
![\left[\frac{\Delta log(P^{S\&P500}_{15:00})}{\sigma_{S\&P}}\right]^2](img70.gif) |
-0.0003 | 0.005 | -0.005 | -0.004 | |
| Panel B: End-of-Day Volatility:
(standard errors) |
0.0005 | 0.003 | 0.013 | 0.002 | |
| Panel B: End-of-Day Volatility:# of Obs. | 250,365 | 684,868 | 1,025,122 | 2,220,766 | 129,799 |
| Panel B: End-of-Day Volatility: |
5.12% | 4.16% | 4.90% | 8.65% | 4.02% |
This table presents the regression results for robustness checks.
, the dependent variable in Panel A, is the return of stock i between 15:00pm(ET) and 16:00pm(ET) scaled by its daily volatility, - the standard deviation of previous 20 days' returns.
is the share of stock i from the total LETF rebalancing flow calculated as a function of the target index return between the previous day's close and 15:00pm. is the past 20 day average dollar trading volume of stock i.
is the return of stock i from the previous day's close to 15:00pm scaled by its daily volatility.
is the return of the underlying index from the previous day's close to 15:00pm scaled by its daily volatility.
is the return of the S&P 500 index from the previous day's close to 15:00pm scaled by its daily volatility.
is the dependent variable in Panel B.
is the absolute value of the share of stock i from the total LETF rebalancing flow scaled by its average dollar trading volume. Standard errors are clustered
daily and reported below the coefficient estimates.
Table IX: Stock Market Indexes and LETFs
| Category | Variables | 2007 | 2008 | 2009 | 2010 | 2011 |
| Financial Stock Index | ADV (in billions) | $29.325 | $36.687 | $28.628 | $24.433 | $22.516 |
| Financial Stock Index | Volatility | 0.013 | 0.037 | 0.034 | 0.015 | 0.018 |
| Financial Stock Index |
 |
0.073 | 0.424 | 1.020 | 1.214 | 1.077 |
| Financial Stock Index |
 (in bps) |
3.353 | 53.506 | 96.992 | 38.548 | 45.083 [b] |
| Large Cap Stock Index | ADV (in billions) | $112.906 | $132.555 | $99.618 | $107.613 | $111.514 |
| Large Cap Stock Index | Volatility | 0.009 | 0.022 | 0.016 | 0.011 | 0.013 |
| Large Cap Stock Index |
|
0.093 | 0.192 | 0.394 | 0.385 | 0.323 |
| Large Cap Stock Index |
(in bps) |
3.121 | 22.405 | 23.221 | 13.656 | 15.578 [b] |
| Mid-Cap Stock Index | ADV (in billions) | $55.021 | $59.520 | $43.432 | $49.387 | $54.263 |
| Mid-Cap Stock Index | Volatility | 0.010 | 0.023 | 0.019 | 0.012 | 0.015 |
| Mid-Cap Stock Index |
|
0.027 | 0.026 | 0.025 | 0.025 | 0.025 |
| Mid-Cap Stock Index |
(in bps) |
0.672 | 2.041 | 1.436 | 0.814 | 1.124 [b] |
| Small Stock Index | ADV (in billions) | $20.748 | $18.103 | $11.306 | $13.311 | $15.512 |
| Small Stock Index | Volatility | 0.012 | 0.025 | 0.022 | 0.015 | 0.019 |
| Small Stock Index |
|
0.129 | 0.414 | 0.776 | 1.127 | 1.212 |
| Small Stock Index |
(in bps) |
3.818 | 25.974 | 31.963 | 31.323 | 51.189 |
| Technology Stock Index | ADV (in billions) | $34.865 | $36.699 | $24.999 | $31.692 | $35.318 |
| Technology Stock Index | Volatility | 0.011 | 0.023 | 0.016 | 0.011 | 0.014 |
| Technology Stock Index |
|
0.309 | 0.307 | 0.365 | 0.328 | 0.297 |
| Technology Stock Index |
(in bps) |
7.303 | 20.768 | 13.110 | 8.358 | 9.800 |
This table presents the daily averages of the variables used in implied price impact computation (, ,).
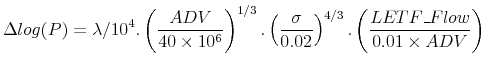
LETF Flow is the total rebalancing flow of LETFs in response to a 1% change in the target stock index. ADV is the total daily dollar volume of the member stocks. Volatility ( ) is defined as the standard deviation of the previous 20 day index returns. is 5.78.
Table X: Investor Flows into the Leveraged and Inverse ETFs
| Investor Flow: parameter | Investor Flow: t-statstic | Investor Flow: parameter | Investor Flow: t-statistic | Investor Flow: parameter | Investor Flow: t-statistic | Investor Net Inflow: parameter | Investor Net Inflow: t-statistic | Investor Net Outflow: parameter | Investor Net Outflow: t-statistic | |
| Intercept | 0.14 | 17.25 | 0.14 | 18.20 | 0.14 | 18.16 | 1.96 | 65.94 | -1.33 | -72.14 |
 |
0.10 | 16.90 | 0.09 | 14.87 | 0.09 | 14.81 | 0.17 | 10.73 | 0.02 | 1.94 |
 |
0.06 | 10.56 | 0.06 | 9.42 | 0.06 | 9.37 | 0.13 | 8.78 | -0.02 | -2.04 |
 |
0.04 | 6.91 | 0.04 | 6.39 | 0.04 | 6.33 | 0.08 | 5.08 | -0.02 | -1.65 |
 |
0.04 | 7.31 | 0.04 | 6.84 | 0.04 | 6.85 | 0.09 | 6.25 | -0.02 | -1.64 |
 |
0.04 | 6.63 | 0.04 | 6.65 | 0.04 | 6.63 | 0.08 | 5.55 | 0.01 | 0.57 |
 |
0.004 | 0.73 | 0.00 | 0.78 | 0.00 | 0.78 | 0.02 | 1.18 | -0.03 | -2.33 |
 |
0.02 | 4.05 | 0.02 | 4.12 | 0.02 | 4.18 | 0.06 | 4.33 | -0.02 | -1.81 |
 |
0.02 | 3.46 | 0.02 | 3.36 | 0.02 | 3.36 | 0.06 | 4.10 | -0.03 | -2.63 |
 |
0.04 | 6.71 | 0.04 | 6.54 | 0.04 | 6.58 | 0.08 | 5.25 | 0.00 | 0.34 |
 |
0.02 | 4.08 | 0.02 | 4.10 | 0.02 | 4.13 | 0.06 | 4.05 | 0.00 | 0.10 |
 |
-0.08 | -24.15 | -0.08 | -24.30 | -0.11 | -11.33 | -0.12 | -16.81 | ||
 |
-0.05 | -15.34 | -0.05 | -15.49 | -0.04 | -4.25 | -0.08 | -12.62 | ||
 |
-0.04 | -10.79 | -0.04 | -10.98 | -0.02 | -1.93 | -0.07 | -10.66 | ||
 |
-0.02 | -5.10 | -0.02 | -5.33 | 0.03 | 2.59 | -0.06 | -8.75 | ||
 |
-0.02 | -5.72 | -0.02 | -5.68 | 0.00 | 0.12 | -0.06 | -8.50 | ||
 |
-0.01 | -2.96 | -0.01 | -3.03 | 0.02 | 1.92 | -0.04 | -6.73 | ||
 |
0.000 | 0.16 | 0.000 | 0.08 | 0.036 | 3.61 | -0.028 | -4.10 | ||
 |
-0.001 | -0.19 | -0.001 | -0.17 | 0.026 | 2.56 | -0.026 | -3.94 | ||
 |
-0.001 | -0.44 | -0.001 | -0.46 | 0.034 | 3.47 | -0.030 | -4.39 | ||
 |
-0.005 | -1.47 | -0.005 | -1.48 | 0.026 | 2.71 | -0.024 | -3.76 | ||
 |
0.01 | 2.96 | 0.05 | 3.43 | -0.06 | -5.58 | ||||
 |
> | 0.02 | 3.32 | 0.08 | 5.00 | -0.06 | -5.05 | |||
 |
0.02 | 3.80 | 0.10 | 6.40 | -0.05 | -5.04 | ||||
 |
0.02 | 5.23 | 0.12 | 7.90 | -0.04 | -3.90 | ||||
 |
-0.002 | -0.52 | 0.04 | 2.55 | -0.07 | -7.02 | ||||
 |
0.01 | 1.63 | 0.08 | 5.02 | -0.07 | -6.26 | ||||
 |
0.01 | 2.34 | 0.09 | 5.45 | -0.07 | -5.66 | ||||
 |
0.002 | 0.36 | 0.02 | 1.54 | -0.03 | -2.76 | ||||
 |
0.003 | 0.70 | 0.05 | 2.98 | -0.06 | -5.78 | ||||
 |
0.003 | 0.81 | 0.05 | 3.05 | -0.04 | -3.56 | ||||
|
3.24% | 3.24% | 5.05% | 5.05% | 5.11% | 5.11% | 9.77% | 9.77% | 7.39% | 7.39% |
| # of Obs | 103,807 | 103,807 | 103,807 | 103,807 | 103,807 | 103,807 | 22,027 | 22,027 | 20,254 | 20,254 |
This table presents the results of the regression of Investor Flows into the LETFs. Dependent variables, Investor Flow, is the product of daily shares outstanding change and net asset value of LETF scaled by its lagged net assets. Explanatory variables are lagged daily Investor Flows, lagged daily LETF returns and lagged changes in VIX. All variables are in percentages. t-statistics are adjusted for heteroskedasticity and reported next to the coefficient estimates. Net Inflows are positive Investor Flows and Net Outflows are negative Investor Flows.
This figure illustrates the share of total hypothetical rebalancing flows for an average stock as a fraction of its daily volume for each category. Total LETF flows are calculated as the sum of all LETFs in that category in response to a 1% increase in the target index and allocated into stocks based on their weights in the target index. Daily volume of a stock is defined as the previous 20 day average of the stock's dollar volume.
Figure 2: Hypothetical LETF Rebalancing Flows as a Fraction of Stock Volume in the Last Hour
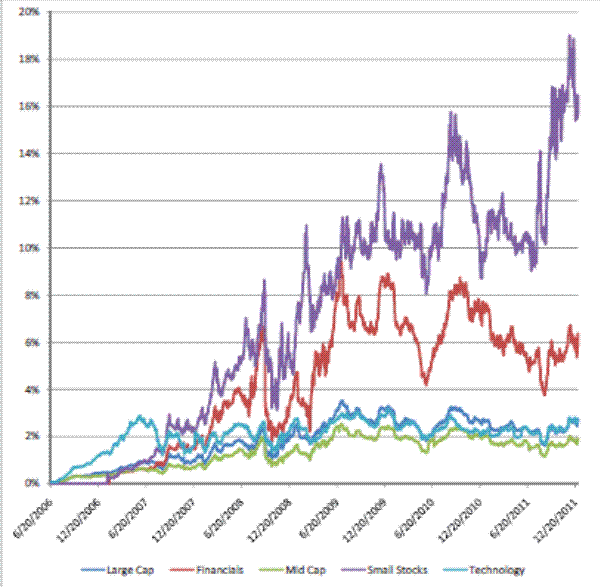Figure 2 Data
This figure illustrates the share of total hypothetical LETF rebalancing flows for an average stock as a fraction of its volume between 15:00pm and 16:00pm for each category. Total LETF flows are calculated as the sum of all LETFs in that category in response to a 1% increase in the target index and allocated into stocks based on their weights in the target index. Volume of a stock is defined as the previous 20 day average of the stock's dollar volume between 15:00pm and 16:00pm.
This figure plots the price impact estimates implied by market microstructure invariance(, ,).
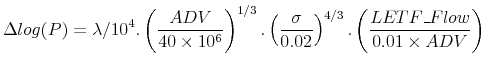
ADV is the total daily dollar volume of the member stocks. is the standard deviation of the previous 20 days' index returns. is 5.78. LETF Flow is the total LETF rebalancing flow in that category in response to a 1% change in the target index.
This figure plots the frequency of a 1% price move in the Russell 1000 Financial Services Index between 3:00pm and 4:00pm given that the index has already moved 1% by 3:00pm in the same direction. This measure is calculated from a month's trading days in which the index moved 1% by 3:00pm. More formally this frequency is:
