Learning from the Test:Raising Selective College Enrollment by Providing Information
Abstract
In the last decade, five U.S. states adopted mandates requiring high school juniors to take a college entrance exam. In the two earliest-adopting states, nearly half of all students were induced into testing, and 40-45% of them earned scores high enough to qualify for selective schools. Selective college enrollment rose by 20% following implementation of the mandates, with no effect on overall attendance. I conclude that a large number of high-ability students appear to dramatically underestimate their candidacy for selective colleges. Policies aimed at reducing this information shortage are likely to increase human capital investment for a substantial number of students.
- Introduction
- ACT Mandates
- The Effect of the Mandates on Test-taking and the Score Distribution
- The Test-taking Decision
- The Effects of the Mandates on College Enrollment
- Potential Effects on Enrollment
- Estimating Enrollment Effects
- Robustness Checks and Extensions
- Assessing the Test-taking Decision
- Discussion
The disparity in college attendance between children from low- and high-income families has been increasing over time (Bailey and Dynarski, 2011).1
Meanwhile, over the past 35 years, earnings have been essentially steady among the college-educated and have dropped substantially for everyone else (The College Board, 2007; Deming and Dynarski, 2010). Earnings are correlated with not just the level of an individual's education, but also the
caliber of college she attends (Hoekstra, 2009; Card and Krueger, 1992; Black and Smith, 2006).2![]() 3 And while disadvantaged students, in particular, appear to gain the most from selective schools
(McPherson, 2006; Dale and Krueger, 2011; Dale and Krueger, 2002; Saavedra, 2008), they are vastly underrepresented at top institutions (Bowen, Kurzweil, and Tobin, 2005; Hill and Winston, 2005; Pallais and Turner, 2006; Hoxby and Avery, 2012).4
3 And while disadvantaged students, in particular, appear to gain the most from selective schools
(McPherson, 2006; Dale and Krueger, 2011; Dale and Krueger, 2002; Saavedra, 2008), they are vastly underrepresented at top institutions (Bowen, Kurzweil, and Tobin, 2005; Hill and Winston, 2005; Pallais and Turner, 2006; Hoxby and Avery, 2012).4![]() 5
5
These trends underscore the importance of education policies that raise access to higher education, and especially highly selective schools, among disadvantaged students. Financial aid programs alone have not been able to close the educational gap that persists between socioeconomic groups (Kane, 1995). It is thus important to understand other factors, amenable to intervention, that contribute to disparities in postsecondary access and enrollment.6
Providing information to students at critical junctures, such as when they are finalizing their postsecondary enrollment decisions, may help address these disparities. Much research, mostly by psychologists and sociologists, has examined the profound effect a student's experiences and the expectations of those around her have on the expectations and goals she sets for herself (see Figure 1 in Jacob and Wilder, 2010).7 Jacob and Wilder (2010) demonstrate that these expectations--however misaligned with ability they may be--are strongly predictive of later enrollment decisions, but that they are also malleable8: high school students' future educational plans appear to fluctuate with the limited new information available in their GPAs.
To shed light on whether an intervention in this area could be successful, this paper examines whether students' beliefs about their own suitability for selective colleges contribute to observed disparities in college attendance. I exploit recent reforms in several states that required high school students to take entrance exams necessary for admission to selective colleges. A side-effect of compulsory testing is the new availability of a salient test score--a direct measure of candidacy for selective schools--for students who would not otherwise have taken the exam. Comparisons of tested students, test results, and college enrollment patterns by state before and after mandate adoption therefore offer a convenient quasi-experiment for measuring the impact of information on students' educational plans.
I demonstrate that the mandates can be linked to large increases in test participation and subsequent selective college enrollment. Many high-ability, low-income students appear to have downward-biased estimates of their probabilities of admission to selective colleges and, as a result, they do not choose to take the exam unless required to. When a mandate is introduced, they take the test, learn that they are admissible, and apply to and attend selective colleges.
This paper makes two important contributions. First, I reveal the existence of a sizable subgroup of high-ability teens interested in attending a selective school who drastically underestimate their candidacy; thus, I offer a new behavioral rationale that can help explain the widening educational attainment and earnings gap. Second, by showing that many students induced into testing by the new requirements go on to attend selective schools, I demonstrate that providing students with low-cost information at very late stages of adolescence can have a large impact on educational choices. Thus, I expose a new and inexpensive area for policy intervention that would likely increase human capital investment among a high-need population of students.
In the last decade, five U.S. states have adopted mandatory ACT testing for their public high school students.9 The ACT, short for the American College Test, is a nationally standardized test, designed to measure preparedness for higher education, that is widely used in selective college admissions in the United States. It was traditionally taken only by students applying to selective colleges, which consider it in admissions, and this remains the situation in all states without mandatory ACT policies.10
Using data on ACT test-takers, I demonstrate that, in each of the two early-adopting states (Colorado and Illinois), between
![]() and
and
![]() of high school students are induced to take the ACT test by the mandates I consider. Large shares of the new test-takers - 40-45% of the total - earn scores that would make them
eligible for competitive-admission schools. Moreover, disproportionately many - of both the new test-takers and the high scorers among them - are from disadvantaged backgrounds.
of high school students are induced to take the ACT test by the mandates I consider. Large shares of the new test-takers - 40-45% of the total - earn scores that would make them
eligible for competitive-admission schools. Moreover, disproportionately many - of both the new test-takers and the high scorers among them - are from disadvantaged backgrounds.
Next, I develop a model of the test-taking decision, and I use this model to show that with plausible parameter values, any student who both prefers to attend a selective college and thinks she stands a non-trivial chance of admission should take the test whether it is required or not. This makes the large share of new test-takers who score highly a puzzle, unless nearly all are uninterested in attending selective schools.11
Unfortunately, I do not have a direct measure of preferences. However, I can examine realized outcomes. In the primary empirical analysis of the paper, I use a difference-in-differences analysis to examine the effect of the mandates on college enrollment outcomes. I show that mandates cause substantial increases in selective college enrollment, with no effect on overall enrollment (which is dominated by unselective schools; see Kane, 1998). Enrollment of students from mandate states in selective colleges rises by 10-20% (depending on the precise selectivity measure) relative to control states in the years following the mandate.
My results imply that about 20% of the new high scorers (or 10% of students induced into testing by the mandates) enroll in selective colleges. This is inconsistent with the hypothesis that lack of interest explains the low test participation rates of students who could earn high scores, and indicates that many students would like to attend competitive colleges but choose not to take the test out of an incorrect belief that they cannot score highly enough to gain admission.
Therefore, this paper addresses two important, policy-relevant questions. The first is the simple question of whether mandates affect college enrollment outcomes. The answer to this is clearly yes. Second, what explains this effect? My results indicate that a significant fraction of secondary school students dramatically underestimate their candidacy for selective colleges. Thus, I provide the first clear evidence of a causal link between secondary students' perceptions of their own ability and their postsecondary educational choices, and of a policy that can successfully exploit this link to improve decision-making. Relative to many existing policies with similar aims, this policy is highly cost-effective.12
The rest of the paper proceeds as follows. Section II provides background on the ACT and the ACT mandates. Section III counts and characterizes the students induced into testing by the mandates. Section IV provides a model of information and test participation decisions. Section V presents estimates of the enrollment effects of the mandates. Section VI uses the empirical results to calibrate the participation model and demonstrates that the former can be explained only if many students have biased predictions of their own admissibility for selective schools. Section VII synthesizes the results and discusses their implications for future policy.
In this section, I describe the ACT mandates that are the source of my identification strategy. I demonstrate that they are almost perfectly binding: test participation rates increase sharply following the introduction of a mandate.
The ACT is a standardized national test for high school achievement and college admissions. It was first administered in 1959 and contains four main sections - English, Math, Reading, and Science - along with (since 2005) an optional Writing section. Students receive scores between 1 and 36 on each section as well as a composite score formed by averaging scores from the four main sections. The ACT competes with an alternative assessment, the SAT, in a fairly stable geographically-differentiated duopoly.13 The ACT has traditionally been more popular in the South and Midwest, and the SAT on the coasts. However, every four-year college and university in the United States that requires such a test will now accept either.14
The ACT is generally taken by students in the 11![]() and 12
and 12![]() grades, and
is offered several times throughout the year. The testing fee is about $50, which includes the option to send score reports to up to four colleges.15 The
scores supplement the student's secondary school record in college admissions, helping to benchmark locally-normed performance measures like GPA. According to a recent ACT Annual Institutional Data Questionnaire, 81% of colleges require or use the ACT or the SAT in admissions.
grades, and
is offered several times throughout the year. The testing fee is about $50, which includes the option to send score reports to up to four colleges.15 The
scores supplement the student's secondary school record in college admissions, helping to benchmark locally-normed performance measures like GPA. According to a recent ACT Annual Institutional Data Questionnaire, 81% of colleges require or use the ACT or the SAT in admissions.
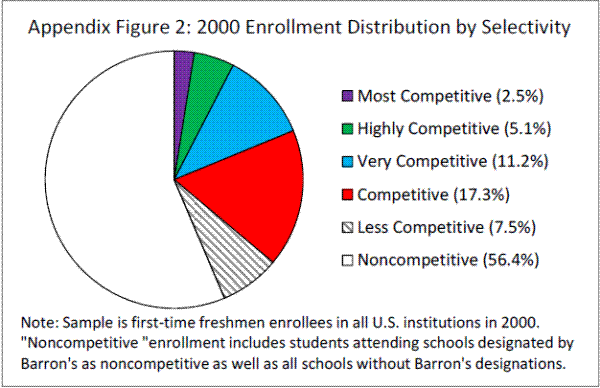
Even so, many students attend noncompetitive schools with open admissions policies. According to recent statistics published by the Carnegie Foundation, nearly 40% of all students who attend postsecondary school are enrolled in two-year associate's-degree-granting programs. Moreover, according to the same data, over 20% of students enrolled full-time at four-year institutions attend schools that either did not report test score data or that report scores indicating they enroll a wide range of students with respect to academic preparation and achievement. Altogether, 55% of students enrolled in either two-year or full-time four year institutions attend noncompetitive schools and likely need not have taken the ACT or the SAT for admission.
Since 2000, five states (Colorado, Illinois, Kentucky, Michigan, and Tennessee) have begun requiring all public high school students to take the ACT.16 There are two primary motivations for these policies. The first relates to the 2001 amendment of the Federal Elementary and Secondary Education Act (ESEA) of 1965, popularly referred to as No Child Left Behind (NCLB). With NCLB, there has been considerable national pressure on states to adopt statewide accountability measures for their public schools. The Act formally requires states to develop assessments in basic skills to be given to all students in particular grades, if those states are to receive federal funding for schools. Specific provisions mandate several rounds of assessment in math, reading, and science proficiency, one of which must occur in grade 10, 11, or 12. Since the ACT is a nationally recognized assessment tool, includes all the requisite material (unlike the SAT), and tests proficiency at the high school level, states can elect to outsource their NCLB accountability testing to the ACT, and thereby avoid a large cost of developing their own metric.17
The second motivation for mandating the ACT relates to the increasingly popular belief that all high school graduates should be "college ready." In an environment where this view dominates, a college entrance exam serves as a natural requirement for high school graduation.
Table 1 displays a full list of the ACT mandates and the testing programs of which they are a part. Of the five, Colorado and Illinois were the earliest adopters: both states have been administering the ACT to all public school students in the 11![]() grade since 2001, and thereby first required the exam for the 2002 graduating cohort.18
Kentucky, Michigan, and Tennessee each adopted mandates more than five years later.
grade since 2001, and thereby first required the exam for the 2002 graduating cohort.18
Kentucky, Michigan, and Tennessee each adopted mandates more than five years later.
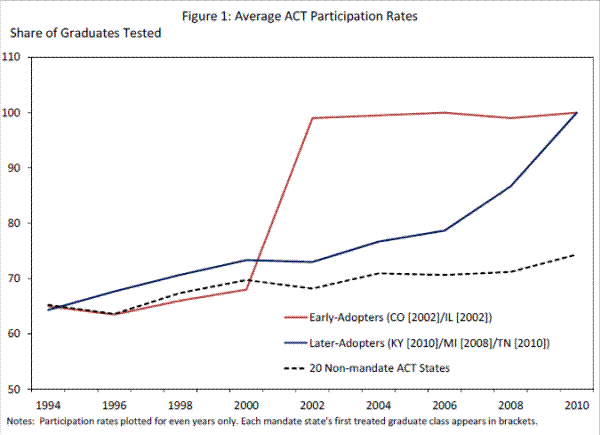
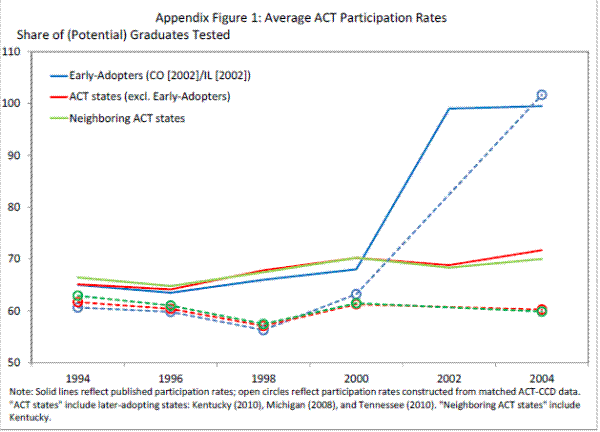
Figure 1 presents graphical evidence that ACT mandates have large impacts on test participation. It shows average ACT participation rates by graduation year for mandate states, divided into two groups by the timing of their adoption, and for the 20 other "ACT states"19 for even numbered years 1994-2010. State-level participation rates reflect the fraction of high school students (public and private) projected to graduate in a given year who take the ACT test within the three academic years prior to graduation, and are published by ACT, Inc.
Prior to the mandate, the three groups of states had similar levels and trends in ACT-taking. The slow upward trend in participation continued through 2010 in the states that never adopted mandates, with average test-taking among graduates rising gradually from 65% to just over 70% over the last 16 years. By contrast, in the early adopting states participation jumped enormously (from 68% to approximately 100%) in 2002, immediately after the mandates were introduced. The later-adopting states had a slow upward trend in participation through 2006, then saw their participation rates jump by over 20 percentage points over the next four years as their mandates were introduced. Altogether, this picture demonstrates that the mandate programs had large effects on ACT participation, that compliance with the mandates is nearly universal, and that in the absence of mandates, participation rates are fairly stable and have been comparable in level and trend between mandate and non-mandate states.
Due to data availability, the majority of the empirical analysis in this paper focuses on the two early adopters. However, I briefly extend the analysis to estimate short-term enrollment effects within the other ACT mandate states, and contextualize them using the longer-term findings from Colorado and Illinois.
In Appendix A, I describe the data on test-takers that I will use to identify mandate-induced test-taking increases and outcomes. In this section, I present key summary statistics demonstrating that the test-takers drawn in by the mandates were disproportionately lower-scoring, minority, and lower-income relative to pre-mandate test-takers. Then, I investigate shifts in the score distribution following the introduction of a mandate. Adjusting for cohort size, many of the new test-takers in mandate states score within a competitive range, suggesting a large portion obtained ACT scores high enough to qualify for admission to competitive colleges.
Table 2 presents average test-taker characteristics in my sample. Note that the sample sizes in each treatment state reflect a substantial jump in test-taking consistent with the timing of the mandates. The number of test-takers more than doubled from the pre-treatment average in Colorado, and increased about 80% in Illinois; in each case the neighboring states saw growth of less than 10%.
Predictably, forcing all students to take the test lowers the average score: both treatment states experienced about 1½-point drops in their mean scores after their respective mandates took effect. Similarly, the mean parental income is lower among the post-treatment test-takers than
among those who voluntarily test.20 Post-treatment, the test-taker population exhibits a more-equal gender and minority balance than the group of students
who opt into testing on their own.21 This is also unsurprising, since more female and white students tend to pursue postsecondary education, especially at
selective schools. Finally, the post-treatment test-takers more often tend to be enrolled in high-minority high schools.22![]() 23
23
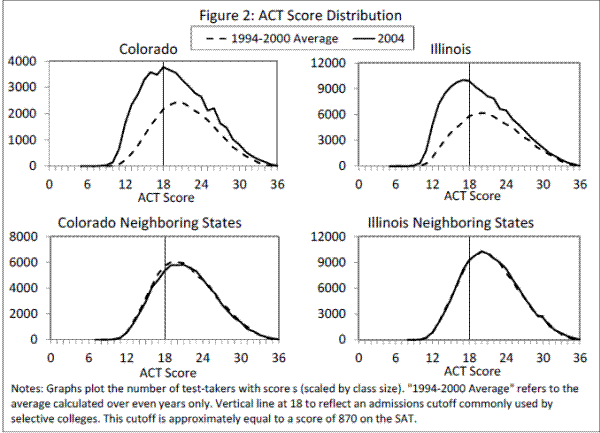
Figure 2 plots the score frequencies for the two treated states and their neighbors for the years before and after treatment.24 The plots include a vertical line at a composite score of 18, reflecting a conventionally used threshold by colleges with the most liberal, but still competitive, admissions processes.25
In both of the treatment states, the change in characteristics presented in the last section appeared to shift the ACT score distribution to the left. Moreover, the distributions, particularly in Colorado, broadened with the influx of new test-takers. In the neighboring states, however, where average test-taker characteristics were mostly unchanged, there were no such shifts. New test-takers tended to earn lower scores, on average, than pre-mandate test-takers, but there is substantial overlap in the distributions. Thus, we see both a decline in mean scores following the mandates and a considerable increase in the number of students scoring above 18. For example, the number of students scoring between 18 and 20 (inclusive) grew by 60% in Colorado and 55% in Illinois, even after adjusting for changes in the size of the graduating class; at scores above 23, the growth rates were 40% and 25%, respectively.
However, since there were (small) changes in score distributions in non-mandate states as well as in mandate states, I employ a difference-in-differences strategy to identify the effect of the mandates on the number of students scoring at each level, net of any trends common to mandate and non-mandate states. Conceptually, students can be separated into two groups: those who will take the ACT whether or not they are required, and those who will take it only if subject to a mandate. Following the program evaluation literature, I refer to these students as "always-takers" and "compliers", respectively (Angrist, Imbens, and Rubin, 1996).26
Because my data pertain to test-takers, compliers are not present in non-mandate state-year cells. In mandate cells, by contrast, they are present but are not directly identifiable. Therefore, characterizing the complier group requires explicit assumptions about the evolution of characteristics
of the "at-risk" population that I cannot observe (i.e. 11![]() grade students planning to graduate high school).
grade students planning to graduate high school).
The first step is to identify the number of compliers. My key assumption is that absent the policy the (voluntary) test-taking rate would have evolved in a mandate state the same way it did in its neighbors. In other words, the likelihood that a randomly selected student elects to take the exam would have increased by the same amount over the sample period, regardless of state lines. The mandates' average effects on test-taking - i.e. the share of students induced to take the exam by the mandates - can be estimated with the equation:
Table 3 summarizes the results. About 45% of 11![]() graders in Colorado, and 39% in Illinois, are "compliers." The bottom panel of the table uses these estimates to decompose the
number of test-takers into compliers and always-takers.
graders in Colorado, and 39% in Illinois, are "compliers." The bottom panel of the table uses these estimates to decompose the
number of test-takers into compliers and always-takers.
It is somewhat more complex to identify the score distribution of compliers and requires an additional assumption about the evolution of score distributions in my sample. My estimator relies on the fact that the fraction of all test-takers scoring at any value, ![]() , in a mandate state can be written as a weighted average of compliers and always-takers scoring at that value, where the weights are the share of students each group represents. I recovered estimates for these weights in the
last exercise; thus, estimating the share of compliers at any given score,
, in a mandate state can be written as a weighted average of compliers and always-takers scoring at that value, where the weights are the share of students each group represents. I recovered estimates for these weights in the
last exercise; thus, estimating the share of compliers at any given score, ![]() , only requires knowing the share of always-takers at
, only requires knowing the share of always-takers at ![]() .
.
The score distribution in non-mandate neighboring states--which by definition, reflects the universe of always-takers in those states--provides a convenient counterfactual for scores among always-takers in mandate states. I assume that, absent the mandate, the likelihood that a randomly selected
always-taker earns a score of ![]() increases (or decreases) by the same amount in mandate states and their neighbors.28 Repeating this exercise for each score cell, I can fully recover the complier score distribution.29
increases (or decreases) by the same amount in mandate states and their neighbors.28 Repeating this exercise for each score cell, I can fully recover the complier score distribution.29
Table 4 summarizes the results for test-takers scoring below 17, between 18 and 20, between 21 and 24, and above 25. The estimates are broadly consistent with Figure 2 and suggest that, while a majority of compliers earned low scores (more than twice as often as their always-taker counterparts from earlier years), many still scored within each of the selective scoring ranges (column 3). As a consequence, a substantial portion of the high scorers in mandate states came from the induced group (column 5). I estimate that around 40-45% of compliers - amounting to about 20% of all post-mandate test-takers - earned scores surpassing conventional thresholds for admission to competitive colleges.
Appendix C shows how I can link the above methodology to test-taker characteristics to estimate complier shares in subgroups of interest (such as, e.g., high-scoring minority students). I demonstrate that in both treatment states, compliers tend to come from poorer families and high-minority high schools, and are more often males and minorities, than those who opt into testing voluntarily. This is true even holding ability levels constant. Altogether, these test-taking and -scoring patterns are consistent with previous literature that finds these same groups are vastly underrepresented at selective colleges, suggesting that early in their educational careers, students from these groups do not consider attending selective colleges at the same rate as other students.
In this section, I model the test-taking decision a student faces in the non-mandate state. I assume that all students are rational and fully informed. Such a student will take the exam if the benefits of doing so exceed the costs.
The primary benefit of taking the exam is potential admission to a selective college, if the resulting score is high enough. The test-taking decision faced by a student in a non-mandate state can be fully characterized by:
The expression captures several important dimensions of the testing decision. A student who prefers to attend the unselective school -- for whom
![]() -- will not take the exam regardless of the values of
-- will not take the exam regardless of the values of ![]() and
and
![]() . A student who prefers the selective school -- for whom
. A student who prefers the selective school -- for whom ![]() -- will
take the exam only if she judges her probability of passing to be sufficiently large,
-- will
take the exam only if she judges her probability of passing to be sufficiently large,
![]() . Finally, note the relevant
. Finally, note the relevant ![]() is not the objective estimate
of a student's chance of earning a high score. The objective estimate, which I denote
is not the objective estimate
of a student's chance of earning a high score. The objective estimate, which I denote ![]() , governs the optimal test-taking decision but might not be a particularly useful guide to the
student's actual decision. Rather, the student forms her own subjective expectation and decides whether to take the exam on that basis. Thus, under
, governs the optimal test-taking decision but might not be a particularly useful guide to the
student's actual decision. Rather, the student forms her own subjective expectation and decides whether to take the exam on that basis. Thus, under ![]() , a high-ability student might choose not
to take the exam because she underestimates her own ability and judges her probability of passing to be small. If students are rational in their self-assessments,
, a high-ability student might choose not
to take the exam because she underestimates her own ability and judges her probability of passing to be small. If students are rational in their self-assessments,
![]() , in which case there should be no evidence that such underestimation is systematically occurring.
, in which case there should be no evidence that such underestimation is systematically occurring.
This framework allows me to enumerate two exhaustive and mutually exclusive subcategories of mandate compliers. There are those who abstain from the exam in the non-mandate state because they simply prefer the unselective college to the selective college, and there are those who abstain from the
exam even though they prefer the selective college, because they judge
![]() .32 I refer to the former
as the "not interested" (NI) compliers and the latter as the "low expectations" (LE) compliers.
.32 I refer to the former
as the "not interested" (NI) compliers and the latter as the "low expectations" (LE) compliers.
The LE group is of particular interest here because if these students have incorrectly low expectations, then a mandate may lead substantial numbers of them to enroll in selective schools. It is thus useful to attempt to bound the ratio
![]() . I sketch out an estimate here, and provide more details in Appendix C.
. I sketch out an estimate here, and provide more details in Appendix C.
I begin with the test-taking cost, ![]() . There are two components to this cost: the direct cost of taking the test - around $50 - and the time cost of sitting for an exam that lasts about 4
hours. A wage rate of $25 would be quite high for a high school student. I thus assume
. There are two components to this cost: the direct cost of taking the test - around $50 - and the time cost of sitting for an exam that lasts about 4
hours. A wage rate of $25 would be quite high for a high school student. I thus assume ![]() is unlikely to be larger than $150.
is unlikely to be larger than $150.
It is more challenging to estimate ![]() . Given the magnitudes of the numbers involved in this calculation - with returns to college attendance in the millions of dollars - it would be
quite unlikely for the choice between a selective and an unselective college to be a knife-edge decision for many students. I rely on findings from the literature on the return to college quality to approximate the difference between the return to attending a selective and a non-selective school.
In the most relevant study for this analysis, Black and Smith (2006) estimate that the average treatment-on-the-treated effect of attending a selective college on subsequent earnings is 4.2%.33 In my case, this implies that
. Given the magnitudes of the numbers involved in this calculation - with returns to college attendance in the millions of dollars - it would be
quite unlikely for the choice between a selective and an unselective college to be a knife-edge decision for many students. I rely on findings from the literature on the return to college quality to approximate the difference between the return to attending a selective and a non-selective school.
In the most relevant study for this analysis, Black and Smith (2006) estimate that the average treatment-on-the-treated effect of attending a selective college on subsequent earnings is 4.2%.33 In my case, this implies that ![]() will average around $80,000.
will average around $80,000.
Combining these estimates, the ratio of
![]() is likely to be on the order of 0.0019 for a large share of students for whom
is likely to be on the order of 0.0019 for a large share of students for whom ![]() . In Appendix D, I present a second, highly conservative calculation that instead estimates
. In Appendix D, I present a second, highly conservative calculation that instead estimates
![]() at around 0.03, so that students opt not to take the test unless
at around 0.03, so that students opt not to take the test unless ![]() . Then the average subjective passage rate among low-expectations compliers must be below 0.03 (
. Then the average subjective passage rate among low-expectations compliers must be below 0.03 (
![]() ), most likely substantially so.
), most likely substantially so.
In Section III, I explored the change in the test score distribution surrounding the implementation of the mandate. The results indicate that about 40-45% of compliers attained high-enough scores to qualify them for admission to selective schools, or that
![]() . In Section V, I will investigate the effect of the mandates on selective college enrollment,
which will identify the share of compliers who both score highly and are interested in attending a selective college. In Section VI, I use these two results to place a lower bound on
. In Section V, I will investigate the effect of the mandates on selective college enrollment,
which will identify the share of compliers who both score highly and are interested in attending a selective college. In Section VI, I use these two results to place a lower bound on
![]() and shed light on whether these compliers' low expectations are indeed rationally-formed.
and shed light on whether these compliers' low expectations are indeed rationally-formed.
In this section, I investigate the mandates' reduced-form effects on college attendance, under the assumption that the shifts in enrollment patterns I identify arise among the group of students induced into testing by the mandates described in Section III. I show that the mandates led to large increases in enrollment at selective colleges, with no discernible effect on overall college attendance. I use this evidence to argue that the students whose postsecondary plans were affected by the mandates were likely already college-bound but attended more-selective schools as a result of the new requirement. To motivate my analysis, I briefly describe the potential effects of compulsory ACT testing on enrollment.
A key byproduct of required testing is the availability of an exam score for students who would not otherwise have taken the ACT.34 The score may contain new information for the mandate compliers, either revealing their true ability or simply their admissibility to selective colleges. Consider two distinct decisions that might be affected by this information: one, the decision to attend college, and two, the decision to attend a selective college (as opposed to an unselective or open admissions college).
Whether to attend college at all is a complex function of individual-specific returns to college attendance and the opportunity cost of college each student faces. Further, it is unclear whether the return to college is an increasing, decreasing, or non-monotonic function of test scores. Note that the ability to attend college does not depend on test scores, as the majority of American college students attend open-enrollment colleges that do not require test scores. Still, it is possible that students use the score as information about whether they can succeed in college (Stange, 2012), in which case the effect on their choice to attend college at all is theoretically ambiguous. Altogether, it appears that the information contained in a student's ACT score would likely have little influence on her decision to enroll in college, and the direction of influence is not obvious.
By contrast, conditional on attending college, it is clear that returns are higher to attending a selective college, and acceptance at a selective college is a direct function of test scores. Therefore, the new availability of a score, on net, could positively influence her decision to attend a selective school.
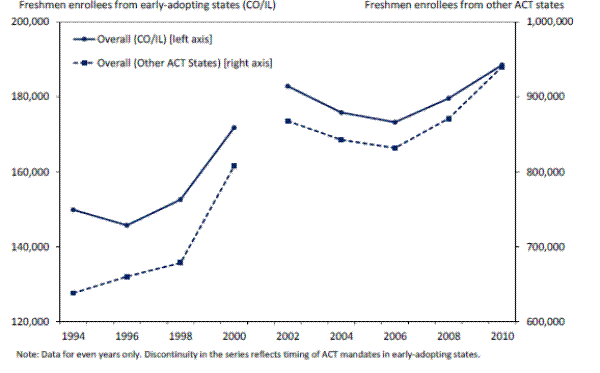
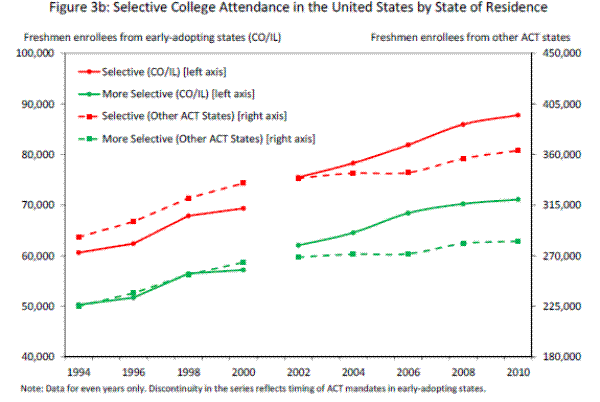
In Appendix A, I describe the data on freshmen enrollment that I will use to identify mandate-induced changes in college attendance. Figures 3a and 3b present suggestive evidence linking the ACT mandates to movements in these data. Figure 3a plots overall enrollment over time by 2002 mandate status for freshmen from all of the ACT states. Students from Illinois and Colorado are plotted on the left axis, and those from the remaining 23 states are on the right. Figure 3b presents the same construction for selective and more selective enrollment. There is a break in each series between 2000 and 2002, corresponding to the introduction of the mandates.
The graphs highlight several important phenomena. First, there are important time trends in all three series: overall enrollment rose by about 30% between 1994 and 2000 (in part, reflecting increased coverage of the IPEDS survey) among freshmen from the non-mandate states and by 15% among freshmen from the mandate states, while selective and more selective enrollment rose by around 15% over this period from each group of states. Second, after 2002, the rate of increase of each series slowed somewhat among freshmen from the non-mandate states. The mandate states experienced a similar slowing in overall enrollment growth for much of that period, but if anything, the growth of selective and more selective enrollment from these states accelerated after 2002. For instance, by 2010, selective enrollment from the mandate states was almost 30% above its 2000 level, but only 9% higher among freshmen from the other states.
Table 5 summarizes levels and changes in average enrollment figures according to mandate status using data from 2000 and 2002. The bolded rows indicate the primary enrollment measures I consider in my baseline regressions, denominated as a share of the at-risk population of 18 year olds. (Note that the mandate states are larger than the average non-mandate state.) The share of 18 year olds attending college increased around 5 percentage points within both groups between 2000 and 2002, whereas attendance at selective and more selective colleges grew around 2 percentage points among students from mandate states but was essentially flat for those from non-mandate states.35
Table 5 also summarizes key characteristics derived from the Current Population Survey that might affect college enrollment: namely, the minority and in-poverty shares, the fraction of adults with a B.A., and the June-May unemployment rate. While mandate states differ somewhat from non-mandate states in these variables, the change over time is similar across the two groups of states. This suggests that differential time trends in these measures are unlikely to confound identification in the difference-in-differences strategy I employ. Nonetheless, I will present some specifications that control for these observables as a robustness check.
To refine the simple difference-in-differences estimate from Table 5, I turn to a regression version of the estimator, using data from 1994 to 2008:
X![]() represents a vector of controls that vary over time within states. For my primary analyses, I consider three specifications
of
represents a vector of controls that vary over time within states. For my primary analyses, I consider three specifications
of
![]() that vary in how I measure students at-risk of enrolling. In the first set of analyses, I do not include an explicit measure of cohort size. In the second, I include the size of
the potential enrolling class (measured as the log of the state population of 16-year-olds in year t-2). And in the third, just of selective and more selective enrollment, I instead use total postsecondary enrollment in the state-of-residence/year cell as a summary statistic for factors influencing
the demand for higher education. Because (as I show below and as Figure 3a makes clear) there is little sign of a relationship between mandates and overall enrollment, this control makes little difference to the results. I estimate each specification with and without the demographic controls from
Table 5.
that vary in how I measure students at-risk of enrolling. In the first set of analyses, I do not include an explicit measure of cohort size. In the second, I include the size of
the potential enrolling class (measured as the log of the state population of 16-year-olds in year t-2). And in the third, just of selective and more selective enrollment, I instead use total postsecondary enrollment in the state-of-residence/year cell as a summary statistic for factors influencing
the demand for higher education. Because (as I show below and as Figure 3a makes clear) there is little sign of a relationship between mandates and overall enrollment, this control makes little difference to the results. I estimate each specification with and without the demographic controls from
Table 5.
Table 6a presents the regression results for the period between 1994 and 2008, where the estimation sample includes all ACT states,38 and the treatment
states are Colorado and Illinois. Each panel reflects a different dependent variable measuring selective enrollment, with the definition of selectivity increasing in stringency from the top to the bottom of the table. Within each panel, I present up to 6 variations of my main equation:
Specification (1) includes no additional controls beyond the state and time effects, specification (2) adds only the demographic controls, specification (3) controls only for the size of the high school cohort, specification (4) adds the demographic controls, and specifications (5) and (6) replace
the size of the high school cohort in (3) and (4) with total college enrollment.39![]()
In order for my strategy to identify the true impact of an ACT mandate on freshmen enrollment, college-going trends among students from mandate states would - absent the new requirement - resemble those observed in non-mandate states. To examine this, I follow Autor (2003) and estimate an event-study version of equation (3) that normalizes the mandate year to 0 and includes lead and lag terms for each year of data between 1994 and 2008 (inclusive). Following Table 6a, I estimate the event-study equation for all three categories of enrollment, with and without the two cohort controls. The omitted year is 2000, corresponding to the year just before the mandate is introduced in early-adopting states.
Table 6b displays the results. The coefficients on all of the lead terms are not significantly different from 0; thus, there is no evidence of anticipatory effects or important heterogeneity in enrollment pre-trends. When either of the selective categories is the outcome of interest, the coefficients on the lag terms are all highly significant. (They are zero when overall enrollment is the outcome.) Moreover, the effect size appears to increase sharply over the first 4 years of the policy and then gradually thereafter. I investigate this further in the next section and elaborate on possible explanations in the discussion.
Results are quite stable across specifications. There is no sign that mandates affect overall enrollment probabilities. However, the mandate does appear to influence enrollment at selective schools: selective and more selective college enrollment each increase by between 10% and 20% when the mandates are introduced. Altogether, the regression results coincide with the descriptive evidence: the mandate is inducing students who would otherwise enroll in nonselective schools to alter their plans and enroll in selective institutions.
This section explores several alternative specifications. To conserve space, I report results for selective enrollment, controlling for overall enrollment (Panel B, Specification (5) in Table 6a).40
Table 7 presents the first set of results. Column (1) reviews the key results from Table 6a. The specification in column (2) extends the sample to include 2010. To do so, I remove Kentucky and Tennessee from the sample, since their ACT mandates potentially affect 2010 enrollment. The treatment coefficient strengthens a bit with the additional year of coverage.
In column (3), I reduce the sample to just the two mandate states and their nine neighbors (as discussed in Section III). Given the demonstrated similarity in test-taking rates and demographic characteristics across state borders, it is plausible that the marginal competitive college-goer within treatment states is better represented by her counterpart in a neighboring state than in the full sample of ACT states. The results are quite similar to those in column (1).
The implicit assumption so far is that, all else equal, the underlying enrollment trends in treatment and control states are the same. In column (4), I add state-specific time trends. The mandate effect vanishes in this specification.41 However, Figures 3a and 3b suggest that the mandate effects appear gradually after the mandates are introduced, a pattern that may be absorbed in a specification with a linear trend and a single step-up mandate effect. So I also explore another specification that allows the treatment effect to phase in:42
Column (7) presents a simple falsification test that extends the treatment period four years earlier to 1998. I estimate:
Columns (8) and (9) present separate estimates of the mandate effect in Illinois and Colorado. The increase in students attending selective schools is essentially the same in each.43
In the last column, I use a similar specification to estimate the effects of more recent ACT mandates in Kentucky, Michigan, and Tennessee. Column (10) presents the results of estimating equation (3) over the full sample period for the late-adopting states, omitting Colorado and Illinois from
the sample.44 An important limitation is that I have only one post-mandate year of data in Kentucky and Tennessee and only two years in Michigan. Thus,
based on column 5 we should expect a smaller treatment effect than was seen for Illinois and Colorado with the same specification. This is indeed what we see.45![]() 46
46
Finally, Tables 8 and 9 present additional analyses for other measures of selectivity. The regression framework mirrors equation (3) but varies the enrollment measure.47 For instance, Table 8 examines the effects of the mandate on enrollment in each of the six Barron's selectivity categories, treated as mutually exclusive rather than as cumulative. The enrollment effect is large and mostly comparable in magnitude across each of the five selective tiers, but negative for non-competitive enrollment.
Table 9 further probes variation across types of institutions. Mandates appear to increase enrollment at all schools primarily offering four-year degrees, as well as enrollment within several subcategories of selective institutions, including land grant schools, both public and private schools, and both in-state and out-of-state schools. The size of the effect (in percentage terms) is larger at private than at public schools, and at out-of-state than at in-state schools; however, taking into account baseline enrollment in each category, attendance levels actually increased more at public and in-state institutions with the mandate.
Rows 8 and 9 try to zero in on "flagship" schools, which are difficult to define precisely. I find large effects for selective in-state land grant schools, but not particularly large effects for an alternative definition that includes all in-state public schools. Applying the estimated increases to baseline enrollment, it appears that state flagships absorb some, but not all, of the estimated in-state increase; a bit more than half of the increase owes to increased enrollment at private schools in Colorado and Illinois. Since the effect for out-of state enrollment (row 7) and in-state selective private enrollment (row 10) are each quite large, any possible public sector responses--which might conceivably have been part of the same policy reforms that led to the mandates (although I have found no evidence, anecdotal or otherwise, of any such reforms)--do not appear to account for the observed boost in enrollment.
In the previous sections, I demonstrated that requiring students to take the ACT leads test-taking rates to rise by about 40-45 percentage points and produces substantial increases in selective college enrollment--between 10% and 20%, on average--with no detectable effect on overall college attendance. When I separately consider the early years of implementation, corresponding to the period covered by the test-taker data, the selective enrollment impact is still around 10%. This implies that the mandates induced about 2,000 students in Colorado and 5,000 students in Illinois to enroll in selective schools in each of the early post-mandate years of these mandates. This corresponds to about 10% of the mandate compliers in 2004, estimated as 23,000 and 53,000, respectively, in Section III. About half of the compliers earned scores above 18, roughly corresponding to the threshold for admission to selective schools. Thus, the enrollment effects indicate that about 20% of selective-college-eligible compliers wound up enrolling in such schools.
In Appendix E, I present a simple calculation to show that the combination of results above - in particular, the high share of mandate compliers who earn high scores and the large effect of the mandates on selective college enrollment - are incompatible with a view in which students make
rational test-taking decisions based on unbiased forecasts of their probabilities of earning high scores. In particular, I show that the true passing probability among compliers who would attend a selective college if admitted (referred to previously as the LE compliers) is roughly 0.16. Because a
passing probability well below that threshold would be sufficient to justify the cost of taking the exam for an LE student, this implies an important divergence between ![]() , the actual rate
at which such students pass the exam, and
, the actual rate
at which such students pass the exam, and ![]() , the students' subjective judgments of their likelihood of passing. In other words, many students must have systematically downwardly biased
forecasts of their performance.
, the students' subjective judgments of their likelihood of passing. In other words, many students must have systematically downwardly biased
forecasts of their performance.
Figure 4 graphs the probability that a student will earn a competitive score against various potential values of the return to selective college attendance. The solid curve represents the locus of points {return to selective college, probability of admission} at which individual students will be indifferent between taking the test or not. For a given anticipated selective college return, students who perceive their probability of earning a high score as above this curve will find it rational to take the ACT even if it is not mandated, while students who perceive their probability of earning a high score as below the line will not. The dashed horizontal line represents my lower-bound estimate for the average passing rate among LE compliers, 16%.48 This crosses the decision threshold at $963, indicating that the observed decisions can be consistent with full information only if students perceive the return to attending a selective college as under $1000.
The vertical lines on Figure 4 depict estimates of the returns to attending a selective college from the literature. These range from $5,000 (Black and Smith [2006] with an adjustment from Cohodes and Goodman [2012]) to $507,000 (Dale and Krueger [2011] for their minority subsample; in the full sample, Dale and Krueger estimate a return of zero).49 All of these are well above the value consistent with the estimated passing rate. They thus imply much lower decision thresholds for students to take the test, ranging from 3% down to 0.03%.
This of course does not count the psychic costs, if any, of attending a more selective school, nor any difference in tuition or other financial costs. It is conceivable that such costs almost exactly offset the wage benefits for some students, but it is extremely unlikely that very many students view the choice as a knife-edge decision, so that removing $150 from the marginal cost of selective college enrollment is decisive in making the benefit exceed the cost. A more plausible explanation for the results is that many compliers held downward-biased estimates of their chances of earning high scores.
My analyses demonstrate that ACT mandates led to large increases in ACT participation, in the number of high-scoring students, and in selective college enrollment. In particular, about 40-45% of students induced to take the ACT exam under a mandate earned competitive scores and many of these new high-scorers--about 20%--ultimately enrolled in competitive schools. The fraction of all mandate compliers who achieved high scores and upwardly revised their enrollment plans--about 10%-- is well beyond the fraction that can be accommodated by an unbiased model of the test-taking decision. Under extremely conservative assumptions, such a fraction would not be higher than 3%.
One concern is that the enrollment effects I find might derive not from the mandates themselves but from the accountability policies of which the mandates were a part. In each of the mandate states but Tennessee, the mandates were accompanied by new standards of progress and achievement imposed on schools and districts. If those reforms had direct effects on student achievement or qualifications for selective college admissions, the reduced-form analyses in Tables 6-9 would attribute those effects to the mandates. There are several reasons, however, to believe that the results indeed derive from the mandates themselves.
The first reason is the absence of an overall enrollment effect of the mandate policies. One would expect that accountability policies that raise students' preparedness would lead some to enroll in college who would not otherwise have. There is no sign of this; effects appear to be concentrated among students who planned to attend college.
Second, National Assessment of Educational Progress (NAEP) state testing results for math and reading in both Colorado and Illinois mirror the national trends over the same period. These results are based on 8![]() grade students, so do not reflect the same cohorts. Nevertheless, I take the stability of NAEP scores as evidence that the school systems in mandate states were not broadly improving student performance.
grade students, so do not reflect the same cohorts. Nevertheless, I take the stability of NAEP scores as evidence that the school systems in mandate states were not broadly improving student performance.
Third, the policies in the later-adopting states and the different ways in which they were implemented provide some insight into the causal role of the testing mandate alone. Beginning in spring 2008, Tennessee mandated that its students take the ACT as part of a battery of required assessments, but did not implement other changes in accountability policy at the same time. A specification mirroring the baseline equation in this section estimates that enrollment of Tennessee students in selective schools rose by 15% in 2010, similar to the estimates for Illinois and Colorado. This strongly suggests that it is the testing mandates themselves--not accountability policies that accompanied them--that account for the enrollment effects.
Finally, one would expect accountability-driven school improvement to take several years to produce increases in selective college enrollment. But my estimates reveal that important effects on selective college enrollment appear immediately after the implementation of the mandates.
Relatedly, it remains an open question why enrollment effects appear to phase in over the first several years of compulsory testing. There are several candidate explanations: 1) selective colleges are accepting more students from mandate states over time; 2) large state schools are gradually expanding to accommodate admissible mandate compliers; 3) more students from mandate states are earning high scores on the exam over time; and 4) students are becoming better informed about their options over time, by, for example, guidance counselors becoming more knowledgeable about placement options, college recruiting efforts increasing, or successes of students in earlier cohorts from similar backgrounds carving pathways for later cohorts. Note that the first two explanations imply that there is disproportionate growth in the seats at selective colleges for students from mandate states, while the latter two imply that there is disproportionate growth in the number of candidates from these states.
Unfortunately, due to data limitations, I cannot investigate the supply-side explanations or evolutions in college admissions patterns. However, Appendix Figure 4 offers some insight into the viability of the first explanation, that large state schools are gradually increasing their slots for in-state candidates. The figure plots selective enrollment growth among students from mandate states by control and location of the college, estimated from a specification that mimics Table 7, Column (5). For example, the leftmost bars plot the estimated increases at public in-state colleges owing to the mandates, where the first column represents growth in matriculants within the first few years of compulsory testing, and the second after compulsory testing has been in effect for at least four years. There is a notable increased presence of students from mandate states at private schools in their home states and in public schools in other states, suggesting that not all of the phase-in owes to an expansion of slots for students at large in-state public schools. Further research in this area is needed.
Another concern might be the generalizability of the policy effects: what could we expect if we were to institute nationwide compulsory testing? For the most part, the estimates I present are based on two widely separated states that implemented mandates. While the total increase in selective enrollment represented about 15% of prior selective enrollment among students from those states, the new enrollees amounted to only 1% of total national selective enrollment and 5% of selective enrollment from the mandate states and their neighbors.
Still, one hurdle to relying on the experiences in Illinois and Colorado to encourage similar policies nationwide is that national policies may create significant congestion in the selective college market, leading either to crowd-out of always-takers by compliers or to reduced enrollment of
compliers (Bound and Turner, 2007; Card and Lemieux, 2000).50![]() 51 This kind of crowd-out would be particularly likely if the selective college sector was unable to expand quickly enough to
accommodate new mandate-induced demand. Over the sample period national selective enrollment grew by about 2% each year. This implies that the increase in enrollment produced by a national mandate, which I estimate at around 15%, would be absorbed with under eight years of normal growth. Thus,
while crowd-out remains a possibility from a national mandate, it seems likely that the supply of selective college seats is elastic enough to avoid large or long-lasting crowd-out effects.
51 This kind of crowd-out would be particularly likely if the selective college sector was unable to expand quickly enough to
accommodate new mandate-induced demand. Over the sample period national selective enrollment grew by about 2% each year. This implies that the increase in enrollment produced by a national mandate, which I estimate at around 15%, would be absorbed with under eight years of normal growth. Thus,
while crowd-out remains a possibility from a national mandate, it seems likely that the supply of selective college seats is elastic enough to avoid large or long-lasting crowd-out effects.
In sum, the evidence overwhelmingly suggests that students are systematically under-predicting their suitability for selective schools. I demonstrate that students on average take admissions tests far less often than they should: mandate compliers earn competitive scores at remarkably high rates and attend more-selective schools with significant probability when they do earn competitive scores. Thus, many students are learning important information from these tests, and these better-informed students, all else equal, are enrolling in better schools. This pattern is not consistent with a model of rational ignorance - students who can collect valuable information at low cost by taking the ACT frequently opt not to do so.
Framed differently, a substantial share of high-ability students prematurely and incorrectly rule out selective colleges from their choice sets. Although my data do not permit me to estimate the characteristics of these students, it seems likely that many of them come from low-income families. Students from low-SES families are much less likely to take the test in the absence of a mandate than are their more advantaged peers, and when the mandate is implemented the low-SES compliers are no less likely to earn high scores than are compliers from high-SES families.
Recent studies have demonstrated that college quality is an important determinant of later success.52 Black and Smith (2006) and Cohodes and Goodman (2012), for example, find that students at lower-quality schools earn less over their lifetimes and are less likely to graduate than their counterparts at higher-quality schools. Since my results demonstrate that mandatory ACT testing leads many students to enroll in more-competitive, higher-quality colleges, requiring students to take the ACT likely enables many students to vastly improve their lifetime earnings trajectories. For instance, using the continuous quality measure I describe in Appendix D, I can link my results to Black and Smith's findings that an additional standard deviation in college quality produces a 4.2% increase in lifetime earnings. The increase in selective enrollment that I estimate translates into a 0.247 standard deviation increase in average college quality. Thus, the roughly 4.5% of students who are induced to change their enrollment status by the mandate should, on average, expect a boost of 23% in their lifetime earnings.53
In a separate but related line of research, Pallais and Turner (2006) establish that underprivileged groups are underrepresented at top schools. They attribute their finding to a combination of information constraints, credit constraints, and pre-collegiate underachievement, but are unable to distinguish among them. My analysis provides additional support for their first explanation - that lack of information can explain at least some of the missing low-income students.
I conclude that increasing information flow between universities and students from these underrepresented groups--so that the potential high scorers know they are indeed suitable candidates--will likely erase some of the enrollment gap found at top schools. This is a potentially fruitful area for further policy development - expanding mandates appears to be a desirable policy on its own, but there may be additional policies that would complement mandates in targeting students' information shortages.
References
Angrist J., G. Imbens, and D. Rubin (1996). Identification of Causal Effects Using Instrumental Variables. Journal of the American Statistical Association 91(434), 444-455.
Autor, D. (2003). Outsourcing at Will: The Contribution of Unjust Dismissal Doctrine to the Growth of Employment Outsourcing. Journal of Labor Economics 21(1).
Avery, C. and T. Kane. (2004). Student Perceptions of College Opportunities: The Boston COACH Program. In C. Hoxby, ed. College Choices: The Economics of Where to Go, When to Go, and How to Pay for It. University of Chicago Press.
Bailey M. and S. Dynarski (2011, December). Gains and Gaps: Changing Inequality in U.S. College Entry and Completion. Working Paper 17633, NBER.
Barron's College Division (2000). Barron's Profiles of American Colleges: 24th Edition, 2001. Barron's Educational Series, Inc.
Bettinger, E., B. Long, P. Oreopoulos, and L. Sanbonmatsu (forthcoming). The Role of Simplification and Information in College Decisions: Results from the H&R Block FAFSA Experiment. Journal of Labor Economics.
Black, D. and J. Smith (2006). Estimating the Returns to College Quality with Multiple Proxies for Quality. Journal of Labor Economics 24(3), 701-728.
Bound, J. and S. Turner (2007). Cohort Crowding: How Resources Affect Collegiate Attainment. Journal of Public Economics 91(5-6), 877-899.
Bowen, W., M. Kurzweil, and E. Tobin (2005). Equity and Excellence in American Higher Education. Reviewed by R. Rothstein. University of Virginia Press.
Card, D. and A. Krueger (1992). Does School Quality Matter? Returns to Education and the Characteristics of Public Schools in the United States. Journal of Political Economy 100(1), 1-40.
Card, D. and T. Lemieux (2000). Dropout and Enrollment Trends in the Post-War Period: What Went Wrong in the 1970s? In J. Gruber, ed. An Economic Analysis of Risky Behavior Among Youth. University of Chicago Press, 439-482.
Clark, M., Rothstein, J., and D. Schanzenbach (2009). Selection Bias in College Admissions Test Scores. Economics of Education Review 28(3), 295-307.
Clotfelter C. and J. Vigdor (2003). Retaking the SAT. Journal of Human Resources 38(1).
Cohodes S. and J. Goodman (2012, August). First Degree Earns: The Impact of College Quality on College Completion Rates. Working Paper RWP12-033. Harvard Kennedy School Faculty Research Working Paper Series.
The College Board (2007). Education Pays. Trends in Higher Education Series.
The College Board (2009, October). ACT and SAT§Concordance Tables. RN-40.
Conley T. and C. Taber (2011). Inference with "Difference in Differences" with a Small Number of Policy Changes. The Review of Economics and Statistics 93(1), 113-125.
Dale, S. and A. Krueger (2002). Estimating the Payoff to Attending a More Selective College: An Application of Selection on Observables and Unobservables. Quarterly Journal of Economics 117(4), 1491-1527.
Dale, S. and A. Krueger (2011, June). Estimating the Return to College Selectivity over the Career Using Administrative Earnings Data. Working Paper 17159, NBER.
Deming, D. and S. Dynarski (2010). Into College, Out of Poverty? Policies to Increase the Postsecondary Attainment of the Poor. In Phil Levine and David Zimmerman, eds. Targeting Investments in Children: Fighting Poverty When Resources are Limited. University of Chicago Press, 283-302.
Dinkelman, T. and C. Martínez (2011, May). Investing in Schooling in Chile: The Role of Information about Financial Aid for Higher Education. Discussion Paper No. DP8375. Centre for Economic Policy Research.
Dynarski, S. (2003). Does Aid Matter? Measuring the Effect of Student Aid on College Attendance and Completion. American Economic Review 93(1), 279-288.
Hansen, C. (2007). Asymptotic Properties of a Robust Variance Matrix Estimator for Panel Data When T is Large. Journal of Econometrics 141, 597-620.
Hill, C. and G. Winston (2005). Access to the Most Selective Private Colleges by High Ability, Low-Income Students: Are They Out There? Discussion Paper No. 69. Williams Project on the Economics of Higher Education.
Hoekstra, M. (2009). The Effect of Attending the Flagship State University on Earnings: A Discontinuity-Based Approach. The Review of Economics and Statistics 91(4), 717-724.
Hoxby, C. (2009). The Changing Selectivity of American Colleges. Journal of Economic Perspectives 23(4), 95-118.
Hoxby, C. and C. Avery (2012, December). The Missing "One-Offs": The Hidden Supply of High-Achieving, Low Income Students. Working Paper 18586, NBER.
Hoxby, C. and S. Turner (2013). Expanding College Opportunities for High-Achieving, Low Income Students. Discussion Paper 12-014. Stanford Institute for Economic Policy Research.
Jacob, B. and T. Wilder (2010, January). Educational Expectations and Attainment. Working Paper 15683, NBER.
Jensen, Robert (2010). The (Perceived) Returns to Education and the Demand for Schooling. The Quarterly Journal of Economics 125 (2): 515-548.
Kane, T. (1995, July). Rising Public College Tuition and College Entry: How Well Do Public Subsidies Promote Access to College? Working Paper 5164, NBER.
Kane, T. (1998). Misconceptions in the Debate over Affirmative Action in College Admissions. In G. Orfield and E. Miller, eds. Chilling Admissions: The Affirmative Action Crisis and the Search for Alternatives. Harvard Education Publishing Group, 17-31.
Manski, C. (2004). Measuring Expectations. Econometrica 72, 1329-1376.
McPherson, M (2006). "Low-Income Access through Different Lenses." Address to WISCAPE. University of Wisconsin, Madison. February 1, 2006.
Orfield, G. and F. Paul. (1994). High Hopes, Long Odds: A Major Report on Hoosier Teens and the American Dream. Indiana Youth Institute.
Oreopoulos, P. and R. Dunn. (2012, November). Information and College Access: Evidence from a Randomized Field Experiment. Working Paper 18551, NBER.
Pallais A. and S. Turner (2006). Opportunities for Low Income Students at Top Colleges and Universities: Policy Initiatives and the Distribution of Students. National Tax Journal 59(2), 357-386.
Pallais, A. (2009, February). Small Differences That Matter: Mistakes in Applying to College. MIT Working Paper.
Pew Research Center Social and Demographic Trends (2011, May 16). Is College Worth It? Retrieved from http://www.pewsocialtrends.org/category/reports/2011/page/2/
Saavedra, Juan (2008). The Returns to College Quality: A Regression Discontinuity Approach. Unpublished Manuscript. Harvard University.
Schneider, B. and D. Stevenson (1999). The Ambitious Generation: American Teenagers Motivated but Directionless. Yale University Press.
Stange, K. (2012). An Empirical Investigation of the Option Value of College Enrollment. American Economic Journal: Applied Economics 4(1), 49-84.
Stinebrickner T. and R. Stinebrickner (2012). Learning about Academic Ability and the College Dropout Decision. Journal of Labor Economics 30(4), 707-748.
Zafar, B. (2011). How Do College Students Form Expectations? Journal of Labor Economics 29(2), 301-348.
Notes: Participation rates plotted for even years only. Each mandate state's first treated graduate class appears in brackets.Figure 4: Implied Test-taking Thresholds for Various Estimates of the Return to College Quality
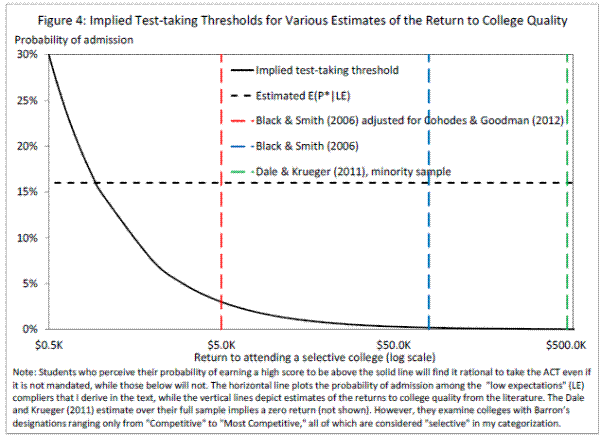 Figure 4 Data
Figure 4 Data
| State | Program Name or Details | First Affected Graduating Class/Enrollment Year |
| Colorado | Colorado ACT | 2002 | Illinois | Prairie State Achievement Exam | 2002 |
| Kentucky | Kentucky Work and College Readiness Examination | 2010 |
| Michigan | Michigan Merit Exam | 2008 |
| Tennessee | Tennessee Code Annotated 49-6-6001(b), amended by Senate Bill No. 2175 | 2010 |
| Period | State or State Group | Number of States | Number of Test-takers | Average ACT Score | Average Income Quintile | Share of Test-takers Attended High-Minority (Minority) | Share of Test-takers Attended High-Minority (HS) | Share of Test-takers Attended High-Minority (Female) |
| 1994 2004 Average | Colorado | 1 | 23,421 | 21.5 | 3.0 | 25% | 30% | 55% |
| 2004 | Colorado | 1 | 51,300 | 20.1 | 2.7 | 34% | 42% | 50% |
| 1994 2000 Average | CO neighbors | 5 | 69,887 | 21.3 | 2.8 | 18% | 21% | 54% |
| 2004 | CO neighbors | 5 | 71,604 | 21.3 | 2.8 | 21% | 26% | 54% |
| 1994-2000 Average | Illinois | 1 | 73,799 | 21.3 | 2.9 | 29% | 36% | 55% |
| 2004 | Illinois | 1 | 135,468 | 19.8 | 2.6 | 36% | 46% | 51% |
| 1994 2000 Average | IL neighbors | 4 | 114,207 | 21.4 | 2.8 | 12% | 12% | 56% |
| 2004 | IL neighbors | 4 | 123,684 | 21.5 | 2.8 | 14% | 15% | 56% |
Note: "1994-2000 Average" refers to the average calculated over even years only. Count of test-takers in neighboring states reflect the average across states in each group.
| Participation Rate (0 to 1) Colorado | Participation Rate (0 to 1) Illinois | |
| treatments*postt | 0.455*** | 0.393*** |
| treatments*postt: Robust Standard Errors | (0.03) | (0.02) |
| postt | 0.019 | 0.005 |
| postt:robust standard errors | (0.02) | (0.01) |
| adj R2 | 0.649 | 0.908 |
| N | 30 | 25 |
| Implied Number of Test takers in Each Group: Compliers | 22,803 | 52,718 |
| Implied Number of Test takers in Each Group: Always Takers | 28,497 | 82,750 |
| Total ACT Test takers | 51,300 | 135,468 |
Notes: Each column in the top panel reports coefficients from an OLS regression, with robust standard errors in parentheses. The participation rate is the share of potential public high school graduates who take the ACT exam in each state time cell. The estimation sample in each column is one of two early adopting states--treated beginning in 2002--and its neighboring states in 1994, 1996, 1998, 2000, and 2004, where the set of neighboring states and the years prior to 2004 serve as control state and period composites. See text for explanation of bottom panel.
| Score Range | (1) Pre (1994-2000 Average): n | (1) Pre (1994-2000 Average): % | (2) Post (2004): n | (2) Post (2004): % | (3) Shares of Compliers (2004): % | (4) Compliers (2004) : n | (5) Complier Share of Test-takers (4)/(2) (2004) % |
| 0-17 (Colorado) | 4,880 | 21% | 17,884 | 35% | 53% | 12,016 | 67% |
| 18-20(Colorado) | 5,507 | 24% | 10,992 | 21% | 19% | 4,417 | 40% |
| 21-24 (Colorado) | 6,973 | 30% | 11,750 | 23% | 13% | 3,021 | 26% |
| 25+ (Colorado) | 6,060 | 26% | 10,674 | 21% | 15% | 3,349 | 31% |
All (Colorado)
| 23,421 |
| 100% | 51,300 | 100% | 100% | 22,803 | 44% |
| 0-17 (Illinois) | 17,984 | 24% | 51,656 | 38% | 60% | 31,394 | 61% |
| 18-20 (Illinois) | 16,256 | 22% | 27,826 | 21% | 19% | 9,797 | 35% |
| 21- 24 (Illinois) | 19,817 | 27% | 29,130 | 22% | 13% | 6,975 | 24% |
| 25+ (Illinois) | 19,741 | 27% | 26,856 | 20% | 9% | 4,554 | 17% |
| All (Illinois) | 73,799 | 100% | 135,468 | 100% | 100% | 52,718 | 39% |
Note: Compliers are students who take the ACT only if subject to a mandate. "1994-2000 Average" refers to the average calculated over even years only.
| Mandate Status in 2002: Mandate CO and IL Average (2000) | Mandate Status in 2002: Mandate CO and IL Difference (2002-2000) | Mandate Status in 2002: No Mandate: Other ACT States Average (2000) | Mandate Status in 2002:No Mandate: Other ACT States Difference (2002-2000) | Mandate Status in 2002: Difference in Difference | |
| Enrollment (as Share of Population) Most Selective | 1.1% | 0.1 p.p. | 0.6% | 0.0 p.p. | 0.1 p.p. |
| Enrollment (as Share of Population) Highly Selective | 4.3% | 0.3 p.p. | 1.8% | 0.0 p.p. | 0.3 p.p. |
| Enrollment (as Share of Population) Very Selective | 12.8% | 1.2 p.p. | 8.0% | 0.1 p.p. | 1.1 p.p. | Enrollment (as Share of Population) More Selective | 23.9% | 1.8 p.p. | 20.8% | 0.3 p.p. | 1.6 p.p. |
| Enrollment (as Share of Population) Selective | 30.4% | 2.3 p.p. | 26.9% | 0.4 p.p. | 1.9 p.p. |
| Enrollment (as Share of Population) Overall | 74.9% | 5.7 p.p. | 65.8% | 4.5 p.p. | 1.1 p.p. |
| Key Demographics 18-year-old Population | 118,114 | 278 | 53,196 | 129 | 407 |
| Minority Share (Fr. of All Residents) | 27.4% | 2.3 p.p. | 18.9% | 1.3 p.p. | 1.0 p.p. |
| Poverty Share (Fr. of All Residents) | 9.4% | 0.2 p.p. | 12.6% | 0.1 p.p. | 0.3 p.p. |
| Unemployment Rate (Fr. of Residents in the Labor Market, Ages 16+) | 3.7% | 1.8 p.p. | 4.0% | 0.8 p.p. | 0.9 p.p. |
| Share with a B.A. (Fr. of Residents, Ages 25+) | 30.8% | 0.7 p.p. | 23.0% | 0.3 p.p. | 0.3 p.p. |
| States in Group ACT Participation Rate (Published) | 2 | 2 | 23 | 23 |
Note: Enrollment categories are cumulative.
| (1) | (2) | (3) | (4) | (5) | (6) | |
| A. Overall mandate st | 0.054 | 0.032 | 0.003 | -0.006 | ||
| A. Overall s.e. | ||||||
| A. Overall adjusted R2 | 0.988 | 0.988 | 0.990 | 0.990 | ||
| B. Selective mandatest | 0.159*** | 0.138** | 0.111*** | 0.102*** | 0.142*** | 0.128*** |
| B. Selective s.e. | (0.057) | (0.053) | (0.034) | (0.033) | (0.018) | (0.021) |
| B. Selective adjusted R2 | 0.995 | 0.995 | 0.996 | 0.996 | 0.996 | 0.996 |
| C. More Selective mandate st | 0.163** | 0.140* | 0.110** | 0.100** | 0.145*** | 0.130*** |
| C. More Selective s.e. | (0.000) | (0.012) | (0.045) | (0.046) | (0.025) | (0.029) |
| C. More Selective adjusted R 2 | 0.995 | 0.995 | 0.996 | 0.996 | 0.996 | 0.996 |
| controls ln(population) | X | X | ||||
| ln(overall enrollment) | X | X | ||||
| demographic controls | X | X | X |
Notes: Each column in each panel represents a separate OLS regression. The dependent variable in each regression is the log of first-time freshmen enrollment of students from state s in year t at a subset of schools, with the definition of selectivity increasing in stringency from the top to the bottom of the table. All regressions include state and year effects. Demographic controls include poverty and minority share, the June-May unemployment rate, and the share of residents over 25 with a B.A.. The estimation sample is all ACT states (excl. Michigan) in even years between 1994-2008 (inclusive). Two states are treated beginning in 2002. Standard errors, clustered on the state, are in parentheses. *, **, and *** reflect significance at the 10%, 5%, and 1% levels.
| (1) Enrollment Measure | (2)Overall | (3)Overall | (4)Selective | (5)Selective | (6)More Selective | (7)More Selective | (8)More Selective | |
| Treatment state x 8 years prior | 0.018 | 0.002 | 0.016 | 0.002 | 0.011 | 0.003 | 0.009 | 0.006 |
| s.e. | (0.177) | (0.151) | (0.053) | (0.034) | (0.025) | (0.026) | (0.072) | (0.048) |
| Treatment state x 6 years prior | -0.073 | -0.063 | -0.022 | -0.013 | 0.001 | 0.02 | -0.005 | 0.005 |
| s.e. | (0.156) | (0.145) | (0.049) | (0.040) | (0.020) | (0.025) | (0.059) | (0.049) |
| Treatment state x 4 years prior | -0.033 | -0.028 | -0.005 | 0.000 | 0.006 | 0.026 | 0.015 | 0.02 |
| s.e. | (0.112) | (0.107) | (0.036) | (0.031) | (0.013) | (0.021) | (0.031) | (0.027) |
| Treatment state x 2 years prior | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| s.e. | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Treatment state x mandate | 0.015 | 0.006 | 0.067*** | 0.060*** | 0.063*** | 0.065*** | 0.070*** | 0.062*** |
| s.e. | (0.035) | (0.030) | (0.012) | (0.019) | (0.019) | (0.015) | (0.014) | (0.017) |
| Treatment state x 2 years after | 0.016 | 0.022 | 0.129*** | 0.096*** | 0.124*** | 0.126*** | 0.132*** | 0.095*** |
| s.e. | (0.039) | (0.025) | (0.035) | (0.022) | (0.024) | (0.026) | (0.037) | (0.023) |
| Treatment state x 4 years after | 0.039 | 0.023 | 0.187*** | 0.132*** | 0.174*** | 0.212*** | 0.226*** | 0.166*** |
| s.e. | (0.054) | (0.040) | (0.038) | (0.027) | (0.025) | (0.043) | (0.058) | (0.041) |
| Treatment state x 6 years after | 0.024 | 0.046 | 0.212*** | 0.150*** | 0.204*** | 0.218*** | 0.227*** | 0.158*** |
| s.e. | (0.034) | (0.032) | (0.046) | (0.034) | (0.039) | (0.053) | (0.061) | (0.043) |
| adjusted R2 | 0.988 | 0.990 | 0.995 | 0.996 | 0.996 | 0.996 | 0.995 | 0.996 |
| controls ln(population) | X | X | X | |||||
| controls ln(overall enrollment) | X | X |
Notes: Each column represents a separate OLS regression. The dependent variable in each regression is the log of first-time freshmen enrollment of students from state s in year t at a subset of schools. All regressions include state and year effects. The estimation sample is all ACT states (excl. Michigan) in even years between 1994-2008 (inclusive). Two states are treated beginning in 2002. Standard errors, clustered on the state, are in parentheses. *, **, and *** reflect significance at the 10%, 5%, and 1% levels.
| Specification | (1) Table 6a, Panel B Spec. (5) | (2) Extended Sample Period: 1994-2010 | (3) Alt. Control Sample: Neighboring States | (4) State Time Trends | (5) Phased-in Treatment | (6) State Time Trends w/ Phased-in Treatment | (7) Placebo Policy Four Years Earlier | (8) Colorado only | (9) Illinois only | (10) Late-adopting States |
| mandatest | 0.142*** | 0.163*** | 0.134*** | 0.043 | 0.139*** | 0.156*** | 0.129*** | |||
| s.e. | (0.018) | (0.019) | (0.020) | (0.044) | (0.018) | (0.025) | (0.016) | |||
treatments*(<4 years of policy)t
| |
| 0.095*** | 0.065** | 0.070** | ||||||
| s.e. | (0.014) | (0.029) | (0.030) | |||||||
| treatments*(.4 years of policy)t | 0.190*** | 0.140*** | ||||||||
| s.e. | (0.029) | (0.034) | ||||||||
treatments*(post1998)t
| |
| 0.007 | ||||||||
| s.e. | (0.018) | |||||||||
| Joint Significance Test F-statistic | 30.962*** | 9.426*** | ||||||||
| Joint Significance Test p-value | 0.000 | 0.000 | ||||||||
| adjusted R2 | 0.996 | 0.995 | 0.997 | 0.997 | 0.996 | 0.997 | 0.996 | 0.995 | 0.996 | 0.995 |
| control states | 22 | 20 | 9 | 22 | 22 | 22 | 22 | 21 | 21 | 20 |
| N | 192 | 198 | 88 | 192 | 192 | 192 | 192 | 184 | 184 | 207 |
Notes: Each column represents a separate OLS regression. Sample and specification for columns (1)-(9) are as in Table 6a, Panel B, Specification (5), except as noted. Sample for (2) excludes Kentucky and Tennessee; sample for (10) excludes Colorado and Illinois and includes Michigan. In (10), one state is treated beginning in 2008 and two states are treated in 2010. Standard errors, clustered on the state (except in columns (4) and (6), which use more conservative robust standard errors), are in parentheses . *, **, and *** reflect significance at the 10%, 5%, and 1% levels, respectively.
| Enrollment Category | Specification | Share of Enrollment (2000) | mandate st |
| Most Competitive | (1) | 1.5% | 0.139*** |
| Most Competitive : standard errors | (0.024) | ||
| Highly Competitive | (2) | 4.4% | 0.205*** |
| Highly Competitive: standard errors | (0.029) | ||
| Very Competitive | (3) | 11.3% | 0.236*** |
| Very Competitive : standard errors | (0.057) | ||
| Competitive | (4) | 14.8% | 0.097*** |
Competitive: standard errors
| |
| (0.021) | |
| Less Competitive | (5) | 8.5% | 0.159** |
Less Competitive: standard errors
| |
| (0.064) | |
| Noncompetitive | (6) | 59.4% | 0.122*** |
| Noncompetitive : standard errors | (0.032) |
| Enrollment Category | Specification | Share of Enrollment (2000) | mandate st |
| Four year | (1) | 47.6% | 0.137*** |
| Four year (standard errors) | (0.020) | ||
| Subcategories of Selective Enrollment Selective Land Grant | (2) | 6.6% | 0.169** |
| Subcategories of Selective Enrollment Selective Land Grant (standard errors) | (0.077) | ||
| Subcategories of Selective Enrollment Selective Public | (3) | 27.8% | 0.104*** |
| Subcategories of Selective Enrollment Selective Public (standard errors) | (0.032) | ||
| Subcategories of Selective Enrollment Selective Private | (4) | 12.7% | 0.230*** |
| Subcategories of Selective Enrollment Selective Private (standard errors) | (0.040) | ||
| Subcategories of Selective Enrollment Selective Private Not for Profit | (5) | 11.8% | 0.227*** |
Subcategories of Selective Enrollment Selective Private Not for Profit (standard errors)
| |
| (0.041) | |
| Subcategories of Selective Enrollment Selective In State | (6) | 29.6% | 0.116*** |
| Subcategories of Selective Enrollment Selective In State (standard errors) | (0.031) | ||
| Subcategories of Selective Enrollment Selective Out of State | (7) | 10.9% | 0.212*** |
| Subcategories of Selective Enrollment Selective Out of State (standard errors) | (0.043) | ||
| More-refined Subcategories Selective-Land Grant-In-State | (8) | 4.9% | 0.167 |
More-refined Subcategories Selective-Land Grant-In-State (standard errors)
| |
| (0.093) | |
| More-refined Subcategories Selective-Public- In-State | (9) | 23.1% | 0.084** |
More-refined Subcategories Selective-Public- In-State (standard errors)
| |
| (0.036) | |
| More-refined Subcategories Selective-Private In State | (10) | 6.5% | 0.311*** |
| More-refined Subcategories Selective-Private In State (standard errors) | (0.095) | ||
| More-refined Subcategories Selective-Land Grant-Out of State | (11) | 1.6% | 0.240*** |
More-refined Subcategories Selective-Land Grant-Out of State (standard errors)
| |
| (0.059) | |
| More-refined Subcategories Selective-Land Public Out of State | (12) | 4.8% | 0.228*** |
| More-refined Subcategories Selective-Land Public Out of State (standard errors) | (0.049) | ||
| More-refined Subcategories Selective-Land Private Out of State | (13) | 6.2% | 0.210*** |
| More-refined Subcategories Selective-Land Private Out of State (standard errors) | (0.067) |
Notes: Each row represents a separate OLS regression. Sample and specification for (1)-(7) and (11)-(13) as in Table 6, Panel B, Specification (5); Specifications (8) and (9) exclude Kansas and specification (10) excludes Wyoming, as there are none of the relevant institutions in these states. Standard errors, clustered on the state, are in parentheses. *, **, and *** reflect significance at the 10%, 5%, and 1% levels. Figures in the third column denote the average share of freshmen enrollment in each category in the treatment states in 2000 (before mandates were introduced).
For Online Publication
Appendix A: Data
- Test-taker Data
- Enrollment Data
My primary test-taker data come from microdata samples of ACT test-takers who graduated in 1994, 1996, 1998, 2000, and 2004, matched to the public high schools that they attended.54 The dataset includes a 50% sample of non-white students and a 25% sample of white students who took the ACT exam each year.
Each student-observation in the ACT dataset includes an ACT "composite" score, which is an integer value ranging between 1 and 36 reflecting the average of the four main tested subjects. The composite score is the metric most relied upon in the college admissions process. Observations also include an array of student survey responses completed before the exam that provide an overview of the test-taker's enrollment status, socioeconomic status, other demographics, and high school.55
The ACT microdata also contain high school identifiers that can be linked to records from the Common Core of Data (CCD), an annual census of public schools. The CCD is useful in quantifying the size and minority share of each school's student body. I use one-year-earlier CCD data describing the
11![]() grade class as the population at risk of test-taking.56
grade class as the population at risk of test-taking.56
The student-level analyses in the text rely on neighboring ACT states to generate a composite counterfactual for the experiences of test-takers from the two early-adopting states.57 In comparison to one formed from all of the ACT states, a counterfactual test-taker constructed from surrounding states is likely to be more demographically and environmentally similar to the marginal test-taker in a mandate state. This is important because these characteristics cannot be fully accounted for in the data but could be linked to particular experiences, such as the likelihood she attends public school (and thus is exposed to the mandate) or her ambitiousness.58
To study enrollment effects, I use information on college matriculation available in the Integrated Postsecondary Education Data System (IPEDS).59 IPEDS
surveys are completed annually by each of the more than 7,500 colleges, universities, and technical and vocational institutions that participate in the federal student financial aid programs. I use data on first-time, first-year enrollment of degree- or certificate-seeking students enrolled in
degree or vocational programs, disaggregated by state of residence, which are reported by each institution in even years.60![]() , 61
, 61
I merge the IPEDS data to classifications of schools into nine selectivity categories from the Barron's "College Admissions Selector."62 A detailed
description of the Barron's selectivity categories can be found in Appendix Table 1. Designations range from noncompetitive, where nearly 100% of an institution's applicants are granted admission and ACT scores are often not required, to most competitive, where less than one third of applicants are
accepted. Matriculates at "competitive" institutions tend to have ACT scores around 24, while those at "less competitive" schools (the category just above "noncompetitive") generally have scores below 21. I create six summary enrollment measures, corresponding to increasing degrees of
selectivity, in order from most to least inclusive: overall (any institution, including those not ranked by Barron's), selective ("less competitive" institutions and above), more selective ("competitive" institutions and above), very selective ("very competitive" institutions and above),
highly selective ("highly competitive" institutions and above), and most selective ("most competitive" institutions, only).63![]() 64
64
I also explore analyses that cross-classify institutions by selectivity and other institutional characteristics, such as program length (4-year vs. other), location (in-state vs. out-of-state), control (public vs. private), and status as a land grant institution,65 constructed from the IPEDS.
Appendix B: Comparing Test-taker Composition to the At-Risk Population
Appendix Tables 2 and 3 compare the gender and racial composition of test-takers, both before and after mandates, to those of the high school student population. I draw data for the latter from the CCD, focusing on 11![]() grade students in public schools that enroll at least one test-taker in the corresponding year - either 2000 or 2004.66
grade students in public schools that enroll at least one test-taker in the corresponding year - either 2000 or 2004.66
Not surprisingly, the composition of high school students changes little over time within states. The composition of test-takers is stable as well in non-mandate states and in mandate states before the mandates are introduced. However, in 2004 the female share of test-takers falls, and the minority share rises, in Illinois and Colorado.
Note that even after the mandates, there are small differences in the minority share of test-takers and high school students in the mandate states. This may reflect differences in the way that race is reported and counted in the two data sets. Gender shares are quite comparable across the two groups.
Appendix C: Describing the Compliers
In this Appendix, I rely on the methods proposed in Section III to characterize the demographic composition of mandate compliers. Assume ![]() is an indicator variable taking on a value of 1
if a test-taker indicates that she has a particular characteristic (i.e., low income, male, minority), and 0 if not.
is an indicator variable taking on a value of 1
if a test-taker indicates that she has a particular characteristic (i.e., low income, male, minority), and 0 if not.
Though the ACT-CCD matched dataset enables me to approximate a limited number of characteristics describing the at-risk population, I cannot observe the full range of student demographics or data years available in the ACT survey. Thus, to best approximate the characteristics of the complier
population, I assume, analogous to the main text, that test-taker composition would evolve similarly across states over time in the absence of mandates.![]() This
assumption is supported by the estimates in Appendix Tables 2 and 3. With this assumption and reasoning parallel to that in Section III, I can express the share of compliers with any characteristic
This
assumption is supported by the estimates in Appendix Tables 2 and 3. With this assumption and reasoning parallel to that in Section III, I can express the share of compliers with any characteristic ![]() in terms of observable quantities.
in terms of observable quantities.
Appendix Table 4 estimates complier characteristics using school reports of their minority enrollment and student reports of their gender, minority status, and parental income bracket. Generally, a majority of students from disadvantaged backgrounds are compliers with the mandates - that is, they would not have taken the exam in the absence of the mandate.67 The middle columns reveal that in both treatment states, compliers are from poorer families, and are more often males and minorities, than those who opt into testing voluntarily. The final column presents these same statistics from a different perspective: a majority of low-income and minority students would not have taken the exam if they had not been forced.
The first columns of Appendix Table 5 present the share of high-scorers who are compliers and always-takers in each demographic. Across groups, a substantial portion of the compliers from every subpopulation wind up with competitive scores, and generally about 30-40% of students with scores above 18 would not have taken the test in the absence of a mandate. Compliers account for around 40% of competitive scoring within groups typically associated with disadvantage (low income and minority students and students from high-minority high schools), and around 30% of competitive scoring within other student groups. Thus, students who can earn high scores are less likely to take the ACT if they are from minority groups.
The last columns of Appendix Table 5 present the share of always-takers and compliers who are high scorers in each demographic. These statistics are useful in calculating the share of high-scoring compliers (or always-takers) with particular characteristics. Using Bayes' Rule,
![]() . Substituting in values from
Appendix Tables 4 and 5, I estimate that 30% of high-scoring compliers in Colorado, and 40% in Illinois, are minority students. These figures can be compared with the 20% of high-scoring always-takers in each mandate state that are minorities. A similar series of calculations demonstrates that
between 30 and 40% of high-scoring compliers are from the bottom income quintiles, compared to just 15% of high-scoring always-takers. Thus, high-scoring compliers are disproportionately likely to be from disadvantaged backgrounds, relative to students with similar scores who take the test
voluntarily.
. Substituting in values from
Appendix Tables 4 and 5, I estimate that 30% of high-scoring compliers in Colorado, and 40% in Illinois, are minority students. These figures can be compared with the 20% of high-scoring always-takers in each mandate state that are minorities. A similar series of calculations demonstrates that
between 30 and 40% of high-scoring compliers are from the bottom income quintiles, compared to just 15% of high-scoring always-takers. Thus, high-scoring compliers are disproportionately likely to be from disadvantaged backgrounds, relative to students with similar scores who take the test
voluntarily.
Appendix D: Bounding ![]() for LE Compliers
for LE Compliers
This exercise generates a rough estimate for the upper bound of ![]() for the LE compliers. Recall from the text that these students would like to enroll in selective schools but perceive that
their probabilities of achieving a high score are below some threshold,
for the LE compliers. Recall from the text that these students would like to enroll in selective schools but perceive that
their probabilities of achieving a high score are below some threshold,
![]() . Define
. Define
![]() .
.
First, I bound the numerator, ![]() - the cost to the student of taking the test. $25/hour would be an implausibly large time cost, incorporating the disutility of sitting for the test. (Note
that this is well above minimum wage, and teenage unemployment rates are high.) The test is about three hours in length, so allowing an additional hour for transportation and administration time, the full amount a student would need in exchange for taking the exam is $100. To this must be added the
direct cost of signing up for the test, $35 in 2012 (for the version of the exam without the writing portion). Therefore, under extremely conservative assumptions, the total cost of taking the exam is $150. Thus, any student who perceives the net present value of taking the exam to be $150 or more
will take the test even without a mandate.
- the cost to the student of taking the test. $25/hour would be an implausibly large time cost, incorporating the disutility of sitting for the test. (Note
that this is well above minimum wage, and teenage unemployment rates are high.) The test is about three hours in length, so allowing an additional hour for transportation and administration time, the full amount a student would need in exchange for taking the exam is $100. To this must be added the
direct cost of signing up for the test, $35 in 2012 (for the version of the exam without the writing portion). Therefore, under extremely conservative assumptions, the total cost of taking the exam is $150. Thus, any student who perceives the net present value of taking the exam to be $150 or more
will take the test even without a mandate.
Next, I consider the denominator, the additional value accrued from attending a selective school. I model the calculation after Cohodes and Goodman (2012). Black and Smith (2006) find that a one standard deviation increase in quality causes earnings to rise by 4.2%. To use this, I need to
convert the difference in quality a student in my sample experiences from electing the selective school over the unselective school into standard deviation units. Following Cohodes and Goodman (2012), I first construct a continuous measure of "college quality" as the first component of a
principal components analysis of available college characteristics; specifically, I use each college's student-faculty ratio, detailed Carnegie classification, dichotomous Barron's competitiveness measure, and open enrollment status.68 The gain in college quality associated with moving from an unselective to selective college--estimated by scaling the average mandate-induced change in college quality by the fraction of students induced to take
the test--is 0.60 standard deviation. Average lifetime earnings for college graduates are approximately $3.3 million (Pew Research Center Social and Demographic Trends, 2011).69 So, according to the Black and Smith result, a student stands to gain
![]() in lifetime earnings for every standard deviation increase in quality, or around $80,000 by switching from unselective to selective enrollment among the
colleges in my sample.
in lifetime earnings for every standard deviation increase in quality, or around $80,000 by switching from unselective to selective enrollment among the
colleges in my sample.
Therefore, for any rational student not to take the exam,
![]() , or
, or ![]() . Hence, a student interested in
attending college must believe she has a less-than-0.19% probability of passing in order to opt out of the exam, or
. Hence, a student interested in
attending college must believe she has a less-than-0.19% probability of passing in order to opt out of the exam, or
![]() .
.
The above calculation assumes that all students value attending a selective college (relative to an unselective college) at $80,000. This might be too high, either due to heterogeneity in the returns to selectivity or to understatement of the discount rate that some students apply to long-run
earnings changes. For instance, Cohodes and Goodman (2012) find that students value differences in college quality with an extremely large discount rate. By their estimates, students are willing to sacrifice about $110,000 of lifetime income for about $7,000 in free tuition. Adjusting my estimates
for these low values of selective schooling, reduces the value of a high score to about $5,000
![]() , and thus increases the estimate of
, and thus increases the estimate of
![]() to 0.03, so that
to 0.03, so that
![]() .
.
Appendix E: Bounding ![]() for LE Compliers
for LE Compliers
I can express the fraction of compliers who are high-scoring as a weighted sum:
The expression on the right hand side is the share of mandate compliers who would attend a selective school if admitted and who earn high enough scores to enroll in a selective school. In other words, it equals the share of compliers who ultimately enroll in a
selective school. Under the assumption that test mandates do not affect the preferences, scores, or behaviors of the always-takers, I can interpret the effect of the mandate on selective college enrollment as an estimate of this share.70 From Section III in the main text, it is approximately 10%. Moreover, in Section V, I demonstrated that roughly 40% of compliers earn scores high enough to be admitted to a selective college; that is,
![]() .
.
Substituting these into the original expression and rearranging, we find that:
Using the rationale established by the model in Section IV, my calculations imply that many high-scoring compliers thought that their chances of passing were lower than their actual chances. Formally,
![]() so that these students must have systematically downwardly biased forecasts of
their performance.
so that these students must have systematically downwardly biased forecasts of
their performance.
Appendix F: Simulating Luck
In Appendix E, I assigned an upper bound on ![]() that could be consistent with the estimated share of compliers who were observed to earn "passing" scores and with the effect
of the mandate on college-going. An even tighter bound that would be consistent with rational decision-making can be obtained by assuming that potential test-takers know their own ability and are uncertain only about how lucky they will be on the test day. In this Appendix, I ask whether this
"luck" effect is large enough to account for the effect I find of the mandates on enrollment, given the full distribution of test scores I observe (rather than only the passing rate).
that could be consistent with the estimated share of compliers who were observed to earn "passing" scores and with the effect
of the mandate on college-going. An even tighter bound that would be consistent with rational decision-making can be obtained by assuming that potential test-takers know their own ability and are uncertain only about how lucky they will be on the test day. In this Appendix, I ask whether this
"luck" effect is large enough to account for the effect I find of the mandates on enrollment, given the full distribution of test scores I observe (rather than only the passing rate).
Under an assumption that students make rational test-taking decisions based on accurate estimates of ![]() , I demonstrate that, in order to match the 10% share of all compliers that go on
to competitive schools, it would have to be the case that students opt out of the exam whenever their pass rates are below 40 to 45%. This far exceeds the threshold implied by any plausible estimate of the ratio of the costs of test-taking to the benefits of attending a selective school.
, I demonstrate that, in order to match the 10% share of all compliers that go on
to competitive schools, it would have to be the case that students opt out of the exam whenever their pass rates are below 40 to 45%. This far exceeds the threshold implied by any plausible estimate of the ratio of the costs of test-taking to the benefits of attending a selective school.
To estimate this, I assume that students are fully informed about their own ability, as measured by the ACT. We can write the ACT test score, ![]() as the sum of ability,
as the sum of ability, ![]() , and a luck component,
, and a luck component,
![]() , which reflects idiosyncratic influences on the test (e.g., the student has a cold on test day). Assume that
, which reflects idiosyncratic influences on the test (e.g., the student has a cold on test day). Assume that ![]() and
and
![]() are normally distributed and independent, with:
are normally distributed and independent, with:
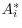 ~N(
~N(
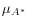 ,
,
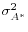 )
)-
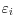 ~N(0,
~N(0,
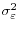 )
)
Suppose there is a known threshold,
![]() , that a student's
, that a student's ![]() must meet or surpass in order to enroll in the
selective college. The condition for a "passing" test score is thus:
must meet or surpass in order to enroll in the
selective college. The condition for a "passing" test score is thus: ![]() =
=
![]() . Student
. Student ![]() 's probability of passing, given her ability, can be
written:
's probability of passing, given her ability, can be
written:
I assume that students take the test voluntarily if ![]() so compliers consist of those students for whom
so compliers consist of those students for whom ![]() . Then the complier pass rate is:
. Then the complier pass rate is:
![\displaystyle E\left[P^*_i\vert P^*_i<c\right]=\int^{P^{*-1}(c)}_0{\left[{1-F}_{\varepsilon }\left(\overline{s}-A^*_i\right)\right]dF_{A^*_i}}](img78.gif)
I assume that the ACT's test-retest reliability is 0.9 and compute
![]() as:
as:
![]() .71 I estimate
.71 I estimate
![]() and
and
![]() from the empirical score distributions in each state in 2004. For each, I generate 1,000,000 draws of
from the empirical score distributions in each state in 2004. For each, I generate 1,000,000 draws of ![]() , which together with my estimate of
, which together with my estimate of
![]() and an assumed value of
and an assumed value of
![]() , yields 1,000,000 observations of
, yields 1,000,000 observations of ![]() . Incrementing values of
. Incrementing values of
![]() by hundredths for values between 0 and 1, I calculate the mean passing rate among test-takers who have
by hundredths for values between 0 and 1, I calculate the mean passing rate among test-takers who have ![]() . Appendix Figure 3 shows the implied mean passing rate among compliers, assuming
. Appendix Figure 3 shows the implied mean passing rate among compliers, assuming
![]() , as a function of
, as a function of ![]() , for Illinois and Colorado.
, for Illinois and Colorado.
The graph also plots dashed horizontal lines at the estimated competitive attendance rate among compliers within each state. This can be taken as a lower bound to the actual pass rate - if there are any high-scoring compliers who are not interested in attending selective colleges, the true pass rate exceeds this rate.
The horizontal lines fall quite high in the distribution. They indicate that one would expect to see the observed effects on selective college enrollment if students take the test only when their anticipated probabilities of passage exceed 40% (in Colorado) or 45% (in Illinois). The calculations in Section IV would support this kind of a decision rule only if the benefit of enrolling in a selective college rather than a nonselective one were smaller than $330.
Note: Solid lines reflect published participation rates; open circles reflect participation rates constructed from matched ACT-CCD data. "ACT states" include later-adopting states: Kentucky (2010), Michigan (2008), and Tennessee (2010). "Neighboring ACT states" include Kentucky.Appendix Figure 4: Effect of Mandates on Subcategories of Selective Enrollment, Allowing Phase-In
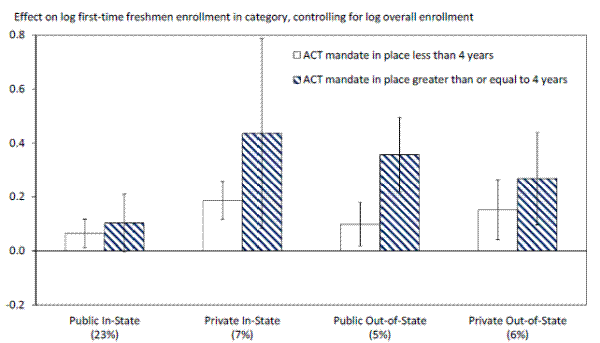 Appendix Figure 4 Data
Appendix Figure 4 Data
| Category | Criteria | Share Admitted | Example Schools |
| Most Competitive | HS rank: top 10-20% | <1/3 | Amherst College, MA |
| Most Competitive | GPA: A to B+ | Brown University | |
| Most Competitive | Median SAT: 1310-1600 | Middlebury, VT | |
| Most Competitive | Median ACT: 29+ | Tufts University, MA | |
| Highly Competitive | HS rank: top 20-35% | 1/3-1/2 | UIUC, IL* |
| Highly Competitive | GPA B+ to B | George Washington University, DC | |
| Highly Competitive | Median SAT: 1240-1308 | SUNY Binghamton, NY | |
| Highly Competitive | Median ACT: 27-28 | Vanderbilt University, TN | |
| Very Competitive | HS rank: top 35-50% | 1/2-3/4 | Colorado State University, CO* |
| Very Competitive | GPA: B- to up | Amercian University, DC | |
| Very Competitive | Median SAT: 1146-1238 | Fordham University, NY | |
| Very Competitive | Median ACT: 24-26 | George Mason University, VA | |
| Competitive | HS rank: top 50-65% | 75-85 | University of Colorado at Boulder, CO* |
| Competitive | GPA: C and up | Quinnipiac University, CT | |
| Competitive | Median SAt: 1000-1133 | SUNY Buffalo, NY | |
| Competitive | Median ACT: 21-23 | UC Davis, CA | |
| Less Competitive | HS rank: top 65% | 85 or more | San Francisco State University, CA |
| Less Competitive | GPA: below C | SUNY Farmingdale, NY | |
| Less Competitive | Median SAT: below 1000 | UT Arlington, TX | |
| Less Competitive | Median ACT: below 21 | UWisconsin/Milwaukee, WI | |
| Noncompetitive | HS graduate | 98 or more | CUNY York, NY |
| Noncompetitive | HS graduate | UT El Paso, TX | |
| Noncompetitive | HS graduate | UT San Antonio, TX | |
| Noncompetitive | HS graduate | Wilmington College, DE |
| ACT Data 1994 | ACT Data 1996 | ACT Data 1998 | ACT Data 2000 | ACT Data 2004 | CCD Data 2000 | CCD Data 2004 | |
| Iowa | 54 | 55 | 56 | 55 | 54 | 49 | 49 |
| Kansas | 54 | 54 | 53 | 55 | 54 | 49 | 49 |
| Kentucky | 56 | 56 | 57 | 57 | 57 | 50 | 50 |
| Missouri | 55 | 56 | 57 | 58 | 56 | 49 | 49 |
| Nebraska | 53 | 53 | 54 | 54 | 54 | 49 | 49 |
| New Mexico | 55 | 56 | 55 | 57 | 57 | 49 | 49 |
| Utah | 53 | 53 | 54 | 54 | 53 | 49 | 50 |
| Wisconsin | 55 | 56 | 57 | 57 | 56 | 49 | 49 |
| Wyoming | 55 | 55 | 58 | 56 | 54 | 49 | 49 |
| Colorado* | 54 | 55 | 56 | 55 | 50 | 50 | 49 |
| Illinois | 54 | 55 | 55 | 55 | 51 | 50 | 50 |
| ACT Data 1994 | ACT Data 1996 | ACT Data 1998 | ACT Data 2000 | ACT Data 2004 | CCD Data 2000 | CCD Data 2004 | |
| Iowa | 7 | 7 | 7 | 7 | 9 | 6 | 8 |
| Kansas | 14 | 15 | 15 | 16 | 18 | 15 | 18 |
| Kentucky | 12 | 13 | 13 | 12 | 15 | 10 | 11 |
| Missouri | 14 | 14 | 15 | 17 | 18 | 16 | 16 |
| Nebraska | 9 | 9 | 10 | 11 | 13 | 11 | 14 |
| New Mexico | 53 | 55 | 57 | 58 | 61 | 58 | 61 |
| Utah | 8 | 9 | 9 | 9 | 13 | 9 | 13 |
| Wisconsin | 10 | 10 | 11 | 11 | 13 | 12 | 14 |
| Wyoming | 11 | 11 | 11 | 11 | 12 | 9 | 10 |
| Colorado* | 23 | 24 | 25 | 26 | 34 | 22 | 27 |
| Illinois | 29 | 28 | 29 | 30 | 36 | 31 | 33 |
| Characteristic | Pre-reform Test-takers: Always- Takers | 2004 Test-takers All | 2004 Test-takers Always-Takers | 2004 Test-takers Compliers | Complier Share of 2004 Test-Takers |
| Female (Colorado) | 55 | 50 | 55 | 45 | 39 |
| Male (Colorado) | 45 | 50 | 45 | 55 | 50 |
| From a High-Minority HS (Colorado) | 30 | 42 | 35 | 50 | 53 |
| Not From a High-Minority HS(Colorado) | 70 | 58 | 65 | 50 | 38 |
| Minority (Colorado) | 25 | 34 | 28 | 41 | 54 |
| Non-minority (Colorado) | 75| 66 |
72 |
59 |
40 |
|
| Bottom Income Quintile (Colorado) | 22 | 26 | 20 | 33 | 57 |
| 2nd - 4th Quintiles (Colorado) | 60 | 61 | 65 | 57 | 41 |
| Top Income Quintile (Colorado) | 18 | 13 | 15 | 10 | 34 |
| Female (Illinois) | 55 | 51 | 55 | 46 | 35 |
| Male (Illinois) | 45 | 49 | 45 | 54 | 43 |
| From a High-Minority HS (Illinois) | 36 | 46 | 39 | 56 | 47 |
| Not From a High Minority HS (Illinois) | 64 | 54 | 61 | 44 | 32 |
| Minority (Illinois) | 29 | 36 | 32 | 42 | 46 |
| Non-minority (Illinois) | 71 | 64 | 68 | 58 | 35 |
| Bottom Income Quintile (Illinois) | 24 | 29 | 22 | 39 | 53 |
| 2nd 4th Quintiles (Illinois) | 58 | 58 | 62 | 51 | 34 |
| Top Income Quintile(Illinois) | 18 13 | 16 | 10 | 29 |
|
Characteristic |
Share of High-Scorers who are Always-takers | Share of High-Scores who are Compliers | Share of Always-takers who Earn High Scores | Share of Compliers who Earn High Scores |
| All (Colorado) | 68 | 32 | 79 | 47 |
| Female(Colorado) | 73 | 27 | 80 | 47 |
| Male(Colorado) | 63 | 37 | 80 | 48 |
| From a High-Minority HS(Colorado) | 63 | 37 | 70 | 37 |
| Not From a High-Minority HS(Colorado) | 71 | 29 | 86 | 58 |
| Minority(Colorado) | 60 | 40 | 64 | 37 |
| Non-Minority(Colorado) | 67 | 33 | 86 | 64 |
| Bottom Income Quintile(Colorado) | 57 | 43 | 64 | 37 |
| 2nd - 4th Quintiles(Colorado) | 70 | 30 | 81 | 49 |
| Top Income Quintile(Colorado) | 71 | 29 | 92 | 74 |
| All (Illionois) | 75 | 25 | 76 | 40 |
| Female(Illionois) | 76 | 24 | 74 | 43 |
| Male(Illionois) | 72 | 28 | 77 | 39 |
| From a High Minority HS(Illionois) | 66 | 34 | 62 | 35 |
| Not From a High Minority HS(Illionois) | 80 | 20 | 85 | 47 |
| Minority(Illionois) | 63 | 37 | 55 | 39 |
| Non-minority(Illionois) | 72 | 28 | 85 | 61 |
| Bottom Income Quintile(Illionois) | 54 | 46 | 50 | 38 |
| 2nd-4th Quintiles(Illionois) | 81 | 19 | 81 | 36 |
| Top Income Quintile(Illionois) | 75 | 25 | 92 | 75 |
| Mandate Status in 2002: Mandate CO and IL (Average (2000)) | Mandate Status in 2002: Mandate CO and IL (Difference (2002-2000)) | Mandate Status in 2002: No Mandate:Other ACT States: (Average (2000)) | Mandate Status in 2002: No Mandate:Other ACT States: (Average (2002-2000)) | Mandate Status in 2002: No Mandate:Other ACT States: Difference in Difference | |
| Subcategories of Enrollment (as Share of Population) Four Year | 35.7 | 2.7p.p. | 36.8 | 1.2p.p. | 1.5p.p. |
| Select and Land Grant | 4.9 | 0.4p.p. | 7.2 | 0.2 p.p | 0.2 p.p |
| Select and Public | 21.0 | 1.5p.p | 20.1 | 0.5p.p | 1.0 p.p |
| Select and Private | 9.3 | 0.7p.p | 6.8 | -0.1 p.p | 0.9 p.p |
| Select and Private Not-for-Profit | 8.7 | 0.7 p.p | 6.6 | -0.1 p.p | 0.8 p.p |
| Select and In-state | 22.3 | 1.4p.p | 20.4 | 0.5p.p | 0.9p.p. |
| Select and Out-of-State | 8.1 | 0.9 p.p | 6.6 | -0.1p.p | 1.0p.p |
| In-State and Selective-Land Grant | 3.7 | 0.3p.p | 6.3 | 0.2 p.p. | 0.1 p.p |
| In-State and Selective-Public | 17.5 | 1.1 p.p | 17.6 | 0.4 p.p | 0.7 p.p |
| In-State and Selective-Private | 4.7 | 0.3 p.p | 3.7 | 0.0p.p | 0.2 p.p |
| Out-of-State and Selective-Land Grant | 1.2 | 0.1p.p | 1.2 | 0.0 p.p | 0.1 p.p |
| Out-of-State and Selective-Public | 3.5 | 0.4p.p | 3.3 | 0.1 p.p | 0.3 p.p |
| Out-of-State and Selective-Private 4.6 | 0.4 p.p | 3.2 | -0.2 p.p | 0.6 p.p | |
| 18-year-old Population | 118,114 | 278 | 53,196 | -129 | 407 |
| States in Group | 2 | 2 | 23 | 23 | 23 |
| ACT Participation Rate (Published) | 68 | 31p.p | 70 | -1 p.p | 32 p.p. |