A Robust Capital Asset Pricing Model*
Abstract:
1 Introduction
The Great Recession of 2008 has prompted calls for a microeconomic theory to predict the behavior of capital markets under Knightian uncertainty.1 Although many insights can be drawn from the capital asset pricing model (CAPM) under risk, and from its many variations2, thus far few studies have explored the effects on equilibrium asset prices of uncertainty in investors' preferences. We develop a robust capital asset pricing model (RCAPM) that offers powerful predictions about how to measure the uncertainty-return tradeoff. Also, the model's analytical tractability renders it immediately applicable to capital-budgeting estimations, to the evaluation of professionally managed portfolios, and so on.
Since the CAPM of Treynor (1962), Sharpe (1964), Lintner (1965), and Mossin (1966) is founded on the formal quantitative theory for optimal portfolio selection of Markowitz (1952) and Tobin (1958), we first propose a general solution for the portfolio-selection problem under uncertainty. Our objective function features the second-order approximation of the certainty equivalent of Maccheroni, Marinacci, and Ruffino (2013a), which is the analoge of the Arrow-Pratt approximation under model uncertainty. It also introduces an ambiguity premium that captures variations in returns due to model uncertainty.
First, we find a mean-variance efficient portfolio that depends on the investor's tastes - his aversion to risk and uncertainty - as well as his beliefs over expected returns. Next, we use the optimal solution to derive a robust version of the two-fund separation theorem: here, all mean-variance efficient portfolios come from combining the riskless asset with the mean-variance efficient portfolio made of ambiguous assets only. Last, assuming that all investors are mean-variance optimizers who make decisions according to the same normative model, we derive the set of prices at which everyone's demand is satisfied in equilibrium.
The resulting relationship between asset returns and uncertainty resembles the CAPM security market line under risk. In addition, it displays a robust beta coefficient that measures an asset's systematic ambiguity. Given the results of our model, we discuss the case in which the existence of superior-performance assets (that is, assets whose robust alpha coefficient is greater than zero) allows for the creation of " super-efficient" portfolios.
Our work is related to recent research on optimal portfolio-selection theory under risk and uncertainty. Maccheroni, Marinacci, and Ruffino (2013a) and Gollier (2011) study the effects of higher ambiguity aversion on optimal portfolio rebalancing. They also set the conditions under which ambiguity reinforces (or mitigates) risk. Izhakian and Benninga (2008) find similar results on the separation of risk and ambiguity. Garlappi, Uppal, and Wang (2007) and Chen, Ju, and Miao (2013) contrast the optimal portfolio allocation from the Bayesian and the ambiguity models. Portfolio optimization under uncertainty also helps to explain some puzzling investor behaviors. For example, Epstein and Miao (2003) and Boyle, Garlappi, Uppal, and Wang (2012) provide a rational justification for holding "familiar" assets. Easley and O'Hara (2009) and Illeditsch (2011) tackle poor investor participation in the stock market.
We share some features with the capital asset-pricing models of Chen and Epstein (2002); Collard, Mukerji, Sheppard, and Tallon (2011); Ju and Miao (2012); and Izhakian (2012). In Chen and Epstein's (2002) model, excess returns also reflect a compensation for risk and a separate compensation for ambiguity. In Collard and others (2011) and Ju and Miao's (2012) models, the investor's pessimistic behavior is tied to a variety of dynamic asset-pricing phenomena (equity premium, risk-free rate, and so forth). In Izhakian's (2012) model, equilibrium prices contain a systematic beta similar to ours. We differ in that his derivation is founded on shadow probability theory, while ours is based on the smooth preferences of Klibanoff, Marinacci, and Mukerji (2005).
The rest of the paper is organized as follows. In Section 2 we introduce the mathematical setup, in Section 3 we derive the mean-variance efficient portfolio and present a robust version of the two-fund separation theorem, in Section 4 we obtain the RCAPM, and in Section 5 we conclude.
2 Theoretical decision framework
The sure amount of money that a von Neumann-Morgenstern expected-utility maximizer with utility ![]() and wealth
and wealth ![]() considers equivalent to a risky investment
considers equivalent to a risky investment ![]() is given by
is given by
where
where
where
where
The last term in (4) - the ambiguity premium - is new relative to (2).3 Specifically, the ambiguity premium changes the certainty equivalent through the decisionmaker's aversion to ambiguity
![]() as well as the variance of the return
as well as the variance of the return
![]() . Hence, this parsimonious extension of the mean-variance model under risk is fully determined by three parameters:
. Hence, this parsimonious extension of the mean-variance model under risk is fully determined by three parameters:
![]() ,
,
![]() , and
, and ![]() . Higher values of
. Higher values of
![]() and
and
![]() indicate stronger negative attitudes toward risk and ambiguity, respectively. Higher values of
indicate stronger negative attitudes toward risk and ambiguity, respectively. Higher values of
![]() indicate poorer information on outcomes and models. In the special case of
indicate poorer information on outcomes and models. In the special case of
![]() (that is, where
(that is, where ![]() is a
trivial measure), there is no source of model uncertainty and (4) reduces to (2). Last, the variance decomposition between state and model uncertainty,
is a
trivial measure), there is no source of model uncertainty and (4) reduces to (2). Last, the variance decomposition between state and model uncertainty,
allows us to rearrange (4) by the Arrow-Pratt coefficients of
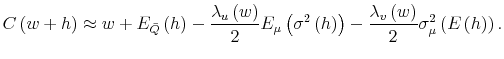 4 4 |
(6) |
In (6), risk aversion and ambiguity aversion determine the decisionmaker's response to the average variance,
![]() , and the variance of averages,
, and the variance of averages,
![]() , respectively.
, respectively.
Next, we set
![]() and
and
![]() . Then, a decisionmaker is risk averse when
. Then, a decisionmaker is risk averse when
![]() and ambiguity averse when
and ambiguity averse when ![]() .5 Last, we assume that
.5 Last, we assume that
- The ratio of
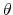 to
to 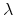 is equal for all investors.
is equal for all investors. 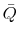 is equal to the baseline probability
is equal to the baseline probability 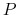 .6
.6
In Section 3 we apply the " enhanced" Arrow-Pratt approximation to the mean-variance model of optimal portfolio-selection theory.
3 Mean-variance portfolio theory
We allow for an arbitrary number of investors who make portfolio decisions based on their prior probability ![]() on the space of possible probabilistic models of their end-of-period
wealth.7 For the normative results that follow, investors need not agree on the prospects of the various investments; thus, in general, beliefs are not
homogenous. The market is formed of
on the space of possible probabilistic models of their end-of-period
wealth.7 For the normative results that follow, investors need not agree on the prospects of the various investments; thus, in general, beliefs are not
homogenous. The market is formed of ![]() ambiguous assets (
ambiguous assets (
![]() ,
, ![]() ) with
expected rate of return
) with
expected rate of return ![]() and a risk-less asset, whose return
and a risk-less asset, whose return ![]() is known
with certainty. Denote by
is known
with certainty. Denote by
![]() the vector of returns on the first
the vector of returns on the first ![]() assets and by
assets and by
![]() the mean-variance efficient portfolio with expected return
the mean-variance efficient portfolio with expected return
where
To deliver the optimality condition, set
Hence, from (8), we have that
![\displaystyle \max_{\mathbf{w}\in \mathbb{R}^{n}}C\left( r_{\mathbf{w}}\right) =\max_{% \mathbf{w}\in \mathbb{R}^{n}}\left( \mathbf{w}\cdot \mathrm{E}_{P}\left[ \mathbf{r}-r_{f}\mathbf{1}\right] -\frac{1}{2}\mathbf{w}^{\mathbf{\intercal }% }\Xi \mathbf{w}\right) .](img55.gif) |
The first-order condition for a maximum is:
which can be solved by matrix inversion assuming that
where
The optimal solution has the merit to naturally adjust the classic risk model to reflect investors' uncertainty over expected returns,
![]() . In fact, if investors are either ambiguity-neutral (
. In fact, if investors are either ambiguity-neutral (![]() ) or approximately unambiguous (
) or approximately unambiguous (
![]() ), the Markowitz-Tobin derivation readily obtains.8 The form of (9) is especially convenient because it allows for a direct application of the ample research on mean-variance preferences developed for problems involving risk to the analysis of
problems involving ambiguity. In particular, provided that information on
), the Markowitz-Tobin derivation readily obtains.8 The form of (9) is especially convenient because it allows for a direct application of the ample research on mean-variance preferences developed for problems involving risk to the analysis of
problems involving ambiguity. In particular, provided that information on ![]() ,
,
![]() ,
,
![]() , and
, and
![]() is available, all mean-variance investors use the normative model (8) to select the
optimal combination of ambiguous assets with the risk-free asset. The resulting allocation is a smooth function of the taste parameters
is available, all mean-variance investors use the normative model (8) to select the
optimal combination of ambiguous assets with the risk-free asset. The resulting allocation is a smooth function of the taste parameters ![]() and
and ![]() , which is particularly well suited for comparative statics analysis. Maccheroni, Marinacci and Ruffino (2013a) exhaustively map the conditions under which higher ambiguity aversion (or higher ambiguity in expectations)
lowers an investor's optimal exposures to the ambiguous assets, spurring severe " flights-to-quality" and investments "in the familiar." 9
, which is particularly well suited for comparative statics analysis. Maccheroni, Marinacci and Ruffino (2013a) exhaustively map the conditions under which higher ambiguity aversion (or higher ambiguity in expectations)
lowers an investor's optimal exposures to the ambiguous assets, spurring severe " flights-to-quality" and investments "in the familiar." 9![]() 10
10
Now assume that investors share the same prior probability ![]() on the space of possible probabilistic models. Then, for
on the space of possible probabilistic models. Then, for
![]() , the allocations to ambiguous assets in (9) have the same relative
proportions, independent of wealth, risk aversion, or ambiguity aversion, as long as
, the allocations to ambiguous assets in (9) have the same relative
proportions, independent of wealth, risk aversion, or ambiguity aversion, as long as ![]() is a fixed proportion of
is a fixed proportion of ![]() equal for all investors. We have that
equal for all investors. We have that
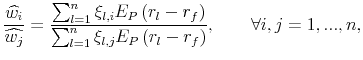 |
where
We define the optimal combination of ambiguous assets (OCAA) as the mean-variance efficient portfolio that contains ambiguous assets only. Labeling
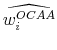 the fraction of OCAA made up by
the fraction of OCAA made up by ![]() , we have that:
, we have that:
-
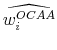 solves (8).
solves (8). -
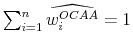 .
.
Thus,
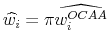 .
.In other words, the mean-variance efficient portfolio with expected return
![]() can be constructed from mixing the optimal combination of ambiguous assets with the risk-less asset - a robust two-fund separation theorem. In particular
can be constructed from mixing the optimal combination of ambiguous assets with the risk-less asset - a robust two-fund separation theorem. In particular
where
4 Equilibrium prices of capital assets
In this section we propose a positive asset-pricing theory that formalizes the relationship between asset returns and uncertainty, assuming that investors follow the mean-variance norm (9). First, we derive the set of prices that clears the market. Then, we discuss superior portfolio performance measurement when the RCAPM fails.
Theorem (1) characterizes an investor's demand function with respect to the mean-variance efficient portfolio that contains ambiguous assets only. Thus, the relative proportion of ![]() to
to ![]() is given by
is given by
The equilibrium implication of (12) is summarized in Theorem (2).
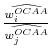 ,
,
That is, only if the market portfolio is mean-variance efficient (equal to the optimal combination of ambiguous assets) is it feasible for all investors to hold ambiguous assets in the same relative proportions as OCAA. Denoting by ![]() the return on the market portfolio, the equilibrium expected return on asset
the return on the market portfolio, the equilibrium expected return on asset ![]() is given by
is given by
| (13) |
with
The Security Market Line (13) features a robust beta,
Observe that if there exists an asset ![]() whose expected return violates (13), then the market portfolio is not the optimal combination of ambiguous assets. Instead,
one can create OCAA by combining
whose expected return violates (13), then the market portfolio is not the optimal combination of ambiguous assets. Instead,
one can create OCAA by combining ![]() with the market portfolio. Define
with the market portfolio. Define
![]() to be the deviation of asset
to be the deviation of asset ![]() from the expected return profile
(13). We decompose the excess return on asset
from the expected return profile
(13). We decompose the excess return on asset ![]() by means of the ordinary least square coefficients to obtain
by means of the ordinary least square coefficients to obtain
Here,
It is easy to show that the sign of
where
- Underpriced if
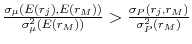 .
. - Overpriced if
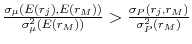 .
. - Fairly priced if
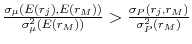 .
.
Finally, we remark that the original capital asset pricing model under risk is nested in our equilibrium model of the capital market under uncertainty. In fact, setting
![]() ,
,
![]() , we have that
, we have that
![]() and
and
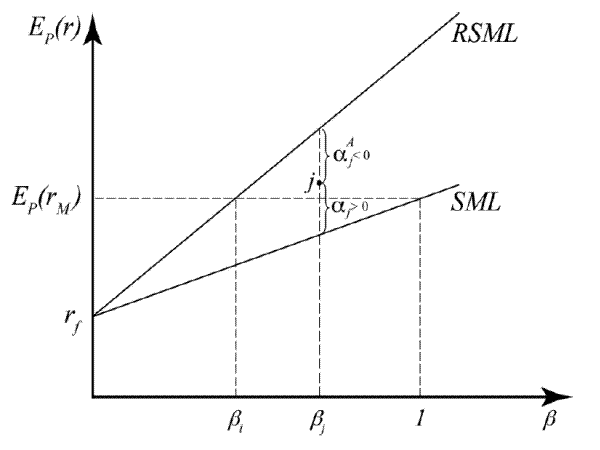
![]() . Figure 1 summarizes our results.
. Figure 1 summarizes our results.
Notes:
![]()
![]() .
.
![]()
![\beta _{i}=\frac{\sigma _{P}\left( r_{i},r_{M}\right) }{% \sigma _{P}^{2}\left( r_{M}\right) }=1-\frac{\theta \left[ \sigma _{\mu }\left( E\left( r_{i}\right) ,E\left( r_{M}\right) \right) \sigma _{P}^{2}\left( r_{M}\right) -\sigma _{P}\left( r_{i},r_{M}\right) \sigma _{\mu }^{2}\left( E\left( r_{M}\right) \right) \right] }{\sigma _{P}^{2}\left( r_{M}\right) \left[ \lambda \sigma _{P}^{2}\left( r_{M}\right) +\theta \sigma _{\mu }^{2}\left( E\left( r_{M}\right) \right) % \right] }](img110.gif) .
.
![]()
![]() has been drawn assuming
has been drawn assuming
![]() .
.
The menu of equilibrium expected returns if the CAPM holds is given by the Security Market Line (SML). If the RCAPM holds, and ambiguity reinforces risk, the robust Security Market Line (RSML) is steeper than SML, reflecting higher returns due to model uncertainty. Instead, asset ![]() is created to violate both SML and RSML. Note
that if an investor makes decisions according to the CAPM, he identifies
is created to violate both SML and RSML. Note
that if an investor makes decisions according to the CAPM, he identifies ![]() as underpriced (
as underpriced (
![]() ) when in fact, properly accounting for model uncertainty,
) when in fact, properly accounting for model uncertainty, ![]() is
overpriced (
is
overpriced (
![]() ). Then, the portfolio constructed by combining
). Then, the portfolio constructed by combining ![]() with the
market portfolio is not a superior performer as the investor believes, but an inferior one.
with the
market portfolio is not a superior performer as the investor believes, but an inferior one.
Finally, if ambiguity mitigates risk, RSML is flatter than ![]() and assets command lower returns for the same level of risk. This result is important in light
of compelling evidence that the U.S. stock market SML is much flatter than the CAPM-implied SML. For example, Black, Jensen, and Scholes (1972) analyze the returns of portfolios formed by ranking U.S. stocks on
and assets command lower returns for the same level of risk. This result is important in light
of compelling evidence that the U.S. stock market SML is much flatter than the CAPM-implied SML. For example, Black, Jensen, and Scholes (1972) analyze the returns of portfolios formed by ranking U.S. stocks on ![]() values. They find that between 1926 and 1966 low-beta stocks earned higher average returns than the CAPM predicts, and vice versa. Even after accounting for measurement errors, the CAPM relation between expected
returns and
values. They find that between 1926 and 1966 low-beta stocks earned higher average returns than the CAPM predicts, and vice versa. Even after accounting for measurement errors, the CAPM relation between expected
returns and ![]() is so weak that the model must be rejected. By contrast, the joint effect of risk and uncertainty on individual decisionmaking allows the RCAPM to predict a proportional
relation between expected returns and
is so weak that the model must be rejected. By contrast, the joint effect of risk and uncertainty on individual decisionmaking allows the RCAPM to predict a proportional
relation between expected returns and ![]() - one that is consistent with the above-mentioned empirical evidence.
- one that is consistent with the above-mentioned empirical evidence.
5 Conclusions
We extend the capital asset pricing model by including Knightian uncertainty about asset returns. First, we derive the mean-variance efficient portfolio using the certainty equivalent approximation of Maccheroni, Marinacci, and Ruffino (2013a). The optimal portfolio holdings decrease with ambiguity aversion and perceived ambiguity - a phenomenon usually referred to as flight to quality. Next, we define the optimal combination of ambiguous assets and propose a robust version of the two-fund separation theorem: we show that all mean-variance efficient portfolios come from combining the optimal combination of ambiguous assets with the risk-free asset. Last, we find the robust security market line and compare it with the security market line under risk. In particular, we show that the interaction of risk and ambiguity can predict a robust security market line whose flatter slope fits the data. We argue that this result is important to address known empirical failures of the capital asset pricing model.
[1] Arrow K. Essays in the Theory of Risk Bearing. Markham Publishing Co., Chicago, IL, (1971).
[2] Black F., Jensen, M., and Scholes, M. "The Capital Asset Pricing Model: Some Empirical Tests." In Studies in the Theory of Capital Markets, Michael C. Jensen, ed., New York (1972), pp. 79-121.
[3] Boyle P., Garlappi, L., Uppal, R. and Wang, T. " Keynes Meets Markowitz: The Tradeoff Between Familiarity and Diversification." Management Science, Vol. 58 (2012), pp. 253-272.
[4] Breeden D. "An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities." Journal of Financial Economics, Vol. 7, (1979), pp. 265-296.
[5] Chen Z., and Epstein, L. "Ambiguity, Risk, and Asset Returns in Continuous Time." Econometrica, Vol. 70, (2002), pp. 1403-1443.
[6] Chen H., Ju, N., and Miao, J. "Dynamic Asset Allocation with Ambiguous Return Predictability." Unpublished manuscript, (2013).
[7] Collard S. Mukerji, S., Sheppard, K., and Tallon, J. "Ambiguity and the historical equity premium." Oxford University Economics Dept. WP 550, (2011).[8] Easley D,. and O'Hara, M. "Ambiguity and Nonparticipation: The Role of Regulation." Review of Financial Studies, Vol. 29, (2009), pp. 1817-1843.
[9] Epstein L., and J. Miao, J., "A Two-person Dynamic Equilibrium Under Ambiguity." Journal of Economic Dynamics and Control, Vol. 27, (2003), pp. 1253-1288.
[10] Garlappi L., Uppal, R. and Wang, T. "Portfolio Selection with Parameter and Model Uncertainty: A Multi-prior Approach." Review of Financial Studies, Vol. 20 (2007), pp. 41-81.
[11] Gollier C. "Portfolio Choices and Asset Prices: The Comparative Statics of Ambiguity Aversion." Review of Economic Studies, Vol. 78, (2011), pp. 1329-1344.
[12] Grossman S., and Shiller R. "The Determinants of the Variability of Stock Market Prices." American Economic Review, Vol. 71, (1981), pp. 222-227.
[13] Huberman G. "Familiarity Breeds Investment." Review of Financial Studies, Vol. 14 (2001), pp. 659-680.
[14] Illeditsch P. "Ambiguous Information, Risk Aversion and Asset Pricing." Journal of Finance, Vol. 66, (2012), pp. 2213-2247.
[15] Izhakian Y. "Capital Asset Pricing Under Ambiguity." NYU WP, 2451/31464 (2012).
[16] Izhakian Y. and Benninga S. "The Uncertainty Premium in An Ambiguous Economy." Unpublished manuscript, (2008).
[17] Jewitt I. and Mukerji, S. "Ordering Ambiguous Acts." Oxford University Economics Dept. WP 553, (2011)
[18] Ju N., and Miao, J. "Ambiguity, Learning and Asset Returns." Econometrica, Vol. 80, (2012), pp. 559-591.
[19] Klibanoff P., Marinacci, M., and Mukerji, S. "A Smooth Model of Decision Making Under Ambiguity." Econometrica, Vol. 73, (2005), pp. 1849-1892.
[20] Knight F. Risk, Uncertainty, and Profit. Hart, Schaffner & Marx; Houghton Mifflin Co., Boston, MA, (1921).
[21] Lintner J. "The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets." Review of Economics and Statistics, Vol. 47, (1965), pp. 13-37.
[22] Lucas R. "Asset Prices in an Exchange Economy." Econometrica, Vol. 46, (1978), pp. 1429-1446.
[23] Maccheroni F., Marinacci, M., and Ruffino D. " Alpha as Ambiguity: Robust Mean-Variance Portfolio Analysis." Econometrica, Vol. 81 (2013a), pp. 1075-1113.
[24] Maccheroni F., Marinacci, M., and Ruffino D. " Does Uncertainty Vanish in the Small? The Smooth Ambiguity Case." IGIER WP391 (2013b), pp., 1085-1088.
[26] Mossin J. "Equilibrium in a Capital Asset Market." Econometrica, Vol. 35, (1966), pp. 768-783.
[27] Nau R. "Uncertainty Aversion With Second-order Utilities and Probabilities." Management Science, Vol. 52, (2006), pp. 136-145, 2006.
[28] Pratt J. "Risk Aversion in the Small and in the Large." Econometrica, Vol. 32, (1964), pp. 122-136
[29] Sharpe W. "Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk." Journal of Finance, Vol. 19, (1964), pp. 425-442.
[30] Treynor J. "Toward a Theory of Market Value of Risly Assets." Unpublished manuscript, (1962). Final version in Asset Pricing and Portfolio Performance, Robert Korajcyzk, ed., London: Risk Books (1999), pp. 15-22.
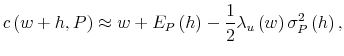
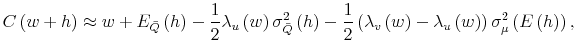
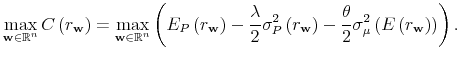
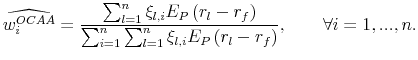
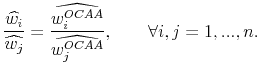
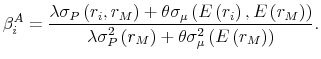
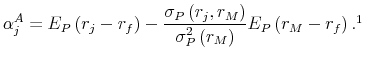
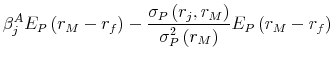
![\displaystyle \frac{\theta \left[ \sigma _{\mu }\left( E\left( r_{j}\right) ,E\left( r_{M}\right) \right) \sigma _{P}^{2}\left( r_{M}\right) -\sigma _{P}\left( r_{j},r_{M}\right) \sigma _{\mu }^{2}\left( E\left( r_{M}\right) \right) % \right] }{\sigma _{P}^{2}\left( r_{M}\right) \left[ \lambda \sigma _{P}^{2}\left( r_{M}\right) +\theta \sigma _{\mu }^{2}\left( E\left( r_{M}\right) \right) \right] }E_{P}\left( r_{M}-r_{f}\right) . \notag](img99.gif)
![\displaystyle \limfunc{sgn}\alpha _{j}^{A}=\limfunc{sgn}\left[ \frac{\sigma _{\mu }\left( E\left( r_{j}\right) ,E\left( r_{M}\right) \right) }{\sigma _{\mu }^{2}\left( E\left( r_{M}\right) \right) }-\frac{\sigma _{P}\left( r_{j},r_{M}\right) }{\sigma _{P}^{2}\left( r_{M}\right) }\right] ,](img100.gif)