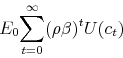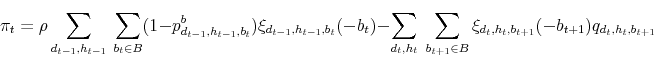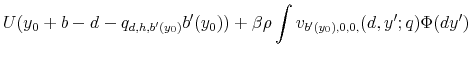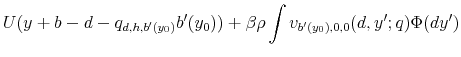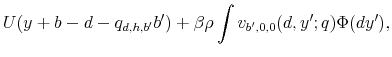The Interplay Between Student Loans and Credit Card Debt: Implications for Default in the Great Recession*
Abstract:
We prove the existence of a steady-state equilibrium and characterize the circumstances under which a household defaults on each of these loans. We demonstrate that the institutional differences between the two markets make borrowers prefer to default on student loans rather than on credit card debt. Our quantitative analysis shows that the increase in student loan debt together with the expansion of the credit card market fully explains the increase in the default rate for student loans in recent normal years (2004-2007). Worse labor outcomes for young borrowers during the Great Recession (2008-2009) significantly amplified student loan default, whereas credit card market contraction during this period helped reduce this effect. At the same time, the accumulation of student loan debt did not affect much the default risk in the credit card market during normal times, but significantly increased it during the Great Recession. An income contingent repayment plan for student loans completely eliminates the default risk in the credit card market and induces important redistribution effects. This policy is beneficial (in a welfare improving sense) during the Great Recession but not during normal times.
JEL Codes: D11; D91; G33; H81; I28;
Keywords: Default, bankruptcy, student loans, credit cards, great recession
1 Introduction
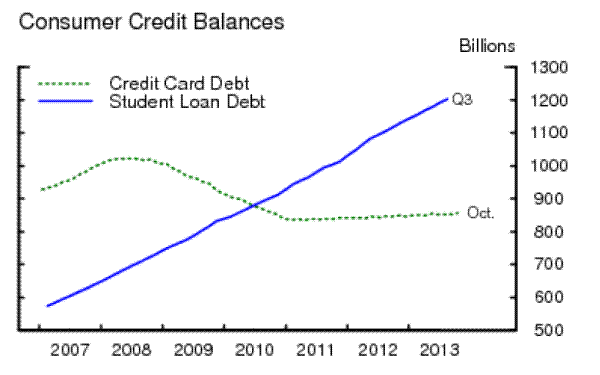
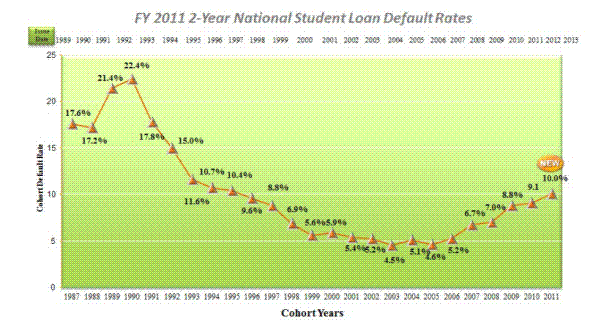
Student loan debt has steadily increased in the last two decades, reaching 1.2 trillion dollars in 2012. In June 2010, total student loan debt surpassed total credit card debt for the first time (see Figure 1 in Section 2). Currently, 70 percent of individuals who enroll in college take out student loans; the graduates of 2013 are the most indebted in history, with an average debt load of $27,300 (College Board, 2013). At the same time, the two-year basis cohort default rate (CDR) for Federal student loans steadily declined from 22.4 percent in 1990 to 4.6 percent in 2005 and has increased ever since, reaching record highs in the last decade (at 10 percent for FY2011).1
The accumulation of student loan debt alone cannot explain the recent increase in student loan default rates of young U.S. households. A second market is needed to understand this behavior: the majority of individuals with student loan debt (66 percent in 2004-2007) also have credit card debt, according to our findings from the Survey of Consumer Finances (SCF). Credit card usage is common among college students, with approximately 84 percent of the student population having at least one credit card in 2008 (Sallie Mae, 2009). While both of these loans represent important components of young households' portfolios in the United States, the financial arrangements in the two markets are very different, in particular with respect to the roles played by bankruptcy arrangements and default pricing. Furthermore, credit terms on credit card accounts have worsened in recent years, adversely affecting households' capability to diversify risk but also limiting the young borrowers' indebtedness.
We propose a theory about the interactions between student loans and credit card loans in the United States and their impact on default incentives of young U.S. households. As we argue in this paper, this interaction between different bankruptcy arrangements induces significant trade-offs in default incentives in the two markets. Understanding these trade-offs is particularly important in the light of recent trends in borrowing and default behavior. Data show that young U.S. households (of which a large percentage have both college and credit card debt) now have the second highest rate of bankruptcy (just after those aged 35 to 44). Furthermore, the bankruptcy rate among 25- to 34-year-olds increased between 1991 and 2001, indicating that this generation is more likely to file for bankruptcy as young adults than were young boomers at the same age.2 Moreover, student loans have a higher default rate than credit card loans or any other type of loan, including car loans and home loans.3
These trends are concerning, considering the large risks that young borrowers face: first, the college dropout rate has increased significantly in the past decade (from 38 percent to 50 percent for the cohorts that enrolled in college in 1995 and 2003, respectively).4 Furthermore, the unemployment rate among young workers with a college education has jumped up significantly during the Great Recession: 8 percent of young college graduates and 14.1 percent of young workers with some college education were unemployed in 2010 (Bureau of Labor Statistics). In addition, in order to begin repaying their student loan debt, many college graduates resort to underemployment outside their fields of study, especially after the Great Recession, a move that may have long-term deleterious financial effects.5
The combination of high indebtedness and high income risk in the Great Recession implies that borrowers are more likely to default on at least one of their loans. A few questions arise immediately: First, which default option do young borrowers find more attractive and why? In particular, is the current environment conducive to higher default incentives in the student loan market? Second, absent the Great Recession, how much of the increase in default on student loans is explained by trends in the student loan market and how much by trends in the credit card market? Lastly, how much does the Great Recession amplify default incentives?
In order to address the proposed issues, we develop a general equilibrium economy that mimics features of student and credit card loans. Infinitely lived agents differ in student loan debt and income levels. Agents face uncertainty in income and may save/borrow and, as in practice, borrowing terms are individual specific. Central to the model is the decision of young college-educated individuals to repay or default on their credit card and student loans. Consequences of defaulting on student and credit card loans differ in several important ways: for student loans, they include a wage garnishment, while for credit card loans, they induce exclusion from borrowing for several periods. More importantly, credit card loans can be discharged in bankruptcy (under Chapter 7), whereas student loans cannot be discharged (borrowers need to reorganize and repay under Chapter 13). Borrowing and default behavior in both markets determine the individual default risk. This risk, in turn, determines the loan terms agents face on their credit card accounts, including loan prices. In contrast, the interest rate in the student loan market does not account for the risk that some borrowers may default.
In the theoretical part of the paper, we first characterize the default behavior and show how it varies with households' characteristics and behavior in both markets. Then we demonstrate the existence of cross-market effects and their implications for default behavior. This represents the main contribution of our paper, a contribution which is two-fold:
1) Our theory delivers the result that in equilibrium, credit card loan prices depend not only on the size of the credit card loan (as in (Chatterjee et al., 2007)), but also on the size of the loan and the default status in the student loan market. This is a direct consequence of the result that the probability of default on any credit card loan decreases with the amount of debt owed in the student loan market. Also, this default probability is higher for an individual with a default flag in the student loan market relative to an individual without a default flag. To our knowledge, these results are new in the literature and provide a rationale for pricing credit card loans based on behavior in all credit markets in which individuals participate.
2) In any steady-state equilibrium, we find a combination of student loan and credit card debt for which the agent defaults on at least one type of her loans. Moreover, we find that for larger levels of student loans or credit card debt than the levels in this combination, default occurs for student loans. This result is novel because it shows that while a high student loan debt is necessary to induce default on student loans, this effect is amplified by indebtedness in the credit card market. This arises from the differences in bankruptcy arrangements in the two markets: the financially constrained borrower finds it optimal to default on student loans (even though she cannot discharge her debt) in order to be able to access the credit card market. Since defaulting on student loans causes a limited effect on her credit card market participation (shortly-lived exclusion and higher costs of loans in the credit card market), this borrower prefers the default penalty in the student loan market over defaulting in the credit card market, an action which would trigger long-term exclusion from the credit card market.
In the quantitative part of our paper, we parametrize the model to match statistics regarding student loan debt, credit card debt, and income of young borrowers with student loans (as delivered by the SCF 2004-2007). There are several sets of results.
First, our findings reveal large gaps in credit card rates across individuals with different levels of student loan debt and default status in the student loan market. This result strengthens our theory and emphasizes the quantitative importance of correctly pricing credit card debt based on behavior in other credit markets.
Second, we find that individuals with no credit card debt have lower default rates on student loans than individuals with credit card debt. Furthermore, individuals with low levels of credit card debt and low levels of student loan debt do not default on credit card debt, but they do default on their student loans. For them, the benefit of discharging their credit card debt is small compared to the large cost associated with default (exclusion from borrowing). Individuals with large levels of credit card and student loan debt are more likely to default on student loans.
Third, we determine combinations of levels of student loans and credit card debt above which borrowers are more likely to default, a result which complements our main theoretical result. Our findings suggest that having debt in the credit card market amplifies the incentive to default on student loans.
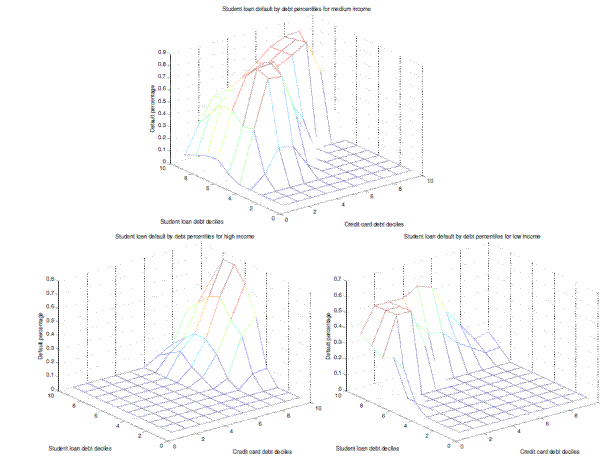
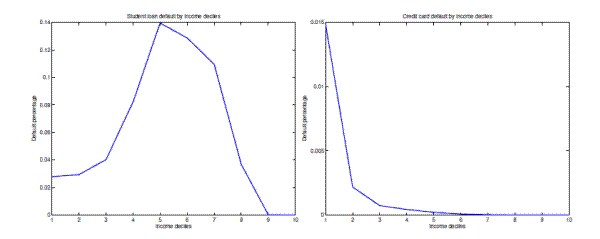
Fourth, an interesting result is that conditional on participating in the credit card market, individuals with medium levels of student loan debt or with low income levels (and large levels of student loans) use credit card debt to reduce their default on student loans. On the one hand, participating in the credit card market pushes borrowers towards increased default on their student loans, while on the other hand, taking on credit card debt helps student loan borrowers smooth consumption and pay their student loan debt, in particular when their student loan debt burdens are large. At the same time, given the importance of student loan borrowing and default behavior in credit card loan pricing, individuals with high levels of credit card debt are mostly "good risk" borrowers, i.e. individuals with low levels of student loan debt. Overall, these three effects induce a hump-shaped profile of student loan default on credit card debt. Similarly, we find a hump-shaped profile of student loan default on income. Individuals with medium levels of income default the most on their student loan debt but not as frequently on their credit card debt.
Next, we use our theory to understand how the interaction between the two credit markets affects default behavior in recent normal times (2004-2007) and in the Great Recession. Specifically, we quantify how much of the recent increase in default rates for student loans is due to an increase in student loan debt and how much is explained by changes in the credit card market. We find that the expansion of both markets in normal times fully explains the increase in student loan default from 5 percent to 6.7 percent during 2004-2007, with 88 percent of the increase in default coming from the increase in student loan debt (by 20.7 percent) during this period. At the same time, a decline of 19 percent in income levels of young borrowers during the Great Recession accounts for a significant portion of the increase in student loan default (to 9 percent in 2010), whereas the changes in the credit card market have no effects on aggregate default rate. Specifically, while a lower risk-free rate (by 1.5 percent during 2007-2010) transfers risk from the credit card market to the student loan market and increases student loan default, a higher transaction cost during this period has the opposite effect. Overall, these two effects offset each other, resulting in a negligible combined effect on default incentives.
Lastly, we explore the policy implications of our model and study the impact of an income contingent repayment plan on student loans.6 We find that this plan completely eliminates the default risk in the credit card market and induces high levels of dischargeability of student loans. Overall, the policy induces an increase in welfare of 2.86 percent in a Great Recession environment but has a negative, although small, effect on welfare in normal times (0.14 percent).7 The elimination of risk in the Great Recession environment more than outweighs the welfare cost associated with high dischargeability and thus with high taxation in the economy. Results show important redistributional effects: poor borrowers with large levels of student loans benefit from the policy, while medium income borrowers with low and medium levels of debt are hurt by it. Medium earners are precisely the group who default the most under the standard repayment plan. Under income contingent repayment plans, these borrowers repay most of the student loan debt without discharging and also pay higher taxes to pay for bailing out delinquent borrowers. In contrast, poor borrowers with large levels of student loans are most likely to discharge their student loan debt under income contingent repayment plans, whereas in the absence of this repayment plan they are most likely to discharge their credit card debt. Our findings are particularly important in the current market conditions in which, due to a significant increase in college costs, students borrow more than ever in both the student loan and the credit card markets, and at the same time, they face worse job outcomes and more severe terms on their credit card accounts.
1.1 Related literature
Our paper is related to two strands of existing literature: credit card debt default and student loans default. The first strand includes important contributions by (Athreya et al., 2009), (Chatterjee et al., 2007), (Chatterjee et al., 2010), and (Livshits et al., 2007). The first two studies explicitly model a menu of credit levels and interest rates offered by credit suppliers with the focus on default under Chapter 7 within the credit card market. (Chatterjee et al., 2010) provide a theory that explores the importance of credit scores for consumer credit based on a limited information environment. (Livshits et al., 2007) quantitatively compare liquidation in the United States to reorganization in Germany in a life-cycle model with incomplete markets, earnings and expense uncertainty.
In the student loan literature, there are several papers closely related to the current study, including research by (Ionescu, 2010), (Ionescu & Simpson, 2010), and (Lochner & Monge, 2010). These papers incorporate the option to default on student loans when analyzing various government policies. Of these studies, the only one that accounts for the role of individual default risk in pricing loans is (Ionescu & Simpson, 2010), who recognize the importance of this risk in the context of the private student loan market. Their model, however, is silent with respect to the role of credit risk for credit cards or for the allocation of consumer credit because the study is restricted to the analysis of the student loan market. (Ionescu, 2010) models both dischargeability and non-dischargeability of loans, but only in the context of the student loan market. Furthermore, as in (Livshits et al., 2007), (Ionescu, 2010) studies various bankruptcy rules in distinct environments that mimic different periods in the student loan program (in (Livshits et al., 2007) in different countries) rather than modeling them as alternative insurance mechanisms available to borrowers.
Our paper builds on this body of work and improves on the modeling of insurance options available to borrowers with student loans and credit card debt. On a methodological level, our paper is related to (Chatterjee et al., 2007). As in their paper, we model a menu of prices for credit card loans based on the individual risk of default. In (Chatterjee et al., 2007), individual probabilities of default are linked to the size of the credit card loan. We take a step further in this direction and condition individual default probabilities not only on the size of the credit card loan, but also on the default status and the amount owed on student loans. All three components determine credit card loan pricing in our model. We argue that this is an important feature to account for in models of consumer default. Furthermore, we allow interest rates to respond to changes in default incentives induced by different bankruptcy arrangements in the two markets. To our knowledge, we are the first to embed such trade-offs into a quantitative dynamic theory of unsecured credit default. But capturing these trade-offs induced by multiple default decisions with different consequences poses obvious technical challenges. We provide mathematical tools to address these issues.
To this end, the novelty of our work consists in providing a theory about interactions between credit markets with different financial arrangements and their role in amplifying consumer default for student loans. Previous research analyzed these two markets separately, mainly focusing on credit card debt. Our paper attempts to bridge this gap. Our results are not specific to the interpretation for student loans and credit cards and speak to consumer default in any environments that feature differences in financial market arrangements and thus induce a trade-off in default incentives. In this respect our paper is related to (Chatterjee et al., 2008), who provide a theory of unsecured credit based on the interaction between unsecured credit and insurance markets. Also related to our paper is research by (Mitman, 2012), who develops a general-equilibrium model of housing and default to jointly analyze the effects of bankruptcy and foreclosure policies. However, our research is different from (Mitman, 2012) in several important ways: our paper focuses on the interplay between two types of unsecured credit that feature dischargeability and non-dischargeability of loans. In addition, we study how this interaction between two credit markets with different bankruptcy arrangements changes during normal times and during the Great Recession.8
The paper is organized as follows. In Section 2, we describe important facts about student loans and credit card terms. We develop the model in Section 3 and present the theoretical results in Section 4. We calibrate the economy to match important features of the markets for student and credit card loans and present quantitative results in Section 5. Section 6 concludes.
2 Data facts
This section contains two sets of facts: 1) facts related to default behavior and loan pricing and 2) facts related to trends in the student loan, credit card, and labor markets for young college-educated individuals during 2004-2010. We build an economy that is consistent with the first set of facts and use the second set of facts to guide our experiments, which explain recent trends in default rates for student loans.
2.1 Default behavior and risk pricing
- High student loan debt increases the likelihood of default for student loans (see (Dynarsky, 1994) and (Ionescu, 2008)).
- High credit card debt increases the likelihood of default on credit card debt (see (Athreya et al., 2009) and (Chatterjee et al., 2007)).
- Low income increases the likelihood of default on credit card debt (see (Sullivan et al., 2001)).
- Individuals with high credit risk receive higher interest rates on their credit card debt (Chatterjee et al., 2010).
2.2 Trends in the student loan and credit card market
Findings documented in this section are primarily based on the SCF data for young borrowers aged 20-30 years old who have some college education (with or without a college degree), who are no longer enrolled in college and who took out student loans to finance their college education.9 We construct these samples using the SCF 2004, the SCF 2007 and SCF 2010. The sample sizes are 466, 430, and 675, respectively. We also use Equifax data, in which similarly constructed samples consists of 15,000 observations, on average, for the years 2004-2010.10
- Student loan debt borrowed by young U.S. households increased significantly in the recent years, passing credit card debt for the first time in 2010 (See Figure 1).11
- According to our samples from the SCF data, the amount of student loans increased by almost 21 percent in both normal times (2004-2007) and in the Great Recession (2007-2010).12
- At the same time, the unemployment rate went up from 4.3% before the Great Recession (2004-2007) to 7.6% (2010) and labor income went down 19 percent, on average.13
- Young borrowers with student loans use credit cards at very high rates: 71 percent of young U.S. households have at least one credit card and 93 percent of credit card users have positive balances.14
- Terms on credit card accounts of young borrowers have changed: the credit card limit increased by 30 percent from 2004 to 2007 but decreased by about the same percentage during the Great Recession (2007-2010). The average amount lent by credit card issuers to young borrowers declined by 31.5 percent from 2007 to 2010.15
- According to statistics from the DoE, the national two-year basis CDR on student loans increased from 5 percent in 2004-2006 to 10 percent in 2011 (see Figure 2).16
3.1 Legal environment
Consumers who participate in the student loan and credit card markets, namely, young college educated individuals with student loans, are small, risk-averse, price takers. They differ in levels of student loan debt, ![]() and income,
and income, ![]() . They are endowed with a line of credit, which they may use for transactions and consumption smoothing. They choose to repay or default on their
student loans as well as on their credit card debt. Both types of loans are not secured by any tangible assets, but eligibility conditions are very different and default has different consequences in each market.
. They are endowed with a line of credit, which they may use for transactions and consumption smoothing. They choose to repay or default on their
student loans as well as on their credit card debt. Both types of loans are not secured by any tangible assets, but eligibility conditions are very different and default has different consequences in each market.
3.1.1 Credit cards
Bankruptcy for credit cards in the model resembles Chapter 7 "total liquidation" bankruptcy. The model captures the fact that in practice, credit card issuers use consumer repayment and borrowing behavior on all types of loans to assess the likelihood that any single borrower will default (as reflected by FICO scores). Loan prices and credit limits imposed by credit card issuers are set to account for the individual default risk and are tailored to each credit account.
Consider a household that starts the period with some credit card debt, ![]() . Depending on the household decision to declare bankruptcy as well as on the household borrowing behavior, the
following things happen:
. Depending on the household decision to declare bankruptcy as well as on the household borrowing behavior, the
following things happen:
- If a household files for bankruptcy,
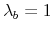 , then the household unsecured debt is discharged and liabilities are set to 0.
, then the household unsecured debt is discharged and liabilities are set to 0. - The household cannot save during the period when default occurs, which is a simple way of modeling that U.S. bankruptcy law does not permit those invoking bankruptcy to simultaneously accumulate assets.
- The household begins the next period with a record of default on credit cards. Let
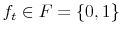 denote the default flag for a household in period
denote the default flag for a household in period 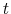 , where
, where
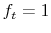 indicates in period
indicates in period 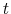 a record of default and
a record of default and 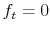 denotes the absence of such a record. Thus a household who defaults on credit in period
denotes the absence of such a record. Thus a household who defaults on credit in period 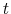 starts period
starts period
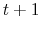 with
with 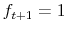 .
. - A household who starts the period with a default flag cannot borrow and the default flag can be erased with a probability
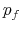 .
. - In contrast, a household who starts the period with
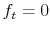 is allowed to borrow and save according to individual credit terms: credit rates assigned to households by credit lenders vary
with individual characteristics. This feature is important to allow for capturing default risk pricing in equilibrium.
is allowed to borrow and save according to individual credit terms: credit rates assigned to households by credit lenders vary
with individual characteristics. This feature is important to allow for capturing default risk pricing in equilibrium.
3.1.2 Student loans
Government-guaranteed student loans are conditioned on financial need, not credit ratings. Agents are eligible to borrow up to the full college cost minus expected family contributions. Once borrowers are out of college, they enter a standard 10-year repayment plan with fixed payments. The
interest rate on student loans does not incorporate the risk that some borrowers might exercise the option to default. The interest rate is set by the government. Several default penalties implemented in the student loan program might bear part of the default risk. Bankruptcy for student loans in
the model resembles Chapter 13 "reorganization" bankruptcy, which requires the reorganization and repayment of defaulted loans. Under the current Federal Student Loan Program (FSLP), students who participate cannot discharge on their student loans except in extreme circumstances. Consequently,
default on student loans in the model at period ![]() (denoted by
(denoted by ![]() ) simply
means a delay in repayment that triggers the following consequences:
) simply
means a delay in repayment that triggers the following consequences:
- There is no debt repayment in period
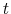 . However, the student loan debt is not discharged. The defaulter must repay the amount owed for payment in period
. However, the student loan debt is not discharged. The defaulter must repay the amount owed for payment in period 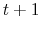 .17
.17 - The defaulter is not allowed to borrow or save in period
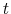 , which is in line with the fact that credit bureaus are notified when default occurs and thus access to the credit card market is
restricted. Also, as in the case of the credit card market, this feature captures the fact that U.S. bankruptcy law does not permit those invoking bankruptcy to simultaneously accumulate assets.
, which is in line with the fact that credit bureaus are notified when default occurs and thus access to the credit card market is
restricted. Also, as in the case of the credit card market, this feature captures the fact that U.S. bankruptcy law does not permit those invoking bankruptcy to simultaneously accumulate assets. - A fraction
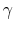 of the defaulter's wages is garnished starting in period
of the defaulter's wages is garnished starting in period 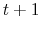 .
Once the defaulter rehabilitates her student loan, the wage garnishment is interrupted. This penalty captures the default risk for student loans in the model.18
.
Once the defaulter rehabilitates her student loan, the wage garnishment is interrupted. This penalty captures the default risk for student loans in the model.18 - The household begins the next period with a record of default on student loans. Let
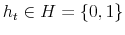 denote the default flag for a household in period
denote the default flag for a household in period 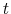 , where
, where
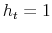 indicates a record of default and
indicates a record of default and 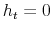 denotes the absence of such a
record. Thus a household who defaults in period
denotes the absence of such a
record. Thus a household who defaults in period 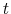 starts period
starts period 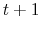 with
with 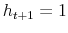 .
. - A household that begins period
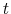 with a record of default must pay the debt owed in period
with a record of default must pay the debt owed in period 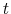 ,
, 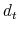 . The default flag is erased with probability
. The default flag is erased with probability 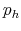 .19
.19 - There are no consequences on credit card market participation during the periods after a default on student loan occurs. However, there are consequences on the pricing of credit card loans from defaulting on student loans, as mentioned above. This assumption is justified by the fact that in practice, student loan default is reported to credit bureaus and so creditors can observe the default status immediately after default occurs. However, immediate repayment and rehabilitation of the defaulted loan will result in the removal of the default status reported by the loan holder to the national credit bureaus. In practice, the majority of defaulters rehabilitate their loans. Therefore, they are still able to access the credit card market (on worse terms, as explained above).
3.2 Preferences and endowments
At any point in time the economy is composed of a continuum of infinitely lived households with unit mass.20 Agents differ in student loan payment
levels,
![]() and income levels,
and income levels,
![]() . There is a constant probability
. There is a constant probability ![]() that households
will die at the end of each period. Households that do not survive are replaced by newborns who have not defaulted on student loans (
that households
will die at the end of each period. Households that do not survive are replaced by newborns who have not defaulted on student loans (![]() ) or credit cards (
) or credit cards (![]() ), have zero assets (
), have zero assets (![]() ), and with labor income and student loan debt drawn independently from the probability
measure space
), and with labor income and student loan debt drawn independently from the probability
measure space
![]() where
where
![]() denotes the Borel sigma algebra and
denotes the Borel sigma algebra and
![]() denotes the joint probability measure. Surviving households independently draw their labor income at time
denotes the joint probability measure. Surviving households independently draw their labor income at time ![]() from a stochastic process. The amount that the household needs to pay on her student loan is the same.21 Household characteristics are then defined on the measurable space
from a stochastic process. The amount that the household needs to pay on her student loan is the same.21 Household characteristics are then defined on the measurable space
![]() . The transition function is given by
. The transition function is given by
![]() , where
, where ![]() is an i.i.d. process and
is an i.i.d. process and
![]() is the probability measure supported at
is the probability measure supported at ![]() .
.
This assumption ensures that even for the worst possible realization of income, the amount owed on student loans each period does not exceed the per period income.22
The preferences of the households are given by the expected value of a discounted lifetime utility, which consists of:
3.3 Market arrangements
There are several similarities as well as important differences between the credit card market and the market for student loans.
3.3.1 Credit cards
The market for privately issued unsecured credit in the United States is characterized by a large, competitive marketplace in which price-taking lenders issue credit through the purchase of securities backed by repayments from those who borrow. These transactions are intermediated principally by
credit card issuers. Given a default option and consequences on the credit record from default behavior, the market arrangement departs from the conventional modeling of borrowing and lending. As in (Chatterjee et al., 2007), our model handles the competitive pricing of
default risk, a risk that varies with household characteristics.23 In this dimension, our model departs from (Chatterjee et al.,
2007) in several important ways: the default risk is based on the borrowing behavior in both markets, i.e. it depends on the size of the loan on credit cards, ![]() as well as the amount of
student loans owed,
as well as the amount of
student loans owed, ![]() . In addition, it depends on the default status on student loans,
. In addition, it depends on the default status on student loans, ![]() . Competitive default pricing is achieved by allowing prices to vary with all three elements. This modeling feature is novel in the literature and is meant to capture the fact that in practice, the price of the loan depends on past repayment and borrowing behavior in all the
markets in which borrowers participate. Unsecured credit card lenders use this behavior (which, in practice, is captured in a credit score) as a signal for household credit risks and thus their probability of default. They tailor loan prices to individual default risk, not only to individual loan
sizes. Obviously, in the case of a default flag on credit cards, no loan is provided.
. Competitive default pricing is achieved by allowing prices to vary with all three elements. This modeling feature is novel in the literature and is meant to capture the fact that in practice, the price of the loan depends on past repayment and borrowing behavior in all the
markets in which borrowers participate. Unsecured credit card lenders use this behavior (which, in practice, is captured in a credit score) as a signal for household credit risks and thus their probability of default. They tailor loan prices to individual default risk, not only to individual loan
sizes. Obviously, in the case of a default flag on credit cards, no loan is provided.
A household can borrow or save by purchasing a single one-period pure discount bond with a face value in a finite set
![]() . The set
. The set
![]() contains 0 and positive and negative elements. Let
contains 0 and positive and negative elements. Let
![]() be the cardinality of this set. Individuals with
be the cardinality of this set. Individuals with ![]() (which is a result of
defaulting on credit cards in one of the previous periods) are limited in their market participation,
(which is a result of
defaulting on credit cards in one of the previous periods) are limited in their market participation, ![]() .24
.24
A purchase of a discount bond in period ![]() with a non-negative face value
with a non-negative face value ![]() means that the household has entered into a contract where it will receive
means that the household has entered into a contract where it will receive ![]() units of the consumption good in period
units of the consumption good in period ![]() . The purchase of a discount bond with a negative face value
. The purchase of a discount bond with a negative face value ![]() means that the household receives
means that the household receives
![]() units of the period-t consumption good and promises to deliver, conditional on not declaring bankruptcy,
units of the period-t consumption good and promises to deliver, conditional on not declaring bankruptcy, ![]() units of the consumption good in period
units of the consumption good in period ![]() ; if it declares bankruptcy, the household delivers nothing. The total
number of credit indexes is
; if it declares bankruptcy, the household delivers nothing. The total
number of credit indexes is
![]() . Let the entire set of
. Let the entire set of
![]() prices in period
prices in period ![]() be denoted by the vector
be denoted by the vector
![]() . We restrict
. We restrict ![]() to lie in a
compact set
to lie in a
compact set
![]() where
where ![]() .
.
3.3.2 Student loans
Student loans represent a different form of unsecured credit. First, loans are primarily provided by the government (either direct or indirect and guaranteed through the FSLP), and do not share the features of a competitive market.25 Unlike credit cards, the interest rate on student loans, ![]() is set by the government and does not
reflect the risk of default in the student loan market.26 However, the penalties for default capture some of this risk. In particular, the wage garnishment
is adjusted to cover default. More generally, loan terms are based on financial need, not on default risk. Second, taking out student loans is a decision made during college years. Once households are out of college, they need to repay their loans in equal rounds over a determined period of time
subject to the fixed interest rate. We model college-loan-bound households that are out of school and need to repay
is set by the government and does not
reflect the risk of default in the student loan market.26 However, the penalties for default capture some of this risk. In particular, the wage garnishment
is adjusted to cover default. More generally, loan terms are based on financial need, not on default risk. Second, taking out student loans is a decision made during college years. Once households are out of college, they need to repay their loans in equal rounds over a determined period of time
subject to the fixed interest rate. We model college-loan-bound households that are out of school and need to repay ![]() per period; there is no borrowing decision for student loans.27 Third, defaulters cannot discharge their debt. Recall that in the case that the household has a default flag (
per period; there is no borrowing decision for student loans.27 Third, defaulters cannot discharge their debt. Recall that in the case that the household has a default flag (![]() ), a wage garnishment is imposed and she keeps repaying the amount owed during the following periods after default occurs.
), a wage garnishment is imposed and she keeps repaying the amount owed during the following periods after default occurs.
We define the state space of credit characteristics of the households by
![]() to represent the asset position, the credit card, and student loan default flags. Let
to represent the asset position, the credit card, and student loan default flags. Let
![]() be the cardinality of this set.
be the cardinality of this set.
To this end, an important note is that the assumption that all debt that young borrowers access is unsecured is made for a specific purpose and is not restrictive. The model is designed to represent the section of households who have student loans and credit card debt. As argued, these borrowers rely on credit cards to smooth consumption and have little or no collateral debt.
3.4 Decision problems
The timing of events in any period is: (i) idiosyncratic shocks, ![]() are drawn for survivors and newborns and student loan debt is drawn for newborns; (ii) households' decisions take
place: they choose to default/repay on both credit card and student loans, make borrowing/savings and consumption decisions, and default flags for the next period are determined. We focus on steady state equilibria where
are drawn for survivors and newborns and student loan debt is drawn for newborns; (ii) households' decisions take
place: they choose to default/repay on both credit card and student loans, make borrowing/savings and consumption decisions, and default flags for the next period are determined. We focus on steady state equilibria where ![]() .
.
3.4.1 Households
We present the households' decision problem in a recursive formulation where any period ![]() variable
variable ![]() is denoted by
is denoted by ![]() and its period
and its period ![]() value by
value by ![]() .
.
Each period, given their student loan debt, ![]() , current income,
, current income, ![]() , and
beginning-of-period assets,
, and
beginning-of-period assets, ![]() , households must choose consumption,
, households must choose consumption, ![]() and asset
holdings to carry forward into the next period,
and asset
holdings to carry forward into the next period, ![]() . In addition, agents may decide to repay/default on their student loans,
. In addition, agents may decide to repay/default on their student loans,
![]() and credit card loans,
and credit card loans,
![]() . As described before, these decisions have different consequences: while default on student loans implies a wage garnishment
. As described before, these decisions have different consequences: while default on student loans implies a wage garnishment ![]() and no effect on market participation (although it may deteriorate terms on credit card accounts), default on credit card payments triggers exclusion from borrowing for several periods and has no effect on income.
and no effect on market participation (although it may deteriorate terms on credit card accounts), default on credit card payments triggers exclusion from borrowing for several periods and has no effect on income.
The household's current budget correspondence,
![]() depends on the exogenously given income,
depends on the exogenously given income, ![]() , student loan debt,
, student loan debt,
![]() , beginning of period asset position,
, beginning of period asset position, ![]() , credit card default record,
, credit card default record, ![]() , student loan default record,
, student loan default record, ![]() , and the prices in the credit card market,
, and the prices in the credit card market, ![]() . It consists of elements of the form
. It consists of elements of the form
![]() such that
such that
and such that the following cases hold:
1. If a household with income ![]() and student loan debt
and student loan debt ![]() has a good student loan
record,
has a good student loan
record, ![]() , and a good credit card record,
, and a good credit card record, ![]() , then we have the following:
, then we have the following:
![]() and
and
![]() if
if ![]() and
and ![]() if
if ![]() . In the case where
. In the case where ![]() or
or ![]() then
then ![]() and in the case
where
and in the case
where
![]() then
then
![]() . Also
. Also ![]() ,
,
![]() ,
,
![]() . The household can choose to pay off both loans (
. The household can choose to pay off both loans (
![]() , in which case the household can borrow freely on the credit card market. If the household chooses to exercise its default option on either of the loans
(
, in which case the household can borrow freely on the credit card market. If the household chooses to exercise its default option on either of the loans
(![]() or
or ![]() ), then the household cannot borrow or accumulate
assets. Since
), then the household cannot borrow or accumulate
assets. Since ![]() , there is no income garnishment (
, there is no income garnishment (![]() ).
).
2. If a household with income ![]() and student loan debt
and student loan debt ![]() has a good student loan
record,
has a good student loan
record, ![]() , and a bad credit card record,
, and a bad credit card record, ![]() , then
, then ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() . In this case, there is no repayment on credit
card debt; the household chooses to pay or default on the student loan debt. The household cannot borrow and the credit card record will stay 1.
. In this case, there is no repayment on credit
card debt; the household chooses to pay or default on the student loan debt. The household cannot borrow and the credit card record will stay 1.
3. If a household with income ![]() and student loan debt
and student loan debt ![]() has a bad student loan
record,
has a bad student loan
record, ![]() , and a good credit card record,
, and a good credit card record, ![]() , then
, then
![]() if
if ![]() and
and ![]() if
if ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() . The household pays back the credit card
debt (if net liabilities,
. The household pays back the credit card
debt (if net liabilities, ![]() ) or defaults, pays the student loan and has its income garnished by a factor of
) or defaults, pays the student loan and has its income garnished by a factor of ![]() . The student record will stay 1. As in case 1,
. The student record will stay 1. As in case 1,
![]() if
if ![]() and
and ![]() if
if ![]() .
.
4. If a household with income ![]() and student loan debt
and student loan debt ![]() has a bad student loan
record,
has a bad student loan
record, ![]() , and a bad credit card record,
, and a bad credit card record, ![]() , then
, then
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() . The household cannot borrow in the credit card market, pays the student loan, and has her income
garnished.
. The household cannot borrow in the credit card market, pays the student loan, and has her income
garnished.
There are several important observations: 1) we account for the fact that the budget constraint may be empty; in particular ,if the household is deep in debt, earnings are low, and new loans are expensive, then the household may not be able to afford non-negative consumption. The implication of
this is that involuntary default may occur; and 2) Repeated default on student loans occurs on a limited basis (i.e. when
![]() ) and is followed by partial dischargeability, an assumption that is in line with the data. All households pay taxes
) and is followed by partial dischargeability, an assumption that is in line with the data. All households pay taxes ![]() .
.
1. For ![]() and
and ![]()
where
2. For ![]() and
and ![]() (in which case
(in which case ![]() and
and ![]() with probability
with probability ![]() and
and ![]() with probability
with probability ![]() )
)
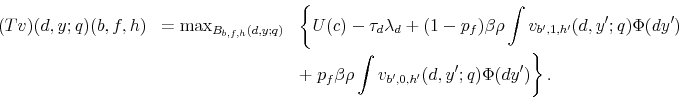
3. For ![]() and
and ![]() (in which case
(in which case ![]() and
and ![]() with probability
with probability ![]() and
and ![]() with probability
with probability ![]() )
)
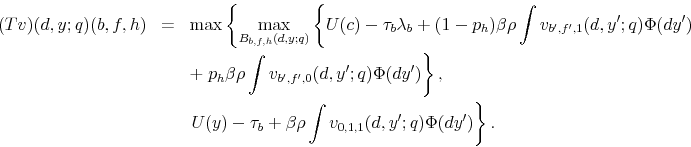
4. For ![]() and
and ![]()
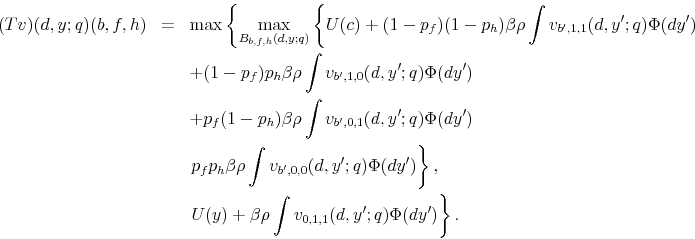
The second part of the definition says that if the household has a good student loan default record and a default flag on credit cards, she will only have the choice to default/repay on student loans since she does not have any credit card debt. Recall that as long as the household carries the default flag in the credit card market, she cannot borrow.
The last two parts represent cases for a household with a bad student loan default record. In these last cases, defaulting on student loans is not an option. In part three, the household has the choice to default on her credit card loan. As before, this is only an option if the associated budget set is non-empty. In the case that all of these sets are empty, then default involuntarily occurs. We assume that when involuntarily default happens it will occur on both markets (this is captured in the second term of the maximization problem).28
In part four, however, there is no choice to default given that ![]() and
and ![]() . Thus,
the household simply solves a consumption/savings decision if the budget set conditional on not defaulting on either loan is non-empty. Otherwise, we assume that default involuntarily occurs. In this case, this happens only in the student loan market since there is no credit card debt.
. Thus,
the household simply solves a consumption/savings decision if the budget set conditional on not defaulting on either loan is non-empty. Otherwise, we assume that default involuntarily occurs. In this case, this happens only in the student loan market since there is no credit card debt.
There are two additional observations: First, in all the cases in which default occurs on credit card debt, the household incurs a utility cost, which is denoted by ![]() . Consistent
with modeling of consumer default in the literature, these utility costs are meant to capture the stigma following default as well as the attorney and collection fees associated with default.29 Second, involuntary default happens when borrowers with very low income realizations and high indebtedness have no choice but default. Note that this case occurs repeatedly in the student loan market, i.e. for a household with
default flag,
. Consistent
with modeling of consumer default in the literature, these utility costs are meant to capture the stigma following default as well as the attorney and collection fees associated with default.29 Second, involuntary default happens when borrowers with very low income realizations and high indebtedness have no choice but default. Note that this case occurs repeatedly in the student loan market, i.e. for a household with
default flag, ![]() . Under these circumstances we assume that the household may discharge her student loan and there is no wage garnishment. This feature captures the fact that in practice, a
small proportion of households partially discharge their student loan debt.
. Under these circumstances we assume that the household may discharge her student loan and there is no wage garnishment. This feature captures the fact that in practice, a
small proportion of households partially discharge their student loan debt.
3.4.2 Financial intermediaries
The (representative) financial intermediary has access to an international credit market where it can borrow or lend at the risk-free interest rate ![]() . The intermediary operates in a
competitive market, takes prices as given, and chooses the number of loans
. The intermediary operates in a
competitive market, takes prices as given, and chooses the number of loans
![]() for all type
for all type
![]() contractsfor each
contractsfor each ![]() to maximize the present discounted
value of current and future cash flows
to maximize the present discounted
value of current and future cash flows
![]() given that
given that
![]() . The period
. The period ![]() cash flow is given by
cash flow is given by
If a solution to the financial intermediary's problem exists, then optimization implies
![]() if
if ![]() and
and
![]() if
if ![]() . If any optimal
. If any optimal
![]() is nonzero then the associate conditions hold with equality.
is nonzero then the associate conditions hold with equality.
3.4.3 Government
The only purpose of the government in this model is to operate the student loan program. The government needs to collect all student loans. The cost to the government is the total amount of college loans plus the interest rate subsidized in college.30 Denote by ![]() this loan price. We compute the per period payment on student loans,
this loan price. We compute the per period payment on student loans,
![]() as the coupon payment of a student loan with its face value equals to its price (a debt instrument priced at par) and infinite maturity (console). Thus the coupon rate equals its yield rate,
as the coupon payment of a student loan with its face value equals to its price (a debt instrument priced at par) and infinite maturity (console). Thus the coupon rate equals its yield rate,
![]() . In practice, this represents the government interest rate on student loans. When no default occurs, the present value of coupon payments from all borrowers (revenue) is equal to the
price of all the loans made (cost), i.e. the government balances its budget.
. In practice, this represents the government interest rate on student loans. When no default occurs, the present value of coupon payments from all borrowers (revenue) is equal to the
price of all the loans made (cost), i.e. the government balances its budget.
However, since default is a possibility, the government's budget constraint may not hold. In this case the government revenue from a household in state ![]() with credit card default status
with credit card default status
![]() , income
, income ![]() and student loan debt
and student loan debt ![]() is given by
is given by
![]() where
where ![]() is the probability that a contract of type
is the probability that a contract of type
![]() experiences default for student loans. The government will choose taxes,
experiences default for student loans. The government will choose taxes, ![]() to recover
the losses incurred when default for student loans arises. The budget constraint is then given by
to recover
the losses incurred when default for student loans arises. The budget constraint is then given by
Taxes are lump-sum and equally distributed in the economy. They are chosen such that the budget constraint balances. We turn now to the definition of equilibrium and characterize the equilibrium in the economy.
3.5 Steady-state equilibrium
In this section we define a steady state equilibrium, prove its existence, and characterize the properties of the price schedule for individuals with different default risks.
-
 ,
,
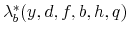 ,
,
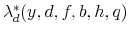 ,
,
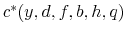 solve the household's optimization problem;
solve the household's optimization problem; 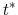 solves the government's budget constraint;
solves the government's budget constraint;-
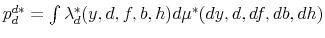 (government consistency);
(government consistency); 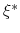 solves the intermediary's optimization problem;
solves the intermediary's optimization problem;-
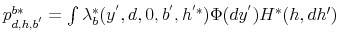 for
for  and
and
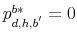 for
for 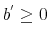 (intermediary consistency);
(intermediary consistency); -
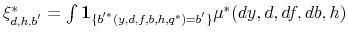 (market clearing conditions (for each type
(market clearing conditions (for each type 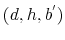 );
); -
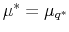 where
where
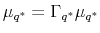 (
(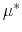 is an invariant probability
measure).
is an invariant probability
measure).
Next, we proceed as following: we provide a first set of results which contains the existence and uniqueness of the household's problem and the existence of the invariant distribution. The second set of results contains the characterization of both default decisions in terms of household characteristics and market arrangements. The last set of results contains the existence of the equilibrium and the characterization of prices. We prove the existence of cross-market effects and characterize how financial arrangements in one market affect default behavior in the other market. All proofs are provided in the Appendix.
Existence and uniqueness of a recursive solution to the household's problem
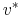 is increasing in
is increasing in 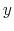 and
and 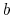 .
.- Default decreases
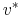 .
. - The optimal policy correspondence implied by
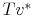 is compact-valued, upper-hemicontinuous.
is compact-valued, upper-hemicontinuous. - Default is strictly preferable to zero consumption and optimal consumption is always positive.
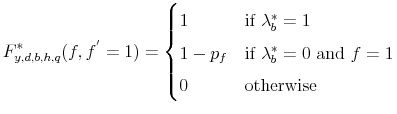
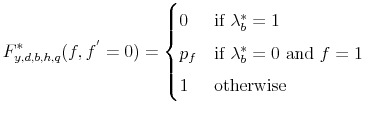
The policy functions determine a transition matrix for the student loan default record,
![H_{y,d,b,f,q}^{*}:H\times H\to[0,1]](img167.gif) which gives the student loan record for the next period,
which gives the student loan record for the next period,
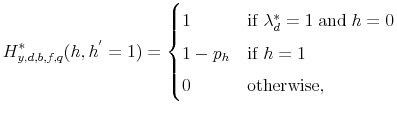
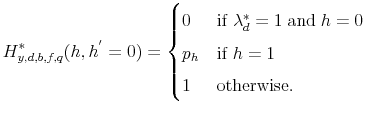
Existence of invariant distribution
Let
![]() be the space of household characteristics. In the following we will write
be the space of household characteristics. In the following we will write
![]() and
and
![]() . Then the transition function for the surviving households' state variable
. Then the transition function for the surviving households' state variable
![]() is given by
is given by
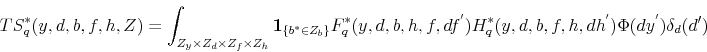
where
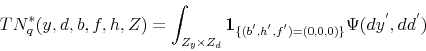
Combining the two transitions, we can define the transition function for the economy,
Given the transition function
4.1 Characterization of the default decisions
We first determine the set for which default occurs for student loans (including involuntary default with partial dischargeability), the set for which default occurs for credit card debt, as well as the set for which default occurs for both of these two loans. Let
![]() be the set for which involuntary default on student loans and partial dischargeability occurs. This set is defined as combinations of earnings,
be the set for which involuntary default on student loans and partial dischargeability occurs. This set is defined as combinations of earnings, ![]() , and student loan amount,
, and student loan amount, ![]() , for which
, for which
![]() in the case
in the case ![]() . For
. For ![]() let
let
![]() be the set of earnings for which the value of defaulting on student loans exceeds the value of not defaulting on student loans. Similarly, let
be the set of earnings for which the value of defaulting on student loans exceeds the value of not defaulting on student loans. Similarly, let
![]() be the set of earnings for which the value of defaulting on credit card debt exceeds the value of not defaulting on credit card debt in the case
be the set of earnings for which the value of defaulting on credit card debt exceeds the value of not defaulting on credit card debt in the case ![]() . Finally, let
. Finally, let
![]() be the set of earnings for which default on both types of loans occurs with
be the set of earnings for which default on both types of loans occurs with ![]() and
and ![]() . Note that the last two sets are defined only in the case
. Note that the last two sets are defined only in the case ![]() , since for
, since for ![]() there is no credit card debt to default on.
there is no credit card debt to default on.
Theorem 3 characterizes the sets when default on student loans occurs (voluntarily or involuntarily). Theorem 4 characterizes the sets when default occurs on credit card debt and Theorem 5 presents the set for which default occurs for both types of loans.
In addition, we show two new results in the literature: 1) the set of default on credit card loans only shrinks when the student loan amount increases and the set of default on both credit card and student loans expands when the student loan amount increases. These findings imply that
individuals with lower levels of student loans are more likely to default only on credit card debt and individuals with higher levels of student loans are more likely to default on both credit card and student loan debt (Theorem 7); and 2) the set of default on credit card
loans is larger when ![]() relative to the case in which
relative to the case in which ![]() . This result implies that
individuals with a default record on student loans are more likely to default on their credit card debt (Theorem 8).
. This result implies that
individuals with a default record on student loans are more likely to default on their credit card debt (Theorem 8).
This last set of theorems shows the importance of accounting for borrowing and default behavior in the student loan market when determining the risk of default on credit card debt. These elements will be considered in the decision of the financial intermediary, which we explain next.
4.2 Existence of equilibrium and characterization
In equilibrium, the credit card loan price vector has the property that all possible face-value loans (household deposits) bear the risk-free rate and negative face-value loans (household borrowings) bear a rate that reflects the risk-free rate and a premium that accounts for the default probability. This probability depends on the characteristics of the student loan markets, such as loan amount and default status, as well as the size of the credit card loan. This result is delivered by the free entry condition of the financial intermediary which implies that cross-subsidization across loans made to individuals of different characteristics in the student loan market is not possible. Each- For any
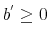 ,
,
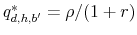 for all
for all 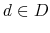 and
and 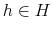 .
. - If the grids of D and
 are sufficiently fine, and
are sufficiently fine, and 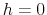 , there are
, there are
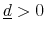 and
and
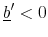 such that
such that
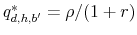 for all
for all
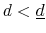 and
and
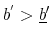 .
. - If the set of income levels for which the household is indifferent between defaulting on credit card debt and any other available option is of measure zero, then
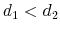 implies
implies
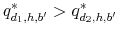 for any
for any  and
and
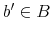 .
. - If the set of income levels for which the household is indifferent between defaulting on credit card debt and any other available option is of measure zero, then
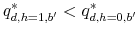 for any
for any 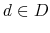 and
and
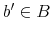 .
.
4.3 The interplay between the two markets
Since the novel feature in this paper is the interaction between different types of unsecured credit markets and its effects on default decisions, we show how the default decision varies not only with the loan amount in the respective market, but also with the loan amount in the other market. We already established that the default probability on credit card loans increases in the amount of student loans. In this section we demonstrate that a borrower with high enough loans will prefer defaulting on her student loans rather than on her credit card debt. Theorem 11 shows that we can find a combination of credit card debt and student loan debt which induces a borrower to default. Furthermore, if the amounts owed to student loans and credit card accounts are higher than the two values in this combination, then the borrower will choose to default on student loans rather than on credit card debt.
To conclude, our theory produces several facts consistent with reality (presented in Section 2): First, the incentive to default on student loans increases in student loan debt burden (debt-to-income ratio), i.e. default on student loans is more likely to occur for individuals with low levels of earnings and high levels of student loan debt. Second, the incentive to default on credit card debt increases in credit card debt, which is consistent with findings in (Chatterjee et al., 2007).
Our theory is innovative because it shows that a household with a high amount of student loans or with a record of default on student loans is more likely to default on credit card debt. This result emphasizes the importance of accounting for other markets in which the individual participates when studying default on credit card debt. Finally, we show that while a high student loan debt burden is necessary to induce default on student loans, this effect is amplified by high indebtedness in the credit card market. The financial arrangements in the two markets, and in particular the differences in bankruptcy rules and default consequences between the two types of credit, certainly play an important role in shifting default incentives. In the next section we quantify the role each of these two types of credit played in the increase in student loan default rates in recent years.
5.1 Mapping the model to the data
There are four sets of parameters that we calibrate: 1) standard parameters, such as the discount factor and the coefficient of risk aversion; 2) parameters for the initial distribution of student loan debt and income; 3) parameters specific to student loan markets such as default consequences and interest rates on student loans; and 4) parameters specific to credit card markets. Our approach includes a combination of setting some parameters to values that are standard in the literature, calibrating some parameters directly to data, and jointly estimating the parameters that we do not observe in the data by matching moments for several observable implications of the model.
Our model is representative for college-educated individuals who are out of college and have student loans. We calibrate the model to 2004-2007 and use the Survey of Consumer Finances in 2004 and 2007 for moments in the distribution of income, student loan, and credit card debt. The sample consists of young households (aged 20-30 years old) with college education and student loan debt. The age group is specifically chosen to include college dropouts and recent graduates. All individuals are out of college and in the labor force. The sample sizes are 466 and 430, respectively. All numbers in the paper are provided in 2004 dollars.31
The model period is one year and the coefficient of risk aversion chosen (![]() ) is in the range of estimates suggested by (Auerbach & Kotlikoff,
1987) and (Prescott, 1986). The discount factor (
) is in the range of estimates suggested by (Auerbach & Kotlikoff,
1987) and (Prescott, 1986). The discount factor (![]() ) is also standard in the literature. We set the interest rate on student loans
) is also standard in the literature. We set the interest rate on student loans ![]() as the most representative rate for student loans.32 The annual risk-free rate is set equal to
as the most representative rate for student loans.32 The annual risk-free rate is set equal to ![]() , which is the average return on capital reported by (McGrattan & Prescott,
2000). Table 1 presents the basic parameters of the model. We set the transaction cost in the credit card market to 0.053 following (Evans & Schmalensee, 1999). We estimate the survival probability
, which is the average return on capital reported by (McGrattan & Prescott,
2000). Table 1 presents the basic parameters of the model. We set the transaction cost in the credit card market to 0.053 following (Evans & Schmalensee, 1999). We estimate the survival probability ![]() to match average years of life to 40.33 The probabilities to keep default flags in the two markets
are set to
to match average years of life to 40.33 The probabilities to keep default flags in the two markets
are set to ![]() for credit card debt and
for credit card debt and ![]() for student loan debt
to match average years of punishments, ten for the credit card market and two for the student loan market. The first is consistent with estimates in the literature (see (Chatterjee et al., 2007) and (Livshits et al., 2007)) and the second is
consistent with regulations from the DoE. Specifically, it takes one period before borrowers restructure and reorganize and another period before completing loan rehabilitation. Borrowers must make 10 consecutive payments to rehabilitate.
for student loan debt
to match average years of punishments, ten for the credit card market and two for the student loan market. The first is consistent with estimates in the literature (see (Chatterjee et al., 2007) and (Livshits et al., 2007)) and the second is
consistent with regulations from the DoE. Specifically, it takes one period before borrowers restructure and reorganize and another period before completing loan rehabilitation. Borrowers must make 10 consecutive payments to rehabilitate.
| Parameter: Name | Value | Target/Source |
| Coef of risk aversion: |
2.00 | standard |
| Discount factor: |
0.96 | standard |
| Interest on student loans: |
0.068 | Dept. of Education |
| Risk-free rate: |
0.04 | Avg rate 2004-2007 (FRB-G19) |
| Transaction cost: |
0. 053 | Evans and Schmalensee (1999) |
| Prob to keep CC default flag: |
0.9 | Avg years of punishment=10 |
| Prob to keep SL default flag: |
0.5 | Avg years of punishment=2 |
| Survival probability: |
0.975 | Avg years of life=40 |
| Wage garnishment if SL default: |
0.028 | Default rate on SL =5% |
| Utility loss from CC default: |
19.5 | CC debt/income ratio=0.057 |
We assume that the default flag is immediately removed after
rehabilitation. We estimate the wage garnishment ![]() and the utility loss from defaulting on credit card loans
and the utility loss from defaulting on credit card loans ![]() to match the two year cohort default rate for student loans of 5 percent during 2004-2006 (see Figure 2 in section 2.2) and the credit card debt to income ratio in our sample from SCF.34
to match the two year cohort default rate for student loans of 5 percent during 2004-2006 (see Figure 2 in section 2.2) and the credit card debt to income ratio in our sample from SCF.34
We use the joint distribution of student loan debt and income for young households as delivered by the SCF 2004 and SCF 2007. The mean of income is $51,510 and the standard deviation $41,688. The mean amount of student loan debt owed per period is $2,741 and the standard deviation $2,400. We
assume a log normal distribution with parameters
![]() on
on
![]() .35 We pick the grid for
assets consistent with the distribution of credit card debt in the SCF 2004-2007, for which the mean and standard deviations are $2,979 and $4,934, respectively.
.35 We pick the grid for
assets consistent with the distribution of credit card debt in the SCF 2004-2007, for which the mean and standard deviations are $2,979 and $4,934, respectively.
5.2.1 Model versus data
The model does a good job of matching debt burdens in the two markets for borrowers in the SCF 2004-2007. It delivers a credit card debt burden of 0.056 and a student loan debt burden of 0.054. The data counterparts are 0.058 and 0.054, respectively. The model predicts that 18 percent of individuals have negative assets (without including student loans). The data counterpart is 34 percent.36
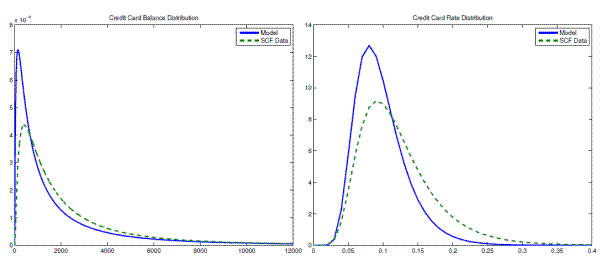
Also, the model replicates the distribution of credit card debt and credit card interest rate quite well , as evident in Figure 3. The model delivers an average credit card debt of $2,990 and an average credit card interest rate of 9.8 percent. The data counterparts are $2,979 and 12 percent, respectively. The interest rate in the model is lower compared to the credit card rate in the data since the interest rate in the model represents the effective rate at which borrowers pay, whereas in the data borrowers pay the high rate only in the case that they roll over their debt.The default rate on credit card debt is 0.3 percent, which is in the range used in the literature (see (Athreya et al., 2009)). Lastly, taxes to cover defaulters in the economy are insignificant (3.615e-004 percent of income, on average).
5.2.2 Credit card default and pricing
We study default behavior in the two markets across individual characteristics (student loan amount, ![]() , credit card debt,
, credit card debt, ![]() , and income,
, and income, ![]() ). Table 2 shows these findings across individuals with high levels of
). Table 2 shows these findings across individuals with high levels of ![]() ,
, ![]() ,
, ![]() (defined as the top 50th percentile) versus individuals with low levels of
(defined as the top 50th percentile) versus individuals with low levels of ![]() ,
, ![]() ,
, ![]() (defined as the bottom 50th percentile) and Figure 4
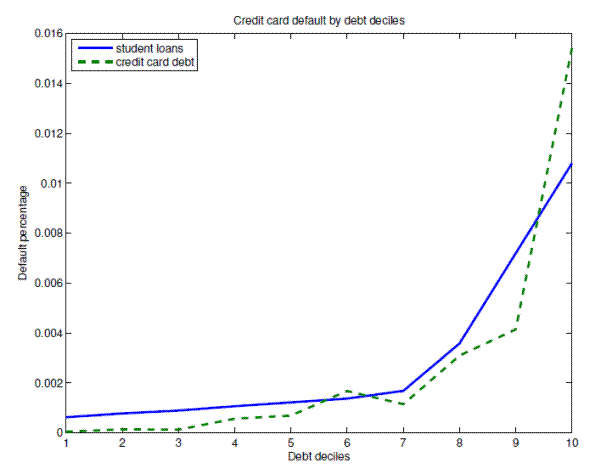
shows credit card default rates by deciles of student loan and credit card debt.
(defined as the bottom 50th percentile) and Figure 4
shows credit card default rates by deciles of student loan and credit card debt.
| Characteristic | Low | High | |
| Default SL | SL debt | 0 | 68% |
| Default SL | CC debt | 6 | 35% |
| Default SL | Income | 8 | 27% |
| Default CC | SL debt | 0 | 28% |
| Default CC | CC debt | 0 | 45% |
| Default CC | Income | 1 | 1% |
Our results are consistent with data facts presented in Section 2.1. Default rates on credit card debt are higher for individuals with high levels of both types of loans. Individuals with high levels of credit card debt are more likely to default on their credit card debt (consistent with fact number 2 in Section 2.1). In addition, having high levels of student loans makes borrowers more likely to default on credit card loans. Recall that our theory predicts that high levels of student loans decrease the incentive to default only on credit card debt but increase the incentive to default on both types of loans. Quantitatively, the second effect dominates. In our model, defaulters on credit card loans default on both their college loans and their credit card debt. As evidenced in Figure 4, default on credit card debt is more sensitive to the debt in the credit card market, but student loan amounts have important effects on the incentive to default on credit card debt.
Lastly, the likelihood of default on credit card debt is higher for individuals with low income relative to that of individuals with high income. This finding is consistent with fact 3 in Section 2.1. However, for the most part, the literature on unsecured default delivers the opposite result. The intuition behind this previous result in the literature is that agents with relatively low income levels stand to lose more from defaulting on their credit card debt relative to individuals with high income levels, for whom the penalties associated with default are less costly in relative terms. In our model, however, individuals also possess other types of loans, i.e. student loans with different default consequences; individuals in our model make a joint default decision. It turns out that this interaction is key in delivering the default probability in the credit market to decrease in income. This finding shows the importance of accounting for other types of loans when analyzing default behavior, a feature that is absent in previous models of consumer default. Details of the interaction between the two markets together with the importance of income for default are discussed in Section 5.2.4.
Consistent with our results on the individual probability of default for credit cards, the model delivers a pricing scheme of credit card loans based on individual default risk as proxied by the size of the loan, the amount owed in the student loan market, and the default status in the student
loan market. Recall that our theoretical results show that the interest rate on credit card debt increases in both amounts of loans and is higher for individuals with a default flag on student loans. These results are consistent with fact number 4 in Section 2.1. Table 3 summarizes our quantitative results regarding credit card loan pricing across these individual characteristics.
| Characteristic | Low | High |
| CC debt | 9 | 35% |
| SL debt | 9 | 44% |
| Income | 9 | 8% |
First, agents with high levels of credit card debt (top 50th percentile) have a credit card rate of 10.1 percent and agents with low credit card debt (bottom 50th percentile) have a credit
card rate of 9.35 percent. Second, agents with high levels of student loans receive a credit card rate of 10.3 percent and agents with low levels of student loans receive a credit card rate of 9.44 percent. The wedge in the interest rates accounts for the gap in the
probabilities of default between these two groups (presented in Table 2). Finally, defaulters on student loans (![]() have a credit card rate of
10 percent and nondefaulters on student loans
have a credit card rate of
10 percent and nondefaulters on student loans ![]() have a credit card rate of
9.7 percent. This last result is driven by the fact that defaulters on student loans have a higher likelihood of default on credit card debt relative to non-defaulters in the student loan
market. There are two main reasons behind this behavior: first, defaulters on student loans do not have the option to default on their student loans, so if they must default they do so in the credit card market; and second, in addition to being asked to repay their student loans, individuals with a
default record on student loans also have part of their earnings garnished. We conclude that the amount of student loan debt and the default status on student loans represent important components of credit card loan pricing. These three findings represent the quantitative counterpart of our
theoretical results in Theorem 10. In addition, our quantitative analysis predicts that agents with low income receive higher rates, on average, than agents with high income, as Table 3 shows. This is a direct implication of the
differences in default rates across income groups presented in Table 2.
have a credit card rate of
9.7 percent. This last result is driven by the fact that defaulters on student loans have a higher likelihood of default on credit card debt relative to non-defaulters in the student loan
market. There are two main reasons behind this behavior: first, defaulters on student loans do not have the option to default on their student loans, so if they must default they do so in the credit card market; and second, in addition to being asked to repay their student loans, individuals with a
default record on student loans also have part of their earnings garnished. We conclude that the amount of student loan debt and the default status on student loans represent important components of credit card loan pricing. These three findings represent the quantitative counterpart of our
theoretical results in Theorem 10. In addition, our quantitative analysis predicts that agents with low income receive higher rates, on average, than agents with high income, as Table 3 shows. This is a direct implication of the
differences in default rates across income groups presented in Table 2.
5.2.3 Student loan default
As Table 2 shows, default rates on student loans are larger for individuals with high amounts owed to the student loan program relative to those with low amounts of student loans. The gap between the default rates for the two groups is significant. Similarly, the default rates for individuals with low income levels are higher than those for individuals with high levels of income, and the difference between the two groups is significant. Overall, the default probability for student loans is higher for individuals with relatively high student loan debt burdens in the student loan market, a fact consistent with the data (fact number 1 in Section 2.1). At the same time, individuals with credit card debt have higher default rates for student loans (5.8 percent) relative to individuals with no credit card debt (4.8 percent). However, an interesting finding is that conditional on having credit card debt, the model delivers that individuals with relatively low levels of credit card debt have a default rate of 6.3 percent, whereas individuals with have high levels of credit card debt have a default rate of 5.2 percent. We further investigate this issue. Figure 5 shows default rates on student loans across deciles of credit card and student loan debt. We find that while default on student loans increases in student loan debt, it is hump-shaped in credit card debt. This result could be interpreted in two ways: individuals use their credit card debt to repay student loans or individuals with high credit card debt levels are individuals with low risk, on average. We analyze this issue in more detail in the next section, which focuses on the interaction between the two markets.
5.2.4 The interplay between the two markets
We turn now to the interaction between the two markets and its effect on default behavior, the main focus of the paper. Recall from Theorem 11 that in any steady-state equilibrium, we can find a combination of student loans and credit card debt such that individuals default. Furthermore, if loan amounts in both markets are larger than these two levels of debt, then default occurs first on student loans. Our quantitative analysis in this subsection complements this theoretical result.
First, recall that in our model, everyone who defaults on credit card debt also defaults on student loan debt.
| 0.65% | 0.85% | 0.76% | |
| NA | 0.00% | 0.23% | |
| 8.37% | 14.8% | 12.7% | |
| NA | 0.12% | 1.1% |
There is no borrower who strictly prefers defaulting on credit card debt to defaulting on student loans. Table 4 shows our findings regarding
default behavior across groups of student loan and credit card debt. We divide individuals in two groups based on the amount owed to the student loan program, ![]() (low and high defined as before)
and in three groups based on the credit card debt,
(low and high defined as before)
and in three groups based on the credit card debt, ![]() : one group with positive assets and two groups with negative assets (low and high defined as before).
: one group with positive assets and two groups with negative assets (low and high defined as before).
We find that individuals with no credit card debt have lower default rates on student loans than individuals with credit card debt, regardless of the amount owed in the student loan market. Second, conditional on having low levels of student loan debt, individuals with low levels of credit card debt do not default on their credit card debt, but rather default on their student loans (if they must default). The benefit of discharging their credit card debt upon default is too small compared to the large cost of being excluded from borrowing. At the same time, the penalties associated with default in the student loan market are not contingent on their credit card debt. Similarly, conditional on having high levels of student loan debt, individuals with high levels of credit card debt have a higher likelihood of defaulting on their credit card debt. Third, the gap between default rates by student loan amounts is higher for individuals with low levels of credit card debt relative to individuals with high levels of credit card debt.
These findings confirm our conjecture that while both types of debt increase incentives to default in both credit markets, some individuals may substitute credit card debt for student loan debt, in particular individuals with high levels of student loans. But these individuals with high levels
of student loans represent high risk for the credit card market and therefore receive worse terms on their credit card accounts. More expensive credit card debt together with the need to access the credit card market may increase incentives to default on student loans. We further examine which
individuals can use the credit card market to pay off student loan debt and which ones are defaulting even more on their student loans because of more (and expensive) credit. We determine combinations of student loans and credit card debt levels such that above these levels of debt in the two
markets, the incentives to default on student loans increase rapidly and no one strictly prefers to default on their credit card debt. This is the quantitative counterpart of our main theoretical result (Theorem 11), which showed that there exists a combination of student loans (![]() and credit card debt (
and credit card debt (![]() ) such that above this threshold
) such that above this threshold ![]() individuals may default first on their student loans. We determine such
individuals may default first on their student loans. We determine such ![]() )
combinations next. In addition, our quantitative analysis establishes that under these thresholds
)
combinations next. In addition, our quantitative analysis establishes that under these thresholds ![]() and
and ![]() , students may be able to use the credit card market to pay off their student loan debt. These findings are evidenced in Figure 6, which
illustrates the default rates in the two markets conditional on both types of debt.
, students may be able to use the credit card market to pay off their student loan debt. These findings are evidenced in Figure 6, which
illustrates the default rates in the two markets conditional on both types of debt.
Note in the left panel of Figure 6 that for a borrower in the 10th decile of student loans, there is a sharp increase in student loan default once the borrower has more credit card debt than in the 5th decile. Similarly, for a borrower in the 9th (8th) decile of student loans, there is a rapid increase in student loan default once the borrower has more debt than in the 6th (8th) decile of credit card debt. Below these levels of credit card debt, however, default on student loans is quite flat across deciles of credit card debt. These findings imply that before hitting a critical credit card debt level, individuals are able to use the credit card market to keep their student loan default rate low. Once they borrow more than this threshold level, their default on student loans is amplified by their credit card debt. This threshold of credit card debt (or critical point) is decreasing with student loan debt, in part because the interest rates on credit card loans increase with student loan levels.
An interesting result is that for borrowers with intermediate levels of student loan debt (5th and 6th deciles) default on student loans is hump-shaped in credit card debt levels.
This result suggests that these borrowers may use credit card debt to pay off their student loans. Their student loan levels are high enough for them to need to borrow in the credit card market, but not high enough to induce high default incentives; at the same time, terms on credit card accounts for these individuals are good enough for them to be able to use the credit card market to keep student loan default rates low. For individuals with very low levels of student loan debt, however, default on student loans is flat across deciles of credit card debt. Their incentive to default on student loans is very low and credit card debt does not affect this decision. The combination of these factors delivers the hump-shaped student loan default pattern across levels of credit card debt (Figure 6). This pattern is a result of a composition effect in addition to a strategic default effect. Borrowers with high levels of credit card debt are mostly low risk individuals with low levels of student loans. They receive lower interest rates and have higher levels of credit card debt in equilibrium. Finally, credit card default increases with both levels of debt (right panel in Figure 6). As expected, a lower credit card level is needed to trigger default on credit card debt for individuals with high levels of student loans relative to individuals with low levels of student loans. Consistent with our theory, all defaulters on credit card debt also default on their student loans.
We conclude that, on average, having debt in one of the two markets amplifies the incentives to default in the other market. However, while student loan debt increases credit card default regardless of loan amount, debt in the credit card market amplifies the incentive to default on student loans only for certain combinations of debt. More importantly, some individuals may use the credit card market to reduce their default on student loans. On the one hand, participating in the credit card market and at worse terms pushes borrowers towards more default on their student loans. On the other hand, taking on credit card debt helps student loan borrowers smooth consumption
and pay their student loan debt. Certainly these channels work differently for individuals with different levels of income. We further investigate this issue and present our findings in Figure 7. First, we find that individuals with medium levels of income (top panel) have higher default rates on student loans than individuals with low or high levels of income; in addition, having credit card debt further increases default on student loans for most borrowers in this income group. Second, individuals with high income levels (middle panel) have lower default rates on student loan debt. As expected, they need larger amounts for both types of loans to default and their incentives to default on student loans are amplified by having more credit card debt. Third, an interesting result is that for individuals with low levels of income (bottom panel), incentives to default on student loans are not amplified by credit card debt. On the contrary, poor individuals with large levels of student loans seem to primarily use credit card debt to lower default on student loans. Notice the decline in default rates for student loans across deciles of credit card debt for top deciles of student loans, shown in the bottom panel.
Overall, individuals with medium levels of income default the most on their student loans (Figure 8, left panel). Those with high levels of income are not financially constrained and the wage garnishment punishment is too costly for them to warrant default on their student loans, while individuals with low levels of income would rather use the credit card market to pay off their student loans. Some of these low income individuals may also default on their credit card debt (Figure 8, right panel). We conjecture that various terms and changes in the credit market affect the default behavior in the student loan market differently across income groups, especially during the Great Recession, when credit card terms worsened and income was negatively affected. We analyze these issues in the next section.
5.3 Analysis: Recent trends in the two markets
In this section, we analyze how the interaction between student loan and credit card markets affects default behavior in normal times (2004-2007) and in the Great Recession (2007-2010). Recall from Section 2.2 that for both periods, student loans increased steadily (about 21 percent in a three year period in both normal times and in the Great Recession). However, the credit card market expanded during normal times and contracted during the Great Recession. Specifically, the credit card limit increased by 30 percent during normal times and declined by about the same percentage during the Great Recession; also, transaction costs and fees increased during the Great Recession. At the same time, the risk-free rate declined by 1.5 percent from 2007 to 2010, on average affecting interest rates in the credit card market. In addition, while the income of young borrowers did not change much during 2004-2007, it declined significantly (by 19 percent on average) during the Great Recession. Lastly, recall that the national default rate for student loans increased by 1.7 percentage points during normal times (from 5 percent in 2004-2006 to 6.7 percent in 2007) and further increased by more than two percentage points during the Great Recession (to 8.95 percent in 2009-2010).37
We conduct several experiments to understand how each of these changes affected default behavior. Specifically, in Section 5.3.1 we 1) quantify the share of the increase in student loan default rates that can be explained by the increase in student loans alone; 2) quantify the effects of the expansion of the credit card market on student loan default rates in normal times and 3) quantify the effects of the Great Recession on student loan default. In Section 5.3.2 we first quantify the share of the increase in student loan default rates during the Great Recession that can be explained by worse labor outcomes for college-educated individuals and the share that can be explained by the changes in the credit card market during the Great Recession. Finally, we disentangle the effects of each channel in the credit card market and study whether there is an amplification effect on student loan default from the Great Recession.
5.3.1 Debt and default: Normal times versus the Great Recession
Table 5 shows our findings for the first set of experiments: the first column represents the benchmark economy, while the second column shows the results from experiment 1 (E1-d only), which assumes an increase in student loan debt by 20.7% on average, relative to
the benchmark economy (fact 2 in Section 2.2). Columns three and four show the results for experiment 2, normal times (E2-Normal) and experiment 3, Great Recession (E3-GR). In experiment 2 we suppose an increase in credit card limits by 30 percent (fact 5 in Section 2.2) in addition to the increase
in student loan debt in experiment 1. To put discipline in this exercise we model the expansion in the credit card market via a decrease in transaction cost, which is exogenous in the economy. We obtain a transaction cost of 3.4 percent (consistent with the number used in (Athreya, 2008))compared to 5.3 percent in the benchmark economy. In experiment 3, Great Recession, we suppose a decline in income by 19 percent, on average, together with a decline in the risk-free rate of 1.5 percent and a decline in the credit card limit by 30 percent.
The decline in income of 19 percent is obtained using the distribution of income in SCF 2010 together with unemployment rates, duration, and eligibility from CPS 2008-2009 (fact 3 in Section 2.2). The decline in credit card limit is modeled via an increase in the transaction cost. We know that
transaction costs and fees increased during the Great Recession, but there is no estimate in the literature, in particular for the group of interest in our paper. Similarly to experiment 2, to put discipline on this exercise we find the transaction cost that delivers a 30 percent decline in credit
card limits (fact 5 in Section 2.2). We obtain a transaction cost of 6.8 percent (compared to 5.3 percent in the benchmark economy).
| Baseline | E1-d only | E2-Normal | E3-GR | |
| SL default | 5.00% | 6.50% | 6.80% | 8.98% |
| CC default | 0.30% | 0.40% | 0.30% | 1.22% |
| Perc with neg assets | 18.00% | 16.00% | 20.00% | 17.00% |
| CC interest rate | 9.80% | 9.83% | 7.90% | 11.20% |
| CC balance | $2,920 | $2,541 | $3,239 | $1,963 |
| Tax rel to bench | - | 1.41% | 1.52% | 1.71% |
Results show that the expansion of both markets fully accounts for the increase in student loan default during normal times, with most of the increase due to the increase in student loan debt (88 percent). The expansion of credit card debt for young borrowers contributes to the increase in default on student loans during this period, although the effect is small. On the one hand, more people are borrowing, and having credit card debt increases the incentive to default on student loan debt. On the other hand, the average level of credit card debt is higher, but the average interest rate on credit cards is lower. This fact, in turn, dampens the effect of credit card debt on default incentives. Recall that individuals with high levels of student loans who are more likely to default on student loan debt borrow lower amounts of credit card debt, on average. At the same time, for individuals with medium and low levels of student loans, high credit card debt does not amplify the incentives to default on student loan debt. The accumulation of student loan debt induces a higher risk in the credit card market, but the effect is small in equilibrium. The credit card market contracts and the average credit card rate increases slightly as a result of relatively riskier borrowers in the credit card market (i.e. borrowers with higher levels of student loan debt and student loan default flags).
From experiment 3, we observe that during the Great Recession, default rates on both student loans and credit card debt increased significantly. Fewer borrowers access the credit card market and they borrow less, on average, relative to the benchmark economy. To account for the extra risk, the interest rate increases significantly relative to the benchmark economy. There are several forces at play: young borrowers have worse labor outcomes, and at the same time there is a higher transaction cost but also a lower risk-free rate in the economy. These three channels may have opposite effects on default rates. In the next section we disentangle these effects.
5.4 Great Recession channels: Implications for default
Table 6 presents our results regarding the effects of various channels during the Great Recession. The first column (experiment E3a-y only) supposes only a decline of 19 percent relative to the benchmark economy, while the second column (experiment E3b-d and y)
supposes a decline of 19 percent relative to the benchmark economy in addition to an increase in student loan debt by 20.7 percent. In experiments E3c and E3d we disentangle the effects coming from the credit card market. We consider the same changes as in experiment E3b together with a decline in
the credit card limit by 30 percent (E3c) or a decline in the risk-free rate of 1.5 percent (E3d).
| E3a-y only | E3b-d and y | E3c-GR | E3d-GR | |
| SL default | 7.1% | 8.98% | 8.68% | 9.29% |
| CC default | 0.84% | 1.26% | 1.35% | 1.1% |
| Perc with neg assets | 17.7% | 15.5% | 14.3% | 19.5% |
| CC balance | $2,513 | $1,992 | $1,701 | $2,409 |
| CC interest rate | 10.6% | 11.24% | 12.9% | 9.5% |
| Tax rel to bench | 1.24% | 1.71% | 1.65% | 1.81% |
Our findings show that the decline in income alone induces a significant increase in default rates in both markets, relative to the benchmark economy. This effect on default rates is larger than the effect induced by an increase in student loan debt in experiment 1. Consequently, the interest rate in the economy is much higher, on average, than in experiment 1. However, the credit card market does not shrink as much as in experiment 1. About the same percentage of individuals as in the benchmark economy take credit card debt given worse income levels, on average, but they borrow at higher rates, resulting from the fact that there is more default in both markets. Recall that the credit card default risk and pricing also depend on the default status for student loans. Experiment 3b shows the results for the cumulative effect of a decline in income and an increase in student loan levels. Note that there is an amplification effect for default behavior in both markets. The combination of lower income levels and higher student loan levels induces higher default rates than simply adding the two effects together. Taking on more student loan debt when post-college job prospects are worse adds extra risk. Consequently, the credit card market shrinks significantly, with only 15.5 percent of individuals borrowing, and the interest rate increases to 11.24 percent.
An interesting result is that the effects on default rates delivered in experiment 3b are the same as those delivered in experiment 3, in which all three channels in the Great Recession are accounted for. This result suggests that most of the risks in the two credit markets are induced by the combination of lower income and higher student loan amounts for young borrowers. When a higher transaction cost and a lower risk-free interest rate are added, there is not much change in terms of borrowing and default behavior on credit card loans and default behavior on student loans. However, as experiments 3c and 3d show, an increase in the transaction cost in column 3 (to 6.8 percent) and a decline in the risk-free interest rate in column 4 (by 1.5 percentage points) impact borrowing and default behavior but with opposite signs. An increase in transaction costs delivers an increase in credit card default but a decrease in student loan default (by 0.3 percentage points). Having more expensive credit card loans makes borrowers borrow less and lower amounts, on average, which in turn lowers their incentives to default on student loans (for the same amount of student loan debt). This effect of a higher transaction cost induces further tightening of the credit card market and higher interest rates. In contrast, the effect coming from a lower risk-free rate relaxes the credit card market; it induces lower interest rates, more borrowers and lower default rates in the credit card market. This change, however, induces a substantial increase in student loan defaults (from 8.98 percent to 9.29 percent). This suggests that a decrease in the risk-free interest rate in the economy induces a transfer of risk from the credit card market to the student loan market, whereas the opposite is true when transaction costs increase in the economy. Overall, the two effects combined allow for more borrowing in the credit card market (17 percent compared to 15.5 percent in experiment 3b) and induce a slightly lower default rate for credit card loans.38
We conclude that the accumulation of debt in the student loan market increased the risk of default in the credit card market, and in particular in the Great Recession when young borrowers faced worse labor income outcomes. At the same time, the expansion of the credit card market induced more default on student loans. A change that relaxes the credit card market during the Great Recession transfers risk from the credit card market into the student loan market, significantly increasing student loan default, whereas the opposite is true when the credit card market tightens. In the former case, borrowers receive lower prices on the same loan sizes, whereas in the latter they receive higher rates on the same loan sizes. More or less expensive credit card debt affects borrowing behavior in the credit card market and consequently affects default behavior in the student loan market.
5.5 Policy analysis: Income contingent repayment
There are currently four versions of student loan repayment plans based on income.39 All of these plans assume loan payments as a percentage of discretionary income. Borrowers who earn less than 150 percent of the poverty line have a loan payment of zero (or $5 depending on the income plan type).40 Borrowers who have an income higher than this threshold pay a fraction of their income (between 10-25 percent, depending on the income plan type). The income contingent repayment plan (ICR) provides more flexibility in eligibility criteria and therefore is used in the current experiment. According to the ICR, borrowers pay 20 percent of discretionary income and any remaining debt after 25 years in repayment is forgiven, including both principal and interest. When the ICR was introduced in 2010 (The Health Care and Education Reconciliation Act of 2010), it resulted in a lot of discussions among policy makers, in particular regarding its cost.
We analyze the quantitative implications of the ICR in both normal times and in the Great Recession. Our analysis takes into account the fact that the amount of student loans discharged is recovered through taxes. Note that our welfare calculations represent an upper bound since we ignore the fact that in reality, other versions of income repayment plans already existed.41
We conduct two experiments: we introduce the ICR in the benchmark economy and then in the Great Recession economy with relatively higher levels of student loans, lower levels of income, and a tight credit card market. We find that dischargeability is high in both experiments and therefore taxes are high when the ICR is introduced: 21 percent of borrowers do not fully repay their student loans when the ICR is introduced in the benchmark economy and 28 percent do not repay the full amount in the Great Recession. With higher amounts to pay and worse income, on average, more borrowers cannot finish their payments under the ICR during the Great Recession. This effect induces a decline in welfare. At the same time, the ICR completely eliminates the risk in the credit card market. The credit card default rate is 0 in both experiments. This effect induces an increase in welfare. Given a relatively higher risk in the credit card market in the Great Recession than in the benchmark economy, this last effect is more important, quantitatively, when the ICR is introduced in the Great Recession economy. More people are borrowing in the credit card market and at lower rates. Participation in the credit card market increases to 30 percent when the ICR is introduced in the benchmark economy and to 45 percent when it is introduced in the Great Recession. Overall, we find that the introduction of the ICR in the benchmark (normal) economy induces a small decrease in welfare (by 0.14 percent), but it induces a significant improvement in welfare when introduced in the Great Recession economy (by 2.86 percent).42
We find that the ICR induces important redistributional effects (see Table 7). In the Great Recession for instance experiment poor borrowers (bottom quartile of income) gain more than 10 percent and those within the top quartile of student loans gain more than 20 percent. Poor borrowers with high levels of student loans benefit the most from discharging their loans after 25 years of repayment under the ICR. At the same time, the other groups lose from the ICR implementation, given that now they have to pay higher taxes to pay for delinquent borrowers. As expected, welfare changes are monotonous in student loan levels, with individuals in the bottom quartile losing the most. However, that is not the case by income groups: middle earners (quartiles 2 and 3 of income) lose the most from the policy.43 They lose about 2 to 2.32 percent while borrowers in the top income quartile only lose 0.35 percent. Middle earners repay most of their student loans under the ICR without discharging; at the same time, they do not benefit from paying their loans faster (as opposed to rich individuals), and they pay higher taxes. They do not have the option to delay their repayment via default either. Recall that middle earners default the most under standard 10-year repayment. The same pattern across income and student loan groups emerges when the ICR is introduced during normal years, although the effects are smaller (Table 7). To conclude, while the ICR improves welfare when it is introduced during the Great Recession, it induces a decline, although small, when it is introduced during normal times. The income contingent repayment policy induces significant redistribution effects, with poor individuals with large levels of student loan debt benefiting from the policy and middle income individuals with low and medium levels of student loan debt being hurt the most.
| Quartile | Q1 | Q2 | Q3 | Q4 |
| Great Recession: Income | +10.73% | -2% | -2.32% | -0.35% |
| Great Recession: Student loan | -6.27% | -5.07% | -3.62% | +21.8% |
| Normal: Income | +0.61% | -0.25% | -0.39% | +0.07% |
| Normal: Student loan | -0.29% | -0.19% | -0.14% | +3.1% |
6 Conclusion
We developed a quantitative theory of unsecured credit and default behavior of young U.S. households based on the interplay between two forms of unsecured credit, and we analyzed the implications of this interaction for default incentives. Our theory is motivated by facts related to borrowing and repayment behavior of young U.S. households with college and credit card debt, and in particular by recent trends in default rates for student loans. Specifically, different financial market arrangements and in particular, different bankruptcy rules in these two markets alter incentives to default.
We built a general equilibrium economy that mimics features of student and credit card loans. In particular, our model accounts for 1) bankruptcy arrangement differences between the two types of loans and 2) differences in pricing default risk in the two markets. Our theory is consistent with observed borrowing and default behavior of young U.S. households: incentives to default on student loans increase in student loan debt and incentives to default on credit card debt increase in credit card debt.
In addition, our model produces four new results in the literature. First, the likelihood to default on credit card debt increases with the amount of student loans. Second, individuals with a default flag in the student loan market have higher default probabilities in the credit card market than individuals who have not defaulted on their student loans. Third, in the quantitative part of our paper we show that individuals with high levels of income are less likely to default in both the student loan and the credit card markets relative to individuals with low levels of income. While this result is intuitive and consistent with empirical evidence, it is not a straightforward result from models of unsecured credit. The fact that individuals in our model also have other types of loans produces this result. Lastly, having more credit card debt induces higher incentives to default in the student loan market. These four results reveal the importance of accounting for interactions between different financial markets in which individuals participate when one analyzes default behavior for unsecured credit.
Our main contribution is that we demonstrate that differences in market arrangements can lead to amplification of default in the student loan market. Our main theoretical result shows that a borrower with high enough student loan debt and credit card debt chooses to default in the student loan market rather than in the credit card market. We further explore this issue in the quantitative part of the paper and show that while an increase in student loan debt is necessary to deliver an increase in the default rate on student loans, this effect is amplified by the expansion of the credit card market in normal times. An interesting finding is that once poor individuals (bottom quartile of income) access the credit card market, they can actually use it to reduce their default incentives on student loans. Good credit card terms for these individuals are essential. Overall, individuals with medium levels of income (quartiles 2 and 3 of income) default the most on their student loans. We find that the decline in income levels of young borrowers during the Great Recession significantly increased the risk in both the student loan and credit card market. At the same time, changes in the credit card market during the Great Recession did not much affect the default behavior: a decrease in the risk-free interest rate that relaxes credit card markets during the Great Recession transfers risk from the credit card market into the student loan market, significantly increasing student loan default, but the opposite is true when the credit card market tightens (transaction costs increase). Overall, the two effects cancel each other.
Lastly, we explore the policy implications of our model and study the impact of income contingent repayment plans on student loans. We find that the proposal induces a welfare gain of 2.86 percent when it is available in a Great Recession economy where individuals face worse job outcomes and tight credit markets. However, the policy has a (small) negative welfare effect when it is available in normal times. The policy induces significant redistributional effects, with poor borrowers with large levels of student loans benefiting the most and middle earners losing the most. Middle earners are precisely the group who choose to default the most under the standard repayment scheme. Our findings suggest that an income contingent repayment scheme is important in the current market conditions when, due to a significant increase in college costs, students borrow more than ever in both the student loan and the credit card markets, and at the same time, they face stringent terms on their credit card accounts and worse job outcomes.
References
College Board (2013). Trends in student aid. College Board Publication.
DoE (2014): "Student Loans Overview: Fiscal Year 2014 Budget Proposal"
Ionescu, F., and N. Simpson (2010): "Credit Scores and College Investment" Working paper.
Lucas, R., N. Stokey, and E. Prescott (1989): "Recursive methods in economic dynamics" Cambridge MA
Mitman, K. (2012). "Macroeconomic effects of bankruptcy & foreclosure policies"
Prescott E. (1986): "Theory ahead of business cycle measurement" Real business cycles: a reader
Rudin W. (1987). Real and complex analysis. McGraw-Hill Book Co., New York, third edn.
A.1 Proofs of Theorems 1 and 2
Let
![]() and
and
![]() . Then, if
. Then, if ![]() is the consumption in any of the
cases in the definition of
is the consumption in any of the
cases in the definition of ![]() , we have that
, we have that
![]() and that
and that ![]() is a feasible consumption.
Recall that
is a feasible consumption.
Recall that
![]() is a finite set and let
is a finite set and let
![]() be the cardinality of
be the cardinality of ![]() .
.
- For all
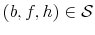 and
and
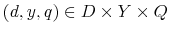
 is increasing in
is increasing in 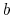 and
and 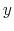 .
.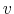 is decreasing in
is decreasing in  :
:
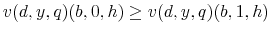 for all
for all 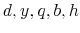 .
.
where the norm of a vector
Then
In the first lemma we show that the two spaces of functions that we defined above are interchangeable.
is a surjective isomorphism.
Proof. We prove first that if
![]() then
then ![]() is continuous.
Let
is continuous.
Let
![]() be a sequence that converges to
be a sequence that converges to ![]() and let
and let ![]() . Since
. Since ![]() is a finite
set it follows that there is some
is a finite
set it follows that there is some ![]() such that
such that ![]() ,
, ![]() , and
, and ![]() for all
for all ![]() . Since
. Since ![]() is continuous then there is
is continuous then there is ![]() such that if
such that if ![]() then
then
Thus
and
Then
for all
because
and, similarly
Thus the condition (3) of Definition A1 is satisfied. To prove that
Since ![]() and
and ![]() are finite spaces, it suffices to show that
are finite spaces, it suffices to show that ![]() is continuous with respect to
is continuous with respect to ![]() and
and ![]() . Since
. Since ![]() is compact and
is compact and ![]() is
uniformly continuous with respect to
is
uniformly continuous with respect to ![]() , it follows by a simple
, it follows by a simple
![]() argument that the integral is continuous with respect
argument that the integral is continuous with respect ![]() . Since
. Since
![]() is continuous with respect to
is continuous with respect to ![]() and
and ![]() is continuous with respect to
is continuous with respect to ![]() and
and ![]() , it follows that
, it follows that ![]() is continuous.
is continuous.
Finally we prove that ![]() is a contraction with factor
is a contraction with factor ![]() by showing that
by showing that
![]() satisfies Blackwell's conditions. For simplicity, we are going to view
satisfies Blackwell's conditions. For simplicity, we are going to view ![]() one more time as a subset of
one more time as a subset of
![]() . Let
. Let
![]() such that
such that
![]() for all
for all
![]() . Then
. Then
for all
Thus
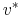 is increasing in
is increasing in 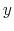 and
and 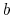 .
.- Default decreases
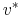 .
. - The optimal policy correspondence implied by
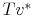 is compact-valued, upper hemi-continuous.
is compact-valued, upper hemi-continuous. - Default is strictly preferable to zero consumption and optimal consumption is always positive.
For simplicity of our notation we will write
and, thus, it is a bounded set. We need to prove that it is closed. Let
Since
Then
Thus
To prove that ![]() is upper hemi-continuous consider
is upper hemi-continuous consider
![]() and let
and let
![]() ,
,
![]() be a sequence that converges to
be a sequence that converges to ![]() .
Since
.
Since ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are finite sets it follows that there is
are finite sets it follows that there is ![]() such that if
such that if ![]() then
then ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let
![]() for all
for all ![]() . We need to find a convergent subsequence of
. We need to find a convergent subsequence of ![]() whose limit point is in
whose limit point is in ![]() . Since
. Since ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are finite sets we can find a subsequence
are finite sets we can find a subsequence ![]() such that
such that
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() for some
for some
![]() ,
,
![]() ,
,
![]()
![]() . Since
. Since
![]() which is a compact interval, there must be a convergent subsequence, which we still label
which is a compact interval, there must be a convergent subsequence, which we still label ![]() for simplicity. Let
for simplicity. Let
![]() and let
and let
![]() for all
for all ![]() . Then
. Then ![]() is a subsequence of
is a subsequence of ![]() such
that
such
that
Moreover, since
and since
Thus
for all
Next, notice that if ![]() then
then
![]() and, thus,
and, thus,
Then Theorem 11.10 of Stockey, Lucas, Prescott (1989) implies the conclusion of the theorem.
A.2 Proofs of Theorems 3-8
Let
![]() and
and ![]() be fixed. Before proving the theorem we will
introduce some notation which will ease the writing of our proofs. For
be fixed. Before proving the theorem we will
introduce some notation which will ease the writing of our proofs. For ![]() ,
, ![]() we define the following maps:
we define the following maps:
for all
for all
for all
for all
and, thus,
Assume now that ![]() and let
and let ![]() be fixed. Let
be fixed. Let ![]() and
and ![]() with
with ![]() be in
be in
![]() . Therefore
. Therefore
for all
for all
If
Therefore
Subtracting (7) from (5) we have that
Since
Consider now
![]() . Then
. Then
![]() and thus
and thus
Thus
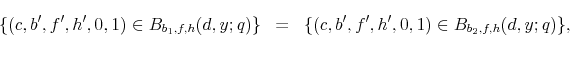
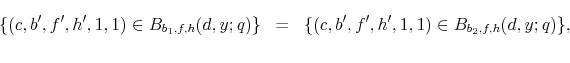
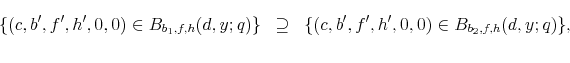
Thus, if for
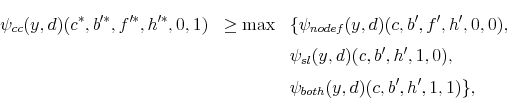
it follows that the same inequality will hold for
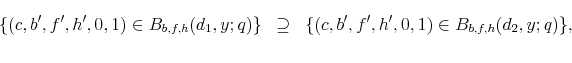
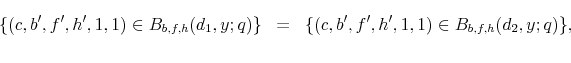
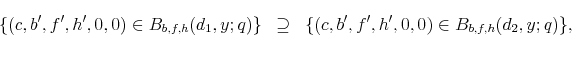
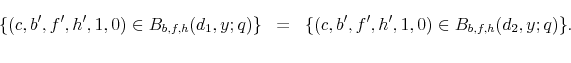
Thus, if
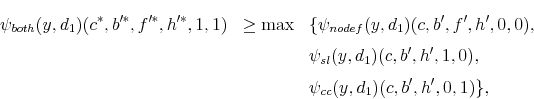
it follows that the same inequality holds for
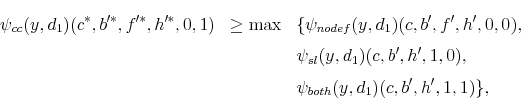
the inequalities can reverse for
and
Therefore, if for
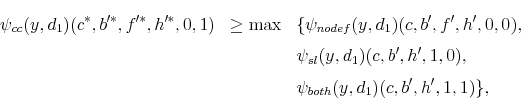
then the same inequalities hold for
A.3 Proofs of Theorems 9 and 10
We see that once ![]() is known, then all the other components of the equilibrium are given by the formulas in Definition 2. We can rewrite part 5 of the
Definition as
is known, then all the other components of the equilibrium are given by the formulas in Definition 2. We can rewrite part 5 of the
Definition as
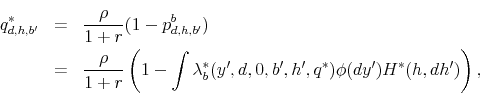
where
Since
is continuous.
Before starting the proof we remark that the above map is well defined because even though apriori the transition matrix ![]() depends on
depends on ![]() , in fact, knowing the pair
, in fact, knowing the pair
![]() completely determines
completely determines
![]() when
when ![]() . If
. If ![]() then
then ![]() ,
,
![]() . Thus
. Thus ![]() ,
, ![]() ,
,
![]() and
and
![]() . Also, if
. Also, if
![]() then
then
![]() by definition.
by definition.
We begin by showing that the sets of discontinuities of
![]() and
and
![]() ,
, ![]() , and
, and
![]() and
and
![]() ,
, ![]() , have measure 0. This will follow from the following lemmas. Let us begin by noticing that the sets of discontinuities of these functions are contained in the sets of indifference.
, have measure 0. This will follow from the following lemmas. Let us begin by noticing that the sets of discontinuities of these functions are contained in the sets of indifference.
We fix ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and we will suppress the dependence of functions on these variables. That is, we study the behavior with respect to
and we will suppress the dependence of functions on these variables. That is, we study the behavior with respect to ![]() . Since
. Since ![]() and
and ![]() are finite sets this will suffice to prove the continuity of
are finite sets this will suffice to prove the continuity of
![]() . The first step is to study in more detail the maximization problem on the no default path. Recall that
. The first step is to study in more detail the maximization problem on the no default path. Recall that
for all
- If
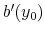 is a single valued then
is a single valued then 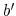 is constant and single valued
on
is constant and single valued
on
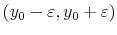 .
. - If
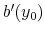 is multi-valued then either
is multi-valued then either 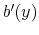 is single valued on
is single valued on
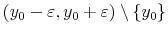 and there is
and there is
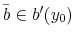 such that
such that
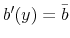 for all
for all
 , or
, or
 for all
for all
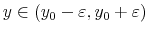 .
.
for all
for all
Suppose now that
![]() is multi-valued. WLOG, assume that
is multi-valued. WLOG, assume that
![]() consists of two elements
consists of two elements
![]() and
and
![]() (we can assume this since
(we can assume this since ![]() is finite). Then
is finite). Then
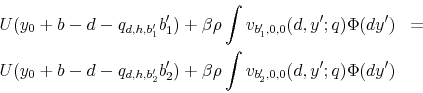
and they both satisfy inequality (10) for all
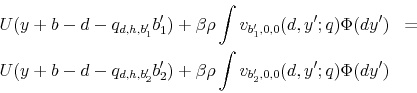
for all
Assume that
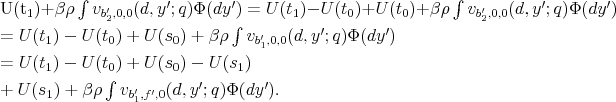
Since
and
and
Therefore
This is a contradiction with
Proof. of Theorem 9 Let
![]() be a sequence that converges to
be a sequence that converges to ![]() . We will show
that
. We will show
that
![]() almost everywhere. Since the sequence
almost everywhere. Since the sequence ![]() is countable, by Lemma A5 we can find a set
is countable, by Lemma A5 we can find a set ![]() of measure 0 that contains all the points of indifference for the prices
of measure 0 that contains all the points of indifference for the prices ![]() ,
,
![]() , and
, and ![]() . Let
. Let
![]() be fixed. Since
be fixed. Since
![]() is continuous and
is continuous and ![]() is a compact space it follows that
is a compact space it follows that
![]() is uniformly continuous. Therefore, since
is uniformly continuous. Therefore, since ![]() is finite, there
is
is finite, there
is ![]() such that if
such that if
![]() and
and
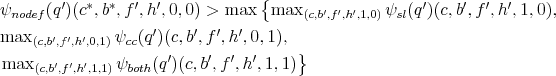
then the same inequality holds for
![]() . In the inequality above we suppressed the dependence on
. In the inequality above we suppressed the dependence on ![]() to simplify the notation. Thus, if
to simplify the notation. Thus, if
![]() and
and
![]() then
then
![]() and
and
![]() . Similar statements hold for all possible combinations of values of
. Similar statements hold for all possible combinations of values of
![]() and
and
![]() . Therefore, by shrinking
. Therefore, by shrinking ![]() if necessary, we have that if
if necessary, we have that if
![]() then
then
![]() . This implies that
. This implies that
![]() for all
for all
![]() . Finally, since
. Finally, since
![]() and
and ![]() is a compact space, the
Lebesgue's Dominated Convergence Theorem (see, for example, (Rudin, 1987, Theorem 1.34)) implies that
is a compact space, the
Lebesgue's Dominated Convergence Theorem (see, for example, (Rudin, 1987, Theorem 1.34)) implies that
Thus the map
- For any
 ,
,
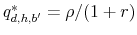 for all
for all  and
and 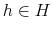 .
. - If the grids of D and
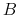 are sufficiently fine, and
are sufficiently fine, and 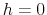 there are
there are
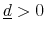 and
and
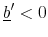 such that
such that
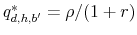 for all
for all
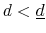 and
and
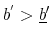 .
. - If the set of income levels for which the household is indifferent between defaulting on credit card debt and any other available option is of measure zero, then
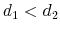 implies
implies
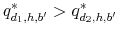 for any
for any  and
and
 .
. - If the set of income levels for which the household is indifferent between defaulting on credit card debt and any other available option is of measure zero, then
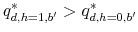 for any
for any 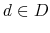 and
and
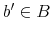 .
.
For the second part, assume that there are ![]() and
and
![]() such that
such that
![]() for all
for all ![]() and consider any household with
and consider any household with ![]() and
and
![]() . In particular the household must have a clean default flag on the credit card market and on the student loan market. If an household with debt
. In particular the household must have a clean default flag on the credit card market and on the student loan market. If an household with debt ![]() defaults only on the credit card market then its utility is
defaults only on the credit card market then its utility is
![]()
On the other hand, one feasible action of the household is to not default on any market, pay off the debt and save in the following period
![]() . The utility from this course of action is
. The utility from this course of action is
![]()
Then property 3) of Definition A1 implies that the utility gain by not defaulting is at least
Assuming that the grid of
Assuming that the set of income levels for which the household is indifferent between defaulting on credit card debt and any other available option, Theorem 7 implies that if ![]() then
then
![]() for any
for any ![]() and
and
![]() . The third part of the theorem follows. One can similarly prove the last part of the theorem.
. The third part of the theorem follows. One can similarly prove the last part of the theorem.
A.4 Proof of Theorem 11
and the utility from not defaulting on either path is
Using the mean value theorem we can find
In particular,
for all
Suppose now that the grids of ![]() and
and ![]() are fine enough so that we can find
are fine enough so that we can find
![]() and
and
![]() such that
such that
![]() is zero or as close to zero as we want. That is, the agent's current utility from defaulting on student loans or credit card are basically
the same. Then, if an agent chooses to default on the credit card market today, in the next period her utility will be
is zero or as close to zero as we want. That is, the agent's current utility from defaulting on student loans or credit card are basically
the same. Then, if an agent chooses to default on the credit card market today, in the next period her utility will be
where
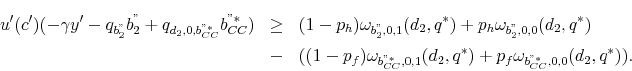
Thus, if
Footnotes
Emails: [email protected]; [email protected]. Return to Text