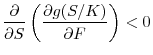Finance and Productivity Growth: Firm-level Evidence*
Abstract
Using data on a broad set of European firms, we find a strong positive relationship between the use of external financing and future productivity (TFP) growth within firms. This relationship is robust to various measures of financing and productivity, and strengthens as financing costs increase. We provide evidence against a reverse-causality explanation by showing that this relationship arises from the component of TFP that is outside the information set of the firm. These findings indicate that financial development supports productivity growth within firms, and helps explain why economic activity remains persistently depressed following financial crisis.
Keywords: Finance-growth nexus, financial crises, total factor productivity (TFP)
JEL classifications: D24, G30, O16
1 Introduction
What is the role of the financial system in influencing economic growth? Following the seminal works of Goldstein (1969) and King & Levine (1993), many studies find that increased financial development leads to higher output and growth. However, the specific reasons for this relationship remain an area of ongoing study. As noted in Levine (2005), there are many channels by which increased financial development can lead to better economic outcomes, including greater business investment, higher household consumption, and better risk-sharing.
Economic output increases with capital, labor, and total factor productivity. A large literature examines how financing affects capital accumulation (see Fazzari et al. (1988)). Some recent studies, such as Jermann & Quadrini (2012), examine the link between the financial system and employment. This study focuses on the link between finance and total factor productivity, which has been shown to be fundamental to understanding economic output.1 An increase in productivity implies that an economy produces a higher level of output, given the same capital and labor inputs. Thus, firm-level evidence of a link between finance and productivity growth suggests an additional and vital channel through which the financial system can impact overall economic activity.
Using data on a broad set of firms in four large European countries, we find a strong positive relationship between the use of external financing and future productivity growth, after controlling for other firm characteristics. We find this result holds for both debt and equity financing, and for various measures of productivity. We directly test whether this can be explained by reverse causality--that firms finance physical investment in expectation of future productivity growth--by using the approach of Levinsohn & Petrin (2003) to identify separately expected and unexpected productivity growth. We find that the data does not support a reverse-causality explanation. Furthermore, we find direct evidence that firms in the UK use financing to invest in productivity-enhancing projects by showing a positive relationship between finance and non-operating expenses, which lead to future productivity growth.
A link between finance and productivity growth may help explain why financial crises lead to persistent declines in output. Recent studies such as Cerra & Saxena (2008), Reinhart & Rogoff (2009a), and Reinhart & Rogoff (2009b) find that economic output does not recover to trend values following financial crises. This pattern contrasts with typical recessions, where output rebounds sharply back to the pre-crisis trend level following the recession. Such a finding is puzzling from a traditional view that financial crises impair only capital accumulation; in this view, overall activity would rebound to the trend level following a financial crisis. However, if financial crises also hamper productivity growth at firms, the underlying level of future aggregate productivity would be lower, leading to persistently lower output and employment.
We carry out our analysis using firm-level data from Europe obtained from the Amadeus data set. Bureau van Dijk constructs this data set from regulatory filings for firms in each European country. In particular, this data set is helpful for our purpose as it includes both data on financing and data on variables such as value-added and wage costs that are necessary to carefully measure productivity at the firm level.2 In order to ensure a robust calculation of productivity, we focus on four of the larger European countries: France, Italy, Spain and UK.3 We carry out our analysis for each of these countries separately, providing an additional degree of robustness.
Our base empirical specification consists of a regression of future productivity growth on its own lags, debt growth and control variables. We measure productivity (hereon referred to as TFP) for each firm-year observation as the residual from a log regression of value-added on capital and labor input. We use debt growth as our primary measure of financing as much of our sample consists of medium-sized private firms for which debt is the primary source of financing. We estimate this equation using the dynamic panel method of Holtz-Eakin et al. (1988) and Arellano & Bond (1991). The dynamic panel method corrects for estimation biases caused by the presence of lagged dependent variables by first-differencing the observation equation and using lagged levels of the regressors as instruments for the differenced equation. This instrument-based approach also helps mitigate endogeneity concerns. Using this approach, we find a statistically significant effect of debt growth on future TFP growth in each of the four countries in our sample: a 10% increase in debt leads to productivity increases of between 0.8% and 2.1%. To the best of our knowledge, we are the first to document such a relationship between the use of finance and productivity growth at the firm-level.
We examine the robustness of the above finding. We obtain similar results with alternative productivity measures such as labor productivity, and TFP measured using the approach of Levinsohn & Petrin (2003).4 We also find similar results when broadening the definition of financing to include debt and equity financing. Finally, the result is consistently strong across various subsamples, including those sorted on firm size and age.
We attempt to shed further light on the mechanism by which the observed relationship arises by using other operating expenses as a proxy for investments in innovative projects. As argued by Eisfeldt & Papanikolaou (2013), other operating expenses include research and development expenses, as well as more general investments that firms make in intangible capital. Indeed, we find that other operating expenses have a positive relationship with future TFP growth at the firm-level. More strikingly, we find that the fitted value from a first-stage regression of other operating expense growth on debt growth has a positive and significant effect on future TFP growth, providing direct evidence that firms rely on financing to invest in productivity-increasing projects.
A potential alternative explanation for our finding is that firms may obtain financing in expectation of future productivity increases--a form of reverse causality. We address this concern by decomposing TFP growth into an expected and unexpected component. This decomposition builds on the insight of Levinsohn & Petrin (2003) that the use of fully flexible inputs, such as materials, should reflect information on productivity available to the firm. That is, one could use data on materials input to decompose measured TFP into a part that is inside the information set of the firm, and a part that is not. Based on this decomposition, we find that the relationship between finance and TFP growth arises mainly in the part of TFP that is outside the information set of the firm, providing evidence against a reverse-causality explanation.
A natural corollary is to examine how the relationship between finance and productivity growth changes as financing costs vary. An increase in financing costs could lead firms to use less finance and invest less in productivity-enhancing projects. Assuming decreasing returns to productivity-enhancing investments, the resulting reduction in productivity would be less than the reduction in the use of finance, implying a strengthening of the relationship between finance and productivity growth. Using the spread on sovereign bonds as a proxy for country-specific financing costs, we find that increases in financing costs result in a stronger relationship between debt growth and future TFP growth. Turning to measures of financing costs at the firm-level, we find that firms with higher leverage have a stronger relationship between the use of finance and future TFP growth.
In order to assess economic significance of our findings, we use data on aggregate debt growth for nonfinancial firms during the recent crisis in Europe as the input to our model to predict firm-level TFP. Using this approach, we find that the observed slowdown in debt growth from 2009 to 2011 implied that aggregate output, keeping labor and capital inputs fixed, was between 0.06 and 0.35 percent below the trend level in 2012. This demonstrates that the finance-productivity growth channel we identify is indeed economically significant and that it may play a role in understanding why economic output remains persistently low following financial crises.
Somewhat surprisingly, there are only limited studies that explicitly examine a relationship between the use of finance by firms and their productivity growth. One such study is Gatti & Love (2008), who use World Bank survey data from Bulgeria and find that firms that self-report lack of access to credit have lower subsequent productivity growth. The limited number of studies may reflect the fact that the census data sets typically used to study firm-level productivity do not include financial variables. Some closely related studies examine the role of aggregate financial development on firm-level productivity: Beck et al. (2000) find that financial development impacts growth mainly through increased productivity; Bakke (2009) shows that an aggregate reduction of credit in Venezuela leads to reduced productivity; Krishnan et al. (2012) demonstrate that bank deregulation leads to increased productivity at US manufacturing firms; and Hsu et al. (2013) examine how better developed equity markets support innovations at the firm-level. Compared to these studies, we focus on the effect of the use of finance by firms on their own productivity growth. Turning to the firm-level, Brown et al. (2009) find that increased equity financing helps explain the boom in R&D in the late 1990s but does not link that explicitly to productivity growth.
The broader literature that examines the link between finance and output includes Jayarathne & Strahan (1996), Butler & Cornaggia (2011), and Guiso et al. (2004), who examine this relationship across US states, counties in some US states, and Italian regions, respectively. Rajan & Zingales (1998) and Beck et al. (2008) focus their analysis across industries. Aghion et al. (2007) find that financial development facilitates firm entry. Jeong & Townsend (2007) and Buera et al. (2011) emphasize financing investment by the most productive firms in the economy. In addition, Demirguc-Kunt & Maksimovic (1998) and Beck et al. (2005) examine the effect of financial development on firm growth using each country's legal origin as an instrument (see La Porta (1998)).
The paper is organized as follows. Section 2 presents a simple model that develops the testable hypotheses. Section 3 presents the data. Section 4 presents the main findings and examines the robustness of our results. Section 5 provides further tests that aim to distinguish our hypothesis on the financing of productivity-increasing projects from a possible alternative hypothesis. Section 6 presents evidence on the effect of variation in financing costs. Section 7 examines the economic impact of the recent financial crisis in Europe and Section 8 concludes.
2 Model
The section presents a simple model that yields a relationship between finance and productivity growth even in the absence of financing frictions. It also establishes our second prediction on how the relationship between finance and productivity growth varies with the cost of finance faced by firms.
2.1 Setup
The model builds on a standard investment model of the firm. Firms use capital, ![]() , and labor,
, and labor, ![]() , to produce output,
, to produce output, ![]() , using the following Cobb-Douglas specification:
, using the following Cobb-Douglas specification:
| (1) |
where ![]() denotes the capital share and
denotes the capital share and ![]() denotes the log productivity of the
firm. The price of output is normalized to 1. Firms hire labor at a fixed wage rate
denotes the log productivity of the
firm. The price of output is normalized to 1. Firms hire labor at a fixed wage rate ![]() . The cash flows of the firm are given by
. The cash flows of the firm are given by
| (2) |
The capital stock depreciates at a rate, ![]() . Firms finance physical investment using internal funds and external finance. We assume that firms face a quadratic adjustment cost of
investment,
. Firms finance physical investment using internal funds and external finance. We assume that firms face a quadratic adjustment cost of
investment,
![]() ; this adjustment cost is only necessary to ensure that investment is well-defined.5
; this adjustment cost is only necessary to ensure that investment is well-defined.5
2.2 Financing productivity increasing projects
Our point of departure is that firms can invest in innovative projects that lead to increases in productivity, ![]() . Let
. Let ![]() denote expenditures in innovative projects. We allow for the outcome from such expenditures to be stochastic (see Doraszelski & Jaumandreu (2013) and Warusawitharana (2013)). The firm realizes an
increase in productivity given by the stochastic function
denote expenditures in innovative projects. We allow for the outcome from such expenditures to be stochastic (see Doraszelski & Jaumandreu (2013) and Warusawitharana (2013)). The firm realizes an
increase in productivity given by the stochastic function ![]() , where the increase in productivity is influenced by expenditures in innovative projects scaled by firm size. This captures
the notion that larger firms must spend greater resources to obtain a similar increase in log productivity, and maintains homotheticity. Log-productivity next period,
, where the increase in productivity is influenced by expenditures in innovative projects scaled by firm size. This captures
the notion that larger firms must spend greater resources to obtain a similar increase in log productivity, and maintains homotheticity. Log-productivity next period,
![]() , is a random variable given by
, is a random variable given by
We assume the function for productivity increases,
The value of the firm, ![]() , can be written as the solution to the following Bellman equation:
, can be written as the solution to the following Bellman equation:
where
Taking first order conditions, it is straightforward to show that the optimal expenditures in innovative projects is given by
where the marginal cost of such expenditures equals 1, and the right-hand-side yields the marginal benefit.6
The amount of external finance used by the firm, ![]() , is given by the sources and uses of funds equations:
, is given by the sources and uses of funds equations:
That is, an increase in expenditures in innovative projects will require firms to obtain additional financing.7
2.3 Model implications
Our first result relating the use of finance to productivity growth follows from the above setup.
![\displaystyle \frac{\partial E[z^{\prime} - z]}{\partial F} > 0](img39.gif)
Intuitively, the above result reflects the fact that increased expenditures in innovative projects that lead to higher productivity growth require increased financing.
Our second, more subtle, result examines the sensitivity of productivity growth to financing as the interest rate faced by the firm varies. That is,
![\displaystyle \frac{\partial}{\partial r} \left(\frac{\partial E[z^{\prime} - z]}{\partial F}\right) > 0](img41.gif)
The intuition for the above result follows from the fact that an increase in financing costs lowers the present value of future cash flows for the firm, resulting in lower expenditures in innovative projects. The diminishing marginal productivity gains from these innovative investments imply that, at lower expenditure levels, productivity growth becomes more sensitive to expenditures on innovative projects. This translates to an increased sensitivity of productivity growth to financing at higher interest rates.
Proposition 1 provides one explanation for a potential finding of a link between the use of finance and future productivity growth within firms. An alternative explanation for such a link would be if firms obtained financing--possibly to fund capital expenditures--in expectation of future productivity increases.8 This is essentially a reverse-causality argument.9 Thus, our Alternate Hypothesis states that:
Alternate Hypothesis: The relationship between finance and productivity growth reflects firms obtaining financing in expectation of future productivity increases.
The distinction matters as, under Proposition 1, the financial system helps increase productivity in the economy, enabling an expansion of the production possibility frontier. Under the Alternate Hypothesis, the financial system enables firms to reach the existing production frontier, not expand it. As such, Proposition 1 implies a greater impact of the financial system on output and growth than the Alternate Hypothesis. The distinction also has implications for the consequences of a financial crisis. Under Proposition 1, a reduction in the availability of finance would lower productivity growth in the economy, leading to a permanent reduction in the future level of productivity and output. In comparison, under the Alternate Hypothesis, the underlying productivity path would not be affected by a financial crisis, implying no permanent effect on output from the financial crisis, absent other frictions.
The subsequent empirical analysis tests the above two propositions and the Alternative Hypothesis on firm-level data from four European countries.
2.4 Discussion
The role of finance in capital allocation typically considers the underlying productivity of firms (or talent of entrepreneurs) as exogenous. Yet, financial development may also help firms pursue innovations, as shown by Cornaggia et al. (2013).10 Assuming that innovations lead to greater productivity growth--a feature of the endogenous growth models (see Romer (1990))--one arrives at the predicted relationship between finance and productivity growth.
Firms could engage in a variety of activities that lead to productivity increases. Recent studies such as Bloom et al. (2012) and Doraszelski & Jaumandreu (2013) emphasize the role of information techonology investments and R&D in generating productivity increases at the firm level. In addition, firms also spend substantial resources on increasing productivity through the training of employees. Our proposition allows for increased financing to lead to higher productivity through all these expenditures.
Proposition 1 does not imply a strictly causal effect of financing on productivity. As our primary financing measure is debt growth, one possible strictly causal channel is that increases in debt lead firms to reduce slack, leading to higher productivity.11 As most of our firms are medium-sized private firms, they are not likely to have much slack. In addition, the literature on the real effects of financial distress suggests that increased debt would lead to lower productivity (see Phillips & Sertsios (2011)).
3 Data
The data we use in our study are obtained from the Amadeus database maintained by Bureau Van Dijk. Bureau Van Dijk constructs this database based on required filings of annual reports for corporations in European countries. The level of detail and the degree of coverage varies across countries, reflecting the reporting requirements of each country. In particular, the filing requirements apply to both public and private firms. As such, the bulk of the sample consists of medium-sized private firms. Thus, the sample is much more comprehensive than those that focus only on publicly traded firms. The sample period extends from 2000 to 2010 and varies slightly across countries, due to the fact that Amadeus only reports 10 years of data for each country. As the data set includes many outliers, we Winsorize the sample at the 2.5 percent level in order to reduce the impact of outliers.
One key benefit of this database is that it includes the variables necessary to carefully construct measures of productivity and use of finance at the firm-year level. As Syverson (2011) discusses, productivity is typically measured either using log regressions of value-added on labor and capital, or using log regressions of revenue on materials input, labor and capital. Amadeus includes information on value-added, capital, labor (both wages and the number of employees) and, for some countries, materials usage. This enables a robust calculation of productivity at the firm level. In addition, the balance sheet component of Amadeus includes information on short-term and long-term debt as well as contributed capital, enabling us to construct measures of financing at the firm level. In comparison, we would not have the necessary detail to carry out this analysis using data sets on US firms. While Compustat provides detailed financing data, it does not enable a careful calculation of productivity as it reports only revenue, capital, and wages. One the other hand, the US Census data sets used in productivity studies do not include firms' financing information.
We restrict the sample to four of the five largest countries in the database: France, Italy, Spain and United Kingdom (UK).12 We exclude Germany, the other large European country, as the Amadeus data is particularly sparse for Germany. This arises due to the fact that the German reporting requirements are less stringent than those in other European countries, and most firms choose to not file detailed annual reports and instead pay the small non-reporting fine. We focus on these countries to provide a large number of observations for our productivity regression, which we carry out at the country-industry level. In order to fully benefit from the scale of the database, we treat the four countries in the sample as four distinct samples throughout. This allows all the coefficients to vary freely across the countries, which would not be achieved by using country fixed effects. Perhaps more importantly, focusing on the four countries separately eliminates potential differences in sample composition across countries and provides an additional degree of robustness to the analysis.
We translate nominal values into real values in order to eliminate the impact of aggregate price changes. We use the price of fixed assets to deflate the capital stock, and the consumer price index for all items excluding food and energy to deflate other variables. The price indices are obtained at the individual country level. As such, we measure both productivity growth and financing in real terms.
3.1 Measurement of productivity
The productivity measure we use in this study is the value-added-based total factor productivity measure, which we denote as TFP. We calculate this measure using the following regression specification:
where
In the baseline specification, we measure capital using the replacement value of capital and measure labor as the staff cost of employees. We calculate the replacement value of capital following the double declining balance method employed by Summers & Salinger (1983). Using the replacement value of capital enables us to incorporate potential differences in the quality of the capital stock by vintage.13 We measure the labor input by the staff cost instead of the number of employees as this captures potential differences in the skill level of employees. We carry out robustness checks using different measures of productivity, detailed in Section 4.4, to tackle concerns regarding the measurement of productivity.
Essentially the TFP measure we use reflects the amount of value-added by the firm beyond what can be explained by its capital and labor inputs. An increase in TFP implies that, holding factor inputs constants, the firm contributes a higher amount of value-added to the economy. There could be a myriad reasons for such an increase: the firm may improve how it utilizes it capital stock; the firm may increase the efficiency with which it employs workers; or the firm may increase the quality of its products, enabling it to charge higher prices. Importantly, such increases in productivity help spur overall growth in the economy.
3.2 Summary statistics
Table 1 presents the summary statistics from the data. The table reports means for each variable, with medians in square brackets and standard deviations in parenthesis. The summary statistics are reported for each country separately, as in the subsequent regression analysis.
The findings indicate that mean TFP growth is slightly negative, consistent with the poor overall productivity growth of these countries. In particluar, TFP declined notably in the years following the recent financial crisis. TFP growth is quite volatile, with significant variation within and across firms. Debt growth, adjusted for inflation, exhibits similar properties with the exception of firms in France, where firms realized substantial debt growth, on average. As most of our sample consists of mid-sized privately held firms, we use debt growth as the primary measure of financing. In order to verify that debt is indeed the marginal source of financing for these firms, we report the fraction of firms that exhibit positive debt and equity growth in the last two lines of the table. The results indicate that while nearly half of the firm-year observations report positive debt growth, only between 5 to 10 percent of firms report an increase in contributed capital, thereby confirming the importance of debt as a source of financing.14
The summary statistics also reveal notable differences in some variables across the countries in the sample. For instance, while firms in the UK are bigger on average, firms in France have smaller leverage. Treating firms in each of these countries as distinct samples enables us to sidestep these cross-country differences.
3.3 Correlations
One concern with any empirical analysis is the presence of multi-collinearity in the regressors. Table 2 presents the cross-correlations for the variables used in the regression for each country in the sample. As the table indicates, there is little cross-correlation in the regressors indicating that multi-collinearity concerns do not arise in our setting.15
The results also indicate a small negative correlation between sales growth and TFP growth. This reflects the fact that while TFP growth measures output per unit of factor input, sales growth incorporates both TFP growth as well as capital and labor input growth. This negative correlation indicates that our results are not merely capturing a relationship between finance and the overall growth of the firm.
4 Results
This section presents our main finding: increases in financing lead to increases in future productivity within firms. We also investigate the robustness of this result to different measures of productivity and financing, and examine how the results vary across subsamples.
4.1 Regression specification
We test Proposition 1 by using the following regression specification:
where
As Holtz-Eakin et al. (1988) note, the presence of lagged dependant variables lead to biased estimates from traditional panel regressions. As such, we employ the dynamic panel estimator developed by Holtz-Eakin et al. (1988) and
Arellano & Bond (1991). This estimator first-differences the observation equation, and uses the lagged dependent variable in levels as instruments for the differenced equation. The resulting system of equations is estimated via GMM. The use of lag variables as
instruments in this GMM-based estimation approach helps alleviate endogeneity concerns. The dynamic panel estimator yields two diagnostic tests: a specification test of whether the error terms in the differenced equation are serially correlated of order 1, and only of order 1, and a GMM-style
![]() -test of overidentification restrictions.17 We
test these condition in all our specifications. We find that the bulk of our specifications satisfy these tests with the main exception being that many of the regressions for Italy do not satisfy the higher-order serial correlation test.
-test of overidentification restrictions.17 We
test these condition in all our specifications. We find that the bulk of our specifications satisfy these tests with the main exception being that many of the regressions for Italy do not satisfy the higher-order serial correlation test.
One concern is that the dynamic panel estimator suffers from a potential weak instruments problem. As such, we do not use the full set of lagged variables that can be potentially used as instruments, but instead use only 2 lags of each of the dependent variables as instruments in our GMM specification (see Cummins et al. (2006)). This approach helps limit the number of instruments to those that may be most informative.
As the estimator begins by first-differencing the observation equation, it sweeps away any firm (or industry) fixed effect and focuses only on within-firm variation. This ensures that any effect we observe does not reflect variation across firms (or industries).
4.2 Main result
Table 3 reports the results from our baseline specification for each of the four countries in our sample.18 The control variables also include unreported year dummies. The results show that debt growth at the firm level has a statistically significant impact on future TFP growth. The results imply that a 1 standard deviation increase in debt growth is associated with between 0.033 to 0.059 standard deviations increase in TFP over the next period. Thus, keeping factor (capital and labor) inputs constant, a rise in debt leads to a rise in value-added by firms. In addition, the fact that the coefficients on lagged changes sum to less than -1 implies that changes in TFP persist over a long period. Therefore, an increase in debt will lead to TFP increases not only in the next period, but also further into the future. In addition, firms may increase their capital and labor inputs following the rise in productivity, amplifying the potential benefit to the economy.
The results demonstrate the persistence of TFP. The coefficient on
![]() implies that following a 10% increase in TFP we will observe a subsequent decline in TFP of between 2.1% to 2.9% next period. Thus, much of the initial increase in TFP
persists. It is this persistence in productivity that led us to employ the dynamic panel estimation method, as fixed effects panel regressions would be biased in the presence of the lagged dependent variable. We report the specification test for serial correlation in the residual, and find serial
correlation of order 1 as expected. We find no evidence of serial correlation of order 2 for the UK, France and Spain, satisfying the specification test. We also carry out the Hansen
implies that following a 10% increase in TFP we will observe a subsequent decline in TFP of between 2.1% to 2.9% next period. Thus, much of the initial increase in TFP
persists. It is this persistence in productivity that led us to employ the dynamic panel estimation method, as fixed effects panel regressions would be biased in the presence of the lagged dependent variable. We report the specification test for serial correlation in the residual, and find serial
correlation of order 1 as expected. We find no evidence of serial correlation of order 2 for the UK, France and Spain, satisfying the specification test. We also carry out the Hansen ![]() -test
of the overidentification restrictions, and find no evidence to reject the model specification.
-test
of the overidentification restrictions, and find no evidence to reject the model specification.
The results for the control variables indicate that smaller firms have higher TFP growth. After controlling for size, age has no further effect on TFP growth. The results also indicate that firms that realize high sales growth have subsequently lower TFP growth, similar to the negative coefficient on lagged productivity growth. In addition, investment enters the regression with a positive coefficient in the regression. This could either reflect firms investing in expectation of future TFP increases, or technical progress embodied in new capital that is not fully captured by our replacement value of capital measure.
4.3 Equity financing
The above specification employed debt as the marginal source of financing. The rationale for this is that as the firms in our sample are mostly private firms they would not be able to obtain equity financing easily. Indeed, this was borne out by the summary statistics on the proportions of firms that used each type of financing with about half the firms having increases in debt while less than 10% of firms having increases in contributed equity. That said, we examine the robustness of our results using the growth of equity financing as the variable of interest.
Table 4 presents the results obtained from regressing future TFP growth on the growth of equity and debt separately.19 The inclusion of equity financing has little effect on the coefficient on debt growth, which remains positive and statistically significant. The estimated coefficient on equity financing varies across the countries, with positive and significant coefficients in the UK and Spain, and insignificant coefficients in France and Italy. The strong positive coefficient in the UK may reflect the fact that these firms tend to be larger and therefore more able to access equity than those in the other countries, or it may reflect the greater role of equity financing in the UK. This mixed finding arises from the fact that most of the firms in our samples exhibit no change in equity financing from year to year, thereby reducing the power of this test. In the subsequent analysis, we will use debt growth to measure the use of finance by firms.
4.4 Measurement of productivity
Difficulties in measuring productivity poses a challenge for our analysis. Our baseline measure of TFP accounts for potential differences in the quality of the capital stock by using a replacement value measure. It also accounts for potential differences in the skill level of workers by using staff costs as the measure of labor input. This section addresses further measurement concerns. In the following tables, we report the results from our baseline specification (9) with different productivity measures.
4.4.1 Endogeneity of labor choice
One concern regarding our productivity measure is that it does not take into account the endogeneity of the labor input in the production function. Levinsohn & Petrin (2003) develop a method that tackles this issue by using materials input as a proxy for the labor input in the production function. We address this concern by replicating the analysis with TFP measured according to their method. As data on materials input is not available for the UK, this limits our analysis to the other three countries in the sample.
Table 5 presents the results obtained using the Levinsohn & Petrin (2003) measure of TFP in our baseline specification. Using this measure of productivity has little impact on our results. The coefficients on debt growth continue to be positive and statistically significant and are mostly unchanged from our baseline results.
4.4.2 Finance and labor productivity
The TFP measure we use measures productivity relative to all factor inputs. Output per worker provides a simpler measure of productivity that is often used in the literature. Table 6 presents the results obtained using value-added per worker as the produtivity measure. Here too, we obtain a positive and statistically significant effect of debt growth on productivity, as in our baseline specification.
Overall, these results indicate that our finding of a positive relationship between debt growth and future productivity growth within firms is robust to different measures of productivity. This follows Syverson (2011), who argues that different methods of measuring productivity generally yield similar results.
4.5 Split sample results
One concern is that our finding reflects a relationship that applies only for a specific subset of firms. We tackle this concern by repeating our analysis after dividing the samples by firm size and age. We divide the samples into three bins based on the size and age of firms when they enter the sample. Fixing each firm into one bin helps with the first-differencing step in the dynamic panel estimator. As age and size are highly persistent, categorizing firms when they enter the sample is unlikely to cause much misclassification.
Table 7 reports the results after the dividing the sample into subsamples. The table reports only the coefficient on debt growth for each of these age and size terciles (we do not report the other coefficients for compactness). We obtain positive coefficients for debt growth within each of the bins. However, we do lose statistical significance for a few of the bins. That said, no clear pattern emerges across the age and size bins for all the countries, indicating that our finding of a positive relationship between debt growth and future productivity growth occurs broadly among the firms in the sample.
5 Tests of Hypotheses
The previous results demonstrated that increased use of finance by firms leads to increases in future productivity. While this finding supports our proposition that firms use financing to invest in innovative projects, it is also consistent with the Alternate Hypothesis that firms obtain financing in expectation of future productivity increases, possibly to finance physical investment. This Alternate Hypothesis is essentially a form of reverse causality. This section provides tests to differentiate between these two competing explanations.
5.1 Other operating expenses as a proxy for investments in innovative projects
The simple model developed in Section 2 emphasizes the financing of innovative projects. One could test this mechanism by examining whether debt growth influences such expenditures by firms, and by examining whether such expenditures influence productivity growth. We carry out this analysis by using other operating expenses as a proxy for investment in innovative projects. Eisfeldt & Papanikolaou (2013) argue that other operating expenses capture both direct investments in research and development as well as indirect investments in intangible assets such as employee training and advertising.20 We perform our analysis using data on UK firms only, as other operating expenses are not available for firms in the other countries in the sample.
We first regress other operating expenses on contemporaneous debt growth using a panel fixed-effects specification. Appendix Table A2 reports the results of this regression, with and without additional control variables. Debt growth has a positive and statistically significant relationship with growth in other operating expenses in all of the specifications, suggesting that firms may use external finance to invest in innovative projects. Using these regression specifications, we derive fitted values for the predicted growth in other operating expenses.
Table 8 reports results of a second stage regression, where we replace debt growth in our baseline specification with either other operating expenses or with the fitted values of other operating expenses from the first-stage regression. As reported in the first column, growth of other operating expenses indeed has a positive and statistically significant effect on future TFP growth, supporting the argument of Eisfeldt & Papanikolaou (2013) that such expenses broadly capture investments in intangible capital that may lead to future increases in productivity. More relevant for our argument, the part of other operating expenses predicted by debt growth has a positive and significant effect on future TFP growth, as reported in the second column. This provides evidence in favor of the channel highlighted in the model, where firms finance investments in innovative projects that lead to future productivity growth. Indeed, the point estimate on the predicted component of other operating expense growth is noticeably larger than that of all other operating expenses, suggesting that the result shown in the first column is strongly influenced by the part of other operating expenses that is predicted by debt growth. Turning to the third column, we find a similar result when we use the predicted value of other operating expenses that is obtained by fitting a more general specification in the first-stage regression.
5.2 Decomposing TFP into expected and unexpected components
An alternative explanation for our finding is that firms have some information about their future productivity that influences their borrowing decisions. This explanation is essentially a form of reverse causality that may occur when managers have more information about the future productivity growth of the firm than the econometrician. In order to address this concern, we decompose TFP growth into two components: one that is potentially inside the information set of the firm and another that is outside the information set. Under the Alternate Hypothesis, the relationship between productivity growth and financing arises mainly from the component of TFP growth that is inside the information set of the firm but unobservable to the econometrician. Conversely, evidence that this relationship arises mainly from the component outside the firm's information set is consistent with Proposition 1.21
The basis of our decomposition builds on the insight of Levinsohn & Petrin (2003) that the use of fully flexible inputs, such as materials, reflects expectations of TFP by the firm's management. That is, if management had information that TFP was going to be elevated, they would increase use of flexible inputs so as to fully benefit from the higher TFP. Levinsohn & Petrin (2003) use this insight to control for the endogeneity of a firm's labor choice each period in the estimation of TFP. As a side product of their approach, one obtains a decomposition of TFP into a part that is potentially inside the information set of the firm and a part that is outside. Formally, Levinsohn & Petrin (2003) employ the following specification:
where
We obtain estimates of the two components of TFP using the above approach and carry out our baseline regression on each of these two components separately. Our insight is that any information a firm had about its
![]() as of time
as of time ![]() would be a subset of its information about its
would be a subset of its information about its
![]() as of
as of ![]() , which would be captured by
, which would be captured by
![]() . Therefore, evidence that the relationship between debt growth and TFP growth arises mainly from the
. Therefore, evidence that the relationship between debt growth and TFP growth arises mainly from the ![]() component would be supportive of the Alternate Hypothesis. Conversely, evidence that the relationship arises mainly from the
component would be supportive of the Alternate Hypothesis. Conversely, evidence that the relationship arises mainly from the ![]() component would be
supportive of Proposition 1. To the best of our knowledge, we are the first to use this decomposition of TFP to address potential reverse-causality concerns in TFP growth regressions.23 As data on materials input is not available for the UK, we carry out this estimation for the other three countries in the sample.
component would be
supportive of Proposition 1. To the best of our knowledge, we are the first to use this decomposition of TFP to address potential reverse-causality concerns in TFP growth regressions.23 As data on materials input is not available for the UK, we carry out this estimation for the other three countries in the sample.
Table 9 presents the results from this regression using
![]() , the component of TFP that is outside the firm's information set when it chooses materials input for the next period. We find that debt growth has a significant positive impact on
this component. Further, the point estimates are similar to those obtained with the corresponding total TFP measure reported in Table 5. This indicates that the relationship between debt growth and TFP growth arises from the component of TFP growth that is unexpected by
the firm.
, the component of TFP that is outside the firm's information set when it chooses materials input for the next period. We find that debt growth has a significant positive impact on
this component. Further, the point estimates are similar to those obtained with the corresponding total TFP measure reported in Table 5. This indicates that the relationship between debt growth and TFP growth arises from the component of TFP growth that is unexpected by
the firm.
Table 10 presents the results of the corresponding regression using the component of TFP that is inside the firm's information set,
![]() . Conversely, we find that debt growth has a statistically insignificant impact on this component of TFP. In comparison to the previous table, the magnitudes of the coefficients
are also much smaller, providing further evidence that debt growth is not driven by the component of TFP growth that is potentially inside the information set of the firm. Taken together, the results in these two tables clearly point against the reverse-causality interpretation of our finding
implied by the Alternate Hypothesis.
. Conversely, we find that debt growth has a statistically insignificant impact on this component of TFP. In comparison to the previous table, the magnitudes of the coefficients
are also much smaller, providing further evidence that debt growth is not driven by the component of TFP growth that is potentially inside the information set of the firm. Taken together, the results in these two tables clearly point against the reverse-causality interpretation of our finding
implied by the Alternate Hypothesis.
5.3 Control for investment in year 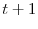
A further test of the Alternate Hypothesis would be to control for contemporaneous investment. Our baseline specification includes as a control variable investment in year ![]() . This helps
partially control for firms borrowing to fund physical investment in expectation of future TFP increases. However, there may be lead times in investment--see Kydland & Prescott (1982)--that make investment in year
. This helps
partially control for firms borrowing to fund physical investment in expectation of future TFP increases. However, there may be lead times in investment--see Kydland & Prescott (1982)--that make investment in year ![]() a poor proxy and motivates adding investment in year
a poor proxy and motivates adding investment in year ![]() as an additional control variable.
as an additional control variable.
Table 11 presents the results of this regression. The estimates indicate that adding future investment has no effect on the coefficients on debt growth, which remain essentially unchanged from Table 3. Future investment itself enters with a negative sign, potentially reflecting the fact that it may take firms some time to obtain the full benefit from the newly installed capital. The above finding provides further evidence that the relationship between debt growth and future productivity growth we find is not mainly due to firms borrowing to finance investment in expectation of future productivity increases.
6 Cost of finance
Proposition 2 argues that an increase in financing costs increases the sensitivity of future productivity growth to debt growth. We test this hypothesis using the following regression specification:
A positive coefficient for
6.1 Variation in aggregate financing costs over time
We first focus on variation in aggregate financing costs over time, where we proxy for aggregate financing costs using the cost of sovereign debt. A rise in sovereign financing costs will likely directly impact the funding costs of banks, given the role of the sovereign in providing support for banks and other financial institutions (for instance, sovereigns provide an implicit guarantee for the debt of major banks). Indeed, the recent sovereign debt crisis in Europe has highlighted the degree to which the health of the banking sector is intertwined with the health of the sovereign. As a rise in financing costs for banks and other financial institutions will directly impact financing costs of the firms in that country--especially for the mid-sized firms that comprise the bulk of our sample--sovereign financing costs provide a good proxy for financing costs faced by firms.
We measure sovereign financing costs using the spread between the 10-year bond of each sovereign and the 10-year German bond. Taking the spread relative to the German bond eliminates potential variation in interest rates arising from changes in inflation expectations, and provides a measure of the riskiness of the sovereign.
Table 12 presents the results of our baseline regression augmented by an interaction term of firm-level debt growth and the spread between the 10-year bond of each country and the 10-year German bond. We find that the relationship between firm-level debt growth and subsequent TFP growth strengthens as the bond spread increases for France, Spain and Italy, consistent with Proposition 2. We find no significant result for the UK, possibly reflecting the fact that there is less variation between the bond spreads on UK and German bonds than for the other countries in the sample. The findings in this table indicate that the relationship between debt growth and future productivity growth strengthens as aggregate financing costs rise.
6.2 Variation in leverage
Models such as Leland (1994) and Hennessy & Whited (2007) imply that the interest rate faced by firms increases as their leverage rises. Thus, one could use leverage as a proxy for variation in financial costs faced by firms. Table 13 presents the results obtained by using book leverage of the firm as of ![]() as a proxy for financing costs. For simplicity, we use dummy variables that reflect which
leverage tercile the firm fell into the previous year.
as a proxy for financing costs. For simplicity, we use dummy variables that reflect which
leverage tercile the firm fell into the previous year.
The results indicate sharp variation in the sensitivity of future productivity growth to debt growth with the leverage of the firm. For firms in the middle tercile, debt growth has a positive and significant impact on future TFP growth. This relationship strengthens/(weakens) significantly for firms in the upper/(lower) leverage tercile. Indeed, the implied coefficient for firms in the upper tercile is many times the coefficient for firms in the lower tercile, providing clear evidence in favor of Proposition 2.
The above analysis shows that variation in financing costs, both in the aggregate and across firms, has an impact on the relationship between the use of finance and future productivity growth within firms.
6.3 Cash holdings and dependency on external finance
We next examine the sensitivity of the finance-productivity growth relationship to variation in financing needs. A firm with greater financing needs would be more likely to obtain external finance to invest in innovative projects, thereby leading to a stronger relationship between debt growth and productivity growth. We first use cash holdings as a measure of financing needs, as a firm with ample cash would be less likely to need external finance.
Table 14 presents the results of our baseline regression across prior year cash holding terciles for the four countries in the sample. We find that debt growth has a statistically significant effect on productivity growth for firms in the lower and middle cash terciles. This likely reflects the fact that the bulk of the mid-sized firms in the sample are dependent on external finance to finance their investments. In comparison, we find that the sensitivity of productivity growth to debt growths weakens notably for firms in the highest cash holding tercile, consistent with these firms financing more investments with internal funds. Statistically, the difference between the debt growth coefficients across the mid- and high-cash holding terciles is significant at the 5 percent level in Italy and the UK, and significant at the 10 percent level in France.
A related analysis examines whether the sensitivity of future TFP growth to financing varies with the external finance dependency of the firm's industry. One would possibly expect that firms in industries that are more dependent on external finance would exhibit a stronger relationship between the use of finance and future productivity growth. We carry out this test by augmenting our baseline regression specification with an interaction term of debt growth times the external finance dependency of the industry. Following Rajan & Zingales (1998), we measure the external finance dependency of firms as the median ratio of fixed assets to sales for US firms in the same 2-digit industry. Table 15 reports the results of this analysis. We find that for firms in France and Italy, a rise in external finance dependency has a statistically significant impact on the relationship between debt growth and future TFP growth (the corresponding result for UK firms is significant only at the 10% level).
We next examine whether the finance-productivity growth relationship we find varies with the financial constraint indices developed by Cleary (1999) and Whited & Wu (2006). These indices were developed to measure financing constraints for public corporations in the US based on firm-level income and balance sheet information. We find no clear relationship between these financial constraint measures and the sensitivity of future TFP growth to debt growth by firms. One possible explanation is that these financial constraint indices--developed for publicly traded US corporations--may not necessarily be applicable for measuring financial constraints for the mostly private medium-sized firms in our sample.
7 Economic impact of productivity channel
The previous sections demonstrated that the use of finance has a statistically significant effect on firms' future productivity growth. This section examines the economic significance of our finding. Specifically, we use our estimates to derive the impact of the ongoing financial crisis in these European countries. This analysis provides an estimate of the economic impact of the finance-productivity growth channel highlighted in the study.
Table 16 presents annual real aggregate nonfinancial firm loan growth for the four countries in our sample. We obtain data on nominal nonfinancial loans outstanding from the corresponding financial accounts for each country. As in the estimation above, we translate nominal debt growth into real terms using the price index on all items excluding food and energy. The data indicate that real nonfinancial firm loan growth was negative, overall, in Italy, Spain and the UK. The decline in debt growth reflects the after-effects of the 2009 recession, the potential impact of increased bank capital requirements and the effects of the sovereign debt crisis that erupted in mid-2010. Debt growth was particularly muted in the UK and Spain as banking sector weakness in these countries limited loan growth.
We use as our counterfactual real debt growth from the US. Using data from the Flow of Funds accounts, we calculate that nonfinancial corporate debt grew at a real rate of about 4.1% from 1958 to 2011. We use data on US debt growth as the corresponding historical data are not available for a sufficient period for the European countries in our sample. We calculate the difference between the real debt growth rates reported in Table 16 and the US counterfactual, and use that as the input in our estimation equation (9) to obtain the predicted impact on TFP growth for 2010, 2011, and 2012. In this calculation, we use the point estimates for debt growth reported in Table 3. We also incorporate the estimated lag structure for TFP growth, which implies that it takes many years for TFP to return to its previous level following a negative shock.
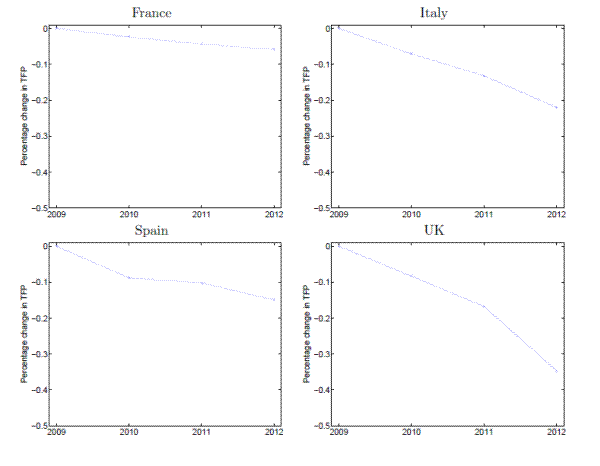
Figure 1 plots the estimated cumulative effect on the level of aggregate TFP predicted by the observed slowdown in real debt growth relative to the US counterfactual for each of the countries in our sample. The decline in TFP reflects the fact that the observed debt growth was below the counterfactual in each of the four countries. We report the cumulative effect as it adds together the total impact of the observed contractions in debt. We construct the aggregate impact as the weighted sum of the predicted firm-level impacts, where the weights are given by each firm's log value-added in 2009. The estimated impact is highest for the UK, reflecting the sharp decline in loans to nonfinancial firms and the fact that the debt growth coefficient is highest for the UK. The estimated impact is the smallest for France as nonfinancial loans expanded slightly in France and because France has a much smaller regression coefficient on debt growth (the estimated impact is negative as the small increase in nonfinancial debt in France is less than the counterfactual trend growth rate of 4.1%). Economically, the results imply that the difference between the cumulative decline in real debt from 2009 to 2011 and the counterfactual US debt growth rate translates to TFP declines of between 0.06 to 0.35 percent relative to trend. Thus, the finance-productivity growth channel emphasized in the study implies that the observed decline in debt growth leads to an economically significant shortfall in output, holding capital and labor inputs fixed, of between 0.06 to 0.35 percent relative to what may have been expected if debt grew at the counterfactual rate. This finding also demonstrates how the finance-productivity growth channel can help explain why output remains persistently below the pre-crisis trend level following a financial crisis.
Clearly, a few caveats are in order. The above analysis ignores heterogeneity in the distribution of firms. However, such heterogeneity may not have much impact on the above analysis, which is essentially calculating a mean effect. Our findings do not indicate that debt growth, by itself, causes declines in productivity. Instead, we interpret the finding as suggesting that reductions in debt reduce investments in productivity increasing projects by firms, thereby leading to lower productivity growth. Firms may mitigate this effect by substituting out of physical investment. On the other hand, the above calcuations are based on the findings from our baseline specification; the findings of Tables 12 indicate a higher debt growth coefficient in times of financial distress, which suggests that the observed cumulative decline in real debt from 2009 to 2011 may have had an even greater impact on output.
8 Conclusion
We examine the relationship between finance and future productivity growth at the firm level. Using data on firms in four European countries, we find that an increase in debt leads to future TFP increases. This result remains robust to a variety of controls, different methods of measuring productivity, and occurs in most subsamples. We also provide evidence that this relationship occurs through other operating expenses, which can be thought of as broadly capturing expenditures in innovative projects. In order to tackle reverse-causality concerns, we use a novel decomposition of TFP into a component that is potentially inside the information set of the firm and a component that is not. We find that the relationship between debt growth and future TFP growth mostly arises from the component outside the firm's information set, providing evidence against reverse causality. We also find that the relationship between the use of finance and future productivity growth strengthens as financing becomes more costly, consistent with economic intuition. Finally, we use our estimates to predict the decline in output resulting from the ongoing contraction in European nonfinancial firm debt and find that the finance-productivity channel highlighted in the study predicts economically meaningful declines in output.
Overall, our findings indicate that, in addition to the well-studied relationship between financing and physical investment, firms use finance to invest in innovative projects that lead to increases in future productivity. These results indicate that the role of finance in supporting investments in innovative projects may be an important link in understanding the effects of financial development (and financial crises) on economic output and growth.
Proofs
![\displaystyle \frac{\partial E[z^{\prime} - z]}{\partial F} > 0](img39.gif)
Equation (4) implies positivity of
Differentiating Equation (7) with respect to ![]() , one obtains
, one obtains
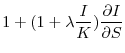 |
|||
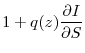 |
Differentiating the first-order conditions for investment with respect to
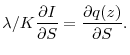
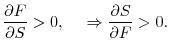
![\displaystyle \frac{\partial E[z^{\prime} - z]}{\partial F} > 0.](img84.gif)
![\displaystyle \frac{\partial}{\partial r} \left(\frac{\partial E[z^{\prime} - z]}{\partial F}\right) > 0](img41.gif)
We first establish that the relationship between interest rates and expenditures on innovative projects is negative. Rewrite the optimal expenditures in innovative projects as
![\displaystyle 1+r = \frac{\partial }{\partial S} E\left[V(K^{\prime}, z^{\prime}) \right].](img86.gif)
![\displaystyle \frac{\partial^2}{\partial S^2} E\left[V(K^{\prime}, z^{\prime}) \right] \notag](img88.gif) |
(A.3) |
The second-order condition for an interior solution to
Effectively, this states that an increase in interest rates lowers optimal expenditures in innovative projects.
We establish negativity of the second expression as follows:
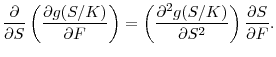 |
The concavity of
Substituting Equations (A.3) and (A.4) into (A.2), one obtains the desired result.
B Additional results
Appendix Table A1 presents the results of our baseline regression using a standard panel fixed-effects specification. We find that debt growth has a positive and statistically significant effect on future TFP growth. As is fairly typical, we find that the point estimates in the un-instrumented regression are smaller than the point estimates of our baseline regression reported in Table 3. Holtz-Eakin et al. (1988) note that the panel fixed-effect specification generates biased point estimates in the presence of lagged-dependent variables, leading us to choose the dynamic panel approach of Arellano & Bond (1991) as our preferred specification.
Appendix Table A2 reports the results from a first stage panel fixed-effects regression of growth in other operating expenses on contemporaneous debt growth. The first column reports the results using only debt growth as the independent variable, while the second column reports the results using additional controls. We find that, in both specifications, debt growth has a positive relationship with other operating expense growth, suggesting that firms may use external finance to invest in intangible capital.
References
Fazzari, Steven M., R. Glenn Hubbard, and Bruce C. Petersen , 1988. Financing constraints and corporate investment. Brookings Papers on Economic Activity 1:141-195.
La Porta, Rafael, Florencio Lopez de Silanes, Andrei Shleifer, and Robert W. Vishny, 1998, Law and finance. Journal of Political Economy 106:1131-1150.Romer, Paul M., 1990, Endogenous technological change. Journal of Political Economy 98:S71-S102.
Schumpeter, Joseph A., 1911, Theorie der Wirtschaftlichen Entwicklung (The Theory of Economic Development)
Syverson, Chad, 2011, What determines productivity. Journal of Economic Literature 49:326-65.
| Italy | Spain | UK | ||
|
|
-0.006 | -0.025 | -0.009 | -0.006 |
|
|
[0.000] | [-0.010] | [0.000] | [0.000] |
|
|
(0.160) | ( 0.224) | ( 0.210) | ( 0.260) |
| Age | 24.999 | 25.144 | 18.379 | 28.761 |
| Age: Median | [20.500] | [ 23.000] | [ 16.000] | [ 21.500] |
| Age: std. deviations | ( 17.037) | ( 15.706) | ( 11.266) | ( 23.078) |
| Assets, mil. USD | 30.422 | 49.354 | 36.451 | 385.044 |
| Assets, mil. USD : Median | [ 2.674] | [ 11.637] | [ 2.353] | [23.209] |
| Assets, mil. USD: std. deviations | (741.729) | (565.914) | (844.770) | (4524.196) |
| Asset turnover | 2.122 | 1.320 | 1.598 | 1.926 |
| Asset turnover: Median | [1.922] | [1.187] | [1.388] | [1.684] |
| Asset turnover: std. deviations | (1.036) | (0.715) | (0.996) | (1.277) |
| Investment | 0.035 | 0.066 | 0.084 | 0.045 |
| Investment: Median | [-0.029] | [-0.012] | [0.004] | [0.015] |
| Investment: std. deviations | (0.366) | (0.351) | (0.377) | (0.306) |
| Sales growth | 0.027 | 0.003 | 0.028 | 0.029 |
| Sales growth: Median | [0.022] | [0.011] | [0.025] | [0.028] |
| Sales growth: std. deviations | (0.139) | (0.194) | (0.217) | (0.197) |
| Book leverage | 0.129 | 0.275 | 0.224 | 0.309 |
| Book leverage: Median | [0.089] | [0.269] | [0.176] | [0.258] |
| Book leverage: std. deviations | (0.125) | (0.173) | (0.190) | (0.252) |
| Debt growth | 0.133 | 0.009 | 0.014 | -0.010 |
| Debt growth: Median | [0.037] | [-0.003] | [-0.081] | [-0.018] |
| Debt growth: std. deviations | (0.955) | (0.625) | (0.766) | (0.727) |
| Debt/Assets growth pos. | 0.060 | 0.061 | 0.084 | 0.076 |
| Debt/Assets growth pos.: Median | [0.037] | [0.044] | [0.049] | [0.047] |
| Debt/Assets growth pos.: std. deviations | (0.062) | (0.058) | (0.097) | (0.083) |
| Equity/Assets growth pos. | 0.012 | 0.011 | 0.012 | 0.011 |
| Equity/Assets growth pos.: Median | [0.005] | [0.004] | [0.004] | [0.001] |
| Equity/Assets growth pos.: std. deviations | (0.017) | (0.015) | (0.019) | (0.022) |
| % Obs. debt growth pos. | 0.504 | 0.499 | 0.384 | 0.474 |
| % Obs. equity growth pos. | 0.053 | 0.094 | 0.054 | 0.065 |
|
|
Log age | Log assets | Investment | Sales growth | Debt growth | |
| France:
|
1.00 | |||||
| France: Log age | -0.00 | 1.00 | ||||
| France: Log assets | -0.02 | 0.30 | 1.00 | |||
| France:Investment | 0.06 | 0.01 | 0.11 | 1.00 | ||
| France:Sales growth | -0.08 | -0.04 | 0.10 | 0.17 | 1.00 | |
| France: Debt growth | 0.06 | 0.01 | 0.04 | 0.25 | 0.06 | 1.00 |
| Italy:
|
1.00 | |||||
| Italy: Log age | -0.01 | 1.00 | ||||
| Italy: Log assets | -0.01 | 0.20 | 1.00 | |||
| Italy: Investment | 0.02 | 0.02 | 0.09 | 1.00 | ||
| Italy: Sales growth | -0.08 | -0.05 | 0.09 | 0.10 | 1.00 | |
| Italy: Debt growth | 0.04 | -0.02 | 0.04 | 0.17 | 0.09 | 1.00 |
| Spain:
|
1.00 | |||||
| Spain: Log age | -0.03 | 1.00 | ||||
| Spain: Log assets | -0.07 | 0.40 | 1.00 | |||
| Spain:Investment | 0.02 | -0.03 | 0.09 | 1.00 | ||
| Spain:Sales growth | -0.07 | -0.07 | 0.04 | 0.10 | 1.00 | |
| Spain:Debt growth | 0.04 | -0.01 | 0.09 | 0.28 | 0.06 | 1.00 |
| UK:
|
1.00 | |||||
| UK: Log age | 0.00 | 1.00 | ||||
| UK: Log assets | 0.00 | 0.16 | 1.00 | |||
| UK:Investment | -0.01 | -0.03 | 0.08 | 1.00 | ||
| UK:Sales growth | -0.08 | -0.05 | 0.06 | 0.18 | 1.00 | |
| UK:Debt growth | 0.03 | 0.01 | 0.06 | 0.23 | 0.10 | 1.00 |
| France | Italy | Spain | UK | |
|
|
-0.25** | -0.21** | -0.29** | -0.27** |
|
|
(-14.23) | (-17.42) | (-14.90) | (-18.13) |
|
|
-0.12** | -0.07** | -0.12** | -0.08** |
|
|
(-7.83) | (-8.26) | (-6.44) | (-5.34) |
|
|
0.52 | 0.75 | 1.03 | 0.22 |
|
|
(0.99) | (1.89) | (1.11) | (0.09) |
|
|
-0.09** | -0.02 | -0.06** | -0.13 |
|
|
(-4.63) | (-1.03) | (-2.84) | (-0.90) |
|
|
-0.15** | -0.15** | -0.13** | -0.15** |
|
|
(-14.09) | (-15.54) | (-24.09) | (-6.03) |
|
|
0.05** | 0.08** | 0.04** | 0.05 |
|
|
(10.83) | (20.05) | (14.42) | (1.83) |
|
|
0.008** | 0.016** | 0.009** | 0.021** |
|
|
(7.32) | (10.91) | (6.72) | (2.82) |
| Obs. | 81,789 | 124,142 | 207,419 | 49,129 |
| Serial corr. test, order 1 (p-val) | ||||
| Serial corr. test, order 2 (p-val) | 0.116 | 0.042 | 0.543 | 0.818 |
| Hansen J-Test (p-val) | 0.504 | 0.187 | 0.058 | 0.402 |
| France | Italy | Spain | UK | |
|
|
-0.25** | -0.21** | -0.29** | -0.29** |
|
|
(-14.21) | (-17.40) | (-14.95) | (-16.25) |
|
|
-0.12** | -0.07** | -0.13** | -0.09** |
|
|
(-7.85) | (-8.25) | (-6.48) | (-5.19) |
|
Log age |
0.61 | 0.75 | 1.02 | -0.23 |
|
Log age |
(1.16) | (1.88) | (1.10) | (-0.07) |
|
Log assets |
-0.09** | -0.02 | -0.06** | -0.17 |
|
Log assets |
(-4.44) | (-1.06) | (-2.89) | (-0.93) |
|
Sales growth |
-0.15** | -0.15** | -0.13** | -0.16** |
|
Sales growth |
(-14.28) | (-15.56) | (-24.06) | (-5.71) |
|
Investment |
0.04** | 0.08** | 0.04** | 0.05 |
|
Investment |
(10.71) | (20.00) | (14.23) | (1.78) |
|
Debt growth |
0.008** | 0.016** | 0.010** | 0.022* |
|
Debt growth |
(7.15) | (10.91) | (6.77) | (2.41) |
|
Equity growth |
0.015 | 0.004 | 0.038** | 0.169** |
|
Equity growth |
(1.62) | (0.58) | (4.78) | (3.86) |
| Obs. | 81,692 | 124,035 | 207,407 | 44,413 |
| Serial corr. test, order 1 (p-val) | 0.004 | |||
| Serial corr. test, order 2 (p-val) | 0.243 | 0.030 | 0.574 | 0.673 |
| Hansen J-Test (p-val) | 0.524 | 0.185 | 0.057 | 0.546 |
| France | Italy | Spain | |
|
|
-0.29** | -0.25** | -0.36** |
|
|
(-14.10) | (-16.05) | (-10.25) |
|
|
-0.14** | -0.07** | -0.17** |
|
|
(-7.73) | (-6.75) | (-4.71) |
|
Log age |
0.77 | 0.92 | -1.26 |
|
Log age |
(1.04) | (1.48) | (-0.69) |
|
Log assets |
-0.11** | -0.03 | -0.13** |
|
Log assets |
(-3.83) | (-1.17) | (-3.29) |
|
Sales growth |
-0.15** | -0.14** | -0.10** |
|
Sales growth |
(-11.43) | (-9.05) | (-14.76) |
|
Investment |
0.04** | 0.08** | 0.03** |
|
Investment |
(7.86) | (15.13) | (4.70) |
|
Debt growth |
0.008** | 0.015** | 0.014** |
|
Debt growth |
(5.82) | (7.81) | (4.67) |
| Obs. | 74,229 | 121,962 | 197,709 |
| Serial corr. test, order 1 (p-val) | |||
| Serial corr. test, order 2 (p-val) | 0.761 | 0.796 | 0.127 |
| Hansen J-Test (p-val) | 0.252 | 0.187 | 0.031 |
| France | Italy | Spain | UK | |
|
|
-0.31** | -0.26** | -0.32** | -0.28** |
|
|
(-27.43) | (-29.42) | (-28.97) | (-18.23) |
|
|
-0.13** | -0.04** | -0.12** | -0.07** |
|
|
(-10.18) | (-5.41) | (-9.93) | (-7.39) |
|
Log age |
-0.48 | -1.07 | 1.70 | 4.58** |
|
Log age |
(-0.60) | (-1.82) | (1.86) | (3.14) |
|
Log assets |
-0.15** | -0.19** | -0.05** | 0.00 |
|
Log assets |
(-4.84) | (-7.15) | (-3.03) | (0.01) |
|
Sales growth |
-0.13** | -0.09** | -0.11** | -0.21** |
|
Sales growth |
(-10.24) | (-3.70) | (-18.21) | (-9.42) |
|
Investment |
0.01* | 0.02** | 0.01** | 0.02 |
|
Investment |
(2.34) | (3.13) | (6.06) | (1.39) |
|
Debt growth |
0.006* | 0.024** | 0.009** | 0.013** |
|
Debt growth |
(2.02) | (10.36) | (6.21) | (2.66) |
| Obs. | 83,671 | 137,377 | 210,088 | 51,437 |
| Serial corr. test, order 1 (p-val) | 0.220 | |||
| Serial corr. test, order 2 (p-val) | 0.979 | 0.137 | 0.006 | |
| Hansen J-Test (p-val) | 0.840 | 0.045 | 0.478 |
| France | Italy | Spain | UK | |
| Small (1) | 0.017** | 0.016** | 0.015 | 0.008 |
| Small (1): t-stat | (7.69) | (7.58) | (1.62) | (0.99) |
| Medium (2) | 0.009** | 0.015** | 0.007** | 0.015 |
| Medium (2): t-stat | (5.14) | (5.33) | (3.09) | (1.81) |
| Large (3) | 0.003* | 0.016** | 0.011** | 0.035** |
| Large (3): t-stat | (1.98) | (5.36) | (4.56) | (3.24) |
| Young (1) | 0.010** | 0.014** | 0.009** | 0.021** |
| Young (1): t-stat | (5.58) | (6.07) | (4.77) | (2.72) |
| Middle (2) | 0.004 | 0.022** | 0.011** | 0.022** |
| Middle (2): t-stat | (1.35) | (7.99) | (5.87) | (3.50) |
| Mature (3) | 0.007** | 0.014** | 0.012** | 0.027** |
| Mature (3): t-stat | (4.34) | (4.67) | (6.22) | (3.73) |
|
|
-0.25** | -0.28** | -0.27** |
|
|
(-16.38) | (-18.01) | (-17.64) |
|
|
-0.08** | -0.08** | -0.08** |
|
|
(-5.43) | (-5.23) | (-4.99) |
|
Log age |
0.70 | -0.05 | 0.66 |
|
Log age |
(0.37) | (-0.02) | (0.34) |
|
Log assets |
-0.07 | -0.14 | -0.35 |
|
Log assets |
(-0.72) | (-1.05) | (-1.93) |
|
Sales growth |
-0.22** | -0.15** | -2.68** |
|
Sales growth |
(-9.33) | (-6.07) | (-2.91) |
|
Investment |
0.06* | 0.05 | -0.27* |
|
Investment |
(2.53) | (1.82) | (-2.08) |
|
OOE growth |
0.132** | ||
|
OOE growth |
(10.18) | ||
|
Pred. OOE growth |
0.742** | ||
|
Pred. OOE growth |
(3.14) | ||
|
Pred. OOE growth, (full) |
5.716** | ||
|
Pred. OOE growth, (full) |
(2.72) | ||
| Obs. | 49,647 | 46,793 | 46,793 |
| Serial corr. test, order 1 (p-val) | |||
| Serial corr. test, order 2 (p-val) | 0.858 | 0.803 | 0.916 |
| Hansen J-Test (p-val) | 0.410 | 0.412 | 0.466 |
| France | Italy | Spain | |
| -0.28** | -0.25** | -0.31** | |
| (-20.44) | (-17.07) | (-16.19) | |
|
|
-0.12** | -0.07** | -0.12** |
|
|
(-9.21) | (-7.23) | (-5.95) |
|
Log age |
0.63 | 0.59 | 1.25 |
|
Log age |
(1.22) | (1.11) | (1.28) |
|
Log assets |
-0.08** | 0.00 | -0.07** |
|
Log assets |
(-4.23) | (0.08) | (-2.98) |
|
Sales growth |
-0.12** | -0.09** | -0.07** |
|
Sales growth |
(-9.31) | (-7.89) | (-9.40) |
|
Investment |
0.03** | 0.06** | 0.03** |
|
Investment |
(8.10) | (15.45) | (12.62) |
|
Debt growth |
0.008** | 0.014** | 0.008** |
|
Debt growth |
(6.50) | (8.14) | (5.28) |
| Obs. | 74,229 | 121,962 | 197,709 |
| Serial corr. test, order 1 (p-val) | |||
| Serial corr. test, order 2 (p-val) | 0.634 | 0.028 | 0.757 |
| Hansen J-Test (p-val) | 0.215 | 0.476 | 0.002 |
| France | Italy | Spain | |
|
|
-0.30** | -0.25** | -0.37** |
|
|
(-10.76) | (-11.54) | (-7.06) |
|
|
-0.12** | -0.05** | -0.15** |
|
|
(-5.79) | (-3.42) | (-2.92) |
|
Log age |
-0.28 | 0.20 | -0.01 |
|
Log age |
(-0.50) | (0.39) | (-0.01) |
|
Log assets |
-0.03 | -0.06* | -0.01 |
|
Log assets |
(-1.61) | (-2.45) | (-0.47) |
|
Sales growth |
-0.03** | -0.08** | -0.04** |
|
Sales growth |
(-3.62) | (-4.43) | (-6.10) |
|
Investment |
0.01** | 0.01 | 0.00** |
|
Investment |
(2.96) | (1.26) | (2.61) |
|
Debt growth |
0.000 | 0.002 | 0.001 |
|
Debt growth |
(0.12) | (1.21) | (0.89) |
| Obs. | 74,229 | 121,962 | 197,709 |
| Serial corr. test, order 1 (p-val) | |||
| Serial corr. test, order 2 (p-val) | 0.153 | 0.718 | 0.251 |
| Hansen J-Test (p-val) | 0.017 | 0.500 | 0.813 |
| France | Italy | Spain | UK | |
|
|
-0.29** | -0.23** | -0.31** | -0.28** |
|
|
(-16.40) | (-18.92) | (-15.20) | (-14.20) |
|
|
-0.12** | -0.07** | -0.13** | -0.08** |
|
|
(-8.29) | (-8.83) | (-6.56) | (-5.29) |
|
Log age |
0.63 | 0.87* | 1.10 | 0.07 |
|
Log age |
(1.23) | (2.24) | (1.20) | (0.02) |
|
Log assets |
-0.11** | -0.06** | -0.08** | -0.16 |
|
Log assets |
(-5.87) | (-2.92) | (-3.65) | (-0.80) |
|
Sales growth |
-0.13** | -0.14** | -0.12** | -0.14** |
|
Sales growth |
(-12.49) | (-13.92) | (-23.17) | (-4.71) |
|
Investment |
-0.01 | 0.01** | -0.01* | -0.02 |
|
Investment |
(-1.21) | (2.94) | (-2.00) | (-0.20) |
|
Debt growth |
0.007** | 0.017** | 0.010** | 0.022* |
|
Debt growth |
(6.42) | (11.68) | (7.28) | (2.32) |
|
Investment |
-0.11** | -0.13** | -0.10** | -0.14 |
|
Investment |
(-43.98) | (-17.31) | (-15.13) | (-0.99) |
| Obs. | 81,704 | 124,066 | 207,107 | 49,073 |
| Serial corr. test, order 1 (p-val) | 0.002 | |||
| Serial corr. test, order 2 (p-val) | 0.670 | 0.402 | 0.419 | 0.866 |
| Hansen J-Test (p-val) | 0.546 | 0.329 | 0.043 | 0.382 |
| France | Italy | Spain | UK | |
|
|
-0.24** | -0.21** | -0.27** | -0.27** |
|
|
(-14.50) | (-17.39) | (-13.34) | (-20.02) |
|
|
-0.11** | -0.07** | -0.10** | -0.07** |
|
|
(-7.41) | (-8.34) | (-5.16) | (-6.19) |
|
Log age |
-0.28 | 0.74 | 1.57 | 0.80 |
|
Log age |
(-0.70) | (1.90) | (1.49) | (0.33) |
|
Log assets |
-0.12** | -0.02 | -0.03 | -0.10 |
|
Log assets |
(-6.10) | (-1.15) | (-1.62) | (-0.69) |
|
Sales growth |
-0.14** | -0.15** | -0.12** | -0.15** |
|
Sales growth |
(-19.33) | (-14.53) | (-28.31) | (-5.62) |
|
Investment |
0.05** | 0.07** | 0.04** | 0.05 |
|
Investment |
(12.16) | (18.86) | (14.97) | (1.75) |
|
Debt growth |
0.005** | 0.008** | 0.007** | 0.027** |
|
Debt growth |
(4.02) | (3.34) | (4.24) | (2.83) |
|
10-yr spread |
-0.756 | 2.024 | -8.883 | -0.325 |
|
10-yr spread |
(-0.56) | (1.01) | (-1.01) | (-0.31) |
|
Debt growth |
0.069** | 0.025** | 0.049* | -0.011 |
|
Debt growth |
(5.98) | (3.86) | (2.54) | (-0.99) |
| Obs. | 81,789 | 124,142 | 207,419 | 49,129 |
| Serial corr. test, order 1 (p-val) | 0.001 | |||
| Serial corr. test, order 2 (p-val) | 0.155 | 0.063 | 0.048 | 0.967 |
| Hansen J-Test (p-val) | 0.265 | 0.239 | 0.008 | 0.327 |
| France | Italy | Spain | UK | |
|
|
-0.27** | -0.22** | -0.29** | -0.28** |
|
|
(-14.79) | (-18.05) | (-14.57) | (-18.34) |
|
|
-0.13** | -0.07** | -0.12** | -0.08** |
|
|
(-8.47) | (-8.42) | (-6.23) | (-5.53) |
|
Log age |
0.87 | 0.48 | 1.16 | 0.05 |
|
Log age |
(1.67) | (1.13) | (1.22) | (0.02) |
|
Log assets |
-0.09** | -0.05* | -0.08** | -0.19 |
|
Log assets |
(-4.40) | (-2.39) | (-3.43) | (-1.20) |
|
Sales growth |
-0.15** | -0.15** | -0.13** | -0.15** |
|
Sales growth |
(-14.42) | (-14.43) | (-22.90) | (-5.60) |
|
Investment |
0.04** | 0.08** | 0.04** | 0.04 |
|
Investment |
(10.48) | (19.04) | (13.78) | (1.71) |
|
Debt growth |
0.020** | 0.047** | 0.027** | 0.052** |
|
Debt growth |
(7.71) | (11.66) | (8.82) | (3.80) |
|
Low leverage dummy |
-0.018** | -0.030** | -0.015** | -0.048** |
|
Low leverage dummy |
(-6.39) | (-8.25) | (-3.72) | (-4.59) |
|
High leverage dummy |
0.025** | 0.025** | 0.019** | 0.039** |
|
High leverage dummy |
(7.86) | (7.59) | (4.62) | (3.18) |
|
Debt growth |
-0.013** | -0.035** | -0.022** | -0.039** |
|
Debt growth |
(-6.29) | (-8.82) | (-10.31) | (-4.00) |
|
Debt growth |
0.008** | 0.019** | 0.021** | 0.047** |
|
Debt growth |
(3.43) | (3.17) | (6.05) | (2.77) |
| Obs. | 79,538 | 114,601 | 197,973 | 48,024 |
| Serial corr. test, order 1 (p-val) | ||||
| Serial corr. test, order 2 (p-val) | 0.770 | 0.005 | 0.399 | 0.815 |
| Hansen J-Test (p-val) | 0.638 | 0.112 | 0.091 | 0.297 |
| France | Italy | Spain | UK | |
|
|
-0.26** | -0.22** | -0.29** | -0.28** |
|
|
(-13.57) | (-17.97) | (-14.61) | (-15.23) |
|
|
-0.13** | -0.07** | -0.12** | -0.08** |
|
|
(-7.69) | (-8.35) | (-6.20) | (-4.67) |
|
Log age |
0.97 | 0.46 | 0.83 | -0.74 |
|
Log age |
(1.75) | (1.09) | (0.85) | (-0.28) |
|
Log assets |
-0.08** | -0.03 | -0.07** | -0.20 |
|
Log assets |
(-3.58) | (-1.40) | (-3.04) | (-1.29) |
|
Sales growth |
-0.16** | -0.15** | -0.14** | -0.15** |
|
Sales growth |
(-13.90) | (-14.50) | (-23.31) | (-5.37) |
|
Investment |
0.04** | 0.08** | 0.04** | 0.04 |
|
Investment |
(9.71) | (19.27) | (13.41) | (1.76) |
|
Debt growth |
0.009** | 0.022** | 0.011** | 0.029** |
|
Debt growth |
(5.77) | (8.30) | (6.00) | (3.57) |
|
Low cash dummy |
0.010** | 0.005* | 0.001 | 0.012* |
|
Low cash dummy |
(4.45) | (1.99) | (0.71) | (2.01) |
|
High cash dummy |
-0.003 | -0.006* | -0.006** | -0.010 |
|
High cash dummy |
(-1.28) | (-2.40) | (-2.83) | (-1.60) |
|
Debt growth |
0.001 | 0.002 | 0.001 | 0.000 |
|
Debt growth |
(0.38) | (0.64) | (0.54) | (0.05) |
|
Debt growth |
-0.003 | -0.011** | -0.002 | -0.012* |
|
Debt growth |
(-1.87) | (-3.78) | (-1.18) | (-2.00) |
| Obs. | 73,942 | 114,379 | 186,529 | 42,594 |
| Serial corr. test, order 1 (p-val) | ||||
| Serial corr. test, order 2 (p-val) | 0.755 | 0.004 | 0.659 | 0.981 |
| Hansen J-Test (p-val) | 0.568 | 0.115 | 0.078 | 0.364 |
| France | Italy | Spain | UK | |
|
|
-0.25** | -0.21** | -0.29** | -0.28** |
|
|
(-14.22) | (-17.37) | (-15.08) | (-17.88) |
|
|
-0.12** | -0.07** | -0.13** | -0.08** |
|
|
(-7.81) | (-8.27) | (-6.57) | (-5.13) |
|
Log age |
0.53 | 0.74 | 0.94 | -0.07 |
|
Log age |
(1.01) | (1.85) | (1.02) | (-0.03) |
|
Log assets |
-0.09** | -0.02 | -0.06** | -0.14 |
|
Log assets |
(-4.64) | (-1.06) | (-2.96) | (-1.00) |
|
Sales growth |
-0.15** | -0.15** | -0.13** | -0.15** |
|
Sales growth |
(-14.12) | (-15.56) | (-23.98) | (-6.07) |
|
Investment |
0.05** | 0.08** | 0.04** | 0.05 |
|
Investment |
(10.80) | (20.00) | (14.39) | (1.74) |
|
Debt growth |
0.005** | 0.014** | 0.009** | 0.019* |
|
Debt growth |
(4.72) | (8.21) | (6.25) | (2.55) |
|
Debt growth |
0.013** | 0.008* | 0.002 | 0.013 |
|
Debt growth |
(5.14) | (2.32) | (0.78) | (1.74) |
| Obs. | 81,748 | 123,683 | 207,106 | 48,542 |
| Serial corr. test, order 1 (p-val) | ||||
| Serial corr. test, order 2 (p-val) | 0.134 | 0.032 | 0.775 | 0.743 |
| Hansen J-Test (p-val) | 0.499 | 0.179 | 0.049 | 0.340 |
| France | Italy | Spain | UK | |
| 2009 | 1.19% | -0.34% | -5.21% | 0.12% |
| 2010 | 0.92% | -0.65% | -0.05% | -1.03% |
| 2011 | 1.28% | -2.51% | -2.52% | -5.87% |
| France | Italy | Spain | UK | |
|
|
-0.68** | -0.53** | -0.69** | -0.58** |
|
|
(-103.15) | (-110.09) | (-164.03) | (-73.53) |
|
|
-0.48** | -0.28** | -0.48** | -0.30** |
|
|
(-75.51) | (-72.06) | (-115.26) | (-44.39) |
|
Log age |
0.03 | 0.03* | 0.01 | 0.02 |
|
Log age |
(1.88) | (2.30) | (0.51) | (1.34) |
|
Log assets |
-0.06** | -0.05** | -0.03** | -0.10** |
|
Log assets |
(-14.27) | (-12.89) | (-9.78) | (-14.40) |
|
Sales growth |
0.03** | 0.04** | 0.02** | 0.05** |
|
Sales growth |
(6.76) | (9.39) | (9.25) | (5.68) |
|
Investment |
-0.01** | -0.01** | -0.01** | -0.04** |
|
Investment |
(-6.65) | (-6.74) | (-12.00) | (-8.61) |
|
Debt growth |
0.002** | 0.005** | 0.007** | 0.008** |
|
Debt growth |
(4.03) | (5.54) | (11.22) | (5.53) |
| Obs. | 134,473 | 174,377 | 312,650 | 69,621 |
| R-square (within) | 0.317 | 0.240 | 0.325 | 0.262 |
|
Debt Growth |
0.028** | 0.012** |
|
Debt Growth |
(34.01) | (14.30) |
|
Log Age |
-0.104** | |
|
Log Age |
(-17.70) | |
|
Log Assets |
0.028** | |
|
Log Assets |
(12.80) | |
|
Sales Growth |
0.445** | |
|
Sales Growth |
(104.91) | |
|
Investment |
0.053** | |
|
Investment |
(24.69) | |
| Obs. | 258,388 | 204,966 |
| R-square (within) | .007 | 0.213 |
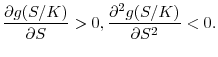
![\displaystyle \max_{I,S} \hspace{.2cm} \Pi - I - \lambda\frac{I^2}{2K} - S + \frac{1}{1+r} E[V(K^{\prime}, z^{\prime})],](img31.gif)
![\displaystyle 1 = \frac{1}{1+r}\frac{\partial}{\partial S} E\left[ V(K^{\prime}, z^{\prime})\right],](img35.gif)
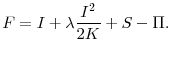
![\displaystyle \frac{\partial E[z^{\prime} - z]}{\partial F} = \frac{\partial E[g(S/K)]}{\partial F} = E\left[\frac{\partial g(S/K)}{\partial S} \frac{\partial S}{\partial F}\right].](img75.gif)
![\displaystyle \frac{\partial}{\partial r} \left(\frac{\partial E[z^{\prime} - z]}{\partial F}\right) = \frac{\partial}{\partial r} \left(\frac{\partial E[g(S/K)]}{\partial F}\right) = E\left[\frac{\partial S}{\partial r} \frac{\partial}{\partial S} \left(\frac{\partial g(S/K)}{\partial F}\right)\right].](img85.gif)