
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 828, February 2005 --- Screen Reader
Version*
Investment-Specific and Multifactor Productivity in Multi-Sector Open Economies: Data and Analysis
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In the last half of the 1990s, labor productivity growth rose in the U.S. and fell almost everywhere in Europe. We document changes in both capital deepening and multifactor productivity (MFP) growth in both the information and communication technology (ICT) and non-ICT sectors. We view MFP growth in the ICT sector as investment-specific productivity (ISP) growth. We perform simulations suggested by the data using a two-country DGE model with traded and nontraded goods. For ISP, we consider level increases and persistent growth rate increases that are symmetric across countries and allow for costs of adjusting capital-labor ratios that are higher in one country because of structural differences. ISP increases generate investment booms unless adjustment costs are too high. For MFP, we consider persistent growth rate shocks that are asymmetric. When such MFP shocks affect only traded goods (as often assumed), movements in 'international' variables are qualitatively similar to those in the data. However, when they also affect nontraded goods (as suggested by the data), movements in some of the variables are not. To obtain plausible results for the growth rate shocks, it is necessary to assume slow recognition.
Keywords: Technology shocks, technical change, dynamic general equilibrium, learning, Harrod-Balassa-Samuelson Effect, nontraded goods
JEL classification: D83, F43, O41
1 Introduction
Changes in labor productivity growth in the U.S. and Europe are among the major economic events of the last fifteen years. There now seems to be general agreement that in the last half of the 1990s, labor productivity growth rose in the U.S. and fell almost everywhere in Europe. In the first half of the 1990s, U.S. growth was significantly below that in European countries, but in the second half the situation was reversed in almost every case. Recently, several analysts have provided breakdowns of changes in labor productivity growth by country, by component, and by sector. 1
Some generalizations are suggested by the data. In both the U.S. and Europe there were increases in multifactor productivity (MFP) growth in the information and communication technology (ICT) sector. It came as a surprise to us that these increases were the same or even greater in Europe. As a consequence, there were sharp reductions in the relative prices of ICT goods.2 At least partly for this reason, capital deepening through investment in information and communication technology (ICT) goods increased in both the U.S. and Europe, but the increase was about twice as great in the U.S. We treat MFP growth in the ICT sector as investment-specific productivity (ISP) growth, a convention adopted by several others.3
MFP growth in the non-ICT-producing sector rose by a significant amount in the U.S. and by comparable amounts in some European countries but fell by more than double these amounts in other European countries. Capital deepening through investment in non-ICT goods increased markedly in the U.S. but decreased in Europe. Increases in both labor productivity growth and MFP growth have been higher in the U.S. in important sectors that produce mostly nontraded goods.
The changes in relative productivity growth rates in the last half of the 1990s were accompanied by some dramatic changes in other variables. In the U.S., there was an investment boom, a deterioration in the trade account, a temporary improvement in the terms of trade, and a significant real appreciation of the dollar.
In an attempt to provide perspective on the data, we perform simulations using a DGE model with two countries (Home and Foreign).4 Each country produces a traded good and a nontraded good, and the two traded goods are imperfect substitutes for each other.5 In each country, consumption and investment goods are aggregates assembled using the two traded goods and the local nontraded good. The baskets of traded goods used in both consumption and investment are biased toward the locally-produced good, but the 'local bias' in consumption is greater. The model nests most two-country DGE models used over the past fifteen years to analyze productivity changes.
Our reading of the disparate productivity-growth experiences of
the U.S. and Europe has determined our choice of simulation
experiments. We focus primarily on two persistent productivity
growth shocks. The first is a symmetric ISP growth shock.
This shock has different effects on the two countries because one
of them has less structural rigidity reflected in lower costs of
adjusting capital-labor (![]() -
-![]() ) ratios. The
second is an MFP growth shock that is (perfectly) asymmetric
across countries. Departing from much previous analysis, we
emphasize the case in which the shock affects both the traded and
nontraded sectors. To take account of slow adjustment of
consumption and slow recognition of persistent growth shocks, we
incorporate habit in consumption and learning about shocks. To fix
ideas, we consider symmetric ISP level shocks before
discussing the two growth shocks.
) ratios. The
second is an MFP growth shock that is (perfectly) asymmetric
across countries. Departing from much previous analysis, we
emphasize the case in which the shock affects both the traded and
nontraded sectors. To take account of slow adjustment of
consumption and slow recognition of persistent growth shocks, we
incorporate habit in consumption and learning about shocks. To fix
ideas, we consider symmetric ISP level shocks before
discussing the two growth shocks.
We calibrate the symmetric ISP growth shock so that it
causes an increase in the rate of decline of the relative price of
investment that closely matches the one in U.S. data. In the
country with low ![]() -
-![]() adjustment costs,
the investment incentive of the shock is large relative to the
wealth effect. As a result, there is an investment boom, an actual
reduction in consumption for several periods, and a modest trade
deficit. In contrast, in the country with high
adjustment costs,
the investment incentive of the shock is large relative to the
wealth effect. As a result, there is an investment boom, an actual
reduction in consumption for several periods, and a modest trade
deficit. In contrast, in the country with high ![]() -
-![]() adjustment costs, the wealth effect
dominates: investment increases very little, but consumption rises
significantly. The movements in the TOT and the
adjustment costs, the wealth effect
dominates: investment increases very little, but consumption rises
significantly. The movements in the TOT and the ![]() are qualitatively quite different from those in the
data.
are qualitatively quite different from those in the
data.
We calibrate the asymmetric MFP growth shock so that for the country receiving the increase, the initial rise in labor productivity growth is the same as for the symmetric ISP shock. With MFP shocks, the wealth effect is large relative to the investment incentive. For positive shocks, both consumption and investment rise, and there is a sizeable trade deficit. The large wealth effect combined with local-good bias keeps the TOT from deteriorating for a while since demand for the local traded good increases by as much as supply.
In succeeding sections, we present data relevant for analyzing productivity shocks in the U.S. and Europe, our model, our simulations, and our conclusions.
2 Data
2.1 Accounting for Changes in Labor Productivity Growth
Much progress has been made in accounting for changes in labor productivity growth in the U.S. and Europe during the 1990s.6 It is no easy task to separate out the contributions of capital deepening and multi-factor productivity growth for the economy as a whole and for individual sectors.7 Data revisions and improvements in methodology continue to have significant effects on conclusions.8
Here we focus primarily on data from three sources: the Groningen Growth and Development Center (GGDC), Dale Jorgenson and his associates, and the Organization for Economic Co-operation and Development (OECD) STandard ANalysis data base.9 Data from all three sources have at least three desirable features: they (1) are reported on a standardized basis across several countries, (2) include estimates of hours instead of only the number of employees for all countries, and (3) include estimates of real investment that are quality adjusted using the same methodology.10
Table 1 contains a comparison of GGDC and Jorgenson data for the U.S., France, Germany, and the U.K.11 In addition, for the GGDC there are data for the Netherlands and an aggregate called the 'EU-4' (France, Germany, the U.K., and the Netherlands).12 For Jorgenson there are data for Italy but there is no aggregate of European countries.13 In our comparisons we use average annual growth rates for the periods 1990-1995 and 1996-2001.14 We focus our attention on changes in average growth rates between the two periods in the U.S. and European countries. Unless stated otherwise, growth rate differences are presented in percentage point (pp) form.
Changes in U.S. growth rates are essentially the same in the data from the GGDC and Jorgenson, and we will treat them as if they were the same in what follows.15 Most of the major qualitative features that we choose to emphasize can be illustrated by comparisons between the U.S. and the EU-4 aggregate in the GGDC data. 16 In the last half of the 1990s, labor productivity growth rose in the U.S. and fell in Europe resulting in a difference between changes in growth rates of 1.5 pp. In the first half of the 1990s, U.S. labor productivity growth was significantly below that in the EU-4, but in the second half it was slightly above.
Using the same data, the changes in labor productivity can be broken down into changes in components. Overall capital deepening increased in the U.S.: there were increases for both ICT capital (0.4 pp) and non-ICT capital (0.2 pp). In contrast, overall capital deepening fell in the EU-4 because the increase in ICT capital deepening (0.2 pp) was only half as much as in the U.S. and was more than offset by the decrease in non-ICT capital deepening (-0.6 pp). The contribution of MFP growth increased in both the U.S. and the EU-4 but the U.S. increase was more than twice as high (0.7 pp versus 0.3 pp).
The Jorgenson data include a breakdown of the contributions of MFP growth into those from ICT-producing sectors and those from all other sectors. 1718 These data confirm earlier findings that there has been a significant increase in the contribution of MFP growth in ICT producing sector in the U.S. (0.3 pp).19 However, it came as a surprise to us that they also imply that the contribution of this sector has been just as high in the European countries. In the non-ICT sectors, MFP growth increased by 0.4 pp in the U.S. and by slightly more in France and the U.K. but fell by 1.2 pp in Italy and by even more in Germany.
There has been much interest in the sectoral breakdown of the changes in labor productivity growth. Using OECD data on value added by sector in the U.S. (a rearrangement of BEA data) we constructed a sectoral breakdown of labor productivity growth for the U.S. which is shown in the leftmost three columns of Table 2.20 It appears that most of the pickup in aggregate growth was accounted for by three sectors: Manufacturing (0.2 pp); Wholesale and Retail Trade; Restaurants and Hotels (0.4 pp); and Finance, Insurance, Real Estate, and Business Services (0.2 pp).
Conceptually, sectoral contributions to changes in aggregate labor productivity growth can be broken down into changes in capital deepening and changes in MFP growth. As it turns out, it is difficult to reach definitive conclusions about the relative importance of these contributions. There is evidence that sectoral changes in ICT capital deepening have been important.21 As an example, the data in Table 2 provide some support for the view that the sectors that have made the largest sectoral contributions are the ones with the biggest increases in investment in ICT goods. Sectoral data for the ratio of nominal gross investment in ICT goods to nominal value added are shown in the rightmost three columns of Table 2. The increases in this ratio for Wholesale and Retail Trade as well as Finance, Insurance, Real Estate & Business Sector Services are significantly larger than for all of the other sectors (except Transportation, Storage, and Communication). These are two of the three sectors that made the largest contributions. However, even though Manufacturing is the third, the increase in its ratio is on the low end. Furthermore, by far the largest increase in the ratio occurred in the Transportation, Storage, and Communication sector, where there was a negative contribution.
There is also evidence that sectoral changes in MFP growth have been important. Inklar et al (2003) show that some of the sectors that have made the largest contributions to the increase in the difference between aggregate U.S. and EU-4 labor productivity growth are sectors in which increases in the difference between MFP growth rates have also been high. 22 According to their data, for some of these sectors the increases in MFP growth were considerably more important than the increases in ICT capital deepening.23 Three sectors which exhibit both of these phenomena are (1) Electrical and Electronic Equipment; Instruments, (2) Repairs and Wholesale Trade, and (3) Retail Trade.24
We believe that the data clearly suggest at least three generalizations regarding the breakdown of the increase in the difference between U.S. and European labor productivity growth rates. First, although MFP growth in the ICT sector was roughly the same in the U.S. and Europe, there have been important increases in differences between ICT capital deepening in both ICT-producing and non-ICT-producing sectors. Second, MFP growth in the non-ICT-producing sectors increased in the U.S. but fell on balance in Europe. Third, in contrast to what some might have expected, there have been significant increases in differentials in MFP growth rates nontraded goods as well as for traded goods. We have taken these generalizations into account in constructing the model that we use to shed light on recent experience.
2.2 More on the U.S. Economy in the 1990s
Some additional data for the U.S. economy relevant for analyzing the effects of productivity shocks are shown in Figure 1. In discussing figures, we use the convention that, for example, 'panel 4 of Figure 1' is referred to simply as 'F1.4'.
In the second half of the 1990s, the decline in prices of investment goods became more rapid. In particular, the rate of decline in the price of aggregate investment relative to GDP (F1.1) increased by 0.69 pp. A greater increase for consumer durables and a smaller increase for private investment (by businesses) more than offset the small decline for government investment. For the subcategory of investment in equipment and software, the increase was 1.28 pp.
At least partly in response to this more rapid rate of price decline, there was an investment boom. The share of investment in GDP (broken line F1.4) rose throughout this period from about 0.19 to about 0.22 . In contrast, the saving rate, the solid line, climbed by 2 pp between 1995 and 1998 but fell back to slightly below its 1994 level by the end of 2000. Since the fraction of GDP devoted to government spending was fairly constant in the late 1990s, the continued increase in investment accompanied by the reduction in savings implied a deterioration in the overall U.S. trade balance (F1.5).
The increase in the nominal investment share does not fully capture the magnitude of the investment boom because of the decline in prices of investment goods. To better capture the relative magnitude of the changes in quality-adjusted real investment, we plot the difference between the growth rates of chain-weighted real investment and chain-weighted real GDP (F1.2). The difference between these two growth rates got at least as high in the last half of the 1990s as in earlier booms and remained high much longer. Furthermore, the drop in the difference in the recession of the early 2000s was significantly less than in earlier recessions.
What is not shown in Figure 1 is that an overwhelming portion of growth in investment can be attributed to outlays for ICT investment (information-processing equipment and computer software); nominal outlays on these item were 9% of total nominal investment in 1990 and 22% in 1999. Real outlays grew faster because computer prices fell. The increase in ICT investment growth accounts for 60% of the increase in all investment. 25
There was an abrupt increase in U.S. labor productivity growth (F1.3) in the second half of the 1990s.26
The overall U.S. trade balance as a ratio of GDP (F1.5, dotted line) deteriorated rapidly in the last half of the 1990s. We are especially interested in a comparison of the U.S. with Europe. The U.S. bilateral trade balance with the European Union (solid line) worsened slightly. After improving for a while, the overall trade balance for Europe (dashed line) fell below its initial level.
The U.S. terms of trade with the rest of the world (F1.6, dotted line) improved by as much as 5% before giving back much of its gain by the end of the decade.27 The dollar appreciated dramatically in real terms against the 'rest of the world' (dashed line) and even more dramatically against the Euro (solid line).
It apparently took some time for government and private analysts to become convinced that the increase in productivity growth was going to be persistent. Both the Congressional Budget Office and the consensus of Blue Chip forecasters produce five-year-ahead forecasts of real GDP growth. As reported by Erceg, Guerreri, and Gust (2002), these forecasts were virtually unchanged until the late 1990s and then increased gradually.
3 Model
In our analysis of the effects of different productivity shocks, we use a DGE model with two countries designated Home and Foreign which are mirror images of one another. We describe the behavior of the representative Home agent.
3.1 Tastes
In period ![]() , the agent maximizes the intertemporal
utility function 28
, the agent maximizes the intertemporal
utility function 28
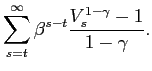
|
(1) |
Period utility is a constant elasticity function of ![]() which, in turn, depends on the current consumption of
the agent (
which, in turn, depends on the current consumption of
the agent (![]() ), lagged total consumption (
), lagged total consumption (
![]() ), and leisure which is
given by one minus labor (
), and leisure which is
given by one minus labor (![]() ):
):
![$\displaystyle V_{s}=V\left( C_{s},\mathcal{C}_{s-1},L_{s}\right) =\left( \frac{C_{s} -\eta\mathcal{C}_{s-1}}{1-\eta}\right) \exp\left\{ \chi_{0}\left[ \frac{\left( 1-L_{s}\right) ^{1-\chi}-1}{1-\chi}\right] \right\} .$](img19.gif)
|
(2) |
That is, there is external habit in consumption. The agent also
chooses holdings of a single bond (![]() ) denominated
in the Home traded good (the numeraire good for the model) and
traded internationally.
) denominated
in the Home traded good (the numeraire good for the model) and
traded internationally.
3.2 Technology
Home technology comprises six sectors. First, there are two
sectors in which traded (![]() ) goods and nontraded
(
) goods and nontraded
(![]() ) goods are produced using identical
Cobb-Douglas production functions scaled by adjustment
costs:29
) goods are produced using identical
Cobb-Douglas production functions scaled by adjustment
costs:29
![$\displaystyle Y_{is}=K_{is}^{\alpha}L_{is}^{1-\alpha}X_{is}^{1-\alpha}\left[ 1-\frac{ \psi_{KL}}{2}\left( \frac{K_{is}}{L_{is}}/\frac{K_{is-1}}{L_{is-1}}\right) ^{2}\right] =F(\underline{K}_{is},\underline{L}_{is})X_{is}^{1-\alpha},$](img23.gif)
|
(3) |
where
![]() and
and
![]() are vectors containing
current and lagged values and
are vectors containing
current and lagged values and![]() . For sector
. For sector
![]() , output (
, output (![]() ) is produced
using sector-specific capital (
) is produced
using sector-specific capital (![]() ) and labor
(
) and labor
(![]() ). The
). The ![]() and
and
![]() sectors use all the labor that is supplied:
sectors use all the labor that is supplied:
| (4) |
There are MFP shocks (![]() ) that may
differ between the two sectors. For sector
) that may
differ between the two sectors. For sector ![]() , there
are quadratic adjustment costs (governed by
, there
are quadratic adjustment costs (governed by ![]() ) associated with changing capital-labor
ratios
) associated with changing capital-labor
ratios![]() 30 Examples of such adjustment costs
are training costs and costs of satisfying regulations.
30 Examples of such adjustment costs
are training costs and costs of satisfying regulations.
Next, there are two sectors in which capital stocks are
accumulated. In each of these sectors, yesterday's sector-specific
capital stock (![]() ) and some of yesterday's
investment good (
) and some of yesterday's
investment good (![]() ) are used to generate
today's sector-specific capital stock :
) are used to generate
today's sector-specific capital stock :
![$\displaystyle K_{is}=\left[ \delta\left( \frac{J_{is-1}}{\delta}\right) ^{1-\phi}+\left( 1-\delta\right) \left( K_{is-1}\right) ^{1-\phi}\right] ^{\frac{1 } {1-\phi}},\quad i=T,N, $](img40.gif)
where ![]() governs the costs of adjusting capital
stocks.31
governs the costs of adjusting capital
stocks.31
Finally, there are two sectors in which goods are assembled into
a consumption good (![]() ) and an investment good
(
) and an investment good
(![]() ).
). ![]() is a constant
elasticity of substitution (CES) function of consumption inputs of
traded goods (
is a constant
elasticity of substitution (CES) function of consumption inputs of
traded goods (![]() ) and of the local nontraded good
(
) and of the local nontraded good
(![]() ):
):
![$\displaystyle C_{s}=\left[ \left( 1-\nu_{C}\right) \left( \frac{C_{Ts}}{1-\nu}\right) ^{1-\theta_{CN}}+\nu_{C}\left( \frac{C_{Ns}}{\nu}\right) ^{1-\theta_{CN}} \right] ^{\frac{1}{1-\theta_{CN}}},$](img47.gif)
|
(5) |
and ![]() is a CES function of 'quality-adjusted'
investment inputs of traded goods (
is a CES function of 'quality-adjusted'
investment inputs of traded goods (
![]() ) and of the local nontraded
good (
) and of the local nontraded
good (![]() ): 32
): 32
![$\displaystyle J_{s}=\left[ \left( 1-\nu_{I}\right) \left( \frac{\mathcal{I}_{Ts}}{1-\nu} \right) ^{1-\theta_{IN}}+\nu_{I}\left( \frac{I_{Ns}}{\nu}\right) ^{1-\theta_{IN}}\right] ^{\frac{1}{1-\theta_{IN}}} ,$](img51.gif)
|
(6) |
where
![]() is the 'quality-adjusted'
input of traded goods defined below. In assembly sector
is the 'quality-adjusted'
input of traded goods defined below. In assembly sector ![]() where
where ![]() the parameters
the parameters ![]() and
and
![]() are, respectively, the weight
given to nontraded goods in production and the elasticity of
substitution between traded and nontraded goods.
are, respectively, the weight
given to nontraded goods in production and the elasticity of
substitution between traded and nontraded goods.
In turn, the consumption input of traded goods is a CES function
of consumption inputs of Home traded goods (![]() )
and of Foreign traded goods (
)
and of Foreign traded goods (![]() ):
):
![$\displaystyle C_{Ts}=\left[ \ell_{C}\left( \frac{C_{Hs}}{\ell_{C}}\right) ^{1-\theta _{CT}}+\left( 1-\ell_{C}\right) \left( \frac{C_{Fs}}{1-\ell_{C}}\right) ^{1-\theta_{CT}}\right] ^{\frac{1}{1-\theta_{CT}}},\qquad\ell_{C} =n+\kappa_{C}.$](img59.gif)
|
(7) |
By analogy, the investment input of quality-adjusted traded goods
is a CES function of quality-adjusted inputs of Home traded goods (
![]() ) and of Foreign traded
goods (
) and of Foreign traded
goods (
![]() ):
):
![$\displaystyle \mathcal{I}_{Ts}=\left[ \ell_{I}\left( \frac{\mathcal{I}_{Hs}}{\ell_{I}} \right) ^{1-\theta_{IT}}+\left( 1-\ell_{I}\right) \left( \frac{\mathcal{I} _{Fs}}{1-\ell_{I}}\right) ^{1-\theta_{IT}}\right] ^{\frac{1}{1-\theta_{IT} }},\qquad\ell_{I}=n+\kappa_{I}.$](img62.gif)
|
(8) |
![]() are,
respectively, the weights on the Home traded good in traded-good
inputs into consumption and investment.
are,
respectively, the weights on the Home traded good in traded-good
inputs into consumption and investment. ![]() is the
proportion of the world's population living in the Home country. In
this paper, we make the simplifying assumption that the two
countries are of equal size (
is the
proportion of the world's population living in the Home country. In
this paper, we make the simplifying assumption that the two
countries are of equal size (
![]() ). The parameters
). The parameters
![]() and
and
![]() (
(
![]() )
determine the amount of local-good bias in the composition of
traded goods inputs into consumption and investment, respectively.
(For example, there is no local-good bias when
)
determine the amount of local-good bias in the composition of
traded goods inputs into consumption and investment, respectively.
(For example, there is no local-good bias when
![]() ). We incorporate the
empirically-based assumption that the local-good bias is greater in
consumption than in investment.
). We incorporate the
empirically-based assumption that the local-good bias is greater in
consumption than in investment.
Traded investment inputs are referred to as 'quality-adjusted', because there are investment-specific productivity (ISP) increases:
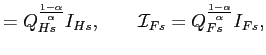
|
||
| (9) | ||
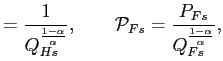
|
where the
![]() are ISP shocks that can
be different.33 If a
are ISP shocks that can
be different.33 If a ![]() increases, a given physical unit of output of good
increases, a given physical unit of output of good ![]() can contribute more to investment good output (
can contribute more to investment good output (![]() ) than the same unit did before.
) than the same unit did before. ![]() and
and
![]() are measured in units of Home and
Foreign traded goods, respectively, whereas
are measured in units of Home and
Foreign traded goods, respectively, whereas
![]() and
and
![]() are measured in performance
units. For example,
are measured in performance
units. For example, ![]() and
and ![]() might be measured in numbers of computers in which
case
might be measured in numbers of computers in which
case
![]() and
and
![]() might be measured in terms
of computing power. Given that the Home traded good is the
numeraire, the price of a unit of
might be measured in terms
of computing power. Given that the Home traded good is the
numeraire, the price of a unit of ![]() is
unity.
is
unity. ![]() is the price of the Foreign traded
good in terms of the Home traded good, and
is the price of the Foreign traded
good in terms of the Home traded good, and
![]() and
and
![]() are prices of Home and
Foreign performance units in terms of the Home traded good.
are prices of Home and
Foreign performance units in terms of the Home traded good.
Our ISP shocks are designed to generate effects similar to those of an increase in multifactor productivity in a separate ICT sector. The traded-goods sector can be thought of as being divided into two sub-sectors--one producing investment inputs that are subject to quality improvements and the other producing consumption inputs that are not--with perfect mobility of capital and labor between the two subsectors. Note that all of the ISP shocks affect output of the investment good, which can be used to increase the capital stock in both the traded and nontraded goods sectors.
![]() shocks are reflected in the relative prices
of investment goods. Using the model results for sectoral prices
and quantities, we can construct aggregate prices and quantities.
In order to generate model results that are comparable to the data,
we construct chain-weighted aggregates. For example, for the
relative price of investment, we use the ratio of Fisher indices
for the investment (
shocks are reflected in the relative prices
of investment goods. Using the model results for sectoral prices
and quantities, we can construct aggregate prices and quantities.
In order to generate model results that are comparable to the data,
we construct chain-weighted aggregates. For example, for the
relative price of investment, we use the ratio of Fisher indices
for the investment (![]() ) deflator and the GDP
deflator, where the deflator for
) deflator and the GDP
deflator, where the deflator for ![]() is calculated
using the prices of
is calculated
using the prices of
![]() ,
,
![]() , and
, and ![]() and the deflator for GDP is calculated using the
prices of
and the deflator for GDP is calculated using the
prices of ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() , and
, and ![]()
3.3 The Budget Constraint
The agent must also take into account a budget constraint. Income from production of traded and nontraded goods plus interest from claims on Foreign last period must be at least enough to cover purchases of both traded goods and the home nontraded good for use in assembling consumption and investment plus claims on Foreign this period and "portfolio management costs'' associated with claims on or liabilities to Foreign:34
![$\displaystyle \begin{tabular}[c]{c} $F(\underline{K}_{Ts},\underline{L}_{Ts})X_{Ts}^{1-\alpha}+F(\underline{K} _{Ns},\underline{L}_{Ns})X_{Ns}^{1-\alpha}+R_{s-1}B_{s-1}\geq$\\ \\ $\left[ C_{Hs}+P_{Fs}C_{Fs}+P_{Ns}C_{Ns}+\frac{\mathcal{I}_{Hs}}{Q_{Hs}^{ \frac{1-\alpha}{\alpha}}}+\frac{P_{Fs}\mathcal{I}_{Fs}}{Q_{Fs}^{\frac{ 1-\alpha}{\alpha}}}+P_{Ns}I_{Ns}+B_{s}+\frac{\zeta}{2}\frac{B_{s}^{2}}{ Z_{Ts}}\right] .$ \end{tabular}$](img107.gif)
|
(10) |
![]() is the price of Home nontraded goods
in term of Home traded goods.
is the price of Home nontraded goods
in term of Home traded goods. ![]() is the gross
return on bonds denominated in the Home traded good. A positive
value of
is the gross
return on bonds denominated in the Home traded good. A positive
value of ![]() indicates claims of Home on Foreign.
indicates claims of Home on Foreign.
3.4 Relative Prices
In this paper, we focus on four relative prices. Two of them are
the relative prices of the two countries' nontraded goods in terms
of their traded goods represented by ![]() and
and
![]() , respectively. An asterisk on
a variable indicates that it relates to Foreign. The terms of trade
(TOT) and real exchange rate (
, respectively. An asterisk on
a variable indicates that it relates to Foreign. The terms of trade
(TOT) and real exchange rate (![]() ) are given
by
) are given
by
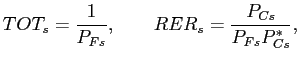
|
(11) |
where
![]() is the price of the Foreign
consumption bundle in terms of the Foreign traded good. The
TOT is defined as the number of Foreign traded goods it
takes to buy a unit of Home traded goods, so an increase is an
improvement. The
is the price of the Foreign
consumption bundle in terms of the Foreign traded good. The
TOT is defined as the number of Foreign traded goods it
takes to buy a unit of Home traded goods, so an increase is an
improvement. The ![]() is the CPI-adjusted exchange
rate defined as the number of Foreign consumption bundles it takes
to buy a Home consumption bundle, so an increase is an appreciation
of the Home currency in real terms. Improvements in the TOT
and increases in
is the CPI-adjusted exchange
rate defined as the number of Foreign consumption bundles it takes
to buy a Home consumption bundle, so an increase is an appreciation
of the Home currency in real terms. Improvements in the TOT
and increases in ![]() cause the Home currency to
appreciate in real terms but increases in
cause the Home currency to
appreciate in real terms but increases in
![]() cause it to depreciate. In the
neighborhood of the steady state
cause it to depreciate. In the
neighborhood of the steady state
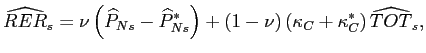
|
(12) |
where a hat over a variable indicates a percentage deviation from
its steady-state value.
![]() is the degree of
local-good bias in consumption in Foreign, and we assume
is the degree of
local-good bias in consumption in Foreign, and we assume
![]() .
.
4 Simulations
In this section we report the results of our simulations. To fix ideas, we first discuss symmetric increases in the levels of ISP in Home and Foreign. Then, we analyze two types of persistent productivity growth shocks suggested by the data: symmetric increases in ISP growth and (perfectly) asymmetric changes in MFP growth. The values of the parameters used in the simulations are in Table A1 in the Appendix. Unless stated otherwise, we assume that Home and Foreign parameters are identical.
In explaining our simulations, we use the terms 'wealth effect'
and 'investment incentive'. For us, a shock has a positive wealth
effect if it gives rise to an increase in the excess of income over
the spending needed to support the initial steady-state path (both
measured in Home traded goods). In calculating this excess, we hold
constant relative prices of physical units, consumption
allocations, effective investment input allocations (
![]() and
and
![]() ), and bond holdings.
35 With MFP shocks, income goes
up. Agents receive the value of production of traded and nontraded
goods through either wages or capital income, and MFP shocks
increase the amounts produced. With ISP shocks, spending
goes down. There is a fall in the relative price of
effective traded-good investment inputs. When there are
positive wealth effects, agents can consume more, increase the
capital stock by more, or work less. What they choose to do depends
on the incentives they face.
), and bond holdings.
35 With MFP shocks, income goes
up. Agents receive the value of production of traded and nontraded
goods through either wages or capital income, and MFP shocks
increase the amounts produced. With ISP shocks, spending
goes down. There is a fall in the relative price of
effective traded-good investment inputs. When there are
positive wealth effects, agents can consume more, increase the
capital stock by more, or work less. What they choose to do depends
on the incentives they face.
A positive investment incentive can arise either because of a
fall in the consumption price of (quality-adjusted) investment or
because of a rise in the marginal product of capital.36
Changes in the consumption price of investment are associated with
changes in the ![]() price of investment in the same
direction. We use the latter variable and call it simply the
'relative price of investment'. U.S. data for this relative price
are in F1.1.
price of investment in the same
direction. We use the latter variable and call it simply the
'relative price of investment'. U.S. data for this relative price
are in F1.1.
4.1 Symmetric ISP Level Increases
In our first experiment,
there are symmetric permanent increases in the levels of
ISP. We compare results for two cases: (1) the identical
(adjustment) costs case in which adjusting capital-labor
(![]() -
-![]() ) ratios is costless in both
countries (
) ratios is costless in both
countries (
![]() ), and (2) the higher Foreign
(adjustment) costs case in which adjusting
), and (2) the higher Foreign
(adjustment) costs case in which adjusting ![]() -
-![]() ratios is very costly in Foreign (
ratios is very costly in Foreign (
![]() ). In both cases, there
are positive costs of adjusting capital stocks that are the same in
both countries.
). In both cases, there
are positive costs of adjusting capital stocks that are the same in
both countries.
In F2A and F2B, we show the effects of 1% increases in the
productivities of Home and Foreign traded goods that are used as
inputs in the assembly of investment goods (![]() and
and ![]() respectively). Since these increases
in the ISP of tradable investment inputs are symmetric, they
have the same positive wealth effects in both countries in both
cases. In each country, it takes fewer resources to support the
initial steady-state path.
respectively). Since these increases
in the ISP of tradable investment inputs are symmetric, they
have the same positive wealth effects in both countries in both
cases. In each country, it takes fewer resources to support the
initial steady-state path.
We use the case with identical costs (dashed lines) as a benchmark. In this case, the two countries are completely symmetric, so all the effects are the same in the two countries. These results are similar to those for a closed economy in many respects.
It comes as no surprise that the shocks create positive investment incentives. Before adjustment of consumption and investment, there are decreases in the relative prices of investment. With optimal adjustment, the relative prices of investment (F2A.1) fall by roughly 0.45%. The magnitudes of these declines reflect the fact that tradables account for roughly half of investment inputs. After their initial drop, the relative prices of investment remain roughly constant.
In our calibration, the costs of adjusting capital stocks are low enough that (gross) investment shares (F2A.3) increase because quantity increases outweigh price declines. The increases in investment shares by 0.09 pp must be matched by equal decreases in consumption shares (F2A.4). The investment incentive is large enough relative to the wealth effect that there are decreases not only in the shares of consumption but also in the chain-weighted levels (F2B.1). Although the shares of consumption remain below baseline for twenty five years, the levels rise above baseline after four years. The hump-shaped responses of consumption shares are due to the effects of habit in consumption. In each country, there are the same spikes in the excess of (quality-adjusted) investment growth over GDP growth (F2A.2), labor productivity growth (F2A.5), and GDP growth (F2A.7) as well as persistent increases in capital deepening (F2A.6) and hours worked (F2A.8).
Now we turn to the case with higher Foreign costs (solid and
dotted lines). Once again, there are positive investment incentives
in both countries. Before adjustment of consumption and investment,
the declines in the relative prices of investment are the same.
However, the positive investment incentive is larger in Home. The
marginal product of capital is higher there because there are no
![]() -
-![]() adjustment costs. The
initial increase in the Home investment share is about twice as
great as in the identical-costs case. About one third of this
change is financed by an additional reduction in the Home
consumption share and the remaining two thirds by borrowing from
Foreign. As in the identical-costs case, the investment incentive
effect is large enough relative to the wealth effects that there
are reductions not only in the share of Home consumption but also
in its the level. There is a major deterrent to increasing
investment further by borrowing more. Nontraded goods constitute a
large share of Home investment-assembly inputs and are complements
to the other inputs, so either the fall in consumption or the rise
in work effort would have to be relatively large.37
adjustment costs. The
initial increase in the Home investment share is about twice as
great as in the identical-costs case. About one third of this
change is financed by an additional reduction in the Home
consumption share and the remaining two thirds by borrowing from
Foreign. As in the identical-costs case, the investment incentive
effect is large enough relative to the wealth effects that there
are reductions not only in the share of Home consumption but also
in its the level. There is a major deterrent to increasing
investment further by borrowing more. Nontraded goods constitute a
large share of Home investment-assembly inputs and are complements
to the other inputs, so either the fall in consumption or the rise
in work effort would have to be relatively large.37
In contrast, in Foreign the investment incentive is small enough relative to the wealth effect that the investment share is reduced rather than increased. Given that investment inputs are now much cheaper, Foreign residents can maintain their capital stocks and even increase them a little, even though they drastically reduce their investment share. They choose to devote the lion's share of the freed resources to increasing their consumption share because there is a relatively small increase in the incentive to lend to Home.
In Home, there is some magnification of the effects on the excess of investment growth over GDP growth, labor productivity growth, GDP growth, capital deepening, and hours worked.38 However, in Foreign, there are significant effects on only three of these variables: GDP growth, labor productivity growth, and hours. The initial spike in labor productivity growth is larger in Foreign (0.14 pp) than in Home (0.1 pp). Output growth increases somewhat less in Foreign, but hours remain virtually unchanged there while they increase significantly in Home. At first, hours in Foreign remain virtually unchanged because of the large cost of changing the capital-labor ratio. Over time, total hours increase as a gradual increase in nontraded hours (not shown) offsets an even more gradual decrease in traded hours (not shown). Two observations help in understanding why: (1) steady-state capital stocks increase in Foreign as much as they do in Home and (2) nontraded investment inputs are complements to traded inputs but do not benefit from an improvement in ISP.
Home runs a trade balance deficit (F2B.3) for about 5 years and a trade surplus for many years thereafter. The higher level of investment in Home increases demand for both tradable investment inputs. The increase in the trade deficit as a share of GDP is at its maximum (-.05 pp) initially when it is about a fourth of the total increase in the Home investment share.
The Home TOT (F2B.4) remains roughly unchanged initially
and then deteriorates slowly over time. At first, the supply of and
demand for traded goods (not shown) are cut back by roughly equal
amounts in Home and in Foreign. In Home, a significant amount of
labor (not shown) is shifted from the traded to the nontraded
sector. However, almost immediately the supply of traded goods
begins to increase faster in Home because the Home traded-good
capital stock increases much more rapidly and because Home
traded-good hours rebound rapidly. In each country, the relative
price of the nontraded goods (F2B.6), ![]() or
or
![]() , rises by roughly the same
amount initially. It continues to rise in Foreign but begins to
fall in Home because of the divergent movements in consumption
assembly, which is relatively intensive in nontraded goods.
Initially, the Home currency appreciates in real terms (F2B.5), and
equation (12) helps in understanding why. The
, rises by roughly the same
amount initially. It continues to rise in Foreign but begins to
fall in Home because of the divergent movements in consumption
assembly, which is relatively intensive in nontraded goods.
Initially, the Home currency appreciates in real terms (F2B.5), and
equation (12) helps in understanding why. The
![]() rises a little initially because the
TOT improves, and the movements in the relative prices of
nontraded goods offset each other. However, it begins to fall
almost immediately because the effects of the divergent movements
in the relative prices of nontraded goods reinforce those of the
deterioration in the TOT.
rises a little initially because the
TOT improves, and the movements in the relative prices of
nontraded goods offset each other. However, it begins to fall
almost immediately because the effects of the divergent movements
in the relative prices of nontraded goods reinforce those of the
deterioration in the TOT.
4.2 Symmetric ISP Growth Rate Increases
The data indicate that there was a persistent increase in MFP growth in the ICT sector in the last half of the 1990s in both the U.S. and Europe. For this reason, it is interesting to analyze persistent symmetric increases in the growth rates of ISP. For simplicity, we restrict our attention to the more relevant case of asymmetric adjustment costs. Like other analysts of persistent growth-rate shocks, we find it necessary to assume that agents must learn the process governing the growth rate shocks in order to obtain results that bear some resemblance to the data.39 We focus on the learning case and show results for the full-information case primarily for purposes of exposition.
We assume that the Home ISP growth rate follows an
![]() process:
process:
| (13) |
where a tilde over a variable indicates a growth rate. We set the coefficient on the lagged growth rate equal to 0.95 so that the relative price of investment (F3a.1) decreases by one percent per year during the first six years of the simulation (1996-2001). This rate of decrease closely matches the one in the U.S. data. The process for the Foreign ISP growth rate is analogous.
In the case with learning, agents hypothesize that
![]() is the sum of a persistent
shock (
is the sum of a persistent
shock (![]() ) and a temporary shock (
) and a temporary shock (![]() ) and that it evolves according to
) and that it evolves according to
| (14) |
where ![]() and
and ![]() are
normally distributed innovations. Having observed
are
normally distributed innovations. Having observed
![]() , the agent infers
, the agent infers ![]() and
and ![]() using a Kalman filter. We
assume that agents set the autoregressive coefficient for their
hypothesized persistent process equal to the true coefficient.
40 The ratio of the variances of
using a Kalman filter. We
assume that agents set the autoregressive coefficient for their
hypothesized persistent process equal to the true coefficient.
40 The ratio of the variances of
![]() and
and ![]() perceived by agents determines how long it takes them to learn. We
choose this ratio so that the part of the observed shock attributed
to the persistent component is 75% after five years and virtually
100% after ten years. The learning process for the Foreign
ISP growth rate is analogous.
perceived by agents determines how long it takes them to learn. We
choose this ratio so that the part of the observed shock attributed
to the persistent component is 75% after five years and virtually
100% after ten years. The learning process for the Foreign
ISP growth rate is analogous.
We choose the ISP growth rate innovations (
![]() for Home) so that they
raise the level of ISP by 1% in the first period. That is,
the first-period effects of the ISP growth rate shocks on
the levels of ISP are the same as those of the ISP
level shock considered in subsection 4.1.
Scaling the shocks in this way makes it easy to compare the initial
effects in the learning and full information cases. However, it has
the implication that the effects of persistent growth rate shocks
are an order of magnitude larger because the ISP shocks
asymptotically approach levels that are 13% higher than their
preshock levels.
for Home) so that they
raise the level of ISP by 1% in the first period. That is,
the first-period effects of the ISP growth rate shocks on
the levels of ISP are the same as those of the ISP
level shock considered in subsection 4.1.
Scaling the shocks in this way makes it easy to compare the initial
effects in the learning and full information cases. However, it has
the implication that the effects of persistent growth rate shocks
are an order of magnitude larger because the ISP shocks
asymptotically approach levels that are 13% higher than their
preshock levels.
Just as in the case of increases in the levels of ISP, the wealth effects are the same in both countries because the shocks are symmetric. However, the wealth effects are smaller in the benchmark case with learning than with full information because agents are not sure that the shock is truly a persistent growth rate shock.
There are positive investment incentives in both countries, but
the incentive in Home is greater. The initial decreases in the
relative prices of investment are the same in both countries, but
the marginal product of capital is higher in Home because there are
no ![]() -
-![]() adjustment costs. With
optimal adjustment, the paths for the relative prices of investment
(F3A.1) in Home and Foreign are slightly different because
investment demand increases by more in Home, limiting the price
decline to some extent. The increase in Home investment demand is
reflected both in the increase in the investment share (F3A.3) over
time and in the rise in the excess of investment growth over output
growth (F3A.2) by about 0.5 pp for the first 5 years. As in the
level shocks case, investment is attractive enough that there are
decreases in both the share (F3A.4) and the level (F3B.1) of
consumption. Also, Home is induced to borrow from Foreign. In
contrast, Foreign residents reduce the share of investment but
increase the level of investment very gradually because of the high
costs of adjusting
adjustment costs. With
optimal adjustment, the paths for the relative prices of investment
(F3A.1) in Home and Foreign are slightly different because
investment demand increases by more in Home, limiting the price
decline to some extent. The increase in Home investment demand is
reflected both in the increase in the investment share (F3A.3) over
time and in the rise in the excess of investment growth over output
growth (F3A.2) by about 0.5 pp for the first 5 years. As in the
level shocks case, investment is attractive enough that there are
decreases in both the share (F3A.4) and the level (F3B.1) of
consumption. Also, Home is induced to borrow from Foreign. In
contrast, Foreign residents reduce the share of investment but
increase the level of investment very gradually because of the high
costs of adjusting ![]() -
-![]() ratios. They
increase the consumption share by somewhat less than they decrease
the investment share, and lend to Home.
ratios. They
increase the consumption share by somewhat less than they decrease
the investment share, and lend to Home.
In order to better understand the adjustment process in the learning case, it is useful to consider the full information case. We show only the results for Home. With full information, the wealth effect is greater. Agents know full well that the relative price of investment will be much lower in the future. For Home residents, investment is unattractive enough initially that they cut the investment share (F3A.3) by roughly 2 pp and the level of investment (F3B.2) by roughly 8%. The growth rate of investment is temporarily below that of output (F3A.2). A little more than half of the decrease in the investment share is used to raise the consumption share, and the rest is lent to Foreign. We do not discuss the full information case any further, except to note that in the early periods the paths for all the variables depart from those in the learning case in the manner implied by a larger perceived wealth effect.
With learning, the response of the Home investment share in the first period is a weighted average of what the response would be for a persistent growth shock with full information (-1.77 pp from F3A.2) and what it would be with a level shock (0.17 pp from F2A.2). Agents initially attribute only 6% of the observed movement in ISP to the persistent component and the other 94% to a level shock. When these percentages are used to weight the effects of the two possible kinds of shocks, the average effect is 0.05 pp (F3A.3). Since the U.S. investment share did not fall in the data when the rate of decline in the relative price of investment became larger, the results with learning seem more plausible to us than those with full information.
Home labor productivity growth (F3A.5) increases on impact by 0.14 pp, roughly the amount of the initial increase in ISP times the share in GDP of traded investment inputs (Home and Foreign). As the large increase in investment raises the contribution of capital deepening (F4A.6), labor productivity growth rises above its initial level. In contrast, in Foreign there is essentially no contribution of capital deepening, so the evolution of labor productivity growth closely matches that of the ISP shock.
In Home, hours (F4A.8) rise relatively rapidly and then fall back toward their initial level. In Foreign, hours increase more slowly and reach a higher level.
The Home trade balance (F3B.3) is in deficit for a time but then moves into surplus. The Home TOT (F3B.4) deteriorate over time, making Home traded goods relatively more attractive. The relative price of the nontraded good rises in Foreign because consumption is intensive in nontraded goods. This rise reinforces the deterioration in the Home TOT both of which cause the Home currency to depreciate in real terms (F3B.4).
4.3 Asymmetric MFP Growth Rate Shocks
According to the data we report above, in the late 90s the U.S. experienced an increase in the rate of growth of MFP in the non-ICT sector, and taken together European countries experienced a reduction. In both regions, there were changes in several sectors, some of which clearly produce nontraded goods. We perform simulations designed to isolate the effects of persistent changes in MFP growth rates.
For clarity, we make two simplifying assumptions. First, we
assume that the shocks are (perfectly) asymmetric by which we mean
that the increase in Home and the decrease in Foreign are equal in
absolute value. Second, we assume that there are no costs of
adjusting ![]() -
-![]() ratios in either
Home or Foreign.41 We report responses only for Home
since with symmetric economic structures and asymmetric shocks,
Foreign responses are the exact opposites of Home responses.
ratios in either
Home or Foreign.41 We report responses only for Home
since with symmetric economic structures and asymmetric shocks,
Foreign responses are the exact opposites of Home responses.
As a benchmark, we take the case in which there are MFP shocks of equal magnitude in the traded and nontraded sectors as suggested by the data. For comparison, we also consider the more familiar case in which there are MFP shocks only in the traded goods sector. This is the case used in discussions of the well-known Harrod-Balassa-Samuelson effect. In both cases, we assume that agents face a learning problem with the same structure as the one described in Subsection 4.2. We also discuss some of the differences between the results for MFP shocks and those for ISP shocks.
In the benchmark case the MFP growth rate increases initially by 0.33 pp in both the traded and nontraded sectors in Home (and declines by 0.33 pp in Foreign).42 We have picked the size of the shocks so that the initial rise in Home labor productivity growth matches the one in the simulation for a 1% ISP growth shock.43
There is a positive wealth effect since the outputs of both traded and nontraded goods increase. Before quantities adjust, there is no change in the relative price of investment goods because MFP rises by the same proportion in the traded and nontraded sectors. Nonetheless, there is still a positive investment incentive in Home because the marginal products of capital rise in both sectors.
The positive investment incentive leads to increases in the Home investment share (F4A.3) and in the excess of investment growth over GDP growth (F4A.2). At the point at which it is the largest (0.8 pp), about half of the increase in the investment share is financed by a reduction in the consumption share (F4A.4), and the remainder is financed by borrowing from Foreign. Although the consumption share falls, the wealth effect is strong enough relative to the investment incentive that the level of consumption rises steadily.
In the benchmark MFP case, the initial rise in Home labor productivity growth (F4B.1, solid line) of roughly 0.2 pp reflects both the 0.33 pp increase in MFP growth across the economy and labor's share of income (0.7 pp). As MFP growth subsides, labor productivity growth declines, and the contribution of capital deepening (F4A.6)--as opposed to the shock itself--accounts for a larger and larger share of labor productivity growth.
For the first several years, Home continues to borrow and run a trade-balance deficit (F4B.3). Since Home and Foreign traded goods are good substitutes, the deterioration is substantial, as much as 0.5% of GDP in our baseline case. Since there is local-good bias in both consumption and investment, the big initial increase in home absorption results in a slight improvement in the terms of trade. However, as Home production continues to expand, the Home terms of trade (F4B.4) deteriorate.
Now we turn to the more familiar case in which the MFP shock is concentrated in the traded sector. We call this case the 'traded-sector-only' case and double the magnitude of the shock since it affects only one sector. The traded-sector-only case is similar to the benchmark case in several ways. In Home there are a positive wealth effect and a positive investment incentive because the output of traded goods and the marginal product of capital in the traded goods sector both rise.
However, there are some differences between the two cases. In the traded-sector-only case, the path for the relative price of investment (F4A.1) is lower everywhere. The reason is that investment assembly is more intensive in traded goods than consumption assembly.44As a result, the investment share of GDP goes up by more. Since the reduction in the consumption share (F4A.4) is about the same in both cases, the higher investment share is reflected in more borrowing from Foreign accompanied by more deterioration in the trade balance (F4B.3).
The most significant differences from the benchmark case lie in
the results for some relative prices. The deterioration of the Home
TOT (F4B.4) in the first few years is not very different
from that in the benchmark case. In sharp contrast, the relative
price of the nontraded good (F4B.6) increases rapidly in Home (and
falls rapidly in Foreign) instead of remaining constant and is
about 7% higher in the long run. The large and divergent movements
in the relative prices of nontraded goods dominate movements in the
TOT, so the ![]() (F4B.5) rises in
accordance with equation (12). That is, in
contrast to the benchmark case, the Home currency appreciates
dramatically in real terms, exemplifying the familiar
Harrod-Balassa-Samuelson effect.
(F4B.5) rises in
accordance with equation (12). That is, in
contrast to the benchmark case, the Home currency appreciates
dramatically in real terms, exemplifying the familiar
Harrod-Balassa-Samuelson effect.
A comparison of the effects of growth rate shocks for MFP with those of ISP reveals some important differences. The MFP and ISP shocks we have chosen are the ones suggested by our reading of the data, not those best suited for a head- to-head comparison of the two kinds of shocks. Nonetheless, our simulations reveal some salient differences between them.
The relative importances of the wealth effect and the investment incentive are opposite in the two cases. With MFP shocks, the relative strength of the wealth effect is great enough that the level of consumption rises from the outset. In contrast, with ISP shocks, the wealth effect is relatively weak, so the level of consumption falls for some time.
The increase in labor productivity can be divided into the contribution of capital deepening and the contribution of the shocks themselves.45 Capital deepening is relatively less important with MFP shocks; that is, it accounts for a smaller fraction of labor productivity growth. For instance, in year 2000 (4 years after the start of the simulation) capital deepening accounts for one fourth of labor productivity growth with MFP shocks (F4A.5 and F4A.6) as opposed to one half with ISP shocks (F3A.5 and F3A.6).
As stated above, we calibrate the shocks so that the initial change in labor productivity growth is the same for MFP and for ISP shocks. Given this normalization and our calibration of the parameters, for example, the trade balance deteriorates more with the MFP shocks.
5 Conclusions
Our analysis highlights the major difference between positive ISP and MFP shocks. Both shocks lead to marked increases in labor productivity growth. However, with ISP shocks, raising labor productivity growth requires much more investment. Increases in labor productivity are accounted for more by increases in capital deepening than by the shock itself. This finding supports the view that ISP shocks played a relatively more important role than MFP shocks in generating the persistent excess of investment growth over GDP growth in the U.S. in the late 1990s.
Lags in recognition are key in explaining our results for persistent growth shocks. Under full information, with positive ISP shocks investment falls initially and remains below its initial level for a few years. Agents postpone investment because they realize that the price of investment goods will be even lower in the future. With learning, our simulation results are closer to the observed outcomes: investment remains constant initially but rises immediately thereafter.
We confirm that the treatment of nontraded goods can make a big
difference. 46 In the case of ISP shocks,
changing the degree of substitutability between traded and
nontraded goods has large effects at the sectoral level. In the
case of MFP shocks, we can reproduce the conventional
Harrod-Balassa-Samuelson result: when a country experiences a
positive shock that affects only traded goods, its currency
appreciates in real terms and its trade balance deteriorates,
changes like those that occurred in the U.S. in the late 1990s.
However, the data suggest that real-life MFP shocks also
affected nontraded goods. Our model implies that such shocks should
have virtually no effect on the ![]() and that they
should generate a smaller trade balance deterioration.
and that they
should generate a smaller trade balance deterioration.
Our simulations provide some insights regarding the effects of observed productivity shocks. However, it is not surprising that they leave some features of the data unaccounted for. We use a two-country model. But it seems clear that a model with more regions, almost certainly including a separate East Asia bloc, is required to analyze some of the developments of the 1990s, such as the big increase in the U.S. trade account deficit--accompanied by little increase in the bilateral trade surplus of Europe with the U.S.--and the large real appreciation of the dollar. We consider only productivity shocks. But other important shocks influenced economic outcomes in the 1990s. A prime example is the Asian crisis.
Appendix
A Lagrangian Expression for Home Agent
The Lagrangian expression for the home agent is
![\begin{displaymath} \begin{array}[c]{c} \sum_{s=t}^{\infty}\beta^{s-t}\left\{ \frac{\left[ V\left( C_{s},\mathcal{C }_{s-1},L_{s}\right) \right] ^{1-\gamma}-1}{1-\gamma}+\Lambda_{Ts}\left[ K\left( J_{Ts-1},K_{Ts-1}\right) -K_{Ts}\right] \right. \ \ +\Lambda_{Ns}\left[ K\left( J_{Ns-1},K_{Ns-1}\right) -K_{Ns}\right] +\Lambda_{Js}\left[ J\left( Q_{Hs}^{\frac{1-\alpha}{\alpha}}\mathcal{I} _{Hs},Q_{Fs}^{\frac{1-\alpha}{\alpha}}\mathcal{I}_{Fs},,I_{Ns}\right) -J_{Ts}-J_{Ns}\right] \ \ +\Lambda_{Cs}\left[ R_{s-1}B_{s-1}+F(\underline{K}_{Ts},\underline{L} _{Ts})X_{Ts}^{1-\alpha}+P_{Ns}F(\underline{K}_{Ns},\underline{L} _{Ns} )X_{Ns}^{1-\alpha}-\frac{\zeta}{2}\frac{B_{s}^{2}}{Z_{Ts}}\right. \ \ \left. -C_{Hs}-P_{Fs}C_{Fs}-P_{Ns}C_{Ns}-\frac{\mathcal{I}_{Hs}}{Q_{Hs}^{ \frac{1-\alpha}{\alpha}}}-\frac{P_{Fs}\mathcal{I}_{Fs}}{Q_{Fs}^{\frac{ 1-\alpha}{\alpha}}}-P_{Ns}I_{Ns}-B_{s}\right] \end{array}\end{displaymath}](img167.gif)
where
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are the shadow prices of
are the shadow prices of
![]() ,
, ![]() ,
,
![]() and income.
and income.
B Parameter Values
The parameter values used in the simulations are given in Table
A1. In the initial steady state ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() and
and
![]() are all unity.
are all unity.
Table A1: Parameter Values
| discount factor | ||
| elasticity of marginal utility
w.r.t. |
||
| share of capital in production | ||
| depreciation rate | ||
| governs capital adjustment costs | ||
| share of nontraded goods in
|
||
| | elasticity of substitution -
|
|
| | elasticity of substitution -
|
|
| relative size of home country | ||
| | local-good bias in |
|
| | local-good bias in |
|
| | elasticity of substitution -
|
|
| | elasticity of substitution -
|
|
| governs capital-labor ratio adjustment costs | 0 |
|
| governs portfolio management costs | ||
| Frisch elasticity of labor supply | ||
| set so steady-state share of time worked is 0.33 |
C Decomposing Labor Productivity Growth
In this section, we show that the usual decomposition of labor productivity growth into a contribution from capital deepening and a contribution from a productivity shock is as relevant for ISP shocks as it is for MFP shocks. For simplicity, we focus on a special case in which all goods are traded, but the argument generalizes.
The Törnqvist index for quality-adjusted, chain-weighted output growth, which approximates the Fisher index, is given by
| (15) |
where
![]() ,
,
![]() , and
, and
![]() are chain-weighted output,
consumption exports, and investment exports, respectively, and, for
example
are chain-weighted output,
consumption exports, and investment exports, respectively, and, for
example ![]() is the average of the shares of the
consumption of the Home good in total output in periods
is the average of the shares of the
consumption of the Home good in total output in periods ![]() and
and ![]() . 47
. 47
Quality-adjusted output at constant prices (
![]() ) and its growth rate (
) and its growth rate (
![]() ) are
) are
| (16) | |
![$\displaystyle \begin{tabular}[c]{l} $\tilde{Y}_{t}^{CP}=S_{CH}\tilde{C}_{Ht}+S_{CH}^{\ast}\tilde{C}_{Ht}^{\ast }+S_{IH}\left( \tilde{I}_{Ht}+\frac{1-\alpha}{\alpha}\tilde{Q}_{Ht}\right) +S_{IH}^{\ast}\left( \tilde{I}_{Ht}^{\ast}+\frac{1-\alpha}{\alpha}\tilde{ Q}_{Ht}\right) ,$ \end{tabular}$](img252.gif)
|
(17) |
where in the initial steady state ![]() , and,
for example,
, and,
for example,
![]() . From equations (15) and (17), it is
clear that growth of GDP at constant prices can be viewed as the
first-order approximation of the Törnqvist index with no trend
growth since
. From equations (15) and (17), it is
clear that growth of GDP at constant prices can be viewed as the
first-order approximation of the Törnqvist index with no trend
growth since
![]() in the steady state.
in the steady state.
Log-linearizing and combining equation (16) and the technology constraint
| (18) |
yield the usual decomposition in terms of percent deviations from the steady state:
![$\displaystyle \begin{tabular}[c]{l} $\hat{Y}_{t}^{CP}-\hat{L}_{t}=\alpha\left( \hat{K}_{t}-\hat{L}_{t}\right) +(1-\alpha)\hat{X}_{Ht}+\left( Sh_{IH}+Sh_{IH^{\ast}}\right) \frac{ 1-\alpha}{\alpha}\hat{Q}_{Ht}.$ \end{tabular}$](img257.gif)
|
(19) |
From equation (19), it is clear that the
ISP shock (
![]() ) can be interpreted as an
MFP shock that affects only the investment-producing sector
of the economy.
) can be interpreted as an
MFP shock that affects only the investment-producing sector
of the economy.
D Defining the Investment Incentive
For us, a positive investment incentive arises for one of two
reasons. The first reason is a decrease in the relative price of
investment. Under perfect competition, prices equal marginal costs,
so this relative price equals the ratio of marginal costs,
![]() , where
, where ![]() and
and ![]() are obtained from the
cost minimization problems
are obtained from the
cost minimization problems
| (20) | |
| (21) |
![]() and
and ![]() are
the CES aggregators (6) and
(5), and
are
the CES aggregators (6) and
(5), and ![]() and
and ![]() are the pre-shock levels of
quality-adjusted investment and consumption. Positive ISP
shocks lower the relative price of investment. The second reason is
an increase in the marginal product of capital. Positive MFP
shocks raise the marginal product of capital.
are the pre-shock levels of
quality-adjusted investment and consumption. Positive ISP
shocks lower the relative price of investment. The second reason is
an increase in the marginal product of capital. Positive MFP
shocks raise the marginal product of capital.
References
Backus, D., P. Kehoe, and F. Kydland. 1994a. "Dyamics of the Trade Balance and the Terms of Trade: The J Curve?" American Economic Review, Vol. 84, pp. 84-103.
Backus, D., P. Kehoe, and F. Kydland. 1994b. "Relative Price Movements in Dynamic General Equilibrium Models of International Trade." In F. van der Ploeg (Ed.), The Handbook of International Macroeconomics. Oxford: Blackwell.
Baxter, M. 1995. "International Trade and Business Cycles." In G. Grossman and K. Rogoff (Eds.), Handbook of International Economics, Vol. 3, pp. 1801-1864. Amsterdam: Elsevier.
Baxter, M. and M. J. Crucini. 1995. "Business Cycles and the Asset Structure of Foreign Trade." International Economic Review Vol. 36, pp. 821-854.
Bergin, P. R. and R. Glick. 2003. "Endogenous Tradability and Macroeconomic Implications." Nber working paper 9739, National Bureau of Economic Research.
Bosworth, B. P. and J. E. Triplett. 2000. "What's New About the New Economy? IT, Economic Growth, and Productivity", processed, Brookings Institution.
Dornbusch, R., S. Fischer, and P. A. Samuelson. 1977. "Comparative Advantage, Trade, and Payments in a Ricardian Model with a Continuum of Goods." American Economic Review, Vol. 67, pp. 823-839.
Dumagan, J. C. 2002. "Comparing the Superlative Törnqvist and Fisher Ideal Indexes." Economic Letters, Vol. 76, pp. 251-58.
Edge, R. M., T. Laubach, and J. C. Williams. 2003. "The Responses of Wages and Prices to Technology Shocks." Finance and economics discussion papers 2003-65, Federal Reserve Board.
Edge, R. M., T. Laubach, and J. C. Williams. 2004. "Learning and Shifts in Long-Run Productivity Growth." Finance and economics discussion papers 2004-21, Federal Reserve Board.
Erceg, C. J., L. Guerrieri, and C. Gust. 2002. "Productivity Growth and the Trade Balance in the 1990s: the Role of Evolving Perceptions", processed, Federal Reserve Board.
Fernald, J. G. and S. Ramnath. 2004. "The Acceleration in U.S. Total Factor Productivity After 1995: The Role of Information Technology." Economic Perspectives, Vol. 1, pp. 52-67.
GGDC. 2004. "60-Industry Database". Groningen Growth and Development Center. (www.ggdc.net).
Ghironi, F. and M. J. Melitz. 2004. "International Trade and Macroeconomic Dynamics with Heterogenous Firms", processed, Harvard.
Greenwood, J., Z. Hercowitz, and P. Krusell. 1997. "Long-Run Implications of Investment-Specific Technological Change." American Economic Review, Vol. 87, pp. 342-362.
Hunt, B. and A. Rebucci. 2003. "The U.S. Dollar and the Trade Deficit: What Accounts for the Late 1990s?", processed, International Monetary Fund.
Inklar, R., M. O'Mahony, K. Robinson, and M. Timmer. 2003. "Productivity and Competitiveness in the EU and in the U.S." In M. O'Mahony and B. van Ark (Eds.), EU Productivity and Competitiveness: An Industry Perspective Can Europe Resume the Catching-up Process?, Luxembourg, pp. 73-147. Office for Official Publications of the European Communities. (www.ggdc.net).
Jorgenson, D. W. 2003. "Information Technology and the G7 Economies." World Economics, Vol. 4, pp. 162-69.
Jorgenson, D. W. 2004a. "Accounting for Growth in the Information Age." In P. Aghion and S. Durlauf (Eds.), Handbook of Economic Growth, North Holland, Amsterdam, forthcoming (http://emlab.berkeley.edu/users/ chad/Handbook.html).
Jorgenson, D. W. 2004b. "Information Technology and the G7 Economies", processed, Harvard. (http://post.economics.harvard.edu/faculty/jorgenson/ papers/handbook.extract.2001update10142004dwj1.pdf).
Kollmann, R. 1998. "U.S. Trade Balance Dynamics: the Role of Fiscal Policy and Productivity Shocks and of Financial Market Linkages." Journal of International Money and Finance, Vol. 17, pp. 637-669.
Laxton, D. and P. Pesenti. 2003. "Monetary Rules for Small, Open, Emerging Economies." Journal of Monetary Economics, Vol. 50, pp. 1109-1146.
Oliner, S. D. and D. E. Sichel. 2000. "The Resurgence of Growth in the Late 1990s: Is Information Technology the Story?" Journal of Economic Perspectives, Vol. 14, pp. 3-22.
Organization for Economic Co-operation and Development. 2004. "STAN Database", (www.oecd.org/sti/stan).
Schmitt-Grohe, S. and M. Uribe. 2003. "Closing Small Open Economy Models." Journal of International Economics, Vol. 61, pp. 163-185.
Schreyer, P. 2001. Measuring Productivity. OECD.
Stockman, A. and L. Tesar. 1995. "Tastes and Technology in a Two-Country Model of the Business Cycle: Explaining International Comovements." American Economic Review, Vol. 85, pp. 168-185.
Table 1: Output Growth for the U.S. and Some European Countries
| Variable | U.S. Groningen | U.S. Jorgenson | EU-4* Groningen | France Groningen | France Jorgenson | German Groningen | German Jorgenson | Italy Jorgenson | Netherlands Groningen | U.K. Groningen | U.K. Jorgenson |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Output 1990-1995 | 2.1 | 2.5 | 1.8 | 1.0 | 1.3 | 2.5 | 2.3 | 1.5 | 2.1 | 1.6 | 1.6 |
| Output 1996-2001 | 3.8 | 4.2 | 2.8 | 2.6 | 2.3 | 2.0 | 1.2 | 1.9 | 3.2 | 3.7 | 2.7 |
| Hours 1990-1995 | 1.1 | 1.0 | -0.5 | -0.4 | -0.4 | -0.1 | -0.7 | -0.6 | 0.8 | -1.3 | -1.2 |
| Hours 1996-2001 | 1.6 | 1.5 | 0.8 | 1.0 | 0.9 | 0.0 | -0.1 | 1.0 | 2.1 | 1.1 | 1.0 |
| Labor Productivity 1990-1995 | 1.0 | 1.5 | 2.3 | 1.4 | 1.7 | 2.6 | 3.1 | 2.1 | 1.4 | 3.3 | 2.8 |
| Labor Productivity 1996-2001 | 2.2 | 2.7 | 2.0 | 1.5 | 1.4 | 2.0 | 1.3 | 0.9 | 1.1 | 2.6 | 1.7 |
| Capital Deepening: Contribution from ICT Capital 1990-1995 | 0.4 | 0.4 | 0.3 | 0.1 | 0.2 | 0.4 | 0.3 | 0.3 | 0.3 | 0.4 | 0.3 |
| Capital Deepening: Contribution from ICT Capital 1996-2001 | 0.8 | 0.9 | 0.5 | 0.3 | 0.4 | 0.5 | 0.5 | 0.5 | 0.6 | 0.7 | 0.7 |
| Capital Deepening: Contribution from non-ICT Capital 1990-1995 | 0.2 | 0.4 | 0.8 | 0.5 | 1.2 | 1.0 | 1.3 | 1.1 | 0.4 | 0.8 | 2.1 |
| Capital Deepening: Contribution from non-ICT Capital 1996-2001 | 0.4 | 0.6 | 0.2 | -0.2 | 0.3 | 0.5 | 0.7 | 0.6 | 0.1 | 0.2 | -0.2 |
| Capital Deepening 1990-1995 | 0.6 | 0.8 | 1.2 | 0.6 | 1.4 | 1.4 | 1.6 | 1.3 | 0.7 | - | 2.4 |
| Capital Deepening 1996-2001 | 1.2 | 1.5 | 0.7 | 0.0 | 0.6 | 1.1 | 1.2 | 1.1 | 0.7 | - | 0.5 |
| Multifactor Productivity: Contribution from ICT 1990-1995 | - | 0.2 | - | - | 0.3 | - | 0.4 | 0.4 | - | - | 0.3 |
| Multifactor Productivity: Contribution from ICT 1996-2001 | - | 0.5 | - | - | 0.6 | - | 0.7 | 0.7 | - | - | 0.8 |
| Multifactor Productivity: Contribution from non-ICT 1990-1995 | - | 0.1 | - | - | -0.6 | - | 0.7 | 0.0 | - | - | -0.4 |
| Multifactor Productivity: Contribution from non-ICT 1996-2001 | - | 0.5 | - | - | 0.0 | - | -0.8 | -1.2 | - | - | 0.1 |
| Multifactor Productivity: 1990-1995 | 0.1 | 0.4 | 0.8 | 0.5 | -0.3 | 1.1 | 1.1 | 0.4 | 0.5 | 1.5 | -0.1 |
| Multifactor Productivity: 1996-2001 | 0.8 | 1.0 | 1.1 | 1.0 | 0.6 | 0.9 | -0.1 | -0.5 | 0.4 | 1.3 | 0.9 |
| Labor Quality 1990-1995 | 0.2 | 0.4 | 0.4 | 0.3 | 0.6 | 0.1 | 0.3 | 0.4 | 0.2 | 0.6 | 0.5 |
| Labor Quality 1996-2001 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.0 | 0.2 | 0.4 | 0.1 | 0.3 | 0.3 |
* Aggregate for France, Germany, the U.K., and the Netherlands.
Table 2:�Labor Productivity Growth and Investment in ICT by Sector (averages) - Panel A: Contribution to Labor Productivity Growth
| Sector | 1990-1995 | 1996-2001 | Increase |
|---|---|---|---|
| Agriculture, hunting, forestry & fishing | 0.00% | 0.00% | 0.00% |
| Mining and quarrying | 0.00% | 0.00% | 0.00% |
| Manufacturing | 0.40% | 0.60% | 0.20% |
| Electricity, gas and water | 0.10% | 0.00% | -0.10% |
| Construction | -0.10% | -0.10% | 0.00% |
| Wholesale & retail | 0.30% | 0.20% | -0.10% |
| Transportation, storage & communication | 0.30% | 0.20% | -0.10% |
| Finance, insurance, real estate & business-sector services | 0.30% | 0.50% | 0.20% |
| Community, social & personal services*** | -0.20% | -0.30% | -0.10% |
| Total | 1.10% | 1.70% | 0.60% |
Table 2:�Labor Productivity Growth and Investment in ICT by Sector (averages) - Panel B: U.S. Nominal Gross Investment in ICT
(percent of value added)**
| Sector | 1990-1995 | 1996-2001 | Increase |
|---|---|---|---|
| Agriculture, hunting, forestry & fishing | 0.7 | 1.0 | 0.3 |
| Mining and quarrying | 3.0 | 3.1 | 0.1 |
| Manufacturing | 3.2 | 3.5 | 0.3 |
| Electricity, gas and water | 5.2 | 4.8 | -0.4 |
| Construction | 0.6 | 0.7 | 0.2 |
| Wholesale & retail | 3.3 | 4.3 | 1.0 |
| Transportation, storage & communication | 10.0 | 13.6 | 3.6 |
| Finance, insurance, real estate & business-sector services | 3.8 | 5.0 | 1.2 |
| Community, social & personal services*** | 1.6 | 2.2 | 0.6 |
* Source: OECD Stan Database.
** Includes other automation equipment. Source: Bureau for Economic Analysis.
*** Excludes government services for nominal gross investment shares.
Figure1: U.S. Stylized Facts
1. Average Percent Declines in Relative Prices
| Componenet | 1990-95 | 1996-01 |
|---|---|---|
| Aggregate Investment | 1.50 | 2.19 |
| Durable Consumer Goods | 1.50 | 3.43 |
| Private Investment | 1.47 | 1.65 |
| Government Investment | 0.69 | 0.45 |
| Equipment and Software | 2.70 | 3.98 |
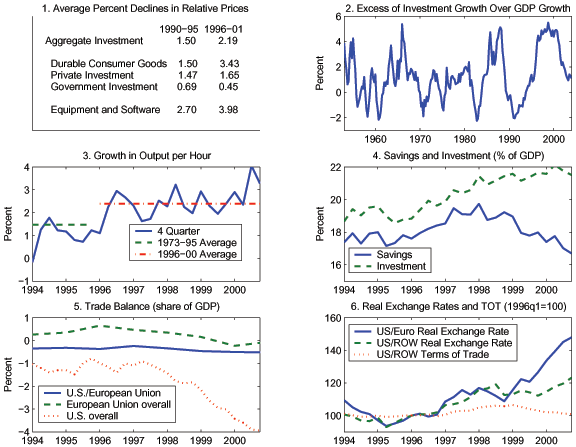
Figure 2A: ISP Level Shocks
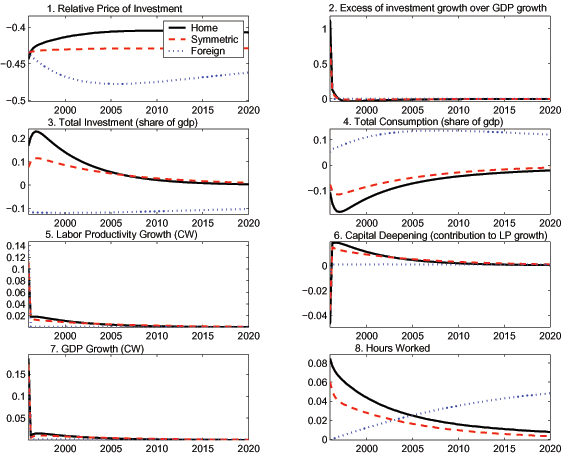
Data for Figure 2A: ISP Level Shocks (Home)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.44360 | 1.12710 | 0.16910 | -0.10820 | 0.10090 | -0.04720 | 0.18550 | 0.08460 |
| 1997 | -0.42440 | -0.00365 | 0.22940 | -0.18480 | 0.01810 | 0.01820 | 0.01520 | 0.06570 |
| 1998 | -0.41960 | -0.03400 | 0.20190 | -0.17110 | 0.01580 | 0.01580 | 0.01380 | 0.05670 |
| 1999 | -0.41600 | -0.03200 | 0.16920 | -0.15030 | 0.01330 | 0.01330 | 0.01160 | 0.04950 |
| 2000 | -0.41360 | -0.02710 | 0.14080 | -0.13160 | 0.01110 | 0.01110 | 0.00970 | 0.04380 |
| 2001 | -0.41120 | -0.02260 | 0.11700 | -0.11560 | 0.00927 | 0.00929 | 0.00810 | 0.03870 |
| 2002 | -0.40960 | -0.01880 | 0.09720 | -0.10200 | 0.00775 | 0.00776 | 0.00670 | 0.03450 |
| 2003 | -0.40800 | -0.01570 | 0.08070 | -0.09040 | 0.00648 | 0.00649 | 0.00560 | 0.03060 |
| 2004 | -0.40680 | -0.01300 | 0.06690 | -0.08050 | 0.00543 | 0.00544 | 0.00470 | 0.02760 |
| 2005 | -0.40600 | -0.01080 | 0.05550 | -0.07200 | 0.00455 | 0.00456 | 0.00390 | 0.02490 |
| 2006 | -0.40560 | -0.00897 | 0.04600 | -0.06470 | 0.00382 | 0.00382 | 0.00330 | 0.02250 |
| 2007 | -0.40520 | -0.00744 | 0.03810 | -0.05840 | 0.00321 | 0.00321 | 0.00270 | 0.02040 |
| 2008 | -0.40480 | -0.00617 | 0.03150 | -0.05300 | 0.00270 | 0.00270 | 0.00230 | 0.01860 |
| 2009 | -0.40480 | -0.00511 | 0.02600 | -0.04820 | 0.00228 | 0.00228 | 0.00190 | 0.01710 |
| 2010 | -0.40480 | -0.00422 | 0.02150 | -0.04400 | 0.00193 | 0.00193 | 0.00160 | 0.01560 |
| 2011 | -0.40480 | -0.00348 | 0.01770 | -0.04040 | 0.00163 | 0.00163 | 0.00130 | 0.01440 |
| 2012 | -0.40480 | -0.00287 | 0.01460 | -0.03710 | 0.00139 | 0.00139 | 0.00110 | 0.01350 |
| 2013 | -0.40520 | -0.00236 | 0.01200 | -0.03420 | 0.00118 | 0.00118 | 0.00090 | 0.01230 |
| 2014 | -0.40520 | -0.00194 | 0.00990 | -0.03170 | 0.00101 | 0.00101 | 0.00080 | 0.01170 |
| 2015 | -0.40560 | -0.00159 | 0.00810 | -0.02940 | 0.00087 | 0.00087 | 0.00070 | 0.01080 |
| 2016 | -0.40560 | -0.00129 | 0.00660 | -0.02730 | 0.00075 | 0.00075 | 0.00060 | 0.00990 |
| 2017 | -0.40600 | -0.00105 | 0.00540 | -0.02540 | 0.00065 | 0.00065 | 0.00050 | 0.00930 |
| 2018 | -0.40640 | -0.00085 | 0.00440 | -0.02370 | 0.00056 | 0.00056 | 0.00040 | 0.00870 |
| 2019 | -0.40680 | -0.00068 | 0.00360 | -0.02210 | 0.00049 | 0.00049 | 0.00040 | 0.00810 |
| 2020 | -0.40720 | -0.00055 | 0.00290 | -0.02070 | 0.00043 | 0.00043 | 0.00030 | 0.00780 |
Data for Figure 2A: ISP Level Shocks (Symmetric)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.43440 | 0.74500 | 0.07650 | -0.07650 | 0.11240 | -0.03600 | 0.17230 | 0.06000 |
| 1997 | -0.43240 | 0.00025 | 0.11530 | -0.11530 | 0.01260 | 0.01270 | 0.01050 | 0.03960 |
| 1998 | -0.43160 | -0.01120 | 0.10610 | -0.10610 | 0.01120 | 0.01120 | 0.01010 | 0.03450 |
| 1999 | -0.43080 | -0.01070 | 0.09520 | -0.09520 | 0.01000 | 0.01000 | 0.00910 | 0.03090 |
| 2000 | -0.43040 | -0.00955 | 0.08530 | -0.08530 | 0.00896 | 0.00899 | 0.00820 | 0.02790 |
| 2001 | -0.43000 | -0.00853 | 0.07650 | -0.07650 | 0.00804 | 0.00806 | 0.00740 | 0.02490 |
| 2002 | -0.42960 | -0.00763 | 0.06860 | -0.06860 | 0.00721 | 0.00722 | 0.00660 | 0.02250 |
| 2003 | -0.42960 | -0.00682 | 0.06150 | -0.06150 | 0.00647 | 0.00648 | 0.00590 | 0.02010 |
| 2004 | -0.42960 | -0.00611 | 0.05510 | -0.05510 | 0.00580 | 0.00581 | 0.00530 | 0.01800 |
| 2005 | -0.42920 | -0.00547 | 0.04940 | -0.04940 | 0.00521 | 0.00522 | 0.00480 | 0.01620 |
| 2006 | -0.42920 | -0.00490 | 0.04430 | -0.04430 | 0.00468 | 0.00468 | 0.00430 | 0.01470 |
| 2007 | -0.42920 | -0.00440 | 0.03980 | -0.03980 | 0.00420 | 0.00420 | 0.00380 | 0.01320 |
| 2008 | -0.42920 | -0.00394 | 0.03570 | -0.03570 | 0.00377 | 0.00377 | 0.00350 | 0.01170 |
| 2009 | -0.42920 | -0.00354 | 0.03200 | -0.03200 | 0.00338 | 0.00339 | 0.00310 | 0.01050 |
| 2010 | -0.42920 | -0.00317 | 0.02870 | -0.02870 | 0.00304 | 0.00304 | 0.00280 | 0.00960 |
| 2011 | -0.42880 | -0.00285 | 0.02570 | -0.02570 | 0.00273 | 0.00273 | 0.00250 | 0.00870 |
| 2012 | -0.42880 | -0.00256 | 0.02300 | -0.02300 | 0.00245 | 0.00245 | 0.00220 | 0.00780 |
| 2013 | -0.42880 | -0.00230 | 0.02070 | -0.02070 | 0.00220 | 0.00220 | 0.00200 | 0.00690 |
| 2014 | -0.42880 | -0.00206 | 0.01850 | -0.01850 | 0.00198 | 0.00198 | 0.00180 | 0.00630 |
| 2015 | -0.42880 | -0.00185 | 0.01660 | -0.01660 | 0.00178 | 0.00177 | 0.00160 | 0.00570 |
| 2016 | -0.42880 | -0.00166 | 0.01490 | -0.01490 | 0.00159 | 0.00159 | 0.00150 | 0.00510 |
| 2017 | -0.42880 | -0.00149 | 0.01330 | -0.01330 | 0.00143 | 0.00143 | 0.00130 | 0.00450 |
| 2018 | -0.42880 | -0.00134 | 0.01190 | -0.01190 | 0.00129 | 0.00129 | 0.00120 | 0.00420 |
| 2019 | -0.42880 | -0.00120 | 0.01070 | -0.01070 | 0.00116 | 0.00115 | 0.00110 | 0.00360 |
| 2020 | -0.42880 | -0.00108 | 0.00950 | -0.00950 | 0.00104 | 0.00104 | 0.00090 | 0.00330 |
Data for Figure 2A: ISP Level Shocks (Foreign)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.43280 | -0.02050 | -0.11330 | 0.05230 | 0.13980 | -0.00850 | 0.13910 | -0.00060 |
| 1997 | -0.44680 | 0.00135 | -0.11850 | 0.07390 | 0.00100 | 0.00100 | 0.00180 | 0.00300 |
| 1998 | -0.45560 | 0.00134 | -0.11920 | 0.08840 | 0.00102 | 0.00102 | 0.00180 | 0.00600 |
| 1999 | -0.46240 | 0.00121 | -0.11970 | 0.10080 | 0.00103 | 0.00103 | 0.00180 | 0.00900 |
| 2000 | -0.46760 | 0.00112 | -0.11980 | 0.11060 | 0.00104 | 0.00104 | 0.00180 | 0.01200 |
| 2001 | -0.47120 | 0.00104 | -0.11970 | 0.11830 | 0.00104 | 0.00104 | 0.00170 | 0.01500 |
| 2002 | -0.47400 | 0.00097 | -0.11940 | 0.12420 | 0.00104 | 0.00104 | 0.00170 | 0.01770 |
| 2003 | -0.47600 | 0.00092 | -0.11900 | 0.12870 | 0.00104 | 0.00104 | 0.00170 | 0.02010 |
| 2004 | -0.47680 | 0.00087 | -0.11830 | 0.13190 | 0.00104 | 0.00104 | 0.00160 | 0.02280 |
| 2005 | -0.47760 | 0.00084 | -0.11760 | 0.13410 | 0.00103 | 0.00103 | 0.00160 | 0.02520 |
| 2006 | -0.47760 | 0.00081 | -0.11680 | 0.13560 | 0.00103 | 0.00103 | 0.00160 | 0.02730 |
| 2007 | -0.47720 | 0.00079 | -0.11590 | 0.13630 | 0.00102 | 0.00102 | 0.00150 | 0.02940 |
| 2008 | -0.47640 | 0.00077 | -0.11500 | 0.13650 | 0.00101 | 0.00101 | 0.00150 | 0.03150 |
| 2009 | -0.47560 | 0.00076 | -0.11410 | 0.13620 | 0.00100 | 0.00101 | 0.00150 | 0.03360 |
| 2010 | -0.47480 | 0.00075 | -0.11310 | 0.13560 | 0.00099 | 0.00100 | 0.00140 | 0.03540 |
| 2011 | -0.47360 | 0.00074 | -0.11200 | 0.13470 | 0.00098 | 0.00099 | 0.00140 | 0.03690 |
| 2012 | -0.47240 | 0.00073 | -0.11100 | 0.13350 | 0.00098 | 0.00098 | 0.00140 | 0.03870 |
| 2013 | -0.47120 | 0.00072 | -0.11000 | 0.13220 | 0.00097 | 0.00097 | 0.00130 | 0.04020 |
| 2014 | -0.47000 | 0.00072 | -0.10890 | 0.13070 | 0.00096 | 0.00096 | 0.00130 | 0.04140 |
| 2015 | -0.46840 | 0.00072 | -0.10790 | 0.12920 | 0.00095 | 0.00095 | 0.00130 | 0.04290 |
| 2016 | -0.46720 | 0.00071 | -0.10680 | 0.12750 | 0.00094 | 0.00094 | 0.00120 | 0.04410 |
| 2017 | -0.46600 | 0.00071 | -0.10580 | 0.12580 | 0.00093 | 0.00093 | 0.00120 | 0.04530 |
| 2018 | -0.46480 | 0.00071 | -0.10480 | 0.12400 | 0.00092 | 0.00092 | 0.00120 | 0.04620 |
| 2019 | -0.46320 | 0.00071 | -0.10380 | 0.12230 | 0.00091 | 0.00091 | 0.00110 | 0.04740 |
| 2020 | -0.46200 | 0.00071 | -0.10270 | 0.12050 | 0.00090 | 0.00090 | 0.00110 | 0.04830 |
Figure 2B: ISP Level Shocks
Data for Figure 2B: ISP Level Shocks (Home)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | -0.10490 | 1.31270 | -0.06090 | 0.01710 | 0.04620 | 0.14120 |
| 1997 | -0.15210 | 1.59090 | -0.04450 | -0.02400 | -0.12350 | 0.00340 |
| 1998 | -0.07730 | 1.53430 | -0.03090 | -0.04670 | -0.17860 | -0.00030 |
| 1999 | -0.00100 | 1.44940 | -0.01890 | -0.06420 | -0.22030 | -0.00030 |
| 2000 | 0.06460 | 1.37410 | -0.00923 | -0.07820 | -0.25130 | -0.00020 |
| 2001 | 0.11990 | 1.31100 | -0.00142 | -0.08940 | -0.27360 | -0.00020 |
| 2002 | 0.16640 | 1.25840 | 0.00481 | -0.09830 | -0.28870 | -0.00010 |
| 2003 | 0.20560 | 1.21480 | 0.00974 | -0.10520 | -0.29810 | -0.00010 |
| 2004 | 0.23860 | 1.17850 | 0.01360 | -0.11060 | -0.30300 | -0.00010 |
| 2005 | 0.26650 | 1.14850 | 0.01650 | -0.11470 | -0.30410 | -0.00010 |
| 2006 | 0.29010 | 1.12370 | 0.01870 | -0.11770 | -0.30240 | -0.00010 |
| 2007 | 0.31010 | 1.10320 | 0.02040 | -0.11980 | -0.29840 | 0.00000 |
| 2008 | 0.32710 | 1.08620 | 0.02150 | -0.12110 | -0.29260 | 0.00000 |
| 2009 | 0.34160 | 1.07230 | 0.02220 | -0.12180 | -0.28550 | 0.00000 |
| 2010 | 0.35410 | 1.06090 | 0.02250 | -0.12200 | -0.27740 | 0.00000 |
| 2011 | 0.36470 | 1.05150 | 0.02260 | -0.12180 | -0.26870 | 0.00000 |
| 2012 | 0.37390 | 1.04390 | 0.02250 | -0.12120 | -0.25950 | 0.00000 |
| 2013 | 0.38190 | 1.03770 | 0.02220 | -0.12040 | -0.25000 | 0.00000 |
| 2014 | 0.38880 | 1.03270 | 0.02180 | -0.11930 | -0.24040 | 0.00000 |
| 2015 | 0.39490 | 1.02860 | 0.02130 | -0.11810 | -0.23080 | 0.00000 |
| 2016 | 0.40020 | 1.02550 | 0.02060 | -0.11670 | -0.22130 | 0.00000 |
| 2017 | 0.40490 | 1.02300 | 0.02000 | -0.11520 | -0.21190 | 0.00000 |
| 2018 | 0.40910 | 1.02100 | 0.01920 | -0.11370 | -0.20280 | 0.00000 |
| 2019 | 0.41290 | 1.01960 | 0.01850 | -0.11200 | -0.19400 | 0.00000 |
| 2020 | 0.41620 | 1.01850 | 0.01770 | -0.11040 | -0.18540 | 0.00000 |
Data for Figure 2B: ISP Level Shocks (Symmetric)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | -0.07530 | 0.91720 | 0.00000 | 0.00000 | 0.00000 | 0.07160 |
| 1997 | -0.09220 | 1.10560 | 0.00000 | 0.00000 | 0.00000 | 0.04390 |
| 1998 | -0.03800 | 1.10990 | 0.00000 | 0.00000 | 0.00000 | 0.03280 |
| 1999 | 0.01480 | 1.10390 | 0.00000 | 0.00000 | 0.00000 | 0.02500 |
| 2000 | 0.06230 | 1.09810 | 0.00000 | 0.00000 | 0.00000 | 0.01930 |
| 2001 | 0.10490 | 1.09310 | 0.00000 | 0.00000 | 0.00000 | 0.01490 |
| 2002 | 0.14310 | 1.08870 | 0.00000 | 0.00000 | 0.00000 | 0.01170 |
| 2003 | 0.17740 | 1.08490 | 0.00000 | 0.00000 | 0.00000 | 0.00920 |
| 2004 | 0.20810 | 1.08150 | 0.00000 | 0.00000 | 0.00000 | 0.00730 |
| 2005 | 0.23570 | 1.07850 | 0.00000 | 0.00000 | 0.00000 | 0.00590 |
| 2006 | 0.26040 | 1.07590 | 0.00000 | 0.00000 | 0.00000 | 0.00470 |
| 2007 | 0.28260 | 1.07360 | 0.00000 | 0.00000 | 0.00000 | 0.00390 |
| 2008 | 0.30250 | 1.07150 | 0.00000 | 0.00000 | 0.00000 | 0.00320 |
| 2009 | 0.32040 | 1.06960 | 0.00000 | 0.00000 | 0.00000 | 0.00270 |
| 2010 | 0.33650 | 1.06800 | 0.00000 | 0.00000 | 0.00000 | 0.00220 |
| 2011 | 0.35090 | 1.06650 | 0.00000 | 0.00000 | 0.00000 | 0.00190 |
| 2012 | 0.36390 | 1.06520 | 0.00000 | 0.00000 | 0.00000 | 0.00160 |
| 2013 | 0.37550 | 1.06400 | 0.00000 | 0.00000 | 0.00000 | 0.00140 |
| 2014 | 0.38590 | 1.06290 | 0.00000 | 0.00000 | 0.00000 | 0.00120 |
| 2015 | 0.39530 | 1.06200 | 0.00000 | 0.00000 | 0.00000 | 0.00110 |
| 2016 | 0.40370 | 1.06110 | 0.00000 | 0.00000 | 0.00000 | 0.00090 |
| 2017 | 0.41130 | 1.06040 | 0.00000 | 0.00000 | 0.00000 | 0.00080 |
| 2018 | 0.41810 | 1.05970 | 0.00000 | 0.00000 | 0.00000 | 0.00070 |
| 2019 | 0.42420 | 1.05910 | 0.00000 | 0.00000 | 0.00000 | 0.00060 |
| 2020 | 0.42970 | 1.05850 | 0.00000 | 0.00000 | 0.00000 | 0.00060 |
Data for Figure 2B: ISP Level Shocks (Foreign)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | 0.06170 | 0.11860 | 0.06100 | -0.01720 | -0.04630 | 0.09120 |
| 1997 | 0.09890 | 0.11940 | 0.04450 | 0.02390 | 0.12350 | 0.16740 |
| 1998 | 0.12540 | 0.13220 | 0.03090 | 0.04660 | 0.17880 | 0.22050 |
| 1999 | 0.14910 | 0.14440 | 0.01890 | 0.06420 | 0.22080 | 0.26310 |
| 2000 | 0.16950 | 0.15610 | 0.00925 | 0.07820 | 0.25190 | 0.29350 |
| 2001 | 0.18700 | 0.16740 | 0.00144 | 0.08950 | 0.27430 | 0.31370 |
| 2002 | 0.20210 | 0.17820 | -0.00480 | 0.09840 | 0.28960 | 0.32570 |
| 2003 | 0.21520 | 0.18880 | -0.00972 | 0.10540 | 0.29910 | 0.33110 |
| 2004 | 0.22650 | 0.19900 | -0.01360 | 0.11090 | 0.30400 | 0.33140 |
| 2005 | 0.23640 | 0.20900 | -0.01650 | 0.11500 | 0.30520 | 0.32760 |
| 2006 | 0.24500 | 0.21860 | -0.01870 | 0.11800 | 0.30340 | 0.32070 |
| 2007 | 0.25270 | 0.22810 | -0.02030 | 0.12010 | 0.29940 | 0.31140 |
| 2008 | 0.25940 | 0.23730 | -0.02150 | 0.12140 | 0.29360 | 0.30030 |
| 2009 | 0.26540 | 0.24630 | -0.02220 | 0.12210 | 0.28650 | 0.28800 |
| 2010 | 0.27070 | 0.25510 | -0.02250 | 0.12230 | 0.27840 | 0.27480 |
| 2011 | 0.27550 | 0.26380 | -0.02260 | 0.12210 | 0.26960 | 0.26110 |
| 2012 | 0.27980 | 0.27220 | -0.02250 | 0.12150 | 0.26030 | 0.24710 |
| 2013 | 0.28380 | 0.28050 | -0.02220 | 0.12070 | 0.25080 | 0.23310 |
| 2014 | 0.28740 | 0.28870 | -0.02180 | 0.11960 | 0.24120 | 0.21920 |
| 2015 | 0.29070 | 0.29670 | -0.02130 | 0.11840 | 0.23150 | 0.20550 |
| 2016 | 0.29370 | 0.30460 | -0.02070 | 0.11700 | 0.22190 | 0.19220 |
| 2017 | 0.29660 | 0.31230 | -0.02000 | 0.11550 | 0.21260 | 0.17930 |
| 2018 | 0.29920 | 0.32000 | -0.01930 | 0.11390 | 0.20340 | 0.16680 |
| 2019 | 0.30170 | 0.32750 | -0.01850 | 0.11230 | 0.19450 | 0.15490 |
| 2020 | 0.30410 | 0.33480 | -0.01780 | 0.11060 | 0.18590 | 0.14360 |
Figure 3A: ISP Growth Shocks
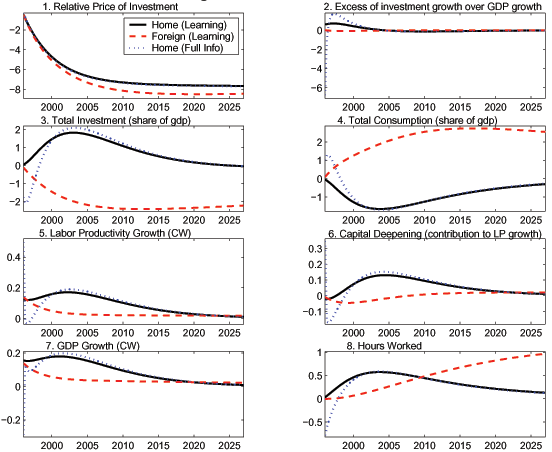
Data for Figure 3A: ISP Growth Shocks (Home - Learning)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.43480 | 0.64210 | 0.05090 | -0.03890 | 0.12490 | -0.02310 | 0.15640 | 0.03150 |
| 1997 | -1.90040 | 0.71860 | 0.36530 | -0.33570 | 0.12210 | -0.01300 | 0.15350 | 0.15510 |
| 1998 | -3.06040 | 0.68140 | 0.77850 | -0.69050 | 0.13250 | 0.01230 | 0.16160 | 0.27660 |
| 1999 | -3.98160 | 0.56750 | 1.16470 | -1.01390 | 0.14700 | 0.04350 | 0.17090 | 0.38100 |
| 2000 | -4.71400 | 0.43260 | 1.47000 | -1.27280 | 0.15960 | 0.07310 | 0.17750 | 0.46200 |
| 2001 | -5.29720 | 0.30340 | 1.67850 | -1.45890 | 0.16790 | 0.09740 | 0.18000 | 0.51900 |
| 2002 | -5.76160 | 0.19130 | 1.79410 | -1.57660 | 0.17120 | 0.11480 | 0.17820 | 0.55410 |
| 2003 | -6.13160 | 0.10000 | 1.83050 | -1.63550 | 0.17000 | 0.12540 | 0.17280 | 0.57120 |
| 2004 | -6.42680 | 0.02920 | 1.80410 | -1.64730 | 0.16500 | 0.13020 | 0.16450 | 0.57390 |
| 2005 | -6.66240 | -0.02350 | 1.73120 | -1.62310 | 0.15720 | 0.13010 | 0.15420 | 0.56550 |
| 2006 | -6.85040 | -0.06070 | 1.62640 | -1.57280 | 0.14740 | 0.12650 | 0.14270 | 0.54870 |
| 2007 | -7.00120 | -0.08560 | 1.50150 | -1.50460 | 0.13650 | 0.12030 | 0.13060 | 0.52680 |
| 2008 | -7.12160 | -0.10070 | 1.36610 | -1.42510 | 0.12510 | 0.11250 | 0.11840 | 0.50100 |
| 2009 | -7.21840 | -0.10840 | 1.22720 | -1.33930 | 0.11360 | 0.10380 | 0.10650 | 0.47340 |
| 2010 | -7.29600 | -0.11060 | 1.09010 | -1.25100 | 0.10230 | 0.09480 | 0.09520 | 0.44490 |
| 2011 | -7.35880 | -0.10880 | 0.95830 | -1.16290 | 0.09170 | 0.08580 | 0.08460 | 0.41640 |
| 2012 | -7.40960 | -0.10430 | 0.83420 | -1.07700 | 0.08170 | 0.07710 | 0.07480 | 0.38850 |
| 2013 | -7.45080 | -0.09800 | 0.71920 | -0.99460 | 0.07240 | 0.06880 | 0.06590 | 0.36180 |
| 2014 | -7.48440 | -0.09060 | 0.61390 | -0.91650 | 0.06400 | 0.06120 | 0.05780 | 0.33630 |
| 2015 | -7.51240 | -0.08270 | 0.51860 | -0.84300 | 0.05630 | 0.05410 | 0.05050 | 0.31230 |
| 2016 | -7.53560 | -0.07480 | 0.43300 | -0.77440 | 0.04950 | 0.04780 | 0.04400 | 0.29010 |
| 2017 | -7.55480 | -0.06690 | 0.35680 | -0.71070 | 0.04340 | 0.04200 | 0.03830 | 0.26910 |
| 2018 | -7.57120 | -0.05940 | 0.28920 | -0.65170 | 0.03790 | 0.03690 | 0.03320 | 0.24990 |
| 2019 | -7.58560 | -0.05240 | 0.22980 | -0.59730 | 0.03310 | 0.03230 | 0.02880 | 0.23190 |
| 2020 | -7.59760 | -0.04590 | 0.17770 | -0.54710 | 0.02890 | 0.02830 | 0.02490 | 0.21540 |
Data for Figure 3A: ISP Growth Shocks (Foreign - Learning)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.45840 | 0.01870 | -0.10990 | 0.09800 | 0.13970 | -0.00827 | 0.13850 | -0.00120 |
| 1997 | -2.06240 | -0.03950 | -0.53650 | 0.50710 | 0.10410 | -0.02980 | 0.10620 | 0.00300 |
| 1998 | -3.31080 | -0.05710 | -0.89810 | 0.81120 | 0.07930 | -0.04130 | 0.08370 | 0.01710 |
| 1999 | -4.29720 | -0.06240 | -1.20230 | 1.05320 | 0.06200 | -0.04530 | 0.06820 | 0.03930 |
| 2000 | -5.08720 | -0.06000 | -1.45660 | 1.26140 | 0.04990 | -0.04430 | 0.05760 | 0.06810 |
| 2001 | -5.72640 | -0.05330 | -1.66750 | 1.44960 | 0.04140 | -0.04010 | 0.05020 | 0.10200 |
| 2002 | -6.24680 | -0.04440 | -1.84070 | 1.62400 | 0.03540 | -0.03430 | 0.04510 | 0.13950 |
| 2003 | -6.67280 | -0.03510 | -1.98150 | 1.78650 | 0.03130 | -0.02760 | 0.04150 | 0.18000 |
| 2004 | -7.02280 | -0.02610 | -2.09460 | 1.93710 | 0.02830 | -0.02100 | 0.03900 | 0.22230 |
| 2005 | -7.31040 | -0.01790 | -2.18450 | 2.07500 | 0.02620 | -0.01460 | 0.03710 | 0.26580 |
| 2006 | -7.54680 | -0.01080 | -2.25490 | 2.19950 | 0.02480 | -0.00882 | 0.03580 | 0.30960 |
| 2007 | -7.74080 | -0.00482 | -2.30900 | 2.31000 | 0.02370 | -0.00369 | 0.03470 | 0.35370 |
| 2008 | -7.90000 | 0.00015 | -2.34970 | 2.40650 | 0.02290 | 0.00077 | 0.03370 | 0.39720 |
| 2009 | -8.03000 | 0.00420 | -2.37910 | 2.48920 | 0.02230 | 0.00457 | 0.03290 | 0.44010 |
| 2010 | -8.13560 | 0.00747 | -2.39940 | 2.55860 | 0.02190 | 0.00776 | 0.03220 | 0.48210 |
| 2011 | -8.22080 | 0.01010 | -2.41210 | 2.61550 | 0.02150 | 0.01040 | 0.03150 | 0.52290 |
| 2012 | -8.28880 | 0.01210 | -2.41860 | 2.66070 | 0.02120 | 0.01260 | 0.03090 | 0.56220 |
| 2013 | -8.34280 | 0.01370 | -2.42000 | 2.69530 | 0.02100 | 0.01440 | 0.03030 | 0.60030 |
| 2014 | -8.38480 | 0.01490 | -2.41730 | 2.72040 | 0.02070 | 0.01590 | 0.02960 | 0.63660 |
| 2015 | -8.41720 | 0.01590 | -2.41120 | 2.73680 | 0.02050 | 0.01700 | 0.02900 | 0.67140 |
| 2016 | -8.44080 | 0.01660 | -2.40240 | 2.74550 | 0.02030 | 0.01790 | 0.02840 | 0.70470 |
| 2017 | -8.45800 | 0.01710 | -2.39130 | 2.74760 | 0.02010 | 0.01860 | 0.02780 | 0.73620 |
| 2018 | -8.46960 | 0.01750 | -2.37850 | 2.74390 | 0.01990 | 0.01920 | 0.02720 | 0.76620 |
| 2019 | -8.47640 | 0.01780 | -2.36420 | 2.73510 | 0.01970 | 0.01960 | 0.02660 | 0.79440 |
| 2020 | -8.47960 | 0.01790 | -2.34870 | 2.72210 | 0.01950 | 0.01990 | 0.02600 | 0.82110 |
Data for Figure 3A: ISP Growth Shocks (Home - Full Information)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.30040 | -6.77340 | -1.76820 | 1.02200 | 0.49590 | 0.34560 | -0.28850 | -0.78030 |
| 1997 | -1.88360 | 1.64630 | -1.52880 | 1.01010 | -0.01140 | -0.14550 | 0.09230 | -0.27240 |
| 1998 | -3.10480 | 1.52660 | -0.25470 | 0.14340 | 0.06050 | -0.06240 | 0.12920 | 0.04740 |
| 1999 | -4.05320 | 1.07620 | 0.74130 | -0.57170 | 0.11820 | 0.01210 | 0.16480 | 0.26460 |
| 2000 | -4.79720 | 0.71280 | 1.41000 | -1.06960 | 0.15650 | 0.06870 | 0.18720 | 0.41010 |
| 2001 | -5.38280 | 0.44640 | 1.81750 | -1.39040 | 0.17870 | 0.10830 | 0.19770 | 0.50250 |
| 2002 | -5.84600 | 0.25460 | 2.03050 | -1.57820 | 0.18880 | 0.13350 | 0.19910 | 0.55620 |
| 2003 | -6.21240 | 0.11820 | 2.10380 | -1.66890 | 0.19000 | 0.14710 | 0.19410 | 0.58110 |
| 2004 | -6.50280 | 0.02270 | 2.08000 | -1.69070 | 0.18500 | 0.15200 | 0.18470 | 0.58590 |
| 2005 | -6.73400 | -0.04250 | 1.99150 | -1.66460 | 0.17590 | 0.15060 | 0.17250 | 0.57660 |
| 2006 | -6.91760 | -0.08520 | 1.86240 | -1.60670 | 0.16430 | 0.14490 | 0.15890 | 0.55770 |
| 2007 | -7.06400 | -0.11150 | 1.71020 | -1.52860 | 0.15140 | 0.13650 | 0.14470 | 0.53280 |
| 2008 | -7.18040 | -0.12590 | 1.54770 | -1.43880 | 0.13790 | 0.12650 | 0.13050 | 0.50400 |
| 2009 | -7.27400 | -0.13170 | 1.38350 | -1.34350 | 0.12450 | 0.11570 | 0.11680 | 0.47340 |
| 2010 | -7.34880 | -0.13150 | 1.22350 | -1.24680 | 0.11160 | 0.10480 | 0.10390 | 0.44250 |
| 2011 | -7.40880 | -0.12720 | 1.07160 | -1.15170 | 0.09950 | 0.09410 | 0.09190 | 0.41190 |
| 2012 | -7.45720 | -0.12030 | 0.93010 | -1.06000 | 0.08820 | 0.08400 | 0.08090 | 0.38220 |
| 2013 | -7.49640 | -0.11170 | 0.80010 | -0.97300 | 0.07780 | 0.07460 | 0.07100 | 0.35430 |
| 2014 | -7.52840 | -0.10240 | 0.68220 | -0.89140 | 0.06850 | 0.06590 | 0.06200 | 0.32760 |
| 2015 | -7.55480 | -0.09280 | 0.57610 | -0.81540 | 0.06010 | 0.05810 | 0.05410 | 0.30300 |
| 2016 | -7.57640 | -0.08330 | 0.48140 | -0.74500 | 0.05250 | 0.05100 | 0.04700 | 0.28020 |
| 2017 | -7.59480 | -0.07420 | 0.39750 | -0.68020 | 0.04590 | 0.04470 | 0.04070 | 0.25890 |
| 2018 | -7.61000 | -0.06560 | 0.32350 | -0.62070 | 0.04000 | 0.03900 | 0.03530 | 0.23940 |
| 2019 | -7.62320 | -0.05760 | 0.25860 | -0.56610 | 0.03480 | 0.03410 | 0.03050 | 0.22140 |
| 2020 | -7.63440 | -0.05030 | 0.20200 | -0.51610 | 0.03030 | 0.02970 | 0.02630 | 0.20520 |
Figure 3B: ISP Growth Shocks
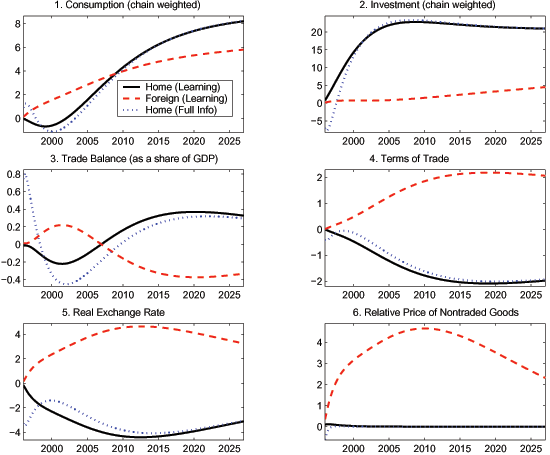
Data for Figure 3B: ISP Growth Shocks (Home - Learning)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | -0.04220 | 0.79850 | -0.01200 | -0.00990 | -0.16480 | 0.09570 |
| 1997 | -0.33620 | 4.22430 | -0.02970 | -0.11970 | -1.06000 | 0.10300 |
| 1998 | -0.59190 | 7.86920 | -0.08800 | -0.22490 | -1.62120 | 0.06900 |
| 1999 | -0.69520 | 11.27860 | -0.15080 | -0.33960 | -2.00250 | 0.04560 |
| 2000 | -0.62230 | 14.24020 | -0.19720 | -0.46940 | -2.30980 | 0.03020 |
| 2001 | -0.38670 | 16.68210 | -0.21950 | -0.61260 | -2.59030 | 0.01990 |
| 2002 | -0.01860 | 18.61190 | -0.21760 | -0.76430 | -2.86070 | 0.01310 |
| 2003 | 0.44780 | 20.07820 | -0.19500 | -0.91910 | -3.12280 | 0.00860 |
| 2004 | 0.97930 | 21.14780 | -0.15680 | -1.07180 | -3.37200 | 0.00550 |
| 2005 | 1.54730 | 21.89150 | -0.10810 | -1.21830 | -3.60240 | 0.00350 |
| 2006 | 2.12840 | 22.37600 | -0.05360 | -1.35560 | -3.80840 | 0.00210 |
| 2007 | 2.70460 | 22.66010 | 0.00309 | -1.48150 | -3.98580 | 0.00120 |
| 2008 | 3.26260 | 22.79380 | 0.05900 | -1.59480 | -4.13230 | 0.00060 |
| 2009 | 3.79340 | 22.81800 | 0.11200 | -1.69500 | -4.24710 | 0.00020 |
| 2010 | 4.29110 | 22.76530 | 0.16090 | -1.78210 | -4.33050 | 0.00000 |
| 2011 | 4.75260 | 22.66130 | 0.20460 | -1.85640 | -4.38400 | -0.00010 |
| 2012 | 5.17650 | 22.52540 | 0.24280 | -1.91870 | -4.40960 | -0.00020 |
| 2013 | 5.56300 | 22.37220 | 0.27540 | -1.96960 | -4.40980 | -0.00020 |
| 2014 | 5.91340 | 22.21230 | 0.30250 | -2.01020 | -4.38730 | -0.00020 |
| 2015 | 6.22950 | 22.05330 | 0.32440 | -2.04140 | -4.34490 | -0.00020 |
| 2016 | 6.51350 | 21.90030 | 0.34140 | -2.06410 | -4.28530 | -0.00020 |
| 2017 | 6.76790 | 21.75680 | 0.35390 | -2.07920 | -4.21110 | -0.00010 |
| 2018 | 6.99540 | 21.62470 | 0.36250 | -2.08770 | -4.12490 | -0.00010 |
| 2019 | 7.19830 | 21.50500 | 0.36750 | -2.09040 | -4.02900 | -0.00010 |
| 2020 | 7.37930 | 21.39810 | 0.36940 | -2.08800 | -3.92550 | 0.00000 |
Data for Figure 3B: ISP Growth Shocks (Foreign - Learning)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | 0.11750 | 0.15720 | 0.01200 | 0.00990 | 0.16510 | 0.34560 |
| 1997 | 0.61000 | 0.52420 | 0.02940 | 0.12000 | 1.07150 | 1.64850 |
| 1998 | 0.97300 | 0.68420 | 0.08700 | 0.22590 | 1.64840 | 2.38790 |
| 1999 | 1.26820 | 0.73420 | 0.14910 | 0.34190 | 2.04460 | 2.83390 |
| 2000 | 1.53560 | 0.73380 | 0.19520 | 0.47390 | 2.36670 | 3.14610 |
| 2001 | 1.79500 | 0.72070 | 0.21790 | 0.62020 | 2.66310 | 3.40150 |
| 2002 | 2.05440 | 0.71700 | 0.21660 | 0.77620 | 2.95100 | 3.63270 |
| 2003 | 2.31500 | 0.73410 | 0.19490 | 0.93630 | 3.23230 | 3.84900 |
| 2004 | 2.57520 | 0.77650 | 0.15750 | 1.09530 | 3.50190 | 4.04920 |
| 2005 | 2.83180 | 0.84470 | 0.10950 | 1.24880 | 3.75280 | 4.22830 |
| 2006 | 3.08180 | 0.93690 | 0.05550 | 1.39340 | 3.97880 | 4.38040 |
| 2007 | 3.32250 | 1.05030 | -0.00095 | 1.52670 | 4.17480 | 4.50130 |
| 2008 | 3.55170 | 1.18140 | -0.05680 | 1.64730 | 4.33780 | 4.58800 |
| 2009 | 3.76820 | 1.32710 | -0.11000 | 1.75450 | 4.46650 | 4.63960 |
| 2010 | 3.97100 | 1.48450 | -0.15920 | 1.84790 | 4.56100 | 4.65650 |
| 2011 | 4.16000 | 1.65070 | -0.20340 | 1.92800 | 4.62250 | 4.64050 |
| 2012 | 4.33520 | 1.82370 | -0.24210 | 1.99520 | 4.65310 | 4.59400 |
| 2013 | 4.49710 | 2.00150 | -0.27530 | 2.05040 | 4.65550 | 4.52020 |
| 2014 | 4.64640 | 2.18260 | -0.30300 | 2.09440 | 4.63270 | 4.42230 |
| 2015 | 4.78360 | 2.36580 | -0.32550 | 2.12830 | 4.58760 | 4.30400 |
| 2016 | 4.90980 | 2.54990 | -0.34320 | 2.15300 | 4.52350 | 4.16860 |
| 2017 | 5.02580 | 2.73430 | -0.35630 | 2.16950 | 4.44330 | 4.01950 |
| 2018 | 5.13250 | 2.91830 | -0.36540 | 2.17870 | 4.34990 | 3.85970 |
| 2019 | 5.23070 | 3.10150 | -0.37090 | 2.18160 | 4.24570 | 3.69210 |
| 2020 | 5.32130 | 3.28340 | -0.37330 | 2.17900 | 4.13320 | 3.51910 |
Data for Figure 3B: ISP Growth Shocks (Home - Full Information)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | 0.91580 | -7.06190 | 0.74620 | -0.42320 | -3.29970 | -0.60070 |
| 1997 | 0.82290 | -4.19420 | 0.51870 | -0.23510 | -2.73130 | -0.00340 |
| 1998 | -0.25620 | 2.74570 | 0.11130 | -0.07500 | -1.89210 | 0.01750 |
| 1999 | -0.92250 | 8.59760 | -0.16950 | -0.06010 | -1.49130 | 0.01240 |
| 2000 | -1.14340 | 13.09920 | -0.34040 | -0.13380 | -1.39930 | 0.00870 |
| 2001 | -1.02780 | 16.45720 | -0.42710 | -0.26210 | -1.51020 | 0.00600 |
| 2002 | -0.67780 | 18.90180 | -0.45240 | -0.42170 | -1.74420 | 0.00410 |
| 2003 | -0.17420 | 20.63300 | -0.43490 | -0.59600 | -2.04340 | 0.00270 |
| 2004 | 0.42160 | 21.81580 | -0.38940 | -0.77340 | -2.36710 | 0.00160 |
| 2005 | 1.06420 | 22.58340 | -0.32690 | -0.94600 | -2.68760 | 0.00090 |
| 2006 | 1.72050 | 23.04210 | -0.25570 | -1.10860 | -2.98720 | 0.00040 |
| 2007 | 2.36750 | 23.27490 | -0.18160 | -1.25830 | -3.25500 | 0.00000 |
| 2008 | 2.98940 | 23.34660 | -0.10880 | -1.39320 | -3.48540 | -0.00020 |
| 2009 | 3.57620 | 23.30650 | -0.04000 | -1.51270 | -3.67620 | -0.00040 |
| 2010 | 4.12220 | 23.19200 | 0.02330 | -1.61700 | -3.82760 | -0.00050 |
| 2011 | 4.62460 | 23.03100 | 0.08000 | -1.70650 | -3.94120 | -0.00050 |
| 2012 | 5.08280 | 22.84390 | 0.12990 | -1.78210 | -4.01980 | -0.00050 |
| 2013 | 5.49780 | 22.64560 | 0.17290 | -1.84490 | -4.06650 | -0.00050 |
| 2014 | 5.87150 | 22.44630 | 0.20920 | -1.89590 | -4.08490 | -0.00040 |
| 2015 | 6.20660 | 22.25330 | 0.23930 | -1.93630 | -4.07840 | -0.00040 |
| 2016 | 6.50600 | 22.07120 | 0.26370 | -1.96720 | -4.05040 | -0.00030 |
| 2017 | 6.77280 | 21.90260 | 0.28280 | -1.98960 | -4.00410 | -0.00030 |
| 2018 | 7.00990 | 21.74910 | 0.29720 | -2.00470 | -3.94250 | -0.00020 |
| 2019 | 7.22050 | 21.61120 | 0.30740 | -2.01320 | -3.86830 | -0.00020 |
| 2020 | 7.40730 | 21.48860 | 0.31410 | -2.01610 | -3.78400 | -0.00010 |
Figure 4A: Home Response to MFP Growth Shocks
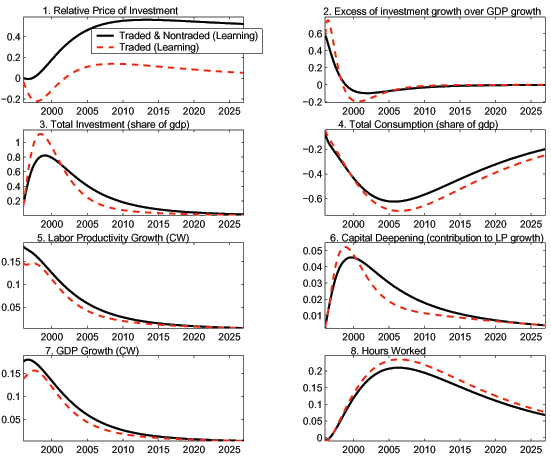
Data for Figure 4A: Home Response to MFP Growth Shocks
(Traded and Nontraded - Learning)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.00080 | 0.59080 | 0.14730 | -0.07140 | 0.18250 | 0.00233 | 0.17630 | -0.00600 |
| 1997 | -0.00560 | 0.32180 | 0.57400 | -0.19260 | 0.17220 | 0.02480 | 0.17910 | 0.00810 |
| 1998 | 0.03280 | 0.11200 | 0.77140 | -0.27310 | 0.15910 | 0.03900 | 0.16870 | 0.04380 |
| 1999 | 0.10080 | -0.00880 | 0.82040 | -0.35550 | 0.14260 | 0.04480 | 0.15210 | 0.08250 |
| 2000 | 0.17840 | -0.06870 | 0.78900 | -0.43260 | 0.12520 | 0.04560 | 0.13360 | 0.11790 |
| 2001 | 0.25360 | -0.09300 | 0.71990 | -0.49820 | 0.10850 | 0.04370 | 0.11530 | 0.14790 |
| 2002 | 0.32040 | -0.09800 | 0.63730 | -0.54950 | 0.09330 | 0.04060 | 0.09850 | 0.17130 |
| 2003 | 0.37760 | -0.09330 | 0.55400 | -0.58640 | 0.07990 | 0.03710 | 0.08370 | 0.18840 |
| 2004 | 0.42440 | -0.08410 | 0.47640 | -0.60990 | 0.06840 | 0.03350 | 0.07080 | 0.20010 |
| 2005 | 0.46160 | -0.07350 | 0.40700 | -0.62170 | 0.05850 | 0.03020 | 0.05980 | 0.20670 |
| 2006 | 0.49120 | -0.06300 | 0.34660 | -0.62360 | 0.05010 | 0.02710 | 0.05050 | 0.20940 |
| 2007 | 0.51360 | -0.05320 | 0.29470 | -0.61760 | 0.04310 | 0.02440 | 0.04270 | 0.20880 |
| 2008 | 0.53040 | -0.04470 | 0.25060 | -0.60520 | 0.03710 | 0.02190 | 0.03620 | 0.20580 |
| 2009 | 0.54240 | -0.03730 | 0.21330 | -0.58800 | 0.03210 | 0.01970 | 0.03070 | 0.20070 |
| 2010 | 0.55080 | -0.03100 | 0.18190 | -0.56730 | 0.02790 | 0.01780 | 0.02610 | 0.19440 |
| 2011 | 0.55600 | -0.02570 | 0.15540 | -0.54420 | 0.02430 | 0.01610 | 0.02230 | 0.18690 |
| 2012 | 0.55880 | -0.02130 | 0.13310 | -0.51940 | 0.02120 | 0.01460 | 0.01910 | 0.17850 |
| 2013 | 0.56000 | -0.01770 | 0.11430 | -0.49380 | 0.01860 | 0.01320 | 0.01650 | 0.16980 |
| 2014 | 0.56000 | -0.01470 | 0.09840 | -0.46780 | 0.01640 | 0.01200 | 0.01420 | 0.16110 |
| 2015 | 0.55840 | -0.01220 | 0.08500 | -0.44200 | 0.01450 | 0.01100 | 0.01230 | 0.15210 |
| 2016 | 0.55640 | -0.01010 | 0.07350 | -0.41650 | 0.01290 | 0.01000 | 0.01070 | 0.14340 |
| 2017 | 0.55360 | -0.00846 | 0.06380 | -0.39170 | 0.01150 | 0.00914 | 0.00940 | 0.13470 |
| 2018 | 0.55040 | -0.00706 | 0.05540 | -0.36780 | 0.01030 | 0.00837 | 0.00820 | 0.12660 |
| 2019 | 0.54720 | -0.00592 | 0.04820 | -0.34480 | 0.00922 | 0.00767 | 0.00720 | 0.11850 |
| 2020 | 0.54360 | -0.00497 | 0.04200 | -0.32290 | 0.00829 | 0.00703 | 0.00640 | 0.11070 |
Data for Figure 4A: Home Response to MFP Growth Shocks
(Traded - Learning)
| Date | 1. Relative Price of Investment | 2. Excess of investment growth over GDP growth | 3. Total Investment (share of gdp) | 4. Total Consumption (share of gdp) | 5. Labor Productivity Growth (CW) | 6. Capital Deepening (contribution to LP growth) | 7. GDP Growth (CW) | 8. Hours Worked |
|---|---|---|---|---|---|---|---|---|
| 1996 | -0.03640 | 0.58100 | 0.13590 | -0.04600 | 0.14670 | 0.00302 | 0.13830 | -0.00840 |
| 1997 | -0.18480 | 0.57720 | 0.79800 | -0.15370 | 0.14570 | 0.02860 | 0.15380 | 0.00810 |
| 1998 | -0.22120 | 0.14370 | 1.09410 | -0.25150 | 0.14360 | 0.04830 | 0.15440 | 0.04860 |
| 1999 | -0.18160 | -0.09680 | 1.08160 | -0.34870 | 0.13000 | 0.05210 | 0.14050 | 0.09150 |
| 2000 | -0.11520 | -0.18440 | 0.93230 | -0.43880 | 0.11130 | 0.04750 | 0.12050 | 0.13080 |
| 2001 | -0.04800 | -0.19360 | 0.74910 | -0.51760 | 0.09240 | 0.04020 | 0.10000 | 0.16380 |
| 2002 | 0.00920 | -0.16980 | 0.57890 | -0.58240 | 0.07570 | 0.03300 | 0.08160 | 0.18990 |
| 2003 | 0.05400 | -0.13640 | 0.43820 | -0.63220 | 0.06190 | 0.02690 | 0.06610 | 0.20940 |
| 2004 | 0.08680 | -0.10410 | 0.32880 | -0.66730 | 0.05080 | 0.02220 | 0.05350 | 0.22260 |
| 2005 | 0.10960 | -0.07690 | 0.24700 | -0.68880 | 0.04210 | 0.01880 | 0.04360 | 0.23070 |
| 2006 | 0.12440 | -0.05560 | 0.18700 | -0.69860 | 0.03530 | 0.01630 | 0.03570 | 0.23400 |
| 2007 | 0.13320 | -0.03960 | 0.14370 | -0.69840 | 0.02990 | 0.01450 | 0.02960 | 0.23370 |
| 2008 | 0.13720 | -0.02800 | 0.11250 | -0.69000 | 0.02580 | 0.01320 | 0.02470 | 0.23070 |
| 2009 | 0.13800 | -0.01970 | 0.09000 | -0.67530 | 0.02240 | 0.01220 | 0.02090 | 0.22530 |
| 2010 | 0.13640 | -0.01400 | 0.07360 | -0.65570 | 0.01970 | 0.01140 | 0.01790 | 0.21840 |
| 2011 | 0.13320 | -0.00994 | 0.06140 | -0.63260 | 0.01750 | 0.01080 | 0.01540 | 0.21000 |
| 2012 | 0.12840 | -0.00717 | 0.05210 | -0.60700 | 0.01570 | 0.01020 | 0.01340 | 0.20100 |
| 2013 | 0.12320 | -0.00526 | 0.04490 | -0.57980 | 0.01410 | 0.00966 | 0.01170 | 0.19140 |
| 2014 | 0.11760 | -0.00395 | 0.03900 | -0.55170 | 0.01280 | 0.00916 | 0.01030 | 0.18150 |
| 2015 | 0.11160 | -0.00304 | 0.03420 | -0.52340 | 0.01160 | 0.00867 | 0.00910 | 0.17160 |
| 2016 | 0.10560 | -0.00241 | 0.03000 | -0.49520 | 0.01060 | 0.00820 | 0.00810 | 0.16200 |
| 2017 | 0.09960 | -0.00196 | 0.02640 | -0.46760 | 0.00967 | 0.00774 | 0.00730 | 0.15210 |
| 2018 | 0.09360 | -0.00164 | 0.02320 | -0.44060 | 0.00886 | 0.00729 | 0.00650 | 0.14280 |
| 2019 | 0.08800 | -0.00140 | 0.02020 | -0.41470 | 0.00812 | 0.00686 | 0.00590 | 0.13380 |
| 2020 | 0.08240 | -0.00122 | 0.01760 | -0.38980 | 0.00746 | 0.00644 | 0.00530 | 0.12510 |
Figure 4B: Home Response to MFP Growth Shocks
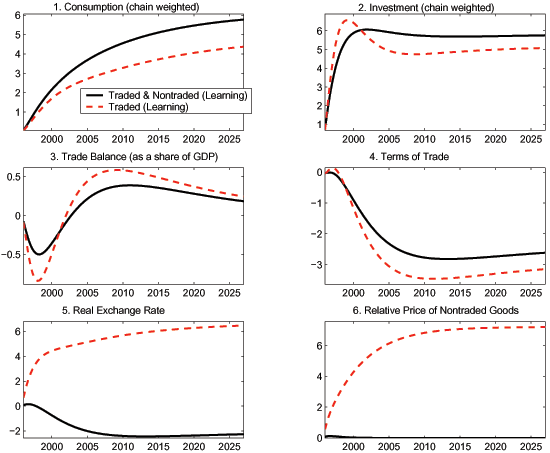
Data for Figure 4B: Home Response to MFP Growth Shocks
(Traded and Nontraded - Learning)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | 0.07700 | 0.76710 | -0.07580 | -0.02700 | 0.07150 | 0.07570 |
| 1997 | 0.63360 | 3.21970 | -0.38140 | -0.02070 | 0.13420 | 0.12130 |
| 1998 | 1.21300 | 4.69910 | -0.49830 | -0.19600 | -0.06840 | 0.08100 |
| 1999 | 1.72320 | 5.49350 | -0.46490 | -0.52350 | -0.39400 | 0.04780 |
| 2000 | 2.16570 | 5.87690 | -0.35640 | -0.90390 | -0.75000 | 0.02680 |
| 2001 | 2.55060 | 6.03040 | -0.22170 | -1.27610 | -1.08820 | 0.01420 |
| 2002 | 2.88760 | 6.06220 | -0.08770 | -1.61040 | -1.38700 | 0.00690 |
| 2003 | 3.18450 | 6.03470 | 0.03240 | -1.89590 | -1.63940 | 0.00280 |
| 2004 | 3.44790 | 5.98260 | 0.13360 | -2.13150 | -1.84620 | 0.00060 |
| 2005 | 3.68300 | 5.92430 | 0.21470 | -2.32070 | -2.01150 | -0.00050 |
| 2006 | 3.89400 | 5.86920 | 0.27710 | -2.46910 | -2.14070 | -0.00090 |
| 2007 | 4.08420 | 5.82140 | 0.32290 | -2.58290 | -2.23940 | -0.00110 |
| 2008 | 4.25630 | 5.78220 | 0.35460 | -2.66780 | -2.31290 | -0.00100 |
| 2009 | 4.41260 | 5.75140 | 0.37470 | -2.72920 | -2.36590 | -0.00080 |
| 2010 | 4.55490 | 5.72820 | 0.38540 | -2.77150 | -2.40240 | -0.00070 |
| 2011 | 4.68480 | 5.71160 | 0.38870 | -2.79870 | -2.42560 | -0.00050 |
| 2012 | 4.80360 | 5.70050 | 0.38630 | -2.81380 | -2.43860 | -0.00030 |
| 2013 | 4.91230 | 5.69390 | 0.37950 | -2.81960 | -2.44340 | -0.00020 |
| 2014 | 5.01200 | 5.69080 | 0.36940 | -2.81820 | -2.44210 | -0.00010 |
| 2015 | 5.10360 | 5.69040 | 0.35700 | -2.81140 | -2.43610 | 0.00000 |
| 2016 | 5.18770 | 5.69220 | 0.34300 | -2.80060 | -2.42660 | 0.00010 |
| 2017 | 5.26510 | 5.69560 | 0.32800 | -2.78690 | -2.41470 | 0.00010 |
| 2018 | 5.33630 | 5.70010 | 0.31240 | -2.77110 | -2.40100 | 0.00020 |
| 2019 | 5.40190 | 5.70550 | 0.29660 | -2.75410 | -2.38620 | 0.00020 |
| 2020 | 5.46240 | 5.71140 | 0.28080 | -2.73630 | -2.37070 | 0.00020 |
Data for Figure 4B: Home Response to MFP Growth Shocks
(Traded - Learning)
| Date | 1. Consumption (chain weighted) | 2. Investment (chain weighted) | 3. Trade Balance (as a share of GDP) | 4. Terms of Trade | 5. Real Exchange Rate | 6. Relative Price of Nontraded Goods |
|---|---|---|---|---|---|---|
| 1996 | 0.05920 | 0.71920 | -0.08990 | -0.04290 | 0.67190 | 0.56390 |
| 1997 | 0.48680 | 4.14140 | -0.64440 | 0.13650 | 2.60560 | 1.95760 |
| 1998 | 0.94750 | 6.03230 | -0.84250 | -0.06060 | 3.62620 | 2.88310 |
| 1999 | 1.35750 | 6.56180 | -0.73290 | -0.57060 | 4.14810 | 3.63680 |
| 2000 | 1.70140 | 6.42560 | -0.49350 | -1.16480 | 4.43310 | 4.26790 |
| 2001 | 1.98280 | 6.05800 | -0.23150 | -1.71900 | 4.61600 | 4.79450 |
| 2002 | 2.21270 | 5.66910 | 0.00347 | -2.18580 | 4.75940 | 5.23120 |
| 2003 | 2.40380 | 5.34210 | 0.19400 | -2.55730 | 4.88930 | 5.59140 |
| 2004 | 2.56680 | 5.09850 | 0.33840 | -2.84190 | 5.01490 | 5.88740 |
| 2005 | 2.71000 | 4.93250 | 0.44190 | -3.05340 | 5.13790 | 6.13010 |
| 2006 | 2.83950 | 4.82940 | 0.51150 | -3.20630 | 5.25740 | 6.32860 |
| 2007 | 2.95910 | 4.77320 | 0.55470 | -3.31310 | 5.37200 | 6.49090 |
| 2008 | 3.07130 | 4.74980 | 0.57750 | -3.38470 | 5.48030 | 6.62330 |
| 2009 | 3.17760 | 4.74850 | 0.58530 | -3.42940 | 5.58170 | 6.73130 |
| 2010 | 3.27890 | 4.76100 | 0.58220 | -3.45390 | 5.67570 | 6.81940 |
| 2011 | 3.37550 | 4.78170 | 0.57120 | -3.46330 | 5.76220 | 6.89120 |
| 2012 | 3.46780 | 4.80660 | 0.55490 | -3.46170 | 5.84170 | 6.94970 |
| 2013 | 3.55580 | 4.83340 | 0.53490 | -3.45210 | 5.91430 | 6.99730 |
| 2014 | 3.63940 | 4.86020 | 0.51270 | -3.43670 | 5.98060 | 7.03620 |
| 2015 | 3.71880 | 4.88620 | 0.48920 | -3.41740 | 6.04120 | 7.06780 |
| 2016 | 3.79400 | 4.91090 | 0.46520 | -3.39540 | 6.09640 | 7.09350 |
| 2017 | 3.86500 | 4.93390 | 0.44120 | -3.37170 | 6.14680 | 7.11450 |
| 2018 | 3.93190 | 4.95510 | 0.41750 | -3.34730 | 6.19280 | 7.13160 |
| 2019 | 3.99480 | 4.97460 | 0.39440 | -3.32250 | 6.23480 | 7.14550 |
| 2020 | 4.05380 | 4.99250 | 0.37220 | -3.29790 | 6.27330 | 7.15680 |
Footnotes
* Helpful comments were received from participants in the conference entitled 'Dynamic Macroeconomic Theory' held at the University of Copenhagen on June 11-13, 2004 and in seminars at the International Finance Division of the Federal Reserve Board and Georgetown University. We had useful discussions with Susantu Basu, David Bowman, Andrea DeMichelis, Charles Engel, Christopher Erceg, Christopher Gust, Jon Faust, Jaime Marquez, Daniel Sichel, and Jonathan Wright. Remaining errors are ours. Return to text
1. Most of our data come from three sources: the Groningen Growth and Development Center, Dale Jorgenson and his associates, and the Organization for Economic Co-operation and Development. Return to text
2. To be more precise, what happened in the last half of the 1990s was an increase in the rate of decline of the relative price of investment goods. Return to text
3. See, for example, Greenwood, Hercowitz, and Krusell (1997). Return to text
4. Pioneering contributions to the analysis of productivity shocks in open-economy DGE models include Backus, Kehoe, and Kydland (1994b), Backus, Kehoe, and Kydland (1994a), Stockman and Tesar (1995), Baxter and Crucinni (1995), and Kollmann (1998). Recent contributions include Erceg, Guerreri, and Gust (2002), Laxton and Pesenti (2003), and Hunt and Rebucci (2003). Closed economy contributions include Edge, Laubach, and Williams (2003, 2004). Return to text
5. Nontraded goods are clearly a large fraction of output in the U.S. (and Europe). The (increasingly unsatisfactory) convention of indentifying goods as traded and services as nontraded leads to the conclusion that 75% or so of output is nontraded. Taking account of the familiar argument that some services are traded, we assume that nontraded goods constitute 63% of consumption and 52 investment. These figures are in the middle of the (admittedly large) range of assumptions in the literature. Return to text
6. In this paper we do not attempt to explain why labor productivity growth was higher in Europe for many years before 1995 or to compare the levels of labor productivity in the U.S. and Europe. Return to text
7. Some analysts also separate out a contribution of changes in labor quality, but in this paper we abstract from such changes. Return to text
8. For example, the estimate of the contribution of MFP growth in the non-ICT sector to the change in labor productivity growth in the U.S. fell from 0.22 in Jorgenson (2003) to 0.03 in Jorgenson (2004a) and then rose to 0.35 in Jorgenson (2004b). Return to text
9. Two GGDC sources are GGDC (2004) and Inkleretal (2003). The work of Jorgenson and his associates is summarized in Jorgenson (2004b). For the OECD STAN data base source, see OECD (2004). Return to text
10. Data from these three sources also have some important differences. The GGDC data take the STAN data as a starting point, include more recent data obtained from national sources, and fill in some of the gaps in the STAN data using industry data. In the GGDC and STAN data, the concepts of output and capital services are the same as those in countries' national accounts, but in the Jorgenson data, these concepts both include imputed services from durable goods (including ITC goods) purchased by consumers and the government. Also,the Jorgenson data include land and inventories in the capital stock. The STAN data include country breakdowns for more countries than either of the others. As far as we know, neither detailed explanations of differences among the data nor all of the data necessary for reconciliation are publicly available. Return to text
11. The GGDC data come from GGDC (2004) and the Jorgenson data come from Jorgenson (2004b). Return to text
12. The Netherlands is included for completeness because we do not have the data necessary to construct an aggregate that includes only the other three EU-4 countries. Return to text
13. We cannot construct a meaningful aggregate for France, Germany, Italy, and the U.K. using the Jorgenson data because the data necessary to determine the appropriate weights for the contributions to labor productivity growth are not reported in his papers. Return to text
14. We use period averages for simplicity. Since we have found the Jorgenson data only in that form, we choose period averages based on data from the same years as his. We begin in 1990 to avoid the break in German data resulting from reunification. We have adopted the labeling convention under which, for example, level hours data for 1989 through 1995 are used to construct the average growth of hours for the period labeled 1990-1995. Jorgenson (2004b) uses a different convention under which the period he labels 1989-1995 corresponds to the period we label 1990-1995. GGDC uses yet another convention under which the period it labels 1990-1995 makes use of level data for 1990 through 1995. Since GGDC provides data on an annual basis we are able to construct the desired period averages. Return to text
15. The possible exceptions to this statement are the growth rates for labor quality which are not considered in this paper. Return to text
16. In the GGDC data, France is the only country where the qualitative pattern is different from that in the EU-4 aggregate. Labor productivity growth rose slightly there as a combination of a relatively large increase in MFP growth (0.5) and a moderate increase in labor quality growth (0.2) a little more than offset a large decrease in capital deepening (-0.6). Return to text
17. There is a similar breakdown of the contributions of MFP growth in Inkleretal (2003). We do not discuss this breakdown because the data used to construct it do not have the same coverage as the data used to construct Table 1. Return to text
18. There are significant differences between the GGDC data and the Jorgenson data which are not important for the points we want to make. They include (1) a larger decline in labor productivity growth in France resulting from both a smaller increase in output growth and a larger increase in hours growth, (2) a bigger increase in MFP growth in France associated with there being a reduction in labor quality growth for Jorgenson because of there being a significant increase in labor quality growth rather than a decrease this is half as large, (3) larger decreases in labor productivity growth and MPF growth in Germany both resulting from a larger decrease in output growth as well as a larger increase in hours growth, (4) a bigger decrease in labor productivity growth in the U.K. largely because of a much lower increase in output growth, and (5) a big increase in MFP growth rather than a small decrease because of a much larger decrease in the contribution of non-ICT capital deepening. Return to text
19. See, for example, Oliner and Sichel (2000). Return to text
20. The contributions in Table 2 are calculated using the standard methodology summarized in equation A.43 on p. 145 of Schreyer (2001). Return to text
21. Inkleretal (2003) present explicit breakdowns of labor productivity growth at the sectoral level, but we have been unable to reconcile them with breakdowns at the aggregate level even for the U.S. Return to text
22. See their Figure III.3.c. The analysis in Fernald and Ramnath (2004) also supports this conclusion. These authors point out that there may be a correlation between ICT capital deepening and MFP growth as conventionally measured because ICT is a 'general purpose technology' that can change ways of doing business. Return to text
23. See their Appendix Tables III.C.1 through III.C.6. Return to text
24. The GCGD sectoral breakdown is somewhat different from the OECD breakdown referred to above, but the difference does not matter for the points we want to make. Return to text
25. See, for example, Bosworth and Triplett (2000). Return to text
26. The quarterly data shown come from the productivity release of the Bureau of Labor Statistics. It differs from the data presented in Table 1 in that it excludes the government and farm sectors. Return to text
27. The US/ROW terms of trade is the ratio of the U.S. import deflator to the U.S. export deflator. We have not calculated a US/EURO terms of trade because there are no bilateral data for some countries in the Euro Area. The U.S./ROW real exchange rate is the ratio of the U.S. CPI to the trade-weighted sum of exchange-rate-adjusted CPIs for 25 major trading partners of the U.S. Return to text
28. The Lagrangian expression for the Home maximization problem is in the Appendix. Return to text
29. It is much easier to characterize the steady state of the model if production functions are identical. Return to text
30. In future work we plan to investigate the case in which there are also costs of changing labor inputs. Return to text
31. It is easier to accommodate trend growth in our formulation of adjustment costs than in the conventional quadratic formulation. Return to text
32. For example, in Edge, Laubach, and Williams (2003, 2004) an investment sector similar to ours is called an IT-producing sector. The IT good produced by this sector is the only capital good. For some purposes, it might be useful to construct a model with both IT capital and other capital, but we do not attempt to do so in this paper. Return to text
33. The qualtity shocks are entered with
the exponent
![]() so that if the
so that if the
![]() are equal, doubling all of them
doubles steady-state outputs. More precisely, if
are equal, doubling all of them
doubles steady-state outputs. More precisely, if
![]() , then
, then
![]() is constant in
the nonstochastic steady state. In this paper we assume that
is constant in
the nonstochastic steady state. In this paper we assume that
![]() remains constant at unity. Return to text
remains constant at unity. Return to text
34. Portfolio management costs are included to insure that the model has a well-defined steady state. Including these costs is the easiest among several roughly equivalent ways of guaranteeing stationarity as explained by Schmitt-Grohe and Uribe (2003). Return to text
35. Since the initial excess is zero, the
wealth effect is given by the first line of equation (10) minus the second where ![]() ,
, ![]() ,
,
![]() , and
, and
![]() are at
their post shock values and all other variables are at their
initial steady state values. Our definition of the term 'wealth
effect' is quite different from the one in
Baxter (1995). Return to text
are at
their post shock values and all other variables are at their
initial steady state values. Our definition of the term 'wealth
effect' is quite different from the one in
Baxter (1995). Return to text
36. For further discussion of the investment incentive see the Appendix. Return to text
37. We find it natural to assume that nontraded goods are complements in the assembly of investment (and consumption) goods. In our simulations the elasticity of substitution between nontraded and traded goods is one-half. Raising it to one has very small quantitative effects. Raising it to four (the value of the elasticity of substitution between the two traded goods) has large effects at the sectoral level and significant but considerably smaller effects at the aggregate level. It is more attractive to use traded goods in both investment and consumption, so investment can be higher without having consumption be any lower. At its peak the trade deficit is 0.10 pp instead of 0.07 pp. Return to text
38. Note that the initial decrease in capital deepening occurs because hours can increase in the period of the shock, but the capital stock cannot. Return to text
39. Learning has been used in the analysis of productivity shocks by Erceg, Guerreri, and Gust (2002) and Edge, Laubach, and Williams (2004). Return to text
40. If agents must also learn the coefficient of the autoregressive process, they figure out the true shock process much more slowly. Return to text
41. Allowing for costs of adjusting
![]() -
-![]() ratios in Foreign would
make less difference in the case of MFP growth shocks since
capital deepening makes a smaller contribution to labor
productivity growth in this case. Return
to text
ratios in Foreign would
make less difference in the case of MFP growth shocks since
capital deepening makes a smaller contribution to labor
productivity growth in this case. Return
to text
42. As before, the ![]() process governing the evolution of MFP growth
has a coefficient of 0.95. Return to
text
process governing the evolution of MFP growth
has a coefficient of 0.95. Return to
text
43. It is not surprising that with MFP shocks of the type we consider, we cannot match the entire path of labor productivity growth. Return to text
44. In our calibration, the traded shares for investment and consumption are 0.48 and 0.37, respectively. Return to text
45. See the Appendix. Return to text
46. Like many others, we assume that the dividing line between traded and nontraded goods is exogenous. There is a clear need for more research on endogenous tradability. An early contribution is Dornbusch, Fischer, and Samuelson (1977), and recent contributions include Bergin and Glick (2003) and Ghironi and Melitz (2004). The outsourcing abroad of record keeping and customer service functions is a familiar concrete example. Return to text
47. Dumagan (2002) shows the relationship between the Törnqvist index and the Fisher ideal index used in computing chain-weighted GDP by the U.S. Bureau of Economic Analysis. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text