The Federal Reserve Board eagle logo links to home page

Optimal Inflation Persistence:
Ramsey Taxation with Capital and Habits

Sanjay Chugh*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Ramsey models of fiscal and monetary policy with perfectly-competitive product markets and a fixed supply of capital predict highly volatile inflation with no serial correlation. In this paper, we show that an otherwise-standard Ramsey model that incorporates capital accumulation and habit persistence predicts highly persistent inflation. The result depends on increases in either the ability to smooth consumption or the preference for doing so. The effect operates through the Fisher relationship: a smoother profile of consumption implies a more persistent real interest rate, which in turn implies persistent optimal inflation. Our work complements a recent strand of the Ramsey literature based on models with nominal rigidities. In these models, inflation volatility is lower but continues to exhibit very little persistence. We quantify the effects of habit and capital on inflation persistence and also relate our findings to recent work on optimal fiscal policy with incomplete markets.

Keywords: Optimal fiscal and monetary policy, inflation persistence, Ramsey model, habit formation

JEL classification: E50, E61, E63


1  Introduction

The work of Chari, Christiano, and Kehoe (1991) showed that under the Ramsey plan, surprise inflation can be used by the government to synthesize state-contingent returns from nominal risk-free debt. Optimal inflation is highly volatile and serially uncorrelated in their environment, which features perfectly-competitive product markets and no capital accumulation. Likewise, little inflation persistence emerges in Ramsey models with nominal rigidities. For example, in the models of Schmitt-Grohe and Uribe (2004b) and Siu (2004), the volatility of inflation is dampened by introducing a cost associated with ex-post inflation. These results lead Chari and Kehoe (1999) to question whether any general equilibrium settings rationalize inflation persistence as part of the Ramsey policy. In this paper, we show that in an otherwise-standard flexible-price Ramsey model, either capital accumulation or habit persistence in preferences generates substantial persistence in optimal inflation. An increased preference for smooth consumption or an increased ability to smooth consumption makes Ramsey inflation persistent. The effect is a Fisherian one: with capital or habits, the real interest rate acquires persistence, which generates persistence in inflation. We thus answer the question posed by Chari and Kehoe (1999) in the affirmative.

Our result depends on consumption-smoothing. In the presence of capital, consumers' ability to smooth consumption in response to shocks is enhanced. This generates a persistent real interest rate, which, given an optimal nominal interest rate that is not too volatile, implies persistent inflation through the Fisher relationship. Alternatively, absent capital but with habit persistence, the preference for consumption-smoothing is greater than without habit. In equilibrium, this also generates persistence in the real rate and thus in inflation. Relative to a model with neither capital nor habit, then, either capital or habit increases the persistence in the real interest rate and thus in inflation. We show that each channel is quantitatively important.

Our results show that neglecting capital accumulation in models of optimal monetary policy is not innocuous. In Ramsey models of only fiscal policy, capital accumulation and capital taxation are central to the analysis. However, since the work of Lucas and Stokey (1983), the tradition in Ramsey analysis of monetary policy has been to assume fixed capital. The long line of studies that have followed this tradition have yielded many important insights regarding optimal monetary policy. Removing an endogenous state variable, though, may change the properties of optimal policy in an important way. Incorporating capital formation, a hallmark of Ramsey models of fiscal policy, allows us to go a long way in generating persistence in inflation. Introducing yet another endogenous state -- lagged consumption, due to habit -- generates even more persistence.

This mechanism of generating persistence in policy by introducing state variables seems to be at work in recent studies of optimal fiscal policy featuring incomplete markets and non-state-contingent debt, both of which necessitate the introduction of additional state variables. These studies successfully revive the Barro (1979) result that tax rates follow a random walk.1 A similar mechanism -- the introduction of a particular state variable leading to increased persistence of a component of optimal policy -- seems be at work in our model as well. However, it is not that introducing any persistent state would achieve the result. The baseline Ramsey monetary model features a persistent state, in the form of persistent exogenous shocks, yet predicts no inflation persistence. The important features in our model are the desire and ability, associated with habits and capital, to smooth out these shocks.

Our work also fits into the existing literature on optimal taxation in another way. In partial equilibrium models of optimal taxation that feature money, a central result is that inflation should be used as part of an optimal program of raising government revenue and should be highly persistent. That inflation should be used at all was argued by, among others, Phelps (1973), and that it should be persistent was discovered by Mankiw (1987). Optimal inflation persistence in partial equilibrium may not be very surprising -- assuming the real rate is constant should deliver an inflation rate that is highly persistent. In general equilibrium formulations, however, exactly the opposite prescription emerges: inflation, although still used to finance government spending, has zero persistence. As noted above, Chari and Kehoe (1999) call attention to this discrepancy and leave as an open question whether inflation persistence can be part of an optimal policy in a general equilibrium formulation. This paper answers this question in the affirmative, thus filling a theoretical gap in the optimal taxation literature.

The rest of the paper is organized as follows. Section 2 presents a Ramsey taxation problem in a standard cash-credit environment, one featuring flexible prices and no capital accumulation. We present the model without capital but with habit first, even though it generates less inflation persistence than the model with capital, because it is closer to existing Ramsey models of fiscal and monetary policy. Through numerical simulation, we show that habit formation does generate inflation persistence due to the Fisherian effect outlined above, but not a tremendous amount. So in Section 3, we extend the baseline model in a different direction and introduce capital accumulation, which to our knowledge makes our work the first in the Ramsey literature on the joint determination of fiscal and monetary policy to do so. Inflation is also optimally persistent in the presence of capital, moreso than with habit alone. The Fisher relation continues to provide the explanation for the result. Introducing habit formation in the model with capital only further increases the inertia in inflation. In Sections 2 and 3, we parameterize our model so that the Friedman Rule of a zero nominal interest rate is always optimal because the link between persistence in the real rate and persistence in inflation is most apparent with a constant nominal interest rate. To demonstrate that our results, neither qualitative nor quantitative, are not driven by the Friedman Rule, we extend our model in Section 4 to allow for a time-varying optimal nominal interest rate. Our results are little changed in this extended model. Section 5 relates our findings to the existing optimal taxation literature, especially the recent work on optimal fiscal policy with incomplete markets. We see an interesting link between our results and this recent branch of the Ramsey literature. We also briefly discuss how our work might connect to the vast recent New Keynesian literature on inflation persistence. Section 6 offers concluding thoughts.

2  An Economy without Capital

We start by studying a simple economy in which firms use only labor to produce output and in which consumers' preferences feature habit formation. Habit formation has been used recently in a number of macroeconomic models, too numerous to cite here, so the idea is by now fairly well-known. Briefly, when preferences display habit persistence, past consumption affects current marginal utility. Past consumption may in general affect current marginal utility in a complicated way, but we follow much of the existing macro literature on habits and assume that it is consumption in only the immediate past that matters, and moreover that it detracts from current consumption in a linear way.2 A useful way of understanding a habit utility function is that it gives rise to a concern for smoothing both the level and the growth of consumption. We begin by describing the economic environment, proceed to construct the Ramsey optimal allocation problem, and then present our numerical findings.

2.1  Representative Consumer

We motivate money demand using a standard cash good/credit good environment. Denote by $ c_{1t}$ consumption of cash goods, $ c_{2t}$ consumption of credit goods, and $ n_{t}$ hours worked. The representative consumer maximizes the sum of lifetime expected discounted utility,

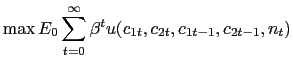
$\displaystyle \max E_{0} \sum_{t=0}^{\infty} \beta^{t} u(c_{1t}, c_{2t}, c_{1t-1}, c_{2t-1}, n_{t})$ (1)

subject to a flow budget constraint

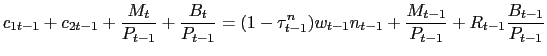
$\displaystyle c_{1t-1} + c_{2t-1} + \frac{M_{t}}{P_{t-1}} + \frac{B_{t}}{P_{t-1}} = (1-\tau^{n}_{t-1})w_{t-1} n_{t-1} + \frac{M_{t-1} }{P_{t-1}} + R_{t-1} \frac{B_{t-1}}{P_{t-1}}$ (2)

and the cash-in-advance constraint

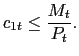$\displaystyle c_{1t} \leq\frac{M_{t}}{P_{t}}.$ (3)

Period utility is increasing in $ c_{1t}$ and $ c_{2t}$ and decreasing in $ c_{1t-1}$, $ c_{2t-1}$, and $ n_{t}$. The notation here is standard: $ M_{t}$ denotes nominal money holdings chosen during securities-market trading in period $ t$, $ B_{t}$ denotes nominal, risk-free one-period bond holdings chosen during securities-market trading in period $ t$, $ R_{t}$ denotes the gross nominal interest rate on these bonds, and $ w_{t}$ denotes the real wage that the consumer takes as given. The tax rate on labor income is denoted $ \tau ^{n}_{t}$. Finally, the consumer is endowed with one unit of time each period to divide between work and leisure.

The lagged consumption terms in the utility function represent habit persistence -- past consumption (negatively) affects current utility.

Finally, the two constraints embody the same timing of markets as in Chari, Christiano, and Kehoe (1991). Specifically, in any given period securities market trading, in which money and bonds are traded, occurs first, followed by simultaneous goods-market and factor-market trading.

Attach the Lagrange multipliers $ \phi_{t}$ and $ \lambda_{t}$ to (2) and (3), respectively. The consumer's first-order conditions with respect to $ c_{1t}$, $ c_{2t}$, $ n_{t}$, $ M_{t}$, and $ B_{t}$ are, respectively,

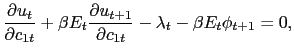
$\displaystyle \frac{\partial u_{t}}{\partial c_{1t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{1t}} - \lambda_{t} - \beta E_{t} \phi_{t+1} = 0,$ (4)

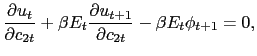
$\displaystyle \frac{\partial u_{t}}{\partial c_{2t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{2t}} - \beta E_{t} \phi_{t+1} = 0,$ (5)

$\displaystyle \frac{\partial u_{t}}{\partial n_{t}} + \beta E_{t}[ \phi_{t+1} w_{t} (1-\tau^{n}_{t}) ] = 0,$ (6)

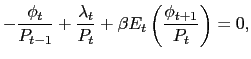
$\displaystyle -\frac{\phi_{t}}{P_{t-1}} + \frac{\lambda_{t}}{P_{t}} + \beta E_{t} \left( \frac{\phi_{t+1}}{P_{t}} \right) = 0,$ (7)

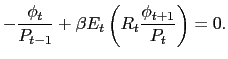
$\displaystyle -\frac{\phi_{t}}{P_{t-1}} + \beta E_{t} \left( R_{t} \frac{\phi_{t+1}}{P_{t}} \right) = 0.$ (8)

The sources of uncertainty in the economy are stochastic productivity and government spending, hence the expectations operators. From (8), we get the usual Fisher relation,

$\displaystyle 1 = \beta R_{t} E_{t} \left[ \frac{\phi_{t+1}}{\phi_{t}} \frac{1}{\pi_{t}} \right] ,$ (9)

where $ \pi_{t} \equiv P_{t}/P_{t-1}$ is the gross rate of inflation between period $ t-1$ and period $ t$. The stochastic discount factor $ \beta E_{t} [ (\phi_{t+1}/\phi_{t}) (1/\pi_{t}) ]$ prices a nominal, risk-free one-period asset. We can express the Fisher relation instead as a pricing equation. Combining (4) and (7), we get

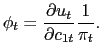
$\displaystyle \phi_{t} = \frac{\partial u_{t}}{\partial c_{1t}} \frac{1}{\pi_{t}}.$ (10)

Substituting this expression into (9) gives us the pricing formula for a one-period risk-free nominal bond,

$\displaystyle 1 = \beta R_{t} E_{t} \left[ \frac{ (\partial u_{t+1} / \partial c_{1t+1}) + \beta E_{t+1} (\partial u_{t+2} / \partial c_{1t+1}) }{ (\partial u_{t} / \partial c_{1t}) + \beta E_{t} (\partial u_{t+1} / \partial c_{1t}) } \frac{1}{\pi_{t+1}} \right] .$ (11)

We will use expression (11) to develop the intuition for our inflation persistence result.

The consumer first-order conditions also imply that the gross nominal interest rate equals the marginal rate of substitution between cash and credit goods, which with habit persistence depends on past, current, and future consumption. Specifcally,

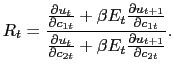
$\displaystyle R_{t} = \frac{\frac{\partial u_{t}}{\partial c_{1t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{1t}}} {\frac{\partial u_{t} }{\partial c_{2t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{2t}}}.$ (12)

This condition collapses to $ R_{t} = (\partial u_{t} / \partial c_{1t}) / (\partial u_{t} / \partial c_{2t})$ , which depends on only consumption in period $ t$, as is standard in cash-credit models without habit.

2.2  Representative Firm

A representative firm produces the aggregate good in a perfectly competitive market by hiring labor in a perfectly competitive spot market. The production technology is

$\displaystyle y_{t} = z_{t} n_{t},$ (13)

with the productivity shock $ z_{t}$ realized before period-$ t$ decisions. Due to perfect competition in the labor market, the (pre-tax) real wage equals the marginal product of labor.

2.3  Government

The government has an exogenous stream of real expenditures $ \{g_{t} \}_{t=0}^{\infty}$ that it must finance through the labor income tax, the inflation tax, and nominal risk-free one-period debt. In nominal terms, its period-$ t$ budget constraint is

$\displaystyle M_{t} - M_{t-1} + B_{t} + P_{t-1} \tau^{n}_{t-1} w_{t-1} n_{t-1} = R_{t-1} B_{t-1} + P_{t-1} g_{t-1}.$ (14)

Government spending is thus a credit good. Nominal liabilities thus serve a fiscal role in this model, although as we show in our results, seignorage revenue is only a small fraction of government spending. In steady-state, the government budget constraint is

$\displaystyle sr + \pi b + \tau^{n} w n = R b + g,$ (15)

where $ b$ denotes steady-state real debt, and $ sr$ is steady-state seignorage revenue. In steady-state, $ sr = c_{1}(\pi-1)$.

2.4  Equilibrium

A competitive monetary equilibrium is stochastic processes for $ c_{1t}$, $ c_{2t}$, $ n_{t}$, $ M_{t+1}$, $ B_{t+1}$, $ w_{t}$, $ \tau^{n}_{t}$, and $ R_{t}$ such that the household maximizes utility with the cash-in-advance constraint holding with equality, taking as given prices and policies; the firm maximizes profit taking as given the wage rate; the labor market clears, the money market clears, the bond market clears, the government budget constraint (14) is satisfied, and the resource constraint

$\displaystyle c_{1t} + c_{2t} + g_{t} = z_{t} n_{t}$ (16)

is satisfied. In addition, if bonds earn a gross nominal return of less than one, the household can make unbounded profits by buying money and selling bonds, which implies that in a monetary equilibrium $ R_{t} \geq1$.

2.5  Ramsey Problem

In a standard way in the Ramsey taxation literature, we adopt the primal approach and derive the present-value implementability constraint facing the Ramsey government. In the present model, the implementability constraint is

$\displaystyle \sum_{t=0}^{\infty} \beta^{t} \left[ \left( \frac{\partial u_{t}}{\partial c_{1t}} + \beta\frac{\partial u_{t+1}}{\partial c_{1t}} \right) c_{1t} + \left( \frac{\partial u_{t}}{\partial c_{2t}} + \beta\frac{\partial u_{t+1}}{\partial c_{2t}} \right) c_{2t} + \frac{\partial u_{t}}{\partial n_{t}} n_{t} \right] = \phi_{0} \left( \frac{M_{-1} + R_{-1} B_{-1}}{P_{0}} \right) ,$ (17)

the derivation of which can be found in, for example, Chari and Kehoe (1999), modified slightly to account for habit persistence. The implementability constraint is in terms of only allocations and is the present-value budget constraint of the consumer with prices and policies substituted out using the consumer's first-order conditions. This constraint describes how distortionary taxation imposes additional restrictions on welfare maximization beyond that encoded in the economy's technology. The novel terms in this implementability constraint compared to others in the Ramsey literature are the $ \partial u_{t+1}/\partial c_{it}$, $ i=1,2$ terms, which arise due to the habit persistence. These terms reflect the fact that the consumer knows that period-$ t$ consumption (negatively) affects his period-$ (t+1)$ utility. To continue to lay the groundwork for the intuition behind our inflation persistence result, we emphasize that the Fisher relation (9) -- alternatively, its pricing formula representation (11) -- is embedded in the implementability constraint. The Ramsey allocations thus respect the Fisher equation, which is the key to understanding our results.

The Ramsey government chooses sequences for $ c_{1t}$, $ c_{2t}$, and $ n_{t}$ to maximize (1) subject to the resource constraint (16) and the implementability constraint (17), taking as given exogenous processes for $ z_{t}$ and $ g_{t}$. In order to ensure that allocations can be supported as a competitive monetary equilibrium, the Ramsey government must also respect the constraint

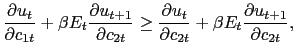
$\displaystyle \frac{\partial u_{t}}{\partial c_{1t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{2t}} \geq\frac{\partial u_{t}}{\partial c_{2t}} + \beta E_{t} \frac{\partial u_{t+1}}{\partial c_{2t}},$ (18)

which guarantees that the gross nominal interest rate is no smaller than one, as inspection of condition (12) shows. In other words, in principle we should impose a zero-lower-bound constraint for the nominal interest rate. However, it can be shown analytically that solving the Ramsey problem without this constraint, and given the implementability constraint (17) and the separable form for utility we use (presented in Section 2.6.1 below), the Friedman Rule of a zero net nominal interest rate is optimal. Thus, $ R_{t}=1$ always and (18) always holds with equality in the less-constrained problem. Thus we can drop (18) from the Ramsey problem. The proof is a special case of that presented by Chari and Kehoe (1999). Define $ \widehat{u}_{j,t} = \frac{\partial u_{t}}{\partial c_{jt}} + \beta \frac{\partial u_{t+1}}{\partial c_{jt}}$ , $ j=1,2$, and substitute in (17) and (18). The proof then follows Chari and Kehoe (1999) exactly.

We focus attention on the Ramsey first-order conditions for $ t>0$ and for our dynamic results assume that the economy starts in the steady-state of the Ramsey plan for $ t>0$. By doing so, we adopt the timeless approach to policy described by Woodford (2003), thus endogenizing the initial state of the economy and concerning ourselves with only the asymptotic dynamics of the economy.

2.6  Quantitative Results

We describe how we choose parameter values, show steady-state results highlighting how seignorage revenue depends on the parameter governing money demand, and then present our dynamic results.

2.6.1  Parameter Values

We choose the period utility function

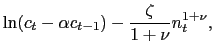
$\displaystyle \ln(c_{t} - \alpha c_{t-1}) - \frac{\zeta}{1+\nu} n_{t}^{1+\nu},$ (19)

in which $ \alpha$ parameterizes the strength of the habit persistence on the consumption aggregate

$\displaystyle c_{t} = \left[ (1-\sigma) c_{1t}^{\upsilon} + \sigma c_{2t}^{\upsilon}\right] ^{1/\upsilon}.$ (20)

Siu (2004) estimates the parameters $ \sigma$ and $ \upsilon$ of the consumption aggregator for the case of time-separable preferences using the consumer's optimality condition (12). It is easy to verify that despite the presence of habit persistence in our model, the estimating equation is identical and so we use Siu's (2004) estimates $ \sigma=0.62$ and $ \upsilon=0.79$ as our baseline. The parameter $ (1-\sigma)$ captures the importance of cash goods in the model and hence the importance of money demand, without which there is no tax base for inflation. If $ (1-\sigma) = 0$, then the model is cashless and seignorage revenue is zero. However, as long as $ (1-\sigma)$ does not equal exactly zero, the dynamic properties of inflation -- in particular, the persistence and volatility -- are independent of $ \sigma$. This is because prices are flexible in our model and thus the only consideration regarding the use of inflation is to generate state-contingent returns from risk-free nominal debt. We explain this mechanism further in Section 2.6.3. On the other hand, if prices were sticky, as in Siu (2004) and Schmitt-Grohe and Uribe (2004b), the optimal inflation rate would balance the insurance value of surprise inflation against the resource misallocation cost. In such a model, the dynamic properties of inflation would be importantly affected by $ \sigma$. We also discuss this point a bit further below.

For the parameters governing disutility of work, we choose $ \nu= 1.7$, in line with Hall's (1997) estimates of the elasticity of marginal disutility of work, and calibrate $ \zeta$ so that in the deterministic steady-state of the Ramsey plan the consumer spends one-third of his time working. The value of $ \zeta$ thus depends on the rest of the parameterization. There is little agreement on realistic values for the habit parameter $ \alpha$, so we simply choose $ \alpha=0.5$ for the main results we describe in the model with habit. This value is in line with other studies using habit in macro models. But we also investigate how inflation persistence in our model varies with $ \alpha$.

The exogenous processes for productivity and government spending each follow an AR(1),

$\displaystyle \ln z_{t+1} = \rho_{z} \ln z_{t} + \epsilon^{z}_{t}$ (21)

$\displaystyle \ln g_{t+1} = \rho_{g} \ln g_{t} + \epsilon^{g}_{t}$ (22)

with $ \epsilon^{z} \sim iid N(0,\sigma_{z}^{2})$ and $ \epsilon^{g} \sim iid N(0,\sigma_{g}^{2})$. We set $ \rho_{z} = 0.95$, $ \rho_{g} = 0.90$, $ \sigma_{z} = 0.007$, and $ \sigma_{g} = 0.02$, in line with evidence for the U.S. economy, as our baseline parameterization. To investigate how much inflation persistence derives from the assumed persistence of the government spending shock, we also consider $ \rho_{g}=0$.

Finally, we set the initial real liabilities of the government $ \frac{M_{-1} + R_{-1} B_{-1}}{P_{0}}$ so that in the non-stochastic Ramsey steady-state the government debt-to-GDP ratio is 0.45, in line with U.S. experience. Table 1 summarizes our baseline calibration.

Table 1:  Baseline parameter values for model without capital

Parameter
Value
Description
$ \beta$
0.99
Quarterly subjective discount factor
$ \sigma$
0.62
Share of credit goods in consumption aggregator
$ \upsilon$
0.79
Elasticity of substitution between cash goods and credit goods
$ \nu$
1.7
Elasticity of marginal disutility of work
$ \zeta$
Varies
Pins down steady-state hours worked
$ \rho_{z}$
0.95
Persistence in log productivity
$ \rho_{g}$
0.90
Persistence in log government spending
$ \sigma_{z}$
0.007
Standard deviation of log productivity
$ \sigma_{g}$
0.02
Standard deviation of log government spending

2.6.2  Steady-State Policy

To elaborate a bit further on how our main result does not depend on $ \sigma$, Table 2 presents steady-state seignorage revenue, real (ex-post) government debt, and labor tax revenue as percentage of government spending for three different values: $ (1-\sigma) = 0.05$ ("cashless" model), $ (1-\sigma)=0.38$ (baseline model), and $ (1-\sigma) = 0.95$ ("cashful" model).3 The first column is the percentage of steady-state government spending that is financed with seignorage revenue, the second column is the percentage that is financed with labor income taxation, and the third column is the percentage financed by net proceeds from bond issuance, inclusive of the costs of retiring maturing debt. The first and third columns show negative values because there is deflation on average in the economy due to the optimality of the Friedman Rule. Because of this lump-sum average inflation subsidy, labor tax revenues are actually more than one hundred percent of government spending on average. As a preview of the dynamic results in the next section, we point out that, in unreported results, seignorage revenue fluctuates very little dynamically regardless of $ \sigma$, so the dynamics of inflation we describe below are not driven by revenue-generation needs.

Finally, the steady-state optimal labor tax rate is $ \tau^{n} = 0.196$, invariant to both $ \sigma$ and $ \alpha$. The labor tax is invariant to the strength of habit because it is internal habit persistence and so does not represent any market failure to which policy would need to respond.

Table 2:  Steady-state financing of government spending as function of 1 - σ, in percentage points. sr denotes seignorage revenue. Habit parameter is α = 0.

Model
1 - σ
sr/g
τnwn/g
b(π - R)/g
"Cashless"
0.05
0.0
102.5
-2.5
Baseline
0.38
-0.4
102.8
-2.5
"Cashful"
0.95
-4.6
107.1
-2.5

2.6.3  Optimal Inflation Persistence

We now describe our first central result, that habit persistence generates inertia in inflation. Tables 3 and 4 present simulation-based moments for the key policy and real variables of the model using first-order and second-order approximation methods, respectively. We approximate the model in levels around the non-stochastic Ramsey steady-state and follow the perturbation algorithm described by Schmitt-Grohe and Uribe (2004c). For each parameterization, we conduct 1000 simulations of 500 periods each and discard the first 100 periods. For each simulation, we then compute first and second moments and report the average of these moments over the 1000 simulations in Tables 3 and 4. To make the comparisons meaningful, the same realizations for the government spending shocks and productivity shocks are used across parameterizations.

The numerical results from the first-order and second-order approximations are virtually identical, suggesting that in this class of models and for a typical calibration, the results of a first-order approximation are not misleading. Schmitt-Grohe and Uribe (2004b) in their sticky-price Ramsey model also report obtaining largely similar results from a first-order and second-order approximation, and Aruoba, Fernandez-Villaverde, and Rubio-Ramirez (2003) show that only for extreme parameterizations of the stochastic growth model does a first-order approximation perform worse than a second-order approximation. These findings suggest that the recent debate about the need for higher-order approximations in optimal policy models applies more forcefully to New Keynesian models rather than the type of Ramsey analysis we conduct.4

Table 3:  First-order approximation. Economy with habit persistence and no capital. π and R reported in annualized percentage points - Panel A: No habit (α = 0)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x, y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.198
0.045
0.934
0.643
-0.140
0.987
$ \pi$
-3.86
4.36
-0.027
-0.098
0.049
-0.173
$ R$
0
0
--
--
--
--
 y
0.330
0.012
0.916
1
0.652
0.758
$ c$
0.270
0.004
0.934
0.643
-0.140
0.987
$ n$
0.330
0.003
0.921
-0.312
0.497
-0.850

Table 3:  First-order approximation. Economy with habit persistence and no capital. π and R reported in annualized percentage points - Panel B: Habit (α = 0.5)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x, y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.198
0.040
0.929
0.340
-0.141
0.986
$ \pi$
-3.70
7.78
0.214
0.017
0.070
-0.247
$ R$
0
0
--
--
--
--
 y
0.330
0.009
0.902
1
0.871
0.486
$ c$
0.270
0.002
0.972
0.357
-0.130
0.975
$ n$
0.330
0.003
0.912
-0.052
0.422
-0.891

Table 4:  Second-order approximation. Economy with habit persistence and no capital. π and R reported in annualized percentage points - Panel A: No habit (α = 0)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x, y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.195
0.045
0.934
0.642
-0.140
0.984
$ \pi$
-3.84
4.37
-0.027
-0.101
0.049
-0.177
$ R$
0
0
--
--
--
--
 y
0.331
0.012
0.916
1
0.650
0.758
$ c$
0.270
0.004
0.934
0.644
-0.140
0.987
$ n$
0.330
0.003
0.921
-0.314
0.496
-0.851

Table 4:  Second-order approximation. Economy with habit persistence and no capital. π and R reported in annualized percentage points - Panel B: Habit (α = 0.5)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x, y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.195
0.044
0.927
0.295
-0.138
0.973
$ \pi$
-3.80
7.78
0.212
0.015
0.068
-0.248
$ R$
0
0
--
--
--
--
$ y$
0.330
0.009
0.902
1
0.873
0.488
$ c$
0.271
0.002
0.972
0.358
-0.124
0.974
$ n$
0.330
0.003
0.910
-0.051
0.418
-0.890

We focus on the dynamic properties of inflation in Tables 3 and 4. Deflation on average at close to the rate of time preference is a feature of the optimal policy, confirming the results of Chari and Kehoe (1999), Siu (2004), and Schmitt-Grohe and Uribe (2004a). As those studies also find, without habits the persistence of inflation, as measured by the first-order autocorrelation, is essentially zero while the volatility of inflation is quite high. The reason for the latter result, which is well-known in the Ramsey literature, is that inflation is used by the Ramsey government to make risk-free nominal debt state-contingent in real terms. Doing so allows the government to maintain a very smooth path for the distortionary labor income tax, as the small standard deviation of $ \tau^{n}$ shows, which supports a smooth path of consumption. Unanticipated inflation is thus used by the Ramsey government as insurance against fluctuations in government spending. The ex-post real return on government debt is $ R_{t}/\pi_{t}$. Because the Friedman Rule ($ R_{t}=1$) is optimal in this model, the real return is simply $ 1/\pi_{t}$ -- so with volatile inflation, the real return is volatile. We point out that this result is standard with flexible prices. With sticky prices, recent results obtained by Siu (2004) and Schmitt-Grohe and Uribe (2004b) suggest that the insurance provided by inflation is dominated by other efficiency considerations, a point we discuss further in Section 5.

Our simulations also confirm that the optimal nominal interest rate is always zero, which, as we noted in Section 2.5, can be shown analytically. The dynamics of real variables are also in line with evidence, and while we do not report results for alternative values of $ \sigma$, our experiments show that the dynamic properties of inflation are unaffected by $ \sigma$, as we mentioned in Section 2.6.2.

Inflation dynamics differ, however, when preferences display habit persistence. With our baseline habit parameter $ \alpha=0.50$, inflation persistence rises from effectively zero to about 0.2 with habit. The standard deviation of inflation also increases markedly with habit persistence. Both the increased persistence and increased volatility can be understood in terms of the pricing equation (11). With habits, the intertemporal marginal rate of substitution (IMRS), or the real risk-free pricing kernel, $ \phi_{t+1}/\phi_{t}$, depends on $ c_{t+2}$, $ c_{t+1}, c_{t}$, and $ c_{t-1}$, rather than just $ c_{t+1}$ and $ c_{t}$, suggesting the riskless real interest rate is more persistent with habit. The increased desire to smooth consumption implies a more persistent (smoother) path for the IMRS, which in equilibrium is the real riskless rate. With a constant nominal interest rate, this means that inflation also becomes more persistent.5 This is the basic way to understand why inflation persistence rises with habit formation.

The theoretical gap between partial equilibrium models and general equilibrium models we identified in the introduction is thus bridged in the following way. In a partial equilibrium model, the real interest rate is fixed by construction. In such a model, Mankiw (1987) argues that inflation should be highly persistent -- indeed, a random walk if the nominal rate is also constant. In general equilibrium models (with neither capital nor habit), the real interest rate of course is not fixed. Such models to date predict very little inflation persistence. Introducing habit (or, as in Section 3, capital) generates persistence in the real interest rate -- the real rate does not become constant, of course, but, loosely speaking, closer to constant. Inflation then must also become more persistent. This is of course simply the Fisher effect described more informally, but it captures the essence of why introducing habit or capital in a general equilibrium model partially revives the implications for inflation that emerge from a partial equilibrium model.

The IMRS also becomes more volatile with habits, causing inflation volatility to rise as well. The IMRS becomes more volatile because the intertemporal margin in effect absorbs the fluctuations in optimal consumption that habit squeezes out. The following informal argument illustrates this effect: starting from a given level of consumption in period $ t$, a consumer receiving a positive income shock in $ t+1$ will increase his consumption by less if he forms habits than if he does not, which makes the IMRS more persistent as described above. In addition, the consumer is closer to his habit stock if he forms habits (the habit stock is of course zero with time-separable utility), making his marginal utility, which is a function of consumption less the habit stock, more sensitive to fluctuations in consumption. This sensitivity of marginal utility leads to increased volatility of the pricing kernel and is the reason that habit-based asset-pricing models help explain volatile stock returns. In our model, the volatile IMRS process allows us to conclude through the Fisher equation that inflation must also become more volatile. This increased inflation volatility is mirrored in a corresponding (slight) drop in the volatility of the labor tax rate. With flexible prices, unanticipated large swings in the price level do not impose any cost.

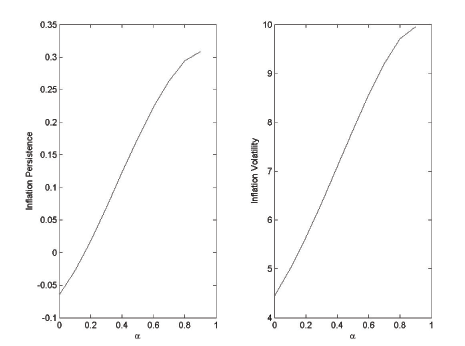
Figure 1 plots the persistence and volatility of inflation as a function of the habit parameter $ \alpha$. Because the results are virtually identical using either a first- or second-order approximation, we summarize results from only the first-order simulations. Inflation persistence and volatility both rise as $ \alpha$ increases, as the discussion above suggests. The plots in Figure 1 are for our baseline serial correlation in government spending shocks of $ \rho_{g} = 0.90$. Figure 2 provides the same plots for serially uncorrelated spending shocks, holding the serial correlation of productivity shocks constant at $ \rho_{z} = 0.95$. Comparison of the two shows that habit generates inflation persistence beyond the persistence in government spending shocks. However, even with very strong habit, inflation persistence only reaches roughly 0.3. As we show in the next section, another natural candidate source of endogenous persistence, capital accumulation, performs even better.

Figure 1:  Inflation persistence (left panel) and volatility (right panel) as a function of the habit parameter α for serially correlated government expenditure shocks. π measured in annualized percentage points, ρg = 0.90, ρz = 0.95. Steady-state π = -3.9 percent.

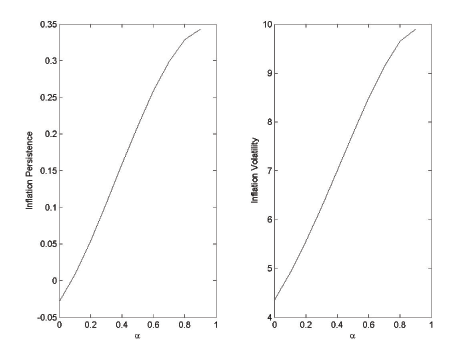
The left panel of Figure 1 shows the inflation persistence on the vertical axis with a scale ranging from negative 0.05 to positive 0.35, as a function of the habit parameter alpha on the horizontal axis with a scale ranging from 0 to 1, for serially correlated government expenditure shocks. When alpha is zero, inflation persistence is about negative 0.025. As alpha approaches one, inflation persistence increases approximately linearly to almost positive 0.35. The right panel of Figure 1 shows the inflation volatility on the vertical axis with a scale ranging from positive 4 to positive 10, as a function of the habit parameter alpha on the horizontal axis with a scale ranging from 0 to 1, for serially correlated government expenditure shocks. When alpha is zero, volatility is about 4.3. As alpha approaches one, volatility increases approximately linearly to about 10.

Figure 2:  Inflation persistence (left panel) and volatility (right panel) as a function of the habit parameter α for serially uncorrelated government expenditure shocks. π measured in annualized percentage points, ρg = 0, ρz = 0.95. Steady-state π = -3.9 percent.

The left panel of Figure 2 shows the inflation persistence on the vertical axis with a scale ranging from negative 0.1 to positive 0.35, as a function of the habit parameter alpha on the horizontal axis with a scale ranging from 0 to 1, for serially uncorrelated government expenditure shocks. When alpha is zero, inflation persistence is about negative 0.06. As alpha approaches one, inflation persistence increases approximately linearly to about positive 0.3. The right panel of Figure 2 shows the inflation volatility on the vertical axis with a scale ranging from positive 4 to positive 10, as a function of the habit parameter alpha on the horizontal axis with a scale ranging from 0 to 1, for serially uncorrelated government expenditure shocks. When alpha is zero, volatility is about 4.5. As alpha approaches one, volatility increases approximately linearly to about 10.

3  An Economy with Capital

In this section, we introduce a second source of endogenous persistence, capital accumulation, to our model. The basic reason that capital accumulation should be expected to generate inflation persistence is again through a more persistent real interest rate, this time due to an increased ability, rather than an increased desire, to smooth consumption. Beyond its implications for inflation inertia, however, characterizing optimal monetary policy in the presence of capital is an understudied area of theoretical research, one that warrants further development to make the policy prescriptions of such models more relevant for policy-makers. We first briefly describe how the economic primitives are modified to accommodate capital accumulation, proceed to show how the Ramsey problem is affected, and then present quantitative results.

3.1  Representative Consumer

The problem of the consumer is as described in Section 2.1 except the flow budget constraint is now

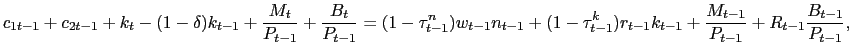
$\displaystyle {\small c_{1t-1} + c_{2t-1} + k_{t} - (1-\delta )k_{t-1} + \frac{M_{t}}{P_{t-1}} + \frac{B_{t}}{P_{t-1}} = (1-\tau^{n} _{t-1})w_{t-1} n_{t-1} + (1-\tau^{k}_{t-1})r_{t-1} k_{t-1} + \frac{M_{t-1} }{P_{t-1}} + R_{t-1} \frac{B_{t-1}}{P_{t-1}},}$ (23)

where $ r_{t}$ is the pre-tax rental rate of capital, $ \tau ^{k}_{t}$ is the tax rate on capital income and $ \delta$ is the depreciation rate of capital. The only new first-order condition is that on capital holdings,

$\displaystyle - E_{t} \phi_{t+1} + \beta E_{t} \left[ \phi_{t+2} \left( 1-\delta+ r_{t+1} \left( 1-\tau^{k}_{t+1} \right) \right) \right] = 0.$ (24)

3.2  Firms

The representative firm's problem is as described in Section 2.2, except now production occurs via the constant-returns technology

$\displaystyle y_{t} = z_{t} f(k_{t},n_{t}).$ (25)

The firm rents capital and labor in competitive spot markets to minimize the cost of producing the demand it must fill. Profit-maximization gives rise to equilibrium values for the (pre-tax) real wage and real rental rate that equal their respective marginal products.

3.3  Government

In addition to the distortionary labor income tax, the government now also has access to a distortionary capital income tax. The government's budget constraint is modified in the obvious way to reflect the capital income taxes it now collects:

$\displaystyle M_{t} - M_{t-1} + B_{t} + P_{t-1} \tau^{n}_{t-1} w_{t-1} n_{t-1} + P_{t-1} \tau^{k}_{t-1} r_{t-1} k_{t-1} = R_{t-1} B_{t-1} + P_{t-1} g_{t-1}.$ (26)

3.4  Ramsey Problem

Finally, the implementability constraint faced by the Ramsey government is now given by

$\displaystyle {\scriptsize\sum_{t=0}^{\infty} \beta^{t} \left[ \left( \frac{\partial u_{t}}{\partial c_{1t}} + \beta\frac{\partial u_{t+1} }{\partial c_{1t}} \right) c_{1t} + \left( \frac{\partial u_{t}}{\partial c_{2t}} + \beta\frac{\partial u_{t+1}}{\partial c_{2t}} \right) c_{2t} + \frac{\partial u_{t}}{\partial n_{t}} n_{t} \right] = \frac{\partial u_{0} }{\partial c_{20}} \left( \frac{M_{-1} + R_{-1} B_{-1}}{P_{0}} \right) + \frac{\partial u_{0}}{\partial c_{20}} \left( 1-\delta+ r_{0} \left( 1-\tau^{k}_{0} \right) \right) k_{0},}$ (27)

which is again derived in the standard way. The second term in the constant arises due to the initial capital stock. The Ramsey government chooses sequences for $ c_{1t}$, $ c_{2t}$, $ n_{t}$, and $ k_{t+1}$ to maximize (1) subject to (27) and the resource constraint

$\displaystyle c_{1t} + c_{2t} + k_{t+1} - (1-\delta)k_{t} + g_{t} = z_{t} f(k_{t},n_{t}).$ (28)

The Friedman Rule is again always optimal, so we can drop the constraint $ R_{t} \geq1$. We again focus attention on only the Ramsey first-order conditions for $ t>0$.

3.5  Quantitative Results

To our previous calibration, we now must specify parameters associated with the use of capital. We use the Cobb-Douglas production function $ f(k_{t}, n_{t}) = k_{t}^{\theta} n_{t}^{1-\theta}$, with capital share $ \theta=0.36$, and a quarterly depreciation rate of capital $ \delta=0.02$, consistent with the RBC literature.

3.5.1  Steady-State Policy

Our numerical results show that in steady-state, the zero-capital taxation result holds, recalling the results of Chari and Kehoe (1999) and others. Zero steady-state capital taxation holds both without and with habit persistence. This result has not previously been obtained in a Ramsey taxation model with money, however, because such models have abstracted from capital, and so is of some interest on its own. It is not surprising that this result should emerge, however, given the demonstration by Atkeson, Chari, and Kehoe (1999) that the zero-capital-taxation result is robust to many features of the environment. The steady-state labor income tax rate is $ \tau^{n} = 0.289$ in this model.

3.5.2  Optimal Inflation Persistence

We complete the central focus of our study with numerical evidence that capital formation generates inertia in inflation. Table 5 presents simulation-based moments using a first-order approximation to the policy function for the model with capital.6

First consider the economy without habit. The capital income tax rate is identically zero dynamically as well as in the steady-state, and the Friedman Rule is again always optimal. Inflation is on average close to the Friedman deflation, but its persistence is now quite high, 0.587, and its standard deviation, compared to the no-capital/no-habit economy in Table 3, is also high. The intuition behind these results is the same as for the economy without capital but with habit discussed in Section 2.6. With capital, the IMRS becomes more persistent for reasons similar to those discussed above -- specifically, with consumption-smoothing opportunities enhanced by the presence of capital, consumption responds more gradually to shocks. The equilibrium real interest rate needed to support this smoother path of consumption is also more persistent than without capital. The Fisher relation shows that the inflation rate also becomes more persistent. Seemingly more subtle to understand than in the model without capital, however, is that the volatility of the IMRS increases as well. Based on the quantitative evidence, the effect seems to be just as described in Section 2.6, namely that the intertemporal margin soaks up the volatility that the smoothing effect of capital on consumption squeezes out. Clearly, though, the quantitative effect of capital on inflation persistence is much stronger than the effect of habit, while the effect on inflation volatility is similar.

Perhaps the most empirically-relevant model, one with both capital and habits, delivers an even larger increase in both inflation persistence and volatility. The persistence of inflation in this model is above 0.7, putting it in the middle of the range of estimates of U.S. inflation persistence. In terms of inflation volatility, the effects of capital and habits are essentially additive.

Finally, note that in the economy with $ \alpha=0.5$ the capital income tax rate, while close to zero on average, is not identically zero. In fact, it fluctuates quite a bit over the business cycle. This result is reminiscent of Chari and Kehoe's (1999) finding in their model of optimal fiscal policy that with high risk-aversion the capital tax rate is slightly negative on average and displays a lot of volatility. One well-known property of habit formation from asset-pricing models is that it induces a form of state-contingent risk aversion.7 The effect of habit on the capital income tax in our model thus seems similar to the effect of high risk-aversion in their model.

Table 5:  First-order approximation. Economy with capital. π and R reported in annualized percentage points - Panel A: No habit (α = 0)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.288
0.065
0.947
0.967
-0.034
0.995
$ \tau^{k}$
0
0
--
--
--
--
$ \pi$
-3.76
7.40
0.587
-0.870
0.036
-0.884
$ R$
0
0
--
--
--
--
$ y$
1.33
0.042
0.927
1
0.180
0.986
$ c$
0.773
0.012
0.947
0.967
-0.034
0.995
$ i$
0.318
0.007
0.837
0.772
-0.003
0.756
$ k$
15.91
0.040
0.995
0.727
0.016
0.768
$ n$
0.329
0.004
0.953
-0.942
0.105
-0.983

Table 5:  First-order approximation. Economy with capital. π and R reported in annualized percentage points - Panel B: Habit (α = 0.5)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
$ \tau^{n}$
0.289
0.056
0.941
0.904
-0.044
0.997
$ \tau^{k}$
-0.011
0.145
0.722
-0.856
0.050
-0.938
$ \pi$
-3.84
16.90
0.721
-0.855
0.046
-0.935
$ R$
0
0
--
--
--
--
$ y$
1.33
0.022
0.924
1
0.364
0.931
$ c$
0.773
0.006
0.967
0.895
-0.041
0.990
$ i$
0.319
0.004
0.674
0.662
-0.032
0.684
$ k$
15.89
0.190
0.999
0.952
-0.074
0.877
$ n$
0.330
0.005
0.942
-0.879
0.094
-0.992

4  Deviations from the Friedman Rule

In this section, we show that the optimality of the Friedman Rule -- or, more generally, any time-invariant nominal interest rate -- does not drive our inflation persistence result. We extend our model to allow for monopolistic competition in product markets, still with flexible prices. Absent a 100 percent profit tax, a positive nominal interest rate indirectly taxes monopoly profits, which from the Ramsey planner's perspective is a lump-sum tax because monopoly power is in fixed supply. The steady-state level of the nominal interest rate is increasing in the degree of monopoly power, and the nominal interest rate thus fluctuates in the presence of shocks as the Ramsey planner finances government spending. These insights are developed by Schmitt-Grohe and Uribe (2004a). Fluctuations in the nominal interest rate make theoretically less clear how increased persistence in the real rate maps into increased persistence in inflation. We show quantitatively, however, that the intuition developed above continues to hold. We first briefly describe how we modify our model to include imperfect competition and then present numerical results.

4.1  Production: Final Goods and Intermediate Goods

We extend both our model without and with capital accumulation. The consumption (and investment) good is a final good and, as is common in New Keynesian models, is produced according to a Dixit-Stiglitz CES aggregator

$\displaystyle y_{t} = \left[ \int_{0}^{1} y(i)^{1/\varepsilon} di\right] ^{\varepsilon},$ (29)

where $ \varepsilon/(\varepsilon-1)$ is the elasticity of substitution between any two intermediate goods and $ \varepsilon$ is the gross markup of price over marginal cost. Here, $ i$ indexes the differentiated intermediate goods. Final goods producers require only the differentiated intermediate goods for production of final goods. Profit maximization by final goods producers gives rise to demand functions for each intermediate good $ i$

$\displaystyle y_{i,t} = \left[ \frac{P_{t}}{P_{i,t}}\right] ^{\frac {\varepsilon}{\varepsilon-1}} y_{t},$ (30)

where aggregate demand $ y_{t}$ and the aggregate price level $ P_{t}$ are both taken as given by each intermediate good producer, and $ P_{i,t}$ denotes the nominal price of intermediate good $ i$. Our analysis will be restricted to symmetric equilibria in which all intermediate goods producers make the same decisions, so that in equilibrium $ y_{t} = y_{i,t}$. Intermediate producers hire labor, or both labor and capital in the model with investment, as in Sections 2 and 3.

It is straightforward to show that, given maximization by firms, profits are given by

$\displaystyle pr_{t} = \left( 1-\frac{1}{\varepsilon} \right) y_{t}.$ (31)

This expression of profits in terms of allocations is needed to modify the Ramsey problem, which we present in the next section.

4.2  Consumers and the Ramsey Problem

Consumers receive the profits of the intermediate goods sector in lump-sum fashion, so the consumer budget constraint is modified slightly,

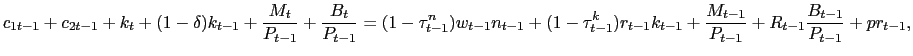
$\displaystyle {\footnotesize c_{1t-1} + c_{2t-1} + k_{t} + (1-\delta) k_{t-1} + \frac{M_{t}}{P_{t-1}} + \frac{B_{t}}{P_{t-1}} = (1-\tau^{n}_{t-1})w_{t-1} n_{t-1} + (1-\tau^{k}_{t-1}) r_{t-1} k_{t-1} + \frac{M_{t-1}}{P_{t-1}} + R_{t-1} \frac{B_{t-1}}{P_{t-1}} + pr_{t-1},}$ (32)

where $ pr_{t}$ denotes real profits. If capital accumulation is not a feature of the environment, the $ k_{t}$ terms of course disappear.

Profits are optimally redistributed by the Ramsey planner to consumers, which is reflected in the implementability constraint. The new implementability constraint is

$\displaystyle \lefteqn{\sum_{t=0}^{\infty} \beta^{t} \left[ \left( \frac{\partial u_{t}}{\partial c_{1t}} + \beta\frac{\partial u_{t+1}}{\partial c_{1t}} \right) c_{1t} + \left( \frac{\partial u_{t}}{\partial c_{2t}} + \beta\frac{\partial u_{t+1}}{\partial c_{2t}} \right) c_{2t} + \frac{\partial u_{t}}{\partial n_{t}} n_{t} - \left( \frac{\partial u_{t}}{\partial c_{2t}} + \beta\frac{\partial u_{t+1}}{\partial c_{2t}} \right) pr_{t} \right] = }$
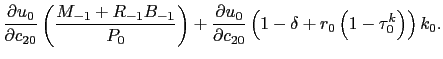
$\displaystyle \frac{\partial u_{0}}{\partial c_{20}} \left( \frac{M_{-1} + R_{-1} B_{-1}}{P_{0}} \right) + \frac{\partial u_{0}}{\partial c_{20}} \left( 1-\delta+ r_{0} \left( 1-\tau^{k}_{0} \right) \right) k_{0}.$

If the economy does not feature capital, the second term in the constant drops out. The resource constraint facing the Ramsey planner is either (16) or (28). Finally, in principle, we again need to impose the zero-lower-bound constraint (18). However, as we show in our quantitative results, for the degree of monopoly power and the size of the shocks we use, the zero-lower-bound was never reached during our simulations of the model without this constraint. So we once again ignore this constraint.

4.3  Quantitative Results

We now present quantitative evidence that capital and habits generate persistence in Ramsey inflation even when the nominal interest rate fluctuates. We describe first the steady-state policy and then the simulation-based results.

4.3.1  Steady-State Policy

Table 6 presents the optimal steady-state policy for various values of $ \varepsilon$. As in Schmitt-Grohe and Uribe (2004a), the nominal interest rate is increasing in the degree of market power. The reason for this is that in the absence of a profit tax, the nominal interest rate can be used to tax monopoly profits. This tax raises revenue in a non-distortionary way because market power represents a fixed factor of production. We do not take literally the prescription that the nominal interest rate should be used or is used in practice to tax monopoly profits. As Uhlig (2004) notes, governments surely are able to levy profit taxes, even at rates approaching confiscation. Rather, we consider the use of the nominal interest rate to tax profits simply a metaphor to move the economy away from the Friedman Rule. Only once we have moved away from the Friedman Rule -- that is, only once a zero nominal interest rate is not always optimal -- can we address the secondary issue of how policy interest rates respond to business cycle shocks in our model.

Table 6:  Optimal steady-state nominal interest rate and labor income tax rate for various degrees of monopoly power in the economy without capital. R reported in annualized percentage points. ε measures the gross markup.

Parameter
ε = 1
ε = 1.1
ε = 1.2
ε = 1.3
R
0
1.85
3.97
7.14
τn
0.198
0.221
0.237
0.256

The labor income tax rate is also increasing in the degree of market power, again as Schmitt-Grohe and Uribe (2004a) find. However, the reason for this is a little more subtle than they describe. In their study, the fraction of time spent working decreases as market power increases, so their claim is that both the decline in hours and the decline in wages (due to stronger market power) call for a higher tax rate to raise a given revenue. However, because we re-calibrate $ \zeta$ so that steady-state hours are constant across all parameterizations, we can conclude that the higher tax rate is required only because of the decline in wages. In either case, it is a shrinking labor tax base that calls for a higher labor tax rate. Finally, note that neither the labor tax rate nor the nominal interest rate varies with $ \alpha$ because habit persistence is modelled as internal rather than external. Introducing habits as external, as in Chugh (2004), would entail another market failure to which policy would respond.

Table 7:  Optimal steady-state nominal interest rate, labor income tax and capital income tax rate for various degrees of monopoly power in the economy with capital. R reported in annualized percentage points. ε measures the gross markup.

Parameter
ε = 1
ε = 1.1
ε = 1.2
ε = 1.3
R
0
3.85
10.31
18.70
τn
0.288
0.357
0.414
0.458
τk
0
-0.074
-0.124
-0.154

Table 7 shows the optimal steady-state nominal interest rate, labor income tax rate, and capital income tax rate for various values of $ \varepsilon$ in the model with capital. The intuition for the behavior of the nominal interest rate and the labor tax is as just discussed in the model without capital, so we focus on the capital income tax. With perfectly competitive product markets, the zero-capital taxation result holds, confirming the results of Chari and Kehoe (1999) and others. However, we find here that the capital income tax rate decreases with market power in product markets. The stronger market power is, the larger a capital subsidy the Ramsey government provides. The reason for this is straightforward: with market power, there is a tendency towards an under-accumulation of capital, so providing a subsidy boosts the capital stock. This result recalls that of Atkeson, Chari, and Kehoe (1999). They show that, as far as possible, an optimal policy should promote efficiency along the capital accumulation margin. With monopoly power and the resulting under-accumulation of capital, providing a capital subsidy achieves this goal. This result extends the steady-state fiscal policy implications of monopoly power studied by Schmitt-Grohe and Uribe (2004a) to a model with capital.

4.3.2  Optimal Inflation Persistence

Table 8 presents simulation results obtained using first-order approximations. The series of shocks used to generate these moments is the same as that used in the models of Sections 2 and 3. We fix the gross markup at $ \varepsilon=1.1$, consistent with empirical estimates. With this parameter choice and the volatility of the shocks driving our models, the zero-lower-bound on the nominal interest rate was never reached during our simulations of the Ramsey solution computed without the zero-lower-bound constraint.

The main result is that inflation is again persistent, despite fluctuations in the nominal interest rate. Indeed, the quantitative results are little changed compared to the models with perfectly-competitive product markets. Comparing these results with those obtained in the models in which the Friedman Rule was always optimal, we conclude that the intuition developed through the Fisher condition -- that increased persistence of the real rate leads to increased persistence of Ramsey inflation -- is robust.

Table 8:  Economies with imperfectly competitive markets. In all simulations, the gross markup is ε = 1.1. π and R reported in annualized percentage points - Panel A: No capital, no habit (α = 0)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
τn
0.221
0.046
0.934
0.602
-0.151
0.985
π
-2.09
4.20
-0.025
0.115
0.060
-0.216
R
1.85
0.208
0.928
-0.429
0.345
-0.927
y
0.330
0.011
0.914
1
0.683
0.730
c
0.270
0.004
0.934
0.622
-0.126
0.989
n
0.330
0.003
0.922
-0.279
0.491
-0.853

Table 8:  Economies with imperfectly competitive markets. In all simulations, the gross markup is ε = 1.1. π and R reported in annualized percentage points - Panel B: No capital, habit (α = 0.5)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
τn
0.221
0.050
0.928
0.281
-0.168
0.981
π
-1.95
7.36
0.222
-0.001
0.057
-0.270
R
1.85
0.165
0.943
-0.090
0.360
-0.919
y
0.330
0.009
0.901
1
0.887
0.456
c
0.270
0.002
0.973
0.363
-0.090
0.980
n
0.330
0.003
0.913
-0.014
0.426
-0.889

Table 8:  Economies with imperfectly competitive markets. In all simulations, the gross markup is ε = 1.1. π and R reported in annualized percentage points - Panel C: Capital, no habit (π = 0)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
τn
0.367
0.056
0.945
0.957
-0.041
0.995
τk
-0.087
0.059
0.560
-0.849
0.043
-0.871
π
0.699
7.30
0.611
-0.873
0.036
-0.895
R
4.65
0.634
0.947
-0.944
0.075
-0.991
y
1.31
0.036
0.926
1
0.218
0.978
c
0.769
0.010
0.945
0.960
-0.030
0.996
i
0.304
0.006
0.836
0.767
-0.003
0.755
k
15.19
0.031
0.995
0.719
0.016
0.769
n
0.329
0.004
0.949
-0.933
0.105
-0.986

Table 8:  Economies with imperfectly competitive markets. In all simulations, the gross markup is ε = 1.1. π and R reported in annualized percentage points - Panel D: Capital, habit (π = 0.5)

Variable
Mean
Std. Dev.
Auto corr.
Corr(x,y)
Corr(x,g)
Corr(x,z)
τn
0.367
0.064
0.940
0.859
-0.053
0.997
τk
-0.093
0.134
0.708
-0.816
0.039
-0.933
π
1.41
15.50
0.717
-0.819
0.036
-0.935
R
4.62
0.479
0.952
-0.838
0.086
-0.992
y
1.31
0.018
0.923
1
0.446
0.895
c
0.770
0.005
0.965
0.863
-0.030
0.992
i
0.304
0.003
0.619
0.594
-0.032
0.650
k
15.21
0.014
0.993
0.690
-0.010
0.814
n
0.330
0.005
0.940
-0.835
0.097
-0.992

5  Discussion

Table 9 summarizes the standard deviation and autocorrelation of inflation in the models in which the Friedman Rule is optimal, for the baseline parameters ρg = 0.90, ρz = 0.95, and σ = 0.62. Starting from the baseline model with neither capital nor habits, introducing either state variable roughly doubles inflation volatility while dramatically increasing inflation persistence, the latter effect being stronger in the presence of capital accumulation. With both capital and habits present, the effects of each on both volatility and persistence are essentially additive.

Table 9:  Persistence and volatility of inflation under the Ramsey policy in economies in which the Friedman Rule is optimal, with ρg = 0.90, ρz = 0.95, and σ = 0.62.

Economy
Mean
Std. Dev.
Auto. corr.
No capital, no habit
-3.86
4.36
-0.027
No capital, habit
-3.70
7.78
0.214
Capital, no habit
-3.76
7.40
0.587
Capital, habit
-3.84
16.90
0.722

In addition to the Fisher effect, another possibly helpful way to understand our results is to recognize that the state vectors in our models are larger than in standard flexible-price Ramsey models. Optimal tax rates may thus be expected to acquire more persistence due to the increased history-dependence in the economy. This conclusion does not immediately follow, but our computed decision rules suggest this intuition goes through. Table 10 presents the numerical coefficients we find for inflation as a function of the state variables in the economy without capital. The time-$ t$ state of the economy in general in that model is given by $ [c_{1t-1}, c_{2t-1}, c_{1t-2}, c_{2t-2}, z_{t}, g_{t}]$. The first lags of consumption appear in the state because of the Fisher equation, which we use to track the evolution of inflation, and the second lags appear when there is habit persistence ($ \alpha>0$). With habit, the coefficient on the first lag of consumption is much larger than without habit, and the coefficient on the second lag of consumption rises from zero.

This numerical evidence of course does not prove the link between persistence in policy and the size of the state vector, but we think this may be a promising way to consider our result, especially given recent studies on optimal fiscal policy with incomplete markets. Aiyagari et al (2002), Angeletos (2002), and Shin (2003) find that under different forms of market incompleteness, tax rates become highly persistent compared to the standard complete-markets Ramsey framework. A common technical aspect of these models is that the state vector expands to include lagged Lagrange multipliers that capture the effects of market incompleteness. At a technical level, then, these models also seemingly rely on increased persistence of the state to generate increased persistence of tax rates. We think this may be an interesting analogy to explore further. We point out, however, that it is not the introduction of a persistent state variable per se that generates persistence in inflation. Indeed, in the model with neither capital nor habits, persistent state variables are present -- the exogenous and persistent technology and government spending shocks -- but inflation is not persistent. Thus, in our model it is the introduction of states that affect the desire and ability of consumers to smooth consumption over time that is important, and these preferences and opportunities are reflected in the real interest rate. Persistent exogenous states do not affect smoothing preferences and opportunities.

Table 10:  Computed linear policy function for inflation in the model without capital for π = 0 and π = 0.50.

π
c1t-1
c2t-1
c1t-2
c2t-2
zt
gt
0
5.78
7.47
0
0
-2.71
0.58
0.50
29.17
30.86
7.24
7.24
-4.72
1.01

We emphasize that our results obtain in flexible-price environments. If nominal rigidities were introduced, the Ramsey government would balance the insurance value of inflation against the resource misallocation of nonzero inflation. In a recent strand of the Ramsey literature, Siu (2004) and Schmitt-Grohe and Uribe (2004b) show that with sticky prices this tension is resolved overwhelmingly in favor of price stability. However, these studies predict little or no inflation persistence.8, 9 Continuing to study the consequences for optimal policy of sticky prices, and of sticky prices together with incomplete markets as Angeletos (2004) suggests, seems to be an important line of research.

Finally, we acknowledge that we have ignored the vast recent New Keynesian literature on inflation persistence. This stems partly from the fact that we have not needed any nominal rigidities to obtain our result, and partly because the New Keynesian literature has evolved largely in isolation from the public finance optimal taxation literature. Our work falls squarely in the latter tradition. The studies by Siu (2004) and Schmitt-Grohe and Uribe (2004b) question the high volatility of inflation predicted by flexible-price Ramsey models, while not taking on the lack of inflation persistence that such models also predict. Our study complements theirs by questioning the low persistence of inflation in Ramsey models without taking on the volatility issue. As we mention in the above footnote, however, we have begun extending our model to incorporate nominal rigidities. Our interest in doing so is to quantify the effects on both inflation persistence and inflation volatility of nominal rigidities coupled with endogenous states. In particular, the goal is to determine whether both the effects on volatility that Siu (2004) and Schmitt-Grohe and Uribe (2004b) identify and the effects on persistence that we identify can coexist. We conjecture that they can.

6  Conclusion

The Ramsey planner respects equilibrium conditions when choosing allocations. These conditions encode, among other features of equilibrium, the desire and ability to smooth consumption over time. Altering this desire or ability, as we do in this paper through habit persistence and capital accumulation, renders the real interest rate persistent. Through the Fisher relation, which is an equilibrium condition the Ramsey planner respects, the optimal inflation rate is persistent. This result stands in contrast to the predictions of the baseline Ramsey model of Chari, Christiano, and Kehoe (1991) as well as the predictions of recent extensions to environments with nominal rigidities. An important point that our results suggest is that Ramsey models of monetary policy that neglect capital formation may have very different predictions about the nature of policy than models that include capital.


Appendix A  Approximation Method

Models with both capital accumulation and habit persistence lead to a greater degree of endogenous persistence than models with either alone. The general method of Schmitt-Grohe and Uribe (2004c) needs to be extended to accommodate such a model. While their general form can accommodate an arbitrary number of lags of variables, it cannot accommodate forward-looking expectations more than one period in the future. With both capital and habits, the Ramsey first-order-conditions feature such further leads.

We extend Schmitt-Grohe and Uribe (2004c) in a straightforward way. Our canonical model is written as

$\displaystyle E_{t} f(y_{t+2}, y_{t+1}, y_{t}, x_{t+2}, x_{t+1}, x_{t}) = 0.$ (33)

The decision rules are given as in Schmitt-Grohe and Uribe (2004c),

$\displaystyle y_{t} = g(x_{t}, \sigma)$ (34)

$\displaystyle x_{t+1} = h(x_{t}, \sigma) + \eta\sigma\epsilon_{t+1}.$ (35)

Define

$\displaystyle {\small F(x,\sigma) \equiv f[ g(h(h(x,\sigma)+\eta\sigma\epsilon^{\prime}) + \eta\sigma\epsilon^{\prime\prime}, \sigma), g(h(x,\sigma)+ \eta\sigma \epsilon^{\prime}, \sigma), g(x,\sigma), h(h(x,\sigma) + \eta\sigma \epsilon^{\prime}) + \eta\sigma\epsilon^{\prime\prime}, h(x,\sigma) + \eta\sigma\epsilon^{\prime}, x] = 0.}$ (36)

We can then can identify the first-order approximations $ g_{x}$ and $ h_{x}$ from the condition

$\displaystyle F_{x}(\bar{x}, 0) = f_{y^{\prime\prime}}g_{x} h_{x} h_{x} + f_{y^{\prime}}g_{x} h_{x} + f_{y} g_{x} + f_{x^{\prime\prime}} h_{x} h_{x} + f_{x^{\prime}} h_{x} + f_{x} = 0,$ (37)

where $ f_{y^{\prime\prime}} g_{x} h_{x} h_{x}$ and $ f_{x^{\prime\prime}} h_{x} h_{x}$ are the novel terms compared with Schmitt-Grohe and Uribe (2004c). Each term on the right-hand-side of (37) is evaluated at the non-stochastic steady-state given by $ (\bar{x}, 0)$.

Constructing the second-order approximation is more tedious but also a straightforward extension of Schmitt-Grohe and Uribe (2004c).


References

Aiyagari, S. Rao, Albert Marcet, Thomas J, Sargent, and Juha Seppala. 2002. "Optimal Taxation without State-Contingent Debt." Journal of Political Economy. Vol. 110, pp. 1220-1254.

Angeletos, George-Marios. 2002. "Fiscal Policy with Noncontingent Debt." Quarterly Journal of Economics. Vol. 117, pp. 1105-1131.

Angeletos, George-Marios. 2004. "Comment on Beningo and Woodford: Optimal Monetary and Fiscal Policy." NBER Macroeconomics Annual 2003.

Aruoba, S. Boragan, Jesus Fernandez-Villaverde, and Juan F. Rubio-Ramirez. 2003. "Comparing Solution Methods for Dynamic Equilibrium Economies." University of Pennsylvania.

Atkeson, Andrew, V. V. Chari, and Patrick J. Kehoe. 1999. "Taxing Capital Income: A Bad Idea." Federal Reserve Bank of Minneapolis Quarterly Review. Vol. 23, pp. 3-17.

Buera, Francisco and Juan Pablo Nicolini. 2004. "Optimal Maturity of Government Debt without State Contingent Bonds." Journal of Monetary Economics. Vol. 51, pp. 531-554.

Calvo, Guillermo A. and Pablo E. Guidotti. 1993. "On the Flexibility of Monetary Policy: The Case of the Optimal Inflation Tax." Review of Economic Studies. Vol. 60, pp. 667-687.

Campbell, John Y. and John H. Cochrane. 1999. "By Force of Habit: A Consumption-Based Explanation of Aggregate Stock Market Behavior." Journal of Political Economy. Vol. 107, pp. 205-251.

Chari, V.V., Lawrence Christiano, and Patrick Kehoe. 1991. "Optimal Monetary and Fiscal Policy: Some Recent Results." Journal of Money, Credit, and Banking. Vol. 23, pp. 519-539.

Chari V. V., and Patrick J. Kehoe. 1999. "Optimal Fiscal and Monetary Policy." Handbook of Macroeconomics. John B. Taylor and Michael Woodford, Vol. 1C. Elsevier.

Chen, Xiaohong and Sydney Ludvigson. 2004. "Land of Addicts? An Empirical Investigation of Habit-Based Asset Pricing Models." New York University.

Chugh, Sanjay K. 2004. "Does Monetary Policy Keep Up with the Joneses? Optimal Interest-Rate Smoothing with Consumption Externalities." International Finance Discussion Paper no. 812, Board of Governors of the Federal Reserve System.

Mankiw, N. Gregory. 1987. "The Optimal Collection of Seignorage." Journal of Monetary Economics. Vol. 20, pp. 327-341.

Phelps, Edmund S. 1973. "Inflation in the Theory of Public Finance." Swedish Journal of Economics. Vol. 75, pp. 67-82.

Schmitt-Grohe, Stephanie and Martin Uribe. 2004a. "Optimal Fiscal and Monetary Policy Under Imperfect Competition." Journal of Macroeconomics. Vol. 26, pp. 183-209.

Schmitt-Grohe, Stephanie and Martin Uribe. 2004b. "Optimal Fiscal and Monetary Policy Under Sticky Prices." Journal of Economic Theory. Vol. 114, pp. 198-230.

Schmitt-Grohe, Stephanie and Martin Uribe. 2004c. "Solving Dynamic General Equilibrium Models Using a Second-Order Approximation to the Policy Function." Journal of Economic Dynamics and Control. Vol. 28, pp. 755-775.

Shin, Yongseok. 2003. "Optimal Fiscal Policy with Incomplete Markets." Stanford University.

Siu, Henry E. 2004. "Optimal Fiscal and Monetary Policy with Sticky Prices." Journal of Monetary Economics. Vol. 51, pp. 576-607.

Uhlig, Harald. 2004. "Comments on Optimal Fiscal and Monetary Policy Under Imperfect Competition." Journal of Macroeconomics. Vol. 26, pp. 211-217.

Footnotes

*  E-mail address: [email protected]. I thank Boragan Aruoba, David Bowman, Chris Erceg, Luca Guerrieri, Dale Henderson, Jinill Kim, Sylvain Leduc, Robert Martin, John Rogers, and Luis-Felipe Zanna for helpful conversations. The views expressed here are solely those of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System. Return to text

1.  Recent papers on Ramsey taxation with incomplete markets or non-state-contingent debt include Aiyagari et al (2002), Angeletos (2002), Shin (2003), and Buera and Nicolini (2004). A feature their models share is that the state vector expands to include lagged multiplier, which capture the nature of market incompleteness. Return to text

2.  See Campbell and Cochrane (1999) for why the additive specification is especially important for resolving the equity premium puzzle. Chen and Ludvigson (2004) argue, however, that more complicated specifications of habit processes fit data better than the simple specifications usually used in macro models. Return to text

3.  We do not set $ 1-\sigma$ exactly equal to zero or one for the "cashless" and "cashful" economies, respectively, because our numerical algorithm cannot handle the limiting cases. Return to text

4.  New Keynesian models are typically specified as linear-quadratic programming problems, so there may be some aspect of this setup that makes them vulnerable to use of first-order approximations. This issue is beyond the scope of this paper but deserves further study. Return to text

5.  The intuition comes through most clearly with a constant nominal interest rate. In Section 4, we extend our model to allow for fluctuations in the nominal interest rate and find that our intuition continues to hold. Return to text

6.   We also computed a second-order approximation for the model with capital but without habit and found very similar results. The second-order approximation for the model with both capital and habit is computationally much more demanding, and we were unable to obtain the second-order approximation for this model. Return to text

7.   This is the property of habit that allows it to explain time-varying risk premia for equity. Return to text

8.   Siu (2004) finds moderate persistence and Schmitt-Grohe and Uribe (2004b) find zero persistence. The two papers model nominal rigidities in different ways, suggesting that the assumed structure of sticky prices may be important for understanding, among other things, inflation dynamics. Return to text

9.   In ongoing work, we have begun studying the role of sticky prices coupled with capital and/or habit in predicting both low inflation volatility and high inflation persistence. We model sticky prices using Taylor staggered contracts, an approach different from both Siu (2004) and Schmitt-Grohe and Uribe (2004b), and find that the price-staggering alone is enough to generate strong inflation persistence under the Ramsey policy. Furthermore, to return to a point mentioned in Section 2.6.1, the importance of money demand -- corresponding to the parameter $ 1-\sigma$ in our model -- does influence inflation dynamics with sticky prices. The less important is money demand, the less volatile is the inflation rate because relative price distortions dominate. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: August 20, 2008