
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 838, August 2005 --- Screen Reader
Version*
General-to-Specific Modeling: An Overview and Selected Bibliography
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper discusses the econometric methodology of general-to-specific modeling, in which the modeler simplifies an initially general model that adequately characterizes the empirical evidence within his or her theoretical framework. Central aspects of this approach include the theory of reduction, dynamic specification, model selection procedures, model selection criteria, model comparison, encompassing, computer automation, and empirical implementation. This paper thus reviews the theory of reduction, summarizes the approach of general-to-specific modeling, and discusses the econometrics of model selection, noting that general-to-specific modeling is the practical embodiment of reduction. This paper then summarizes fifty-seven articles key to the development of general-to-specific modeling.
Keywords: cointegration, conditional models, data mining, diagnostic testing, dynamic specification, econometric methodology, encompassing, equilibrium correction models, error correction models, exogeneity, general-to-specific modeling, model comparison, model design, model evaluation, model selection, non-nested hypotheses, PcGets, PcGive, reduction, specific-to-general modeling
JEL classification: C1, C5
1 Motivation and Overview
This paper focuses on a central method for selecting useful empirical models, called general-to-specific modeling. In this method, the modeler simplifies an initially general model that adequately characterizes the empirical evidence within his or her theoretical framework. While the methodological, statistical, and empirical foundations for general-to-specific modeling have been laid down over the last several decades, a burst of activity has occurred in the last half-dozen years, stimulated in fair part by Hoover and Perez's (1999a) development and analysis of a computer algorithm for general-to-specific modeling. The papers discussed herein detail how the subject has advanced to its present stage of success and convey the promise of these developments for future empirical research. The remainder of this overview motivates the interest in general-to-specific modeling and summarizes the structure of the subsequent sections (Sections 2-5).
Economists have long sought to develop quantitative models of economic behavior by blending economic theory with data evidence. The task has proved an arduous one because of the nature of the economy modeled, the economic theory, and the data evidence. The economy is a complicated, dynamic, nonlinear, simultaneous, high-dimensional, and evolving entity; social systems alter over time; laws change; and technological innovations occur. Thus, the target is not only a moving one; it behaves in a distinctly nonstationary manner, both evolving over time and being subject to sudden and unanticipated shifts. Economic theories are highly abstract and simplified; and they also change over time, with conflicting rival explanations sometimes coexisting. The data evidence is tarnished: economic magnitudes are inaccurately measured and subject to substantive revisions, and many important variables are not even observable. The data themselves are often time series where samples are short, highly aggregated, heterogeneous, time-dependent, and inter-dependent. Econometric modeling of economic time series has nevertheless strived to discover sustainable and interpretable relationships between observed economic variables. This paper focuses on general-to-specific modeling, in which the modeler simplifies an initially general model that adequately characterizes the empirical evidence within his or her theoretical framework. This method has proved useful in practice for selecting empirical economic models.
The difficulties of empirical modeling are well reflected in the slowness of empirical progress, providing plenty of ammunition for critics. However, part of the problem may be internal to the discipline, deriving from inappropriate modeling methods. The "conventional" approach insists on a complete theoretical model of the phenomena of interest prior to data analysis, leaving the empirical evidence as little more than quantitative clothing. Unfortunately, the complexity and nonstationarity of economies makes it improbable than anyone--however brilliant--could deduce a priori the multitude of quantitative equations characterizing the behavior of millions of disparate and competing agents. Without a radical change in the discipline's methodology, empirical progress seems doomed to remain slow.
The situation is not as bleak as just described, for two reasons. First, the accumulation of knowledge is progressive, implying that one does not need to know all the answers at the start. Otherwise, no science could have advanced. Although the best empirical model at any given time may be supplanted later, it can provide a springboard for further discovery. Data-based model selection need not raise serious concerns: this implication is established below and is demonstrated by the actual behavior of model selection algorithms.
Second, inconsistencies between the implications of any conjectured model and the observed data are often easy to detect. The ease of model rejection worries some economists, yet it is also a powerful advantage by helping sort out which models are empirically adequate and which are not. Constructive progress may still be difficult because "we don't know what we don't know, and so we cannot know how best to find out what we don't know". The dichotomy between model destruction and model construction is an old one in the philosophy of science. While critical evaluation of empirical evidence is a destructive use of econometrics, it can also establish a legitimate basis for empirical models.
To undertake empirical modeling, one must begin by assuming a probability structure for the data, which is tantamount to conjecturing the data generating process. Because the economic mechanism is itself unknown, the relevant probability structure is also unknown, so one must proceed iteratively: conjecture the data generation process (DGP), develop the associated probability theory, use that theory for modeling empirical evidence, and revise the starting point when the results do not match consistently. The development of econometric theory highlights this iterative progression: from stationarity assumptions, through integrated-cointegrated systems, to general nonstationary mixing processes, as empirical evidence revealed the inadequacy of each earlier step. Further developments will undoubtedly occur, leading to a still more useful foundation for empirical modeling. See Hendry (1995a) for an extensive treatment of progressive research strategies.
Having postulated a reasonable probability basis for the DGP, including the procedures used for data measurement and its collection, the next issue concerns what classes of model might be useful. The theory of reduction (discussed in Section 2) explains how empirical models arise and what their status is, noting that they are not facsimiles of the DGP. Specifically, empirical models describe the behavior of a relatively small set of variables--often from one to several hundred--and never the many millions of distinct variables present in most economies.
A key concept here is that of the local DGP, which is the probability mechanism in the space of those variables under analysis. The theory of reduction shows how the local DGP arises as a simplification of a vastly more general DGP involving millions of variables. The usefulness of a given local DGP depends on it capturing sustainable links, which in turn depends partly on the theoretical framework and partly on data accuracy. An econometric model cannot do better than capture the salient characteristics of its corresponding local DGP. The extent to which the model does capture those characteristics depends both on its specification at least embedding the local DGP and on the goodness of its selection.
There are thus two distinct conceptual steps in modeling, albeit ones closely related in practice. First, specify a useful information set for a "well-behaved" local DGP. Second, select a "good" empirical model of that local DGP.
A viable methodology for empirical modeling is an integral component of achieving the second step. Despite the controversy surrounding every aspect of econometric methodology, the "LSE" (or London School of Economics) approach has emerged as a leading methodology for empirical modeling; see Hendry (1993) for an overview. One of the LSE approach's main tenets is general-to-specific modeling, sometimes abbreviated as Gets. In general-to-specific modeling, empirical analysis starts with a general statistical model that captures the essential characteristics of the underlying dataset, i.e., that general model is congruent. Then, that general model is reduced in complexity by eliminating statistically insignificant variables, checking the validity of the reductions at every stage to ensure congruence of the finally selected model.
The papers discussed below articulate many reasons for adopting a general-to-specific approach. First amongst these reasons is that general-to-specific modeling implements the theory of reduction in an empirical context. Section 2 summarizes the theory of reduction, and Section 3 discusses general-to-specific modeling as the empirical analogue of reduction.
General-to-specific modeling also has excellent characteristics for model selection, as documented in Monte Carlo studies of automatic general-to-specific modeling algorithms. Hoover and Perez (1999a) were the first to evaluate the performance of general-to-specific modeling as a general approach to econometric model building. To analyze the general-to-specific approach systematically, Hoover and Perez mechanized the decisions in general-to-specific modeling by coding them in a computer algorithm. In doing so, Hoover and Perez also made important advances in practical modeling.
To appreciate Hoover and Perez's contributions to general-to-specific modeling, consider the most basic steps that such an algorithm follows.
- Ascertain that the general statistical model is congruent.
- Eliminate a variable (or variables) that satisfies the
selection (i.e., simplification) criteria.
- Check that the simplified model remains congruent.
- Continue steps 2 and 3 until none of the remaining variables
can be eliminated.
Pagan (1987) and other critics have argued that the outcome of general-to-specific modeling may depend on the simplification path chosen--that is, on the order in which variables are eliminated and on the data transformations adopted--and so the selected model might vary with the investigator. Many reduction paths certainly could be considered from an initial general model.
Hoover and Perez (1999a) turned this potential drawback into a virtue by exploring many feasible paths and seeing which models result. When searches do lead to different model selections, encompassing tests can be used to discriminate between these models, with only the surviving (possibly non-nested) specifications retained. If multiple models are found that are both congruent and encompassing, a new general model can be formed from their union, and the simplification process is then re-applied. If that union model re-occurs, a final selection among the competing models can be made by using (say) information criteria. Otherwise, a unique, congruent, encompassing reduction has been located.
Hoover and Perez (1999a) re-analyzed the Monte Carlo experiments in Lovell (1983) and found that their (Hoover and Perez's) general-to-specific algorithm performed much better than any method investigated by Lovell. Hendry and Krolzig (1999) demonstrated improvements on Hoover and Perez's general-to-specific algorithm, and Hoover and Perez (2004) showed how their algorithm could be successfully modified for analyzing cross-section data; see also Hendry and Krolzig (2004)
Automating the general-to-specific approach throws light on several methodological issues and prompts many new ideas, several of which are discussed in Section 3.1. Three common concerns with the general-to-specific approach are repeated testing, recursive procedures, and selection of variables.
First, critics such as Ed Leamer have worried about the interpretation of mis-specification tests that are repeatedly applied during simplification; see Hendry, Leamer, and Poirier (1990). Automation of the general-to-specific approach reveals two distinct roles for mis-specification tests: their initial application to test the congruence of the general model, and their subsequent use to guard against invalid reductions during simplification. The mis-specification tests are thus applied only once as statistical mis-specification tests--to the general model--so no doubts of interpretation arise. Their subsequent role in diagnostic checking during reduction does not alter their statistical properties as applied to the general model.
Second, recursive procedures such as subsample estimation play two roles. Recursive procedures help investigate parameter constancy, which is essential for congruence and for any practical use of the resulting model. Recursive procedures also assist in checking that estimated effects are significant over subsamples, and not just over the whole sample. Specifically, if a variable is only occasionally significant over various subsamples, that occasional significance may reflect chance rather than substance, especially if the variable's significance does not increase as the sample size grows. Eliminating such occasionally significant variables may be useful for parsimony.
Third, model selection procedures that use diagnostic testing and are based on multiple criteria have eluded most attempts at theoretical analysis. However, computer implementation of the model selection process has allowed evaluation of such strategies by Monte Carlo simulation. Krolzig and Hendry (2001) and Hendry and Krolzig (2003) present the results of many Monte Carlo experiments to investigate whether the model selection process works well or fails badly for time series processes. The implications for the calibration of their econometrics computer program PcGets are also noted below; see Hendry and Krolzig (2001).
The remainder of this paper is organized into four sections. Section 2 reviews the theory of reduction as a major background component to general-to-specific modeling. Section 3 reviews the basis for general-to-specific modeling and discusses the econometrics of model selection, noting that general-to-specific modeling is the practical embodiment of reduction. Section 4 then summarizes, paper by paper, fifty-seven papers key to the development of general-to-specific modeling. These papers are reprinted in Campos, Ericsson, and Hendry (2005) and are grouped into nine parts across the two volumes of Campos, Ericsson, and Hendry (2005): see the Appendix below for a listing of these papers. This nine-part division is also paralleled by the subsections in Section 4, as follows.
Volume I
Part I. Introduction to the methodology (Section 4.1);
Part II. Theory of reduction (Section 4.2);
Part III. Dynamic specification (Section 4.3);
Part IV. Model selection procedures (Section 4.4);
Volume II
Part I. Model selection criteria (Section 4.5);
Part II. Model comparison (Section 4.6);
Part III. Encompassing (Section 4.7);
Part IV. Computer automation (Section 4.8); and
Part V. Empirical applications (Section 4.9).
Section 5 concludes.
For ease of reference, when an article reprinted in Campos, Ericsson, and Hendry (2005) is initially cited in Sections 2-3, text in square brackets immediately following the citation indicates the volume and chapter where the reprint appears: for instance, "Hoover and Perez (1999a) [Volume II: Chapter 22]". Thereafter--except in Section 4's actual summary of the article--citation to an article reprinted in Campos, Ericsson, and Hendry (2005) is indicated by a trailing asterisk, as in "Hoover and Perez (1999a)*". On a separate issue, the mathematical notation in Section 2 differs somewhat from that used in Section 3, owing to the different strands of literature on which those two sections are based. The mathematical notation in Section 4 generally follows the notation in the article being described.
2 Theory of Reduction
This section examines the relationship between the data generation process and an empirical model. Section 2.1 defines what an empirical model is, Section 2.2 defines what the data generation process is, and Section 2.3 shows how an empirical model is obtained as a reduction or simplification of the data generation process. Sections 2.4, 2.5, and 2.6 thus examine how models can be compared, how to measure the information losses associated with a model, and what information is used in evaluating models. Section 2.7 turns to explicit model design, which recognizes and utilizes the relationship between empirical models and the data generation process.
The exposition in this section draws on Hendry (1995a). Hendry (1987) [Volume I: Chapter 8] presents a non-technical exposition of the theory of reduction. Important contributions to its development include Florens and Mouchart (1980, 1985), Hendry and Richard (1982) [Volume I: Chapter 9], Engle, Hendry, and Richard (1983) [Volume I: Chapter 13], and Florens, Mouchart, and Rolin (1990).
Before proceeding to the theory of reduction, a few comments are in order. First, data are generated from an unknown high-dimensional probability distribution (the DGP), which is indexed by a set of parameters. Some functions of those parameters are of interest to an investigator. A central aim of modeling is to determine the numerical values of those parameters, which can be used for testing theories, forecasting, conducting economic policy, and learning about the economy.
Second, the DGP itself involves far too many parameters to estimate on available data, so reductions of the DGP are essential to produce an operational model. The key feature of every reduction is whether or not it involves a loss of information about the parameters of interest. Such a loss may be total (as when the parameters of interest no longer enter the model) or partial (as when some parameters can be gleaned but others not, or when some cease to be constant), or it may just lower the statistical efficiency with which the parameters may be estimated. Logically, reductions lead from the original DGP--which involves the universe of variables--to the distribution of a small subset thereof--which is the local DGP.
Third, an empirical model of that subset of variables then approximates their local DGP. Estimation of the parameters of that model comes last, logically speaking. That model's estimation has been extensively analyzed in econometrics for many postulated types of model. A variety of approaches are still extant, such as "classical" and "Bayesian", and with varying degrees of emphasis on least squares, instrumental variables, maximum likelihood, method of moments, and so on. Many of these approaches are minor variants on the basic likelihood score equations; see Hendry (1976).
Fourth, an empirical model may include variables that do not actually enter the local DGP, in which case a more parsimonious representation can be selected from the sample evidence. Such a data-based simplification is a major focus of this paper. As noted in the previous section, model selection procedures have been debated extensively, with little professional accord. The discussion below shows how the general-to-specific approach is the analogue in modeling of reduction in theory. Critiques of the general-to-specific approach and the practical arguments in its favor are also considered.
2.1 Theory Models and Empirical Models
Both economic theory and data are important in empirical economic modeling, so this subsection compares theory models and empirical models. Theory models are freely created, whereas empirical models are derived and not autonomous. That distinction in a model's status has direct implications for the roles that sequential reduction and mis-specification testing play in empirical modeling. At a more general level, theory models play a key part in interpreting economic data, but theory models in themselves are not sufficient for doing so in a reliable fashion. To illustrate the distinction between theory models and empirical models, consider a standard linear model that is subsequently estimated by least squares.
From the outset, it is important to distinguish between the
economic theory-model and the empirical model that the theory model
serves to interpret. A theory model is freely created by the human
imagination. For instance, economic theory might specify a
relationship between two variables
![]() and
and ![]() :
:
| yt = b´zt + et | (1) |
| [output] [transformed input] [perturbation] |
where the coefficient vector
![]() is the partial derivative
is the partial derivative
![]() ,
the variables
,
the variables
![]() and
and
![]() (in sans serif font) denote the
economic theoretic variables at time
(in sans serif font) denote the
economic theoretic variables at time ![]() , and the
error
, and the
error
![]() is an independent perturbation
at time
is an independent perturbation
at time ![]() . The theory model is defined by how it
is constructed. In equation (1),
. The theory model is defined by how it
is constructed. In equation (1),
![]() is constructed from
is constructed from
![]() and the error
and the error
![]() , and the relationship between
, and the relationship between
![]() and
and
![]() can be treated as if it were a
causal mechanism.
can be treated as if it were a
causal mechanism.
A corresponding empirical model is anything but freely created, with the properties of the empirical model being determined by reductions of the DGP. The mapping between variables and disturbances also differs. To demonstrate, consider the following empirical model:
| yt = b´zt + et | (2) |
| [observed variable [explanation] [remainder] of interest] |
where ![]() and
and ![]() (in italic) are
economic data at time
(in italic) are
economic data at time ![]() , the conditional
expectation
, the conditional
expectation
![]() is zero (by
assumption), and
is zero (by
assumption), and
![]() is the expectations
operator. The orthogonality assumption that
is the expectations
operator. The orthogonality assumption that
![]() defines the
parameter vector
defines the
parameter vector ![]() from equation (2) in terms of the
data's properties:
from equation (2) in terms of the
data's properties:
| (3) |
The error ![]() in
equation (2)
is also defined as a function of the data:
in
equation (2)
is also defined as a function of the data:
| (4) |
In particular, equation (4) shows
explicitly that the error ![]() contains
everything in
contains
everything in ![]() that is not modeled by
that is not modeled by ![]() . From a slightly different perspective,
. From a slightly different perspective, ![]() can always be decomposed into two components:
can always be decomposed into two components:
![]() (the explained part) and
(the explained part) and
![]() (the unexplained part). Such a
partition is feasible, even when
(the unexplained part). Such a
partition is feasible, even when ![]() does not depend
on
does not depend
on ![]() in any way and so is not caused by
in any way and so is not caused by
![]() .
.
From equations (3)
and (4), the
properties of ![]() and
and ![]() vary with the
choice of
vary with the
choice of ![]() and the orthogonality assumption.
Equivalently, the properties of
and the orthogonality assumption.
Equivalently, the properties of ![]() and
and ![]() vary with the choice of variables ignored and with the
conditioning assumption. The coefficients and errors of empirical
models are thus derived and not autonomous.
vary with the choice of variables ignored and with the
conditioning assumption. The coefficients and errors of empirical
models are thus derived and not autonomous.
As an immediate implication, empirical models can be designed
through the selection of ![]() : changing
: changing ![]() redesigns the error
redesigns the error ![]() and the
coefficients
and the
coefficients ![]() . Consequently, design
criteria can be analyzed. For example, what makes one design better
than another? Sections 2.5-2.7 address this
issue, leading to the notion of a congruent model--one that
matches the data evidence on all the measured attributes. Any given
sample may have more than one congruent model. That leads to the
requirement of a dominant congruent model, which entails an
ordering over congruent models. Indeed, successive congruent models
of a given phenomenon should be able to explain or encompass
previous models, thereby achieving progress in modeling.
. Consequently, design
criteria can be analyzed. For example, what makes one design better
than another? Sections 2.5-2.7 address this
issue, leading to the notion of a congruent model--one that
matches the data evidence on all the measured attributes. Any given
sample may have more than one congruent model. That leads to the
requirement of a dominant congruent model, which entails an
ordering over congruent models. Indeed, successive congruent models
of a given phenomenon should be able to explain or encompass
previous models, thereby achieving progress in modeling.
2.2 The Data Generation Process
This subsection formally (and briefly) discusses the statistical basis for the data generation process.
Let
![]() denote a
stochastic process for a vector
denote a
stochastic process for a vector
![]() of random variables at
time
of random variables at
time ![]() that is defined on the probability
space
that is defined on the probability
space
![]() , where
, where
![]() is the sample space,
is the sample space,
![]() is the event space (sigma field),
and
is the event space (sigma field),
and
![]() is the probability measure. Let
is the probability measure. Let
![]() denote a vector of parameters,
which are entities that do not depend on
denote a vector of parameters,
which are entities that do not depend on
![]() .
.
Consider the full sample
![]() , which is for
, which is for
![]() where the notation
where the notation
![]() means
means
![]() for
for
![]() ; and denote the initial (pre-sample)
conditions by
; and denote the initial (pre-sample)
conditions by
![]() . The distribution function
. The distribution function
![]() of
of
![]() , conditional on
, conditional on
![]() , is denoted by
, is denoted by
![]() , which is often called the Haavelmo distribution; see
Spanos (1989) [Volume I: Chapter 4]. To make explicit
the observed phenomenon of parameter nonconstancy,
, which is often called the Haavelmo distribution; see
Spanos (1989) [Volume I: Chapter 4]. To make explicit
the observed phenomenon of parameter nonconstancy,
![]() is represented parametrically by the
is represented parametrically by the ![]() -dimensional
vector of parameters
-dimensional
vector of parameters
![]() , where each time period has an associated parameter
, where each time period has an associated parameter
![]()
![]() . Thus, elements of
. Thus, elements of
![]() need not be the same at each
time
need not be the same at each
time ![]() , and some of the
, and some of the
![]() may reflect
transient effects or regime shifts. The parameter space is
may reflect
transient effects or regime shifts. The parameter space is
![]() , so
, so
![]() .
.
The data generating process of
![]() is therefore
written as:
is therefore
written as:
| (A5) |
From equation (5), the complete
sample
![]() is generated from
is generated from
![]() by a population parameter value, which is denoted
by a population parameter value, which is denoted
![]() .
.
2.3 The Reduction Sequence
This subsection considers the sequence of reductions that
obtains the empirical model from the DGP. Because
![]() is unmanageably large,
operational models are defined by a sequence of data reductions,
which can be viewed in ten stages:
is unmanageably large,
operational models are defined by a sequence of data reductions,
which can be viewed in ten stages:
- parameters of interest,
- data transformations and aggregation,
- sequential factorization,
- data partition,
- marginalization,
- mapping to stationarity,
- conditional factorization,
- constancy,
- lag truncation, and
- functional form.
It is assumed that empirical modeling aims to determine the values of a set of parameters of interest that are relevant to an investigator's objectives, such as testing theories or undertaking policy analysis. The key concern of any given reduction is its effect on the parameters of interest. To derive that effect, this subsection briefly considers each of these ten stages in turn, while noting that some of these stages do not involve a reduction per se.
Parameters of interest. Let the parameters of interest be
denoted by
![]() . Both economic
theory and empirical properties may suggest that certain parameters
are parameters of interest. Parameters that are identifiable and
invariant to an empirically relevant class of interventions are
likely to be of interest. Other parameters may be of interest,
depending on the purpose of the exercise.
. Both economic
theory and empirical properties may suggest that certain parameters
are parameters of interest. Parameters that are identifiable and
invariant to an empirically relevant class of interventions are
likely to be of interest. Other parameters may be of interest,
depending on the purpose of the exercise.
Also, if
![]() is not a function of
is not a function of
![]() , then the modeling
exercise will be vacuous, so assume that
, then the modeling
exercise will be vacuous, so assume that
![]() .
After each reduction, it is essential to check that
.
After each reduction, it is essential to check that
![]() can still be retrieved from the
parameters characterizing the lower-dimensional data density.
can still be retrieved from the
parameters characterizing the lower-dimensional data density.
Data transformations and aggregation. Consider a
one-to-one mapping of
![]() to a new dataset
to a new dataset
![]() :
:
![]() . The
variables in
. The
variables in
![]() may include aggregates of
the original variables, their growth rates, etc. The transformation
from
may include aggregates of
the original variables, their growth rates, etc. The transformation
from
![]() to
to
![]() affects the parameter space, so
affects the parameter space, so
![]() is transformed into
is transformed into
![]() (say). Because densities are
equivariant under one-to-one transformations, the DGP of
(say). Because densities are
equivariant under one-to-one transformations, the DGP of
![]() is characterized by the
joint density of
is characterized by the
joint density of
![]() :
:
| (6) |
where
![]() is the set of
transformed parameters, with
is the set of
transformed parameters, with
![]() .
.
For
![]() in equation (6),
the key issue is how the transformation from
in equation (6),
the key issue is how the transformation from
![]() to
to
![]() alters the properties
of the parameters. Some parameters in
alters the properties
of the parameters. Some parameters in
![]() may be more constant
than ones in
may be more constant
than ones in
![]() ; others may be less
constant; and a smaller (or larger) number of the parameters in
; others may be less
constant; and a smaller (or larger) number of the parameters in
![]() may be needed to
characterize the parameters of interest
may be needed to
characterize the parameters of interest
![]() .
.
Sequential factorization. Using the basic result that a
joint probability equals the product of the conditional and
marginal probabilities, and noting that time is irreversible, then
sequentially factorize the density of
![]() into its
(martingale-difference) components:
into its
(martingale-difference) components:
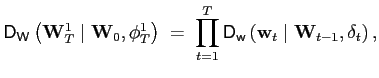
|
(7) |
where
![]() ,
,
![]() is the
is the ![]() -th column in
-th column in
![]() , and
, and
![]() is the parameterization
resulting from the sequential factorization. The right-hand side of
equation (7)
implicitly defines an innovation process
is the parameterization
resulting from the sequential factorization. The right-hand side of
equation (7)
implicitly defines an innovation process
![]() , which equals
, which equals
![]() .
.
Data partition. Now, partition
![]() into two sets, one set to
be analyzed (
into two sets, one set to
be analyzed (![]() ) and one set to be
marginalized (
) and one set to be
marginalized (![]() ):
):
| (8) |
where
![]() is an
is an ![]() matrix. Consequently, everything about
matrix. Consequently, everything about
![]() must be learnt from
must be learnt from
![]() alone, which entails that
alone, which entails that
![]() must not be essential to
inference about
must not be essential to
inference about
![]() .
.
Marginalization. Actual marginalization proceeds as
follows. Using the partition in equation (8), and noting
that
![]() , factorize
, factorize
![]() into the conditional distribution of
into the conditional distribution of
![]() given
given
![]() , and the marginal
distribution of
, and the marginal
distribution of
![]() :
:
![$\displaystyle \begin{tabular}[b]{l} $\mathsf{D}_{\mathsf{w}}\left( \mathbf{w}_{t}\mid\mathbf{W}_{t-1} ,\mathbf{\delta}_{t}\right) \bigskip $\\ $\hspace*{0.5in}=\;\mathsf{D}_{\mathsf{v\vert x}}\left( \mathbf{v}_{t} \mid\mathbf{x}_{t},\mathbf{W}_{t-1},\mathbf{\delta}_{a,t}\right) \cdot\mathsf{D}_{\mathsf{x}}\left( \mathbf{x}_{t}\mid\mathbf{V}_{t-1} ^{1},\mathbf{X}_{t-1}^{1},\mathbf{W}_{0},\mathbf{\delta}_{b,t}\right) .$ \end{tabular}$](img136.gif)
|
(9) |
If only
![]() is to be
analyzed, with only
is to be
analyzed, with only
![]() retained, then
retained, then
![]() must be obtainable from
must be obtainable from
![]() alone.
alone.
If lagged information about
![]() is also to be eliminated, then
is also to be eliminated, then
![]() must be marginalized with respect to
must be marginalized with respect to
![]() , requiring the very
strong condition that:
, requiring the very
strong condition that:
| (10) |
There is no loss of information from eliminating the history
![]() if and only if
if and only if
![]() , in which case the conditional sequential distribution of
, in which case the conditional sequential distribution of
![]() does not
depend on
does not
depend on
![]() . That is,
. That is,
![]() does not Granger-cause
does not Granger-cause
![]() ; see Granger (1969). In
modeling, another important condition is that there is no loss of
relevant information when
; see Granger (1969). In
modeling, another important condition is that there is no loss of
relevant information when
![]() . That is still a strong condition, but less stringent than
. That is still a strong condition, but less stringent than
![]() . Also, marginalizing
. Also, marginalizing
![]() will entail a loss of information
unless
will entail a loss of information
unless
![]() for parameter spaces
for parameter spaces
![]() and
and
![]() . Otherwise, the
parameters of the conditional and marginal distributions in
equation (9)
are cross-linked.
. Otherwise, the
parameters of the conditional and marginal distributions in
equation (9)
are cross-linked.
The above discussion implies that modeling aggregated data (say) can be viewed as a two-step process. First, the disaggregated series for a given variable (such as expenditure) are transformed by a one-to-one transformation into the corresponding aggregated series and all but one of those disaggregated series. Second, those disaggregated series are marginalized.
Mapping to stationarity. An economy may generate
integrated data, where a variable that is integrated of order
![]() (denoted I(
(denoted I(![]() )) must
be differenced
)) must
be differenced ![]() times to eliminate all unit roots.
Mapping such data to stationarity is a reduction from
I(
times to eliminate all unit roots.
Mapping such data to stationarity is a reduction from
I(![]() ) to I(0). This mapping is generally
useful for interpreting the resulting models, and it is needed to
ensure that conventional inference is valid for all parameters.
Still, many inferences will be valid even if this reduction is not
enforced; see Sims, Stock, and Watson (1990). While differencing the data
can map the data to stationarity, cointegration can also eliminate
unit roots between linear combinations of variables. Cointegration
is merely noted here, as it is treated extensively in numerous
books and expository articles: see Banerjee and Hendry (1992),
Ericsson (1992a), Banerjee, Dolado, Galbraith, and Hendry (1993),
Johansen (1995), Hatanaka (1996), Doornik, Hendry, and Nielsen (1998),
and Hendry and Juselius (2001) inter alia.
) to I(0). This mapping is generally
useful for interpreting the resulting models, and it is needed to
ensure that conventional inference is valid for all parameters.
Still, many inferences will be valid even if this reduction is not
enforced; see Sims, Stock, and Watson (1990). While differencing the data
can map the data to stationarity, cointegration can also eliminate
unit roots between linear combinations of variables. Cointegration
is merely noted here, as it is treated extensively in numerous
books and expository articles: see Banerjee and Hendry (1992),
Ericsson (1992a), Banerjee, Dolado, Galbraith, and Hendry (1993),
Johansen (1995), Hatanaka (1996), Doornik, Hendry, and Nielsen (1998),
and Hendry and Juselius (2001) inter alia.
Conditional factorization. Typically in empirical
modeling, some variables are treated as endogenous and others are
treated as given or non-modeled. Formally, this partitioning of the
variables arises by factorizing the density of ![]() variables in
variables in
![]() into sets of
into sets of ![]() and
and ![]() variables
variables
![]() and
and
![]() :
:
| (11) |
where
![]() denotes the endogenous
variables in
denotes the endogenous
variables in
![]() ,
,
![]() denotes the non-modeled
variables in
denotes the non-modeled
variables in
![]() , and
, and
![]() . Using the partition in
equation (11),
the joint distribution of
. Using the partition in
equation (11),
the joint distribution of
![]() on the right-hand side of
equation (10)
can always be factorized as:
on the right-hand side of
equation (10)
can always be factorized as:
![$\displaystyle \begin{tabular}[b]{l} $\mathsf{D}_{\mathsf{x}}\left( \mathbf{x}_{t}\mid\mathbf{X}_{t-1} ^{1},\mathbf{W}_{0},\mathbf{\delta}_{b,t}^{\ast}\right) \bigskip $\\ $\hspace*{0.5in}=\mathsf{D}_{\mathsf{y\vert z}}\left( \mathbf{y}_{t}\mid \mathbf{z}_{t},\mathbf{X}_{t-1}^{1},\mathbf{W}_{0},\mathbf{\theta} _{a,t}\right) \cdot\mathsf{D}_{\mathsf{z}}\left( \mathbf{z}_{t} \mid\mathbf{X}_{t-1}^{1},\mathbf{W}_{0},\mathbf{\theta}_{b,t}\right) ,$ \end{tabular}$](img174.gif)
|
(12) |
where
![]() is the conditional density of
is the conditional density of
![]() given
given
![]() ,
,
![]() is the marginal density of
is the marginal density of
![]() , and
, and
![]() and
and
![]() are those densities'
parameters. Modeling only
are those densities'
parameters. Modeling only
![]() and treating
and treating
![]() as given corresponds to
modeling only
as given corresponds to
modeling only
![]() and discarding the marginal distribution
and discarding the marginal distribution
![]() on the right-hand side of equation (12). No loss of
information in this reduction corresponds to the condition that
on the right-hand side of equation (12). No loss of
information in this reduction corresponds to the condition that
![]() is weakly exogenous for
is weakly exogenous for
![]() . Specifically, weak exogeneity
requires that
. Specifically, weak exogeneity
requires that
![]() alone and that
alone and that
![]() for parameter spaces
for parameter spaces
![]() and
and
![]() ; see
Engle, Hendry, and Richard (1983)*.
; see
Engle, Hendry, and Richard (1983)*.
Constancy. Complete parameter constancy in the
conditional density
![]() means that
means that
![]() , where
, where
![]() . In such a
situation, if weak exogeneity holds,
. In such a
situation, if weak exogeneity holds,
![]() itself is constant because
itself is constant because
![]() is a function of only
is a function of only
![]() . While appearing simple
enough, constancy is actually a subtle concept; see Hendry (1996)
and Ericsson, Hendry, and Prestwich (1998).
. While appearing simple
enough, constancy is actually a subtle concept; see Hendry (1996)
and Ericsson, Hendry, and Prestwich (1998).
Lag truncation. Lag truncation limits the extent of the
history
![]() in the conditional
density
in the conditional
density
![]() in equation (12).
For instance, truncation at
in equation (12).
For instance, truncation at ![]() lags implies:
lags implies:
| (13) |
In equation (13), no loss of
relevant information requires that
![]() .
.
Functional form. Functional form could be treated as a
set of data transformations, but it merits some discussion on its
own. Specifically, map
![]() into
into
![]() (
(
![]() ) and
) and
![]() into
into
![]() (
(
![]() ), and denote the
resulting data by
), and denote the
resulting data by
![]() . Assume that the
transformations
. Assume that the
transformations
![]() and
and
![]() together make
together make
![]() approximately normal and homoscedastic, denoted
approximately normal and homoscedastic, denoted
![]() .
Then there is no loss of information--and no change in the
specification--if:
.
Then there is no loss of information--and no change in the
specification--if:
| (14) |
A well-known example in which no loss of information occurs is
transforming the log-normal density of a variable to the normal
density in the logarithm of that variable. The left-hand side
density in equation (14) defines the
local (conditional) DGP of
![]() . When joint
normality holds, as is assumed here, that final conditional model
is linear in the transformed space.
. When joint
normality holds, as is assumed here, that final conditional model
is linear in the transformed space.
The derived model. This sequence of reductions delivers the following specification:
| (15) |
where
![]() is a mean-zero,
homoscedastic, mean-innovation process with variance
is a mean-zero,
homoscedastic, mean-innovation process with variance
![]() , and
, and
![]() and
and
![]() are
constant-parameter polynomial matrices of order
are
constant-parameter polynomial matrices of order ![]() in the lag operator
in the lag operator ![]() . That is,
. That is,
![]() and
and
![]() are matrices
whose elements are polynomials. The error
are matrices
whose elements are polynomials. The error
![]() is a derived
process that is defined by:
is a derived
process that is defined by:
| (16) |
so
![]() as given in
equation (16)
is not autonomous. For the same reason, equation (15) is a derived
model, rather than an autonomous model. Equations (15)
and (16)
parallel and generalize Section 2.1's discussion of
the empirical model in equation (2) and its derived
error in equation (4).
Section 4.3
discusses further aspects of model formulation, focusing on dynamic
specification, noting that equation (15) is an
autoregressive distributed lag model.
as given in
equation (16)
is not autonomous. For the same reason, equation (15) is a derived
model, rather than an autonomous model. Equations (15)
and (16)
parallel and generalize Section 2.1's discussion of
the empirical model in equation (2) and its derived
error in equation (4).
Section 4.3
discusses further aspects of model formulation, focusing on dynamic
specification, noting that equation (15) is an
autoregressive distributed lag model.
Reduction from the DGP to the generic econometric equation in
(15) involves all
ten stages of reduction discussed above, thereby transforming the
parameters
![]() in the DGP to the
coefficients of the empirical model. Because the DGP is congruent
with itself, equation (15) would be an
undominated congruent model if there were no information losses
from the corresponding reductions. More generally,
equation (15)
is congruent under the conditions stated, but it still could be
dominated, as the next subsection discusses.
in the DGP to the
coefficients of the empirical model. Because the DGP is congruent
with itself, equation (15) would be an
undominated congruent model if there were no information losses
from the corresponding reductions. More generally,
equation (15)
is congruent under the conditions stated, but it still could be
dominated, as the next subsection discusses.
2.4 Dominance
Comparison of empirical models is often of interest, and dominance is a useful criterion when comparing models. Dominance can be summarized, as follows.
Consider two distinct scalar empirical models, denoted
![]() and
and
![]() , with mean innovation
processes (MIPs)
, with mean innovation
processes (MIPs)
![]() and
and
![]() relative
to their own information sets, where
relative
to their own information sets, where
![]() and
and
![]() have constant finite
variances
have constant finite
variances
![]() and
and
![]() respectively. Model
respectively. Model
![]() variance-dominates
model
variance-dominates
model
![]() if
if
![]() . That
property is denoted
. That
property is denoted
![]() .
.
Several implications follow immediately from the definition of variance dominance in terms of the models' variances.
- Variance dominance is transitive: if
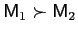 and
and
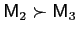 , then
, then
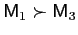 .
. - Variance dominance is also anti-symmetric: if
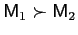 , then it
cannot be true that
, then it
cannot be true that
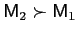 .
. - On a common dataset, a model without a MIP error can be variance-dominated by a model with a MIP error.
- In the population, the DGP cannot be variance-dominated by any models thereof; see Theil (1971), p. 543].
- A model with an innovation error cannot be variance-dominated by a model that uses only a subset of the same information.
- If (e.g.)
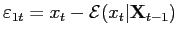 , then
, then
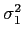 is no larger than the
variance of any other empirical model's error
is no larger than the
variance of any other empirical model's error
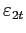 that is defined by
that is defined by
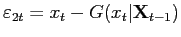 ,
whatever the choice of
,
whatever the choice of 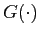 . This result follows
because the conditional expectation is the minimum mean-square
error predictor.
. This result follows
because the conditional expectation is the minimum mean-square
error predictor. - Thus, a model that nests all contending explanations as special cases must variance-dominate in that class of models.
- Variance dominance and parsimony may be considered together.
Let model
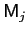 be characterized by a
parameter vector with
be characterized by a
parameter vector with
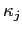 elements. Then model
elements. Then model
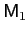 is parsimoniously undominated
in the class
is parsimoniously undominated
in the class
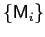 if
if
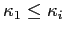 and no
and no
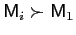
 . Hendry and Richard (1982)* define
this property; see also Section 4.2.
. Hendry and Richard (1982)* define
this property; see also Section 4.2. - Model selection procedures such as the Akaike information criterion and the Schwarz criterion seek parsimoniously undominated models, but they usually do not check for congruence; see Akaike (1981) [Volume II: Chapter 1] and Schwarz (1978) [Volume II: Chapter 2], and Section 4.5.
These implications favor starting with general rather than simple empirical models, given any choice of information set; and they suggest modeling the conditional expectation.
2.5 Measuring Information Loss
Valid reductions involve no losses in information. Econometrics has created concepts that correspond to avoiding possible losses, as the following list highlights.
- Aggregation entails no loss of information when
marginalizing with respect to disaggregates if the retained
(aggregated) information provides a set of sufficient statistics
for the parameters of interest
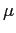 .
. - Sequential factorization involves no loss if the derived error process is an innovation relative to the history of the random variables.
- Marginalizing with respect to
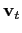 is without loss, provided
that the remaining data are sufficient for
is without loss, provided
that the remaining data are sufficient for
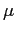 .
. - Marginalizing with respect to
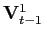 is without loss,
provided that
is without loss,
provided that
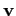 does not Granger-cause
does not Granger-cause
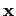 and that the parameters are
variation free.
and that the parameters are
variation free. - Cointegration and differencing can reduce integrated data to I(0) without loss.
- Conditional factorization leads to no loss of
information if the conditioning variables are weakly exogenous for
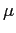 .
. - Parameter constancy over time and with respect to interventions on the marginal processes (invariance) are essential for sustainable relationships.
- Lag truncation involves no loss when the error process remains an innovation.
- Choice of functional form likewise involves no loss when the error process remains an innovation.
At a more general level, encompassing implies that no loss of information arises from ignoring another model's data, conditional on retaining the data in one's own model.
To provide some insight into encompassing, note that the local DGP is a reduction of the DGP itself and is nested within that DGP. The properties of the local DGP are explained by the reduction process: knowledge of the DGP entails knowledge of all reductions thereof. Thus, when knowledge of one model entails knowledge of another, the first model is said to encompass the second. Several relevant papers on encompassing are reprinted in Campos, Ericsson, and Hendry (2005); see Sections 4.6 and 4.7.
2.6 Information for Model Evaluation
Given the potential information losses that can occur in
reduction, it is natural to evaluate the extent to which there is
evidence of invalid reductions. A taxonomy of information sources
arises from the data themselves, theory and measurement
information, and data used in rival models. In this taxonomy, it is
useful to partition the data used in modeling (
![]() ) into its relative past,
relative present, and relative future:
) into its relative past,
relative present, and relative future:
| (17) |
The taxonomy of information sources is thus:
- past data
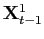 ;
; - present data
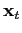 ;
; - future data
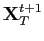 ;
; - theory information, which often motivates the choice of parameters of interest;
- measurement information, including price index theory, constructed identities, and data accuracy; and
- data of rival models, which is partitioned into its relative past, present, and future, paralleling the partition of the model's own data in equation (17).
Each source of information implies a criterion for evaluating an empirical model:
- homoscedastic innovation errors;
- weakly exogenous conditioning variables for the parameters of interest;
- constant invariant parameters of interest;
- theory-consistent identifiable structures;
- data-admissible formulations on accurate observations; and
- encompassing of rival models.
Models that satisfy the criteria for the first five information sets are said to be congruent. An encompassing congruent model satisfies all six criteria; see Sections 4.6 and 4.7.
2.7 Model Design
Model design can be either implicit or explicit. Implicit model design typically occurs when modeling aims to address the symptoms of existing mis-specification. For instance, a simple model might be initially specified and then tested for problems such as autocorrelation, heteroscedasticity, and omitted variables, correcting such problems as they are discovered. The model is thus implicitly designed to minimize (or control) the values of the test statistics that are computed.
Explicit model design aims to mimic reduction theory in empirical modeling, thereby minimizing the losses due to the reductions imposed. Explicit model design leads to general-to-specific modeling; see the following section. Gilbert (1986) [Volume I: Chapter 1] discusses and contrasts implicit and explicit model design in detail.
3 General-to-specific Modeling
General-to-specific modeling is the practical embodiment of reduction. The introduction to the current section summarizes important aspects of that relationship, focusing on implications for automated general-to-specific modeling algorithms. See Gilbert (1986)* and Ericsson, Campos, and Tran (1990) [Volume I: Chapter 7] for detailed expositions on general-to-specific modeling and Phillips (1988) [Volume I: Chapter 6] for a constructive critique.
As background to the methodology of general-to-specific modeling, consider the local DGP, which is the joint distribution of the subset of variables under analysis. A general unrestricted model such as equation (15) is formulated to provide a congruent approximation to that local DGP, given the theoretical, institutional, and existing empirical background. The empirical analysis commences from this general specification, which is assessed for discrepancies from congruency by using mis-specification tests. If no mis-specification is apparent, the general unrestricted model (or GUM) is simplified to a parsimonious congruent representation, with each step in the simplification being checked by diagnostic testing.
Simplification can proceed in many ways. Although the goodness of a model is intrinsic to the model and is not a property of the selection route, poor routes seem unlikely to deliver useful models. Consequently, some economists worry about how selection rules may affect the properties of the resulting models, thus advocating the use of a priori specifications. To be a viable empirical approach, these a priori specifications require knowledge of the answer before starting; and they deny any useful role to empirical modeling. Conversely, good routes may have a high chance of delivering congruent representations of the local DGP. Section 4.4 addresses model selection procedures and summarizes the papers reprinted in Campos, Ericsson, and Hendry (2005).
Several studies have recently investigated how well
general-to-specific modeling does in model selection. In
particular, the pathbreaking Monte Carlo study by
Hoover and Perez (1999a) [Volume II: Chapter 22] reconsiders
earlier Monte Carlo results by Lovell (1983) [Volume II:
Chapter 20]. Hoover and Perez start with series on 20
macroeconomic variables (![]() ) and generate a new variable
(denoted
) and generate a new variable
(denoted ![]() ) as a function of zero to five of the
) as a function of zero to five of the
![]() 's and an error. Hoover and
Perez then regress
's and an error. Hoover and
Perez then regress ![]() on all twenty
on all twenty
![]() 's plus lags thereof (
's plus lags thereof (![]() ), and they
let their general-to-specific algorithm simplify that general
unrestricted model until it finds an irreducible, congruent,
encompassing result. Their algorithm checks up to 10 different
simplification paths, testing for mis-specification at every step.
It then collects the models from those different simplification
paths and selects the one that variance-dominates the others. By
following many paths, the algorithm guards against choosing a
misleading route; and it delivers an undominated congruent
model.
), and they
let their general-to-specific algorithm simplify that general
unrestricted model until it finds an irreducible, congruent,
encompassing result. Their algorithm checks up to 10 different
simplification paths, testing for mis-specification at every step.
It then collects the models from those different simplification
paths and selects the one that variance-dominates the others. By
following many paths, the algorithm guards against choosing a
misleading route; and it delivers an undominated congruent
model.
HooverPerez (1999a)* stimulated a flurry of activity on the methodology of general-to-specific modeling. Hendry and Krolzig (1999) [Volume II: Chapter 23] improved on Hoover and Perez's algorithm. More recently, Hoover and Perez (2004) extended their investigations to cross-section datasets and found equally impressive performance by general-to-specific modeling in model selection. Hendry and Krolzig (2003) also reported a wide range of simulation studies used to calibrate their algorithm.
To see why general-to-specific modeling does well, the current section examines this approach from several standpoints. Section 3.1 summarizes generic difficulties in model selection. Section 3.2 reviews the debates about general-to-specific modeling prior to the publication of Hoover and Perez (1999a)*. Section 3.3 develops the analytics for several procedures in general-to-specific modeling, drawing on Hendry (2000), from which Section 3.4 derives various costs of search. Section 3.5 reports recent simulation evidence on the properties of general-to-specific modeling.
3.1 The Econometrics of Model Selection
There are four potential basic mistakes in selecting a model from data evidence:
- mis-specifying the general unrestricted model;
- failing to retain variables that should be included;
- retaining variables that should be omitted; and
- selecting a noncongruent representation, which renders conventional inference hazardous.
The first mistake is outside the purview of selection issues, although mis-specification testing of the general unrestricted model can alert the investigator to potential problems with that model. When the general unrestricted model is congruent, the fourth mistake can be avoided by ensuring that all simplifications are valid. That leaves the second and third mistakes as the two central problems for model selection. In what follows, the resulting costs of selection are typically considered for situations in which the general unrestricted model is much larger than the required model.
The conventional statistical analysis of repeated testing provides a pessimistic background for model selection. Every test has a nonzero null rejection frequency (or size, if independent of nuisance parameters), so type I errors accumulate across tests. Setting a tight significance level for tests would counteract that phenomenon, but would also induce low power to detect the influences that really matter. Thus, the conventional view concludes that incorrect decisions in model search must be commonplace.
As a contrasting view, in a progressive research strategy that utilizes general-to-specific modeling, evidence accumulates over time against irrelevant influences and in favor of relevant influences. White (1990) [Volume I: Chapter 23] showed that, with sufficiently rigorous testing, the selected model will converge to the DGP, so overfitting and mis-specification problems are primarily finite sample issues. Sections 3.3, 3.4, and 3.5 show that general-to-specific modeling has relatively low search costs, with sizes close to their nominal levels and powers near those attainable when commencing from the correct specification.
3.2 Past Debates
In addition to the four potential mistakes above, critics of general-to-specific methods have voiced concerns about data-based model selection, measurement without theory, pre-test biases, ignored selection effects, data mining, repeated testing, lack of identification, and the potential path dependence of any selected model. This subsection highlights central references in these debates and considers various responses to the critics.
Keynes (1939, 1940), Tinbergen (1940), Koopmans (1947), Judge and Bock (1978), Leamer (1978), Lovell (1983)*, Pagan (1987) [Volume I: Chapter 5], Hendry, Leamer, and Poirier (1990), and Faust and Whiteman (1997) inter alia critique general-to-specific methods in several key exchanges in the literature. Although Hendry and Krolzig (2001) address numerous concerns raised about general-to-specific modeling, it has taken a considerable time to develop the conceptual framework within which that rebuttal is possible. For instance, when Hendry (1980) was written, it was unclear how to counter earlier attacks, such as those by Keynes on Tinbergen (1939) or by Koopmans on Burns and Mitchell (1946). These debates set the scene for doubting any econometric analysis that failed to commence from a pre-specified model. Leamer (1978) also worried about the effects of data mining, which he defined as "the data-dependent process of selecting a statistical model" (p. 1). After Lovell83* found low success rates for selecting a small relation hidden in a large database, an adverse view of data-based model selection became entrenched in the profession. This view was reinforced by two additional results: the apparent coefficient bias that arises when variables are selected by significance tests, and the claimed under-estimation in reported coefficient standard errors that arises from treating a selected model as if it were certain.
Consequently, many empirical econometric studies have tried to appear to commence from pre-specified models, whether they did so or not. Econometric evidence became theory dependent: empirical evidence provided little value added, and it was likely to be discarded when fashions in theory changed. Confusion over the role of econometric evidence was so great that (e.g.) Summers (1991) failed to notice that theory dependence was a source of the problem, not the use of "sophisticated" econometrics.
Keynes and others claimed that valid econometric analysis must be based on models pre-specified by economic theory. The fallacy in that approach is that theoretical models are themselves incomplete and incorrect. Similarly, Koopmans inter alia relied on the (unstated) assumption that only one form of economic theory was applicable, that it was correct, and that it was immutable; see Hendry and Morgan (1995). That said, it is actually not necessary (or even possible) to know everything in advance when commencing statistical work in economics. If it were necessary, no one would ever discover anything not already known! Partial explanations are likewise valuable empirically, as the development of the natural sciences has demonstrated. Progressive research can discover invariant features of reality without prior knowledge of the whole; see Hendry (1995b).
A critic might well grant the force of such arguments, yet remain skeptical that data mining could produce anything useful, thereby undermining an evidence-based approach. However, as Gilbert (1986)* discusses, pejorative forms of data mining can be discovered from conflicting evidence or by rival models that cannot be encompassed. Stringent and critical model evaluation can detect and avoid these forms of data mining. See Hendry (1995a, Ch. 15] and Campos and Ericsson (1999) [Volume II: Chapter 33] for further discussion of data mining, including other less pejorative senses. Even when an undominated congruent model is data-based, it can provide a good approximation to the local DGP; and it can help reveal pejorative data mining.
3.3 Probabilities of Deletion and Retention
At first blush, the theory of repeated testing appears to wreak havoc with general-to-specific model selection, so this subsection addresses that issue. In fact, the probabilities of deleting irrelevant variables are relatively high. The greater difficulty is retaining relevant effects, even if the analysis commences from the "correct" model, i.e., the local DGP. This subsection re-examines the probabilities associated with deleting irrelevant variables and retaining relevant variables when adopting a general-to-specific modeling strategy.
Deleting irrelevant variables. To illustrate the
probabilities associated with deleting irrelevant variables in
general-to-specific model selection, consider a classical
regression model in which ![]() regressors are
irrelevant, i.e., have regression parameters equal to zero. Under
that null hypothesis, the probability p
regressors are
irrelevant, i.e., have regression parameters equal to zero. Under
that null hypothesis, the probability p![]() that at least one of
that at least one of ![]() corresponding
corresponding
![]() -tests rejects at the
-tests rejects at the
![]() level is one minus the
probability that none of those
level is one minus the
probability that none of those
![]() -tests rejects:
-tests rejects:
![\begin{displaymath}\begin{array}[b]{lll} \mathsf{p}_{\alpha} & = & 1-\mathsf{P}(\vert\mathsf{t}_{i}\vert<c_{\alpha}\;\forall i=1,\ldots,n)\medskip\\ & = & 1-\left( 1-\alpha\right) ^{n}, \end{array}\end{displaymath}](img282.gif)
|
(18) |
where
![]() is the critical value associated
with an
is the critical value associated
with an ![]() rejection frequency. For example,
when
rejection frequency. For example,
when ![]() tests of correct null hypotheses are
conducted at
tests of correct null hypotheses are
conducted at
![]() (say), then
(say), then
![]() from
equation (18).
With approximately 87% probability, at least
one
t-test spuriously rejects at the
5% level. Such a high
p-value is usually the focus of
worry with repeated testing.
from
equation (18).
With approximately 87% probability, at least
one
t-test spuriously rejects at the
5% level. Such a high
p-value is usually the focus of
worry with repeated testing.
One solution is to use larger critical values. The
t-distribution is thin-tailed,
leading Sargan (2001a) to note how difficult it is to obtain
spurious
t-values exceeding three in
absolute value; see also Sargan (2001b). A critical value of three
corresponds to (approximately) the 0.5% critical
value for a
t-test with ![]() ,
for which
,
for which
![]() when
when
![]() . While an 18% chance
of a false rejection may still be high from some perspectives, this
situation has other interpretations, as is now shown.
. While an 18% chance
of a false rejection may still be high from some perspectives, this
situation has other interpretations, as is now shown.
To better grasp the issues involved in false rejection,
reconsider the probability of irrelevant variables being
significant on a
t-test at significance
level ![]() . That probability
distribution
. That probability
distribution![]() is given by the
is given by the
![]() terms of the binomial expansion of
terms of the binomial expansion of
![]() ,
namely:
,
namely:
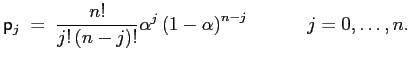
|
(19) |
Thus, the probability of all ![]() coefficients being
significant is
coefficients being
significant is
![]() , the probability of
, the probability of ![]() being significant is
being significant is
![]() , and
(as used in equation (18)) the
probability of none being significant is
, and
(as used in equation (18)) the
probability of none being significant is
![]() . Using
equation (19),
the average number of variables found significant by chance
is:
. Using
equation (19),
the average number of variables found significant by chance
is:
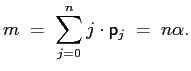
|
(20) |
If
![]() and
and ![]() , then
, then
![]() equals two, which explains the high
probability of at least one spurious rejection. Even so,
38 out of the 40 variables
will be deleted (on average) when using individual
t-tests at this relatively loose
significance level. Moreover, from equation (20),
equals two, which explains the high
probability of at least one spurious rejection. Even so,
38 out of the 40 variables
will be deleted (on average) when using individual
t-tests at this relatively loose
significance level. Moreover, from equation (20), ![]() falls to 0.4 for
falls to 0.4 for
![]() and to 0.2 for
and to 0.2 for
![]() . That is, when using a critical
value of three, one variable out of forty is retained just once in
five attempts, on average. That value of
. That is, when using a critical
value of three, one variable out of forty is retained just once in
five attempts, on average. That value of ![]() explains why
explains why
![]() . It also
reveals that such a rejection rate does not correspond to the usual
interpretation of size but to the rare occurrence of a selection
error, despite a large number of irrelevant variables. Even if
repeated
t-tests are used, few spurious
variables will typically be retained for
. It also
reveals that such a rejection rate does not correspond to the usual
interpretation of size but to the rare occurrence of a selection
error, despite a large number of irrelevant variables. Even if
repeated
t-tests are used, few spurious
variables will typically be retained for
![]() . Unfortunately, small values
of
. Unfortunately, small values
of ![]() often imply difficulty in detecting
relevant variables, leading to the issue of retention.
often imply difficulty in detecting
relevant variables, leading to the issue of retention.
Retaining relevant variables. Unless the relevant variables are highly significant in the population, retaining them appears inherently difficult, whether or not general-to-specific modeling is used. The difficulty in retaining relevant variables can be illustrated in a framework similar to the one used above for calculating the probabilities of deleting irrelevant variables, but with the t-ratios having noncentral distributions.
Consider drawing from a
t-distribution
![]() with
with
![]() degrees of freedom and a noncentrality
parameter
degrees of freedom and a noncentrality
parameter ![]() , which is approximately the
t-statistic's mean. The null
hypothesis
, which is approximately the
t-statistic's mean. The null
hypothesis
![]() is
is ![]() ,
the alternative hypothesis
,
the alternative hypothesis
![]() is
is ![]() , and assume that the alternative hypothesis is
true. For a critical value
, and assume that the alternative hypothesis is
true. For a critical value
![]() , the probability
, the probability
![]() determines the size, whereas power is given by:
determines the size, whereas power is given by:
| (21) |
Suppose that ![]() , which corresponds to an
expected
t-value of approximately two in
the population. That is,
, which corresponds to an
expected
t-value of approximately two in
the population. That is,
![]() for a
fixed
for a
fixed ![]() . Because the
t-distribution is nearly symmetric
around its mean, the probability of that
t-ratio exceeding two is about
50%:
. Because the
t-distribution is nearly symmetric
around its mean, the probability of that
t-ratio exceeding two is about
50%:
| (22) |
For even relatively small ![]() ,
equation (22) is the power in
equation (21)
when calculated for the alternative hypothesis
,
equation (22) is the power in
equation (21)
when calculated for the alternative hypothesis
![]() , noting that then
, noting that then
![]() roughly corresponds to
roughly corresponds to
![]() and
and
![]() is
approximately zero. The probability of rejecting the null
hypothesis that
is
approximately zero. The probability of rejecting the null
hypothesis that ![]() is thus only 50% under the alternative hypothesis that
is thus only 50% under the alternative hypothesis that ![]() , even although the local DGP is known and only a
single variable is involved. For three such variables, the
probability of detecting all three is:
, even although the local DGP is known and only a
single variable is involved. For three such variables, the
probability of detecting all three is:
| (23) |
where the estimated model is the local DGP and includes no additional irrelevant variables, and the included variables are orthogonal. From equation (23), all three variables are deemed significant only about one-eighth of the time (12.5%)--the same probability that no variables are retained. This low power represents an inexorable cost of inference from the given evidence, even when commencing from a correctly specified model.
This difficulty with power is exacerbated if the critical value
is increased (e.g.) to offset problems of "overfitting". For
example,
![]() for even large
for even large ![]() , implying only about a 2% chance of keeping all three variables. Despite knowing
the local DGP, such a variable will only occasionally be retained
using
t-tests if the null hypothesis is
tested. If there are many such variables, retaining all of them is
highly unlikely.
, implying only about a 2% chance of keeping all three variables. Despite knowing
the local DGP, such a variable will only occasionally be retained
using
t-tests if the null hypothesis is
tested. If there are many such variables, retaining all of them is
highly unlikely.
These calculations paint a potentially gloomy picture for data-based model selection. However, the situation is more promising than it might appear. As Section 3.4 explains, general-to-specific modeling can have surprisingly small search costs--i.e., the additional costs that arise by commencing from a general unrestricted model that nests the local DGP, rather than by commencing from the local DGP and knowing that it is the local DGP. These search costs are typically positive: it is difficult to improve on model selection if the local DGP is known. However, multiple-variable procedures such as F-tests can improve on single-variable procedures such as the t-tests above.
3.4 Costs of Inference and Costs of Search
The costs associated with model selection can be usefully separated into the costs of inference and the costs of search, as the following example illustrates.
The costs of inference are those costs associated with
inference about variables in a model when the model is the local
DGP but the modeler does not know that. Consider a local DGP with
![]() variables (all relevant), and denote those
variables by the set
variables (all relevant), and denote those
variables by the set ![]() (
(![]() for relevant). Let
for relevant). Let
![]() denote the
probability of retaining the
denote the
probability of retaining the ![]() variable at
significance level
variable at
significance level ![]() when commencing from
the local DGP as the initial specification. The probability of
dropping the
when commencing from
the local DGP as the initial specification. The probability of
dropping the ![]() relevant variable is
relevant variable is
![]() , so a
measure of the total costs of inference in this situation is:
, so a
measure of the total costs of inference in this situation is:
|
(24) |
While equation (24) is one measure of the costs of inference, other measures are feasible as well, such as unity minus the probability of selecting the local DGP; cf. equation (23).
The costs of search are those costs associated with
inference about variables in a general unrestricted model that
nests the local DGP, relative to inferences in the local DGP
itself. Let
![]() denote the
probability of retaining the
denote the
probability of retaining the ![]() variable when
commencing from a general unrestricted model with
variable when
commencing from a general unrestricted model with ![]() variables, applying the same selection tests and significance
levels as before. Thecost of search is
variables, applying the same selection tests and significance
levels as before. Thecost of search is
![]() for a
relevant variable (
for a
relevant variable (
![]() ), and it is
), and it is
![]() for an
irrelevant variable (
for an
irrelevant variable (
![]() ), where
), where ![]() is
the set of
is
the set of ![]() irrelevant variables in the general
unrestricted model. By construction, the local DGP has no
irrelevant variables, so the whole cost of keeping irrelevant
variables in model selection is attributed to search. Thus, a
measure of the pure search costs is:
irrelevant variables in the general
unrestricted model. By construction, the local DGP has no
irrelevant variables, so the whole cost of keeping irrelevant
variables in model selection is attributed to search. Thus, a
measure of the pure search costs is:
|
(25) |
In principle, the pure search costs given in equation (25) could be negative if the algorithm for selection from a general unrestricted model were different from that for testing in a local DGP. The complexities of multiple-variable problems typically preclude analytical answers, so Section 3.5 reports some simulation evidence. Before examining that evidence, consider conditions under which search might do well.
Reducing search costs. To keep search costs low, the model selection process should satisfy a number of requirements. These include starting with a congruent general unrestricted model and using a well-designed simplification algorithm, as is now discussed.
- The search should start from a congruent statistical model to ensure that selection inferences are reliable. Problems such as residual autocorrelation and heteroscedasticity not only reveal mis-specification. They can deliver incorrect coefficient standard errors for test calculations. Consequently, the algorithm must test for model mis-specification in the initial general model. The tests used at this stage should be few in number (four or five, say), at relatively stringent significance levels (such as 1%), and well calibrated, i.e., so that their nominal sizes are close to the actual size. These choices help avoid spurious rejections of the general unrestricted model at the outset. For instance, five independent mis-specification tests at the 1% level induce an overall size of about 5%. Alternatively, a single general portmanteau test could be applied at the 5% level. Once congruence of the general unrestricted model is established, selection can reliably commence.
- The search algorithm should avoid getting stuck in search paths that inadvertently delete relevant variables early on and then retain many other variables as proxies, leading to very non-parsimonious selections. The algorithm should consequently both filter out genuinely irrelevant variables and search down many paths to avoid path dependence. The former points towards F-testing, the latter towards exploring all statistically reasonable paths.
- The algorithm should check that diagnostic tests remain insignificant throughout the search process. If eliminating a variable induced a significant diagnostic test, the associated reduction would appear to be invalid, and later inferences would be distorted. Even if model mis-specification tests are computed at every simplification step, this form of repeated testing does not affect the probabilities of spurious rejections because the general unrestricted model is already known to be congruent. There are thus three protections against inappropriate simplification: the reduction test itself, the reduction's consequences for the residuals, and the outcomes of different paths. Such protections act together, rather like error correction: each reduces the chances of a mistake.
- The algorithm should ensure that any candidate model parsimoniously encompasses the general unrestricted model, so that no loss of information has occurred. Searching down various paths may result in several different (perhaps non-nested) terminal models. Each of these models can be tested against the general unrestricted model to ensure that the cumulative losses from simplification are small enough: i.e., that the general unrestricted model is parsimoniously encompassed. These models can also be tested against each other to eliminate any dominated findings. A coherent approach is to form the union of the models' variables, test each model against that union to check whether it (the model) parsimoniously encompasses the union, and drop any model that does not parsimoniously encompass the union.
- The algorithm should have a high probability of retaining relevant variables. To achieve this requires both a relatively loose significance level and powerful selection tests. Decisions about significance levels should probably be made by the user because the trade-off between costs of over- and under-selection depend on the problem, including such features as the likely numbers of relevant variables and irrelevant variables, and the likely noncentrality parameters of the former.
- The algorithm should have a low probability of retaining variables that are actually irrelevant. This objective clashes with the fifth objective in part and so requires an alternative use of the available information. As noted previously, false rejection frequencies of the null can be lowered by increasing the required significance levels of the selection tests, but only at the cost of reducing power. However, it may be feasible to simultaneously lower the former and raise the latter by improving the search algorithm.
- The algorithm should have powerful procedures to select between the candidate models and any models derived from them--with an aim of good model choice. Tests of parsimonious encompassing are natural here, particularly because all of the candidate models are congruent relative to the general unrestricted model by design.
Section 4.8 summarizes the relevant papers that are reprinted in Campos, Ericsson, and Hendry (2005) on this topic. Assuming now that the chosen algorithm satisfies the first four requirements--which are relatively easy to ensure--the current subsection examines the fifth and sixth requirements in greater detail.
Improving deletion probabilities. To highlight how the
choice of algorithm may improve deletion probabilities, consider
the extreme case in which the model includes many variables but
none of those variables actually matters. Low deletion
probabilities of those irrelevant variables might entail high
search costs. One solution is to check whether the general
unrestricted model can be reduced to the empty (or null) model, as
with a one-off
F-test (
![]() , say) of the general
unrestricted model against the null model using a critical
value
, say) of the general
unrestricted model against the null model using a critical
value
![]() . This approach would have size
. This approach would have size
![]() under the null hypothesis if
under the null hypothesis if
![]() were the only test
implemented. Because the null is true, model searches along more
complicated paths would occur only if
were the only test
implemented. Because the null is true, model searches along more
complicated paths would occur only if
![]() rejected, i.e., only
rejected, i.e., only
![]() of the time. Even for those
searches, some could terminate at the null model as well,
especially if
of the time. Even for those
searches, some could terminate at the null model as well,
especially if
![]() were set more stringently than
were set more stringently than
![]() .
.
A specific example helps clarify the benefits of this two-stage
strategy. For a general unrestricted model with ![]() regressors, suppose
regressors, suppose
![]() rejects
rejects
![]() of the time, as above. Also,
suppose that
t-test selection in the general
unrestricted model is used if the null model is rejected by
of the time, as above. Also,
suppose that
t-test selection in the general
unrestricted model is used if the null model is rejected by
![]() , with (say)
, with (say) ![]() regressors being retained on average from the
t-test selection. Overall, the
average number of variables retained by this two-stage search
procedure is:
regressors being retained on average from the
t-test selection. Overall, the
average number of variables retained by this two-stage search
procedure is:
| (26) |
It is difficult to determine ![]() analytically
because the model searches using
t-test selection condition on
analytically
because the model searches using
t-test selection condition on
![]() . Because
. Because
![]() variables are retained on average
when the test
variables are retained on average
when the test
![]() is not utilized, it
seems reasonable to assume that
is not utilized, it
seems reasonable to assume that ![]() is larger than
is larger than
![]() , e.g.,
, e.g.,
![]() . Under that assumption, the
expected number of variables retained by this two-stage algorithm
is
. Under that assumption, the
expected number of variables retained by this two-stage algorithm
is
![]() , using
equation (26). For
, using
equation (26). For
![]() (a moderate value),
(a moderate value),
![]() , and
, and ![]() , only
0.4 variables are retained on average,
implying a size of just 1%, and without the
consequential adverse implications for power that were present when
the search algorithm used only
t-tests.
, only
0.4 variables are retained on average,
implying a size of just 1%, and without the
consequential adverse implications for power that were present when
the search algorithm used only
t-tests.
For comparison, Hendry and Krolzig (1999)* found that this two-stage
algorithm selected the (correct) null model 97.2% of
the time, with a very small size, when
![]() and
and ![]() in their
Monte Carlo re-run of Hoover and Perez's experiments. Hendry and
Krolzig's value of
in their
Monte Carlo re-run of Hoover and Perez's experiments. Hendry and
Krolzig's value of ![]() now seems too
stringent, over-emphasizing size relative to power. Nevertheless,
by using relatively tight significance levels or a reasonable
probability for looser significance levels, it is feasible to
obtain a high probability of locating the null model, even when
40 irrelevant variables are included.
now seems too
stringent, over-emphasizing size relative to power. Nevertheless,
by using relatively tight significance levels or a reasonable
probability for looser significance levels, it is feasible to
obtain a high probability of locating the null model, even when
40 irrelevant variables are included.
Improving selection probabilities. A generic pre-search
filter can improve selection probabilities, even when
![]() by itself is not very
useful. Notably,
by itself is not very
useful. Notably,
![]() may well reject much of the
time if the general unrestricted model includes even a relatively
small number of relevant variables, in which case
may well reject much of the
time if the general unrestricted model includes even a relatively
small number of relevant variables, in which case
![]() has little value in the
search algorithm. To illustrate the use of a pre-search filter,
suppose that the general unrestricted model has 40
variables, of which 30 are irrelevant and
10 are relevant, and where the latter have
population
t-values equal to two in absolute
value. The test
has little value in the
search algorithm. To illustrate the use of a pre-search filter,
suppose that the general unrestricted model has 40
variables, of which 30 are irrelevant and
10 are relevant, and where the latter have
population
t-values equal to two in absolute
value. The test
![]() will almost always reject
at standard levels. However, a pre-search filter generalizing on
will almost always reject
at standard levels. However, a pre-search filter generalizing on
![]() can help eliminate the
irrelevant variables. One appealing pre-search filter focuses on a
single decision--"What is to be excluded?"--thereby entailing
what is to be included. Ideally, the general model's variables
would be split into the two sets
can help eliminate the
irrelevant variables. One appealing pre-search filter focuses on a
single decision--"What is to be excluded?"--thereby entailing
what is to be included. Ideally, the general model's variables
would be split into the two sets ![]() and
and ![]() , with the
F-test applied to the latter set
(the irrelevant variables). Although that particular split cannot
be accomplished with any certainty due to the sampling variability
of estimated coefficients, the overall approach is useful.
, with the
F-test applied to the latter set
(the irrelevant variables). Although that particular split cannot
be accomplished with any certainty due to the sampling variability
of estimated coefficients, the overall approach is useful.
One feasible pre-search filter in this spirit can be constructed
as follows. Consider a procedure comprising two
F-tests, denoted
![]() and
and
![]() , where
, where
![]() is conducted at the
is conducted at the
![]() level (as above), and
level (as above), and
![]() is conducted at the
is conducted at the
![]() level (say). The
level (say). The ![]() variables to be tested are first ordered by their
variables to be tested are first ordered by their
![]() -values in the general
unrestricted model, such that
-values in the general
unrestricted model, such that
![]() . The statistic
. The statistic
![]() tests the
significance of the first
tests the
significance of the first ![]() variables, where
variables, where
![]() is chosen such that
is chosen such that
![]() (
(
![]() ) and
) and
![]() but
that either
but
that either
![]() or
or
![]() .
The first
.
The first ![]() variables are eliminated, provided
that the diagnostic statistics for the corresponding reduction
remain insignificant. Then,
variables are eliminated, provided
that the diagnostic statistics for the corresponding reduction
remain insignificant. Then,
![]() tests whether the
remaining
tests whether the
remaining ![]() variables are jointly significant,
i.e., that
variables are jointly significant,
i.e., that
![]() . If so, those
remaining variables are retained.
. If so, those
remaining variables are retained.
The number of variables eliminated (![]() ) is central
to this procedure. To illustrate this procedure's appeal, calculate
the likely values of
) is central
to this procedure. To illustrate this procedure's appeal, calculate
the likely values of ![]() for
for ![]() ,
with 30 irrelevant variables and 10
relevant variables (as above). For ease of exposition, further
assume that the variables are independent of each other. From the
definitions of
,
with 30 irrelevant variables and 10
relevant variables (as above). For ease of exposition, further
assume that the variables are independent of each other. From the
definitions of ![]() and
and
![]() , it follows that
, it follows that
![]() ,
that
,
that
![]() , and
that:
, and
that:
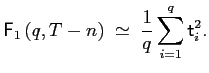
|
(27) |
When 30 variables are irrelevant, approximately
20 of those variables will have absolute
t-ratios less than unity because
![]() . From equation (27), every
additional
. From equation (27), every
additional
![]() that is less than unity
reduces the value of
that is less than unity
reduces the value of
![]() , implying that typically
, implying that typically
![]() .
Moreover,
.
Moreover,
![]() , so on average only three irrelevant variables have absolute
t-ratios larger than 1.65, with seven variables having absolute
t-ratios between unity and
1.65. Hence, the expected value of
, so on average only three irrelevant variables have absolute
t-ratios larger than 1.65, with seven variables having absolute
t-ratios between unity and
1.65. Hence, the expected value of
![]() for the first 27
variables is approximately:
for the first 27
variables is approximately:
![\begin{displaymath}\begin{array}[b]{lll} \mathsf{F}_{1}\left( 27,T-n\right) & \simeq & \dfrac{1}{27}[(20\times 1.00^{2})+(4\times1.33^{2})+(3\times1.65^{2})]\bigskip\vspace{-0.05in}\\ & \simeq & 1.31, \end{array}\end{displaymath}](img484.gif)
|
(28) |
which is insignificant at the 19% level for
![]() . For even this very moderate level of
. For even this very moderate level of
![]() implied by equation (28),
implied by equation (28), ![]() is likely to be close to the total number of irrelevant
variables, with only a few irrelevant variables inadvertently
retained. Also, few relevant variables are likely to be deleted
because
is likely to be close to the total number of irrelevant
variables, with only a few irrelevant variables inadvertently
retained. Also, few relevant variables are likely to be deleted
because
![]() .
.
3.5 Simulation Evidence
Monte Carlo findings on the econometrics software package PcGets suggest that its operational characteristics are well described by the above analysis. Hendry and Krolzig (2001) present full details of the algorithm in PcGets. This subsection summarizes the accumulating evidence on the excellent--and still rapidly improving--performance of implemented general-to-specific selection procedures.
Hoover and Perez (1999a)* is the first major Monte Carlo study of general-to-specific selection procedures. Hoover and Perez demonstrated both the feasibility of automatic model selection procedures and the highly superior properties of general-to-specific modeling over any of the selection approaches considered by Lovell (1983)*. Hoover and Perez found that the size (null rejection frequency) of their automated general-to-specific model selection procedure was close to the nominal value. Moreover, they found that power was sufficiently high to detect many of the models hidden in very large general unrestricted models, e.g., when seeking models with from zero to five variables when the general unrestricted model had 44 variables.
Building on Hoover and Perez (1999a)*, Hendry and Krolzig (1999)* used early versions of many of the ideas discussed above and substantially improved Hoover and Perez's algorithm. While Hendry and Krolzig's algorithm performed exceptionally well in some states of nature--as when the DGP was the null model--the algorithm did less well in other situations. Hendry and Krolzig (2003) have shown that a more recent version of their algorithm achieves good performance across all the states considered, with controlled size and power close to those that would be achieved if the analysis commenced from the local DGP.
HendryKrolzig (2001) present an array of simulations at different choices of the many critical values in PcGets and confirm the algorithm's "error correction" behavior, in that poor choices for some decision criteria can be offset by more sensible choices elsewhere. For instance, too loose a pre-search criterion can be offset by multi-path searches. Finally, Krolzig (2001, 2003) finds that the general-to-specific search procedure does well in selecting the equations in a vector autoregression.
All of these experiments concerned time series datasets. Hoover and Perez (2004) have reported simulations representing cross-country regressions. Again, Hoover and Perez found well-controlled size and power close to those attainable when the local DGP is the model. Hoover and Perez contrast that outcome with the poor properties of procedures such as extreme bounds analysis; see Leamer (1985). To summarize, the available analytics and simulation evidence concur: general-to-specific modeling can work almost as well as commencing from the local DGP, and search costs are remarkably low.
4 A Selected Bibliography
This section summarizes fifty-seven papers key to the development of general-to-specific modeling. These papers are reprinted in the two volumes of Campos, Ericsson, and Hendry (2005). Selecting the papers was not easy, as literally hundreds of exemplars are available. We considered the pivotal role of each paper and the ease of access to that paper, including through existing reprints of it--although previous reprinting in itself signaled importance. We included many papers on specific tests and procedures, while narrowing the topic by excluding papers that arose as implications of general-to-specific modeling approaches. We also omitted papers on alternative methodologies, while including some expository evaluations of general-to-specific modeling.
The fifty-seven papers are divided topically into nine parts,
which are discussed in this section's nine subsections.
Volume I
Part I. Introduction to the methodology (Section 4.1);
Part II. Theory of reduction (Section 4.2);
Part III. Dynamic specification (Section 4.3);
Part IV. Model selection procedures (Section 4.4);
Volume II
Part I. Model selection criteria (Section 4.5);
Part II. Model comparison (Section 4.6);
Part III. Encompassing (Section 4.7);
Part IV. Computer automation (Section 4.8); and
Part V. Empirical applications (Section 4.9).
These divisions are convenient but not always clearcut. For instance, some applications have a strong methodological slant; and some analyses of econometric theory report substantive empirical findings. The remainder of this section summarizes the fifty-seven papers, part by part, following the structure indicated above.
4.1 Introduction to the Methodology
This subsection focuses on two common, alternative approaches to modeling the economy: specific-to-general and general-to-specific. In the first approach, the researcher starts from a simple relationship, with the intent of generalizing it in light of any discrepancies between the model and the data. In the second approach, the researcher postulates the most general model that is feasible, which is then reduced as far as its congruence with the data permits. While both procedures may lead to a congruent model, they have substantial differences that may greatly affect the chances of selecting a good representation.
Any specific-to-general strategy faces a key problem: diagnostic statistics are unable to provide enough information to identify the causes of the symptoms detected by diagnostic statistics themselves. For instance, a test for parameter constancy may reject, but the parameters' apparent nonconstancy may have arisen because relevant variables are omitted or because conditioning upon the included variables is invalid. Hence, in the specific-to-general approach, it is crucial to correctly guess the interpretation of a rejected null hypothesis because fixing the wrong cause does not solve the actual problem. For example, adding variables to a model may not lead to constant parameters if joint modeling is in fact required. Likewise, correcting for residual autocorrelation may not lead to a better model if inappropriate functional form is the root cause of the autocorrelation.
General-to-specific strategies also face challenges, as documented in Section 3. That section also considers how those challenges are addressable in practice.
Gilbert (1986) [Volume I: Chapter 1] offers a clear explanation of the general-to-specific approach to econometric modeling, emphasizing the approach's foundations and its advantages over specific-to-general modeling. Hendry (1983) [Volume I: Chapter 2] exposits the main aspects of general-to-specific modeling, illustrating throughout with the modeling of U.K. consumers' expenditure.
Gilbert (1989) [Volume I: Chapter 3] discusses the origins of general-to-specific modeling at the London School of Economics (LSE), and he summarizes the approach's major developments through the 1970s. Understanding these circumstances is of interest in order to avoid repeating earlier mistakes. Spanos (1989) [Volume I: Chapter 4] outlines a framework based on the Haavelmo distribution, in which the LSE approach may be embedded. Mizon (1995) notes further recent improvements in general-to-specific modeling and discusses model evaluation.
Three additional papers evaluate a range of alternative approaches. Pagan (1987) [Volume I: Chapter 5] compares Hendry's, Leamer's, and Sims's methodologies for constructing econometric models; see Hendry (1983) [Volume I: Chapter 2], Leamer (1978), and Sims (1980) respectively, and see Hendry and Leamer, and Poirier (1990) for further discussion. Phillips (1988) [Volume I: Chapter 6] evaluates Aigner's, Granger's, Leamer's, and Pesaran's views on econometric methodology, with reflections on Hendry's methodology, including general-to-specific modeling. Ericsson, Campos, and Tran (1990) [Volume I: Chapter 7] provide a general exposition of Hendry's methodology, linking it to the econometrics software program PcGive.
4.1.1 Professor Hendry's Econometric Methodology by C.L. Gilbert (1986)
Gilbert (1986) offers a clear yet quite complete explanation of the general-to-specific approach to econometric modeling, emphasizing the approach's foundations and its advantages over specific-to-general modeling. Gilbert (1986) contrasts these two approaches, referring to the latter as Average Economic Regression (AER) and the former as Professor Hendry's econometric methodology. The two approaches differ in several respects: the interpretation of the econometric model, the interpretation of any evidence of the model's mis-specification, the solutions advocated to correct for that mis-specification, the consequences of the strategy followed to obtain a final representation, and the independence of the final representation from the approach by which it has been obtained.
Gilbert characterizes the AER as follows. First, the econometric model is viewed as a representation of economic theory. Second, statistical properties such as residual autocorrelation, heteroscedasticity, collinearity, and simultaneity are regarded as inherent to the model, so the modeler's goal becomes one of re-specifying the model in order to eliminate those undesirable features, thereby permitting estimation with desirable properties. Third, because the AER treats the model as a representation of economic theory, the AER approach is naturally specific-to-general: it starts from a simple model, which is re-specified to adjust for any of its undesirable empirical properties.
Gilbert characterizes Hendry's approach as follows. First, the econometric model is viewed as a representation of the process or probability distribution generating the sample of data, i.e., the DGP. Second, the model's properties arise from operations applied to the DGP to obtain the empirical model. The modeler's goal is thus to find evidence on whether the model's properties are sustained by the data, and so whether those properties are satisfied by the DGP. Third, because Hendry's approach views the model as a simplification of the unknown DGP, Hendry's approach is naturally a general-to-specific modeling strategy. Model specification starts from the most general feasible model and arrives at a parsimonious model by imposing acceptable restrictions.
Gilbert considers one important consequence of the choice of strategy: the likelihood of arriving at a unique representation. Whichever approach is used, there are many routes from the initial model to a final representation. However, a general-to-specific modeling approach appears to be more efficient in finding such a representation.
Gilbert (1986) reformulates Leamer's (1978, p. 4) "Axiom of Correct Specification" as an axiom of route independence of the final specification from the strategy by which the modeler has arrived at that final representation. Gilbert explains the criteria in Hendry and Richard (1982*, 1983) under which a model is congruent with data; and he concludes that there is no surefire recipe for discovering a suitable final representation. That said, there are a few guidelines: models are designed for particular purposes; models must be robust to changes in the properties of the sample; parameters must be economically interpretable; and models must be reasonably simple.
4.1.2 Econometric Modelling: The "Consumption Function" in Retrospect by D.F. Hendry (1983)
Hendry (1983) summarizes all of the main issues in the theory of reduction and general-to-specific modeling, focusing on model evaluation and model design. He first observes that every empirical model is a reduction of the DGP. A model's disturbances are thus a derived process, suggesting that the model (and so its residuals) could be designed to have specific desirable properties. Those properties are characterized by a set of criteria against which the model can be tested or evaluated. In model design, the model is revised after a diagnostic statistic's failure, rather than being rejected. While a revised model may reflect a successful design procedure, it need not be a good representation of the DGP, emphasizing the importance of general-to-specific rather than specific-to-general modeling.
Hendry (1983) illustrates model evaluation with the quarterly model of U.K. consumers' expenditure in Davidson, Hendry, Srba, and Yeo (1978)*, testing that model for data coherence, valid conditioning, parameter constancy, data admissibility, theory consistency, and encompassing. Hendry discusses what test statistics are associated with which criterion, shows that white noise is a weak property, and tries to find evidence as to whether simultaneity is due to time aggregation. Hendry examines the issue of parameter constancy in detail, implementing standard tests, considering changes in correlations over subperiods, and checking the model against earlier (pre-sample) annual data. He checks for data admissibility by constructing a savings equation and by considering the model's robustness to data revisions; he discusses the role of economic theory and examines the consistency of the model with the life-cycle hypothesis; he interprets the model's long-run solution, highlighting the importance of regressors that are orthogonal; and he discusses sequential simplification.
Hendry advocates a modeling strategy that incorporates encompassing. Variance dominance is necessary but not sufficient for parameter encompassing, so the latter criterion is of greater interest in practice. Finally, he notes that none of the available models may be encompassing, that unions of models need not be meaningful to provide a test baseline, and that a minimal nesting model may not exist. While attaining innovation errors is important, innovations are defined with respect to a given information set: hence, an encompassing model may itself be encompassed on a different information set.
4.1.3 LSE and the British Approach to Time Series Econometrics by C.L. Gilbert (1989)
Gilbert (1989) describes the joint evolution of econometrics and time series analysis at the LSE through the 1970s. He argues that the methodology of general-to-specific modeling was motivated by the uniformly most powerful testing procedure proposed by Anderson (1971), and that Sargan's (1980b)* COMFAC procedure was derived in this framework. Gilbert also discusses two additional papers that provided major contributions to econometrics: Sargan's (1964) Colston paper on modeling wages and prices, and Davidson, Hendry, Srba, and Yeo's (1978)* paper on modeling consumer's expenditure. The former appears to be the first empirical implementation of an error correction model; the latter introduces the encompassing procedure, albeit informally.
4.1.4 On Rereading Haavelmo: A Retrospective View of Econometric Modeling by A. Spanos (1989)
Spanos (1989) proposes a methodological framework based on the probabilistic approach in Haavelmo (1944), focusing on Haavelmo's concepts of statistical adequacy and identification. Spanos's framework is closely tied to the LSE (or Hendry's) modeling strategy and addresses various common criticisms of empirical modeling.
In the context of statistical adequacy, Spanos (1989) discusses how the statistical model is a relationship between observables, with a set of distributional assumptions on those observables. The statistical model can be interpreted as a reduction of the Haavelmo distribution and is derived from a distribution that is conditional on factors suggested by theory and data. A model is statistically adequate if the distributional assumptions embedded in that model are compatible with the data's properties. Spanos then considers how specification, mis-specification, and re-specification are all well-defined aspects concerning statistical adequacy.
Spanos also distinguishes between statistical identification and structural identification. Statistical identification is a concept related to the parameters in the statistical model and so concerns the estimability of those parameters. Structural identification is a concept relating the economic theory's parameters to the parameters in the statistical model, so it reparameterizes or restricts the statistical model to provide it with a theory interpretation. Testing over-identifying restrictions thus checks whether the data are consistent with the underlying economic theory. Spanos also suggests considering reparameterizations induced by data as a valid interim alternative to finding more realistic economic theories.
Spanos contrasts his approach with the "textbook" approach. The latter has been criticized because it has generated empirical models with questionable forecasting abilities, and because those models have used a priori information without adequately accounting for the time series properties of the observed data. Spanos's framework addresses two common elements that underlie these criticisms--the experimental interpretation of the statistical model, and statistical adequacy.
Spanos (1989) discusses how his framework provides support for and is compatible with most features of the LSE methodology. In particular, his framework helps clarify the roles of mis-specification, diagnostic checking, statistical adequacy, and model selection; and it provides arguments in favor of a general-to-specific modeling approach.
4.1.5 Three Econometric Methodologies:A Critical Appraisal by A. Pagan (1987)
Pagan (1987) compares Hendry's, Leamer's, and Sims's
methodologies for constructing econometric models. Pagan notes that
all three methodologies are general-to-specific in nature, albeit
each with a different procedure for simplifying and each with
limited reporting of the procedure. Hendry's and Sims's
methodologies reduce their general models by testing restrictions
on parameters, whereas Leamer's relies on extreme bounds analysis.
Both Hendry's and Leamer's methodologies base decisions on the
value of a ![]() statistic, but in a different
way, and hence their conclusions may differ. At the time of writing
(in 1985), none of these methodologies provided a complete set of
techniques for analyzing data. For instance, they had been
developed mainly for macroeconomic time series and would require
modification for large microeconomic datasets.
statistic, but in a different
way, and hence their conclusions may differ. At the time of writing
(in 1985), none of these methodologies provided a complete set of
techniques for analyzing data. For instance, they had been
developed mainly for macroeconomic time series and would require
modification for large microeconomic datasets.
All three methodologies perform data transformations, but with different purposes. Hendry's approach reparameterizes his general model to obtain orthogonal regressors, keeping in mind the issue of interpretable parameters. Leamer's approach reparameterizes in terms of parameters of interest. Sims's approach seeks stationarity with orthogonal innovations, despite orthogonality implying restrictions on the model in its structural form and hence defeating a main purpose of Sims's methodology--to avoid imposing a priori restrictions. Pagan indicates that it is difficult to decide which parameters are of interest at the outset, especially because Hendry's and Sims's methodologies are responding to different economic questions.
In Pagan's view, precise control of the overall significance level is not very important. Rather, the crucial issue is how the likelihood changes as simplification decisions are made. Model evaluation is performed in Hendry's and Leamer's methodologies, but in very different ways. Evaluation in Hendry's methodology is performed by diagnostic testing. Evaluation in Leamer's methodology proceeds by analyzing the sensitivity of the mean of the posterior distribution to changes in prior variances. Pagan suggests that all the methodologies need to improve on their reporting of information about model validity. While useful information is provided, Pagan feels that too many statistics appear in Hendry's approach, restrictions on prior variances are hard to understand in Leamer's approach, and graphs and impulse responses are difficult to interpret in Sims's approach.
In summary, Pagan advocates clarifying and combining these methodologies in order to extract the greatest information from the available data. Hendry's methodology may benefit from extreme bounds analysis and sensitivity analysis, which may provide information on the shape of the likelihood, whereas Sims's and Leamer's methodologies may find that an analysis of residuals can help assess the sensitivity of the likelihood to including variables.
4.1.6 Reflections on Econometric Methodology by P.C.B. Phillips (1988)
Phillips (1988) discusses Aigner's, Granger's, Leamer's, and Pesaran's views on econometric methodology and illustrates how econometric methods can be used for evaluating modeling strategies. Phillips also shows, under quite general conditions, how Hendry's methodology provides an optimal or near-optimal procedure for estimating a cointegrating relationship.
Phillips (1988) argues for progressive modeling strategies, which are amenable to being improved and capable of providing explanations for changing economic mechanisms. Phillips identifies several properties that are desirable in a modeling strategy, as follows. Economic theory must play a role. The modeling strategy must guide the choice of econometric technique, model specification, and dataset. It must warn against its own weaknesses and provide advice on how to sort out those weaknesses. It must be implemented in software for carrying out computations, drawing graphs, and performing Monte Carlo studies that can assess how good the strategy is in discovering an adequate representation of the economic mechanism. Phillips also discusses several key issues in empirical modeling, including the limited role of more and better data, procedures for model comparisons, the relationship between econometric models and DGPs, the use of sharp hypotheses, the use and misuse of diagnostic testing and graphical analysis, asymptotic and finite sample approximations, nuisance parameters, maximum likelihood methods, and the role of economic theory.
Phillips (1988) then discusses the role of econometric theory in evaluating modeling strategies, illustrating with Hendry's methodology applied to a cointegrated vector autoregression in triangular form. For disturbances that are independently and identically distributed normal, the maximum likelihood estimates of this triangular system coincide with least squares for an equivalent equilibrium correction representation of the conditional equation in Hendry's methodology. For more general stationary error processes, the general-to-specific methodology performs a set of corrections that make it an optimal procedure under weak exogeneity.
4.1.7 PC-GIVE and David Hendry's Econometric Methodology by N.R. Ericsson, J. Campos, and H.-A. Tran (1990)
Ericsson, Campos, and Tran (1990) describe Hendry's methodology in detail. They then consider how that methodology is implemented in the software package PC-GIVE (now known as PcGive) and illustrate key aspects of that methodology with empirical examples.
In Hendry's methodology, econometric models of the economic mechanism are constructed, based on statistical data and economic theory. Statistical data are realizations from a probability distribution (the DGP); economic theory guides the econometric model's specification; and the DGP determines the model's properties because the model arises from a sequence of reductions applied to the DGP.
Ericsson, Campos, and Tran describe those reductions, discuss why they may lead to losses of information (and hence to invalid inference), establish the relationship between those reductions and tests of the corresponding assumptions, and illustrate how this framework leads to a constructive modeling strategy, such as simplifying a general autoregressive distributed lag model in a multiple-path search. The autoregressive distributed lag model is the most general model in its class and includes many other model types as special cases. Evidence on the autoregressive distributed lag model thus may suggest directions in which it may be simplified, while keeping in mind the importance of evaluating the final specification and of isolating invariants to changes in the economy.
Many results follow immediately by noting that an econometric model is an entity derived from the DGP. Specifically, the model's disturbances are derived and not autonomous; simply leaving some variables as unmodeled does not make them exogenous; and model evaluation is a structured procedure, not an ad hoc one.
Ericsson, Campos, and Tran (1990) also illustrate Hendry's methodology in practice. First, they re-analyze Hendry and Ericsson's (1991) data on U.K. narrow money demand, demonstrating cointegration and weak exogeneity; see also Johansen (1992b)* and Johansen and Juselius (1990)*. In light of those results, Ericsson, Campos, and Tran estimate a general unrestricted autoregressive distributed lag model of U.K. money demand, reparameterize it with a relatively orthogonal and economically interpretable set of regressors, and simplify, describing that simplification path in detail. Second, Ericsson, Campos, and Tran replicate a key money demand equation from Friedman and Schwartz (1982) and demonstrate that that equation is mis-specified by employing various diagnostic tests. Finally, Ericsson, Campos, and Tran test for exogeneity in a model of consumers' expenditure from Campos and Ericsson (1988), later published as Campos and Ericsson (1999)*.
Mizon (1995) provides a complementary assessment of the LSE methodology, beginning with its origins and evolution. Mizon describes the general-to-specific modeling strategy, emphasizing the roles of two main evaluation criteria--congruence and encompassing; and he contrasts that strategy with the specific-to-general modeling strategy. Mizon illustrates the LSE methodology for both single-equation and system modeling with an empirical analysis of wages, prices, and unemployment in the United Kingdom over 1965-1993.
4.2 Theory of Reduction
Section 2 summarizes the structure of the theory of reduction. The current subsection summarizes two papers that help clarify that structure: Hendry (1987) [Volume I: Chapter 8], and Hendry and Richard (1982) [Volume I: Chapter 9]. The first systematizes the components in the theory of reduction and thereby accounts for the origins and properties of empirical models. The second investigates the concepts underlying model formulation. Hendry (1983)* illustrates the concepts developed in both papers by demonstrating empirically how to build models and evaluate their properties.
The remaining papers associated with this subsection concentrate on the issue of exogeneity and the reductions associated with that concept. Koopmans (1950) [Volume I: Chapter 10] ties exogeneity to the feasibility of obtaining consistent and asymptotically unbiased maximum likelihood estimators of the parameters of interest when the equations explaining some of the variables in the analysis are disregarded. The general problem is viewed as one of completeness of models in a statistical framework, and it is solved by providing informal definitions of exogeneity, predeterminedness, and joint dependence. Koopmans's concept of exogeneity can be interpreted as what is later called weak exogeneity. Phillips (1956) [Volume I: Chapter 11] investigates the validity of these results for discrete approximations to continuous time variables.
Richard (1980) [Volume I: Chapter 12] provides a formal definition of weak exogeneity for dynamic systems and derives a sufficient condition for it. Richard also defines strong exogeneity and generalizes the sufficient condition for it to include models with changing regimes. Some of the assumptions leading to Koopmans's sufficient conditions for exogeneity imply that the disturbances in the subsystem of interest are uncorrelated with the predetermined variables. Richard (1980)* warns against relying on that zero covariance. More than one representation may have a zero covariance; a zero covariance need not provide information on causality; and, in models with several regimes, that covariance may alter as economic variables switch their status between being endogenous and exogenous.
Engle, Hendry, and Richard (1983) [Volume I: Chapter 13] separate the problem of model completeness from that of efficient model estimation, and they add to Richard's (1980)* results by providing the definition of super exogeneity. With the conceptual tools that they developed, Engle, Hendry, and Richard then clarify the implications that predeterminedness, Granger causality, and weak, strong, super, and strict exogeneity have for the economic analysis of dynamic econometric models with possibly autocorrelated errors.
Subsequent work re-assesses these concepts for cointegrated systems. Johansen (1992a), Johansen (1992b)*, and Urbain (1992) derive sufficient conditions for weak exogeneity for short-run and long-run parameters in a conditional subsystem from a cointegrated vector autoregression. Harbo, Johansen, Nielsen, and Rahbek (1998) provide critical values for the likelihood ratio test for that form of cointegration; and Johansen and Juselius (1990)* develop a general framework for testing restrictions on cointegrated systems, including exogeneity restrictions. Ericsson (1992a) and Ericsson, Hendry, and Mizon (1998) provide expository syntheses of cointegration and exogeneity.
4.2.1 Econometric Methodology: A Personal Perspective by D.F. Hendry (1987)
Hendry (1987) begins with four prescriptions for successful empirical econometric research: "think brilliantly, ... be infinitely creative, ... be outstandingly lucky, ... [and] stick to being a theorist" (pp. 29-30). While tongue in cheek, Hendry's prescriptions emphasize key aspects of substantive empirical analysis, particularly the "respective roles of theory and evidence and discovery and justification as well as the credibility of econometric models" (p. 30).
Hendry then focuses on how models are reductions of the DGP, and on what implications follow therefrom. Hendry outlines the principal reductions (see Section 2), discusses the implied derived status of empirical models, and explains how errors on empirical equations can be either implicitly or explicitly redesigned to achieve desirable criteria, such as being white noise. The theory of reduction clarifies how an empirical model is entailed by the DGP, while economic-theory models help motivate, formulate, and interpret the empirical model. The validity of reductions can be evaluated by diagnostic tests derived from a taxonomy of information, which underpins the notion of a congruent model.
By establishing the link between DGPs and empirical models, the theory of reduction justifies both evaluative and constructive aspects of econometric modeling. That said, Hendry argues against mechanically redesigning an empirical model to "correct" whatever econometric problems arise, such as residual autocorrelation. Hendry instead proposes designing an empirical model to satisfy all of the criteria that underlie congruence. Extreme bounds analysis is unhelpful in empirical modeling because a congruent dominating model may be fragile in Leamer's sense. Finally, Hendry emphasizes the value of a progressive research strategy and cites empirical examples where later studies have successfully encompassed earlier ones.
4.2.2 On the Formulation of Empirical Models in Dynamic Econometrics by D.F. Hendry and J.-F. Richard (1982)
Hendry and Richard (1982) formally derive an information taxonomy from the theory of reduction, they propose a corresponding set of criteria for evaluating econometric models (see Section 2.6), and they illustrate these results with an empirical model of mortgage repayments.
Hendry and Richard propose the following model evaluation criteria.
- The empirical model's error is an innovation with respect to the selected information set.
- Conditioning variables are weakly exogenous for the parameters of interest.
- The model's parameters are constant.
- The econometric model is consistent with the underlying economic theory.
- The model is data admissible.
- The model encompasses all rival models.
A specification meeting these criteria is said to be a tentatively adequate conditional data characterization (TACD) or (in later publications) a congruent model. Hendry and Richard also discuss the value of reparameterizing equations to have near-orthogonal regressors and the value of having a parsimonious final specification.
Hendry and Richard highlight the differences between an economic-theory model, an empirical econometric model, a statistical model, and the DGP. The economic-theory model and the empirical econometric model complement each other in that they both help explain the same phenomenon. However, they are distinct in that the properties of an empirical model are implicitly derived from the DGP, rather than being a consequence of the postulated economic theory.
In this context, Hendry and Richard discuss problems with some traditional approaches to empirical modeling. For instance, they demonstrate that adding a hypothesized stochastic process to an economic-theory model need not obtain an adequate characterization of the data. Hendry and Richard also highlight difficulties with mechanically correcting problems in an empirical specification, e.g., when starting from a strict economic-theory representation and reformulating that specification to correct for residual autocorrelation, heteroscedasticity, etc. Rejection of the null hypothesis does not imply the alternative hypothesis: hence, underlying causes cannot be inferred from effects detected by diagnostic tests. For example, rejection of the null hypothesis of white-noise residuals does not imply any specific alternative, e.g., autoregressive errors.
Hendry and Richard suggest a different perspective on empirical modeling. An unknown DGP generates measurements on economic variables, which are represented by an econometric specification in which the residuals include everything not in that specification. In that light, empirical models and their errors may be designed to have specified properties, turning the evaluation criteria discussed above into design criteria. One minimal design criterion is white-noise errors. That is, the errors should be unpredictable on their own past. Otherwise, the model could be improved by accounting for the errors' predictability. More generally, modeling should aim for representations with innovation errors, which also ensure variance dominance of other models using the same information set.
The remaining design criteria--weak exogeneity, parameter constancy, theory consistency, data admissibility, and encompassing--also have clear justifications. For instance, econometric models often have fewer equations than variables, so Hendry and Richard examine the conditions for excluding equations for some of the variables. The required concept is weak exogeneity, which sustains inference about the parameters of interest without loss of information. If the process for the unmodeled variables alters, invalid conditioning on those variables may induce parameter nonconstancy in the model itself, rendering the model less useful for forecasting and policy analysis.
The theory of reduction also sheds light on the concept of encompassing. For instance, all empirical models are reductions of the underlying DGP and so are nested in the DGP. Hence, comparisons of rival econometric models are feasible. This result underpins the principle of encompassing, in which a given model accounts for the results of rival models. Hendry and Richard provide examples in which the encompassing model predicts parameter nonconstancy and residual autocorrelation in the encompassed model. Variance dominance is an aspect of encompassing--rather than an independent criterion--because variance dominance is necessary but not sufficient for encompassing. Hendry and Richard then illustrate model evaluation and model design with an empirical example of mortgage repayments, and they examine the role of dynamic simulation in evaluating econometric models.
4.2.3 When Is an Equation System Complete for Statistical Purposes? by T.C. Koopmans (1950)
Koopmans (1950) addresses the problem of completeness in models. A model is complete if it includes equations for all variables in the system that are neither exogenous nor predetermined. Conversely, variables are regarded as exogenous if consistent and asymptotically unbiased maximum likelihood estimates of the parameters of interest can be obtained, even though the (marginal) equations explaining those exogenous variables have been neglected. Non-exogenous variables are called predetermined if consistent and asymptotically unbiased estimates of the parameters of the subsystem of non-exogenous non-predetermined variables can be obtained separately from those of the subsystem of predetermined variables.
Koopmans provides sufficient conditions for this definition of exogeneity. Specifically, the variables explained by the conditional equations must not enter the marginal equations; all parameters of interest must be located in the conditional equations; conditional and marginal parameters must be unrelated; and error terms across conditional and marginal subsystems must be mutually independent. The sufficient conditions for predeterminedness are analogous and require that the subsystem for the predetermined variables not be a function of the remaining current-dated non-exogenous variables, with error terms across subsystems of these variables being mutually independent.
Koopmans (1950) derives his sufficient conditions, assuming that the error terms are serially independent. Serial independence appears to be a satisfactory assumption, provided that the lengths of lagged reactions are not smaller than the time unit of observation. Koopmans also re-examines the issue of identification and argues that, if the parameters in the estimated subsystem are identified, they also will be so in the whole system.
4.2.4 Some Notes on the Estimation of Time-forms of Reactions in Interdependent Dynamic Systems by A.W. Phillips (1956)
Phillips (1956) provides theoretical justifications for lagged responses of agents to changing conditions and for the interdependence of economic variables. He examines the effects of time aggregation and the feasibility of estimating "time-forms" (i.e., distributed lags) between economic variables.
Phillips analyzes the effects of time aggregation by postulating linear relationships between economic variables in continuous time and aggregating over time. He shows that the reaction over time of one variable to another coincides with the change of the explained variable to a unit step change of the explanatory variable at the origin. Because discrete-time observations on flow variables may be interpreted as cumulations of corresponding continuous-time observations, Phillips then considers the estimation of time-forms of linear relationships between variables that are measured in discrete time. Phillips notes that, because of the effects of time aggregation, the time-lag reactions in discrete-time relationships generally do not reveal the precise nature of the underlying continuous-time relationship. Additionally, Phillips shows that variables in discrete time are related over at least two periods unless the time-form reaction in continuous time is instantaneous. That observation has direct implications for empirical modeling.
Phillips (1956) also derives conditions under which least squares estimation of the coefficients in the discrete-time relationship is a reasonable procedure. In doing so, he considers distributed-lag and feedback reactions within a system, and reactions of the system to variables determined outside the system. Phillips shows that errors correlated with explanatory variables can be avoided by including in the estimated equation all factors affecting directly or indirectly the explained variable as well as exogenous factors. Finally, Phillips proposes a strategy for empirical work, focusing on choice of explanatory variables, observation frequency, length of lags, seasonal components, trends, and multicollinearity.
4.2.5 Models with Several Regimes and Changes in Exogeneity by J.-F. Richard (1980)
Richard (1980) develops two key concepts--weak exogeneity and strong exogeneity--and he considers maximum likelihood estimation of models with switching regimes. Richard motivates his approach by re-examining Goldfeld and Quandt's (1973) model with two regimes. Goldfeld and Quandt's model is statistically incomplete in the sense of Koopmans (1950)* and so is inappropriate for detecting changes in the exogeneity status of variables. Richard also uses that model to distinguish between causality, exogeneity, and assumptions of "zero covariances between some variables and so-called 'disturbance terms"' (p. 3), showing in particular that the last property can be obtained by definition.
Richard (1980) then sets up a linear dynamic framework and specifies conditions for weak exogeneity, which permits conditioning on a variable with no loss of information for the model's purpose--here, specifically, for estimation and testing. He interprets those conditions from an economic viewpoint; and he proposes a likelihood ratio statistic for testing for weak exogeneity when the model is identified, as well as one that can be applied for complete dynamic simultaneous equations models. Richard also considers a model with several regimes when the regimes are known and the conditioning variables in each regime are weakly exogenous. In that case, the likelihood function for all regimes can be factorized into a product of conditional densities times a product of marginal densities, and the marginal densities can be ignored for statistical inference. Richard analyzes two types of restrictions on the conditional parameters: restrictions corresponding to parameters in the structural model having columns in common across regimes, and restrictions arising from the connection between reduced form and structural form parameters.
Richard also describes limited information maximum likelihood (LIML) procedures for estimating the conditional parameters, both when the switching times are known and when they are unknown. If the marginal parameters are not of interest and the switching times are known, then only the conditional densities need be analyzed. If the switching times are unknown, then conditional and marginal densities share the (unknown) switching times and so must be analyzed jointly, even if all other parameters in the marginal densities are not of interest.
4.2.6 Exogeneity by R.F. Engle, D.F. Hendry, and J.-F. Richard (1983)
Engle, Hendry, and Richard (1983) find sufficient conditions for a variable to be exogenous, where the conditions depend upon the purpose of the model at hand. Engle, Hendry, and Richard show that the distinct purposes of statistical inference, forecasting, and policy analysis define the three distinct concepts of weak, strong, and super exogeneity. Valid exogeneity assumptions may permit simpler modeling strategies, reduce computational expense, and help isolate invariants of the economic mechanism. Invalid exogeneity assumptions may lead to inefficient or inconsistent inferences and result in misleading forecasts and policy simulations. Engle, Hendry, and Richard demonstrate the relationship between these three concepts of exogeneity and the concepts of predeterminedness, orthogonality conditions, strict exogeneity, Granger causality, and Wold's causal ordering; and Engle, Hendry, and Richard illustrate these concepts with bivariate models and the dynamic simultaneous equations model.
As in Richard (1980)*, Engle, Hendry, and Richard (1983) start with the joint distribution of all variables relevant to the phenomenon under study. Engle, Hendry, and Richard then ask whether the marginal distribution for a certain subset of those variables (the supposedly exogenous variables) can be ignored without loss of information. The answer to that question depends on the purpose of the model, the choice of marginal variables, the parameters of interest, and the underlying process generating the data. The authors also discuss the close connection between their approach to exogeneity and the approach in Koopmans (1950)*.
The paper's examples show how to apply the sufficient conditions for exogeneity, and they highlight the importance of parameters of interest. The examples also demonstrate several general propositions. Strict exogeneity, predeterminedness, and the absence of Granger causality are neither necessary nor sufficient for valid conditional inference and policy analysis. Behavioral models with structurally invariant parameters of interest need not lead to models with conditional parameters that are invariant to interventions on the marginal model's parameters. And, irrelevant current-dated variables need not be weakly exogenous.
4.3 Dynamic Specification
The theory of reduction in Section 2 presents a straightforward framework in which to discuss dynamic specification. The current subsection considers how that theory aids in understanding both the structure of dynamic specification and the tests of dynamic specification. One recent and important special case of dynamic specification is cointegration.
The theory of reduction leads to a model typology for dynamic specification. Economic data are realizations of a probability distribution (the DGP), and an econometric model is constructed to characterize that DGP and represent the economic phenomena under study. As Phillips (1956)* and Hendry, Pagan, and Sargan (1984) [Volume I: Chapter 14] inter alia discuss, theoretical justifications exist for why agents might base their current decisions on past information. Thus, it is sensible to write the DGP as the product of joint distributions of current variables conditional on past observations; see also Section 2.3. This sequential factorization implies econometric models with lagged variables, which may enter explicitly as "variable dynamics" or implicitly as "error dynamics". In the latter, an equation includes lagged errors, as with an autoregressive error process. However, lagged errors are functions of lagged variables in the equation and hence are interpretable as imposing a set of restrictions on variable dynamics. The roots of the lag polynomials are also important, with a zero root allowing lag simplification, a unit root implying a nonstationary component, etc. Dynamic specification also focuses on the properties of alternative model formulations. The model typology in Hendry, Pagan, and Sargan (1984)* greatly eases that comparison by interpreting those formulations as special cases of an autoregressive distributed lag (ADL) specification: see equation (15).
Tests of dynamic specification are typically part of the simplification procedure for models involving time series data, so dynamic specification has figured prominently in the general-to-specific modeling methodology. Models with autoregressive errors can be viewed as imposing a restriction of common factors in the lag polynomials of an ADL--a restriction called "comfac": see Sargan (1964). Because of the ubiquity of autoregressive errors in econometric modeling, several papers discussed below focus on the comfac reduction. Sargan (1980b) [Volume I: Chapter 16] derives a determinantal procedure for testing common factors in dynamics for single equations. Based on that work, Hendry and Mizon (1978) [Volume I: Chapter 15] clarify how autoregressive errors imply restrictions on a general ADL model, rather than simply offering a way of generalizing a static model with innovation errors. Hendry and Anderson (1977) develop Sargan's (1980b)* procedure for simultaneous equations systems. A suitable estimation procedure is required if an autoregressive restriction is valid: Sargan (1961) [Volume I: Chapter 17] describes the corresponding maximum likelihood procedure. Whether or not the autoregressive restrictions are valid, the choice of lag length and the shape of the lag distribution are of interest, as discussed in Hendry, Pagan, and Sargan (1984)*; see also Phillips (1956)*.
Modeling nonstationarities due to unit roots in the dynamics has also attracted considerable attention; see Dickey and Fuller (1979, 1981) and Engle and Granger (1987). Johansen and Juselius (1990) [Volume I: Chapter 18] focus specifically on cointegration and differencing as reductions to I(0), developing corresponding inferential procedures and applying them to small monetary systems for Denmark and Finland. Dynamic specification in cointegrated systems also arises in several papers discussed in other subsections: see Phillips (1991 [Volume I: Chapter 24], Hendry and Mizon (1993) [Volume II: Chapter 19], MacDonald and Taylor (1992) [Volume II: Chapter 30], and Johansen (1992b) [Volume II: Chapter 31], and Metin (1998) [Volume II: Chapter 32] inter alia.
4.3.1 Dynamic Specification by D.F. Hendry, A. Pagan, and J.D. Sargan (1984)
Hendry, Pagan, and Sargan (1984) examine two related issues--dynamic specification ("variable dynamics") and stochastic specification ("error dynamics")--in the context of model formulation and model selection for single equations and systems. This examination leads to a general model typology for dynamic specification. Hendry, Pagan, and Sargan also summarize maximum likelihood methods for estimation and the three main principles for testing.
Hendry, Pagan, and Sargan (1984) systematize their study of dynamic specification by creating a model typology that includes all major model types as special (restricted) cases of an ADL. Those model types are:
- a static regression,
- a univariate time series model,
- a differenced data (growth rate) model,
- a leading indicator model,
- a distributed lag model,
- a partial adjustment model,
- a common factor (autoregressive error) model,
- a homogeneous error correction model, and
- a reduced form (dead start) model.
The restrictions implied by each model type are testable against the ADL. If accepted, the restrictions achieve greater parsimony through the associated reduction. If the restrictions are rejected, then the associated model ignores valuable information in the dataset.
The relationship between dynamic specification and stochastic specification is illustrated by showing that apparently alternative specifications (dynamic and stochastic) may be equivalent representations. Some of those representations may be more parsimonious than others, so some justification is required to choose between them.
Two criteria appear fundamental: data coherency and theory consistency. However, these criteria can be regarded as only necessary conditions for choosing a model. Lack of sufficiency arises because alternative representations entailing different behavior may be consistent with the same economic theory, and data coherence may be unclear due to measurement errors and various sorts of mis-specification. Further criteria are mentioned for in-sample testing, in addition to a measure of the model's ability to encompass any extant models.
Hendry, Pagan, and Sargan (1984) give several theoretical justifications for dynamics, including non-instantaneous adjustment by agents and the formation of expectations by agents. Empirically, dynamics can be represented by ADL models, which are the unrestricted (and hence most general) parameterization for a class of models, with each model type having its own properties. To illustrate, Hendry, Pagan, and Sargan analyze in detail nine distinct models that are all special cases of a bivariate, single-lag ADL model. A general-to-specific modeling approach emerges from this model typology as a natural way to design models. The model typology also has implications for the usefulness of several existing empirical procedures. For instance, autocorrelated residuals are not interpretable as autoregressive errors unless common factor restrictions are valid; tests for the significance of autoregressive coefficients condition on the existence of a common factor, which itself is testable; the insignificance of autoregressive error coefficients does not imply the absence of dynamics; and white-noise residuals do not imply data coherency. Error correction models (ECMs; also called equilibrium correction models) are convenient reparameterizations of ADL models and are supported by their relation to cointegration.
Hendry, Pagan, and Sargan (1984) also examine high- (but finite-) order distributed lag models and infinite-order distributed lag models. Because these models may entail estimation problems due to a large number of parameters, various forms of restrictions have been considered in the literature to reduce dimensionality. Hendry, Pagan, and Sargan discuss various polynomial distributed-lag restrictions (such as Almon distributed lags), procedures for choosing lag lengths and lag shapes, and the effects on estimates of incorrect choices. Hendry, Pagan, and Sargan propose reparameterizing the distributed lag model as an error correction model whenever convenient. Sargan (1980a) also proposes a lag shape that further reduces the required number of parameters. Hendry, Pagan, and Sargan (1984) emphasize the consequences of stochastic mis-specification, the effect of Granger causality on the properties of diagnostic tests, the merits of general error correction models, the suitability of normality as an approximation to the distribution of the estimated mean lag, and the value of economic theory and the importance of correct dynamic specification in determining long-run parameters.
Model selection in the (infinite-order) ARMAX class is more complex, no matter which model representation is considered. Hypotheses may be non-uniquely nested, there may be too many parameters relative to the sample size, and roots may be close to the unit circle. Hendry, Pagan, and Sargan (1984) consider various simplifications of the model representation and discuss procedures to determine the maximal lag, including a variation on Sargan's (1980b)* COMFAC procedure. In COMFAC, first the maximal lag order is determined, with no comfac restrictions. Then hypotheses of polynomial common factors are tested by a sequence of Wald tests. Likelihood-ratio and Lagrange multiplier tests are also discussed. Finally, Hendry, Pagan, and Sargan (1984) generalize their model typology to systems of equations and consider issues of reduced form, final form, dynamic multipliers, and alternative model representations. On the last, various disequilibrium models are shown to be derivable as optimal control rules.
4.3.2 Serial Correlation as a Convenient Simplification, Not a Nuisance: A Comment on a Study of the Demand for Money by the Bank of England by D.F. Hendry and G.E. Mizon (1978)
Hendry and Mizon (1978) exposit how the comfac analysis proposed in Sargan (1980b)* tests for dynamic mis-specification. Comfac analysis involves a two-step procedure. The first step tests for common factor restrictions in the equation's dynamics by applying (e.g.) Wald tests to check the validity of an autoregressive error interpretation. The second step tests whether the common factor polynomial has any zero roots to see if an autoregressive error is required.
Hendry and Mizon (1978) discuss several key issues in comfac analysis.
- Common factor dynamics imply autoregressive errors, so this form of dynamic specification is testable.
- Residual autocorrelation does not necessarily imply autoregressive errors. Residual autocorrelation may also arise from incorrect functional form, parameter nonconstancy, incorrect seasonal adjustment, and other forms of dynamic mis-specification inter alia.
- Growth-rate models impose common factors with unit roots.
- Choosing a growth-rate model as the most general model prevents one from detecting invalid restrictions imposed on the levels of the variables.
- The Durbin-Watson statistic is not a test for a common factor, and hence it is not testing for autoregressive errors. Rather, the Durbin-Watson statistic is a test for a zero root, assuming a common factor exists.
Hendry and Mizon (1978) illustrate comfac analysis by re-examining the growth-rate model for U.K. money demand in Hacche (1974). Hacche's model is rejected against an ADL model in levels. Thus, Hacche's model imposes invalid common factor restrictions and incorrectly excludes certain levels of the variables.
4.3.3 Some Tests of Dynamic Specification for a Single Equation by J.D. Sargan (1980b)
Sargan (1980b) proposes a procedure for model selection in a single-equation time series model with multiple variables and illustrates it empirically. His procedure formulates an unrestricted ADL model and tests (with a Wald test) that all lag polynomials on the variables in the equation have a polynomial of a given degree in common (the "common factor"). A single ADL may permit common factors corresponding to different lag lengths (or degrees), and those common factors describe a sequence of uniquely ordered nested hypotheses. Each hypothesis can be written as a less restrictive hypothesis plus a set of additional restrictions; and the corresponding incremental Wald statistics are mutually independently distributed, so that the overall significance level can be controlled, as in Anderson (1971).
Sargan derives a necessary and sufficient condition for the lag polynomials to have a common factor in terms of a determinantal condition for a particular matrix. The lag polynomials associated with the variables in the ADL model may be of different degrees, but they all have a common factor of a certain degree under suitable restrictions. Sargan develops an algorithm for testing whether those restrictions are satisfied.
Sargan (1980b) compares his procedure to the traditional procedure in which a model with autoregressive errors is estimated. Sargan's procedure may be inefficient due to unrestricted estimation, but the traditional procedure seems to be incapable of distinguishing between models with the same total maximal lag order but with different degrees of variable and stochastic dynamics.
Sargan provides two justifications for choosing the Wald test. First, Wald statistics can be defined for any estimation method, with their properties depending upon the restrictions tested and the properties of the estimator. Second, if the true common factor has complex roots and if the degree of the (tested) common factor is set too low, the likelihood-ratio statistic has problems because the likelihood has multiple maxima.
Sargan also considers shortcomings of his procedure. First, a
Jacobian condition must be satisfied in order to write the most
restricted hypothesis as a less restrictive hypothesis plus a set
of additional restrictions. Second, if that Jacobian condition is
not satisfied, then the Wald statistic for testing those additional
restrictions does not converge to a ![]() distribution.
distribution.
Sargan illustrates the comfac procedure with a model for U.K. wages, and the procedure's performance is compared to the likelihood-ratio test.
Hendry and Anderson (1977) generalize Sargan's comfac analysis to include simultaneous equations systems. Hendry and Anderson (1977) also discuss the advantages of system-based likelihood-ratio statistics over single-equation instrumental variable statistics. Hendry and Anderson apply their procedure to a simultaneous equations model of U.K. building societies. Hendry and Anderson construct an economic-theory model by minimizing a loss function that is believed to explain how building societies set borrowing and lending rates and volumes. Minimization of that loss function results in a simultaneous equations model, with many testable implications. See Anderson and Hendry (1984) for a follow-up study.
4.3.4 The Maximum Likelihood Estimation of Economic Relationships with Autoregressive Residuals by J.D. Sargan (1961)
Sargan (1961) proposes procedures to compute full information and limited information estimators--denoted ARFIML and ARLIML respectively--of parameters in a dynamic simultaneous equations model with autoregressive errors.
The procedure for ARFIML depends upon whether the system is over-identified or just identified. If the system is over-identified, ARFIML is obtained by maximizing the log-likelihood of the original system. If the system is just identified, ARFIML estimates can be obtained from the system's reduced form, with the precise approach depending upon whether the system is closed or open. Closed systems have vector autoregressions as reduced forms. The maximum likelihood estimates of the vector autoregression provide non-unique (but equally good) maximum likelihood estimates of the parameters in the unrestricted reduced form of the original system, from which a unique ARFIML solution can be obtained. If the system is open, maximum likelihood estimates of the unrestricted transformed reduced form parameters must be obtained directly, as with an iterative procedure or by a successive maximization procedure proposed by Sargan.
Sargan also derives the ARLIML estimator for a single equation in the system. If the errors of the estimated equation are the only errors that appear at a lag in that equation, then ARLIML coincides with Sargan's (1959) autoregressive instrumental variables estimator. If a lag of another equation's errors also appears in the estimated equation, estimation is more involved. The log-likelihood is more complicated, and its maximum must be found by an iterative procedure. Sargan (1961) also provides necessary and sufficient conditions for identification, and he formulates a mis-specification test.
4.3.5 Maximum Likelihood Estimation and Inference on Cointegration--With Applications to the Demand for Money by S. Johansen and K. Juselius (1990)
Johansen and Juselius (1990) develop procedures for analyzing vector autoregressions (VARs) that are possibly cointegrated, focusing on tests of cointegration and tests of restrictions on the cointegrating vectors and feedback coefficients. In the context of general-to-specific modeling, cointegration permits a reduction from I(1) to I(0); and valid restrictions on the cointegrating vectors and feedback coefficients permit yet additional reductions. Johansen and Juselius (1990) illustrate their approach by estimating and testing small monetary systems for Denmark and Finland.
Johansen and Juselius (1990) discuss the determination of the number of cointegration relations, the estimation of the cointegrating relations, and the testing of further restrictions in a cointegrated system. Johansen and Juselius also consider the role of deterministic terms in the underlying VAR. For instance, an intercept in the VAR is associated with both the mean of the cointegration relations and the mean of the variables' growth rates. A linear trend in the VAR is associated with both a linear trend in the cointegration relations and a linear trend in the variables' growth rates, with the latter implying a quadratic trend in the levels of the variables--an unrealistic property for most economic data. Care is thus required to ensure that the estimated model does not inadvertently allow for quadratic trends in the levels of the variables and ever-increasing growth rates. Johansen and Juselius distinguish clearly between inference about coefficients on nonstationary variables and inference about coefficients on I(0) variables.
Johansen and Juselius (1990) apply their procedures to small
monetary systems of Denmark and Finland that involve money, income,
prices, and the opportunity cost of holding money. The two datasets
are distinctly different and thus illustrate the versatility of
Johansen and Juselius's procedures, particularly regarding trends,
determination of cointegration, and subsequent testing. First,
their procedures can be applied to datasets with or without trends
in the underlying VAR, as exemplified by the Finnish data and
Danish data respectively. Second, the hypotheses concerning the
order of cointegrating rank are formulated as a sequence of nested
hypotheses and are tested using likelihood-ratio statistics, albeit
ones that are not asymptotically ![]() .
Johansen and Juselius (1990, Tables A1-A3) list critical values
for these statistics--tabulations that the profession has used
heavily since their publication. Third, remaining inferences based
on the likelihood ratio are asymptotically
.
Johansen and Juselius (1990, Tables A1-A3) list critical values
for these statistics--tabulations that the profession has used
heavily since their publication. Third, remaining inferences based
on the likelihood ratio are asymptotically ![]() because, once the order of cointegrating rank is determined, the
variables involved have all been transformed to I(0).
Fourth, the conjectured presence or absence of linear trends can be
tested. Fifth, likelihood-ratio statistics are derived for linear
restrictions on all cointegration vectors. These restrictions
include hypotheses such as stationarity and proportionality. Sixth,
Wald statistics are developed and are compared with the
likelihood-ratio statistics. Finally, likelihood-ratio statistics
are derived for linear restrictions on the weighting matrix,
including restrictions that imply valid conditioning (weak
exogeneity).
because, once the order of cointegrating rank is determined, the
variables involved have all been transformed to I(0).
Fourth, the conjectured presence or absence of linear trends can be
tested. Fifth, likelihood-ratio statistics are derived for linear
restrictions on all cointegration vectors. These restrictions
include hypotheses such as stationarity and proportionality. Sixth,
Wald statistics are developed and are compared with the
likelihood-ratio statistics. Finally, likelihood-ratio statistics
are derived for linear restrictions on the weighting matrix,
including restrictions that imply valid conditioning (weak
exogeneity).
Although the reduction to I(0) is but one of many possible reductions, its correct treatment is important for valid inference on other reductions and for the proper interpretation of dynamic economic systems. Moreover, the empirical presence of unit roots in many macroeconomic time series confirms the value of a sound statistical framework for analyzing nonstationary processes.
4.4 Model Selection Procedures
The theory of reduction in Section 2 helps clarify the nature of various model selection procedures. This overview to the current subsection focuses on sequential simplification tests, progressive modeling strategies, and cointegrated systems. The associated literature is closely related to the literature on dynamic specification, discussed in Section 4.3 above.
Sequential simplification tests have an important place in general-to-specific modeling strategies. Anderson (1962) [Volume I: Chapter 19] develops sequential simplification tests for determining the order of a polynomial in an index, such as time. That model structure generates a naturally ordered sequence of hypotheses. Anderson (1971, Ch. 6.4) carries over that approach to sequential simplification tests for autoregressive models. Using Monte Carlo methods, Yancey and Judge (1976) [Volume I: Chapter 20] assess the effects of model selection on the implied coefficient estimators. Mizon (1977b) [Volume I: Chapter 21] generalizes Anderson's approach for a special form of non-ordered hypotheses for nonlinear restrictions that arise in common factor analysis. Savin (1980) [Volume I: Chapter 22] shows how to use Bonferroni and Scheffé procedures to compute the overall significance level of a set of tests.
Two additional papers examine key aspects of model selection procedures. White (1990) [Volume I: Chapter 23] provides a consistent procedure for testing model mis-specification. The overall size of the test can be controlled, even when the set of hypotheses to be tested may not be representable by a sequence of nested hypotheses. Control of the overall significance level is gained by combining a set of indicator functions into a single indicator. However, combining indicators entails a loss of information regarding the potential directions in which the model is mis-specified. Phillips (1991) [Volume I: Chapter 24] discusses the relative advantages of unrestricted VARs, single-equation error correction models, and system error correction models for conducting inference in cointegrated systems, where that inference concerns reductions in those cointegrated systems.
4.4.1 The Choice of the Degree of a Polynomial Regression as a Multiple Decision Problem by T.W. Anderson (1962)
Anderson (1962) proposes a uniformly most powerful (UMP) procedure for testing hypotheses on a set of parameters, where those hypotheses have a natural ordering. Specifically, Anderson considers a model in which the independent variables are polynomials in a deterministic index (such as time), and the modeler wants to determine the order of polynomial required. Anderson assumes that the coefficients of the polynomial are:
| (29) |
where ![]() and
and ![]() in
equation (29) are the minimum
and maximum possible orders of the polynomial, both known a
priori. Additionally, Anderson assumes that the signs of the
coefficients are irrelevant and that the hypothesis
in
equation (29) are the minimum
and maximum possible orders of the polynomial, both known a
priori. Additionally, Anderson assumes that the signs of the
coefficients are irrelevant and that the hypothesis
![]() is of interest if and only if
is of interest if and only if
![]() for all
for all
![]() or
or ![]() . Under these assumptions, Anderson represents the
multiple-decision problem in terms of a set of mutually exclusive
hypotheses, from which he derives a uniquely ordered nested
sequence of hypotheses.
. Under these assumptions, Anderson represents the
multiple-decision problem in terms of a set of mutually exclusive
hypotheses, from which he derives a uniquely ordered nested
sequence of hypotheses.
Anderson shows that this procedure is similar and uniformly most powerful, and that the hypotheses (suitably defined) can be tested at the same significance level. Anderson (1962) notes that this procedure can be applied in testing the significance of other types of regressors, so long as the coefficients of these variables can be ordered as described above. Anderson (1971, pp. 270-276) develops that generalization for data densities in the exponential family.
While the construction of econometric models requires solving more complicated problems than the order of a polynomial, Anderson's results have three direct implications for general-to-specific modeling. First, they provide the basis for developing statistically powerful procedures for testing the relevance of explanatory variables in general; see Mizon (1977b)*. Second, the significance level can be kept constant by suitably redefining the sequence of hypotheses being tested. Third, as Anderson demonstrates, a simple-to-general procedure that starts from the lowest-order polynomial and incrementally increases the order of the polynomial is non-optimal. That contrasts with the optimality of the general-to-specific approach that he advocates.
4.4.2 A Monte Carlo Comparison of Traditional and Stein-rule Estimators Under Squared Error Loss by T.A. Yancey and G.G. Judge (1976)
Yancey and Judge (1976) assess the effects of model selection on the implied coefficient estimators, examining a single-equation model with normally distributed, independent errors. Yancey and Judge focus on the efficiency of least squares (which is maximum likelihood in their case), the pre-test estimator, the Stein rule estimator, the Stein rule positive estimator, and the Stein-modified positive rule estimator. Because of the complicated risk functions involved, Yancey and Judge use Monte Carlo techniques to evaluate and compare these different approaches to model selection. For the critical values examined, all estimators have higher gains in efficiency over least squares when the null and alternative hypotheses are close to each other. Yancey and Judge also show that the choice of the critical value is crucial to the results obtained.
4.4.3 Model Selection Procedures by G.E. Mizon (1977b)
Mizon (1977b) proposes a procedure for testing the dynamic specification of an econometric model. Mizon's approach generalizes Anderson's (1962*, 1971) approach to include a special form of non-ordered hypotheses for nonlinear restrictions that arise in Sargan's (1980b)* common factor analysis.
Mizon's procedure is not uniformly most powerful because a single set of uniquely ordered nested hypotheses cannot be defined. However, the testing problem can be represented by two main sequences of nested hypotheses. The first main sequence consists of a set of hypotheses on the maximal lag order of dynamics in a single-equation or simultaneous equations system ADL. That sequence is a set of subsequences of hypotheses, one subsequence for each variable in the model. Anderson's procedure is asymptotically uniformly most powerful for each subsequence. However, the combination of subsequences is not uniformly most powerful because tests across subsequences are not independent. The second main sequence evaluates how many common factors are present in the model's dynamics, as in Sargan (1980b)* and Hendry and Anderson (1977). This sequence is subsidiary to the first main sequence, in that the number of common factors is determined after the maximal lag length has been chosen.
The two-stage procedure is not uniformly most powerful, so Mizon
discusses situations in which more powerful procedures exist, and
he considers how to improve power after the maximal lag order and
the degree of common factors have been determined. First, tests of
mis-specification and the use of larger-than-conventional
significance levels in the first main sequence may improve the
power of Mizon's procedure. Second, Anderson's procedure assumes
that, if
![]() , then
, then
![]() for all
for all ![]() , precluding holes in the lag distributions. In
practice, such holes may be present, both in the general lag
distributions and in the (presumed) autoregressive error's
coefficients. Both economic theory and statistical regularities in
the data--such as seasonality--may provide hypotheses about holes
that can help improve power. Third, if some roots of an
autoregressive process are complex, first-order autocorrelation may
be rejected in favor of no autocorrelation. Thus, testing
simultaneously for autoregressive factors in pairs is recommended
in order to allow for complex roots.
, precluding holes in the lag distributions. In
practice, such holes may be present, both in the general lag
distributions and in the (presumed) autoregressive error's
coefficients. Both economic theory and statistical regularities in
the data--such as seasonality--may provide hypotheses about holes
that can help improve power. Third, if some roots of an
autoregressive process are complex, first-order autocorrelation may
be rejected in favor of no autocorrelation. Thus, testing
simultaneously for autoregressive factors in pairs is recommended
in order to allow for complex roots.
In a closely related paper, Mizon (1977a) analyzes selection procedures for nonlinear models. Mizon focuses on several issues: direct estimation of the nonlinear models; existence of a uniformly most powerful procedure for a composite hypothesis; and the importance of singling out which of the constituent hypotheses causes rejection of that composite hypothesis, if rejection occurs. Mizon distinguishes between three kinds of composite hypotheses.
- The composite hypothesis is formed by a set of independent constituent hypotheses. The composite hypothesis can then be tested by testing each constituent hypothesis separately.
- The constituent hypotheses are not independent, but they do have a natural and unique ordering. Specifically, if the constituent hypotheses are ordered from the least restrictive to the most restrictive, rejection of a given hypothesis implies rejection of all succeeding ones. Mizon discusses why Anderson's (1971) procedure is asymptotically valid in this situation, even for nonlinear models.
- The constituent hypotheses are not independent and do not have a natural ordering. Mizon suggests either (a) applying enough additional structure to achieve a unique ordering, or (b) applying an optimal procedure to every path of nested hypotheses--his "exhaustive testing procedure" (p. 1229). The exhaustive procedure may lead to multiple final models that are non-nested, so Mizon considers three ways for choosing between such models: the Cox (1961* procedure, Sargan's (1964) approach based on maximized likelihood values, and the Akaike (1973) information criterion; see also Akaike (1981)*.
Mizon (1977a) applies this structure for model selection to testing and choosing between nine nonlinear production functions.
4.4.4 The Bonferroni and the Scheffé Multiple Comparison Procedures by N.E. Savin (1980)
Savin (1980) considers testing composite hypotheses about the parameters in a regression model, both as a single-decision problem and as a multiple-decision problem. A single-decision procedure (i.e., using a joint test) is straightforward because the distribution of the test statistic--either exact or asymptotic--can usually be derived. If the decision on the composite hypothesis is derived from separate decisions on the constituent hypotheses, the situation is more complex because the individual test statistics may not be independent of each other. Savin provides a graphical example in which single-decision and multiple-decision approaches can lead to conflicting results and have different power.
Savin proposes both a Bonferroni procedure and a Scheffé procedure for testing restrictions on the model's parameters. The Bonferroni procedure is based on the Bonferroni inequality and allows one to compute an upper bound to the overall significance level in a multiple-decision problem. Savin also provides an expression for simultaneous confidence intervals for restrictions of primary interest. The composite hypothesis is rejected if and only if any of the individual hypotheses is rejected, so rejection of the composite hypothesis depends upon what restrictions are chosen to be of primary interest.
The Scheffé procedure is based on a theorem by Scheffé (1953) and provides the exact overall significance level. The overall Scheffé acceptance region of tests of individual hypotheses coincides with that of the joint test, so it is reasonable to carry out the joint test first and then test separate hypotheses if and only if the joint test rejects the composite hypothesis.
Savin (1980) compares the lengths of the Bonferroni and Scheffé confidence intervals, distinguishing between restrictions of primary interest and those of secondary interest. Bonferroni confidence intervals seem to be wider than Scheffé confidence intervals if the number of linear combinations of restrictions of primary interest is sufficiently large, and shorter if sufficiently small. Bonferroni confidence intervals are generally shorter than Scheffé confidence intervals for restrictions of primary interest and wider for restrictions of secondary interest. Savin also indicates how simultaneous confidence intervals can be derived for restrictions of secondary interest. Savin briefly discusses possible data-based inference, he extends both procedures for large samples, and he provides two empirical examples to show how to compute the confidence intervals.
4.4.5 A Consistent Model Selection Procedure Based on m-testing by H. White (1990)
White's (1990) framework is similar to that in
Section 2
and consists of a DGP, a parametric stochastic specification (a
model) of the mean of the conditional distribution, and a set of
requirements that a stochastic specification must satisfy to be
regarded as a correct specification. White proposes a model
selection procedure known as ![]() -testing, which
uses a single statistic for jointly testing a set of specification
requirements. Under suitable conditions,
-testing, which
uses a single statistic for jointly testing a set of specification
requirements. Under suitable conditions, ![]() -testing
selects the correct specification with a probability approaching
unity as the sample size becomes large.
-testing
selects the correct specification with a probability approaching
unity as the sample size becomes large.
The idea underlying ![]() -testing is as follows. If a
model with parameters
-testing is as follows. If a
model with parameters
![]() of a dataset
of a dataset
![]() is correctly specified,
then a collection of
is correctly specified,
then a collection of ![]() indicator functions
indicator functions
![]() for
for
![]() must satisfy
must satisfy
![]() for
for
![]() . Testing for correct
specification can thus be performed with a single test on the
sample average of
. Testing for correct
specification can thus be performed with a single test on the
sample average of ![]() . White proposes four
sets of requirements for correct specification, and they are
closely related to the model evaluation criteria in
Hendry and Richard (1982)* and Hendry (1987)*. Each set of
requirements represents a degree of closeness to correct
specification, and each has a joint indicator function.
. White proposes four
sets of requirements for correct specification, and they are
closely related to the model evaluation criteria in
Hendry and Richard (1982)* and Hendry (1987)*. Each set of
requirements represents a degree of closeness to correct
specification, and each has a joint indicator function.
White describes the implications of his results for the Hendry methodology.
Thus, we have an-testing model selection procedure which rejects sufficiently mis-specified models and retains sufficiently correctly specified models with confidence approaching certainty as [the sample size becomes large]. Use of such procedures has the potential to remove some of the capriciousness associated with certain empirical work in economics and other fields. For this reason we wholeheartedly endorse progressive research strategies such as that of Hendry and Richard (1982) and Hendry (1987) for arriving at sufficiently well specified characterizations of the DGP. We believe the
-testing framework set forth here can be a convenient vehicle for such strategies. (p. 381)
White's article thus helps formalize the statistical basis for model evaluation and design, as summarized in Sections 2 and 3.
4.4.6 Optimal Inference in Cointegrated Systems by P.C.B. Phillips (1991)
Phillips (1991) derives conditions for optimal inferences in a cointegrated system, focusing on conditions that obtain distributions in the locally asymptotically mixed normal family. In essence, asymptotic normal inference is feasible, once the presence of unit roots is known and the system can be written in a triangular representation. Inferences about the presence of unit roots themselves (and so of cointegration) involve non-standard distributions, as discussed in Johansen (1988) and Johansen and Juselius (1990)*.
Phillips's results are particularly important for general-to-specific modeling because they partition inferences into two stages:
- one about unit roots, and involving non-standard distribution theory; and
- one conditioning upon the presence of (and upon a certain amount of structure about) unit roots, but involving only standard distribution theory.
In addition to being an important conceptual clarification, this partitioning has a valuable empirical implication: it is advantageous to sort out issues of integration and cointegration at the outset of an empirical analysis, and then proceed to the remaining inferences. Otherwise, it can be very difficult to conduct proper inferences.
Phillips's results include the following. First, if the
triangular system's errors are independently and identically
distributed normal, then maximum likelihood estimates of the
long-run parameters coincide with least squares applied to a
suitably augmented version of the triangular representation; see
Phillips's equation (7). Second, the asymptotic distribution
of these estimates is in the locally asymptotically mixed normal
family. Third, these estimates are asymptotically optimal. Fourth,
the maximum likelihood estimates of the triangular form have
different asymptotic properties from those obtained from a VAR
representation or an unrestricted error correction model because
the VAR and the ECM implicitly estimate unit roots. Fifth, the
results can be (and are) generalized to account for error processes
that are not independently and identically distributed normal.
Sixth, joint estimation of long-run parameters and short-run
dynamics is not required for optimal estimation of the long-run
parameters. Seventh, subsystem and single-equation estimation are
equivalent to full system maximum likelihood under only very
specific conditions. Eighth, statistics for testing hypotheses on
the long-run parameters are asymptotically ![]() .
.
Through its focus on cointegrated systems, Phillips (1991) has close links with the articles in Section 4.3 on dynamic specification.
4.5 Model Selection Criteria
Model selection criteria in the form of information criteria are utilized in three aspects of general-to-specific modeling: model selection after multiple path searches, the reduction of lag length, and the choice of maximal lag length. On the first, if several undominated congruent models are found after multiple path searches, a selection needs to be made. Information criteria provide a tool for model selection. On the second, the lag order may be determined in practice by information criteria--rather than by significance testing--when constructing econometric models of time series. On the third, the maximal lag order is often determined by the number of observations available. Large values of an information criterion may suggest invalid exclusion of higher-order lags, so a consistent procedure using an information criterion can function as part of a progressive research strategy.
Many information criteria have been proposed, including:
- the Akaike (1973) information criterion (denoted AIC), as discussed in detail by Akaike (1981) [Volume II: Chapter 1];
- the Schwarz criterion (denoted SC, or sometimes BIC for Bayesian information criterion), developed in Schwarz (1978) [Volume II: Chapter 2];
- the Hannan-Quinn criterion (denoted HQ), developed in Hannan and Quinn (1979) [Volume II: Chapter 3]; and
- the posterior information forecast evaluation criterion (denoted PIC), developed and analyzed in Phillips (1996) [Volume II: Chapter 6].
Atkinson (1981) [Volume II: Chapter 4] constructs a criterion generating equation, which helps clarify the relationships between the various criteria. Sawyer (1983) [Volume II: Chapter 5] constructs a criterion based on the Kullback-Leibler information measure.
4.5.1 Likelihood of a Model and Information Criteria by H. Akaike (1981)
Akaike (1981) shows that his 1973 "AIC" information criterion is a maximum predictive likelihood selection procedure. He also compares the AIC with other then-extant information criteria.
Akaike uses a paradox in Bayesian model selection to justify the AIC. If the modeler has diffuse priors about the parameters of a given model, then the likelihood of that model tends to zero as the prior becomes sufficiently diffuse. To clarify the nature of this problem, Akaike decomposes the log-likelihood into the prior log-likelihood--which is the "expected log likelihood under the assumption of the model" (pp. 5-6)--and an incremental log-likelihood--which is the deviation of the actual log-likelihood of the model from its expectation. The incremental log-likelihood converges to a finite quantity, but the prior log-likelihood converges to minus infinity as the measure of diffuseness becomes large, thereby creating the paradox.
Following this course of thought, Akaike defines the predictive log-likelihood as the sum of the prior predictive log-likelihood and the incremental predictive log-likelihood. He then shows that (aside from a constant term) the AIC is simply minus twice the log of the predictive log-likelihood:
| (30) |
where ![]() is the log-likelihood for the model,
and
is the log-likelihood for the model,
and ![]() is the number of parameters in the model.
Minimizing the AIC as a model selection procedure is thus
equivalent to maximizing the predictive log-likelihood.
is the number of parameters in the model.
Minimizing the AIC as a model selection procedure is thus
equivalent to maximizing the predictive log-likelihood.
Akaike (1981) then discusses why the Schwarz (1978)* criterion is not based on the expected behavior of the likelihood, and that it is valid only if the priors are strongly held. Akaike also analyzes certain modifications to the AIC--as in Sawa (1978)--and finds some shortcomings with them.
4.5.2 Estimating the Dimension of a Model by G. Schwarz (1978)
Schwarz (1978) proposes an alternative information criterion for choosing between linear models when the joint distribution of the data belongs to the Koopman-Darmois family. Schwarz's criterion is:
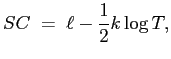 |
(31) |
where ![]() is the sample size. Schwarz formulates his
procedure in a Bayesian framework and analyzes its asymptotic
properties. If the priors assign positive probability to all
subspaces corresponding to contending models, and if there is a
fixed penalty for choosing the wrong model, then a Bayesian
analysis leads to choosing the model that maximizes SC. Because of
its relationship to Bayesian analysis, the Schwarz criterion is
sometimes known as the Bayesian information criterion. That said,
the asymptotic properties of SC as a selection criterion do not
depend upon the priors, making the Schwarz criterion appealing
beyond the Bayesian context.
is the sample size. Schwarz formulates his
procedure in a Bayesian framework and analyzes its asymptotic
properties. If the priors assign positive probability to all
subspaces corresponding to contending models, and if there is a
fixed penalty for choosing the wrong model, then a Bayesian
analysis leads to choosing the model that maximizes SC. Because of
its relationship to Bayesian analysis, the Schwarz criterion is
sometimes known as the Bayesian information criterion. That said,
the asymptotic properties of SC as a selection criterion do not
depend upon the priors, making the Schwarz criterion appealing
beyond the Bayesian context.
Schwarz notes that his information criterion and the AIC differ
only in the way that they treat the additive term involving the
number of parameters in the model. Specifically, SC weights![]() by ½logT, relative to AIC. SC thus
tends to favor models with fewer parameters, particularly in larger
samples. Because of this different treatment of
by ½logT, relative to AIC. SC thus
tends to favor models with fewer parameters, particularly in larger
samples. Because of this different treatment of ![]() ,
AIC is not a consistent model selection procedure for certain
classes of models; see also Atkinson (1981)*.
,
AIC is not a consistent model selection procedure for certain
classes of models; see also Atkinson (1981)*.
4.5.3 The Determination of the Order of an Autoregression by E.J. Hannan and B.G. Quinn (1979)
Hannan and Quinn (1979) provide a criterion for estimation of the
order ![]() of a stationary, ergodic, finite-order
autoregressive process. Their estimator
of a stationary, ergodic, finite-order
autoregressive process. Their estimator ![]() of the true order
of the true order ![]() is
obtained by minimizing the criterion function:
is
obtained by minimizing the criterion function:
| (32) |
with respect to ![]() , where
, where
![]() is the estimate of
is the estimate of
![]() obtained from solving the
Yule-Walker equations for a
obtained from solving the
Yule-Walker equations for a ![]() th-order
autoregressive model, and
th-order
autoregressive model, and ![]() .
.
Hannan and Quinn show that ![]() is strongly
consistent for
is strongly
consistent for ![]() when the postulated maximum
order of the autoregressive process is greater than or equal to the
true order. By the same token,
when the postulated maximum
order of the autoregressive process is greater than or equal to the
true order. By the same token, ![]() is strongly
consistent for
is strongly
consistent for ![]() when the postulated maximum
order of the process is allowed to increase at a suitable rate with
the sample size. Hannan and Quinn simulate a first-order
autoregressive process by Monte Carlo and show that HQ performs
better than AIC for moderately to highly autoregressive processes
and larger sample sizes. Hannan and Quinn (1979) thus recommend HQ for
larger sample sizes when an autoregressive process is a good
approximation to the DGP.
when the postulated maximum
order of the process is allowed to increase at a suitable rate with
the sample size. Hannan and Quinn simulate a first-order
autoregressive process by Monte Carlo and show that HQ performs
better than AIC for moderately to highly autoregressive processes
and larger sample sizes. Hannan and Quinn (1979) thus recommend HQ for
larger sample sizes when an autoregressive process is a good
approximation to the DGP.
4.5.4 Likelihood Ratios, Posterior Odds and Information Criteria by A.C. Atkinson (1981)
Atkinson (1981) provides a general function that includes
various existing model selection criteria as special cases,
including AIC, SC, HQ, final prediction error (FPE), Mallows's
C![]() criterion, and Atkinson's posterior
odds. For autoregressive processes, Atkinson's criterion generating
function is the negative of the log-likelihood, plus some weighting
times the number of parameters in the model. For a
criterion, and Atkinson's posterior
odds. For autoregressive processes, Atkinson's criterion generating
function is the negative of the log-likelihood, plus some weighting
times the number of parameters in the model. For a ![]() th-order autoregressive model, the criterion generating
function (CGF) is equivalent to:
th-order autoregressive model, the criterion generating
function (CGF) is equivalent to:
| (33) |
where ![]() (Atkinson's "
(Atkinson's "![]() ") is a
value or function associated with the particular information
criterion. Thus, in equation (33),
") is a
value or function associated with the particular information
criterion. Thus, in equation (33), ![]() for AIC,
for AIC, ![]() for SC, and
for SC, and
![]() for HQ;
cf. equations (30), (31),
and (32). See
Campos, Hendry, and Krolzig (2003, Figures 1-3) for a graphical
comparison of these and other model selection criteria; see also
Hendry and Krolzig (2005).
for HQ;
cf. equations (30), (31),
and (32). See
Campos, Hendry, and Krolzig (2003, Figures 1-3) for a graphical
comparison of these and other model selection criteria; see also
Hendry and Krolzig (2005).
Atkinson shows that the criterion increases with the sample size
for false models, and that the probability of choosing an
over-parameterized model can be controlled by appropriately setting
![]() . Atkinson also discusses the optimum
choice of
. Atkinson also discusses the optimum
choice of ![]() .
.
4.5.5 Testing Separate Families of Hypotheses: An Information Criterion by K.R. Sawyer (1983)
Cox (1961*, 1962*) derives a test for comparing two non-nested hypotheses, basing the test on the likelihood ratio of those hypotheses relative to what that likelihood ratio would be if one of the hypotheses were the DGP. Sawyer (1983) derives a similar test that uses the Kullback-Leibler information criterion rather than the likelihood ratio. Sawyer's statistic is asymptotically normally distributed when the assumed hypothesis is actually the DGP.
Sawyer illustrates his procedure with the choice between two non-nested models that have non-stochastic regressors and Gaussian errors. When one model's regressors are orthogonal to the other model's regressors, Cox's test does not exist, but Sawyer's test is still valid, and it is equivalent to the F-test applied to the minimal nesting model. Sawyer also compares the finite sample properties of the two tests for the Monte Carlo experiments in Pesaran (1974)*, focusing on the statistics' moments, size, and power.
4.5.6 Econometric Model Determination by P.C.B. Phillips (1996)
Phillips (1996) develops, analyzes, and justifies automated model selection procedures, focusing on the updating of forecasting models when data properties change and when the DGP is nonconstant. Phillips commences with the Bayesian data density, constructs the conditional density (conditional on past observations), links it to the posterior information criterion (PIC) for forecasts, discusses how PIC is an extension of SC, and derives asymptotic properties of model selection using PIC.
Phillips's numerous results include the following. Maximizing PIC is asymptotically equivalent to maximizing the penalized log-likelihood. When the DGP is constant over time, PIC is valid for stationary data, integrated data, and cointegrated data. PIC leads to the best model that can be chosen from a parametric class, even if the true density does not belong to that class. When the DGP is nonconstant, PIC achieves the lower bound of closeness to the evolving true density.
Phillips shows how PIC can help detect when an existing model using historical data may no longer adequately capture the behavior of recent data. For model selection, such a situation may lead to discarding some data or to weeding out certain models. Phillips also illustrates PIC for the joint selection of cointegration rank, lag length, and trend in a VAR, and for the choice between unrestricted VARs, cointegrated VARs, and Bayesian VARs (such as ones with Minnesota priors).
4.6 Model Comparison
The literature on model comparison is closely tied to the literature on model selection criteria, as Sawyer (1983)* in particular highlights. The literature on model comparison also spurred the development of encompassing, both as a concept and as a practical tool; see Section 4.7. The articles discussed below focus on comparing non-nested models: Section 4.4 focuses on nested models.
As a pair, Cox (1961) and Cox (1962) [Volume II:
Chapters 7 and 8] provide the key source on model
comparison. Cox proposes a modified likelihood-ratio statistic for
comparing non-nested models, derives its asymptotic distribution,
and illustrates its application for several specific classes of
models. Cox (1961)* and Cox (1962)* seed a large literature on
testing non-nested hypotheses; see MacKinnon (1983),
Mizon and Richard (1986)*, and Hendry and Richard (1989)* for summaries.
Dhrymes, Howrey, Hymans, Kmenta, Leamer, Quandt, Ramsey, Shapiro,
and Zarnowitz (1972) [Volume II: Chapter 9] assess
numerous procedures for comparing and evaluating models, including
(for non-nested models) Ramsey's (1969) test, Cox's test, the
Bayesian approach, and the use of R![]() .
Pesaran (1974) [Volume II: Chapter 10] derives the
explicit form of the Cox statistic for non-nested linear regression
models, and he compares its finite sample properties with the
F-statistic that evaluates each
model of interest directly against the comprehensive model that
nests the two competing non-nested models. This subsection on model
comparison thus segues directly to Section 4.7 on
encompassing.
.
Pesaran (1974) [Volume II: Chapter 10] derives the
explicit form of the Cox statistic for non-nested linear regression
models, and he compares its finite sample properties with the
F-statistic that evaluates each
model of interest directly against the comprehensive model that
nests the two competing non-nested models. This subsection on model
comparison thus segues directly to Section 4.7 on
encompassing.
4.6.1 Tests of Separate Families of Hypotheses by D.R. Cox (1961)
Drawing on the framework for the Neyman-Pearson likelihood ratio, Cox (1961) proposes a procedure for testing two separate families of hypotheses, assuming that the parameters are continuous and are interior to their parameter spaces. Cox defines his test statistic as the deviation of the Neyman-Pearson likelihood ratio from its expected value under the hypothesis chosen to be the null hypothesis.
The asymptotic distribution of Cox's statistic is non-trivial to derive. However, if both hypotheses belong to the Koopman-Darmois family of densities, then, under suitable conditions, the statistic can be written in terms of the estimates of the parameters of the null hypothesis, the estimates of the parameters of the alternative hypothesis, and the value that the latter converge to under the null hypothesis. Cox derives the asymptotic covariance matrix for the estimates of both models, from which he obtains the statistic's asymptotic variance; and he shows that the statistic is asymptotically normally distributed.
Cox then suggests how to proceed for more general cases. He also notes a number of caveats for some specific classes of hypotheses. In particular, for some classes of hypotheses, the statistic's asymptotic distribution may not be normal.
4.6.2 Further Results on Tests of Separate Families of Hypotheses by D.R. Cox (1962)
Cox (1962) derives the asymptotic distribution of the Cox (1961)* test statistic under maximum likelihood estimation when the sample is independently and identically distributed and when the assumption of identical distributions is relaxed. Cox's procedure is also valid for estimators that are asymptotically equivalent to the maximum likelihood estimator. Cox discusses how to compute the statistic; and he illustrates it with detailed derivations for examples of testing log-normal versus exponential distributions, Poisson versus geometric distributions, and multiplicative versus additive models.
4.6.3 Criteria for Evaluation of Econometric Models by P.J. Dhrymes, E.P. Howrey, S.H. Hymans, J. Kmenta, E.E. Leamer, R.E. Quandt, J.B. Ramsey, H.T. Shapiro, and V. Zarnowitz (1972)
Dhrymes, Howrey, Hymans, Kmenta, Leamer, Quandt, Ramsey, Shapiro, and Zarnowitz (1972) aim to systematize both parametric and non-parametric evaluation of econometric models. Parametric evaluation includes model selection, estimation, hypothesis testing, computation of ex post forecasts and structural stability tests, and testing against new datasets. The authors associate the first four activities with model design and the last activity with model evaluation. Non-parametric evaluation includes examination of goodness-of-fit statistics (such as the mean square forecast error) and spectral methods, and it can help check whether the model is useful for particular purposes. In the context of general-to-specific modeling, the framework in Dhrymes et al. can be interpreted as a loose categorization similar to the taxonomy of model evaluation and design criteria developed later by Hendry and Richard (1982)*; see also Section 2.6.
Dhrymes et al. view model selection as an activity for
discriminating between functional forms. They first examine
discrimination between non-nested specifications, comparing
Ramsey's (1969) test, Cox's (1961*, 1962*) test, the Bayesian
approach, and the use of R![]() . Dhrymes et
al. then consider testing of sequences of nested hypotheses,
focusing on the Lagrange multiplier statistic and the comparable
F-statistic; and they generalize
the Chow (1960) statistic for predictive failure to forecasts from
a system. They consider various methods for evaluating a model
after its initial construction, as by regressing actual values on
predicted values and testing hypotheses about the coefficients.
That approach is the basis for forecast encompassing; see
Chong and Hendry (1986)* and Ericsson (1992b)*. Finally, Dhrymes et
al. outline possible non-parametric measures for model
evaluation, including measures such as the mean square forecast
error. The usefulness of many of these measures is reconsidered by
Clements and Hendry (1998, 1999).
. Dhrymes et
al. then consider testing of sequences of nested hypotheses,
focusing on the Lagrange multiplier statistic and the comparable
F-statistic; and they generalize
the Chow (1960) statistic for predictive failure to forecasts from
a system. They consider various methods for evaluating a model
after its initial construction, as by regressing actual values on
predicted values and testing hypotheses about the coefficients.
That approach is the basis for forecast encompassing; see
Chong and Hendry (1986)* and Ericsson (1992b)*. Finally, Dhrymes et
al. outline possible non-parametric measures for model
evaluation, including measures such as the mean square forecast
error. The usefulness of many of these measures is reconsidered by
Clements and Hendry (1998, 1999).
4.6.4 On the General Problem of Model Selection by M.H. Pesaran (1974)
Pesaran (1974) considers how to choose between non-nested linear regression models, deriving the explicit form of the Cox statistic for this situation. The Cox statistic is asymptotically distributed as standardized normal, provided that the contending sets of regressors are not orthogonal to each other.
Pesaran compares the finite sample properties of the Cox test
(Pesaran's "![]() -test") with those of the exact
F-test in a Monte Carlo study. The
F-test compares the model of
interest directly against the comprehensive model that nests the
two competing non-nested models. Pesaran finds that the
small-sample size of the Cox test is much larger than its nominal
size, but that its Type II error is smaller than that associated
with the
F-test. Pesaran argues against
calculating a test's power from its Type II error alone because
there is a nonzero probability of rejecting both models. Pesaran
proposes an alternative measure of power--the probability of
jointly accepting the correct specification and rejecting the
incorrect specification. In Pesaran's Monte Carlo study, the Cox
test performs better than the
F-test on this measure. Pesaran
also presents three conceptual reasons for using the Cox test
rather than the
F-test: the comprehensive model is
arbitrary, the
F-test may be inconclusive, and the
F-test may be affected by high
collinearity between the competing sets of regressors.
Pesaran and Deaton (1978) subsequently derive the Cox statistic for
nonlinear regression models, and Ericsson (1983) derives it for
instrumental variables estimators.
-test") with those of the exact
F-test in a Monte Carlo study. The
F-test compares the model of
interest directly against the comprehensive model that nests the
two competing non-nested models. Pesaran finds that the
small-sample size of the Cox test is much larger than its nominal
size, but that its Type II error is smaller than that associated
with the
F-test. Pesaran argues against
calculating a test's power from its Type II error alone because
there is a nonzero probability of rejecting both models. Pesaran
proposes an alternative measure of power--the probability of
jointly accepting the correct specification and rejecting the
incorrect specification. In Pesaran's Monte Carlo study, the Cox
test performs better than the
F-test on this measure. Pesaran
also presents three conceptual reasons for using the Cox test
rather than the
F-test: the comprehensive model is
arbitrary, the
F-test may be inconclusive, and the
F-test may be affected by high
collinearity between the competing sets of regressors.
Pesaran and Deaton (1978) subsequently derive the Cox statistic for
nonlinear regression models, and Ericsson (1983) derives it for
instrumental variables estimators.
4.7 Encompassing
Encompassing provides a basis for constructing tests of a given model against an alternative specification, whether those models are nested or non-nested. In general-to-specific modeling, one common application of encompassing arises when comparing congruent models obtained from alternative simplification paths.
An encompassing test evaluates a given model against the information content in an alternative specification that is not a special case of the given model. Equivalently, an encompassing test assesses whether a given model is able to explain why the alternative explanation obtains the results that it does. If the given model were the DGP, then the alternative specification would be derivable from the given model; see Section 2.1. Thus, an encompassing model explains the results obtained by an alternative model. More generally, an encompassing model may predict unnoticed features of an alternative model, such as error autocorrelation or parameter nonconstancy; and it may help explain why the alternative model was selected. As with the evaluation of a model on its own data, evaluation of a model by encompassing can utilize (relative) past, current, and future information sets, with the relevant concepts being variance and parameter encompassing, exogeneity encompassing, and forecast encompassing.
Mizon and Richard (1986), Hendry and Richard (1989), Wooldridge (1990),
and Lu and Mizon (1996) [Volume II: Chapters 11, 12, 13,
and 14, respectively] focus on variance and parameter
encompassing. Mizon and Richard (1986)* consider a wide range of
possible encompassing test statistics and show that Cox-type tests
of non-nested hypotheses are tests of variance encompassing.
Hendry and Richard (1989)* summarize the encompassing literature to
date, generalize certain aspects of encompassing, and consider
various nuances to encompassing when the models are dynamic.
Wooldridge (1990)* derives a conditional mean encompassing test
and compares it to the Cox and Mizon-Richard tests.
Lu and Mizon (1996)* establish an equivalence of ![]() -testing (as in White (1990)*) and the encompassing
procedures.
-testing (as in White (1990)*) and the encompassing
procedures.
Hendry (1988) [Volume II: Chapter 15] develops statistics for exogeneity encompassing, focusing on the Lucas (1976) critique and the role of expectations in econometric models. In empirical analysis, contending models often differ in their treatment of expectations. Two common forms are feedforward (or expectations-based) models such as rational expectations models, and feedback (or conditional) models such as the conditional model in equation (15). Expectations-based models are of particular interest to economists: they have an intuitive appeal, and they are ubiquitous, in fair part because of the Lucas critique. Lucas (1976) shows that, under an assumption of rational expectations, coefficients in conditional econometric equations are nonconstant when policy rules change. That nonconstancy is an encompassing implication, and it provides the basis for Hendry's exogeneity encompassing statistics.
Chong and Hendry (1986), Ericsson (1992b), and Ericsson and Marquez (1993) [Volume II: Chapters 16, 17, and 18, respectively] develop tests of forecast encompassing. Chong and Hendry (1986)* discuss the usefulness of various methods for evaluating econometric systems and propose a forecast encompassing test, which assesses a model's ability to explain the forecasts obtained from an alternative model. In addition, mean square forecast errors have often been used to compare models' forecast performance. Ericsson (1992b)* shows that achieving the smallest mean square forecast error is neither necessary nor sufficient for parameter constancy. This separation of properties leads to a forecast-model encompassing test, which assesses a given model's ability to explain the model used to generate the alternative model's forecasts. Ericsson and Marquez (1993)* extend the results in Chong and Hendry (1986)* and Ericsson (1992b)* to nonlinear systems.
Hendry and Mizon (1993) [Volume II: Chapter 19] focus specifically on encompassing in dynamic systems. Hendry and Mizon develop a test for whether a structural econometric model parsimoniously encompasses the VAR from which it is derived.
4.7.1 The Encompassing Principle and its Application to Testing Non-nested Hypotheses by G.E. Mizon and J-F. Richard (1986)
Mizon and Richard (1986) develop a class of Wald encompassing test statistics that unifies testing of both nested and non-nested hypotheses. The Wald encompassing test statistic (or "WET statistic") compares a parameter estimate for the alternative hypothesis with an estimate of what the null hypothesis implies that the alternative hypothesis's parameter estimate would be, if the null hypothesis were correct. If these two estimates are close together, given the uncertainty of estimation, then the null hypothesis encompasses the alternative hypothesis--at least for the parameter estimated. If these two estimates are far apart, then the alternative hypothesis contains information that the null hypothesis has difficulty explaining, in which case the null hypothesis does not encompass the alternative hypothesis. While the test is "against" the alternative hypothesis, it is the null hypothesis that is being evaluated. Specifically, the null hypothesis is being evaluated against information in the alternative hypothesis that is not contained in the null hypothesis. Mizon and Richard derive the asymptotic distribution of the Wald encompassing test statistic, and they demonstrate its asymptotic equivalence to likelihood ratio and Lagrange multiplier statistics under certain conditions.
Mizon and Richard also show that the Wald encompassing test statistic is asymptotically equivalent to the Cox statistic for linear regression models when the parameter being estimated is the model's error variance. The Cox statistic is thus a variance encompassing test statistic. The Cox statistic is not equivalent (even asymptotically) to the Wald encompassing test statistic for the regression parameters. That distinction leads to a discussion of the implicit null hypothesis defined by a test statistic, helping clarify the relationships between the various test statistics. In particular, the Cox statistic has an implicit null hypothesis that is larger than its nominal null hypothesis, implying power equal to size for some regions of the comprehensive hypothesis.
In related work, Mizon (1984) shows that the Wald encompassing
test statistic is a test generating equation, in that it generates
numerous other extant test statistics as special cases. These
statistics include the Cox statistic when the parameter being
encompassed is the other model's error variance, Sawyer's (1983)*
statistic based on the information criterion, a non-nested
hypothesis test statistic based on the empirical moment generating
function, the conventional
![]() -statistic that tests for invalid
exclusion of regressors, Sargan's (1980b)* comfac statistic,
Sargan's (1964) statistic for testing the validity of instruments,
Hausman's (1978) mis-specification test statistic, and
specification-robust Wald and Largrange multiplier test statistics.
Encompassing is a criterion for comparing models, rather than a
tool for choosing between them. Mizon also discusses the role of
encompassing in a progressive research strategy. In subsequent
work, Kent (1986) examines the properties of the Cox and Wald
encompassing tests when the joint distribution is degenerate, he
proposes an additional test that combines features of both the Cox
test and the Wald encompassing test, and he analyzes the geometry
of the tests.
-statistic that tests for invalid
exclusion of regressors, Sargan's (1980b)* comfac statistic,
Sargan's (1964) statistic for testing the validity of instruments,
Hausman's (1978) mis-specification test statistic, and
specification-robust Wald and Largrange multiplier test statistics.
Encompassing is a criterion for comparing models, rather than a
tool for choosing between them. Mizon also discusses the role of
encompassing in a progressive research strategy. In subsequent
work, Kent (1986) examines the properties of the Cox and Wald
encompassing tests when the joint distribution is degenerate, he
proposes an additional test that combines features of both the Cox
test and the Wald encompassing test, and he analyzes the geometry
of the tests.
4.7.2 Recent Developments in the Theory of Encompassing by D.F. Hendry and J.-F. Richard (1989)
Hendry and Richard (1989) summarize numerous then-extant results on encompassing in a unifying framework; and they develop further results, particularly for dynamic models. Hendry and Richard first define concepts such as parametric encompassing, parsimonious encompassing, encompassing with respect to an estimator, the minimal nesting model, and the minimal completing model. Analytical examples then illustrate these concepts and various results. In particular, encompassing analysis can be carried out by encompassing the minimal nesting model; exact distributions are derivable in some situations; and variance dominance is necessary but not sufficient for parameter encompassing in linear models. Hendry and Richard propose a Monte Carlo procedure for calculating the empirical distribution of the Wald encompassing test statistic--a procedure that is particularly useful when no explicit analytical results are available. Hendry and Richard also discuss the choice between encompassing tests in terms of power, invariance, and computational burden, highlighting how the Wald encompassing test statistic arises naturally from a theory of reduction.
Hendry and Richard then develop a theory of encompassing for dynamic systems, including ones with Granger causality. If Granger causality is present, the marginal model features much more prominently in calculating the encompassing statistic than if Granger causality is lacking. Govaerts, Hendry, and Richard (1994) provide additional details. Hendry and Richard (1989) finish by considering the concept of encompassing in a Bayesian framework.
4.7.3 An Encompassing Approach to Conditional Mean Tests with Applications to Testing Nonnested Hypotheses by J.M. Wooldridge (1990)
Wooldridge (1990) derives an easily computable encompassing
test that is robust to heteroscedasticity. This conditional mean
encompassing test (or "CME test") does not require computation of
the asymptotic covariance matrix of estimates of either model under
the null hypothesis. Wooldridge derives the conditional mean
encompassing test statistic for nonlinear least squares and shows
that it has asymptotic ![]() distributions under
both the null hypothesis and a local alternative hypothesis. This
test statistic may utilize any
distributions under
both the null hypothesis and a local alternative hypothesis. This
test statistic may utilize any ![]() -consistent
estimator of the parameters of the null hypothesis.
-consistent
estimator of the parameters of the null hypothesis.
Wooldridge derives the conditional mean encompassing test statistic for non-nested linear models, linear versus loglinear models, and linear versus exponential models, showing that the test statistic is asymptotically equivalent to a suitably constructed Lagrange multiplier statistic. Wooldridge extends his results for weighted nonlinear least squares; notes additional relationships with the Lagrange multiplier statistic, Wald encompassing statistic, Hausman statistic, and Davidson and MacKinnon's (1981) statistic; and proposes heteroscedasticity-robust versions of the last.
4.7.4 The Encompassing Principle and Hypothesis Testing by M. Lu and G.E. Mizon (1996)
Lu and Mizon (1996) establish several relationships between
statistics developed for testing the specification of econometric
models. Lu and Mizon show that the ![]() -testing
procedure and the encompassing principle can generate equivalent
test statistics, which are Lagrange multiplier in nature. That
said, the two principles have different motivations:
-testing
procedure and the encompassing principle can generate equivalent
test statistics, which are Lagrange multiplier in nature. That
said, the two principles have different motivations: ![]() -testing is performed mainly to check for model
mis-specification, whereas encompassing tests are viewed as
specification tests, particularly in the context of
general-to-specific modeling.
-testing is performed mainly to check for model
mis-specification, whereas encompassing tests are viewed as
specification tests, particularly in the context of
general-to-specific modeling.
4.7.5 The Encompassing Implications of Feedback Versus Feedforward Mechanisms in Econometrics by D.F. Hendry (1988)
Hendry (1988) proposes and implements a test of super exogeneity that is based on tests of constancy. Super exogeneity is the concept relevant for valid conditioning when regimes change, so it is of particular interest to economists. Hendry's test is interpretable as an encompassing test of feedback versus feedforward models, and it provides a means of testing the Lucas critique.
Specifically, Hendry develops procedures for discriminating between feedback and feedforward models, highlighting the role of changes in the marginal models for the expectations processes. Sufficient changes in the marginal processes permit distinguishing between feedback and feedforward models, which advocates testing the constancy of the proposed marginal models. Recursive estimation and recursive testing are useful tools for doing so. Hendry illustrates his approach, empirically rejecting Cuthbertson's (1988) expectations interpretation of a constant conditional model for U.K. M1 demand. Such conditional models still have a forward-looking interpretation, albeit one formulated in terms of data-based rather than model-based predictors; see Campos and Ericsson (1988, 1999*] and Hendry and Ericsson (1991).
In a rejoinder, Cuthbertson (1991) qualifies Hendry's (1988) results, emphasizing finite sample issues and model design. Favero and Hendry (1992) discuss and rebut Cuthbertson's (1991) criticisms of Hendry (1988), focusing on the asymptotic and finite sample power of the encompassing tests. Favero and Hendry also examine different tests of super exogeneity and invariance, and they generalize results in Hendry (1988) by considering expectations about future values of variables. Ericsson and Hendry (1999) derive additional encompassing implications of conditional models for rational expectations models. Despite the importance of testing the Lucas critique, it remains untested in much empirical work; see Ericsson and Irons (1995).
4.7.6 Econometric Evaluation of Linear Macro-economic Models by Y.Y. Chong and D.F. Hendry (1986)
Chong and Hendry (1986) develop and analyze a forecast encompassing test as a feasible device for evaluating multi-equation econometric models. Chong and Hendry first critique several common procedures for evaluating econometric systems, including dynamic simulation, inter-model ex ante forecast performance, and the economic plausibility of the model. Chong and Hendry propose four alternative devices for model evaluation: forecast encompassing, multi-step ahead forecast errors, long-run properties, and inter-equation feedbacks. Chong and Hendry focus on forecast encompassing and multi-step ahead forecast errors, simulating finite sample properties of the latter.
Chong and Hendry construct their forecast encompassing test
statistic from an artificial regression in which the dependent
variable is the variable being forecast and the regressors are the
forecasts from two competing models. Under the null hypothesis that
the first model is correct, the coefficients in that regression
should be unity on the correct model's forecasts and zero on the
incorrect model's forecasts. From that property, Chong and Hendry
base their actual forecast encompassing test statistic on a
(modified) artificial regression of the forecast errors for the
model of the null hypothesis on the forecasts of the alternative
model. Their forecast encompassing test statistic is the
![]() -ratio for the regressor's coefficient. The
distribution of this statistic is found under the null hypothesis,
and the authors argue that power functions can also be derived for
alternatives that embed the two rival models.
-ratio for the regressor's coefficient. The
distribution of this statistic is found under the null hypothesis,
and the authors argue that power functions can also be derived for
alternatives that embed the two rival models.
Chong and Hendry also formulate test statistics based on
![]() -step ahead forecast errors and on averages
of forecast errors, derive their asymptotic distributions, and
analyze their finite sample properties in a Monte Carlo study.
Chong and Hendry note that the variance of the
-step ahead forecast errors and on averages
of forecast errors, derive their asymptotic distributions, and
analyze their finite sample properties in a Monte Carlo study.
Chong and Hendry note that the variance of the ![]() -step ahead forecast error is not necessarily monotonically
increasing in the forecast horizon, so forecast modifications such
as pooling and intercept adjustment may be worthwhile.
-step ahead forecast error is not necessarily monotonically
increasing in the forecast horizon, so forecast modifications such
as pooling and intercept adjustment may be worthwhile.
4.7.7 Parameter Constancy, Mean Square Forecast Errors, and Measuring Forecast Performance: An Exposition, Extensions, and Illustration by N.R. Ericsson (1992b)
Ericsson (1992b) focuses on the issues of parameter constancy and predictive accuracy. He begins with an exposition of the statistical criteria for model evaluation and design, including various criteria based on forecasts. Using Hendry and Richard's (1982*, 1983) taxonomy for model criteria, Ericsson resolves a debate between modelers emphasizing parameter constancy and those running competitions based on mean square forecast errors (MSFEs). By explicit consideration of the information sets involved, Ericsson clarifies the roles that each plays in analyzing a model's forecast accuracy. Both parameter constancy and minimizing MSFE across a set of models are necessary for good forecast performance, but neither (nor both) is sufficient. Both criteria also fit into Hendry and Richard's general taxonomy of model evaluation statistics. Simple linear models illustrate how these criteria bear on forecasting.
Hendry and Richard's taxonomy also leads to a new test statistic, which is for forecast-model encompassing. Ericsson applies that and other forecast-related test statistics to two models of U.K. money demand. Properties of several of the forecast-based tests are affected by the presence of integrated and cointegrated variables. Ericsson's Table 2 categorizes numerous model evaluation and design criteria according to Hendry and Richard's taxonomy. This table provides a useful reference, as many of these criteria appear elsewhere in this collection.
In discussing Hendry and Richard's taxonomy, Ericsson re-examines the concepts of variance dominance, variance encompassing, and parameter encompassing, derives relationships between these concepts, and formulates the corresponding hypotheses and testing procedures. This discussion leads to a similar discussion for the equivalent forecast-related concepts: MSFE dominance, forecast encompassing, and forecast-model encompassing. Because Chong and Hendry's forecast encompassing test is generally not invariant to nonsingular linear transformations of the data, Ericsson reformulates their testing procedure to attain invariance, and he evaluates the properties of that modified test statistic. Ericsson also shows that models with time-varying coefficients do not necessarily attain smaller MSFEs than models with fixed coefficients.
Lu and Mizon (1991) re-interpret the forecast tests in Ericsson (1992b) and Chong and Hendry (1986)* by examining the implicit null hypotheses associated with parameter encompassing, parameter constancy, and forecast encompassing. Additionally, some of the results in Chong and Hendry (1986)*, Lu and Mizon (1991), and Ericsson (1992b) may be affected by transformations of the models' variables. For instance, Ericsson, Hendry, and Tran (1994) show that variance dominance is not necessary for a model using seasonally unadjusted data to encompass a model using seasonally adjusted data. Ericsson, Hendry, and Tran then design encompassing tests for comparing two such models and discuss the effects of seasonal adjustment on other properties, such as cointegration and weak exogeneity. Ericsson, Hendry, and Tran illustrate their analytical results empirically with models of quarterly U.K. narrow money demand over 1964-1989.
4.7.8 Encompassing the Forecasts of U.S. Trade Balance Models by N.R. Ericsson and J. Marquez (1993)
Chong and Hendry (1986)* propose the concept of forecast encompassing, which corresponds to the lack of additional information in another model's forecasts. Chong and Hendry's test statistic for forecast encompassing is based on the regression of one model's forecast errors on the other model's forecasts. Ericsson and Marquez (1993) generalize Chong and Hendry's statistic to include sets of dynamic nonlinear models with uncertain estimated coefficients generating multi-step forecasts with possibly systematic biases. Using Monte Carlo simulation, Ericsson and Marquez apply their generalized forecast encompassing test statistic to forecasts over 1985Q1-1987Q4 from six models of the U.S. merchandise trade balance, revealing mis-specification in all models.
4.7.9 Evaluating Dynamic Econometric Models by Encompassing the VAR by D.F. Hendry and G.E. Mizon (1993)
Hendry and Mizon (1993) propose a procedure for comparing econometric models, whether those models' variables are I(0) or I(1) and whether those models are closed or open. Hendry and Mizon's procedure consists of formulating a congruent VAR that embeds all the contending dynamic structural econometric models (SEMs) being evaluated, and testing which of those models is a valid reduction of that VAR. The variables' orders of integration can affect inferential procedures, so Hendry and Mizon first test for cointegration--which is a reduction in itself--and then examine parsimonious congruence in the cointegrated VAR, which is transformed to have I(0) variables.
Closed SEMs are transformed restrictions of the congruent VAR, providing a necessary and sufficient condition for the SEM to encompass the VAR. While this condition does not necessarily lead to a unique encompassing model, parameter invariance provides an additional criterion for narrowing the class of acceptable models.
Open SEMs condition on a set of variables, which may be I(1). If it is known which of those variables are I(1) and which cointegrate, then the open SEM can be tested against a VAR formulated in terms of differences of the I(1) variables and the cointegrating relationships. If there is no information about unit roots and cointegration vectors, then Hendry and Mizon suggest the following procedure: formulate a VAR on all variables in I(0) form, construct a closed SEM by augmenting the open SEM with equations for all conditioning variables, test each closed form against the general VAR, and finally test the validity of the weak exogeneity (conditioning) assumptions of each closed model. Hendry and Mizon illustrate their approach with system models of quarterly U.K. narrow money demand over 1963-1984.
In a subsequent and related paper, Hendry and Doornik (1997) examine potential sources of predictive failure, including parameter nonconstancy, model mis-specification, collinearity, and lack of parsimony. Parameter changes associated with deterministic factors typically have larger effects on the forecasts than changes in coefficients associated with stochastic variables. Model mis-specification per se can not induce forecast failure, although model mis-specification in the presence of parameter nonconstancy can augment the effects of the latter. Likewise, multi-collinearity per se can not induce forecast failure, although it can affect forecasts when the marginal process alters.
Hendry and Doornik (1997) distinguish between error correction and equilibrium correction, and show that forecasts from equilibrium correction models generally have biased forecasts if the equilibrium mean alters. Changes in equilibrium means typically have larger effects on the forecasts than changes in growth rates. Hendry and Doornik also discuss the concept of extended model constancy, in which a model that is constant in sample may require extensions out-of-sample if it is to remain constant in a world of structural change.
4.8 Computer Automation
Computers have long played an essential role in the operational development of econometrics, particularly for estimation, inference, and simulation. Beale, Kendall, and Mann (1967) and Coen, Gomme, and Kendall (1969) set a backdrop for more recent developments in computer-automated model selection.
Beale, Kendall, and Mann (1967) propose an early algorithm for model selection that aims to maximize the adjusted R2 of a regression with an initially specified set of potential regressors. Coen, Gomme, and Kendall (1969) empirically apply that algorithm to modeling the Financial Times ordinary share index, starting from pure distributed lags, with the lag order and lag length chosen informally. Coen, Gomme, and Kendall model seasonally adjusted data, which in some cases is detrended or differenced. They then graphically analyze forecasts for different models over different forecast periods. The published discussion of Coen, Gomme, and Kendall (1969) is critical and raises numerous issues, including the role of statistics in economic analysis, goodness of fit and the choice of model selection criterion, dynamics and dynamic specification, expectations and endogeneity, causality, policy analysis, institutional and structural changes, the effects of seasonal adjustment on modeling, the purpose of a model (e.g., whether for policy, economic analysis, or forecasting), and the use of spectral methods.
Lovell (1983) [Volume II: Chapter 20] re-examines the appropriateness of automated selection procedures in a quasi-empirical Monte Carlo study. Denton (1985) [Volume II: Chapter 21] extends Lovell's critique of data mining to a profession that chooses which papers to publish, based on their empirical results, even when the papers' authors themselves do not data-mine. While Lovell (1983)* and Denton (1985)* (and others) cast a pejorative light on data mining, Lovell (1983)* in particular stimulated a more recent and constructive view of data mining by Hoover and Perez (1999a)*.
Hoover and Perez (1999a) [Volume II: Chapter 22] implement and analyze a general-to-specific model selection algorithm that mimics the theory of reduction for model simplification. Hendry and Krolzig (1999) [Volume II: Chapter 23] comment on Hoover and Perez (1999a)* and improve upon Hoover and Perez's algorithm in what has become the econometrics software package PcGets. Hoover and Perez (1999b) [Volume II: Chapter 24] reply to their discussants, which include Hendry and Krolzig (1999)* and Campos and Ericsson (1999)*. Perez, Amaral, Gallo, and White (2003) develop, simulate, and apply a specific-to-general algorithm called RETINA that uses a forecast-based criterion for model selection. Castle (2005) evaluates and compares the simulated and empirical performance of PcGets and RETINA. The remarkable performance of general-to-specific algorithms has already been discussed in Section 3; and they seem bound to improve in the years ahead.
4.8.1 Data Mining by M.C. Lovell (1983)
Lovell (1983) criticizes the use of nominal significance levels when model selection depends on the dataset. Lovell addresses this problem in two ways. First, he develops a rule of thumb that approximates the actual significance level when a given number of explanatory variables are selected from a larger set of variables, assuming that those variables are orthogonal. Second, Lovell simulates selection probabilities by Monte Carlo for several DGPs that use actual macroeconomic time series as explanatory variables but construct the dependent variable by adding a simulated disturbance.
For simulations from each of those DGPs, Lovell considers three automated procedures that may mimic actual empirical model selection:
- stepwise regression,
- maximum adjusted
 , and
, and - max-min
 .
.
For each procedure and at various significance levels, Lovell
calculates how frequently the DGP is found and how frequently each
variable is selected. Estimated finite sample significance levels
are much larger than nominal levels, but employing Lovell's
proposed rule helps to some extent. Also, stepwise regression and
the adjusted
![]() criterion appear to
outperform the
t-value criterion, in that the
first two procedures find the relevant variables more often.
Nevertheless, no method is uniformly successful.
criterion appear to
outperform the
t-value criterion, in that the
first two procedures find the relevant variables more often.
Nevertheless, no method is uniformly successful.
4.8.2 Data Mining as an Industry by F.T. Denton (1985)
Denton (1985) shows that re-using data can affect the probability of incorrectly retaining variables, whether a single researcher tests several hypotheses on the data and selects the best model (Lovell's example), or whether many researchers test one hypothesis each and only significant results are reported (as might occur with a publication filter). The probabilities in these two situations coincide when either the number of researchers is large or the number of hypotheses tested is large. Under certain simplifying assumptions, Denton shows that the probability of false inclusion increases with the number of researchers involved and with the total number of possible explanatory variables. Denton thus urges using smaller significance levels and computing Lovell's (1983)* rule of thumb to interpret published results.
4.8.3 Data Mining Reconsidered: Encompassing and the General-to-specific Approach to Specification Search by K.D. Hoover and S.J. Perez (1999a)
Hoover and Perez (1999a) assess the practical efficacy of the LSE's general-to-specific approach for building econometric models. Hoover and Perez characterize the LSE approach as a search procedure for finding a parsimonious econometric model by imposing restrictions on a more general representation. Hoover and Perez design a computerized general-to-specific modeling algorithm that mimics the LSE approach, they simulate several DGPs that are similar to those used by Lovell (1983)*, and they examine how well their algorithm does in selecting the DGP as its final model.
Hoover and Perez find that their algorithm performs remarkably well, and that the size and power of t-tests in the final model are not very much affected by the algorithm's search procedure. In addition to these surprising and innovative findings, Hoover and Perez make major contributions to the LSE methodology itself, including development of a computer algorithm to perform general-to-specific modeling, formalization of multi-path searches, and encompassing-based comparisons of multiple terminal models.
Prior to conducting their Monte Carlo analysis, Hoover and Perez (1999a) examine several criticisms of the LSE modeling approach.
- Multiple search paths--whether by a single researcher or several--may give rise to multiple parsimonious terminal models, which require comparison. Encompassing procedures can distinguish between those terminal models.
- Overfitting could occur from an approach that selects regressors from many intercorrelated variables where selection is based (in part) on goodness of fit. Chance empirical correlations in the data may thus favor retaining some regressors that are actually irrelevant in the DGP. However, the LSE approach emphasizes a progressive research strategy, in which such mistakes become detectable as additional data accrue.
- The interpretation of test statistics in the final model may be at issue because of the potential consequences of empirical model selection. In proceeding along a simplification path, tests are applied to a sequence of models to check whether each new model is a congruent reduction of the previous one. Because the dataset is the same at every stage of simplification, some critics have questioned the tests' independence and the critical values used. However, this view confuses two distinct roles of such tests: as mis-specification tests when applied to the initial model to check congruence; and as diagnostics for detecting inappropriate reductions, which are not followed if they induce a lack of congruence.
To investigate whether these concerns have merit in practice, Hoover and Perez construct a computerized search algorithm that mimics the LSE general-to-specific modeling approach. In the LSE approach, the general-to-specific procedure should obtain a final model that satisfies the criteria discussed in Section 2.6: consistency with economic theory, innovation errors, data admissibility, constant parameters, weak exogeneity of conditioning variables, and encompassing of competing specifications. Because of the experimental design chosen in Hoover and Perez's Monte Carlo simulations, some of these criteria--such as theory consistency and weak exogeneity--are irrelevant, allowing Hoover and Perez to focus on other aspects of the general-to-specific approach. Their algorithm follows several search paths to obtain parsimonious reductions of the general model that satisfy the standard diagnostic statistics. Because variance dominance is necessary for parameter encompassing, the algorithm then selects among those terminal models to obtain the one with the smallest equation standard error.
Hoover and Perez simulate several DGPs that are similar to Lovell's, and they then examine how well their algorithm does in selecting the DGP as the procedure's final model. The DGPs include 0, 1, or 2 regressors and an error that is independently and identically distributed normal or first-order autoregressive in such an error, with observations spanning approximately 35 years of quarterly data. The potential regressors are 18 standard economic variables, the first lag of those variables, and the first four lags of the dependent variable. The algorithm uses tests at nominal sizes of 1%, 5% and 10%.
Hoover and Perez summarize their results, as follows.
- Their algorithm does remarkably well at simplifying to the DGP
or to a model very much like the DGP. For instance, when using a
nominal size of 5%, their algorithm typically chooses the DGP as
its final model, albeit augmented by about two irrelevant
regressors on average. Noting that there are approximately 40
irrelevant regressors in the general model, a 5% nominal size for
one-off
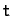 -tests should retain about
two irrelevant regressors on average. Overfitting--such as it
is--resembles the classical statistical calculation, not the one
derived by Lovell. However, Lovell did not consider
general-to-specific modeling algorithms.
-tests should retain about
two irrelevant regressors on average. Overfitting--such as it
is--resembles the classical statistical calculation, not the one
derived by Lovell. However, Lovell did not consider
general-to-specific modeling algorithms. - A smaller nominal size typically reduces the number of falsely significant variables and retained insignificant variables, with little loss in power, although power itself does depend upon the particular signal-to-noise ratios for the variables in the DGP. That said, the observed size-power tradeoff may justify using a nominal size for the algorithm's tests that is smaller than the commonly used 5% value.
- The size and power of t-tests in the final model are not very much affected by the search procedure.
- Overfitting may be reduced by splitting the sample into two possibly overlapping subsamples, applying the algorithm to each subsample separately, and selecting the final model as the intersection of the two subsample models. Hoover and Perez (in their Figure 1) find only a small reduction in empirical power for subsamples that are at least 80% of the full sample.
In summary, Hoover and Perez show that general-to-specific modeling can often attain a final specification that is the DGP or that nests the DGP and has few spuriously included regressors. A judicious choice of the nominal size enhances their algorithm's ability in model search, whereas variables with low signal-to-noise ratios pose challenges. Searches along multiple simplification paths--in conjunction with encompassing comparisons of the resulting terminal models--can help the algorithm avoid getting stuck in dead ends.
4.8.4 Improving on "Data Mining Reconsidered" by K.D. Hoover and S.J. Perez by D.F. Hendry and H.-M. Krolzig (1999)
Hendry and Krolzig (1999) develop and analyze the econometrics software package PcGets, which offers several improvements on Hoover and Perez's (1999a)* algorithm for model selection.
- PcGets expands the range of feasible paths searched by including block tests for sets of potentially insignificant coefficients, rather than just individual coefficient tests.
- The dimensionality of the general unrestricted model may be reduced by conducting a pre-search simplification, which uses a significance level that is less stringent than conventional. Pre-search simplification can reduce the number of subsequent paths that need to be examined and so can help avoid overfitting.
- Tests of parsimonious encompassing help discern between distinct terminal models arising from multiple search paths. If multiple search paths give rise to distinct terminal models, PcGets constructs the most parsimonious union model that nests those terminal models, tests each terminal model against that union model, and retains only those terminal models that pass this test of parsimonious encompassing. If more than one terminal model parsimoniously encompasses that union model, a new union model is constructed, and the simplification algorithm is applied to it. Parsimonious encompassing helps protect against overfitting, and it can recover relevant variables that were accidentally dropped during some search paths.
- If repeated simplification searches still obtain multiple parsimoniously encompassing terminal models, model choice relies on information criteria.
- If a diagnostic test is significant in the general unrestricted model, the test is re-assessed at a more stringent significance level rather than being excluded in subsequent simplifications. That modification can prevent rejection caused by overfitting and so can avoid simplifying to a poor specification because of insufficient diagnostic testing.
- Significance tests over subsamples help bring to light variables that were adventitiously significant in the whole sample.
Hendry and Krolzig discuss Hoover and Perez's experimental design, they consider differences between the costs of search and the costs of inference for algorithmic model simplification, and they enumerate key features of Hoover and Perez's and PcGets's algorithms. Hendry and Krolzig compare PcGets with Hoover and Perez's algorithm for some of the equations in Hoover and Perez (1999a)*. Pre-search simplification in particular increases the chances of finding the DGP and reduces the average number of falsely included variables. For the simulations conducted, a better model often would not have been chosen, even if the search had begun with the DGP as the general unrestricted model.
Hendry and Krolzig also examine potential roles of data nonstationarity and data non-orthogonality. Nonstationarity does not appear to affect the results because most diagnostic test statistics are unaffected by nonstationarity. However, tests of some reductions are affected, so Hendry and Krolzig (1999) suggest that these reductions be based on suitable cointegration tests, and that appropriate transformations be performed prior to applying PcGets. Regressor non-orthogonality can work adversely by confusing model selection.
Hendry and Krolzig (1999) finish by modeling U.S. narrow money demand on Baba, Hendry, and Starr's (1992) data with PcGets. The selected model is remarkably similar to the final model in Baba, Hendry, and Starr (1992) and is insensitive to the use of pre-selection tests and the particular significance level chosen. Hendry and Krolzig conclude that PcGets is a marked improvement on an already powerful algorithm developed by Hoover and Perez (1999a)*. The empirical modeler still plays a central role in modeling, including through the choice of economic theory, the formulation of the general unrestricted model, and the parameterization of the general unrestricted model.
4.8.5 Reply to Our Discussants by K.D. Hoover and S.J. Perez (1999b)
Hoover and Perez (1999b) identify and respond to several key issues raised by their discussants.
- While Hoover and Perez (1999a)* failed to use heteroscedasticity-consistent standard errors, such standard errors should not affect their results because the dependent variable has been generated with homoscedastic disturbances. Hendry and Krolzig (1999)* also discuss this point.
- Also, while Hoover and Perez (1999a)* did not use information criteria in their algorithm, they could have done so, and Hendry and Krolzig (1999)* do so.
- In designing their algorithm, Hoover and Perez (1999a)* aimed to mimic certain key features of the LSE approach, not capture it in its entirety.
- Truth is relevant to econometric modeling for several reasons. In particular, some notion of the truth is required for assessing the adequacy of a model. Also, both policy analysis and forecasting require some notion of what the true structure is like--specifically, about what aspects of structure are constant or invariant. Conversely, predictive performance alone is insufficient for describing how Hoover and Perez's algorithm works. In Hoover and Perez's simulations, the DGP is in the model space, but it does not need to be so in empirical practice. The central question is whether the DGP can be eventually uncovered by the LSE approach; see also White (1990)*.
4.9 Empirical Applications
The following empirical applications represent several vintages of models across numerous countries and different sectors of the economy. The different vintages highlight the progressivity of the methodology. The range of sectors examined and the range of countries--which include Argentina, Turkey, Venezuela, the United Kingdom, and the United States--emphasize the breadth of interest in and applicability of coherent modeling approaches. While each paper focuses on different aspects of the general-to-specific modeling approach, some common strands include dynamic specification, model evaluation and design criteria, parameter constancy and predictive failure, sequential reductions and multiple-path searches, data mining, exogeneity, and encompassing.
The first five papers--Trivedi (1970b), Davidson, Hendry, Srba, and Yeo (1978), Davidson and Hendry (1981), Hendry (1979), and Ahumada (1985) [Volume II: Chapters 25, 26, 27, 28, and 29, respectively]--capture the general-to-specific methodology at various stages of development, initially focusing on model simplification and then expanding to include diagnostic testing and encompassing. Trivedi (1970b)* illustrates the general-to-specific approach for a particular form of dynamic specification--the Almon (1965) lag polynomial--with an application to the lag structure relating orders to deliveries in the U.K. engineering industry. Davidson, Hendry, Srba, and Yeo (1978)* model the U.K. consumption function, providing a pivotal and substantive empirical application that emphasizes both general-to-specific modeling and encompassing. Davidson and Hendry (1981)* compare the final model in Davidson, Hendry, Srba, and Yeo (1978)* with a similar model based on the rational expectations hypothesis by deriving encompassing implications of both models. Hendry (1979)* highlights the differences between simple-to-general and general-to-specific approaches, modeling U.K. narrow money demand. In her modeling of the Argentine balance of trade, Ahumada (1985)* illustrates various features of the evolving general-to-specific methodology, such as empirical implementation of the theory of reduction, and encompassing as a tool for assessing alternative models that result from different path searches.
The next three papers--MacDonald and Taylor (1992),
Johansen (1992b), and Metin (1998) [Volume II:
Chapters 30, 31, and 32, respectively]--add cointegration
analysis as a central feature in the general-to-specific
methodology, with both cointegration and weak exogeneity forming
possible key reductions in modeling. MacDonald and Taylor (1992)*
construct a congruent econometric model for U.S. real money demand
from an ADL, with cointegration determined in a VAR by the Johansen
procedure. Johansen (1992b)* applies his cointegration analysis to
U.K. money demand, emphasizing tests of weak exogeneity and the
empirical determination of the order of integration. The latter
leads to an I(![]() ) cointegration analysis,
which is contrasted with the more common I(
) cointegration analysis,
which is contrasted with the more common I(![]() )
analysis. Metin (1998)* models the determinants of Turkish
inflation. Because no variables are weakly exogenous for her
cointegration vectors, Metin imposes the system-based estimates of
the cointegrating coefficients in her single equation analysis of
inflation. The resulting model encompasses an extant model in
Metin (1995) with different economic foundations.
)
analysis. Metin (1998)* models the determinants of Turkish
inflation. Because no variables are weakly exogenous for her
cointegration vectors, Metin imposes the system-based estimates of
the cointegrating coefficients in her single equation analysis of
inflation. The resulting model encompasses an extant model in
Metin (1995) with different economic foundations.
The final paper--Campos and Ericsson (1999) [Volume II: Chapter 33]--examines and implements the general-to-specific approach with automated model selection procedures. Campos and Ericsson first examine the concept of data mining and show that automated model selection procedures such as PcGets can help avoid data mining in its pejorative senses. Campos and Ericsson then illustrate constructive data mining by empirically modeling Venezuelan consumers' expenditure, both manually and with PcGets.
4.9.1 The Relation Between the Order-delivery Lag and the Rate of Capacity Utilization in the Engineering Industry in the United Kingdom, 1958-1967 by P.K. Trivedi (1970b)
Trivedi (1970b) investigates the lag structure involving orders in the U.K. engineering industry and the delivery of those orders in domestic and foreign markets over 1958Q1-1967Q2. Trivedi assumes that all orders are eventually delivered, and that the speed at which orders are met depends upon the degree of capacity utilization. The econometric models for deliveries are Almon (1965) polynomial distributed lag models of orders received. Coefficients of a distributed lag are interpreted as the proportions of orders delivered at the corresponding lags. Those coefficients are expected to be non-negative, to add up to unity, and to depend on capacity utilization.
Trivedi (1970b) is methodologically important for its treatment of distributed lags in a (albeit informal) general-to-specific framework. To determine the precise nature of the distributed lags, Trivedi examines overall lag length, the order of the polynomial, end-point constraints, dependence of the lag coefficients on capacity utilization, and the functional form of the latter. These aspects are examined by extensive sequential simplifications that imply multiple search paths. Trivedi evaluates alternative simplifications by F-tests and t-tests, by comparison of residual variances (i.e., variance dominance), and by diagnostic tests.
Empirically, Trivedi finds that only equations in which the lag weights are linear functions of utilized capacity are sensible. Models of home deliveries fit better than those for foreign deliveries, mainly due to seamen's strikes affecting the latter. The proportion of home orders met in the first year is somewhat larger than the proportion of foreign orders delivered over the same interval. Trivedi's models omit lagged dependent variables, although he does note a lack of success with rational distributed lag models. In a companion paper, Trivedi (1970a) builds autoregressive distributed lag models with moving average errors for inventories of the U.K. manufacturing sector; see also Trivedi (1973, 1975).
4.9.2 Econometric Modelling of the Aggregate Time-series Relationship Between Consumers' Expenditure and Income in the United Kingdom by J.E.H. Davidson, D.F. Hendry, F. Srba, and S. Yeo (1978)
Davidson, Hendry, Srba, and Yeo (1978) (often abbreviated DHSY) provide a comprehensive and unified treatment of the empirical relationship between consumers' expenditure and disposable income in the United Kingdom. Their methodological treatment and resulting empirical model have served as templates for much subsequent empirical economic modeling.
DHSY make substantial contributions in several areas related to general-to-specific modeling.
- Encompassing. DHSY explicitly adopt an encompassing approach to compare different models and to explain why different models were obtained by their designers. Specifically, DHSY first standardize three contending models to eliminate tangential differences arising from differing data samples, treatments of seasonality, functional forms, and levels of data aggregation. DHSY then nest those standardized models in a union model (DHSY's equation (25)) and test those models against the union model.
- Dynamic specification. The union model is an autoregressive distributed lag, and tests of the contending models involve alternative claims about dynamic specification, leading to a discussion of error correction models and their properties. DHSY also consider how seasonality and seasonal adjustment may affect dynamic specification.
- Evaluation criteria. DHSY introduce and explicitly use a battery of test statistics for evaluating the contending models and their own (new) model. These statistics include ones for testing parameter constancy, residual autocorrelation, innovation error (relative to the ADL), validity of instruments, theory consistency (through the role of the error correction term), and common factors. Graphs of the data help clarify key features of the data that must be captured by any congruent empirical model.
DHSY's final empirical model is an error correction model, which reconciles previously observed low short-run income elasticities with a hypothesized (and testable) unit long-run income elasticity. DHSY also observe that a nearly constant error correction term may lead to the exclusion of the intercept, that effects of multicollinearity may be dampened by adding variables, and that seasonal adjustment need not imply low-order dynamics. DHSY fail to detect important liquidity effects, which are investigated in Hendry and von Ungern-Sternberg (1981).
4.9.3 Interpreting Econometric Evidence: The Behaviour of Consumers' Expenditure in the UK by J.E.H. Davidson and D.F. Hendry (1981)
Davidson and Hendry (1981) focus on several areas central to general-to-specific modeling: encompassing, dynamic specification, parameter constancy and predictive failure, model evaluation criteria, exogeneity, and model reduction. Davidson and Hendry's immediate aim is to reconcile the error correction models developed in Davidson, Hendry, Srba, and Yeo (1978)* and Hendry and von Ungern-Sternberg (1981) with claims by Hall (1978) that consumers' expenditure is a random walk, as implied by the rational expectations hypothesis. Davidson and Hendry update these error correction models on a longer data sample and show that these models encompass Hall's model. Davidson and Hendry also discuss some qualifications about white noise as a criterion for data congruency, and they consider implications that result from the random walk model being a derived process through model reductions.
Both in a Monte Carlo study and empirically with U.K. data, Davidson and Hendry (1981) show how and why consumers' expenditure might appear to be a random walk, even when the data are generated by a conditional error correction model. In essence, tests of deviations from the random walk hypothesis have low power to detect the deviations implied by economically sensible values for parameters in the DGP for an error correction mechanism. That said, Davidson and Hendry do detect statistically significant improvements from adding additional variables to the random walk model. Davidson and Hendry also discuss the potential effects of endogeneity, measurement errors, time aggregation, and identities. While Davidson and Hendry note that mis-specification and the lack of weak exogeneity both imply predictive failure when data correlations change, the associated implications are not fleshed out until Hendry (1988)* and Engle and Hendry (1993).
4.9.4 Predictive Failure and Econometric Modelling in Macroeconomics: The Transactions Demand for Money by D.F. Hendry (1979)
Hendry (1979) designs an error correction model of narrow money demand in the United Kingdom that encompasses extant models in levels and in differences, and that remains constant, in spite of predictive failure by other models.
Hendry begins by empirically illustrating the simple-to-general approach and highlighting its difficulties. In particular, he notes how "every test is conditional on arbitrary assumptions which are to be tested later, and if these are rejected, all earlier inferences are invalidated, whether 'reject' or 'not reject' decisions" (p. 226). Through this illustration, Hendry links such inappropriate modeling procedures to (likely) model mis-specifications such as parameter nonconstancy.
Hendry then models U.K. narrow money demand following a general-to-specific approach, sequentially simplifying from an autoregressive distributed lag to a parsimonious error correction model. That error correction model is empirically constant, and it encompasses extant equations in levels and in differences. Hendry notes several potential shortcomings of the general-to-specific approach: a general model that is not general enough, inadequate information in the sample, multiple simplification paths with different terminal models, and the costs of search and of inference.
4.9.5 An Encompassing Test of Two Models of the Balance of Trade for Argentina by H.A. Ahumada (1985)
Following a general-to-specific modeling approach, Ahumada (1985) formulates two empirical models of the Argentine balance of trade--one based on the excess supply of tradable goods and the other on the monetary model for the balance of trade--and she compares the two models using encompassing tests. The first model appears more satisfactory, both statistically and economically. Ahumada (1985) exemplifies general-to-specific modeling in practice. Ahumada (1985) also highlights how an empirical model can be designed to satisfy a range of criteria on a given dataset, even while additional data may be informative against that model. This result reiterates the value of encompassing tests.
Ahumada starts with a fourth-order ADL model for the trade surplus in terms of income, agricultural output, the inverse of the real wage, and deviations from purchasing power parity. She simplifies this ADL to a parsimonious ECM, setting small and statistically insignificant coefficients to zero, and reparameterizing the ADL as an ECM to achieve near orthogonality of the regressors. The model's residuals are innovations, its parameters are empirically constant, weak exogeneity appears satisfied, and the model is consistent with an economic theory for the excess supply of tradable goods.
Ahumada also formulates a fourth-order ADL model for the trade surplus in terms of income, the money stock, and an interest rate, and she simplifies that ADL to an ECM. The resulting ECM also appears congruent with the data, and it is generally consistent with the monetary model for the balance of trade.
Ahumada uses a battery of encompassing tests to compare and evaluate the ECMs based on the two different economic theories for the balance of trade. Overall, the first ECM encompasses the second, but not conversely.
4.9.6 A Stable US Money Demand Function, 1874-1975 by R. MacDonald and M.P. Taylor (1992)
Following a general-to-specific modeling approach, MacDonald and Taylor (1992) construct a congruent econometric model for U.S. money demand from the annual data in Friedman and Schwartz (1982). MacDonald and Taylor establish that a second-order VAR in nominal money, prices, real income, and a long-term interest rate satisfies various diagnostic statistics and, using the Johansen (1988) procedure, they show that those variables are cointegrated. Long-run unit price homogeneity is a statistically acceptable restriction, but jointly long-run unit price homogeneity and long-run unit income homogeneity are not.
MacDonald and Taylor then develop a parsimonious congruent single-equation error correction model that has long-run properties matching those obtained by the Johansen procedure. MacDonald and Taylor start from an ADL in the VAR's variables, with short-term interest rates added as well, and they then sequentially simplify that ADL. MacDonald and Taylor demonstrate the super exogeneity of prices in their money demand equation by showing that that equation is empirically constant, whereas its inversion with prices as the dependent variable is not.
4.9.7 Testing Weak Exogeneity and the Order of Cointegration in UK Money Demand Data by S. Johansen (1992b)
Johansen (1992b) summarizes his 1988 procedure for testing cointegration of I(1) variables, his generalization of that procedure to include I(2) variables, and his 1992 test of weak exogeneity for cointegrating vectors; see Johansen (1988), Johansen (1995, Ch. 9), and Johansen (1992a). Each of these three contributions analyzes a reduction or simplification in the data's distribution, and all three appear highly important in general empirical practice.
Johansen (1992b) also illustrates how to implement each contribution by considering Hendry and Ericsson's (1991) quarterly data for narrow U.K. money demand. Empirically, nominal money and prices appear to be I(2), and they cointegrate as real money to become I(1). Real money in turn cointegrates with real total final expenditure (the scale variable), interest rates, and inflation to generate an I(0) linear combination. Prices, income, and interest rates appear weakly exogenous for the single I(1) cointegrating vector in the system, whereas money is clearly not exogenous.
In a closely related paper, Urbain (1992) derives conditions for weak exogeneity for short- and long-run parameters in a single equation of a cointegrated VAR. Urbain also clarifies the role of orthogonality tests in testing for weak exogeneity, and he illustrates the procedures for testing weak exogeneity with two empirical applications.
4.9.8 The Relationship Between Inflation and the Budget Deficit in Turkey by K. Metin (1998)
Metin (1998) models the determinants of Turkish inflation, following a general-to-specific approach. The resulting model encompasses an extant model in Metin (1995) with different economic foundations.
Metin (1998) bases her empirical analysis on an economic theory for a closed economy that relates inflation to the budget deficit and real income growth. Metin's cointegration analysis of real income growth, inflation, the budget deficit, and base money finds three cointegration vectors, interpretable as stationary real income growth, a relationship between inflation and the budget deficit (augmented by base money), and a relationship between inflation and the budget deficit (augmented by a trend). No variables are weakly exogenous for the cointegration vectors, so Metin imposes the system-based estimates of the cointegrating coefficients in her single equation analysis of inflation.
Metin simplifies her initial ADL to obtain a parsimonious and congruent error correction model of inflation. In the short run, changes in inflation depend on their own past and on growth rates of the budget deficit, money base, and real income. In the long run, inflation depends on the deficit and the money base through the error correction terms for the two (non-trivial) cointegrating relationships. This error correction model also encompasses Metin's (1995) previous specification in which inflation is driven by disequilibrium in money demand and deviations from purchasing power parity and uncovered interest-rate parity.
4.9.9 Constructive Data Mining: Modeling Consumers' Expenditure in Venezuela by J. Campos and N.R. Ericsson (1999)
Campos and Ericsson (1999) systematically examine the concept of data mining in econometric modeling. Their discussion provides support for the automated model selection procedures developed by Hoover and Perez (1999a)* and improved upon by Hendry and Krolzig (1999)*. Campos and Ericsson illustrate these model selection procedures by empirically modeling Venezuelan consumers' expenditure.
Campos and Ericsson (1999) first distinguish between four pejorative senses of data mining, which are repeated testing, data interdependence, corroboration, and over-parameterization. Data mining, in each of its pejorative senses, is empirically detectable. Campos and Ericsson show how Hoover and Perez's (1999a)* modified general-to-specific modeling strategy can counter each of these senses of data mining in practice.
Campos and Ericsson then use PcGets to model Venezuelan consumers' expenditure over 1970-1985. In the selected model, income, liquidity, and inflation determine expenditure in an economically sensible fashion; and that model is robust and has constant, well-determined parameter estimates. Even with relatively few observations, high information content in the data helps counter claims of pejorative data mining.
Campos and Ericsson identify two limitations to algorithmically based data mining: the initial general model, and data transformations. Campos and Ericsson demonstrate how these limitations are opportunities for the researcher qua economist to contribute value added to the empirical analysis.
5 Conclusions
This paper focuses on general-to-specific modeling--a central method for selecting useful empirical models. Using this method, the modeler simplifies an initially general model that adequately characterizes the empirical evidence within his or her theoretical framework. The papers reprinted in Campos, Ericsson, and Hendry (2005) articulate many reasons for adopting a general-to-specific approach. In particular, general-to-specific modeling implements the theory of reduction in an empirical context; and it has excellent model selection abilities, as documented in empirical practice and in Monte Carlo studies of automated general-to-specific modeling algorithms.
Studies of those algorithms have also clarified and helped resolve key issues in general-to-specific modeling, including path simplification and path dependence, the interpretation of mis-specification tests, the roles of recursive estimation, the value of model selection procedures, and the distinction between the almost inevitable costs of inference and the relatively low costs of search. This paper details how the subject has advanced to its present stage of success and should convey the promise of these developments for future empirical research.
Appendix A Selected Bibliography
This appendix lists the fifty-seven publications that are reprinted in Campos, Ericsson, and Hendry (2005) and summarized in Section 4 above. The titles of the reprints are listed in the order in which they appear in Campos, Ericsson, and Hendry (2005) and Section 4, and are grouped into the nine parts that span the two volumes of Campos, Ericsson, and Hendry (2005).
Volume I
Part I. Introduction to the Methodology (Section 4.1)
1. Gilbert, C. L. (1986) "Professor Hendry's Econometric Methodology", Oxford Bulletin of Economics and Statistics, 48, 3, 283-307.
2. Hendry, D. F. (1983) "Econometric Modelling: The 'Consumption Function' in Retrospect", Scottish Journal of Political Economy, 30, 3, 193-220.
3. Gilbert, C. L. (1989) "LSE and the British Approach to Time Series Econometrics", Oxford Economic Papers, 41, 1, 108-128.
4. Spanos, A. (1989) "On Rereading Haavelmo: A Retrospective View of Econometric Modeling", Econometric Theory, 5, 3, 405-429.
5. Pagan, A. (1987) "Three Econometric Methodologies: A Critical Appraisal", Journal of Economic Surveys, 1, 1, 3-24.
6. Phillips, P. C. B. (1988) "Reflections on Econometric Methodology", Economic Record, 64, 187, 344-359.
7. Ericsson, N. R., J. Campos, and H.-A. Tran (1990) "PC-GIVE and David Hendry's Econometric Methodology", Revista de Econometria, 10, 1, 7-117.
Part II. Theory of Reduction (Section 4.2)
8. Hendry, D. F. (1987) "Econometric Methodology: A Personal Perspective", Chapter 10 in T. F. Bewley (ed.) Advances in Econometrics: Fifth World Congress, Volume 2, Cambridge University Press, Cambridge, 29-48.
9. Hendry, D. F., and J.-F. Richard (1982) "On the Formulation of Empirical Models in Dynamic Econometrics", Journal of Econometrics, 20, 1, 3-33.
10. Koopmans, T. C. (1950) "When Is an Equation System Complete for Statistical Purposes?", Chapter 17 in T. C. Koopmans (ed.) Statistical Inference in Dynamic Economic Models (Cowles Commission Monograph No. 10), John Wiley, New York, 393-409.
11. Phillips, A. W. (1956) "Some Notes on the Estimation of Time-forms of Reactions in Interdependent Dynamic Systems", Economica, 23, 90, 99-113.
12. Richard, J.-F. (1980) "Models with Several Regimes and Changes in Exogeneity", Review of Economic Studies, 47, 1, 1-20.
13. Engle, R. F., D. F. Hendry, and J.-F. Richard (1983) "Exogeneity", Econometrica, 51, 2, 277-304.
Part III. Dynamic Specification (Section 4.3)
14. Hendry, D. F., A. Pagan, and J. D. Sargan (1984) "Dynamic Specification", Chapter 18 in Z. Griliches and M. D. Intriligator (eds.) Handbook of Econometrics, Volume 2, North-Holland, Amsterdam, 1023-1100.
15. Hendry, D. F., and G. E. Mizon (1978) "Serial Correlation as a Convenient Simplification, Not a Nuisance: A Comment on a Study of the Demand for Money by the Bank of England", Economic Journal, 88, 351, 549-563.
16 Sargan, J. D. (1980b) "Some Tests of Dynamic Specification for a Single Equation", Econometrica, 48, 4, 879-897.
17. Sargan, J. D. (1961) "The Maximum Likelihood Estimation of Economic Relationships with Autoregressive Residuals", Econometrica, 29, 3, 414-426.
18. Johansen, S., and K. Juselius (1990) "Maximum Likelihood Estimation and Inference on Cointegration -- With Applications to the Demand for Money", Oxford Bulletin of Economics and Statistics, 52, 2, 169-210.
Part IV. Model Selection Procedures (Section 4.4)
19. Anderson, T. W. (1962) "The Choice of the Degree of a Polynomial Regression as a Multiple Decision Problem", Annals of Mathematical Statistics, 33, 1, 255-265.
20. Yancey, T. A., and G. G. Judge (1976) "A Monte Carlo Comparison of Traditional and Stein-rule Estimators Under Squared Error Loss", Journal of Econometrics, 4, 3, 285-294.
21. Mizon, G. E. (1977b) "Model Selection Procedures", Chapter 4 in M. J. Artis and A. R. Nobay (eds.) Studies in Modern Economic Analysis, Basil Blackwell, Oxford, 97-120.
22. Savin, N. E. (1980) "The Bonferroni and the Scheffé Multiple Comparison Procedures", Review of Economic Studies, 47, 1, 255-273.
23. White, H. (1990) "A Consistent Model Selection Procedure Based
on ![]() -testing", Chapter 16 in
C. W. J. Granger (ed.) Modelling Economic Series:
Readings in Econometric Methodology, Oxford University Press,
Oxford, 369-383.
-testing", Chapter 16 in
C. W. J. Granger (ed.) Modelling Economic Series:
Readings in Econometric Methodology, Oxford University Press,
Oxford, 369-383.
24. Phillips, P. C. B. (1991) "Optimal Inference in Cointegrated Systems", Econometrica, 59, 2, 283-306.
Volume II
Part I. Model Selection Criteria (Section 4.5)
1. Akaike, H. (1981) "Likelihood of a Model and Information Criteria", Journal of Econometrics, 16, 1, 3-14.
2. Schwarz, G. (1978) "Estimating the Dimension of a Model", Annals of Statistics, 6, 2, 461-464.
3. Hannan, E. J., and B. G. Quinn (1979) "The Determination of the Order of an Autoregression", Journal of the Royal Statistical Society , Series B, 41, 2, 190-195.
4. Atkinson, A. C. (1981) "Likelihood Ratios, Posterior Odds and Information Criteria", Journal of Econometrics, 16, 1, 15-20.
5. Sawyer, K. R. (1983) "Testing Separate Families of Hypotheses: An Information Criterion", Journal of the Royal Statistical Society , Series B, 45, 1, 89-99.
6. Phillips, P. C. B. (1996) "Econometric Model Determination", Econometrica, 64, 4, 763-812.
Part II. Model Comparison (Section 4.6)
7. Cox, D. R. (1961) "Tests of Separate Families of Hypotheses", in J. Neyman (ed.) Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1, University of California Press, Berkeley, California, 105-123.
8. Cox, D. R. (1962) "Further Results on Tests of Separate Families of Hypotheses", Journal of the Royal Statistical Society , Series B, 24, 2, 406-424.
9. Dhrymes, P. J., E. P. Howrey, S. H. Hymans, J. Kmenta, E. E. Leamer, R. E. Quandt, J. B. Ramsey, H. T. Shapiro, and V. Zarnowitz (1972) "Criteria for Evaluation of Econometric Models", Annals of Economic and Social Measurement, 1, 3, 291-324.
10. Pesaran, M. H. (1974) "On the General Problem of Model Selection", Review of Economic Studies, 41, 2, 153-171.
Part III. Encompassing (Section 4.7)
11. Mizon, G. E., and J.-F. Richard (1986) "The Encompassing Principle and its Application to Testing Non-nested Hypotheses", Econometrica, 54, 3, 657-678.
12. Hendry, D. F., and J.-F. Richard (1989) "Recent Developments in the Theory of Encompassing", Chapter 12 in B. Cornet and H. Tulkens (eds.) Contributions to Operations Research and Economics: The Twentieth Anniversary of CORE, MIT Press, Cambridge, 393-440.
13. Wooldridge, J. M. (1990) "An Encompassing Approach to Conditional Mean Tests with Applications to Testing Nonnested Hypotheses", Journal of Econometrics, 45, 3, 331-350.
14. Lu, M., and G. E. Mizon (1996) "The Encompassing Principle and Hypothesis Testing", Econometric Theory, 12, 5, 845-858.
15 Hendry, D. F. (1988) "The Encompassing Implications of Feedback Versus Feedforward Mechanisms in Econometrics", Oxford Economic Papers, 40, 1, 132-149.
16 Chong, Y. Y., and D. F. Hendry (1986) "Econometric Evaluation of Linear Macro-economic Models", Review of Economic Studies, 53, 4, 671-690.
17. Ericsson, N. R. (1992b) "Parameter Constancy, Mean Square Forecast Errors, and Measuring Forecast Performance: An Exposition, Extensions, and Illustration", Journal of Policy Modeling, 14, 4, 465-495.
18. Ericsson, N. R., and J. Marquez (1993) "Encompassing the Forecasts of U.S. Trade Balance Models", Review of Economics and Statistics, 75, 1, 19-31.
19. Hendry, D. F., and G. E. Mizon (1993) "Evaluating Dynamic Econometric Models by Encompassing the VAR", Chapter 18 in P. C. B. Phillips (ed.) Models, Methods, and Applications of Econometrics: Essays in Honor of A. R. Bergstrom, Basil Blackwell, Cambridge, 272-300.
Part IV. Computer Automation (Section 4.8)
20. Lovell, M. C. (1983) "Data Mining", Review of Economics and Statistics, 65, 1, 1-12.
21. Denton, F. T. (1985) "Data Mining as an Industry", Review of Economics and Statistics, 67, 1, 124-127.
22. Hoover, K. D., and S. J. Perez (1999a) "Data Mining Reconsidered: Encompassing and the General-to-specific Approach to Specification Search", Econometrics Journal, 2, 2, 167-191.
23. Hendry, D. F., and H.-M. Krolzig (1999) "Improving on 'Data Mining Reconsidered' by K. D. Hoover and S. J. Perez", Econometrics Journal, 2, 2, 202-219.
24 Hoover, K. D., and S. J. Perez (1999b) "Reply to Our Discussants", Econometrics Journal, 2, 2, 244-247.
Part V. Empirical Applications (Section 4.9)
25. Trivedi, P. K. (1970b) "The Relation Between the Order-delivery Lag and the Rate of Capacity Utilization in the Engineering Industry in the United Kingdom, 1958-1967", Economica, 37, 145, 54-67.
26. Davidson, J. E. H., D. F. Hendry, F. Srba, and S. Yeo (1978) "Econometric Modelling of the Aggregate Time-series Relationship Between Consumers' Expenditure and Income in the United Kingdom", Economic Journal, 88, 352, 661-692.
27. Davidson, J. E. H., and D. F. Hendry (1981) "Interpreting Econometric Evidence: The Behaviour of Consumers' Expenditure in the UK", European Economic Review, 16, 1, 177-192.
28. Hendry, D. F. (1979) "Predictive Failure and Econometric Modelling in Macroeconomics: The Transactions Demand for Money", Chapter 9 in P. Ormerod (ed.) Economic Modelling: Current Issues and Problems in Macroeconomic Modelling in the UK and the US, Heinemann Education Books, London, 217-242.
29. Ahumada, H. A. (1985) "An Encompassing Test of Two Models of the Balance of Trade for Argentina", Oxford Bulletin of Economics and Statistics, 47, 1, 51-70.
30. MacDonald, R., and M. P. Taylor (1992) "A Stable US Money Demand Function, 1874-1975", Economics Letters, 39, 2, 191-198.
31. Johansen, S. (1992b) "Testing Weak Exogeneity and the Order of Cointegration in UK Money Demand Data", Journal of Policy Modeling, 14, 3, 313-334.
32. Metin, K. (1998) "The Relationship Between Inflation and the Budget Deficit in Turkey", Journal of Business and Economic Statistics, 16, 4, 412-422.
33. Campos, J., and N. R. Ericsson (1999) "Constructive Data Mining: Modeling Consumers' Expenditure in Venezuela", Econometrics Journal, 2, 2, 226-240.
References
Ahumada, H. A. (1985) "An Encompassing Test of Two Models of the Balance of Trade for Argentina", Oxford Bulletin of Economics and Statistics, 47, 1, 51-70.
Akaike, H. (1973) "Information Theory and an Extension of the Maximum Likelihood Principle", in B. N. Petrov and F. Csaki (eds.) Second International Symposium on Information Theory, Akademiai Kiado, Budapest, 267-281.
Akaike, H. (1981) "Likelihood of a Model and Information Criteria", Journal of Econometrics, 16, 1, 3-14.
Almon, S. (1965) "The Distributed Lag Between Capital Appropriations and Expenditures", Econometrica, 33, 1, 178-196.
Anderson, G. J., and D. F. Hendry (1984) "An Econometric Model of United Kingdom Building Societies", Oxford Bulletin of Economics and Statistics, 46, 3, 185-210.
Anderson, T. W. (1962) "The Choice of the Degree of a Polynomial Regression as a Multiple Decision Problem", Annals of Mathematical Statistics, 33, 1, 255-265.
Anderson, T. W. (1971) The Statistical Analaysis of Time Series, John Wiley, New York.
Atkinson, A. C. (1981) "Likelihood Ratios, Posterior Odds and Information Criteria", Journal of Econometrics, 16, 1, 15-20.
Baba, Y., D. F. Hendry, and R. M. Starr (1992) "The Demand for M1 in the U.S.A., 1960-1988", Review of Economic Studies, 59, 1, 25-61.
Banerjee, A., J. J. Dolado, J. w. Galbraith, and D. F. Hendry (1993) Co-integration, Error Correction, and the Econometric Analysis of Non-stationary Data, Oxford University Press, Oxford.
Banerjee, A., and D. F. Hendry (1992) "Testing Integration and Cointegration: An Overview", Oxford Bulletin of Economics and Statistics, 54, 3, 225-255.
Beale, E. M. L., M. G. Kendall, and D. W. Mann (1967) "The Discarding of Variables in Multivariate Analysis", Biometrika, 54, 3/4, 357-366.
Burns, A. F., and W. C. Mitchell (1946) Measuring Business Cycles, National Bureau of Economic Research, New York.
Campos, J., and N. R. Ericsson (1988) "Econometric Modeling of Consumers' Expenditure in Venezuela", International Finance Discussion Paper No. 325, Board of Governors of the Federal Reserve System, Washington, D. C., June.
Campos, J., and N. R. Ericsson (1999) "Constructive Data Mining: Modeling COnsumers' Expenditure Venezuela", Econometrics Journal, 2, 2, 226-240.
Campos, J., N. R. Ericsson, and D. F. Hendry (2005) General-to-Specific Modeling, Edward Elgar, Cheltenham.
Campos, J., D. F. Hendry, and H.-M. Krolzig (2003) "Consistent Model Selectin by an Automatic Gets Approach", Oxford Bulletin of Economics and Statistics, 65, supplement, 803-819.
Castle, J. (2005) "Evaluating PcGets and RETINA as Automatic Model Selection Algorithms", mimeo, Nuffield College, Oxford University, Oxford, England, January.
Chong, Y. Y., and D. F. Hendry (1986) "Econometric Evaluation of Linear Macroeconomic Models", Review of Economic Studies, 53, 4, 671-690.
Chow, G. C. (1960) "Tests of Equality Between Sets of Coefficients in Two Linear Regressions", Econometrica, 28, 3, 591-605.
Clements, M. P., and D. F. Hendry (1998) Forecasting Economic Time Series, Cambridge University Press, Cambridge.
Clements, M. P., and D. F. Hendry (1999) Forecasting Non-stationary Economic Time Series, MIT Press, Cambridge.
Coen, P. J., E. D. Gomme, and M. G. Kendall (1969) "Lagged Relationships in Economic Forecasting", Journal of the Royal Statistical Society, Series A, 132, 2, 133-152.
Cox, D. R. (1961) "Tests of Separate Families of Hypotheses", in J. Neyman (ed.) Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1, University of California Press, Berkeley, California, 105-123.
Cox, D. R. (1962) "Further Results on Tests of Separate Families of Hypotheses", Journal of the Royal Statistical Society, Series B, 24, 2, 406-424.
Cuthbertson, K. (1988) "The Demand for M1: A Forward Looking Buffer Shock Model", Oxford Economic Papers, 40, 1, 110-131.
Cutherbertson, K. (1991) "The Encompassing Implications of Feedforward Versus Feedback Mechanisms: A Reply to Hendry", Oxford Economic Papers, 43, 2, 344-350.
Davidson, J. E. H., and D. F. Hendry (1981) "Interpreting Econometric Evidence: The Behaviour of Consumers' Expenditure in the UK", European Economic Review, 16, 1, 177-192 (with discussion).
Davidson, J. E. H., D. F. Hendry, F. Srba, and S. Yeo (1978) "Econometric Modelling of the Aggregate Time-series Relationship between Consumers' Expenditure and Income in the United Kingdom", Economic Journal, 88, 352, 661-692.
Davidson, R., and J. G. MacKinnon (1981) "Several Tests for Model Specification in the Presence of Alternative Hypotheses", Econometrica, 49, 3, 781-793.
Denton, F. T. (1985) "Data Mining as an Industry", Review of Economics and Statistics, 67, 1, 124-127.
Dhrymes, P. J., E. P. Howrey, S. H. Hymans, J. Kmenta, E. E. Leamer, R. E. Quandt, J. B. Ramsey, H. T. Shapiro, and V. Zarnowitz (1972) "Criteria for Evaluation of Econometric Models", Annals of Economic and Social Measurement, 1, 3, 291-324.
Dickey, D. A., and W. A. Fuller (1979) "Distribution of the Estimators for Autoregressive Time Series with a Unit Root", Journal of the American Statistical Association, 74, 366, 427-431.
Dickey, D. A., and W. A. Fuller (1981) "Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root", Econometrica, 49, 4, 1057-1072.
Doornik, J. A., D. F. Hendry, and B. Nielsen (1998) "Inference in Cointegrating Models: UK M1 Revisited", Journal of Economic Surveys, 12, 5, 533-572.
Engle, R. F., and C. W. J. Granger (1987) "Co-integration and Error Correction: Representation, Estimation, and Testing", Econometrica, 55, 2, 251-276.
Engle, R. F., and D. F. Hendry (1993) "Testing Super Exogeneity and Invariance in Regression Models", Journal of Econometrics, 56, 1/2, 119-139.
Engle, R. F., D. F. Hendry, and J.-F. Richard (1983) "Exogeneity", Econometrica, 51, 2, 277-304.
Ericsson, N. R. (1983) "Asymptotic Properties of Instrumental Variables Statistics for Testing Non-nested Hypotheses", Review of Economic Studies, 50, 2, 287-304.
Ericsson, N. R. (1992a) "Cointegration, Exogeneity, and Policy Analysis: An Overview", Journal of Policy Modeling, 14, 3, 251-280.
Ericsson, N. R. (1992b) "Parameter Constancy, Mean Square Forecast Errors, and Measuring Forecast Performance: An Exposition, Extensions, and Illustration", Journal of Policy Modeling, 14, 4, 465-495.
Ericsson, N. R., J. Campos, and H.-A. Tran (1990) "PC-GIVE and David Hendry's Econometric Methodology", Revista de Econometria, 10, 1, 7-117.
Ericsson, N. R., and D. F. Hendry (1999) "Encompassing and Rational Expectations: How Sequential Corroboration Can Imply Refutation", Empirical Economics, 24, 1, 1-21.
Ericsson, N. R., D. F. Hendry, and G. E. Mizon (1998) "Exogeneity, Cointegration, and Economic Policy Analysis", Journal of Business and Economic Statistics, 16, 4, 370-387.
Ericsson, N. R., D. F. Hendry, and K. M. Prestwich (1998) "The Demand for Broad Money in the United Kingdom, 1878-1993", Scandinavian Journal of Economics, 100, 1, 289-324 (with discussion).
Ericsson, N. R., D. F. Hendry, and H.-A. Tran (1994) "Cointegration, Seasonality, Encompassing, and the Demand for Money in the United Kingdom", Chapter 7 in C. P. Hargreaves (ed.) Nonstationary Time Series Analysis and Cointegration, Oxford University Press, Oxford, 179-224.
Ericsson, N. R., and J. S. Irons (1995) "The Lucas Critique in Practice: Theory Without Measurement", Chapter 8 in K. D. Hoover (ed.) Macroeconometrics: Developments, Tensions, and Prospects, Kluwer Academic Publishers, Boston, Massachusetts, 263-312 (with discussion).
Ericsson, N. R., and J. Marquez (1993) "Encompassing the Forecasts of U. S. Trade Balance Models", Review of Economics and Statistics, 75, 1, 19-31.
Faust, J., and C. H. Whiteman (1997) "General-to-specific Procedures for Fitting a Data-admissible, Theory-inspired, Congruent, Parsimonious, Encompassing, Weakly-exogenous, Identified, Structural Model to the DGP: A Translation and Critique", Carnegie-Rochester Conference Series on Public Policy, 47, December 121-161.
Favero, C., and D. F. Hendry (1992) "Testing the Lucas Critique: A Review", Econometric Reviews. 11, 3, 265-306 (with discussion).
Florens, J.-P., and M. Mouchart (1980) "Initial and Sequential Reduction of Bayesian Experiments", CORE Discussion Paper No. 8015, CORE, Louvain-La-Neuve, Belgium, April.
Florens, J.-P., and M. Mouchart (1985) "Conditioning in Dynamic Models", Journal of Time Series Analysis, 6, 1, 15-34.
Florens, J.-P., M. Mouchart, and J.-M. Rolin (1990) "Elements of Bayesian Statistics", Marcel Dekker, New York.
Friedman, M., and A. J. Schwartz (1982) Monetary Trends in the United States and the United Kingdom: Their Relation to Income, Prices, and Interest Rates, 1867-1975, University of Chicago Press, Chicago.
Gilbert, C. L. (1986) "Professor Hendry's Econometric Methodology", Oxford Bulletin of Economics and Statistics, 48, 3, 283-307.
Gilbert, C. L. (1989) "LSE and the British Approach to Time Series Econometrics", Oxford Economic Papers, 41, 1, 108-128.
Goldfeld, S. M., and R. E. Quandt (1973) "The Estimation of Structural Shifts by Switching Regressions", Annals of Economic and Social Measurement, 2, 4, 475-485.
Govaerts, B., D. F. Hendry, and J.-F. Richard (1994) "Encompassing in Stationary Linear Dynamic Models", Journal of Econometrics, 63, 1, 245-270.
Granger, C. W. J. (1969) "Investigating Causal Relations by Econometric Models and Cross-Spectral Methods", Econometrica, 37, 3, 424-438.
Haavelmo, T. (1944) "The Probability Approach in Econometrics", Econometrica, 12, Supplement, i-viii, 1-118.
Hacche, G. (1974) "The Demand for Money in the United Kingdom: Experience Since 1971", Bank of England Quarterly Bulletin, 14, 3, 284-305.
Hall, R. E. (1978) "Stochastic Implications of the Life Cycle-Permanent Income Hypothesis: Theory and Evidence", Journal of Political Economy, 86, 6, 971-987.
Hannan, E. J., and B. G. Quinn (1979) "The Determination of the Order of an Autoregression", Journal of the Royal Statistical Society, Series B, 41, 2, 190-195.
Harbo, I., S. Johansen, B. Nielsen, and A. Rahbek (1998) "Asymptotic Inference on Cointegrating Rank in Partial Systems", Journal of Business and Economic Statistics, 16, 4, 388-399.
Hatanaka, M. (1996) Time-series-based Econometrics: Unit Roots and Cointegrations, Oxford University Press, Oxford.
Hausman, J. A. (1978) "Specification Tests in Econometrics", Econometrica, 46, 6, 1251-1271.
Hendry, D. F. (1976) "The Structure of Simultaneous Equations Estimators", Journal of Econometrics, 4, 1, 51-88.
Hendry, D. F. (1979) "Predictive Failure and Econometric Modelling in Macroeconomics: The Transactions Demand for Money", Chapter 9 in P. Ormerod (ed.) Economic Modelling: Current Issues and Problems in Macroeconomic Modelling in the UK and the US, Heinemann Education Books, London, 217-242.
Hendry, D. F. (1980) "Econometrics - Alchemy or Science?", Economica, 47, 188, 387-406.
Hendry, D. F. (1983) "Econometric Modelling: The 'Consumption Function' in Retrospect", Scottish Journal of Politicial Economy, 30, 3, 193-220.
Hendry, D. F. (1987) "Econometric Methodology: A Personal Perspective", Chapter 10 in T. F. Bewley (ed.) Advances in Econometrics: Fifth World Congress, Volume 2, Cambridge University Press, Cambridge, 29-48.
Hendry, D. F. (1988) "The Encompassing Implications of Feedback Versus Feedforward Mechanisms in Econometrics", Oxford Economic Papers, 40, 1, 132-149.
Hendry, D. F. (1993) Econometrics: Alchemy or Science? Essays in Econometric Methodology, Blackwell Publishers, Oxford.
Hendry, D. F. (1995a) Dynamic Econometrics, Oxford University Press, Oxford.
Hendry, D. F. (1995b) "Econometrics and Business Cycle Empirics", Economic Journal, 105, 433, 1622-1636.
Hendry, D. F. (1996) "On the Constancy of Time-series Econometric Equations", Economic and Social Review, 27, 5, 401-422.
Hendry, D. F. (2000) "Epilogue: The Success of General-to-specific Model Selection", Chapter 20 in D. F. Hendry (ed.) Econometrics: Alchemy or Science? Essays in Econometric Methodology, Oxford University Press, Oxford, New Edition, 467-490.
Hendry, D. F., and G. J. Anderson (1977) "Testing Dynamic Specification in Small Simultaneous Systems: An Application to a Model of Building Society Behaviour in the United Kingdom", Chapter 8c in M. D. Intriligator (ed.) Frontiers of Quantitative Economics, Volume 3A, North-Holland, Amsterdam, 361-383.
Hendry, D. F., and J. A. Doornik (1997) "The Implications for Econometric Modelling of Forecast Failure", Scottish Journal of Political Economy, 44, 4, 437-461.
Hendry, D. F., and N. R. Ericsson (1991) "Modelling the Demand for Narrow Money in the United Kingdom and the United States", European Economic Review, 35, 4, 833-883 (with discussion).
Hendry, D. F., and K. Juselius (2001) "Explaining Cointegration Analysis: Part II", Energy Journal, 22, 1, 75-120.
Hendry, D. F., and H.-M. Krolzig (1999) "Improving on 'Data Mining Reconsidered' by K. D. Hoover and S. J. Perez", Econometrics Journal, 2, 2, 202-219.
Hendry, D. F., and H.-M. Krolzig (2001) Automatic Econometric Model Selection Using PcGets 1.0, Timberlake Consultants Press, London.
Hendry, D. F., and H.-M. Krolzig (2003) "New Developments in Automatic General-to-specific Modelling", Chapter 16 in B. P. Stigum (ed.) Econometrics and the Philosophy of Economics: Theory-Data Confrontations in Economics, Princeton University Press, Princeton, 379-419.
Hendry, D. F., and H.-M. Krolzig (2004) "We Ran One Regression", Oxford Bulletin of Economics and Statistics, 66, 5, 799-810.
Hendry, D. F., and H.-M. Krolzig (2005) "The Properties of Automatic Gets Modelling", Economic Journal, 115, 502, C32-C61.
Hendry, D. F., E. E. Leamer, and D. J. Poirer (1990) "The ET Dialogue: A Conversation on Econometric Methodology", Econometric Theory, 6, 2, 171-261.
Hendry, D. F., and G. E. Mizon (1978) "Serial Correlation as a Convenient Simplification, Not a Nuisance: A Comment on a Study of the Demand for Money by the Bank of England", Economic Journal, 88, 351, 549-563.
Hendry, D. F., and G. E. Mizon (1993) "Evaluating Dynamic Econometric Models by Encompassing the VAR", Chapter 18 in P. C. B. Phillips (ed.) Models, Methods, and Applications of Econometrics: Essays in Honor of A. R. Bergstrom, Basil Blackwell, Cambridge, 272-300.
Hendry, D. F., and M. S. Morgan (eds.) (1995) The Foundations of Econometric Analysis, Cambridge University Press, Cambridge.
Hendry, D. F., A. Pagan, and J. D. Sargan (1984) "Dynamic Specification", Chapter 18 in Z. Griliches and M. D. Intriligator (eds.) Handbook of Econometrics, Volume 2, North-Holland, Amsterdam, 1023-1100.
Hendry, D. F., and J.-F. Richard (1982) "On the Formulation of Empirical Models in Dynamic Econometrics", Journal of Econometrics, 20, 1, 3-33.
Hendry, D. F., and J.-F. Richard (1983) "The Econometric Analysis of Economic Time Series", International Statistical Review, 51, 2, 111-148 (with discussion).
Hendry, D. F., and J.-F. Richard (1989) "Recent Developments in the Theory of Encompassing", Chapter 12 in B. Cornet and H. Tulkens (eds.) Contributions to Operations Research and Economics: The Twentieth Anniversary of CORE, MIT Press, Cambridge, 393-440.
Hendry, D. F., and T. von Ungern-Sternberg (1981) "Liquidity and Inflation Effects on Consumers' Expenditure", Chapter 9 in A. S. Deaton (ed.) Essays in the Theory and Measurement of Consumer Behaviour: In Honour of Sir Richard Stone, Cambridge University Press, Cambridge, 237-260.
Hoover, K. D., and S. J. Perez (1999a) "Data Mining Reconsidered: Encompassing and the General-to-specific Approach to Specification Search", Econometrics Journal, 2, 2, 167-191.
Hoover, K. D., and S. J. Perez (1999b) "Reply to Our Discussants", Econometrics Journal, 2, 2, 244-247.
Hoover, K. D., and S. J. Perez (2004) "Truth and Robustness in Cross-country Growth Regressions", Oxford Bulletin of Economics and Statistics, 66, 5, 765-798.
Johansen, S. (1988) "Statistical Analysis of Cointegration Vectors", Journal of Economic Dynamics and Control, 12, 2/3, 231-254.
Johansen, S. (1992a) "Cointegration in Partial Systems and the Efficiency of Single-equation Analysis", Journal of Econometrics, 52, 3, 389-402.
Johansen, S. (1992b) "Testing Weak Exogeneity and the Order of Cointegration in UK Money Demand Data", Journal of Policy Modeling, 14, 3, 313-334.
Johansen, S. (1995) Likelihood-based Inference in Cointegrated Vector Autoregressive Models, Oxford University Press, Oxford.
Johansen, S., and K. Juselius (1990) "Maximum Likelihood Estimation and Inference on Cointegration - With Applications to the Demand for Money", Oxford Bulletin of Economics and Statistics, 52, 2, 169-210.
Judge, G. G., and M. E. Bock (1978) The Statistical Implications of Pre-test and Stein-rule Estimators in Econometrics, North-Holland, Amsterdam.
Kent, J. T. (1986) "The Underlying Structure of Nonnested Hypothesis Tests", Biometrika, 73, 2, 333-343.
Keynes, J. M. (1939) "Professor Tinbergen's Method", Economic Journal, 49, 195, 558-568.
Keynes, J. M. (1940) "Comment", Economic Journal, 50, 197, 154-156.
Koopmans, T. C. (1947) "Measurement Without Theory", Review of Economics and Statistics (formerly the Review of Economic Statistics), 29, 3, 161-172.
Koopmans, T. C. (1950) "When Is an Equation System Complete for Statistical Purposes?", Chapter 17 in T. C. Koopmans (ed.) Statistical Inference in Dynamic Economic Models (Cowles Comission Monograph No. 10), John Wiley, New York, 393-409.
Krolzig, H.-M. (2001) "General-to-specific Reductions of Vector Autoregressive Processes", in R. Friedmann, L. Knüppel, and H. Lütkepohl (eds.) Econometric Studies: A Festschrift in Honour of Joachim Frohn, LIT Verlag, Munster, 129-157.
Krolzig, H.-M. (2003) "General-to-specific Model Selection Procedures for Structural Vector Autoregressions", Oxford Bulletin of Economics and Statistics, 65, supplement, 769-801.
Krolzig, H.-M., and D. F. Hendry (2001) "Computer Automation of General-to-specific Model Selection Procedures", Journal of Economic Dynamics and Control, 25, 6-7, 831-866.
Leamer, E. E. (1978) Specification Searches: Ad Hoc Inference With Nonexperimental Data, John Wiley, New York.
Leamer, E. E. (1985) "Sensitivity Analyses Would Help", American Economic Review, 75, 3, 308-313.
Lovell, M. C. (1983) "Data Mining", Review of Economics and Statistics, 65, 1, 1-12.
Lu, M., and G. E. Mizon (1991) "Forecast Encompassing and Model Evaluation", Chapter 9 in P. Hackl and A. H. Westlund (eds.) Economic Structural change: Analysis and Forecasting, Springer-Verlag, Berlin, 123-138.
Lu, M., and G. E. Mizon (1996) "The Encompassing Principle and Hypothesis Testing", Econometric Theory, 12, 5, 845-858.
Lucas, Jr., R. E. (1976) "Econometric Policy Evaluation: A Critique", in K. Brunner and A. H. Meltzer (eds.) The Phillips Curve and Labor Markets, North-Holland, Amsterdam, Carnegie-Rochester Conference Series on Public Policy, Volume 1, Journal of Monetary Economics, Supplement, 19-46 (with discussion).
MacDonald, R., and M. P. Taylor (1992) "A Stable US Money Demand Function, 1874-1975", Economics Letters, 39, 2, 191-198.
MacKinnon, J. G. (1983) "Model Specification Tests Against Non-nested Alternatives", Econometric Reviews, 2, 1, 85-110 (with discussion).
Metin, K. (1995) "An Integrated Analysis of Turkish Inflation", Oxford Bulletin of Economics and Statistics, 57, 4, 513-531.
Mizon, G. E. (1977a) "Inferential Procedures in Nonlinear Models: An Application in a UK Industrial Cross Section Study of Factor Substitution and Returns to Scale", Econometrica, 45, 5, 1221-1242.
Mizon, G. E. (1977b) "Model Selection Procedures", Chapter 4 in M. J. Artis and A. R. Nobay (eds.) Studies in Modern Economic Analysis, Basil Blackwell, Oxford, 97-120.
Mizon, G. E. (1984) "The Encompassing Approach in Econometrics", Chapter 6 in D. F. Hendry and K. F. Wallis (eds.) Econometrics and Quantitative Economics, Basil Blackwell, Oxford, 135-172.
Mizon, G. E. (1995) "Progressive Modeling of Macroeconomic Time Series: The LSE Methodology", Chapter 4 in K. D. Hoover (ed.) Macroeconometrics: Developments, Tensions, and Prospects, Kluwer Academic Publishers, Boston, Massachusetts, 107-170 (with discussion).
Mizon, G. E., and J.-F. Richard (1986) "The Encompassing Principle and its Application to Testing Non-nested Hypotheses", Econometrica, 54, 3, 657-678.
Pagan, A. (1987) "Three Econometric Methodologies: A Critical Appraisal", Journal of Economic Surveys, 1, 1, 3-24.
Perez-Amaral, T., G. M. Gallo, and H. White (2003) "A Flexible Tool for Model Building: The Relevant Transformation of the Inputs Network Approach (RETINA)", Oxford Bulletin of Economics and Statistics, 65, Supplement, 821-838.
Pesaran, M. H. (1974) "On the General Problem of Model Selection", Review of Economic Studies, 41, 2, 153-171.
Pesaran, M. H., and A. S. Deaton (1978) "Testing Non-nested Nonlinear Regression Models", Econometrica, 46, 3, 677-694.
Phillips, A. W. (1956) "Some Notes on the Estimation of Time-forms of Reactions in Interdependent Dynamic Systems", Economica, 23, 90, 99-113.
Phillips, P. C. B. (1988) "Reflections on Econometric Methodology", Economic Record, 64, 187, 344-359.
Phillips, P. C. B. (1991) "Optimal Inference in Cointegrated Systems", Econometrica, 59, 2, 283-306.
Phllips, P. C. B. (1996) "Econometric Model Determination", Econometrica, 64, 4, 763-812.
Ramsey, J. B. (1969) "Tests for Specification Errors in Classical Linear Least-squares Regression Analysis", Journal of the Royal Statistical Society, Series B, 31, 2, 350-371.
Richard, J.-F. (1980) "Models with Several Regimes and Changes in Exogeneity", Review of Economic Studies, 47, 1, 1-20.
Sargan, J. D. (1959) "The Estimation of Relationships with Autocorrelated Residuals by the Use of Instrumental Variables", Journal of the Royal Statistical Society, Series B, 21, 1, 91-105.
Sargan, J. D. (1961) "The Maximum Likelihood Estimation of Economic Relationships with Autoregressive Residuals", Econometrica, 29, 3, 414-426.
Sargan, J. D. (1964) "Wages and Prices in the United Kingdom: A Study in Econometric Methodology", in P. E. Hart, G. Mills, and J. K. Whitaker (eds.) Econometric Analysis for National Economic Planning, Volume 16 of Colston Papers, Buttersworths, London, 25-54. (with discussion).
Sargan, J. D. (1980a) "The Consumer Price Equation in the Post War British Economy: An Exercise in Equation Specification Testing", Review of Economic Studies, 47, 1, 113-135.
Sargan, J. D. (1980b) "Some Tests of Dynamic Specification for a Single Equation", Econometrica, 48, 4, 879-897.
Sargan, J. D. (2001a) "The Choice Between Sets of Regressors", Econometric Reviews, 20, 2, 171-186. (reprint of a June 1981 manuscript).
Sargan, J. D. (2001b) "Model Building and Data Mining", Econometric Reviews, 20, 2, 159-170.
Savin, N. E. (1980) "The Bonferroni and the Scheffé Multiple Comparison Procedures", Review of Economic Studies, 47, 1, 255-273.
Sawa, T. (1978) "Information Criteria for Discriminating Among Alternative Regression Models", Econometrica, 46, 6, 1273-1291.
Sawyer, K. R. (1983) "Testing Separate Families of Hypotheses: An Infomation Criterion", Journal of the Royal Statistical Society, Series B, 45, 1, 89-99.
Scheffé, H. (1953) "A Method for Judging All Contrasts in the Analysis of Variance", Biometrika, 40, 1/2, 87-104.
Schwarz, G. (1978) "Estimating the Dimension of a Model", Annals of Statistics, 6, 2, 461-464.
Sims, C. A. (1980) "Macroeconomics and Reality", Econometrica, 48, 1, 1-48.
Sims, C. A., J. H. Stock, and M. W. Watson (1990) "Inference in Linear Time Series Models with Some Unit Roots", Econometrica, 58, 1, 113-144.
Spanos, A. (1989) "On Rereading Haavelmo: A Retrospective View of Econometric Modeling", Econometric Theory, 5, 3, 405-429.
Summers, L. H. (1991) "The Scientific Illusion in Empirical Macroeconomics", Scandinavian Journal of Economics, 93, 2, 129-148.
Theil, H. (1971) Principles of Econometrics, John Wiley, New York.
Tinbergen, J. (1939) Statistical Testing of Business-Cycle Theories, League of Nations, Geneva.
Tinbergen, J. (1940) "On a Method of Statistical Business-cycle Research. A Reply", Economic Journal, 50, 197, 141-154.
Trivedi, P. K. (1970a) "Inventory Behaviour in U.K. Manufacturing 1956-67", Review of Economic Studies, 37, 4, 517-536.
Trivedi, P. K. (1970b) "The Relation Between the Order-delivery Lag and the Rate of Capacity Utilization in the Engineering Industry in the United Kingdom, 1958-1967", Economica, 37, 145, 54-67.
Trivedi, P. K. (1973) "Retail Inventory Investment Behaviour", Journal of Econometrics, 1, 1, 61-80.
Trivedi, P. K. (1975) "Time Series Versus Structural Models: A Case Study of Canadiann Manufacturing Inventory Behaviour", International Economic Review, 16, 3, 587-608.
Urbain, J.-P. (1992) "On Weak Exogeneity in Error Correction Models", Oxford Bulletin of Economics and Statistics, 54, 2, 187-207.
White, H. (1990) "A Consistent Model Selection Procedure Based on m-testing", Chapter 16 in C. W. J. Granger (ed.) Modelling Economic Series: Readings in Econometric Methodology, Oxford University Press, Oxford, 369-383.
Wooldridge, J. M. (1990) "An Encompassing Approach to Conditional Mean Tests with Applications to Testing Nonnested Hypotheses", Journal of Econometrics, 45, 3, 331-350.
Yancey, T. A., and G. G. Judge (1976) "A Monte Carlo Comparison of Traditional and Stein-rule Estimators Under Squared Error Loss", Journal of Econometrics, 4, 3, 285-294.
Footnotes
* Forthcoming as the editors' introduction to a two-volume set of readings entitled General-to-Specific Modelling, Julia Campos, Neil R. Ericsson, and David F. Hendry (eds.), Edward Elgar Publishing, Cheltenham, 2005. The first author is a professor of econometrics in the Departmento de Economía e Historia Económica, Facultad de Economía y Empresa, Universidad de Salamanca, Salamanca 37008 España (Spain). The second author is a staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. The third author is an ESRC Professorial Research Fellow and the head of the Economics Department at the University of Oxford, Oxford, England. They may be reached on the Internet at [email protected], [email protected], and [email protected] respectively. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. The authors are indebted to Jonathan Halket, Jaime Marquez, and Kristin Rogers for helpful comments; and to Nicola Mills for seeing the production of this work through to completion. Scientific Workplace (MacKichan Software, Inc., Poulsbo, Washington, U.S.A.) eased the preparation of this paper in LaTeX. This discussion paper is available from the authors and at www.federalreserve.gov/pubs/ifdp/2005/838/default.htm on the World Wide Web. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text