
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 839, September 2005--- Screen Reader
Version*
Effects of Financial Autarky and Integration: The Case of the South Africa Embargo
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The economic embargo imposed on South Africa between 1985 and 1993 brought the country closer to financial isolation. This paper interprets the imposition and removal of the embargo as financial autarky and financial integration `natural experiments', and studies the effects on the economy. The aggregate data indicate a decrease in the levels and growth rates of investment, capital, and output during the embargo period relative to the pre-embargo and post-embargo periods. To further rationalize the findings in the aggregate data, we calibrate a neoclassical growth model to the South African economy. During the transition to steady-state, we model the embargo by limiting the country's ability to borrow for a period corresponding to the duration of the embargo. The derived dynamics for investment, capital, and output support the view of a positive (negative) link between financial integration (isolation) and economic growth.
Keywords: International finance, embargo, autarky, financial integration, financial isolation, econmic growth
JEL classification: F3, F41, E13, O4, O11, O16
1 Introduction
Between 1985 and 1993 the world imposed economic sanctions on South Africa to put pressure on its apartheid regime (a political system that granted different rights to citizens based on race). At that time, foreign investors withdrew their capital from the country and stopped making new investments in and loans to South Africa. As a result, net capital inflows declined drastically. In this paper, we exploit the unique reversion toward financial autarky during the embargo period and reintegration into the world economy in the post-embargo period to study the economic benefits of financial integration for an emerging economy.
Until recently, it seemed obvious that financial integration yields important economic benefits for emerging economies. The conventional view of financial integration suggests that when countries are integrated, capital flows from capital-abundant to capital-scarce countries to achieve a more efficient allocation of global savings. The inflow of capital speeds up capital formation, and increases economic growth and welfare in the recipient country (see e.g. Obstfeld, 1994; Fischer, 1998; Eichengreen and Mussa, 1998).1
The financial crises that devastated the emerging economies of Asia and Latin America in the mid to late 1990s following the liberalization of their capital accounts challenged the conventional view on the economic effect of financial integration, and prompted a renewed research interest in the subject.2 Since then, several empirical studies have assessed the economic effect of capital account liberalizations with mixed resulting evidence. (see Edison et al., 2003 for a survey). Part of the challenge to resolve this issue can be traced to the difficulty in measuring financial integration as noted in Edison et al. (2002). The literature uses four broad measures.
The first measure is based on the International Monetary Fund's (IMF) Annual Report on Exchange Arrangements and Exchange Restrictions (AREAER). It constructs a binary zero-one indicator for whether the country maintains restrictions on foreign exchanges. When averaged over a period, the constructed indicator measures the fraction of time when the country maintained an open capital account. Rodrick (1998) uses such a measure as an independent variable in a panel regression of one hundred countries. He finds no evidence that capital account liberalization increases investment or economic growth.
The second measure, proposed by Quinn (1997), aims to improve upon the first measure by capturing the intensity of the restrictions. It departs from the binary coding and assigns numerical values based on detailed information in the AREAER. The resulting 0-14 measure attempts to provide a more informative measure by capturing the extent of the countries' financial integration. In contrast to findings in Rodrick (1998), he finds a positive relationship between capital account liberalization and economic growth.
The third set of measures is based on the flow of capital or the stock of foreign liabilities to Gross Domestic Product (GDP) ratios. Based on these measures, the higher the capital flows between a country and the rest of the world, or the higher the country's stock of foreign liabilities as a share of GDP, the more financially integrated the country is. Using this measure, Kraay (1998) finds some positive relationship between financial integration and economic growth, while Edison et al. (2002) finds no significant relationship.
The last measure is based on official dates of stock market liberalizations. This approach, used in Henry (2003) and Bekaert et al. (2001), considers that the countries are more financially integrated after they open their stock markets to foreign investors. Both authors find a positive significant relationship between the liberalization of stock markets and growth in investment and output. (see Edison et al., 2002 for a detailed survey on various measures).
In this study, the financial isolation is the imposition of the embargo, and the financial integration is the removal of the embargo. The experiment, therefore, circumvents the challenges of measuring financial integration. A related and often mentioned reservation about some of the previous measures of financial integration is the endogeneity of the integration measure itself. Financial integration, skeptics argue, is a process that does not occur in isolation. It is usually induced by contemporaneous or prospective changes to the economy. In this case, the direction of causality between integration to economic performance is not obvious.
In this study, we posit that the isolation and reintegration due to the imposition and removal of the embargo, can be interpreted as events less subject to the endogeneity encountered in some of the previous studies. The decision by the world to impose an economic embargo on South Africa was not related to the country's economic performance, but to the desire to change its political regime. Similarly, the decision to remove the embargo followed a host of political reforms that dismantled the apartheid regime. The reforms were instituted under a new and more moderate prime minister following the resignation of his predecessor for unexpected health problems.
The study further contributes to the literature by analyzing the benefits of financial integration through the lenses of the adverse effects of financial isolation. A corollary of the view that greater financial integration yields economic benefits is that financial isolation should adversely affect the economy. Since South Africa was integrated prior to the economic embargo and reintegrated into the world financial markets after the embargo period, we can analyze both the negative effects of financial isolation as well as the positive effects of financial integration.
There are, however, potential challenges to using this embargo event study which make it difficult to isolate the effect of the financial isolation. First, the sanctions against South Africa included an embargo on trade, and the effects of the embargo on the economy could have resulted from the trade sanctions, and not necessarily from the financial isolation. Second, domestic policy changes induced by the sanctions, if any, could have been the cause of any distortions to the economy during the embargo period. Third, the embargo took place in an environment of political instability. The risk stemming from the instability could have adversely affected the economy during the embargo period. Last, possible shocks to the global economy during the embargo period could have also affected the South African economy irrespective of the financial isolation. Despite these potential limitations, which we address later in the study, the South Africa embargo offers a unique alternative experiment not explored in the literature to analyze the economic importance of financial integration (isolation) for an emerging economy.
The study begins in section 2 with a documentation of the embargo event and the financial isolation. In section 3, we analyze the effect of the embargo on investment, capital, and output using time series data of the South Africa economy. According to the integration hypothesis, the growth rates and levels for these variables should decrease during the embargo period compared to the pre-embargo and post-embargo years. The data support these predictions.
During the embargo period, average growth rates fell from 0.2 percent to -2.6 percent for investment, from 3.5 to 1.3 percent for capital per worker, and from 2.2 to 0.8 percent for output per worker. After the embargo, the average growth rates for investment, and capital and output per worker increased to 5.0 percent, 2.0 percent, and 3.7 percent, respectively. The statistics further indicate that the levels of investment, capital, and output fell by 25.6 percent, 12.5 percent, and 9.5 percent during the embargo period compared to the levels that would have prevailed if the variables had maintained the pre-embargo average growth rates. In the post-embargo period, the levels of investment, capital, and output rose 37.3 percent, 2.2 percent, and 8.4 percent above the levels that would have prevailed if the variables had continued to grow at the embargo period average growth rates.
To further rationalize the observations of a positive (negative) effect of financial integration (isolation) on economic performance, we present in section 4, a small open economy neoclassical growth model calibrated to the South African economy. During the transition to steady-state, we model the embargo event by limiting the country's ability to borrow, and by imposing a tax on output to capture the disinvestment during the embargo period. The resulting dynamics for investment, capital, and output confirm the observations of a positive (negative) link between financial integration (isolation) and economic growth. In section 5, we address the challenges, noted earlier, with using the South Africa embargo experiment, and conclude in section 6.
2 The South Africa Embargo
2.1 Historical Context
In 1948, the Nationalist party assumed power in South Africa and passed legislations that instituted the apartheid system; a system under which citizens from different racial groups had different rights. The institution of the apartheid system prompted a worldwide condemnation and marked the beginning of sanctions against the country. The United Nations (U.N.) and several countries imposed various forms of sanctions on South Africa to end the apartheid regime. However, the economic sanctions did not intensify until 1985, and they continued until the apartheid regime was dismantled around 1993. In the remainder of the study, the period 1985-1993 is considered the embargo period. The choice of these dates is guided by historical accounts of the embargo and by the changes in economic variables such as foreign liabilities, net capital flows, and the current account.
To assess the effect of the embargo on foreign investment and trade in South Africa, the next sections document some anecdotal evidence of the disinvestment, and present data obtained from the South Africa Reserve Bank on net capital inflows (Figure 1), foreign liabilities (Figures 2 and 3) and the current account (Figure 4).
2.3 Foreign Investment prior to the Embargo
Prior to the 1985 economic sanctions, South Africa had an open capital account and foreigners invested in the country. The following statistics document the magnitude and composition of foreign liabilities (Foreign Direct Investment, Portfolio investment, and Loans) in the period leading up to the 1985 embargo.
Between 1970 and 1985, net capital inflows and total foreign liabilities as percentages of GDP averaged 2.2 percent and 53 percent, respectively (see Figures 1 and 2). Figure 4 indicates that current account was mostly in deficit (except in 1977-1980), averaging over 2 percent of GDP. Figure 3 presents the composition of the liabilities. On average, 45 percent of the total liabilities were in Foreign Direct Investment (FDI), followed by loans (40 percent). Portfolio investments made up the remaining 15 percent; two-thirds of which were held in equity.
By 1985, total foreign liabilities as a percentage of GDP had increased from 53 percent to nearly 70 percent (the public sector held 37 percent of the liabilities, and the banking and non-banking sectors held the remaining 63 percent), and the composition changed. The share of FDI and portfolio investments declined to 25 percent and 13 percent, respectively. The share of loans, on the other hand, increased from 40 percent of total liabilities to over 60 percent; 70 percent of which was due to mature within a year. The shift in liabilities from FDI and portfolio to debt reflected, perhaps, foreign investors' desire to reduce their risk exposure in South Africa (in light of the prevailing fragile political situation), forcing the country to rely on loans rather than on FDI and equity capital to fulfill its investment needs. The government had, reportedly, facilitated foreign borrowing by reassuring foreign banks and by stabilizing the indebtedness through gold swaps, or by borrowing from the IMF.
2.3 Foreign Investment during the Embargo
In September 1984, the ruling party in South Africa instituted a new constitution that established separate parliamentary chambers for Indian and colored representatives, and continued to exclude Blacks. The new constitution signaled an uncompromising position on the apartheid issue, and sparked widespread protests and riots. The unrest resulted in an intensification of economic sanctions and marked the beginning of the disinvestment period.
Several foreign companies operating in South Africa decided to disinvest and/or stop making new investments or reinvestments of earnings in the country. For example, of the approximately 350-400 United States (U.S.) companies with direct investment in South Africa in January 1984, the Investor Responsibility Research Center estimated that seven withdrew in 1984 and 39 in 1985. During 1986 the pace quickened. Forty companies left and thirteen announced their intention of leaving. By June 1987, 39 additional firms had left or announced their intention of leaving. By mid-1988, only 136 U.S. companies reportedly remained in the country (Lipton 1998, 64; Baker 1989, 59).
In addition to private companies, several countries and some U.S. states passed laws forbidding investment of municipal or state funds in companies operating in South Africa. In 1986, California announced a gradual disinvestment of its $11 billion held in companies with ties to South Africa. By the end of 1988, 23 states, 19 counties, and 79 cities had adopted various economic measures to distance themselves from South Africa. (Chettle 1982, 106-08; New York Times, 28 October 1984, A18; Los Angeles Times, 25 December 1984, A1; Lipton 1988, 23-24; Baker 61). In 1985, France also banned new investment in or loans to South Africa.
Foreign banks joined in on the sanctions. In the first half of 1985, U.S. banks reportedly withdrew $1 billion. In the Fall of 1986, Barclays Bank (the largest British investor in the country) disinvested as well. Other British banks, that had lent South Africa more than $3 billion in debt due to mature in 1987, were also unwilling to make new loans to the country (Washington Post, 1 September 1985, A1).3
As a result of the economic sanctions, the U.S. General Accounting Office (GAO) estimated that $10.8 billion flowed out of South Africa from January 1985 through June 1989, including $3.7 billion in loan repayments to banks, $7.1 billion in other debt repayments and capital flight (GAO 1990, 12, 17). Similarly, Trust Bank (a South Africa commercial bank) calculated that the country had forgone nearly $14 billion in loans and direct investments between 1985 and 1990 in comparison to what loans and direct investments would have been had money flown in at the rate that had prevailed before 1985 (The Economist, 10 February 1990, 69). The IMF estimated that South Africa had forgone $8 billion in foreign investment between 1985 and 1991, which amounted to 3 percent of the 1985-1991 period cumulative GDP.
Figures 1-4 document the effect of the embargo on net capital inflows, foreign liabilities, and the current account. Net capital inflows reversed to net outflows of approximately 2 percent of GDP per year. The current account reversed from an average of 2 percent of GDP deficit prior to the embargo to a 2.4 percent surplus during the embargo period. Foreign liabilities as a percentage of GDP fell from 53 percent prior to 1985, to 44 percent during the embargo period. The composition of the liabilities shifted from loans to portfolio investment, most likely, reflecting a 1987 debt renegotiation agreement that allowed foreign investors to convert loans into equity.
2.4 Foreign Investment after the Embargo
In 1989, the Prime minister suffered a stroke, and resigned unexpectedly. His successor initiated a series of reforms in the early 1990s that resulted in the abolishment of the apartheid system. Accordingly, the international community began to lift the sanctions. In 1992, the European Commission lifted its sanctions against South Africa. The United States, Norway, and India followed in 1993. In 1994, the remaining United Nations sanctions were removed.
With the removal of the economic sanctions and the reintegration of South Africa in the global economy, foreign investment in the country resumed. For example, the World Bank announced $1 billion worth of development projects for South Africa in 1993. The South Africa Reserve Bank estimated that capital flows switched from large outflows prior to 1994 to net inflows of approximately 2.6 billion rands ($730 million) in 1994, and to 16.6 billion rands ($4.6 billion) in 1995 (Wesso, 2001). The share of foreign portfolio investment in the JSE increased from 6 percent in 1985 to approximately 15 percent in 1994. At the end of 1995, South Africa had the largest weight in the International Finance Corporation's (IFC) global emerging market index (15 percent) and investible emerging market index (27 percent).
Figures 1-4 document the effect of the removal of the embargo on net capital inflows, foreign liabilities, and the current account. Capital flows reversed again from net outflows during the embargo period to net inflows of approximately 2 percent of GDP per year between 1994 and 2001. During the same period, the current account also reversed from a surplus during the embargo period to a 1 percent per year deficit. The effect of the post embargo inflows is also reflected in the stock of foreign liabilities. Total liabilities as a percentage of GDP increased from its 1985-1993 average of 40 percent to 63 percent between 1994 and 2001, exceeding the pre-1985 average of 53 percent.
In summary, consistent with historical accounts on the disinvesment, net capital flows which were positive prior to the embargo, reversed to net outflows during the embargo period, and the amount of foreign liabilities declined significantly. Reflecting, in part, the disinvestment, the current account reversed from a deficit to a surplus. When the sanctions were lifted, foreign investment returned to South Africa. Net capital flows switched from net outflows during the embargo to net inflows. The stock of foreign liabilities increased significantly in the post embargo period, and the current account reversed back to a deficit. Both the historical accounts of the disinvestment and the data on foreign investment support a reduction of foreign investment in South Africa between 1985 and 1993 reverting the country to quasi-autarky. The following section analyzes the effect, if any, of the financial isolation on fixed investment, capital, and output.
3 Economic Effect of the Embargo
We plot in figures 5 through 7, annual fixed investment, and capital and output per worker for South Africa from 1970 to 2001. The vertical bars denote the 1985-1993 embargo period. The figures indicate that during the embargo period, the growth rates of investment, capital and output per worker decreased in comparison to the pre-embargo and post-embargo periods growth rates.
Table 1 compares the growth rates of investment, capital, and output before, during, and after the embargo. The results indicate that average growth rate of investment fell during the embargo period to -2.6 percent from 0.2 percent in the eight years prior to the embargo, and increased to 5.0 percent between 1994 and 2001. The average growth rate for capital also fell during the embargo period to 1.3 percent from 3.5 percent in the eight years prior to the embargo, and increased to 2.0 percent in the post-embargo period. Similarly, the average growth rate of output fell from 2.2 percent prior to the embargo to 0.8 during the embargo period, and increased to 3.7 percent after the embargo.
To measure the investment, capital, and output loss due to the embargo, we plot also, in figures 5 through 7, the paths assuming the variables maintained their eight-year pre-embargo period average growth rates during the embargo period (upper dotted lines between 1985 and 1993). To measure the investment, capital, and output gains due to the removal of the embargo, we also plot in figures 5 through 7, the paths assuming the variables maintained their eight-year embargo period average growth rates (lower dotted lines between 1994 and 2001). To quantify the losses (gains), we compare, also in Table 1, the levels of investment, capital, and output to those that would have prevailed if the variables had maintained the pre-embargo (embargo) period average growth rates.
Results indicate that the average level of investment fell by 25.6 percent during the embargo period compared to the level that would have prevailed if investment had grown at its pre-embargo growth rate. For capital and output, the corresponding declines in average levels were 12.5 and 9.5 percent, respectively. After the embargo, the levels of investment, output and capital increased 37.3 percent, 2.2 percent, and 8.4 percent from the levels that would have prevailed if the variables had grown at the embargo period average growth rates.
In summary, the descriptive statistics of investment, capital, and output suggest that the embargo adversely affected the economy, and that the economy benefited from the removal of the embargo. To further rationalize these findings, the next section presents a neoclassical growth model calibrated to the South Africa economy to capture the effects of the embargo.
4 A Theoretical Growth Model
The theoretical framework is a simple neoclassical growth model in the context of a small open economy with perfect capital mobility and capital adjustment costs. The adjustment costs are introduced to avoid instantaneous convergence to steady-state. A central planner makes all the production, consumption, and investment decisions. The agents in the economy are infinitely lived. There are no uncertainties, except that the imposition and removal of embargo are unexpected, and there is no government. Markets are competitive, and the production technology has constant returns to scale.
The model further assumes that population and labor (supplied
inelastically) are identical. Labor grows at a constant rate so
that labor at a time ![]() is given by
is given by
![]() Technology
Technology ![]() evolves at a constant rate
evolves at a constant rate ![]() and
and
![]() . Zero subscripts denote the
initial value of the economic variable, e.g.
. Zero subscripts denote the
initial value of the economic variable, e.g.
![]() Let
Let ![]() and
and
![]() The effective unit of labor at a
time
The effective unit of labor at a
time ![]() is given by
is given by
![]() All lower case variables
are expressed in effective units of labor; e.g.,
All lower case variables
are expressed in effective units of labor; e.g.,
![]() .
.
4.1 Financial Integration
In absence of the embargo, the economy accumulates capital using savings of its residents, and by attracting foreign capital. Since the country is open and small, the interest rate is set exogenously at the world rate. The social planner has perfect foresight and determines each period's allocation by maximizing the welfare subject to the budget constraint:
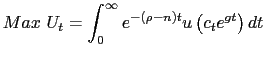
![$\displaystyle \dot{d}_{t}=c_{t}+\left( r^{w}-n-g\right) d_{t}+i_{t}\left[ 1+\phi\left( \frac{i_{t}}{k_{t}}\right) \right] -f\left( k_{t}\right)$](img17.gif)
|
(1) |
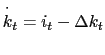 |
(2) |
Where
![]() is the utility
function,
is the utility
function, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote
consumption, the stock of foreign debt, capital stock, output, and
investment in effective units of labor, respectively.
denote
consumption, the stock of foreign debt, capital stock, output, and
investment in effective units of labor, respectively. ![]() is the world interest rate. It is costly to adjust
capital.
is the world interest rate. It is costly to adjust
capital.
![]() is the adjustment
cost function. Parameters
is the adjustment
cost function. Parameters ![]() ,
, ![]() , and
, and ![]() represent the rate of
depreciation, the utility discount rate, and the share of capital
in output production, respectively.
represent the rate of
depreciation, the utility discount rate, and the share of capital
in output production, respectively.
Equation
(1)
is the resource flow constraint. The change in the net foreign debt
is the excess spending (consumption, investment, transfers) over
production net of capital adjustment costs. Equation
(2)
states that capital accumulates through investment net of
depreciation. Further, assume a constant relative risk aversion
(CRRA) utility function of the following form:
![]() for
for
![]() and
and
![]() for
for
![]() , where
, where ![]() is the
inverse intertemporal elasticity of substitution for consumption
(risk aversion parameter). Let
is the
inverse intertemporal elasticity of substitution for consumption
(risk aversion parameter). Let
![]() , and
, and
![]() so that lifetime utility
does not diverge. Let
so that lifetime utility
does not diverge. Let
![]() and
and ![]() be the
marginal valuation of wealth and uninstalled capital, respectively.
The necessary and sufficient conditions characterizing the social
planner's optimal path are as follows:
be the
marginal valuation of wealth and uninstalled capital, respectively.
The necessary and sufficient conditions characterizing the social
planner's optimal path are as follows:
| (3) |
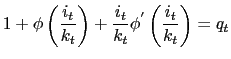
|
(4) |
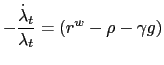
|
(5) |
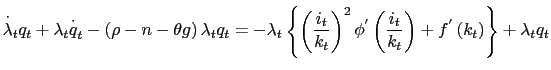
|
(6) |
The transvervsality conditions are as follows:
| (7) |
| (8) |
Equations
(3)
through
(8) along
with the initial conditions for capital and debt characterize the
solution to the maximization problem. Equation
(3)
states that at the optimal level of consumption, the marginal
utility and the marginal valuation for wealth are identical.
Equation
(4)
contains a strong implication that the rate of investment relative
to capital stock depends only on ![]() ; the shadow
price (in terms of consumption goods) of a unit of installed
capital. Equations
(5) and
(6) are
the Euler equations associated with
; the shadow
price (in terms of consumption goods) of a unit of installed
capital. Equations
(5) and
(6) are
the Euler equations associated with
![]() and
and ![]() ,
respectively. Equations
(7) and
(8) are
the corresponding transversality conditions. Combining
(5) and
(6), and
substituting out
,
respectively. Equations
(7) and
(8) are
the corresponding transversality conditions. Combining
(5) and
(6), and
substituting out
![]() and
and ![]() using
(5),
results in the the equation of motion for
using
(5),
results in the the equation of motion for ![]() .
.
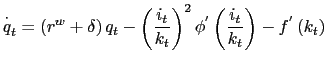
|
(9) |
4.2 Financial Autarky
The theoretical specification for the embargo period is similar
to the framework under financial integration in the previous
section. It differs in the economy's ability to run current account
deficits. The economy can only accumulate capital with the savings
of its residents. It can no longer raise new foreign capital as in
the previous section. To allow for capital flight and some debt
servicing during the embargo, we introduce a parameter ![]() as a temporary tax on output. It captures the net
outflow of capital (as a percentage of GDP) observed during the
embargo period. With these assumptions, the embargo period resource
constraint is as follows:
as a temporary tax on output. It captures the net
outflow of capital (as a percentage of GDP) observed during the
embargo period. With these assumptions, the embargo period resource
constraint is as follows:
![$\displaystyle f\left( k_{t}\right) =c_{t}+\tau f\left( k_{t}\right) +i_{t}\left[ 1+\phi\left( \frac{i_{t}}{k_{t}}\right) \right]$](img66.gif)
|
(10) |
Where ![]() for
for ![]() and
and
![]() for
for ![]() .
. ![]() is period of time from beginning of the embargo until debt
accumulated up to the embargo is completely serviced at a rate of
is period of time from beginning of the embargo until debt
accumulated up to the embargo is completely serviced at a rate of
![]() percent of output per year. Let
percent of output per year. Let
![]() denote the initial level of capital
disinvested and foreign debt repayments at the eve of the embargo
that subsequently leaves the country during the embargo period.
denote the initial level of capital
disinvested and foreign debt repayments at the eve of the embargo
that subsequently leaves the country during the embargo period.
![]() is such that
is such that
![]() . Constraint
(10)
indicates that output is allocated between consumption,
investment, adjustment costs, and some debt servicing and capital
flight during the embargo. The country can no longer borrow, and
the current account surplus is equal to the amount of outflows
. Constraint
(10)
indicates that output is allocated between consumption,
investment, adjustment costs, and some debt servicing and capital
flight during the embargo. The country can no longer borrow, and
the current account surplus is equal to the amount of outflows
![]() . Let
. Let
![]() , and let
, and let
![]() denote the marginal valuation for a unit
of uninstalled capital measured in utility. The central planner
maximizes lifetime welfare subject to
(2) and
(10)
. The necessary and sufficient conditions characterizing the social
planner's optimal path are as follows:
denote the marginal valuation for a unit
of uninstalled capital measured in utility. The central planner
maximizes lifetime welfare subject to
(2) and
(10)
. The necessary and sufficient conditions characterizing the social
planner's optimal path are as follows:
![$\displaystyle \left[ 1+\phi\left( \frac{i_{t}}{k_{t}}\right) +\frac{i_{t}}{k_{t}} \phi^{^{\prime}}\left( \frac{i_{t}}{k_{t}}\right) \right] u^{^{\prime} }\left( c_{t}\right) =\mu_{t}$](img82.gif)
|
(11) |
| (12) |
| (13) |
For notational convenience, let
![]() . Time differentiating equation
(11)
and substituting out
. Time differentiating equation
(11)
and substituting out
![]() and
and
![]() in equation
(12),
provides the following equation of motion for
in equation
(12),
provides the following equation of motion for
![]() .
.
![$\displaystyle \left[ G^{^{\prime}}\left( x_{t}\right) -G^{2}\left( x_{t}\right) \frac{u^{^{}}\left( c_{t}\right) }{u^{^{\prime}}\left( c_{t}\right) }k_{t}\right] \overset{\cdot}{x}_{t}$](img91.gif) |
(14) | |
![$\displaystyle -x_{t}^{2}\phi^{^{\prime}}\left( x_{t}\right) -G\left( x_{t}\right) \frac{u^{^{}}\left( c_{t}\right) }{u^{^{\prime}}\left( c_{t}\right) }\left[ \left( 1-\tau\right) f^{^{\prime}}\left( k_{t}\right) -x_{t}\left( 1+\phi\left( x_{t}\right) \right) \right] \overset{\cdot} {k}_{t}$](img93.gif)
|
(15) |
Equations (2) and (14) characterize the optimal solution during the embargo period.
4.3 Steady-state
To characterize the steady-state, we assume the following
functional forms for production and adjustment costs. Output is
produced using a cobb-douglas production technology with capital
and labor:
![]() so that
so that
![]() . Let
. Let
![]() .
From equation
(4),
.
From equation
(4),
![]() , and
, and
![]() .
Substituting these functions in equations
(9) and
(14), the
equations of motion for the
.
Substituting these functions in equations
(9) and
(14), the
equations of motion for the ![]() ,
, ![]() and
and ![]() are summarized as follows:
are summarized as follows:
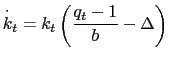
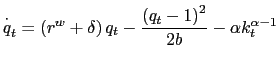
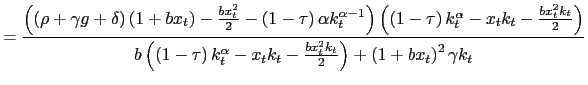
|
|
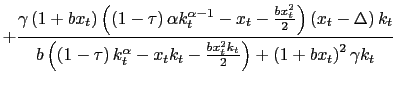
|
Setting
![]() ,
,
![]() , and
, and
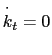 results in the following steady-states for
results in the following steady-states for ![]() , and
, and
![]() for the open economy:
for the open economy:
| (16) |
![$\displaystyle k^{\ast}=\left[ \frac{2\alpha}{2\left( r^{w}+\delta\right) \left( 1+b\Delta\right) -b\Delta^{2}}\right] ^{\frac{1}{1-\alpha}}$](img118.gif)
|
(17) |
and steady-states ![]() , and
, and ![]() for the closed economy:
for the closed economy:
| (18) |
![$\displaystyle k^{\ast}=\left[ \frac{2\alpha}{2\left( \rho+\gamma g+\delta\right) \left( 1+b\Delta\right) -b\Delta^{2}}\right] ^{\frac{1}{1-\alpha}}$](img122.gif)
|
(19) |
The steady-state value of ![]() exceeds 1 because
adjustment costs are borne in the steady state for the gross
investment that replaces the capital that depreciates at a rate
exceeds 1 because
adjustment costs are borne in the steady state for the gross
investment that replaces the capital that depreciates at a rate
![]() , and there is further depreciation of
capital in efficiency units due growth in effective labor at a rate
, and there is further depreciation of
capital in efficiency units due growth in effective labor at a rate
![]() . In both the closed and open
economy models, the steady-state value of capital depends on the
share of capital in production, the capital adjustment cost
parameter, the growth rates of labor and technology, and the rate
of capital depreciation. The steady-states, however, differ when
the world rate
. In both the closed and open
economy models, the steady-state value of capital depends on the
share of capital in production, the capital adjustment cost
parameter, the growth rates of labor and technology, and the rate
of capital depreciation. The steady-states, however, differ when
the world rate
![]() is different from the
effective utility discount rate
is different from the
effective utility discount rate
![]() . Assuming
the small open economy is as patient as the rest of the world,
. Assuming
the small open economy is as patient as the rest of the world,
![]() . If
. If
![]() , the small open
economy will accumulate capital forever and will eventually violate
the "small open economy" assumption. Alternatively, if
, the small open
economy will accumulate capital forever and will eventually violate
the "small open economy" assumption. Alternatively, if
![]() , the small open
economy is more impatient and will de-accumulate its capital
rapidly. With
, the small open
economy is more impatient and will de-accumulate its capital
rapidly. With
![]() , the steady-state values
for capital are identical in both economies. In other words,
openness of the economy does not affect the steady-state value of
capital and output.
, the steady-state values
for capital are identical in both economies. In other words,
openness of the economy does not affect the steady-state value of
capital and output.
4.4 Calibration and Dynamics
The model is calibrated to the South African economy using the following benchmark parameters:
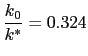 |
The growth rate of labor
![]() is consistent with the
South African average annual labor growth between 1970 and 2001.
is consistent with the
South African average annual labor growth between 1970 and 2001.
![]() is the average multifactor productivity
and
is the average multifactor productivity
and ![]() is measured as the average annual
rate of depreciation for physical capital from 1970 to 2001. Annual
depreciation is the ratio of capital consumption to the previous
year's capital stock. The calibration for
is measured as the average annual
rate of depreciation for physical capital from 1970 to 2001. Annual
depreciation is the ratio of capital consumption to the previous
year's capital stock. The calibration for ![]() is
computed as the average of the ratio of total employee compensation
to the sum of total employee compensation, capital depreciation,
and net operating surplus over the 1970-2001 period.4 The
data used for the calibration are obtained from the South African
Trade and Industrial Policy Strategies database (TIPS). The
calibration for
is
computed as the average of the ratio of total employee compensation
to the sum of total employee compensation, capital depreciation,
and net operating surplus over the 1970-2001 period.4 The
data used for the calibration are obtained from the South African
Trade and Industrial Policy Strategies database (TIPS). The
calibration for ![]() is consistent with the
steady-state value of
is consistent with the
steady-state value of ![]() . Blanchard, Rhee, and
Summers (1993) estimate
. Blanchard, Rhee, and
Summers (1993) estimate ![]() for the US Stock Market
between 1900 and 1990. The estimated values are below 1.5. Assuming
the marginal value for capital in the United States reflects the
steady-state value, and with
for the US Stock Market
between 1900 and 1990. The estimated values are below 1.5. Assuming
the marginal value for capital in the United States reflects the
steady-state value, and with
![]() , the calibrated parameter for
, the calibrated parameter for
![]() is 6.944.5
is 6.944.5
![]() and
and ![]() are set
to 1.00 and 0.053, respectively. The implied world interest rate is
0.06 as in Barro et al. (1995), consistent with long-term averages
of real rates of return on the US stock market.6
are set
to 1.00 and 0.053, respectively. The implied world interest rate is
0.06 as in Barro et al. (1995), consistent with long-term averages
of real rates of return on the US stock market.6
With the parameters above, the system of equations
(2) and
(9), and
(2) and
(14) are
solved using the time-elimination method following Mulligan and
Sala-i-Martin (1991), and numerical estimation methods as further
described in Appendix
A. During the
transition to steady-state, we limit the country's ability to
borrow for eight years consistent with the duration of the South
Africa embargo. For comparison, we derive the dynamics for the same
economy assuming it was never subjected to the embargo. We'll refer
to the first case as the "embargo" economy and to the second case
as the "no embargo" economy. In addition to the calibration
parameters specified above, we set the initial debt to GDP ratio to
0.64 consistent with the ratio of the stock of foreign liabilities
(FDI, Portfolios, and Loans) to GDP in the theoretical initial
period - 1976. To capture the capital outflows during the embargo
period, we set ![]() to 0.024 consistent with the
average ratio of net capital outflows to GDP during the embargo
period.
to 0.024 consistent with the
average ratio of net capital outflows to GDP during the embargo
period.
Figure 10 indicates that the current account to GDP ratio reverses from negative in the pre-embargo period to a surplus during the embargo period; reflecting both the country's inability to borrow and the disinvestment. When the embargo is lifted, the current account reverses again to a deficit. Figure 11 indicates that during the financial isolation, investment fell, increased gradually, and jumped up when the country regained access to world markets before converging gradually to steady state. Figures 12 and 13 display the dynamics for capital and output per worker. For comparison, we include an additional scenario to capture the paths of capital and output that would have prevailed if the embargo were indefinite. We refer to this scenario as the "Indefinite Embargo" scenario (dotted line). The figures indicate that during the financial isolation, the levels and growth rates for capital and output decreased relative to growth rates and levels in the "no embargo" economy. When the embargo is lifted, the growth rates and levels increase relative to the growth rates and levels in the "indefinite embargo" economy.
To assess the robustness of the results, we conduct a number
sensitivity tests by varying some parameters in the model. The
results are presented in Table 3. The benchmark
results are in bold. In the sensitivity analysis, we vary the
initial level of capital
![]() , the
share of capital in the production technology
, the
share of capital in the production technology
![]() , and the capital
adjustment cost parameter
, and the capital
adjustment cost parameter
![]() . The results are robust to
various parameter specifications and indicate a negative (positive)
effect of financial isolation (integration) on economic
performance. The results further indicate that the effect of
integration (isolation) increases the higher the initial distance
from steady-state
. The results are robust to
various parameter specifications and indicate a negative (positive)
effect of financial isolation (integration) on economic
performance. The results further indicate that the effect of
integration (isolation) increases the higher the initial distance
from steady-state
![]() , the
higher the share of capital
, the
higher the share of capital
![]() in the production
technology, and the less costly it is for the economy to adjust its
capital stock
in the production
technology, and the less costly it is for the economy to adjust its
capital stock
![]() .
.
5 Caveats
The results from the data analysis indicated a negative effect of the embargo on the economy and a positive effect following the removal of the embargo. There are several possible factors, unrelated to financial isolation, that could have affected the economy during the embargo period as noted in the introduction. In the sections that follow, we evaluate the merit of each one of the factors.
5.1 Effect of Trade Sanctions
The economic embargo against South Africa was intended to affect both investment and trade. To the extent that the trade embargo was effective, it could have influenced investment, capital, and output. Trade data and historical accounts of the trade embargo suggest that the trade embargo, unlike the financial embargo, was ineffective. Figures 8 and 9 present exports and imports, and the trade-balance to GDP ratios, respectively. The figures show no reduction in trade during the embargo period. Both exports and imports continued to grow at a healthier rate than in the pre-embargo period, and the trade balance improved a bit on average during the embargo period.
A source of failure of the trade embargo can be attributed to the ease with which trade sanctions can be circumvented. The lack of cooperation of one country is sufficient to render the trade sanctions ineffective, as the [uncooperative] country becomes the primary trading partner for the goods and services that fall under the sanctions.
Some observers also attribute the failure of the trade embargo to the vague language of the trade sanctions, and others, to the lack of a commitment to enforce it aggressively (Journal of Commerce, 15 May 1990, 1A). For example, protectionist lobbies within the U.S. were reportedly active in shaping the items affected by the sanctions under the 1986 Comprehensive Anti-Apartheid Act (CAAA). The selection of items reflected more special groups' interests than their ability to dent the country's economy (Lipton 1988, 52). Coal exports, one of South Africa's main export products, continued to grow in the late 1980's and earned vital foreign exchange well in excess of 3 billion rands in the late 1980's despite the embargo, placing coal second behind gold in terms of contributions to the balance of payments. This export growth in the face of sanctions suggested the inefficacy of the coal embargo (ILO 1992a, 1-12).
The vagueness of the language in which the trade sanctions were written further contributed to their ineffectiveness. The following examples illustrate. CAAA did not clearly define when a product is South African. Tuna shipped from South Africa, for example, was allowed in the U.S. as long as it was caught in international waters by non-South African fishermen. Also, lobster tails caught by South African fishermen in South African waters were also allowed in the U.S. if they were processed on non-South African vessels. Fabricated iron and steel of various types were permitted in Europe if their specific shapes were not banned by the European Commission's text on the products affected by the sanctions. The narrow definition of petroleum products allowed certain petroleum-based products to continue being shipped to South Africa despite the ban on exports of petroleum products. (Journal of Commerce, 15 May 1990, 1A).
While it is possible (and likely) that the trade sanctions affected specific products, and bilateral trade between South Africa and some individual countries, the aggregate trade value was mainly unaffected; earning trade sanctions the phrase " paper tiger" by a Journal of Commerce observer: "...the sanctions passed by Congress have scarcely put a dent in the volume of trade between the U.S. and South Africa....why did the sanctions turn out to be a paper tiger? " (Journal of Commerce, 15 May 1990, 1A).
Given the evidence, both in trade data and in historical accounts, that the trade embargo was ineffective overall, and is not likely the source of the decrease in growth rates and levels of investment, capital, and output observed in the data between 1985-1993.
5.2 Effect of Domestic Policy Response
The major policies adopted by the government during the embargo period do not support the hypothesis that domestic policy changes adversely affected the economy. At the beginning of the disinvestment in 1985, when the exchange rate (pegged to the U.S. dollar) collapsed, the government announced two major domestic policies to contain the crisis.
First, it introduced a dual exchange rate system; a financial exchange rate and a commercial exchange rate. The new financial rand, used primarily for movement of nonresident funds, traded at a discount relative to the commercial rand. The objective of the dual exchange rate system was to discourage disinvestment, and it remained in effect until March 1995.
Second, in September 1985, the government announced a temporary standstill on repayments of commercial debt principal, including short-term interbank loans. The standstill reportedly affected $13.6 billion in debt or 60 percent of the country's total debt. South Africa, however, continued regular payments on its public bonds, debts guaranteed by the government, and outstanding debts to international financial institutions such as the IMF (Ovenden 1989, 85). In December 1985, the government was unable to reach an agreement with its creditors and extended the freeze on debt repayments until 31 March 1986. In March 1987, the government reached a three-year agreement with foreign banks on rescheduling its debt. Under the agreement, South Africa continued to service all its debt, and made principal payments as originally scheduled, and by June 1990, the country had repaid 13 percent of the total principal of debt in standstill. The agreement also contained two exit options, one that allowed banks to convert frozen short-term claims into repayable long-term debt, and another that allowed creditors to use claims to purchase equities in South Africa. (Financial Times, 25 March 1987, 1; Ovenden 1989, 91-93).
The government decisions to institute capital controls and to freeze some of the debt repayments contributed to containing the crisis. This is evidenced in the unexpected resilience of the stock market during the embargo period.7 After a brief and moderate decline in 1988, the Johannesburg Stock Exchange (JSE) Index recovered quickly and registered a continuous increase throughout the embargo period. The effect of major domestic policies undertaken during the embargo period contributed to containing, not causing, the fall in investment, capital, and output.
5.3 Effect of Political Instability
The hypotheses that political instability within the country could have caused the fall in investment, capital, and output does not seem tenable. The political situation during the 1985-1993 period was unstable, but no worse than in previous years. The country risk measures for South Africa in Erb et. al (1995) indicate that the political and overall country risk level at the eve of the embargo was higher than the average risk level during the embargo period.8 Historical accounts of the apartheid regime, in support of these risk measures, indicate a wave of political and social protests within the country since the institution of apartheid in 1948- one of which resulted in the arrest of Nelson Mandela and other anti-apartheid leaders in 1964. For example, the political situation deteriorated in April 1960 during violent protests against new laws restricting the movements of blacks and minorities. In 1976, hundreds of minorities were killed during violent protests against inequalities in the educational system. In summary, the available risk data and historical accounts of the political situation do not support the hypothesis that increased instability caused the fall in investment, capital, and output observed in the data.
5.4 Effect of Global Factors
The 1980s is mostly remembered as a period of sovereign debt crisis in the global economy. At the beginning of the embargo around 1985, several emerging countries were recovering from the crisis. We evaluate whether this global factor and others could have caused the distortions to the South African economy observed between 1985 and 1993.
Figure 14 compares the current account to GDP ratio for South Africa to that of other middle-income countries using data from the World Bank World Development Indicator database.9 The figure indicates that the current account to GDP ratio of the middle-income countries remained in deficit between 1985 and 1993, and did not reverse in 1985 or in 1993 as in the case of South Africa. In addition, real GDP per capita statistics indicate that world output per capita grew on average by 0.63 percent between 1976 and 1984, by 1.32 percent between 1985 and 1993, and by 1.62 percent between 1994 and 2001. For the middle-income countries subcategory, the average growth rates for these periods were 0.78, 1.26, and 2.52 percent, respectively. For South Africa, the corresponding growth rates of output per worker were 2.2, 0.8, and 3.7 percent, respectively. In other words, output growth fell more during the embargo period and increased more in the post-embargo period in South Africa than it did in the world economy and in comparable middle-income economies.
6 Conclusion
This paper exploited the 1985-1993 South Africa embargo to study the effect of financial isolation and integration on an emerging economy. The experiment is interesting for three reasons. First, it circumvents the need to measure financial integration. Second, because the country was integrated prior to the embargo, we were able to evaluate both the adverse effect of financial isolation as well as the benefits of financial integration for the same economy. Third, the imposition and removal of the embargo was not directly related to the country's economic performance, but to the desire to change its political regime. We can, therefore, interpret the embargo as an event less subject to the endogeneity encountered in some previous studies.
The analysis indicated that during the embargo, which turned out to be a financial embargo, the average growth rates of investment, and capital and output per worker fell 2.8 percent, 1.2 percent, and 1.4 percent, respectively, below the average growth rates in the pre-embargo period. When the embargo was lifted in 1993, the average growth rates for investment, capital, and output rose 7.6 percent, 0.7 percent, and 2.9 percent, respectively, above the average growth rates during the embargo period.
The analysis further indicated that the lower growth rates during the embargo resulted in lower levels of investment, capital, and output. The average levels of investment, and capital and output per worker decreased 25.6 percent, 12.5 percent, and 9.5 percent, respectively, during the embargo period relative to the levels that would have prevailed if the variables had maintained their eight-year pre-embargo period average growth rates. When the embargo was lifted, the average levels of investment, and capital and output per capita increased 37.3 percent, 2.2 percent, and 8.4 percent, respectively, relative to the levels that would have prevailed if the variables had maintained their embargo period average growth rates.
To ensure that the above results were not driven by factors other than the embargo, we assess the merits of some obvious suspects such as trade sanctions, domestic policy changes, political instability, and global factors. The analyses and evidence presented did not support the hypothesis that one or some of these factors caused the distortions to the South Africa economy observed during the embargo and post-embargo periods. The results in this study lend support to findings in previous studies that financial integration yields economic benefits for emerging economies, and suggest that issues related to the measurement and endogeneity of financial integration did not necessarily drive the results in those studies.
References
Bhagwati Jadish, (1998). " The Capital Myth: The difference between trade in widgets and dollars", Foreign Affairs 3, (May/June).
Baker, Pauline H. (1989). The United States and South Africa: The Reagan Years. South Africa UPDATE Series. New York: Ford Foundation-Foreign Policy Association.
Barro J. Robert and Xavier Sala-I-Martin (1992). " Convergence", Journal of Political Economy, 100 (2), 223-51
Barro J. Robert, N. Gregory Mankiw, and Xavier Sala-I-Martin (1995), " Capital Mobility in Neoclassical Models of Growth", The American Economic Review, Vol. 85, No. 1 (Mars), 103-115.
Bernanke, Ben S. and Gürkaynak S. Refet (2001). " Is Growth Exogenous? Taking Mankiw, Romer, and Weil Seriously", NBER Working Paper No. 8365 (Cambridge, Massachussetts: National Bureau of Economic Research)
Bekaert, Geert and Harvey, Campbell (2000). " Foreign speculators and emerging markets equity Markets" , Journal of Finance, 55, pp 565-612.
_________ Harvey, Campbell and Lundblad, Christian (2001). " Does Financial Liberalization Spur Growth?" NBER Working Paper No. 8245 (Cambridge, Massachussetts: National Bureau of Economic Research)
Blanchard, Olivier, Changyong Rhee, and Lawrence H. Summers (1993). " The Stock Market, Profit, and Investment", Quarterly Journal of Economics, 108, 1(February), 115-136
Chettle, John H. (1982). "The Divestment of South African Stock: Is it Practical, Desirable, or Constitutional?" Paper submitted to Georgetown University Law School, Washington, October.
Edison, H., Klein, M., Ricci, L., and Slok, T., (2003). " Capital Account Liberalization and Economic Performance: Survey and Synthesis", IMF Working Paper 02/120, Washington: International Monetary Fund
Edison, H., Klein, M., Ricci, L., and Slok, T., (2002). " International Financial Integration and Economic Growth," Journal of International Money and Finance, Vol. 21, pp 749-776
Eichengreen, Barry and Michael Mussa. (1998) " Capital Account Liberalization: Theoretical and Practical Aspects," International Monetary Fund, Washington DC. with G. Dell' Ariccia, E. Detragiache, G.M. Milesi-Ferreti and A. Tweedie. Occasional Paper No. 172.
Erb, Claude B., Campbell R. Havery, and Tada E. VIskanta. "Political Risk, Economic Risk and Financial Risk" Financial Analysts Journal, Vol. 52, 6 (November/December 1996), pp. 28-46.
Fischer, Stanley (1998). " Capital Account Liberalization and the Role of the IMF," in " Should the IMF pursue Capital-Account Convertibility?" Vol. 207, Essays in International Finance, Department of Economics, Princeton University, pp. 1-10
General Accounting Office. (1990). "South Africa: Relationship with Western Financial Institutions", GAO/NSIAD-90-189. Washington, June.
Gollin, Douglas (1998). " Getting Income Shares Right: Self Employment, Unincorporated Enterprise, and the Cobb-Douglas Hypothesis", unpublished paper, Williams College, June.
Hall, Robert E. (2002). " Industry Dynamics With Adjustment Costs, NBER Working Paper No. 8849 (Cambridge, Massachussetts: National Bureau of Economic Research)
Henry, Peter Blair. (2000a). " Stock Market Liberalization, Economic Reform, and Emerging Market Equity Prices," Journal of Finance, Vol. 55, No. 2, pp. 529-64.
______________. (2000b). " Do Stock Market Liberalizations Cause Investment Booms?" Journal of Financial Economics, Vol. 58, Nos. 1-2, pp. 301-334
______________. (2003). " Capital Account Liberalization, The Cost of Capital, and Economic Growth", American Economic Review, Papers and Proceedings, Vol. 93, (May), p. 91-96.
Klein, W. Michael. (2004). " Capital Account Liberalization, Institutional Quality and Economic Growth: Theory and Evidence," Tufts University Manuscript.
Kraay, Aart. (1998). " In Search of the Macroeconomic Effects of Capital Account Liberalization," unpublished; (Washington: The World Bank)
Lipton, Merle (1988). "Sanctions and South Africa: The Dynamics of Economic Isolation". The Economist Intelligence Unit Special Report No 1119. London: The Economist Publications Limited.
Mankiw, N. Gregory, David Romer, and David Weil (1992). " A Contribution to the Empirics of Economic Growth," Quarterly Journal of Economics, 107 (2), 407-38
Mulligan, Casey and Sala-i-Martin, Xavier (1991). " A Note on the Time-elimination Method for Solving Recursive Dynamic Economic Models", NBER Working Paper No. 116, (Cambridge, Massachussetts: National Bureau of Economic Research)
Obstfeld, Maurice (1994). " Risk-taking, global diversification, and growth", American Economic Review, 84, Issue 5, 1310-1329.
Ovenden, Keith, and Tony Cole (1989). "Apartheid and International Finance: A Program for Change" Ringwood, Victoria, Australia: Penguin Books.
Quinn, Dennis (1997), " The Correlates of Change in International Financial Regulations," American Political Science Review, Vol. 91, No. 3, pp. 531-51
Rodrick, Dani (1998). " Who needs capital account convertibility?" Princeton Essays in International Finance 207, 55-65.
Shapiro, Matthew D. (1986)." The Dynamic Demand for Capital and Labor," The Quarterly Journal of Economics, 101 (3), (Aug.), 513-542.
Stiglitz, Joseph (2000). " Capital Market Liberalization, Economic Growth, and Instability" World Development, June, Vol. 28, No. 6, pp. 1075-1086.
Stulz, Rene, M. (1999). " Globalization of Equity Markets and The Cost of Capital." NBER Working paper No. 7021 (Cambridge, Massachussetts: National Bureau of Economic Research)
Summers, Lawrence H. (2000). " International Financial Crises: Causes, Prevention, and Cures," American Economic Review, Vol. 90, No 2, pp. 1-16.
Wesso, G. R. (2001). " The Dynamics of Capital Flows in South Africa: an Empirical Investigation", Quarterly Bulletin, South African Reserve Bank
Appendix A: Solving the model
The Time-Elimination method consists of two stages. The first stage estimates the policy function which is used to reduce the dimensionality of the system of two equations to a single equation. The following section describes the methodology for the case of the open economy. Recall the equations describing the dynamics of the of the open economy
| (2) | |
| (9) |
The ratio of the two equations describe the slope of the policy
function
![]() .
.
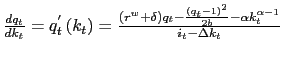 |
Given initial values of ![]() and
and
![]() , one can estimate the entire slope of
the policy function by linear approximation. Since the initial
value of
, one can estimate the entire slope of
the policy function by linear approximation. Since the initial
value of ![]() is unknown, the approximation starts
with the steady-state values
is unknown, the approximation starts
with the steady-state values ![]() and
and
![]() which are known. Note however that
the slope is indeterminate in steady-state. An application of
l'hopital's rule resolves this issue. Given the steady-state slope
which are known. Note however that
the slope is indeterminate in steady-state. An application of
l'hopital's rule resolves this issue. Given the steady-state slope
![]() , estimate the entire policy
function as follows:
, estimate the entire policy
function as follows:
![]() . Re-estimating the slope at
. Re-estimating the slope at
![]() and
and
![]() , and repeating the
process until
, and repeating the
process until ![]() , traces out the entire policy
function
, traces out the entire policy
function
![]() and completes the first
stage of the estimation process.
and completes the first
stage of the estimation process.
In the second stage, the policy function is used to eliminate
![]() from the differential equations.
from the differential equations.
| (2) | |
| (9) |
To derive the time paths for each variable, repeat the process with respect to time using the given initial level of capital.
The solution method for the closed economy uses an identical method for the following equations:
| (2) | |
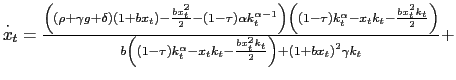 |
(14) |
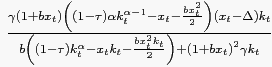 |
Table 1: Average Annual Growth Rates for Investment, Capital, and Output (percentage)
| Period | Investment1 | Capital Stock2 | Output2 |
|---|---|---|---|
| Pre-embargo (1976-1984) | 0.2 | 3.5 | 2.2 |
| Embago (1985-1993) | -2.6 | 1.3 | 0.8 |
| Post-embargo (1994-2001) | 5.0 | 2.0 | 3.7 |
Notes:
1 Aggregate fixed investment.
2 In units per worker.
The growth rates are annual growth rates averaged over the indicated period.
Table 2: Percentage difference in levels of Investment, Capital, and Output (annual rate)
| Period | Investment1 | Capital Stock2 | Output2 |
|---|---|---|---|
| Pre-embargo (1976-1984) | 0.0 | 0.0 | 0.0 |
| Embago (1985-1993) | -25.6 | -12.5 | -9.5 |
| Post-embargo (1994-2001) | 37.3 | 2.2 | 8.4 |
Notes:
1 Aggregate fixed investment.
2 In units per worker.
The difference in levels for the embargo
period are computed as percentage decrease from the levels that
would have prevailed if the variables had grown at the pre-embargo
average growth rates. The difference in levels for the post-embargo
period are computed as percentage increase from the levels that
would haveprevailed if the variables had grown at the
embargo-period average growth rates
Table 3: Effect of Financial Isolation and Integration on Output for various Parameter Specifications
| Parameter | Embargo Isolation effect: Growth Effect | Embargo Isolation effect: Level Effect | Post-embargo Integration effect: Growth Effect | Post-embargo Integration effect: Level Effect |
|---|---|---|---|---|
-0.43 | -4.74 | 0.34 | 2.67 | |
-0.33 | -3.48 | 0.33 | 2.28 | |
-0.24 | -2.33 | 0.19 | 2.03 | |
| α = 0.33 | -0.11 | -1.19 | 0.07 | 0.42 |
| α = 0.41 | -0.33 | -3.48 | 0.33 | 2.28 |
| α = 0.70 | -2.92 | -38.93 | 2.91 | 23.63 |
| b = 6.94 | -0.33 | -3.48 | 0.33 | -2.28 |
| b = 10.00 | -0.30 | 2.69 | 0.30 | 2.20 |
| b = 20.00 | -0.13 | 1.08 | 0.09 | 0.42 |
The first column specifies the parameters of the model. The benchmark specification is in bold. The column 2 contains the average reduction in annual growth rate of output per capita due to the financial isolation. Column 3 contains the average reduction in the level of output due to the financial isolation. Columns 4 and 5 Columns 4 and 5 contain the same data for the effect of financial integration. The average of the effect are computed over an eight-year period corresponding to the duration of the embargo
Figure 1: Net Capital Inflows to GDP Ratio
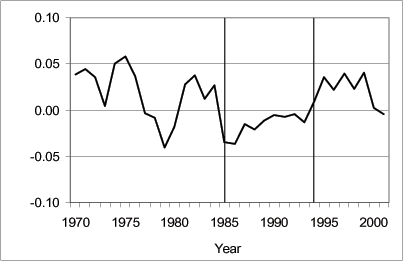
Inflows include FDI, Portfolio, and Loans. Net inflows is the outflow less the inflow of capital. The inflow data are obtained from the South Africa Reserve Bank and are available through the web site (http://www.resbank.co.za). The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 1
| Year | Net Capital Inflows to GDP Ratio |
|---|---|
| 1970 | 0.038 |
| 1971 | 0.044 |
| 1972 | 0.036 |
| 1973 | 0.005 |
| 1974 | 0.050 |
| 1975 | 0.058 |
| 1976 | 0.036 |
| 1977 | -0.004 |
| 1978 | -0.008 |
| 1979 | -0.041 |
| 1980 | -0.018 |
| 1981 | 0.028 |
| 1982 | 0.038 |
| 1983 | 0.012 |
| 1984 | 0.027 |
| 1985 | -0.034 |
| 1986 | -0.037 |
| 1987 | -0.015 |
| 1988 | -0.021 |
| 1989 | -0.011 |
| 1990 | -0.005 |
| 1991 | -0.008 |
| 1992 | -0.004 |
| 1993 | -0.013 |
| 1994 | 0.009 |
| 1995 | 0.036 |
| 1996 | 0.022 |
| 1997 | 0.039 |
| 1998 | 0.023 |
| 1999 | 0.041 |
| 2000 | 0.002 |
| 2001 | -0.004 |
Figure 2: Stock of Capital Inflows to GDP Ratio
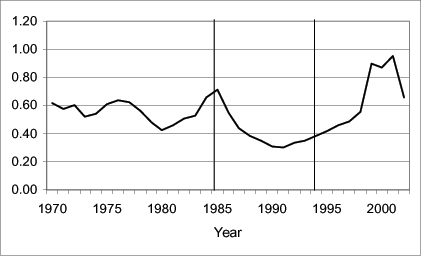
The foreign liabilities data are obtained from the Balance of Payment section of the Reserve Bank of South Africa. Foreign Liabilities are defined as Portfolio, Direct Investment, and Loans invested by foreigners in South Africa. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 2
| Year | Stock of Capital Inflows to GDP Ratio |
|---|---|
| 1970 | 0.617 |
| 1971 | 0.575 |
| 1972 | 0.603 |
| 1973 | 0.519 |
| 1974 | 0.544 |
| 1975 | 0.613 |
| 1976 | 0.639 |
| 1977 | 0.622 |
| 1978 | 0.565 |
| 1979 | 0.479 |
| 1980 | 0.424 |
| 1981 | 0.456 |
| 1982 | 0.510 |
| 1983 | 0.525 |
| 1984 | 0.657 |
| 1985 | 0.712 |
| 1986 | 0.552 |
| 1987 | 0.439 |
| 1988 | 0.383 |
| 1989 | 0.347 |
| 1990 | 0.311 |
| 1991 | 0.304 |
| 1992 | 0.335 |
| 1993 | 0.351 |
| 1994 | 0.384 |
| 1995 | 0.417 |
| 1996 | 0.458 |
| 1997 | 0.487 |
| 1998 | 0.554 |
| 1999 | 0.899 |
| 2000 | 0.871 |
| 2001 | 0.954 |
| 2002 | 0.657 |
Figure 3: Composition of Foreign Liabilities
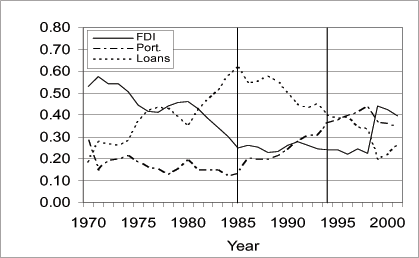
The foreign liabilities data are obtained from the Balance of Payment section of the Reserve Bank of South Africa. Foreign Liabilities are defined as Portfolio, Direct Investment, and Loans invested by foreigners in South Africa. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 3
| Year | FDI | Portfolio | Loans |
|---|---|---|---|
| 1970 | 0.53 | 0.29 | 0.18 |
| 1971 | 0.57 | 0.15 | 0.28 |
| 1972 | 0.54 | 0.19 | 0.27 |
| 1973 | 0.54 | 0.19 | 0.26 |
| 1974 | 0.51 | 0.21 | 0.28 |
| 1975 | 0.44 | 0.18 | 0.37 |
| 1976 | 0.42 | 0.16 | 0.42 |
| 1977 | 0.41 | 0.15 | 0.43 |
| 1978 | 0.44 | 0.13 | 0.43 |
| 1979 | 0.46 | 0.15 | 0.39 |
| 1980 | 0.46 | 0.19 | 0.35 |
| 1981 | 0.43 | 0.15 | 0.42 |
| 1982 | 0.38 | 0.15 | 0.47 |
| 1983 | 0.34 | 0.15 | 0.51 |
| 1984 | 0.30 | 0.12 | 0.58 |
| 1985 | 0.25 | 0.13 | 0.62 |
| 1986 | 0.26 | 0.20 | 0.54 |
| 1987 | 0.25 | 0.20 | 0.55 |
| 1988 | 0.23 | 0.19 | 0.58 |
| 1989 | 0.23 | 0.21 | 0.55 |
| 1990 | 0.26 | 0.24 | 0.50 |
| 1991 | 0.28 | 0.28 | 0.44 |
| 1992 | 0.26 | 0.31 | 0.43 |
| 1993 | 0.24 | 0.31 | 0.45 |
| 1994 | 0.24 | 0.36 | 0.39 |
| 1995 | 0.24 | 0.37 | 0.39 |
| 1996 | 0.22 | 0.39 | 0.39 |
| 1997 | 0.24 | 0.41 | 0.34 |
| 1998 | 0.22 | 0.44 | 0.34 |
| 1999 | 0.44 | 0.36 | 0.20 |
| 2000 | 0.43 | 0.36 | 0.22 |
| 2001 | 0.39 | 0.34 | 0.26 |
Figure 4: Current Account Balance to GDP Ratio
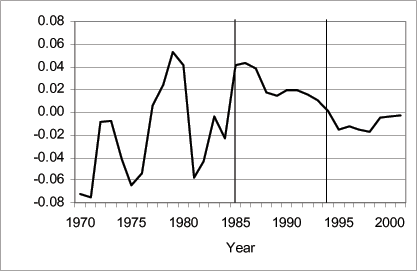
The current account data are obtained from the South Africa Reserve Bank (http://www.resbank.co.za). The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 4
| Year | Current Account Balance to GDP Ratio |
|---|---|
| 1970 | -0.07 |
| 1971 | -0.08 |
| 1972 | -0.01 |
| 1973 | -0.01 |
| 1974 | -0.04 |
| 1975 | -0.07 |
| 1976 | -0.05 |
| 1977 | 0.01 |
| 1978 | 0.02 |
| 1979 | 0.05 |
| 1980 | 0.04 |
| 1981 | -0.06 |
| 1982 | -0.04 |
| 1983 | 0.00 |
| 1984 | -0.02 |
| 1985 | 0.04 |
| 1986 | 0.04 |
| 1987 | 0.04 |
| 1988 | 0.02 |
| 1989 | 0.01 |
| 1990 | 0.02 |
| 1991 | 0.02 |
| 1992 | 0.02 |
| 1993 | 0.01 |
| 1994 | 0.00 |
| 1995 | -0.02 |
| 1996 | -0.01 |
| 1997 | -0.02 |
| 1998 | -0.02 |
| 1999 | -0.01 |
| 2000 | 0.00 |
| 2001 | 0.00 |
Figure 5: Real Domestic Fixed Investment in billions of 1995 Rands
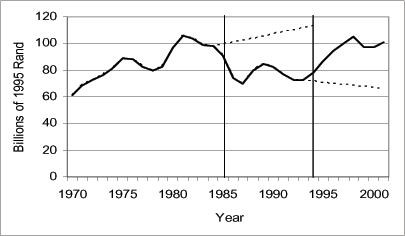
The investment data are obtained from the TIPS available through the web site (http://www.tips.org.za). Investment refers to fixed domestic investment in buildings and construction works, transportation equipment, machinery and other equipment and transfer costs. The upper dotted line is the hypothetical path for investment assuming embargo period investment grew at the eight-year pre-embargo period average growth rate. The lower dotted line is the hypothetical path for investment assuming post-embargo investment grew at the embargo period average growth rate. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 5
| Year | Actual Investment (solid line) | Assuming embargo period capital grew at the 8-year pre-embargo period average growth rate (top dash line) | Assuming post-embargo capital grew at the embargo period average growth rate (bottom dash line) |
|---|---|---|---|
| 1970 | 61.7 | 61.7 | 61.7 |
| 1971 | 68.5 | 68.5 | 68.5 |
| 1972 | 72.4 | 72.4 | 72.4 |
| 1973 | 76.0 | 76.0 | 76.0 |
| 1974 | 81.0 | 81.0 | 81.0 |
| 1975 | 89.1 | 89.1 | 89.1 |
| 1976 | 88.0 | 88.0 | 88.0 |
| 1977 | 82.5 | 82.5 | 82.5 |
| 1978 | 79.9 | 79.9 | 79.9 |
| 1979 | 82.8 | 82.8 | 82.8 |
| 1980 | 96.9 | 96.9 | 96.9 |
| 1981 | 106.1 | 106.1 | 106.1 |
| 1982 | 103.5 | 103.5 | 103.5 |
| 1983 | 99.0 | 99.0 | 99.0 |
| 1984 | 97.8 | 97.8 | 97.8 |
| 1985 | 90.9 | 99.3 | 90.9 |
| 1986 | 74.2 | 100.8 | 74.2 |
| 1987 | 70.2 | 102.3 | 70.2 |
| 1988 | 79.9 | 103.9 | 79.9 |
| 1989 | 84.9 | 105.4 | 84.9 |
| 1990 | 82.8 | 107.0 | 82.8 |
| 1991 | 77.2 | 108.6 | 77.2 |
| 1992 | 73.0 | 110.2 | 73.0 |
| 1993 | 72.6 | 111.9 | 72.6 |
| 1994 | 78.6 | 113.6 | 71.8 |
| 1995 | 87.0 | - | 70.9 |
| 1996 | 94.9 | - | 70.1 |
| 1997 | 100.3 | - | 69.2 |
| 1998 | 105.4 | - | 68.4 |
| 1999 | 97.1 | - | 67.6 |
| 2000 | 97.4 | - | 66.8 |
| 2001 | 100.7 | - | 66.0 |
Figure 6: Real Capital per Worker in 000's 1995 Rands
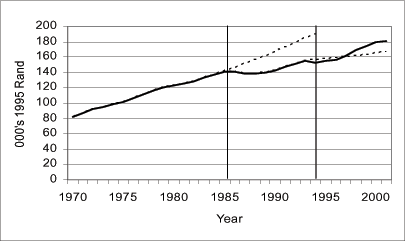
The capital stock data include buildings and construction works, transportation equipment machinery and other equipment, and transfer costs. They are obtained from the Trade and Industrial Policy Strategies Database available through the web site (http://www.tips.org.za). The upper dotted line is the hypothetical path for capital assuming embargo period capital grew at the eight-year pre-embargo period average growth rate. The lower dotted line is the hypothetical path for capital assuming post-embargo capitral grew at the embargo period average growth rate. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 6
| Year | Actual Capital Stock (Solid line) | Assuming embargo period capital grew at the 8-year pre-embargo period average growth rate (top dash line) | Assuming post-embargo capital grew at the embargo period average growth rate (bottom dash line) |
|---|---|---|---|
| 1970 | 82 | 82 | 82 |
| 1971 | 87 | 87 | 87 |
| 1972 | 92 | 92 | 92 |
| 1973 | 95 | 95 | 95 |
| 1974 | 99 | 99 | 99 |
| 1975 | 101 | 101 | 101 |
| 1976 | 106 | 106 | 106 |
| 1977 | 111 | 111 | 111 |
| 1978 | 117 | 117 | 117 |
| 1979 | 120 | 120 | 120 |
| 1980 | 123 | 123 | 123 |
| 1981 | 126 | 126 | 126 |
| 1982 | 129 | 129 | 129 |
| 1983 | 134 | 134 | 134 |
| 1984 | 137 | 137 | 137 |
| 1985 | 141 | 142 | 141 |
| 1986 | 141 | 147 | 141 |
| 1987 | 139 | 151 | 139 |
| 1988 | 138 | 156 | 138 |
| 1989 | 140 | 162 | 140 |
| 1990 | 143 | 167 | 143 |
| 1991 | 148 | 172 | 148 |
| 1992 | 151 | 178 | 151 |
| 1993 | 155 | 184 | 155 |
| 1994 | 153 | 190 | 156 |
| 1995 | 155 | - | 158 |
| 1996 | 157 | - | 159 |
| 1997 | 161 | - | 160 |
| 1998 | 169 | - | 162 |
| 1999 | 174 | - | 163 |
| 2000 | 179 | - | 165 |
| 2001 | 181 | - | 166 |
Figure 7: Real Output per Worker in 000's 1995 Rands
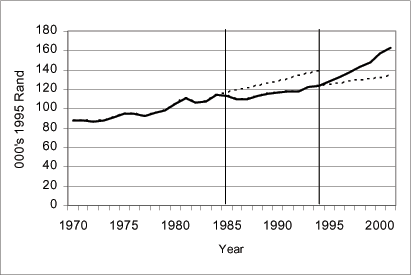
Output data are obtained from the Trade and Industrial Policy Strategies Database available through the web site (http://www.tips.org.za). The vertical bars mark the embargo period 1985-1993. The upper dotted line is the hypothetical path for output assuming the embargo period output grew at the eight-year pre-embargo period average growth rate. The lower dotted line is the hypothetical path for capital assuming post-embargo output grew at the embargo period average growth rate. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 7
| Year | Actual Output (Solid line) | Assuming embargo period output grew at the 8-year pre-embargo period average growth rate (top dash line) | Assuming post-embargo output grew at the embargo period average growth rate (bottom dash line) |
|---|---|---|---|
| 1970 | 87.5 | 87.5 | 87.5 |
| 1971 | 87.7 | 87.7 | 87.7 |
| 1972 | 86.7 | 86.7 | 86.7 |
| 1973 | 88.2 | 88.2 | 88.2 |
| 1974 | 90.8 | 90.8 | 90.8 |
| 1975 | 94.3 | 94.3 | 94.3 |
| 1976 | 94.5 | 94.5 | 94.5 |
| 1977 | 92.8 | 92.8 | 92.8 |
| 1978 | 96.1 | 96.1 | 96.1 |
| 1979 | 98.5 | 98.5 | 98.5 |
| 1980 | 105.5 | 105.5 | 105.5 |
| 1981 | 111.0 | 111.0 | 111.0 |
| 1982 | 105.7 | 105.7 | 105.7 |
| 1983 | 107.2 | 107.2 | 107.2 |
| 1984 | 113.9 | 113.9 | 113.9 |
| 1985 | 112.6 | 116.2 | 112.6 |
| 1986 | 109.2 | 118.5 | 109.2 |
| 1987 | 109.7 | 120.9 | 109.7 |
| 1988 | 113.1 | 123.3 | 113.1 |
| 1989 | 115.9 | 125.8 | 115.9 |
| 1990 | 116.0 | 128.3 | 116.0 |
| 1991 | 117.9 | 130.9 | 117.9 |
| 1992 | 118.1 | 133.5 | 118.1 |
| 1993 | 122.2 | 136.1 | 122.2 |
| 1994 | 123.8 | 138.9 | 123.6 |
| 1995 | 128.4 | - | 125.0 |
| 1996 | 132.5 | - | 126.3 |
| 1997 | 137.7 | - | 127.7 |
| 1998 | 142.6 | - | 129.1 |
| 1999 | 147.9 | - | 130.5 |
| 2000 | 157.3 | - | 132.0 |
| 2001 | 162.9 | - | 133.4 |
Figure 8: Real Exports and Imports of Goods and Services in billions of 1995 Rands
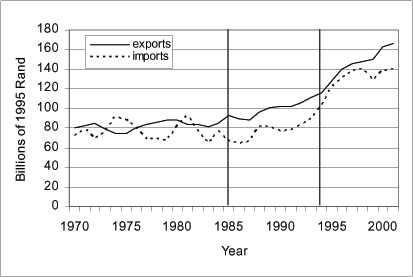
Trade data are obtained through the Trade and Industrial Policy Strategies web site (http://www.tips.org.za). The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 8
| Year | Exports | Imports |
|---|---|---|
| 1970 | 80.8 | 71.9 |
| 1971 | 83.0 | 79.1 |
| 1972 | 84.4 | 69.2 |
| 1973 | 78.9 | 77.0 |
| 1974 | 74.3 | 91.6 |
| 1975 | 74.6 | 88.6 |
| 1976 | 79.7 | 79.7 |
| 1977 | 83.8 | 68.8 |
| 1978 | 86.5 | 68.9 |
| 1979 | 88.0 | 68.2 |
| 1980 | 88.2 | 81.2 |
| 1981 | 83.9 | 92.4 |
| 1982 | 83.1 | 76.3 |
| 1983 | 81.3 | 64.1 |
| 1984 | 85.1 | 76.7 |
| 1985 | 92.5 | 66.0 |
| 1986 | 89.2 | 64.3 |
| 1987 | 87.8 | 66.6 |
| 1988 | 96.2 | 81.2 |
| 1989 | 101.0 | 81.4 |
| 1990 | 102.5 | 76.7 |
| 1991 | 102.4 | 78.3 |
| 1992 | 105.7 | 82.5 |
| 1993 | 111.0 | 89.0 |
| 1994 | 115.7 | 103.3 |
| 1995 | 128.1 | 121.1 |
| 1996 | 139.5 | 131.2 |
| 1997 | 145.3 | 138.3 |
| 1998 | 148.3 | 140.3 |
| 1999 | 149.9 | 129.8 |
| 2000 | 162.4 | 139.2 |
| 2001 | 166.3 | 139.8 |
Figure 9: Trade Balance to GDP ratio
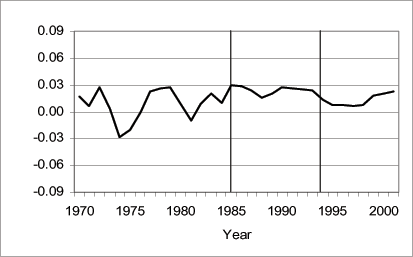
The trade data are obtained from the Trade and Industrial Policy Strategies Database available through the web site (http://www.tips.org.za). The trade balance is the value of exports of goods and services less the value of imports of goods and services. The vertical bars denote the embargo period estimated to be between 1985 and 1993.
Data for Figure 9
| Year | Trade Balance to GDP ratio |
|---|---|
| 1970 | 0.02 |
| 1971 | 0.01 |
| 1972 | 0.03 |
| 1973 | 0.00 |
| 1974 | -0.03 |
| 1975 | -0.02 |
| 1976 | 0.00 |
| 1977 | 0.02 |
| 1978 | 0.03 |
| 1979 | 0.03 |
| 1980 | 0.01 |
| 1981 | -0.01 |
| 1982 | 0.01 |
| 1983 | 0.02 |
| 1984 | 0.01 |
| 1985 | 0.03 |
| 1986 | 0.03 |
| 1987 | 0.02 |
| 1988 | 0.02 |
| 1989 | 0.02 |
| 1990 | 0.03 |
| 1991 | 0.03 |
| 1992 | 0.03 |
| 1993 | 0.02 |
| 1994 | 0.01 |
| 1995 | 0.01 |
| 1996 | 0.01 |
| 1997 | 0.01 |
| 1998 | 0.01 |
| 1999 | 0.02 |
| 2000 | 0.02 |
| 2001 | 0.02 |
Figure 10: Current Account to GDP ratio
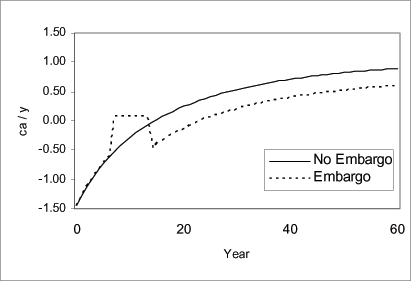
Estimated from the neoclassical growth model with adjustment costs.
Data for Figure 10
| Year | No Embargo | Embargo |
|---|---|---|
| 0 | -1.43 | -1.43 |
| 1 | -1.26 | -1.26 |
| 2 | -1.10 | -1.10 |
| 3 | -0.96 | -0.96 |
| 4 | -0.82 | -0.82 |
| 5 | -0.72 | -0.72 |
| 6 | -0.61 | -0.61 |
| 7 | -0.51 | 0.07 |
| 8 | -0.43 | 0.07 |
| 9 | -0.35 | 0.07 |
| 10 | -0.27 | 0.07 |
| 11 | -0.21 | 0.07 |
| 12 | -0.15 | 0.07 |
| 13 | -0.09 | 0.07 |
| 14 | -0.03 | -0.45 |
| 15 | 0.02 | -0.39 |
| 16 | 0.07 | -0.33 |
| 17 | 0.12 | -0.28 |
| 18 | 0.17 | -0.22 |
| 19 | 0.21 | -0.18 |
| 20 | 0.25 | -0.13 |
| 21 | 0.29 | -0.09 |
| 22 | 0.32 | -0.05 |
| 23 | 0.35 | -0.01 |
| 24 | 0.38 | 0.03 |
| 25 | 0.41 | 0.07 |
| 26 | 0.44 | 0.10 |
| 27 | 0.47 | 0.13 |
| 28 | 0.49 | 0.15 |
| 29 | 0.51 | 0.18 |
| 30 | 0.54 | 0.21 |
| 31 | 0.56 | 0.23 |
| 32 | 0.58 | 0.25 |
| 33 | 0.60 | 0.27 |
| 34 | 0.62 | 0.29 |
| 35 | 0.64 | 0.31 |
| 36 | 0.65 | 0.33 |
| 37 | 0.67 | 0.35 |
| 38 | 0.68 | 0.37 |
| 39 | 0.70 | 0.38 |
| 40 | 0.71 | 0.40 |
| 41 | 0.73 | 0.41 |
| 42 | 0.74 | 0.43 |
| 43 | 0.75 | 0.44 |
| 44 | 0.76 | 0.46 |
| 45 | 0.78 | 0.47 |
| 46 | 0.79 | 0.48 |
| 47 | 0.80 | 0.49 |
| 48 | 0.81 | 0.50 |
| 49 | 0.81 | 0.51 |
| 50 | 0.82 | 0.52 |
| 51 | 0.83 | 0.53 |
| 52 | 0.84 | 0.54 |
| 53 | 0.85 | 0.55 |
| 54 | 0.85 | 0.55 |
| 55 | 0.86 | 0.56 |
| 56 | 0.87 | 0.57 |
| 57 | 0.87 | 0.58 |
| 58 | 0.88 | 0.58 |
| 59 | 0.89 | 0.59 |
| 60 | 0.89 | 0.60 |
Figure 11: Investment relative to steady-state Investment
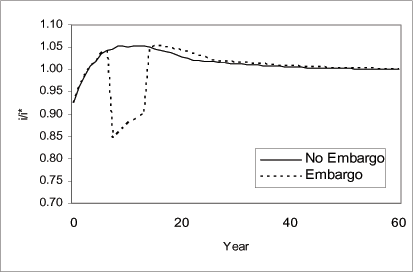
Estimated from the neoclassical growth model with adjustment costs.
Data for Figure 11
| Year | No Embargo | Embargo |
|---|---|---|
| 0 | 0.93 | 0.93 |
| 1 | 0.96 | 0.96 |
| 2 | 0.99 | 0.99 |
| 3 | 1.01 | 1.01 |
| 4 | 1.02 | 1.02 |
| 5 | 1.03 | 1.03 |
| 6 | 1.04 | 1.04 |
| 7 | 1.04 | 0.85 |
| 8 | 1.05 | 0.86 |
| 9 | 1.05 | 0.87 |
| 10 | 1.05 | 0.88 |
| 11 | 1.05 | 0.89 |
| 12 | 1.05 | 0.89 |
| 13 | 1.05 | 0.90 |
| 14 | 1.05 | 1.05 |
| 15 | 1.05 | 1.05 |
| 16 | 1.04 | 1.05 |
| 17 | 1.04 | 1.05 |
| 18 | 1.04 | 1.05 |
| 19 | 1.03 | 1.05 |
| 20 | 1.03 | 1.04 |
| 21 | 1.02 | 1.04 |
| 22 | 1.02 | 1.04 |
| 23 | 1.02 | 1.03 |
| 24 | 1.02 | 1.03 |
| 25 | 1.02 | 1.02 |
| 26 | 1.02 | 1.02 |
| 27 | 1.02 | 1.02 |
| 28 | 1.01 | 1.02 |
| 29 | 1.01 | 1.02 |
| 30 | 1.01 | 1.02 |
| 31 | 1.01 | 1.02 |
| 32 | 1.01 | 1.01 |
| 33 | 1.01 | 1.01 |
| 34 | 1.01 | 1.01 |
| 35 | 1.01 | 1.01 |
| 36 | 1.01 | 1.01 |
| 37 | 1.01 | 1.01 |
| 38 | 1.01 | 1.01 |
| 39 | 1.01 | 1.01 |
| 40 | 1.01 | 1.01 |
| 41 | 1.01 | 1.01 |
| 42 | 1.00 | 1.01 |
| 43 | 1.00 | 1.01 |
| 44 | 1.00 | 1.01 |
| 45 | 1.00 | 1.01 |
| 46 | 1.00 | 1.00 |
| 47 | 1.00 | 1.00 |
| 48 | 1.00 | 1.00 |
| 49 | 1.00 | 1.00 |
| 50 | 1.00 | 1.00 |
| 51 | 1.00 | 1.00 |
| 52 | 1.00 | 1.00 |
| 53 | 1.00 | 1.00 |
| 54 | 1.00 | 1.00 |
| 55 | 1.00 | 1.00 |
| 56 | 1.00 | 1.00 |
| 57 | 1.00 | 1.00 |
| 58 | 1.00 | 1.00 |
| 59 | 1.00 | 1.00 |
| 60 | 1.00 | 1.00 |
Figure 12: Capital relative to steady-state capital
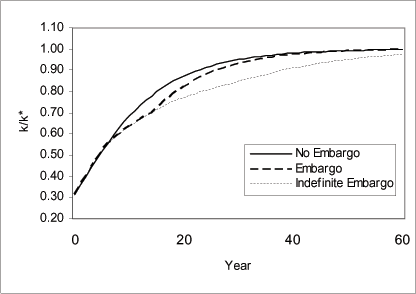
Estimates from the neoclassical growth model with adjustment costs.
Data for Figure 12
| Year | No Embargo (solid line) | Embargo (dashed line) | Indefinite Embargo (dotted line) |
|---|---|---|---|
| 0 | 0.31 | 0.31 | 0.31 |
| 1 | 0.36 | 0.36 | 0.36 |
| 2 | 0.40 | 0.40 | 0.40 |
| 3 | 0.44 | 0.44 | 0.44 |
| 4 | 0.48 | 0.48 | 0.48 |
| 5 | 0.52 | 0.52 | 0.52 |
| 6 | 0.56 | 0.56 | 0.56 |
| 7 | 0.59 | 0.58 | 0.58 |
| 8 | 0.63 | 0.60 | 0.60 |
| 9 | 0.66 | 0.62 | 0.62 |
| 10 | 0.69 | 0.63 | 0.63 |
| 11 | 0.71 | 0.65 | 0.65 |
| 12 | 0.74 | 0.67 | 0.67 |
| 13 | 0.76 | 0.69 | 0.69 |
| 14 | 0.78 | 0.70 | 0.70 |
| 15 | 0.80 | 0.72 | 0.72 |
| 16 | 0.82 | 0.75 | 0.73 |
| 17 | 0.83 | 0.77 | 0.74 |
| 18 | 0.85 | 0.79 | 0.75 |
| 19 | 0.86 | 0.81 | 0.76 |
| 20 | 0.87 | 0.82 | 0.77 |
| 21 | 0.89 | 0.84 | 0.78 |
| 22 | 0.90 | 0.85 | 0.79 |
| 23 | 0.90 | 0.87 | 0.80 |
| 24 | 0.91 | 0.88 | 0.81 |
| 25 | 0.92 | 0.89 | 0.81 |
| 26 | 0.93 | 0.90 | 0.82 |
| 27 | 0.93 | 0.91 | 0.83 |
| 28 | 0.94 | 0.92 | 0.83 |
| 29 | 0.95 | 0.92 | 0.84 |
| 30 | 0.95 | 0.93 | 0.85 |
| 31 | 0.95 | 0.94 | 0.86 |
| 32 | 0.96 | 0.94 | 0.86 |
| 33 | 0.96 | 0.95 | 0.87 |
| 34 | 0.97 | 0.95 | 0.87 |
| 35 | 0.97 | 0.96 | 0.88 |
| 36 | 0.97 | 0.96 | 0.89 |
| 37 | 0.97 | 0.96 | 0.89 |
| 38 | 0.98 | 0.97 | 0.90 |
| 39 | 0.98 | 0.97 | 0.91 |
| 40 | 0.98 | 0.97 | 0.91 |
| 41 | 0.98 | 0.98 | 0.92 |
| 42 | 0.98 | 0.98 | 0.92 |
| 43 | 0.99 | 0.98 | 0.93 |
| 44 | 0.99 | 0.98 | 0.93 |
| 45 | 0.99 | 0.98 | 0.93 |
| 46 | 0.99 | 0.99 | 0.94 |
| 47 | 0.99 | 0.99 | 0.94 |
| 48 | 0.99 | 0.99 | 0.95 |
| 49 | 0.99 | 0.99 | 0.95 |
| 50 | 0.99 | 0.99 | 0.95 |
| 51 | 0.99 | 0.99 | 0.95 |
| 52 | 0.99 | 0.99 | 0.96 |
| 53 | 0.99 | 0.99 | 0.96 |
| 54 | 1.00 | 0.99 | 0.96 |
| 55 | 1.00 | 0.99 | 0.96 |
| 56 | 1.00 | 0.99 | 0.97 |
| 57 | 1.00 | 1.00 | 0.97 |
| 58 | 1.00 | 1.00 | 0.97 |
| 59 | 1.00 | 1.00 | 0.97 |
| 60 | 1.00 | 1.00 | 0.97 |
Figure 13: Output relative to steady-state output
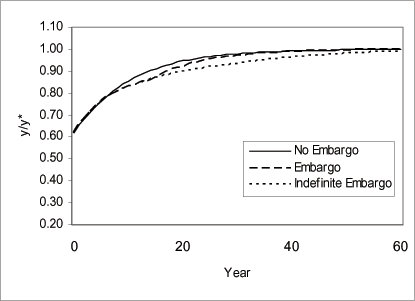
Estimates from the neoclassical growth model with adjustment costs.
Data for Figure 13
| Year | No Embargo (solid line) | Embargo (dashed line) | Indefinite Embargo (dotted line) |
|---|---|---|---|
| 0 | 0.62 | 0.62 | 0.62 |
| 1 | 0.66 | 0.66 | 0.66 |
| 2 | 0.69 | 0.69 | 0.69 |
| 3 | 0.72 | 0.72 | 0.72 |
| 4 | 0.74 | 0.74 | 0.74 |
| 5 | 0.77 | 0.77 | 0.77 |
| 6 | 0.79 | 0.79 | 0.79 |
| 7 | 0.81 | 0.80 | 0.80 |
| 8 | 0.83 | 0.81 | 0.81 |
| 9 | 0.84 | 0.82 | 0.82 |
| 10 | 0.86 | 0.83 | 0.83 |
| 11 | 0.87 | 0.84 | 0.84 |
| 12 | 0.88 | 0.85 | 0.85 |
| 13 | 0.89 | 0.86 | 0.86 |
| 14 | 0.90 | 0.86 | 0.86 |
| 15 | 0.91 | 0.88 | 0.87 |
| 16 | 0.92 | 0.89 | 0.88 |
| 17 | 0.93 | 0.90 | 0.88 |
| 18 | 0.93 | 0.91 | 0.89 |
| 19 | 0.94 | 0.92 | 0.90 |
| 20 | 0.95 | 0.92 | 0.90 |
| 21 | 0.95 | 0.93 | 0.90 |
| 22 | 0.96 | 0.94 | 0.91 |
| 23 | 0.96 | 0.94 | 0.91 |
| 24 | 0.96 | 0.95 | 0.92 |
| 25 | 0.97 | 0.95 | 0.92 |
| 26 | 0.97 | 0.96 | 0.92 |
| 27 | 0.97 | 0.96 | 0.93 |
| 28 | 0.97 | 0.96 | 0.93 |
| 29 | 0.98 | 0.97 | 0.93 |
| 30 | 0.98 | 0.97 | 0.93 |
| 31 | 0.98 | 0.97 | 0.94 |
| 32 | 0.98 | 0.98 | 0.94 |
| 33 | 0.98 | 0.98 | 0.94 |
| 34 | 0.99 | 0.98 | 0.95 |
| 35 | 0.99 | 0.98 | 0.95 |
| 36 | 0.99 | 0.98 | 0.95 |
| 37 | 0.99 | 0.99 | 0.95 |
| 38 | 0.99 | 0.99 | 0.96 |
| 39 | 0.99 | 0.99 | 0.96 |
| 40 | 0.99 | 0.99 | 0.96 |
| 41 | 0.99 | 0.99 | 0.96 |
| 42 | 0.99 | 0.99 | 0.97 |
| 43 | 0.99 | 0.99 | 0.97 |
| 44 | 0.99 | 0.99 | 0.97 |
| 45 | 1.00 | 0.99 | 0.97 |
| 46 | 1.00 | 0.99 | 0.97 |
| 47 | 1.00 | 0.99 | 0.98 |
| 48 | 1.00 | 0.99 | 0.98 |
| 49 | 1.00 | 1.00 | 0.98 |
| 50 | 1.00 | 1.00 | 0.98 |
| 51 | 1.00 | 1.00 | 0.98 |
| 52 | 1.00 | 1.00 | 0.98 |
| 53 | 1.00 | 1.00 | 0.98 |
| 54 | 1.00 | 1.00 | 0.98 |
| 55 | 1.00 | 1.00 | 0.99 |
| 56 | 1.00 | 1.00 | 0.99 |
| 57 | 1.00 | 1.00 | 0.99 |
| 58 | 1.00 | 1.00 | 0.99 |
| 59 | 1.00 | 1.00 | 0.99 |
| 60 | 1.00 | 1.00 | 0.99 |
Figure 14: Current Account to GDP ratios: South Africa vs. Middle-income Countries
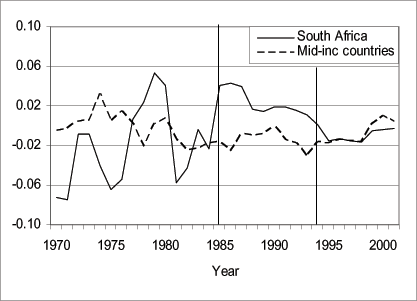
Current Account data are obtained from the 2005 World Development Indicator database. The middle income countries, it is the GDP weighted average of the Current Account to GDP ratios for countries classified in the middle-income category by the World Bank.
Data for Figure 14
| Year | South Africa | Mid-Income countries |
|---|---|---|
| 1970 | -0.07 | -0.005 |
| 1971 | -0.08 | -0.003 |
| 1972 | -0.01 | 0.003 |
| 1973 | -0.01 | 0.005 |
| 1974 | -0.04 | 0.032 |
| 1975 | -0.07 | 0.004 |
| 1976 | -0.05 | 0.014 |
| 1977 | 0.01 | 0.002 |
| 1978 | 0.02 | -0.021 |
| 1979 | 0.05 | 0.002 |
| 1980 | 0.04 | 0.008 |
| 1981 | -0.06 | -0.014 |
| 1982 | -0.04 | -0.025 |
| 1983 | 0.00 | -0.024 |
| 1984 | -0.02 | -0.018 |
| 1985 | 0.04 | -0.016 |
| 1986 | 0.04 | -0.026 |
| 1987 | 0.04 | -0.009 |
| 1988 | 0.02 | -0.009 |
| 1989 | 0.01 | -0.008 |
| 1990 | 0.02 | -0.001 |
| 1991 | 0.02 | -0.015 |
| 1992 | 0.02 | -0.018 |
| 1993 | 0.01 | -0.031 |
| 1994 | 0.00 | -0.017 |
| 1995 | -0.02 | -0.018 |
| 1996 | -0.01 | -0.015 |
| 1997 | -0.02 | -0.015 |
| 1998 | -0.02 | -0.017 |
| 1999 | -0.01 | 0.001 |
| 2000 | 0.00 | 0.009 |
| 2001 | 0.00 | 0.004 |
Footnotes
* Mailing address: Division of International Finance, Board of Governors ,Federal Reserve System, Mail Stop 24, Washington DC 20551,USA; email: [email protected]. Tel.: (202)-452-2609; fax: (202)-736-5638. The author thanks Linda Tesar for encouragement and constructive feedback, Matthew Shapiro, Miles Kimball, and Herman Kamil for helpful comments and discussions. I am indebted to David Gale at the South Africa Trade and Industrial Policy Strategies for providing access to some of the data, and to David Lam for funding a data set used to explore earlier versions of the study. I am also grateful to Dale Henderson, Sylvain LeDuc, David Bowman, Sanjay Chugh, Luis-Felipe Zanna, and to seminar participants at the Board of Governors of the Federal Reserve System for helpful comments, and to Jon Faust for constructive feedback. Work on this project started while I was a graduate student in the Department of Economics and a Research Associate at the Institute for Social Research at the University of Michigan. The views expressed in the paper are those of the author and do not necessarily reflect those of the Board of Governors or the Federal Reserve System. Return to text
1. Additional references on positive effect of financial integration include Henry (2000a,b), Bekaert et al. (2001), and Summers (2000). Return to text
2. See for example Stiglitz, 2000 and Bagwhati, 1998 for arguments against the conventional view of a positive effect of financial liberalization. Return to text
3. Detailed historical accounts of the
economic embargo and the disinvestment are available on the
Institute for International Economics website at the following
addresses:http://www.iie.com/research/topics/sanctions/southafrica3.htm#economic
http://www.iie.com/research/topics/sanctions/southafrica.htm#chronology
Return to text
4. Bernanke and Gurkaynak (2001) estimated a labor share of 0.59 for South Africa. After correcting the estimate to account for self-employed workers based on recommendations in Gollin (1998), the share of labor increases to 0.62-0.63. The estimates of labor share obtained imply a share of capital between 0.37 and 0.41, consistent with the estimate in this study. Barro and Xala-I-Martin (1992), and Mankiw et al. (1992), note that a high capital share - around 0.75 - is necessary to obtain empirically reasonable convergence rates. Models that include human capital are able to justify such a high share. In this study, human capital is omitted. The presence of adjustment costs for capital can control the speed of convergence, and when set high enough, it delivers a reasonable convergence rate without the inclusion of human capital. Return to text
5. This estimate is higher than empirical estimates for the United States in Shapiro (1986) and Hall (2002) where the estimates at annual frequencies are 2 and 1.5 respectively. Sensitivity analyses with different parameter values will explore the robustnes of the results to various values of the adjustement cost parameter. Return to text
6. Barro et. al (1995) uses the following estimates for the US economy: f = 0.02, ρ = 0.02, and γ = 2 which imply rω = 0.06. Return to text
7. The recent experience of emerging markets in Asia and South America reveal that reversal of capital flows usually result in significant declines in the stock market indices. For example, the Mexican market index fell by approximately 50 percent during the 1994 Mexican crisis, and by 20 percent in Brazil and Argentina in the same period. In the 1997 Asia crisis, the Hong-Kong and South Korean markets declined by 20 percent and by 70 percent respectively. Return to text
8. Risk measures for South Africa are available on the following website address: http://www.duke.edu/~ charvey/Country_risk/risk/southa.gif Return to text
9. We follow the classification provided by the World Bank; according to which, South Africa is a middle-income country. The current account to GDP ratio is GDP weighted. The unweigthed simple average measure does not reverse the results. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text