
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 849, December 2005 --- Screen Reader
Version*
Interest Rate Rules, Endogenous Cycles and Chaotic Dynamics in Open Economies*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In this paper we present an extensive analysis of the consequences for global equilibrium determinacy of implementing active interest rate rules (i.e. monetary rules where the nominal interest rate responds more than proportionally to changes in inflation) in flexible-price open economies. We show that conditions under which these rules generate aggregate instability by inducing cyclical and chaotic equilibrium dynamics depend on particular characteristics of open economies such as the degree of (trade) openness and the degree of exchange rate pass-through implied by the presence of non-traded distribution costs. For instance, we find that a forward-looking rule is more prone to induce endogenous cyclical and chaotic dynamics the more open the economy and the higher the degree of exchange rate pass-through. The existence of these dynamics and their dependence on the degree of openness are in general robust to different timings of the rule (forward-looking versus contemporaneous rules), to the use of alternative measures of inflation in the rule (CPI versus Core inflation), as well as to changes in the timing of real money balances in liquidity services ("cash-when-I-am-done" timing versus "cash-in-advance" timing).
Keywords: Small open economy, interest rate rules, Taylor Rules, multiple equilibria, chaos and endogenous fluctuations
JEL classification: E32, E52, F41
1 Introduction
In recent years there has been a revival of theoretical and empirical literature aimed at understanding the macroeconomic consequences of implementing diverse monetary rules in the Small Open Economy (SOE).1 In this literature the study of interest rate rules whose interest rate response coefficient to inflation is greater than one, generally referred to as Taylor rules or active rules, has received particular attention.2 To some extent the importance given to these rules in the SOE literature is just a consequence of some of the benefits that the closed economy literature has claimed for them. For instance, Bernanke and Woodford (1997) and Clarida, Galí and Gertler (2000), among others, have argued that active rules are desirable because they guarantee a unique Rational Expectations Equilibrium (REE) whereas rules whose interest rate response coefficient to inflation is less than one, also called passive rules, induce aggregate instability in the economy by generating multiple equilibria. Despite these arguments supporting active rules in closed economies, Benhabib, Schmitt-Grohé and Uribe (2001b, 2002a,b) have pointed out that they are based on results that rely on the type of equilibrium analysis that is adopted. In fact these policy prescriptions are usually derived from a local determinacy of equilibrium analysis, i.e. identifying conditions for rules that guarantee equilibrium uniqueness in an arbitrarily small neighborhood of the target steady state. In contrast by pursuing a global equilibrium analysis in tandem with the observation that nominal interest rates are bounded below by zero, Benhabib et al. have shown that active rules can induce aggregate instability in closed economies through endogenous cycles, chaotic dynamics and liquidity traps.3
What motivates our paper is the fact that the open economy literature on interest rate rules has also restricted its attention to local dynamics and not to global dynamics, often disregarding the zero bound on the nominal interest rate. By doing this, the literature has gained in tractability but has also overlooked a possibly wider set of equilibrium dynamics.
To the best of our knowledge, our work is the first attempt in the open economy literature to understand how interest rate rules may lead to global endogenous fluctuations. We pursue a global and non-linear equilibrium analysis of a traditional flexible-price SOE model with traded and non-traded goods, whose government follows an active forward-looking rule by responding to the expected future CPI-inflation. We show that conditions under which active rules induce aggregate instability by generating cyclical and chaotic dynamics depend on some specific features of an open economy such as the degree of openness of the economy (measured as the share of traded goods in consumption) and the degree of exchange rate pass-through into import prices (implied by the presence of non-traded distribution services). For example, we find that a forward-looking rule is more prone to induce cyclical equilibria and chaotic dynamics the more open the economy and the higher the degree of exchange rate pass-through. If consumption and money are Edgeworth complements in utility these dynamics occur around an extremely low interest rate steady state. On the other hand if consumption and money are substitutes these dynamics appear around the high interest rate target set by the monetary authority.4
For a given specification of the rule, we show that the existence of these dynamics and their dependence on the degree of openness are in general robust to different timings of the rule (forward-looking versus contemporaneous rules), to the use of alternative measures of inflation in the rule (CPI versus Core inflation), as well as to changes in the timing of real money balances in liquidity services ("cash-when-I-am-done" timing versus "cash-in-advance" timing.)
Table 1
| Country | Degree of Openness (Imports/GDP) | Response Coefficient to Inflation (ρπ) | Type of Interest Rate Rule |
|---|---|---|---|
| France | 0.22 | 1.13† | Forward-Looking |
| Costa Rica | 0.42 | 1.47* | Forward-Looking |
| Colombia | 0.20 | 1.31× | Forward-Looking |
| Chile | 0.28 | 2.10о | Forward-Looking |
| United Kingdom | 0.28 | 1.84‡ | Contemporaneous |
| Australia | 0.19 | 2.10‡ | Contemporaneous |
| Canada | 0.31 | 2.24‡ | Contemporaneous |
| New Zealand | 0.28 | 2.49‡ | Contemporaneous |
Note: Data from IFS were used to calculate the Imports/GDP share, while the significant estimates for the interest rate response coefficient to the CPI-inflation (ρπ) come from : × Bernal (2003),† Clarida et al. (1998), * Corbo (2000), ‡ Lubik and Schorfheide (2003), and о Restrepo (1999). The degree of openness of the economy is the annual average of imports to GDP share for the period of time used for the estimation of ρπ.
The relevance of our results stems from the fact that they point out the importance of considering particular features of the open economy in the design of monetary policy. Clearly both the degree of openness and the degree of exchange rate pass-through are open economy features that have been neglected by previous closed economy studies. Furthermore, both are characteristics that vary significantly among economies that follow (or followed) active interest rate rules. For instance Table 1 shows the diverse degrees of openness, measured as the share of imports to GDP, for some industrialized and developing economies that have been claimed to follow interest rate rules. In addition Campa and Goldberg (2004) and Frankel, Parsley and Wei (2005), among others, provide empirical evidence suggesting that the degree of exchange rate pass-through into import prices not only varies across industrialized and developing economies; but it has also varied over time within these economies.
This paper is different from closed economy contributions such as Benhabib et al. (2002a) in some key aspects. First, our analysis shows that the assumption of money in the production function used by Benhabib et al. is not necessary to obtain cyclical and chaotic equilibrium dynamics under rules. We introduce money in the utility function and show that the existence of these global dynamics depends on whether consumption and money are Edgeworth complements or substitutes in the utility function. This observation was raised by Benhabib et al. (2001a) in the local determinacy of equilibrium analysis context but to the best of our knowledge it has not been raised in the context of a global equilibrium analysis.
Second, we show that if consumption and money are complements then it is possible to have " non-monotonic liquidity traps" featuring periodic and aperiodic oscillations around an extremely low interest rate steady state that is different from the target steady state. On the contrary if consumption and money are substitutes then cyclical and chaotic dynamics occur only around the target steady state. Although this case is reminiscent of the one in Benhabib et al. (2002a), it also presents a subtle difference. In their closed economy model period-3 cycles and therefore chaos always occur only for sufficiently low coefficients of relative risk aversion. Our results show that these dynamics can basically appear for any coefficient of relative risk aversion greater than one and provided that the economy is sufficiently open. In this sense open economies are more prone than closed economies to display these cyclical dynamics.
Third, we identify necessary and sufficient conditions for the design of active forward looking rules that do not generate cyclical and chaotic equilibria. For some given structural parameters, these conditions generally entail an appropriate choice of the rule's responsiveness to inflation. Although cyclical dynamics can be ruled out, liquidity traps and (hyper) inflationary paths remain viable equilibria. Previous works on monetary economics, however, have proposed solutions on how to deal with these equilibria.5
There are previous works in the SOE literature that have tried to identify conditions under which interest rate rules may lead to local multiple equilibria.6 For instance, De Fiore and Liu (2003), Linnemann and Schabert (2002), and Zanna (2003), among others, discuss the importance of the degree of openness of the economy in the local equilibrium analysis. The last work also points out the key role played by the degree of the exchange rate pass-through. Although our work is related to these previous studies it is different from them in the type of equilibrium analysis that is pursued. To the extent that our work considers the zero lower bound for the interest rate and pursues a global equilibrium analysis, it is able to focus on a wider set of equilibrium dynamics.
In contrast to the above mentioned works in the SOE literature, this paper does not consider nominal price rigidities. In this sense it is similar to the closed economy works of Benhabib et al. (2002a,b), Carlstrom and Fuerst (2001), and Leeper (1991) among others. In Airaudo and Zanna (2005) we introduce price stickiness and study, through a Hopf bifurcation analysis, how rules can induce cyclical dynamics that never converge to the target steady state. As in the current paper, the existence of equilibrium cycles depends on some open economy features.
The remainder of this paper is organized as follows. In Section 2 we present a flexible-price model with its main assumptions. We define the open economy equilibrium and derive some basic steady state results. In Section 3 we pursue a local and a global equilibrium analyses for an active forward-looking interest rate rule. In Section 4 we study active forward-looking rules that can preclude the existence of cyclical equilibria. In Section 5 we investigate how the degree of exchange rate pass-through can affect the existence of cyclical dynamics for forward-looking rules. We pursue a sensitivity analysis to gauge the robustness of our main results in Section 6. Finally Section 7 concludes.
2 A Flexible-Price Model
2.1 The Household-Firm Unit
Consider a Small Open Economy (SOE)
populated by a large number of infinitely lived household-firm
units. They are identical. Each unit derives utility from
consumption (![]() ), real money balances (
), real money balances (![]() ), and not working (
), and not working (
![]() ) according to
) according to
![$\displaystyle E_{0}\sum_{t=0}^{\infty}\beta^{t}\left\{ \frac{\left[ \left( c_{t}\right) ^{\gamma}\left( m_{t}^{d}\right) ^{1-\gamma}\right] ^{1-\sigma}-1} {1-\sigma}+\psi(1-h_{t}^{T}-h_{t}^{N})\right\}$](img20.gif)
|
(1) |
| (2) |
where ![]()
![]() and
and
![]() but
but
![]() 7
7 ![]() is the expectations operator conditional on the set of
information available at time 0;
is the expectations operator conditional on the set of
information available at time 0; ![]() and
and
![]() denote the consumption of traded
and non-traded goods in period
denote the consumption of traded
and non-traded goods in period ![]() respectively;
respectively;
![]() are real
money balances (domestic currency money balances deflated by the
Consumer Price Index, CPI,
are real
money balances (domestic currency money balances deflated by the
Consumer Price Index, CPI, ![]() to be defined
below);
to be defined
below); ![]() and
and
![]() stand for labor supplied to the
production of traded and non-traded goods respectively and
stand for labor supplied to the
production of traded and non-traded goods respectively and
![]() is the share of traded goods
in the consumption aggregator (2). We
interpret this share as a measure of the degree of (trade) openness
of the economy. As
is the share of traded goods
in the consumption aggregator (2). We
interpret this share as a measure of the degree of (trade) openness
of the economy. As ![]() goes to zero, domestic
agents do not value internationally traded goods for consumption.
Then the economy is fundamentally closed. Whereas if
goes to zero, domestic
agents do not value internationally traded goods for consumption.
Then the economy is fundamentally closed. Whereas if ![]() goes to one, non-traded goods are negligible in
consumption. We refer to this case as the completely open economy.
goes to one, non-traded goods are negligible in
consumption. We refer to this case as the completely open economy.
Although we use specific functional forms, they are general
enough to convey the main message of this paper. They will allow us
to show analytically how cyclical dynamics induced by the
interest rate rule depend on the degree of openness ![]() .8 They also allow us to study how
these dynamics are affected by whether consumption,
.8 They also allow us to study how
these dynamics are affected by whether consumption, ![]() and money,
and money, ![]() are either Edgeworth
substitutes or complements. By defining
are either Edgeworth
substitutes or complements. By defining
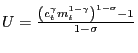 and noticing that the sign of the cross partial derivative
and noticing that the sign of the cross partial derivative
![]() satisfies
satisfies
![]() then we can distinguish between the case of Edgeworth substitutes
when
then we can distinguish between the case of Edgeworth substitutes
when ![]() (
(![]() or
the case of complements when
or
the case of complements when ![]() (
(![]() . Moreover, given that
. Moreover, given that
![]() and that the coefficient of
relative risk aversion (CRRA) can be expressed as
and that the coefficient of
relative risk aversion (CRRA) can be expressed as
![]() then
then
![]() implies
implies
![]() As a result
of this we will refer to
As a result
of this we will refer to ![]() as the " risk aversion
parameter."
as the " risk aversion
parameter."
The representative unit produces traded and non-traded goods by employing labor according to the technologies
| (3) |
where
![]() and
and ![]() and
and ![]() are
productivity shocks following stationary AR
are
productivity shocks following stationary AR
![]() stochastic processes. We
assume that these shocks are the sole source of fundamental
uncertainty.
stochastic processes. We
assume that these shocks are the sole source of fundamental
uncertainty.
As standard in the literature, we assume that the Law of One
Price holds for traded goods and normalize the foreign price of the
traded good to one.9 Hence
![]() , where
, where ![]() is the domestic currency price of traded goods and
is the domestic currency price of traded goods and
![]() is the nominal exchange rate.
This simplification together with (2) can
be used to derive the Consumer Price Index (CPI)
is the nominal exchange rate.
This simplification together with (2) can
be used to derive the Consumer Price Index (CPI)
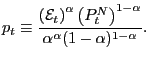
|
(4) |
Using equation (4) and defining the gross
nominal devaluation rate as
![]() and the
gross non-traded goods inflation rate as
and the
gross non-traded goods inflation rate as
![]() we
derive the gross CPI-inflation rate
we
derive the gross CPI-inflation rate
| (5) |
where
![]() It is
just a weighted average of different goods inflations whose weights
are related to the degree of openness,
It is
just a weighted average of different goods inflations whose weights
are related to the degree of openness, ![]() . The
real exchange rate (
. The
real exchange rate (![]() ) is defined as the ratio
of the price of traded goods (nominal exchange rate) and the price
of non-traded goods
) is defined as the ratio
of the price of traded goods (nominal exchange rate) and the price
of non-traded goods
| (6) |
Then the gross real exchange rate depreciation,
![]() can be written as
can be written as
| (7) |
As has become very common in the open economy literature such as
Clarida et al. (2001) and Galí and Monacelli (2004) among
others, we assume that the household-firm units have access to a
complete set of internationally traded claims. In each period
![]() the agents can purchase two types of
financial assets: fiat money
the agents can purchase two types of
financial assets: fiat money ![]() and nominal
state contingent claims,
and nominal
state contingent claims, ![]() The latter pay one
unit of (foreign) currency for a specific realization of the
fundamental shocks in
The latter pay one
unit of (foreign) currency for a specific realization of the
fundamental shocks in ![]() Although the existence of
complete markets is a very strong assumption, it is well known that
they can be approximated by a set of non-state contingent
instruments featuring a wide range of maturities and
indexations.10 In this paper the assumption of
complete markets serves the sole purpose of ruling out the unit
root problem of the small open economy, allowing us to pursue a
meaningful local determinacy of equilibrium analysis. In this way,
we can compare the results from the global equilibrium analysis to
the ones from the local equilibrium analysis.11Nevertheless our
global results on the existence of cyclical and chaotic equilibrium
dynamics will still hold if instead we assume incomplete markets,
as we will show in Section 6.
Although the existence of
complete markets is a very strong assumption, it is well known that
they can be approximated by a set of non-state contingent
instruments featuring a wide range of maturities and
indexations.10 In this paper the assumption of
complete markets serves the sole purpose of ruling out the unit
root problem of the small open economy, allowing us to pursue a
meaningful local determinacy of equilibrium analysis. In this way,
we can compare the results from the global equilibrium analysis to
the ones from the local equilibrium analysis.11Nevertheless our
global results on the existence of cyclical and chaotic equilibrium
dynamics will still hold if instead we assume incomplete markets,
as we will show in Section 6.
Under complete markets the representative agent's flow constraint for each period can be written as
| (8) |
where
![]() denotes the cost of all
contingent claims bought at the beginning of period
denotes the cost of all
contingent claims bought at the beginning of period ![]() and
and ![]() refers to the period-
refers to the period-![]() price of a claim to one unit of currency delivered in a
particular state of period
price of a claim to one unit of currency delivered in a
particular state of period ![]() divided by the
probability of occurrence of that state and conditional of
information available in period
divided by the
probability of occurrence of that state and conditional of
information available in period ![]() . Constraint
(8) says that the total end-of-period nominal
value of the financial assets can be worth no more than the value
of the financial wealth brought into the period,
. Constraint
(8) says that the total end-of-period nominal
value of the financial assets can be worth no more than the value
of the financial wealth brought into the period, ![]() , plus non-financial income during the period net of the
value of taxes,
, plus non-financial income during the period net of the
value of taxes,
![]() , and the
value of consumption spending.
, and the
value of consumption spending.
To derive the period-by-period budget constraint, we use the
definition of the total beginning-of-period wealth, in the
following period,
![]() and the fact that
the period-
and the fact that
the period-![]() price of a claim that pays one unit of
currency in every state in period
price of a claim that pays one unit of
currency in every state in period ![]() is equal to
the inverse of the risk-free gross nominal interest rate; that is
is equal to
the inverse of the risk-free gross nominal interest rate; that is
![]() From this,
the definition of
From this,
the definition of ![]() and (8) we obtain
and (8) we obtain
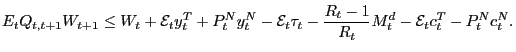
|
(9) |
The representative unit is also subject to a Non-Ponzi game condition
| (10) |
at all dates and under all contingencies where ![]() represents the period-zero price of one unit of
currency to be delivered in a particular state of period
represents the period-zero price of one unit of
currency to be delivered in a particular state of period
![]() divided by the probability of occurrence of
that state and given information available at time
divided by the probability of occurrence of
that state and given information available at time ![]() It satisfies
It satisfies
![]() with
with
![]() .
.
The problem of the representative household-firm unit reduces to
choosing the sequences
![]()
![]()
![]()
![]()
![]()
![]() in order to
maximize (1) subject to (2), (3), (9) and (10), given
in order to
maximize (1) subject to (2), (3), (9) and (10), given
![]() and the time paths of
and the time paths of ![]() ,
,
![]() ,
,
![]()
![]() and
and
![]() Note that since the utility
function specified in (1) implies that the
preferences of the agent display non-satiation then both
constraints (9) and (10) hold with equality.
Note that since the utility
function specified in (1) implies that the
preferences of the agent display non-satiation then both
constraints (9) and (10) hold with equality.
The first order conditions correspond to (9) and (10) with equality and
| (11) |
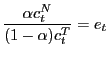
|
(12) |
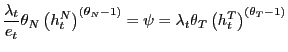
|
(13) |
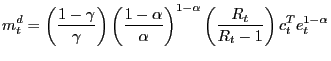
|
(14) |
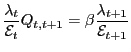
|
(15) |
where
![]() is the Lagrange
multiplier of the flow budget constraint.
is the Lagrange
multiplier of the flow budget constraint.
The interpretation of the first order conditions is
straightforward. Equation (11) is the usual
intertemporal envelope condition that makes the marginal utility of
consumption of traded goods equal to the marginal utility of wealth
measure in terms of traded goods (
![]() ). Condition (12) implies that the marginal rate of substitution
between traded and non-traded goods must be equal to the real
exchange rate. Condition (13) equalizes the
value of the marginal products of labor in both sectors. Equation
(14) represents the demand for real money
balances. And finally condition (15) describes
a standard pricing equation for one-step-ahead nominal contingent
claims for each period
). Condition (12) implies that the marginal rate of substitution
between traded and non-traded goods must be equal to the real
exchange rate. Condition (13) equalizes the
value of the marginal products of labor in both sectors. Equation
(14) represents the demand for real money
balances. And finally condition (15) describes
a standard pricing equation for one-step-ahead nominal contingent
claims for each period ![]() and for each possible state
of nature.
and for each possible state
of nature.
2.2 The Government
The government issues two nominal
liabilities: money, ![]() , and a one period
risk-free domestic bond,
, and a one period
risk-free domestic bond,
![]() that pays a gross risk-free
nominal interest rate
that pays a gross risk-free
nominal interest rate ![]() . We assume that it
cannot issue or hold state contingent claims. It also levies taxes,
. We assume that it
cannot issue or hold state contingent claims. It also levies taxes,
![]() pays interest on its debt, (
pays interest on its debt, (
![]() , and receives revenues
from seigniorage
, and receives revenues
from seigniorage![]() Then the government's budget
constraint can be written as
Then the government's budget
constraint can be written as
![]() where
where
![]()
We proceed to describe the fiscal and monetary policies. The
former corresponds to a generic Ricardian policy: the government
picks the path of the lump-sum transfers, ![]() in order to satisfy the intertemporal version of its budget
constraint in conjunction with the transversality condition
in order to satisfy the intertemporal version of its budget
constraint in conjunction with the transversality condition
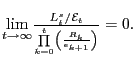 The latter is described as an interest rate feedback rule whereby
the government sets the nominal interest rate,
The latter is described as an interest rate feedback rule whereby
the government sets the nominal interest rate, ![]() , as a continuous and increasing function of the
deviation of the expected future CPI-inflation rate,
, as a continuous and increasing function of the
deviation of the expected future CPI-inflation rate,
![]() , from a
target,
, from a
target,
![]() 12 For analytical and
computational purposes, as in Benhabib et al. (2002a) and
Christiano and Rostagno (2001), we use the following specific
non-linear rule13
12 For analytical and
computational purposes, as in Benhabib et al. (2002a) and
Christiano and Rostagno (2001), we use the following specific
non-linear rule13
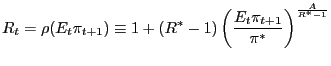
|
(16) |
where
![]() and
and ![]() corresponds to the target interest rate. (16) always satisfies the zero bound on the nominal
interest rate, i.e.
corresponds to the target interest rate. (16) always satisfies the zero bound on the nominal
interest rate, i.e.
![]() In addition
we assume that the government responds aggressively to inflation.
This means that at the inflation target, the rule's elasticity to
inflation
In addition
we assume that the government responds aggressively to inflation.
This means that at the inflation target, the rule's elasticity to
inflation
![]() is strictly bigger than 1. Following Leeper (1991) we call rules
with this property active rules.
is strictly bigger than 1. Following Leeper (1991) we call rules
with this property active rules.
Assumption 0:
![]() That is, the
rule is active.
That is, the
rule is active.
2.3 International Capital Markets
Besides complete markets there is free
international capital mobility. Then the no-arbitrage condition
![]() holds, where
holds, where
![]() refers to the
period-
refers to the
period-![]() foreign currency price of a claim to one
unit of foreign currency delivered in a particular state of period
foreign currency price of a claim to one
unit of foreign currency delivered in a particular state of period
![]() divided by the probability of occurrence
of that state and conditional of information available in period
divided by the probability of occurrence
of that state and conditional of information available in period
![]() .
.
Furthermore under the assumption of complete markets a condition
similar to (15) must hold from the
maximization problem of the representative agent in the Rest of The
World (ROW). That is,
![]() where
where
![]() represents the marginal
utility of nominal wealth in the ROW,
represents the marginal
utility of nominal wealth in the ROW, ![]() denotes the subjective discount rate of the ROW and
denotes the subjective discount rate of the ROW and
![]() is the foreign price of traded
goods. Since we normalize this price to one (
is the foreign price of traded
goods. Since we normalize this price to one (
![]() then assuming that
then assuming that
![]() leads to
leads to
![]()
Combining this last equation, with condition (15) and the fact that
![]() yields
yields
![]() which holds at all dates and under all contingencies. This
condition implies that the domestic marginal utility of wealth is
proportional to its foreign counterpart:
which holds at all dates and under all contingencies. This
condition implies that the domestic marginal utility of wealth is
proportional to its foreign counterpart:
![]() where
where
![]() refers to a constant parameter that
determines the wealth difference between the SOE and the ROW. From
the perspective of a SOE,
refers to a constant parameter that
determines the wealth difference between the SOE and the ROW. From
the perspective of a SOE,
![]() can be taken as an exogenous
variable. For simplicity we assume that
can be taken as an exogenous
variable. For simplicity we assume that
![]() is constant and equal to
is constant and equal to
![]() As a result of this
As a result of this
![]() becomes a constant. Then
becomes a constant. Then
| (17) |
This allows us to write condition (15) as
![]() that together with
that together with
![]() yields
yields
![$\displaystyle R_{t}=\beta^{-1}\left[ E_{t}\frac{1}{\epsilon_{t+1}}\right] ^{-1}$](img158.gif)
|
(18) |
which is similar to an uncovered interest parity condition.
2.4 The Definition of Equilibrium
In this paper we will focus on perfect
foresight equilibria. In other words, we assume the all the agents
in the economy, including the government, forecast correctly all
the anticipated variables. Hence for any variable ![]() we have that
we have that
![]() with
with ![]() implying that we can drop the expectation operator in
the previous equations. For instance, under perfect foresight,
condition (18) becomes
implying that we can drop the expectation operator in
the previous equations. For instance, under perfect foresight,
condition (18) becomes
| (19) |
that corresponds to the typical uncovered interest parity condition
as long as
![]() represents the foreign
international interest rate.14
represents the foreign
international interest rate.14
In order to provide a definition of the equilibrium dynamics
subject of our study, we find a reduced non-linear form of the
model. To do so we use the definitions (5)
and (7) together with conditions (11)-(14), (17), (19), and the market clearing
conditions for money and the non-traded good,
![]() and
and
![]() to
obtain
to
obtain
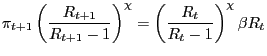
|
(20) |
where
![$\displaystyle \chi=\frac{(\sigma-1)(1-\alpha)(1-\gamma)(1-\theta_{N})}{\sigma\lbrack \theta_{N}+\alpha(1-\theta_{N})]+\left( 1-\alpha\right) (1-\theta_{N} )}.$](img168.gif)
|
(21) |
Combining (16) and (20) and dropping the expectation operator yields
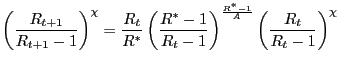
|
(22) |
which corresponds to the reduced non-linear form of the model that can be used to pursue the local and global determinacy of equilibrium analyses.15 We use this equation in order to provide a definition of a Perfect Foresight Equilibrium (PFE).
Definition
1 Given the target ![]() and the initial condition
and the initial condition ![]() a Perfect
Foresight Equilibrium (PFE) is a deterministic process
a Perfect
Foresight Equilibrium (PFE) is a deterministic process
![]() with
with ![]() for any
for any ![]() that satisfies equation
(22) if the interest rate rule is
forward-looking.
that satisfies equation
(22) if the interest rate rule is
forward-looking.
Although Definition 1 is stated
exclusively in terms of the nominal interest rate (![]() ), it must be clear that multiple perfect foresight
equilibrium solutions to (22) imply real
local and/or global indeterminacy of all the endogenous
variables.16 In other words the indeterminacy of
the nominal interest rate implies real indeterminacy in our model
because of the non-separability in the utility function between
money and consumption.17
), it must be clear that multiple perfect foresight
equilibrium solutions to (22) imply real
local and/or global indeterminacy of all the endogenous
variables.16 In other words the indeterminacy of
the nominal interest rate implies real indeterminacy in our model
because of the non-separability in the utility function between
money and consumption.17
In order to pursue the equilibrium analysis we need to identify
the steady state(s) of the economy. From (5), (7) and (20) we obtain that at the steady-state(s),
![]() and
and
![]() Using these and the
rule (16) we have that
Using these and the
rule (16) we have that
| (23) |
Clearly
![]() is a solution to
(23), and therefore a feasible steady
state. But if the rule is active at
is a solution to
(23), and therefore a feasible steady
state. But if the rule is active at ![]() that
is if
that
is if
![]() then another
lower steady state
then another
lower steady state
![]() exists and
it is unique. At this low steady state the elasticity of the rule
to inflation satisfies
exists and
it is unique. At this low steady state the elasticity of the rule
to inflation satisfies
![]() The following
proposition formalizes the existence of the low steady state
The following
proposition formalizes the existence of the low steady state
![]() .
.
Proposition
1 If
![]() (an active rule) and
(an active rule) and
![]() (the zero lower bound) then
there exists a solution
(the zero lower bound) then
there exists a solution
![]() solving (23) besides the trivial
solution
solving (23) besides the trivial
solution
![]() .
.
Proof. See the Appendix.
The existence of two steady states plays a crucial role in the
derivation of our results as in the closed economy model of
Benhabib et al. (2002a). As a matter of fact, the steady state
equation (23) of our SOE is identical to
theirs. It is independent of the non-policy structural parameters.
Hence no fold bifurcation (i.e. appearance/disappearance of steady
states) occurs because of changes in these parameters![]() What distinguishes our model from theirs are the equilibrium
dynamics off the two steady states. This is a consequence of the
following two features of our model. First, by introducing traded
and non-traded goods we present an economy with two sectors that
although homogeneous in terms of price setting behavior (both
feature flexible prices), are fundamentally different in terms of
the degree of openness to international trade. As we will see below
this degree, measured by
What distinguishes our model from theirs are the equilibrium
dynamics off the two steady states. This is a consequence of the
following two features of our model. First, by introducing traded
and non-traded goods we present an economy with two sectors that
although homogeneous in terms of price setting behavior (both
feature flexible prices), are fundamentally different in terms of
the degree of openness to international trade. As we will see below
this degree, measured by ![]() will influence the
equilibrium dynamics. Second, by considering money in the
non-separable utility function we are able to study how the
existence of cyclical dynamics depend on whether money and
consumption are either Edgeworth complements (
will influence the
equilibrium dynamics. Second, by considering money in the
non-separable utility function we are able to study how the
existence of cyclical dynamics depend on whether money and
consumption are either Edgeworth complements (![]() ) or substitutes (
) or substitutes (![]() ).
).
In the analysis to follow we will study how ![]() and
and ![]() affect the local and global
equilibrium dynamics in our SOE model while keeping constant the
other structural parameters (
affect the local and global
equilibrium dynamics in our SOE model while keeping constant the
other structural parameters (![]()
![]() and
and
![]() ) and the policy parameters
(
) and the policy parameters
(![]() and
and ![]() ). This will
allow us to compare economies that implement the same monetary rule
but differ in the degree of openness
). This will
allow us to compare economies that implement the same monetary rule
but differ in the degree of openness ![]() and the
risk aversion parameter
and the
risk aversion parameter ![]() To accomplish this
goal we will proceed in two steps. First we will analyze how these
dynamics are affected by the composite parameter
To accomplish this
goal we will proceed in two steps. First we will analyze how these
dynamics are affected by the composite parameter ![]() defined in (21). Second by taking into
account the dependence of
defined in (21). Second by taking into
account the dependence of ![]() on both
on both
![]() and
and ![]() we will
unveil the effect of the degree of openness and the risk aversion
parameter on the existence of local and global dynamics (cycles and
chaos). In this sense we will regard
we will
unveil the effect of the degree of openness and the risk aversion
parameter on the existence of local and global dynamics (cycles and
chaos). In this sense we will regard ![]() as a
function of
as a
function of ![]() and
and ![]() 18That is
18That is
![]() For the second step we
will use and refer to (21), and to Lemmata
4 and 5
in the Appendix.In turn, these Lemmata and subsequent propositions
will use the following definitions
For the second step we
will use and refer to (21), and to Lemmata
4 and 5
in the Appendix.In turn, these Lemmata and subsequent propositions
will use the following definitions
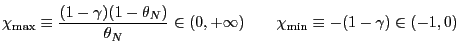
|
(24) |
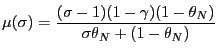
|
(25) |
where
![]() and
and
![]() are considered scalars and
are considered scalars and
![]() is considered a function of
is considered a function of
![]()
Definition
2 Using (24) and
(25) define the scalars
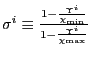 and the functions
and the functions
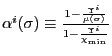 for
for ![]() where
where
![]()
![]()
![]() and
and
![]() and the functions
and the functions
![]() are characterized in
Lemma 4 when
are characterized in
Lemma 4 when ![]() and in Lemma 5 when
and in Lemma 5 when
![]() .
.
3 Equilibrium Dynamics under Forward-Looking Rules
Our study of forward-looking rules is motivated by the evidence provided by Clarida et al. (1998) for industrialized economies and by Corbo (2000) for developing economies. Both works suggest that these economies have followed forward-looking rules.
In order to derive analytical results for both the local and the
global equilibrium analyses we will assume that the constant
parameters ![]()
![]()
![]() and
and
![]() satisfy the following
assumptions.19,20
satisfy the following
assumptions.19,20
Assumption 1:
![]()
Assumption 2:
![]()
Assumption 3:
![]()
3.1 The Local Determinacy of Equilibrium Analysis
The local determinacy of equilibrium
analysis for forward-looking rules is pursued by log-linearizing
equation (22) around the target steady state
![]() , yielding
, yielding
![$\displaystyle \hat{R}_{t+1}=\left[ 1+\frac{\frac{R^{\ast}}{A}-1}{\frac{\chi}{R^{\ast}-1} }\right] \hat{R}_{t}.$](img253.gif)
|
(26) |
Since ![]() is a non-predetermined variable,
studying local determinacy is equivalent to finding conditions that
make the linear difference equation (26)
explosive. The next Lemma shows how local equilibrium determinacy
depends on
is a non-predetermined variable,
studying local determinacy is equivalent to finding conditions that
make the linear difference equation (26)
explosive. The next Lemma shows how local equilibrium determinacy
depends on ![]() .
.
Lemma 1 Define
![]() and consider
and consider
![]() . Suppose the government
follows an active forward-looking rule then: 1) the equilibrium is
locally unique if
. Suppose the government
follows an active forward-looking rule then: 1) the equilibrium is
locally unique if
![]() 2) there exist locally
multiple equilibria if
2) there exist locally
multiple equilibria if
![]() .
.
Proof. See the Appendix.
These simple determinacy of equilibrium conditions for
![]() can be reinterpreted in terms of the
degree of openness
can be reinterpreted in terms of the
degree of openness ![]() and the risk aversion
parameter
and the risk aversion
parameter ![]() in the following Proposition.
in the following Proposition.
Proposition 2 Consider
![]() and
and
![]() in Definition 2 where
in Definition 2 where
![]() and
and
![]() . Suppose that the government follows an active forward-looking
rule.
. Suppose that the government follows an active forward-looking
rule.
1. There exists a locally unique equilibrium(a) if consumption and money are Edgeworth complements, i.e.
and for any degree of openness, i.e.
(b) if consumption and money are Edgeworth substitutes, i.e.
and the economy is sufficiently open satisfying
where
is positive and strictly increasing for
but constant and equal to zero for any
2. There exist locally multiple equilibria if consumption and money are Edgeworth substitutes satisfying
, and the economy is sufficiently closed satisfying
Proof. See the Appendix.
The results of this proposition show the importance of
![]() and
and ![]() in the
local characterization of the equilibrium. In a nutshell, active
forward-looking rules guarantee local uniqueness in the following
cases: when regardless of the degree of openness the risk aversion
parameter
in the
local characterization of the equilibrium. In a nutshell, active
forward-looking rules guarantee local uniqueness in the following
cases: when regardless of the degree of openness the risk aversion
parameter ![]() is sufficiently low; and when the
economy is sufficiently open for high values of
is sufficiently low; and when the
economy is sufficiently open for high values of ![]() .21 It is in this sense that an active
rule might be viewed as stabilizing. Local equilibrium determinacy,
however, does not guarantee global equilibrium determinacy. To see
this we pursue a global characterization of the equilibrium
dynamics in the following subsection.
.21 It is in this sense that an active
rule might be viewed as stabilizing. Local equilibrium determinacy,
however, does not guarantee global equilibrium determinacy. To see
this we pursue a global characterization of the equilibrium
dynamics in the following subsection.
3.2 The Global Determinacy of Equilibrium Analysis
To pursue the global equilibrium
analysis we rewrite equation (22) as the
forward mapping
![]() where
where
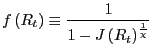
|
(27) |
and
![$\displaystyle J\left( R_{t}\right) \equiv\frac{R^{\ast}}{\left[ R^{\ast}-1\right] ^{\frac{R^{\ast}-1}{A}}}\frac{\left[ R_{t}-1\right] ^{\chi+\frac{R^{\ast} -1}{A}}}{R_{t}^{1+\chi}}.$](img284.gif)
|
(28) |
Then the global analysis corresponds to studying the global PFE
dynamics that satisfy
![]() given an
initial condition
given an
initial condition ![]() and subject to the
zero-lower-bound condition
and subject to the
zero-lower-bound condition
![]() for any
for any
![]() The types of cyclical and chaotic
dynamics we will be referring to are those conforming to the
following definitions.
The types of cyclical and chaotic
dynamics we will be referring to are those conforming to the
following definitions.
Definition
3 Period-n cycle. A value "
![]() " is a point of a period-n cycle if it is
a fixed point of the n-th iterate of the mapping
" is a point of a period-n cycle if it is
a fixed point of the n-th iterate of the mapping ![]() , i.e.
, i.e.
![]() but not a fixed
point of an iterate of any lower order. If "
but not a fixed
point of an iterate of any lower order. If " ![]() " is such, we call the sequence
" is such, we call the sequence
![]() a period-n cycle.
a period-n cycle.
Definition
4 Topological chaos. The mapping
![]() is topologically chaotic if there
exists a set " S" of uncountable many initial points, belonging
to its domain, such that no orbit that starts in " S" will
converge to one another or to any existing period orbit.
is topologically chaotic if there
exists a set " S" of uncountable many initial points, belonging
to its domain, such that no orbit that starts in " S" will
converge to one another or to any existing period orbit.
The global analysis requires a full characterization of
![]() in (27) not only
around its stationary solutions, like in the local analysis, but
over its entire domain. In this characterization it is useful to
take into account that a necessary condition for the existence of
cyclical dynamics in continuously differentiable maps is that the
mapping
in (27) not only
around its stationary solutions, like in the local analysis, but
over its entire domain. In this characterization it is useful to
take into account that a necessary condition for the existence of
cyclical dynamics in continuously differentiable maps is that the
mapping
![]() slopes negatively at
either one of the two steady states.22 Lemma 6 in the Appendix investigates the properties of
the mapping
slopes negatively at
either one of the two steady states.22 Lemma 6 in the Appendix investigates the properties of
the mapping ![]() showing that they depend critically
on
showing that they depend critically
on ![]() . Here we only provide a big picture of
the analysis. First of all, the Lemma specifies conditions under
which
. Here we only provide a big picture of
the analysis. First of all, the Lemma specifies conditions under
which
![]() satisfies the
zero-lower-bound requirement. Second, it makes use of the following
conditions
satisfies the
zero-lower-bound requirement. Second, it makes use of the following
conditions
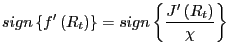 and
and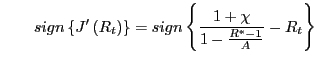
|
(29) |
which imply that for ![]() then
then
![]() is a
critical point of
is a
critical point of
![]() as long as
as long as ![]() . With these conditions the Lemma shows that the
mapping
. With these conditions the Lemma shows that the
mapping
![]() is always
single-peaked for
is always
single-peaked for ![]() whereas for
whereas for
![]() it is single-troughed only if
it is single-troughed only if
![]() .
.
Figure 1 displays a graphical representation of the cases where
the equilibrium mapping
![]() has a critical
point between the two steady states
has a critical
point between the two steady states![]() The right
panel considers the case of
The right
panel considers the case of ![]() and
and
![]() while the
left panel the case of
while the
left panel the case of ![]() In the left one,
In the left one,
![]() always satisfies the
equilibrium conditions for any
always satisfies the
equilibrium conditions for any
![]() and crosses
the 45 degree line twice at
and crosses
the 45 degree line twice at ![]() and
and
![]() (the two steady states).
Furthermore,
(the two steady states).
Furthermore,
![]() and there is a maximum at
and there is a maximum at
![]() In
the right panel, all equilibrium conditions are satisfied only
within a subset
In
the right panel, all equilibrium conditions are satisfied only
within a subset
![]() defined in Lemma 6. Within
that set,
defined in Lemma 6. Within
that set,
![]() crosses the 45 degree line
at
crosses the 45 degree line
at ![]() and
and
![]() as in the previous case,
but now
as in the previous case,
but now
![]() is a
minimum and
is a
minimum and
![]() These are clearly the cases in which we are interested, as they
imply a negative derivative of
These are clearly the cases in which we are interested, as they
imply a negative derivative of ![]() at either one
of the two steady states.
at either one
of the two steady states.
Figure 1
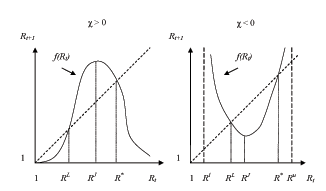
Figure 1: This Figure shows the mapping Rt+1 = f(Rt) for χ > 0, and χ < 0 but
![]() and Rt denotes the nominal interest rate. A formal characterization of this mapping is provided in Lemma 6 in the Appendix.
and Rt denotes the nominal interest rate. A formal characterization of this mapping is provided in Lemma 6 in the Appendix.
Figure 1 together with Lemma 6
suggest that depending on the sign of ![]() cycles
may appear around either the active steady state or the passive
steady state. Hence we proceed to look for flip bifurcation
thresholds for
cycles
may appear around either the active steady state or the passive
steady state. Hence we proceed to look for flip bifurcation
thresholds for ![]() i.e. critical values of
i.e. critical values of
![]() that determine a change in the
stability properties of the steady state where the map
that determine a change in the
stability properties of the steady state where the map ![]()
![]() is negatively sloped. If
the steady state is stable, any equilibrium orbit, that starts in a
map invariant set centered around this state, will asymptotically
converge to the steady state itself, monotonically or spirally.
Thus equilibrium cycles are impossible. On the contrary if the
steady state is unstable, such orbit will keep oscillating within
the map invariant set and either it converge to a stable
is negatively sloped. If
the steady state is stable, any equilibrium orbit, that starts in a
map invariant set centered around this state, will asymptotically
converge to the steady state itself, monotonically or spirally.
Thus equilibrium cycles are impossible. On the contrary if the
steady state is unstable, such orbit will keep oscillating within
the map invariant set and either it converge to a stable
![]() -period cycle, or not converge at all
displaying aperiodic but bounded dynamics (chaotic equilibrium
paths). We first consider the case of
-period cycle, or not converge at all
displaying aperiodic but bounded dynamics (chaotic equilibrium
paths). We first consider the case of
![]() and show that endogenous cyclical dynamics of period 2 can occur
around the passive steady state.
and show that endogenous cyclical dynamics of period 2 can occur
around the passive steady state.
Lemma 2
Let
![]() and define the points
and define the points
![]() i.e. the image of
i.e. the image of ![]() (the critical point of
(the critical point of
![]() and
and
![]() i.e. the
inverse image of the high steady state. Consider
i.e. the
inverse image of the high steady state. Consider
![]() and
assume that
and
assume that
![]() 23 Then:
23 Then:
1.
and
2. the set
is invariant under the mapping
and attractive for any
where
3. period-2 cycles within
and centered around the passive steady state occur when
Proof. See Appendix.
For the case of
![]() endogenous cyclical dynamics of period 2 exist around the active
steady state, instead.
endogenous cyclical dynamics of period 2 exist around the active
steady state, instead.
Lemma 3
Let
![]() and define the points
and define the points
![]() i.e. the image of
i.e. the image of ![]() (the critical point of
(the critical point of
![]() and
and
![]() i.e. the
inverse image of the high steady state. Consider
i.e. the
inverse image of the high steady state. Consider
![]() and
assume
and
assume
![]() Then:
Then:
1.
and
2. the set
is invariant under the mapping
and attractive for any
where
3. period-2 cycles within
and centered around the active steady state occur when
Proof. See Appendix.
Similarly to the local determinacy analysis, the conditions for
endogenous cycles derived in terms of ![]() can be
easily translated into conditions described in terms of the degree
of openness
can be
easily translated into conditions described in terms of the degree
of openness ![]() and the risk aversion parameter
and the risk aversion parameter
![]() The next Proposition accomplishes
this goal.
The next Proposition accomplishes
this goal.
Proposition 3 Suppose that the government follows an active forward-looking rule.
1. Consider
and
in Definition 2 where
and
and assume that consumption and money are Edgeworth complements, i.e.
Then period-2 equilibrium cycles exist around the passive steady state if the economy is sufficiently open satisfying
where
is positive and strictly decreasing for
but constant and equal to zero for any
2. Consider
and
in Definition 2 where
and
and assume that consumption and money are Edgeworth substitutes, i.e.
Then period-2 equilibrium cycles exist around the active steady state if the economy is sufficiently open satisfying
where
is positive and strictly increasing for
but constant and equal to zero for any
Proof. See the Appendix.
Proposition 3 is one of
the main contributions of our paper. It states that at either
sufficiently low or sufficiently high risk aversion coefficients
(![]() ), forward looking rules are more
prone to induce endogenous cyclical dynamics the more open the
economy; while for
), forward looking rules are more
prone to induce endogenous cyclical dynamics the more open the
economy; while for ![]() sufficiently close to
1, but different from it, forward looking rules will lead to those
dynamics regardless of the degree of openness.24
sufficiently close to
1, but different from it, forward looking rules will lead to those
dynamics regardless of the degree of openness.24
The second point of this Proposition is also useful to make the
following interesting argument. The sufficient condition for the
existence of period-2 cycles when ![]() and the local determinacy condition stated in Point 1b) of
Proposition 2 are exactly the
same. This is a clear example of why local analysis can be
misleading. By log-linearizing around the steady state, local
analysis implicitly assumes that any path starting arbitrarily
close to it and diverging cannot be part of an equilibrium since it
will eventually explode and thus violate some transversality
condition. This is not the case here as the global analysis proves
that the true non-linear map features a bounded map-invariant and
attractive set around the active steady state. It is then possible
to have equilibrium paths that starting arbitrarily close to the
target steady state will converge to a stable deterministic
cycle.
and the local determinacy condition stated in Point 1b) of
Proposition 2 are exactly the
same. This is a clear example of why local analysis can be
misleading. By log-linearizing around the steady state, local
analysis implicitly assumes that any path starting arbitrarily
close to it and diverging cannot be part of an equilibrium since it
will eventually explode and thus violate some transversality
condition. This is not the case here as the global analysis proves
that the true non-linear map features a bounded map-invariant and
attractive set around the active steady state. It is then possible
to have equilibrium paths that starting arbitrarily close to the
target steady state will converge to a stable deterministic
cycle.
Given the functional form of
![]() in (27) it is very difficult to derive analytical
conditions for
in (27) it is very difficult to derive analytical
conditions for ![]() and
and ![]() under which forward-looking rules induce either cycles of period
higher than 2 or chaotic dynamics. Therefore in order to shed some
light on the role of both
under which forward-looking rules induce either cycles of period
higher than 2 or chaotic dynamics. Therefore in order to shed some
light on the role of both ![]() and
and
![]() in delivering these dynamics, as well
as to find some empirical confirmation of our analytical results,
we pursue a simple calibration-simulation exercise.
in delivering these dynamics, as well
as to find some empirical confirmation of our analytical results,
we pursue a simple calibration-simulation exercise.
Table 2: Parametrization
θN |
β |
π* |
R* |
1 - γ |
A/R* |
0.56 |
0.99 |
1.031¼ |
1.072¼ |
0.03 |
2.24 |
We set the time unit to be a quarter and use Canada as the
representative economy. From Mendoza (1995) we borrow the labor
income shares for the non-traded sector and set
![]() The steady-state inflation,
The steady-state inflation,
![]() and the steady state nominal
interest rate,
and the steady state nominal
interest rate, ![]() , are calculated as the
average of the CPI-inflation and the Central Bank discount rate
between 1983-2002. This yields
, are calculated as the
average of the CPI-inflation and the Central Bank discount rate
between 1983-2002. This yields
![]() and
and
![]() Then the
subjective discount rate is determined by
Then the
subjective discount rate is determined by
![]() We use the
estimate of Lubik and Schorfheide (2003) for the Canadian interest
rate response coefficient to inflation which corresponds to
We use the
estimate of Lubik and Schorfheide (2003) for the Canadian interest
rate response coefficient to inflation which corresponds to
![]() . Estimates for the
share of expenditures on real money balances,
. Estimates for the
share of expenditures on real money balances, ![]() , for Canada are not available. For the US, estimates
of this parameter vary from 0.0146 to 0.039 depending on the
specification of the utility function and method of estimation. We
set
, for Canada are not available. For the US, estimates
of this parameter vary from 0.0146 to 0.039 depending on the
specification of the utility function and method of estimation. We
set ![]() equal to 0.03 that is in line with
the estimates provided by previous works.25 Table 2 gathers the
parametrization.
equal to 0.03 that is in line with
the estimates provided by previous works.25 Table 2 gathers the
parametrization.
As in the analytical study, in the simulation exercise we vary
![]() and
and ![]() keeping
the remaining parameters as in Table 2
keeping
the remaining parameters as in Table 2![]() Nevertheless, an estimate of
Nevertheless, an estimate of ![]() for Canada
can be obtained from the average imports to GDP share during
1983-2002, yielding
for Canada
can be obtained from the average imports to GDP share during
1983-2002, yielding
![]() In contrast, obtaining an
estimate of
In contrast, obtaining an
estimate of ![]() is more difficult. As explained
before,
is more difficult. As explained
before, ![]() is related to the CRRA coefficient
is related to the CRRA coefficient
![]() through
through
![]() which
spans over a wide range. The RBC literature usually sets
which
spans over a wide range. The RBC literature usually sets
![]() . This value and
. This value and
![]() imply
imply
![]() Since the value of
Since the value of ![]() determines whether consumption and real money balances
are either Edgeworth substitutes or complements we will use
different values for the CRRA
determines whether consumption and real money balances
are either Edgeworth substitutes or complements we will use
different values for the CRRA
![]() . For instance, we let
. For instance, we let
![]() which in
tandem with
which in
tandem with
![]() leads to
leads to
![]() respectively
respectively![]()
Given
![]() which
corresponds to CRRA of
which
corresponds to CRRA of
![]() we
construct Figure 2. It presents the bifurcation (or orbit) diagrams
for the degree of openness
we
construct Figure 2. It presents the bifurcation (or orbit) diagrams
for the degree of openness ![]() The left
panel considers the case when money and consumption are complements
by setting
The left
panel considers the case when money and consumption are complements
by setting
![]() The right panel
corresponds to the case when they are substitutes as
The right panel
corresponds to the case when they are substitutes as
![]() With
With
![]() on the
horizontal axis and
on the
horizontal axis and ![]() on the vertical
axis, the solid lines in the diagram correspond to stable solutions
of period
on the vertical
axis, the solid lines in the diagram correspond to stable solutions
of period ![]() The left and right panels of the
figure show how by increasing
The left and right panels of the
figure show how by increasing ![]() an active
forward-looking rule can drive the economy into period-2 cycles,
period-4 cycles,...period-
an active
forward-looking rule can drive the economy into period-2 cycles,
period-4 cycles,...period-![]() cycles and
eventually chaotic dynamics. Starting from
cycles and
eventually chaotic dynamics. Starting from ![]() both panels show that for low degrees of openness the economy, that
is described by the mapping
both panels show that for low degrees of openness the economy, that
is described by the mapping
![]() in (27), always settles on a stable steady state
equilibrium after a long enough series of iterations. It settles on
the passive steady state,
in (27), always settles on a stable steady state
equilibrium after a long enough series of iterations. It settles on
the passive steady state, ![]() for
for
![]() and on the active steady
state,
and on the active steady
state, ![]() for
for
![]() . Once
. Once ![]() reaches some threshold a stable period-2 cycle
appears, as indicated by the first split into two branches in both
panels. As we increase
reaches some threshold a stable period-2 cycle
appears, as indicated by the first split into two branches in both
panels. As we increase ![]() further in both
panels, both branches split again yielding a period-4 stable cycle.
A cascade of further period doubling occurs as we keep increasing
further in both
panels, both branches split again yielding a period-4 stable cycle.
A cascade of further period doubling occurs as we keep increasing
![]() , yielding cycles of period-8,
period-16 and so on. Finally for sufficiently high
, yielding cycles of period-8,
period-16 and so on. Finally for sufficiently high ![]() values, the rule produces aperiodic chaotic dynamics,
i.e. the attractor of the map (27) changes from
a finite to an infinite set of points.
values, the rule produces aperiodic chaotic dynamics,
i.e. the attractor of the map (27) changes from
a finite to an infinite set of points.
Figure 2: Orbit-Bifurcation Diagrams
Forward-Looking Rules
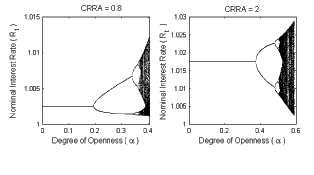
Figure 2: Orbit-bifurcation diagrams for the degree of openness, α. Rt denotes the nominal interest rate. The diagrams show the set of limit points as a function of α, under two different coefficients of risk aversion (CRRA)
![]() and
and
![]() , and under an active forward-looking rule. Depending on α, an active forward-looking rule may drive the economy into period-2 cycles, period-4 cycles, ... period-n cycles and even chaotic dynamics.
, and under an active forward-looking rule. Depending on α, an active forward-looking rule may drive the economy into period-2 cycles, period-4 cycles, ... period-n cycles and even chaotic dynamics.
From Figure 2 we also see that when consumption and money are complements then cyclical and chaotic dynamics occur around the passive steady state; whereas if they are substitutes then these dynamics appear around the target active steady state. Nevertheless for both cases, forward-looking rules are more prone to induce cycles and chaos the more open the economy.
In order to summarize and compare the results of the local and
global determinacy of equilibrium analyses we construct Figure 3.
It shows the combinations of the degree of openness and the risk
aversion parameter, ![]() and
and ![]() for which there is local and/or global
(in)determinacy. For
for which there is local and/or global
(in)determinacy. For
![]() and
and
![]() we plot two
threshold frontiers: the flip bifurcation frontier for period-2
cycles around the passive steady state,
we plot two
threshold frontiers: the flip bifurcation frontier for period-2
cycles around the passive steady state,
![]() and the frontier
and the frontier
![]() for both local
determinacy and period-2 cycles around the active steady state.
Regions featuring a locally unique equilibrium are labeled with a
"U", while those featuring locally multiple equilibria are
labeled with an "M". Clearly, "U" appears everywhere but
below the curve
for both local
determinacy and period-2 cycles around the active steady state.
Regions featuring a locally unique equilibrium are labeled with a
"U", while those featuring locally multiple equilibria are
labeled with an "M". Clearly, "U" appears everywhere but
below the curve
![]() implying that local
determinacy occurs for a wide range of
implying that local
determinacy occurs for a wide range of
![]() combinations.
In fact note how local determinacy coexists with global
indeterminacy.
combinations.
In fact note how local determinacy coexists with global
indeterminacy.
Figure 3
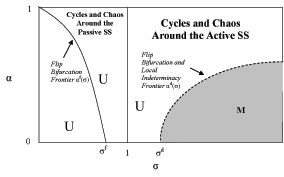
Figure 3: Equilibrium analysis for an active forward-looking interest rate rule. This figure shows a comparison between the local equilibrium analysis and the global equilibrium analysis as the degree of openness α and the coefficient of risk aversion σ vary. "M" stands for local multiple equilibria and "U" stands for a local unique equilibrium.
It is also interesting to compare our results with the ones in
Benhabib et al. (2002a). There are some important differences.
First our results derived in a money-in-the-utility-function set-up
point out that it is not necessary to assume a productive role for
money to obtain cyclical and chaotic equilibria. Second if
consumption and money are complements then it is possible to have
liquidity traps as in Benhabib et al. (2002a). But some of them may
be "non-monotonic" and converge to a cycle around an extremely
low interest rate steady state. On the contrary if consumption and
money are substitutes then cyclical and chaotic dynamics occur only
around the active steady state. Although this case is reminiscent
of the one in Benhabib et al. (2002a), it also presents a subtle
difference. In their closed economy model period-3 cycles always
occur only for sufficiently low ![]() while our
results show that they can basically appear for any
while our
results show that they can basically appear for any ![]() provided that there is enough degree of openness
in the economy. In this sense and with respect to closed economies,
open economies are more prone to display these cyclical
dynamics.
provided that there is enough degree of openness
in the economy. In this sense and with respect to closed economies,
open economies are more prone to display these cyclical
dynamics.
4 Stabilizing Endogenous Fluctuations
The rule's elasticity to inflation was
treated as given in the previous analysis, since the objective was
to compare the performance of a particular rule across economies
differing in trade openness and risk aversion. But this parameter
is actually a policy choice. Recognizing this poses the following
question. Given all the non-policy structural parameters, in
particular, given the degree of openness ![]() and the risk aversion parameter
and the risk aversion parameter ![]() what
elasticity to inflation will eliminate cyclical and chaotic
dynamics? To answer this question we can do the following simple
exercise.26
what
elasticity to inflation will eliminate cyclical and chaotic
dynamics? To answer this question we can do the following simple
exercise.26
The bifurcation thresholds that determine the existence of
cyclical dynamics can be implicitly represented by
![]() where
where ![]() depends on
depends on ![]()
![]()
![]() and
and
![]() and
and ![]() depends on
depends on ![]() and
and
![]() Then we can keep
Then we can keep
![]() fixed as well as
fixed as well as ![]()
![]()
![]() and
and
![]() (that determine
(that determine ![]() ) and use
) and use
![]() to solve for the bifurcation
thresholds in terms of the elasticity
to solve for the bifurcation
thresholds in terms of the elasticity
![]() subject to
subject to
![]() This will help us to find values
of
This will help us to find values
of ![]() that preclude the existence of
cycles.
that preclude the existence of
cycles.
It is simple to show that, for the case of ![]() there cannot exist cycles when27
there cannot exist cycles when27
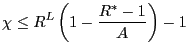
|
(30) |
and for the case of ![]() when
when
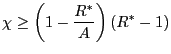
|
(31) |
Let's consider the case of ![]() We notice
that if the interest rate target is set such that
We notice
that if the interest rate target is set such that
![]() then inequality
(31) always holds for any active interest rate
rule. If instead,
then inequality
(31) always holds for any active interest rate
rule. If instead,
![]() then inequality
(31) is equivalent to
then inequality
(31) is equivalent to
![]() ,
which means that cycles are ruled out if the interest rate rule is
not too active. To illustrate this we use the calibration in Table
2 and set
,
which means that cycles are ruled out if the interest rate rule is
not too active. To illustrate this we use the calibration in Table
2 and set
![]() and CRRA
and CRRA ![]() (or
equivalently
(or
equivalently
![]() Under this parametrization
Under this parametrization
![]() and the right panel of Figure 2
suggests that there are period-2 cycles around the active steady
state. In order to rule out them the elasticity to inflation should
be below 1.35.
and the right panel of Figure 2
suggests that there are period-2 cycles around the active steady
state. In order to rule out them the elasticity to inflation should
be below 1.35.
In the case of ![]() , inequality
(30) can be written as
, inequality
(30) can be written as
![]() for
for
![]() First of all we notice that, since in equilibrium
First of all we notice that, since in equilibrium ![]() , then the last inequality always holds when
, then the last inequality always holds when
![]() , i.e.
, i.e.
![]() Given the definition of
elasticity, the latter can also be written as
Given the definition of
elasticity, the latter can also be written as
![]() where
where
![]() Hence a sufficiently active rule satisfying
Hence a sufficiently active rule satisfying
![]() does not allow for
equilibrium cycles. Nevertheless, even if we had
does not allow for
equilibrium cycles. Nevertheless, even if we had
![]() still
still
![]() could
hold. From the implicit definition of
could
hold. From the implicit definition of ![]() in
equation (23) and the related proof in
Proposition 1, the last inequality is
equivalent to
in
equation (23) and the related proof in
Proposition 1, the last inequality is
equivalent to
![$ \frac{1}{1-\Upsilon }\left[ \frac{R^{\ast}-1}{1-\Upsilon}\left( \chi+\Upsilon\right) \right] ^{\Upsilon}\geq\frac{R^{\ast}}{1+\chi}$](img504.gif) , which depends solely on
, which depends solely on ![]()
![]() and
and ![]() This inequality defines
implicitly a threshold
This inequality defines
implicitly a threshold ![]() below which cycles
are ruled out. Summarizing when
below which cycles
are ruled out. Summarizing when ![]() then rules
with elasticities
then rules
with elasticities ![]() that satisfy either
that satisfy either
![]() or
or
![]() will preclude the existence
of cyclical dynamics. For instance, using the calibration in Table
2 and setting
will preclude the existence
of cyclical dynamics. For instance, using the calibration in Table
2 and setting
![]() and CRRA
and CRRA![]() (or
equivalently
(or
equivalently
![]() , we know that the left panel of
Figure 2 suggests that there are chaotic dynamics around the
passive steady state. But for this parametrization we obtain
, we know that the left panel of
Figure 2 suggests that there are chaotic dynamics around the
passive steady state. But for this parametrization we obtain
![]() and
and
![]() Thus these complex dynamics
can be ruled out as long as the elasticity to inflation is either
Thus these complex dynamics
can be ruled out as long as the elasticity to inflation is either
![]() or
or ![]()
According to these results, the Taylor principle
![]() can be
still a viable policy recommendation for equilibrium determinacy,
even from a global equilibrium dynamics perspective. But there is
an additional requirement: an upper bound on the rule's elasticity
to inflation.28
can be
still a viable policy recommendation for equilibrium determinacy,
even from a global equilibrium dynamics perspective. But there is
an additional requirement: an upper bound on the rule's elasticity
to inflation.28
5 Distribution Costs and Imperfect Exchange Rate Pass-Through
The previous results were derived assuming that the Law of One Price held at the consumption level for traded goods and normalizing their foreign price to one. This in turn implied that there was a perfect exchange rate pass-through into import prices. In this Section we relax this assumption by introducing non-traded distribution costs which in turn implies imperfect exchange rate pass-through into import prices. Our goal is to understand how this can affect the previous global results of Section 3.
We follow Burnstein, Neves and Rebelo (2003) by assuming that
the traded good needs to be combined with some non-traded
distribution services before it is consumed. In order to consume
one unit of the traded good it is required ![]() units of the non-traded good. Let
units of the non-traded good. Let
![]() and
and ![]() be the prices in the domestic currency of the
small open economy that producers of traded goods receive and that
consumers pay, respectively. Hence the consumer price of the traded
good can be written as
be the prices in the domestic currency of the
small open economy that producers of traded goods receive and that
consumers pay, respectively. Hence the consumer price of the traded
good can be written as
| (32) |
To simplify the analysis we assume that the Law of One Price holds
for traded goods at the production level and normalize the foreign
price of the traded good to one (
![]() ). Thus
). Thus
![]()
The presence of distribution services leads to imperfect
exchange rate pass-through into import prices. To see this we
combine (32),
![]() and
and
![]() to obtain
to obtain
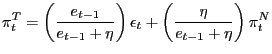
where
![]()
![]() and
and
![]() correspond to
the (gross) inflation of import prices, the (gross) nominal
depreciation rate and the (gross) non-traded inflation
respectively. Clearly if
correspond to
the (gross) inflation of import prices, the (gross) nominal
depreciation rate and the (gross) non-traded inflation
respectively. Clearly if ![]() then there is perfect
pass-through of the nominal depreciation rate into the inflation of
import prices and it is measured by
then there is perfect
pass-through of the nominal depreciation rate into the inflation of
import prices and it is measured by
![]() This
is the case that we already studied. But if
This
is the case that we already studied. But if ![]() then we obtain imperfect exchange rate pass-through measured by
then we obtain imperfect exchange rate pass-through measured by
![]() As the parameter of distribution costs,
As the parameter of distribution costs, ![]() ,
increases then the degree of exchange rate pass-through decreases.
,
increases then the degree of exchange rate pass-through decreases.
In order to pursue a determinacy of equilibrium analysis we
proceed as before. We obtain a reduced non-linear form of the model
that describes the dynamics of this economy. Nevertheless in
contrast to the case of perfect exchange rate pass-through it is
not possible to derive explicitly a difference equation similar to
(22) that depends exclusively on the nominal
interest rate ![]() . Under imperfect exchange rate
pass-through the dynamics of the economy are determined by the
system
. Under imperfect exchange rate
pass-through the dynamics of the economy are determined by the
system
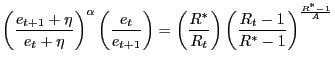
![$\displaystyle \left( \frac{e_{t}+\eta}{e_{t+1}+\eta}\right) ^{\left[ \alpha (1-\sigma)+\sigma\right] }\left( \frac{(1-\alpha)e_{t+1}+\eta} {(1-\alpha)e_{t}+\eta}\right) ^{\sigma}\left( \frac{e_{t+1}}{e_{t}}\right) ^{\left( 1+\frac{\sigma\theta_{N}}{1-\theta_{N}}\right) }=\left[ \left( \frac{R_{t+1}-1}{R_{t+1}}\right) \left( \frac{R_{t}}{R_{t}-1}\right) \right] ^{(1-\gamma)(1-\sigma)}. $](img540.gif)
Since it is not possible to derive analytical results we rely on
numerical simulations. The objective of the simulations is to
assess the impact of varying the distribution costs parameter
![]() (and therefore the degree of exchange
rate pass-through) on the previous results about cyclical and
chaotic dynamics. To do so we use the parametrization of Table 2
and construct Figure 4.
(and therefore the degree of exchange
rate pass-through) on the previous results about cyclical and
chaotic dynamics. To do so we use the parametrization of Table 2
and construct Figure 4.
Figure 4: Orbit-Bifurcation Diagrams
Forward-Looking Rules
Distribution Costs - Degree of Exchange Rate Pass-Through
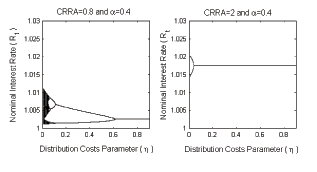
Figure 4: Orbit-bifurcation diagrams for the distribution costs parameter (η). Rt denotes the nominal interest rate. The diagrams show the set of limit points as a function of η, under two different sets of values of the degree of openness and the CRRA, (
![]() , α) = (0.8, 0.4) and (
, α) = (0.8, 0.4) and (
![]() , α) = (2, 0.4), and under an active forward-looking rule. Depending on η which is related to the degree of exchange rate pass-through, an active forward-looking rule may lead the economy into cyclical and chaotic dynamics.
, α) = (2, 0.4), and under an active forward-looking rule. Depending on η which is related to the degree of exchange rate pass-through, an active forward-looking rule may lead the economy into cyclical and chaotic dynamics.
We use two pairs of values for the degree of openness and the
CRRA (that depends on ![]() . The first pair sets
. The first pair sets
![]() and CRRA=0.8. According to the
left panel of Figure 2 for theses values there are chaotic dynamics
around the passive steady state. The second pair sets
and CRRA=0.8. According to the
left panel of Figure 2 for theses values there are chaotic dynamics
around the passive steady state. The second pair sets
![]() and CRRA=2. For these values the
right panel of Figure 2 suggests that there are period-2 cycles
around the active steady state. In the context of the present
discussion these results associated with the selected pairs
correspond to perfect exchange rate pass-through or
and CRRA=2. For these values the
right panel of Figure 2 suggests that there are period-2 cycles
around the active steady state. In the context of the present
discussion these results associated with the selected pairs
correspond to perfect exchange rate pass-through or ![]() Increasing
Increasing ![]() , or in other words
decreasing the degree of exchange rate pass-through, has a
non-trivial impact on these results as can be confirmed by Figure
4. Consider the left panel first, where
, or in other words
decreasing the degree of exchange rate pass-through, has a
non-trivial impact on these results as can be confirmed by Figure
4. Consider the left panel first, where
![]() and CRRA=0.8. Starting from
and CRRA=0.8. Starting from
![]() as
as ![]() increases (as
the degree of exchange rate pass-through declines) then the economy
moves from displaying chaotic dynamics into displaying periodic
cyclical dynamics. As
increases (as
the degree of exchange rate pass-through declines) then the economy
moves from displaying chaotic dynamics into displaying periodic
cyclical dynamics. As ![]() continues increasing the
period of cycles decrease. Beyond
continues increasing the
period of cycles decrease. Beyond
![]() cycles disappear and the only
fixed point that subsists corresponds to the passive steady state.
On the other hand, the right panel of Figure 4 shows the results
for
cycles disappear and the only
fixed point that subsists corresponds to the passive steady state.
On the other hand, the right panel of Figure 4 shows the results
for
![]() and CRRA=2. For
and CRRA=2. For ![]() the economy presents period-2 cycles around the active
steady state as mentioned before. However as
the economy presents period-2 cycles around the active
steady state as mentioned before. However as ![]() increases (as the degree of exchange rate pass-through
declines) cycles also disappear and the only attractor that
subsists is the active steady state.
increases (as the degree of exchange rate pass-through
declines) cycles also disappear and the only attractor that
subsists is the active steady state.
The results of this analysis can be summarized in the following Proposition.
Proposition 4 Forward-looking rules are more prone to induce cyclical and chaotic dynamics the higher the degree of exchange rate pass-through.
6 Sensitivity Analysis
Throughout the whole paper, the analysis was pursued under the following assumptions: 1) international complete financial markets, 2) the measure of inflation in the rule was the CPI-inflation, 3) a forward-looking rule and 4) real money balances entered into utility via what Carlstrom and Fuerst (2001) call a "cash-when-I'm-done" timing. In this section, we study the consequences of relaxing these assumptions. To simplify the analysis we still assume perfect exchange rate pass-through. We will show that our previous global findings of Section 3 hold even if we consider incomplete financial markets or if we introduce a forward-looking rule that responds to a different measure of inflation such as the non-traded inflation. That is, the degree of openness still plays an important role for the existence of cyclical and chaotic dynamics.
We also argue that cyclical and chaotic dynamics are less likely to occur under backward-looking rules while they can still appear under contemporaneous rules depending on the degrees of trade openness and risk aversion. And finally we prove that the alternative timing for real money balances, known as the "Cash-in-Advance" timing, affects the previously derived bifurcation thresholds, but does not preclude the existence of cyclical and chaotic dynamics.
6.1 Incomplete Markets
The assumption about complete markets
is not essential for the results derived in Section 3 about
cyclical and chaotic dynamics. Assuming incomplete markets leads to
the same global dynamics results. To see this assume that the agent
is blessed with perfect foresight and has access to an
international bond ![]() and a domestic bond
and a domestic bond
![]() issued by the government
issued by the government![]() The former pays a constant international interest rate,
The former pays a constant international interest rate, ![]() and the latter pays an interest rate,
and the latter pays an interest rate, ![]() Using this and the assumptions in the Subsection 2.1
we can rewrite the agent's budget constraint as
Using this and the assumptions in the Subsection 2.1
we can rewrite the agent's budget constraint as
The agent chooses the sequences
![]()
![]()
![]()
![]()
![]()
![]()
![]() in order to maximize
(1) subject to (2)
and (3), the previously mentioned budget
constraint and corresponding transversality conditions, given
in order to maximize
(1) subject to (2)
and (3), the previously mentioned budget
constraint and corresponding transversality conditions, given
![]()
![]() and
and ![]() and the
time paths of
and the
time paths of ![]() ,
,
![]() ,
,
![]()
![]() and
and
![]() The first order conditions of this
problem for
The first order conditions of this
problem for ![]() and
and ![]() correspond to
correspond to
| (33) |
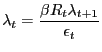
|
(34) |
whereas the conditions for
![]() can be
written as (11)-(14).
can be
written as (11)-(14).
As is common in the small open economy literature, we assume
![]() , which implies by (33) that
, which implies by (33) that
![]() This in turn
means that there is a unit root in the system of equations that
describe the dynamics of the economy. This prevents us from using
(log)linearization techniques in order to pursue a meaningful local
determinacy of equilibrium analysis. Hence we cannot derive local
results similar to the ones in the Subsection 3.1.
This in turn
means that there is a unit root in the system of equations that
describe the dynamics of the economy. This prevents us from using
(log)linearization techniques in order to pursue a meaningful local
determinacy of equilibrium analysis. Hence we cannot derive local
results similar to the ones in the Subsection 3.1.
But this does not change the previous results from the global
determinacy of equilibrium analysis, since the global dynamics are
still governed by (22). To see this use
![]() and (34) to obtain
and (34) to obtain
![]() which is identical
to (19). This condition together with
which is identical
to (19). This condition together with
![]() (5), (7), (11)-(14), and market clearing
conditions can be used to derive an identical equation to (20) which in tandem with a forward-looking rule
allows us to find an identical difference equation to (22). Then the cyclical and chaotic dynamics results
that we derived before still hold under incomplete markets.
(5), (7), (11)-(14), and market clearing
conditions can be used to derive an identical equation to (20) which in tandem with a forward-looking rule
allows us to find an identical difference equation to (22). Then the cyclical and chaotic dynamics results
that we derived before still hold under incomplete markets.
Nevertheless, introducing incomplete markets has an interesting
consequence for the behavior of the current account. To explore
this, recall that indeterminacy of the nominal interest rate in our
model implies real indeterminacy because of the non-separability in
the utility function between consumption and money. That
is![]() one can obtain all the remaining real
endogenous variables as a functions of
one can obtain all the remaining real
endogenous variables as a functions of ![]() . In
particular
. In
particular
![]() ,
,
![]() and
and
![]() Using these and the
definition of the current account
Using these and the
definition of the current account
we can deduce that cycles of the nominal interest rate may cause cycles of the accumulation of foreign bonds and therefore cycles of the current account.
6.2 Choosing A Different Measure of Inflation: The Core Inflation
In the specification of the rule, the
government can react to a measure of inflation different from the
CPI-inflation. For instance it can respond to the core-inflation
which can be defined as either the inflation of the traded goods or
the inflation of the non-traded goods. These two cases can be
considered as extreme cases of cases of a rule that reacts to the
full-inflation
![]() when the government picks the weight
when the government picks the weight
![]() 29 In
the former case it picks
29 In
the former case it picks ![]() whereas in the
latter case it chooses
whereas in the
latter case it chooses ![]()
To analyze these cases we derive a difference equation similar
to (22) where the only difference is that
the parameter ![]() is substituted by
is substituted by
![$\displaystyle \chi^{f}\equiv\frac{(\sigma-1)(1-\omega)(1-\gamma)(1-\theta_{N})} {\sigma\lbrack\theta_{N}+\alpha(1-\theta_{N})]+\left( 1-\alpha\right) (1-\theta_{N})}. $](img598.gif)
Using this difference equation and setting sequentially
![]() and
and ![]() in
in
![]() we obtain the following. Cyclical
and chaotic dynamics are not present under a rule that reacts to
the future traded inflation,
we obtain the following. Cyclical
and chaotic dynamics are not present under a rule that reacts to
the future traded inflation,
![]() (
(![]() ;
only liquidity traps are possible in this case. Nevertheless by
reacting to the future non-traded inflation
;
only liquidity traps are possible in this case. Nevertheless by
reacting to the future non-traded inflation
![]() forward-looking rules can
still induce cycles and their existence can depend on the degree of
openness of the economy.
forward-looking rules can
still induce cycles and their existence can depend on the degree of
openness of the economy.
To illustrate this point we rely on simulations and using the
parametrization in Table 2 we construct Figure 5. It presents the
orbit-diagram for a forward-looking rule that reacts exclusively to
the non-traded inflation where the relative risk aversion
coefficient CRRA is
![]() (or equivalently
(or equivalently
![]() From this figure it is clear
that for low degrees of openness (
From this figure it is clear
that for low degrees of openness (![]() ), the
previously mentioned rule leads the economy to the active steady
state. But as the degree of openness increases the same rule can
induce period-2 cycles in the economy. Hence the appearance of
these cycles depend on the degree of openness
), the
previously mentioned rule leads the economy to the active steady
state. But as the degree of openness increases the same rule can
induce period-2 cycles in the economy. Hence the appearance of
these cycles depend on the degree of openness![]()
Figure 5: Responding to Non-Traded Inflation (ω = 0)
CRRA = 1.5
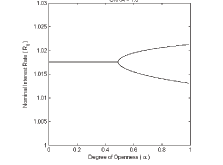
Figure 5: Orbit-bifurcation diagram for the degree of openness, α. Rt denotes the nominal interest rate. The diagram shows the set of limit points as a function of α, when the coefficient of relative risk aversion (CRRA)
![]() = 1.5 and when the active forward-looking rule responds exclusively to the non-traded inflation. Depending on α this rule can induce cyclical dynamics in the economy.
= 1.5 and when the active forward-looking rule responds exclusively to the non-traded inflation. Depending on α this rule can induce cyclical dynamics in the economy.
6.3 Contemporaneous and Backward-Looking Rules
In this subsection we consider varying the timing of the rule. We will study contemporaneous and backward-looking rules that still respond to the CPI inflation.
6.3.1Contemporaneous Rules
Motivated by the recent estimations by
Lubik and Schorfheide (2003) for the United kingdom, Canada,
Australia and New Zealand, we study the determinacy of equilibrium
for rules that respond to current CPI inflation:
![]() with
with
![]() and
and ![]() Under these rules the equilibrium dynamics are
described by
Under these rules the equilibrium dynamics are
described by
![$\displaystyle \left[ \frac{R_{t+1}-1}{R_{t+1}}\right] ^{\chi}\left[ \frac{R^{\ast} -1}{R_{t+1}-1}\right] ^{\frac{R^{\ast}-1}{A}}=\left[ \frac{R_{t}-1}{R_{t} }\right] ^{\chi}\frac{R^{\ast}}{R_{t}}$](img612.gif)
|
(35) |
where ![]() defined in (21)
depends on
defined in (21)
depends on ![]() and
and ![]() An
explicit representation for either the forward or the backward
dynamics of (35) is not available in
this case. Although it is feasible to derive some analytical
results as before, for reasons of space, we only present some
numerical simulations. These are sufficient to make the point that
the degree of openness still affects the appearance of complex
dynamics.30
An
explicit representation for either the forward or the backward
dynamics of (35) is not available in
this case. Although it is feasible to derive some analytical
results as before, for reasons of space, we only present some
numerical simulations. These are sufficient to make the point that
the degree of openness still affects the appearance of complex
dynamics.30
In addition in the subsequent analysis we will focus on characterizing the existence of cycles of period 2 and 3 because of the following reasons. By Sarkovskii (1964)'s Theorem the existence of period-2 cycles is a necessary (but not a sufficient) condition for the existence of cycles of any higher order, while the existence of period-3 cycles implies the existence of cycles of every possible period. Furthermore, by Li and Yorke (1975), if a map possesses a period-3 cycle then it also features topologically chaotic trajectories.31
Using the parametrization of Table 2 we construct Figure 6. This
Figure presents some qualitative properties of the global dynamics
of the model for contemporaneous rules for different degrees of
openness while setting
![]() (when consumption and money are
Edgeworth substitutes)
(when consumption and money are
Edgeworth substitutes)![]() Each row of panels in
Figure 6 contains plots of the map
Each row of panels in
Figure 6 contains plots of the map
![]() implicitly
defined in the difference equation (35), its second iterate
implicitly
defined in the difference equation (35), its second iterate
![]() and its third iterate
and its third iterate
![]() respectively, for a
given degree of openness
respectively, for a
given degree of openness ![]() .
.
Figure 6: Active Contemporaneous Rules
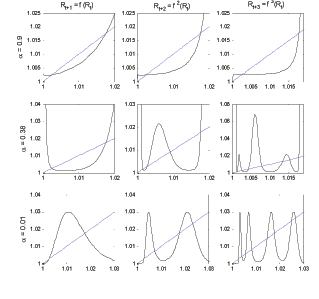
Figure 6: This graph shows the first, the second and the third iterates of the implicit mapping Rt+1 = f(Rt) defined in (35) for different degrees of openness of the economy (α). From the figure it is possible to infer that depending on α, two-period cycles and three period cycles around the active and the passive steady states may arise.
Going from the bottom to the top row we increase openness by
considering
![]() . In all the panels
the straight line corresponds to the 45
. In all the panels
the straight line corresponds to the 45![]() degree
line
degree
line![]() The first result to notice is that for
The first result to notice is that for
![]() namely an almost
closed and moderately open economy respectively, the second and
third iterates,
namely an almost
closed and moderately open economy respectively, the second and
third iterates,
![]() and
and
![]() have fixed points
different from the steady state values
have fixed points
different from the steady state values ![]() and
and
![]() , implying the existence of cycles of
period-2 and 3. Then by the Sarkovskii's (1964) Theorem and the Li
and Yorke's (1975) Theorem,
, implying the existence of cycles of
period-2 and 3. Then by the Sarkovskii's (1964) Theorem and the Li
and Yorke's (1975) Theorem, ![]() features
cycles of any order, as well as aperiodic cyclical dynamics
(chaos). But there is an important difference between the dynamics
for
features
cycles of any order, as well as aperiodic cyclical dynamics
(chaos). But there is an important difference between the dynamics
for
![]() and those for
and those for
![]() . In the former case, cycles and
chaos appear around the active steady state, while in the latter
they occur around the passive steady state. Finally, for very open
economies (
. In the former case, cycles and
chaos appear around the active steady state, while in the latter
they occur around the passive steady state. Finally, for very open
economies (
![]() ), no cycles and chaotic dynamics
appear at all. The monotonicity of the map
), no cycles and chaotic dynamics
appear at all. The monotonicity of the map ![]() implies that liquidity traps are the only type of global
equilibrium multiplicity in this case.
implies that liquidity traps are the only type of global
equilibrium multiplicity in this case.
Given
![]() (or equivalently
(or equivalently
![]() it is possible to
find the exact numerical values of the
it is possible to
find the exact numerical values of the ![]() thresholds triggering a qualitative switch in dynamics. We find
that period-2 cycles appear around the active steady state when
thresholds triggering a qualitative switch in dynamics. We find
that period-2 cycles appear around the active steady state when
![]() and period-3 cycles
occur around the active steady state when
and period-3 cycles
occur around the active steady state when
![]() Pushing
Pushing ![]() up, period-2 cycles appear around the passive steady
state for
up, period-2 cycles appear around the passive steady
state for
![]() , whereas period-3
cycles (and therefore chaos) exist for
, whereas period-3
cycles (and therefore chaos) exist for
![]() . Finally for
. Finally for
![]() only liquidity traps
exist.
only liquidity traps
exist.
Overall the existence of cyclical and chaotic dynamics is robust
to changing the timing of the rule from forward-looking to
contemporaneous. The key difference is that now endogenous global
fluctuations can only occur for the case when consumption and money
are Edgeworth substitutes. Nevertheless for this case conclusions
are quite different in the following sense: very open economies
seem to be the less prone to endogenous cycles. Furthermore the
qualitative changes induced by a variation in the degree of
openness, for a fixed ![]() can be even more
dramatic under a contemporaneous rule since they might even trigger
a switch from one steady state to the other as the focus of
fluctuations.
can be even more
dramatic under a contemporaneous rule since they might even trigger
a switch from one steady state to the other as the focus of
fluctuations.
The following proposition summarizes these results.
Proposition 5 Suppose the government follows an active contemporaneous rule. Then:
1. if consumption and money are Edgeworth complements, i.e.
, there cannot be equilibrium cycles of any periodicity for any degree of openness
2. if consumption and money are Edgeworth substitutes, i.e.
(a) there cannot be equilibrium cycles of any periodicity if the economy is sufficiently open;
(b) cyclical and chaotic dynamics occur around the passive steady state for intermediate degrees of openness;
(c) cyclical and chaotic dynamics appear around the active steady state occur if the economy is sufficiently closed.
6.3.2 Backward-Looking Rules
We conclude the analysis of different
timings for the rule by studying backward-looking rules defined as
![]() with
with
![]() . This
specification in tandem with (20) conform a
system of two first-order difference equations that can be used to
pursue the global determinacy of equilibrium analysis. Since it is
very difficult to derive analytical results, we rely on simulations
in order to assess whether for different values of
. This
specification in tandem with (20) conform a
system of two first-order difference equations that can be used to
pursue the global determinacy of equilibrium analysis. Since it is
very difficult to derive analytical results, we rely on simulations
in order to assess whether for different values of ![]() and
and ![]() the system presents cycles
or chaos. The simulation results show that these types of dynamics
are not present regardless of the degree of openness
the system presents cycles
or chaos. The simulation results show that these types of dynamics
are not present regardless of the degree of openness ![]() when
when
![]() (or
equivalently when the CRRA coefficient
(or
equivalently when the CRRA coefficient
![]() ). The
interest rate converges to either the active or the passive
steady-state.
). The
interest rate converges to either the active or the passive
steady-state.
Nevertheless this is not sufficient evidence to conclude that backward-looking rules will preclude the existence of cyclical dynamics. In fact in Airaudo and Zanna (2005) we show that these rules may still lead to these dynamics in open economies that face nominal price rigidities.
6.4 Real money balances timing and cycles
In our set-up the real money balances that provide transaction services, and therefore utility, are those left after leaving the goods market. This is the traditional timing adopted in money-in-utility-function models. Carlstrom and Fuerst (2001) call this timing the "Cash-When-I'm-Done" (CWID) timing and argue that is counterintuitive.32 They suggest an alternative timing: the standard "Cash-In-Advance" (CIA) timing, where the real money balances entering the agent's utility are those left after leaving the bond market but before entering the goods market.
In this Subsection we construct a simple example showing that the results presented in Section 3 for active forward-looking rules are not driven by the CWID timing. Following Woodford (2003), we introduce a CIA timing by altering the budget constraint of the representative agent as follows
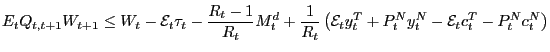
while leaving unchanged all the remaining elements of the model presented in Section 2. By the same analysis we pursued in that section we obtain the non-linear reduced form
![$\displaystyle \left[ \frac{R_{t+1}-1}{R_{t+1}^{\Psi}}\right] ^{\chi}=\frac{R^{\ast} }{\left( R^{\ast}-1\right) ^{\frac{R^{\ast}-1}{A}}}\frac{\left( R_{t}-1\right) }{R_{t}^{1+\Psi\chi}}^{\chi+\frac{R^{\ast}-1}{A} }$](img656.gif)
|
(36) |
that describes the equilibrium dynamics of the economy under
forward-looking rules. The difference between (36) and its CWID counterpart (22) is the coefficient
![]() , which is positive for
, which is positive for
![]() and negative for
and negative for
![]() .33 The structural
parameter
.33 The structural
parameter ![]() is unchanged and still defined by
(21). The following Proposition suggests that
under the CIA timing, cycles are still possible and their existence
depends on the degree of openness
is unchanged and still defined by
(21). The following Proposition suggests that
under the CIA timing, cycles are still possible and their existence
depends on the degree of openness ![]() Nevertheless this different timing implies different bifurcation
thresholds for
Nevertheless this different timing implies different bifurcation
thresholds for ![]() from the ones derived in
Section 3.
from the ones derived in
Section 3.
Proposition
6 Consider the definition of ![]() in (21) and define
in (21) and define
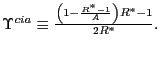 Suppose
Suppose
![]() and that the government
follows an active forward-looking rule. If consumption and money
are Edgeworth substitutes, i.e.
and that the government
follows an active forward-looking rule. If consumption and money
are Edgeworth substitutes, i.e. ![]() , then
there exist period-2 cycles when
, then
there exist period-2 cycles when
![]() a condition that is
satisfied for sufficiently open economies, i.e
a condition that is
satisfied for sufficiently open economies, i.e
![]() .
.
Proof. See the Appendix. ![]()
7 Conclusions
In this paper we show that active interest rate rules can have perverse effects in a small open economy by inducing endogenous cyclical and chaotic dynamics. Our main contribution is to show that the existence of these dynamics depends on some particular features of open economies such as the degree of openness (measured by the share of tradable goods in consumers' preferences) and the degree of exchange rate pass-through (implied by the presence of non-traded distribution services). In our model a forward-looking rule that responds to CPI-inflation is more prone to lead to cyclical and chaotic dynamics the more open the economy and the higher the degree of exchange rate pass-through. If consumption and money are Edgeworth complements these dynamics occur around an extremely low interest rate steady state. On the other hand if consumption and money are substitutes these dynamics appear around the interest rate target set by the monetary authority.
We also discuss how the government could design a forward-looking rule in order to rule out complex dynamics, while still preserving the Taylor principle at the target steady state. The analysis implies a "modified Taylor principle": for a given interest rate target, the interest rate rule responsiveness to CPI inflation should satisfy some lower (upper) bound depending on whether consumption and real balances are Edgeworth complements or substitutes.
The existence of cyclical and chaotic dynamics and their dependence on the degree of openness are in general robust to different inflation timings in the rule (forward-looking versus contemporaneous rules), to the use of alternative measures of inflation (CPI versus Core inflation), as well as to changes in the timing of real money balances in liquidity services ("Cash-When-I'm-Done" timing versus "Cash-In-Advance" timing).
Clearly the analytical tractability of our model comes from one of its limitations: we are considering a flexible price and perfectly competitive economy. Without any sort of nominal rigidity, monetary policy does not have any role for active stabilization. Nevertheless as we show in Airaudo and Zanna (2005), the existence of cycles induced by interest rate rules and the important role played by some open economy features in the characterization of the equilibrium are not precluded by introducing sticky-prices.
This paper leaves open some interesting research questions. First as standard in the literature, we model the government as an automaton that always follows the same monetary rule. That is, it implements an active interest rate rule with a given parametrization, independently from the evolution of inflation itself and other monetary variables. One might consider the possibility of an endogenous monetary policy regime switching featuring a change in the monetary instrument (from an interest rate rule to money growth and viceversa) or a change in the responsiveness to inflation triggered by an endogenous variable monitored by the central bank.
Finally we have implicitly assumed that agents in the economy can coordinate their actions and learn the particular equilibria that we studied. Relaxing this assumption and introducing learning as in Evans and Honkapojha (2001) can be another avenue to explore in future research.
Appendix A
This first part of the appendix presents the statements of some Lemmata and their proofs as well as some of the proofs of the Lemmata stated in the paper. The second part presents the proofs of the main Propositions of the paper.
A.1 Lemmata and Proofs
A.1.1 Proof of Lemma 1
Proof. Let
![]() be the slope of (26) and define
be the slope of (26) and define
![]() Since
Since ![]() is a non-predetermined variable, the
equilibrium is locally unique if and only if
is a non-predetermined variable, the
equilibrium is locally unique if and only if
![]() , i.e.
the linearized mapping (26) is explosive and
therefore the target steady state is the unique bounded PFE.
, i.e.
the linearized mapping (26) is explosive and
therefore the target steady state is the unique bounded PFE.
First suppose that ![]() . This together with
Assumption 0 (
. This together with
Assumption 0 (
![]() and the zero lower
bound
and the zero lower
bound ![]() implies that
implies that
![]() Hence
Hence![]() the
equilibrium is locally unique. Now suppose that
the
equilibrium is locally unique. Now suppose that ![]() This in tandem with Assumption 0 and the zero
lower bound leads to
This in tandem with Assumption 0 and the zero
lower bound leads to
![]() meaning that in order to have
a unique equilibrium we need
meaning that in order to have
a unique equilibrium we need
![]() Simple algebra shows that
Simple algebra shows that
![]() implies
implies
![]() . Then the map is explosive
and the equilibrium is unique.
. Then the map is explosive
and the equilibrium is unique.
On the other hand, it is simple to show that if
![]() then
then
![]() . Hence the map is
non-explosive, i.e. from any initial condition
. Hence the map is
non-explosive, i.e. from any initial condition ![]() off the target steady state
off the target steady state ![]() ,
,
![]() will eventually converge to
will eventually converge to
![]() . This continuity of PFE paths is
the source of local multiple equilibria.
. This continuity of PFE paths is
the source of local multiple equilibria. ![]()
A.1.2 Proof of Lemma 2
Proof. From point 2 of Lemma 6, the assumption
![]() implies
that the mapping
implies
that the mapping
![]() satisfies the
zero-lower-bound condition only for
satisfies the
zero-lower-bound condition only for
![]() Moreover within
Moreover within
![]() the mapping
the mapping
![]() looks like an inverted
logistic mapping with a minimum at
looks like an inverted
logistic mapping with a minimum at ![]() and
and
![]() (see the right panel
of Figure 1). With these properties of
(see the right panel
of Figure 1). With these properties of
![]() the proof of Point 1
follows from the fact that
the proof of Point 1
follows from the fact that
![]() for any
for any
![]() .
.
To prove Point 2, take any
![]() whose first
iterate is
whose first
iterate is
![$ R_{t+1}=\left[ 1-J\left( R_{t}\right) ^{\frac {1}{\chi\left( \alpha,\sigma\right) }}\right] ^{-1}.$](img704.gif) If
If
![]() then
then
![]() since
since
![]() for any
for any
![]() moreover
moreover
![]() if
if
![]() Similarly, if
Similarly, if
![]() then
then
![]() since
since
![]() for
for
![]() as well as
as well as
![]() Hence we have shown that for any
Hence we have shown that for any
![]()
![]() Then
Then
![]() The attractive property of the set is straightforward to show and
therefore omitted.
The attractive property of the set is straightforward to show and
therefore omitted.
Point 3 is based on the fact that a sufficient condition for the
existence of period-2 cycles is
![]() which implies an
unstable passive steady state. To show this we define an auxiliary
function
which implies an
unstable passive steady state. To show this we define an auxiliary
function
![]() such that period-2 cycles are the zeros of
such that period-2 cycles are the zeros of ![]() The assumption
The assumption
![]() requires a distinction between the two cases: a)
requires a distinction between the two cases: a)
![]() and
b)
and
b)
![]()
In case a), the map-invariant set is
![]() Clearly
Clearly
![]() and
and
![]() Also,
by the chain rule,
Also,
by the chain rule,
![]() with
with ![]() being either one of the two steady
states. But then
being either one of the two steady
states. But then
![]() implies that
implies that
![]() . What
is ambiguous is the sign of
. What
is ambiguous is the sign of
![]() If
If
![]() then the period-2
cycle is obviously
then the period-2
cycle is obviously
![]() If
If
![]() by continuity of
by continuity of
![]() on
on
![]() , then
there exists a point
, then
there exists a point
![]() such
that
such
that
![]() Since the set
Since the set
![]() is map
invariant the second point of the period-2 cycle belongs to the
same set.34 If instead
is map
invariant the second point of the period-2 cycle belongs to the
same set.34 If instead
![]() nothing
guarantees that the function
nothing
guarantees that the function ![]() has zeros other
than the two steady states. A sufficient condition for having
another zero is that
has zeros other
than the two steady states. A sufficient condition for having
another zero is that
![]() i.e.
i.e.
![]() If
this holds, then
If
this holds, then
![]() at some point between
at some point between
![]() and
and ![]() From the
definition of
From the
definition of ![]() it is simple to show that
it is simple to show that
![]() is equivalent to
is equivalent to
![]() where
where
![]() Since we are considering
Since we are considering ![]()
![]() in case a) period-2
cycles around the passive steady state occur when
in case a) period-2
cycles around the passive steady state occur when
![]() In case
b) all conditions of case a) hold, although in this
case
In case
b) all conditions of case a) hold, although in this
case
![]() is always true.
Therefore by a similar argument there are always period-2 cycles.
is always true.
Therefore by a similar argument there are always period-2 cycles.
![]()
A.1.3 Proof of Lemma 3
Proof. Let
![]() The restriction
The restriction
![]() implies, by Point 1 of Lemma 6, that the
mapping
implies, by Point 1 of Lemma 6, that the
mapping
![]() looks like a logistic map
with a maximum at
looks like a logistic map
with a maximum at ![]()
![]() and
and
![]() (see the left
panel of Figure 1).
(see the left
panel of Figure 1).
The proofs of Points 1 and 2 are similar to their counterparts in Lemma 2, so both are omitted.
Point 3 involves searching for a flip bifurcation at the active
steady state. Let's define an auxiliary function
![]() Period 2 cycles are then zeros of
Period 2 cycles are then zeros of
![]() The assumption
The assumption
![]() requires a distinction between the two cases:
requires a distinction between the two cases:
![]() and
and
![]()
If
![]() the
set invariant under mapping
the
set invariant under mapping ![]() is
is
![]() Clearly
Clearly
![]() and
and
![]() but
but
![]() If
If
![]() a period-2 cycle
is, by construction,
a period-2 cycle
is, by construction,
![]() If
If
![]() by continuity of
the function
by continuity of
the function
![]() there must exist a point
there must exist a point
![]() such
that
such
that
![]() As
As ![]() belongs to the map invariant set
belongs to the map invariant set
![]()
![]() as well: a period-2 cycle exists. If instead
as well: a period-2 cycle exists. If instead
![]() by continuity, a
sufficient condition for period-2 cycles is that
by continuity, a
sufficient condition for period-2 cycles is that
![]() i.e.
i.e.
![]() given that over these parametric ranges
given that over these parametric ranges
![]() always. Using the definition of
always. Using the definition of
![]() in (27) and by simple differentiation, this is in fact
equivalent to
in (27) and by simple differentiation, this is in fact
equivalent to
![]()
The case of
![]()
![]() is trivial. All the properties of the
previous case hold, but now
is trivial. All the properties of the
previous case hold, but now
![]() always. So by similar arguments, a period-2 cycle always exists.
always. So by similar arguments, a period-2 cycle always exists.
![]()
A.1.4 Lemma 4
Lemma
4 Keep ![]() and
and
![]() constant and let
constant and let
![]()
![]()
![]() and
and
![]() be defined as in (21), (24) and (25)
be defined as in (21), (24) and (25)![]() Consider any real number
Consider any real number
![]() and define a function
and define a function
![$ \alpha^{i}(\sigma)\equiv\frac{\left[ 1-\frac{\Upsilon^{i} }{\mu(\sigma)}\right] }{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min}}\right] }$](img801.gif) for
for ![]()
1. Over the domain
the function
satisfies the following properties:
(a) it is continuously differentiable, strictly increasing and strictly concave;
(b)
and
![$ \underset{\sigma\rightarrow+\infty}{lim}\alpha^{i}(\sigma)=\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min}}\right] ^{-1}\left[ 1-\frac{\Upsilon^{i} }{\chi_{\max}}\right] \in\left( 0,1\right) $](img806.gif)
(c)
for
where
2. For any given
if and only if
3. For
and
we have that
if and only if
Proof. First of all recall the definitions of
![]()
![]()
![]() and
and
![]() in (21),
(24) and (25>). Then take any
real number
in (21),
(24) and (25>). Then take any
real number
![]() and any
and any ![]() If we solve explicitly the
equation
If we solve explicitly the
equation
![]() with respect to
with respect to
![]() for a given
for a given ![]() after some simple algebra, the solution is a function
after some simple algebra, the solution is a function
![$ \alpha^{i}(\sigma)\equiv\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min}}\right] ^{-1}\left[ 1-\frac{\Upsilon^{i}}{\mu(\sigma)}\right] .$](img827.gif) We first prove point 1 for
We first prove point 1 for
![]()
The statement that
![]() is continuously
differentiable, strictly increasing and strictly concave over the
domain
is continuously
differentiable, strictly increasing and strictly concave over the
domain
![]() follows from its
definition,
follows from its
definition,
![]()
![]()
![]() and the fact
that for
and the fact
that for ![]() the function
the function
![]() defined in (25) satisfies the following.
defined in (25) satisfies the following.
![]() it is
continuously differentiable, strictly increasing and strictly
concave with respect to
it is
continuously differentiable, strictly increasing and strictly
concave with respect to ![]() and satisfies
and satisfies
![]() and
and
![]() This proves Point 1(a).
This proves Point 1(a).
Given that
![]() and
and
![]() then for
then for
![]() and
and
![]() we have
that
we have
that
![]() and
and
![$ \underset {\sigma\rightarrow+\infty}{lim}\alpha^{i}(\sigma)=\left[ 1-\frac{\Upsilon ^{i}}{\chi_{\min}}\right] ^{-1}\left[ 1-\frac{\Upsilon^{i}}{\chi_{\max} }\right] $](img845.gif) . The assumption of
. The assumption of
![]() together with
together with
![]() guarantees
that
guarantees
that
![$ \left[ 1-\frac{\Upsilon^{i}}{\chi_{\min}}\right] ^{-1}\left[ 1-\frac{\Upsilon^{i} }{\chi_{\max}}\right] \in\left( 0,1\right) .$](img848.gif) This proves Point 1(b).
This proves Point 1(b).
Point 1(c) follows from solving
![]() with respect to
with respect to
![]() and obtaining
and obtaining
![$ \sigma^{i}=\frac{\left[ 1-\frac{\Upsilon^{i}} {\chi_{\min}}\right] }{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\max}}\right] }.$](img851.gif) As
As
![]() and
and
![]() it must
be that
it must
be that
![]() Using the definition of
Using the definition of
![]() and the previous two points 1(a)
and 1(b) then the rest of 1(c) follows.
and the previous two points 1(a)
and 1(b) then the rest of 1(c) follows.
Since for ![]() and
and
![]() the function
the function
![]()
![]() is
continuously differentiable, strictly decreasing with respect to
is
continuously differentiable, strictly decreasing with respect to
![]() and satisfies
and satisfies
![]() then
it follows that
then
it follows that
![]() if
and only if
if
and only if
![]() This
proves Point 2.
This
proves Point 2.
To prove Point 3 we proceed as follows. From point 2 of the
present Lemma, we know that
![]() if and only
if
if and only
if
![]() From point
1(c) of the same Lemma we have also that
From point
1(c) of the same Lemma we have also that
![]() for
for
![]() Since
Since
![]() then
then
![]() for any
for any
![]() when
when
![]() as in this case
as in this case
![]() while
while
![]() only for
only for
![]() if
if
![]() If we write this
compactly, we have that
If we write this
compactly, we have that
![]() if and only
if
if and only
if
![]()
![]()
A.1.5 Lemma 5
Lemma
5 Keep ![]() and
and
![]() constant and let
constant and let
![]()
![]()
![]() and
and
![]() be defined as in (21), (24) and (25).
Consider any real number
be defined as in (21), (24) and (25).
Consider any real number
![]() and define a function
and define a function
![$ \alpha^{i}(\sigma)\equiv\frac{\left[ 1-\frac{\Upsilon^{i} }{\mu(\sigma)}\right] }{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min}}\right] }$](img885.gif) for
for
![]()
1. Over the domain
the function
satisfies the following properties:
(a) it is continuously differentiable
strictly decreasing and strictly concave;
(b)
and
;
(c)
for
where
2. For any given
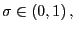
if and only if
3. For
and
we have that
if and only if
Proof. The proof is omitted since it is very similar
to the proof of Lemma 4. ![]()
A.1.6 Lemma 6
Lemma
6 Define the scalars
![]()
![]() and
and
![]() Recall the definition of
Recall the definition of ![]() in (27)-(28) for
in (27)-(28) for
![]()
1. Suppose that
Then a)
and it is continuously differentiable; b)
has a global maximum at
with
; c)
d)
always, while
depending on
2. Suppose that
Let
and
be the solutions to
with
and
Then a)
and it is continuously differentiable ; b) within
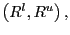
has a unique minimum at
c)
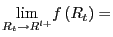
; d)
always, while
depending on
with
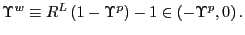
Proof. In order to simplify the notation in the proof
and the statements, we define the following scalars: ![]()
![]()
![]()
![]() and
and
![]() From the zero-lower-bound restriction and the assumption of an
active rule, it is clear that
From the zero-lower-bound restriction and the assumption of an
active rule, it is clear that
![]() and
and
![]()
Recall the definition of
![]() in (27). From (28),
in (27). From (28),
![]() is always positive and
continuously differentiable for any
is always positive and
continuously differentiable for any
![]() and any
and any
![]() . Furthermore, since
. Furthermore, since
![]() and
and ![]()
![]()
![]() (as
(as
![]() then
then
| (37) |
and
![$\displaystyle \underset{R_{t}\rightarrow1^{+}}{\lim}J\left( R_{t}\right) =\left\{ \begin{array}[c]{c} 0\text{ \ \ \ if }\chi>-\Upsilon^{p}\\ +\infty\text{ if }\chi<-\Upsilon^{p} \end{array} \right.$](img952.gif)
|
(38) |
From (29) we also observe that
![]() if and only if
if and only if
![]() as well as
that
as well as
that
![]() if
and only if
if
and only if
![]() As a
consequence of these inequalities, when
As a
consequence of these inequalities, when
![]() we have
we have
![]() and
therefore
and
therefore
![]() for any
for any
![]()
Next we prove point 1. Suppose that ![]() . As
. As
![]() then from (29) and (37) we infer that
then from (29) and (37) we infer that
![]() is single-peaked at
is single-peaked at
![]() with
with
![]() An inspection of (27) shows that for
An inspection of (27) shows that for
![]()
![]() and it is
continuous over the domain
and it is
continuous over the domain
![]() if and only if
if and only if
![]() But
But
![]() and with a
maximum at
and with a
maximum at ![]() when
when ![]() Then since
Then since
![]() holds, we have
that
holds, we have
that
![]() for any
for any
![]() .35
This in turn implies that
.35
This in turn implies that
![]() Furthermore,
Furthermore,
![]() is continuously
differentiable since
is continuously
differentiable since
![]() is continuously
differentiable as well. This proves Point 1(a). Point 1(b) follows
from (29) together with
is continuously
differentiable as well. This proves Point 1(a). Point 1(b) follows
from (29) together with ![]() ; while Point 1(c) is obtained from the definition
of
; while Point 1(c) is obtained from the definition
of
![]() in (27) and (37)-(38)
in (27) and (37)-(38)![]() The complete
characterization of
The complete
characterization of
![]() for
for ![]() is achieved by noticing that being continuous and
crossing the 45 degree line twice within its domain (see
Proposition 1) it must necessarily be that
is achieved by noticing that being continuous and
crossing the 45 degree line twice within its domain (see
Proposition 1) it must necessarily be that
![]() . But then
. But then
![]() must cross the 45 degree
line at the low steady state
must cross the 45 degree
line at the low steady state ![]() with a slope
bigger than 1. That is
with a slope
bigger than 1. That is
![]() 36
Nevertheless the sign of
36
Nevertheless the sign of
![]() remains
ambiguous because
remains
ambiguous because
![]() and
and
![]() . Simple algebra
shows that this last inequality is equivalent to
. Simple algebra
shows that this last inequality is equivalent to
![]() This proves
Point 1(d).
This proves
Point 1(d).
Suppose that
![]() then
the function
then
the function
![]() has the same properties we
derived at the beginning of the proof for the case of
has the same properties we
derived at the beginning of the proof for the case of ![]() Thus
Thus
![]() is single-peaked at
is single-peaked at
![]() with
with
![]() . However the fact that
. However the fact that
![]() (see Proposition 1) combined with
(see Proposition 1) combined with ![]() imply
that although
imply
that although
![]() we
now have that
we
now have that
![]() As
As
![]() is a global maximum,
is a global maximum,
![]() as
well
as
well![]() These properties together with
These properties together with
![]() imply that there exist two values,
imply that there exist two values, ![]() and
and
![]() , such that
, such that
![]() where
where
![]() and
and
![]() 37 Given the
definition (27) of
37 Given the
definition (27) of ![]()
![]() we can see that it is not
well-defined at both
we can see that it is not
well-defined at both ![]() and
and ![]() . Moreover, as
. Moreover, as
![]() and
and
![]() for any
for any
![]() and any
and any
![]() then any
initial condition
then any
initial condition
![]() would violate the zero-lower-bound condition and therefore cannot
be part of a PFE of our model. The range
would violate the zero-lower-bound condition and therefore cannot
be part of a PFE of our model. The range
![]() is
therefore necessary for an iterated sequence to be supported as an
equilibrium. Within the interval
is
therefore necessary for an iterated sequence to be supported as an
equilibrium. Within the interval
![]() ,
,
![]() satisfies
satisfies
![]() and is continuously
differentiable
and is continuously
differentiable![]() implying
implying
![]() for any
for any ![]() It follows that
It follows that
![]() and
and
![]() is continuously
differentiable for any
is continuously
differentiable for any
![]() . This
proves Point 2(a). Point 2(b) follows from (29) together with
. This
proves Point 2(a). Point 2(b) follows from (29) together with ![]() , while
Point 2(c) is obtained from the definition of
, while
Point 2(c) is obtained from the definition of
![]() in (27) and (37)-(38)
in (27) and (37)-(38)![]() Since
Since
![]() crosses the 45 degree
line at both
crosses the 45 degree
line at both ![]() and
and ![]() (see
Proposition 1) it must be that
(see
Proposition 1) it must be that
![]() Nevertheless the sign of
Nevertheless the sign of
![]() remains
ambiguous as
remains
ambiguous as
![]() and
and
![]() Simple algebra
shows that this last inequality is equivalent to
Simple algebra
shows that this last inequality is equivalent to
![]() Finally
Observe that an active rule implies
Finally
Observe that an active rule implies
![]() and that, from Assumption 3,
and that, from Assumption 3,
![]() Then
Then
![]() such that
such that
![]() Using
this and
Using
this and
![]() we conclude that
we conclude that
![]() This completes
the proof for Point 2(d).
This completes
the proof for Point 2(d).
For
![]() it can be shown
that the mapping
it can be shown
that the mapping
![]() features no critical
point and it is strictly increasing.
features no critical
point and it is strictly increasing. ![]()
A.2 Proofs of the Propositions
A.2.1 Proof of Proposition 1
Proof. Let the left hand side and the right hand side
of equation (23>) be denoted as
![]() and
and
![]() respectively. Since
respectively. Since
![]() we have that
we have that
It is simple to verify that given
![]() and
and ![]() then
then
![]() is linear in
is linear in ![]() with slope
with slope
![]() and
and
![]() slopes upwards as well,
slopes upwards as well,
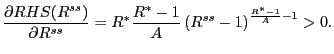
Moreover
![]()
![]() and
and ![]() are sufficient conditions for
are sufficient conditions for
![]() to be strictly concave. That is
to be strictly concave. That is
![]()
Given that
![]() is continuous and linear and
is continuous and linear and
![]() is continuous and strictly
concave for any
is continuous and strictly
concave for any ![]() a sufficient condition
for a second solution
a sufficient condition
for a second solution
![]() to
exist is that the slope of the
to
exist is that the slope of the
![]() at
at ![]() is
smaller than the slope of
is
smaller than the slope of
![]() at
at ![]() In
other words,
In
other words,
![]() or equivalently
or equivalently
![]() Moreover since
Moreover since
![]() is strictly concave then no
other solution to (23) different from
is strictly concave then no
other solution to (23) different from
![]() and
and ![]() exists.
exists.
![]()
A.2.2 Proof of Proposition 2
Proof. Recall the definition of
![]() in
(21). For
in
(21). For
![]() and
and
![]() we have that
we have that
![]()
![]() Then Point
1(a) follows from point 1 of Lemma 1 and the fact that
Then Point
1(a) follows from point 1 of Lemma 1 and the fact that
![]() if
if
![]() and
and
![]()
Next we prove point 1(b). For
![]() and
and
![]() we have that
we have that
![]()
![]() . Define
. Define
![]() The proof of point 1(a) of Lemma 1 makes clear that
The proof of point 1(a) of Lemma 1 makes clear that
![]() is the threshold value of
is the threshold value of
![]() that differentiates between active
rules leading to either a unique equilibrium or multiple
equilibria. Since we are interested in how the pair
that differentiates between active
rules leading to either a unique equilibrium or multiple
equilibria. Since we are interested in how the pair
![]() affects local
equilibrium determinacy, we look for values of
affects local
equilibrium determinacy, we look for values of ![]() that, for given
that, for given ![]() solve
solve
![]() Simple
algebra shows that this solution is
Simple
algebra shows that this solution is
![$ \alpha^{d}(\sigma)=\left[ 1-\frac{\Upsilon^{d}}{\chi_{\min}}\right] ^{-1}\left[ 1-\frac{\Upsilon^{d}}{\mu(\sigma)}\right] ,$](img1102.gif) a function relating
a function relating ![]() to
to ![]() Since Assumption 1 holds, that is
Since Assumption 1 holds, that is
![]() then we can use
Lemma 4 to deduce that the function
then we can use
Lemma 4 to deduce that the function
![]() is equivalent to the
function
is equivalent to the
function
![]() defined in that Lemma,
for
defined in that Lemma,
for
![]() Therefore,
Therefore,
![]() inherits all the
properties of
inherits all the
properties of
![]() .
.
From Point 3 of Lemma 4, we can
conclude that for any ![]() then
then
![]() with
with
![]() This is a necessary and sufficient condition for
This is a necessary and sufficient condition for
![]() to hold.
Which, by Lemma 1, implies local
equilibrium determinacy.
to hold.
Which, by Lemma 1, implies local
equilibrium determinacy.
To prove point 2 we follow the same steps of proving 1(b) taking
into account that from point 2 of Lemma 4 we can deduce that
![]() and
and
![]() leads to
leads to
![]() Which by
point 2 of Lemma 1 implies
multiple equilibria.
Which by
point 2 of Lemma 1 implies
multiple equilibria. ![]()
A.2.3 Proof of Proposition 3
Proof. The proof of Point 1 combines the results of Point 3 in Lemma 2 with Lemma 5.
Define
![]()
![]() and
and
![]() From Point 3 of Lemma 2,
the flip bifurcation threshold is
From Point 3 of Lemma 2,
the flip bifurcation threshold is
![]() Since
Since ![]() is a function of
is a function of ![]() and
and
![]() then this threshold can be expressed
in the
then this threshold can be expressed
in the
![]() -space as the
solution to
-space as the
solution to
![]() with respect
to
with respect
to ![]() for any arbitrary
for any arbitrary
![]() . Simple algebra
shows that the solution is a function
. Simple algebra
shows that the solution is a function
![$ \alpha^{f}(\sigma)\equiv\left[ 1-\frac{\Upsilon^{f}}{\chi_{\min} }\right] ^{-1}\left[ 1-\frac{\Upsilon^{f}}{\mu(\sigma)}\right] .$](img1130.gif) Observe that an active rule implies
Observe that an active rule implies
![]() and that, from Assumption 3,
and that, from Assumption 3,
![]() Then
Then
![]() which implies that
which implies that
![]() Using
this and
Using
this and
![]() we conclude that
we conclude that
![]() From this and
Assumption 2 we can see that
From this and
Assumption 2 we can see that
![]() satisfying the assumptions in Lemma 5. Hence
satisfying the assumptions in Lemma 5. Hence
![]() shares all the
properties of the function
shares all the
properties of the function
![]() for
for
![]() stated in that
Lemma
stated in that
Lemma![]() By Point 3 of Lemma 5, for an arbitrary
By Point 3 of Lemma 5, for an arbitrary
![]() the flip
bifurcation condition
the flip
bifurcation condition
![]() in Lemma
2 is therefore equivalent
to
in Lemma
2 is therefore equivalent
to
![]() where
where
![]() . From an application of Point 1 of Lemma 5 we can also see that such minimum degree of
openness,
. From an application of Point 1 of Lemma 5 we can also see that such minimum degree of
openness,
![]() , is positive and
decreasing in
, is positive and
decreasing in ![]() for
for
![]() but
constant and equal to zero for
but
constant and equal to zero for
![]()
The proof of Point 2 is omitted since it is very similar to the
proof of Point 1. But it uses the fact that ![]() and Point 3 of Lemma 3 together with Lemma 4 instead.
and Point 3 of Lemma 3 together with Lemma 4 instead. ![]()
A.2.4 Proof of Proposition 6
Proof. We provide a sketch of the proof. Let
![]() and
and
![]() be the left and the
right hand sides of (36) respectively.
First of all notice that for
be the left and the
right hand sides of (36) respectively.
First of all notice that for ![]() we
have
we
have ![]() and
and ![]() . To
simplify the notation let
. To
simplify the notation let
![]()
Then consider the function
![]() Since
Since ![]() it is simple to show that
it is simple to show that
![]() and
and
![]() Furthermore simple algebra shows that
Furthermore simple algebra shows that
![]() is strictly increasing
over the entire domain
is strictly increasing
over the entire domain
![]() . But then
. But then
![]() is also globally
invertible such that there exist a well defined function
is also globally
invertible such that there exist a well defined function
![]() describing the forward equilibrium dynamics.
describing the forward equilibrium dynamics.
Then consider the function
![]() Since
Since
![]() for any
for any
![]() then
then
![]() while:
while:
![\begin{displaymath} \underset{R_{t}\rightarrow+\infty}{\lim}J\left( R_{t}\right) =\left\{ \begin{array}[c]{c} +\infty\text{ if }\Gamma>\left( 1-\frac{R^{\ast}-1}{A}\right) \ 0\text{ \ \ \ if }\Gamma<\left( 1-\frac{R^{\ast}-1}{A}\right) \end{array}\right. \end{displaymath}](img1170.gif)
Using the definition of ![]() let's consider the
case of
let's consider the
case of
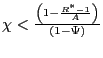 such that
such that
![]() It is possible to show that
It is possible to show that
![]() has a critical point at
has a critical point at
![]() Therefore if
Therefore if
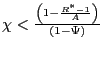 the function
the function
![]() is single-peaked. This in
turn in tandem with the fact that
is single-peaked. This in
turn in tandem with the fact that
![]() is strictly increasing
over the entire domain
is strictly increasing
over the entire domain
![]() implies that the
equilibrium mapping
implies that the
equilibrium mapping
![]() looks like a logistic
map. Then if cycles exist they have to be centered around the
active steady state. To show this we can use a similar argument to
the one developed in Lemma 3. That is a sufficient condition
for period-2 cycles to exist is
looks like a logistic
map. Then if cycles exist they have to be centered around the
active steady state. To show this we can use a similar argument to
the one developed in Lemma 3. That is a sufficient condition
for period-2 cycles to exist is
![]() By
computing this derivative at the target steady state and after some
algebra this condition is equivalent to
By
computing this derivative at the target steady state and after some
algebra this condition is equivalent to
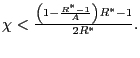 Given
Given ![]() it is possible to show that
there exists
it is possible to show that
there exists
![]() such that
such that
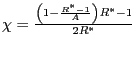 and that for
and that for
![]()
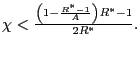
References
Airaudo, M. and L.F. Zanna, (2005), "Stabilizing Taylor Rules in Open Economies: Finding the 'Right' Measure of Inflation for the Rules," Manuscript, Board of Governors of the Federal Reserve System.
Alstadheim, R. and D. Henderson, (2004), "Price-level Determinacy, Lower Bounds on the Nominal Interest Rate, and Liquidity Traps," IFDP No. 795, Board of Governors of the Federal Reserve System.
Angeletos, M. (2002), "Fiscal Policy with Non-Contingent Debt and the Optimal Maturity Structure", Quarterly Journal of Economics, 117 (2).
Azariadis, C. (1993), Intertemporal Macroeconomics, Blackwell, Cambridge, Massachusetts.
Ball, L. (1999), " Policy Rules for Open Economies," in Monetary Policy Rules, edited by John B. Taylor, Chicago, National Bureau of Economic Research, 127-144.
Batini, N., P. Levine and J. Pearlman, (2004), "Indeterminacy with Inflation-Forecast-Based Rules in a Two-Bloc Model," IFDP No. 797, Board of Governors of the Federal Reserve System.
Benhabib, J., S. Schmitt-Grohé and M. Uribe (2001a), "Monetary Policy Rules and Multiple Equilibria," American Economic Review, 91, 167-184.
Benhabib, J., S. Schmitt-Grohé and M. Uribe (2001b), "The Perils of the Taylor Rules," Journal of Economic Theory, 96, 40-69.
Benhabib, J., S. Schmitt-Grohé and M. Uribe (2002a), "Chaotic Interest Rate Rules," American Economic Review Papers and Proceedings, 92, 72-78.
Benhabib, J., S. Schmitt-Grohé and M. Uribe (2002b), "Avoiding Liquidity Traps", Journal of Political Economy, 110, 3, 535-563.
Bernal, R. (2003), "Monetary Policy Rules in Practice: The Case of Colombia," Desarrollo y Sociedad, Universidad de Los Andes, 51, 37-53.
Bernanke, B. and M. Woodford, (1997). "Inflation Forecasts and Monetary Policy," Journal of Money, Credit and Banking, 29(4), 653-684.
Burnstein, A., Neves J. and S. Rebelo (2003), "Distribution Costs and Real Exchange Rate Dynamics," Journal of Monetary Economics, Forthcoming.
Boldrin, M., K. Nishimura, T. Shigoka and M. Yana (2001), "Chaotic Equilibrium Dynamics in Endogenous Growth Models", Journal of Economic Theory, 96, 97-132.
Campa, J. M. and L. Goldberg (2004), "Exchange Rate Pass-Through into Import Prices: A Macro or a Micro Phenomenon," NBER Working Paper No. 8934.
Carlstrom, C. and T. Fuerst (2001), "Timing and Real Indeterminacy in Monetary Models," Journal of Monetary Economics, 47, 285-298.
Clarida, J., J. Galí and M. Gertler (1998), "Monetary Policy Rules in Practice: Some International Evidence," European Economic Review, 42, 1033-1067.
Clarida, J., J. Galí and M. Gertler (2000), "Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory," Quarterly Journal of Economics, 115, 147-180.
Clarida, J., J. Galí and M. Gertler (2001), "Optimal Monetary Policy in Open vs Closed Economies: An Integrated Approach," American Economic Review, 91, 248-252.
Christiano, L. and M. Rostagno (2001), "Money Growth Monitoring and the Taylor Rule", NBER Working Paper 8539.
Corbo, V. (2000), "Monetary Policy in Latin America in the 90s," Working Papers, No. 78, Central Bank of Chile.
De Fiore, F.and L. Zheng (2003), " Does Trade Openness Matters for Aggregate Instability?," Manuscript, Emory University.
Evans, G, and S. Honkapohja (2001), Learning and Expectations in Macroeconomics, Princeton University Press, New Jersey.
Frankel, J., D. Parsley and S. Wei (2005), "Slow Passthrough Around the World: A New Import for Developing Countries?," NBER Working Paper 11199.
Fukuda, S. (1993), "The Emergence of Equilibrium Cycles in a Monetary Economy with a Separable Utility Function", Journal of Monetary Economics, 32, 321-334.
Fukuda, S. (1997), "The Role of Monetary Policy in Eliminating Nonconvergent Dynamic Paths", International Economic Review, 38, 249-261.
Galí, J. and T. Monacelli (2004), "Monetary Policy and Exchange Rate Volatility in a Small Open Economy," Manuscript, CREI, forthcoming Review of Economic Studies.
Holman, J. (1998), "GMM Estimation of a Money-in-the-Utility-Function Model: The Implications of Functional Forms," Journal of Money, Credit and Banking, 30(4), 679-698.
Kollmann, R. (2002), "Monetary Policy Rules in the Open Economy: Effects on Welfare and Business Cycles," Journal of Monetary Economics, 49(5), 989-1015.
Leeper, E. (1991), "Equilibria Under `Active' and `Passive' Monetary and Fiscal Policies," Journal of Monetary Economics, 27(1), 129-147
Li, T. and J. Yorke, (1975), "Period Three Implies Chaos," American Mathematical Monthly, 82, 985-992.
Linnemann, L. and L. Schabert (2002), "Monetary Policy, Exchange Rates and Real Indeterminacy," University of Cologne, Manuscript.
Lorenz, H. (1993), Nonlinear Dynamical Economics and Chaotic Motion, Springer-Verlag, New York.
Lubik, T and F. Schorfheide (2003), "Do Central Banks Target Exchange Rates? A Structural Investigation", Manuscript, University of Pennsylvania.
Matsuyama, K. (1991), "Endogenous Price Fluctuations in an Optimizing Model of a Monetary Economy", Econometrica, 59, 6, 1617-1631.
Mendoza, E. (1995), "The Terms of Trade, The Real Exchange rate and Economic Fluctuations," International Economic Review, 36, 101-137.
Obstfeld, M. and K. Rogoff (1983), "Speculative Hyperinflations in Maximizing Models: Can We Rule Them Out?", Journal of Political Economy, 91, 675-687.
Restrepo-Londono, J. (1999), "Monetary Rules in Colombia and Chile", Departamento Nacional de Planeacion, Colombia, Manuscript.
Sarkovskii, A. (1964), "Coexistence of Cycles of a Continuous Map of the Line Into Itself," Ukraine Math. Zhur., 16, 61-71.
Schmitt-Grohé, S. and M. Uribe (2003), "Closing Small Open Economy Models," Journal of International Economics, 59,137-139.
Svensson, L. E. O. (2000), "Open-economy Inflation Targeting," Journal of International Economics, 50, 155-184.
Taylor, J. B. (1993), "Discretion Versus Policy Rules in Practice," Carnegie-Rochester Conference Series on Public Policy, 39, 195-214.
Woodford, M. (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton,Princeton University Press.
Zanna, L. F. (2003), "Interest Rate Rules and Multiple Equilibria in the Small Open Economy", IFDP No. 785, Board of Governors of the Federal Reserve System.
Footnotes
* The authors would like to thank the following people for comments and suggestions: Gian-Italo Bischi, David Bowman, Chris Erceg, Jon Faust, Laura Gardini, Dale Henderson, Salvatore Nisticò, and the seminar participants at the Board of Governors, the LUISS University, the University of Urbino, the 2004 Meeting of the Society for Nonlinear Dynamics and Econometrics (SNDE), the 2004 MMF Group Symposium on Banking and Monetary Economics and the 2004 Latin American Meeting of the Econometric Society. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the view of the Institute of Economic Policy or the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
† Institute of Economic Policy I, Humboldt University, Spandauer Strasse 1, Berlin D-10178, Germany. Email: [email protected] Return to text
‡ Board of Governors of the Federal Reserve System, 20th Street and Constitution Avenue, NW, Washington, D.C., 20551. Phone: (202)452-2337. Fax: (202)736-5638. E-mail: [email protected]. Return to text
1. See Ball (1999), Clarida, Galí and Gertler (1998, 2001), Galí and Monacelli (2004), Kollman (2002), Lubik and Schorfheide (2003), and Svensson (2000), among others. Return to text
2. See Taylor (1993). Return to text
3. In this context a liquidity trap is understood as a decelerating inflation dynamics where the economy is headed to a situation of low and possibly negative inflation and low and possibly zero interest rates and in which monetary policy is ineffective to stop this process. Return to text
4. The existence of two stationary equilibria is a consequence of combining active interest rate rules with the zero lower bound on nominal interest rates as shown by Benhabib et al. (2001b). Return to text
5. See Alstadheim and Henderson (2004), Benhabib et al. (2002b) or Christiano and Rostagno (2001) for the liquidity traps case and Obstfelf and Rogoff (1983) for the inflationary paths case. Return to text
6. For two country models see Batini, Levine and Pearlman (2004) among others. Return to text
7. The case of ![]() corresponds to the case of separability among consumption and money
in the utility function. It implies no distortionary effects of
transaction money demand. It can be easily shown that no
equilibrium cycles occur in this case. Hence, we do not consider it
in the analysis. Return to text
corresponds to the case of separability among consumption and money
in the utility function. It implies no distortionary effects of
transaction money demand. It can be easily shown that no
equilibrium cycles occur in this case. Hence, we do not consider it
in the analysis. Return to text
8. We could consider a CES function for aggregate consumption (2) to emphasize the fact that the intratemporal elasticity of substitution between the two types of consumption can be different from one. However, this would not affect our conclusions on the role of openness, but simply prevent us from obtaining analytical results. Return to text
9. In Section 5 we will relax the assumption of the Law of One Price" at the consumption level by introducing non-traded distribution costs. This will allow us to model an imperfect degree of exchange rate pass-through into import prices. Return to text
10. See Angeletos (2002). Return to text
11. See Schmitt-Grohé and Uribe (2003). Return to text
12. In the sensitivity analysis presented in Section 6 we also study contemporaneous and backward-looking rules. Return to text
13. Cycles and chaos would also occur if the interest rate rule was a linear function of inflation. Return to text
14. This holds by the previous analysis
since
![]() Return to text
Return to text
15. This equation abstracts from possible effects that fiscal policies can have on the equilibrium dynamics of the economy. The reason is that we have assumed a Ricardian fiscal policy under which the intertemporal version of the government's budget constraint and its transversality condition will be always satisfied. Return to text
16. By indeterminacy we refer to a situation where one or more real variables are not pinned down by the model. We use the terms indeterminacy and multiple equlibria interchangeably. The same comment applies to determinacy and a unique equilibrium. Return to text
17. In fact, for any given ![]() by simply manipulating equations (5), (7), (11)- (14), (17), (19), and the market clearing
conditions for money and the non-traded good, we can obtain all the
remaining real endogenous variables. For instance the labor
allocated for the production of the non-traded good and the real
exchange rate can be expressed as functions of the gross interest
rate only,
by simply manipulating equations (5), (7), (11)- (14), (17), (19), and the market clearing
conditions for money and the non-traded good, we can obtain all the
remaining real endogenous variables. For instance the labor
allocated for the production of the non-traded good and the real
exchange rate can be expressed as functions of the gross interest
rate only,
![]() and
and
![]() , respectively,
whereas from the market clearing condition,
, respectively,
whereas from the market clearing condition,
![]() we obtain
we obtain
![]() Return to text
Return to text
18. ![]() also depends on
also depends on
![]() and
and
![]() . However we will not pursue any
bifurcation analysis with respect to these
parameters. Return to text
. However we will not pursue any
bifurcation analysis with respect to these
parameters. Return to text
19. Assumption 1 is necessary and
sufficient for the existence of ranges of ![]() and
and ![]() where local indeterminacy occurs, as
well as for the existence of a flip bifurcation frontier in the
case of
where local indeterminacy occurs, as
well as for the existence of a flip bifurcation frontier in the
case of ![]() . Assumption 2 allows monotonic
liquidity traps for low values of
. Assumption 2 allows monotonic
liquidity traps for low values of ![]() . It
could therefore be dropped without affecting the possibility of
cycles around the passive steady state. Assumption 3 - which
basically requires enough separation between the two steady states
- is useful in proving the existence of a flip bifurcation frontier
in the case of
. It
could therefore be dropped without affecting the possibility of
cycles around the passive steady state. Assumption 3 - which
basically requires enough separation between the two steady states
- is useful in proving the existence of a flip bifurcation frontier
in the case of ![]() Extensive algebra (not
reported here for reasons of space) shows that Assumption 3 holds
if, for a given target
Extensive algebra (not
reported here for reasons of space) shows that Assumption 3 holds
if, for a given target ![]() the rule is
sufficiently active. Return to
text
the rule is
sufficiently active. Return to
text
20. The calibration exercise that we
present below suggests that these assumptions are not unrealistic.
For given monetary policy parameters and for given ![]() both Assumptions 1 and 2 imply a minimum share of
real balances in utility. We can in fact rewrite Assumption 1 as
both Assumptions 1 and 2 imply a minimum share of
real balances in utility. We can in fact rewrite Assumption 1 as
![]() For the calibration used in Table 2, the right hand side of this
inequality is about 0.006, while we set
For the calibration used in Table 2, the right hand side of this
inequality is about 0.006, while we set
![]() consistently with the
literature. Similarly, Assumption 2 can be written as
consistently with the
literature. Similarly, Assumption 2 can be written as
![]() with the
right hand side equal to 0.007 in our calibration. Return to text
with the
right hand side equal to 0.007 in our calibration. Return to text
21. In fact this result is more general since a quick inspection of Proposition 2 suggests that if the the economy is very open, an active rule leads to a unique equilibrium regardless of the values of the other structural parameters. Return to text
22. See Lorenz (1993). Return to text
23. This assumption rules out explosive
paths for initial conditions between the two steady states. It is
similar in flavor to the one used by Boldrin et al. (2001) and
Matsuyama (1991). If
![]() there would
not be a non-trivial mapping-invariant set. This case displays a
different type of multiplicity. It can be shown that there exists a
set of points within the set
there would
not be a non-trivial mapping-invariant set. This case displays a
different type of multiplicity. It can be shown that there exists a
set of points within the set
![]() that
leave such a set after a finite number of iterations, and settle to
an exploding path diverging from the active steady state (see
Matsuyama, 1991). Return to text
that
leave such a set after a finite number of iterations, and settle to
an exploding path diverging from the active steady state (see
Matsuyama, 1991). Return to text
24. As mentioned before, the
discountinuity of the model with respect to ![]() corresponds to a utility function that is separable in money and
consumption. In this case it is possible to show that no cyclical
dynamics can occur. Return to
text
corresponds to a utility function that is separable in money and
consumption. In this case it is possible to show that no cyclical
dynamics can occur. Return to
text
25. 0.5 See Holman (1998) among others. Return to text
26. Assumptions 0-3 will not be violated by the following analysis. Return to text
27. The formal derivation is available upon request. Return to text
28. Note that although it is possible to rule out cyclical and chaotic dynamics, liquidity traps are still feasible. To eliminate them it is necessary to implement some of the fiscal-monetary regimes proposed by Benhabib et al. (2002a). Return to text
29. CPI inflation is clearly a specific
case of full inflation for
![]() Return to text
Return to text
30. The analytical results of this part of the paper are available upon request. Return to text
31. See Lorenz (1993) for a precise statement of these two theorems. Return to text
32. A discussion on money-in-utility timing and cycles is already present in the papers of Fukuda (1993, 1995), pointing out that, under money growth rules, non-separability between consumption and real balances is not a necessary condition for cycles to exist (as one might have conjectured from the previous works of Matsuyama (1991) and Obstfeld and Rogoff (1983)). Under CIA timing cycles occur even under full separability. Return to text
33. One could think of the CWID set up as
one where ![]() . Return to text
. Return to text
34. We could actually show that this
second point belong to the intervak
![]() meaning
that the equilibrium path jumps deterministically from the left to
the right neighborhood of the passive steady state. Return to text
meaning
that the equilibrium path jumps deterministically from the left to
the right neighborhood of the passive steady state. Return to text
35. Proving that
![]() involes some
algebra. It is available from us upon request. Return to text
involes some
algebra. It is available from us upon request. Return to text
36. Simple algebra also proves that
![]() Return to text
Return to text
37. This should be clear from drwaing the
function
![]() which is continous,
hump-shaped, with maximum bigger than 1 and limits equal to
zero. Return to text
which is continous,
hump-shaped, with maximum bigger than 1 and limits equal to
zero. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
![$ \sigma^{i}\equiv\frac{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min} }\right] }{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\max}}\right] }>1;$](img809.gif)
![$ \sigma^{i}\equiv\frac{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\min} }\right] }{\left[ 1-\frac{\Upsilon^{i}}{\chi_{\max}}\right] }\in\left( 0,1\right) .$](img894.gif)