
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 853, October 2008 --- Screen Reader
Version*
Inference in Long-Horizon Regressions
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
I develop new results for long-horizon predictive regressions with overlapping observations. I show that rather than using auto-correlation robust standard errors, the standard t-statistic can simply be divided by the square root of the forecasting horizon to correct for the effects of the overlap in the data; this is asymptotically an exact correction and not an approximate result. Further, when the regressors are persistent and endogenous, the long-run OLS estimator suffers from the same problems as does the short-run OLS estimator, and it is shown how similar corrections and test procedures as those proposed for the short-run case can also be implemented in the long-run. New results for the power properties of long-horizon tests are also developed. The theoretical results are illustrated with an application to long-run stock-return predictability, where it is shown that once correctly sized tests are used, the evidence of predictability is generally much stronger at short rather than long horizons.
Keywords: Predictive regressions, long-horizon regressions, stock return predictability
JEL classification: C22, G1
1 Introduction
Predictive regressions are used frequently in empirical finance and economics. The underlying economic motivation is often the test of a rational expectations model, which implies that the innovations to the dependent variable should be orthogonal to all past information; i.e., the dependent variable should not be predictable using any lagged regressors. Although this orthogonality condition should hold at any time horizon, it is popular to test for predictability by regressing sums of future values of the dependent variable onto the current value of the regressor. A leading example is the question of stock return predictability, where regressions with 5 or 10 year returns are often used (e.g. Campbell and Shiller, 1988, and Fama and French, 1988). While stock return predictability will also serve as the motivating example in this paper, the results derived are applicable to a much wider range of empirical questions.1
The main inferential issue in long-horizon regressions has been the uncertainty regarding the proper calculation of standard errors. Since overlapping observations are typically used, the regression residuals will exhibit strong serial correlation; standard errors failing to account for this fact will lead to biased inference. Typically, auto-correlation robust estimation of the standard errors (e.g. Newey and West, 1987) is therefore used. However, these robust estimators tend to perform poorly in finite samples since the serial correlation induced in the error terms by overlapping data is often very strong.2
The main contribution of this paper is the development of new
asymptotic results for long-run regressions with overlapping
observations. Using a framework where the predictors are highly
persistent variables, as in Stambaugh (1999) and Campbell and Yogo
(2006), I show how to obtain asymptotically correct
test-statistics, with good small sample properties, for the null
hypothesis of no predictability.3 Rather than using robust standard
errors, I find that the standard ![]() statistic can simply
be divided by the square root of the forecasting horizon to correct
for the effects of the overlap in the data. This is not an
approximation, but rather an exact asymptotic result. Further, when
the regressor is persistent and endogenous, the long-run OLS
estimator suffers from the same problems as does the short-run OLS
estimator, and similar corrections and test procedures as those
proposed by Campbell and Yogo (2006) for the short-run case should
also be used in the long-run; again, the resulting test statistics
should be scaled due to the overlap.4 Thus, these results lead
to simple and more efficient inference in long-run regressions by
obviating the need for robust standard error estimation methods and
controlling for the endogeneity and persistence of the
regressor.
statistic can simply
be divided by the square root of the forecasting horizon to correct
for the effects of the overlap in the data. This is not an
approximation, but rather an exact asymptotic result. Further, when
the regressor is persistent and endogenous, the long-run OLS
estimator suffers from the same problems as does the short-run OLS
estimator, and similar corrections and test procedures as those
proposed by Campbell and Yogo (2006) for the short-run case should
also be used in the long-run; again, the resulting test statistics
should be scaled due to the overlap.4 Thus, these results lead
to simple and more efficient inference in long-run regressions by
obviating the need for robust standard error estimation methods and
controlling for the endogeneity and persistence of the
regressor.
The results in this paper are derived under the assumption that the forecasting horizon increases with the sample size, but at a slower pace. Most previous work, e.g. Richardson and Stock (1989) and Valkanov (2003), rely on the assumption that the forecasting horizon grows at the same pace as the sample size so that the forecasting horizon remains a fraction of the sample size asymptotically. In some related work, Moon et al. (2004) consider both asymptotic approaches and find that although the asymptotic distributions are seemingly quite different under the two assumptions, they both tend to provide good approximations for the finite sample properties. Indeed, Valkanov (2003), who studies a similar econometric model to the one analyzed in this paper, derives a similar scaling result to the one found here. Asymptotic results are, of course, only useful to the extent that they provide us with relevant information regarding the finite sample properties of an econometric procedure. As shown in Monte Carlo simulations, both the asymptotic results derived under the assumptions in this paper and those derived under the assumptions in Valkanov's paper provide good approximations of finite sample behavior.
In relation to Valkanov's study, the current paper makes two
important contributions. First, I show that with exogenous
regressors the scaled standard ![]() statistic will be
normally distributed and standard inference can thus be performed.
Second, when the regressors are endogenous, the inferential methods
can be suitably modified to correct for the biasing endogeneity
effects; this can be seen as an analogue of the inferential
procedures developed by Campbell and Yogo (2006) for short-run,
one-period horizon, regressions. Importantly, the modified
test-statistic in the endogenous case is again normally
distributed. In contrast, Valkanov's test statistics have highly
non-standard distributions, both for exogenous and endogenous
regressors, which require simulation of the critical values for
each specific case.
statistic will be
normally distributed and standard inference can thus be performed.
Second, when the regressors are endogenous, the inferential methods
can be suitably modified to correct for the biasing endogeneity
effects; this can be seen as an analogue of the inferential
procedures developed by Campbell and Yogo (2006) for short-run,
one-period horizon, regressions. Importantly, the modified
test-statistic in the endogenous case is again normally
distributed. In contrast, Valkanov's test statistics have highly
non-standard distributions, both for exogenous and endogenous
regressors, which require simulation of the critical values for
each specific case.
Monte Carlo simulations show that the asymptotic normal distribution of the test statistics derived in this paper provides a good approximation in finite samples, resulting in rejection rates that are very close to the nominal size of the test under the null hypothesis. This is also true when the overlap in the data is large. This shows that although the asymptotic results are derived under an assumption that the forecasting horizon is small compared to the sample size, the normal distribution of the scaled test statistics is not very sensitive to this restriction. In fact, the tests tend to become somewhat conservative and under reject, rather than over reject, as the forecasting horizon becomes large.
Since the size properties of both the tests proposed here and those of Valkanov (2003) are good, it becomes interesting to compare the power properties. Using Monte Carlo simulations, it is evident that for exogenous regressors the power properties of the test proposed here are quite similar to that of Valkanov, although there are typically some slight power advantages to the current procedure. When the regressors are endogenous, however, the test procedure derived here is often much more powerful than the test proposed by Valkanov. This stems partly from the fact that the test here explicitly takes into account, and controls for, the biasing effects of the endogenous regressors, whereas Valkanov's test only adjusts the critical values of the test statistic. Part of the power gains are also achieved by using a Bonferroni method, as in Campbell and Yogo (2006), to control for the unknown persistence in the regressors, whereas Valkanov relies on a sup-bound method, which is typically less efficient; Campbell and Yogo (2006) find the same result in the one-period case when they compare their method to the sup-bound method proposed by Lewellen (2004).
In fact, the power simulations, and additional asymptotic
results, reveal three interesting facts about the properties of
long-run predictive tests. First, the power of long-run tests
increases only with the sample size relative to the forecasting
horizon. Keeping this ratio fixed as the sample size increases does
not lead to any power gains for the larger sample size. This result
also suggests that for a given sample size, the power of a test
will generally decrease as the forecasting horizon increases;
additional simulations also support this conjecture and find that
in general the one-period test will be the most powerful test.
Second, when the regressors are endogenous, tests that are based on
the standard long-run OLS estimator will result in power curves
that are sometimes decreasing in the magnitude of the slope
coefficient. That is, as the model drifts further away from the
null hypothesis, the power may decrease. This is true both for
Valkanov's test, but also if one uses, for instance, Newey-West
standard errors in a normal ![]() statistic. The test
proposed here for the case of endogenous regressors does not suffer
from this problem. The third finding is related to the second one,
and shows that although the power of the long-horizon tests
increases with the magnitude of the slope coefficient for
alternatives close to the null hypothesis, there are no gains in
power as the slope coefficient grows large. That is, the power
curve is asymptotically horizontal when viewed as a function of the
slope coefficient. Both the second and third findings arise from
the fact that when forecasting over multiple horizons, there is
uncertainty not just regarding the future path of the outcome
variable (e.g. future excess stock returns), but also about the
future path of the forecasting variable over these multiple
horizons. These results therefore add a further note of caution to
attempts at forecasting at very long-horizons relative to the
sample size: even though correctly sized tests are available, the
power properties of the test can be very poor. The sometimes
decreasing power curves for endogenous regressors also makes the
case stronger for using test of the type proposed here, which
attempts to correct for the bias and inefficiency induced in the
estimation procedure by the endogeneity, and not just correct the
critical values.
statistic. The test
proposed here for the case of endogenous regressors does not suffer
from this problem. The third finding is related to the second one,
and shows that although the power of the long-horizon tests
increases with the magnitude of the slope coefficient for
alternatives close to the null hypothesis, there are no gains in
power as the slope coefficient grows large. That is, the power
curve is asymptotically horizontal when viewed as a function of the
slope coefficient. Both the second and third findings arise from
the fact that when forecasting over multiple horizons, there is
uncertainty not just regarding the future path of the outcome
variable (e.g. future excess stock returns), but also about the
future path of the forecasting variable over these multiple
horizons. These results therefore add a further note of caution to
attempts at forecasting at very long-horizons relative to the
sample size: even though correctly sized tests are available, the
power properties of the test can be very poor. The sometimes
decreasing power curves for endogenous regressors also makes the
case stronger for using test of the type proposed here, which
attempts to correct for the bias and inefficiency induced in the
estimation procedure by the endogeneity, and not just correct the
critical values.
The theoretical results in the paper are illustrated with an application to stock-return predictability. I use a U.S. data set with excess returns on the S&P 500, as well as the value weighted CRSP index as dependent variables. The dividend price ratio, the smoothed earnings price ratio suggested by Campbell and Shiller (1988), the short interest rate and the yield spread are used as predictor variables. In addition, I also analyze an international data set with nine additional countries with monthly data spanning at least fifty years for each country. The predictor variables in the international data include the dividend-price ratio and measures of both the short interest rate and the term spread.
The evidence of predictability using the dividend- and
earnings-price ratios is overall fairly weak, both in the U.S. and
the international data, once the endogeneity and persistence in the
regressors have been controlled for. The empirical results are more
favorable of predictability when using either of the interest rate
variables as predictors. This is particularly true in the U.S.
data, but also to some extent in other countries. Contrary to some
popular beliefs, however, the case for predictability does not
increase with the forecast horizon. In fact, the near opposite is
true, with generally declining ![]() statistics as the
forecasting horizon increases (similar results are also found by
Torous et al., 2004, and Ang and Bekaert, 2007). Given the fairly
weak evidence of predictability at the short horizon, these results
are consistent with a loss of power as the forecasting horizon
increases, which is in line with the theoretical results derived in
this paper.
statistics as the
forecasting horizon increases (similar results are also found by
Torous et al., 2004, and Ang and Bekaert, 2007). Given the fairly
weak evidence of predictability at the short horizon, these results
are consistent with a loss of power as the forecasting horizon
increases, which is in line with the theoretical results derived in
this paper.
The rest of the paper is organized as follows. Section 2 sets up the model and derives the theoretical results and Section 3 discusses the practical implementation of the methods in the paper. Section 4 describes the Monte-Carlo simulations that illustrate the finite sample properties of the methods and Section 5 provides further discussion and analysis of the power properties of long-horizon tests under an alternative of predictability. The empirical application is given in Section 6 and Section 7 concludes. Technical proofs are found in the Appendix.
2 Long-run estimation
2.1 Model and assumptions
Although the results derived in this paper are of general
applicability, it is helpful to discuss the model and derivations
in light of the specific question of stock return predictability.
Thus, let the dependent variable be denoted ![]() ,
which would typically represent excess stock returns when analyzing
return predictability, and the corresponding regressor,
,
which would typically represent excess stock returns when analyzing
return predictability, and the corresponding regressor, ![]() .5 The behavior of
.5 The behavior of ![]() and
and ![]() are assumed to satisfy,
are assumed to satisfy,
| (1) | ||
| (2) |
where
![]()
![]() , and
, and
![]() is the sample size. The error processes are
assumed to satisfy the following conditions.
is the sample size. The error processes are
assumed to satisfy the following conditions.
1.
![]()
2.
![]()
3.
![]() ,
,
![]() ,
and
,
and
![]() .
.
The model described by equations (1) and (2) and Assumption 1 captures the
essential features of a predictive regression with a nearly
persistent regressor. It states the usual martingale difference
assumption for the error terms and allows the innovations to be
conditionally heteroskedastic, as long as they are covariance
stationary. The error terms ![]() and
and ![]() are also often highly correlated; the regressor will be
referred to as endogenous whenever this correlation, which will be
labelled
are also often highly correlated; the regressor will be
referred to as endogenous whenever this correlation, which will be
labelled
![]() , is
non-zero.
, is
non-zero.
The auto-regressive root of the regressor is parameterized as
being local-to-unity, which captures the near unit-root, or highly
persistent, behavior of many predictor variables, but is less
restrictive than a pure unit-root assumption. The near unit-root
construction, where the autoregressive root drifts closer to unity
as the sample size increases, is used as a tool to enable an
asymptotic analysis where the persistence in the data remains large
relative to the sample size, also as the sample size increases to
infinity. That is, if ![]() is treated as fixed and
strictly less than unity, then as the sample size grows, the
process
is treated as fixed and
strictly less than unity, then as the sample size grows, the
process ![]() will behave as a strictly stationary
process asymptotically, and the standard first order asymptotic
results will not provide a good guide to the actual small sample
properties of the model. For
will behave as a strictly stationary
process asymptotically, and the standard first order asymptotic
results will not provide a good guide to the actual small sample
properties of the model. For ![]() , the usual
unit-root asymptotics apply to the model, but this is clearly a
restrictive assumption for most potential predictor variables.
Instead, by letting
, the usual
unit-root asymptotics apply to the model, but this is clearly a
restrictive assumption for most potential predictor variables.
Instead, by letting
![]() , the effects from the high
persistence in the regressor will appear also in the asymptotic
results, but without imposing the strict assumption of a unit root.
Cavanagh et al. (1995), Lanne (2002), Valkanov (2003), Torous et
al. (2004), and Campbell and Yogo (2006) all use similar models,
with a near unit-root construct, to analyze the predictability of
stock returns.
, the effects from the high
persistence in the regressor will appear also in the asymptotic
results, but without imposing the strict assumption of a unit root.
Cavanagh et al. (1995), Lanne (2002), Valkanov (2003), Torous et
al. (2004), and Campbell and Yogo (2006) all use similar models,
with a near unit-root construct, to analyze the predictability of
stock returns.
The greatest problem in dealing with regressors that are near
unit-root processes is the nuisance parameter ![]() ;
;
![]() is generally unknown and not consistently
estimable.6 It is nevertheless useful to first
derive inferential methods under the assumption that
is generally unknown and not consistently
estimable.6 It is nevertheless useful to first
derive inferential methods under the assumption that ![]() is known, and then use the arguments of Cavanagh et al.
(1995) to construct feasible tests. The remainder of this section
derives and outlines the inferential methods used for estimating
and performing tests on
is known, and then use the arguments of Cavanagh et al.
(1995) to construct feasible tests. The remainder of this section
derives and outlines the inferential methods used for estimating
and performing tests on ![]() in equation (1), treating
in equation (1), treating
![]() as known. Section 3 discusses how
the methods of Cavanagh et al. (1995), and Campbell and Yogo
(2006), can be used to construct feasible tests with
as known. Section 3 discusses how
the methods of Cavanagh et al. (1995), and Campbell and Yogo
(2006), can be used to construct feasible tests with ![]() unknown.
unknown.
2.2 The fitted regression
In long-run regressions, the focus of interest is the fitted regression,
| (3) |
where
Let the OLS estimator of ![]() in equation
(3), using
overlapping observations, be denoted by
in equation
(3), using
overlapping observations, be denoted by
![]() . A long-standing issue is the
calculation of correct standard errors for
. A long-standing issue is the
calculation of correct standard errors for
![]() . Since overlapping
observations are used to form the estimates, the residuals
. Since overlapping
observations are used to form the estimates, the residuals
![]() will exhibit serial
correlation; standard errors failing to account for this fact will
lead to biased inference. The common solution to this problem has
been to calculate auto-correlation robust standard errors, using
methods described by Hansen and Hodrick (1980) and Newey and West
(1987). However, these robust estimators tend to have rather poor
finite sample properties.
will exhibit serial
correlation; standard errors failing to account for this fact will
lead to biased inference. The common solution to this problem has
been to calculate auto-correlation robust standard errors, using
methods described by Hansen and Hodrick (1980) and Newey and West
(1987). However, these robust estimators tend to have rather poor
finite sample properties.
In this section, I derive the asymptotic properties of
![]() under the assumption that the
forecasting horizon
under the assumption that the
forecasting horizon ![]() grows with the sample size
but at a slower pace. The results complement those of Valkanov
(2003), who treats the case where the forecasting horizon grows at
the same rate as the sample size. Simulation results in Valkanov
(2003) and later on in this paper show that both asymptotic
approaches provide limiting distributions that are good proxies for
the finite sample behavior of the long-run estimators. The
asymptotic results derived here also provide additional
understanding of the properties of the long-run estimators. In
particular, the results here show the strong connection between the
limiting distributions of the short- and long-run estimators. This
finding has important implications for the construction of more
efficient estimators and test-statistics that control for the
endogeneity and persistence in the regressors. Unlike Valkanov
(2003), the procedures in this paper avoid the need for simulation
methods; the proposed test-statistics have limiting normal
distributions, although in the case of endogenous regressors with
unknown persistence, Bonferroni type methods need to be used to
construct feasible tests.
grows with the sample size
but at a slower pace. The results complement those of Valkanov
(2003), who treats the case where the forecasting horizon grows at
the same rate as the sample size. Simulation results in Valkanov
(2003) and later on in this paper show that both asymptotic
approaches provide limiting distributions that are good proxies for
the finite sample behavior of the long-run estimators. The
asymptotic results derived here also provide additional
understanding of the properties of the long-run estimators. In
particular, the results here show the strong connection between the
limiting distributions of the short- and long-run estimators. This
finding has important implications for the construction of more
efficient estimators and test-statistics that control for the
endogeneity and persistence in the regressors. Unlike Valkanov
(2003), the procedures in this paper avoid the need for simulation
methods; the proposed test-statistics have limiting normal
distributions, although in the case of endogenous regressors with
unknown persistence, Bonferroni type methods need to be used to
construct feasible tests.
2.3 The limiting distribution of the long-run OLS estimator
The following theorem states the asymptotic distribution of the
long-run OLS estimator of equation (3), and provides
the key building block for the rest of the analysis. The result is
derived under the null hypothesis of no predictability, in which
case the one period data generating process is simply
![]() , and the long-run coefficient
, and the long-run coefficient
![]() will also be equal to zero.
will also be equal to zero.
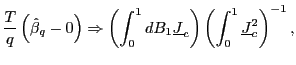 |
(4) |
where
Theorem 1 shows
that under the null of no predictability, the limiting distribution
of
![]() is identical to that of the
standard short-run, one-period, OLS estimator
is identical to that of the
standard short-run, one-period, OLS estimator
![]() in equation (1), which is
easily shown to converge to this distribution at a rate
in equation (1), which is
easily shown to converge to this distribution at a rate ![]() (Cavanagh et al., 1995), although
(Cavanagh et al., 1995), although
![]() needs to be standardized by
needs to be standardized by
![]() . This additional standardization
follows since the estimated parameter
. This additional standardization
follows since the estimated parameter ![]() is of
an order
is of
an order ![]() times larger than the original short-run
parameter
times larger than the original short-run
parameter ![]() , as discussed at length in Boudoukh
et al. (2005).
, as discussed at length in Boudoukh
et al. (2005).
The convergence rate of ![]() for the long-run
estimator also confirms the conjecture made by Nelson and Kim
(1993), regarding the size of the bias in a long-run regression
with endogenous regressors. They conjecture, based on simulation
results, that the size of the bias is consistent with Stambaugh's
(1999) approximation of the one-period bias, if one takes the total
number of non-overlapping observations as the relevant
sample size. In the near unit-root framework analyzed here, the
Stambaugh bias is revealed in the non-standard asymptotic
distribution of
for the long-run
estimator also confirms the conjecture made by Nelson and Kim
(1993), regarding the size of the bias in a long-run regression
with endogenous regressors. They conjecture, based on simulation
results, that the size of the bias is consistent with Stambaugh's
(1999) approximation of the one-period bias, if one takes the total
number of non-overlapping observations as the relevant
sample size. In the near unit-root framework analyzed here, the
Stambaugh bias is revealed in the non-standard asymptotic
distribution of
![]() , which has a non-zero mean
whenever the correlation between
, which has a non-zero mean
whenever the correlation between ![]() and
and ![]() differs from zero. Thus, since the rate of convergence
is
differs from zero. Thus, since the rate of convergence
is ![]() , the size of the bias in a given finite
sample will be proportional to the number of non-overlapping
observations.
, the size of the bias in a given finite
sample will be proportional to the number of non-overlapping
observations.
The equality between the long-run asymptotic distribution under the null hypothesis, shown in Theorem 1, and that of the short-run OLS estimator may seem puzzling. The intuition behind this result stems from the persistent nature of the regressors. In a (near) unit-root process, the long-run movements dominate the behavior of the process. Therefore, regardless of whether one focuses on the long-run behavior, as is done in a long-horizon regression, or includes both the short-run and long-run information as is done in a standard one-period OLS estimation, the asymptotic result is the same since, asymptotically, the long-run movements are all that matter.7
The limiting distribution of
![]() is non-standard and a
function of the local-to-unity parameter
is non-standard and a
function of the local-to-unity parameter ![]() . Since
. Since
![]() is not known, and not consistently
estimable, the exact limiting distribution is therefore not known
in practice, which makes valid inference difficult. Cavanagh et al.
(1995) suggest putting bounds on
is not known, and not consistently
estimable, the exact limiting distribution is therefore not known
in practice, which makes valid inference difficult. Cavanagh et al.
(1995) suggest putting bounds on ![]() in some manner, and
find the most conservative value of the limiting distribution for
some value of
in some manner, and
find the most conservative value of the limiting distribution for
some value of ![]() within these bounds. Campbell and Yogo
(2006) suggest first modifying the estimator or, ultimately, the
resulting test-statistic, in an optimal manner for a known value of
within these bounds. Campbell and Yogo
(2006) suggest first modifying the estimator or, ultimately, the
resulting test-statistic, in an optimal manner for a known value of
![]() , which results in more powerful tests.
Again using a bounds procedure, the most conservative value of the
modified test-statistic can be chosen for a value of
, which results in more powerful tests.
Again using a bounds procedure, the most conservative value of the
modified test-statistic can be chosen for a value of ![]() within these bounds. I will pursue a long-run analogue of
this latter approach here since it leads to more efficient tests
and because the relevant limiting distribution is standard normal,
which greatly simplifies practical inference. Before deriving the
modified estimator and test statistic, however, it is instructive
to consider the special case of exogenous regressors where no
modifications are needed.
within these bounds. I will pursue a long-run analogue of
this latter approach here since it leads to more efficient tests
and because the relevant limiting distribution is standard normal,
which greatly simplifies practical inference. Before deriving the
modified estimator and test statistic, however, it is instructive
to consider the special case of exogenous regressors where no
modifications are needed.
2.4 The special case of exogenous regressors
Suppose the regressor ![]() is exogenous in the
sense that
is exogenous in the
sense that ![]() is uncorrelated with
is uncorrelated with ![]() and thus
and thus
![]() . In this case, the
limiting processes
. In this case, the
limiting processes ![]() and
and ![]() are orthogonal to each other and the limiting
distribution in (4)
simplifies. In particular, it follows that
are orthogonal to each other and the limiting
distribution in (4)
simplifies. In particular, it follows that
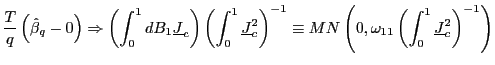
|
(5) |
where
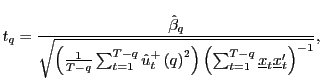 |
(6) |
where
| (7) |
Thus, by standardizing the ![]() statistic for
statistic for
![]() by the square root of the
forecasting horizon, the effects of the overlap in the data are
controlled for and a standard normal distribution is obtained.
Although the mechanics behind this result are spelled out in the
proof in the Appendix, it is useful to outline the intuition. Note
that the result in (5)
implies that
by the square root of the
forecasting horizon, the effects of the overlap in the data are
controlled for and a standard normal distribution is obtained.
Although the mechanics behind this result are spelled out in the
proof in the Appendix, it is useful to outline the intuition. Note
that the result in (5)
implies that
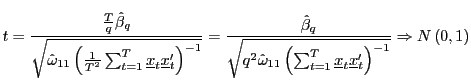
|
(8) |
for some consistent estimator
2.5 Endogeneity corrections
As discussed above, the long-run OLS estimator suffers from the
same endogeneity problems as the short-run estimator; that is, when
the regressors are endogenous, the limiting distribution is
non-standard and a function of the unknown parameter ![]() . To address this issue, I consider a version of the
augmented regression of Phillips (1991a), together with the
Bonferroni methods of Campbell and Yogo (2006). For now, I assume
that
. To address this issue, I consider a version of the
augmented regression of Phillips (1991a), together with the
Bonferroni methods of Campbell and Yogo (2006). For now, I assume
that ![]() , or equivalently
, or equivalently ![]() ,
is known and derive an estimator and test statistic under this
assumption.
,
is known and derive an estimator and test statistic under this
assumption.
Note that, for a given ![]() , the
innovations
, the
innovations ![]() can be obtained from
can be obtained from
![]() . Consider first the
one-period regression. Once the innovations
. Consider first the
one-period regression. Once the innovations ![]() are
obtained, an implementation of the augmented regression equation of
Phillips (1991a), which he proposed for the pure unit-root case, is
now possible:
are
obtained, an implementation of the augmented regression equation of
Phillips (1991a), which he proposed for the pure unit-root case, is
now possible:
| (9) |
Here
As discussed in Hjalmarsson (2007), there is a close
relationship between inference based on the augmented regression
equation (9) and the
inferential procedures proposed by Campbell and Yogo (2006). To see
this, suppose first that the covariance matrix for the innovation
process, ![]() , is known, and hence also
, is known, and hence also
![]() and
and
![]() . The
. The ![]() test for
test for ![]() in (9) is then
asymptotically equivalent to
in (9) is then
asymptotically equivalent to
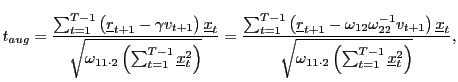
|
(10) |
which is, in fact, identical to Campbell and Yogo's
In the current context, the augmented regression equation is attractive since it can easily be generalized to the long-horizon case. Thus, consider the augmented long-run regression equation
| (11) |
where
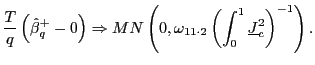
|
(12) |
The only difference from the result for the exogenous regressor
case is the variance
![]() , which reflects the fact
that the variation in
, which reflects the fact
that the variation in ![]() that is correlated with
that is correlated with
![]() has been removed. As in the exogenous
case, given the asymptotically mixed normal distributions of
has been removed. As in the exogenous
case, given the asymptotically mixed normal distributions of
![]() , standard test
procedures can now be applied to test the null of no
predictability. In particular, the scaled
, standard test
procedures can now be applied to test the null of no
predictability. In particular, the scaled ![]() statistic corresponding to
statistic corresponding to
![]() will be normally
distributed, as shown in the following corollary.
will be normally
distributed, as shown in the following corollary.
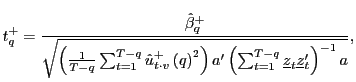
|
(13) |
where
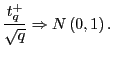
|
(14) |
Thus, for a given ![]() , inference becomes
trivial also in the case with endogenous regressors since the
scaled
, inference becomes
trivial also in the case with endogenous regressors since the
scaled ![]() statistic corresponding to the estimate of
statistic corresponding to the estimate of
![]() from the augmented regression
equation (11) is
normally distributed. In practice,
from the augmented regression
equation (11) is
normally distributed. In practice, ![]() is
typically unknown and the next section outlines methods for
implementing a feasible test.
is
typically unknown and the next section outlines methods for
implementing a feasible test.
3 Feasible methods
To implement the methods for endogenous regressors described in
the previous section, knowledge of the parameter ![]() (or equivalently, for a given sample size,
(or equivalently, for a given sample size, ![]() ) is
required. Since
) is
required. Since ![]() is typically unknown and not
estimable in general, the bounds procedures of Cavanagh et al.
(1995) and Campbell and Yogo (2006) can be used to obtain feasible
tests.
is typically unknown and not
estimable in general, the bounds procedures of Cavanagh et al.
(1995) and Campbell and Yogo (2006) can be used to obtain feasible
tests.
Although ![]() is not estimable, a confidence
interval for
is not estimable, a confidence
interval for ![]() can be obtained, as described by Stock
(1991). By evaluating the estimator and corresponding
test-statistic for each value of
can be obtained, as described by Stock
(1991). By evaluating the estimator and corresponding
test-statistic for each value of ![]() in that confidence
interval, a range of possible estimates and values of the
test-statistic are obtained. A conservative test can then be formed
by choosing the most conservative value of the test statistic,
given the alternative hypothesis. If the confidence interval for
in that confidence
interval, a range of possible estimates and values of the
test-statistic are obtained. A conservative test can then be formed
by choosing the most conservative value of the test statistic,
given the alternative hypothesis. If the confidence interval for
![]() has a coverage rate of
has a coverage rate of
![]() and the
nominal size of the test is
and the
nominal size of the test is
![]() percent, then by Bonferroni's
inequality, the final conservative test will have a size no greater
than
percent, then by Bonferroni's
inequality, the final conservative test will have a size no greater
than
![]() percent.
percent.
Thus, suppose that one wants to test
![]() versus
versus
![]() . The first step is to
obtain a confidence interval for
. The first step is to
obtain a confidence interval for ![]() , with confidence
level
, with confidence
level
![]() , which is
denoted
, which is
denoted
![]() .
For all values of
.
For all values of
![]() ,
,
![]() and the corresponding
and the corresponding
![]() are
calculated, where the estimator and test statistic are written as
functions of
are
calculated, where the estimator and test statistic are written as
functions of ![]() to emphasize the fact that a
different value is obtained for each
to emphasize the fact that a
different value is obtained for each
![]() . Let
. Let
![]() be the minimum value of
be the minimum value of
![]() that is
obtained for
that is
obtained for
![]() and
and
![]() be the maximum value. A conservative test of the null hypothesis
of no predictability, against a positive alternative, is then given
by evaluating
be the maximum value. A conservative test of the null hypothesis
of no predictability, against a positive alternative, is then given
by evaluating
![]() against the critical values of a standard normal distribution; the
null is rejected if
against the critical values of a standard normal distribution; the
null is rejected if
![]() , where
, where
![]() denotes the
denotes the
![]() quantile of the standard normal
distribution. The resulting test of the null hypothesis will have a
size no greater than
quantile of the standard normal
distribution. The resulting test of the null hypothesis will have a
size no greater than
![]() . An analogous
procedure can be used to test against a negative
alternative.8
. An analogous
procedure can be used to test against a negative
alternative.8
Unlike in the short-run methods in Campbell and Yogo (2006),
there is no guarantee that
![]() and
and
![]() will be the endpoints of the confidence interval for
will be the endpoints of the confidence interval for ![]() , although for most values of
, although for most values of ![]() they
typically are; in fact, it is easy to show that asymptotically the
minimum and maximum will always be at the endpoints, but this does
not hold in finite samples for
they
typically are; in fact, it is easy to show that asymptotically the
minimum and maximum will always be at the endpoints, but this does
not hold in finite samples for ![]() . The
test-statistic should thus be evaluated for all values in
. The
test-statistic should thus be evaluated for all values in
![]() in
order to find
in
order to find
![]() and
and
![]() ; for
; for ![]() , the
same result as in Campbell and Yogo (2006) holds and the extreme
values of the test statistic will always be obtained at the
endpoints.
, the
same result as in Campbell and Yogo (2006) holds and the extreme
values of the test statistic will always be obtained at the
endpoints.
In general, Bonferroni's inequality will be strict and the
overall size of the test just outlined will be less than
![]() . A test with a pre-specified size can
be achieved by fixing
. A test with a pre-specified size can
be achieved by fixing
![]() and adjusting
and adjusting
![]() . That is, by shrinking the size
of the confidence interval for
. That is, by shrinking the size
of the confidence interval for ![]() , a test of a
desired size can be achieved. Such procedures are discussed at
length in Campbell and Yogo (2006) and I rely on their results
here. That is, since, for all values of
, a test of a
desired size can be achieved. Such procedures are discussed at
length in Campbell and Yogo (2006) and I rely on their results
here. That is, since, for all values of ![]() , the
asymptotic properties of the estimators and corresponding
test-statistics derived here are identical to those in Campbell and
Yogo, it is reasonable to test if their adjustments to the
confidence level of the interval for
, the
asymptotic properties of the estimators and corresponding
test-statistics derived here are identical to those in Campbell and
Yogo, it is reasonable to test if their adjustments to the
confidence level of the interval for ![]() also work in
the long-run case considered here. Since the Campbell and Yogo
methods are frequently used in one-period regressions, this allows
the use of very similar procedures in long-run regressions. As
discussed below in conjunction with the Monte Carlo results, using
the Campbell and Yogo adjustments in the long-run case appear to
work well, although there is a tendency to under reject when the
forecasting horizon is large relative to the sample size. The power
properties of the test still remain good, however. Thus, there may
be some scope for improving the procedure by size adjusting the
confidence interval for
also work in
the long-run case considered here. Since the Campbell and Yogo
methods are frequently used in one-period regressions, this allows
the use of very similar procedures in long-run regressions. As
discussed below in conjunction with the Monte Carlo results, using
the Campbell and Yogo adjustments in the long-run case appear to
work well, although there is a tendency to under reject when the
forecasting horizon is large relative to the sample size. The power
properties of the test still remain good, however. Thus, there may
be some scope for improving the procedure by size adjusting the
confidence interval for ![]() differently for different
combinations of
differently for different
combinations of ![]() and
and ![]() , but at the
expense of much simplicity. Since the potential gains do not appear
large, I do not pursue that here, although it would be relatively
easy to implement on a case by case basis in applied work.
, but at the
expense of much simplicity. Since the potential gains do not appear
large, I do not pursue that here, although it would be relatively
easy to implement on a case by case basis in applied work.
Campbell and Yogo fix
![]() at ten percent, so that the
nominal size of the tests evaluated for each
at ten percent, so that the
nominal size of the tests evaluated for each ![]() is equal to ten percent. They also set the desired
size of the overall Bonferroni test, which they label
is equal to ten percent. They also set the desired
size of the overall Bonferroni test, which they label
![]() , to ten percent. Since the
degree of endogeneity, and hence the size of the biasing effects,
is a function of the correlation
, to ten percent. Since the
degree of endogeneity, and hence the size of the biasing effects,
is a function of the correlation ![]() between the
innovations
between the
innovations ![]() and
and ![]() , they
then search for each value of
, they
then search for each value of ![]() , for values
of
, for values
of
![]() , such that the overall size of
the test will be no greater than
, such that the overall size of
the test will be no greater than
![]() .9
.9
The practical implementation of the methods in this paper can be summarized as follows:
- (i)
- Using OLS estimation for each equation, obtain the estimated
residuals from equations (1) and (2). Calculate the
correlation
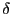 from these residuals.
from these residuals. - (ii)
- Calculate the DF-GLS unit-root test statistic of Elliot et al.
(1996), and obtain
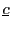 and
and
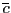 from Tables 2-11 in Campbell
and Yogo (2005) corresponding to the estimated value of
from Tables 2-11 in Campbell
and Yogo (2005) corresponding to the estimated value of 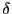 .
. - (iii)
- For a grid of values
![$ \tilde{c}\in\left[ \underline {c},\overline{c}\right] $](img228.gif) ,
calculate
,
calculate
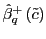 and
and
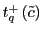 and find
and find
![$ t_{q,\min }^{+}\equiv\min_{\tilde{c}\in\left[ \underline{c},\overline{c}\right] } t_{q}^{+}\left( \tilde{c}\right) $](img231.gif) , and
, and
![$ t_{q,\max}^{+}\equiv\max_{\tilde {c}\in\left[ \underline{c},\overline{c}\right] }t_{q}^{+}\left( \tilde {c}\right) $](img232.gif) .
. - (iv)
- If the alternative hypothesis is
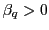 , compare
, compare
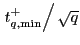 to the
to the
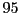 percent critical values of the standard
normal distribution (i.e.
percent critical values of the standard
normal distribution (i.e. 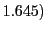 and if the
alternative hypothesis is
and if the
alternative hypothesis is
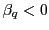 , compare
, compare
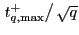 to the
five percent critical values of the standard normal
distribution.
to the
five percent critical values of the standard normal
distribution.
The above procedure results in a one-sided test at the five
percent level, or alternatively a two-sided test at the ten percent
level. Note that, although the analysis in Section 2.5 proposes an
improved point estimator,
![]() , for a given
, for a given ![]() , in practice it is merely used as a device to deliver an
improved and feasible test statistic. That is, since
, in practice it is merely used as a device to deliver an
improved and feasible test statistic. That is, since ![]() is not known in practice, the scope for improving upon
the standard (long-run) OLS estimator is limited, even though
improved test statistics are obtained.
is not known in practice, the scope for improving upon
the standard (long-run) OLS estimator is limited, even though
improved test statistics are obtained.
The estimate of ![]() and the confidence
interval for
and the confidence
interval for ![]() can be made more robust by allowing
the regressors to follow an autoregressive process with
can be made more robust by allowing
the regressors to follow an autoregressive process with ![]() lags
lags
![]() , rather
than an
, rather
than an
![]() process. That is, an
process. That is, an
![]() process can be estimated
for the regressor, and the DF-GLS statistic can be calculated using
process can be estimated
for the regressor, and the DF-GLS statistic can be calculated using
![]() lags. Since the outcome of
lags. Since the outcome of
![]() and
and ![]() can be quite sensitive to the choice of
can be quite sensitive to the choice of ![]() , when
, when ![]() is large in absolute terms, it
can be important to pin down the confidence interval
is large in absolute terms, it
can be important to pin down the confidence interval
![]() as
well as possible. Although the augmented regression equation is
only formally justified for the
as
well as possible. Although the augmented regression equation is
only formally justified for the
![]() case, the outcome of
case, the outcome of
![]() and
and ![]() will in general be much more sensitive to the
choice of
will in general be much more sensitive to the
choice of ![]() than the effects of a, typically
small, serially correlated component for higher order lags in the
regressor. Thus, the main benefits from allowing for a richer
auto-correlation structure in the regressor come from the proper
calculation of
than the effects of a, typically
small, serially correlated component for higher order lags in the
regressor. Thus, the main benefits from allowing for a richer
auto-correlation structure in the regressor come from the proper
calculation of
![]() ;
the effects of using the augmented regression equation rather than
a method that explicitly controls for higher order
auto-correlations should be small on the other hand. In practice,
as evidenced in Campbell and Yogo (2006), the difference between
results based on an
;
the effects of using the augmented regression equation rather than
a method that explicitly controls for higher order
auto-correlations should be small on the other hand. In practice,
as evidenced in Campbell and Yogo (2006), the difference between
results based on an
![]() and an
and an
![]() assumption seems to be
fairly small. However, in order to keep the analysis as robust as
possible, the empirical results in Section 6 are obtained
using the
assumption seems to be
fairly small. However, in order to keep the analysis as robust as
possible, the empirical results in Section 6 are obtained
using the
![]() specification; the
implementation follows the methods described in Campbell and Yogo
(2005), using the Bayesian information criterion (BIC) to choose
the appropriate lag length.
specification; the
implementation follows the methods described in Campbell and Yogo
(2005), using the Bayesian information criterion (BIC) to choose
the appropriate lag length.
4 Monte Carlo results
All of the above asymptotic results are derived under the
assumption that the forecasting horizon grows with the sample size,
but at a slower rate. Valkanov (2003) also studies long-run
regressions with near-integrated regressors, but derives his
asymptotic results under the assumption that
![]() as
as
![]() . That is, he assumes
that the forecasting horizon grows at the same pace as the sample
size. Under such conditions, the asymptotic results are, at least
at first glance, quite different from those derived in this paper.
There is, of course, no right or wrong way to perform the
asymptotic analysis; what matters in the end is how well the
asymptotic distributions capture the actual finite sample
properties of the test statistics. To this end, Monte Carlo
simulations are therefore conducted. Since Valkanov's methods are
known to have good size properties, I merely present power results
for his tests.
. That is, he assumes
that the forecasting horizon grows at the same pace as the sample
size. Under such conditions, the asymptotic results are, at least
at first glance, quite different from those derived in this paper.
There is, of course, no right or wrong way to perform the
asymptotic analysis; what matters in the end is how well the
asymptotic distributions capture the actual finite sample
properties of the test statistics. To this end, Monte Carlo
simulations are therefore conducted. Since Valkanov's methods are
known to have good size properties, I merely present power results
for his tests.
4.1 Size properties
I start with analyzing the size properties of the scaled
![]() statistics proposed earlier in the paper.
Equations (1) and
(2) are simulated,
with
statistics proposed earlier in the paper.
Equations (1) and
(2) are simulated,
with ![]() and
and ![]() drawn from an
drawn from an
![]() bivariate normal distribution with mean
zero, unit variance and correlations
bivariate normal distribution with mean
zero, unit variance and correlations
![]() and
and ![]() . The intercept
. The intercept ![]() is set to
zero and the local-to-unity parameter
is set to
zero and the local-to-unity parameter ![]() is set to
either 0 or
is set to
either 0 or ![]() . The sample size is either equal to
. The sample size is either equal to
![]() or
or ![]() . Since the
size of the tests are evaluated, the slope coefficient
. Since the
size of the tests are evaluated, the slope coefficient ![]() is set to zero, which implies that
is set to zero, which implies that
![]() as well. All results are based
on
as well. All results are based
on ![]() repetitions.
repetitions.
Three different test statistics are considered: the scaled
![]() statistic corresponding to the long-run
OLS estimate
statistic corresponding to the long-run
OLS estimate
![]() , the scaled Bonferroni
, the scaled Bonferroni
![]() statistic described above
statistic described above
![]() , and the scaled infeasible
, and the scaled infeasible ![]() statistic
corresponding to the infeasible estimate
statistic
corresponding to the infeasible estimate
![]() for a known value of
for a known value of
![]() . In practice, of course, the infeasible
test is not feasible but in the Monte Carlo simulations the
parameter
. In practice, of course, the infeasible
test is not feasible but in the Monte Carlo simulations the
parameter ![]() is known, and the test based on the
infeasible estimate thus provides a benchmark. All tests are
evaluated against a positive one-sided alternative at the five
percent level; i.e. the null is rejected if the scaled test
statistic exceeds
is known, and the test based on the
infeasible estimate thus provides a benchmark. All tests are
evaluated against a positive one-sided alternative at the five
percent level; i.e. the null is rejected if the scaled test
statistic exceeds ![]() .
.
The results are shown in Table 1. The first set
of columns shows the rejection rates for the scaled OLS ![]() statistic under the null hypothesis of no predictability.
When the regressors are exogenous, such that
statistic under the null hypothesis of no predictability.
When the regressors are exogenous, such that ![]() , this test statistic should be asymptotically
normally distributed. The normal distribution appears to work well
in finite samples, with rejection rates close to the nominal five
percent size. For
, this test statistic should be asymptotically
normally distributed. The normal distribution appears to work well
in finite samples, with rejection rates close to the nominal five
percent size. For ![]() and for large
and for large
![]() relative to
relative to ![]() , the size
drops and the test becomes somewhat conservative; this is primarily
true for forecasting horizons that span more than
, the size
drops and the test becomes somewhat conservative; this is primarily
true for forecasting horizons that span more than ![]() percent of the sample size. Overall, however, the scaling by
percent of the sample size. Overall, however, the scaling by
![]() of the standard
of the standard
![]() test appears to work well in practice for
exogenous regressors. As is expected from the asymptotic analysis
previously, the scaled OLS
test appears to work well in practice for
exogenous regressors. As is expected from the asymptotic analysis
previously, the scaled OLS ![]() test tends to over
reject for endogenous regressors with
test tends to over
reject for endogenous regressors with ![]() ,
which highlights that the biasing effects of endogenous regressors
are a great problem also in long-horizon regressions.
,
which highlights that the biasing effects of endogenous regressors
are a great problem also in long-horizon regressions.
The next set of columns shows the results for the scaled
Bonferroni test. The rejection rates for all ![]() are now typically close to, or below, five percent,
indicating that the proposed correction in the augmented
regressions equation (9)
works well in finite samples. Only for
are now typically close to, or below, five percent,
indicating that the proposed correction in the augmented
regressions equation (9)
works well in finite samples. Only for ![]() and
and
![]() is there a slight tendency to over
reject when
is there a slight tendency to over
reject when ![]() is small, but the average rejection
rates are still well within the acceptable range; Campbell and Yogo
(2006) find similar rejection rates in their one-period test, for
is small, but the average rejection
rates are still well within the acceptable range; Campbell and Yogo
(2006) find similar rejection rates in their one-period test, for
![]() . Again, as in the OLS case, there is a
tendency to under reject for large
. Again, as in the OLS case, there is a
tendency to under reject for large ![]() relative to
the sample size
relative to
the sample size ![]() . Since the Bonferroni test is
formed based on the shrunk confidence intervals for
. Since the Bonferroni test is
formed based on the shrunk confidence intervals for ![]() with the confidence levels provided in Table 2 of Campbell and Yogo
(2006), this could perhaps be somewhat remedied by adjusting these
confidence levels for large
with the confidence levels provided in Table 2 of Campbell and Yogo
(2006), this could perhaps be somewhat remedied by adjusting these
confidence levels for large ![]() .10
However, as seen in the power simulations below, the Bonferroni
test is not dramatically less powerful than the infeasible test,
and there seems to be little need for complicating the procedure by
requiring different tables for the confidence level for
.10
However, as seen in the power simulations below, the Bonferroni
test is not dramatically less powerful than the infeasible test,
and there seems to be little need for complicating the procedure by
requiring different tables for the confidence level for ![]() , for different combinations of
, for different combinations of ![]() and
and
![]() .
.
Finally, the last set of columns in Table 1 shows the
rejection rates for the scaled infeasible ![]() test
test
![]() , resulting
from the infeasible estimate
, resulting
from the infeasible estimate
![]() , which uses knowledge of
the true value of
, which uses knowledge of
the true value of ![]() . As in the case of the
Bonferroni test, the rejection rates are all close to the nominal
five percent level, although there is still a tendency to under
reject when
. As in the case of the
Bonferroni test, the rejection rates are all close to the nominal
five percent level, although there is still a tendency to under
reject when ![]() is large.
is large.
In summary, the above simulations confirm the main conclusions
from the formal asymptotic analysis: (i) when the regressor is
exogenous, the standard ![]() statistic scaled by the
square root of the forecasting horizon will be normally
distributed, and (ii) when the regressor is endogenous, the scaled
statistic scaled by the
square root of the forecasting horizon will be normally
distributed, and (ii) when the regressor is endogenous, the scaled
![]() statistic corresponding to the augmented
regression equation will be normally distributed. The simulations
also show that these scaled tests tend to be somewhat conservative
when
statistic corresponding to the augmented
regression equation will be normally distributed. The simulations
also show that these scaled tests tend to be somewhat conservative
when ![]() is large relative to
is large relative to ![]() ;
this observation is further discussed in the context of the power
properties of the tests, analyzed below.
;
this observation is further discussed in the context of the power
properties of the tests, analyzed below.
The size simulations were also performed under the assumption
that the innovation processes were drawn from ![]() distributions with five degrees of freedom, to proxy for
the fat tails that are observed in returns data. The results were
very similar to those presented here and are available upon
request.
distributions with five degrees of freedom, to proxy for
the fat tails that are observed in returns data. The results were
very similar to those presented here and are available upon
request.
4.2 Power properties
Since the test procedures proposed in this paper appear to have
good size properties and, if anything, under reject rather than
over reject the null, the second important consideration is their
power to reject the null when the alternative is in fact true. The
same simulation design as above is used, with the data generated by
equations (1) and
(2). In order to
assess the power of the tests, however, the slope coefficient
![]() in equation (1) now varies
between 0 and
in equation (1) now varies
between 0 and ![]() . For simplicity, I only consider the
cases of
. For simplicity, I only consider the
cases of ![]() and
and
![]() .
.
In addition to the three scaled ![]() statistics
considered in the size simulations - i.e. the scaled OLS
statistics
considered in the size simulations - i.e. the scaled OLS
![]() test, the scaled Bonferroni test, and the
scaled infeasible test - I now also study two additional
test-statistics based on Valkanov (2003). Valkanov derives his
asymptotic results under the assumption that
test, the scaled Bonferroni test, and the
scaled infeasible test - I now also study two additional
test-statistics based on Valkanov (2003). Valkanov derives his
asymptotic results under the assumption that
![]() as
as
![]() , and shows that under
this assumption,
, and shows that under
this assumption,
![]() will have a well defined
distribution. That is, he proposes to scale the standard OLS
will have a well defined
distribution. That is, he proposes to scale the standard OLS
![]() statistic by the square root of the sample
size, rather than by the square root of the forecasting horizon, as
suggested in this paper. The scaled
statistic by the square root of the sample
size, rather than by the square root of the forecasting horizon, as
suggested in this paper. The scaled ![]() statistic in
Valkanov's analysis is not normally distributed. It's asymptotic
distribution is a function of the parameters
statistic in
Valkanov's analysis is not normally distributed. It's asymptotic
distribution is a function of the parameters ![]() (the degree of overlap), the local-to-unity parameter
(the degree of overlap), the local-to-unity parameter
![]() , and the degree of endogeneity
, and the degree of endogeneity ![]() ; critical values must be obtained by simulation for a
given combination of these three parameters.11 Since the
critical values are a function of
; critical values must be obtained by simulation for a
given combination of these three parameters.11 Since the
critical values are a function of ![]() , Valkanov's
scaled
, Valkanov's
scaled ![]() test is generally infeasible since this
parameter is unknown. He therefore proposes a so-called sup-bound
test, where the test is evaluated at some bound for
test is generally infeasible since this
parameter is unknown. He therefore proposes a so-called sup-bound
test, where the test is evaluated at some bound for ![]() ,
outside of which it is assumed that
,
outside of which it is assumed that ![]() will not
lie. Ruling out explosive processes, he suggests using
will not
lie. Ruling out explosive processes, he suggests using ![]() in the sup-bound test, which results in a conservative
one-sided test against
in the sup-bound test, which results in a conservative
one-sided test against ![]() for
for ![]() .12 In the results below, I report the
power curves for both the infeasible test and the sup-bound test;
for
.12 In the results below, I report the
power curves for both the infeasible test and the sup-bound test;
for ![]() , they are identical. To avoid confusion,
I will continue to refer to the tests proposed in this paper as
scaled tests, whereas I will refer to the tests suggested by
Valkanov explicitly as Valkanov's infeasible and sup-bound tests.
Following Valkanov's exposition, I focus on the case of
, they are identical. To avoid confusion,
I will continue to refer to the tests proposed in this paper as
scaled tests, whereas I will refer to the tests suggested by
Valkanov explicitly as Valkanov's infeasible and sup-bound tests.
Following Valkanov's exposition, I focus on the case of ![]() , but given the apparently conservative nature of the
tests proposed here for large
, but given the apparently conservative nature of the
tests proposed here for large ![]() , I also consider
some results for
, I also consider
some results for ![]() .
.
Figure 1 shows
the power curves for the scaled OLS ![]() test
proposed in this paper and the two tests suggested by Valkanov, for
test
proposed in this paper and the two tests suggested by Valkanov, for
![]()
![]() , and
, and
![]() . For
. For ![]() , the power
curves are virtually identical, whereas for
, the power
curves are virtually identical, whereas for ![]() ,
Valkanov's infeasible test has some power advantages. The scaled
OLS
,
Valkanov's infeasible test has some power advantages. The scaled
OLS ![]() test is, however, marginally more powerful
than Valkanov's sup-bound test for
test is, however, marginally more powerful
than Valkanov's sup-bound test for ![]() .
Overall, for the case of exogenous regressors, there appears to be
no loss of power from using the simple scaled and normally
distributed
.
Overall, for the case of exogenous regressors, there appears to be
no loss of power from using the simple scaled and normally
distributed ![]() test suggested here.
test suggested here.
Figure 2
shows the results for endogenous regressors with
![]()
![]() , and
, and
![]() . Since the scaled
. Since the scaled ![]() test based on the OLS estimator is known to be biased in
this case, I only show the results for the scaled Bonferroni test
and the scaled infeasible test based on the augmented regression,
along with Valkanov's two tests. The results are qualitatively
similar to those for exogenous regressors with
test based on the OLS estimator is known to be biased in
this case, I only show the results for the scaled Bonferroni test
and the scaled infeasible test based on the augmented regression,
along with Valkanov's two tests. The results are qualitatively
similar to those for exogenous regressors with ![]() . For
. For ![]() , the power curves for the
three tests are nearly identical, although the scaled infeasible
test proposed in this paper tends to slightly dominate Valkanov's
infeasible test. For
, the power curves for the
three tests are nearly identical, although the scaled infeasible
test proposed in this paper tends to slightly dominate Valkanov's
infeasible test. For ![]() , the scaled infeasible
test is still the most powerful, and Valkanov's infeasible test is
somewhat more powerful than the scaled Bonferroni test. The least
powerful test is Valkanov's (feasible) sup-bound test. Note that
one would expect the scaled infeasible test proposed here to be
more powerful than Valkanov's infeasible test, since the test
proposed here attempts to correct the bias in the estimation
procedure and not just adjust the critical values of the test; this
comparison is thus the analogue of the comparison between the
infeasible (short-run)
, the scaled infeasible
test is still the most powerful, and Valkanov's infeasible test is
somewhat more powerful than the scaled Bonferroni test. The least
powerful test is Valkanov's (feasible) sup-bound test. Note that
one would expect the scaled infeasible test proposed here to be
more powerful than Valkanov's infeasible test, since the test
proposed here attempts to correct the bias in the estimation
procedure and not just adjust the critical values of the test; this
comparison is thus the analogue of the comparison between the
infeasible (short-run) ![]() test proposed by Campbell
and Yogo and the infeasible
test proposed by Campbell
and Yogo and the infeasible ![]() test proposed by
Cavanagh et al. (1995). Finally, it is noteworthy that the power of
Valkanov's sup-bound test appears to decrease for large
values of
test proposed by
Cavanagh et al. (1995). Finally, it is noteworthy that the power of
Valkanov's sup-bound test appears to decrease for large
values of ![]() when
when ![]() . A
similar pattern is also hinted at for Valkanov's test with
. A
similar pattern is also hinted at for Valkanov's test with
![]() . These patterns become clearer as the
forecasting horizon increases and will be analyzed at length
below.
. These patterns become clearer as the
forecasting horizon increases and will be analyzed at length
below.
Given that the scaled Bonferroni test, in particular, seemed to
be under sized for large values of ![]() relative to
relative to
![]() , it is interesting to see if this also
translates into poor power properties. Figure 3 shows the
results for
, it is interesting to see if this also
translates into poor power properties. Figure 3 shows the
results for
![]() ,
, ![]() , and
, and
![]() . Two observations are immediately
obvious from studying the plots. First, the scaled Bonferroni test
is reasonably powerful when compared to the infeasible scaled test,
and very powerful compared to Valkanov's sup-bound test. Second,
the declining pattern in the power curves for Valkanov's two tests
that were hinted at in Figure 2 are now evident;
as
. Two observations are immediately
obvious from studying the plots. First, the scaled Bonferroni test
is reasonably powerful when compared to the infeasible scaled test,
and very powerful compared to Valkanov's sup-bound test. Second,
the declining pattern in the power curves for Valkanov's two tests
that were hinted at in Figure 2 are now evident;
as ![]() becomes larger, the power of these two
tests decline. This result is of course perplexing, since
Valkanov's tests were explicitly derived under the assumption that
becomes larger, the power of these two
tests decline. This result is of course perplexing, since
Valkanov's tests were explicitly derived under the assumption that
![]() is large relative to the sample size
is large relative to the sample size
![]() . In the following section, additional
analytical results are derived that will shed some light on these
findings. However, before turning to the formal analysis, results
shown in Figure 4
provide further confirmation of the results in Figure 3, as well as
highlight some additional findings.
. In the following section, additional
analytical results are derived that will shed some light on these
findings. However, before turning to the formal analysis, results
shown in Figure 4
provide further confirmation of the results in Figure 3, as well as
highlight some additional findings.
Figure 4
confirms and elaborates on the findings in Figure 3. The right hand
graph shows the power curves for
![]()
![]() ,
,
![]() , and
, and ![]() . Using
. Using
![]() confirms that the previous findings
were not just a small sample artefact. The same pattern as in
Figure 3
emerges for Valkanov's two tests: after an initial increase in
power as
confirms that the previous findings
were not just a small sample artefact. The same pattern as in
Figure 3
emerges for Valkanov's two tests: after an initial increase in
power as ![]() becomes larger, the power starts to
decrease. Further results for larger values of
becomes larger, the power starts to
decrease. Further results for larger values of ![]() , which are not shown, indicate that the power curves do
not converge to zero as
, which are not shown, indicate that the power curves do
not converge to zero as ![]() grows large; rather,
they seem to level out after the initial decrease. Furthermore, the
power curves for the scaled Bonferroni test and the scaled
infeasible test do not seem to converge to one as
grows large; rather,
they seem to level out after the initial decrease. Furthermore, the
power curves for the scaled Bonferroni test and the scaled
infeasible test do not seem to converge to one as ![]() increases, although they do not decrease either, and
stabilize at a much higher level than the power curves for
Valkanov's tests. In addition, the power curve for the scaled OLS
increases, although they do not decrease either, and
stabilize at a much higher level than the power curves for
Valkanov's tests. In addition, the power curve for the scaled OLS
![]() test is also shown. This test is biased
for
test is also shown. This test is biased
for
![]() but provides an interesting
comparison to the power curves of Valkanov's test. As is seen, the
scaled OLS
but provides an interesting
comparison to the power curves of Valkanov's test. As is seen, the
scaled OLS ![]() test behaves in a very similar manner
to Valkanov's infeasible test. It is thus apparent that the
difference in behavior between the Bonferroni test and Valkanov's
tests stems primarily from the endogeneity correction and not the
manner in which they are scaled. Finally, the right hand graph in
Figure 4 also shows
that the patterns established for the power curves of the tests
proposed both in this paper and in Valkanov (2003) are not a result
of scaling the test statistic by either the sample size or the
forecasting horizon. As shown, if one uses Newey-West standard
errors to calculate the (non scaled)
test behaves in a very similar manner
to Valkanov's infeasible test. It is thus apparent that the
difference in behavior between the Bonferroni test and Valkanov's
tests stems primarily from the endogeneity correction and not the
manner in which they are scaled. Finally, the right hand graph in
Figure 4 also shows
that the patterns established for the power curves of the tests
proposed both in this paper and in Valkanov (2003) are not a result
of scaling the test statistic by either the sample size or the
forecasting horizon. As shown, if one uses Newey-West standard
errors to calculate the (non scaled) ![]() statistic
from the long-run OLS regression, a similar pattern emerges; note
that the test based on Newey-West standard errors will be biased
both for the well established reason that the standard errors do
not properly control for the overlap in the data, but also because
the
statistic
from the long-run OLS regression, a similar pattern emerges; note
that the test based on Newey-West standard errors will be biased
both for the well established reason that the standard errors do
not properly control for the overlap in the data, but also because
the ![]() statistic from the long-run OLS regression
does not control for the endogeneity in the regressors. The
Newey-West standard errors were calculated using
statistic from the long-run OLS regression
does not control for the endogeneity in the regressors. The
Newey-West standard errors were calculated using ![]() lags.
lags.
It is worth pointing out that Valkanov (2003) also performs a
Monte Carlo experiment of the power properties of his proposed
test-statistics, without finding the sometimes decreasing patterns
in the power curves reported here. However, Valkanov (2003) only
considers the case with
![]()
![]() , and
, and
![]() , for values of
, for values of ![]() between 0 and
between 0 and ![]() . As seen in Figurehere, the power
curves of all the tests are strictly increasing in
. As seen in Figurehere, the power
curves of all the tests are strictly increasing in ![]() for these parameter values.
for these parameter values.
The left hand graph in Figure 4 further
illustrates the above observations for the scaled OLS ![]() statistic in the case of
statistic in the case of ![]() . Here, with
. Here, with
![]() ,
, ![]() and
and
![]() , the power of the scaled OLS
, the power of the scaled OLS ![]() statistic and Valkanov's (infeasible) test statistic are
almost identical and again seem to converge to some fixed level
less than one. The results also suggest that the decrease in power
seen for Valkanov's test in the previous plots does not occur when
the regressors are exogenous. The
statistic and Valkanov's (infeasible) test statistic are
almost identical and again seem to converge to some fixed level
less than one. The results also suggest that the decrease in power
seen for Valkanov's test in the previous plots does not occur when
the regressors are exogenous. The ![]() statistic
based on Newey-West standard errors is also shown to exhibit the
same pattern; here, the bias in this test resulting from the
overlap in the data alone is evident, with a rejection rate around
20 percent under the null.
statistic
based on Newey-West standard errors is also shown to exhibit the
same pattern; here, the bias in this test resulting from the
overlap in the data alone is evident, with a rejection rate around
20 percent under the null.
To sum up, the simulations show that both the scaled OLS
![]() test and the scaled Bonferroni test have
good (local) power properties when compared to the tests proposed
by Valkanov (2003). This is especially true for the Bonferroni test
used with endogenous regressors, which tends to dominate Valkanov's
sup test for all values of
test and the scaled Bonferroni test have
good (local) power properties when compared to the tests proposed
by Valkanov (2003). This is especially true for the Bonferroni test
used with endogenous regressors, which tends to dominate Valkanov's
sup test for all values of ![]() , and also
dominates Valkanov's infeasible test for large values of
, and also
dominates Valkanov's infeasible test for large values of
![]() .
.
However, all of the tests discussed here, including the standard
![]() test based on Newey-West standard errors,
seem to behave in a non-standard way as the value of the slope
coefficient drift further away from the null hypothesis: rather
than converging to one as
test based on Newey-West standard errors,
seem to behave in a non-standard way as the value of the slope
coefficient drift further away from the null hypothesis: rather
than converging to one as ![]() grows large,
the power of the tests seem to converge to some value less than
unity. In the next section, I provide an analytical explanation of
these findings and discuss its implications.
grows large,
the power of the tests seem to converge to some value less than
unity. In the next section, I provide an analytical explanation of
these findings and discuss its implications.
5 Long-run inference under the alternative of predictability
5.1 Asymptotic power properties of long-run tests
The simulation evidence in the previous section raises questions
about the properties of long-run tests under the alternative of
predictability. In particular, the power of the tests does not seem
to converge to one as the slope coefficient increases and, in
addition, the power curves appear to sometimes decrease as
the slope coefficient drifts away from the null hypothesis. In this
section, I therefore derive some analytical results for the power
properties of long-run tests. I first start by considering a fixed
alternative, which provides the answer to why the power does not
converge to unity when the slope coefficient increases. In the
following sub-section, I consider the power against a local
alternative, which helps explain the hump shaped pattern in the
power curves. These analytical results also reveal some interesting
features about the consistency of long-run tests. I focus on the
standard (scaled) OLS ![]() statistic, since the
behavior of the
statistic, since the
behavior of the
![]() statistic is similar to the
former with exogenous regressors.
statistic is similar to the
former with exogenous regressors.
The following theorem provides the asymptotic results for the
distribution of the ![]() statistic under a fixed
alternative of predictability. Results are given both for the
asymptotics considered so far in this paper, i.e.
statistic under a fixed
alternative of predictability. Results are given both for the
asymptotics considered so far in this paper, i.e.
![]() , as well as the type
of asymptotics considered by Valkanov (2003).
, as well as the type
of asymptotics considered by Valkanov (2003).
(i) As
![]() , such that
, such that
![]() ,
,
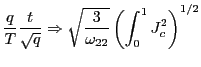 and thus
and thus 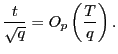
|
(15) |
(ii) As
![]() , such that
, such that
![]() ,
,
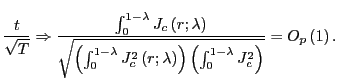
|
(16) |
where
The asymptotic results in Theorem 3 help shed light
on the general patterns seen in the figures above. Part (i)
of the theorem, which provides the limiting distribution of the
scaled ![]() test analyzed in this paper, shows that
the power of this test will increase with the relative size of the
sample to the forecasting horizon; thus, as long as the ratio
between
test analyzed in this paper, shows that
the power of this test will increase with the relative size of the
sample to the forecasting horizon; thus, as long as the ratio
between ![]() and
and ![]() is fixed, there
are no asymptotic power gains. The power is also independent of the
value of the slope coefficient
is fixed, there
are no asymptotic power gains. The power is also independent of the
value of the slope coefficient ![]() , as long as it
is different from zero. This explains the leveling out of the power
curves as
, as long as it
is different from zero. This explains the leveling out of the power
curves as ![]() grows large, and their failure to
converge to one for large values of
grows large, and their failure to
converge to one for large values of ![]() . The
intuition behind the independence of
. The
intuition behind the independence of ![]() in the
limiting distribution is best understood by explicitly writing out
the equation for the long-run returns under the alternative of
predictability. That is, since the true model is given by equations
(1) and (2), the long-run
regression equation is a fitted regression, rather than the data
generating process. As shown in the proof of Theorem 3 in the Appendix,
under the alternative of predictability, the long-run returns
in the
limiting distribution is best understood by explicitly writing out
the equation for the long-run returns under the alternative of
predictability. That is, since the true model is given by equations
(1) and (2), the long-run
regression equation is a fitted regression, rather than the data
generating process. As shown in the proof of Theorem 3 in the Appendix,
under the alternative of predictability, the long-run returns
![]() actually satisfy the
following relationship when ignoring the constant, derived from
equations (1) and
(2):
actually satisfy the
following relationship when ignoring the constant, derived from
equations (1) and
(2):
|
(17) |
There are now, in effect, two error terms, the usual
Part (ii) of the theorem states that Valkanov's scaled
![]() statistic converges to a well defined
limiting distribution that is independent of
statistic converges to a well defined
limiting distribution that is independent of ![]() and
and ![]() , although it is a function of
, although it is a function of
![]() . Thus, under the assumptions on
. Thus, under the assumptions on
![]() and
and ![]() maintained by
Valkanov, the
maintained by
Valkanov, the ![]() statistic scaled by
statistic scaled by ![]() does not diverge and hence the power of the test
does not converge to one. Of course, for a fixed
does not diverge and hence the power of the test
does not converge to one. Of course, for a fixed
![]() , the same heuristic result
follows from part (i), since as long as
, the same heuristic result
follows from part (i), since as long as ![]() does not change, there are no power gains. Thus, although
some caution is required when comparing the results in parts
(i) and (ii) of the theorem, since they are derived
under different assumptions, they lead to the same heuristic
result. Indeed, for a fixed
does not change, there are no power gains. Thus, although
some caution is required when comparing the results in parts
(i) and (ii) of the theorem, since they are derived
under different assumptions, they lead to the same heuristic
result. Indeed, for a fixed
![]() , it follows that
, it follows that
![]() and that the
results for the scaled tests in this paper should be similar to
those of Valkanov's tests.
and that the
results for the scaled tests in this paper should be similar to
those of Valkanov's tests.
The main message of Theorem 3 is thus that the
only way to achieve power gains in long-run regressions is by
increasing the sample size relative to the forecasting horizon; as
long as this ratio is fixed, there are no asymptotic power gains as
the sample size increases. The results in Theorem 3 also provide
some intuition to a somewhat counter intuitive result in Valkanov
(2003). As shown there, under the assumption that
![]() asymptotically, the estimator of
the long-run coefficient
asymptotically, the estimator of
the long-run coefficient ![]() is not consistent;
however, a scaled version of the
is not consistent;
however, a scaled version of the ![]() statistic has a
well defined distribution. That is, even though the coefficient is
not estimated consistently, valid tests can still be performed.
Theorem 3 shows the
limitation of this result: like the estimator, the test is not
consistent since there are no asymptotic power gains for a fixed
statistic has a
well defined distribution. That is, even though the coefficient is
not estimated consistently, valid tests can still be performed.
Theorem 3 shows the
limitation of this result: like the estimator, the test is not
consistent since there are no asymptotic power gains for a fixed
![]() .
.
Part (i) of Theorem 3 also suggests
that for a fixed sample size, more powerful tests of predictability
are achieved by setting the forecasting horizon as small as
possible. That is, in general, one might expect power to be
decreasing with the forecasting horizon. This is merely a heuristic
argument, since the result in part (i) of Theorem 3 is an asymptotic
result based on the assumption that
![]() . Nevertheless, it is
interesting to briefly compare the finite sample power properties
between tests at different horizons. The simulation results in the
previous section already support the conjecture that power is
decreasing with the horizon, in finite samples, as evidenced by the
rather poor power properties for the really long horizons studied
in Figures 3
and 4. The simulations
in Figure 5
make these results even clearer. The simulation setup is the same
as before, with
. Nevertheless, it is
interesting to briefly compare the finite sample power properties
between tests at different horizons. The simulation results in the
previous section already support the conjecture that power is
decreasing with the horizon, in finite samples, as evidenced by the
rather poor power properties for the really long horizons studied
in Figures 3
and 4. The simulations
in Figure 5
make these results even clearer. The simulation setup is the same
as before, with ![]() and
and ![]() . The
left hand graph shows the power curves for the scaled OLS
. The
left hand graph shows the power curves for the scaled OLS
![]() test, when
test, when ![]() , for
three different forecasting horizons,
, for
three different forecasting horizons, ![]() and
and
![]() . It is evident that as
. It is evident that as ![]() increases, the power uniformly decreases. The right hand graph
shows the case of
increases, the power uniformly decreases. The right hand graph
shows the case of
![]() , and illustrates the power
curves for the scaled Bonferroni test, for
, and illustrates the power
curves for the scaled Bonferroni test, for ![]() and
and ![]() . Again, there is a clear ranking of the
power curves from short to long horizon. Qualitatively identical
results, which are not shown, are obtained for
. Again, there is a clear ranking of the
power curves from short to long horizon. Qualitatively identical
results, which are not shown, are obtained for ![]() , and for
, and for ![]() .
.
Overall, the results here are thus supportive of the notion that
tests of predictability generally lose power as the forecasting
horizon increases. This is in line with what one might expect based
on classical statistical and econometric theory. In the case of
exogenous regressors, the OLS estimates of the single period
![]() regression in equation
(1) are identical
to the full information maximum likelihood estimates and in the
endogenous regressor case, OLS estimation of the one-period
augmented regression equation (9) is likewise
efficient. Standard analysis of power against a sequence of local
alternatives then implies that a one-period Wald test (or,
equivalently, a
regression in equation
(1) are identical
to the full information maximum likelihood estimates and in the
endogenous regressor case, OLS estimation of the one-period
augmented regression equation (9) is likewise
efficient. Standard analysis of power against a sequence of local
alternatives then implies that a one-period Wald test (or,
equivalently, a ![]() test) is asymptotically optimal
(Engle, 1984). Campbell (2001) makes this point, but also finds
that some alternative ways of comparing asymptotic power across
horizons suggest that there may be power gains from using longer
horizons; however, he finds little support for this in his Monte
Carlo simulations.
test) is asymptotically optimal
(Engle, 1984). Campbell (2001) makes this point, but also finds
that some alternative ways of comparing asymptotic power across
horizons suggest that there may be power gains from using longer
horizons; however, he finds little support for this in his Monte
Carlo simulations.
5.2 Local asymptotic power
The asymptotic power properties in the previous section were
derived under the assumption of a fixed alternative
![]() . As seen in the power curves in
the figures above, it is clear that for small values of
. As seen in the power curves in
the figures above, it is clear that for small values of ![]() , the power of the long-run tests is a function of
, the power of the long-run tests is a function of
![]() . And, in particular, there appears to
be regions of the parameter space where the power of the tests are
decreasing in the magnitude of the slope coefficient. These facts
are not reflected in the results in Theorem 3, however, and
the power properties in these regions of the parameter space are
therefore likely better analyzed with a local alternative for
. And, in particular, there appears to
be regions of the parameter space where the power of the tests are
decreasing in the magnitude of the slope coefficient. These facts
are not reflected in the results in Theorem 3, however, and
the power properties in these regions of the parameter space are
therefore likely better analyzed with a local alternative for
![]() , as is common in the literature on
evaluating the power of statistical tests. The following theorem
provides a guide to the local power properties of the scaled OLS
, as is common in the literature on
evaluating the power of statistical tests. The following theorem
provides a guide to the local power properties of the scaled OLS
![]() test proposed in this paper.
test proposed in this paper.
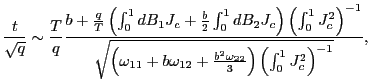
|
(18) |
where `
This theorem heuristically shows the approximate distribution of
the scaled OLS ![]() statistic for alternatives that
are close to the null hypothesis, in the sense that the slope
coefficient
statistic for alternatives that
are close to the null hypothesis, in the sense that the slope
coefficient ![]() shrinks towards zero with the
forecasting horizon. For small to moderate values of
shrinks towards zero with the
forecasting horizon. For small to moderate values of ![]() , it is evident that the
, it is evident that the ![]() statistic, and
hence the power of the test, will depend on the value of
statistic, and
hence the power of the test, will depend on the value of
![]() . For large
. For large ![]() , and small
, and small
![]() relative to
relative to ![]() , it follows
that
, it follows
that
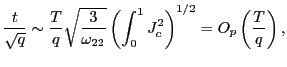
|
(19) |
which is independent of
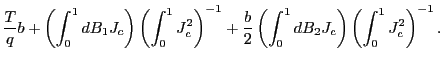
|
(20) |
Here the first term is the pure drift part, which will dominate asymptotically provided that
For large ![]() , the denominator is increasing in
, the denominator is increasing in
![]() but, in the case of
but, in the case of
![]() , there is a range of
, there is a range of
![]() for which the denominator is decreasing in
for which the denominator is decreasing in
![]() ; this explains the hump-shaped pattern in
the power curves that was documented in the Monte Carlo study. To
form an intuition behind these results, consider again the
representation of the long-run regression in equation (17). Under the
assumption that
; this explains the hump-shaped pattern in
the power curves that was documented in the Monte Carlo study. To
form an intuition behind these results, consider again the
representation of the long-run regression in equation (17). Under the
assumption that ![]() , the usual error term
, the usual error term
![]() and the additional
term
and the additional
term
![]() will both be of the same order of magnitude. When calculating the
variance of the fitted residual, which enters into the denominator
of the
will both be of the same order of magnitude. When calculating the
variance of the fitted residual, which enters into the denominator
of the ![]() statistic, the variance of both of these
terms as well as their covariance will thus enter. The covariance
statistic, the variance of both of these
terms as well as their covariance will thus enter. The covariance
![]() , when it is negative, will
induce the non-monotonicity in the
, when it is negative, will
induce the non-monotonicity in the ![]() statistic as
a function of
statistic as
a function of ![]() . Initially, as the slope coefficient
drifts away from zero, the first term will dominate and the power
of the test is increasing in
. Initially, as the slope coefficient
drifts away from zero, the first term will dominate and the power
of the test is increasing in ![]() , since the
variance of
, since the
variance of
![]() is independent of
is independent of
![]() . In a middle stage, the covariance term
becomes important as well and the
. In a middle stage, the covariance term
becomes important as well and the ![]() statistic
decreases with the slope coefficient. Finally, as
statistic
decreases with the slope coefficient. Finally, as ![]() grows large, the last term dominates and will exactly cancel out
the dependence on
grows large, the last term dominates and will exactly cancel out
the dependence on ![]() in the numerator and
denominator.
in the numerator and
denominator.
Figure 6
shows the average power curves that result from direct simulations
of the limiting random variables in equation (18). As in the
previous simulations, the variances
![]() and
and
![]() are both set equal to one. I let
are both set equal to one. I let
![]() so that the results correspond to the
finite sample power curves shown in Figures 3 and 4, where the
forecasting horizon is equal to 20 percent of the sample size. The
local-to-unity parameter
so that the results correspond to the
finite sample power curves shown in Figures 3 and 4, where the
forecasting horizon is equal to 20 percent of the sample size. The
local-to-unity parameter ![]() is set equal to zero and
is set equal to zero and
![]() repetitions are used.
repetitions are used.
The left hand graph in Figure 6 shows the case
of exogenous regressors
![]() . The
local power curve is weakly increasing and looks very similar to
the finite sample results seen in Figure 4. For endogenous
regressors with
. The
local power curve is weakly increasing and looks very similar to
the finite sample results seen in Figure 4. For endogenous
regressors with
![]() , shown in the right hand graph
in Figure 6,
the same hump shaped pattern as in Figures 3 and 4 is evident; the
biased nature of the OLS
, shown in the right hand graph
in Figure 6,
the same hump shaped pattern as in Figures 3 and 4 is evident; the
biased nature of the OLS ![]() test with endogenous
regressors is also clearly evident with a rejection rate around 40
percent under the null. The power curves based directly on the
asymptotic results in Theorem 4 thus seem to
correspond well to the finite sample ones.
test with endogenous
regressors is also clearly evident with a rejection rate around 40
percent under the null. The power curves based directly on the
asymptotic results in Theorem 4 thus seem to
correspond well to the finite sample ones.
5.3 Practical implications
The results in this section help shed more light on the
properties of long-run tests under the alternative of
predictability. The main lesson is that the power of long-horizon
tests only grows with the size of the sample relative to the
forecasting horizon; keeping ![]() fixed as
fixed as
![]() increases does not result in any power
gains. The practical implications and recommendations must
therefore be that inference on forecasts at very long horizons will
be imprecise, and caution should be used in extending the
forecasting horizon as larger samples become available. The results
here also show that the asymptotic device used in this paper, where
increases does not result in any power
gains. The practical implications and recommendations must
therefore be that inference on forecasts at very long horizons will
be imprecise, and caution should be used in extending the
forecasting horizon as larger samples become available. The results
here also show that the asymptotic device used in this paper, where
![]() , provides an important
benchmark comparison to the commonly used framework with
, provides an important
benchmark comparison to the commonly used framework with
![]() , since the test statistics are
only consistent under the former assumption. The theoretical
results here also help explain the puzzling non-monotonicity in the
power curves for long-run regressors, a finding which adds an
additional note of caution to the use of long forecasting horizons.
Note that the turning point of the power curve is not outside the
relevant parameter region. As seen in Figure 3, for
, since the test statistics are
only consistent under the former assumption. The theoretical
results here also help explain the puzzling non-monotonicity in the
power curves for long-run regressors, a finding which adds an
additional note of caution to the use of long forecasting horizons.
Note that the turning point of the power curve is not outside the
relevant parameter region. As seen in Figure 3, for ![]() , the power is already declining for
, the power is already declining for ![]() ; the results in Campbell and Yogo (2006) show that
in annual data, which the 100 observations in each simulated sample
used to generate Figure 3 might represent,
the estimates of
; the results in Campbell and Yogo (2006) show that
in annual data, which the 100 observations in each simulated sample
used to generate Figure 3 might represent,
the estimates of ![]() are between
are between ![]() and
and ![]() for the dividend and earnings-price
ratios. This also provides a strong case for the test based on the
long-run augmented regression equation suggested in this paper,
since it does not suffer from non-monotone power.
for the dividend and earnings-price
ratios. This also provides a strong case for the test based on the
long-run augmented regression equation suggested in this paper,
since it does not suffer from non-monotone power.
The results here also suggest that the power of predictive tests may be decreasing with the forecasting horizon, which would seem to imply that using one period tests is the best approach. The simulation results are supportive of this conjecture and the empirical results presented in the next section can also be interpreted as favorable of this view. However, the power comparisons across different forecasting horizons conducted in this paper are all informal and heuristic; a more thorough analysis, which is outside the scope of the current study, is required before any definitive statements can be made. Finally, one should recall one important caveat. The power results are all derived under the assumption that the true model is the one given by equations (1) and (2). This is a standard assumption used by, for instance, Nelson and Kim (1993) and Campbell (2001), but clearly other potential data generating processes that might lead to different results are possible. The results under the model analyzed here, however, can be considered a point of reference against which to compare other specifications.
6 Long-run stock return predictability
To illustrate the theoretical results derived in this paper, I revisit the question of stock return predictability. There have been many conflicting results regarding the existence of a predictable component in stock returns. However, recent work by Lewellen (2004) and Campbell and Yogo (2006), which rely on both more robust as well as more efficient methods of inference than previous research, do find evidence that stock returns are predictable to some degree. In this section, I extend their empirical analysis to the long-horizon case. Since the scaled long-run Bonferroni test, which controls for the endogeneity and persistence in the regressors, is effectively a long-run version of the methods developed in Campbell and Yogo (2006), the empirical results presented here provide a direct comparison with previous work. In the first part of the empirical analysis, I therefore analyze the same data as those used by Campbell and Yogo. I then consider the evidence in an international data set from nine additional countries. The section ends with a discussion of the results.
6.1 The data
6.1.1 The U.S. data
The data on U.S. stock returns and predictor variables are the
same as those used by Campbell and Yogo (2006).13The returns data
consist of the monthly and annual excess returns on the CRSP
NYSE/AMEX value-weighted index over the period 1926-2002, as well
as annual returns on the S&P 500 index over the period
1880-2002. The excess returns are calculated as the stock returns
over the risk free rate, measured by the return on the one-month
T-bill for the monthly data, and by the return on the three-month
T-bill rolled over quarterly for the annual data. The predictor
variables are the dividend-price ratio
![]() , the smoothed
earnings-price ratio
, the smoothed
earnings-price ratio
![]() suggested by Campbell and
Shiller (1988), the 3-month T-bill rate
suggested by Campbell and
Shiller (1988), the 3-month T-bill rate
![]() , and the long-short
yield spread
, and the long-short
yield spread
![]() , which is defined as
the difference between Moody's seasoned Aaa corporate bond yield
and the one month T-bill rate. The dividend-price ratio is
calculated as dividends over the past year divided by the current
price and the (smoothed) earnings-price ratio as the average
earnings of the past 10 years divided by the current price. Since
earnings are not available for the CRSP data, the corresponding
S&P 500 earnings are used. All regressions are run using
log-transformed variables with the log excess returns as the
dependent variable. The regressions involving the short-rate and
the yield-spread as predictors are estimated over the period
1952-2002, since prior to this time period the interest rate was
pegged by the Federal Reserve. The regressions with the CRSP data,
using the dividend- and earnings-price ratios as predictors, are
also analyzed over this period as a comparison to the full sample
results.
, which is defined as
the difference between Moody's seasoned Aaa corporate bond yield
and the one month T-bill rate. The dividend-price ratio is
calculated as dividends over the past year divided by the current
price and the (smoothed) earnings-price ratio as the average
earnings of the past 10 years divided by the current price. Since
earnings are not available for the CRSP data, the corresponding
S&P 500 earnings are used. All regressions are run using
log-transformed variables with the log excess returns as the
dependent variable. The regressions involving the short-rate and
the yield-spread as predictors are estimated over the period
1952-2002, since prior to this time period the interest rate was
pegged by the Federal Reserve. The regressions with the CRSP data,
using the dividend- and earnings-price ratios as predictors, are
also analyzed over this period as a comparison to the full sample
results.
6.1.2 The international data
The international data used in this paper come from Global Financial Data. Total returns, including direct returns from dividends, on market-wide indices in nine countries with at least 50 years of data were obtained, as well as the corresponding dividend-price ratios. Earnings data were typically only available over much shorter time periods and long-run regressions with the earnings-price ratio as a predictor are therefore not included in the international analysis. In addition, for each country, measures of the short and long interest rates were obtained, from which measures of the term spread were constructed. The variable definitions follow the usual conventions in the literature. The dividend-price ratio is defined as the sum of dividends during the past year, divided by the current price. The measure of the short interest rate comes from the interest rate series constructed by Global Financial Data and uses rates on 3-month T-bills when available or, otherwise, private discount rates or interbank rates. The long rate is measured by the yield on long-term government bonds. When available, a 10 year bond is used; otherwise, I use that with the closest maturity to 10 years. The term spread is defined as the log difference between the long and the short rate. Excess stock returns are defined as the return on stocks, in the local currency, over the local short rate, which provides the international analogue of the typical forecasting regressions estimated for U.S. data.
The predictor variables used in the international sample are
therefore the dividend-price ratio
![]() , the short interest rate
, the short interest rate
![]() and the term spread
and the term spread
![]() , where the latter
two are meant to capture similar features of stock return
predictability as the corresponding interest rate variables in the
U.S. sample, even though they are not defined in an identical
manner.
, where the latter
two are meant to capture similar features of stock return
predictability as the corresponding interest rate variables in the
U.S. sample, even though they are not defined in an identical
manner.
The countries in the data are: Australia, Belgium, Canada, France, Germany, Italy, Japan, Sweden, and the U.K. The end date for each series is March 2004, although the starting date varies between the countries. The longest series is for Australia, which dates back to 1882, and the shortest for Germany, which goes back to 1953. All returns and interest rate data are on a monthly frequency. For a few of the older observations, the dividend-price ratios are given on an annual basis; these are transformed to monthly data by filling in the monthly dividends over the year with the previous year's values.14
All regressions are run using log-transformed variables with the log excess returns over the domestic short rate as the dependent variable. Following the convention used in the U.S. data, the data used in all interest rate regressions are restricted to start in 1952 or after.15 Again, as a comparison, the predictive regression with the dividend price ratios are also run over this restricted sample period; in the international data, this is particularly useful, since the starting points of the series vary from country to country and imposing a common starting date allows for easier cross-country comparison.
6.2 Characteristics of the predictor variables
The two key data characteristics that define the properties of
the regression estimators analyzed in this paper are the near
persistence and endogeneity of the regressors. For the U.S. data,
Table 2 shows
confidence intervals for the autoregressive root ![]() , and the analogue intervals for the local-to-unity
parameter
, and the analogue intervals for the local-to-unity
parameter ![]() , calculated by inverting the DF-GLS
unit-root test, as well as estimates of the correlation between the
innovations to returns and the innovations to the regressors
, calculated by inverting the DF-GLS
unit-root test, as well as estimates of the correlation between the
innovations to returns and the innovations to the regressors
![]() . The results are shown
both for the full sample period, as well as for the post 1952
sample. As is evident, there is a large negative correlation
between the innovations to the returns and the valuation-ratios.
The short interest rate is nearly exogenous, however. The yield
spread is also almost exogenous in the monthly data, although it
exhibits a somewhat larger correlation in the annual data. Standard
OLS inference might thus be expected to work fairly well when using
the short rate or the yield spread as predictor variables. In
addition, all variables, except perhaps the annual yield spread,
show signs of having autoregressive roots that are close to
unity.
. The results are shown
both for the full sample period, as well as for the post 1952
sample. As is evident, there is a large negative correlation
between the innovations to the returns and the valuation-ratios.
The short interest rate is nearly exogenous, however. The yield
spread is also almost exogenous in the monthly data, although it
exhibits a somewhat larger correlation in the annual data. Standard
OLS inference might thus be expected to work fairly well when using
the short rate or the yield spread as predictor variables. In
addition, all variables, except perhaps the annual yield spread,
show signs of having autoregressive roots that are close to
unity.
The corresponding results for the international data are given
in Table 3, where
the sample period available for each country is also given.
Overall, the international predictor variables are similar to the
corresponding U.S. ones. The dividend-price ratio is highly
persistent in all countries, and the null hypothesis of a unit root
can typically not be rejected based on the DF-GLS test statistic.
Furthermore, the dividend-price ratio is generally fairly
endogenous, in the sense that the estimates of ![]() , the correlation between the innovations to the
returns and the predictor process, are large in absolute value.
Compared to the U.S. data, however, the estimates of
, the correlation between the innovations to the
returns and the predictor process, are large in absolute value.
Compared to the U.S. data, however, the estimates of ![]() for the dividend-price ratio are generally somewhat
smaller in absolute value, typically ranging from
for the dividend-price ratio are generally somewhat
smaller in absolute value, typically ranging from ![]() to
to ![]() , whereas in the U.S. data absolute
values above
, whereas in the U.S. data absolute
values above ![]() are common. The short interest rate
and the term spread also behave similar to the U.S. counterparts.
They are mostly exogenous but still highly persistent.
are common. The short interest rate
and the term spread also behave similar to the U.S. counterparts.
They are mostly exogenous but still highly persistent.
Both the U.S. and the international data thus seem to fit well the assumptions under which the results in this paper are derived. In addition, at least for the valuation ratios, there is a strong case for using test statistics that take into account the bias induced by the endogeneity and persistence in the regressors. For the interest rate variables, OLS inference should be fairly accurate.
6.3 Long-run regression results for the U.S. data
The results from the long-run regressions are presented
graphically as plots of the scaled ![]() statistics
against the forecasting horizon
statistics
against the forecasting horizon ![]() . Although the
results in previous sections suggest that using very long
forecasting horizons are generally not advisable, I will show
results for forecasting horizons out to 20 years in the annual data
and 10 years in the monthly data, to illustrate the properties of
the test statistics across most potential forecasting horizons that
may be used in applied work.
. Although the
results in previous sections suggest that using very long
forecasting horizons are generally not advisable, I will show
results for forecasting horizons out to 20 years in the annual data
and 10 years in the monthly data, to illustrate the properties of
the test statistics across most potential forecasting horizons that
may be used in applied work.
In each plot, the values of the scaled OLS ![]() statistics along with the scaled Bonferroni
statistics along with the scaled Bonferroni ![]() statistics are plotted against the forecasting horizon; as
a point of reference, the five percent significance level in a one
sided test is also shown, i.e. a flat line equal to
statistics are plotted against the forecasting horizon; as
a point of reference, the five percent significance level in a one
sided test is also shown, i.e. a flat line equal to ![]() . The Bonferroni test statistic is calculated in the
same manner as described in Section 3. Given the
asymptotic results developed previously, the scaled Bonferroni
. The Bonferroni test statistic is calculated in the
same manner as described in Section 3. Given the
asymptotic results developed previously, the scaled Bonferroni
![]() statistic will be approximately normally
distributed for all predictor variables, whereas for the scaled OLS
statistic will be approximately normally
distributed for all predictor variables, whereas for the scaled OLS
![]() test, the normal approximation will only
be satisfied for exogenous variables and might thus be expected to
work well with the interest rate variables. In addition to the
scaled Bonferroni test statistic, I also show the value of the
scaled
test, the normal approximation will only
be satisfied for exogenous variables and might thus be expected to
work well with the interest rate variables. In addition to the
scaled Bonferroni test statistic, I also show the value of the
scaled ![]() statistic evaluated for
statistic evaluated for
![]() (i.e.
(i.e. ![]() ). The
maximum of this test statistic and the Bonferroni test
statistic can be seen as the value of the Bonferroni test when
explosive
). The
maximum of this test statistic and the Bonferroni test
statistic can be seen as the value of the Bonferroni test when
explosive
![]() roots are ruled out
a priori.16 This additional statistic is not
shown for the interest rate variables where the Bonferroni and OLS
statistics are already very close to each other.17
roots are ruled out
a priori.16 This additional statistic is not
shown for the interest rate variables where the Bonferroni and OLS
statistics are already very close to each other.17
The first set of results are displayed in Figure 7, which shows
the scaled OLS and Bonferroni ![]() statistics from
the regressions with the dividend- and earnings-price ratios in the
annual full sample U.S. data. As is to be expected, the results for
the one period forecasting horizon are qualitatively identical to
those in Campbell and Yogo (2006). Thus, at the shorter horizons,
there is some mixed evidence of predictability, with the null
rejected for both the S&P 500 and the CRSP returns when using
the earnings-price ratio, but only for the CRSP returns when using
the dividend-price ratio. It is interesting to note that although
the Bonferroni test is more robust than the OLS test, the numerical
outcome of the Bonferroni test need not always be smaller than the
biased OLS
statistics from
the regressions with the dividend- and earnings-price ratios in the
annual full sample U.S. data. As is to be expected, the results for
the one period forecasting horizon are qualitatively identical to
those in Campbell and Yogo (2006). Thus, at the shorter horizons,
there is some mixed evidence of predictability, with the null
rejected for both the S&P 500 and the CRSP returns when using
the earnings-price ratio, but only for the CRSP returns when using
the dividend-price ratio. It is interesting to note that although
the Bonferroni test is more robust than the OLS test, the numerical
outcome of the Bonferroni test need not always be smaller than the
biased OLS ![]() statistic. In addition, in Figure
7,
the
statistic. In addition, in Figure
7,
the ![]() statistics based on Newey-West standard
errors are also shown, calculated using
statistics based on Newey-West standard
errors are also shown, calculated using ![]() lags.
Comparing the plots of these against the properly scaled
lags.
Comparing the plots of these against the properly scaled
![]() statistics, it is apparent that Newey-West
errors can fail substantially in controlling the size of
long-horizon test. They also illustrate why long-run predictability
is often thought to be stronger than short-run predictability.
Given the well known biases in the Newey-West statistics, in the
subsequent figures they are not shown in order to keep the graphs
more easily readable.
statistics, it is apparent that Newey-West
errors can fail substantially in controlling the size of
long-horizon test. They also illustrate why long-run predictability
is often thought to be stronger than short-run predictability.
Given the well known biases in the Newey-West statistics, in the
subsequent figures they are not shown in order to keep the graphs
more easily readable.
Similar results to those in Figure 7 are also
found in Figure 8, which shows the
results for monthly CRSP returns, both for the full sample from
1926 and in the post 1952 sample, using the dividend- and
earnings-price ratios as predictors. Again, there is mixed evidence
of predictability. The results in Figure 8 also
illustrates that ruling out explosive processes, i.e. restricting
![]() to be less than or equal to one, can
have a substantial impact on the results. In the sub sample from
1952-2002, the evidence in favour of predictability is
substantially greater when ruling out explosive processes. This
great sensitivity stems from the extreme endogeneity of the
dividend- and earnings-price ratios in the U.S. data, with absolute
values of
to be less than or equal to one, can
have a substantial impact on the results. In the sub sample from
1952-2002, the evidence in favour of predictability is
substantially greater when ruling out explosive processes. This
great sensitivity stems from the extreme endogeneity of the
dividend- and earnings-price ratios in the U.S. data, with absolute
values of ![]() upwards of
upwards of ![]() .
.
From the perspective of the theoretical analysis in the current
paper, the results in Figures 7 and 8 illustrate
two key findings. First, and contrary to many popular beliefs, the
evidence of predictability does not typically become stronger at
longer forecasting horizons. There are some exceptions, such as the
results for the dividend-price ratio in the full CRSP sample in
Figure 8, but overall
there is little tendency for the results to look stronger at longer
horizons. If anything, there is a tendency for the properly scaled
![]() statistics to become smaller as the
horizon increases, which would be consistent with a loss of power.
Second, these results show that it is important to control for the
biasing effect of persistent and endogenous regressors also in
long-horizon regressions, as seen from the often large difference
between the OLS and the Bonferroni test statistics.
statistics to become smaller as the
horizon increases, which would be consistent with a loss of power.
Second, these results show that it is important to control for the
biasing effect of persistent and endogenous regressors also in
long-horizon regressions, as seen from the often large difference
between the OLS and the Bonferroni test statistics.
Figure 9 shows the results for the short rate and the yield spread, both for the annual and the monthly data. As expected, the OLS and Bonferroni results are now very close to each other, reflecting the nearly exogenous nature of the interest rate variables. For the short rate, the one-sided alternative is now a negative coefficient. In order to achieve easy comparison with the rest of the results in general, and the yield-spread in particular, the negative of the test statistics are plotted for the short rate. As seen, there is evidence of predictability at very short horizons, which disappears very fast as the horizon increases. In fact, the evidence is already gone in the annual data at the one-period horizon. A similar result is found for the yield spread, where the expected coefficient under the alternative of predictability is again positive.
The one-period, or short-run, empirical findings for the U.S. data are qualitatively identical to those of Campbell and Yogo (2006). The bottom line is that there is fairly robust evidence of predictability in U.S. data in the short run when using the two interest rate variables as predictors, whereas the evidence for the valuation ratios is more mixed. The results from the regressions with the dividend- and earnings-price ratios are made more difficult to interpret given the large endogeneity of the regressors. As is seen, for instance, restricting the autoregressive root to be less than or equal to unity can change the results rather dramatically, a point which is discussed in detail in Campbell and Yogo (2006); these results thus illustrate well the power gains that can be made with additional knowledge regarding the true autoregressive root in the process. Although restricting the regressor to be a non-explosive process seems like a fairly sensible restriction in most cases, it should also be stressed that imposing a non-explosive condition on the dividend-price ratio, for instance, is not necessarily completely innocuous. Lettau and Van Nieuwerburgh (2007) show that there is evidence of structural breaks in the valuation ratios in U.S. data and that if one takes into account these breaks, the predictive ability of these ratios improves. A structural break process is inherently non-stationary and is indeed very hard to distinguish from a highly persistent process of the kinds analyzed in this paper, especially if one allows for explosive roots. Some caution is therefore required in ruling out explosive processes, a point also made by Campbell and Yogo (2006).
6.4 Long-run regression results for the international data
The results for the international data are shown in Figures 10-13. The results for the dividend-price ratio are shown in Figure 10 for the full sample and in Figure 11 for the post 1952 sample. Given the somewhat mixed and overall fairly weak results in the U.S. data, the international results are close to what one might expect. There is some weak evidence of predictability in the full sample for Canada, as well as for Japan. In both the Canadian and Japanese cases, however, these results are no longer significant in the post 1952 sample, which is particularly striking for Japan since the full sample only stretches back to 1949. The results for both Canada and Japan are also sensitive to the exclusion of explosive roots. The only country for which there is consistently strong evidence is the U.K. Again, there is little evidence of stronger predictability in the long-run. The only significant result in this direction is for the full Canadian sample where there is no predictability at the first few horizons; the results are far from striking, however.
The results for the interest rate variables, shown in Figures 12 and 13, are somewhat more favorable of predictability. For the short-rate, shown in Figure 12, where again the alternative hypothesis is a negative coefficient and the negative of the test statistic is plotted, significance is found at short horizons in Canada and Germany, and close to significance in Australia, France, and Italy. The corrections for endogeneity have little effect, and the OLS and Bonferroni results are very close to each other. The only exception is at long horizons for Japan where there is some discrepancy, although not enough to change any conclusions if one were to rely on the OLS analysis.
For the term spread, shown in Figure 13, the results look similar but somewhat stronger, with significant short-run coefficients found for Canada, France, Germany, and Italy, and for a few horizons for Australia. Again, with the exception of Australia, the evidence of predictability disappears very fast as the horizon increases.
The results from the international data support the U.S.
conclusions to some extent. The evidence in favour of
predictability using the dividend-price ratio in international data
is overall weak, with the only solid evidence coming from the U.K.
data. The evidence from Canada and Japan is weaker and more
sensitive to the sampling period. Although the scaled Bonferroni
statistic is generally much smaller than the scaled OLS ![]() statistic in the international data as well, the evidence
based on the OLS results themselves is not that supportive of a
predictive relationship either. Thus, although some power gains
would still be had from a more precise knowledge of the
autoregressive root in the data, the international results may be
somewhat less susceptible to this critique than the U.S. results.
The international results for the interest rate variables are again
similar to those of the U.S. data, but do not fully support any
generic statements about the predictive ability of these variables.
However, there is some commonality across the country results for
these variables. This is particularly true for Australia, Canada,
France, Germany, and Italy, where the significant results are
found.
statistic in the international data as well, the evidence
based on the OLS results themselves is not that supportive of a
predictive relationship either. Thus, although some power gains
would still be had from a more precise knowledge of the
autoregressive root in the data, the international results may be
somewhat less susceptible to this critique than the U.S. results.
The international results for the interest rate variables are again
similar to those of the U.S. data, but do not fully support any
generic statements about the predictive ability of these variables.
However, there is some commonality across the country results for
these variables. This is particularly true for Australia, Canada,
France, Germany, and Italy, where the significant results are
found.
6.5 Discussion of the empirical findings
The empirical findings can broadly be summed up as follows: (i) The evidence of predictability using the valuation ratios is overall fairly weak, both in the U.S. and the international data. (ii) The predictive ability of the interest rate variables appears fairly robust in the U.S. data and extends to some degree to the international data. (iii) With few exceptions, all evidence of predictability is found for the shortest horizons and any evidence that does exist tends to disappear as the forecasting horizon increases; this is particularly true for the interest rate variables where the test statistics are often almost monotonically declining in value with the forecasting horizons.
Points (i) and (ii) are discussed at some length in Campbell and Yogo (2006) and Ang and Bekaert (2007), although the international sample used by the latter is somewhat smaller than the one used here. Instead, I will focus on the third point regarding the long-run results. Contrary to many popular beliefs, the results here show that evidence of predictability in the long-run is not stronger than in the short-run. In fact, in most cases the opposite appears true.
If the data are generated by the standard model in equations (1) and (2), predictability in the short-run also implies predictability in the long-run. However, the analytical results in this paper also show that tests lose power as the horizon increases, which could explain the findings presented here. That is, even if the results from the one-period regressions are correct, and there is predictability in some cases, there is no guarantee that this predictability will be evident at longer horizons, given a decrease in the power to detect it. In practice, the evidence of predictability is weak also at short horizons, and it should therefore not be surprising that the null of no predictability cannot be rejected for longer horizons.18 The empirical results are thus consistent with the model in equations (1) and (2), under which the analytical results were derived. Consistent empirical findings of long-run, but not short-run, predictability, on the other hand, would suggest that equations (1) and (2) are not adequate tools for modelling return predictability.
Torous et al. (2004) and Ang and Bekaert (2007) also find that the evidence of predictability tends to be strongest at shorter horizons, although they do not suggest the possibility that this may be due to a lack of power in long horizon tests. Boudoukh et al. (2005) explicitly question the prevailing view of long-horizon predictability and reach similar conclusions to those presented here, although their focus is on the joint properties of the regression estimators across different horizons. Taken together, there is thus mounting evidence against the previously prevailing view that stock return predictability is more apparent in the long-run than in the short-run.
7 Conclusion
I derive several new results for long-horizon regressions that use overlapping observations when the regressors are endogenous and highly persistent. I show how to properly correct for the overlap in the data in a simple manner that obviates the need for auto-correlation robust standard error methods in these regressions. Further, when the regressors are persistent and endogenous, I show how to correct the long-run OLS estimators and test procedures in a manner similar to that proposed by Campbell and Yogo (2006) for the short-run case.
The analysis also highlights the boundaries of long-horizon regressions. Analytical results, supported by Monte Carlo simulations, show that there are no power gains to long-run tests as long as the ratio between the forecasting horizon and the sample size is fixed. Thus, increasing the forecasting horizon as more data becomes available is not a good strategy.
An empirical application to stock-return predictability illustrates these results and shows that, in line with the theoretical results of this paper, the evidence for predictability is typically weaker as the forecasting horizon gets longer, reflecting at least to some extent the loss of power in long-run tests.
A Proofs
For ease of notation the case with no intercept is treated. The
results generalize immediately to regressions with fitted
intercepts by replacing all variables by their demeaned versions.
Unless otherwise noted, all limits as
![]() are under the condition
that
are under the condition
that
![]() .
.
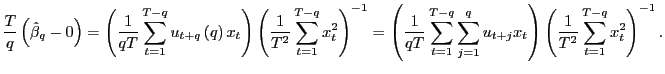
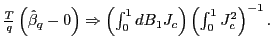
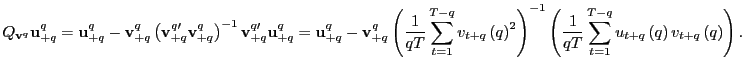
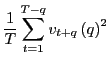 |
||
Now, observe that
![$\displaystyle \frac{1}{qT}\sum_{t=1}^{T-q}v_{t+q}\left( q\right) ^{2}\overset{d}{=} \frac{1}{q}\left[ q\hat{\gamma}_{vv}\left( 0\right) +\left( q-1\right) \hat{\gamma}_{vv}\left( -1\right) +...+\hat{\gamma}_{vv}\left( -\left( q-1\right) \right) +\hat{\gamma}_{vv}\left( q-1\right) +...+\left( q-1\right) \hat{\gamma}_{vv}\left( 1\right) \right]$](img638.gif) |
||
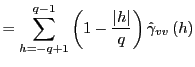 |
and as
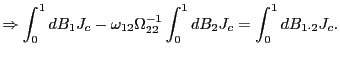 |
Finally, as
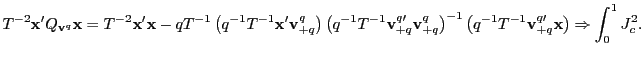
![]()
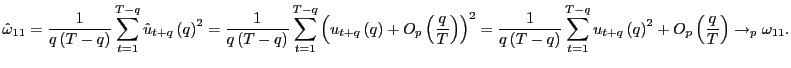
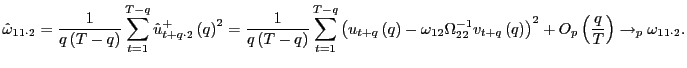
![]()
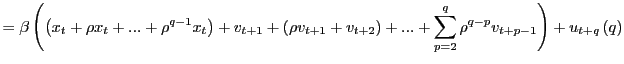
|
||
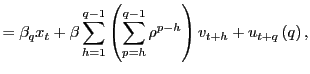
|
where
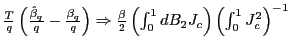 , and thus
, and thus
![$\displaystyle \frac{1}{q^{3}T}\beta^{2}\sum_{t=1}^{T-q}\left( \sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) v_{t+h}\right) ^{2}=\frac{1}{q^{3}T} \beta^{2}\sum_{t=1}^{T-q}\left[ \sum_{h=1}^{q-1}\sum_{k=1}^{q-1}\left( q-h\right) \left( q-k\right) v_{t+h}v_{t+k}\right] +o_{p}\left( 1\right)$](img672.gif)
|
||
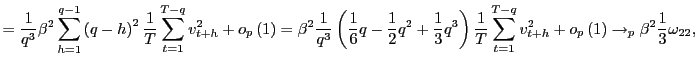
|
where the first equality follows from the local-to-unity nature of
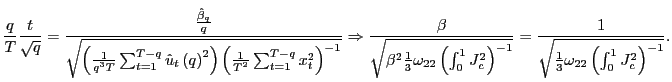
(ii) Consider next the case when
![]() as
as
![]() . By summing up on both
sides in equation (1),
. By summing up on both
sides in equation (1),
![]() , and the fitted regression is
, and the fitted regression is
![]() .
It follows that,
.
It follows that,
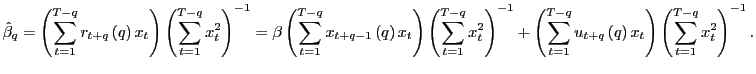
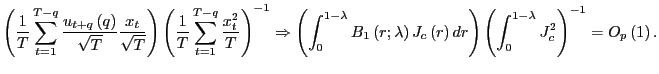
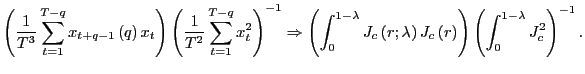
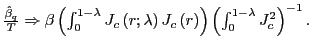 The fitted residuals satisfy
The fitted residuals satisfy
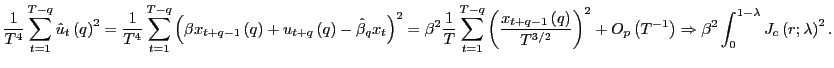
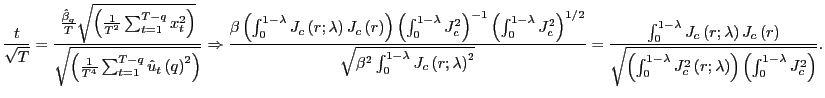
![]()
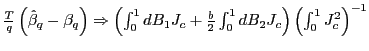 , where
, where
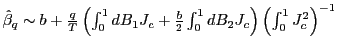 . As before,
. As before,
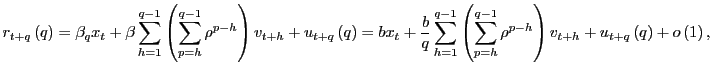
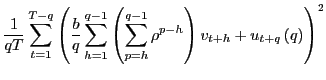
|
||
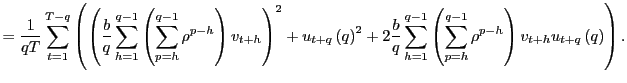
|
By previous results,
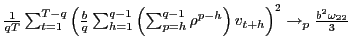 and
and
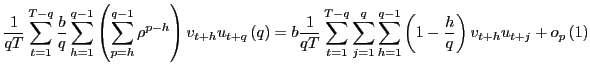
|
||
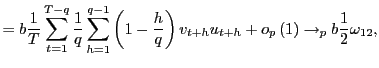
|
since
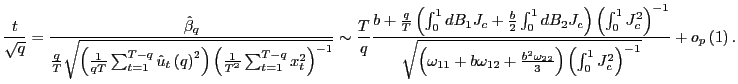
References
Andrews, D.W.K., 1991. Heteroskedasticity and autocorrelation consistent covariance matrix estimation, Econometrica 59, 817-858.
Ang, A., and G. Bekaert, 2007. Stock return predictability: is it there? Review of Financial Studies 20, 651-707.
Boudoukh J., and M. Richardson, 1993. Stock returns and inflation: a long-horizon perspective, American Economic Review 83, 1346-1355.
Boudoukh J., M. Richardson, and R.F. Whitelaw, 2005. The myth of long-horizon predictability, forthcoming Review of Financial Studies.
Berkowitz, J., and L. Giorgianni, 2001. Long-horizon exchange rate predictability?, Review of Economics and Statistics 83, 81-91.
Campbell, J.Y., 2001. Why long horizons? A study of power against persistent alternatives, Journal of Empirical Finance 8, 459-491.
Campbell, J.Y., and R. Shiller, 1988. Stock prices, earnings, and expected dividends, Journal of Finance 43, 661-676.
Campbell, J.Y., and M. Yogo, 2005. Implementing the econometric methods in `` Efficient tests of stock return predictability''. Working paper, University of Pennsylvania.
Campbell, J.Y., and M. Yogo, 2006. Efficient tests of stock return predictability, Journal of Financial Economics 81, 27-60.
Cavanagh, C., G. Elliot, and J. Stock, 1995. Inference in models with nearly integrated regressors, Econometric Theory 11, 1131-1147.
Corbae D., S. Ouliaris, and P.C.B. Phillips, 2002. Band spectral regression with trending data, Econometrica 70, 1067-1109.
Daniel, K., 2001. The power and size of mean reversion tests, Journal of Empirical Finance 8, 493-535.
Elliot G., T.J. Rothenberg, and J.H. Stock, 1996. Efficient tests for an autoregressive unit root, Econometrica 64, 813-836.
Engle, R.F., 1984. Wald, likelihood ratio and lagrange multiplier tests in econometrics, in Handbook of Econometrics, vol II., edited by Z. Griliches, and M.D. Intriligator. Amsterdam, North Holland.
Fama, E.F., and K.R. French, 1988. Dividend yields and expected stock returns, Journal of Financial Economics 22, 3-25.
Fisher, M.E., and J.J. Seater, 1993. Long-run neutrality and superneutrality in an ARIMA Framework, American Economic Review 83, 402-415.
Goetzman W.N., and P. Jorion, 1993. Testing the predictive power of dividend yields, Journal of Finance 48, 663-679.
Hansen, L.P., and R.J. Hodrick, 1980. Forward exchange rates as optimal predictors of future spot rates: An Econometric Analysis, Journal of Political Economy 88, 829-853.
Hjalmarsson, E., 2007. Fully modified estimation with nearly integrated regressors, Finance Research Letters 4, 92-94.
Hjalmarsson, E., 2008. Interpreting long-horizon estimates in predictive regressions, Finance Research Letters 5, 104-117.
Hodrick, R.J., 1992. Dividend yields and expected stock returns: alternative procedures for inference and measurement, Review of Financial Studies 5, 357-386.
Jansson, M., and M.J. Moreira, 2006. Optimal inference in regression models with nearly integrated regressors, Econometrica 74, 681-714.
Kaminsky G.L., and S.L. Schmukler, 2002. Short-run pain, long-run gain: the effects of financial liberalization, Working Paper, George Washington University.
Lanne, M., 2002. Testing the predictability of stock returns, Review of Economics and Statistics 84, 407-415.
Lettau, M., and S. Van Nieuwerburgh, 2007. Reconciling the return predictability evidence, forthcoming Review of Financial Studies.
Lewellen, J., 2004. Predicting returns with financial ratios, Journal of Financial Economics, 74, 209-235.
Mankiw, N.G., and M.D. Shapiro, 1986. Do we reject too often? Small sample properties of tests of rational expectations models, Economics Letters 20, 139-145.
Mark, N.C., 1995. Exchange rates and fundamentals: evidence on long-horizon predictability, American Economic Review 85, 201-218.
Mark, N.C., and D. Sul, 2004. The use of predictive regressions at alternative horizons in finance and economics, NBER Technical Working Paper 298.
Mishkin, F.S., 1990. What does the term structure tell us about future inflation?, Journal of Monetary Economics 25, 77-95.
Mishkin, F.S., 1992. Is the Fisher effect for real?, Journal of Monetary Economics 30, 195-215.
Moon, R., A. Rubia, and R. Valkanov, 2004. Long-horizon regressions when the predictor is slowly varying, Working Paper, UCLA, Anderson School of Management.
Nelson, C.R., and M.J. Kim, 1993. Predictable stock returns: the role of small sample bias, Journal of Finance 48, 641-661.
Newey, W., and K. West, 1987. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix, Econometrica 55, 703-708.
Phillips, P.C.B, 1987. Towards a unified asymptotic theory of autoregression, Biometrika 74, 535-547.
Phillips, P.C.B, 1988. Regression theory for near-integrated time series, Econometrica 56, 1021-1043.
Phillips, P.C.B, 1991a. Optimal inference in cointegrated systems, Econometrica 59, 283-306.
Phillips, P.C.B, 1991b. Spectral regression for cointegrated time series, in Nonparametric and Semiparametric Methods in Economics and Statistics, edited by W. Barnett, J. Powell, and G. Tauchen. Cambridge, Cambridge University Press.
Polk, C., S. Thompson, and T. Vuolteenaho, 2006. Cross-sectional forecasts of the equity premium, Journal of Financial Economics 81, 101-141.
Rapach D.E., and M.E. Wohar, 2005. Valuation ratios and long-horizon stock price predictability, Journal of Applied Econometrics 20, 327-344.
Richardson, M., and T. Smith, 1991. Tests of financial models in the presence of overlapping observations, Review of Financial Studies 4, 227-254.
Richardson, M., and J.H. Stock, 1989. Drawing inferences from statistics based on multiyear asset returns, Journal of Financial Economics 25, 323-348.
Rossi, B., 2005. Testing long-horizon predictive ability with high persistence, and the Meese-Rogoff puzzle, International Economic Review 46, 61-92.
Stambaugh, R., 1999. Predictive regressions, Journal of Financial Economics 54, 375-421.
Stock, J.H., 1991. Confidence intervals for the largest autoregressive root in U.S. economic time-series. Journal of Monetary Economics 28, 435-460.
Torous, W., R. Valkanov, and S. Yan, 2004. On predicting stock returns with nearly integrated explanatory variables, Journal of Business 77, 937-966.
Valkanov, R., 2003. Long-horizon regressions: theoretical results and applications, Journal of Financial Economics 68, 201-232.
Table 1.1a - Long-Run OLS t-Test: T = 100, c = 0
Finite sample sizes for the scaled long-run OLS t-test, the scaled Bonferroni test and the scaled infeasible test. The first column gives the forecasting horizon q, and the top row below the labels gives the value of the parameter ![]() , the correlation between the innovation processes. The remaining entires show, for each combination of q and
, the correlation between the innovation processes. The remaining entires show, for each combination of q and ![]() , the average rejection rates under the null hypothesis of no predictability for the corresponding test. The results are based on the Monte Carlo simulation described in the main text and the average rejection rates are calculated over 10,000 repetitions. Results for the sample sizes T equal to 100 and 500 and for local-to-unity parameters c equal to 0 and -10 are shown; for T=100, these values correspond to autoregressive roots
, the average rejection rates under the null hypothesis of no predictability for the corresponding test. The results are based on the Monte Carlo simulation described in the main text and the average rejection rates are calculated over 10,000 repetitions. Results for the sample sizes T equal to 100 and 500 and for local-to-unity parameters c equal to 0 and -10 are shown; for T=100, these values correspond to autoregressive roots ![]() =1 and
=1 and ![]() =0.9, respectively, and for T=500, they correspond to
=0.9, respectively, and for T=500, they correspond to ![]() =1 and
=1 and ![]() =0.98.
=0.98.
| q | ||||||
|---|---|---|---|---|---|---|
1 | 0.058 | 0.102 | 0.188 | 0.295 | 0.385 | 0.419 |
| 5 | 0.052 | 0.110 | 0.186 | 0.303 | 0.399 | 0.434 |
| 10 | 0.048 | 0.102 | 0.185 | 0.306 | 0.421 | 0.458 |
| 15 | 0.048 | 0.101 | 0.171 | 0.294 | 0.405 | .0451 |
| 20 | 0.043 | 0.088 | 0.166 | 0.289 | 0.392 | 0.435 |
| 25 | 0.040 | 0.082 | 0.154 | 0.261 | 0.365 | 0.403 |
Table 1.1b - Long-Run OLS t-Test: T = 500, c = 0
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.051 | 0.099 | 0.176 | 0.298 | 0.381 | 0.415 |
| 25 | 0.051 | 0.100 | 0.179 | 0.305 | 0.407 | 0.438 |
| 50 | 0.053 | 0.108 | 0.181 | 0.301 | 0.410 | 0.458 |
| 75 | 0.051 | 0.099 | 0.177 | 0.287 | 0.398 | 0.450 |
| 100 | 0.045 | 0.092 | 0.161 | 0.280 | 0.382 | 0.436 |
| 125 | 0.039 | 0.080 | 0.146 | 0.258 | 0.363 | 0.406 |
Table 1.1c - Long-Run OLS t-Test: T = 100, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.052 | 0.071 | 0.097 | 0.123 | 0.137 | 0.143 |
| 5 | 0.044 | 0.058 | 0.083 | 0.102 | 0.117 | 0.130 |
| 10 | 0.033 | 0.045 | 0.063 | 0.082 | 0.098 | 0.108 |
| 15 | 0.022 | 0.036 | 0.048 | 0.067 | 0.082 | 0.089 |
| 20 | 0.018 | 0.027 | 0.039 | 0.056 | 0.064 | 0.069 |
| 25 | 0.011 | 0.019 | 0.028 | 0.039 | 0.046 | 0.048 |
Table 1.1d - Long-Run OLS t-Test: T = 500, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.050 | 0.069 | 0.091 | 0.122 | 0.136 | 0.140 |
| 25 | 0.038 | 0.059 | 0.078 | 0.106 | 0.123 | 0.128 |
| 50 | 0.033 | 0.045 | 0.070 | 0.087 | 0.104 | 0.104 |
| 75 | 0.024 | 0.036 | 0.054 | 0.076 | 0.086 | 0.091 |
| 100 | 0.018 | 0.029 | 0.040 | 0.057 | 0.064 | 0.071 |
| 125 | 0.010 | 0.020 | 0.031 | 0.038 | 0.051 | 0.053 |
1.2a - Bonferroni Test: T = 100, c = 0
| q | ||||||
|---|---|---|---|---|---|---|
1 | 0.044 | 0.045 | 0.042 | 0.046 | 0.053 | 0.068 |
| 5 | 0.043 | 0.046 | 0.042 | 0.043 | 0.053 | 0.057 |
| 10 | 0.041 | 0.048 | 0.046 | 0.042 | 0.044 | 0.048 |
| 15 | 0.042 | 0.047 | 0.044 | 0.035 | 0.032 | 0.034 |
| 20 | 0.041 | 0.042 | 0.043 | 0.031 | 0.025 | 0.023 |
| 25 | 0.033 | 0.036 | 0.034 | 0.025 | 0.016 | 0.013 |
1.2b - Bonferroni Test: T = 500, c = 0
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.045 | 0.043 | 0.034 | 0.034 | 0.040 | 0.043 |
| 25 | 0.043 | 0.042 | 0.036 | 0.029 | 0.034 | 0.041 |
| 50 | 0.045 | 0.042 | 0.039 | 0.033 | 0.028 | 0.035 |
| 75 | 0.042 | 0.045 | 0.036 | 0.030 | 0.024 | 0.022 |
| 100 | 0.036 | 0.039 | 0.035 | 0.023 | 0.017 | 0.018 |
| 125 | 0.032 | 0.029 | 0.025 | 0.017 | 0.014 | 0.012 |
1.2c - Bonferroni Test: T = 100, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.044 | 0.04 | 0.032 | 0.034 | 0.043 | 0.051 |
| 5 | 0.030 | 0.033 | 0.026 | 0.025 | 0.034 | 0.037 |
| 10 | 0.027 | 0.024 | 0.021 | 0.016 | 0.017 | 0.020 |
| 15 | 0.021 | 0.022 | 0.017 | 0.011 | 0.009 | 0.011 |
| 20 | 0.017 | 0.014 | 0.012 | 0.007 | 0.006 | 0.007 |
| 25 | 0.013 | 0.011 | 0.009 | 0.005 | 0.005 | 0.003 |
1.2d - Bonferroni Test: T = 500, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.047 | 0.033 | 0.027 | 0.023 | 0.033 | 0.039 |
| 25 | 0.033 | 0.031 | 0.023 | 0.020 | 0.021 | 0.027 |
| 50 | 0.022 | 0.030 | 0.022 | 0.014 | 0.014 | 0.016 |
| 75 | 0.024 | 0.023 | 0.016 | 0.010 | 0.009 | 0.008 |
| 100 | 0.018 | 0.018 | 0.015 | 0.008 | 0.005 | 0.006 |
| 125 | 0.015 | 0.015 | 0.01 | 0.005 | 0.004 | 0.003 |
1.3a Infeasible Test (using true value of c): T = 100, c = 0
| q | ||||||
|---|---|---|---|---|---|---|
1 | 0.053 | 0.056 | 0.051 | 0.057 | 0.057 | 0.052 |
| 5 | 0.054 | 0.065 | 0.061 | 0.057 | 0.047 | 0.041 |
| 10 | 0.065 | 0.063 | 0.064 | 0.060 | 0.050 | 0.043 |
| 15 | 0.066 | 0.066 | 0.064 | 0.060 | 0.049 | 0.041 |
| 20 | 0.064 | 0.063 | 0.060 | 0.059 | 0.048 | 0.044 |
| 25 | 0.060 | 0.059 | 0.061 | 0.053 | 0.046 | 0.040 |
1.3b Infeasible Test (using true value of c): T = 500, c = 0
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.050 | 0.054 | 0.052 | 0.048 | 0.051 | 0.048 |
| 25 | 0.059 | 0.058 | 0.064 | 0.049 | 0.047 | 0.039 |
| 50 | 0.067 | 0.066 | 0.063 | 0.055 | 0.048 | 0.037 |
| 75 | 0.064 | 0.067 | 0.068 | 0.058 | 0.050 | 0.036 |
| 100 | 0.067 | 0.062 | 0.067 | 0.059 | 0.047 | 0.036 |
| 125 | 0.058 | 0.055 | 0.056 | 0.054 | 0.044 | 0.042 |
1.3c Infeasible Test (using true value of c): T = 100, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.054 | 0.053 | 0.054 | 0.053 | 0.057 | 0.059 |
| 5 | 0.049 | 0.047 | 0.047 | 0.049 | 0.046 | 0.050 |
| 10 | 0.044 | 0.043 | 0.044 | 0.046 | 0.041 | 0.038 |
| 15 | 0.041 | 0.037 | 0.040 | 0.040 | 0.034 | 0.031 |
| 20 | 0.035 | 0.035 | 0.030 | 0.031 | 0.028 | 0.029 |
| 25 | 0.026 | 0.029 | 0.028 | 0.029 | 0.025 | 0.023 |
1.3d Infeasible Test (using true value of c): T = 500, c = -10
| q | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.049 | 0.056 | 0.052 | 0.052 | 0.053 | 0.055 |
| 25 | 0.046 | 0.049 | 0.043 | 0.048 | 0.044 | 0.041 |
| 50 | 0.044 | 0.045 | 0.044 | 0.043 | 0.038 | 0.039 |
| 75 | 0.039 | 0.040 | 0.039 | 0.041 | 0.038 | 0.030 |
| 100 | 0.034 | 0.035 | 0.034 | 0.031 | 0.029 | 0.027 |
| 125 | 0.029 | 0.025 | 0.028 | 0.026 | 0.022 | 0.022 |
Table 2
Characteristics of the predictor
variables in the U.S. data. This table reports the key time-series
characteristics of the dividend-price ratio ![]() ,
the earnings-price ratio
,
the earnings-price ratio ![]() , the short interest
rate
, the short interest
rate ![]() , and the yield spread
, and the yield spread ![]() . The S&P 500 variables are on an annual
frequency, whereas results for both the annual and monthly CRSP
data are reported. All series end in
. The S&P 500 variables are on an annual
frequency, whereas results for both the annual and monthly CRSP
data are reported. All series end in ![]() . The
first two columns indicate the data set and predictor variable
being used. The following three columns show the sampling
frequency, the start date of the sample period, and the number of
observations in that sample. The column labeled DF-GLS gives the
value of the DF-GLS unit-root test statistic, and the column
labeled
. The
first two columns indicate the data set and predictor variable
being used. The following three columns show the sampling
frequency, the start date of the sample period, and the number of
observations in that sample. The column labeled DF-GLS gives the
value of the DF-GLS unit-root test statistic, and the column
labeled ![]() gives the estimated correlations
between the innovations to the predictor variables and the
innovations to the corresponding excess returns. The last two
columns give the 95% confidence intervals for the autoregressive
root
gives the estimated correlations
between the innovations to the predictor variables and the
innovations to the corresponding excess returns. The last two
columns give the 95% confidence intervals for the autoregressive
root ![]() and the corresponding local-to-unity
parameter
and the corresponding local-to-unity
parameter ![]() , obtained by inverting the DF-GLS
unit-root test statistic.
, obtained by inverting the DF-GLS
unit-root test statistic.
| Series | Variable | Sample Freq. | Sample Begins | Obs. | DF-GLS | |||
|---|---|---|---|---|---|---|---|---|
| S&P 500 | Annual |
|
|
|||||
| S&P 500 | Annual |
|
|
|||||
| CRSP | Annual |
|
|
|||||
| CRSP | Annual |
|
|
|||||
| CSRP | Monthly |
|
|
|||||
| CRSP | Monthly |
|
|
|||||
| CRSP | Monthly |
|
|
|||||
| CRSP | Monthly |
|
|
|||||
| CSRP | Annual |
|
|
|||||
| CRSP | Annual |
|
|
|||||
| CSRP | Monthly |
|
|
|||||
| CRSP | Monthly |
|
|
Table 3
Characteristics of the predictor
variables in the international data. This table reports the key
time-series characteristics of the dividend-price ratio ![]() , the short interest rate
, the short interest rate ![]() , and the
term spread
, and the
term spread ![]() . All data are on a monthly
frequency, and all series end in 2004. The first two columns
indicate the country and predictor variable being used, and the
next two columns show the start date of the sample period and the
number of observations in that sample. The column labeled DF-GLS
gives the value of the DF-GLS unit-root test statistic, and the
column labeled
. All data are on a monthly
frequency, and all series end in 2004. The first two columns
indicate the country and predictor variable being used, and the
next two columns show the start date of the sample period and the
number of observations in that sample. The column labeled DF-GLS
gives the value of the DF-GLS unit-root test statistic, and the
column labeled ![]() gives the estimated
correlations between the innovations to the predictor variables and
the innovations to the corresponding excess returns. The last two
columns give the 95% confidence intervals for the autoregressive
root
gives the estimated
correlations between the innovations to the predictor variables and
the innovations to the corresponding excess returns. The last two
columns give the 95% confidence intervals for the autoregressive
root ![]() and the corresponding local-to-unity
parameter
and the corresponding local-to-unity
parameter ![]() , obtained by inverting the DF-GLS
unit-root test statistic.
, obtained by inverting the DF-GLS
unit-root test statistic.
| Country | Variable | Sample Begins | Obs. | DF-GLS | |||
|---|---|---|---|---|---|---|---|
| Australia |
|
|
|||||
| Belgium |
|
|
|||||
| Canada |
|
|
|||||
| France |
|
|
|||||
| Germany |
|
|
|||||
| Italy |
|
|
|||||
| Japan |
|
|
|||||
| Sweden |
|
|
|||||
| UK |
|
|
|||||
| Australia |
|
|
|||||
| Belgium |
|
|
|||||
| Canada |
|
|
|||||
| France |
|
|
|||||
| Germany |
|
|
|||||
| Italy |
|
|
|||||
| Japan |
|
|
|||||
| Sweden |
|
|
|||||
| UK |
|
|
|||||
| Australia |
|
|
|||||
| Belgium |
|
|
|||||
| Canada |
|
|
|||||
| France |
|
|
|||||
| Germany |
|
|
|||||
| Italy |
|
|
|||||
| Japan |
|
|
|||||
| Sweden |
|
|
|||||
| UK |
|
|
|||||
| Australia |
|
|
|
||||
| Belgium |
|
|
|
||||
| Canada |
|
|
|
||||
| France |
|
|
|
||||
| Germany |
|
|
|
||||
| Italy |
|
|
|
||||
| Japan |
|
|
|
||||
| Sweden |
|
|
|
||||
| UK |
|
|
|
Figure 1
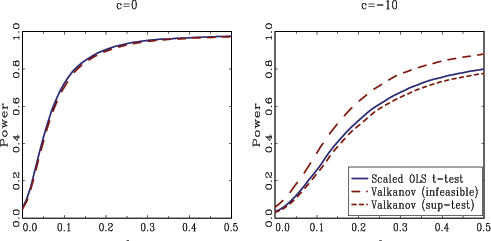
Power curves for exogenous regressors with ![]() ,
, ![]() , and
, and
![]() The graphs show the average
rejection rates for a one-sided
The graphs show the average
rejection rates for a one-sided ![]() percent test of
the null hypothesis of
percent test of
the null hypothesis of ![]() against a positive
alternative. The
against a positive
alternative. The ![]() axis shows the true value of the
parameter
axis shows the true value of the
parameter ![]() , and the
, and the ![]() axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of
axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of ![]()
![]() , and the right-hand
graph gives the results for
, and the right-hand
graph gives the results for ![]()
![]() . The results for
the scaled OLS
. The results for
the scaled OLS ![]() test derived in this paper are
given by the solid lines, the results for Valkanov's infeasible
test are given by the long dashed lines, and the results for
Valkanov's feasible sup-bound test are given by the short dashed
lines. The results are based on the Monte Carlo simulations
described in the main text, and the power is calculated as the
average rejection rates over 10,000
repetitions.
test derived in this paper are
given by the solid lines, the results for Valkanov's infeasible
test are given by the long dashed lines, and the results for
Valkanov's feasible sup-bound test are given by the short dashed
lines. The results are based on the Monte Carlo simulations
described in the main text, and the power is calculated as the
average rejection rates over 10,000
repetitions.
Figure 2
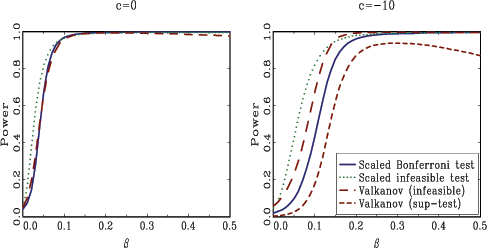
Power curves for endogenous regressors with ![]() ,
, ![]() , and
, and
![]() The graphs show the average
rejection rates for a one-sided
The graphs show the average
rejection rates for a one-sided ![]() percent test of
the null hypothesis of
percent test of
the null hypothesis of ![]() against a positive
alternative. The
against a positive
alternative. The ![]() axis shows the true value of the
parameter
axis shows the true value of the
parameter ![]() , and the
, and the ![]() axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of
axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of ![]()
![]() , and the right-hand
graph gives the results for
, and the right-hand
graph gives the results for ![]()
![]() . The results for
the scaled Bonferroni test are given by the solid lines, the
results for the scaled infeasible
. The results for
the scaled Bonferroni test are given by the solid lines, the
results for the scaled infeasible ![]() test
test
![]() from the
augmented regression equation, which uses knowledge of the true
value of
from the
augmented regression equation, which uses knowledge of the true
value of ![]() , are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, and the results for Valkanov's feasible sup-bound test are
given by the short dashed lines. The results are based on the Monte
Carlo simulations described in the main text, and the power is
calculated as the average rejection rates over 10,000 repetitions.
, are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, and the results for Valkanov's feasible sup-bound test are
given by the short dashed lines. The results are based on the Monte
Carlo simulations described in the main text, and the power is
calculated as the average rejection rates over 10,000 repetitions.
Figure 3
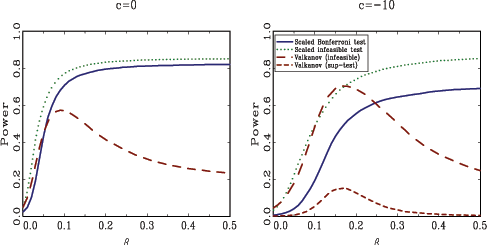
Power curves for endogenous regressors with ![]() ,
, ![]() , and
, and
![]() The graphs show the average
rejection rates for a one-sided
The graphs show the average
rejection rates for a one-sided ![]() percent test of
the null hypothesis of
percent test of
the null hypothesis of ![]() against a positive
alternative. The
against a positive
alternative. The ![]() axis shows the true value of the
parameter
axis shows the true value of the
parameter ![]() , and the
, and the ![]() axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of
axis
indicates the average rejection rate. The left-hand graph gives the
results for the case of ![]()
![]() , and the right-hand
graph gives the results for
, and the right-hand
graph gives the results for ![]()
![]() . The results for
the scaled Bonferroni test are given by the solid lines, the
results for the scaled infeasible
. The results for
the scaled Bonferroni test are given by the solid lines, the
results for the scaled infeasible ![]() test
test
![]() from the
augmented regression equation, which uses knowledge of the true
value of
from the
augmented regression equation, which uses knowledge of the true
value of ![]() , are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, and the results for Valkanov's feasible sup-bound test are
given by the short dashed lines. The results are based on the Monte
Carlo simulations described in the main text, and the power is
calculated as the average rejection rates over 10,000 repetitions.
, are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, and the results for Valkanov's feasible sup-bound test are
given by the short dashed lines. The results are based on the Monte
Carlo simulations described in the main text, and the power is
calculated as the average rejection rates over 10,000 repetitions.
Figure 4
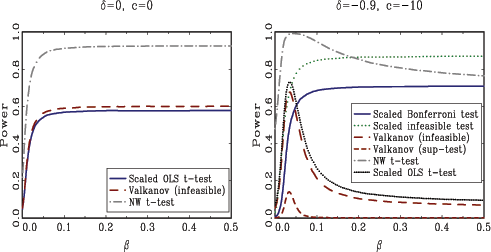
Power curves for ![]() , and
, and ![]() . The
graphs show the average rejection rates for a one-sided
. The
graphs show the average rejection rates for a one-sided ![]() percent test of the null hypothesis of
percent test of the null hypothesis of ![]() against a positive alternative. The
against a positive alternative. The ![]() axis shows the true value of the parameter
axis shows the true value of the parameter ![]() , and the
, and the ![]() axis indicates the average
rejection rate. The left hand graph gives the results for the case
of exogenous regressors with
axis indicates the average
rejection rate. The left hand graph gives the results for the case
of exogenous regressors with ![]() and
and
![]() . The results for the scaled OLS
. The results for the scaled OLS
![]() test are given by the solid lines, the
results for Valkanov's infeasible test, which coincides with
Valkanov's sup-bound test for
test are given by the solid lines, the
results for Valkanov's infeasible test, which coincides with
Valkanov's sup-bound test for ![]() , are given by
the long dashed lines, and the results for the (non-scaled)
, are given by
the long dashed lines, and the results for the (non-scaled)
![]() test using Newey-West standard errors are
given by the dotted and dashed line. The right hand graph gives the
results for the case of endogenous regressors with
test using Newey-West standard errors are
given by the dotted and dashed line. The right hand graph gives the
results for the case of endogenous regressors with
![]() and
and ![]() . The
results for the scaled Bonferroni test are given by the solid
lines, the results for the scaled infeasible
. The
results for the scaled Bonferroni test are given by the solid
lines, the results for the scaled infeasible ![]() test
test
![]() from the
augmented regression equation, which uses knowledge of the true
value of
from the
augmented regression equation, which uses knowledge of the true
value of ![]() , are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, the results for Valkanov's feasible sup-bound test are given
by the short dashed lines, the results for the (non-scaled)
, are given by the dotted line, the
results for Valkanov's infeasible test are given by the long dashed
lines, the results for Valkanov's feasible sup-bound test are given
by the short dashed lines, the results for the (non-scaled)
![]() test using Newey-West standard errors are
given by the dotted and dashed line, and the results for the scaled
OLS
test using Newey-West standard errors are
given by the dotted and dashed line, and the results for the scaled
OLS ![]() test are given by the finely dotted line.
The results are based on the Monte Carlo simulations described in
the main text, and the power is calculated as the average rejection
rates over 10,000 repetitions.
test are given by the finely dotted line.
The results are based on the Monte Carlo simulations described in
the main text, and the power is calculated as the average rejection
rates over 10,000 repetitions.
Figure 5
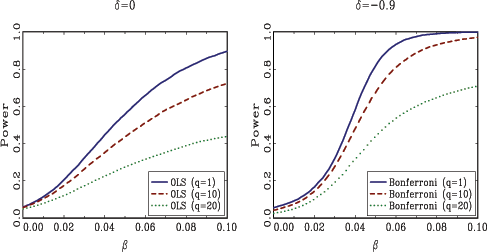
Comparison of power across horizons for ![]() and
and
![]() . The graphs show the average rejection
rates for a one-sided
. The graphs show the average rejection
rates for a one-sided ![]() percent test of the null
hypothesis of
percent test of the null
hypothesis of ![]() against a positive alternative.
The
against a positive alternative.
The ![]() axis shows the true value of the
parameter
axis shows the true value of the
parameter ![]() , and the
, and the ![]() axis
indicates the average rejection rate. The left hand graph gives the
results for the case of exogenous regressors with
axis
indicates the average rejection rate. The left hand graph gives the
results for the case of exogenous regressors with ![]() . The results for the one period OLS
. The results for the one period OLS ![]() test are given by the solid line (
test are given by the solid line (![]() ),
and the results for the scaled OLS
),
and the results for the scaled OLS ![]() tests for
tests for
![]() and
and ![]() are given by
the the short dashed line and the dotted line, respectively. The
right hand graph gives the results for the case of endogenous
regressors with
are given by
the the short dashed line and the dotted line, respectively. The
right hand graph gives the results for the case of endogenous
regressors with
![]() . The results for the one period
(
. The results for the one period
(![]() ) Bonferroni test are given by the solid
line, and the results for the scaled Bonferroni tests for
) Bonferroni test are given by the solid
line, and the results for the scaled Bonferroni tests for
![]() and
and ![]() are given by
the the short dashed line and the dotted line, respectively. The
results are based on the Monte Carlo simulations described in the
main text, and the power is calculated as the average rejection
rates over 10,000 repetitions.
are given by
the the short dashed line and the dotted line, respectively. The
results are based on the Monte Carlo simulations described in the
main text, and the power is calculated as the average rejection
rates over 10,000 repetitions.
Figure 6
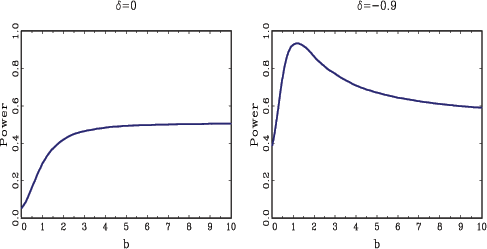
Local power curves for ![]() and
and ![]() . The
graphs show the average power curves for a one-sided
. The
graphs show the average power curves for a one-sided ![]() percent test of the null hypothesis against a positive
local alternative, based on the distribution of the scaled OLS
percent test of the null hypothesis against a positive
local alternative, based on the distribution of the scaled OLS
![]() statistic derived in Theorem 4. The
statistic derived in Theorem 4. The ![]() axis shows the true value of the parameter
axis shows the true value of the parameter ![]() , and the
, and the ![]() axis indicates the average
rejection rate. The left-hand graph gives the results for exogenous
regressors with
axis indicates the average
rejection rate. The left-hand graph gives the results for exogenous
regressors with ![]() , and the right-hand graph
gives the results for endogeneous regressors with
, and the right-hand graph
gives the results for endogeneous regressors with
![]() . The results are obtained from
direct simulation of the limiting random variables in equation
(18), and the power
is calculated as the average rejection rate over 10,000 repetitions.
. The results are obtained from
direct simulation of the limiting random variables in equation
(18), and the power
is calculated as the average rejection rate over 10,000 repetitions.
Figure 7
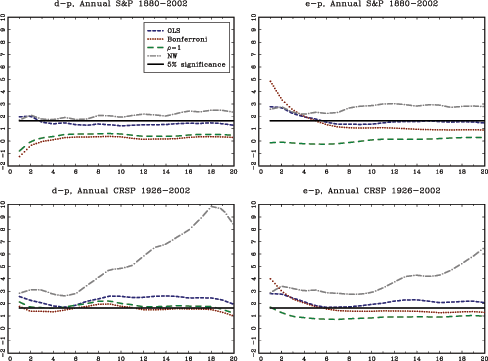
Empirical results for the annual U.S. data with valuation ratios as predictors. The
graphs show the outcomes of the long-run test statistics as
functions of the forecasting horizon. The ![]() axis
shows the forecasting horizon
axis
shows the forecasting horizon ![]() , and the
, and the
![]() axis shows the value of the test
statistic. The left-hand graphs give the results for the dividend
price ratio
axis shows the value of the test
statistic. The left-hand graphs give the results for the dividend
price ratio
![]() , and the right-hand
graphs give the results for the earnings-price ratio
, and the right-hand
graphs give the results for the earnings-price ratio
![]() . Results for the S&P
500 data are shown in the top graphs and results for the CRSP data
in the bottom graphs. The results for the scaled OLS
. Results for the S&P
500 data are shown in the top graphs and results for the CRSP data
in the bottom graphs. The results for the scaled OLS ![]() test are given by the short dashed lines, the results for
the scaled Bonferroni test are given by the dotted lines, the
results for the scaled
test are given by the short dashed lines, the results for
the scaled Bonferroni test are given by the dotted lines, the
results for the scaled ![]() test from the augmented
regression equation under the assumption of
test from the augmented
regression equation under the assumption of ![]() are given by the long dashed lines, and the results for the
(non-scaled)
are given by the long dashed lines, and the results for the
(non-scaled) ![]() test using Newey-West standard errors
are given by the dotted and dashed line. The flat solid line shows
the 5% significance level, equal to
1.645 based on the normal distribution,
for the one sided test.
test using Newey-West standard errors
are given by the dotted and dashed line. The flat solid line shows
the 5% significance level, equal to
1.645 based on the normal distribution,
for the one sided test.
Figure 8
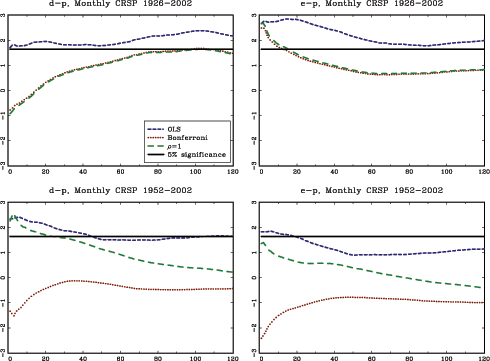
Empirical results for the monthly U.S. data with valuation ratios as predictors. The
graphs show the outcomes of the long-run test statistics as
functions of the forecasting horizon. The ![]() axis
shows the forecasting horizon
axis
shows the forecasting horizon ![]() , and the
, and the
![]() axis shows the value of the test
statistic. The left-hand graphs give the results for the dividend
price ratio
axis shows the value of the test
statistic. The left-hand graphs give the results for the dividend
price ratio
![]() , and the right-hand
graphs give the results for the earnings-price ratio
, and the right-hand
graphs give the results for the earnings-price ratio
![]() . Results for the full
CRSP sample from 1926-2002 are shown in the top graphs and results
for the restricted CRSP sample from 1952-2002 in the bottom graphs.
The results for the scaled OLS
. Results for the full
CRSP sample from 1926-2002 are shown in the top graphs and results
for the restricted CRSP sample from 1952-2002 in the bottom graphs.
The results for the scaled OLS ![]() test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
![]() test from the augmented regression
equation under the assumption of
test from the augmented regression
equation under the assumption of ![]() are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
Figure 9
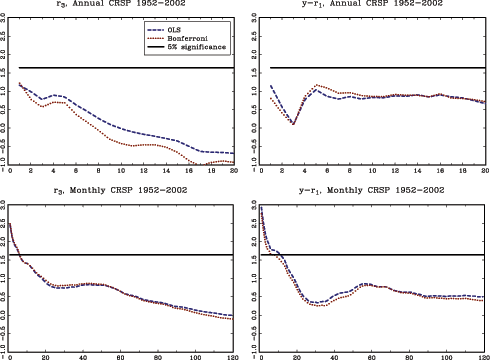
Empirical results for the U.S. data with interest rate variables as predictors. The
graphs show the outcomes of the long-run test statistics as
functions of the forecasting horizon. The ![]() axis
shows the forecasting horizon
axis
shows the forecasting horizon ![]() , and the
, and the
![]() axis shows the value of the test
statistic. The left-hand graphs give the results for the short
interest rate
axis shows the value of the test
statistic. The left-hand graphs give the results for the short
interest rate
![]() , and the right-hand
graphs give the results for the yield spread
, and the right-hand
graphs give the results for the yield spread
![]() . Results for the
annual data are shown in the top graphs and results for the monthly
data in the bottom graphs. The results for the scaled OLS
. Results for the
annual data are shown in the top graphs and results for the monthly
data in the bottom graphs. The results for the scaled OLS
![]() test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
Figure 10
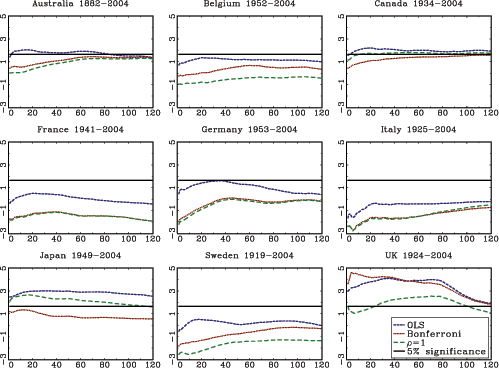
Empirical results for the international data with the dividend-price ratio as
predictor, using the full sample for each country. The graphs show
the outcomes of the long-run test statistics as functions of the
forecasting horizon. The ![]() axis shows the forecasting
horizon
axis shows the forecasting
horizon ![]() , and the
, and the ![]() axis shows
the value of the test statistic. The title of each graph indicates
the country and sample period to which the results correspond. The
results for the scaled OLS
axis shows
the value of the test statistic. The title of each graph indicates
the country and sample period to which the results correspond. The
results for the scaled OLS ![]() test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
![]() test from the augmented regression
equation under the assumption of
test from the augmented regression
equation under the assumption of ![]() are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
Figure 11
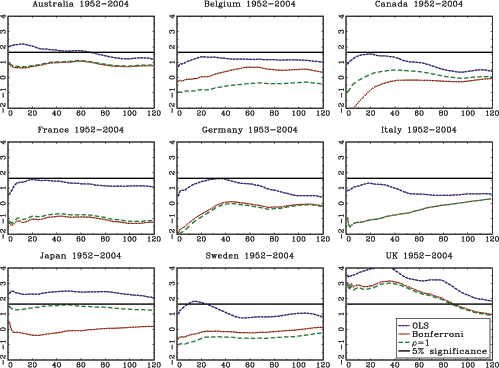
Empirical results for the international data with the dividend-price ratio as
predictor, using data after 1952. The graphs show the outcomes of
the long-run test statistics as functions of the forecasting
horizon. The ![]() axis shows the forecasting horizon
axis shows the forecasting horizon
![]() , and the
, and the ![]() axis shows
the value of the test statistic. The title of each graph indicates
the country and sample period to which the results correspond. The
results for the scaled OLS
axis shows
the value of the test statistic. The title of each graph indicates
the country and sample period to which the results correspond. The
results for the scaled OLS ![]() test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
test are given by
the short dashed lines, the results for the scaled Bonferroni test
are given by the dotted lines, and the results for the scaled
![]() test from the augmented regression
equation under the assumption of
test from the augmented regression
equation under the assumption of ![]() are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
are given by
the long dashed lines. The flat solid line shows the 5% significance level, equal to 1.645 based
on the normal distribution, for the one sided test.
Figure 12
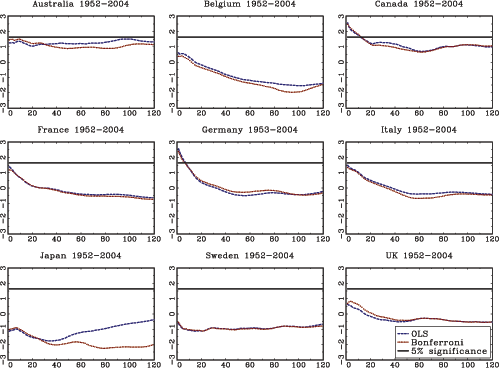
Empirical results for the international data with the short interest rate as
predictor. The graphs show the outcomes of the long-run test
statistics as functions of the forecasting horizon. The ![]() axis shows the forecasting horizon
axis shows the forecasting horizon ![]() , and
the
, and
the ![]() axis shows the value of the test
statistic. The title of each graph indicates the country and sample
period to which the results correspond. The results for the scaled
OLS
axis shows the value of the test
statistic. The title of each graph indicates the country and sample
period to which the results correspond. The results for the scaled
OLS ![]() test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
Figure 13
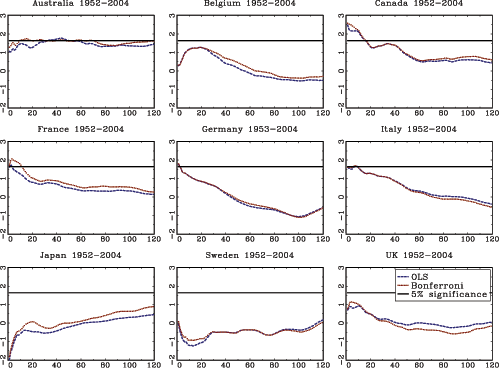
Empirical results for the international data with the term spread as predictor. The
graphs show the outcomes of the long-run test statistics as
functions of the forecasting horizon. The ![]() axis
shows the forecasting horizon
axis
shows the forecasting horizon ![]() , and the
, and the
![]() axis shows the value of the test
statistic. The title of each graph indicates the country and sample
period to which the results correspond. The results for the scaled
OLS
axis shows the value of the test
statistic. The title of each graph indicates the country and sample
period to which the results correspond. The results for the scaled
OLS ![]() test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
test are given by the short dashed lines
and the results for the scaled Bonferroni test are given by the
dotted lines. The flat solid line shows the 5%
significance level, equal to 1.645 based on the
normal distribution, for the one sided test.
Footnotes
* I have greatly benefitted from advice by Peter Phillips and Robert Shiller. Other helpful comments have also been provided by Don Andrews, John Campbell, Dobrislav Dobrev, Ray Fair, Jon Faust, Lennart Hjalmarsson, Randi Hjalmarsson, Yuichi Kitamura, Taisuke Otsu, as well as participants in the econometrics seminar and workshop at Yale University, the international finance seminar at the Federal Reserve Board, the finance seminar at Göteborg University, the World meeting of the Econometric Society in London, 2005, and the Copenhagen Conference on Stock Return Predictability, 2007. Excellent research assistance has been provided by Benjamin Chiquoine. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: [email protected]. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. Other applications of long-horizon regressions include tests of exchange rate predictability (Mark, 1995, Berkowitz and Giorgianni, 2001, and Rossi 2005), the Fisher effect (Mishkin, 1990, 1992, and Boudoukh and Richardson, 1993), and the neutrality of money (Fisher and Seater, 1993). Return to text
2. Ang and Bekaert (2007) suggest using Hodrick (1992) auto-correlation robust standard errors, which they argue have good finite sample properties. However, these rely on the regressors being covariance stationary, which is a restrictive assumption for most forecasting variables as evidenced by the results in the empirical analysis in this paper. Return to text
3. There is now a large literature on regressions with overlapping observations. Additional references to those mentioned previously include Hansen and Hodrick (1980), Richardson and Stock (1989), Richardson and Smith (1991), Nelson and Kim (1993), Goetzman and Jorion (1993), Campbell (2001), Daniel (2001), Mark and Sul (2004), Moon et al. (2004), Torous et al. (2004), Boudoukh et al. (2005), and Rapach and Wohar (2005). The study by Valkanov (2003) is the most closely related to this paper and is discussed in more detail below. Studies on (short-run) predictive regressions in the context of persistent regressors include Mankiw and Shapiro (1986), Cavanagh et al. (1995), Stambaugh (1999), Lewellen (2004), Campbell and Yogo (2006), Janson and Moreira (2006), and Polk et al. (2006). Return to text
4. A predictive regressor is generally referred to as endogenous if the innovations to the returns are contemporaneously correlated with the innovations to the regressor. When the regressor is strictly stationary, such endogeneity has no impact on the properties of the estimator, but when the regressor is persistent in some manner, the properties of the estimator will be affected (e.g. Stambaugh, 1999). Nelson and Kim (1993) may be the first to raise the biasing problems of endogenous regressors in the long-horizon case. Return to text
5. The asymptotic results presented in Section 2 all generalize immediately to the case of multiple regressors. However, the Bonferroni methods described in Section 3 are currently only developed for the case of a single regressor. Return to text
6. That is, ![]() can be
estimated consistently, but not with enough precision to identify
can be
estimated consistently, but not with enough precision to identify
![]() . Return to text
. Return to text
7. A similar point is made by Phillips (1991b) and Corbae et al. (2002) in regards to frequency domain estimation with persistent variables. They show that the asympototic distribution of the narrow band least squares estimator, which only uses frequencies close to zero and thus captures the long-run relationship in the data, is identical to the asymptotic distribution of the full frequency estimator (which is identical to standard OLS). Return to text
8. An alternative approach is to invert the test-statistics and form conservative confidence intervals instead. This approach will deliver qualitatively identical results, in terms of whether the null hypothesis is rejected or not. However, the distribution of the long-run estimator under the alternative hypothesis is not the same as under the null hypothesis (see the proofs of Theorems 3 and 4 in the Appendix), in which case the confidence intervals are only valid under the null hypothesis. Presenting confidence intervals based on the distribution under the null hypothesis may therefore be misleading. Return to text
9. In practice, the confidence levels of
the lower and upper bounds in the shrunk confidence interval are
not symmetrical, and Campbell and Yogo (2006) find separate
confidence levels
![]() and
and
![]() that correspond to the
lower and upper bounds. Return to
text
that correspond to the
lower and upper bounds. Return to
text
10. Table 2 in Campbell and Yogo (2006)
gives the confidence levels for the confidence interval for
![]() that is used in the Bonferroni test, for a
given
that is used in the Bonferroni test, for a
given ![]() . Tables 2-11 in Campbell and Yogo
(2005) give the actual confidence intervals for
. Tables 2-11 in Campbell and Yogo
(2005) give the actual confidence intervals for ![]() ,
for a given
,
for a given ![]() and value of the DF-GLS unit-root
test statistic. That is, for a given value of
and value of the DF-GLS unit-root
test statistic. That is, for a given value of ![]() and the DF-GLS statistic, Tables 2-11 in Campbell and
Yogo (2005) present the confidence intervals for
and the DF-GLS statistic, Tables 2-11 in Campbell and
Yogo (2005) present the confidence intervals for ![]() with confidence levels corresponding to those in Table 2 in
Campbell and Yogo (2006). Return to
text
with confidence levels corresponding to those in Table 2 in
Campbell and Yogo (2006). Return to
text
11. Valkanov (2003) provides critical
values for ![]() , for different combinations of
, for different combinations of
![]() and
and ![]() , and I use
these values when applicable. In the power simulations below where
, and I use
these values when applicable. In the power simulations below where
![]() , I simulate critical values in the
same manner as in the original paper, with
, I simulate critical values in the
same manner as in the original paper, with ![]() ,
and using
,
and using ![]() repetitions. Return to text
repetitions. Return to text
12. Lewellen (2004) suggests a similar procedure in one-period (short-run) regressions. Return to text
13. These data were downloaded from Professor Yogo's website: http://finance.wharton.upenn.edu/~yogo/. Return to text
14. Certain countries had longer periods over which, for instance, data on dividends were missing (e.g. the U.K.), or where no data at all were available during some periods, such as the years around the two world wars (e.g. Germany). In these cases, I restrict myself to the longest available consecutive time-series, and do not attempt to parse together the discontinuous series. Return to text
15. In the U.S., the interest rate was pegged by the Federal Reserve before this date. Of course, in other countries, deregulation of the interest rate markets occurred at different times, most of which are later than 1952. As seen in the international finance literature (e.g. Kaminsky and Schmukler, 2002), however, it is often difficult to determine the exact date of deregulation. And, if one follows classification schemes, such as those in Kaminsky and Schmukler (2002), then most markets are not considered to be fully deregulated until the 1980s, resulting in a very small sample period to study. Thus, the extent to which observed interest rates reflect actual market rates is hard to determine and one should keep this caveat in mind when interpreting the results. Return to text
16. For ![]() ,
the
,
the ![]() statistic is asymptotically
decreasing in
statistic is asymptotically
decreasing in ![]() , and restricting
, and restricting ![]() to be less than or equal to one (or equivalently
to be less than or equal to one (or equivalently
![]() ) thus results in a more powerful
test. In finite samples, the
) thus results in a more powerful
test. In finite samples, the ![]() statistic
is not always monotonically decreasing in
statistic
is not always monotonically decreasing in ![]() and the
statement in the text is thus not always necesarrily true. That is,
there could be some value for
and the
statement in the text is thus not always necesarrily true. That is,
there could be some value for
![]() , with
, with
![]() such that
such that
![]() , in which case even though explosive roots are ruled out, the most
conservative value is not obtained for
, in which case even though explosive roots are ruled out, the most
conservative value is not obtained for ![]() . In
this case, the procedure described in the text is not correct since
it could lead to a test that over rejects. However, in all but one
of the cases considered here, the statement in the text holds true
and it is only marginally wrong once, with no qualitative impact at
all. In fact, interior optima seems very rare in
practice. Return to text
. In
this case, the procedure described in the text is not correct since
it could lead to a test that over rejects. However, in all but one
of the cases considered here, the statement in the text holds true
and it is only marginally wrong once, with no qualitative impact at
all. In fact, interior optima seems very rare in
practice. Return to text
17. Note also that it is only for
![]() and an alternative of
and an alternative of
![]() for which
for which ![]() will provide a conservative upper bound. For other parameter
combinations, the conservative bound might be achieved for small
values of
will provide a conservative upper bound. For other parameter
combinations, the conservative bound might be achieved for small
values of ![]() . Return
to text
. Return
to text
18. In making statements about multiple horizons, there is always the issue of multiple testing, which is not adressed here. However, since the baseline assumption that would arise from the theoretical analysis is that the short-run results should be stronger than the long-run results, and these predictions are reflected in the actual results, the multiple testing issue seems less of a concern in the current discussion. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text