
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 879, October 2008 --- Screen Reader Version*
Efficiency in Housing Markets: Which Home Buyers Know how to Discount?
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We test for efficiency in the market for Swedish co-ops by examining the negative relationship between the sales price and the present value of future monthly payments or `rents'. If the co-op housing market is efficient, the present value of co-op rental payments due to underlying debt obligations of the cooperative should be fully reflected in the sales price. However, we find that, on average, a one hundred kronor increase in the present value of future rents only leads to an approximately 75 kronor reduction in the sales price; co-ops with higher rents are thus relatively overpriced compared to those with lower rents. We also find that these inefficiencies are larger at the lower end of the housing market and in poorer, less educated regions (though they are still observed in all geographic regions). These findings appear to reflect both the role played by liquidity constraints in price formation and there being more informed and `sophisticated' buyers in higher educated areas who push prices closer to efficiency. Overall, our findings suggest that there is some systematic failure to properly discount the future stream of rent payments relative to the up front sales price.
Keywords: Housing markets, market efficiency, cooperative housing
JEL classification: G14, R21, R31
1. Introduction
For the majority of households, the purchase of a home is the largest financial decision of their lives. One may therefore assume that housing market transactions are conducted by agents who have carefully evaluated all available information and that the resulting prices reflect that information. A growing number of studies, many of which are based on time-series of home sales and rental data, therefore test whether housing prices are in fact informationally efficient.1 This paper takes advantage of the nature of the cooperative housing market in Sweden to provide an alternative test of market efficiency.
Cooperatives are distinct from condominiums in that the purchaser of a unit in a cooperative housing association is formally buying a share in the cooperative, along with the non-time-restricted right to occupy the unit, i.e. the actual apartment. Owners of a co-op unit must make a monthly payment comprised of maintenance fees and the capital costs attributed to the cooperative's debt. For the remainder of the paper, we will refer to the total of these monthly payments as `rents'. The capital costs component derives from the fact that the formal owner of a co-op unit is the cooperative association; the cooperative can have its own debts, which are serviced through the collection of rents from the members of the cooperative, i.e. the indirect owners of the cooperative apartments. These implicit interest payments in the monthly co-op rents are on top of any direct mortgage service obligations that the home buyer may have incurred. Thus, only part of the true cost of owning a co-op unit is reflected in the actual sales price; the remaining cost is reflected in the monthly rent. The total value of a co-op unit can therefore be expressed as the sum of its sales price and the discounted value of the cooperative financing component of the future monthly rent payments, i.e. rent excluding the maintenance fee component.
This simple present value relationship provides the starting point for our analysis. In particular, if markets are efficient, there should be an inverse one-to-one relationship between prices and discounted rents. That is, if the present value of rents goes up by one unit, prices should decrease by one unit.
Although this analysis relies on Swedish data, there is no reason to believe that the findings cannot be extended to housing markets in other countries or, indeed, to non-cooperative forms of housing. Co-ops are also quite common in many other countries, including Finland and Canada, and in certain cities in the U.S., such as New York, where they tend to dominate the market for owner occupied apartments.2 More generally, our test of market efficiency is a test of proper discounting, or comparison, of future payments relative to upfront costs. This is strongly related to traditional tests of housing market efficiency, which compare house price indices to present values of rent-cost indices (e.g., Meese and Wallace, 1994). The major drawback of this traditional approach is that rent and price indices are, for obvious reasons, not based on the same housing units or, more importantly, units that necessarily have comparable characteristics; Glaeser and Gyourko (2007) provide evidence that this is in fact the case and argue against the robustness of empirical analyses based on rent-price comparisons. In addition, these types of analyses rely on the time-series properties of the housing market data, which may be partly determined by frictions in the market; Meese and Wallace (1994) try to get around this second issue by considering tests of efficiency in the long-run, where short-run market frictions should play no role.
In contrast, by utilizing the fact that a co-op has both a price and a rent component, we can test a present value relationship by comparing across co-op units, rather than between rental and owner occupied units. This offers several advantages. The buy versus rent decision is a very large one for most households, and may depend on many factors, not all of which are of a financial nature. By focusing on actual co-op purchases, we eliminate this part of the decision making process and therefore expect a cleaner present value relationship. Cross-sectional transaction data also alleviates concerns about the time-series properties of the data. Finally, in our setup, there is a clear theoretical cross-sectional relationship between rents and prices; deviations from this relationship are easily translated into actual measures of miss-pricing.
Our analysis is based on a data set of more than 30,000 Swedish co-op transactions between 2002 and 2005 and hedonic price regressions that relate co-op sales prices to the present value of future rents.3 Our preferred specification controls for a variety of apartment characteristics, unobservable neighborhood characteristics through zip code fixed effects, and national and regional time trends. We find that an increase in discounted rents of 100 Swedish kronor (SEK) only leads to a decrease in price of about 75 SEK. On average, co-ops with high rents are thus relatively over-priced. This result cannot be explained away by potential changes in future rents or interest rates. For instance, buyers need to have extremely risk-averse beliefs regarding the paths of future interest rates to reconcile our estimates with market efficiency.
An alternative hypothesis that may explain these findings is that not all buyers have a common discount rate, as our baseline specification assumes. Rather, some may have substantially higher discount rates due to liquidity constraints; that is, home buyers who cannot make the necessary down payment will face a higher marginal mortgage rate. To explore this scenario, we redo our analysis for sub-samples of the data grouped on apartment size. One may expect apartment size to be a reasonable proxy for liquidity, as poorer and first time buyers, i.e. those most likely to be constrained, are those most likely to buy the smallest apartments. Even for the largest apartments, however, we find evidence of inefficiency; it is thus hard to argue that liquidity constraints can be the sole explanation for our findings. In addition, even if we allow a two percent top loan markup, which should be at the high end of the spectrum, there is still strong evidence of inefficiency at the lower end of the market (i.e. small apartments). Thus, liquidity constraints potentially play a role in the price formation in certain parts of the market, but cannot explain the overall inefficiency observed.
Similarly, we estimate our basic model separately for each parish or county in our data. We find evidence of inefficiency in 57 of 70 parishes, including those at both ends of the socioeconomic spectrum. However, these inefficiencies tend to be greater in poorer and less educated parishes. While these findings are likely to partly reflect the liquidity constraints described above, they are also consistent with there being more informed and `sophisticated' buyers in higher educated areas who push prices closer to efficiency. Further analyses that group the data jointly on apartment size and education level provide evidence that both liquidity constraints and `sophistication' are relevant to explain our findings.
Overall, our findings suggest that there is some systematic failure to properly discount the future stream of rent payments relative to the upfront sales price. This is in line with the time-series results reported in the literature, which typically show that house prices tend not to be efficient (e.g Case and Shiller, 1989, 1990). The heterogeneity across different groups of buyers is also consistent with recent findings in the emerging household finance literature. In a series of papers, Campbell (2006) and Calvet, Campbell, and Sodini (2007, 2008) document that higher-educated and wealthier households are more likely to satisfy the predictions of standard financial models.
The rest of the paper proceeds as follows. Section 2 provides background information about the Swedish co-op housing market. Section 3 outlines the theoretical relationship between prices and rents and discusses the calculation of the present value of future rent payments. In addition, it presents the econometric model and discusses the potential identification issue of omitted variables. Section 4 describes the data and Section 5 presents the main empirical results, including an analysis of how sensitive the findings are to assumptions about future rents and interest rates. Section 6 explores whether the findings of inefficiency are heterogeneous across parishes and socioeconomic characteristics and discusses alternative explanations of these findings, including the potential role of risk premia. Section 7 concludes.
2. The Swedish Cooperative Market
2.1 Overview and Market Characteristics
Cooperative (co-op) ownership is the only way to own an apartment in Sweden; condominiums do not exist as an alternative. Apart from single family houses, co-ops are therefore the only other form of owner-occupied housing, and in central areas of most cities, the only alternative to rental apartments. The Swedish housing market, and especially the co-op market, is generally characterized by few market frictions and low transaction costs, including minimal mortgage fees.
The purchase of a co-op unit entails ownership of a share of the cooperative, as well as membership in the cooperative association. The share ownership is not time-restricted in any sense. Though co-op purchasers do not have actual property rights over the apartment unit, they are free to renovate and otherwise modify their apartments in the same manner as a condominium owner.
Technically, a new owner of a co-op share needs to be approved by the co-op board, but this is primarily a formality and rejections are extremely rare. Co-ops in Sweden are intended to be occupied by their actual owners and cannot be rented out to a third party without board approval; the co-op board does commonly exercise its powers in this respect. There are some time limited exceptions, such as studying or working abroad for a fixed period of time, but it is usually difficult to get permission for more than a few years. The motivation behind these rules is that the co-op is not intended as an investment vehicle but as an owner-occupied form of living.4
2.2 Rent Determination
The cooperative association faces two sorts of costs. First, there are the costs of maintaining all interior and exterior common areas as well as other maintenance costs that may be shared among the members. Second, the cooperative as a whole may have loans that need to be serviced. These costs are met by collecting monthly payments, or `rents', from the association members, which are based on the size of their shares in the cooperative and typically are fairly linear functions of apartment size.
When a co-op is initially formed and the shares are sold, either by a residential developer or through a conversion of rental units to co-op units, the founders can decide how much of the total cost of the shares will be paid upfront by the buyers and how much of it will be financed by mortgages taken out by the cooperative itself. If the cooperative opts to finance a larger amount, then higher monthly rents are necessary. Ceteris paribus, higher rents should therefore imply a lower price. It should be stressed that given the size of an apartment's share in the cooperative, the rent will not be affected by individual characteristics of the apartment. That is, if an apartment gets renovated by the current owner, the increased standard of the apartment will only be reflected in the price of the apartment when it is next sold, not in its rent.
Differences in the capital cost component of the rent can thus arise from differences in the initial loans taken out by the cooperative at the time of its foundation.5 In addition, a cooperative may at times acquire new loans to finance major renovations that are conducted by the cooperative as a whole, such as changing the electricity or sewage systems in the entire building. The initial variation is clearly predetermined and exogenous to our analysis. However, if the buyer of a certain co-op expects future renovations and, consequently, rent increases to occur, this could bias our results since the buyer perceives the long-run rent as higher than what we observe. Of course, this is only a problem for anticipated renovations, and subsequent rent increases.6 Our empirical analysis therefore includes a test of whether such rent increases are in fact anticipated and finds no evidence that they are.
3 Modeling the Relationship between Prices and Rents
The purpose of this paper is to estimate the degree to which differing rents across apartments are accounted for in the sales prices of co-ops. The basic idea is that given two identical apartments with different rents, the difference in price between the two apartments should equal the difference between the present values of all future rent payments. To account for the fact that apartments differ in dimensions other than rents, we rely on hedonic price regressions and control for a variety of apartment and neighborhood characteristics as well as trends over time.
3.1 Theoretical Motivation
As discussed previously, the rent on a co-op is comprised of a maintenance fee
component and a capital cost component, which covers the cooperatives'
financial costs in terms of mortgages and loans. In effect, a co-op purchaser
takes on a share of the cooperatives' debt obligations, commensurate with the
size of his share in the cooperative. Thus, the true price, or intrinsic
value, of the co-op is actually the sum of the sales price and the present
value of this future stream of capital cost payments. Consequently, the sales
price should equal the intrinsic value less the present value of the capital
cost payments. That is, for co-op ![]() ,
,
| (1) |
where
Equation (1) captures the fundamental relationship that should hold
between prices and discounted rents, if co-ops are priced efficiently. The
primary aim of this paper is to evaluate the empirical validity of this
theoretical relationship and test whether the present value of the future rent
payments, PV(C![]() , is in fact fully reflected in the sales price,
, is in fact fully reflected in the sales price,
![]() . Thus, if the variables in equation (1) were all observed, one
could run the empirical regression,
. Thus, if the variables in equation (1) were all observed, one
could run the empirical regression,
| (2) |
where it follows that under rational, or efficient, pricing, ![]() .
However, since the intrinsic value
.
However, since the intrinsic value ![]() is not observed, equation
(2) is not a directly testable relationship.
is not observed, equation
(2) is not a directly testable relationship.
We therefore rely on hedonic price regressions to test this relationship. In such a framework, it is assumed that a vector of characteristics capture the value of the good. That is,
| (3) |
where ![]() includes the relevant characteristics of the co-op and
includes the relevant characteristics of the co-op and
![]() is a mean zero error term uncorrelated with
is a mean zero error term uncorrelated with ![]() .
Consequently,
.
Consequently,
| (4) |
where, under the null hypothesis of efficient pricing, ![]() .
.
3.2 Calculating the Present Value of the Rent
Consider two co-ops that have the same intrinsic value, but one costs ![]() and the other
and the other ![]() , and assume that the home buyers borrow at the
prevailing mortgage rate
, and assume that the home buyers borrow at the
prevailing mortgage rate ![]() . If the efficient market hypothesis holds, it
follows that the annual capital costs for these two co-ops should be
identical:
. If the efficient market hypothesis holds, it
follows that the annual capital costs for these two co-ops should be
identical:
| (5) |
where ![]() is the tax rate at which interest rate payments are deductible
and
is the tax rate at which interest rate payments are deductible
and ![]() and C
and C![]() are the annual capital cost components of the
rents.
are the annual capital cost components of the
rents.![]() 7
7![]() 8Divide through by the effective interest rate,
8Divide through by the effective interest rate,
![]() ,
and it follows that
,
and it follows that
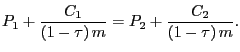 |
(6) |
The terms on each side of this equation are, of course, equal to the price
plus the discounted value of the future rent payments, under the assumption of
a fixed discount rate equal to the (tax-adjusted) mortgage rate,
![]() , and fixed rents. The present value of the rent can easily
be adjusted to allow for changing rents. Suppose rents were to decrease by
, and fixed rents. The present value of the rent can easily
be adjusted to allow for changing rents. Suppose rents were to decrease by ![]() percent every year after the first year. In this case, it follows that
percent every year after the first year. In this case, it follows that
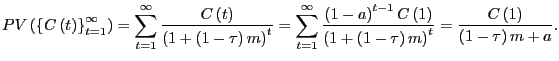 |
(7) |
The capital cost part of the rent reflects the servicing of loans that the cooperative as a whole has incurred. If the rent covers only the interest rate payments on these loans, one would expect the rent to stay fixed in the future since the loan remains the same each year, provided interest rates stay constant. On the other hand, if the rent payments also include an amortization on these loans, one would expect the rent to decrease over time as the loan becomes smaller. That is, if the cooperative were to pay off one percent of their loans each year, this should translate into an average decrease in the rent of one percent per year. In practice, there might be a desire to smooth rents and decreases in the loan might therefore not be immediately reflected in the rents, but over the long-run, the relationship should hold. We discuss plausible levels of rent decreases and amortization rates in the empirical section.9 Use of equation (7) to calculate present values also assumes that the rent payments continue indefinitely in the future. We find no evidence to the contrary when looking at annual statements for more than 100 cooperatives in Gothenburg; thus, most loans that cooperatives have are, for our purposes, infinitely lived. That is, the rents paid to service these loans cover only interest rate payments plus the potential (proportional) amortization rates discussed in the empirical section.10
We thus calculate the present value of future discounted rents as
![]() , where
, where
![]() and
and ![]() is the mortgage rate faced by the
purchaser of co-op
is the mortgage rate faced by the
purchaser of co-op ![]() ,
, ![]() is the rent decrease or, alternatively
interpreted, the amortization rate, and
is the rent decrease or, alternatively
interpreted, the amortization rate, and ![]() is the tax rate at which
interest rate payments are deductible and equal to 30 percent; the 30 percent
tax deduction applies to all home owners in Sweden, regardless of their income
level. In addition, the effect of changing future interest rates is explicitly
addressed in the empirical sections.
is the tax rate at which
interest rate payments are deductible and equal to 30 percent; the 30 percent
tax deduction applies to all home owners in Sweden, regardless of their income
level. In addition, the effect of changing future interest rates is explicitly
addressed in the empirical sections.
The discount factor proposed here is somewhat different from the one used, for instance, by, Meese and Wallace (1994). It is worth briefly discussing the differences, which stem from the fact that we compare co-op units with each other rather than rental apartments with owner occupied residences, as done by Meese and Wallace. Similar to Meese and Wallace, we use the mortgage rate adjusted for (income) tax deductions as the basic interest rate component in the discount rate. However, Meese and Wallace also adjust for property taxes, depreciation, and rental inflation. In our setup, property taxes are paid for by the cooperative as a whole and are not linked to the purchase prices of the individual units; rather, they are determined by the value of the entire cooperative and are thus independent of the capital structure. The depreciation term in Meese and Wallace accounts for the capital depreciation of the home-owner's property, which is a cost that is not incurred when renting. However, in the context of our application, capital depreciation does not affect the trade off between purchase prices and rents since it should be the same across units, once other factors have been controlled for. Similarly, rental inflation plays no role in our analysis. Finally, Meese and Wallace also include a risk premium on housing investments. While this could also be added to our current discount factor, its interpretation is not as straightforward since we are comparing between investments in co-ops rather than between buying and renting. However, since the personal mortgage is in a sense riskier to the home buyer than the mortgage carried by the cooperative, which has a form of limited liability attached to it from the perspective of the individual home buyer, a risk premium could be added to the discount factor. Because there is no obvious way of estimating this premium, we assume throughout the analysis that it is zero, but discuss it qualitatively at the end of Section 6.
3.3 Total Rent, Capital Costs, and Maintenance Fees
An additional empirical issue that must be dealt with is the fact that the
capital cost component of the rent is not directly observed in our data;
rather, we only observe the total rent, i.e. maintenance plus capital costs.
Therefore, we rewrite equation (4), letting the total annual rent of
co-op ![]() be
be
![]() , where
, where ![]() and
and ![]() denote the
annual capital cost and maintenance components of the rent, respectively:
denote the
annual capital cost and maintenance components of the rent, respectively:
![\begin{displaymath}\begin{array}[c]{l} P_{i} =\theta PV\left( {C_{i} } \right) +X_{i} \beta+\varepsilon_{i}\\ \quad=\theta\frac{C_{i} }{k_{i} }+\theta\frac{M_{i} }{k_{i} }-\theta \frac{M_{i} }{k_{i} }+X_{i} \beta+\varepsilon_{i}\\ \quad=\theta\frac{rent_{i} }{k_{i} }-\theta\frac{M_{i} }{k_{i} }+X_{i} \beta+\varepsilon_{i} .\\ \end{array}\end{displaymath}](img53.gif) |
(8) |
Thus, the coefficient in front of the total rent is still identical to the
original one in front of the capital cost component, but an additional
variable,
![]() , which represents the discounted value of
the maintenance fee, is now present. To control for this additional term
empirically, we proxy for the maintenance fee with a linear combination of the
characteristics in
, which represents the discounted value of
the maintenance fee, is now present. To control for this additional term
empirically, we proxy for the maintenance fee with a linear combination of the
characteristics in ![]() . That is, under the assumption that
. That is, under the assumption that
![]() , it follows that
, it follows that
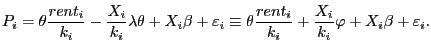 |
(9) |
This effectively assumes that conditional on ![]() , the maintenance fee is
constant. For instance, if
, the maintenance fee is
constant. For instance, if ![]() represents the size of the co-op, the
maintenance fee per square meter would be equal across cooperatives. More
generally, potential differences in the maintenance fee across other apartment
or neighborhood characteristics can also be controlled for by interacting
these observable control variables (or neighborhood dummies) with the inverse
of the discount rate. Empirically, however, it is evident that once we
interact the square meter size of the co-op with the inverse of the discount
rate, additional interaction terms (such as floor, number of floors, and
parish dummies) do not alter the results. There is thus strong support for the
notion that the maintenance fee per square meter is fairly constant across
cooperatives in the sample. This is consistent with the nature of typical
Swedish housing cooperatives, i.e. they generally have no common area rooms or
other elements, such as pools or doormen, that would add variation to the
maintenance fee.
represents the size of the co-op, the
maintenance fee per square meter would be equal across cooperatives. More
generally, potential differences in the maintenance fee across other apartment
or neighborhood characteristics can also be controlled for by interacting
these observable control variables (or neighborhood dummies) with the inverse
of the discount rate. Empirically, however, it is evident that once we
interact the square meter size of the co-op with the inverse of the discount
rate, additional interaction terms (such as floor, number of floors, and
parish dummies) do not alter the results. There is thus strong support for the
notion that the maintenance fee per square meter is fairly constant across
cooperatives in the sample. This is consistent with the nature of typical
Swedish housing cooperatives, i.e. they generally have no common area rooms or
other elements, such as pools or doormen, that would add variation to the
maintenance fee.
3.4 Empirical Specification
The basic specification taken to the data is presented in equation
(10). The dependent variable, ![]() , is the sales price for transaction
, is the sales price for transaction ![]() on day
on day ![]() , and in parish
, and in parish ![]() and zip code
and zip code ![]() .
.
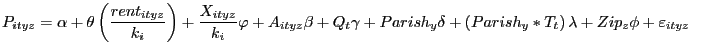 |
(10) |
Thus, the aim of this paper is to test whether ![]() is significantly
different from negative one. We control for a number of observable and
unobservable characteristics. Specifically,
is significantly
different from negative one. We control for a number of observable and
unobservable characteristics. Specifically, ![]() includes apartment
characteristics, such as size, number of rooms, floor number, number of floors
in the building, building age, and whether or not heat is included in the
rent. We use quarterly dummies (
includes apartment
characteristics, such as size, number of rooms, floor number, number of floors
in the building, building age, and whether or not heat is included in the
rent. We use quarterly dummies (![]() to control for the increasing trend in
co-op prices observed nationwide over the sample period. In addition, we allow
for the possibility that trends vary across geographic areas by including
parish specific time trends (Parish
to control for the increasing trend in
co-op prices observed nationwide over the sample period. In addition, we allow
for the possibility that trends vary across geographic areas by including
parish specific time trends (Parish
![]() . In Sweden, a parish
is comparable to a U.S. county.
. In Sweden, a parish
is comparable to a U.S. county.
Of course, given the cross-sectional nature of our analysis, one must also address the concern of omitted variable bias. In particular, an omitted variable that is positively correlated with both price and rents would bias our results away from market efficiency and towards a coefficient of zero.11 The most obvious omission is a measure of the overall standard of the apartment. Unfortunately, the available data does not include any variables, such as whether the kitchen has been renovated, that would help characterize apartment quality. We do not believe that this is as problematic as it may seem for two reasons. First, strict building codes in conjunction with thin tails in the income distribution contribute to fairly homogeneous housing standards in Sweden. Second, many indicators of standard are unlikely to be correlated with the rent; specifically, idiosyncratic upgrades done by the co-op owner, such as a kitchen renovation, would be reflected in the price of an apartment but not in the rent, as discussed previously.
Of course, not all variation in standard is idiosyncratic across units. It is
certainly feasible that some cooperatives with an overall greater standard
have a higher level of debt. Such overall building standard may be
neighborhood specific; for instance, cooperatives in wealthy neighborhoods may
be more inclined to invest money in the building to keep it in superior
condition, thereby keeping rents high. To the extent that this is the case, we
control for unobservable neighborhood characteristics in two ways. First, we
control for parish dummies, Parish![]() . However, it is certainly
possible that neighborhood characteristics vary within a parish. Thus, our
preferred specifications also include neighborhood fixed effects in the form
of zip code dummies, Zip
. However, it is certainly
possible that neighborhood characteristics vary within a parish. Thus, our
preferred specifications also include neighborhood fixed effects in the form
of zip code dummies, Zip![]() . There are 77 parishes and 1,081 zip
codes in our data.12
. There are 77 parishes and 1,081 zip
codes in our data.12
4 Data
Our data set consists of over 30,000 transactions of Swedish co-ops between January 2002 and September 2005 for the three largest cities in Sweden: Stockholm, Gothenburg, and Malmo. The data come from a company called Värderingsdata AB, which collects data on all co-op transactions conducted by members of Svenska Mäklarsamfundet (the Swedish association of real estate agents), as well as by Föreningssparbankens Fastighetsbyrå and Svensk Fastighetsförmedling, which are the two largest real estate agencies on the market. The data is believed to cover approximately 70 percent of all co-op transactions that occur in Sweden.
For each transaction, the following data are recorded: the transaction date, the actual sales price, the annual rent, the size of the apartment measured in square meters, the number of rooms, the apartment's floor number, the number of floors in the building, the build year, and whether heating is included in the rent.13 In addition, the address of the apartment, including the zip code and parish, and the name of the co-op in which it is sold are reported.
Table 1 presents summary statistics for the entire sample. The average price of co-ops sold is 1,250,685 SEK; at an exchange rate of 6.0 SEK per U.S. dollar, this is approximately $208,000. Prices vary substantially across the three cities, ranging from an average of 1.6 million SEK in Stockholm to 1.0 million SEK in Gothenburg and just 0.7 million SEK in Malmo. Figure 1 plots the average transaction price for each quarter from January 2002 through September 2005, and indicates an increase of more than 35 percent over the period.
The average annual rent is 37,629 SEK across all cities. Compared to the price, there is much less variation in the annual rent across cities and over time; the average annual rents in the first and last quarters, respectively, are 37,307 SEK and 37,232 SEK. To calculate the present value of future rent payments, we rely on the mortgage rate as of the transaction date. This is measured as the average of the five-year rates from three different lenders (SBAB, Nordea, and Stadshypotek); the average mortgage rate faced by purchasers in our sample is 4.8 percent and decreases substantially over the sample period from 6.7 percent, on average, in the first quarter to 3.6 percent in the final quarter. Assuming no amortizations, the average present discounted value of annual rent payments is 1,150,926 SEK. Thus, the present value of future rent payments is not an inconsequential amount; on average, it almost equals the purchase price.14
The average apartment in the entire sample is 66 square meters and two room apartments are the most common. Overall, 73 percent of the co-ops include heat in the rent. Seven mutually exclusive variables are created to indicate the age of an apartment, where the age is defined to be the transaction year minus the build year. Overall, 5.2 percent of the units are less than 10 years old and about two-thirds of the units are more than 50 years old.
5 Empirical Results
5.1 Baseline Results
Table 2 presents the main empirical results. The baseline specifications are presented in Panel 1; the remaining panels of Table 2 allow for rent decreases or, equivalently, amortization of the cooperatives' loans. The first row of columns (1) and (2) of each panel present the coefficient on the present value of the discounted rent stream that results from estimating equation (10) when zip code fixed effects are excluded and included, respectively. Whether or not the estimated rent coefficients differ significantly from minus one, i.e. the value under the null hypothesis of market efficiency, are indicated with stars throughout the tables.
As seen in columns (1) and (2) of Panel 1, the estimated rent coefficient is equal to -0.61 when zip code fixed effects are not included and equal to -0.56 with zip code fixed effects.15 That is, on average, increasing the present value of the annual rent by 100 SEK decreases the transaction price by 56 to 61 SEK. Thus, the results so far strongly reject the efficient market hypothesis. Given the concerns about omitted variables, our preferred specification includes zip code fixed effects to control for neighborhood unobservables. Including zip code fixed effects does not decrease the precision of the estimates; in fact, the standard errors actually decrease somewhat (from 0.03 to 0.02).
5.2 Rent Changes
We continue the analysis by assessing the sensitivity of these baseline
estimates to relaxing the assumptions that future rents and mortgage rates
will not change. Specifically, Panels 2 and 3 of Table 2 assume
an annual rent decrease or, equivalently, amortization rate of one and two
percent, respectively. Intuitively, and as is evident from the discount
formula presented in equation (7), rent decreases will result in a
lower present value of future rents; therefore,
![]() must increase
in absolute value. With zip code fixed effects included, assuming a one
percent amortization rate results in a rent coefficient of -0.74 that is
highly significantly different from minus one. Increasing the amortization
rate to two percent brings the rent coefficient much closer to minus one,
although the point estimate of -0.92 is still significantly different.
must increase
in absolute value. With zip code fixed effects included, assuming a one
percent amortization rate results in a rent coefficient of -0.74 that is
highly significantly different from minus one. Increasing the amortization
rate to two percent brings the rent coefficient much closer to minus one,
although the point estimate of -0.92 is still significantly different.
As is evident, decreasing rents or amortizations can substantially impact the results; it is therefore important to identify the value of a realistic amortization rate. To get a sense of this, we examined the annual statements from 125 cooperatives in Gothenburg and recorded the amortization rate of their loans as well as the change in overall rents.16 The results are shown in Table 3. The average change in overall rent from one year to the next for the 125 cooperatives is 1.2 percent; this is very similar to the average annual increase in rent per square meter of 1.3 percent observed in our primary data. As is seen from the percentiles of the rent changes, very few of these 125 cooperatives lower their rents, although more than half keep their rents fixed for the year of the annual statement. As discussed previously, short term rent changes may not reflect expected longer term patterns that might result from persistent annual amortization of the cooperatives' loans. The average amortization rate is 1.7 percent, although this may be somewhat misleading since the median rate is only 0.53 percent. The high average is driven by a few large amortizations, which were primarily the results of some windfall gain for the cooperative, such as the conversion and sale of previous rental apartments. These high amortization rates are therefore almost exclusively one time events and do not represent long term averages. The final row in the table gives the statistics for those cooperatives that amortized between zero and five percent of their loans, and for which the average amortization rate is 0.71 percent.
Therefore, based on a reading of the annual statements, we believe that a long-term average amortization rate closer to one percent (and probably even lower than one percent) is more realistic than a two percent rate. That is, the results in Panel 2 of Table 2 should provide the most accurate estimated rent coefficient (i.e. -0.74).
A separate issue that is also related to rent changes is whether co-ops with relatively low rents today have some unobservable characteristics that make them more likely to have higher rents in the future. For example, low rents today may signal that renovations have not recently taken place and are thus more likely to occur in the near future. If this is true, then we are clearly underestimating the magnitude of the coefficient since low rent apartments will seem more attractive to the researcher than to the actual homebuyer, who can infer that rents are likely to increase in the future. Of course, whether or not this is actually an issue in our empirical analysis depends on whether homebuyers take such potential rent increases into account.
We test this by taking advantage of the fact that our data contains multiple transactions within the same cooperative. We identify a subset of cooperatives that potentially incurred significant renovations over the sample period, as proxied for by those cooperatives with large rent increases between the first and last observed transactions. Specifically, we observe 602 cooperatives in which the annual rent per squared meter increased by more than 15 percent, 384 cooperatives in which it increased by at least 20 percent, and 253 cooperatives in which it increased by at least 25 percent. We then estimate equation (10), excluding parish specific time trends and zip code fixed effects, separately for these sub-samples of first and last transactions. The estimated rent coefficients are presented in Table 4.17
If such renovations and subsequent rent increases are fully anticipated, then the rent coefficients for the post-renovation transactions should be less biased since the researcher and homebuyer have more similar information than in the pre-renovation transactions. Hence, the post-renovation coefficients should be closer to minus one. However, the estimates shown in Table 4 indicate the exact opposite. For instance, when considering the sample of cooperatives with a 15 percent or more rent increase, we find that the estimated rent coefficient decreases in magnitude from -0.70 for the pre-renovation transactions to -0.46 for the post-renovation transactions. The same pattern of results is seen for the cooperatives with 20 and 25 percent rent increases, though the estimates become more imprecise due to the decreased sample sizes. Thus, there is little evidence that this kind of rent increase is anticipated and that our empirical analysis would be biased by omitting expectations about future renovations and subsequent rent changes.
5.3 Interest Rate Changes Over Time
The interest rate used in the discount formula, which is equal to the five-year mortgage rate, obviously has a large effect on the present value of the discounted rent.18 The interest rate is fairly low during parts of the sample, particularly towards the end (3.6 percent during the last quarter); this is most likely well below what can be expected over the long-run. Thus, there might be some concern that our findings can be explained by expectations about interest rates increasing in the future, which would reduce the present value of future rent payments.
A first diagnostic of the validity of these concerns is to see if the rent coefficient changes dramatically over the sample period. If the evidence of market inefficiency is due to a failure to account for expectations about high future interest rates, we would expect the rent coefficient to be closer to efficiency at the beginning of the sample, where the interest rate is closer to a long-run average. Although not shown here, estimating equation (10) quarter by quarter indicates that the rent coefficient does not change systematically over time. Thus, the results are not driven by lower discount rates at the end of the sample.
Alternatively, we can estimate the implied interest rate for each quarter that
is consistent with market efficiency. That is, we set ![]() = -1, and
treat the interest rate as the free parameter to be estimated. We still assume
a 30 percent tax-deduction, but that there is no amortization. For each
quarter, Figure 2 plots the actual five-year rate as well as two
estimates of the implied interest rate. The first estimate shows the implied
interest rate that would have to prevail in all future periods in
order for market efficiency to hold. The second estimate is the implied rate
necessary in all periods after the first five years, assuming that the current
five-year rate is used to discount during the initial five years. On average,
the implied rate is about three percent higher than the five-year mortgage
rate in each quarter, and ranges from about 10 percent in the first quarter to
six percent in the last. Apart from a couple of outliers, which are most
likely due to less precision in the quarterly estimates, the implied interest
rate when the current five-year rate is used for the first five years is
substantially higher and varies between approximately 16 and 10 percent.
= -1, and
treat the interest rate as the free parameter to be estimated. We still assume
a 30 percent tax-deduction, but that there is no amortization. For each
quarter, Figure 2 plots the actual five-year rate as well as two
estimates of the implied interest rate. The first estimate shows the implied
interest rate that would have to prevail in all future periods in
order for market efficiency to hold. The second estimate is the implied rate
necessary in all periods after the first five years, assuming that the current
five-year rate is used to discount during the initial five years. On average,
the implied rate is about three percent higher than the five-year mortgage
rate in each quarter, and ranges from about 10 percent in the first quarter to
six percent in the last. Apart from a couple of outliers, which are most
likely due to less precision in the quarterly estimates, the implied interest
rate when the current five-year rate is used for the first five years is
substantially higher and varies between approximately 16 and 10 percent.
Though five-year fixed rate loans are available, many home buyers still choose floating interest rates. It is therefore reasonable to assume that most of the uncertainty (and risk-aversion) regarding future interest rates is beyond the five-year horizon; that is, we can view the five-year rate as a conservative (i.e. high) expectation of rates for the first five years. Otherwise, the fixed rate loan would be more frequently used. Based on the implied interest rate beyond the five year horizon, it is clear that home buyers would have to have very risk-averse beliefs regarding the path of future interest rates to justify the lack of market efficiency found thus far.
Finally, it should be stressed that future increases in the interest rate are likely to be associated with increases in the capital cost part of the rent, since this also reflects interest rate payments. Thus, future increases in the interest rate are likely to be more or less offset by increases in the rent, leaving the present value of future discounted rents fairly unchanged. Consequently, our analysis may be less sensitive to changing interest rates than it appears at first glance.19
5.4 Liquidity Constraints and Heterogeneous Discount Rates Across Agents
The results described above are hard to reconcile with an efficient market where all agents at a given point in time face the same discount rate. In reality, however, some buyers may face a higher marginal discount rate as a result of being liquidity constrained and having to take out a larger fraction of the price as a loan. For instance, most lending institutions charge a higher marginal rate of interest (i.e. a top loan) if the buyer does not provide a certain percentage in down payment. A survey of Swedish lending institutions suggests that top loans are provided at a one to two percentage point higher rate than the floating mortgage rates offered. Although we have no information on actual buyers, certain groups, such as poorer buyers or first time buyers, are more likely to be liquidity constrained than others.
Therefore, this section allows those most likely to be liquidity constrained to face a higher mortgage rate and assesses the impact of this on estimates of market efficiency. We proxy for buyer liquidity with apartment size and assume that the buyers of the smallest apartments face the greatest constraints and those of the largest face few to none. Table 5 presents the results of estimating equation (10) for various sub-samples based on apartment size. The results in the first row assume a one percent amortization rate to calculate the present value of rents while the second row additionally assumes a two percent markup on the 5-year mortgage rate used in our baseline analysis. This is likely to be a very conservative markup, i.e. resulting in a high interest rate, given: (i) the range seen in markups for top loans, (ii) that we are applying the markup to all buyers within a group, and (iii) that the five year rate used here may be conservative to begin with since most loans are floating (see footnote ).20
The results presented when there is no markup (row 1) indicate that the estimated rent coefficient is further from efficiency for buyers in smaller apartments. In particular, the estimated coefficient for the bottom size decile is equal to -0.39 and increases in absolute value as apartment size increases, such that it is equal to -0.70 for the top decile. If one assumes that the buyers of these largest apartments face minimal liquidity constraints, then it is hard to argue that liquidity constraints can be the sole explanation for our findings of inefficiency.
However, row 2 of Table 5 indicates that liquidity constraints can explain some of the inefficiencies observed at the lower end of the market. When using the two percent markup, the estimated rent coefficients naturally get closer to minus one. While we apply this markup to apartments of all sizes in row 2, this is not a realistic scenario. In practice, such a markup would be most relevant for the smallest apartments and least relevant for the largest. Specifically, we find an estimated rent coefficient of -0.52 for the bottom decile. Thus, even when allowing for this conservative top loan, there is still strong evidence of inefficiency. Liquidity constraints may, therefore, explain some efficiency differences across buyer group; but, it does not account for the overall inefficiencies seen in the market.
6 Heterogeneity Across Parishes and Correlates of Efficiency
To further understand potential sources and explanations of inefficiency, we estimate equation (10) separately for each parish, assuming a one percent amortization rate. While there are 77 parishes in Stockholm, Gothenburg, and Malmo, we only present the results for those 70 parishes with 50 or more transactions in the sample. The estimated rent coefficient is significantly different from minus one in 57 of the 70 parishes. The mean and median estimates of the rent coefficient are -0.50 and -0.53, respectively There is also a fair amount of variation in the rent coefficients across parishes; the standard deviation of the estimates is 0.31.
What explains this variation in the estimated rent coefficient? We explore this question in two ways. First, we examine the relationship between the estimated parish-by-parish rent coefficients and parish income and wealth. These results are presented in panels A through C of Figure 3, which ranks parishes from low to high on the x-axis according to average gross labor income (column 1) or average assets (column 2). Panels A and B show cumulative and moving averages of the rent coefficient, respectively, while Panel C plots the actual point estimates along with the estimated least squares relationship. All six graphs tell the same basic story. The estimated rent coefficient gets closer to minus one as wealth or income increases.
Table 6 reinforces these observations by grouping the parishes into two samples, most and least efficient, and comparing measures of socioeconomic status: the amount of education, average income and wealth, and the income distribution.21 The first four columns compare parishes with rent coefficients below (more efficient or closer to minus one) and above (less efficient) the median point estimate. The last four columns look at parishes in the most and least efficient quartiles. Of note is that the differences in the education and income variables across the two groups are both statistically and economically significant. On average, 14 percent more of the population has attended college in the relatively more efficient parishes; this gap increases to 22 percent when comparing parishes in the top and bottom quartiles. Average income and wealth are also significantly higher in more efficient parishes; for instance, average net wealth, including the value of housing, is more than 500,000 SEK greater when comparing the top and bottom quartiles. Thus, Table 6 indicates that there are significant differences in socioeconomic characteristics between parishes that, on average, more accurately discount the rent. In general, these parishes are more educated and have greater wealth and income.
These findings are consistent with multiple hypotheses. One possibility is that of liquidity constraints, as described in the previous section. One would expect buyers in poorer, less educated parishes to be more constrained and more likely to face marked up interest rates. Alternatively, these findings also line up well with a scenario of more `sophisticated' buyers in higher educated, wealthier markets who push prices towards efficiency. To try to further distinguish between these two hypotheses, we group the data jointly according to both apartment size (as in Table 5) and education level. Specifically, we rank the parishes' education level, measured by the percent with college as the highest education; high educated parishes are those with an education level above the median. Panel A of Table 7 presents the results for the low-educated parishes and Panel B for the high-educated parishes. Two distinct patterns stand out. First, the estimated rent coefficient increases almost monotonically from the smallest to largest apartment groups for both low- and high-educated parishes. Second, for any given apartment size, the estimated rent coefficient is closer to minus one, sometimes substantially so, in the higher-educated parishes. Thus, to the extent that apartment size proxies for liquidity and parish education level proxies for `sophistication', these results provide evidence that both of the above hypotheses are relevant to explain our findings.
The above findings are also consistent with Campbell (2006), who analyzes household decisions regarding financial matters, and finds that a minority of households make significant investment mistakes and that this group tends to be poorer and less well educated than the majority of more successful investors. More generally, Campbell (2006) and Calvet, Campbell, and Sodini (2007, 2008) document that higher-educated and wealthier households are more likely to satisfy the predictions of standard financial models.
Lastly, our analysis implicitly assumes that agents are risk neutral in their decision making. Risk-averse agents may prefer, and thus pay a premium for, co-ops with lower sales prices and higher rents since the owner of a co-op faces a limited liability on the loans taken out by the cooperative; in the case of a failure to meet his rent obligations, the unit will be returned to the cooperative. On his personal mortgage, on the other hand, there is no limited liability. Thus, if the prices of co-ops reflect such preferences, which would enter into our discount formula as a risk premium on housing investment, they may be the outcome of an efficient market process.
All of the scenarios described above can potentially account for some or all of the inefficiencies uncovered in our analysis. However, these explanations would seem to be most valid at the lower end of the market and appear less convincing in explaining inefficiencies at the higher end of the market. Yet, the efficiency hypothesis is rejected in the overwhelming majority of parishes, even those that are characterized by high income, suggesting that there is a systematic failure to fully discount rent differences.
7 Conclusion
We test for efficiency in housing markets using a new and novel approach. We capitalize on the fact that only part of the true price of a co-op is captured by the actual sales price, with the rest paid through monthly rents that reflect the underlying debts of the cooperative. There is thus a simple present value relationship between co-op sales prices and rents. Using hedonic price regressions, we find that, on average, higher rents are not fully compensated for by lower prices. Under realistic assumptions regarding future interest and amortization rates, a 100 SEK increase in the discounted value of future rent payments yields a reduction in the sales price of about 75 SEK. A number of explanations are discussed throughout the paper for the findings of inefficiencies. Though our data does not allow us to explicitly test one hypothesis versus another, there are strong indications that at least some of the inefficiencies are due to a fundamental failure to properly compare future rent payments with up front costs at the time of purchase.
In most markets, one would expect inefficiencies to be exploited by investors and arbitraged away over time. This is less likely to be true in the current context since owners of Swedish co-ops are not allowed to rent out their apartments, thereby preventing speculators from entering this market. Thus, the inefficiencies found in this paper can only be taken advantage of by `smart' buyers who realize that lower rent apartments are, in general, of better value, and the market may therefore only slowly converge towards efficient pricing.
References
Berg L., and J. Lyhagen, 1998. The dynamics in Swedish house prices - an empirical time series analysis, Working Paper No. 12, Institute for Housing Research, Uppsala University.
Calvet, L., J.Y. Campbell, and P. Sodini, 2007. Down or Out: Assessing the Welfare Costs of Household Investment Mistakes, Journal of Political Economy 115, 707-747.
Calvet, L., J.Y. Campbell, and P. Sodini, 2008. Fight or Flight? Portfolio Rebalancing by Individual Investors, Working Paper Harvard University.
Campbell, J.Y., 2006. Household Finance, Journal of Finance 61, 1553-1604.
Case, B., and J.M. Quigley, 1991. The Dynamics of Real Estate Prices, Review of Economics and Statistics 73, 50-58.
Case, K.E., and R.J. Shiller, 1989. The Efficiency of the Market for Single-Family Homes, American Economic Review 79, 125-137.
Case, K.E., and R.J. Shiller, 1990. Forecasting Prices and Excess Returns in the Housing Market, Journal of the American Real Estate and Urban Economics Association 18, 253-273.
Englund, P., T.M. Gordon, and J.M. Quigley, 1999. The Valuation of Real Capital: A Random Walk down Kungsgatan, Journal of Housing Economics 8, 205-216.
Gallin, J., 2005. The Long-Run Relationship between House Prices and Rents, Working Paper, Federal Reserve Board.
Gatzlaff, D.H., 1994. Excess Returns, Inflation and the Efficiency of the Housing Market, Journal of the American Real Estate and Urban Economics Association 22, 553-581.
Glaeser, E.L, and J. Gyourko, 2007. Arbitrage in Housing Markets, Working Paper, Harvard University.
Guntermann K.L., and S.C. Norrbin, 1991. Empirical Tests of Real Estate Market Efficiency, Journal of Real Estate Finance and Economics 4, 297-313.
Hill, R.C., C.F. Sirmans, and J.R. Knight, 1999. A random walk down main street?, Regional Science and Urban Economics 29, 89-103.
Hwang, M., and J. Quigley, 2002. Price Discovery in Time and Space: The Course of Condominium Prices in Singapore, Working Paper, Department of Economics, University of California, Berkeley.
Hwang, M., and J. Quigley, 2004. Selectivity, quality adjustment and mean reversion in the measurement of house values, Journal of Real Estate Finance and Economics 28, 161-178.
Hwang, M., J. Quigley, and J. Son, 2006. The Dividend Pricing Model: New Evidence from the Korean Housing Market, Journal of Real Estate Finance and Economics 32, 205-228.
Linneman, P., 1986. An Empirical Test of the Efficiency of the Housing Market, Journal of Urban Economics 20, 140-154.
Malpezzi, S., 1999. A Simple Error Correction Model of House Prices, Journal of Housing Economics 8, 27-62.
Meese R., and N. Wallace, 1994. Testing the Present Value Relation for Housing Prices: Should I Leave My House in San Francisco?, Journal of Urban Economics 35, 245-266.
Rosenthal, Stuart, 1999. Residential Buildings and the Cost of Construction: New Evidence on the Efficiency of the Housing Market, The Review of Economics and Statistics 81(2), 288-302.
Schill, M.H., I. Voicu, and J. Miller, 2004. The Condominium v. Cooperative Puzzle: An Empirical Analysis of Housing in New York City, Law and Economics Research Paper Series, Working Paper No. 04-003, New York University.
Turner B., 1997. Housing Cooperatives in Sweden: The Effects of Financial Deregulation, Journal of Real Estate Finance and Economics 15, 193-217.
Table 1: Summary Statistics
| Variable | Mean | Std. Dev. | Within Parish Std. Dev.(1) | Within Zipcode Std. Dev.(2) | Min | Max |
|---|---|---|---|---|---|---|
| Price (kronor) | 1,250,685 | 934,297 | 706,249 | 614,146 | 17,500 | 9,450,000 |
| Price per Meter | 19,903 | 11,436 | 5,120 | 4,420 | 179 | 86,667 |
| Annual Rent (kronor) | 37,629 | 17,022 | 15,541 | 12,499 | 0 | 199,044 |
| PV Annual Rent | 1,150,926 | 562,249 | 520,712 | 439,384 | 0 | 4,335,367 |
| Meter | 65.78 | 27.19 | 25.39 | 22.09 | 12 | 276 |
| 1 Room | .18 | .39 | .37 | .35 | 0 | 1 |
| 2 Rooms | .42 | .49 | .48 | .46 | 0 | 1 |
| 3 Rooms | .25 | .43 | .42 | .40 | 0 | 1 |
| 4 Rooms | .11 | .31 | .31 | .29 | 0 | 1 |
| 5 or More Rooms | .037 | .19 | .19 | .17 | 0 | 1 |
| Floor | 2.85 | 1.70 | 1.64 | 1.49 | 1 | 21 |
| # Floors | 4.73 | 2.02 | 1.82 | 1.36 | 1 | 24 |
| Heat | .73 | .44 | .43 | .42 | 0 | 1 |
| Stockholm | .51 | .50 | .066 | 0 | 0 | 1 |
| Malmo | .22 | .42 | .049 | 0 | 0 | 1 |
| Gothenburg | .26 | .44 | .058 | 0 | 0 | 1 |
| < 10 Years Old | .052 | .22 | .21 | .14 | 0 | 1 |
| 10-20 Years Old | .061 | .24 | .23 | .17 | 0 | 1 |
| 20-30 Years Old | .049 | .22 | .19 | .15 | 0 | 1 |
| 30-40 Years Old | .076 | .27 | .23 | .19 | 0 | 1 |
| 40-50 Years Old | .094 | .29 | .26 | .20 | 0 | 1 |
| 50-60 Years Old | .29 | .45 | .42 | .37 | 0 | 1 |
| > 60 Years Old | .38 | .48 | .38 | .30 | 0 | 1 |
| Mortgage Rate | .048 | .0086 | .0085 | .0083 | .035 | .070 |
Note - (1) Within standard deviation is the variation within parishes. There are 77 parishes in the sample and 30,479 observations in total.
(2) Within standard deviation is the variation within zip codes. There are 1081 zip codes in the sample and 30,479 observations in total.
Table 2: Main Results: The Relationship Between the Present Value of Rents and Prices - Panel 1: Baseline Specifications
Variable | (1) |
(1) Robust Standard Error |
(2) | (2) Robust Standard Error |
|---|---|---|---|---|
| PV Annual Rent | -0.61*** |
(0.03) |
-0.56*** | (0.02) |
| Meter | 580.49*** |
(33.28) |
556.29*** | (26.90) |
| Meter | 11,255.88*** |
(2,545.26) |
11,126.89*** | (2,510.50) |
| (Meter | 17.46 |
(11.88) |
15.38 | (11.11) |
| 1 Room | 241,239.08*** |
(79,433.96) |
200,195.51*** | (72,701.20) |
| 2 Rooms | 280,674.19*** |
(71,521.99) |
233,813.92*** | (65,055.43) |
| 3 Rooms | 255,070.18*** |
(59,758.85) |
212,065.76*** | (53,361.58) |
| 4 Rooms | 181,657.75*** |
(42,588.27) |
158,118.47*** | (38,777.54) |
| Floor | 35,188.55*** |
(4,786.49) |
35,397.63*** | (4,732.94) |
| # Floors | -11,045.60** |
(4,573.03) |
-3,824.09 | (2,716.37) |
| Heat | -1,637.66 |
(7,523.14) |
379.29 | (5,821.00) |
| 10-20 Years Old | -224,058.49*** |
(55,504.88) |
-135,430.97*** | (48,085.29) |
| 20-30 Years Old | -286,181.97*** |
(64,931.95) |
-164,090.86*** | (47,794.73) |
| 30-40 Years Old | -309,361.45*** |
(57,500.95) |
-183,188.18*** | (44,331.12) |
| 40-50 Years Old | -241,103.39*** |
(55,045.47) |
-137,920.21*** | (43,073.21) |
| 50-60 Years Old | -145,779.93** |
(57,186.24) |
-99,457.99** | (41,546.63) |
| > 60 Years Old | -118,056.31* |
(62,979.64) |
-96,871.18* | (50,046.04) |
| Controls for Quarter Dummies | YES |
-- |
YES | -- |
| Controls for Parish Dummies | YES |
-- |
YES | -- |
| Controls for Parish Specific Time Trends | YES |
-- |
YES | -- |
| Controls for Zip Code Dummies | NO |
-- |
YES | -- |
| Discount Rate Assumes 30% tax deduction | YES |
-- |
YES | -- |
| Discount Rate Assumes 1% amortization | NO |
-- |
NO | -- |
| Discount Rate Assumes 2% amortization | NO |
-- |
NO | -- |
| Observations | 30,475 |
-- |
30,475 | -- |
| R-squared | 0.85 |
-- |
0.89 | -- |
Table 2: Main Results: The Relationship Between the Present Value of Rents and Prices - Panel 2: Assumes 1% Amortization or Rent Change
Variable |
(1) |
(1) Robust Standard Error |
(2) |
(2) Robust Standard Error |
|---|---|---|---|---|
| PV Annual Rent | -0.81*** |
(0.04) |
-0.74*** |
(0.03) |
| Meter |
889.71*** |
(55.74) |
858.76*** |
(47.42) |
| Meter |
8,330.42*** |
(2,538.57) |
8,226.15*** |
(2,469.69) |
| (Meter |
17.63 |
(11.81) |
15.44 |
(11.04) |
| 1 Room | 241,028.69*** |
(79,227.66) |
199,926.45*** |
(72,494.96) |
| 2 Rooms | 280,628.11*** |
(71,317.57) |
233,699.23*** |
(64,820.78) |
| 3 Rooms | 255,365.27*** |
(59,565.74) |
212,133.58*** |
(53,147.19) |
| 4 Rooms | 182,283.63*** |
(42,505.71) |
158,574.82*** |
(38,708.78) |
| Floor | 35,318.80*** |
(4,802.67) |
35,524.84*** |
(4,747.05) |
| # Floors | -11,109.26** |
(4,574.30) |
-3,850.35 |
(2,720.53) |
| Heat | -1,467.51 |
(7,478.91) |
587.14 |
(5,832.61) |
| 10-20 Years Old | -224,585.86*** |
(55,488.60) |
-139,068.26*** |
(47,915.21) |
| 20-30 Years Old | -291,606.02*** |
(64,838.18) |
-171,036.66*** |
(47,549.33) |
| 30-40 Years Old | -314,507.39*** |
(57,293.49) |
-189,037.28*** |
(44,064.67) |
| 40-50 Years Old | -245,881.37*** |
(54,884.63) |
-143,074.28*** |
(42,889.24) |
| 50-60 Years Old | -150,183.88** |
(56,975.72) |
-104,791.85** |
(41,239.28) |
| > 60 Years Old | -122,585.05* |
(62,843.18) |
-102,343.08** |
(49,758.88) |
| Controls for Quarter Dummies | YES |
-- |
YES |
-- |
| Controls for Parish Dummies | YES |
-- |
YES |
-- |
| Controls for Parish Specific Time Trends | YES |
-- |
YES |
-- |
| Controls for Zip Code Dummies | NO |
-- |
YES |
-- |
| Discount Rate Assumes 30% tax deduction | YES |
-- |
YES |
-- |
| Discount Rate Assumes 1% amortization | YES |
-- |
YES |
-- |
| Discount Rate Assumes 2% amortization | NO |
-- |
NO |
-- |
| Observations | 30,475 |
-- |
30,475 |
-- |
| R-squared | 0.85 |
-- |
0.89 |
-- |
Table 2: Main Results: The Relationship Between the Present Value of Rents and Prices - Panel 3: Assumes 2% Amortization or Rent Change
Variable |
(1) |
(1) Robust Standard Error |
(2) |
(2) Robust Standard Error |
|---|---|---|---|---|
| PV Annual Rent | -1.00 |
(0.05) |
-0.92*** |
(0.03) |
| Meter |
1,251.55*** |
(84.23) |
1,213.45*** |
(73.77) |
| Meter |
5,474.08** |
(2,571.06) |
5,387.27** |
(2,464.50) |
| (Meter2)2 | 17.79 |
(11.77) |
15.55 |
(11.00) |
| 1 Room | 241,164.15*** |
(79,105.32) |
200,087.21*** |
(72,373.00) |
| 2 Rooms | 280,859.77*** |
(71,201.06) |
233,954.37*** |
(64,687.99) |
| 3 Rooms | 255,740.19*** |
(59,455.75) |
212,432.83*** |
(53,025.50) |
| 4 Rooms | 182,758.57*** |
(42,469.45) |
158,980.05*** |
(38,676.41) |
| Floor | 35,385.95*** |
(4,812.52) |
35,588.90*** |
(4,755.90) |
| # Floors | -11,140.86** |
(4,575.47) |
-3,861.22 |
(2,723.81) |
| Heat | -1,391.77 |
(7,455.10) |
688.43 |
(5,842.48) |
| 10-20 Years Old | -225,144.86*** |
(55,474.77) |
-141,618.70*** |
(47,806.06) |
| 20-30 Years Old | -294,427.70*** |
(64,773.29) |
-174,938.11*** |
(47,424.35) |
| 30-40 Years Old | -316,960.22*** |
(57,178.64) |
-192,097.49*** |
(43,924.02) |
| 40-50 Years Old | -248,043.49*** |
(54,795.14) |
-145,638.31*** |
(42,802.47) |
| 50-60 Years Old | -152,329.11*** |
(56,863.35) |
-107,648.87** |
(41,076.06) |
| > 60 Years Old | -124,758.56* |
(62,777.91) |
-105,268.86** |
(49,610.18) |
| Controls for Quarter Dummies | YES |
-- |
YES |
-- |
| Controls for Parish Dummies | YES |
-- |
YES |
-- |
| Controls for Parish Specific Time Trends | YES |
-- |
YES |
-- |
| Controls for Zip Code Dummies | NO |
-- |
YES |
-- |
| Discount Rate Assumes 30% tax deduction | YES |
-- |
YES |
-- |
| Discount Rate Assumes 1% amortization | NO |
-- |
NO |
-- |
| Discount Rate Assumes 2% amortization | YES |
-- |
YES |
-- |
| Observations | 30,475 |
-- |
30,475 |
-- |
| R-squared | 0.85 |
-- |
0.89 |
-- |
Note - Robust standard errors that are clustered at the parish level are in parentheses. * indicates significance at the 10% level, ** at the 5% level, *** at the 1% level. For the PV Annual Rent coefficient, the *�s indicate a significant difference from minus one; for all other coefficients, the *�s indicate a significant difference from zero. The discount rate in Panel 1 is calculated using a 30% tax deduction. In panels 2 and 3, respectively, amortization rates of 1% and 2% are also included. Columns (1) and (2) of each panel estimate equation (10) when excluding and including zip code fixed effects, respectively. The omitted category for number of rooms is 5 or more rooms and for apartment age is < than 10 years old.
Table 3a: Descriptive Statistics of Amortization and Annual Rent Changes in Sample of Gothenburg Cooperatives
Variable | N | Mean | Std. Dev. | 10 Percentile | 25 Percentile | 50 Percentile | 75 Percentile | 90 Percentile |
|---|---|---|---|---|---|---|---|---|
| % Change In Rent | 125 | 1.24 | 8.76 | 0.00 | 0.00 | 0.00 | 2.00 | 7.00 |
| Amortization Rate (%) | 125 | 1.70 | 7.82 | 0.00 | 0.00 | 0.53 | 1.67 | 7.27 |
Table 3b: Descriptive Statistics of Amortization and Annual Rent Changes in Sample of Gothenburg Cooperatives With Amortization Rates Between 0 and 5%
Variable | N | Mean | Std. Dev. | 10 Percentile | 25 Percentile | 50 Percentile | 75 Percentile | 90 Percentile |
|---|---|---|---|---|---|---|---|---|
| % Change In Rent | 125 | 1.24 | 8.76 | 0.00 | 0.00 | 0.00 | 2.00 | 7.00 |
| Amortization Rate (%) | 103 | 0.71 | 0.86 | 0.00 | 0.00 | 0.35 | 1.06 | 2.09 |
Note - Data in these tables are based on annual statements for 125 cooperatives in Gothenburg. Almost all of the annual statements were from either 2004 or 2005.
Table 4a: Are Changes in Rent Expected? Cooperatives with at least 15% in annual rent per meter squared between first and last transactions (N=602)
Transactions | PDV Annual Rent | Robust Standard Error |
|---|---|---|
| First Transaction in Cooperative Over the Sample Period | -0.70*** | (0.09) |
| Last Transaction in Cooperative Over the Sample Period | -0.46*** | (0.08) |
Table 4b: Are Changes in Rent Expected? Cooperatives with at 20% increase in annual rent per meter squared between first and last transactions (N =384)
Transactions | PDV Annual Rent | Robust Standard Error |
|---|---|---|
| First Transaction in Cooperative Over the Sample Period | -0.82 | (0.16) |
| Last Transaction in Cooperative Over the Sample Period | -0.45*** | (0.10) |
Table 4c: Are Changes in Rent Expected? Cooperatives with at least 25% increase in annual rent per meter squared between first and last transactions (N = 253)
Transactions | PDV Annual Rent | Robust Standard Error |
|---|---|---|
| First Transaction in Cooperative Over the Sample Period | -0.90 | (0.25) |
| Last Transaction in Cooperative Over the Sample Period | -0.48*** | (0.13) |
Note - Robust standard errors in parentheses. * indicates significantly different from minus one at 10% level; ** indicates significantly different from minus one at 5% level; *** indicates significantly different from minus one at 1% level. We cannot directly observe which cooperatives underwent renovations. However, we proxy for this by considering those cooperatives that had a large increase in the annual rent per square meter between the first and last transactions (i.e. a 15%, 20% or 25% increase). We then use the sub-samples of first and last transactions to estimate our basic model. Specifically, each cell presents the coefficient on the present value of annual rents that result from estimating equation (10) when excluding parish specific time trends and zip code fixed effects. All specifications still include controls for apartment size (as a quadratic), dummy variables indicating the number of rooms, dummy variables indicating the age of the building, the floor of the apartment, the number of floors in the building, whether heat is included in the rent, and apartment size over the discount rate. The discount rate takes into account the 30 percent tax deduction in all specifications.
Table 5: Heterogeneity in Transaction Level Estimates Across Apartment Size, with and without a Top Loan
Apartment Size | Apartment Percentile | PV Annual Rent (1) | PV (1) Robust Standard Error | PV Annual Rent (2) | PV (2) Robust Standard Error | Observations |
|---|---|---|---|---|---|---|
| All Apartments | -- | -0.74*** | (0.03) | -0.99 | (0.04) | 30475 |
| < 37 m |
0-10 | -0.39*** | (0.07) | -0.52*** | (0.10) | 3467 |
| 37-46 m | 10-25 | -0.43*** | (0.03) | -0.58*** | (0.04) | 4284 |
| 46-62 m | 25-50 | -0.51*** | (0.04) | -0.68*** | (0.05) | 7936 |
| 63-80 m | 50-75 | -0.66*** | (0.04) | -0.89** | (0.05) | 7364 |
| 80-101 m | 75-90 | -0.60*** | (0.06) | -0.80** | (0.08) | 4426 |
| > 101 m | 90-100 | -0.70*** | (0.06) | -0.93 | (0.08) | 2998 |
Note - Robust standard errors that are clustered at the parish level are in parentheses. * indicates significantly different from minus one at 10% level; ** indicates significantly different from minus one at 5% level; *** indicates significantly different from minus one at 1% level. Each cell presents the coefficient on the present value of rents that results from estimating equation (10) for the sub-sample denoted at the top of each column with zip code fixed effects, parish specific time trends, and the full set of observable controls: apartment size (as a quadratic), dummy variables indicating the number of rooms, dummy variables indicating the age of the building, the floor of the apartment, the number of floors in the building, whether heat is included in the rent, and apartment size over the discount rate. The discount rate used in PV Annual Rent (1) takes the tax deduction and an amortization rate of 1 percent into account. PV Annual Rent (2) accounts for the tax deduction, 1 percent amortization, and a 2 percent top loan.
Table 6: Comparison of Average Parish Characteristics for Parishes with More and Less Efficiency
Outcome Variable | Mean for Most Efficient Parishes (n=35) | Mean for Least Efficient Parishes (n=35) | Difference | t-stat on Difference | Mean for Most Efficient Parishes (n=18) | Mean for Least Efficient Parishes (n=19) | Difference | t-stat on Difference |
|---|---|---|---|---|---|---|---|---|
| % with grade school as highest education | 0.11 | 0.17 | -0.06 | -3.44 | 0.09 | 0.19 | -0.10 | -4.55 |
| % with high school as highest education | 0.35 | 0.43 | -0.08 | -4.20 | 0.33 | 0.45 | -0.12 | -5.10 |
| % with college as highest education | 0.54 | 0.40 | 0.14 | 4.27 | 0.58 | 0.36 | 0.22 | 5.54 |
| average gross labor income | 183,160 | 152,493 | 30,667 | 2.99 | 201,552 | 150,156 | 51,396 | 3.50 |
| average net income | 188,512 | 154,686 | 33,826 | 3.01 | 211,095 | 153,125 | 57,970 | 3.55 |
| average disposable income | 177,848 | 160,493 | 17,355 | 2.57 | 193,895 | 161,191 | 32,704 | 3.42 |
| average net wealth | 635,070 | 402,238 | 232,832 | 2.66 | 904,848 | 392,538 | 512,310 | 4.11 |
| average financial wealth | 257,101 | 174,718 | 82,383 | 2.62 | 340,055 | 170,897 | 169,158 | 3.56 |
| % with income in bottom quartile | 0.27 | 0.31 | -0.04 | -2.34 | 0.27 | 0.32 | -0.05 | -2.09 |
| % with income in middle two quartiles | 0.44 | 0.48 | -0.04 | -2.92 | 0.41 | 0.48 | -0.07 | -3.88 |
| % with income in upper quartile | 0.29 | 0.21 | 0.08 | 3.60 | 0.32 | 0.20 | 0.12 | 3.95 |
Note - The first group of columns looks at average socioeconomic characteristics for parishes with the estimated rent coefficient above and below the median. The last four columns compare those parishes in the top and bottom quartiles. Rankings are based on coefficient estimates resulting from estimating equation (10), with zip code fixed effects, separately for each parish with more than 50 transactions in the sample; the discount rate accounts for the 30 percent tax deduction and assumes a one percent amortization rate. Bolded test statistics indicate differences that are significant at the 5 percent level.
Table 7: Heterogenity in Transcation Level Estimates Across Apartment Size and Parish Education Level - Panel A: For Parishes with Less than Median Percent Attended College
| Apartment Size (meters) | Apartment Percentile | PV Annual Rent | Robust Standard Error | Observations | R-squared |
|---|---|---|---|---|---|
| < 36 | 0-10 | -0.24*** | (0.09) | 660 | 0.92 |
| 36-46 | 10-25 | -0.25*** | (0.08) | 1188 | 0.92 |
| 46-62 | 25-50 | -0.31*** | (0.03) | 3536 | 0.89 |
| 62-80 | 50-75 | -0.39*** | (0.06) | 3466 | 0.88 |
| 80-101 | 75-90 | -0.57*** | (0.06) | 2024 | 0.91 |
| > 101 | 90-100 | -0.43*** | (0.11) | 1136 | 0.94 |
Table 7: Heterogenity in Transcation Level Estimates Across Apartment Size and Parish Education Level -Panel B: For Parishes with Greater than Median Percent Attended College
| Apartment Size (meters) | Apartment Percentile | PV Annual Rent | Robust Standard Error | Observations | R-squared |
|---|---|---|---|---|---|
| < 36 | 0-10 | -0.40*** | (0.08) | 2807 | 0.86 |
| 36-46 | 10-25 | -0.47*** | (0.04) | 3096 | 0.89 |
| 46-62 | 25-50 | -0.59*** | (0.04) | 4400 | 0.89 |
| 62-80 | 50-75 | -0.72*** | (0.04) | 3898 | 0.88 |
| 80-101 | 75-90 | -0.63*** | (0.07) | 2402 | 0.89 |
| > 101 | 90-100 | -0.73*** | (0.06) | 1862 | 0.91 |
Note - Robust standard errors that are clustered at the parish level are in parentheses. * indicates significantly different from minus one at 10% level; ** indicates significantly different from minus one at 5% level; *** indicates significantly different from minus one at 1% level. Each cell presents the coefficient on the present value of rents that results from estimating equation (10) for the sub-sample denoted at the top of each column. Panel A includes the sample of least educated parishes, as measured by college education; that is, it includes only those parishes with less than the median amount of college attendance. Panel B includes the sample of more educated parishes; i.e. with more than the median amount of college attendance. Each specification includes zip code fixed effects, parish specific time trends, and the full set of observable controls: apartment size (as a quadratic), dummy variables indicating the number of rooms, dummy variables indicating the age of the building, the floor of the apartment, the number of floors in the building, whether heat is included in the rent, and apartment size over the discount rate. The discount rate takes the tax deduction and an amortization rate of 1 percent into account.
Figure 1: Average Quarterly Co-op Transaction Price from 2002 to 2005
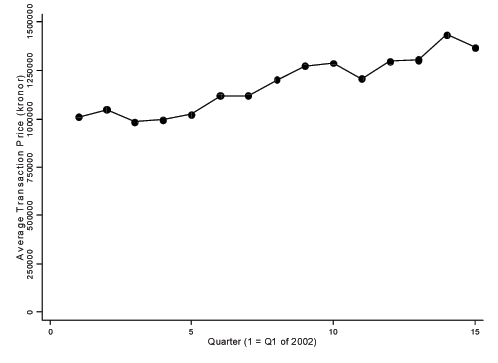
Figure 2: Implied Interest Rate, Quarter by Quarter, versus Actual 5-Year Mortgage Rate
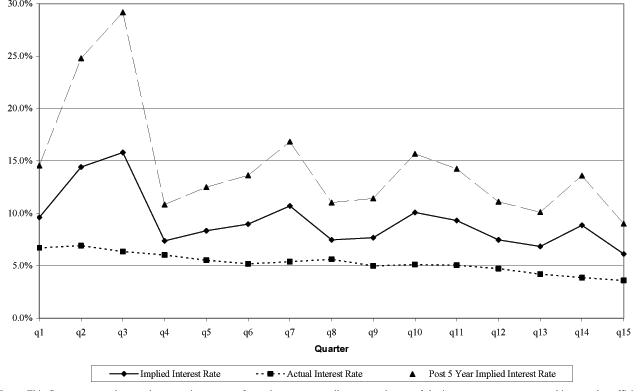
Note - This figure presents the actual average interest rate for each quarter
as well as two estimates of the interest rate necessary to achieve market
efficiency. We estimate the implied measures from quarterly regressions, which
still include zip code fixed effects, that assume market efficiency (i.e. that
set ![]() = -1) and treat the interest rate as the free parameter. The
first estimate, labeled `Implied Interest Rate', is the interest rate
necessary in all future periods to achieve efficiency. The second
estimate, labeled `Post 5 Year Implied Interest Rate', is the interest rate
necessary in all periods after the first five years to achieve
efficiency; we assume that the buyer discounts at the current 5-year fixed
rate during the initial five years.
= -1) and treat the interest rate as the free parameter. The
first estimate, labeled `Implied Interest Rate', is the interest rate
necessary in all future periods to achieve efficiency. The second
estimate, labeled `Post 5 Year Implied Interest Rate', is the interest rate
necessary in all periods after the first five years to achieve
efficiency; we assume that the buyer discounts at the current 5-year fixed
rate during the initial five years.
Figure 3: Estimated Rent Coefficients By Parish Characteristics
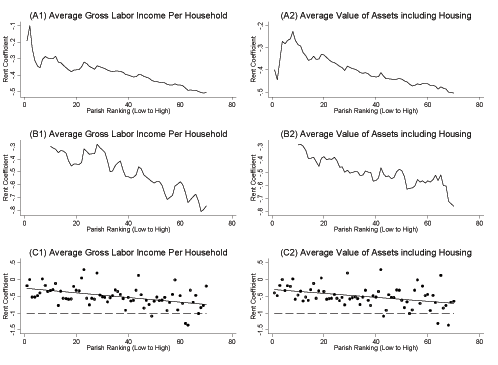
Note - Parishes are ranked from low to high on the x-axis according to the characteristics listed at the top of each figure: average disposable gross labor income or average asset value. Panel A plots the average cumulative rent coefficient; that, is the first point represents the estimated rent coefficient for the lowest ranking parish, the second point is the average coefficient for the two lowest parishes, etc. Panel B plots a 10 parish moving average of the rent coefficient. Panel C plots the actual point estimates for each parish; the solid line is the estimated least squares relationship and the dashed line is equal to minus one. Rent coefficients result from estimating equation (10), with zip code fixed effects, separately for each parish with more than 50 transactions in the sample; the discount rate accounts for the 30 percent tax deduction and assumes a one percent amortization rate.
Footnotes
*. This paper has greatly benefited from many helpful comments by Malin Adolfson, John Ammer, Pat Bayer, Anders Boman, Sean Campbell, Evert Carlsson, Mikael Carlsson, Dale Henderson, Lennart Hjalmarsson, Tor Jacobson, George Korniotis, Mico Loretan, Kasper Roszbach, Robert Shiller, Karl Walentin, Jon Wongswan, Pär Österholm, and participants in seminars at the Federal Reserve Board, Göteborg University, and Sveriges Riksbank. We are also grateful to Berndt Ringdahl and Värderingsdata AB for kindly providing the data, as well as to Tobias Skillbäck who helped answer many of our data questions. Finally, we would like to thank Lennart Flood for performing all the calculations involving the parish-level socio-economic data. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any person associated with the Federal Reserve System. Erik Hjalmarsson is with the Division of International Finance, Federal Reserve Board, Mail Stop 20, Washington, DC 20551, USA. Randi Hjalmarsson is at the University of Maryland, School of Public Policy, 4131 Van Munching Hall, College Park, Maryland 20742. Corresponding author: Erik Hjalmarsson. Email: [email protected] tel.: +1-202-452-2426; fax: +1-202-263-4850. Return to text
1. Most related to the current paper are Meese and Wallace (1994) and Gallin (2005). Other studies that consider aspects of housing market efficiency include Case and Shiller (1989, 1990), Case and Quigley (1991), Guntermann and Norrbin (1991), Gatzlaff (1994), Berg and Lyhagen (1998), Englund et al. (1999), Hill et al. (1999), Malpezzi (1999), Rosenthal (1999), Hwang and Quigley (2002, 2004), and Hwang et. al. (2006). Return to text
2. Co-ops have also been increasing in popularity in the 1990s and 2000s in a number of U.S. cities, including Chicago, Washington, D.C, and Miami. For an extensive analysis of co-ops in New York, see Schill et. al. (2004). Return to text
3. Linneman (1986) also relies on hedonic price regressions to determine what the `fair' value of houses are and classifies the market as inefficient if the pricing errors based on the fitted hedonic regression exceed the transaction costs in the market for a substantial number of observations. Return to text
4. Turner (1997) provides some additional information on the cooperative housing market in Sweden. Return to text
5. It is not clear what determines the proportions in this initial split. Indeed, given that the cooperative generally enjoys less advantageous tax deductions on its loans, it would typically be more efficient for the individual buyers to pay the total value of the co-op unit directly and carry all of the capital costs in the form of private mortgages. Return to text
6. Cooperatives typically have funds put aside over time to at least partially cover the costs of future renovations. Thus, many anticipated renovations should cause only minor, and most likely transient, changes in rents. Return to text
7. The mortgage rate ![]() is the rate faced by the
individual purchaser of the co-op. While the rate faced by the cooperatives
may differ from
is the rate faced by the
individual purchaser of the co-op. While the rate faced by the cooperatives
may differ from ![]() (and across cooperatives), this is reflected in the
capital costs,
(and across cooperatives), this is reflected in the
capital costs, ![]() and
and![]() , which represent the servicing costs of
their mortgages at the cooperatives' prevailing mortgage rates. Since
, which represent the servicing costs of
their mortgages at the cooperatives' prevailing mortgage rates. Since ![]() and
and![]() are taken as given in our analysis, the cooperatives' mortgage
rates do not explicitly enter into our analysis. To the extent that the
cooperatives' interest rate payments are tax deductible, this will also
already be reflected in the values of
are taken as given in our analysis, the cooperatives' mortgage
rates do not explicitly enter into our analysis. To the extent that the
cooperatives' interest rate payments are tax deductible, this will also
already be reflected in the values of ![]() and
and![]() , which explains why
the personal mortgage payments are tax adjusted, but not
, which explains why
the personal mortgage payments are tax adjusted, but not![]() and
and![]() ; no
portion of the rent (i.e. the capital cost or maintenance fee) is tax
deductible by the individual co-op purchaser. Return to text
; no
portion of the rent (i.e. the capital cost or maintenance fee) is tax
deductible by the individual co-op purchaser. Return to text
8. In practice, the home buyer might not borrow the entire amount, and the prevailing mortgage rate might therefore not represent, on average, the true cost of capital for the home buyer. However, it is reasonable to assume that at the margin, most home buyers will borrow at the prevailing mortgage rate. In particular, it seems a natural assumption that the marginal cost of capital is equal to the mortgage rate when choosing between two co-ops with different sales prices. Return to text
9. As discussed previously, new loans could also be taken on due to the need, for instance, to raise new capital for major renovations. This could raise rents in the future and we explicitly address this possibility in the empirical section. Return to text
10. That is, we do not find evidence of cooperatives paying off their loans with fixed monthly payments rather than in proportional amounts, which supports our hypothesis that the rate of amortization translates into an equivalent rent decrease and that the loans are, for our purposes, infinitely lived. Return to text
11. However, it is also possible, though perhaps less likely, that
omitted variables are not positively correlated with both rent and prices. For
instance, high rents, and consequently large debt levels, might in some
circumstances send a signal that the cooperative is poorly managed or in some
economic distress. If high rents were indeed a signal of economic problems for
the cooperatives, one would expect low rent apartments to be relatively more
attractive than high rent apartments; that is, the coefficient in front of the
discounted rent, ![]() , should be less than minus one in an
efficient market. Given that we consistently find
, should be less than minus one in an
efficient market. Given that we consistently find ![]() to be
greater than minus one in the empirical results, we do not investigate this
conjecture further. However, it potentially adds to the strength with which we
reject the efficient market hypothesis. Return to text
to be
greater than minus one in the empirical results, we do not investigate this
conjecture further. However, it potentially adds to the strength with which we
reject the efficient market hypothesis. Return to text
12. Note that it is possible, though not common, for a zip code to be located in more than one parish; thus parish and zip code fixed effects can be included simultaneously in the analysis. In addition, note that Table 1 presents within parish and within zip code standard deviations for each of the variables; i.e. the standard deviation after subtracting the parish or zip code mean from each observation. While there is slightly less variation within parishes and zip codes than in the entire sample, there is still a sufficient amount of variation for identification. Return to text
13. In Sweden, `number of rooms' refers to the number of rooms besides the kitchen and bathroom. So, a one-room apartment is a studio, a two-room apartment is a one bedroom, etc. Number of bathrooms is not reported in the data; but, this is largely a reflection of the lack of emphasis placed on bathrooms in the market. Return to text
14. As stated previously, we do not directly have data on the size of the capital component of the rent. To give a ballpark estimate of the present value of the capital cost component by itself, one can assume a maintenance fee of 350 SEK per square meter; this appears to be a reasonable estimate based on annual statements from Swedish cooperatives. In this scenario, the average discounted value of the capital component of the rent is 448,351 SEK, which is still almost 40 percent of the average sales price. As discussed previously, however, our empirical analysis is based on the total rent and not this back-of-the-envelope calculation. Return to text
15. Throughout the paper, all analyses use robust standard errors that are clustered at the parish-level. Return to text
16. The annual statements were obtained from the website of the realtor firm Ahre, www.ahre.se. Most of the statements cover either the year 2004 or 2005. In cases where there were multiple years available for one cooperative, we recorded the results from the most recent statement. Return to text
17. While we can identify multiple transactions for the same cooperative, we cannot, unfortunately, take advantage of this in our main specifications by including cooperative fixed effects. As should be expected, there is very little variation in rent per square meter within cooperatives. That is, apart from special circumstances, there is little change in the debt structure and, hence, rents within the cooperative over our fairly short sample period. Return to text
18. The five year fixed-rate mortgage interest rate that we use should be a conservative (high) estimate of the interest rate facing the home buyer at the time of the purchase, given that most home buyers in Sweden take at least a part of their loans with a floating rate. For instance, according to the mortgage lender SBAB's website (www.sbab.se), less than 10 percent of their loans have interest rates that are fixed for five or more years. In fact, 69 percent of their loans have floating rates; these statistics are for July 2006. Return to text
19. Home buyers may of course base some of their decisions on worst-case scenarios. For instance, as indicated by a loan officer at Handelsbanken (a Swedish bank), most banks today require that borrowers can handle an interest rate of seven to eight percent in the future. This is not inconsistent with the implied interest rates necessary in all future periods estimated in the final quarters of our data. Thus, one can raise these worst-case calculations as a potential explanation for our findings of market inefficiency. However, a permanent shift to an eight percent interest rate would also necessitate a higher capital cost component of the rent, which would once again more or less offset the increased discount rate. This leaves the worst-case scenario explanation of inefficiency somewhat unsatisfactory. Return to text
20. In particular, all top loans have floating rates and the markup will be on the current short rate, which could be significantly lower than our five year rate. That is, the top loan rate could actually be lower than the five year rate used here; thus, the 2 percent markup used in our analysis should be conservative. Return to text
21. We are grateful to Lennart Flood for performing all calculations involving these variables, which are sourced from the Swedish Linda dataset. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text