The Federal Reserve Board eagle logo links to home page

Real-Time Measurement of Business Conditions*

S. Borağan Aruoba† , University of Maryland
Francis X. Diebold, University of Pennsylvannia and NBER
Chiara Scotti, Federal Reserve Board

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We construct a framework for measuring economic activity in real time (e.g., minute-by-minute), using a variety of stock and flow data observed at mixed frequencies. Specifically, we propose a dynamic factor model that permits exact filtering, and we explore the efficacy of our methods both in a simulation study and in a detailed empirical example.

Keywords: Business cycle, expansion, recession, state space model, macroeconomic forecasting, dynamic factor model

JEL classification: E32, E37, C01, C22

1  Introduction

Aggregate business conditions are of central importance in the business, finance, and policy communities, worldwide, and huge resources are devoted to assessment of the continuously-evolving state of the real economy. Literally thousands of newspapers, newsletters, television shows, and blogs, not to mention armies of employees in manufacturing and service industries, including the financial services industries, central banks, government and non-government organizations, grapple daily with the real-time measurement and forecasting of evolving business conditions.

Against this background, we propose and illustrate a framework for real-time business conditions assessment in a systematic, replicable, and statistically optimal manner. Our framework has four key ingredients.

Ingredient 1. We work with a dynamic factor model, treating business conditions as an unobserved variable, related to observed indicators. The appeal of latency of business conditions comes from its close coherence with economic theory, which emphasizes that the business cycle is not about any single variable, whether GDP, industrial production, sales, employment, or anything else. Rather, the business cycle is about the dynamics and interactions ("co-movements") of many variables, as forcefully argued by Lucas (1977) among many others.

Treating business conditions as latent is also a venerable tradition in empirical business cycle analysis, ranging from the earliest work to the most recent, and from the statistically informal to the statistically formal. On the informal side, latency of business conditions is central to many approaches, from the classic early work of Burns and Mitchell (1946) to the recent workings of the NBER business cycle dating committee, as described for example by Hall et al. (2003). On the formal side, latency of business conditions is central to the popular dynamic factor framework, whether from the "small data" perspective of Geweke (1977), Sargent and Sims (1977), Stock and Watson (1989, 1991), and Diebold and Rudebusch (1996), or the more recent "large data" perspective of Stock and Watson (2002) and Forni, Hallin, Lippi and Reichlin (2000).1

Ingredient 2. We explicitly incorporate business conditions indicators measured at different frequencies. Important business conditions indicators do in fact arrive at a variety of frequencies, including quarterly (e.g., GDP), monthly (e.g., industrial production), weekly (e.g., employment), and continuously (e.g., asset prices), and we want to be able to incorporate all of them, to provide continuously-updated assessments in real time.

Ingredient 3. We explicitly incorporate a continuously-evolving indicator. Given that our goal is to track the evolution of real activity in real time, it is crucial to incorporate (or at least not exclude from the outset) the real-time information flow associated with continuously-evolving indicators, such as the yield curve. For practical purposes, in this paper we equate "continuously-evolving" with "daily," but intra-day information could be used as well.

Ingredient 4. We extract and forecast latent business conditions using linear yet statistically optimal procedures, which involve no approximations. The appeal of exact as opposed to approximate procedures is obvious, but achieving exact optimality is not trivial and has proved elusive in the literature, due to complications arising from temporal aggregation of stocks vs. flows in systems with mixed-frequency data.

Related to our concerns and framework is a small but nevertheless significant literature, including Stock and Watson (1989, 1991), Mariano and Murasawa (2003), Evans (2005) and Proietti and Moauro (2006). Our contribution, however, differs from the others, as follows.2

Stock and Watson (1989, 1991) work in a dynamic factor framework with exact linear filtering, but they don't consider data at different frequencies or at high frequencies. We include data at different and high frequencies, while still achieving exact linear filtering. This turns out to be a non-trivial task, requiring an original modeling approach.

Mariano and Murasawa (2003) work in a dynamic factor framework and consider data at different frequencies, but not high frequencies, and their filtering algorithm is not exact. In particular, they invoke an approximation essentially equivalent to assuming that the log of a sum equals the sum of the logs.

Evans (2005) does not use a dynamic factor framework and does not use high-frequency data. Instead, he equates business conditions with GDP growth, and he uses state space methods to estimate daily GDP growth using data on preliminary, advanced and final releases of GDP, as well as a variety of other macroeconomic variables.

Proietti and Moauro (2006) work in the Mariano-Murasawa framework and are able to avoid the Mariano-Murasawa approximation, but only at the cost of moving to a non-linear model, resulting in a filtering scheme that is more tedious than the Kalman filter and that involves approximations of its own.

We proceed as follows. In Section 2 we provide a detailed statement of our methodological framework, covering the state space formulation with missing data, optimal filtering and smoothing, and estimation. In Section 3 we report the results of a small simulation exercise, which lets us illustrate our methods and assess their efficacy in a controlled environment. In Section 4 we report the results of a four-indicator empirical analysis, using quarterly GDP, monthly employment, weekly initial claims, and the daily yield curve term premium. In Section 5 we conclude and offer directions for future research.

2  Methodology

Here we propose a state space macroeconomic model with an ultra-high base observational frequency, treating specification, estimation, state extraction and state prediction. Our framework facilitates exactly optimal filtering and forecasting, which we achieve throughout.

2.1  Missing Observations and Temporal Aggregation

We assume that the state of the economy evolves at a very high frequency; without loss of generality, call it "daily."3 Similarly, we assume that all economic and financial variables evolve daily, although many are not observed daily. For example, an end-of-year wealth variable is observed each December 31, and is "missing" for every other day of the year.

Let $ y_{t}^{i}$ denote a daily economic or financial variable, and let $ \tilde{y}_{t}^{i}$ denote the same variable observed at a lower frequency (without loss of generality, call it the "tilde" frequency). The relationship between $ \tilde{y}_{t}^{i}$ and $ y_{t}^{i}$ depends on whether $ y_{t}^{i}$ is a stock or flow variable. In the case of a stock variable, which by definition is a point-in-time snapshot, we have:

\begin{displaymath} \tilde{y}_{t}^{i}=\left\{ \begin{array}[c]{cl} y_{t}^{i} & \text{if $y_{t}^{i}$\ is observed}\ NA & \text{otherwise,} \end{array}\right. \end{displaymath}

where NA denotes missing data. In the case of a flow variable, the lower-frequency observations of which are functions of current and past daily observations, we have

\begin{displaymath} \tilde{y}_{t}^{i}=\left\{ \begin{array}[c]{cl} f(y_{t}^{i},y_{t-1}^{i},...,y_{t-D_{i}}^{i}) & \text{if $y_{t}^{i}$\ is observed}\ NA & \text{otherwise,} \end{array}\right. \end{displaymath}

where $ D_{i}$ denotes the relevant number of days for the temporal aggregation.ease of exposition we assume for now that $ D_{i}$ is fixed, but in our subsequent implementation and empirical work we allow for time-varying $ D_{i}$, which allows us to accommodate, for example, the fact that some months have 28 days, some have 29, some have 30, and some have 31.

Satisfactory treatment of temporal aggregation remains elusive in the literature. Most authors work in logarithms and are effectively forced into the unappealing "approximation" that the log of a sum equals the sum of the logs. Mariano and Murasawa (2003), for example, assume that quarterly GDP is the geometric average of the intra-quarter monthly GDPs.

In contrast, our framework permits exact aggregation. We work in levels, so that flow variables aggregate linearly and exactly. Specifically, we model the levels of all observed variables as stationary deviations from polynomial trends of arbitrary order. The result is a linear state space system for which the standard Kalman filter is optimal, as we now describe in detail.

2.2  The Model

We assume that underlying business conditions $ x_{t}$ evolve daily with $ AR(p)$ dynamics,

$\displaystyle x_{t}=\rho_{1}x_{t-1}+...+\rho_{p}x_{t-p}+v_{t},$ (1)

where $ v_{t}$ is a white noise innovation with unit variance.4 We are interested in tracking and forecasting real activity, so we use a single-factor model; that is, $ x_{t}$ is a scalar, as for example in Stock and Watson (1989). Additional factors could of course be introduced to track, for example, nominal wage/price developments.

We assume that all economic variables $ y_{t}^{i}$ evolve daily, although they are not necessarily observed daily. We assume that $ y_{t}^{i}$ depends linearly on $ x_{t}$ and possibly also various exogenous variables and/or lags of $ y_{t}^{i}$:

$\displaystyle y_{t}^{i}=c_{i}+\beta_{i}x_{t}+\delta_{i1}w_{t}^{1}+...+\delta_{ik}w_{t} ^{k}+\gamma_{i1}y_{t-D_{i}}^{i}+...+\gamma_{in}y_{t-nD_{i}}^{i}+u _{t} ^{i},$ (2)

where the $ w_{t}$ are exogenous variables, we include $ n$ lags of the dependent variable, and the $ u_{t}^{i}$ are contemporaneously and serially uncorrelated innovations. Notice that we introduce lags of the dependent variable $ y_{t}^{i}$ in multiples of $ D_{i}$, because the persistence in $ y_{t}^{i}$ is actually linked to the lower (tilde) observational frequency of $ \tilde{y}_{t}^{i}$. Persistence modeled only in the higher daily frequency would be inadequate, as it would decay too quickly. We use (2) as the measurement equation for all stock variables.

Temporal aggregation in our framework is very simple: flow variables observed at a tilde frequency lower than daily are the sums of the corresponding daily variables,

\begin{displaymath} \tilde{y}_{t}^{i}=\left\{ \begin{array}[c]{cl} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} y_{t-j}^{i} & \text{if ${y}_{t}^{i}$\ is observed}\ NA & \text{otherwise.} \end{array}\right. \end{displaymath}

The relationship between an observed flow variable and the factor then follows from (2),

$\displaystyle \tilde{y}_{t}^{i}=\left\{ \begin{array}[c]{cl} \begin{array}[c]{c} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} c_{i}+\beta_{i} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} x_{t-j}^{i}+\delta_{i1} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} w_{t-j}^{1}+...+\delta_{ik} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} w_{t-j}^{k}\\ +\gamma_{i1} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} y_{t-D_{i}-j}^{i}+...+\gamma_{in} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} y_{t-nD_{i}-j}^{i}+u_{t}^{\ast i} \end{array} & \text{if $y_{t}^{i}$\ is observed}\\ NA & \text{otherwise, } \end{array} \right.$ (3)

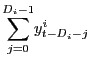where $ {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} y_{t-D_{i}-j}^{i}$ is by definition the observed flow variable one period ago ( $ \tilde{y}_{t-D_{i}}^{i}$), and $ u_{t}^{\ast i}$ is the sum of the $ u_{t} ^{i}$ over the tilde period. Note that although $ u_{t}^{\ast i}$ follows a serially correlated moving average process of order $ D_{i}-1$ at the daily frequency, it nevertheless remains white noise when observed at the tilde frequency, due to the cutoff in the autocorrelation function of an $ MA(D_{i}-1)$ process at displacement $ D_{i}-1$. Hence we will appropriately treat $ u_{t}^{\ast i}$ as white noise in what follows, and we have $ var\left( u_{t}^{\ast i}\right) =Dvar\left( u _{t}^{i}\right) .$

The exogenous variables $ w_{t}$ are the key to handling trend. In particular, in the important special case where the $ w_{t}$ are simply deterministic polynomial trend terms ( $ w_{t-j}^{1}=t-j$, $ w_{t-j}^{2}=(t-j)^{2}$ and so on) we have that

$\displaystyle {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} \left[ c_{i}+\delta_{i1}\left( t-j\right) +...+\delta_{ik}\left( t-j\right) ^{k}\right] \equiv c_{i}^{\ast}+\delta_{i1}^{\ast}t+...+\delta _{ik}^{\ast}t^{k},$ (4)

which yields

$\displaystyle \tilde{y}_{t}^{i}=\left\{ \begin{array}[c]{cl} c_{i}^{\ast}+\beta_{i} {\displaystyle\sum\limits_{j=0}^{D_{i}-1}} x_{t-j}^{i}+\delta_{i1}^{\ast}t+...+\delta_{ik}^{\ast}t^{k}+\gamma_{i1} \tilde{y}_{t-D_{i}}^{i}+...+\gamma_{in}\tilde{y}_{t-nD_{i}}^{i}+u _{t}^{\ast i} & \text{if $y_{t}^{i}$\ is observed}\\ NA & \text{otherwise}. \end{array} \right.$ (5)

We use (5) as the measurement equation for all flow variables. In the appendix we derive the mapping between $ \left( c,\delta_{1},\delta _{2},\delta_{3}\right) $ and $ \left( c^{\ast},\delta_{1}^{\ast},\delta _{2}^{\ast},\delta_{3}^{\ast}\right) $ for cubic trends, which we use throughout this paper.5

This completes the specification of our model, which has a natural state space form, to which we now turn.

2.3  State Space Representation, Filtering and Smoothing

Assembling the discussion thus far, the state space representation of our model is

$\displaystyle y_{t}=Z_{t}\alpha_{t}+\Gamma_{t} w_{t}+\varepsilon_{t}$   
$\displaystyle \alpha_{t+1}=T\alpha_{t}+R\eta_{t}$ (6)
$\displaystyle \varepsilon_{t}\sim\left( 0,H_{t}\right) ,\eta_{t}\sim\left( 0,Q\right) ,$   

$ t=1,...,\mathcal{T}$, where $ \mathcal{T}$ denotes the last time-series observation, $ y_{t}$ is an $ N\times1$ vector of observed variables, $ \alpha_{t}$ is an $ m\times1$ vector of state variables, $ w_{t}$ is a $ e\times1$ vector of exogenous variables, and $ \varepsilon_{t}$ and $ \eta_{t}$ are vectors of measurement and transition shocks which will collectively contain $ v_{t}$ and $ u_{t}^{i}$. The vector $ w_{t}$ includes an entry of unity for the constant, $ k$ trend terms and $ N\times n$ lagged dependent variables, $ n$ for each of the $ N$ elements of the $ y_{t}$ vector. The exact structure of these vectors will vary across the different setups we consider below. The observed data vector $ y_{t}$ will have many missing values, reflecting those variables observed at a frequency lower than daily, as well as missing daily data due to holidays. At a minimum, the state vector $ \alpha_{t}$ will include $ p$ lags of $ x_{t}$, as implied by (1). Moreover, because the presence of flow variables requires a state vector containing all lags of $ x_{t}$ inside the aggregation period, in practice the dimension of $ \alpha_{t}$ will be much greater than $ p$. The system parameter matrices $ T,R$ and $ Q$, are constant, while $ Z_{t}$, $ \Gamma_{t} $ and $ H_{t}$ are not, because of the variation in the number of days in a quarter or month ($ D_{i}$ for each $ i$).6

With the model cast in state space form, we can immediately apply the Kalman filter and smoother. We first present the algorithm assuming no missing data values, and then we incorporate missing data. For given parameters, we initialize the Kalman filter using $ \alpha_{1}\sim N\left( a_{1} ,P_{1}\right) $ where $ a_{1}=0_{m\times1}$ and $ P_{1}$ solves

$\displaystyle \left( I-T\otimes T\right) vec\left( P_{1}\right) =vec\left( RQR^{\prime }\right) .$ (7)

Given $ a_{1}$ and $ P_{1},$ for $ t=1,...,\mathcal{T},$ we use the contemporaneous Kalman filtering equations, which incorporate the computation of the state vector estimate and its associated covariance matrix, denoted by $ a_{t\vert t}$ and $ P_{t\vert t}$.7 Denote $ \left\{ y_{1},...,y_{t}\right\} $ by $ \mathcal{Y}_{t}$ for $ t=1,...,\mathcal{T}$. Then, given $ a_{t}\equiv E\left( \alpha _{t}\vert\mathcal{Y}_{t-1}\right) $ and $ P_{t}=var\left( \alpha_{t} \vert\mathcal{Y}_{t-1}\right) $, the prediction equations that produce $ a_{t+1}$ and $ P_{t+1}$ are

$\displaystyle a_{t\vert t} = a_{t}+P_{t}Z_{t}^{\prime}F_{t}^{-1}v_{t}$ (8)

$\displaystyle P_{t\vert t} =P_{t}-P_{t}Z_{t}^{\prime}F_{t}^{-1}Z_{t}P_{t}^{\prime}$ (9)

$\displaystyle a_{t+1} =Ta_{t\vert t}$ (10)

$\displaystyle P_{t+1} =TP_{t\vert t}T^{\prime}+RQR^{\prime},$ (11)

where

$\displaystyle v_{t} =y_{t}-Z_{t}a_{t}-\Gamma_{t} w_{t}$ (12)

$\displaystyle F_{t} =Z_{t}P_{t}Z_{t}^{\prime}+H_{t}.$ (13)

The Kalman smoother computes the conditional expectation of the state vector and its covariance matrix using all the information in the data set, which we denote by $ \hat{\alpha}_{t}\equiv E\left( \alpha_{t}\vert\mathcal{Y} _{\mathcal{T}}\right) $ and $ V_{t}\equiv var\left( \alpha_{t}\vert\mathcal{Y} _{\mathcal{T}}\right) $ for $ t=1,...,\mathcal{T}.$ The Kalman smoother recursions start from $ t=\mathcal{T}$ and work backward. The vector $ r_{t}$ is a weighted average of the innovations $ v_{t}$ that happen after period $ t$ with the variance matrix $ N_{t}.$ We initialize the smoother with $ r_{\mathcal{T}}=0_{m\times1}$ and $ N_{\mathcal{T}}=0_{m\times m}$, and for $ t=1,...,\mathcal{T}\emph{-1}$ we use

$\displaystyle K_{t} =TPZ_{t}^{\prime}F_{t}^{-1}$ (14)

$\displaystyle L_{t} =T-K_{t}Z_{t}$ (15)

$\displaystyle r_{t-1} =Z_{t}^{\prime}F_{t}^{-1}v_{t}+L_{t}^{\prime}r_{t}$ (16)

$\displaystyle N_{t-1} =Z_{t}^{\prime}F_{t}^{-1}Z_{t}+L_{t}^{\prime}N_{t}L_{t}$ (17)

$\displaystyle \hat{\alpha}_{t} =a_{t}+P_{t}r_{t-1}$ (18)

$\displaystyle V_{t} =P_{t}-P_{t}N_{t-1}P_{t},$ (19)

where we store the matrices $ \left\{ F_{t},v_{t},a_{t},P_{t}\right\} _{t=1}^{\mathcal{T}}$ from one run of the Kalman filter. We use the appropriate element of the $ \hat{\alpha}_{t}$ vector as the extracted factor and the corresponding diagonal element of $ V_{t}$ as its standard error to compute confidence bands.

We now describe how we handle missing observations (that is, how the Kalman filter optimally handles missing observations). If all elements of the vector $ y_{t}$ are missing for period $ t$, we skip updating and the recursion becomes

$\displaystyle a_{t+1} =Ta_{t}$ (20)
$\displaystyle P_{t+1} =TP_{t}T^{\prime}+RQR .$ (21)

If some (but not all) elements of $ y_{t}$ are missing, we replace the observation equation with

$\displaystyle y_{t}^{\ast} =Z_{t}^{\ast}\alpha_{t}+\Gamma_{t} w_{t}+\varepsilon_{t}^{\ast}$ (22)
$\displaystyle \varepsilon_{t}^{\ast} \sim N\left( 0,H_{t}^{\ast}\right) ,$ (23)

where $ y_{t}^{\ast}$ are the elements of the $ y_{t}$ vector that are observed.8 The two vectors are linked by $ y_{t}^{\ast}=W_{t}y_{t}$, where $ W_{t}$ is a matrix that carries the appropriate rows or $ I_{N\times N}$, $ Z_{t}^{\ast }=W_{t}Z_{t},$ $ \varepsilon_{t}^{\ast}=W_{t}\varepsilon_{t}$ and $ H_{t}^{\ast }=W_{t}H_{t}W_{t}^{\prime}.$ The Kalman filter and smoother work exactly as described above replacing $ y_{t},$ $ Z_{t}$ and $ H$ with $ y_{t}^{\ast},$ $ Z_{t}^{\ast}$ and $ H_{t}^{\ast}$ for period $ t.$

2.4  A Costless Generalization

Note that in the model as specified thus far, current observables depend only on the current state vector. More generally, we might want to allow current observables to depend on both the present state vector and various of its leads or lags. This turns out to introduce significant complications in situations such as ours that involve temporal aggregation. Hence we will not pursue it, with one notable exception: For daily variables we can easily accommodate dynamic interaction between observables and the state because there is no temporal aggregation.a

In our subsequent empirical work, for example, we allow daily observables to depend on a distributed lag of the state. To promote parsimony, we use a polynomial distributed lag (PDL) specification. Specifically, the measurement equation for a daily variable is

$\displaystyle y_{t}^{i}=c_{i}+\beta_{i}^{0} x_{t}+\beta_{i}^{1}x_{t-1}+...+\beta^{\tilde{D} }_{i}x_{t-\tilde{D}}+\delta_{i1}w_{t}^{1}+...+\delta_{ik}w_{t}^{k}+\gamma _{i1}y_{t-1}^{i}+...+\gamma_{in}y_{t-n}^{i}+\varepsilon_{t}^{i} ,$ (24)

where the elements of $ \{\beta_{i}^{j}\}_{j=0}^{\tilde{D}}$ follow a low-ordered polynomial given by

$\displaystyle \beta_{i}^{j} = \xi_{i}^{1} + \xi_{i}^{2} (j-\bar{c}) + \xi_{i}^{3} (j-\bar {c})^{2} + .. + \xi_{i}^{\tilde{D}+1} (j-\bar{c})^{\tilde{D}},$ (25)

where $ \bar{c}$ is equal to $ k/2$ if $ k$ is even and to $ (k-1)/2$ if $ k$ is odd.9 We shall use a third-order polynomial.

2.5  Estimation

As is well-known, the Kalman filter supplies all of the ingredients needed for evaluating the Gaussian pseudo log likelihood function via the prediction error decomposition,

$\displaystyle \log L=-\frac{1}{2}\sum_{t=1}^{\mathcal{T}}\left[ N\log2\pi+\left( \log\left\vert F_{t}\right\vert +v_{t}^{\prime}F_{t}^{-1}v_{t}\right) \right]$ (26)

In calculating the log likelihood, if all elements of $ y_{t}$ are missing, the contribution of period $ t$ to the likelihood is zero. When some elements of $ y_{t}$ are observed, the contribution of period $ t$ is $ \left[ N^{\ast} \log2\pi+\left( \log\left\vert F_{t}^{\ast}\right\vert +v_{t}^{\ast\prime }F_{t}^{\ast-1}v_{t}^{\ast}\right) \right] $ where $ N^{\ast}$ is the number of observed variables and the other matrices and vectors are obtained using the Kalman filter recursions on the modified system with $ y_{t}^{\ast}.$

Armed with the ability to evaluate the log likelihood for any given set of parameters, we proceed with estimation using standard methods. In particular, we use a quasi-Newton optimization routine with BFGS updating of the inverse Hessian.

We impose several constraints in our estimation. First, to impose stationarity of $ x_{t}$ we use a result of Barndorff-Nielsen and Schou (1973), who show that under stationarity there is a one-to-one correspondence between the parameters of an $ AR(p)$ process and the first $ p$ partial autocorrelations. Hence we can parameterize the likelihood in terms of the relevant partial autocorrelations, which requires searching only over the unit interval. In our subsequent empirical analysis, we use an $ AR(3)$ process for the factor, which allows for a rich variety of dynamics. Denoting the $ AR(3)$ parameters by $ \rho_{i}$ and the partial autocorrelations by $ \pi_{i},$ the Barndorff-Nielsen-Schou mapping between the two is

$\displaystyle \rho_{1} =\pi_{1}-\pi_{1}\pi_{2}-\pi_{3}\pi_{2}$ (27)

$\displaystyle \rho_{2} =\pi_{2}-\pi_{1}\pi_{3}+\pi_{1}\pi_{2}\pi_{3}$ (28)

$\displaystyle \rho_{3} =\pi_{3}.$ (29)

We then optimize over $ \pi_{i}\in\left[ -1,1\right] $.10

Second, we impose non-negativity of the variance terms in the diagonal elements of $ Q$ and $ H_{t}$ matrices by estimating natural logarithms of these elements. Similarly, we restrict the factor loadings on some of the variables to have a certain sign (e.g., positive for GDP and negative for initial jobless claims) using the same transformation.

Searching for a global optimum in a parameter space with more than $ 30$ dimensions is a challenging problem. It is not intractable, however, if the iterations are initialized cleverly. To do so, we exploit knowledge gained from a simulation study, to which we now turn.

3  A Simulation-Based Example

Here we illustrate our methods in a simulation. This allows us to assess their efficacy in a controlled environment, and to gain insights of relevance to our subsequent fitting of the model to real data. We work with an $ AR(1)$ real activity factor and three observed indicators, which are driven by the factor and linear trend.11 We generate forty years of daily data, and then we transform them to obtain the data observed by the econometrician. Specifically, $ y_{t}^{1}$ is a daily financial variable so we eliminate weekend observations, $ y_{t}^{2}$ is a monthly stock variable so we eliminate all observations except the last observation of each month, and $ y_{t}^{3}$ is a quarterly flow variable so we eliminate all observations except the last observation of the quarter, which we set equal to the sum of the intra-quarter daily observations. After obtaining the observed data we estimate the model given in (6), with the system vectors and matrices are defined as:

$\displaystyle y_{t}=\left[ \begin{array}[c]{c} \tilde{y}_{t}^{1}\\ \tilde{y}_{t}^{2}\\ \tilde{y}_{t}^{3} \end{array} \right] , \alpha_{t}=\left[ \begin{array}[c]{c} x_{t}\\ x_{t-1}\\ x_{t-2}\\ \vdots\\ x_{t-\bar{q}+1}\\ x_{t-\bar{q}} \end{array} \right] ,w_{t}=\left[ \begin{array}[c]{c} 1\\ t \end{array} \right] ,\varepsilon_{t}=\left[ \begin{array}[c]{c} u _{t}^{1}\\ u _{t}^{2}\\ u _{t}^{\ast3} \end{array} \right] ,v_{t}=\eta_{t},R=\left[ \begin{array}[c]{c} 1\\ 0\\ \vdots\\ 0\\ 0\\ 0\\ 0 \end{array} \right] \\ $    

$\displaystyle Z_{t}=\left[ \begin{array}[c]{ccc} \beta_{1} & \beta_{2} & \beta_{3}\\ 0 & 0 & \beta_{3}\\ \vdots & \vdots & \vdots\\ 0 & 0 & \beta_{3}\text{ or }0\\ 0 & 0 & \beta_{3}\text{ or }0\\ 0 & 0 & \beta_{3}\text{ or }0\\ & & \end{array} \right] ^{\prime},\Gamma_{t} =\left[ \begin{array}[c]{cc} c_{1} & \delta_{1}\\ c_{2} & \delta_{2}\\ c_{3t}^{\ast} & \delta_{3t}^{\ast} \end{array} \right] ,T=\left[ \begin{array}[c]{cccccc} \rho_{1} & \rho_{2} & \rho_{3} & \cdots & 0 & 0\\ 1 & 0 & 0 & \cdots & 0 & 0\\ 0 & 1 & 0 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & \cdots & 0 & 0\\ 0 & 0 & 0 & \cdots & 1 & 0 \end{array} \right]\\ $ (30)

$\displaystyle \left[ \begin{array}[c]{c} \varepsilon_{t}\\ v_{t} \end{array} \right] \sim N\left( \left[ \begin{array}[c]{c} 0_{3\times1}\\ 0 \end{array} \right] ,\left[ \begin{array}[c]{cc} H_{t} & 0\\ 0 & Q \end{array} \right] \right), H_{t}=\left[ \begin{array}[c]{ccc} \sigma_{1}^{2} & 0 & 0\\ 0 & \sigma_{2}^{2} & 0\\ 0 & 0 & \sigma_{3t}^{\ast2} \end{array} \right] , Q=1$  

where $ \bar{q}$ is the maximum number of days in a quarter. For convenience, in our notation we treat $ q$, the number of days in a quarter (the counterpart of $ D_{i}$ in the previous section), as fixed. In our implementation, however, we make the necessary adjustments to account for the exact number of days in a quarter, which is either 90, 91 or 92, depending on the quarter and whether or not the year is a leap year. All of the relevant matrices and vectors allow for the largest possible value, $ \bar{q}$, and we adjust the matrices $ Z_{t},$ $ \Gamma_{t} $ and $ H_{t}$ every quarter as follows.12 Each quarter, if $ q<\bar{q}$, we first set the first $ q$ elements of the third row of $ Z_{t}$ to $ \beta_{3}$ and we set the remaining elements to zero. Next, we use $ D=q$ in the formulas derived in the appendix that map our original parameters $ c_{3}$ and $ \delta_{3}$ into $ c_{3t}^{\ast}$ and $ \delta _{3t}^{\ast}$, and we substitute in $ \Gamma_{t} .$ Finally, we set the third diagonal element of $ H_{t}$ to $ \sigma_{3t}^{\ast2}=q\sigma_{3}^{2}.$ All of the adjustments follow from the discussion in the previous section. First, the quarterly flow variable requires summing the factors over the quarter, and our adjustment of the third row of $ Z_{t}$ ensures that we sum only the relevant factors. Second, the adjustment of the elements of $ \Gamma_{t}$ is obvious. Finally, because $ \varepsilon_{t}^{\ast3}$ is the sum of $ q$ iid normal innovations each with variance $ \sigma_{3}^{2},$ its variance is $ q\sigma _{3}^{2}.$

We use a multi-step estimation procedure that helps us obtain accurate startup values for certain of the model parameters, after which we estimate all parameters simultaneously. This approach is of course most helpful in higher-dimensional systems than the simple one at hand, but we illustrate it here because we use it in our subsequent (higher-dimensional) empirical work.

Specifically, we first use only the first two variables, estimating the model using naive startup values and experimenting with them to make sure we reach the global maxima. Because we exclude the quarterly flow variable from this model, the system estimated is small and the cost of experimentation is low. Once the model is estimated, we use the Kalman smoother to extract the factor, $ \hat{x}_{t}$. Then we obtain startup values for the third equation via least-squares estimation of the auxiliary model,

$\displaystyle \tilde{y}_{t}^{3}=\sum_{j=0}^{q-1}\left[ a+d\left( t-j\right) \right] +b\left( \hat{x}_{t}+\hat{x}_{t-1}+...+\hat{x}_{t-q}\right) +e_{t} .$ (31)

We then estimate the full model using the estimates of $ a,$ $ b,$ $ d$ and $ var\left( e_{t}\right) /\bar{q}$ obtained from this auxiliary regression as startup values for the third equation's parameters, and the originally-estimated parameters of the first and second equations as startup values for those equations' parameters.

To illustrate the performance of our methodology we compare the true and smoothed factor and indicators. To obtain the "smoothed indicators," we run the smoothed factor through equation (2). In Figure 1 we plot the true and smoothed versions of the factor, and the high-frequency (true), observed and smoothed versions of two indicators (the daily financial variable and the monthly stock variable) over a 6-month period in the sample. The first panel shows the very close relationship between the smoothed and the true factor. In fact, over the full sample the correlation between the two is greater than 0.96. In the second panel, the observed and high-frequency (true) indicators are identical except for weekends, and the smoothed signal tries to fill in the missing values in the observed indicator by using the information from other variables. Finally, in the third panel, the observed indicator is represented by dots, which are the end-of-month-values of the true signal. Our smoothed signal tries to fill in the remaining values and performs quite well. Over the full sample, the correlations between the smoothed and true indicators for both $ Y1$ and $ Y2$ are 0.997. Overall, this example shows that our methodology is well-suited to extract the factor in an environment with missing data and/or time aggregation issues.

4  Empirical Analysis

Now we apply our framework to real data. First, we describe the data, and then we discuss our empirical results.

4.1  Data

Our analysis covers the period from April 1, 1962 through February 20, 2007, which is over 45 years of daily data. Because it is not realistic to assume that economic activity stops over the weekends is not realistic, we use a seven-day week instead of using only business days. We use four variables in our analysis. Below we list these variables and describe how we handle missing data and time-aggregation issues.13

4.2  Model

The state variable $ x_{t}$ follows an $ AR(3)$ process and we also assume $ AR(3)$ structures for the observed variables at their observation frequency. For weekly initial claims, monthly employment and quarterly GDP, this simply means that the lagged values of these variables are elements of the $ w_{t}$ vector. We denote these by $ \tilde{y}_{t-iW}^{2},$ $ \tilde{y}_{t-iM}^{3}$ and $ \tilde{y}_{t-iq}^{4}$ for $ i=1,2,3$, where $ W$ denotes the number of days in a week, $ M$ denotes the number of days in a month and $ q$ denotes the number of days in a quarter.14 For the term premium, on the other hand, we choose to model the autocorrelation structure using an $ AR(3)$ process for the measurement equation innovation, $ u_{t}^{1}$, instead of adding three lags of the term premium in $ w_{t}$. We choose to follow this route because of the missing term premium observations due to non-business days. If we used the lagged term premium as an element of $ w_{t}$ this would yield only two valid observations for each week and it would make the analysis less reliable.15

The matrices that define the model are given by

$\displaystyle y_{t}=\left[ \begin{array}[c]{c} \tilde{y}_{t}^{1}\\ \tilde{y}_{t}^{2}\\ \tilde{y}_{t}^{3}\\ \tilde{y}_{t}^{4} \end{array} \right] ,\\ \alpha_{t}=\left[ \begin{array}[c]{c} x_{t}\\ x_{t-1}\\ \vdots\\ x_{t-\bar{q}-1}\\ x_{t-\bar{q}}\\ u_{t}^{1}\\ u_{t-1}^{1}\\ u_{t-2}^{1} \end{array} \right] ,\\ w_{t}=\left[ \begin{array}[c]{c} 1\\ t\\ t^{2}\\ t^{3}\\ \tilde{y}_{t-W}^{2}\\ \tilde{y}_{t-2W}^{2}\\ \tilde{y}_{t-3W}^{2}\\ \tilde{y}_{t-M}^{3}\\ \tilde{y}_{t-2M}^{3}\\ \tilde{y}_{t-3M}^{3}\\ \tilde{y}_{t-q}^{4}\\ \tilde{y}_{t-2q}^{4}\\ \tilde{y}_{t-3q}^{4} \end{array} \right] ,\\ \varepsilon_{t}=\left[ \begin{array}[c]{c} 0\\ u_{t}^{*2}\\ u_{t}^{3}\\ u _{t}^{*4} \end{array} \right] ,\\ v_{t}=\left[ \begin{array}[c]{c} \eta_{t}\\ \zeta{t} \end{array} \right] ,\\ R=\left[ \begin{array}[c]{cc} 1 & 0\\ 0 & 0\\ \vdots & \vdots\\ 0 & 0\\ 0 & 0\\ 0 & 1\\ 0 & 0\\ 0 & 0 \end{array} \right]$  
$\displaystyle Z_{t}=\left[ \begin{array}[c]{cccc} \beta_{1}^{0} & \beta_{2} & \beta_{3} & \beta_{4}\\ \beta_{1}^{1} & \beta_{2} & 0 & \beta_{4}\\ \vdots & \vdots & \vdots & \vdots\\ \beta_{1}^{6} & \beta_{2} & 0 & \beta_{4}\\ \beta_{1}^{7} & 0 & 0 & \beta_{4}\\ \vdots & \vdots & \vdots & \vdots\\ \beta_{1}^{\bar{q}-2} & 0 & 0 & \beta_{4}\text{ or } 0\\ \beta_{1}^{\bar{q}-1} & 0 & 0 & \beta_{4}\text{ or } 0\\ \beta_{1}^{\bar{q}} & 0 & 0 & \beta_{4}\text{ or } 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{array} \right] ^{\prime},\\ \Gamma_{t} =\left[ \begin{array}[c]{cccc} c_{1} & c_{2t}^{\ast} & c_{3} & c_{4t}^{\ast}\\ \delta_{11} & \delta_{21t}^{\ast} & \delta_{31} & \delta_{41t}^{\ast}\\ \delta_{12} & \delta_{22t}^{\ast} & \delta_{32} & \delta_{42t}^{\ast}\\ \delta_{13} & \delta_{23t}^{\ast} & \delta_{33} & \delta_{43t}^{\ast}\\ 0 & \gamma_{21} & 0 & 0\\ 0 & \gamma_{22} & 0 & 0\\ 0 & \gamma_{23} & 0 & 0\\ 0 & 0 & \gamma_{31} & 0\\ 0 & 0 & \gamma_{32} & 0\\ 0 & 0 & \gamma_{33} & 0\\ 0 & 0 & 0 & \gamma_{41}\\ 0 & 0 & 0 & \gamma_{42}\\ 0 & 0 & 0 & \gamma_{43} \end{array} \right] ^{\prime}$ (32)
$\displaystyle T=\left[ \begin{array}[c]{cccccccccc} \rho_{1} & \rho_{2} & \rho_{3} & 0 & \cdots & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots\\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \cdots & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & \gamma_{11} & \gamma_{12} & \gamma_{13}\\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 & 0 \end{array} \right]$  
$\displaystyle H_{t}=\left[ \begin{array}[c]{cccc} 0 & 0 & 0 & 0\\ 0 & \sigma_{2t}^{\ast2} & 0 & 0\\ 0 & 0 & \sigma_{3}^{2} & 0\\ 0 & 0 & 0 & \sigma_{4t}^{\ast2} \end{array} \right] \, \\ Q=\left[ \begin{array}[c]{cc} 1 & 0\\ 0 & \sigma_{1}^{2} \end{array} \right]$  

where the matrices and vectors correspond to the system in Section 2.2 and we have $ N=4,$ $ k=13,$ $ m=95$, $ p=3$ and $ r=2$. We use the current and $ 91$ lags of the factor in our state vector because the maximum of days possible in a quarter is 92, which we denote by $ \bar{q}$.16 As we did in the simulation example, we use the transformation given in the appendix to convert the coefficients with "$ *$" to those without. Also in every quarter, we adjust the number of non-zero elements in the fourth row of the $ Z_{t}$ matrix to reflect the number of days in that quarter. When estimating this system, we restrict $ \beta_{3}$ and $ \beta_{4}$ to be positive and $ \beta_{2}$ to be negative to reflect our expectation of the relationship between these variables and the common factor.17

4.3  Results

4.3.1  Estimation

It is worth emphasizing the size of this model. We have 16,397 daily observations, 95 state variables and 42 coefficients. Using a fairly efficiently programmed Kalman filter routine in MATLAB, one evaluation of the log-likelihood takes about 25 seconds. As such, one iteration (including the calculation of the Jacobian) takes a minimum of eighteen minutes. Clearly, it is very costly to look over an "irrelevant'' part of the parameter space as it may take the estimation routine many hours or days to find the "right'' path, if at all. To tackle this problem, we follow the algorithm outlined earlier: We start by a smaller system, one that has only the term premium and employment. Once we estimate this system we get the smoothed factor and estimate the auxiliary regression for real GDP. Using the estimated values from the smaller system and the auxiliary regression as the starting guesses, we estimate the system with real GDP. We repeat this for initial claims.

4.3.2  Factor

First we focus on the factor and its properties. In Figure 2 we plot the smoothed factor from the estimation along with 95% confidence bands, with NBER recessions shaded. Because theprovides only months of the turning points, we assume recessions start on the first day of the month and end on the last day of the month. We can make a few important observations. First, the smoothed factor declines sharply around the recession start dates announced by the NBER. Although the beginning of recessions and the decline of the smoothed factor do not always coincide, the factor shows the same sharp decline pattern at the start of each of the six recessions in the sample. Second, recoveries do not all have the same pattern. For the recessions in 1974, 1980 and 1982 the recoveries coincide with as sharp reversals in the factor as the recessions. For the three remaining recessions, as well as the 1961 recession which ends just before our sample starts, the factor is more sluggish during the recoveries, especially so for the 1990 recession as is well-known. We will turn to this in more detail when we zoom in around turning points below. Finally, there seem to be few, if any, "false positives'' where our factor shows patterns similar to recessions in a period which is not a recession. Overall, we conclude that our smoothed factor tracks the U.S. business cycle well.

4.3.3  Smoothed Indicators, Smoothed Factor, and Turning Points

One of the most powerful aspects of our framework is its ability to produce high frequency measures of indicators that are observed in much lower frequencies. To demonstrate this, and to investigate how our indicators behave around turning points, we compute the smoothed daily signals for our four indicators. To do this, we use the relationship given by (2) for all non-daily variables and by (26) for term premium. Given the presence of lagged terms, we initialize each variable by the mean implied by the steady state of signal equation. To avoid small-sample problems with this initialization, we drop about 4.5 years' worth of data and use the daily indicators starting from 01/01/1969.18

As a first task, we want to verify that the daily smoothed versions of the indicators are consistent with their lower frequency counterparts. For a stock variable such as employment, the daily observation at the end of the observation period (month in this case) will be comparable with the observed value. On the other hand, for a flow variable such as initial claims, we use the appropriate temporal aggregation (adding over the days of the week in this case). In Figure 3 we plot the actual and smoothed term premium. Perhaps not surprisingly, because the term premium is observed on all business days, there is a very close match between the two and the correlation is over 0.99. In Figure 4 we plot the seven-day sum of the daily smoothed initial claims (dark circles) versus the actual weekly initial claims (light circles) and the correlation here is 0.76. It seems that the smoothed version is, by its nature, not as extreme as the actual series but the match between the two is very high. In the first panel of Figure 5 we plot the actual monthly (circles) and the smoothed daily (solid line) employment. Because the non-stationary nature of the variable can be deceiving, we also plot the detrended versions of the two series, where we detrend using cubic polynomials in trend. The correlations are over 0.99 in both cases. In Figure 6 we plot the actual quarterly (light circles) and the smoothed quarterly (dark circles) GDP both as level and as deviation from a cubic trend. The match between the two are weaker compared to the other variables with a correlation of 0.31. This is because GDP is very infrequently observed compared to the other variables with only 128 observations. Overall, we conclude that the smoothed daily indicators that we obtain are very reliable.

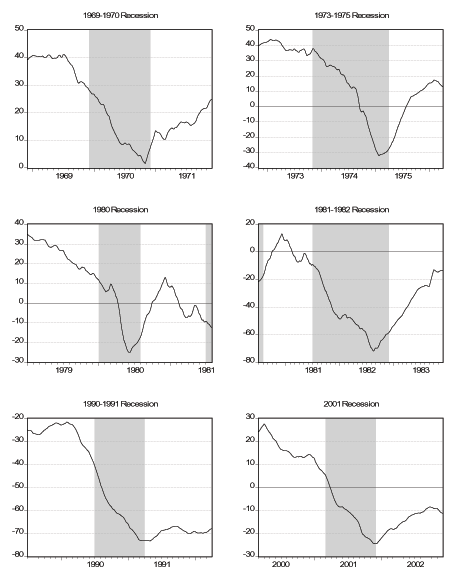
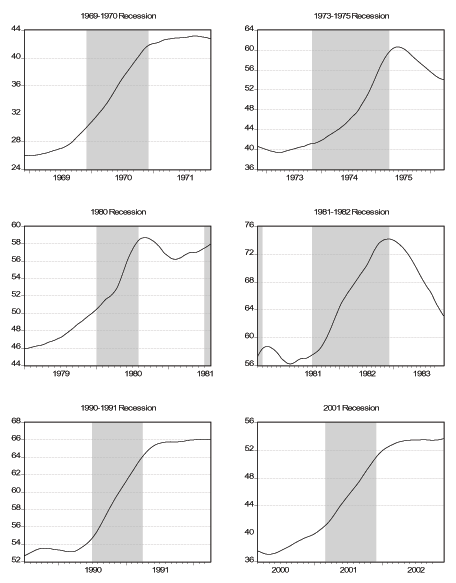
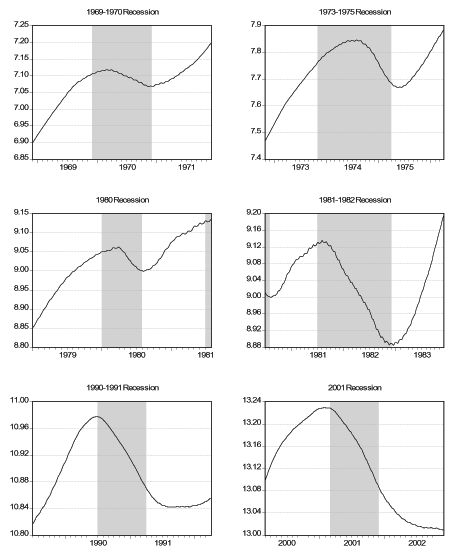
Next we zoom in around the turning points of the six business cycles that are in our sample, as determined by the NBER.19 We consider a window that starts twelve months before the month of the peak and ends twelve months after the month of the trough. First, we look at the smoothed daily factor in the six windows, which we plot in Figure 7, where we superimpose NBER Recession dates. Two things that are of interest is how the turning points of the daily factor compare with the official turning points and the behavior of the factor during recessions. We should keep in mind that neither matching the NBER dates is a success, nor not matching them is a failure, at least because there might be some discrepancy due to the lower frequency (monthly) the NBER uses. Generally speaking our factor is decreasing during most of the recessions but there is quite a bit of disagreement about the turning points, especially the peaks. In all recessions except for the 1973-1975 recession, our factor reaches its peak and starts falling at least five months before the official peak of the expansion. For the 1980 recession, the peak of the factor seems to be beyond our twelve-month window. As for the troughs, in all but the last two recessions our factor has already picked up before the trough of the recession even though the difference is at most three months. For the last two recessions, the turning point of the factor seems to exactly match the official end of the recession. In Figure 8 we plot daily smoothed initial claims in the same six windows. We see that initial claims are either relatively flat (i.e. non-decreasing) or increasing even a year before the official start of a recession in all the six episodes. Moreover, the increase in initial claims that is sustained during all the recessions starts to slow down or get reversed either exactly at the trough or shortly thereafter in all six episodes. In Figure 9 we plot daily smoothed employment in the six windows. The cyclical behavior of employment over the business cycle is very clearly visible in the figures. In the first three recessions, employment reaches its peak after the economy falls in to recession while in the latter three recessions the peak of employment coincides with the peak of the business cycle. As for the troughs, the trough of employment coincides with the trough of the business cycle for the first four episodes while it significantly lags the business cycle for the latter two episodes. This finding reinforces the "jobless recovery'' description commonly attributed to the 1990-1991 recession. Moreover it is an indication that the 2001 recession is similar to the 1990-1991 recession and these two episodes are different from the previous recessions in the US. In fact, comparing the lower two panels of Figures 7-9 with the other panels, this observation is very apparent. Finally, in Figure 10 we plot daily smoothed GDP over the last four recessions in our sample. Except for the 1980 recession, GDP starts to decline right about the same time as the official peak date and continues the decline past the official trough. In fact, the trough of GDP for these three recessions are all beyond our twelve-month window. Despite a slowdown during the 1980 recession, GDP does not start to decline until the peak of the 1981-1982 recession.

5  Summary and Concluding Remarks

We have constructed a framework for measuring macroeconomic activity in real time, using a variety of stock and flow data observed at mixed frequencies, including ultra-high frequencies. Specifically, we have proposed a dynamic factor model that permits exactly optimal extraction of the latent state of macroeconomic activity, and we have illustrated it both in simulation environments and in a sequence of progressively richer empirical examples. We also provided some examples of the applications of the framework which yield useful insights for understanding comovements of variables over the business cycle.

We look forward to a variety of variations and extensions of our basic theme, including but not limited to:

(1) Incorporation of indicators beyond macroeconomic and financial data. In particular, it will be of interest to attempt inclusion of qualitative information such as headline news.

(2) Construction of a real time composite leading index (CLI). Thus far we have focused only on construction of a composite coincident index (CCI), which is the more fundamental problem, because a CLI is simply a forecast of a CCI. Explicit construction of a leading index will nevertheless be of interest.

(3) Allowance for nonlinear regime-switching dynamics. The linear methods used in this paper provide only a partial (linear) statistical distillation of the rich business cycle literature. A more complete approach would incorporate the insight that expansions and contractions may be probabilistically different regimes, separated by the "turning points" corresponding to peaks and troughs, as emphasized for many decades in the business cycle literature and rigorously embodied Hamilton's (1989) Markov-switching model. Diebold and Rudebusch (1996) and Kim and Nelson (1998) show that the linear and nonlinear traditions can be naturally joined via dynamic factor modeling with a regime-switching factor. Such an approach could be productively implemented in the present context, particularly if interest centers on turning points, which are intrinsically well-defined only in regime-switching environments.

(4) Comparative assessment of experiences and results from "small data" approaches, such as ours, vs. "big data" approaches. Although much professional attention has recently turned to big data approaches, as for example in Forni, Hallin, Lippi and Reichlin (2000) and Stock and Watson (2002), recent theoretical work by Boivin and Ng (2006) shows that bigger is not necessarily better. The matter is ultimately empirical, requiring detailed comparative assessment. It would be of great interest, for example, to compare results from our approach to those from the Altissimo et al. (2002) EuroCOIN approach, for the same economy and time period. Such comparisons are very difficult, of course, because the "true" state of the economy is never known, even ex post.

References

Abeysinghe, T. (2000), " Modeling Variables of Different Frequencies,''Journal of Forecasting, 16, 117-119.

Altissimo, F., Bassanetti, A., Cristadoro, R., Forni, M., Hallin, M., Lippi, M., Reichlin, L. and Veronese, G. (2001), " Eurocoin: A Real Time Coincident Indicator of the Euro Area Business Cycle,''Discussion Paper No. 3108.

Barndorf-Nielsen, O. and G. Schou (1973), " On the Parametrization of Autoregressive Models by Partial Autocorrelations,''of Multivariate Analysis, 3, 408-419.

Boivin, J. and Ng, S. (2006), " Are More Data Always Better for Factor Analysis,''of Econometrics, 127, 169-194.

Burns, A.F. and Mitchell, W.C. (1946), Measuring Business Cycles, New York, NBER.

Diebold, F.X. (2003), "'Big Data' Dynamic Factor Models for Macroeconomic Measurement and Forecasting" (Discussion of Reichlin and Watson papers), in M. Dewatripont, L.P. Hansen and S. Turnovsky (Eds.), Advances in Economics and Econometrics, Eighth World Congress of the Econometric Society . Cambridge: Cambridge University Press, 115 122.

Diebold, F.X. and Rudebusch, G. (1996), "Measuring Business Cycles: A Modern Perspective," Review of Economics and Statistics, 78, 67 77.

Durbin and Koopman (2001), Time Series Analysis by State Space Methods, Oxford University Press.

Evans, M.D.D. (2005), "Where Are We Now?: Real Time Estimates of the Macro Economy," The International Journal of Central Banking, September.

Forni, M., Hallin, M., Lippi, M. and Reichlin, L. (2000), " The Generalized Factor Model: Identification and Estimation,''of Economics and Statistics, 82, 540-554.

Geweke, J.F. (1977), "The Dynamic Factor Analysis of Economic Timeseries Models,'' in D. Aigner and A. Goldberger (eds.), Latent Variables in Socio economic Models, North Holland, 1977, pp. 365 383.

Ghysels, E., Santa-Clara, P. and Valkanov, R.(2004), "The MIDAS Touch: Mixed Data Sampling Regression Models," Manuscript, University of North Carolina.

Hall, R.E., et al. (2003), "The NBER's Recession Dating Procedure," Available at http://www.nber.org/cycles/recessions.html

Hamilton, J.D. (1989), "A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle,'' Econometrica, 57, 357 384.

Kim, C.-J. and Nelson, C.R. (1998), State Space Models with Regime Switching: Classical and Gibbs Sampling Approaches with Applications. Cambridge, Mass.: MIT Press.

Liu, H. and Hall, S.G. (2001), " Creating High-frequency National Accounts with State-Space Modelling: A Monte Carlo Experiment,'' Journal of Forecasting, 20, 441-449.

Lucas, R.E. (1977), "Understanding Business Cycles," Carnegie Rochester Conference Series on Public Policy, 5, 7 29.

Mariano, R.S. and Murasawa, Y. (2003), "A New Coincident Index of Business Cycles Based on Monthly and Quarterly Series," Journal of Applied Econometrics, 18, 427 443.

McGuckin, R.H., Ozyildirim, A. and Zarnowitz, V. (2003), " A More Timely and Useful Index of Leading Indicators,'', Conference Board.

Proietti, T. and Moauro, F. (2006), "Dynamic Factor Analysis with Non Linear Temporal Aggregation Constraints," Applied Statistics, 55, 281-300.

Sargent, T.J. and Sims, C.A. (1977), "Business Cycle Modeling Without Pretending to Have Too Much A Priori Economic Theory," in C. Sims (ed.), New Methods in Business Research. Minneapolis: Federal Reserve Bank of Minneapolis.

Shen, C.-H. (1996), " Forecasting Macroeconomic Variables Using Data of Different Periodicities,''Journal of Forecasting, 12, 269-282.

Stock, J.H. and Watson, M.W. (1989), " New Indexes of Coincident and Leading Economic Indicators,'' Macro Annual, Volume 4. Cambridge, Mass.: MIT Press.

Stock, J.H. and Watson, M.W. (1991), "A Probability Model of the Coincident Economic Indicators." In K. Lahiri and G. Moore (eds.), Leading Economic Indicators: New Approaches and Forecasting Records. Cambridge: Cambridge University Press, 63 89.

Stock, J.H. and Watson, M.W. (2002), "Macroeconomic Forecasting Using Diffusion Indexes," Journal of Business and Economic Statistics, 20, 147-162.

Appendix

A  The Mapping for Third-Order Trend Polynomial Coefficients

Here we establish the mapping between two sets of parameters. On the one hand, we have

$\displaystyle \sum_{j=0}^{D-1}\left[ c+\delta_{1}\left( \frac{t-j}{1000}\right) +\delta_{2}\left( \frac{t-j}{1000}\right) ^{2}+\delta_{3}\left( \frac {t-j}{1000}\right) ^{3}\right] ,$  

and on the other hand we have

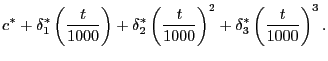
$\displaystyle c^{\ast}+\delta_{1}^{\ast}\left( \frac{t}{1000}\right) +\delta_{2}^{\ast }\left( \frac{t}{1000}\right) ^{2}+\delta_{3}^{\ast}\left( \frac{t} {1000}\right) ^{3} .$  

We want to establish the mapping between $ \left( c,\delta_{1},\delta _{2},\delta_{3}\right) $ and $ \left( c^{\ast},\delta_{1}^{\ast},\delta _{2}^{\ast},\delta_{3}^{\ast}\right) .$ We have

\begin{equation*}\begin{align}& \sum_{j=0}^{D-1}\left[ c+\delta_{1}\left( \frac{t-j}{1000}\right) +\delta_{2}\left( \frac{t-j}{1000}\right) ^{2}+\delta_{3}\left( \frac {t-j}{1000}\right) ^{3}\right] \\ & =\sum_{j=0}^{D-1}c+\delta_{1}\sum_{j=0}^{D-1}\left( \frac{t}{1000}-\frac {j}{1000}\right) +\delta_{2}\sum_{j=0}^{D-1}\left( \frac{t}{1000}-\frac {j}{1000}\right) ^{2}+\delta_{3}\sum_{j=0}^{D-1}\left( \frac{t}{1000} -\frac{j}{1000}\right) ^{3} \end{align}\end{equation*}

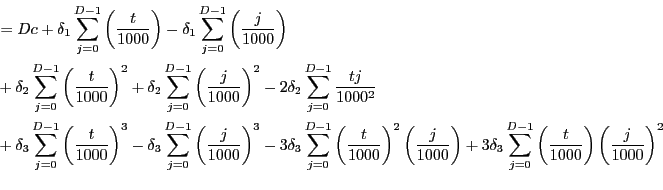
\begin{equation*}\begin{align}& =Dc+\delta_{1}\sum_{j=0}^{D-1}\left( \frac{t}{1000}\right) -\delta_{1} \sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) \\ & +\delta_{2}\sum_{j=0}^{D-1}\left( \frac{t}{1000}\right) ^{2}+\delta _{2}\sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) ^{2}-2\delta_{2}\sum _{j=0}^{D-1}\frac{tj}{1000^{2}}\\ & +\delta_{3}\sum_{j=0}^{D-1}\left( \frac{t}{1000}\right) ^{3}-\delta _{3}\sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) ^{3}-3\delta_{3}\sum _{j=0}^{D-1}\left( \frac{t}{1000}\right) ^{2}\left( \frac{j}{1000}\right) +3\delta_{3}\sum_{j=0}^{D-1}\left( \frac{t}{1000}\right) \left( \frac {j}{1000}\right) ^{2} \end{align}\end{equation*}

\begin{equation*}\begin{align}& =Dc-\delta_{1}\sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) +\delta_{2} \sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) ^{2}-\delta_{3}\sum_{j=0} ^{D-1}\left( \frac{j}{1000}\right) ^{3}\\ & +\frac{t}{1000}\left[ D\delta_{1}-2\delta_{2}\sum_{j=0}^{D-1}\frac{j} {1000}+3\delta_{3}\sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) ^{2}\right] \\ & +\left( \frac{t}{1000}\right) ^{2}\left[ D\delta_{2}-3\delta_{3} \sum_{j=0}^{D-1}\left( \frac{j}{1000}\right) \right] \\ & +\left( \frac{t}{1000}\right) ^{3}\left( D\delta_{3}\right) . \end{align}\end{equation*}

Now, note that

\begin{equation*}\begin{align}\sum_{j=0}^{D-1}j & =\frac{D\left( D-1\right) }{2}\\ \sum_{j=0}^{D-1}j^{2} & =\frac{D\left( D-1\right) \left[ 2\left( D-1\right) +1\right] }{6}=\frac{D\left( D-1\right) \left( 2D-1\right) }{6}\\ \sum_{j=0}^{D-1}j^{3} & =\left[ \frac{D\left( D-1\right) }{2}\right] ^{2}. \end{align}\end{equation*}

Hence we obtain

\begin{equation*}\begin{align}c^{\ast} & =Dc-\frac{\delta_{1}D\left( D-1\right) }{2000}+\frac{\delta _{2}D\left( D-1\right) \left( 2D-1\right) }{6\times10^{6}}-\frac {\delta_{3}\left[ D\left( D-1\right) \right] ^{2}}{4\times10^{9}}\\ \delta_{1}^{\ast} & =D\delta_{1}-\frac{\delta_{2}D\left( D-1\right) } {1000}+\frac{\delta_{3}D\left( D-1\right) \left( 2D-1\right) } {2\times10^{6}}\\ \delta_{2}^{\ast} & =D\delta_{2}-\frac{3\delta_{3}D\left( D-1\right) }{2000}\\ \delta_{3}^{\ast} & =D\delta_{3} . \end{align}\end{equation*}

Figure 1 - Simulation:  Smoothed Factors and Indicators

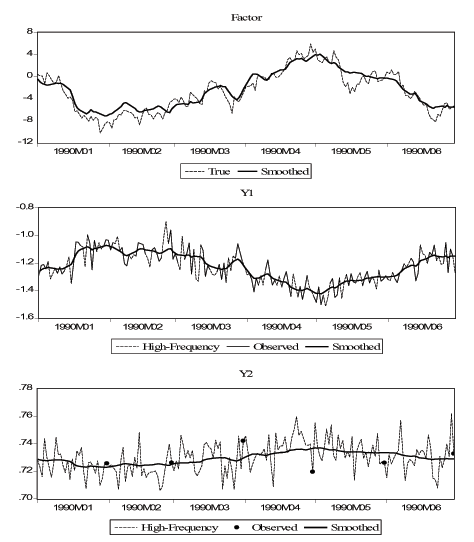
Figure 1 shows the results of our simulation exercise over a six-month period. The first panel shows the true and smoothed values of the latent real activity factor. The x-axis displays the dates, from month 1 to month 6; the y-axis displays the values of the factor, from a minimum of -12 to a maximum of +8. The true factor has a lot more fluctuations than the smoothed factor, but the latter tracks the former very well. Both factors start around zero, decrease to the negative territory in the first half of the sample, become positive between the fourth and fifth month, and then become negative again. The second panel shows the high-frequency (daily) values of indicator Y1, the observed values of Y1, and the smoothed daily values of Y1 obtained by running the smoothed values of the factor through equation (2) for Y1. The x-axis displays the dates, from month 1 to month 6; the y-axis displays the values of Y1, from a minimum of -1.6 to a maximum of -0.8. The high-frequency line is the latent series which has values for all days in the six-month period. The observed line overlaps the high-frequency line for the dates in which the variable is observed by the econometrician. The smoothed line tracks the former to lines very well, but has less fluctuation. All line starts just below -1.2, rise above -1.2 for the first three months, decrease and reach a trough at the end of the fourth month, and then rise again to about -1.2. The third panel shows the high-frequency (daily) values of indicator Y2, the observed values of Y2, and the smoothed daily values of Y2 obtained by running the smoothed values of the factor through equation (2) for Y2. The x-axis displays the dates, from month 1 to month 6; the y-axis displays the values of Y2, from a minimum of 0.70 to a maximum of -0.78. The high-frequency line is the latent series which has values for all days in the six-month period. The observed series is represented by dots overlapping the high-frequency line for the dates in which the variable is observed by the econometrician. The smoothed line tracks the former to lines very well, but has less fluctuation. All line starts just below 0.73 and fluctuate mainly in the 0.71 to 0.75 band.

Notes: The first panel shows the true and smoothed values of the latent real activity factor. The second panel shows the high-frequency ("daily") values of indicator Y1, the observed values of Y1, and the "smoothed" daily values of Y1 obtained by running the smoothed values of the factor through equation (2) for Y1. The third panel shows the high-frequency ("daily") values of indicator Y2, the observed values of Y2, and the "smoothed" daily values of Y2 obtained by running the smoothed values of the factor through equation (2) for Y2. See text for details.

Figure 2 - Smoothed U.S. Real Activity Factor

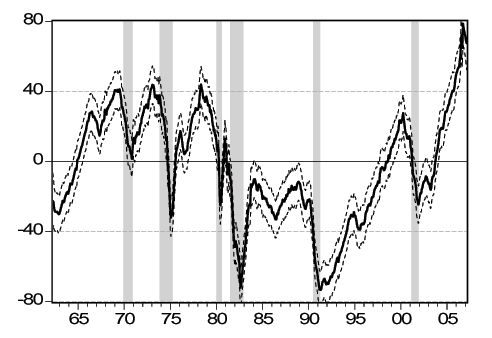
Figure 2 shows the smoothed U.S. real activity factor during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. The x-axis displays the dates, from April 1962 to February 2007; the y-axis displays the values of the factor, from a minimum of -80 to a maximum of +80. The factor is generally decreasing during recessions. The peak does not always coincide with the beginning of the recession as defined by the NBER, while the trough tends to coincide.

Notes: We show the smoothed factor together with ninety-five percent confidence bands (dashed lines). The shaded bars denote NBER recessions. See text for details.

Figure 3 - Smoothed Indicators I: Term Premium

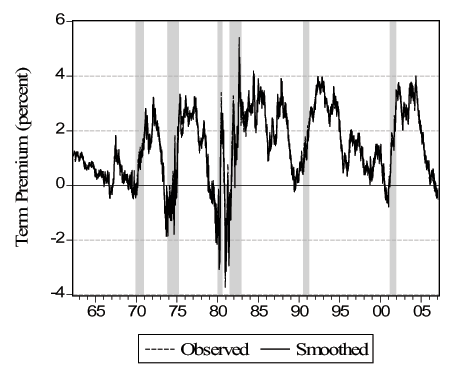
Figure 3 shows smoothed and observed term premium during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. The x-axis displays the dates, from April 1962 to February 2007; the y-axis displays the values of the term premium, from a minimum of -4 to a maximum of +6. The smoothed line overlaps the observed one and it almost impossible to distinguish them. The term premium is generally decreasing just before the onset of the recessions as defined by the NBER.

Notes: We show the oberved and "smoothed" daily term premium. We obtain the smoothed daily term premium by running the smoothed values of the factor through equation (24) for the term premium. See text for details.

Figure 4 - Smoothed Indicators II: Initial Jobless Claims

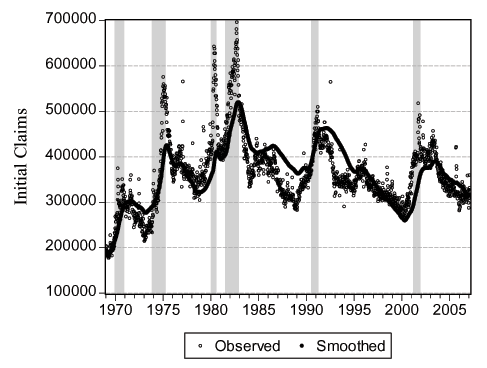
Figure 4 shows smoothed and observed values of initial jobless claims during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. The x-axis displays the dates, from April 1962 to February 2007; the y-axis displays the values of initial jobless claims, from a minimum of 100,000 to a maximum of 700,000. The smoothed line does a good job in tracing the observed one. Initial jobless claims are generally increasing during recession period, as they are defined by the NBER.

Notes: We show the observed and "smoothed" weekly initial jobless claims. We obtain the smoothed daily initial claims by running the smoothed values of the factor through equation (2) for initial claims. We obtain smoothed weekly initial claims (Saturdays) by summing daily smoothed initial claims over the last seven days. See text for details.

Figure 5 - Smoothed Indicators III: Employment

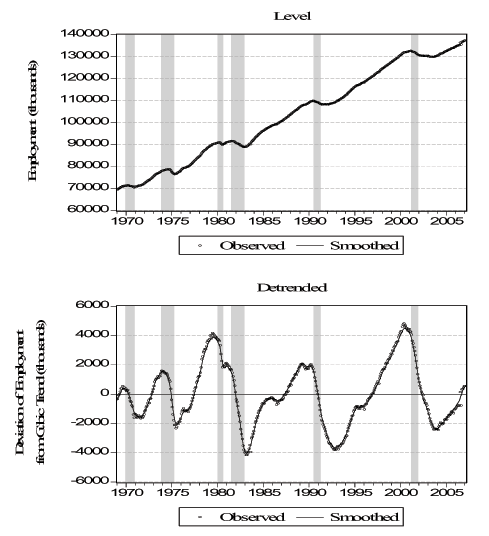
Figure 5 shows smoothed and observed employment during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. In the first panel, the x-axis displays the dates, from 1969 to February 2007; the y-axis displays the values of employment, from a minimum of 60,000 to a maximum of 140,000. In the second panel, the x-axis displays the dates, from 1969 to February 2007; the y-axis displays the values of detrended employment, from a minimum of -6,000 to a maximum of+6000. The smoothed line overlaps the observed one and it almost impossible to distinguish them. Employment is generally decreasing during recession periods, as they are defined by the NBER.

Notes: We show observed (monthly) and "smoothed" (daily) employment. The top panel shows observed and smoothed values of total employment, and the bottom panel shows observed and smoothed values of detrended employment. We obtain smoothed daily employment by running smoothed values of the factor through equation (2) for employment. See text for details.

Figure 6 - Smoothed Indicators IV: GDP

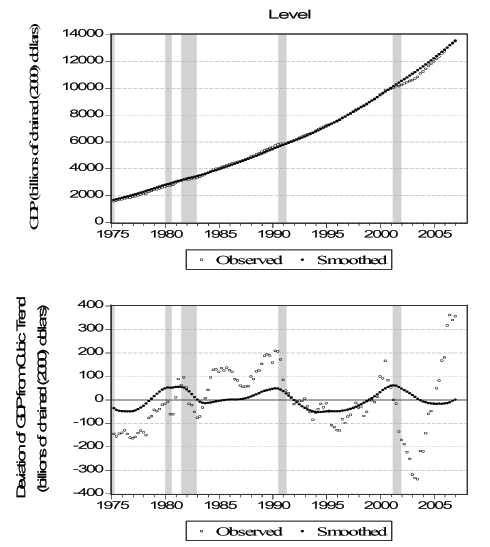
Figure 6 shows smoothed and observed GDP during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. In the first panel, the x-axis displays the dates, from 1975 to February 2007; the y-axis displays GDP values, from 0 to a maximum of 14,000. In the second panel, the x-axis displays the dates, from 1975 to February 2007; the y-axis displays GDP detrended values, from a minimum of -400 to a maximum of+400. The smoothed line does a good job in tracing the observed one both in the level and in the detrended series. GDP is generally decreasing during recession periods, as they are defined by the NBER.

Notes: We show observed (monthly) and "smoothed" (quarterly) GDP. We obtain the smoothed daily GDP by running the smoothed values of the factor through equation (2) for GDP. We obtain smoothed quarterly GDP by summing daily smoothed GDP over the last 91 days. The top panel shows observed and smoothed values of GDP, and the bottom panel shows observed and smoothed values of detrended GDP. See text for details.

Figure 7 - Smoothed Factor During Recessions

Figure 7 shows the smoothed daily real activity factor during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. In all the panels, a shaded area indicates the recession. The six months before the beginning of the shaded area indicate the six months preceding the recession. The six months after the end of the shaded area indicate the six months following the recession. In all the panels (all the recessions), the factor seems to pick before the beginning of the shaded area, which is the recession as defined by the NBER. In the first four panels/recessions, the factor reaches a trough before the end of the shaded area, while in the last two recessions, the trough of the factor coincides with the end of the recession as defined by the NBER.

Notes: We show the smoothed daily real activity factor during and near the six NBER recessions in our sample. See text for details.

Figure 8 - Smoothed Initial Claims During Recessions

Figure 8 shows the smoothed daily initial jobless claims during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. In all the panels, a shaded area indicates the recession. The six months before the beginning of the shaded area indicate the six months preceding the recession. The six months after the end of the shaded area indicate the six months following the recession. In all the panels (all the recessions), the smoothed initial claims line is increasing during the recession (shaded area), it seems to have reached a trough in the month preceding the recession, and in the 1973-75, 1980 and 1981-82 recessions, it reaches a peak very close to or at the end of the recession. In the 1990-91 and 2001 recessions, the smoothed initial jobless claim line seems to reach a high value after the recession and stay around that value for the following months.

Notes: We show the smoothed daily initial claims during and near the six NBER recessions in our sample. See text for details.

Figure 9 - Smoothed Employment During Recessions

Figure 9 shows the smoothed employment during and near the six NBER recessions in our sample: 1969-1970, 1973-1975, 1980, 1981-1982, 1990-1991, and 2001. In all the panels, a shaded area indicates the recession. The six months before the beginning of the shaded area indicate the six months preceding the recession. The six months after the end of the shaded area indicate the six months following the recession. In the first four panels (four recessions), the smoothed employment line reaches a peak after the beginning of the recession, as defined by the NBER, decreases during the recession, reaches a trough very close to the end of the shaded area, and then rises. In the last two panels (recessions), the employment smoothed line peaks at the beginning of the shaded area, decreases in the shaded area, and reaches a trough after the end of the shaded area.

Notes: We show the smoothed daily employment during and near the six NBER recessions in our sample. See text for details.

Figure 10 - Smoothed GDP During Recessions

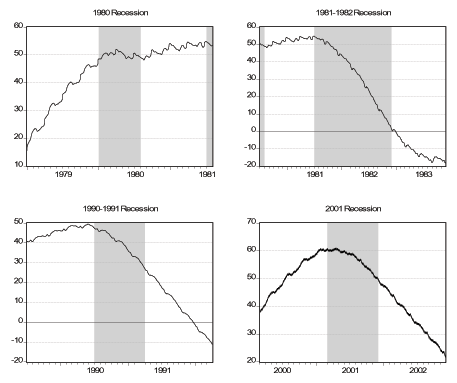
Figure 10 shows smoothed GDP during and near four NBER recessions: 1980, 1981-1982, 1990-1991, and 2001. In all the panels, a shaded area indicates the recession. The six months before the beginning of the shaded area indicate the six months preceding the recession. The six months after the end of the shaded area indicate the six months following the recession. In the first panel, the smoothed GDP line is increasing throughout the six months before the recession (as defined by the NBER), the line in flat during the recession itself and then increases again during the six months after. In the last three panels, the GDP smoothed line increases in the six months before the recession (as defined by the NBER), and decreases during the recession and in the six months after.

Notes: We show the smoothed daily GDP during and near the six NBER recessions in our sample. See text for details.

Footnotes

*  For helpful discussion we thank seminar and conference participants at the Board of Governors of the Federal Reserve System, the Federal Reserve Bank of Philadelphia, SCE Cyprus, and American University. We are especially grateful to Carlos Capistran, Martin Evans, Jon Faust, Eric Ghysels, Sharon Kozicki, Alexi Onatski, Frank Schorfheide and Jonathan Wright. We thank the National Science Foundation for research support. The usual disclaimer applies. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System.  Return to text

†   Corresponding author. Department of Economics, University of Maryland, College Park, MD 20742. [email protected] Return to text

1.  For definition and discussion of small-data vs. large-data dynamic factor modeling, see Diebold (2003). Return to text

2.  Other related and noteworthy contributions include Shen (1996), Abeysinghe (2000), Altissimo et al. (2002), Liu and Hall (2001), McGuckin, Ozyildirim and Zarnowitz (2003), and Ghysels, Santa Clara and Valkanov (2004). Return to text

3.  In our subsequent empirical work, we will indeed use a daily base observational frequency, but much higher (intra-day) frequencies could be used if desired. Return to text

4.  As is well-known, identification of factor models requires normalization either on a factor loading or on the factor variance, and we choose to normalize the factor variance to unity. Return to text

5.  For numerical stability we use $ t/1000,$ $ \left( t/1000\right) ^{2}$ and $ \left( t/1000\right) ^{3}$ instead of simply $ t,$ $ t^{2}$ and $ t^{3}$ in specifying our cubic trend polynomial. This is simply a normalization and does not affect the other parameters of interest or the log-likelihood. We impose it because in our subsequent empirical work we have over 16,000 daily observations, in which case $ t^{3}$ can be very large, which might create numerical problems. Return to text

6.  Time-varying system matrices pose no problem for the Kalman filter. Return to text

7.  We find that using this version of the filter improves the efficiency of the algorithm. See Durbin and Koopman (2001) for details. Return to text

8.  By construction, whenever there is an observation for a particular element of $ y_{t}$, there is a corresponding element of $ w_{t}$. Return to text

9.  Because we assume that daily frequency is the highest available, we can treat flow and stock variables identically when they are observed daily. Return to text

10.  We use a hyperbolic tangent function to search over $ \pi_{i} $, because for $ y\in R$, $ x=\tanh(y)\in\left[ -1,1\right] .$ Return to text

11.  For simplicity in the simulation, we do not use higher order trend terms, lagged dependent variables, or polynomial distributed lags. Return to text

12.  Note that the third rows of $ Z_{t}$, $ \Gamma_{t} $ and $ H_{t}$ are only relevant when $ \tilde{y}_{t}^{3}$ is observed. For all other days, the contents of the third rows of these matrices do not affect any calculations. When there is an observation for $ \tilde{y}_{t}^{3}$ we look at the number of days in that particular quarter, $ q,$ and make the adjustments. Return to text

13.  For numerical stability we adjust the units of some of our observed variables. (e.g. we divide employment by 10,000 and initial jobless claims by 1,000) Return to text

14.  Once again, the notation in the paper assumes $ M$ and $ q$ are constant over time but in the implementation we adjust them according to the number of days in the relevant month or quarter. The number of days in a week is always seven. Return to text

15.  Alternatively we could have used $ AR(3)$ measurement errors for all variables. But this persistence in the daily frequency would essentially disappear when we aggregate the variables to the monthly or quarterly frequency. Return to text

16.  If there are $ q$ days in a quarter, on the last day of the quarter, we need the current and the $ q-1$ lags of the factor for the measurement equation of GDP. Return to text

17.  In our experience with smaller systems, when we do not impose a sign restriction the estimation may yield a factor which is negatively correlated with GDP. Imposing the sign restriction reverses the correlation with virtually no change in the likelihood. Return to text

18.  Because the number of days in a quarter is not fixed, we assume this number is 91 in (2) for GDP and in the temporal aggregation for Figure 6 below. We also start from 01/01/1975 for GDP because it is less frequently observed and hence more time is needed to remove the effects of initialization. Return to text

19.  These are December 1969-November 1970, November 1973-March 1975, January 1980-July 1980, July 1981-November 1982, July 1990-March 1991 and March 2001-November 2001. Return to text


This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: September 18, 2007