
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 907, October 2007--- Screen Reader
Version*
A Residual-Based Cointegration Test for Near Unit Root Variables*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Methods of inference based on a unit root assumption in the data are typically not robust to even small deviations from this assumption. In this paper, we propose robust procedures for a residual-based test of cointegration when the data are generated by a near unit root process. A Bonferroni method is used to address the uncertainty regarding the exact degree of persistence in the process. We thus provide a method for valid inference in multivariate near unit root processes where standard cointegration tests may be subject to substantial size distortions and standard OLS inference may lead to spurious results. Empirical illustrations are given by: (i) a re-examination of the Fisher hypothesis, and (ii) a test of the validity of the cointegrating relationship between aggregate consumption, asset holdings, and labor income, which has attracted a great deal of attention in the recent finance literature.
Keywords: Bonferroni test, cointegration, near unit roots
JEL classification: C12, C22
1 Introduction
Cointegration tests have been among the most important and influential tools in empirical economics since their introduction over two decades ago. In essence, cointegration tests attempt to identify common driving factors in stochastically trending data, thus identifying long-run equilibrium relationships between economic variables. The most common cointegration tests are based on the assumption that the individual variables are unit root processes. The unit root assumption, however, is often hard to fully justify for actual economic data. In finite samples, many economic variables appear highly, but not totally, persistent; that is, the largest autoregressive root is close to, but not necessarily equal to, unity. Unfortunately, inferencial procedures designed for unit root data tend not to be robust to even small deviations from the unit root assumption. For instance, Elliot (1998) shows that large size distortions can occur when performing inference on the cointegrating vector in a system where the individual variables follow near unit root processes rather than pure unit root processes.
Unit root tests go some way toward alleviating the uncertainty regarding the persistence in a given time series but do not provide a definitive answer. Since unit root tests have low power against local alternatives, a failure to reject the null hypothesis of a unit root does not rule out the possibility of a root slightly different from unity. On the other hand, rejecting the null of a unit root does not rule out that the process is still fairly persistent and leaves open the possibility of spurious regressions. It is thus far from obvious how to deal with a multivariate near unit root process: Standard cointegration tests will not be valid under deviations from the pure unit root assumption and the possibility of spurious regressions invalidates standard OLS inference.1
The aim of this paper is to design a test of cointegration that is robust to deviations from the pure unit root assumption. In particular, we extend the standard framework to the case where the original data possess autoregressive roots that are local-to-unity, rather than identically equal to unity. The methods developed here are useful from two different perspectives. First, they provide a robustness check to standard cointegration tests in the typical situation where it is not known with certainty that there is an exact unit root in the data. Second, and just as importantly, the test procedures in this paper allow for valid inference in the case when the data is likely not a pure unit root process, but still highly persistent.
While there is a large literature on cointegrating regressions with near unit root regressors, the focus has been on inference on the slope parameter in these regressions, rather than actual tests of cointegration; see, for example, Cavanagh et al. (1995), Elliot (1998), Campbell and Yogo (2006) and Jansson and Moreira (2006). Typically, the models in this literature have been specified such that under the null hypothesis of a zero slope coefficient, the dependent variable is a stationary process. Tests on the slope coefficient therefore become joint tests of cointegration as well, and the issue of spurious regressions never occurs. Although this is a useful specification, for instance, in tests of stock-return predictability which motivated much of this literature, it is less convenient in most typical economic applications where both dependent and independent variables are near-integrated. The closest related literature to the current paper is the work on stationarity tests (Leybourne and McCabe, 1993, and Shin, 1994) and the work by Wright (2000). In particular, Wright (2000) develops a joint test of a specific hypothesis regarding the cointegrating vector and a test of the null hypothesis of cointegration that is robust to deviations from the pure unit root framework.
We focus on a residual-based test of cointegration. Following the work of Phillips and Ouliaris (1990), we extend the asymptotic results for a residual-based test to the case of near-integrated processes. Unlike the pure unit root case, the asymptotic distribution of the test statistic now depends on an unknown nuisance parameter; the local-to-unity root. Since this parameter is not consistently estimable, feasible tests cannot be directly constructed from the asymptotic distribution. Instead, we propose to replace the unknown parameter value for the local-to-unity root with a conservative estimate.
In order to understand the intuition behind our procedure, it is useful to consider the potential errors when applying a standard, pure unit root case, cointegration test to a set of near unit root variables. A residual-based cointegration test evaluates whether the residuals from the empirical regression contain a unit root. Now, if the original data are in fact near-integrated, with a root less than unity, the test will over-reject since the residuals will not contain a unit root even if there is no cointegration. But, by instead using critical values based on a conservative estimate of the local-to-unity root in the original data, a valid test is obtained. Intuitively, if one views a residual-based test of cointegration as a test of whether there is less persistence in the residuals than in the original data, then this test is only valid if the persistence of the original data is not overstated.2 In a spirit similar to the Bonferroni methods proposed by Cavanagh et al. (1995), we show how an appropriately conservative estimate of the local-to-unity root is obtained.
The rest of the paper is organized as follows. Section 2 outlines the modelling assumptions and the theoretical results. Section 3 describes the Bonferroni methods. In Section 4, the proposed procedure is evaluated using Monte Carlo simulations. We show that once the conservative estimate for the local-to-unity parameter is chosen appropriately, the resulting test has both good size and power properties. This is in contrast to standard cointegration tests, based on the unit root assumption, which are shown to severely over-reject as the data generating process deviates from a pure unit root setup. As an illustration of the method, two empirical applications are considered in Section 5. First, we re-examine the Fisher hypothesis and show that using the robust methods proposed in this paper, one can no longer find significant support for a long-run equilibrium relationship between nominal interest rates and inflation; using standard unit root based cointegration tests on the other hand, the null hypothesis of no cointegration is rejected. In a second illustration, we consider the robustness of the long-run relationship between aggregate consumption, asset holdings, and labor income, which was initially studied by Lettau and Ludvigson (2001) and has since received a great deal of attention in the finance literature. We find that after controlling for the unknown persistence in the variables, there is still strong evidence of cointegration between the three variables. Section 6 concludes and the Appendix contains tables of critical values for the test statistic.
2 Theoretical framework
2.1 Model and assumptions
Let
![]() be an
be an
![]() vector of nearly integrated processes, such
that the data generating process satisfies
vector of nearly integrated processes, such
that the data generating process satisfies
| (1) |
where
![]() is an
is an ![]() matrix with
matrix with
![]() and
and
![]() , and
, and
![]() is the sample size. That is, each component
process in
is the sample size. That is, each component
process in ![]() is generated as a near unit root
process with individual local-to-unity parameters
is generated as a near unit root
process with individual local-to-unity parameters ![]() ,
, ![]() . The initial conditions are set
at
. The initial conditions are set
at ![]() and
and ![]() is assumed
randomly distributed with finite variance. Although none of the
formal results depend upon it, we will work under the assumption
that
is assumed
randomly distributed with finite variance. Although none of the
formal results depend upon it, we will work under the assumption
that
![]() for all
for all ![]() , which
rules out explosive processes. The innovations
, which
rules out explosive processes. The innovations ![]() satisfy a general linear process.
satisfy a general linear process.
2.
![]() is iid with mean zero, variance
matrix
is iid with mean zero, variance
matrix
![]() , and finite fourth-order
moment.
, and finite fourth-order
moment.
By standard results, e.g. Phillips and Solo (1992),
![]() , where
, where
![]() is a Brownian motion with
covariance matrix
is a Brownian motion with
covariance matrix
![]() . Partition
. Partition
![]() such that
such that
![]() is a scalar and
is a scalar and ![]() is
an
is
an ![]() vector
vector
![]() . Let
. Let
![]() ,
,
![]() , and
, and
![]() be conformable partitions of
be conformable partitions of
![]() ,
, ![]() ,
and
,
and ![]() , respectively. We assume that
, respectively. We assume that
![]() and write
and write
![]() . Denote an
. Denote an ![]() vector standard Brownian motion as
vector standard Brownian motion as
![]() , and it follows that
, and it follows that
![]() . Further, as
. Further, as
![]() ,
,
![]() . Partition
. Partition ![]() conformably with
conformably with ![]() and let
and let
![]()
We consider residual-based tests of the null of no cointegration
using the regression residuals,
![]() , from the following empirical
regression:
, from the following empirical
regression:
| (2) |
2.2 The test statistic
We focus on the traditional Augmented Engle-Granger ![]() test (Engle and Granger, 1987) of the null of no
cointegration, which is probably the most commonly used
residual-based test of cointegration. Our analysis could easily be
extended to cover the
test (Engle and Granger, 1987) of the null of no
cointegration, which is probably the most commonly used
residual-based test of cointegration. Our analysis could easily be
extended to cover the
![]() and
and ![]() cointegration tests proposed by Phillips and Ouliaris (1990), but
for brevity we restrict ourselves to the Augmented Engle-Granger
test (henceforth denoted AEG test).
cointegration tests proposed by Phillips and Ouliaris (1990), but
for brevity we restrict ourselves to the Augmented Engle-Granger
test (henceforth denoted AEG test).
The AEG test is defined as the ![]() statistic for
statistic for
![]() from the regression
from the regression
![]() . The below result follows from the results in Phillips and
Ouliaris (1990) and the results for near-integrated processes in
Phillips (1987,1988).
. The below result follows from the results in Phillips and
Ouliaris (1990) and the results for near-integrated processes in
Phillips (1987,1988).
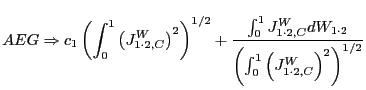
|
(3) |
where
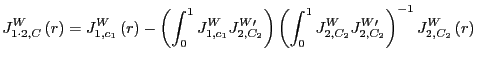
|
(4) |
and
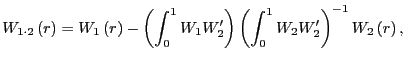
|
(5) |
are the
![]() projection residuals of
projection residuals of
![]() and
and ![]() on
the spaces spanned by
on
the spaces spanned by
![]() and
and ![]() respectively.
respectively.
3 Feasible implementation
For a known ![]() , the above test is trivial to use
once critical values for the asymptotic distribution are obtained.
Unfortunately,
, the above test is trivial to use
once critical values for the asymptotic distribution are obtained.
Unfortunately, ![]() is typically not known. We
therefore consider a Bonferroni test approach, which is similar to
that used by Cavanagh et al. (1995) and Campbell and Yogo
(2006) in their pursuit of inference in predictive regression with
near-integrated variables.
is typically not known. We
therefore consider a Bonferroni test approach, which is similar to
that used by Cavanagh et al. (1995) and Campbell and Yogo
(2006) in their pursuit of inference in predictive regression with
near-integrated variables.
Consider confidence intervals for ![]() ,
,
![]() , of the shape
, of the shape
![]() with an overall coverage rate equal to
with an overall coverage rate equal to
![]() percent.
Let
percent.
Let
![]() be the set of parameter values in this confidence region for which
the critical value of the asymptotic distribution of the
be the set of parameter values in this confidence region for which
the critical value of the asymptotic distribution of the
![]() statistic is most conservative, for some
given
statistic is most conservative, for some
given
![]() percent level (e.g. five percent).
If the
percent level (e.g. five percent).
If the ![]() statistic is evaluated using this
conservative critical value, calculated at the
statistic is evaluated using this
conservative critical value, calculated at the
![]() percent level, the size of the
resulting cointegration test will be less than or equal to
percent level, the size of the
resulting cointegration test will be less than or equal to
![]() , by Bonferroni's
inequality.
, by Bonferroni's
inequality.
However, relative to the Cavanagh et al. (1995) and
Campbell and Yogo (2006) studies, there is an additional
complication in the current setup. In those papers, there is only
one local-to-unity process, whereas here there are at least two in
the simplest case with just one regressor. In the univariate case,
confidence intervals of the local-to-unity parameter can be
obtained by inverting a unit root test statistic (Stock, 1991). In
the ![]() dimensional case, a confidence region for
dimensional case, a confidence region for
![]() could be obtained by inverting individual
unit root test statistics in order to obtain confidence intervals
could be obtained by inverting individual
unit root test statistics in order to obtain confidence intervals
![]() ,
,
![]() , each with coverage rate
, each with coverage rate
![]() . The overall confidence level
of
. The overall confidence level
of
![]() is at least
is at least
![]() percent,
again by Bonferroni's inequality. Although theoretically sound,
such an approach suffers from the practical disadvantage that it
would be virtually impossible to tabulate the critical values for
the asymptotic distribution beyond the simple two-dimensional case.
We therefore propose a simpler approach that allows for tabulation
of critical values and seems to give up little in robustness.
percent,
again by Bonferroni's inequality. Although theoretically sound,
such an approach suffers from the practical disadvantage that it
would be virtually impossible to tabulate the critical values for
the asymptotic distribution beyond the simple two-dimensional case.
We therefore propose a simpler approach that allows for tabulation
of critical values and seems to give up little in robustness.
Intuitively, the AEG test evaluates whether the
persistence, or autoregressive root, in the regression residuals,
![]() , is less than in the original data,
, is less than in the original data,
![]() . As seen in equations (3) and (4), the critical
values of the test depend on both the persistence in the
`dependent' variable,
. As seen in equations (3) and (4), the critical
values of the test depend on both the persistence in the
`dependent' variable, ![]() , and the regressors,
, and the regressors,
![]() , denoted
, denoted ![]() and
and
![]() respectively. However, it seems
reasonable to conjecture that the main determinant of the
asymptotic distribution will be
respectively. However, it seems
reasonable to conjecture that the main determinant of the
asymptotic distribution will be ![]() , rather than
, rather than
![]() . Thus, using
. Thus, using
![]() for some
for some
![]() , rather than
, rather than
![]() , to form critical values might not cause a large size distortion
in the test. Although this conjecture is difficult to evaluate
analytically, extensive simulation evidence supports it. For
instance, Figure 1 shows the critical values for the AEG
test in the two-dimensional case with an intercept in the empirical
regression. As is evident, the primary changes come from changing
, to form critical values might not cause a large size distortion
in the test. Although this conjecture is difficult to evaluate
analytically, extensive simulation evidence supports it. For
instance, Figure 1 shows the critical values for the AEG
test in the two-dimensional case with an intercept in the empirical
regression. As is evident, the primary changes come from changing
![]() , whereas the critical values are
almost constant across
, whereas the critical values are
almost constant across ![]() . Additional evidence
supporting this conclusion is provided by simulations in the
following section.
. Additional evidence
supporting this conclusion is provided by simulations in the
following section.
Furthermore, if
![]() is
used to calculate the critical values for the asymptotic
distribution in Theorem 1, the
is
used to calculate the critical values for the asymptotic
distribution in Theorem 1, the ![]() cointegration test will be more conservative as the
value of
cointegration test will be more conservative as the
value of ![]() decreases; that is, as
decreases; that is, as ![]() becomes more negative, so do the corresponding critical
values, as shown in Table A3. Only the lower
bound on
becomes more negative, so do the corresponding critical
values, as shown in Table A3. Only the lower
bound on ![]() , say
, say
![]() , is therefore of interest
in constructing a conservative test; for a given confidence level,
such a lower bound can be obtained from a one-sided confidence
interval for
, is therefore of interest
in constructing a conservative test; for a given confidence level,
such a lower bound can be obtained from a one-sided confidence
interval for ![]() ,
,
![]() .
.
By restricting the attention to the parameter ![]() , and calculating critical values based on
, and calculating critical values based on
![]() , it now becomes easy to implement the Bonferroni method. The lower
confidence bound for
, it now becomes easy to implement the Bonferroni method. The lower
confidence bound for ![]() ,
,
![]() , is obtained by inverting
a unit root test statistic for the variable
, is obtained by inverting
a unit root test statistic for the variable ![]() .
Based on this lower bound of
.
Based on this lower bound of ![]() , the test is
evaluated using the corresponding critical value for
, the test is
evaluated using the corresponding critical value for
![]() . If the lower bound
. If the lower bound
![]() has confidence level
has confidence level
![]() and the AEG test is
evaluated at the
and the AEG test is
evaluated at the
![]() level, the resulting test will
have a size no larger than
level, the resulting test will
have a size no larger than
![]() .3
.3
In general, Bonferroni's inequality is strict, and the size of
the test will be less than ![]() . To obtain a
correctly sized test of size
. To obtain a
correctly sized test of size
![]() , which is distinct from
, which is distinct from
![]() , we first fix
, we first fix
![]() at some level and then find
at some level and then find
![]() such that the resulting test has
size
such that the resulting test has
size
![]() . Finding
. Finding
![]() is effectively a trial and error
exercise. In the simulations below, we let
is effectively a trial and error
exercise. In the simulations below, we let
![]() and show
that setting
and show
that setting
![]() equal to
equal to ![]() percent will approximately result in an overall five percent test.
Thus, by effectively using a median unbiased estimate of
percent will approximately result in an overall five percent test.
Thus, by effectively using a median unbiased estimate of
![]() , an approximately correctly-sized test
is obtained. These results are discussed more extensively in
conjunction with the Monte Carlo simulations in the next
section.
, an approximately correctly-sized test
is obtained. These results are discussed more extensively in
conjunction with the Monte Carlo simulations in the next
section.
In terms of practical implementation, we follow Campbell and
Yogo (2006) and invert Elliot et al.'s (1996) DF-GLS unit
root test statistic to obtain a lower bound for ![]() . Table A1 provides the
lower 95th, 75th, 50th, 25th, and 5th percent confidence bounds of
. Table A1 provides the
lower 95th, 75th, 50th, 25th, and 5th percent confidence bounds of
![]() , given a value of the DF-GLS test
statistic.4 For instance, the lower confidence
bound that corresponds to
, given a value of the DF-GLS test
statistic.4 For instance, the lower confidence
bound that corresponds to
![]() is given in the
is given in the
![]() column. Table A2 provides the
corresponding bounds when a trend is allowed for in the DF-GLS
regression. Table A3 tabulates the
five percent critical values for the AEG statistic, for
column. Table A2 provides the
corresponding bounds when a trend is allowed for in the DF-GLS
regression. Table A3 tabulates the
five percent critical values for the AEG statistic, for
![]() to
to ![]() ,
assuming that
,
assuming that
![]() ; values for one to
five regressors are provided for the cases of no intercept,
intercept, and intercept and a linear trend in the empirical
regression.
; values for one to
five regressors are provided for the cases of no intercept,
intercept, and intercept and a linear trend in the empirical
regression.
Henceforth, we will refer to the cointegration test constructed
in the manner above as the Bonferroni AEG test, with the
additional specification of the value of
![]() when necessary. Unless otherwise
noted, we let
when necessary. Unless otherwise
noted, we let
![]() .
.
4 Finite-sample properties
4.1 Size properties
We analyze the finite-sample properties of the proposed test
procedure through a series of Monte Carlo simulations. Starting
with the size properties, it is assumed that the data generating
process (DGP) is given by equation (1), with the
innovations ![]() drawn from a multivariate normal
distribution such that
drawn from a multivariate normal
distribution such that
![]() and
and
![]() . The
sample size is set to either
. The
sample size is set to either ![]() or
or ![]() and the number of regressors,
and the number of regressors, ![]() , is
equal to either one or three. The regression
, is
equal to either one or three. The regression
| (6) |
is estimated, which is a spurious regression given the above DGP,
and the cointegration tests are applied to the fitted residuals,
![]() . Each simulated
. Each simulated ![]() dimensional time-series
dimensional time-series ![]() is thus
partitioned as
is thus
partitioned as
![]() , as
described previously. When all components in
, as
described previously. When all components in ![]() are ex-ante identical, i.e. have the same persistence
are ex-ante identical, i.e. have the same persistence
![]() , the first component series is set to
, the first component series is set to
![]() and the remainder to
and the remainder to ![]() . When
. When ![]() varies between each
series, we describe explicitly which series are set as
varies between each
series, we describe explicitly which series are set as ![]() and
and ![]() . All tests are performed at
the five percent significance level and are evaluated using the
critical values given in Table A3. The results are
based on 10,000 repetitions.
. All tests are performed at
the five percent significance level and are evaluated using the
critical values given in Table A3. The results are
based on 10,000 repetitions.
In the first round of simulations, we let the local-to-unity
matrix for ![]() be given by
be given by
![]() , so that all
the series have identical persistence. The local-to-unity parameter
, so that all
the series have identical persistence. The local-to-unity parameter
![]() varies from 0 to -30.
varies from 0 to -30.
Figure 2 shows the size properties for the traditional
![]() cointegration test, which by definition
is evaluated at
cointegration test, which by definition
is evaluated at ![]() , as a function of the
local-to-unity parameter
, as a function of the
local-to-unity parameter ![]() . The nominal size of the
test is five percent, and for
. The nominal size of the
test is five percent, and for ![]() close to zero, the
actual rejection rate is also close to five percent. However, as
close to zero, the
actual rejection rate is also close to five percent. However, as
![]() decreases in value, the test starts
over-rejecting and the rejection rates already approach ten percent
for
decreases in value, the test starts
over-rejecting and the rejection rates already approach ten percent
for ![]() . The rejection rates become even larger
and approach one as
. The rejection rates become even larger
and approach one as ![]() becomes even smaller. It
should be stressed that this is not a small-sample bias, but a
reflection of the inconsistency of the test when
becomes even smaller. It
should be stressed that this is not a small-sample bias, but a
reflection of the inconsistency of the test when ![]() . Since the autoregressive root of the residual in
equation (6)
is less than one for
. Since the autoregressive root of the residual in
equation (6)
is less than one for ![]() , the AEG test,
evaluated under the assumption of
, the AEG test,
evaluated under the assumption of ![]() , will
reject the null of a unit root in the residuals more frequently
than its nominal size. For time series that do not necessarily have
a unit root, standard cointegration tests can thus be highly
misleading. This raises questions regarding previous studies that
have relied on cointegrating methods, despite having found evidence
of stationarity of the included variables; see, for example,
Crowder and Hoffman (1996).
, will
reject the null of a unit root in the residuals more frequently
than its nominal size. For time series that do not necessarily have
a unit root, standard cointegration tests can thus be highly
misleading. This raises questions regarding previous studies that
have relied on cointegrating methods, despite having found evidence
of stationarity of the included variables; see, for example,
Crowder and Hoffman (1996).
We next consider the size properties of the Bonferroni
AEG test using a conservative estimate of ![]() .
As discussed in the previous section, we use
.
As discussed in the previous section, we use
![]() where
where
![]() is the lower bound on the
persistence in
is the lower bound on the
persistence in ![]() . A direct application of the
Bonferroni method suggests choosing
. A direct application of the
Bonferroni method suggests choosing
![]() such that the one-sided
confidence interval
such that the one-sided
confidence interval
![]() has confidence level
has confidence level
![]() percent, and then evaluating the AEG test-statistic at the
percent, and then evaluating the AEG test-statistic at the
![]() percent level for a total size of
percent level for a total size of
![]() percent. In
practice, however, such an approach will deliver extremely
conservative tests. For instance, if
percent. In
practice, however, such an approach will deliver extremely
conservative tests. For instance, if
![]() , the rejection
rate for the resulting test is virtually identical to zero in the
simulations considered here. Instead, we follow the approach
outlined above and fix
, the rejection
rate for the resulting test is virtually identical to zero in the
simulations considered here. Instead, we follow the approach
outlined above and fix
![]() and choose
and choose
![]() such that the size of the overall
test is close to five percent. In particular, we consider setting
such that the size of the overall
test is close to five percent. In particular, we consider setting
![]() and
and ![]() . That is,
. That is,
![]() is chosen as the lower
bound in one-sided confidence intervals with confidence levels
equal to
is chosen as the lower
bound in one-sided confidence intervals with confidence levels
equal to ![]() ,
, ![]() , and
, and ![]() percent, respectively. To obtain these values for
percent, respectively. To obtain these values for
![]() , the DF-GLS unit root
test-statistic is inverted, using the values in Table A1.5
, the DF-GLS unit root
test-statistic is inverted, using the values in Table A1.5
Figure 3 shows the results for the Bonferroni AEG test
using these different estimates of
![]() . It is immediately
apparent that for small values of
. It is immediately
apparent that for small values of ![]() , the test
tends to over-reject when
, the test
tends to over-reject when
![]() , and under-reject when
, and under-reject when
![]() . For
. For
![]() , the test still tends to
under-reject somewhat, except for small values of
, the test still tends to
under-reject somewhat, except for small values of ![]() in the case of
in the case of ![]() and
and ![]() ,
where there is instead a slight over-rejection. Overall, however,
for
,
where there is instead a slight over-rejection. Overall, however,
for
![]() , the rejection rate is
typically between two and five percent. One could achieve rejection
rates that are somewhat closer to the nominal size by letting
, the rejection rate is
typically between two and five percent. One could achieve rejection
rates that are somewhat closer to the nominal size by letting
![]() vary with
vary with
![]() in some manner, but at the
cost of a substantially more cumbersome procedure. Using a fixed
value of
in some manner, but at the
cost of a substantially more cumbersome procedure. Using a fixed
value of
![]()
![]() , for all
values of
, for all
values of
![]() , yields a very simple test
to implement. The procedure would simply be given as:
, yields a very simple test
to implement. The procedure would simply be given as:
- (i)
- Obtain the value of the AEG test statistic from a standard implementation of the Engle and Granger test.
- (ii)
- Calculate the DF-GLS unit root statistic for the
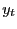 variable and obtain the corresponding value of
variable and obtain the corresponding value of
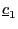 from Table A1 or A2.
from Table A1 or A2. - (iii)
- Compare the AEG test statistic to the critical value
corresponding to
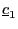 in Table A3.
in Table A3.
It may seem surprising that using, for instance, a lower bound
with only a 25 percent confidence level, does not result in a
larger size distortion. Figure 4 helps shed some light on this
puzzle. The results in the figure are based on ![]() simulations of a univariate local-to-unity process,
with local-to-unity parameter
simulations of a univariate local-to-unity process,
with local-to-unity parameter ![]() ,
, ![]() normal innovations and sample size
normal innovations and sample size ![]() . It shows estimates of the lower bounds of
. It shows estimates of the lower bounds of ![]() , with confidence levels of 25, 50, and 75 percent, using
the inversion of the DF-GLS statistic in Table A1. The panels in
Figure 4 show the densities for the lower-bounds estimates for
, with confidence levels of 25, 50, and 75 percent, using
the inversion of the DF-GLS statistic in Table A1. The panels in
Figure 4 show the densities for the lower-bounds estimates for
![]() and
and ![]() . As
expected, the bounds estimates at the 75 percent confidence level
are furthest to the left. However, the densities are far from
symmetric, especially for
. As
expected, the bounds estimates at the 75 percent confidence level
are furthest to the left. However, the densities are far from
symmetric, especially for ![]() close to zero; the
density for the 25 percent confidence bound is also less symmetric
than the density for the 75 percent bound. Thus, although the
density is shifted further to the right as the confidence level
decreases, which leads to estimates of
close to zero; the
density for the 25 percent confidence bound is also less symmetric
than the density for the 75 percent bound. Thus, although the
density is shifted further to the right as the confidence level
decreases, which leads to estimates of ![]() closer to
zero, the shift is not symmetric and the risk of vastly
over-estimating
closer to
zero, the shift is not symmetric and the risk of vastly
over-estimating ![]() is not increased dramatically.
This explains, to some extent, why the rejection rates in the
cointegration test only increase slowly as the confidence level of
the lower bound is decreased.
is not increased dramatically.
This explains, to some extent, why the rejection rates in the
cointegration test only increase slowly as the confidence level of
the lower bound is decreased.
In the last set of size simulations, shown in Figure 5, we
analyze the properties of the Bonferroni AEG test when the
local-to-unity parameters ![]() ,
, ![]() are not identical; i.e. when the processes in
are not identical; i.e. when the processes in
![]() do not have the same persistence. Two
different cases are considered. In the first case, there are two
regressors with persistence parameters equal to
do not have the same persistence. Two
different cases are considered. In the first case, there are two
regressors with persistence parameters equal to ![]() and
and ![]() . In the second setup, there are
three regressors with persistence parameters
. In the second setup, there are
three regressors with persistence parameters ![]() , and
, and ![]() . In both cases, it is assumed
that the persistence in
. In both cases, it is assumed
that the persistence in ![]() ,
, ![]() , varies between 0 and
, varies between 0 and ![]() . Thus, in
the first case,
. Thus, in
the first case,
![]() , and in
the second case
, and in
the second case
![]() . The
same methods as in the case with identical
. The
same methods as in the case with identical ![]() are used and the results for
are used and the results for
![]() and
and ![]() , are shown. Overall, the results in Figure 5 are very
similar to those in Figure 3. Using
, are shown. Overall, the results in Figure 5 are very
similar to those in Figure 3. Using
![]() and a nominal size of five
percent results in actual rejection rates around three percent.
Given the results shown previously in Figure 1, it is not
surprising that the test also performs well when the
and a nominal size of five
percent results in actual rejection rates around three percent.
Given the results shown previously in Figure 1, it is not
surprising that the test also performs well when the ![]() are not identical.
are not identical.
In summary, the proposed procedure for tests of cointegration in
data with an unknown ![]() appears to work well in
finite samples, once the confidence level of the lower bound is
chosen appropriately. Additional fine tuning of this confidence
level could be done to bring the actual size even closer to the
nominal size, but at the cost of adding some complexity.
appears to work well in
finite samples, once the confidence level of the lower bound is
chosen appropriately. Additional fine tuning of this confidence
level could be done to bring the actual size even closer to the
nominal size, but at the cost of adding some complexity.
4.2 Power properties
We next perform a second Monte Carlo simulation to evaluate the
finite-sample rejection rates under the alternative of
cointegration. The `independent' variable ![]() is
still generated according to equation (1) using
is
still generated according to equation (1) using
![]() standard normal innovations. However,
the `dependent' variable
standard normal innovations. However,
the `dependent' variable ![]() , is now generated
as
, is now generated
as
| (7) |
where ![]() is an
is an
![]() process with an
auto-regressive root
process with an
auto-regressive root ![]() ; the innovations to this
; the innovations to this
![]() process are
process are ![]() standard
normal.
standard
normal. ![]() is set to an
is set to an ![]() -vector
of ones. The same empirical regression, including the constant, as
in the size simulations is estimated, and the Bonferroni AEG
test with
-vector
of ones. The same empirical regression, including the constant, as
in the size simulations is estimated, and the Bonferroni AEG
test with
![]() is applied to the estimated
residuals
is applied to the estimated
residuals
![]() . The critical values that are
used are thus for the case with a constant in the regression. Two
different sample sizes,
. The critical values that are
used are thus for the case with a constant in the regression. Two
different sample sizes, ![]() and
and ![]() , and
, and ![]() and
and ![]() regressors,
are considered. In the case of one regressor, the persistence in
regressors,
are considered. In the case of one regressor, the persistence in
![]() is set equal to either
is set equal to either
![]() or
or ![]() . In the
case of three regressors, it is assumed that
. In the
case of three regressors, it is assumed that
![]() .
.
Figure 6 shows the results in four sub-plots corresponding to
the different combinations of sample size and number of regressors.
The vertical axes of the graphs show the power of the Bonferroni
AEG test plotted against the persistence ![]() in the error term
in the error term ![]() . In the case
of
. In the case
of ![]() , results for
, results for
![]() are shown and
for the
are shown and
for the ![]() , results for
, results for
![]() are shown. As is
to be expected, power is a monotone and declining function of the
persistence,
are shown. As is
to be expected, power is a monotone and declining function of the
persistence, ![]() . It should be noted that for very
large values of
. It should be noted that for very
large values of ![]() , we expect the test to have low
power; for example, in the bivariate case, a residual that is less
persistent than
, we expect the test to have low
power; for example, in the bivariate case, a residual that is less
persistent than ![]() cannot be generated by
regressing
cannot be generated by
regressing ![]() on
on ![]() when
when
![]() . For most values of
. For most values of
![]() , however, the test appears to exhibit
good power properties and appears sufficiently powerful that it
would be a useful tool in many empirical applications, including
those with relatively small sample sizes.
, however, the test appears to exhibit
good power properties and appears sufficiently powerful that it
would be a useful tool in many empirical applications, including
those with relatively small sample sizes.
5 Empirical illustrations
To illustrate the empirical use of the Bonferroni AEG test, we next consider two applications where the variables in question are all fairly persistent, but not necessarily pure unit root processes. As a comparison to the robust methodology proposed in this paper, we will also conduct the traditional AEG test.
5.1 The Fisher hypothesis
It is well known that both nominal interest rates and inflation are fairly persistent in most countries. Accordingly, cointegration techniques have been a popular approach to test the Fisher hypothesis in more recent years; see, for example, Mishkin (1992), Wallace and Warner (1993), Evans and Lewis (1995), and Crowder and Hoffman (1996). However, the assumption made in most of these studies of exact unit roots in both nominal interest rates and inflation can be questioned on both theoretical and empirical grounds.6 It is therefore worth re-interesting this issue using the Bonferroni AEG test.
A common formulation of the Fisher hypothesis is that the
![]() -period nominal interest rate (
-period nominal interest rate (![]() ) is related to the real interest rate (
) is related to the real interest rate (![]() ) and inflation (
) and inflation (
![]() ) according to
) according to
| (8) |
Relying on the commonly made assumption of a constant or mean-reverting real interest rate, an empirical version of the Fisher hypothesis can be written as
| (9) |
where the constant ![]() has the interpretation
of the (constant) equilibrium real interest rate, the error term
has the interpretation
of the (constant) equilibrium real interest rate, the error term
![]() is assumed to be a stationary ARMA
process and
is assumed to be a stationary ARMA
process and ![]() , in the most traditional
interpretation, should be equal to unity.7
, in the most traditional
interpretation, should be equal to unity.7
Monthly data on the short nominal interest rate - given by the
three month treasury bill - and CPI inflation from January 1955 to
October 2006 in the United States were provided by the Board of
Governors of the Federal Reserve System. Table 1 shows the
results from the DF-GLS unit root test and the KPSS stationarity
test, as well as the median unbiased estimate of ![]() ,
denoted
,
denoted ![]() , and a 90 percent confidence
interval for
, and a 90 percent confidence
interval for ![]() ; the estimates and confidence
intervals of
; the estimates and confidence
intervals of ![]() are derived using the values in Table
A1 and linear
interpolation.8 As can be seen, the evidence for a
unit root in the interest rate appears reasonably strong; the
DF-GLS test fails to reject the null of a unit root whereas the
KPSS test rejects the null of stationarity. For inflation, on the
other hand, the evidence is more mixed since the DF-GLS test
rejects a unit root but the KPSS test rejects stationarity.9
are derived using the values in Table
A1 and linear
interpolation.8 As can be seen, the evidence for a
unit root in the interest rate appears reasonably strong; the
DF-GLS test fails to reject the null of a unit root whereas the
KPSS test rejects the null of stationarity. For inflation, on the
other hand, the evidence is more mixed since the DF-GLS test
rejects a unit root but the KPSS test rejects stationarity.9
Table 1: Unit root tests.
Unit root tests for the monthly short interest rate and CPI inflation in the U.S. The sample spans January 1955 to October 2006. Result for the DF-GLS and KPSS tests are presented, along with the median unbiased estimate of c and a 90 percent confidence interval for c.
| Test | ||
|---|---|---|
| DF-GLS | -1.40 | -2.54 |
| KPSS | 0.53 | 0.52 |
-3.40 | -12.91 | |
| 90% CI for | [-9.06, 2.00] | [-21.37, -3.46] |
Notes: * indicates significance at the five percent level.
The cointegration tests are conducted using a significance level
of five percent. For the Bonferroni AEG test, based on the
simulation results in the previous section, we set
![]() ; thus
; thus
![]() , the median unbiased estimate
for the nominal interest rate, is used to establish the critical
value in the Bonferroni AEG test. The results from the
cointegration tests based on the specification in equation
(9) are given in
Table 2.10Asymptotic critical values are used
for both the standard Engle-Granger test (denoted
, the median unbiased estimate
for the nominal interest rate, is used to establish the critical
value in the Bonferroni AEG test. The results from the
cointegration tests based on the specification in equation
(9) are given in
Table 2.10Asymptotic critical values are used
for both the standard Engle-Granger test (denoted ![]() ) and the Bonferroni AEG test (denoted
) and the Bonferroni AEG test (denoted ![]() ) and are provided in Table 2; the
) and are provided in Table 2; the
![]() critical value is obtained from
Table A3 and
linear interpolation.
critical value is obtained from
Table A3 and
linear interpolation.
Table 2: Cointegration tests.
Cointegration tests between the short interest rate and the CPI inflation in monthly U.S. data spanning January 1955 to October 2006. The outcome of the augmented Engle-Granger test statistic along with the standard critical values and the Bonferroni critical values are presented.
| Test statistic |
-3.43 |
|---|---|
| Critical value | -3.47 |
| Critical value | -3.34 |
Notes: Nominal size is 0.05.
As can be seen, the null hypothesis of no cointegration is rejected if the standard method is used, as the test statistic is smaller than the critical value for the traditional AEG test. However, when the Bonferroni AEG test is used, the null hypothesis is not rejected. Thus, performing inference using robust methods, there is no strong evidence of cointegration, or co-movement, between the nominal interest rate and inflation in U.S. data. This raises doubts about the validity of the Fisher hypothesis, and also illustrates the importance of controlling for the unknown degree of persistence in the data; assuming unit roots in the data, the cointegration test would have resulted in evidence favorable of the Fisher hypothesis. Having looked at a traditional application from the macroeconomic literature, we next turn to a recent issue from financial economics.
5.2 Consumption, aggregate wealth and stock returns
Many studies argue that financial valuation ratios such as the
dividend- and earnings-price ratios may have predictive power for
excess stock returns over the risk-free rate. In a novel attempt to
tie macroeconomic variables more closely to financial markets,
Lettau and Ludvigson (2001) argue that consumption is a function of
aggregate wealth. Based on this claim, they suggest that aggregate
consumption (![]() ), asset holdings (
), asset holdings (![]() ) and labour income (
) and labour income (![]() ) are
cointegrated and that the deviation from equilibrium is useful in
terms of predicting both excess stock returns and real stock
returns. The empirical specification used by Lettau and Ludvigson
accordingly takes its starting point in a cointegrating
relationship of the type
) are
cointegrated and that the deviation from equilibrium is useful in
terms of predicting both excess stock returns and real stock
returns. The empirical specification used by Lettau and Ludvigson
accordingly takes its starting point in a cointegrating
relationship of the type
| (10) |
where the error term ![]() is assumed to be a
stationary ARMA process which has predictive power for future
returns.
is assumed to be a
stationary ARMA process which has predictive power for future
returns.
However, there is no strong a priori reason to assume that the above variables contain pure unit roots.11 We therefore investigate the sensitivity of Lettau and Ludvigson's results when the uncertainty regarding the persistence in the data is taken into account. Quarterly data on US consumption, asset holdings and labour income ranging from the first quarter 1952 to the fourth quarter 2006 were obtained from Professor Ludvigson's web page;12 all variables are given by the natural logarithm of real, per capita data.
Table 3 shows the
results from unit root tests and stationarity tests for all
variables and also provides the median unbiased estimates of
![]() ,
, ![]() , as well as
90 percent confidence intervals.13 The evidence for unit
roots in consumption and labour income seems strong, whereas it is
mixed for asset holdings.
, as well as
90 percent confidence intervals.13 The evidence for unit
roots in consumption and labour income seems strong, whereas it is
mixed for asset holdings.
Table 3: Unit root tests.
Unit root tests for U.S. aggregate consumption, asset holdings and labour income. The data are on quarterly frequency and spans quarter 1, 1952, to quarter 4, 2006. Result for the DF-GLS and KPSS tests are presented, along with the median unbiased estimate of c and a 90 percent confidence interval for c.
| Test | |||||
|---|---|---|---|---|---|
| DF-GLS | -1.95 | -2.54 | -0.78 | ||
| KPSS | 0.36 | 0.20 | 0.38 | ||
-4.06 | -9.98 | 2.32 | |||
| 90% CI for | [-12.28, 3.35] | [-19.63, 2.32] | [-2.18, 4.44] |
Notes: * indicates significance at the five percent level.
As in the previous application, we choose a significance level
of five percent for the cointegration tests and set
![]() . The results from the
AEG and Bonferroni AEG cointegration tests are shown
in Table 4. The null
hypothesis of no cointegration is rejected regardless of which test
is used. The robust cointegration methods developed here thus
support the conclusion of Lettau and Ludvigson that US consumption,
asset holdings and labour income are cointegrated.
. The results from the
AEG and Bonferroni AEG cointegration tests are shown
in Table 4. The null
hypothesis of no cointegration is rejected regardless of which test
is used. The robust cointegration methods developed here thus
support the conclusion of Lettau and Ludvigson that US consumption,
asset holdings and labour income are cointegrated.
Table 4: Cointegration tests.
Cointegration tests between aggregate consumption, asset holdings and labour income in U.S. quarterly data spanning quarter 1, 1952, to quarter 4, 2006. The outcome of the augmented Engle-Granger test statistic along with the standard critical values and the Bonferroni critical values are presented.
| Test statistic | -4.03 |
|---|---|
| Critical value | -3.86 |
| Critical value | -3.77 |
Notes: Nominal size is 0.05.
6 Conclusion
For many economic time series, it is difficult to justify theoretically that they are generated by unit root processes. This is problematic from an empirical point of view since cointegration tests may be misleading when the data follow near-integrated, rather than pure unit root, processes. The size distortions of cointegration tests relying on the unit root assumption - combined with the fact that standard OLS inference could lead to spurious results - makes it unclear how to analyze a multivariate time series of near-integrated variables.
In this paper, we have extended a standard residual-based cointegration test to allow for an unknown local deviation from the unit root assumption. This more robust test is easy to implement and Monte Carlo simulations show that it works well in finite samples. Unlike standard cointegration tests, the methods developed in this paper thus provide a means of performing valid inference on a multivariate near unit root process. The framework suggested in this paper therefore takes another step towards addressing the problems associated with inference when variables are near-integrated. The methods presented here take their starting point in the work of Engle and Granger (1987). In future research it would also be of interest to see Johansen's (1988,1991) VAR-based framework extended to a setting with near-integrated variables.
References
Campbell, J.Y. and M. Yogo, 2006. Efficient Tests of Stock Return Predictability, Journal of Financial Economics 81, 27-60.
Casares, M., 2007. The New Keynesian Model and the Euro Area Business Cycle, Oxford Bulletin of Economics and Statistics 69, 209-244.
Cavanagh, C., G. Elliot, and J. Stock, 1995. Inference in models with nearly integrated regressors, Econometric Theory 11, 1131-1147.
Cooper, R. and J. Ejarque, 2000. Financial Intermediation and Aggregate Fluctuations: A Quantitative Analysis, Macroeconomic Dynamics 4, 423-447.
Crowder, W.J., and D.L. Hoffman, 1996. The Long-Run Relationship between Nominal Interest Rates and Inflation: The Fisher Equation Revisited, Journal of Money, Credit and Banking 28, 102-118.
Culver, S.E. and D.H. Papell, 1997. Is There a Unit Root in the Inflation Rate? Evidence from Sequential Break and Panel Data Models, Journal of Applied Econometrics 12, 435-444.
Diebold, F.X. and A.S. Senhadji, 1996. The Uncertain Unit Root in Real GNP: Comment, American Economic Review 86, 1291-1298.
Elliot, G., 1998. On the Robustness of Cointegration Methods When Regressors Almost Have Unit Roots, Econometrica 66, 149-158.
Elliot G., T.J. Rothenberg, and J.H. Stock, 1996. Efficient Tests for an Autoregressive Unit Root, Econometrica 64, 813-836.
Engle, R.F. and C.W.J. Granger, 1987. Co-Integration and Error Correction: Representation, Estimation, and Testing, Econometrica 55, 251-276.
Evans, M. and K. Lewis, 1995. Do Expected Shifts in Inflation Affect Estimates of the Long-Run Fisher Relation?, Journal of Finance 50, 225-253.
Flavin, M., 1981. The Adjustment of Consumption to Changing Expectations about Future Income, Journal of Political Economy 89, 974-1009.
Gali, J., 1993. Variability of Durable and Nondurable Consumption: Evidence for Six O.E.C.D. Countries, Review of Economics and Statistics 75, 418-428.
Hall, R.E., 1978. Stochastic Implications of the Life-Cycle-Permanent-Income Hypothesis: Theory and Evidence, Journal of Political Economy 86, 971-987.
Hjalmarsson, E., and P. Österholm, 2007. Testing for Cointegration Using the Johansen Methodology when Variables are Near-Integrated, IMF Working Paper 07/141, International Monetary Fund.
Jansson, M., and M.J. Moreira, 2006. Optimal Inference in Regression Models with Nearly Integrated Regressors, Econometrica 74, 681-714.
Johansen, S., 1988. Statistical Analysis of Cointegration Vectors, Journal of Economic Dynamics and Control 12, 231-254.
Johansen, S., 1991. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models, Econometrica 59, 1551-1580.
Lettau, M. and S. Ludvigson, 2001. Consumption, Aggregate Wealth and Expected Stock Returns, Journal of Finance 56, 815-849.
Leybourne, S.J. and B.P.M. McCabe, 1993. A Simple Test for Cointegration, Oxford Bulletin of Economics and Statistics 55, 97-103.
Mishkin, F.S., 1992. Is the Fisher effect for real?, Journal of Monetary Economics 30, 195-215.
Phillips, P.C.B., 1987. Towards a Unified Asymptotic Theory of Autoregression, Biometrika 74, 535-547.
Phillips, P.C.B., 1988. Regression Theory for Near-Integrated Time Series, Econometrica 56, 1021-1043.
Phillips, P.C.B., ans S. Ouliaris, 1990. Asymptotic Properties of Residual Based Tests for Cointegration, Econometrica 58, 165-193.
Phillips, P.C.B., and V. Solo, 1992. Asymptotics for Linear Processes, Annals of Statistics, 20, 971-1001.
Schwarz, G., 1978. Estimating the Dimension of a Model, Annals of Statistics 6, 461-464.
Shin, Y., 1994. A Residual-Based Test of the Null of Cointegration Against the Alternative of No Cointegration, Econometric Theory 10, 91-115.
Stock, J.H., 1991. Confidence intervals for the largest autoregressive root in U.S. economic time-series. Journal of Monetary Economics 28, 435-460.
Stock, J.H., 1997. Cointegration, Long-Run Comovements, and Long-Horizon Forecasting, in D. Kreps and K.F. Wallis (eds), Advances in Econometrics: Proceedings of the Seventh World Congress of the Econometric Society, vol. III. Cambridge: Cambridge University Press, 34-60.
Wallace, M. and J. Warner, 1993. The Fisher Effect and the Term Structure of Interest Rates: Test of Cointegration. Review of Economics and Statistics 75, 320-324.
Wright J.H., 2000. Confidence Sets for Cointegrating Coefficients Based on Stationarity Tests, Journal of Business and Economic Statistics 18, 211-222.
Wu, J.-L. and S.-L. Chen, 2001. Mean Reversion of Interest Rates in the Eurocurrency Market, Oxford Bulletin of Economics and Statistics 63, 459-474.
Wu, Y. and H. Zhang, (1996). Mean Reversion in Interest Rates: New Evidence from a Panel of OECD Countries, Journal of Money, Credit and Banking 28, 604-621.
Table A1: Lower confidence bounds for c based on the DF-GLS statistic.
For a given value of the DF-GLS statistic, without a time trend included, the following columns give lower confidence bounds of the local-to-unity parameter c with confidence levels of 95, 75, 50, 25, and 5 percent, respectively.
| DF-GLS | 95% | 75% | 50% | 25% | 5% |
|---|---|---|---|---|---|
| 1.0 | -0.29 | 0.72 | 1.47 | 2.39 | 4.23 |
| 0.9 | -0.40 | 0.65 | 1.41 | 2.34 | 4.19 |
| 0.8 | -0.50 | 0.57 | 1.35 | 2.29 | 4.15 |
| 0.7 | -0.63 | 0.49 | 1.29 | 2.24 | 4.12 |
| 0.6 | -0.76 | 0.40 | 1.23 | 2.19 | 4.08 |
| 0.5 | -0.91 | 0.30 | 1.15 | 2.13 | 4.04 |
| 0.4 | -1.07 | 0.20 | 1.07 | 2.07 | 4.00 |
| 0.3 | -1.25 | 0.09 | 0.99 | 2.02 | 3.95 |
| 0.2 | -1.46 | -0.03 | 0.90 | 1.94 | 3.90 |
| 0.1 | -1.66 | -0.17 | 0.80 | 1.87 | 3.85 |
| 0.0 | -1.89 | -0.31 | 0.70 | 1.79 | 3.80 |
| -0.1 | -2.14 | -0.46 | 0.59 | 1.71 | 3.75 |
| -0.2 | -2.41 | -0.63 | 0.48 | 1.62 | 3.69 |
| -0.3 | -2.72 | -0.82 | 0.34 | 1.53 | 3.63 |
| -0.4 | -3.05 | -1.03 | 0.18 | 1.42 | 3.57 |
| -0.5 | -3.45 | -1.29 | -0.02 | 1.30 | 3.51 |
| -0.6 | -3.84 | -1.60 | -0.23 | 1.15 | 3.40 |
| -0.7 | -4.31 | -1.94 | -0.47 | 0.98 | 3.28 |
| -0.8 | -4.87 | -2.32 | -0.75 | 0.78 | 3.17 |
| -0.9 | -5.44 | -2.78 | -1.10 | 0.54 | 3.06 |
| -1.0 | -6.04 | -3.27 | -1.47 | 0.28 | 2.91 |
| -1.1 | -6.73 | -3.79 | -1.90 | -0.06 | 2.71 |
| -1.2 | -7.45 | -4.37 | -2.35 | -0.39 | 2.49 |
| -1.3 | -8.19 | -4.97 | -2.88 | -0.76 | 2.29 |
| -1.4 | -9.04 | -5.66 | -3.40 | -1.18 | 2.01 |
| -1.5 | -9.90 | -6.33 | -3.97 | -1.65 | 1.74 |
| -1.6 | -10.82 | -7.05 | -4.60 | -2.15 | 1.38 |
| -1.7 | -11.75 | -7.85 | -5.23 | -2.72 | 1.03 |
| -1.8 | -12.78 | -8.65 | -5.94 | -3.27 | 0.59 |
| -1.9 | -13.84 | -9.51 | -6.69 | -3.86 | 0.22 |
| -2.0 | -14.90 | -10.41 | -7.44 | -4.51 | -0.31 |
| -2.1 | -15.95 | -11.37 | -8.25 | -5.21 | -0.88 |
| -2.2 | -17.14 | -12.35 | -9.09 | -5.94 | -1.36 |
| -2.3 | -18.34 | -13.38 | -9.97 | -6.74 | -1.98 |
| -2.4 | -19.57 | -14.42 | -10.92 | -7.48 | -2.55 |
| -2.5 | -20.84 | -15.48 | -11.89 | -8.32 | -3.28 |
| -2.6 | -22.15 | -16.61 | -12.91 | -9.19 | -3.95 |
| -2.7 | -23.53 | -17.78 | -13.95 | -10.06 | -4.69 |
| -2.8 | -24.93 | -18.98 | -15.03 | -11.06 | -5.52 |
| -2.9 | -26.34 | -20.20 | -16.13 | -12.06 | -6.28 |
| -3.0 | -27.71 | -21.49 | -17.29 | -13.08 | -7.14 |
| -3.1 | -29.27 | -22.81 | -18.45 | -14.12 | -7.97 |
| -3.2 | -30.86 | -24.17 | -19.62 | -15.21 | -8.88 |
| -3.3 | -32.44 | -25.53 | -20.87 | -16.33 | -9.84 |
| -3.4 | -34.06 | -26.94 | -22.15 | -17.52 | -10.83 |
| -3.5 | -35.78 | -28.39 | -23.49 | -18.70 | -11.80 |
| -3.6 | -37.43 | -29.87 | -24.85 | -19.87 | -12.87 |
| -3.7 | -39.09 | -31.44 | -26.24 | -21.16 | -13.96 |
| -3.8 | -40.85 | -32.98 | -27.65 | -22.48 | -15.09 |
| -3.9 | -42.69 | -34.55 | -29.11 | -23.82 | -16.25 |
| -4.0 | -44.52 | -36.22 | -30.62 | -25.18 | -17.52 |
| -4.1 | -46.35 | -37.87 | -32.17 | -26.55 | -18.71 |
| -4.2 | -48.24 | -39.50 | -33.70 | -27.93 | -19.87 |
| -4.3 | -50.14 | -41.27 | -35.31 | -29.44 | -21.22 |
| -4.4 | -52.14 | -43.07 | -36.94 | -30.94 | -22.57 |
| -4.5 | -53.96 | -44.86 | -38.58 | -32.45 | -23.89 |
| -4.6 | -56.08 | -46.68 | -40.23 | -34.00 | -25.21 |
| -4.7 | -58.20 | -48.54 | -41.95 | -35.67 | -26.59 |
| -4.8 | -60.27 | -50.39 | -43.70 | -37.29 | -28.05 |
| -4.9 | -62.38 | -52.31 | -45.50 | -38.90 | -29.53 |
Table A2: Lower confidence bounds for c based on the DF-GLS statistic with a linear time trend included.
For a given value of the DF-GLS statistic, allowing for linear time trend, the following columns give lower confidence bounds of the local-to-unity parameter c with confidence levels of 95, 75, 50, 25, and 5 percent, respectively.
| DF-GLS | 95% | 75% | 50% | 25% | 5% |
|---|---|---|---|---|---|
| 1.0 | 2.20 | 2.63 | 3.07 | 3.72 | 5.24 |
| 0.9 | 2.16 | 2.60 | 3.04 | 3.69 | 5.20 |
| 0.8 | 2.12 | 2.57 | 3.01 | 3.65 | 5.16 |
| 0.7 | 2.09 | 2.53 | 2.97 | 3.62 | 5.13 |
| 0.6 | 2.05 | 2.50 | 2.93 | 3.58 | 5.09 |
| 0.5 | 2.02 | 2.46 | 2.90 | 3.55 | 5.05 |
| 0.4 | 1.97 | 2.42 | 2.86 | 3.51 | 5.01 |
| 0.3 | 1.93 | 2.38 | 2.82 | 3.47 | 4.97 |
| 0.2 | 1.88 | 2.34 | 2.78 | 3.42 | 4.93 |
| 0.1 | 1.83 | 2.30 | 2.74 | 3.38 | 4.88 |
| 0.0 | 1.78 | 2.26 | 2.70 | 3.33 | 4.84 |
| -0.1 | 1.72 | 2.22 | 2.65 | 3.29 | 4.79 |
| -0.2 | 1.64 | 2.17 | 2.61 | 3.24 | 4.75 |
| -0.3 | 1.56 | 2.12 | 2.56 | 3.20 | 4.70 |
| -0.4 | 1.47 | 2.07 | 2.52 | 3.15 | 4.64 |
| -0.5 | 1.32 | 2.02 | 2.47 | 3.10 | 4.59 |
| -0.6 | -0.81 | 1.95 | 2.42 | 3.05 | 4.54 |
| -0.7 | -1.58 | 1.89 | 2.36 | 3.01 | 4.49 |
| -0.8 | -2.29 | 1.82 | 2.31 | 2.95 | 4.43 |
| -0.9 | -2.95 | 1.75 | 2.26 | 2.89 | 4.37 |
| -1.0 | -3.70 | 1.61 | 2.18 | 2.82 | 4.31 |
| -1.1 | -4.43 | 1.45 | 2.10 | 2.76 | 4.25 |
| -1.2 | -5.15 | -0.72 | 2.03 | 2.69 | 4.17 |
| -1.3 | -6.01 | -1.85 | 1.92 | 2.60 | 4.09 |
| -1.4 | -6.83 | -2.75 | 1.80 | 2.52 | 4.01 |
| -1.5 | -7.74 | -3.62 | 1.63 | 2.42 | 3.91 |
| -1.6 | -8.69 | -4.46 | 1.36 | 2.31 | 3.81 |
| -1.7 | -9.67 | -5.33 | -1.56 | 2.19 | 3.69 |
| -1.8 | -10.65 | -6.22 | -2.69 | 2.06 | 3.56 |
| -1.9 | -11.76 | -7.17 | -3.64 | 1.89 | 3.42 |
| -2.0 | -12.90 | -8.15 | -4.56 | 1.69 | 3.27 |
| -2.1 | -14.04 | -9.15 | -5.54 | 1.28 | 3.12 |
| -2.2 | -15.26 | -10.17 | -6.48 | -2.10 | 2.95 |
| -2.3 | -16.52 | -11.28 | -7.47 | -3.22 | 2.76 |
| -2.4 | -17.85 | -12.40 | -8.49 | -4.26 | 2.58 |
| -2.5 | -19.14 | -13.55 | -9.59 | -5.30 | 2.39 |
| -2.6 | -20.49 | -14.77 | -10.67 | -6.33 | 2.19 |
| -2.7 | -21.97 | -16.04 | -11.80 | -7.41 | 1.96 |
| -2.8 | -23.44 | -17.35 | -12.98 | -8.47 | 1.61 |
| -2.9 | -24.97 | -18.67 | -14.20 | -9.62 | -1.55 |
| -3.0 | -26.55 | -20.02 | -15.47 | -10.75 | -3.10 |
| -3.1 | -28.14 | -21.48 | -16.78 | -11.91 | -4.27 |
| -3.2 | -29.86 | -22.97 | -18.10 | -13.19 | -5.55 |
| -3.3 | -31.64 | -24.49 | -19.51 | -14.48 | -6.68 |
| -3.4 | -33.42 | -26.05 | -20.96 | -15.80 | -7.91 |
| -3.5 | -35.21 | -27.67 | -22.45 | -17.15 | -9.12 |
| -3.6 | -37.09 | -29.37 | -23.95 | -18.53 | -10.30 |
| -3.7 | -38.99 | -31.09 | -25.56 | -19.93 | -11.62 |
| -3.8 | -40.97 | -32.85 | -27.19 | -21.42 | -12.96 |
| -3.9 | -43.06 | -34.64 | -28.85 | -22.97 | -14.34 |
| -4.0 | -45.18 | -36.50 | -30.56 | -24.57 | -15.79 |
| -4.1 | -47.18 | -38.45 | -32.34 | -26.18 | -17.31 |
| -4.2 | -49.36 | -40.35 | -34.13 | -27.89 | -18.77 |
| -4.3 | -51.66 | -42.37 | -36.01 | -29.56 | -20.19 |
| -4.4 | -53.91 | -44.46 | -37.90 | -31.31 | -21.83 |
| -4.5 | -56.27 | -46.60 | -39.83 | -33.15 | -23.44 |
| -4.6 | -58.74 | -48.74 | -41.89 | -35.04 | -25.00 |
| -4.7 | -61.20 | -50.98 | -43.94 | -36.99 | -26.66 |
| -4.8 | -63.78 | -53.32 | -46.07 | -38.96 | -28.52 |
| -4.9 | -66.25 | -55.64 | -48.29 | -40.95 | -30.28 |
Table A3 - Panel 1: No constant: Five percent critical values for the AEG statistic
This table gives the critical values for the AEG statistic at the five percent level, for different values of c under the assumption that c1 = ... = cm = c, and for one to five regressors. The first set of values provide the critical values when no intercept is included in the cointegrating regression. The second set provides the values when an intercept, but no time trend is included and the third set of values represent the case with both an intercept and a linear time trend. The values are based on 100,000 repetitions with T = 1,000.
| c | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0 | -2.77 | -3.30 | -3.73 | -4.09 | -4.41 |
| -1 | -2.80 | -3.32 | -3.74 | -4.09 | -4.42 |
| -2 | -2.88 | -3.35 | -3.75 | -4.10 | -4.42 |
| -3 | -2.96 | -3.39 | -3.78 | -4.12 | -4.44 |
| -4 | -3.05 | -3.45 | -3.82 | -4.15 | -4.45 |
| -5 | -3.15 | -3.51 | -3.86 | -4.17 | -4.46 |
| -6 | -3.23 | -3.58 | -3.91 | -4.21 | -4.51 |
| -7 | -3.32 | -3.64 | -3.96 | -4.26 | -4.53 |
| -8 | -3.41 | -3.72 | -4.01 | -4.30 | -4.57 |
| -9 | -3.50 | -3.79 | -4.07 | -4.34 | -4.61 |
| -10 | -3.58 | -3.86 | -4.13 | -4.40 | -4.65 |
| -11 | -3.68 | -3.93 | -4.19 | -4.45 | -4.69 |
| -12 | -3.75 | -4.01 | -4.26 | -4.50 | -4.73 |
| -13 | -3.84 | -4.08 | -4.33 | -4.56 | -4.78 |
| -14 | -3.92 | -4.16 | -4.38 | -4.60 | -4.83 |
| -15 | -4.01 | -4.23 | -4.44 | -4.66 | -4.88 |
| -16 | -4.06 | -4.30 | -4.50 | -4.72 | -4.94 |
| -17 | -4.15 | -4.37 | -4.57 | -4.78 | -4.98 |
| -18 | -4.22 | -4.43 | -4.63 | -4.83 | -5.03 |
| -19 | -4.29 | -4.50 | -4.69 | -4.89 | -5.07 |
| -20 | -4.37 | -4.57 | -4.76 | -4.94 | -5.13 |
| -21 | -4.44 | -4.62 | -4.81 | -5.00 | -5.19 |
| -22 | -4.51 | -4.69 | -4.87 | -5.04 | -5.23 |
| -23 | -4.57 | -4.76 | -4.93 | -5.11 | -5.28 |
| -24 | -4.65 | -4.81 | -5.00 | -5.16 | -5.34 |
| -25 | -4.71 | -4.88 | -5.04 | -5.22 | -5.39 |
| -26 | -4.77 | -4.93 | -5.11 | -5.27 | -5.44 |
| -27 | -4.84 | -5.00 | -5.16 | -5.32 | -5.49 |
| -28 | -4.90 | -5.06 | -5.21 | -5.38 | -5.53 |
| -29 | -4.96 | -5.12 | -5.28 | -5.43 | -5.59 |
| -30 | -5.02 | -5.18 | -5.32 | -5.47 | -5.64 |
| -31 | -5.09 | -5.23 | -5.39 | -5.53 | -5.69 |
| -32 | -5.14 | -5.30 | -5.44 | -5.59 | -5.74 |
| -33 | -5.20 | -5.35 | -5.49 | -5.63 | -5.79 |
| -34 | -5.26 | -5.41 | -5.54 | -5.69 | -5.83 |
| -35 | -5.32 | -5.46 | -5.60 | -5.75 | -5.89 |
| -36 | -5.38 | -5.51 | -5.65 | -5.80 | -5.94 |
| -37 | -5.44 | -5.56 | -5.71 | -5.84 | -5.98 |
| -38 | -5.50 | -5.63 | -5.76 | -5.90 | -6.03 |
| -39 | -5.55 | -5.68 | -5.81 | -5.94 | -6.07 |
| -40 | -5.60 | -5.73 | -5.86 | -5.99 | -6.12 |
| -41 | -5.65 | -5.78 | -5.91 | -6.04 | -6.17 |
| -42 | -5.71 | -5.84 | -5.96 | -6.09 | -6.22 |
| -43 | -5.77 | -5.89 | -6.01 | -6.13 | -6.26 |
| -44 | -5.81 | -5.93 | -6.06 | -6.18 | -6.30 |
| -45 | -5.87 | -5.98 | -6.11 | -6.23 | -6.36 |
| -46 | -5.92 | -6.04 | -6.16 | -6.28 | -6.41 |
| -47 | -5.96 | -6.09 | -6.20 | -6.33 | -6.44 |
| -48 | -6.01 | -6.14 | -6.26 | -6.37 | -6.49 |
| -49 | -6.07 | -6.19 | -6.30 | -6.43 | -6.54 |
| -50 | -6.13 | -6.23 | -6.36 | -6.47 | -6.59 |
| -51 | -6.17 | -6.29 | -6.40 | -6.51 | -6.63 |
| -52 | -6.22 | -6.33 | -6.44 | -6.56 | -6.67 |
| -53 | -6.27 | -6.39 | -6.49 | -6.60 | -6.71 |
| -54 | -6.31 | -6.43 | -6.54 | -6.65 | -6.76 |
| -55 | -6.38 | -6.47 | -6.58 | -6.69 | -6.80 |
| -56 | -6.41 | -6.52 | -6.62 | -6.75 | -6.85 |
| -57 | -6.46 | -6.57 | -6.68 | -6.78 | -6.89 |
| -58 | -6.51 | -6.62 | -6.72 | -6.83 | -6.93 |
| -59 | -6.56 | -6.66 | -6.77 | -6.87 | -6.98 |
| -60 | -6.60 | -6.71 | -6.82 | -6.92 | -7.02 |
Table A3 - Panel 2: Constant: Five percent critical values for the AEG statistic
| c | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0 | -3.34 | -3.77 | -4.10 | -4.42 | -4.72 |
| -1 | -3.37 | -3.76 | -4.12 | -4.43 | -4.73 |
| -2 | -3.40 | -3.78 | -4.12 | -4.44 | -4.73 |
| -3 | -3.45 | -3.82 | -4.15 | -4.46 | -4.75 |
| -4 | -3.50 | -3.86 | -4.17 | -4.47 | -4.76 |
| -5 | -3.56 | -3.89 | -4.21 | -4.49 | -4.77 |
| -6 | -3.62 | -3.94 | -4.24 | -4.53 | -4.80 |
| -7 | -3.68 | -4.00 | -4.28 | -4.56 | -4.81 |
| -8 | -3.75 | -4.05 | -4.33 | -4.60 | -4.86 |
| -9 | -3.82 | -4.11 | -4.37 | -4.64 | -4.89 |
| -10 | -3.89 | -4.16 | -4.43 | -4.68 | -4.92 |
| -11 | -3.97 | -4.22 | -4.47 | -4.72 | -4.95 |
| -12 | -4.03 | -4.29 | -4.52 | -4.76 | -4.99 |
| -13 | -4.10 | -4.34 | -4.58 | -4.81 | -5.03 |
| -14 | -4.18 | -4.41 | -4.64 | -4.85 | -5.07 |
| -15 | -4.25 | -4.47 | -4.69 | -4.90 | -5.11 |
| -16 | -4.30 | -4.54 | -4.74 | -4.96 | -5.16 |
| -17 | -4.38 | -4.60 | -4.80 | -5.00 | -5.20 |
| -18 | -4.44 | -4.66 | -4.85 | -5.05 | -5.25 |
| -19 | -4.50 | -4.72 | -4.90 | -5.11 | -5.29 |
| -20 | -4.58 | -4.77 | -4.97 | -5.16 | -5.34 |
| -21 | -4.65 | -4.83 | -5.01 | -5.21 | -5.39 |
| -22 | -4.70 | -4.89 | -5.07 | -5.25 | -5.42 |
| -23 | -4.77 | -4.96 | -5.13 | -5.30 | -5.47 |
| -24 | -4.83 | -5.00 | -5.19 | -5.35 | -5.52 |
| -25 | -4.89 | -5.06 | -5.23 | -5.41 | -5.57 |
| -26 | -4.95 | -5.11 | -5.29 | -5.45 | -5.62 |
| -27 | -5.01 | -5.18 | -5.34 | -5.50 | -5.67 |
| -28 | -5.08 | -5.23 | -5.39 | -5.55 | -5.70 |
| -29 | -5.13 | -5.29 | -5.45 | -5.60 | -5.76 |
| -30 | -5.19 | -5.34 | -5.49 | -5.64 | -5.81 |
| -31 | -5.25 | -5.39 | -5.55 | -5.70 | -5.85 |
| -32 | -5.30 | -5.46 | -5.61 | -5.75 | -5.90 |
| -33 | -5.36 | -5.51 | -5.66 | -5.80 | -5.94 |
| -34 | -5.42 | -5.56 | -5.70 | -5.85 | -5.99 |
| -35 | -5.47 | -5.61 | -5.76 | -5.90 | -6.04 |
| -36 | -5.53 | -5.66 | -5.81 | -5.95 | -6.09 |
| -37 | -5.58 | -5.71 | -5.86 | -5.99 | -6.13 |
| -38 | -5.64 | -5.77 | -5.91 | -6.04 | -6.18 |
| -39 | -5.69 | -5.82 | -5.95 | -6.09 | -6.22 |
| -40 | -5.74 | -5.87 | -6.00 | -6.13 | -6.27 |
| -41 | -5.79 | -5.92 | -6.05 | -6.18 | -6.31 |
| -42 | -5.84 | -5.97 | -6.10 | -6.22 | -6.35 |
| -43 | -5.90 | -6.02 | -6.15 | -6.27 | -6.40 |
| -44 | -5.94 | -6.06 | -6.19 | -6.32 | -6.44 |
| -45 | -6.00 | -6.11 | -6.24 | -6.36 | -6.49 |
| -46 | -6.04 | -6.17 | -6.29 | -6.41 | -6.54 |
| -47 | -6.09 | -6.22 | -6.33 | -6.45 | -6.58 |
| -48 | -6.14 | -6.26 | -6.38 | -6.49 | -6.61 |
| -49 | -6.19 | -6.32 | -6.43 | -6.55 | -6.67 |
| -50 | -6.25 | -6.36 | -6.48 | -6.59 | -6.72 |
| -51 | -6.29 | -6.41 | -6.53 | -6.63 | -6.76 |
| -52 | -6.35 | -6.45 | -6.56 | -6.68 | -6.80 |
| -53 | -6.39 | -6.50 | -6.62 | -6.72 | -6.83 |
| -54 | -6.43 | -6.55 | -6.66 | -6.76 | -6.88 |
| -55 | -6.49 | -6.59 | -6.70 | -6.81 | -6.92 |
| -56 | -6.52 | -6.64 | -6.74 | -6.86 | -6.97 |
| -57 | -6.58 | -6.68 | -6.80 | -6.89 | -7.01 |
| -58 | -6.62 | -6.73 | -6.83 | -6.94 | -7.05 |
| -59 | -6.67 | -6.77 | -6.89 | -6.98 | -7.09 |
| -60 | -6.71 | -6.82 | -6.93 | -7.03 | -7.13 |
Table A3 - Panel 3: Constant and trend: Five percent critical values for the AEG statistic
| c | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0 | -3.79 | -4.14 | -4.44 | -4.73 | -5.00 |
| -1 | -3.79 | -4.14 | -4.46 | -4.72 | -5.01 |
| -2 | -3.82 | -4.16 | -4.45 | -4.74 | -5.01 |
| -3 | -3.86 | -4.18 | -4.48 | -4.76 | -5.03 |
| -4 | -3.89 | -4.21 | -4.50 | -4.78 | -5.03 |
| -5 | -3.94 | -4.24 | -4.53 | -4.79 | -5.05 |
| -6 | -3.98 | -4.27 | -4.56 | -4.81 | -5.07 |
| -7 | -4.03 | -4.32 | -4.58 | -4.85 | -5.09 |
| -8 | -4.08 | -4.36 | -4.63 | -4.89 | -5.11 |
| -9 | -4.14 | -4.41 | -4.66 | -4.91 | -5.16 |
| -10 | -4.19 | -4.44 | -4.71 | -4.93 | -5.18 |
| -11 | -4.26 | -4.51 | -4.74 | -4.98 | -5.21 |
| -12 | -4.32 | -4.56 | -4.79 | -5.02 | -5.23 |
| -13 | -4.37 | -4.60 | -4.84 | -5.06 | -5.28 |
| -14 | -4.44 | -4.66 | -4.88 | -5.09 | -5.30 |
| -15 | -4.50 | -4.71 | -4.93 | -5.14 | -5.34 |
| -16 | -4.55 | -4.78 | -4.97 | -5.19 | -5.39 |
| -17 | -4.61 | -4.82 | -5.02 | -5.23 | -5.42 |
| -18 | -4.67 | -4.88 | -5.07 | -5.27 | -5.46 |
| -19 | -4.73 | -4.94 | -5.12 | -5.32 | -5.50 |
| -20 | -4.79 | -4.99 | -5.18 | -5.37 | -5.55 |
| -21 | -4.85 | -5.04 | -5.21 | -5.41 | -5.59 |
| -22 | -4.91 | -5.08 | -5.27 | -5.45 | -5.62 |
| -23 | -4.97 | -5.15 | -5.33 | -5.49 | -5.67 |
| -24 | -5.03 | -5.19 | -5.38 | -5.54 | -5.72 |
| -25 | -5.08 | -5.25 | -5.42 | -5.59 | -5.76 |
| -26 | -5.14 | -5.29 | -5.47 | -5.64 | -5.81 |
| -27 | -5.19 | -5.36 | -5.53 | -5.69 | -5.85 |
| -28 | -5.25 | -5.41 | -5.56 | -5.72 | -5.88 |
| -29 | -5.30 | -5.47 | -5.63 | -5.77 | -5.93 |
| -30 | -5.36 | -5.52 | -5.66 | -5.82 | -5.98 |
| -31 | -5.41 | -5.57 | -5.72 | -5.86 | -6.02 |
| -32 | -5.47 | -5.62 | -5.76 | -5.92 | -6.07 |
| -33 | -5.52 | -5.67 | -5.82 | -5.95 | -6.11 |
| -34 | -5.57 | -5.72 | -5.86 | -6.01 | -6.15 |
| -35 | -5.62 | -5.76 | -5.91 | -6.05 | -6.20 |
| -36 | -5.67 | -5.82 | -5.96 | -6.10 | -6.24 |
| -37 | -5.72 | -5.87 | -6.01 | -6.14 | -6.28 |
| -38 | -5.79 | -5.92 | -6.06 | -6.19 | -6.33 |
| -39 | -5.84 | -5.97 | -6.10 | -6.24 | -6.36 |
| -40 | -5.88 | -6.01 | -6.15 | -6.28 | -6.41 |
| -41 | -5.93 | -6.06 | -6.20 | -6.32 | -6.46 |
| -42 | -5.99 | -6.11 | -6.24 | -6.37 | -6.49 |
| -43 | -6.04 | -6.16 | -6.28 | -6.41 | -6.54 |
| -44 | -6.08 | -6.20 | -6.33 | -6.45 | -6.58 |
| -45 | -6.13 | -6.25 | -6.38 | -6.49 | -6.63 |
| -46 | -6.18 | -6.30 | -6.42 | -6.55 | -6.68 |
| -47 | -6.22 | -6.35 | -6.46 | -6.59 | -6.71 |
| -48 | -6.27 | -6.40 | -6.51 | -6.63 | -6.75 |
| -49 | -6.32 | -6.44 | -6.56 | -6.68 | -6.80 |
| -50 | -6.37 | -6.48 | -6.60 | -6.72 | -6.84 |
| -51 | -6.42 | -6.54 | -6.65 | -6.76 | -6.89 |
| -52 | -6.47 | -6.58 | -6.69 | -6.81 | -6.92 |
| -53 | -6.51 | -6.63 | -6.74 | -6.85 | -6.95 |
| -54 | -6.55 | -6.67 | -6.78 | -6.89 | -7.00 |
| -55 | -6.60 | -6.71 | -6.82 | -6.93 | -7.04 |
| -56 | -6.64 | -6.76 | -6.86 | -6.98 | -7.09 |
| -57 | -6.69 | -6.80 | -6.91 | -7.01 | -7.13 |
| -58 | -6.74 | -6.85 | -6.95 | -7.06 | -7.16 |
| -59 | -6.78 | -6.88 | -7.00 | -7.10 | -7.21 |
| -60 | -6.82 | -6.93 | -7.04 | -7.15 | -7.25 |
Figure 1: Critical values at the five percent level for the AEG test as a function of c1 and c2.
The top panel shows the surface describing the five percent critical values of the AEG test, in the case of an intercept and one regressor, when c1 and c2 are non-identical. The bottom panel shows the corresponding contour plot. The values are based on 10,000 repetitions with T = 1,000.
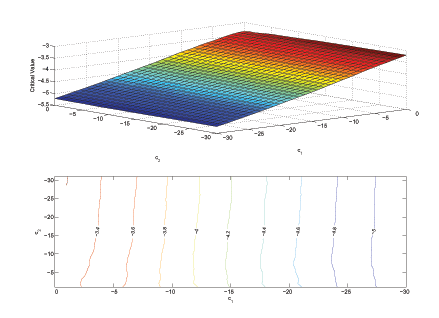
Figure 2: Size properties of the Engle and Granger (1987) test of cointegration, as a function of the local-to-unity parameter c.
The graph shows the average rejection rates under the null hypothesis of no cointegration for the Engle and Granger test of cointegration, i.e. the standard AEG test evaluated under the assumption that c = 0, for the different true values of c. The sample size is equal to either T = 100 or 500, and the number of regressors equal to either n = 1 or 3. The true persistence in the data is equal to C = diag (c, ..., c), where c varies between 0 and -30. The results are based on 10,000 repetitions.
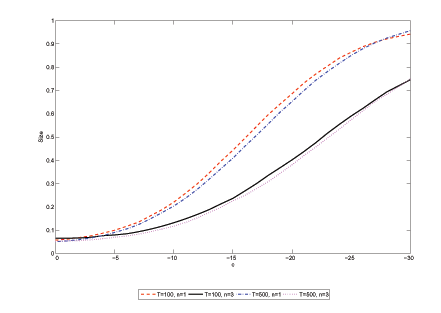
Figure 3: Size properties of the Bonferroni AEG test when the variables all have equal persistence.
The graphs show the average rejection rates for the Bonferroni AEG test, under the null hypothesis of no cointegration, for α1 = 0.75, 0.50, and 0.25. The sample size is equal to either T = 100 or 500, and the number of regressors is equal to either n = 1 or 3. The true persistence in the data is equal to C = diag (c, ..., c), where c varies between 0 and -30. The results are based on 10,000 repetitions.
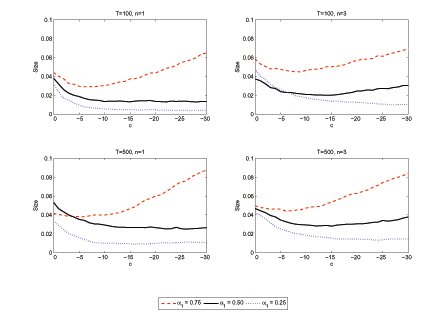
Figure 4: Estimates of the lower bounds of c.
The graphs show the density of the estimates of the lower bounds of c, with confidence levels of 75, 50, and 25 percent, based on inversion of the DF-GLS statistic. The results are obtained from 10,000 simulations of a univariate local-to-unity process, with local-to-unity parameter c, iid normal innovations and sample size T = 500.
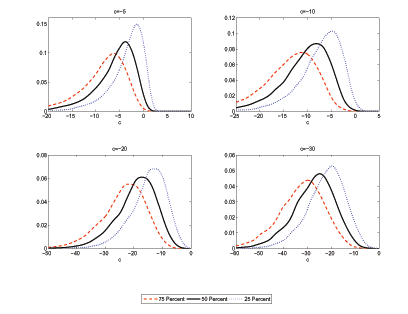
Figure 5: Size properties of the Bonferroni AEG test when ci is not identical for all i.
The graphs show the average rejection rates for the Bonferroni AEG test, under the null hypothesis of no cointegration, for α1 = 0.75,0.50, and 0.25. The sample size is equal to either T = 100 or 500, and the number of regressors is equal to either n = 2 or 3. For n = 2, the true persistence in the data is equal to C = diag (c1, -10, -20), and for n = 3, C = diag (c1, 0, -10, -20), where c1 varies between 0 and -30. The results are based on 10,000 repetitions.
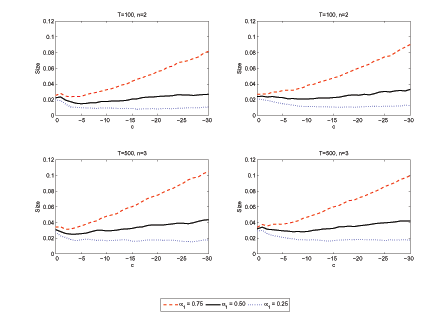
Figure 6: Power properties of the Bonferroni AEG test.
The graphs show the average rejection rates of the Bonferroni AEG test, for α1 = 0.50, under the alternative of cointegration. The power is plotted as a function of ρ, the AR(1) persistence parameter in the cointegrating residuals. The sample size is set equal to either T = 100 or 500. The left column gives results for the case of one regressor with persistence C2 = -2, -10, or -20. The right column gives the results for the case with three regressors and C2 = diag (0,-10,-20). The results are based on 10,000 repetitions.
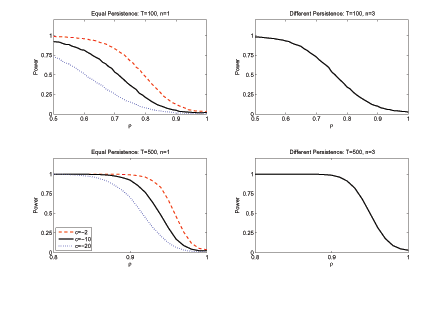
Footnotes
* We have benefitted from comments by Meredith Beechey, David Bowman, Mike McCracken, Chris Erceg, Dale Henderson, Lennart Hjalmarsson, Randi Hjalmarsson, George Korniotos, Rolf Larsson, Andy Levin, Johan Lyhagen, John Rogers, Jonathan Wright, and seminar participants at the Federal Reserve Board. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Österholm gratefully acknowledges financial support from Jan Wallander's and Tom Hedelius' Foundation. Return to text
† Division of International Finance, Federal Reserve Board, Mail Stop 20, Washington, DC 20551, USA. email: [email protected] Phone: +1 202 452 2426 Return to text
‡ Department of Economics, Uppsala University, Box 513, 751 20 Uppsala, Sweden. email: [email protected] Phone: +1 202 378 4135 Return to text
1. In most cointegration studies, the regressors are endogenous, in which case OLS inference would be further complicated and invalid even in the strictly stationary case. Stock (1997) provides a detailed discussion on many of the issues that arise in inference with near unit root variables. Return to text
2. Although, perhaps, less obvious, the same also holds true for non-residual-based tests, such as those of Johansen (1988,1991); see Hjalmarsson and Österholm (2007). Return to text
3. Since ![]() is
assumed not to play an important role in the distribution of the
test-statistic, the only uncertainty regarding the persistence of
the data comes from uncertainty regarding
is
assumed not to play an important role in the distribution of the
test-statistic, the only uncertainty regarding the persistence of
the data comes from uncertainty regarding ![]() .
The confidence level of the lower bound
.
The confidence level of the lower bound
![]() is therefore
is therefore
![]() rather than
rather than
![]() , as discussed
above. Return to text
, as discussed
above. Return to text
4. Note that, for instance, the two lower confidence bounds at the 5 percent and 95 percent level provide a two-sided confidence interval with confidence level 90 percent. Return to text
5. The number of lags included in the
DF-GLS test is chosen using the Schwarz (1978) information
critierion, with a maximum number of two allowed in order to keep
the simulation times managable. The same number of lags is also
included in the ![]() regression; that is, in
regression; that is, in
![]() . Return to text
. Return to text
6. See, for example, Wu and Zhang (1996), Culver and Papell (1997), and Wu and Chen (2001). Return to text
7. Note that in the estimations below,
time ![]() inflation is given as future inflation
between
inflation is given as future inflation
between ![]() and
and ![]() . This can be
motivated by assuming rational expectations; see, for example,
Mishkin (1992). Return to text
. This can be
motivated by assuming rational expectations; see, for example,
Mishkin (1992). Return to text
8. Regarding the specification of deterministic terms in the unit root tests, it should be noted that we test for mean reversion around a constant level. Return to text
9. Lag length in the DF-GLS test was determined using the Schwarz (1978) information criterion. For the KPSS test, a Newey-West estimator was employed to correct for serial correlation. Return to text
10. As in the DF-GLS test, lag length in the test equation is determined using the Schwarz (1978) criterion. Return to text
11. As was shown above, the persistence of the dependent variable is of special importance when using the AEG test. The assumption of a unit root in consumption is thus of particular interest. Although this conjecture finds some support - see, for example, Hall (1978) and Gali (1993) - the opinion in the litterature is far from unanimous. For instance, the vast literatue that uses linear trends to detrend consumption - see, for example, Cooper and Ejarque (2000) and Casares (2007) - implicitly or explicitly assumes that consumption is trend stationary rather than generated by a unit root process. Furthermore, it has been argued that consumption and output should be integrated of the same order. Thus, if output is trend stationary (e.g. Flavin, 1981 and Diebold and Senhadji, 1996) then consumption should be as well. Return to text
12. http://www.econ.nyu.edu/user/ludvigsons/ Return to text
13. Note that in this application, the
unit root tests have both constant and trend included in the
specification. Thus, the estimates and confidence intervals of
![]() are derived using the values in Table
A2; again, linear interpolation is used. Return to text
are derived using the values in Table
A2; again, linear interpolation is used. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text