
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 918, January 2008---Screen Reader
Version*
International Competition and Inflation: A New Keynesian Perspective*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We develop and estimate an open economy New Keynesian Phillips curve (NKPC) in which variable demand elasticities give rise to changes in desired markups in response to changes in competitive pressure from abroad. A parametric restriction on our specification yields the standard NKPC, in which the elasticity is constant, and there is no role for foreign competition to influence domestic inflation. By comparing the unrestricted and restricted specifications, we provide evidence that foreign competition plays an important role in accounting for the behavior of inflation in the traded goods sector. Our estimates suggest that foreign competition has lowered domestic goods inflation about 1 percentage point over the 2000-2006 period. Our results also provide evidence against demand curves with a constant elasticity in the context of models of monopolistic competition.
Keywords: Inflation, New Keynesian Phillips curve, variable markups
JEL classification: F41, E31, E32
1 Introduction
An important question in macroeconomics is the extent to which global factors influence the behavior of aggregate prices. While it is widely recognized that import prices have a direct effect on consumer prices, there is less agreement about the extent to which global factors influence domestic prices. One prominent view is that the prices of U.S. domestic producers mainly depend on domestic variables, with international factors having only a limited impact. Recent work has challenged this view, arguing that the intensifying trend of global economic integration has changed the behavior of inflation, and international considerations have become an important determinant of inflation dynamics.1
We address this question in the context of a structural model of inflation in the spirit of Dornbusch and Fischer (1984) and Dornbusch (1985), who emphasized how variations in the desired markups of domestic firms could arise in response to changes in competitive pressures from abroad. These competitiveness effects arise in our model, because a firm faces an elasticity of demand as in Kimball (1995), which depends on its price relative to its competitors. As a result, a reduction in the prices of foreign competitors can induce domestic firms to lower their desired markups. We embed these non-constant elasticity preferences into a short-run model of inflation in which firms only infrequently re-optimize their prices due to the presence of Calvo (1983) contracts.
We derive a specification for domestic inflation that depends not only on real marginal cost, but on the prices of imported or foreign goods relative to domestic prices.2 A parametric restriction on our specification yields the standard New Keynesian Phillips curve (NKPC) in which the elasticity of demand is constant, and there is no role for competition abroad to directly influence inflation.3 By comparing the unrestricted and restricted versions of our model, we are able to evaluate the extent to which foreign competition influences the behavior of inflation. In addition, we empirically assess the hypothesis of a constant elasticity of substitution (CES), which is often used by researchers due to its analytical convenience rather than its empirical validity.
Our methodology for estimating inflation closely parallels the present-value approach used in the empirical finance literature. To estimate our model, we use data on the prices of U.S. domestic tradable goods rather than a broader price measure. While this choice represents a departure from most of the empirical literature on inflation, it is motivated by two considerations. First, tradable prices are appropriate given our theoretical model, which focuses on the interactions between foreign and domestic producers of tradable products. Second, the behavior of domestic tradable prices should be particularly revealing regarding the influence of global factors on the domestic economy. We view substantiating that domestic tradeable prices are influenced by global factors as an important first step in building a similar case for broader measures of domestic inflation that include non-tradables.
Our results provide evidence that foreign competition has played
an important role in explaining the behavior of traded goods
inflation. For instance, we estimate that foreign competition, by
reducing the desired markups of domestic producers, has lowered the
annual inflation rate for domestic goods about 1 percentage point,
on average, over the 2000-2006 period. In addition, movements in
relative import prices associated with changes in foreign
competition account for over
![]() of the volatility of goods price
inflation over the 1983-2006 sample period.
of the volatility of goods price
inflation over the 1983-2006 sample period.
Our benchmark estimate for the degree of nominal rigidities are consistent with firms that re-optimize prices, on average, once every 3 to 4 quarters.4 We also find that once we account for the endogenous changes in desired markups, there is a limited, if not negligible, role for backward-looking price setting behavior in explaining the dynamics of traded goods inflation. In contrast, much of the NKPC literature including Galí and Gertler (1999) and Eichenbaum and Fischer (2007) estimate degrees of backward-looking behavior that are significantly different from zero. The difference in our results with these earlier papers reflects our focus on inflation for tradeable goods, which inherits a considerable degree of persistence from movements in relative import prices.
Another contribution of our work is that we show that in an open economy the variability in desired markups can be separately identified from changes in markups arising from nominal rigidities. As demonstrated by Eichenbaum and Fischer (2007), in a closed economy, it is not possible to separately identify the frequency of price re-optimization from the real rigidity associated with changes in desired markups. To estimate the frequency of price adjustment in closed economy models, researchers frequently resort to calibrating the parameter governing the variation in the demand elasticity with little empirical guidance. In an open economy, relative import prices are informative about the competitive interaction between foreign and domestic firms, and can shed light on the nature of the demand curve. In this context, our estimates provide evidence against CES demand curves. In particular, we find a large and statistically significant departure from a constant elasticity of substitution, and our estimates for the demand curve are consistent with the calibrated values used in closed economy contexts by Eichenbaum and Fischer (2007), Coenen, Levin, and Christoffel (2007), and Dotsey and King (2005).
The rest of this paper proceeds as follows. Section 2 describes our open economy model with a variable demand elasticity and discusses the issue of identification. Section 3 and 4 describe our data and empirical methodology. Section 5 discusses our estimation results, while Section 6 concludes.
2 An Open Economy Model with a Variable Demand Elasticity
In this section, we describe the analytical framework that leads to the open economy New Keynesian Phillips curve that we estimate. Our framework can be viewed as part of a general equilibrium model which also includes households and the producers of non-tradable goods and services. However, in order to help minimize model misspecification, we employ a limited information approach in estimating traded goods inflation, and only describe the part of the model that is relevant for our estimation approach. In doing so, we emphasize how the international dimension of our model allows us to separately identify the degree to which markups vary due to nominal rigidities from variation in desired markups arising from changes in competition.
2.1 Final Good Producers
At time ![]() , an aggregate final good,
, an aggregate final good, ![]() , is produced by perfectly competitive firms. The
representative firm combines a continuum of intermediate goods
produced at home and another continuum produced abroad. The firm
chooses domestically-produced goods,
, is produced by perfectly competitive firms. The
representative firm combines a continuum of intermediate goods
produced at home and another continuum produced abroad. The firm
chooses domestically-produced goods, ![]() ,
,
![]() , imported goods,
, imported goods, ![]() ,
,
![]() , and
, and ![]() to
maximize profits:
to
maximize profits:
![$\displaystyle \max P_{At}A_{t}-\left[ \int_{0}^{1}P_{Dt}(i)A_{Dt}(i)di-\int_{0}^{1} P_{Mt}(i)A_{Mt}(i)di\right] ,$](img9.gif)
|
(1) |
subject to
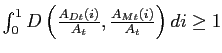 . In maximizing profits, the firm takes the prices of the domestic,
. In maximizing profits, the firm takes the prices of the domestic,
![]() , imported goods,
, imported goods, ![]() , and the final good,
, and the final good, ![]() , as
given.
, as
given.
For
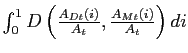 , we adopt the aggregator used by Gust, Leduc, and Vigfusson (2006), who extend the
one discussed in Dotsey and King (2005) to an international environment.
This aggregator is given by:
, we adopt the aggregator used by Gust, Leduc, and Vigfusson (2006), who extend the
one discussed in Dotsey and King (2005) to an international environment.
This aggregator is given by:
![$\displaystyle \int^{1}_{0} D\left( \frac{A_{Dt}(i)}{A_{t}},\frac{A_{Mt}(i)}{A_{t}}\right) di = \left[ V_{Dt}^{1/\rho}+V_{Mt}^{1/\rho}\right] ^{\rho}-\frac{1} {(1-\nu)\gamma_{t}}+1 .$](img15.gif)
|
(2) |
In turn, ![]() is an aggregator of
domestically-produced goods given by
is an aggregator of
domestically-produced goods given by
![$\displaystyle V_{Dt}=\int_{0}^{1}\frac{(1-\omega)^{\rho}}{(1-\nu)\gamma_{t}}\left[ \frac{1-\nu}{1-\omega}\frac{A_{Dt}(i)}{A_{t}}+\nu\right] ^{\gamma_{t} }di,$](img17.gif)
|
(3) |
and ![]() is an aggregator of imported goods
given by
is an aggregator of imported goods
given by
![$\displaystyle V_{Mt}=\int_{0}^{1}\frac{\omega^{\rho}}{(1-\nu)\gamma_{t}}\left[ \frac {(1-\nu)}{\omega}\frac{A_{Mt}(i)}{A_{t}}+\nu\right] ^{\gamma_{t} }di.$](img19.gif)
|
(4) |
In the above, ![]() influences the substitutability
between domestic and foreign goods. The share parameter
influences the substitutability
between domestic and foreign goods. The share parameter ![]() is related to the degree of home bias in preferences
and can be thought of as indexing the degree of trade openness.
is related to the degree of home bias in preferences
and can be thought of as indexing the degree of trade openness.
Our estimation strategy explicitly requires us to model an error
to our structural equation for inflation. We let
![]() be an exogenous shock influencing
the elasticity of substitution between varieties produced within a
given country, which, as we discuss later, introduces exogenous
variations in markups and in aggregate inflation. We specify that
be an exogenous shock influencing
the elasticity of substitution between varieties produced within a
given country, which, as we discuss later, introduces exogenous
variations in markups and in aggregate inflation. We specify that
![]() evolves according to:
evolves according to:
| (5) |
where
![]() is an identically and
independently distributed (iid) process with zero-mean and
standard deviation,
is an identically and
independently distributed (iid) process with zero-mean and
standard deviation,
![]() . Later, we verify that once
you take into account endogenous variations of the markup, this
error is in fact white noise and thus makes no contribution to
inflation persistence. In contrast, recent empirical applications
such as Ireland (2004) and Smets and Wouters (2007) have generally assumed
that the exogenous movements in the markup are serially
autocorrelated.
. Later, we verify that once
you take into account endogenous variations of the markup, this
error is in fact white noise and thus makes no contribution to
inflation persistence. In contrast, recent empirical applications
such as Ireland (2004) and Smets and Wouters (2007) have generally assumed
that the exogenous movements in the markup are serially
autocorrelated.
To understand our aggregator, it is useful to abstract from the
iid markup shock. In that case, when ![]() and
and
![]() , the elasticity of demand
is variable (VES) and the (absolute value of the) demand elasticity
can be expressed as an increasing function of a firm's relative
price. When
, the elasticity of demand
is variable (VES) and the (absolute value of the) demand elasticity
can be expressed as an increasing function of a firm's relative
price. When ![]() and
and
![]() , the demand aggregator
has a constant elasticity of substitution (CES) and can be thought
of as the combination of a Dixit-Stiglitz and Armington (1969) aggregators. In particular, in this case, our aggregator can be
rewritten as:
, the demand aggregator
has a constant elasticity of substitution (CES) and can be thought
of as the combination of a Dixit-Stiglitz and Armington (1969) aggregators. In particular, in this case, our aggregator can be
rewritten as:
![$\displaystyle A_{t}=\left[ (1-\omega)A_{Dt}^{\frac{\gamma}{\rho}}+\omega A_{Mt} ^{\frac{\gamma}{\rho}}\right] ^{\frac{\rho}{\gamma}}, $](img31.gif)
where
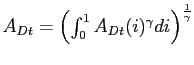 and
and
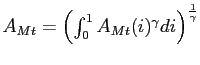 .
.
As shown in Appendix A, profit
maximization by the representative final good producer implies that
its demand for domestic good ![]() is given by:
is given by:
![$\displaystyle A_{Dt}(i)=(1-\omega)\left[ \frac{1}{1-\nu}\left( \frac{P_{Dt}(i)}{P_{Dt} }\right) ^{\frac{1}{\gamma_{t}-1}}\left( \frac{P_{Dt}}{P_{Ft}}\right) ^{\frac{\rho}{\gamma_{t}-\rho}}-\frac{\nu}{1-\nu}\right] A_{t} .$](img35.gif)
|
(6) |
In these demand curves, ![]() , and
, and ![]() are price indices of domestic and imported goods given
by:
are price indices of domestic and imported goods given
by:
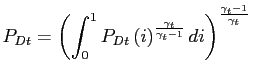 and
and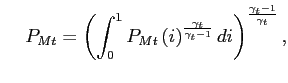
|
(7) |
while ![]() is a price index consisting of all the
prices of a firm's competitors:
is a price index consisting of all the
prices of a firm's competitors:
![$\displaystyle P_{Ft}=\left[ (1-\omega)P_{Dt}^{\frac{\gamma_{t}}{\gamma_{t}-\rho}}+\omega P_{Mt}^{\frac{\gamma_{t}}{\gamma_{t}-\rho}}\right] ^{\frac{\gamma_{t}-\rho }{\gamma_{t}}}.$](img41.gif)
|
(8) |
As in Dotsey and King (2005), when ![]() , these
demand curves have a linear term which implies that the elasticity
of demand depends on a firm's price relative to the prices of its
competitors,
, these
demand curves have a linear term which implies that the elasticity
of demand depends on a firm's price relative to the prices of its
competitors, ![]() .
.
2.2 Intermediate Good Producers
Intermediate good ![]() is produced by a
monopolistically competitive firm, whose technology is Cobb-Douglas
over capital and labor. Intermediate goods producers face perfectly
competitive factor input markets within a country. Capital and
labor are assumed to be immobile across countries but completely
mobile within a country. Thus, within a country, all firms have the
same marginal cost,
is produced by a
monopolistically competitive firm, whose technology is Cobb-Douglas
over capital and labor. Intermediate goods producers face perfectly
competitive factor input markets within a country. Capital and
labor are assumed to be immobile across countries but completely
mobile within a country. Thus, within a country, all firms have the
same marginal cost, ![]() .
.
Intermediate goods producers sell their products to the
consumption goods distributors, and we assume that markets are
segmented so that firms can charge different prices at home and
abroad (i.e., price to market). The domestic price is determined
according to Calvo-style contracts. In particular, firm ![]() faces a constant probability
faces a constant probability ![]() of
being able to re-optimize its price. This probability is assumed to
be independent across time, firms, and countries. If firm
of
being able to re-optimize its price. This probability is assumed to
be independent across time, firms, and countries. If firm
![]() can not re-optimize its price at time
can not re-optimize its price at time
![]() , the firms resets its price based on lagged
inflation as in Christiano, Eichenbaum, and Evans (2005) and Smets and Wouters (2003). In
particular,
, the firms resets its price based on lagged
inflation as in Christiano, Eichenbaum, and Evans (2005) and Smets and Wouters (2003). In
particular,
![]() , where
, where
![]() , and the parameter
, and the parameter
![]() captures the degree of
indexation to past inflation. In this specification
captures the degree of
indexation to past inflation. In this specification
![]() corresponds to indexation to
steady state inflation (
corresponds to indexation to
steady state inflation (![]() ), and
), and
![]() implies full indexation to past
inflation. When firm
implies full indexation to past
inflation. When firm ![]() can re-optimize in period
can re-optimize in period
![]() , it maximizes:
, it maximizes:
![$\displaystyle E_{t}\sum_{j=0}^{\infty} \xi_{t+j} \theta^{j} \left[ I_{Dt+j}P_{Dt}\left( i\right) -MC_{t+j}\right] A_{Dt+j}(i),$](img58.gif)
|
(9) |
taking ![]() , its demand schedule, and the
indexing scheme,
, its demand schedule, and the
indexing scheme,
![]() as given. In the above,
as given. In the above, ![]() is the stochastic
discount factor with steady state value,
is the stochastic
discount factor with steady state value,
![]() , and
, and ![]() denotes the conditional expectations operator at date
denotes the conditional expectations operator at date ![]() . The first-order condition from this problem is:
. The first-order condition from this problem is:
![$\displaystyle E_{t}\sum_{j=0}^{\infty} \xi_{t+j} \theta^{j}\left[ 1-\left( 1-\frac {MC_{t+j} }{I_{Dt+j}P_{Dt}(i)}\right) \epsilon_{t+j}(i)\right] A_{Dt+j}(i)=0,$](img65.gif)
|
(10) |
where the elasticity of demand for good ![]() in the
domestic market is:
in the
domestic market is:
![$\displaystyle \epsilon_{t}(i)=\frac{1}{1-\gamma_{t}}\left[ 1-\nu\left( \frac{P_{Dt} (i)}{P_{Dt}}\right) ^{\frac{1}{1-\gamma_{t}}}\left( \frac{P_{Dt}}{P_{Ft} }\right) ^{\frac{\rho}{\rho-\gamma_{t}}}\right] ^{-1}.$](img67.gif)
|
(11) |
This elasticity results in a time-varying markup of the form:
![$\displaystyle \mu_{t}(i)=\frac{\epsilon_{t}(i)}{\epsilon_{t}(i)-1}=\left[ \gamma_{t} +\nu(1-\gamma_{t})p_{Dt}(i)^{\frac{1}{1-\gamma_{t}}}p_{Ft}^{\frac{\rho} {\gamma_{t}-\rho}}\right] ^{-1},$](img68.gif)
|
(12) |
where the lower case variables denote relative prices (i.e.,
![]() and
and
![]() ).
).
To understand variations in the desired markup (i.e., the markup
in the absence of price rigidities and the exogenous shock
![]() ), it is useful to log-linearize
this expression around a steady state in which relative prices are
equal to one and write it as:
), it is useful to log-linearize
this expression around a steady state in which relative prices are
equal to one and write it as:
| (13) |
where
![]() is the log-linearized
desired markup and
is the log-linearized
desired markup and
![]() . The desired
markup is given by:
. The desired
markup is given by:
![$\displaystyle \hat{\mu}_{Dt}(i)=-\left[ \frac{\partial\epsilon(i)}{\partial p_{D}(i)} \frac{1}{\epsilon}\right] (\mu-1)\hat{p}_{Dt}(i)+\left[ \frac{\partial \epsilon(i)}{\partial p_{M}}\frac{1}{\epsilon}\right] (\mu-1)\hat{p} _{Mt}.$](img75.gif)
|
(14) |
The steady state markup of an intermediate good producer is given by
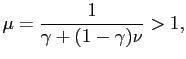 |
(15) |
and
![]() is the
steady state demand elasticity.
is the
steady state demand elasticity.
According to equation (14), there are two
sources of variations in desired markups. The first reflects
variations arising from deviations in a firm's price relative to
the prices of its domestic competitors. Variations in desired
markups arising from this source depend on
![]() , which is the elasticity of the elasticity with respect to a
firm's relative price. For
, which is the elasticity of the elasticity with respect to a
firm's relative price. For ![]() , this
elasticity measures how much
, this
elasticity measures how much
![]() rises when a firm raises its
price above the prices of its domestic competitors. In that case, a
firm will lower its desired markup so that its desired price does
not deviate too far from those of its domestic competitors. If
rises when a firm raises its
price above the prices of its domestic competitors. In that case, a
firm will lower its desired markup so that its desired price does
not deviate too far from those of its domestic competitors. If
![]() , then the demand curves are CES absent
the markup shock, and
, then the demand curves are CES absent
the markup shock, and
![]() .
.
The second source of variation in a firm's desired markup arises
from foreign competition. This effect depends on
![]() , where
, where
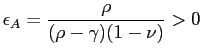
|
(16) |
is the elasticity of substitution between home and foreign goods.
The elasticity of the elasticity with respect to the relative
import price,
![]() ,
measures how much
,
measures how much
![]() rises when relative import
prices fall. In that case, a firm faces stiffer competition from
abroad and will lower its desired markup. For
rises when relative import
prices fall. In that case, a firm faces stiffer competition from
abroad and will lower its desired markup. For ![]() , the CES case, there is no effect of foreign
competitiveness on domestic markups and
, the CES case, there is no effect of foreign
competitiveness on domestic markups and
![]() . The importance of foreign competitiveness on the desired markups
of domestic firms depends on the degree of trade openness
(
. The importance of foreign competitiveness on the desired markups
of domestic firms depends on the degree of trade openness
(![]() ) and the elasticity of substitution
between home and foreign goods. International competition has a
larger influence on desired markups when an economy is more open or
its goods are closer substitutes with foreign goods.
) and the elasticity of substitution
between home and foreign goods. International competition has a
larger influence on desired markups when an economy is more open or
its goods are closer substitutes with foreign goods.
Substituting out
![]() and
and
![]() ,
the desired markup can be expressed as:
,
the desired markup can be expressed as:
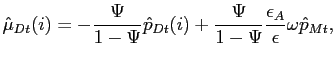
|
(17) |
where the parameter ![]() reflects the variations
in the desired markup associated with competition from other firms
and is given by:
reflects the variations
in the desired markup associated with competition from other firms
and is given by:
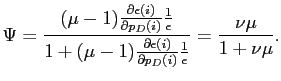
|
(18) |
In our empirical work, we focus on estimating ![]() while calibrating the values of
while calibrating the values of ![]() and
and
![]() . These three parameters uniquely
determine the demand curve parameters discussed earlier -
. These three parameters uniquely
determine the demand curve parameters discussed earlier -
![]() ,
, ![]() , and
, and
![]() - via equations (15), (16), and (18).
- via equations (15), (16), and (18).
2.3 Inflation Dynamics
To understand the role of variations in desired markups for inflation, we log-linearize the firm's first-order condition for price re-optimization, equation (10). As detailed in Appendix A, after some algebraic manipulation, a first-order approximation to this equation yields:
![$\displaystyle \hat{\pi}_{t}-\delta_{D}\hat{\pi}_{t-1}=\beta E_{t}[\hat{\pi}_{t+1} -\delta_{D}\hat{\pi}_{t}]+ \kappa\left[ (1-\Psi) \hat{s}_{t}+ \Psi\omega \frac{\epsilon_{A}}{\epsilon}\hat{p}_{Mt}+\varphi\widehat{\gamma}_{t}\right] ,$](img101.gif)
|
(19) | |
where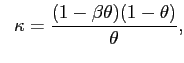
|
and where
![]() is domestic price inflation
expressed as a log deviation from steady state,
is domestic price inflation
expressed as a log deviation from steady state, ![]() represents real marginal cost (defined using
represents real marginal cost (defined using
![]() ), and the composite parameter,
), and the composite parameter,
![]() , influences the sensitivity of
inflation to exogenous variations in the markup and is given by
, influences the sensitivity of
inflation to exogenous variations in the markup and is given by
![]() .5
.5
Since we allow for partial indexation to lagged inflation,
current inflation is affected by inflation in the previous period.
Similar to a standard new Keynesian Phillips curve (e.g.,
Galí and Gertler (1999)), the Calvo price setting parameter, ![]() , affects the responsiveness of inflation to real
marginal cost through its effect on
, affects the responsiveness of inflation to real
marginal cost through its effect on ![]() .
However, equation (19) differs from
the standard specification, since relative import prices also
affect inflation. In an open economy, a domestic firm must take
into account the prices of its foreign competitors on its desired
markup.6 If foreign goods become relatively
less expensive, then domestic firms will respond by lowering their
desired markups in order to maintain a competitive price; hence,
this puts downward pressure on
.
However, equation (19) differs from
the standard specification, since relative import prices also
affect inflation. In an open economy, a domestic firm must take
into account the prices of its foreign competitors on its desired
markup.6 If foreign goods become relatively
less expensive, then domestic firms will respond by lowering their
desired markups in order to maintain a competitive price; hence,
this puts downward pressure on ![]() .
.
The importance of this foreign competitiveness effect on
domestic inflation depends on the degree of trade openness
(![]() ) and the import price elasticity (
) and the import price elasticity (
![]() ) as well as
) as well as ![]() . We use
. We use ![]() to gauge the extent of
the real rigidity associated with pricing complementarities between
firms. A higher value of
to gauge the extent of
the real rigidity associated with pricing complementarities between
firms. A higher value of ![]() reduces the sensitivity
of inflation to real marginal cost and raises the sensitivity of
inflation to relative import prices.
reduces the sensitivity
of inflation to real marginal cost and raises the sensitivity of
inflation to relative import prices.
Identifying the Real
Rigidity. Equation (19)
nests two important cases. With ![]() , the CES
case, there is no direct effect of international competition on
domestic prices. Equation (19>) is
observationally-equivalent to the specification estimated by
Galí and Gertler (1999) among others. Another interesting case is the one
considered by Eichenbaum and Fischer (2007) in which
, the CES
case, there is no direct effect of international competition on
domestic prices. Equation (19>) is
observationally-equivalent to the specification estimated by
Galí and Gertler (1999) among others. Another interesting case is the one
considered by Eichenbaum and Fischer (2007) in which ![]() . In
this case, the domestic economy does not import foreign goods, and
a domestic firm, while willing to vary its desired markup in
response to domestic competition, need not be concerned with
foreign competition. Accordingly, relative import prices do not
affect domestic price inflation.
. In
this case, the domestic economy does not import foreign goods, and
a domestic firm, while willing to vary its desired markup in
response to domestic competition, need not be concerned with
foreign competition. Accordingly, relative import prices do not
affect domestic price inflation.
As discussed by Eichenbaum and Fischer (2007), one can not separately
identify ![]() and
and ![]() in the closed
economy (
in the closed
economy (![]() ) using equation (19). As a result,
many researchers opt to calibrate the value of
) using equation (19). As a result,
many researchers opt to calibrate the value of ![]() with little empirical guidance. However, when
with little empirical guidance. However, when
![]() , relative import prices are
informative about the extent to which firms vary their desired
markups, and it is clear from equation (19) that it is
possible to jointly identify both
, relative import prices are
informative about the extent to which firms vary their desired
markups, and it is clear from equation (19) that it is
possible to jointly identify both ![]() and
and
![]() .
.
Coenen, Levin, and Christoffel (2007) alter the standard Calvo framework and show how one can separately identify real and nominal rigidities in a closed economy framework in which there are nominal pricing contracts of different durations. Their approach exploits the more complex dynamics between inflation and real marginal cost induced by their contracting structure and they use simulated methods of moments to estimate the parameters. Instead, we use the baseline Calvo model and exploit variation in relative import prices to provide information regarding the nature of demand curves and endogenous changes in desired markups.
2.4 Firm-Specific Capital
We now extend the analysis to incorporate firm-specific capital.
To do so, we assume that the production function for intermediate
good ![]() is given by:
is given by:
| (20) |
where ![]() is a firm's demand for labor and
is a firm's demand for labor and
![]() is a common technological factor.
Finally,
is a common technological factor.
Finally, ![]() denotes each firm's fixed stock of
capital. As discussed in Coenen, Levin, and Christoffel (2007), the firm specific level of
capital can be interpreted more broadly as production factors that
remain fixed in the short run (such as land and overhead labor),
while
denotes each firm's fixed stock of
capital. As discussed in Coenen, Levin, and Christoffel (2007), the firm specific level of
capital can be interpreted more broadly as production factors that
remain fixed in the short run (such as land and overhead labor),
while ![]() can be interpreted as those factors
which are variable in the short run.
can be interpreted as those factors
which are variable in the short run.
Under these assumptions, firm ![]() 's marginal cost is
given by:
's marginal cost is
given by:
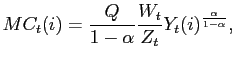
|
(21) |
where
![]() and
and
![]() can be
interpreted as the short-run elasticity of a firm's marginal cost
to output. Because capital specificity implies that a firm's
marginal cost is an increasing function of its output, it acts as
another source of real rigidity. In particular, following an
increase in nominal demand, a firm with the opportunity to raise
its price will have a weaker incentive to do so, since the fall in
the relative demand for its good reduces its marginal cost.
can be
interpreted as the short-run elasticity of a firm's marginal cost
to output. Because capital specificity implies that a firm's
marginal cost is an increasing function of its output, it acts as
another source of real rigidity. In particular, following an
increase in nominal demand, a firm with the opportunity to raise
its price will have a weaker incentive to do so, since the fall in
the relative demand for its good reduces its marginal cost.
In the benchmark economy, a domestic producer may set different
prices at home and abroad, and its pricing decision in its home
market is completely independent of its pricing decision in its
foreign market. With firm-specific capital, this is no longer true.
A firm's export price affects a firm's domestic price through its
effect on the demand for its product, ![]() ,
which alters its marginal cost. To keep our analysis tractable, we
abstract from these effects and assume that the domestic firms who
compete with foreign firms in the domestic market are distinct from
those firms which export. While this assumption simplifies our
analysis, it is also more in line with the empirical evidence
discussed in Bernard, Eaton, Jensen, and Kortum (2003) than the standard assumption in which
all domestic goods producers export their goods. In particular,
Bernard, Eaton, Jensen, and Kortum (2003) document that in 1992 only 21 percent of
manufacturing establishments were exporters.
,
which alters its marginal cost. To keep our analysis tractable, we
abstract from these effects and assume that the domestic firms who
compete with foreign firms in the domestic market are distinct from
those firms which export. While this assumption simplifies our
analysis, it is also more in line with the empirical evidence
discussed in Bernard, Eaton, Jensen, and Kortum (2003) than the standard assumption in which
all domestic goods producers export their goods. In particular,
Bernard, Eaton, Jensen, and Kortum (2003) document that in 1992 only 21 percent of
manufacturing establishments were exporters.
With a firm's production equal to its domestic demand (i.e.,
![]()
![]() ), the first order condition for a firm that
re-optimizes its price at date
), the first order condition for a firm that
re-optimizes its price at date ![]() is:
is:
![$\displaystyle E_{t}\sum_{j=0}^{\infty} \xi_{t+j} \theta^{j} \left[ 1-\left( 1-\frac {MC_{t+j}(i)}{V_{Dt+j}P_{Dt}(i)}\right) \epsilon_{Dt+j}(i)\right] A_{Dt+j}(i)=0.$](img144.gif)
|
(22) |
The log-linearized expression for domestic inflation in this case is given by:
![$\displaystyle \hat{\pi}_{t}-\delta_{D}\hat{\pi}_{t-1}=\beta E_{t}[\hat{\pi}_{t+1}-\delta _{D}\hat{\pi}_{t}]+ \kappa_{D} \left[ (1-\Psi) \hat{s}_{t}+ \Psi\omega \frac{\epsilon_{A}}{\epsilon}\hat{p}_{Mt}+\varphi\widehat{\gamma}_{t}\right] ,$](img145.gif)
|
(23) |
where
![]() , and
, and ![]() and
and ![]() are defined
as before. Comparing equation (23) with equation
(19), it is
clear that capital specificity does not alter the form of the NKPC
but lowers the reduced-form slope coefficient since
are defined
as before. Comparing equation (23) with equation
(19), it is
clear that capital specificity does not alter the form of the NKPC
but lowers the reduced-form slope coefficient since
![]() with
with ![]() . An implication of this result is that we can
not separately identify the real rigidity associated with
firm-specific capital from the Calvo-price setting parameter.
However, the real rigidity associated with variations in desired
markups can still be separately identified and estimated provided
information on either
. An implication of this result is that we can
not separately identify the real rigidity associated with
firm-specific capital from the Calvo-price setting parameter.
However, the real rigidity associated with variations in desired
markups can still be separately identified and estimated provided
information on either ![]() or
or ![]() .
.
3 Data
We use quarterly data on inflation, marginal cost, and relative import prices from 1983-2006 to estimate our model. We focus on this sample period to help abstract from changes in monetary policy regimes. Since our theoretical analysis is for the prices of tradables, we construct on inflation measure based on goods prices (from NIPA Table 1.2.4). We also net out the prices of exported goods, reflecting that prices at home and abroad can differ.7 The upper panel of Figure 1 plots goods inflation and inflation in the non-farm business sector from 1979-2006. The two series are positively correlated with each other (the correlation is 0.5). Goods price inflation, however, has been lower, on average, than overall inflation, as well as more volatile, particularly over the past 15 years.
To measure real marginal cost, ![]() , we use
data on the labor share in the non-farm business sector defined as
nominal labor compensation divided by nominal output. This measure
is the standard one used by Galí and Gertler (1999), Sbordone (2002), and
Eichenbaum and Fischer (2007) among others.8 The lower panel of Figure
1 plots the labor
share in the non-farm business sector along with GDP goods
inflation. The labor share declined throughout the first half of
the 1990s, rose noticeably at the end of the 1990s, and then
dropped sharply from 2001-2005.
, we use
data on the labor share in the non-farm business sector defined as
nominal labor compensation divided by nominal output. This measure
is the standard one used by Galí and Gertler (1999), Sbordone (2002), and
Eichenbaum and Fischer (2007) among others.8 The lower panel of Figure
1 plots the labor
share in the non-farm business sector along with GDP goods
inflation. The labor share declined throughout the first half of
the 1990s, rose noticeably at the end of the 1990s, and then
dropped sharply from 2001-2005.
We measure relative import prices by dividing the NIPA price deflator for non-oil imported goods by the deflator for domestic goods prices.9 This series is shown in Figure 2 along with domestic goods inflation. Relative import prices are positively correlated with goods inflation, rising and falling with inflation in the 1980s and moving lower in the 1990s before trending upward in the past five years.
The top panel of Figure 3 shows the correlations between the current value of inflation and the leads of relative import prices. The correlation between traded goods inflation and relative import prices is above 0.3 for the first twelve leads of import prices. These correlations are consistent with our theoretical model, which links inflation to expected future values of relative import prices. The bottom panel of Figure 3 also shows these dynamic correlations between inflation and real unit labor costs. Inflation is also positively correlated with leads of real unit labor costs, as suggested by our theoretical model.
4 Empirical Methodology
Our methodology closely parallels the present-value approach used in the empirical finance literature.10 In particular, we rewrite equation (19) as a relationship between inflation and the expected discounted value of the future values of real marginal cost and relative import prices:
![$\displaystyle \widehat{\pi}_{t}=\delta_{D}\widehat{\pi}_{t-1}+ \kappa_{D} \sum_{k=0} ^{\infty}\beta^{k} E_{t}\left[ (1-\Psi) \hat{s}_{t+k}+ \Psi\omega \frac{\epsilon_{A}}{\epsilon} \hat{p}_{Mt+k}+\varphi\hat{\gamma}_{t+k} \right] ,$](img154.gif) |
(24) |
where
![]() if capital is not firm
specific. As discussed in Appendix B, we choose to
estimate our model using equation (24) rather than
applying a generalized method of moments' (GMM) estimator to
equation (23),
because we found that the small-sample properties of our approach
were superior.
if capital is not firm
specific. As discussed in Appendix B, we choose to
estimate our model using equation (24) rather than
applying a generalized method of moments' (GMM) estimator to
equation (23),
because we found that the small-sample properties of our approach
were superior.
To estimate the parameters of interest using (24), we need
forecasts of real marginal cost and relative import prices, which
we obtain through a VAR. Defining ![]() as a
vector of variables that includes
as a
vector of variables that includes ![]() and
and
![]() , our VAR in companion form can be
written as:
, our VAR in companion form can be
written as:
| (25) |
where ![]() is a matrix of VAR coefficients, and
is a matrix of VAR coefficients, and
![]() is a vector of iid innovations
that may be correlated with each other. With the VAR expressed in
this way, we compute the forecasts of
is a vector of iid innovations
that may be correlated with each other. With the VAR expressed in
this way, we compute the forecasts of ![]() using
the relationship:
using
the relationship:
![]()
![]() .
.
For our benchmark specification of the VAR, we include only
measures of real unit labor costs and relative import prices in
![]() . Furthermore, we used the Box-Jenkins
methodology to test down from an unrestricted VAR with longer lag
length. We choose an AR(1) process for real unit labor costs and an
AR(2) process for relative import prices. Later, we conduct
sensitivity analysis in which we allow for feedback between unit
labor costs and import prices in our VAR. For our benchmark
specification of the VAR, the equation for inflation that we
estimate is:
. Furthermore, we used the Box-Jenkins
methodology to test down from an unrestricted VAR with longer lag
length. We choose an AR(1) process for real unit labor costs and an
AR(2) process for relative import prices. Later, we conduct
sensitivity analysis in which we allow for feedback between unit
labor costs and import prices in our VAR. For our benchmark
specification of the VAR, the equation for inflation that we
estimate is:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa_{D} \left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t},$](img166.gif)
|
(26) |
where ![]() is the lag operator, and
is the lag operator, and ![]() is the autoregressive coefficient for unit labor
costs, and
is the autoregressive coefficient for unit labor
costs, and ![]() , and
, and ![]() are the autoregressive coefficients for import prices. We jointly
estimate the VAR, equation (25), along with the
process for inflation, equation (26).
are the autoregressive coefficients for import prices. We jointly
estimate the VAR, equation (25), along with the
process for inflation, equation (26).
Our estimation strategy explicitly requires us to model an error
to equation (26). In
our model, this error reflects iid shocks to the markup and
is given by
![]() . Since the
exogenous variation in markups may be correlated with unit labor
costs and import prices, we use lagged variables as
instruments.11 Our benchmark set of instruments
includes one lag of traded goods inflation, one lag of real unit
labor costs, two lags of relative import prices, two lags of a
measure of commodity price inflation, two lags of
quadratically-detrended output in the goods sector, and four lags
of the spread between the 10-year Treasury note and the 3-month
Treasury bill.12
. Since the
exogenous variation in markups may be correlated with unit labor
costs and import prices, we use lagged variables as
instruments.11 Our benchmark set of instruments
includes one lag of traded goods inflation, one lag of real unit
labor costs, two lags of relative import prices, two lags of a
measure of commodity price inflation, two lags of
quadratically-detrended output in the goods sector, and four lags
of the spread between the 10-year Treasury note and the 3-month
Treasury bill.12
Since it is possible that our instruments are only weakly
correlated with the endogenous variables in our model, we follow
Stock, Wright, and Yogo (2002) and Stock and Yogo (2004) and check for the presence of weak
instruments based on the ![]() statistic of Cragg
and Donald (1993). We compare this statistic against the critical
values for the null hypothesis of weak instruments compiled by
Stock and Yogo (2004). Finally, as robustness, we also use maximum
likelihood estimation as an alternative to GMM.
statistic of Cragg
and Donald (1993). We compare this statistic against the critical
values for the null hypothesis of weak instruments compiled by
Stock and Yogo (2004). Finally, as robustness, we also use maximum
likelihood estimation as an alternative to GMM.
Identification and
Calibration. We estimate ![]() ,
, ![]() ,
,
![]() , as well as
, as well as ![]() , the
coefficients from the VAR used to forecast unit labor costs and
import prices (for our benchmark specification, the relevant
elements of
, the
coefficients from the VAR used to forecast unit labor costs and
import prices (for our benchmark specification, the relevant
elements of ![]() are
are ![]() ,
,
![]() , and
, and ![]() ). We
calibrate
). We
calibrate ![]() ,
, ![]() , and
, and
![]() . Given considerable
uncertainty about the values of these parameters, we report results
for alternative calibrations in our sensitivity analysis.
Throughout our analysis, we set
. Given considerable
uncertainty about the values of these parameters, we report results
for alternative calibrations in our sensitivity analysis.
Throughout our analysis, we set
![]() .
.
For our benchmark calibration, we choose ![]() ,
which is at the midpoint of the estimates surveyed by
Rotemberg and Woodford (1995) but higher than the estimate of Basu and Fernald (1997).
This value of
,
which is at the midpoint of the estimates surveyed by
Rotemberg and Woodford (1995) but higher than the estimate of Basu and Fernald (1997).
This value of ![]() implies
implies
![]() . We choose
. We choose
![]() , the elasticity of substitution
between home and foreign goods, to be 1.5. This estimate is toward
the higher end of estimates using macroeconomic data, which are
typically below unity in the short run and near unity in the long
run (e.g., Hooper, Johnson, and Marquez (2000)). Nevertheless, estimates of this
elasticity following a tariff change are typically much
higher.13
, the elasticity of substitution
between home and foreign goods, to be 1.5. This estimate is toward
the higher end of estimates using macroeconomic data, which are
typically below unity in the short run and near unity in the long
run (e.g., Hooper, Johnson, and Marquez (2000)). Nevertheless, estimates of this
elasticity following a tariff change are typically much
higher.13
We choose ![]() based on the ratio of non-oil
imported goods to total goods production. Because of a secular rise
in the share of imports, it is difficult to determine an
appropriate value for
based on the ratio of non-oil
imported goods to total goods production. Because of a secular rise
in the share of imports, it is difficult to determine an
appropriate value for ![]() , which in our model
corresponds to the steady state import share. For our benchmark
calibration, we choose
, which in our model
corresponds to the steady state import share. For our benchmark
calibration, we choose
![]() , which is the sample average for
the 1983:Q1-2006:Q4 period that we use throughout our analysis. For
the version of the model with firm-specific capital, following
Coenen, Levin, and Christoffel (2004), we set
, which is the sample average for
the 1983:Q1-2006:Q4 period that we use throughout our analysis. For
the version of the model with firm-specific capital, following
Coenen, Levin, and Christoffel (2004), we set
![]() .
.
5 Estimation Results
Table 1
reports our estimates of ![]() ,
, ![]() , and
, and
![]() for the version of the model in
which capital moves instantaneously across domestic firms. Table
2 shows
these results for the version of the model in which capital is
firm-specific. (For our estimates of the auxiliary VAR, see
Appendix C.)
Comparing Tables 1 and 2, it is apparent
that with the exception of the parameter
for the version of the model in
which capital moves instantaneously across domestic firms. Table
2 shows
these results for the version of the model in which capital is
firm-specific. (For our estimates of the auxiliary VAR, see
Appendix C.)
Comparing Tables 1 and 2, it is apparent
that with the exception of the parameter ![]() ,
the estimates are very similar. With firm-specific capital, the
second column of Table 2 shows that our
estimate of
,
the estimates are very similar. With firm-specific capital, the
second column of Table 2 shows that our
estimate of ![]() is 0.75 for the model with a
variable elasticity (VES), which implies that a firm, on average,
re-optimizes its price every four quarters. In contrast, without
capital specificity,
is 0.75 for the model with a
variable elasticity (VES), which implies that a firm, on average,
re-optimizes its price every four quarters. In contrast, without
capital specificity,
![]() , implying an average contract
duration of over 5 quarters.14 Since our estimate of
, implying an average contract
duration of over 5 quarters.14 Since our estimate of ![]() is the only difference in results between these two
specifications, and it is quite reasonable to believe that some
production factors are firm-specific, we now proceed to focus
exclusively on the model in which capital is firm-specific.
is the only difference in results between these two
specifications, and it is quite reasonable to believe that some
production factors are firm-specific, we now proceed to focus
exclusively on the model in which capital is firm-specific.
Table 2
shows that our estimate of ![]() implies a
demand elasticity that is far from constant, as the value of
implies a
demand elasticity that is far from constant, as the value of
![]() is 0.73 and also statistically
significant. To understand what this estimate implies for an
individual firm's demand, the upper left panel of Figure 4 plots the demand
curve of good
is 0.73 and also statistically
significant. To understand what this estimate implies for an
individual firm's demand, the upper left panel of Figure 4 plots the demand
curve of good ![]() for different values of
for different values of
![]() and compares it to
the CES demand curve (i.e.,
and compares it to
the CES demand curve (i.e., ![]() ). As shown
there, because the elasticity increases as a firm raises its price,
demand falls more for the VES demand curve than the CES demand
curve. With a rising elasticity of demand, the upper right panel
shows that a firm will reduce its desired markup as its price rises
above those of its domestic competitors.
). As shown
there, because the elasticity increases as a firm raises its price,
demand falls more for the VES demand curve than the CES demand
curve. With a rising elasticity of demand, the upper right panel
shows that a firm will reduce its desired markup as its price rises
above those of its domestic competitors.
Our estimate of ![]() implies that demand for
good
implies that demand for
good ![]() falls about 14 percent in response to a 2
percent increase in a firm's price above its steady-state value and
about 45 percent in response to a 5 percent increase.
Correspondingly, these relative price movements are associated with
6 and 12 percentage point falls in desired markups, respectively.
These estimates seem quite reasonable in contrast to the values
discussed in Chari, Kehoe, and McGrattan (2000). They criticize the calibration of the
demand curve in Kimball (1995), because 2 percent and 2.3 percent
increases in a firm's price induce a 78 percent and 100 percent
fall in demand.
falls about 14 percent in response to a 2
percent increase in a firm's price above its steady-state value and
about 45 percent in response to a 5 percent increase.
Correspondingly, these relative price movements are associated with
6 and 12 percentage point falls in desired markups, respectively.
These estimates seem quite reasonable in contrast to the values
discussed in Chari, Kehoe, and McGrattan (2000). They criticize the calibration of the
demand curve in Kimball (1995), because 2 percent and 2.3 percent
increases in a firm's price induce a 78 percent and 100 percent
fall in demand.
The lower right panel of Figure 4 shows that a
decrease in foreign prices relative to domestic prices induces a
domestic firm to lower its desired markup. However, a firm's
desired markup varies much less in response to a change in foreign
prices than in response to its own price, reflecting home bias in
tradable consumption (i.e., the calibrated value of ![]() ) and the lower elasticity between home and foreign
goods (
) and the lower elasticity between home and foreign
goods (
![]() ) than between home goods
(
) than between home goods
(![]() ). A 10 percent fall in the relative
import price from its steady state value induces a firm to lower
its desired markup only about 2 percentage points. Still, as
discussed below, such movements in relative import prices and
desired markups of firms are enough to have substantial effects on
domestic price inflation.
). A 10 percent fall in the relative
import price from its steady state value induces a firm to lower
its desired markup only about 2 percentage points. Still, as
discussed below, such movements in relative import prices and
desired markups of firms are enough to have substantial effects on
domestic price inflation.
The results in Table 2 also suggest that there is upward bias in the degree of indexation for the CES demand curves. In particular, there is a relatively large and significant coefficient on lagged inflation in this case. In contrast, in the unrestricted VES specification, the coefficient on lagged inflation is smaller and not statistically significant. Intuitively, with the VES demand curves, inflation is inheriting persistence from movements in relative import prices, and as a result, one does not need the partial indexation scheme to compensate. Later, we report results from a Monte Carlo exercise that substantiate this interpretation.
Table 2 reports the Ljung-Box Q-statistic at lags 1 and 4. For the VES specification with indexation, we can reject the presence of serially correlated markup shocks. For the CES specification without indexation, there is strong evidence that the markup shocks are serially correlated, suggesting that the model is misspecified. Although there appears to be less serial correlation for the CES specification with indexation, the Q-statistic at lag 4 still suggests model misspecification. In contrast, even if we omit indexation from the VES specification, the Q-statistics are consistent with no serial correlation.
Table 2
computes the ![]() statistic, which can be used to
test for the presence of weak instruments using the critical values
from Stock and Yogo (2004). Based on both definitions of weak instruments
discussed there, we can reject that the instrument set is weak for
all four specifications shown in Table 2.15
statistic, which can be used to
test for the presence of weak instruments using the critical values
from Stock and Yogo (2004). Based on both definitions of weak instruments
discussed there, we can reject that the instrument set is weak for
all four specifications shown in Table 2.15
To assess the fit of our model without indexation (shown in the
third column of Table 2), Figure
5 plots
predicted inflation,
![]() , defined as:
, defined as:
![$\displaystyle \hat{\pi}^{F}_{t}= \kappa\left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac{\Psi(1+\beta\rho_{M2}L)}{1-\beta \rho_{M1}-\beta^{2} \rho_{M2}} \hat{p}_{Mt}\right] ,$](img215.gif)
|
(27) |
using our estimates for ![]() and
and ![]() . The dashed red line in the figure shows a four-quarter
moving-average of
. The dashed red line in the figure shows a four-quarter
moving-average of
![]() , while the solid black
line shows a four-quarter moving average of actual inflation.
Predicted inflation tracks the broad contours of observed
inflation. In particular, the predicted series rises in the mid to
late 1980s, trends downward with inflation in the 1990s, and rises
and falls with actual inflation in the first half of this decade.
, while the solid black
line shows a four-quarter moving average of actual inflation.
Predicted inflation tracks the broad contours of observed
inflation. In particular, the predicted series rises in the mid to
late 1980s, trends downward with inflation in the 1990s, and rises
and falls with actual inflation in the first half of this decade.
An important implication of our estimate of ![]() is that international competition plays an important
role in influencing domestic inflation. To assess this role, the
dashed blue line in Figure 5 plots predicted
inflation for the CES specification in which
is that international competition plays an important
role in influencing domestic inflation. To assess this role, the
dashed blue line in Figure 5 plots predicted
inflation for the CES specification in which ![]() and foreign prices do not influence the desired
markups of domestic firms. As shown there, without this foreign
competitiveness channel, the model fails to account for the
increase in inflation in the late 1980s and its subsequent reversal
in the early 1990s. More disconcerting, the CES specification
overstates the level of inflation for the last seven years of our
sample: the model predicts an average, annualized inflation rate of
0.5 percent from 2000-2006 compared to a slight deflation of 0.4
percent. In contrast, the average value of predicted inflation for
the VES specification is very close to the observed value over this
period. Since the difference between these two specifications
reflects the influence of foreign competition on desired markups,
our estimates suggest that foreign competition has lowered domestic
goods inflation nearly 1 percentage point over the last seven
years.
and foreign prices do not influence the desired
markups of domestic firms. As shown there, without this foreign
competitiveness channel, the model fails to account for the
increase in inflation in the late 1980s and its subsequent reversal
in the early 1990s. More disconcerting, the CES specification
overstates the level of inflation for the last seven years of our
sample: the model predicts an average, annualized inflation rate of
0.5 percent from 2000-2006 compared to a slight deflation of 0.4
percent. In contrast, the average value of predicted inflation for
the VES specification is very close to the observed value over this
period. Since the difference between these two specifications
reflects the influence of foreign competition on desired markups,
our estimates suggest that foreign competition has lowered domestic
goods inflation nearly 1 percentage point over the last seven
years.
We can also assess the role of foreign competition for inflation
dynamics by computing its contribution to the volatility of the
four-quarter change in domestic goods prices. For the VES
specification, as shown in Table 2 in the row
labelled "![]() ",
predicted inflation accounts for nearly 75 percent of the
volatility of observed inflation, with movements in relative import
prices accounting for about a
",
predicted inflation accounts for nearly 75 percent of the
volatility of observed inflation, with movements in relative import
prices accounting for about a
![]() of actual inflation volatility.
In comparison, the CES specification that allows for lagged
indexation only accounts for 35 percent of the volatility of
inflation. Accordingly, these variance decompositions offer
additional evidence that foreign competition has played an
important role in accounting for movements in domestic goods
prices.
of actual inflation volatility.
In comparison, the CES specification that allows for lagged
indexation only accounts for 35 percent of the volatility of
inflation. Accordingly, these variance decompositions offer
additional evidence that foreign competition has played an
important role in accounting for movements in domestic goods
prices.
Model Misspecification and
Indexation. The results shown in Table 2 suggested that
the CES model, by excluding import prices is misspecified. In
particular, this specification appears to generate upward biased
estimates of
![]() , the degree of indexation. We
investigate this hypothesis by considering the following Monte
Carlo experiment. We use the VES specification with pseudo-true
values of
, the degree of indexation. We
investigate this hypothesis by considering the following Monte
Carlo experiment. We use the VES specification with pseudo-true
values of
![]() ,
,
![]() ,
,
![]() to bootstrap 10,000 repetitions
of artificial data, each with 96 observations (i.e., the length of
1983Q1-2006Q4 sample period).16 For each Monte Carlo sample, we
re-estimated the VES and CES specifications with indexation. We
also repeated this exercise by generating bootstrapped data with an
alternative parameterization of
to bootstrap 10,000 repetitions
of artificial data, each with 96 observations (i.e., the length of
1983Q1-2006Q4 sample period).16 For each Monte Carlo sample, we
re-estimated the VES and CES specifications with indexation. We
also repeated this exercise by generating bootstrapped data with an
alternative parameterization of ![]() .
.
The top panels of Figure 6 plot the
sampling distributions of our estimates for
![]() and
and ![]() for the
first Monte Carlo experiment in which the pseudo-true value of
for the
first Monte Carlo experiment in which the pseudo-true value of
![]() is
is ![]() . The estimate
of
. The estimate
of
![]() from the VES specification
appears to be unbiased with the mass of the distribution narrowly
concentrated around its pseudo-true value, while the estimate of
from the VES specification
appears to be unbiased with the mass of the distribution narrowly
concentrated around its pseudo-true value, while the estimate of
![]() displays some small sample bias and a
bit wider distribution than implied by the asymptotic standard
errors provided in Table 2. Still, these
results suggest that our GMM estimator fares well in small
samples.17
displays some small sample bias and a
bit wider distribution than implied by the asymptotic standard
errors provided in Table 2. Still, these
results suggest that our GMM estimator fares well in small
samples.17
Figure 6 also
shows that the misspecification bias of the CES formulation leads
to estimates of
![]() and
and ![]() above
their pseudo-true values. As shown in the bottom panels, the bias
for
above
their pseudo-true values. As shown in the bottom panels, the bias
for
![]() and
and ![]() becomes
more severe, when we increase the value of
becomes
more severe, when we increase the value of ![]() from
0.67 to 0.9 and lower
from
0.67 to 0.9 and lower ![]() from 0.75 to
0.67.18 In particular, the mean estimate of
from 0.75 to
0.67.18 In particular, the mean estimate of
![]() is 0.47 compared to its
pseudo-true value of
is 0.47 compared to its
pseudo-true value of ![]() when
when ![]() . This upward bias arises, because the
misspecification associated with the omitted import price variable
gives rise to serially correlated markup shocks. As a result, the
estimate of
. This upward bias arises, because the
misspecification associated with the omitted import price variable
gives rise to serially correlated markup shocks. As a result, the
estimate of
![]() rises above its pseudo-true value
to help soak up this residual autocorrelation. Thus, an
econometrician, who ignored the influence of foreign competition on
inflation, may mistakenly conclude that lagged indexation plays an
important role in explaining inflation.
rises above its pseudo-true value
to help soak up this residual autocorrelation. Thus, an
econometrician, who ignored the influence of foreign competition on
inflation, may mistakenly conclude that lagged indexation plays an
important role in explaining inflation.
Comparison with the
Literature. As discussed earlier, ![]() can be used to gauge the
degree of real rigidities associated with variations in desired
markups arising from domestic competition. From equation (18), we can see
that
can be used to gauge the
degree of real rigidities associated with variations in desired
markups arising from domestic competition. From equation (18), we can see
that ![]() depends on both the steady state demand
elasticity or markup, and the elasticity of the demand elasticity
with respect to a firm's price,
depends on both the steady state demand
elasticity or markup, and the elasticity of the demand elasticity
with respect to a firm's price,
![]() . It is therefore a useful metric to compare our estimates with
calibrated values of the Kimball (1995) preferences used in the
literature.
. It is therefore a useful metric to compare our estimates with
calibrated values of the Kimball (1995) preferences used in the
literature.
Table 3 shows
our estimated value for ![]() as well as the
elasticity of the elasticity with respect to a firm's price.
Although our estimates suggest that those discussed in
Chari, Kehoe, and McGrattan (2000) are high, a number of researchers use calibrations
that are validated by our results. In contrast, Dossche, Heylen, and den Poel (2007) use
scanner data from a euro-area supermarket chain to argue that most
calibrations of the Kimball (1995) aggregator impose too high a
value of
as well as the
elasticity of the elasticity with respect to a firm's price.
Although our estimates suggest that those discussed in
Chari, Kehoe, and McGrattan (2000) are high, a number of researchers use calibrations
that are validated by our results. In contrast, Dossche, Heylen, and den Poel (2007) use
scanner data from a euro-area supermarket chain to argue that most
calibrations of the Kimball (1995) aggregator impose too high a
value of
![]() , as the median estimate for the goods they consider is only 0.8.
However, given that they estimate a demand elasticity with a (net)
markup of 250%, their implied estimate of
, as the median estimate for the goods they consider is only 0.8.
However, given that they estimate a demand elasticity with a (net)
markup of 250%, their implied estimate of ![]() is
0.67, quite close to our estimate. In our view,
is
0.67, quite close to our estimate. In our view, ![]() is the relevant metric for comparing results, since
is the relevant metric for comparing results, since
![]() is not a sufficient statistic for describing the demand curve or
the degree of variation in desired markups.19
is not a sufficient statistic for describing the demand curve or
the degree of variation in desired markups.19
Our results are also related to Batini, Jackson, and Nickell (2005), who estimate an open economy NKPC for the United Kingdom in which foreign prices affect inflation due to both variations in desired markups and the presence of imported intermediate goods. In contrast to our results, they find that their measure of external competitiveness does not have a statistically significant role in explaining the variation in inflation. However, there are a number of important differences in their paper from ours. Most notably, they adopt an ad hoc specification for variations in desired markups.
In our purely forward-looking model, we estimate a value of
![]() , which implies an average contract
duration of four quarters. This estimate is broadly consistent with
the micro evidence of Nakamura and Steinsson (2007), who find a median duration
of non-sale prices of 8-11 months using prices for both consumers
and producer's finished goods.20 Our estimates are also broadly in
line though slightly higher than those of Coenen, Levin, and Christoffel (2004) and
Eichenbaum and Fischer (2007), who incorporate both VES demand curves and
firm-specific capital into New Keynesian Phillips curves.
, which implies an average contract
duration of four quarters. This estimate is broadly consistent with
the micro evidence of Nakamura and Steinsson (2007), who find a median duration
of non-sale prices of 8-11 months using prices for both consumers
and producer's finished goods.20 Our estimates are also broadly in
line though slightly higher than those of Coenen, Levin, and Christoffel (2004) and
Eichenbaum and Fischer (2007), who incorporate both VES demand curves and
firm-specific capital into New Keynesian Phillips curves.
Our estimate of an insignificant degree of indexation are in line with two recent papers by Ireland (2004) and Coenen, Levin, and Christoffel (2004). Ireland (2004) finds no role for indexation in a closed economy model when he allows for serially autocorrelated markup shocks. In contrast, we use iid markup shocks to show that once we allow for endogenous variations in markups, lagged indexation is not significant. Coenen, Levin, and Christoffel (2004) estimate a closed economy Phillips curve and argue that backward-looking price-setting is not needed to explain aggregate inflation in the context of a stable monetary policy regime. Contrary to their analysis, our results do not hinge on the use of a dummy variable to account for a change in the U.S. monetary policy regime occurring in 1991.21
5.1 Alternative Model Calibrations
Table 4
considers the sensitivity of our estimates to the calibrated values
of ![]() ,
,
![]() , and
, and ![]() . As a
point of comparison, Table 4 also reports our
estimates from the VES specification with firm-specific capital and
lagged indexation using the benchmark calibration of these
parameters.
. As a
point of comparison, Table 4 also reports our
estimates from the VES specification with firm-specific capital and
lagged indexation using the benchmark calibration of these
parameters.
The parameter ![]() determines the share of
imports in goods production. For our benchmark calibration, we
choose
determines the share of
imports in goods production. For our benchmark calibration, we
choose
![]() , the sample average of the
ratio of nonfuel goods imports to goods production from 1983-2006.
As an alternative, we set
, the sample average of the
ratio of nonfuel goods imports to goods production from 1983-2006.
As an alternative, we set
![]() , its value in 2004. With
, its value in 2004. With
![]() , our estimate of
, our estimate of ![]() declines slightly from 0.73 in our benchmark calibration
to 0.66.
declines slightly from 0.73 in our benchmark calibration
to 0.66.
The third column of Table 4 shows the effect
of lowering the import price elasticity,
![]() , from its benchmark value of
1.5 to 0.5, a value consistent with short-run estimates. In this
case, the estimate of
, from its benchmark value of
1.5 to 0.5, a value consistent with short-run estimates. In this
case, the estimate of ![]() rises to 0.84, still
within the 90% confidence interval of the benchmark model.
Alternatively, an increase in
rises to 0.84, still
within the 90% confidence interval of the benchmark model.
Alternatively, an increase in
![]() to 2 lowers our estimate of
to 2 lowers our estimate of
![]() to 0.56. This fall in
to 0.56. This fall in ![]() , however, does not necessarily imply that foreign
competition has a smaller effect on the desired markups of domestic
firms. In particular, for a given value of
, however, does not necessarily imply that foreign
competition has a smaller effect on the desired markups of domestic
firms. In particular, for a given value of ![]() , a
higher import price elasticity raises the responsiveness of
domestic firms' desired markups to foreign prices. The final column
of Table 4 shows
the estimation results using a markup of 10%, a value in line with
the estimates of Basu and Fernald (1997). In this case, our benchmark estimate
for
, a
higher import price elasticity raises the responsiveness of
domestic firms' desired markups to foreign prices. The final column
of Table 4 shows
the estimation results using a markup of 10%, a value in line with
the estimates of Basu and Fernald (1997). In this case, our benchmark estimate
for ![]() rises from 0.73 to 0.82.
rises from 0.73 to 0.82.
Although the point estimates for the parameters governing the nominal and real rigidities are somewhat dependent on our calibration choices, the qualitative results are not. For a wide set of parameter choices, as evidenced in Table 4, we find that nominal contracts last on average between 3 and 4 quarters, and that foreign competition by inducing changes in the desired markups plays a significant role in explaining the dynamic of inflation.
5.2 Alternative Instruments, Data, and Estimation Procedures
Table 5
compares the structural estimates for the VES model assuming
firm-specific capital with a number of alternatives. The first
alternative examines the estimation results when we use a smaller
instrument set. In particular, in this case, we include two lags of
relative import prices, two lags of inflation, and one lag of real
unit labor costs. While the point estimate for ![]() does not change, we find that the degree of real
rigidities is modestly lower in this case.
does not change, we find that the degree of real
rigidities is modestly lower in this case.
In our benchmark specification for forecasting unit labor costs
and import prices, we ignored any feedback between these variables
by considering separate AR processes for these variables. In the
third column, we consider an alternative forecasting process in
which these variables are modeled as a VAR(2):
![]() with
with
![]()
![]()
![]()
![]() and
and
![]()
![]() 0
0
![]() .22 For the VAR, it is
useful to define the vectors
.22 For the VAR, it is
useful to define the vectors
![]() 0 0
0 0 ![]() and
and
![]()
![]() 0
0
![]() to pick out the the first element,
to pick out the the first element,
![]() , and the second element,
, and the second element,
![]() , from the vector
, from the vector ![]() . Using the previous definitions, we can solve equation
(23), the second
order difference equation governing inflation dynamics and rewrite
it as:
. Using the previous definitions, we can solve equation
(23), the second
order difference equation governing inflation dynamics and rewrite
it as:
![$\displaystyle \widehat{\pi}_{t}=\delta_{D}\widehat{\pi}_{t-1}+\kappa_{D}[(1-\Psi )e_{1}^{\prime}(I-\beta A)^{-1}X_{t}+\omega\frac{\epsilon_{A}}{ \epsilon}\Psi e_{2}^{\prime}(I-\beta A)^{-1}X_{t}]+\epsilon_{\pi t}.$](img291.gif)
|
(28) |
The third column of Table 5 reports the
estimation results under this alternative forecasting model, and
Appendix C
reports our estimate of ![]() . As shown in Table 5, the estimate of
. As shown in Table 5, the estimate of
![]() is somewhat larger; however, overall,
the restrictions we place on the forecasting model do not
appreciably alter the estimates vis-à-vis our benchmark
model.
is somewhat larger; however, overall,
the restrictions we place on the forecasting model do not
appreciably alter the estimates vis-à-vis our benchmark
model.
To be consistent with our theoretical model, it would be ideal to have data on a basket of imported goods that matches the basket of domestically-produced goods. However, no such series are available, and instead our benchmark measure of imported prices excludes oil prices, reflecting that oil's share of imports is much larger than its share of domestic goods production. Since the same argument is applicable to other commodities, the third column of Table 5 presents results based on a measure of import prices that excludes oil, materials, and industrial goods. As shown there, our estimates only change slightly from the benchmark case; the most noticeable difference is for the indexation parameter, which equals 0.18 instead of the benchmark estimate of 0.1.
The last column of Table 5 presents results from estimating our system of equations (i.e., the structural inflation equation and the two AR processes for unit labor costs and import prices) using maximum likelihood estimation (MLE). Despite this different estimation strategy, the results are remarkably similar to our GMM estimates.
Overall, we conclude that our results are robust to some broad changes in the instrument set, the forecasting process, the import price series, and the estimation method. In particular, in all cases, these estimates suggest that movements in relative import prices have been an important factor in accounting for traded goods inflation; once we account for endogenous markup variation, there is a limited, if not negligible, contribution of indexation to traded goods inflation.
6 Conclusions
In this paper, we developed a structural model and showed that foreign competition has played an important role in accounting for the behavior of goods inflation through changes in desired markups of domestic firms. In particular, we found that foreign competition has lowered domestic goods inflation by nearly 1 percentage point over the 2000-2006 period. In addition, our results also provided evidence in favor of demand curves which lead to endogenous variations in markups. In contrast to previous work, we found that an inflation specification without backward-looking behavior performed reasonably well in explaining movements in traded goods inflation due to endogenous changes in desired markups.
Although we view this as an important step in understanding how
international factors influence domestic prices, goods production
is about
![]() of overall GDP. A rough estimate
would suggest that foreign competition has lowered overall GDP
inflation about
of overall GDP. A rough estimate
would suggest that foreign competition has lowered overall GDP
inflation about
![]() of 1 percentage point over the
2000-2006 period. However, this estimate does not take into account
any interaction between the traded and non-traded sectors, which
may magnify these effects. We leave the exploration of this issue
to future research.
of 1 percentage point over the
2000-2006 period. However, this estimate does not take into account
any interaction between the traded and non-traded sectors, which
may magnify these effects. We leave the exploration of this issue
to future research.
References
Armington, P. (1969). A Theory of Demand for Products Distinguished by Place of Production. IMF Staff Papers 16, 159-176.
Ball, L. (2006). Has Globalization Changed Inflation. NBER Working Paper No. W12687.
Basu, S. and J. G. Fernald (1997). Returns to Scale in U.S. Production: Estimates and Implications. Journal of Political Economy 105, 249-83.
Batini, N., B. Jackson, and S. Nickell (2005). An Open-Economy New Keynesian Phillips Curve for the U.K. Journal of Monetary Economics 52, 1061-1071.
Bernard, A. B., J. Eaton, J. B. Jensen, and S. Kortum (2003). Plants and Productivity in International Trade. American Economic Review 93, 1668-90.
Bils, M. and P. Klenow (2004). Some Evidence on the Importance of Sticky Prices. Journal of Political Economy 112, 947-985.
Borio, C. and A. Filardo (2006). Globalisation and Inflation: New Cross-Country Evidence on the Global Determinants of Domestic Inflation. Mimeo, Bank for International Settlements.
Calvo, G. A. (1983). Staggered Prices in a Utility-Maximizing Framework. Journal of Monetary Economics 12, 383-398.
Chari, V. V., P. J. Kehoe, and E. R. McGrattan (2000). Sticky Price Models of the Business Cycle: Can the Contract Multiplier Solve the Persistence Problem? Econometrica 68(5), 1151-1179
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy 113(1), 1-45.
Coenen, G., A. T. Levin, and K. Christoffel (2007). Identifying the Influences of Nominal and Real Rigidities in Aggregate Price-Setting Behavior. Journal of Monetary Economics. Forthcoming.
Dornbusch, R. (1985). Inflation, Exchange Rates, and Stabilization. NBER WOrking Paper No. 1739.
Dornbusch, R. and S. Fischer (1984). The Open Economy: Implications for Monetary and Fiscal Policy. In R. J. Gordon (Ed.), The American Business Cycle: Continuity and Change, pp. 459-516. The University of Chicago Press.
Dossche, M., F. Heylen, and D. V. den Poel (2007). The Kinked Demand Curve and Price Rigidity: Evidence from Scanner Data. Mimeo, National Bank of Belgium.
Dotsey, M. and R. G. King (2005). Implications of State-Dependent Pricing for Dynamic Macroeconomic Models. Journal of Monetary Economics 52, 213-42.
Eichenbaum, M. and J. D. Fischer (2007). Estimating the Frequency of Price Re-Optimization in Calvo-style Models. Journal of Monetary Economics. Forthcoming.
Galí, J. and M. Gertler (1999). Inflation Dynamics: A Structural Econometric Analysis. Journal of Monetary Economics 44(2), 195-222.
Galí, J., M. Gertler, and J. D. López-Salido (2001). European Inflation Dynamics. European Economic Review 45, 1237-1270.
Gordon, R. J. (1973). The Response of Wages and Prices to the First Two Years of Controls. Brookings Papers on Economic Activity 3, 765-778.
Gust, C., S. Leduc, and R. J. Vigfusson (2006). Trade Integration, Competition, and the Decline in Exchange-Rate Pass-Through. International Finance Discussion Papers, Number 864, Board of Governors of the Federal Reserve System.
Hooper, P., K. Johnson, and J. Marquez (2000). Trade Elasticities for the G-7 Countries. Princeton Studies in International Economics.
Ihrig, J., S. B. Kamin, D. Lindner, and J. Marquez (2007). Some Simple Tests of the Globalization and Inflation Hypothesis. International Finance Discussion Paper 893.
Ireland, P. N. (2004). Technology Shocks in the New Keynesian Model. Review of Economics and Statistics 86(4), 923-936.
Kimball, M. S. (1995). The Quantitative Analytics of the Neomonetarist Model. Journal of Money, Credit and Banking 27, 1241-77.
Nakamura, E. and J. Steinsson (2007). Five Facts About Prices: A Reevaluation of Menu Cost Models. Mimeo, Harvard University.
Podivinsky, J. M. (1999). Finite Sample Properties of GMM Estimators and Tests. In L. Mátyás (Ed.), Generalized Method of Moments Estimators, pp. 128-148. Cambridge University Press.
Rogoff, K. (2003). Globalization and Global Disinflation. Paper prepared for the Federal Reserve Bank of Kansas City conference on "Monetary Policy and Uncertainty: Adapting to a Changing Economy", Jackson Hole, WY.
Rotemberg, J. (1982). Sticky Prices in the United States. Journal of Political Economy 90, 1187-1211.
Rotemberg, J. J. and M. Woodford (1995). Dynamic General Equilibrium Models with Imperfectly Competitive Markets. In T. F. Cooley (Ed.), Frontiers of Business Cycle Research, pp. 243-293. Princeton: Princeton University Press.
Ruhl, K. (2005). The Elasticity Puzzle in International Economics. University of Texas at Austin, mimeo.
Sbordone, A. M. (2002). Prices and Unit Labor Costs: A New Test of Price Stickiness. Journal of Monetary Economics 49(2), 265-292.
Sbordone, A. M. (2007). Globalization and Inflation Dynamics: The Impact of Increased Competition. National Bureau of Economic Research Working Paper No. 13556.
Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1(5), 1124-1175.
Smets, F. and R. Wouters (2007). Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach. Centre for Economic Policy Research Working Paper No. 6112.
Stock, J. H., J. H. Wright, and M. Yogo (2002). A Survey of Weak Instruments and Weak Identification in Generalized Methods of Moments. Journal of Business and Economic Statistics 20, 518-529.
Stock, J. H. and M. Yogo (2004). Testing for Weak Instruments in Linear IV Regression. Mimeo, Harvard University.
Taylor, J. B. (1999). Staggered Price and Wage Setting in Macroeconomics. In J. Taylor and M. Woodford (Eds.), Handbook of Macroeconomics, Volume 1 of Handbooks in Economics Series. Elsevier Science B.V.
Vega, M. and D. Winkelried (2005). How Does Global Disinflation Drag Inflation in Small Open Economies? Central Bank of Peru Working Paper No. 2005-01.
Table 1: Estimates of Open Economy Calvo Model (Capital Not Firm Specific) 1983:Q1 - 2006Q4 a,b
| Parameter | VES with indexation | VES without indexation | CES with indexation | CES without indexation |
|---|---|---|---|---|
| θ | 0.82 (0.03) | 0.82 (0.03) | 0.92 (0.02) | 0.91 (0.02) |
| ψ | 0.73 (0.11) | 0.72 (0.12) | 0 (-) | 0 (-) |
| δD | 0.10 (0.08) | 0 (-) | 0.34 (0.08) | 0 (-) |
| | 0.73 | 0.76 | 0.34 | 0.28 |
| | 0.33 | 0.40 | 0.00 | 0.00 |
| Q-Statistic(1) | 0.20 [0.65] | 2.22 [0.14] | 0.38 [0.54] | 11.43 [0.00] |
| Q-Statistic(4) | 3.93 [0.42] | 6.87 [0.14] | 11.34 [0.02] | 44.33 [0.00] |
| gmin | 71.64 | 62.03 | 72.30 | 62.33 |
a Standard errors are reported in parentheses. A dash in
lieu of a standard error indicates that we restricted the corresponding parameter. Q-statistic refers to the
Ljung-Box test for serial correlation of
![]() at lags 1 and 4.
Probability values of Q-statistics are reported in brackets.
at lags 1 and 4.
Probability values of Q-statistics are reported in brackets.
![]() refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation, and
refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation, and
![]() refers to the contribution of the relative import price to
inflation volatility.
refers to the contribution of the relative import price to
inflation volatility.
b The estimated inflation equation from Section 4 is:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa\left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t}, $](img311.gif)
where
![]() .
.
Table 2: Estimates of Open Economy Calvo Model (Firm-Specific Capital) 1983Q1 - 2006Q4 a,b
| Parameter | VES with indexation | VES without indexation | CES with indexation | CES without indexation |
|---|---|---|---|---|
| θ | 0.75 (0.03) | 0.74 (0.03) | 0.83 (0.03) | 0.80 (0.04) |
| ψ | 0.73 0.11) | 0.72 (0.12) | 0 (-) | 0 (-) |
| δD | 0.10 (0.08) | 0 (-) | 0.34 (0.08) | 0 (-) |
| | 0.73 | 0.76 | 0.34 | 0.28 |
| | 0.33 | 0.40 | 0.00 | 0.00 |
| Q-Statistic(1) | 0.20 [0.65] | 2.22 [0.14] | 0.38 [0.54] | 11.43 [0.00] |
| Q-Statistic(4) | 3.93 [0.42] | 6.87 [0.14] | 11.34 [0.02] | 44.33 [0.00] |
| gmin | 71.64 | 62.03 | 72.30 | 62.33 |
a Standard errors are reported in parentheses. A dash in
lieu of a standard error indicates that we restricted the corresponding parameter. Q-statistic refers to the
Ljung-Box test for serial correlation of
![]() at lags 1 and 4.
Probability values of Q-statistics are reported in brackets.
at lags 1 and 4.
Probability values of Q-statistics are reported in brackets.
![]() refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation, and
refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation, and
![]() refers to the contribution of the relative import price to
inflation volatility.
refers to the contribution of the relative import price to
inflation volatility.
b The estimated inflation equation is:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa_{D} \left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t}, $](img326.gif)
where
![]() .
.
Table 3: Comparison of Benchmark Estimates and Calibrated Demand Curves in the Literature
| Study | ||||
|---|---|---|---|---|
| Benchmark Estimates | 6 | 1.2 | 13.67 | 0.73 |
| Chari, Kehoe, and McGrattan (2000) | 10 | 0.11 | 300 | 0.97 |
| Coenen, Levin, and Christoffel (2007) | 5-20 | 0.05-0.25 | 10-33 | 0.47-0.89 |
| Eichenbaum and Fischer (2007) | 11 | 0.1 | 10-33 | 0.5-0.77 |
| Dossche, Heylen, and den Poel (2007)b | 1.4 | 2.5 | 0.8 | 0.67 |
| Dotsey and King (2005) | 10 | 0.11 | 60 | 0.87 |
| Gust, Leduc, and Vigfusson (2006) | 6 | 0.2 | 18.30 | 0.78 |
b Median estimated demand elasticity and curvature from Table 5.
Table 4: Estimates of VES Specification Under Alternative Calibrations
| Parameter | Benchmark* | ω = 0.35 | εA = 0.5 | εA = 2 | μ = 0.1 |
|---|---|---|---|---|---|
| θ | 0.75 (0.03) | 0.77 (0.03) | 0.72 (0.04) | 0.77 (0.03) | 0.69 (0.04) |
| ψ | 0.73 (0.11) | 0.66 (0.14) | 0.84 (0.08) | 0.56 (0.14) | 0.82 (0.08) |
| δD | 0.10 (0.08) | 0.10 (0.08) | 0.10 (0.08) | 0.10 (0.08) | 0.10 (0.08) |
* The benchmark column refers to the model including firm-specific capital. The estimated inflation equation is:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa_{D} \left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t}, $](img343.gif)
where
![]() .
.
Table 5: Estimates of VES Specification Under Alternative Assumptions a
| Parameter | Benchmark VESb | Smaller Instrument Setc | VAR(2) Forecasting Modeld | Alternative Import Price Seriese | Maximum Likelihood |
|---|---|---|---|---|---|
| θ | 0.75 (0.03) | 0.75 (0.04) | 0.72 (0.05) | 0.75 (0.03) | 0.77 (0.05) |
| ψ | 0.73 (0.11) | 0.67 (0.17) | 0.82 (0.16) | 0.76 (0.12) | 0.71 (0.18) |
| δD | 0.10 (0.08) | 0.16 (0.09) | 0.11 (0.08) | 0.18 (0.09) | 0.11 (0.08) |
| | 0.73 | 0.77 | 0.69 | 0.74 | 0.74 |
| Q-Statistic(1) | 0.20 [0.65] | 0.00 [0.99] | 0.29 [0.59] | 0.12 [0.72] | 0.15 [0.70] |
| Q-Statistic(4) | 3.93 [0.42] | 3.43 [0.49] | 3.82 [0.43] | 5.56 [0.23] | 3.37 [0.50] |
| gmin | 71.64 | 156.81 | 71.03 | 84.07 | - |
a Standard errors are reported in parentheses. Q-statistic
refers to the Ljung-Box test for serial correlation of
![]() at lags 1 and 4,
respectively. Probability values of the Q-statistics are reported
in brackets.
at lags 1 and 4,
respectively. Probability values of the Q-statistics are reported
in brackets.
![]() refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation.
refers
to the ratio of the volatility of predicted inflation to the
volatility of actual inflation.
b The benchmark column refers to the model including firm-specific capital. The estimated inflation equation is:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa_{D} \left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t}, $](img360.gif)
where
![]() .
.
c The benchmark instrument set includes two lags of relative import prices, commodity price inflation, and quadratically-detrended output in the traded goods sector, 4 lags of the interest rate spread, and one lag of real unit labor costs and inflation. The smaller instrument set includes two lags of relative import prices, two lags of inflation, and one lag of real unit labor costs.
d The benchmark system includes an AR(1) process for real unit labor costs and an AR(2) for relative import prices. The VAR(2) model refers to replacing these part of the benchmark system with an unrestricted VAR(2) model for real unit labor costs and relative import prices.
e The benchmark relative import price series is the NIPA price deflator for non-oil imported goods divided by domestic goods prices. The alternative series excludes import prices of industrial goods and materials in addition to fuel prices.
Figure 1: Tradable Goods Inflation and Unit Labor Costs, 1983-2006
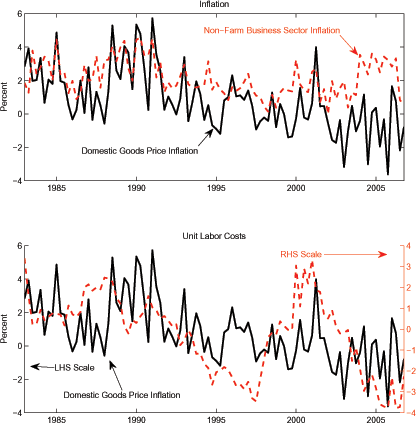
Data for Figure1
| Dates | Domestic Goods Price Inflation | Non-Farm Business Sector Inflation | Unit Labor Costs |
|---|---|---|---|
| 1983 | 2.8390 | 1.8553 | 3.3911 |
| 1983.25 | 3.9175 | 1.2721 | 1.5894 |
| 1983.5 | 1.9786 | 3.7874 | 0.2259 |
| 1983.75 | 2.0320 | 2.3771 | 0.2612 |
| 1984 | 3.3539 | 2.7976 | 0.9329 |
| 1984.25 | 0.6681 | 3.4265 | 0.4333 |
| 1984.5 | 2.0522 | 3.1707 | 0.6021 |
| 1984.75 | 1.7985 | 1.9937 | 0.7526 |
| 1985 | 4.8667 | 4.4514 | 0.7372 |
| 1985.25 | 1.9664 | 2.3090 | 0.6983 |
| 1985.5 | 1.8678 | 2.4543 | 0.1822 |
| 1985.75 | 0.5355 | 1.2463 | 1.1360 |
| 1986 | -0.3250 | 1.9776 | 0.7175 |
| 1986.25 | 0.2367 | 0.8868 | 0.5865 |
| 1986.5 | 1.9943 | 1.2382 | 0.8277 |
| 1986.75 | 0.0566 | 2.9350 | 2.0034 |
| 1987 | 2.7829 | 1.9729 | 2.1472 |
| 1987.25 | -0.3525 | 2.0822 | 1.8502 |
| 1987.5 | 1.3277 | 3.4704 | 2.0007 |
| 1987.75 | 0.5075 | 1.5697 | 1.9133 |
| 1988 | -0.5784 | 3.1992 | 2.4675 |
| 1988.25 | 1.3514 | 3.2521 | 2.4381 |
| 1988.5 | 5.2921 | 4.0455 | 2.2711 |
| 1988.75 | 2.6042 | 3.1522 | 1.5122 |
| 1989 | 2.0836 | 3.9879 | 1.2261 |
| 1989.25 | 4.0562 | 4.3763 | 0.1547 |
| 1989.5 | 3.6807 | 2.7329 | -0.2027 |
| 1989.75 | 1.4782 | 1.9931 | 0.4384 |
| 1990 | 5.3471 | 4.4436 | 0.2994 |
| 1990.25 | 4.7997 | 4.5670 | 0.6130 |
| 1990.5 | 2.6994 | 3.4917 | 0.8619 |
| 1990.75 | 0.2351 | 3.4966 | 1.5854 |
| 1991 | 5.7227 | 4.4916 | 1.0451 |
| 1991.25 | 3.5588 | 2.1808 | 0.9132 |
| 1991.5 | 2.5889 | 3.0999 | 0.5089 |
| 1991.75 | 0.2515 | 1.2932 | 0.6331 |
| 1992 | 1.0400 | 1.8833 | 0.4089 |
| 1992.25 | 0.5457 | 1.5246 | 0.1443 |
| 1992.5 | -0.0294 | 1.6933 | 0.2372 |
| 1992.75 | 0.9115 | 2.2596 | -0.7603 |
| 1993 | 3.3976 | 2.9483 | -0.5355 |
| 1993.25 | -0.4375 | 1.7784 | -0.0315 |
| 1993.5 | 0.6595 | 1.6005 | -0.4020 |
| 1993.75 | 1.9460 | 1.5836 | -1.1852 |
| 1994 | 1.2021 | 1.6559 | -1.1418 |
| 1994.25 | -0.3595 | 1.7437 | -1.6586 |
| 1994.5 | 0.5197 | 3.1456 | -1.8575 |
| 1994.75 | -0.6822 | 1.4510 | -2.6545 |
| 1995 | -0.8997 | 1.9080 | -2.0581 |
| 1995.25 | -1.1882 | 1.4568 | -1.9789 |
| 1995.5 | 0.8094 | 1.2324 | -1.8100 |
| 1995.75 | 1.0045 | 0.8248 | -1.9503 |
| 1996 | 2.3045 | 1.6015 | -2.3052 |
| 1996.25 | 1.0560 | 1.3863 | -2.7168 |
| 1996.5 | 1.1070 | 1.5432 | -2.6384 |
| 1996.75 | 0.8429 | 1.9244 | -2.8660 |
| 1997 | 1.3992 | 2.4015 | -2.5176 |
| 1997.25 | 0.5054 | 1.4543 | -3.3062 |
| 1997.5 | -0.9303 | 1.0973 | -3.4545 |
| 1997.75 | -0.4448 | 1.0181 | -2.3995 |
| 1998 | -0.2187 | 0.4408 | -1.4227 |
| 1998.25 | -0.4110 | 0.1393 | -0.3860 |
| 1998.5 | 1.2764 | 1.1461 | -0.1596 |
| 1998.75 | -0.7948 | 0.3709 | -0.2606 |
| 1999 | 0.5943 | 1.2786 | 0.3754 |
| 1999.25 | -0.0240 | 1.5594 | 0.1563 |
| 1999.5 | -1.3982 | 1.4016 | -0.0304 |
| 1999.75 | -1.3468 | 1.3491 | -0.0477 |
| 2000 | -0.2779 | 3.2462 | 3.0463 |
| 2000.25 | 1.5568 | 1.7692 | 1.0945 |
| 2000.5 | -0.2134 | 1.4300 | 2.9124 |
| 2000.75 | -0.3365 | 1.3068 | 2.1898 |
| 2001 | 0.6231 | 2.5208 | 3.3219 |
| 2001.25 | 3.9925 | 2.7078 | 1.8680 |
| 2001.5 | 0.4587 | 0.7057 | 1.7860 |
| 2001.75 | 0.4751 | 1.4847 | 0.6883 |
| 2002 | -0.5486 | -0.0137 | 0.5147 |
| 2002.25 | -1.5601 | 1.9666 | 0.9178 |
| 2002.5 | -1.7272 | 0.9129 | 0.1306 |
| 2002.75 | -0.3690 | 1.5506 | -0.1971 |
| 2003 | -3.1754 | 1.9408 | -0.1774 |
| 2003.25 | -1.0376 | 0.3836 | -0.0365 |
| 2003.5 | 0.4889 | 1.2930 | -1.5192 |
| 2003.75 | -1.0384 | 1.1261 | -0.8640 |
| 2004 | -0.4198 | 3.5424 | -1.8877 |
| 2004.25 | 1.1612 | 3.0094 | -2.9529 |
| 2004.5 | -3.0142 | 2.3606 | -2.5238 |
| 2004.75 | 0.0885 | 3.6080 | -2.1693 |
| 2005 | 0.3693 | 3.2671 | -2.8145 |
| 2005.25 | -1.9514 | 2.4909 | -3.5902 |
| 2005.5 | -0.3220 | 3.4302 | -3.7031 |
| 2005.75 | -3.6163 | 3.2297 | -3.7721 |
| 2006 | 1.6565 | 2.8366 | -2.3027 |
| 2006.25 | 0.7587 | 3.3286 | -3.7783 |
| 2006.5 | -2.1775 | 0.8359 | -3.7241 |
| 2006.75 | -0.7866 | 0.5262 | -2.2646 |
Figure 2: Relative Import Prices, 1983-2006
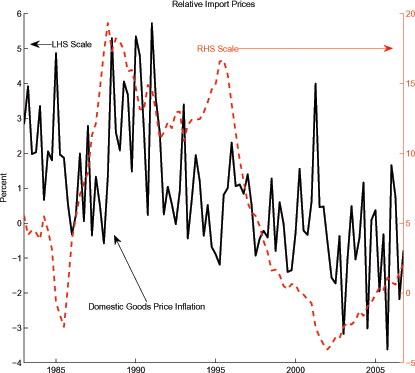
Data for Figure 2
| Dates | Domestic Goods Price Inflation | Relative Import Prices |
|---|---|---|
| 1983 | 2.8390 | 5.5375 |
| 1983.25 | 3.9175 | 4.1483 |
| 1983.5 | 1.9786 | 4.4951 |
| 1983.75 | 2.0320 | 4.3155 |
| 1984 | 3.3539 | 3.8445 |
| 1984.25 | 0.6681 | 5.4790 |
| 1984.5 | 2.0522 | 4.4800 |
| 1984.75 | 1.7985 | 3.1225 |
| 1985 | 4.8667 | -0.6729 |
| 1985.25 | 1.9664 | -1.5823 |
| 1985.5 | 1.8678 | -2.4255 |
| 1985.75 | 0.5355 | 0.5466 |
| 1986 | -0.3250 | 3.8426 |
| 1986.25 | 0.2367 | 5.4281 |
| 1986.5 | 1.9943 | 7.0653 |
| 1986.75 | 0.0566 | 7.8847 |
| 1987 | 2.7829 | 8.6348 |
| 1987.25 | -0.3525 | 11.3002 |
| 1987.5 | 1.3277 | 12.1361 |
| 1987.75 | 0.5075 | 14.6368 |
| 1988 | -0.5784 | 17.2440 |
| 1988.25 | 1.3514 | 19.3260 |
| 1988.5 | 5.2921 | 17.3124 |
| 1988.75 | 2.6042 | 18.2270 |
| 1989 | 2.0836 | 17.9804 |
| 1989.25 | 4.0562 | 17.4079 |
| 1989.5 | 3.6807 | 15.8572 |
| 1989.75 | 1.4782 | 15.9689 |
| 1990 | 5.3471 | 14.7110 |
| 1990.25 | 4.7997 | 13.1674 |
| 1990.5 | 2.6994 | 13.0817 |
| 1990.75 | 0.2351 | 14.8954 |
| 1991 | 5.7227 | 14.6210 |
| 1991.25 | 3.5588 | 13.0388 |
| 1991.5 | 2.5889 | 11.0222 |
| 1991.75 | 0.2515 | 11.4805 |
| 1992 | 1.0400 | 12.2291 |
| 1992.25 | 0.5457 | 11.8010 |
| 1992.5 | -0.0294 | 12.9427 |
| 1992.75 | 0.9115 | 12.9829 |
| 1993 | 3.3976 | 10.8832 |
| 1993.25 | -0.4375 | 12.0155 |
| 1993.5 | 0.6595 | 12.4006 |
| 1993.75 | 1.9460 | 12.4081 |
| 1994 | 1.2021 | 12.4506 |
| 1994.25 | -0.3595 | 12.9318 |
| 1994.5 | 0.5197 | 13.6667 |
| 1994.75 | -0.6822 | 14.5583 |
| 1995 | -0.8997 | 14.9775 |
| 1995.25 | -1.1882 | 16.5707 |
| 1995.5 | 0.8094 | 16.6688 |
| 1995.75 | 1.0045 | 15.6307 |
| 1996 | 2.3045 | 13.5245 |
| 1996.25 | 1.0560 | 11.4663 |
| 1996.5 | 1.1070 | 9.5401 |
| 1996.75 | 0.8429 | 8.0172 |
| 1997 | 1.3992 | 6.4488 |
| 1997.25 | 0.5054 | 5.7724 |
| 1997.5 | -0.9303 | 5.5154 |
| 1997.75 | -0.4448 | 4.7928 |
| 1998 | -0.2187 | 3.7051 |
| 1998.25 | -0.4110 | 2.8980 |
| 1998.5 | 1.2764 | 1.6000 |
| 1998.75 | -0.7948 | 1.6680 |
| 1999 | 0.5943 | 1.2777 |
| 1999.25 | -0.0240 | 0.4939 |
| 1999.5 | -1.3982 | 0.2705 |
| 1999.75 | -1.3468 | 0.6392 |
| 2000 | -0.2779 | 0.5775 |
| 2000.25 | 1.5568 | -0.0017 |
| 2000.5 | -0.2134 | -0.1238 |
| 2000.75 | -0.3365 | -0.4679 |
| 2001 | 0.6231 | -0.7365 |
| 2001.25 | 3.9925 | -2.4355 |
| 2001.5 | 0.4587 | -3.1608 |
| 2001.75 | 0.4751 | -3.6826 |
| 2002 | -0.5486 | -4.0461 |
| 2002.25 | -1.5601 | -3.7026 |
| 2002.5 | -1.7272 | -3.1703 |
| 2002.75 | -0.3690 | -3.2598 |
| 2003 | -3.1754 | -2.4228 |
| 2003.25 | -1.0376 | -2.1257 |
| 2003.5 | 0.4889 | -2.2644 |
| 2003.75 | -1.0384 | -1.9621 |
| 2004 | -0.4198 | -1.2941 |
| 2004.25 | 1.1612 | -1.6468 |
| 2004.5 | -3.0142 | -0.9593 |
| 2004.75 | 0.0885 | -0.6691 |
| 2005 | 0.3693 | -0.1165 |
| 2005.25 | -1.9514 | 0.3880 |
| 2005.5 | -0.3220 | 0.2094 |
| 2005.75 | -3.6163 | 1.0969 |
| 2006 | 1.6565 | 0.7607 |
| 2006.25 | 0.7587 | 0.5993 |
| 2006.5 | -2.1775 | 1.5311 |
| 2006.75 | -0.7866 | 2.0188 |
Figure 3: Cross-Correlogram for Inflation, 1983-2006
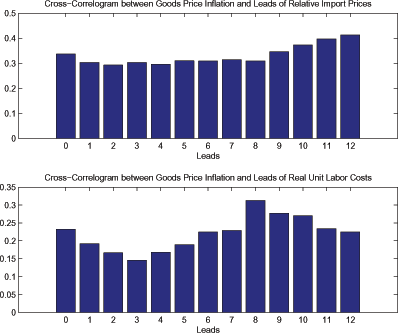
Data for Figure 3
| Leads | Cross-correlogram with Relative Import Prices | Cross-correlograms with Real Unit Labor Costs |
|---|---|---|
| 0 | 0.3370 | 0.2325 |
| 1 | 0.3031 | 0.1918 |
| 2 | 0.2929 | 0.1665 |
| 3 | 0.3029 | 0.1459 |
| 4 | 0.2962 | 0.1684 |
| 5 | 0.3101 | 0.1895 |
| 6 | 0.3089 | 0.2246 |
| 7 | 0.3142 | 0.2291 |
| 8 | 0.3089 | 0.3125 |
| 9 | 0.3457 | 0.2772 |
| 10 | 0.3733 | 0.2697 |
| 11 | 0.3971 | 0.2338 |
| 12 | 0.4132 | 0.2251 |
Figure 4: Properties of Estimated Demand Curve
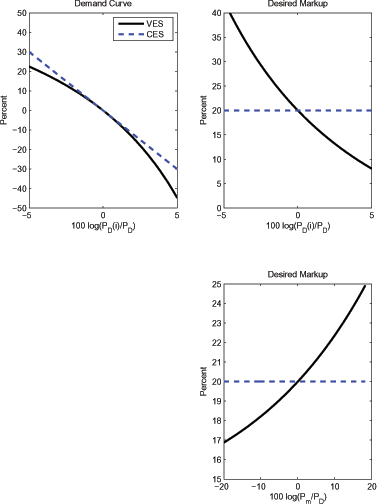
Figure 5: Actual and Predicted Inflation from Alternative Specifications (4-Quarter Moving Average)
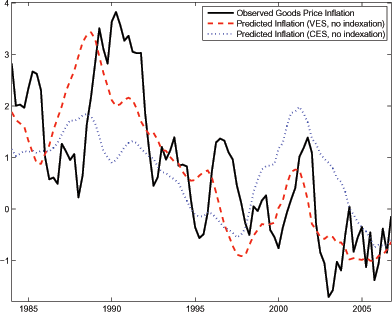
Predicted inflation is defined in equation (27) in the text. The estimated parameters used in constructing the predicted series for the VES specification are reported in the second column of Table 2, labelled "VES without indexation." The parameters used for the CES case appear in the fourth column of Table 2, labelled "CES without indexation."
Data for Figure 5
| Dates | Predicted Inflation (CES, no indexation) | Predicted Inflation (VES, no indexation) | Observed Goods Price Inflation |
|---|---|---|---|
| 1984 | 1.1602 | 1.8822 | 2.8205 |
| 1984.25 | 1.0296 | 1.7314 | 2.0081 |
| 1984.5 | 1.0721 | 1.6632 | 2.0266 |
| 1984.75 | 1.1276 | 1.6001 | 1.9682 |
| 1985 | 1.1055 | 1.3242 | 2.3464 |
| 1985.25 | 1.1354 | 1.0966 | 2.6709 |
| 1985.5 | 1.0880 | 0.8859 | 2.6248 |
| 1985.75 | 1.1313 | 0.8786 | 2.3091 |
| 1986 | 1.1291 | 1.0739 | 1.0112 |
| 1986.25 | 1.1165 | 1.2357 | 0.5787 |
| 1986.5 | 1.1894 | 1.5331 | 0.6104 |
| 1986.75 | 1.2873 | 1.7655 | 0.4906 |
| 1987 | 1.4488 | 1.9962 | 1.2676 |
| 1987.25 | 1.5916 | 2.2868 | 1.1203 |
| 1987.5 | 1.7241 | 2.4928 | 0.9537 |
| 1987.75 | 1.7139 | 2.6838 | 1.0664 |
| 1988 | 1.7501 | 2.9674 | 0.2261 |
| 1988.25 | 1.8165 | 3.2363 | 0.6520 |
| 1988.5 | 1.8471 | 3.3777 | 1.6431 |
| 1988.75 | 1.8017 | 3.4319 | 2.1673 |
| 1989 | 1.6615 | 3.3012 | 2.8328 |
| 1989.25 | 1.4036 | 2.9599 | 3.5090 |
| 1989.5 | 1.1241 | 2.6424 | 3.1062 |
| 1989.75 | 1.0028 | 2.3844 | 2.8247 |
| 1990 | 0.8982 | 2.1127 | 3.6406 |
| 1990.25 | 0.9499 | 2.0001 | 3.8264 |
| 1990.5 | 1.0702 | 2.0352 | 3.5811 |
| 1990.75 | 1.1998 | 2.1228 | 3.2703 |
| 1991 | 1.2840 | 2.1616 | 3.3642 |
| 1991.25 | 1.3179 | 2.1182 | 3.0540 |
| 1991.5 | 1.2780 | 1.9411 | 3.0264 |
| 1991.75 | 1.1705 | 1.7012 | 3.0305 |
| 1992 | 1.0986 | 1.5601 | 1.8598 |
| 1992.25 | 1.0117 | 1.4419 | 1.1065 |
| 1992.5 | 0.9811 | 1.4793 | 0.4519 |
| 1992.75 | 0.8237 | 1.3409 | 0.6169 |
| 1993 | 0.7170 | 1.1473 | 1.2063 |
| 1993.25 | 0.6971 | 1.1297 | 0.9605 |
| 1993.5 | 0.6249 | 1.0112 | 1.1328 |
| 1993.75 | 0.5769 | 0.9181 | 1.3914 |
| 1994 | 0.5084 | 0.8832 | 0.8425 |
| 1994.25 | 0.3246 | 0.7234 | 0.8620 |
| 1994.5 | 0.1602 | 0.6119 | 0.8271 |
| 1994.75 | -0.0058 | 0.5500 | 0.1700 |
| 1995 | -0.1093 | 0.5639 | -0.3554 |
| 1995.25 | -0.1454 | 0.6506 | -0.5626 |
| 1995.5 | -0.1401 | 0.7140 | -0.4902 |
| 1995.75 | -0.0605 | 0.7500 | -0.0685 |
| 1996 | -0.0884 | 0.6102 | 0.7325 |
| 1996.25 | -0.1718 | 0.3228 | 1.2936 |
| 1996.5 | -0.2654 | 0.0078 | 1.3680 |
| 1996.75 | -0.3688 | -0.3016 | 1.3276 |
| 1997 | -0.3928 | -0.5039 | 1.1013 |
| 1997.25 | -0.4594 | -0.7148 | 0.9636 |
| 1997.5 | -0.5516 | -0.8836 | 0.4543 |
| 1997.75 | -0.4989 | -0.9140 | 0.1324 |
| 1998 | -0.3752 | -0.9017 | -0.2721 |
| 1998.25 | -0.0453 | -0.6980 | -0.5012 |
| 1998.5 | 0.3269 | -0.5182 | 0.0505 |
| 1998.75 | 0.5685 | -0.4053 | -0.0370 |
| 1999 | 0.7716 | -0.2913 | 0.1662 |
| 1999.25 | 0.8328 | -0.3073 | 0.2630 |
| 1999.5 | 0.8474 | -0.2925 | -0.4057 |
| 1999.75 | 0.8715 | -0.2665 | -0.5437 |
| 2000 | 1.1732 | 0.0248 | -0.7617 |
| 2000.25 | 1.2792 | 0.1557 | -0.3665 |
| 2000.5 | 1.6116 | 0.4826 | -0.0703 |
| 2000.75 | 1.8643 | 0.7199 | 0.1823 |
| 2001 | 1.8955 | 0.7661 | 0.4075 |
| 2001.25 | 1.9828 | 0.7547 | 1.0164 |
| 2001.5 | 1.8556 | 0.4996 | 1.1844 |
| 2001.75 | 1.6860 | 0.1765 | 1.3873 |
| 2002 | 1.3689 | -0.2873 | 1.0944 |
| 2002.25 | 1.2616 | -0.4055 | -0.2937 |
| 2002.5 | 1.0746 | -0.5431 | -0.8402 |
| 2002.75 | 0.9745 | -0.5792 | -1.0512 |
| 2003 | 0.8964 | -0.5143 | -1.7079 |
| 2003.25 | 0.7886 | -0.5428 | -1.5773 |
| 2003.5 | 0.6022 | -0.6572 | -1.0233 |
| 2003.75 | 0.5269 | -0.6481 | -1.1906 |
| 2004 | 0.3337 | -0.7621 | -0.5017 |
| 2004.25 | 0.0042 | -0.9778 | 0.0480 |
| 2004.5 | -0.1092 | -0.9541 | -0.8278 |
| 2004.75 | -0.2567 | -0.9723 | -0.5461 |
| 2005 | -0.3613 | -0.9884 | -0.3488 |
| 2005.25 | -0.4333 | -0.9427 | -1.1269 |
| 2005.5 | -0.5666 | -1.0036 | -0.4539 |
| 2005.75 | -0.7476 | -1.0101 | -1.3801 |
| 2006 | -0.6898 | -0.9091 | -1.0583 |
| 2006.25 | -0.7110 | -0.8919 | -0.3808 |
| 2006.5 | -0.7134 | -0.7882 | -0.8446 |
| 2006.75 | -0.5431 | -0.6416 | -0.1372 |
Figure 6: Sampling Distribution of Estimates from Alternative Specifications
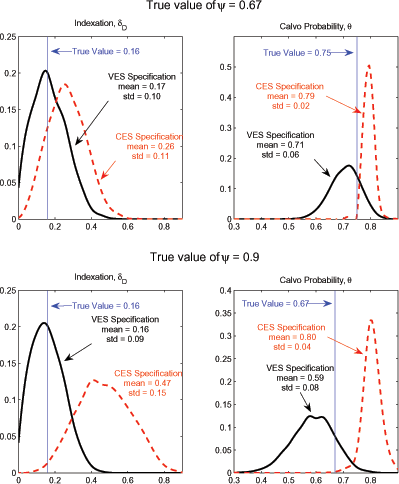
The VES specification described in equation (26) in the text is used as the data-generating process.
Data for Figure 6 - Panel A: Indexation, δD
Indexation, δD | True Value of ψ = 0.67: Probability Density Function of Estimator from CES Specification | True Value of ψ = 0.67: Probability Density Function of Estimator from VES specification | True Value of ψ = 0.9: Probability Density Function of Estimator from CES Specification | True Value of ψ = 0.9: Probability Density Function of Estimator from VES specification |
|---|---|---|---|---|
0.000 |
0.0019293 |
0.0431689 |
0.0001354 |
0.0414185 |
0.005 |
0.0026540 |
0.0557006 |
0.0000155 |
0.0556164 |
0.010 |
0.0037207 |
0.0671857 |
-0.0000699 |
0.0688779 |
0.015 |
0.0051167 |
0.0776919 |
-0.0001216 |
0.0812418 |
0.020 |
0.0068292 |
0.0872867 |
-0.0001401 |
0.0927468 |
0.025 |
0.0088453 |
0.0960378 |
-0.0001263 |
0.1034317 |
0.030 |
0.0111522 |
0.1040130 |
-0.0000806 |
0.1133354 |
0.035 |
0.0137371 |
0.1112798 |
-0.0000039 |
0.1224965 |
0.040 |
0.0165871 |
0.1179060 |
0.0001032 |
0.1309538 |
0.045 |
0.0196895 |
0.1239591 |
0.0002401 |
0.1387461 |
0.050 |
0.0230315 |
0.1295068 |
0.0004061 |
0.1459123 |
0.055 |
0.0266001 |
0.1346168 |
0.0006005 |
0.1524910 |
0.060 |
0.0303826 |
0.1393568 |
0.0008226 |
0.1585210 |
0.065 |
0.0343662 |
0.1437943 |
0.0010719 |
0.1640412 |
0.070 |
0.0385379 |
0.1479971 |
0.0013476 |
0.1690902 |
0.075 |
0.0428851 |
0.1520328 |
0.0016490 |
0.1737069 |
0.080 |
0.0473949 |
0.1559691 |
0.0019755 |
0.1779300 |
0.085 |
0.0520544 |
0.1598736 |
0.0023265 |
0.1817983 |
0.090 |
0.0568509 |
0.1638139 |
0.0027012 |
0.1853506 |
0.095 |
0.0617715 |
0.1678578 |
0.0030990 |
0.1886256 |
0.100 |
0.0668033 |
0.1720728 |
0.0035192 |
0.1916622 |
0.105 |
0.0719306 |
0.1764914 |
0.0039634 |
0.1944858 |
0.110 |
0.0771249 |
0.1810044 |
0.0044415 |
0.1970694 |
0.115 |
0.0823549 |
0.1854675 |
0.0049660 |
0.1993725 |
0.120 |
0.0875892 |
0.1897363 |
0.0055490 |
0.2013548 |
0.125 |
0.0927965 |
0.1936664 |
0.0062028 |
0.2029759 |
0.130 |
0.0979452 |
0.1971134 |
0.0069398 |
0.2041954 |
0.135 |
0.1030042 |
0.1999330 |
0.0077720 |
0.2049729 |
0.140 |
0.1079418 |
0.2019808 |
0.0087120 |
0.2052682 |
0.145 |
0.1127269 |
0.2031124 |
0.0097718 |
0.2050407 |
0.150 |
0.1173279 |
0.2031834 |
0.0109637 |
0.2042501 |
0.155 |
0.1217237 |
0.2021023 |
0.0122960 |
0.2028732 |
0.160 |
0.1259339 |
0.1999889 |
0.0137600 |
0.2009546 |
0.165 |
0.1299885 |
0.1970160 |
0.0153430 |
0.1985561 |
0.170 |
0.1339171 |
0.1933563 |
0.0170325 |
0.1957397 |
0.175 |
0.1377498 |
0.1891825 |
0.0188158 |
0.1925671 |
0.180 |
0.1415163 |
0.1846673 |
0.0206802 |
0.1891001 |
0.185 |
0.1452465 |
0.1799833 |
0.0226130 |
0.1854005 |
0.190 |
0.1489702 |
0.1753034 |
0.0246015 |
0.1815302 |
0.195 |
0.1527172 |
0.1708003 |
0.0266331 |
0.1775510 |
0.200 |
0.1565175 |
0.1666466 |
0.0286952 |
0.1735246 |
0.205 |
0.1603816 |
0.1629686 |
0.0307781 |
0.1694974 |
0.210 |
0.1642430 |
0.1597069 |
0.0328847 |
0.1654535 |
0.215 |
0.1680157 |
0.1567557 |
0.0350208 |
0.1613613 |
0.220 |
0.1716140 |
0.1540091 |
0.0371925 |
0.1571894 |
0.225 |
0.1749521 |
0.1513612 |
0.0394056 |
0.1529063 |
0.230 |
0.1779440 |
0.1487062 |
0.0416660 |
0.1484806 |
0.235 |
0.1805041 |
0.1459382 |
0.0439797 |
0.1438809 |
0.240 |
0.1825463 |
0.1429513 |
0.0463525 |
0.1390755 |
0.245 |
0.1839849 |
0.1396398 |
0.0487905 |
0.1340331 |
0.250 |
0.1847341 |
0.1358977 |
0.0512994 |
0.1287223 |
0.255 |
0.1847366 |
0.1316511 |
0.0538813 |
0.1231275 |
0.260 |
0.1840494 |
0.1269531 |
0.0565227 |
0.1172976 |
0.265 |
0.1827581 |
0.1218887 |
0.0592060 |
0.1112975 |
0.270 |
0.1809483 |
0.1165430 |
0.0619137 |
0.1051920 |
0.275 |
0.1787055 |
0.1110011 |
0.0646284 |
0.0990460 |
0.280 |
0.1761155 |
0.1053479 |
0.0673325 |
0.0929243 |
0.285 |
0.1732637 |
0.0996685 |
0.0700086 |
0.0868918 |
0.290 |
0.1702357 |
0.0940479 |
0.0726391 |
0.0810135 |
0.295 |
0.1671172 |
0.0885711 |
0.0752066 |
0.0753540 |
0.300 |
0.1639937 |
0.0833233 |
0.0776936 |
0.0699783 |
0.305 |
0.1609314 |
0.0783704 |
0.0800897 |
0.0649368 |
0.310 |
0.1579181 |
0.0737026 |
0.0824138 |
0.0602214 |
0.315 |
0.1549224 |
0.0692911 |
0.0846916 |
0.0558096 |
0.320 |
0.1519128 |
0.0651072 |
0.0869490 |
0.0516789 |
0.325 |
0.1488577 |
0.0611220 |
0.0892120 |
0.0478068 |
0.330 |
0.1457257 |
0.0573067 |
0.0915064 |
0.0441708 |
0.335 |
0.1424853 |
0.0536325 |
0.0938581 |
0.0407484 |
0.340 |
0.1391048 |
0.0500707 |
0.0962930 |
0.0375171 |
0.345 |
0.1355529 |
0.0465925 |
0.0988370 |
0.0344544 |
0.350 |
0.1317979 |
0.0431689 |
0.1015160 |
0.0315376 |
0.355 |
0.1278182 |
0.0397806 |
0.1043402 |
0.0287490 |
0.360 |
0.1236315 |
0.0364447 |
0.1072580 |
0.0260888 |
0.365 |
0.1192651 |
0.0331879 |
0.1102018 |
0.0235619 |
0.370 |
0.1147465 |
0.0300366 |
0.1131044 |
0.0211732 |
0.375 |
0.1101032 |
0.0270174 |
0.1158983 |
0.0189275 |
0.380 |
0.1053626 |
0.0241569 |
0.1185162 |
0.0168298 |
0.385 |
0.1005521 |
0.0214815 |
0.1208907 |
0.0148849 |
0.390 |
0.0956993 |
0.0190179 |
0.1229543 |
0.0130978 |
0.395 |
0.0908314 |
0.0167924 |
0.1246398 |
0.0114733 |
0.400 |
0.0859761 |
0.0148318 |
0.1258798 |
0.0100162 |
0.405 |
0.0811589 |
0.0131529 |
0.1266297 |
0.0087284 |
0.410 |
0.0763982 |
0.0117342 |
0.1269365 |
0.0075989 |
0.415 |
0.0717104 |
0.0105448 |
0.1268701 |
0.0066136 |
0.420 |
0.0671120 |
0.0095535 |
0.1265002 |
0.0057584 |
0.425 |
0.0626196 |
0.0087294 |
0.1258967 |
0.0050193 |
0.430 |
0.0582497 |
0.0080414 |
0.1251294 |
0.0043822 |
0.435 |
0.0540188 |
0.0074584 |
0.1242682 |
0.0038329 |
0.440 |
0.0499433 |
0.0069494 |
0.1233829 |
0.0033575 |
0.445 |
0.0460398 |
0.0064833 |
0.1225432 |
0.0029418 |
0.450 |
0.0423249 |
0.0060292 |
0.1218192 |
0.0025717 |
0.455 |
0.0388121 |
0.0055622 |
0.1212630 |
0.0022354 |
0.460 |
0.0355042 |
0.0050834 |
0.1208573 |
0.0019292 |
0.465 |
0.0324010 |
0.0045998 |
0.1205672 |
0.0016519 |
0.470 |
0.0295024 |
0.0041187 |
0.1203578 |
0.0014022 |
0.475 |
0.0268083 |
0.0036473 |
0.1201941 |
0.0011786 |
0.480 |
0.0243184 |
0.0031928 |
0.1200414 |
0.0009798 |
0.485 |
0.0220327 |
0.0027624 |
0.1198646 |
0.0008045 |
0.490 |
0.0199511 |
0.0023634 |
0.1196290 |
0.0006514 |
0.495 |
0.0180734 |
0.0020029 |
0.1192995 |
0.0005190 |
0.500 |
0.0163994 |
0.0016882 |
0.1188414 |
0.0004061 |
0.505 |
0.0149253 |
0.0014243 |
0.1182273 |
0.0003111 |
0.510 |
0.0136323 |
0.0012076 |
0.1174610 |
0.0002327 |
0.515 |
0.0124981 |
0.0010323 |
0.1165536 |
0.0001690 |
0.520 |
0.0115001 |
0.0008928 |
0.1155165 |
0.0001185 |
0.525 |
0.0106158 |
0.0007832 |
0.1143609 |
0.0000795 |
0.530 |
0.0098228 |
0.0006977 |
0.1130981 |
0.0000504 |
0.535 |
0.0090986 |
0.0006307 |
0.1117395 |
0.0000295 |
0.540 |
0.0084208 |
0.0005763 |
0.1102962 |
0.0000153 |
0.545 |
0.0077669 |
0.0005287 |
0.1087796 |
0.0000060 |
0.550 |
0.0071144 |
0.0004823 |
0.1072009 |
0.0000000 |
0.555 |
0.0064465 |
0.0004325 |
0.1055704 |
-0.0000041 |
0.560 |
0.0057687 |
0.0003793 |
0.1038943 |
-0.0000066 |
0.565 |
0.0050921 |
0.0003243 |
0.1021779 |
-0.0000080 |
0.570 |
0.0044279 |
0.0002687 |
0.1004263 |
-0.0000082 |
0.575 |
0.0037872 |
0.0002139 |
0.0986447 |
-0.0000077 |
0.580 |
0.0031812 |
0.0001613 |
0.0968384 |
-0.0000065 |
0.585 |
0.0026210 |
0.0001123 |
0.0950125 |
-0.0000050 |
0.590 |
0.0021177 |
0.0000681 |
0.0931722 |
-0.0000032 |
0.595 |
0.0016824 |
0.0000302 |
0.0913228 |
-0.0000015 |
0.600 |
0.0013264 |
0.0000000 |
0.0894694 |
0.0000000 |
0.605 |
0.0010569 |
-0.0000217 |
0.0876161 |
0.0000011 |
0.610 |
0.0008658 |
-0.0000355 |
0.0857619 |
0.0000018 |
0.615 |
0.0007411 |
-0.0000426 |
0.0839049 |
0.0000021 |
0.620 |
0.0006709 |
-0.0000441 |
0.0820431 |
0.0000022 |
0.625 |
0.0006432 |
-0.0000412 |
0.0801743 |
0.0000021 |
0.630 |
0.0006460 |
-0.0000350 |
0.0782966 |
0.0000018 |
0.635 |
0.0006674 |
-0.0000266 |
0.0764078 |
0.0000013 |
0.640 |
0.0006954 |
-0.0000172 |
0.0745060 |
0.0000009 |
0.645 |
0.0007181 |
-0.0000080 |
0.0725891 |
0.0000004 |
0.650 |
0.0007235 |
0.0000000 |
0.0706551 |
0.0000000 |
0.655 |
0.0007024 |
0.0000058 |
0.0687018 |
-0.0000003 |
0.660 |
0.0006570 |
0.0000095 |
0.0667266 |
-0.0000005 |
0.665 |
0.0005920 |
0.0000114 |
0.0647268 |
-0.0000006 |
0.670 |
0.0005124 |
0.0000118 |
0.0626997 |
-0.0000006 |
0.675 |
0.0004230 |
0.0000110 |
0.0606425 |
-0.0000006 |
0.680 |
0.0003287 |
0.0000094 |
0.0585525 |
-0.0000005 |
0.685 |
0.0002344 |
0.0000071 |
0.0564270 |
-0.0000004 |
0.690 |
0.0001449 |
0.0000046 |
0.0542634 |
-0.0000002 |
0.695 |
0.0000652 |
0.0000021 |
0.0520588 |
-0.0000001 |
0.700 |
0.0000000 |
0.0000000 |
0.0498105 |
0.0000000 |
0.705 |
-0.0000469 |
-0.0000016 |
0.0475185 |
0.0000001 |
0.710 |
-0.0000768 |
-0.0000025 |
0.0451930 |
0.0000001 |
0.715 |
-0.0000922 |
-0.0000031 |
0.0428470 |
0.0000002 |
0.720 |
-0.0000955 |
-0.0000032 |
0.0404934 |
0.0000002 |
0.725 |
-0.0000892 |
-0.0000030 |
0.0381451 |
0.0000001 |
0.730 |
-0.0000758 |
-0.0000025 |
0.0358150 |
0.0000001 |
0.735 |
-0.0000577 |
-0.0000019 |
0.0335161 |
0.0000001 |
0.740 |
-0.0000374 |
-0.0000012 |
0.0312613 |
0.0000001 |
0.745 |
-0.0000173 |
-0.0000006 |
0.0290635 |
0.0000000 |
0.750 |
0.0000000 |
0.0000000 |
0.0269356 |
0.0000000 |
0.755 |
0.0000127 |
0.0000004 |
0.0248888 |
0.0000000 |
0.760 |
0.0000208 |
0.0000007 |
0.0229280 |
0.0000000 |
0.765 |
0.0000250 |
0.0000008 |
0.0210560 |
0.0000000 |
0.770 |
0.0000260 |
0.0000009 |
0.0192758 |
0.0000000 |
0.775 |
0.0000243 |
0.0000008 |
0.0175906 |
0.0000000 |
0.780 |
0.0000208 |
0.0000007 |
0.0160032 |
0.0000000 |
0.785 |
0.0000159 |
0.0000005 |
0.0145168 |
0.0000000 |
0.790 |
0.0000104 |
0.0000003 |
0.0131343 |
0.0000000 |
0.795 |
0.0000049 |
0.0000002 |
0.0118587 |
0.0000000 |
0.800 |
0.0000000 |
0.0000000 |
0.0106930 |
0.0000000 |
0.805 |
-0.0000037 |
-0.0000001 |
0.0096385 |
0.0000000 |
0.810 |
-0.0000062 |
-0.0000002 |
0.0086890 |
0.0000000 |
0.815 |
-0.0000077 |
-0.0000003 |
0.0078367 |
0.0000000 |
0.820 |
-0.0000083 |
-0.0000003 |
0.0070735 |
0.0000000 |
0.825 |
-0.0000081 |
-0.0000003 |
0.0063917 |
0.0000000 |
0.830 |
-0.0000073 |
-0.0000002 |
0.0057833 |
0.0000000 |
0.835 |
-0.0000059 |
-0.0000002 |
0.0052403 |
0.0000000 |
0.840 |
-0.0000042 |
-0.0000001 |
0.0047550 |
0.0000000 |
0.845 |
-0.0000021 |
-0.0000001 |
0.0043192 |
0.0000000 |
0.850 |
0.0000000 |
0.0000000 |
0.0039253 |
0.0000000 |
0.855 |
0.0000021 |
0.0000001 |
0.0035652 |
0.0000000 |
0.860 |
0.0000042 |
0.0000001 |
0.0032310 |
0.0000000 |
0.865 |
0.0000059 |
0.0000002 |
0.0029148 |
0.0000000 |
0.870 |
0.0000073 |
0.0000002 |
0.0026087 |
0.0000000 |
0.875 |
0.0000081 |
0.0000003 |
0.0023048 |
0.0000000 |
0.880 |
0.0000083 |
0.0000003 |
0.0019952 |
0.0000000 |
0.885 |
0.0000077 |
0.0000003 |
0.0016720 |
0.0000000 |
0.890 |
0.0000062 |
0.0000002 |
0.0013272 |
0.0000000 |
0.895 |
0.0000037 |
0.0000001 |
0.0009530 |
0.0000000 |
0.900 |
0.0000000 |
0.0000000 |
0.0005414 |
0.0000000 |
Data for Figure 6 - Panel B: Calvo Probability, θ
Calvo Probability, θ | True Value of ψ = 0.67: Probability Density Function of Estimator from CES Specification | True Value of ψ = 0.67: Probability Density Function of Estimator from VES specification | True Value of ψ = 0.9: Probability Density Function of Estimator from CES Specification | True Value of ψ = 0.9: Probability Density Function of Estimator from VES specification |
|---|---|---|---|---|
0.300 |
0.0000000 |
0.0000000 |
0.0009475 |
0.0002707 |
0.305 |
0.0000000 |
0.0000002 |
0.0006967 |
0.0006234 |
0.310 |
0.0000000 |
0.0000003 |
0.0004958 |
0.0008889 |
0.315 |
0.0000000 |
0.0000002 |
0.0003391 |
0.0010864 |
0.320 |
0.0000000 |
0.0000001 |
0.0002208 |
0.0012349 |
0.325 |
0.0000000 |
0.0000000 |
0.0001354 |
0.0013535 |
0.330 |
0.0000000 |
-0.0000001 |
0.0000769 |
0.0014613 |
0.335 |
0.0000000 |
-0.0000002 |
0.0000399 |
0.0015773 |
0.340 |
0.0000000 |
-0.0000003 |
0.0000185 |
0.0017207 |
0.345 |
0.0000000 |
-0.0000002 |
0.0000071 |
0.0019104 |
0.350 |
0.0000000 |
0.0000000 |
0.0000000 |
0.0021657 |
0.355 |
0.0000000 |
0.0000003 |
-0.0000072 |
0.0025015 |
0.360 |
0.0000000 |
0.0000006 |
-0.0000133 |
0.0029175 |
0.365 |
0.0000000 |
0.0000008 |
-0.0000158 |
0.0034092 |
0.370 |
0.0000000 |
0.0000006 |
-0.0000122 |
0.0039722 |
0.375 |
0.0000000 |
0.0000000 |
0.0000000 |
0.0046021 |
0.380 |
0.0000000 |
-0.0000011 |
0.0000221 |
0.0052959 |
0.385 |
0.0000000 |
-0.0000023 |
0.0000511 |
0.0060573 |
0.390 |
0.0000000 |
-0.0000029 |
0.0000825 |
0.0068914 |
0.395 |
0.0000000 |
-0.0000023 |
0.0001120 |
0.0078032 |
0.400 |
0.0000000 |
0.0000000 |
0.0001354 |
0.0087981 |
0.405 |
0.0000000 |
0.0000043 |
0.0001492 |
0.0098839 |
0.410 |
0.0000000 |
0.0000086 |
0.0001544 |
0.0110807 |
0.415 |
0.0000000 |
0.0000109 |
0.0001526 |
0.0124113 |
0.420 |
0.0000000 |
0.0000088 |
0.0001457 |
0.0138987 |
0.425 |
0.0000000 |
0.0000000 |
0.0001354 |
0.0155658 |
0.430 |
0.0000000 |
-0.0000159 |
0.0001238 |
0.0174361 |
0.435 |
0.0000000 |
-0.0000322 |
0.0001143 |
0.0195356 |
0.440 |
0.0000000 |
-0.0000406 |
0.0001106 |
0.0218912 |
0.445 |
0.0000000 |
-0.0000327 |
0.0001164 |
0.0245294 |
0.450 |
0.0000000 |
0.0000000 |
0.0001354 |
0.0274770 |
0.455 |
0.0000000 |
0.0000641 |
0.0001690 |
0.0307379 |
0.460 |
0.0000000 |
0.0001588 |
0.0002094 |
0.0342246 |
0.465 |
0.0000000 |
0.0002819 |
0.0002465 |
0.0378270 |
0.470 |
0.0000000 |
0.0004307 |
0.0002703 |
0.0414347 |
0.475 |
0.0000000 |
0.0006029 |
0.0002707 |
0.0449377 |
0.480 |
0.0000000 |
0.0007938 |
0.0002410 |
0.0482666 |
0.485 |
0.0000000 |
0.0009896 |
0.0001884 |
0.0515152 |
0.490 |
0.0000000 |
0.0011743 |
0.0001236 |
0.0548184 |
0.495 |
0.0000000 |
0.0013321 |
0.0000573 |
0.0583110 |
0.500 |
0.0000000 |
0.0014470 |
0.0000000 |
0.0621278 |
0.505 |
0.0000001 |
0.0015119 |
-0.0000393 |
0.0663530 |
0.510 |
0.0000001 |
0.0015552 |
-0.0000590 |
0.0708680 |
0.515 |
0.0000002 |
0.0016143 |
-0.0000589 |
0.0755039 |
0.520 |
0.0000001 |
0.0017266 |
-0.0000393 |
0.0800913 |
0.525 |
0.0000000 |
0.0019293 |
0.0000000 |
0.0844613 |
0.530 |
-0.0000003 |
0.0022575 |
0.0000571 |
0.0885035 |
0.535 |
-0.0000005 |
0.0027364 |
0.0001232 |
0.0923436 |
0.540 |
-0.0000007 |
0.0033888 |
0.0001878 |
0.0961657 |
0.545 |
-0.0000005 |
0.0042376 |
0.0002405 |
0.1001543 |
0.550 |
0.0000000 |
0.0053057 |
0.0002707 |
0.1044938 |
0.555 |
0.0000010 |
0.0066128 |
0.0002724 |
0.1092571 |
0.560 |
0.0000020 |
0.0081663 |
0.0002571 |
0.1140718 |
0.565 |
0.0000025 |
0.0099707 |
0.0002410 |
0.1184539 |
0.570 |
0.0000020 |
0.0120303 |
0.0002402 |
0.1219195 |
0.575 |
0.0000000 |
0.0143495 |
0.0002707 |
0.1239848 |
0.580 |
-0.0000037 |
0.0169405 |
0.0003424 |
0.1243521 |
0.585 |
-0.0000075 |
0.0198478 |
0.0004402 |
0.1234689 |
0.590 |
-0.0000094 |
0.0231236 |
0.0005427 |
0.1219689 |
0.595 |
-0.0000076 |
0.0268202 |
0.0006287 |
0.1204859 |
0.600 |
0.0000000 |
0.0309900 |
0.0006768 |
0.1196535 |
0.605 |
0.0000138 |
0.0356756 |
0.0006732 |
0.1199039 |
0.610 |
0.0000279 |
0.0408814 |
0.0006341 |
0.1208625 |
0.615 |
0.0000352 |
0.0466023 |
0.0005833 |
0.1219530 |
0.620 |
0.0000284 |
0.0528330 |
0.0005445 |
0.1225994 |
0.625 |
0.0000000 |
0.0595683 |
0.0005414 |
0.1222252 |
0.630 |
-0.0000514 |
0.0667958 |
0.0005924 |
0.1203973 |
0.635 |
-0.0001043 |
0.0744738 |
0.0006941 |
0.1172534 |
0.640 |
-0.0001315 |
0.0825535 |
0.0008381 |
0.1130744 |
0.645 |
-0.0001058 |
0.0909861 |
0.0010157 |
0.1081411 |
0.650 |
0.0000000 |
0.0997227 |
0.0012182 |
0.1027342 |
0.655 |
0.0001917 |
0.1086750 |
0.0014435 |
0.0971026 |
0.660 |
0.0003891 |
0.1175968 |
0.0017155 |
0.0913681 |
0.665 |
0.0004907 |
0.1262027 |
0.0020642 |
0.0856204 |
0.670 |
0.0003949 |
0.1342070 |
0.0025201 |
0.0799495 |
0.675 |
0.0000000 |
0.1413240 |
0.0031132 |
0.0744450 |
0.680 |
-0.0007134 |
0.1473591 |
0.0038652 |
0.0691750 |
0.685 |
-0.0014368 |
0.1524807 |
0.0047634 |
0.0641189 |
0.690 |
-0.0017793 |
0.1569482 |
0.0057863 |
0.0592344 |
0.695 |
-0.0013502 |
0.1610210 |
0.0069128 |
0.0544790 |
0.700 |
0.0002412 |
0.1649584 |
0.0081213 |
0.0498105 |
0.705 |
0.0030740 |
0.1688898 |
0.0093946 |
0.0452002 |
0.710 |
0.0059811 |
0.1724248 |
0.0107319 |
0.0406751 |
0.715 |
0.0074839 |
0.1750433 |
0.0121364 |
0.0362759 |
0.720 |
0.0061037 |
0.1762248 |
0.0136112 |
0.0320434 |
0.725 |
0.0003618 |
0.1754492 |
0.0151597 |
0.0280184 |
0.730 |
-0.0099618 |
0.1723481 |
0.0169862 |
0.0242418 |
0.735 |
-0.0200519 |
0.1671618 |
0.0201000 |
0.0207552 |
0.740 |
-0.0238346 |
0.1602823 |
0.0257115 |
0.0176003 |
0.745 |
-0.0152362 |
0.1521017 |
0.0350310 |
0.0148188 |
0.750 |
0.0118172 |
0.1430122 |
0.0492691 |
0.0124526 |
0.755 |
0.0611784 |
0.1333655 |
0.0692906 |
0.0105245 |
0.760 |
0.1278157 |
0.1233520 |
0.0945789 |
0.0089821 |
0.765 |
0.2044764 |
0.1131213 |
0.1242717 |
0.0077540 |
0.770 |
0.2839077 |
0.1028235 |
0.1575067 |
0.0067689 |
0.775 |
0.3588569 |
0.0926082 |
0.1934218 |
0.0059556 |
0.780 |
0.4226355 |
0.0826146 |
0.2307651 |
0.0052508 |
0.785 |
0.4708121 |
0.0729386 |
0.2667267 |
0.0046236 |
0.790 |
0.4995195 |
0.0636650 |
0.2981071 |
0.0040509 |
0.795 |
0.5048905 |
0.0548791 |
0.3217067 |
0.0035100 |
0.800 |
0.4830580 |
0.0466659 |
0.3343259 |
0.0029778 |
0.805 |
0.4325537 |
0.0391042 |
0.3337561 |
0.0024397 |
0.810 |
0.3615047 |
0.0322484 |
0.3217518 |
0.0019140 |
0.815 |
0.2804372 |
0.0261469 |
0.3010584 |
0.0014273 |
0.820 |
0.1998773 |
0.0208478 |
0.2744213 |
0.0010060 |
0.825 |
0.1303509 |
0.0163994 |
0.2445858 |
0.0006768 |
0.830 |
0.0799476 |
0.0128187 |
0.2139852 |
0.0004575 |
0.835 |
0.0470104 |
0.0099978 |
0.1838036 |
0.0003320 |
0.840 |
0.0274455 |
0.0077976 |
0.1549132 |
0.0002756 |
0.845 |
0.0171594 |
0.0060789 |
0.1281859 |
0.0002634 |
0.850 |
0.0120584 |
0.0047028 |
0.1044938 |
0.0002707 |
0.855 |
0.0087035 |
0.0035510 |
0.0844905 |
0.0002770 |
0.860 |
0.0062749 |
0.0025899 |
0.0679563 |
0.0002791 |
0.865 |
0.0046073 |
0.0018067 |
0.0544530 |
0.0002781 |
0.870 |
0.0035354 |
0.0011888 |
0.0435423 |
0.0002749 |
0.875 |
0.0028940 |
0.0007235 |
0.0347861 |
0.0002707 |
0.880 |
0.0025179 |
0.0003981 |
0.0277462 |
0.0002665 |
0.885 |
0.0022419 |
0.0001998 |
0.0219845 |
0.0002633 |
0.890 |
0.0019007 |
0.0001160 |
0.0170626 |
0.0002623 |
0.895 |
0.0013290 |
0.0001340 |
0.0125425 |
0.0002644 |
0.900 |
0.0003618 |
0.0002412 |
0.0079859 |
0.0002707 |
Appendix
This appendix is divided into three sections. In Appendix A, we derive the demand curves of the final goods producer as well as the log-linearized expression for inflation, i.e., equation (19). Appendix B compares the small sample properties of our approach with estimating the moment condition implied by equation (23). In Appendix C, we show the results from the system estimation of the forecasting VAR.
A Theoretical Derivations
A.1 Deriving the Demand of a Domestically-Produced Good
To derive the demand curves for domestically-produced goods, recall that the representative final goods producer maximizes equation (1) subject to the demand aggregator implied by equations (2)-(4). The first order conditions associated with this problem are:
![$\displaystyle P_{Dt}(i) = \frac{\Lambda_{t}}{A_{t}}\left[ \frac{1-\nu}{1-\omega} \frac{A_{Dt}(i)}{A_{t}}+\nu\right] ^{\gamma_{t}-1} \left[ V_{Dt}^{1/\rho }+V_{Mt}^{1/\rho}\right] ^{\rho-1} V_{Dt}^{\frac{1}{\rho}-1} (1-\omega )^{\rho-1},$](img371.gif)
|
(A.1) |
![$\displaystyle P_{Mt}(i) = \frac{\Lambda_{t}}{A_{t}}\left[ \frac{1-\nu}{\omega} \frac {A_{Mt}(i)}{A_{t}}+\nu\right] ^{\gamma_{t}-1} \left[ V_{Dt}^{1/\rho} +V_{Mt}^{1/\rho}\right] ^{\rho-1} V_{Mt}^{\frac{1}{\rho}-1} \omega^{\rho -1},$](img372.gif)
|
(A.2) |
where
![]() is the Lagrange multiplier
associated with equation (2). Before
deriving the demand curves, we need to define
is the Lagrange multiplier
associated with equation (2). Before
deriving the demand curves, we need to define
![]() and show
that
and show
that ![]() satisfies equation (8).
satisfies equation (8).
To do so, rewrite equations (A.1)-(A.2) as:
![$\displaystyle \left[ \frac{1-\nu}{\omega} \frac{A_{Dt}(i)}{A_{t}}+\nu\right] = \left( \frac{P_{Dt}(i)}{P_{Ft}}\right) ^{\frac{1}{\gamma_{t}-1}} \left[ V_{Dt}^{1/\rho}+V_{Mt}^{1/\rho}\right] ^{\frac{1-\rho}{\gamma_{t}-1}} V_{Dt}^{\frac{\rho-1}{\rho(\gamma_{t}-1)}} (1-\omega)^{\frac{1-\rho} {\gamma_{t}-1}}, $](img377.gif)
![$\displaystyle \left[ \frac{1-\nu}{\omega} \frac{A_{Mt}(i)}{A_{t}}+\nu\right] = \left( \frac{P_{Mt}(i)}{P_{Ft}}\right) ^{\frac{1}{\gamma_{t}-1}} \left[ V_{Dt}^{1/\rho}+V_{Mt}^{1/\rho}\right] ^{\frac{1-\rho}{\gamma_{t}-1}} V_{Mt}^{\frac{\rho-1}{\rho(\gamma_{t}-1)}} \omega^{\frac{1-\rho}{\gamma_{t} -1}}. $](img378.gif)
Substituting these expressions into equations (3)-(4), we can express
![]() and
and ![]() as:
as:
![$\displaystyle V_{Dt} = \frac{1}{(1-\nu)\gamma_{t}} \left( \frac{P_{Dt}}{P_{Ft}}\right) ^{\frac{\gamma_{t}}{\gamma_{t}-1}} \left[ V_{Dt}^{1/\rho}+V_{Mt}^{1/\rho }\right] ^{\frac{\gamma_{t}(1-\rho)}{\gamma_{t}-1}} V_{Dt}^{\frac{\gamma _{t}(\rho-1)}{(\gamma_{t}-1)\rho}} (1-\omega)^{\frac{\gamma_{t}-\rho} {\gamma_{t}-1}}$](img381.gif)
|
(A.3) |
![$\displaystyle V_{Mt} = \frac{1}{(1-\nu)\gamma_{t}} \left( \frac{P_{Mt}}{P_{Ft}}\right) ^{\frac{\gamma_{t}}{\gamma_{t}-1}} \left[ V_{Dt}^{1/\rho}+V_{Mt}^{1/\rho }\right] ^{\frac{\gamma_{t}(1-\rho)}{\gamma_{t}-1}} V_{Mt}^{\frac{\gamma _{t}(\rho-1)}{(\gamma_{t}-1)\rho}} \omega^{\frac{\gamma_{t}-\rho}{\gamma _{t}-1}},$](img382.gif)
|
(A.4) |
where the price indices, ![]() and
and ![]() , are defined in equation (7). Using
equations (A.3)
and (A.4), the
ratio of
, are defined in equation (7). Using
equations (A.3)
and (A.4), the
ratio of ![]() to
to ![]() is given by:
is given by:
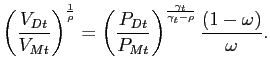
|
(A.5) |
Since optimal behavior by a final goods producer implies that equation (2) holds with equality, we can rewrite it as:
![$\displaystyle \left[ \left( \frac{V_{Dt}}{V_{Mt}}\right) ^{\frac{1}{\rho}} + 1 \right] ^{\rho} V_{Mt} = \frac{1}{(1-\nu)\gamma_{t}}.$](img388.gif)
|
(A.6) |
It is useful to express equation (A.4) as:
![$\displaystyle V_{Mt} = \frac{1}{(1-\nu)\gamma_{t}} \left( \frac{P_{Mt}}{P_{Ft}}\right) ^{\frac{\gamma_{t}}{\gamma_{t}-1}} \left[ \left( \frac{V_{Dt}}{V_{Mt}}\right) ^{\frac{1}{\rho}} + 1 \right] ^{\frac{\gamma_{t}(1-\rho)}{\gamma_{t}-1}} \omega^{\frac{\gamma_{t}-\rho}{\gamma_{t}-1}}. $](img389.gif)
Substituting this expression and equation (A.5) into equation (A.6), we have:
![$\displaystyle \left[ \left( \frac{P_{Dt}}{P_{Mt}}\right) ^{\frac{\gamma_{t}}{\gamma_{t} -\rho}} \frac{(1-\omega)}{\omega} + 1 \right] ^{\frac{\gamma_{t}-\rho} {\gamma_{t}-1}} \omega^{\frac{\gamma_{t}-\rho}{\gamma_{t}-1}} P_{Mt} ^{\frac{\gamma_{t}}{\gamma_{t}-1}}=P_{Ft}^{\frac{\gamma_{t}}{\gamma_{t}-1}}. $](img390.gif)
This expression, with some manipulation, can be written as:
![$\displaystyle P_{Ft}=\left[ (1-\omega)P_{Dt}^{\frac{\gamma_{t}}{\gamma_{t}-\rho}}+\omega P_{Mt}^{\frac{\gamma_{t}}{\gamma_{t}-\rho}}\right] ^{\frac{\gamma_{t}-\rho }{\gamma_{t}}}, $](img391.gif)
which is equation (8).
With ![]() defined in this way, we can now turn
to deriving the demand curve for a domestically-produced good,
i.e., equation (6). We begin by
re-expressing equation (A.1) as:
defined in this way, we can now turn
to deriving the demand curve for a domestically-produced good,
i.e., equation (6). We begin by
re-expressing equation (A.1) as:
![$\displaystyle \left[ \frac{1-\nu}{1-\omega} \frac{A_{Dt}(i)}{A_{t}}+\nu\right] = \left( \frac{P_{Dt}(i)}{P_{Ft}}\right) ^{\frac{1}{\gamma_{t}-1}} \left[ 1 + \left( \frac{V_{Mt}}{V_{Dt}}\right) ^{\frac{1}{\rho}} \right] ^{\frac{1-\rho} {\gamma_{t}-1}} (1-\omega)^{\frac{1-\rho}{\gamma_{t}-1}}.$](img393.gif)
|
(A.7) |
Note that equation (A.5) implies:
![$\displaystyle 1 + \left( \frac{V_{Mt}}{V_{Dt}}\right) ^{\frac{1}{\rho}} = \frac {P_{Dt}^{\frac{\gamma_{t}}{\rho-\gamma_{t}}}}{1-\omega} \left[ (1-\omega )P_{Dt}^{\frac{\gamma_{t}}{\gamma_{t}-\rho}}+\omega P_{Mt}^{\frac{\gamma_{t} }{\gamma_{t}-\rho}}\right] , $](img394.gif)
or
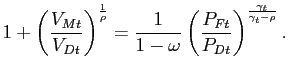
|
(A.8) |
Substituting equation (A.8) into equation (A.7) yields:
![$\displaystyle \left[ \frac{1-\nu}{1-\omega} \frac{A_{Dt}(i)}{A_{t}}+\nu\right] = \left( \frac{P_{Dt}(i)}{P_{Ft}}\right) ^{\frac{1}{\gamma_{t}-1}} \left( \frac{P_{Dt} }{P_{Ft}}\right) ^{\frac{\gamma_{t}}{\gamma_{t}-\rho}\frac{1-\rho}{\gamma _{t}-1}}. $](img396.gif)
Rearranging this expression, we get equation (6):
![$\displaystyle A_{Dt}(i)=(1-\omega)\left[ \frac{1}{1-\nu}\left( \frac{P_{Dt}(i)}{P_{Dt} }\right) ^{\frac{1}{\gamma_{t}-1}}\left( \frac{P_{Dt}}{P_{Ft}}\right) ^{\frac{\rho}{\gamma_{t}-\rho}}-\frac{\nu}{1-\nu}\right] A_{t}. $](img397.gif)
A.2 Deriving the Log-Linearized Pricing Equation
To derive equation (19), we begin by
defining the contract price,
![]() ,
for a firm that optimally chooses its price at date
,
for a firm that optimally chooses its price at date ![]() .
Using this definition in equation (10) and
log-linearizing, we get:
.
Using this definition in equation (10) and
log-linearizing, we get:
![$\displaystyle \hat{P}^{c}_{Dt}(i) = \sum^{\infty}_{j=1} (\beta\theta)^{j} (\hat{\pi} _{Dt+j}-\delta_{D} \hat{\pi}_{Dt+j-1})+ (1-\beta\theta) \sum^{\infty}_{j=0} (\beta\theta)^{j} \left[ \hat{s}_{t+j} - \frac{1}{\epsilon-1} \hat{\epsilon }_{t+j}(i) \right] .$](img400.gif)
|
(A.9) |
In the above equation,
![]() is the log-linearized
version of the elasticity of demand for good
is the log-linearized
version of the elasticity of demand for good ![]() given by:
given by:
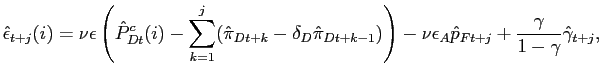
|
(A.10) |
where
![]() is the log-linearized price
index consisting of all of the prices of a firm's competitors
relative to the domestic price index, (i.e.,
is the log-linearized price
index consisting of all of the prices of a firm's competitors
relative to the domestic price index, (i.e.,
![]() ). Substituting
this expression for the elasticity of demand into equation
(A.9), we have:
). Substituting
this expression for the elasticity of demand into equation
(A.9), we have:
![$\displaystyle \hat{P}^{c}_{Dt}(i) = \sum^{\infty}_{j=1} (\beta\theta)^{j} (\hat{\pi} _{Dt+j}-\delta_{D} \hat{\pi}_{Dt+j-1})+ \frac{1-\beta\theta}{1+\frac {\nu\epsilon}{\epsilon-1}} \left[ \hat{s}_{t+j} + \frac{\nu\epsilon} {\epsilon-1} \frac{\epsilon_{A}}{\epsilon} \hat{p}_{Ft+j} - \left( \frac {1}{\epsilon-1}\right) \left( \frac{\gamma}{1-\gamma}\right) \hat{\gamma }_{t+j}\right] . $](img406.gif)
Using the definition of the steady state markup (i.e.,
![]() ) and the
definition of
) and the
definition of ![]() (i.e.,
(i.e.,
![]() ), this
expression, after quasi-differencing, can be rewritten as:
), this
expression, after quasi-differencing, can be rewritten as:
![$\displaystyle \hat{P}^{c}_{Dt}(i) - \beta\theta\hat{P}^{c}_{Dt+1}(i) = \beta\theta(\hat{\pi }_{Dt+1}-\delta_{D} \hat{\pi}_{Dt}) + (1-\beta\theta) \left[ (1-\Psi) \hat {s}_{t} + \Psi\frac{\epsilon_{A}}{\epsilon} \hat{p}_{Ft} + (2 \Psi-1) \hat{\gamma}_{t} \right] .$](img410.gif)
|
(A.11) |
From the log-linearized version of the first expression in
equation (7), the
contract price at date ![]() can be related to traded
goods inflation via:
can be related to traded
goods inflation via:
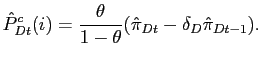
|
(A.12) |
Substituting this expression into equation (A.11), we get an
expression relating domestic price inflation to real marginal cost
and ![]() :
:
![$\displaystyle \hat{\pi}_{Dt}-\delta_{D} \hat{\pi}_{Dt-1} = \beta(\hat{\pi}_{Dt+1}-\delta_{D} \hat{\pi}_{Dt}) + \kappa\left[ (1-\Psi) \hat{s}_{t} + \Psi\frac{\epsilon_{A} }{\epsilon} \hat{p}_{Ft} + (2 \Psi-1) \hat{\gamma}_{t} \right] .$](img414.gif)
|
(A.13) |
The log-linearized version of equation (8) implies that
Using this expression in equation (A.13) yields equation (<19).
B Small Sample Properties of our GMM Estimator
This appendix investigates the small-sample properties of our estimator through a Monte Carlo exercise. We bootstrapped 10,000 Monte Carlo samples for traded goods inflation, relative import prices, and the labor share using equation (26), and its auxiliary forecasting processes, which we have reproduced below:
![$\displaystyle \hat{\pi}_{t}=\delta_{D}\hat{\pi}_{t-1}+\kappa_{D} \left[ \frac{1-\Psi} {1-\beta\rho_{s}} \hat{s}_{t}+ \omega\frac{\epsilon_{A}}{\epsilon} \frac {\Psi(1+\beta\rho_{M2}L)}{1-\beta\rho_{M1}-\beta^{2} \rho_{M2}} \hat{p} _{Mt}\right] + \epsilon_{\pi t}$](img416.gif)
|
(B.1) | |
As pseudo-true parameter values for our Monte Carlo exercise, we
used the GMM estimates of ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() , and
, and ![]() from
equations (B.1)
with the following instrument set: one lag of the labor share, two
lags of goods inflation, and two lags of relative import prices as
instruments (see the second column of Table 5). In
bootstrapping, we jointly sampled with replacement from this
model's estimates of
from
equations (B.1)
with the following instrument set: one lag of the labor share, two
lags of goods inflation, and two lags of relative import prices as
instruments (see the second column of Table 5). In
bootstrapping, we jointly sampled with replacement from this
model's estimates of
![]() and the residuals from the
two autoregressive processes, which maintains the correlation
structure across residuals. Each bootstrapped sample had a length
of 96 observations, which is the same length as the 1983Q1-2006Q4
sample.
and the residuals from the
two autoregressive processes, which maintains the correlation
structure across residuals. Each bootstrapped sample had a length
of 96 observations, which is the same length as the 1983Q1-2006Q4
sample.
For each sample of artificial data, we used the generalized
method of moments to re-estimate ![]() ,
, ![]() , and
, and
![]() based, again, on equations
(B.1) using the
same instrument set as above. The solid lines in Figure 7 show the
parameters' sampling distributions. As discussed earlier in the
text, the estimates of
based, again, on equations
(B.1) using the
same instrument set as above. The solid lines in Figure 7 show the
parameters' sampling distributions. As discussed earlier in the
text, the estimates of ![]() and
and
![]() based on the closed form solution
do not display much small-sample bias. The estimate of
based on the closed form solution
do not display much small-sample bias. The estimate of ![]() does display some modest upward bias, and the
small-sample confidence intervals appear a little wider than
intervals based on asymptotic derivations. Overall, however, our
GMM estimator performs well in small samples.
does display some modest upward bias, and the
small-sample confidence intervals appear a little wider than
intervals based on asymptotic derivations. Overall, however, our
GMM estimator performs well in small samples.
Figure 7 also compares the performance of our baseline estimator with an alternative GMM estimator that uses equation (23) as the moment condition (reproduced below):
![$\displaystyle \hat{\pi}_{t}-\delta_{D}\hat{\pi}_{t-1}=\beta E_{t}[\hat{\pi}_{t+1} -\delta_{D}\hat{\pi}_{t}]+ \kappa_{D} \left[ (1-\Psi) \hat{s}_{t}+ \Psi \omega\frac{\epsilon_{A}}{\epsilon}\hat{p}_{Mt}+\varphi\widehat{\gamma} _{t}\right]$](img432.gif)
|
(B.2) | |
![$\displaystyle \kappa_{D} = \frac{(1-\beta\theta)(1-\theta)}{\theta[1+\epsilon\frac {\alpha}{1-\alpha} (1-\Psi)]}.$](img433.gif)
|
For convenience, we shall refer to our baseline estimator as "closed-form", while we dub the alternative, based on equation (B.2), "single-equation."
In contrast to our closed-form estimator, we find that
single-equation GMM estimator performs poorly in small samples. In
particular, we found that estimates of ![]() were
severely upward-biased with the mass of the distribution near unity
- the upper bound of feasible values for
were
severely upward-biased with the mass of the distribution near unity
- the upper bound of feasible values for ![]() .
Accordingly, we do not show sampling distributions when we jointly
estimate
.
Accordingly, we do not show sampling distributions when we jointly
estimate ![]() with
with ![]() and
and
![]() . Instead, the dashed lines
labelled "Single-Equation Estimates" in the middle and lower
panels of Figure 7
show the sampling distributions for
. Instead, the dashed lines
labelled "Single-Equation Estimates" in the middle and lower
panels of Figure 7
show the sampling distributions for ![]() and
and
![]() , conditional on
, conditional on ![]() being at its pseudo-true value of
being at its pseudo-true value of ![]() . We find it remarkable that, despite using the
pseudo-true value of
. We find it remarkable that, despite using the
pseudo-true value of ![]() , the GMM estimator based
on equation (B.2) still performs
worse in small samples than the GMM estimator based on the closed
form solution. The former yields estimates of
, the GMM estimator based
on equation (B.2) still performs
worse in small samples than the GMM estimator based on the closed
form solution. The former yields estimates of
![]() that are more upward-biased and
the distribution of estimates for
that are more upward-biased and
the distribution of estimates for ![]() has
fatter tails.
has
fatter tails.
Figure 7: Comparison of Small Sample Properties of Alternative Estimators
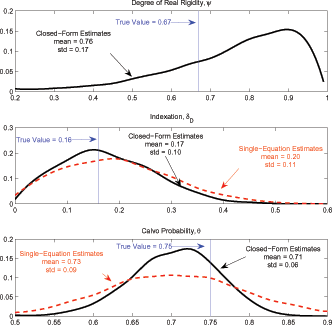
Data for Figure 7 - Panel A: Degree of Real Rigidity, ψ
Degree of Real Rigidity (ψ) | Probability Density Function of Closed-Form Estimates |
|---|---|
0.200 |
0.0072431 |
0.205 |
0.0068022 |
0.210 |
0.0064418 |
0.215 |
0.0061571 |
0.220 |
0.0059434 |
0.225 |
0.0057958 |
0.230 |
0.0057097 |
0.235 |
0.0056804 |
0.240 |
0.0057029 |
0.245 |
0.0057727 |
0.250 |
0.0058850 |
0.255 |
0.0060350 |
0.260 |
0.0062180 |
0.265 |
0.0064292 |
0.270 |
0.0066639 |
0.275 |
0.0069173 |
0.280 |
0.0071847 |
0.285 |
0.0074614 |
0.290 |
0.0077426 |
0.295 |
0.0080235 |
0.300 |
0.0082994 |
0.305 |
0.0085670 |
0.310 |
0.0088286 |
0.315 |
0.0090882 |
0.320 |
0.0093495 |
0.325 |
0.0096162 |
0.330 |
0.0098924 |
0.335 |
0.0101816 |
0.340 |
0.0104878 |
0.345 |
0.0108148 |
0.350 |
0.0111664 |
0.355 |
0.0115450 |
0.360 |
0.0119468 |
0.365 |
0.0123669 |
0.370 |
0.0128002 |
0.375 |
0.0132415 |
0.380 |
0.0136859 |
0.385 |
0.0141281 |
0.390 |
0.0145632 |
0.395 |
0.0149861 |
0.400 |
0.0153916 |
0.405 |
0.0157777 |
0.410 |
0.0161543 |
0.415 |
0.0165342 |
0.420 |
0.0169304 |
0.425 |
0.0173558 |
0.430 |
0.0178232 |
0.435 |
0.0183456 |
0.440 |
0.0189358 |
0.445 |
0.0196067 |
0.450 |
0.0203712 |
0.455 |
0.0212378 |
0.460 |
0.0221970 |
0.465 |
0.0232349 |
0.470 |
0.0243376 |
0.475 |
0.0254913 |
0.480 |
0.0266821 |
0.485 |
0.0278959 |
0.490 |
0.0291191 |
0.495 |
0.0303376 |
0.500 |
0.0315376 |
0.505 |
0.0327079 |
0.510 |
0.0338477 |
0.515 |
0.0349589 |
0.520 |
0.0360435 |
0.525 |
0.0371034 |
0.530 |
0.0381406 |
0.535 |
0.0391570 |
0.540 |
0.0401544 |
0.545 |
0.0411350 |
0.550 |
0.0421005 |
0.555 |
0.0430547 |
0.560 |
0.0440083 |
0.565 |
0.0449738 |
0.570 |
0.0459638 |
0.575 |
0.0469906 |
0.580 |
0.0480669 |
0.585 |
0.0492051 |
0.590 |
0.0504177 |
0.595 |
0.0517171 |
0.600 |
0.0531160 |
0.605 |
0.0546209 |
0.610 |
0.0562148 |
0.615 |
0.0578746 |
0.620 |
0.0595775 |
0.625 |
0.0613004 |
0.630 |
0.0630205 |
0.635 |
0.0647148 |
0.640 |
0.0663602 |
0.645 |
0.0679340 |
0.650 |
0.0694130 |
0.655 |
0.0707830 |
0.660 |
0.0720639 |
0.665 |
0.0732845 |
0.670 |
0.0744732 |
0.675 |
0.0756588 |
0.680 |
0.0768699 |
0.685 |
0.0781350 |
0.690 |
0.0794829 |
0.695 |
0.0809420 |
0.700 |
0.0825411 |
0.705 |
0.0843017 |
0.710 |
0.0862173 |
0.715 |
0.0882740 |
0.720 |
0.0904583 |
0.725 |
0.0927565 |
0.730 |
0.0951550 |
0.735 |
0.0976399 |
0.740 |
0.1001978 |
0.745 |
0.1028149 |
0.750 |
0.1054776 |
0.755 |
0.1081706 |
0.760 |
0.1108727 |
0.765 |
0.1135609 |
0.770 |
0.1162126 |
0.775 |
0.1188047 |
0.780 |
0.1213146 |
0.785 |
0.1237193 |
0.790 |
0.1259959 |
0.795 |
0.1281218 |
0.800 |
0.1300739 |
0.805 |
0.1318384 |
0.810 |
0.1334362 |
0.815 |
0.1348972 |
0.820 |
0.1362514 |
0.825 |
0.1375285 |
0.830 |
0.1387586 |
0.835 |
0.1399715 |
0.840 |
0.1411970 |
0.845 |
0.1424651 |
0.850 |
0.1438056 |
0.855 |
0.1452345 |
0.860 |
0.1467115 |
0.865 |
0.1481826 |
0.870 |
0.1495935 |
0.875 |
0.1508902 |
0.880 |
0.1520185 |
0.885 |
0.1529243 |
0.890 |
0.1535534 |
0.895 |
0.1538516 |
0.900 |
0.1537649 |
0.905 |
0.1532391 |
0.910 |
0.1522200 |
0.915 |
0.1506535 |
0.920 |
0.1484855 |
0.925 |
0.1456618 |
0.930 |
0.1421282 |
0.935 |
0.1378307 |
0.940 |
0.1327151 |
0.945 |
0.1267272 |
0.950 |
0.1198129 |
0.955 |
0.1119180 |
0.960 |
0.1029885 |
0.965 |
0.0929701 |
0.970 |
0.0818088 |
0.975 |
0.0694503 |
0.980 |
0.0558406 |
0.985 |
0.0409254 |
0.990 |
0.0246507 |
Data for Figure 7 -Panel B: Indexation, δD
Indexation (δD) | Probability Density Function of Single Equation Estimates | Probability Density Function of Closed-Form Estimates |
|---|---|---|
0.000 |
0.0341029 |
0.0179568 |
0.005 |
0.0418360 |
0.0305635 |
0.010 |
0.0493784 |
0.0423497 |
0.015 |
0.0567244 |
0.0533660 |
0.020 |
0.0638681 |
0.0636630 |
0.025 |
0.0708038 |
0.0732914 |
0.030 |
0.0775256 |
0.0823017 |
0.035 |
0.0840278 |
0.0907444 |
0.040 |
0.0903044 |
0.0986702 |
0.045 |
0.0963497 |
0.1061297 |
0.050 |
0.1021578 |
0.1131734 |
0.055 |
0.1077231 |
0.1198519 |
0.060 |
0.1130395 |
0.1262159 |
0.065 |
0.1181014 |
0.1323158 |
0.070 |
0.1229029 |
0.1382023 |
0.075 |
0.1274382 |
0.1439260 |
0.080 |
0.1317015 |
0.1495375 |
0.085 |
0.1356870 |
0.1550873 |
0.090 |
0.1393888 |
0.1606260 |
0.095 |
0.1428011 |
0.1662043 |
0.100 |
0.1459182 |
0.1718726 |
0.105 |
0.1487417 |
0.1776501 |
0.110 |
0.1513031 |
0.1834294 |
0.115 |
0.1536415 |
0.1890717 |
0.120 |
0.1557959 |
0.1944381 |
0.125 |
0.1578053 |
0.1993898 |
0.130 |
0.1597088 |
0.2037880 |
0.135 |
0.1615454 |
0.2074937 |
0.140 |
0.1633541 |
0.2103681 |
0.145 |
0.1651739 |
0.2122724 |
0.150 |
0.1670439 |
0.2130678 |
0.155 |
0.1689824 |
0.2126664 |
0.160 |
0.1709251 |
0.2111852 |
0.165 |
0.1727867 |
0.2087923 |
0.170 |
0.1744821 |
0.2056555 |
0.175 |
0.1759264 |
0.2019430 |
0.180 |
0.1770342 |
0.1978228 |
0.185 |
0.1777206 |
0.1934628 |
0.190 |
0.1779003 |
0.1890311 |
0.195 |
0.1774884 |
0.1846958 |
0.200 |
0.1763996 |
0.1806247 |
0.205 |
0.1745805 |
0.1769411 |
0.210 |
0.1721045 |
0.1735885 |
0.215 |
0.1690764 |
0.1704655 |
0.220 |
0.1656013 |
0.1674709 |
0.225 |
0.1617841 |
0.1645032 |
0.230 |
0.1577298 |
0.1614611 |
0.235 |
0.1535433 |
0.1582432 |
0.240 |
0.1493296 |
0.1547483 |
0.245 |
0.1451936 |
0.1508749 |
0.250 |
0.1412404 |
0.1465218 |
0.255 |
0.1375473 |
0.1416206 |
0.260 |
0.1340814 |
0.1362353 |
0.265 |
0.1307825 |
0.1304630 |
0.270 |
0.1275900 |
0.1244006 |
0.275 |
0.1244436 |
0.1181453 |
0.280 |
0.1212828 |
0.1117940 |
0.285 |
0.1180473 |
0.1054437 |
0.290 |
0.1146767 |
0.0991916 |
0.295 |
0.1111105 |
0.0931346 |
0.300 |
0.1072884 |
0.0873699 |
0.305 |
0.1031708 |
0.0819719 |
0.310 |
0.0988020 |
0.0769264 |
0.315 |
0.0942471 |
0.0721962 |
0.320 |
0.0895712 |
0.0677445 |
0.325 |
0.0848395 |
0.0635344 |
0.330 |
0.0801171 |
0.0595291 |
0.335 |
0.0754690 |
0.0556915 |
0.340 |
0.0709605 |
0.0519849 |
0.345 |
0.0666567 |
0.0483722 |
0.350 |
0.0626226 |
0.0448167 |
0.355 |
0.0589076 |
0.0412924 |
0.360 |
0.0554976 |
0.0378181 |
0.365 |
0.0523628 |
0.0344235 |
0.370 |
0.0494732 |
0.0311384 |
0.375 |
0.0467989 |
0.0279924 |
0.380 |
0.0443101 |
0.0250154 |
0.385 |
0.0419769 |
0.0222370 |
0.390 |
0.0397694 |
0.0196871 |
0.395 |
0.0376577 |
0.0173954 |
0.400 |
0.0356119 |
0.0153916 |
0.405 |
0.0336077 |
0.0136945 |
0.410 |
0.0316433 |
0.0122792 |
0.415 |
0.0297223 |
0.0111097 |
0.420 |
0.0278486 |
0.0101502 |
0.425 |
0.0260257 |
0.0093646 |
0.430 |
0.0242576 |
0.0087172 |
0.435 |
0.0225478 |
0.0081720 |
0.440 |
0.0209001 |
0.0076931 |
0.445 |
0.0193182 |
0.0072445 |
0.450 |
0.0178059 |
0.0067904 |
0.455 |
0.0163663 |
0.0063026 |
0.460 |
0.0149994 |
0.0057840 |
0.465 |
0.0137051 |
0.0052454 |
0.470 |
0.0124828 |
0.0046974 |
0.475 |
0.0113322 |
0.0041507 |
0.480 |
0.0102528 |
0.0036159 |
0.485 |
0.0092442 |
0.0031039 |
0.490 |
0.0083061 |
0.0026252 |
0.495 |
0.0074380 |
0.0021906 |
0.500 |
0.0066395 |
0.0018108 |
0.505 |
0.0059098 |
0.0014936 |
0.510 |
0.0052462 |
0.0012359 |
0.515 |
0.0046459 |
0.0010318 |
0.520 |
0.0041058 |
0.0008753 |
0.525 |
0.0036229 |
0.0007604 |
0.530 |
0.0031942 |
0.0006814 |
0.535 |
0.0028167 |
0.0006321 |
0.540 |
0.0024875 |
0.0006066 |
0.545 |
0.0022035 |
0.0005991 |
0.550 |
0.0019617 |
0.0006036 |
0.555 |
0.0017591 |
0.0006141 |
0.560 |
0.0015928 |
0.0006247 |
0.565 |
0.0014597 |
0.0006294 |
0.570 |
0.0013569 |
0.0006224 |
0.575 |
0.0012813 |
0.0005976 |
0.580 |
0.0012300 |
0.0005492 |
0.585 |
0.0011999 |
0.0004712 |
0.590 |
0.0011880 |
0.0003576 |
0.595 |
0.0011915 |
0.0002025 |
0.600 |
0.0012072 |
0.0000000 |
Data for Figure 7 -Panel C: Calvo Probability, θ
Calvo Probability (θ) | Probability Density Function of Single Equation Estimates | Probability Density Function of Closed-Form Estimates |
|---|---|---|
0.500 |
0.0098084 |
0.0025653 |
0.505 |
0.0100779 |
0.0021378 |
0.510 |
0.0107764 |
0.0018524 |
0.515 |
0.0118381 |
0.0017205 |
0.520 |
0.0131972 |
0.0017531 |
0.525 |
0.0147880 |
0.0019617 |
0.530 |
0.0165599 |
0.0023573 |
0.535 |
0.0185226 |
0.0029513 |
0.540 |
0.0207008 |
0.0037549 |
0.545 |
0.0231196 |
0.0047794 |
0.550 |
0.0258035 |
0.0060359 |
0.555 |
0.0287533 |
0.0075318 |
0.560 |
0.0318728 |
0.0092582 |
0.565 |
0.0350414 |
0.0112025 |
0.570 |
0.0381387 |
0.0133518 |
0.575 |
0.0410442 |
0.0156934 |
0.580 |
0.0436867 |
0.0182365 |
0.585 |
0.0461916 |
0.0210786 |
0.590 |
0.0487333 |
0.0243392 |
0.595 |
0.0514862 |
0.0281378 |
0.600 |
0.0546250 |
0.0325939 |
0.605 |
0.0582772 |
0.0377815 |
0.610 |
0.0623830 |
0.0435922 |
0.615 |
0.0668356 |
0.0498724 |
0.620 |
0.0715283 |
0.0564683 |
0.625 |
0.0763543 |
0.0632262 |
0.630 |
0.0811919 |
0.0700522 |
0.635 |
0.0858595 |
0.0770921 |
0.640 |
0.0901605 |
0.0845519 |
0.645 |
0.0938983 |
0.0926374 |
0.650 |
0.0968764 |
0.1015542 |
0.655 |
0.0989711 |
0.1113649 |
0.660 |
0.1003507 |
0.1215579 |
0.665 |
0.1012563 |
0.1314780 |
0.670 |
0.1019292 |
0.1404704 |
0.675 |
0.1026105 |
0.1478799 |
0.680 |
0.1034747 |
0.1532625 |
0.685 |
0.1044287 |
0.1570180 |
0.690 |
0.1053128 |
0.1597571 |
0.695 |
0.1059672 |
0.1620907 |
0.700 |
0.1062321 |
0.1646295 |
0.705 |
0.1060044 |
0.1677632 |
0.710 |
0.1054081 |
0.1709967 |
0.715 |
0.1046239 |
0.1736141 |
0.720 |
0.1038323 |
0.1748993 |
0.725 |
0.1032141 |
0.1741361 |
0.730 |
0.1028707 |
0.1708065 |
0.735 |
0.1025864 |
0.1651843 |
0.740 |
0.1020664 |
0.1577411 |
0.745 |
0.1010158 |
0.1489487 |
0.750 |
0.0991399 |
0.1392787 |
0.755 |
0.0962446 |
0.1291501 |
0.760 |
0.0925398 |
0.1187703 |
0.765 |
0.0883360 |
0.1082942 |
0.770 |
0.0839439 |
0.0978764 |
0.775 |
0.0796741 |
0.0876716 |
0.780 |
0.0757615 |
0.0778191 |
0.785 |
0.0721382 |
0.0683954 |
0.790 |
0.0686603 |
0.0594616 |
0.795 |
0.0651843 |
0.0510786 |
0.800 |
0.0615663 |
0.0433077 |
0.805 |
0.0577150 |
0.0362031 |
0.810 |
0.0537481 |
0.0297927 |
0.815 |
0.0498357 |
0.0240977 |
0.820 |
0.0461480 |
0.0191394 |
0.825 |
0.0428550 |
0.0149389 |
0.830 |
0.0400754 |
0.0114980 |
0.835 |
0.0377224 |
0.0087410 |
0.840 |
0.0356576 |
0.0065727 |
0.845 |
0.0337427 |
0.0048979 |
0.850 |
0.0318394 |
0.0036215 |
0.855 |
0.0298348 |
0.0026565 |
0.860 |
0.0277173 |
0.0019486 |
0.865 |
0.0255004 |
0.0014515 |
0.870 |
0.0231981 |
0.0011191 |
0.875 |
0.0208239 |
0.0009054 |
0.880 |
0.0184262 |
0.0007641 |
0.885 |
0.0161914 |
0.0006490 |
0.890 |
0.0143407 |
0.0005141 |
0.895 |
0.0130950 |
0.0003131 |
0.900 |
0.0126754 |
0.0000000 |
C Empirical Estimates of the Forecasting VAR
Before we show the estimates of the forecasting VAR, recall that the VAR that we use can be rewritten in companion form as:
where
![]()
![]()
![]()
![]() , and
, and
![]()
![]() 0
0
![]() . Accordingly, the first row of
the matrix
. Accordingly, the first row of
the matrix ![]() corresponds to the estimated process
for the labor share (
corresponds to the estimated process
for the labor share (
![]() ) and the second row corresponds
to the estimated process for relative import prices (
) and the second row corresponds
to the estimated process for relative import prices (
![]() ).
).
Table 6 shows
the estimates of ![]() for three different
specifications: the benchmark VES, CES with lagged indexation, and
the VES specification using an unrestricted VAR(2). (We show only
the results in which capital is firm-specific, since the estimates
of
for three different
specifications: the benchmark VES, CES with lagged indexation, and
the VES specification using an unrestricted VAR(2). (We show only
the results in which capital is firm-specific, since the estimates
of ![]() are unchanged under the alternative
assumption of full capital mobility within a country.) The table
confirms that both the labor share and relative import prices are
well-approximated by simple, univariate processes. In particular,
for the benchmark VES specification, there is no evidence of
feedback between the two variables (i.e.,
are unchanged under the alternative
assumption of full capital mobility within a country.) The table
confirms that both the labor share and relative import prices are
well-approximated by simple, univariate processes. In particular,
for the benchmark VES specification, there is no evidence of
feedback between the two variables (i.e.,
![]() ).
).
Table 6: System Estimates of VAR
| Parameters | Benchmark VES | CES with indexation | VAR(2) Forecasting Model |
|---|---|---|---|
| Labor Share Equation: A11 | 0.89 (0.03) | 0.91 (0.03) | 0.71 (0.14) |
| Labor Share Equation: A12 | 0 (-) | 0 (-) | 0.00 (0.05) |
| Labor Share Equation: A13 | 0 (-) | 0 (-) | 0.21 (0.16) |
| Labor Share Equation: A14 | 0 (-) | 0 (-) | 0.00 (0.05) |
| Labor Share Equation: R2 | 0.83 | 0.83 | 0.83 |
| Labor Share Equation: Durbin-Watson Statistic | 2.26 | 2.32 | 1.78 |
| Relative Import Price Equation: A21 | 0 (-) | NA | -0.01 (0.11) |
| Relative Import Price Equation: A22 | 1.37 (0.06) | NA | 1.39 (0.06) |
| Relative Import Price Equation: A23 | 0 (-) | NA | 0.00 (0.1) |
| Relative Import Price Equation: A24 | -0.39 (0.06) | NA | -0.41 (0.06) |
| Relative Import Price Equation: R2 | 0.98 | NA | 0.98 |
| Relative Import Price Equation: Durbin-Watson Statistic | 1.91 | NA | 1.92 |
a Standard errors are reported in parentheses.
Footnotes
* The authors thank Chris Erceg, Alejandro Justiniano, Mike Kiley, Sylvain Leduc, Andy Levin, Andrea Pescatori, Argia Sbordone, Rob Vigfusson, and Jonathan Wright as well as seminar participants at the Federal Reserve Board and Federal Reserve Bank of Philadelphia for useful comments and suggestions. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
† Corresponding Author: Christopher Gust, Telephone 202-452-2383, Fax 202-452-4926. Email addresses: [email protected], [email protected], [email protected] Return to text
1. For arguments in favor of view that global factors have changed the behavior of inflation, see Borio and Filardo (2006) and Rogoff (2003). For evidence that the effect has been limited, see Ihrig, Kamin, Lindner, and Marquez (2007). Ball (2006) takes an even more extreme position, arguing that there is no effect of foreign variables on U.S. inflation. Return to text
2. Our paper is related to a longstanding literature that includes import prices in the estimation of reduced-form Phillips curves such as Gordon (1973) and Dornbusch and Fischer (1984). However, our paper differs from these earlier works by providing estimates from a structural model. Return to text
3. Important work estimating the standard NKPC includes Galí and Gertler (1999), Galí, Gertler, and López-Salido (2001) and Sbordone (2002). Return to text
4. This estimate is broadly consistent with the micro evidence of Nakamura and Steinsson (2007), who find a median duration of non-sale prices of 8-11 months using prices for both consumers and producer's finished goods. Return to text
5. For
simplicity, we assume that the underlying dynamic general
equilibrium model implies zero growth in both the tradable and
non-tradable sectors. As a result, ![]() has the
interpretation as the representative household's discount factor.
If we did allow for positive and differential growth rates in these
two sectors, the appropriate discount rate in equation (19) would be
has the
interpretation as the representative household's discount factor.
If we did allow for positive and differential growth rates in these
two sectors, the appropriate discount rate in equation (19) would be
![]() , where
, where
![]() is the steady state inflation rate for
tradable goods,
is the steady state inflation rate for
tradable goods, ![]() is the steady state
inflation rate of consumer prices, and
is the steady state
inflation rate of consumer prices, and ![]() is the
growth rate of consumption. For U.S. data, consumption growth and
the inflation differential between traded goods prices and consumer
prices are small enough that taking into account these extra terms
in equation (19)
has a negligible effect on our results. Return to text
is the
growth rate of consumption. For U.S. data, consumption growth and
the inflation differential between traded goods prices and consumer
prices are small enough that taking into account these extra terms
in equation (19)
has a negligible effect on our results. Return to text
6. Our specification has some similarities with Vega and Winkelried (2005), who derive a NKPC in which world prices affect domestic inflation in a small open economy with Rotemberg (1982) style price contracts and a translog demand curve. Also, Sbordone (2007) analyzes how the entry of new competitors affects the slope of the NKPC in a closed economy context using the preferences of Dotsey and King (2005). Return to text
7. We construct a Laspeyres index for domestic goods prices by netting out the index for export prices from the overall index for goods prices. Return to text
8. A measure that corresponded more closely to costs in the tradable sector is the labor share for the manufacturing sector, but it is only available on an annual basis beginning in 1986. Return to text
9. Ideally, we would like to have data on a basket of imported goods that matches the basket of domestically-produced goods. However, no such series are available, and instead our measure of imported prices excludes oil prices, reflecting that oil's share of imports is much larger than its share of domestic goods production. Later, as sensitivity analysis, we use an import price series that excludes other commodity prices. Return to text
10. For a summary of this literature, see chapter 7 of Campbell, Lo, and MacKinlay (1997). For an early application of this approach to inflation dynamics, see Sbordone (2002). Return to text
11. If the markup shock evolved according to an AR(1) process, then the lagged endogenous variables that we use would be invalid instruments. In our empirical work, we test for the presence of serially correlated errors to evaluate this possibility. Return to text
12. For our commodity price measure, we use the raw industrials spot commodity price series from the Commodity Research Bureau. Return to text
13. For a discussion of the macro estimates and estimates after trade liberalizations, see Ruhl (2005). Return to text
14. For the CES demand curves, we exclude relative import prices from the instrument set, since the estimated system of equations no longer involves import prices. Return to text
15. More
specifically, we use the critical values from Tables 1 and 2 of
Stock and Yogo (2004). For the VES specification with
![]() , we have 2 endogenous
regressors (
, we have 2 endogenous
regressors (![]() ), and 9 instruments (
), and 9 instruments (![]() ) excluding exogenous variables such as the
constant. The critical value for the test based on a desired
maximal bias of 5 percent relative to OLS is 18.76, and the
critical value for a 10 percent desired maximal size of a 5 percent
Wald test is 29.32. Return to
text
) excluding exogenous variables such as the
constant. The critical value for the test based on a desired
maximal bias of 5 percent relative to OLS is 18.76, and the
critical value for a 10 percent desired maximal size of a 5 percent
Wald test is 29.32. Return to
text
16. These
values for ![]() ,
,
![]() , and
, and ![]() correspond to the GMM estimates of the VES specification using a
smaller set of instruments. In particular, we eliminated the lags
of commodity price inflation and the interest rate spread from the
instrument set to facilitate the Monte Carlo exercise. The results
of this smaller instrument set are shown in Table 5. For additional
details regarding the Monte Carlo experiment, see Appendix B.
Return to text
correspond to the GMM estimates of the VES specification using a
smaller set of instruments. In particular, we eliminated the lags
of commodity price inflation and the interest rate spread from the
instrument set to facilitate the Monte Carlo exercise. The results
of this smaller instrument set are shown in Table 5. For additional
details regarding the Monte Carlo experiment, see Appendix B.
Return to text
17. See Podivinsky (1999) for a review of the literature using Monte Carlo simulations to evaluate the small sample properties of GMM. Return to text
18. This
alternative parameterization holds fixed the value of
![]() , the reduced-form slope
coefficient of real unit labor cost in equation (23).
Return to text
, the reduced-form slope
coefficient of real unit labor cost in equation (23).
Return to text
19. For example, for a very high markup, such as the one estimated by Dossche, Heylen, and den Poel (2007), the variation in the desired markup can be substantial without much variation in the demand elasticity. Return to text
20. The findings of Nakamura and Steinsson (2007) are also in line with earlier micro studies surveyed in Taylor (1999). In contrast, Bils and Klenow (2004) find a much higher frequency of price adjustment using micro data on consumer prices. The lower frequency of price changes in Nakamura and Steinsson (2007) largely reflects that they exclude temporary sales in measuring price changes, while Bils and Klenow (2004) include sales. Return to text
21. If we
included the 1991 dummy into our analysis, the estimates of
![]() and
and
![]() would fall and the overall fit of
the model would improve. However, we take a more conservative
approach and exclude the dummy from our
analysis. Return to text
would fall and the overall fit of
the model would improve. However, we take a more conservative
approach and exclude the dummy from our
analysis. Return to text
22. In this case, we use the benchmark set of instruments. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text