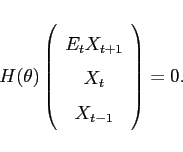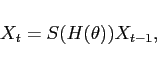Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 920, February 2008 --- Screen Reader
Version*
On the Application of Automatic Differentiation to the Likelihood Function for Dynamic General Equilibrium Models*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
A key application of automatic differentiation (AD) is to facilitate numerical optimization problems. Such problems are at the core of many estimation techniques, including maximum likelihood. As one of the first applications of AD in the field of economics, we used Tapenade to construct derivatives for the likelihood function of any linear or linearized general equilibrium model solved under the assumption of rational expectations. We view our main contribution as providing an important check on finite-difference (FD) numerical derivatives. We also construct Monte Carlo experiments to compare maximum-likelihood estimates obtained with and without the aid of automatic derivatives. We find that the convergence rate of our optimization algorithm can increase substantially when we use AD derivatives.
Keywords: General equilibrium models, Kalman filter, maximum likelihood
JEL classification: C52, C61, C63
1 Introduction
While applications of automatic differentiation have spread across many different disciplines, they have remained less common in the field of economics.1 Based on the successes reported in facilitating optimization exercises in other disciplines, we deployed AD techniques to assist with the estimation of dynamic general equilibrium (DGE) models. These models are becoming a standard tool that central banks use to inform monetary policy decisions. However, the estimation of these models is complicated by the many parameters of interest. Thus, typically, the optimization method of choice makes use of derivatives. However, the complexity of the models does not afford a closed-form representation for the likelihood function. Finite-difference methods have been the standard practice to obtain numerical derivatives in this context. Using Tapenade (see [Hascoët 2004], [Hascoët et al. 2005], [Hascoët et al. 2005]), we constructed derivatives for a general formulation of the likelihood function, which takes as essential input the linear representation of the model's conditions for an equilibrium.
The programming task was complicated by the fact that the numerical solution of a DGE model under rational expectations relies on fairly complex algorithms.2 We use Lapack routines for the implementation of the solution algorithm. In turn, our top Lapack routines make use of a large number of Blas routines. A byproduct of our project has been the implementation of numerous AD derivatives of the double precision subset of Blas routines. Table 1 lists the routines involved.
In the remainder of this paper, Section 2 lays out the general structure of a DGE model and describes our approach to setting up the model's likelihood function. Section 3 outlines the step we took to implement the AD derivatives and how we built confidence in our results. Section 4 gives an example of a DGE model that we used to construct Monte Carlo experiments to compare maximum-likelihood estimates that rely, alternatively, on AD or FD derivatives, reported in Section 5. Section 6 concludes.
2 General Model Description and Estimation Strategy
The class of DGE models that is the focus of this paper take the general form:
In the equation above, ![]() is a matrix whose entries are
a function of the structural parameter vector
is a matrix whose entries are
a function of the structural parameter vector ![]() , while
, while ![]() is a vector of the model's
variables (including the stochastic innovations to the shock
processes). The term
is a vector of the model's
variables (including the stochastic innovations to the shock
processes). The term ![]() is an expectation operator,
conditional on information available at time
is an expectation operator,
conditional on information available at time ![]() and the model's structure as in equation 1. Notice that allowing for only one lead
and one lag of
and the model's structure as in equation 1. Notice that allowing for only one lead
and one lag of ![]() in the above equation implies no
loss of generality.
in the above equation implies no
loss of generality.
The model's solution takes the form:
thus, given knowledge of the model's variables at time ![]() , a solution determines the model's variables at time
, a solution determines the model's variables at time
![]() uniquely. The entries of the matrix
uniquely. The entries of the matrix
![]() are themselves functions of the matrix
are themselves functions of the matrix
![]() and, in turn, of the parameter vector
and, in turn, of the parameter vector
![]() .
.
Partitioning ![]() such that
such that
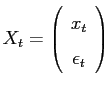 , where
, where ![]() is a collection of all the
innovations to the exogenous shock processes (and possibly
rearranging the system) it is convenient to rewrite the model's
solution as
is a collection of all the
innovations to the exogenous shock processes (and possibly
rearranging the system) it is convenient to rewrite the model's
solution as
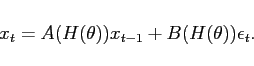
|
(3) |
Without loss of generality, we restrict the matrix
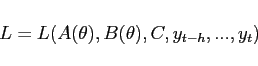
|
(6) |
The routines we developed, given an input ![]() , produce the derivative of the likelihood function
with respect to the structural parameters,
, produce the derivative of the likelihood function
with respect to the structural parameters,
![]() , and as an
intermediate product,
, and as an
intermediate product,
![]() , the
derivative of the model's reduced-form parameters with respect to
the structural parameters.
, the
derivative of the model's reduced-form parameters with respect to
the structural parameters.
3 Implementing AD Derivatives
To obtain AD derivatives of the likelihood function, we used Tapenade in tangent mode. Tapenade required limited manual intervention on our part. This is remarkable given that the code to be differentiated consisted of approximately 80 subroutines for a total of over 17,000 lines of code. The derivative-augmented code produced by Tapenade covers approximately 25,000 lines (the original code has a size of 554 kilobytes and the differentiated code is 784 kilobytes in size).
Recoding became necessary when the Lapack or Blas routines we called did not explicitly declare the sizes of the arguments in the calling structure and instead allowed for arbitrary sizing (possibly exceeding the storage requirements). A more limited recoding was required when we encountered the use of ``GOTO'' statements in the Fortran 77 code of the Blas library, which Tapenade could not process.
More substantially, two of the decompositions involved in the model solution, the real Schur decomposition and the singular-value decomposition, are not always unique. Parametric restrictions of the models we tested could ensure uniqueness of these decompositions. In those cases, we verified that AD derivatives obtained through Tapenade satisfied some basic properties of the decompositions that we derived analytically, but our test failed whenever we relaxed those parametric restrictions to allow for more general model specifications
In particular, we relied on the Lapack routine DGEESX to
implement the real Schur decomposition. For a given real matrix
![]() , this decomposition produces a unitary
matrix
, this decomposition produces a unitary
matrix ![]() , such that
, such that ![]() is
quasitriangular. Given
is
quasitriangular. Given
![]() , we need
that the derivative
, we need
that the derivative
![]() satisfy
satisfy
![]() , where
, where
![]() is itself
quasitriangular. This property failed to be met by our AD
derivatives when our choice of E implied a non-unique Schur
decomposition. To obviate this problem, we substituted the AD
derivative for the DGEESX routine with the analytical derivative of
the Schur decomposition as outlined in [Anderson 1987].
is itself
quasitriangular. This property failed to be met by our AD
derivatives when our choice of E implied a non-unique Schur
decomposition. To obviate this problem, we substituted the AD
derivative for the DGEESX routine with the analytical derivative of
the Schur decomposition as outlined in [Anderson 1987].
Similarly, the singular value decomposition, implemented through
the DGESVD routine in the Lapack library, given a real matrix
![]() , produces unitary matrices
, produces unitary matrices ![]() and
and ![]() and a diagonal matrix
and a diagonal matrix ![]() ,
such that
,
such that ![]() . Given
. Given
![]() , it can be
shown that
, it can be
shown that
![]() , where
, where
![]() is diagonal and
is diagonal and
![]() and
and
![]() are both
antisymmetric. Our AD derivative of the routine DGESVD failed to
satisfy this property when the matrix
are both
antisymmetric. Our AD derivative of the routine DGESVD failed to
satisfy this property when the matrix ![]() had repeated
singular values (making the decomposition non-unique). We
substituted our AD derivative with the analytical derivative
derived by [Papadopoulo and Lourakis 2000].
had repeated
singular values (making the decomposition non-unique). We
substituted our AD derivative with the analytical derivative
derived by [Papadopoulo and Lourakis 2000].
To test the derivative of the likelihood function, we used a
two-pronged approach. For special cases of our model that could be
simplified enough as to yield a closed-form analytical solution, we
computed analytical derivatives and found them in agreement with
our AD derivatives, accounting for numerical imprecision. To test
the derivatives for more complex models that we could not solve
analytically, we relied on comparisons with centered FD
derivatives. Generally with a step size of ![]() we
found broad agreement between our AD derivatives and FD
derivatives. Plotting AD and FD side by side, and varying the value
at which the derivatives were evaluated, we noticed that the FD
derivatives appeared noisier than the AD derivatives. We quantify
the ``noise'' we observed in an example below.
we
found broad agreement between our AD derivatives and FD
derivatives. Plotting AD and FD side by side, and varying the value
at which the derivatives were evaluated, we noticed that the FD
derivatives appeared noisier than the AD derivatives. We quantify
the ``noise'' we observed in an example below.
4 Example Application
As a first application of our derivatives, we consider a real business cycle model augmented with sticky prices and sticky wages, as well as several real rigidities, following the work of [Smets and Wouters 2003]. Below, we give a brief description of the optimization problems solved by agents in the model, which allows us to interpret the parameters estimated in the Monte Carlo exercises that follow.
There is a continuum of households of measure 1, indexed by
![]() , whose objective is to maximize a discounted
stream of utility according to the following setup:
, whose objective is to maximize a discounted
stream of utility according to the following setup:
![\begin{eqnarray*} && \max_{[C_t(h), W_t(h), I_t(h), K_{t+1}(h), B_{t+1}(h)]} E_t \sum^{\infty}_{j=0} \beta^j \left( U(C_{t+j}(h),C_{t+j-1}(h)) \right. \ && \left. + V(L_{t+j}(h)) \right) + \beta^j\lambda_{t+j}(h) \left[ \Pi_t(h) + T_{t+j}(h) + (1-\tau_{Lt}) W_{t+j}(h)L_{t+j}(h) \right. \ && \left. +(1-\tau_{Kt})R_{kt+j}K_{t+j}(h) -\frac{1}{2}\psi_I P_{t+j} \frac{ \left( I_{t+j}(h) - I_{t+j-1}(h) \right)^2}{I_{t+j-1}(h)} \right. \ && \left. -P_{t+j} C_{t+j}(h) - P_{t+j} I_{t+j}(h) - \int_s \psi_{t+j+1, t+j}B_{t+j+1}(h) + B_{t+j}(h) \right] \ && +\beta^j Q_{t+j}(h) \left[ (1-\delta) K_{t+j}(h) + I_{t+j} (h) -K_{t+j+1}(h) \right]. \end{eqnarray*}](img57.gif)
The utility function depends on consumption ![]() and
labor supplied
and
labor supplied ![]() . The parameter
. The parameter ![]() is a discount factor for future utility. Households
choose streams for consumption
is a discount factor for future utility. Households
choose streams for consumption ![]() , wages
, wages
![]() , investment
, investment ![]() , capital
, capital
![]() and bond holdings
and bond holdings ![]() , subject to the budget constraint, whose Lagrangian
multiplier is
, subject to the budget constraint, whose Lagrangian
multiplier is ![]() , capital accumulation
equation, whose Lagrangian multiplier is
, capital accumulation
equation, whose Lagrangian multiplier is ![]() , and
the labor demand schedule
, and
the labor demand schedule
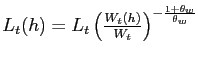 . Households rent to firms (described below) both capital, at the
rental rate
. Households rent to firms (described below) both capital, at the
rental rate ![]() , and labor at the rental rate
, and labor at the rental rate
![]() , subject to labor taxes at the rate
, subject to labor taxes at the rate
![]() and to capital taxes at the rate
and to capital taxes at the rate
![]() . There are quadratic adjustment
costs for investment, governed by the parameter
. There are quadratic adjustment
costs for investment, governed by the parameter ![]() , and capital depreciates at a per-period rate
, and capital depreciates at a per-period rate
![]() . We introduce Calvo-type contracts for
wages following [Erceg et al. 2000]. According to these
contracts, the ability to reset wages for a household
. We introduce Calvo-type contracts for
wages following [Erceg et al. 2000]. According to these
contracts, the ability to reset wages for a household ![]() in any period
in any period ![]() follows a Poisson
distribution. A household is allowed to reset wages with
probability
follows a Poisson
distribution. A household is allowed to reset wages with
probability ![]() . If the wage is not reset, it is
updated according to
. If the wage is not reset, it is
updated according to
![]() (where
(where ![]() is the steady-state inflation rate), as in [Yun 1996]. Finally,
is the steady-state inflation rate), as in [Yun 1996]. Finally,
![]() and
and ![]() represent,
respectively, net lump-sum transfers from the government and an
aliquot share of the profits of firms.
represent,
respectively, net lump-sum transfers from the government and an
aliquot share of the profits of firms.
In the production sector, we have a standard Dixit-Stiglitz setup with nominal rigidities. Competitive final producers aggregate intermediate products for resale. Their production function is
![$\displaystyle Y_t= \left[ \int_0^1 Y_t(f)^{\frac{1}{1+\theta_p}} \right]^{1+\theta_p}$](img82.gif)
|
(7) |
and from the zero profit condition the price for final goods is
![$\displaystyle P_{t}= \left[ \int_0^1 P_t(f)^{-\frac{1}{\theta_p}} \right] ^{-\theta_p}.$](img83.gif)
|
(8) |
where ![]() is the price for a unit of output for
the intermediate firm
is the price for a unit of output for
the intermediate firm ![]() .
.
Intermediate firms are monopolistically competitive. There is
complete mobility of capital and labor across firms. Their
production technology is given by
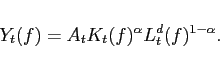
|
(9) |
Intermediate firms take input prices as given. ![]() , which enters the intermediate firms' production
function, is an aggregate over the skills supplied by each
household, and takes the form
, which enters the intermediate firms' production
function, is an aggregate over the skills supplied by each
household, and takes the form
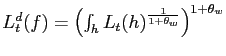 .
. ![]() is the technology level and evolves
according to an autoregressive (AR) process:
is the technology level and evolves
according to an autoregressive (AR) process:
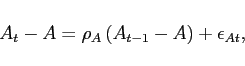
|
(10) |
where ![]() is an
is an ![]() innovation with standard deviation
innovation with standard deviation ![]() , and
, and
![]() is the steady-state level for technology.
Intermediate firms set their prices
is the steady-state level for technology.
Intermediate firms set their prices ![]() according
to Calvo-type contracts with reset probabilities
according
to Calvo-type contracts with reset probabilities ![]() . When prices are not reset, they are updated
according to
. When prices are not reset, they are updated
according to
![]() .
.
Finally, the government sector sets a nominal risk-free interest
rate according to the reaction function:
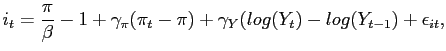
|
(11) |
where inflation
![]() , and
, and
![]() is itself an AR process of
order 1. For this process, we denote the AR coefficient with
is itself an AR process of
order 1. For this process, we denote the AR coefficient with
![]() ; the stochastic innovation is iid with
standard deviation
; the stochastic innovation is iid with
standard deviation ![]() . Notice that, in this
setting, households are Ricardian, hence the time-profile of net
lump-sum transfers is not distortionary. We assume that these
transfers are set according to:
. Notice that, in this
setting, households are Ricardian, hence the time-profile of net
lump-sum transfers is not distortionary. We assume that these
transfers are set according to:
|
(12) |
Labor taxes, ![]() , and capital taxes,
, and capital taxes, ![]() , follow exogenous AR processes
, follow exogenous AR processes
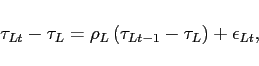
|
(13) |
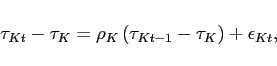
|
(14) |
as does Government spending (expressed as a share of output)
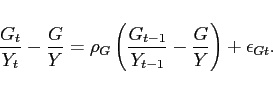
|
(15) |
In the equations above, the exogenous innovations
![]() are
are ![]() with standard deviations
with standard deviations ![]() ,
, ![]() , and
, and ![]() , respectively. The parameters
, respectively. The parameters ![]() ,
,
![]() , and
, and ![]() ,
without a time subscript, denote steady-state levels.
,
without a time subscript, denote steady-state levels.
The calibration strategy follows [Erceg et al. 2005] and parameter values are reported in Table 2. By linearizing the necessary conditions for the solution of the model, we can express them in the format of Equation (1).
5 Monte Carlo Results
Using the model described in Section 4 as the data-generating process, we set up a Monte Carlo experiment to compare maximum-likelihood estimates obtained through two different optimization methods. One of the methods relies on our AD derivative of the model's likelihood function. The alternative method, uses a two-point, centered, finite-difference approximation to the derivative.
In setting up the likelihood function, we limit our choices for
the observed variables in the vector ![]() of equation
(5) to four series, namely:
growth rate of output
of equation
(5) to four series, namely:
growth rate of output
![]() , price inflation
, price inflation
![]() , wage inflation
, wage inflation
![]() , and the
policy interest rate
, and the
policy interest rate ![]() . For each Monte Carlo
sample, we generate 200 observations, equivalent to 50 years of
data given our quarterly calibration, a sample length often used in
empirical studies. We attempt to estimate the parameters
. For each Monte Carlo
sample, we generate 200 observations, equivalent to 50 years of
data given our quarterly calibration, a sample length often used in
empirical studies. We attempt to estimate the parameters
![]() ,
, ![]() , governing
the exogenous shock process for the interest rate reaction
function;
, governing
the exogenous shock process for the interest rate reaction
function; ![]() ,
, ![]() , the
Calvo contract parameters for wages and prices; and
, the
Calvo contract parameters for wages and prices; and ![]() , and
, and ![]() the weights in the
monetary policy reaction function for inflation and activity. In
the estimation exercises, we kept the remaining parameters at their
values in the data-generating process as detailed in Table 2. We considered 1,000 Monte Carlo
samples.3 The two experiments described below
differ only insofar as we chose two different initialization points
for the optimization routines we used to maximize the likelihood
function.
the weights in the
monetary policy reaction function for inflation and activity. In
the estimation exercises, we kept the remaining parameters at their
values in the data-generating process as detailed in Table 2. We considered 1,000 Monte Carlo
samples.3 The two experiments described below
differ only insofar as we chose two different initialization points
for the optimization routines we used to maximize the likelihood
function.
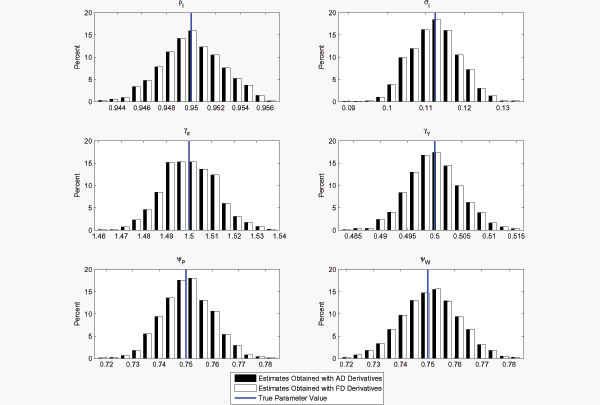
Figure 1 shows the sampling distribution for the parameter estimates from our Monte Carlo exercise when we initialize the optimization routine at the true parameter values used in the data-generating process. The black bars in the various panels denote the estimates that rely on AD derivatives, while the white bars denote the estimates obtained with FD derivatives. The optimization algorithm converged for all of the 1,000 Monte Carlo samples.4We verified that the optimization routine did move away from the initial point towards higher likelihood values, so that clustering of the estimates around the truth do not merely reflect the initialization point. For our experiment, the figure makes clear that when the optimization algorithm is initiated at the true value for the parameters of interest, reliance on FD derivatives minimally affects the maximum-likelihood estimates for those parameters.5
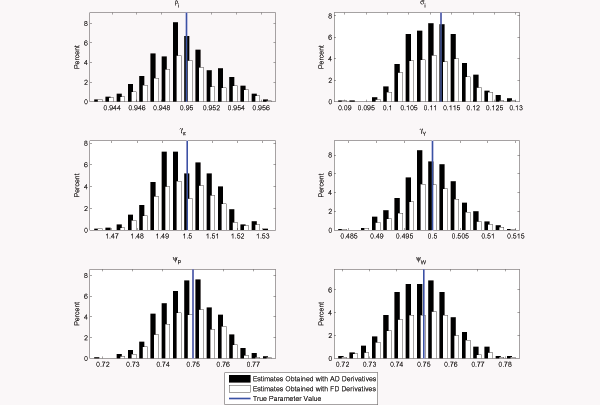
Of course, the true value of the parameters do not necessarily
coincide with the ML parameter estimates for small samples. Yet, it
is unrealistic to assume that a researcher would happen on such
good starting values. Figure 2 reports the sampling distribution of estimates obtained when we
initialize the optimization algorithm at arbitrary values for the
parameters being estimated, away from their true values. For the
estimates reported in Figure 2, we
chose ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() . The bars in Figure 2 show the frequency of estimates in a given
range as a percentage of the 1,000 experiments we performed. We
excluded results for which our optimization algorithm failed to
converge. The figure makes clear that the convergence rate is much
higher when using AD derivatives (47.2% instead of 28.3% for FD
derivatives). Moreover, it is also remarkable that the higher
convergence rate is not accompanied by a deterioration of the
estimates (the increased height of the black bars in the figure is
proportional to that of the white bars).
. The bars in Figure 2 show the frequency of estimates in a given
range as a percentage of the 1,000 experiments we performed. We
excluded results for which our optimization algorithm failed to
converge. The figure makes clear that the convergence rate is much
higher when using AD derivatives (47.2% instead of 28.3% for FD
derivatives). Moreover, it is also remarkable that the higher
convergence rate is not accompanied by a deterioration of the
estimates (the increased height of the black bars in the figure is
proportional to that of the white bars).
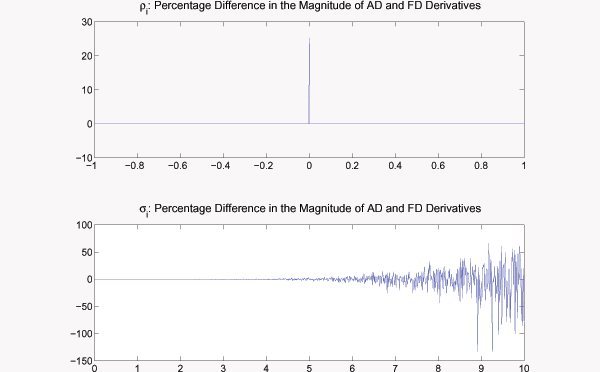
To quantify the difference between AD and FD derivatives of the
likelihood function for one of our samples, we varied the
parameters we estimated one at a time. Figure 3 shows the percentage difference in
the magnitude of the AD and FD derivatives for ![]() and
and ![]() . We discretized the ranges
shown using a grid of 1,000 equally spaced points. The differences
are generally small percentage-wise, although, on occasion, they
spike up, or creep up as we move away from the true value, as in
the case of
. We discretized the ranges
shown using a grid of 1,000 equally spaced points. The differences
are generally small percentage-wise, although, on occasion, they
spike up, or creep up as we move away from the true value, as in
the case of ![]() . For the other parameters we
estimated, we did not observe differences in the magnitudes of the
AD and FD derivatives larger than
. For the other parameters we
estimated, we did not observe differences in the magnitudes of the
AD and FD derivatives larger than ![]() over
ranges consistent with the existence of a rational expectations
equilibrium for our model.
over
ranges consistent with the existence of a rational expectations
equilibrium for our model.
6 Conclusion
Given that the approximation error for a first derivative of the likelihood function of a DGE model computed through FD methods depends on the size of the second derivative, which itself is subject to approximation error, we view having an independent check in the form of automatic derivatives as a major contribution of our work. As an example application, we showed that AD derivatives can facilitate the computation of maximum-likelihood estimates for the parameters of a DGE model.
Bibliography
Anderson, G. (1987). A Procedure for Differentiating Perfect-Foresight-Model Reduced-Form Coefficients. Journal of Economic Dynamics and Control 11, 465-81.
Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.
C. H. Bischof, H. M. Bücher, B. L. (2002). Automatic Differentiation for Computational Finance. In B. R. E. J. Kontoghiorghes and S. Siokos (Eds.), Computational Methods in Decision-Making. springer.
Erceg, C. J., L. Guerrieri, and C. Gust (2005). Can Long-Run Restrictions Identify Technology Shocks? Journal of the European Economic Association 3(6), 1237-1278.
Erceg, C. J., D. W. Henderson, and A. T. Levin (2000). Optimal monetary policy with staggered wage and price contracts. Journal of Monetary Economics 46(2), 281-313.
Giles, M. (2007). Monte Carlo Evaluation of Sensitivities in Computational Finance. In E. A. Lipitakis (Ed.), HERCMA – The 8th Hellenic European Research on Computer Mathematics and its Applications Conference.
Hascoët, L. (2004). TAPENADE: a tool for Automatic Differentiation of programs. In Proceedings of 4![]() European Congress on Computational Methods, ECCOMAS'2004, Jyvaskyla, Finland.
European Congress on Computational Methods, ECCOMAS'2004, Jyvaskyla, Finland.
Hascoët, L., R.-M. Greborio, and V. Pascual (2005). Computing Adjoints by Automatic Differentiation with TAPENADE. Springer. Forthcoming.
Hascoët, L., V. Pascual, and D. Dervieux (2005). Automatic Differentiation with TAPENADE. Springer. Forthcoming.
M. Giles, P. G. (2006). Smoking Adjoints: Fast Monte Carlo Greeks. Risk Magazine 19, 88-92.
Papadopoulo, T. and M. I. A. Lourakis (2000). Estimating the Jacobian of the Singular Value Decomposition: Theory and Applications. Lecture Notes in Computer Science 1842/2000, 554-570.
Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1(5), 1123-1175.
Yun, T. (1996). Nominal price rigidity, money supply endogeneity, and business cycles. Journal of Monetary Economics 37, 345-370.
Table 1: List of library functions
| Blas Functions | daxpy.f, dcopy.f, ddot.f, dgemm.f, dgemv.f, dger.f, dnrm2.f, drot.f, dscal.f, dswap.f, dtrmm.f, dtrmv.f, dtrsm.f |
|---|---|
| Lapack Functions | dgebak.f, dgebal.f, dgeesx.f, dgehd2.f, dgehrd.f, dgeqp3.f, dgeqr2.f, dgeqrf.f, dgesv.f, dgetf2.f, dgetrf.f, dgetrs.f, dhseqr.f, dlacn2.f, dlacpy.f, dladiv.f, dlaexc.f, dlahqr.f, dlahr2.f, dlaln2.f, dlange.f, dlanv2.f, dlapy2.f, dlaqp2.f, dlaqps.f, dlaqr0.f, dlaqr1.f, dlaqr2.f, dlaqr3.f, dlaqr4.f, dlaqr5.f, dlarfb.f, dlarf.f, dlarfg.f, dlarft.f, dlarfx.f, dlartg.f, dlascl.f, dlaset.f, dlassq.f, dlaswp.f, dlasy2.f, dorg2r.f, dorghr.f, dorgqr.f, dorm2r.f, dormqr.f, dtrexc.f, dtrsen.f, dtrsyl.f, dtrtrs.f |
Table 2a: Calibration - Parameters Governing Households' and Firms' Behavior
| Parameter | Used to Determine |
|---|---|
| discount factor | |
| steady state labor tax rate | |
| Calvo price parameter | |
|
|
depreciation rate |
| investment adj. cost | |
| steady state capital tax rate | |
| Calvo wage parameter |
Table 2b: Calibration - Monetary Policy Reaction Function
| Parameter | Used to Determine |
|---|---|
|
|
inflation weight |
| output weight |
Table 2c: Calibration - Exogenous Processes
| Parameter | Used to Determine |
|---|---|
| AR(1) Coefficient - labor tax rate | |
| AR(1) Coefficient - capital tax rate | |
| AR(1) Coefficient - govt spending | |
| AR(1) Coefficient - monetary policy | |
| AR(1) Coefficient - technology | |
| Standard Deviation - labor tax rate innovation | |
| Standard Deviation - capital tax innovation | |
| Standard Deviation - govt spending innovation | |
| Standard Deviation - monetary policy innovation | |
| Standard Deviation - labor tax innovation |
Figure 1: Sampling Distribution of Parameter Estimates; the Initial Guesses Concided with the True Values in the Data-Generating Process
Data for Figure 1
variable | true parameter value | bin | finite differences (%) | automatic differentiation (%) |
|---|---|---|---|---|
\rho_i | 0.95 |
0.942808 |
0.3 |
0.3 |
\rho_i | 0.95 |
0.943721 |
0.6 |
0.6 |
\rho_i | 0.95 |
0.944633 |
0.9 |
0.9 |
\rho_i | 0.95 |
0.945545 |
3.4 |
3.4 |
\rho_i | 0.95 |
0.946458 |
4.8 |
4.8 |
\rho_i | 0.95 |
0.94737 |
7.8 |
7.8 |
\rho_i | 0.95 |
0.948283 |
11.2 |
11.2 |
\rho_i | 0.95 |
0.949195 |
14.2 |
14.2 |
\rho_i | 0.95 |
0.950108 |
15.9 |
15.9 |
\rho_i | 0.95 |
0.95102 |
12.3 |
12.3 |
\rho_i | 0.95 |
0.951932 |
10.5 |
10.5 |
\rho_i | 0.95 |
0.952845 |
7.6 |
7.6 |
\rho_i | 0.95 |
0.953757 |
5.2 |
5.2 |
\rho_i | 0.95 |
0.95467 |
3.7 |
3.7 |
\rho_i | 0.95 |
0.955582 |
1.4 |
1.4 |
\rho_i | 0.95 |
0.956495 |
0.2 |
0.2 |
\sigma_i | 0.1125 |
0.089507 |
0.1 |
0.1 |
\sigma_i | 0.1125 |
0.092423 |
0.1 |
0.1 |
\sigma_i | 0.1125 |
0.095339 |
0.2 |
0.2 |
\sigma_i | 0.1125 |
0.098255 |
1 |
1 |
\sigma_i | 0.1125 |
0.101171 |
3.8 |
3.8 |
\sigma_i | 0.1125 |
0.104087 |
9.9 |
9.9 |
\sigma_i | 0.1125 |
0.107003 |
11.9 |
11.9 |
\sigma_i | 0.1125 |
0.109919 |
16.2 |
16.2 |
\sigma_i | 0.1125 |
0.112835 |
18.4 |
18.4 |
\sigma_i | 0.1125 |
0.115751 |
16 |
16 |
\sigma_i | 0.1125 |
0.118667 |
10.5 |
10.5 |
\sigma_i | 0.1125 |
0.121582 |
7.2 |
7.2 |
\sigma_i | 0.1125 |
0.124498 |
3 |
3 |
\sigma_i | 0.1125 |
0.127414 |
1.3 |
1.3 |
\sigma_i | 0.1125 |
0.13033 |
0.2 |
0.2 |
\sigma_i | 0.1125 |
0.133246 |
0.2 |
0.2 |
\gamma_{\pi} | 1.5 |
1.461714 |
0.1 |
0.1 |
\gamma_{\pi} | 1.5 |
1.466688 |
0.1 |
0.1 |
\gamma_{\pi} | 1.5 |
1.471662 |
0.7 |
0.7 |
\gamma_{\pi} | 1.5 |
1.476636 |
2.3 |
2.3 |
\gamma_{\pi} | 1.5 |
1.48161 |
4.6 |
4.6 |
\gamma_{\pi} | 1.5 |
1.486584 |
8.5 |
8.5 |
\gamma_{\pi} | 1.5 |
1.491557 |
15.2 |
15.2 |
\gamma_{\pi} | 1.5 |
1.496531 |
15.3 |
15.3 |
\gamma_{\pi} | 1.5 |
1.501505 |
15.3 |
15.3 |
\gamma_{\pi} | 1.5 |
1.506479 |
13.7 |
13.7 |
\gamma_{\pi} | 1.5 |
1.511453 |
12.4 |
12.4 |
\gamma_{\pi} | 1.5 |
1.516427 |
6 |
6 |
\gamma_{\pi} | 1.5 |
1.5214 |
3.1 |
3.1 |
\gamma_{\pi} | 1.5 |
1.526374 |
1.7 |
1.7 |
\gamma_{\pi} | 1.5 |
1.531348 |
0.8 |
0.8 |
\gamma_{\pi} | 1.5 |
1.536322 |
0.2 |
0.2 |
\gamma_Y | 0.5 |
0.483826 |
0.1 |
0.1 |
\gamma_Y | 0.5 |
0.485893 |
0.4 |
0.4 |
\gamma_Y | 0.5 |
0.487959 |
0.4 |
0.4 |
\gamma_Y | 0.5 |
0.490026 |
2.4 |
2.4 |
\gamma_Y | 0.5 |
0.492093 |
4 |
4 |
\gamma_Y | 0.5 |
0.494159 |
8.4 |
8.4 |
\gamma_Y | 0.5 |
0.496226 |
13 |
13 |
\gamma_Y | 0.5 |
0.498293 |
16.8 |
16.8 |
\gamma_Y | 0.5 |
0.500359 |
17.4 |
17.4 |
\gamma_Y | 0.5 |
0.502426 |
14.4 |
14.4 |
\gamma_Y | 0.5 |
0.504493 |
10 |
10 |
\gamma_Y | 0.5 |
0.506559 |
6.2 |
6.2 |
\gamma_Y | 0.5 |
0.508626 |
3.9 |
3.9 |
\gamma_Y | 0.5 |
0.510693 |
1.6 |
1.6 |
\gamma_Y | 0.5 |
0.51276 |
0.7 |
0.7 |
\gamma_Y | 0.5 |
0.514826 |
0.3 |
0.3 |
\psi_P | 0.75 |
0.718549 |
0.1 |
0.1 |
\psi_P | 0.75 |
0.722793 |
0.2 |
0.2 |
\psi_P | 0.75 |
0.727037 |
0.6 |
0.6 |
\psi_P | 0.75 |
0.731281 |
1.8 |
1.8 |
\psi_P | 0.75 |
0.735526 |
5.5 |
5.5 |
\psi_P | 0.75 |
0.73977 |
9.4 |
9.4 |
\psi_P | 0.75 |
0.744014 |
13.6 |
13.6 |
\psi_P | 0.75 |
0.748258 |
17.6 |
17.6 |
\psi_P | 0.75 |
0.752502 |
18 |
18 |
\psi_P | 0.75 |
0.756746 |
13 |
13 |
\psi_P | 0.75 |
0.76099 |
10.6 |
10.6 |
\psi_P | 0.75 |
0.765234 |
5.4 |
5.4 |
\psi_P | 0.75 |
0.769478 |
2.9 |
2.9 |
\psi_P | 0.75 |
0.773722 |
0.8 |
0.8 |
\psi_P | 0.75 |
0.777966 |
0.4 |
0.4 |
\psi_P | 0.75 |
0.78221 |
0.1 |
0.1 |
\psi_W | 0.75 |
0.720129 |
0.2 |
0.2 |
\psi_W | 0.75 |
0.724272 |
0.8 |
0.8 |
\psi_W | 0.75 |
0.728415 |
1.8 |
1.8 |
\psi_W | 0.75 |
0.732558 |
3.3 |
3.3 |
\psi_W | 0.75 |
0.736702 |
6.5 |
6.5 |
\psi_W | 0.75 |
0.740845 |
9.7 |
9.7 |
\psi_W | 0.75 |
0.744988 |
13 |
13 |
\psi_W | 0.75 |
0.749131 |
14.7 |
14.7 |
\psi_W | 0.75 |
0.753275 |
15.6 |
15.5 |
\psi_W | 0.75 |
0.757418 |
12.8 |
12.9 |
\psi_W | 0.75 |
0.761561 |
9.4 |
9.4 |
\psi_W | 0.75 |
0.765704 |
6.5 |
6.5 |
\psi_W | 0.75 |
0.769848 |
3.1 |
3.1 |
\psi_W | 0.75 |
0.773991 |
1.8 |
1.8 |
\psi_W | 0.75 |
0.778134 |
0.5 |
0.5 |
\psi_W | 0.75 |
0.782277 |
0.3 |
0.3 |
Figure 2: Sampling Distribution of Parameter Estimates; the Initial Guesses Did Not Concide with the True Values in the Data-Generating Process
Data for Figure 2
variable |
true parameter value |
bin |
finite differences (%) |
automatic differentiation (%) |
|---|---|---|---|---|
\rho_i | 0.95 |
0.942894 |
0.2 |
0.2 |
\rho_i | 0.95 |
0.9438 |
0.4 |
0.5 |
\rho_i | 0.95 |
0.944706 |
0.5 |
0.8 |
\rho_i | 0.95 |
0.945612 |
1 |
1.8 |
\rho_i | 0.95 |
0.946518 |
1.7 |
2.6 |
\rho_i | 0.95 |
0.947425 |
2.4 |
4.9 |
\rho_i | 0.95 |
0.948331 |
3.3 |
4.6 |
\rho_i | 0.95 |
0.949237 |
4.7 |
8.1 |
\rho_i | 0.95 |
0.950143 |
4.2 |
6.7 |
\rho_i | 0.95 |
0.951049 |
3.5 |
5.3 |
\rho_i | 0.95 |
0.951955 |
1.5 |
3.2 |
\rho_i | 0.95 |
0.952862 |
1.4 |
3.4 |
\rho_i | 0.95 |
0.953768 |
1.6 |
2.5 |
\rho_i | 0.95 |
0.954674 |
1.2 |
1.6 |
\rho_i | 0.95 |
0.95558 |
0.6 |
0.8 |
\rho_i | 0.95 |
0.956486 |
0.1 |
0.2 |
\sigma_i | 0.1125 |
0.089486 |
0.1 |
0.1 |
\sigma_i | 0.1125 |
0.092113 |
0 |
0.1 |
\sigma_i | 0.1125 |
0.09474 |
0 |
0 |
\sigma_i | 0.1125 |
0.097366 |
0.2 |
0.4 |
\sigma_i | 0.1125 |
0.099993 |
0.9 |
1.4 |
\sigma_i | 0.1125 |
0.102619 |
2.7 |
3.5 |
\sigma_i | 0.1125 |
0.105246 |
3.8 |
6.3 |
\sigma_i | 0.1125 |
0.107873 |
3.9 |
6.6 |
\sigma_i | 0.1125 |
0.110499 |
4.3 |
7.3 |
\sigma_i | 0.1125 |
0.113126 |
3.7 |
7.2 |
\sigma_i | 0.1125 |
0.115753 |
4 |
6.3 |
\sigma_i | 0.1125 |
0.118379 |
2.3 |
3.6 |
\sigma_i | 0.1125 |
0.121006 |
1.3 |
2.5 |
\sigma_i | 0.1125 |
0.123633 |
0.9 |
1 |
\sigma_i | 0.1125 |
0.126259 |
0.1 |
0.6 |
\sigma_i | 0.1125 |
0.128886 |
0.1 |
0.3 |
\gamma_{\pi} | 1.5 |
1.464618 |
0.1 |
0.1 |
\gamma_{\pi} | 1.5 |
1.46909 |
0 |
0.2 |
\gamma_{\pi} | 1.5 |
1.473563 |
0.2 |
0.5 |
\gamma_{\pi} | 1.5 |
1.478035 |
0.9 |
1.4 |
\gamma_{\pi} | 1.5 |
1.482507 |
1.3 |
2.3 |
\gamma_{\pi} | 1.5 |
1.48698 |
3.1 |
4.4 |
\gamma_{\pi} | 1.5 |
1.491452 |
4 |
7.2 |
\gamma_{\pi} | 1.5 |
1.495925 |
4.5 |
7.2 |
\gamma_{\pi} | 1.5 |
1.500397 |
2.9 |
5.2 |
\gamma_{\pi} | 1.5 |
1.50487 |
4.1 |
6.2 |
\gamma_{\pi} | 1.5 |
1.509342 |
3.2 |
5.2 |
\gamma_{\pi} | 1.5 |
1.513815 |
2.4 |
4 |
\gamma_{\pi} | 1.5 |
1.518287 |
0.7 |
1.9 |
\gamma_{\pi} | 1.5 |
1.52276 |
0.4 |
0.5 |
\gamma_{\pi} | 1.5 |
1.527232 |
0.5 |
0.8 |
\gamma_{\pi} | 1.5 |
1.531704 |
-1.1E-16 |
0.1 |
\gamma_Y | 0.5 |
0.483832 |
0.1 |
0.1 |
\gamma_Y | 0.5 |
0.485855 |
0 |
0 |
\gamma_Y | 0.5 |
0.487877 |
0.2 |
0.2 |
\gamma_Y | 0.5 |
0.489899 |
0.8 |
1.4 |
\gamma_Y | 0.5 |
0.491921 |
1.2 |
2.1 |
\gamma_Y | 0.5 |
0.493944 |
1.8 |
3.4 |
\gamma_Y | 0.5 |
0.495966 |
3 |
5.6 |
\gamma_Y | 0.5 |
0.497988 |
4.9 |
8.5 |
\gamma_Y | 0.5 |
0.50001 |
4.8 |
7.3 |
\gamma_Y | 0.5 |
0.502033 |
4.4 |
7 |
\gamma_Y | 0.5 |
0.504055 |
3.3 |
5.2 |
\gamma_Y | 0.5 |
0.506077 |
1.9 |
2.9 |
\gamma_Y | 0.5 |
0.508099 |
0.9 |
2 |
\gamma_Y | 0.5 |
0.510122 |
0.6 |
0.9 |
\gamma_Y | 0.5 |
0.512144 |
0.3 |
0.5 |
\gamma_Y | 0.5 |
0.514166 |
0.1 |
0.1 |
\psi_P | 0.75 |
0.718544 |
0 |
0.1 |
\psi_P | 0.75 |
0.722281 |
0 |
0 |
\psi_P | 0.75 |
0.726019 |
0.2 |
0.4 |
\psi_P | 0.75 |
0.729757 |
0.4 |
0.8 |
\psi_P | 0.75 |
0.733494 |
1.1 |
1.6 |
\psi_P | 0.75 |
0.737232 |
2.3 |
4.3 |
\psi_P | 0.75 |
0.74097 |
3.3 |
5.3 |
\psi_P | 0.75 |
0.744707 |
4.4 |
6.5 |
\psi_P | 0.75 |
0.748445 |
4.2 |
7.5 |
\psi_P | 0.75 |
0.752183 |
4.7 |
7.6 |
\psi_P | 0.75 |
0.755921 |
2.8 |
4.9 |
\psi_P | 0.75 |
0.759658 |
3.1 |
4.2 |
\psi_P | 0.75 |
0.763396 |
1.3 |
2.3 |
\psi_P | 0.75 |
0.767134 |
0.3 |
1 |
\psi_P | 0.75 |
0.770871 |
0.1 |
0.5 |
\psi_P | 0.75 |
0.774609 |
0.1 |
0.2 |
\psi_W | 0.75 |
0.720031 |
0.1 |
0.2 |
\psi_W | 0.75 |
0.72418 |
0.4 |
0.5 |
\psi_W | 0.75 |
0.728329 |
0.5 |
1.1 |
\psi_W | 0.75 |
0.732478 |
1.4 |
1.9 |
\psi_W | 0.75 |
0.736627 |
2.4 |
3.8 |
\psi_W | 0.75 |
0.740776 |
3.4 |
5.8 |
\psi_W | 0.75 |
0.744925 |
3.8 |
6.5 |
\psi_W | 0.75 |
0.749074 |
3.8 |
6.5 |
\psi_W | 0.75 |
0.753223 |
4.1 |
6.8 |
\psi_W | 0.75 |
0.757372 |
3.8 |
5.8 |
\psi_W | 0.75 |
0.761521 |
2 |
3.6 |
\psi_W | 0.75 |
0.765669 |
1.6 |
2.3 |
\psi_W | 0.75 |
0.769818 |
0.3 |
1 |
\psi_W | 0.75 |
0.773967 |
0.5 |
1 |
\psi_W | 0.75 |
0.778116 |
0.1 |
0.2 |
\psi_W | 0.75 |
0.782265 |
0.1 |
0.2 |
Figure 3: Percentage Difference Between AD and FD Derivatives
Data for Figure 3 - \rho_i: Percentage Difference in the Magnitude of AD and FD Derivatives
Parameter Value | Percentage Difference |
|---|---|
-0.999 |
-4.4E-05 |
-0.997 |
-2.7E-05 |
-0.995 |
0.000378 |
-0.99301 |
-4.3E-05 |
-0.99101 |
-2E-05 |
-0.98901 |
-0.00022 |
-0.98701 |
-0.00017 |
-0.98501 |
-0.00025 |
-0.98302 |
-3.2E-05 |
-0.98102 |
-5.1E-05 |
-0.97902 |
-0.00026 |
-0.97702 |
-5.3E-05 |
-0.97502 |
8.3E-05 |
-0.97303 |
-9.2E-05 |
-0.97103 |
1.03E-05 |
-0.96903 |
-0.00017 |
-0.96703 |
-0.00028 |
-0.96503 |
-1.9E-05 |
-0.96304 |
0.00019 |
-0.96104 |
5.99E-05 |
-0.95904 |
4.74E-05 |
-0.95704 |
0.000168 |
-0.95504 |
-0.00032 |
-0.95305 |
5.11E-05 |
-0.95105 |
9.21E-05 |
-0.94905 |
0.000108 |
-0.94705 |
7.23E-06 |
-0.94505 |
-0.00011 |
-0.94306 |
-0.00026 |
-0.94106 |
-7.9E-05 |
-0.93906 |
0.000209 |
-0.93706 |
5.22E-05 |
-0.93506 |
-4.4E-06 |
-0.93307 |
-0.0002 |
-0.93107 |
-0.00011 |
-0.92907 |
-9.8E-05 |
-0.92707 |
-8.2E-05 |
-0.92507 |
-3.9E-05 |
-0.92308 |
-5.3E-05 |
-0.92108 |
-4.7E-05 |
-0.91908 |
-0.00024 |
-0.91708 |
-7E-05 |
-0.91508 |
4.28E-05 |
-0.91309 |
0.000124 |
-0.91109 |
-0.00019 |
-0.90909 |
-0.00025 |
-0.90709 |
5.47E-06 |
-0.90509 |
8.31E-05 |
-0.9031 |
0.000125 |
-0.9011 |
4.57E-05 |
-0.8991 |
-0.00016 |
-0.8971 |
-9.8E-05 |
-0.8951 |
0.00014 |
-0.89311 |
-0.0001 |
-0.89111 |
5.34E-05 |
-0.88911 |
3.68E-05 |
-0.88711 |
0.000184 |
-0.88511 |
-0.00015 |
-0.88312 |
0.000176 |
-0.88112 |
0.000139 |
-0.87912 |
-3.5E-05 |
-0.87712 |
0.000126 |
-0.87512 |
9.19E-06 |
-0.87313 |
-0.00012 |
-0.87113 |
-0.00027 |
-0.86913 |
-6.2E-05 |
-0.86713 |
-1.2E-05 |
-0.86513 |
3.78E-06 |
-0.86314 |
-0.00011 |
-0.86114 |
0.000193 |
-0.85914 |
0.000156 |
-0.85714 |
-9.5E-05 |
-0.85514 |
-4.6E-05 |
-0.85315 |
0.00012 |
-0.85115 |
3.12E-05 |
-0.84915 |
-0.00024 |
-0.84715 |
-0.00013 |
-0.84515 |
0.000128 |
-0.84316 |
0.000132 |
-0.84116 |
2.81E-05 |
-0.83916 |
-1.5E-05 |
-0.83716 |
-0.00028 |
-0.83516 |
-0.00013 |
-0.83317 |
-0.00013 |
-0.83117 |
4.74E-05 |
-0.82917 |
-4.1E-05 |
-0.82717 |
-0.00016 |
-0.82517 |
-9.5E-05 |
-0.82318 |
1.95E-05 |
-0.82118 |
0.000202 |
-0.81918 |
-0.00021 |
-0.81718 |
-0.00023 |
-0.81518 |
0.000167 |
-0.81319 |
0.000111 |
-0.81119 |
-9.1E-05 |
-0.80919 |
-1.6E-05 |
-0.80719 |
-5E-05 |
-0.80519 |
-0.00034 |
-0.8032 |
2.35E-05 |
-0.8012 |
0.000145 |
-0.7992 |
0.00013 |
-0.7972 |
4.62E-05 |
-0.7952 |
0.000109 |
-0.79321 |
-9E-05 |
-0.79121 |
0.000153 |
-0.78921 |
-0.00026 |
-0.78721 |
-2E-05 |
-0.78521 |
1.39E-05 |
-0.78322 |
-0.00033 |
-0.78122 |
8.92E-05 |
-0.77922 |
7.51E-05 |
-0.77722 |
-0.00014 |
-0.77522 |
-9.2E-05 |
-0.77323 |
0.000303 |
-0.77123 |
2.86E-05 |
-0.76923 |
1.91E-05 |
-0.76723 |
-1.6E-05 |
-0.76523 |
0.000117 |
-0.76324 |
-7.1E-06 |
-0.76124 |
-7.9E-05 |
-0.75924 |
-9.1E-05 |
-0.75724 |
-8.5E-05 |
-0.75524 |
-9.8E-05 |
-0.75325 |
-0.00017 |
-0.75125 |
-0.00014 |
-0.74925 |
-0.0002 |
-0.74725 |
1.99E-05 |
-0.74525 |
8.02E-05 |
-0.74326 |
-4.1E-05 |
-0.74126 |
6.17E-05 |
-0.73926 |
4.08E-05 |
-0.73726 |
0.000116 |
-0.73526 |
6.27E-05 |
-0.73327 |
7.47E-05 |
-0.73127 |
0.000128 |
-0.72927 |
9.41E-06 |
-0.72727 |
5.35E-05 |
-0.72527 |
6.24E-05 |
-0.72328 |
0.000252 |
-0.72128 |
8.26E-05 |
-0.71928 |
0.000108 |
-0.71728 |
-0.00017 |
-0.71528 |
5.2E-05 |
-0.71329 |
-9.9E-05 |
-0.71129 |
-4E-05 |
-0.70929 |
0.000123 |
-0.70729 |
-0.00012 |
-0.70529 |
0.00012 |
-0.7033 |
-0.00024 |
-0.7013 |
3.55E-05 |
-0.6993 |
4.47E-05 |
-0.6973 |
0.000274 |
-0.6953 |
-0.00016 |
-0.69331 |
2.23E-05 |
-0.69131 |
0.000183 |
-0.68931 |
1.27E-05 |
-0.68731 |
0.000156 |
-0.68531 |
-1.5E-05 |
-0.68332 |
-0.00033 |
-0.68132 |
-0.00022 |
-0.67932 |
-1.5E-05 |
-0.67732 |
0.000239 |
-0.67532 |
-0.00011 |
-0.67333 |
-0.00028 |
-0.67133 |
0.00012 |
-0.66933 |
5.49E-05 |
-0.66733 |
0.000156 |
-0.66533 |
0.000244 |
-0.66334 |
-8.5E-06 |
-0.66134 |
1.58E-05 |
-0.65934 |
-0.00028 |
-0.65734 |
-2.6E-05 |
-0.65534 |
-5.6E-05 |
-0.65335 |
5.17E-05 |
-0.65135 |
0.00017 |
-0.64935 |
-1.4E-05 |
-0.64735 |
-0.00022 |
-0.64535 |
-4.9E-05 |
-0.64336 |
0.000288 |
-0.64136 |
0.00025 |
-0.63936 |
0.000124 |
-0.63736 |
-0.00019 |
-0.63536 |
0.00014 |
-0.63337 |
-0.0003 |
-0.63137 |
-0.00015 |
-0.62937 |
5.12E-05 |
-0.62737 |
5.28E-05 |
-0.62537 |
4.5E-05 |
-0.62338 |
0.000226 |
-0.62138 |
1.24E-05 |
-0.61938 |
0.000247 |
-0.61738 |
-2.7E-07 |
-0.61538 |
-0.00016 |
-0.61339 |
0.000184 |
-0.61139 |
-0.00016 |
-0.60939 |
3.98E-05 |
-0.60739 |
-6.9E-05 |
-0.60539 |
-0.00013 |
-0.6034 |
-3.1E-05 |
-0.6014 |
0.000341 |
-0.5994 |
0.000174 |
-0.5974 |
-7.1E-05 |
-0.5954 |
-0.00021 |
-0.59341 |
-7.2E-05 |
-0.59141 |
-0.00017 |
-0.58941 |
-0.00017 |
-0.58741 |
-6.2E-05 |
-0.58541 |
-5.1E-05 |
-0.58342 |
-0.00012 |
-0.58142 |
0.000123 |
-0.57942 |
-4.9E-05 |
-0.57742 |
-9.5E-05 |
-0.57542 |
-0.0003 |
-0.57343 |
-0.00014 |
-0.57143 |
0.000278 |
-0.56943 |
-0.00014 |
-0.56743 |
-0.00015 |
-0.56543 |
-1.8E-05 |
-0.56344 |
-4.6E-06 |
-0.56144 |
0.000231 |
-0.55944 |
-2.1E-05 |
-0.55744 |
3.3E-05 |
-0.55544 |
0.000308 |
-0.55345 |
0.000121 |
-0.55145 |
-0.00034 |
-0.54945 |
-2E-05 |
-0.54745 |
0.000178 |
-0.54545 |
-0.00023 |
-0.54346 |
-0.00035 |
-0.54146 |
7.25E-05 |
-0.53946 |
-1.8E-05 |
-0.53746 |
0.000122 |
-0.53546 |
0.00014 |
-0.53347 |
1.97E-05 |
-0.53147 |
0.000117 |
-0.52947 |
-4.3E-06 |
-0.52747 |
0.000147 |
-0.52547 |
0.00022 |
-0.52348 |
1E-05 |
-0.52148 |
0.000263 |
-0.51948 |
-5.9E-05 |
-0.51748 |
6.05E-05 |
-0.51548 |
0.00024 |
-0.51349 |
0.00011 |
-0.51149 |
-9.1E-05 |
-0.50949 |
-9E-05 |
-0.50749 |
0.000218 |
-0.50549 |
-0.00014 |
-0.5035 |
-0.00023 |
-0.5015 |
-0.00025 |
-0.4995 |
0.000368 |
-0.4975 |
0.000197 |
-0.4955 |
0.000193 |
-0.49351 |
-8.3E-05 |
-0.49151 |
7.46E-05 |
-0.48951 |
1.05E-06 |
-0.48751 |
-5.1E-05 |
-0.48551 |
-0.00028 |
-0.48352 |
-0.00012 |
-0.48152 |
-0.00021 |
-0.47952 |
-0.00018 |
-0.47752 |
6.43E-05 |
-0.47552 |
7.1E-05 |
-0.47353 |
-0.00016 |
-0.47153 |
-0.00032 |
-0.46953 |
0.000227 |
-0.46753 |
-0.00034 |
-0.46553 |
0.00018 |
-0.46354 |
0.000111 |
-0.46154 |
-1.3E-05 |
-0.45954 |
0.000264 |
-0.45754 |
-4.7E-05 |
-0.45554 |
-2.2E-05 |
-0.45355 |
-3.9E-05 |
-0.45155 |
0.000262 |
-0.44955 |
-0.00021 |
-0.44755 |
-0.0003 |
-0.44555 |
-0.0002 |
-0.44356 |
-0.00034 |
-0.44156 |
-2.1E-05 |
-0.43956 |
-3.3E-05 |
-0.43756 |
0.000211 |
-0.43556 |
1.1E-05 |
-0.43357 |
3.33E-05 |
-0.43157 |
-3.2E-05 |
-0.42957 |
4.8E-05 |
-0.42757 |
-6.6E-06 |
-0.42557 |
-3.5E-07 |
-0.42358 |
0.000305 |
-0.42158 |
-0.00014 |
-0.41958 |
6.74E-05 |
-0.41758 |
4.66E-05 |
-0.41558 |
-3E-05 |
-0.41359 |
-4.7E-05 |
-0.41159 |
-5.3E-05 |
-0.40959 |
5.96E-05 |
-0.40759 |
0.000103 |
-0.40559 |
-9.1E-05 |
-0.4036 |
4.49E-05 |
-0.4016 |
0.000131 |
-0.3996 |
0.000279 |
-0.3976 |
-6.6E-06 |
-0.3956 |
-2.4E-05 |
-0.39361 |
0.000336 |
-0.39161 |
0.000167 |
-0.38961 |
-0.00021 |
-0.38761 |
-0.00022 |
-0.38561 |
-0.0003 |
-0.38362 |
-0.0003 |
-0.38162 |
6.72E-05 |
-0.37962 |
-0.00016 |
-0.37762 |
-1E-05 |
-0.37562 |
2.55E-05 |
-0.37363 |
0.000236 |
-0.37163 |
0.000321 |
-0.36963 |
7.49E-06 |
-0.36763 |
-4.5E-05 |
-0.36563 |
-0.00015 |
-0.36364 |
-1.1E-05 |
-0.36164 |
-8.1E-05 |
-0.35964 |
0.000207 |
-0.35764 |
0.000102 |
-0.35564 |
-0.00018 |
-0.35365 |
4.22E-05 |
-0.35165 |
-0.00021 |
-0.34965 |
-0.00022 |
-0.34765 |
0.000336 |
-0.34565 |
-5.8E-05 |
-0.34366 |
0.000123 |
-0.34166 |
-7.2E-05 |
-0.33966 |
0.000139 |
-0.33766 |
0.000247 |
-0.33566 |
-0.00016 |
-0.33367 |
0.00021 |
-0.33167 |
1.58E-05 |
-0.32967 |
-4E-05 |
-0.32767 |
-0.0002 |
-0.32567 |
-0.00024 |
-0.32368 |
-0.00023 |
-0.32168 |
0.000101 |
-0.31968 |
0.000228 |
-0.31768 |
0.000217 |
-0.31568 |
-1.6E-06 |
-0.31369 |
0.000119 |
-0.31169 |
0.000304 |
-0.30969 |
0.000362 |
-0.30769 |
8.39E-05 |
-0.30569 |
-6.6E-05 |
-0.3037 |
-0.00024 |
-0.3017 |
0.000111 |
-0.2997 |
3.32E-05 |
-0.2977 |
-6.1E-05 |
-0.2957 |
-7.2E-06 |
-0.29371 |
4.09E-06 |
-0.29171 |
-5.8E-05 |
-0.28971 |
-0.00018 |
-0.28771 |
-8.4E-05 |
-0.28571 |
0.000187 |
-0.28372 |
-0.00028 |
-0.28172 |
-5.4E-05 |
-0.27972 |
8.58E-05 |
-0.27772 |
0.000147 |
-0.27572 |
-0.00017 |
-0.27373 |
0.000159 |
-0.27173 |
0.000171 |
-0.26973 |
-0.00011 |
-0.26773 |
-3.4E-05 |
-0.26573 |
-0.00013 |
-0.26374 |
3.97E-05 |
-0.26174 |
0.000127 |
-0.25974 |
-0.00017 |
-0.25774 |
0.00014 |
-0.25574 |
-7E-05 |
-0.25375 |
-2.7E-05 |
-0.25175 |
0.000184 |
-0.24975 |
0.000202 |
-0.24775 |
7.97E-05 |
-0.24575 |
0.000188 |
-0.24376 |
0.000126 |
-0.24176 |
-0.00011 |
-0.23976 |
0.000158 |
-0.23776 |
-0.00011 |
-0.23576 |
-0.00017 |
-0.23377 |
-9.1E-05 |
-0.23177 |
0.000149 |
-0.22977 |
1.1E-05 |
-0.22777 |
0.000496 |
-0.22577 |
-0.00016 |
-0.22378 |
3.54E-05 |
-0.22178 |
-0.00015 |
-0.21978 |
-0.0001 |
-0.21778 |
-0.00018 |
-0.21578 |
0.000142 |
-0.21379 |
0.000436 |
-0.21179 |
-9.9E-05 |
-0.20979 |
9.38E-05 |
-0.20779 |
-0.00025 |
-0.20579 |
2.97E-05 |
-0.2038 |
-0.00012 |
-0.2018 |
4.45E-05 |
-0.1998 |
0.0002 |
-0.1978 |
0.000195 |
-0.1958 |
0.000218 |
-0.19381 |
-0.00018 |
-0.19181 |
-0.0001 |
-0.18981 |
0.00011 |
-0.18781 |
3.44E-05 |
-0.18581 |
2.71E-05 |
-0.18382 |
-0.00017 |
-0.18182 |
2.87E-05 |
-0.17982 |
-1.2E-05 |
-0.17782 |
-9.5E-05 |
-0.17582 |
0.000191 |
-0.17383 |
6.39E-05 |
-0.17183 |
0.000132 |
-0.16983 |
4.1E-05 |
-0.16783 |
-0.00023 |
-0.16583 |
-3E-05 |
-0.16384 |
8.86E-05 |
-0.16184 |
8.49E-05 |
-0.15984 |
2.26E-05 |
-0.15784 |
0.000188 |
-0.15584 |
0.00025 |
-0.15385 |
0.000408 |
-0.15185 |
6.63E-05 |
-0.14985 |
-1.5E-05 |
-0.14785 |
-6.9E-05 |
-0.14585 |
-5.6E-05 |
-0.14386 |
-0.00012 |
-0.14186 |
-0.00014 |
-0.13986 |
0.000215 |
-0.13786 |
-0.00015 |
-0.13586 |
-0.00025 |
-0.13387 |
6.62E-05 |
-0.13187 |
-5.4E-05 |
-0.12987 |
3.95E-05 |
-0.12787 |
-0.00036 |
-0.12587 |
0.000164 |
-0.12388 |
0.000228 |
-0.12188 |
2.06E-05 |
-0.11988 |
-0.00011 |
-0.11788 |
0.000327 |
-0.11588 |
0.000388 |
-0.11389 |
0.000128 |
-0.11189 |
-0.00022 |
-0.10989 |
-0.00019 |
-0.10789 |
-0.00014 |
-0.10589 |
-9.4E-05 |
-0.1039 |
3.99E-05 |
-0.1019 |
7.95E-06 |
-0.0999 |
6.43E-05 |
-0.0979 |
-0.00017 |
-0.0959 |
1.57E-05 |
-0.09391 |
0.000105 |
-0.09191 |
0.000181 |
-0.08991 |
-6E-05 |
-0.08791 |
0.000296 |
-0.08591 |
-8.6E-05 |
-0.08392 |
-2.8E-05 |
-0.08192 |
-0.00032 |
-0.07992 |
5.36E-05 |
-0.07792 |
-7E-05 |
-0.07592 |
6.23E-05 |
-0.07393 |
-1.3E-05 |
-0.07193 |
5.35E-05 |
-0.06993 |
0.000155 |
-0.06793 |
-3.2E-05 |
-0.06593 |
0.000342 |
-0.06394 |
-8.3E-05 |
-0.06194 |
-5E-05 |
-0.05994 |
0.000261 |
-0.05794 |
0.000116 |
-0.05594 |
-6.4E-05 |
-0.05395 |
-0.00021 |
-0.05195 |
2.29E-06 |
-0.04995 |
2.94E-05 |
-0.04795 |
0.000251 |
-0.04595 |
-7E-05 |
-0.04396 |
-3E-06 |
-0.04196 |
0.000303 |
-0.03996 |
1.06E-05 |
-0.03796 |
-7.3E-05 |
-0.03596 |
-1.1E-05 |
-0.03397 |
0.000163 |
-0.03197 |
-0.00023 |
-0.02997 |
-1.9E-06 |
-0.02797 |
-3.6E-05 |
-0.02597 |
-0.00016 |
-0.02398 |
-6.5E-05 |
-0.02198 |
0.000204 |
-0.01998 |
-3.2E-05 |
-0.01798 |
0.000225 |
-0.01598 |
4.58E-05 |
-0.01399 |
2.1E-06 |
-0.01199 |
5.52E-05 |
-0.00999 |
-0.00015 |
-0.00799 |
-5.2E-05 |
-0.00599 |
0.000133 |
-0.004 |
-1.2E-05 |
-0.002 |
-0.00012 |
1.11E-16 |
25.29392 |
0.001998 |
1.76E-05 |
0.003996 |
0.00039 |
0.005994 |
5.11E-05 |
0.007992 |
-1.5E-05 |
0.00999 |
0.000278 |
0.011988 |
1.48E-05 |
0.013986 |
-0.00017 |
0.015984 |
2.12E-05 |
0.017982 |
0.000109 |
0.01998 |
-0.00013 |
0.021978 |
-0.00015 |
0.023976 |
0.00025 |
0.025974 |
0.000324 |
0.027972 |
0.000166 |
0.02997 |
-0.00011 |
0.031968 |
0.000148 |
0.033966 |
-0.00019 |
0.035964 |
-7.2E-05 |
0.037962 |
0.000148 |
0.03996 |
-0.00013 |
0.041958 |
-0.00016 |
0.043956 |
-0.00023 |
0.045954 |
-7.2E-05 |
0.047952 |
0.000272 |
0.04995 |
-0.00013 |
0.051948 |
-0.00017 |
0.053946 |
0.000304 |
0.055944 |
0.000277 |
0.057942 |
-4.4E-06 |
0.05994 |
0.000168 |
0.061938 |
-8.2E-05 |
0.063936 |
-0.00016 |
0.065934 |
7.1E-05 |
0.067932 |
0.000157 |
0.06993 |
-2.4E-05 |
0.071928 |
0.000266 |
0.073926 |
0.000125 |
0.075924 |
0.00032 |
0.077922 |
-0.00039 |
0.07992 |
7.63E-05 |
0.081918 |
0.000269 |
0.083916 |
0.000154 |
0.085914 |
0.000126 |
0.087912 |
-9.3E-05 |
0.08991 |
-0.00018 |
0.091908 |
-0.00028 |
0.093906 |
5.79E-05 |
0.095904 |
-0.00022 |
0.097902 |
-0.00024 |
0.0999 |
0.00018 |
0.101898 |
0.000108 |
0.103896 |
-0.00011 |
0.105894 |
-0.00016 |
0.107892 |
0.0004 |
0.10989 |
8.99E-05 |
0.111888 |
-0.0003 |
0.113886 |
-2.4E-05 |
0.115884 |
-0.00012 |
0.117882 |
8.16E-05 |
0.11988 |
0.000106 |
0.121878 |
7.62E-05 |
0.123876 |
0.000139 |
0.125874 |
-0.00027 |
0.127872 |
-0.00024 |
0.12987 |
-3.2E-05 |
0.131868 |
0.000286 |
0.133866 |
-0.00042 |
0.135864 |
-0.00019 |
0.137862 |
0.000253 |
0.13986 |
0.000173 |
0.141858 |
0.000398 |
0.143856 |
-8.6E-05 |
0.145854 |
0.000343 |
0.147852 |
-0.00016 |
0.14985 |
7.61E-05 |
0.151848 |
-3.5E-05 |
0.153846 |
-0.00034 |
0.155844 |
-2.5E-05 |
0.157842 |
0.000378 |
0.15984 |
-0.00011 |
0.161838 |
-7E-05 |
0.163836 |
0.000432 |
0.165834 |
-0.0002 |
0.167832 |
0.000279 |
0.16983 |
7.88E-05 |
0.171828 |
-0.00011 |
0.173826 |
-2E-05 |
0.175824 |
3.34E-05 |
0.177822 |
-0.00032 |
0.17982 |
0.000129 |
0.181818 |
-0.00017 |
0.183816 |
0.000305 |
0.185814 |
-0.00023 |
0.187812 |
7.58E-05 |
0.18981 |
-0.00023 |
0.191808 |
0.000209 |
0.193806 |
-0.00016 |
0.195804 |
-5.8E-05 |
0.197802 |
0.000203 |
0.1998 |
0.000117 |
0.201798 |
-0.0003 |
0.203796 |
1.5E-05 |
0.205794 |
0.000344 |
0.207792 |
0.000202 |
0.20979 |
0.000202 |
0.211788 |
0.00027 |
0.213786 |
-0.00011 |
0.215784 |
0.000159 |
0.217782 |
-0.00013 |
0.21978 |
-0.00011 |
0.221778 |
-7.8E-05 |
0.223776 |
-1.8E-05 |
0.225774 |
-8.7E-05 |
0.227772 |
-5.8E-05 |
0.22977 |
-8.6E-05 |
0.231768 |
-5.9E-05 |
0.233766 |
-8.7E-05 |
0.235764 |
0.000193 |
0.237762 |
0.000165 |
0.23976 |
9.95E-05 |
0.241758 |
0.000183 |
0.243756 |
0.00032 |
0.245754 |
0.000289 |
0.247752 |
0.000244 |
0.24975 |
0.000447 |
0.251748 |
-3.3E-05 |
0.253746 |
-4.1E-06 |
0.255744 |
-0.00019 |
0.257742 |
8.66E-06 |
0.25974 |
-0.00023 |
0.261738 |
0.00024 |
0.263736 |
-0.00015 |
0.265734 |
-4.7E-06 |
0.267732 |
-9.2E-05 |
0.26973 |
0.000398 |
0.271728 |
2.64E-05 |
0.273726 |
0.000115 |
0.275724 |
-0.00035 |
0.277722 |
-6E-05 |
0.27972 |
-1.6E-05 |
0.281718 |
0.000142 |
0.283716 |
0.000164 |
0.285714 |
0.000213 |
0.287712 |
-0.00015 |
0.28971 |
0.000168 |
0.291708 |
-1.6E-05 |
0.293706 |
-2.8E-05 |
0.295704 |
-0.00015 |
0.297702 |
-0.00011 |
0.2997 |
0.000288 |
0.301698 |
0.000155 |
0.303696 |
8.56E-05 |
0.305694 |
-6.6E-05 |
0.307692 |
-0.00043 |
0.30969 |
0.000443 |
0.311688 |
-1.2E-05 |
0.313686 |
-0.00021 |
0.315684 |
7.96E-05 |
0.317682 |
-0.0002 |
0.31968 |
9.96E-05 |
0.321678 |
-7.2E-05 |
0.323676 |
-0.00021 |
0.325674 |
-9.5E-05 |
0.327672 |
0.000111 |
0.32967 |
-0.00011 |
0.331668 |
-5.1E-05 |
0.333666 |
-0.00025 |
0.335664 |
-1.7E-05 |
0.337662 |
-0.00011 |
0.33966 |
-0.00021 |
0.341658 |
-2.7E-07 |
0.343656 |
-0.0002 |
0.345654 |
0.00031 |
0.347652 |
-5.6E-05 |
0.34965 |
-1E-05 |
0.351648 |
-5.4E-05 |
0.353646 |
4.23E-05 |
0.355644 |
-4E-05 |
0.357642 |
0.000225 |
0.35964 |
4.74E-05 |
0.361638 |
-9.7E-05 |
0.363636 |
-2.6E-05 |
0.365634 |
-1.3E-05 |
0.367632 |
-6.8E-05 |
0.36963 |
0.000113 |
0.371628 |
-0.00035 |
0.373626 |
0.000115 |
0.375624 |
-7.8E-05 |
0.377622 |
-0.00026 |
0.37962 |
8.75E-05 |
0.381618 |
-0.00012 |
0.383616 |
5.16E-05 |
0.385614 |
-4.5E-05 |
0.387612 |
5.9E-05 |
0.38961 |
9.35E-05 |
0.391608 |
-0.00019 |
0.393606 |
-9E-05 |
0.395604 |
0.000114 |
0.397602 |
1.99E-07 |
0.3996 |
-0.00027 |
0.401598 |
7.41E-05 |
0.403596 |
4.73E-05 |
0.405594 |
-8.9E-05 |
0.407592 |
0.000172 |
0.40959 |
-0.00012 |
0.411588 |
9.16E-05 |
0.413586 |
2.36E-05 |
0.415584 |
0.000159 |
0.417582 |
5.11E-06 |
0.41958 |
8.3E-05 |
0.421578 |
-0.00016 |
0.423576 |
-4.8E-05 |
0.425574 |
-0.00012 |
0.427572 |
4.89E-05 |
0.42957 |
-0.00013 |
0.431568 |
0.000127 |
0.433566 |
0.000107 |
0.435564 |
-0.00016 |
0.437562 |
-0.00015 |
0.43956 |
5E-05 |
0.441558 |
0.00022 |
0.443556 |
0.000149 |
0.445554 |
-0.0001 |
0.447552 |
-0.00017 |
0.44955 |
7.66E-05 |
0.451548 |
0.00021 |
0.453546 |
0.000202 |
0.455544 |
-8.6E-05 |
0.457542 |
-0.0001 |
0.45954 |
-8.9E-05 |
0.461538 |
1.87E-05 |
0.463536 |
-0.00012 |
0.465534 |
4.92E-05 |
0.467532 |
-1.1E-05 |
0.46953 |
0.000112 |
0.471528 |
-2.6E-05 |
0.473526 |
-5.7E-05 |
0.475524 |
3.35E-05 |
0.477522 |
0.000163 |
0.47952 |
-4E-05 |
0.481518 |
0.000239 |
0.483516 |
2.7E-05 |
0.485514 |
-0.00013 |
0.487512 |
3.59E-05 |
0.48951 |
-3.4E-05 |
0.491508 |
1.93E-05 |
0.493506 |
2.04E-05 |
0.495504 |
-5.7E-05 |
0.497502 |
7.59E-05 |
0.4995 |
-4.2E-05 |
0.501498 |
5.6E-05 |
0.503496 |
-4.1E-05 |
0.505494 |
-0.00017 |
0.507492 |
-0.00012 |
0.50949 |
-7.8E-05 |
0.511488 |
4.24E-05 |
0.513486 |
3.57E-06 |
0.515484 |
5.07E-05 |
0.517482 |
-2.4E-05 |
0.51948 |
0.000151 |
0.521478 |
-0.00013 |
0.523476 |
-0.00027 |
0.525474 |
-7.9E-05 |
0.527472 |
0.000143 |
0.52947 |
-4.5E-05 |
0.531468 |
-6.6E-05 |
0.533466 |
-5.7E-05 |
0.535464 |
-3.2E-05 |
0.537462 |
2.35E-05 |
0.53946 |
0.000107 |
0.541458 |
-9.6E-06 |
0.543456 |
7.64E-05 |
0.545454 |
-8.7E-05 |
0.547452 |
-0.00014 |
0.54945 |
2.62E-05 |
0.551448 |
-2.1E-05 |
0.553446 |
3.25E-05 |
0.555444 |
4.01E-05 |
0.557442 |
8.2E-05 |
0.55944 |
-3.3E-05 |
0.561438 |
-7.2E-05 |
0.563436 |
0.000115 |
0.565434 |
-0.00016 |
0.567432 |
4.85E-05 |
0.56943 |
-2.8E-06 |
0.571428 |
9.9E-06 |
0.573426 |
-2.3E-05 |
0.575424 |
5.2E-05 |
0.577422 |
-8E-05 |
0.57942 |
1.91E-05 |
0.581418 |
-8.9E-05 |
0.583416 |
7.14E-05 |
0.585414 |
-3E-05 |
0.587412 |
-0.00011 |
0.58941 |
0.000102 |
0.591408 |
-1.6E-05 |
0.593406 |
6.1E-05 |
0.595404 |
0.000174 |
0.597402 |
-7.5E-06 |
0.5994 |
4.62E-05 |
0.601398 |
3.03E-05 |
0.603396 |
-1.6E-05 |
0.605394 |
5.02E-05 |
0.607392 |
1.03E-05 |
0.60939 |
-3.1E-05 |
0.611388 |
-1.6E-05 |
0.613386 |
3.97E-05 |
0.615384 |
-6.7E-05 |
0.617382 |
0.000142 |
0.61938 |
-9.9E-05 |
0.621378 |
1.14E-05 |
0.623376 |
2.84E-05 |
0.625374 |
0.000112 |
0.627372 |
-6.8E-06 |
0.62937 |
-4.7E-05 |
0.631368 |
-1.6E-06 |
0.633366 |
-3.1E-05 |
0.635364 |
2.22E-05 |
0.637362 |
-6E-05 |
0.63936 |
-1.5E-05 |
0.641358 |
-4E-05 |
0.643356 |
-1.1E-05 |
0.645354 |
4.69E-05 |
0.647352 |
-8.6E-05 |
0.64935 |
-7.4E-05 |
0.651348 |
-6.3E-05 |
0.653346 |
5.65E-05 |
0.655344 |
-7.2E-05 |
0.657342 |
-2.3E-05 |
0.65934 |
9.09E-05 |
0.661338 |
-6.3E-06 |
0.663336 |
5.17E-05 |
0.665334 |
5.14E-05 |
0.667332 |
1.12E-05 |
0.66933 |
-9.3E-05 |
0.671328 |
1.77E-05 |
0.673326 |
2.99E-05 |
0.675324 |
8.44E-05 |
0.677322 |
2.41E-05 |
0.67932 |
2E-05 |
0.681318 |
-9.2E-05 |
0.683316 |
5.66E-05 |
0.685314 |
-6.7E-06 |
0.687312 |
4.21E-05 |
0.68931 |
-4.8E-05 |
0.691308 |
1.83E-05 |
0.693306 |
-4.8E-05 |
0.695304 |
9.8E-06 |
0.697302 |
4.03E-05 |
0.6993 |
4.47E-06 |
0.701298 |
2.1E-05 |
0.703296 |
-7.4E-06 |
0.705294 |
5.33E-05 |
0.707292 |
-4.1E-05 |
0.70929 |
2.69E-05 |
0.711288 |
2.93E-05 |
0.713286 |
4.96E-06 |
0.715284 |
2.43E-06 |
0.717282 |
-2.6E-05 |
0.71928 |
-1.6E-05 |
0.721278 |
3.19E-05 |
0.723276 |
9.3E-06 |
0.725274 |
-6.4E-05 |
0.727272 |
1.02E-05 |
0.72927 |
1.92E-05 |
0.731268 |
9.4E-06 |
0.733266 |
-6.4E-05 |
0.735264 |
1.07E-05 |
0.737262 |
4.83E-05 |
0.73926 |
2.15E-05 |
0.741258 |
-7.2E-05 |
0.743256 |
-2.3E-05 |
0.745254 |
-4.7E-05 |
0.747252 |
2.17E-05 |
0.74925 |
-4E-05 |
0.751248 |
-3.5E-06 |
0.753246 |
1.95E-05 |
0.755244 |
-7.5E-06 |
0.757242 |
2.98E-05 |
0.75924 |
-5E-06 |
0.761238 |
3.26E-05 |
0.763236 |
3.01E-05 |
0.765234 |
-4.1E-05 |
0.767232 |
3.23E-05 |
0.76923 |
2.96E-06 |
0.771228 |
-1.3E-05 |
0.773226 |
-5.5E-05 |
0.775224 |
6.93E-06 |
0.777222 |
-2.6E-05 |
0.77922 |
3.36E-05 |
0.781218 |
5.59E-05 |
0.783216 |
3.12E-05 |
0.785214 |
-3.2E-06 |
0.787212 |
-4.9E-05 |
0.78921 |
1.06E-05 |
0.791208 |
3.26E-05 |
0.793206 |
1.15E-07 |
0.795204 |
5.41E-05 |
0.797202 |
2.4E-05 |
0.7992 |
6.71E-06 |
0.801198 |
1.61E-05 |
0.803196 |
7.03E-06 |
0.805194 |
-1.9E-05 |
0.807192 |
1.58E-05 |
0.80919 |
-2.2E-05 |
0.811188 |
5.29E-05 |
0.813186 |
-1.9E-05 |
0.815184 |
3.82E-05 |
0.817182 |
-2.4E-06 |
0.81918 |
-3.8E-05 |
0.821178 |
-1.9E-05 |
0.823176 |
2.71E-05 |
0.825174 |
-5.3E-06 |
0.827172 |
-1.1E-05 |
0.82917 |
2.5E-06 |
0.831168 |
1.18E-06 |
0.833166 |
1.12E-05 |
0.835164 |
-3.7E-06 |
0.837162 |
-3.8E-05 |
0.83916 |
-1.8E-05 |
0.841158 |
-9.8E-06 |
0.843156 |
-5.3E-06 |
0.845154 |
1.36E-05 |
0.847152 |
-9.8E-06 |
0.84915 |
-2.2E-05 |
0.851148 |
-7.7E-06 |
0.853146 |
-8.2E-06 |
0.855144 |
1.99E-05 |
0.857142 |
1.13E-05 |
0.85914 |
-7.3E-07 |
0.861138 |
1.02E-05 |
0.863136 |
-3.9E-06 |
0.865134 |
1.44E-05 |
0.867132 |
-5.1E-06 |
0.86913 |
-9.1E-06 |
0.871128 |
1.83E-06 |
0.873126 |
3.4E-06 |
0.875124 |
2.16E-05 |
0.877122 |
-9.5E-06 |
0.87912 |
3.78E-06 |
0.881118 |
2.71E-06 |
0.883116 |
1.47E-05 |
0.885114 |
-8.2E-06 |
0.887112 |
-8.6E-08 |
0.88911 |
-1.1E-06 |
0.891108 |
-2.6E-06 |
0.893106 |
-2.5E-06 |
0.895104 |
1.86E-05 |
0.897102 |
-1E-05 |
0.8991 |
-9.9E-06 |
0.901098 |
2.36E-05 |
0.903096 |
1.16E-05 |
0.905094 |
-1.1E-05 |
0.907092 |
-1.1E-05 |
0.90909 |
-5.5E-06 |
0.911088 |
2.71E-06 |
0.913086 |
-1.8E-07 |
0.915084 |
-8.2E-06 |
0.917082 |
8.69E-06 |
0.91908 |
-8.9E-06 |
0.921078 |
1.23E-06 |
0.923076 |
-5.1E-06 |
0.925074 |
-7E-06 |
0.927072 |
-6.8E-06 |
0.92907 |
-4.5E-06 |
0.931068 |
-7E-06 |
0.933066 |
6.68E-06 |
0.935064 |
3.05E-06 |
0.937062 |
4.52E-06 |
0.93906 |
1.79E-06 |
0.941058 |
4.27E-07 |
0.943056 |
-1.9E-06 |
0.945054 |
-2.9E-06 |
0.947052 |
-8E-06 |
0.94905 |
-5.5E-05 |
0.951048 |
-1E-06 |
0.953046 |
-9.2E-06 |
0.955044 |
7.84E-07 |
0.957042 |
-8.6E-07 |
0.95904 |
-6.3E-07 |
0.961038 |
7.35E-07 |
0.963036 |
-6.1E-06 |
0.965034 |
2.63E-06 |
0.967032 |
-2E-06 |
0.96903 |
-9.2E-06 |
0.971028 |
2.88E-06 |
0.973026 |
5.05E-06 |
0.975024 |
4.21E-06 |
0.977022 |
2.59E-07 |
0.97902 |
-1.4E-05 |
0.981018 |
5.08E-07 |
0.983016 |
1.54E-07 |
0.985014 |
-4.3E-06 |
0.987012 |
2.76E-06 |
0.98901 |
-8.7E-07 |
0.991008 |
-4.1E-07 |
0.993006 |
5.39E-06 |
0.995004 |
-7E-07 |
0.997002 |
1.37E-06 |
0.999 |
4.67E-07 |
Data for Figure 3 - \sigma_i: Percentage Difference in the Magnitude of AD and FD Derivatives
Parameter Value | Percentage Difference |
|---|---|
0.01 |
-3.96877E-08 |
0.01999 |
6.48469E-07 |
0.02998 |
-5.29766E-08 |
0.03997 |
-2.28593E-07 |
0.04996 |
-1.08174E-07 |
0.05995 |
4.09006E-07 |
0.06994 |
-4.56715E-07 |
0.07993 |
-6.62141E-07 |
0.08992 |
-2.20146E-07 |
0.09991 |
1.12202E-06 |
0.1099 |
-4.11395E-05 |
0.11989 |
2.34058E-05 |
0.12988 |
-6.96191E-06 |
0.13987 |
6.58076E-06 |
0.14986 |
-2.10937E-06 |
0.15985 |
-1.18189E-06 |
0.16984 |
3.83503E-06 |
0.17983 |
-2.1921E-06 |
0.18982 |
4.62295E-06 |
0.19981 |
-9.91955E-06 |
0.2098 |
7.58087E-06 |
0.21979 |
-7.87446E-06 |
0.22978 |
-5.97855E-06 |
0.23977 |
-4.0015E-06 |
0.24976 |
1.98007E-06 |
0.25975 |
-6.68415E-06 |
0.26974 |
-3.09489E-07 |
0.27973 |
2.55194E-06 |
0.28972 |
5.68727E-06 |
0.29971 |
4.56569E-06 |
0.3097 |
7.43372E-06 |
0.31969 |
1.97156E-05 |
0.32968 |
-3.47164E-05 |
0.33967 |
9.76026E-07 |
0.34966 |
-9.81611E-06 |
0.35965 |
2.32309E-05 |
0.36964 |
8.5459E-06 |
0.37963 |
9.067E-06 |
0.38962 |
-3.62126E-06 |
0.39961 |
1.1713E-05 |
0.4096 |
4.49508E-06 |
0.41959 |
-2.35838E-05 |
0.42958 |
2.06114E-05 |
0.43957 |
4.97628E-05 |
0.44956 |
1.2314E-05 |
0.45955 |
-7.25996E-05 |
0.46954 |
8.99336E-05 |
0.47953 |
9.20955E-06 |
0.48952 |
-3.31398E-05 |
0.49951 |
-6.27868E-05 |
0.5095 |
-1.22621E-05 |
0.51949 |
4.52273E-05 |
0.52948 |
2.89833E-05 |
0.53947 |
-6.88488E-05 |
0.54946 |
0.000107057 |
0.55945 |
6.06651E-05 |
0.56944 |
-2.17505E-05 |
0.57943 |
-1.22109E-05 |
0.58942 |
6.43894E-05 |
0.59941 |
0.000163699 |
0.6094 |
-3.8241E-05 |
0.61939 |
4.71372E-05 |
0.62938 |
-7.13947E-05 |
0.63937 |
-0.0002762 |
0.64936 |
-8.46217E-05 |
0.65935 |
0.000155337 |
0.66934 |
-7.09724E-05 |
0.67933 |
-3.21982E-05 |
0.68932 |
-5.24646E-05 |
0.69931 |
-8.78236E-05 |
0.7093 |
-6.18672E-05 |
0.71929 |
9.49142E-05 |
0.72928 |
0.000243485 |
0.73927 |
0.00013932 |
0.74926 |
0.000314872 |
0.75925 |
-0.000124351 |
0.76924 |
8.50423E-05 |
0.77923 |
-8.63151E-05 |
0.78922 |
-1.64694E-05 |
0.79921 |
0.000164676 |
0.8092 |
0.000265555 |
0.81919 |
-0.000307406 |
0.82918 |
-1.23651E-05 |
0.83917 |
3.61386E-05 |
0.84916 |
0.00044652 |
0.85915 |
1.59146E-06 |
0.86914 |
-0.000395419 |
0.87913 |
0.000456902 |
0.88912 |
0.000651542 |
0.89911 |
-3.57253E-05 |
0.9091 |
-0.00053729 |
0.91909 |
0.000769805 |
0.92908 |
0.000273671 |
0.93907 |
-0.000218437 |
0.94906 |
3.48831E-05 |
0.95905 |
-0.000332814 |
0.96904 |
0.001117121 |
0.97903 |
-0.001130212 |
0.98902 |
-0.000263866 |
0.99901 |
-0.000163197 |
1.009 |
-0.000208994 |
1.01899 |
-0.000374421 |
1.02898 |
0.000336126 |
1.03897 |
0.000282565 |
1.04896 |
-0.001595435 |
1.05895 |
0.000495463 |
1.06894 |
0.000452591 |
1.07893 |
-0.00201085 |
1.08892 |
-0.000397415 |
1.09891 |
-0.000350685 |
1.1089 |
0.000928867 |
1.11889 |
-0.000561568 |
1.12888 |
0.000508868 |
1.13887 |
0.000814731 |
1.14886 |
-0.002802407 |
1.15885 |
0.000362299 |
1.16884 |
0.001455951 |
1.17883 |
-6.97061E-05 |
1.18882 |
0.000621271 |
1.19881 |
6.02856E-05 |
1.2088 |
-0.000699996 |
1.21879 |
-0.002227497 |
1.22878 |
0.001179491 |
1.23877 |
-0.000516196 |
1.24876 |
4.50089E-05 |
1.25875 |
0.001601458 |
1.26874 |
0.00160209 |
1.27873 |
0.00189171 |
1.28872 |
-0.001077334 |
1.29871 |
-0.001603421 |
1.3087 |
0.001325701 |
1.31869 |
-0.004663514 |
1.32868 |
0.000634452 |
1.33867 |
0.003889639 |
1.34866 |
-0.000284269 |
1.35865 |
0.000412849 |
1.36864 |
-9.22171E-05 |
1.37863 |
-0.004192731 |
1.38862 |
0.003338652 |
1.39861 |
-0.003310565 |
1.4086 |
0.002849925 |
1.41859 |
-0.000930183 |
1.42858 |
0.001272808 |
1.43857 |
-0.002017839 |
1.44856 |
-0.002537633 |
1.45855 |
-9.00879E-05 |
1.46854 |
-0.000155696 |
1.47853 |
-0.002481056 |
1.48852 |
-0.000849573 |
1.49851 |
0.00193324 |
1.5085 |
-0.004297459 |
1.51849 |
-0.005088258 |
1.52848 |
-0.003518983 |
1.53847 |
-0.003229269 |
1.54846 |
0.003454289 |
1.55845 |
-0.003544026 |
1.56844 |
-0.006972998 |
1.57843 |
0.003580213 |
1.58842 |
-5.36557E-05 |
1.59841 |
0.000432053 |
1.6084 |
-0.000854915 |
1.61839 |
0.000346479 |
1.62838 |
-0.001578174 |
1.63837 |
0.001283971 |
1.64836 |
-0.009277005 |
1.65835 |
0.004472234 |
1.66834 |
0.013075701 |
1.67833 |
-0.007077093 |
1.68832 |
-0.000690782 |
1.69831 |
0.004974698 |
1.7083 |
-0.004641906 |
1.71829 |
0.002639456 |
1.72828 |
-0.005265245 |
1.73827 |
0.000447386 |
1.74826 |
0.014707016 |
1.75825 |
0.007348583 |
1.76824 |
-0.005149853 |
1.77823 |
0.006576411 |
1.78822 |
-0.005236408 |
1.79821 |
0.001944835 |
1.8082 |
0.005926127 |
1.81819 |
-0.007223866 |
1.82818 |
-0.006268839 |
1.83817 |
-0.001773626 |
1.84816 |
-0.010354035 |
1.85815 |
-0.015054949 |
1.86814 |
0.007653617 |
1.87813 |
0.00526347 |
1.88812 |
0.009641695 |
1.89811 |
-0.006412724 |
1.9081 |
0.002281007 |
1.91809 |
0.012492301 |
1.92808 |
0.003350477 |
1.93807 |
0.003394441 |
1.94806 |
0.014816535 |
1.95805 |
0.021855077 |
1.96804 |
-0.013213585 |
1.97803 |
0.002160541 |
1.98802 |
-0.005039198 |
1.99801 |
-0.010563593 |
2.008 |
0.008635265 |
2.01799 |
-0.031717033 |
2.02798 |
0.009133299 |
2.03797 |
-0.007894147 |
2.04796 |
0.018757868 |
2.05795 |
-0.01324823 |
2.06794 |
-0.002004265 |
2.07793 |
-0.011499035 |
2.08792 |
0.009815134 |
2.09791 |
0.009518511 |
2.1079 |
0.01064589 |
2.11789 |
0.000377019 |
2.12788 |
-0.024614273 |
2.13787 |
0.014874272 |
2.14786 |
0.008235022 |
2.15785 |
-0.006766763 |
2.16784 |
-0.022747364 |
2.17783 |
0.003169547 |
2.18782 |
-0.000913344 |
2.19781 |
-0.009747998 |
2.2078 |
0.02520474 |
2.21779 |
0.001894996 |
2.22778 |
0.046891146 |
2.23777 |
0.016244258 |
2.24776 |
-0.011028587 |
2.25775 |
0.021795705 |
2.26774 |
0.027841795 |
2.27773 |
0.014638432 |
2.28772 |
0.047085755 |
2.29771 |
-0.021070552 |
2.3077 |
-0.039191432 |
2.31769 |
0.022905241 |
2.32768 |
-0.013740324 |
2.33767 |
0.107181959 |
2.34766 |
-0.069878194 |
2.35765 |
0.053631579 |
2.36764 |
0.048182504 |
2.37763 |
0.003864745 |
2.38762 |
-0.018128614 |
2.39761 |
0.018663038 |
2.4076 |
0.049571901 |
2.41759 |
-0.013083277 |
2.42758 |
0.07329303 |
2.43757 |
-0.045605495 |
2.44756 |
0.042140188 |
2.45755 |
-0.087341824 |
2.46754 |
0.003435201 |
2.47753 |
0.029372072 |
2.48752 |
0.061167154 |
2.49751 |
0.034581095 |
2.5075 |
0.026092388 |
2.51749 |
0.007108562 |
2.52748 |
0.020812154 |
2.53747 |
-0.030838067 |
2.54746 |
0.002904707 |
2.55745 |
-0.036377965 |
2.56744 |
0.030085422 |
2.57743 |
0.010296082 |
2.58742 |
-0.044198563 |
2.59741 |
0.002531108 |
2.6074 |
0.03316495 |
2.61739 |
-0.067622638 |
2.62738 |
0.050418355 |
2.63737 |
0.000496448 |
2.64736 |
-0.01682244 |
2.65735 |
-0.04428689 |
2.66734 |
-0.091288902 |
2.67733 |
0.041684072 |
2.68732 |
-0.033597688 |
2.69731 |
-0.106993774 |
2.7073 |
0.067596013 |
2.71729 |
0.138248335 |
2.72728 |
0.028022751 |
2.73727 |
0.138605644 |
2.74726 |
-0.073778287 |
2.75725 |
0.00773288 |
2.76724 |
0.029443872 |
2.77723 |
-0.036924222 |
2.78722 |
0.033303102 |
2.79721 |
-0.014555263 |
2.8072 |
0.056129447 |
2.81719 |
0.152095118 |
2.82718 |
-0.078277941 |
2.83717 |
-0.044073956 |
2.84716 |
0.00513116 |
2.85715 |
0.017732749 |
2.86714 |
-0.034575097 |
2.87713 |
0.070604964 |
2.88712 |
-0.101639745 |
2.89711 |
-0.029395598 |
2.9071 |
-0.008760552 |
2.91709 |
0.02145164 |
2.92708 |
-0.018067586 |
2.93707 |
0.107131216 |
2.94706 |
0.119651981 |
2.95705 |
-0.057496302 |
2.96704 |
0.158329372 |
2.97703 |
-0.237455979 |
2.98702 |
-0.108366732 |
2.99701 |
-0.190315661 |
3.007 |
0.213910274 |
3.01699 |
0.195708797 |
3.02698 |
0.026184198 |
3.03697 |
0.157274053 |
3.04696 |
0.154837068 |
3.05695 |
-0.158021903 |
3.06694 |
-0.13439084 |
3.07693 |
-0.0254591 |
3.08692 |
-0.040765655 |
3.09691 |
0.063631682 |
3.1069 |
-0.064880099 |
3.11689 |
-0.084626113 |
3.12688 |
-0.123212892 |
3.13687 |
0.043233872 |
3.14686 |
0.140379283 |
3.15685 |
0.096374861 |
3.16684 |
0.312001099 |
3.17683 |
-0.045421552 |
3.18682 |
-0.296464778 |
3.19681 |
0.038066049 |
3.2068 |
0.111023716 |
3.21679 |
0.003168512 |
3.22678 |
-0.292922012 |
3.23677 |
-0.054163051 |
3.24676 |
-0.088100772 |
3.25675 |
-0.406600097 |
3.26674 |
0.120831644 |
3.27673 |
-0.201064827 |
3.28672 |
0.215296567 |
3.29671 |
0.09814241 |
3.3067 |
0.029356501 |
3.31669 |
0.03174842 |
3.32668 |
0.216128388 |
3.33667 |
-0.059964772 |
3.34666 |
-0.123651331 |
3.35665 |
0.239678629 |
3.36664 |
-0.17848257 |
3.37663 |
-0.267338814 |
3.38662 |
-0.023772706 |
3.39661 |
-0.100758895 |
3.4066 |
-0.276827159 |
3.41659 |
0.383283156 |
3.42658 |
0.012010949 |
3.43657 |
-0.337610875 |
3.44656 |
-0.05610203 |
3.45655 |
-0.093951885 |
3.46654 |
0.022365621 |
3.47653 |
0.517832249 |
3.48652 |
0.120126135 |
3.49651 |
0.128296043 |
3.5065 |
0.204951246 |
3.51649 |
0.267242627 |
3.52648 |
-0.346222344 |
3.53647 |
0.129650974 |
3.54646 |
-0.201627158 |
3.55645 |
0.282335349 |
3.56644 |
0.273765576 |
3.57643 |
0.228555113 |
3.58642 |
-0.084699595 |
3.59641 |
0.405033164 |
3.6064 |
0.248520044 |
3.61639 |
-0.350943113 |
3.62638 |
-0.327395235 |
3.63637 |
-0.062768803 |
3.64636 |
-0.143781568 |
3.65635 |
-0.229931636 |
3.66634 |
-0.018432376 |
3.67633 |
0.206033764 |
3.68632 |
-0.194614569 |
3.69631 |
-0.152012052 |
3.7063 |
-0.07908664 |
3.71629 |
0.125636769 |
3.72628 |
0.269251197 |
3.73627 |
-0.341253097 |
3.74626 |
0.208672439 |
3.75625 |
0.385092083 |
3.76624 |
-0.374845026 |
3.77623 |
0.73918495 |
3.78622 |
0.097636288 |
3.79621 |
0.166283383 |
3.8062 |
0.399442767 |
3.81619 |
-0.180518044 |
3.82618 |
-0.654735899 |
3.83617 |
0.13858508 |
3.84616 |
0.095061293 |
3.85615 |
0.453359619 |
3.86614 |
0.070247205 |
3.87613 |
-0.429842409 |
3.88612 |
0.187571672 |
3.89611 |
-0.234928833 |
3.9061 |
-0.314250186 |
3.91609 |
-0.180418344 |
3.92608 |
-0.354799875 |
3.93607 |
-0.604014261 |
3.94606 |
-0.110337563 |
3.95605 |
0.174374171 |
3.96604 |
-0.160455419 |
3.97603 |
-0.28631089 |
3.98602 |
-0.177105 |
3.99601 |
0.368682216 |
4.006 |
0.204512271 |
4.01599 |
-0.400762623 |
4.02598 |
-0.770853869 |
4.03597 |
0.305887116 |
4.04596 |
-0.06962491 |
4.05595 |
0.579802654 |
4.06594 |
-0.745907085 |
4.07593 |
0.273547747 |
4.08592 |
-0.186052552 |
4.09591 |
-0.142593768 |
4.1059 |
-0.123200517 |
4.11589 |
-0.341450691 |
4.12588 |
-0.765388357 |
4.13587 |
-0.42435896 |
4.14586 |
-0.895251684 |
4.15585 |
0.443510309 |
4.16584 |
-0.349988838 |
4.17583 |
0.514071864 |
4.18582 |
-0.188285972 |
4.19581 |
0.383990561 |
4.2058 |
-0.529451376 |
4.21579 |
-0.16666036 |
4.22578 |
-0.96653815 |
4.23577 |
-0.042394231 |
4.24576 |
0.599618013 |
4.25575 |
-0.609576154 |
4.26574 |
-0.67591996 |
4.27573 |
-0.554447365 |
4.28572 |
0.314351425 |
4.29571 |
0.731247629 |
4.3057 |
0.338736943 |
4.31569 |
1.012173515 |
4.32568 |
-0.361984316 |
4.33567 |
0.722617547 |
4.34566 |
0.352490528 |
4.35565 |
0.256865944 |
4.36564 |
-0.322912405 |
4.37563 |
-0.037718714 |
4.38562 |
-0.085526486 |
4.39561 |
1.715952157 |
4.4056 |
-0.78272069 |
4.41559 |
-0.308478321 |
4.42558 |
0.487817437 |
4.43557 |
0.591985473 |
4.44556 |
0.744869489 |
4.45555 |
0.814542532 |
4.46554 |
-0.553067196 |
4.47553 |
-0.095014385 |
4.48552 |
-0.831056876 |
4.49551 |
0.290170715 |
4.5055 |
-1.38411522 |
4.51549 |
0.810222985 |
4.52548 |
-1.9511412 |
4.53547 |
0.601204828 |
4.54546 |
0.615424482 |
4.55545 |
-1.276971364 |
4.56544 |
0.390523733 |
4.57543 |
0.372830305 |
4.58542 |
2.514527767 |
4.59541 |
1.325533004 |
4.6054 |
-2.465868476 |
4.61539 |
0.549509733 |
4.62538 |
-0.004738761 |
4.63537 |
0.443569047 |
4.64536 |
-1.563103184 |
4.65535 |
-0.151346019 |
4.66534 |
0.924846042 |
4.67533 |
-1.05375765 |
4.68532 |
0.759577783 |
4.69531 |
-1.445624268 |
4.7053 |
0.602208018 |
4.71529 |
-1.326783785 |
4.72528 |
-1.174592542 |
4.73527 |
-0.230072473 |
4.74526 |
1.613201595 |
4.75525 |
1.865835853 |
4.76524 |
-1.094008979 |
4.77523 |
-0.425154431 |
4.78522 |
-0.15848223 |
4.79521 |
0.531131748 |
4.8052 |
-0.087066681 |
4.81519 |
-2.028190976 |
4.82518 |
-1.406162827 |
4.83517 |
-0.911841745 |
4.84516 |
1.04471736 |
4.85515 |
1.153402865 |
4.86514 |
-1.506180238 |
4.87513 |
0.133896158 |
4.88512 |
2.413476011 |
4.89511 |
1.464809107 |
4.9051 |
0.272294116 |
4.91509 |
0.013181951 |
4.92508 |
-2.446395403 |
4.93507 |
1.814888953 |
4.94506 |
1.257497989 |
4.95505 |
-0.483299894 |
4.96504 |
2.284245894 |
4.97503 |
1.28220478 |
4.98502 |
2.861925554 |
4.99501 |
0.970736495 |
5.005 |
0.010081567 |
5.01499 |
0.481625529 |
5.02498 |
-0.55365966 |
5.03497 |
0.895968233 |
5.04496 |
-0.807633926 |
5.05495 |
-1.125771653 |
5.06494 |
-0.827432532 |
5.07493 |
-0.612119526 |
5.08492 |
0.647815067 |
5.09491 |
-3.824112449 |
5.1049 |
-0.509791505 |
5.11489 |
-1.451690569 |
5.12488 |
-1.516537804 |
5.13487 |
-0.13680297 |
5.14486 |
0.594323978 |
5.15485 |
-0.711330341 |
5.16484 |
0.656807597 |
5.17483 |
0.818482522 |
5.18482 |
-2.535392741 |
5.19481 |
-0.848627539 |
5.2048 |
0.776310291 |
5.21479 |
2.033679614 |
5.22478 |
-0.516817219 |
5.23477 |
-1.867873925 |
5.24476 |
1.611213241 |
5.25475 |
-1.06636093 |
5.26474 |
-0.4537674 |
5.27473 |
1.286242124 |
5.28472 |
-0.405156143 |
5.29471 |
0.648046252 |
5.3047 |
1.648578728 |
5.31469 |
0.972123065 |
5.32468 |
0.790488628 |
5.33467 |
-2.313246184 |
5.34466 |
2.090885642 |
5.35465 |
3.882659195 |
5.36464 |
-1.192351923 |
5.37463 |
-1.058225293 |
5.38462 |
-0.671480351 |
5.39461 |
-0.729906689 |
5.4046 |
-0.916962491 |
5.41459 |
2.127354159 |
5.42458 |
0.132916844 |
5.43457 |
-3.172969664 |
5.44456 |
-3.134014773 |
5.45455 |
-1.50914063 |
5.46454 |
2.287247341 |
5.47453 |
2.312678782 |
5.48452 |
2.328075937 |
5.49451 |
1.679661068 |
5.5045 |
-0.268964654 |
5.51449 |
-0.322079329 |
5.52448 |
4.566327785 |
5.53447 |
1.606437119 |
5.54446 |
-3.628161599 |
5.55445 |
2.783671064 |
5.56444 |
-4.10672208 |
5.57443 |
1.313018151 |
5.58442 |
2.128598333 |
5.59441 |
0.091390122 |
5.6044 |
-3.16573364 |
5.61439 |
-3.076581848 |
5.62438 |
-0.269592086 |
5.63437 |
1.510146414 |
5.64436 |
-0.67252471 |
5.65435 |
0.593766983 |
5.66434 |
0.072879549 |
5.67433 |
-5.441288456 |
5.68432 |
5.432172158 |
5.69431 |
-5.926369783 |
5.7043 |
1.005221215 |
5.71429 |
-0.658170661 |
5.72428 |
-4.851538908 |
5.73427 |
-0.722095791 |
5.74426 |
1.566054183 |
5.75425 |
1.711425543 |
5.76424 |
1.091098002 |
5.77423 |
-0.961971767 |
5.78422 |
-1.893103584 |
5.79421 |
-0.793448647 |
5.8042 |
1.765624908 |
5.81419 |
-4.290377901 |
5.82418 |
2.534772755 |
5.83417 |
-2.912263667 |
5.84416 |
-6.460139504 |
5.85415 |
2.940745857 |
5.86414 |
4.119445903 |
5.87413 |
0.825363783 |
5.88412 |
5.274593492 |
5.89411 |
-1.587335847 |
5.9041 |
-0.398332442 |
5.91409 |
-0.453563579 |
5.92408 |
-5.517795299 |
5.93407 |
1.546685736 |
5.94406 |
5.860173244 |
5.95405 |
-2.017061722 |
5.96404 |
4.324785205 |
5.97403 |
3.329251114 |
5.98402 |
3.360053688 |
5.99401 |
0.129011249 |
6.004 |
0.913432303 |
6.01399 |
-1.184345231 |
6.02398 |
-3.284400011 |
6.03397 |
0.495091412 |
6.04396 |
-1.575702961 |
6.05395 |
6.029598956 |
6.06394 |
2.949179326 |
6.07393 |
-2.818349991 |
6.08392 |
3.330001659 |
6.09391 |
-0.075304364 |
6.1039 |
-1.021214056 |
6.11389 |
3.803012714 |
6.12388 |
-5.145019263 |
6.13387 |
-1.601383628 |
6.14386 |
-4.678307996 |
6.15385 |
-1.172392235 |
6.16384 |
0.519721361 |
6.17383 |
-0.752733576 |
6.18382 |
-6.77871065 |
6.19381 |
-3.277476162 |
6.2038 |
2.447728734 |
6.21379 |
-2.376101809 |
6.22378 |
-0.58242244 |
6.23377 |
-4.771415791 |
6.24376 |
6.336227984 |
6.25375 |
-1.230860392 |
6.26374 |
3.737564155 |
6.27373 |
10.44768439 |
6.28372 |
0.636640239 |
6.29371 |
-8.492809485 |
6.3037 |
1.54264236 |
6.31369 |
-5.535318052 |
6.32368 |
-0.161101152 |
6.33367 |
-0.943692972 |
6.34366 |
6.167403207 |
6.35365 |
-2.325637235 |
6.36364 |
2.715224354 |
6.37363 |
0.665249177 |
6.38362 |
4.110332468 |
6.39361 |
6.355059233 |
6.4036 |
1.337127072 |
6.41359 |
-1.39848632 |
6.42358 |
-0.059626176 |
6.43357 |
3.846205763 |
6.44356 |
5.023300395 |
6.45355 |
-2.471063661 |
6.46354 |
13.32871005 |
6.47353 |
-10.76310665 |
6.48352 |
6.87093098 |
6.49351 |
-1.155886837 |
6.5035 |
13.01744219 |
6.51349 |
-4.794541109 |
6.52348 |
6.173363552 |
6.53347 |
-5.837301831 |
6.54346 |
-7.331183929 |
6.55345 |
5.274081294 |
6.56344 |
1.722591097 |
6.57343 |
-5.413858372 |
6.58342 |
-3.333021488 |
6.59341 |
-1.858750554 |
6.6034 |
7.098760966 |
6.61339 |
-0.641575928 |
6.62338 |
6.484658465 |
6.63337 |
-0.860808054 |
6.64336 |
-13.68047734 |
6.65335 |
1.492050407 |
6.66334 |
6.163276336 |
6.67333 |
3.833679415 |
6.68332 |
-8.409774186 |
6.69331 |
4.29869495 |
6.7033 |
5.23685778 |
6.71329 |
14.65120908 |
6.72328 |
-3.120336206 |
6.73327 |
2.360000164 |
6.74326 |
-9.011145498 |
6.75325 |
1.903090614 |
6.76324 |
-6.631856487 |
6.77323 |
7.793663765 |
6.78322 |
1.945032825 |
6.79321 |
8.669966298 |
6.8032 |
0.116513367 |
6.81319 |
-25.55801513 |
6.82318 |
11.93859995 |
6.83317 |
-15.183429 |
6.84316 |
5.180656091 |
6.85315 |
-7.06179701 |
6.86314 |
8.274075236 |
6.87313 |
12.3700884 |
6.88312 |
-12.95494251 |
6.89311 |
0.156741754 |
6.9031 |
-0.509014585 |
6.91309 |
-8.458626806 |
6.92308 |
-0.083351781 |
6.93307 |
3.470766516 |
6.94306 |
-14.46932313 |
6.95305 |
13.77043702 |
6.96304 |
5.313923448 |
6.97303 |
4.931846114 |
6.98302 |
-10.01036614 |
6.99301 |
-8.767449648 |
7.003 |
10.06318732 |
7.01299 |
-3.423666569 |
7.02298 |
-15.36949847 |
7.03297 |
2.608538509 |
7.04296 |
7.878140082 |
7.05295 |
0.913242327 |
7.06294 |
0.348155247 |
7.07293 |
-2.231988584 |
7.08292 |
-0.345359839 |
7.09291 |
1.278247058 |
7.1029 |
-20.02808536 |
7.11289 |
5.03468863 |
7.12288 |
3.260527942 |
7.13287 |
5.309746077 |
7.14286 |
-2.189574223 |
7.15285 |
-2.284912632 |
7.16284 |
-5.403491633 |
7.17283 |
0.092657462 |
7.18282 |
4.518721706 |
7.19281 |
3.580857128 |
7.2028 |
-10.17322989 |
7.21279 |
7.806021794 |
7.22278 |
-4.73421844 |
7.23277 |
-3.415076116 |
7.24276 |
-7.290820809 |
7.25275 |
-14.45068133 |
7.26274 |
8.169200723 |
7.27273 |
-2.825292145 |
7.28272 |
-4.296237892 |
7.29271 |
-8.983454369 |
7.3027 |
9.182327102 |
7.31269 |
-1.197272811 |
7.32268 |
13.76200883 |
7.33267 |
3.133104226 |
7.34266 |
3.867411 |
7.35265 |
-3.03035123 |
7.36264 |
-6.542621009 |
7.37263 |
1.945815673 |
7.38262 |
-2.549595601 |
7.39261 |
-0.158160279 |
7.4026 |
-6.978950597 |
7.41259 |
-25.47934976 |
7.42258 |
-6.789221764 |
7.43257 |
-6.099270412 |
7.44256 |
2.415213572 |
7.45255 |
-18.23976869 |
7.46254 |
-1.982576687 |
7.47253 |
3.640569181 |
7.48252 |
-20.03419854 |
7.49251 |
0.935736146 |
7.5025 |
10.70330205 |
7.51249 |
1.635202361 |
7.52248 |
-15.63194684 |
7.53247 |
-5.953008561 |
7.54246 |
12.78808847 |
7.55245 |
-0.235570553 |
7.56244 |
5.667988363 |
7.57243 |
-6.787869386 |
7.58242 |
-0.388372962 |
7.59241 |
7.247156358 |
7.6024 |
3.438966323 |
7.61239 |
-14.54662266 |
7.62238 |
13.86340422 |
7.63237 |
4.689593496 |
7.64236 |
-20.13647163 |
7.65235 |
4.067467358 |
7.66234 |
-4.778943212 |
7.67233 |
14.60034375 |
7.68232 |
22.76778605 |
7.69231 |
5.17666876 |
7.7023 |
-9.189985809 |
7.71229 |
-6.353035545 |
7.72228 |
-6.663864973 |
7.73227 |
0.091541848 |
7.74226 |
5.785591763 |
7.75225 |
-25.02702468 |
7.76224 |
7.537635024 |
7.77223 |
18.27125711 |
7.78222 |
-1.461704695 |
7.79221 |
33.05832628 |
7.8022 |
11.68769856 |
7.81219 |
25.67116899 |
7.82218 |
20.33666274 |
7.83217 |
-2.010092134 |
7.84216 |
6.497586595 |
7.85215 |
0.01999981 |
7.86214 |
1.03601428 |
7.87213 |
-1.248522738 |
7.88212 |
-18.05622089 |
7.89211 |
15.30589029 |
7.9021 |
11.5075216 |
7.91209 |
-22.61471602 |
7.92208 |
11.64299033 |
7.93207 |
-15.40346174 |
7.94206 |
-12.47251092 |
7.95205 |
10.77204641 |
7.96204 |
18.76912227 |
7.97203 |
0.015044285 |
7.98202 |
-27.31686912 |
7.99201 |
12.69931385 |
8.002 |
20.30772335 |
8.01199 |
-11.9474597 |
8.02198 |
-18.52025157 |
8.03197 |
15.77094464 |
8.04196 |
-43.49125262 |
8.05195 |
9.084368073 |
8.06194 |
17.26108046 |
8.07193 |
4.464399403 |
8.08192 |
7.912643385 |
8.09191 |
-1.624458961 |
8.1019 |
12.15870055 |
8.11189 |
-15.66592129 |
8.12188 |
-17.47127329 |
8.13187 |
18.04342416 |
8.14186 |
23.80072274 |
8.15185 |
-1.750750433 |
8.16184 |
15.46223445 |
8.17183 |
-11.89620932 |
8.18182 |
2.91360712 |
8.19181 |
-8.505649879 |
8.2018 |
-25.60973519 |
8.21179 |
0.005208679 |
8.22178 |
-12.10138741 |
8.23177 |
3.455382617 |
8.24176 |
12.11794773 |
8.25175 |
14.95958598 |
8.26174 |
1.087300074 |
8.27173 |
19.17679081 |
8.28172 |
-13.10055028 |
8.29171 |
-3.856950248 |
8.3017 |
1.039740918 |
8.31169 |
9.235484747 |
8.32168 |
-7.318417776 |
8.33167 |
-13.69754917 |
8.34166 |
-4.9012421 |
8.35165 |
2.757833328 |
8.36164 |
-22.70424622 |
8.37163 |
-3.589292127 |
8.38162 |
-7.466987742 |
8.39161 |
-22.08249183 |
8.4016 |
-3.312592718 |
8.41159 |
-10.87803484 |
8.42158 |
10.30753535 |
8.43157 |
6.758907671 |
8.44156 |
-13.93415176 |
8.45155 |
19.18052855 |
8.46154 |
-4.835784579 |
8.47153 |
-29.94474599 |
8.48152 |
9.971936678 |
8.49151 |
21.57896021 |
8.5015 |
-27.48496393 |
8.51149 |
-41.6081291 |
8.52148 |
38.54556796 |
8.53147 |
1.442754966 |
8.54146 |
22.5982067 |
8.55145 |
-15.99858065 |
8.56144 |
36.24111148 |
8.57143 |
-34.76076236 |
8.58142 |
33.51314598 |
8.59141 |
0.40099877 |
8.6014 |
-12.34154269 |
8.61139 |
-3.559646004 |
8.62138 |
38.98898358 |
8.63137 |
7.336385871 |
8.64136 |
19.57460441 |
8.65135 |
20.83607076 |
8.66134 |
4.448777787 |
8.67133 |
-26.79773139 |
8.68132 |
13.39250856 |
8.69131 |
8.48305462 |
8.7013 |
11.94815434 |
8.71129 |
-3.776316282 |
8.72128 |
-7.76026753 |
8.73127 |
-7.194562262 |
8.74126 |
-18.64066092 |
8.75125 |
38.20635534 |
8.76124 |
6.995308791 |
8.77123 |
0.473593066 |
8.78122 |
-34.88025295 |
8.79121 |
19.5511043 |
8.8012 |
23.20638403 |
8.81119 |
9.470860955 |
8.82118 |
-6.983990891 |
8.83117 |
15.95592639 |
8.84116 |
-10.98617491 |
8.85115 |
16.8233729 |
8.86114 |
13.73180328 |
8.87113 |
26.80460098 |
8.88112 |
7.185254247 |
8.89111 |
-44.08013475 |
8.9011 |
4.68717189 |
8.91109 |
-7.779397578 |
8.92108 |
-133.0817014 |
8.93107 |
-43.50435301 |
8.94106 |
21.67831422 |
8.95105 |
-39.18134171 |
8.96104 |
7.396364548 |
8.97103 |
-24.58140489 |
8.98102 |
-40.15176149 |
8.99101 |
-52.92060766 |
9.001 |
-3.762063297 |
9.01099 |
-16.89308882 |
9.02098 |
-40.18753397 |
9.03097 |
21.59453121 |
9.04096 |
19.35019069 |
9.05095 |
25.87086349 |
9.06094 |
22.41312237 |
9.07093 |
29.08038094 |
9.08092 |
-21.29083289 |
9.09091 |
10.78272625 |
9.1009 |
-38.76330939 |
9.11089 |
-34.58911739 |
9.12088 |
9.959079743 |
9.13087 |
19.19832944 |
9.14086 |
17.38748543 |
9.15085 |
-17.86247991 |
9.16084 |
-9.261927615 |
9.17083 |
-2.403220487 |
9.18082 |
65.92464211 |
9.19081 |
13.53711071 |
9.2008 |
-22.96353242 |
9.21079 |
-1.576541898 |
9.22078 |
36.58492527 |
9.23077 |
-32.44643058 |
9.24076 |
33.76451211 |
9.25075 |
-53.15802996 |
9.26074 |
-133.5729399 |
9.27073 |
-14.57939329 |
9.28072 |
0.727994201 |
9.29071 |
-5.897097507 |
9.3007 |
3.679698617 |
9.31069 |
10.83397033 |
9.32068 |
24.35973637 |
9.33067 |
-41.70409998 |
9.34066 |
6.562819052 |
9.35065 |
-18.53171364 |
9.36064 |
-26.86253805 |
9.37063 |
-13.76559009 |
9.38062 |
24.27873479 |
9.39061 |
7.618845528 |
9.4006 |
-101.8975949 |
9.41059 |
18.98590718 |
9.42058 |
-42.55085027 |
9.43057 |
-19.66291584 |
9.44056 |
34.00565921 |
9.45055 |
13.94016878 |
9.46054 |
-29.32953584 |
9.47053 |
61.60881424 |
9.48052 |
-83.51621761 |
9.49051 |
-62.95248752 |
9.5005 |
-35.9292256 |
9.51049 |
22.10187011 |
9.52048 |
27.27135858 |
9.53047 |
19.4115128 |
9.54046 |
-36.48796336 |
9.55045 |
-6.410382387 |
9.56044 |
49.00213791 |
9.57043 |
8.781002361 |
9.58042 |
-12.07864908 |
9.59041 |
-77.95703268 |
9.6004 |
-2.670473139 |
9.61039 |
-6.110824879 |
9.62038 |
-53.66229896 |
9.63037 |
-15.01723026 |
9.64036 |
6.272267353 |
9.65035 |
19.17851145 |
9.66034 |
11.96531963 |
9.67033 |
-69.63230314 |
9.68032 |
-18.62619523 |
9.69031 |
-79.80169635 |
9.7003 |
-3.505735099 |
9.71029 |
18.53903242 |
9.72028 |
40.20569826 |
9.73027 |
31.31606569 |
9.74026 |
56.38691391 |
9.75025 |
-5.042841889 |
9.76024 |
-10.60264086 |
9.77023 |
53.41597802 |
9.78022 |
15.39006761 |
9.79021 |
-100.2898206 |
9.8002 |
45.41666654 |
9.81019 |
-42.6718043 |
9.82018 |
31.98359875 |
9.83017 |
-19.06598401 |
9.84016 |
-19.67787487 |
9.85015 |
-71.86271035 |
9.86014 |
47.12437275 |
9.87013 |
-10.25191798 |
9.88012 |
11.61134253 |
9.89011 |
0.710566802 |
9.9001 |
60.71120752 |
9.91009 |
38.06149416 |
9.92008 |
33.29985731 |
9.93007 |
-18.41128956 |
9.94006 |
-76.3326217 |
9.95005 |
19.39548829 |
9.96004 |
-69.22075904 |
9.97003 |
-85.63781011 |
9.98002 |
19.98373354 |
9.99001 |
-64.2646008 |
10 |
-78.2711671 |
Footnotes
*The authors thank Chris Gust, Alejandro Justiniano, and seminar participants at the 2007 meeting of the Society for Computational Economics. We are particularly grateful to Gary Anderson for countless helpful conversations, as well as for generously sharing his programs with us. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
**Corresponding author. Telephone (202) 452-2550. E-mail [email protected]. Return to text
1. Examples of AD contributions to the computational finance literature are [C. H. Bischof 2002], [M. Giles 2006], [Giles 2007]. Return to text
2. In this paper we focus on the first-order approximation to the solution of a DGE model. Many alternative approaches have been advanced. We use the algorithm described by [Anderson and Moore 1985] which has the marked advantage of not relying on complex decompositions. Return to text
3. Our maximum-likelihood estimates were constructed using the MATLAB optimization routine FMINUNC. When the optional argument ``LargeScale'' is set to ``OFF'', this routine uses a limited memory quasi-Newton conjugate gradient method, which takes as input first derivatives of the objective function, or an acceptable FD approximation. Return to text
4. For our MATLAB optimization routine, we
set the convergence criterion to require a change in the objective
function smaller than to ![]() , implying 6
significant figures for our specific likelihood function. This
choice seemed appropriate given the limited precision of observed
series in practical applications. Return
to text
, implying 6
significant figures for our specific likelihood function. This
choice seemed appropriate given the limited precision of observed
series in practical applications. Return
to text
5. We experimented with a broad set of Monte Carlo experiments by varying the choice of estimation parameters, so as to encompass the near totality of parameters in the calibration table, or so as to study individual parameters in isolation. We found results broadly in line with the particular Monte Carlo experiments we are reporting below. Our results also appear robust to broad variation in the calibration choice. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text