Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 929, April 2008--- Screen Reader Version*

Competitive Search Equilibrium in a DSGE Model

David M. Arseneau, Federal Reserve Board^*
Sanjay K. Chugh, University of Maryland^†

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We show how to implement a competitive search equilibrium in a fully-specified DSGE environment. Competitive search, an equilibrium concept well-understood in labor market theory, offers an alternative to the commonly-used Nash bargaining in search-based macro models. Our simulation-based results show that business cycle fluctuations under competitive search equilibrium are virtually identical to those under Nash bargaining for a broad range of calibrations of Nash bargaining power. We also prove that business cycle fluctuations under competitive search equilibrium are exactly identical to those under Nash bargaining restricted to the popularly-used Hosios condition for search efficiency. This latter result extends the efficiency properties of competitive search equilibrium to a DSGE environment. Our results thus provide a foundation for researchers interested in studying business cycle fluctuations using search-based environments to claim that the sometimes-awkward assumption of bargaining per se does not obscure interpretation of results.

Keywords: Search models, customer markets, business cycle fluctuations

JEL classification: E10, E30, E32

1  Introduction

DSGE models featuring search and matching frictions have exploded in popularity in the past few years.¹Invariably, this recent vintage of models has assumed that transactions prices are determined according to bilateral bargaining between a buyer and a seller, and Nash bargaining has been by far the most common bargaining specification adopted. While bargaining may be plausible in some circumstances, it seems desirable to also consider price-setting mechanisms that retain the competitive nature familiar to most macroeconomists while still allowing for fundamental search and matching frictions. We show how to implement the concept of competitive search equilibrium developed by Moen (1997) in a fully-specified DSGE environment. We show using stochastic simulations of a simple DSGE model featuring search and matching frictions that competitive search equilibrium gives rise to fluctuations nearly identical to those that arise in an environment featuring Nash bargaining. Furthermore, if Nash bargaining is coupled with the well-known Hosios (1990) parameterization that has become a focal point in the recent vintage of search-DSGE models, we show analytically that business cycle fluctuations are identical under either bargaining or competitive search. Our results thus provide a foundation for researchers interested in studying business cycle fluctuations using search-based environments to claim that the sometimes-awkward assumption of bargaining per se does not obscure interpretation of results.

Moen (1997) developed the concept of competitive search equilibrium in its current form and on which we build. As described by Rogerson, Shimer, and Wright (2005, p. 29), an important conceptual advantage of the competitive search framework over the search and bargaining framework is that it endogenizes the surplus-splitting mechanism between parties. Nash equilibrium assigns arbitrary bargaining powers to parties in a bilateral trade. However, there is typically no empirical guidance on the calibration of these bargaining powers in a quantitative model. Absent empirical guidance, many search-based models focus on the well-known Hosios (1990) parameterization, which places a specific parameter restriction across bargaining powers and matching technology parameters that delivers Pareto-efficiency in search markets. Competitive search does away with this arbitrary bargaining parameter and yet, as shown by Moen (1997), endogenously delivers the efficiency delivered by the Hosios parameter setting. We show that the Moen (1997) result extends to a full dynamic stochastic general equilibrium environment.² Furthermore, and especially of interest to quantitative practitioners, we show that even if one departs from the Hosios parameter setting, the business-cycle fluctuations that arise from either competitive search equilibrium or Nash bargaining are extremely similar.

Moen's (1997) framework was developed in a search-based model of the labor market. However, we develop our results in a search-based model of the goods market. Specifically, we build on the quantitative search-based model of goods markets developed in Arseneau and Chugh (2007b). Their model, as does Hall's (2007) model, uses the search-and-matching framework familiar from labor market theory as a basis for a model of goods markets. In both Arseneau and Chugh (2007b) and Hall (2007), the search frictions that both consumers and firms must overcome before goods trade can occur make customer relationships valuable to both parties. The novel feature of our search-based goods market compared to Arseneau and Chugh (2007b) and Hall (2007) is a competitive mechanism in which firms post prices and consumers optimally direct their search based on these posted prices, rather than prices being determined by ad-hoc bargaining or surplus-splitting rules. We think the combination of all three features -- search frictions, firms posting prices unilaterally, and consumers directing their search towards firms based on posted prices -- is a potentially very natural description of goods markets. As such, the model development we do in this paper is also a building block to richer applications of the Arseneau and Chugh (2007b) and Hall (2007) environments.

Nevertheless, our results cover a wide class of existing DSGE labor search models as well. We describe how one would adapt our implementation of competitive search for a labor search framework. There is no reason to think that our virtual equivalence results would not readily extend to a baseline DSGE labor search model. Regardless of in which market one articulates our ideas, one virtue of replacing bargaining with competitive search equilibrium in a full DSGE model is that it avoids the Coles and Wright (1998) criticism of bilateral bargaining in a dynamic environment. Rather, prices are set unilaterally by firms in competitive search equilibrium, and price-setting is forward-looking, as it is in, say, a typical New Keynesian sticky-price model.

The rest of the paper is organized as follows. In Section 2, we sketch how price posting and directed search works. Section 3 details the model, including a precise description of how to implement a competitive search equilibrium. In Section 4, we analytically extend Moen's (1997) results to a dynamic stochastic general equilibrium environment, proving that business cycle fluctuations under competitive search are identical to those under Nash bargaining at the Hosios condition. We also provide a simple MRS = MRT interpretation of pricing outcomes in search models that should prove useful in other search models, as well. Section 5 presents quantitative results. Section 6 demonstrates the robustness of our results to alternative sources of business cycle fluctuations. Section 7 outlines how one could adapt our implementation of competitive search to a DSGE labor search model. Section 8 concludes and offers thoughts for ongoing work.

2  General Description of the Environment

Before going into details, we outline the basic structure of goods markets in our model. Our environment builds on Arseneau and Chugh (2007b), which posits that, for some goods trades, households and firms each have to expend time and resources finding individuals on the other side of the market with whom to trade. The resource costs for consumers involve time. The resource costs for firms involve time and direct costs of activities we interpret as advertising, which are meant to attract potential customers.

The key feature of the environment on which we focus is the method by which transactions prices are determined. One alternative is Nash bargaining, whose use is standard in DSGE search-based models. The focus of our study, however, is on a system in which prices are unilaterally posted by firms. These posted prices play a crucial role in governing how many potential customers are attracted to the firm's location. As Rogerson, Shimer, and Wright (2005) emphasize, it is the combination of these features -- price-posting by firms and search activity directed by these posted prices -- that is necessary for the concept of competitive search equilibrium. Merely attracting customers to a location is not enough, however; once a set of potential customers has arrived at a location, some randomness governs how many of them actually purchase goods at the posted price. The probability of purchase depends on how many potential customers a store attracts.³ To introduce some basic terminology of our model, posted prices maximize the expected value of each good "advertised" by a firm or, equivalently, (to use Hall's (2007) terminology) the expected value of each "customer opening" or, equivalently, (to use Moen's (1997) terminology) the expected value of each "submarket."

We will rely most on the "submarket" terminology, which evokes an especially interesting interpretation. The submarket interpretation of our environment is that some product markets exist locally. Consumers and firms in a given submarket search for trading partners in the same submarket. We assume that there is a continuum $[0,1]$ of goods submarkets. In each submarket $j$, a homogenous product is sold by firms that are competitive in a sense to be described further below. In any two submarkets $j \neq j^{\prime}$, goods may be different, although in the end we will analyze an equilibrium symmetric across submarkets.

3  Model

We now proceed to lay out the important details of our model economy.

3.1  Households

There is a measure one of identical households, with a measure one of individuals that live within each household. In a given period, an individual member of the representative household can be engaged in one of four types of activities: purchasing goods (shopping) at a firm, working, searching for goods, or leisure. More specifically, $l_{t}$ members of the household are working in a given period; $s_{jt}$ members are searching for stores in submarket $j$ from which to buy goods; $N^{h}_{jt}$ members are shopping at stores in submarket $j$; and $1 - l_{t} - \int_{0}^{1} s_{jt} dj - \int_{0}^{1} N^{h}_{jt} dj$ members are enjoying leisure.

Note our distinction between shopping and searching for goods. Individuals who are searching are looking to form relationships with firms, which takes time. Individuals who are shopping were previously successful in forming customer relationships, but the act of acquiring and bringing home goods itself takes time.⁴ We assume that the members of a household share equally the consumption that shoppers acquire.

In very general terms, we can express the representative household's total lifetime utility as

$$E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(x_{t}) + \vartheta v\left( \int_{0}^{1} \int_{0}^{N^{h}_{jt}} c_{ijt} di dj \right) + g\left( 1-l_{t} - \int_{0}^{1} s_{jt}dj - \int_{0}^{1} N^{h}_{jt} dj\right) \right] ,$$ (1)

where $j$ indexes submarkets and $i$ indexes a given family member in submarket $j$. However, anticipating the symmetric equilibrium on which we will focus and because we lose no clarity by doing so, we specialize right away to

$$E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(x_{t}) + \vartheta v\left( \int_{0}^{1} N^{h}_{jt} \bar{c} \right) + g\left( 1-l_{t} - \int_{0}^{1} s_{jt} dj - \int_{0}^{1} N^{h}_{jt} dj \right) \right] .$$ (2)

In writing (2), we have also imposed that each transaction, regardless of submarket, results in the exchange of $\bar{c}$ units of goods. Thus, we close down the intensive margin of consumption purchases to emphasize the concept of competitive search equilibrium.⁵

The household faces a sequence of flow budget constraints

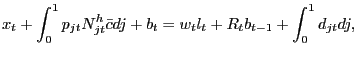
$$x_{t} + \int_{0}^{1} p_{jt} N^{h}_{jt} \bar{c} dj + b_{t} = w_{t} l_{t} + R_{t} b_{t-1} + \int_{0}^{1} d_{jt} dj,$$ (3)

where $b_{t-1}$ is holdings of a state-contingent one-period real private bond at the end of period $t-1$, which has gross payoff $R_{t}$ at the beginning of period $t$, $w_{t}$ is the real wage, and $d_{jt}$ is firm dividends of submarket $j$ received lump-sum by the household. The Walrasian good $x$ serves as the numeraire, hence the price $p_{j}$ of a given submarket's good is measured in units of $x$.

The household also faces a sequence of perceived laws of motion for the number of active customer relationships in each submarket $j$,

$$N^{h}_{jt} = (1-\rho^{x})N^{h}_{jt-1} + s_{jt} k^{h}(\theta_{jt}),$$ (4)

where $k^{h}(\theta_{jt})$ is the probability that a searcher forms a customer relationship in submarket $j$. This matching probability depends on $\theta_{jt}$, which measures the tightness of goods submarket $j$ -- how many advertisements there are per searcher -- and is taken as given by the household.⁶ With fixed probability $\rho^{x}$, which is known to both households and firms, an existing customer relationship dissolves at the beginning of a period. The dissolution of a customer relationship may occur for any of a number of reasons: the customer may move away, the firm may close shop, the customer may simply choose to stop visiting the same store for some reason, and so on. A natural potential future extension would be to endogenize the rate at which customer-firm relationships break up. Finally, note the timing of events embodied by the flow budget constraint and the flow utility function: period-$t$ search and matching precedes period-$t$ purchases of goods. That is, successful search in period $t$ leads to the purchase of goods in period $t$ (and possibly beyond, as well).

The representative household chooses decision rules for $\{x_{t}, l_{t}, s_{jt}, N^{h}_{jt}\}$, taking as given $\{w_{t}\}$ and $\{\theta_{jt}, p_{jt}\}$ $\forall j$. Optimization yields a standard consumption-leisure optimality condition,

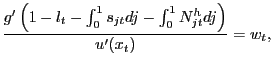
$$\frac{g^{\prime}\left( 1-l_{t} - \int _{0}^{1} s_{jt}dj - \int_{0}^{1} N^{h}_{jt} dj\right) }{u^{\prime}(x_{t})} = w_{t},$$ (5)

a standard consumption-savings optimality condition

$$u^{\prime}(x_{t}) = \beta E_{t} \left\{ u^{\prime}(x_{t+1}) R_{t+1}\right\} ,$$ (6)

and a condition that we refer to as the household shopping condition

$$\frac{\left[ 1 + k^{h}(\theta_{jt})\right] g^{\prime }_{t}}{k^{h}(\theta_{jt})} = \left[ \vartheta v^{\prime}_{t} - p_{jt} u^{\prime}_{t}\right] \bar{c} + \beta(1-\rho^{x}) E_{t} \left\{ \frac{g^{\prime}_{t+1}}{k^{h}(\theta_{jt+1})}\right\} .$$ (7)

A shopping condition exists for each submarket $j$. As in Arseneau and Chugh (2007b), the shopping condition for each submarket simply states that at the optimum, the household should send a number of individuals out to search for goods in market $j$ such that the expected marginal cost of shopping (the left-hand-side of (7)) equals the expected marginal benefit of shopping (the right-hand-side of (7)). The expected marginal benefit of shopping is composed of two parts: the utility gain from obtaining $\bar{c}$ more goods via the search market rather than via the Walrasian market (net of the direct disutility $g^{\prime}$ of shopping) and the benefit to the household of having one additional pre-existing customer relationship entering period $t+1$. If all trades were frictionless, household optimal choices would imply $\vartheta v^{\prime}_{t} = p_{t} u^{\prime} (x_{t})$. With frictions, in order to engage in costly search, it must be that on the margin, the household expects $\vartheta v^{\prime}_{t+1} > p_{t+1} u^{\prime}(x_{t+1})$. This positive flow return ensures that the household finds it worthwhile to send some of its members shopping.

3.2  Walrasian Firms

To make pricing labor simple, we assume that there is a representative firm that buys labor in and sells the Walrasian good $x$ in competitive spot markets. The firm operates a linear production technology that is subject to aggregate TFP fluctuations, $y_{t} = z_{t} l_{t}$. Profit-maximization yields the standard result that

$$w_{t} = z_{t},$$ (8)

which all participants in the economy, including the non-Walrasian firms described next, take as given.⁷

3.3  Non-Walrasian Firms and the Submarkets for Goods

We assume that a representative "large" firm produces and sells the entire continuum $[0,1]$ of goods. Specifically, the firm sells output in each submarket. Our assumption of a representative large firm facilitates aggregation, allowing us to avoid tracking the particular history of trades at any particular "trading post" within a submarket. In each submarket, the firm must decide how much advertising in which to engage. Ex-ante, and this is key for the concept of competitive search equilibrium, the intensity of advertising can vary across submarkets, which means that queue lengths, the numbers of customers, and prices can vary across submarkets. In constructing the equilibrium, however, we will restrict attention to an equilibrium that is symmetric across submarkets.

With this structure, the firm's dynamic profit function is

$$E_{0} \sum_{t=0}^{\infty} \Xi_{t\vert}\left[ \int_{0}^{1} N^{f}_{jt} p_{jt} \bar{c} dj - \int_{0}^{1} N^{f}_{jt} mc_{t} \bar{c} dj - \gamma\int_{0}^{1} a_{jt} dj \right] ,$$ (9)

where $\Xi_{t\vert}$ is the period-0 value to the household of period-$t$ goods, which we assume the firm uses to discount profit flows because the households are the ultimate owners of firms.⁸ The firm's choice of advertising $a_{jt}$ in any submarket $j$ is costly; each advertisement, irrespective of submarket, entails a flow cost $\gamma$. The real marginal cost of production is $mc_{t}$, also identical across submarkets. As for Walrasian firms, production is assumed to be linear in labor and subject to a common TFP shock; hence, in equilibrium, $mc_{t} = w_{t}/z_{t}$.

The firm faces a sequence of perceived laws of motion for the number of customer relationships in each submarket $j$,

$$N^{f}_{jt} = (1-\rho^{x})N^{f}_{jt-1} + a_{jt} k^{f}(\theta_{jt}),$$ (10)

where $k^{f}(\theta_{jt})$ is the probability that one of the firm's advertisements attracts a customer in submarket $j$. As with customer matching probabilites, firm matching probabilities depend only on the relative number of participants in a submarket and are taken as given by the firm.

In the "stage-one" (i.e., before making any decisions regarding prices -- pricing decisions are made after entering a market) profit-maximization problem, the firm's choice variables are $\{a_{jt}, N^{f}_{jt}\}$. Optimization leads to an optimal advertising condition for each submarket,

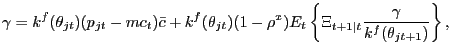
$$\gamma= k^{f}(\theta_{jt})(p_{jt} - mc_{t})\bar{c} + k^{f}(\theta_{jt})(1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \frac{\gamma}{k^{f}(\theta_{jt+1})}\right\} ,$$ (11)

which states that at the optimum, the expected marginal cost of posting an ad in submarket $j$ (the left-hand-side of (11)) equals the expected marginal benefit of forming a relationship with a new customer in submarket $j$ (the right-hand-side of (11)). The expected marginal benefit takes into account the revenue from selling to one extra customer, the production costs incurred for producing to sell those extra units, and the cost savings of finding another customer in the future due to the pre-existing (in time $t+1$) customer relationship. Condition (11) is a free-entry condition in advertising in submarket $j$.

3.4  Price Determination

Our main objective is to compare the dynamics implied by the two alternative pricing protocols, Nash bargaining and competitive pricing with directed search.

3.4.1  Nash Bargaining

We show in Appendix A that the Nash-bargained transactions price $p_{jt}$ in submarket $j$ satisfies

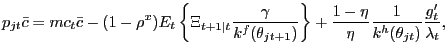
$$p_{jt} \bar{c} = mc_{t} \bar{c} - (1-\rho^{x}) E_{t}\left\{ \Xi_{t+1\vert t}\frac{\gamma}{k^{f}(\theta_{jt+1})} \right\} + \frac{1-\eta}{\eta} \frac{1}{k^{h}(\theta_{jt})}\frac{g^{\prime}_{t}} {\lambda_{t}},$$ (12)

in which arguments of $g^{\prime}(.)$ and $v^{\prime}(.)$ have been suppressed. In equilibrium, the household's marginal value of wealth $\lambda_{t} = u^{\prime}(x_{t})$. Condition (12) shows that the Nash price depends on firms' marginal production costs (the first term on the right hand side), net of the asset value to a firm of forming a long-term relationship with a customer (the second term on the right hand side), and the share of the surplus that consumers can extract from firms (the third term on the right hand side). If goods markets were perfectly competitive, we would have $\gamma=0$, because there would be no search costs, and $\eta=1$, which means that firms have no market power; in this case, we recover the usual result that $p_{jt}=mc_{t}$.

3.4.2  Competitive Search

We now describe how to implement price posting with directed search. This kind of pricing mechanism has not yet been incorporated into search-based DSGE models; in section 7, we describe how one would implement this mechanism in a labor search model.

If firms post prices, the firm chooses the price $p_{jt}$ following entry into a submarket $j$. The firm's choice of $p_{jt}$ maximizes the value of selling (i.e., post-entry) in submarket $j$ and takes into account the relationship that describes how many customers "queue up" in the submarket as a function of the posted price. This latter relationship is described by the shopping condition (7) for submarket $j$. Formally, the posted price maximizes the value of the $j$-th submarket, described by the right-hand-side of (11), subject to the constraint of the shopping condition (7) for the $j$-th submarket.⁹. From the perspective of the firm, condition (7) describes how a change in the price $p_{jt}$ it charges in submarket $j$ affects the queue length $\theta_{jt}$ in that submarket. Thus, the formal objects of choice in this maximization problem are both $p_{jt}$ and $\theta_{jt}$.

Solving this optimization problem, the optimal posted price $p_{jt}$ is characterized by

$$k^{f^{\prime}}(\theta_{jt}) \left[ (p_{jt}-mc_{t} )\bar{c} + (1-\rho^{x}) \Gamma_{t}\right] = \varphi_{t} k^{h^{\prime}} (\theta_{jt}) \left[ g^{\prime}_{t} - (\vartheta v^{\prime}_{t} - p_{jt}u^{\prime}_{t}) \bar{c} - \beta(1-\rho^{x}) \Lambda_{t} \right] ,$$ (13)

where $\varphi_{t} \equiv\frac{k^{f}(\theta_{jt})}{k^{h}(\theta_{jt}) u^{\prime}_{t}}$ , $\Gamma_{t} \equiv E_{t} \left[ \Xi_{t+1\vert t} \frac{\gamma }{k^{f}(\theta_{jt+1})}\right]$ , and $\Lambda_{t} \equiv E_{t} \left[ \frac{g^{\prime}_{t+1}}{k^{h}(\theta_{jt+1})} \right]$ . Together, conditions (13) and (7) characterize the competitive search outcome $(p_{jt}, \theta_{jt})$ in goods-submarket $j$, taking as given outcomes in labor markets, capital markets, Walrasian goods markets, and all other goods submarkets.

3.5  Goods Market Matching

In equilibrium, the number of active customer matches in submarket $j$ evolves according to

$$N_{jt} = (1-\rho^{x})N_{jt-1} + m(s_{jt}, a_{jt}),$$ (14)

where $m(.)$ is a constant-returns-to-scale matching function that governs the flow of new customer relationships that form in each submarket $j$. As is standard in search-based models, constant-returns matching implies that the transition probabilities $k^{h}(.)$ and $k^{f}(.)$ depend only on the tightness of each submarket, which is already reflected in our notation. Imposing symmetry across submarkets and aggregating over $j \in[0,1]$ yields the aggregate law of motion for customer relationships

$$N_{t} = (1-\rho^{x}) N_{t-1} + m(s_{t}, a_{t}).$$ (15)

3.6  Equilibrium

The conditions describing a symmetric (across submarkets) search equilibrium are the consumption-leisure optimality condition (5), the consumption-savings optimality condition (6), the shopping condition (7), the equilibrium wage condition (8), the advertising condition (11), the law of motion for the aggregate stock of customer relationships (15), and the aggregate resource constraint of the economy

$$x_{t} + N_{t} \bar{c} + \gamma a_{t} = z_{t} l_{t}.$$ (16)

Note in (16) that aggregate advertising costs $\gamma a_{t}$ are a real resource cost for the economy.

Depending on whether price-posting or Nash bargaining is the pricing mechanism, either condition (12) or (13) completes the set of conditions characterizing equilibrium. If prices are posted, we refer to the equilibrium as a competitive search equilibrium; if prices are bargained, we refer to the equilibrium as a bargaining equilibrium. The unknown stochastic processes are $\{p_{t}, \theta_{t}, N_{t}, a_{t}, x_{t}, l_{t}, w_{t}, R_{t}\}_{t=0} ^{\infty}$ , for exogenous stochastic process $\{z_{t}\}_{t=0}^{\infty}$. Finally, as we noted above, by construction, $mc_{t} = w_{t}/z_{t} = 1$ $\forall t$.

4  Equivalence Between Competitive Search and Nash Bargaining

We now prove that if in the bargaining economy the elasticity of the aggregate matching function with respect to the number of searching individuals (we denote this elasticity $\xi$) equals the Nash bargaining power of customers ($\eta$), then the competitive search price and the Nash price are identical. This extends the results of Moen (1997) to a dynamic stochastic general equilibrium environment.

To show this, begin with the competitive search outcome (13). Given the Cobb-Douglas specification $m(s,a)=\psi s^{\xi} a^{1-\xi}$ we assume below, we have $k^{f}(\theta)/k^{h}(\theta) = \theta^{-1}$, $k^{h^{\prime}}(\theta)/k^{f^{\prime}}(\theta) = -(1-\xi)\theta/\xi$ , and thus $(k^{f}(\theta)/k^{h}(\theta))(k^{h^{\prime}}(\theta_{t})/k^{f^{\prime} }(\theta_{t})) = -(1-\xi)/\xi$ . Using these, we can simplify (13) to

$$\lefteqn{u'_{t} \left[ (p_{jt}-mc_{t}) \bar{c} + (1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \frac{\gamma}{k^{f}(\theta_{jt+1})}\right\} \right] }$$ (17)

$$= -\left( \frac{1-\xi}{\xi}\right) \left[ g^{\prime}_{t} - ( \vartheta v^{\prime}_{t} - p_{jt} u^{\prime}_{t}) \bar{c} - \beta(1-\rho^{x}) E_{t} \left\{ \frac{g^{\prime}_{t+1}}{k^{h}(\theta_{jt+1})}\right\} \right] .$$

Next, use the advertising condition (11) to substitute for the term in square brackets on the first line, and use the shopping condition (7) to substitute for the term in square brackets on the second line; doing so yields

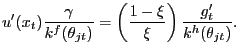
$$u^{\prime}(x_{t}) \frac{\gamma}{k^{f}(\theta_{jt})} = \left( \frac{1-\xi}{\xi}\right) \frac{g^{\prime}_{t}}{k^{h}(\theta_{jt})}.$$ (18)

Expression (18) defines $p_{jt}$ -- the price is implicit in the time-$t$ asset values of a customer relationship for firms and households that appear on the left- and right-hand-sides, respectively.

Again using the result $k^{h}(\theta_{jt})/k^{f}(\theta_{jt}) = \theta_{jt}$, one more rearrangement gives

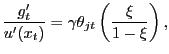
$$\frac{g^{\prime}_{t}}{u^{\prime}(x_{t})} = \gamma\theta_{jt} \left( \frac{\xi}{1-\xi}\right) ,$$ (19)

which has a standard MRS = MRT interpretation. That the left-hand-side of (19) is the MRS between consumption and leisure is obvious. To understand why the right-hand-side measures the corresponding MRT, consider the algebraic units of each term. The units of $\gamma$ is goods per advertisement, the units of $\theta_{jt}$ (which, recall, $\equiv a_{t} / s_{t}$), is advertisements per searching individual, and $\xi/(1-\xi)$, because it is the ratio of elasticities in the Cobb-Douglas matching function, is a unitless number. The latter term measures the social (technological) contribution of a searching individual to the aggregate formation of customer relationships in goods submarket $j$. Thus, $\gamma\theta_{jt} \xi/(1-\xi)$ measures how many search goods are produced for each individual who is searching; it is thus the economy's MRT between time spent searching for goods and production of search-market goods.

Expression (19) was obtained starting with the competitive search outcome (13); we arrive at the same result starting with the Nash outcome (12) provided $\eta= \xi$. Rewrite (12) as

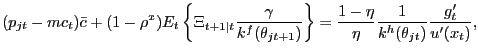
$$(p_{jt}-mc_{t}) \bar{c} + (1-\rho^{x}) E_{t}\left\{ \Xi_{t+1\vert t} \frac{\gamma }{k^{f}(\theta_{jt+1})} \right\} = \frac{1-\eta}{\eta} \frac{1}{k^{h} (\theta_{jt})} \frac{g^{\prime}_{t}}{u^{\prime}(x_{t})},$$ (20)

in which we have used the equilibrium condition $\lambda_{t} = u^{\prime }(x_{t})$. Using the advertising condition (11) on the left-hand-side, we have

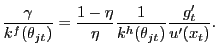
$$\frac{\gamma}{k^{f}(\theta_{jt})} = \frac{1-\eta}{\eta} \frac{1}{k^{h} (\theta_{jt})} \frac{g^{\prime}_{t}}{u^{\prime}(x_{t})}.$$ (21)

Using the result $k^{h}(\theta_{jt})/k^{f}(\theta_{jt}) = \theta_{jt}$ and the parameter restriction $\eta= \xi_{u}$, we again obtain condition (19). Thus, Nash bargaining coupled with the Hosios (1990) parameter setting and competitive search yield identical equilibrium prices in each period; hence, business cycle fluctuations under the two alternative price-setting protocols are guaranteed to be the same.

5  Quantitative Results

We characterize the deterministic steady state and the dynamics of our model numerically. Our primary interest is in just comparing fluctuations under competitive search equilibrium to those under bargaining equilibria, thus parameter values are only illustrative. We use the calibrated values of Arseneau and Chugh (2007b), and we refer the interested reader there for a complete description of calibration targets and both individual time-use and advertising data used to calibrate search and matching parameters of the goods market. As in Arseneau and Chugh (2007b), we choose standard, simple functional forms: $u(x) = \log(x)$, $v(y) = \log(y)$, $g(z) = \frac{\zeta z^{1-\nu}}{1-\nu}$, and $m(s,a) = \psi s^{\xi} a^{1-\xi}$. We assume, as is standard, that TFP follows an AR(1) in logs: $\log z_{t+1} = \rho_{z} \log z_{t} + \epsilon^{z}_{t+1}$. Finally, when we consider Nash bargaining, the Hosios parameterization requires setting $\eta= \xi$, although we also consider different values of $\eta$. Table 1 lists parameter settings.

Table 1:  Parameter settings

Variable	Value	Description
$\beta$	0.99	Subjective discount factor
$\vartheta$	1	Relative preference for search consumption
$\nu$	0.40	Elasticity of leisure with respect to real wage
$\zeta$	4.3	Calibrating parameter
$\rho^{x}$	0.10	Probability of dissolution of a customer relationship
$\xi$	0.50	Elasticity of matches with respect to number of shoppers
$\psi$	0.45	Calibrating parameter
$\gamma$	0.48	Fixed cost of posting an advertisement/entering a submarket
$\rho_{z}$	0.95	Persistence of log TFP shocks
$\sigma_{z}$	0.007	Standard deviation of shocks to log TFP
$\bar{c}$	1	Quantity traded in each customer transaction

To study dynamics, we approximate our model by linearizing in levels the equilibrium conditions of the model around the deterministic steady state. Our numerical method is our own implementation of the perturbation algorithm described by Schmitt-Grohe and Uribe (2004b). We conduct 1000 simulations, each 200 periods long. For each simulation, we compute first and second moments and report the medians of these moments across the 1000 simulations. To make the comparisons meaningful, we use the same realizations for productivity shocks as we switch between competitive search equilibrium and bargaining equilibria.

Figure 1

Time-series simulation of price (top panel) and market tightness (lower panel) under price posting (red line) and Nash bargaining satisfying the Hosios condition (blue line).

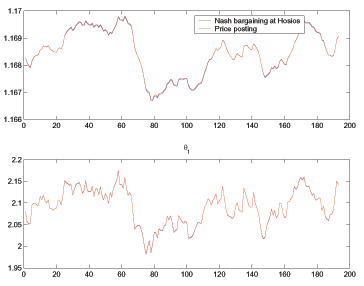
Figure 1 displays dynamic $\{p_{t}, \theta_{t}\}$ realizations for a represenative simulation of our model under competitive search equilibrium and bargaining at the Hosios condition. As is obvious, the fluctuations are identical, numerically verifying our proof in Section 4. This finding extends Moen's (1997) equivalence between competitive search equilibrium and Nash bargaining at the Hosios condition to a stochastic general equilibrium environment. Thus, if one were to implement competitive search equilibrium in a DSGE model featuring labor search frictions (we sketch the implementation of this in Section 7), one would expect identical fluctuations to also arise under competitive search and Nash bargaining coupled at the Hosios condition. Given that most DSGE labor-search models focus on this parameterization, we think this equivalence is important to know.

Table 2 - Panel A: Competitive Search Equilibrium

Simulation-based moments under competitive search equilibrium, Nash bargaining at the Hosios condition ( $\eta= \alpha= 0.50$), Nash bargaining with low customer bargaining power ( $\eta= 0.20$), and Nash bargaining with high customer bargaining power ($\eta=0.80$).

Variable	Mean	Std. Dev.	SD%	Auto corr.	Corr(x, gdp)
$p$	1.1685	0.0009	0.0008	0.9884	0.8901
$\theta$	2.0931	0.0415	0.0198	0.9279	0.9989
$gdp$	0.2870	0.0049	0.0171	0.9097	1
$N$	0.0266	0.0010	0.0365	0.3791	0.7388
$a$	0.0823	0.0008	0.0099	0.9484	0.9071

Table 2 - Panel B: Nash bargaining, Hosios condition

Variable	Mean	Std. Dev.	SD%	Auto corr.	Corr(x, gdp)
$p$	1.1685	0.0009	0.0008	0.9884	0.8901
$\theta$	2.0931	0.0415	0.0198	0.9279	0.9989
$gdp$	0.2870	0.0049	0.0171	0.9097	1
$N$	0.0266	0.0010	0.0365	0.3791	0.7388
$a$	0.0823	0.0008	0.0099	0.9484	0.9071

Table 2 - Panel C: Nash bargaining, low customer bargaining power

Variable	Mean	Std. Dev.	SD%	Auto corr.	Corr(x, gdp)
$p$	1.3269	0.0019	0.0014	0.9747	0.9513
$\theta$	7.8739	0.1537	0.0195	0.9278	0.9955
$gdp$	0.2957	0.0052	0.0176	0.8880	1
$N$	0.0500	0.0018	0.0362	0.4090	0.7797
$a$	0.0797	0.0008	0.0101	0.9520	0.8846

Table 2 - Panel D: Nash bargaining, high customer bargaining power

Variable	Mean	Std. Dev.	SD%	Auto corr.	Corr(x, gdp)
$p$	1.0843	0.0004	0.0004	0.9939	0.7911
$\theta$	0.5233	0.0106	0.0203	0.9280	0.9999
$gdp$	0.2776	0.0047	0.0169	0.9262	1
$N$	0.0129	0.0005	0.0355	0.4209	0.7311
$a$	0.0795	0.0008	0.0097	0.9522	0.9227

However, the properties of cyclical fluctuations do not vary much between competitive search equilibrium and bargaining equilibria with non-Hosios parameter settings ( $\eta\neq\xi$) either. In Table 2, we tabulate business cycle statistics obtained through simulations of our model under competitive search, bargaining under the Hosios condition, and bargaining under two deviations from the Hosios condition. Comparing first moments, second moments, and salient correlations across specifications of our model reveals that fluctuations display very nearly identical dynamics in all cases. Perhaps the largest differences are in the volatility of prices in search markets -- nevertheless, in all cases, this volatility is near 0.1 percent or less. This virtual equivalence of fluctuations between competitive search equilibrium and bargaining equilibria holds for the entire spectrum of values of $\eta \in(0,1)$.

The levels of variables, however, of course differ for non-Hosios parameterizations of the bargaining equilibria, as the first column of Table 2 shows. As Arseneau and Chugh (2007b) show analytically, variations in $\eta$ essentially vary the degree of "market power" firms wield over customers, which thus makes the levels of prices (and hence all endogenous variables) change. But if one's interests lie primarily in the cyclical properties of fluctuations, all bargaining equilibria are extremely similar to the competitive search equilibrium. This result would also readily extend to DSGE labor-search models; thus, to the extent that some such models do deviate from the Hosios parameterization, this equivalence of fluctuations is also important to know.

6  Robustness

We have so far only compared bargaining equilibria with competitive search equilibrium in the presence of TFP shocks. One may wonder how the dynamics of competitive search equilibrium compare to the dynamics of bargaining equilibria in the face of other kinds of shocks, such as exogenous movements in tax rates or exogenous shifts in government consumption. Our equivalence results carry over to these types of disturbances.

It is straightforward to introduce a proportional labor income tax and/or government purchases in our model. Denoting by $\tau^{n}_{t}$ a proportional labor income tax, the only equilibrium condition that would be affected is the household consumption-leisure optimality condition (5), which of course would now have the after-tax wage rate $(1-\tau^{n}_{t})w_{t}$ on the right-hand-side. Adding exogenous government consumption $g_{t}$ is also straightforward -- modify the resource constraint (16) so that $g_{t}$ appears on the left-hand-side. In introducing these (exogenous) policy-related variables, we assume the government also appropriately adjusts a lump-sum tax or transfer so that government financing is not an issue.

We parameterize stochastic processes for $\tau^{n}_{t}$ and $g_{t}$ in standard ways: we assume each follows an AR(1) in logs, with persistence parameter $\rho_{\tau^{n}} = 0.8$ for the labor income tax process and $\rho_{g} = 0.8$ for the government purchase process. Standard deviations of i.i.d. Gaussian shocks to these processes are assumed to be $\sigma_{\tau^{n}} = 0.01$ and $\sigma_{g} = 0.03$, respectively. Finally, we set the means of these processes to $\bar{\tau}^{n} = 0.2$ and a $\bar{g}$ such that government spending absorbs 20 percent of output in the steady state. As before, our parameter settings are meant to be illustrative rather than precise calibrations.

Simulating our model economy under competitive search equilibrium and bargaining equilibria in the presence of these alternative disturbances, in isolation or in combination, we find the same results as before: if bargaining occurs with the Hosios condition in place, fluctuations are identical to those with competitive search, whereas if bargaining occurs away from the Hosios condition, the levels of variables are once again different, but the cyclical properties of fluctuations are again virtually the same.

5  Adapting the Framework for a Labor Search Model

We have chosen to illustrate our ideas in a search-based model of the goods market because we think the combination of search frictions, firms posting prices unilaterally, and consumers directing their search based on posted prices is an appealing description of product markets. A similar description could plausibly be offered for labor markets as well. In light of the fact that the recent surge in search-based DSGE model-building has mostly been concentrated in labor search models, we offer here the outlines of how one would need to modify a typical labor-search-based DSGE model in order to incorporate price (more precisely, wage) posting. Our sketch has nothing to do whether it is real or nominal wages that are posted.

Many recent labor-search-based macro models allow an endogenous labor-force participation margin, so we will sketch our outline based on such a model.¹⁰ In this type of model, the household's optimal labor-participation margin is the analog of our model's shopping condition -- households would optimally choose how many family members to send to look for jobs in each labor submarket as a function of the posted wages in those submarkets. Some models -- for example, Walsh (2005) and Krause and Lubik (2007) -- do not allow for a labor-force participation margin. We emphasize that such models do not admit a competitive search equilibrium -- this is simply a manifestation of the point emphasized by Rogerson, Shimer, and Wright (2005, p. 972-973) that both price-posting and directed search are required for the concept of competitive search equilibrium. "Directed search" is nothing more than a synonym for (optimal) participation decisions.

On the firms' side, the job-creation condition (see, as an example, Krause and Lubik (2007, equation 13) or Arseneau and Chugh (2007a, equation 19)) is the analog of our model's advertising condition. This condition would pin down how many job openings a (large, representative) firm would post in a given labor submarket. The wage-posting problem would then be a firm's choice of a wage and labor (sub)market tightness to maximize the expected value of a job in that submarket subject to the household's labor-force participation condition for that labor submarket.

Thus, adapting our setup to a DSGE labor search model is a straightforward adaptation of our model here provided a labor force participation margin - i.e., directed search -- is allowed. Business cycle dynamics under competitive search equilibrium would then be identical to business cycle dynamics in bargaining equilibria, subject again to the caveat that the levels of variables of course depend on exogenous bargaining power in a bargaining equilibrium.

8  Conclusion

One contribution of our paper is methodological. We show how to implement the concept of competitive search equilibrium in a fully-specified DSGE environment. Competitive search equilibrium is well-understood in labor market theory, but its implications for business cycle dynamics have until now not been explored. We develop our model and results in a search-based model of the goods market, a market in which, building on Arseneau and Chugh (2007b) and Hall (2007), we think search frictions are quite plausible. However, as we describe, our modeling strategy readily extends to macro models featuring search-based labor markets.

Another contribution of our paper is conceptual. We show a vitual equivalence of business cycle fluctuations with either competitive search equilibrium or Nash bargaining. Moreover, we prove that business cycle fluctuations are identical under either competitive search or Nash bargaining restricted to the Hosios (1990) condition. As a methodological by-product of our analysis, we provide for these latter cases a simple MRS = MRT interpretation of pricing outcomes in search models that should provde useful in other search models, as well. Given the recent surge in interest in developing search-based macro models and because of what we view as the intuitive appeal of competitive search, our results provide a foundation for researchers to claim that the sometimes-awkward assumption of bargaining per se does not obscure interpretation of results. We think this is an important result to know. At the same time, we acknowledge our point is demonstrated in a simple framework. Although this framework must be at the core of virtually any DSGE search-based model, and hence there is reason to think our equivalence result would lie in the background of richer models, we cannot claim that every DSGE search-based model ever developed, especially as they become richer in features, must display this virtual equivalence of fluctuations. Some forms of proportional taxation, for example, are likely to break the equivalence.

Policy predictions of search-based models are bound to be sensitive to the use of competitive search equilibrium or bargaining equilibria. This is because, as we mentioned above, the competitive search framework endogenizes the surplus-splitting mechanism between parties engaged in bilateral trade, as opposed to the exogenous surplus-splitting imposed by Nash bargaining. A growing body of work -- for example, Cooley and Quadrini (2004), Faia (2007), Thomas (2007), and Arseneau and Chugh (2007a, 2007c) -- studies optimal policy in the presence of search frictions, and one common theme that emerges is that long-run policy prescriptions are quite sensitive to the assumption of exogenous bargaining power. This is not surprising because the levels of variables can be quite sensitive to this exogenous feature of bargaining models, as we showed. As interest grows in using search-based models for policy prescriptions, it is important to know and perhaps even extremely appealing to be able to use a framework that avoids this prediction.

Finally, as we mentioned at the outset, part of our work here is in the spirit of pure model development, specifically to enrich the Arseneau and Chugh (2007b) and Hall (2007) environments in a "competitive" vein. We think one particularly natural application of the goods-market price-posting model we have developed here is to try to model "sale prices" in the context of a full macro model. Nakamura and Steinsson (2007) have shown that the dynamics of temporary sale prices may be quite important to understand and model. A quite natural explanation of why firms may engage in sales is to attract customers. Our price-posting model naturally articulates such a relationship -- there is an inverse relationship between the price posted in a submarket and the number of customers attracted to that submarket.

Appendix A:  Nash Bargaining

Here we derive the Nash-bargaining solution between an individual customer and the firm. We suppress indices referring to submarkets, but it is understood in the following that asset values are all indexed by submarket, as are prices $p$ and (sub)market tightness $\theta$.

The marginal value to the household of a family member who is already engaged in a relationship (a shopper) with a firm is and thus obtains $\bar{c}$ consumption goods for the households is

$$\mathbf{M_{t}} = \frac{\vartheta v^{\prime}_{t}}{\lambda_{t}} - \frac {g^{\prime}_{t}}{\lambda_{t}} - p_{it} \bar{c} + E_{t} \left[ \Xi _{t+1\vert t}\left( (1-\rho^{x}) \mathbf{M_{t+1}} + \rho^{x} \mathbf{S_{t+1} }\right) \right] .$$ (22)

Because the units of $v^{\prime}$ and $g^{\prime}$ are utils, we convert them into units of the final composite by dividing by the period-$t$ marginal utility of wealth for the household, $\lambda_{t}$, which has units of utils per final good. In equilibrium, $\lambda_{t} = u^{\prime}(x_{t})$.

The marginal value to the household of an individual who is searching for goods is

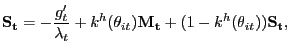
$$\mathbf{S_{t}} = -\frac{g^{\prime}_{t}}{\lambda_{t}} + k^{h}(\theta_{it}) \mathbf{M_{t}} + (1-k^{h}(\theta_{it})) \mathbf{S_{t}},$$ (23)

where, note the continuation values on the right-hand-side are dated time $t$, which follows from our assumption that successful search leads to shopping that begins in the same period as the successful search.

The value to a firm of an existing customer is

$$\mathbf{A_{t}} = p_{it} \bar{c} - mc_{t} \bar{c} + (1-\rho^{x})E_{t} \left[ \Xi_{t+1\vert t} \mathbf{A_{t+1}}\right] .$$ (24)

The Nash bargaining problem is standard; the firm and customer choose $p_{it}$ every period to maximize a Cobb-Douglas function of the gains from trade for both the customer and the firm,

$$(\mathbf{M_{t}}-\mathbf{S_{t}})^{\eta} \mathbf{A_{t}}^{1-\eta},$$ (25)

where $\eta$ is the exogenous bargaining power of customers.

The outcome of bargaining is the standard Nash sharing rule

$$(1-\eta) (\mathbf{M_{t}}-\mathbf{S_{t}}) = \eta\mathbf{A_{t}}.$$ (26)

Using the definitions of $\mathbf{M_{t}}$, $\mathbf{S_{t}}$, and $\mathbf{A_{t}}$ and after several straightforward steps of algebra, we can express the Nash price in submarket $j$ as

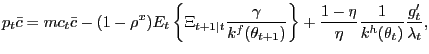
$$p_{t} \bar{c} = mc_{t} \bar{c} - (1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \frac{\gamma}{k^{f}(\theta_{t+1})} \right\} + \frac{1-\eta}{\eta} \frac {1}{k^{h}(\theta_{t})}\frac{g^{\prime}_{t}}{\lambda_{t}},$$ (27)

where we have dropped the $j$ subscripts because we focus on a symmetric equilibrium. In symmetric equilibrium, this condition characterizes the Nash price in every submarket.

References

Andolfatto, David. 1996. "Business Cycles and Labor-Market Search." American Economic Review, Vol. 86, pp. 112-132.

Arseneau, David M. and Sanjay K. Chugh. 2007a. "Optimal Fiscal and Monetary Policy with Costly Wage Bargaining." International Finance Discussion Paper no. 893, Board of Governors of the Federal Reserve System.

Arseneau, David M. and Sanjay K. Chugh. 2007b. "Bargaining and Price Rigidity in a DSGE Environment." International Finance Discussion Paper no. 900, Board of Governors of the Federal Reserve System.

Arseneau, David M. and Sanjay K. Chugh. 2007c. "Optimal Fiscal and Monetary Policy in Customer Markers." University of Maryland.

Blanchard, Olivier and Jordi Gali. 2007. "Real Wage Rigidities and the New Keynesian Model." Journal of Money, Credit, and Banking, Vol. 39, pp. 35-65.

Coles, Mervyn G. and Randall Wright. 1998. "A Dynamic Equilibrium Model of Search, Bargaining, and Money." Journal of Economic Theory, Vol. 78, pp. 32-54.

Cooley, Thomas F. and Vincenzo Quadrini. 2004. "Optimal Monetary Policy in a Phillips-Curve World." Journal of Economic Theory, Vol. 118, pp. 174-208.

den Haan, Wouter J, Garey Ramey, and Joel Watson. 2000. "Job Destruction and Propagation of Shocks." American Economic Review, Vol. 90, pp. 482-498.

Faia, Ester. 2007. "Optimal Monetary Policy Rules with Labor Market Frictions." Journal Economic Dynamics and Control. Forthcoming.

Gertler, Mark and Antonella Trigari. 2006. "Unemployment Fluctuations with Staggered Nash Bargaining." New York University.

Hall, Robert E. 2005. "Equilibrium Wage Stickiness". American Economic Review, Vol. 95, pp. 50-65.

Hall, Robert E. 2007. "Equilibrium Sticky Prices." Stanford University.

Krause, Michael U. and Thomas A. Lubik. 2007. "The (Ir)relevance of Real Wage Rigidity in the New Keynesian Model with Search Frictions." Journal of Monetary Economics, Vol. 54, pp. 706-727.

Menzio, Guido and Espen Moen. 2006. "Incomplete Self-Enforcing Labor Contracts." University of Pennsylvania.

Merz, Monika. 1995. "Search in the Labor Market and the Real Business Cycle." Journal of Monetary Economics, Vol. 36, pp. 269-300.

Moen, Espen. 1997. "Competitive Search Equilibrium." Journal of Political Economy, Vol. 105, pp. 385-411.

Nakamura, Emi and Jon Steinsson. 2007. "Five Facts About Prices." Columbia University.

Rocheteau, Guillaume and Randall Wright. 2005. "Money in Search equilibrium, in Competitive Equilibrium, and in Competitive Search Equilibrium." Econometrica, Vol. 73, pp. 175-202.

Rogerson, Richard, Robert Shimer, and Randall Wright. 2005. "Search-Theoretic Models of the Labor Market: A Survey." Journal of Economic Literature, Vol. 43, pp. 959-988.

Shimer, Robert. 2005. "The Cyclical Behavior of Equilibrium Unemployment and Vacancies." American Economic Review, Vol. 95, pp. 25-49.

Pissarides, Christopher A. 2000. Equilibrium Unemployment Theory. MIT Press.

Thomas, Carlos. 2007. "Search and Matching Frictions and Optimal Monetary Policy." London School of Economics.

Trigari, Antonella. 2006. "The Role of Search Frictions and Bargaining for Inflation Dynamics." Bocconi University.

Walsh, Carl E. 2005. "Labor Market Search, Sticky Prices, and Interest Rate Policies." Review of Economic Dynamics, Vol. 8, pp. 829-849.

Footnotes

*  E-mail address: [email protected]. Return to text

†  E-mail address: [email protected].  Return to text

1.  As just a few recent examples, studies using this framework include Walsh (2005), Trigari (2006), Gertler and Trigari (2006), Krause and Lubik (2007), Blanchard and Gali (2007), Faia (2007), and Thomas (2007). The recent outburst of work using this framework was initiated by the results of Shimer (2005) and Hall (2005). Of course, Merz (1995), Andolfatto (1996), and den Haan, Ramey, and Watson (2000) are early examples of incorporating a search framework in a standard DSGE model. Return to text

2.  We should also note that Rocheteau and Wright (2005) and Menzio and Moen (2006) also extend the concept of competitive search equilibrium to a general equilibrium setting. Rocheteau and Wright (2005) present a money-search environment where buyer-seller pairs end after just one period of trade. In contrast, the long-lasting nature of buyer-seller pairs is important in our model. Menzio and Moen (2006) do allow for long-lasting (labor) relationships; however, their focus is on incomplete contracts and not on business cycle dynamics. Return to text

3.  We think the distinction between customers being attracted to a location and actually purchasing goods is quite intuitive -- a "sale," for example, may attract many people to a location, but it is likely not all people will actually purchase the sale good. Return to text

4.  For example, even if one knows exactly where to go to buy certain goods, one may still have to walk around the aisles, stand in the checkout line, etc. Return to text

5.  As Arseneau and Chugh (2007b) show, one can allow for an endogenous intensive margin of consumption in this model. Doing so requires assuming imperfect substitutability between the goods of different submarkets in preferences. This of course may be a natural feature one wants to model, and details are provided in Arseneau and Chugh (2007b), but it does not affect the main points we illustrate here. Return to text

6.  Rogerson, Shimer, and Wright's (2005) exposition of models of posting and directed search is in terms of the "queue length" in a given market. The queue length in a submarket is simply the inverse of our definition of market tightness. Return to text

7.  A structure isomorphic to our division into Walrasian firms and non-Walrasian firms described next is to suppose that there is a single representative firm that hires labor to produce output, some of which it sells directly to consumers via Walrasian markets and some of which it sells via search-based channels. One could labels these two channels of sales to consumers as "wholesale" and "retail" channels, which would make the environment look more similar to that of Hall (2007). Either way, we use the presence of these "Walrasian firms" as a simple way of ensuring that markets clear. Return to text

8.  Technically, of course, it is the real interest rate with which firms discount profits, and in equilibrium the real interest rate between time zero and time $t$ is measured by $\Xi_{t\vert}$. Because there will be no confusion using this equilibrium result "too early," we skip this intermediate level of notation and structure. Return to text

9.  Intuitively, the shopping condition describes the optimal price/queue length tradeoff made by households and can be thought of as the "participation condition" for submarket $j$ Return to text

10.  Despite the fact that the pure labor search literature often does not consider the participation margin. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: April 22, 2008