Jackknifing Stock Return Predictions

Benjamin Chiquoine and Erik Hjalmarsson^*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We show that the general bias reducing technique of jackknifing can be successfully applied to stock return predictability regressions. Compared to standard OLS estimation, the jackknifing procedure delivers virtually unbiased estimates with mean squared errors that generally dominate those of the OLS estimates. The jackknifing method is very general, as well as simple to implement, and can be applied to models with multiple predictors and overlapping observations. Unlike most previous work on inference in predictive regressions, no specific assumptions regarding the data generating process for the predictors are required. A set of Monte Carlo experiments show that the method works well in finite samples and the empirical section finds that out-of-sample forecasts based on the jackknifed estimates tend to outperform those based on the plain OLS estimates. The improved forecast ability also translates into economically relevant welfare gains for an investor who uses the predictive regression, with jackknifed estimates, to time the market.

Keywords: Bias correction, jackknifing, predictive regression, stock return predictability

JEL classification: C22, G1

1 Introduction

Ordinary Least Squares (OLS) estimation of predictive regressions for stock returns generally results in biased estimates. This is true in particular when valuation ratios, such as the dividend- and earnings-price ratios, are used as predictor variables. The bias has been analyzed and discussed in numerous articles and a number of potential solutions have been suggested (e.g., Mankiw and Shapiro, 1986, Stambaugh, 1999, and Jansson and Moreira, 2006). However, most of the attention in the literature has been directed at constructing valid tests in the case of a single regressor that follows an auto-regressive process, and much less attention has been given to the problem of obtaining better estimators, both in the case of single or multiple predictor variables.¹

Although the testing problem is arguably the more fundamental issue from a strictly statistical point of view, the estimation problem is of great interest from an economic and practical perspective. The statistical tests answer the question whether there is predictability, but the coefficient estimate speaks more directly to the economic magnitude of the relationship. Since there is an emerging consensus in the finance profession that stock returns are to some extent predictable, it is of vital interest to determine the economic importance of this predictability. In addition, if forecasting regressions are to be used for out-of-sample forecasts, which is often their ultimate purpose, the point estimate obviously takes on the main role.

In this paper, we propose the application of a general bias reduction technique, the jackknife, to obtain better point estimates in predictive regressions. Unlike most other methods that have been proposed, this procedure does not assume a particular data generating process for the regressor and allows for multiple predictor variables. The jackknifed estimator, which is based on a combination of OLS estimates for a small number of subsamples, is also trivial to implement and could easily be used with common statistical packages. In relation to previous work, the current paper contributes to both the emerging literature on bias-reducing techniques in predictive regressions, such as Amihud and Hurvich (2004) and Eliasz (2005), as well as the ongoing debate on out-of-sample predictability in stock-returns, as exemplified by Goyal and Welch (2003, 2007) and Campbell and Thompson (2007).

In a series of Monte Carlo experiments, we show that the jackknifed estimator can reduce the bias in the estimates of the slope coefficients in predictive regressions. This applies both to the standard one-regressor, one-period regression as well as to the case of multiple regressors and longer forecasting horizons. Although the jackknifed estimates have a larger variance than the OLS estimates, the jackknifed estimates still often outperform the OLS ones in a mean squared error sense. Thus, to the extent that it is desirable to have as small a bias as possible, for a given mean squared error, the jackknifed estimator tends to dominate the OLS estimator.

In the empirical section of the paper, we consider forecasting of aggregate U.S. stock returns, using five different predictor variables: the dividend- and earnings-price ratios, the smoothed earnings-price ratio suggested by Campbell and Shiller (1988), the book-to-market ratio, and the short interest rate. Although many other stock return predictors have been proposed (see, for instance, Goyal and Welch, 2007), the above valuation ratios are of most interest here, since they tend to result in the largest biases in the OLS estimates. The short interest rate is also analyzed since some recent work by Ang and Bekaert (2007) suggests that it works well as a predictor together with the dividend-price ratio, which thus provides an opportunity to study the performance of the jackknifed estimator with multiple regressors.

The in-sample results show that the jackknifed estimates, in some cases, deviate substantially from the OLS estimates. For instance, the magnitude of the coefficient for the book-to-market ratio is often drastically smaller when using the jackknife procedure. On average, the OLS estimates often overstate the magnitude of predictability compared to the jackknife estimates.

In order to evaluate whether these discrepancies in the full-sample estimates actually translate into better real time forecasting ability, we perform two different out-of-sample exercises. First, we calculate the out-of-sample R²s for the different predictor variables, and find that the forecasts based on the jackknifed estimates typically dominate those based on the OLS estimates; this is true also if one imposes some of the forecast restrictions proposed by Campbell and Thompson (2007). In a second out-of-sample exercise, we estimate the welfare gains to a mean-variance investor who uses either the OLS estimates or the jackknifed estimates to form his portfolio weights in order to time the market. In this case, the jackknifed estimates produce even clearer gains, dominating both the portfolio choices based on the OLS estimates as well as the baseline choice based on the historical average returns. Overall, the promising results seen in the Monte Carlo simulations carry over to the real data.

The rest of the paper is organized as follows. Section 2 outlines the jackknife procedure and provides an explicit example of how it works in a predictive regression. Section 3 presents the results from the Monte Carlo exercises. The empirical analysis is performed in Section 4 and Section 5 concludes.

2 The Jackknife

Let T be the sample size available for the estimation of some parameter $\theta$ . Decompose the sample into m consecutive subsamples, each with l observations, so that T = m × l. The jackknife estimator, which was introduced by Quenoille (1956), is given by

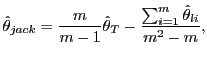
$\displaystyle \hat{\theta}_{jack}=\frac{m}{m-1}\hat{\theta}_{T}-\frac{\sum_{i=1}^{m} \hat{\theta}_{li}}{m^{2}-m},$

(1)

where $\hat{\theta}_{T}$ and $\hat{\theta}_{li}$ are the estimates of $\theta$ based on the full sample and the th subsample, respectively, using some given estimation method such as OLS or maximum likelihood. In the current paper, we rely only on OLS for obtaining $\hat{\theta}_{li}$ . Under fairly general conditions, which ensure that the bias of $\hat{\theta}_{T}$ and $\hat{\theta}_{li}$ can be expanded in powers of $T^{-1}$ , it can be shown that the bias of $\hat{\theta}_{jack}$ will be of an order $O\left( T^{-2}\right)$ instead of $O\left( T^{-1}\right)$ ; Phillips and Yu (2005) provide a longer discussion on this.

Note that $\theta$ may be a single parameter, or a vector of parameters, estimated from some model using any feasible estimation method. Furthermore, $\theta$ may also represent a combination, or complicated function, of estimated parameters. For instance, Phillips and Yu (2005) show how jackknifing bond option prices directly, rather than the estimated parameters that enters the bond option formula, can help reduce the bias in the estimated option prices. The jackknife is thus a very generally applicable method. Within the context of estimating models for stock return predictability, we consider, in addition to the standard single regressor case, also a case with multiple regressors, as well as overlapping observations. Whereas the bias in the single regressor case is well analyzed, less is understood about the biases in the case of multiple regressors or the case of long-run forecasting regressions with overlapping observations. Again, in all three cases the analysis of the bias is usually restricted to the case where the regressors follow an auto-regressive process; see, for instance, Amihud and Hurvich (2004) for a discussion on some bias reduction methods for the case of multiple regressors.

A simple example helps to illustrate how the jackknifing procedure reduces the bias in estimates. Consider the traditional predictive regression with a single regressor which follows an $AR\left( 1\right)$ process:

$\displaystyle r_{t}$	$\displaystyle =\mu+\beta x_{t-1}+u_{t},$	(2)
$\displaystyle x_{t}$	$\displaystyle =\gamma+\rho x_{t-1}+v_{t}.$	(3)

Suppose $u_{t}$ and $v_{t}$ are bivariate normally distributed with mean zero and covariance matrix $\left[ \left( \sigma_{u}^{2},\sigma_{uv}\right) ,\left( \sigma_{uv},\sigma_{v}^{2}\right) \right] ^{\prime}$ ; the correlation between $u_{t}$ and $v_{t}$ is denoted by $\delta$ in the simulations below. As shown in Stambaugh (1999), the bias in the OLS estimator of $\beta$ is given by

$\displaystyle E\left[ \hat{\beta}_{OLS}-\beta\right] =-\frac{\sigma_{uv}}{\sigma_{v}^{2} }\left( \frac{1+3\rho}{T}\right) +O\left( T^{-2}\right) =O\left( T^{-1}\right) .$

(4)

The jackknife estimator of $\beta$ for , based on OLS estimation, is equal to

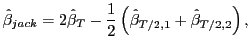
$\displaystyle \hat{\beta}_{jack}=2\hat{\beta}_{T}-\frac{1}{2}\left( \hat{\beta} _{T/2,1}+\hat{\beta}_{T/2,2}\right) ,$

(5)

and

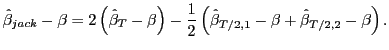
$\displaystyle \hat{\beta}_{jack}-\beta=2\left( \hat{\beta}_{T}-\beta\right) -\frac{1} {2}\left( \hat{\beta}_{T/2,1}-\beta+\hat{\beta}_{T/2,2}-\beta\right) .$

(6)

Taking expectations on both sides and using the expression in (4), it follows that

$\displaystyle E\left[ \hat{\beta}_{jack}-\beta\right] =-2\frac{\sigma_{uv}}{\sigma_{v} ^{2}}\left( \frac{1+3\rho}{T}\right) +\frac{\sigma_{uv}}{\sigma_{v}^{2} }\left( \frac{1+3\rho}{T/2}\right) +O\left( \left( \frac{T}{2}\right) ^{-2}\right) =O\left( T^{-2}\right) .$

(7)

Thus, the bias is reduced from $O\left( T^{-1}\right)$ to $O\left( T^{-2}\right)$ .

This result would hold for any m, which raises the question of what value m should be set to in practice. As shown by the simulations in the following section, setting m = 2 works very well and usually eliminates almost all of the bias. However, the simulations also show that an increase in m (to 3 or 4) can reduce the variance of the jackknife estimate without any substantial increase in the bias. In general, the root mean squared error is smallest for m = 4 in the simulations presented below. Phillips and Yu (2005) present results along similar lines and provide some brief theoretical arguments that support these findings. In a given context, an optimal choice of m may therefore exist, although there appears to be no studies on how to choose this optimal m. The empirical section, which presents results for m = 2, 3, and 4, m = 3 may be the best choice on average, although the differences are generally not great between the three alternatives, and there appears to be no choice of m that strictly dominates empirically.

3 Monte Carlo Simulations

We analyze the finite sample performance of the jackknife method by simulating data from the model defined by equations (2) and (3). The assumption that the predictor variable follows an AR(1) process is probably the most common one in the analysis of stock-return predictability. This stems primarily from the relative ease with which the properties of estimators of β can be analyzed in this setup, and because the model captures the most salient features of typical forecasting variables such as valuation ratios and interest rates. The results from the AR(1) specification should also be qualitatively similar to those from a more general AR(p) model. In general, the jackknife procedure should help reduce bias in other setups as well, but we focus on its properties for this familiar model which is easy to parametrize in a realistic manner, such that the OLS estimator will be biased in finite samples. In addition to considering the case with a single regressor, we also simulate from a model with two forecasting variables, where each of these follows an AR(1) process as specified in detail below. Finally, we also consider the case when forecasts are formed at a horizon different from that at which the data were sampled.

3.1 The single regressor case

Equations (2) and (3) are simulated for the case when $x_{t}$ is a scalar. The innovation terms $u_{t}$ and $v_{t}$ are drawn from a multivariate normal distribution with unit variances. The correlation between $u_{t}$ and $v_{t}$ , denoted $\delta$ , takes on three different values: -0.9, -0.95, and -0.99. The auto-regressive root $\rho$ is set equal to either 0.9, 0.95, or 0.999. The sample size, T, is equal to 100 or 500 observations. The parameters $\mu,\beta,$ and $\gamma$ are all set to zero, although an intercept is still estimated in the predictive regression; since the bias in the OLS estimator is not a function of the values of these parameters (e.g. Stambaugh, 1999), this standardization does not affect the results. Campbell and Yogo (2006) show that values such as these for $\delta$ and $\rho$ are often encountered empirically, when using valuation ratios as predictors.

Note that, if $\delta=0$ , so that the error terms $u_{t}$ and $v_{t}$ are uncorrelated, the OLS estimator is unbiased and equal to the full information maximum likelihood estimator. Furthermore, for $\rho$ close to zero, the OLS estimator will also be unbiased, even when $\delta\neq0$ . In general, the bias for the OLS estimator is thus greater as $\rho$ gets closer to unity, and the closer the absolute value of $\delta$ is to one. We therefore restrict the analysis to the part of the parameter space where there actually is a bias to correct in the OLS estimator. Results for $\delta<0$ are shown since this is the empirically most relevant case and the case of $\delta>0$ is completely analogous.

The Monte Carlo simulation is conducted by generating 10,000 sample paths from equations (2) and (3), for each combination of parameter values. From each set of generated returns and regressors, the OLS estimate of $\beta$ and the jackknife estimates for m = 2, 3 and 4, are calculated. The average bias and root-mean-squared errors (RMSE) for these estimators are then calculated across the 10,000 samples. The results are reported in Table 1, which shows the bias and the RMSE in parentheses below, for each parameter combination.

An inspection of the results in Table 1 quickly reveals three distinct findings: (i) the OLS estimates are upward biased for all of the parameter combinations under consideration, (ii) the jackknife estimates are virtually unbiased in all cases, and (iii) the RMSEs for the jackknife estimates are always less than or equal to the RMSE for the OLS estimates for m = 3 and 4, and fairly similar to the RMSE for the OLS estimates for m = 2. These simulation results thus suggest that the jackknifing procedure reduces the bias without inducing enough variance to inflate the RMSE.

Figure 1 provides some additional insights into the workings of the jackknifed estimator. It shows density plots for the OLS estimator as well as the jackknife estimators for m = 2, 3 and 4. The densities are estimated with kernel methods from 100,000 samples, with T = 100, $\rho=0.999$ and $\delta=-0.99$ . The density of the OLS estimate is almost completely to the right of the true value for $\beta$ , and is also highly skewed towards the right. The jackknifed estimates are both more centered around the true value as well as more symmetric. For m = 2, the jackknife estimator has a distribution that is centered almost exactly at the true value and is also fairly symmetric. For m = 3 and 4, the densities are more peaked, reflecting the lower RMSEs shown in Table 1, but also slightly less centered at the true value; these densities are also somewhat more skewed. As mentioned in the previous section, these results indicate that there is a trade off between bias and variance in the choice of m, and an optimal choice of m in terms of RMSE may therefore exist. However, no formal results along these lines appear to be available.

In order to understand the magnitude of the bias in the OLS estimator, and the importance of the bias reduction achieved with the jackknife estimators, it is useful to consider typical values of the estimates of $\beta$ in actual data. The results in Campbell and Yogo (2006) are particularly convenient for such a comparison since they present their estimates in a standardized manner conforming with the model simulated here; that is, they scale the estimate of $\beta$ to correspond to a model with unit variance in $u_{t}$ and $v_{t}$ . Campbell and Yogo (2006) consider stock return predictability for aggregate U.S. stock returns. They show that OLS estimates of $\beta$ are typically in the range of 0.1 to 0.2 in annual data and most often in the range of 0.01 to 0.02 in monthly data. Thus, if one uses 100 years of annual data, the bias in the OLS estimate may be between 20 and 50 percent of the actual parameter value, as seen from the results in Table 1. If one relies on a shorter (in years covered) monthly series with 500 observations, the bias could easily be as large as the parameter value itself. In proportion to the size of the parameter value, the bias reduction in the jackknifing procedure is therefore at least substantial and potentially huge.

3.2 Multiple regressors

Although the simple forecasting regression with just one predictor is by far the most studied and commonly used in the literature, there are instances when the use of several forecasting variables may be advantageous. For instance, Ang and Beekaert (2007) argue that the dividend-price ratio works much better as a predictor when used jointly with the short rate, rather than on its own.

In order to evaluate the properties of the jackknife estimator in the multiple regressor case, we restrict the attention to the case with two forecasting variables and follow a similar setup to the one used in the single regressor case. In particular, it is assumed that the data is generated by a multivariate version of the model described by equations (2) and (3). The auto-regressive matrix for the two predictor variables is set to $A=\left[ \left( a_{11},0\right) ,\left( 0,a_{22}\right) \right] ^{\prime}\,$ and the innovations $u_{t}$ and $v_{t}=\left( v_{1t} ,v_{2t}\right)$ are again normally distributed with unit variance. The correlation vector between $u_{t}$ and $v_{t}$ is labeled $\omega_{uv}$ and the correlation between $v_{1t}$ and $v_{2t}$ is labeled $\eta$ , such that the variance-covariance matrix for $v_{t}$ is equal to $\Omega_{vv}=\left[ \left( 1,\eta\right) ,\left( \eta,1\right) \right] ^{\prime}$ . Table 2 shows the results for the estimates of the two coefficients, $\beta_{1}\,$ and $\beta_{2}$ , that correspond to the first and second predictor variable, for various values of A and different correlations between the innovations. Results for T = 100 and T = 500 are presented and the results are based on 10,000 repetitions.

The first two columns of results in Table 2 represent perhaps the most empirically interesting case. For these results, $a_{11}=0.999$ , $a_{22}=0.95$ , $\omega_{uv}=\left( -0.9,0\right) ^{\prime}$ and $\eta=0.4$ . That is, the first predictor is the most persistent one and is also highly endogenous, whereas the second predictor is exogenous and less persistent. This setup corresponds fairly well to the case with the dividend-price ratio and the short interest rate as predictors, since the dividend-price ratio is highly endogenous whereas the short rate is nearly exogenous, and usually somewhat less persistent than the dividend-price ratio (Campbell and Yogo, 2006). The correlation of 0.4 between the innovations to the two regressors results in an average correlation of around 0.25 between the levels of the regressors, which is similar to the empirical correlation between the dividend-price ratio and the short interest rate observed in the data used in this paper.²

Intuitively, given the results for the single regressor case, one would expect the OLS estimate for the coefficient for the first regressor $\left( \beta_{1}\right)$ to be highly biased whereas the second estimate $\left( \beta_{2}\right)$ should perform better, since it is only indirectly affected by the endogeneity bias through the correlation of the two regressors. This intuition is bourne out to some extent by the simulation results, which show a large bias for the first predictor but a smaller, although still substantial, bias for the second. The jackknife works very well for $\beta_{1}$ , resulting in almost unbiased estimates with only a small increase in RMSE for m = 2 and a significant reduction in RMSE for m = 3 and 4. Jackknifing the estimates for $\beta_{2}$ also results in unbiased estimates, but with a slight increase in RMSE, particularly for T = 100.

The following two sets of results in Table 2 represent cases where both regressors are endogenous. In order for the overall covariance matrix between $u_{t}$ and $v_{t}$ to be well defined, this forces $v_{1t}$ and $v_{2t}$ to be fairly highly correlated as well. In particular, $\omega_{uv}=\left( -0.7,-0.7\right) ^{\prime}$ and $\eta=0.5$ in the first case and $\omega_{uv}=\left( -0.9,-0.9\right) ^{\prime}$ and $\eta=0.8$ in the second case. The persistence parameters are set to $a_{11}=0.999$ and $a_{22}=0.95$ in the first specification, and to $a_{11}=a_{22}=0.999$ in the second one. Thus, both variables are highly endogenous and highly co-linear. In the first specification, the first predictor is more persistent than the other, whereas in the latter specification both have the same persistence. These parametrizations could correspond to, for instance, various combinations of valuation ratios, which may have somewhat different degrees of persistence and endogeneity, and may also have different correlations with each other.

As seen in Table 2, both of these parametrizations result in OLS estimates that are biased, both for $\beta_{1}$ and $\beta_{2}$ . The jackknifing reduces the bias substantially, although there is a little bias left in the jackknifed estimates when using the first parameter specification for T = 100, as seen in the middle columns of Table 2. For m = 3 and 4, the RMSE for the jackknifed estimates are similar to the OLS ones. The second specification, shown in the last two columns of Table 2, is symmetric for the two regressors and the OLS biases for the two coefficients are virtually identical. For T = 100 the jackknifed estimates are now virtually unbiased, with only a small increase in the RMSE relative to the OLS estimates. For T = 500, the bias is completely removed by the jackknifing.

In summary, the jackknife appears to work well in the multivariate case and generally results in virtually unbiased estimates. Given the multitude of possible parameter combinations that arise as soon as one leaves the simplicity of the single regressor case, the results presented in this section are far from exhaustive but hopefully capture some of the more salient features of biases in multivariate regressions.

3.3 Overlapping observations

Finally, we consider the performance of the jackknife estimator for predictive regression with overlapping observations. Inference with overlapping observations is a topic that has a long history in the finance literature, but most of the effort has been directed at constructing valid test statistics rather than reducing the bias in OLS estimates.³ The jackknife procedure provides a simple but flexible way of addressing the estimation problem.

To keep things tractable, the single regressor case is analyzed. The data is generated in exactly the same manner as described in Section 3.1, generating sample paths from equations (2) and (3). However, instead of estimating equation (2), the sums of future q-period returns are now regressed on the value of $x_{t}$ . The forecasting horizon q is set equal to 10 for T = 100 and equal to 12 for T = 500. These two cases capture common applications of long-run forecasts using a century of annual data and annual forecasts based on monthly data.

The results are shown in Table 3. The bias in the OLS estimates is of an order of magnitude larger than the ones shown in Table 1. This is entirely in line with the analytical results of Bodoukh et al. (2006), who show that one should expect the estimate, and hence the bias, to increase almost linearly with the forecasting horizon. The jackknifing reduces the bias substantially in all cases, although not always completely. The RMSEs for the jackknifed estimates is slightly larger than those for the OLS estimates in some cases, although there are also substantial reductions for some parameter combinations.

It is evident that the jackknife is also applicable in long-horizon regressions. From the results presented here, it appears to be most useful when the overlap is not too large relative to the number of observations; the results for q = 12 and T = 500 are generally stronger than those for q = 10 and T = 100. Overall, however, the results are very promising and the jackknife clearly presents a simple way of alleviating estimation biases in long-horizon regressions, an issue which is often ignored in applied work.

4 Empirical analysis

We next apply the jackknife method to real stock market data. Since the purpose of the jackknife method is to obtain better point estimates, we primarily evaluate its usefulness by an out-of-sample (OOS) forecasting exercise. However, it is also of interest to analyze the full sample point estimates, since they directly show the differences between the plain OLS estimates and the bias corrected jackknifed estimates.

As the dependent variable, we use monthly total excess returns on the S&P 500 index, starting in February 1872 and ending December 2005; after 1920, the T-Bill rate is used to form excess returns and before that, commercial paper rates. Five separate forecasting variables are used: the dividend- and earnings-price ratios (D/P and E/P), the smoothed earnings-price ratio of Campbell and Shiller (1988), the book-to-market ratio (B/M), and the short term interest rate as measured by the three-month T-Bill rate. The smoothed earnings-price ratio is defined as the ratio of the 10-year moving average of real earnings to the current real price. Although many other stock return predictors have been proposed (see, for instance, Goyal and Welch, 2007), the above valuation ratios are of most interest here since they tend to result in the largest biases in the OLS estimates (e.g. Campbell and Yogo, 2006). The short interest rate is also analyzed, since recent work by Ang and Bekaert (2007) suggests that it works well as a predictor together with the dividend-price ratio, which provides an opportunity to study the performance of the jackknifed estimator with multiple regressors; the short interest rate is generally negatively related to future stock returns, and we therefore flip the sign on this predictor variable in all regressions so that the expected sign is always positive. All data are recorded on a monthly basis and regressions are run either at this monthly frequency or at an annual frequency, using overlapping observations based on the original monthly data. The annual results thus provide an illustration of the jackknifed procedures applied to regressions with overlapping observations. In all cases, excess stock returns are regressed on the lagged predictor variable(s) and an intercept, following the basic structure of equation (2).

These are a subset of the same data as those used by Campbell and Thompson (2007) in their study of out-of-sample return predictability.⁴ The jackknifed OOS predictions can thus be directly compared to their results. In line with Campbell and Thompson, we use the level, and not logs, of the predictor variables as well as simple rather than log-returns.

4.1 In-sample results

The first set of empirical results is given in Table 4 and shows the full sample OLS estimates, t-statistics and R², along with the jackknifed estimates; the t-statistics for the annual data with overlapping observations are formed using Newey and West (1987) standard errors. Results for the monthly and annual frequencies are displayed, and two different sample periods are considered: the longest available sample for each predictor variable, as well as the forecast period used in the out-of-sample forecasts below.

As is well established, predictive regressions like these tend to generate significant t-statistics but fairly small R², which increase with the horizon. Inference based on the t-statistics is generally subject to pitfalls, as documented in, for instance, Stambaugh (1999) and Campbell and Yogo (2006), and they are primarily shown here for completeness. The focus in this paper is on the point estimates in the predictive regression, which are also shown in Table 4. Four sets of estimates are shown: the standard OLS ones and the jackknifed ones using m = 2, 3, and 4 subsamples. Within the standard stock return predictability model, where the regressors follow an auto-regressive process, the OLS estimates for the valuation ratios are generally upward biased, whereas for the short interest rate the OLS estimator should be nearly unbiased. This suggests that the jackknifed estimates, which attempt to correct the OLS bias, should generally be smaller than the OLS estimates. Overall, this is the case, especially when using m > 2. This is particularly true for the book-to-market ratio in the shorter sample, and for the coefficient on the dividend-price ratio in the regressions that include the dividend-price ratio and the short rate jointly. The jackknifed estimates using m = 2 are often close to the OLS estimates, although they sometimes deviate substantially as well. Qualitatively, the results are similar for the monthly and annual data.

The results in Table 4 suggests that standard OLS estimates are likely to exaggerate the size of the slope coefficient in these predictive regressions. However, from these full sample estimates alone, it is difficult to tell whether the jackknifed estimates are actually more accurate than the OLS estimates and we therefore turn to out-of-sample exercises to evaluate this question.

4.2 Out-of-sample results

In order to evaluate the OOS performance of the jackknifed estimates, we calculate an OOS $R^{2}$ , defined as

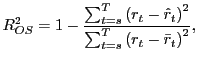
$\displaystyle R_{OS}^{2}=1-\frac{\sum_{t=s}^{T}\left( r_{t}-\hat{r}_{t}\right) ^{2}} {\sum_{t=s}^{T}\left( r_{t}-\bar{r}_{t}\right) ^{2}},$

(8)

where $\hat{r}_{t}$ is the fitted value from a predictive regression estimated using data up till time t - 1 and $\bar{r}_{t}$ is the historical average return estimated using all available data up till time t - 1. The out-of-sample forecasts begin in 1927, at which point high quality monthly CRSP data becomes available, or 20 years after the first available observation for a given predictor variable, whichever comes later. Thus, s, in equation (8), represents the length of this initial 'training-sample', which is used to obtain the estimates on which the first round of forecasts is based. Note that the historical average forecast, $\bar{r}_{t}$ , is always based on all the data back to 1872, which preserves its real world advantage. The $R_{OS}^{2}$ statistic is positive when the conditional forecast based on the predictive regression outperforms the historical mean. Thus, the out-of-sample R² is positive when the root mean squared error of the conditional forecast is less than that of the historical mean forecast. Given that the out-of-sample R² and a comparison of the root mean squared errors yield identical qualitative results, we focus on the out-of-sample R² since it is measured in comparable units to the in-sample R² and thus allows for more direct comparison.

In addition to the standard forecasts based on the predictive regression and the historical mean, we also analyze the effects of imposing some of the forecast restrictions proposed by Campbell and Thompson (2007). That is, Campbell and Thompson argue that rather than mechanically forecasting stock returns based on the estimated forecasting equation, it is reasonable to impose the following restrictions: if an estimated coefficient does not have the expected sign, it is set equal to zero, and if the forecast of the equity premium is negative, the forecast is set equal to zero. These restrictions rule out some of the perverse results that can otherwise occur in the rolling regressions that are used in the out-of-sample forecasts.⁵

Table 5 shows the OOS R²s for the OLS estimator and the jackknifed estimator with m = 2, 3 and 4, for both the restricted forecasts, which impose the Campbell and Thompson restrictions, and the unrestricted ones. For each predictor, the highest OOS R² is shown in bold type. In general, the results show that the forecasts based on the jackknifed estimates tend to outperform the ones based on the plain OLS estimates, although there is no given value of m that consistently produces the highest OOS R². The jackknifing procedure appears to be somewhat more useful on the monthly, rather than the annual data, in line with the simulation results above, although the results are somewhat mixed. Qualitatively, the results are similar for both the unrestricted and restricted forecasts. As might be expected from the full-sample coefficient estimates in Table 4, where the full-sample jackknifed estimates were drastically different from the OLS estimate, the advantages of the jackknifing are particularly clear for the book-to-market ratio.

With regards to the choice of m, there is no value that clearly produces the best results. However, using m = 3 in the restricted forecasts consistently dominates the OLS forecasts in the monthly data and is close to, or better, in the annual data; only for the smoothed earnings price ratio in the annual data is there a material difference in favor of the OLS forecasts. In the unrestricted case, there is no m for which the jackknifed estimates consistently dominate the OLS ones for all predictor variables. This is clearly a drawback, since, as mentioned before, there are no clear guidelines for choosing m. However, as shown in the section below, the results become clearer when one considers the implementation of actual portfolio strategies.

In summary, the jackknifed estimator often improves upon the OLS estimator in out-of-sample forecasts. This seems to be particularly true when one also imposes the forecast restrictions proposed by Campbell and Thompson (2007), in which case the jackknifed estimator with m = 3 almost completely dominates the OLS estimator.

4.3 Portfolio strategies

Campbell and Thompson (2007) discuss how the OOS R² can be translated into gains in economic terms for an investor that attempts to time the market using these predictor variables. However, practical considerations such as short selling constraints may render such theoretical relationships less accurate; a more reliable approach to gauging the economic importance of the improvement in out-of-sample forecasts is to directly simulate a portfolio choice strategy. To keep the calculations tractable, consider an investor with a single-period investment horizon and mean-variance preferences; that is, in each period the investor myopically chooses the optimal portfolio based on his quadratic preferences. The investor's utility function is the expected excess return minus $\left( \gamma/2\right)$ times the portfolio variance, where $\gamma$ can be viewed as the coefficient of relative risk aversion. The weight on the risky asset for this investor is given by

$\displaystyle \alpha_{t}=\left( \frac{1}{\gamma}\right) \left( \frac{E_{t}\left[ r_{t+1}\right] }{Var_{t}\left( r_{t+1}\right) }\right) ,$

(9)

where $E_{t}\left[ r_{t+1}\right]$ and $Var_{t}\left( r_{t+1}\right)$ represents the expected value and variance of the excess returns over the next period, conditional on the information at time t. If the investor does not use the predictive regression (2), it follows that

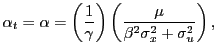
$\displaystyle \alpha_{t}=\alpha=\left( \frac{1}{\gamma}\right) \left( \frac{\mu} {\beta^{2}\sigma_{x}^{2}+\sigma_{u}^{2}}\right) ,$

(10)

where $\sigma_{x}^{2}=Var\left( x_{t}\right)$ and $\sigma_{u} ^{2}=Var\left( u_{t}\right)$ . If the investor does use regression (2),

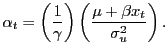
$\displaystyle \alpha_{t}=\left( \frac{1}{\gamma}\right) \left( \frac{\mu+\beta x_{t} }{\sigma_{u}^{2}}\right) .$

(11)

The out-of-sample economic gains of the predictive ability of equation (2) are evaluated by comparing the utilities from an investor who uses the weights in (11) to one who disregards the predictability in returns and uses the weights in (10).

The weights $\alpha_{t}$ are calculated using only information available at time t. When the predictive regression is not used, the weights at each time t are estimated by

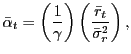
$\displaystyle \bar{\alpha}_{t}=\left( \frac{1}{\gamma}\right) \left( \frac{\bar{r}_{t} }{\bar{\sigma}_{r}^{2}}\right) ,$

(12)

where $\bar{r}_{t}$ is the historical average return estimated using all available data up till time t and $\bar{\sigma}_{r}^{2}$ is the variance of returns estimated using a five year rolling window of data; i.e. $\bar{\sigma }_{r}^{2}$ is estimated using the last five years of data before time t. The weights based on the predictive regression are given by

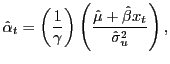
$\displaystyle \hat{\alpha}_{t}=\left( \frac{1}{\gamma}\right) \left( \frac{\hat{\mu} +\hat{\beta}x_{t}}{\hat{\sigma}_{u}^{2}}\right) ,$

(13)

where $\hat{\mu}$ and $\hat{\beta}$ are the estimates of the intercept and slope coefficient in the predictive regression, using the data up till time t, and $\hat{\sigma}_{u}^{2}$ is the variance of the residuals, again estimated using a five year rolling window of data.⁶ In order for the portfolio weights to be compatible with real world constraints, we impose a no short selling restriction and a maximum of 50% leverage, so that the portfolio weights are restricted to lie between 0 and 150%. Finally, the risk aversion parameter $\gamma$ is set equal to three.

Table 6 reports the welfare benefits from using the weights $\hat{\alpha}_{t}$ , using either the OLS estimator or the jackknifed estimators, instead of the weights $\bar{\alpha}_{t}$ . The utility differences are expressed in terms of expected annualized returns and can thus be interpreted as the (maximum) management fee that an investor would be willing to pay a portfolio manager that exploits the predictive ability of equation (2). As in Table 5, we consider both the forecasts that impose the Campbell and Thompson restrictions and those that do not. Qualitatively, the results in Table 6 tell the same story as those in Table 5. The portfolio strategies based on the jackknifed estimates tend to outperform those based on the OLS estimates, and, importantly, offer welfare gains over the strategies based purely on historical average returns. Again, the jackknifed estimator appears to work best for the monthly data.

The portfolio results in Table 6 provides even stronger support of the benefit of the jackknifed estimates than the OOS R²s reported in Table 5. In the monthly data, the results for the OLS portfolio weights are dominated by the jackknife weights, for any m, in almost all cases. This is true both for the restricted and unrestricted forecasts. If one were to choose a single m for all predictors, m = 3 would appear to be the best choice; in the monthly data, it dominates the OLS results in all cases.

Compared to the OLS weights, the utility gains from using the jackknife procedure are relatively large, often between 50 and 100 basis points. Although this may not sound that large in absolute terms, the gains from using the predictive regression (with OLS estimates) in the first place, instead of the historical average return, are typically no larger than 50-60 basis points. In fact, the welfare gains from the OLS weights are quite often negative, whereas the jackknife weights, especially for m = 3, are almost always positive. The welfare gains from the jackknife weights are also similar to those reported by Campbell and Thompson (2007) based on their completely restricted forecasts where the coefficient in the predictive regression is totally pinned down by theoretical arguments and not estimated at all. The results here thus suggest that improving the estimation procedures can lead to at least as big an improvement as the imposition of theoretical constraints. These result also add further evidence to the case that returns are predictable out-of-sample, in contrast to the conclusions of Goyal and Welch (2003, 2007).

5 Conclusion

A simple bias reducing method, the jackknife, is proposed for predictive regressions of stock returns. Unlike most previous work on inference in stock return predictability regressions, this paper puts the focus on obtaining good point estimates rather than correctly sized tests, a task which has become increasingly more important as the focus in the literature has shifted towards out-of-sample forecasts and practical portfolio choice based on return forecasts. In addition, the jackknife is a general method that does not rely on specific assumptions on the data generating process.

Monte Carlo simulations show that the jackknife method works well in finite samples and virtually eliminates the bias in OLS estimates of predictive regressions. Most importantly, it also works well on actual stock returns data, and leads to substantial improvements in out-of-sample forecasts. This is illustrated not only by purely statistical measures such as out-of-sample R², but also through simulated portfolio strategies, which often perform significantly better when the forecasts are based on the jackknifed estimates rather than the OLS ones.

References

Amihud, Y., and Hurvich, C., 2004. Predictive Regressions: A Reduced-Bias Estimation Method, Journal of Financial and Quantitative Analysis 39, 813-841.

Ang, A., and G. Bekaert, 2007. Stock Return Predictability: Is it There? Review of Financial Studies 20, 651-707.

Boudoukh J., M. Richardson, and R.F. Whitelaw, 2006. The Myth of Long-Horizon Predictability, Review of Financial Studies, forthcoming.

Campbell, J.Y., 2001. Why long horizons? A study of power against persistent alternatives, Journal of Empirical Finance 8, 459-491.

Campbell, J.Y., and R. Shiller, 1988. Stock Prices, Earnings, and Expected Dividends, Journal of Finance 43, 661-676.

Campbell., J.Y., and S.B. Thompson, 2007. Predicting Excess Stock Returns Out of Sample: Can Anything Beat the Historical Average?, Review of Financial Studies, forthcoming.

Campbell, J.Y., and M. Yogo, 2006. Efficient Tests of Stock Return Predictability, Journal of Financial Economics 81, 27-60.

Cavanagh, C., G. Elliot, and J. Stock, 1995. Inference in Models with Nearly Integrated Regressors, Econometric Theory 11, 1131-1147.

Eliasz, P., 2005. Optimal Median Unbiased Estimation of Coefficients on Highly Persistent Regressors, Mimeo, Princeton University.

Goetzman W.N., and P. Jorion, 1993. Testing the predictive power of dividend yields, Journal of Finance 48, 663-679.

Goyal A., and I. Welch, 2003. Predicting the Equity Premium with Dividend Ratios, Management Science 49, 639-654.

Goyal, A., and I. Welch, 2007. A Comprehensive Look at the Empirical Performance of Equity Premium Prediction, Review of Financial Studies, forthcoming.

Hansen, L.P., and R.J. Hodrick, 1980. Forward exchange rates as optimal predictors of future spot rates: An Econometric Analysis, Journal of Political Economy 88, 829-853.

Jansson, M., and M.J. Moreira, 2006. Optimal Inference in Regression Models with Nearly Integrated Regressors, Econometrica 74, 681-714.

Lewellen, J., 2004. Predicting Returns with Financial Ratios, Journal of Financial Economics, 74, 209-235.

Mankiw, N.G., and M.D. Shapiro, 1986. Do We Reject Too Often? Small Sample Properties of Tests of Rational Expectations Models, Economics Letters 20, 139-145.

Nelson, C.R., and M.J. Kim, 1993. Predictable stock returns: the role of small sample bias, Journal of Finance 48, 641-661.

Newey, W., and K. West, 1987. A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix, Econometrica 55, 703-708.

Paye, B.S., and A. Timmermann, 2006. Instability of Return Prediction Models, Journal of Empirical Finance 13, 274-315.

Phillips, P.C.B., and J. Yu, 2005. Jackknifing Bond Option Prices, Review of Financial Studies 18, 707-742.

Quenouille, M. H., 1956. Notes on Bias in Estimation, Biometrika 43, 353-360.

Richardson, M., and T. Smith, 1991. Tests of financial models in the presence of overlapping observations, Review of Financial Studies 4, 227-254.

Richardson, M., and J.H. Stock, 1989. Drawing inferences from statistics based on multiyear asset returns, Journal of Financial Economics 25, 323-348.

Stambaugh, R., 1999. Predictive Regressions, Journal of Financial Economics 54, 375-421.

Torous, W., R. Valkanov, and S. Yan, 2004. On predicting stock returns with nearly integrated explanatory variables, Journal of Business 77, 937-966.

Valkanov, R., 2003. Long-horizon regressions: theoretical results and applications, Journal of Financial Economics 68, 201-232.

Table 1: Monte Carlo results for the Single Regressor Case - Panel A: T = 100

The table shows the mean bias and root mean squared error (in parentheses) for the OLS estimator and the jackknifed estimators with m = 2, 3, and 4 subsamples. The differing values of δ, the correlation between the innovations to the returns and the regressor, are given in the top row. The sample size (T) and the value of the auto-regressive root (ρ) are given above each set of results. All results are based on 10,000 repetitions.

Estimator	T=100 ρ=0.9 δ=-0.90	T=100 ρ=0.9 δ=-0.95	T=100 ρ=0.9 δ=-0.99	T=100 ρ=0.95 δ=-0.90	T=100 ρ=0.95 δ=-0.95	T=100 ρ=0.95 δ=-0.99	T=100 ρ=0.999 δ=-0.90	T=100 ρ=0.999 δ=-0.95	T=100 ρ=0.999 δ=-0.99
OLS: Mean	0.038	0.040	0.041	0.042	0.044	0.046	0.048	0.051	0.053
OLS: RMSE	(0.069)	(0.070)	(0.072)	(0.066)	(0.068)	(0.069)	(0.065)	(0.067)	(0.068)
m = 2: Mean	-0.001	-0.002	-0.002	-0.002	-0.002	-0.002	0.003	0.003	0.002
m = 2: RMSE	(0.074)	(0.075)	(0.076)	(0.071)	(0.073)	(0.073)	(0.066)	(0.067)	(0.069)
m = 3: Mean	-0.002	-0.003	-0.002	-0.001	-0.002	-0.002	0.003	0.004	0.003
m = 3: RMSE	(0.068)	(0.069)	(0.070)	(0.061)	(0.064)	(0.064)	(0.056)	(0.056)	(0.057)
m = 4: Mean	-0.002	-0.002	-0.002	0.000	-0.001	-0.001	0.004	0.004	0.004
m = 4: RMSE	(0.065)	(0.066)	(0.067)	(0.058)	(0.060)	(0.061)	(0.052)	(0.052)	(0.053)

Table 1: Monte Carlo results for the Single Regressor Case - Panel B: T = 500

Estimator	T=500 ρ=0.9 δ=-0.90	T=500 ρ=0.9 δ=-0.95	T=500 ρ=0.9 δ=-0.99	T=500 ρ=0.95 δ=-0.90	T=500 ρ=0.95 δ=-0.95	T=500 ρ=0.95 δ=-0.99	T=500 ρ=0.999 δ=-0.90	T=500 ρ=0.999 δ=-0.95	T=500 ρ=0.999 δ=-0.99
OLS: Mean	0.007	0.007	0.008	0.008	0.008	0.008	0.010	0.010	0.011
OLS: RMSE	(0.022)	(0.022)	(0.022)	(0.018)	(0.018)	(0.018)	(0.013)	(0.014)	(0.014)
m = 2: Mean	0.000	0.000	0.000	0.000	-0.001	-0.001	0.000	0.000	0.000
m = 2: RMSE	(0.022)	(0.022)	(0.023)	(0.018)	(0.018)	(0.018)	(0.014)	(0.014)	(0.014)
m = 3: Mean	0.000	0.000	0.000	0.000	-0.001	-0.001	0.000	0.000	0.000
m = 3: RMSE	(0.021)	(0.022)	(0.022)	(0.017)	(0.018)	(0.017)	(0.011)	(0.012)	(0.012)
m = 4: Mean	0.000	0.000	0.000	0.000	-0.001	-0.001	0.000	0.000	0.000
m = 4: RMSE	(0.021)	(0.022)	(0.022)	(0.017)	(0.017)	(0.017)	(0.011)	(0.011)	(0.011)

Table 2: Monte Carlo results for the Multiple Regressor Case - Panel A: T = 100

The table shows the mean bias and root mean squared error (in parentheses) for the OLS estimator and the jackknifed estimators with m = 2, 3, and 4 subsamples, for the two slope coefficients in a predictive regression with two predictor variables. The top row indicates the value of the auto-regressive roots for the two regressors, with the auto-regressive matrix given by A = [(a₁₁, 0), (0, a₂₂)]´. The second row indicates the correlation vector, ω_uv , between the innovations to the returns and the two regressors. The third row gives the variance-covariance matrix Ω_uv, for the innovation processes of the two regressors. The sample size, T, is equal to either 100 or 500, and indicated above each set of results. All results are based on 10,000 repetitions.

Estimator	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.9,0)´ Ω_uv=[(1,0.4),(0.4,1)]´ β₁	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.9,0)´ Ω_uv=[(1,0.4),(0.4,1)]´ β₂	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.7,-0.7)´ Ω_uv=[(1,0.5),(0.5,1)]´ β₁	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.7,-0.7)´ Ω_uv=[(1,0.5),(0.5,1)]´ β₂	a₁₁=0.999 a₂₂=0.999 ω_uv=(-0.9,-0.9)´ Ω_uv=[(1,0.8),(0.8,1)]´ β₁	a₁₁=0.999 a₂₂=0.999 ω_uv=(-0.9,-0.9)´ Ω_uv=[(1,0.8),(0.8,1)]´ β₂
OLS: Mean	0.064	-0.028	0.038	0.026	0.035	0.036
OLS: RMSE	(0.084)	(0.068)	(0.062)	(0.068)	(0.093)	(0.093)
m = 2: Mean	-0.004	-0.001	0.005	-0.003	0.002	0.002
m = 2: RMSE	(0.085)	(0.085)	(0.075)	(0.085)	(0.123)	(0.123)
m = 3: Mean	-0.004	-0.001	0.005	-0.003	0.002	0.003
m = 3: RMSE	(0.072)	(0.075)	(0.064)	(0.076)	(0.106)	(0.105)
m = 4: Mean	-0.002	-0.002	0.007	-0.002	0.003	0.004
m = 4: RMSE	(0.066)	(0.071)	(0.059)	(0.071)	(0.100)	(0.100)

Table 2: Monte Carlo results for the Multiple Regressor Case - Panel B: T = 500

Estimator	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.9,0)´ Ω_uv=[(1,0.4),(0.4,1)]´ β₁	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.9,0)´ Ω_uv=[(1,0.4),(0.4,1)]´ β₂	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.7,-0.7)´ Ω_uv=[(1,0.5),(0.5,1)]´ β₁	a₁₁=0.999 a₂₂=0.95 ω_uv=(-0.7,-0.7)´ Ω_uv=[(1,0.5),(0.5,1)]´ β₂	a₁₁=0.999 a₂₂=0.999 ω_uv=(-0.9,-0.9)´ Ω_uv=[(1,0.8),(0.8,1)]´ β₁	a₁₁=0.999 a₂₂=0.999 ω_uv=(-0.9,-0.9)´ Ω_uv=[(1,0.8),(0.8,1)]´ β₂
OLS: Mean	0.011	-0.005	0.008	0.004	0.007	0.007
OLS: RMSE	(0.015)	(0.018)	(0.012)	(0.018)	(0.019)	(0.019)
m = 2: Mean	-0.001	0.000	0.000	-0.001	0.000	0.000
m = 2: RMSE	(0.015)	(0.020)	(0.013)	(0.020)	(0.025)	(0.025)
m = 3: Mean	-0.002	0.000	0.000	-0.001	0.000	0.000
m = 3: RMSE	(0.013)	(0.019)	(0.011)	(0.019)	(0.022)	(0.022)
m = 4: Mean	-0.002	0.000	0.000	-0.001	0.000	0.000
m = 4: RMSE	(0.012)	(0.019)	(0.011)	(0.018)	(0.021)	(0.020)

Table 3: Monte Carlo results for long-horizon regressions with overlapping observations - Panel A: T = 100 and q = 10

The table shows the mean bias and root mean squared error (in parentheses) for the OLS estimator and the jackknifed estimators with m = 2, 3, and 4 subsamples, for the slope coefficient in a long-horizon predictive regression with overlapping observations and forecast horizon q. A single regressor is used in the regression. The differing values of δ, the correlation between the innovations to the returns and the regressor, are given in the top row. The sample size T, the forecast horizon q, and the value of the auto-regressive root ρ, are given above each set of results. All results are based on 10,000 repetitions.

Estimator	T=100 q=10 ρ=0.9 δ=-0.90	T=100 q=10 ρ=0.9 δ=-0.95	T=100 q=10 ρ=0.9 δ=-0.99	T=100 q=10 ρ=0.95 δ=-0.90	T=100 q=10 ρ=0.95 δ=-0.95	T=100 q=10 ρ=0.95 δ=-0.99	T=100 q=10 ρ=0.999 δ=-0.90	T=100 q=10 ρ=0.999 δ=-0.95	T=100 q=10 ρ=0.999 δ=-0.99
OLS: Mean	0.284	0.307	0.316	0.339	0.361	0.368	0.401	0.419	0.435
OLS: RMSE	(0.469)	(0.481)	(0.482)	(0.480)	(0.492)	(0.495)	(0.496)	(0.513)	(0.523)
m = 2: Mean	0.043	0.052	0.050	0.086	0.098	0.084	0.166	0.175	0.171
m = 2: RMSE	(0.573)	(0.577)	(0.577)	(0.549)	(0.550)	(0.554)	(0.506)	(0.521)	(0.515)
m = 3: Mean	0.076	0.086	0.087	0.133	0.146	0.139	0.223	0.229	0.238
m = 3: RMSE	(0.507)	(0.510)	(0.506)	(0.480)	(0.480)	(0.476)	(0.454)	(0.464)	(0.462)
m = 4: Mean	0.106	0.120	0.121	0.173	0.188	0.186	0.267	0.277	0.286
m = 4: RMSE	(0.480)	(0.482)	(0.475)	(0.460)	(0.461)	(0.457)	(0.454)	(0.465)	(0.463)

Table 3: Monte Carlo results for long-horizon regressions with overlapping observations - Panel B: T = 500 and q = 12

Estimator	T=500 q=12 ρ=0.9 δ=-0.90	T=500 q=12 ρ=0.9 δ=-0.95	T=500 q=12 ρ=0.9 δ=-0.99	T=500 q=12 ρ=0.95 δ=-0.90	T=500 q=12 ρ=0.95 δ=-0.95	T=500 q=12 ρ=0.95 δ=-0.99	T=500 q=12 ρ=0.999 δ=-0.90	T=500 q=12 ρ=0.999 δ=-0.95	T=500 q=12 ρ=0.999 δ=-0.99
OLS: Mean	0.063	0.067	0.073	0.078	0.080	0.084	0.113	0.121	0.123
OLS: RMSE	(0.206)	(0.208)	(0.208)	(0.180)	(0.181)	(0.181)	(0.147)	(0.155)	(0.157)
m = 2: Mean	-0.001	-0.001	0.001	0.002	-0.002	-0.002	0.013	0.016	0.013
m = 2: RMSE	(0.226)	(0.228)	(0.226)	(0.196)	(0.199)	(0.198)	(0.149)	(0.152)	(0.154)
m = 3: Mean	-0.001	-0.002	0.002	0.002	-0.001	0.000	0.018	0.022	0.019
m = 3: RMSE	(0.218)	(0.221)	(0.218)	(0.187)	(0.188)	(0.188)	(0.125)	(0.130)	(0.130)
m = 4: Mean	-0.001	-0.001	0.002	0.004	0.000	0.001	0.023	0.027	0.024
m = 4: RMSE	(0.215)	(0.218)	(0.215)	(0.182)	(0.184)	(0.183)	(0.118)	(0.122)	(0.121)

Table 4: In-Sample Empirical Results - Panel A: Monthly, Full Sample

The table shows the OLS and jackknifed point estimates of the slope coefficients in predictive regressions of excess stock returns, using the predictor variables indicated in the first column. In addition, the OLS t-statistics and R² (expressed in percent) are shown. Four sets of results are shown, using either monthly or annual overlapping data, based on the original monthly observations, and either the longest available full sample for each predictor variable or the forecast sample used in the subsequent out-of-sample exercises. The first column in the table indicates the predictor variable(s) used in the predictive regression, and the second column shows the start date of the sample; all samples end in December 2005. The next four columns show the OLS and jackknifed point estimates, with m = 2, 3, and 4 subsamples, for the slope coefficient of the first (and typically only) predictor in the forecasting regression. The next four columns show the estimates of the slope coefficient for the second regressor; this is only applicable in the regression with both the dividend-price ratio and the T-Bill rate included jointly. The final three columns show the OLS $t-$statistics for the two slope coefficients and the OLS R² in percent. The t-statistics for the annual data with overlapping observations are calculated using Newey and West (1987) standard errors.

Predictor(s)	Sample Begins	_1,OLS	_1,m=2	_1,m=3	_1,m=4	_2,OLS	_2,m=2	_2,m=3	_2,m=4	t_1,OLS	t_2,OLS	R²_OLS (%)
D/P	1872m2	1.99	0.93	2.03	1.84	-	-	-	-	1.02	-	0.37
E/P	1872m2	1.05	1.04	1.32	1.13	-	-	-	-	1.73	-	0.24
Smoothed E/P	1881m2	1.49	1.34	1.23	1.38	-	-	-	-	1.77	-	0.56
B/M	1926m6	0.21	0.24	0.15	0.12	-	-	-	-	1.28	-	1.19
T-Bill rate	1920m1	1.37	1.01	0.74	1.22	-	-	-	-	1.88	-	0.38
D/P and T-Bill rate	1920m1	1.87	0.53	1.36	1.13	1.65	-0.57	0.38	1.01	1.79	2.08	1.21

Table 4: In-Sample Empirical Results - Panel B: Monthly, Forecast Sample

Predictor(s)	Sample Begins	_1,OLS	_1,m=2	_1,m=3	_1,m=4	_2,OLS	_2,m=2	_2,m=3	_2,m=4	t_1,OLS	t_2,OLS	R²_OLS (%)
D/P	1927m1	3.93	4.22	2.68	3.00	-	-	-	-	1.25	-	1.12
E/P	1927m1	2.06	2.06	2.01	1.62	-	-	-	-	2.28	-	0.71
Smoothed E/P	1927m1	3.02	2.57	2.76	2.62	-	-	-	-	1.85	-	1.35
B/M	1946m6	0.18	0.01	0.01	0.05	-	-	-	-	1.96	-	0.61
T-Bill rate	1940m1	1.53	0.88	1.50	1.73	-	-	-	-	2.46	-	0.87
D/P and T-Bill rate	1940m1	2.91	0.10	-1.74	0.21	1.35	-0.22	0.28	1.23	2.33	2.13	1.56

Table 4: In-Sample Empirical Results - Panel C: Annual, Full Sample

Predictor(s)	Sample Begins	_1,OLS	_1,m=2	_1,m=3	_1,m=4	_2,OLS	_2,m=2	_2,m=3	_2,m=4	t_1,OLS	t_2,OLS	R²_OLS (%)
D/P	1872m2	2.55	1.41	2.53	2.32	-	-	-	-	2.41	-	5.14
E/P	1872m2	1.52	1.49	1.70	1.51	-	-	-	-	2.76	-	4.30
Smoothed E/P	1881m2	1.77	1.65	1.48	1.46	-	-	-	-	2.35	-	6.89
B/M	1926m6	0.23	0.25	0.15	0.15	-	-	-	-	4.05	-	13.71
T-Bill rate	1920m1	0.99	1.33	0.63	0.98	-	-	-	-	1.75	-	1.91
D/P and T-Bill rate	1920m1	2.66	2.38	2.29	2.16	1.32	0.78	0.50	1.35	3.75	2.32	16.01

Table 4: In-Sample Empirical Results - Panel D: Annual, Forecast Sample

Predictor(s)	Sample Begins	_1,OLS	_1,m=2	_1,m=3	_1,m=4	_2,OLS	_2,m=2	_2,m=3	_2,m=4	t_1,OLS	t_2,OLS	R²_OLS (%)
D/P	1927m1	3.97	4.33	2.47	3.11	-	-	-	-	3.24	-	10.89
E/P	1927m1	2.05	2.07	1.97	1.76	-	-	-	-	3.12	-	6.78
Smoothed E/P	1927m1	3.09	2.66	2.85	2.74	-	-	-	-	3.25	-	13.57
B/M	1946m6	0.22	0.04	0.05	0.10	-	-	-	-	2.09	-	8.26
T-Bill rate	1940m1	1.12	0.53	1.16	1.34	-	-	-	-	2.18	-	4.26
D/P and T-Bill rate	1940m1	3.70	2.16	0.50	1.18	0.87	0.57	0.55	0.94	2.87	1.82	14.28

Table 5: Out-of-Sample Results - Panel A: Monthly

The table shows the out-of-sample R² (expressed in percent) that result from the forecasts of excess stock returns using the predictor variables indicated in the first column. The forecasts are formed using either the OLS estimates or the jackknifed estimates, with m = 2, 3, and 4, and with or without imposing the restrictions on the forecasts recommended by Campbell and Thompson (2007). Results for both the monthly and annual data are shown. For each row, and for both the unrestricted and restricted sets of forecasts, the highest out-of-sample R² is shown in bold type. The first column indicates the predictor variable(s) that the forecasts are based on, and the following two columns show the date at which the sample begins and the date at which the out-of-sample forecasts begin, respectively. The difference between columns two and three represents the 'training-sample' that is used to form the initial estimates for the first forecast. The following four columns show the out-of-sample R² for the unrestricted forecasts that do not impose the Campbell and Thompson restrictions, and the last four columns show the correpsonding results with the Campbell and Thompson restrictions in place.

Predictor(s)	Sample Begins	Forecast Begins	Unrestricted: R²_OLS	Unrestricted: R²_m=2	Unrestricted: R²_m=3	Unrestricted: R²_m=4	Restricted: R²_OLS	Restricted: R²_m=2	Restricted: R²_m=3	Restricted: R²_m=4
D/P	1872m2	1927m1	-0.66	-0.31	-0.62	-0.54	0.16	0.44	0.33	0.36
E/P	1872m2	1927m1	0.12	0.39	0.31	0.29	0.24	0.46	0.37	0.38
Smoothed E/P	1881m2	1927m1	0.32	0.67	0.17	0.10	0.44	0.74	0.56	0.41
B/M	1926m6	1946m6	-0.44	-0.38	0.72	0.42	-0.01	0.13	0.78	0.47
T-Bill rate	1920m1	1940m1	0.54	-13.74	-0.29	-4.30	0.58	-13.75	0.84	-0.10
D/P and T-Bill rate	1920m1	1940m1	0.12	-10.50	-1.22	-3.00	0.17	-9.21	1.09	0.22

Table 5: Out-of-Sample Results - Panel B: Annual

Predictor(s)	Sample Begins	Forecast Begins	Unrestricted: R²_OLS	Unrestricted: R²_m=2	Unrestricted: R²_m=3	Unrestricted: R²_m=4	Restricted: R²_OLS	Restricted: R²_m=2	Restricted: R²_m=3	Restricted: R²_m=4
D/P	1872m2	1927m1	5.53	7.69	4.72	5.29	5.63	7.73	4.79	5.27
E/P	1872m2	1927m1	4.93	5.23	4.65	3.92	4.94	5.24	4.72	3.97
Smoothed E/P	1881m2	1927m1	7.89	5.67	3.15	2.01	7.85	5.70	4.23	2.61
B/M	1926m6	1946m6	-3.38	-10.80	4.47	2.94	1.39	-3.61	5.83	3.81
T-Bill rate	1920m1	1940m1	5.54	-2.24	8.20	-0.98	7.47	0.34	9.45	7.40
D/P and T-Bill rate	1920m1	1940m1	8.84	1.95	9.24	11.31	7.87	12.94	10.40	9.46

Table 6: Portfolio Choice Results - Panel A: Monthly

The table shows the utility gains, expressed in percent annualized expected returns, for an investor who uses the predictor variables indicated in the first column, instead of the historical mean, to time the market; the investor has mean-variance preferences with relative risk aversion equal to three. The portfolio weights are based on forecasts of the excess stock returns, formed using either the OLS estimates or the jackknifed estimates, with m = 2, 3, and 4, and with or without imposing the restrictions on the forecasts recommended by Campbell and Thompson (2007). Results for both the monthly and annual data are shown. For each row, and for both the unrestricted and restricted sets of forecasts, the highest utility gain is shown in bold type. The first column indicates the predictor variable(s) that the forecasts are based on, and the following two columns show the date at which the sample begins and the date at which the out-of-sample forecasts begin respectively. The difference between columns two and three represents the 'training-sample' that is used to form the initial estimates for the first forecast. The following four columns show the utility gains from the portfolio decisions based on the unrestricted forecats that do not impose the Campbell and Thompson restrictions, and the last four columns show the corresponding results with the Campbell and Thompson restrictions in place.

Predictor(s)	Sample Begins	Forecast Begins	Unrestricted: OLS	Unrestricted: m=2	Unrestricted: m=3	Unrestricted: m=4	Restricted: OLS	Restricted: m=2	Restricted: m=3	Restricted: m=4
D/P	1872m2	1927m1	-0.52	0.41	-0.06	-0.09	-0.43	0.50	0.08	0.03
E/P	1872m2	1927m1	0.23	0.53	0.51	0.56	0.37	0.65	0.63	0.71
Smoothed E/P	1881m2	1927m1	-0.30	-0.11	0.08	-0.09	-0.26	-0.07	0.38	0.08
B/M	1926m6	1946m6	-0.70	-0.64	0.39	0.20	-0.71	-0.64	0.38	0.20
T-Bill rate	1920m1	1940m1	1.68	2.12	2.15	1.55	1.67	2.11	2.22	1.75
D/P and T-Bill rate	1920m1	1940m1	-0.65	0.92	0.77	1.01	-0.65	0.50	0.89	2.47

Table 6: Portfolio Choice Results - Panel B: Annual

Predictor(s)	Sample Begins	Forecast Begins	Unrestricted: OLS	Unrestricted: m=2	Unrestricted: m=3	Unrestricted: m=4	Restricted: OLS	Restricted: m=2	Restricted: m=3	Restricted: m=4
D/P	1872m2	1927m1	-0.54	0.30	-0.30	-0.35	-0.55	0.28	-0.30	-0.35
E/P	1872m2	1927m1	0.62	0.58	0.46	0.42	0.62	0.58	0.46	0.42
Smoothed E/P	1881m2	1927m1	0.52	0.14	-0.26	0.16	0.52	0.14	0.03	0.33
B/M	1926m6	1946m6	-0.57	-1.64	-0.02	-0.45	-0.62	-1.63	-0.03	-0.46
T-Bill rate	1920m1	1940m1	1.55	1.42	1.95	1.52	1.53	1.41	1.89	1.56
D/P and T-Bill rate	1920m1	1940m1	0.00	1.33	0.95	2.07	-0.06	-0.51	-0.31	0.23

Figure 1: Density Plots

Density plots for the OLS and jackknife estimates, based on 100,000 simulations for T = 100, ρ = 0.999 and δ = -0.99. The graphs shows the kernel density estimates of the bias in the OLS and jackknifed estimates, with m = 2, 3, and 4. The vertical solid line indicates a zero bias.

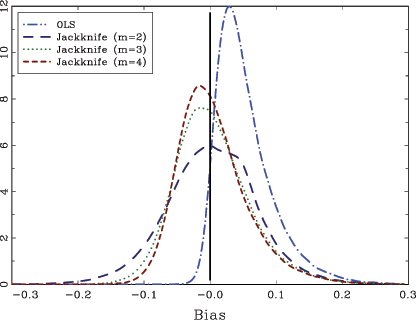
Footnotes

* Helpful comments have been provided by Daniel Beltran, Lennart Hjalmarsson, Randi Hjalmarsson, and Mike McCracken. Corresponding author: Erik Hjalmarsson. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: erik.hjalmarsson@frb.gov. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1. The only bias corrections, in predictive regressions, that have been used to any great extent are ad hoc corrections for the bias dervied by Stambaugh (1999), for the case of a single regressor that follows an AR(1) process. Amihud and Hurvich (2004) provide justifications for similar corrections in the case of multiple regressors. Lewellen (2004) provides a 'conservative' bias correction, also based on a single AR(1) regressor, which is primarily useful as a tool for obtaining conservative test statistics, since in general the corrected estimate will not be unbiased but, rather, underestimate the true parameter value. In fact, one of the main reasons that testing, rather than estimation, has been the main focus is that most studies on inference in predictive regressions resort to some conservative test, which does not deliver a unique estimation analogue; e.g., Cavanagh et al. (1995) and Campbell and Yogo (2006). Return to text

2. The case when the regressors are completely orthogonal to each other is obviously most desirable in empirical specifications, although it is not often likely to hold. In that case, however, there will be little to no difference between the individual coefficient estimates from separate regressions on each regressor and the estimates obtained from a multiple regression. Thus, there is little point in analyzing this case, since it would merely confirm the results obtained in the previous section. Return to text

3. See, for instance, Hansen and Hodrick (1980), Richardson and Stock (1989), Richardson and Smith (1991), Goetzman and Jorion (1993), Campbell (2001), Valkanov (2003), Torous et al. (2004), and Boudoukh et al. (2006). Nelson and Kim (1993) briefly discuss the magnitude of the Stambaugh (1999) bias in regressions with overlapping observations. Return to text

4. The data were obtained from Professor John Campbell's website and are described in more detail in Campbell and Thompson (2007). Return to text

5. One could consider various ways of implementing the restrictions on the jackknife estimates. Here we take the simplest approach and set the parameter estimate equal to zero if it has the wrong sign. Alternatively, one could restrict the individual sub-sample estimates in the jackknife estimator to have the right sign. Since the first approach immediately generalizes to the case of multiple regressors, unlike the second one which would become complicated to implement for more than one regressor, we use the first approach. In all cases, the intercepts are calculated to line up with the, potentially restricted, slope coefficient such that the residuals have mean zero. In the regressions with two predictor variables, each coefficient is restricted separately and the intercept is again estimated to produce zero mean residuals. Return to text

6. The use of a five-year window to estimate the variance of the (unexpected) returns conforms with the approach taken by Campbell and Thompson (2007). It can be justified by the fact that it is easier to calculate the variance of returns, as opposed to the expected value, over shorter time horizons, and there is a large literature that shows that variances change over time. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text