
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 934, June 2008--- Screen Reader
Version*
Trade Elasticity of Substitution and Equilibrium Dynamics*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The empirical literature provides a wide range of estimates for trade elasticities at the aggregate level. Furthermore, recent contributions in international macroeconomics suggest that low (implied) values of the trade elasticity of substitution may play an important role in understanding the disconnect between international prices and real variables. However, a standard model of the international business cycle displays multiple locally isolated equilibria if the trade elasticity of substitution is sufficiently low. The main contribution of this paper is to compute and characterize some dynamic properties of these equilibria. While multiple steady states clearly signal equilibrium multiplicity in the dynamic setup, this is not a necessary condition. Solutions based on log-linearization around a deterministic steady state are of limited to no help in computing the true dynamics. However, the log-linear solution can hint at the presence of multiple dynamic equilibria.
Keywords: Multiple equilibria, linearization, DSGE models
JEL classification: C68, F41
1 Introduction
General equilibrium theory is plagued with the problem of equilibrium multiplicity.1 This paper analyzes a standard model of the international business cycle that is based on the seminal contribution of Backus, Kehoe, and Kydland (1995). If the elasticity of substitution between the home and the foreign good is sufficiently low, this model displays multiple locally isolated equilibria.2 The main contribution of this paper is to characterize the dynamic properties of these multiple equilibria in a model with endogenous capital accumulation and incomplete international financial markets for borrowing and lending. The two major computational issues that arise are to identify conditions that indicate the existence of multiple equilibria and to find a reliable method to compute these equilibria.
To build intuition, consider an endowment economy with two countries and two traded goods that are imperfect substitutes. The countries are mirroring each other with respect to preferences and endowments.3 There is always one equilibrium with the relative price of the traded goods equal to unity. However, there can be two more equilibria. Let the price of the domestic good be high relative to the price of the foreign good, so that domestic agents have high purchasing power relative to the foreign agents. If the elasticity of substitution is low, foreigners are willing to give up most of their good in order to consume at least some of the domestic good, and domestic agents end up consuming most of the domestic and the foreign good. The reverse is true as well. Foreign agents consume most of the two goods, if the foreign good is very expensive in relative terms. Of course, these last two scenarios cannot be an equilibrium for high values of the elasticity of substitution. In the limiting case of perfect substitutability the unique equilibrium features each country consuming its own endowment. Such a model of multiple locally unique equilibria allows for the construction of sunspot equilibria, meaning there are equilibria for which allocations are different across different states of nature, even though nothing fundamental has changed.4
In a model with endogenous state variables the computation of dynamic multiple equilibria cannot be separated from considering sunspot equilibria. To eliminate these complications I conduct the following experiment. In the first period the economy experiences an unforeseen shock to technology. This is the only period in which agents are free to coordinate on any of the possible equilibrium paths. Starting from the second period onwards, agents have perfect foresight and they keep coordinating on the equilibrium path that has been chosen in the first period.
Under these assumptions I can typically find three equilibria provided that the elasticity of substitution is sufficiently low. Along the first equilibrium path the dynamics are solely driven by the impact of the technology shock and all variables stay in the neighborhood of their pre-shock level. The dynamics of the other two equilibria are mostly driven by the shifts in relative purchasing power due to self-fulfilling changes in the relative price of the home and foreign good. The effects of the technology shock are negligible in these cases.
Whereas for a given calibration the existence of multiple equilibria mostly depends on the magnitude of the trade elasticity of substitution, it can also depend on the magnitude and the persistence of the shock. In some cases, two of the three equilibria cease to exists if the shock is sufficiently large or permanent. At least in the cases presented in this paper, the now unique equilibrium involves a large shift in relative purchasing power.
Although equilibrium multiplicity in the dynamic model mostly goes along with multiple steady states, one can also find multiple equilibria in cases with a unique steady state. In a model with a slow-moving capital stock the short-run excess demand function behaves differently from the long-run excess demand, as the economy is less flexible in the short run.
The major challenge in computing equilibria in an environment with multiple locally unique equilibria is to generate a good starting guess. Fortunately, it is possible to derive a starting guess for the model economy with capital and incomplete financial markets from an endowment economy with incomplete financial markets. Using a combination of backward and forward shooting algorithms the impulse response functions for a technology shock are derived under the aforementioned assumption that in the period of the shock agents coordinate once and for all on one equilibrium path.
Linearization or higher-order perturbation methods that approximate the equilibrium policy functions around a deterministic steady state are of limited use in an environment with low trade elasticities. First, these methods can only detect one of the three equilibria. In particular, the method cannot detect those equilibria that are associated with the large shifts in relative purchasing power. Second, in some cases of large shocks local approximation techniques are inappropriate. This issue is not just due to the declining accuracy of the approximation method with increasing distance from the deterministic steady state. The real problem is that the method searches for an equilibrium path where it can be shown that no such equilibrium path exists for a shock of the considered size. Hence, even if one is willing to abstract from equilibrium multiplicity and the possibility of sunspot equilibria, global non-linear methods are preferred to local approximation methods. However, the linear approximation to the policy functions can be put to use in detecting the presence multiple equilibria.
The literature provides a large range of estimates for the trade elasticity of substitution. Using aggregate data Whalley (1995) reports an elasticity of 1.5. In a recent study, Hooper, Johnson and Marquez (2000) estimate trade elasticities for the G7 countries. They report a short-run trade elasticity of 0.6 for the U.S. and values between 0 and 0.6 for the remaining G7 countries. Taylor (1993) estimates an import demand equation for the U.S. and finds a short-run elasticity of 0.22 and a long-run trade elasticity of 0.39. Obviously, these macro estimates are in sharp contrasts to the estimates from lower levels of aggregation. In Broda and Weinstein (2005), for example, the mean estimates are between 4 and 6. Most relevant for this paper, it is common in many applied macroeconomic models to choose values of the elasticity of substitution between 1 and 1.5. Examples include Backus et al (1995), Chari, Kehoe, and McGrattan (2003), and Heathcote and Perri (2002). Recently, however, models with (implied) low elasticities of substitution between home and foreign goods have received considerable attention - Corsetti, Dedola, and Leduc (2008), Collard and Dellas (2004), Benigno and Thoenissen (2008), Thoenissen (2008), and Enders and Mueller (2008) - as such models seem to provide a better fit to the international business cycle. In particular, this has been shown for the case of the puzzling negative correlation between the real exchange rate and relative consumption (Backus and Smith (1993)), cross-country consumption correlations, and the volatility of the real exchange rate. Furthermore, Rabanal and Tuesta (2005) and Lubik and Schorfheide (2005) show estimates for the elasticity of substitution well below unity in DSGE models using Bayesian techniques. In a model that is akin to Corsetti et al (2008), de Walque, Smets and Wouters (2005) find that the data speaks in favor of a low implied elasticity of substitution.
This paper does not take a stand on the value of the trade elasticity of substitution in macro models. However, as there seems to be considerable interest in models with low trade elasticities, it is important to search for tools that allow a complete analysis of models with multiple equilibria and to investigate the extent to which the results of these models and their support through the data hinge on the value of the elasticity of substitution between traded goods being so low that the model admits multiple equilibria.5
The remainder of the paper is organized as follows. Section 2 introduces the problem of multiple equilibria in a static endowment economy. Section 3 presents a dynamic model with endogenous capital accumulation and international borrowing and lending. Computational issues are addressed in Section 4. In Section 5, the equilibrium multiplicity in the dynamic economy is illustrated with the help of impulse response functions. Some sensitivity aspects of the results are discussed in Section 6. Section 7 concludes.
2 Multiple Equilibria
The analysis begins with the well-known example of a static
exchange economy with two agents and two goods.6 Let agent
![]() (
(![]() ) receive an endowment of
) receive an endowment of
![]() units of good
units of good ![]() . Agents
can trade their endowments with each other and they have constant
elasticity of substitution preferences over the two goods. The
problem of agent
. Agents
can trade their endowments with each other and they have constant
elasticity of substitution preferences over the two goods. The
problem of agent ![]() is given by
is given by
![$\displaystyle \max_{c_{i1}, c_{i2}}c_{i}=\left[ \left( \alpha_{i1}\right) ^{1-\rho }c_{i1}^{\rho}+\left( \alpha_{i2}\right) ^{1-\rho}c_{i2}^{\rho}\right] ^{ \frac{1}{\rho}}$](img27.gif)
|
(1) | |
| s.t. | ||
| (2) |
where ![]() and
and
![]() ,
, ![]() .
.
![]() is the
elasticity of substitution between the two goods.
is the
elasticity of substitution between the two goods. ![]() denotes the amount of good
denotes the amount of good ![]() that is
consumed by agent
that is
consumed by agent ![]() .
.
![]() is the price of good
is the price of good ![]() . Absent trading frictions both agents face the same prices.
Market clearing requires
. Absent trading frictions both agents face the same prices.
Market clearing requires
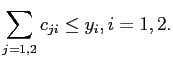 |
(3) |
An equilibrium in this economy is defined as follows.
Define
![]() , and
let
, and
let ![]() denote the excess demand for good
2. A competitive equilibrium is then fully
summarized by
denote the excess demand for good
2. A competitive equilibrium is then fully
summarized by
| (4) | |
| (5) |
Since agents' preferences over goods in (1) are
strictly monotone, the equilibrium price is strictly positive, and
![]() .
.
Standard theorems establish the existence of a competitive
equilibrium. However, the equilibrium may not be unique. Let
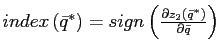 be the index of an equilibrium with the relative price
be the index of an equilibrium with the relative price
![]() . If all equilibria are locally
unique, the sum of the indices across equilibria equals
. If all equilibria are locally
unique, the sum of the indices across equilibria equals ![]() by virtue of the index theorem. Hence, the number of
equilibria is finite. If there is an equilibrium with
by virtue of the index theorem. Hence, the number of
equilibria is finite. If there is an equilibrium with
![]() , there are at least two more equilibria.7
, there are at least two more equilibria.7
Figure 1 plots the excess
demand for good 2 as a function of a monotone transformation of the
relative price,
![]() , for two different
values of the elasticity of substitution,
, for two different
values of the elasticity of substitution,
![]() and
and
![]() .8 There is a unique
equilibrium with
.8 There is a unique
equilibrium with ![]()
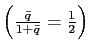 for
for
![]() , but there are three equilibria
with
, but there are three equilibria
with ![]() equal to 0.47
equal to 0.47
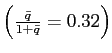 , 1, and 2.12
, 1, and 2.12
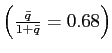 for
for
![]() . Notice, that in the latter
case the slope of the excess demand function is positive for
. Notice, that in the latter
case the slope of the excess demand function is positive for
![]() and all the equilibria are locally
unique.9 To understand how multiple equilibria
arise at low values of the elasticity of substitution consider the
first equilibrium in the second panel of Figure 1. As the
price of good 1 is high relative to the price of good
2,
and all the equilibria are locally
unique.9 To understand how multiple equilibria
arise at low values of the elasticity of substitution consider the
first equilibrium in the second panel of Figure 1. As the
price of good 1 is high relative to the price of good
2,
![]() , the value of the endowment of
country 1 is high relative to country 2.
Agents in country 2 are willing to pay the high
price for good 1 and country 1 ends up
consuming most of the two goods. The same logic applies in the
third equilibrium,
, the value of the endowment of
country 1 is high relative to country 2.
Agents in country 2 are willing to pay the high
price for good 1 and country 1 ends up
consuming most of the two goods. The same logic applies in the
third equilibrium,
![]() , with the roles of country
1 and 2 being reversed. The
second equilibrium is the symmetric equilibrium featuring
, with the roles of country
1 and 2 being reversed. The
second equilibrium is the symmetric equilibrium featuring
![]() . If the elasticity of substitution
is high, equilibria 1 and 3 cannot
exist.
. If the elasticity of substitution
is high, equilibria 1 and 3 cannot
exist.
The dynamic extension of the static economy with a low
elasticity of substitution delivers a simple example of an economy
with sunspot equilibria. Let preferences admit an expected utility
representation. Agents receive a fixed endowment every period and
there are no international financial markets. The dynamic economy
is then simply the repeated static economy. A sunspot equilibrium
is given by a system of the three spot prices and a probability
distribution ![]() over the three spot prices: although
the fundamentals of the economy, i.e., the endowments, are
unaffected by the realization of the state, the equilibrium prices
and allocations differ across states.10
over the three spot prices: although
the fundamentals of the economy, i.e., the endowments, are
unaffected by the realization of the state, the equilibrium prices
and allocations differ across states.10
3 General Model
The model is quite standard in the international business cycle
literature and it is closely related to the seminal work of Backus
et al (1995). There are two countries
![]() , each populated by an
infinite number of households of measure one. Each country produces
one good and the home and foreign good are imperfect substitutes in
the households' utility functions. The two goods are produced under
perfect competition using capital and labor. Agents have access to
a non-contingent bond that pays one unit of country 1's
currency.
, each populated by an
infinite number of households of measure one. Each country produces
one good and the home and foreign good are imperfect substitutes in
the households' utility functions. The two goods are produced under
perfect competition using capital and labor. Agents have access to
a non-contingent bond that pays one unit of country 1's
currency.
Time is discrete and each period the economy experiences one of
finitely many events ![]() .
.
![]() denotes the history of events up through and including period
denotes the history of events up through and including period
![]() . The probability, as of period 0, of any
particular history
. The probability, as of period 0, of any
particular history ![]() is
is
![]() . The initial
realization
. The initial
realization ![]() is given.
is given.
3.1 Households
Households in country
![]() maximize their expected discounted
lifetime utility subject to their budget constraint. All variables
are expressed in per household units
maximize their expected discounted
lifetime utility subject to their budget constraint. All variables
are expressed in per household units
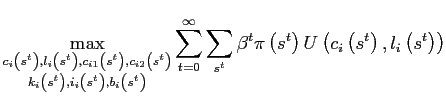
|
(6) | |
| s.t. | ||
| (7) | ||
| (8) |
where ![]() ,
, ![]() ,
, ![]() and
and ![]() denote consumption,
investment, labor, and capital, respectively.
denote consumption,
investment, labor, and capital, respectively. ![]() is the price of the final consumption-investment good,
is the price of the final consumption-investment good,
![]() is the price of good
is the price of good ![]() ,
,
![]() and
and
![]() are the nominal rental rate
of capital and the nominal wage,
are the nominal rental rate
of capital and the nominal wage,
![]() denotes nominal profits,
and
denotes nominal profits,
and ![]() denotes holdings of a non-contingent
bond.
denotes holdings of a non-contingent
bond. ![]() is the price of the bond. To rule out
Ponzi-schemes, I assume that agents face an upper bound for
borrowing
is the price of the bond. To rule out
Ponzi-schemes, I assume that agents face an upper bound for
borrowing
![]() that is large enough to never
bind in this application.
that is large enough to never
bind in this application.
3.2 Firms
Firms utilize labor and capital in order to produce the traded good under perfect competition. The technology is assumed to be of the constant elasticity of substitution type. Since capital is owned by households and rented out to firms, the solution to the firms' maximization problem can be found from
| (9) | ||
| s.t. | ||
![$\displaystyle F_{i}\left( l_{i},k_{i}\right) =\left[ \omega_{li}^{1-\kappa}\left( A_{i}\left( s^{t}\right) l_{i}\left( s^{t}\right) \right) ^{\kappa }+\omega_{ki}^{1-\kappa}k_{i}\left( s^{t-1}\right) ^{\kappa}\right] ^{\frac{1}{\kappa}},$](img121.gif)
|
(10) | |
| if |
||
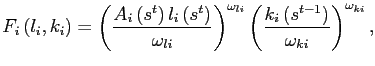
|
(11) | |
| if |
3.3 International trade
Households in country ![]() demand a
consumption-investment good
demand a
consumption-investment good
![]()
![]() .
.
![]() is an aggregate of the
domestically produced good and the imports of the foreign good
according to
is an aggregate of the
domestically produced good and the imports of the foreign good
according to
![$\displaystyle \tilde{c}_{i}\left( s^{t}\right) =c_{i}\left( s^{t}\right) +i_{i}\left( s^{t}\right) =\left[ \alpha_{i1}^{1-\rho}c_{i1}\left( s^{t}\right) ^{\rho }+\alpha_{i2}^{1-\rho}c_{i2}\left( s^{t}\right) ^{\rho}\right] ^{\frac{1}{ \rho}},$](img129.gif)
|
(12) |
with
![]() . The parameters
. The parameters
![]() will be calibrated to match
aggregate trade shares in the data.11
will be calibrated to match
aggregate trade shares in the data.11 ![]() and
and
![]() measures the
elasticity of substitution between traded goods.
measures the
elasticity of substitution between traded goods.
A household's optimal choices for consumption of the home and the foreign good are determined from the cost minimization problem
| (13) | ||
| s.t. | ||
![$\displaystyle \tilde{c}_{i}\left( s^{t}\right) = \left[ \alpha_{i1}^{1-\rho} c_{i1}\left( s^{t}\right) ^{\rho}+\alpha_{i2}^{1-\rho}c_{i2}\left( s^{t}\right) ^{\rho}\right] ^{\frac{1}{\rho}}.$](img136.gif)
|
(14) |
The first order conditions for country ![]() 's households
imply
's households
imply
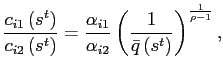
|
(15) |
where I have defined the relative price to be
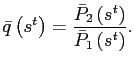
|
(16) |
This relative price relates to the real exchange rate as follows
![$\displaystyle q\left( s^{t}\right) =\frac{P_{2}\left( s^{t}\right) }{P_{1}\left( s^{t}\right) }=\frac{\tau_{22}}{\tau_{11}}\left[ \frac{\alpha_{11} +\alpha_{12}\left( \frac{\tau_{11}}{\tau_{12}}\bar{q}\left( s^{t}\right) \right) ^{\frac{\rho}{1-\rho}}}{\alpha_{21}\left( \frac{\tau_{21}}{\tau _{22}} \right) ^{\frac{\rho}{\rho-1}}+\alpha_{22}\left( \bar{q}\left( s^{t}\right) \right) ^{\frac{\rho}{\rho-1}}}\right] ^{\frac{1-\rho}{\rho} }.$](img140.gif)
|
(17) |
In what follows
![]() is normalized to
unity. Using goods market clearing, budget constraints, and
optimality conditions the demand for good 2 in
countries 1 and 2 can be expressed
as
is normalized to
unity. Using goods market clearing, budget constraints, and
optimality conditions the demand for good 2 in
countries 1 and 2 can be expressed
as
![$\displaystyle c_{12}\left( s^{t}\right) =\frac{\alpha_{12}\bar{q}\left( s^{t}\right) ^{ \frac{1}{\rho-1}}}{\alpha_{11}+\alpha_{12}\bar{q}\left( s^{t}\right) ^{ \frac{\rho}{\rho-1}}}\left[ y_{1}\left( s^{t}\right) +\frac{ b_{1}\left( s^{t-1}\right) -Q_{1}\left( s^{t}\right) b_{1}\left( s^{t}\right) } {\Phi_{1}\left( s^{t}\right) } \right] ,$](img145.gif)
|
(18) |
![$\displaystyle c_{22}\left( s^{t}\right) =\frac{\alpha_{22}}{\alpha_{21}\left( \frac{1}{ \bar{q}\left( s^{t}\right) }\right) ^{\frac{\rho}{\rho-1}}+\alpha_{22}} \left[ y_{2}\left( s^{t}\right) +\frac{ b_{2}\left( s^{t-1}\right) -Q_{2}\left( s^{t}\right) b_{2}\left( s^{t}\right) }{\Phi_{1}\left( s^{t}\right) \bar{q }\left( s^{t}\right) } \right] ,$](img146.gif)
|
(19) |
and
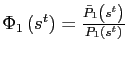 .
.
3.4 Definition of Equilibrium
A competitive equilibrium in the dynamic model is defined as follows:
4 Computation and Calibration
In a static model, the computation of the possibly multiple equilibria can be separated from the consideration of sunspot equilibria. However, in a dynamic model this is no longer possible. Each equilibrium path depends on the probability distribution over all the possible equilibria. To impose more discipline on the analysis, the following assumptions are made in the subsequent computations.
4.1 More Assumptions
As argued in Section 2, equilibrium multiplicity occurs because changes in the relative price lead to a shift in purchasing power that can be supported as equilibrium if the trade elasticity is low. In a dynamic economy with capital, labor, and internationally traded bonds the same intuition applies provided that markets are not complete.12
In order to characterize the equilibrium multiplicity in the general model, I impose two assumptions:
- At time 1 country 2 experiences an unexpected rise in its technology. The shock follows an AR(1) process with known persistence. Once the shock is realized agents perfectly foresee the future path of technology.
- The agents' problem is modified to yield stationarity of the net foreign asset position under the first assumption. Two alternatives are considered:
(a) Agents face a convex cost for holding/issuing bonds as in Heathcote and Perri (2002), and Schmitt-Grohé and Uribe (2003). The collected fees are reimbursed to the agents by a lump-sum transfer.
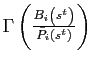 denotes the portfolio costs in terms of country
denotes the portfolio costs in terms of country 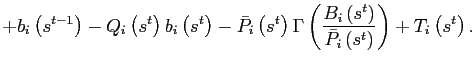
|
(20) |
(b) Agents' intertemporal discount factors are endogenous as in Uzawa (1968).13 More specifically, the problem of the representative household is given by
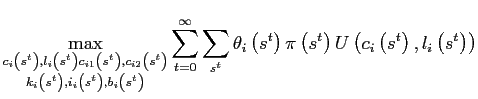
|
(21) | |
| s.t. | ||
| (22) |
and equations (7) and (8).
The first assumption eliminates all uncertainty including sunspots from period 2 onwards. This assumption allows the characterization of the equilibrium multiplicity without the additional complications that arise in a fully stochastic model with incomplete markets, borrowing constraints and endogenous capital accumulation. Identifying multiple equilibria is a tedious task, but without this assumption, one does not even know where to look for the equilibrium multiplicity.
The second assumption is a direct consequence of the first. Since I assume perfect foresight from period 2 onwards, the long-run equilibrium value of the net foreign asset position changes in response to the temporary shock.14 Unfortunately, this long-run value and therefore the long-run equilibrium are unknown thereby making the computational procedure suggested below inapplicable. Under the second assumption, however, net foreign assets are known to return to their pre-shock level.15
4.2 Solution Method
I describe the solution algorithm for finding the equilibrium path of the endogenous variables for the (perfect-foresight) experiment described above.
The major step in accounting for equilibrium multiplicity is to generate a good starting guess. Unfortunately, local approximation methods such as linearization or second-order perturbation methods are of little help. These methods can only find one equilibrium. While the suggested algorithm does not guarantee the detection of all equilibria, it does detect some.16
To find the equilibrium paths I use a combination of forward and backward shooting algorithms. Since shooting algorithms with many state variable are computationally intensive, the algorithm starts under the assumption of fixed capital. Endogenous capital accumulation is then reintroduced once a starting guess is found. Without loss in generality, the stationarity inducing devices introduced under assumption 2 are parameterized to induce zero net-foreign asset positions in any steady state.
- Choose the parametrization of the model, set
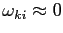 , and assume that
capital is fixed at its steady level, i.e., remove the Euler
equation for capital from the model. Assume that there are no
shocks.
, and assume that
capital is fixed at its steady level, i.e., remove the Euler
equation for capital from the model. Assume that there are no
shocks. - For each locally stable steady state compute the stable
manifold using a reverse shooting algorithm as described in Judd
(1998). I reduce the dimension of the problem to the relative price
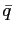 , and bond holdings
, and bond holdings 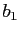 . The resulting manifold shows the path along which the
economy converges to a steady state from the initial net foreign
asset position
. The resulting manifold shows the path along which the
economy converges to a steady state from the initial net foreign
asset position
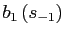 and the initial
value of the relative price
and the initial
value of the relative price
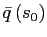 .
. - Compute the equilibrium path of the endogenous variables to a
purely transitory shock in time 1,
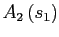 . Prior to the
shock the economy is assumed to be in steady state. Since bond
holdings can freely adjust from one period to the other, the
economy must move along the stable manifold(s) computed under step
2 starting from the second period on. To
find a candidate equilibrium path:
. Prior to the
shock the economy is assumed to be in steady state. Since bond
holdings can freely adjust from one period to the other, the
economy must move along the stable manifold(s) computed under step
2 starting from the second period on. To
find a candidate equilibrium path:
(a) choose a pair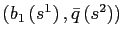 on the manifold as a guess for the position of the economy in the
second period, the period right after the shock,
on the manifold as a guess for the position of the economy in the
second period, the period right after the shock,
(b) use the first order conditions of the model to compute the implied value of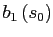 if
if
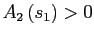 . Since bond
holdings are 0 in the steady state, a bond-price pair
. Since bond
holdings are 0 in the steady state, a bond-price pair
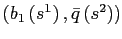 is an equilibrium only if the implied bond holdings for state
is an equilibrium only if the implied bond holdings for state
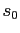 satisfy
satisfy
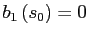 .
. - This candidate impulse response is used as starting guess in a code that solves non-linear perfect foresight problems using a Newton method. The solution algorithm for this step borrows heavily from the DYNARE code "simul" and is implemented in FORTRAN.
- Once an equilibrium path has been computed, I reintroduce the
dynamic investment decision and increase
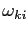 to its desired value. At this
stage it is also convenient to increase the persistence of the
shock if desired.
to its desired value. At this
stage it is also convenient to increase the persistence of the
shock if desired.
Figure 2 shows
the stable manifolds computed under step 2 for the
case of convex portfolio costs (top panel) and endogenous
discounting (lower panel) with
![]() and
and
![]() . In the case of convex
portfolio costs the two stable steady states which are marked by
the filled in circles feature different capital stocks and
therefore the two manifolds do not "connect". As argued in
Bodenstein (2007), the third steady state with
. In the case of convex
portfolio costs the two stable steady states which are marked by
the filled in circles feature different capital stocks and
therefore the two manifolds do not "connect". As argued in
Bodenstein (2007), the third steady state with ![]() is unstable. In the case of endogenous discounting
the steady state is always unique and stable as indicated by the
black arrows.
is unstable. In the case of endogenous discounting
the steady state is always unique and stable as indicated by the
black arrows.
4.3 Calibration
Most parameter choices are taken straight from the international business cycle literature and are summarized in Table 1. The utility function is assumed to be additive separable between labor and consumption
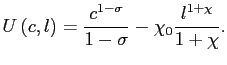
|
(23) |
Following assumption 2a the convex portfolio costs are chosen to be quadratic
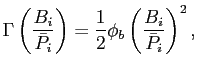
|
(24) |
and under assumption 2b the endogenous discount factor is given by
![$\displaystyle \beta\left( c_{i},l_{i}\right) =\left[ 1+\exp\left( \frac{c^{1-\sigma} }{1-\sigma}-\chi_{0}\frac{l^{1+\chi}}{1+\chi}\right) \right] ^{-\psi_{i}}.$](img208.gif)
|
(25) |
The ![]() 's are chosen such that
's are chosen such that
![]() takes on the
value of
takes on the
value of ![]() at the steady state. The parameters
at the steady state. The parameters
![]() and
and
![]() determine the home bias in
consumption. Following the applied DSGE literature, these
consumption weights are chosen to match the import to GDP ratio for
the U.S., which is about 13% .17
determine the home bias in
consumption. Following the applied DSGE literature, these
consumption weights are chosen to match the import to GDP ratio for
the U.S., which is about 13% .17
5 Results
Before discussing the results for the dynamic economy a look at
the steady state equilibria for this economy seems instructive.
Similar to the endowment economy in Section 2, there are
three steady states absent international financial markets provided
that the elasticity of substitution between the traded goods
![]() is sufficiently low. For the
above calibration this is true for
is sufficiently low. For the
above calibration this is true for ![]() .18 The same steady states arise with
incomplete markets under the additional restriction that steady
state bond holdings are zero.
.18 The same steady states arise with
incomplete markets under the additional restriction that steady
state bond holdings are zero.
For an elasticity of substitution
![]()
![]() the three
different values of the relative price that are consistent with an
equilibrium are given in the first column of Table 2. Furthermore,
Table 2
summarizes how capital, employment and output in country
1 differ across steady states. The value of
variable
the three
different values of the relative price that are consistent with an
equilibrium are given in the first column of Table 2. Furthermore,
Table 2
summarizes how capital, employment and output in country
1 differ across steady states. The value of
variable
![]() for
country 2 coincides with
for
country 2 coincides with
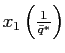 . In contrast to
the endowment economy, the differences in purchasing power across
equilibria also have an impact on the supply side of the economy.
For example, if the relative price is in favor of country
1, i.e.,
. In contrast to
the endowment economy, the differences in purchasing power across
equilibria also have an impact on the supply side of the economy.
For example, if the relative price is in favor of country
1, i.e.,
![]() , country 1
accumulates higher capital, enjoys higher output and uses less
labor in the production process.
, country 1
accumulates higher capital, enjoys higher output and uses less
labor in the production process.
5.1 Convex Portfolio Costs
Under the above specification of the portfolio cost function the steady state value of bond holdings is uniquely determined to be zero. Thus, the steady states of the model with portfolio costs are the same as in the economy without international financial markets.
Similar to Bodenstein (2007), the steady state with ![]() is dynamically unstable, while the remaining two
are stable. Prior to the realization of the positive technology
shock in the foreign country, the economy is assumed to be in the
steady state with
is dynamically unstable, while the remaining two
are stable. Prior to the realization of the positive technology
shock in the foreign country, the economy is assumed to be in the
steady state with
![]() . The size of the shock is set
equal to 0.01%.
. The size of the shock is set
equal to 0.01%.
5.1.1 Impulse Response Functions
Figure 3
plots the impulse response functions for selected variables in
percentage deviations from the original steady state. Paths
1 (solid line) and 2 (dashed
line) lead back to the original steady state, whereas path
3 (dotted line) converges to the other
stable steady state with
![]() . As the magnitude of the
responses is considerably smaller for path 1 than
for the other two paths, Figure 4 plots
the responses of the variables for the non-linear solution of path
1 (solid line).
. As the magnitude of the
responses is considerably smaller for path 1 than
for the other two paths, Figure 4 plots
the responses of the variables for the non-linear solution of path
1 (solid line).
The reasoning behind the equilibrium multiplicity in the dynamic
economy is the same as in the static endowment economy: given the
predetermined capital stock, there are three locally isolated price
equilibria each associated with a different distribution of
relative purchasing power. If the capital stock adjusted quickly,
one would expect that there is one path in the neighborhood of each
of the three steady states. However, the capital stock is
predetermined relative to the shock and adjusts slowly afterwards.
Hence, only path 1 starts in the neighborhood of a
steady state - the original steady state in the case of path
1. In particular, path 3,
which converges to the steady state with
![]() , starts with allocations and
prices that are far away from their long run values. This fact is
driven by the differences in the capital stock in the original
steady state (
, starts with allocations and
prices that are far away from their long run values. This fact is
driven by the differences in the capital stock in the original
steady state (![]() ) and the new one (
) and the new one (![]() ) as reported in Table 2.
) as reported in Table 2.
Path 1 is the sole path that linearization around
the original steady state detects. In response to the transitory
technology shock output rises in the foreign country for a few
periods. Simultaneously, the real exchange rate appreciates for the
home country reflecting a change of the relative price ![]() against the foreign country. Even more purchasing
power is shifted to the home country and the home country's
consumption rises relative to the foreign country's.
against the foreign country. Even more purchasing
power is shifted to the home country and the home country's
consumption rises relative to the foreign country's.
While the dynamics for path 1 are solely driven by the increase in foreign technology, the dynamics for paths 2 and 3 are driven mostly by the large shifts in relative purchasing power towards the foreign country that are associated with the rise in the relative price of the foreign good. The effects of the technology shock are negligible in these two cases. In fact, the same responses would be obtained if the technology shock was replaced by a pure sunspot shock. Demand in the home country (consumption plus investment) falls considerably. Home output falls as well, but by less than home consumption, as the foreign country raises its demand for the home good due to generally stronger foreign demand. Furthermore, the trade balance to GDP ratio falls on impact, indicating that the home country borrows funds to smooth the consequences of the shock.
5.1.2 Local Approximation
As shown in Figure 4, path 1 can be reliably approximated using (log-)linearization techniques around the model's non-stochastic steady state. However, this is not the case for paths 2 and 3.
Consider path 3 first. In general, one should be
able to compute an approximate path using local approximation
techniques around the new steady state with
![]() . The values of the
predetermined variables (capital stocks and bonds) in the original
steady state are then taken as starting values of the system. While
this approach works reasonably well if the share of capital in
production is low, Figure 5 shows
that this is not true for the chosen calibration. The linear
approximation to path 3 (solid line) and the actual
path 3 (dotted line) differ considerably. These
differences are most obvious in the exaggerated response of the
real exchange rate and the relative price
. The values of the
predetermined variables (capital stocks and bonds) in the original
steady state are then taken as starting values of the system. While
this approach works reasonably well if the share of capital in
production is low, Figure 5 shows
that this is not true for the chosen calibration. The linear
approximation to path 3 (solid line) and the actual
path 3 (dotted line) differ considerably. These
differences are most obvious in the exaggerated response of the
real exchange rate and the relative price ![]() in the linearized framework. A second order perturbation approach
yields results that are even further away from the true path.
Equally disappointing results are obtained with a starting guess
that uses knowledge about the actual path 3, namely
the values that the state variables assume for the period right
after the shock. These observations suggest, that for a realistic
calibration of the model the deviations of the starting values from
their new steady state values are simply too large for path
3 to be correctly approximated by local
approximation methods.
in the linearized framework. A second order perturbation approach
yields results that are even further away from the true path.
Equally disappointing results are obtained with a starting guess
that uses knowledge about the actual path 3, namely
the values that the state variables assume for the period right
after the shock. These observations suggest, that for a realistic
calibration of the model the deviations of the starting values from
their new steady state values are simply too large for path
3 to be correctly approximated by local
approximation methods.
In the case of path 2 the attempt of using local
approximation techniques is even less successful. Prior to
computing path 2 it is not even known whether path
2 converges back to the original steady
state or to the other stable steady state. Depending on the
magnitude of the technology shock and the share of capital in
production
![]() , one can find either behavior.
Even if the convergence properties of path 2 are
known, one faces the question how to approximate this path by a
first- or second-order approximation technique that expands the
equilibrium system around the steady state to which the system will
converge. For a given realization of the state variables
(technology, home and foreign capital, international bond holdings)
these methods prescribe a unique adjustment path. As the economy is
in steady state prior to the shock, the adjustment path that is
recovered using perturbation methods is path 1.
Using the values of the state variables of the first period after
the shock along the true path 2 rather than those
of the period of the shock as starting values in the approximated
decision rules does not recover path 2 either.
, one can find either behavior.
Even if the convergence properties of path 2 are
known, one faces the question how to approximate this path by a
first- or second-order approximation technique that expands the
equilibrium system around the steady state to which the system will
converge. For a given realization of the state variables
(technology, home and foreign capital, international bond holdings)
these methods prescribe a unique adjustment path. As the economy is
in steady state prior to the shock, the adjustment path that is
recovered using perturbation methods is path 1.
Using the values of the state variables of the first period after
the shock along the true path 2 rather than those
of the period of the shock as starting values in the approximated
decision rules does not recover path 2 either.
5.2 Endogenous Discount Factor
As discussed in more detail in Bodenstein (2007), there is
always a unique steady state irrespective of the value of the trade
elasticity if the agents' discount factors are endogenous. In the
following I calibrate the free parameters in the functional form of
the endogenous discount factor such that the unique stable steady
state features ![]() . Obviously, this
uniqueness is somewhat artificial, since the underlying economy
without endogenous discounting still has multiple steady states
with zero bond holdings if
. Obviously, this
uniqueness is somewhat artificial, since the underlying economy
without endogenous discounting still has multiple steady states
with zero bond holdings if
![]() for the above calibration.
for the above calibration.
However, the analysis with an endogenous discount factor
provides insights that go beyond those gained in the model with
convex portfolio costs. First, the version of the model allows for
the construction of equilibria around the symmetric steady state as
in Corsetti et al (2008) and Thoenissen (2008). Second, it turns
out that there can be multiple equilibria even if
![]() , i.e., for calibrations that
never admit multiple steady states.
, i.e., for calibrations that
never admit multiple steady states.
5.2.1 Impulse Response Functions
Figure 6 plots the
impulse response functions for selected endogenous variables for
![]() to a purely transitory
shock to the foreign country's technology level of 0.01%. Similar to the analysis under convex portfolio costs,
the technology shock is the major determinant of the equilibrium
dynamics for only one of the three paths. The other two paths are
associated with large shifts in relative purchasing power and the
effects of the technology shock are negligible. However, all these
paths lead the economy back to the original steady state with
to a purely transitory
shock to the foreign country's technology level of 0.01%. Similar to the analysis under convex portfolio costs,
the technology shock is the major determinant of the equilibrium
dynamics for only one of the three paths. The other two paths are
associated with large shifts in relative purchasing power and the
effects of the technology shock are negligible. However, all these
paths lead the economy back to the original steady state with
![]() .
.
Path 1 (solid line) implies a persistent decline
of the relative price ![]() that increases the
purchasing power of the home country. Consequently, home
consumption, investment, and output show a strong rise. The foreign
country is willing to trade at the low relative price in order to
receive at least some of the home good from which it can hardly
substitute away. The roles are reversed for path 3
(dotted line) which features a strong rise in the relative
price.
that increases the
purchasing power of the home country. Consequently, home
consumption, investment, and output show a strong rise. The foreign
country is willing to trade at the low relative price in order to
receive at least some of the home good from which it can hardly
substitute away. The roles are reversed for path 3
(dotted line) which features a strong rise in the relative
price.
Path 2 (dashed line) has received considerable
attention in the recent literature, see, e.g., the work of Corsetti
et al (2008) and Thoenissen (2008). Subject to some caveats
discussed below, this is the unique path that is recovered by
linearization around the model's steady state.19 The increase in
foreign technology raises foreign output. In contrast to the
dynamics under a high elasticity of substitution the price of the
foreign good does not need to fall under a low elasticity of
substitution: if ![]() rises, the value of the
foreign country's production increases, while it falls in the home
country. In both countries there is a tendency to substitute away
from the more expensive foreign good. This situation can only be an
equilibrium if the increase in purchasing power in the foreign
country offsets the negative impact that the higher price and lower
home income exert on overall demand for the foreign good.
rises, the value of the
foreign country's production increases, while it falls in the home
country. In both countries there is a tendency to substitute away
from the more expensive foreign good. This situation can only be an
equilibrium if the increase in purchasing power in the foreign
country offsets the negative impact that the higher price and lower
home income exert on overall demand for the foreign good.
Corsetti et al (2008) refer to the appreciation of the terms of
trade in light of a positive supply shock as "negative
transmission mechanism".20 From an applied point of view, path
2 has certain appealing features. In a
richer model with distribution costs and nontraded goods, Corsetti
et al (2008) invoke this mechanism to address two important puzzles
in the international macroeconomics literature, namely the
Backus-Smith puzzle (Backus and Smith (1993)) and the real exchange
rate volatility puzzle. If the implied elasticity of substitution
between foreign and domestic goods is low enough, an appreciation
of the relative price and the real exchange rate for the home
country goes along with an increase in the home country's
consumption relative to the foreign country's. In addition, the
real exchange rate is about as volatile as in the data.
Furthermore, just as the model presented in Thoenissen (2008) and
in line with the data their model predicts a negative cross-country
correlation for consumption and a negative correlation of output
with the real exchange rate - a major step forward relative to
previous attempts in the literature. The model presented here can
replicate all of these findings if ![]() is
sufficiently close to but less than a critical value of -1.4685. The next section sheds more light on this critical
value of the trade elasticity of substitution.
is
sufficiently close to but less than a critical value of -1.4685. The next section sheds more light on this critical
value of the trade elasticity of substitution.
5.2.2 Multiple Equilibria and the Short-Run Excess Demand Function
In Section 5.1 the analysis of
the multiple equilibrium paths relies on the presence of multiple
steady state equilibria, i.e.,
![]() . However, as just shown
equilibrium multiplicity can also occurs if there is a unique
steady state with
. However, as just shown
equilibrium multiplicity can also occurs if there is a unique
steady state with
![]() . The reason for this finding
lies in the behavior of the economy in the short-run: the capital
stock is not fully flexible. Consequently, if the relative price
moves against country
. The reason for this finding
lies in the behavior of the economy in the short-run: the capital
stock is not fully flexible. Consequently, if the relative price
moves against country ![]() its agents' ability to
lower the production of good
its agents' ability to
lower the production of good ![]() and offset some of
the adverse movements in the relative price is diminished. Hence,
multiple equilibria can exist in the short run but may be absent in
the long run.
and offset some of
the adverse movements in the relative price is diminished. Hence,
multiple equilibria can exist in the short run but may be absent in
the long run.
More formally, the short-run excess demand function can be
upward-sloping while the long-run excess demand function is
downward-sloping. Figure 7 plots the slope
of the excess demand function around
![]() , i.e., the partial derivative of
the excess demand for good 2 with respect to
the relative price, denoted by
, i.e., the partial derivative of
the excess demand for good 2 with respect to
the relative price, denoted by
![]() ,
for the two horizons as a function of
,
for the two horizons as a function of ![]() . The
underlying derivations are provided in Appendix A.
The scale for the short-run and the long-run slopes are depicted on
the left and the right vertical axis, respectively. A positive
value of the slope indicates the presence of multiple equilibria.
The curve labeled "long run excess demand'' intersects the
horizontal axis at
. The
underlying derivations are provided in Appendix A.
The scale for the short-run and the long-run slopes are depicted on
the left and the right vertical axis, respectively. A positive
value of the slope indicates the presence of multiple equilibria.
The curve labeled "long run excess demand'' intersects the
horizontal axis at
![]() , whereas the curve labeled
"short run excess demand'' intersects with the horizontal axis for
the higher value of
, whereas the curve labeled
"short run excess demand'' intersects with the horizontal axis for
the higher value of
![]() .
.
The change in the sign of the slope of the excess demand
function,
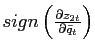 , can be easily detected by looking at the policy function for the
relative price
, can be easily detected by looking at the policy function for the
relative price ![]() that is obtained from
linearization around the steady state with
that is obtained from
linearization around the steady state with
![]() . If
. If
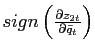 changes sign so do the coefficients on the endogenous state
variables in the policy function for the relative price.
changes sign so do the coefficients on the endogenous state
variables in the policy function for the relative price.
To offer an economic interpretation, consider the coefficient on
current bond holdings which is denoted by
![]() . This
coefficient is positive if
. This
coefficient is positive if
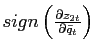 is positive and negative otherwise. Suppose
is positive and negative otherwise. Suppose
![]() , i.e., the home country lends
funds to the foreign country in period t - 1. In order
to pay back its debt obligations in time t, the
foreign country has to increase its total export revenue which
implies that the price and/or the number of exported units have to
rise. If
, i.e., the home country lends
funds to the foreign country in period t - 1. In order
to pay back its debt obligations in time t, the
foreign country has to increase its total export revenue which
implies that the price and/or the number of exported units have to
rise. If
![]() , the
foreign country increases the number of units determined for
exports and the relative price of the foreign good falls. Since the
elasticity of substitution is high, a small decline in the price
leads to a relatively large increase in exports and the total
export revenue rises. If
, the
foreign country increases the number of units determined for
exports and the relative price of the foreign good falls. Since the
elasticity of substitution is high, a small decline in the price
leads to a relatively large increase in exports and the total
export revenue rises. If
![]() , the
relative price of the foreign good increases and the number of
exported units falls. However, since the substitutability between
the traded goods is low, a large price increase leads to a
relatively small decline in the number of exported units and the
total export revenue rises.21
, the
relative price of the foreign good increases and the number of
exported units falls. However, since the substitutability between
the traded goods is low, a large price increase leads to a
relatively small decline in the number of exported units and the
total export revenue rises.21
Remember, that the slope of the short-run excess demand function
is close to zero in the neighborhood of
![]() for the equilibrium with
for the equilibrium with
![]() . When deriving the linear
approximation to the law of motion of the relative price one
divides by a number that is arbitrarily close to zero. This finding
explains why Thoenissen (2008), Corsetti et al (2008), de Walque et
al (2005), and Benigno and Thoenissen (2008) find that in each of
their models there is a critical value of the trade elasticity of
substitution for which the volatility of the real exchange rate is
infinite. Such behavior of the model is again indicative of
equilibrium multiplicity.22
. When deriving the linear
approximation to the law of motion of the relative price one
divides by a number that is arbitrarily close to zero. This finding
explains why Thoenissen (2008), Corsetti et al (2008), de Walque et
al (2005), and Benigno and Thoenissen (2008) find that in each of
their models there is a critical value of the trade elasticity of
substitution for which the volatility of the real exchange rate is
infinite. Such behavior of the model is again indicative of
equilibrium multiplicity.22
5.2.3 Local Approximation
The existence of multiple equilibria poses some challenges to
applying the model with a low trade elasticity of substitution. For
example, it turns out that for a sufficiently large technology
shock only one of the three equilibrium paths exists. For
![]() the maximum size of the
technology shock in the foreign country for which all three paths
exists is around 0.1%. For shocks larger than
0.1%, only path 1
exists.23
the maximum size of the
technology shock in the foreign country for which all three paths
exists is around 0.1%. For shocks larger than
0.1%, only path 1
exists.23
In particular, this finding poses a problem if relying on local approximation techniques. Log-linearization around the model's unique steady state delivers an approximation of path 2 as the sole equilibrium path. Figures 8 and 9 show the possible computational errors for a calibration of the technology shock that follows Backus et al (1995). The shock to the foreign country's technology is 0.85% with persistence of 0.95. The solid line in Figure 8 shows the unique equilibrium path for this technology shock. The dashed line is the suggested solution path derived from log-linearization around the steady state. The discrepancy between the two paths is obviously large. To convince the reader of the (in-)accuracy of the two suggested solution paths Figure 9 plots the approximation errors in the three dynamic equations of the model: the two Euler equations for capital and the risk sharing condition. The systematic nature of the approximation error indicates, that the dashed line (path 2) is not a solution of the model for a technology shock of size 0.85%.
The closer the value of the elasticity of substitution is to the
threshold level of
![]() (meaning
(meaning ![]() close to -1.4685, the smaller is the size of the
technology shock for which path 2 exists. For a
calibration of
close to -1.4685, the smaller is the size of the
technology shock for which path 2 exists. For a
calibration of
![]() as in Section 5.1, all three
impulse responses exist for a 0.85% technology
shock.
as in Section 5.1, all three
impulse responses exist for a 0.85% technology
shock.
6 Sensitivity
The results are sensitive to three types of changes: parameters, model specification and the assumptions about financial markets. If financial markets are complete with respect to all states of nature (fundamental and non-fundamental), the equilibrium is always unique. However, if agents cannot insure against self-fulfilling fluctuations, sunspot equilibria can be constructed and there will be multiple equilibria provided that the trade elasticity is sufficiently low. Therefore, multiple equilibria will also be present in models with a richer set of assets, unless the assets span the complete market. As noted earlier, fundamental shocks are not really needed in the analysis, but they facilitate the computations and allow for comparisons of my results to the literature.
6.1 Sensitivity to Parametrization
Changes in the underlying model parameters affect the threshold
level of the trade elasticity
![]() for which the model
displays multiple equilibria as follows:
for which the model
displays multiple equilibria as follows:
![$\displaystyle \begin{tabular}[c]{lllll} $\omega_{ki}$\ & $\downarrow$\ & $\Longrightarrow$\ & $\bar{\varepsilon}$\ & $\uparrow$\\ $\kappa$\ & $\downarrow$\ & $\Longrightarrow$\ & $\bar{\varepsilon}$\ & $\uparrow $\\ $\alpha_{ii}$\ & $\uparrow$\ & $\Longrightarrow$\ & $\bar{\varepsilon}$\ & $\uparrow$\\ $\chi$\ & $\uparrow$\ & $\Longrightarrow$\ & $\bar{\varepsilon}$\ & $\downarrow$ \end{tabular}$](img326.gif)
|
(26) |
Both lowering the share of capital in production
![]() or the elasticity of
substitution between capital and labor
or the elasticity of
substitution between capital and labor ![]() makes
the economy look more like an endowment economy and raises the
threshold level
makes
the economy look more like an endowment economy and raises the
threshold level
![]() for which multiple
equilibria are observed. Increasing home bias, i.e., a rise in
for which multiple
equilibria are observed. Increasing home bias, i.e., a rise in
![]() , also leads to a higher value of
, also leads to a higher value of
![]() as shifts in relative
purchasing power become less relevant with each country consuming
mostly its own good.
as shifts in relative
purchasing power become less relevant with each country consuming
mostly its own good.
The effect of lowering the labor supply elasticity (raising
![]() ) depends on the value of
) depends on the value of ![]() . If
. If ![]() , the threshold level
, the threshold level
![]() falls in response to a
rise in
falls in response to a
rise in ![]() . However, if
. However, if ![]() , a rise in
, a rise in ![]() lowers
lowers
![]() . All these results can be
obtained more formally from the derivations of the long- and
short-run excess demand function that are provided in Appendix
A.
. All these results can be
obtained more formally from the derivations of the long- and
short-run excess demand function that are provided in Appendix
A.
6.2 Sensitivity to Model Specification
Multiple equilibria of the type discussed here can also occur in richer models with a low trade elasticity of substitution. A prominent example is the model with nontraded goods and distribution costs that is at the core of Corsetti et al (2008). In that model the implied elasticity of substitution between the home and foreign good at the consumer level is endogenous. Corsetti and Dedola (2005) mention the possibility of multiple steady states in such a model but do not analyze the dynamic case.
The following example serves to highlight some additional
challenges that arise in models with distribution costs. Assume
that agents in country ![]() are endowed with
are endowed with
![]() units of the traded good
units of the traded good ![]() and
and ![]() units of a nontraded good. Agents
consume the two traded goods and their own nontraded good. However,
in order to consume one unit of a traded good, agents have to
forgive
units of a nontraded good. Agents
consume the two traded goods and their own nontraded good. However,
in order to consume one unit of a traded good, agents have to
forgive ![]() units of their nontraded good. In the
static economy agent
units of their nontraded good. In the
static economy agent ![]() solves
solves
![$\displaystyle \max_{{ c_{iT},c_{iN},c_{i1},c_{i2}}}c_{i}=\left[ \left( \alpha _{iT}\right) ^{1-\phi}c_{iT}^{\phi}+\left( \alpha_{iN}\right) ^{1-\phi }c_{iN}^{\phi}\right] ^{\frac{1}{\phi}}$](img346.gif)
|
(27) | |
| s.t. | ||
| (28) |
where
![$ c_{iT}=\left[ \left( \alpha_{i1}\right) ^{1-\rho}c_{i1}^{\rho }+\left( \alpha_{i2}\right) ^{1-\rho}c_{i2}^{\rho}\right] ^{\frac{1}{\rho} }$](img348.gif) . The market clearing conditions for this economy are
. The market clearing conditions for this economy are
| (29) | ||
| (30) | ||
| (31) |
with ![]() . Following Corsetti et al (2008), let
. Following Corsetti et al (2008), let
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
, ![]() ,
,
![]() , and
, and
![]() . I set the ratio of nontraded to
traded goods
. I set the ratio of nontraded to
traded goods
![]() equal to 2.25, which is of similar magnitude as the ratio of service
to manufacturing output in the U.S., the common proxies for traded
and nontraded goods. For this parametrization, the trade elasticity
of substitution between the foreign and the domestic good is around
0.27, the producer price elasticity of
traded goods is around 0.68, and the consumer price
elasticity of traded goods is
equal to 2.25, which is of similar magnitude as the ratio of service
to manufacturing output in the U.S., the common proxies for traded
and nontraded goods. For this parametrization, the trade elasticity
of substitution between the foreign and the domestic good is around
0.27, the producer price elasticity of
traded goods is around 0.68, and the consumer price
elasticity of traded goods is
![]() .
.
This endowment economy features a unique equilibrium with the
relative price
![]() . Consider,
however, a 3 percent decline of the endowment with both traded
goods while keeping the endowment with nontraded goods constant.
Two new equilibria arise, one with
. Consider,
however, a 3 percent decline of the endowment with both traded
goods while keeping the endowment with nontraded goods constant.
Two new equilibria arise, one with
![]() and the other one with
and the other one with
![]() . However, the equilibrium
remains unique if the endowment with traded goods increases in both
countries by the same amount. Hence, with an endogenous trade
elasticity of substitution symmetric shocks can have very different
implications for the number of equilibria and the resulting
dynamics of the model.
. However, the equilibrium
remains unique if the endowment with traded goods increases in both
countries by the same amount. Hence, with an endogenous trade
elasticity of substitution symmetric shocks can have very different
implications for the number of equilibria and the resulting
dynamics of the model.
7 Conclusions
Dynamic models with multiple equilibria can give rise to complex dynamics. As a first step, I characterize the dynamics of three equilibrium paths in a standard model of the international business cycle under the assumption that the elasticity of substitution between traded goods is low.
The empirical literature reports a wide range of trade elasticities at the aggregate level from 0 to 1.5. Recent macroeconomic research has pointed towards low trade elasticities: Corsetti, Dedola, and Leduc (2008), Thoenissen (2008) and others have shown that business cycle models with low trade elasticities may explain several puzzles in international macroeconomics, such as the Backus-Smith puzzle, the real exchange rate volatility puzzle, or the cross country correlation puzzles for consumption and output (see Thoenissen (2008) for a comprehensive list). In estimated DSGE models Rabanal and Tuesta (2005), Lubik and Schorfheide (2005), and de Walque, Smets, and Wouters (2005) show estimates for the trade elasticity that are very low and in some cases close to zero. At least in some of these cases the results hinge on values of the trade elasticity of substitution that imply the presence of multiple equilibria. However, no study has discussed the presence multiple equilibria in these DSGE models in depth, let alone the possible dynamics.24
Going forward the literature faces two major possibilities to address the aforementioned aspects of the data. Using the insights of this paper, one can proceed by building fully stochastic general equilibrium models with low trade elasticities that explicitly allow for sunspot equilibria. Such work requires the use of global approximation methods and is computationally intensive. It also seems important to continue the search for alternative models. Oil shocks as in Backus and Crucini (1998) and Bodenstein, Erceg, Guerrieri (2008), or investment-specific shocks as in Raffo (2008) are potentially promising. In the meantime trade adjustment costs as in Erceg, Guerrieri and Gust (2006) and taste shocks as in Corsetti et al (2008) can serve as simple fixes in the estimation of DSGE models to prevent the estimation algorithm from forcing the elasticity of substitution towards very low values in the attempt of fitting the model to the data.
References
Azariadis, C. (1981). Self-fulfillling Prophecies. Journal of Economic Theory 25, 380-396.
Backus, D., and M. Crucini (1998). Oil Prices and the Terms of Trade. Journal of International Economics 50, 185-213.
Backus, D., P. Kehoe, and F. Kydland (1995). International Business Cycles: Theory and Evidence. In T. Cooley (ed.) Frontiers of Business Cycle Research Princeton University Press, 331-356.
Backus, D. and G. Smith (1993). Consumption and Real Exchange Rates in Dynamic Economies with Non-traded Goods. Journal of International Economics 35, 297-316.
Benhabib, J. and R. Farmer (1994). Indeterminacy and Increasing Returns. Journal of Economic Theory 63, 19-46.
Benigno, G. and C. Thoenissen (2008). Consumption and Real Exchange Rates with Incomplete Markets and Non-traded Goods. Journal of International Money and Finance, forthcoming.
Bodenstein, M. (2007). Closing Large Open Economy Models. International Finance Discussion Papers 867, Board of Governors of the Federal Reserve System.
Bodenstein, M., C. Erceg, and L. Guerrieri (2007). Oil Shocks and External Adjustment. International Finance Discussion Papers 897, Board of Governors of the Federal Reserve System.
Boileau, M. and M. Normandin (2005). Closing International Real Business Cycle Models with Restricted Financial Markets. Center for Economic Analysis, University of Colorado at Boulder.
Broda, C. and D. Weinstein (2006). Globalization and the Gains from Variety. Quarterly Journal of Economics 121, 541-585.
Cass, D. and K. Shell (1983). Do Sunspots Matter? Journal of Political Economy 91, 193-227.
Chari, V.V., P. Kehoe, and E. McGrattan (2002). Can Sticky Prices Generate Volatile and Persistent Real Exchange Rates? Review of Economic Studies 69, 633-63.
Chiappori, P. and R. Guesnerie (1991). Sunspot Equilibria in Sequential Market Models. In W. Hildenbrand and H. Sonnenschein (eds.) Handbook of Mathematical Economics, vol.4. Amsterdam: North Holland.
Collard, F. and H. Dellas (2002). Technology Shocks and Employment. CEPR Discussion Papers 3680.
Corsetti, G. and L. Dedola (2005). A Macroeconomic Model of International Price Discrimination. Journal of International Economics 67, 129-155.
Corsetti, G., L. Dedola, and S. Leduc (2005). International Risk-sharing and the Transmission of Productivity Shocks. Review of Economic Studies 75, 443-473.
de Walque, G., F. Smets, and R. Wouters (2005). An Estimated Two Country DSGE Model for the Euro Area and the US Economy. Working Paper.
Enders, Z. and G. Mueller (2008). On the International Transmission of Technology Shocks. EUI Working Paper ECO 2006/36.
Epstein, L. (1983). Stationary Cardinal Utility and Optimal Growth under Uncertainty. Journal of Economic Theory 31, 133-152.
Epstein, L. (1987). A Simple Dynamic General Equilibrium Model. Journal of Economic Theory 41, 68-95.
Erceg C., C. Gust, and L. Guerrieri (2006). SIGMA: A New Open Economy Model for Policy Analysis. International Journal of Central Banking 2, 1-50.
Ghironi, F. (2003). Macroeconomic Interdependence under Incomplete Markets. Journal of International Economics 70, 428-450.
Heathcote, J. and F. Perri (2002). Financial Autarchy and International Business Cycles. Journal of Monetary Economics 49, 601-627.
Hooper, P., K. Johnson, and J. Marquez (2000). Trade Elasticities for the G-7 Countries. Princeton Studies in International Economics 87.
Kehoe, T. (1980). An Index Theorem for General Equilibrium Models with Production. Econometrica 48, 1211-1232.
Kehoe, T. (1991). Computation and Multiplicity of Equilibria. In W. Hildenbrand and H. Sonnenschein (eds.) Handbook of Mathematical Economics, vol.4. Amsterdam: North Holland.
Kim, S. and M. Kose (2003). Dynamics of Open Economy Business Cycle Models: Role of the Discount Factor. Macroeconomic Dynamics 7, 263-290.
Lubik, T. and Schorfheide F. (2005). A Bayesian Look at New Open Economy Macroeconomics. NBER Macroeconomics Annual 2005.
Mas-Colell, A., M. Whinston and J. Green (1995). Microeconomic Analysis. Oxford University Press, Oxford, UK.
Mendoza, E. (1991). Real Business Cycles in a Small Open Economy. American Economic Review 81, 797-818.
Rabanal, P. and V. Tuesta (2005). Euro-Dollar Real Exchange Rate Dynamics in an Estimated Two-country Model: What is Important and What is Not. International Monetary Fund.
Raffo, A. (2008). Technology Shocks: Novel Implications for International Business Cycles. Board of Governors of the Federal Reserve System.
Schmitt-Grohé, S. and M. Uribe (2003). Closing Small Open Economy Models. Journal of International Economics 61, 163-185.
Taylor, J. (1993). Macroeconomic Policy in a World Economy: from Economic Design to Practical Operation. Norton, New York, NY.
Thoenissen, C. (2008). Exchange Rate Dynamics, Asset Market Structure, and the Role of the Trade Elasticity. CDMA Working Paper Series 0803.
Uzawa, H. (1968). Time Preference, the Consumption Function and Optimum Asset Holdings. In J. Wolfe (ed), Value, capital and growth: papers in honor of Sir John Hicks. The University of Edinburgh Press, Edinburgh, 485-504.
Whalley, J. (1985). Trade Liberalization among Major World Trading Areas. MIT Press, Cambridge, MA.
Table 1: Calibration of Baseline Model - Panel A: Parameters Governing Households' Behavior
| Parameter | Used to Determine |
|---|---|
| β = 0.99 | discount factor |
| σ = 1 | intertemporal consumption elasticity |
| α11 = 0.87 | weight on good 1 country 1's cons. basket |
| α21 = 0.13 | weight on good 1 country 2's cons. basket |
| χ = 5 | labor supply elasticitya |
| ρ = -1.65 | elasticity between traded goods |
| α12 = 0.13 | weight on good 2 country 1's cons. basket |
| α22 = 0.87 | weight on good 2 country 2's cons. basket |
a The Frisch elasticity is 1/χ = 0.2.
Table 1: Calibration of Baseline Model - Panel B: Parameters Governing Firms' Behavior
| Parameter | Used to Determine |
|---|---|
| ωk = 0.33 | share of capital in production |
| δ = 0.025 | depreciation rate of capital |
| ωl = 0.67 | share of capital in production |
Table 1: Calibration of Baseline Model - Panel C: Parameters Governing Asset Dynamics
| Parameter | Used to Determine |
|---|---|
| ψ1 = 0.0275 | endogenous discounting |
| φb = 0.0025 | adjustment costs |
| ψ2 = 0.0275 | endogenous discounting |
Table 2: Steady State Values of Selected Prices and Allocations
Relative Price: | Domestic Output: | Domestic Capital: | Domestic Labor: |
|---|---|---|---|
0.35 |
1.87 |
19.5 |
0.22 |
1.00 |
1.81 |
17.0 |
0.23 |
2.86 |
1.72 |
13.5 |
0.24 |
Steady state values
for country 2 are mirroring the values for country
1. The value for variable x2, at the equilibrium with
![]() coincides with the
equilibrium value for variable x1 at the
equilibrium
coincides with the
equilibrium value for variable x1 at the
equilibrium
![]() .
.
Figure 1: Excess Demand Function in the Endowment Economy
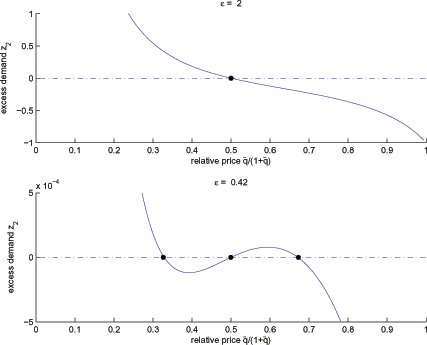
Data for Figure 1
Relative Price: epsilon = 2 | Excess Demand: epsilon = 2 | Relative Price: epsilon = 0.42 | Excess Demand: epsilon = 0.42 |
|---|---|---|---|
0.010000 |
92.729934 |
0.010000 |
0.357704 |
0.014945 |
59.834305 |
0.014945 |
0.244339 |
0.019890 |
43.381403 |
0.019890 |
0.181651 |
0.024835 |
33.544174 |
0.024835 |
0.141842 |
0.029780 |
27.023144 |
0.029780 |
0.114399 |
0.034725 |
22.398591 |
0.034725 |
0.094418 |
0.039670 |
18.958927 |
0.039670 |
0.079287 |
0.044615 |
16.308235 |
0.044615 |
0.067483 |
0.049560 |
14.208765 |
0.049560 |
0.058059 |
0.054505 |
12.509170 |
0.054505 |
0.050394 |
0.059450 |
11.108562 |
0.059450 |
0.044062 |
0.064395 |
9.937125 |
0.064395 |
0.038764 |
0.069340 |
8.945029 |
0.069340 |
0.034284 |
0.074285 |
8.095772 |
0.074285 |
0.030458 |
0.079230 |
7.362013 |
0.079230 |
0.027165 |
0.084175 |
6.722880 |
0.084175 |
0.024311 |
0.089120 |
6.162169 |
0.089120 |
0.021821 |
0.094065 |
5.667114 |
0.094065 |
0.019637 |
0.099010 |
5.227529 |
0.099010 |
0.017711 |
0.103955 |
4.835186 |
0.103955 |
0.016007 |
0.108900 |
4.483376 |
0.108900 |
0.014491 |
0.113845 |
4.166570 |
0.113845 |
0.013139 |
0.118790 |
3.880177 |
0.118790 |
0.011928 |
0.123735 |
3.620353 |
0.123735 |
0.010841 |
0.128680 |
3.383859 |
0.128680 |
0.009863 |
0.133625 |
3.167944 |
0.133625 |
0.008980 |
0.138570 |
2.970261 |
0.138570 |
0.008182 |
0.143515 |
2.788793 |
0.143515 |
0.007458 |
0.148460 |
2.621802 |
0.148460 |
0.006801 |
0.153405 |
2.467779 |
0.153405 |
0.006203 |
0.158350 |
2.325411 |
0.158350 |
0.005659 |
0.163295 |
2.193548 |
0.163295 |
0.005162 |
0.168240 |
2.071181 |
0.168240 |
0.004709 |
0.173185 |
1.957421 |
0.173185 |
0.004294 |
0.178130 |
1.851481 |
0.178130 |
0.003915 |
0.183075 |
1.752664 |
0.183075 |
0.003567 |
0.188020 |
1.660349 |
0.188020 |
0.003248 |
0.192965 |
1.573980 |
0.192965 |
0.002956 |
0.197910 |
1.493063 |
0.197910 |
0.002687 |
0.202855 |
1.417150 |
0.202855 |
0.002440 |
0.207800 |
1.345843 |
0.207800 |
0.002214 |
0.212745 |
1.278779 |
0.212745 |
0.002005 |
0.217690 |
1.215631 |
0.217690 |
0.001814 |
0.222635 |
1.156105 |
0.222635 |
0.001638 |
0.227580 |
1.099931 |
0.227580 |
0.001476 |
0.232525 |
1.046865 |
0.232525 |
0.001327 |
0.237470 |
0.996685 |
0.237470 |
0.001190 |
0.242415 |
0.949188 |
0.242415 |
0.001064 |
0.247360 |
0.904188 |
0.247360 |
0.000949 |
0.252305 |
0.861514 |
0.252305 |
0.000842 |
0.257250 |
0.821012 |
0.257250 |
0.000745 |
0.262195 |
0.782537 |
0.262195 |
0.000656 |
0.267140 |
0.745958 |
0.267140 |
0.000574 |
0.272085 |
0.711152 |
0.272085 |
0.000499 |
0.277030 |
0.678009 |
0.277030 |
0.000430 |
0.281975 |
0.646425 |
0.281975 |
0.000368 |
0.286920 |
0.616303 |
0.286920 |
0.000311 |
0.291865 |
0.587554 |
0.291865 |
0.000259 |
0.296810 |
0.560097 |
0.296810 |
0.000211 |
0.301755 |
0.533856 |
0.301755 |
0.000169 |
0.306700 |
0.508758 |
0.306700 |
0.000130 |
0.311645 |
0.484738 |
0.311645 |
0.000095 |
0.316590 |
0.461735 |
0.316590 |
0.000064 |
0.321535 |
0.439690 |
0.321535 |
0.000036 |
0.326480 |
0.418551 |
0.326480 |
0.000011 |
0.331425 |
0.398267 |
0.331425 |
-0.000012 |
0.336370 |
0.378792 |
0.336370 |
-0.000031 |
0.341315 |
0.360081 |
0.341315 |
-0.000048 |
0.346260 |
0.342094 |
0.346260 |
-0.000063 |
0.351205 |
0.324792 |
0.351205 |
-0.000076 |
0.356150 |
0.308139 |
0.356150 |
-0.000087 |
0.361095 |
0.292101 |
0.361095 |
-0.000096 |
0.366040 |
0.276646 |
0.366040 |
-0.000103 |
0.370985 |
0.261744 |
0.370985 |
-0.000109 |
0.375930 |
0.247367 |
0.375930 |
-0.000113 |
0.380875 |
0.233488 |
0.380875 |
-0.000117 |
0.385820 |
0.220082 |
0.385820 |
-0.000118 |
0.390765 |
0.207126 |
0.390765 |
-0.000119 |
0.395710 |
0.194596 |
0.395710 |
-0.000119 |
0.400655 |
0.182472 |
0.400655 |
-0.000118 |
0.405600 |
0.170734 |
0.405600 |
-0.000116 |
0.410545 |
0.159362 |
0.410545 |
-0.000113 |
0.415490 |
0.148340 |
0.415490 |
-0.000110 |
0.420435 |
0.137648 |
0.420435 |
-0.000106 |
0.425380 |
0.127273 |
0.425380 |
-0.000101 |
0.430325 |
0.117198 |
0.430325 |
-0.000096 |
0.435270 |
0.107408 |
0.435270 |
-0.000090 |
0.440215 |
0.097890 |
0.440215 |
-0.000085 |
0.445160 |
0.088631 |
0.445160 |
-0.000078 |
0.450105 |
0.079617 |
0.450105 |
-0.000072 |
0.455050 |
0.070838 |
0.455050 |
-0.000065 |
0.459995 |
0.062282 |
0.459995 |
-0.000058 |
0.464940 |
0.053937 |
0.464940 |
-0.000051 |
0.469885 |
0.045794 |
0.469885 |
-0.000044 |
0.474830 |
0.037842 |
0.474830 |
-0.000037 |
0.479775 |
0.030072 |
0.479775 |
-0.000029 |
0.484720 |
0.022474 |
0.484720 |
-0.000022 |
0.489665 |
0.015041 |
0.489665 |
-0.000015 |
0.494610 |
0.007764 |
0.494610 |
-0.000008 |
0.499555 |
0.000635 |
0.499555 |
-0.000001 |
0.504500 |
-0.006355 |
0.504500 |
0.000006 |
0.509445 |
-0.013212 |
0.509445 |
0.000013 |
0.514390 |
-0.019943 |
0.514390 |
0.000020 |
0.519335 |
-0.026555 |
0.519335 |
0.000026 |
0.524280 |
-0.033056 |
0.524280 |
0.000032 |
0.529225 |
-0.039450 |
0.529225 |
0.000038 |
0.534170 |
-0.045746 |
0.534170 |
0.000043 |
0.539115 |
-0.051947 |
0.539115 |
0.000049 |
0.544060 |
-0.058061 |
0.544060 |
0.000053 |
0.549005 |
-0.064092 |
0.549005 |
0.000058 |
0.553950 |
-0.070046 |
0.553950 |
0.000062 |
0.558895 |
-0.075929 |
0.558895 |
0.000066 |
0.563840 |
-0.081745 |
0.563840 |
0.000069 |
0.568785 |
-0.087500 |
0.568785 |
0.000072 |
0.573730 |
-0.093198 |
0.573730 |
0.000074 |
0.578675 |
-0.098844 |
0.578675 |
0.000076 |
0.583620 |
-0.104442 |
0.583620 |
0.000078 |
0.588565 |
-0.109997 |
0.588565 |
0.000079 |
0.593510 |
-0.115514 |
0.593510 |
0.000079 |
0.598455 |
-0.120997 |
0.598455 |
0.000079 |
0.603400 |
-0.126450 |
0.603400 |
0.000078 |
0.608345 |
-0.131877 |
0.608345 |
0.000077 |
0.613290 |
-0.137282 |
0.613290 |
0.000075 |
0.618235 |
-0.142670 |
0.618235 |
0.000072 |
0.623180 |
-0.148044 |
0.623180 |
0.000069 |
0.628125 |
-0.153409 |
0.628125 |
0.000065 |
0.633070 |
-0.158768 |
0.633070 |
0.000060 |
0.638015 |
-0.164125 |
0.638015 |
0.000055 |
0.642960 |
-0.169484 |
0.642960 |
0.000049 |
0.647905 |
-0.174850 |
0.647905 |
0.000042 |
0.652850 |
-0.180225 |
0.652850 |
0.000035 |
0.657795 |
-0.185614 |
0.657795 |
0.000027 |
0.662740 |
-0.191021 |
0.662740 |
0.000018 |
0.667685 |
-0.196449 |
0.667685 |
0.000008 |
0.672630 |
-0.201903 |
0.672630 |
-0.000003 |
0.677575 |
-0.207386 |
0.677575 |
-0.000015 |
0.682520 |
-0.212902 |
0.682520 |
-0.000027 |
0.687465 |
-0.218456 |
0.687465 |
-0.000041 |
0.692410 |
-0.224051 |
0.692410 |
-0.000055 |
0.697355 |
-0.229692 |
0.697355 |
-0.000070 |
0.702300 |
-0.235382 |
0.702300 |
-0.000086 |
0.707245 |
-0.241127 |
0.707245 |
-0.000103 |
0.712190 |
-0.246929 |
0.712190 |
-0.000122 |
0.717135 |
-0.252794 |
0.717135 |
-0.000141 |
0.722080 |
-0.258727 |
0.722080 |
-0.000161 |
0.727025 |
-0.264731 |
0.727025 |
-0.000182 |
0.731970 |
-0.270811 |
0.731970 |
-0.000205 |
0.736915 |
-0.276973 |
0.736915 |
-0.000229 |
0.741860 |
-0.283222 |
0.741860 |
-0.000253 |
0.746805 |
-0.289561 |
0.746805 |
-0.000279 |
0.751750 |
-0.295998 |
0.751750 |
-0.000307 |
0.756695 |
-0.302537 |
0.756695 |
-0.000335 |
0.761640 |
-0.309183 |
0.761640 |
-0.000365 |
0.766585 |
-0.315944 |
0.766585 |
-0.000396 |
0.771530 |
-0.322824 |
0.771530 |
-0.000429 |
0.776475 |
-0.329830 |
0.776475 |
-0.000463 |
0.781420 |
-0.336969 |
0.781420 |
-0.000498 |
0.786365 |
-0.344247 |
0.786365 |
-0.000535 |
0.791310 |
-0.351672 |
0.791310 |
-0.000574 |
0.796255 |
-0.359251 |
0.796255 |
-0.000614 |
0.801200 |
-0.366992 |
0.801200 |
-0.000655 |
0.806145 |
-0.374902 |
0.806145 |
-0.000699 |
0.811090 |
-0.382991 |
0.811090 |
-0.000744 |
0.816035 |
-0.391267 |
0.816035 |
-0.000791 |
0.820980 |
-0.399739 |
0.820980 |
-0.000839 |
0.825925 |
-0.408417 |
0.825925 |
-0.000890 |
0.830870 |
-0.417313 |
0.830870 |
-0.000943 |
0.835815 |
-0.426435 |
0.835815 |
-0.000997 |
0.840760 |
-0.435797 |
0.840760 |
-0.001054 |
0.845705 |
-0.445410 |
0.845705 |
-0.001113 |
0.850650 |
-0.455286 |
0.850650 |
-0.001174 |
0.855595 |
-0.465440 |
0.855595 |
-0.001238 |
0.860540 |
-0.475885 |
0.860540 |
-0.001304 |
0.865485 |
-0.486638 |
0.865485 |
-0.001372 |
0.870430 |
-0.497713 |
0.870430 |
-0.001444 |
0.875375 |
-0.509128 |
0.875375 |
-0.001517 |
0.880320 |
-0.520902 |
0.880320 |
-0.001594 |
0.885265 |
-0.533054 |
0.885265 |
-0.001673 |
0.890210 |
-0.545604 |
0.890210 |
-0.001756 |
0.895155 |
-0.558575 |
0.895155 |
-0.001841 |
0.900100 |
-0.571991 |
0.900100 |
-0.001930 |
0.905045 |
-0.585876 |
0.905045 |
-0.002022 |
0.909990 |
-0.600259 |
0.909990 |
-0.002117 |
0.914935 |
-0.615169 |
0.914935 |
-0.002216 |
0.919880 |
-0.630637 |
0.919880 |
-0.002319 |
0.924825 |
-0.646698 |
0.924825 |
-0.002425 |
0.929770 |
-0.663387 |
0.929770 |
-0.002534 |
0.934715 |
-0.680745 |
0.934715 |
-0.002647 |
0.939660 |
-0.698815 |
0.939660 |
-0.002764 |
0.944605 |
-0.717644 |
0.944605 |
-0.002883 |
0.949550 |
-0.737281 |
0.949550 |
-0.003005 |
0.954495 |
-0.757783 |
0.954495 |
-0.003129 |
0.959440 |
-0.779209 |
0.959440 |
-0.003253 |
0.964385 |
-0.801626 |
0.964385 |
-0.003375 |
0.969330 |
-0.825106 |
0.969330 |
-0.003491 |
0.974275 |
-0.849727 |
0.974275 |
-0.003596 |
0.979220 |
-0.875576 |
0.979220 |
-0.003676 |
0.984165 |
-0.902751 |
0.984165 |
-0.003709 |
0.989110 |
-0.931357 |
0.989110 |
-0.003644 |
0.994055 |
-0.961511 |
0.994055 |
-0.003330 |
Figure 2: Stable Manifolds
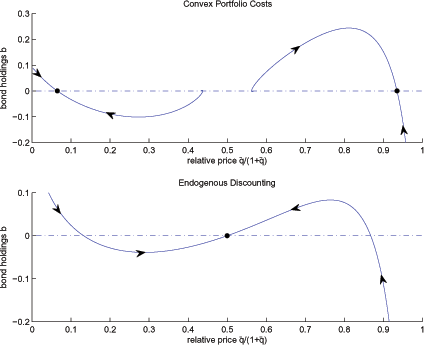
Figure 3: Impulse Responses for Selected Variables: Convex Portfolio Costs
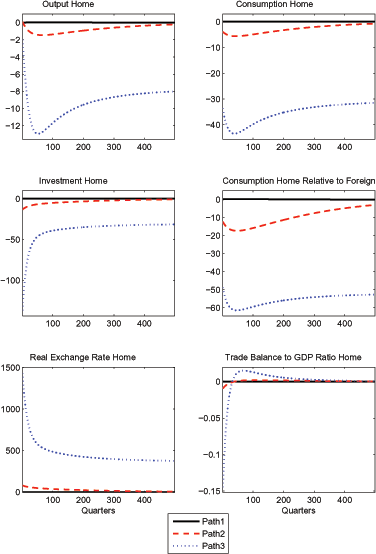
Data for Figure 3 - Panel A
Quarters | Output Home: Path 3 | Output Home: Path 2 | Output Home: Path 1 | Consumption Home: Path 3 | Consumption Home: Path 2 | Consumption Home: Path 1 | Investment Home: Path 3 | Investment Home: Path 2 | Investment Home: Path 1 |
|---|---|---|---|---|---|---|---|---|---|
1 | -1.984 | 0.089 | 0.000 | -33.624 | -3.923 | 0.049 | -136.725 | -13.470 | -0.103 |
2 | -2.544 | 0.007 | -0.002 | -34.328 | -4.033 | 0.051 | -129.735 | -12.792 | 0.190 |
3 | -3.085 | -0.068 | 0.000 | -34.996 | -4.138 | 0.052 | -124.097 | -12.518 | 0.186 |
4 | -3.616 | -0.140 | 0.001 | -35.629 | -4.237 | 0.054 | -118.835 | -12.256 | 0.182 |
5 | -4.134 | -0.208 | 0.002 | -36.228 | -4.332 | 0.055 | -113.926 | -12.006 | 0.177 |
6 | -4.638 | -0.274 | 0.003 | -36.793 | -4.421 | 0.056 | -109.348 | -11.767 | 0.173 |
7 | -5.126 | -0.337 | 0.004 | -37.327 | -4.506 | 0.058 | -105.081 | -11.538 | 0.170 |
8 | -5.599 | -0.397 | 0.005 | -37.830 | -4.587 | 0.059 | -101.102 | -11.319 | 0.166 |
9 | -6.055 | -0.454 | 0.006 | -38.303 | -4.663 | 0.060 | -97.393 | -11.109 | 0.162 |
10 | -6.493 | -0.509 | 0.006 | -38.747 | -4.735 | 0.061 | -93.935 | -10.907 | 0.159 |
11 | -6.913 | -0.561 | 0.007 | -39.163 | -4.803 | 0.062 | -90.710 | -10.714 | 0.156 |
12 | -7.316 | -0.611 | 0.008 | -39.553 | -4.867 | 0.063 | -87.703 | -10.529 | 0.152 |
13 | -7.701 | -0.659 | 0.009 | -39.918 | -4.928 | 0.064 | -84.897 | -10.352 | 0.149 |
14 | -8.067 | -0.704 | 0.009 | -40.258 | -4.985 | 0.065 | -82.278 | -10.181 | 0.146 |
15 | -8.416 | -0.748 | 0.010 | -40.575 | -5.039 | 0.065 | -79.834 | -10.018 | 0.144 |
16 | -8.748 | -0.789 | 0.011 | -40.869 | -5.090 | 0.066 | -77.551 | -9.860 | 0.141 |
17 | -9.062 | -0.828 | 0.011 | -41.142 | -5.138 | 0.067 | -75.417 | -9.709 | 0.138 |
18 | -9.360 | -0.866 | 0.012 | -41.395 | -5.183 | 0.067 | -73.423 | -9.564 | 0.136 |
19 | -9.641 | -0.902 | 0.012 | -41.628 | -5.225 | 0.068 | -71.557 | -9.424 | 0.133 |
20 | -9.906 | -0.936 | 0.013 | -41.843 | -5.265 | 0.068 | -69.811 | -9.289 | 0.131 |
21 | -10.156 | -0.968 | 0.013 | -42.041 | -5.301 | 0.069 | -68.177 | -9.159 | 0.128 |
22 | -10.390 | -0.999 | 0.014 | -42.221 | -5.336 | 0.069 | -66.645 | -9.034 | 0.126 |
23 | -10.611 | -1.029 | 0.014 | -42.386 | -5.368 | 0.070 | -65.209 | -8.914 | 0.124 |
24 | -10.817 | -1.057 | 0.014 | -42.536 | -5.398 | 0.070 | -63.863 | -8.797 | 0.122 |
25 | -11.010 | -1.083 | 0.015 | -42.671 | -5.426 | 0.070 | -62.598 | -8.685 | 0.120 |
26 | -11.190 | -1.109 | 0.015 | -42.793 | -5.451 | 0.071 | -61.411 | -8.577 | 0.118 |
27 | -11.358 | -1.133 | 0.015 | -42.903 | -5.475 | 0.071 | -60.295 | -8.473 | 0.116 |
28 | -11.514 | -1.155 | 0.016 | -43.000 | -5.497 | 0.071 | -59.246 | -8.372 | 0.114 |
29 | -11.659 | -1.177 | 0.016 | -43.086 | -5.517 | 0.071 | -58.259 | -8.274 | 0.113 |
30 | -11.793 | -1.197 | 0.016 | -43.161 | -5.535 | 0.072 | -57.329 | -8.180 | 0.111 |
31 | -11.917 | -1.217 | 0.016 | -43.225 | -5.551 | 0.072 | -56.452 | -8.089 | 0.109 |
32 | -12.032 | -1.235 | 0.017 | -43.281 | -5.566 | 0.072 | -55.626 | -8.001 | 0.108 |
33 | -12.137 | -1.252 | 0.017 | -43.327 | -5.580 | 0.072 | -54.847 | -7.915 | 0.106 |
34 | -12.233 | -1.269 | 0.017 | -43.365 | -5.592 | 0.072 | -54.110 | -7.833 | 0.105 |
35 | -12.322 | -1.284 | 0.017 | -43.394 | -5.603 | 0.072 | -53.415 | -7.752 | 0.103 |
36 | -12.402 | -1.299 | 0.017 | -43.416 | -5.612 | 0.072 | -52.757 | -7.675 | 0.102 |
37 | -12.475 | -1.312 | 0.018 | -43.432 | -5.620 | 0.072 | -52.135 | -7.600 | 0.100 |
38 | -12.541 | -1.325 | 0.018 | -43.440 | -5.627 | 0.072 | -51.545 | -7.526 | 0.099 |
39 | -12.600 | -1.337 | 0.018 | -43.442 | -5.632 | 0.072 | -50.987 | -7.456 | 0.098 |
40 | -12.653 | -1.349 | 0.018 | -43.439 | -5.637 | 0.072 | -50.458 | -7.387 | 0.097 |
41 | -12.700 | -1.360 | 0.018 | -43.430 | -5.640 | 0.072 | -49.955 | -7.320 | 0.095 |
42 | -12.742 | -1.370 | 0.018 | -43.415 | -5.643 | 0.072 | -49.479 | -7.255 | 0.094 |
43 | -12.778 | -1.379 | 0.018 | -43.397 | -5.644 | 0.072 | -49.025 | -7.192 | 0.093 |
44 | -12.809 | -1.388 | 0.018 | -43.373 | -5.644 | 0.072 | -48.594 | -7.130 | 0.092 |
45 | -12.836 | -1.396 | 0.019 | -43.345 | -5.644 | 0.072 | -48.184 | -7.071 | 0.091 |
46 | -12.859 | -1.403 | 0.019 | -43.314 | -5.643 | 0.072 | -47.794 | -7.012 | 0.090 |
47 | -12.877 | -1.410 | 0.019 | -43.279 | -5.641 | 0.072 | -47.422 | -6.956 | 0.089 |
48 | -12.891 | -1.417 | 0.019 | -43.240 | -5.638 | 0.071 | -47.067 | -6.901 | 0.088 |
49 | -12.902 | -1.423 | 0.019 | -43.198 | -5.634 | 0.071 | -46.729 | -6.847 | 0.087 |
50 | -12.910 | -1.428 | 0.019 | -43.154 | -5.630 | 0.071 | -46.406 | -6.794 | 0.086 |
51 | -12.914 | -1.434 | 0.019 | -43.106 | -5.625 | 0.071 | -46.097 | -6.743 | 0.085 |
52 | -12.915 | -1.438 | 0.019 | -43.057 | -5.619 | 0.071 | -45.802 | -6.693 | 0.084 |
53 | -12.914 | -1.442 | 0.019 | -43.004 | -5.613 | 0.071 | -45.519 | -6.644 | 0.083 |
54 | -12.910 | -1.446 | 0.019 | -42.950 | -5.606 | 0.070 | -45.249 | -6.597 | 0.083 |
55 | -12.903 | -1.449 | 0.019 | -42.894 | -5.598 | 0.070 | -44.990 | -6.550 | 0.082 |
56 | -12.895 | -1.452 | 0.019 | -42.835 | -5.590 | 0.070 | -44.741 | -6.505 | 0.081 |
57 | -12.884 | -1.455 | 0.019 | -42.776 | -5.581 | 0.070 | -44.503 | -6.460 | 0.080 |
58 | -12.871 | -1.457 | 0.019 | -42.714 | -5.572 | 0.070 | -44.274 | -6.417 | 0.079 |
59 | -12.857 | -1.459 | 0.019 | -42.651 | -5.563 | 0.069 | -44.054 | -6.374 | 0.079 |
60 | -12.841 | -1.461 | 0.019 | -42.587 | -5.553 | 0.069 | -43.842 | -6.332 | 0.078 |
61 | -12.823 | -1.462 | 0.019 | -42.522 | -5.542 | 0.069 | -43.639 | -6.291 | 0.077 |
62 | -12.804 | -1.463 | 0.019 | -42.456 | -5.531 | 0.069 | -43.443 | -6.251 | 0.077 |
63 | -12.783 | -1.464 | 0.019 | -42.389 | -5.520 | 0.068 | -43.254 | -6.212 | 0.076 |
64 | -12.761 | -1.465 | 0.019 | -42.320 | -5.508 | 0.068 | -43.072 | -6.173 | 0.075 |
65 | -12.739 | -1.465 | 0.019 | -42.252 | -5.496 | 0.068 | -42.897 | -6.136 | 0.075 |
66 | -12.715 | -1.465 | 0.019 | -42.182 | -5.484 | 0.068 | -42.727 | -6.098 | 0.074 |
67 | -12.690 | -1.465 | 0.019 | -42.112 | -5.471 | 0.067 | -42.563 | -6.062 | 0.073 |
68 | -12.664 | -1.464 | 0.019 | -42.041 | -5.458 | 0.067 | -42.405 | -6.026 | 0.073 |
69 | -12.637 | -1.464 | 0.019 | -41.970 | -5.445 | 0.067 | -42.252 | -5.991 | 0.072 |
70 | -12.610 | -1.463 | 0.019 | -41.899 | -5.431 | 0.067 | -42.104 | -5.956 | 0.072 |
71 | -12.582 | -1.462 | 0.019 | -41.827 | -5.418 | 0.066 | -41.960 | -5.922 | 0.071 |
72 | -12.553 | -1.461 | 0.019 | -41.755 | -5.403 | 0.066 | -41.821 | -5.889 | 0.070 |
73 | -12.524 | -1.459 | 0.018 | -41.682 | -5.389 | 0.066 | -41.686 | -5.856 | 0.070 |
74 | -12.494 | -1.458 | 0.018 | -41.610 | -5.375 | 0.065 | -41.556 | -5.824 | 0.069 |
75 | -12.464 | -1.456 | 0.018 | -41.537 | -5.360 | 0.065 | -41.429 | -5.792 | 0.069 |
76 | -12.434 | -1.454 | 0.018 | -41.465 | -5.345 | 0.065 | -41.305 | -5.760 | 0.068 |
77 | -12.403 | -1.452 | 0.018 | -41.392 | -5.329 | 0.065 | -41.185 | -5.729 | 0.068 |
78 | -12.372 | -1.450 | 0.018 | -41.319 | -5.314 | 0.064 | -41.069 | -5.699 | 0.067 |
79 | -12.340 | -1.448 | 0.018 | -41.247 | -5.299 | 0.064 | -40.955 | -5.669 | 0.067 |
80 | -12.309 | -1.445 | 0.018 | -41.174 | -5.283 | 0.064 | -40.845 | -5.639 | 0.066 |
81 | -12.277 | -1.443 | 0.018 | -41.102 | -5.267 | 0.063 | -40.737 | -5.609 | 0.066 |
82 | -12.245 | -1.440 | 0.018 | -41.030 | -5.251 | 0.063 | -40.632 | -5.580 | 0.065 |
83 | -12.213 | -1.437 | 0.018 | -40.958 | -5.235 | 0.063 | -40.530 | -5.552 | 0.065 |
84 | -12.180 | -1.434 | 0.018 | -40.886 | -5.218 | 0.063 | -40.430 | -5.524 | 0.064 |
85 | -12.148 | -1.431 | 0.018 | -40.814 | -5.202 | 0.062 | -40.333 | -5.496 | 0.064 |
86 | -12.116 | -1.428 | 0.018 | -40.743 | -5.185 | 0.062 | -40.238 | -5.468 | 0.064 |
87 | -12.083 | -1.425 | 0.018 | -40.672 | -5.169 | 0.062 | -40.145 | -5.441 | 0.063 |
88 | -12.051 | -1.422 | 0.018 | -40.601 | -5.152 | 0.061 | -40.054 | -5.414 | 0.063 |
89 | -12.018 | -1.419 | 0.017 | -40.531 | -5.135 | 0.061 | -39.965 | -5.387 | 0.062 |
90 | -11.986 | -1.415 | 0.017 | -40.460 | -5.118 | 0.061 | -39.878 | -5.361 | 0.062 |
91 | -11.954 | -1.412 | 0.017 | -40.391 | -5.101 | 0.060 | -39.793 | -5.335 | 0.061 |
92 | -11.921 | -1.408 | 0.017 | -40.321 | -5.084 | 0.060 | -39.709 | -5.309 | 0.061 |
93 | -11.889 | -1.404 | 0.017 | -40.252 | -5.067 | 0.060 | -39.628 | -5.284 | 0.061 |
94 | -11.857 | -1.401 | 0.017 | -40.183 | -5.049 | 0.060 | -39.547 | -5.258 | 0.060 |
95 | -11.825 | -1.397 | 0.017 | -40.115 | -5.032 | 0.059 | -39.469 | -5.233 | 0.060 |
96 | -11.793 | -1.393 | 0.017 | -40.047 | -5.014 | 0.059 | -39.392 | -5.208 | 0.059 |
97 | -11.762 | -1.389 | 0.017 | -39.980 | -4.997 | 0.059 | -39.316 | -5.184 | 0.059 |
98 | -11.730 | -1.385 | 0.017 | -39.912 | -4.980 | 0.058 | -39.242 | -5.159 | 0.059 |
99 | -11.699 | -1.381 | 0.017 | -39.846 | -4.962 | 0.058 | -39.169 | -5.135 | 0.058 |
100 | -11.667 | -1.377 | 0.017 | -39.779 | -4.944 | 0.058 | -39.097 | -5.111 | 0.058 |
101 | -11.636 | -1.373 | 0.017 | -39.714 | -4.927 | 0.058 | -39.027 | -5.088 | 0.058 |
102 | -11.605 | -1.369 | 0.016 | -39.648 | -4.909 | 0.057 | -38.958 | -5.064 | 0.057 |
103 | -11.575 | -1.365 | 0.016 | -39.583 | -4.891 | 0.057 | -38.890 | -5.041 | 0.057 |
104 | -11.544 | -1.361 | 0.016 | -39.519 | -4.874 | 0.057 | -38.823 | -5.018 | 0.056 |
105 | -11.514 | -1.357 | 0.016 | -39.455 | -4.856 | 0.056 | -38.757 | -4.995 | 0.056 |
106 | -11.484 | -1.352 | 0.016 | -39.391 | -4.838 | 0.056 | -38.692 | -4.972 | 0.056 |
107 | -11.454 | -1.348 | 0.016 | -39.328 | -4.820 | 0.056 | -38.628 | -4.949 | 0.055 |
108 | -11.424 | -1.344 | 0.016 | -39.266 | -4.802 | 0.055 | -38.565 | -4.927 | 0.055 |
109 | -11.394 | -1.339 | 0.016 | -39.203 | -4.785 | 0.055 | -38.503 | -4.904 | 0.055 |
110 | -11.365 | -1.335 | 0.016 | -39.142 | -4.767 | 0.055 | -38.442 | -4.882 | 0.054 |
111 | -11.336 | -1.330 | 0.016 | -39.080 | -4.749 | 0.055 | -38.382 | -4.860 | 0.054 |
112 | -11.307 | -1.326 | 0.016 | -39.020 | -4.731 | 0.054 | -38.323 | -4.838 | 0.054 |
113 | -11.278 | -1.322 | 0.016 | -38.959 | -4.713 | 0.054 | -38.264 | -4.817 | 0.053 |
114 | -11.250 | -1.317 | 0.016 | -38.899 | -4.695 | 0.054 | -38.207 | -4.795 | 0.053 |
115 | -11.222 | -1.313 | 0.015 | -38.840 | -4.677 | 0.053 | -38.150 | -4.773 | 0.053 |
116 | -11.194 | -1.308 | 0.015 | -38.781 | -4.660 | 0.053 | -38.094 | -4.752 | 0.053 |
117 | -11.166 | -1.304 | 0.015 | -38.723 | -4.642 | 0.053 | -38.038 | -4.731 | 0.052 |
118 | -11.138 | -1.299 | 0.015 | -38.665 | -4.624 | 0.053 | -37.983 | -4.710 | 0.052 |
119 | -11.111 | -1.295 | 0.015 | -38.607 | -4.606 | 0.052 | -37.929 | -4.689 | 0.052 |
120 | -11.084 | -1.290 | 0.015 | -38.550 | -4.588 | 0.052 | -37.876 | -4.668 | 0.051 |
121 | -11.057 | -1.285 | 0.015 | -38.493 | -4.570 | 0.052 | -37.823 | -4.648 | 0.051 |
122 | -11.031 | -1.281 | 0.015 | -38.437 | -4.553 | 0.052 | -37.771 | -4.627 | 0.051 |
123 | -11.004 | -1.276 | 0.015 | -38.382 | -4.535 | 0.051 | -37.720 | -4.606 | 0.050 |
124 | -10.978 | -1.272 | 0.015 | -38.326 | -4.517 | 0.051 | -37.669 | -4.586 | 0.050 |
125 | -10.952 | -1.267 | 0.015 | -38.271 | -4.499 | 0.051 | -37.619 | -4.566 | 0.050 |
126 | -10.926 | -1.262 | 0.015 | -38.217 | -4.482 | 0.050 | -37.569 | -4.546 | 0.050 |
127 | -10.901 | -1.258 | 0.015 | -38.163 | -4.464 | 0.050 | -37.520 | -4.526 | 0.049 |
128 | -10.876 | -1.253 | 0.014 | -38.110 | -4.446 | 0.050 | -37.471 | -4.506 | 0.049 |
129 | -10.851 | -1.248 | 0.014 | -38.057 | -4.429 | 0.050 | -37.423 | -4.486 | 0.049 |
130 | -10.826 | -1.244 | 0.014 | -38.004 | -4.411 | 0.049 | -37.376 | -4.466 | 0.048 |
131 | -10.801 | -1.239 | 0.014 | -37.952 | -4.393 | 0.049 | -37.329 | -4.447 | 0.048 |
132 | -10.777 | -1.235 | 0.014 | -37.900 | -4.376 | 0.049 | -37.282 | -4.427 | 0.048 |
133 | -10.753 | -1.230 | 0.014 | -37.849 | -4.358 | 0.049 | -37.236 | -4.408 | 0.048 |
134 | -10.729 | -1.225 | 0.014 | -37.798 | -4.341 | 0.048 | -37.190 | -4.388 | 0.047 |
135 | -10.705 | -1.221 | 0.014 | -37.748 | -4.323 | 0.048 | -37.145 | -4.369 | 0.047 |
136 | -10.682 | -1.216 | 0.014 | -37.698 | -4.306 | 0.048 | -37.101 | -4.350 | 0.047 |
137 | -10.659 | -1.211 | 0.014 | -37.648 | -4.289 | 0.048 | -37.056 | -4.331 | 0.046 |
138 | -10.636 | -1.207 | 0.014 | -37.599 | -4.271 | 0.047 | -37.013 | -4.312 | 0.046 |
139 | -10.613 | -1.202 | 0.014 | -37.550 | -4.254 | 0.047 | -36.969 | -4.293 | 0.046 |
140 | -10.590 | -1.197 | 0.014 | -37.502 | -4.236 | 0.047 | -36.926 | -4.274 | 0.046 |
141 | -10.568 | -1.193 | 0.013 | -37.454 | -4.219 | 0.047 | -36.884 | -4.255 | 0.045 |
142 | -10.546 | -1.188 | 0.013 | -37.406 | -4.202 | 0.046 | -36.842 | -4.237 | 0.045 |
143 | -10.524 | -1.183 | 0.013 | -37.359 | -4.185 | 0.046 | -36.800 | -4.218 | 0.045 |
144 | -10.502 | -1.179 | 0.013 | -37.312 | -4.168 | 0.046 | -36.759 | -4.200 | 0.045 |
145 | -10.480 | -1.174 | 0.013 | -37.266 | -4.151 | 0.046 | -36.718 | -4.181 | 0.044 |
146 | -10.459 | -1.170 | 0.013 | -37.220 | -4.133 | 0.045 | -36.677 | -4.163 | 0.044 |
147 | -10.438 | -1.165 | 0.013 | -37.174 | -4.116 | 0.045 | -36.637 | -4.145 | 0.044 |
148 | -10.417 | -1.160 | 0.013 | -37.129 | -4.099 | 0.045 | -36.597 | -4.127 | 0.044 |
149 | -10.396 | -1.156 | 0.013 | -37.084 | -4.082 | 0.045 | -36.558 | -4.108 | 0.043 |
150 | -10.376 | -1.151 | 0.013 | -37.040 | -4.066 | 0.044 | -36.519 | -4.090 | 0.043 |
151 | -10.355 | -1.147 | 0.013 | -36.996 | -4.049 | 0.044 | -36.480 | -4.072 | 0.043 |
152 | -10.335 | -1.142 | 0.013 | -36.952 | -4.032 | 0.044 | -36.442 | -4.055 | 0.043 |
153 | -10.315 | -1.138 | 0.013 | -36.909 | -4.015 | 0.044 | -36.403 | -4.037 | 0.042 |
154 | -10.295 | -1.133 | 0.013 | -36.866 | -3.998 | 0.043 | -36.366 | -4.019 | 0.042 |
155 | -10.276 | -1.128 | 0.013 | -36.823 | -3.982 | 0.043 | -36.328 | -4.001 | 0.042 |
156 | -10.256 | -1.124 | 0.012 | -36.781 | -3.965 | 0.043 | -36.291 | -3.984 | 0.042 |
157 | -10.237 | -1.119 | 0.012 | -36.739 | -3.948 | 0.043 | -36.254 | -3.966 | 0.042 |
158 | -10.218 | -1.115 | 0.012 | -36.697 | -3.932 | 0.042 | -36.218 | -3.949 | 0.041 |
159 | -10.199 | -1.110 | 0.012 | -36.656 | -3.915 | 0.042 | -36.182 | -3.931 | 0.041 |
160 | -10.180 | -1.106 | 0.012 | -36.615 | -3.899 | 0.042 | -36.146 | -3.914 | 0.041 |
161 | -10.162 | -1.101 | 0.012 | -36.574 | -3.882 | 0.042 | -36.110 | -3.897 | 0.041 |
162 | -10.143 | -1.097 | 0.012 | -36.534 | -3.866 | 0.042 | -36.075 | -3.880 | 0.040 |
163 | -10.125 | -1.092 | 0.012 | -36.494 | -3.849 | 0.041 | -36.040 | -3.862 | 0.040 |
164 | -10.107 | -1.088 | 0.012 | -36.454 | -3.833 | 0.041 | -36.005 | -3.845 | 0.040 |
165 | -10.089 | -1.083 | 0.012 | -36.415 | -3.817 | 0.041 | -35.971 | -3.828 | 0.040 |
166 | -10.071 | -1.079 | 0.012 | -36.376 | -3.801 | 0.041 | -35.937 | -3.812 | 0.040 |
167 | -10.054 | -1.074 | 0.012 | -36.338 | -3.785 | 0.040 | -35.903 | -3.795 | 0.039 |
168 | -10.036 | -1.070 | 0.012 | -36.299 | -3.768 | 0.040 | -35.869 | -3.778 | 0.039 |
169 | -10.019 | -1.066 | 0.012 | -36.261 | -3.752 | 0.040 | -35.836 | -3.761 | 0.039 |
170 | -10.002 | -1.061 | 0.012 | -36.224 | -3.736 | 0.040 | -35.803 | -3.744 | 0.039 |
171 | -9.985 | -1.057 | 0.011 | -36.186 | -3.720 | 0.040 | -35.770 | -3.728 | 0.038 |
172 | -9.968 | -1.052 | 0.011 | -36.149 | -3.704 | 0.039 | -35.737 | -3.711 | 0.038 |
173 | -9.952 | -1.048 | 0.011 | -36.112 | -3.689 | 0.039 | -35.705 | -3.695 | 0.038 |
174 | -9.935 | -1.044 | 0.011 | -36.076 | -3.673 | 0.039 | -35.673 | -3.678 | 0.038 |
175 | -9.919 | -1.039 | 0.011 | -36.040 | -3.657 | 0.039 | -35.641 | -3.662 | 0.038 |
176 | -9.903 | -1.035 | 0.011 | -36.004 | -3.641 | 0.038 | -35.610 | -3.646 | 0.037 |
177 | -9.887 | -1.031 | 0.011 | -35.968 | -3.625 | 0.038 | -35.578 | -3.629 | 0.037 |
178 | -9.871 | -1.026 | 0.011 | -35.933 | -3.610 | 0.038 | -35.547 | -3.613 | 0.037 |
179 | -9.855 | -1.022 | 0.011 | -35.898 | -3.594 | 0.038 | -35.516 | -3.597 | 0.037 |
180 | -9.840 | -1.018 | 0.011 | -35.863 | -3.579 | 0.038 | -35.486 | -3.581 | 0.037 |
181 | -9.824 | -1.013 | 0.011 | -35.829 | -3.563 | 0.037 | -35.455 | -3.565 | 0.036 |
182 | -9.809 | -1.009 | 0.011 | -35.794 | -3.548 | 0.037 | -35.425 | -3.549 | 0.036 |
183 | -9.794 | -1.005 | 0.011 | -35.761 | -3.532 | 0.037 | -35.395 | -3.533 | 0.036 |
184 | -9.779 | -1.001 | 0.011 | -35.727 | -3.517 | 0.037 | -35.366 | -3.517 | 0.036 |
185 | -9.764 | -0.996 | 0.011 | -35.693 | -3.502 | 0.037 | -35.336 | -3.502 | 0.036 |
186 | -9.749 | -0.992 | 0.011 | -35.660 | -3.486 | 0.036 | -35.307 | -3.486 | 0.035 |
187 | -9.734 | -0.988 | 0.011 | -35.627 | -3.471 | 0.036 | -35.278 | -3.470 | 0.035 |
188 | -9.720 | -0.984 | 0.010 | -35.595 | -3.456 | 0.036 | -35.249 | -3.455 | 0.035 |
189 | -9.705 | -0.979 | 0.010 | -35.563 | -3.441 | 0.036 | -35.220 | -3.439 | 0.035 |
190 | -9.691 | -0.975 | 0.010 | -35.530 | -3.426 | 0.036 | -35.192 | -3.424 | 0.035 |
191 | -9.677 | -0.971 | 0.010 | -35.499 | -3.411 | 0.035 | -35.164 | -3.408 | 0.034 |
192 | -9.663 | -0.967 | 0.010 | -35.467 | -3.396 | 0.035 | -35.136 | -3.393 | 0.034 |
193 | -9.649 | -0.963 | 0.010 | -35.436 | -3.381 | 0.035 | -35.108 | -3.378 | 0.034 |
194 | -9.635 | -0.959 | 0.010 | -35.405 | -3.366 | 0.035 | -35.080 | -3.362 | 0.034 |
195 | -9.622 | -0.955 | 0.010 | -35.374 | -3.351 | 0.035 | -35.053 | -3.347 | 0.034 |
196 | -9.608 | -0.950 | 0.010 | -35.343 | -3.337 | 0.034 | -35.026 | -3.332 | 0.033 |
197 | -9.595 | -0.946 | 0.010 | -35.313 | -3.322 | 0.034 | -34.999 | -3.317 | 0.033 |
198 | -9.581 | -0.942 | 0.010 | -35.283 | -3.307 | 0.034 | -34.972 | -3.302 | 0.033 |
199 | -9.568 | -0.938 | 0.010 | -35.253 | -3.293 | 0.034 | -34.945 | -3.287 | 0.033 |
200 | -9.555 | -0.934 | 0.010 | -35.223 | -3.278 | 0.034 | -34.919 | -3.272 | 0.033 |
201 | -9.542 | -0.930 | 0.010 | -35.194 | -3.263 | 0.034 | -34.893 | -3.257 | 0.033 |
202 | -9.529 | -0.926 | 0.010 | -35.164 | -3.249 | 0.033 | -34.867 | -3.242 | 0.032 |
203 | -9.517 | -0.922 | 0.010 | -35.135 | -3.235 | 0.033 | -34.841 | -3.228 | 0.032 |
204 | -9.504 | -0.918 | 0.010 | -35.107 | -3.220 | 0.033 | -34.815 | -3.213 | 0.032 |
205 | -9.492 | -0.914 | 0.010 | -35.078 | -3.206 | 0.033 | -34.790 | -3.198 | 0.032 |
206 | -9.479 | -0.910 | 0.009 | -35.050 | -3.192 | 0.033 | -34.765 | -3.184 | 0.032 |
207 | -9.467 | -0.906 | 0.009 | -35.022 | -3.177 | 0.032 | -34.739 | -3.169 | 0.032 |
208 | -9.455 | -0.902 | 0.009 | -34.994 | -3.163 | 0.032 | -34.715 | -3.155 | 0.031 |
209 | -9.443 | -0.898 | 0.009 | -34.966 | -3.149 | 0.032 | -34.690 | -3.140 | 0.031 |
210 | -9.431 | -0.894 | 0.009 | -34.938 | -3.135 | 0.032 | -34.665 | -3.126 | 0.031 |
211 | -9.419 | -0.890 | 0.009 | -34.911 | -3.121 | 0.032 | -34.641 | -3.112 | 0.031 |
212 | -9.407 | -0.886 | 0.009 | -34.884 | -3.107 | 0.032 | -34.617 | -3.097 | 0.031 |
213 | -9.395 | -0.883 | 0.009 | -34.857 | -3.093 | 0.031 | -34.592 | -3.083 | 0.030 |
214 | -9.384 | -0.879 | 0.009 | -34.831 | -3.079 | 0.031 | -34.569 | -3.069 | 0.030 |
215 | -9.372 | -0.875 | 0.009 | -34.804 | -3.065 | 0.031 | -34.545 | -3.055 | 0.030 |
216 | -9.361 | -0.871 | 0.009 | -34.778 | -3.052 | 0.031 | -34.521 | -3.041 | 0.030 |
217 | -9.349 | -0.867 | 0.009 | -34.752 | -3.038 | 0.031 | -34.498 | -3.027 | 0.030 |
218 | -9.338 | -0.863 | 0.009 | -34.726 | -3.024 | 0.031 | -34.475 | -3.013 | 0.030 |
219 | -9.327 | -0.859 | 0.009 | -34.700 | -3.011 | 0.030 | -34.451 | -2.999 | 0.030 |
220 | -9.316 | -0.856 | 0.009 | -34.675 | -2.997 | 0.030 | -34.429 | -2.985 | 0.029 |
221 | -9.305 | -0.852 | 0.009 | -34.649 | -2.983 | 0.030 | -34.406 | -2.971 | 0.029 |
222 | -9.294 | -0.848 | 0.009 | -34.624 | -2.970 | 0.030 | -34.383 | -2.958 | 0.029 |
223 | -9.283 | -0.844 | 0.009 | -34.599 | -2.956 | 0.030 | -34.361 | -2.944 | 0.029 |
224 | -9.273 | -0.841 | 0.009 | -34.575 | -2.943 | 0.030 | -34.338 | -2.930 | 0.029 |
225 | -9.262 | -0.837 | 0.009 | -34.550 | -2.930 | 0.029 | -34.316 | -2.917 | 0.029 |
226 | -9.252 | -0.833 | 0.008 | -34.526 | -2.916 | 0.029 | -34.294 | -2.903 | 0.028 |
227 | -9.241 | -0.829 | 0.008 | -34.502 | -2.903 | 0.029 | -34.272 | -2.890 | 0.028 |
228 | -9.231 | -0.826 | 0.008 | -34.478 | -2.890 | 0.029 | -34.251 | -2.876 | 0.028 |
229 | -9.221 | -0.822 | 0.008 | -34.454 | -2.877 | 0.029 | -34.229 | -2.863 | 0.028 |
230 | -9.210 | -0.818 | 0.008 | -34.430 | -2.864 | 0.029 | -34.208 | -2.850 | 0.028 |
231 | -9.200 | -0.815 | 0.008 | -34.407 | -2.851 | 0.028 | -34.187 | -2.837 | 0.028 |
232 | -9.190 | -0.811 | 0.008 | -34.383 | -2.838 | 0.028 | -34.165 | -2.823 | 0.027 |
233 | -9.180 | -0.807 | 0.008 | -34.360 | -2.825 | 0.028 | -34.144 | -2.810 | 0.027 |
234 | -9.170 | -0.804 | 0.008 | -34.337 | -2.812 | 0.028 | -34.124 | -2.797 | 0.027 |
235 | -9.161 | -0.800 | 0.008 | -34.314 | -2.799 | 0.028 | -34.103 | -2.784 | 0.027 |
236 | -9.151 | -0.796 | 0.008 | -34.292 | -2.786 | 0.028 | -34.082 | -2.771 | 0.027 |
237 | -9.141 | -0.793 | 0.008 | -34.269 | -2.773 | 0.028 | -34.062 | -2.758 | 0.027 |
238 | -9.132 | -0.789 | 0.008 | -34.247 | -2.761 | 0.027 | -34.042 | -2.745 | 0.027 |
239 | -9.122 | -0.786 | 0.008 | -34.225 | -2.748 | 0.027 | -34.022 | -2.732 | 0.026 |
240 | -9.113 | -0.782 | 0.008 | -34.203 | -2.735 | 0.027 | -34.002 | -2.719 | 0.026 |
241 | -9.104 | -0.779 | 0.008 | -34.181 | -2.723 | 0.027 | -33.982 | -2.707 | 0.026 |
242 | -9.094 | -0.775 | 0.008 | -34.159 | -2.710 | 0.027 | -33.962 | -2.694 | 0.026 |
243 | -9.085 | -0.772 | 0.008 | -34.138 | -2.698 | 0.027 | -33.942 | -2.681 | 0.026 |
244 | -9.076 | -0.768 | 0.008 | -34.116 | -2.685 | 0.026 | -33.923 | -2.669 | 0.026 |
245 | -9.067 | -0.765 | 0.008 | -34.095 | -2.673 | 0.026 | -33.904 | -2.656 | 0.026 |
246 | -9.058 | -0.761 | 0.008 | -34.074 | -2.661 | 0.026 | -33.884 | -2.644 | 0.025 |
247 | -9.049 | -0.758 | 0.008 | -34.053 | -2.648 | 0.026 | -33.865 | -2.631 | 0.025 |
248 | -9.040 | -0.754 | 0.008 | -34.032 | -2.636 | 0.026 | -33.846 | -2.619 | 0.025 |
249 | -9.032 | -0.751 | 0.007 | -34.011 | -2.624 | 0.026 | -33.827 | -2.606 | 0.025 |
250 | -9.023 | -0.747 | 0.007 | -33.991 | -2.612 | 0.026 | -33.809 | -2.594 | 0.025 |
251 | -9.014 | -0.744 | 0.007 | -33.971 | -2.599 | 0.025 | -33.790 | -2.582 | 0.025 |
252 | -9.006 | -0.741 | 0.007 | -33.950 | -2.587 | 0.025 | -33.772 | -2.570 | 0.025 |
253 | -8.997 | -0.737 | 0.007 | -33.930 | -2.575 | 0.025 | -33.753 | -2.558 | 0.024 |
254 | -8.989 | -0.734 | 0.007 | -33.911 | -2.563 | 0.025 | -33.735 | -2.545 | 0.024 |
255 | -8.981 | -0.731 | 0.007 | -33.891 | -2.551 | 0.025 | -33.717 | -2.533 | 0.024 |
256 | -8.972 | -0.727 | 0.007 | -33.871 | -2.540 | 0.025 | -33.699 | -2.521 | 0.024 |
257 | -8.964 | -0.724 | 0.007 | -33.852 | -2.528 | 0.025 | -33.681 | -2.509 | 0.024 |
258 | -8.956 | -0.721 | 0.007 | -33.832 | -2.516 | 0.025 | -33.664 | -2.497 | 0.024 |
259 | -8.948 | -0.717 | 0.007 | -33.813 | -2.504 | 0.024 | -33.646 | -2.486 | 0.024 |
260 | -8.940 | -0.714 | 0.007 | -33.794 | -2.493 | 0.024 | -33.628 | -2.474 | 0.024 |
261 | -8.932 | -0.711 | 0.007 | -33.775 | -2.481 | 0.024 | -33.611 | -2.462 | 0.023 |
262 | -8.924 | -0.707 | 0.007 | -33.756 | -2.469 | 0.024 | -33.594 | -2.450 | 0.023 |
263 | -8.916 | -0.704 | 0.007 | -33.737 | -2.458 | 0.024 | -33.577 | -2.439 | 0.023 |
264 | -8.908 | -0.701 | 0.007 | -33.719 | -2.446 | 0.024 | -33.560 | -2.427 | 0.023 |
265 | -8.900 | -0.698 | 0.007 | -33.700 | -2.435 | 0.024 | -33.543 | -2.415 | 0.023 |
266 | -8.893 | -0.694 | 0.007 | -33.682 | -2.423 | 0.023 | -33.526 | -2.404 | 0.023 |
267 | -8.885 | -0.691 | 0.007 | -33.664 | -2.412 | 0.023 | -33.509 | -2.392 | 0.023 |
268 | -8.877 | -0.688 | 0.007 | -33.646 | -2.401 | 0.023 | -33.492 | -2.381 | 0.023 |
269 | -8.870 | -0.685 | 0.007 | -33.628 | -2.389 | 0.023 | -33.476 | -2.369 | 0.022 |
270 | -8.862 | -0.682 | 0.007 | -33.610 | -2.378 | 0.023 | -33.459 | -2.358 | 0.022 |
271 | -8.855 | -0.678 | 0.007 | -33.593 | -2.367 | 0.023 | -33.443 | -2.347 | 0.022 |
272 | -8.848 | -0.675 | 0.007 | -33.575 | -2.356 | 0.023 | -33.427 | -2.336 | 0.022 |
273 | -8.840 | -0.672 | 0.007 | -33.558 | -2.345 | 0.023 | -33.411 | -2.324 | 0.022 |
274 | -8.833 | -0.669 | 0.007 | -33.540 | -2.334 | 0.022 | -33.395 | -2.313 | 0.022 |
275 | -8.826 | -0.666 | 0.006 | -33.523 | -2.322 | 0.022 | -33.379 | -2.302 | 0.022 |
276 | -8.819 | -0.663 | 0.006 | -33.506 | -2.311 | 0.022 | -33.363 | -2.291 | 0.022 |
277 | -8.812 | -0.660 | 0.006 | -33.489 | -2.301 | 0.022 | -33.348 | -2.280 | 0.021 |
278 | -8.805 | -0.657 | 0.006 | -33.472 | -2.290 | 0.022 | -33.332 | -2.269 | 0.021 |
279 | -8.798 | -0.654 | 0.006 | -33.455 | -2.279 | 0.022 | -33.317 | -2.258 | 0.021 |
280 | -8.791 | -0.651 | 0.006 | -33.439 | -2.268 | 0.022 | -33.301 | -2.247 | 0.021 |
281 | -8.784 | -0.647 | 0.006 | -33.422 | -2.257 | 0.022 | -33.286 | -2.236 | 0.021 |
282 | -8.777 | -0.644 | 0.006 | -33.406 | -2.247 | 0.021 | -33.271 | -2.226 | 0.021 |
283 | -8.770 | -0.641 | 0.006 | -33.390 | -2.236 | 0.021 | -33.256 | -2.215 | 0.021 |
284 | -8.763 | -0.638 | 0.006 | -33.373 | -2.225 | 0.021 | -33.241 | -2.204 | 0.021 |
285 | -8.757 | -0.635 | 0.006 | -33.357 | -2.215 | 0.021 | -33.226 | -2.193 | 0.021 |
286 | -8.750 | -0.632 | 0.006 | -33.341 | -2.204 | 0.021 | -33.211 | -2.183 | 0.020 |
287 | -8.743 | -0.629 | 0.006 | -33.325 | -2.194 | 0.021 | -33.196 | -2.172 | 0.020 |
288 | -8.737 | -0.626 | 0.006 | -33.310 | -2.183 | 0.021 | -33.182 | -2.162 | 0.020 |
289 | -8.730 | -0.624 | 0.006 | -33.294 | -2.173 | 0.021 | -33.167 | -2.151 | 0.020 |
290 | -8.724 | -0.621 | 0.006 | -33.279 | -2.162 | 0.021 | -33.153 | -2.141 | 0.020 |
291 | -8.718 | -0.618 | 0.006 | -33.263 | -2.152 | 0.020 | -33.139 | -2.130 | 0.020 |
292 | -8.711 | -0.615 | 0.006 | -33.248 | -2.142 | 0.020 | -33.124 | -2.120 | 0.020 |
293 | -8.705 | -0.612 | 0.006 | -33.233 | -2.131 | 0.020 | -33.110 | -2.110 | 0.020 |
294 | -8.699 | -0.609 | 0.006 | -33.217 | -2.121 | 0.020 | -33.096 | -2.099 | 0.020 |
295 | -8.692 | -0.606 | 0.006 | -33.202 | -2.111 | 0.020 | -33.082 | -2.089 | 0.019 |
296 | -8.686 | -0.603 | 0.006 | -33.187 | -2.101 | 0.020 | -33.068 | -2.079 | 0.019 |
297 | -8.680 | -0.600 | 0.006 | -33.173 | -2.091 | 0.020 | -33.055 | -2.069 | 0.019 |
298 | -8.674 | -0.598 | 0.006 | -33.158 | -2.081 | 0.020 | -33.041 | -2.059 | 0.019 |
299 | -8.668 | -0.595 | 0.006 | -33.143 | -2.071 | 0.020 | -33.027 | -2.049 | 0.019 |
300 | -8.662 | -0.592 | 0.006 | -33.129 | -2.061 | 0.019 | -33.014 | -2.039 | 0.019 |
301 | -8.656 | -0.589 | 0.006 | -33.114 | -2.051 | 0.019 | -33.000 | -2.029 | 0.019 |
302 | -8.650 | -0.586 | 0.006 | -33.100 | -2.041 | 0.019 | -32.987 | -2.019 | 0.019 |
303 | -8.644 | -0.583 | 0.006 | -33.086 | -2.031 | 0.019 | -32.974 | -2.009 | 0.019 |
304 | -8.638 | -0.581 | 0.006 | -33.072 | -2.021 | 0.019 | -32.961 | -1.999 | 0.018 |
305 | -8.633 | -0.578 | 0.006 | -33.058 | -2.012 | 0.019 | -32.947 | -1.989 | 0.018 |
306 | -8.627 | -0.575 | 0.005 | -33.044 | -2.002 | 0.019 | -32.934 | -1.980 | 0.018 |
307 | -8.621 | -0.572 | 0.005 | -33.030 | -1.992 | 0.019 | -32.921 | -1.970 | 0.018 |
308 | -8.615 | -0.570 | 0.005 | -33.016 | -1.983 | 0.019 | -32.909 | -1.960 | 0.018 |
309 | -8.610 | -0.567 | 0.005 | -33.002 | -1.973 | 0.019 | -32.896 | -1.951 | 0.018 |
310 | -8.604 | -0.564 | 0.005 | -32.989 | -1.964 | 0.018 | -32.883 | -1.941 | 0.018 |
311 | -8.599 | -0.562 | 0.005 | -32.975 | -1.954 | 0.018 | -32.871 | -1.931 | 0.018 |
312 | -8.593 | -0.559 | 0.005 | -32.962 | -1.945 | 0.018 | -32.858 | -1.922 | 0.018 |
313 | -8.588 | -0.556 | 0.005 | -32.948 | -1.935 | 0.018 | -32.846 | -1.912 | 0.018 |
314 | -8.582 | -0.554 | 0.005 | -32.935 | -1.926 | 0.018 | -32.833 | -1.903 | 0.017 |
315 | -8.577 | -0.551 | 0.005 | -32.922 | -1.916 | 0.018 | -32.821 | -1.894 | 0.017 |
316 | -8.571 | -0.548 | 0.005 | -32.909 | -1.907 | 0.018 | -32.809 | -1.884 | 0.017 |
317 | -8.566 | -0.546 | 0.005 | -32.896 | -1.898 | 0.018 | -32.796 | -1.875 | 0.017 |
318 | -8.561 | -0.543 | 0.005 | -32.883 | -1.889 | 0.018 | -32.784 | -1.866 | 0.017 |
319 | -8.555 | -0.540 | 0.005 | -32.870 | -1.879 | 0.018 | -32.772 | -1.857 | 0.017 |
320 | -8.550 | -0.538 | 0.005 | -32.857 | -1.870 | 0.017 | -32.760 | -1.847 | 0.017 |
321 | -8.545 | -0.535 | 0.005 | -32.845 | -1.861 | 0.017 | -32.749 | -1.838 | 0.017 |
322 | -8.540 | -0.533 | 0.005 | -32.832 | -1.852 | 0.017 | -32.737 | -1.829 | 0.017 |
323 | -8.535 | -0.530 | 0.005 | -32.820 | -1.843 | 0.017 | -32.725 | -1.820 | 0.017 |
324 | -8.530 | -0.527 | 0.005 | -32.807 | -1.834 | 0.017 | -32.714 | -1.811 | 0.017 |
325 | -8.525 | -0.525 | 0.005 | -32.795 | -1.825 | 0.017 | -32.702 | -1.802 | 0.016 |
326 | -8.520 | -0.522 | 0.005 | -32.783 | -1.816 | 0.017 | -32.691 | -1.793 | 0.016 |
327 | -8.515 | -0.520 | 0.005 | -32.770 | -1.807 | 0.017 | -32.679 | -1.784 | 0.016 |
328 | -8.510 | -0.517 | 0.005 | -32.758 | -1.798 | 0.017 | -32.668 | -1.775 | 0.016 |
329 | -8.505 | -0.515 | 0.005 | -32.746 | -1.790 | 0.017 | -32.656 | -1.767 | 0.016 |
330 | -8.500 | -0.512 | 0.005 | -32.734 | -1.781 | 0.016 | -32.645 | -1.758 | 0.016 |
331 | -8.495 | -0.510 | 0.005 | -32.723 | -1.772 | 0.016 | -32.634 | -1.749 | 0.016 |
332 | -8.490 | -0.507 | 0.005 | -32.711 | -1.764 | 0.016 | -32.623 | -1.740 | 0.016 |
333 | -8.485 | -0.505 | 0.005 | -32.699 | -1.755 | 0.016 | -32.612 | -1.732 | 0.016 |
334 | -8.481 | -0.502 | 0.005 | -32.687 | -1.746 | 0.016 | -32.601 | -1.723 | 0.016 |
335 | -8.476 | -0.500 | 0.005 | -32.676 | -1.738 | 0.016 | -32.590 | -1.715 | 0.016 |
336 | -8.471 | -0.498 | 0.005 | -32.664 | -1.729 | 0.016 | -32.579 | -1.706 | 0.015 |
337 | -8.467 | -0.495 | 0.005 | -32.653 | -1.721 | 0.016 | -32.569 | -1.697 | 0.015 |
338 | -8.462 | -0.493 | 0.005 | -32.642 | -1.712 | 0.016 | -32.558 | -1.689 | 0.015 |
339 | -8.457 | -0.490 | 0.005 | -32.630 | -1.704 | 0.016 | -32.548 | -1.681 | 0.015 |
340 | -8.453 | -0.488 | 0.005 | -32.619 | -1.695 | 0.016 | -32.537 | -1.672 | 0.015 |
341 | -8.448 | -0.486 | 0.005 | -32.608 | -1.687 | 0.016 | -32.527 | -1.664 | 0.015 |
342 | -8.444 | -0.483 | 0.004 | -32.597 | -1.679 | 0.015 | -32.516 | -1.656 | 0.015 |
343 | -8.439 | -0.481 | 0.004 | -32.586 | -1.670 | 0.015 | -32.506 | -1.647 | 0.015 |
344 | -8.435 | -0.479 | 0.004 | -32.575 | -1.662 | 0.015 | -32.495 | -1.639 | 0.015 |
345 | -8.430 | -0.476 | 0.004 | -32.564 | -1.654 | 0.015 | -32.485 | -1.631 | 0.015 |
346 | -8.426 | -0.474 | 0.004 | -32.553 | -1.646 | 0.015 | -32.475 | -1.623 | 0.015 |
347 | -8.422 | -0.472 | 0.004 | -32.543 | -1.638 | 0.015 | -32.465 | -1.615 | 0.015 |
348 | -8.417 | -0.469 | 0.004 | -32.532 | -1.630 | 0.015 | -32.455 | -1.606 | 0.014 |
349 | -8.413 | -0.467 | 0.004 | -32.521 | -1.621 | 0.015 | -32.445 | -1.598 | 0.014 |
350 | -8.409 | -0.465 | 0.004 | -32.511 | -1.613 | 0.015 | -32.435 | -1.590 | 0.014 |
351 | -8.405 | -0.462 | 0.004 | -32.500 | -1.605 | 0.015 | -32.425 | -1.582 | 0.014 |
352 | -8.400 | -0.460 | 0.004 | -32.490 | -1.597 | 0.015 | -32.416 | -1.574 | 0.014 |
353 | -8.396 | -0.458 | 0.004 | -32.480 | -1.590 | 0.015 | -32.406 | -1.566 | 0.014 |
354 | -8.392 | -0.456 | 0.004 | -32.470 | -1.582 | 0.014 | -32.396 | -1.559 | 0.014 |
355 | -8.388 | -0.453 | 0.004 | -32.459 | -1.574 | 0.014 | -32.387 | -1.551 | 0.014 |
356 | -8.384 | -0.451 | 0.004 | -32.449 | -1.566 | 0.014 | -32.377 | -1.543 | 0.014 |
357 | -8.380 | -0.449 | 0.004 | -32.439 | -1.558 | 0.014 | -32.367 | -1.535 | 0.014 |
358 | -8.376 | -0.447 | 0.004 | -32.429 | -1.550 | 0.014 | -32.358 | -1.527 | 0.014 |
359 | -8.372 | -0.444 | 0.004 | -32.419 | -1.543 | 0.014 | -32.349 | -1.520 | 0.014 |
360 | -8.368 | -0.442 | 0.004 | -32.409 | -1.535 | 0.014 | -32.339 | -1.512 | 0.014 |
361 | -8.364 | -0.440 | 0.004 | -32.400 | -1.527 | 0.014 | -32.330 | -1.504 | 0.013 |
362 | -8.360 | -0.438 | 0.004 | -32.390 | -1.520 | 0.014 | -32.321 | -1.497 | 0.013 |
363 | -8.356 | -0.436 | 0.004 | -32.380 | -1.512 | 0.014 | -32.312 | -1.489 | 0.013 |
364 | -8.352 | -0.434 | 0.004 | -32.370 | -1.505 | 0.014 | -32.303 | -1.482 | 0.013 |
365 | -8.348 | -0.431 | 0.004 | -32.361 | -1.497 | 0.014 | -32.294 | -1.474 | 0.013 |
366 | -8.344 | -0.429 | 0.004 | -32.351 | -1.490 | 0.014 | -32.285 | -1.467 | 0.013 |
367 | -8.340 | -0.427 | 0.004 | -32.342 | -1.482 | 0.013 | -32.276 | -1.459 | 0.013 |
368 | -8.337 | -0.425 | 0.004 | -32.333 | -1.475 | 0.013 | -32.267 | -1.452 | 0.013 |
369 | -8.333 | -0.423 | 0.004 | -32.323 | -1.468 | 0.013 | -32.258 | -1.445 | 0.013 |
370 | -8.329 | -0.421 | 0.004 | -32.314 | -1.460 | 0.013 | -32.249 | -1.437 | 0.013 |
371 | -8.325 | -0.419 | 0.004 | -32.305 | -1.453 | 0.013 | -32.241 | -1.430 | 0.013 |
372 | -8.322 | -0.417 | 0.004 | -32.296 | -1.446 | 0.013 | -32.232 | -1.423 | 0.013 |
373 | -8.318 | -0.415 | 0.004 | -32.286 | -1.438 | 0.013 | -32.223 | -1.416 | 0.013 |
374 | -8.314 | -0.413 | 0.004 | -32.277 | -1.431 | 0.013 | -32.215 | -1.408 | 0.013 |
375 | -8.311 | -0.411 | 0.004 | -32.268 | -1.424 | 0.013 | -32.206 | -1.401 | 0.012 |
376 | -8.307 | -0.408 | 0.004 | -32.260 | -1.417 | 0.013 | -32.198 | -1.394 | 0.012 |
377 | -8.304 | -0.406 | 0.004 | -32.251 | -1.410 | 0.013 | -32.189 | -1.387 | 0.012 |
378 | -8.300 | -0.404 | 0.004 | -32.242 | -1.403 | 0.013 | -32.181 | -1.380 | 0.012 |
379 | -8.296 | -0.402 | 0.004 | -32.233 | -1.396 | 0.013 | -32.173 | -1.373 | 0.012 |
380 | -8.293 | -0.400 | 0.004 | -32.224 | -1.389 | 0.013 | -32.164 | -1.366 | 0.012 |
381 | -8.289 | -0.398 | 0.004 | -32.216 | -1.382 | 0.012 | -32.156 | -1.359 | 0.012 |
382 | -8.286 | -0.396 | 0.004 | -32.207 | -1.375 | 0.012 | -32.148 | -1.352 | 0.012 |
383 | -8.283 | -0.394 | 0.004 | -32.199 | -1.368 | 0.012 | -32.140 | -1.345 | 0.012 |
384 | -8.279 | -0.392 | 0.004 | -32.190 | -1.361 | 0.012 | -32.132 | -1.339 | 0.012 |
385 | -8.276 | -0.391 | 0.004 | -32.182 | -1.354 | 0.012 | -32.124 | -1.332 | 0.012 |
386 | -8.272 | -0.389 | 0.004 | -32.173 | -1.347 | 0.012 | -32.116 | -1.325 | 0.012 |
387 | -8.269 | -0.387 | 0.004 | -32.165 | -1.340 | 0.012 | -32.108 | -1.318 | 0.012 |
388 | -8.266 | -0.385 | 0.003 | -32.157 | -1.334 | 0.012 | -32.100 | -1.311 | 0.012 |
389 | -8.262 | -0.383 | 0.003 | -32.148 | -1.327 | 0.012 | -32.092 | -1.305 | 0.012 |
390 | -8.259 | -0.381 | 0.003 | -32.140 | -1.320 | 0.012 | -32.084 | -1.298 | 0.011 |
391 | -8.256 | -0.379 | 0.003 | -32.132 | -1.314 | 0.012 | -32.077 | -1.291 | 0.011 |
392 | -8.252 | -0.377 | 0.003 | -32.124 | -1.307 | 0.012 | -32.069 | -1.285 | 0.011 |
393 | -8.249 | -0.375 | 0.003 | -32.116 | -1.300 | 0.012 | -32.061 | -1.278 | 0.011 |
394 | -8.246 | -0.373 | 0.003 | -32.108 | -1.294 | 0.012 | -32.054 | -1.272 | 0.011 |
395 | -8.243 | -0.371 | 0.003 | -32.100 | -1.287 | 0.012 | -32.046 | -1.265 | 0.011 |
396 | -8.240 | -0.370 | 0.003 | -32.092 | -1.281 | 0.011 | -32.039 | -1.259 | 0.011 |
397 | -8.237 | -0.368 | 0.003 | -32.084 | -1.274 | 0.011 | -32.031 | -1.252 | 0.011 |
398 | -8.233 | -0.366 | 0.003 | -32.076 | -1.268 | 0.011 | -32.024 | -1.246 | 0.011 |
399 | -8.230 | -0.364 | 0.003 | -32.069 | -1.261 | 0.011 | -32.017 | -1.240 | 0.011 |
400 | -8.227 | -0.362 | 0.003 | -32.061 | -1.255 | 0.011 | -32.009 | -1.233 | 0.011 |
401 | -8.224 | -0.360 | 0.003 | -32.053 | -1.249 | 0.011 | -32.002 | -1.227 | 0.011 |
402 | -8.221 | -0.359 | 0.003 | -32.046 | -1.242 | 0.011 | -31.995 | -1.221 | 0.011 |
403 | -8.218 | -0.357 | 0.003 | -32.038 | -1.236 | 0.011 | -31.988 | -1.214 | 0.011 |
404 | -8.215 | -0.355 | 0.003 | -32.030 | -1.230 | 0.011 | -31.980 | -1.208 | 0.011 |
405 | -8.212 | -0.353 | 0.003 | -32.023 | -1.223 | 0.011 | -31.973 | -1.202 | 0.011 |
406 | -8.209 | -0.351 | 0.003 | -32.016 | -1.217 | 0.011 | -31.966 | -1.196 | 0.011 |
407 | -8.206 | -0.350 | 0.003 | -32.008 | -1.211 | 0.011 | -31.959 | -1.190 | 0.010 |
408 | -8.203 | -0.348 | 0.003 | -32.001 | -1.205 | 0.011 | -31.952 | -1.183 | 0.010 |
409 | -8.200 | -0.346 | 0.003 | -31.993 | -1.199 | 0.011 | -31.945 | -1.177 | 0.010 |
410 | -8.197 | -0.344 | 0.003 | -31.986 | -1.193 | 0.011 | -31.938 | -1.171 | 0.010 |
411 | -8.194 | -0.343 | 0.003 | -31.979 | -1.187 | 0.011 | -31.931 | -1.165 | 0.010 |
412 | -8.192 | -0.341 | 0.003 | -31.972 | -1.181 | 0.010 | -31.925 | -1.159 | 0.010 |
413 | -8.189 | -0.339 | 0.003 | -31.965 | -1.174 | 0.010 | -31.918 | -1.153 | 0.010 |
414 | -8.186 | -0.337 | 0.003 | -31.958 | -1.169 | 0.010 | -31.911 | -1.147 | 0.010 |
415 | -8.183 | -0.336 | 0.003 | -31.951 | -1.163 | 0.010 | -31.904 | -1.141 | 0.010 |
416 | -8.180 | -0.334 | 0.003 | -31.944 | -1.157 | 0.010 | -31.898 | -1.136 | 0.010 |
417 | -8.178 | -0.332 | 0.003 | -31.937 | -1.151 | 0.010 | -31.891 | -1.130 | 0.010 |
418 | -8.175 | -0.331 | 0.003 | -31.930 | -1.145 | 0.010 | -31.885 | -1.124 | 0.010 |
419 | -8.172 | -0.329 | 0.003 | -31.923 | -1.139 | 0.010 | -31.878 | -1.118 | 0.010 |
420 | -8.169 | -0.327 | 0.003 | -31.916 | -1.133 | 0.010 | -31.871 | -1.112 | 0.010 |
421 | -8.167 | -0.326 | 0.003 | -31.909 | -1.127 | 0.010 | -31.865 | -1.107 | 0.010 |
422 | -8.164 | -0.324 | 0.003 | -31.903 | -1.122 | 0.010 | -31.859 | -1.101 | 0.010 |
423 | -8.161 | -0.322 | 0.003 | -31.896 | -1.116 | 0.010 | -31.852 | -1.095 | 0.010 |
424 | -8.159 | -0.321 | 0.003 | -31.889 | -1.110 | 0.010 | -31.846 | -1.090 | 0.010 |
425 | -8.156 | -0.319 | 0.003 | -31.883 | -1.104 | 0.010 | -31.840 | -1.084 | 0.009 |
426 | -8.153 | -0.317 | 0.003 | -31.876 | -1.099 | 0.010 | -31.833 | -1.078 | 0.009 |
427 | -8.151 | -0.316 | 0.003 | -31.869 | -1.093 | 0.010 | -31.827 | -1.073 | 0.009 |
428 | -8.148 | -0.314 | 0.003 | -31.863 | -1.088 | 0.010 | -31.821 | -1.067 | 0.009 |
429 | -8.146 | -0.313 | 0.003 | -31.856 | -1.082 | 0.010 | -31.815 | -1.062 | 0.009 |
430 | -8.143 | -0.311 | 0.003 | -31.850 | -1.076 | 0.009 | -31.808 | -1.056 | 0.009 |
431 | -8.140 | -0.309 | 0.003 | -31.844 | -1.071 | 0.009 | -31.802 | -1.051 | 0.009 |
432 | -8.138 | -0.308 | 0.003 | -31.837 | -1.065 | 0.009 | -31.796 | -1.045 | 0.009 |
433 | -8.135 | -0.306 | 0.003 | -31.831 | -1.060 | 0.009 | -31.790 | -1.040 | 0.009 |
434 | -8.133 | -0.305 | 0.003 | -31.825 | -1.055 | 0.009 | -31.784 | -1.034 | 0.009 |
435 | -8.130 | -0.303 | 0.003 | -31.818 | -1.049 | 0.009 | -31.778 | -1.029 | 0.009 |
436 | -8.128 | -0.302 | 0.003 | -31.812 | -1.044 | 0.009 | -31.772 | -1.024 | 0.009 |
437 | -8.125 | -0.300 | 0.003 | -31.806 | -1.038 | 0.009 | -31.767 | -1.018 | 0.009 |
438 | -8.123 | -0.299 | 0.003 | -31.800 | -1.033 | 0.009 | -31.761 | -1.013 | 0.009 |
439 | -8.121 | -0.297 | 0.003 | -31.794 | -1.028 | 0.009 | -31.755 | -1.008 | 0.009 |
440 | -8.118 | -0.295 | 0.003 | -31.788 | -1.022 | 0.009 | -31.749 | -1.003 | 0.009 |
441 | -8.116 | -0.294 | 0.003 | -31.782 | -1.017 | 0.009 | -31.743 | -0.997 | 0.009 |
442 | -8.113 | -0.292 | 0.003 | -31.776 | -1.012 | 0.009 | -31.738 | -0.992 | 0.009 |
443 | -8.111 | -0.291 | 0.003 | -31.770 | -1.007 | 0.009 | -31.732 | -0.987 | 0.009 |
444 | -8.109 | -0.289 | 0.003 | -31.764 | -1.002 | 0.009 | -31.726 | -0.982 | 0.009 |
445 | -8.106 | -0.288 | 0.003 | -31.758 | -0.996 | 0.009 | -31.721 | -0.977 | 0.008 |
446 | -8.104 | -0.287 | 0.003 | -31.752 | -0.991 | 0.009 | -31.715 | -0.972 | 0.008 |
447 | -8.102 | -0.285 | 0.003 | -31.746 | -0.986 | 0.009 | -31.709 | -0.967 | 0.008 |
448 | -8.099 | -0.284 | 0.002 | -31.740 | -0.981 | 0.009 | -31.704 | -0.962 | 0.008 |
449 | -8.097 | -0.282 | 0.002 | -31.735 | -0.976 | 0.009 | -31.698 | -0.957 | 0.008 |
450 | -8.095 | -0.281 | 0.002 | -31.729 | -0.971 | 0.008 | -31.693 | -0.952 | 0.008 |
451 | -8.093 | -0.279 | 0.002 | -31.723 | -0.966 | 0.008 | -31.688 | -0.947 | 0.008 |
452 | -8.090 | -0.278 | 0.002 | -31.718 | -0.961 | 0.008 | -31.682 | -0.942 | 0.008 |
453 | -8.088 | -0.276 | 0.002 | -31.712 | -0.956 | 0.008 | -31.677 | -0.937 | 0.008 |
454 | -8.086 | -0.275 | 0.002 | -31.707 | -0.951 | 0.008 | -31.671 | -0.932 | 0.008 |
455 | -8.084 | -0.274 | 0.002 | -31.701 | -0.946 | 0.008 | -31.666 | -0.927 | 0.008 |
456 | -8.082 | -0.272 | 0.002 | -31.695 | -0.941 | 0.008 | -31.661 | -0.922 | 0.008 |
457 | -8.079 | -0.271 | 0.002 | -31.690 | -0.936 | 0.008 | -31.656 | -0.918 | 0.008 |
458 | -8.077 | -0.269 | 0.002 | -31.685 | -0.932 | 0.008 | -31.650 | -0.913 | 0.008 |
459 | -8.075 | -0.268 | 0.002 | -31.679 | -0.927 | 0.008 | -31.645 | -0.908 | 0.008 |
460 | -8.073 | -0.267 | 0.002 | -31.674 | -0.922 | 0.008 | -31.640 | -0.903 | 0.008 |
461 | -8.071 | -0.265 | 0.002 | -31.668 | -0.917 | 0.008 | -31.635 | -0.898 | 0.008 |
462 | -8.069 | -0.264 | 0.002 | -31.663 | -0.912 | 0.008 | -31.630 | -0.894 | 0.008 |
463 | -8.067 | -0.262 | 0.002 | -31.658 | -0.908 | 0.008 | -31.625 | -0.889 | 0.008 |
464 | -8.065 | -0.261 | 0.002 | -31.653 | -0.903 | 0.008 | -31.620 | -0.884 | 0.008 |
465 | -8.062 | -0.260 | 0.002 | -31.647 | -0.898 | 0.008 | -31.615 | -0.880 | 0.008 |
466 | -8.060 | -0.258 | 0.002 | -31.642 | -0.894 | 0.008 | -31.610 | -0.875 | 0.008 |
467 | -8.058 | -0.257 | 0.002 | -31.637 | -0.889 | 0.008 | -31.605 | -0.871 | 0.007 |
468 | -8.056 | -0.256 | 0.002 | -31.632 | -0.884 | 0.008 | -31.600 | -0.866 | 0.007 |
469 | -8.054 | -0.254 | 0.002 | -31.627 | -0.880 | 0.008 | -31.595 | -0.862 | 0.007 |
470 | -8.052 | -0.253 | 0.002 | -31.622 | -0.875 | 0.008 | -31.590 | -0.857 | 0.007 |
471 | -8.050 | -0.252 | 0.002 | -31.617 | -0.871 | 0.008 | -31.585 | -0.853 | 0.007 |
472 | -8.048 | -0.251 | 0.002 | -31.612 | -0.866 | 0.008 | -31.581 | -0.848 | 0.007 |
473 | -8.046 | -0.249 | 0.002 | -31.607 | -0.862 | 0.007 | -31.576 | -0.844 | 0.007 |
474 | -8.044 | -0.248 | 0.002 | -31.602 | -0.857 | 0.007 | -31.571 | -0.839 | 0.007 |
475 | -8.042 | -0.247 | 0.002 | -31.597 | -0.853 | 0.007 | -31.566 | -0.835 | 0.007 |
476 | -8.040 | -0.245 | 0.002 | -31.592 | -0.848 | 0.007 | -31.562 | -0.830 | 0.007 |
477 | -8.039 | -0.244 | 0.002 | -31.587 | -0.844 | 0.007 | -31.557 | -0.826 | 0.007 |
478 | -8.037 | -0.243 | 0.002 | -31.582 | -0.839 | 0.007 | -31.552 | -0.822 | 0.007 |
479 | -8.035 | -0.242 | 0.002 | -31.577 | -0.835 | 0.007 | -31.548 | -0.817 | 0.007 |
480 | -8.033 | -0.240 | 0.002 | -31.572 | -0.831 | 0.007 | -31.543 | -0.813 | 0.007 |
481 | -8.031 | -0.239 | 0.002 | -31.568 | -0.826 | 0.007 | -31.539 | -0.809 | 0.007 |
482 | -8.029 | -0.238 | 0.002 | -31.563 | -0.822 | 0.007 | -31.534 | -0.805 | 0.007 |
483 | -8.027 | -0.237 | 0.002 | -31.558 | -0.818 | 0.007 | -31.530 | -0.800 | 0.007 |
484 | -8.025 | -0.235 | 0.002 | -31.554 | -0.814 | 0.007 | -31.525 | -0.796 | 0.007 |
485 | -8.024 | -0.234 | 0.002 | -31.549 | -0.809 | 0.007 | -31.521 | -0.792 | 0.007 |
486 | -8.022 | -0.233 | 0.002 | -31.544 | -0.805 | 0.007 | -31.516 | -0.788 | 0.007 |
487 | -8.020 | -0.232 | 0.002 | -31.540 | -0.801 | 0.007 | -31.512 | -0.784 | 0.007 |
488 | -8.018 | -0.231 | 0.002 | -31.535 | -0.797 | 0.007 | -31.507 | -0.780 | 0.007 |
489 | -8.016 | -0.229 | 0.002 | -31.531 | -0.793 | 0.007 | -31.503 | -0.776 | 0.007 |
490 | -8.015 | -0.228 | 0.002 | -31.526 | -0.788 | 0.007 | -31.499 | -0.771 | 0.007 |
491 | -8.013 | -0.227 | 0.002 | -31.522 | -0.784 | 0.007 | -31.494 | -0.767 | 0.007 |
492 | -8.011 | -0.226 | 0.002 | -31.517 | -0.780 | 0.007 | -31.490 | -0.763 | 0.007 |
493 | -8.009 | -0.225 | 0.002 | -31.513 | -0.776 | 0.007 | -31.486 | -0.759 | 0.006 |
494 | -8.008 | -0.223 | 0.002 | -31.508 | -0.772 | 0.007 | -31.482 | -0.755 | 0.006 |
495 | -8.006 | -0.222 | 0.002 | -31.504 | -0.768 | 0.007 | -31.477 | -0.751 | 0.006 |
496 | -8.004 | -0.221 | 0.002 | -31.500 | -0.764 | 0.007 | -31.473 | -0.747 | 0.006 |
497 | -8.002 | -0.220 | 0.002 | -31.495 | -0.760 | 0.007 | -31.469 | -0.743 | 0.006 |
498 | -8.001 | -0.219 | 0.002 | -31.491 | -0.756 | 0.006 | -31.465 | -0.740 | 0.006 |
499 | -7.999 | -0.218 | 0.002 | -31.487 | -0.752 | 0.006 | -31.461 | -0.736 | 0.006 |
Data for Figure 3 - Panel B
Quarters | Consumption Home Relative to Foreign: Path 3 | Consumption Home Relative to Foreign Path 2 | Consumption Home Relative to Foreign Path 1 | Real Exchange Rate Home Path 3 | Real Exchange Rate Home Path 2 | Real Exchange Rate Home Path 1 | Trade Balance to GDP Ratio Home Path 3 | Trade Balance to GDP Ratio Home Path 2 | Trade Balance to GDP Ratio Home Path 1 |
|---|---|---|---|---|---|---|---|---|---|
1 | -48.876 | -12.234 | 0.169 | 1432.772 | 78.605 | -0.959 | -0.144592 | -0.008430 | 0.000848 |
2 | -49.765 | -12.555 | 0.177 | 1378.950 | 77.281 | -0.941 | -0.139647 | -0.008916 | 0.000114 |
3 | -50.599 | -12.860 | 0.185 | 1328.396 | 76.014 | -0.924 | -0.129174 | -0.008403 | 0.000106 |
4 | -51.381 | -13.148 | 0.192 | 1280.942 | 74.801 | -0.908 | -0.119334 | -0.007916 | 0.000100 |
5 | -52.115 | -13.421 | 0.199 | 1236.422 | 73.639 | -0.893 | -0.110104 | -0.007453 | 0.000093 |
6 | -52.804 | -13.679 | 0.205 | 1194.669 | 72.525 | -0.878 | -0.101458 | -0.007013 | 0.000087 |
7 | -53.449 | -13.923 | 0.211 | 1155.520 | 71.455 | -0.863 | -0.093368 | -0.006593 | 0.000081 |
8 | -54.054 | -14.154 | 0.217 | 1118.817 | 70.429 | -0.849 | -0.085803 | -0.006194 | 0.000075 |
9 | -54.621 | -14.373 | 0.222 | 1084.408 | 69.442 | -0.835 | -0.078734 | -0.005814 | 0.000070 |
10 | -55.152 | -14.579 | 0.227 | 1052.147 | 68.493 | -0.822 | -0.072132 | -0.005452 | 0.000065 |
11 | -55.649 | -14.774 | 0.232 | 1021.897 | 67.581 | -0.809 | -0.065969 | -0.005107 | 0.000060 |
12 | -56.114 | -14.959 | 0.237 | 993.527 | 66.702 | -0.797 | -0.060218 | -0.004778 | 0.000055 |
13 | -56.549 | -15.133 | 0.241 | 966.913 | 65.856 | -0.785 | -0.054851 | -0.004465 | 0.000050 |
14 | -56.955 | -15.297 | 0.245 | 941.939 | 65.041 | -0.774 | -0.049845 | -0.004166 | 0.000046 |
15 | -57.334 | -15.452 | 0.249 | 918.495 | 64.254 | -0.762 | -0.045176 | -0.003881 | 0.000042 |
16 | -57.689 | -15.598 | 0.252 | 896.481 | 63.495 | -0.752 | -0.040822 | -0.003609 | 0.000038 |
17 | -58.019 | -15.736 | 0.255 | 875.799 | 62.762 | -0.741 | -0.036761 | -0.003349 | 0.000034 |
18 | -58.326 | -15.865 | 0.259 | 856.361 | 62.054 | -0.731 | -0.032975 | -0.003101 | 0.000030 |
19 | -58.613 | -15.987 | 0.261 | 838.083 | 61.369 | -0.721 | -0.029445 | -0.002865 | 0.000027 |
20 | -58.879 | -16.101 | 0.264 | 820.887 | 60.707 | -0.711 | -0.026155 | -0.002640 | 0.000024 |
21 | -59.126 | -16.209 | 0.267 | 804.702 | 60.066 | -0.702 | -0.023087 | -0.002424 | 0.000021 |
22 | -59.356 | -16.310 | 0.269 | 789.459 | 59.446 | -0.693 | -0.020229 | -0.002218 | 0.000018 |
23 | -59.568 | -16.404 | 0.271 | 775.096 | 58.845 | -0.684 | -0.017564 | -0.002022 | 0.000015 |
24 | -59.765 | -16.492 | 0.273 | 761.554 | 58.262 | -0.676 | -0.015081 | -0.001834 | 0.000012 |
25 | -59.947 | -16.575 | 0.275 | 748.779 | 57.697 | -0.668 | -0.012768 | -0.001655 | 0.000009 |
26 | -60.115 | -16.652 | 0.277 | 736.720 | 57.148 | -0.660 | -0.010613 | -0.001484 | 0.000007 |
27 | -60.269 | -16.723 | 0.278 | 725.330 | 56.616 | -0.652 | -0.008606 | -0.001320 | 0.000005 |
28 | -60.411 | -16.790 | 0.280 | 714.565 | 56.099 | -0.644 | -0.006737 | -0.001164 | 0.000002 |
29 | -60.541 | -16.852 | 0.281 | 704.385 | 55.596 | -0.637 | -0.004997 | -0.001015 | 0.000000 |
30 | -60.660 | -16.909 | 0.282 | 694.751 | 55.107 | -0.630 | -0.003377 | -0.000872 | -0.000002 |
31 | -60.769 | -16.961 | 0.283 | 685.628 | 54.631 | -0.623 | -0.001870 | -0.000736 | -0.000004 |
32 | -60.867 | -17.009 | 0.284 | 676.984 | 54.168 | -0.616 | -0.000468 | -0.000605 | -0.000006 |
33 | -60.957 | -17.054 | 0.285 | 668.788 | 53.717 | -0.610 | 0.000835 | -0.000481 | -0.000008 |
34 | -61.037 | -17.094 | 0.285 | 661.010 | 53.278 | -0.603 | 0.002047 | -0.000362 | -0.000009 |
35 | -61.109 | -17.131 | 0.286 | 653.626 | 52.849 | -0.597 | 0.003172 | -0.000248 | -0.000011 |
36 | -61.174 | -17.164 | 0.287 | 646.610 | 52.431 | -0.591 | 0.004218 | -0.000139 | -0.000012 |
37 | -61.231 | -17.193 | 0.287 | 639.939 | 52.024 | -0.585 | 0.005187 | -0.000035 | -0.000014 |
38 | -61.282 | -17.219 | 0.287 | 633.591 | 51.625 | -0.579 | 0.006087 | 0.000064 | -0.000015 |
39 | -61.325 | -17.243 | 0.288 | 627.548 | 51.237 | -0.573 | 0.006921 | 0.000159 | -0.000017 |
40 | -61.363 | -17.263 | 0.288 | 621.789 | 50.857 | -0.568 | 0.007693 | 0.000250 | -0.000018 |
41 | -61.395 | -17.280 | 0.288 | 616.299 | 50.485 | -0.562 | 0.008407 | 0.000337 | -0.000019 |
42 | -61.422 | -17.295 | 0.288 | 611.060 | 50.122 | -0.557 | 0.009067 | 0.000420 | -0.000020 |
43 | -61.444 | -17.307 | 0.288 | 606.057 | 49.766 | -0.552 | 0.009677 | 0.000499 | -0.000021 |
44 | -61.461 | -17.316 | 0.288 | 601.276 | 49.418 | -0.547 | 0.010240 | 0.000575 | -0.000022 |
45 | -61.473 | -17.323 | 0.288 | 596.705 | 49.077 | -0.542 | 0.010758 | 0.000647 | -0.000023 |
46 | -61.481 | -17.328 | 0.287 | 592.331 | 48.743 | -0.537 | 0.011235 | 0.000717 | -0.000024 |
47 | -61.485 | -17.330 | 0.287 | 588.142 | 48.416 | -0.533 | 0.011673 | 0.000783 | -0.000025 |
48 | -61.486 | -17.330 | 0.287 | 584.127 | 48.095 | -0.528 | 0.012075 | 0.000846 | -0.000026 |
49 | -61.483 | -17.329 | 0.286 | 580.277 | 47.780 | -0.523 | 0.012443 | 0.000906 | -0.000027 |
50 | -61.477 | -17.325 | 0.286 | 576.582 | 47.471 | -0.519 | 0.012779 | 0.000964 | -0.000027 |
51 | -61.468 | -17.319 | 0.286 | 573.034 | 47.168 | -0.515 | 0.013085 | 0.001019 | -0.000028 |
52 | -61.455 | -17.312 | 0.285 | 569.623 | 46.869 | -0.510 | 0.013363 | 0.001072 | -0.000029 |
53 | -61.441 | -17.303 | 0.284 | 566.343 | 46.576 | -0.506 | 0.013615 | 0.001122 | -0.000029 |
54 | -61.423 | -17.292 | 0.284 | 563.186 | 46.289 | -0.502 | 0.013843 | 0.001170 | -0.000030 |
55 | -61.403 | -17.280 | 0.283 | 560.146 | 46.005 | -0.498 | 0.014047 | 0.001216 | -0.000030 |
56 | -61.381 | -17.266 | 0.283 | 557.215 | 45.727 | -0.494 | 0.014230 | 0.001259 | -0.000031 |
57 | -61.357 | -17.250 | 0.282 | 554.389 | 45.453 | -0.490 | 0.014393 | 0.001301 | -0.000031 |
58 | -61.331 | -17.234 | 0.281 | 551.661 | 45.183 | -0.487 | 0.014538 | 0.001341 | -0.000032 |
59 | -61.304 | -17.216 | 0.280 | 549.027 | 44.917 | -0.483 | 0.014664 | 0.001379 | -0.000032 |
60 | -61.274 | -17.196 | 0.280 | 546.481 | 44.656 | -0.479 | 0.014774 | 0.001415 | -0.000033 |
61 | -61.243 | -17.176 | 0.279 | 544.018 | 44.398 | -0.476 | 0.014869 | 0.001450 | -0.000033 |
62 | -61.211 | -17.154 | 0.278 | 541.635 | 44.144 | -0.472 | 0.014949 | 0.001483 | -0.000033 |
63 | -61.177 | -17.131 | 0.277 | 539.328 | 43.893 | -0.469 | 0.015016 | 0.001514 | -0.000034 |
64 | -61.142 | -17.107 | 0.276 | 537.092 | 43.646 | -0.465 | 0.015071 | 0.001544 | -0.000034 |
65 | -61.105 | -17.082 | 0.275 | 534.924 | 43.402 | -0.462 | 0.015113 | 0.001572 | -0.000034 |
66 | -61.068 | -17.056 | 0.274 | 532.821 | 43.161 | -0.459 | 0.015144 | 0.001600 | -0.000034 |
67 | -61.029 | -17.029 | 0.273 | 530.779 | 42.923 | -0.455 | 0.015166 | 0.001625 | -0.000035 |
68 | -60.990 | -17.001 | 0.272 | 528.796 | 42.689 | -0.452 | 0.015177 | 0.001650 | -0.000035 |
69 | -60.950 | -16.973 | 0.272 | 526.868 | 42.457 | -0.449 | 0.015180 | 0.001673 | -0.000035 |
70 | -60.909 | -16.943 | 0.271 | 524.993 | 42.228 | -0.446 | 0.015174 | 0.001696 | -0.000035 |
71 | -60.867 | -16.913 | 0.269 | 523.169 | 42.001 | -0.443 | 0.015160 | 0.001717 | -0.000035 |
72 | -60.824 | -16.881 | 0.268 | 521.392 | 41.778 | -0.440 | 0.015140 | 0.001737 | -0.000036 |
73 | -60.781 | -16.850 | 0.267 | 519.662 | 41.556 | -0.437 | 0.015112 | 0.001756 | -0.000036 |
74 | -60.738 | -16.817 | 0.266 | 517.975 | 41.337 | -0.434 | 0.015078 | 0.001774 | -0.000036 |
75 | -60.693 | -16.784 | 0.265 | 516.331 | 41.121 | -0.431 | 0.015039 | 0.001791 | -0.000036 |
76 | -60.649 | -16.750 | 0.264 | 514.726 | 40.907 | -0.428 | 0.014993 | 0.001807 | -0.000036 |
77 | -60.603 | -16.715 | 0.263 | 513.159 | 40.695 | -0.425 | 0.014943 | 0.001823 | -0.000036 |
78 | -60.558 | -16.680 | 0.262 | 511.629 | 40.485 | -0.422 | 0.014888 | 0.001837 | -0.000036 |
79 | -60.512 | -16.644 | 0.261 | 510.133 | 40.277 | -0.420 | 0.014829 | 0.001851 | -0.000036 |
80 | -60.466 | -16.608 | 0.260 | 508.672 | 40.071 | -0.417 | 0.014766 | 0.001864 | -0.000036 |
81 | -60.420 | -16.571 | 0.259 | 507.242 | 39.867 | -0.414 | 0.014699 | 0.001876 | -0.000036 |
82 | -60.373 | -16.534 | 0.258 | 505.843 | 39.665 | -0.412 | 0.014629 | 0.001888 | -0.000036 |
83 | -60.326 | -16.496 | 0.256 | 504.473 | 39.465 | -0.409 | 0.014555 | 0.001899 | -0.000036 |
84 | -60.279 | -16.458 | 0.255 | 503.132 | 39.266 | -0.406 | 0.014479 | 0.001909 | -0.000036 |
85 | -60.232 | -16.419 | 0.254 | 501.818 | 39.070 | -0.404 | 0.014400 | 0.001918 | -0.000036 |
86 | -60.185 | -16.380 | 0.253 | 500.530 | 38.875 | -0.401 | 0.014318 | 0.001928 | -0.000036 |
87 | -60.137 | -16.341 | 0.252 | 499.267 | 38.681 | -0.399 | 0.014235 | 0.001936 | -0.000036 |
88 | -60.090 | -16.301 | 0.251 | 498.028 | 38.490 | -0.396 | 0.014149 | 0.001944 | -0.000036 |
89 | -60.042 | -16.261 | 0.250 | 496.812 | 38.299 | -0.394 | 0.014061 | 0.001951 | -0.000036 |
90 | -59.995 | -16.220 | 0.248 | 495.618 | 38.111 | -0.391 | 0.013972 | 0.001958 | -0.000036 |
91 | -59.947 | -16.179 | 0.247 | 494.446 | 37.923 | -0.389 | 0.013881 | 0.001965 | -0.000036 |
92 | -59.899 | -16.138 | 0.246 | 493.295 | 37.737 | -0.387 | 0.013789 | 0.001971 | -0.000036 |
93 | -59.852 | -16.097 | 0.245 | 492.164 | 37.553 | -0.384 | 0.013696 | 0.001976 | -0.000036 |
94 | -59.804 | -16.055 | 0.244 | 491.052 | 37.370 | -0.382 | 0.013601 | 0.001981 | -0.000036 |
95 | -59.757 | -16.013 | 0.243 | 489.959 | 37.188 | -0.380 | 0.013506 | 0.001986 | -0.000036 |
96 | -59.710 | -15.971 | 0.241 | 488.883 | 37.008 | -0.377 | 0.013409 | 0.001990 | -0.000036 |
97 | -59.662 | -15.928 | 0.240 | 487.825 | 36.828 | -0.375 | 0.013312 | 0.001994 | -0.000036 |
98 | -59.615 | -15.885 | 0.239 | 486.784 | 36.650 | -0.373 | 0.013215 | 0.001997 | -0.000036 |
99 | -59.568 | -15.842 | 0.238 | 485.759 | 36.474 | -0.371 | 0.013117 | 0.002001 | -0.000036 |
100 | -59.521 | -15.799 | 0.237 | 484.750 | 36.298 | -0.368 | 0.013018 | 0.002003 | -0.000036 |
101 | -59.474 | -15.755 | 0.236 | 483.756 | 36.124 | -0.366 | 0.012919 | 0.002006 | -0.000036 |
102 | -59.428 | -15.712 | 0.234 | 482.777 | 35.950 | -0.364 | 0.012820 | 0.002008 | -0.000035 |
103 | -59.381 | -15.668 | 0.233 | 481.812 | 35.778 | -0.362 | 0.012721 | 0.002010 | -0.000035 |
104 | -59.335 | -15.624 | 0.232 | 480.861 | 35.607 | -0.360 | 0.012621 | 0.002012 | -0.000035 |
105 | -59.289 | -15.580 | 0.231 | 479.923 | 35.437 | -0.358 | 0.012522 | 0.002013 | -0.000035 |
106 | -59.243 | -15.536 | 0.230 | 478.999 | 35.268 | -0.355 | 0.012422 | 0.002014 | -0.000035 |
107 | -59.197 | -15.491 | 0.229 | 478.087 | 35.100 | -0.353 | 0.012323 | 0.002015 | -0.000035 |
108 | -59.151 | -15.446 | 0.228 | 477.187 | 34.933 | -0.351 | 0.012223 | 0.002015 | -0.000035 |
109 | -59.106 | -15.402 | 0.226 | 476.300 | 34.767 | -0.349 | 0.012124 | 0.002016 | -0.000035 |
110 | -59.061 | -15.357 | 0.225 | 475.424 | 34.601 | -0.347 | 0.012025 | 0.002016 | -0.000035 |
111 | -59.016 | -15.312 | 0.224 | 474.559 | 34.437 | -0.345 | 0.011927 | 0.002016 | -0.000034 |
112 | -58.971 | -15.267 | 0.223 | 473.706 | 34.274 | -0.343 | 0.011828 | 0.002016 | -0.000034 |
113 | -58.926 | -15.222 | 0.222 | 472.863 | 34.112 | -0.341 | 0.011730 | 0.002015 | -0.000034 |
114 | -58.882 | -15.176 | 0.221 | 472.031 | 33.950 | -0.339 | 0.011633 | 0.002014 | -0.000034 |
115 | -58.838 | -15.131 | 0.219 | 471.209 | 33.790 | -0.337 | 0.011536 | 0.002013 | -0.000034 |
116 | -58.794 | -15.086 | 0.218 | 470.397 | 33.630 | -0.335 | 0.011439 | 0.002012 | -0.000034 |
117 | -58.750 | -15.040 | 0.217 | 469.595 | 33.471 | -0.334 | 0.011343 | 0.002011 | -0.000034 |
118 | -58.707 | -14.995 | 0.216 | 468.802 | 33.313 | -0.332 | 0.011247 | 0.002010 | -0.000034 |
119 | -58.664 | -14.949 | 0.215 | 468.019 | 33.156 | -0.330 | 0.011151 | 0.002008 | -0.000033 |
120 | -58.621 | -14.903 | 0.214 | 467.244 | 33.000 | -0.328 | 0.011057 | 0.002007 | -0.000033 |
121 | -58.578 | -14.857 | 0.213 | 466.478 | 32.844 | -0.326 | 0.010963 | 0.002005 | -0.000033 |
122 | -58.536 | -14.812 | 0.212 | 465.721 | 32.689 | -0.324 | 0.010869 | 0.002003 | -0.000033 |
123 | -58.493 | -14.766 | 0.211 | 464.973 | 32.535 | -0.322 | 0.010776 | 0.002001 | -0.000033 |
124 | -58.451 | -14.720 | 0.209 | 464.233 | 32.382 | -0.320 | 0.010684 | 0.001998 | -0.000033 |
125 | -58.410 | -14.674 | 0.208 | 463.501 | 32.230 | -0.319 | 0.010592 | 0.001996 | -0.000033 |
126 | -58.368 | -14.628 | 0.207 | 462.776 | 32.078 | -0.317 | 0.010501 | 0.001994 | -0.000032 |
127 | -58.327 | -14.582 | 0.206 | 462.060 | 31.927 | -0.315 | 0.010410 | 0.001991 | -0.000032 |
128 | -58.286 | -14.536 | 0.205 | 461.351 | 31.777 | -0.313 | 0.010320 | 0.001988 | -0.000032 |
129 | -58.245 | -14.490 | 0.204 | 460.650 | 31.627 | -0.311 | 0.010231 | 0.001985 | -0.000032 |
130 | -58.205 | -14.444 | 0.203 | 459.955 | 31.478 | -0.310 | 0.010143 | 0.001982 | -0.000032 |
131 | -58.165 | -14.398 | 0.202 | 459.268 | 31.330 | -0.308 | 0.010055 | 0.001979 | -0.000032 |
132 | -58.125 | -14.352 | 0.201 | 458.589 | 31.183 | -0.306 | 0.009968 | 0.001976 | -0.000032 |
133 | -58.085 | -14.306 | 0.200 | 457.915 | 31.036 | -0.305 | 0.009882 | 0.001973 | -0.000031 |
134 | -58.046 | -14.260 | 0.199 | 457.249 | 30.890 | -0.303 | 0.009796 | 0.001970 | -0.000031 |
135 | -58.007 | -14.214 | 0.198 | 456.590 | 30.745 | -0.301 | 0.009711 | 0.001966 | -0.000031 |
136 | -57.968 | -14.167 | 0.197 | 455.936 | 30.600 | -0.299 | 0.009627 | 0.001963 | -0.000031 |
137 | -57.929 | -14.121 | 0.195 | 455.290 | 30.456 | -0.298 | 0.009543 | 0.001960 | -0.000031 |
138 | -57.891 | -14.075 | 0.194 | 454.649 | 30.312 | -0.296 | 0.009460 | 0.001956 | -0.000031 |
139 | -57.852 | -14.029 | 0.193 | 454.015 | 30.170 | -0.294 | 0.009378 | 0.001952 | -0.000031 |
140 | -57.814 | -13.983 | 0.192 | 453.387 | 30.028 | -0.293 | 0.009297 | 0.001949 | -0.000030 |
141 | -57.777 | -13.937 | 0.191 | 452.765 | 29.886 | -0.291 | 0.009216 | 0.001945 | -0.000030 |
142 | -57.739 | -13.891 | 0.190 | 452.148 | 29.745 | -0.290 | 0.009136 | 0.001941 | -0.000030 |
143 | -57.702 | -13.845 | 0.189 | 451.538 | 29.605 | -0.288 | 0.009057 | 0.001937 | -0.000030 |
144 | -57.665 | -13.799 | 0.188 | 450.933 | 29.466 | -0.286 | 0.008979 | 0.001933 | -0.000030 |
145 | -57.629 | -13.753 | 0.187 | 450.333 | 29.327 | -0.285 | 0.008901 | 0.001929 | -0.000030 |
146 | -57.592 | -13.708 | 0.186 | 449.740 | 29.188 | -0.283 | 0.008824 | 0.001925 | -0.000029 |
147 | -57.556 | -13.662 | 0.185 | 449.151 | 29.051 | -0.282 | 0.008747 | 0.001921 | -0.000029 |
148 | -57.520 | -13.616 | 0.184 | 448.568 | 28.913 | -0.280 | 0.008672 | 0.001916 | -0.000029 |
149 | -57.485 | -13.570 | 0.183 | 447.991 | 28.777 | -0.278 | 0.008597 | 0.001912 | -0.000029 |
150 | -57.449 | -13.524 | 0.182 | 447.418 | 28.641 | -0.277 | 0.008523 | 0.001908 | -0.000029 |
151 | -57.414 | -13.479 | 0.181 | 446.851 | 28.506 | -0.275 | 0.008449 | 0.001904 | -0.000029 |
152 | -57.379 | -13.433 | 0.180 | 446.288 | 28.371 | -0.274 | 0.008376 | 0.001899 | -0.000029 |
153 | -57.344 | -13.387 | 0.179 | 445.731 | 28.237 | -0.272 | 0.008304 | 0.001895 | -0.000029 |
154 | -57.310 | -13.342 | 0.178 | 445.178 | 28.103 | -0.271 | 0.008233 | 0.001890 | -0.000028 |
155 | -57.276 | -13.296 | 0.177 | 444.630 | 27.970 | -0.269 | 0.008162 | 0.001886 | -0.000028 |
156 | -57.242 | -13.251 | 0.176 | 444.087 | 27.838 | -0.268 | 0.008092 | 0.001881 | -0.000028 |
157 | -57.208 | -13.205 | 0.175 | 443.549 | 27.706 | -0.266 | 0.008022 | 0.001877 | -0.000028 |
158 | -57.175 | -13.160 | 0.175 | 443.015 | 27.575 | -0.265 | 0.007954 | 0.001872 | -0.000028 |
159 | -57.141 | -13.114 | 0.174 | 442.486 | 27.444 | -0.263 | 0.007886 | 0.001867 | -0.000028 |
160 | -57.108 | -13.069 | 0.173 | 441.962 | 27.314 | -0.262 | 0.007818 | 0.001863 | -0.000027 |
161 | -57.076 | -13.024 | 0.172 | 441.441 | 27.184 | -0.261 | 0.007751 | 0.001858 | -0.000027 |
162 | -57.043 | -12.979 | 0.171 | 440.926 | 27.055 | -0.259 | 0.007685 | 0.001853 | -0.000027 |
163 | -57.011 | -12.934 | 0.170 | 440.414 | 26.926 | -0.258 | 0.007620 | 0.001849 | -0.000027 |
164 | -56.979 | -12.888 | 0.169 | 439.907 | 26.798 | -0.256 | 0.007555 | 0.001844 | -0.000027 |
165 | -56.947 | -12.843 | 0.168 | 439.404 | 26.671 | -0.255 | 0.007491 | 0.001839 | -0.000027 |
166 | -56.915 | -12.798 | 0.167 | 438.905 | 26.544 | -0.253 | 0.007427 | 0.001834 | -0.000027 |
167 | -56.884 | -12.754 | 0.166 | 438.410 | 26.418 | -0.252 | 0.007364 | 0.001829 | -0.000027 |
168 | -56.852 | -12.709 | 0.165 | 437.920 | 26.292 | -0.251 | 0.007302 | 0.001825 | -0.000026 |
169 | -56.821 | -12.664 | 0.164 | 437.433 | 26.167 | -0.249 | 0.007240 | 0.001820 | -0.000026 |
170 | -56.791 | -12.619 | 0.164 | 436.950 | 26.042 | -0.248 | 0.007179 | 0.001815 | -0.000026 |
171 | -56.760 | -12.575 | 0.163 | 436.472 | 25.918 | -0.247 | 0.007119 | 0.001810 | -0.000026 |
172 | -56.730 | -12.530 | 0.162 | 435.997 | 25.794 | -0.245 | 0.007059 | 0.001805 | -0.000026 |
173 | -56.700 | -12.486 | 0.161 | 435.526 | 25.671 | -0.244 | 0.007000 | 0.001800 | -0.000026 |
174 | -56.670 | -12.441 | 0.160 | 435.059 | 25.548 | -0.242 | 0.006941 | 0.001795 | -0.000026 |
175 | -56.640 | -12.397 | 0.159 | 434.595 | 25.426 | -0.241 | 0.006883 | 0.001790 | -0.000025 |
176 | -56.611 | -12.352 | 0.158 | 434.135 | 25.304 | -0.240 | 0.006825 | 0.001785 | -0.000025 |
177 | -56.581 | -12.308 | 0.157 | 433.679 | 25.183 | -0.239 | 0.006769 | 0.001780 | -0.000025 |
178 | -56.552 | -12.264 | 0.157 | 433.227 | 25.062 | -0.237 | 0.006712 | 0.001775 | -0.000025 |
179 | -56.523 | -12.220 | 0.156 | 432.778 | 24.942 | -0.236 | 0.006656 | 0.001770 | -0.000025 |
180 | -56.495 | -12.176 | 0.155 | 432.332 | 24.823 | -0.235 | 0.006601 | 0.001765 | -0.000025 |
181 | -56.466 | -12.132 | 0.154 | 431.890 | 24.704 | -0.233 | 0.006546 | 0.001760 | -0.000025 |
182 | -56.438 | -12.088 | 0.153 | 431.452 | 24.585 | -0.232 | 0.006492 | 0.001755 | -0.000025 |
183 | -56.410 | -12.044 | 0.152 | 431.017 | 24.467 | -0.231 | 0.006438 | 0.001749 | -0.000024 |
184 | -56.382 | -12.001 | 0.151 | 430.585 | 24.349 | -0.229 | 0.006385 | 0.001744 | -0.000024 |
185 | -56.354 | -11.957 | 0.151 | 430.157 | 24.232 | -0.228 | 0.006333 | 0.001739 | -0.000024 |
186 | -56.327 | -11.913 | 0.150 | 429.732 | 24.116 | -0.227 | 0.006281 | 0.001734 | -0.000024 |
187 | -56.300 | -11.870 | 0.149 | 429.310 | 24.000 | -0.226 | 0.006229 | 0.001729 | -0.000024 |
188 | -56.273 | -11.827 | 0.148 | 428.892 | 23.884 | -0.224 | 0.006178 | 0.001724 | -0.000024 |
189 | -56.246 | -11.783 | 0.147 | 428.476 | 23.769 | -0.223 | 0.006128 | 0.001719 | -0.000024 |
190 | -56.219 | -11.740 | 0.147 | 428.064 | 23.654 | -0.222 | 0.006078 | 0.001714 | -0.000024 |
191 | -56.192 | -11.697 | 0.146 | 427.655 | 23.540 | -0.221 | 0.006028 | 0.001708 | -0.000023 |
192 | -56.166 | -11.654 | 0.145 | 427.250 | 23.427 | -0.220 | 0.005979 | 0.001703 | -0.000023 |
193 | -56.140 | -11.611 | 0.144 | 426.847 | 23.313 | -0.218 | 0.005930 | 0.001698 | -0.000023 |
194 | -56.114 | -11.568 | 0.143 | 426.447 | 23.201 | -0.217 | 0.005882 | 0.001693 | -0.000023 |
195 | -56.088 | -11.525 | 0.143 | 426.051 | 23.088 | -0.216 | 0.005835 | 0.001688 | -0.000023 |
196 | -56.063 | -11.482 | 0.142 | 425.657 | 22.977 | -0.215 | 0.005787 | 0.001682 | -0.000023 |
197 | -56.037 | -11.440 | 0.141 | 425.266 | 22.865 | -0.214 | 0.005741 | 0.001677 | -0.000023 |
198 | -56.012 | -11.397 | 0.140 | 424.878 | 22.755 | -0.212 | 0.005695 | 0.001672 | -0.000022 |
199 | -55.987 | -11.354 | 0.140 | 424.493 | 22.644 | -0.211 | 0.005649 | 0.001667 | -0.000022 |
200 | -55.962 | -11.312 | 0.139 | 424.111 | 22.535 | -0.210 | 0.005603 | 0.001662 | -0.000022 |
201 | -55.937 | -11.270 | 0.138 | 423.732 | 22.425 | -0.209 | 0.005559 | 0.001656 | -0.000022 |
202 | -55.913 | -11.227 | 0.137 | 423.356 | 22.316 | -0.208 | 0.005514 | 0.001651 | -0.000022 |
203 | -55.888 | -11.185 | 0.137 | 422.982 | 22.208 | -0.207 | 0.005470 | 0.001646 | -0.000022 |
204 | -55.864 | -11.143 | 0.136 | 422.612 | 22.100 | -0.206 | 0.005426 | 0.001641 | -0.000022 |
205 | -55.840 | -11.101 | 0.135 | 422.244 | 21.992 | -0.204 | 0.005383 | 0.001636 | -0.000022 |
206 | -55.816 | -11.059 | 0.134 | 421.878 | 21.885 | -0.203 | 0.005341 | 0.001630 | -0.000022 |
207 | -55.793 | -11.018 | 0.134 | 421.516 | 21.779 | -0.202 | 0.005298 | 0.001625 | -0.000021 |
208 | -55.769 | -10.976 | 0.133 | 421.156 | 21.672 | -0.201 | 0.005256 | 0.001620 | -0.000021 |
209 | -55.746 | -10.934 | 0.132 | 420.798 | 21.567 | -0.200 | 0.005215 | 0.001615 | -0.000021 |
210 | -55.722 | -10.893 | 0.131 | 420.443 | 21.462 | -0.199 | 0.005174 | 0.001609 | -0.000021 |
211 | -55.699 | -10.851 | 0.131 | 420.091 | 21.357 | -0.198 | 0.005133 | 0.001604 | -0.000021 |
212 | -55.676 | -10.810 | 0.130 | 419.742 | 21.252 | -0.197 | 0.005092 | 0.001599 | -0.000021 |
213 | -55.654 | -10.769 | 0.129 | 419.395 | 21.149 | -0.196 | 0.005053 | 0.001594 | -0.000021 |
214 | -55.631 | -10.727 | 0.129 | 419.050 | 21.045 | -0.195 | 0.005013 | 0.001589 | -0.000021 |
215 | -55.609 | -10.686 | 0.128 | 418.708 | 20.942 | -0.193 | 0.004974 | 0.001583 | -0.000021 |
216 | -55.587 | -10.645 | 0.127 | 418.368 | 20.840 | -0.192 | 0.004935 | 0.001578 | -0.000020 |
217 | -55.564 | -10.604 | 0.126 | 418.031 | 20.738 | -0.191 | 0.004896 | 0.001573 | -0.000020 |
218 | -55.542 | -10.564 | 0.126 | 417.696 | 20.636 | -0.190 | 0.004858 | 0.001568 | -0.000020 |
219 | -55.521 | -10.523 | 0.125 | 417.364 | 20.535 | -0.189 | 0.004821 | 0.001562 | -0.000020 |
220 | -55.499 | -10.482 | 0.124 | 417.034 | 20.434 | -0.188 | 0.004783 | 0.001557 | -0.000020 |
221 | -55.477 | -10.442 | 0.124 | 416.707 | 20.334 | -0.187 | 0.004746 | 0.001552 | -0.000020 |
222 | -55.456 | -10.401 | 0.123 | 416.381 | 20.234 | -0.186 | 0.004710 | 0.001547 | -0.000020 |
223 | -55.435 | -10.361 | 0.122 | 416.059 | 20.134 | -0.185 | 0.004673 | 0.001542 | -0.000020 |
224 | -55.414 | -10.321 | 0.122 | 415.738 | 20.035 | -0.184 | 0.004637 | 0.001536 | -0.000020 |
225 | -55.393 | -10.281 | 0.121 | 415.420 | 19.937 | -0.183 | 0.004602 | 0.001531 | -0.000019 |
226 | -55.372 | -10.241 | 0.120 | 415.104 | 19.838 | -0.182 | 0.004566 | 0.001526 | -0.000019 |
227 | -55.351 | -10.201 | 0.120 | 414.790 | 19.741 | -0.181 | 0.004531 | 0.001521 | -0.000019 |
228 | -55.331 | -10.161 | 0.119 | 414.478 | 19.643 | -0.180 | 0.004497 | 0.001516 | -0.000019 |
229 | -55.311 | -10.121 | 0.118 | 414.169 | 19.547 | -0.179 | 0.004462 | 0.001510 | -0.000019 |
230 | -55.290 | -10.081 | 0.118 | 413.861 | 19.450 | -0.178 | 0.004428 | 0.001505 | -0.000019 |
231 | -55.270 | -10.042 | 0.117 | 413.556 | 19.354 | -0.177 | 0.004395 | 0.001500 | -0.000019 |
232 | -55.250 | -10.002 | 0.116 | 413.253 | 19.258 | -0.176 | 0.004361 | 0.001495 | -0.000019 |
233 | -55.231 | -9.963 | 0.116 | 412.953 | 19.163 | -0.175 | 0.004328 | 0.001490 | -0.000019 |
234 | -55.211 | -9.924 | 0.115 | 412.654 | 19.068 | -0.174 | 0.004296 | 0.001485 | -0.000019 |
235 | -55.191 | -9.884 | 0.115 | 412.357 | 18.974 | -0.173 | 0.004263 | 0.001479 | -0.000018 |
236 | -55.172 | -9.845 | 0.114 | 412.063 | 18.880 | -0.172 | 0.004231 | 0.001474 | -0.000018 |
237 | -55.153 | -9.806 | 0.113 | 411.770 | 18.787 | -0.171 | 0.004199 | 0.001469 | -0.000018 |
238 | -55.134 | -9.767 | 0.113 | 411.480 | 18.694 | -0.170 | 0.004167 | 0.001464 | -0.000018 |
239 | -55.114 | -9.729 | 0.112 | 411.192 | 18.601 | -0.170 | 0.004136 | 0.001459 | -0.000018 |
240 | -55.096 | -9.690 | 0.111 | 410.905 | 18.509 | -0.169 | 0.004105 | 0.001454 | -0.000018 |
241 | -55.077 | -9.651 | 0.111 | 410.621 | 18.417 | -0.168 | 0.004074 | 0.001449 | -0.000018 |
242 | -55.058 | -9.613 | 0.110 | 410.338 | 18.325 | -0.167 | 0.004044 | 0.001443 | -0.000018 |
243 | -55.040 | -9.574 | 0.110 | 410.058 | 18.234 | -0.166 | 0.004014 | 0.001438 | -0.000018 |
244 | -55.021 | -9.536 | 0.109 | 409.779 | 18.144 | -0.165 | 0.003984 | 0.001433 | -0.000018 |
245 | -55.003 | -9.498 | 0.108 | 409.502 | 18.053 | -0.164 | 0.003954 | 0.001428 | -0.000017 |
246 | -54.985 | -9.460 | 0.108 | 409.228 | 17.963 | -0.163 | 0.003925 | 0.001423 | -0.000017 |
247 | -54.967 | -9.422 | 0.107 | 408.955 | 17.874 | -0.162 | 0.003896 | 0.001418 | -0.000017 |
248 | -54.949 | -9.384 | 0.107 | 408.684 | 17.785 | -0.161 | 0.003867 | 0.001413 | -0.000017 |
249 | -54.931 | -9.346 | 0.106 | 408.415 | 17.696 | -0.160 | 0.003839 | 0.001408 | -0.000017 |
250 | -54.914 | -9.308 | 0.105 | 408.147 | 17.608 | -0.160 | 0.003810 | 0.001403 | -0.000017 |
251 | -54.896 | -9.271 | 0.105 | 407.882 | 17.520 | -0.159 | 0.003782 | 0.001398 | -0.000017 |
252 | -54.879 | -9.233 | 0.104 | 407.618 | 17.433 | -0.158 | 0.003754 | 0.001393 | -0.000017 |
253 | -54.861 | -9.196 | 0.104 | 407.357 | 17.346 | -0.157 | 0.003727 | 0.001387 | -0.000017 |
254 | -54.844 | -9.159 | 0.103 | 407.096 | 17.259 | -0.156 | 0.003699 | 0.001382 | -0.000017 |
255 | -54.827 | -9.121 | 0.103 | 406.838 | 17.173 | -0.155 | 0.003672 | 0.001377 | -0.000017 |
256 | -54.810 | -9.084 | 0.102 | 406.582 | 17.087 | -0.154 | 0.003646 | 0.001372 | -0.000016 |
257 | -54.793 | -9.047 | 0.101 | 406.327 | 17.001 | -0.154 | 0.003619 | 0.001367 | -0.000016 |
258 | -54.776 | -9.010 | 0.101 | 406.074 | 16.916 | -0.153 | 0.003593 | 0.001362 | -0.000016 |
259 | -54.760 | -8.974 | 0.100 | 405.822 | 16.831 | -0.152 | 0.003566 | 0.001357 | -0.000016 |
260 | -54.743 | -8.937 | 0.100 | 405.573 | 16.747 | -0.151 | 0.003541 | 0.001352 | -0.000016 |
261 | -54.727 | -8.900 | 0.099 | 405.325 | 16.663 | -0.150 | 0.003515 | 0.001347 | -0.000016 |
262 | -54.710 | -8.864 | 0.099 | 405.078 | 16.580 | -0.149 | 0.003489 | 0.001342 | -0.000016 |
263 | -54.694 | -8.827 | 0.098 | 404.834 | 16.496 | -0.149 | 0.003464 | 0.001337 | -0.000016 |
264 | -54.678 | -8.791 | 0.098 | 404.591 | 16.414 | -0.148 | 0.003439 | 0.001332 | -0.000016 |
265 | -54.662 | -8.755 | 0.097 | 404.349 | 16.331 | -0.147 | 0.003414 | 0.001327 | -0.000016 |
266 | -54.646 | -8.719 | 0.097 | 404.110 | 16.249 | -0.146 | 0.003390 | 0.001322 | -0.000016 |
267 | -54.631 | -8.683 | 0.096 | 403.871 | 16.167 | -0.145 | 0.003366 | 0.001318 | -0.000015 |
268 | -54.615 | -8.647 | 0.095 | 403.635 | 16.086 | -0.145 | 0.003341 | 0.001313 | -0.000015 |
269 | -54.599 | -8.611 | 0.095 | 403.400 | 16.005 | -0.144 | 0.003317 | 0.001308 | -0.000015 |
270 | -54.584 | -8.575 | 0.094 | 403.167 | 15.924 | -0.143 | 0.003294 | 0.001303 | -0.000015 |
271 | -54.568 | -8.540 | 0.094 | 402.935 | 15.844 | -0.142 | 0.003270 | 0.001298 | -0.000015 |
272 | -54.553 | -8.504 | 0.093 | 402.704 | 15.764 | -0.141 | 0.003247 | 0.001293 | -0.000015 |
273 | -54.538 | -8.469 | 0.093 | 402.476 | 15.685 | -0.141 | 0.003224 | 0.001288 | -0.000015 |
274 | -54.523 | -8.434 | 0.092 | 402.248 | 15.606 | -0.140 | 0.003201 | 0.001283 | -0.000015 |
275 | -54.508 | -8.399 | 0.092 | 402.023 | 15.527 | -0.139 | 0.003178 | 0.001278 | -0.000015 |
276 | -54.493 | -8.363 | 0.091 | 401.798 | 15.449 | -0.138 | 0.003155 | 0.001273 | -0.000015 |
277 | -54.478 | -8.328 | 0.091 | 401.576 | 15.371 | -0.138 | 0.003133 | 0.001269 | -0.000015 |
278 | -54.464 | -8.294 | 0.090 | 401.354 | 15.293 | -0.137 | 0.003111 | 0.001264 | -0.000015 |
279 | -54.449 | -8.259 | 0.090 | 401.134 | 15.216 | -0.136 | 0.003089 | 0.001259 | -0.000015 |
280 | -54.435 | -8.224 | 0.089 | 400.916 | 15.139 | -0.135 | 0.003067 | 0.001254 | -0.000014 |
281 | -54.420 | -8.190 | 0.089 | 400.699 | 15.062 | -0.135 | 0.003046 | 0.001249 | -0.000014 |
282 | -54.406 | -8.155 | 0.088 | 400.484 | 14.986 | -0.134 | 0.003024 | 0.001244 | -0.000014 |
283 | -54.392 | -8.121 | 0.088 | 400.270 | 14.910 | -0.133 | 0.003003 | 0.001240 | -0.000014 |
284 | -54.377 | -8.087 | 0.087 | 400.057 | 14.834 | -0.132 | 0.002982 | 0.001235 | -0.000014 |
285 | -54.363 | -8.052 | 0.087 | 399.846 | 14.759 | -0.132 | 0.002961 | 0.001230 | -0.000014 |
286 | -54.350 | -8.018 | 0.086 | 399.636 | 14.684 | -0.131 | 0.002940 | 0.001225 | -0.000014 |
287 | -54.336 | -7.984 | 0.086 | 399.427 | 14.610 | -0.130 | 0.002920 | 0.001220 | -0.000014 |
288 | -54.322 | -7.951 | 0.086 | 399.220 | 14.536 | -0.129 | 0.002899 | 0.001216 | -0.000014 |
289 | -54.308 | -7.917 | 0.085 | 399.014 | 14.462 | -0.129 | 0.002879 | 0.001211 | -0.000014 |
290 | -54.295 | -7.883 | 0.085 | 398.810 | 14.388 | -0.128 | 0.002859 | 0.001206 | -0.000014 |
291 | -54.281 | -7.850 | 0.084 | 398.607 | 14.315 | -0.127 | 0.002839 | 0.001202 | -0.000014 |
292 | -54.268 | -7.816 | 0.084 | 398.405 | 14.242 | -0.127 | 0.002820 | 0.001197 | -0.000014 |
293 | -54.254 | -7.783 | 0.083 | 398.204 | 14.170 | -0.126 | 0.002800 | 0.001192 | -0.000013 |
294 | -54.241 | -7.750 | 0.083 | 398.005 | 14.098 | -0.125 | 0.002781 | 0.001187 | -0.000013 |
295 | -54.228 | -7.717 | 0.082 | 397.807 | 14.026 | -0.125 | 0.002761 | 0.001183 | -0.000013 |
296 | -54.215 | -7.684 | 0.082 | 397.611 | 13.955 | -0.124 | 0.002742 | 0.001178 | -0.000013 |
297 | -54.202 | -7.651 | 0.081 | 397.415 | 13.884 | -0.123 | 0.002723 | 0.001173 | -0.000013 |
298 | -54.189 | -7.618 | 0.081 | 397.221 | 13.813 | -0.122 | 0.002705 | 0.001169 | -0.000013 |
299 | -54.176 | -7.585 | 0.080 | 397.028 | 13.742 | -0.122 | 0.002686 | 0.001164 | -0.000013 |
300 | -54.163 | -7.553 | 0.080 | 396.837 | 13.672 | -0.121 | 0.002668 | 0.001159 | -0.000013 |
301 | -54.151 | -7.520 | 0.080 | 396.647 | 13.602 | -0.120 | 0.002649 | 0.001155 | -0.000013 |
302 | -54.138 | -7.488 | 0.079 | 396.457 | 13.533 | -0.120 | 0.002631 | 0.001150 | -0.000013 |
303 | -54.126 | -7.455 | 0.079 | 396.270 | 13.464 | -0.119 | 0.002613 | 0.001146 | -0.000013 |
304 | -54.113 | -7.423 | 0.078 | 396.083 | 13.395 | -0.118 | 0.002595 | 0.001141 | -0.000013 |
305 | -54.101 | -7.391 | 0.078 | 395.897 | 13.327 | -0.118 | 0.002578 | 0.001136 | -0.000013 |
306 | -54.089 | -7.359 | 0.077 | 395.713 | 13.259 | -0.117 | 0.002560 | 0.001132 | -0.000013 |
307 | -54.076 | -7.327 | 0.077 | 395.530 | 13.191 | -0.117 | 0.002543 | 0.001127 | -0.000012 |
308 | -54.064 | -7.296 | 0.077 | 395.348 | 13.123 | -0.116 | 0.002525 | 0.001123 | -0.000012 |
309 | -54.052 | -7.264 | 0.076 | 395.167 | 13.056 | -0.115 | 0.002508 | 0.001118 | -0.000012 |
310 | -54.040 | -7.232 | 0.076 | 394.988 | 12.989 | -0.115 | 0.002491 | 0.001114 | -0.000012 |
311 | -54.028 | -7.201 | 0.075 | 394.809 | 12.923 | -0.114 | 0.002474 | 0.001109 | -0.000012 |
312 | -54.017 | -7.169 | 0.075 | 394.632 | 12.856 | -0.113 | 0.002458 | 0.001105 | -0.000012 |
313 | -54.005 | -7.138 | 0.075 | 394.456 | 12.791 | -0.113 | 0.002441 | 0.001100 | -0.000012 |
314 | -53.993 | -7.107 | 0.074 | 394.281 | 12.725 | -0.112 | 0.002424 | 0.001096 | -0.000012 |
315 | -53.982 | -7.076 | 0.074 | 394.107 | 12.660 | -0.112 | 0.002408 | 0.001091 | -0.000012 |
316 | -53.970 | -7.045 | 0.073 | 393.934 | 12.595 | -0.111 | 0.002392 | 0.001087 | -0.000012 |
317 | -53.959 | -7.014 | 0.073 | 393.762 | 12.530 | -0.110 | 0.002376 | 0.001082 | -0.000012 |
318 | -53.947 | -6.983 | 0.072 | 393.592 | 12.466 | -0.110 | 0.002360 | 0.001078 | -0.000012 |
319 | -53.936 | -6.953 | 0.072 | 393.422 | 12.402 | -0.109 | 0.002344 | 0.001074 | -0.000012 |
320 | -53.925 | -6.922 | 0.072 | 393.254 | 12.338 | -0.108 | 0.002328 | 0.001069 | -0.000012 |
321 | -53.914 | -6.892 | 0.071 | 393.086 | 12.274 | -0.108 | 0.002313 | 0.001065 | -0.000012 |
322 | -53.903 | -6.861 | 0.071 | 392.920 | 12.211 | -0.107 | 0.002297 | 0.001060 | -0.000011 |
323 | -53.892 | -6.831 | 0.071 | 392.755 | 12.149 | -0.107 | 0.002282 | 0.001056 | -0.000011 |
324 | -53.881 | -6.801 | 0.070 | 392.591 | 12.086 | -0.106 | 0.002267 | 0.001052 | -0.000011 |
325 | -53.870 | -6.771 | 0.070 | 392.427 | 12.024 | -0.106 | 0.002252 | 0.001047 | -0.000011 |
326 | -53.859 | -6.741 | 0.069 | 392.265 | 11.962 | -0.105 | 0.002237 | 0.001043 | -0.000011 |
327 | -53.848 | -6.711 | 0.069 | 392.104 | 11.900 | -0.104 | 0.002222 | 0.001039 | -0.000011 |
328 | -53.837 | -6.682 | 0.069 | 391.944 | 11.839 | -0.104 | 0.002207 | 0.001034 | -0.000011 |
329 | -53.827 | -6.652 | 0.068 | 391.785 | 11.778 | -0.103 | 0.002192 | 0.001030 | -0.000011 |
330 | -53.816 | -6.622 | 0.068 | 391.627 | 11.717 | -0.103 | 0.002178 | 0.001026 | -0.000011 |
331 | -53.806 | -6.593 | 0.067 | 391.470 | 11.657 | -0.102 | 0.002163 | 0.001021 | -0.000011 |
332 | -53.795 | -6.564 | 0.067 | 391.314 | 11.596 | -0.102 | 0.002149 | 0.001017 | -0.000011 |
333 | -53.785 | -6.534 | 0.067 | 391.158 | 11.537 | -0.101 | 0.002135 | 0.001013 | -0.000011 |
334 | -53.775 | -6.505 | 0.066 | 391.004 | 11.477 | -0.100 | 0.002121 | 0.001009 | -0.000011 |
335 | -53.765 | -6.476 | 0.066 | 390.851 | 11.418 | -0.100 | 0.002107 | 0.001004 | -0.000011 |
336 | -53.754 | -6.447 | 0.066 | 390.699 | 11.359 | -0.099 | 0.002093 | 0.001000 | -0.000011 |
337 | -53.744 | -6.419 | 0.065 | 390.548 | 11.300 | -0.099 | 0.002079 | 0.000996 | -0.000011 |
338 | -53.734 | -6.390 | 0.065 | 390.397 | 11.242 | -0.098 | 0.002065 | 0.000992 | -0.000011 |
339 | -53.724 | -6.361 | 0.065 | 390.248 | 11.183 | -0.098 | 0.002052 | 0.000988 | -0.000010 |
340 | -53.714 | -6.333 | 0.064 | 390.099 | 11.126 | -0.097 | 0.002038 | 0.000983 | -0.000010 |
341 | -53.705 | -6.304 | 0.064 | 389.952 | 11.068 | -0.097 | 0.002025 | 0.000979 | -0.000010 |
342 | -53.695 | -6.276 | 0.063 | 389.805 | 11.011 | -0.096 | 0.002012 | 0.000975 | -0.000010 |
343 | -53.685 | -6.248 | 0.063 | 389.659 | 10.954 | -0.096 | 0.001999 | 0.000971 | -0.000010 |
344 | -53.675 | -6.220 | 0.063 | 389.515 | 10.897 | -0.095 | 0.001986 | 0.000967 | -0.000010 |
345 | -53.666 | -6.192 | 0.062 | 389.371 | 10.840 | -0.094 | 0.001973 | 0.000963 | -0.000010 |
346 | -53.656 | -6.164 | 0.062 | 389.228 | 10.784 | -0.094 | 0.001960 | 0.000959 | -0.000010 |
347 | -53.647 | -6.136 | 0.062 | 389.086 | 10.728 | -0.093 | 0.001947 | 0.000954 | -0.000010 |
348 | -53.637 | -6.108 | 0.061 | 388.944 | 10.673 | -0.093 | 0.001934 | 0.000950 | -0.000010 |
349 | -53.628 | -6.081 | 0.061 | 388.804 | 10.617 | -0.092 | 0.001922 | 0.000946 | -0.000010 |
350 | -53.619 | -6.053 | 0.061 | 388.664 | 10.562 | -0.092 | 0.001909 | 0.000942 | -0.000010 |
351 | -53.609 | -6.026 | 0.060 | 388.526 | 10.507 | -0.091 | 0.001897 | 0.000938 | -0.000010 |
352 | -53.600 | -5.998 | 0.060 | 388.388 | 10.453 | -0.091 | 0.001885 | 0.000934 | -0.000010 |
353 | -53.591 | -5.971 | 0.060 | 388.251 | 10.398 | -0.090 | 0.001872 | 0.000930 | -0.000010 |
354 | -53.582 | -5.944 | 0.059 | 388.115 | 10.344 | -0.090 | 0.001860 | 0.000926 | -0.000010 |
355 | -53.573 | -5.917 | 0.059 | 387.980 | 10.290 | -0.089 | 0.001848 | 0.000922 | -0.000010 |
356 | -53.564 | -5.890 | 0.059 | 387.845 | 10.237 | -0.089 | 0.001836 | 0.000918 | -0.000010 |
357 | -53.555 | -5.863 | 0.058 | 387.712 | 10.184 | -0.088 | 0.001824 | 0.000914 | -0.000009 |
358 | -53.546 | -5.836 | 0.058 | 387.579 | 10.131 | -0.088 | 0.001813 | 0.000910 | -0.000009 |
359 | -53.537 | -5.810 | 0.058 | 387.447 | 10.078 | -0.087 | 0.001801 | 0.000906 | -0.000009 |
360 | -53.528 | -5.783 | 0.057 | 387.316 | 10.025 | -0.087 | 0.001789 | 0.000902 | -0.000009 |
361 | -53.520 | -5.757 | 0.057 | 387.186 | 9.973 | -0.086 | 0.001778 | 0.000898 | -0.000009 |
362 | -53.511 | -5.730 | 0.057 | 387.056 | 9.921 | -0.086 | 0.001767 | 0.000895 | -0.000009 |
363 | -53.502 | -5.704 | 0.057 | 386.928 | 9.870 | -0.085 | 0.001755 | 0.000891 | -0.000009 |
364 | -53.494 | -5.678 | 0.056 | 386.800 | 9.818 | -0.085 | 0.001744 | 0.000887 | -0.000009 |
365 | -53.485 | -5.652 | 0.056 | 386.673 | 9.767 | -0.085 | 0.001733 | 0.000883 | -0.000009 |
366 | -53.477 | -5.626 | 0.056 | 386.546 | 9.716 | -0.084 | 0.001722 | 0.000879 | -0.000009 |
367 | -53.468 | -5.600 | 0.055 | 386.421 | 9.665 | -0.084 | 0.001711 | 0.000875 | -0.000009 |
368 | -53.460 | -5.574 | 0.055 | 386.296 | 9.615 | -0.083 | 0.001700 | 0.000871 | -0.000009 |
369 | -53.452 | -5.549 | 0.055 | 386.172 | 9.565 | -0.083 | 0.001689 | 0.000868 | -0.000009 |
370 | -53.444 | -5.523 | 0.054 | 386.048 | 9.515 | -0.082 | 0.001678 | 0.000864 | -0.000009 |
371 | -53.435 | -5.498 | 0.054 | 385.926 | 9.465 | -0.082 | 0.001668 | 0.000860 | -0.000009 |
372 | -53.427 | -5.472 | 0.054 | 385.804 | 9.416 | -0.081 | 0.001657 | 0.000856 | -0.000009 |
373 | -53.419 | -5.447 | 0.053 | 385.683 | 9.366 | -0.081 | 0.001646 | 0.000852 | -0.000009 |
374 | -53.411 | -5.422 | 0.053 | 385.563 | 9.317 | -0.080 | 0.001636 | 0.000849 | -0.000009 |
375 | -53.403 | -5.397 | 0.053 | 385.443 | 9.269 | -0.080 | 0.001626 | 0.000845 | -0.000009 |
376 | -53.395 | -5.372 | 0.053 | 385.324 | 9.220 | -0.080 | 0.001615 | 0.000841 | -0.000009 |
377 | -53.387 | -5.347 | 0.052 | 385.206 | 9.172 | -0.079 | 0.001605 | 0.000837 | -0.000009 |
378 | -53.379 | -5.322 | 0.052 | 385.089 | 9.124 | -0.079 | 0.001595 | 0.000834 | -0.000008 |
379 | -53.371 | -5.297 | 0.052 | 384.972 | 9.076 | -0.078 | 0.001585 | 0.000830 | -0.000008 |
380 | -53.364 | -5.273 | 0.051 | 384.856 | 9.029 | -0.078 | 0.001575 | 0.000826 | -0.000008 |
381 | -53.356 | -5.248 | 0.051 | 384.741 | 8.981 | -0.077 | 0.001565 | 0.000823 | -0.000008 |
382 | -53.348 | -5.224 | 0.051 | 384.626 | 8.934 | -0.077 | 0.001555 | 0.000819 | -0.000008 |
383 | -53.341 | -5.199 | 0.051 | 384.512 | 8.888 | -0.077 | 0.001545 | 0.000815 | -0.000008 |
384 | -53.333 | -5.175 | 0.050 | 384.399 | 8.841 | -0.076 | 0.001535 | 0.000812 | -0.000008 |
385 | -53.326 | -5.151 | 0.050 | 384.287 | 8.795 | -0.076 | 0.001526 | 0.000808 | -0.000008 |
386 | -53.318 | -5.127 | 0.050 | 384.175 | 8.749 | -0.075 | 0.001516 | 0.000804 | -0.000008 |
387 | -53.311 | -5.103 | 0.049 | 384.064 | 8.703 | -0.075 | 0.001507 | 0.000801 | -0.000008 |
388 | -53.303 | -5.079 | 0.049 | 383.953 | 8.657 | -0.074 | 0.001497 | 0.000797 | -0.000008 |
389 | -53.296 | -5.055 | 0.049 | 383.843 | 8.612 | -0.074 | 0.001488 | 0.000794 | -0.000008 |
390 | -53.289 | -5.032 | 0.049 | 383.734 | 8.566 | -0.074 | 0.001478 | 0.000790 | -0.000008 |
391 | -53.281 | -5.008 | 0.048 | 383.626 | 8.521 | -0.073 | 0.001469 | 0.000786 | -0.000008 |
392 | -53.274 | -4.985 | 0.048 | 383.518 | 8.477 | -0.073 | 0.001460 | 0.000783 | -0.000008 |
393 | -53.267 | -4.961 | 0.048 | 383.411 | 8.432 | -0.072 | 0.001451 | 0.000779 | -0.000008 |
394 | -53.260 | -4.938 | 0.048 | 383.304 | 8.388 | -0.072 | 0.001442 | 0.000776 | -0.000008 |
395 | -53.253 | -4.915 | 0.047 | 383.198 | 8.344 | -0.072 | 0.001433 | 0.000772 | -0.000008 |
396 | -53.246 | -4.892 | 0.047 | 383.093 | 8.300 | -0.071 | 0.001424 | 0.000769 | -0.000008 |
397 | -53.239 | -4.869 | 0.047 | 382.989 | 8.256 | -0.071 | 0.001415 | 0.000765 | -0.000008 |
398 | -53.232 | -4.846 | 0.047 | 382.885 | 8.213 | -0.070 | 0.001406 | 0.000762 | -0.000008 |
399 | -53.225 | -4.823 | 0.046 | 382.781 | 8.170 | -0.070 | 0.001397 | 0.000759 | -0.000008 |
400 | -53.218 | -4.800 | 0.046 | 382.678 | 8.127 | -0.070 | 0.001389 | 0.000755 | -0.000007 |
401 | -53.211 | -4.777 | 0.046 | 382.576 | 8.084 | -0.069 | 0.001380 | 0.000752 | -0.000007 |
402 | -53.204 | -4.755 | 0.046 | 382.475 | 8.041 | -0.069 | 0.001372 | 0.000748 | -0.000007 |
403 | -53.197 | -4.732 | 0.045 | 382.374 | 7.999 | -0.068 | 0.001363 | 0.000745 | -0.000007 |
404 | -53.191 | -4.710 | 0.045 | 382.274 | 7.957 | -0.068 | 0.001355 | 0.000741 | -0.000007 |
405 | -53.184 | -4.688 | 0.045 | 382.174 | 7.915 | -0.068 | 0.001346 | 0.000738 | -0.000007 |
406 | -53.177 | -4.665 | 0.045 | 382.075 | 7.873 | -0.067 | 0.001338 | 0.000735 | -0.000007 |
407 | -53.171 | -4.643 | 0.044 | 381.976 | 7.832 | -0.067 | 0.001330 | 0.000731 | -0.000007 |
408 | -53.164 | -4.621 | 0.044 | 381.878 | 7.790 | -0.067 | 0.001321 | 0.000728 | -0.000007 |
409 | -53.158 | -4.599 | 0.044 | 381.781 | 7.749 | -0.066 | 0.001313 | 0.000725 | -0.000007 |
410 | -53.151 | -4.577 | 0.044 | 381.684 | 7.709 | -0.066 | 0.001305 | 0.000721 | -0.000007 |
411 | -53.145 | -4.555 | 0.043 | 381.588 | 7.668 | -0.065 | 0.001297 | 0.000718 | -0.000007 |
412 | -53.138 | -4.534 | 0.043 | 381.492 | 7.627 | -0.065 | 0.001289 | 0.000715 | -0.000007 |
413 | -53.132 | -4.512 | 0.043 | 381.397 | 7.587 | -0.065 | 0.001281 | 0.000711 | -0.000007 |
414 | -53.125 | -4.491 | 0.043 | 381.303 | 7.547 | -0.064 | 0.001273 | 0.000708 | -0.000007 |
415 | -53.119 | -4.469 | 0.042 | 381.209 | 7.507 | -0.064 | 0.001265 | 0.000705 | -0.000007 |
416 | -53.113 | -4.448 | 0.042 | 381.116 | 7.468 | -0.064 | 0.001258 | 0.000702 | -0.000007 |
417 | -53.107 | -4.427 | 0.042 | 381.023 | 7.428 | -0.063 | 0.001250 | 0.000698 | -0.000007 |
418 | -53.100 | -4.405 | 0.042 | 380.930 | 7.389 | -0.063 | 0.001242 | 0.000695 | -0.000007 |
419 | -53.094 | -4.384 | 0.041 | 380.839 | 7.350 | -0.063 | 0.001235 | 0.000692 | -0.000007 |
420 | -53.088 | -4.363 | 0.041 | 380.748 | 7.311 | -0.062 | 0.001227 | 0.000689 | -0.000007 |
421 | -53.082 | -4.342 | 0.041 | 380.657 | 7.272 | -0.062 | 0.001220 | 0.000686 | -0.000007 |
422 | -53.076 | -4.322 | 0.041 | 380.567 | 7.234 | -0.062 | 0.001212 | 0.000682 | -0.000007 |
423 | -53.070 | -4.301 | 0.041 | 380.477 | 7.196 | -0.061 | 0.001205 | 0.000679 | -0.000007 |
424 | -53.064 | -4.280 | 0.040 | 380.388 | 7.158 | -0.061 | 0.001197 | 0.000676 | -0.000007 |
425 | -53.058 | -4.260 | 0.040 | 380.300 | 7.120 | -0.061 | 0.001190 | 0.000673 | -0.000007 |
426 | -53.052 | -4.239 | 0.040 | 380.212 | 7.082 | -0.060 | 0.001183 | 0.000670 | -0.000006 |
427 | -53.046 | -4.219 | 0.040 | 380.124 | 7.045 | -0.060 | 0.001176 | 0.000667 | -0.000006 |
428 | -53.040 | -4.199 | 0.039 | 380.038 | 7.007 | -0.060 | 0.001168 | 0.000664 | -0.000006 |
429 | -53.035 | -4.178 | 0.039 | 379.951 | 6.970 | -0.059 | 0.001161 | 0.000660 | -0.000006 |
430 | -53.029 | -4.158 | 0.039 | 379.865 | 6.933 | -0.059 | 0.001154 | 0.000657 | -0.000006 |
431 | -53.023 | -4.138 | 0.039 | 379.780 | 6.897 | -0.059 | 0.001147 | 0.000654 | -0.000006 |
432 | -53.017 | -4.118 | 0.039 | 379.695 | 6.860 | -0.058 | 0.001140 | 0.000651 | -0.000006 |
433 | -53.012 | -4.098 | 0.038 | 379.611 | 6.824 | -0.058 | 0.001133 | 0.000648 | -0.000006 |
434 | -53.006 | -4.078 | 0.038 | 379.527 | 6.788 | -0.058 | 0.001126 | 0.000645 | -0.000006 |
435 | -53.001 | -4.059 | 0.038 | 379.443 | 6.752 | -0.057 | 0.001120 | 0.000642 | -0.000006 |
436 | -52.995 | -4.039 | 0.038 | 379.360 | 6.716 | -0.057 | 0.001113 | 0.000639 | -0.000006 |
437 | -52.989 | -4.020 | 0.038 | 379.278 | 6.680 | -0.057 | 0.001106 | 0.000636 | -0.000006 |
438 | -52.984 | -4.000 | 0.037 | 379.196 | 6.645 | -0.056 | 0.001099 | 0.000633 | -0.000006 |
439 | -52.978 | -3.981 | 0.037 | 379.115 | 6.609 | -0.056 | 0.001093 | 0.000630 | -0.000006 |
440 | -52.973 | -3.961 | 0.037 | 379.034 | 6.574 | -0.056 | 0.001086 | 0.000627 | -0.000006 |
441 | -52.968 | -3.942 | 0.037 | 378.953 | 6.540 | -0.055 | 0.001079 | 0.000624 | -0.000006 |
442 | -52.962 | -3.923 | 0.036 | 378.873 | 6.505 | -0.055 | 0.001073 | 0.000621 | -0.000006 |
443 | -52.957 | -3.904 | 0.036 | 378.794 | 6.470 | -0.055 | 0.001066 | 0.000618 | -0.000006 |
444 | -52.952 | -3.885 | 0.036 | 378.715 | 6.436 | -0.055 | 0.001060 | 0.000615 | -0.000006 |
445 | -52.946 | -3.866 | 0.036 | 378.636 | 6.402 | -0.054 | 0.001054 | 0.000612 | -0.000006 |
446 | -52.941 | -3.847 | 0.036 | 378.558 | 6.368 | -0.054 | 0.001047 | 0.000610 | -0.000006 |
447 | -52.936 | -3.828 | 0.035 | 378.480 | 6.334 | -0.054 | 0.001041 | 0.000607 | -0.000006 |
448 | -52.931 | -3.810 | 0.035 | 378.403 | 6.300 | -0.053 | 0.001035 | 0.000604 | -0.000006 |
449 | -52.925 | -3.791 | 0.035 | 378.326 | 6.267 | -0.053 | 0.001028 | 0.000601 | -0.000006 |
450 | -52.920 | -3.773 | 0.035 | 378.250 | 6.233 | -0.053 | 0.001022 | 0.000598 | -0.000006 |
451 | -52.915 | -3.754 | 0.035 | 378.174 | 6.200 | -0.052 | 0.001016 | 0.000595 | -0.000006 |
452 | -52.910 | -3.736 | 0.034 | 378.098 | 6.167 | -0.052 | 0.001010 | 0.000592 | -0.000006 |
453 | -52.905 | -3.718 | 0.034 | 378.023 | 6.135 | -0.052 | 0.001004 | 0.000590 | -0.000006 |
454 | -52.900 | -3.699 | 0.034 | 377.949 | 6.102 | -0.052 | 0.000998 | 0.000587 | -0.000006 |
455 | -52.895 | -3.681 | 0.034 | 377.875 | 6.069 | -0.051 | 0.000992 | 0.000584 | -0.000006 |
456 | -52.890 | -3.663 | 0.034 | 377.801 | 6.037 | -0.051 | 0.000986 | 0.000581 | -0.000006 |
457 | -52.885 | -3.645 | 0.034 | 377.728 | 6.005 | -0.051 | 0.000980 | 0.000578 | -0.000005 |
458 | -52.880 | -3.627 | 0.033 | 377.655 | 5.973 | -0.050 | 0.000974 | 0.000576 | -0.000005 |
459 | -52.875 | -3.610 | 0.033 | 377.582 | 5.941 | -0.050 | 0.000968 | 0.000573 | -0.000005 |
460 | -52.871 | -3.592 | 0.033 | 377.510 | 5.910 | -0.050 | 0.000963 | 0.000570 | -0.000005 |
461 | -52.866 | -3.574 | 0.033 | 377.439 | 5.878 | -0.050 | 0.000957 | 0.000567 | -0.000005 |
462 | -52.861 | -3.557 | 0.033 | 377.368 | 5.847 | -0.049 | 0.000951 | 0.000565 | -0.000005 |
463 | -52.856 | -3.539 | 0.032 | 377.297 | 5.816 | -0.049 | 0.000945 | 0.000562 | -0.000005 |
464 | -52.851 | -3.522 | 0.032 | 377.227 | 5.785 | -0.049 | 0.000940 | 0.000559 | -0.000005 |
465 | -52.847 | -3.504 | 0.032 | 377.157 | 5.754 | -0.048 | 0.000934 | 0.000557 | -0.000005 |
466 | -52.842 | -3.487 | 0.032 | 377.087 | 5.723 | -0.048 | 0.000929 | 0.000554 | -0.000005 |
467 | -52.837 | -3.470 | 0.032 | 377.018 | 5.693 | -0.048 | 0.000923 | 0.000551 | -0.000005 |
468 | -52.833 | -3.453 | 0.032 | 376.949 | 5.662 | -0.048 | 0.000918 | 0.000549 | -0.000005 |
469 | -52.828 | -3.436 | 0.031 | 376.881 | 5.632 | -0.047 | 0.000912 | 0.000546 | -0.000005 |
470 | -52.824 | -3.419 | 0.031 | 376.813 | 5.602 | -0.047 | 0.000907 | 0.000543 | -0.000005 |
471 | -52.819 | -3.402 | 0.031 | 376.746 | 5.572 | -0.047 | 0.000901 | 0.000541 | -0.000005 |
472 | -52.815 | -3.385 | 0.031 | 376.678 | 5.542 | -0.047 | 0.000896 | 0.000538 | -0.000005 |
473 | -52.810 | -3.368 | 0.031 | 376.612 | 5.513 | -0.046 | 0.000891 | 0.000536 | -0.000005 |
474 | -52.806 | -3.352 | 0.031 | 376.545 | 5.483 | -0.046 | 0.000885 | 0.000533 | -0.000005 |
475 | -52.801 | -3.335 | 0.030 | 376.479 | 5.454 | -0.046 | 0.000880 | 0.000530 | -0.000005 |
476 | -52.797 | -3.319 | 0.030 | 376.414 | 5.425 | -0.046 | 0.000875 | 0.000528 | -0.000005 |
477 | -52.792 | -3.302 | 0.030 | 376.349 | 5.396 | -0.045 | 0.000870 | 0.000525 | -0.000005 |
478 | -52.788 | -3.286 | 0.030 | 376.284 | 5.367 | -0.045 | 0.000865 | 0.000523 | -0.000005 |
479 | -52.784 | -3.270 | 0.030 | 376.219 | 5.339 | -0.045 | 0.000859 | 0.000520 | -0.000005 |
480 | -52.779 | -3.253 | 0.030 | 376.155 | 5.310 | -0.045 | 0.000854 | 0.000518 | -0.000005 |
481 | -52.775 | -3.237 | 0.029 | 376.092 | 5.282 | -0.044 | 0.000849 | 0.000515 | -0.000005 |
482 | -52.771 | -3.221 | 0.029 | 376.028 | 5.254 | -0.044 | 0.000844 | 0.000513 | -0.000005 |
483 | -52.767 | -3.205 | 0.029 | 375.965 | 5.225 | -0.044 | 0.000839 | 0.000510 | -0.000005 |
484 | -52.762 | -3.189 | 0.029 | 375.903 | 5.198 | -0.044 | 0.000834 | 0.000508 | -0.000005 |
485 | -52.758 | -3.173 | 0.029 | 375.840 | 5.170 | -0.043 | 0.000829 | 0.000505 | -0.000005 |
486 | -52.754 | -3.157 | 0.029 | 375.779 | 5.142 | -0.043 | 0.000825 | 0.000503 | -0.000005 |
487 | -52.750 | -3.142 | 0.028 | 375.717 | 5.115 | -0.043 | 0.000820 | 0.000500 | -0.000005 |
488 | -52.746 | -3.126 | 0.028 | 375.656 | 5.087 | -0.043 | 0.000815 | 0.000498 | -0.000005 |
489 | -52.742 | -3.110 | 0.028 | 375.595 | 5.060 | -0.042 | 0.000810 | 0.000495 | -0.000005 |
490 | -52.738 | -3.095 | 0.028 | 375.535 | 5.033 | -0.042 | 0.000805 | 0.000493 | -0.000005 |
491 | -52.733 | -3.080 | 0.028 | 375.474 | 5.006 | -0.042 | 0.000800 | 0.000491 | -0.000005 |
492 | -52.729 | -3.064 | 0.028 | 375.415 | 4.979 | -0.042 | 0.000796 | 0.000488 | -0.000005 |
493 | -52.725 | -3.049 | 0.027 | 375.355 | 4.953 | -0.041 | 0.000791 | 0.000486 | -0.000004 |
494 | -52.721 | -3.034 | 0.027 | 375.296 | 4.926 | -0.041 | 0.000786 | 0.000483 | -0.000004 |
495 | -52.717 | -3.018 | 0.027 | 375.237 | 4.900 | -0.041 | 0.000782 | 0.000481 | -0.000004 |
496 | -52.714 | -3.003 | 0.027 | 375.179 | 4.874 | -0.041 | 0.000777 | 0.000479 | -0.000004 |
497 | -52.710 | -2.988 | 0.027 | 375.121 | 4.847 | -0.041 | 0.000773 | 0.000476 | -0.000004 |
498 | -52.706 | -2.973 | 0.027 | 375.063 | 4.821 | -0.040 | 0.000768 | 0.000474 | -0.000004 |
499 | -52.702 | -2.958 | 0.027 | 375.006 | 4.796 | -0.040 | 0.000764 | 0.000472 | -0.000004 |
Figure 4: Linear vs Nonlinear Impulse Responses: Path 1
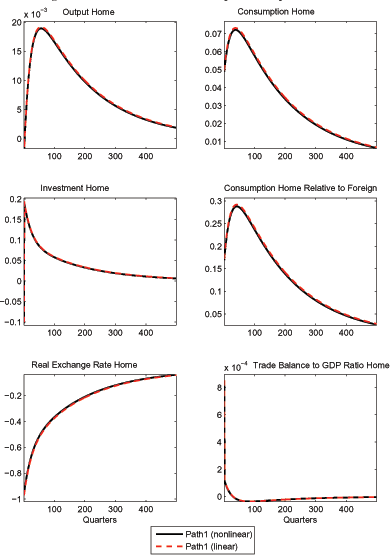
Data for Figure 4
Quarters | Output Home: Path 1 (nonlinear) | Output Home: Path 1 (linear) | Consumption Home: Path 1 (nonlinear) | Consumption Home: Path 1 (linear) | Investment Home: Path 1 (nonlinear) | Investment Home: Path 1 (linear) | Real Exchange Rate Home: Path 1 (nonlinear) | Real Exchange Rate Home: Path 1 (linear) | Real Exchange Rate Home: Path 1 (nonlinear) | Real Exchange Rate Home: Path 1 (linear) | Trade Balance to GDP Ratio Home: Path 1 (nonlinear) | Trade Balance to GDP Ratio Home: Path 1 (linear) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 | 0.0000 | 0.0000 | 0.0497 | 0.0489 | -0.1003 | -0.1025 | 0.1719 | 0.1692 | -0.9719 | -0.9585 | 0.00085272 | 0.00084798 |
2 | -0.0016 | -0.0016 | 0.0514 | 0.0506 | 0.1926 | 0.1904 | 0.1799 | 0.1772 | -0.9543 | -0.9412 | 0.00011781 | 0.00011357 |
3 | -0.0004 | -0.0004 | 0.0530 | 0.0522 | 0.1881 | 0.1859 | 0.1875 | 0.1847 | -0.9374 | -0.9245 | 0.00011051 | 0.00010644 |
4 | 0.0007 | 0.0007 | 0.0545 | 0.0537 | 0.1837 | 0.1816 | 0.1947 | 0.1918 | -0.9210 | -0.9083 | 0.00010353 | 0.00009964 |
5 | 0.0018 | 0.0018 | 0.0560 | 0.0552 | 0.1795 | 0.1774 | 0.2016 | 0.1986 | -0.9052 | -0.8927 | 0.00009686 | 0.00009314 |
6 | 0.0028 | 0.0028 | 0.0573 | 0.0565 | 0.1755 | 0.1734 | 0.2080 | 0.2050 | -0.8899 | -0.8776 | 0.00009048 | 0.00008691 |
7 | 0.0038 | 0.0037 | 0.0586 | 0.0578 | 0.1716 | 0.1696 | 0.2141 | 0.2110 | -0.8752 | -0.8630 | 0.00008438 | 0.00008095 |
8 | 0.0047 | 0.0047 | 0.0598 | 0.0589 | 0.1679 | 0.1659 | 0.2199 | 0.2167 | -0.8609 | -0.8489 | 0.00007855 | 0.00007526 |
9 | 0.0056 | 0.0055 | 0.0609 | 0.0601 | 0.1643 | 0.1623 | 0.2254 | 0.2221 | -0.8471 | -0.8353 | 0.00007297 | 0.00006983 |
10 | 0.0064 | 0.0064 | 0.0620 | 0.0611 | 0.1608 | 0.1589 | 0.2305 | 0.2272 | -0.8338 | -0.8221 | 0.00006765 | 0.00006461 |
11 | 0.0072 | 0.0071 | 0.0630 | 0.0621 | 0.1575 | 0.1556 | 0.2354 | 0.2320 | -0.8209 | -0.8094 | 0.00006255 | 0.00005964 |
12 | 0.0080 | 0.0079 | 0.0639 | 0.0630 | 0.1542 | 0.1524 | 0.2399 | 0.2366 | -0.8085 | -0.7970 | 0.00005769 | 0.00005492 |
13 | 0.0087 | 0.0086 | 0.0648 | 0.0639 | 0.1511 | 0.1493 | 0.2442 | 0.2408 | -0.7964 | -0.7851 | 0.00005304 | 0.00005035 |
14 | 0.0094 | 0.0093 | 0.0656 | 0.0647 | 0.1482 | 0.1464 | 0.2483 | 0.2448 | -0.7847 | -0.7735 | 0.00004860 | 0.00004599 |
15 | 0.0100 | 0.0099 | 0.0664 | 0.0654 | 0.1453 | 0.1435 | 0.2521 | 0.2486 | -0.7734 | -0.7624 | 0.00004435 | 0.00004186 |
16 | 0.0106 | 0.0105 | 0.0671 | 0.0661 | 0.1425 | 0.1408 | 0.2556 | 0.2521 | -0.7625 | -0.7515 | 0.00004030 | 0.00003789 |
17 | 0.0112 | 0.0111 | 0.0677 | 0.0668 | 0.1398 | 0.1381 | 0.2590 | 0.2554 | -0.7519 | -0.7410 | 0.00003642 | 0.00003411 |
18 | 0.0118 | 0.0116 | 0.0683 | 0.0674 | 0.1372 | 0.1356 | 0.2621 | 0.2585 | -0.7416 | -0.7309 | 0.00003273 | 0.00003050 |
19 | 0.0123 | 0.0121 | 0.0689 | 0.0679 | 0.1347 | 0.1331 | 0.2650 | 0.2614 | -0.7316 | -0.7210 | 0.00002919 | 0.00002705 |
20 | 0.0128 | 0.0126 | 0.0694 | 0.0684 | 0.1323 | 0.1307 | 0.2677 | 0.2641 | -0.7220 | -0.7114 | 0.00002582 | 0.00002376 |
21 | 0.0132 | 0.0131 | 0.0699 | 0.0689 | 0.1300 | 0.1284 | 0.2703 | 0.2666 | -0.7126 | -0.7022 | 0.00002260 | 0.00002061 |
22 | 0.0137 | 0.0135 | 0.0703 | 0.0694 | 0.1278 | 0.1262 | 0.2726 | 0.2689 | -0.7035 | -0.6932 | 0.00001953 | 0.00001761 |
23 | 0.0141 | 0.0139 | 0.0707 | 0.0697 | 0.1256 | 0.1240 | 0.2748 | 0.2711 | -0.6947 | -0.6844 | 0.00001660 | 0.00001474 |
24 | 0.0145 | 0.0143 | 0.0711 | 0.0701 | 0.1235 | 0.1220 | 0.2768 | 0.2731 | -0.6861 | -0.6759 | 0.00001380 | 0.00001203 |
25 | 0.0148 | 0.0147 | 0.0714 | 0.0704 | 0.1215 | 0.1200 | 0.2787 | 0.2749 | -0.6778 | -0.6677 | 0.00001113 | 0.00000938 |
26 | 0.0152 | 0.0150 | 0.0717 | 0.0707 | 0.1196 | 0.1180 | 0.2804 | 0.2766 | -0.6697 | -0.6597 | 0.00000858 | 0.00000690 |
27 | 0.0155 | 0.0153 | 0.0720 | 0.0710 | 0.1177 | 0.1162 | 0.2820 | 0.2781 | -0.6619 | -0.6519 | 0.00000615 | 0.00000454 |
28 | 0.0158 | 0.0156 | 0.0723 | 0.0712 | 0.1158 | 0.1144 | 0.2834 | 0.2795 | -0.6542 | -0.6444 | 0.00000383 | 0.00000227 |
29 | 0.0161 | 0.0159 | 0.0725 | 0.0714 | 0.1141 | 0.1126 | 0.2847 | 0.2808 | -0.6468 | -0.6370 | 0.00000163 | 0.00000011 |
30 | 0.0164 | 0.0162 | 0.0726 | 0.0716 | 0.1124 | 0.1109 | 0.2859 | 0.2820 | -0.6396 | -0.6299 | -0.00000048 | -0.00000192 |
31 | 0.0166 | 0.0164 | 0.0728 | 0.0718 | 0.1107 | 0.1093 | 0.2869 | 0.2830 | -0.6326 | -0.6229 | -0.00000249 | -0.00000390 |
32 | 0.0169 | 0.0167 | 0.0729 | 0.0719 | 0.1091 | 0.1077 | 0.2878 | 0.2839 | -0.6257 | -0.6162 | -0.00000440 | -0.00000577 |
33 | 0.0171 | 0.0169 | 0.0730 | 0.0720 | 0.1076 | 0.1062 | 0.2887 | 0.2847 | -0.6191 | -0.6096 | -0.00000622 | -0.00000753 |
34 | 0.0173 | 0.0171 | 0.0731 | 0.0721 | 0.1061 | 0.1047 | 0.2894 | 0.2854 | -0.6126 | -0.6031 | -0.00000795 | -0.00000922 |
35 | 0.0175 | 0.0173 | 0.0732 | 0.0721 | 0.1046 | 0.1032 | 0.2900 | 0.2860 | -0.6063 | -0.5969 | -0.00000960 | -0.00001084 |
36 | 0.0177 | 0.0175 | 0.0732 | 0.0722 | 0.1032 | 0.1018 | 0.2905 | 0.2866 | -0.6001 | -0.5908 | -0.00001117 | -0.00001234 |
37 | 0.0178 | 0.0176 | 0.0733 | 0.0722 | 0.1019 | 0.1005 | 0.2910 | 0.2870 | -0.5941 | -0.5848 | -0.00001267 | -0.00001383 |
38 | 0.0180 | 0.0178 | 0.0733 | 0.0722 | 0.1005 | 0.0992 | 0.2913 | 0.2873 | -0.5883 | -0.5790 | -0.00001409 | -0.00001520 |
39 | 0.0181 | 0.0179 | 0.0733 | 0.0722 | 0.0993 | 0.0979 | 0.2916 | 0.2876 | -0.5826 | -0.5734 | -0.00001544 | -0.00001653 |
40 | 0.0183 | 0.0180 | 0.0732 | 0.0722 | 0.0980 | 0.0967 | 0.2918 | 0.2878 | -0.5770 | -0.5679 | -0.00001673 | -0.00001776 |
41 | 0.0184 | 0.0182 | 0.0732 | 0.0721 | 0.0968 | 0.0955 | 0.2919 | 0.2879 | -0.5715 | -0.5625 | -0.00001795 | -0.00001897 |
42 | 0.0185 | 0.0183 | 0.0731 | 0.0721 | 0.0956 | 0.0943 | 0.2920 | 0.2879 | -0.5662 | -0.5572 | -0.00001911 | -0.00002009 |
43 | 0.0186 | 0.0184 | 0.0730 | 0.0720 | 0.0945 | 0.0932 | 0.2919 | 0.2879 | -0.5610 | -0.5520 | -0.00002021 | -0.00002117 |
44 | 0.0187 | 0.0184 | 0.0730 | 0.0719 | 0.0934 | 0.0921 | 0.2918 | 0.2878 | -0.5560 | -0.5470 | -0.00002126 | -0.00002217 |
45 | 0.0188 | 0.0185 | 0.0729 | 0.0718 | 0.0923 | 0.0910 | 0.2917 | 0.2876 | -0.5510 | -0.5421 | -0.00002225 | -0.00002311 |
46 | 0.0188 | 0.0186 | 0.0727 | 0.0717 | 0.0913 | 0.0900 | 0.2915 | 0.2874 | -0.5461 | -0.5373 | -0.00002319 | -0.00002404 |
47 | 0.0189 | 0.0187 | 0.0726 | 0.0715 | 0.0903 | 0.0890 | 0.2912 | 0.2871 | -0.5414 | -0.5326 | -0.00002408 | -0.00002492 |
48 | 0.0190 | 0.0187 | 0.0725 | 0.0714 | 0.0893 | 0.0880 | 0.2909 | 0.2868 | -0.5367 | -0.5280 | -0.00002492 | -0.00002573 |
49 | 0.0190 | 0.0188 | 0.0723 | 0.0713 | 0.0883 | 0.0871 | 0.2905 | 0.2865 | -0.5322 | -0.5234 | -0.00002572 | -0.00002652 |
50 | 0.0191 | 0.0188 | 0.0722 | 0.0711 | 0.0874 | 0.0861 | 0.2901 | 0.2860 | -0.5277 | -0.5190 | -0.00002648 | -0.00002726 |
51 | 0.0191 | 0.0188 | 0.0720 | 0.0709 | 0.0865 | 0.0852 | 0.2896 | 0.2856 | -0.5234 | -0.5147 | -0.00002719 | -0.00002794 |
52 | 0.0191 | 0.0189 | 0.0718 | 0.0708 | 0.0856 | 0.0843 | 0.2891 | 0.2851 | -0.5191 | -0.5105 | -0.00002787 | -0.00002858 |
53 | 0.0191 | 0.0189 | 0.0717 | 0.0706 | 0.0847 | 0.0835 | 0.2886 | 0.2845 | -0.5149 | -0.5063 | -0.00002850 | -0.00002919 |
54 | 0.0192 | 0.0189 | 0.0715 | 0.0704 | 0.0839 | 0.0826 | 0.2880 | 0.2839 | -0.5108 | -0.5022 | -0.00002910 | -0.00002976 |
55 | 0.0192 | 0.0189 | 0.0713 | 0.0702 | 0.0830 | 0.0818 | 0.2874 | 0.2833 | -0.5067 | -0.4982 | -0.00002967 | -0.00003031 |
56 | 0.0192 | 0.0189 | 0.0711 | 0.0700 | 0.0822 | 0.0810 | 0.2867 | 0.2826 | -0.5028 | -0.4943 | -0.00003020 | -0.00003086 |
57 | 0.0192 | 0.0189 | 0.0708 | 0.0698 | 0.0815 | 0.0803 | 0.2860 | 0.2819 | -0.4989 | -0.4904 | -0.00003070 | -0.00003130 |
58 | 0.0192 | 0.0189 | 0.0706 | 0.0696 | 0.0807 | 0.0795 | 0.2853 | 0.2812 | -0.4950 | -0.4866 | -0.00003117 | -0.00003179 |
59 | 0.0192 | 0.0189 | 0.0704 | 0.0693 | 0.0799 | 0.0788 | 0.2845 | 0.2804 | -0.4913 | -0.4829 | -0.00003162 | -0.00003219 |
60 | 0.0192 | 0.0189 | 0.0702 | 0.0691 | 0.0792 | 0.0780 | 0.2837 | 0.2796 | -0.4876 | -0.4793 | -0.00003203 | -0.00003261 |
61 | 0.0192 | 0.0189 | 0.0699 | 0.0689 | 0.0785 | 0.0773 | 0.2829 | 0.2788 | -0.4840 | -0.4757 | -0.00003242 | -0.00003296 |
62 | 0.0191 | 0.0189 | 0.0697 | 0.0686 | 0.0778 | 0.0766 | 0.2821 | 0.2780 | -0.4804 | -0.4721 | -0.00003278 | -0.00003330 |
63 | 0.0191 | 0.0189 | 0.0694 | 0.0684 | 0.0771 | 0.0760 | 0.2812 | 0.2771 | -0.4769 | -0.4687 | -0.00003312 | -0.00003362 |
64 | 0.0191 | 0.0188 | 0.0692 | 0.0681 | 0.0765 | 0.0753 | 0.2803 | 0.2762 | -0.4735 | -0.4653 | -0.00003343 | -0.00003391 |
65 | 0.0191 | 0.0188 | 0.0689 | 0.0679 | 0.0758 | 0.0746 | 0.2794 | 0.2753 | -0.4701 | -0.4619 | -0.00003373 | -0.00003421 |
66 | 0.0190 | 0.0188 | 0.0687 | 0.0676 | 0.0752 | 0.0740 | 0.2785 | 0.2744 | -0.4667 | -0.4586 | -0.00003400 | -0.00003447 |
67 | 0.0190 | 0.0187 | 0.0684 | 0.0674 | 0.0745 | 0.0734 | 0.2776 | 0.2735 | -0.4634 | -0.4553 | -0.00003425 | -0.00003471 |
68 | 0.0189 | 0.0187 | 0.0682 | 0.0671 | 0.0739 | 0.0728 | 0.2766 | 0.2725 | -0.4602 | -0.4521 | -0.00003448 | -0.00003493 |
69 | 0.0189 | 0.0187 | 0.0679 | 0.0668 | 0.0733 | 0.0722 | 0.2756 | 0.2715 | -0.4570 | -0.4490 | -0.00003470 | -0.00003512 |
70 | 0.0189 | 0.0186 | 0.0676 | 0.0666 | 0.0727 | 0.0716 | 0.2746 | 0.2705 | -0.4539 | -0.4458 | -0.00003489 | -0.00003532 |
71 | 0.0188 | 0.0186 | 0.0673 | 0.0663 | 0.0722 | 0.0710 | 0.2736 | 0.2695 | -0.4508 | -0.4428 | -0.00003507 | -0.00003546 |
72 | 0.0188 | 0.0185 | 0.0671 | 0.0660 | 0.0716 | 0.0705 | 0.2726 | 0.2685 | -0.4477 | -0.4397 | -0.00003523 | -0.00003562 |
73 | 0.0187 | 0.0185 | 0.0668 | 0.0657 | 0.0710 | 0.0699 | 0.2715 | 0.2674 | -0.4447 | -0.4368 | -0.00003538 | -0.00003576 |
74 | 0.0187 | 0.0184 | 0.0665 | 0.0654 | 0.0705 | 0.0694 | 0.2705 | 0.2664 | -0.4417 | -0.4338 | -0.00003551 | -0.00003585 |
75 | 0.0186 | 0.0184 | 0.0662 | 0.0652 | 0.0700 | 0.0688 | 0.2694 | 0.2653 | -0.4388 | -0.4309 | -0.00003563 | -0.00003596 |
76 | 0.0186 | 0.0183 | 0.0659 | 0.0649 | 0.0694 | 0.0683 | 0.2683 | 0.2642 | -0.4359 | -0.4280 | -0.00003574 | -0.00003607 |
77 | 0.0185 | 0.0182 | 0.0656 | 0.0646 | 0.0689 | 0.0678 | 0.2672 | 0.2632 | -0.4331 | -0.4252 | -0.00003583 | -0.00003617 |
78 | 0.0184 | 0.0182 | 0.0654 | 0.0643 | 0.0684 | 0.0673 | 0.2661 | 0.2621 | -0.4303 | -0.4224 | -0.00003591 | -0.00003623 |
79 | 0.0184 | 0.0181 | 0.0651 | 0.0640 | 0.0679 | 0.0668 | 0.2650 | 0.2610 | -0.4275 | -0.4197 | -0.00003598 | -0.00003629 |
80 | 0.0183 | 0.0181 | 0.0648 | 0.0637 | 0.0674 | 0.0663 | 0.2639 | 0.2599 | -0.4247 | -0.4169 | -0.00003604 | -0.00003632 |
81 | 0.0183 | 0.0180 | 0.0645 | 0.0634 | 0.0669 | 0.0658 | 0.2628 | 0.2587 | -0.4220 | -0.4142 | -0.00003608 | -0.00003638 |
82 | 0.0182 | 0.0179 | 0.0642 | 0.0631 | 0.0665 | 0.0654 | 0.2617 | 0.2576 | -0.4193 | -0.4116 | -0.00003612 | -0.00003638 |
83 | 0.0181 | 0.0179 | 0.0639 | 0.0628 | 0.0660 | 0.0649 | 0.2605 | 0.2565 | -0.4167 | -0.4090 | -0.00003615 | -0.00003640 |
84 | 0.0181 | 0.0178 | 0.0636 | 0.0626 | 0.0655 | 0.0644 | 0.2594 | 0.2553 | -0.4141 | -0.4064 | -0.00003616 | -0.00003641 |
85 | 0.0180 | 0.0177 | 0.0633 | 0.0623 | 0.0651 | 0.0640 | 0.2582 | 0.2542 | -0.4115 | -0.4038 | -0.00003617 | -0.00003643 |
86 | 0.0179 | 0.0177 | 0.0630 | 0.0620 | 0.0646 | 0.0635 | 0.2571 | 0.2531 | -0.4089 | -0.4013 | -0.00003617 | -0.00003641 |
87 | 0.0178 | 0.0176 | 0.0627 | 0.0617 | 0.0642 | 0.0631 | 0.2559 | 0.2519 | -0.4064 | -0.3987 | -0.00003617 | -0.00003640 |
88 | 0.0178 | 0.0175 | 0.0624 | 0.0614 | 0.0638 | 0.0627 | 0.2548 | 0.2508 | -0.4039 | -0.3963 | -0.00003615 | -0.00003635 |
89 | 0.0177 | 0.0174 | 0.0621 | 0.0611 | 0.0633 | 0.0623 | 0.2536 | 0.2496 | -0.4014 | -0.3938 | -0.00003613 | -0.00003635 |
90 | 0.0176 | 0.0174 | 0.0618 | 0.0608 | 0.0629 | 0.0618 | 0.2525 | 0.2484 | -0.3989 | -0.3914 | -0.00003610 | -0.00003632 |
91 | 0.0176 | 0.0173 | 0.0615 | 0.0605 | 0.0625 | 0.0614 | 0.2513 | 0.2473 | -0.3965 | -0.3890 | -0.00003606 | -0.00003626 |
92 | 0.0175 | 0.0172 | 0.0612 | 0.0602 | 0.0621 | 0.0610 | 0.2501 | 0.2461 | -0.3941 | -0.3866 | -0.00003602 | -0.00003621 |
93 | 0.0174 | 0.0172 | 0.0609 | 0.0599 | 0.0617 | 0.0606 | 0.2490 | 0.2450 | -0.3917 | -0.3842 | -0.00003597 | -0.00003614 |
94 | 0.0173 | 0.0171 | 0.0606 | 0.0596 | 0.0613 | 0.0602 | 0.2478 | 0.2438 | -0.3893 | -0.3819 | -0.00003592 | -0.00003609 |
95 | 0.0173 | 0.0170 | 0.0603 | 0.0593 | 0.0609 | 0.0598 | 0.2466 | 0.2426 | -0.3870 | -0.3796 | -0.00003586 | -0.00003605 |
96 | 0.0172 | 0.0169 | 0.0600 | 0.0590 | 0.0605 | 0.0594 | 0.2454 | 0.2415 | -0.3847 | -0.3773 | -0.00003579 | -0.00003597 |
97 | 0.0171 | 0.0169 | 0.0597 | 0.0587 | 0.0601 | 0.0591 | 0.2443 | 0.2403 | -0.3824 | -0.3750 | -0.00003572 | -0.00003588 |
98 | 0.0170 | 0.0168 | 0.0594 | 0.0584 | 0.0597 | 0.0587 | 0.2431 | 0.2391 | -0.3801 | -0.3728 | -0.00003565 | -0.00003579 |
99 | 0.0170 | 0.0167 | 0.0591 | 0.0581 | 0.0593 | 0.0583 | 0.2419 | 0.2380 | -0.3779 | -0.3705 | -0.00003557 | -0.00003571 |
100 | 0.0169 | 0.0166 | 0.0588 | 0.0578 | 0.0590 | 0.0579 | 0.2408 | 0.2368 | -0.3757 | -0.3683 | -0.00003549 | -0.00003562 |
101 | 0.0168 | 0.0165 | 0.0585 | 0.0575 | 0.0586 | 0.0576 | 0.2396 | 0.2356 | -0.3735 | -0.3661 | -0.00003540 | -0.00003553 |
102 | 0.0167 | 0.0165 | 0.0582 | 0.0572 | 0.0582 | 0.0572 | 0.2384 | 0.2345 | -0.3713 | -0.3640 | -0.00003531 | -0.00003543 |
103 | 0.0166 | 0.0164 | 0.0579 | 0.0569 | 0.0579 | 0.0568 | 0.2372 | 0.2333 | -0.3691 | -0.3618 | -0.00003522 | -0.00003535 |
104 | 0.0166 | 0.0163 | 0.0577 | 0.0567 | 0.0575 | 0.0565 | 0.2361 | 0.2321 | -0.3669 | -0.3597 | -0.00003512 | -0.00003522 |
105 | 0.0165 | 0.0162 | 0.0574 | 0.0564 | 0.0572 | 0.0561 | 0.2349 | 0.2310 | -0.3648 | -0.3576 | -0.00003502 | -0.00003513 |
106 | 0.0164 | 0.0162 | 0.0571 | 0.0561 | 0.0568 | 0.0558 | 0.2337 | 0.2298 | -0.3627 | -0.3555 | -0.00003492 | -0.00003503 |
107 | 0.0163 | 0.0161 | 0.0568 | 0.0558 | 0.0565 | 0.0555 | 0.2326 | 0.2287 | -0.3606 | -0.3534 | -0.00003481 | -0.00003490 |
108 | 0.0162 | 0.0160 | 0.0565 | 0.0555 | 0.0561 | 0.0551 | 0.2314 | 0.2275 | -0.3585 | -0.3513 | -0.00003470 | -0.00003478 |
109 | 0.0162 | 0.0159 | 0.0562 | 0.0552 | 0.0558 | 0.0548 | 0.2303 | 0.2264 | -0.3565 | -0.3493 | -0.00003459 | -0.00003468 |
110 | 0.0161 | 0.0158 | 0.0559 | 0.0549 | 0.0555 | 0.0544 | 0.2291 | 0.2252 | -0.3544 | -0.3473 | -0.00003447 | -0.00003455 |
111 | 0.0160 | 0.0158 | 0.0556 | 0.0546 | 0.0551 | 0.0541 | 0.2279 | 0.2241 | -0.3524 | -0.3453 | -0.00003436 | -0.00003445 |
112 | 0.0159 | 0.0157 | 0.0553 | 0.0543 | 0.0548 | 0.0538 | 0.2268 | 0.2229 | -0.3504 | -0.3433 | -0.00003424 | -0.00003431 |
113 | 0.0159 | 0.0156 | 0.0550 | 0.0541 | 0.0545 | 0.0535 | 0.2256 | 0.2218 | -0.3484 | -0.3413 | -0.00003412 | -0.00003419 |
114 | 0.0158 | 0.0155 | 0.0548 | 0.0538 | 0.0541 | 0.0532 | 0.2245 | 0.2206 | -0.3464 | -0.3393 | -0.00003400 | -0.00003406 |
115 | 0.0157 | 0.0155 | 0.0545 | 0.0535 | 0.0538 | 0.0528 | 0.2234 | 0.2195 | -0.3444 | -0.3374 | -0.00003387 | -0.00003390 |
116 | 0.0156 | 0.0154 | 0.0542 | 0.0532 | 0.0535 | 0.0525 | 0.2222 | 0.2184 | -0.3425 | -0.3354 | -0.00003375 | -0.00003380 |
117 | 0.0155 | 0.0153 | 0.0539 | 0.0529 | 0.0532 | 0.0522 | 0.2211 | 0.2172 | -0.3405 | -0.3335 | -0.00003362 | -0.00003368 |
118 | 0.0155 | 0.0152 | 0.0536 | 0.0527 | 0.0529 | 0.0519 | 0.2199 | 0.2161 | -0.3386 | -0.3316 | -0.00003349 | -0.00003351 |
119 | 0.0154 | 0.0151 | 0.0533 | 0.0524 | 0.0526 | 0.0516 | 0.2188 | 0.2150 | -0.3367 | -0.3297 | -0.00003336 | -0.00003339 |
120 | 0.0153 | 0.0151 | 0.0531 | 0.0521 | 0.0523 | 0.0513 | 0.2177 | 0.2139 | -0.3348 | -0.3278 | -0.00003323 | -0.00003327 |
121 | 0.0152 | 0.0150 | 0.0528 | 0.0518 | 0.0520 | 0.0510 | 0.2166 | 0.2127 | -0.3329 | -0.3260 | -0.00003309 | -0.00003312 |
122 | 0.0152 | 0.0149 | 0.0525 | 0.0515 | 0.0517 | 0.0507 | 0.2155 | 0.2116 | -0.3310 | -0.3241 | -0.00003296 | -0.00003296 |
123 | 0.0151 | 0.0148 | 0.0522 | 0.0513 | 0.0514 | 0.0504 | 0.2143 | 0.2105 | -0.3292 | -0.3223 | -0.00003282 | -0.00003285 |
124 | 0.0150 | 0.0148 | 0.0520 | 0.0510 | 0.0511 | 0.0501 | 0.2132 | 0.2094 | -0.3273 | -0.3204 | -0.00003269 | -0.00003269 |
125 | 0.0149 | 0.0147 | 0.0517 | 0.0507 | 0.0508 | 0.0498 | 0.2121 | 0.2083 | -0.3255 | -0.3186 | -0.00003255 | -0.00003258 |
126 | 0.0148 | 0.0146 | 0.0514 | 0.0505 | 0.0505 | 0.0495 | 0.2110 | 0.2072 | -0.3237 | -0.3168 | -0.00003241 | -0.00003242 |
127 | 0.0148 | 0.0145 | 0.0511 | 0.0502 | 0.0502 | 0.0492 | 0.2099 | 0.2061 | -0.3219 | -0.3150 | -0.00003228 | -0.00003227 |
128 | 0.0147 | 0.0145 | 0.0509 | 0.0499 | 0.0499 | 0.0490 | 0.2088 | 0.2051 | -0.3201 | -0.3133 | -0.00003214 | -0.00003213 |
129 | 0.0146 | 0.0144 | 0.0506 | 0.0497 | 0.0496 | 0.0487 | 0.2077 | 0.2040 | -0.3183 | -0.3115 | -0.00003200 | -0.00003199 |
130 | 0.0145 | 0.0143 | 0.0503 | 0.0494 | 0.0494 | 0.0484 | 0.2067 | 0.2029 | -0.3165 | -0.3097 | -0.00003186 | -0.00003185 |
131 | 0.0145 | 0.0142 | 0.0501 | 0.0491 | 0.0491 | 0.0481 | 0.2056 | 0.2018 | -0.3148 | -0.3080 | -0.00003172 | -0.00003170 |
132 | 0.0144 | 0.0142 | 0.0498 | 0.0489 | 0.0488 | 0.0478 | 0.2045 | 0.2007 | -0.3130 | -0.3063 | -0.00003158 | -0.00003155 |
133 | 0.0143 | 0.0141 | 0.0495 | 0.0486 | 0.0485 | 0.0476 | 0.2034 | 0.1997 | -0.3113 | -0.3046 | -0.00003143 | -0.00003140 |
134 | 0.0142 | 0.0140 | 0.0493 | 0.0483 | 0.0482 | 0.0473 | 0.2024 | 0.1986 | -0.3096 | -0.3028 | -0.00003129 | -0.00003127 |
135 | 0.0142 | 0.0139 | 0.0490 | 0.0481 | 0.0480 | 0.0470 | 0.2013 | 0.1976 | -0.3078 | -0.3011 | -0.00003115 | -0.00003114 |
136 | 0.0141 | 0.0139 | 0.0488 | 0.0478 | 0.0477 | 0.0468 | 0.2002 | 0.1965 | -0.3061 | -0.2995 | -0.00003101 | -0.00003098 |
137 | 0.0140 | 0.0138 | 0.0485 | 0.0476 | 0.0474 | 0.0465 | 0.1992 | 0.1955 | -0.3044 | -0.2978 | -0.00003086 | -0.00003081 |
138 | 0.0139 | 0.0137 | 0.0482 | 0.0473 | 0.0472 | 0.0462 | 0.1981 | 0.1944 | -0.3028 | -0.2961 | -0.00003072 | -0.00003067 |
139 | 0.0139 | 0.0136 | 0.0480 | 0.0470 | 0.0469 | 0.0460 | 0.1971 | 0.1934 | -0.3011 | -0.2945 | -0.00003058 | -0.00003055 |
140 | 0.0138 | 0.0136 | 0.0477 | 0.0468 | 0.0466 | 0.0457 | 0.1960 | 0.1923 | -0.2994 | -0.2928 | -0.00003044 | -0.00003040 |
141 | 0.0137 | 0.0135 | 0.0475 | 0.0465 | 0.0464 | 0.0455 | 0.1950 | 0.1913 | -0.2978 | -0.2912 | -0.00003029 | -0.00003025 |
142 | 0.0137 | 0.0134 | 0.0472 | 0.0463 | 0.0461 | 0.0452 | 0.1940 | 0.1903 | -0.2961 | -0.2896 | -0.00003015 | -0.00003011 |
143 | 0.0136 | 0.0134 | 0.0470 | 0.0460 | 0.0459 | 0.0449 | 0.1929 | 0.1893 | -0.2945 | -0.2880 | -0.00003001 | -0.00002993 |
144 | 0.0135 | 0.0133 | 0.0467 | 0.0458 | 0.0456 | 0.0447 | 0.1919 | 0.1883 | -0.2929 | -0.2864 | -0.00002986 | -0.00002983 |
145 | 0.0134 | 0.0132 | 0.0465 | 0.0455 | 0.0454 | 0.0444 | 0.1909 | 0.1872 | -0.2913 | -0.2848 | -0.00002972 | -0.00002966 |
146 | 0.0134 | 0.0131 | 0.0462 | 0.0453 | 0.0451 | 0.0442 | 0.1899 | 0.1862 | -0.2897 | -0.2832 | -0.00002958 | -0.00002949 |
147 | 0.0133 | 0.0131 | 0.0460 | 0.0450 | 0.0449 | 0.0439 | 0.1889 | 0.1852 | -0.2881 | -0.2816 | -0.00002944 | -0.00002938 |
148 | 0.0132 | 0.0130 | 0.0457 | 0.0448 | 0.0446 | 0.0437 | 0.1879 | 0.1842 | -0.2865 | -0.2800 | -0.00002929 | -0.00002924 |
149 | 0.0132 | 0.0129 | 0.0455 | 0.0446 | 0.0444 | 0.0434 | 0.1869 | 0.1832 | -0.2849 | -0.2785 | -0.00002915 | -0.00002909 |
150 | 0.0131 | 0.0129 | 0.0452 | 0.0443 | 0.0441 | 0.0432 | 0.1859 | 0.1823 | -0.2834 | -0.2769 | -0.00002901 | -0.00002894 |
151 | 0.0130 | 0.0128 | 0.0450 | 0.0441 | 0.0439 | 0.0430 | 0.1849 | 0.1813 | -0.2818 | -0.2754 | -0.00002887 | -0.00002879 |
152 | 0.0129 | 0.0127 | 0.0447 | 0.0438 | 0.0436 | 0.0427 | 0.1839 | 0.1803 | -0.2803 | -0.2739 | -0.00002872 | -0.00002864 |
153 | 0.0129 | 0.0127 | 0.0445 | 0.0436 | 0.0434 | 0.0425 | 0.1829 | 0.1793 | -0.2788 | -0.2724 | -0.00002858 | -0.00002850 |
154 | 0.0128 | 0.0126 | 0.0443 | 0.0434 | 0.0432 | 0.0422 | 0.1820 | 0.1784 | -0.2772 | -0.2709 | -0.00002844 | -0.00002838 |
155 | 0.0127 | 0.0125 | 0.0440 | 0.0431 | 0.0429 | 0.0420 | 0.1810 | 0.1774 | -0.2757 | -0.2694 | -0.00002830 | -0.00002821 |
156 | 0.0127 | 0.0124 | 0.0438 | 0.0429 | 0.0427 | 0.0418 | 0.1800 | 0.1764 | -0.2742 | -0.2679 | -0.00002816 | -0.00002808 |
157 | 0.0126 | 0.0124 | 0.0436 | 0.0427 | 0.0424 | 0.0415 | 0.1791 | 0.1755 | -0.2727 | -0.2664 | -0.00002802 | -0.00002794 |
158 | 0.0125 | 0.0123 | 0.0433 | 0.0424 | 0.0422 | 0.0413 | 0.1781 | 0.1745 | -0.2712 | -0.2649 | -0.00002788 | -0.00002776 |
159 | 0.0125 | 0.0122 | 0.0431 | 0.0422 | 0.0420 | 0.0411 | 0.1771 | 0.1736 | -0.2698 | -0.2635 | -0.00002774 | -0.00002764 |
160 | 0.0124 | 0.0122 | 0.0429 | 0.0420 | 0.0417 | 0.0409 | 0.1762 | 0.1727 | -0.2683 | -0.2620 | -0.00002760 | -0.00002750 |
161 | 0.0123 | 0.0121 | 0.0426 | 0.0417 | 0.0415 | 0.0406 | 0.1753 | 0.1717 | -0.2668 | -0.2606 | -0.00002746 | -0.00002736 |
162 | 0.0123 | 0.0120 | 0.0424 | 0.0415 | 0.0413 | 0.0404 | 0.1743 | 0.1708 | -0.2654 | -0.2591 | -0.00002732 | -0.00002723 |
163 | 0.0122 | 0.0120 | 0.0422 | 0.0413 | 0.0411 | 0.0402 | 0.1734 | 0.1699 | -0.2639 | -0.2577 | -0.00002719 | -0.00002707 |
164 | 0.0121 | 0.0119 | 0.0419 | 0.0411 | 0.0408 | 0.0400 | 0.1725 | 0.1689 | -0.2625 | -0.2563 | -0.00002705 | -0.00002696 |
165 | 0.0121 | 0.0119 | 0.0417 | 0.0408 | 0.0406 | 0.0397 | 0.1715 | 0.1680 | -0.2611 | -0.2549 | -0.00002691 | -0.00002682 |
166 | 0.0120 | 0.0118 | 0.0415 | 0.0406 | 0.0404 | 0.0395 | 0.1706 | 0.1671 | -0.2596 | -0.2534 | -0.00002678 | -0.00002666 |
167 | 0.0119 | 0.0117 | 0.0413 | 0.0404 | 0.0402 | 0.0393 | 0.1697 | 0.1662 | -0.2582 | -0.2521 | -0.00002664 | -0.00002653 |
168 | 0.0119 | 0.0117 | 0.0410 | 0.0402 | 0.0400 | 0.0391 | 0.1688 | 0.1653 | -0.2568 | -0.2507 | -0.00002650 | -0.00002639 |
169 | 0.0118 | 0.0116 | 0.0408 | 0.0400 | 0.0397 | 0.0389 | 0.1679 | 0.1644 | -0.2554 | -0.2493 | -0.00002637 | -0.00002625 |
170 | 0.0118 | 0.0115 | 0.0406 | 0.0397 | 0.0395 | 0.0387 | 0.1670 | 0.1635 | -0.2540 | -0.2479 | -0.00002623 | -0.00002610 |
171 | 0.0117 | 0.0115 | 0.0404 | 0.0395 | 0.0393 | 0.0384 | 0.1661 | 0.1626 | -0.2526 | -0.2465 | -0.00002610 | -0.00002600 |
172 | 0.0116 | 0.0114 | 0.0402 | 0.0393 | 0.0391 | 0.0382 | 0.1652 | 0.1617 | -0.2513 | -0.2452 | -0.00002597 | -0.00002582 |
173 | 0.0116 | 0.0113 | 0.0400 | 0.0391 | 0.0389 | 0.0380 | 0.1643 | 0.1609 | -0.2499 | -0.2438 | -0.00002583 | -0.00002571 |
174 | 0.0115 | 0.0113 | 0.0397 | 0.0389 | 0.0387 | 0.0378 | 0.1634 | 0.1600 | -0.2486 | -0.2425 | -0.00002570 | -0.00002559 |
175 | 0.0114 | 0.0112 | 0.0395 | 0.0387 | 0.0385 | 0.0376 | 0.1625 | 0.1591 | -0.2472 | -0.2412 | -0.00002557 | -0.00002543 |
176 | 0.0114 | 0.0112 | 0.0393 | 0.0385 | 0.0382 | 0.0374 | 0.1617 | 0.1582 | -0.2459 | -0.2398 | -0.00002543 | -0.00002531 |
177 | 0.0113 | 0.0111 | 0.0391 | 0.0382 | 0.0380 | 0.0372 | 0.1608 | 0.1574 | -0.2445 | -0.2385 | -0.00002530 | -0.00002515 |
178 | 0.0113 | 0.0110 | 0.0389 | 0.0380 | 0.0378 | 0.0370 | 0.1599 | 0.1565 | -0.2432 | -0.2372 | -0.00002517 | -0.00002506 |
179 | 0.0112 | 0.0110 | 0.0387 | 0.0378 | 0.0376 | 0.0368 | 0.1591 | 0.1557 | -0.2419 | -0.2359 | -0.00002504 | -0.00002489 |
180 | 0.0111 | 0.0109 | 0.0385 | 0.0376 | 0.0374 | 0.0366 | 0.1582 | 0.1548 | -0.2406 | -0.2346 | -0.00002491 | -0.00002476 |
181 | 0.0111 | 0.0109 | 0.0383 | 0.0374 | 0.0372 | 0.0364 | 0.1574 | 0.1540 | -0.2393 | -0.2333 | -0.00002478 | -0.00002463 |
182 | 0.0110 | 0.0108 | 0.0381 | 0.0372 | 0.0370 | 0.0362 | 0.1565 | 0.1531 | -0.2380 | -0.2320 | -0.00002466 | -0.00002453 |
183 | 0.0110 | 0.0107 | 0.0378 | 0.0370 | 0.0368 | 0.0360 | 0.1557 | 0.1523 | -0.2367 | -0.2308 | -0.00002453 | -0.00002439 |
184 | 0.0109 | 0.0107 | 0.0376 | 0.0368 | 0.0366 | 0.0358 | 0.1548 | 0.1515 | -0.2354 | -0.2295 | -0.00002440 | -0.00002427 |
185 | 0.0108 | 0.0106 | 0.0374 | 0.0366 | 0.0364 | 0.0356 | 0.1540 | 0.1506 | -0.2341 | -0.2282 | -0.00002427 | -0.00002413 |
186 | 0.0108 | 0.0106 | 0.0372 | 0.0364 | 0.0362 | 0.0354 | 0.1532 | 0.1498 | -0.2328 | -0.2270 | -0.00002415 | -0.00002402 |
187 | 0.0107 | 0.0105 | 0.0370 | 0.0362 | 0.0360 | 0.0352 | 0.1524 | 0.1490 | -0.2316 | -0.2257 | -0.00002402 | -0.00002387 |
188 | 0.0107 | 0.0105 | 0.0368 | 0.0360 | 0.0358 | 0.0350 | 0.1515 | 0.1482 | -0.2303 | -0.2245 | -0.00002389 | -0.00002373 |
189 | 0.0106 | 0.0104 | 0.0366 | 0.0358 | 0.0356 | 0.0348 | 0.1507 | 0.1474 | -0.2291 | -0.2232 | -0.00002377 | -0.00002363 |
190 | 0.0105 | 0.0103 | 0.0364 | 0.0356 | 0.0354 | 0.0346 | 0.1499 | 0.1466 | -0.2278 | -0.2220 | -0.00002365 | -0.00002352 |
191 | 0.0105 | 0.0103 | 0.0362 | 0.0354 | 0.0352 | 0.0344 | 0.1491 | 0.1458 | -0.2266 | -0.2208 | -0.00002352 | -0.00002336 |
192 | 0.0104 | 0.0102 | 0.0360 | 0.0352 | 0.0351 | 0.0342 | 0.1483 | 0.1450 | -0.2254 | -0.2196 | -0.00002340 | -0.00002323 |
193 | 0.0104 | 0.0102 | 0.0359 | 0.0350 | 0.0349 | 0.0340 | 0.1475 | 0.1442 | -0.2242 | -0.2184 | -0.00002328 | -0.00002310 |
194 | 0.0103 | 0.0101 | 0.0357 | 0.0348 | 0.0347 | 0.0339 | 0.1467 | 0.1434 | -0.2229 | -0.2172 | -0.00002315 | -0.00002301 |
195 | 0.0103 | 0.0101 | 0.0355 | 0.0346 | 0.0345 | 0.0337 | 0.1459 | 0.1426 | -0.2217 | -0.2160 | -0.00002303 | -0.00002287 |
196 | 0.0102 | 0.0100 | 0.0353 | 0.0345 | 0.0343 | 0.0335 | 0.1451 | 0.1418 | -0.2205 | -0.2148 | -0.00002291 | -0.00002277 |
197 | 0.0102 | 0.0100 | 0.0351 | 0.0343 | 0.0341 | 0.0333 | 0.1443 | 0.1411 | -0.2193 | -0.2136 | -0.00002279 | -0.00002263 |
198 | 0.0101 | 0.0099 | 0.0349 | 0.0341 | 0.0339 | 0.0331 | 0.1436 | 0.1403 | -0.2182 | -0.2125 | -0.00002267 | -0.00002250 |
199 | 0.0100 | 0.0098 | 0.0347 | 0.0339 | 0.0337 | 0.0329 | 0.1428 | 0.1395 | -0.2170 | -0.2113 | -0.00002255 | -0.00002236 |
200 | 0.0100 | 0.0098 | 0.0345 | 0.0337 | 0.0336 | 0.0328 | 0.1420 | 0.1388 | -0.2158 | -0.2101 | -0.00002243 | -0.00002228 |
201 | 0.0099 | 0.0097 | 0.0343 | 0.0335 | 0.0334 | 0.0326 | 0.1413 | 0.1380 | -0.2146 | -0.2090 | -0.00002232 | -0.00002218 |
202 | 0.0099 | 0.0097 | 0.0341 | 0.0333 | 0.0332 | 0.0324 | 0.1405 | 0.1373 | -0.2135 | -0.2078 | -0.00002220 | -0.00002203 |
203 | 0.0098 | 0.0096 | 0.0340 | 0.0332 | 0.0330 | 0.0322 | 0.1397 | 0.1365 | -0.2123 | -0.2067 | -0.00002208 | -0.00002192 |
204 | 0.0098 | 0.0096 | 0.0338 | 0.0330 | 0.0328 | 0.0320 | 0.1390 | 0.1358 | -0.2112 | -0.2056 | -0.00002197 | -0.00002180 |
205 | 0.0097 | 0.0095 | 0.0336 | 0.0328 | 0.0327 | 0.0319 | 0.1382 | 0.1350 | -0.2100 | -0.2044 | -0.00002185 | -0.00002168 |
206 | 0.0097 | 0.0095 | 0.0334 | 0.0326 | 0.0325 | 0.0317 | 0.1375 | 0.1343 | -0.2089 | -0.2033 | -0.00002173 | -0.00002156 |
207 | 0.0096 | 0.0094 | 0.0332 | 0.0324 | 0.0323 | 0.0315 | 0.1367 | 0.1335 | -0.2078 | -0.2022 | -0.00002162 | -0.00002143 |
208 | 0.0096 | 0.0094 | 0.0331 | 0.0323 | 0.0321 | 0.0313 | 0.1360 | 0.1328 | -0.2066 | -0.2011 | -0.00002151 | -0.00002134 |
209 | 0.0095 | 0.0093 | 0.0329 | 0.0321 | 0.0320 | 0.0312 | 0.1353 | 0.1321 | -0.2055 | -0.2000 | -0.00002139 | -0.00002122 |
210 | 0.0095 | 0.0093 | 0.0327 | 0.0319 | 0.0318 | 0.0310 | 0.1345 | 0.1314 | -0.2044 | -0.1989 | -0.00002128 | -0.00002111 |
211 | 0.0094 | 0.0092 | 0.0325 | 0.0317 | 0.0316 | 0.0308 | 0.1338 | 0.1306 | -0.2033 | -0.1978 | -0.00002117 | -0.00002099 |
212 | 0.0094 | 0.0092 | 0.0323 | 0.0316 | 0.0314 | 0.0307 | 0.1331 | 0.1299 | -0.2022 | -0.1967 | -0.00002105 | -0.00002089 |
213 | 0.0093 | 0.0091 | 0.0322 | 0.0314 | 0.0313 | 0.0305 | 0.1324 | 0.1292 | -0.2011 | -0.1956 | -0.00002094 | -0.00002076 |
214 | 0.0093 | 0.0091 | 0.0320 | 0.0312 | 0.0311 | 0.0303 | 0.1317 | 0.1285 | -0.2000 | -0.1945 | -0.00002083 | -0.00002066 |
215 | 0.0092 | 0.0090 | 0.0318 | 0.0310 | 0.0309 | 0.0302 | 0.1310 | 0.1278 | -0.1989 | -0.1935 | -0.00002072 | -0.00002052 |
216 | 0.0092 | 0.0090 | 0.0317 | 0.0309 | 0.0308 | 0.0300 | 0.1302 | 0.1271 | -0.1979 | -0.1924 | -0.00002061 | -0.00002044 |
217 | 0.0091 | 0.0089 | 0.0315 | 0.0307 | 0.0306 | 0.0298 | 0.1295 | 0.1264 | -0.1968 | -0.1914 | -0.00002050 | -0.00002034 |
218 | 0.0091 | 0.0089 | 0.0313 | 0.0305 | 0.0304 | 0.0297 | 0.1288 | 0.1257 | -0.1957 | -0.1903 | -0.00002039 | -0.00002023 |
219 | 0.0090 | 0.0088 | 0.0311 | 0.0304 | 0.0303 | 0.0295 | 0.1281 | 0.1250 | -0.1947 | -0.1893 | -0.00002029 | -0.00002009 |
220 | 0.0090 | 0.0088 | 0.0310 | 0.0302 | 0.0301 | 0.0293 | 0.1275 | 0.1243 | -0.1936 | -0.1882 | -0.00002018 | -0.00002001 |
221 | 0.0089 | 0.0087 | 0.0308 | 0.0300 | 0.0299 | 0.0292 | 0.1268 | 0.1237 | -0.1926 | -0.1872 | -0.00002007 | -0.00001989 |
222 | 0.0089 | 0.0087 | 0.0306 | 0.0299 | 0.0298 | 0.0290 | 0.1261 | 0.1230 | -0.1915 | -0.1862 | -0.00001997 | -0.00001977 |
223 | 0.0088 | 0.0086 | 0.0305 | 0.0297 | 0.0296 | 0.0289 | 0.1254 | 0.1223 | -0.1905 | -0.1851 | -0.00001986 | -0.00001966 |
224 | 0.0088 | 0.0086 | 0.0303 | 0.0295 | 0.0295 | 0.0287 | 0.1247 | 0.1216 | -0.1895 | -0.1841 | -0.00001975 | -0.00001956 |
225 | 0.0087 | 0.0085 | 0.0301 | 0.0294 | 0.0293 | 0.0285 | 0.1240 | 0.1210 | -0.1884 | -0.1831 | -0.00001965 | -0.00001948 |
226 | 0.0087 | 0.0085 | 0.0300 | 0.0292 | 0.0291 | 0.0284 | 0.1234 | 0.1203 | -0.1874 | -0.1821 | -0.00001954 | -0.00001936 |
227 | 0.0086 | 0.0084 | 0.0298 | 0.0291 | 0.0290 | 0.0282 | 0.1227 | 0.1197 | -0.1864 | -0.1811 | -0.00001944 | -0.00001926 |
228 | 0.0086 | 0.0084 | 0.0297 | 0.0289 | 0.0288 | 0.0281 | 0.1221 | 0.1190 | -0.1854 | -0.1801 | -0.00001934 | -0.00001914 |
229 | 0.0085 | 0.0084 | 0.0295 | 0.0287 | 0.0287 | 0.0279 | 0.1214 | 0.1183 | -0.1844 | -0.1791 | -0.00001923 | -0.00001905 |
230 | 0.0085 | 0.0083 | 0.0293 | 0.0286 | 0.0285 | 0.0278 | 0.1207 | 0.1177 | -0.1834 | -0.1781 | -0.00001913 | -0.00001894 |
231 | 0.0084 | 0.0083 | 0.0292 | 0.0284 | 0.0284 | 0.0276 | 0.1201 | 0.1171 | -0.1824 | -0.1772 | -0.00001903 | -0.00001884 |
232 | 0.0084 | 0.0082 | 0.0290 | 0.0283 | 0.0282 | 0.0275 | 0.1194 | 0.1164 | -0.1814 | -0.1762 | -0.00001893 | -0.00001874 |
233 | 0.0084 | 0.0082 | 0.0289 | 0.0281 | 0.0281 | 0.0273 | 0.1188 | 0.1158 | -0.1804 | -0.1752 | -0.00001883 | -0.00001864 |
234 | 0.0083 | 0.0081 | 0.0287 | 0.0280 | 0.0279 | 0.0272 | 0.1181 | 0.1151 | -0.1795 | -0.1743 | -0.00001873 | -0.00001854 |
235 | 0.0083 | 0.0081 | 0.0286 | 0.0278 | 0.0278 | 0.0270 | 0.1175 | 0.1145 | -0.1785 | -0.1733 | -0.00001863 | -0.00001843 |
236 | 0.0082 | 0.0080 | 0.0284 | 0.0277 | 0.0276 | 0.0269 | 0.1169 | 0.1139 | -0.1775 | -0.1724 | -0.00001853 | -0.00001832 |
237 | 0.0082 | 0.0080 | 0.0283 | 0.0275 | 0.0275 | 0.0267 | 0.1162 | 0.1133 | -0.1766 | -0.1714 | -0.00001843 | -0.00001824 |
238 | 0.0081 | 0.0079 | 0.0281 | 0.0274 | 0.0273 | 0.0266 | 0.1156 | 0.1126 | -0.1756 | -0.1705 | -0.00001833 | -0.00001814 |
239 | 0.0081 | 0.0079 | 0.0279 | 0.0272 | 0.0272 | 0.0264 | 0.1150 | 0.1120 | -0.1747 | -0.1695 | -0.00001824 | -0.00001803 |
240 | 0.0080 | 0.0079 | 0.0278 | 0.0271 | 0.0270 | 0.0263 | 0.1144 | 0.1114 | -0.1737 | -0.1686 | -0.00001814 | -0.00001795 |
241 | 0.0080 | 0.0078 | 0.0276 | 0.0269 | 0.0269 | 0.0261 | 0.1138 | 0.1108 | -0.1728 | -0.1677 | -0.00001804 | -0.00001783 |
242 | 0.0080 | 0.0078 | 0.0275 | 0.0268 | 0.0267 | 0.0260 | 0.1131 | 0.1102 | -0.1719 | -0.1668 | -0.00001795 | -0.00001772 |
243 | 0.0079 | 0.0077 | 0.0273 | 0.0266 | 0.0266 | 0.0259 | 0.1125 | 0.1096 | -0.1709 | -0.1658 | -0.00001785 | -0.00001766 |
244 | 0.0079 | 0.0077 | 0.0272 | 0.0265 | 0.0264 | 0.0257 | 0.1119 | 0.1090 | -0.1700 | -0.1649 | -0.00001776 | -0.00001758 |
245 | 0.0078 | 0.0077 | 0.0271 | 0.0263 | 0.0263 | 0.0256 | 0.1113 | 0.1084 | -0.1691 | -0.1640 | -0.00001766 | -0.00001746 |
246 | 0.0078 | 0.0076 | 0.0269 | 0.0262 | 0.0262 | 0.0254 | 0.1107 | 0.1078 | -0.1682 | -0.1631 | -0.00001757 | -0.00001736 |
247 | 0.0077 | 0.0076 | 0.0268 | 0.0260 | 0.0260 | 0.0253 | 0.1101 | 0.1072 | -0.1673 | -0.1622 | -0.00001747 | -0.00001728 |
248 | 0.0077 | 0.0075 | 0.0266 | 0.0259 | 0.0259 | 0.0252 | 0.1095 | 0.1066 | -0.1664 | -0.1613 | -0.00001738 | -0.00001718 |
249 | 0.0077 | 0.0075 | 0.0265 | 0.0258 | 0.0257 | 0.0250 | 0.1089 | 0.1060 | -0.1655 | -0.1605 | -0.00001729 | -0.00001709 |
250 | 0.0076 | 0.0074 | 0.0263 | 0.0256 | 0.0256 | 0.0249 | 0.1083 | 0.1054 | -0.1646 | -0.1596 | -0.00001719 | -0.00001699 |
251 | 0.0076 | 0.0074 | 0.0262 | 0.0255 | 0.0255 | 0.0247 | 0.1078 | 0.1049 | -0.1637 | -0.1587 | -0.00001710 | -0.00001690 |
252 | 0.0075 | 0.0074 | 0.0260 | 0.0253 | 0.0253 | 0.0246 | 0.1072 | 0.1043 | -0.1628 | -0.1578 | -0.00001701 | -0.00001681 |
253 | 0.0075 | 0.0073 | 0.0259 | 0.0252 | 0.0252 | 0.0245 | 0.1066 | 0.1037 | -0.1619 | -0.1570 | -0.00001692 | -0.00001674 |
254 | 0.0075 | 0.0073 | 0.0258 | 0.0251 | 0.0250 | 0.0243 | 0.1060 | 0.1031 | -0.1610 | -0.1561 | -0.00001683 | -0.00001663 |
255 | 0.0074 | 0.0072 | 0.0256 | 0.0249 | 0.0249 | 0.0242 | 0.1054 | 0.1026 | -0.1602 | -0.1552 | -0.00001674 | -0.00001653 |
256 | 0.0074 | 0.0072 | 0.0255 | 0.0248 | 0.0248 | 0.0241 | 0.1049 | 0.1020 | -0.1593 | -0.1544 | -0.00001665 | -0.00001643 |
257 | 0.0073 | 0.0072 | 0.0254 | 0.0246 | 0.0246 | 0.0239 | 0.1043 | 0.1015 | -0.1584 | -0.1535 | -0.00001656 | -0.00001636 |
258 | 0.0073 | 0.0071 | 0.0252 | 0.0245 | 0.0245 | 0.0238 | 0.1037 | 0.1009 | -0.1576 | -0.1527 | -0.00001647 | -0.00001629 |
259 | 0.0073 | 0.0071 | 0.0251 | 0.0244 | 0.0244 | 0.0237 | 0.1032 | 0.1003 | -0.1567 | -0.1519 | -0.00001639 | -0.00001618 |
260 | 0.0072 | 0.0070 | 0.0249 | 0.0242 | 0.0242 | 0.0235 | 0.1026 | 0.0998 | -0.1559 | -0.1510 | -0.00001630 | -0.00001610 |
261 | 0.0072 | 0.0070 | 0.0248 | 0.0241 | 0.0241 | 0.0234 | 0.1021 | 0.0992 | -0.1551 | -0.1502 | -0.00001621 | -0.00001602 |
262 | 0.0071 | 0.0070 | 0.0247 | 0.0240 | 0.0240 | 0.0233 | 0.1015 | 0.0987 | -0.1542 | -0.1494 | -0.00001613 | -0.00001592 |
263 | 0.0071 | 0.0069 | 0.0245 | 0.0238 | 0.0239 | 0.0232 | 0.1010 | 0.0982 | -0.1534 | -0.1485 | -0.00001604 | -0.00001583 |
264 | 0.0071 | 0.0069 | 0.0244 | 0.0237 | 0.0237 | 0.0230 | 0.1004 | 0.0976 | -0.1526 | -0.1477 | -0.00001595 | -0.00001575 |
265 | 0.0070 | 0.0069 | 0.0243 | 0.0236 | 0.0236 | 0.0229 | 0.0999 | 0.0971 | -0.1517 | -0.1469 | -0.00001587 | -0.00001566 |
266 | 0.0070 | 0.0068 | 0.0241 | 0.0235 | 0.0235 | 0.0228 | 0.0993 | 0.0965 | -0.1509 | -0.1461 | -0.00001578 | -0.00001559 |
267 | 0.0070 | 0.0068 | 0.0240 | 0.0233 | 0.0233 | 0.0227 | 0.0988 | 0.0960 | -0.1501 | -0.1453 | -0.00001570 | -0.00001550 |
268 | 0.0069 | 0.0067 | 0.0239 | 0.0232 | 0.0232 | 0.0225 | 0.0983 | 0.0955 | -0.1493 | -0.1445 | -0.00001562 | -0.00001541 |
269 | 0.0069 | 0.0067 | 0.0238 | 0.0231 | 0.0231 | 0.0224 | 0.0977 | 0.0950 | -0.1485 | -0.1437 | -0.00001553 | -0.00001532 |
270 | 0.0068 | 0.0067 | 0.0236 | 0.0229 | 0.0230 | 0.0223 | 0.0972 | 0.0944 | -0.1477 | -0.1429 | -0.00001545 | -0.00001526 |
271 | 0.0068 | 0.0066 | 0.0235 | 0.0228 | 0.0228 | 0.0222 | 0.0967 | 0.0939 | -0.1469 | -0.1421 | -0.00001537 | -0.00001518 |
272 | 0.0068 | 0.0066 | 0.0234 | 0.0227 | 0.0227 | 0.0220 | 0.0962 | 0.0934 | -0.1461 | -0.1414 | -0.00001528 | -0.00001508 |
273 | 0.0067 | 0.0066 | 0.0232 | 0.0226 | 0.0226 | 0.0219 | 0.0956 | 0.0929 | -0.1453 | -0.1406 | -0.00001520 | -0.00001498 |
274 | 0.0067 | 0.0065 | 0.0231 | 0.0224 | 0.0225 | 0.0218 | 0.0951 | 0.0924 | -0.1445 | -0.1398 | -0.00001512 | -0.00001489 |
275 | 0.0067 | 0.0065 | 0.0230 | 0.0223 | 0.0224 | 0.0217 | 0.0946 | 0.0919 | -0.1437 | -0.1390 | -0.00001504 | -0.00001483 |
276 | 0.0066 | 0.0065 | 0.0229 | 0.0222 | 0.0222 | 0.0216 | 0.0941 | 0.0914 | -0.1430 | -0.1383 | -0.00001496 | -0.00001476 |
277 | 0.0066 | 0.0064 | 0.0227 | 0.0221 | 0.0221 | 0.0214 | 0.0936 | 0.0909 | -0.1422 | -0.1375 | -0.00001488 | -0.00001466 |
278 | 0.0065 | 0.0064 | 0.0226 | 0.0220 | 0.0220 | 0.0213 | 0.0931 | 0.0904 | -0.1414 | -0.1368 | -0.00001480 | -0.00001460 |
279 | 0.0065 | 0.0063 | 0.0225 | 0.0218 | 0.0219 | 0.0212 | 0.0926 | 0.0899 | -0.1407 | -0.1360 | -0.00001472 | -0.00001453 |
280 | 0.0065 | 0.0063 | 0.0224 | 0.0217 | 0.0218 | 0.0211 | 0.0921 | 0.0894 | -0.1399 | -0.1353 | -0.00001464 | -0.00001443 |
281 | 0.0064 | 0.0063 | 0.0223 | 0.0216 | 0.0216 | 0.0210 | 0.0916 | 0.0889 | -0.1391 | -0.1345 | -0.00001456 | -0.00001436 |
282 | 0.0064 | 0.0062 | 0.0221 | 0.0215 | 0.0215 | 0.0209 | 0.0911 | 0.0884 | -0.1384 | -0.1338 | -0.00001449 | -0.00001428 |
283 | 0.0064 | 0.0062 | 0.0220 | 0.0214 | 0.0214 | 0.0207 | 0.0906 | 0.0879 | -0.1376 | -0.1330 | -0.00001441 | -0.00001421 |
284 | 0.0063 | 0.0062 | 0.0219 | 0.0212 | 0.0213 | 0.0206 | 0.0901 | 0.0874 | -0.1369 | -0.1323 | -0.00001433 | -0.00001410 |
285 | 0.0063 | 0.0061 | 0.0218 | 0.0211 | 0.0212 | 0.0205 | 0.0896 | 0.0870 | -0.1362 | -0.1316 | -0.00001426 | -0.00001403 |
286 | 0.0063 | 0.0061 | 0.0217 | 0.0210 | 0.0211 | 0.0204 | 0.0891 | 0.0865 | -0.1354 | -0.1309 | -0.00001418 | -0.00001398 |
287 | 0.0062 | 0.0061 | 0.0215 | 0.0209 | 0.0209 | 0.0203 | 0.0887 | 0.0860 | -0.1347 | -0.1301 | -0.00001410 | -0.00001388 |
288 | 0.0062 | 0.0060 | 0.0214 | 0.0208 | 0.0208 | 0.0202 | 0.0882 | 0.0855 | -0.1340 | -0.1294 | -0.00001403 | -0.00001380 |
289 | 0.0062 | 0.0060 | 0.0213 | 0.0207 | 0.0207 | 0.0201 | 0.0877 | 0.0851 | -0.1332 | -0.1287 | -0.00001395 | -0.00001375 |
290 | 0.0061 | 0.0060 | 0.0212 | 0.0206 | 0.0206 | 0.0200 | 0.0872 | 0.0846 | -0.1325 | -0.1280 | -0.00001388 | -0.00001367 |
291 | 0.0061 | 0.0059 | 0.0211 | 0.0204 | 0.0205 | 0.0199 | 0.0868 | 0.0841 | -0.1318 | -0.1273 | -0.00001380 | -0.00001359 |
292 | 0.0061 | 0.0059 | 0.0210 | 0.0203 | 0.0204 | 0.0197 | 0.0863 | 0.0837 | -0.1311 | -0.1266 | -0.00001373 | -0.00001351 |
293 | 0.0060 | 0.0059 | 0.0209 | 0.0202 | 0.0203 | 0.0196 | 0.0858 | 0.0832 | -0.1304 | -0.1259 | -0.00001366 | -0.00001342 |
294 | 0.0060 | 0.0058 | 0.0207 | 0.0201 | 0.0202 | 0.0195 | 0.0854 | 0.0828 | -0.1297 | -0.1252 | -0.00001358 | -0.00001337 |
295 | 0.0060 | 0.0058 | 0.0206 | 0.0200 | 0.0201 | 0.0194 | 0.0849 | 0.0823 | -0.1290 | -0.1245 | -0.00001351 | -0.00001331 |
296 | 0.0059 | 0.0058 | 0.0205 | 0.0199 | 0.0199 | 0.0193 | 0.0844 | 0.0818 | -0.1283 | -0.1238 | -0.00001344 | -0.00001324 |
297 | 0.0059 | 0.0057 | 0.0204 | 0.0198 | 0.0198 | 0.0192 | 0.0840 | 0.0814 | -0.1276 | -0.1232 | -0.00001337 | -0.00001317 |
298 | 0.0059 | 0.0057 | 0.0203 | 0.0197 | 0.0197 | 0.0191 | 0.0835 | 0.0809 | -0.1269 | -0.1225 | -0.00001329 | -0.00001311 |
299 | 0.0058 | 0.0057 | 0.0202 | 0.0196 | 0.0196 | 0.0190 | 0.0831 | 0.0805 | -0.1262 | -0.1218 | -0.00001322 | -0.00001299 |
300 | 0.0058 | 0.0057 | 0.0201 | 0.0195 | 0.0195 | 0.0189 | 0.0826 | 0.0801 | -0.1255 | -0.1211 | -0.00001315 | -0.00001294 |
301 | 0.0058 | 0.0056 | 0.0200 | 0.0193 | 0.0194 | 0.0188 | 0.0822 | 0.0796 | -0.1249 | -0.1205 | -0.00001308 | -0.00001286 |
302 | 0.0057 | 0.0056 | 0.0199 | 0.0192 | 0.0193 | 0.0187 | 0.0817 | 0.0792 | -0.1242 | -0.1198 | -0.00001301 | -0.00001280 |
303 | 0.0057 | 0.0056 | 0.0198 | 0.0191 | 0.0192 | 0.0186 | 0.0813 | 0.0787 | -0.1235 | -0.1191 | -0.00001294 | -0.00001274 |
304 | 0.0057 | 0.0055 | 0.0197 | 0.0190 | 0.0191 | 0.0185 | 0.0809 | 0.0783 | -0.1228 | -0.1185 | -0.00001287 | -0.00001267 |
305 | 0.0057 | 0.0055 | 0.0195 | 0.0189 | 0.0190 | 0.0184 | 0.0804 | 0.0779 | -0.1222 | -0.1178 | -0.00001280 | -0.00001258 |
306 | 0.0056 | 0.0055 | 0.0194 | 0.0188 | 0.0189 | 0.0183 | 0.0800 | 0.0775 | -0.1215 | -0.1172 | -0.00001274 | -0.00001251 |
307 | 0.0056 | 0.0054 | 0.0193 | 0.0187 | 0.0188 | 0.0182 | 0.0796 | 0.0770 | -0.1209 | -0.1165 | -0.00001267 | -0.00001247 |
308 | 0.0056 | 0.0054 | 0.0192 | 0.0186 | 0.0187 | 0.0181 | 0.0791 | 0.0766 | -0.1202 | -0.1159 | -0.00001260 | -0.00001238 |
309 | 0.0055 | 0.0054 | 0.0191 | 0.0185 | 0.0186 | 0.0180 | 0.0787 | 0.0762 | -0.1196 | -0.1153 | -0.00001253 | -0.00001233 |
310 | 0.0055 | 0.0054 | 0.0190 | 0.0184 | 0.0185 | 0.0179 | 0.0783 | 0.0758 | -0.1189 | -0.1146 | -0.00001246 | -0.00001227 |
311 | 0.0055 | 0.0053 | 0.0189 | 0.0183 | 0.0184 | 0.0178 | 0.0779 | 0.0753 | -0.1183 | -0.1140 | -0.00001240 | -0.00001220 |
312 | 0.0054 | 0.0053 | 0.0188 | 0.0182 | 0.0183 | 0.0177 | 0.0774 | 0.0749 | -0.1176 | -0.1134 | -0.00001233 | -0.00001212 |
313 | 0.0054 | 0.0053 | 0.0187 | 0.0181 | 0.0182 | 0.0176 | 0.0770 | 0.0745 | -0.1170 | -0.1127 | -0.00001227 | -0.00001205 |
314 | 0.0054 | 0.0052 | 0.0186 | 0.0180 | 0.0181 | 0.0175 | 0.0766 | 0.0741 | -0.1164 | -0.1121 | -0.00001220 | -0.00001200 |
315 | 0.0054 | 0.0052 | 0.0185 | 0.0179 | 0.0180 | 0.0174 | 0.0762 | 0.0737 | -0.1157 | -0.1115 | -0.00001213 | -0.00001193 |
316 | 0.0053 | 0.0052 | 0.0184 | 0.0178 | 0.0179 | 0.0173 | 0.0758 | 0.0733 | -0.1151 | -0.1109 | -0.00001207 | -0.00001185 |
317 | 0.0053 | 0.0051 | 0.0183 | 0.0177 | 0.0178 | 0.0172 | 0.0754 | 0.0729 | -0.1145 | -0.1103 | -0.00001200 | -0.00001181 |
318 | 0.0053 | 0.0051 | 0.0182 | 0.0176 | 0.0177 | 0.0171 | 0.0750 | 0.0725 | -0.1139 | -0.1097 | -0.00001194 | -0.00001173 |
319 | 0.0052 | 0.0051 | 0.0181 | 0.0175 | 0.0176 | 0.0170 | 0.0745 | 0.0721 | -0.1133 | -0.1091 | -0.00001188 | -0.00001168 |
320 | 0.0052 | 0.0051 | 0.0180 | 0.0174 | 0.0175 | 0.0169 | 0.0741 | 0.0717 | -0.1126 | -0.1085 | -0.00001181 | -0.00001160 |
321 | 0.0052 | 0.0050 | 0.0179 | 0.0173 | 0.0174 | 0.0168 | 0.0737 | 0.0713 | -0.1120 | -0.1079 | -0.00001175 | -0.00001153 |
322 | 0.0052 | 0.0050 | 0.0178 | 0.0172 | 0.0173 | 0.0167 | 0.0733 | 0.0709 | -0.1114 | -0.1073 | -0.00001169 | -0.00001148 |
323 | 0.0051 | 0.0050 | 0.0177 | 0.0171 | 0.0172 | 0.0166 | 0.0730 | 0.0705 | -0.1108 | -0.1067 | -0.00001162 | -0.00001142 |
324 | 0.0051 | 0.0050 | 0.0176 | 0.0170 | 0.0171 | 0.0165 | 0.0726 | 0.0701 | -0.1102 | -0.1061 | -0.00001156 | -0.00001137 |
325 | 0.0051 | 0.0049 | 0.0175 | 0.0169 | 0.0171 | 0.0165 | 0.0722 | 0.0697 | -0.1096 | -0.1055 | -0.00001150 | -0.00001129 |
326 | 0.0050 | 0.0049 | 0.0174 | 0.0169 | 0.0170 | 0.0164 | 0.0718 | 0.0694 | -0.1090 | -0.1049 | -0.00001144 | -0.00001123 |
327 | 0.0050 | 0.0049 | 0.0174 | 0.0168 | 0.0169 | 0.0163 | 0.0714 | 0.0690 | -0.1085 | -0.1043 | -0.00001138 | -0.00001117 |
328 | 0.0050 | 0.0048 | 0.0173 | 0.0167 | 0.0168 | 0.0162 | 0.0710 | 0.0686 | -0.1079 | -0.1038 | -0.00001132 | -0.00001109 |
329 | 0.0050 | 0.0048 | 0.0172 | 0.0166 | 0.0167 | 0.0161 | 0.0706 | 0.0682 | -0.1073 | -0.1032 | -0.00001125 | -0.00001104 |
330 | 0.0049 | 0.0048 | 0.0171 | 0.0165 | 0.0166 | 0.0160 | 0.0702 | 0.0678 | -0.1067 | -0.1026 | -0.00001119 | -0.00001098 |
331 | 0.0049 | 0.0048 | 0.0170 | 0.0164 | 0.0165 | 0.0159 | 0.0699 | 0.0675 | -0.1061 | -0.1021 | -0.00001113 | -0.00001092 |
332 | 0.0049 | 0.0047 | 0.0169 | 0.0163 | 0.0164 | 0.0158 | 0.0695 | 0.0671 | -0.1056 | -0.1015 | -0.00001107 | -0.00001086 |
333 | 0.0049 | 0.0047 | 0.0168 | 0.0162 | 0.0163 | 0.0157 | 0.0691 | 0.0667 | -0.1050 | -0.1009 | -0.00001102 | -0.00001080 |
334 | 0.0048 | 0.0047 | 0.0167 | 0.0161 | 0.0162 | 0.0157 | 0.0687 | 0.0664 | -0.1044 | -0.1004 | -0.00001096 | -0.00001074 |
335 | 0.0048 | 0.0047 | 0.0166 | 0.0160 | 0.0162 | 0.0156 | 0.0684 | 0.0660 | -0.1039 | -0.0998 | -0.00001090 | -0.00001071 |
336 | 0.0048 | 0.0046 | 0.0165 | 0.0159 | 0.0161 | 0.0155 | 0.0680 | 0.0656 | -0.1033 | -0.0993 | -0.00001084 | -0.00001065 |
337 | 0.0048 | 0.0046 | 0.0164 | 0.0159 | 0.0160 | 0.0154 | 0.0676 | 0.0653 | -0.1027 | -0.0987 | -0.00001078 | -0.00001058 |
338 | 0.0047 | 0.0046 | 0.0163 | 0.0158 | 0.0159 | 0.0153 | 0.0673 | 0.0649 | -0.1022 | -0.0982 | -0.00001072 | -0.00001051 |
339 | 0.0047 | 0.0046 | 0.0163 | 0.0157 | 0.0158 | 0.0152 | 0.0669 | 0.0646 | -0.1016 | -0.0976 | -0.00001067 | -0.00001045 |
340 | 0.0047 | 0.0045 | 0.0162 | 0.0156 | 0.0157 | 0.0151 | 0.0665 | 0.0642 | -0.1011 | -0.0971 | -0.00001061 | -0.00001042 |
341 | 0.0047 | 0.0045 | 0.0161 | 0.0155 | 0.0156 | 0.0151 | 0.0662 | 0.0638 | -0.1005 | -0.0966 | -0.00001055 | -0.00001034 |
342 | 0.0046 | 0.0045 | 0.0160 | 0.0154 | 0.0156 | 0.0150 | 0.0658 | 0.0635 | -0.1000 | -0.0960 | -0.00001049 | -0.00001028 |
343 | 0.0046 | 0.0045 | 0.0159 | 0.0153 | 0.0155 | 0.0149 | 0.0655 | 0.0631 | -0.0995 | -0.0955 | -0.00001044 | -0.00001024 |
344 | 0.0046 | 0.0044 | 0.0158 | 0.0153 | 0.0154 | 0.0148 | 0.0651 | 0.0628 | -0.0989 | -0.0950 | -0.00001038 | -0.00001020 |
345 | 0.0046 | 0.0044 | 0.0157 | 0.0152 | 0.0153 | 0.0147 | 0.0648 | 0.0624 | -0.0984 | -0.0945 | -0.00001033 | -0.00001010 |
346 | 0.0045 | 0.0044 | 0.0157 | 0.0151 | 0.0152 | 0.0147 | 0.0644 | 0.0621 | -0.0979 | -0.0939 | -0.00001027 | -0.00001007 |
347 | 0.0045 | 0.0044 | 0.0156 | 0.0150 | 0.0151 | 0.0146 | 0.0641 | 0.0618 | -0.0973 | -0.0934 | -0.00001022 | -0.00000999 |
348 | 0.0045 | 0.0043 | 0.0155 | 0.0149 | 0.0151 | 0.0145 | 0.0637 | 0.0614 | -0.0968 | -0.0929 | -0.00001016 | -0.00000995 |
349 | 0.0045 | 0.0043 | 0.0154 | 0.0148 | 0.0150 | 0.0144 | 0.0634 | 0.0611 | -0.0963 | -0.0924 | -0.00001011 | -0.00000987 |
350 | 0.0044 | 0.0043 | 0.0153 | 0.0148 | 0.0149 | 0.0143 | 0.0630 | 0.0607 | -0.0958 | -0.0919 | -0.00001005 | -0.00000986 |
351 | 0.0044 | 0.0043 | 0.0152 | 0.0147 | 0.0148 | 0.0143 | 0.0627 | 0.0604 | -0.0952 | -0.0914 | -0.00001000 | -0.00000979 |
352 | 0.0044 | 0.0042 | 0.0152 | 0.0146 | 0.0147 | 0.0142 | 0.0623 | 0.0601 | -0.0947 | -0.0909 | -0.00000994 | -0.00000975 |
353 | 0.0044 | 0.0042 | 0.0151 | 0.0145 | 0.0147 | 0.0141 | 0.0620 | 0.0597 | -0.0942 | -0.0904 | -0.00000989 | -0.00000967 |
354 | 0.0043 | 0.0042 | 0.0150 | 0.0144 | 0.0146 | 0.0140 | 0.0617 | 0.0594 | -0.0937 | -0.0899 | -0.00000984 | -0.00000965 |
355 | 0.0043 | 0.0042 | 0.0149 | 0.0144 | 0.0145 | 0.0139 | 0.0613 | 0.0591 | -0.0932 | -0.0894 | -0.00000979 | -0.00000958 |
356 | 0.0043 | 0.0042 | 0.0148 | 0.0143 | 0.0144 | 0.0139 | 0.0610 | 0.0588 | -0.0927 | -0.0889 | -0.00000973 | -0.00000953 |
357 | 0.0043 | 0.0041 | 0.0148 | 0.0142 | 0.0143 | 0.0138 | 0.0607 | 0.0584 | -0.0922 | -0.0884 | -0.00000968 | -0.00000949 |
358 | 0.0042 | 0.0041 | 0.0147 | 0.0141 | 0.0143 | 0.0137 | 0.0604 | 0.0581 | -0.0917 | -0.0879 | -0.00000963 | -0.00000943 |
359 | 0.0042 | 0.0041 | 0.0146 | 0.0140 | 0.0142 | 0.0136 | 0.0600 | 0.0578 | -0.0912 | -0.0874 | -0.00000958 | -0.00000935 |
360 | 0.0042 | 0.0041 | 0.0145 | 0.0140 | 0.0141 | 0.0136 | 0.0597 | 0.0575 | -0.0907 | -0.0869 | -0.00000953 | -0.00000932 |
361 | 0.0042 | 0.0040 | 0.0144 | 0.0139 | 0.0140 | 0.0135 | 0.0594 | 0.0572 | -0.0902 | -0.0864 | -0.00000947 | -0.00000929 |
362 | 0.0042 | 0.0040 | 0.0144 | 0.0138 | 0.0140 | 0.0134 | 0.0591 | 0.0568 | -0.0897 | -0.0860 | -0.00000942 | -0.00000923 |
363 | 0.0041 | 0.0040 | 0.0143 | 0.0137 | 0.0139 | 0.0133 | 0.0587 | 0.0565 | -0.0893 | -0.0855 | -0.00000937 | -0.00000918 |
364 | 0.0041 | 0.0040 | 0.0142 | 0.0137 | 0.0138 | 0.0133 | 0.0584 | 0.0562 | -0.0888 | -0.0850 | -0.00000932 | -0.00000913 |
365 | 0.0041 | 0.0040 | 0.0141 | 0.0136 | 0.0137 | 0.0132 | 0.0581 | 0.0559 | -0.0883 | -0.0846 | -0.00000927 | -0.00000910 |
366 | 0.0041 | 0.0039 | 0.0140 | 0.0135 | 0.0137 | 0.0131 | 0.0578 | 0.0556 | -0.0878 | -0.0841 | -0.00000922 | -0.00000904 |
367 | 0.0040 | 0.0039 | 0.0140 | 0.0134 | 0.0136 | 0.0130 | 0.0575 | 0.0553 | -0.0873 | -0.0836 | -0.00000917 | -0.00000898 |
368 | 0.0040 | 0.0039 | 0.0139 | 0.0134 | 0.0135 | 0.0130 | 0.0572 | 0.0550 | -0.0869 | -0.0832 | -0.00000912 | -0.00000893 |
369 | 0.0040 | 0.0039 | 0.0138 | 0.0133 | 0.0134 | 0.0129 | 0.0569 | 0.0547 | -0.0864 | -0.0827 | -0.00000908 | -0.00000888 |
370 | 0.0040 | 0.0038 | 0.0137 | 0.0132 | 0.0134 | 0.0128 | 0.0566 | 0.0544 | -0.0859 | -0.0822 | -0.00000903 | -0.00000881 |
371 | 0.0040 | 0.0038 | 0.0137 | 0.0131 | 0.0133 | 0.0128 | 0.0562 | 0.0541 | -0.0855 | -0.0818 | -0.00000898 | -0.00000879 |
372 | 0.0039 | 0.0038 | 0.0136 | 0.0131 | 0.0132 | 0.0127 | 0.0559 | 0.0538 | -0.0850 | -0.0813 | -0.00000893 | -0.00000873 |
373 | 0.0039 | 0.0038 | 0.0135 | 0.0130 | 0.0131 | 0.0126 | 0.0556 | 0.0535 | -0.0845 | -0.0809 | -0.00000888 | -0.00000868 |
374 | 0.0039 | 0.0038 | 0.0135 | 0.0129 | 0.0131 | 0.0126 | 0.0553 | 0.0532 | -0.0841 | -0.0804 | -0.00000883 | -0.00000864 |
375 | 0.0039 | 0.0037 | 0.0134 | 0.0129 | 0.0130 | 0.0125 | 0.0550 | 0.0529 | -0.0836 | -0.0800 | -0.00000879 | -0.00000858 |
376 | 0.0039 | 0.0037 | 0.0133 | 0.0128 | 0.0129 | 0.0124 | 0.0547 | 0.0526 | -0.0832 | -0.0796 | -0.00000874 | -0.00000855 |
377 | 0.0038 | 0.0037 | 0.0132 | 0.0127 | 0.0129 | 0.0123 | 0.0544 | 0.0523 | -0.0827 | -0.0791 | -0.00000869 | -0.00000852 |
378 | 0.0038 | 0.0037 | 0.0132 | 0.0126 | 0.0128 | 0.0123 | 0.0542 | 0.0520 | -0.0823 | -0.0787 | -0.00000865 | -0.00000843 |
379 | 0.0038 | 0.0037 | 0.0131 | 0.0126 | 0.0127 | 0.0122 | 0.0539 | 0.0517 | -0.0818 | -0.0782 | -0.00000860 | -0.00000839 |
380 | 0.0038 | 0.0036 | 0.0130 | 0.0125 | 0.0127 | 0.0121 | 0.0536 | 0.0515 | -0.0814 | -0.0778 | -0.00000855 | -0.00000836 |
381 | 0.0037 | 0.0036 | 0.0130 | 0.0124 | 0.0126 | 0.0121 | 0.0533 | 0.0512 | -0.0810 | -0.0774 | -0.00000851 | -0.00000832 |
382 | 0.0037 | 0.0036 | 0.0129 | 0.0124 | 0.0125 | 0.0120 | 0.0530 | 0.0509 | -0.0805 | -0.0769 | -0.00000846 | -0.00000828 |
383 | 0.0037 | 0.0036 | 0.0128 | 0.0123 | 0.0125 | 0.0119 | 0.0527 | 0.0506 | -0.0801 | -0.0765 | -0.00000842 | -0.00000820 |
384 | 0.0037 | 0.0036 | 0.0127 | 0.0122 | 0.0124 | 0.0119 | 0.0524 | 0.0503 | -0.0797 | -0.0761 | -0.00000837 | -0.00000816 |
385 | 0.0037 | 0.0035 | 0.0127 | 0.0122 | 0.0123 | 0.0118 | 0.0521 | 0.0500 | -0.0792 | -0.0757 | -0.00000833 | -0.00000812 |
386 | 0.0036 | 0.0035 | 0.0126 | 0.0121 | 0.0123 | 0.0117 | 0.0519 | 0.0498 | -0.0788 | -0.0753 | -0.00000828 | -0.00000808 |
387 | 0.0036 | 0.0035 | 0.0125 | 0.0120 | 0.0122 | 0.0117 | 0.0516 | 0.0495 | -0.0784 | -0.0748 | -0.00000824 | -0.00000804 |
388 | 0.0036 | 0.0035 | 0.0125 | 0.0120 | 0.0121 | 0.0116 | 0.0513 | 0.0492 | -0.0780 | -0.0744 | -0.00000819 | -0.00000800 |
389 | 0.0036 | 0.0035 | 0.0124 | 0.0119 | 0.0121 | 0.0116 | 0.0510 | 0.0490 | -0.0775 | -0.0740 | -0.00000815 | -0.00000796 |
390 | 0.0036 | 0.0034 | 0.0123 | 0.0118 | 0.0120 | 0.0115 | 0.0507 | 0.0487 | -0.0771 | -0.0736 | -0.00000810 | -0.00000789 |
391 | 0.0036 | 0.0034 | 0.0123 | 0.0118 | 0.0119 | 0.0114 | 0.0505 | 0.0484 | -0.0767 | -0.0732 | -0.00000806 | -0.00000789 |
392 | 0.0035 | 0.0034 | 0.0122 | 0.0117 | 0.0119 | 0.0114 | 0.0502 | 0.0481 | -0.0763 | -0.0728 | -0.00000802 | -0.00000781 |
393 | 0.0035 | 0.0034 | 0.0121 | 0.0116 | 0.0118 | 0.0113 | 0.0499 | 0.0479 | -0.0759 | -0.0724 | -0.00000797 | -0.00000777 |
394 | 0.0035 | 0.0034 | 0.0121 | 0.0116 | 0.0117 | 0.0112 | 0.0497 | 0.0476 | -0.0755 | -0.0720 | -0.00000793 | -0.00000775 |
395 | 0.0035 | 0.0034 | 0.0120 | 0.0115 | 0.0117 | 0.0112 | 0.0494 | 0.0473 | -0.0751 | -0.0716 | -0.00000789 | -0.00000769 |
396 | 0.0035 | 0.0033 | 0.0119 | 0.0114 | 0.0116 | 0.0111 | 0.0491 | 0.0471 | -0.0746 | -0.0712 | -0.00000785 | -0.00000768 |
397 | 0.0034 | 0.0033 | 0.0119 | 0.0114 | 0.0115 | 0.0111 | 0.0489 | 0.0468 | -0.0742 | -0.0708 | -0.00000780 | -0.00000760 |
398 | 0.0034 | 0.0033 | 0.0118 | 0.0113 | 0.0115 | 0.0110 | 0.0486 | 0.0466 | -0.0738 | -0.0704 | -0.00000776 | -0.00000756 |
399 | 0.0034 | 0.0033 | 0.0117 | 0.0113 | 0.0114 | 0.0109 | 0.0483 | 0.0463 | -0.0734 | -0.0700 | -0.00000772 | -0.00000753 |
400 | 0.0034 | 0.0033 | 0.0117 | 0.0112 | 0.0114 | 0.0109 | 0.0481 | 0.0461 | -0.0730 | -0.0696 | -0.00000768 | -0.00000746 |
401 | 0.0034 | 0.0032 | 0.0116 | 0.0111 | 0.0113 | 0.0108 | 0.0478 | 0.0458 | -0.0727 | -0.0692 | -0.00000764 | -0.00000745 |
402 | 0.0033 | 0.0032 | 0.0116 | 0.0111 | 0.0112 | 0.0107 | 0.0476 | 0.0456 | -0.0723 | -0.0689 | -0.00000760 | -0.00000741 |
403 | 0.0033 | 0.0032 | 0.0115 | 0.0110 | 0.0112 | 0.0107 | 0.0473 | 0.0453 | -0.0719 | -0.0685 | -0.00000756 | -0.00000738 |
404 | 0.0033 | 0.0032 | 0.0114 | 0.0109 | 0.0111 | 0.0106 | 0.0470 | 0.0450 | -0.0715 | -0.0681 | -0.00000752 | -0.00000734 |
405 | 0.0033 | 0.0032 | 0.0114 | 0.0109 | 0.0111 | 0.0106 | 0.0468 | 0.0448 | -0.0711 | -0.0677 | -0.00000748 | -0.00000729 |
406 | 0.0033 | 0.0032 | 0.0113 | 0.0108 | 0.0110 | 0.0105 | 0.0465 | 0.0445 | -0.0707 | -0.0673 | -0.00000744 | -0.00000726 |
407 | 0.0033 | 0.0031 | 0.0113 | 0.0108 | 0.0109 | 0.0105 | 0.0463 | 0.0443 | -0.0703 | -0.0670 | -0.00000740 | -0.00000722 |
408 | 0.0032 | 0.0031 | 0.0112 | 0.0107 | 0.0109 | 0.0104 | 0.0460 | 0.0441 | -0.0700 | -0.0666 | -0.00000736 | -0.00000717 |
409 | 0.0032 | 0.0031 | 0.0111 | 0.0106 | 0.0108 | 0.0103 | 0.0458 | 0.0438 | -0.0696 | -0.0662 | -0.00000732 | -0.00000712 |
410 | 0.0032 | 0.0031 | 0.0111 | 0.0106 | 0.0108 | 0.0103 | 0.0455 | 0.0436 | -0.0692 | -0.0659 | -0.00000728 | -0.00000710 |
411 | 0.0032 | 0.0031 | 0.0110 | 0.0105 | 0.0107 | 0.0102 | 0.0453 | 0.0433 | -0.0688 | -0.0655 | -0.00000724 | -0.00000704 |
412 | 0.0032 | 0.0030 | 0.0110 | 0.0105 | 0.0106 | 0.0102 | 0.0450 | 0.0431 | -0.0685 | -0.0651 | -0.00000720 | -0.00000699 |
413 | 0.0032 | 0.0030 | 0.0109 | 0.0104 | 0.0106 | 0.0101 | 0.0448 | 0.0429 | -0.0681 | -0.0648 | -0.00000716 | -0.00000697 |
414 | 0.0031 | 0.0030 | 0.0108 | 0.0104 | 0.0105 | 0.0101 | 0.0446 | 0.0426 | -0.0677 | -0.0644 | -0.00000712 | -0.00000692 |
415 | 0.0031 | 0.0030 | 0.0108 | 0.0103 | 0.0105 | 0.0100 | 0.0443 | 0.0424 | -0.0673 | -0.0641 | -0.00000708 | -0.00000690 |
416 | 0.0031 | 0.0030 | 0.0107 | 0.0102 | 0.0104 | 0.0099 | 0.0441 | 0.0421 | -0.0670 | -0.0637 | -0.00000704 | -0.00000687 |
417 | 0.0031 | 0.0030 | 0.0107 | 0.0102 | 0.0104 | 0.0099 | 0.0438 | 0.0419 | -0.0666 | -0.0633 | -0.00000701 | -0.00000682 |
418 | 0.0031 | 0.0030 | 0.0106 | 0.0101 | 0.0103 | 0.0098 | 0.0436 | 0.0417 | -0.0663 | -0.0630 | -0.00000697 | -0.00000679 |
419 | 0.0031 | 0.0029 | 0.0105 | 0.0101 | 0.0102 | 0.0098 | 0.0434 | 0.0414 | -0.0659 | -0.0626 | -0.00000693 | -0.00000674 |
420 | 0.0030 | 0.0029 | 0.0105 | 0.0100 | 0.0102 | 0.0097 | 0.0431 | 0.0412 | -0.0656 | -0.0623 | -0.00000689 | -0.00000670 |
421 | 0.0030 | 0.0029 | 0.0104 | 0.0100 | 0.0101 | 0.0097 | 0.0429 | 0.0410 | -0.0652 | -0.0620 | -0.00000686 | -0.00000665 |
422 | 0.0030 | 0.0029 | 0.0104 | 0.0099 | 0.0101 | 0.0096 | 0.0427 | 0.0408 | -0.0648 | -0.0616 | -0.00000682 | -0.00000663 |
423 | 0.0030 | 0.0029 | 0.0103 | 0.0099 | 0.0100 | 0.0096 | 0.0424 | 0.0405 | -0.0645 | -0.0613 | -0.00000678 | -0.00000660 |
424 | 0.0030 | 0.0029 | 0.0103 | 0.0098 | 0.0100 | 0.0095 | 0.0422 | 0.0403 | -0.0641 | -0.0609 | -0.00000675 | -0.00000656 |
425 | 0.0030 | 0.0028 | 0.0102 | 0.0097 | 0.0099 | 0.0095 | 0.0420 | 0.0401 | -0.0638 | -0.0606 | -0.00000671 | -0.00000651 |
426 | 0.0029 | 0.0028 | 0.0102 | 0.0097 | 0.0099 | 0.0094 | 0.0418 | 0.0399 | -0.0635 | -0.0603 | -0.00000668 | -0.00000648 |
427 | 0.0029 | 0.0028 | 0.0101 | 0.0096 | 0.0098 | 0.0094 | 0.0415 | 0.0396 | -0.0631 | -0.0599 | -0.00000664 | -0.00000645 |
428 | 0.0029 | 0.0028 | 0.0100 | 0.0096 | 0.0098 | 0.0093 | 0.0413 | 0.0394 | -0.0628 | -0.0596 | -0.00000660 | -0.00000642 |
429 | 0.0029 | 0.0028 | 0.0100 | 0.0095 | 0.0097 | 0.0093 | 0.0411 | 0.0392 | -0.0624 | -0.0593 | -0.00000657 | -0.00000639 |
430 | 0.0029 | 0.0028 | 0.0099 | 0.0095 | 0.0097 | 0.0092 | 0.0409 | 0.0390 | -0.0621 | -0.0589 | -0.00000653 | -0.00000635 |
431 | 0.0029 | 0.0027 | 0.0099 | 0.0094 | 0.0096 | 0.0091 | 0.0406 | 0.0388 | -0.0618 | -0.0586 | -0.00000650 | -0.00000632 |
432 | 0.0028 | 0.0027 | 0.0098 | 0.0094 | 0.0096 | 0.0091 | 0.0404 | 0.0386 | -0.0614 | -0.0583 | -0.00000646 | -0.00000629 |
433 | 0.0028 | 0.0027 | 0.0098 | 0.0093 | 0.0095 | 0.0090 | 0.0402 | 0.0383 | -0.0611 | -0.0579 | -0.00000643 | -0.00000626 |
434 | 0.0028 | 0.0027 | 0.0097 | 0.0093 | 0.0094 | 0.0090 | 0.0400 | 0.0381 | -0.0608 | -0.0576 | -0.00000639 | -0.00000622 |
435 | 0.0028 | 0.0027 | 0.0097 | 0.0092 | 0.0094 | 0.0089 | 0.0398 | 0.0379 | -0.0604 | -0.0573 | -0.00000636 | -0.00000617 |
436 | 0.0028 | 0.0027 | 0.0096 | 0.0092 | 0.0093 | 0.0089 | 0.0396 | 0.0377 | -0.0601 | -0.0570 | -0.00000632 | -0.00000613 |
437 | 0.0028 | 0.0027 | 0.0096 | 0.0091 | 0.0093 | 0.0088 | 0.0393 | 0.0375 | -0.0598 | -0.0567 | -0.00000629 | -0.00000612 |
438 | 0.0028 | 0.0026 | 0.0095 | 0.0091 | 0.0092 | 0.0088 | 0.0391 | 0.0373 | -0.0595 | -0.0564 | -0.00000626 | -0.00000609 |
439 | 0.0027 | 0.0026 | 0.0095 | 0.0090 | 0.0092 | 0.0088 | 0.0389 | 0.0371 | -0.0591 | -0.0560 | -0.00000622 | -0.00000606 |
440 | 0.0027 | 0.0026 | 0.0094 | 0.0090 | 0.0091 | 0.0087 | 0.0387 | 0.0369 | -0.0588 | -0.0557 | -0.00000619 | -0.00000599 |
441 | 0.0027 | 0.0026 | 0.0094 | 0.0089 | 0.0091 | 0.0087 | 0.0385 | 0.0367 | -0.0585 | -0.0554 | -0.00000616 | -0.00000599 |
442 | 0.0027 | 0.0026 | 0.0093 | 0.0089 | 0.0090 | 0.0086 | 0.0383 | 0.0365 | -0.0582 | -0.0551 | -0.00000612 | -0.00000594 |
443 | 0.0027 | 0.0026 | 0.0093 | 0.0088 | 0.0090 | 0.0086 | 0.0381 | 0.0363 | -0.0579 | -0.0548 | -0.00000609 | -0.00000593 |
444 | 0.0027 | 0.0026 | 0.0092 | 0.0088 | 0.0090 | 0.0085 | 0.0379 | 0.0361 | -0.0576 | -0.0545 | -0.00000606 | -0.00000587 |
445 | 0.0027 | 0.0025 | 0.0092 | 0.0087 | 0.0089 | 0.0085 | 0.0377 | 0.0359 | -0.0573 | -0.0542 | -0.00000602 | -0.00000586 |
446 | 0.0026 | 0.0025 | 0.0091 | 0.0087 | 0.0089 | 0.0084 | 0.0375 | 0.0357 | -0.0569 | -0.0539 | -0.00000599 | -0.00000582 |
447 | 0.0026 | 0.0025 | 0.0091 | 0.0086 | 0.0088 | 0.0084 | 0.0373 | 0.0355 | -0.0566 | -0.0536 | -0.00000596 | -0.00000578 |
448 | 0.0026 | 0.0025 | 0.0090 | 0.0086 | 0.0088 | 0.0083 | 0.0371 | 0.0353 | -0.0563 | -0.0533 | -0.00000593 | -0.00000575 |
449 | 0.0026 | 0.0025 | 0.0090 | 0.0085 | 0.0087 | 0.0083 | 0.0369 | 0.0351 | -0.0560 | -0.0530 | -0.00000590 | -0.00000573 |
450 | 0.0026 | 0.0025 | 0.0089 | 0.0085 | 0.0087 | 0.0082 | 0.0367 | 0.0349 | -0.0557 | -0.0527 | -0.00000586 | -0.00000569 |
451 | 0.0026 | 0.0025 | 0.0089 | 0.0084 | 0.0086 | 0.0082 | 0.0365 | 0.0347 | -0.0554 | -0.0524 | -0.00000583 | -0.00000565 |
452 | 0.0026 | 0.0024 | 0.0088 | 0.0084 | 0.0086 | 0.0081 | 0.0363 | 0.0345 | -0.0551 | -0.0521 | -0.00000580 | -0.00000561 |
453 | 0.0025 | 0.0024 | 0.0088 | 0.0083 | 0.0085 | 0.0081 | 0.0361 | 0.0343 | -0.0548 | -0.0518 | -0.00000577 | -0.00000560 |
454 | 0.0025 | 0.0024 | 0.0087 | 0.0083 | 0.0085 | 0.0081 | 0.0359 | 0.0341 | -0.0545 | -0.0515 | -0.00000574 | -0.00000558 |
455 | 0.0025 | 0.0024 | 0.0087 | 0.0082 | 0.0084 | 0.0080 | 0.0357 | 0.0339 | -0.0542 | -0.0513 | -0.00000571 | -0.00000555 |
456 | 0.0025 | 0.0024 | 0.0086 | 0.0082 | 0.0084 | 0.0080 | 0.0355 | 0.0337 | -0.0539 | -0.0510 | -0.00000568 | -0.00000553 |
457 | 0.0025 | 0.0024 | 0.0086 | 0.0082 | 0.0083 | 0.0079 | 0.0353 | 0.0336 | -0.0536 | -0.0507 | -0.00000565 | -0.00000545 |
458 | 0.0025 | 0.0024 | 0.0085 | 0.0081 | 0.0083 | 0.0079 | 0.0351 | 0.0334 | -0.0534 | -0.0504 | -0.00000562 | -0.00000544 |
459 | 0.0025 | 0.0024 | 0.0085 | 0.0081 | 0.0083 | 0.0078 | 0.0349 | 0.0332 | -0.0531 | -0.0501 | -0.00000559 | -0.00000539 |
460 | 0.0024 | 0.0023 | 0.0084 | 0.0080 | 0.0082 | 0.0078 | 0.0347 | 0.0330 | -0.0528 | -0.0498 | -0.00000556 | -0.00000539 |
461 | 0.0024 | 0.0023 | 0.0084 | 0.0080 | 0.0082 | 0.0077 | 0.0345 | 0.0328 | -0.0525 | -0.0496 | -0.00000553 | -0.00000535 |
462 | 0.0024 | 0.0023 | 0.0084 | 0.0079 | 0.0081 | 0.0077 | 0.0344 | 0.0326 | -0.0522 | -0.0493 | -0.00000550 | -0.00000536 |
463 | 0.0024 | 0.0023 | 0.0083 | 0.0079 | 0.0081 | 0.0077 | 0.0342 | 0.0325 | -0.0519 | -0.0490 | -0.00000547 | -0.00000531 |
464 | 0.0024 | 0.0023 | 0.0083 | 0.0078 | 0.0080 | 0.0076 | 0.0340 | 0.0323 | -0.0517 | -0.0487 | -0.00000544 | -0.00000526 |
465 | 0.0024 | 0.0023 | 0.0082 | 0.0078 | 0.0080 | 0.0076 | 0.0338 | 0.0321 | -0.0514 | -0.0485 | -0.00000541 | -0.00000525 |
466 | 0.0024 | 0.0023 | 0.0082 | 0.0078 | 0.0079 | 0.0075 | 0.0336 | 0.0319 | -0.0511 | -0.0482 | -0.00000538 | -0.00000520 |
467 | 0.0024 | 0.0022 | 0.0081 | 0.0077 | 0.0079 | 0.0075 | 0.0334 | 0.0317 | -0.0508 | -0.0479 | -0.00000535 | -0.00000518 |
468 | 0.0023 | 0.0022 | 0.0081 | 0.0077 | 0.0079 | 0.0074 | 0.0333 | 0.0316 | -0.0505 | -0.0477 | -0.00000532 | -0.00000516 |
469 | 0.0023 | 0.0022 | 0.0080 | 0.0076 | 0.0078 | 0.0074 | 0.0331 | 0.0314 | -0.0503 | -0.0474 | -0.00000529 | -0.00000512 |
470 | 0.0023 | 0.0022 | 0.0080 | 0.0076 | 0.0078 | 0.0074 | 0.0329 | 0.0312 | -0.0500 | -0.0471 | -0.00000526 | -0.00000510 |
471 | 0.0023 | 0.0022 | 0.0080 | 0.0075 | 0.0077 | 0.0073 | 0.0327 | 0.0310 | -0.0497 | -0.0469 | -0.00000524 | -0.00000507 |
472 | 0.0023 | 0.0022 | 0.0079 | 0.0075 | 0.0077 | 0.0073 | 0.0325 | 0.0309 | -0.0495 | -0.0466 | -0.00000521 | -0.00000503 |
473 | 0.0023 | 0.0022 | 0.0079 | 0.0075 | 0.0077 | 0.0072 | 0.0324 | 0.0307 | -0.0492 | -0.0464 | -0.00000518 | -0.00000501 |
474 | 0.0023 | 0.0022 | 0.0078 | 0.0074 | 0.0076 | 0.0072 | 0.0322 | 0.0305 | -0.0489 | -0.0461 | -0.00000515 | -0.00000499 |
475 | 0.0023 | 0.0022 | 0.0078 | 0.0074 | 0.0076 | 0.0072 | 0.0320 | 0.0304 | -0.0487 | -0.0458 | -0.00000512 | -0.00000495 |
476 | 0.0022 | 0.0021 | 0.0077 | 0.0073 | 0.0075 | 0.0071 | 0.0319 | 0.0302 | -0.0484 | -0.0456 | -0.00000510 | -0.00000491 |
477 | 0.0022 | 0.0021 | 0.0077 | 0.0073 | 0.0075 | 0.0071 | 0.0317 | 0.0300 | -0.0481 | -0.0453 | -0.00000507 | -0.00000490 |
478 | 0.0022 | 0.0021 | 0.0077 | 0.0073 | 0.0074 | 0.0070 | 0.0315 | 0.0298 | -0.0479 | -0.0451 | -0.00000504 | -0.00000487 |
479 | 0.0022 | 0.0021 | 0.0076 | 0.0072 | 0.0074 | 0.0070 | 0.0313 | 0.0297 | -0.0476 | -0.0448 | -0.00000502 | -0.00000485 |
480 | 0.0022 | 0.0021 | 0.0076 | 0.0072 | 0.0074 | 0.0070 | 0.0312 | 0.0295 | -0.0474 | -0.0446 | -0.00000499 | -0.00000480 |
481 | 0.0022 | 0.0021 | 0.0075 | 0.0071 | 0.0073 | 0.0069 | 0.0310 | 0.0294 | -0.0471 | -0.0443 | -0.00000496 | -0.00000482 |
482 | 0.0022 | 0.0021 | 0.0075 | 0.0071 | 0.0073 | 0.0069 | 0.0308 | 0.0292 | -0.0469 | -0.0441 | -0.00000493 | -0.00000479 |
483 | 0.0022 | 0.0021 | 0.0075 | 0.0071 | 0.0072 | 0.0068 | 0.0307 | 0.0290 | -0.0466 | -0.0438 | -0.00000491 | -0.00000473 |
484 | 0.0021 | 0.0020 | 0.0074 | 0.0070 | 0.0072 | 0.0068 | 0.0305 | 0.0289 | -0.0464 | -0.0436 | -0.00000488 | -0.00000470 |
485 | 0.0021 | 0.0020 | 0.0074 | 0.0070 | 0.0072 | 0.0068 | 0.0303 | 0.0287 | -0.0461 | -0.0433 | -0.00000486 | -0.00000469 |
486 | 0.0021 | 0.0020 | 0.0073 | 0.0069 | 0.0071 | 0.0067 | 0.0302 | 0.0285 | -0.0459 | -0.0431 | -0.00000483 | -0.00000468 |
487 | 0.0021 | 0.0020 | 0.0073 | 0.0069 | 0.0071 | 0.0067 | 0.0300 | 0.0284 | -0.0456 | -0.0429 | -0.00000480 | -0.00000464 |
488 | 0.0021 | 0.0020 | 0.0073 | 0.0069 | 0.0071 | 0.0067 | 0.0298 | 0.0282 | -0.0454 | -0.0426 | -0.00000478 | -0.00000461 |
489 | 0.0021 | 0.0020 | 0.0072 | 0.0068 | 0.0070 | 0.0066 | 0.0297 | 0.0281 | -0.0451 | -0.0424 | -0.00000475 | -0.00000458 |
490 | 0.0021 | 0.0020 | 0.0072 | 0.0068 | 0.0070 | 0.0066 | 0.0295 | 0.0279 | -0.0449 | -0.0421 | -0.00000473 | -0.00000456 |
491 | 0.0021 | 0.0020 | 0.0071 | 0.0067 | 0.0069 | 0.0065 | 0.0294 | 0.0278 | -0.0446 | -0.0419 | -0.00000470 | -0.00000453 |
492 | 0.0021 | 0.0020 | 0.0071 | 0.0067 | 0.0069 | 0.0065 | 0.0292 | 0.0276 | -0.0444 | -0.0417 | -0.00000468 | -0.00000451 |
493 | 0.0020 | 0.0019 | 0.0071 | 0.0067 | 0.0069 | 0.0065 | 0.0290 | 0.0275 | -0.0441 | -0.0414 | -0.00000465 | -0.00000448 |
494 | 0.0020 | 0.0019 | 0.0070 | 0.0066 | 0.0068 | 0.0064 | 0.0289 | 0.0273 | -0.0439 | -0.0412 | -0.00000462 | -0.00000445 |
495 | 0.0020 | 0.0019 | 0.0070 | 0.0066 | 0.0068 | 0.0064 | 0.0287 | 0.0271 | -0.0437 | -0.0410 | -0.00000460 | -0.00000443 |
496 | 0.0020 | 0.0019 | 0.0069 | 0.0066 | 0.0068 | 0.0064 | 0.0286 | 0.0270 | -0.0434 | -0.0408 | -0.00000458 | -0.00000440 |
497 | 0.0020 | 0.0019 | 0.0069 | 0.0065 | 0.0067 | 0.0063 | 0.0284 | 0.0268 | -0.0432 | -0.0405 | -0.00000455 | -0.00000437 |
498 | 0.0020 | 0.0019 | 0.0069 | 0.0065 | 0.0067 | 0.0063 | 0.0283 | 0.0267 | -0.0430 | -0.0403 | -0.00000453 | -0.00000437 |
499 | 0.0020 | 0.0019 | 0.0068 | 0.0065 | 0.0066 | 0.0063 | 0.0281 | 0.0265 | -0.0427 | -0.0401 | -0.00000450 | -0.00000436 |
Figure 5: Linear vs Nonlinear Impulse Responses: Path 3
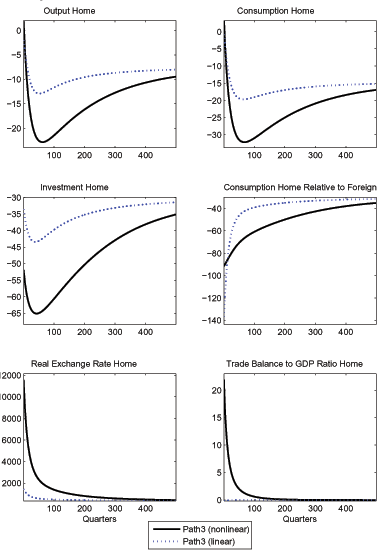
Data for Figure 5
Quarters | Output Home: Path 3 (linear) | Output Home: Path 3 (nonlinear) | Consumption Home Path 3 (linear) | Consumption Home: Path 3 (nonlinear) | Investment Home: Path 3 (linear) | Investment Home: Path 3 (nonlinear) | Consumption Home Relative to Foreign: Path 3 (linear) | Consumption Home Relative to Foreign: Path 3 (nonlinear) | Real Exchange Rate Home: Path 3 (linear) | Real Exchange Rate Home: Path 3 (nonlinear) | Trade Balance to GDP Ratio Home: Path 3 (linear) | Trade Balance to GDP Ratio Home: Path 3 (nonlinear) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 | -1.98 | 1.94 | -0.85 | 3.07 | -33.62 | -51.88 | -136.72 | -91.61 | 1432.77 | 11562.23 | -0.145 | 21.899 |
2 | -2.54 | 0.40 | -1.23 | 1.56 | -34.33 | -52.90 | -129.74 | -91.06 | 1378.95 | 10847.56 | -0.140 | 19.860 |
3 | -3.09 | -1.03 | -2.26 | -0.54 | -35.00 | -53.84 | -124.10 | -90.59 | 1328.40 | 10199.91 | -0.129 | 18.347 |
4 | -3.62 | -2.37 | -3.24 | -2.50 | -35.63 | -54.71 | -118.83 | -90.11 | 1280.94 | 9611.59 | -0.119 | 16.987 |
5 | -4.13 | -3.63 | -4.18 | -4.34 | -36.23 | -55.52 | -113.93 | -89.62 | 1236.42 | 9075.91 | -0.110 | 15.763 |
6 | -4.64 | -4.82 | -5.08 | -6.06 | -36.79 | -56.28 | -109.35 | -89.14 | 1194.67 | 8587.08 | -0.101 | 14.658 |
7 | -5.13 | -5.94 | -5.94 | -7.68 | -37.33 | -56.98 | -105.08 | -88.65 | 1155.52 | 8140.01 | -0.093 | 13.658 |
8 | -5.60 | -6.99 | -6.76 | -9.19 | -37.83 | -57.63 | -101.10 | -88.15 | 1118.82 | 7730.30 | -0.086 | 12.752 |
9 | -6.05 | -7.99 | -7.54 | -10.61 | -38.30 | -58.24 | -97.39 | -87.66 | 1084.41 | 7354.06 | -0.079 | 11.927 |
10 | -6.49 | -8.92 | -8.28 | -11.95 | -38.75 | -58.81 | -93.93 | -87.16 | 1052.15 | 7007.88 | -0.072 | 11.177 |
11 | -6.91 | -9.80 | -8.98 | -13.20 | -39.16 | -59.33 | -90.71 | -86.67 | 1021.90 | 6688.75 | -0.066 | 10.491 |
12 | -7.32 | -10.63 | -9.65 | -14.38 | -39.55 | -59.82 | -87.70 | -86.17 | 993.53 | 6394.03 | -0.060 | 9.864 |
13 | -7.70 | -11.41 | -10.28 | -15.49 | -39.92 | -60.28 | -84.90 | -85.68 | 966.91 | 6121.37 | -0.055 | 9.290 |
14 | -8.07 | -12.15 | -10.88 | -16.53 | -40.26 | -60.70 | -82.28 | -85.19 | 941.94 | 5868.68 | -0.050 | 8.762 |
15 | -8.42 | -12.84 | -11.45 | -17.51 | -40.57 | -61.10 | -79.83 | -84.70 | 918.50 | 5634.12 | -0.045 | 8.276 |
16 | -8.75 | -13.50 | -11.99 | -18.44 | -40.87 | -61.47 | -77.55 | -84.21 | 896.48 | 5416.04 | -0.041 | 7.829 |
17 | -9.06 | -14.12 | -12.50 | -19.31 | -41.14 | -61.81 | -75.42 | -83.73 | 875.80 | 5212.95 | -0.037 | 7.416 |
18 | -9.36 | -14.70 | -12.98 | -20.13 | -41.40 | -62.12 | -73.42 | -83.24 | 856.36 | 5023.55 | -0.033 | 7.033 |
19 | -9.64 | -15.25 | -13.44 | -20.90 | -41.63 | -62.42 | -71.56 | -82.77 | 838.08 | 4846.66 | -0.029 | 6.679 |
20 | -9.91 | -15.76 | -13.87 | -21.63 | -41.84 | -62.69 | -69.81 | -82.30 | 820.89 | 4681.21 | -0.026 | 6.351 |
21 | -10.16 | -16.25 | -14.27 | -22.32 | -42.04 | -62.94 | -68.18 | -81.83 | 804.70 | 4526.25 | -0.023 | 6.045 |
22 | -10.39 | -16.71 | -14.65 | -22.96 | -42.22 | -63.17 | -66.65 | -81.37 | 789.46 | 4380.92 | -0.020 | 5.761 |
23 | -10.61 | -17.14 | -15.01 | -23.57 | -42.39 | -63.39 | -65.21 | -80.91 | 775.10 | 4244.45 | -0.018 | 5.496 |
24 | -10.82 | -17.55 | -15.35 | -24.15 | -42.54 | -63.58 | -63.86 | -80.46 | 761.55 | 4116.14 | -0.015 | 5.248 |
25 | -11.01 | -17.94 | -15.67 | -24.69 | -42.67 | -63.76 | -62.60 | -80.01 | 748.78 | 3995.34 | -0.013 | 5.017 |
26 | -11.19 | -18.30 | -15.97 | -25.20 | -42.79 | -63.93 | -61.41 | -79.57 | 736.72 | 3881.48 | -0.011 | 4.800 |
27 | -11.36 | -18.64 | -16.25 | -25.68 | -42.90 | -64.08 | -60.30 | -79.14 | 725.33 | 3774.04 | -0.009 | 4.597 |
28 | -11.51 | -18.96 | -16.52 | -26.13 | -43.00 | -64.22 | -59.25 | -78.71 | 714.57 | 3672.54 | -0.007 | 4.407 |
29 | -11.66 | -19.26 | -16.76 | -26.56 | -43.09 | -64.35 | -58.26 | -78.29 | 704.38 | 3576.55 | -0.005 | 4.228 |
30 | -11.79 | -19.54 | -17.00 | -26.96 | -43.16 | -64.46 | -57.33 | -77.87 | 694.75 | 3485.67 | -0.003 | 4.059 |
31 | -11.92 | -19.81 | -17.21 | -27.34 | -43.23 | -64.57 | -56.45 | -77.46 | 685.63 | 3399.53 | -0.002 | 3.900 |
32 | -12.03 | -20.06 | -17.42 | -27.70 | -43.28 | -64.66 | -55.63 | -77.06 | 676.98 | 3317.81 | 0.000 | 3.751 |
33 | -12.14 | -20.29 | -17.61 | -28.03 | -43.33 | -64.74 | -54.85 | -76.66 | 668.79 | 3240.20 | 0.001 | 3.609 |
34 | -12.23 | -20.51 | -17.78 | -28.35 | -43.36 | -64.81 | -54.11 | -76.27 | 661.01 | 3166.43 | 0.002 | 3.476 |
35 | -12.32 | -20.72 | -17.95 | -28.65 | -43.39 | -64.87 | -53.41 | -75.89 | 653.63 | 3096.23 | 0.003 | 3.349 |
36 | -12.40 | -20.91 | -18.11 | -28.92 | -43.42 | -64.93 | -52.76 | -75.51 | 646.61 | 3029.37 | 0.004 | 3.229 |
37 | -12.47 | -21.09 | -18.25 | -29.19 | -43.43 | -64.97 | -52.13 | -75.14 | 639.94 | 2965.63 | 0.005 | 3.116 |
38 | -12.54 | -21.26 | -18.38 | -29.43 | -43.44 | -65.01 | -51.55 | -74.78 | 633.59 | 2904.82 | 0.006 | 3.008 |
39 | -12.60 | -21.41 | -18.51 | -29.66 | -43.44 | -65.04 | -50.99 | -74.42 | 627.55 | 2846.74 | 0.007 | 2.906 |
40 | -12.65 | -21.56 | -18.62 | -29.88 | -43.44 | -65.07 | -50.46 | -74.07 | 621.79 | 2791.23 | 0.008 | 2.808 |
41 | -12.70 | -21.69 | -18.73 | -30.08 | -43.43 | -65.08 | -49.96 | -73.73 | 616.30 | 2738.14 | 0.008 | 2.716 |
42 | -12.74 | -21.82 | -18.83 | -30.27 | -43.42 | -65.09 | -49.48 | -73.39 | 611.06 | 2687.30 | 0.009 | 2.627 |
43 | -12.78 | -21.93 | -18.92 | -30.44 | -43.40 | -65.10 | -49.03 | -73.05 | 606.06 | 2638.60 | 0.010 | 2.543 |
44 | -12.81 | -22.04 | -19.00 | -30.61 | -43.37 | -65.09 | -48.59 | -72.73 | 601.28 | 2591.89 | 0.010 | 2.463 |
45 | -12.84 | -22.14 | -19.08 | -30.76 | -43.35 | -65.09 | -48.18 | -72.41 | 596.71 | 2547.08 | 0.011 | 2.386 |
46 | -12.86 | -22.23 | -19.15 | -30.90 | -43.31 | -65.08 | -47.79 | -72.09 | 592.33 | 2504.04 | 0.011 | 2.313 |
47 | -12.88 | -22.31 | -19.22 | -31.04 | -43.28 | -65.06 | -47.42 | -71.78 | 588.14 | 2462.67 | 0.012 | 2.243 |
48 | -12.89 | -22.39 | -19.28 | -31.16 | -43.24 | -65.04 | -47.07 | -71.48 | 584.13 | 2422.89 | 0.012 | 2.176 |
49 | -12.90 | -22.46 | -19.33 | -31.27 | -43.20 | -65.01 | -46.73 | -71.18 | 580.28 | 2384.61 | 0.012 | 2.111 |
50 | -12.91 | -22.52 | -19.38 | -31.38 | -43.15 | -64.98 | -46.41 | -70.89 | 576.58 | 2347.73 | 0.013 | 2.050 |
51 | -12.91 | -22.57 | -19.43 | -31.47 | -43.11 | -64.94 | -46.10 | -70.60 | 573.03 | 2312.20 | 0.013 | 1.991 |
52 | -12.92 | -22.62 | -19.47 | -31.56 | -43.06 | -64.90 | -45.80 | -70.32 | 569.62 | 2277.93 | 0.013 | 1.934 |
53 | -12.91 | -22.67 | -19.50 | -31.64 | -43.00 | -64.86 | -45.52 | -70.05 | 566.34 | 2244.86 | 0.014 | 1.880 |
54 | -12.91 | -22.71 | -19.53 | -31.71 | -42.95 | -64.81 | -45.25 | -69.77 | 563.19 | 2212.92 | 0.014 | 1.827 |
55 | -12.90 | -22.74 | -19.56 | -31.78 | -42.89 | -64.76 | -44.99 | -69.51 | 560.15 | 2182.07 | 0.014 | 1.777 |
56 | -12.89 | -22.77 | -19.59 | -31.84 | -42.84 | -64.71 | -44.74 | -69.24 | 557.22 | 2152.23 | 0.014 | 1.728 |
57 | -12.88 | -22.79 | -19.61 | -31.89 | -42.78 | -64.65 | -44.50 | -68.99 | 554.39 | 2123.37 | 0.014 | 1.682 |
58 | -12.87 | -22.81 | -19.62 | -31.94 | -42.71 | -64.59 | -44.27 | -68.73 | 551.66 | 2095.44 | 0.015 | 1.637 |
59 | -12.86 | -22.83 | -19.64 | -31.98 | -42.65 | -64.53 | -44.05 | -68.48 | 549.03 | 2068.38 | 0.015 | 1.594 |
60 | -12.84 | -22.84 | -19.65 | -32.02 | -42.59 | -64.47 | -43.84 | -68.24 | 546.48 | 2042.16 | 0.015 | 1.552 |
61 | -12.82 | -22.85 | -19.66 | -32.05 | -42.52 | -64.40 | -43.64 | -68.00 | 544.02 | 2016.74 | 0.015 | 1.512 |
62 | -12.80 | -22.85 | -19.67 | -32.07 | -42.46 | -64.33 | -43.44 | -67.76 | 541.64 | 1992.07 | 0.015 | 1.473 |
63 | -12.78 | -22.85 | -19.67 | -32.10 | -42.39 | -64.26 | -43.25 | -67.53 | 539.33 | 1968.13 | 0.015 | 1.436 |
64 | -12.76 | -22.85 | -19.68 | -32.11 | -42.32 | -64.18 | -43.07 | -67.30 | 537.09 | 1944.88 | 0.015 | 1.399 |
65 | -12.74 | -22.84 | -19.68 | -32.13 | -42.25 | -64.11 | -42.90 | -67.08 | 534.92 | 1922.29 | 0.015 | 1.364 |
66 | -12.71 | -22.83 | -19.67 | -32.13 | -42.18 | -64.03 | -42.73 | -66.86 | 532.82 | 1900.33 | 0.015 | 1.331 |
67 | -12.69 | -22.82 | -19.67 | -32.14 | -42.11 | -63.95 | -42.56 | -66.64 | 530.78 | 1878.97 | 0.015 | 1.298 |
68 | -12.66 | -22.80 | -19.67 | -32.14 | -42.04 | -63.86 | -42.41 | -66.42 | 528.80 | 1858.19 | 0.015 | 1.266 |
69 | -12.64 | -22.79 | -19.66 | -32.14 | -41.97 | -63.78 | -42.25 | -66.21 | 526.87 | 1837.95 | 0.015 | 1.236 |
70 | -12.61 | -22.77 | -19.65 | -32.13 | -41.90 | -63.69 | -42.10 | -66.01 | 524.99 | 1818.24 | 0.015 | 1.206 |
71 | -12.58 | -22.74 | -19.64 | -32.12 | -41.83 | -63.61 | -41.96 | -65.80 | 523.17 | 1799.04 | 0.015 | 1.177 |
72 | -12.55 | -22.72 | -19.63 | -32.11 | -41.75 | -63.52 | -41.82 | -65.60 | 521.39 | 1780.32 | 0.015 | 1.149 |
73 | -12.52 | -22.69 | -19.62 | -32.09 | -41.68 | -63.43 | -41.69 | -65.40 | 519.66 | 1762.07 | 0.015 | 1.122 |
74 | -12.49 | -22.66 | -19.61 | -32.08 | -41.61 | -63.34 | -41.56 | -65.20 | 517.98 | 1744.26 | 0.015 | 1.096 |
75 | -12.46 | -22.63 | -19.59 | -32.06 | -41.54 | -63.24 | -41.43 | -65.01 | 516.33 | 1726.87 | 0.015 | 1.071 |
76 | -12.43 | -22.60 | -19.58 | -32.03 | -41.46 | -63.15 | -41.31 | -64.82 | 514.73 | 1709.90 | 0.015 | 1.046 |
77 | -12.40 | -22.57 | -19.56 | -32.01 | -41.39 | -63.05 | -41.19 | -64.63 | 513.16 | 1693.32 | 0.015 | 1.022 |
78 | -12.37 | -22.53 | -19.55 | -31.98 | -41.32 | -62.96 | -41.07 | -64.45 | 511.63 | 1677.12 | 0.015 | 0.999 |
79 | -12.34 | -22.50 | -19.53 | -31.95 | -41.25 | -62.86 | -40.96 | -64.27 | 510.13 | 1661.28 | 0.015 | 0.976 |
80 | -12.31 | -22.46 | -19.51 | -31.92 | -41.17 | -62.76 | -40.84 | -64.09 | 508.67 | 1645.79 | 0.015 | 0.955 |
81 | -12.28 | -22.42 | -19.49 | -31.88 | -41.10 | -62.66 | -40.74 | -63.91 | 507.24 | 1630.64 | 0.015 | 0.933 |
82 | -12.24 | -22.38 | -19.47 | -31.85 | -41.03 | -62.56 | -40.63 | -63.73 | 505.84 | 1615.82 | 0.015 | 0.913 |
83 | -12.21 | -22.33 | -19.45 | -31.81 | -40.96 | -62.46 | -40.53 | -63.56 | 504.47 | 1601.30 | 0.015 | 0.892 |
84 | -12.18 | -22.29 | -19.43 | -31.77 | -40.89 | -62.36 | -40.43 | -63.39 | 503.13 | 1587.09 | 0.014 | 0.873 |
85 | -12.15 | -22.25 | -19.41 | -31.73 | -40.81 | -62.26 | -40.33 | -63.22 | 501.82 | 1573.17 | 0.014 | 0.854 |
86 | -12.12 | -22.20 | -19.39 | -31.69 | -40.74 | -62.15 | -40.24 | -63.05 | 500.53 | 1559.54 | 0.014 | 0.835 |
87 | -12.08 | -22.15 | -19.36 | -31.64 | -40.67 | -62.05 | -40.14 | -62.88 | 499.27 | 1546.17 | 0.014 | 0.817 |
88 | -12.05 | -22.11 | -19.34 | -31.60 | -40.60 | -61.95 | -40.05 | -62.72 | 498.03 | 1533.06 | 0.014 | 0.800 |
89 | -12.02 | -22.06 | -19.32 | -31.55 | -40.53 | -61.84 | -39.96 | -62.56 | 496.81 | 1520.21 | 0.014 | 0.783 |
90 | -11.99 | -22.01 | -19.30 | -31.51 | -40.46 | -61.73 | -39.88 | -62.40 | 495.62 | 1507.60 | 0.014 | 0.766 |
91 | -11.95 | -21.96 | -19.27 | -31.46 | -40.39 | -61.63 | -39.79 | -62.24 | 494.45 | 1495.23 | 0.014 | 0.750 |
92 | -11.92 | -21.91 | -19.25 | -31.41 | -40.32 | -61.52 | -39.71 | -62.08 | 493.30 | 1483.09 | 0.014 | 0.734 |
93 | -11.89 | -21.86 | -19.22 | -31.36 | -40.25 | -61.42 | -39.63 | -61.93 | 492.16 | 1471.17 | 0.014 | 0.719 |
94 | -11.86 | -21.81 | -19.20 | -31.30 | -40.18 | -61.31 | -39.55 | -61.77 | 491.05 | 1459.47 | 0.014 | 0.704 |
95 | -11.83 | -21.75 | -19.17 | -31.25 | -40.11 | -61.20 | -39.47 | -61.62 | 489.96 | 1447.97 | 0.014 | 0.689 |
96 | -11.79 | -21.70 | -19.15 | -31.20 | -40.05 | -61.09 | -39.39 | -61.47 | 488.88 | 1436.67 | 0.013 | 0.675 |
97 | -11.76 | -21.65 | -19.12 | -31.14 | -39.98 | -60.98 | -39.32 | -61.32 | 487.83 | 1425.57 | 0.013 | 0.661 |
98 | -11.73 | -21.59 | -19.10 | -31.09 | -39.91 | -60.87 | -39.24 | -61.17 | 486.78 | 1414.66 | 0.013 | 0.647 |
99 | -11.70 | -21.54 | -19.07 | -31.03 | -39.85 | -60.77 | -39.17 | -61.03 | 485.76 | 1403.93 | 0.013 | 0.634 |
100 | -11.67 | -21.48 | -19.05 | -30.97 | -39.78 | -60.66 | -39.10 | -60.88 | 484.75 | 1393.39 | 0.013 | 0.621 |
101 | -11.64 | -21.43 | -19.02 | -30.92 | -39.71 | -60.55 | -39.03 | -60.74 | 483.76 | 1383.01 | 0.013 | 0.609 |
102 | -11.61 | -21.37 | -19.00 | -30.86 | -39.65 | -60.44 | -38.96 | -60.60 | 482.78 | 1372.81 | 0.013 | 0.597 |
103 | -11.57 | -21.32 | -18.97 | -30.80 | -39.58 | -60.33 | -38.89 | -60.45 | 481.81 | 1362.76 | 0.013 | 0.585 |
104 | -11.54 | -21.26 | -18.95 | -30.74 | -39.52 | -60.22 | -38.82 | -60.31 | 480.86 | 1352.88 | 0.013 | 0.573 |
105 | -11.51 | -21.20 | -18.92 | -30.68 | -39.45 | -60.11 | -38.76 | -60.17 | 479.92 | 1343.16 | 0.013 | 0.561 |
106 | -11.48 | -21.15 | -18.90 | -30.62 | -39.39 | -60.00 | -38.69 | -60.04 | 479.00 | 1333.58 | 0.012 | 0.550 |
107 | -11.45 | -21.09 | -18.87 | -30.56 | -39.33 | -59.88 | -38.63 | -59.90 | 478.09 | 1324.15 | 0.012 | 0.539 |
108 | -11.42 | -21.03 | -18.84 | -30.50 | -39.27 | -59.77 | -38.57 | -59.76 | 477.19 | 1314.86 | 0.012 | 0.529 |
109 | -11.39 | -20.97 | -18.82 | -30.44 | -39.20 | -59.66 | -38.50 | -59.63 | 476.30 | 1305.72 | 0.012 | 0.518 |
110 | -11.36 | -20.92 | -18.79 | -30.38 | -39.14 | -59.55 | -38.44 | -59.50 | 475.42 | 1296.70 | 0.012 | 0.508 |
111 | -11.34 | -20.86 | -18.77 | -30.31 | -39.08 | -59.44 | -38.38 | -59.36 | 474.56 | 1287.83 | 0.012 | 0.498 |
112 | -11.31 | -20.80 | -18.74 | -30.25 | -39.02 | -59.33 | -38.32 | -59.23 | 473.71 | 1279.08 | 0.012 | 0.489 |
113 | -11.28 | -20.74 | -18.72 | -30.19 | -38.96 | -59.22 | -38.26 | -59.10 | 472.86 | 1270.45 | 0.012 | 0.479 |
114 | -11.25 | -20.69 | -18.69 | -30.13 | -38.90 | -59.11 | -38.21 | -58.97 | 472.03 | 1261.95 | 0.012 | 0.470 |
115 | -11.22 | -20.63 | -18.66 | -30.06 | -38.84 | -59.00 | -38.15 | -58.84 | 471.21 | 1253.57 | 0.012 | 0.461 |
116 | -11.19 | -20.57 | -18.64 | -30.00 | -38.78 | -58.89 | -38.09 | -58.71 | 470.40 | 1245.30 | 0.011 | 0.452 |
117 | -11.17 | -20.51 | -18.61 | -29.94 | -38.72 | -58.78 | -38.04 | -58.58 | 469.59 | 1237.15 | 0.011 | 0.444 |
118 | -11.14 | -20.45 | -18.59 | -29.87 | -38.66 | -58.67 | -37.98 | -58.46 | 468.80 | 1229.12 | 0.011 | 0.435 |
119 | -11.11 | -20.39 | -18.56 | -29.81 | -38.61 | -58.56 | -37.93 | -58.33 | 468.02 | 1221.19 | 0.011 | 0.427 |
120 | -11.08 | -20.34 | -18.54 | -29.74 | -38.55 | -58.45 | -37.88 | -58.21 | 467.24 | 1213.37 | 0.011 | 0.419 |
121 | -11.06 | -20.28 | -18.51 | -29.68 | -38.49 | -58.33 | -37.82 | -58.08 | 466.48 | 1205.65 | 0.011 | 0.411 |
122 | -11.03 | -20.22 | -18.49 | -29.62 | -38.44 | -58.22 | -37.77 | -57.96 | 465.72 | 1198.03 | 0.011 | 0.403 |
123 | -11.00 | -20.16 | -18.46 | -29.55 | -38.38 | -58.11 | -37.72 | -57.83 | 464.97 | 1190.52 | 0.011 | 0.396 |
124 | -10.98 | -20.10 | -18.44 | -29.49 | -38.33 | -58.00 | -37.67 | -57.71 | 464.23 | 1183.10 | 0.011 | 0.389 |
125 | -10.95 | -20.05 | -18.42 | -29.42 | -38.27 | -57.89 | -37.62 | -57.59 | 463.50 | 1175.78 | 0.011 | 0.381 |
126 | -10.93 | -19.99 | -18.39 | -29.36 | -38.22 | -57.78 | -37.57 | -57.47 | 462.78 | 1168.55 | 0.011 | 0.374 |
127 | -10.90 | -19.93 | -18.37 | -29.29 | -38.16 | -57.67 | -37.52 | -57.35 | 462.06 | 1161.41 | 0.010 | 0.367 |
128 | -10.88 | -19.87 | -18.34 | -29.23 | -38.11 | -57.56 | -37.47 | -57.23 | 461.35 | 1154.36 | 0.010 | 0.361 |
129 | -10.85 | -19.81 | -18.32 | -29.17 | -38.06 | -57.46 | -37.42 | -57.11 | 460.65 | 1147.40 | 0.010 | 0.354 |
130 | -10.83 | -19.76 | -18.29 | -29.10 | -38.00 | -57.35 | -37.38 | -56.99 | 459.96 | 1140.53 | 0.010 | 0.348 |
131 | -10.80 | -19.70 | -18.27 | -29.04 | -37.95 | -57.24 | -37.33 | -56.88 | 459.27 | 1133.74 | 0.010 | 0.341 |
132 | -10.78 | -19.64 | -18.25 | -28.97 | -37.90 | -57.13 | -37.28 | -56.76 | 458.59 | 1127.04 | 0.010 | 0.335 |
133 | -10.75 | -19.58 | -18.22 | -28.91 | -37.85 | -57.02 | -37.24 | -56.64 | 457.92 | 1120.41 | 0.010 | 0.329 |
134 | -10.73 | -19.53 | -18.20 | -28.84 | -37.80 | -56.91 | -37.19 | -56.53 | 457.25 | 1113.87 | 0.010 | 0.323 |
135 | -10.71 | -19.47 | -18.18 | -28.78 | -37.75 | -56.80 | -37.15 | -56.41 | 456.59 | 1107.41 | 0.010 | 0.317 |
136 | -10.68 | -19.41 | -18.15 | -28.72 | -37.70 | -56.69 | -37.10 | -56.30 | 455.94 | 1101.02 | 0.010 | 0.312 |
137 | -10.66 | -19.36 | -18.13 | -28.65 | -37.65 | -56.59 | -37.06 | -56.18 | 455.29 | 1094.70 | 0.010 | 0.306 |
138 | -10.64 | -19.30 | -18.11 | -28.59 | -37.60 | -56.48 | -37.01 | -56.07 | 454.65 | 1088.47 | 0.009 | 0.301 |
139 | -10.61 | -19.24 | -18.09 | -28.52 | -37.55 | -56.37 | -36.97 | -55.96 | 454.01 | 1082.30 | 0.009 | 0.295 |
140 | -10.59 | -19.19 | -18.06 | -28.46 | -37.50 | -56.26 | -36.93 | -55.84 | 453.39 | 1076.21 | 0.009 | 0.290 |
141 | -10.57 | -19.13 | -18.04 | -28.40 | -37.45 | -56.16 | -36.88 | -55.73 | 452.76 | 1070.18 | 0.009 | 0.285 |
142 | -10.55 | -19.08 | -18.02 | -28.33 | -37.41 | -56.05 | -36.84 | -55.62 | 452.15 | 1064.23 | 0.009 | 0.280 |
143 | -10.52 | -19.02 | -18.00 | -28.27 | -37.36 | -55.94 | -36.80 | -55.51 | 451.54 | 1058.34 | 0.009 | 0.275 |
144 | -10.50 | -18.96 | -17.98 | -28.21 | -37.31 | -55.84 | -36.76 | -55.40 | 450.93 | 1052.52 | 0.009 | 0.270 |
145 | -10.48 | -18.91 | -17.95 | -28.14 | -37.27 | -55.73 | -36.72 | -55.29 | 450.33 | 1046.76 | 0.009 | 0.265 |
146 | -10.46 | -18.85 | -17.93 | -28.08 | -37.22 | -55.63 | -36.68 | -55.18 | 449.74 | 1041.07 | 0.009 | 0.261 |
147 | -10.44 | -18.80 | -17.91 | -28.02 | -37.17 | -55.52 | -36.64 | -55.07 | 449.15 | 1035.45 | 0.009 | 0.256 |
148 | -10.42 | -18.74 | -17.89 | -27.96 | -37.13 | -55.41 | -36.60 | -54.96 | 448.57 | 1029.88 | 0.009 | 0.252 |
149 | -10.40 | -18.69 | -17.87 | -27.89 | -37.08 | -55.31 | -36.56 | -54.85 | 447.99 | 1024.38 | 0.009 | 0.247 |
150 | -10.38 | -18.63 | -17.85 | -27.83 | -37.04 | -55.20 | -36.52 | -54.75 | 447.42 | 1018.93 | 0.009 | 0.243 |
151 | -10.36 | -18.58 | -17.83 | -27.77 | -37.00 | -55.10 | -36.48 | -54.64 | 446.85 | 1013.55 | 0.008 | 0.239 |
152 | -10.33 | -18.53 | -17.81 | -27.71 | -36.95 | -55.00 | -36.44 | -54.53 | 446.29 | 1008.22 | 0.008 | 0.235 |
153 | -10.31 | -18.47 | -17.79 | -27.65 | -36.91 | -54.89 | -36.40 | -54.43 | 445.73 | 1002.96 | 0.008 | 0.231 |
154 | -10.30 | -18.42 | -17.77 | -27.58 | -36.87 | -54.79 | -36.37 | -54.32 | 445.18 | 997.75 | 0.008 | 0.227 |
155 | -10.28 | -18.36 | -17.74 | -27.52 | -36.82 | -54.68 | -36.33 | -54.22 | 444.63 | 992.59 | 0.008 | 0.223 |
156 | -10.26 | -18.31 | -17.72 | -27.46 | -36.78 | -54.58 | -36.29 | -54.11 | 444.09 | 987.49 | 0.008 | 0.219 |
157 | -10.24 | -18.26 | -17.70 | -27.40 | -36.74 | -54.48 | -36.25 | -54.01 | 443.55 | 982.44 | 0.008 | 0.216 |
158 | -10.22 | -18.21 | -17.69 | -27.34 | -36.70 | -54.38 | -36.22 | -53.90 | 443.02 | 977.45 | 0.008 | 0.212 |
159 | -10.20 | -18.15 | -17.67 | -27.28 | -36.66 | -54.27 | -36.18 | -53.80 | 442.49 | 972.51 | 0.008 | 0.209 |
160 | -10.18 | -18.10 | -17.65 | -27.22 | -36.61 | -54.17 | -36.15 | -53.70 | 441.96 | 967.62 | 0.008 | 0.205 |
161 | -10.16 | -18.05 | -17.63 | -27.16 | -36.57 | -54.07 | -36.11 | -53.59 | 441.44 | 962.78 | 0.008 | 0.202 |
162 | -10.14 | -18.00 | -17.61 | -27.10 | -36.53 | -53.97 | -36.07 | -53.49 | 440.93 | 957.99 | 0.008 | 0.198 |
163 | -10.12 | -17.94 | -17.59 | -27.04 | -36.49 | -53.87 | -36.04 | -53.39 | 440.41 | 953.25 | 0.008 | 0.195 |
164 | -10.11 | -17.89 | -17.57 | -26.98 | -36.45 | -53.77 | -36.01 | -53.29 | 439.91 | 948.56 | 0.008 | 0.192 |
165 | -10.09 | -17.84 | -17.55 | -26.92 | -36.42 | -53.67 | -35.97 | -53.19 | 439.40 | 943.92 | 0.007 | 0.189 |
166 | -10.07 | -17.79 | -17.53 | -26.86 | -36.38 | -53.57 | -35.94 | -53.08 | 438.91 | 939.33 | 0.007 | 0.186 |
167 | -10.05 | -17.74 | -17.51 | -26.80 | -36.34 | -53.47 | -35.90 | -52.98 | 438.41 | 934.78 | 0.007 | 0.183 |
168 | -10.04 | -17.69 | -17.49 | -26.74 | -36.30 | -53.37 | -35.87 | -52.88 | 437.92 | 930.28 | 0.007 | 0.180 |
169 | -10.02 | -17.64 | -17.48 | -26.68 | -36.26 | -53.27 | -35.84 | -52.78 | 437.43 | 925.82 | 0.007 | 0.177 |
170 | -10.00 | -17.59 | -17.46 | -26.63 | -36.22 | -53.17 | -35.80 | -52.69 | 436.95 | 921.41 | 0.007 | 0.174 |
171 | -9.99 | -17.54 | -17.44 | -26.57 | -36.19 | -53.07 | -35.77 | -52.59 | 436.47 | 917.04 | 0.007 | 0.171 |
172 | -9.97 | -17.49 | -17.42 | -26.51 | -36.15 | -52.97 | -35.74 | -52.49 | 436.00 | 912.72 | 0.007 | 0.168 |
173 | -9.95 | -17.44 | -17.40 | -26.45 | -36.11 | -52.87 | -35.70 | -52.39 | 435.53 | 908.43 | 0.007 | 0.165 |
174 | -9.94 | -17.39 | -17.39 | -26.39 | -36.08 | -52.77 | -35.67 | -52.29 | 435.06 | 904.20 | 0.007 | 0.163 |
175 | -9.92 | -17.34 | -17.37 | -26.34 | -36.04 | -52.68 | -35.64 | -52.20 | 434.60 | 900.00 | 0.007 | 0.160 |
176 | -9.90 | -17.29 | -17.35 | -26.28 | -36.00 | -52.58 | -35.61 | -52.10 | 434.14 | 895.84 | 0.007 | 0.158 |
177 | -9.89 | -17.24 | -17.34 | -26.22 | -35.97 | -52.48 | -35.58 | -52.00 | 433.68 | 891.73 | 0.007 | 0.155 |
178 | -9.87 | -17.19 | -17.32 | -26.17 | -35.93 | -52.39 | -35.55 | -51.91 | 433.23 | 887.65 | 0.007 | 0.153 |
179 | -9.86 | -17.14 | -17.30 | -26.11 | -35.90 | -52.29 | -35.52 | -51.81 | 432.78 | 883.62 | 0.007 | 0.150 |
180 | -9.84 | -17.10 | -17.28 | -26.06 | -35.86 | -52.19 | -35.49 | -51.72 | 432.33 | 879.62 | 0.007 | 0.148 |
181 | -9.82 | -17.05 | -17.27 | -26.00 | -35.83 | -52.10 | -35.46 | -51.62 | 431.89 | 875.66 | 0.007 | 0.146 |
182 | -9.81 | -17.00 | -17.25 | -25.94 | -35.79 | -52.00 | -35.43 | -51.53 | 431.45 | 871.74 | 0.006 | 0.143 |
183 | -9.79 | -16.95 | -17.23 | -25.89 | -35.76 | -51.91 | -35.40 | -51.43 | 431.02 | 867.86 | 0.006 | 0.141 |
184 | -9.78 | -16.91 | -17.22 | -25.83 | -35.73 | -51.81 | -35.37 | -51.34 | 430.59 | 864.02 | 0.006 | 0.139 |
185 | -9.76 | -16.86 | -17.20 | -25.78 | -35.69 | -51.72 | -35.34 | -51.24 | 430.16 | 860.21 | 0.006 | 0.137 |
186 | -9.75 | -16.81 | -17.19 | -25.72 | -35.66 | -51.62 | -35.31 | -51.15 | 429.73 | 856.44 | 0.006 | 0.135 |
187 | -9.73 | -16.77 | -17.17 | -25.67 | -35.63 | -51.53 | -35.28 | -51.06 | 429.31 | 852.70 | 0.006 | 0.132 |
188 | -9.72 | -16.72 | -17.15 | -25.62 | -35.59 | -51.44 | -35.25 | -50.97 | 428.89 | 849.00 | 0.006 | 0.130 |
189 | -9.71 | -16.67 | -17.14 | -25.56 | -35.56 | -51.34 | -35.22 | -50.87 | 428.48 | 845.33 | 0.006 | 0.128 |
190 | -9.69 | -16.63 | -17.12 | -25.51 | -35.53 | -51.25 | -35.19 | -50.78 | 428.06 | 841.70 | 0.006 | 0.126 |
191 | -9.68 | -16.58 | -17.11 | -25.45 | -35.50 | -51.16 | -35.16 | -50.69 | 427.66 | 838.10 | 0.006 | 0.125 |
192 | -9.66 | -16.54 | -17.09 | -25.40 | -35.47 | -51.07 | -35.14 | -50.60 | 427.25 | 834.54 | 0.006 | 0.123 |
193 | -9.65 | -16.49 | -17.08 | -25.35 | -35.44 | -50.97 | -35.11 | -50.51 | 426.85 | 831.01 | 0.006 | 0.121 |
194 | -9.64 | -16.45 | -17.06 | -25.29 | -35.40 | -50.88 | -35.08 | -50.42 | 426.45 | 827.51 | 0.006 | 0.119 |
195 | -9.62 | -16.40 | -17.05 | -25.24 | -35.37 | -50.79 | -35.05 | -50.33 | 426.05 | 824.05 | 0.006 | 0.117 |
196 | -9.61 | -16.36 | -17.03 | -25.19 | -35.34 | -50.70 | -35.03 | -50.24 | 425.66 | 820.61 | 0.006 | 0.115 |
197 | -9.59 | -16.31 | -17.02 | -25.14 | -35.31 | -50.61 | -35.00 | -50.15 | 425.27 | 817.21 | 0.006 | 0.114 |
198 | -9.58 | -16.27 | -17.00 | -25.09 | -35.28 | -50.52 | -34.97 | -50.06 | 424.88 | 813.84 | 0.006 | 0.112 |
199 | -9.57 | -16.22 | -16.99 | -25.03 | -35.25 | -50.43 | -34.95 | -49.97 | 424.49 | 810.50 | 0.006 | 0.110 |
200 | -9.56 | -16.18 | -16.97 | -24.98 | -35.22 | -50.34 | -34.92 | -49.88 | 424.11 | 807.19 | 0.006 | 0.109 |
201 | -9.54 | -16.14 | -16.96 | -24.93 | -35.19 | -50.25 | -34.89 | -49.79 | 423.73 | 803.91 | 0.006 | 0.107 |
202 | -9.53 | -16.09 | -16.95 | -24.88 | -35.16 | -50.16 | -34.87 | -49.71 | 423.36 | 800.67 | 0.006 | 0.105 |
203 | -9.52 | -16.05 | -16.93 | -24.83 | -35.14 | -50.07 | -34.84 | -49.62 | 422.98 | 797.45 | 0.005 | 0.104 |
204 | -9.50 | -16.01 | -16.92 | -24.78 | -35.11 | -49.98 | -34.82 | -49.53 | 422.61 | 794.26 | 0.005 | 0.102 |
205 | -9.49 | -15.96 | -16.90 | -24.73 | -35.08 | -49.90 | -34.79 | -49.45 | 422.24 | 791.09 | 0.005 | 0.101 |
206 | -9.48 | -15.92 | -16.89 | -24.68 | -35.05 | -49.81 | -34.76 | -49.36 | 421.88 | 787.96 | 0.005 | 0.099 |
207 | -9.47 | -15.88 | -16.88 | -24.63 | -35.02 | -49.72 | -34.74 | -49.27 | 421.52 | 784.86 | 0.005 | 0.098 |
208 | -9.45 | -15.84 | -16.86 | -24.58 | -34.99 | -49.63 | -34.71 | -49.19 | 421.16 | 781.78 | 0.005 | 0.097 |
209 | -9.44 | -15.80 | -16.85 | -24.53 | -34.97 | -49.55 | -34.69 | -49.10 | 420.80 | 778.73 | 0.005 | 0.095 |
210 | -9.43 | -15.75 | -16.84 | -24.48 | -34.94 | -49.46 | -34.67 | -49.02 | 420.44 | 775.71 | 0.005 | 0.094 |
211 | -9.42 | -15.71 | -16.82 | -24.43 | -34.91 | -49.38 | -34.64 | -48.93 | 420.09 | 772.71 | 0.005 | 0.092 |
212 | -9.41 | -15.67 | -16.81 | -24.38 | -34.88 | -49.29 | -34.62 | -48.85 | 419.74 | 769.74 | 0.005 | 0.091 |
213 | -9.40 | -15.63 | -16.80 | -24.33 | -34.86 | -49.20 | -34.59 | -48.76 | 419.39 | 766.80 | 0.005 | 0.090 |
214 | -9.38 | -15.59 | -16.78 | -24.29 | -34.83 | -49.12 | -34.57 | -48.68 | 419.05 | 763.88 | 0.005 | 0.088 |
215 | -9.37 | -15.55 | -16.77 | -24.24 | -34.80 | -49.03 | -34.54 | -48.60 | 418.71 | 760.99 | 0.005 | 0.087 |
216 | -9.36 | -15.51 | -16.76 | -24.19 | -34.78 | -48.95 | -34.52 | -48.51 | 418.37 | 758.12 | 0.005 | 0.086 |
217 | -9.35 | -15.47 | -16.74 | -24.14 | -34.75 | -48.87 | -34.50 | -48.43 | 418.03 | 755.28 | 0.005 | 0.085 |
218 | -9.34 | -15.43 | -16.73 | -24.10 | -34.73 | -48.78 | -34.47 | -48.35 | 417.70 | 752.47 | 0.005 | 0.084 |
219 | -9.33 | -15.39 | -16.72 | -24.05 | -34.70 | -48.70 | -34.45 | -48.27 | 417.36 | 749.68 | 0.005 | 0.082 |
220 | -9.32 | -15.35 | -16.71 | -24.00 | -34.67 | -48.61 | -34.43 | -48.18 | 417.03 | 746.91 | 0.005 | 0.081 |
221 | -9.30 | -15.31 | -16.69 | -23.95 | -34.65 | -48.53 | -34.41 | -48.10 | 416.71 | 744.17 | 0.005 | 0.080 |
222 | -9.29 | -15.27 | -16.68 | -23.91 | -34.62 | -48.45 | -34.38 | -48.02 | 416.38 | 741.45 | 0.005 | 0.079 |
223 | -9.28 | -15.23 | -16.67 | -23.86 | -34.60 | -48.37 | -34.36 | -47.94 | 416.06 | 738.75 | 0.005 | 0.078 |
224 | -9.27 | -15.19 | -16.66 | -23.82 | -34.57 | -48.28 | -34.34 | -47.86 | 415.74 | 736.08 | 0.005 | 0.077 |
225 | -9.26 | -15.15 | -16.65 | -23.77 | -34.55 | -48.20 | -34.32 | -47.78 | 415.42 | 733.43 | 0.005 | 0.076 |
226 | -9.25 | -15.11 | -16.63 | -23.72 | -34.53 | -48.12 | -34.29 | -47.70 | 415.10 | 730.80 | 0.005 | 0.075 |
227 | -9.24 | -15.07 | -16.62 | -23.68 | -34.50 | -48.04 | -34.27 | -47.62 | 414.79 | 728.20 | 0.005 | 0.074 |
228 | -9.23 | -15.04 | -16.61 | -23.63 | -34.48 | -47.96 | -34.25 | -47.54 | 414.48 | 725.61 | 0.004 | 0.073 |
229 | -9.22 | -15.00 | -16.60 | -23.59 | -34.45 | -47.88 | -34.23 | -47.46 | 414.17 | 723.05 | 0.004 | 0.072 |
230 | -9.21 | -14.96 | -16.59 | -23.54 | -34.43 | -47.80 | -34.21 | -47.38 | 413.86 | 720.52 | 0.004 | 0.071 |
231 | -9.20 | -14.92 | -16.58 | -23.50 | -34.41 | -47.72 | -34.19 | -47.31 | 413.56 | 718.00 | 0.004 | 0.070 |
232 | -9.19 | -14.89 | -16.57 | -23.45 | -34.38 | -47.64 | -34.17 | -47.23 | 413.25 | 715.50 | 0.004 | 0.069 |
233 | -9.18 | -14.85 | -16.55 | -23.41 | -34.36 | -47.56 | -34.14 | -47.15 | 412.95 | 713.03 | 0.004 | 0.068 |
234 | -9.17 | -14.81 | -16.54 | -23.37 | -34.34 | -47.48 | -34.12 | -47.07 | 412.65 | 710.58 | 0.004 | 0.067 |
235 | -9.16 | -14.77 | -16.53 | -23.32 | -34.31 | -47.40 | -34.10 | -47.00 | 412.36 | 708.14 | 0.004 | 0.066 |
236 | -9.15 | -14.74 | -16.52 | -23.28 | -34.29 | -47.32 | -34.08 | -46.92 | 412.06 | 705.73 | 0.004 | 0.065 |
237 | -9.14 | -14.70 | -16.51 | -23.24 | -34.27 | -47.25 | -34.06 | -46.84 | 411.77 | 703.34 | 0.004 | 0.064 |
238 | -9.13 | -14.66 | -16.50 | -23.19 | -34.25 | -47.17 | -34.04 | -46.77 | 411.48 | 700.97 | 0.004 | 0.063 |
239 | -9.12 | -14.63 | -16.49 | -23.15 | -34.22 | -47.09 | -34.02 | -46.69 | 411.19 | 698.62 | 0.004 | 0.063 |
240 | -9.11 | -14.59 | -16.48 | -23.11 | -34.20 | -47.01 | -34.00 | -46.62 | 410.91 | 696.28 | 0.004 | 0.062 |
241 | -9.10 | -14.56 | -16.47 | -23.07 | -34.18 | -46.94 | -33.98 | -46.54 | 410.62 | 693.97 | 0.004 | 0.061 |
242 | -9.09 | -14.52 | -16.46 | -23.02 | -34.16 | -46.86 | -33.96 | -46.47 | 410.34 | 691.68 | 0.004 | 0.060 |
243 | -9.09 | -14.49 | -16.45 | -22.98 | -34.14 | -46.78 | -33.94 | -46.39 | 410.06 | 689.40 | 0.004 | 0.059 |
244 | -9.08 | -14.45 | -16.44 | -22.94 | -34.12 | -46.71 | -33.92 | -46.32 | 409.78 | 687.15 | 0.004 | 0.059 |
245 | -9.07 | -14.41 | -16.43 | -22.90 | -34.09 | -46.63 | -33.90 | -46.24 | 409.50 | 684.91 | 0.004 | 0.058 |
246 | -9.06 | -14.38 | -16.41 | -22.86 | -34.07 | -46.56 | -33.88 | -46.17 | 409.23 | 682.69 | 0.004 | 0.057 |
247 | -9.05 | -14.35 | -16.40 | -22.81 | -34.05 | -46.48 | -33.87 | -46.10 | 408.95 | 680.49 | 0.004 | 0.056 |
248 | -9.04 | -14.31 | -16.39 | -22.77 | -34.03 | -46.41 | -33.85 | -46.02 | 408.68 | 678.31 | 0.004 | 0.056 |
249 | -9.03 | -14.28 | -16.38 | -22.73 | -34.01 | -46.33 | -33.83 | -45.95 | 408.41 | 676.14 | 0.004 | 0.055 |
250 | -9.02 | -14.24 | -16.37 | -22.69 | -33.99 | -46.26 | -33.81 | -45.88 | 408.15 | 673.99 | 0.004 | 0.054 |
251 | -9.01 | -14.21 | -16.36 | -22.65 | -33.97 | -46.19 | -33.79 | -45.80 | 407.88 | 671.86 | 0.004 | 0.054 |
252 | -9.01 | -14.17 | -16.35 | -22.61 | -33.95 | -46.11 | -33.77 | -45.73 | 407.62 | 669.75 | 0.004 | 0.053 |
253 | -9.00 | -14.14 | -16.35 | -22.57 | -33.93 | -46.04 | -33.75 | -45.66 | 407.36 | 667.66 | 0.004 | 0.052 |
254 | -8.99 | -14.11 | -16.34 | -22.53 | -33.91 | -45.97 | -33.74 | -45.59 | 407.10 | 665.58 | 0.004 | 0.052 |
255 | -8.98 | -14.07 | -16.33 | -22.49 | -33.89 | -45.89 | -33.72 | -45.52 | 406.84 | 663.52 | 0.004 | 0.051 |
256 | -8.97 | -14.04 | -16.32 | -22.45 | -33.87 | -45.82 | -33.70 | -45.45 | 406.58 | 661.47 | 0.004 | 0.050 |
257 | -8.96 | -14.01 | -16.31 | -22.41 | -33.85 | -45.75 | -33.68 | -45.38 | 406.33 | 659.45 | 0.004 | 0.050 |
258 | -8.96 | -13.97 | -16.30 | -22.37 | -33.83 | -45.68 | -33.66 | -45.31 | 406.07 | 657.43 | 0.004 | 0.049 |
259 | -8.95 | -13.94 | -16.29 | -22.33 | -33.81 | -45.61 | -33.65 | -45.24 | 405.82 | 655.44 | 0.004 | 0.048 |
260 | -8.94 | -13.91 | -16.28 | -22.30 | -33.79 | -45.54 | -33.63 | -45.17 | 405.57 | 653.46 | 0.004 | 0.048 |
261 | -8.93 | -13.88 | -16.27 | -22.26 | -33.77 | -45.46 | -33.61 | -45.10 | 405.32 | 651.50 | 0.004 | 0.047 |
262 | -8.92 | -13.84 | -16.26 | -22.22 | -33.76 | -45.39 | -33.59 | -45.03 | 405.08 | 649.55 | 0.003 | 0.047 |
263 | -8.92 | -13.81 | -16.25 | -22.18 | -33.74 | -45.32 | -33.58 | -44.96 | 404.83 | 647.61 | 0.003 | 0.046 |
264 | -8.91 | -13.78 | -16.24 | -22.14 | -33.72 | -45.25 | -33.56 | -44.89 | 404.59 | 645.70 | 0.003 | 0.045 |
265 | -8.90 | -13.75 | -16.23 | -22.10 | -33.70 | -45.18 | -33.54 | -44.82 | 404.35 | 643.80 | 0.003 | 0.045 |
266 | -8.89 | -13.72 | -16.22 | -22.07 | -33.68 | -45.12 | -33.53 | -44.76 | 404.11 | 641.91 | 0.003 | 0.044 |
267 | -8.88 | -13.69 | -16.22 | -22.03 | -33.66 | -45.05 | -33.51 | -44.69 | 403.87 | 640.04 | 0.003 | 0.044 |
268 | -8.88 | -13.65 | -16.21 | -21.99 | -33.65 | -44.98 | -33.49 | -44.62 | 403.63 | 638.18 | 0.003 | 0.043 |
269 | -8.87 | -13.62 | -16.20 | -21.95 | -33.63 | -44.91 | -33.48 | -44.55 | 403.40 | 636.34 | 0.003 | 0.043 |
270 | -8.86 | -13.59 | -16.19 | -21.92 | -33.61 | -44.84 | -33.46 | -44.49 | 403.17 | 634.51 | 0.003 | 0.042 |
271 | -8.85 | -13.56 | -16.18 | -21.88 | -33.59 | -44.77 | -33.44 | -44.42 | 402.93 | 632.70 | 0.003 | 0.042 |
272 | -8.85 | -13.53 | -16.17 | -21.84 | -33.57 | -44.71 | -33.43 | -44.36 | 402.70 | 630.90 | 0.003 | 0.041 |
273 | -8.84 | -13.50 | -16.16 | -21.81 | -33.56 | -44.64 | -33.41 | -44.29 | 402.48 | 629.11 | 0.003 | 0.041 |
274 | -8.83 | -13.47 | -16.16 | -21.77 | -33.54 | -44.57 | -33.39 | -44.22 | 402.25 | 627.34 | 0.003 | 0.040 |
275 | -8.83 | -13.44 | -16.15 | -21.74 | -33.52 | -44.50 | -33.38 | -44.16 | 402.02 | 625.59 | 0.003 | 0.040 |
276 | -8.82 | -13.41 | -16.14 | -21.70 | -33.51 | -44.44 | -33.36 | -44.09 | 401.80 | 623.84 | 0.003 | 0.039 |
277 | -8.81 | -13.38 | -16.13 | -21.66 | -33.49 | -44.37 | -33.35 | -44.03 | 401.58 | 622.11 | 0.003 | 0.039 |
278 | -8.80 | -13.35 | -16.12 | -21.63 | -33.47 | -44.31 | -33.33 | -43.96 | 401.35 | 620.40 | 0.003 | 0.038 |
279 | -8.80 | -13.32 | -16.11 | -21.59 | -33.46 | -44.24 | -33.32 | -43.90 | 401.13 | 618.69 | 0.003 | 0.038 |
280 | -8.79 | -13.29 | -16.11 | -21.56 | -33.44 | -44.17 | -33.30 | -43.84 | 400.92 | 617.00 | 0.003 | 0.037 |
281 | -8.78 | -13.26 | -16.10 | -21.52 | -33.42 | -44.11 | -33.29 | -43.77 | 400.70 | 615.33 | 0.003 | 0.037 |
282 | -8.78 | -13.23 | -16.09 | -21.49 | -33.41 | -44.04 | -33.27 | -43.71 | 400.48 | 613.66 | 0.003 | 0.037 |
283 | -8.77 | -13.20 | -16.08 | -21.45 | -33.39 | -43.98 | -33.26 | -43.65 | 400.27 | 612.01 | 0.003 | 0.036 |
284 | -8.76 | -13.18 | -16.08 | -21.42 | -33.37 | -43.92 | -33.24 | -43.58 | 400.06 | 610.37 | 0.003 | 0.036 |
285 | -8.76 | -13.15 | -16.07 | -21.39 | -33.36 | -43.85 | -33.23 | -43.52 | 399.85 | 608.75 | 0.003 | 0.035 |
286 | -8.75 | -13.12 | -16.06 | -21.35 | -33.34 | -43.79 | -33.21 | -43.46 | 399.64 | 607.13 | 0.003 | 0.035 |
287 | -8.74 | -13.09 | -16.05 | -21.32 | -33.33 | -43.72 | -33.20 | -43.40 | 399.43 | 605.53 | 0.003 | 0.035 |
288 | -8.74 | -13.06 | -16.04 | -21.28 | -33.31 | -43.66 | -33.18 | -43.33 | 399.22 | 603.94 | 0.003 | 0.034 |
289 | -8.73 | -13.03 | -16.04 | -21.25 | -33.29 | -43.60 | -33.17 | -43.27 | 399.01 | 602.37 | 0.003 | 0.034 |
290 | -8.72 | -13.01 | -16.03 | -21.22 | -33.28 | -43.54 | -33.15 | -43.21 | 398.81 | 600.80 | 0.003 | 0.033 |
291 | -8.72 | -12.98 | -16.02 | -21.18 | -33.26 | -43.47 | -33.14 | -43.15 | 398.61 | 599.25 | 0.003 | 0.033 |
292 | -8.71 | -12.95 | -16.01 | -21.15 | -33.25 | -43.41 | -33.12 | -43.09 | 398.40 | 597.71 | 0.003 | 0.033 |
293 | -8.70 | -12.92 | -16.01 | -21.12 | -33.23 | -43.35 | -33.11 | -43.03 | 398.20 | 596.18 | 0.003 | 0.032 |
294 | -8.70 | -12.89 | -16.00 | -21.08 | -33.22 | -43.29 | -33.10 | -42.97 | 398.01 | 594.66 | 0.003 | 0.032 |
295 | -8.69 | -12.87 | -15.99 | -21.05 | -33.20 | -43.23 | -33.08 | -42.91 | 397.81 | 593.16 | 0.003 | 0.032 |
296 | -8.69 | -12.84 | -15.99 | -21.02 | -33.19 | -43.16 | -33.07 | -42.85 | 397.61 | 591.66 | 0.003 | 0.031 |
297 | -8.68 | -12.81 | -15.98 | -20.99 | -33.17 | -43.10 | -33.05 | -42.79 | 397.42 | 590.18 | 0.003 | 0.031 |
298 | -8.67 | -12.79 | -15.97 | -20.96 | -33.16 | -43.04 | -33.04 | -42.73 | 397.22 | 588.71 | 0.003 | 0.031 |
299 | -8.67 | -12.76 | -15.96 | -20.92 | -33.14 | -42.98 | -33.03 | -42.67 | 397.03 | 587.25 | 0.003 | 0.030 |
300 | -8.66 | -12.73 | -15.96 | -20.89 | -33.13 | -42.92 | -33.01 | -42.61 | 396.84 | 585.80 | 0.003 | 0.030 |
301 | -8.66 | -12.71 | -15.95 | -20.86 | -33.11 | -42.86 | -33.00 | -42.56 | 396.65 | 584.36 | 0.003 | 0.030 |
302 | -8.65 | -12.68 | -15.94 | -20.83 | -33.10 | -42.80 | -32.99 | -42.50 | 396.46 | 582.93 | 0.003 | 0.029 |
303 | -8.64 | -12.65 | -15.94 | -20.80 | -33.09 | -42.74 | -32.97 | -42.44 | 396.27 | 581.51 | 0.003 | 0.029 |
304 | -8.64 | -12.63 | -15.93 | -20.77 | -33.07 | -42.69 | -32.96 | -42.38 | 396.08 | 580.10 | 0.003 | 0.029 |
305 | -8.63 | -12.60 | -15.92 | -20.74 | -33.06 | -42.63 | -32.95 | -42.32 | 395.90 | 578.71 | 0.003 | 0.028 |
306 | -8.63 | -12.58 | -15.92 | -20.70 | -33.04 | -42.57 | -32.93 | -42.27 | 395.71 | 577.32 | 0.003 | 0.028 |
307 | -8.62 | -12.55 | -15.91 | -20.67 | -33.03 | -42.51 | -32.92 | -42.21 | 395.53 | 575.94 | 0.003 | 0.028 |
308 | -8.62 | -12.53 | -15.90 | -20.64 | -33.02 | -42.45 | -32.91 | -42.15 | 395.35 | 574.58 | 0.003 | 0.027 |
309 | -8.61 | -12.50 | -15.90 | -20.61 | -33.00 | -42.40 | -32.90 | -42.10 | 395.17 | 573.22 | 0.003 | 0.027 |
310 | -8.60 | -12.48 | -15.89 | -20.58 | -32.99 | -42.34 | -32.88 | -42.04 | 394.99 | 571.88 | 0.002 | 0.027 |
311 | -8.60 | -12.45 | -15.88 | -20.55 | -32.98 | -42.28 | -32.87 | -41.99 | 394.81 | 570.54 | 0.002 | 0.026 |
312 | -8.59 | -12.42 | -15.88 | -20.52 | -32.96 | -42.22 | -32.86 | -41.93 | 394.63 | 569.21 | 0.002 | 0.026 |
313 | -8.59 | -12.40 | -15.87 | -20.49 | -32.95 | -42.17 | -32.85 | -41.87 | 394.46 | 567.90 | 0.002 | 0.026 |
314 | -8.58 | -12.38 | -15.86 | -20.46 | -32.94 | -42.11 | -32.83 | -41.82 | 394.28 | 566.59 | 0.002 | 0.026 |
315 | -8.58 | -12.35 | -15.86 | -20.43 | -32.92 | -42.05 | -32.82 | -41.76 | 394.11 | 565.29 | 0.002 | 0.025 |
316 | -8.57 | -12.33 | -15.85 | -20.40 | -32.91 | -42.00 | -32.81 | -41.71 | 393.93 | 564.01 | 0.002 | 0.025 |
317 | -8.57 | -12.30 | -15.84 | -20.37 | -32.90 | -41.94 | -32.80 | -41.66 | 393.76 | 562.73 | 0.002 | 0.025 |
318 | -8.56 | -12.28 | -15.84 | -20.35 | -32.88 | -41.89 | -32.78 | -41.60 | 393.59 | 561.46 | 0.002 | 0.025 |
319 | -8.56 | -12.25 | -15.83 | -20.32 | -32.87 | -41.83 | -32.77 | -41.55 | 393.42 | 560.20 | 0.002 | 0.024 |
320 | -8.55 | -12.23 | -15.83 | -20.29 | -32.86 | -41.78 | -32.76 | -41.49 | 393.25 | 558.95 | 0.002 | 0.024 |
321 | -8.54 | -12.21 | -15.82 | -20.26 | -32.84 | -41.72 | -32.75 | -41.44 | 393.09 | 557.71 | 0.002 | 0.024 |
322 | -8.54 | -12.18 | -15.81 | -20.23 | -32.83 | -41.67 | -32.74 | -41.39 | 392.92 | 556.48 | 0.002 | 0.024 |
323 | -8.53 | -12.16 | -15.81 | -20.20 | -32.82 | -41.61 | -32.73 | -41.33 | 392.75 | 555.25 | 0.002 | 0.023 |
324 | -8.53 | -12.14 | -15.80 | -20.17 | -32.81 | -41.56 | -32.71 | -41.28 | 392.59 | 554.04 | 0.002 | 0.023 |
325 | -8.52 | -12.11 | -15.80 | -20.15 | -32.79 | -41.51 | -32.70 | -41.23 | 392.43 | 552.83 | 0.002 | 0.023 |
326 | -8.52 | -12.09 | -15.79 | -20.12 | -32.78 | -41.45 | -32.69 | -41.18 | 392.27 | 551.64 | 0.002 | 0.023 |
327 | -8.51 | -12.07 | -15.78 | -20.09 | -32.77 | -41.40 | -32.68 | -41.12 | 392.10 | 550.45 | 0.002 | 0.022 |
328 | -8.51 | -12.04 | -15.78 | -20.06 | -32.76 | -41.35 | -32.67 | -41.07 | 391.94 | 549.27 | 0.002 | 0.022 |
329 | -8.50 | -12.02 | -15.77 | -20.04 | -32.75 | -41.29 | -32.66 | -41.02 | 391.78 | 548.10 | 0.002 | 0.022 |
330 | -8.50 | -12.00 | -15.77 | -20.01 | -32.73 | -41.24 | -32.65 | -40.97 | 391.63 | 546.94 | 0.002 | 0.022 |
331 | -8.49 | -11.97 | -15.76 | -19.98 | -32.72 | -41.19 | -32.63 | -40.92 | 391.47 | 545.78 | 0.002 | 0.022 |
332 | -8.49 | -11.95 | -15.76 | -19.95 | -32.71 | -41.14 | -32.62 | -40.87 | 391.31 | 544.64 | 0.002 | 0.021 |
333 | -8.49 | -11.93 | -15.75 | -19.93 | -32.70 | -41.09 | -32.61 | -40.82 | 391.16 | 543.50 | 0.002 | 0.021 |
334 | -8.48 | -11.91 | -15.74 | -19.90 | -32.69 | -41.03 | -32.60 | -40.77 | 391.00 | 542.37 | 0.002 | 0.021 |
335 | -8.48 | -11.88 | -15.74 | -19.87 | -32.68 | -40.98 | -32.59 | -40.72 | 390.85 | 541.25 | 0.002 | 0.021 |
336 | -8.47 | -11.86 | -15.73 | -19.85 | -32.66 | -40.93 | -32.58 | -40.67 | 390.70 | 540.13 | 0.002 | 0.020 |
337 | -8.47 | -11.84 | -15.73 | -19.82 | -32.65 | -40.88 | -32.57 | -40.62 | 390.55 | 539.03 | 0.002 | 0.020 |
338 | -8.46 | -11.82 | -15.72 | -19.79 | -32.64 | -40.83 | -32.56 | -40.57 | 390.40 | 537.93 | 0.002 | 0.020 |
339 | -8.46 | -11.80 | -15.72 | -19.77 | -32.63 | -40.78 | -32.55 | -40.52 | 390.25 | 536.84 | 0.002 | 0.020 |
340 | -8.45 | -11.78 | -15.71 | -19.74 | -32.62 | -40.73 | -32.54 | -40.47 | 390.10 | 535.76 | 0.002 | 0.020 |
341 | -8.45 | -11.75 | -15.71 | -19.72 | -32.61 | -40.68 | -32.53 | -40.42 | 389.95 | 534.68 | 0.002 | 0.020 |
342 | -8.44 | -11.73 | -15.70 | -19.69 | -32.60 | -40.63 | -32.52 | -40.37 | 389.81 | 533.62 | 0.002 | 0.019 |
343 | -8.44 | -11.71 | -15.70 | -19.67 | -32.59 | -40.58 | -32.51 | -40.32 | 389.66 | 532.56 | 0.002 | 0.019 |
344 | -8.43 | -11.69 | -15.69 | -19.64 | -32.57 | -40.53 | -32.50 | -40.28 | 389.51 | 531.50 | 0.002 | 0.019 |
345 | -8.43 | -11.67 | -15.68 | -19.61 | -32.56 | -40.48 | -32.49 | -40.23 | 389.37 | 530.46 | 0.002 | 0.019 |
346 | -8.43 | -11.65 | -15.68 | -19.59 | -32.55 | -40.43 | -32.48 | -40.18 | 389.23 | 529.42 | 0.002 | 0.019 |
347 | -8.42 | -11.63 | -15.67 | -19.56 | -32.54 | -40.38 | -32.47 | -40.13 | 389.09 | 528.39 | 0.002 | 0.018 |
348 | -8.42 | -11.61 | -15.67 | -19.54 | -32.53 | -40.34 | -32.46 | -40.09 | 388.94 | 527.37 | 0.002 | 0.018 |
349 | -8.41 | -11.59 | -15.66 | -19.51 | -32.52 | -40.29 | -32.45 | -40.04 | 388.80 | 526.35 | 0.002 | 0.018 |
350 | -8.41 | -11.57 | -15.66 | -19.49 | -32.51 | -40.24 | -32.44 | -39.99 | 388.66 | 525.35 | 0.002 | 0.018 |
351 | -8.40 | -11.54 | -15.65 | -19.47 | -32.50 | -40.19 | -32.43 | -39.95 | 388.53 | 524.35 | 0.002 | 0.018 |
352 | -8.40 | -11.52 | -15.65 | -19.44 | -32.49 | -40.14 | -32.42 | -39.90 | 388.39 | 523.35 | 0.002 | 0.018 |
353 | -8.40 | -11.50 | -15.64 | -19.42 | -32.48 | -40.10 | -32.41 | -39.85 | 388.25 | 522.36 | 0.002 | 0.017 |
354 | -8.39 | -11.48 | -15.64 | -19.39 | -32.47 | -40.05 | -32.40 | -39.81 | 388.12 | 521.38 | 0.002 | 0.017 |
355 | -8.39 | -11.46 | -15.63 | -19.37 | -32.46 | -40.00 | -32.39 | -39.76 | 387.98 | 520.41 | 0.002 | 0.017 |
356 | -8.38 | -11.44 | -15.63 | -19.34 | -32.45 | -39.96 | -32.38 | -39.72 | 387.85 | 519.44 | 0.002 | 0.017 |
357 | -8.38 | -11.42 | -15.62 | -19.32 | -32.44 | -39.91 | -32.37 | -39.67 | 387.71 | 518.48 | 0.002 | 0.017 |
358 | -8.38 | -11.40 | -15.62 | -19.30 | -32.43 | -39.86 | -32.36 | -39.63 | 387.58 | 517.53 | 0.002 | 0.017 |
359 | -8.37 | -11.39 | -15.62 | -19.27 | -32.42 | -39.82 | -32.35 | -39.58 | 387.45 | 516.58 | 0.002 | 0.016 |
360 | -8.37 | -11.37 | -15.61 | -19.25 | -32.41 | -39.77 | -32.34 | -39.54 | 387.32 | 515.64 | 0.002 | 0.016 |
361 | -8.36 | -11.35 | -15.61 | -19.23 | -32.40 | -39.73 | -32.33 | -39.49 | 387.19 | 514.71 | 0.002 | 0.016 |
362 | -8.36 | -11.33 | -15.60 | -19.20 | -32.39 | -39.68 | -32.32 | -39.45 | 387.06 | 513.78 | 0.002 | 0.016 |
363 | -8.36 | -11.31 | -15.60 | -19.18 | -32.38 | -39.64 | -32.31 | -39.40 | 386.93 | 512.86 | 0.002 | 0.016 |
364 | -8.35 | -11.29 | -15.59 | -19.16 | -32.37 | -39.59 | -32.30 | -39.36 | 386.80 | 511.94 | 0.002 | 0.016 |
365 | -8.35 | -11.27 | -15.59 | -19.13 | -32.36 | -39.55 | -32.29 | -39.32 | 386.67 | 511.04 | 0.002 | 0.016 |
366 | -8.34 | -11.25 | -15.58 | -19.11 | -32.35 | -39.50 | -32.28 | -39.27 | 386.55 | 510.13 | 0.002 | 0.015 |
367 | -8.34 | -11.23 | -15.58 | -19.09 | -32.34 | -39.46 | -32.28 | -39.23 | 386.42 | 509.24 | 0.002 | 0.015 |
368 | -8.34 | -11.21 | -15.57 | -19.07 | -32.33 | -39.41 | -32.27 | -39.19 | 386.30 | 508.35 | 0.002 | 0.015 |
369 | -8.33 | -11.19 | -15.57 | -19.04 | -32.32 | -39.37 | -32.26 | -39.14 | 386.17 | 507.46 | 0.002 | 0.015 |
370 | -8.33 | -11.18 | -15.56 | -19.02 | -32.31 | -39.33 | -32.25 | -39.10 | 386.05 | 506.59 | 0.002 | 0.015 |
371 | -8.33 | -11.16 | -15.56 | -19.00 | -32.30 | -39.28 | -32.24 | -39.06 | 385.93 | 505.71 | 0.002 | 0.015 |
372 | -8.32 | -11.14 | -15.56 | -18.98 | -32.30 | -39.24 | -32.23 | -39.02 | 385.80 | 504.85 | 0.002 | 0.015 |
373 | -8.32 | -11.12 | -15.55 | -18.96 | -32.29 | -39.20 | -32.22 | -38.98 | 385.68 | 503.99 | 0.002 | 0.014 |
374 | -8.31 | -11.10 | -15.55 | -18.93 | -32.28 | -39.15 | -32.21 | -38.93 | 385.56 | 503.14 | 0.002 | 0.014 |
375 | -8.31 | -11.09 | -15.54 | -18.91 | -32.27 | -39.11 | -32.21 | -38.89 | 385.44 | 502.29 | 0.002 | 0.014 |
376 | -8.31 | -11.07 | -15.54 | -18.89 | -32.26 | -39.07 | -32.20 | -38.85 | 385.32 | 501.44 | 0.002 | 0.014 |
377 | -8.30 | -11.05 | -15.53 | -18.87 | -32.25 | -39.03 | -32.19 | -38.81 | 385.21 | 500.61 | 0.002 | 0.014 |
378 | -8.30 | -11.03 | -15.53 | -18.85 | -32.24 | -38.98 | -32.18 | -38.77 | 385.09 | 499.78 | 0.002 | 0.014 |
379 | -8.30 | -11.01 | -15.53 | -18.83 | -32.23 | -38.94 | -32.17 | -38.73 | 384.97 | 498.95 | 0.002 | 0.014 |
380 | -8.29 | -11.00 | -15.52 | -18.81 | -32.22 | -38.90 | -32.16 | -38.69 | 384.86 | 498.13 | 0.002 | 0.014 |
381 | -8.29 | -10.98 | -15.52 | -18.78 | -32.22 | -38.86 | -32.16 | -38.65 | 384.74 | 497.32 | 0.002 | 0.013 |
382 | -8.29 | -10.96 | -15.51 | -18.76 | -32.21 | -38.82 | -32.15 | -38.61 | 384.63 | 496.51 | 0.002 | 0.013 |
383 | -8.28 | -10.94 | -15.51 | -18.74 | -32.20 | -38.78 | -32.14 | -38.57 | 384.51 | 495.71 | 0.002 | 0.013 |
384 | -8.28 | -10.93 | -15.51 | -18.72 | -32.19 | -38.74 | -32.13 | -38.53 | 384.40 | 494.91 | 0.002 | 0.013 |
385 | -8.28 | -10.91 | -15.50 | -18.70 | -32.18 | -38.70 | -32.12 | -38.49 | 384.29 | 494.11 | 0.002 | 0.013 |
386 | -8.27 | -10.89 | -15.50 | -18.68 | -32.17 | -38.66 | -32.12 | -38.45 | 384.17 | 493.33 | 0.002 | 0.013 |
387 | -8.27 | -10.88 | -15.49 | -18.66 | -32.16 | -38.62 | -32.11 | -38.41 | 384.06 | 492.55 | 0.002 | 0.013 |
388 | -8.27 | -10.86 | -15.49 | -18.64 | -32.16 | -38.58 | -32.10 | -38.37 | 383.95 | 491.77 | 0.001 | 0.013 |
389 | -8.26 | -10.84 | -15.49 | -18.62 | -32.15 | -38.54 | -32.09 | -38.33 | 383.84 | 491.00 | 0.001 | 0.013 |
390 | -8.26 | -10.83 | -15.48 | -18.60 | -32.14 | -38.50 | -32.08 | -38.29 | 383.73 | 490.23 | 0.001 | 0.012 |
391 | -8.26 | -10.81 | -15.48 | -18.58 | -32.13 | -38.46 | -32.08 | -38.25 | 383.63 | 489.47 | 0.001 | 0.012 |
392 | -8.25 | -10.79 | -15.47 | -18.56 | -32.12 | -38.42 | -32.07 | -38.21 | 383.52 | 488.71 | 0.001 | 0.012 |
393 | -8.25 | -10.78 | -15.47 | -18.54 | -32.12 | -38.38 | -32.06 | -38.18 | 383.41 | 487.96 | 0.001 | 0.012 |
394 | -8.25 | -10.76 | -15.47 | -18.52 | -32.11 | -38.34 | -32.05 | -38.14 | 383.30 | 487.22 | 0.001 | 0.012 |
395 | -8.24 | -10.74 | -15.46 | -18.50 | -32.10 | -38.30 | -32.05 | -38.10 | 383.20 | 486.48 | 0.001 | 0.012 |
396 | -8.24 | -10.73 | -15.46 | -18.48 | -32.09 | -38.26 | -32.04 | -38.06 | 383.09 | 485.74 | 0.001 | 0.012 |
397 | -8.24 | -10.71 | -15.45 | -18.46 | -32.08 | -38.22 | -32.03 | -38.02 | 382.99 | 485.01 | 0.001 | 0.012 |
398 | -8.23 | -10.70 | -15.45 | -18.44 | -32.08 | -38.18 | -32.02 | -37.99 | 382.88 | 484.28 | 0.001 | 0.012 |
399 | -8.23 | -10.68 | -15.45 | -18.42 | -32.07 | -38.15 | -32.02 | -37.95 | 382.78 | 483.56 | 0.001 | 0.012 |
400 | -8.23 | -10.66 | -15.44 | -18.40 | -32.06 | -38.11 | -32.01 | -37.91 | 382.68 | 482.84 | 0.001 | 0.011 |
401 | -8.22 | -10.65 | -15.44 | -18.38 | -32.05 | -38.07 | -32.00 | -37.88 | 382.58 | 482.13 | 0.001 | 0.011 |
402 | -8.22 | -10.63 | -15.44 | -18.37 | -32.05 | -38.03 | -31.99 | -37.84 | 382.47 | 481.42 | 0.001 | 0.011 |
403 | -8.22 | -10.62 | -15.43 | -18.35 | -32.04 | -38.00 | -31.99 | -37.80 | 382.37 | 480.72 | 0.001 | 0.011 |
404 | -8.22 | -10.60 | -15.43 | -18.33 | -32.03 | -37.96 | -31.98 | -37.77 | 382.27 | 480.02 | 0.001 | 0.011 |
405 | -8.21 | -10.59 | -15.43 | -18.31 | -32.02 | -37.92 | -31.97 | -37.73 | 382.17 | 479.33 | 0.001 | 0.011 |
406 | -8.21 | -10.57 | -15.42 | -18.29 | -32.02 | -37.89 | -31.97 | -37.70 | 382.07 | 478.64 | 0.001 | 0.011 |
407 | -8.21 | -10.56 | -15.42 | -18.27 | -32.01 | -37.85 | -31.96 | -37.66 | 381.98 | 477.96 | 0.001 | 0.011 |
408 | -8.20 | -10.54 | -15.42 | -18.25 | -32.00 | -37.81 | -31.95 | -37.62 | 381.88 | 477.28 | 0.001 | 0.011 |
409 | -8.20 | -10.53 | -15.41 | -18.24 | -31.99 | -37.78 | -31.95 | -37.59 | 381.78 | 476.60 | 0.001 | 0.011 |
410 | -8.20 | -10.51 | -15.41 | -18.22 | -31.99 | -37.74 | -31.94 | -37.55 | 381.68 | 475.93 | 0.001 | 0.011 |
411 | -8.19 | -10.50 | -15.40 | -18.20 | -31.98 | -37.70 | -31.93 | -37.52 | 381.59 | 475.26 | 0.001 | 0.010 |
412 | -8.19 | -10.48 | -15.40 | -18.18 | -31.97 | -37.67 | -31.92 | -37.48 | 381.49 | 474.60 | 0.001 | 0.010 |
413 | -8.19 | -10.47 | -15.40 | -18.16 | -31.96 | -37.63 | -31.92 | -37.45 | 381.40 | 473.94 | 0.001 | 0.010 |
414 | -8.19 | -10.45 | -15.39 | -18.15 | -31.96 | -37.60 | -31.91 | -37.41 | 381.30 | 473.29 | 0.001 | 0.010 |
415 | -8.18 | -10.44 | -15.39 | -18.13 | -31.95 | -37.56 | -31.90 | -37.38 | 381.21 | 472.64 | 0.001 | 0.010 |
416 | -8.18 | -10.42 | -15.39 | -18.11 | -31.94 | -37.53 | -31.90 | -37.35 | 381.12 | 472.00 | 0.001 | 0.010 |
417 | -8.18 | -10.41 | -15.38 | -18.09 | -31.94 | -37.49 | -31.89 | -37.31 | 381.02 | 471.36 | 0.001 | 0.010 |
418 | -8.17 | -10.39 | -15.38 | -18.08 | -31.93 | -37.46 | -31.88 | -37.28 | 380.93 | 470.72 | 0.001 | 0.010 |
419 | -8.17 | -10.38 | -15.38 | -18.06 | -31.92 | -37.42 | -31.88 | -37.24 | 380.84 | 470.09 | 0.001 | 0.010 |
420 | -8.17 | -10.36 | -15.37 | -18.04 | -31.92 | -37.39 | -31.87 | -37.21 | 380.75 | 469.46 | 0.001 | 0.010 |
421 | -8.17 | -10.35 | -15.37 | -18.03 | -31.91 | -37.35 | -31.87 | -37.18 | 380.66 | 468.83 | 0.001 | 0.010 |
422 | -8.16 | -10.34 | -15.37 | -18.01 | -31.90 | -37.32 | -31.86 | -37.14 | 380.57 | 468.21 | 0.001 | 0.010 |
423 | -8.16 | -10.32 | -15.37 | -17.99 | -31.90 | -37.29 | -31.85 | -37.11 | 380.48 | 467.60 | 0.001 | 0.010 |
424 | -8.16 | -10.31 | -15.36 | -17.97 | -31.89 | -37.25 | -31.85 | -37.08 | 380.39 | 466.98 | 0.001 | 0.009 |
425 | -8.16 | -10.29 | -15.36 | -17.96 | -31.88 | -37.22 | -31.84 | -37.05 | 380.30 | 466.38 | 0.001 | 0.009 |
426 | -8.15 | -10.28 | -15.36 | -17.94 | -31.88 | -37.19 | -31.83 | -37.01 | 380.21 | 465.77 | 0.001 | 0.009 |
427 | -8.15 | -10.27 | -15.35 | -17.92 | -31.87 | -37.15 | -31.83 | -36.98 | 380.12 | 465.17 | 0.001 | 0.009 |
428 | -8.15 | -10.25 | -15.35 | -17.91 | -31.86 | -37.12 | -31.82 | -36.95 | 380.04 | 464.57 | 0.001 | 0.009 |
429 | -8.15 | -10.24 | -15.35 | -17.89 | -31.86 | -37.09 | -31.81 | -36.92 | 379.95 | 463.98 | 0.001 | 0.009 |
430 | -8.14 | -10.23 | -15.34 | -17.87 | -31.85 | -37.05 | -31.81 | -36.89 | 379.87 | 463.39 | 0.001 | 0.009 |
431 | -8.14 | -10.21 | -15.34 | -17.86 | -31.84 | -37.02 | -31.80 | -36.85 | 379.78 | 462.81 | 0.001 | 0.009 |
432 | -8.14 | -10.20 | -15.34 | -17.84 | -31.84 | -36.99 | -31.80 | -36.82 | 379.69 | 462.23 | 0.001 | 0.009 |
433 | -8.14 | -10.19 | -15.33 | -17.83 | -31.83 | -36.96 | -31.79 | -36.79 | 379.61 | 461.65 | 0.001 | 0.009 |
434 | -8.13 | -10.17 | -15.33 | -17.81 | -31.82 | -36.92 | -31.78 | -36.76 | 379.53 | 461.07 | 0.001 | 0.009 |
435 | -8.13 | -10.16 | -15.33 | -17.79 | -31.82 | -36.89 | -31.78 | -36.73 | 379.44 | 460.50 | 0.001 | 0.009 |
436 | -8.13 | -10.15 | -15.33 | -17.78 | -31.81 | -36.86 | -31.77 | -36.70 | 379.36 | 459.94 | 0.001 | 0.009 |
437 | -8.13 | -10.13 | -15.32 | -17.76 | -31.81 | -36.83 | -31.77 | -36.67 | 379.28 | 459.37 | 0.001 | 0.009 |
438 | -8.12 | -10.12 | -15.32 | -17.75 | -31.80 | -36.80 | -31.76 | -36.64 | 379.20 | 458.82 | 0.001 | 0.008 |
439 | -8.12 | -10.11 | -15.32 | -17.73 | -31.79 | -36.77 | -31.75 | -36.60 | 379.11 | 458.26 | 0.001 | 0.008 |
440 | -8.12 | -10.09 | -15.31 | -17.72 | -31.79 | -36.74 | -31.75 | -36.57 | 379.03 | 457.71 | 0.001 | 0.008 |
441 | -8.12 | -10.08 | -15.31 | -17.70 | -31.78 | -36.70 | -31.74 | -36.54 | 378.95 | 457.16 | 0.001 | 0.008 |
442 | -8.11 | -10.07 | -15.31 | -17.69 | -31.78 | -36.67 | -31.74 | -36.51 | 378.87 | 456.61 | 0.001 | 0.008 |
443 | -8.11 | -10.06 | -15.30 | -17.67 | -31.77 | -36.64 | -31.73 | -36.48 | 378.79 | 456.07 | 0.001 | 0.008 |
444 | -8.11 | -10.04 | -15.30 | -17.66 | -31.76 | -36.61 | -31.73 | -36.45 | 378.71 | 455.53 | 0.001 | 0.008 |
445 | -8.11 | -10.03 | -15.30 | -17.64 | -31.76 | -36.58 | -31.72 | -36.42 | 378.64 | 455.00 | 0.001 | 0.008 |
446 | -8.10 | -10.02 | -15.30 | -17.62 | -31.75 | -36.55 | -31.72 | -36.40 | 378.56 | 454.47 | 0.001 | 0.008 |
447 | -8.10 | -10.01 | -15.29 | -17.61 | -31.75 | -36.52 | -31.71 | -36.37 | 378.48 | 453.94 | 0.001 | 0.008 |
448 | -8.10 | -9.99 | -15.29 | -17.60 | -31.74 | -36.49 | -31.70 | -36.34 | 378.40 | 453.41 | 0.001 | 0.008 |
449 | -8.10 | -9.98 | -15.29 | -17.58 | -31.73 | -36.46 | -31.70 | -36.31 | 378.33 | 452.89 | 0.001 | 0.008 |
450 | -8.09 | -9.97 | -15.29 | -17.57 | -31.73 | -36.43 | -31.69 | -36.28 | 378.25 | 452.37 | 0.001 | 0.008 |
451 | -8.09 | -9.96 | -15.28 | -17.55 | -31.72 | -36.40 | -31.69 | -36.25 | 378.17 | 451.86 | 0.001 | 0.008 |
452 | -8.09 | -9.95 | -15.28 | -17.54 | -31.72 | -36.37 | -31.68 | -36.22 | 378.10 | 451.35 | 0.001 | 0.008 |
453 | -8.09 | -9.93 | -15.28 | -17.52 | -31.71 | -36.34 | -31.68 | -36.19 | 378.02 | 450.84 | 0.001 | 0.008 |
454 | -8.09 | -9.92 | -15.27 | -17.51 | -31.71 | -36.31 | -31.67 | -36.16 | 377.95 | 450.33 | 0.001 | 0.007 |
455 | -8.08 | -9.91 | -15.27 | -17.49 | -31.70 | -36.29 | -31.67 | -36.14 | 377.87 | 449.83 | 0.001 | 0.007 |
456 | -8.08 | -9.90 | -15.27 | -17.48 | -31.70 | -36.26 | -31.66 | -36.11 | 377.80 | 449.33 | 0.001 | 0.007 |
457 | -8.08 | -9.89 | -15.27 | -17.46 | -31.69 | -36.23 | -31.66 | -36.08 | 377.73 | 448.84 | 0.001 | 0.007 |
458 | -8.08 | -9.87 | -15.26 | -17.45 | -31.68 | -36.20 | -31.65 | -36.05 | 377.65 | 448.35 | 0.001 | 0.007 |
459 | -8.08 | -9.86 | -15.26 | -17.44 | -31.68 | -36.17 | -31.65 | -36.03 | 377.58 | 447.86 | 0.001 | 0.007 |
460 | -8.07 | -9.85 | -15.26 | -17.42 | -31.67 | -36.14 | -31.64 | -36.00 | 377.51 | 447.37 | 0.001 | 0.007 |
461 | -8.07 | -9.84 | -15.26 | -17.41 | -31.67 | -36.11 | -31.64 | -35.97 | 377.44 | 446.89 | 0.001 | 0.007 |
462 | -8.07 | -9.83 | -15.25 | -17.39 | -31.66 | -36.09 | -31.63 | -35.94 | 377.37 | 446.41 | 0.001 | 0.007 |
463 | -8.07 | -9.82 | -15.25 | -17.38 | -31.66 | -36.06 | -31.62 | -35.92 | 377.30 | 445.93 | 0.001 | 0.007 |
464 | -8.06 | -9.81 | -15.25 | -17.37 | -31.65 | -36.03 | -31.62 | -35.89 | 377.23 | 445.45 | 0.001 | 0.007 |
465 | -8.06 | -9.80 | -15.25 | -17.35 | -31.65 | -36.00 | -31.61 | -35.86 | 377.16 | 444.98 | 0.001 | 0.007 |
466 | -8.06 | -9.78 | -15.24 | -17.34 | -31.64 | -35.98 | -31.61 | -35.84 | 377.09 | 444.51 | 0.001 | 0.007 |
467 | -8.06 | -9.77 | -15.24 | -17.33 | -31.64 | -35.95 | -31.60 | -35.81 | 377.02 | 444.05 | 0.001 | 0.007 |
468 | -8.06 | -9.76 | -15.24 | -17.31 | -31.63 | -35.92 | -31.60 | -35.78 | 376.95 | 443.59 | 0.001 | 0.007 |
469 | -8.05 | -9.75 | -15.24 | -17.30 | -31.63 | -35.90 | -31.60 | -35.76 | 376.88 | 443.13 | 0.001 | 0.007 |
470 | -8.05 | -9.74 | -15.23 | -17.29 | -31.62 | -35.87 | -31.59 | -35.73 | 376.81 | 442.67 | 0.001 | 0.007 |
471 | -8.05 | -9.73 | -15.23 | -17.27 | -31.62 | -35.84 | -31.59 | -35.70 | 376.75 | 442.22 | 0.001 | 0.007 |
472 | -8.05 | -9.72 | -15.23 | -17.26 | -31.61 | -35.82 | -31.58 | -35.68 | 376.68 | 441.77 | 0.001 | 0.007 |
473 | -8.05 | -9.71 | -15.23 | -17.25 | -31.61 | -35.79 | -31.58 | -35.65 | 376.61 | 441.32 | 0.001 | 0.007 |
474 | -8.04 | -9.70 | -15.23 | -17.23 | -31.60 | -35.76 | -31.57 | -35.63 | 376.55 | 440.87 | 0.001 | 0.006 |
475 | -8.04 | -9.69 | -15.22 | -17.22 | -31.60 | -35.74 | -31.57 | -35.60 | 376.48 | 440.43 | 0.001 | 0.006 |
476 | -8.04 | -9.68 | -15.22 | -17.21 | -31.59 | -35.71 | -31.56 | -35.58 | 376.41 | 439.99 | 0.001 | 0.006 |
477 | -8.04 | -9.66 | -15.22 | -17.20 | -31.59 | -35.68 | -31.56 | -35.55 | 376.35 | 439.55 | 0.001 | 0.006 |
478 | -8.04 | -9.65 | -15.22 | -17.18 | -31.58 | -35.66 | -31.55 | -35.53 | 376.28 | 439.12 | 0.001 | 0.006 |
479 | -8.03 | -9.64 | -15.21 | -17.17 | -31.58 | -35.63 | -31.55 | -35.50 | 376.22 | 438.68 | 0.001 | 0.006 |
480 | -8.03 | -9.63 | -15.21 | -17.16 | -31.57 | -35.61 | -31.54 | -35.48 | 376.16 | 438.26 | 0.001 | 0.006 |
481 | -8.03 | -9.62 | -15.21 | -17.15 | -31.57 | -35.58 | -31.54 | -35.45 | 376.09 | 437.83 | 0.001 | 0.006 |
482 | -8.03 | -9.61 | -15.21 | -17.13 | -31.56 | -35.56 | -31.53 | -35.43 | 376.03 | 437.41 | 0.001 | 0.006 |
483 | -8.03 | -9.60 | -15.20 | -17.12 | -31.56 | -35.53 | -31.53 | -35.40 | 375.97 | 436.98 | 0.001 | 0.006 |
484 | -8.03 | -9.59 | -15.20 | -17.11 | -31.55 | -35.51 | -31.53 | -35.38 | 375.90 | 436.57 | 0.001 | 0.006 |
485 | -8.02 | -9.58 | -15.20 | -17.10 | -31.55 | -35.48 | -31.52 | -35.35 | 375.84 | 436.15 | 0.001 | 0.006 |
486 | -8.02 | -9.57 | -15.20 | -17.08 | -31.54 | -35.46 | -31.52 | -35.33 | 375.78 | 435.74 | 0.001 | 0.006 |
487 | -8.02 | -9.56 | -15.20 | -17.07 | -31.54 | -35.43 | -31.51 | -35.30 | 375.72 | 435.33 | 0.001 | 0.006 |
488 | -8.02 | -9.55 | -15.19 | -17.06 | -31.54 | -35.41 | -31.51 | -35.28 | 375.66 | 434.92 | 0.001 | 0.006 |
489 | -8.02 | -9.54 | -15.19 | -17.05 | -31.53 | -35.38 | -31.50 | -35.26 | 375.59 | 434.51 | 0.001 | 0.006 |
490 | -8.01 | -9.53 | -15.19 | -17.04 | -31.53 | -35.36 | -31.50 | -35.23 | 375.53 | 434.11 | 0.001 | 0.006 |
491 | -8.01 | -9.52 | -15.19 | -17.02 | -31.52 | -35.33 | -31.49 | -35.21 | 375.47 | 433.71 | 0.001 | 0.006 |
492 | -8.01 | -9.51 | -15.18 | -17.01 | -31.52 | -35.31 | -31.49 | -35.19 | 375.41 | 433.31 | 0.001 | 0.006 |
493 | -8.01 | -9.50 | -15.18 | -17.00 | -31.51 | -35.29 | -31.49 | -35.16 | 375.36 | 432.91 | 0.001 | 0.006 |
494 | -8.01 | -9.49 | -15.18 | -16.99 | -31.51 | -35.26 | -31.48 | -35.14 | 375.30 | 432.52 | 0.001 | 0.006 |
495 | -8.01 | -9.48 | -15.18 | -16.98 | -31.50 | -35.24 | -31.48 | -35.12 | 375.24 | 432.13 | 0.001 | 0.006 |
496 | -8.00 | -9.47 | -15.18 | -16.97 | -31.50 | -35.22 | -31.47 | -35.09 | 375.18 | 431.74 | 0.001 | 0.006 |
497 | -8.00 | -9.47 | -15.17 | -16.95 | -31.50 | -35.19 | -31.47 | -35.07 | 375.12 | 431.35 | 0.001 | 0.006 |
498 | -8.00 | -9.46 | -15.17 | -16.94 | -31.49 | -35.17 | -31.46 | -35.05 | 375.06 | 430.97 | 0.001 | 0.005 |
499 | -8.00 | -9.45 | -15.17 | -16.93 | -31.49 | -35.15 | -31.46 | -35.03 | 375.01 | 430.59 | 0.001 | 0.005 |
Figure 6: Impulse Responses for Selected Variables: Endogenous Discounting
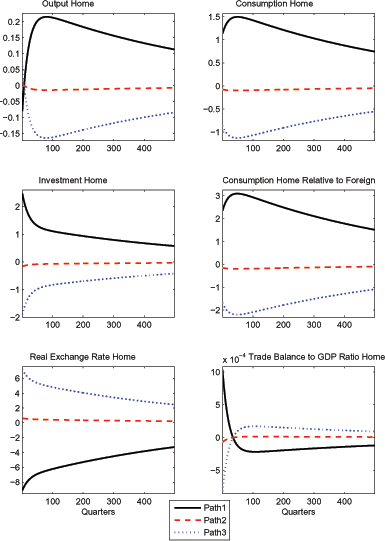
Data for Figure 6 - Panel A
Quarters | Output Home: Path 3 | Output Home: Path 2 | Output Home: Path 1 | Consumption Home: Path3 | Consumption Home: Path 2 | Consumption Home: Path1 | Investment Home: Path 3 | Investment Home: Path 2 | Investment Home: Path 1 |
|---|---|---|---|---|---|---|---|---|---|
1 | 0.060 | 0.005 | -0.080 | -0.862 | -0.075 | 1.137 | -1.907 | -0.169 | 2.472 |
2 | 0.048 | 0.004 | -0.065 | -0.879 | -0.076 | 1.160 | -1.856 | -0.160 | 2.420 |
3 | 0.037 | 0.003 | -0.050 | -0.895 | -0.078 | 1.181 | -1.812 | -0.156 | 2.365 |
4 | 0.027 | 0.002 | -0.037 | -0.910 | -0.079 | 1.201 | -1.771 | -0.152 | 2.313 |
5 | 0.017 | 0.001 | -0.024 | -0.924 | -0.080 | 1.220 | -1.731 | -0.149 | 2.263 |
6 | 0.007 | 0.001 | -0.011 | -0.938 | -0.081 | 1.238 | -1.694 | -0.146 | 2.215 |
7 | -0.002 | 0.000 | 0.001 | -0.951 | -0.082 | 1.255 | -1.658 | -0.143 | 2.169 |
8 | -0.011 | -0.001 | 0.012 | -0.963 | -0.084 | 1.271 | -1.623 | -0.140 | 2.126 |
9 | -0.019 | -0.002 | 0.023 | -0.974 | -0.084 | 1.287 | -1.591 | -0.137 | 2.084 |
10 | -0.027 | -0.002 | 0.033 | -0.985 | -0.085 | 1.301 | -1.559 | -0.134 | 2.044 |
11 | -0.034 | -0.003 | 0.043 | -0.995 | -0.086 | 1.315 | -1.529 | -0.132 | 2.006 |
12 | -0.041 | -0.003 | 0.052 | -1.005 | -0.087 | 1.328 | -1.501 | -0.129 | 1.969 |
13 | -0.048 | -0.004 | 0.061 | -1.014 | -0.088 | 1.340 | -1.473 | -0.127 | 1.935 |
14 | -0.054 | -0.005 | 0.069 | -1.022 | -0.089 | 1.351 | -1.447 | -0.125 | 1.901 |
15 | -0.060 | -0.005 | 0.077 | -1.030 | -0.089 | 1.362 | -1.422 | -0.123 | 1.869 |
16 | -0.066 | -0.006 | 0.085 | -1.038 | -0.090 | 1.372 | -1.399 | -0.121 | 1.839 |
17 | -0.071 | -0.006 | 0.092 | -1.045 | -0.091 | 1.382 | -1.376 | -0.119 | 1.810 |
18 | -0.077 | -0.007 | 0.099 | -1.052 | -0.091 | 1.391 | -1.354 | -0.117 | 1.782 |
19 | -0.082 | -0.007 | 0.105 | -1.058 | -0.092 | 1.400 | -1.333 | -0.115 | 1.755 |
20 | -0.086 | -0.007 | 0.111 | -1.064 | -0.092 | 1.408 | -1.314 | -0.113 | 1.730 |
21 | -0.091 | -0.008 | 0.117 | -1.069 | -0.093 | 1.415 | -1.294 | -0.112 | 1.705 |
22 | -0.095 | -0.008 | 0.123 | -1.075 | -0.093 | 1.422 | -1.276 | -0.110 | 1.682 |
23 | -0.099 | -0.008 | 0.128 | -1.079 | -0.094 | 1.429 | -1.259 | -0.109 | 1.659 |
24 | -0.103 | -0.009 | 0.133 | -1.084 | -0.094 | 1.435 | -1.242 | -0.107 | 1.638 |
25 | -0.107 | -0.009 | 0.138 | -1.088 | -0.094 | 1.441 | -1.226 | -0.106 | 1.618 |
26 | -0.110 | -0.009 | 0.142 | -1.092 | -0.095 | 1.446 | -1.211 | -0.105 | 1.598 |
27 | -0.113 | -0.010 | 0.147 | -1.096 | -0.095 | 1.451 | -1.196 | -0.103 | 1.579 |
28 | -0.116 | -0.010 | 0.151 | -1.099 | -0.095 | 1.456 | -1.182 | -0.102 | 1.561 |
29 | -0.119 | -0.010 | 0.155 | -1.102 | -0.096 | 1.460 | -1.169 | -0.101 | 1.544 |
30 | -0.122 | -0.010 | 0.158 | -1.105 | -0.096 | 1.464 | -1.156 | -0.100 | 1.527 |
31 | -0.125 | -0.011 | 0.162 | -1.108 | -0.096 | 1.468 | -1.144 | -0.099 | 1.511 |
32 | -0.127 | -0.011 | 0.165 | -1.110 | -0.096 | 1.471 | -1.132 | -0.098 | 1.496 |
33 | -0.130 | -0.011 | 0.168 | -1.113 | -0.097 | 1.474 | -1.121 | -0.097 | 1.481 |
34 | -0.132 | -0.011 | 0.171 | -1.115 | -0.097 | 1.477 | -1.110 | -0.096 | 1.467 |
35 | -0.134 | -0.011 | 0.174 | -1.116 | -0.097 | 1.480 | -1.100 | -0.095 | 1.454 |
36 | -0.136 | -0.012 | 0.177 | -1.118 | -0.097 | 1.482 | -1.090 | -0.094 | 1.441 |
37 | -0.138 | -0.012 | 0.179 | -1.120 | -0.097 | 1.484 | -1.080 | -0.093 | 1.428 |
38 | -0.140 | -0.012 | 0.182 | -1.121 | -0.097 | 1.486 | -1.071 | -0.093 | 1.416 |
39 | -0.141 | -0.012 | 0.184 | -1.122 | -0.097 | 1.488 | -1.062 | -0.092 | 1.405 |
40 | -0.143 | -0.012 | 0.186 | -1.123 | -0.097 | 1.489 | -1.053 | -0.091 | 1.394 |
41 | -0.145 | -0.012 | 0.188 | -1.124 | -0.098 | 1.491 | -1.045 | -0.090 | 1.383 |
42 | -0.146 | -0.013 | 0.190 | -1.125 | -0.098 | 1.492 | -1.037 | -0.090 | 1.373 |
43 | -0.147 | -0.013 | 0.192 | -1.126 | -0.098 | 1.493 | -1.030 | -0.089 | 1.363 |
44 | -0.149 | -0.013 | 0.194 | -1.126 | -0.098 | 1.494 | -1.023 | -0.088 | 1.354 |
45 | -0.150 | -0.013 | 0.195 | -1.126 | -0.098 | 1.494 | -1.016 | -0.088 | 1.345 |
46 | -0.151 | -0.013 | 0.197 | -1.127 | -0.098 | 1.495 | -1.009 | -0.087 | 1.336 |
47 | -0.152 | -0.013 | 0.198 | -1.127 | -0.098 | 1.495 | -1.003 | -0.087 | 1.328 |
48 | -0.153 | -0.013 | 0.199 | -1.127 | -0.098 | 1.495 | -0.996 | -0.086 | 1.320 |
49 | -0.154 | -0.013 | 0.201 | -1.127 | -0.098 | 1.496 | -0.990 | -0.086 | 1.312 |
50 | -0.155 | -0.013 | 0.202 | -1.127 | -0.098 | 1.496 | -0.984 | -0.085 | 1.304 |
51 | -0.156 | -0.013 | 0.203 | -1.127 | -0.098 | 1.495 | -0.979 | -0.085 | 1.297 |
52 | -0.156 | -0.013 | 0.204 | -1.127 | -0.098 | 1.495 | -0.973 | -0.084 | 1.290 |
53 | -0.157 | -0.014 | 0.205 | -1.126 | -0.098 | 1.495 | -0.968 | -0.084 | 1.283 |
54 | -0.158 | -0.014 | 0.206 | -1.126 | -0.098 | 1.495 | -0.963 | -0.083 | 1.277 |
55 | -0.158 | -0.014 | 0.207 | -1.125 | -0.098 | 1.494 | -0.958 | -0.083 | 1.270 |
56 | -0.159 | -0.014 | 0.208 | -1.125 | -0.098 | 1.493 | -0.954 | -0.083 | 1.264 |
57 | -0.160 | -0.014 | 0.208 | -1.124 | -0.098 | 1.493 | -0.949 | -0.082 | 1.258 |
58 | -0.160 | -0.014 | 0.209 | -1.124 | -0.098 | 1.492 | -0.945 | -0.082 | 1.253 |
59 | -0.161 | -0.014 | 0.210 | -1.123 | -0.097 | 1.491 | -0.940 | -0.081 | 1.247 |
60 | -0.161 | -0.014 | 0.210 | -1.122 | -0.097 | 1.490 | -0.936 | -0.081 | 1.242 |
61 | -0.161 | -0.014 | 0.211 | -1.121 | -0.097 | 1.489 | -0.932 | -0.081 | 1.237 |
62 | -0.162 | -0.014 | 0.211 | -1.120 | -0.097 | 1.488 | -0.928 | -0.080 | 1.231 |
63 | -0.162 | -0.014 | 0.212 | -1.120 | -0.097 | 1.487 | -0.925 | -0.080 | 1.227 |
64 | -0.162 | -0.014 | 0.212 | -1.119 | -0.097 | 1.486 | -0.921 | -0.080 | 1.222 |
65 | -0.163 | -0.014 | 0.213 | -1.118 | -0.097 | 1.485 | -0.917 | -0.079 | 1.217 |
66 | -0.163 | -0.014 | 0.213 | -1.117 | -0.097 | 1.484 | -0.914 | -0.079 | 1.213 |
67 | -0.163 | -0.014 | 0.213 | -1.115 | -0.097 | 1.482 | -0.911 | -0.079 | 1.208 |
68 | -0.163 | -0.014 | 0.214 | -1.114 | -0.097 | 1.481 | -0.907 | -0.079 | 1.204 |
69 | -0.164 | -0.014 | 0.214 | -1.113 | -0.097 | 1.479 | -0.904 | -0.078 | 1.200 |
70 | -0.164 | -0.014 | 0.214 | -1.112 | -0.097 | 1.478 | -0.901 | -0.078 | 1.196 |
71 | -0.164 | -0.014 | 0.214 | -1.111 | -0.096 | 1.477 | -0.898 | -0.078 | 1.192 |
72 | -0.164 | -0.014 | 0.215 | -1.110 | -0.096 | 1.475 | -0.895 | -0.077 | 1.188 |
73 | -0.164 | -0.014 | 0.215 | -1.108 | -0.096 | 1.473 | -0.892 | -0.077 | 1.184 |
74 | -0.164 | -0.014 | 0.215 | -1.107 | -0.096 | 1.472 | -0.890 | -0.077 | 1.181 |
75 | -0.164 | -0.014 | 0.215 | -1.106 | -0.096 | 1.470 | -0.887 | -0.077 | 1.177 |
76 | -0.164 | -0.014 | 0.215 | -1.104 | -0.096 | 1.468 | -0.884 | -0.077 | 1.174 |
77 | -0.164 | -0.014 | 0.215 | -1.103 | -0.096 | 1.467 | -0.882 | -0.076 | 1.170 |
78 | -0.164 | -0.014 | 0.215 | -1.102 | -0.096 | 1.465 | -0.879 | -0.076 | 1.167 |
79 | -0.164 | -0.014 | 0.215 | -1.100 | -0.096 | 1.463 | -0.876 | -0.076 | 1.164 |
80 | -0.164 | -0.014 | 0.215 | -1.099 | -0.095 | 1.461 | -0.874 | -0.076 | 1.161 |
81 | -0.164 | -0.014 | 0.215 | -1.097 | -0.095 | 1.460 | -0.872 | -0.075 | 1.158 |
82 | -0.164 | -0.014 | 0.215 | -1.096 | -0.095 | 1.458 | -0.869 | -0.075 | 1.155 |
83 | -0.164 | -0.014 | 0.215 | -1.095 | -0.095 | 1.456 | -0.867 | -0.075 | 1.152 |
84 | -0.164 | -0.014 | 0.215 | -1.093 | -0.095 | 1.454 | -0.865 | -0.075 | 1.149 |
85 | -0.164 | -0.014 | 0.215 | -1.092 | -0.095 | 1.452 | -0.863 | -0.075 | 1.146 |
86 | -0.164 | -0.014 | 0.215 | -1.090 | -0.095 | 1.450 | -0.860 | -0.074 | 1.143 |
87 | -0.164 | -0.014 | 0.215 | -1.089 | -0.095 | 1.448 | -0.858 | -0.074 | 1.140 |
88 | -0.164 | -0.014 | 0.215 | -1.087 | -0.094 | 1.446 | -0.856 | -0.074 | 1.137 |
89 | -0.164 | -0.014 | 0.215 | -1.085 | -0.094 | 1.444 | -0.854 | -0.074 | 1.135 |
90 | -0.164 | -0.014 | 0.215 | -1.084 | -0.094 | 1.442 | -0.852 | -0.074 | 1.132 |
91 | -0.164 | -0.014 | 0.214 | -1.082 | -0.094 | 1.440 | -0.850 | -0.074 | 1.130 |
92 | -0.163 | -0.014 | 0.214 | -1.081 | -0.094 | 1.438 | -0.848 | -0.073 | 1.127 |
93 | -0.163 | -0.014 | 0.214 | -1.079 | -0.094 | 1.436 | -0.846 | -0.073 | 1.124 |
94 | -0.163 | -0.014 | 0.214 | -1.078 | -0.094 | 1.434 | -0.844 | -0.073 | 1.122 |
95 | -0.163 | -0.014 | 0.214 | -1.076 | -0.093 | 1.432 | -0.842 | -0.073 | 1.120 |
96 | -0.163 | -0.014 | 0.214 | -1.074 | -0.093 | 1.430 | -0.840 | -0.073 | 1.117 |
97 | -0.163 | -0.014 | 0.213 | -1.073 | -0.093 | 1.428 | -0.839 | -0.073 | 1.115 |
98 | -0.163 | -0.014 | 0.213 | -1.071 | -0.093 | 1.426 | -0.837 | -0.072 | 1.112 |
99 | -0.162 | -0.014 | 0.213 | -1.070 | -0.093 | 1.424 | -0.835 | -0.072 | 1.110 |
100 | -0.162 | -0.014 | 0.213 | -1.068 | -0.093 | 1.422 | -0.833 | -0.072 | 1.108 |
101 | -0.162 | -0.014 | 0.213 | -1.066 | -0.093 | 1.420 | -0.832 | -0.072 | 1.106 |
102 | -0.162 | -0.014 | 0.212 | -1.065 | -0.092 | 1.418 | -0.830 | -0.072 | 1.103 |
103 | -0.162 | -0.014 | 0.212 | -1.063 | -0.092 | 1.416 | -0.828 | -0.072 | 1.101 |
104 | -0.161 | -0.014 | 0.212 | -1.061 | -0.092 | 1.414 | -0.826 | -0.072 | 1.099 |
105 | -0.161 | -0.014 | 0.212 | -1.060 | -0.092 | 1.411 | -0.825 | -0.071 | 1.097 |
106 | -0.161 | -0.014 | 0.212 | -1.058 | -0.092 | 1.409 | -0.823 | -0.071 | 1.095 |
107 | -0.161 | -0.014 | 0.211 | -1.056 | -0.092 | 1.407 | -0.821 | -0.071 | 1.092 |
108 | -0.161 | -0.014 | 0.211 | -1.055 | -0.092 | 1.405 | -0.820 | -0.071 | 1.090 |
109 | -0.160 | -0.014 | 0.211 | -1.053 | -0.091 | 1.403 | -0.818 | -0.071 | 1.088 |
110 | -0.160 | -0.014 | 0.211 | -1.052 | -0.091 | 1.401 | -0.817 | -0.071 | 1.086 |
111 | -0.160 | -0.014 | 0.210 | -1.050 | -0.091 | 1.399 | -0.815 | -0.071 | 1.084 |
112 | -0.160 | -0.014 | 0.210 | -1.048 | -0.091 | 1.397 | -0.813 | -0.070 | 1.082 |
113 | -0.160 | -0.014 | 0.210 | -1.047 | -0.091 | 1.394 | -0.812 | -0.070 | 1.080 |
114 | -0.159 | -0.014 | 0.209 | -1.045 | -0.091 | 1.392 | -0.810 | -0.070 | 1.078 |
115 | -0.159 | -0.014 | 0.209 | -1.043 | -0.091 | 1.390 | -0.809 | -0.070 | 1.076 |
116 | -0.159 | -0.014 | 0.209 | -1.042 | -0.090 | 1.388 | -0.807 | -0.070 | 1.074 |
117 | -0.159 | -0.014 | 0.209 | -1.040 | -0.090 | 1.386 | -0.806 | -0.070 | 1.072 |
118 | -0.159 | -0.014 | 0.208 | -1.038 | -0.090 | 1.384 | -0.804 | -0.070 | 1.070 |
119 | -0.158 | -0.014 | 0.208 | -1.037 | -0.090 | 1.381 | -0.803 | -0.070 | 1.068 |
120 | -0.158 | -0.014 | 0.208 | -1.035 | -0.090 | 1.379 | -0.801 | -0.069 | 1.066 |
121 | -0.158 | -0.014 | 0.208 | -1.033 | -0.090 | 1.377 | -0.800 | -0.069 | 1.064 |
122 | -0.158 | -0.014 | 0.207 | -1.032 | -0.090 | 1.375 | -0.798 | -0.069 | 1.062 |
123 | -0.157 | -0.014 | 0.207 | -1.030 | -0.089 | 1.373 | -0.797 | -0.069 | 1.061 |
124 | -0.157 | -0.014 | 0.207 | -1.028 | -0.089 | 1.371 | -0.795 | -0.069 | 1.059 |
125 | -0.157 | -0.014 | 0.206 | -1.027 | -0.089 | 1.369 | -0.794 | -0.069 | 1.057 |
126 | -0.157 | -0.013 | 0.206 | -1.025 | -0.089 | 1.366 | -0.793 | -0.069 | 1.055 |
127 | -0.156 | -0.013 | 0.206 | -1.023 | -0.089 | 1.364 | -0.791 | -0.069 | 1.053 |
128 | -0.156 | -0.013 | 0.206 | -1.022 | -0.089 | 1.362 | -0.790 | -0.068 | 1.051 |
129 | -0.156 | -0.013 | 0.205 | -1.020 | -0.089 | 1.360 | -0.788 | -0.068 | 1.049 |
130 | -0.156 | -0.013 | 0.205 | -1.018 | -0.088 | 1.358 | -0.787 | -0.068 | 1.048 |
131 | -0.156 | -0.013 | 0.205 | -1.017 | -0.088 | 1.356 | -0.786 | -0.068 | 1.046 |
132 | -0.155 | -0.013 | 0.204 | -1.015 | -0.088 | 1.353 | -0.784 | -0.068 | 1.044 |
133 | -0.155 | -0.013 | 0.204 | -1.013 | -0.088 | 1.351 | -0.783 | -0.068 | 1.042 |
134 | -0.155 | -0.013 | 0.204 | -1.012 | -0.088 | 1.349 | -0.781 | -0.068 | 1.040 |
135 | -0.155 | -0.013 | 0.203 | -1.010 | -0.088 | 1.347 | -0.780 | -0.068 | 1.039 |
136 | -0.154 | -0.013 | 0.203 | -1.008 | -0.088 | 1.345 | -0.779 | -0.067 | 1.037 |
137 | -0.154 | -0.013 | 0.203 | -1.007 | -0.087 | 1.343 | -0.777 | -0.067 | 1.035 |
138 | -0.154 | -0.013 | 0.203 | -1.005 | -0.087 | 1.341 | -0.776 | -0.067 | 1.033 |
139 | -0.154 | -0.013 | 0.202 | -1.003 | -0.087 | 1.338 | -0.775 | -0.067 | 1.032 |
140 | -0.153 | -0.013 | 0.202 | -1.002 | -0.087 | 1.336 | -0.773 | -0.067 | 1.030 |
141 | -0.153 | -0.013 | 0.202 | -1.000 | -0.087 | 1.334 | -0.772 | -0.067 | 1.028 |
142 | -0.153 | -0.013 | 0.201 | -0.998 | -0.087 | 1.332 | -0.771 | -0.067 | 1.026 |
143 | -0.153 | -0.013 | 0.201 | -0.997 | -0.087 | 1.330 | -0.769 | -0.067 | 1.025 |
144 | -0.152 | -0.013 | 0.201 | -0.995 | -0.086 | 1.328 | -0.768 | -0.066 | 1.023 |
145 | -0.152 | -0.013 | 0.200 | -0.993 | -0.086 | 1.326 | -0.767 | -0.066 | 1.021 |
146 | -0.152 | -0.013 | 0.200 | -0.992 | -0.086 | 1.324 | -0.765 | -0.066 | 1.020 |
147 | -0.152 | -0.013 | 0.200 | -0.990 | -0.086 | 1.321 | -0.764 | -0.066 | 1.018 |
148 | -0.151 | -0.013 | 0.199 | -0.988 | -0.086 | 1.319 | -0.763 | -0.066 | 1.016 |
149 | -0.151 | -0.013 | 0.199 | -0.987 | -0.086 | 1.317 | -0.761 | -0.066 | 1.014 |
150 | -0.151 | -0.013 | 0.199 | -0.985 | -0.086 | 1.315 | -0.760 | -0.066 | 1.013 |
151 | -0.151 | -0.013 | 0.199 | -0.984 | -0.085 | 1.313 | -0.759 | -0.066 | 1.011 |
152 | -0.150 | -0.013 | 0.198 | -0.982 | -0.085 | 1.311 | -0.757 | -0.066 | 1.009 |
153 | -0.150 | -0.013 | 0.198 | -0.980 | -0.085 | 1.309 | -0.756 | -0.065 | 1.008 |
154 | -0.150 | -0.013 | 0.198 | -0.979 | -0.085 | 1.307 | -0.755 | -0.065 | 1.006 |
155 | -0.150 | -0.013 | 0.197 | -0.977 | -0.085 | 1.304 | -0.754 | -0.065 | 1.004 |
156 | -0.149 | -0.013 | 0.197 | -0.975 | -0.085 | 1.302 | -0.752 | -0.065 | 1.003 |
157 | -0.149 | -0.013 | 0.197 | -0.974 | -0.085 | 1.300 | -0.751 | -0.065 | 1.001 |
158 | -0.149 | -0.013 | 0.196 | -0.972 | -0.084 | 1.298 | -0.750 | -0.065 | 0.999 |
159 | -0.149 | -0.013 | 0.196 | -0.971 | -0.084 | 1.296 | -0.748 | -0.065 | 0.998 |
160 | -0.148 | -0.013 | 0.196 | -0.969 | -0.084 | 1.294 | -0.747 | -0.065 | 0.996 |
161 | -0.148 | -0.013 | 0.195 | -0.967 | -0.084 | 1.292 | -0.746 | -0.065 | 0.994 |
162 | -0.148 | -0.013 | 0.195 | -0.966 | -0.084 | 1.290 | -0.745 | -0.064 | 0.993 |
163 | -0.148 | -0.013 | 0.195 | -0.964 | -0.084 | 1.288 | -0.743 | -0.064 | 0.991 |
164 | -0.147 | -0.013 | 0.195 | -0.963 | -0.084 | 1.286 | -0.742 | -0.064 | 0.990 |
165 | -0.147 | -0.013 | 0.194 | -0.961 | -0.083 | 1.284 | -0.741 | -0.064 | 0.988 |
166 | -0.147 | -0.013 | 0.194 | -0.959 | -0.083 | 1.281 | -0.740 | -0.064 | 0.986 |
167 | -0.147 | -0.013 | 0.194 | -0.958 | -0.083 | 1.279 | -0.738 | -0.064 | 0.985 |
168 | -0.147 | -0.013 | 0.193 | -0.956 | -0.083 | 1.277 | -0.737 | -0.064 | 0.983 |
169 | -0.146 | -0.013 | 0.193 | -0.955 | -0.083 | 1.275 | -0.736 | -0.064 | 0.981 |
170 | -0.146 | -0.013 | 0.193 | -0.953 | -0.083 | 1.273 | -0.735 | -0.064 | 0.980 |
171 | -0.146 | -0.013 | 0.192 | -0.951 | -0.083 | 1.271 | -0.733 | -0.064 | 0.978 |
172 | -0.146 | -0.013 | 0.192 | -0.950 | -0.082 | 1.269 | -0.732 | -0.063 | 0.977 |
173 | -0.145 | -0.013 | 0.192 | -0.948 | -0.082 | 1.267 | -0.731 | -0.063 | 0.975 |
174 | -0.145 | -0.013 | 0.191 | -0.947 | -0.082 | 1.265 | -0.730 | -0.063 | 0.973 |
175 | -0.145 | -0.012 | 0.191 | -0.945 | -0.082 | 1.263 | -0.729 | -0.063 | 0.972 |
176 | -0.145 | -0.012 | 0.191 | -0.944 | -0.082 | 1.261 | -0.727 | -0.063 | 0.970 |
177 | -0.144 | -0.012 | 0.191 | -0.942 | -0.082 | 1.259 | -0.726 | -0.063 | 0.969 |
178 | -0.144 | -0.012 | 0.190 | -0.940 | -0.082 | 1.257 | -0.725 | -0.063 | 0.967 |
179 | -0.144 | -0.012 | 0.190 | -0.939 | -0.082 | 1.255 | -0.724 | -0.063 | 0.965 |
180 | -0.144 | -0.012 | 0.190 | -0.937 | -0.081 | 1.253 | -0.722 | -0.063 | 0.964 |
181 | -0.143 | -0.012 | 0.189 | -0.936 | -0.081 | 1.251 | -0.721 | -0.062 | 0.962 |
182 | -0.143 | -0.012 | 0.189 | -0.934 | -0.081 | 1.249 | -0.720 | -0.062 | 0.961 |
183 | -0.143 | -0.012 | 0.189 | -0.933 | -0.081 | 1.247 | -0.719 | -0.062 | 0.959 |
184 | -0.143 | -0.012 | 0.188 | -0.931 | -0.081 | 1.245 | -0.718 | -0.062 | 0.958 |
185 | -0.142 | -0.012 | 0.188 | -0.930 | -0.081 | 1.243 | -0.716 | -0.062 | 0.956 |
186 | -0.142 | -0.012 | 0.188 | -0.928 | -0.081 | 1.241 | -0.715 | -0.062 | 0.954 |
187 | -0.142 | -0.012 | 0.188 | -0.926 | -0.080 | 1.239 | -0.714 | -0.062 | 0.953 |
188 | -0.142 | -0.012 | 0.187 | -0.925 | -0.080 | 1.237 | -0.713 | -0.062 | 0.951 |
189 | -0.141 | -0.012 | 0.187 | -0.923 | -0.080 | 1.235 | -0.712 | -0.062 | 0.950 |
190 | -0.141 | -0.012 | 0.187 | -0.922 | -0.080 | 1.233 | -0.710 | -0.062 | 0.948 |
191 | -0.141 | -0.012 | 0.186 | -0.920 | -0.080 | 1.231 | -0.709 | -0.061 | 0.947 |
192 | -0.141 | -0.012 | 0.186 | -0.919 | -0.080 | 1.229 | -0.708 | -0.061 | 0.945 |
193 | -0.141 | -0.012 | 0.186 | -0.917 | -0.080 | 1.227 | -0.707 | -0.061 | 0.944 |
194 | -0.140 | -0.012 | 0.185 | -0.916 | -0.080 | 1.225 | -0.706 | -0.061 | 0.942 |
195 | -0.140 | -0.012 | 0.185 | -0.914 | -0.079 | 1.223 | -0.704 | -0.061 | 0.941 |
196 | -0.140 | -0.012 | 0.185 | -0.913 | -0.079 | 1.221 | -0.703 | -0.061 | 0.939 |
197 | -0.140 | -0.012 | 0.185 | -0.911 | -0.079 | 1.219 | -0.702 | -0.061 | 0.937 |
198 | -0.139 | -0.012 | 0.184 | -0.910 | -0.079 | 1.217 | -0.701 | -0.061 | 0.936 |
199 | -0.139 | -0.012 | 0.184 | -0.908 | -0.079 | 1.215 | -0.700 | -0.061 | 0.934 |
200 | -0.139 | -0.012 | 0.184 | -0.907 | -0.079 | 1.213 | -0.699 | -0.060 | 0.933 |
201 | -0.139 | -0.012 | 0.183 | -0.905 | -0.079 | 1.211 | -0.697 | -0.060 | 0.931 |
202 | -0.138 | -0.012 | 0.183 | -0.904 | -0.078 | 1.209 | -0.696 | -0.060 | 0.930 |
203 | -0.138 | -0.012 | 0.183 | -0.902 | -0.078 | 1.207 | -0.695 | -0.060 | 0.928 |
204 | -0.138 | -0.012 | 0.182 | -0.901 | -0.078 | 1.205 | -0.694 | -0.060 | 0.927 |
205 | -0.138 | -0.012 | 0.182 | -0.899 | -0.078 | 1.203 | -0.693 | -0.060 | 0.925 |
206 | -0.138 | -0.012 | 0.182 | -0.898 | -0.078 | 1.201 | -0.692 | -0.060 | 0.924 |
207 | -0.137 | -0.012 | 0.182 | -0.896 | -0.078 | 1.199 | -0.690 | -0.060 | 0.922 |
208 | -0.137 | -0.012 | 0.181 | -0.895 | -0.078 | 1.197 | -0.689 | -0.060 | 0.921 |
209 | -0.137 | -0.012 | 0.181 | -0.893 | -0.078 | 1.195 | -0.688 | -0.060 | 0.919 |
210 | -0.137 | -0.012 | 0.181 | -0.892 | -0.077 | 1.193 | -0.687 | -0.059 | 0.918 |
211 | -0.136 | -0.012 | 0.180 | -0.890 | -0.077 | 1.191 | -0.686 | -0.059 | 0.916 |
212 | -0.136 | -0.012 | 0.180 | -0.889 | -0.077 | 1.189 | -0.685 | -0.059 | 0.915 |
213 | -0.136 | -0.012 | 0.180 | -0.887 | -0.077 | 1.187 | -0.684 | -0.059 | 0.913 |
214 | -0.136 | -0.012 | 0.180 | -0.886 | -0.077 | 1.185 | -0.682 | -0.059 | 0.912 |
215 | -0.135 | -0.012 | 0.179 | -0.884 | -0.077 | 1.183 | -0.681 | -0.059 | 0.910 |
216 | -0.135 | -0.012 | 0.179 | -0.883 | -0.077 | 1.181 | -0.680 | -0.059 | 0.909 |
217 | -0.135 | -0.012 | 0.179 | -0.881 | -0.077 | 1.180 | -0.679 | -0.059 | 0.907 |
218 | -0.135 | -0.012 | 0.178 | -0.880 | -0.076 | 1.178 | -0.678 | -0.059 | 0.906 |
219 | -0.135 | -0.012 | 0.178 | -0.878 | -0.076 | 1.176 | -0.677 | -0.059 | 0.904 |
220 | -0.134 | -0.012 | 0.178 | -0.877 | -0.076 | 1.174 | -0.676 | -0.058 | 0.903 |
221 | -0.134 | -0.012 | 0.178 | -0.875 | -0.076 | 1.172 | -0.675 | -0.058 | 0.901 |
222 | -0.134 | -0.012 | 0.177 | -0.874 | -0.076 | 1.170 | -0.673 | -0.058 | 0.900 |
223 | -0.134 | -0.012 | 0.177 | -0.873 | -0.076 | 1.168 | -0.672 | -0.058 | 0.899 |
224 | -0.133 | -0.012 | 0.177 | -0.871 | -0.076 | 1.166 | -0.671 | -0.058 | 0.897 |
225 | -0.133 | -0.011 | 0.176 | -0.870 | -0.076 | 1.164 | -0.670 | -0.058 | 0.896 |
226 | -0.133 | -0.011 | 0.176 | -0.868 | -0.075 | 1.162 | -0.669 | -0.058 | 0.894 |
227 | -0.133 | -0.011 | 0.176 | -0.867 | -0.075 | 1.161 | -0.668 | -0.058 | 0.893 |
228 | -0.133 | -0.011 | 0.176 | -0.865 | -0.075 | 1.159 | -0.667 | -0.058 | 0.891 |
229 | -0.132 | -0.011 | 0.175 | -0.864 | -0.075 | 1.157 | -0.666 | -0.058 | 0.890 |
230 | -0.132 | -0.011 | 0.175 | -0.862 | -0.075 | 1.155 | -0.664 | -0.058 | 0.888 |
231 | -0.132 | -0.011 | 0.175 | -0.861 | -0.075 | 1.153 | -0.663 | -0.057 | 0.887 |
232 | -0.132 | -0.011 | 0.174 | -0.860 | -0.075 | 1.151 | -0.662 | -0.057 | 0.885 |
233 | -0.131 | -0.011 | 0.174 | -0.858 | -0.075 | 1.149 | -0.661 | -0.057 | 0.884 |
234 | -0.131 | -0.011 | 0.174 | -0.857 | -0.074 | 1.147 | -0.660 | -0.057 | 0.883 |
235 | -0.131 | -0.011 | 0.174 | -0.855 | -0.074 | 1.145 | -0.659 | -0.057 | 0.881 |
236 | -0.131 | -0.011 | 0.173 | -0.854 | -0.074 | 1.144 | -0.658 | -0.057 | 0.880 |
237 | -0.131 | -0.011 | 0.173 | -0.852 | -0.074 | 1.142 | -0.657 | -0.057 | 0.878 |
238 | -0.130 | -0.011 | 0.173 | -0.851 | -0.074 | 1.140 | -0.656 | -0.057 | 0.877 |
239 | -0.130 | -0.011 | 0.172 | -0.850 | -0.074 | 1.138 | -0.655 | -0.057 | 0.875 |
240 | -0.130 | -0.011 | 0.172 | -0.848 | -0.074 | 1.136 | -0.653 | -0.057 | 0.874 |
241 | -0.130 | -0.011 | 0.172 | -0.847 | -0.074 | 1.134 | -0.652 | -0.056 | 0.873 |
242 | -0.129 | -0.011 | 0.172 | -0.845 | -0.073 | 1.132 | -0.651 | -0.056 | 0.871 |
243 | -0.129 | -0.011 | 0.171 | -0.844 | -0.073 | 1.131 | -0.650 | -0.056 | 0.870 |
244 | -0.129 | -0.011 | 0.171 | -0.843 | -0.073 | 1.129 | -0.649 | -0.056 | 0.868 |
245 | -0.129 | -0.011 | 0.171 | -0.841 | -0.073 | 1.127 | -0.648 | -0.056 | 0.867 |
246 | -0.129 | -0.011 | 0.171 | -0.840 | -0.073 | 1.125 | -0.647 | -0.056 | 0.866 |
247 | -0.128 | -0.011 | 0.170 | -0.838 | -0.073 | 1.123 | -0.646 | -0.056 | 0.864 |
248 | -0.128 | -0.011 | 0.170 | -0.837 | -0.073 | 1.121 | -0.645 | -0.056 | 0.863 |
249 | -0.128 | -0.011 | 0.170 | -0.836 | -0.073 | 1.120 | -0.644 | -0.056 | 0.861 |
250 | -0.128 | -0.011 | 0.169 | -0.834 | -0.072 | 1.118 | -0.643 | -0.056 | 0.860 |
251 | -0.128 | -0.011 | 0.169 | -0.833 | -0.072 | 1.116 | -0.642 | -0.056 | 0.859 |
252 | -0.127 | -0.011 | 0.169 | -0.831 | -0.072 | 1.114 | -0.641 | -0.055 | 0.857 |
253 | -0.127 | -0.011 | 0.169 | -0.830 | -0.072 | 1.112 | -0.639 | -0.055 | 0.856 |
254 | -0.127 | -0.011 | 0.168 | -0.829 | -0.072 | 1.111 | -0.638 | -0.055 | 0.854 |
255 | -0.127 | -0.011 | 0.168 | -0.827 | -0.072 | 1.109 | -0.637 | -0.055 | 0.853 |
256 | -0.126 | -0.011 | 0.168 | -0.826 | -0.072 | 1.107 | -0.636 | -0.055 | 0.852 |
257 | -0.126 | -0.011 | 0.167 | -0.824 | -0.072 | 1.105 | -0.635 | -0.055 | 0.850 |
258 | -0.126 | -0.011 | 0.167 | -0.823 | -0.071 | 1.103 | -0.634 | -0.055 | 0.849 |
259 | -0.126 | -0.011 | 0.167 | -0.822 | -0.071 | 1.102 | -0.633 | -0.055 | 0.847 |
260 | -0.126 | -0.011 | 0.167 | -0.820 | -0.071 | 1.100 | -0.632 | -0.055 | 0.846 |
261 | -0.125 | -0.011 | 0.166 | -0.819 | -0.071 | 1.098 | -0.631 | -0.055 | 0.845 |
262 | -0.125 | -0.011 | 0.166 | -0.818 | -0.071 | 1.096 | -0.630 | -0.055 | 0.843 |
263 | -0.125 | -0.011 | 0.166 | -0.816 | -0.071 | 1.094 | -0.629 | -0.054 | 0.842 |
264 | -0.125 | -0.011 | 0.166 | -0.815 | -0.071 | 1.093 | -0.628 | -0.054 | 0.841 |
265 | -0.125 | -0.011 | 0.165 | -0.814 | -0.071 | 1.091 | -0.627 | -0.054 | 0.839 |
266 | -0.124 | -0.011 | 0.165 | -0.812 | -0.071 | 1.089 | -0.626 | -0.054 | 0.838 |
267 | -0.124 | -0.011 | 0.165 | -0.811 | -0.070 | 1.087 | -0.625 | -0.054 | 0.836 |
268 | -0.124 | -0.011 | 0.165 | -0.810 | -0.070 | 1.086 | -0.624 | -0.054 | 0.835 |
269 | -0.124 | -0.011 | 0.164 | -0.808 | -0.070 | 1.084 | -0.623 | -0.054 | 0.834 |
270 | -0.124 | -0.011 | 0.164 | -0.807 | -0.070 | 1.082 | -0.622 | -0.054 | 0.832 |
271 | -0.123 | -0.011 | 0.164 | -0.805 | -0.070 | 1.080 | -0.621 | -0.054 | 0.831 |
272 | -0.123 | -0.011 | 0.163 | -0.804 | -0.070 | 1.078 | -0.620 | -0.054 | 0.830 |
273 | -0.123 | -0.011 | 0.163 | -0.803 | -0.070 | 1.077 | -0.618 | -0.054 | 0.828 |
274 | -0.123 | -0.011 | 0.163 | -0.801 | -0.070 | 1.075 | -0.617 | -0.053 | 0.827 |
275 | -0.123 | -0.011 | 0.163 | -0.800 | -0.069 | 1.073 | -0.616 | -0.053 | 0.826 |
276 | -0.122 | -0.011 | 0.162 | -0.799 | -0.069 | 1.071 | -0.615 | -0.053 | 0.824 |
277 | -0.122 | -0.011 | 0.162 | -0.797 | -0.069 | 1.070 | -0.614 | -0.053 | 0.823 |
278 | -0.122 | -0.011 | 0.162 | -0.796 | -0.069 | 1.068 | -0.613 | -0.053 | 0.822 |
279 | -0.122 | -0.010 | 0.162 | -0.795 | -0.069 | 1.066 | -0.612 | -0.053 | 0.820 |
280 | -0.122 | -0.010 | 0.161 | -0.793 | -0.069 | 1.064 | -0.611 | -0.053 | 0.819 |
281 | -0.121 | -0.010 | 0.161 | -0.792 | -0.069 | 1.063 | -0.610 | -0.053 | 0.818 |
282 | -0.121 | -0.010 | 0.161 | -0.791 | -0.069 | 1.061 | -0.609 | -0.053 | 0.816 |
283 | -0.121 | -0.010 | 0.161 | -0.790 | -0.069 | 1.059 | -0.608 | -0.053 | 0.815 |
284 | -0.121 | -0.010 | 0.160 | -0.788 | -0.068 | 1.058 | -0.607 | -0.053 | 0.814 |
285 | -0.121 | -0.010 | 0.160 | -0.787 | -0.068 | 1.056 | -0.606 | -0.052 | 0.812 |
286 | -0.120 | -0.010 | 0.160 | -0.786 | -0.068 | 1.054 | -0.605 | -0.052 | 0.811 |
287 | -0.120 | -0.010 | 0.160 | -0.784 | -0.068 | 1.052 | -0.604 | -0.052 | 0.810 |
288 | -0.120 | -0.010 | 0.159 | -0.783 | -0.068 | 1.051 | -0.603 | -0.052 | 0.808 |
289 | -0.120 | -0.010 | 0.159 | -0.782 | -0.068 | 1.049 | -0.602 | -0.052 | 0.807 |
290 | -0.119 | -0.010 | 0.159 | -0.780 | -0.068 | 1.047 | -0.601 | -0.052 | 0.806 |
291 | -0.119 | -0.010 | 0.159 | -0.779 | -0.068 | 1.046 | -0.600 | -0.052 | 0.804 |
292 | -0.119 | -0.010 | 0.158 | -0.778 | -0.068 | 1.044 | -0.599 | -0.052 | 0.803 |
293 | -0.119 | -0.010 | 0.158 | -0.776 | -0.067 | 1.042 | -0.598 | -0.052 | 0.802 |
294 | -0.119 | -0.010 | 0.158 | -0.775 | -0.067 | 1.040 | -0.597 | -0.052 | 0.800 |
295 | -0.119 | -0.010 | 0.157 | -0.774 | -0.067 | 1.039 | -0.596 | -0.052 | 0.799 |
296 | -0.118 | -0.010 | 0.157 | -0.773 | -0.067 | 1.037 | -0.595 | -0.052 | 0.798 |
297 | -0.118 | -0.010 | 0.157 | -0.771 | -0.067 | 1.035 | -0.594 | -0.051 | 0.797 |
298 | -0.118 | -0.010 | 0.157 | -0.770 | -0.067 | 1.034 | -0.593 | -0.051 | 0.795 |
299 | -0.118 | -0.010 | 0.156 | -0.769 | -0.067 | 1.032 | -0.592 | -0.051 | 0.794 |
300 | -0.118 | -0.010 | 0.156 | -0.767 | -0.067 | 1.030 | -0.591 | -0.051 | 0.793 |
301 | -0.117 | -0.010 | 0.156 | -0.766 | -0.067 | 1.029 | -0.590 | -0.051 | 0.791 |
302 | -0.117 | -0.010 | 0.156 | -0.765 | -0.066 | 1.027 | -0.589 | -0.051 | 0.790 |
303 | -0.117 | -0.010 | 0.155 | -0.764 | -0.066 | 1.025 | -0.588 | -0.051 | 0.789 |
304 | -0.117 | -0.010 | 0.155 | -0.762 | -0.066 | 1.024 | -0.587 | -0.051 | 0.787 |
305 | -0.117 | -0.010 | 0.155 | -0.761 | -0.066 | 1.022 | -0.586 | -0.051 | 0.786 |
306 | -0.116 | -0.010 | 0.155 | -0.760 | -0.066 | 1.020 | -0.585 | -0.051 | 0.785 |
307 | -0.116 | -0.010 | 0.154 | -0.759 | -0.066 | 1.019 | -0.584 | -0.051 | 0.784 |
308 | -0.116 | -0.010 | 0.154 | -0.757 | -0.066 | 1.017 | -0.583 | -0.051 | 0.782 |
309 | -0.116 | -0.010 | 0.154 | -0.756 | -0.066 | 1.015 | -0.582 | -0.050 | 0.781 |
310 | -0.116 | -0.010 | 0.154 | -0.755 | -0.066 | 1.014 | -0.582 | -0.050 | 0.780 |
311 | -0.115 | -0.010 | 0.153 | -0.754 | -0.065 | 1.012 | -0.581 | -0.050 | 0.779 |
312 | -0.115 | -0.010 | 0.153 | -0.752 | -0.065 | 1.010 | -0.580 | -0.050 | 0.777 |
313 | -0.115 | -0.010 | 0.153 | -0.751 | -0.065 | 1.009 | -0.579 | -0.050 | 0.776 |
314 | -0.115 | -0.010 | 0.153 | -0.750 | -0.065 | 1.007 | -0.578 | -0.050 | 0.775 |
315 | -0.115 | -0.010 | 0.152 | -0.749 | -0.065 | 1.005 | -0.577 | -0.050 | 0.773 |
316 | -0.114 | -0.010 | 0.152 | -0.747 | -0.065 | 1.004 | -0.576 | -0.050 | 0.772 |
317 | -0.114 | -0.010 | 0.152 | -0.746 | -0.065 | 1.002 | -0.575 | -0.050 | 0.771 |
318 | -0.114 | -0.010 | 0.152 | -0.745 | -0.065 | 1.000 | -0.574 | -0.050 | 0.770 |
319 | -0.114 | -0.010 | 0.151 | -0.744 | -0.065 | 0.999 | -0.573 | -0.050 | 0.768 |
320 | -0.114 | -0.010 | 0.151 | -0.742 | -0.064 | 0.997 | -0.572 | -0.050 | 0.767 |
321 | -0.113 | -0.010 | 0.151 | -0.741 | -0.064 | 0.996 | -0.571 | -0.049 | 0.766 |
322 | -0.113 | -0.010 | 0.151 | -0.740 | -0.064 | 0.994 | -0.570 | -0.049 | 0.765 |
323 | -0.113 | -0.010 | 0.150 | -0.739 | -0.064 | 0.992 | -0.569 | -0.049 | 0.763 |
324 | -0.113 | -0.010 | 0.150 | -0.737 | -0.064 | 0.991 | -0.568 | -0.049 | 0.762 |
325 | -0.113 | -0.010 | 0.150 | -0.736 | -0.064 | 0.989 | -0.567 | -0.049 | 0.761 |
326 | -0.113 | -0.010 | 0.150 | -0.735 | -0.064 | 0.988 | -0.566 | -0.049 | 0.760 |
327 | -0.112 | -0.010 | 0.150 | -0.734 | -0.064 | 0.986 | -0.565 | -0.049 | 0.758 |
328 | -0.112 | -0.010 | 0.149 | -0.733 | -0.064 | 0.984 | -0.564 | -0.049 | 0.757 |
329 | -0.112 | -0.010 | 0.149 | -0.731 | -0.063 | 0.983 | -0.563 | -0.049 | 0.756 |
330 | -0.112 | -0.010 | 0.149 | -0.730 | -0.063 | 0.981 | -0.562 | -0.049 | 0.755 |
331 | -0.112 | -0.010 | 0.149 | -0.729 | -0.063 | 0.979 | -0.562 | -0.049 | 0.754 |
332 | -0.111 | -0.010 | 0.148 | -0.728 | -0.063 | 0.978 | -0.561 | -0.049 | 0.752 |
333 | -0.111 | -0.010 | 0.148 | -0.726 | -0.063 | 0.976 | -0.560 | -0.048 | 0.751 |
334 | -0.111 | -0.010 | 0.148 | -0.725 | -0.063 | 0.975 | -0.559 | -0.048 | 0.750 |
335 | -0.111 | -0.010 | 0.148 | -0.724 | -0.063 | 0.973 | -0.558 | -0.048 | 0.749 |
336 | -0.111 | -0.010 | 0.147 | -0.723 | -0.063 | 0.972 | -0.557 | -0.048 | 0.747 |
337 | -0.110 | -0.010 | 0.147 | -0.722 | -0.063 | 0.970 | -0.556 | -0.048 | 0.746 |
338 | -0.110 | -0.010 | 0.147 | -0.720 | -0.063 | 0.968 | -0.555 | -0.048 | 0.745 |
339 | -0.110 | -0.009 | 0.147 | -0.719 | -0.062 | 0.967 | -0.554 | -0.048 | 0.744 |
340 | -0.110 | -0.009 | 0.146 | -0.718 | -0.062 | 0.965 | -0.553 | -0.048 | 0.743 |
341 | -0.110 | -0.009 | 0.146 | -0.717 | -0.062 | 0.964 | -0.552 | -0.048 | 0.741 |
342 | -0.110 | -0.009 | 0.146 | -0.716 | -0.062 | 0.962 | -0.551 | -0.048 | 0.740 |
343 | -0.109 | -0.009 | 0.146 | -0.714 | -0.062 | 0.960 | -0.550 | -0.048 | 0.739 |
344 | -0.109 | -0.009 | 0.145 | -0.713 | -0.062 | 0.959 | -0.550 | -0.048 | 0.738 |
345 | -0.109 | -0.009 | 0.145 | -0.712 | -0.062 | 0.957 | -0.549 | -0.047 | 0.737 |
346 | -0.109 | -0.009 | 0.145 | -0.711 | -0.062 | 0.956 | -0.548 | -0.047 | 0.735 |
347 | -0.109 | -0.009 | 0.145 | -0.710 | -0.062 | 0.954 | -0.547 | -0.047 | 0.734 |
348 | -0.108 | -0.009 | 0.145 | -0.709 | -0.061 | 0.953 | -0.546 | -0.047 | 0.733 |
349 | -0.108 | -0.009 | 0.144 | -0.707 | -0.061 | 0.951 | -0.545 | -0.047 | 0.732 |
350 | -0.108 | -0.009 | 0.144 | -0.706 | -0.061 | 0.950 | -0.544 | -0.047 | 0.731 |
351 | -0.108 | -0.009 | 0.144 | -0.705 | -0.061 | 0.948 | -0.543 | -0.047 | 0.729 |
352 | -0.108 | -0.009 | 0.144 | -0.704 | -0.061 | 0.946 | -0.542 | -0.047 | 0.728 |
353 | -0.108 | -0.009 | 0.143 | -0.703 | -0.061 | 0.945 | -0.541 | -0.047 | 0.727 |
354 | -0.107 | -0.009 | 0.143 | -0.702 | -0.061 | 0.943 | -0.540 | -0.047 | 0.726 |
355 | -0.107 | -0.009 | 0.143 | -0.700 | -0.061 | 0.942 | -0.540 | -0.047 | 0.725 |
356 | -0.107 | -0.009 | 0.143 | -0.699 | -0.061 | 0.940 | -0.539 | -0.047 | 0.723 |
357 | -0.107 | -0.009 | 0.142 | -0.698 | -0.061 | 0.939 | -0.538 | -0.047 | 0.722 |
358 | -0.107 | -0.009 | 0.142 | -0.697 | -0.060 | 0.937 | -0.537 | -0.046 | 0.721 |
359 | -0.106 | -0.009 | 0.142 | -0.696 | -0.060 | 0.936 | -0.536 | -0.046 | 0.720 |
360 | -0.106 | -0.009 | 0.142 | -0.695 | -0.060 | 0.934 | -0.535 | -0.046 | 0.719 |
361 | -0.106 | -0.009 | 0.141 | -0.693 | -0.060 | 0.933 | -0.534 | -0.046 | 0.718 |
362 | -0.106 | -0.009 | 0.141 | -0.692 | -0.060 | 0.931 | -0.533 | -0.046 | 0.716 |
363 | -0.106 | -0.009 | 0.141 | -0.691 | -0.060 | 0.930 | -0.532 | -0.046 | 0.715 |
364 | -0.106 | -0.009 | 0.141 | -0.690 | -0.060 | 0.928 | -0.532 | -0.046 | 0.714 |
365 | -0.105 | -0.009 | 0.141 | -0.689 | -0.060 | 0.927 | -0.531 | -0.046 | 0.713 |
366 | -0.105 | -0.009 | 0.140 | -0.688 | -0.060 | 0.925 | -0.530 | -0.046 | 0.712 |
367 | -0.105 | -0.009 | 0.140 | -0.687 | -0.060 | 0.924 | -0.529 | -0.046 | 0.711 |
368 | -0.105 | -0.009 | 0.140 | -0.685 | -0.059 | 0.922 | -0.528 | -0.046 | 0.709 |
369 | -0.105 | -0.009 | 0.140 | -0.684 | -0.059 | 0.921 | -0.527 | -0.046 | 0.708 |
370 | -0.105 | -0.009 | 0.139 | -0.683 | -0.059 | 0.919 | -0.526 | -0.046 | 0.707 |
371 | -0.104 | -0.009 | 0.139 | -0.682 | -0.059 | 0.918 | -0.525 | -0.045 | 0.706 |
372 | -0.104 | -0.009 | 0.139 | -0.681 | -0.059 | 0.916 | -0.524 | -0.045 | 0.705 |
373 | -0.104 | -0.009 | 0.139 | -0.680 | -0.059 | 0.915 | -0.524 | -0.045 | 0.704 |
374 | -0.104 | -0.009 | 0.139 | -0.679 | -0.059 | 0.913 | -0.523 | -0.045 | 0.702 |
375 | -0.104 | -0.009 | 0.138 | -0.677 | -0.059 | 0.912 | -0.522 | -0.045 | 0.701 |
376 | -0.104 | -0.009 | 0.138 | -0.676 | -0.059 | 0.910 | -0.521 | -0.045 | 0.700 |
377 | -0.103 | -0.009 | 0.138 | -0.675 | -0.059 | 0.909 | -0.520 | -0.045 | 0.699 |
378 | -0.103 | -0.009 | 0.138 | -0.674 | -0.058 | 0.907 | -0.519 | -0.045 | 0.698 |
379 | -0.103 | -0.009 | 0.137 | -0.673 | -0.058 | 0.906 | -0.518 | -0.045 | 0.697 |
380 | -0.103 | -0.009 | 0.137 | -0.672 | -0.058 | 0.904 | -0.518 | -0.045 | 0.696 |
381 | -0.103 | -0.009 | 0.137 | -0.671 | -0.058 | 0.903 | -0.517 | -0.045 | 0.694 |
382 | -0.102 | -0.009 | 0.137 | -0.670 | -0.058 | 0.901 | -0.516 | -0.045 | 0.693 |
383 | -0.102 | -0.009 | 0.137 | -0.668 | -0.058 | 0.900 | -0.515 | -0.045 | 0.692 |
384 | -0.102 | -0.009 | 0.136 | -0.667 | -0.058 | 0.898 | -0.514 | -0.044 | 0.691 |
385 | -0.102 | -0.009 | 0.136 | -0.666 | -0.058 | 0.897 | -0.513 | -0.044 | 0.690 |
386 | -0.102 | -0.009 | 0.136 | -0.665 | -0.058 | 0.895 | -0.512 | -0.044 | 0.689 |
387 | -0.102 | -0.009 | 0.136 | -0.664 | -0.058 | 0.894 | -0.512 | -0.044 | 0.688 |
388 | -0.101 | -0.009 | 0.135 | -0.663 | -0.058 | 0.892 | -0.511 | -0.044 | 0.687 |
389 | -0.101 | -0.009 | 0.135 | -0.662 | -0.057 | 0.891 | -0.510 | -0.044 | 0.685 |
390 | -0.101 | -0.009 | 0.135 | -0.661 | -0.057 | 0.889 | -0.509 | -0.044 | 0.684 |
391 | -0.101 | -0.009 | 0.135 | -0.660 | -0.057 | 0.888 | -0.508 | -0.044 | 0.683 |
392 | -0.101 | -0.009 | 0.135 | -0.659 | -0.057 | 0.887 | -0.507 | -0.044 | 0.682 |
393 | -0.101 | -0.009 | 0.134 | -0.657 | -0.057 | 0.885 | -0.506 | -0.044 | 0.681 |
394 | -0.100 | -0.009 | 0.134 | -0.656 | -0.057 | 0.884 | -0.506 | -0.044 | 0.680 |
395 | -0.100 | -0.009 | 0.134 | -0.655 | -0.057 | 0.882 | -0.505 | -0.044 | 0.679 |
396 | -0.100 | -0.009 | 0.134 | -0.654 | -0.057 | 0.881 | -0.504 | -0.044 | 0.678 |
397 | -0.100 | -0.009 | 0.133 | -0.653 | -0.057 | 0.879 | -0.503 | -0.044 | 0.677 |
398 | -0.100 | -0.009 | 0.133 | -0.652 | -0.057 | 0.878 | -0.502 | -0.043 | 0.675 |
399 | -0.100 | -0.009 | 0.133 | -0.651 | -0.056 | 0.876 | -0.501 | -0.043 | 0.674 |
400 | -0.099 | -0.009 | 0.133 | -0.650 | -0.056 | 0.875 | -0.501 | -0.043 | 0.673 |
401 | -0.099 | -0.009 | 0.133 | -0.649 | -0.056 | 0.874 | -0.500 | -0.043 | 0.672 |
402 | -0.099 | -0.009 | 0.132 | -0.648 | -0.056 | 0.872 | -0.499 | -0.043 | 0.671 |
403 | -0.099 | -0.009 | 0.132 | -0.647 | -0.056 | 0.871 | -0.498 | -0.043 | 0.670 |
404 | -0.099 | -0.009 | 0.132 | -0.646 | -0.056 | 0.869 | -0.497 | -0.043 | 0.669 |
405 | -0.099 | -0.009 | 0.132 | -0.644 | -0.056 | 0.868 | -0.496 | -0.043 | 0.668 |
406 | -0.098 | -0.008 | 0.132 | -0.643 | -0.056 | 0.867 | -0.496 | -0.043 | 0.667 |
407 | -0.098 | -0.008 | 0.131 | -0.642 | -0.056 | 0.865 | -0.495 | -0.043 | 0.666 |
408 | -0.098 | -0.008 | 0.131 | -0.641 | -0.056 | 0.864 | -0.494 | -0.043 | 0.665 |
409 | -0.098 | -0.008 | 0.131 | -0.640 | -0.056 | 0.862 | -0.493 | -0.043 | 0.663 |
410 | -0.098 | -0.008 | 0.131 | -0.639 | -0.055 | 0.861 | -0.492 | -0.043 | 0.662 |
411 | -0.098 | -0.008 | 0.130 | -0.638 | -0.055 | 0.859 | -0.492 | -0.043 | 0.661 |
412 | -0.097 | -0.008 | 0.130 | -0.637 | -0.055 | 0.858 | -0.491 | -0.042 | 0.660 |
413 | -0.097 | -0.008 | 0.130 | -0.636 | -0.055 | 0.857 | -0.490 | -0.042 | 0.659 |
414 | -0.097 | -0.008 | 0.130 | -0.635 | -0.055 | 0.855 | -0.489 | -0.042 | 0.658 |
415 | -0.097 | -0.008 | 0.130 | -0.634 | -0.055 | 0.854 | -0.488 | -0.042 | 0.657 |
416 | -0.097 | -0.008 | 0.129 | -0.633 | -0.055 | 0.852 | -0.487 | -0.042 | 0.656 |
417 | -0.097 | -0.008 | 0.129 | -0.632 | -0.055 | 0.851 | -0.487 | -0.042 | 0.655 |
418 | -0.097 | -0.008 | 0.129 | -0.631 | -0.055 | 0.850 | -0.486 | -0.042 | 0.654 |
419 | -0.096 | -0.008 | 0.129 | -0.630 | -0.055 | 0.848 | -0.485 | -0.042 | 0.653 |
420 | -0.096 | -0.008 | 0.129 | -0.629 | -0.055 | 0.847 | -0.484 | -0.042 | 0.652 |
421 | -0.096 | -0.008 | 0.128 | -0.628 | -0.054 | 0.846 | -0.483 | -0.042 | 0.651 |
422 | -0.096 | -0.008 | 0.128 | -0.627 | -0.054 | 0.844 | -0.483 | -0.042 | 0.650 |
423 | -0.096 | -0.008 | 0.128 | -0.625 | -0.054 | 0.843 | -0.482 | -0.042 | 0.648 |
424 | -0.096 | -0.008 | 0.128 | -0.624 | -0.054 | 0.841 | -0.481 | -0.042 | 0.647 |
425 | -0.095 | -0.008 | 0.128 | -0.623 | -0.054 | 0.840 | -0.480 | -0.042 | 0.646 |
426 | -0.095 | -0.008 | 0.127 | -0.622 | -0.054 | 0.839 | -0.479 | -0.041 | 0.645 |
427 | -0.095 | -0.008 | 0.127 | -0.621 | -0.054 | 0.837 | -0.479 | -0.041 | 0.644 |
428 | -0.095 | -0.008 | 0.127 | -0.620 | -0.054 | 0.836 | -0.478 | -0.041 | 0.643 |
429 | -0.095 | -0.008 | 0.127 | -0.619 | -0.054 | 0.835 | -0.477 | -0.041 | 0.642 |
430 | -0.095 | -0.008 | 0.126 | -0.618 | -0.054 | 0.833 | -0.476 | -0.041 | 0.641 |
431 | -0.094 | -0.008 | 0.126 | -0.617 | -0.054 | 0.832 | -0.475 | -0.041 | 0.640 |
432 | -0.094 | -0.008 | 0.126 | -0.616 | -0.053 | 0.830 | -0.475 | -0.041 | 0.639 |
433 | -0.094 | -0.008 | 0.126 | -0.615 | -0.053 | 0.829 | -0.474 | -0.041 | 0.638 |
434 | -0.094 | -0.008 | 0.126 | -0.614 | -0.053 | 0.828 | -0.473 | -0.041 | 0.637 |
435 | -0.094 | -0.008 | 0.125 | -0.613 | -0.053 | 0.826 | -0.472 | -0.041 | 0.636 |
436 | -0.094 | -0.008 | 0.125 | -0.612 | -0.053 | 0.825 | -0.472 | -0.041 | 0.635 |
437 | -0.093 | -0.008 | 0.125 | -0.611 | -0.053 | 0.824 | -0.471 | -0.041 | 0.634 |
438 | -0.093 | -0.008 | 0.125 | -0.610 | -0.053 | 0.822 | -0.470 | -0.041 | 0.633 |
439 | -0.093 | -0.008 | 0.125 | -0.609 | -0.053 | 0.821 | -0.469 | -0.041 | 0.632 |
440 | -0.093 | -0.008 | 0.124 | -0.608 | -0.053 | 0.820 | -0.468 | -0.041 | 0.631 |
441 | -0.093 | -0.008 | 0.124 | -0.607 | -0.053 | 0.818 | -0.468 | -0.040 | 0.630 |
442 | -0.093 | -0.008 | 0.124 | -0.606 | -0.053 | 0.817 | -0.467 | -0.040 | 0.629 |
443 | -0.093 | -0.008 | 0.124 | -0.605 | -0.052 | 0.816 | -0.466 | -0.040 | 0.628 |
444 | -0.092 | -0.008 | 0.124 | -0.604 | -0.052 | 0.814 | -0.465 | -0.040 | 0.627 |
445 | -0.092 | -0.008 | 0.123 | -0.603 | -0.052 | 0.813 | -0.465 | -0.040 | 0.626 |
446 | -0.092 | -0.008 | 0.123 | -0.602 | -0.052 | 0.812 | -0.464 | -0.040 | 0.625 |
447 | -0.092 | -0.008 | 0.123 | -0.601 | -0.052 | 0.810 | -0.463 | -0.040 | 0.624 |
448 | -0.092 | -0.008 | 0.123 | -0.600 | -0.052 | 0.809 | -0.462 | -0.040 | 0.622 |
449 | -0.092 | -0.008 | 0.123 | -0.599 | -0.052 | 0.808 | -0.461 | -0.040 | 0.621 |
450 | -0.091 | -0.008 | 0.122 | -0.598 | -0.052 | 0.806 | -0.461 | -0.040 | 0.620 |
451 | -0.091 | -0.008 | 0.122 | -0.597 | -0.052 | 0.805 | -0.460 | -0.040 | 0.619 |
452 | -0.091 | -0.008 | 0.122 | -0.596 | -0.052 | 0.804 | -0.459 | -0.040 | 0.618 |
453 | -0.091 | -0.008 | 0.122 | -0.595 | -0.052 | 0.802 | -0.458 | -0.040 | 0.617 |
454 | -0.091 | -0.008 | 0.122 | -0.594 | -0.052 | 0.801 | -0.458 | -0.040 | 0.616 |
455 | -0.091 | -0.008 | 0.121 | -0.593 | -0.051 | 0.800 | -0.457 | -0.040 | 0.615 |
456 | -0.091 | -0.008 | 0.121 | -0.592 | -0.051 | 0.798 | -0.456 | -0.039 | 0.614 |
457 | -0.090 | -0.008 | 0.121 | -0.591 | -0.051 | 0.797 | -0.455 | -0.039 | 0.613 |
458 | -0.090 | -0.008 | 0.121 | -0.590 | -0.051 | 0.796 | -0.455 | -0.039 | 0.612 |
459 | -0.090 | -0.008 | 0.121 | -0.589 | -0.051 | 0.795 | -0.454 | -0.039 | 0.611 |
460 | -0.090 | -0.008 | 0.120 | -0.588 | -0.051 | 0.793 | -0.453 | -0.039 | 0.610 |
461 | -0.090 | -0.008 | 0.120 | -0.587 | -0.051 | 0.792 | -0.452 | -0.039 | 0.609 |
462 | -0.090 | -0.008 | 0.120 | -0.586 | -0.051 | 0.791 | -0.452 | -0.039 | 0.608 |
463 | -0.090 | -0.008 | 0.120 | -0.585 | -0.051 | 0.789 | -0.451 | -0.039 | 0.607 |
464 | -0.089 | -0.008 | 0.120 | -0.584 | -0.051 | 0.788 | -0.450 | -0.039 | 0.606 |
465 | -0.089 | -0.008 | 0.119 | -0.583 | -0.051 | 0.787 | -0.449 | -0.039 | 0.605 |
466 | -0.089 | -0.008 | 0.119 | -0.582 | -0.051 | 0.786 | -0.449 | -0.039 | 0.604 |
467 | -0.089 | -0.008 | 0.119 | -0.581 | -0.050 | 0.784 | -0.448 | -0.039 | 0.603 |
468 | -0.089 | -0.008 | 0.119 | -0.580 | -0.050 | 0.783 | -0.447 | -0.039 | 0.602 |
469 | -0.089 | -0.008 | 0.119 | -0.579 | -0.050 | 0.782 | -0.446 | -0.039 | 0.601 |
470 | -0.088 | -0.008 | 0.118 | -0.578 | -0.050 | 0.780 | -0.446 | -0.039 | 0.600 |
471 | -0.088 | -0.008 | 0.118 | -0.578 | -0.050 | 0.779 | -0.445 | -0.038 | 0.600 |
472 | -0.088 | -0.008 | 0.118 | -0.577 | -0.050 | 0.778 | -0.444 | -0.038 | 0.599 |
473 | -0.088 | -0.008 | 0.118 | -0.576 | -0.050 | 0.777 | -0.443 | -0.038 | 0.598 |
474 | -0.088 | -0.008 | 0.118 | -0.575 | -0.050 | 0.775 | -0.443 | -0.038 | 0.597 |
475 | -0.088 | -0.008 | 0.118 | -0.574 | -0.050 | 0.774 | -0.442 | -0.038 | 0.596 |
476 | -0.088 | -0.008 | 0.117 | -0.573 | -0.050 | 0.773 | -0.441 | -0.038 | 0.595 |
477 | -0.087 | -0.008 | 0.117 | -0.572 | -0.050 | 0.772 | -0.440 | -0.038 | 0.594 |
478 | -0.087 | -0.008 | 0.117 | -0.571 | -0.050 | 0.770 | -0.440 | -0.038 | 0.593 |
479 | -0.087 | -0.008 | 0.117 | -0.570 | -0.049 | 0.769 | -0.439 | -0.038 | 0.592 |
480 | -0.087 | -0.008 | 0.117 | -0.569 | -0.049 | 0.768 | -0.438 | -0.038 | 0.591 |
481 | -0.087 | -0.007 | 0.116 | -0.568 | -0.049 | 0.766 | -0.438 | -0.038 | 0.590 |
482 | -0.087 | -0.007 | 0.116 | -0.567 | -0.049 | 0.765 | -0.437 | -0.038 | 0.589 |
483 | -0.087 | -0.007 | 0.116 | -0.566 | -0.049 | 0.764 | -0.436 | -0.038 | 0.588 |
484 | -0.086 | -0.007 | 0.116 | -0.565 | -0.049 | 0.763 | -0.435 | -0.038 | 0.587 |
485 | -0.086 | -0.007 | 0.116 | -0.564 | -0.049 | 0.761 | -0.435 | -0.038 | 0.586 |
486 | -0.086 | -0.007 | 0.115 | -0.563 | -0.049 | 0.760 | -0.434 | -0.038 | 0.585 |
487 | -0.086 | -0.007 | 0.115 | -0.562 | -0.049 | 0.759 | -0.433 | -0.037 | 0.584 |
488 | -0.086 | -0.007 | 0.115 | -0.561 | -0.049 | 0.758 | -0.432 | -0.037 | 0.583 |
489 | -0.086 | -0.007 | 0.115 | -0.561 | -0.049 | 0.757 | -0.432 | -0.037 | 0.582 |
490 | -0.086 | -0.007 | 0.115 | -0.560 | -0.049 | 0.755 | -0.431 | -0.037 | 0.581 |
491 | -0.085 | -0.007 | 0.115 | -0.559 | -0.048 | 0.754 | -0.430 | -0.037 | 0.580 |
492 | -0.085 | -0.007 | 0.114 | -0.558 | -0.048 | 0.753 | -0.430 | -0.037 | 0.579 |
493 | -0.085 | -0.007 | 0.114 | -0.557 | -0.048 | 0.752 | -0.429 | -0.037 | 0.578 |
494 | -0.085 | -0.007 | 0.114 | -0.556 | -0.048 | 0.750 | -0.428 | -0.037 | 0.577 |
495 | -0.085 | -0.007 | 0.114 | -0.555 | -0.048 | 0.749 | -0.427 | -0.037 | 0.576 |
496 | -0.085 | -0.007 | 0.114 | -0.554 | -0.048 | 0.748 | -0.427 | -0.037 | 0.575 |
497 | -0.085 | -0.007 | 0.113 | -0.553 | -0.048 | 0.747 | -0.426 | -0.037 | 0.575 |
498 | -0.084 | -0.007 | 0.113 | -0.552 | -0.048 | 0.745 | -0.425 | -0.037 | 0.574 |
499 | -0.084 | -0.007 | 0.113 | -0.551 | -0.048 | 0.744 | -0.425 | -0.037 | 0.573 |
Data for Figure 6 - Panel B
Quarters | Consumption Home Relative to Foreign: Path 3 | Consumption Home Relative to Foreign: Path 2 | Consumption Home Relative to Foreign: Path 1 | Real Exchange Rate Home: Path 3 | Real Exchange Rate Home: Path 2 | Real Exchange Rate Home: Path 1 | Trade Balance to GDP Ratio Home: Path 3 | Trade Balance to GDP Ratio Home: Path 2 | Trade Balance to GDP Ratio Home: Path 1 |
|---|---|---|---|---|---|---|---|---|---|
1 | -1.684 | -0.150 | 2.353 | 7.223 | 0.614 | -9.112 | -0.00082 | -0.00006 | 0.00103 |
2 | -1.716 | -0.153 | 2.400 | 7.140 | 0.608 | -9.015 | -0.00078 | -0.00007 | 0.00096 |
3 | -1.747 | -0.155 | 2.444 | 7.060 | 0.601 | -8.922 | -0.00073 | -0.00006 | 0.00090 |
4 | -1.777 | -0.158 | 2.486 | 6.984 | 0.595 | -8.833 | -0.00069 | -0.00006 | 0.00085 |
5 | -1.804 | -0.160 | 2.526 | 6.910 | 0.589 | -8.748 | -0.00065 | -0.00005 | 0.00080 |
6 | -1.831 | -0.163 | 2.563 | 6.840 | 0.583 | -8.666 | -0.00061 | -0.00005 | 0.00075 |
7 | -1.856 | -0.165 | 2.599 | 6.773 | 0.577 | -8.587 | -0.00057 | -0.00005 | 0.00070 |
8 | -1.879 | -0.167 | 2.632 | 6.709 | 0.572 | -8.511 | -0.00053 | -0.00004 | 0.00066 |
9 | -1.901 | -0.169 | 2.664 | 6.647 | 0.567 | -8.439 | -0.00050 | -0.00004 | 0.00062 |
10 | -1.922 | -0.171 | 2.694 | 6.588 | 0.562 | -8.369 | -0.00046 | -0.00004 | 0.00057 |
11 | -1.942 | -0.172 | 2.723 | 6.531 | 0.557 | -8.302 | -0.00043 | -0.00004 | 0.00054 |
12 | -1.961 | -0.174 | 2.750 | 6.476 | 0.553 | -8.237 | -0.00040 | -0.00003 | 0.00050 |
13 | -1.978 | -0.176 | 2.775 | 6.424 | 0.548 | -8.175 | -0.00037 | -0.00003 | 0.00046 |
14 | -1.995 | -0.177 | 2.799 | 6.373 | 0.544 | -8.115 | -0.00035 | -0.00003 | 0.00043 |
15 | -2.011 | -0.179 | 2.821 | 6.325 | 0.540 | -8.058 | -0.00032 | -0.00003 | 0.00040 |
16 | -2.025 | -0.180 | 2.843 | 6.278 | 0.536 | -8.003 | -0.00030 | -0.00003 | 0.00037 |
17 | -2.039 | -0.181 | 2.863 | 6.233 | 0.533 | -7.949 | -0.00027 | -0.00002 | 0.00034 |
18 | -2.052 | -0.182 | 2.881 | 6.190 | 0.529 | -7.898 | -0.00025 | -0.00002 | 0.00031 |
19 | -2.064 | -0.183 | 2.899 | 6.148 | 0.526 | -7.849 | -0.00023 | -0.00002 | 0.00029 |
20 | -2.076 | -0.184 | 2.916 | 6.109 | 0.522 | -7.801 | -0.00021 | -0.00002 | 0.00026 |
21 | -2.087 | -0.185 | 2.931 | 6.070 | 0.519 | -7.755 | -0.00019 | -0.00002 | 0.00024 |
22 | -2.097 | -0.186 | 2.946 | 6.033 | 0.516 | -7.711 | -0.00017 | -0.00001 | 0.00021 |
23 | -2.106 | -0.187 | 2.959 | 5.997 | 0.513 | -7.668 | -0.00015 | -0.00001 | 0.00019 |
24 | -2.115 | -0.188 | 2.972 | 5.963 | 0.510 | -7.627 | -0.00014 | -0.00001 | 0.00017 |
25 | -2.123 | -0.189 | 2.984 | 5.929 | 0.507 | -7.587 | -0.00012 | -0.00001 | 0.00015 |
26 | -2.131 | -0.189 | 2.995 | 5.897 | 0.505 | -7.549 | -0.00011 | -0.00001 | 0.00013 |
27 | -2.138 | -0.190 | 3.005 | 5.866 | 0.502 | -7.511 | -0.00009 | -0.00001 | 0.00012 |
28 | -2.145 | -0.190 | 3.015 | 5.836 | 0.500 | -7.475 | -0.00008 | -0.00001 | 0.00010 |
29 | -2.151 | -0.191 | 3.024 | 5.807 | 0.497 | -7.441 | -0.00007 | -0.00001 | 0.00008 |
30 | -2.156 | -0.191 | 3.032 | 5.779 | 0.495 | -7.407 | -0.00005 | 0.00000 | 0.00007 |
31 | -2.162 | -0.192 | 3.039 | 5.752 | 0.493 | -7.374 | -0.00004 | 0.00000 | 0.00005 |
32 | -2.166 | -0.192 | 3.046 | 5.726 | 0.490 | -7.343 | -0.00003 | 0.00000 | 0.00004 |
33 | -2.171 | -0.193 | 3.053 | 5.700 | 0.488 | -7.312 | -0.00002 | 0.00000 | 0.00002 |
34 | -2.175 | -0.193 | 3.058 | 5.675 | 0.486 | -7.283 | -0.00001 | 0.00000 | 0.00001 |
35 | -2.179 | -0.193 | 3.064 | 5.651 | 0.484 | -7.254 | 0.00000 | 0.00000 | 0.00000 |
36 | -2.182 | -0.194 | 3.069 | 5.628 | 0.482 | -7.226 | 0.00001 | 0.00000 | -0.00001 |
37 | -2.185 | -0.194 | 3.073 | 5.606 | 0.480 | -7.199 | 0.00002 | 0.00000 | -0.00002 |
38 | -2.188 | -0.194 | 3.077 | 5.584 | 0.479 | -7.172 | 0.00003 | 0.00000 | -0.00003 |
39 | -2.190 | -0.194 | 3.080 | 5.563 | 0.477 | -7.147 | 0.00003 | 0.00000 | -0.00004 |
40 | -2.192 | -0.195 | 3.083 | 5.542 | 0.475 | -7.122 | 0.00004 | 0.00000 | -0.00005 |
41 | -2.194 | -0.195 | 3.086 | 5.522 | 0.473 | -7.098 | 0.00005 | 0.00000 | -0.00006 |
42 | -2.195 | -0.195 | 3.088 | 5.502 | 0.472 | -7.074 | 0.00006 | 0.00000 | -0.00007 |
43 | -2.197 | -0.195 | 3.090 | 5.483 | 0.470 | -7.051 | 0.00006 | 0.00001 | -0.00008 |
44 | -2.198 | -0.195 | 3.092 | 5.465 | 0.469 | -7.029 | 0.00007 | 0.00001 | -0.00009 |
45 | -2.199 | -0.195 | 3.093 | 5.447 | 0.467 | -7.007 | 0.00007 | 0.00001 | -0.00009 |
46 | -2.199 | -0.195 | 3.094 | 5.429 | 0.466 | -6.986 | 0.00008 | 0.00001 | -0.00010 |
47 | -2.200 | -0.195 | 3.095 | 5.412 | 0.464 | -6.965 | 0.00008 | 0.00001 | -0.00011 |
48 | -2.200 | -0.195 | 3.095 | 5.395 | 0.463 | -6.944 | 0.00009 | 0.00001 | -0.00011 |
49 | -2.200 | -0.195 | 3.095 | 5.379 | 0.461 | -6.925 | 0.00009 | 0.00001 | -0.00012 |
50 | -2.200 | -0.195 | 3.095 | 5.363 | 0.460 | -6.905 | 0.00010 | 0.00001 | -0.00012 |
51 | -2.200 | -0.195 | 3.095 | 5.347 | 0.459 | -6.886 | 0.00010 | 0.00001 | -0.00013 |
52 | -2.200 | -0.195 | 3.094 | 5.332 | 0.457 | -6.868 | 0.00011 | 0.00001 | -0.00013 |
53 | -2.199 | -0.195 | 3.093 | 5.317 | 0.456 | -6.849 | 0.00011 | 0.00001 | -0.00014 |
54 | -2.198 | -0.195 | 3.092 | 5.302 | 0.455 | -6.832 | 0.00011 | 0.00001 | -0.00014 |
55 | -2.197 | -0.195 | 3.091 | 5.287 | 0.454 | -6.814 | 0.00012 | 0.00001 | -0.00015 |
56 | -2.196 | -0.195 | 3.090 | 5.273 | 0.453 | -6.797 | 0.00012 | 0.00001 | -0.00015 |
57 | -2.195 | -0.195 | 3.088 | 5.259 | 0.451 | -6.780 | 0.00012 | 0.00001 | -0.00016 |
58 | -2.194 | -0.195 | 3.086 | 5.246 | 0.450 | -6.764 | 0.00013 | 0.00001 | -0.00016 |
59 | -2.193 | -0.195 | 3.084 | 5.232 | 0.449 | -6.747 | 0.00013 | 0.00001 | -0.00016 |
60 | -2.191 | -0.194 | 3.082 | 5.219 | 0.448 | -6.731 | 0.00013 | 0.00001 | -0.00017 |
61 | -2.190 | -0.194 | 3.080 | 5.206 | 0.447 | -6.716 | 0.00014 | 0.00001 | -0.00017 |
62 | -2.188 | -0.194 | 3.078 | 5.194 | 0.446 | -6.700 | 0.00014 | 0.00001 | -0.00017 |
63 | -2.187 | -0.194 | 3.075 | 5.181 | 0.445 | -6.685 | 0.00014 | 0.00001 | -0.00018 |
64 | -2.185 | -0.194 | 3.073 | 5.169 | 0.444 | -6.670 | 0.00014 | 0.00001 | -0.00018 |
65 | -2.183 | -0.194 | 3.070 | 5.157 | 0.443 | -6.655 | 0.00014 | 0.00001 | -0.00018 |
66 | -2.181 | -0.193 | 3.067 | 5.145 | 0.442 | -6.641 | 0.00015 | 0.00001 | -0.00018 |
67 | -2.179 | -0.193 | 3.065 | 5.133 | 0.441 | -6.627 | 0.00015 | 0.00001 | -0.00019 |
68 | -2.177 | -0.193 | 3.061 | 5.121 | 0.440 | -6.613 | 0.00015 | 0.00001 | -0.00019 |
69 | -2.175 | -0.193 | 3.058 | 5.110 | 0.439 | -6.599 | 0.00015 | 0.00001 | -0.00019 |
70 | -2.173 | -0.193 | 3.055 | 5.099 | 0.438 | -6.585 | 0.00015 | 0.00001 | -0.00019 |
71 | -2.170 | -0.193 | 3.052 | 5.088 | 0.437 | -6.571 | 0.00015 | 0.00001 | -0.00019 |
72 | -2.168 | -0.192 | 3.049 | 5.077 | 0.436 | -6.558 | 0.00016 | 0.00001 | -0.00020 |
73 | -2.166 | -0.192 | 3.045 | 5.066 | 0.435 | -6.545 | 0.00016 | 0.00001 | -0.00020 |
74 | -2.163 | -0.192 | 3.042 | 5.055 | 0.434 | -6.532 | 0.00016 | 0.00001 | -0.00020 |
75 | -2.161 | -0.192 | 3.038 | 5.044 | 0.433 | -6.519 | 0.00016 | 0.00001 | -0.00020 |
76 | -2.158 | -0.191 | 3.034 | 5.034 | 0.432 | -6.506 | 0.00016 | 0.00001 | -0.00020 |
77 | -2.156 | -0.191 | 3.031 | 5.023 | 0.432 | -6.493 | 0.00016 | 0.00001 | -0.00020 |
78 | -2.153 | -0.191 | 3.027 | 5.013 | 0.431 | -6.481 | 0.00016 | 0.00001 | -0.00020 |
79 | -2.150 | -0.191 | 3.023 | 5.003 | 0.430 | -6.468 | 0.00016 | 0.00001 | -0.00021 |
80 | -2.148 | -0.190 | 3.019 | 4.993 | 0.429 | -6.456 | 0.00016 | 0.00001 | -0.00021 |
81 | -2.145 | -0.190 | 3.015 | 4.983 | 0.428 | -6.444 | 0.00016 | 0.00001 | -0.00021 |
82 | -2.142 | -0.190 | 3.011 | 4.973 | 0.427 | -6.432 | 0.00017 | 0.00001 | -0.00021 |
83 | -2.140 | -0.190 | 3.007 | 4.963 | 0.426 | -6.420 | 0.00017 | 0.00001 | -0.00021 |
84 | -2.137 | -0.189 | 3.003 | 4.953 | 0.426 | -6.408 | 0.00017 | 0.00001 | -0.00021 |
85 | -2.134 | -0.189 | 2.999 | 4.944 | 0.425 | -6.396 | 0.00017 | 0.00001 | -0.00021 |
86 | -2.131 | -0.189 | 2.995 | 4.934 | 0.424 | -6.384 | 0.00017 | 0.00001 | -0.00021 |
87 | -2.128 | -0.189 | 2.991 | 4.925 | 0.423 | -6.373 | 0.00017 | 0.00001 | -0.00021 |
88 | -2.125 | -0.188 | 2.987 | 4.915 | 0.422 | -6.361 | 0.00017 | 0.00001 | -0.00021 |
89 | -2.122 | -0.188 | 2.983 | 4.906 | 0.422 | -6.350 | 0.00017 | 0.00001 | -0.00021 |
90 | -2.119 | -0.188 | 2.978 | 4.897 | 0.421 | -6.338 | 0.00017 | 0.00001 | -0.00021 |
91 | -2.116 | -0.188 | 2.974 | 4.887 | 0.420 | -6.327 | 0.00017 | 0.00001 | -0.00021 |
92 | -2.113 | -0.187 | 2.970 | 4.878 | 0.419 | -6.316 | 0.00017 | 0.00001 | -0.00022 |
93 | -2.110 | -0.187 | 2.965 | 4.869 | 0.418 | -6.305 | 0.00017 | 0.00001 | -0.00022 |
94 | -2.107 | -0.187 | 2.961 | 4.860 | 0.418 | -6.294 | 0.00017 | 0.00001 | -0.00022 |
95 | -2.104 | -0.187 | 2.957 | 4.851 | 0.417 | -6.282 | 0.00017 | 0.00001 | -0.00022 |
96 | -2.101 | -0.186 | 2.952 | 4.842 | 0.416 | -6.272 | 0.00017 | 0.00001 | -0.00022 |
97 | -2.098 | -0.186 | 2.948 | 4.833 | 0.415 | -6.261 | 0.00017 | 0.00001 | -0.00022 |
98 | -2.095 | -0.186 | 2.943 | 4.824 | 0.415 | -6.250 | 0.00017 | 0.00001 | -0.00022 |
99 | -2.092 | -0.185 | 2.939 | 4.816 | 0.414 | -6.239 | 0.00017 | 0.00001 | -0.00022 |
100 | -2.089 | -0.185 | 2.934 | 4.807 | 0.413 | -6.228 | 0.00017 | 0.00001 | -0.00022 |
101 | -2.086 | -0.185 | 2.930 | 4.798 | 0.412 | -6.218 | 0.00017 | 0.00001 | -0.00022 |
102 | -2.083 | -0.185 | 2.925 | 4.789 | 0.412 | -6.207 | 0.00017 | 0.00001 | -0.00022 |
103 | -2.080 | -0.184 | 2.921 | 4.781 | 0.411 | -6.196 | 0.00017 | 0.00001 | -0.00022 |
104 | -2.076 | -0.184 | 2.916 | 4.772 | 0.410 | -6.186 | 0.00017 | 0.00001 | -0.00022 |
105 | -2.073 | -0.184 | 2.912 | 4.764 | 0.409 | -6.175 | 0.00017 | 0.00001 | -0.00022 |
106 | -2.070 | -0.183 | 2.907 | 4.755 | 0.409 | -6.165 | 0.00017 | 0.00001 | -0.00022 |
107 | -2.067 | -0.183 | 2.903 | 4.747 | 0.408 | -6.155 | 0.00017 | 0.00001 | -0.00022 |
108 | -2.064 | -0.183 | 2.898 | 4.738 | 0.407 | -6.144 | 0.00017 | 0.00001 | -0.00022 |
109 | -2.061 | -0.183 | 2.894 | 4.730 | 0.407 | -6.134 | 0.00017 | 0.00001 | -0.00022 |
110 | -2.058 | -0.182 | 2.889 | 4.722 | 0.406 | -6.124 | 0.00017 | 0.00001 | -0.00022 |
111 | -2.054 | -0.182 | 2.885 | 4.713 | 0.405 | -6.113 | 0.00017 | 0.00001 | -0.00022 |
112 | -2.051 | -0.182 | 2.880 | 4.705 | 0.404 | -6.103 | 0.00017 | 0.00001 | -0.00022 |
113 | -2.048 | -0.181 | 2.875 | 4.697 | 0.404 | -6.093 | 0.00017 | 0.00001 | -0.00022 |
114 | -2.045 | -0.181 | 2.871 | 4.688 | 0.403 | -6.083 | 0.00017 | 0.00001 | -0.00022 |
115 | -2.042 | -0.181 | 2.866 | 4.680 | 0.402 | -6.073 | 0.00017 | 0.00001 | -0.00022 |
116 | -2.038 | -0.181 | 2.862 | 4.672 | 0.402 | -6.063 | 0.00017 | 0.00001 | -0.00022 |
117 | -2.035 | -0.180 | 2.857 | 4.664 | 0.401 | -6.053 | 0.00017 | 0.00001 | -0.00022 |
118 | -2.032 | -0.180 | 2.853 | 4.656 | 0.400 | -6.043 | 0.00017 | 0.00001 | -0.00022 |
119 | -2.029 | -0.180 | 2.848 | 4.648 | 0.400 | -6.033 | 0.00017 | 0.00001 | -0.00022 |
120 | -2.026 | -0.179 | 2.843 | 4.640 | 0.399 | -6.023 | 0.00017 | 0.00001 | -0.00022 |
121 | -2.022 | -0.179 | 2.839 | 4.631 | 0.398 | -6.013 | 0.00017 | 0.00001 | -0.00022 |
122 | -2.019 | -0.179 | 2.834 | 4.623 | 0.398 | -6.003 | 0.00017 | 0.00001 | -0.00022 |
123 | -2.016 | -0.179 | 2.830 | 4.615 | 0.397 | -5.993 | 0.00017 | 0.00001 | -0.00022 |
124 | -2.013 | -0.178 | 2.825 | 4.607 | 0.396 | -5.983 | 0.00017 | 0.00001 | -0.00022 |
125 | -2.010 | -0.178 | 2.820 | 4.599 | 0.396 | -5.974 | 0.00017 | 0.00001 | -0.00022 |
126 | -2.007 | -0.178 | 2.816 | 4.592 | 0.395 | -5.964 | 0.00017 | 0.00001 | -0.00022 |
127 | -2.003 | -0.177 | 2.811 | 4.584 | 0.394 | -5.954 | 0.00017 | 0.00001 | -0.00022 |
128 | -2.000 | -0.177 | 2.807 | 4.576 | 0.393 | -5.944 | 0.00017 | 0.00001 | -0.00022 |
129 | -1.997 | -0.177 | 2.802 | 4.568 | 0.393 | -5.935 | 0.00017 | 0.00001 | -0.00022 |
130 | -1.994 | -0.177 | 2.797 | 4.560 | 0.392 | -5.925 | 0.00017 | 0.00001 | -0.00022 |
131 | -1.991 | -0.176 | 2.793 | 4.552 | 0.391 | -5.915 | 0.00017 | 0.00001 | -0.00022 |
132 | -1.987 | -0.176 | 2.788 | 4.544 | 0.391 | -5.906 | 0.00017 | 0.00001 | -0.00022 |
133 | -1.984 | -0.176 | 2.784 | 4.537 | 0.390 | -5.896 | 0.00017 | 0.00001 | -0.00021 |
134 | -1.981 | -0.175 | 2.779 | 4.529 | 0.389 | -5.886 | 0.00017 | 0.00001 | -0.00021 |
135 | -1.978 | -0.175 | 2.775 | 4.521 | 0.389 | -5.877 | 0.00017 | 0.00001 | -0.00021 |
136 | -1.975 | -0.175 | 2.770 | 4.513 | 0.388 | -5.867 | 0.00017 | 0.00001 | -0.00021 |
137 | -1.972 | -0.175 | 2.765 | 4.506 | 0.388 | -5.858 | 0.00017 | 0.00001 | -0.00021 |
138 | -1.968 | -0.174 | 2.761 | 4.498 | 0.387 | -5.848 | 0.00017 | 0.00001 | -0.00021 |
139 | -1.965 | -0.174 | 2.756 | 4.490 | 0.386 | -5.839 | 0.00017 | 0.00001 | -0.00021 |
140 | -1.962 | -0.174 | 2.752 | 4.483 | 0.386 | -5.829 | 0.00017 | 0.00001 | -0.00021 |
141 | -1.959 | -0.173 | 2.747 | 4.475 | 0.385 | -5.820 | 0.00017 | 0.00001 | -0.00021 |
142 | -1.956 | -0.173 | 2.743 | 4.467 | 0.384 | -5.811 | 0.00017 | 0.00001 | -0.00021 |
143 | -1.953 | -0.173 | 2.738 | 4.460 | 0.384 | -5.801 | 0.00017 | 0.00001 | -0.00021 |
144 | -1.949 | -0.173 | 2.734 | 4.452 | 0.383 | -5.792 | 0.00017 | 0.00001 | -0.00021 |
145 | -1.946 | -0.172 | 2.729 | 4.445 | 0.382 | -5.782 | 0.00017 | 0.00001 | -0.00021 |
146 | -1.943 | -0.172 | 2.725 | 4.437 | 0.382 | -5.773 | 0.00017 | 0.00001 | -0.00021 |
147 | -1.940 | -0.172 | 2.720 | 4.429 | 0.381 | -5.764 | 0.00017 | 0.00001 | -0.00021 |
148 | -1.937 | -0.171 | 2.716 | 4.422 | 0.380 | -5.754 | 0.00017 | 0.00001 | -0.00021 |
149 | -1.934 | -0.171 | 2.711 | 4.414 | 0.380 | -5.745 | 0.00017 | 0.00001 | -0.00021 |
150 | -1.931 | -0.171 | 2.707 | 4.407 | 0.379 | -5.736 | 0.00016 | 0.00001 | -0.00021 |
151 | -1.927 | -0.171 | 2.702 | 4.399 | 0.378 | -5.727 | 0.00016 | 0.00001 | -0.00021 |
152 | -1.924 | -0.170 | 2.698 | 4.392 | 0.378 | -5.717 | 0.00016 | 0.00001 | -0.00021 |
153 | -1.921 | -0.170 | 2.693 | 4.385 | 0.377 | -5.708 | 0.00016 | 0.00001 | -0.00021 |
154 | -1.918 | -0.170 | 2.689 | 4.377 | 0.377 | -5.699 | 0.00016 | 0.00001 | -0.00021 |
155 | -1.915 | -0.169 | 2.684 | 4.370 | 0.376 | -5.690 | 0.00016 | 0.00001 | -0.00021 |
156 | -1.912 | -0.169 | 2.680 | 4.362 | 0.375 | -5.681 | 0.00016 | 0.00001 | -0.00021 |
157 | -1.909 | -0.169 | 2.675 | 4.355 | 0.375 | -5.672 | 0.00016 | 0.00001 | -0.00021 |
158 | -1.906 | -0.169 | 2.671 | 4.347 | 0.374 | -5.662 | 0.00016 | 0.00001 | -0.00021 |
159 | -1.903 | -0.168 | 2.666 | 4.340 | 0.373 | -5.653 | 0.00016 | 0.00001 | -0.00021 |
160 | -1.899 | -0.168 | 2.662 | 4.333 | 0.373 | -5.644 | 0.00016 | 0.00001 | -0.00021 |
161 | -1.896 | -0.168 | 2.658 | 4.325 | 0.372 | -5.635 | 0.00016 | 0.00001 | -0.00021 |
162 | -1.893 | -0.167 | 2.653 | 4.318 | 0.372 | -5.626 | 0.00016 | 0.00001 | -0.00021 |
163 | -1.890 | -0.167 | 2.649 | 4.311 | 0.371 | -5.617 | 0.00016 | 0.00001 | -0.00021 |
164 | -1.887 | -0.167 | 2.644 | 4.304 | 0.370 | -5.608 | 0.00016 | 0.00001 | -0.00021 |
165 | -1.884 | -0.167 | 2.640 | 4.296 | 0.370 | -5.599 | 0.00016 | 0.00001 | -0.00021 |
166 | -1.881 | -0.166 | 2.636 | 4.289 | 0.369 | -5.590 | 0.00016 | 0.00001 | -0.00021 |
167 | -1.878 | -0.166 | 2.631 | 4.282 | 0.368 | -5.581 | 0.00016 | 0.00001 | -0.00021 |
168 | -1.875 | -0.166 | 2.627 | 4.275 | 0.368 | -5.572 | 0.00016 | 0.00001 | -0.00020 |
169 | -1.872 | -0.166 | 2.622 | 4.267 | 0.367 | -5.563 | 0.00016 | 0.00001 | -0.00020 |
170 | -1.869 | -0.165 | 2.618 | 4.260 | 0.367 | -5.554 | 0.00016 | 0.00001 | -0.00020 |
171 | -1.866 | -0.165 | 2.614 | 4.253 | 0.366 | -5.545 | 0.00016 | 0.00001 | -0.00020 |
172 | -1.863 | -0.165 | 2.609 | 4.246 | 0.365 | -5.536 | 0.00016 | 0.00001 | -0.00020 |
173 | -1.860 | -0.164 | 2.605 | 4.239 | 0.365 | -5.527 | 0.00016 | 0.00001 | -0.00020 |
174 | -1.857 | -0.164 | 2.601 | 4.231 | 0.364 | -5.518 | 0.00016 | 0.00001 | -0.00020 |
175 | -1.854 | -0.164 | 2.596 | 4.224 | 0.364 | -5.510 | 0.00016 | 0.00001 | -0.00020 |
176 | -1.851 | -0.164 | 2.592 | 4.217 | 0.363 | -5.501 | 0.00016 | 0.00001 | -0.00020 |
177 | -1.848 | -0.163 | 2.588 | 4.210 | 0.362 | -5.492 | 0.00016 | 0.00001 | -0.00020 |
178 | -1.845 | -0.163 | 2.583 | 4.203 | 0.362 | -5.483 | 0.00016 | 0.00001 | -0.00020 |
179 | -1.842 | -0.163 | 2.579 | 4.196 | 0.361 | -5.474 | 0.00016 | 0.00001 | -0.00020 |
180 | -1.839 | -0.163 | 2.575 | 4.189 | 0.361 | -5.465 | 0.00016 | 0.00001 | -0.00020 |
181 | -1.836 | -0.162 | 2.570 | 4.182 | 0.360 | -5.457 | 0.00016 | 0.00001 | -0.00020 |
182 | -1.833 | -0.162 | 2.566 | 4.175 | 0.359 | -5.448 | 0.00016 | 0.00001 | -0.00020 |
183 | -1.830 | -0.162 | 2.562 | 4.168 | 0.359 | -5.439 | 0.00016 | 0.00001 | -0.00020 |
184 | -1.827 | -0.161 | 2.558 | 4.161 | 0.358 | -5.430 | 0.00016 | 0.00001 | -0.00020 |
185 | -1.824 | -0.161 | 2.553 | 4.154 | 0.357 | -5.422 | 0.00016 | 0.00001 | -0.00020 |
186 | -1.821 | -0.161 | 2.549 | 4.147 | 0.357 | -5.413 | 0.00016 | 0.00001 | -0.00020 |
187 | -1.818 | -0.161 | 2.545 | 4.140 | 0.356 | -5.404 | 0.00016 | 0.00001 | -0.00020 |
188 | -1.815 | -0.160 | 2.541 | 4.133 | 0.356 | -5.396 | 0.00016 | 0.00001 | -0.00020 |
189 | -1.812 | -0.160 | 2.536 | 4.126 | 0.355 | -5.387 | 0.00015 | 0.00001 | -0.00020 |
190 | -1.809 | -0.160 | 2.532 | 4.119 | 0.355 | -5.378 | 0.00015 | 0.00001 | -0.00020 |
191 | -1.806 | -0.160 | 2.528 | 4.112 | 0.354 | -5.370 | 0.00015 | 0.00001 | -0.00020 |
192 | -1.803 | -0.159 | 2.524 | 4.105 | 0.353 | -5.361 | 0.00015 | 0.00001 | -0.00020 |
193 | -1.800 | -0.159 | 2.519 | 4.098 | 0.353 | -5.352 | 0.00015 | 0.00001 | -0.00020 |
194 | -1.797 | -0.159 | 2.515 | 4.091 | 0.352 | -5.344 | 0.00015 | 0.00001 | -0.00020 |
195 | -1.794 | -0.159 | 2.511 | 4.084 | 0.352 | -5.335 | 0.00015 | 0.00001 | -0.00020 |
196 | -1.791 | -0.158 | 2.507 | 4.077 | 0.351 | -5.327 | 0.00015 | 0.00001 | -0.00020 |
197 | -1.788 | -0.158 | 2.503 | 4.070 | 0.350 | -5.318 | 0.00015 | 0.00001 | -0.00020 |
198 | -1.785 | -0.158 | 2.498 | 4.063 | 0.350 | -5.310 | 0.00015 | 0.00001 | -0.00020 |
199 | -1.782 | -0.157 | 2.494 | 4.057 | 0.349 | -5.301 | 0.00015 | 0.00001 | -0.00020 |
200 | -1.779 | -0.157 | 2.490 | 4.050 | 0.349 | -5.293 | 0.00015 | 0.00001 | -0.00020 |
201 | -1.776 | -0.157 | 2.486 | 4.043 | 0.348 | -5.284 | 0.00015 | 0.00001 | -0.00019 |
202 | -1.774 | -0.157 | 2.482 | 4.036 | 0.347 | -5.276 | 0.00015 | 0.00001 | -0.00019 |
203 | -1.771 | -0.156 | 2.478 | 4.029 | 0.347 | -5.267 | 0.00015 | 0.00001 | -0.00019 |
204 | -1.768 | -0.156 | 2.474 | 4.023 | 0.346 | -5.259 | 0.00015 | 0.00001 | -0.00019 |
205 | -1.765 | -0.156 | 2.469 | 4.016 | 0.346 | -5.250 | 0.00015 | 0.00001 | -0.00019 |
206 | -1.762 | -0.156 | 2.465 | 4.009 | 0.345 | -5.242 | 0.00015 | 0.00001 | -0.00019 |
207 | -1.759 | -0.155 | 2.461 | 4.002 | 0.345 | -5.233 | 0.00015 | 0.00001 | -0.00019 |
208 | -1.756 | -0.155 | 2.457 | 3.996 | 0.344 | -5.225 | 0.00015 | 0.00001 | -0.00019 |
209 | -1.753 | -0.155 | 2.453 | 3.989 | 0.343 | -5.217 | 0.00015 | 0.00001 | -0.00019 |
210 | -1.751 | -0.155 | 2.449 | 3.982 | 0.343 | -5.208 | 0.00015 | 0.00001 | -0.00019 |
211 | -1.748 | -0.154 | 2.445 | 3.975 | 0.342 | -5.200 | 0.00015 | 0.00001 | -0.00019 |
212 | -1.745 | -0.154 | 2.441 | 3.969 | 0.342 | -5.191 | 0.00015 | 0.00001 | -0.00019 |
213 | -1.742 | -0.154 | 2.437 | 3.962 | 0.341 | -5.183 | 0.00015 | 0.00001 | -0.00019 |
214 | -1.739 | -0.154 | 2.433 | 3.955 | 0.341 | -5.175 | 0.00015 | 0.00001 | -0.00019 |
215 | -1.736 | -0.153 | 2.428 | 3.949 | 0.340 | -5.166 | 0.00015 | 0.00001 | -0.00019 |
216 | -1.733 | -0.153 | 2.424 | 3.942 | 0.339 | -5.158 | 0.00015 | 0.00001 | -0.00019 |
217 | -1.731 | -0.153 | 2.420 | 3.936 | 0.339 | -5.150 | 0.00015 | 0.00001 | -0.00019 |
218 | -1.728 | -0.153 | 2.416 | 3.929 | 0.338 | -5.142 | 0.00015 | 0.00001 | -0.00019 |
219 | -1.725 | -0.152 | 2.412 | 3.922 | 0.338 | -5.133 | 0.00015 | 0.00001 | -0.00019 |
220 | -1.722 | -0.152 | 2.408 | 3.916 | 0.337 | -5.125 | 0.00015 | 0.00001 | -0.00019 |
221 | -1.719 | -0.152 | 2.404 | 3.909 | 0.337 | -5.117 | 0.00015 | 0.00001 | -0.00019 |
222 | -1.717 | -0.152 | 2.400 | 3.903 | 0.336 | -5.109 | 0.00015 | 0.00001 | -0.00019 |
223 | -1.714 | -0.151 | 2.396 | 3.896 | 0.335 | -5.100 | 0.00015 | 0.00001 | -0.00019 |
224 | -1.711 | -0.151 | 2.392 | 3.889 | 0.335 | -5.092 | 0.00015 | 0.00001 | -0.00019 |
225 | -1.708 | -0.151 | 2.388 | 3.883 | 0.334 | -5.084 | 0.00015 | 0.00001 | -0.00019 |
226 | -1.705 | -0.151 | 2.384 | 3.876 | 0.334 | -5.076 | 0.00015 | 0.00001 | -0.00019 |
227 | -1.703 | -0.150 | 2.380 | 3.870 | 0.333 | -5.068 | 0.00015 | 0.00001 | -0.00019 |
228 | -1.700 | -0.150 | 2.376 | 3.863 | 0.333 | -5.060 | 0.00014 | 0.00001 | -0.00019 |
229 | -1.697 | -0.150 | 2.372 | 3.857 | 0.332 | -5.051 | 0.00014 | 0.00001 | -0.00019 |
230 | -1.694 | -0.150 | 2.368 | 3.850 | 0.332 | -5.043 | 0.00014 | 0.00001 | -0.00019 |
231 | -1.691 | -0.149 | 2.364 | 3.844 | 0.331 | -5.035 | 0.00014 | 0.00001 | -0.00019 |
232 | -1.689 | -0.149 | 2.360 | 3.837 | 0.330 | -5.027 | 0.00014 | 0.00001 | -0.00019 |
233 | -1.686 | -0.149 | 2.357 | 3.831 | 0.330 | -5.019 | 0.00014 | 0.00001 | -0.00019 |
234 | -1.683 | -0.149 | 2.353 | 3.825 | 0.329 | -5.011 | 0.00014 | 0.00001 | -0.00018 |
235 | -1.680 | -0.148 | 2.349 | 3.818 | 0.329 | -5.003 | 0.00014 | 0.00001 | -0.00018 |
236 | -1.678 | -0.148 | 2.345 | 3.812 | 0.328 | -4.995 | 0.00014 | 0.00001 | -0.00018 |
237 | -1.675 | -0.148 | 2.341 | 3.805 | 0.328 | -4.987 | 0.00014 | 0.00001 | -0.00018 |
238 | -1.672 | -0.148 | 2.337 | 3.799 | 0.327 | -4.979 | 0.00014 | 0.00001 | -0.00018 |
239 | -1.669 | -0.147 | 2.333 | 3.792 | 0.327 | -4.971 | 0.00014 | 0.00001 | -0.00018 |
240 | -1.667 | -0.147 | 2.329 | 3.786 | 0.326 | -4.963 | 0.00014 | 0.00001 | -0.00018 |
241 | -1.664 | -0.147 | 2.325 | 3.780 | 0.326 | -4.955 | 0.00014 | 0.00001 | -0.00018 |
242 | -1.661 | -0.147 | 2.321 | 3.773 | 0.325 | -4.947 | 0.00014 | 0.00001 | -0.00018 |
243 | -1.658 | -0.146 | 2.317 | 3.767 | 0.324 | -4.939 | 0.00014 | 0.00001 | -0.00018 |
244 | -1.656 | -0.146 | 2.314 | 3.761 | 0.324 | -4.931 | 0.00014 | 0.00001 | -0.00018 |
245 | -1.653 | -0.146 | 2.310 | 3.754 | 0.323 | -4.923 | 0.00014 | 0.00001 | -0.00018 |
246 | -1.650 | -0.146 | 2.306 | 3.748 | 0.323 | -4.915 | 0.00014 | 0.00001 | -0.00018 |
247 | -1.648 | -0.145 | 2.302 | 3.742 | 0.322 | -4.907 | 0.00014 | 0.00001 | -0.00018 |
248 | -1.645 | -0.145 | 2.298 | 3.736 | 0.322 | -4.899 | 0.00014 | 0.00001 | -0.00018 |
249 | -1.642 | -0.145 | 2.294 | 3.729 | 0.321 | -4.891 | 0.00014 | 0.00001 | -0.00018 |
250 | -1.640 | -0.145 | 2.291 | 3.723 | 0.321 | -4.884 | 0.00014 | 0.00001 | -0.00018 |
251 | -1.637 | -0.144 | 2.287 | 3.717 | 0.320 | -4.876 | 0.00014 | 0.00001 | -0.00018 |
252 | -1.634 | -0.144 | 2.283 | 3.710 | 0.320 | -4.868 | 0.00014 | 0.00001 | -0.00018 |
253 | -1.632 | -0.144 | 2.279 | 3.704 | 0.319 | -4.860 | 0.00014 | 0.00001 | -0.00018 |
254 | -1.629 | -0.144 | 2.275 | 3.698 | 0.319 | -4.852 | 0.00014 | 0.00001 | -0.00018 |
255 | -1.626 | -0.143 | 2.272 | 3.692 | 0.318 | -4.844 | 0.00014 | 0.00001 | -0.00018 |
256 | -1.624 | -0.143 | 2.268 | 3.686 | 0.317 | -4.837 | 0.00014 | 0.00001 | -0.00018 |
257 | -1.621 | -0.143 | 2.264 | 3.679 | 0.317 | -4.829 | 0.00014 | 0.00001 | -0.00018 |
258 | -1.618 | -0.143 | 2.260 | 3.673 | 0.316 | -4.821 | 0.00014 | 0.00001 | -0.00018 |
259 | -1.616 | -0.142 | 2.256 | 3.667 | 0.316 | -4.813 | 0.00014 | 0.00001 | -0.00018 |
260 | -1.613 | -0.142 | 2.253 | 3.661 | 0.315 | -4.806 | 0.00014 | 0.00001 | -0.00018 |
261 | -1.610 | -0.142 | 2.249 | 3.655 | 0.315 | -4.798 | 0.00014 | 0.00001 | -0.00018 |
262 | -1.608 | -0.142 | 2.245 | 3.649 | 0.314 | -4.790 | 0.00014 | 0.00001 | -0.00018 |
263 | -1.605 | -0.142 | 2.241 | 3.643 | 0.314 | -4.782 | 0.00014 | 0.00001 | -0.00018 |
264 | -1.602 | -0.141 | 2.238 | 3.636 | 0.313 | -4.775 | 0.00014 | 0.00001 | -0.00018 |
265 | -1.600 | -0.141 | 2.234 | 3.630 | 0.313 | -4.767 | 0.00014 | 0.00001 | -0.00018 |
266 | -1.597 | -0.141 | 2.230 | 3.624 | 0.312 | -4.759 | 0.00014 | 0.00001 | -0.00018 |
267 | -1.595 | -0.141 | 2.226 | 3.618 | 0.312 | -4.752 | 0.00014 | 0.00001 | -0.00018 |
268 | -1.592 | -0.140 | 2.223 | 3.612 | 0.311 | -4.744 | 0.00014 | 0.00001 | -0.00018 |
269 | -1.589 | -0.140 | 2.219 | 3.606 | 0.311 | -4.736 | 0.00014 | 0.00001 | -0.00017 |
270 | -1.587 | -0.140 | 2.215 | 3.600 | 0.310 | -4.729 | 0.00014 | 0.00001 | -0.00017 |
271 | -1.584 | -0.140 | 2.212 | 3.594 | 0.310 | -4.721 | 0.00013 | 0.00001 | -0.00017 |
272 | -1.582 | -0.139 | 2.208 | 3.588 | 0.309 | -4.714 | 0.00013 | 0.00001 | -0.00017 |
273 | -1.579 | -0.139 | 2.204 | 3.582 | 0.309 | -4.706 | 0.00013 | 0.00001 | -0.00017 |
274 | -1.576 | -0.139 | 2.201 | 3.576 | 0.308 | -4.698 | 0.00013 | 0.00001 | -0.00017 |
275 | -1.574 | -0.139 | 2.197 | 3.570 | 0.308 | -4.691 | 0.00013 | 0.00001 | -0.00017 |
276 | -1.571 | -0.139 | 2.193 | 3.564 | 0.307 | -4.683 | 0.00013 | 0.00001 | -0.00017 |
277 | -1.569 | -0.138 | 2.190 | 3.558 | 0.307 | -4.676 | 0.00013 | 0.00001 | -0.00017 |
278 | -1.566 | -0.138 | 2.186 | 3.552 | 0.306 | -4.668 | 0.00013 | 0.00001 | -0.00017 |
279 | -1.564 | -0.138 | 2.182 | 3.546 | 0.306 | -4.661 | 0.00013 | 0.00001 | -0.00017 |
280 | -1.561 | -0.138 | 2.179 | 3.540 | 0.305 | -4.653 | 0.00013 | 0.00001 | -0.00017 |
281 | -1.558 | -0.137 | 2.175 | 3.534 | 0.305 | -4.646 | 0.00013 | 0.00001 | -0.00017 |
282 | -1.556 | -0.137 | 2.171 | 3.528 | 0.304 | -4.638 | 0.00013 | 0.00001 | -0.00017 |
283 | -1.553 | -0.137 | 2.168 | 3.522 | 0.303 | -4.631 | 0.00013 | 0.00001 | -0.00017 |
284 | -1.551 | -0.137 | 2.164 | 3.516 | 0.303 | -4.623 | 0.00013 | 0.00001 | -0.00017 |
285 | -1.548 | -0.136 | 2.161 | 3.510 | 0.302 | -4.616 | 0.00013 | 0.00001 | -0.00017 |
286 | -1.546 | -0.136 | 2.157 | 3.504 | 0.302 | -4.608 | 0.00013 | 0.00001 | -0.00017 |
287 | -1.543 | -0.136 | 2.153 | 3.499 | 0.301 | -4.601 | 0.00013 | 0.00001 | -0.00017 |
288 | -1.541 | -0.136 | 2.150 | 3.493 | 0.301 | -4.594 | 0.00013 | 0.00001 | -0.00017 |
289 | -1.538 | -0.136 | 2.146 | 3.487 | 0.300 | -4.586 | 0.00013 | 0.00001 | -0.00017 |
290 | -1.536 | -0.135 | 2.143 | 3.481 | 0.300 | -4.579 | 0.00013 | 0.00001 | -0.00017 |
291 | -1.533 | -0.135 | 2.139 | 3.475 | 0.299 | -4.571 | 0.00013 | 0.00001 | -0.00017 |
292 | -1.531 | -0.135 | 2.135 | 3.469 | 0.299 | -4.564 | 0.00013 | 0.00001 | -0.00017 |
293 | -1.528 | -0.135 | 2.132 | 3.464 | 0.298 | -4.557 | 0.00013 | 0.00001 | -0.00017 |
294 | -1.526 | -0.134 | 2.128 | 3.458 | 0.298 | -4.549 | 0.00013 | 0.00001 | -0.00017 |
295 | -1.523 | -0.134 | 2.125 | 3.452 | 0.297 | -4.542 | 0.00013 | 0.00001 | -0.00017 |
296 | -1.521 | -0.134 | 2.121 | 3.446 | 0.297 | -4.535 | 0.00013 | 0.00001 | -0.00017 |
297 | -1.518 | -0.134 | 2.118 | 3.440 | 0.296 | -4.527 | 0.00013 | 0.00001 | -0.00017 |
298 | -1.516 | -0.134 | 2.114 | 3.435 | 0.296 | -4.520 | 0.00013 | 0.00001 | -0.00017 |
299 | -1.513 | -0.133 | 2.111 | 3.429 | 0.295 | -4.513 | 0.00013 | 0.00001 | -0.00017 |
300 | -1.511 | -0.133 | 2.107 | 3.423 | 0.295 | -4.506 | 0.00013 | 0.00001 | -0.00017 |
301 | -1.508 | -0.133 | 2.104 | 3.417 | 0.295 | -4.498 | 0.00013 | 0.00001 | -0.00017 |
302 | -1.506 | -0.133 | 2.100 | 3.412 | 0.294 | -4.491 | 0.00013 | 0.00001 | -0.00017 |
303 | -1.503 | -0.132 | 2.097 | 3.406 | 0.294 | -4.484 | 0.00013 | 0.00001 | -0.00017 |
304 | -1.501 | -0.132 | 2.093 | 3.400 | 0.293 | -4.477 | 0.00013 | 0.00001 | -0.00017 |
305 | -1.498 | -0.132 | 2.090 | 3.394 | 0.293 | -4.469 | 0.00013 | 0.00001 | -0.00016 |
306 | -1.496 | -0.132 | 2.086 | 3.389 | 0.292 | -4.462 | 0.00013 | 0.00001 | -0.00016 |
307 | -1.493 | -0.132 | 2.083 | 3.383 | 0.292 | -4.455 | 0.00013 | 0.00001 | -0.00016 |
308 | -1.491 | -0.131 | 2.079 | 3.377 | 0.291 | -4.448 | 0.00013 | 0.00001 | -0.00016 |
309 | -1.489 | -0.131 | 2.076 | 3.372 | 0.291 | -4.441 | 0.00013 | 0.00001 | -0.00016 |
310 | -1.486 | -0.131 | 2.072 | 3.366 | 0.290 | -4.433 | 0.00013 | 0.00001 | -0.00016 |
311 | -1.484 | -0.131 | 2.069 | 3.360 | 0.290 | -4.426 | 0.00013 | 0.00001 | -0.00016 |
312 | -1.481 | -0.130 | 2.065 | 3.355 | 0.289 | -4.419 | 0.00013 | 0.00001 | -0.00016 |
313 | -1.479 | -0.130 | 2.062 | 3.349 | 0.289 | -4.412 | 0.00013 | 0.00001 | -0.00016 |
314 | -1.476 | -0.130 | 2.058 | 3.344 | 0.288 | -4.405 | 0.00013 | 0.00001 | -0.00016 |
315 | -1.474 | -0.130 | 2.055 | 3.338 | 0.288 | -4.398 | 0.00013 | 0.00001 | -0.00016 |
316 | -1.472 | -0.130 | 2.052 | 3.332 | 0.287 | -4.391 | 0.00012 | 0.00001 | -0.00016 |
317 | -1.469 | -0.129 | 2.048 | 3.327 | 0.287 | -4.384 | 0.00012 | 0.00001 | -0.00016 |
318 | -1.467 | -0.129 | 2.045 | 3.321 | 0.286 | -4.377 | 0.00012 | 0.00001 | -0.00016 |
319 | -1.464 | -0.129 | 2.041 | 3.316 | 0.286 | -4.369 | 0.00012 | 0.00001 | -0.00016 |
320 | -1.462 | -0.129 | 2.038 | 3.310 | 0.285 | -4.362 | 0.00012 | 0.00001 | -0.00016 |
321 | -1.460 | -0.128 | 2.035 | 3.305 | 0.285 | -4.355 | 0.00012 | 0.00001 | -0.00016 |
322 | -1.457 | -0.128 | 2.031 | 3.299 | 0.284 | -4.348 | 0.00012 | 0.00001 | -0.00016 |
323 | -1.455 | -0.128 | 2.028 | 3.293 | 0.284 | -4.341 | 0.00012 | 0.00001 | -0.00016 |
324 | -1.452 | -0.128 | 2.024 | 3.288 | 0.283 | -4.334 | 0.00012 | 0.00001 | -0.00016 |
325 | -1.450 | -0.128 | 2.021 | 3.282 | 0.283 | -4.327 | 0.00012 | 0.00001 | -0.00016 |
326 | -1.448 | -0.127 | 2.018 | 3.277 | 0.282 | -4.320 | 0.00012 | 0.00001 | -0.00016 |
327 | -1.445 | -0.127 | 2.014 | 3.271 | 0.282 | -4.313 | 0.00012 | 0.00001 | -0.00016 |
328 | -1.443 | -0.127 | 2.011 | 3.266 | 0.282 | -4.306 | 0.00012 | 0.00001 | -0.00016 |
329 | -1.441 | -0.127 | 2.008 | 3.260 | 0.281 | -4.300 | 0.00012 | 0.00001 | -0.00016 |
330 | -1.438 | -0.127 | 2.004 | 3.255 | 0.281 | -4.293 | 0.00012 | 0.00001 | -0.00016 |
331 | -1.436 | -0.126 | 2.001 | 3.250 | 0.280 | -4.286 | 0.00012 | 0.00001 | -0.00016 |
332 | -1.433 | -0.126 | 1.998 | 3.244 | 0.280 | -4.279 | 0.00012 | 0.00001 | -0.00016 |
333 | -1.431 | -0.126 | 1.994 | 3.239 | 0.279 | -4.272 | 0.00012 | 0.00001 | -0.00016 |
334 | -1.429 | -0.126 | 1.991 | 3.233 | 0.279 | -4.265 | 0.00012 | 0.00001 | -0.00016 |
335 | -1.426 | -0.126 | 1.988 | 3.228 | 0.278 | -4.258 | 0.00012 | 0.00001 | -0.00016 |
336 | -1.424 | -0.125 | 1.984 | 3.222 | 0.278 | -4.251 | 0.00012 | 0.00001 | -0.00016 |
337 | -1.422 | -0.125 | 1.981 | 3.217 | 0.277 | -4.244 | 0.00012 | 0.00001 | -0.00016 |
338 | -1.419 | -0.125 | 1.978 | 3.212 | 0.277 | -4.237 | 0.00012 | 0.00001 | -0.00016 |
339 | -1.417 | -0.125 | 1.974 | 3.206 | 0.276 | -4.231 | 0.00012 | 0.00001 | -0.00016 |
340 | -1.415 | -0.124 | 1.971 | 3.201 | 0.276 | -4.224 | 0.00012 | 0.00001 | -0.00016 |
341 | -1.412 | -0.124 | 1.968 | 3.195 | 0.275 | -4.217 | 0.00012 | 0.00001 | -0.00016 |
342 | -1.410 | -0.124 | 1.965 | 3.190 | 0.275 | -4.210 | 0.00012 | 0.00001 | -0.00016 |
343 | -1.408 | -0.124 | 1.961 | 3.185 | 0.275 | -4.203 | 0.00012 | 0.00001 | -0.00016 |
344 | -1.406 | -0.124 | 1.958 | 3.179 | 0.274 | -4.197 | 0.00012 | 0.00001 | -0.00015 |
345 | -1.403 | -0.123 | 1.955 | 3.174 | 0.274 | -4.190 | 0.00012 | 0.00001 | -0.00015 |
346 | -1.401 | -0.123 | 1.951 | 3.169 | 0.273 | -4.183 | 0.00012 | 0.00001 | -0.00015 |
347 | -1.399 | -0.123 | 1.948 | 3.164 | 0.273 | -4.176 | 0.00012 | 0.00001 | -0.00015 |
348 | -1.396 | -0.123 | 1.945 | 3.158 | 0.272 | -4.170 | 0.00012 | 0.00001 | -0.00015 |
349 | -1.394 | -0.123 | 1.942 | 3.153 | 0.272 | -4.163 | 0.00012 | 0.00001 | -0.00015 |
350 | -1.392 | -0.122 | 1.938 | 3.148 | 0.271 | -4.156 | 0.00012 | 0.00001 | -0.00015 |
351 | -1.390 | -0.122 | 1.935 | 3.142 | 0.271 | -4.149 | 0.00012 | 0.00001 | -0.00015 |
352 | -1.387 | -0.122 | 1.932 | 3.137 | 0.270 | -4.143 | 0.00012 | 0.00001 | -0.00015 |
353 | -1.385 | -0.122 | 1.929 | 3.132 | 0.270 | -4.136 | 0.00012 | 0.00001 | -0.00015 |
354 | -1.383 | -0.122 | 1.926 | 3.127 | 0.270 | -4.129 | 0.00012 | 0.00001 | -0.00015 |
355 | -1.380 | -0.121 | 1.922 | 3.121 | 0.269 | -4.123 | 0.00012 | 0.00001 | -0.00015 |
356 | -1.378 | -0.121 | 1.919 | 3.116 | 0.269 | -4.116 | 0.00012 | 0.00001 | -0.00015 |
357 | -1.376 | -0.121 | 1.916 | 3.111 | 0.268 | -4.109 | 0.00012 | 0.00001 | -0.00015 |
358 | -1.374 | -0.121 | 1.913 | 3.106 | 0.268 | -4.103 | 0.00012 | 0.00001 | -0.00015 |
359 | -1.371 | -0.121 | 1.910 | 3.101 | 0.267 | -4.096 | 0.00012 | 0.00001 | -0.00015 |
360 | -1.369 | -0.120 | 1.906 | 3.095 | 0.267 | -4.089 | 0.00012 | 0.00001 | -0.00015 |
361 | -1.367 | -0.120 | 1.903 | 3.090 | 0.266 | -4.083 | 0.00012 | 0.00001 | -0.00015 |
362 | -1.365 | -0.120 | 1.900 | 3.085 | 0.266 | -4.076 | 0.00012 | 0.00001 | -0.00015 |
363 | -1.362 | -0.120 | 1.897 | 3.080 | 0.266 | -4.070 | 0.00012 | 0.00001 | -0.00015 |
364 | -1.360 | -0.120 | 1.894 | 3.075 | 0.265 | -4.063 | 0.00012 | 0.00001 | -0.00015 |
365 | -1.358 | -0.119 | 1.891 | 3.069 | 0.265 | -4.057 | 0.00011 | 0.00001 | -0.00015 |
366 | -1.356 | -0.119 | 1.887 | 3.064 | 0.264 | -4.050 | 0.00011 | 0.00001 | -0.00015 |
367 | -1.354 | -0.119 | 1.884 | 3.059 | 0.264 | -4.043 | 0.00011 | 0.00001 | -0.00015 |
368 | -1.351 | -0.119 | 1.881 | 3.054 | 0.263 | -4.037 | 0.00011 | 0.00001 | -0.00015 |
369 | -1.349 | -0.119 | 1.878 | 3.049 | 0.263 | -4.030 | 0.00011 | 0.00001 | -0.00015 |
370 | -1.347 | -0.118 | 1.875 | 3.044 | 0.262 | -4.024 | 0.00011 | 0.00001 | -0.00015 |
371 | -1.345 | -0.118 | 1.872 | 3.039 | 0.262 | -4.017 | 0.00011 | 0.00001 | -0.00015 |
372 | -1.342 | -0.118 | 1.869 | 3.034 | 0.262 | -4.011 | 0.00011 | 0.00001 | -0.00015 |
373 | -1.340 | -0.118 | 1.866 | 3.029 | 0.261 | -4.004 | 0.00011 | 0.00001 | -0.00015 |
374 | -1.338 | -0.118 | 1.862 | 3.024 | 0.261 | -3.998 | 0.00011 | 0.00001 | -0.00015 |
375 | -1.336 | -0.117 | 1.859 | 3.018 | 0.260 | -3.991 | 0.00011 | 0.00001 | -0.00015 |
376 | -1.334 | -0.117 | 1.856 | 3.013 | 0.260 | -3.985 | 0.00011 | 0.00001 | -0.00015 |
377 | -1.332 | -0.117 | 1.853 | 3.008 | 0.259 | -3.979 | 0.00011 | 0.00001 | -0.00015 |
378 | -1.329 | -0.117 | 1.850 | 3.003 | 0.259 | -3.972 | 0.00011 | 0.00001 | -0.00015 |
379 | -1.327 | -0.117 | 1.847 | 2.998 | 0.259 | -3.966 | 0.00011 | 0.00001 | -0.00015 |
380 | -1.325 | -0.116 | 1.844 | 2.993 | 0.258 | -3.959 | 0.00011 | 0.00001 | -0.00015 |
381 | -1.323 | -0.116 | 1.841 | 2.988 | 0.258 | -3.953 | 0.00011 | 0.00001 | -0.00015 |
382 | -1.321 | -0.116 | 1.838 | 2.983 | 0.257 | -3.947 | 0.00011 | 0.00001 | -0.00015 |
383 | -1.318 | -0.116 | 1.835 | 2.978 | 0.257 | -3.940 | 0.00011 | 0.00001 | -0.00015 |
384 | -1.316 | -0.116 | 1.832 | 2.973 | 0.256 | -3.934 | 0.00011 | 0.00001 | -0.00015 |
385 | -1.314 | -0.115 | 1.829 | 2.968 | 0.256 | -3.927 | 0.00011 | 0.00001 | -0.00015 |
386 | -1.312 | -0.115 | 1.826 | 2.963 | 0.256 | -3.921 | 0.00011 | 0.00001 | -0.00014 |
387 | -1.310 | -0.115 | 1.823 | 2.958 | 0.255 | -3.915 | 0.00011 | 0.00001 | -0.00014 |
388 | -1.308 | -0.115 | 1.820 | 2.953 | 0.255 | -3.908 | 0.00011 | 0.00001 | -0.00014 |
389 | -1.306 | -0.115 | 1.816 | 2.949 | 0.254 | -3.902 | 0.00011 | 0.00001 | -0.00014 |
390 | -1.303 | -0.115 | 1.813 | 2.944 | 0.254 | -3.896 | 0.00011 | 0.00001 | -0.00014 |
391 | -1.301 | -0.114 | 1.810 | 2.939 | 0.253 | -3.889 | 0.00011 | 0.00001 | -0.00014 |
392 | -1.299 | -0.114 | 1.807 | 2.934 | 0.253 | -3.883 | 0.00011 | 0.00001 | -0.00014 |
393 | -1.297 | -0.114 | 1.804 | 2.929 | 0.253 | -3.877 | 0.00011 | 0.00001 | -0.00014 |
394 | -1.295 | -0.114 | 1.801 | 2.924 | 0.252 | -3.871 | 0.00011 | 0.00001 | -0.00014 |
395 | -1.293 | -0.114 | 1.798 | 2.919 | 0.252 | -3.864 | 0.00011 | 0.00001 | -0.00014 |
396 | -1.291 | -0.113 | 1.795 | 2.914 | 0.251 | -3.858 | 0.00011 | 0.00001 | -0.00014 |
397 | -1.289 | -0.113 | 1.792 | 2.909 | 0.251 | -3.852 | 0.00011 | 0.00001 | -0.00014 |
398 | -1.286 | -0.113 | 1.789 | 2.904 | 0.250 | -3.846 | 0.00011 | 0.00001 | -0.00014 |
399 | -1.284 | -0.113 | 1.786 | 2.900 | 0.250 | -3.839 | 0.00011 | 0.00001 | -0.00014 |
400 | -1.282 | -0.113 | 1.784 | 2.895 | 0.250 | -3.833 | 0.00011 | 0.00001 | -0.00014 |
401 | -1.280 | -0.112 | 1.781 | 2.890 | 0.249 | -3.827 | 0.00011 | 0.00001 | -0.00014 |
402 | -1.278 | -0.112 | 1.778 | 2.885 | 0.249 | -3.821 | 0.00011 | 0.00001 | -0.00014 |
403 | -1.276 | -0.112 | 1.775 | 2.880 | 0.248 | -3.815 | 0.00011 | 0.00001 | -0.00014 |
404 | -1.274 | -0.112 | 1.772 | 2.875 | 0.248 | -3.809 | 0.00011 | 0.00001 | -0.00014 |
405 | -1.272 | -0.112 | 1.769 | 2.871 | 0.248 | -3.802 | 0.00011 | 0.00001 | -0.00014 |
406 | -1.270 | -0.112 | 1.766 | 2.866 | 0.247 | -3.796 | 0.00011 | 0.00001 | -0.00014 |
407 | -1.268 | -0.111 | 1.763 | 2.861 | 0.247 | -3.790 | 0.00011 | 0.00001 | -0.00014 |
408 | -1.265 | -0.111 | 1.760 | 2.856 | 0.246 | -3.784 | 0.00011 | 0.00001 | -0.00014 |
409 | -1.263 | -0.111 | 1.757 | 2.851 | 0.246 | -3.778 | 0.00011 | 0.00001 | -0.00014 |
410 | -1.261 | -0.111 | 1.754 | 2.847 | 0.245 | -3.772 | 0.00011 | 0.00001 | -0.00014 |
411 | -1.259 | -0.111 | 1.751 | 2.842 | 0.245 | -3.766 | 0.00011 | 0.00001 | -0.00014 |
412 | -1.257 | -0.110 | 1.748 | 2.837 | 0.245 | -3.759 | 0.00011 | 0.00001 | -0.00014 |
413 | -1.255 | -0.110 | 1.745 | 2.832 | 0.244 | -3.753 | 0.00011 | 0.00001 | -0.00014 |
414 | -1.253 | -0.110 | 1.742 | 2.828 | 0.244 | -3.747 | 0.00011 | 0.00001 | -0.00014 |
415 | -1.251 | -0.110 | 1.739 | 2.823 | 0.243 | -3.741 | 0.00011 | 0.00001 | -0.00014 |
416 | -1.249 | -0.110 | 1.737 | 2.818 | 0.243 | -3.735 | 0.00011 | 0.00001 | -0.00014 |
417 | -1.247 | -0.109 | 1.734 | 2.813 | 0.243 | -3.729 | 0.00011 | 0.00001 | -0.00014 |
418 | -1.245 | -0.109 | 1.731 | 2.809 | 0.242 | -3.723 | 0.00011 | 0.00001 | -0.00014 |
419 | -1.243 | -0.109 | 1.728 | 2.804 | 0.242 | -3.717 | 0.00010 | 0.00001 | -0.00014 |
420 | -1.241 | -0.109 | 1.725 | 2.799 | 0.241 | -3.711 | 0.00010 | 0.00001 | -0.00014 |
421 | -1.239 | -0.109 | 1.722 | 2.795 | 0.241 | -3.705 | 0.00010 | 0.00001 | -0.00014 |
422 | -1.237 | -0.109 | 1.719 | 2.790 | 0.241 | -3.699 | 0.00010 | 0.00001 | -0.00014 |
423 | -1.235 | -0.108 | 1.716 | 2.785 | 0.240 | -3.693 | 0.00010 | 0.00001 | -0.00014 |
424 | -1.233 | -0.108 | 1.714 | 2.781 | 0.240 | -3.687 | 0.00010 | 0.00001 | -0.00014 |
425 | -1.231 | -0.108 | 1.711 | 2.776 | 0.239 | -3.681 | 0.00010 | 0.00001 | -0.00014 |
426 | -1.229 | -0.108 | 1.708 | 2.771 | 0.239 | -3.675 | 0.00010 | 0.00001 | -0.00014 |
427 | -1.227 | -0.108 | 1.705 | 2.767 | 0.239 | -3.669 | 0.00010 | 0.00001 | -0.00014 |
428 | -1.225 | -0.108 | 1.702 | 2.762 | 0.238 | -3.663 | 0.00010 | 0.00001 | -0.00014 |
429 | -1.223 | -0.107 | 1.699 | 2.758 | 0.238 | -3.657 | 0.00010 | 0.00001 | -0.00014 |
430 | -1.221 | -0.107 | 1.697 | 2.753 | 0.237 | -3.651 | 0.00010 | 0.00001 | -0.00013 |
431 | -1.219 | -0.107 | 1.694 | 2.748 | 0.237 | -3.646 | 0.00010 | 0.00001 | -0.00013 |
432 | -1.217 | -0.107 | 1.691 | 2.744 | 0.237 | -3.640 | 0.00010 | 0.00001 | -0.00013 |
433 | -1.215 | -0.107 | 1.688 | 2.739 | 0.236 | -3.634 | 0.00010 | 0.00001 | -0.00013 |
434 | -1.213 | -0.106 | 1.685 | 2.735 | 0.236 | -3.628 | 0.00010 | 0.00001 | -0.00013 |
435 | -1.211 | -0.106 | 1.683 | 2.730 | 0.235 | -3.622 | 0.00010 | 0.00001 | -0.00013 |
436 | -1.209 | -0.106 | 1.680 | 2.725 | 0.235 | -3.616 | 0.00010 | 0.00001 | -0.00013 |
437 | -1.207 | -0.106 | 1.677 | 2.721 | 0.235 | -3.610 | 0.00010 | 0.00001 | -0.00013 |
438 | -1.205 | -0.106 | 1.674 | 2.716 | 0.234 | -3.604 | 0.00010 | 0.00001 | -0.00013 |
439 | -1.203 | -0.106 | 1.671 | 2.712 | 0.234 | -3.599 | 0.00010 | 0.00001 | -0.00013 |
440 | -1.201 | -0.105 | 1.669 | 2.707 | 0.233 | -3.593 | 0.00010 | 0.00001 | -0.00013 |
441 | -1.199 | -0.105 | 1.666 | 2.703 | 0.233 | -3.587 | 0.00010 | 0.00001 | -0.00013 |
442 | -1.197 | -0.105 | 1.663 | 2.698 | 0.233 | -3.581 | 0.00010 | 0.00001 | -0.00013 |
443 | -1.195 | -0.105 | 1.660 | 2.694 | 0.232 | -3.575 | 0.00010 | 0.00001 | -0.00013 |
444 | -1.193 | -0.105 | 1.657 | 2.689 | 0.232 | -3.570 | 0.00010 | 0.00001 | -0.00013 |
445 | -1.191 | -0.104 | 1.655 | 2.685 | 0.232 | -3.564 | 0.00010 | 0.00001 | -0.00013 |
446 | -1.189 | -0.104 | 1.652 | 2.680 | 0.231 | -3.558 | 0.00010 | 0.00001 | -0.00013 |
447 | -1.187 | -0.104 | 1.649 | 2.676 | 0.231 | -3.552 | 0.00010 | 0.00001 | -0.00013 |
448 | -1.185 | -0.104 | 1.646 | 2.671 | 0.230 | -3.546 | 0.00010 | 0.00001 | -0.00013 |
449 | -1.183 | -0.104 | 1.644 | 2.667 | 0.230 | -3.541 | 0.00010 | 0.00001 | -0.00013 |
450 | -1.181 | -0.104 | 1.641 | 2.662 | 0.230 | -3.535 | 0.00010 | 0.00001 | -0.00013 |
451 | -1.179 | -0.103 | 1.638 | 2.658 | 0.229 | -3.529 | 0.00010 | 0.00001 | -0.00013 |
452 | -1.177 | -0.103 | 1.636 | 2.653 | 0.229 | -3.524 | 0.00010 | 0.00001 | -0.00013 |
453 | -1.175 | -0.103 | 1.633 | 2.649 | 0.228 | -3.518 | 0.00010 | 0.00001 | -0.00013 |
454 | -1.173 | -0.103 | 1.630 | 2.645 | 0.228 | -3.512 | 0.00010 | 0.00001 | -0.00013 |
455 | -1.172 | -0.103 | 1.627 | 2.640 | 0.228 | -3.506 | 0.00010 | 0.00001 | -0.00013 |
456 | -1.170 | -0.103 | 1.625 | 2.636 | 0.227 | -3.501 | 0.00010 | 0.00001 | -0.00013 |
457 | -1.168 | -0.102 | 1.622 | 2.631 | 0.227 | -3.495 | 0.00010 | 0.00001 | -0.00013 |
458 | -1.166 | -0.102 | 1.619 | 2.627 | 0.227 | -3.489 | 0.00010 | 0.00001 | -0.00013 |
459 | -1.164 | -0.102 | 1.617 | 2.623 | 0.226 | -3.484 | 0.00010 | 0.00001 | -0.00013 |
460 | -1.162 | -0.102 | 1.614 | 2.618 | 0.226 | -3.478 | 0.00010 | 0.00001 | -0.00013 |
461 | -1.160 | -0.102 | 1.611 | 2.614 | 0.225 | -3.472 | 0.00010 | 0.00001 | -0.00013 |
462 | -1.158 | -0.102 | 1.609 | 2.609 | 0.225 | -3.467 | 0.00010 | 0.00001 | -0.00013 |
463 | -1.156 | -0.101 | 1.606 | 2.605 | 0.225 | -3.461 | 0.00010 | 0.00001 | -0.00013 |
464 | -1.154 | -0.101 | 1.603 | 2.601 | 0.224 | -3.456 | 0.00010 | 0.00001 | -0.00013 |
465 | -1.152 | -0.101 | 1.601 | 2.596 | 0.224 | -3.450 | 0.00010 | 0.00001 | -0.00013 |
466 | -1.151 | -0.101 | 1.598 | 2.592 | 0.224 | -3.444 | 0.00010 | 0.00001 | -0.00013 |
467 | -1.149 | -0.101 | 1.595 | 2.588 | 0.223 | -3.439 | 0.00010 | 0.00001 | -0.00013 |
468 | -1.147 | -0.101 | 1.593 | 2.583 | 0.223 | -3.433 | 0.00010 | 0.00001 | -0.00013 |
469 | -1.145 | -0.100 | 1.590 | 2.579 | 0.222 | -3.428 | 0.00010 | 0.00001 | -0.00013 |
470 | -1.143 | -0.100 | 1.587 | 2.575 | 0.222 | -3.422 | 0.00010 | 0.00001 | -0.00013 |
471 | -1.141 | -0.100 | 1.585 | 2.570 | 0.222 | -3.417 | 0.00010 | 0.00001 | -0.00013 |
472 | -1.139 | -0.100 | 1.582 | 2.566 | 0.221 | -3.411 | 0.00010 | 0.00001 | -0.00013 |
473 | -1.137 | -0.100 | 1.579 | 2.562 | 0.221 | -3.406 | 0.00010 | 0.00001 | -0.00013 |
474 | -1.136 | -0.100 | 1.577 | 2.558 | 0.221 | -3.400 | 0.00010 | 0.00001 | -0.00013 |
475 | -1.134 | -0.099 | 1.574 | 2.553 | 0.220 | -3.395 | 0.00010 | 0.00001 | -0.00013 |
476 | -1.132 | -0.099 | 1.572 | 2.549 | 0.220 | -3.389 | 0.00010 | 0.00001 | -0.00013 |
477 | -1.130 | -0.099 | 1.569 | 2.545 | 0.219 | -3.384 | 0.00010 | 0.00001 | -0.00013 |
478 | -1.128 | -0.099 | 1.566 | 2.541 | 0.219 | -3.378 | 0.00010 | 0.00001 | -0.00012 |
479 | -1.126 | -0.099 | 1.564 | 2.536 | 0.219 | -3.373 | 0.00009 | 0.00001 | -0.00012 |
480 | -1.124 | -0.099 | 1.561 | 2.532 | 0.218 | -3.367 | 0.00009 | 0.00001 | -0.00012 |
481 | -1.123 | -0.098 | 1.558 | 2.528 | 0.218 | -3.362 | 0.00009 | 0.00001 | -0.00012 |
482 | -1.121 | -0.098 | 1.556 | 2.524 | 0.218 | -3.356 | 0.00009 | 0.00001 | -0.00012 |
483 | -1.119 | -0.098 | 1.553 | 2.519 | 0.217 | -3.351 | 0.00009 | 0.00001 | -0.00012 |
484 | -1.117 | -0.098 | 1.551 | 2.515 | 0.217 | -3.345 | 0.00009 | 0.00001 | -0.00012 |
485 | -1.115 | -0.098 | 1.548 | 2.511 | 0.217 | -3.340 | 0.00009 | 0.00001 | -0.00012 |
486 | -1.113 | -0.098 | 1.546 | 2.507 | 0.216 | -3.334 | 0.00009 | 0.00001 | -0.00012 |
487 | -1.112 | -0.097 | 1.543 | 2.503 | 0.216 | -3.329 | 0.00009 | 0.00001 | -0.00012 |
488 | -1.110 | -0.097 | 1.540 | 2.498 | 0.216 | -3.324 | 0.00009 | 0.00001 | -0.00012 |
489 | -1.108 | -0.097 | 1.538 | 2.494 | 0.215 | -3.318 | 0.00009 | 0.00001 | -0.00012 |
490 | -1.106 | -0.097 | 1.535 | 2.490 | 0.215 | -3.313 | 0.00009 | 0.00001 | -0.00012 |
491 | -1.104 | -0.097 | 1.533 | 2.486 | 0.214 | -3.308 | 0.00009 | 0.00001 | -0.00012 |
492 | -1.103 | -0.097 | 1.530 | 2.482 | 0.214 | -3.302 | 0.00009 | 0.00001 | -0.00012 |
493 | -1.101 | -0.096 | 1.528 | 2.478 | 0.214 | -3.297 | 0.00009 | 0.00001 | -0.00012 |
494 | -1.099 | -0.096 | 1.525 | 2.474 | 0.213 | -3.291 | 0.00009 | 0.00001 | -0.00012 |
495 | -1.097 | -0.096 | 1.523 | 2.469 | 0.213 | -3.286 | 0.00009 | 0.00001 | -0.00012 |
496 | -1.095 | -0.096 | 1.520 | 2.465 | 0.213 | -3.281 | 0.00009 | 0.00001 | -0.00012 |
497 | -1.093 | -0.096 | 1.518 | 2.461 | 0.212 | -3.275 | 0.00009 | 0.00001 | -0.00012 |
498 | -1.092 | -0.096 | 1.515 | 2.457 | 0.212 | -3.270 | 0.00009 | 0.00001 | -0.00012 |
499 | -1.090 | -0.096 | 1.513 | 2.453 | 0.212 | -3.265 | 0.00009 | 0.00001 | -0.00012 |
Figure 7: Slope of the Excess Demand Function
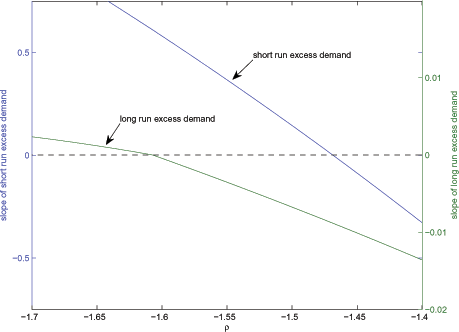
Data for Figure 7
rho | slope of long run excess demand | slope of short run excess demand |
|---|---|---|
-1.7000 | 0.0024 | 0.9787 |
-1.6990 | 0.0023 | 0.9749 |
-1.6980 | 0.0023 | 0.9711 |
-1.6970 | 0.0023 | 0.9673 |
-1.6960 | 0.0023 | 0.9634 |
-1.6950 | 0.0022 | 0.9596 |
-1.6940 | 0.0022 | 0.9557 |
-1.6930 | 0.0022 | 0.9519 |
-1.6920 | 0.0022 | 0.9480 |
-1.6910 | 0.0022 | 0.9442 |
-1.6900 | 0.0021 | 0.9403 |
-1.6890 | 0.0021 | 0.9365 |
-1.6880 | 0.0021 | 0.9326 |
-1.6870 | 0.0021 | 0.9287 |
-1.6860 | 0.0020 | 0.9249 |
-1.6850 | 0.0020 | 0.9210 |
-1.6840 | 0.0020 | 0.9171 |
-1.6830 | 0.0020 | 0.9133 |
-1.6820 | 0.0020 | 0.9094 |
-1.6810 | 0.0019 | 0.9055 |
-1.6800 | 0.0019 | 0.9016 |
-1.6790 | 0.0019 | 0.8977 |
-1.6780 | 0.0019 | 0.8938 |
-1.6770 | 0.0018 | 0.8899 |
-1.6760 | 0.0018 | 0.8860 |
-1.6750 | 0.0018 | 0.8821 |
-1.6740 | 0.0018 | 0.8782 |
-1.6730 | 0.0018 | 0.8743 |
-1.6720 | 0.0017 | 0.8704 |
-1.6710 | 0.0017 | 0.8665 |
-1.6700 | 0.0017 | 0.8626 |
-1.6690 | 0.0017 | 0.8587 |
-1.6680 | 0.0016 | 0.8547 |
-1.6670 | 0.0016 | 0.8508 |
-1.6660 | 0.0016 | 0.8469 |
-1.6650 | 0.0016 | 0.8429 |
-1.6640 | 0.0015 | 0.8390 |
-1.6630 | 0.0015 | 0.8351 |
-1.6620 | 0.0015 | 0.8311 |
-1.6610 | 0.0015 | 0.8272 |
-1.6600 | 0.0014 | 0.8232 |
-1.6590 | 0.0014 | 0.8193 |
-1.6580 | 0.0014 | 0.8153 |
-1.6570 | 0.0014 | 0.8114 |
-1.6560 | 0.0013 | 0.8074 |
-1.6550 | 0.0013 | 0.8034 |
-1.6540 | 0.0013 | 0.7995 |
-1.6530 | 0.0013 | 0.7955 |
-1.6520 | 0.0012 | 0.7915 |
-1.6510 | 0.0012 | 0.7876 |
-1.6500 | 0.0012 | 0.7836 |
-1.6490 | 0.0012 | 0.7796 |
-1.6480 | 0.0011 | 0.7756 |
-1.6470 | 0.0011 | 0.7716 |
-1.6460 | 0.0011 | 0.7676 |
-1.6450 | 0.0011 | 0.7636 |
-1.6440 | 0.0010 | 0.7596 |
-1.6430 | 0.0010 | 0.7556 |
-1.6420 | 0.0010 | 0.7516 |
-1.6410 | 0.0010 | 0.7476 |
-1.6400 | 0.0009 | 0.7436 |
-1.6390 | 0.0009 | 0.7396 |
-1.6380 | 0.0009 | 0.7356 |
-1.6370 | 0.0008 | 0.7315 |
-1.6360 | 0.0008 | 0.7275 |
-1.6350 | 0.0008 | 0.7235 |
-1.6340 | 0.0008 | 0.7195 |
-1.6330 | 0.0007 | 0.7154 |
-1.6320 | 0.0007 | 0.7114 |
-1.6310 | 0.0007 | 0.7073 |
-1.6300 | 0.0007 | 0.7033 |
-1.6290 | 0.0006 | 0.6993 |
-1.6280 | 0.0006 | 0.6952 |
-1.6270 | 0.0006 | 0.6911 |
-1.6260 | 0.0005 | 0.6871 |
-1.6250 | 0.0005 | 0.6830 |
-1.6240 | 0.0005 | 0.6790 |
-1.6230 | 0.0005 | 0.6749 |
-1.6220 | 0.0004 | 0.6708 |
-1.6210 | 0.0004 | 0.6667 |
-1.6200 | 0.0004 | 0.6627 |
-1.6190 | 0.0003 | 0.6586 |
-1.6180 | 0.0003 | 0.6545 |
-1.6170 | 0.0003 | 0.6504 |
-1.6160 | 0.0003 | 0.6463 |
-1.6150 | 0.0002 | 0.6422 |
-1.6140 | 0.0002 | 0.6381 |
-1.6130 | 0.0002 | 0.6340 |
-1.6120 | 0.0001 | 0.6299 |
-1.6110 | 0.0001 | 0.6258 |
-1.6100 | 0.0001 | 0.6217 |
-1.6090 | 0.0001 | 0.6176 |
-1.6080 | 0.0000 | 0.6135 |
-1.6070 | 0.0000 | 0.6093 |
-1.6060 | -0.0001 | 0.6052 |
-1.6050 | -0.0001 | 0.6010 |
-1.6040 | -0.0002 | 0.5969 |
-1.6030 | -0.0003 | 0.5927 |
-1.6020 | -0.0003 | 0.5885 |
-1.6010 | -0.0004 | 0.5843 |
-1.6000 | -0.0004 | 0.5802 |
-1.5990 | -0.0005 | 0.5760 |
-1.5980 | -0.0006 | 0.5718 |
-1.5970 | -0.0006 | 0.5676 |
-1.5960 | -0.0007 | 0.5634 |
-1.5950 | -0.0007 | 0.5592 |
-1.5940 | -0.0008 | 0.5550 |
-1.5930 | -0.0009 | 0.5508 |
-1.5920 | -0.0009 | 0.5466 |
-1.5910 | -0.0010 | 0.5424 |
-1.5900 | -0.0010 | 0.5382 |
-1.5890 | -0.0011 | 0.5339 |
-1.5880 | -0.0012 | 0.5297 |
-1.5870 | -0.0012 | 0.5255 |
-1.5860 | -0.0013 | 0.5213 |
-1.5850 | -0.0014 | 0.5170 |
-1.5840 | -0.0014 | 0.5128 |
-1.5830 | -0.0015 | 0.5086 |
-1.5820 | -0.0015 | 0.5043 |
-1.5810 | -0.0016 | 0.5001 |
-1.5800 | -0.0017 | 0.4958 |
-1.5790 | -0.0017 | 0.4916 |
-1.5780 | -0.0018 | 0.4873 |
-1.5770 | -0.0018 | 0.4831 |
-1.5760 | -0.0019 | 0.4788 |
-1.5750 | -0.0020 | 0.4745 |
-1.5740 | -0.0020 | 0.4703 |
-1.5730 | -0.0021 | 0.4660 |
-1.5720 | -0.0022 | 0.4617 |
-1.5710 | -0.0022 | 0.4575 |
-1.5700 | -0.0023 | 0.4532 |
-1.5690 | -0.0023 | 0.4489 |
-1.5680 | -0.0024 | 0.4446 |
-1.5670 | -0.0025 | 0.4403 |
-1.5660 | -0.0025 | 0.4360 |
-1.5650 | -0.0026 | 0.4317 |
-1.5640 | -0.0027 | 0.4274 |
-1.5630 | -0.0027 | 0.4231 |
-1.5620 | -0.0028 | 0.4188 |
-1.5610 | -0.0028 | 0.4145 |
-1.5600 | -0.0029 | 0.4102 |
-1.5590 | -0.0030 | 0.4058 |
-1.5580 | -0.0030 | 0.4015 |
-1.5570 | -0.0031 | 0.3972 |
-1.5560 | -0.0032 | 0.3929 |
-1.5550 | -0.0032 | 0.3885 |
-1.5540 | -0.0033 | 0.3842 |
-1.5530 | -0.0033 | 0.3798 |
-1.5520 | -0.0034 | 0.3755 |
-1.5510 | -0.0035 | 0.3711 |
-1.5500 | -0.0035 | 0.3668 |
-1.5490 | -0.0036 | 0.3624 |
-1.5480 | -0.0037 | 0.3581 |
-1.5470 | -0.0037 | 0.3537 |
-1.5460 | -0.0038 | 0.3494 |
-1.5450 | -0.0038 | 0.3450 |
-1.5440 | -0.0039 | 0.3406 |
-1.5430 | -0.0040 | 0.3362 |
-1.5420 | -0.0040 | 0.3319 |
-1.5410 | -0.0041 | 0.3275 |
-1.5400 | -0.0042 | 0.3231 |
-1.5390 | -0.0042 | 0.3187 |
-1.5380 | -0.0043 | 0.3143 |
-1.5370 | -0.0044 | 0.3099 |
-1.5360 | -0.0044 | 0.3055 |
-1.5350 | -0.0045 | 0.3011 |
-1.5340 | -0.0045 | 0.2967 |
-1.5330 | -0.0046 | 0.2923 |
-1.5320 | -0.0047 | 0.2879 |
-1.5310 | -0.0047 | 0.2834 |
-1.5300 | -0.0048 | 0.2790 |
-1.5290 | -0.0049 | 0.2746 |
-1.5280 | -0.0049 | 0.2702 |
-1.5270 | -0.0050 | 0.2657 |
-1.5260 | -0.0051 | 0.2613 |
-1.5250 | -0.0051 | 0.2568 |
-1.5240 | -0.0052 | 0.2524 |
-1.5230 | -0.0053 | 0.2480 |
-1.5220 | -0.0053 | 0.2435 |
-1.5210 | -0.0054 | 0.2390 |
-1.5200 | -0.0054 | 0.2346 |
-1.5190 | -0.0055 | 0.2301 |
-1.5180 | -0.0056 | 0.2257 |
-1.5170 | -0.0056 | 0.2212 |
-1.5160 | -0.0057 | 0.2167 |
-1.5150 | -0.0058 | 0.2122 |
-1.5140 | -0.0058 | 0.2077 |
-1.5130 | -0.0059 | 0.2033 |
-1.5120 | -0.0060 | 0.1988 |
-1.5110 | -0.0060 | 0.1943 |
-1.5100 | -0.0061 | 0.1898 |
-1.5090 | -0.0062 | 0.1853 |
-1.5080 | -0.0062 | 0.1808 |
-1.5070 | -0.0063 | 0.1763 |
-1.5060 | -0.0064 | 0.1718 |
-1.5050 | -0.0064 | 0.1672 |
-1.5040 | -0.0065 | 0.1627 |
-1.5030 | -0.0066 | 0.1582 |
-1.5020 | -0.0066 | 0.1537 |
-1.5010 | -0.0067 | 0.1492 |
-1.5000 | -0.0068 | 0.1446 |
-1.4990 | -0.0068 | 0.1401 |
-1.4980 | -0.0069 | 0.1355 |
-1.4970 | -0.0069 | 0.1310 |
-1.4960 | -0.0070 | 0.1264 |
-1.4950 | -0.0071 | 0.1219 |
-1.4940 | -0.0071 | 0.1173 |
-1.4930 | -0.0072 | 0.1128 |
-1.4920 | -0.0073 | 0.1082 |
-1.4910 | -0.0073 | 0.1036 |
-1.4900 | -0.0074 | 0.0991 |
-1.4890 | -0.0075 | 0.0945 |
-1.4880 | -0.0075 | 0.0899 |
-1.4870 | -0.0076 | 0.0853 |
-1.4860 | -0.0077 | 0.0808 |
-1.4850 | -0.0077 | 0.0762 |
-1.4840 | -0.0078 | 0.0716 |
-1.4830 | -0.0079 | 0.0670 |
-1.4820 | -0.0079 | 0.0624 |
-1.4810 | -0.0080 | 0.0578 |
-1.4800 | -0.0081 | 0.0532 |
-1.4790 | -0.0081 | 0.0485 |
-1.4780 | -0.0082 | 0.0439 |
-1.4770 | -0.0083 | 0.0393 |
-1.4760 | -0.0083 | 0.0347 |
-1.4750 | -0.0084 | 0.0300 |
-1.4740 | -0.0085 | 0.0254 |
-1.4730 | -0.0085 | 0.0208 |
-1.4720 | -0.0086 | 0.0161 |
-1.4710 | -0.0087 | 0.0115 |
-1.4700 | -0.0087 | 0.0068 |
-1.4690 | -0.0088 | 0.0022 |
-1.4680 | -0.0089 | -0.0025 |
-1.4670 | -0.0089 | -0.0071 |
-1.4660 | -0.0090 | -0.0118 |
-1.4650 | -0.0091 | -0.0165 |
-1.4640 | -0.0092 | -0.0211 |
-1.4630 | -0.0092 | -0.0258 |
-1.4620 | -0.0093 | -0.0305 |
-1.4610 | -0.0094 | -0.0352 |
-1.4600 | -0.0094 | -0.0399 |
-1.4590 | -0.0095 | -0.0445 |
-1.4580 | -0.0096 | -0.0492 |
-1.4570 | -0.0096 | -0.0539 |
-1.4560 | -0.0097 | -0.0586 |
-1.4550 | -0.0098 | -0.0633 |
-1.4540 | -0.0098 | -0.0681 |
-1.4530 | -0.0099 | -0.0728 |
-1.4520 | -0.0100 | -0.0775 |
-1.4510 | -0.0100 | -0.0822 |
-1.4500 | -0.0101 | -0.0869 |
-1.4490 | -0.0102 | -0.0917 |
-1.4480 | -0.0102 | -0.0964 |
-1.4470 | -0.0103 | -0.1011 |
-1.4460 | -0.0104 | -0.1059 |
-1.4450 | -0.0104 | -0.1106 |
-1.4440 | -0.0105 | -0.1154 |
-1.4430 | -0.0106 | -0.1201 |
-1.4420 | -0.0107 | -0.1249 |
-1.4410 | -0.0107 | -0.1297 |
-1.4400 | -0.0108 | -0.1344 |
-1.4390 | -0.0109 | -0.1392 |
-1.4380 | -0.0109 | -0.1440 |
-1.4370 | -0.0110 | -0.1488 |
-1.4360 | -0.0111 | -0.1535 |
-1.4350 | -0.0111 | -0.1583 |
-1.4340 | -0.0112 | -0.1631 |
-1.4330 | -0.0113 | -0.1679 |
-1.4320 | -0.0113 | -0.1727 |
-1.4310 | -0.0114 | -0.1775 |
-1.4300 | -0.0115 | -0.1823 |
-1.4290 | -0.0116 | -0.1871 |
-1.4280 | -0.0116 | -0.1920 |
-1.4270 | -0.0117 | -0.1968 |
-1.4260 | -0.0118 | -0.2016 |
-1.4250 | -0.0118 | -0.2064 |
-1.4240 | -0.0119 | -0.2113 |
-1.4230 | -0.0120 | -0.2161 |
-1.4220 | -0.0120 | -0.2209 |
-1.4210 | -0.0121 | -0.2258 |
-1.4200 | -0.0122 | -0.2306 |
-1.4190 | -0.0122 | -0.2355 |
-1.4180 | -0.0123 | -0.2403 |
-1.4170 | -0.0124 | -0.2452 |
-1.4160 | -0.0125 | -0.2501 |
-1.4150 | -0.0125 | -0.2549 |
-1.4140 | -0.0126 | -0.2598 |
-1.4130 | -0.0127 | -0.2647 |
-1.4120 | -0.0127 | -0.2696 |
-1.4110 | -0.0128 | -0.2745 |
-1.4100 | -0.0129 | -0.2794 |
-1.4090 | -0.0130 | -0.2842 |
-1.4080 | -0.0130 | -0.2891 |
-1.4070 | -0.0131 | -0.2941 |
-1.4060 | -0.0132 | -0.2990 |
-1.4050 | -0.0132 | -0.3039 |
-1.4040 | -0.0133 | -0.3088 |
-1.4030 | -0.0134 | -0.3137 |
-1.4020 | -0.0135 | -0.3186 |
-1.4010 | -0.0135 | -0.3236 |
-1.4000 | -0.0136 | -0.3285 |
Figure 8: Existence of Equilibrium Paths: Path Comparison
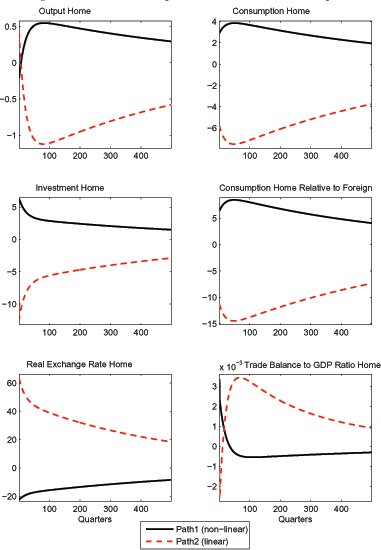
Data for Figure 8
Quarters | Output Home Path 1 (non-linear) | Output Home: Path 2 (linear) | Consumption Home: Path 1 (non-linear) | Consumption Home: Path 2 (linear) | Investment Home: Path 1 (non-linear) | Investment Home: Path 2 (linear) | Consumption Home Relative to Foreign: Path 1 (non-linear) | Consumption Home Relative to Foreign: Path 2 (linear) | Real Exchange Rate Home: Path 1 (non-linear) | Real Exchange Rate Home: Path 2 (linear) | Trade Balance to GDP Ratio Home: Path 1 (non-linear) | Trade Balance to GDP Ratio Home: Path 2 (linear) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 | 0.421 | -0.207 | -5.793 | 2.915 | -12.596 | 5.917 | -11.276 | 6.371 | 63.119 | -22.479 | -0.00127 | 0.00336 |
2 | 0.336 | -0.171 | -5.902 | 2.973 | -11.943 | 6.163 | -11.481 | 6.502 | 62.236 | -22.257 | -0.00263 | 0.00231 |
3 | 0.260 | -0.134 | -6.006 | 3.029 | -11.685 | 6.027 | -11.675 | 6.626 | 61.395 | -22.043 | -0.00229 | 0.00217 |
4 | 0.188 | -0.099 | -6.104 | 3.081 | -11.438 | 5.897 | -11.859 | 6.744 | 60.593 | -21.838 | -0.00196 | 0.00204 |
5 | 0.119 | -0.066 | -6.197 | 3.131 | -11.201 | 5.772 | -12.032 | 6.856 | 59.827 | -21.640 | -0.00166 | 0.00192 |
6 | 0.054 | -0.034 | -6.284 | 3.178 | -10.975 | 5.653 | -12.195 | 6.961 | 59.096 | -21.450 | -0.00136 | 0.00180 |
7 | -0.008 | -0.003 | -6.367 | 3.223 | -10.757 | 5.539 | -12.350 | 7.062 | 58.398 | -21.268 | -0.00109 | 0.00169 |
8 | -0.068 | 0.026 | -6.445 | 3.265 | -10.550 | 5.430 | -12.496 | 7.156 | 57.731 | -21.092 | -0.00083 | 0.00159 |
9 | -0.124 | 0.053 | -6.519 | 3.305 | -10.351 | 5.326 | -12.633 | 7.246 | 57.094 | -20.924 | -0.00058 | 0.00148 |
10 | -0.177 | 0.079 | -6.589 | 3.343 | -10.160 | 5.226 | -12.763 | 7.331 | 56.484 | -20.761 | -0.00034 | 0.00139 |
11 | -0.228 | 0.104 | -6.655 | 3.378 | -9.978 | 5.131 | -12.885 | 7.411 | 55.900 | -20.605 | -0.00012 | 0.00129 |
12 | -0.276 | 0.128 | -6.717 | 3.412 | -9.803 | 5.039 | -13.001 | 7.487 | 55.342 | -20.455 | 0.00009 | 0.00120 |
13 | -0.322 | 0.150 | -6.776 | 3.444 | -9.636 | 4.952 | -13.109 | 7.558 | 54.807 | -20.310 | 0.00029 | 0.00112 |
14 | -0.366 | 0.172 | -6.831 | 3.474 | -9.476 | 4.868 | -13.212 | 7.626 | 54.294 | -20.170 | 0.00048 | 0.00104 |
15 | -0.408 | 0.192 | -6.883 | 3.502 | -9.323 | 4.788 | -13.308 | 7.690 | 53.803 | -20.036 | 0.00066 | 0.00096 |
16 | -0.447 | 0.211 | -6.932 | 3.529 | -9.176 | 4.711 | -13.399 | 7.750 | 53.332 | -19.907 | 0.00083 | 0.00089 |
17 | -0.485 | 0.230 | -6.978 | 3.554 | -9.035 | 4.638 | -13.484 | 7.806 | 52.880 | -19.782 | 0.00099 | 0.00082 |
18 | -0.520 | 0.247 | -7.021 | 3.578 | -8.901 | 4.568 | -13.563 | 7.859 | 52.446 | -19.662 | 0.00114 | 0.00075 |
19 | -0.554 | 0.264 | -7.062 | 3.600 | -8.772 | 4.500 | -13.638 | 7.909 | 52.029 | -19.546 | 0.00129 | 0.00069 |
20 | -0.586 | 0.280 | -7.100 | 3.621 | -8.648 | 4.436 | -13.709 | 7.956 | 51.628 | -19.435 | 0.00143 | 0.00062 |
21 | -0.617 | 0.295 | -7.135 | 3.641 | -8.530 | 4.374 | -13.775 | 8.000 | 51.243 | -19.327 | 0.00155 | 0.00057 |
22 | -0.646 | 0.309 | -7.169 | 3.660 | -8.417 | 4.315 | -13.836 | 8.041 | 50.873 | -19.223 | 0.00168 | 0.00051 |
23 | -0.673 | 0.323 | -7.200 | 3.677 | -8.308 | 4.259 | -13.894 | 8.080 | 50.517 | -19.122 | 0.00179 | 0.00046 |
24 | -0.700 | 0.335 | -7.229 | 3.693 | -8.204 | 4.204 | -13.947 | 8.116 | 50.174 | -19.025 | 0.00190 | 0.00041 |
25 | -0.724 | 0.348 | -7.256 | 3.708 | -8.104 | 4.152 | -13.997 | 8.149 | 49.843 | -18.932 | 0.00201 | 0.00036 |
26 | -0.748 | 0.359 | -7.282 | 3.723 | -8.009 | 4.103 | -14.044 | 8.181 | 49.525 | -18.841 | 0.00210 | 0.00031 |
27 | -0.770 | 0.370 | -7.305 | 3.736 | -7.917 | 4.055 | -14.087 | 8.210 | 49.218 | -18.753 | 0.00220 | 0.00027 |
28 | -0.791 | 0.381 | -7.327 | 3.748 | -7.829 | 4.009 | -14.127 | 8.237 | 48.922 | -18.669 | 0.00228 | 0.00023 |
29 | -0.812 | 0.391 | -7.347 | 3.760 | -7.745 | 3.965 | -14.165 | 8.262 | 48.636 | -18.587 | 0.00236 | 0.00019 |
30 | -0.831 | 0.400 | -7.366 | 3.770 | -7.664 | 3.923 | -14.199 | 8.285 | 48.360 | -18.507 | 0.00244 | 0.00015 |
31 | -0.849 | 0.409 | -7.383 | 3.780 | -7.586 | 3.883 | -14.230 | 8.307 | 48.093 | -18.430 | 0.00252 | 0.00012 |
32 | -0.866 | 0.418 | -7.399 | 3.789 | -7.512 | 3.844 | -14.259 | 8.326 | 47.835 | -18.356 | 0.00258 | 0.00008 |
33 | -0.882 | 0.426 | -7.413 | 3.798 | -7.440 | 3.807 | -14.286 | 8.345 | 47.585 | -18.284 | 0.00265 | 0.00005 |
34 | -0.897 | 0.433 | -7.427 | 3.805 | -7.372 | 3.772 | -14.310 | 8.361 | 47.344 | -18.213 | 0.00271 | 0.00002 |
35 | -0.912 | 0.441 | -7.439 | 3.812 | -7.306 | 3.738 | -14.332 | 8.376 | 47.110 | -18.145 | 0.00277 | -0.00001 |
36 | -0.926 | 0.447 | -7.450 | 3.819 | -7.243 | 3.705 | -14.352 | 8.390 | 46.883 | -18.079 | 0.00282 | -0.00004 |
37 | -0.939 | 0.454 | -7.459 | 3.825 | -7.182 | 3.673 | -14.370 | 8.402 | 46.663 | -18.015 | 0.00287 | -0.00007 |
38 | -0.951 | 0.460 | -7.468 | 3.830 | -7.123 | 3.643 | -14.386 | 8.413 | 46.450 | -17.953 | 0.00292 | -0.00009 |
39 | -0.963 | 0.466 | -7.476 | 3.835 | -7.067 | 3.614 | -14.400 | 8.423 | 46.243 | -17.892 | 0.00296 | -0.00012 |
40 | -0.974 | 0.471 | -7.483 | 3.839 | -7.013 | 3.586 | -14.413 | 8.432 | 46.042 | -17.833 | 0.00301 | -0.00014 |
41 | -0.984 | 0.477 | -7.489 | 3.843 | -6.961 | 3.559 | -14.424 | 8.439 | 45.847 | -17.776 | 0.00304 | -0.00016 |
42 | -0.994 | 0.482 | -7.494 | 3.846 | -6.911 | 3.533 | -14.433 | 8.446 | 45.657 | -17.720 | 0.00308 | -0.00018 |
43 | -1.003 | 0.486 | -7.498 | 3.849 | -6.863 | 3.509 | -14.441 | 8.451 | 45.473 | -17.666 | 0.00311 | -0.00020 |
44 | -1.012 | 0.491 | -7.502 | 3.851 | -6.817 | 3.485 | -14.447 | 8.456 | 45.293 | -17.613 | 0.00315 | -0.00022 |
45 | -1.020 | 0.495 | -7.505 | 3.853 | -6.772 | 3.462 | -14.452 | 8.459 | 45.118 | -17.561 | 0.00318 | -0.00024 |
46 | -1.028 | 0.499 | -7.507 | 3.855 | -6.729 | 3.439 | -14.456 | 8.462 | 44.947 | -17.510 | 0.00320 | -0.00026 |
47 | -1.035 | 0.502 | -7.508 | 3.856 | -6.688 | 3.418 | -14.458 | 8.464 | 44.781 | -17.461 | 0.00323 | -0.00027 |
48 | -1.042 | 0.506 | -7.509 | 3.857 | -6.648 | 3.397 | -14.459 | 8.465 | 44.619 | -17.413 | 0.00325 | -0.00029 |
49 | -1.049 | 0.509 | -7.509 | 3.858 | -6.609 | 3.378 | -14.460 | 8.465 | 44.460 | -17.366 | 0.00327 | -0.00030 |
50 | -1.055 | 0.512 | -7.509 | 3.858 | -6.572 | 3.358 | -14.459 | 8.465 | 44.306 | -17.320 | 0.00329 | -0.00032 |
51 | -1.061 | 0.515 | -7.508 | 3.858 | -6.536 | 3.340 | -14.457 | 8.464 | 44.154 | -17.275 | 0.00331 | -0.00033 |
52 | -1.066 | 0.518 | -7.506 | 3.858 | -6.502 | 3.322 | -14.454 | 8.462 | 44.007 | -17.231 | 0.00333 | -0.00034 |
53 | -1.071 | 0.521 | -7.504 | 3.857 | -6.468 | 3.305 | -14.450 | 8.460 | 43.862 | -17.187 | 0.00334 | -0.00036 |
54 | -1.076 | 0.523 | -7.502 | 3.857 | -6.436 | 3.288 | -14.446 | 8.457 | 43.720 | -17.145 | 0.00336 | -0.00037 |
55 | -1.080 | 0.525 | -7.499 | 3.856 | -6.405 | 3.272 | -14.440 | 8.454 | 43.582 | -17.104 | 0.00337 | -0.00038 |
56 | -1.084 | 0.527 | -7.496 | 3.854 | -6.374 | 3.257 | -14.434 | 8.450 | 43.446 | -17.063 | 0.00338 | -0.00039 |
57 | -1.088 | 0.529 | -7.492 | 3.853 | -6.345 | 3.242 | -14.427 | 8.446 | 43.313 | -17.023 | 0.00339 | -0.00040 |
58 | -1.091 | 0.531 | -7.488 | 3.851 | -6.317 | 3.227 | -14.419 | 8.441 | 43.182 | -16.984 | 0.00340 | -0.00041 |
59 | -1.094 | 0.533 | -7.484 | 3.849 | -6.289 | 3.213 | -14.411 | 8.436 | 43.054 | -16.945 | 0.00341 | -0.00042 |
60 | -1.097 | 0.534 | -7.479 | 3.847 | -6.263 | 3.199 | -14.402 | 8.430 | 42.928 | -16.907 | 0.00342 | -0.00042 |
61 | -1.100 | 0.536 | -7.474 | 3.845 | -6.237 | 3.186 | -14.393 | 8.424 | 42.805 | -16.870 | 0.00342 | -0.00043 |
62 | -1.103 | 0.537 | -7.468 | 3.842 | -6.212 | 3.173 | -14.382 | 8.417 | 42.683 | -16.833 | 0.00343 | -0.00044 |
63 | -1.105 | 0.539 | -7.463 | 3.840 | -6.188 | 3.161 | -14.372 | 8.410 | 42.564 | -16.797 | 0.00343 | -0.00045 |
64 | -1.107 | 0.540 | -7.457 | 3.837 | -6.164 | 3.149 | -14.360 | 8.403 | 42.446 | -16.762 | 0.00343 | -0.00045 |
65 | -1.109 | 0.541 | -7.450 | 3.834 | -6.141 | 3.137 | -14.349 | 8.396 | 42.330 | -16.727 | 0.00344 | -0.00046 |
66 | -1.111 | 0.542 | -7.444 | 3.831 | -6.119 | 3.126 | -14.337 | 8.388 | 42.217 | -16.692 | 0.00344 | -0.00047 |
67 | -1.113 | 0.543 | -7.437 | 3.828 | -6.097 | 3.115 | -14.324 | 8.379 | 42.104 | -16.658 | 0.00344 | -0.00047 |
68 | -1.114 | 0.543 | -7.430 | 3.825 | -6.076 | 3.104 | -14.311 | 8.371 | 41.994 | -16.625 | 0.00344 | -0.00048 |
69 | -1.115 | 0.544 | -7.423 | 3.821 | -6.056 | 3.094 | -14.297 | 8.362 | 41.885 | -16.592 | 0.00344 | -0.00048 |
70 | -1.117 | 0.545 | -7.415 | 3.818 | -6.036 | 3.083 | -14.284 | 8.353 | 41.777 | -16.559 | 0.00344 | -0.00049 |
71 | -1.118 | 0.545 | -7.408 | 3.814 | -6.016 | 3.073 | -14.269 | 8.344 | 41.671 | -16.527 | 0.00344 | -0.00049 |
72 | -1.118 | 0.546 | -7.400 | 3.810 | -5.997 | 3.064 | -14.255 | 8.335 | 41.566 | -16.495 | 0.00343 | -0.00050 |
73 | -1.119 | 0.546 | -7.392 | 3.806 | -5.979 | 3.054 | -14.240 | 8.325 | 41.463 | -16.463 | 0.00343 | -0.00050 |
74 | -1.120 | 0.547 | -7.384 | 3.803 | -5.961 | 3.045 | -14.225 | 8.315 | 41.361 | -16.432 | 0.00343 | -0.00050 |
75 | -1.120 | 0.547 | -7.376 | 3.799 | -5.943 | 3.036 | -14.209 | 8.305 | 41.260 | -16.401 | 0.00342 | -0.00051 |
76 | -1.121 | 0.547 | -7.367 | 3.794 | -5.926 | 3.027 | -14.194 | 8.295 | 41.160 | -16.371 | 0.00342 | -0.00051 |
77 | -1.121 | 0.548 | -7.358 | 3.790 | -5.909 | 3.019 | -14.178 | 8.284 | 41.061 | -16.341 | 0.00342 | -0.00051 |
78 | -1.121 | 0.548 | -7.350 | 3.786 | -5.892 | 3.010 | -14.161 | 8.274 | 40.963 | -16.311 | 0.00341 | -0.00052 |
79 | -1.121 | 0.548 | -7.341 | 3.782 | -5.876 | 3.002 | -14.145 | 8.263 | 40.867 | -16.281 | 0.00341 | -0.00052 |
80 | -1.121 | 0.548 | -7.332 | 3.777 | -5.860 | 2.994 | -14.128 | 8.252 | 40.771 | -16.252 | 0.00340 | -0.00052 |
81 | -1.121 | 0.548 | -7.323 | 3.773 | -5.845 | 2.986 | -14.111 | 8.241 | 40.676 | -16.223 | 0.00339 | -0.00052 |
82 | -1.121 | 0.548 | -7.313 | 3.768 | -5.830 | 2.979 | -14.094 | 8.230 | 40.583 | -16.194 | 0.00339 | -0.00053 |
83 | -1.121 | 0.548 | -7.304 | 3.764 | -5.815 | 2.971 | -14.076 | 8.218 | 40.490 | -16.166 | 0.00338 | -0.00053 |
84 | -1.120 | 0.548 | -7.295 | 3.759 | -5.800 | 2.964 | -14.059 | 8.207 | 40.398 | -16.137 | 0.00338 | -0.00053 |
85 | -1.120 | 0.548 | -7.285 | 3.754 | -5.786 | 2.956 | -14.041 | 8.196 | 40.306 | -16.109 | 0.00337 | -0.00053 |
86 | -1.119 | 0.548 | -7.276 | 3.749 | -5.772 | 2.949 | -14.023 | 8.184 | 40.216 | -16.081 | 0.00336 | -0.00053 |
87 | -1.119 | 0.548 | -7.266 | 3.745 | -5.758 | 2.942 | -14.005 | 8.172 | 40.126 | -16.054 | 0.00335 | -0.00054 |
88 | -1.118 | 0.547 | -7.256 | 3.740 | -5.744 | 2.935 | -13.987 | 8.160 | 40.037 | -16.026 | 0.00335 | -0.00054 |
89 | -1.118 | 0.547 | -7.246 | 3.735 | -5.731 | 2.929 | -13.969 | 8.148 | 39.948 | -15.999 | 0.00334 | -0.00054 |
90 | -1.117 | 0.547 | -7.236 | 3.730 | -5.718 | 2.922 | -13.950 | 8.136 | 39.861 | -15.972 | 0.00333 | -0.00054 |
91 | -1.116 | 0.547 | -7.226 | 3.725 | -5.705 | 2.915 | -13.932 | 8.124 | 39.774 | -15.945 | 0.00332 | -0.00054 |
92 | -1.115 | 0.546 | -7.216 | 3.720 | -5.692 | 2.909 | -13.913 | 8.112 | 39.687 | -15.918 | 0.00331 | -0.00054 |
93 | -1.115 | 0.546 | -7.206 | 3.715 | -5.679 | 2.903 | -13.894 | 8.100 | 39.601 | -15.891 | 0.00330 | -0.00054 |
94 | -1.114 | 0.546 | -7.196 | 3.710 | -5.667 | 2.896 | -13.876 | 8.088 | 39.516 | -15.865 | 0.00330 | -0.00054 |
95 | -1.113 | 0.545 | -7.186 | 3.705 | -5.654 | 2.890 | -13.857 | 8.076 | 39.431 | -15.839 | 0.00329 | -0.00055 |
96 | -1.112 | 0.545 | -7.176 | 3.700 | -5.642 | 2.884 | -13.838 | 8.063 | 39.347 | -15.812 | 0.00328 | -0.00055 |
97 | -1.111 | 0.545 | -7.165 | 3.695 | -5.630 | 2.878 | -13.818 | 8.051 | 39.263 | -15.786 | 0.00327 | -0.00055 |
98 | -1.110 | 0.544 | -7.155 | 3.689 | -5.619 | 2.872 | -13.799 | 8.038 | 39.180 | -15.761 | 0.00326 | -0.00055 |
99 | -1.109 | 0.544 | -7.145 | 3.684 | -5.607 | 2.866 | -13.780 | 8.026 | 39.097 | -15.735 | 0.00325 | -0.00055 |
100 | -1.107 | 0.543 | -7.134 | 3.679 | -5.596 | 2.861 | -13.761 | 8.013 | 39.015 | -15.709 | 0.00324 | -0.00055 |
101 | -1.106 | 0.543 | -7.124 | 3.674 | -5.584 | 2.855 | -13.741 | 8.001 | 38.933 | -15.684 | 0.00323 | -0.00055 |
102 | -1.105 | 0.542 | -7.113 | 3.669 | -5.573 | 2.849 | -13.722 | 7.988 | 38.852 | -15.658 | 0.00322 | -0.00055 |
103 | -1.104 | 0.542 | -7.103 | 3.663 | -5.562 | 2.844 | -13.702 | 7.975 | 38.771 | -15.633 | 0.00321 | -0.00055 |
104 | -1.103 | 0.541 | -7.092 | 3.658 | -5.551 | 2.838 | -13.683 | 7.963 | 38.691 | -15.608 | 0.00320 | -0.00055 |
105 | -1.101 | 0.541 | -7.082 | 3.653 | -5.540 | 2.833 | -13.663 | 7.950 | 38.610 | -15.583 | 0.00319 | -0.00055 |
106 | -1.100 | 0.540 | -7.071 | 3.647 | -5.529 | 2.827 | -13.643 | 7.937 | 38.531 | -15.558 | 0.00318 | -0.00055 |
107 | -1.099 | 0.539 | -7.061 | 3.642 | -5.518 | 2.822 | -13.624 | 7.924 | 38.451 | -15.533 | 0.00317 | -0.00055 |
108 | -1.097 | 0.539 | -7.050 | 3.637 | -5.508 | 2.816 | -13.604 | 7.912 | 38.373 | -15.508 | 0.00316 | -0.00055 |
109 | -1.096 | 0.538 | -7.039 | 3.631 | -5.497 | 2.811 | -13.584 | 7.899 | 38.294 | -15.484 | 0.00315 | -0.00055 |
110 | -1.095 | 0.538 | -7.029 | 3.626 | -5.487 | 2.806 | -13.564 | 7.886 | 38.216 | -15.459 | 0.00314 | -0.00055 |
111 | -1.093 | 0.537 | -7.018 | 3.621 | -5.477 | 2.801 | -13.544 | 7.873 | 38.138 | -15.434 | 0.00313 | -0.00055 |
112 | -1.092 | 0.536 | -7.007 | 3.615 | -5.466 | 2.796 | -13.524 | 7.860 | 38.060 | -15.410 | 0.00312 | -0.00055 |
113 | -1.090 | 0.536 | -6.997 | 3.610 | -5.456 | 2.791 | -13.505 | 7.847 | 37.983 | -15.386 | 0.00311 | -0.00055 |
114 | -1.089 | 0.535 | -6.986 | 3.604 | -5.446 | 2.786 | -13.485 | 7.835 | 37.906 | -15.361 | 0.00310 | -0.00055 |
115 | -1.088 | 0.535 | -6.975 | 3.599 | -5.436 | 2.781 | -13.465 | 7.822 | 37.829 | -15.337 | 0.00309 | -0.00055 |
116 | -1.086 | 0.534 | -6.965 | 3.594 | -5.426 | 2.776 | -13.445 | 7.809 | 37.753 | -15.313 | 0.00308 | -0.00055 |
117 | -1.085 | 0.533 | -6.954 | 3.588 | -5.416 | 2.771 | -13.425 | 7.796 | 37.677 | -15.289 | 0.00307 | -0.00055 |
118 | -1.083 | 0.533 | -6.943 | 3.583 | -5.406 | 2.766 | -13.405 | 7.783 | 37.601 | -15.265 | 0.00306 | -0.00055 |
119 | -1.082 | 0.532 | -6.932 | 3.577 | -5.397 | 2.761 | -13.385 | 7.770 | 37.526 | -15.241 | 0.00305 | -0.00055 |
120 | -1.080 | 0.531 | -6.922 | 3.572 | -5.387 | 2.756 | -13.365 | 7.757 | 37.451 | -15.218 | 0.00304 | -0.00055 |
121 | -1.079 | 0.531 | -6.911 | 3.567 | -5.377 | 2.751 | -13.345 | 7.744 | 37.376 | -15.194 | 0.00303 | -0.00055 |
122 | -1.077 | 0.530 | -6.900 | 3.561 | -5.368 | 2.746 | -13.325 | 7.731 | 37.301 | -15.170 | 0.00302 | -0.00055 |
123 | -1.075 | 0.529 | -6.889 | 3.556 | -5.358 | 2.742 | -13.305 | 7.719 | 37.227 | -15.146 | 0.00301 | -0.00055 |
124 | -1.074 | 0.528 | -6.879 | 3.550 | -5.349 | 2.737 | -13.285 | 7.706 | 37.153 | -15.123 | 0.00300 | -0.00055 |
125 | -1.072 | 0.528 | -6.868 | 3.545 | -5.339 | 2.732 | -13.265 | 7.693 | 37.079 | -15.099 | 0.00298 | -0.00055 |
126 | -1.071 | 0.527 | -6.857 | 3.539 | -5.330 | 2.728 | -13.245 | 7.680 | 37.005 | -15.076 | 0.00297 | -0.00055 |
127 | -1.069 | 0.526 | -6.847 | 3.534 | -5.321 | 2.723 | -13.225 | 7.667 | 36.932 | -15.053 | 0.00296 | -0.00055 |
128 | -1.068 | 0.526 | -6.836 | 3.529 | -5.312 | 2.718 | -13.205 | 7.654 | 36.858 | -15.029 | 0.00295 | -0.00055 |
129 | -1.066 | 0.525 | -6.825 | 3.523 | -5.302 | 2.714 | -13.185 | 7.641 | 36.785 | -15.006 | 0.00294 | -0.00054 |
130 | -1.064 | 0.524 | -6.814 | 3.518 | -5.293 | 2.709 | -13.165 | 7.628 | 36.713 | -14.983 | 0.00293 | -0.00054 |
131 | -1.063 | 0.523 | -6.804 | 3.512 | -5.284 | 2.705 | -13.145 | 7.616 | 36.640 | -14.960 | 0.00292 | -0.00054 |
132 | -1.061 | 0.523 | -6.793 | 3.507 | -5.275 | 2.700 | -13.125 | 7.603 | 36.568 | -14.936 | 0.00291 | -0.00054 |
133 | -1.060 | 0.522 | -6.782 | 3.502 | -5.266 | 2.695 | -13.105 | 7.590 | 36.496 | -14.913 | 0.00290 | -0.00054 |
134 | -1.058 | 0.521 | -6.772 | 3.496 | -5.257 | 2.691 | -13.085 | 7.577 | 36.424 | -14.890 | 0.00289 | -0.00054 |
135 | -1.056 | 0.521 | -6.761 | 3.491 | -5.248 | 2.686 | -13.065 | 7.564 | 36.352 | -14.867 | 0.00288 | -0.00054 |
136 | -1.055 | 0.520 | -6.750 | 3.485 | -5.239 | 2.682 | -13.045 | 7.552 | 36.281 | -14.844 | 0.00287 | -0.00054 |
137 | -1.053 | 0.519 | -6.739 | 3.480 | -5.230 | 2.678 | -13.025 | 7.539 | 36.210 | -14.822 | 0.00286 | -0.00054 |
138 | -1.051 | 0.518 | -6.729 | 3.474 | -5.221 | 2.673 | -13.005 | 7.526 | 36.139 | -14.799 | 0.00285 | -0.00054 |
139 | -1.050 | 0.518 | -6.718 | 3.469 | -5.212 | 2.669 | -12.985 | 7.513 | 36.068 | -14.776 | 0.00284 | -0.00054 |
140 | -1.048 | 0.517 | -6.707 | 3.464 | -5.204 | 2.664 | -12.965 | 7.501 | 35.997 | -14.753 | 0.00283 | -0.00054 |
141 | -1.047 | 0.516 | -6.697 | 3.458 | -5.195 | 2.660 | -12.945 | 7.488 | 35.927 | -14.731 | 0.00282 | -0.00054 |
142 | -1.045 | 0.515 | -6.686 | 3.453 | -5.186 | 2.656 | -12.926 | 7.475 | 35.856 | -14.708 | 0.00281 | -0.00054 |
143 | -1.043 | 0.515 | -6.676 | 3.448 | -5.177 | 2.651 | -12.906 | 7.462 | 35.786 | -14.685 | 0.00280 | -0.00054 |
144 | -1.042 | 0.514 | -6.665 | 3.442 | -5.169 | 2.647 | -12.886 | 7.450 | 35.717 | -14.663 | 0.00279 | -0.00054 |
145 | -1.040 | 0.513 | -6.654 | 3.437 | -5.160 | 2.643 | -12.866 | 7.437 | 35.647 | -14.640 | 0.00278 | -0.00053 |
146 | -1.038 | 0.512 | -6.644 | 3.431 | -5.151 | 2.638 | -12.846 | 7.424 | 35.577 | -14.618 | 0.00277 | -0.00053 |
147 | -1.037 | 0.512 | -6.633 | 3.426 | -5.143 | 2.634 | -12.827 | 7.412 | 35.508 | -14.595 | 0.00276 | -0.00053 |
148 | -1.035 | 0.511 | -6.623 | 3.421 | -5.134 | 2.630 | -12.807 | 7.399 | 35.439 | -14.573 | 0.00275 | -0.00053 |
149 | -1.033 | 0.510 | -6.612 | 3.415 | -5.125 | 2.625 | -12.787 | 7.387 | 35.370 | -14.550 | 0.00274 | -0.00053 |
150 | -1.032 | 0.509 | -6.602 | 3.410 | -5.117 | 2.621 | -12.767 | 7.374 | 35.301 | -14.528 | 0.00273 | -0.00053 |
151 | -1.030 | 0.509 | -6.591 | 3.405 | -5.108 | 2.617 | -12.748 | 7.362 | 35.232 | -14.506 | 0.00272 | -0.00053 |
152 | -1.028 | 0.508 | -6.580 | 3.399 | -5.100 | 2.613 | -12.728 | 7.349 | 35.164 | -14.484 | 0.00271 | -0.00053 |
153 | -1.027 | 0.507 | -6.570 | 3.394 | -5.091 | 2.608 | -12.708 | 7.336 | 35.096 | -14.461 | 0.00270 | -0.00053 |
154 | -1.025 | 0.506 | -6.559 | 3.389 | -5.083 | 2.604 | -12.689 | 7.324 | 35.028 | -14.439 | 0.00269 | -0.00053 |
155 | -1.023 | 0.506 | -6.549 | 3.383 | -5.075 | 2.600 | -12.669 | 7.311 | 34.960 | -14.417 | 0.00268 | -0.00053 |
156 | -1.022 | 0.505 | -6.538 | 3.378 | -5.066 | 2.596 | -12.650 | 7.299 | 34.892 | -14.395 | 0.00267 | -0.00053 |
157 | -1.020 | 0.504 | -6.528 | 3.373 | -5.058 | 2.592 | -12.630 | 7.287 | 34.824 | -14.373 | 0.00266 | -0.00053 |
158 | -1.019 | 0.503 | -6.518 | 3.367 | -5.049 | 2.587 | -12.610 | 7.274 | 34.757 | -14.351 | 0.00265 | -0.00053 |
159 | -1.017 | 0.502 | -6.507 | 3.362 | -5.041 | 2.583 | -12.591 | 7.262 | 34.689 | -14.329 | 0.00264 | -0.00052 |
160 | -1.015 | 0.502 | -6.497 | 3.357 | -5.033 | 2.579 | -12.571 | 7.249 | 34.622 | -14.307 | 0.00263 | -0.00052 |
161 | -1.014 | 0.501 | -6.486 | 3.351 | -5.024 | 2.575 | -12.552 | 7.237 | 34.555 | -14.285 | 0.00263 | -0.00052 |
162 | -1.012 | 0.500 | -6.476 | 3.346 | -5.016 | 2.571 | -12.533 | 7.225 | 34.488 | -14.263 | 0.00262 | -0.00052 |
163 | -1.010 | 0.499 | -6.466 | 3.341 | -5.008 | 2.567 | -12.513 | 7.212 | 34.422 | -14.241 | 0.00261 | -0.00052 |
164 | -1.009 | 0.499 | -6.455 | 3.336 | -5.000 | 2.563 | -12.494 | 7.200 | 34.355 | -14.219 | 0.00260 | -0.00052 |
165 | -1.007 | 0.498 | -6.445 | 3.330 | -4.991 | 2.558 | -12.474 | 7.188 | 34.289 | -14.198 | 0.00259 | -0.00052 |
166 | -1.005 | 0.497 | -6.434 | 3.325 | -4.983 | 2.554 | -12.455 | 7.175 | 34.223 | -14.176 | 0.00258 | -0.00052 |
167 | -1.004 | 0.496 | -6.424 | 3.320 | -4.975 | 2.550 | -12.436 | 7.163 | 34.157 | -14.154 | 0.00257 | -0.00052 |
168 | -1.002 | 0.496 | -6.414 | 3.315 | -4.967 | 2.546 | -12.416 | 7.151 | 34.091 | -14.133 | 0.00256 | -0.00052 |
169 | -1.001 | 0.495 | -6.404 | 3.309 | -4.959 | 2.542 | -12.397 | 7.139 | 34.025 | -14.111 | 0.00255 | -0.00052 |
170 | -0.999 | 0.494 | -6.393 | 3.304 | -4.951 | 2.538 | -12.378 | 7.126 | 33.959 | -14.089 | 0.00254 | -0.00052 |
171 | -0.997 | 0.493 | -6.383 | 3.299 | -4.942 | 2.534 | -12.359 | 7.114 | 33.894 | -14.068 | 0.00253 | -0.00052 |
172 | -0.996 | 0.493 | -6.373 | 3.294 | -4.934 | 2.530 | -12.339 | 7.102 | 33.829 | -14.046 | 0.00252 | -0.00052 |
173 | -0.994 | 0.492 | -6.362 | 3.289 | -4.926 | 2.526 | -12.320 | 7.090 | 33.764 | -14.025 | 0.00251 | -0.00051 |
174 | -0.992 | 0.491 | -6.352 | 3.283 | -4.918 | 2.522 | -12.301 | 7.078 | 33.699 | -14.003 | 0.00251 | -0.00051 |
175 | -0.991 | 0.490 | -6.342 | 3.278 | -4.910 | 2.518 | -12.282 | 7.066 | 33.634 | -13.982 | 0.00250 | -0.00051 |
176 | -0.989 | 0.490 | -6.332 | 3.273 | -4.902 | 2.514 | -12.263 | 7.054 | 33.569 | -13.960 | 0.00249 | -0.00051 |
177 | -0.987 | 0.489 | -6.322 | 3.268 | -4.894 | 2.510 | -12.244 | 7.042 | 33.505 | -13.939 | 0.00248 | -0.00051 |
178 | -0.986 | 0.488 | -6.311 | 3.263 | -4.886 | 2.506 | -12.225 | 7.030 | 33.440 | -13.918 | 0.00247 | -0.00051 |
179 | -0.984 | 0.487 | -6.301 | 3.257 | -4.878 | 2.502 | -12.206 | 7.017 | 33.376 | -13.896 | 0.00246 | -0.00051 |
180 | -0.983 | 0.487 | -6.291 | 3.252 | -4.870 | 2.498 | -12.187 | 7.005 | 33.312 | -13.875 | 0.00245 | -0.00051 |
181 | -0.981 | 0.486 | -6.281 | 3.247 | -4.862 | 2.494 | -12.168 | 6.994 | 33.248 | -13.854 | 0.00244 | -0.00051 |
182 | -0.979 | 0.485 | -6.271 | 3.242 | -4.854 | 2.490 | -12.149 | 6.982 | 33.184 | -13.833 | 0.00243 | -0.00051 |
183 | -0.978 | 0.484 | -6.261 | 3.237 | -4.846 | 2.486 | -12.130 | 6.970 | 33.120 | -13.811 | 0.00243 | -0.00051 |
184 | -0.976 | 0.484 | -6.251 | 3.232 | -4.838 | 2.482 | -12.111 | 6.958 | 33.057 | -13.790 | 0.00242 | -0.00051 |
185 | -0.975 | 0.483 | -6.241 | 3.227 | -4.830 | 2.478 | -12.092 | 6.946 | 32.993 | -13.769 | 0.00241 | -0.00051 |
186 | -0.973 | 0.482 | -6.231 | 3.222 | -4.822 | 2.474 | -12.073 | 6.934 | 32.930 | -13.748 | 0.00240 | -0.00050 |
187 | -0.971 | 0.481 | -6.221 | 3.216 | -4.815 | 2.470 | -12.054 | 6.922 | 32.867 | -13.727 | 0.00239 | -0.00050 |
188 | -0.970 | 0.481 | -6.211 | 3.211 | -4.807 | 2.466 | -12.036 | 6.910 | 32.804 | -13.706 | 0.00238 | -0.00050 |
189 | -0.968 | 0.480 | -6.201 | 3.206 | -4.799 | 2.462 | -12.017 | 6.898 | 32.741 | -13.685 | 0.00238 | -0.00050 |
190 | -0.967 | 0.479 | -6.191 | 3.201 | -4.791 | 2.458 | -11.998 | 6.887 | 32.678 | -13.664 | 0.00237 | -0.00050 |
191 | -0.965 | 0.478 | -6.181 | 3.196 | -4.783 | 2.454 | -11.979 | 6.875 | 32.616 | -13.643 | 0.00236 | -0.00050 |
192 | -0.963 | 0.478 | -6.171 | 3.191 | -4.775 | 2.450 | -11.961 | 6.863 | 32.553 | -13.622 | 0.00235 | -0.00050 |
193 | -0.962 | 0.477 | -6.161 | 3.186 | -4.768 | 2.447 | -11.942 | 6.851 | 32.491 | -13.601 | 0.00234 | -0.00050 |
194 | -0.960 | 0.476 | -6.151 | 3.181 | -4.760 | 2.443 | -11.923 | 6.840 | 32.429 | -13.580 | 0.00233 | -0.00050 |
195 | -0.959 | 0.475 | -6.141 | 3.176 | -4.752 | 2.439 | -11.905 | 6.828 | 32.367 | -13.560 | 0.00233 | -0.00050 |
196 | -0.957 | 0.475 | -6.131 | 3.171 | -4.744 | 2.435 | -11.886 | 6.816 | 32.305 | -13.539 | 0.00232 | -0.00050 |
197 | -0.955 | 0.474 | -6.121 | 3.166 | -4.737 | 2.431 | -11.867 | 6.805 | 32.243 | -13.518 | 0.00231 | -0.00050 |
198 | -0.954 | 0.473 | -6.111 | 3.161 | -4.729 | 2.427 | -11.849 | 6.793 | 32.182 | -13.497 | 0.00230 | -0.00050 |
199 | -0.952 | 0.473 | -6.101 | 3.156 | -4.721 | 2.423 | -11.830 | 6.781 | 32.120 | -13.477 | 0.00229 | -0.00049 |
200 | -0.951 | 0.472 | -6.091 | 3.151 | -4.713 | 2.420 | -11.812 | 6.770 | 32.059 | -13.456 | 0.00228 | -0.00049 |
201 | -0.949 | 0.471 | -6.082 | 3.146 | -4.706 | 2.416 | -11.793 | 6.758 | 31.997 | -13.435 | 0.00228 | -0.00049 |
202 | -0.948 | 0.470 | -6.072 | 3.141 | -4.698 | 2.412 | -11.775 | 6.747 | 31.936 | -13.415 | 0.00227 | -0.00049 |
203 | -0.946 | 0.470 | -6.062 | 3.136 | -4.690 | 2.408 | -11.757 | 6.735 | 31.875 | -13.394 | 0.00226 | -0.00049 |
204 | -0.944 | 0.469 | -6.052 | 3.131 | -4.683 | 2.404 | -11.738 | 6.723 | 31.815 | -13.373 | 0.00225 | -0.00049 |
205 | -0.943 | 0.468 | -6.043 | 3.126 | -4.675 | 2.400 | -11.720 | 6.712 | 31.754 | -13.353 | 0.00225 | -0.00049 |
206 | -0.941 | 0.467 | -6.033 | 3.121 | -4.668 | 2.397 | -11.702 | 6.701 | 31.693 | -13.332 | 0.00224 | -0.00049 |
207 | -0.940 | 0.467 | -6.023 | 3.116 | -4.660 | 2.393 | -11.683 | 6.689 | 31.633 | -13.312 | 0.00223 | -0.00049 |
208 | -0.938 | 0.466 | -6.013 | 3.111 | -4.652 | 2.389 | -11.665 | 6.678 | 31.573 | -13.292 | 0.00222 | -0.00049 |
209 | -0.937 | 0.465 | -6.004 | 3.106 | -4.645 | 2.385 | -11.647 | 6.666 | 31.512 | -13.271 | 0.00221 | -0.00049 |
210 | -0.935 | 0.465 | -5.994 | 3.101 | -4.637 | 2.381 | -11.629 | 6.655 | 31.452 | -13.251 | 0.00221 | -0.00049 |
211 | -0.934 | 0.464 | -5.984 | 3.096 | -4.630 | 2.378 | -11.610 | 6.643 | 31.392 | -13.230 | 0.00220 | -0.00049 |
212 | -0.932 | 0.463 | -5.975 | 3.091 | -4.622 | 2.374 | -11.592 | 6.632 | 31.333 | -13.210 | 0.00219 | -0.00049 |
213 | -0.930 | 0.462 | -5.965 | 3.086 | -4.615 | 2.370 | -11.574 | 6.621 | 31.273 | -13.190 | 0.00218 | -0.00048 |
214 | -0.929 | 0.462 | -5.955 | 3.081 | -4.607 | 2.366 | -11.556 | 6.609 | 31.213 | -13.170 | 0.00218 | -0.00048 |
215 | -0.927 | 0.461 | -5.946 | 3.076 | -4.599 | 2.362 | -11.538 | 6.598 | 31.154 | -13.149 | 0.00217 | -0.00048 |
216 | -0.926 | 0.460 | -5.936 | 3.072 | -4.592 | 2.359 | -11.520 | 6.587 | 31.095 | -13.129 | 0.00216 | -0.00048 |
217 | -0.924 | 0.460 | -5.926 | 3.067 | -4.584 | 2.355 | -11.502 | 6.576 | 31.036 | -13.109 | 0.00215 | -0.00048 |
218 | -0.923 | 0.459 | -5.917 | 3.062 | -4.577 | 2.351 | -11.484 | 6.564 | 30.977 | -13.089 | 0.00215 | -0.00048 |
219 | -0.921 | 0.458 | -5.907 | 3.057 | -4.570 | 2.348 | -11.466 | 6.553 | 30.918 | -13.069 | 0.00214 | -0.00048 |
220 | -0.920 | 0.457 | -5.898 | 3.052 | -4.562 | 2.344 | -11.448 | 6.542 | 30.859 | -13.049 | 0.00213 | -0.00048 |
221 | -0.918 | 0.457 | -5.888 | 3.047 | -4.555 | 2.340 | -11.430 | 6.531 | 30.800 | -13.029 | 0.00212 | -0.00048 |
222 | -0.917 | 0.456 | -5.879 | 3.042 | -4.547 | 2.336 | -11.412 | 6.520 | 30.742 | -13.009 | 0.00212 | -0.00048 |
223 | -0.915 | 0.455 | -5.869 | 3.038 | -4.540 | 2.333 | -11.394 | 6.508 | 30.683 | -12.989 | 0.00211 | -0.00048 |
224 | -0.914 | 0.455 | -5.860 | 3.033 | -4.532 | 2.329 | -11.376 | 6.497 | 30.625 | -12.969 | 0.00210 | -0.00048 |
225 | -0.912 | 0.454 | -5.850 | 3.028 | -4.525 | 2.325 | -11.358 | 6.486 | 30.567 | -12.949 | 0.00209 | -0.00048 |
226 | -0.911 | 0.453 | -5.841 | 3.023 | -4.518 | 2.322 | -11.340 | 6.475 | 30.509 | -12.929 | 0.00209 | -0.00047 |
227 | -0.909 | 0.452 | -5.831 | 3.018 | -4.510 | 2.318 | -11.323 | 6.464 | 30.451 | -12.909 | 0.00208 | -0.00047 |
228 | -0.908 | 0.452 | -5.822 | 3.013 | -4.503 | 2.314 | -11.305 | 6.453 | 30.393 | -12.889 | 0.00207 | -0.00047 |
229 | -0.906 | 0.451 | -5.813 | 3.009 | -4.496 | 2.310 | -11.287 | 6.442 | 30.335 | -12.869 | 0.00207 | -0.00047 |
230 | -0.905 | 0.450 | -5.803 | 3.004 | -4.488 | 2.307 | -11.270 | 6.431 | 30.278 | -12.849 | 0.00206 | -0.00047 |
231 | -0.903 | 0.450 | -5.794 | 2.999 | -4.481 | 2.303 | -11.252 | 6.420 | 30.220 | -12.830 | 0.00205 | -0.00047 |
232 | -0.902 | 0.449 | -5.784 | 2.994 | -4.474 | 2.299 | -11.234 | 6.409 | 30.163 | -12.810 | 0.00205 | -0.00047 |
233 | -0.900 | 0.448 | -5.775 | 2.990 | -4.466 | 2.296 | -11.217 | 6.398 | 30.106 | -12.790 | 0.00204 | -0.00047 |
234 | -0.899 | 0.447 | -5.766 | 2.985 | -4.459 | 2.292 | -11.199 | 6.387 | 30.049 | -12.770 | 0.00203 | -0.00047 |
235 | -0.897 | 0.447 | -5.756 | 2.980 | -4.452 | 2.289 | -11.181 | 6.376 | 29.992 | -12.751 | 0.00202 | -0.00047 |
236 | -0.896 | 0.446 | -5.747 | 2.975 | -4.445 | 2.285 | -11.164 | 6.365 | 29.935 | -12.731 | 0.00202 | -0.00047 |
237 | -0.894 | 0.445 | -5.738 | 2.971 | -4.437 | 2.281 | -11.146 | 6.355 | 29.878 | -12.712 | 0.00201 | -0.00047 |
238 | -0.893 | 0.445 | -5.728 | 2.966 | -4.430 | 2.278 | -11.129 | 6.344 | 29.822 | -12.692 | 0.00200 | -0.00047 |
239 | -0.891 | 0.444 | -5.719 | 2.961 | -4.423 | 2.274 | -11.111 | 6.333 | 29.765 | -12.672 | 0.00200 | -0.00047 |
240 | -0.890 | 0.443 | -5.710 | 2.956 | -4.416 | 2.270 | -11.094 | 6.322 | 29.709 | -12.653 | 0.00199 | -0.00046 |
241 | -0.888 | 0.443 | -5.701 | 2.952 | -4.409 | 2.267 | -11.076 | 6.311 | 29.653 | -12.633 | 0.00198 | -0.00046 |
242 | -0.887 | 0.442 | -5.691 | 2.947 | -4.401 | 2.263 | -11.059 | 6.300 | 29.597 | -12.614 | 0.00198 | -0.00046 |
243 | -0.885 | 0.441 | -5.682 | 2.942 | -4.394 | 2.260 | -11.042 | 6.290 | 29.541 | -12.595 | 0.00197 | -0.00046 |
244 | -0.884 | 0.441 | -5.673 | 2.938 | -4.387 | 2.256 | -11.024 | 6.279 | 29.485 | -12.575 | 0.00196 | -0.00046 |
245 | -0.882 | 0.440 | -5.664 | 2.933 | -4.380 | 2.252 | -11.007 | 6.268 | 29.429 | -12.556 | 0.00196 | -0.00046 |
246 | -0.881 | 0.439 | -5.655 | 2.928 | -4.373 | 2.249 | -10.990 | 6.258 | 29.374 | -12.536 | 0.00195 | -0.00046 |
247 | -0.879 | 0.438 | -5.646 | 2.924 | -4.366 | 2.245 | -10.972 | 6.247 | 29.318 | -12.517 | 0.00194 | -0.00046 |
248 | -0.878 | 0.438 | -5.636 | 2.919 | -4.358 | 2.242 | -10.955 | 6.236 | 29.263 | -12.498 | 0.00194 | -0.00046 |
249 | -0.877 | 0.437 | -5.627 | 2.914 | -4.351 | 2.238 | -10.938 | 6.226 | 29.207 | -12.479 | 0.00193 | -0.00046 |
250 | -0.875 | 0.436 | -5.618 | 2.910 | -4.344 | 2.235 | -10.921 | 6.215 | 29.152 | -12.459 | 0.00192 | -0.00046 |
251 | -0.874 | 0.436 | -5.609 | 2.905 | -4.337 | 2.231 | -10.904 | 6.204 | 29.097 | -12.440 | 0.00192 | -0.00046 |
252 | -0.872 | 0.435 | -5.600 | 2.900 | -4.330 | 2.227 | -10.887 | 6.194 | 29.042 | -12.421 | 0.00191 | -0.00046 |
253 | -0.871 | 0.434 | -5.591 | 2.896 | -4.323 | 2.224 | -10.869 | 6.183 | 28.987 | -12.402 | 0.00190 | -0.00046 |
254 | -0.869 | 0.434 | -5.582 | 2.891 | -4.316 | 2.220 | -10.852 | 6.173 | 28.933 | -12.383 | 0.00190 | -0.00045 |
255 | -0.868 | 0.433 | -5.573 | 2.887 | -4.309 | 2.217 | -10.835 | 6.162 | 28.878 | -12.363 | 0.00189 | -0.00045 |
256 | -0.866 | 0.432 | -5.564 | 2.882 | -4.302 | 2.213 | -10.818 | 6.152 | 28.824 | -12.344 | 0.00189 | -0.00045 |
257 | -0.865 | 0.432 | -5.555 | 2.877 | -4.295 | 2.210 | -10.801 | 6.141 | 28.769 | -12.325 | 0.00188 | -0.00045 |
258 | -0.864 | 0.431 | -5.546 | 2.873 | -4.288 | 2.206 | -10.784 | 6.131 | 28.715 | -12.306 | 0.00187 | -0.00045 |
259 | -0.862 | 0.430 | -5.537 | 2.868 | -4.281 | 2.203 | -10.767 | 6.120 | 28.661 | -12.287 | 0.00187 | -0.00045 |
260 | -0.861 | 0.430 | -5.528 | 2.864 | -4.274 | 2.199 | -10.750 | 6.110 | 28.607 | -12.268 | 0.00186 | -0.00045 |
261 | -0.859 | 0.429 | -5.519 | 2.859 | -4.267 | 2.196 | -10.733 | 6.099 | 28.553 | -12.249 | 0.00185 | -0.00045 |
262 | -0.858 | 0.428 | -5.510 | 2.854 | -4.260 | 2.192 | -10.716 | 6.089 | 28.499 | -12.231 | 0.00185 | -0.00045 |
263 | -0.856 | 0.428 | -5.501 | 2.850 | -4.253 | 2.189 | -10.700 | 6.079 | 28.445 | -12.212 | 0.00184 | -0.00045 |
264 | -0.855 | 0.427 | -5.492 | 2.845 | -4.246 | 2.185 | -10.683 | 6.068 | 28.392 | -12.193 | 0.00184 | -0.00045 |
265 | -0.854 | 0.426 | -5.483 | 2.841 | -4.239 | 2.182 | -10.666 | 6.058 | 28.338 | -12.174 | 0.00183 | -0.00045 |
266 | -0.852 | 0.426 | -5.474 | 2.836 | -4.232 | 2.178 | -10.649 | 6.048 | 28.285 | -12.155 | 0.00182 | -0.00045 |
267 | -0.851 | 0.425 | -5.466 | 2.832 | -4.225 | 2.175 | -10.632 | 6.037 | 28.232 | -12.136 | 0.00182 | -0.00045 |
268 | -0.849 | 0.424 | -5.457 | 2.827 | -4.218 | 2.171 | -10.616 | 6.027 | 28.179 | -12.118 | 0.00181 | -0.00045 |
269 | -0.848 | 0.424 | -5.448 | 2.823 | -4.212 | 2.168 | -10.599 | 6.017 | 28.126 | -12.099 | 0.00181 | -0.00044 |
270 | -0.847 | 0.423 | -5.439 | 2.818 | -4.205 | 2.165 | -10.582 | 6.006 | 28.073 | -12.080 | 0.00180 | -0.00044 |
271 | -0.845 | 0.422 | -5.430 | 2.814 | -4.198 | 2.161 | -10.566 | 5.996 | 28.020 | -12.062 | 0.00179 | -0.00044 |
272 | -0.844 | 0.422 | -5.421 | 2.809 | -4.191 | 2.158 | -10.549 | 5.986 | 27.967 | -12.043 | 0.00179 | -0.00044 |
273 | -0.842 | 0.421 | -5.413 | 2.805 | -4.184 | 2.154 | -10.532 | 5.976 | 27.915 | -12.024 | 0.00178 | -0.00044 |
274 | -0.841 | 0.420 | -5.404 | 2.800 | -4.177 | 2.151 | -10.516 | 5.966 | 27.862 | -12.006 | 0.00178 | -0.00044 |
275 | -0.840 | 0.420 | -5.395 | 2.796 | -4.171 | 2.147 | -10.499 | 5.955 | 27.810 | -11.987 | 0.00177 | -0.00044 |
276 | -0.838 | 0.419 | -5.386 | 2.791 | -4.164 | 2.144 | -10.483 | 5.945 | 27.758 | -11.969 | 0.00177 | -0.00044 |
277 | -0.837 | 0.418 | -5.378 | 2.787 | -4.157 | 2.141 | -10.466 | 5.935 | 27.705 | -11.950 | 0.00176 | -0.00044 |
278 | -0.835 | 0.418 | -5.369 | 2.782 | -4.150 | 2.137 | -10.450 | 5.925 | 27.653 | -11.932 | 0.00175 | -0.00044 |
279 | -0.834 | 0.417 | -5.360 | 2.778 | -4.143 | 2.134 | -10.433 | 5.915 | 27.601 | -11.913 | 0.00175 | -0.00044 |
280 | -0.833 | 0.416 | -5.352 | 2.774 | -4.137 | 2.130 | -10.417 | 5.905 | 27.550 | -11.895 | 0.00174 | -0.00044 |
281 | -0.831 | 0.416 | -5.343 | 2.769 | -4.130 | 2.127 | -10.400 | 5.895 | 27.498 | -11.876 | 0.00174 | -0.00044 |
282 | -0.830 | 0.415 | -5.334 | 2.765 | -4.123 | 2.124 | -10.384 | 5.885 | 27.446 | -11.858 | 0.00173 | -0.00044 |
283 | -0.828 | 0.414 | -5.326 | 2.760 | -4.116 | 2.120 | -10.367 | 5.875 | 27.395 | -11.840 | 0.00173 | -0.00043 |
284 | -0.827 | 0.414 | -5.317 | 2.756 | -4.110 | 2.117 | -10.351 | 5.865 | 27.343 | -11.821 | 0.00172 | -0.00043 |
285 | -0.826 | 0.413 | -5.308 | 2.751 | -4.103 | 2.113 | -10.335 | 5.855 | 27.292 | -11.803 | 0.00171 | -0.00043 |
286 | -0.824 | 0.412 | -5.300 | 2.747 | -4.096 | 2.110 | -10.318 | 5.845 | 27.241 | -11.785 | 0.00171 | -0.00043 |
287 | -0.823 | 0.412 | -5.291 | 2.743 | -4.090 | 2.107 | -10.302 | 5.835 | 27.190 | -11.766 | 0.00170 | -0.00043 |
288 | -0.822 | 0.411 | -5.282 | 2.738 | -4.083 | 2.103 | -10.286 | 5.825 | 27.139 | -11.748 | 0.00170 | -0.00043 |
289 | -0.820 | 0.410 | -5.274 | 2.734 | -4.076 | 2.100 | -10.270 | 5.815 | 27.088 | -11.730 | 0.00169 | -0.00043 |
290 | -0.819 | 0.410 | -5.265 | 2.730 | -4.070 | 2.097 | -10.254 | 5.805 | 27.037 | -11.712 | 0.00169 | -0.00043 |
291 | -0.818 | 0.409 | -5.257 | 2.725 | -4.063 | 2.093 | -10.237 | 5.795 | 26.987 | -11.694 | 0.00168 | -0.00043 |
292 | -0.816 | 0.409 | -5.248 | 2.721 | -4.056 | 2.090 | -10.221 | 5.785 | 26.936 | -11.676 | 0.00168 | -0.00043 |
293 | -0.815 | 0.408 | -5.240 | 2.716 | -4.050 | 2.087 | -10.205 | 5.776 | 26.886 | -11.658 | 0.00167 | -0.00043 |
294 | -0.813 | 0.407 | -5.231 | 2.712 | -4.043 | 2.083 | -10.189 | 5.766 | 26.835 | -11.640 | 0.00167 | -0.00043 |
295 | -0.812 | 0.407 | -5.223 | 2.708 | -4.037 | 2.080 | -10.173 | 5.756 | 26.785 | -11.621 | 0.00166 | -0.00043 |
296 | -0.811 | 0.406 | -5.214 | 2.703 | -4.030 | 2.077 | -10.157 | 5.746 | 26.735 | -11.603 | 0.00165 | -0.00043 |
297 | -0.809 | 0.405 | -5.206 | 2.699 | -4.023 | 2.073 | -10.141 | 5.736 | 26.685 | -11.585 | 0.00165 | -0.00043 |
298 | -0.808 | 0.405 | -5.197 | 2.695 | -4.017 | 2.070 | -10.125 | 5.727 | 26.635 | -11.568 | 0.00164 | -0.00042 |
299 | -0.807 | 0.404 | -5.189 | 2.691 | -4.010 | 2.067 | -10.109 | 5.717 | 26.585 | -11.550 | 0.00164 | -0.00042 |
300 | -0.805 | 0.403 | -5.181 | 2.686 | -4.004 | 2.063 | -10.093 | 5.707 | 26.535 | -11.532 | 0.00163 | -0.00042 |
301 | -0.804 | 0.403 | -5.172 | 2.682 | -3.997 | 2.060 | -10.077 | 5.697 | 26.486 | -11.514 | 0.00163 | -0.00042 |
302 | -0.803 | 0.402 | -5.164 | 2.678 | -3.991 | 2.057 | -10.061 | 5.688 | 26.436 | -11.496 | 0.00162 | -0.00042 |
303 | -0.801 | 0.402 | -5.155 | 2.673 | -3.984 | 2.054 | -10.045 | 5.678 | 26.387 | -11.478 | 0.00162 | -0.00042 |
304 | -0.800 | 0.401 | -5.147 | 2.669 | -3.978 | 2.050 | -10.029 | 5.668 | 26.337 | -11.460 | 0.00161 | -0.00042 |
305 | -0.799 | 0.400 | -5.139 | 2.665 | -3.971 | 2.047 | -10.013 | 5.659 | 26.288 | -11.443 | 0.00161 | -0.00042 |
306 | -0.797 | 0.400 | -5.130 | 2.661 | -3.965 | 2.044 | -9.997 | 5.649 | 26.239 | -11.425 | 0.00160 | -0.00042 |
307 | -0.796 | 0.399 | -5.122 | 2.656 | -3.958 | 2.041 | -9.982 | 5.640 | 26.190 | -11.407 | 0.00160 | -0.00042 |
308 | -0.795 | 0.398 | -5.114 | 2.652 | -3.952 | 2.037 | -9.966 | 5.630 | 26.141 | -11.389 | 0.00159 | -0.00042 |
309 | -0.793 | 0.398 | -5.105 | 2.648 | -3.945 | 2.034 | -9.950 | 5.620 | 26.092 | -11.372 | 0.00159 | -0.00042 |
310 | -0.792 | 0.397 | -5.097 | 2.644 | -3.939 | 2.031 | -9.934 | 5.611 | 26.044 | -11.354 | 0.00158 | -0.00042 |
311 | -0.791 | 0.397 | -5.089 | 2.639 | -3.932 | 2.028 | -9.919 | 5.601 | 25.995 | -11.336 | 0.00158 | -0.00042 |
312 | -0.789 | 0.396 | -5.081 | 2.635 | -3.926 | 2.024 | -9.903 | 5.592 | 25.947 | -11.319 | 0.00157 | -0.00042 |
313 | -0.788 | 0.395 | -5.072 | 2.631 | -3.920 | 2.021 | -9.887 | 5.582 | 25.898 | -11.301 | 0.00157 | -0.00042 |
314 | -0.787 | 0.395 | -5.064 | 2.627 | -3.913 | 2.018 | -9.872 | 5.573 | 25.850 | -11.284 | 0.00156 | -0.00041 |
315 | -0.786 | 0.394 | -5.056 | 2.623 | -3.907 | 2.015 | -9.856 | 5.563 | 25.802 | -11.266 | 0.00156 | -0.00041 |
316 | -0.784 | 0.393 | -5.048 | 2.618 | -3.900 | 2.011 | -9.841 | 5.554 | 25.754 | -11.249 | 0.00155 | -0.00041 |
317 | -0.783 | 0.393 | -5.039 | 2.614 | -3.894 | 2.008 | -9.825 | 5.544 | 25.706 | -11.231 | 0.00155 | -0.00041 |
318 | -0.782 | 0.392 | -5.031 | 2.610 | -3.888 | 2.005 | -9.809 | 5.535 | 25.658 | -11.214 | 0.00154 | -0.00041 |
319 | -0.780 | 0.392 | -5.023 | 2.606 | -3.881 | 2.002 | -9.794 | 5.526 | 25.610 | -11.196 | 0.00154 | -0.00041 |
320 | -0.779 | 0.391 | -5.015 | 2.602 | -3.875 | 1.999 | -9.778 | 5.516 | 25.562 | -11.179 | 0.00153 | -0.00041 |
321 | -0.778 | 0.390 | -5.007 | 2.597 | -3.869 | 1.995 | -9.763 | 5.507 | 25.514 | -11.162 | 0.00153 | -0.00041 |
322 | -0.776 | 0.390 | -4.999 | 2.593 | -3.862 | 1.992 | -9.747 | 5.497 | 25.467 | -11.144 | 0.00152 | -0.00041 |
323 | -0.775 | 0.389 | -4.991 | 2.589 | -3.856 | 1.989 | -9.732 | 5.488 | 25.420 | -11.127 | 0.00152 | -0.00041 |
324 | -0.774 | 0.388 | -4.982 | 2.585 | -3.850 | 1.986 | -9.717 | 5.479 | 25.372 | -11.110 | 0.00151 | -0.00041 |
325 | -0.773 | 0.388 | -4.974 | 2.581 | -3.843 | 1.983 | -9.701 | 5.469 | 25.325 | -11.092 | 0.00151 | -0.00041 |
326 | -0.771 | 0.387 | -4.966 | 2.577 | -3.837 | 1.980 | -9.686 | 5.460 | 25.278 | -11.075 | 0.00150 | -0.00041 |
327 | -0.770 | 0.387 | -4.958 | 2.573 | -3.831 | 1.976 | -9.671 | 5.451 | 25.231 | -11.058 | 0.00150 | -0.00041 |
328 | -0.769 | 0.386 | -4.950 | 2.568 | -3.825 | 1.973 | -9.655 | 5.442 | 25.184 | -11.041 | 0.00150 | -0.00041 |
329 | -0.767 | 0.385 | -4.942 | 2.564 | -3.818 | 1.970 | -9.640 | 5.432 | 25.137 | -11.024 | 0.00149 | -0.00040 |
330 | -0.766 | 0.385 | -4.934 | 2.560 | -3.812 | 1.967 | -9.625 | 5.423 | 25.090 | -11.007 | 0.00149 | -0.00040 |
331 | -0.765 | 0.384 | -4.926 | 2.556 | -3.806 | 1.964 | -9.609 | 5.414 | 25.044 | -10.989 | 0.00148 | -0.00040 |
332 | -0.764 | 0.384 | -4.918 | 2.552 | -3.800 | 1.961 | -9.594 | 5.405 | 24.997 | -10.972 | 0.00148 | -0.00040 |
333 | -0.762 | 0.383 | -4.910 | 2.548 | -3.793 | 1.957 | -9.579 | 5.396 | 24.951 | -10.955 | 0.00147 | -0.00040 |
334 | -0.761 | 0.382 | -4.902 | 2.544 | -3.787 | 1.954 | -9.564 | 5.386 | 24.904 | -10.938 | 0.00147 | -0.00040 |
335 | -0.760 | 0.382 | -4.894 | 2.540 | -3.781 | 1.951 | -9.549 | 5.377 | 24.858 | -10.921 | 0.00146 | -0.00040 |
336 | -0.759 | 0.381 | -4.886 | 2.536 | -3.775 | 1.948 | -9.534 | 5.368 | 24.812 | -10.904 | 0.00146 | -0.00040 |
337 | -0.757 | 0.381 | -4.878 | 2.532 | -3.769 | 1.945 | -9.518 | 5.359 | 24.766 | -10.887 | 0.00145 | -0.00040 |
338 | -0.756 | 0.380 | -4.870 | 2.528 | -3.762 | 1.942 | -9.503 | 5.350 | 24.720 | -10.870 | 0.00145 | -0.00040 |
339 | -0.755 | 0.379 | -4.862 | 2.524 | -3.756 | 1.939 | -9.488 | 5.341 | 24.674 | -10.853 | 0.00145 | -0.00040 |
340 | -0.754 | 0.379 | -4.854 | 2.520 | -3.750 | 1.936 | -9.473 | 5.332 | 24.628 | -10.836 | 0.00144 | -0.00040 |
341 | -0.752 | 0.378 | -4.847 | 2.516 | -3.744 | 1.933 | -9.458 | 5.323 | 24.582 | -10.820 | 0.00144 | -0.00040 |
342 | -0.751 | 0.378 | -4.839 | 2.511 | -3.738 | 1.930 | -9.443 | 5.314 | 24.537 | -10.803 | 0.00143 | -0.00040 |
343 | -0.750 | 0.377 | -4.831 | 2.507 | -3.732 | 1.926 | -9.428 | 5.305 | 24.491 | -10.786 | 0.00143 | -0.00040 |
344 | -0.749 | 0.376 | -4.823 | 2.503 | -3.726 | 1.923 | -9.413 | 5.296 | 24.446 | -10.769 | 0.00142 | -0.00040 |
345 | -0.747 | 0.376 | -4.815 | 2.499 | -3.720 | 1.920 | -9.398 | 5.287 | 24.400 | -10.752 | 0.00142 | -0.00039 |
346 | -0.746 | 0.375 | -4.807 | 2.495 | -3.714 | 1.917 | -9.384 | 5.278 | 24.355 | -10.736 | 0.00141 | -0.00039 |
347 | -0.745 | 0.375 | -4.800 | 2.491 | -3.707 | 1.914 | -9.369 | 5.269 | 24.310 | -10.719 | 0.00141 | -0.00039 |
348 | -0.744 | 0.374 | -4.792 | 2.487 | -3.701 | 1.911 | -9.354 | 5.260 | 24.265 | -10.702 | 0.00141 | -0.00039 |
349 | -0.742 | 0.373 | -4.784 | 2.483 | -3.695 | 1.908 | -9.339 | 5.251 | 24.220 | -10.686 | 0.00140 | -0.00039 |
350 | -0.741 | 0.373 | -4.776 | 2.479 | -3.689 | 1.905 | -9.324 | 5.242 | 24.175 | -10.669 | 0.00140 | -0.00039 |
351 | -0.740 | 0.372 | -4.768 | 2.476 | -3.683 | 1.902 | -9.309 | 5.233 | 24.130 | -10.652 | 0.00139 | -0.00039 |
352 | -0.739 | 0.372 | -4.761 | 2.472 | -3.677 | 1.899 | -9.295 | 5.224 | 24.085 | -10.636 | 0.00139 | -0.00039 |
353 | -0.737 | 0.371 | -4.753 | 2.468 | -3.671 | 1.896 | -9.280 | 5.215 | 24.041 | -10.619 | 0.00138 | -0.00039 |
354 | -0.736 | 0.370 | -4.745 | 2.464 | -3.665 | 1.893 | -9.265 | 5.207 | 23.996 | -10.603 | 0.00138 | -0.00039 |
355 | -0.735 | 0.370 | -4.737 | 2.460 | -3.659 | 1.890 | -9.250 | 5.198 | 23.952 | -10.586 | 0.00138 | -0.00039 |
356 | -0.734 | 0.369 | -4.730 | 2.456 | -3.653 | 1.887 | -9.236 | 5.189 | 23.907 | -10.570 | 0.00137 | -0.00039 |
357 | -0.733 | 0.369 | -4.722 | 2.452 | -3.647 | 1.884 | -9.221 | 5.180 | 23.863 | -10.553 | 0.00137 | -0.00039 |
358 | -0.731 | 0.368 | -4.714 | 2.448 | -3.641 | 1.881 | -9.206 | 5.171 | 23.819 | -10.537 | 0.00136 | -0.00039 |
359 | -0.730 | 0.368 | -4.707 | 2.444 | -3.635 | 1.878 | -9.192 | 5.163 | 23.775 | -10.520 | 0.00136 | -0.00039 |
360 | -0.729 | 0.367 | -4.699 | 2.440 | -3.629 | 1.875 | -9.177 | 5.154 | 23.731 | -10.504 | 0.00136 | -0.00039 |
361 | -0.728 | 0.366 | -4.691 | 2.436 | -3.623 | 1.872 | -9.163 | 5.145 | 23.687 | -10.487 | 0.00135 | -0.00039 |
362 | -0.727 | 0.366 | -4.684 | 2.432 | -3.618 | 1.869 | -9.148 | 5.136 | 23.643 | -10.471 | 0.00135 | -0.00038 |
363 | -0.725 | 0.365 | -4.676 | 2.428 | -3.612 | 1.866 | -9.134 | 5.128 | 23.599 | -10.455 | 0.00134 | -0.00038 |
364 | -0.724 | 0.365 | -4.669 | 2.424 | -3.606 | 1.863 | -9.119 | 5.119 | 23.556 | -10.438 | 0.00134 | -0.00038 |
365 | -0.723 | 0.364 | -4.661 | 2.421 | -3.600 | 1.860 | -9.105 | 5.110 | 23.512 | -10.422 | 0.00134 | -0.00038 |
366 | -0.722 | 0.364 | -4.653 | 2.417 | -3.594 | 1.857 | -9.090 | 5.102 | 23.469 | -10.406 | 0.00133 | -0.00038 |
367 | -0.721 | 0.363 | -4.646 | 2.413 | -3.588 | 1.854 | -9.076 | 5.093 | 23.425 | -10.390 | 0.00133 | -0.00038 |
368 | -0.719 | 0.362 | -4.638 | 2.409 | -3.582 | 1.851 | -9.061 | 5.084 | 23.382 | -10.373 | 0.00132 | -0.00038 |
369 | -0.718 | 0.362 | -4.631 | 2.405 | -3.576 | 1.848 | -9.047 | 5.076 | 23.339 | -10.357 | 0.00132 | -0.00038 |
370 | -0.717 | 0.361 | -4.623 | 2.401 | -3.570 | 1.845 | -9.033 | 5.067 | 23.296 | -10.341 | 0.00132 | -0.00038 |
371 | -0.716 | 0.361 | -4.616 | 2.397 | -3.565 | 1.842 | -9.018 | 5.058 | 23.253 | -10.325 | 0.00131 | -0.00038 |
372 | -0.715 | 0.360 | -4.608 | 2.393 | -3.559 | 1.839 | -9.004 | 5.050 | 23.210 | -10.309 | 0.00131 | -0.00038 |
373 | -0.713 | 0.360 | -4.601 | 2.390 | -3.553 | 1.836 | -8.990 | 5.041 | 23.167 | -10.293 | 0.00130 | -0.00038 |
374 | -0.712 | 0.359 | -4.593 | 2.386 | -3.547 | 1.833 | -8.975 | 5.033 | 23.124 | -10.277 | 0.00130 | -0.00038 |
375 | -0.711 | 0.358 | -4.586 | 2.382 | -3.541 | 1.830 | -8.961 | 5.024 | 23.082 | -10.261 | 0.00130 | -0.00038 |
376 | -0.710 | 0.358 | -4.578 | 2.378 | -3.536 | 1.827 | -8.947 | 5.016 | 23.039 | -10.245 | 0.00129 | -0.00038 |
377 | -0.709 | 0.357 | -4.571 | 2.374 | -3.530 | 1.824 | -8.932 | 5.007 | 22.997 | -10.229 | 0.00129 | -0.00038 |
378 | -0.707 | 0.357 | -4.563 | 2.371 | -3.524 | 1.821 | -8.918 | 4.999 | 22.954 | -10.213 | 0.00128 | -0.00038 |
379 | -0.706 | 0.356 | -4.556 | 2.367 | -3.518 | 1.819 | -8.904 | 4.990 | 22.912 | -10.197 | 0.00128 | -0.00037 |
380 | -0.705 | 0.356 | -4.548 | 2.363 | -3.512 | 1.816 | -8.890 | 4.982 | 22.870 | -10.181 | 0.00128 | -0.00037 |
381 | -0.704 | 0.355 | -4.541 | 2.359 | -3.507 | 1.813 | -8.876 | 4.973 | 22.827 | -10.165 | 0.00127 | -0.00037 |
382 | -0.703 | 0.354 | -4.534 | 2.355 | -3.501 | 1.810 | -8.862 | 4.965 | 22.785 | -10.149 | 0.00127 | -0.00037 |
383 | -0.702 | 0.354 | -4.526 | 2.352 | -3.495 | 1.807 | -8.848 | 4.957 | 22.743 | -10.133 | 0.00127 | -0.00037 |
384 | -0.700 | 0.353 | -4.519 | 2.348 | -3.490 | 1.804 | -8.834 | 4.948 | 22.701 | -10.117 | 0.00126 | -0.00037 |
385 | -0.699 | 0.353 | -4.512 | 2.344 | -3.484 | 1.801 | -8.819 | 4.940 | 22.660 | -10.101 | 0.00126 | -0.00037 |
386 | -0.698 | 0.352 | -4.504 | 2.340 | -3.478 | 1.798 | -8.805 | 4.931 | 22.618 | -10.086 | 0.00125 | -0.00037 |
387 | -0.697 | 0.352 | -4.497 | 2.337 | -3.472 | 1.795 | -8.791 | 4.923 | 22.576 | -10.070 | 0.00125 | -0.00037 |
388 | -0.696 | 0.351 | -4.490 | 2.333 | -3.467 | 1.793 | -8.777 | 4.915 | 22.535 | -10.054 | 0.00125 | -0.00037 |
389 | -0.695 | 0.351 | -4.482 | 2.329 | -3.461 | 1.790 | -8.763 | 4.906 | 22.493 | -10.038 | 0.00124 | -0.00037 |
390 | -0.694 | 0.350 | -4.475 | 2.325 | -3.455 | 1.787 | -8.750 | 4.898 | 22.452 | -10.023 | 0.00124 | -0.00037 |
391 | -0.692 | 0.349 | -4.468 | 2.322 | -3.450 | 1.784 | -8.736 | 4.890 | 22.410 | -10.007 | 0.00124 | -0.00037 |
392 | -0.691 | 0.349 | -4.460 | 2.318 | -3.444 | 1.781 | -8.722 | 4.882 | 22.369 | -9.991 | 0.00123 | -0.00037 |
393 | -0.690 | 0.348 | -4.453 | 2.314 | -3.438 | 1.778 | -8.708 | 4.873 | 22.328 | -9.976 | 0.00123 | -0.00037 |
394 | -0.689 | 0.348 | -4.446 | 2.310 | -3.433 | 1.775 | -8.694 | 4.865 | 22.287 | -9.960 | 0.00123 | -0.00037 |
395 | -0.688 | 0.347 | -4.439 | 2.307 | -3.427 | 1.772 | -8.680 | 4.857 | 22.246 | -9.945 | 0.00122 | -0.00037 |
396 | -0.687 | 0.347 | -4.431 | 2.303 | -3.422 | 1.770 | -8.666 | 4.849 | 22.205 | -9.929 | 0.00122 | -0.00036 |
397 | -0.685 | 0.346 | -4.424 | 2.299 | -3.416 | 1.767 | -8.653 | 4.840 | 22.164 | -9.913 | 0.00121 | -0.00036 |
398 | -0.684 | 0.346 | -4.417 | 2.296 | -3.410 | 1.764 | -8.639 | 4.832 | 22.123 | -9.898 | 0.00121 | -0.00036 |
399 | -0.683 | 0.345 | -4.410 | 2.292 | -3.405 | 1.761 | -8.625 | 4.824 | 22.083 | -9.882 | 0.00121 | -0.00036 |
400 | -0.682 | 0.344 | -4.403 | 2.288 | -3.399 | 1.758 | -8.611 | 4.816 | 22.042 | -9.867 | 0.00120 | -0.00036 |
401 | -0.681 | 0.344 | -4.395 | 2.285 | -3.394 | 1.756 | -8.598 | 4.808 | 22.002 | -9.852 | 0.00120 | -0.00036 |
402 | -0.680 | 0.343 | -4.388 | 2.281 | -3.388 | 1.753 | -8.584 | 4.800 | 21.961 | -9.836 | 0.00120 | -0.00036 |
403 | -0.679 | 0.343 | -4.381 | 2.277 | -3.383 | 1.750 | -8.570 | 4.791 | 21.921 | -9.821 | 0.00119 | -0.00036 |
404 | -0.678 | 0.342 | -4.374 | 2.274 | -3.377 | 1.747 | -8.557 | 4.783 | 21.881 | -9.805 | 0.00119 | -0.00036 |
405 | -0.676 | 0.342 | -4.367 | 2.270 | -3.371 | 1.744 | -8.543 | 4.775 | 21.840 | -9.790 | 0.00119 | -0.00036 |
406 | -0.675 | 0.341 | -4.360 | 2.266 | -3.366 | 1.741 | -8.529 | 4.767 | 21.800 | -9.775 | 0.00118 | -0.00036 |
407 | -0.674 | 0.341 | -4.353 | 2.263 | -3.360 | 1.739 | -8.516 | 4.759 | 21.760 | -9.759 | 0.00118 | -0.00036 |
408 | -0.673 | 0.340 | -4.345 | 2.259 | -3.355 | 1.736 | -8.502 | 4.751 | 21.720 | -9.744 | 0.00118 | -0.00036 |
409 | -0.672 | 0.340 | -4.338 | 2.255 | -3.349 | 1.733 | -8.489 | 4.743 | 21.680 | -9.729 | 0.00117 | -0.00036 |
410 | -0.671 | 0.339 | -4.331 | 2.252 | -3.344 | 1.730 | -8.475 | 4.735 | 21.641 | -9.714 | 0.00117 | -0.00036 |
411 | -0.670 | 0.339 | -4.324 | 2.248 | -3.338 | 1.728 | -8.462 | 4.727 | 21.601 | -9.698 | 0.00117 | -0.00036 |
412 | -0.669 | 0.338 | -4.317 | 2.244 | -3.333 | 1.725 | -8.448 | 4.719 | 21.561 | -9.683 | 0.00116 | -0.00036 |
413 | -0.667 | 0.337 | -4.310 | 2.241 | -3.328 | 1.722 | -8.435 | 4.711 | 21.522 | -9.668 | 0.00116 | -0.00036 |
414 | -0.666 | 0.337 | -4.303 | 2.237 | -3.322 | 1.719 | -8.421 | 4.703 | 21.482 | -9.653 | 0.00116 | -0.00035 |
415 | -0.665 | 0.336 | -4.296 | 2.234 | -3.317 | 1.717 | -8.408 | 4.695 | 21.443 | -9.638 | 0.00115 | -0.00035 |
416 | -0.664 | 0.336 | -4.289 | 2.230 | -3.311 | 1.714 | -8.394 | 4.687 | 21.404 | -9.623 | 0.00115 | -0.00035 |
417 | -0.663 | 0.335 | -4.282 | 2.226 | -3.306 | 1.711 | -8.381 | 4.679 | 21.364 | -9.608 | 0.00115 | -0.00035 |
418 | -0.662 | 0.335 | -4.275 | 2.223 | -3.300 | 1.708 | -8.368 | 4.671 | 21.325 | -9.592 | 0.00114 | -0.00035 |
419 | -0.661 | 0.334 | -4.268 | 2.219 | -3.295 | 1.706 | -8.354 | 4.663 | 21.286 | -9.577 | 0.00114 | -0.00035 |
420 | -0.660 | 0.334 | -4.261 | 2.216 | -3.290 | 1.703 | -8.341 | 4.655 | 21.247 | -9.562 | 0.00114 | -0.00035 |
421 | -0.659 | 0.333 | -4.254 | 2.212 | -3.284 | 1.700 | -8.328 | 4.648 | 21.208 | -9.547 | 0.00113 | -0.00035 |
422 | -0.658 | 0.333 | -4.247 | 2.209 | -3.279 | 1.697 | -8.314 | 4.640 | 21.169 | -9.532 | 0.00113 | -0.00035 |
423 | -0.656 | 0.332 | -4.240 | 2.205 | -3.273 | 1.695 | -8.301 | 4.632 | 21.131 | -9.518 | 0.00113 | -0.00035 |
424 | -0.655 | 0.332 | -4.233 | 2.202 | -3.268 | 1.692 | -8.288 | 4.624 | 21.092 | -9.503 | 0.00112 | -0.00035 |
425 | -0.654 | 0.331 | -4.227 | 2.198 | -3.263 | 1.689 | -8.275 | 4.616 | 21.053 | -9.488 | 0.00112 | -0.00035 |
426 | -0.653 | 0.331 | -4.220 | 2.194 | -3.257 | 1.686 | -8.261 | 4.608 | 21.015 | -9.473 | 0.00112 | -0.00035 |
427 | -0.652 | 0.330 | -4.213 | 2.191 | -3.252 | 1.684 | -8.248 | 4.601 | 20.976 | -9.458 | 0.00111 | -0.00035 |
428 | -0.651 | 0.329 | -4.206 | 2.187 | -3.247 | 1.681 | -8.235 | 4.593 | 20.938 | -9.443 | 0.00111 | -0.00035 |
429 | -0.650 | 0.329 | -4.199 | 2.184 | -3.241 | 1.678 | -8.222 | 4.585 | 20.900 | -9.428 | 0.00111 | -0.00035 |
430 | -0.649 | 0.328 | -4.192 | 2.180 | -3.236 | 1.676 | -8.209 | 4.577 | 20.861 | -9.414 | 0.00110 | -0.00035 |
431 | -0.648 | 0.328 | -4.185 | 2.177 | -3.231 | 1.673 | -8.196 | 4.570 | 20.823 | -9.399 | 0.00110 | -0.00035 |
432 | -0.647 | 0.327 | -4.179 | 2.173 | -3.225 | 1.670 | -8.183 | 4.562 | 20.785 | -9.384 | 0.00110 | -0.00034 |
433 | -0.646 | 0.327 | -4.172 | 2.170 | -3.220 | 1.668 | -8.169 | 4.554 | 20.747 | -9.369 | 0.00110 | -0.00034 |
434 | -0.645 | 0.326 | -4.165 | 2.166 | -3.215 | 1.665 | -8.156 | 4.546 | 20.709 | -9.355 | 0.00109 | -0.00034 |
435 | -0.644 | 0.326 | -4.158 | 2.163 | -3.210 | 1.662 | -8.143 | 4.539 | 20.671 | -9.340 | 0.00109 | -0.00034 |
436 | -0.642 | 0.325 | -4.151 | 2.159 | -3.204 | 1.660 | -8.130 | 4.531 | 20.634 | -9.325 | 0.00109 | -0.00034 |
437 | -0.641 | 0.325 | -4.145 | 2.156 | -3.199 | 1.657 | -8.117 | 4.523 | 20.596 | -9.311 | 0.00108 | -0.00034 |
438 | -0.640 | 0.324 | -4.138 | 2.152 | -3.194 | 1.654 | -8.104 | 4.516 | 20.558 | -9.296 | 0.00108 | -0.00034 |
439 | -0.639 | 0.324 | -4.131 | 2.149 | -3.189 | 1.652 | -8.092 | 4.508 | 20.521 | -9.281 | 0.00108 | -0.00034 |
440 | -0.638 | 0.323 | -4.124 | 2.146 | -3.183 | 1.649 | -8.079 | 4.501 | 20.483 | -9.267 | 0.00107 | -0.00034 |
441 | -0.637 | 0.323 | -4.118 | 2.142 | -3.178 | 1.646 | -8.066 | 4.493 | 20.446 | -9.252 | 0.00107 | -0.00034 |
442 | -0.636 | 0.322 | -4.111 | 2.139 | -3.173 | 1.644 | -8.053 | 4.485 | 20.408 | -9.238 | 0.00107 | -0.00034 |
443 | -0.635 | 0.322 | -4.104 | 2.135 | -3.168 | 1.641 | -8.040 | 4.478 | 20.371 | -9.223 | 0.00107 | -0.00034 |
444 | -0.634 | 0.321 | -4.097 | 2.132 | -3.163 | 1.638 | -8.027 | 4.470 | 20.334 | -9.209 | 0.00106 | -0.00034 |
445 | -0.633 | 0.321 | -4.091 | 2.128 | -3.157 | 1.636 | -8.014 | 4.463 | 20.297 | -9.194 | 0.00106 | -0.00034 |
446 | -0.632 | 0.320 | -4.084 | 2.125 | -3.152 | 1.633 | -8.001 | 4.455 | 20.260 | -9.180 | 0.00106 | -0.00034 |
447 | -0.631 | 0.320 | -4.077 | 2.122 | -3.147 | 1.631 | -7.989 | 4.448 | 20.223 | -9.165 | 0.00105 | -0.00034 |
448 | -0.630 | 0.319 | -4.071 | 2.118 | -3.142 | 1.628 | -7.976 | 4.440 | 20.186 | -9.151 | 0.00105 | -0.00034 |
449 | -0.629 | 0.319 | -4.064 | 2.115 | -3.137 | 1.625 | -7.963 | 4.433 | 20.149 | -9.137 | 0.00105 | -0.00034 |
450 | -0.628 | 0.318 | -4.058 | 2.111 | -3.132 | 1.623 | -7.950 | 4.425 | 20.112 | -9.122 | 0.00104 | -0.00034 |
451 | -0.627 | 0.318 | -4.051 | 2.108 | -3.126 | 1.620 | -7.938 | 4.418 | 20.076 | -9.108 | 0.00104 | -0.00033 |
452 | -0.626 | 0.317 | -4.044 | 2.104 | -3.121 | 1.617 | -7.925 | 4.410 | 20.039 | -9.094 | 0.00104 | -0.00033 |
453 | -0.625 | 0.317 | -4.038 | 2.101 | -3.116 | 1.615 | -7.912 | 4.403 | 20.003 | -9.079 | 0.00104 | -0.00033 |
454 | -0.624 | 0.316 | -4.031 | 2.098 | -3.111 | 1.612 | -7.900 | 4.395 | 19.966 | -9.065 | 0.00103 | -0.00033 |
455 | -0.622 | 0.316 | -4.025 | 2.094 | -3.106 | 1.610 | -7.887 | 4.388 | 19.930 | -9.051 | 0.00103 | -0.00033 |
456 | -0.621 | 0.315 | -4.018 | 2.091 | -3.101 | 1.607 | -7.874 | 4.381 | 19.893 | -9.037 | 0.00103 | -0.00033 |
457 | -0.620 | 0.315 | -4.011 | 2.088 | -3.096 | 1.605 | -7.862 | 4.373 | 19.857 | -9.022 | 0.00102 | -0.00033 |
458 | -0.619 | 0.314 | -4.005 | 2.084 | -3.091 | 1.602 | -7.849 | 4.366 | 19.821 | -9.008 | 0.00102 | -0.00033 |
459 | -0.618 | 0.314 | -3.998 | 2.081 | -3.086 | 1.599 | -7.837 | 4.358 | 19.785 | -8.994 | 0.00102 | -0.00033 |
460 | -0.617 | 0.313 | -3.992 | 2.078 | -3.081 | 1.597 | -7.824 | 4.351 | 19.749 | -8.980 | 0.00102 | -0.00033 |
461 | -0.616 | 0.313 | -3.985 | 2.074 | -3.075 | 1.594 | -7.812 | 4.344 | 19.713 | -8.966 | 0.00101 | -0.00033 |
462 | -0.615 | 0.312 | -3.979 | 2.071 | -3.070 | 1.592 | -7.799 | 4.336 | 19.677 | -8.952 | 0.00101 | -0.00033 |
463 | -0.614 | 0.312 | -3.972 | 2.068 | -3.065 | 1.589 | -7.787 | 4.329 | 19.641 | -8.937 | 0.00101 | -0.00033 |
464 | -0.613 | 0.311 | -3.966 | 2.064 | -3.060 | 1.587 | -7.774 | 4.322 | 19.605 | -8.923 | 0.00101 | -0.00033 |
465 | -0.612 | 0.311 | -3.959 | 2.061 | -3.055 | 1.584 | -7.762 | 4.314 | 19.570 | -8.909 | 0.00100 | -0.00033 |
466 | -0.611 | 0.310 | -3.953 | 2.058 | -3.050 | 1.581 | -7.749 | 4.307 | 19.534 | -8.895 | 0.00100 | -0.00033 |
467 | -0.610 | 0.310 | -3.946 | 2.054 | -3.045 | 1.579 | -7.737 | 4.300 | 19.499 | -8.881 | 0.00100 | -0.00033 |
468 | -0.609 | 0.309 | -3.940 | 2.051 | -3.040 | 1.576 | -7.725 | 4.293 | 19.463 | -8.867 | 0.00099 | -0.00033 |
469 | -0.608 | 0.309 | -3.933 | 2.048 | -3.035 | 1.574 | -7.712 | 4.285 | 19.428 | -8.853 | 0.00099 | -0.00033 |
470 | -0.607 | 0.308 | -3.927 | 2.044 | -3.030 | 1.571 | -7.700 | 4.278 | 19.392 | -8.839 | 0.00099 | -0.00032 |
471 | -0.606 | 0.308 | -3.921 | 2.041 | -3.025 | 1.569 | -7.688 | 4.271 | 19.357 | -8.826 | 0.00099 | -0.00032 |
472 | -0.605 | 0.307 | -3.914 | 2.038 | -3.020 | 1.566 | -7.675 | 4.264 | 19.322 | -8.812 | 0.00098 | -0.00032 |
473 | -0.604 | 0.307 | -3.908 | 2.034 | -3.015 | 1.564 | -7.663 | 4.257 | 19.287 | -8.798 | 0.00098 | -0.00032 |
474 | -0.603 | 0.306 | -3.901 | 2.031 | -3.011 | 1.561 | -7.651 | 4.249 | 19.252 | -8.784 | 0.00098 | -0.00032 |
475 | -0.602 | 0.306 | -3.895 | 2.028 | -3.006 | 1.559 | -7.638 | 4.242 | 19.217 | -8.770 | 0.00098 | -0.00032 |
476 | -0.601 | 0.305 | -3.889 | 2.025 | -3.001 | 1.556 | -7.626 | 4.235 | 19.182 | -8.756 | 0.00097 | -0.00032 |
477 | -0.600 | 0.305 | -3.882 | 2.021 | -2.996 | 1.554 | -7.614 | 4.228 | 19.147 | -8.743 | 0.00097 | -0.00032 |
478 | -0.599 | 0.304 | -3.876 | 2.018 | -2.991 | 1.551 | -7.602 | 4.221 | 19.112 | -8.729 | 0.00097 | -0.00032 |
479 | -0.598 | 0.304 | -3.870 | 2.015 | -2.986 | 1.549 | -7.590 | 4.214 | 19.078 | -8.715 | 0.00096 | -0.00032 |
480 | -0.597 | 0.303 | -3.863 | 2.012 | -2.981 | 1.546 | -7.577 | 4.207 | 19.043 | -8.701 | 0.00096 | -0.00032 |
481 | -0.596 | 0.303 | -3.857 | 2.008 | -2.976 | 1.544 | -7.565 | 4.199 | 19.008 | -8.688 | 0.00096 | -0.00032 |
482 | -0.595 | 0.302 | -3.851 | 2.005 | -2.971 | 1.541 | -7.553 | 4.192 | 18.974 | -8.674 | 0.00096 | -0.00032 |
483 | -0.594 | 0.302 | -3.844 | 2.002 | -2.966 | 1.539 | -7.541 | 4.185 | 18.939 | -8.660 | 0.00095 | -0.00032 |
484 | -0.593 | 0.301 | -3.838 | 1.999 | -2.961 | 1.536 | -7.529 | 4.178 | 18.905 | -8.647 | 0.00095 | -0.00032 |
485 | -0.592 | 0.301 | -3.832 | 1.995 | -2.957 | 1.534 | -7.517 | 4.171 | 18.871 | -8.633 | 0.00095 | -0.00032 |
486 | -0.591 | 0.300 | -3.826 | 1.992 | -2.952 | 1.531 | -7.505 | 4.164 | 18.836 | -8.619 | 0.00095 | -0.00032 |
487 | -0.590 | 0.300 | -3.819 | 1.989 | -2.947 | 1.529 | -7.493 | 4.157 | 18.802 | -8.606 | 0.00094 | -0.00032 |
488 | -0.589 | 0.299 | -3.813 | 1.986 | -2.942 | 1.526 | -7.481 | 4.150 | 18.768 | -8.592 | 0.00094 | -0.00032 |
489 | -0.588 | 0.299 | -3.807 | 1.983 | -2.937 | 1.524 | -7.469 | 4.143 | 18.734 | -8.579 | 0.00094 | -0.00032 |
490 | -0.587 | 0.299 | -3.801 | 1.979 | -2.932 | 1.522 | -7.457 | 4.136 | 18.700 | -8.565 | 0.00094 | -0.00031 |
491 | -0.586 | 0.298 | -3.794 | 1.976 | -2.928 | 1.519 | -7.445 | 4.129 | 18.666 | -8.552 | 0.00093 | -0.00031 |
492 | -0.585 | 0.298 | -3.788 | 1.973 | -2.923 | 1.517 | -7.433 | 4.122 | 18.632 | -8.538 | 0.00093 | -0.00031 |
493 | -0.584 | 0.297 | -3.782 | 1.970 | -2.918 | 1.514 | -7.421 | 4.115 | 18.599 | -8.525 | 0.00093 | -0.00031 |
494 | -0.583 | 0.297 | -3.776 | 1.967 | -2.913 | 1.512 | -7.409 | 4.108 | 18.565 | -8.511 | 0.00093 | -0.00031 |
495 | -0.582 | 0.296 | -3.770 | 1.964 | -2.908 | 1.509 | -7.397 | 4.101 | 18.531 | -8.498 | 0.00092 | -0.00031 |
496 | -0.581 | 0.296 | -3.764 | 1.960 | -2.904 | 1.507 | -7.386 | 4.094 | 18.498 | -8.484 | 0.00092 | -0.00031 |
497 | -0.580 | 0.295 | -3.757 | 1.957 | -2.899 | 1.504 | -7.374 | 4.088 | 18.464 | -8.471 | 0.00092 | -0.00031 |
498 | -0.580 | 0.295 | -3.751 | 1.954 | -2.894 | 1.502 | -7.362 | 4.081 | 18.431 | -8.458 | 0.00092 | -0.00031 |
499 | -0.579 | 0.294 | -3.745 | 1.951 | -2.889 | 1.500 | -7.350 | 4.074 | 18.397 | -8.444 | 0.00091 | -0.00031 |
Figure 9: Existence of Equilibrium Paths: Approximation Errors
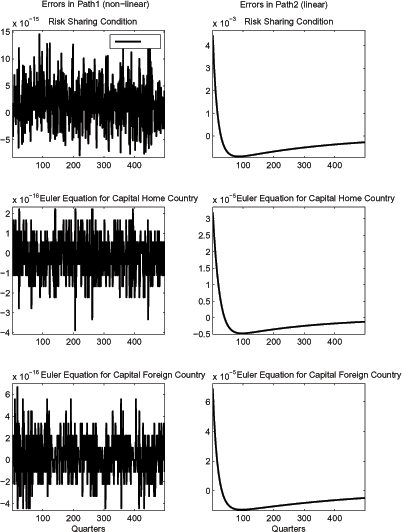
Data for Figure 9
Quarters | Risk Sharing Condition (true solution) | Risk Sharing Condition (linearized solution) | Euler Equation for Capital Home Country (true solution) | Euler Equation for Capital Home Country (linearized solution) | Euler Equation for Capital Foreign Country (true solution) | Euler Equation for Capital Foreign Country (linearized solution) |
|---|---|---|---|---|---|---|
1 | -4.2E-15 | 4.4E-03 | -5.6E-17 | 3.2E-05 | -2.2E-16 | 6.9E-05 |
2 | -6.7E-16 | 4.1E-03 | 1.1E-16 | 3.0E-05 | 0.0E+00 | 6.4E-05 |
3 | -4.3E-15 | 3.8E-03 | 5.6E-17 | 2.9E-05 | 0.0E+00 | 5.9E-05 |
4 | 1.7E-15 | 3.5E-03 | -1.1E-16 | 2.7E-05 | 2.2E-16 | 5.4E-05 |
5 | -8.9E-16 | 3.2E-03 | 1.7E-16 | 2.6E-05 | 1.1E-16 | 5.0E-05 |
6 | 1.1E-16 | 2.9E-03 | -5.6E-17 | 2.4E-05 | 0.0E+00 | 4.6E-05 |
7 | 7.0E-15 | 2.7E-03 | 0.0E+00 | 2.3E-05 | 1.1E-16 | 4.3E-05 |
8 | -4.4E-16 | 2.4E-03 | -1.1E-16 | 2.2E-05 | -2.2E-16 | 3.9E-05 |
9 | 2.3E-15 | 2.2E-03 | 5.6E-17 | 2.0E-05 | 5.6E-16 | 3.6E-05 |
10 | -5.6E-16 | 2.0E-03 | -5.6E-17 | 1.9E-05 | -1.1E-16 | 3.3E-05 |
11 | 4.6E-15 | 1.8E-03 | 1.7E-16 | 1.8E-05 | 2.2E-16 | 3.0E-05 |
12 | -2.1E-15 | 1.7E-03 | -1.1E-16 | 1.7E-05 | 0.0E+00 | 2.8E-05 |
13 | 4.9E-15 | 1.5E-03 | 5.6E-17 | 1.6E-05 | 0.0E+00 | 2.5E-05 |
14 | 3.2E-15 | 1.3E-03 | -5.6E-17 | 1.5E-05 | 3.3E-16 | 2.3E-05 |
15 | 2.2E-16 | 1.2E-03 | 1.1E-16 | 1.4E-05 | -1.1E-16 | 2.1E-05 |
16 | 1.1E-16 | 1.1E-03 | 0.0E+00 | 1.3E-05 | -2.2E-16 | 1.9E-05 |
17 | 8.0E-15 | 9.4E-04 | -1.1E-16 | 1.2E-05 | 6.7E-16 | 1.7E-05 |
18 | -1.1E-15 | 8.2E-04 | -1.1E-16 | 1.1E-05 | -4.4E-16 | 1.5E-05 |
19 | 3.1E-15 | 7.1E-04 | 5.6E-17 | 1.0E-05 | 1.1E-16 | 1.4E-05 |
20 | 2.0E-15 | 6.1E-04 | 1.1E-16 | 9.6E-06 | 2.2E-16 | 1.2E-05 |
21 | -6.4E-15 | 5.1E-04 | 1.1E-16 | 8.8E-06 | 0.0E+00 | 1.0E-05 |
22 | 1.2E-14 | 4.2E-04 | -2.8E-16 | 8.1E-06 | 3.3E-16 | 9.1E-06 |
23 | -1.0E-15 | 3.3E-04 | 2.2E-16 | 7.4E-06 | 2.2E-16 | 7.8E-06 |
24 | 0.0E+00 | 2.6E-04 | -1.7E-16 | 6.8E-06 | 0.0E+00 | 6.6E-06 |
25 | 1.7E-15 | 1.8E-04 | 0.0E+00 | 6.2E-06 | -3.3E-16 | 5.4E-06 |
26 | -1.4E-15 | 1.1E-04 | 5.6E-17 | 5.6E-06 | 2.2E-16 | 4.4E-06 |
27 | -6.7E-16 | 4.6E-05 | 0.0E+00 | 5.0E-06 | 1.1E-16 | 3.3E-06 |
28 | 1.6E-15 | -1.6E-05 | -5.6E-17 | 4.5E-06 | -3.3E-16 | 2.4E-06 |
29 | -2.4E-15 | -7.3E-05 | 1.1E-16 | 4.0E-06 | 1.1E-16 | 1.5E-06 |
30 | 3.2E-15 | -1.3E-04 | -1.1E-16 | 3.5E-06 | 0.0E+00 | 6.4E-07 |
31 | -2.2E-16 | -1.8E-04 | 0.0E+00 | 3.1E-06 | -1.1E-16 | -1.7E-07 |
32 | -5.8E-15 | -2.3E-04 | 0.0E+00 | 2.6E-06 | 0.0E+00 | -9.2E-07 |
33 | 5.1E-15 | -2.7E-04 | 5.6E-17 | 2.2E-06 | -1.1E-16 | -1.6E-06 |
34 | 3.0E-15 | -3.1E-04 | -1.1E-16 | 1.8E-06 | 0.0E+00 | -2.3E-06 |
35 | 8.8E-15 | -3.5E-04 | 0.0E+00 | 1.5E-06 | 5.6E-16 | -2.9E-06 |
36 | -5.3E-15 | -3.9E-04 | 0.0E+00 | 1.1E-06 | -4.4E-16 | -3.5E-06 |
37 | 7.7E-15 | -4.2E-04 | 1.7E-16 | 7.7E-07 | 4.4E-16 | -4.1E-06 |
38 | 1.8E-15 | -4.6E-04 | 0.0E+00 | 4.5E-07 | -2.2E-16 | -4.6E-06 |
39 | 8.5E-15 | -4.9E-04 | -5.6E-17 | 1.4E-07 | 3.3E-16 | -5.1E-06 |
40 | -1.3E-15 | -5.2E-04 | 1.1E-16 | -1.4E-07 | -2.2E-16 | -5.6E-06 |
41 | 6.2E-15 | -5.4E-04 | 0.0E+00 | -4.2E-07 | 0.0E+00 | -6.0E-06 |
42 | -3.8E-15 | -5.7E-04 | 5.6E-17 | -6.8E-07 | -2.2E-16 | -6.5E-06 |
43 | 1.7E-15 | -5.9E-04 | 0.0E+00 | -9.2E-07 | 0.0E+00 | -6.9E-06 |
44 | -7.8E-16 | -6.1E-04 | 1.1E-16 | -1.2E-06 | -1.1E-16 | -7.2E-06 |
45 | 7.2E-15 | -6.3E-04 | -1.1E-16 | -1.4E-06 | 0.0E+00 | -7.6E-06 |
46 | 1.9E-15 | -6.5E-04 | 1.7E-16 | -1.6E-06 | 2.2E-16 | -7.9E-06 |
47 | -1.2E-15 | -6.7E-04 | -1.1E-16 | -1.8E-06 | -4.4E-16 | -8.2E-06 |
48 | -1.9E-15 | -6.9E-04 | -5.6E-17 | -2.0E-06 | 1.1E-16 | -8.5E-06 |
49 | 5.3E-15 | -7.1E-04 | -5.6E-17 | -2.2E-06 | 0.0E+00 | -8.8E-06 |
50 | 3.8E-15 | -7.2E-04 | -1.1E-16 | -2.3E-06 | -1.1E-16 | -9.1E-06 |
51 | 3.2E-15 | -7.4E-04 | 5.6E-17 | -2.5E-06 | 2.2E-16 | -9.3E-06 |
52 | 5.3E-15 | -7.5E-04 | -5.6E-17 | -2.6E-06 | -1.1E-16 | -9.6E-06 |
53 | -1.3E-15 | -7.6E-04 | 0.0E+00 | -2.8E-06 | 4.4E-16 | -9.8E-06 |
54 | 3.0E-15 | -7.7E-04 | -5.6E-17 | -2.9E-06 | -4.4E-16 | -1.0E-05 |
55 | 6.3E-15 | -7.8E-04 | -1.7E-16 | -3.0E-06 | 2.2E-16 | -1.0E-05 |
56 | 3.9E-15 | -7.9E-04 | 0.0E+00 | -3.2E-06 | 1.1E-16 | -1.0E-05 |
57 | 4.4E-15 | -8.0E-04 | -1.1E-16 | -3.3E-06 | 1.1E-16 | -1.1E-05 |
58 | -3.4E-15 | -8.1E-04 | -1.7E-16 | -3.4E-06 | -4.4E-16 | -1.1E-05 |
59 | 8.7E-15 | -8.2E-04 | 5.6E-17 | -3.5E-06 | 2.2E-16 | -1.1E-05 |
60 | -5.2E-15 | -8.3E-04 | 5.6E-17 | -3.6E-06 | -2.2E-16 | -1.1E-05 |
61 | 7.7E-15 | -8.4E-04 | -1.1E-16 | -3.7E-06 | 0.0E+00 | -1.1E-05 |
62 | 4.4E-15 | -8.4E-04 | 1.7E-16 | -3.8E-06 | 4.4E-16 | -1.1E-05 |
63 | 2.1E-15 | -8.5E-04 | -2.8E-16 | -3.8E-06 | 0.0E+00 | -1.1E-05 |
64 | 1.8E-15 | -8.5E-04 | 0.0E+00 | -3.9E-06 | 4.4E-16 | -1.2E-05 |
65 | -2.2E-15 | -8.6E-04 | 1.1E-16 | -4.0E-06 | -3.3E-16 | -1.2E-05 |
66 | 4.7E-15 | -8.6E-04 | -5.6E-17 | -4.0E-06 | 2.2E-16 | -1.2E-05 |
67 | 1.9E-15 | -8.7E-04 | 1.1E-16 | -4.1E-06 | -2.2E-16 | -1.2E-05 |
68 | 4.7E-15 | -8.7E-04 | -1.7E-16 | -4.2E-06 | 2.2E-16 | -1.2E-05 |
69 | 5.6E-16 | -8.8E-04 | 0.0E+00 | -4.2E-06 | 2.2E-16 | -1.2E-05 |
70 | 2.9E-15 | -8.8E-04 | 1.1E-16 | -4.3E-06 | 2.2E-16 | -1.2E-05 |
71 | 2.8E-15 | -8.8E-04 | -1.7E-16 | -4.3E-06 | -1.1E-16 | -1.2E-05 |
72 | 1.0E-14 | -8.9E-04 | 1.1E-16 | -4.4E-06 | 2.2E-16 | -1.2E-05 |
73 | 3.4E-15 | -8.9E-04 | 5.6E-17 | -4.4E-06 | -1.1E-16 | -1.2E-05 |
74 | 5.6E-16 | -8.9E-04 | 0.0E+00 | -4.4E-06 | 0.0E+00 | -1.2E-05 |
75 | 2.9E-15 | -8.9E-04 | -1.7E-16 | -4.5E-06 | 3.3E-16 | -1.2E-05 |
76 | 2.2E-15 | -9.0E-04 | 0.0E+00 | -4.5E-06 | 2.2E-16 | -1.2E-05 |
77 | 4.9E-15 | -9.0E-04 | 5.6E-17 | -4.5E-06 | 0.0E+00 | -1.2E-05 |
78 | -1.0E-15 | -9.0E-04 | 5.6E-17 | -4.6E-06 | 0.0E+00 | -1.2E-05 |
79 | 1.7E-15 | -9.0E-04 | -5.6E-17 | -4.6E-06 | -1.1E-16 | -1.3E-05 |
80 | 3.1E-15 | -9.0E-04 | 1.1E-16 | -4.6E-06 | 2.2E-16 | -1.3E-05 |
81 | 7.4E-15 | -9.0E-04 | -5.6E-17 | -4.6E-06 | 1.1E-16 | -1.3E-05 |
82 | -3.1E-15 | -9.0E-04 | 5.6E-17 | -4.7E-06 | 1.1E-16 | -1.3E-05 |
83 | 5.8E-15 | -9.0E-04 | -1.1E-16 | -4.7E-06 | -1.1E-16 | -1.3E-05 |
84 | -5.6E-16 | -9.0E-04 | 0.0E+00 | -4.7E-06 | 2.2E-16 | -1.3E-05 |
85 | 2.8E-15 | -9.0E-04 | 0.0E+00 | -4.7E-06 | -2.2E-16 | -1.3E-05 |
86 | 5.1E-15 | -9.0E-04 | -1.1E-16 | -4.7E-06 | 3.3E-16 | -1.3E-05 |
87 | 4.0E-15 | -9.0E-04 | -5.6E-17 | -4.7E-06 | -1.1E-16 | -1.3E-05 |
88 | -3.3E-16 | -9.0E-04 | 0.0E+00 | -4.7E-06 | 2.2E-16 | -1.3E-05 |
89 | 1.5E-14 | -9.0E-04 | -5.6E-17 | -4.7E-06 | 2.2E-16 | -1.3E-05 |
90 | -7.8E-16 | -9.0E-04 | -5.6E-17 | -4.7E-06 | 1.1E-16 | -1.3E-05 |
91 | 2.8E-15 | -9.0E-04 | -2.2E-16 | -4.8E-06 | -2.2E-16 | -1.3E-05 |
92 | 1.0E-15 | -9.0E-04 | 0.0E+00 | -4.8E-06 | -1.1E-16 | -1.3E-05 |
93 | 8.8E-15 | -9.0E-04 | 0.0E+00 | -4.8E-06 | 0.0E+00 | -1.3E-05 |
94 | -1.9E-15 | -9.0E-04 | 1.1E-16 | -4.8E-06 | 2.2E-16 | -1.3E-05 |
95 | 8.5E-15 | -9.0E-04 | -1.7E-16 | -4.8E-06 | 3.3E-16 | -1.3E-05 |
96 | -3.3E-15 | -9.0E-04 | 5.6E-17 | -4.8E-06 | -2.2E-16 | -1.3E-05 |
97 | 5.6E-16 | -9.0E-04 | -1.1E-16 | -4.8E-06 | 0.0E+00 | -1.3E-05 |
98 | 1.1E-14 | -8.9E-04 | -5.6E-17 | -4.8E-06 | 2.2E-16 | -1.3E-05 |
99 | 3.3E-16 | -8.9E-04 | -1.1E-16 | -4.8E-06 | 0.0E+00 | -1.3E-05 |
100 | -5.6E-16 | -8.9E-04 | 5.6E-17 | -4.8E-06 | -2.2E-16 | -1.3E-05 |
101 | 6.3E-15 | -8.9E-04 | -1.1E-16 | -4.8E-06 | 1.1E-16 | -1.3E-05 |
102 | -8.9E-16 | -8.9E-04 | 5.6E-17 | -4.8E-06 | -1.1E-16 | -1.3E-05 |
103 | 7.5E-15 | -8.9E-04 | -1.7E-16 | -4.8E-06 | 0.0E+00 | -1.3E-05 |
104 | 6.1E-15 | -8.9E-04 | -5.6E-17 | -4.7E-06 | 0.0E+00 | -1.3E-05 |
105 | -1.0E-15 | -8.8E-04 | -1.1E-16 | -4.7E-06 | 0.0E+00 | -1.3E-05 |
106 | 6.0E-15 | -8.8E-04 | -5.6E-17 | -4.7E-06 | 2.2E-16 | -1.3E-05 |
107 | 3.9E-15 | -8.8E-04 | -5.6E-17 | -4.7E-06 | 3.3E-16 | -1.3E-05 |
108 | 3.3E-16 | -8.8E-04 | 1.1E-16 | -4.7E-06 | -1.1E-16 | -1.3E-05 |
109 | 2.7E-15 | -8.8E-04 | -1.7E-16 | -4.7E-06 | 3.3E-16 | -1.3E-05 |
110 | 2.6E-15 | -8.8E-04 | 5.6E-17 | -4.7E-06 | 0.0E+00 | -1.3E-05 |
111 | 1.6E-15 | -8.7E-04 | 0.0E+00 | -4.7E-06 | 1.1E-16 | -1.3E-05 |
112 | 2.9E-15 | -8.7E-04 | -1.1E-16 | -4.7E-06 | 1.1E-16 | -1.3E-05 |
113 | 6.7E-16 | -8.7E-04 | -1.1E-16 | -4.7E-06 | -1.1E-16 | -1.3E-05 |
114 | 1.3E-14 | -8.7E-04 | 1.1E-16 | -4.7E-06 | 5.6E-16 | -1.3E-05 |
115 | 1.7E-15 | -8.7E-04 | 5.6E-17 | -4.7E-06 | 3.3E-16 | -1.3E-05 |
116 | -1.7E-15 | -8.6E-04 | 0.0E+00 | -4.6E-06 | -3.3E-16 | -1.3E-05 |
117 | 1.1E-15 | -8.6E-04 | -5.6E-17 | -4.6E-06 | 1.1E-16 | -1.3E-05 |
118 | 2.6E-15 | -8.6E-04 | -5.6E-17 | -4.6E-06 | -1.1E-16 | -1.2E-05 |
119 | -3.6E-15 | -8.6E-04 | -5.6E-17 | -4.6E-06 | 1.1E-16 | -1.2E-05 |
120 | 6.1E-15 | -8.6E-04 | 5.6E-17 | -4.6E-06 | -1.1E-16 | -1.2E-05 |
121 | 5.3E-15 | -8.5E-04 | -5.6E-17 | -4.6E-06 | 4.4E-16 | -1.2E-05 |
122 | -2.6E-15 | -8.5E-04 | 0.0E+00 | -4.6E-06 | -2.2E-16 | -1.2E-05 |
123 | 1.3E-14 | -8.5E-04 | -2.2E-16 | -4.6E-06 | 2.2E-16 | -1.2E-05 |
124 | -5.2E-15 | -8.5E-04 | 0.0E+00 | -4.6E-06 | -1.1E-16 | -1.2E-05 |
125 | -4.4E-15 | -8.5E-04 | -5.6E-17 | -4.5E-06 | -2.2E-16 | -1.2E-05 |
126 | 2.2E-15 | -8.4E-04 | 0.0E+00 | -4.5E-06 | 0.0E+00 | -1.2E-05 |
127 | 8.9E-16 | -8.4E-04 | 5.6E-17 | -4.5E-06 | 1.1E-16 | -1.2E-05 |
128 | 4.8E-15 | -8.4E-04 | -5.6E-17 | -4.5E-06 | 2.2E-16 | -1.2E-05 |
129 | 5.0E-15 | -8.4E-04 | 5.6E-17 | -4.5E-06 | 1.1E-16 | -1.2E-05 |
130 | 4.4E-15 | -8.4E-04 | -5.6E-17 | -4.5E-06 | 0.0E+00 | -1.2E-05 |
131 | 4.4E-15 | -8.3E-04 | 5.6E-17 | -4.5E-06 | 1.1E-16 | -1.2E-05 |
132 | -2.2E-16 | -8.3E-04 | 0.0E+00 | -4.5E-06 | 0.0E+00 | -1.2E-05 |
133 | 1.8E-15 | -8.3E-04 | -1.1E-16 | -4.4E-06 | 0.0E+00 | -1.2E-05 |
134 | 4.1E-15 | -8.3E-04 | 0.0E+00 | -4.4E-06 | -1.1E-16 | -1.2E-05 |
135 | -3.9E-15 | -8.2E-04 | 1.1E-16 | -4.4E-06 | -1.1E-16 | -1.2E-05 |
136 | 2.4E-15 | -8.2E-04 | -1.7E-16 | -4.4E-06 | 0.0E+00 | -1.2E-05 |
137 | 7.1E-15 | -8.2E-04 | 5.6E-17 | -4.4E-06 | 0.0E+00 | -1.2E-05 |
138 | 3.9E-15 | -8.2E-04 | -2.2E-16 | -4.4E-06 | -1.1E-16 | -1.2E-05 |
139 | -2.0E-15 | -8.2E-04 | 5.6E-17 | -4.4E-06 | -1.1E-16 | -1.2E-05 |
140 | -4.9E-15 | -8.1E-04 | 2.2E-16 | -4.4E-06 | 0.0E+00 | -1.2E-05 |
141 | -5.6E-16 | -8.1E-04 | 2.2E-16 | -4.3E-06 | 1.1E-16 | -1.2E-05 |
142 | -4.2E-15 | -8.1E-04 | 0.0E+00 | -4.3E-06 | 0.0E+00 | -1.2E-05 |
143 | 3.2E-15 | -8.1E-04 | -2.2E-16 | -4.3E-06 | 0.0E+00 | -1.2E-05 |
144 | 5.9E-15 | -8.0E-04 | 5.6E-17 | -4.3E-06 | 0.0E+00 | -1.2E-05 |
145 | -4.2E-15 | -8.0E-04 | -1.7E-16 | -4.3E-06 | 0.0E+00 | -1.2E-05 |
146 | -2.4E-15 | -8.0E-04 | -5.6E-17 | -4.3E-06 | 0.0E+00 | -1.2E-05 |
147 | -2.7E-15 | -8.0E-04 | 5.6E-17 | -4.3E-06 | -2.2E-16 | -1.2E-05 |
148 | 3.6E-15 | -8.0E-04 | 0.0E+00 | -4.2E-06 | 2.2E-16 | -1.2E-05 |
149 | -3.7E-15 | -7.9E-04 | -5.6E-17 | -4.2E-06 | 1.1E-16 | -1.2E-05 |
150 | 9.5E-15 | -7.9E-04 | 5.6E-17 | -4.2E-06 | 1.1E-16 | -1.2E-05 |
151 | 1.3E-15 | -7.9E-04 | -1.7E-16 | -4.2E-06 | 1.1E-16 | -1.2E-05 |
152 | 4.4E-15 | -7.9E-04 | 1.1E-16 | -4.2E-06 | 1.1E-16 | -1.2E-05 |
153 | 4.0E-15 | -7.8E-04 | 0.0E+00 | -4.2E-06 | 2.2E-16 | -1.2E-05 |
154 | 5.8E-15 | -7.8E-04 | 0.0E+00 | -4.2E-06 | 1.1E-16 | -1.2E-05 |
155 | 1.4E-15 | -7.8E-04 | 0.0E+00 | -4.1E-06 | -2.2E-16 | -1.2E-05 |
156 | 3.1E-15 | -7.8E-04 | -5.6E-17 | -4.1E-06 | 1.1E-16 | -1.2E-05 |
157 | -3.6E-15 | -7.7E-04 | 1.1E-16 | -4.1E-06 | 0.0E+00 | -1.2E-05 |
158 | 7.9E-15 | -7.7E-04 | 0.0E+00 | -4.1E-06 | 3.3E-16 | -1.2E-05 |
159 | 3.1E-15 | -7.7E-04 | -5.6E-17 | -4.1E-06 | 1.1E-16 | -1.2E-05 |
160 | -2.3E-15 | -7.7E-04 | 1.1E-16 | -4.1E-06 | 0.0E+00 | -1.1E-05 |
161 | 1.1E-14 | -7.7E-04 | -1.1E-16 | -4.1E-06 | 0.0E+00 | -1.1E-05 |
162 | 1.0E-15 | -7.6E-04 | 1.1E-16 | -4.0E-06 | 1.1E-16 | -1.1E-05 |
163 | -3.7E-15 | -7.6E-04 | 5.6E-17 | -4.0E-06 | -2.2E-16 | -1.1E-05 |
164 | -1.2E-15 | -7.6E-04 | 0.0E+00 | -4.0E-06 | 1.1E-16 | -1.1E-05 |
165 | -2.2E-16 | -7.6E-04 | 5.6E-17 | -4.0E-06 | 0.0E+00 | -1.1E-05 |
166 | 7.4E-15 | -7.5E-04 | 5.6E-17 | -4.0E-06 | 1.1E-16 | -1.1E-05 |
167 | 3.3E-16 | -7.5E-04 | 0.0E+00 | -4.0E-06 | -1.1E-16 | -1.1E-05 |
168 | -5.2E-15 | -7.5E-04 | 1.7E-16 | -4.0E-06 | -1.1E-16 | -1.1E-05 |
169 | 7.2E-15 | -7.5E-04 | -1.1E-16 | -4.0E-06 | 3.3E-16 | -1.1E-05 |
170 | -2.2E-16 | -7.5E-04 | -5.6E-17 | -3.9E-06 | 0.0E+00 | -1.1E-05 |
171 | 5.4E-15 | -7.4E-04 | -1.1E-16 | -3.9E-06 | 1.1E-16 | -1.1E-05 |
172 | 6.0E-15 | -7.4E-04 | -1.1E-16 | -3.9E-06 | 0.0E+00 | -1.1E-05 |
173 | 1.4E-15 | -7.4E-04 | 5.6E-17 | -3.9E-06 | 1.1E-16 | -1.1E-05 |
174 | -6.0E-15 | -7.4E-04 | -5.6E-17 | -3.9E-06 | 1.1E-16 | -1.1E-05 |
175 | 5.1E-15 | -7.4E-04 | 0.0E+00 | -3.9E-06 | -1.1E-16 | -1.1E-05 |
176 | 6.9E-15 | -7.3E-04 | -1.7E-16 | -3.9E-06 | 4.4E-16 | -1.1E-05 |
177 | 3.6E-15 | -7.3E-04 | 1.7E-16 | -3.8E-06 | 1.1E-16 | -1.1E-05 |
178 | 5.3E-15 | -7.3E-04 | 0.0E+00 | -3.8E-06 | 2.2E-16 | -1.1E-05 |
179 | 1.4E-15 | -7.3E-04 | 0.0E+00 | -3.8E-06 | 0.0E+00 | -1.1E-05 |
180 | 4.0E-15 | -7.2E-04 | 0.0E+00 | -3.8E-06 | 1.1E-16 | -1.1E-05 |
181 | -4.4E-16 | -7.2E-04 | -5.6E-17 | -3.8E-06 | 1.1E-16 | -1.1E-05 |
182 | 1.4E-15 | -7.2E-04 | 1.1E-16 | -3.8E-06 | 1.1E-16 | -1.1E-05 |
183 | 1.4E-15 | -7.2E-04 | -1.1E-16 | -3.8E-06 | -2.2E-16 | -1.1E-05 |
184 | 7.8E-16 | -7.2E-04 | 0.0E+00 | -3.7E-06 | 3.3E-16 | -1.1E-05 |
185 | 2.2E-15 | -7.1E-04 | 0.0E+00 | -3.7E-06 | -2.2E-16 | -1.1E-05 |
186 | -3.3E-15 | -7.1E-04 | 1.7E-16 | -3.7E-06 | -1.1E-16 | -1.1E-05 |
187 | 4.7E-15 | -7.1E-04 | -1.7E-16 | -3.7E-06 | 0.0E+00 | -1.1E-05 |
188 | 2.1E-15 | -7.1E-04 | 5.6E-17 | -3.7E-06 | 2.2E-16 | -1.1E-05 |
189 | -5.6E-16 | -7.1E-04 | -1.1E-16 | -3.7E-06 | -1.1E-16 | -1.1E-05 |
190 | -1.8E-15 | -7.0E-04 | 5.6E-17 | -3.7E-06 | -1.1E-16 | -1.1E-05 |
191 | -3.3E-16 | -7.0E-04 | 0.0E+00 | -3.7E-06 | -1.1E-16 | -1.1E-05 |
192 | 4.4E-15 | -7.0E-04 | -1.1E-16 | -3.6E-06 | 5.6E-16 | -1.1E-05 |
193 | 2.2E-16 | -7.0E-04 | 1.7E-16 | -3.6E-06 | 0.0E+00 | -1.1E-05 |
194 | -5.6E-16 | -6.9E-04 | -1.1E-16 | -3.6E-06 | -2.2E-16 | -1.1E-05 |
195 | 6.7E-16 | -6.9E-04 | -1.1E-16 | -3.6E-06 | 2.2E-16 | -1.1E-05 |
196 | 1.0E-14 | -6.9E-04 | 5.6E-17 | -3.6E-06 | -2.2E-16 | -1.1E-05 |
197 | -5.0E-15 | -6.9E-04 | 0.0E+00 | -3.6E-06 | -1.1E-16 | -1.1E-05 |
198 | 5.6E-16 | -6.9E-04 | -1.7E-16 | -3.6E-06 | -2.2E-16 | -1.1E-05 |
199 | 1.3E-14 | -6.8E-04 | 0.0E+00 | -3.6E-06 | 2.2E-16 | -1.0E-05 |
200 | -4.7E-15 | -6.8E-04 | 0.0E+00 | -3.5E-06 | -1.1E-16 | -1.0E-05 |
201 | 6.7E-16 | -6.8E-04 | -5.6E-17 | -3.5E-06 | 0.0E+00 | -1.0E-05 |
202 | -1.1E-16 | -6.8E-04 | 5.6E-17 | -3.5E-06 | 0.0E+00 | -1.0E-05 |
203 | 3.6E-15 | -6.8E-04 | 0.0E+00 | -3.5E-06 | 0.0E+00 | -1.0E-05 |
204 | 2.7E-15 | -6.7E-04 | -5.6E-17 | -3.5E-06 | -1.1E-16 | -1.0E-05 |
205 | -2.6E-15 | -6.7E-04 | 1.1E-16 | -3.5E-06 | 3.3E-16 | -1.0E-05 |
206 | 3.9E-15 | -6.7E-04 | -3.9E-16 | -3.5E-06 | -1.1E-16 | -1.0E-05 |
207 | -1.9E-15 | -6.7E-04 | 2.2E-16 | -3.5E-06 | 1.1E-16 | -1.0E-05 |
208 | 1.6E-15 | -6.7E-04 | -5.6E-17 | -3.4E-06 | 0.0E+00 | -1.0E-05 |
209 | 5.6E-16 | -6.6E-04 | -2.2E-16 | -3.4E-06 | -2.2E-16 | -1.0E-05 |
210 | -3.8E-15 | -6.6E-04 | -5.6E-17 | -3.4E-06 | 2.2E-16 | -1.0E-05 |
211 | 6.0E-15 | -6.6E-04 | 0.0E+00 | -3.4E-06 | 0.0E+00 | -1.0E-05 |
212 | -3.1E-15 | -6.6E-04 | 0.0E+00 | -3.4E-06 | -2.2E-16 | -1.0E-05 |
213 | 2.7E-15 | -6.6E-04 | -5.6E-17 | -3.4E-06 | 0.0E+00 | -1.0E-05 |
214 | 3.1E-15 | -6.5E-04 | 5.6E-17 | -3.4E-06 | 0.0E+00 | -1.0E-05 |
215 | -1.3E-15 | -6.5E-04 | -5.6E-17 | -3.4E-06 | 0.0E+00 | -1.0E-05 |
216 | 6.6E-15 | -6.5E-04 | 1.7E-16 | -3.3E-06 | 1.1E-16 | -1.0E-05 |
217 | -4.6E-15 | -6.5E-04 | 0.0E+00 | -3.3E-06 | 0.0E+00 | -1.0E-05 |
218 | 7.7E-15 | -6.5E-04 | 0.0E+00 | -3.3E-06 | 0.0E+00 | -1.0E-05 |
219 | 3.6E-15 | -6.4E-04 | 0.0E+00 | -3.3E-06 | 0.0E+00 | -1.0E-05 |
220 | -2.1E-15 | -6.4E-04 | 0.0E+00 | -3.3E-06 | 0.0E+00 | -1.0E-05 |
221 | -7.9E-15 | -6.4E-04 | -5.6E-17 | -3.3E-06 | -1.1E-16 | -9.9E-06 |
222 | 2.4E-15 | -6.4E-04 | 1.1E-16 | -3.3E-06 | 0.0E+00 | -9.9E-06 |
223 | 3.0E-15 | -6.4E-04 | -5.6E-17 | -3.3E-06 | -1.1E-16 | -9.9E-06 |
224 | 2.2E-15 | -6.4E-04 | 0.0E+00 | -3.3E-06 | 3.3E-16 | -9.9E-06 |
225 | -1.7E-15 | -6.3E-04 | 1.7E-16 | -3.2E-06 | 0.0E+00 | -9.9E-06 |
226 | 4.4E-15 | -6.3E-04 | -1.7E-16 | -3.2E-06 | 1.1E-16 | -9.8E-06 |
227 | 4.1E-15 | -6.3E-04 | 1.1E-16 | -3.2E-06 | 0.0E+00 | -9.8E-06 |
228 | 6.3E-15 | -6.3E-04 | -5.6E-17 | -3.2E-06 | 1.1E-16 | -9.8E-06 |
229 | 6.2E-15 | -6.3E-04 | -1.1E-16 | -3.2E-06 | 3.3E-16 | -9.8E-06 |
230 | -4.2E-15 | -6.2E-04 | 1.7E-16 | -3.2E-06 | -3.3E-16 | -9.7E-06 |
231 | 2.9E-15 | -6.2E-04 | 0.0E+00 | -3.2E-06 | 2.2E-16 | -9.7E-06 |
232 | 2.1E-15 | -6.2E-04 | 0.0E+00 | -3.2E-06 | 2.2E-16 | -9.7E-06 |
233 | 6.3E-15 | -6.2E-04 | -1.1E-16 | -3.2E-06 | 1.1E-16 | -9.7E-06 |
234 | 1.0E-14 | -6.2E-04 | -1.1E-16 | -3.1E-06 | -1.1E-16 | -9.6E-06 |
235 | 5.6E-16 | -6.1E-04 | 1.1E-16 | -3.1E-06 | 0.0E+00 | -9.6E-06 |
236 | 2.1E-15 | -6.1E-04 | -1.1E-16 | -3.1E-06 | 2.2E-16 | -9.6E-06 |
237 | 6.0E-15 | -6.1E-04 | 1.1E-16 | -3.1E-06 | 0.0E+00 | -9.6E-06 |
238 | 1.3E-15 | -6.1E-04 | 5.6E-17 | -3.1E-06 | 0.0E+00 | -9.5E-06 |
239 | 7.3E-15 | -6.1E-04 | -2.2E-16 | -3.1E-06 | 1.1E-16 | -9.5E-06 |
240 | -4.7E-15 | -6.1E-04 | 5.6E-17 | -3.1E-06 | 0.0E+00 | -9.5E-06 |
241 | 4.1E-15 | -6.0E-04 | 0.0E+00 | -3.1E-06 | 0.0E+00 | -9.5E-06 |
242 | -2.1E-15 | -6.0E-04 | -1.1E-16 | -3.1E-06 | 2.2E-16 | -9.4E-06 |
243 | 4.2E-15 | -6.0E-04 | -5.6E-17 | -3.0E-06 | 1.1E-16 | -9.4E-06 |
244 | 5.3E-15 | -6.0E-04 | -1.1E-16 | -3.0E-06 | 0.0E+00 | -9.4E-06 |
245 | 4.1E-15 | -6.0E-04 | 1.7E-16 | -3.0E-06 | 3.3E-16 | -9.4E-06 |
246 | -3.1E-15 | -5.9E-04 | 1.7E-16 | -3.0E-06 | -2.2E-16 | -9.4E-06 |
247 | 7.2E-15 | -5.9E-04 | -2.2E-16 | -3.0E-06 | 1.1E-16 | -9.3E-06 |
248 | -3.7E-15 | -5.9E-04 | 5.6E-17 | -3.0E-06 | 0.0E+00 | -9.3E-06 |
249 | -5.7E-15 | -5.9E-04 | 0.0E+00 | -3.0E-06 | -1.1E-16 | -9.3E-06 |
250 | -1.2E-15 | -5.9E-04 | -1.1E-16 | -3.0E-06 | 2.2E-16 | -9.3E-06 |
251 | 8.1E-15 | -5.9E-04 | -2.2E-16 | -3.0E-06 | -1.1E-16 | -9.2E-06 |
252 | 7.8E-16 | -5.8E-04 | 5.6E-17 | -2.9E-06 | -1.1E-16 | -9.2E-06 |
253 | -4.0E-15 | -5.8E-04 | -5.6E-17 | -2.9E-06 | 1.1E-16 | -9.2E-06 |
254 | 1.1E-16 | -5.8E-04 | 1.7E-16 | -2.9E-06 | -1.1E-16 | -9.2E-06 |
255 | 8.0E-15 | -5.8E-04 | -5.6E-17 | -2.9E-06 | 2.2E-16 | -9.1E-06 |
256 | -1.8E-15 | -5.8E-04 | 0.0E+00 | -2.9E-06 | 1.1E-16 | -9.1E-06 |
257 | 2.8E-15 | -5.7E-04 | -1.1E-16 | -2.9E-06 | -3.3E-16 | -9.1E-06 |
258 | 7.8E-15 | -5.7E-04 | 0.0E+00 | -2.9E-06 | 2.2E-16 | -9.1E-06 |
259 | 1.0E-15 | -5.7E-04 | -5.6E-17 | -2.9E-06 | -1.1E-16 | -9.1E-06 |
260 | 3.1E-15 | -5.7E-04 | -5.6E-17 | -2.9E-06 | 0.0E+00 | -9.0E-06 |
261 | -7.8E-16 | -5.7E-04 | 2.2E-16 | -2.9E-06 | -2.2E-16 | -9.0E-06 |
262 | 2.9E-15 | -5.7E-04 | -3.3E-16 | -2.8E-06 | 0.0E+00 | -9.0E-06 |
263 | 4.4E-16 | -5.6E-04 | 2.2E-16 | -2.8E-06 | 2.2E-16 | -9.0E-06 |
264 | 5.4E-15 | -5.6E-04 | -1.7E-16 | -2.8E-06 | 0.0E+00 | -8.9E-06 |
265 | 7.4E-15 | -5.6E-04 | -1.7E-16 | -2.8E-06 | 3.3E-16 | -8.9E-06 |
266 | 1.1E-16 | -5.6E-04 | 1.1E-16 | -2.8E-06 | -3.3E-16 | -8.9E-06 |
267 | 1.1E-15 | -5.6E-04 | -1.7E-16 | -2.8E-06 | 1.1E-16 | -8.9E-06 |
268 | -1.1E-15 | -5.6E-04 | 5.6E-17 | -2.8E-06 | 1.1E-16 | -8.9E-06 |
269 | 6.7E-15 | -5.5E-04 | 0.0E+00 | -2.8E-06 | 2.2E-16 | -8.8E-06 |
270 | 9.9E-15 | -5.5E-04 | -1.7E-16 | -2.8E-06 | 0.0E+00 | -8.8E-06 |
271 | 0.0E+00 | -5.5E-04 | 0.0E+00 | -2.8E-06 | -3.3E-16 | -8.8E-06 |
272 | 3.3E-15 | -5.5E-04 | -5.6E-17 | -2.7E-06 | 3.3E-16 | -8.8E-06 |
273 | 1.9E-15 | -5.5E-04 | 1.7E-16 | -2.7E-06 | 0.0E+00 | -8.7E-06 |
274 | 3.0E-15 | -5.5E-04 | -1.7E-16 | -2.7E-06 | 3.3E-16 | -8.7E-06 |
275 | 3.7E-15 | -5.4E-04 | -5.6E-17 | -2.7E-06 | 1.1E-16 | -8.7E-06 |
276 | -6.4E-15 | -5.4E-04 | 1.1E-16 | -2.7E-06 | -3.3E-16 | -8.7E-06 |
277 | 6.1E-15 | -5.4E-04 | 1.1E-16 | -2.7E-06 | 2.2E-16 | -8.7E-06 |
278 | -2.2E-15 | -5.4E-04 | -5.6E-17 | -2.7E-06 | 0.0E+00 | -8.6E-06 |
279 | 2.1E-15 | -5.4E-04 | 1.1E-16 | -2.7E-06 | -1.1E-16 | -8.6E-06 |
280 | 4.7E-15 | -5.4E-04 | 0.0E+00 | -2.7E-06 | 1.1E-16 | -8.6E-06 |
281 | 0.0E+00 | -5.3E-04 | -1.7E-16 | -2.7E-06 | -1.1E-16 | -8.6E-06 |
282 | 2.6E-15 | -5.3E-04 | 0.0E+00 | -2.7E-06 | 1.1E-16 | -8.6E-06 |
283 | 2.0E-15 | -5.3E-04 | 0.0E+00 | -2.6E-06 | -1.1E-16 | -8.5E-06 |
284 | 5.8E-15 | -5.3E-04 | 0.0E+00 | -2.6E-06 | 0.0E+00 | -8.5E-06 |
285 | 7.8E-15 | -5.3E-04 | -1.7E-16 | -2.6E-06 | 0.0E+00 | -8.5E-06 |
286 | -2.2E-16 | -5.3E-04 | 1.1E-16 | -2.6E-06 | 1.1E-16 | -8.5E-06 |
287 | 2.0E-15 | -5.2E-04 | -5.6E-17 | -2.6E-06 | 0.0E+00 | -8.4E-06 |
288 | -2.3E-15 | -5.2E-04 | 5.6E-17 | -2.6E-06 | 1.1E-16 | -8.4E-06 |
289 | 7.3E-15 | -5.2E-04 | 1.1E-16 | -2.6E-06 | -1.1E-16 | -8.4E-06 |
290 | -1.9E-15 | -5.2E-04 | -1.7E-16 | -2.6E-06 | 0.0E+00 | -8.4E-06 |
291 | 0.0E+00 | -5.2E-04 | 1.1E-16 | -2.6E-06 | 0.0E+00 | -8.4E-06 |
292 | 4.0E-15 | -5.2E-04 | -1.1E-16 | -2.6E-06 | -1.1E-16 | -8.3E-06 |
293 | 6.3E-15 | -5.2E-04 | -5.6E-17 | -2.6E-06 | 0.0E+00 | -8.3E-06 |
294 | 8.1E-15 | -5.1E-04 | -5.6E-17 | -2.5E-06 | 1.1E-16 | -8.3E-06 |
295 | -2.8E-15 | -5.1E-04 | 5.6E-17 | -2.5E-06 | 0.0E+00 | -8.3E-06 |
296 | 7.1E-15 | -5.1E-04 | -5.6E-17 | -2.5E-06 | -2.2E-16 | -8.3E-06 |
297 | 1.2E-15 | -5.1E-04 | -1.1E-16 | -2.5E-06 | 0.0E+00 | -8.2E-06 |
298 | -2.0E-15 | -5.1E-04 | 0.0E+00 | -2.5E-06 | 0.0E+00 | -8.2E-06 |
299 | -2.7E-15 | -5.1E-04 | -5.6E-17 | -2.5E-06 | -2.2E-16 | -8.2E-06 |
300 | 2.3E-15 | -5.0E-04 | 5.6E-17 | -2.5E-06 | -2.2E-16 | -8.2E-06 |
301 | 1.6E-15 | -5.0E-04 | -5.6E-17 | -2.5E-06 | -1.1E-16 | -8.1E-06 |
302 | -4.4E-15 | -5.0E-04 | 1.7E-16 | -2.5E-06 | -1.1E-16 | -8.1E-06 |
303 | 3.4E-15 | -5.0E-04 | -5.6E-17 | -2.5E-06 | 1.1E-16 | -8.1E-06 |
304 | -7.8E-16 | -5.0E-04 | -1.1E-16 | -2.5E-06 | 0.0E+00 | -8.1E-06 |
305 | -3.0E-15 | -5.0E-04 | 5.6E-17 | -2.4E-06 | -4.4E-16 | -8.1E-06 |
306 | 5.0E-15 | -5.0E-04 | 5.6E-17 | -2.4E-06 | -1.1E-16 | -8.0E-06 |
307 | 1.0E-14 | -4.9E-04 | -1.7E-16 | -2.4E-06 | 1.1E-16 | -8.0E-06 |
308 | -4.9E-15 | -4.9E-04 | 5.6E-17 | -2.4E-06 | 3.3E-16 | -8.0E-06 |
309 | 2.3E-15 | -4.9E-04 | -5.6E-17 | -2.4E-06 | -2.2E-16 | -8.0E-06 |
310 | 2.8E-15 | -4.9E-04 | 0.0E+00 | -2.4E-06 | 1.1E-16 | -8.0E-06 |
311 | 6.9E-15 | -4.9E-04 | -5.6E-17 | -2.4E-06 | 2.2E-16 | -7.9E-06 |
312 | 1.1E-15 | -4.9E-04 | 0.0E+00 | -2.4E-06 | 2.2E-16 | -7.9E-06 |
313 | 1.1E-14 | -4.8E-04 | -1.1E-16 | -2.4E-06 | -2.2E-16 | -7.9E-06 |
314 | 5.6E-16 | -4.8E-04 | 1.1E-16 | -2.4E-06 | 0.0E+00 | -7.9E-06 |
315 | -5.2E-15 | -4.8E-04 | 5.6E-17 | -2.4E-06 | 2.2E-16 | -7.9E-06 |
316 | -7.1E-15 | -4.8E-04 | -1.1E-16 | -2.4E-06 | 0.0E+00 | -7.8E-06 |
317 | 3.0E-15 | -4.8E-04 | -1.1E-16 | -2.3E-06 | 1.1E-16 | -7.8E-06 |
318 | -1.7E-15 | -4.8E-04 | 5.6E-17 | -2.3E-06 | -2.2E-16 | -7.8E-06 |
319 | 2.3E-15 | -4.8E-04 | -1.7E-16 | -2.3E-06 | 1.1E-16 | -7.8E-06 |
320 | 4.0E-15 | -4.7E-04 | 0.0E+00 | -2.3E-06 | 1.1E-16 | -7.8E-06 |
321 | 3.0E-15 | -4.7E-04 | -5.6E-17 | -2.3E-06 | 0.0E+00 | -7.7E-06 |
322 | 2.8E-15 | -4.7E-04 | -5.6E-17 | -2.3E-06 | 1.1E-16 | -7.7E-06 |
323 | -1.2E-15 | -4.7E-04 | 0.0E+00 | -2.3E-06 | 0.0E+00 | -7.7E-06 |
324 | 5.3E-15 | -4.7E-04 | 0.0E+00 | -2.3E-06 | -1.1E-16 | -7.7E-06 |
325 | -4.0E-15 | -4.7E-04 | -5.6E-17 | -2.3E-06 | -1.1E-16 | -7.7E-06 |
326 | 2.2E-16 | -4.7E-04 | 5.6E-17 | -2.3E-06 | 0.0E+00 | -7.6E-06 |
327 | 4.8E-15 | -4.6E-04 | 0.0E+00 | -2.3E-06 | 2.2E-16 | -7.6E-06 |
328 | -4.7E-15 | -4.6E-04 | -1.1E-16 | -2.3E-06 | 0.0E+00 | -7.6E-06 |
329 | 7.1E-15 | -4.6E-04 | -1.7E-16 | -2.2E-06 | 4.4E-16 | -7.6E-06 |
330 | 4.7E-15 | -4.6E-04 | 0.0E+00 | -2.2E-06 | 0.0E+00 | -7.6E-06 |
331 | -1.9E-15 | -4.6E-04 | -5.6E-17 | -2.2E-06 | 2.2E-16 | -7.5E-06 |
332 | 5.0E-15 | -4.6E-04 | 5.6E-17 | -2.2E-06 | -1.1E-16 | -7.5E-06 |
333 | 3.3E-15 | -4.6E-04 | -1.1E-16 | -2.2E-06 | -2.2E-16 | -7.5E-06 |
334 | 4.4E-16 | -4.5E-04 | 1.7E-16 | -2.2E-06 | 2.2E-16 | -7.5E-06 |
335 | 3.1E-15 | -4.5E-04 | -5.6E-17 | -2.2E-06 | 0.0E+00 | -7.5E-06 |
336 | 2.3E-15 | -4.5E-04 | -5.6E-17 | -2.2E-06 | 1.1E-16 | -7.4E-06 |
337 | 8.9E-16 | -4.5E-04 | 1.7E-16 | -2.2E-06 | 1.1E-16 | -7.4E-06 |
338 | 4.3E-15 | -4.5E-04 | 1.1E-16 | -2.2E-06 | 3.3E-16 | -7.4E-06 |
339 | 3.8E-15 | -4.5E-04 | -1.1E-16 | -2.2E-06 | 0.0E+00 | -7.4E-06 |
340 | -2.1E-15 | -4.5E-04 | -5.6E-17 | -2.2E-06 | 1.1E-16 | -7.4E-06 |
341 | 2.0E-15 | -4.4E-04 | 1.1E-16 | -2.2E-06 | 0.0E+00 | -7.3E-06 |
342 | -2.9E-15 | -4.4E-04 | 0.0E+00 | -2.1E-06 | 2.2E-16 | -7.3E-06 |
343 | 1.7E-15 | -4.4E-04 | -1.1E-16 | -2.1E-06 | 0.0E+00 | -7.3E-06 |
344 | 3.7E-15 | -4.4E-04 | -1.1E-16 | -2.1E-06 | 1.1E-16 | -7.3E-06 |
345 | 5.6E-16 | -4.4E-04 | 1.7E-16 | -2.1E-06 | 2.2E-16 | -7.3E-06 |
346 | -4.2E-15 | -4.4E-04 | 0.0E+00 | -2.1E-06 | -2.2E-16 | -7.3E-06 |
347 | 5.4E-15 | -4.4E-04 | 1.1E-16 | -2.1E-06 | 2.2E-16 | -7.2E-06 |
348 | -1.1E-16 | -4.4E-04 | -5.6E-17 | -2.1E-06 | 1.1E-16 | -7.2E-06 |
349 | -2.2E-15 | -4.3E-04 | 5.6E-17 | -2.1E-06 | -1.1E-16 | -7.2E-06 |
350 | 1.2E-15 | -4.3E-04 | -1.1E-16 | -2.1E-06 | 0.0E+00 | -7.2E-06 |
351 | 5.9E-15 | -4.3E-04 | 1.1E-16 | -2.1E-06 | 2.2E-16 | -7.2E-06 |
352 | 3.0E-15 | -4.3E-04 | -2.2E-16 | -2.1E-06 | 0.0E+00 | -7.1E-06 |
353 | 2.1E-15 | -4.3E-04 | 1.7E-16 | -2.1E-06 | 0.0E+00 | -7.1E-06 |
354 | 9.2E-15 | -4.3E-04 | 0.0E+00 | -2.1E-06 | 1.1E-16 | -7.1E-06 |
355 | -7.3E-15 | -4.3E-04 | 0.0E+00 | -2.1E-06 | -1.1E-16 | -7.1E-06 |
356 | 8.5E-15 | -4.2E-04 | -5.6E-17 | -2.0E-06 | 5.6E-16 | -7.1E-06 |
357 | -3.2E-15 | -4.2E-04 | 0.0E+00 | -2.0E-06 | -4.4E-16 | -7.0E-06 |
358 | 4.0E-15 | -4.2E-04 | 1.1E-16 | -2.0E-06 | 1.1E-16 | -7.0E-06 |
359 | 3.8E-15 | -4.2E-04 | 0.0E+00 | -2.0E-06 | 0.0E+00 | -7.0E-06 |
360 | 8.1E-15 | -4.2E-04 | -1.7E-16 | -2.0E-06 | 0.0E+00 | -7.0E-06 |
361 | -1.1E-15 | -4.2E-04 | 1.1E-16 | -2.0E-06 | 0.0E+00 | -7.0E-06 |
362 | 4.3E-15 | -4.2E-04 | -5.6E-17 | -2.0E-06 | 1.1E-16 | -7.0E-06 |
363 | 1.3E-14 | -4.2E-04 | -1.7E-16 | -2.0E-06 | 4.4E-16 | -6.9E-06 |
364 | -2.1E-15 | -4.1E-04 | 0.0E+00 | -2.0E-06 | -1.1E-16 | -6.9E-06 |
365 | 3.7E-15 | -4.1E-04 | 5.6E-17 | -2.0E-06 | 0.0E+00 | -6.9E-06 |
366 | -2.4E-15 | -4.1E-04 | -1.1E-16 | -2.0E-06 | -2.2E-16 | -6.9E-06 |
367 | 2.2E-15 | -4.1E-04 | 0.0E+00 | -2.0E-06 | 1.1E-16 | -6.9E-06 |
368 | 2.6E-15 | -4.1E-04 | -5.6E-17 | -2.0E-06 | 0.0E+00 | -6.8E-06 |
369 | -1.1E-16 | -4.1E-04 | -5.6E-17 | -2.0E-06 | -1.1E-16 | -6.8E-06 |
370 | 4.6E-15 | -4.1E-04 | 0.0E+00 | -1.9E-06 | 2.2E-16 | -6.8E-06 |
371 | -3.8E-15 | -4.1E-04 | 0.0E+00 | -1.9E-06 | -1.1E-16 | -6.8E-06 |
372 | -3.3E-16 | -4.0E-04 | -5.6E-17 | -1.9E-06 | 2.2E-16 | -6.8E-06 |
373 | 2.2E-15 | -4.0E-04 | 1.7E-16 | -1.9E-06 | 1.1E-16 | -6.8E-06 |
374 | 5.6E-15 | -4.0E-04 | -2.2E-16 | -1.9E-06 | -2.2E-16 | -6.7E-06 |
375 | 3.8E-15 | -4.0E-04 | -5.6E-17 | -1.9E-06 | 2.2E-16 | -6.7E-06 |
376 | 5.3E-15 | -4.0E-04 | -5.6E-17 | -1.9E-06 | -1.1E-16 | -6.7E-06 |
377 | 2.2E-16 | -4.0E-04 | 5.6E-17 | -1.9E-06 | 0.0E+00 | -6.7E-06 |
378 | 2.6E-15 | -4.0E-04 | -5.6E-17 | -1.9E-06 | 1.1E-16 | -6.7E-06 |
379 | 8.5E-15 | -4.0E-04 | -5.6E-17 | -1.9E-06 | 1.1E-16 | -6.7E-06 |
380 | 4.7E-15 | -3.9E-04 | 5.6E-17 | -1.9E-06 | 2.2E-16 | -6.6E-06 |
381 | 2.8E-15 | -3.9E-04 | 0.0E+00 | -1.9E-06 | 0.0E+00 | -6.6E-06 |
382 | 8.0E-15 | -3.9E-04 | 0.0E+00 | -1.9E-06 | 1.1E-16 | -6.6E-06 |
383 | -5.9E-15 | -3.9E-04 | 1.7E-16 | -1.9E-06 | -1.1E-16 | -6.6E-06 |
384 | 6.1E-15 | -3.9E-04 | -2.2E-16 | -1.9E-06 | -1.1E-16 | -6.6E-06 |
385 | 5.3E-15 | -3.9E-04 | 1.1E-16 | -1.8E-06 | 2.2E-16 | -6.5E-06 |
386 | -7.5E-15 | -3.9E-04 | -5.6E-17 | -1.8E-06 | 2.2E-16 | -6.5E-06 |
387 | 7.8E-16 | -3.9E-04 | 1.7E-16 | -1.8E-06 | 0.0E+00 | -6.5E-06 |
388 | 1.7E-15 | -3.8E-04 | -1.7E-16 | -1.8E-06 | -2.2E-16 | -6.5E-06 |
389 | 2.8E-15 | -3.8E-04 | 1.1E-16 | -1.8E-06 | 0.0E+00 | -6.5E-06 |
390 | 1.1E-14 | -3.8E-04 | -2.2E-16 | -1.8E-06 | 1.1E-16 | -6.5E-06 |
391 | -2.4E-15 | -3.8E-04 | 1.7E-16 | -1.8E-06 | 1.1E-16 | -6.4E-06 |
392 | 2.6E-15 | -3.8E-04 | 5.6E-17 | -1.8E-06 | 0.0E+00 | -6.4E-06 |
393 | 5.1E-15 | -3.8E-04 | -1.7E-16 | -1.8E-06 | 0.0E+00 | -6.4E-06 |
394 | 7.8E-16 | -3.8E-04 | -1.1E-16 | -1.8E-06 | 0.0E+00 | -6.4E-06 |
395 | -5.1E-15 | -3.8E-04 | 2.2E-16 | -1.8E-06 | 1.1E-16 | -6.4E-06 |
396 | 4.2E-15 | -3.8E-04 | 1.7E-16 | -1.8E-06 | 0.0E+00 | -6.4E-06 |
397 | -7.8E-16 | -3.7E-04 | 0.0E+00 | -1.8E-06 | 0.0E+00 | -6.3E-06 |
398 | 5.6E-15 | -3.7E-04 | 0.0E+00 | -1.8E-06 | 0.0E+00 | -6.3E-06 |
399 | -2.7E-15 | -3.7E-04 | -5.6E-17 | -1.8E-06 | -1.1E-16 | -6.3E-06 |
400 | -2.3E-15 | -3.7E-04 | -1.1E-16 | -1.8E-06 | -1.1E-16 | -6.3E-06 |
401 | 8.9E-16 | -3.7E-04 | -2.2E-16 | -1.7E-06 | 0.0E+00 | -6.3E-06 |
402 | -6.9E-15 | -3.7E-04 | 1.1E-16 | -1.7E-06 | -1.1E-16 | -6.3E-06 |
403 | 4.8E-15 | -3.7E-04 | 0.0E+00 | -1.7E-06 | -1.1E-16 | -6.2E-06 |
404 | 3.3E-15 | -3.7E-04 | -1.7E-16 | -1.7E-06 | 0.0E+00 | -6.2E-06 |
405 | 3.2E-15 | -3.7E-04 | -1.1E-16 | -1.7E-06 | 5.6E-16 | -6.2E-06 |
406 | 1.8E-15 | -3.6E-04 | 5.6E-17 | -1.7E-06 | 0.0E+00 | -6.2E-06 |
407 | 2.7E-15 | -3.6E-04 | 5.6E-17 | -1.7E-06 | 0.0E+00 | -6.2E-06 |
408 | -5.2E-15 | -3.6E-04 | 5.6E-17 | -1.7E-06 | 0.0E+00 | -6.2E-06 |
409 | -2.1E-15 | -3.6E-04 | 5.6E-17 | -1.7E-06 | 0.0E+00 | -6.1E-06 |
410 | 4.6E-15 | -3.6E-04 | -5.6E-17 | -1.7E-06 | 1.1E-16 | -6.1E-06 |
411 | 2.2E-16 | -3.6E-04 | -5.6E-17 | -1.7E-06 | -1.1E-16 | -6.1E-06 |
412 | -6.7E-16 | -3.6E-04 | 0.0E+00 | -1.7E-06 | 0.0E+00 | -6.1E-06 |
413 | 4.2E-15 | -3.6E-04 | 0.0E+00 | -1.7E-06 | 2.2E-16 | -6.1E-06 |
414 | 0.0E+00 | -3.6E-04 | -5.6E-17 | -1.7E-06 | 1.1E-16 | -6.1E-06 |
415 | 2.3E-15 | -3.5E-04 | 5.6E-17 | -1.7E-06 | -4.4E-16 | -6.0E-06 |
416 | 1.0E-14 | -3.5E-04 | -2.2E-16 | -1.7E-06 | 4.4E-16 | -6.0E-06 |
417 | -5.2E-15 | -3.5E-04 | 5.6E-17 | -1.7E-06 | -1.1E-16 | -6.0E-06 |
418 | 8.1E-15 | -3.5E-04 | -1.7E-16 | -1.6E-06 | -2.2E-16 | -6.0E-06 |
419 | 3.4E-15 | -3.5E-04 | 0.0E+00 | -1.6E-06 | 1.1E-16 | -6.0E-06 |
420 | -5.4E-15 | -3.5E-04 | 1.1E-16 | -1.6E-06 | 1.1E-16 | -6.0E-06 |
421 | -1.4E-15 | -3.5E-04 | 0.0E+00 | -1.6E-06 | 1.1E-16 | -5.9E-06 |
422 | -2.6E-15 | -3.5E-04 | 5.6E-17 | -1.6E-06 | -3.3E-16 | -5.9E-06 |
423 | 3.3E-16 | -3.5E-04 | 5.6E-17 | -1.6E-06 | 0.0E+00 | -5.9E-06 |
424 | -7.8E-16 | -3.4E-04 | 0.0E+00 | -1.6E-06 | 0.0E+00 | -5.9E-06 |
425 | 5.1E-15 | -3.4E-04 | 5.6E-17 | -1.6E-06 | 0.0E+00 | -5.9E-06 |
426 | 4.0E-15 | -3.4E-04 | 0.0E+00 | -1.6E-06 | -1.1E-16 | -5.9E-06 |
427 | 4.6E-15 | -3.4E-04 | 5.6E-17 | -1.6E-06 | -1.1E-16 | -5.9E-06 |
428 | -3.3E-15 | -3.4E-04 | -1.1E-16 | -1.6E-06 | 3.3E-16 | -5.8E-06 |
429 | 6.9E-15 | -3.4E-04 | 5.6E-17 | -1.6E-06 | -1.1E-16 | -5.8E-06 |
430 | 3.6E-15 | -3.4E-04 | -2.2E-16 | -1.6E-06 | 1.1E-16 | -5.8E-06 |
431 | 6.3E-15 | -3.4E-04 | -1.1E-16 | -1.6E-06 | 0.0E+00 | -5.8E-06 |
432 | -7.5E-15 | -3.4E-04 | 5.6E-17 | -1.6E-06 | -4.4E-16 | -5.8E-06 |
433 | 4.8E-15 | -3.3E-04 | -2.2E-16 | -1.6E-06 | 2.2E-16 | -5.8E-06 |
434 | 1.7E-15 | -3.3E-04 | -5.6E-17 | -1.6E-06 | -2.2E-16 | -5.7E-06 |
435 | -3.4E-15 | -3.3E-04 | 1.1E-16 | -1.6E-06 | 0.0E+00 | -5.7E-06 |
436 | -3.3E-15 | -3.3E-04 | 5.6E-17 | -1.5E-06 | 2.2E-16 | -5.7E-06 |
437 | -7.2E-15 | -3.3E-04 | 5.6E-17 | -1.5E-06 | -1.1E-16 | -5.7E-06 |
438 | 5.0E-15 | -3.3E-04 | 0.0E+00 | -1.5E-06 | 1.1E-16 | -5.7E-06 |
439 | -4.6E-15 | -3.3E-04 | 0.0E+00 | -1.5E-06 | -1.1E-16 | -5.7E-06 |
440 | 5.2E-15 | -3.3E-04 | -1.1E-16 | -1.5E-06 | 0.0E+00 | -5.6E-06 |
441 | 4.4E-16 | -3.3E-04 | 0.0E+00 | -1.5E-06 | 1.1E-16 | -5.6E-06 |
442 | 6.9E-15 | -3.3E-04 | -5.6E-17 | -1.5E-06 | -2.2E-16 | -5.6E-06 |
443 | 5.6E-16 | -3.2E-04 | -5.6E-17 | -1.5E-06 | -1.1E-16 | -5.6E-06 |
444 | -3.9E-15 | -3.2E-04 | 1.7E-16 | -1.5E-06 | 2.2E-16 | -5.6E-06 |
445 | 1.4E-14 | -3.2E-04 | -3.3E-16 | -1.5E-06 | 2.2E-16 | -5.6E-06 |
446 | 2.0E-15 | -3.2E-04 | 0.0E+00 | -1.5E-06 | -2.2E-16 | -5.6E-06 |
447 | -6.6E-15 | -3.2E-04 | 1.1E-16 | -1.5E-06 | 2.2E-16 | -5.5E-06 |
448 | -6.7E-16 | -3.2E-04 | -1.1E-16 | -1.5E-06 | -3.3E-16 | -5.5E-06 |
449 | 2.6E-15 | -3.2E-04 | 0.0E+00 | -1.5E-06 | 0.0E+00 | -5.5E-06 |
450 | 3.4E-15 | -3.2E-04 | 0.0E+00 | -1.5E-06 | 0.0E+00 | -5.5E-06 |
451 | 1.4E-14 | -3.2E-04 | -1.1E-16 | -1.5E-06 | 1.1E-16 | -5.5E-06 |
452 | -4.0E-15 | -3.2E-04 | -1.1E-16 | -1.5E-06 | -2.2E-16 | -5.5E-06 |
453 | 9.4E-15 | -3.1E-04 | -1.7E-16 | -1.5E-06 | 1.1E-16 | -5.5E-06 |
454 | 1.7E-15 | -3.1E-04 | 1.1E-16 | -1.5E-06 | 1.1E-16 | -5.4E-06 |
455 | -5.9E-15 | -3.1E-04 | 5.6E-17 | -1.4E-06 | -2.2E-16 | -5.4E-06 |
456 | 8.3E-15 | -3.1E-04 | 5.6E-17 | -1.4E-06 | 0.0E+00 | -5.4E-06 |
457 | -3.7E-15 | -3.1E-04 | 5.6E-17 | -1.4E-06 | -2.2E-16 | -5.4E-06 |
458 | 6.9E-15 | -3.1E-04 | 0.0E+00 | -1.4E-06 | 2.2E-16 | -5.4E-06 |
459 | 2.3E-15 | -3.1E-04 | -1.7E-16 | -1.4E-06 | 1.1E-16 | -5.4E-06 |
460 | 6.7E-16 | -3.1E-04 | 0.0E+00 | -1.4E-06 | -2.2E-16 | -5.3E-06 |
461 | 3.1E-15 | -3.1E-04 | 5.6E-17 | -1.4E-06 | 0.0E+00 | -5.3E-06 |
462 | 1.4E-15 | -3.1E-04 | -1.1E-16 | -1.4E-06 | 1.1E-16 | -5.3E-06 |
463 | 8.9E-16 | -3.0E-04 | -5.6E-17 | -1.4E-06 | 2.2E-16 | -5.3E-06 |
464 | 2.1E-15 | -3.0E-04 | -5.6E-17 | -1.4E-06 | -3.3E-16 | -5.3E-06 |
465 | 1.8E-15 | -3.0E-04 | -1.1E-16 | -1.4E-06 | 3.3E-16 | -5.3E-06 |
466 | -3.4E-15 | -3.0E-04 | 0.0E+00 | -1.4E-06 | -2.2E-16 | -5.3E-06 |
467 | 1.1E-15 | -3.0E-04 | 1.1E-16 | -1.4E-06 | 0.0E+00 | -5.2E-06 |
468 | 7.8E-16 | -3.0E-04 | -5.6E-17 | -1.4E-06 | -3.3E-16 | -5.2E-06 |
469 | -5.6E-16 | -3.0E-04 | 0.0E+00 | -1.4E-06 | 1.1E-16 | -5.2E-06 |
470 | 4.0E-15 | -3.0E-04 | -5.6E-17 | -1.4E-06 | -1.1E-16 | -5.2E-06 |
471 | 8.9E-16 | -3.0E-04 | -5.6E-17 | -1.4E-06 | -1.1E-16 | -5.2E-06 |
472 | -4.3E-15 | -3.0E-04 | 5.6E-17 | -1.4E-06 | 1.1E-16 | -5.2E-06 |
473 | -1.1E-15 | -3.0E-04 | -5.6E-17 | -1.4E-06 | 2.2E-16 | -5.2E-06 |
474 | -1.1E-16 | -2.9E-04 | -1.1E-16 | -1.4E-06 | 1.1E-16 | -5.1E-06 |
475 | 0.0E+00 | -2.9E-04 | 0.0E+00 | -1.3E-06 | 0.0E+00 | -5.1E-06 |
476 | -3.0E-15 | -2.9E-04 | 1.1E-16 | -1.3E-06 | 2.2E-16 | -5.1E-06 |
477 | 5.6E-15 | -2.9E-04 | -1.7E-16 | -1.3E-06 | 0.0E+00 | -5.1E-06 |
478 | -1.1E-15 | -2.9E-04 | 5.6E-17 | -1.3E-06 | 0.0E+00 | -5.1E-06 |
479 | 3.4E-15 | -2.9E-04 | 5.6E-17 | -1.3E-06 | 0.0E+00 | -5.1E-06 |
480 | 7.8E-16 | -2.9E-04 | 0.0E+00 | -1.3E-06 | -1.1E-16 | -5.1E-06 |
481 | -3.2E-15 | -2.9E-04 | 1.1E-16 | -1.3E-06 | 3.3E-16 | -5.1E-06 |
482 | 5.9E-15 | -2.9E-04 | -1.7E-16 | -1.3E-06 | 0.0E+00 | -5.0E-06 |
483 | -4.4E-16 | -2.9E-04 | -5.6E-17 | -1.3E-06 | -1.1E-16 | -5.0E-06 |
484 | 3.0E-15 | -2.9E-04 | 5.6E-17 | -1.3E-06 | 2.2E-16 | -5.0E-06 |
485 | 5.6E-16 | -2.8E-04 | -1.1E-16 | -1.3E-06 | -2.2E-16 | -5.0E-06 |
486 | -3.8E-15 | -2.8E-04 | 5.6E-17 | -1.3E-06 | 2.2E-16 | -5.0E-06 |
487 | 4.7E-15 | -2.8E-04 | -5.6E-17 | -1.3E-06 | 0.0E+00 | -5.0E-06 |
488 | 3.3E-16 | -2.8E-04 | 5.6E-17 | -1.3E-06 | 3.3E-16 | -5.0E-06 |
489 | -5.6E-16 | -2.8E-04 | 0.0E+00 | -1.3E-06 | -1.1E-16 | -4.9E-06 |
490 | -2.0E-15 | -2.8E-04 | 5.6E-17 | -1.3E-06 | -2.2E-16 | -4.9E-06 |
491 | 2.9E-15 | -2.8E-04 | -1.1E-16 | -1.3E-06 | 0.0E+00 | -4.9E-06 |
492 | 2.1E-15 | -2.8E-04 | -5.6E-17 | -1.3E-06 | 0.0E+00 | -4.9E-06 |
493 | -2.9E-15 | -2.8E-04 | -5.6E-17 | -1.3E-06 | 1.1E-16 | -4.9E-06 |
494 | 8.9E-16 | -2.8E-04 | 0.0E+00 | -1.3E-06 | 2.2E-16 | -4.9E-06 |
495 | 1.1E-15 | -2.8E-04 | 5.6E-17 | -1.3E-06 | 1.1E-16 | -4.9E-06 |
496 | 2.8E-15 | -2.8E-04 | -1.1E-16 | -1.3E-06 | 3.3E-16 | -4.8E-06 |
497 | -1.1E-16 | -2.7E-04 | 0.0E+00 | -1.3E-06 | 0.0E+00 | -4.8E-06 |
498 | 4.0E-15 | -2.7E-04 | 5.6E-17 | -1.2E-06 | 2.2E-16 | -4.8E-06 |
499 | -3.0E-15 | -2.7E-04 | 0.0E+00 | -1.2E-06 | -1.1E-16 | -4.8E-06 |
A Appendix: Derivation of the Short- and Long-Run Excess Demand Function
Preliminaries To derive the slope of the short- and
long-run excess demand function with respect to the relative price,
![]() ,
the following derivations will be of help. Let
,
the following derivations will be of help. Let ![]() denotes the absolute deviation of variable
denotes the absolute deviation of variable ![]() from its steady state value. Trade is assumed to be
balanced in the steady state.
from its steady state value. Trade is assumed to be
balanced in the steady state.
Linearizing equations (18) and (19) delivers
expressions for ![]() and
and ![]()
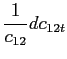 |
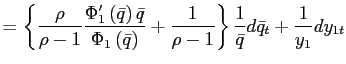
|
|
![$\displaystyle +\frac{1}{y_{1}\Phi_{1}\left( \bar{q}\right) }\left[ db_{1t-1}-\beta db_{1t}\right] ,$](img429.gif)
|
(32) |
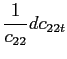 |
![$\displaystyle =\frac{\rho}{\rho-1}\frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\frac{1}{\bar{q} }d\bar{q}_{t}+\frac{1}{y_{2}}dy_{2t}-\frac{1}{\bar{q}\Phi_{1}\left( \bar {q}\right) y_{2}}\left[ db_{1t-1}-\beta db_{1t}\right] .$](img431.gif)
|
(33) |
Furthermore, the production function of firms (equation 12) implies
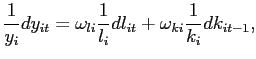
|
(34) |
and the capital accumulation constraint (equation 8) delivers
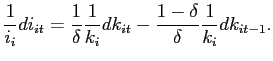
|
(35) |
From the household's optimal allocation between consumption and
leisure,
![]() , and the utility function (23), the labor
supply can be approximated by
, and the utility function (23), the labor
supply can be approximated by
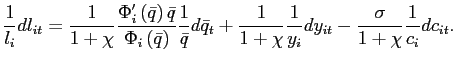
|
(36) |
Combining equations (32) to (36) the output deviations can be expressed as
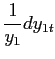 |
![$\displaystyle =\tau_{\bar{q}1}\frac{\Phi_{1}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{1}\left( \bar{q}\right) }\frac{1}{\bar{q} }d\bar{q}_{t}-\tau_{b1}\frac{1}{\Phi_{1}\left( \bar{q}\right) y_{1}}\left[ db_{1t-1}-\beta db_{1t}\right] +\tau_{i1}\frac{1}{i_{1}}di_{1t}+\tau _{k1}\frac{1}{k_{1}}k_{1t-1},$](img437.gif)
|
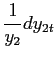 |
![$\displaystyle =\tau_{\bar{q}2}\frac{\Phi_{2}^{\prime}\left( \bar{q}\right) \bar{q}}{\Phi_{2}\left( \bar{q}\right) }\frac{1}{\bar{q} }d\bar{q}_{t}+\tau_{b2}\frac{1}{\Phi_{1}\left( \bar{q}\right) \bar{q}y_{2} }\left[ db_{1t-1}-\beta db_{1t}\right] +\tau_{i2}\frac{1}{i_{2}}di_{2t} +\tau_{k2}\frac{1}{k_{2}}k_{2t-1},$](img439.gif)
|
where
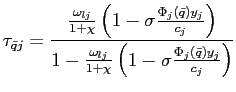 ,
, 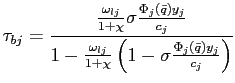 ,
, |
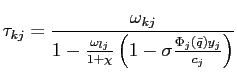 ,
, 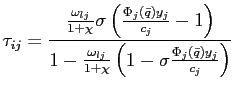 ,
, |
for j = 1, 2.
Slope of the Excess Demand Function Excess demand for good
2 is given by
![]() with
with
![]() in equilibrium.
Linearization of this relationship around a steady state delivers
in equilibrium.
Linearization of this relationship around a steady state delivers
Substituting in expressions (32) and (33) and using the
facts that
![]() ,
,
![]() ,
,
![]() , and
, and
![]() in any steady state with balanced trade
in any steady state with balanced trade
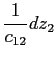 |
![$\displaystyle =\left[ -\left( 1+\frac{1}{1-\rho}\frac{c_{11} }{c_{21}}\right) \frac{c_{21}}{y_{1}}+\left( 1-\frac{1}{1-\rho}\right) \frac{c_{22}}{c_{12}}\frac{c_{12}}{y_{2}}\right] \frac{1}{\bar{q}}d\bar {q}_{t}$](img454.gif)
|
![$\displaystyle -\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}}\left( 1-\frac{c_{21}}{y_{1}}-\frac{c_{12}}{y_{2}}\right) \left[ db_{1t-1}-\beta db_{1t}\right]$](img455.gif)
|
|
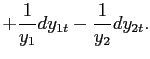 |
and substituting in the approximations for output
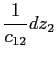 |
![$\displaystyle =\left[ -\left( 1+\frac{1}{1-\rho}\frac{c_{11} }{c_{21}}+\tau_{\bar{q}1}\right) \frac{c_{21}}{y_{1}}+\left( \left( 1-\frac{1}{1-\rho}\right) \frac{c_{22}}{c_{12}}-\tau_{\bar{q}2}\right) \frac{c_{12}}{y_{2}}\right] \frac{1}{\bar{q}}d\bar{q}_{t}$](img458.gif)
|
|
![$\displaystyle -\frac{1}{\bar{q}\Phi_{1}\left( \bar{q}\right) c_{12}}\left( 1-\left( 1-\tau_{b1}\right) \frac{c_{21}}{y_{1}}-\left( 1-\tau_{b2}\right) \frac{c_{12}}{y_{2}}\right) \left[ db_{1t-1}-\beta db_{1t}\right]$](img459.gif)
|
||
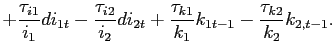
|
(37) |
In the case of a static endowment economy as in Section 2,
![]() and
and
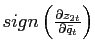 is given by the sign of
is given by the sign of
![$ \left[ -\left( 1+\frac{1}{1-\rho}\frac{c_{11}}{c_{21}}\right) \frac{c_{21}}{y_{1} }+\left( \left( 1-\frac{1}{1-\rho}\right) \frac{c_{22}}{c_{12}}\right) \frac{c_{12}}{y_{2}}\right] $](img463.gif) .25 For the above calibration, the
steady state allocations and prices in the equilibrium with
.25 For the above calibration, the
steady state allocations and prices in the equilibrium with
![]() , do not depend on the value of
the trade elasticity of substitution
, do not depend on the value of
the trade elasticity of substitution
![]() . Therefore,
it can easily be seen that the slope of the excess demand function
becomes positive if
. Therefore,
it can easily be seen that the slope of the excess demand function
becomes positive if
![]() is sufficiently low and multiple
equilibria appear.
is sufficiently low and multiple
equilibria appear.
In the dynamic production economy with flexible labor and
capital, additional terms determine
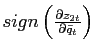 . With flexible labor
. With flexible labor
![]() and
and
![]() are different from zero and
the threshold value of
are different from zero and
the threshold value of ![]() for which
for which
![]() switches sign can be higher or lower depending on the relative
magnitudes of the remaining parameters. The contemporaneous choices
for investment (or capital) and bond holdings also affect the
relative price through the equilibrium requirement of zero excess
demand. Since bond holdings, foreign and domestic capital are the
three endogenous state variables of the model,
switches sign can be higher or lower depending on the relative
magnitudes of the remaining parameters. The contemporaneous choices
for investment (or capital) and bond holdings also affect the
relative price through the equilibrium requirement of zero excess
demand. Since bond holdings, foreign and domestic capital are the
three endogenous state variables of the model, ![]() ,
, ![]() ,
, ![]() , and
, and
![]() can be expressed as functions of
can be expressed as functions of
![]() ,
, ![]() , and
, and
![]() .26
.26
To obtain the sign of
![]() it is key to rewrite the decision rules for
it is key to rewrite the decision rules for ![]() ,
,
![]() ,
, ![]() in terms of
in terms of
![]() using the decision rule for
using the decision rule for
![]() and substitute the results into
(37). Let
and substitute the results into
(37). Let
![]() denote the coefficient on the state
variable
denote the coefficient on the state
variable ![]() in the (linear) decision rule for variable
in the (linear) decision rule for variable
![]() . The sign of
. The sign of
![]() is positive in the short run if
is positive in the short run if
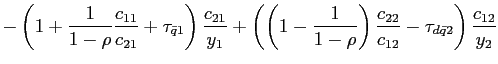
|
||
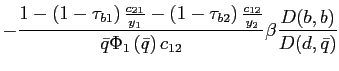
|
||
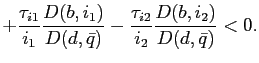
|
(38) |
In the short run the capital stock is fixed and bond holdings effect the relative price through their reallocative effects of purchasing power.27
By contrast, the sign of
![]() for the long run is affected by the full flexibility of the capital
stock in the long run. At the same time, bond holdings are
restricted to be zero. Hence,
for the long run is affected by the full flexibility of the capital
stock in the long run. At the same time, bond holdings are
restricted to be zero. Hence,
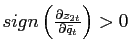 if
if
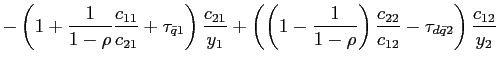
|
||
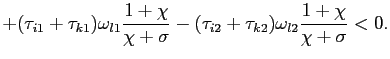
|
(39) |
While the slope of the excess demand function is the same in the
short and the long run for an endowment economy, equations
(38) and
(39) reveal that
these slopes can be very different in a model with endogenous
capital an international bond holdings. Figure 7 plots
expressions (38) and (39) as functions of
![]() at the steady state with
at the steady state with
![]() in the model with endogenous
discounting.
in the model with endogenous
discounting.
Footnotes
* Telephone (202) 452 3796. E-mail [email protected]. Return to text
** I thank Roc Armenter, Christopher Gust, Jonathan Heathcote, and Ricardo Nunes for valuable comments and discussion. I am also grateful to an anonymous associate editor whose suggestions greatly improved this paper. Previously, the paper circulated under the title "Closing Open Economy Models". The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. See Kehoe (1991). Return to text
2. The equilibrium multiplicity discussed in this paper does not stem from equilibrium indeterminacy as in Benhabib and Farmer (1994). Return to text
3. By mirroring I mean that good 1 (2) enters the utility function of agents in country 1 the same way that good 2 (1) enters the utility function of agents in country 2. The same holds true for agents' endowments with goods 1 and 2. Return to text
4. There is a large literature on sunspot equilibria. Most prominent are the seminal contributions of Cass and Shell (1983) and Azariadis (1981). Return to text
5. Corsetti et al (2008), Thoenissen (2008), and de Walque et al (2005) emphasize that there is a critical value of the elasticity of substitution for which the real exchange rate becomes very volatile. At least in the context of the simple model presented in this paper, it can be shown that such a critical point coincides with the appearance of multiple equilibria. Return to text
6. Mas-Colell, Whinston, and Green (1995) and Kehoe (1991) provide an excellent treatment of general equilibrium analysis. Return to text
7. See Kehoe (1980) for a discussion of the index theorem. Return to text
8. The parameter values underlying Figure 1 are summarized in Table 1 and discussed in Section 4.3. Return to text
9. For the chosen parametrization of the
model it is easily shown that for ε < 0.425 there are multiple
equilibria and that the equilibrium is unique for ε > 0.425. For ε = 0.425, however, there is a
continuum of equilibria as the slope of the excess demand function
is zero at
![]() . See also Appendix A. Return to text
. See also Appendix A. Return to text
10. See in particular Cass and Shell (1983). Chiappori and Guesnerie provide an excellent introduction to the topic. Return to text
11. This modelling strategy leads to
(indentical) home-bias in consumption and investment
![]() . An
alternative yet equivalent strategy in this model is to introduce
trading costs of the iceberg type. Return to text
. An
alternative yet equivalent strategy in this model is to introduce
trading costs of the iceberg type. Return to text
12. In this model financial markets are complete only if they also provide insurance against the possible equilibrium multiplicity that I am about to discuss. See also Section 6. Return to text
13. See Mendoza (1991), Corsetti et al (2008), and Schmitt-Grohe and Uribe (2003) for applications of this concept. Preferences with intertemporal dependences were introduced by Uzawa (1968) and the concept has been extended and clarified by Epstein (1983, 1987). Return to text
14. This problem is similar to the non-stationarity problem in linearized models with incomplete markets. Endogenous discounting and convex portfolio costs are only two possibilities to address the non-stationarity problem. See Schmitt-Grohé and Uribe (2003), Kim and Kose (2003), and Boileau and Normandin (2005) to obtain a complete overview about this topic. An interesting approach using a perpetual youth model is due to Ghironi (2003). Return to text
15. If solving a fully stochastic version of the model, the second assumption can be omitted. In ongoing research I analyze equilibrium multiplicity in an endowment economy with borrowing constraints and sunspot shocks. Return to text
16. As in static general equilibrium theory, little is known about the number of equilibria in a model unless uniqueness is proven. Return to text
17. Absent home bias in consumption the equilibrium is always unique in the symmetric economy. Return to text
18. In Appendix A, I provide more details on the derivation of this threshold value. See also the discussion in Section 5.2.2. Return to text
19. In fact, Crosetti et al (2008) do not consider the case of multiple equilibria as they restrict attention to the solution obtained by log-linearizing the model around its symmetric deterministic steady state. See also footnote 7 of their work. Return to text
20. In particular, see the exposition in Section 3 of Corsetti et al (2008). In most of their analysis the authors focus on the case of a low trade elasticity of substitution. However, they also identify a case of negative transmission for a high trade elasticity of substitution that is unrelated to the analysis presented in this paper. Return to text
21. The exact value for which
![]() switches
sign depends on the second assumption in Section 4.1. With convex
portfolio costs the sign switch occurs at ρ = -1.53. It can be shown that for -1.65 < ρ < -1.53
there are at least
three equilibrium paths each converging to the unique steady state
with
switches
sign depends on the second assumption in Section 4.1. With convex
portfolio costs the sign switch occurs at ρ = -1.53. It can be shown that for -1.65 < ρ < -1.53
there are at least
three equilibrium paths each converging to the unique steady state
with ![]() in response to a technology shock.
Obviously, this situation is somewhat of a knife-edge case, as the
steady state with
in response to a technology shock.
Obviously, this situation is somewhat of a knife-edge case, as the
steady state with ![]() becomes unstable
for ρ < -1.65 and the uniqueness of the
equilibrium for ρ > -1.53. Return to text
becomes unstable
for ρ < -1.65 and the uniqueness of the
equilibrium for ρ > -1.53. Return to text
22. Benigno and Thoenissen (2008) and de Walque et al (2005) do not assume that the agents' discount factors are endogenous to invoke stationarity of the net foreign assets. Benigno and Thoenissen (2008) assume convex portfolio costs, whereas de Walque et al (2005) do not invoke stationarity at all. Nevertheless, the finding about the slope of the short-run excess demand function and the volatility of the real exchange rate fully applies to their models. Return to text
23. If the positive shock to technology occurs in the home country, only path 3 exists. Similar logic applies to negative technology shocks. Return to text
24. Corsetti and Dedola (2005) mention the possibility of multiple in such a framework. The working paper version of that paper provides some analysis of the steady state case. Return to text
25. In the endowment economy, the contemporaneous decision on bond holdings does not affect the slope of the excess demand function in the short run. This is different from the economy with endogenous capital. Return to text
26. The decision rules for the endogenous variables in terms of the state variables can be found by using standard techniques for solving linearized rational expectations models. Return to text
27. The policy functions depend on the assumption that induces a stationary net foreign asset position. Hence, the exact value of the threshold and the occurance of multiple equilibria differ between the model with endogenous discounting and the model with convex portfolio costs. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text