
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 938, First version July 2008, current version September 2011 --- Screen Reader Version*
Lack of Commitment and the Level of Debt1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The tendency of countries to accumulate public debt has been rationalized in models of political disagreement and lack of commitment. We analyze in a benchmark model how the evolution of public debt is affected by lack of commitment per se. While commitment introduces indeterminacy in the level of debt, lack of commitment creates incentives for debt to converge to specific levels. One of the levels that debt often converges to implies no debt accumulation at all. In a simple example we prove analytically that debt converges to zero, and we analyze numerically more complex models. We also show in an imperfect credibility setting that a small deviation from full-commitment is enough to obtain these results.
Keywords: Fiscal policy, debt, imperfect commitment
JEL classification: C61, E61, E62, P16
1. Introduction
The recent accumulation of debt in most countries and the debt crises in Europe and in the U.S. have highlighted the importance of understanding why governments accumulate debt. The focus of our analysis is on economies where debt is used to smooth over time the deadweight losses associated with distortionary taxation, following Barro (1979) and Lucas and Stokey (1983). These theories can account for several aspects of the debt evolution in many countries. However, these models do not provide an explanation of why public debt is a sizable fraction of GDP in many developed countries.2
In a world where markets are complete and fiscal policy is chosen optimally by a benevolent government with full-commitment - as in Lucas and Stokey (1983) - the long-run level of debt depends on initial conditions. Countries starting with high debt will have high debt forever, and countries with low debt will have low debt forever. Since initial conditions are exogenous to the model and empirically difficult to determine, such a theory cannot explain what induces countries to accumulate debt. If markets are incomplete - as in Aiyagari, Marcet, Sargent, and Seppala (2002) - matters are even worse since the government accumulates assets.
One possibility to rationalize debt accumulation is to depart from the idealized benevolent planner environment. Some studies in the political economy literature, following Alesina and Tabellini (1990) and Persson and Svensson (1989), have shown that disagreement among different policymakers leads to an inefficiently high level of debt. Political disagreement constitutes a natural limitation to the governments' ability to commit. For this reason, lack of commitment is a concurrent assumption of many political economy models.3
The purpose of this paper is to analyze the role of commitment per se, which has not been fully examined in the political economy literature.4 Our analysis builds on the Lucas and Stokey (1983) model with endogenous public expenditure, which constitutes the building block of many works in the macro and political economy literature. The role of commitment is related to the time-inconsistency problem in optimal policy choices, as illustrated by Kydland and Prescott (1977) and Barro and Gordon (1983). If a government with full-commitment were allowed to revise its plans, it would run a deficit and accumulate debt. It would then be natural to conjecture that lack of commitment per se leads to debt accumulation.
We explore this conjecture and find that it does not necessarily hold. When governments cannot commit, debt converges to specific steady-state levels that are no longer indeterminate.5 And, more interestingly, the economy often converges to a steady-state with no debt accumulation at all. In a simple example, we prove analytically that debt converges to zero. We then analyze numerically a more general case and find that such result still holds for quite standard calibrations and initial debt holdings. This result clarifies that lack of commitment per se does not necessarily lead to positive debt levels.
Because of the striking difference in the behavior of debt between the full-commitment and the no-commitment cases, we check how debt evolves under intermediate commitment settings. We study the behavior of debt in a framework where the planner has access to a commitment technology, but under some circumstances she may renege on her past promises with a given and fixed probability. We find that a small deviation from full-commitment - in the context of the model a negligible probability of reneging on previous commitments - recovers the properties of the no-commitment solution. This result suggests that departing from the full-commitment assumption is enough to obtain a determinate steady-state, but cannot help explaining why the level of debt is a sizeable fraction of GDP.
There are other factors affecting debt accumulation. The presence of a wider array of tax instruments, the possibility to default on debt, idiosyncratic uncertainty, other assets, and social redistribution are some examples. We abstract from a multiplicity of such factors in our model, which should not be interpreted as us passing judgement that those are not important. Instead, we aim at characterizing some key effects in a simple and standard framework. We comment briefly on the literature below.
In a related work Krusell, Martin, and Rios-Rull (2006) analyze the no-commitment solution when government expenditure is exogenous and find a multiplicity of steady-states that are similar to those under full-commitment. In our model, government expenditure is endogenous as this is a crucial feature of models with political interactions.6 Ortigueira and Pereira (2008) examine debt dynamics with no-commitment in an economy with capital accumulation, but with exogenous labor and where the tax rate is equal for all sources of income. The authors find that one of the equilibria is associated with issuance of public debt. These papers are complementary to ours as they shed light on different mechanisms influencing the level of debt.
Some recent works have studied the role of commitment in dynamic political economy frameworks. Song, Storesletten, and Zilibotti (2006) consider an overlapping generation model with inter-generational political conflicts over public goods, where the commitment problem arises because of the endogenous voting behavior. Yared (2010) examines the optimal management of taxes and debt in an environment with self-interested politicians and citizens. The author focuses on sustainable equilibria where politicians can choose extractive policies and citizens can throw politicians out of power. In our work, the commitment problem arises because of the endogenous determination of interest rates. It is not our claim that considering endogenous interest rates changes the results in the political economy literature. Instead, we aim at clarifying the role of lack of commitment per se in the determination of long-run debt.
The effects of lack of commitment have been widely analyzed in monetary economies (e.g. Ellison and Rankin (2007), Diaz-Gimenez, Giovannetti, Marimon, and Teles (2008), and Martin (2009)). They find that, depending on the degree of substitutability of cash-goods, the steady-state level of debt can be positive, negative or zero. We believe that focusing on a real economy is a reasonable assumption. The debt accumulation and the provision of the public good are made by the fiscal authority. Further, in most countries central banks are independent and committed to price stability. Our result that debt converges to zero is neither due to the real erosion of nominal bonds nor to the presence of a cash-in-advance constraint.7
Finally, Lucas and Stokey (1983) and Persson, Persson, and Svensson (2006) show that a carefully chosen maturity of nominal and indexed debt for each contingent state of nature and at each maturity can solve the time-consistency problem. As in many papers in the literature, we do not consider this possibility. This is for three reasons. First, the necessary structure of debt to implement such a policy is not observed in reality. Second, as shown in Fraglia, Marcet, and Scott (2010), strategies of that kind are intricate to implement and very sensitive to specific modeling assumptions. Finally and more importantly, this paper will consider a model with an endogenous public good. Rogers (1989) showed that in such case debt restructuring cannot enforce the commitment solution.
The paper is organized as follows: Section 2 introduces the model. Section 3 examines the no-commitment solution and illustrates some analytical results. Section 4 considers numerical solutions in an extended model. We examine an imperfect credibility setting in Section 5. Section 6 concludes.
2 The Model
We consider an economy where labor is the only factor of production, technology is linear, and there is no uncertainty.8 Output can be used either for private consumption (![]() ) or for
public consumption (
) or for
public consumption (![]() ). The economy's aggregate budget constraint is
). The economy's aggregate budget constraint is
| (1) |
where ![]() denotes leisure.
denotes leisure.
The public good is endogenously supplied by a benevolent government, and financed through a proportional labor income tax (![]() ) and by issuing a one-period discount bond (
) and by issuing a one-period discount bond (![]() ) with price
) with price ![]() . At any point in time, the government budget constraint is
. At any point in time, the government budget constraint is
| (2) |
In a competitive equilibrium, given prices and government policies, the representative household chooses consumption, savings and leisure by solving the following problem
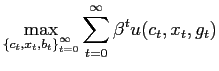 |
(3) | |
| (4) |
where the term ![]() denotes private bond holdings. The utility function
denotes private bond holdings. The utility function ![]() is assumed to be separable in its three arguments, twice continuously differentiable, and with partial derivatives
is assumed to be separable in its three arguments, twice continuously differentiable, and with partial derivatives ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and
![]() .9
.9
The competitive equilibrium is characterized by equations (2), (4), bond market clearing (
![]() ), the optimality conditions in the labor and bond markets
), the optimality conditions in the labor and bond markets
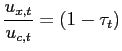 |
(5) |
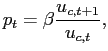 |
(6) |
and the transversality condition
![]() .
.
2.1 Debt Policies Under Full-Commitment
As a benchmark for our analysis and following Lucas and Stokey (1983), we characterize the government solution under full-commitment. For a given initial level of debt (![]() ), the benevolent government maximizes equation (3), subject to the aggregate feasibility constraint (1) and the implementability constraint10
), the benevolent government maximizes equation (3), subject to the aggregate feasibility constraint (1) and the implementability constraint10
| (7) |
Taking derivatives to the associated Lagrangean problem, the optimality conditions are
| (8) | ||
| (9) | ||
| 0 | (10) |
where
![]() denotes the Lagrange multipliers attached to the constraint (7) and, as implied by eq. (10), must be constant for all
denotes the Lagrange multipliers attached to the constraint (7) and, as implied by eq. (10), must be constant for all ![]() .11
.11
As shown in Lucas and Stokey (1983), in this class of models the steady-state level of debt is not determined. This feature can be easily seen in this economy without uncertainty. Given that ![]() must be constant, all the remaining conditions are identical for any
must be constant, all the remaining conditions are identical for any ![]() , and thus the values of
, and thus the values of ![]() and
and ![]() must also be constant from
must also be constant from ![]() onwards. Clearly, the steady-state allocations depend on
onwards. Clearly, the steady-state allocations depend on ![]() . Equation (9) evaluated at
. Equation (9) evaluated at ![]() shows that
shows that ![]() depends on the initial level of debt
depends on the initial level of debt ![]() . As a result, the steady-state level of debt is not unique and depends on initial conditions.
. As a result, the steady-state level of debt is not unique and depends on initial conditions.
The time-inconsistency problem arises from the incentive to manipulate the bond price given by eq. (6). In a generic period ![]() current consumption influences both
current consumption influences both ![]() and
and ![]() . As a consequence, if the government uses taxes and public expenditure to increase the price of the bond
. As a consequence, if the government uses taxes and public expenditure to increase the price of the bond ![]() , other things equal,
, other things equal, ![]() decreases. Instead at
decreases. Instead at ![]() consumers' savings and previous prices (
consumers' savings and previous prices (![]() ) are given. Therefore, if the
government inherits a positive level of debt, it can benefit from
an increase in the price of the bond (
) are given. Therefore, if the
government inherits a positive level of debt, it can benefit from
an increase in the price of the bond (![]() ) without incurring any
additional cost. A suitable public policy that increases initial consumption (
) without incurring any
additional cost. A suitable public policy that increases initial consumption (![]() ), thus fostering the demand for saving, allows the government to sell its bonds at a more convenient price.
), thus fostering the demand for saving, allows the government to sell its bonds at a more convenient price.
3 Debt Policies Under No-Commitment
In the no-commitment solution, we keep the assumption that the planner can credibly commit to repay her loans. Due to the reasons explained in the introduction, we are not considering the possibility of enforcing the time-inconsistent solution through the debt maturity structure. We also assume that reputation mechanisms are not operative, and focus only on Markov-Perfect equilibria as defined for instance in Krusell, Quadrini, and Rios-Rull (1997), and Hassler, Mora, Storesletten, and Zilibotti (2003).12 We assume that the planner moves first in each period and her maximization problem is accordingly defined as:13
| (11) | ||
| (12) | ||
The function
![]() in constraint (12) determines the quantity of consumption expected for period
in constraint (12) determines the quantity of consumption expected for period ![]() as a function of the debt level outstanding at the beginning of next period
as a function of the debt level outstanding at the beginning of next period ![]() . Since the current planner cannot make credible commitments about her future actions, the future stream of consumption is not under her direct control. By taking as given the policy
. Since the current planner cannot make credible commitments about her future actions, the future stream of consumption is not under her direct control. By taking as given the policy
![]() , the current planner can only influence future consumption through her current debt policy. Being the function
, the current planner can only influence future consumption through her current debt policy. Being the function
![]() unknown, the solution of the problem relies on solving a fixed point problem in
unknown, the solution of the problem relies on solving a fixed point problem in
![]() . In what follows, we look at equilibria where the function
. In what follows, we look at equilibria where the function
![]() is differentiable.14
is differentiable.14
More formally, a differentiable Markov-Perfect equilibrium consists of a set of policy functions
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , such that (i) the function
, such that (i) the function
![]() is differentiable and (ii) given
is differentiable and (ii) given
![]() and for any
and for any ![]() , the allocation
, the allocation
![]() ,
,
![]() ,
,
![]() ,
,
![]() is feasible and solve the planner's problem, i.e. satisfy the system of equations (1), (8), (12), and
is feasible and solve the planner's problem, i.e. satisfy the system of equations (1), (8), (12), and
| (13) | |
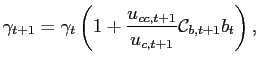 |
(14) |
where
![]() .
.
The generalized Euler equation (14) is a crucial element determining the debt steady-state. The term
![]() - measuring how the debt level affects next period bond prices - constitutes the only difference with respect to the corresponding full-commitment equation (10). Without this term, the equation simplifies to
- measuring how the debt level affects next period bond prices - constitutes the only difference with respect to the corresponding full-commitment equation (10). Without this term, the equation simplifies to
![]() and would always be satisfied in steady-state regardless of the level of debt, which would remain indeterminate. Instead, for equation (14) to be satisfied in a steady-state with no-commitment, it must be that
and would always be satisfied in steady-state regardless of the level of debt, which would remain indeterminate. Instead, for equation (14) to be satisfied in a steady-state with no-commitment, it must be that
| (15) |
which indicates the presence of three possible types of steady-state.15 In the first steady-state, the planner holds enough assets to implement the first-best solution (![]() ). In the second steady-state, there are also no incentives to manipulate the bond price because debt is zero. The third type of steady-state corresponds to
). In the second steady-state, there are also no incentives to manipulate the bond price because debt is zero. The third type of steady-state corresponds to
![]() , where a marginal change in the debt level does not induce any change in private consumption and therefore the price of debt also remains unchanged. More generally, as discussed below, both the steady-state properties and the transition dynamics crucially depend on the derivative
, where a marginal change in the debt level does not induce any change in private consumption and therefore the price of debt also remains unchanged. More generally, as discussed below, both the steady-state properties and the transition dynamics crucially depend on the derivative
![]() .
.
3.1 An Example With an Analytical Solution
We first consider a particular utility function that allows for an analytical solution. Some recent works have considered linear utility in consumption (e.g. (), ()), where bond prices are therefore constant. To preserve the time-inconsistency nature of our problem we instead maintain strict concavity in consumption, but assume linearity in leisure and government expenditure. In particular, we specify the utility function
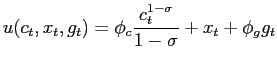 |
(16) |
and impose the non-negativity constraints
![]() . In addition, in order to preserve the main features of optimal taxation problems, we need to impose some parameter restrictions. First, it must be that
. In addition, in order to preserve the main features of optimal taxation problems, we need to impose some parameter restrictions. First, it must be that ![]() . Otherwise, the planner would never provide the public good and there would be no scope for raising taxes or issuing debt. We also impose the restrictions
. Otherwise, the planner would never provide the public good and there would be no scope for raising taxes or issuing debt. We also impose the restrictions
![]() and
and
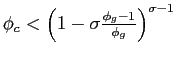 . As explained in Appendix C, these conditions are required to guarantee that the solution is interior, and that a differentiable time-consistent equilibrium exists for
. As explained in Appendix C, these conditions are required to guarantee that the solution is interior, and that a differentiable time-consistent equilibrium exists for
![]() , with
, with
![]() .16
.16
In this case, equations (8) and (12)-(14) specialize to
| (17) | ||
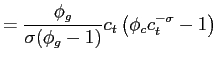 |
(18) | |
| (19) |
where we used the equality
![]() as implied by eq. (8).17
as implied by eq. (8).17
Equation (19) is analogous to the steady-state condition (15). An important difference is that such an equation must hold in every period ![]() and not only in steady-state. Therefore, the solution must either imply
and not only in steady-state. Therefore, the solution must either imply ![]() or
or
![]() , for all
, for all ![]() . The function
. The function
![]() is implicitly defined by equation (18), which totally differentiating w.r.t.
is implicitly defined by equation (18), which totally differentiating w.r.t. ![]() and rearranging gives
and rearranging gives
![$\displaystyle \mathcal{C}_{b,t}\left[\left(\phi_{g}-1\right) \frac{b_{t-1}} {c_{t}}+\frac{\phi_{g}}{\phi_{c}}c_{t}^{\sigma}\right] =\phi _{g}-1.$](img115.gif) |
(20) |
This equation clearly shows that as long ![]() - a necessary condition to preserve the time-inconsistency feature - it must be that
- a necessary condition to preserve the time-inconsistency feature - it must be that
![]() .
.
From equation (20) we can also determine that
![]() . The inequality follows immediately for
. The inequality follows immediately for ![]() . Also, by continuity and noticing that
. Also, by continuity and noticing that
![]() , the inequality must also hold for
, the inequality must also hold for ![]() .18 From equation (19) it then follows that
.18 From equation (19) it then follows that ![]()
![]() is the only interior time-consistent equilibrium.
is the only interior time-consistent equilibrium.
Comparison With Full-Commitment
The full-commitment solution preserves the general features discussed in Section 2.1, namely the steady-state level of debt is not determined. The main difference is that a given initial debt position ![]() can be associated with multiple levels of steady-state debt.19 All the equilibria feature the same level of consumption but differ in the composition of leisure, public expenditure, and debt.
can be associated with multiple levels of steady-state debt.19 All the equilibria feature the same level of consumption but differ in the composition of leisure, public expenditure, and debt.
The commitment assumption is crucial for the indeterminacy of the steady-state debt level. A planner with full-commitment can sustain different debt levels by committing to different spending plans without altering consumption (only leisure adjusts to ensure feasibility). Since consumption does not change, neither do bond prices. Because of the quasi-linear preferences, life-time utility remains unchanged as well.
We have provided a simple example where we could show analytically that debt needs to converge to zero in a time-consistent but not in a time-inconsistent equilibrium. The planner with full-commitment can commit to future allocations regardless of the steady-state level of debt. However, without commitment debt distorts the optimal decisions of the planner and must be reduced to zero. In addition to other incentives regarding debt management, lack of commitment creates an incentive to alleviate the time-inconsistency and reach a steady-state where the incentive to manipulate the interest rate disappears.
4 Generalizing the Model
We now look at numerical solutions for a more general utility function that is not linear in any argument and is given by
![$\displaystyle u(c,x,g)=(1-\phi_{g})\left[\phi_{c}\frac{c^{1-\sigma_{c}}-1}{1-\sigma_{c}}+(1-\phi_{c})\frac{x^{1-\sigma_{x}}-1}{1-\sigma_{x}}\right] +\phi_{g}\frac{g^{1-\sigma_{g}}-1}{1-\sigma_{g}},$](img127.gif) |
(21) |
where ![]() and
and ![]() denote the preference weights on
private and public consumption.
denote the preference weights on
private and public consumption.
We use a standard calibration for an annualized model that matches some key statistics and long-run ratios. Table 1 summarizes the parameter values. The implied long-run values are ![]() , income taxes
, income taxes ![]() , the fraction of time devoted to leisure
, the fraction of time devoted to leisure ![]() , and an annual real interest rate of about 4%. These values change only minimally under different commitment scenarios. The numerical algorithm is described in Appendix D.
, and an annual real interest rate of about 4%. These values change only minimally under different commitment scenarios. The numerical algorithm is described in Appendix D.
Table 1. Parameter Values
| Parameter | Value | Description |
|---|---|---|
| .96 | Discount factor | |
| .3 | Weight of consumption (priv. + publ.) vs. leisure | |
| .1 | Weight of public vs. private consumption | |
| | 1 | Elasticity of leisure |
| | 1 | Elasticity of private consumption |
| | 1 | Elasticity of public consumption |
The transition dynamics shown in Figure 1 resemble the pattern discussed in the analytical example. Debt is reduced over time and approaches zero in the no-commitment solution. The debt reduction is accompanied with a decreasing pattern of private consumption and an increasing interest rate. This pattern is achieved by lowering taxation and increasing public consumption over time. Such policies allow not only to influence favorably the bond price, but also to decrease debt. As the level of debt and interest payments are reduced, public expenditure is raised and taxes are reduced. The increase in public expenditure is matched with a reduction in private consumption and an increase in hours worked.20
Finally, even though the interest rate does not display large movements, one should not conclude that the government does not face a severe time-inconsistency problem related specifically to the interest rate. In fact, lack of commitment is present in the model and has dramatic effects on the debt level.
4.1 Discussion of Results
In this economy and in agreement with section 3.1, we recovered the result that debt converges to zero. Several arguments and results regarding debt convergence are worth discussing.
Debt Movements Under Full-Commitment
A common intuition is that a government with full-commitment has a temptation to deviate and increase the debt level. Our result that under no-commitment debt converges to zero may therefore look surprising and unexpected. To gain a better understanding of the debt dynamics under full-commitment, the bottom-left panel of Figure 1 plots steady-state debt as a function of initial conditions ![]() .
.
The behavior of debt is determined by equation
(2). On the one hand, the tax cut
necessary to foster initial consumption (and influence favorably the bond price) implies a reduction in tax revenues. On the other hand, the resulting lower interest rate
allows the government to sell bonds at a higher price.
The panel plots the level of debt chosen in
the first period (the steady-state level of debt), as a
function of ![]() . For low levels of
. For low levels of ![]() , the government
accumulates debt. Conversely, if the initial level of debt is large
enough, the increase in bond prices applies to a larger base. As a
consequence, the tax cut can be self-financed and decrease debt.
, the government
accumulates debt. Conversely, if the initial level of debt is large
enough, the increase in bond prices applies to a larger base. As a
consequence, the tax cut can be self-financed and decrease debt.
These results clarify that in the initial period, when past promises are not binding, debt does not necessarily increase. Therefore, the full-commitment model does not suggest, intuitively or otherwise, that debt should increase in the absence of commitment.
Figure 1. Commitment vs. No-Commitment Time Pattern of Allocations
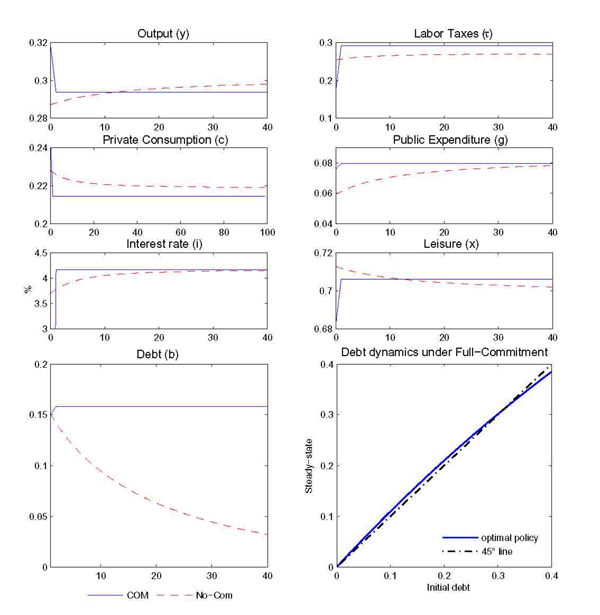
Note: The figure plots the equilibrium allocations over time, for an initial condition of b = .15 (about 50 of GDP). The bottom-left figure plots the steady-state level of debt under full-commitment as a function of the initial debt.
Convergence Properties and the Derivative
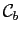
In contrast to our analytical example, a steady-state with
![]() cannot be ruled out. Nevertheless, it is possible to describe how the convergence to the steady-state with
cannot be ruled out. Nevertheless, it is possible to describe how the convergence to the steady-state with ![]() crucially depends on the sign of the derivative
crucially depends on the sign of the derivative
![]() . This can be understood by examining equation (14). In particular - and as opposed to the full-commitment case where the Lagrange multiplier
. This can be understood by examining equation (14). In particular - and as opposed to the full-commitment case where the Lagrange multiplier ![]() is constant - such an equation indicates that
is constant - such an equation indicates that ![]() must follow an autoregressive process with a time varying coefficient
must follow an autoregressive process with a time varying coefficient
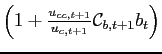 .
.
Consider for simplicity an economy starting with debt ![]() . Because the term
. Because the term
![]() , the multiplier
, the multiplier ![]() decreases over time if and only if consumption is an increasing function of debt (
decreases over time if and only if consumption is an increasing function of debt (![]() ). A decreasing
). A decreasing ![]() means that the constraint (12) becomes less binding and the time-inconsistency problem becomes less severe. Both of these effects should be associated with a reduction in the level of debt. In other words, these considerations show that as debt converges to zero the Lagrange multiplier should decrease and
means that the constraint (12) becomes less binding and the time-inconsistency problem becomes less severe. Both of these effects should be associated with a reduction in the level of debt. In other words, these considerations show that as debt converges to zero the Lagrange multiplier should decrease and
![]() , at least in a neighborhood of
, at least in a neighborhood of ![]() .
.
The economic intuition for the positive derivative of consumption follows from the transition dynamics shown in Figure 1. Whenever a government inherits a positive amount of debt, it has the incentive to use the instruments at its disposal to reduce the interest rate payments. To do so, the demand for savings should increase, which will happen if current consumption increases more than future consumption. If
![]() , the current government needs to leave a lower debt to its successor. If it does not do so, the successor will raise consumption even more, and the anticipated positive consumption growth would harm the current bond price. It follows that debt is reduced until a level of zero debt is reached.21
, the current government needs to leave a lower debt to its successor. If it does not do so, the successor will raise consumption even more, and the anticipated positive consumption growth would harm the current bond price. It follows that debt is reduced until a level of zero debt is reached.21
The Role of Endogenous Expenditure
We have considered a model with endogenous government expenditure because such a feature often serves as a base for political economy models featuring disagreement on the public expenditure level or composition. Such an assumption is also realistic as governments can ultimately decide to increase or decrease their expenditures. In what follows, we show that such an assumption is not innocuous.
A marginal increase in debt causes an increase in distortionary taxes and an increase in leisure (
![]() ).22 In addition, the government changes the supply of public expenditure. The composite effect on private consumption can be understood by examining the aggregate resource constraint. Differentiating equation (1)
with respect to debt (
).22 In addition, the government changes the supply of public expenditure. The composite effect on private consumption can be understood by examining the aggregate resource constraint. Differentiating equation (1)
with respect to debt (![]() ) yields
) yields
| (22) |
In a model where public expenditure is exogenous, as in Krusell, Martin, and Rios-Rull (2006), it must be that
![]() and therefore
and therefore
![]() . Instead, when
public expenditure is endogenous it is possible to obtain
. Instead, when
public expenditure is endogenous it is possible to obtain
![]() . Given our previous considerations, a positive derivative of consumption implies that the economy can converge to a steady-state with zero debt.23 As discussed before, it is also possible that the economy converges to a steady-state with
. Given our previous considerations, a positive derivative of consumption implies that the economy can converge to a steady-state with zero debt.23 As discussed before, it is also possible that the economy converges to a steady-state with
![]() and
and
![]() . We have found calibrations where debt converges to such a steady-state, and discuss these in the next section.
. We have found calibrations where debt converges to such a steady-state, and discuss these in the next section.
4.2 Robustness Checks
As discussed above, the convergence properties of our model crucially depend on the response of public expenditure to changes in debt. We solve the model for different values of the curvature parameter ![]() . Typical estimates for this parameter are about 1.1 for the U.S. (Amano and Wirjanto (1997)) and do not exceed .8 in panel studies for the OECD countries (Nieh and Ho (2006)). Also, in theoretical models with political disagreement the parameter
. Typical estimates for this parameter are about 1.1 for the U.S. (Amano and Wirjanto (1997)) and do not exceed .8 in panel studies for the OECD countries (Nieh and Ho (2006)). Also, in theoretical models with political disagreement the parameter ![]() is typically set below unity.24 To be conservative, we let the parameter
is typically set below unity.24 To be conservative, we let the parameter ![]() to vary in between .5 and 2.
to vary in between .5 and 2.
We also explore the properties of our model for economies where the ratio between public and private consumption (![]() ) ranges from .25 to .45. This interval is large enough to include the average observations over the past 10 years for all the G7 economies.25 Figure 2 shows that debt usually, but not always, converges to zero.
) ranges from .25 to .45. This interval is large enough to include the average observations over the past 10 years for all the G7 economies.25 Figure 2 shows that debt usually, but not always, converges to zero.
Figure 2. Stability Properties Under Alternative Calibrations
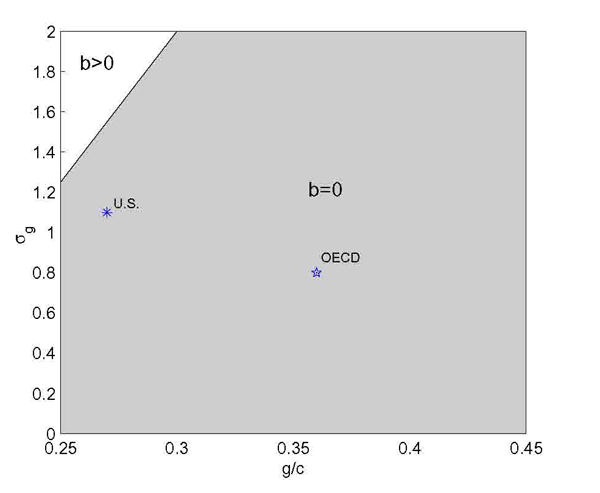
Note: The shaded area indicates calibrations where the steady-state with zero debt is stable. The white area indicates calibrations where the steady-state with a positive debt level is stable - such steady-states correspond to the cases with
![]() . For any value of
. For any value of ![]() (vertical axis), the parameters
(vertical axis), the parameters ![]() and
and ![]() are adjusted so that in the first-best equilibrium leisure is set at 2/3 of total hours, and the ratio
are adjusted so that in the first-best equilibrium leisure is set at 2/3 of total hours, and the ratio ![]() (horizontal axis) matches the corresponding target. The parameters
(horizontal axis) matches the corresponding target. The parameters ![]() and
and ![]() are kept constant at their baseline values.
are kept constant at their baseline values.
Debt converges to a positive level for calibrations where the ratio ![]() is small enough and
is small enough and ![]() is large enough, so that government expenditure is relative unresponsive to changes in debt. Such possibilities still accord with the message that lack of commitment per se does not necessarily lead to debt accumulation. The highest value of steady-state debt found in those calibrations corresponds to 20% of GDP. For initial conditions above that level - which correspond to the situation of most developed economies - our model suggests that debt should be reduced over time and converge to that steady-state. More importantly, the figure shows that debt converges to zero for the relevant empirical estimates and for the calibrations used in many theoretical studies in the political economy literature.
is large enough, so that government expenditure is relative unresponsive to changes in debt. Such possibilities still accord with the message that lack of commitment per se does not necessarily lead to debt accumulation. The highest value of steady-state debt found in those calibrations corresponds to 20% of GDP. For initial conditions above that level - which correspond to the situation of most developed economies - our model suggests that debt should be reduced over time and converge to that steady-state. More importantly, the figure shows that debt converges to zero for the relevant empirical estimates and for the calibrations used in many theoretical studies in the political economy literature.
5 Loose Commitment
Because the evolution of debt is dramatically different with full and no-commitment, we analyze an intermediate loose commitment setting. We consider that governments have the ability to commit, but policy plans are reneged on under some exogenous circumstances such as wars, political pressures, etc. Loose commitment is introduced into the basic model following the methodology developed in Debortoli and Nunes (2010).26
For simplicity, the ability to commit is driven by an exogenous shock
![]() . At any point in time
. At any point in time ![]() , with probability
, with probability ![]() the previously announced plans are fulfilled (
the previously announced plans are fulfilled (![]() ), while with probability
), while with probability ![]() plans are revised (
plans are revised (![]() ). The policymaker's problem becomes
). The policymaker's problem becomes
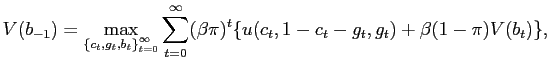 |
(23) |
| (24) |
The objective function (23) contains two parts. The first term in the summation refers to the plan currently made by the planner. The possibility of future reoptimizations decreases the discount rate to ![]() . The second term reflects that, at any point in time, a new plan will be made with probability
. The second term reflects that, at any point in time, a new plan will be made with probability ![]() yielding the value
yielding the value ![]() . Equation (24) is obtained by expanding the term
. Equation (24) is obtained by expanding the term
![]() . With probability
. With probability ![]() , promises are kept. With probability
, promises are kept. With probability ![]() , promises will be disregarded and new policies
, promises will be disregarded and new policies
![]() will be implemented. The optimality conditions to this problem are given by (8), (9), (24) and the generalized Euler equation
will be implemented. The optimality conditions to this problem are given by (8), (9), (24) and the generalized Euler equation
| (25) |
where the superscript R denotes allocations implemented when previous promises are reneged on and plans are reoptimized (![]() ).
).
Steady-State Properties
As long as a small deviation from full-commitment is present (
![]()
![]() ), equation (25) evaluated in steady-state becomes indistinguishable from equation (15). It then follows that under loose commitment there can only be three types of steady-states. This result shows that the indeterminacy of debt illustrated by () is not robust to small deviations from the full-commitment assumption, and the characterization under no-commitment described in this paper is the relevant one.
), equation (25) evaluated in steady-state becomes indistinguishable from equation (15). It then follows that under loose commitment there can only be three types of steady-states. This result shows that the indeterminacy of debt illustrated by () is not robust to small deviations from the full-commitment assumption, and the characterization under no-commitment described in this paper is the relevant one.
Transition Dynamics
For the utility function considered in section 3.1 it is possible to characterize analytically the transition dynamics. Noticing that ![]() is constant and equals
is constant and equals ![]() , the generalized Euler equation (25) collapses into equation (19). Moreover, in periods where promises are reneged on (
, the generalized Euler equation (25) collapses into equation (19). Moreover, in periods where promises are reneged on (![]() ), eq. (9) is equivalent to eq. (18) and fully characterizes the function
), eq. (9) is equivalent to eq. (18) and fully characterizes the function
![]() . As explained in section 3.1, it then follows that
. As explained in section 3.1, it then follows that
![]() and that
and that ![]() from period
from period ![]() onwards.
onwards.
The planner with full-commitment could support and was indifferent between different levels of debt. The prospect of reoptimizing led the planner with no-commitment to hold zero debt in order not to distort its optimal decisions. With loose commitment, the prospects of reoptimizing are present as long as commitment is not perfect, and therefore the planner
chooses zero debt for next period. In that way, tomorrow's decisions will not
be distorted regardless of whether a reoptimization occurs or not. This result shows that a small deviation from full-commitment, i.e.
![]()
![]() makes this economy to behave indistinguishably from an economy with no-commitment.
makes this economy to behave indistinguishably from an economy with no-commitment.
Finally, Figure 3 plots the evolution of average debt under several degrees of commitment for the utility function considered in section 4. Even a relatively small departure from the full-commitment assumption makes the economy to behave very similarly to the no-commitment case. If at period ![]() the government holds debt, it accumulates surpluses, until the level of zero debt is reached. These numerical exercises confirm that the dependency of steady-state debt on the initial conditions is not robust to small deviations from full-commitment.
the government holds debt, it accumulates surpluses, until the level of zero debt is reached. These numerical exercises confirm that the dependency of steady-state debt on the initial conditions is not robust to small deviations from full-commitment.
Figure 3. Loose Commitment: Time Pattern of Debt
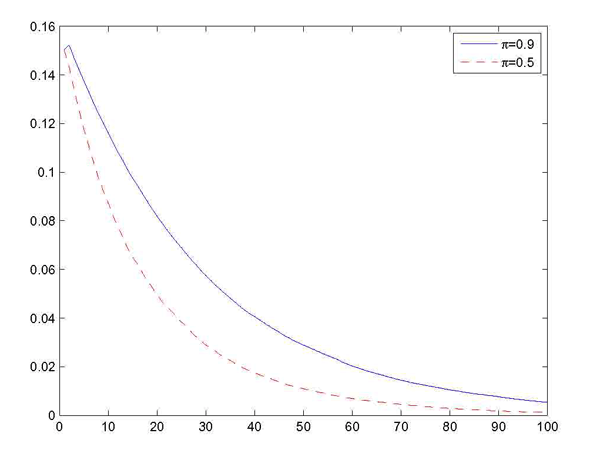
Note: The figure plots the evolution of debt over time,
for values of the parameter ![]() (solid line) and
(solid line) and ![]() (dashed line). Averages across simulations of the histories of the shock
(dashed line). Averages across simulations of the histories of the shock
![]() are reported. The initial condition is
are reported. The initial condition is ![]() (roughly 50% of GDP).
(roughly 50% of GDP).
6 Concluding Remarks
In the aftermath of the Great Recession, public debt increased and large efforts have been laid out to make plans committing to debt reduction. Such plans and their need have been widely discussed across the world and more specifically in the three largest economies - Euro Area, U.S., and Japan.
Our analysis shows that lack of commitment per se is not likely to lead to excessive debt accumulation. Governments without commitment may instead realize that debt distorts their decisions - or might do so with a small probability in the future - and that therefore debt should be optimally reduced. Our results also suggest that debt is more likely to be reduced in economies where public expenditure is a high portion of GDP and where governments are more willing to cut public expenditure.
Our model purposefully assumes an ideal world where governments are benevolent and never disagree. Models with political disagreement and lack of commitment can explain debt accumulation. This paper does not claim any shortcoming of such approaches, nor does it claim that commitment never matters for debt reduction plans. Commitment may well be the solution to political disagreement, intergenerational conflicts, and other akin problems. Giving more prominence to the studies in these areas and specially including them in the current political debate seems of first order importance and urgency.
References
Aiyagari, R., Marcet, A., Sargent, T. J., Seppala, J., 2002. Optimal taxation without state-contingent debt. Journal of Political Economy 110, 1220-1254.
Alesina, A., Tabellini, G., 1990. A positive theory of fiscal deficits and government debt. Review of Economic Studies 57 (3), 403-14.
Amano, R. A., Wirjanto, T. S., November 1997. Intratemporal substitution and government spending. Review of Economic and Statistics 79 (4), 605-609.
Azzimonti-Renzo, M., 2011. Barriers to investment in polarized societies. American Economic Review 101 (5), 2182-2204.
Barro, R. J., 1979. On the determination of the public debt. Journal of Political Economy 87, 940-71.
Barro, R. J., Gordon, D. B., 1983. A positive theory of monetary policy in a natural rate model. Journal of Political Economy 91 (4), 589-610.
Battaglini, M., Coate, S., 2008. A dynamic theory of public spending, taxation and debt. American Economic Review 98 (1), 201-236.
Debortoli, D., Nunes, R., 2010. Fiscal policy under loose commitment. Journal of Economic Theory 145 (3), 1005-1032.
Diaz-Gimenez, J., Giovannetti, G., Marimon, R., Teles, P., 2008. Nominal debt as a burden to monetary policy. Review of Economic Dynamics 11(3), 493-514.
Dominguez, B., 2007. Public debt and optimal taxes without commitment. Journal of Economic Theory 135 (1), 159-170.
Ellison, M., Rankin, N., 2007. Optimal monetary policy when lump-sum taxes are unavailable: A reconsideration of the outcomes under commitment and discretion. Journal of Economic Dynamics and Control 31, 219-243.
Faraglia, E., Marcet, A., Scott, A., 2010. In search of a theory of debt management. Journal of Monetary Economics 57 (7), 821-836.
Hassler, J., Mora, J., Storesletten, K., Zilibotti, F., 2003. The survival of the welfare state. American Economic Review 93 (1), 87-112.
Judd, K. L., 1992. Projection methods for solving aggregate growth models. Journal of Economic Theory 58 (2), 410-452.
Judd, K. L., 2004. Existence, uniqueness, and computational theory for time consistent equilibria: A hyperbolic discounting example. Stanford University. Manuscript.
Klein, P., Krusell, P., Ríos-Rull, J.-V., 2005. Time consistent public policy. Review of Economic Studies 75, 789-808.
Krusell, P., Martin, F., Rios-Rull, J.-V., 2006. Time-consistent debt. Manuscript.
Krusell, P., Quadrini, V., Rios-Rull, J.-V., 1997. Politico-economic equilibrium and economic growth. Journal of Economic Dynamics and Control 21 (1), 243-272.
Kydland, F. E., Prescott, E. C., 1977. Rules rather than discretion: The inconsistency of optimal plans. Journal of Political Economy 85 (3), 473-91.
Ljungqvist, L., Sargent, T. J., January 2004. Recursive Macroeconomic Theory, 2nd Edition. Vol. 1 of MIT Press Books. The MIT Press.
Lucas, R. E., Stokey, N. L., 1983. Optimal fiscal and monetary policy in an economy without capital. Journal of Monetary Economics 12 (1), 55-93.
Martin, F., 2009. A positive theory of government debt. Review of Economic Dynamics 12 (4), 608-631.
Nicolini, J. P., 1998. More on the time consistency of monetary policy. Journal of Monetary Economics 41, 333-350.
Nieh, C.-C., Ho, T., 2006. Does the expansionary government spending crowd out the private consumption? Cointegration analysis in panel data. The Quarterly Review of Economics and Finance 46, 133-148.
Niepelt, D., 2006. Relative asset holdings as a commitment device. Manuscript.
Ortigueira, S., 2006. Markov-perfect taxation. Review of Economic Dynamics 9, 153-178.
Ortigueira, S., Pereira, J., 2008. Markov-perfect optimal ¯scal policy: The case of unbalanced budgets. Manuscript.
Persson, M., Persson, T., Svensson, L., 2006. Time consistency of fiscal and monetary policy: a solution. Econometrica 74, 193-212.
Persson, T., Svensson, L. E. O., 1989. Why a stubborn conservative would run a deficit: Policy with time-inconsistent preferences. The Quarterly Journal of Economics 104 (2), 325-45.
Reis, C., 2008. Taxation without commitment. Manuscript.
Roberds, W., 1987. Models of policy under stochastic replanning. International Economic Review 28 (3), 731-755.
Rogers, C., 1989. Debt restructuring with a public good. Scandinavian Journal of Economics 91, 117-130.
Schaumburg, E., Tambalotti, A., 2007. An investigation of the gains from commitment in monetary policy. Journal of Monetary Economics 54, 302-324.
Song, Z., Storesletten, K., Zilibotti, F., 2006. Rotten parents and disciplined children: A politico-economic theory of public expenditure and debt. Manuscript.
Yared, P., 2010. Politicians, taxes and debt. Review of Economic Studies 77 (2), 806-840.
Appendix:
A Data and Calibration
Table A-1. Debt in the OECD Countries in 2006
| gross | net | |
|---|---|---|
| Australia | 15.0 | -2.8 |
| Austria | 69.1 | 41.8 |
| Belgium | 91.2 | 76.8 |
| Canada | 68.0 | 27.6 |
| Czech Republic | 39.3 | 2.8 |
| Denmark | 39.7 | 6.9 |
| Finland | 48.2 | -60.6 |
| France | 75.3 | 43.0 |
| Germany | 71.3 | 51.9 |
| Greece | 120.6 | 86.9 |
| Hungary | 68.8 | 43.9 |
| Iceland | 24.5 | 8.5 |
| Ireland | 32.5 | 4.9 |
| Italy | 120.8 | 95.4 |
| Japan | 176.2 | 89.5 |
| Korea | 27.9 | -30.2 |
| Luxembourg | 6.6 | . |
| Netherlands | 59.4 | 33.7 |
| New Zealand | 29.8 | -3.5 |
| Norway | 48.1 | -149.3 |
| Poland | 51.7 | 16.6 |
| Portugal | 74.3 | 46.6 |
| Slovak Republic | 38.4 | -11.7 |
| Spain | 46.8 | 26.7 |
| Sweden | 56.0 | -15.0 |
| Switzerland | 54.2 | 21.0 |
| United Kingdom | 47.9 | 41.7 |
| United States | 60.9 | 42.8 |
| Euro Area | 76.8 | 51.3 |
| Total OECD | 76.9 | 44.4 |
Note: The table displays the general government financial liabilities as percent of nominal GDP. The source is the OECD Economic Outlook.
B The No-Commitment Case With Non-Separable Utility
This section shows that a steady-state with zero debt exists even when the utility function is non-separable. The first-order condition with respect to debt becomes
| (B-0.1) |
where
![]() ,
,
![]() , and
, and
![]() denote respectively the derivatives of the policy functions of private consumption, public consumption, and leisure with respect to debt.
The previous equation implies that in a steady-steady
denote respectively the derivatives of the policy functions of private consumption, public consumption, and leisure with respect to debt.
The previous equation implies that in a steady-steady
| (B-0.2) |
There are then three possible steady-states. First, the undistorted equilibrium (![]() ). Second, the level of debt is zero (
). Second, the level of debt is zero (![]() ). Third, the steady-state where the equality
). Third, the steady-state where the equality
![]() holds. Therefore, a steady-state with
holds. Therefore, a steady-state with ![]() exists even with a more generic utility function. As discussed in the main text, the stability properties of the three classes of steady-states depend on the relative weight of public and private consumption and leisure in the utility function and on its curvature.
exists even with a more generic utility function. As discussed in the main text, the stability properties of the three classes of steady-states depend on the relative weight of public and private consumption and leisure in the utility function and on its curvature.
C Particular Case With an Analytical Solution
In this section we provide more detailed derivations of the equilibrium conditions for the particular case analyzed in section 3.1.
C.1 Existence of an Interior Time-Consistent Equilibrium
The purpose of this subsection is to show that if the conditions
| (C-1.1) | |
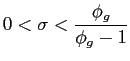 |
(C-1.2) |
 |
(C-1.3) |
are satisfied, there exists an interval
![]() containing
containing ![]() such that an interior and differentiable time-consistent equilibrium exists.
such that an interior and differentiable time-consistent equilibrium exists.
The consumption policy function
![]() is implicitly defined by eq. (18). At the point where
is implicitly defined by eq. (18). At the point where ![]() we have
we have
![$\displaystyle \mathcal{C}(0) = \left[\phi_{c}\left(1-\sigma\frac{\phi_{g}-1}{\phi_{g}}\right)\right]^{\frac{1}{\sigma}}>0,$](img233.gif) |
(C-1.4) |
where the inequality follows directly from conditions (C-1.1) and (C-1.2). Also, consider the corresponding policy functions
![]() and
and
![]() , which can be obtained using the feasibility and implementability constraints. It is easy to verify that given (C-1.3)
, which can be obtained using the feasibility and implementability constraints. It is easy to verify that given (C-1.3)
| (C-1.5) | |
| (C-1.6) |
Thus, the conjectured solution is interior at ![]() . By continuity of
. By continuity of
![]() , it follows that there exist two real numbers
, it follows that there exist two real numbers
![]() and
and
![]() such that
such that
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and all equilibrium conditions are satisfied. Differentiability of the policy function
, and all equilibrium conditions are satisfied. Differentiability of the policy function
![]() is guaranteed by condition (20). Finally, we can denote with
is guaranteed by condition (20). Finally, we can denote with
![]() the largest interval such that an interior and differentiable solution exists. Those bounds are characterized in the following subsection.
the largest interval such that an interior and differentiable solution exists. Those bounds are characterized in the following subsection.
C.2 Characterization of the Interval (
 )
)
As shown in the main text, in an interior equilibrium it must be that ![]() . Thus conditions (17) and (18) simplify to
. Thus conditions (17) and (18) simplify to
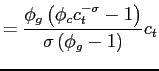 |
(C-2.1) | |
| (C-2.2) |
From these conditions it follows that the solution will be interior as long as ![]() and the marginal utility of consumption satisfies
and the marginal utility of consumption satisfies
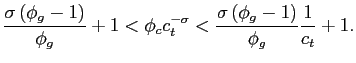 |
(C-2.3) |
The marginal utility of consumption would hit the lower bound when the constraint ![]() is binding, and the upper bound when the constraint
is binding, and the upper bound when the constraint ![]() is binding.
is binding.
The Lower Bound
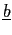
Using condition (C-2.3), constraint ![]() becomes binding at a level of debt
becomes binding at a level of debt ![]() such that
such that
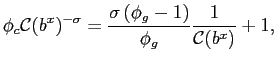 |
(C-2.4) |
or equivalently
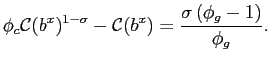 |
(C-2.5) |
We claim that ![]() , and prove this result by contradiction.
, and prove this result by contradiction.
Assume that
![]() and consider the function
and consider the function
![]() , with partial derivative
, with partial derivative
![$\displaystyle \frac{\partial f}{\partial b} = \mathcal{C}_b\left[(1-\sigma)\phi_c\mathcal{C}(b)^{-\sigma} - 1\right].$](img266.gif) |
(C-2.6) |
Such a derivative is clearly negative for
![]() . To determine its sign when
. To determine its sign when ![]() we can evaluate the derivative at
we can evaluate the derivative at ![]() . Recalling that
. Recalling that
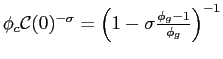 we get
we get
![$\displaystyle \left.{\frac{\partial f}{\partial b}}\right\vert _{b=0} = \mathcal{C}_b(0) \left[(1-\sigma)\left(1 - \sigma \frac{\phi_{g}-1 }{\phi_{g}} \right)^{-1} - 1\right] < 0.$](img271.gif) |
(C-2.7) |
Because
![]() , it follows from equation (C-2.6) that
, it follows from equation (C-2.6) that
![]() remains negative for all
remains negative for all ![]() . So the function
. So the function ![]() is strictly decreasing in
is strictly decreasing in ![]() ,
, ![]() . Since the constraint
. Since the constraint ![]() is not binding when
is not binding when ![]() , it must also be that
, it must also be that
![]() . Because
. Because ![]() is strictly decreasing in
is strictly decreasing in ![]() , there cannot exist a positive debt level satisfying eq. (C-2.5), which contradicts our assumption that
, there cannot exist a positive debt level satisfying eq. (C-2.5), which contradicts our assumption that ![]() . Thus
. Thus ![]() .
.
Finally, given that consumption is strictly increasing in debt, we must have
![]() . It must also be that
. It must also be that
![]() , otherwise there must be a
, otherwise there must be a
![]() such that the constraint
such that the constraint ![]() becomes binding, but this is not possible, as explained below.
becomes binding, but this is not possible, as explained below.
The lower bound of our domain
![]() is thus at a level of debt such that the constraint
is thus at a level of debt such that the constraint ![]() becomes binding.
becomes binding.
The Upper Bound
The constraint ![]() becomes binding at a level of debt
becomes binding at a level of debt ![]() such that
such that
![$\displaystyle \mathcal{C}(b^g) = \left[ \phi_{c}\frac{\phi_{g}}{\sigma\left(\phi_{g}-1\right) +\phi_{g}}\right] ^{\frac{1}{\sigma}},$](img294.gif) |
(C-2.8) |
which substituted into (C-2.1) gives
![$\displaystyle b^{g} = \frac{\sigma\left( \phi_{g}-1\right) }{\sigma\left( \phi_{g}-1\right) +\phi_{g}}\left[ \phi_{c}\frac{\phi_{g}}{\sigma\left( \phi_{g}-1\right) +\phi_{g}}\right] ^{\frac{1}{\sigma}} >0.$](img295.gif) |
(C-2.9) |
Given that consumption is strictly increasing in debt, we must have
![]() . Also, it must be that
. Also, it must be that
![]() , otherwise there must exist a
, otherwise there must exist a
![]() such that the constraint
such that the constraint ![]() becomes binding. But this is not possible as shown above. It must then be that the upperbound
becomes binding. But this is not possible as shown above. It must then be that the upperbound
![]() . In other words, the solution is interior as long as the government does not hold so much debt that it chooses not to provide public expenditure.
. In other words, the solution is interior as long as the government does not hold so much debt that it chooses not to provide public expenditure.
C.3 Characterization of the Policy Functions
We can characterize the behavior of leisure and government expenditure. The optimality conditions (17)-(19) imply that
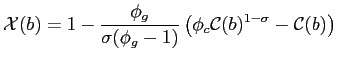 |
(C-3.1) |
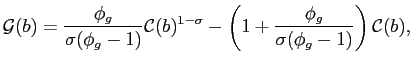 |
(C-3.2) |
and
![$\displaystyle \mathcal{X}_b = - \frac{\phi_g }{\sigma (\phi_g-1)} \mathcal{C}_{b}\left[(1-\sigma)\phi_c\mathcal{C}(b)^{-\sigma}-1\right]$](img303.gif) |
(C-3.3) |
![$\displaystyle \mathcal{G}_b = \mathcal{C}_{b}\left[(1-\sigma)\frac{\phi_g}{\sigma (\phi_g-1)}\phi_c \mathcal{C}(b)^{-\sigma} - \left(1 +\frac{\phi_g}{\sigma (\phi_g-1)}\right)\right].$](img304.gif) |
(C-3.4) |
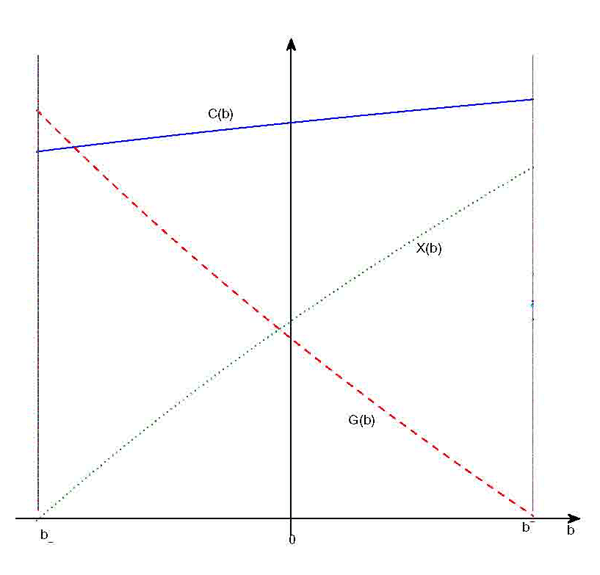
It follows from our previous considerations that
![]() ,
,
![]() and thus when debt is positive
and thus when debt is positive
![]() and
and
![]() . A qualitative description of the policy function is provided in Figure 4.
. A qualitative description of the policy function is provided in Figure 4.
Figure 4. Policy Functions Under No-Commitment
C.4 First-Best Solution
The first best solution can be analyzed in a static form
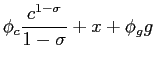 |
|
At an optimum, it must be that
|
|
(C-4.1) |
Since
![]() - otherwise the public good is not provided - the solution is given by
- otherwise the public good is not provided - the solution is given by ![]() ,
,
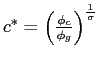 and
and
![]() .27
.27
C.5 Full-Commitment Solution
In an interior equilibrium the allocations must satisfy the feasibility constraint (1), the implementability condition (7), and the optimality conditions (8)-(10). Rearranging these equations one obtains:
| (C-5.1) | |
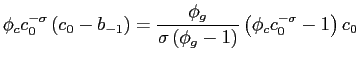 |
(C-5.2) |
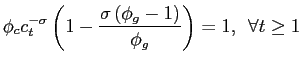 |
(C-5.3) |
| (C-5.4) |
where we have already used the feasibility constraint to substitute for ![]() and the condition
and the condition
![]() as implied by eq. (8). The levels of consumption
as implied by eq. (8). The levels of consumption ![]() and
and ![]() are determined by eqs. (C-5.2) and (C-5.3). Such values can be supported by several levels of leisure and public consumption at different points in time.
are determined by eqs. (C-5.2) and (C-5.3). Such values can be supported by several levels of leisure and public consumption at different points in time.
The indeterminacy between initial allocations
![]() and
allocations at any future date
and
allocations at any future date
![]() can be illustrated as follows.28 Solving forward the
implementability constraint (C-5.1) one obtains
can be illustrated as follows.28 Solving forward the
implementability constraint (C-5.1) one obtains
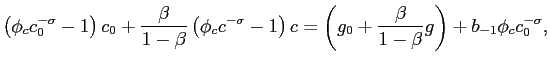 |
(C-5.5) |
where ![]() is given and
is given and ![]() and
and ![]() are set at their optimal levels. Clearly several combinations of
are set at their optimal levels. Clearly several combinations of ![]() and
and ![]() can satisfy this equation. The steady-state level of debt is given by
can satisfy this equation. The steady-state level of debt is given by
![$\displaystyle b=\frac{1}{\beta}\left[(c_{0}+g_{0})\frac{1}{\phi_c c^{-\sigma}} +\frac{c_0^{-\sigma}}{c^{-\sigma}}\left( b_{-1}-c_{0}\right) \right]$](img341.gif) |
(C-5.6) |
and since ![]() is not determined neither is
is not determined neither is ![]() .
.
It is easy to verify that all the solutions yield the same utility level. Totally differentiating the implementability and feasibility constraints, one obtains
![]() ,
,
![]() , and
, and
![]() . Thus, differentiating life-time utility we get
. Thus, differentiating life-time utility we get
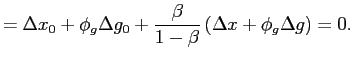 |
(C-5.7) |
The existence of an interior equilibrium for
![]() can be proved as follows. First, notice that one of the solutions under full-commitment coincides with the time-consistent solution derived in section 3.1. Indeed, equation (C-5.2) and (13) coincide, and equation (C-5.3) is satisfied for
can be proved as follows. First, notice that one of the solutions under full-commitment coincides with the time-consistent solution derived in section 3.1. Indeed, equation (C-5.2) and (13) coincide, and equation (C-5.3) is satisfied for
![]() . Thus
. Thus ![]() and
and ![]() are the same as in a time-consistent equilibrium, and thus the allocation
are the same as in a time-consistent equilibrium, and thus the allocation
![]() and
and
![]() ,
, ![]()
![]() must satisfy the feasibility and the implementability constraint, and give an interior solution. It then follows that an interior solution must exist for
must satisfy the feasibility and the implementability constraint, and give an interior solution. It then follows that an interior solution must exist for
![]() also under full-commitment.
also under full-commitment.
D Numerical Algorithm
No-Commitment
For the reasons presented in the text, the policy functions are not linear and
depend on the bond position. Hence, neither local approximations nor linear
approximations of the policy function are well suited for the problem at hand.
We use global methods where the state-variable (![]() ) is defined over a
grid. We solve for the policy functions directly with non-linear functions. We
experimented with splines, Chebyshev polynomials, and different
approximation orders of those. These techniques are described, for instance, in Judd (1992) and Judd (2004).
) is defined over a
grid. We solve for the policy functions directly with non-linear functions. We
experimented with splines, Chebyshev polynomials, and different
approximation orders of those. These techniques are described, for instance, in Judd (1992) and Judd (2004).
The generalized Euler equation poses additional difficulties because the derivative (besides the level) appears in the FOCs. As mentioned in Judd (2004), this issue per se may call for the use of global techniques. Define the set of FOCs in a compact form as:
| (D-0.1) |
where ![]() summarizes the set of all control variables, i.e.
summarizes the set of all control variables, i.e.
![]() .The collocation on first order conditions approximates the policy functions
.The collocation on first order conditions approximates the policy functions
![]() such that for a grid of points
such that for a grid of points ![]()
| (D-0.2) |
where ![]() is the first element of the policy function, i.e.
is the first element of the policy function, i.e.
![]()
The solution algorithm can be compactly summarized as follows:
- Define a grid on the state-variable
 , and choose the class and
order of the approximation functions
, and choose the class and
order of the approximation functions 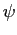 . Guess an initial
. Guess an initial
 where
where 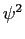 is the second element of
is the second element of 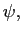 i.e.
i.e.
 .
.
- Update the function
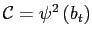 and
and
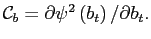
- For a fixed
 and
and
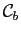 , solve for the functions
, solve for the functions 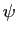 such
that equation (D-0.2) holds.
such
that equation (D-0.2) holds.
- Check convergence of the function
 (and
(and
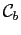 ). If
convergence is not achieved, go back to step 2.
). If
convergence is not achieved, go back to step 2.
We also use another algorithm that uses the same principles but is more
convenient. Note that since
![]() and
and
![]() , equation
(D-0.2) can be compactly written as
, equation
(D-0.2) can be compactly written as
| (D-0.3) |
Therefore, the numerical procedure can directly search for the approximating
functions ![]() and there is no need to fix the function
and there is no need to fix the function
![]() . In this way,
the iterative procedure is incorporated inside the root finding numerical procedure.
Both types of algorithms yield the same solution.
. In this way,
the iterative procedure is incorporated inside the root finding numerical procedure.
Both types of algorithms yield the same solution.
Well suited algorithms are also described in Klein et al. (2005). Earlier numerical implementations of these algorithms can be found in Krusell, Quadrini, and Rios-Rull (1997). Hassler, Mora, Storesletten, and Zilibotti (2003) provide analytical solutions.
Loose Commitment
Global methods are specifically appropriate for this case. For the solution to be accurate, one needs to perform a good approximation of the policy functions both when promises are and are not fulfilled (![]() and
and ![]() ). These two events and the corresponding policy functions are not necessarily similar. This issue raises the challenge of finding an appropriate
value around which to approximate the solution, thus increasing the suitability of global methods.
). These two events and the corresponding policy functions are not necessarily similar. This issue raises the challenge of finding an appropriate
value around which to approximate the solution, thus increasing the suitability of global methods.
We use the method described in Debortoli and nunes (2010). There is no need to approximate separate policy functions for the cases in which promises are and are not kept. Using
their results, the set of control variables in case promises are honored can be
approximated as
![]() The variables in case a
default occurs correspond to
The variables in case a
default occurs correspond to
![]() The
policy functions
The
policy functions
![]() and its derivative correspond to default states and
are approximated with the corresponding element of
and its derivative correspond to default states and
are approximated with the corresponding element of
![]() The overall algorithm is then very similar to the
one described for the time-consistent solution.
The overall algorithm is then very similar to the
one described for the time-consistent solution.
Footnotes
1. We are thankful to Klaus Adam, Alberto Bisin, Jordi Galí, Juan Hatchondo, Albert Marcet, Michael Reiter, Victor Rios-Rull, Kjetil Storesletten, Fabrizio Zilibotti and seminar participants at the SED (2007, 2011), EEA (2007), Federal Reserve System macro conference (2007), Vigo Macrodynamic Workshop (2007), SAEe (2007), RES (2008), Bank of England, Bank of Italy, Boston Fed, Collegio Carlo Alberto, ECB, Federal Reserve Board, LSE, Maryland, Minneapolis Fed, Norges Bank, New York Fed, Pompeu Fabra, Toulouse, UCSD, UCLA, and West Virginia for for many helpful comments. We gratefully acknowledge financial support from CREA and IAE-CSIC (Debortoli) and Fundação para a Ciência e Tecnologia (Nunes). Any remaining errors are our own. The views expressed in the paper are those of the authors and do not necessarily reflect those of the Board of Governors or the Federal Reserve System. Contacts: Davide Debortoli (University of California San Diego), Ricardo Nunes (Federal Reserve Board) Return to text
2. The appendix shows that even before the Great Recession the vast majority of OECD countries were characterized by positive and non-negligible debt over GDP ratios. Return to text
3. In the political economy literature, the no-commitment assumption rules out intricate game-theoretical dynamics between different governments. Return to text
4. For instance, Alesina and Tabellini (1990) assumed an initial zero debt position where the time-inconsistency disappears. Other works assumed quasi-linear utility in consumption, which leads to an exogenous interest rate and no time-inconsistency. Return to text
5. We assume that there is still commitment to honor debt payments. Niepelt (2006) discusses this issue in more detail. Return to text
6. In section 4 we extensively discuss the differences between the two cases. Return to text
7. Ellison and Rankin (2007) also examine indexed debt in a framework similar to Nicolini (1998). Return to text
8. We assume no uncertainty for simplicity. Our considerations are still valid with exogenous shocks and complete financial markets. Return to text
9. The assumption of a separable utility function is standard in models with political disagreement, such that the provisions of public good does not affect private decisions. Relaxing this assumption does not affect the possible classes of steady-states under either full-commitment or no-commitment. The detailed derivations are shown in Appendix B. Return to text
10. The implementability constraint is obtained by using eqs. (5)-(6) and bond market clearing to substitute for taxes, bond prices, and government debt into eq. (4). Return to text
11. See e.g. Ljungqvist and Sargent (2004), pp. 516-517 for a formal proof that
![]() . In particular,
. In particular, ![]() is only possible if the government holds an asset position larger than the one required to implement the first-best solution. The government could then use positive lump-sum transfers to return this excess wealth and implement the first-best allocation (
is only possible if the government holds an asset position larger than the one required to implement the first-best solution. The government could then use positive lump-sum transfers to return this excess wealth and implement the first-best allocation (![]() ). Return to text
). Return to text
12. Dominguez (2007) and Reis (2008) provide an interesting analysis of debt policies with trigger strategies. Return to text
13. Ortigueira (2006) analyzes different assumptions regarding the government's intra-period commitment. Return to text
14. We are assuming differentiability of the function
![]() . We do not have a formal proof about the existence (or uniqueness) of this solution for a general utility function. However, existence can be shown in the particular example of the next section and in our numerical exercises we do find a continuous and differentiable solution. Return to text
. We do not have a formal proof about the existence (or uniqueness) of this solution for a general utility function. However, existence can be shown in the particular example of the next section and in our numerical exercises we do find a continuous and differentiable solution. Return to text
15. The result that ![]() must be constant in a steady-state with constant
must be constant in a steady-state with constant ![]() ,
, ![]() and
and ![]() follows from eq. (13). Return to text
follows from eq. (13). Return to text
16. The domain
![]() encompasses all the cases where public expenditure is provided and taxes are distortionary. For our purposes, focusing our attention to this domain is, therefore, not restrictive. Return to text
encompasses all the cases where public expenditure is provided and taxes are distortionary. For our purposes, focusing our attention to this domain is, therefore, not restrictive. Return to text
17. The equality
![]() indicates that if
indicates that if
![]() an interior solution must be one where the first-best allocation is implemented (
an interior solution must be one where the first-best allocation is implemented (
![]() ), or taxes are negative. Return to text
), or taxes are negative. Return to text
18. In principle, the policy function is not differentiable at a point where the term in parenthesis in eq. (20) equals zero. Since this must occur when ![]() , without loss of generality it is always possible to choose
, without loss of generality it is always possible to choose
![]() to preserve differentiability. The remaining policy functions are fully characterized in Appendix C. Return to text
to preserve differentiability. The remaining policy functions are fully characterized in Appendix C. Return to text
19. This multiplicity is different from the general case considered in Section 2.1, where there is a one-to-one correspondence between initial conditions and steady-states. The detailed derivations for this particular case are contained in Appendix C.5. Return to text
20. Also notice that the natural debt limit cannot be a steady-state. The natural debt limit implies ![]() where the model is not well defined. Return to text
where the model is not well defined. Return to text
21. With a symmetric argument, if the government starts with assets, but to the right of the point where
![]() , asset holdings will be reduced until the zero debt level is reached. Return to text
, asset holdings will be reduced until the zero debt level is reached. Return to text
22. Leisure increases both because of a substitution effect due to more distortionary labor taxation, and because of a wealth effect due to higher private asset holdings. Return to text
23. This reasoning provides an explanation for why the model of Krusell et at. (2006) does not display a differentiable equilibrium where debt converges to zero. Return to text
24. See for example the recent works of Battaglini and Coate (2008). Return to text
25. The lower bound is .27 (U.S.), while the upper bound is .41 (France). The OECD average is .36. Return to text
26. An earlier application of these limited commitment settings can be found in Roberds (1987). Schaumburg and Tambalotti (2007) developed a similar methodology than can be applied only to linear-quadratic problems. The formulation in Debortoli and Nunes (2010) applies to a general class of models including the current one. The proofs and derivations presented there apply here and are omitted for brevity. Return to text
27. For the inequality (![]() ) to be satisfied, we also need that
) to be satisfied, we also need that ![]() , or equivalently
, or equivalently
![]() . The latter condition is always satisfied when the restriction (C-1.3) holds. Return to text
. The latter condition is always satisfied when the restriction (C-1.3) holds. Return to text
28.
The allocations are assumed to be equal from ![]() onwards, thus we are referring to steady-state allocations for expositional simplicity and without loss of generality. With similar arguments one can also show the indeterminacy between allocations at future dates. Return to text
onwards, thus we are referring to steady-state allocations for expositional simplicity and without loss of generality. With similar arguments one can also show the indeterminacy between allocations at future dates. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text