The Federal Reserve Board eagle logo links to home page

Optimal Monetary Policy with Distinct Core and Headline Inflation Rates*

Martin Bodenstein, Christopher J. Erceg, and Luca Guerrieri**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

In a stylized DSGE model with an energy sector, the optimal policy response to an adverse energy supply shock implies a rise in core inflation, a larger rise in headline inflation, and a decline in wage inflation. The optimal policy is well-approximated by policies that stabilize the output gap, but also by a wide array of "dual mandate" policies that are not overly aggressive in stabilizing core inflation. Finally, policies that react to a forecast of headline inflation following a temporary energy shock imply markedly different effects than policies that react to a forecast of core, with the former inducing greater volatility in core inflation and the output gap.

Keywords: Energy-price shocks, monetary policy tradeoffs, DSGE models

JEL classification: E32


1  Introduction

The pronounced divergence between headline and core inflation rates in response to the substantial energy price hikes of the past few years has intensified debate over which inflation measure is the more appropriate focus of policy. Some central banks, such as the Bank of England and European Central Bank, focus on headline inflation both in framing objectives, and as an operational guide to policy; while others appear relatively more concerned with the behavior of core inflation, at least in describing the basis for policy decisions.1

This paper uses a stylized optimization-based DSGE model to assess the implications of alternative monetary policies in response to energy shocks, as well as to compare such policies to the "optimal" policy that maximizes the utility of households. The model economy is formulated to allow a distinction between core and headline inflation, as in recent work by Blanchard and Galí.2 In particular, goods comprising the core basket are produced by monopolistically-competitive retailers that set prices in staggered Calvo-style contracts, so that core prices are sticky. By contrast, energy prices are flexible, and determined to equate the sum of household and firm demand to the available supply (a stochastic endowment process). Because wages are sticky, shocks that depress energy supply raise marginal cost even for a policy that keeps output at potential, pushing up both core and headline price inflation; thus, monetary policy faces a stabilization tradeoff.

We derive a quadratic approximation to welfare following the seminal analysis of Rrotemberg and Woodford 1997. As in the model of Erceg, Henderson, and Levin (2000), the deviation of welfare from its Pareto-optimal level depends on the variance of price inflation, wage inflation, and the employment (or output) gap. But corroborating the insight of Goodfriend and King (1997), King and Wolman (1998), and Aoki (2001), it is core price inflation that matters for welfare, since the price of energy is assumed to be completely flexible.3 Welfare also turns out to depend on the price markup, which affects the intratemporal allocation of energy across households and firms.

Given that the supply block of our model also parallels Erceg, Henderson, and Levin (2000) quite closely, some key prescriptions about optimal policy derived in that setting for technology shocks carry over to energy supply shocks. In particular, in the case of a contractionary supply shock that pushes up the energy price, it is optimal for the required fall in the real wage to occur through a combination of a temporary rise in core inflation, and fall in wage inflation (with headline inflation increasing by more than core). Policies that keep output close to potential turn out to be nearly optimal even though the output gap receives a small weight in the welfare function, reflecting such policies perform well in achieving the wage and price adjustment that occurs under the optimal policy.

Perhaps surprisingly, "dual mandate" objective functions that simply penalize volatility in core inflation and the employment gap also perform remarkably well compared to the welfare-maximizing policy for a wide range of relative weights on these objectives, unless the policymaker only cares about stabilizing inflation. Following the seminal approach of Taylor (1979), this reflects that the variance tradeoff frontier (or "Taylor Curve") implies that the cost of reducing inflation volatility in terms of employment gap volatility is very high. As a result, even a policymaker with a strong aversion to inflation variation does not find it worthwhile to bear the high cost of reducing inflation volatility, and chooses a policy that keeps employment close to potential.

Finally, the performance of simple policy rules that respond to a forecast of either headline or core inflation is examined. This analysis is useful because many central banks describe their policy as aimed at adjusting policy rates so that a forecast of inflation reverts to target over a "medium-term" horizon of roughly two or three years, with most focusing on a forecast of headline inflation. Our model implies that forecasts of headline and core inflation can diverge markedly following a temporary shock to energy supply: as documented in Section 2, Federal Reserve Greenbook forecasts suggest numerous episodes in which such divergence occurred following large but temporary shocks to energy prices. Under such conditions, the particular inflation forecast measure (headline or core) to which the central bank chooses to react can have sizeable macroeconomic implications for the implied response to an energy price shock.

Model simulations illustrate how a temporary rise in the energy price induces a much more accommodative policy response under the rule that responds to a headline inflation forecast, as expected headline inflation falls well below core due to predicted mean-reversion in the energy price. As a result, a policy of responding to a forecast of headline inflation fuels a much larger rise in core inflation and the output gap than a policy of stabilizing a forecast of core (which more closely resembles the optimal policy). In the presence of uncertainty about the persistence of the shock, focusing on headline inflation may even contribute to greater volatility in realized headline inflation than the alternative of focusing on core.

This paper is organized as follows. Section 2 provides some empirical motivation. Section 3 describes the workhorse model, Section 4 the model's log-linearized behavioral equations, and Section 5 the calibration. Section 6 describes the derivation of the welfare function, while Section 7 analyzes optimal policy and various simple rules. Section 8 concludes.


2  Headline and Core Inflation Data and Forecasts

Figure 1 reports the evolution of headline CPI inflation and core CPI inflation between 1990 and the second quarter of 2007 (both series are reported as four quarter changes). The core inflation measure excludes food and energy prices.4 Headline inflation is clearly more volatile than the core CPI inflation rate. Despite the higher weight on food compared with energy in the headline CPI basket (the weights are 15% and 9%, respectively), the energy component accounts for most of the higher volatility of headline inflation. It is also evident from the figure that headline and core inflation exhibit fairly persistent divergence during certain periods, both in the early 1990s, and in the wake of the large escalation in energy prices of the past few years.

There have also been numerous episodes in which forecasts of headline and core inflation have shown large and persistent gaps, especially following energy price changes that were expected to be transitory. Figure 2 provides some examples of episodes in which Federal Reserve Greenbook forecasts for headline and core inflation exhibited a persistent gap. In each panel, the thick lines show data or Greenbook projections for periods prior to final editing of the Greenbook, while the thin lines denote the forecast.5 For each episode, energy price movements dominated the gap between the forecast of core and headline CPI inflation. For example, the Greenbook narrative dated 05/09/2000 is insightful in providing a rationale for the staff's forecast. Several developments that had pushed up energy prices sharply during the previous year - including higher oil prices, regulatory changes in California, capacity problems in electricity production, and the transition to MTBE as an additive in gasoline - were expected to continue to push up headline inflation (measured as a four quarter change) over the remainder of that year. However, as these pressures were expected to be partly reversed, energy prices were projected to drop sharply in the subsequent two years, with the headline inflation rate expected to average roughly 3/4 percentage point less than core.


3  Model Description

The model is similar in form to that of Erceg, Henderson, and Levin (2000). The main difference is the inclusion of an energy sector. Because the household consumption basket includes both energy and a composite good produced by monopolistically-competitive retailers, there is a distinction between headline and core inflation. The model also includes competitive "wholesale" producers that use energy in combination with other inputs, and sell their output to retailers. Against the backdrop of this vertical production structure, variation in the markup of retail over wholesale prices generates an inefficient allocation of energy between households and firms.

3.1  Households and Wage Setting

There is a continuum of monopolistically competitive households indexed by $ h \in[0,1]$, each of which supplies a differentiated labor service to a representative labor aggregator. The aggregator's demand for each household's labor is equal to the sum of firms' demands. The aggregate labor index $ L_{t}$ has the Dixit-Stiglitz form:

$\displaystyle L_{t}=\left[ \int_{0}^{1}\left( N_{t}\left( h\right) \right) ^{\frac {1}{1+\theta_{w}}}dh\right] ^{1+\theta_{w}},$ (1)

where $ \theta_{w}>0$ and $ N_{t}(h)$ is hours worked by each member of household $ h$. The aggregator minimizes the cost of producing a given amount of the aggregate labor index, taking each household's wage rate $ W_{t}\left( h\right) $ as given, and then sells units of the labor index to the production sector at their unit cost $ W_{t}$:

$\displaystyle W_{t}=\left[ \int_{0}^{1}W_{t}{}\left( h\right) ^{\frac{-1}{\theta_{w}} }dh\right] ^{-\theta_{w}}.$ (2)

$ W_{t}$ is interpreted as the aggregate wage index. The aggregator's demand for the labor services of household $ h$ is given by:

$\displaystyle N_{t}\left( h\right) =\left[ \frac{W_{t}\left( h\right) }{W_{t}}\right] ^{-\frac{1+\theta_{w}}{\theta_{w}}}L_{t}.$ (3)

The utility functional of household $ h$ is:

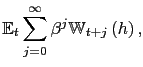
$\displaystyle \mathbb{E}_{t}\sum_{j=0}^{\infty}\beta^{j}\mathbb{W}_{t+j}\left( h\right) ,$ (4)

where the period utility function $ \mathbb{W}_{t}\left( h\right) $ has the time separable form:

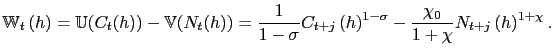
$\displaystyle \mathbb{W}_{t}\left( h\right) = \mathbb{U}(C_{t}(h)) - \mathbb{V}(N_{t}(h)) = \frac{1}{1-\sigma} C_{t+j}\left( h\right) ^{1-\sigma} - \frac{\chi_{0} }{1+\chi}N_{t+j}\left( h\right) ^{1+\chi}.$ (5)

Here $ C_{t}\left( h\right) $ and $ N_{t}\left( h\right) $ denote each household's total consumption and hours of labor in period $ t$, respectively. The intertemporal elasticity of consumption, $ \frac{1}{\sigma}$, satisfies $ \frac{1}{\sigma} > 0$, and $ 0<\beta<1$, $ \chi> 0$, and $ \chi_{0} > 0$.

A household's total consumption in each period depends in turn on its purchases both of a composite nonenergy consumption good $ C_{nt}$, and of energy $ O_{ct}$, according to a Cobb-Douglas production function:

$\displaystyle C_{t}= C_{nt}^{1-\omega_{oc}} \, O_{ct}^{\omega_{oc}}.$ (6)

The parameter $ \omega_{oc}$ in equation (6) equals the share of energy in total consumption.

Household $ h$ faces a flow budget constraint in period $ t$ which requires that combined expenditure on goods and on the net accumulation of financial assets must equal disposable income:

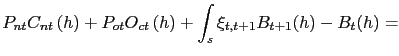
$\displaystyle P_{nt}C_{nt}\left( h\right) + P_{ot}O_{ct}\left( h\right) + \int_{s} \xi_{t,t+1}B_{t+1}(h) - B_{t}(h) =$    
$\displaystyle (1+\tau_{w})W_{t}\left( h\right) N_{t}\left( h\right) + R_{kt} K_{t}(h) + P_{ot} Y_{ot} + \Gamma_{t}\left( h\right) - T_{t}\left( h\right) .$ (7)

Household $ h$'s expenditures consist of purchases of the nonenergy consumption good at a unit price of $ P_{nt}$, of energy at a unit price of $ P_{ot}$, and of net purchases of state-contingent claims. Each household earns labor income of $ (1+\tau_{w})W_{t}\left( h\right) N_{t}\left( h\right) $, where $ \tau_{w}$ is an employment subsidy designed to allow the flexible wage economy to be efficient. Households also earn capital income $ R_{kt} K_{t}(h)$ (though the aggregate capital stock is fixed at $ \bar{K}$). Each household also derives income from receiving an aliquot share $ Y_{ot}$ of the economy's random flow endowment of energy. Households sell their energy endowment at a price of $ P_{ot}$ either to other households, or to those firms in the economy (called "wholesalers" below) that use energy as a productive input. Finally, each household receives an aliquot share $ \Gamma_{t}\left( h\right) $ of the profits of all firms and pays a lump sum tax of $ T_{t}\left( h\right) $ to the government. Household $ h$ maximizes the utility functional (4), subject to (3), (6), and (7), with respect to its consumption of energy, the nonenergy good, and its holdings of contingent claims, taking the prices of consumption goods (energy and nonenergy) and of bonds as given.

Household wages are determined by Calvo-style staggered contracts subject to static wage indexation. In particular, with probability $ 1-\xi_{w} $, each household is allowed to re-optimize its wage contract. If a household is not allowed to optimize its wage rate, it resets its wage according to $ W_{t}(h) = \pi W_{t-1}(h)$, where $ \pi$ is the steady state inflation rate. For a household that can choose its wage optimally, the first order condition for $ W_{t}(h)$ is:

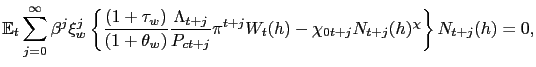
$\displaystyle \mathbb{E}_{t}\sum_{j=0}^{\infty}\beta^{j}\xi_{w}^{j}\left\{ \frac {(1+\tau_{w})}{(1+\theta_{w}) }\frac{\Lambda_{t+j}}{P_{ct+j}}\pi^{t+j} W_{t}(h)- \chi_{0t+j}N_{t+j}(h)^{\chi}\right\} N_{t+j}(h) =0,$ (8)

where $ \Lambda_{t}$ is the marginal value of a unit of consumption. Roughly speaking, equation (8) says that the household chooses its contract wage to equate the present discounted value of working an additional unit of time to the discounted marginal cost. In the calibration, the employment subsidy $ \tau_{w}$ exactly offsets the monopolistic distortion $ \theta_{w}$, so that the household's marginal rate of substitution would equal the consumption real wage in the absence of nominal wage rigidities.

3.2  Firms and Price-Setting

The nonenergy consumption good $ C_{Nt}$ is a composite of a continuum of different "retail" goods. The composite good is produced by a representative firm (or "bundler") according to the technology:

$\displaystyle C_{nt}= Y_{nt}= \left[ \int_{0}^{1}\left( Y_{nt}\left( f\right) \right) ^{\frac{1}{1+\theta_{p}}}df\right] ^{1+\theta_{p}},$ (9)

where $ \theta_{p}>0$ and $ Y_{nt}(f)$ is the input of retail good $ f$. The representative firm purchases the underlying retail goods at prices $ P_{nt}(f)$, and sells the composite good to households at a price of $ P_{nt}$ (which it takes as given). The representative firm's demand for retail good $ f$ is:

$\displaystyle Y_{nt}\left( f\right) =\left[ \frac{P_{nt}\left( f\right) }{P_{nt} }\right] ^{-\frac{1+\theta_{p}}{\theta_{p}}}Y_{nt}.$ (10)

Retail goods are produced by monopolistically competitive firms. Each retailer $ f$ purchases a homogenous "wholesale" good $ Y_{wt}$, and transforms it into a particular type of retail good according to a simple linear production function:

$\displaystyle Y_{nt}\left( f\right) = Y_{wt} \left( f\right) ,$ (11)

where $ Y_{wt} \left( f\right) $ denotes purchases of the wholesale good by producer $ f$. Retailers set the price of their respective output goods in Calvo-style staggered contracts. Thus, each retailer $ f$ faces a constant probability, $ 1-\xi_{p}$, of receiving a signal to re-optimize its contract price, $ P_{nt}(f)$. Those firms not receiving a signal to re-optimize simply adjust their price by the steady state inflation rate. A firm $ f$ that receives a signal to adjust sets its contract price to maximize the profit functional:

$\displaystyle \mathbb{E}_{t}\sum_{j=0}^{\infty}\xi_{p}^{j}\psi_{t,t+j}\left[ (1+\tau_{p} )\pi^{t+j}P_{nt}\left( f\right) Y_{nt+j}\left( f\right) -P_{wt+j} Y_{nt+j}\left( f\right) \right] ,$ (12)

taking its demand schedule (10) and the price of wholesale goods $ P_{wt}$ as given. The term $ \psi_{t,t+j}$ represents the stochastic discount factor, and the constant $ \tau_{p}$ is a production subsidy that is set to exactly offset the distortion due to monopolistic competition; together with the wage subsidy, it ensures that the allocation under flexible prices and wages is Pareto-optimal.

The wholesale good $ Y_{wt}$ is produced by a representative firm according to the technology:

$\displaystyle Y_{wt} = \left( K_{t}^{\alpha} (Z_{t}L_{t})^{1-\alpha} \right) ^{1- \omega_{op}} O_{pt}^{\omega_{op}},$ (13)

where $ O_{pt}$ is energy used in production, $ Z_{t}$ is an exogenous technology shock, and $ \omega_{op}$ is the energy share of gross output. The representative firm purchases energy and hires labor and capital in competitive factor markets (at prices $ P_{ot}$, $ W_{t}$, and $ R_{kt}$ respectively), and sells its output to retail firms at the wholesale price of $ P_{wt}$.

In addition to the constraint in equation (9) that all output of the nonenergy good is consumed by households, clearing of the wholesale market requires that the cumulative demand of retailers equals the available supply:

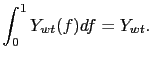$\displaystyle \int_{0}^{1}Y_{wt}(f)df = Y_{wt}.$ (14)

Moreover, energy market clearing implies that the energy demand of households and wholesale firms equal the exogenous flow endowment:

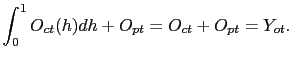
$\displaystyle \int_{0}^{1} O_{ct}(h)dh + O_{pt} = O_{ct} + O_{pt}= Y_{ot} .$ (15)

The exogenous flow endowment, $ Y_{ot}$, is itself the sum of a (nearly) permanent and temporary component, so that $ Y_{ot} = Y^{P}_{ot} +Y^{T}_{ot}$. The permanent and temporary components, represented as log-deviations from their steady-state values, evolve according to:6

$\displaystyle y^{P}_{ot} = \rho^{P} y^{P}_{ot-1} + \epsilon^{P}_{t},$ (16)
$\displaystyle y^{T}_{ot} = \rho^{T} y^{T}_{ot-1} + \epsilon^{T}_{t} .$ (17)

Finally, the technology shock is assumed to follow an AR(1) with persistence parameter $ \rho_{z}$.

3.3  Monetary and Fiscal Policy

The central bank follows an interest rate reaction function of the form:

$\displaystyle i_{t} = \gamma_{1} \pi_{nt} + \gamma_{2} \pi_{ct}+ \gamma_{1f} \pi_{nt+1\vert t} + \gamma_{2f} \pi_{ct+1\vert t} + \gamma_{y} (y_{nt}-y^{*}_{nt}).$ (18)

In this equation, all variables are measured as percentage point deviations from their steady state values. The variable $ i_{t}$ denotes the short-term nominal interest rate. The variable $ \pi_{nt}$ is the logarithmic percentage change in the retail price index $ P_{nt}$, which is interpreted as the core inflation rate in this model. The variable $ \pi_{ct}$ is the logarithmic percentage change in the household's price deflator for consumption $ P_{ct}$ implied by (6), which is interpreted as the headline inflation rate. The instrument rule is sufficiently general to also consider policies that react to one quarter ahead forecasts of core inflation ( $ \pi_{nt+1\vert t}$) or headline inflation ( $ \pi_{ct+1\vert t}$), as well as to the true output gap in the non-energy sector $ (y_{nt}-y^{*}_{nt})$.

Finally, the subsidies to firms and households are assumed to be financed by lump-sum taxes. Given the Ricardian structure of the model, it is convenient to assume that the government budget is balanced each period.


4  Log-Linearized Equations

Table 1 presents the behavioral equations of the model in log-linearized form.7 Equations T1-T6 represent the supply block of the model. Equation T1 is the familiar price-setting equation under Calvo contracts, linking core inflation ($ \pi_{nt}$) to expected core inflation ( $ \pi_{nt+1}$) and real marginal cost ($ mc_{t}$). The first line of T2 expresses real marginal cost as a weighted average of the cost of the non-energy inputs (capital and labor), and of the relative price of energy. Each of the cost components is represented in "gap" form as a deviation from the level that would prevail in the flexible price equilibrium. Thus, marginal cost rises above its steady state level if the employment gap ( $ l_{t}-l^{*}_{t}$) is positive (reflecting diminishing returns), if the product real wage gap ( $ \eta_{t}-\eta^{*}_{t}$) is positive, or if the relative price of oil gap ( $ \psi_{ot}-\psi^{*}_{ot}$) is positive.8

Equation T3 is the usual wage-setting equation under Calvo contracts, linking wage inflation ($ \omega_{t}$) to expected wage inflation and to the gap between the average household's marginal rate of substitution and the real wage ($ MRS_{t}-\eta_{t}$). Because the real wage is expressed as a product real wage (i.e., it is deflated by $ P_{nt}$ rather than the overall consumer price index $ P_{ct}$), the MRS gap given in the first line of T4 depends on the relative price of the overall consumption basket to core goods (i.e., $ \frac{P_{ct}}{P_{nt}}$, or $ \omega_{oc}\psi_{t}$ in log-linearized form). Accordingly, the MRS gap depends on the relative price of oil gap, as well as on the usual arguments reflecting the disutility of working, $ \chi(l_{t}-l^{*}_{t}$), and wealth effect on consumption, $ s_{L} (l_{t} -l^{*}_{t})$. Equation T5 is simply an identity for the evolution of the product real wage, while T6 expresses the relative price of oil gap in terms of the employment gap and real wage gap. A rise in either employment or the real wage increases oil demand (the latter through a substitution effects towards energy), which puts upward pressure on the relative price of oil. Equations T9-T11 give expressions for the flexible price employment level ($ l^{*}_{t}$), real wage ( $ \eta^{*}_{t}$), and oil price ( $ \psi^{*}_{t}$) that can be regarded as "reduced form" shocks in the model's supply block.9

Equations T7 and T8 can be regarded as characterizing the demand block (in conjunction with the monetary rule, which is omitted from the table). Equation T7 is derived from the consumption Euler equation, and links the employment gap directly to the future employment gap, and inversely to the real interest rate gap. The latter is the difference between the consumption-based real interest rate ($ r_{ct}$) and the real interest rate that would prevail under flexible prices and wages ( $ r^{*}_{ct}$, whose evolution is described in T12 and T13). Equation T8 links overall or "headline" consumer price inflation ($ \pi_{ct}$) to core inflation ($ \pi_{nt}$). Clearly, a change in the relative price of energy $ \psi _{ot}-\psi_{ot-1}$ induces a wedge between headline and core inflation.

As shown in Table 1, it is possible to solve out for the relative energy price in order to represent the marginal cost and MRS gap expressions in T2 and T4 solely in terms of the real wage and employment gaps. For example, the "reduced form" sensitivity of marginal cost to the employment gap is given by the parameter $ \lambda_{MPL}$, which captures how employment fluctuations affect marginal cost both directly through diminishing returns, and indirectly through the relative price of energy. Under this "gap" representation, the supply block of the model - consisting of the price-setting, wage-setting, and real wage evolution equation - is formally similar to the equation structure of the Erceg, Henderson, and Levin (2000) model (henceforth, EHL 2000), notwithstanding differences in the magnitude of the reduced form parameters linking marginal cost (or the MRS gap) to the real wage and employment gaps. This similarity will be discussed in more detail in Section 6 when considering the model's properties under a welfare-maximizing policy. But in addition to affecting these transmission channels, the inclusion of energy also introduces a key distinction between headline and core inflation. This allows for the evaluation of monetary rules that may differ in their response to these alternative inflation measures, in contrast to one sector model's such as EHL (2000) that were confined to focusing on a single measure of price inflation.


5  Calibration

The model is calibrated at a quarterly frequency. The discount factor β is 0.993, consistent with an annualized real interest rate of 3 percent. The subutility function over consumption is chosen to be logarithmic ($ \sigma= 1$) and the Frisch elasticity of labor supply is set to unity ($ \chi= 1$).

The capital share parameter is set at 0.3. Consistent with NIPA data, the energy component of consumption (gasoline and fuel, plus gas and electricity) equals 6%, so that $ \omega_{oc} = 0.06$. Based on value-added data at the industry level (mining and utilities), as well as data for imports of oil, gas, coal and electricity, the share of energy in production is fixed at 2%, which implies $ \omega_{op} = 0.02$.

Price and wage contracts are assumed to have a duration of four quarters, so that $ \xi_{p} = 0.75$, and $ \xi_{w} = 0.75$. The wage markup parameter $ \theta_{w}$ and price markup parameter $ \theta_{p}$ are each set to 1/5 ( $ \theta_{p}$ has no effect on the behavior of the log-linearized behavioral equations, and matters only for determining the coefficients of the optimal policy rule). Finally, the persistence of the (nearly) permanent shock to oil supply ($ \rho_{p}$) is arbitrarily close to unity (0.999), while the persistence of the temporary shock both to oil supply and technology are set to 0.8 ( $ \rho_{p}= \rho_{z} = 0.8$).


6  The Welfare Loss Function

To provide a normative assessment of alternative monetary policy choices, social welfare is measured as the conditional expectation of average household lifetime utility:

$\displaystyle \mathbb{E}_{0} \int_{0}^{1} \left[ \sum_{t=0}^{\infty} \beta^{t} \mathbb{W}_{t}\left( h\right) \right] {dh} = \mathbb{E}_{0}\sum _{t=0}^{\infty} \beta^{t} \left[ \int_{0}^{1} \mathbb{W}_{t}\left( h\right) {dh} \right] = \mathbb{E}_{0}\sum_{t=0}^{\infty} \beta^{t} \mathbb{W} _{t}.$ (19)

Upon taking a second-order approximation to the welfare function, the period loss function - the deviation of period social welfare $ \mathbb{W}_{t}$ from the level that would prevail under flexible prices and wages $ \mathbb{W}^{*}_{t}$ - is given by:10

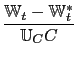
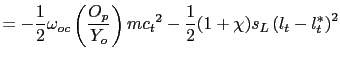
$\displaystyle \frac{\mathbb{W}_{t}-\mathbb{W}^{*}_{t}}{\mathbb{U}_{C}{C}}$ $\displaystyle = -\frac{1} {2}\omega_{oc}\left( \frac{O_{p}}{Y_{o}}\right) {mc_{t}}^{2} -\frac{1} {2}(1+\chi)s_{L}\left( l_{t} -l^{*}_{t} \right) ^{2}$ (20)
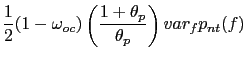
$\displaystyle -$ $\displaystyle \frac{1}{2}(1-\omega_{oc}) \left( \frac{1+\theta_{p}}{\theta_{p}}\right) var_{f}p_{nt}(f)$    
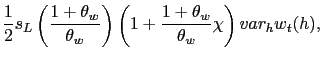
$\displaystyle -$ $\displaystyle \frac{1}{2}s_{L} \left( \frac{1+\theta_{w}}{\theta_{w}}\right) \left( 1+ \frac{1+\theta_{w}}{\theta_{w}} \chi\right) var_{h} w_{t}(h),$    

with $ s_{L} = (1-\alpha)(1-\omega_{oc})(1-\omega_{op})$. The scaling factor $ \mathbb{U}_{C}C$ expresses the period loss as a share of steady state consumption. This period loss function is similar to that derived by EHL (2000) insofar as it depends on cross-sectional dispersion in prices across monopolistically-competitive retailers $ var_{f}p_{nt}(f)$, cross-sectional dispersion in wages across households $ var_{h} w_{t}(h)$, and the square of the employment gap $ (l_{t}-l^{*}_{t})^{2}$. As in that model, the assumption that all firms have identical marginal costs - so that there is no factor attachment in the production of goods - creates a noticeable disparity between the coefficient multiplying the price and wage dispersion terms.

The salient difference relative to EHL (2000) is the presence of the additional term involving the square of the price markup, or equivalently, the square of real marginal cost $ mc_{t}$. This term reflects costs arising from the inefficient allocation of energy across sectors compared to the flexible price equilibrium, and provides some additional rationale for monetary policy to stabilize real marginal cost. Monopolistic competition in the non-energy sector distorts the relative prices faced by households and firms compared to the Pareto-optimal flexible price equilibrium. This is easily seen upon comparing the demand functions of households and firms for energy. The linearized household demand is given by $ o_{ct} = -\log \frac{P_{ot}}{P_{nt}} + y_{wt}$, and hence varies inversely with the price of energy relative to the price index of retail goods; while the linearized energy demand of wholesale producers is given by $ o_{pt} = - \log\frac{P_{ot} }{P_{wt}} + y_{wt}$, and hence depends on the price of energy relative to the wholesale price index. Accordingly, the energy demand of households relative to wholesalers can be expressed:

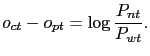$\displaystyle o_{ct}-o_{pt} = \log\frac{P_{nt}}{P_{wt}}.$ (21)

Given the assumption of subsidies to retailers, the gross markup $ \frac {P_{nt}}{P_{wt}}$ simply assumes the constant value of unity under flexible prices and wages. Thus, $ o_{ct}-o_{pt}$ equals zero in the Pareto optimal flexible price equilibrium, and each sector consumes a fixed proportion of the aggregate energy endowment $ Y_{ot}$. By contrast, the markup of the index of retail over wholesale goods varies in the equilibrium with sticky prices, which causes the term $ o_{ct}-o_{pt}$ to fluctuate inefficiently. For example, a shock which lowers the markup causes household demand to fall relative to producer demand, reflecting that the relative price of energy faced by households ($ \frac{P_{ot}}{P_{nt}}$) rises compared with the relative price faced by wholesalers ($ \frac{P_{ot}}{P_{wt}}$).

Because this inefficiency term is scaled by the steady state energy share of production - a small number under any reasonable calibration - its quantitative contribution to welfare turns out to be quite small, so that the welfare loss function does not differ substantially from that of the EHL (2000) model. Even so, it is useful to analyze how this term arises, and to observe that its weight in the welfare loss function would be greater if the variable input that was allocated across sectors comprised a greater share of the input mix of each sector.

With a Calvo-Yun contract structure, the price dispersion term $ {var_{f}} p_{nt}(f)$ evolves according to $ {var_{f}} p_{nt}(f) = (1-\xi_{p}) {var_{f}} p_{nt-1}(f)+ \xi_{p} \pi^{2}_{nt}$ , and similarly for wage dispersion. Using this result and the period loss (20), the discounted conditional welfare loss functional may be expressed as:

  $\displaystyle \mathbb{E}_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ \frac{\mathbb{W} _{t}-\mathbb{W}_{t}^{*}}{\mathbb{U}_{c} {C}} \right] = - \frac{1}{2} (1+\chi)s_{L}\sum_{t=0}^{\infty} \beta^{t} \mathbb{E}_{0} \left( l_{t} -l^{*}_{t} \right) ^{2}$ (22)
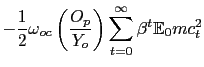
  $\displaystyle -\frac{1}{2}\omega_{oc}\left( \frac{O_{p}}{Y_{o}}\right) \sum_{t=0} ^{\infty} \beta^{t} \mathbb{E}_{0} mc_{t}^{2}$    
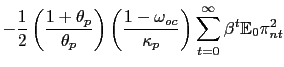
  $\displaystyle -\frac{1}{2} \left( \frac{1+\theta_{p}}{\theta_{p}}\right) \left( \frac{1-\omega_{oc}}{\kappa_{p}}\right) \sum_{t=0}^{\infty} \beta^{t} \mathbb{E}_{0} \pi^{2}_{nt}$    
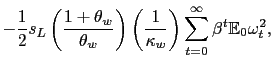
  $\displaystyle - \frac{1}{2} s_{L} \left( \frac{1+\theta_{w}}{\theta_{w}}\right) \left( \frac{1}{\kappa_{w}}\right) \sum_{t=0}^{\infty} \beta^{t} \mathbb{E}_{0} \omega^{2}_{t},$    

with $ \kappa_{p} = \frac{(1-\beta\xi_{p})(1-\xi_{p})}{\xi_{p}}$ and $ \kappa_{w} = \frac{(1-\beta\xi_{w})(1-\xi_{w})}{\xi_{w} \left( 1+\chi \frac{1+\theta_{w}}{\theta_{w}} \right) }$ .

Below, this welfare loss functional is employed both to evaluate the performance of various simple instrument and targeting rules, as well as to derive the optimal full commitment targeting rule following the approach of Woodford (2003) and Svensson and Woodford (2005).


7  The Optimal Policy Rule and Some Alternatives

To derive the full commitment rule, one can use the time invariant first-order conditions obtained from maximizing the conditional loss function (22) subject to the log-linearized behavioral equations. This full commitment rule will be referred to as the optimal rule.

Given this loss function, the characteristics of the optimal rule turn out to depend only on the model's supply block. As noted above, real marginal cost and the MRS gap - the forcing variables in the price- and wage-setting equations - depend only on employment and the real wage (as well as on the reduced form shock $ \eta^{*}_{t}$, recalling that $ l^{*}_{t}=0$). Moreover, after substituting for marginal cost, it is evident that the quadratic loss function (22) also depends only on the same four endogenous variables ( $ \pi_{nt}, \omega_{t}, \eta_{t}, l_{t}$) that enter into the supply block of the model. Thus, by analogy with the simple New Keynesian model, the optimal rule can be derived simply by minimizing the discounted quadratic loss function (22) subject to the price-setting equation (T1 from Table 1, substituting for marginal cost using T2), the wage setting equation (T3, substituting T4), and the real wage evolution equation T5. Accordingly, the responses of core inflation, wage inflation, the employment gap, and real wage gap under the optimal policy depend exclusively on the welfare loss function, and the supply block equations.

Turning next to the optimal responses, Figure 3 examines the effects of a temporary contraction in energy supply ($ y_{ot}$) that is scaled so that the energy price would rise initially by 20 percent in the flexible price and wage equilibrium.11 The panels compare impulse responses of key variables derived under the optimal policy rule with corresponding responses from the flexible price and wage equilibrium. The response of employment under the optimal rule is very small (declining 0.03 percent in response to the 20 percent energy hike), and hence comes close to replicating the flexible price response in which employment is unaffected. Because the (nonenergy) output gap is essentially proportional to the employment gap, it also moves very little, notwithstanding a drop in the level of production due to the lower supply of energy. Real interest rates rise, reflecting an expected recovery in consumption as the effects of the energy shock wear off.

Although the fall in energy supply has an immediate depressing effect on the product real wage in the flexible price equilibrium (equation T10), real wages fall gradually under the optimal policy due to price and wage rigidities. To understand the mechanism underlying the rise in core inflation, note that marginal cost in T2 depends positively on both the real wage gap and employment gap. Despite a slightly negative employment gap, the positive gap between the actual real wage $ \eta_{t}$ and the flexible price real wage $ \eta^{*}_{t}$ puts substantial upward pressure on marginal cost, inducing core prices to rise. Similarly, the expression for the MRS gap in T4 shows that wage inflation falls because the real wage gap is positive (n.b., the coefficient on the real wage gap is close to $ -1$), and the employment gap is negative, both of which induce households to lower their wage (though the quantitative influence of the latter is very small). As capital is freely mobile across firms, prices bear somewhat more of the burden of bringing about the real wage decline, reflecting both that prices are effectively less sticky than wages ($ \kappa_{w} < \kappa_{p}$), and that the welfare weight on price inflation stabilization is correspondingly lower. But the more general implication is that both a rise in core prices, and decline in the nominal wage, are key features of the optimal policy response. Insofar as pure employment gap targeting distributes the price and wage adjustment in nearly the same way as the optimal policy - namely, in a manner proportional to their relative degree of stickiness - it comes very close to replicating the optimal responses.12

The figure also shows how nominal rigidities affect the allocation of energy across sectors compared with the flexible price equilibrium (in which there is no change in the relative proportions of the total endowment consumed by households and firms). As discussed above, the rise in marginal cost - and fall in the markup - means that households experience a larger rise in the relative price of energy than firms. This accounts for some shift in the relative amount of energy demanded towards firms.

The simplified representation of the supply block also facilitates assessment of any targeting rule derived from an objective function that depends on the same variables as the utility-based loss function (22), though with different weights. A natural candidate of interest is a loss function that penalizes variation in core inflation and the employment (or output) gap:

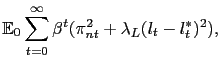
$\displaystyle \mathbb{E}_{0}\sum_{t=0}^{\infty}\beta^{t} ({\pi^{2}_{nt} + \lambda_{L} {(l_{t}-l^{*}_{t})^{2}}}) ,$ (23)

where $ \lambda_{L}$ is the relative weight on the employment gap. This loss function has been widely employed in the literature - dating at least to Kydland and Prescott (1977) - as a stylized characterization of the objective function of many central banks, which appear to care about minimizing volatility in both price inflation and in real activity. Given this "dual mandate" loss function, the responses of core inflation, wage inflation, and the employment gap clearly depend only on the supply block.

Within this class of dual-mandate objective functions, policies that place a large relative weight on stabilizing core price inflation (a low $ \lambda_{L}$) depart markedly from the optimal policy that maximizes social welfare. As shown in Figure 4, such an "aggressive core" policy (for which $ \lambda_{L}$ equals 16/500, when inflation is annualized) succeeds in reducing inflation by generating a substantial negative employment gap, and by putting downward pressure on the real wage. As seen by comparing the first two rows of Table 2, the welfare loss under aggressive core targeting is several times larger than under the optimal policy: the components of the loss presented in columns 2-4 show that the larger loss is attributable to much higher employment gap and wage inflation volatility. Similarly, an aggressive response to headline inflation would precipitate an even larger downturn. The caution against an overly aggressive response to core inflation clearly echoes previous analysis, as in EHL (2000).

But interestingly, Figure 4 suggests that a simple targeting rule that places equal weights on inflation and employment gap stabilization ( $ \lambda_{L}$ = 1/16) performs very well relative to the optimal policy. This is corroborated by Table 2, which reports relatively small losses under this policy compared with the optimum.

This result may seem surprising, given that the objective (23) places no direct weight on wage stabilization (in sharp contrast to the social welfare-based loss function (22)), while according a sizeable weight to stabilizing price inflation. However, it reflects two factors. First, as noted above, output gap stabilization is a close approximation to the optimal policy. Second, the variance tradeoff frontier derived from the simple loss function (22) is quite flat when represented in the volatility of inflation and employment gap space, as can be seen in Figure 5. Following the seminal approach of Taylor (1979), this tradeoff frontier - or "Taylor Curve" - is obtained by minimizing the policymaker's loss function (23) over all possible values of $ \lambda_{L}$ subject to the log-linearized behavioral equations. As suggested by the alternative dual mandate policies examined in Figure 4 - where the aggressive rule only reduced inflation modestly at the cost of a much more substantial output contraction - it is very costly to reduce inflation volatility in the model. The flatness of the Taylor Curve means that a policymaker with preferences of the form (23) would only be willing to depart markedly from employment gap targeting if he placed a very large weight on inflation stabilization ($ \lambda_{L}$ close to zero). As a corollary, a wide range of values of the preference parameter $ \lambda_{L}$ imply policy rules close to output gap targeting. Thus, the dual mandate rule with balanced weights depicted by point C in Figure 5 has implications very close to the rule implying strict employment gap targeting (the latter achieves zero volatility in employment, which in the figure lies at the intersection of the Taylor Curve and vertical axis).

Evaluating the results from a broader perspective, wage rigidities play a central role in determining the tradeoffs facing monetary policymakers, and hence in the transmission of shocks. While the inefficiency associated with the allocation of energy across sectors is a new consideration relative to the models of both Aoki (2001) and EHL (2000), it would not introduce a stabilization tradeoff in the absence of wage stickiness. This is because the policymaker could simply eliminate this allocative inefficiency by stabilizing marginal cost (equivalently, the price markup), which would be achieved by keeping employment at potential, and core inflation at its target level. Thus, the prescription of Aoki's flexible wage model to completely stabilize core prices (and allow the nominal energy price to bring about any changes in the relative price of energy) would indeed emerge in a variant of the model with flexible wages.

But given the inclusion of wage rigidities, the transmission of energy shocks under monetary rules oriented towards stabilizing core inflation (and presumably other goal variables) closely resembles that of a technology shock in the one sector model of EHL (2000); and from a normative perspective, what constitutes good policy is also very similar (for example, employment gap targeting). This reflects that the quantitative implications of the changes introduced into the loss function and into the "reduced form" parameters of the supply block equations appear quite small using reasonable weights for the importance of energy. Thus, the addition of an energy sector has small effects on the transmission of shocks under policies rules that are oriented towards stabilizing core inflation (and other typical goal variables). However, it remains possible that even with a fairly modest share of energy in the consumption bundle (such as the chosen six percent), energy shocks could cause headline and core inflation to diverge enough that policies oriented towards stabilizing the former could exert markedly different effects on the economy. It is to this issue that we next turn.

7.1  Taylor rules that respond to alternative inflation forecasts

Many inflation-targeting central banks have an explicit goal of adjusting policy so that their forecast of inflation reverts to some target level within a specified period of roughly two to three years. Typically, this objective is expressed in terms of a measure of headline inflation, on the grounds that its high degree of public visibility facilitates central bank communication. While it is acknowledged that reacting to realized core and headline inflation would imply very different policy actions in the face of energy price shocks, it is often presumed that responding to a forecast of either headline or core inflation would have similar operational implications for the conduct of policy.13

The conjecture that targeting a forecast of headline or core inflation has similar implications in response to a permanent shock certainly appears correct. As seen by taking the lead of equation T8:

$\displaystyle \pi_{ct+1\vert t} = \pi_{nt+1\vert t} + \omega_{oc} \left( \psi_{ot+1\vert t}-\psi _{ot}\right) ,$ (24)

it is evident that rational forecast of headline and core inflation should be equal in the case of a permanent shock to the relative price of energy. However, Section 2 presented evidence that energy price shocks are often temporary, and that reasonable forecasts of headline and core inflation have exhibited pronounced divergence on this account. In the case of a temporary energy price shock, the wedge between the forecast of headline and core inflation due to predicted mean reversion in the energy price - clearly evident from equation (24) - has important implications for monetary policy. In particular, policies that respond to forecasts of core and headline inflation imply significantly different reactions, with consequent effects on output and inflation.

This is illustrated in Figure 6, which shows the effects of the temporary energy supply shock (considered in Figures 3 and 4) under the optimal policy, and also under two Taylor-style policy rules that respond to alternative inflation forecasts. The latter rules are described by the general interest rate reaction function (18), with the "core CPI forecast" rule setting the coefficient on one period ahead core inflation to 1.5 (i.e., $ \gamma_{1f} = 1.5$), and the "headline CPI forecast" rule setting the coefficient on one period ahead headline inflation to 1.5 (i.e., $ \gamma_{2f} = 1.5$). The coefficient on the output gap is set to 0.5 in each of the instrument rules ($ \gamma_{y} = 0.5$) when expressed at an annualized rate.

Figure 6 indicates that the one quarter ahead forecast of headline inflation nearly reverts to baseline after 3 years under either rule. Thus, either policy appears to succeed in keeping a forecast of headline inflation near baseline over the "medium-term" horizon that is the focus of most inflation-targeting central banks. However, the macroeconomic effects are considerably different over shorter horizons. The policy of responding to a forecast of core inflation appears reasonably similar to the optimal policy insofar as policy tightens in response to higher near-term forecasts of core inflation. There are still some differences relative to the optimal rule: the calibrated policy rule is not aggressive enough to keep the output gap from rising, wage inflation rises, and core inflation increases more substantially; but overall, the macroeconomic implications do not appear very different. By contrast, the policy that responds to a forecast of headline inflation is much more accommodative, reflecting the expected persistent decline in energy price inflation below baseline. Low real interest rates fuel a large and persistent employment gap, core inflation remains significantly above baseline even after a year, and wage inflation exhibits a persistent increase.

Thus, the rule responding to a forecast of headline inflation performs poorly on the dimensions which the model indicates are important for welfare; notably, rather than bringing about real wage adjustment with minimal movements in wage inflation and core price inflation, it induces large movements in both variables in the same direction (Table 2 indicates welfare losses are large). Nevertheless, this rule might still appear somewhat attractive from the perspective of a central bank with a strong desire to control variability in headline inflation. In particular, it is clear from the panel showing the headline inflation forecast in Figure 6 that realized headline inflation is in fact more stable after the impact period than under the alternative policies.

But even the enhanced ability of the headline forecast rule to reduce the variability of realized headline inflation hinges on the assumption that agents correctly perceive the underlying shock. In a more realistic setting in which agents are unsure if the energy shock is temporary or permanent, the rule responding to a forecast of headline inflation may cause realized headline inflation to stray more persistently from target, as well as induce large and persistent deviations in core inflation and the employment gap. This uncertainty about the underlying shock is modeled through a signal extraction framework in which agents observe only the total energy supply $ Y_{ot}$, but not the individual shock components. Given that agents are assumed to understand the law of motion for these exogenous shocks, i.e., equations (16), and (17), they solve a Kalman filtering problem to make optimal forecasts of the energy price.

Within this framework, Figure 7 shows the effects of a permanent contraction in energy supply that agents initially perceive as largely transitory. The relative size of innovations to the permanent and temporary component are calibrated so that the Kalman gain parameter is 0.10. Accordingly, agents initially forecast that about 90 percent of the price hike will eventually be reversed, and only gradually revise their beliefs about the permanence of the shock. Because energy price inflation is incorrectly projected to be negative for a protracted period, the headline forecast rule implies a persistently accommodative policy. Real rates remain very low, which fuels a persistent rise in both the employment gap and core inflation. Because the expected drop in energy prices never materializes, headline inflation tracks core inflation after the initial price spike, and thus remains very elevated until agents finally grasp the permanent nature of the shock.


8  Conclusion

This paper has investigated the performance of alternative monetary rules in response to an energy supply shock, using the optimal rule that maximizes household welfare as the benchmark of comparison. A key finding is that the optimal response to an adverse energy supply shock involves a persistent rise in core and headline inflation. Moreover, under plausible conditions, policies responding to a forecast of headline inflation can induce very different macroeconomic effects than policies responding to a forecast of core inflation. The related finding that the latter type of policies exhibit better stabilization properties seems relevant for both the operational conduct of central banks and their communication strategies.

There are some aspects that merit further investigation in subsequent work. In particular, the model assumes that monetary policy can commit to a time invariant rule, and that the central bank's inflation target is both known to private agents and fully credible. While the model implies that core inflation rises in response to higher energy prices under the optimal policy, many central banks perceive that their credibility depends on forestalling "second round" spillovers into core inflation. Accordingly, it would be interesting to examine the robustness of these conclusions to a setting in which monetary policy might not be fully credible, or in which the public may be uncertain about policymaker's objectives.


References

Anderson, G. (1997). A Reliable and Computationally Efficient Algorithm for Imposing the Saddle Point Property in Dynamic Models. Federal Reserve Board, Occasional Staff's Studies 4.

Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.

Aoki, K. (2001). Optimal Monetary Policy Responses to Relative-Price Changes. Journal of Monetary Economics 48, 55-80.

Aucremanne, L. and R. Wouters (1999). A Structural VAR Approach to Core Inflation and its Relevance for Monetary Policy. In Measures of Underlying Inflation and their Role in the Conduct of Monetary Policy: Workshop Proceedings. Basel: BIS.

Bernanke, B., T. Laubach, F. S. Mishkin, and A. S. Posen (1999). Inflation Targeting: Lessons from the International Experience. Princeton, NJ: Princeton University Press.

Blanchard, O. J. and J. Galí (2007). The Macroeconomic Effects of Oil Price Shocks: Why are the 2000s so different from the 1970s? Working Papers, Pompeu Frabra University.

Blanchard, O. J. and C. M. Kahn (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica 48(5), 1305-1312.

Bryan, M. F. and S. G. Cecchetti (1994). Measuring Core Inflation. In N. G. Mankiw (Ed.), Monetary Policy.

Bryan, M. F. and C. J. Pike (1991). Median price changes: an alternative approach to measuring current monetary inflation. Economic Commentary, 1-4.

Dhawan, R. and K. Jeske (2007). Taylor Rules with Headline Inflation: A Bad Idea. Federal Reserve Bank of Atlanta, Working Paper Number 2007-14.

Erceg, C. J., D. W. Henderson, and A. T. Levin (2000). Optimal Monetary Policy with Staggered Wage and Price Contracts. Journal of Monetary Economics 46, 281-313.

Faust, J. and D. Henderson (2004). Is Inflation Targeting Best Practice Monetary Policy. International Finance Discussion Papers, Number 807.

Goodfriend, M. and R. King (1997). The New Neoclassical Synthesis and the Role of Monetary Policy. NBER Macroeconomics Annual, 231-281.

King, R. G. and A. L. Wolman (1998). What Should the Monetary Authority Do When Prices Are Sticky? In J. B. Taylor (Ed.), Monetary Policy Rules. The University of Chicago Press.

Kydland, F. E. and E. C. Prescott (1977). Rules Rather than Discretion: The Inconsistency of Optimal Plans. The Journal of Political Economy 85(3), 473-492.

Leduc, S. and K. Sill (2004). A Quantitative Analysis of Oil-Price Shocks, Systematic Monetary Policy, and Economic Downturns. Journal of Monetary Economics 51, 781-808.

Mishkin, F. S. (2007). Headline versus Core Inflation in the Conduct of Monetary Policy. Presentation given at the Business Cycles, International Transmission and Macroeconomic Policies Conference. HEC Montreal.

Quah, D. and S. Vehey (1995). Measuring Core Inflation. The Economic Journal, 1130-1144.

Rotemberg, J. and M. Woodford (1997). An Optimization-Based Econometric Frame-work for the Evaluation of Monetary Policy. NBER Macroeconomics Annual 12, 297-346.

Svensson, L. and M. Woodford (2005). Implementing Optimal Policy through Inflation-Forecast Targeting. In B. Bernanke and M. Woodford (Eds.), The Inflation-Targeting Debate, pp. 19-92. Chicago: The University of Chicago Press.

Taylor, J. B. (1979). Estimation and Control of a Macroeconomic Model with Rational Expectations. Econometrica 47(5), 1267-1286.

Woodford, M. (2003). Interest and Prices. Princeton, NJ: Princeton University Press.

Table 1:  Log-Linearized Model Equations

$ \pi_{nt} = \beta\pi_{nt+1\vert t} + \kappa_{p} mc_{t} $Price setting T1
$ mc_{t} = (1-\omega_{op})\left[ (\eta_{t} - \eta^{*}_{t}) + \alpha(l_{t} - l^{*}_{t}) \right] + \omega_{op} \left( \psi_{ot} - \psi^{*}_{ot} \right) $
$ \,\,\,\,\,\,\,\,\,\,\,= \vartheta_{1}(\eta_{t} - \eta^{*}_{t}) + \lambda_{MPL}(l_{t}-l^{*}_{t}) $		Marginal cost T2
$ \omega_{t} = \beta\omega_{t+1\vert t} + \kappa_{w}(MRS_{t} - \eta_{t}) $Wage Setting T3
$ MRS_{t} - \eta_{t} = \omega_{oc}(\psi_{ot}-\psi^{*}_{ot}) + \left( \chi+ s_{L} \right) (l_{t}-l^{*}_{t}) - (\eta_{t} - \eta^{*}_{t})$
$ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= -\vartheta_{1} (\eta_{t} - \eta^{*}_{t}) + \lambda_{MRS} (l_{t} - l^{*}_{t}) $		MRS Gap T4
$ \eta_{t} - \eta_{t-1} = \omega_{t} - \pi_{nt}$Real wage T5
$ \psi_{ot} - \psi^{*}_{ot} = \left( \frac{\omega_{op}}{\omega_{op}+\omega _{oc}}\right) (\eta_{t} - \eta^{*}_{t})+ \vartheta_{2} (l_{t} - l^{*}_{t}) \nonumber $Oil price T6
$ (l_{t} - l_{t}^{*} ) =( l_{t+1} -l_{t+1}^{*}) - \frac{1}{ \sigma s_{L}}\left( i_{t} - \pi_{ct+1} - r_{ct}^{*}\right) $IS curve T7
$ \pi_{ct} = \pi_{nt} + \omega_{oc} \left( \psi_{ot}-\psi_{ot-1} \right) $CPI inflation T8
$ l^{*}_{t} = 0 $Flex Price Employment T9
$ \eta^{*}_{t} = \omega_{op}y_{ot} + (1-\alpha)(1-\omega_{op})z_{t} $Flex Price Real Wage T10
$ \psi^{*}_{ot} = -y_{ot} + \eta^{*}_{t} = -(1-\omega_{op})y_{ot} + (1-\alpha)(1-\omega_{op})z_{t} $Flex Price Oil Price T11
$ r^{*}_{ct} = c^{*}_{t+1\vert t} - c^{*}_{t} $Flex Price Real Rate T12
$ c^{*}_{t} = s_{L} z_{t} + \left[ \omega_{oc}+\omega_{op}(1-\omega _{oc})\right] y_{ot} $Flex Price Consumption T13

where

$ \kappa_{p} = \frac{(1-\beta\xi_{p})(1-\xi_{p})}{\xi_{p}}$, $ \kappa_{w} = \frac{(1-\beta\xi_{w})(1-\xi_{w})}{\xi_{w}(1+\chi\frac {1+\theta_{w}}{\theta_{w}})}$ ,
$ \vartheta_{1} =\left( \frac{\omega_{oc}+\omega_{op}-\omega_{oc}\omega_{op} }{\omega_{op}+\omega_{oc}}\right) ,$ $ \vartheta_{2} = \left[ \frac {\alpha\omega_{op} + (1-\alpha) \left( \omega_{oc}+\omega_{op}-\omega _{oc}\omega_{op}\right) }{\omega_{op}+\omega_{oc}}\right] , $
$ s_{L}=(1-\alpha)(1-\omega_{oc})(1-\omega_{op})$,      $ \lambda_{MPL} = \alpha+ (1-\alpha)\omega_{op}$,
$ \lambda_{MRS} = \omega_{oc}\vartheta_{2} + s_{L} + \chi. $

Table 2:  Welfare Loss under Alternative Policies (as a percent of steady state consumption, multiplied by 102)

Policy Rule
Welfare loss due to volatility in:
Employment Gap**
Welfare loss due to volatility in:
Price Inflation
Welfare loss due to volatility in:
Wage Inflation
Total
A. Optimal Policy
0.00
0.17
0.03
0.20
B. Dual Mandate (aggressive core)
0.34
0.03
0.51
0.88
C. Dual Mandate (balanced weights)
0.01
0.15
0.05
0.22
D. Taylor (forecast of core)
0.14
0.49
0.42
1.05
E. Taylor (forecast headline)
4.11
3.83
11.16
19.11

**  The employment gap term above includes losses due to volatility in both employment and the price markup, corresponding to the first two terms of the loss function given in (22).

Figure 1:  CPI Inflation

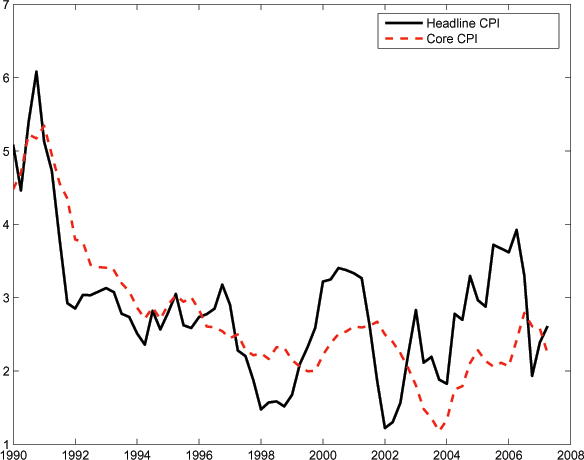
Data for Figure 1 immediately follows.

Data for Figure 1

Quarters
Headline CPI
Core CPI
1990.00
5.09
4.48
1990.25
4.46
4.71
1990.50
5.40
5.23
1990.75
6.08
5.17
1991.00
5.13
5.34
1991.25
4.73
4.95
1991.50
3.79
4.56
1991.75
2.92
4.35
1992.00
2.85
3.79
1992.25
3.04
3.76
1992.50
3.03
3.45
1992.75
3.08
3.42
1993.00
3.13
3.41
1993.25
3.08
3.37
1993.50
2.78
3.20
1993.75
2.74
3.08
1994.00
2.51
2.86
1994.25
2.36
2.71
1994.50
2.82
2.87
1994.75
2.57
2.71
1995.00
2.79
2.90
1995.25
3.05
3.03
1995.50
2.62
2.94
1995.75
2.59
3.01
1996.00
2.74
2.83
1996.25
2.78
2.61
1996.50
2.85
2.60
1996.75
3.18
2.54
1997.00
2.90
2.45
1997.25
2.28
2.50
1997.50
2.20
2.29
1997.75
1.88
2.21
1998.00
1.48
2.24
1998.25
1.57
2.17
1998.50
1.59
2.32
1998.75
1.52
2.32
1999.00
1.67
2.15
1999.25
2.09
2.06
1999.50
2.32
2.00
1999.75
2.59
2.00
2000.00
3.22
2.22
2000.25
3.25
2.38
2000.50
3.40
2.51
2000.75
3.38
2.54
2001.00
3.33
2.61
2001.25
3.27
2.59
2001.50
2.64
2.62
2001.75
1.86
2.67
2002.00
1.22
2.50
2002.25
1.30
2.40
2002.50
1.57
2.24
2002.75
2.22
2.04
2003.00
2.83
1.80
2003.25
2.11
1.48
2003.50
2.19
1.36
2003.75
1.88
1.18
2004.00
1.83
1.33
2004.25
2.78
1.75
2004.50
2.70
1.79
2004.75
3.30
2.11
2005.00
2.97
2.28
2005.25
2.88
2.14
2005.50
3.72
2.06
2005.75
3.67
2.11
2006.00
3.62
2.06
2006.25
3.92
2.42
2006.50
3.30
2.79
2006.75
1.93
2.61
2007.00
2.39
2.58
2007.25
2.61
2.24

Figure 2:  CPI Inflation Forecasts

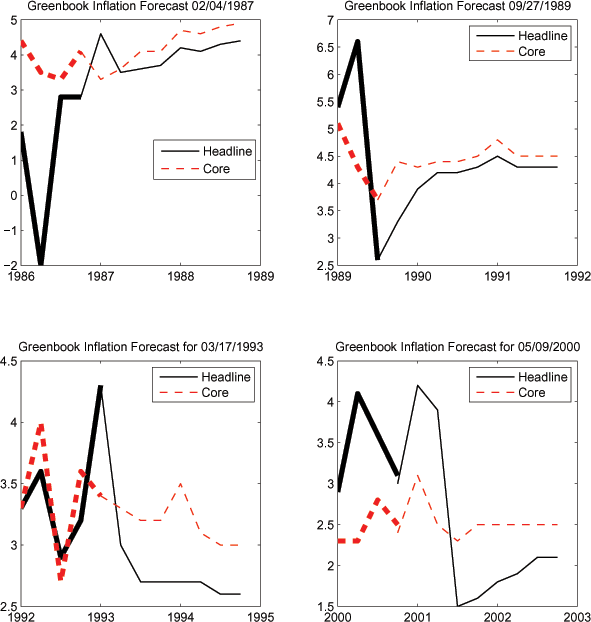
Data for Figure 2 immediately follows.

Data for Figure 2 - Panel A: CPI Inflation Forecasts: Greenbook Inflation Forecast 02/04/1987 (bold indicates forecast values)

Quarters
Headline
Core
1986.00
1.8
4.4
1986.25
-2.0
3.5
1986.50
2.8
3.3
1986.75
2.8
4.1
1987.00
4.6
3.3
1987.25
3.5
3.6
1987.50
3.6
4.1
1987.75
3.7
4.1
1988.00
4.2
4.7
1988.25
4.1
4.6
1988.50
4.3
4.8
1988.75
4.4
4.9

Data for Figure 2 - Panel B: CPI Inflation Forecasts: Greenbook Inflation Forecast 09/27/1989 (bold indicates forecast values)

Quarters
Headline
Core
1989.00
5.4
5.1
1989.25
6.6
4.3
1989.50
2.6
3.7
1989.75
3.3
4.4
1990.00
3.9
4.3
1990.25
4.2
4.4
1990.50
4.2
4.4
1990.75
4.3
4.5
1991.00
4.5
4.8
1991.25
4.3
4.5
1991.50
4.3
4.5
1991.75
4.3
4.5

Data for Figure 2 - Panel C: CPI Inflation Forecasts: Greenbook Inflation Forecast 03/17/1993 (bold indicates forecast values)

Quarters
Headline
Core
1992.00
3.3
3.3
1992.25
3.6
4.0
1992.50
2.9
2.7
1992.75
3.2
3.6
1993.00
4.3
3.4
1993.25
3.0
3.3
1993.50
2.7
3.2
1993.75
2.7
3.2
1994.00
2.7
3.5
1994.25
2.7
3.1
1994.50
2.6
3.0
1994.75
2.6
3.0

Data for Figure 2 - Panel D: CPI Inflation Forecasts: Greenbook Inflation Forecast 05/09/2000 (bold indicates forecast values)

Quarters
Headline
Core
2000.00
2.9
2.3
2000.25
4.1
2.3
2000.50
3.6
2.8
2000.75
3.1
2.5
2001.00
4.2
3.1
2001.25
3.9
2.5
2001.50
1.5
2.3
2001.75
1.6
2.5
2002.00
1.8
2.5
2002.25
1.9
2.5
2002.50
2.1
2.5
2002.75
2.1
2.5


Figure 3:  Temporary Contraction in Energy Supply
Optimal Policy vs. Flexible Prices

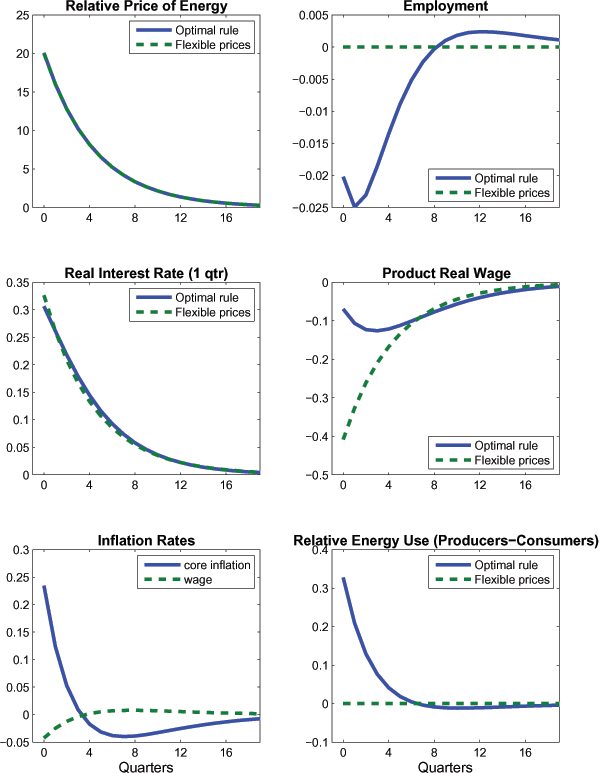
Data for Figure 3 immediately follows.

Data for Figure 3

Quarters
Relative Price of Energy:
Optimal Rule
Relative Price of Energy:
Flexible Prices
Employment:
Optimal Rule
Employment:
Flexible Prices
Real Interest Rate (1 qtr):
Optimal Rule
Real Interest Rate (1 qtr):
Flexible Prices
Product Real Wage:
Optimal Rule
Product Real Wage:
Flexible Prices
Inflation Rates:
Optimal Rule
Inflation Rates:
Flexible Prices
Relative Energy Use (Producers-Consumers):
Optimal Rule
Relative Energy Use (Producers-Consumers):
Flexible Prices
1
20.06931
20.00004
-0.02021
0
0.30637
0.32653
-0.06926
-0.40816
0.23449
-0.04255
0.32757
0
2
16.03600
16.00003
-0.02493
0
0.26153
0.26122
-0.10641
-0.32653
0.12377
-0.02482
0.20911
0
3
12.81704
12.80002
-0.02304
0
0.21810
0.20898
-0.12270
-0.26122
0.05289
-0.01230
0.12932
0
4
10.24662
10.24002
-0.01854
0
0.17889
0.16718
-0.12587
-0.20898
0.00888
-0.00379
0.07613
0
5
8.19321
8.19201
-0.01349
0
0.14496
0.13375
-0.12114
-0.16718
-0.01720
0.00174
0.04118
0
6
6.55224
6.55361
-0.00891
0
0.11642
0.10700
-0.11200
-0.13375
-0.03147
0.00509
0.01867
0
7
5.24051
5.24289
-0.00516
0
0.09287
0.08560
-0.10074
-0.10700
-0.03812
0.00692
0.00457
0
8
4.19173
4.19431
-0.00232
0
0.07371
0.06848
-0.08882
-0.08560
-0.03997
0.00770
-0.00389
0
9
3.35305
3.35545
-0.00031
0
0.05830
0.05478
-0.07713
-0.06848
-0.03894
0.00780
-0.00862
0
10
2.68229
2.68436
0.00102
0
0.04599
0.04383
-0.06620
-0.05478
-0.03627
0.00747
-0.01093
0
11
2.14577
2.14749
0.00183
0
0.03622
0.03506
-0.05628
-0.04383
-0.03279
0.00689
-0.01170
0
12
1.71660
1.71799
0.00225
0
0.02850
0.02805
-0.04748
-0.03506
-0.02902
0.00619
-0.01153
0
13
1.37329
1.37439
0.00239
0
0.02241
0.02244
-0.03979
-0.02805
-0.02528
0.00545
-0.01083
0
14
1.09863
1.09951
0.00236
0
0.01762
0.01795
-0.03318
-0.02244
-0.02175
0.00472
-0.00985
0
15
0.87891
0.87961
0.00222
0
0.01387
0.01436
-0.02753
-0.01795
-0.01854
0.00404
-0.00875
0
16
0.70313
0.70369
0.00201
0
0.01092
0.01149
-0.02276
-0.01436
-0.01567
0.00343
-0.00765
0
17
0.56250
0.56295
0.00178
0
0.00860
0.00919
-0.01875
-0.01149
-0.01316
0.00288
-0.00660
0
18
0.44999
0.45036
0.00154
0
0.00679
0.00735
-0.01540
-0.00919
-0.01100
0.00240
-0.00564
0
19
0.35998
0.36029
0.00132
0
0.00536
0.00588
-0.01261
-0.00735
-0.00915
0.00199
-0.00477
0
20
0.28797
0.28823
0.00111
0
0.00424
0.00471
-0.01031
-0.00588
-0.00758
0.00164
-0.00402
0


Figure 4:  Temporary Contraction in Energy Supply
Alternative Targeting Rules

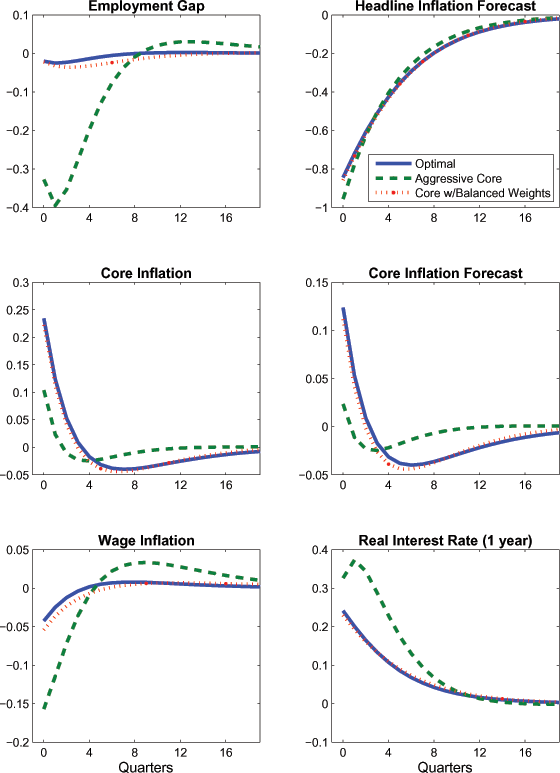
Data for Figure 4 immediately follows.

Data for Figure 4

Quarters
Employment Gap:
Optimal
Employment Gap:
Aggressive Core
Employment Gap:
Core w/Balance Weights
Headline Inflation Forecast:
Optimal
Headline Inflation Forecast:
Aggressive Core
Headline Inflation Forecast:
Core w/Balance Weights
Core Inflation:
Optimal
Core Inflation:
Aggressive Core
Core Inflation:
Core w/Balance Weights
Core Inflation Forecast:
Optimal
Core Inflation Forecast:
Aggressive Core
Core Inflation Forecast:
Core w/Balance Weights
Wage Inflation:
Optimal
Wage Inflation:
Aggressive Core
Wage Inflation:
Core w/Balance Weights
Real Interest Rate (1 year):
Optimal
Real Interest Rate (1 year):
Aggressive Core
Real Interest Rate (1 year):
Core w/Balance Weights
1
-0.02021
-0.32746
-0.02187
-0.84423
-0.95583
-0.85750
0.23449
0.10393
0.22223
0.12377
0.02350
0.11154
-0.04255
-0.15703
-0.05417
0.24122
0.32624
0.22952
2
-0.02493
-0.39478
-0.03235
-0.71966
-0.77636
-0.73227
0.12377
0.02350
0.11154
0.05289
-0.01111
0.04125
-0.02482
-0.11449
-0.03638
0.20087
0.37292
0.19278
3
-0.02304
-0.35346
-0.03579
-0.60802
-0.62680
-0.61925
0.05289
-0.01111
0.04125
0.00888
-0.02316
-0.00166
-0.01230
-0.07165
-0.02332
0.16459
0.34373
0.16062
4
-0.01854
-0.27671
-0.03508
-0.51001
-0.50400
-0.51946
0.00888
-0.02316
-0.00166
-0.01720
-0.02471
-0.02627
-0.00379
-0.03580
-0.01381
0.13329
0.28784
0.13293
5
-0.01349
-0.19772
-0.03211
-0.42530
-0.40412
-0.43280
-0.01720
-0.02471
-0.02627
-0.03147
-0.02187
-0.03887
0.00174
-0.00873
-0.00696
0.10699
0.22820
0.10939
6
-0.00891
-0.12966
-0.02806
-0.35293
-0.32341
-0.35849
-0.03147
-0.02187
-0.03887
-0.03812
-0.01764
-0.04380
0.00509
0.01018
-0.00209
0.08532
0.17448
0.08958
7
-0.00516
-0.07616
-0.02367
-0.29168
-0.25845
-0.29544
-0.03812
-0.01764
-0.04380
-0.03997
-0.01340
-0.04399
0.00692
0.02235
0.00131
0.06772
0.12984
0.07304
8
-0.00232
-0.03665
-0.01939
-0.24022
-0.20633
-0.24237
-0.03997
-0.01340
-0.04399
-0.03894
-0.00969
-0.04144
0.00770
0.02936
0.00362
0.05356
0.09445
0.05933
9
-0.00031
-0.00895
-0.01545
-0.19726
-0.16460
-0.19802
-0.03894
-0.00969
-0.04144
-0.03627
-0.00669
-0.03742
0.00780
0.03264
0.00514
0.04225
0.06727
0.04803
10
0.00102
0.00944
-0.01196
-0.16156
-0.13124
-0.16116
-0.03627
-0.00669
-0.03742
-0.03279
-0.00438
-0.03280
0.00747
0.03332
0.00608
0.03328
0.04686
0.03875
11
0.00183
0.02085
-0.00897
-0.13202
-0.10460
-0.13070
-0.03279
-0.00438
-0.03280
-0.02902
-0.00265
-0.02808
0.00689
0.03231
0.00660
0.02619
0.03182
0.03117
12
0.00225
0.02721
-0.00645
-0.10768
-0.08333
-0.10563
-0.02902
-0.00265
-0.02808
-0.02528
-0.00140
-0.02358
0.00619
0.03026
0.00682
0.02060
0.02092
0.02500
13
0.00239
0.03004
-0.00437
-0.08767
-0.06638
-0.08508
-0.02528
-0.00140
-0.02358
-0.02175
-0.00053
-0.01947
0.00545
0.02764
0.00683
0.01620
0.01315
0.01999
14
0.00236
0.03050
-0.00269
-0.07127
-0.05286
-0.06829
-0.02175
-0.00053
-0.01947
-0.01854
0.00006
-0.01582
0.00472
0.02477
0.00670
0.01275
0.00770
0.01594
15
0.00222
0.02943
-0.00135
-0.05786
-0.04208
-0.05461
-0.01854
0.00006
-0.01582
-0.01567
0.00043
-0.01265
0.00404
0.02188
0.00647
0.01004
0.00395
0.01267
16
0.00201
0.02746
-0.00030
-0.04692
-0.03350
-0.04351
-0.01567
0.00043
-0.01265
-0.01316
0.00066
-0.00995
0.00343
0.01910
0.00618
0.00792
0.00144
0.01004
17
0.00178
0.02501
0.00051
-0.03800
-0.02667
-0.03453
-0.01316
0.00066
-0.00995
-0.01100
0.00078
-0.00768
0.00288
0.01652
0.00586
0.00625
-0.00018
0.00792
18
0.00154
0.02237
0.00111
-0.03075
-0.02122
-0.02727
-0.01100
0.00078
-0.00768
-0.00915
0.00082
-0.00579
0.00240
0.01418
0.00552
0.00494
-0.00118
0.00623
19
0.00132
0.01972
0.00156
-0.02486
-0.01689
-0.02143
-0.00915
0.00082
-0.00579
-0.00758
0.00081
-0.00424
0.00199
0.01208
0.00517
0.00390
-0.00175
0.00487
20
0.00111
0.01719
0.00187
-0.02008
-0.01344
-0.01674
-0.00758
0.00081
-0.00424
-0.00625
0.00078
-0.00298
0.00164
0.01024
0.00483
0.00309
-0.00202
0.00379


Figure 5:  Policy Tradeoff Frontier for Temporary Energy Supply Shock

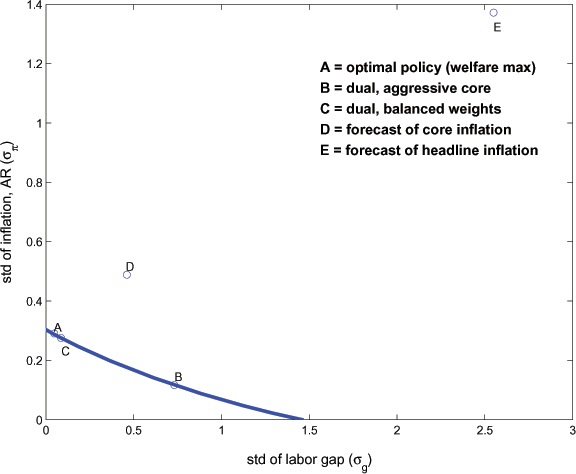
In Figure 5, following the seminal approach of Taylor, this tradeoff frontier - or Taylor Curve - is obtained by minimizing the policymaker's loss function over all possible values of of lambda subject to the log-linearized behavioral equations. As suggested by the alternative dual mandate policies examined in Figure 4 - where the aggressive rule only reduced inflation modestly at the cost of a much more substantial output contraction - it is very costly to reduce inflation volatility in the model. In the figure the Taylor frontier appears flat, intersecting the y axis (showing the standard deviation of inflation at an annualized rate) at 0.3, and the x axis (showing the standard deviation of the output gap) at 1.5. The flatness of the Taylor Curve means that a policymaker with preferences of the form (\ref{policyloss1}) would only be willing to depart markedly from employment gap targeting if he placed a very large weight on inflation stabilization.



Figure 6:  Temporary Contraction in Energy Supply
Forecast-Based Taylor Rules

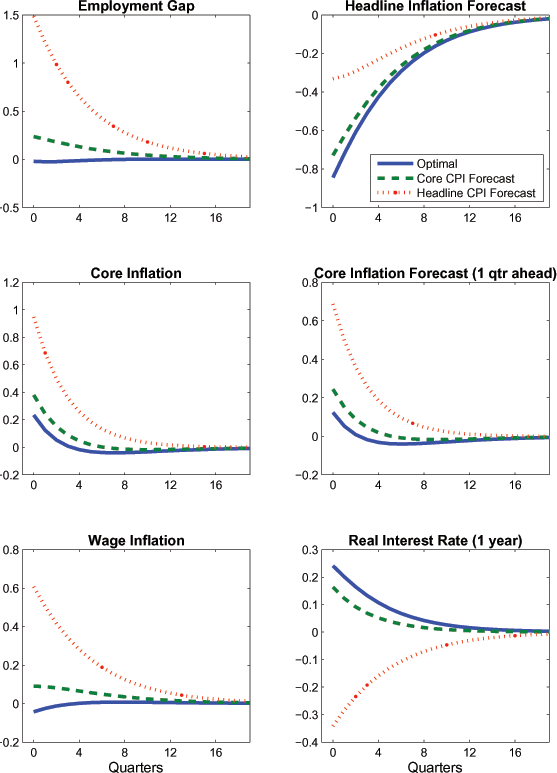
Data for Figure 6 immediately follows.

Data for Figure 6

Quarters
Employment Gap:
Optimal
Employment Gap:
Core CPI Forecast
Employment Gap:
Headline CPI Forecast
Headline Inflation Forecast:
Optimal
Headline Inflation Forecast:
Core CPI Forecast
Headline Inflation Forecast:
Headline CPI Forecast
Core Inflation:
Optimal
Core Inflation:
Core CPI Forecast
Core Inflation:
Headline CPI Forecast
Core Inflation Forecast (1 qtr ahead):
Optimal
Core Inflation Forecast (1 qtr ahead):
Core CPI Forecast
Core Inflation Forecast (1 qtr ahead):
Headline CPI Forecast
Wage Inflation:
Optimal
Wage Inflation:
Core CPI Forecast
Wage Inflation:
Headline CPI Forecast
Real Interest Rate (1 year):
Optimal
Real Interest Rate (1 year):
Core CPI Forecast
Real Interest Rate (1 year):
Headline CPI Forecast
1
-0.02021
0.23686
1.48595
-0.84423
-0.72842
-0.33108
0.23449
0.37995
0.94696
0.12377
0.24405
0.68702
-0.04255
0.09088
0.60642
0.24122
0.16371
-0.34146
2
-0.02493
0.20832
1.21104
-0.71966
-0.62710
-0.31710
0.12377
0.24405
0.68702
0.05289
0.15095
0.49746
-0.02482
0.08815
0.50336
0.20087
0.12241
-0.28330
3
-0.02304
0.18058
0.98530
-0.60802
-0.53447
-0.29230
0.05289
0.15095
0.49746
0.00888
0.08801
0.35941
-0.01230
0.08194
0.41617
0.16459
0.09160
-0.23413
4
-0.01854
0.15476
0.80042
-0.51001
-0.45183
-0.26239
0.00888
0.08801
0.35941
-0.01720
0.04620
0.25902
-0.00379
0.07400
0.34290
0.13329
0.06860
-0.19284
5
-0.01349
0.13142
0.64934
-0.42530
-0.37938
-0.23102
-0.01720
0.04620
0.25902
-0.03147
0.01906
0.18614
0.00174
0.06544
0.28168
0.10699
0.05142
-0.15836
6
-0.00891
0.11076
0.52612
-0.35293
-0.31676
-0.20042
-0.03147
0.01906
0.18614
-0.03812
0.00202
0.13333
0.00509
0.05697
0.23079
0.08532
0.03858
-0.12972
7
-0.00516
0.09277
0.42582
-0.29168
-0.26320
-0.17188
-0.03812
0.00202
0.13333
-0.03997
-0.00817
0.09514
0.00692
0.04898
0.18866
0.06772
0.02897
-0.10601
8
-0.00232
0.07729
0.34429
-0.24022
-0.21781
-0.14603
-0.03997
-0.00817
0.09514
-0.03894
-0.01377
0.06760
0.00770
0.04171
0.15390
0.05356
0.02178
-0.08646
9
-0.00031
0.06410
0.27812
-0.19726
-0.17960
-0.12313
-0.03894
-0.01377
0.06760
-0.03627
-0.01636
0.04778
0.00780
0.03523
0.12532
0.04225
0.01639
-0.07039
10
0.00102
0.05296
0.22449
-0.16156
-0.14764
-0.10317
-0.03627
-0.01636
0.04778
-0.03279
-0.01704
0.03357
0.00747
0.02956
0.10189
0.03328
0.01235
-0.05722
11
0.00183
0.04361
0.18106
-0.13202
-0.12104
-0.08598
-0.03279
-0.01704
0.03357
-0.02902
-0.01656
0.02341
0.00689
0.02467
0.08271
0.02619
0.00931
-0.04644
12
0.00225
0.03581
0.14593
-0.10768
-0.09899
-0.07133
-0.02902
-0.01656
0.02341
-0.02528
-0.01541
0.01619
0.00619
0.02049
0.06706
0.02060
0.00703
-0.03765
13
0.00239
0.02933
0.11755
-0.08767
-0.08079
-0.05895
-0.02528
-0.01541
0.01619
-0.02175
-0.01392
0.01107
0.00545
0.01695
0.05430
0.01620
0.00532
-0.03048
14
0.00236
0.02396
0.09464
-0.07127
-0.06582
-0.04855
-0.02175
-0.01392
0.01107
-0.01854
-0.01232
0.00746
0.00472
0.01397
0.04393
0.01275
0.00403
-0.02466
15
0.00222
0.01954
0.07615
-0.05786
-0.05353
-0.03987
-0.01854
-0.01232
0.00746
-0.01567
-0.01073
0.00494
0.00404
0.01148
0.03550
0.01004
0.00305
-0.01993
16
0.00201
0.01591
0.06124
-0.04692
-0.04347
-0.03266
-0.01567
-0.01073
0.00494
-0.01316
-0.00923
0.00319
0.00343
0.00941
0.02867
0.00792
0.00232
-0.01609
17
0.00178
0.01293
0.04923
-0.03800
-0.03525
-0.02669
-0.01316
-0.00923
0.00319
-0.01100
-0.00786
0.00199
0.00288
0.00769
0.02313
0.00625
0.00176
-0.01298
18
0.00154
0.01049
0.03956
-0.03075
-0.02856
-0.02177
-0.01100
-0.00786
0.00199
-0.00915
-0.00664
0.00118
0.00240
0.00628
0.01865
0.00494
0.00134
-0.01046
19
0.00132
0.00851
0.03178
-0.02486
-0.02311
-0.01772
-0.00915
-0.00664
0.00118
-0.00758
-0.00557
0.00064
0.00199
0.00511
0.01503
0.00390
0.00102
-0.00843
20
0.00111
0.00689
0.02552
-0.02008
-0.01868
-0.01441
-0.00758
-0.00557
0.00064
-0.00625
-0.00465
0.00028
0.00164
0.00416
0.01210
0.00309
0.00078
-0.00679


Figure 7:  Temporary Contraction in Energy Supply Perceived as Temporary Imperfect Information

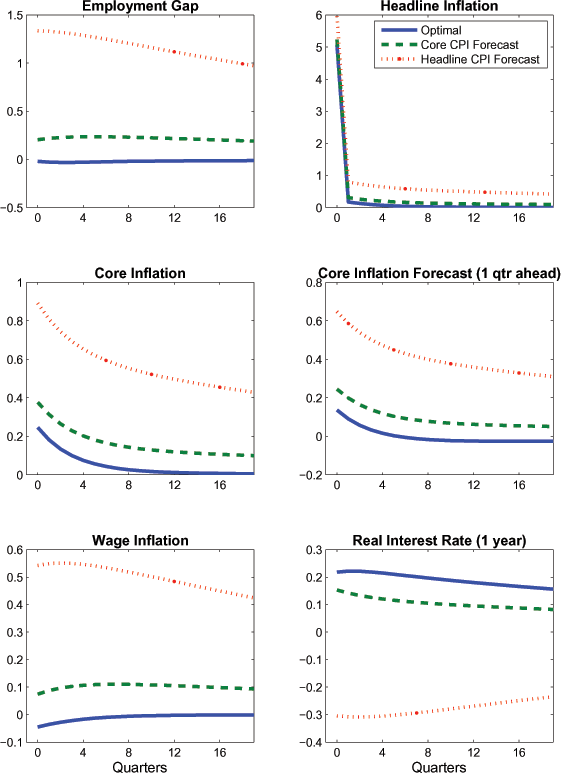
Data for Figure 7 immediately follows.

Data for Figure 7

Quarters
Employment Gap:
Optimal
Employment Gap:
Core CPI Forecast
Employment Gap:
Headline CPI Forecast
Headline Inflation:
Optimal
Headline Inflation:
Core CPI Forecast
Headline Inflation:
Headline CPI Forecast
Core Inflation:
Optimal
Core Inflation:
Core CPI Forecast
Core Inflation:
Headline CPI Forecast
Core Inflation Forecast (1 qtr ahead):
Optimal
Core Inflation Forecast (1 qtr ahead):
Core CPI Forecast
Core Inflation Forecast (1 qtr ahead):
Headline CPI Forecast
Wage Inflation:
Optimal
Wage Inflation:
Core CPI Forecast
Wage Inflation:
Headline CPI Forecast
Real Interest Rate (1 year):
Optimal
Real Interest Rate (1 year):
Core CPI Forecast
Real Interest Rate (1 year):
Headline CPI Forecast
1
-0.02019
0.20453
1.33597
5.06258
5.23384
5.95552
0.24615
0.37634
0.89113
0.13672
0.24492
0.64737
-0.04503
0.07450
0.54267
0.21827
0.15300
-0.30454
2
-0.02874
0.21817
1.33040
0.17144
0.30705
0.79826
0.18108
0.31275
0.80798
0.09052
0.19858
0.58620
-0.03560
0.08760
0.54929
0.22185
0.14198
-0.30795
3
-0.03154
0.22693
1.31951
0.12625
0.25934
0.73395
0.13401
0.26508
0.74365
0.05723
0.16399
0.53893
-0.02787
0.09667
0.55134
0.22143
0.13326
-0.30882
4
-0.03128
0.23211
1.30484
0.09327
0.22341
0.68361
0.09986
0.22917
0.69327
0.03320
0.13809
0.50198
-0.02167
0.10277
0.55007
0.21877
0.12627
-0.30785
5
-0.02957
0.23467
1.28749
0.06911
0.19622
0.64367
0.07499
0.20199
0.65327
0.01585
0.11863
0.47269
-0.01678
0.10667
0.54641
0.21493
0.12056
-0.30556
6
-0.02730
0.23532
1.26830
0.05138
0.17549
0.61146
0.05682
0.18126
0.62099
0.00335
0.10393
0.44911
-0.01297
0.10898
0.54102
0.21052
0.11581
-0.30232
7
-0.02496
0.23458
1.24787
0.03833
0.15955
0.58503
0.04350
0.16532
0.59448
-0.00565
0.09275
0.42978
-0.01003
0.11011
0.53442
0.20592
0.11178
-0.29840
8
-0.02280
0.23284
1.22664
0.02869
0.14717
0.56291
0.03371
0.15293
0.57228
-0.01211
0.08418
0.41364
-0.00779
0.11038
0.52696
0.20132
0.10829
-0.29402
9
-0.02090
0.23038
1.20495
0.02155
0.13743
0.54403
0.02648
0.14317
0.55332
-0.01670
0.07756
0.39989
-0.00609
0.11004
0.51893
0.19683
0.10521
-0.28932
10
-0.01929
0.22741
1.18303
0.01624
0.12966
0.52761
0.02112
0.13538
0.53681
-0.01994
0.07237
0.38794
-0.00481
0.10924
0.51053
0.19248
0.10245
-0.28442
11
-0.01795
0.22409
1.16106
0.01228
0.12335
0.51304
0.01713
0.12905
0.52216
-0.02219
0.06825
0.37736
-0.00384
0.10812
0.50189
0.18830
0.09992
-0.27939
12
-0.01686
0.22054
1.13917
0.00932
0.11813
0.49989
0.01415
0.12381
0.50892
-0.02371
0.06493
0.36783
-0.00312
0.10677
0.49313
0.18428
0.09759
-0.27430
13
-0.01595
0.21682
1.11744
0.00709
0.11373
0.48785
0.01191
0.11939
0.49679
-0.02470
0.06220
0.35910
-0.00258
0.10527
0.48433
0.18041
0.09540
-0.26919
14
-0.01521
0.21302
1.09595
0.00540
0.10994
0.47666
0.01022
0.11559
0.48552
-0.02530
0.05992
0.35100
-0.00218
0.10366
0.47554
0.17667
0.09333
-0.26410
15
-0.01460
0.20917
1.07474
0.00412
0.10663
0.46614
0.00893
0.11225
0.47492
-0.02561
0.05797
0.34340
-0.00188
0.10198
0.46680
0.17306
0.09136
-0.25904
16
-0.01408
0.20530
1.05384
0.00313
0.10366
0.45618
0.00794
0.10927
0.46487
-0.02572
0.05627
0.33620
-0.00166
0.10026
0.45815
0.16956
0.08947
-0.25403
17
-0.01364
0.20144
1.03327
0.00237
0.10097
0.44666
0.00717
0.10655
0.45527
-0.02567
0.05476
0.32933
-0.00149
0.09852
0.44961
0.16616
0.08764
-0.24908
18
-0.01325
0.19761
1.01306
0.00177
0.09849
0.43752
0.00657
0.10405
0.44605
-0.02552
0.05340
0.32273
-0.00136
0.09677
0.44119
0.16284
0.08588
-0.24420
19
-0.01291
0.19382
0.99320
0.00130
0.09618
0.42869
0.00609
0.10172
0.43714
-0.02528
0.05215
0.31636
-0.00126
0.09502
0.43289
0.15961
0.08416
-0.23940
20
-0.01260
0.19007
0.97370
0.00091
0.09400
0.42014
0.00570
0.09952
0.42851
-0.02499
0.05099
0.31019
-0.00118
0.09329
0.42474
0.15646
0.08250
-0.23468

Footnotes

*   The authors thank Brian Doyle, Marvin Goodfriend, Chris Gust, Dale Henderson, Steve Kamin, Robert King (the editor), John Taylor, Paul Wood, and an anonymous referee for insightful comments and discussions. Hilary Croke provided excellent research assistance. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

**   Corresponding author. Telephone (202) 452 2550. E-mail Luca.Guerrieri@frb.gov. Return to text

1.   For example, the Bank of England has a target of 2% that is expressed in terms of headline inflation. It describes operational policy as adjusting interest rates so that its forecast of headline inflation reverts to target within a reasonable time frame without inducing undue instability in real activity (see http://www.bankofengland.co.uk/monetarypolicy/framework.htm). By contrast, the U.S. Federal Reserve has emphasized a measure of core inflation that excludes energy in guiding its operational decisions, even while acknowledging that it may be sensible to express longer-run objectives in terms of headline inflation (for a very useful discussion, see Mishkin (2007)). Return to text

2.   Leduc and Sill (2004) and Dhawan and Jeske (2007) analyzed the implications of alternative policy responses to oil shocks in a DSGE setting with nominal rigidities, but did not consider the optimal policy using a utility-based welfare metric. Return to text

3.   Goodfriend and King (1997) argued that monetary policy should be concerned with stabilizing the components of the price index that are sticky, rather than the overall index. Aoki (2001) formalized this insight by constructing a model with both a flexible-price sector, and a sticky-price sector. Because the welfare losses depend exclusively on the variance of the sticky price components, the optimal policy consists of stabilizing those components. Our model is similar to Aoki's insofar as it can also be regarded as including a flexible price sector and sticky price sector; however, it differs mainly by introducing energy as an input into the demand functions of firms and households, and because wages are assumed to be sticky. Return to text

4.   There is an extensive literature analyzing the properties of some alternative measures of core inflation derived from various statistical procedures; a nice overview is provided in Aucremanne and Wouters (1999). Some notable early contributions include Bryan and Pike (1991), Bryan and Cecchetti (1994), and Quah and Vehey (1995). Return to text

5.   The data underlying each panel was obtained from the Greenbooks dated 02/04/1987, 09/27/1989, 03/17/1993, and 05/09/2000. Greenbooks for 2001 are the latest publicly available. Return to text

6.   Lower case letters are used to denote the logarithmic percentage deviation of a variable from its steady value (or the arithmetic percentage point deviation for variables that are expressed in percentage points). Return to text

7.   For expositional simplicity, Table 1 sets the intertemporal elasticity of substitution in consumption equal to unity, i.e., $ \sigma=1$, which is consistent with the calibration described below. The more general case is reported in the technical appendix. Return to text

8.   The product real wage and the relative price of oil are deflated by the retail price index. Thus, $ \eta_{t}$ is defined as $ log(\frac{W_{t}}{P_{nt}})-log(\frac{W}{P_{n}})$, and $ \psi_{ot}$ as $ log(\frac{P_{ot}}{P_{nt}})-log(\frac{P_{o}}{P_{n}})$.  Return to text

9.   In the special case of logarithmic utility and Cobb-Douglas production, the response of $ l^{*}_{t}$ is zero. More generally, the employment response under flexible prices depends on the relative magnitude of the intertemporal elasticity of substitution in consumption, and the elasticity of substitution between oil and other inputs. Return to text

10.   The technical appendix accompanying this paper provides a detailed derivation of the welfare loss function, as well as of the log-linearized equations given in Table 1. The welfare function assumes that the subutility function over consumption is logarithmic. Return to text

11.   The reduced-form solution of the model is obtained by using the numerical algorithm of Anderson and Moore (1985), which provides an efficient implementation of the method proposed by Blanchard and Kahn (1980) (see also Anderson (1997)). Return to text

12.   With employment equal to potential, it is apparent from equations T1-T4 that the real wage gap is the only forcing variable in the price and wage-setting equations. Because the real wage gap affects marginal cost and the MRS gap in an identical manner in absolute terms, the relative magnitude of price and wage adjustment depends only on the size of $ \kappa_{p}$ to $ \kappa_{w}$. Return to text

13.   Bernanke, Laubach, Mishkin, and Posen (1999) argued that a focus on a forecast of inflation, rather than realized inflation, is also justified by an attempt to reconcile inflation targeting with dual-mandate considerations. Faust and Henderson (2004) stressed that best-practice monetary policy should take account not only of the implications for inflation but also for output gap variability. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: August 20, 2008