Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 952, October 2008 --- Screen Reader Version*

Do Fundamentals Explain the International Impact of U.S. Interest Rates? Evidence at the Firm Level

John Ammer, Clara Vega and Jon Wongswan^*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper analyzes the impact of U.S. monetary policy announcement surprises on U.S. and foreign firm-level equity prices. We find that U.S. monetary policy has important influences on foreign equity prices on average, but with considerable variation across firms. We have found that this differing response reflects a range of factors, including the extent of a foreign firm's exposure to U.S. demand, its dependence on external financing, the behavior of interest rates in its home country, and its sensitivity to portfolio adjustment by U.S. investors. The cross-firm variation in the response is correlated with the firm's CAPM beta; but it cannot fully explain this variation. More generally, we see these results as shedding some additional light on the nature and extent of the monetary and financial linkages between the United States and the rest of the world. In particular, since we are able to explain differences across foreign firms' responses through established theories of monetary transmission, our results are consistent with the surprisingly large average foreign response to U.S. rates reflecting fundamentals, rather than an across-the-board behavioral over-reaction.

Keywords: Monetary policy announcements, high-frequency data, credit channel

JEL classification: E44, E52, G14, G15

1.  Introduction

What are the global shocks that drive the cross-country correlation of stock returns? This question, central to many topics in international finance, is deeply associated with another fundamental question: What are the transmission channels through which these shocks dissipate? Previous literature has documented that U.S. monetary policy is one such global shock (Ehrmann and Fratzscher (2006) and Wongswan (2006 and 2005)), and in this paper we aim to answer the latter question. Specifically, we examine the following four channels of monetary policy transmission: the demand channel, the credit channel, the portfolio channel, and the foreign interest rate channel. Let us discuss them in turn.

The demand channel reflects the fact that foreign firms that produce cyclically-sensitive goods and firms that depend on U.S. sales may respond more to FOMC announcements. According to the demand channel or conventional monetary policy transmission channel, the FOMC affects short-term real interest rates because prices are sticky.¹ In turn, the change in real interest rates affects aggregate demand, as higher rates induce U.S. and foreign consumers to decrease current spending. To assess the importance of this channel, we estimate the response of firms in the relatively cyclical consumer durables sector compared to the non-durables sector. We also assess the response of foreign firms that do not directly depend on U.S. sales, such as firms in the retail services sector. In support of the demand channel, we show that U.S. monetary policy surprises elicit larger reactions from foreign firms in the durables sector, with much smaller effects on firms in the non-durables and retail services sectors. These differences are economically and statistically significant. In addition to these industry effects, we also show evidence that foreign firms react slightly more to FOMC announcement surprises if more of their revenue is generated outside their home country, which should tend to increase their exposure to the U.S. economy. However, this difference is small.

The credit channel posits that U.S. monetary policy shocks could have a large impact on firms with low credit ratings and firms that are largely dependent on external financing. More specifically, opaque firms and firms that have poor credit ratings may find it more difficult to access bank loans or other financing when credit conditions become tighter, as credit lines to opaque firms and customers in poor financial health will often be cut first (See, for example, Bernanke and Blinder (1992), Kashyap, Stein, and Wilcox (1993), and Gertler and Gilchrist (1994)). Worsening credit market conditions also affect firms by weakening their balance sheets as the present value of collateral falls with rising interest rates, and this effect is stronger for firms that depend more heavily on external financing.² According to this channel, U.S. monetary policy shocks can affect foreign firms to the extent that they depend on U.S. credit or if U.S. monetary policy affects credit supplied by foreign institutions.

We find evidence in favor of this channel. The stock price of a typical foreign firm with a speculative-grade credit rating rises about 1.5 percent after a 25-basis-point surprise decrease in the federal funds rate, compared to only about 1.2 percent for foreign firms with an investment-grade rating. Furthermore, FOMC surprises have a smaller effect on foreign firms that pay dividends; such firms are likely to face fewer financial constraints. We also find similar results, for firms that are largely dependent on external financing as measured by the firm's ratio of capital expenditures minus cash flows to market capitalization. These results provide compelling evidence in support of the credit channel.

We also examine the portfolio channel which is based on theoretical models that emphasize the role of investor's asset holdings in transmitting shocks across markets (e.g., Kyle and Xiong (2001), Kodres and Pritsker (2002), and Yuan (2005)). According to the portfolio channel, U.S. investors' portfolio adjustments may create co-movement between U.S. and foreign equity prices. For example, U.S. investors may have to liquidate their positions in other countries when they suffer a negative wealth shock as a result of a Fed funds surprise, thus causing equity prices to decline elsewhere even in the absence of credit or demand effects. We provide weak evidence in favor of the portfolio channel. We find that firms with greater U.S. investor ownership, captured by the ratio of the foreign firm's shares traded in the United States to the total trading volume of the firm, react more to U.S. monetary policy surprises. However, the significance of this variable goes away when we include other control variables.

Previous research shows that U.S. monetary policy also affects foreign short- and long-term interest rates (Hausman and Wongswan (2006), Kim (2001), Canova (2005)). In particular, Kim (2001) finds that the interest rate reaction in other countries is the most important channel of transmission. With the foreign interest rate channel, equity prices of firms that are more sensitive to home country interest rate moves on FOMC announcement days may react more to U.S. monetary policy surprises, as these firms are affected by interest rate movements both in the United States and in their home country. Similarly, countries that peg their currencies to the U.S. dollar may have to adjust their domestic interest rates more than countries with flexible exchange rates. We find that this transmission channel is very important; but, the reaction of foreign equity prices to FOMC announcements is not fully explained by the local interest rate reaction to FOMC announcements, suggesting that U.S. credit and demand transmission channels are also important.

Interestingly, we find that foreign firms react as much as or slightly more to FOMC announcements than U.S. firms.³ To illustrate this, we show in Figure 1 the path of stock prices around the recent FOMC announcement on September 18, 2007, when the announced target federal funds rate came in 20 basis points below market expectations. Within five minutes of the announcement the S&P 500 index moved up 1.5 percent, and it showed a cumulative gain of 1.9 percent after one hour. Strikingly, foreign equity prices, represented by the MSCI Europe and Far East Index, rose slightly more than U.S. equity prices (the cumulative gain was 2.03 percent). This pattern has been typical in our sample period. On average, we find that the foreign firms' reaction is 5 to 10 basis points higher than that of U.S. firms. Our study can at least provide a partial explanation to this apparent puzzle. The credit channel cannot explain the difference in the response, because our foreign firm sample is comprised of financially healthier firms than our U.S. sample. The demand-channel and the foreign interest rate channel, on the other hand, provide an explanation. First, our sample of foreign firms produces more cyclically sensitive goods than the sample of U.S. firms. In fact, once we control for industry fixed effects, we find that foreign firms on average react similarly or 6 basis points less to FOMC announcements than U.S. firms for a 25-basis-point surprise change in the target rate. Second, many of our firms are based in countries either where their home currencies are pegged to the U.S. dollar, or where local interest rates move closely to U.S. rates.

Finally, we test whether our results based on FOMC days are different from the average co-movement between foreign and U.S. equity prices during non-FOMC days. To answer this question we consider whether reactions to FOMC announcement surprises are explained principally by how sensitive a stock is to U.S. market-wide shocks in general, as reflected in its estimated U.S. market beta from the Capital Asset Pricing Model (CAPM). We find that the cross-firm variation in the response is correlated with the CAPM beta, but the other estimated effects generally remain significant even after controlling for CAPM beta. In particular, financially constrained firms have larger reactions to U.S. monetary policy than is explained by CAPM beta alone, as do firms from countries where interest rates are more closely linked to U.S. rates. We thus conclude that stock price co-movement across foreign firms is somewhat different in the wake of news about U.S. monetary policy than it is at other times, with the differences reflecting the importance of the credit and foreign interest rate policy transmission channels.

The remainder of the paper is organized as follows. In Section 2 we relate our study to recent literature. In Section 3 we describe the data, and in Section 4 we develop our hypothesis tests and present the empirical results. We conclude in Section 5 and discuss the implications of our findings. Finally, Section 6 contains an appendix with a detailed definition of each variable we use in our empirical tests.

2.  Related Literature

A number of studies have documented significant effects of U.S. monetary policy announcements on U.S. equity prices.⁴ However, only a few papers have examined how foreign equity indexes react to FOMC surprises (Ehrmann and Fratzscher (2006) and Wongswan (2006 and 2005)), and no prior study has analyzed the firm-level foreign equity response to FOMC announcements. The advantage of studying firm level data is that we will be able to test policy transmission channels that we would otherwise not be able to explore with aggregate equity price data. Furthermore, firm-level data will allow us to understand why foreign firms on average react slightly more to FOMC surprises than domestic firms.

Our paper is most closely related to two recent studies of U.S. equity market reaction to FOMC announcement surprises (Ehrmann and Fratzscher (2004) and Bernanke and Kuttner (2005)), and two recent studies of foreign aggregate equity indexes reaction to FOMC surprises (Wongswan (2005) and Ehrmann and Fratzscher (2006)). Ehrmann and Fratzscher (2004) analyze the daily response of the 500 individual firms comprising the S&P 500 in early 2003 and find that firms that are financially constrained respond more to monetary policy surprises. Bernanke and Kuttner (2005) analyze the daily response of the CRSP value-weighted index and Fama-French industry portfolios. They find that U.S. monetary policy surprises affect U.S. equity markets mainly through their effects on expected future risk premiums and expected future cash flows. Wongswan (2005) studies the impact FOMC announcement surprises have on 15 equity indexes from different countries, while Ehrmann and Fratzscher (2006) analyzes 50 different countries. They both find that the exchange rate regime of the country and financial development are important determinants of the cross-country variation in the response.

Similar to these studies, we are interested in understanding the stock market reaction to FOMC announcements, cross-country and cross-firm variation in the response. However, we extend the existing literature in at least three important dimensions. First, we analyze returns of assets that trade contemporaneously with their U.S. counterparts and trade when FOMC decisions are released. One potential problem in previous studies of the response of international equity prices to FOMC announcements and co-movement with the U.S. stock market is non-synchronous trading (see, Karolyi and Stulz, 1996). Both Wongswan (2005) and Ehrmann and Fratzscher (2006) examine the impact of FOMC announcements, which occur during U.S. trading times, on foreign (overnight) returns. In this paper, we avoid this problem by using foreign assets that trade contemporaneously with American stocks. Second, we study a wider range of U.S. and foreign firms (over 10,000 U.S. firms and 1,501 foreign firms) compared to other studies, allowing us to better understand the effect FOMC surprises have on foreign firms, small firms, firms that depend more heavily on external financing, and firms with higher information asymmetries. To our knowledge, this is the first paper that examines the response of firm-level foreign equity prices to U.S. monetary policy announcements, and as we mentioned above, this in turn allows us to investigate different transmission channels that we would otherwise not be able to analyze. Third, we separately identify interest rate risk exposure from CAPM beta risk exposure.

3.  Data Description

The sample period we analyze includes all FOMC announcements from February 4, 1994 through December 12, 2006, excluding the September 17, 2001 FOMC announcement.⁵ The latter is an extreme example of a joint response by the Federal Reserve, several other central banks, and financial markets to the September 11, 2001 terrorist attacks. The sample covers 108 FOMC announcements, 104 scheduled meeting decisions and 4 intermeeting decisions.

The empirical tests of this paper require data from six different sources: Center for Research in Securities Prices (CRSP), Trade and Quote (TAQ), Compustat, Chicago Board of Trade, I\B\E\S and Bloomberg data. CRSP data is used to compute daily returns on FOMC announcement days, TAQ data is used to compute hourly returns, and Compustat data is used to compute firm characteristics. We exclude from our U.S. sample closed-end funds, Real Estate Investment Trusts, American Depository Receipts, and foreign stocks (we only use stocks with CRSP share code 10 or 11 and Compustat state variable not equal to 99), and for the foreign sample we use American Depository Receipts (CRSP share code 30 or 31) and firms incorporated outside the U.S. excluding closed-end funds (Compustat state variable equal to 99 and CRSP share code 12). We also exclude firms with prices less than $1 per share and above $10,000 per share, and firms we could not compute hourly returns using TAQ data. Merging CRSP, TAQ and Compustat data together, we obtain a final sample of 11,204 U.S. firms and a total of 420,043 firm-FOMC date observations and a sample of 1,501 foreign cross-listed firms and a total of 56,707 firm-FOMC date observations. Table 1 provides the sample coverage by country. The Chicago Board of Trade data is used to compute federal funds rate surprises, the I\B\E\S data is used to estimate the firm's analyst coverage, and Bloomberg data is used to compute the ratio of U.S. trading volume divided by total trading volume. Below we discuss in detail the different variables we use in the empirical tests and potential sample biases.

3.1  Measure of Monetary Policy Surprises

The federal funds rate surprise, $TSt$, is defined as the difference between the announced target for the federal funds rate and expectations derived from the federal funds futures contract (Kuttner, 2001). We compute the target surprise as the change in the current-month federal funds futures contract rate in a thirty-minute window around the FOMC announcement (ten minutes before to twenty minutes after) with some minor adjustments.⁶

We also analyze, what Gürkaynak, Sack, and Swanson (2005) label the path surprise, $PSt$, which is defined as the component of the change in one-year-ahead eurodollar interest rate futures in a thirty-minute window around the announcement that is uncorrelated with the target rate surprise. The path surprise reflects news that market participants have learned from the FOMC's statement about the expected future path of policy over and above what they have learned about the level of the target rate. To derive the path surprise, we run a regression of the change in one-year-ahead eurodollar interest rate futures in a thirty-minute window around the FOMC announcement ($\Delta ed$) on a constant and the target surprise ($TS$):

$$\Delta ed_{t-10,t+20}=a_{0}+a_{1}\ast TS_{t}+PS_{t}$$ (1)

where $PSt$ is the error term from the regression and is the path surprise.⁷ However, consistent with previous studies (e.g., Wongswan (2005, 2006) and Gürkaynak, Sack, and Swanson (2005)), we find that foreign and domestic equity prices mainly react to target surprises, so we do not report these results.

Even though many researchers have used federal funds futures rates as measures of financial markets expectations of future monetary policy, these measures reflect risk premia and may be a biased measure of financial market expectations. Piazzesi and Swanson (2008) conclude that Kuttner (2001)'s method, which is the method we use, is not contaminated by risk premia because this method essentially "differences it out." The method does not completely eliminate the risk premia because risk premia is time-varying. Thus, as a robustness check, we also measure the market's expectation according to a Reuters poll of market participants.⁸ This measure should not be contaminated by risk premia. An additional advantage of survey based forecasts is that there is no room for biases due to endogeneity (the fed funds futures market may be responding not only to the FOMC announcement, but also to the stock market response to the announcement). One disadvantage of the survey based forecast, though, is that it does not contain up to the minute information available to the market, as the survey is conducted on the Friday before each FOMC meeting. This bias is particularly important on inter-meeting FOMC decisions, since Reuters does not poll economist prior to this decisions. All told, we find our results to be qualitatively robust to either using forecasts based on the Reuters survey or based on federal funds future contracts. For conciseness, we only report our results based on the federal funds futures contracts and the survey based results are available upon request. We note that our adjusted R-squares are slightly higher when we measure the surprise using federal funds futures contracts, this is consistent with our observations that survey-based forecasts contain stale information.

3.2  Cross-listed Firms and Potential Sample Biases

There are two main advantages of analyzing firms that list their shares in U.S. markets. First, the majority of the FOMC announcements in our study occur at 2:15 pm ET when Asian and European stock markets are closed, while U.S. stock exchanges are open so that prices of cross-listed firms allow us to capture the high frequency foreign equity response contemporaneously to that of their U.S. counterparts. Second, they allow us to capture the firm-level response as opposed to the aggregate index response. However, since our sample of foreign firms are large relative to the average local firm, and for the most part have access to and use U.S. credit, one may worry that our sample is biased towards foreign firms that react more to U.S. shocks than the average foreign firm.⁹

Nevertheless, we find that our sample firms comprise a considerable percentage of the home country's total market capitalization and, consistent with the literature on cross-listed firms and the law of one price, we find that our sample firms move closely with the country's value-weighted index.¹⁰ To put in perspective our panel-regression estimate of the average effect FOMC announcement surprises have on foreign firms, we also estimate the effect FOMC announcement surprises have on the value-weighted MSCI global index which excludes Canadian and U.S. firms (ticker symbol EFA). The MSCI global index started trading in the American Stock Exchange on August 17, 2001, so this comparison is constrained to the sample period from August 17, 2001 to December 31, 2006, which includes 44 FOMC announcements and no intermeeting moves. A 25-basis-point target rate surprise tightening decreases the MSCI global index by 0.88 percent compared to our panel-data estimate of 0.93 percent, and the coefficient estimates are not statistically different from each other (the $\chi^{2}$of the likelihood ratio testing that the two coefficients in a seemingly unrelated system of equations estimation are equal to each other is 0.16 with a p-value equal to 0.68). We thus conclude that our average effect estimate is equivalent to a value-weighted global response.

3.3  Proxy for Information Asymmetry

A large number of studies have used firm size as a proxy for information asymmetry. It seems plausible that the information about small firms is harder to obtain; this would happen if, for example, investors face fixed costs of information acquisition, and hence choose to devote more effort to learning about those stocks in which they can take large positions. Unfortunately, even if firm size is a useful measure for information asymmetry, it is likely to capture other things as well, so it is only an imperfect proxy for the degree of information asymmetry. Our approach is to use a more direct measure of how opaque firms may be by using the number of analysts that cover a particular firm in our sample. This proxy is used in several empirical studies, e.g., Bhushan (1989), Brennan, Jegadeesh and Swaminathan (1993), Hong, Lim, and Stein (2000), as a proxy for the degree of transparency of the firm and as a measure of the mass of informed agents, e.g., Chordia, Huh and Subrahmanyam (2007). The idea is that stocks with lower analyst coverage should, all else equal, be ones where firm-specific information moves more slowly across investors. We use I/B/E/S detailed history files and define analyst coverage as the average number of analysts that covered a particular firm the previous year.

3.4 Proxies for Real and Financial Integration

We use the ratio of each firm's foreign sales to its total sales to capture the firm's reliance on foreign consumption and assuming the foreign consumption is mainly U.S. consumption, this variable measures the firm's exposure to the U.S. demand channel of monetary policy transmission. This ratio is taken from World Scope.¹¹

Several papers emphasize the role of investor's asset holdings in transmitting shocks across markets (e.g., Kyle and Xiong (2001), Kodres and Pritsker (2002), and Yuan (2005)). To test this hypothesis we compute the percentage of each firm's equity traded in the U.S. versus its total monthly equity trading volume as a proxy for the size of U.S. investors' holdings of each firm. This is computed using Bloomberg data. We note that in computing this variable it is important to control for what fraction of a share ADRs represent.

3.5  Proxies for Local Interest Rate Exposure, Exchange Rate Flexibility, and Exchange Rate Exposure

Previous literature shows that U.S. monetary policy not only affects U.S. short- and long- term interest rates, but it also affects foreign short- and long- term interest rates (e.g., Hausman and Wongswan (2006), Kim (2001) and Canova (2005)). With this empirical result in mind, we expect firms that are sensitive to home country interest rate moves on FOMC announcement days to react more to U.S. monetary policy surprises, as these firms are affected by both the U.S. and home country demand and credit channels. To measure the firm's sensitivity to home country interest rate movements on FOMC announcement days we estimate the following equation,

$$R_{iht}\times\Delta S_{ht}=\beta_{0LCRih}+\beta_{LCRih}\Delta LCR_{ht} \mathit{\ }+\varepsilon_{iht}$$ (2)

where $R_{iht}$ is firm $i$'s dollar-denominated return on FOMC announcement day $t$, the index $h$ denotes which country firm $i$ is located in; $\Delta S_{ht}$ is the foreign currency/US dollar exchange rate change on day $t$ of country $h$, when country $h$ has a flexible exchange rate regime, and 1 otherwise; $\Delta LCR_{ht}$ is either the change in the three-month money market interest rate for country $h$, as a proxy for short-term interest rate changes, or the change in ten-year government bond yield for country $h$, as a proxy for long-term interest rate changes.¹² Our measure of the firm's sensitivity to home country interest rate movements on FOMC announcement days is the absolute value of the slope coefficient $\beta_{LCRih}$ estimated using equation (2).

Because of data availability, we have interest rate data for only 20 foreign countries highlighted in Table 1 with an asterisk. These countries are all industrialized countries, so that our foreign interest rate channel hypothesis test is restricted to this sample. However, we consider an indirect test of this hypothesis that includes our full sample of firms, firms located in developed and developing countries. This indirect test consists of allowing the equity response to vary across exchange rate regimes. The conventional wisdom is that countries with a more flexible exchange rate regime can insulate their local interest rates more from changes in global interest rates (e.g., Shambaugh (2004) and Frankel, Schmukler, and Serven (2004)), so that, holding everything else constant, we expect firms located in countries with flexible exchange rates to react less to U.S. monetary policy surprises than firms located in countries with a fixed exchange rate.

Since there is no consensus on the "correct" exchange rate classification for each country, in this paper we consider several classifications but focus on Levy-Yeyati and Sturzenegger (2005)'s exchange rate regime classification for two reasons. First, their methodology is a de facto classification based on actual data on exchange rates and international reserves. This has an advantage over the de jure classification from the IMF's Annual Report on Exchange Arrangements and Exchange Restrictions, because actual exchange rate regimes often differ from officially announced regimes (Reinhart and Rogoff (2004), Shambaugh (2004), and Levy-Yeyati and Sturzenegger (2005)). Second, Levy-Yeyati and Sturzenegger (2005)'s classification is available for all our countries except Taiwan and is available for almost our entire sample period. In contrast, Reinhart and Rogoff's classification ends in 2001. Levy-Yeyati and Sturzenegger create a discrete variable equal to one for a fully floating regime, equal to two for a limited-flexibility or a managed float regime, and equal to three for a fixed or currency board regime. As a robustness check for our results, we use both Shambaugh's and Reinhart and Rogoff's classifications for the available sample period. The results are qualitatively the same.

We also consider the effect a foreign firm's exchange rate exposure has on the firm's reaction to FOMC announcements. A number of studies show that FOMC announcement surprises (the path surprise more so than the target surprise) affect exchange rates (e.g., Hausman and Wongswan (2006)), so that a foreign firm's sensitivity of the value of the firm to exchange rate fluctuations may affect this firm's reaction to FOMC announcements. To measure this sensitivity we follow Jorion (1990) and estimate the following equation,

$$R_{iht}=\beta_{0Sih}+\beta_{Sih}\Delta S_{ht}+\varepsilon_{iht}$$ (3)

where the absolute value of the estimated slope coefficient $\beta_{Sih}$ is our measure of the foreign firm's exposure to exchange rate movements. Similar to our measure of a firm's sensitivity to local interest rate movements, we estimate equation (3) only using FOMC announcement days. The logic behind this approach is to capture the firm's reaction to exchange rate movements due to U.S. target rate surprises.

Assuming firms do not hedge their currency exposure, we expect foreign firms that are sensitive to exchange rate movements to also react more strongly to FOMC announcement surprises, since these firms must be heavily exposed to U.S. economic fluctuations. However, this result relies on the assumption that either firms chose not to hedge their currency risk exposure (e.g., Loderer and Pichler (2000) find that many Swiss industrial corporations that are heavily exposed to exchange rate fluctuations do not hedge this risk), or firms are not able to hedge the long-term effects of exchange rate changes (Bartov and Bodnar (1994)). If all firms successfully hedge their currency risk exposure, then the firm's sensitivity to exchange rate movements should be close to zero and the relationship between the firm's sensitivity to exchange rate movements and the firm's reaction to FOMC announcement surprises should be insignificant.¹³ If some firms hedge their currency exposure and others don't, our estimated exchange rate exposure effect will have a downward bias.

3.6  Proxies for the Firm's Financial Constraints

We are interested in measuring the amount of desired investment that cannot be financed through internal cash flows generated by the firm itself. Therefore, similar to Rajan and Zingales (1998), we define a firm's dependence on external finance as capital expenditures (Compustat item # 128) minus cash flow from operations (sum of Compustat items # 123, 125, 126, 106, 213, and 217) divided by the market capitalization of the firm. We also examine the following popular proxies for the financial health of the firm: debt to market capital share, dividend payout policy, and Standard and Poor's long term credit rating of the firm.¹⁴ All else equal, we expect firms that are more financially constraint to be more sensitive to federal funds rate surprises.

3.7  Proxies for Time-Varying Periods of Stress

We use a junk-bond spread, measured as the average yield spread over the Treasury curve of six rating-specific indices of seven-year U.S. corporate bonds, based on Bloomberg's daily estimated yield curves for bonds rated BB+, BB, BB-, B+, B, and B-, respectively. The constructed series is shown in Figure 2. High-yield credit spreads are well-known to spike up during stress periods, such as in the summer of 1998 after a Russian debt default and the failure of the Long-Term Capital Management hedge fund.

We show summary statistics for all of these variables in Table 2A for our sample of foreign firms and Table 2B for our sample of U.S. firms. As we mentioned before, our sample of foreign firms are much larger relative to the U.S. sample and the external finance dependence is smaller, so that the credit channel transmission of monetary policy should be more important for U.S. firms than our sample of foreign firms.

4.  Empirical Results

4.1  Baseline Event Study Results

We first estimate the average effect target rate surprises have on equity prices. This analysis does not take advantage of our firm-level data. However, it will allow us to compare our results with previous findings and analyze potential asymmetries in the response at the aggregate level. Specifically, we estimate the following pooled regression:¹⁵

$$R_{it}=\beta_{D0}+\beta_{DTS}TS_{t}+\beta_{F0}I(ForeignFirm)_{i}+\beta _{FTS}TS\mathit{\ }_{t}\times\quad I(ForeignFirm)_{i}+\varepsilon_{it},$$ (4)

where $R_{it}$ is the firm $i$'s return on day $t$, $TS_{t}$ is the FOMC target rate surprise on day $t$, and $I(ForeignFirm)_{i}$ is an indicator variable equal to 1 if firm $i$ is based outside the U.S., zero otherwise. The pooled regression is estimated using ordinary least squares (OLS) and we account for heteroskedasticity and contemporaneous correlation across panels in the residuals by using Panel-Corrected Standard Errors (PCSE). The estimates are based only on those observations when announcements were made.

In Table 3 Panel A and Panel B, we show the coefficient estimates of equation (4) using daily and hourly returns, respectively.¹⁶ Focusing on the daily return results, we find that an unexpected monetary policy tightening of 25 basis points is associated with a decrease of 1.85 percent in U.S. equity prices and a decrease of 1.90 percent in foreign equity prices. Our U.S. equity price response is in line with the findings of Rigobon and Sack (2004), who find a decrease of 2.35 percent in the Nasdaq Composite index. Our estimate is slightly higher than that found in Bernanke and Kuttner (2005), who find a 1 percent decrease in the CRSP value-weighted index, and Ehrmann and Fratzscher (2004), who find a 1.4 percent decrease in the S&P 500, consistent with the fact that our pooled regression puts equal weight on each firm and that our sample contains more financially constraint firms than the S&P 500 sample analyzed by Ehrmann and Fratzscher (2004).

Interestingly, we find that foreign firms react as much as or slightly more to FOMC announcements than U.S. firms (this difference is only statistically significant in the hourly return regression). This finding is consistent with the reaction to the September 18, 2007 announcement shown in Figure 1 and with Wongswan (2005) and Ehrmann and Fratzscher (2006), who analyze the response of stock market indexes in 15 and 50 different countries, respectively, to FOMC announcements, and also find that several countries react more strongly to FOMC announcements than the U.S. equity index itself. In Section 4 we explore different explanations for this phenomenon.

The advantage of using hourly returns is reflected in the nearly doubling of the adjusted R-squared, i.e., in the above equation the adjusted R-squared using daily returns is 1.62% (Table 3 Panel A), while using hourly returns we obtain an adjusted R-squared equal to 3% (Table 3 Panel B), and the tighter standard errors associated with our coefficient estimates. In part, this improvement is due to the fact that during our sample period several FOMC meetings coincided with other major macroeconomic announcements, and the daily return not only reflects the market response to federal funds rate surprises, but it also includes the response to these other data releases.¹⁷ The difference in the coefficient estimates between the hourly and daily return is relatively small, consistent with the view that the stock market response to public announcements is almost immediate.

4.2  Explaining the Cross-Firm Variation in the Response

We have seen that FOMC surprises significantly affect stock market returns. We next explore four main channels of transmission of U.S. monetary policy to foreign equity prices: the demand channel, the credit channel, the portfolio channel, and the foreign interest rate channel.

4.2.1  Industry Effects

The demand channel reflects the fact that foreign firms that produce cyclically-sensitive goods and firms that depend on U.S. sales may respond more to FOMC announcements. The price elasticity of goods differs across industries, so we expect firms belonging to different industries to react differently to FOMC announcements. Furthermore, foreign firms that produce non-tradable goods should not be affected by FOMC surprises as much as the U.S. firm counterparts. To investigate these possibilities we allow the impact of the response coefficient to vary across ten industry classifications and allow FOMC surprises to have a different impact on foreign firms,

$$R_{it} =\beta_{D0}I\left( Firm_{i}\in Industry_{j}\right) +\beta _{Dj}TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right)$$ (5)

$$+\beta_{F0}I\left( Firm_{i}\in Industry_{j}\right) \times I\left( ForeignFirm\right) _{i}$$

$$+\beta_{Fj}TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right) \times I\left( ForeignFirm\right) _{i}+\varepsilon_{it}$$

where $j=1,\ldots10$ industry classifications according to the Fama-French 10 industry portfolio classification, which is based on the firm's SIC code as of the end of the previous fiscal year.

In Table 4, we show that there is considerable cross-industry variation. Consistent with Bernanke and Kuttner (2005), we find that the most responsive industries are high tech and telecommunications, and the least responsive are utilities and energy. In contrast to Bernanke and Kuttner (2005), though, our coefficient estimates are sufficiently precise that we are able to reject the null of equal coefficients across industries both in the daily and hourly return regressions. On average, foreign firms and U.S. firms belonging to a particular industry react very similarly to FOMC surprises. The three exceptions (using daily returns) are the telecom, utilities and the wholesale services sectors. Foreign firms that belong to the telecom and wholesale services sector react less strongly to FOMC announcements than the U.S. counterparts. This is consistent with the demand channel transmission of U.S. monetary policy to foreign economies, since firms in the telecom service and wholesale service sectors produce non-tradable goods and should not be affected by lower U.S. aggregate demand as a result of U.S. monetary policy tightening surprise. Foreshadowing some of the results, U.S. FOMC decisions affect foreign interest rates, so the service sector abroad may still be affected by U.S. monetary policy through the foreign interest rate channel, which we consider in the next section. The demand channel cannot explain why the utilities sector (electric, water, and natural gas supply) abroad reacts more to FOMC surprises than the U.S. counterpart. We note, though, that the foreign utility sector reaction is very small compare to the reaction of other foreign firm sectors. Focusing on the hourly return results, we also find that the foreign health services sector reacts less to FOMC surprises than the U.S. health service sector, consistent with the demand channel theory, while the manufacturing and high-tech sector (which are sectors with relatively high foreign sales) react more to FOMC surprises than the U.S. counterparts, again, consistent with the demand channel transmission of U.S. monetary policy to firms abroad.

Interestingly in Table 5 Panel A, the daily return regression shows that once we control for industry fixed effects foreign firms react, on average, 6 basis points less than U.S. firms for a 25-basis-point target rate surprise (this difference is not statistically significant in the hourly return regression). This result provides a partial explanation to the apparent puzzling result presented in Table 3- that foreign firms, on average, react more to FOMC announcements than U.S. firms. In Table 5 Panel B, we present the ratio of total market capitalization of each industry for our foreign firm sample divided by the domestic firm sample. We can observe that the foreign sample contains twice as much market capitalization in the durables good sector than the domestic sample. Since this sector is very sensitive to interest rate changes, it is natural that foreign firms in our sample react slightly more to FOMC announcements than the U.S. firms.

In addition to these industry effects, we also show in Table 6 evidence that foreign firms react slightly more to FOMC announcement surprises if more of their revenue is generated outside their home country, which should tend to increase their exposure to the U.S. economy. However, this difference is only statistically significant in the hourly return regression.

We now consider the second channel of transmission of U.S. monetary policy to equity prices and ask whether opaque firms and firms that depend more heavily on external finances react more to FOMC announcements.

4.2.2  Credit Channel

The credit channel posits that U.S. monetary policy shocks could have a large impact on firms with low credit ratings and firms that are largely dependent on external financing. More specifically, opaque firms and firms that have poor credit ratings may find it more difficult to access bank loans or other financing when credit conditions become tighter, as credit lines to opaque firms and customers in poor financial health will often be cut first. U.S. monetary policy shocks can affect foreign firms to the extent that they depend on U.S. credit or if U.S. monetary policy affects credit supplied by foreign institutions. Furthermore, U.S. banks may cut credit lines first to foreign customers and then to U.S. customers, so that given a credit grade, foreign firms may react more to FOMC announcements.

Bernanke and Blinder (1992) and Kashyap, Stein and Wilcox (1993) show that a tightening of monetary policy has a particularly strong impact on firms that are highly bank-dependent borrowers as banks reduce their overall supply of credit. The literature on the credit channel of monetary policy conjectures that a tightening of monetary policy should affect not only bank-dependent firms but firms that are financially constrained in general. To analyze the role external costs of funds play in the firm's reaction to federal funds rate surprises we estimate the following equation,

$$R_{it} =\beta_{D0}+\beta_{D1}TS_{t}+\beta_{D2}TS_{t}\times X_{it} +\beta_{F0}I\left( ForeignFirm\right) _{i}$$ (6)

$$+\beta_{F1}TS_{t}\times I\left( ForeignFirm\right) _{i}+\beta_{2} TS_{t}\times X_{it}\times I\left( ForeignFirm\right) _{i}+\varepsilon _{it},$$

where the independent variables, $X_{it}$, measure the extent of the firm's financial constraints. We first consider three external finance dependence measures in isolation: the debt credit rating of the firm, the dividend payout policy and the capital expenditures minus cash flow from operations divided by the market capitalization of the firm. We show these estimation results in Table 7.

Irrespective of our proxy for external finance dependence, we find that more financially constrained firms are more sensitive to target rate surprises, consistent with the credit channel theory. Furthermore, we find that this effect is statistically and economically significant. For example, a typical U.S. and foreign firm that does not payout dividends decreases about 2.4 percent after a 25-basis point unexpected increase in the federal funds rate, compared to only 1 percent for a U.S. firm that pays out dividends and 1.3 percent for a foreign firm that pays out dividends (the comparison with hourly return responses is 2 percent vs 1 percent). Similarly, a typical U.S. and foreign firm with speculative-grade credit rating decreases about 1.5 percent compared to only about 1 percent for a U.S. firm with investment-grade credit rating and 1.2 percent for a foreign firm with investment-grade credit rating. The credit channel transmission of U.S. monetary policy appears to be slightly more important for domestic firms than for foreign firms (i.e., the premium for paying out dividends is larger for U.S. firms than for foreign firms), but the reaction is surprisingly similar.

In Table 8 we show the results of estimating equation (8) controlling for industry fixed-effects, or the demand channel transmission of U.S. monetary policy, other proxies for external finance dependence, our proxy for the degree of transparency of the firm, analyst coverage, a time-varying proxy for financial stress, and a time trend. This table contains a number of noteworthy features.¹⁸

First, as in Table 7 the signs of many of our coefficient estimates are consistent with the credit channel theories; more financially constrained firms are more sensitive to target rate surprises, even after controlling for industry fixed-effects, suggesting that the credit channel still plays an important role over and above the traditional monetary policy transmission channel. For example, we find that the more a firm must finance investment from sources other than its own cash flow (more External Finance Dependence), the more sensitive it is to a target surprise. On the other hand, a firm that pays high dividends or has an investment-grade bond rating has a relatively muted response to U.S. interest rates. In addition, a firm that is less opaque (more Analyst Coverage) response less to target surprises. We also find that responses vary over time. In particular, in relatively stressful periods, as indicated by the level of the junk bond spread, the stock price of a typical firm is more sensitive to a monetary shock. Firms also appear to react less to monetary policy surprises over time. This result coincides with the increased transparency of Fed communications over time, but it also coincides with very low volatility in the financial market (which is captured by our junk bond spread, but perhaps not perfectly). Finally, controlling for asymmetric information and the firm's exposure to other frictions that prevent it from funding all desired investments, large firms react more strongly to federal funds target rate surprises than small firms. Foreshadowing some of the subsequent results, in part this is due to the fact that large firms' systemic risk has changed over time (Schwert, 2003, and Guo, 2002). A little later we consider the possibility that the cross-firm variation in the response is mainly explained by the firm's CAPM beta, but first we turn to potential channels of transmission that are specific to foreign firms in our sample - portfolio balance effects and transmission of U.S. rate shocks through spillovers to local interest rates.

4.2.3  Portfolio balance effects and local interest rate spillovers

The portfolio balance channel posits that U.S. investors will tend to retreat from positions in other risky assets when their domestic investment portfolios undergo an adverse shock, reducing asset values and/or increasing forward-going risk. Accordingly, foreign stocks with a relatively large U.S. investor base ought to be more sensitive to a U.S. rate shock, all else equal. We proxy U.S. holdings by the relative share of U.S. trading volume to home-market trading volume (Panel A of Table 9) and find statistically significant support for this proposition.

U.S. monetary policy can also influence foreign asset prices indirectly through its effect on local interest rates. Equity prices in a country that is more sensitive to changes in U.S. interest rate will respond more to FOMC announcements. We measure each firm's local interest rate sensitivity on FOMC announcement days by calculating each firm's response to the home country's local interest rate change (short- and long-term interest rates) on FOMC announcement days--the beta from a regression of changes in stock market price on local interest rate changes during FOMC announcement days. The country's exchange rate regime can also play a role in transmitting U.S. monetary policy surprises to local interest rates. The estimated responses from this channel are shown in Panel B. We find that U.S. policy has a stronger effect on a foreign stock if its country either (i) has more interest rate co-movement with U.S. rates and/or (ii) pegs its exchange rate. This finding is consistent with Hausman and Wongswan (2006) for the case of foreign aggregate indexes.

4.2.4  One-Factor CAPM Beta

At least to some extent, we expect stocks that are more sensitive to economy-wide shocks in general, all else equal, to show a stronger response to FOMC announcement surprises. As shown in Table 10, we can capture much of the cross-firm variation in the response, simply by including an interaction term between CS and the stock's beta with the CRSP value-weighted daily market return, estimated over the 365 calendar days preceding the event date. However, as is documented in Tables 11 and 12, most of the other results are robust (in sign and statistical significance) to the inclusion of this interaction term, although it still comes in strong. The fact that we find a stronger response in stocks that, ex ante, ought to be particularly sensitive to U.S. rates - suggests that monetary policy news is more than just a generic macroeconomic shock. Note also that the adjusted R-squared increases when we include the beta cross-term, along with the other explanatory variables, consistent with the view that the firm's cost of capital as measured by CAPM beta is an important factor in the cross-variation of the firm's response. Nevertheless, the fact that most of the variables remain statistically significant in Table 11 means that asymmetric information and the health of the firm also play a role.

Table 12 shows estimates only for foreign firms and includes our proxies for the foreign rate and portfolio balance transmission channels. After accounting for the systematic risk, CAPM beta, we still find evidence that for the credit channel (debt to market capital share, dividend dummy, dividend yield, and junk spread), the portfolio balance channel (U.S. trading volume), and the local interest rate channel (Short-Term Interest Rate Beta). Once again, although CAPM beta can pick up some important variation across firms, possibly including mismeasurement of our other variables, monetary shocks appear to have special features that make the cross-sectional pattern of price movements differ systematically from generic market movements.

4.3 Home currency returns

A number of studies show that FOMC announcement surprises affect exchange rates (the path surprise more so than the target surprise). Since we are using dollar-denominated foreign equity prices, changes in the exchange rate, rather than changes in the equity price, may be driving our results. To show that the results of our previous section are not solely due to exchange rate movements we re-estimate our benchmark equation using home-currency equity returns. The results in Table 13 show that most of the response is due to changes in local equity prices rather than movements in the exchange rate.

5.  Conclusion

The results presented here show that U.S. monetary policy has important influences on foreign equity prices on average, but with considerable variation across firms. We have found that this differing response reflects a range of factors, including the extent of a foreign firm's exposure to U.S. demand, its dependence on external financing, the behavior of interest rates in its home country, and its sensitivity to portfolio adjustment by U.S. investors. More generally, we see these results as shedding some additional light on the nature and extent of the monetary and financial linkages between the United States and the rest of the world. In particular, since we are able to explain differences across foreign firms' responses through established theories of monetary transmission, our results are consistent with the surprisingly large average foreign response to U.S. rates reflecting fundamentals, rather than an across-the-board behavioral overreaction.

6.  Data Appendix

Analyst Coverage: We obtain data on analyst coverage from the I/B/E/S Historical Summary files. For each firm $i$ on CRSP/COMPUSTAT merged data, we measure the analyst coverage for firm $i$ in any given FOMC announcement in year $t$ as the number of analysts who provide fiscal-year-1-ahead earnings estimation for this particular firm. If no I/B/E/S value is available (i.e., CRSP is not match with I/B/E/S data using the CUSIP number), we set coverage equal to zero.

CAPM Beta: Estimated CAPM Beta using all of the stock's daily returns on non-FOMC days in the previous 365 calendar days (only for stocks with at least 100 data points in that period) relative to the CRSP value-weighted daily market return (EWRETD field in CRSP).

Debt to Market Capital Share, $DMK_{it}$: Ratio of debt to market capitalization plus debt at the end of the previous fiscal year. Debt is calculated as the sum of the firm's long-term debt (Compustat item #9) and debt in current liabilities (Compustat #34). Market capitalization is the number of shares outstanding (Compustat #25) multiplied by the stock price (Compustat #199).

Dividend Yield, $Div_{it}$: Dividends over the prior 12-month period as a percentage of the price at the beginning of that period. Dividend Yield $=100\times\sum_{k=-11}^{0}\frac{D_{t+k} }{P_{t-12}}$, where D and P are dividends and prices appropriately adjusted for splits. The data are from the CRSP monthly stocks files.

Firm Pays Dividends Indicator Variable, $I(Dividend)_{it}$: Equals 1 if Dividend Yield $>$ 0; equals 0 otherwise.

External Finance Dependence, $EFD_{it}$: Capital expenditures minus cash flows divided by market capitalization. All variables are measured as of the previous fiscal year. Much like the variable used by Rajan and Zingales (1998), our variable uses the sum of Compustat items # 123, 125, 126, 106, 213, and 217 for Cash Flow. Capital Expenditures is Compustat item # 128.

Indicator Variable for Intermeeting moves, $I\left( IM_{t}=1\right)$ : Equals 0 if FOMC announcement took place on a pre-scheduled meeting date, equals 1 otherwise. In our sample period there are four intermeeting moves, three of which were easing surprises.

Junk Bond Spread, $JSpread_{it}$: The average spread on six indices of seven-year junk bonds, minus the seven-year Treasury bond yield. The Junk Bond Spread variable is lagged one trading day.

Log Market Capital, $Size_{it}$: The natural log of the firm's market capitalization; market capitalization is the number of shares outstanding (Compustat #25, expressed in millions) multiplied by the stock price (Compustat #199).

Indicator Variable for Standard and Poors Investment Grade Debt Credit Rating,

$I$(S&P investment grade debt rating)$_{it }$: Dummy for S&P investment-grade credit rating. Equals 1 if the firm had an S&P LT credit rating the previous fiscal year and that credit rating was BBB- or better; equals 0 otherwise.

Indicator Variable for Standard and Poors Speculative Grade Debt Credit Rating,

$I$(S&P speculative grade debt rating)$_{it }$: Dummy for S&P non-investment-grade credit rating. Equals 1 if the firm had an S&P LT credit rating the previous fiscal year and that credit rating was not BBB- or better; equals 0 if the firm did not have an S&P LT credit rating or it had an investment-grade credit rating. [Note: for a firm with no S&P LT credit rating, Rated1=Rated2=0.]

Hourly Return: $\frac{M_{t+0:45:00}-M_{t-0:15:00}}{M_{t-0:15:00} }\times100$, where $M_{s}\,$is the mid-quote $\left( \frac{Bid+Ask} {2}\right)$ for the most recent set of quotes as of time s, and t is the time of the FOMC announcement. For example, if the FOMC announcement takes place at 2:15 PM, then $M_{t-0:15:00}$ is the last set of quotes prior to 2:00 PM (but later than 9:30 AM), and $M_{t+0:45:00}$ is the last set of quotes prior to 3:00 PM.

Daily Return: Daily return, expressed in percent terms; the variable RET (already adjusted for dividends and splits) is from the CRSP monthly stocks files.

Target Rate Surprise: The change in the current-month Fed funds futures contract in a thirty minute window around the FOMC announcement (ten minutes before to twenty minutes after) with some minor adjustments. In particular, because federal funds futures contracts have a payout that is based on the average effective federal funds rate that prevails over the calendar month specified in the contract, we adjust the federal funds futures rate by a factor related to the number of days in the month affected by the change in the target rate. For further details please refer to Kuttner (2001). We also use Reuters survey of professional forecasters to estimate the market expectation of FOMC decisions.

Path Surprise: The component of the change in one-year-ahead Eurodollar interest rate futures in a thirty-minute around the announcement window (ten minutes before to twenty minutes after) that is uncorrelated with the Target Surprise.

Industry classifications: Our industry classification dummies are largely based on the Fama-French 10 Industry Portfolios, http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/Data_Library/det_ 10_ind_port.html. The definitions for nine industries--Non-durables, Durables, Manufacturing, Energy, High-tech, Telecom, Wholesale/Retail, Health, and Utilities--are taken directly from the Fama-French classifications, which are based on the firm's SIC code as of the end of the previous fiscal year. We have partitioned the tenth Fama-French industry category (which they call "Other") into several more categories: Construction, Materials, Transportation, Finance/Banking, Services, and Unknown.

Market to Book Ratio: Market value of equity divided by book value of equity at the end of the previous fiscal year (data199xdata25)/data 60.

US trading volume to total trading volume ratio: This variable is estimated using Bloomberg data. We note that in computing this variable it is important to control for what fraction of a share ADRs represent.

References

Bartov, E., and Bodnar, G., 1994, Firm Valuation, Earnings Expectations, and the Exchange-rate Exposure Effect, Journal of Finance, 44, 1755-1786.

Bernanke, Ben S. and Alan S. Blinder, 1992, The federal funds Rate and the Channels of Monetary Transmission, American Economic Review, 82, 901-21.

Bernanke, Ben S. and Mark Gertler, 1989, Agency Costs, Net Worth, and Business Fluctuations, American Economic Review, 79, 14-31.

Bernanke, Ben S and Mark Gertler, 1995, Inside the Black Box: The Credit Channel of Monetary Policy Transmission, Journal of Economic Perspectives, 9, 27-48.

Bernanke, Ben S. and Kenneth Kuttner, 2005, What Explains the Stock Market's Reaction to Federal Reserve Policy?, Journal of Finance 60, 1221-1257.

Bertolotti, A. and B. Enyeart, 1995, Investing in ADRs: Characteristics of an ADR Portfolio, BARRA Newsletter, 156, 1-3.

Brennan, Michael, J., Narasimhan Jegadeesh, and Avanidhar Swaminathan, 1993, Investment Analysis and Price Formation in Securities Markets, Journal of Financial Economics, 38, 361-381.

Bushan, Ravi, 1989, Firm Characteristics and Analyst Following, Journal of Accounting and Economics 11, 255-274.

Canova, Fabio, 2005, The Transmission of U.S. Shocks to Latin America, Journal of Applied Econometrics, 20, 229-251.

Chordia, Tarun, Sahn-Wook Huh, and Avanidhar Subrahmanyam, 2007, The Cross-Section of Expected Trading Activity, Review of Financial Studies, 20, 709-740.

Ehrmann, Michael and Marcel Fratzscher, 2004, Taking Stock: Monetary Policy Transmission to Equity Markets, Journal of Money, Credit, and Banking 36, 719-737.

Ehrmann, Michael and Marcel Fratzscher, 2006, Global Financial Transmission of Monetary Policy Shocks, ECB Working Paper No 616.

Fama, E. and French, K., 2001, Disappearing dividends: changing firm characteristics or lower propensity to pay? Journal of Financial Economics 60, 3-43.

Fleming, M. and Piazzesi, M., 2005, Monetary Policy Tick-by-Tick, Working Paper.

Frank, Murray and Vidhan K. Goyal, 2003, Testing the pecking order theory of capital structure, Journal of Financial Economics, 67, 217-248.

Frankel, Jeffrey, Sergio L. Schmukler, and Luis Serven, 2004, Global Transmission of Interest Rates: Monetary Independence and Currency Regime, Journal of International Money and Finance, 23, 701-733.

Gertler, Mark, 1992, Financial Capacity and Output Fluctuations in an Economy with Multiperiod Financial Relationships, Review of Economic Studies, 59, 455-472.

Gertler, Mark and Simon Gilchrist, 1994, Monetary Policy, Business Cycles, and the Behavior of Small Manufacturing Firms, The Quarterly Journal of Economics, 109, 309-340.

Gürkaynak, Refet, Brian Sack, and Eric Swanson, 2005, Do Actions Speak Louder than Words? The Response of Asset Prices to Monetary Policy Actions and Statements, International Journal of Central Banking 1, 55-93.

Hausman, Joshua K., and Jon Wongswan, 2006, Global Asset Prices and FOMC Announcements, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 886.

Hong, H., T. Lim and J.C. Stein, 2000, Bad News Travels Slowly: Size, Analyst Coverage, and the Profitability of Momentum Strategies, Journal of Finance, 55, 265-295.

Jensen, Gerald R. and Robert R. Johnson, 1995, Discount Rate Changes and Security Returns in the U.S., 1962-1991, Journal of Banking and Finance 19, 79-95.

Jensen, Gerald R., Jeffrey M. Mercer, and Robert R. Johnson, 1996, Business Conditions, Monetary Policy, and Expected Security Returns, Journal of Financial Economics 40, 213-237.

Jorion, Philippe, 1990, The Exchange-Rate Exposure of U.S. Multinationals, Journal of Business, 63, 331-345.

Karolyi, G. Andrew, 1998, Why Do Companies List Shares Abroad? A Survey of the Evidence and Its Managerial Implications, Financial Markets, Institutions and Money, 7, 1-60.

Karolyi, G. Andrew, 2006, The World of Cross-Listings and Cross-Listings of the World: Challenging Conventional Wisdom. Review of Finance, 10, 99-152.

Karolyi, G. Andrew, and René M. Stulz, 1996, Why Do Markets Move Together? An Investigation of U.S.-Japan Stock Return Comovements, Journal of Finance, 51, 951-986.

Kashyap, Anil K., Jeremy Stein, and David Wilcox, 1993, Monetary Policy and Credit Conditions: Evidence from the Composition of External Finance, American Economic Review, 83, 78-98.

Kato, K, Linn, S., and Schallheim, J., 1991, Are There Arbitrage Opportunities in the Market for American Depositary Receipts? Journal of International Financial Markets, Insitutions and Money, 1, 73-89.

Kaplan, S. N., and L. Zingales, 1997, Do Financing Constraints Explain Why Investment Is Correlated with Cash Flow? Quarterly Journal of Economics, 112, 168-216.

Kim, Soyoung, 2001, International Transmission of U.S. Monetary Policy Shocks: Evidence from VAR's, Journal of Monetary Economics, 48, 339-372.

Kiyotaki, Nobuhiro, and John Moore, 1997, Credit Cycles, The Journal of Political Economy, 105, 211-248.

Kodres, Laura E., and Matthew Pritsker, 2002, A Rational Expectations Model of Financial Contagion, Journal of Finance, 57, 769-799.

Kuttner, Kenneth N., 2001, Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market, Journal of Monetary Economics 47, 523-544.

Kyle, Albert S., and Wei Xiong, 2001, Contagion as a Wealth Effect, Journal of Finance, 56, 1401-1440.

Lamont, Owen, Christopher Polk, and Jesus Saa-Requejo, 2002, Financial Constraints and Stock Returns, Review of Financial Studies, 14, 529-554.

Levy-Yeyati, Eduardo, and Federico Sturzenegger, 2005, Classifying Exchange Rate Regimes: Deeds vs. Words, European Economic Review 49, 1603-1635.

Loderer, C., and Pichler, 2000, Firms, Do you Know Your Currency Risk Exposure? Survey Results, Journal of Empirical Finance, 7, 317-344.

Nance, D., Smith, C., and Smithson, C., 1993, On the Determinants of Corporate Hedging, Journal of Finance, 47, 267-284.

Piazzesi, Monika, and Swanson, Eric, 2008, Futures Prices as Risk-adjusted Forecasts of Monetary Policy, Journal of Monetary Economics, forthcoming.

Rajan, Raghuram, and Luigi Zingales, 1998, Financial Dependence and Growth, American Economic Review, 88, 559-586.

Reinhart, Carmen M. and Kenneth S. Rogoff, 2004, The Modern History of Exchange Rate Arrangements: A Reinterpretation, Quarterly Journal of Economics 119, 1-48.

Rigobon, Roberto and Brian Sack, 2004, The Impact of Monetary Policy on Asset Prices, Journal of Monetary Economics 51, 1553-1575.

Rosentahl, L., 1983, An Empirical Test of the Efficiency of the ADR Market, Journal of Banking and Finance, 7, 17-29.

Schwert, W.G., 2003, Anomalies and Market Efficiency, Handbook of the Economics and Finance, eds. George Constantinides, Milton Harris, and Rene M. Stulz, Horth-Holland, Ch. 15, pp937-972

Shambaugh, Jay C., 2004, The Effect of Fixed Exchange Rates on Monetary Policy, Quarterly Journal of Economics 119, 301-352.

Thorbecke, Willem, 1997, On Stock Market Returns and Monetary Policy, Journal of Finance, 52, 635-654.

Webb, S., Officer, D., Boyd, B., 1995, An Examination of International Equity Markets Using American Depository Receipts, Journal of Business Finance and Accounting, 22, 415-430.

Wongswan, Jon, 2005, The Response of Global Equity Indexes to U.S. Monetary Policy Announcements, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 844.

Wongswan, Jon, 2006, Transmission of Information across International Equity Markets, Review of Financial Studies, 19, 1157-1189.

Yuan, Kathy, 2005, Asymmetric Price Movements and Borrowing Constraints: A Rational Expectations Equilibrium Model of Crises, Contagion, and Confusion, Journal of Finance, 60, 379-411.

Table 1.  Country Representation

In this table we present the number of observations for each country and the number of firms within each country. Asterisk mark those countries for which we have short and long interest rate data.

Country	Observations	Firms
Argentina	903	18
Australia*	1,177	36
Austria*	53	2
Bahamas	252	4
Belgium*	155	5
Bermuda	2,727	72
Brazil	521	13
British Virgin Islands	177	6
Canada*	14,223	441
Cayman Islands	591	16
Chile	1,468	27
China	1,773	60
Colombia	19	1
Denmark*	315	6
Dominican Republic	36	1
Finland*	302	8
France*	1,969	42
Germany*	1,098	33
Ghana	57	1
Greece	370	17
Hong Kong*	1,578	45
Hungary	126	2
Iceland	50	1
India	480	14
Indonesia	269	5
Ireland*	841	20
Israel	4,925	130
Japan*	2,055	38
Jordan	15	1
Korea	542	15
Luxembourg	438	11
Mexico	1,993	37
Netherland Antilles	258	5
Netherlands*	2,500	51
New Zealand*	319	11
Norway*	327	10
Panama	178	3
Papua New Guinea	48	1
Peru	210	3
Philippines	126	4
Poland	11	1
Portugal*	194	3
Russia	365	7
Singapore	428	9
South Africa	719	23
Spain*	739	10
Sweden*	536	19
Switzerland*	700	16
Taiwan	460	11
Thailand	24	2
Turkey	49	1
United Kingdom*	5,971	161
United States*	420,043	11,204
Venezuela	138	4
Italy*	909	18

Table 2A.  Summary Statistics: Foreign Firm Sample

In this table we present summary statistics for the variables used in empirical tests. The summary statistics are calculated using 1,501 foreign firms sampled during all FOMC announcement dates, 108 in total, from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement and in total there are 56,707 firm-FOMC date observations. For a detailed description of the variables please refer to the Appendix.

	Mean	Std. Dev.	Min.	Max.
Dependent Variable: Daily Return	0.300	4.407	-57.863	301.515
Dependent Variable: Hourly Return	0.082	2.751	-45.136	103.125
Firm Characteristsics: Debt to Market Capital Share	0.237	0.232	0.000	0.990
Firm Characteristsics: Market to Book Ratio	3.205	4.404	-10.415	29.119
Firm Characteristsics: External Finance Dependence	0.025	0.240	-0.541	2.477
Firm Characteristsics: Log Market Capital	7.050	2.208	0.229	12.739
Firm Characteristsics: Investment Grade Rating	0.202	0.401	0.000	1.000
Firm Characteristsics: Non-investment Grade Rating	0.174	0.379	0.000	1.000
Firm Characteristsics: Dividend Dummy	0.502	0.500	0.000	1.000
Firm Characteristsics: Dividend Yield	1.524	2.432	0.000	12.245
Firm Characteristsics: Analyst Coverage	5.287	5.020	0.000	33.000
Firm Characteristsics: US Trading Volume/Total Trading Volume	0.425	0.432	0.000	1.000
Firm Characteristsics: Foreign Sales/Total Sales Ratio	0.476	0.520	0.000	1.000
Firm Characteristsics: US CAPM beta	0.792	0.602	-3.983	5.342
Firm Characteristsics: Foreign Exchange Beta	-0.147	5.024	-16.018	32.498
Firm Characteristsics: L.C. Short-Term Interest Rate Beta	-0.079	0.382	-9.297	12.443
Firm Characteristsics: L. C. Long-Term Interest Rate Beta	-0.019	0.149	-2.979	4.660
Business Cycle/Stress Measure: Junk Bond Spread	3.309	1.073	1.960	6.150
Country Factor: Exchange Rate Regime	1.355	0.722	1.000	3.000
FOMC Surprise: Target Surprise	-1.253	8.406	-43.749	16.333
FOMC Surprise: Intermeeting FOMC decision	0.037	0.190	0.000	1.000

Table 2B.  Summary Statistics: U.S. Firm Sample

In this table we present summary statistics for the variables we use in our empirical tests. The summary statistics are calculated using 11,204 U.S. firms sampled during all FOMC announcement dates, 108 in total, from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement and in total there are 420,043 firm-FOMC date observations. For a detailed description of the variables please refer to the Appendix.

	Mean	Std. Dev.	Min.	Max.
Dependent Variable: Daily Return	0.230	4.846	-91.667	412.500
Dependent Variable: Hourly Return	0.066	3.046	-45.136	170.000
Firm Characteristics: Debt to Market Capital Share	0.229	0.239	0.000	1.000
Firm Characteristics: Market to Book Ratio	3.233	4.521	-10.415	29.119
Firm Characteristics: External Finance Dependence	0.014	0.221	-0.541	2.477
Firm Characteristics: Log Market Capital	5.819	1.912	-0.064	13.139
Firm Characteristics: Investment Grade Rating	0.087	0.282	0.000	1.000
Firm Characteristics: Non-investment Grade Rating	0.173	0.378	0.000	1.000
Firm Characteristics: Dividend Dummy	0.360	0.480	0.000	1.000
Firm Characteristics: Dividend Yield	0.888	1.629	0.000	12.245
Firm Characteristics: Analysts Coverage	6.220	6.210	0.000	38.000
Firm Characteristics: US CAPM beta	0.755	0.655	-0.921	3.049

Table 3a.  Panel A - Response of asset prices to federal funds rate surprises - Daily Return

In this table we present estimates of the following equation:

$$R_{it}=\beta_{D0}+\beta_{DTS}TS_{t}+\beta_{F0}I(ForeignFirm)_{i}+\beta _{FTS}TS_{t}\times I(ForeignFirm)_{i}+\varepsilon_{it}$$

where $R_{it}$ is the daily return of asset $i$ on day $t$, $TS_{t}$ is the target rate surprise on day $t$, and $I(ForeignFirm)_{i}$ is an indicator variable equal to 1 if firm $i$ is based outside the U.S., zero otherwise. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement and in total there are 56,707 firm-FOMC date observations for the sample of foreign firms and 420,043 firm-FOMC date observations for the sample of U.S. firms. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test the null hypothesis that the sum of two coefficients is equal to zero. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	Coefficient	t-stat
Target Surprise	-0.0743***	-77.76
Target Surprise $\times I(ForeignFirm)$	-0.0020***	-0.80
$H_{0}:\beta_{DTS}+\beta_{FTS}=0\left( \chi^{2}-statistic\right)$	-0.0763***	1080.6
Adj. $R^{2}$	1.62%

Table 3b.  Panel B - Response of asset prices to federal funds rate surprises - Hourly Return

	Coefficient	t-statistic
Target Surprise	-0.0635***	-106.19
Target Surprise $\times I(ForeignFirm)$	-0.0047***	-2.99
$H_{0}:\beta_{DTS}+\beta_{FTS}=0\left( \chi^{2}-statistic\right)$	-0.0682***	2191.18
Adj. $R^{2}$	3.01%

Table 4a.  Panel A - Industry Response to FOMC Surprises - Daily Returns

In this table we present estimates of the following equation:

$$R_{it} =\beta_{Dj0}I\left( Firm_{i}\in Industry_{j}\right) +\beta _{Dj}TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right) +\beta _{Fj0}I(ForeignFirm)_{i}\times I\left( Firm_{i}\in Industry_{j}\right)$$

$$+\beta_{Fj}TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right) \times I(ForeignFirm)_{i}+\varepsilon_{it},$$

where $R_{it}$ is the daily or hourly return of asset $i$ on day $t$, $TS_{t}$ is the target rate surprise on day $t$,and $j=1,\ldots 10$ industry classifications using Fama-French's 10 industry portfolio classification, which is based on the firm's SIC code as of the end of the previous fiscal year, and $I(ForeignFirm)_{i}$ is an indicator variable equal to 1 if firm $i$ is based outside the U.S., zero otherwise. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement and in total there are 56,707 firm-FOMC date observations for the sample of foreign firms and 420,043 firm-FOMC date observations for the sample of U.S. firms. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-statistic$
$TS\times$ Non-durables	-0.0337***	-10.48	0.001	0.12	-0.0327***	16.62
$TS\times$ Durables	-0.0838***	-15.45	0.0196*	1.73	-0.0642***	42.07
$TS\times$ Manufacturing	-0.0541***	-24.92	-0.0011	-0.2	-0.0552***	109.92
$TS\times$ Energy	0.0042	1.11	-0.0038	-0.48	0.0004	0
$TS\times$ High-tech	-0.1495***	-59.32	-0.0131*	-1.87	-0.1625***	625.13
$TS\times$ Telecom	-0.1319***	-20.26	0.0202**	2.16	-0.1117***	274.97
$TS\times$ Whole/Retail	-0.0624***	-21.47	0.0272**	2.08	-0.0352***	7.61
$TS\times$ Health	-0.0604***	-19.27	0.015	1.58	-0.0454***	25.66
$TS\times$ Utilities	0.0069***	3.36	-0.0263***	-2.73	-0.0194**	4.26
$TS\times$ Other	-0.0502***	-30.74	0.0063	1.5	-0.0439***	129.21
Adj. $R^{2}$	2.29%

Table 4b.  Panel B - Industry Response to FOMC Surprises - Hourly Returns

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-statistic$
$TS\times$ Non-durables	-0.0278***	-10.97	0.003	0.57	-0.0248***	28.52
$TS\times$ Durables	-0.0536***	-17.47	0.0052	0.87	-0.0484***	86.98
$TS\times$ Manufacturing	-0.0473***	-32.2	-0.0089**	-2.17	-0.0562***	215.6
$TS\times$ Energy	-0.0153***	-6.08	-0.0064	-1.43	-0.0217***	34.85
$TS\times$ High-tech	-0.1203***	-77.68	-0.0162***	-4.09	-0.1365***	1392.41
$TS\times$ Telecom	-0.1052***	-25.17	0.015**	2.56	-0.0902***	481.01
$TS\times$ Whole/Retail	-0.0521***	-29.7	0.0246**	2.09	-0.0275**	5.57
$TS\times$ Health	-0.0563***	-28.06	0.0123**	2.32	-0.0441***	80.7
$TS\times$ Utilities	-0.0054***	-3.82	-0.012**	-2.1	-0.0174***	9.87
$TS\times$ Other	-0.0461***	-47.86	0.0015	0.51	-0.0446***	275.09
Adj. $R^{2}$	3.94%

Table 5a.  Panel A - Industry Response to FOMC Surprises - Regression Results

In Panel A we present estimates of the following equation:

$$R_{it}=\beta_{0j}I\left( Firm_{i}\in Industry_{j}\right) +\beta_{Dj} TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right) +\beta_{F}TS_{t}\times I(ForeignFirm)_{i}+\varepsilon_{it,}$$

where $R_{it}$ is the daily or hourly return of asset $i$on day $t$, $TS_{t}$ is the target rate surprise on day $t$,and $j=1,\ldots 10$ industry classifications using Fama-French's 10 industry portfolio classification, which is based on the firm's SIC code as of the end of the previous fiscal year, and $I(ForeignFirm)_{i}$ is an indicator variable equal to 1 if firm $i$ is based outside the U.S., zero otherwise. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement and in total there are 56,707 firm-FOMC date observations for the sample of foreign firms and 420,043 firm-FOMC date observations for the sample of U.S. firms. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively. In Panel B we present the ratio of total market capitalization of each industry for our foreign firm sample divided by the domestic firm sample counterpart.

	Daily Returns: Coefficient	Daily Returns: t-stat	Hourly Returns: Coefficient	Hourly Returns: t-stat
$TS\times I(ForeignFirms)$	0.0026**	2.01	-0.0013	-0.81
$TS\times$ Non-durables	-0.0339***	-11.27	-0.0272***	-11.81
$TS\times$ Durables	-0.0809***	-16.74	-0.0525***	-19.34
$TS\times$ Manufacturing	-0.0545***	-26.66	-0.0481***	-34.68
$TS\times$ Energy	0.0029	0.87	-0.0163***	-7.49
$TS\times$ High-tech	-0.1514***	-63.68	-0.122***	-83.93
$TS\times$ Telecom	-0.126***	-25.00	-0.0998***	-31.08
$TS\times$ Whole/Retail	-0.0611***	-21.55	-0.0507***	-28.73
$TS\times$ Health	-0.0593***	-19.91	-0.0552***	-29.13
$TS\times$ Utilities	0.0041**	1.98	-0.0064***	-4.62
$TS\times$ Other	-0.0498***	-32.03	-0.0458***	-49.44
Adj. $R^{2}$	2.28%		3.94%

Table 5b.  Panel B - Industry Response to FOMC Surprises - Industry Composition

	Foreign Sample/U.S. Sample-Market Cap Ratio
Non-durables	0.329
Durables	1.917
Manufacturing	0.276
Energy	1.077
High-tech	0.235
Telecom	1.011
Whole/Retail	0.084
Health	0.319
Utilities	0.356
Other	0.414

Table 6.  Test of Demand Channel of Monetary Policy Transmission

In this table we present estimates of the following equation:

$$R_{it} =\beta_{D0}+\beta_{D1}TS_{t}+\beta_{DX}TS_{t}\times X_{it} +\beta_{F0}I(ForeignFirm)_{i}+\beta_{F1}TS_{t}\times I(ForeignFirm)_{i}$$

$$+\beta_{FX}TS_{t}\times X_{it}\times I(ForeignFirm)_{i}+\varepsilon_{it,}$$

where $R_{it}$ is the daily or hourly return of asset $i$on day $t$, $TS_{t}$ is the target rate surprise on day $t$, and $X_{it}$ is the ratio of foreign sales to total sales of firm $i$ at time $t$. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement. The total number of observations varies depending on the availability of the data. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	Daily Return: Coefficient	Daily Return: t-value	Hourly Return: Coefficient	Hourly Return: t-value
Target Surprise	-0.0714***	-19.13	-0.0679***	-29.76
Adj. $R^{2}$	3.09%		6.15%
Target Surprise	-0.0636***	-8.22	-0.0518***	-12.14
Target Surprise $\times$ Foreign Sales	-0.0153	-1.18	-0.0313***	-4.10
Adj. $R^{2}$	3.10%		6.27%
Observations	14,854

Table 7a.  Panel A - Financial Constraints - Daily Return

In this table we present estimates of the following equation:

$$R_{it} =\beta_{D0}+\beta_{D}TS_{t}+\beta_{DX}TS_{t}\times X_{it}+\beta _{F0}I(ForeignFirm)_{i}+\beta_{F}TS_{t}\times I(ForeignFirm)_{i}$$

$$+\beta_{FX}TS_{t}\times X_{it}\times I(ForeignFirm)_{i}+\varepsilon_{it,}$$

We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-statistic$
$TS$	-0.0809***	-73.31	-0.0027	-0.9	-0.0837***	866.09
$TS\times$ Ex. Finance Dep.	-0.0515***	-9.22	-0.0177	-1.02	-0.0692***	17.76
Adj. $R^{2}$	1.81%
$TS$	-0.0812***	-66.38	-0.0069*	-1.93	-0.0881***	686.54
$TS\times$ Inv. Grade Rating	0.0367***	19.94	0.0033	0.72	0.04***	89.67
$TS\times$ Non-Inv. Grade Rating	0.0219***	11.32	0.0033	0.58	0.0252***	22.96
Adj. $R^{2}$	1.67%
$TS$	-0.0951***	-68.75	-0.0017	-0.43	-0.0969***	648.57
$TS\times$ Dividend Dummy	0.06***	37.16	-0.0138***	-2.98	0.0462***	112.55
Adj. $R^{2}$	1.86%
$TS$	-0.0895***	-74.55	0.0009	0.28	-0.0886***	908.91
$TS\times$ Dividend Yield	0.0163***	42.61	-0.0064***	-6.98	0.0099***	143.04
Adj. $R^{2}$	1.84%

Table 7b.  Panel B - Financial Constraints - Hourly Return

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$			$\chi^{2}-statistic$
$TS$	-0.0687***	-99.56	-0.0053***	-2.78	-0.074***			1743.35
$TS\times$ Ex. Finance Dep.	-0.0295***	-8.25	0.0121	1.03	-0.0174***			2.39
Adj. $R^{2}$	3.23%
$TS$	-0.0673***	-88.27	-0.0061***	-2.73	-0.0734***			1226
$TS\times$ Inv. Grade Rating	0.0176***	14.68	0.004	1.35	0.0216***			63.78
$TS\times$ Non-Inv. Grade Rating	0.0135***	10.94	-0.0068*	-1.91	0.0067**			3.94
Adj. $R^{2}$	3.05%
$TS$	-0.0779***	-90.56	-0.005**	-2.03	-0.0829***			1293.35
$TS\times$ Dividend Dummy	0.0415***	40.65	-0.0085***	-2.87	0.033***			142.33
Adj. $R^{2}$	3.30%
$TS$	-0.0743***	-99.53	-0.0035*	-1.78	-0.0779***			1816.46
$TS\times$ Dividend Yield	0.0116***	46.94	-0.0038***	-5.69	0.0078***			154.93
Adj. $R^{2}$	3.30%

Table 8a.  Panel A - Financial Constraints, Stress Periods and Time Trend - Daily Return

In this table we present estimates of the following equation:

$$R_{it} =\beta_{D0j}I\left( Firm_{i}\in Industry_{j}\right) +\beta _{Dj}TS_{t}\times I\left( Firm_{i}\in Industry_{j}\right) +\beta_{DX} TS_{t}\times X_{it}$$

$$+\beta_{F0j}I\left( Firm_{i}\in Industry_{j}\right) \times I(ForeignFirm)_{i}+\beta_{Fj}TS_{t}\times I\left( Firm_{i}\in Industry_{j} \right) \times I(ForeignFirm)_{i}$$

$$+\beta_{FX}TS_{t}\times X_{it}\times I(ForeignFirm)_{i}+\varepsilon_{it},$$

We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-stat$
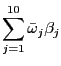$$\sum_{j=1}^{10}\bar{\omega}_{j}\beta_{j}$$ ($\chi^{2}-stat$)	0.1834***	695.2	-0.1597***	49.85	0.0237	1.21
$TS\times$Ex. Finance Dep.	-0.0364***	-6.71	-0.0565***	-2.56	-0.0929***	18.84
$TS\times$Market to Book Ratio	-0.0015***	-5.19	-0.0016*	-1.75	-0.0031***	13.17
$TS\times$Debt to Market Capital	-0.0022	-0.41	0.0308	1.53	0.0287	2.16
$TS\times$ log(market capital)	-0.0164***	-14.91	0.0063**	2.25	-0.0101***	15.78
$TS\times$Inv. Grade Rating	0.039***	12.47	-0.0092	-0.95	0.0298***	10.33
$TS\times$Non-Inv. Grade Rating	0.022***	8.8	-0.0099	-1.22	0.0121	2.45
$TS\times$Dividend Dummy	0.032***	11.88	-0.0131	-1.42	0.0189**	4.56
$TS\times$Dividend Yield	0.0041***	5.69	-0.0025	-1.51	0.0016	1.09
$TS\times$Analyst Coverage	0.0005*	1.71	0.0006	0.86	0.0011	2.59
$TS\times$Junk Spread	-0.0618***	-38.4	0.0385***	8.6	-0.0233***	31.27
$TS\times$Time Trend	0.2028***	23.58	-0.0973***	-3.8	0.1055***	19.16
Adj. $R^{2}$	3.42%

Table 8b.  Panel A - Financial Constraints, Stress Periods and Time Trend - Daily Return

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-stat$
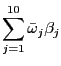$$\sum_{j=1}^{10}\bar{\omega}_{j}\beta_{j}$$ ($\chi^{2}-stat$)	0.1908***	2019.19	-0.1221***	82.73	0.0687***	29.13
$TS\times$Ex. Finance Dep.	-0.0262***	-7.79	0.0076	0.4	-0.0186	1
$TS\times$Market to Book Ratio	-0.0022***	-12.71	-0.001*	-1.79	-0.0032***	36.49
$TS\times$Debt to Market Capital	-0.0026	-0.79	0.0036	0.3	0.0009	0.01
$TS\times$log(market capital)	-0.0185***	-26.77	0.0109***	6.57	-0.0075***	24.81
$TS\times$Inv. Grade Rating	0.0351***	17.14	-0.0159**	-2.41	0.0192***	9.35
$TS\times$Non-Inv. Grade Rating	0.0182***	11.35	-0.0164***	-2.97	0.0018	0.12
$TS\times$Dividend Dummy	0.0248***	14.58	-0.0057	-0.91	0.0191***	10.11
$TS\times$Dividend Yield	0.0028***	6.05	-0.0019*	-1.68	0.0008	0.63
$TS\times$Analyst Coverage	0.0010***	6.25	0.0027***	5.79	0.0037***	14.6
$TS\times$Junk Spread	-0.0600***	-60.51	0.0312***	11.14	-0.0288***	120.71
$TS\times$Time Trend	0.2235***	41.91	-0.1204***	-7.65	0.1031***	48.52
Adj. $R^{2}$	6.79%

Table 9a.  Panel A - Test of Portfolio and Interest Rate Channel of Monetary Policy Transmission - Test of Portfolio Channel

In this table we present estimates of the following equation:

$$R_{it}=\beta_{0}+\beta_{1}TS_{t}+\beta_{2}TS_{t}\times X_{it}+\varepsilon _{it},$$

where $R_{it}$ is the daily or hourly return of asset $i$on day $t$, $TS_{t}$ is the target rate surprise on day $t$, and $X_{it}$ is a vector of firm characteristics. The variable FX regime takes three values, 1 indicates a de facto flexible exchange rate, 2 indicates a managed float regime, and 3 a de facto fixed exchange rate, according to Levy-Yeyati and Sturzenegger (2005)'s exchange rate regime classification. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement. The total number of observations varies depending on the availability of the data and we only consider the sample of foreign firms. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	Daily Return: Coefficient	Daily Return: t-value	Hourly Return: Coefficient	Hourly Return: t-value
Target Surprise	-0.0749***	-28.56	-0.0657***	-40.76
Adj. $R^{2}$	2.43%		4.97%
Target Surprise	-0.0591***	-19.31	-0.0522***	-28.33
$TS\times$US-Local Trading Volume Ratio	-0.0378***	-5.58	-0.0322***	-7.75
Adj. $R^{2}$	2.55%		5.20%
Observations	47,509

Table 9b.  Panel B - Test of Portfolio and Interest Rate Channel of Monetary Policy Transmission - Test of Interest Rate Channel

	Daily Return: Coefficient	Daily Return: t-value	Hourly Return: Coefficient	Hourly Return: t-value
Target Surprise	-0.0608***	-21.37	-0.0574***	-31.08
Adj. $R^{2}$	1.55%		3.16%
Target Surprise	-0.041***	-11.36	-0.0451***	-20.73
$TS\times$FX Exposure	-0.0046***	-3.8	-0.0024***	-3.53
$TS\times$LC Short-Term Int.	-0.1367***	-6.51	-0.0807***	-5.74
$TS\times$LC Long-Term Int.	0.1154***	3.27	0.0538***	3.76
Adj. $R^{2}$	2.35%		3.79%
Observations	35,408
Target Surprise	-0.0763***	-32.6	-0.068***	-46.27
Adj. $R^{2}$	2.03%		4.16%
Target Surprise	-0.056***	-11.46	-0.0616***	-19.96
$TS\times$ FX Regime	-0.0148***	-4.62	-0.0047**	-2.26
Adj. $R^{2}$	2.07%		4.17%
Observations	56,605

Table 10a.  Panel A - CAPM Beta - Daily Return

In this table we present estimates of the following equation:

$$R_{it} =\beta_{D0}+\beta_{D1}TS_{t}+\beta_{D2}TS_{t}\times X_{it} +\beta_{F0}\times I(ForeignFirm)_{i}+\beta_{F1}TS_{t}\times I(ForeignFirm)_{i}$$

$$+\beta_{F2}TS_{t}\times X_{it}\times I(ForeignFirm)_{i}+\varepsilon_{it},$$

where $R_{it}$ is the daily or hourly return of asset $i$ on day $t$, $TS_{t}$ is the target rate surprise on day $t$, and $X_{it}$ is the time-varying estimated CAPM beta for firm $i$ on day $t$. The sample period includes all FOMC announcements, 108 in total (104 scheduled meeting decisions and 4 intermeeting decisions), from February 4, 1994 to December 12, 2006, excluding the September 17, 2001 FOMC announcement. The total number of observations varies depending on the availability of the data. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A " $^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-stat$
$TS$	-0.001	-0.69	0.0046	1.22	0.0036	1.06
$TS\times$ CAPM Beta	-0.0853***	-54.3	-0.0187***	-4.08	-0.1039***	582.86
Adj. $R^{2}$	2.87%

Table 10b.  Panel B - CAPM Beta - Hourly Return

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-stat$
$TS$	-0.0058***	-6.3	-0.002	-0.88	-0.0078***	13.97
$TS\times$ CAPM Beta	-0.0666***	-67.9	-0.0111***	-4.28	-0.0777***	1042.4
Adj. $R^{2}$	4.88%

Table 11a.  Panel A - CAPM Beta Revisited - Daily Return

In this table we present estimates of the following equation:

$$R_{it} =\beta_{D0}+\beta_{D1}TS_{t}+\beta_{D2}TS_{t}\times X_{it} +\beta_{F0}\times I(ForeignFirm)_{i}+\beta_{F1}TS_{t}\times I(ForeignFirm)_{i}$$

$$+\beta_{F2}TS_{t}\times X_{it}\times I(ForeignFirm)_{i}+\varepsilon_{it},$$

where $R_{it}$ is the daily or hourly return of asset $i$ on day $t$, $TS_{t}$ is the target rate surprise on day $t$, and $X_{it\text{ }}$is a vector of firm characteristics. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates, as well as the $\chi^{2}$-statistic to test joint null hypothesis. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	$\beta_{Dj}\quad$	t-stat	$\beta_{Fj}\quad$	t-stat	$\beta_{Dj}+\beta_{Fj}$	$\chi^{2}-stat$
$TS$	0.2089***	30.59	-0.1201***	-5.36	0.0888***	17.34
$TS\times$Ex. Finance Dep.	-0.0087	-1.6	-0.0465**	-2.23	-0.0552***	7.53
$TS\times$Market to Book Ratio	-0.0005*	-1.75	-0.0008	-0.91	-0.0013	2.49
$TS\times$Debt to Market Capital	-0.0164***	-3.25	0.0215	1.23	0.0051	0.09
$TS\times$log(market capital)	-0.0001	-0.1	-0.0007	-0.27	-0.0008	0.12
$TS\times$Inv. Grade Rating	0.0142***	4.56	0.0043	0.47	0.0185**	4.54
$TS\times$Non-Inv. Grade Rating	0.011***	4.43	-0.0054	-0.69	0.0056	0.55
$TS\times$Dividend Dummy	-0.0015	-0.58	-0.0185**	-2.04	-0.0201**	5.33
$TS\times$Dividend Yield	0.0042***	6.94	-0.0035**	-2.18	0.0007	0.25
$TS\times$Analyst Coverage	-0.0005*	-1.9	0.0018**	2.57	0.0013**	4.05
$TS\times$Junk Spread	-0.0635***	-39.58	0.0379***	8.54	-0.0256***	38.45
$TS\times$Time Trend	0.1732***	20.13	-0.0951***	-3.72	0.0781***	10.52
$TS\times$CAPM Beta	-0.0888***	-44.06	-0.0224***	-3.42	-0.1112***	318.84
Adj. $R^{2}$	4.03%

Table 11a.  Panel A - CAPM Beta Revisited - Daily Return

$TS$	0.207***	49.46	-0.0945***	-7.14	0.1125***	80.33
$TS\times$Ex. Finance Dep.	-0.0072**	-2.12	0.0105	0.57	0.0033	0.03
$TS\times$Market to Book Ratio	-0.0016***	-9.05	-0.0005	-0.92	-0.0021***	15.83
$TS\times$Debt to Market Capital	-0.0098***	-3.06	0.0054	0.49	-0.0044	0.17
$TS\times$log(market capital)	-0.007	-1.02	0.0057	1.54	-0.0012	0.73
$TS\times$Inv. Grade Rating	0.018***	9.01	-0.0015	-0.24	0.0165***	7.88
$TS\times$Non-Inv. Grade Rating	0.0105***	6.68	-0.0127**	-2.34	-0.0022	0.17
$TS\times$Dividend Dummy	0.0022	1.33	-0.0078	-1.27	-0.0056	0.91
$TS\times$Dividend Yield	0.003***	7.77	-0.0025**	-2.25	0.0006	0.3
$TS\times$Analyst Coverage	0.0003*	1.94	0.0019***	4.25	0.0022***	14.48
$TS\times$Junk Spread	-0.0612***	-62	0.0306***	11.04	-0.0306***	139.25
$TS\times$Time Trend	0.2026***	37.99	-0.1202***	-7.66	0.0823***	31.09
$TS\times$CAPM Beta	-0.0613***	-47.82	-0.0164***	-4.11	-0.0778***	420.95
Adj. $R^{2}$	7.57%

Table 12a.  Panel A - CAPM Beta Revisited for Foreign Firms - Daily Returns

In this table we present estimates of the following equation:

$$R_{it}=\beta_{0}+\beta_{1}TS_{t}+\beta_{2}TS_{t}\times X_{it}+\varepsilon _{it},$$

We only consider the sample of foreign firms. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

 

	Coefficient (1)	t-value (1)	Coefficient (2)	t-value (2)
Target Surprise	0.034	0.97	0.0444	1.28
$TS\times$Ext. Finance Dependence	-0.0688*	-1.95	-0.0365	-1.06
$TS\times$Market to Book Ratio	-0.0008	-0.91	0.0004	0.52
$TS\times$Debt to Market Capital Ratio	0.081***	3.48	0.0466**	2.03
$TS\times$log(market capital)	-0.0079**	-2.39	0.0024	0.7
$TS\times$Inv. Grade Rating	0.0166	1.42	0.0038	0.33
$TS\times$Non-Inv. Grade Rating	-0.0036	-0.34	-0.0058	-0.55
$TS\times$Dividend Dummy	-0.0117	-1.03	-0.0355***	-3.18
$TS\times$Dividend Yield	0.0068***	2.74	0.0043*	1.76
$TS\times$Analyst Coverage	0.0003	0.10	0.0001	0.08
$TS\times$FX Exposure	-0.0002	-0.07	0.0012	0.47
$TS\times$LC Short-Term Interest Rate	-0.2051***	-7.01	-0.1184***	-4.25
$TS\times$LC Long-Term Interest Rate	0.096	0.86	0.094	0.85
$TS\times$US-Local Trading Volume Ratio	-0.0201	-1.44	-0.0003	-0.02
$TS\times$Regime	-0.01	-0.68	-0.0132	-0.9
$TS\times$Junk Spread	-0.0157***	-2.95	-0.0167***	-3.15
$TS\times$Time Trend	0.0931***	2.94	0.077**	2.43
$TS\times$US CAPM Beta			-0.0945***	-10.79
Adj. $R^{2}$	3.70%		4.79%

Table 12b.  Panel B - CAPM Beta Revisited for Foreign Firms - Panel B: Hourly Return

	Coefficient (1)	t-value (1)	Coefficient (2)	t-value (2)
Target Surprise	0.0932***	4.94	0.101***	5.38
$TS\times$Ext. Finance Dependence	-0.0107	-0.6	0.0139	0.81
$TS\times$Market to Book Ratio	-0.0017***	-3.39	-0.0008	-1.55
$TS\times$Debt to Market Capital Ratio	0.0423***	2.97	0.0153	1.08
$TS\times$log(market capital)	-0.0108***	-5.64	-0.0026	-1.34
$TS\times$Inv. Grade Rating	0.0192***	2.63	0.0091	1.28
$TS\times$Non-Inv. Grade Rating	-0.0075	-1.1	-0.0092	-1.36
$TS\times$Dividend Dummy	0.0106	1.46	-0.008	-1.13
$TS\times$Dividend Yield	0.0014	0.79	-0.0005	-0.3
$TS\times$Analyst Coverage	0.0019***	3.91	0.0018***	3.89
$TS\times$FX Exposure	-0.0046***	-3.35	-0.0036***	-2.66
$TS\times$LC Short-Term Interest Rate	-0.1224***	-7.59	-0.0531***	-3.99
$TS\times$LC Long-Term Interest Rate	0.0437	1.4	0.0429	1.4
$TS\times$US-Local Trading Volume Ratio	-0.0313***	-4.29	-0.0157**	-2.21
$TS\times$Regime	0.0189**	2.31	0.0167**	2.06
$TS\times$Junk Spread	-0.0242***	-7.68	-0.0252***	-8.07
$TS\times$Time Trend	0.0872***	4.82	0.0749***	4.15
$TS\times$US CAPM Beta			-0.075***	-15.21
Adj. $R^{2}$	8.02%		10.08%

Table 13a.  Panel A - Response of local currency asset prices to federal funds rate surprises - USD Equity Returns

In this table we present estimates of the following equation:

$$R_{it}=\beta_{0}+\beta_{1}TS_{t}+\varepsilon_{it},$$

where $R_{it}$ is either the USD (Panel A) or the local currency (Panel B) daily return of asset $i$ on day $t$, and $TS_{t}$ is the target rate surprise on day $t$. We use Panel-Corrected Standard Errors (PCSE) to compute the t-statistics reported next to the coefficient estimates. A "$^{\ast}$", "$^{\ast\ast}$", or "$^{\ast\ast\ast}$" indicate significance level at the 10%, 5% and 1% level, respectively.

	Coefficient	t-stat
Target Surprise	-0.0697***	-35.75
Intercept	0.156***	9.39
Adj. $R^{2}$	1.69%

Table 13b.  Panel B - Response of local currency asset prices to federal funds rate surprises - Local Currency Equity Returns

	Coefficient	t-stat
Target Surprise	-0.0713***	-32.50
Intercept	0.1079***	10.23
Adj. $R^{2}$	1.69%

Figure 1: Case Study: Stock Market Reactions to September 18, 2007 FOMC Announcement

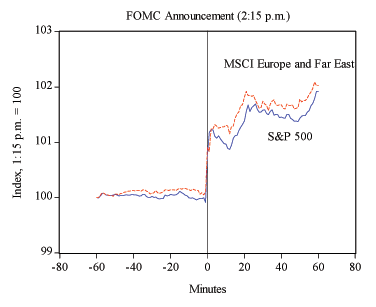
Figure 2. We plot our measure of financial stress periods, the junk-bond spread. It is measured as the average yield spread over the Treasury curve of six rating-specific indices of seven-year U.S. corporate bonds, based on Bloomberg's daily estimated yield curves for bonds rated BB+, BB, BB-, B+, B, and B-, respectively.

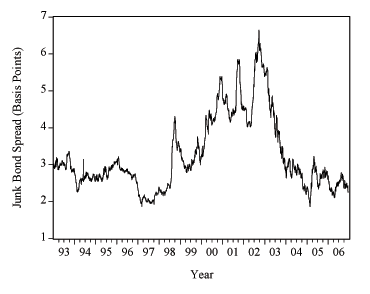
Footnotes

*  Ammer and Vega are affiliated with the Division of International Finance of the Board of Governors of the Federal Reserve System and Wongswan is at Barclays Global Investors. Please address comments to [email protected] and [email protected]. We thank Michael Furchtgott for his contributions to an earlier project that this work extends, Refet G�rkaynak for providing some of the data on monetary policy announcement surprises, Christian S. Miller and Nicholas Klagge for excellent research assistance, and workshop participants at the Federal Reserve Board for helpful comments. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1  See Bernanke and Gertler (1995) for a description of the conventional monetary policy transmission channel. Return to text

2  Theoretical examples of financial propagation mechanisms that stress the role of borrower�s balance sheets include Bernanke and Gertler (1989), Gertler (1992), and Kiyotaki and Moore (1993) among others. Return to text

3  Wongswan (2005) and Ehrmann and Fratzscher (2006), who analyze the response of stock market indexes in 15 and 50 different countries, respectively, to FOMC announcements, also find that several countries react more strongly to FOMC announcements than the U.S. equity index itself. Return to text

4  For example, Jensen and Johnson (1995), Jensen, Mercer, and Johnson (1996), Thorbecke (1997), Patelis (1997), Ehrmann and Fratzscher (2004), Rigobon and Sack (2004), G�rkaynak, Sack, and Swanson (2005), and Bernanke and Kuttner (2005). Return to text

5  Prior to 1994, the FOMC did not explicitly announce changes in its target for the federal funds rate, but such changes were implicitly communicated to financial markets through the size and type of open market operation. Thus, we start our sample when the announcement dates and times were explicitly known to the market. Most of the FOMC press releases have occurred at about 2:15 pm ET; however press releases for intermeeting policy moves and FOMC decisions prior to 1996 were released at varying times throughout the day. We obtain all of these dates and times from the Office of the Secretary of the Federal Reserve Board, for a list of the dates and times please refer to Appendix A1 of G�rkaynak, Sack and Swanson (2005).  Return to text

6  Because federal funds futures contracts have a payout that is based on the average effective federal funds rate that prevails over the calendar month specified in the contract, we adjust the federal funds futures rate by a factor related to the number of days in the month affected by the change in the target rate. For further details please refer to Kuttner (2001). We note that our results are qualitatively similar when we compute the target surprise using a one-hour window around the announcement (fifteen minutes before to forty-five minutes after). We use federal funds futures contracts, as opposed to other short-term interest rate futures contracts like the eurodollar, because G�rkaynak, Sack, and Swanson (2002) showed that these contracts are the best predictors of target fed funds rate changes 1-5 months ahead. Return to text

7  Coefficient estimates for equation (1) are: $\Delta ed_{t-10,t+20} =-0.75+0.49\ast TS_{t}$, and the adjusted R-squared is 0.28. Return to text

8  We thank Michael Ehrmann and Marcel Fratzscher for providing the data and the contact at Reuters ([email protected]) to update the data.  Return to text

9  For non-U.S. firms to be listed in U.S. exchanges they must furnish an annual report on a Form 20-F with a reconciliation of financial accounts with U.S. Generally Accepted Accounting Principles (GAAP). So our sample of firms have higher corporate governance standards than the average foreign firm. For more details on non-U.S. firm requirements to list in U.S. exchanges, please refer to Karolyi (1998). Return to text

10  There are numerous studies that investigate whether the law of one price holds (i.e., the dollar return at time t for the shares of foreign company i listed in its home country is equal to the dollar return for the shares of the same company listed in the U.S.). Karolyi (1998, 2006) provides an extensive survey of these studies and concludes that in general the law of one price holds (e.g., Rosenthal (1983), Kato et al. (1992), Webb et al. (1995), Bertollotti and Enyeart (1995), Karolyi and Stulz (1996)). Return to text

11  Ideally we would like to measure the foreign firm�s U.S. sales, but this data is not available. Return to text

12  Daily exchange rates, short- and long-term interest rate data are from Bloomberg except for interest rate data for Finland and Spain, which are from Thompson Datastream. To account for time-zone differences, we measure changes in foreign exchange rates and interest rates in all countries, except those in Canada, from the day of the FOMC through the next day�s close. In our sample, a few FOMC announcements occur before 1:00 pm Eastern time. In this case some European markets were open at the time of the announcement. To account for theses special cases, we carefully constructed data on the closing time of each market in our sample, adjusting for daylight savings time conventions as needed.  Return to text

13  Jorion (1990) estimates that a firm�s sensitivity to exchange rate movements is not zero, so this scenario may be unrealistic. Return to text

14  However, dividend payments may be a flawed measure of changes in a firm�s financial condition over time -- Fama and French (2001) find a declining propensity of U.S. firms to pay dividends over the period from 1978 to 1999.  Return to text

15  Because we do not want to increase the notational burden, throughout the paper we reuse the same coefficient symbols for the constant; however the coefficients are different in each equation. Return to text

16  We compute hourly returns from fifteen minutes before to forty-five minutes after the FOMC announcement, and the daily returns from the close of the day before the FOMC to the close of the day of the FOMC. Return to text

17  For a complete list of macroeconomic data releases that occurred on the same day as FOMC meetings, please refer to G�rkaynak, Sack and Swanson (2005). Return to text

18  We additional proxies for the extent of the firm�s external finance dependence we consider here: market to book ratio, debt to market capital share, and firm size, are more ambiguous than the proxies we consider in isolation in Table 9. On one hand, a high market to book ratio indicates that the firm has ample investment opportunities, which may imply, ceteris paribus, that the firm has higher financial constraints by requiring more external funds to finance these investments. On the other hand, a firm with a high market value of its assets, a high market to book ratio, may find it easier to raise external funds. Similarly, a highly leveraged firm, a firm with a high debt to market capital ratio, may find it harder to raise external funds, but it may also mean that a firm holds high levels of debt because it can, i.e. it is easy for this firm to raise external funds. Finally, we conjecture that large firms are less financially constraint and more transparent than small firms, but even if firm size is a useful proxy for the financial health of the firm and degree of opaqueness, it is likely to capture other things as well.  Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: November 10, 2008