The Taylor Rule and Interval Forecast For Exchange Rates¹

Jian Wang² and Jason J. Wu³

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper attacks the Meese-Rogoff puzzle from a different perspective: out-of-sample interval forecasting. Most studies in the literature focus on point forecasts. In this paper, we apply Robust Semiparametric (RS) interval forecasting to a group of Taylor rule models. Forecast intervals for twelve OECD exchange rates are generated and modified tests of Giacomini and White (2006) are conducted to compare the performance of Taylor rule models and the random walk. Our contribution is twofold. First, we find that in general, Taylor rule models generate tighter forecast intervals than the random walk, given that their intervals cover out-of-sample exchange rate realizations equally well. This result is more pronounced at longer horizons. Our results suggest a connection between exchange rates and economic fundamentals: economic variables contain information useful in forecasting the distributions of exchange rates. The benchmark Taylor rule model is also found to perform better than the monetary and PPP models. Second, the inference framework proposed in this paper for forecast-interval evaluation can be applied in a broader context, such as inflation forecasting, not just to the models and interval forecasting methods used in this paper.

Keywords: The exchange rate disconnect puzzle, exchange rate forecast, interval forecasting

JEL classification: F31, C14, C53

1. Introduction

Recent studies explore the role of monetary policy rules, such as Taylor rules, in exchange rate determination. They find empirical support in these models for the linkage between exchange rates and economic fundamentals. Our paper extends this literature from a different perspective: interval forecasting. We find that the Taylor rule models can outperform the random walk, especially at long horizons, in forecasting twelve OECD exchange rates based on relevant out-of-sample interval forecasting criteria. The benchmark Taylor rule model is also found to perform relatively better than the standard monetary model and the purchasing power parity (PPP) model.

In a seminal paper, Meese and Rogoff (1983) find that economic fundamentals - such as the money supply, trade balance and national income - are of little use in forecasting exchange rates. They show that existing models cannot forecast exchange rates better than the random walk in terms of out-of-sample forecasting accuracy. This finding suggests that exchange rates may be determined by something purely random rather than economic fundamentals. Meese and Rogoff's (1983) finding has been named the Meese-Rogoff puzzle in the literature.

In defending fundamental-based exchange rate models, various combinations of economic variables and econometric methods have been used in attempts to overturn Meese and Rogoff's finding. For instance, Mark (1995) finds greater exchange rate predictability at longer horizons.⁴ Groen (2000) and Mark and Sul (2001) detect exchange rate predictability by using panel data. Kilian and Taylor (2003) find that exchange rates can be predicted from economic models at horizons of 2 to 3 years, after taking into account the possibility of nonlinear exchange rate dynamics. Faust, Rogers, and Wright (2003) find that the economic models consistently perform better using real-time data than revised data, though they do not perform better than the random walk.

Recently, there is a growing strand of literature that uses Taylor rules to model exchange rate determination. Engel and West (2005) derive the exchange rate as a present-value asset price from a Taylor rule model. They also find a positive correlation between the model-based exchange rate and the actual real exchange rate between the US dollar and the Deutschmark (Engel and West, 2006). Mark (2007) examines the role of Taylor-rule fundamentals for exchange rate determination in a model with learning. In his model, agents use least-square learning rules to acquire information about the numerical values of the model's coefficients. He finds that the model is able to capture six major swings of the real Deutschmark-Dollar exchange rate from 1973 to 2005. Molodtsova and Papell (2009) find significant short-term out-of-sample predictability of exchange rates with Taylor-rule fundamentals for 11 out of 12 currencies vis-á-vis the U.S. dollar over the post-Bretton Woods period. Molodtsova, Nikolsko-Rzhevskyy, and Papell (2008a, 2008b) find evidence of out-of-sample predictability for the dollar/mark nominal exchange rate with forecasts based on Taylor rule fundamentals using real-time data, but not revised data. Chinn (forthcoming) also finds that Taylor rule fundamentals do better than other models at the one year horizon. With a present-value asset pricing model as discussed in Engel and West (2005), Chen and Tsang (2009) find that information contained in the cross-country yield curves are useful in predicting exchange rates.

Our paper joins the above literature of Taylor-rule exchange rate models. However, we address the Meese and Rogoff puzzle from a different perspective: interval forecasting. A forecast interval captures a range in which the exchange rate may lie with a certain probability, given a set of predictors available at the time of forecast. Our contribution to the literature is twofold. First, we find that for twelve OECD exchange rates, the Taylor rule models in general generate tighter forecast intervals than the random walk, given that their intervals cover the realized exchange rates (statistically) equally well. This finding suggests an intuitive connection between exchange rates and economic fundamentals beyond point forecasting: the use of economic variables as predictors helps narrow down the range in which future exchange rates may lie, compared to random walk forecast intervals. Second, we propose an inference framework for cross-model comparison of out-of-sample forecast intervals. The proposed framework can be used for forecast-interval evaluation in a broader context, not just for the models and methods used in this paper. For instance, the framework can also be used to evaluate out-of-sample inflation forecasting.

As we will discuss later, we in fact derive forecast intervals from estimates of the distribution of changes in the exchange rate. Hence, in principle, evaluations across models can be done based on distributions instead of forecast intervals. However, focusing on interval forecasting performance allows us to compare models in two dimensions that are more relevant to practitioners: empirical coverage and length.

While the literature on interval forecasting for exchange rates is sparse, several authors have studied out-of-sample exchange rate density (distribution) forecasts, from which interval forecasts can be derived. Diebold, Hahn and Tay (1999) use the RiskMetrics model of JP Morgan (1996) to compute half-hour-ahead density forecasts for Deutschmark/Dollar and Yen/Dollar returns. Christoffersen and Mazzotta (2005) provide option-implied density and interval forecasts for four major exchange rates. Boero and Marrocu (2004) obtain one-day-ahead density forecasts for the Euro nominal effective exchange rate using self-exciting threshold autoregressive (SETAR) models. Sarno and Valente (2005) evaluate the exchange rate density forecasting performance of the Markov-switching vector equilibrium correction model that is developed by Clarida, Sarno, Taylor and Valente (2003). They find that information from the term structure of forward premia help the model to outperform the random walk in forecasting out-of-sample densities of the spot exchange rate. More recently, Hong, Li, and Zhao (2007) construct half-hour-ahead density forecasts for Euro/Dollar and Yen/Dollar exchange rates using a comprehensive set of univariate time series models that capture fat tails, time-varying volatility and regime switches.

There are several common features across the studies listed above, which make them different from our paper. First, the focus of the above studies is not to make connections between the exchange rate and economic fundamentals. These studies use high frequency data, which are not available for most conventional economic fundamentals. For instance, Diebold, Hahn, and Tay (1999) and Hong, Li, and Zhao (2007) use intra-day data. With the exception of Sarno and Valente (2005), all the studies focus only on univariate time series models. Second, these studies do not consider multi-horizon-ahead forecasts, perhaps due to the fact that their models are often highly nonlinear. Iterating nonlinear density models multiple horizons ahead is analytically difficult, if not infeasible. Lastly, the above studies assume that the densities are analytically defined for a given model. The semiparametric method used in this paper does not impose such restrictions.

Our choice of the semiparametric method is motivated by the difficulty of using macroeconomic models in exchange rate interval forecasting: these models typically do not describe the future distributions of exchange rates. For instance, the Taylor rule models considered in this paper do not describe any features of the data beyond the conditional means of future exchange rates. We address this difficulty by applying Robust Semiparametric forecast intervals (hereon RS forecast intervals) of Wu (2009).⁵ This method is useful since it does not require the model be correctly specified, or contain parametric assumptions about the future distribution of exchange rates.

We apply RS forecast intervals to a set of Taylor rule models that differ in terms of the assumptions on policy and interest rate smoothing rules. Following Molodtsova and Papell (2009), we include twelve OECD exchange rates (relative to the US dollar) over the post-Bretton Woods period in our dataset. For these twelve exchange rates, the out-of-sample RS forecast intervals at different forecast horizons are generated from the Taylor rule models and then compared with those of the random walk. The empirical coverages and lengths of forecast intervals are used as the evaluation criteria. Our empirical coverage and length tests are modified from Giacomini and White's (2006) predictive accuracy tests in the case of rolling, but fixed-size, estimation samples.

For a given nominal coverage (probability), the empirical coverage of forecast intervals derived from a forecasting model is the probability that the out-of-sample realizations (exchange rates) lie in the intervals. The length of the intervals is a measure of its tightness: the distance between its upper and lower bound. In general, the empirical coverage is not the same as its nominal coverage. Significantly missing the nominal coverage indicates poor quality of the model and intervals. One certainly wants the forecast intervals to contain out-of-sample realizations as close as possible to the probability they target. Most evaluation methods in the literature focus on comparing empirical coverages across models, following the seminal work of Christoffersen (1998). Following this literature, we first test whether forecast intervals of the Taylor rule models and the random walk have equally accurate empirical coverages. The model with more accurate coverages is considered the better model. In the cases where equal coverage accuracy cannot be rejected, we further test whether the lengths of forecast intervals are the same. The model with tighter forecast intervals provides more useful information about future values of the data, and hence is considered as a more useful forecasting model.

It is also important to establish what this paper is not attempting. First, the inference procedure does not carry the purpose of finding the correct model specification. Rather, inference is on how useful models are in generating forecast intervals, measured in terms of empirical coverages and lengths. Second, this paper does not consider the possibility that there might be alternatives to RS forecast intervals for the exchange rate models we consider. Some models might perform better if parametric distribution assumptions (e.g. the forecast errors are conditionally heteroskedastic and distributed) or other assumptions (e.g. the forecast errors are independent of the predictors) are added. One could presumably estimate the forecast intervals differently based on the same models, and then compare those with the RS forecast intervals, but this is out of the scope of this paper. As we described, we choose the RS method for the robustness and flexibility achieved by the semiparametric approach.

First, the models considered in this paper are standard macroeconomic models for exchange rate determination. These models do not contain theory about the underlying distributions. Using RS forecast intervals allows us to refrain from having to impose subjective additional structures on the models. Our goal is to use existing models to generate forecast intervals, instead of developing new models. Second, RS forecast intervals are good candidates as they always consistently estimates their population counterparts, independent of the properties of the models and error terms ( $\varepsilon_{m,\tau+h}$ ). With the sample sizes we have, RS forecast intervals are deemed good approximations to the truth.

Our benchmark Taylor rule model is from Engel and West (2005) and Engel, Wang, and Wu (2008). For the purpose of comparison, several alternative Taylor rule models are also considered. These setups have been studied by Molodtsova and Papell (2009) and Engel, Mark, and West (2007). In general, we find that the Taylor rule models perform better than the random walk model, especially at long horizons: the models either have more accurate empirical coverages than the random walk, or in cases of equal coverage accuracy, the models have tighter forecast intervals than the random walk. The evidence of exchange rate predictability is much weaker in coverage tests than in length tests. In most cases, the Taylor rule models and the random walk have statistically equally accurate empirical coverages. So, under the conventional coverage test, the random walk model and the Taylor rule models perform equally well. However, the results of length tests suggest that Taylor rule fundamentals are useful in generating tighter forecasts intervals without losing accuracy in empirical coverages.

We also consider two other popular models in the literature: the monetary model and the model of purchasing power parity (PPP). Based on the same criteria, both models are found to perform better than the random walk in interval forecasting. As with the Taylor rule models, most evidence of exchange rate predictability comes from the length test: economic models have tighter forecast intervals than the random walk given statistically equivalent coverage accuracy. The PPP model performs worse than the benchmark Taylor rule model and the monetary model at short horizons. The benchmark Taylor rule model performs slightly better than the monetary model at most horizons.

Our findings suggest that exchange rate movements are linked to economic fundamentals. However, we acknowledge that the Meese-Rogoff puzzle remains difficult to understand. Although Taylor rule models offer statistically significant length reductions over the random walk, the reduction of length is quantitatively small, especially at short horizons. Forecasting exchange rates remains a difficult task in practice. There are some impressive advances in the literature, but most empirical findings remain fragile. As mentioned in Cheung, Chinn, and Pascual (2005), forecasts from economic fundamentals may work well for some currencies during certain sample periods but not for other currencies or sample periods. Engel, Mark, and West (2007) recently show that a relatively robust finding is that exchange rates are more predictable at longer horizons, especially when using panel data. We find greater predictability at longer horizons in our exercise. It would be of interest to investigate connections between our findings and theirs.

Several recent studies have attacked the puzzle from a different angle: there are reasons that economic fundamentals cannot forecast the exchange rate, even if the exchange rate is determined by these fundamentals. Engel and West (2005) show that existing exchange rate models can be written in a present-value asset-pricing format. In these models, exchange rates are determined not only by current fundamentals but also by expectations of what the fundamentals will be in the future. When the discount factor is large (close to one), current fundamentals receive very little weight in determining the exchange rate. Not surprisingly, the fundamentals are not very useful in forecasting. Nason and Rogers (2008) generalize the Engel-West theorem to a class of open-economy dynamic stochastic general equilibrium (DSGE) models. Other factors such as parameter instability and mis-specification (for instance, Rossi 2005) may also play important roles in understanding the puzzle. It is interesting to investigate conditions under which we can reconcile our findings with these studies.

The remainder of this paper is organized as follows. Section two describes the forecasting models we use, as well as the data. In section three, we illustrate how the RS forecast intervals are constructed from a given model. We also propose loss criteria to evaluate the quality of the forecast intervals and test statistics that are based on Giacomini and White (2006). Section four presents results of out-of-sample forecast evaluation. Finally, section five contains concluding remarks.

2. Models and Data

Seven models are considered in this paper. Let be the index of these models and the first model be the benchmark model. A general setup of the models takes the form of:

$\displaystyle s_{t+h}-s_{t}=\alpha_{m,h}+\beta^{\prime}_{m,h}\mathbf{X}_{m,t}+\varepsilon _{m,t+h},$

(1)

where $s_{t+h}-s_{t}$ is -period changes of the (log) exchange rate, and $\mathbf{X}_{m,t}$ contains economic variables that are used in model . Following the literature of long-horizon regressions, both short- and long-horizon forecasts are considered. Models differ in economic variables that are included in matrix $\mathbf{X}_{m,t}$ . In the benchmark model,

$\displaystyle \mathbf{X}_{1,t}\equiv\left[ \begin{array}[c]{ccc} \pi_{t}-\pi_{t}^{\ast} & y_{t}^{gap}-y_{t}^{gap\ast} & q_{t}\\ & & \end{array} \right] ,$

where $\pi_{t}$ ( $\pi_{t}^{\ast}$ ) is the inflation rate, and $y_{t}^{gap}$ ( $y_{t}^{gap\ast}$ ) is the output gap in the home (foreign) country. The real exchange rate $q_{t}$ is defined as $q_{t}\equiv s_{t}+p_{t}^{\ast}-p_{t}$ , where $p_{t}$ ( $p_{t}^{\ast}$ ) is the (log) consumer price index in the home (foreign) country. This setup is motivated by the Taylor rule model in Engel and West (2005) and Engel, Wang, and Wu (2008). The next subsection describes this benchmark Taylor rule model in detail.

We also consider the following models that have been studied in the literature:

Model 2:	$\begin{displaymath}\mathbf{X}_{2,t}\equiv\left[ \begin{array}[c]{cc} \pi_{t}-\pi_{t}^{\ast} & y_{t}^{gap}-y_{t}^{gap\ast}\ & \end{array}\right] \end{displaymath}$
Model 3:	$\begin{displaymath}\mathbf{X}_{3,t}\equiv\left[ \begin{array}[c]{ccc} \pi_{t}-\pi_{t}^{\ast} & y_{t}^{gap}-y_{t}^{gap\ast} & i_{t-1}-i_{t-1}^{\ast }\ & & \end{array}\right] \end{displaymath}$ ,
	where $i_{t}$ ( $i_{t}^{\ast}$ ) is the short-term interest rate in the home (foreign) country.
Model 4:	$\begin{displaymath}\mathbf{X}_{4,t}\equiv\left[ \begin{array}[c]{cccc} \pi_{t}-\pi_{t}^{\ast} & y_{t}^{gap}-y_{t}^{gap\ast} & q_{t} & i_{t-1} -i_{t-1}^{\ast}\ & & & \end{array}\right] \end{displaymath}$
Model 5:	$\mathbf{X}_{5,t}\equiv q_{t}$
Model 6:	$\begin{displaymath}\mathbf{X}_{6,t}\equiv\left[ \begin{array}[c]{c} s_{t}-\left[ (m_{t}-m_{t}^{\ast})-(y_{t}-y_{t}^{\ast})\right] \ \end{array}\right] \end{displaymath}$ ,
	where $m_{t}$ ( $m_{t}^{\ast}$ ) is the money supply and $y_{t}$ ( $y_{t}^{\ast}$ ) is total output in the home (foreign) country.
Model 7:	$\mathbf{X}_{7,t}\equiv0$

Models 2-4 are the Taylor rule models studied in Molodtsova and Papell (2009). Model 2 can be considered as the constrained benchmark model in which PPP always holds. Molodtsova and Papell (2009) include interest rate lags in models 3 and 4 to take into account potential interest rate smoothing rules of the central bank.⁶ Model 5 is the purchasing power parity (PPP) model and model 6 is the monetary model. Both models have been widely used in the literature. See Molodtsova and Papell (2009) for the PPP model and Mark (1995) for the monetary model. Model 7 is the driftless random walk model ( $\alpha _{7,h}\equiv0$ ).⁷ Given a date $\tau$ and horizon , the objective is to estimate the forecast distribution of $s_{\tau+h}-s_{\tau}$ conditional on $\mathbf{X}_{m,\tau}$ , and subsequently build forecast intervals from the estimated forecast distribution. Before moving to the econometric method, we first describe the Taylor rule model that motivates the setup of our benchmark model.

2.1 Benchmark Taylor Rule Model

Our benchmark model is the Taylor rule model that is derived in Engel and West (2005) and Engel, Wang, and Wu (2008). Following Molodtsova and Papell (2009), we focus on models that depend only on current levels of inflation and the output gap.⁸ The Taylor rule in the home country takes the form of:

$\displaystyle \bar{i}_{t}=\bar{i}+\delta_{\pi}(\pi_{t}-\bar{\pi})+\delta_{y}y_{t} ^{gap}+u_{t},$

(2)

where $\bar{i}_{t}$ is the central bank's target for the short-term interest rate at time , $\bar{i}$ is the equilibrium long-term rate, $\pi_{t}$ is the inflation rate, $\bar{\pi}$ is the target inflation rate, and $y_{t} ^{gap}$ is the output gap. The foreign country is assumed to follow a similar Taylor rule. In addition, we follow Engel and West (2005) to assume that the foreign country targets the exchange rate in its Taylor rule:

$\displaystyle \bar{i}_{t}^{\ast}=\bar{i}+\delta_{\pi}(\pi_{t}^{\ast}-\bar{\pi})+\delta _{y}y_{t}^{gap\ast}+\delta_{s}(s_{t}-\bar{s}_{t})+u_{t}^{\ast} ,$

(3)

where $\bar{s}_{t}$ is the targeted exchange rate. Assume that the foreign country targets the PPP level of the exchange rate: $\bar{s}_{t}=p_{t} -p_{t}^{\ast}$ , where $p_{t}$ and $p_{t}^{\ast}$ are logarithms of home and foreign aggregate prices. In equation (3), we assume that the policy parameters take the same values in the home and foreign countries. Molodtsova and Papell (2009) denote this case as "homogeneous Taylor rules". Our empirical results also hold in the case of heterogenous Taylor rules. To simplify our presentation, we assume that the home and foreign countries have the same long-term inflation and interest rates. Such restrictions have been relaxed in our econometric model after we include a constant term in estimations.

We do not consider interest rate smoothing in our benchmark model. That is, the actual interest rate ( $i_{t}$ ) is identical to the target rate in the benchmark model:

$\displaystyle i_{t}=\bar{i}_{t}.$

(4)

Molodtsova and Papell (2009) consider the following interest rate smoothing rule:

$\displaystyle i_{t}=(1-\rho)\bar{i}_{t}+\rho i_{t-1}+\nu_{t},$

(5)

where $\rho$ is the interest rate smoothing parameter. We include these setups in models 3 and 4. Note that our estimation methods do not require the monetary policy shock $u_{t}$ and the interest rate smoothing shock $\nu_{t}$ to satisfy any assumptions, aside from smoothness of their distributions when conditioned on predictors.

Substituting the difference of equations (2) and (3) into Uncovered Interest-rate Parity (UIP), we have:

$\displaystyle s_{t}=E_{t}\left\{ (1-b)\sum_{j=0}^{\infty }b^{j}(p_{t+j}-p^{*}_{t+j})-b\sum_{j=0}^{\infty}b^{j}\left[ \delta_{y} (y^{gap}_{t+j}-y_{t+j}^{gap\ast})+\delta_{\pi}(\pi_{t+j}-\pi^{*}_{t+j})\right] \right\} ,$

(6)

where the discount factor $b=\frac{1}{1+\delta_{s}}$ . Under some conditions, the present value asset pricing format in equation (6) can be written into an error-correction form:⁹

$\displaystyle s_{t+h}-s_{t}=\alpha_{h}+\beta _{h}z_{t}+\varepsilon_{t+h},$

(7)

where the deviation of the exchange rate from its equilibrium level is defined as:

$\displaystyle z_{t}=s_{t}-p_{t}+p_{t}^{\ast}+\frac{b}{1-b}\left[ \delta_{y}(y_{t}^{gap}-y_{t}^{gap\ast})+\delta_{\pi}(\pi_{t}-\pi_{t}^{\ast })\right] .$

(8)

We use equation (7) as our benchmark setup in calculating h-horizon-ahead out-of-sample forecasting intervals. According to equation (8), the matrix $\mathbf{X} _{1,t}$ in equation (1) includes economic variables $q_{t}\equiv s_{t}+p_{t}^{\ast}-p_{t}$ , $y_{t}^{gap}-y_{t}^{gap\ast}$ , and $\pi_{t}-\pi_{t}^{\ast}$ .¹⁰

2.2 Data

The forecasting models and the corresponding forecast intervals are estimated using monthly data for twelve OECD countries. The United States is treated as the foreign country in all cases. For each country we synchronize the beginning and end dates of the data across all models estimated. The twelve countries and periods considered are: Australia (73:03-06:6), Canada (75:01-06:6), Denmark (73:03-06:6), France (77:12-98:12), Germany (73:03-98:12), Italy (74:12-98:12), Japan (73:03-06:6), Netherlands (73:03-98:12), Portugal (83:01-98:12), Sweden (73:03-04:11), Switzerland (75:09-06:6), and the United Kingdom (73:03-06:4).

The data is taken from Molodtsova and Papell (2009).¹¹ With the exception of interest rates, the data is transformed by taking natural logs and then multiplying by 100. The nominal exchange rates are end-of-month rates taken from the Federal Reserve Bank of St. Louis database. Output data ( $y_{t}$ ) are proxied by Industrial Production (IP) from the International Financial Statistics (IFS) database. IP data for Australia and Switzerland are only available at a quarterly frequency, and hence are transformed from quarterly to monthly observations using the quadratic-match average option in Eviews 4.0 by Molodtsova and Papell (2009). Following Engel and West (2006), the output gap ( $y_{t}^{gap}$ ) is calculated by quadratically de-trending the industrial production for each country.

Prices data ( $p_{t}$ ) are proxied by Consumer Price Index (CPI) from the IFS database. Again, CPI for Australia is only available at a quarterly frequency and the quadratic-match average is used to impute monthly observations. Inflation rates are calculated by taking the first differences of the logs of CPIs. The money market rate from IFS (or "call money rate") is used as a measure of the short-term interest rate set by the central bank. Finally, M1 is used to measure the money supply for most countries. M0 for the UK and M2 for Italy and Netherlands is used due to the unavailability of M1 data.

3. Econometric Method

For a given model , the objective is to estimate from equation (1) the distribution of $s_{\tau +h}-s_{\tau}$ conditional on data $\mathbf{X}_{m,\tau}$ that is observed up to time $\tau$ . This is the -horizon-ahead forecast distribution of the exchange rate, from which the corresponding forecast interval can be derived. For a given $\alpha$ , the forecast interval of coverage $\alpha \in(0,1)$ is an interval in which $s_{\tau+h}-s_{\tau}$ is supposed to lie with a probability of $\alpha$ .

Models in equation (1) provide only point forecasts of $s_{\tau+h}-s_{\tau}$ . In order to construct forecast intervals for a given model, we apply robust semiparametric (RS) forecast intervals to all models. The nominal $\alpha$ -coverage forecast interval of $s_{\tau +h}-s_{\tau}$ conditional on $\mathbf{X}_{m,\tau}$ can be obtained by the following three-step procedure:

Step 1.

Estimate model

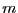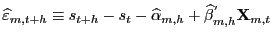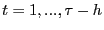by OLS and obtain residuals $\widehat{\varepsilon}_{m,t+h}\equiv s_{t+h}-s_{t}-\widehat{\alpha} _{m,h}+\widehat{\beta}^{^{\prime}}_{m,h}\mathbf{X}_{m,t}$ , for $t=1,...,\tau -h$ .

Step 2.

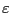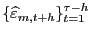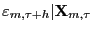For a range of values of $\varepsilon$ (sorted residuals $\{\widehat{\varepsilon}_{m,t+h}\}_{t=1}^{\tau-h}$ ), estimate the conditional distribution of $\varepsilon_{m,\tau+h}\vert\mathbf{X}_{m,\tau}$ by:

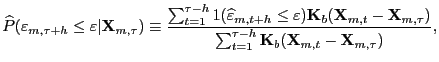
$\displaystyle \widehat{P}(\varepsilon_{m,\tau+h}\le\varepsilon\vert\mathbf{X}_{m,\tau} )\equiv\frac{\sum_{t=1}^{\tau-h}1(\widehat{\varepsilon}_{m,t+h}\le\varepsilon) \mathbf{K}_{b}(\mathbf{X}_{m,t}-\mathbf{X}_{m,\tau})}{\sum_{t=1}^{\tau -h}\mathbf{K}_{b}(\mathbf{X}_{m,t}-\mathbf{X}_{m,\tau})},$

(9)

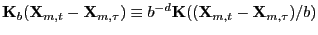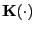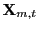where $\mathbf{K}_{b}(\mathbf{X}_{m,t}-\mathbf{X}_{m,\tau})\equiv b^{-d}\mathbf{K}((\mathbf{X}_{m,t}-\mathbf{X}_{m,\tau})/b)$ , $\mathbf{K} (\cdot)$ is a multivariate Gaussian kernel with a dimension the same as that of $\mathbf{X}_{m,t}$ , and 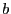is the smoothing parameter or bandwidth.¹²

Step 3.

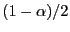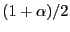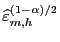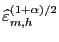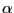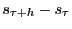Find the $(1-\alpha)/2$ and $(1+\alpha)/2$ quantiles of the estimated distribution, which are denoted by $\widehat{\varepsilon }_{m,h}^{(1-\alpha)/2}$ and $\widehat{\varepsilon}_{m,h}^{(1+\alpha)/2}$ , repectively. The estimate of the $\alpha$ -coverage forecast interval for $s_{\tau+h}-s_{\tau}$ conditional on 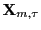$\mathbf{X}_{m,\tau}$ is:

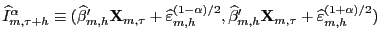
$\displaystyle \widehat{I}^{\alpha}_{m,\tau+h}\equiv(\widehat{\beta}_{m,h}^{\prime} \mathbf{X}_{m,\tau}+\widehat{\varepsilon}_{m,h}^{(1-\alpha)/2}, \widehat {\beta}_{m,h}^{\prime}\mathbf{X}_{m,\tau}+\widehat{\varepsilon}_{m,h} ^{(1+\alpha)/2})$

(10)

For each model , the above method uses the forecast models in equation (1) to estimate the location of the forecast distribution, while the nonparametric kernel distribution estimate is used to estimate the shape. As a result, the interval obtained from this method is semiparametric. Wu (2009) shows that under some weak regularity conditions, this method consistently estimates the forecast distribution,¹³ and hence the forecast intervals of $s_{\tau+h}-s_{\tau}$ conditional on $\mathbf{X} _{m,\tau}$ , regardless of the quality of model . That is, the forecast intervals are robust. Stationarity of economic variables is one of those regularity conditions. In our models, exchange rate differences, interest rates and inflation rates are well-known to be stationary, while empirical tests for real exchange rates and output gaps generate mixed results. These results may be driven by the difficulty of distinguishing a stationary, but persistent, variable from a non-stationary one. In this paper, we take the stationarity of these variables as given.

Model 7 is the random walk model. The estimator in equation (9) becomes the Empirical Distribution Function (EDF) of the exchange rate innovations. Under regularity conditions, equation (9) consistently estimates the unconditional distribution of $s_{\tau+h}-s_{\tau}$ , and can be used to form forecast intervals for $s_{\tau+h}$ . The forecast intervals of economic models and the random walk are compared. Our interest is to test whether RS forecast intervals based on economic models are more accurate than those based on the random walk model. We focus on the empirical coverage and the length of forecast intervals in our tests.

Following Christoffersen (1998) and related work, the first standard we use is the empirical coverage. The empirical coverage should be as close as possible to the nominal coverage ( $\alpha$ ). Significantly missing the nominal coverage indicates the inadequacy of the model and predictors for the given sample size. For instance, if 90% forecast intervals calculated from a model contain only 50% of out-of-sample observations, the model can hardly be identified as useful for interval forecasting. This case is called under-coverage. In contrast, over-coverage implies that the intervals could be reduced in length (or improved in tightness), but the forecast interval method and model are unable to do that for the given sample size. An economic model is said to outperform the random walk if its empirical coverage is more accurate than that of the random walk.

On the other hand, the empirical coverage of an economic model may be equally accurate as that of the random walk model, but the economic model has tighter forecast intervals than the random walk. We argue that the lengths of forecast intervals signify the informativeness of the intervals given that these intervals have equally accurate empirical coverages. In this case, the economic model is also considered to outperform the random walk in forecasting exchange rates. The empirical coverage and length tests are conducted at both short and long horizons for the six economic models relative to the random walk for each of the twelve OECD exchange rates.

We use tests that are applications of the unconditional predictive accuracy inference framework of Giacomini and White (2006). Unlike the tests of Diebold and Mariano (1995) and West (1996), our forecast evaluation tests do not focus on the asymptotic features of the forecasts. Rather, in the spirit of Giacomini and White (2006), we are comparing the population features of forecasts generated by rolling samples of fixed sample size. This contrasts to the traditional forecast evaluation methods in that although it uses asymptotic approximations to do the testing, the inference is not on the asymptotic properties of forecasts, but on their population finite sample properties. We acknowledge that the philosophy of this inference framework remains a point of contention, but it does tackle three important evaluation difficulties in this paper. First, it allows for evaluation of forecast intervals that are not parametrically derived. The density evaluation methods developed in well-known studies such as Diebold, Gunther, Tay (1998), Corradi and Swanson (2006a) and references within Corradi and Swanson (2006b) require that the forecast distributions be parametrically specified. Giacomini and White's (2006) method overcomes this challenge by allowing comparisons among parametric, semiparametric and nonparametric forecasts. As a result, in the cases of semiparametric and nonparametric forecasts, it also allows comparison of models with predictors of different dimensions, as evident in our exercise. Second, by comparing the finite sample properties of RS forecast intervals derived from different models, we avoid rejecting models that are mis-specified,¹⁴ but are nonetheless good approximations useful for forecasting. Finally, we can individually (though not jointly) test whether the forecast intervals differ in terms of empirical coverages and lengths, for the given estimation sample, and are not confined to focus only on empirical coverages or holistic properties of forecast distribution, such as probability integral transform.

3.1 Test of Equal Empirical Coverages

Suppose the sample size available to the researcher is and all data are collected in a vector $\mathbf{W}_{t}$ . Our inference procedure is based on a rolling estimation scheme, with the size of the rolling window fixed while $T\rightarrow\infty$ . Let and be the size of the rolling window. For each horizon and model , a sequence of $\alpha$ -coverage forecast intervals are generated using rolling data: $\{\mathbf{W} _{t}\}_{t=1}^{R}$ for forecast for date , $\{\mathbf{W}_{t}\}_{t=2} ^{R+1}$ for forecast for date , and so on, until forecast for date is generated using $\{\mathbf{W}_{t}\}_{t=N(h)}^{R+N(h)-1}$ .

Under this fixed-sample-size rolling scheme, for each finite we have observations to compare the empirical coverages and lengths across models ( ). By fixing , we allow the finite sample properties of the forecast intervals to be preserved as $T\rightarrow\infty$ . Thus, the forecast intervals and the associated forecast losses are simply functions of a finite and fixed number of random variables. We are interested in approximating the population moments of these objects by taking $N(h)\rightarrow\infty$ . A loose analogy would be finding the finite-sample properties of a certain parameter estimator when the sample size is fixed at , by a bootstrap with an arbitrarily large number of bootstrap replications.

We conduct individual tests for the empirical coverages and lengths. In each test, we define a corresponding forecast loss, propose a test statistic and derive its asymptotic distribution. As defined in equation (10), let $\widehat{I}^{\alpha}_{m,\tau+h}$ be the horizon ahead RS forecast interval of model with a nominal coverage of $\alpha$ . For out-of-sample forecast evaluation, we require $\widehat{I}^{\alpha}_{m,\tau+h}$ to be constructed using data from $t=\tau-R+1$ to $t=\tau$ . The coverage accuracy loss is defined as:

$\displaystyle CL_{m,h}^{\alpha}=\left[ P(Y_{\tau+h}\in\widehat{I}^{\alpha}_{m,\tau +h})-\alpha\right] ^{2}.$

(11)

For economic models (), the goal is to compare the coverage accuracy loss of RS forecast intervals of model with that of the random walk (). The null and alternative hypotheses are:

$\displaystyle H_{0}$	$\displaystyle : \Delta CL_{m,h}^{\alpha}\equiv CL_{7,h}^{\alpha}-CL_{m,h}^{\alpha }=0$
$\displaystyle H_{A}$	$\displaystyle : \Delta CL_{m,h}^{\alpha}\ne0.$

Define the sample analog of the coverage accuracy loss in equation (11):

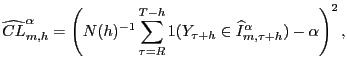$\displaystyle \widehat{CL}_{m,h}^{\alpha}=\left( N(h)^{-1}\sum_{\tau=R}^{T-h}1(Y_{\tau+h} \in\widehat{I}^{\alpha}_{m,\tau+h})-\alpha\right) ^{2},$

where $1(Y_{\tau+h}\in\widehat{I}^{\alpha}_{m,\tau+h})$ is an index function that equals one when $Y_{\tau+h}\in\widehat{I}^{\alpha}_{m,\tau+h}$ , and equals zero otherwise. Applying the asymptotic test of Giacomini and White (2006) to the sequence $\{1(Y_{\tau+h}\in\widehat{I}^{\alpha}_{m,\tau +h})\}_{\tau=R}^{T-h}$ and applying the Delta method, we can show that

$\displaystyle \sqrt{N(h)}(\Delta\widehat{CL}_{m,h}^{\alpha}-\Delta CL_{m,h}^{\alpha })\overset{d}{\rightarrow}N(0,\Gamma_{m,h}^{^{\prime}}\Omega_{m,h}\Gamma _{m,h}),$

(12)

where $\overset{d}{\rightarrow}$ denotes convergence in distribution, and $\Omega_{m,h}$ is the long-run covariance matrix between $1(Y_{\tau+h} \in\widehat{I}^{\alpha}_{m,\tau+h})$ and $1(Y_{\tau+h}\in\widehat{I}^{\alpha }_{7,\tau+h})$ . The matrix $\Gamma_{m,h}$ is defined as:

$\displaystyle \Gamma_{m,h}\equiv\left[ \begin{array}[c]{cc} 2\left( P\left( Y_{\tau+h}\in\widehat{I}^{\alpha}_{m,\tau+h}\right) -\alpha\right) & 2\left( P\left( Y_{\tau+h}\in\widehat{I}^{\alpha}_{7,\tau +h}\right) -\alpha\right) \end{array} \right] ^{\prime}.$

$\Gamma_{m,h}$ can be estimated consistently by its sample analog $\widehat{\Gamma}_{m,h}$ , while $\Omega_{m,h}$ can be estimated by some HAC estimator $\widehat{\Omega}_{m,h}$ , such as Newey and West (1987).¹⁵The test statistic for coverage test is defined as:

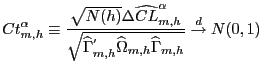
$\displaystyle Ct_{m,h}^{\alpha}\equiv\frac{\sqrt{N(h)}\Delta\widehat{CL}_{m,h}^{\alpha} }{\sqrt{\widehat{\Gamma}_{m,h}^{^{\prime}}\widehat{\Omega}_{m,h} \widehat{\Gamma}_{m,h}}}\overset{d}{\rightarrow}N(0,1)$

(13)

3.2 Test of Equal Empirical Lengths

Define the length loss as:

$\displaystyle LL^{\alpha}_{m,h}\equiv E\left[ leb\left( \widehat{I}^{\alpha}_{m,\tau +h}\right) \right] ,$

(14)

where $leb(\cdot)$ is the Lesbesgue measure. To compare the length loss of RS forecast intervals of economic models with that of the random walk (, the null and alternative hypotheses are:

$\displaystyle H_{0}$	$\displaystyle : \Delta LL_{m,h}^{\alpha}\equiv LL_{7,h}^{\alpha}-LL_{m,h}^{\alpha }=0$
$\displaystyle H_{A}$	$\displaystyle : \Delta LL_{m,h}^{\alpha}\ne0.$

The sample analog of the length loss for model is defined as:

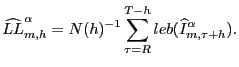$\displaystyle \widehat{LL}_{m,h}^{\alpha}=N(h)^{-1}\sum_{\tau=R}^{T-h}leb(\widehat {I}^{\alpha}_{m,\tau+h}).$

Directly applying the test of Giacomini and White (2006), we have

$\displaystyle \sqrt{N(h)}(\Delta\widehat{LL}_{m,h}^{\alpha}-\Delta LL_{m,h}^{\alpha })\overset{d}{\rightarrow}N(0,\Sigma_{m,h}),$

(15)

where $\Sigma_{m,h}$ is the long-run variance of $leb\left( \widehat {I}^{\alpha}_{7,\tau+h}\right) -leb\left( \widehat{I}^{\alpha}_{m,\tau +h}\right)$ . Let $\widehat{\Sigma}_{m,h}$ be the HAC estimator of $\Sigma_{m,h}$ . The test statistic for empirical length is defined as:

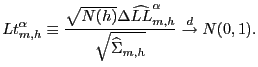
$\displaystyle Lt_{m,h}^{\alpha}\equiv\frac{\sqrt{N(h)}\Delta\widehat{LL}_{m,h}^{\alpha} }{\sqrt{\widehat{\Sigma}_{m,h}}}\overset{d}{\rightarrow}N(0,1).$

(16)

3.3 Discussion

The coverage accuracy loss function is symmetric in our paper. In practice, an asymmetric loss function may be better when looking for an exchange rate forecast model to help make policy or business decisions. Under-coverage is arguably a more severe problem than over-coverage in practical situations. However, the focus of this paper is the disconnect between economic fundamentals and the exchange rate. Our goal is to investigate which model comes closer to the data: the random walk or fundamental-based models. It is not critical in this case whether coverage inaccuracy comes from the under- or over-coverage. We acknowledge that the use of symmetric coverage loss remains a caveat, especially since we are using the coverage accuracy test as a pre-test for the tests of length. Clearly, there is a tradeoff between the empirical coverage and the length of forecast intervals. Given the same center,¹⁶ intervals with under-coverage have shorter lengths than intervals with over-coverage. In this case, the length test is in favor of models that systematically under-cover the targeted nominal coverage when compared to a model that systematically over-covers. This problem cannot be detected by the coverage accuracy test with symmetric loss function because over- and under-coverage are treated equally. However, our results in section 4 show that there is no evidence of systematic under-coverage for the economic models considered in this paper. For instance, in Table 1, one-month-ahead () forecast intervals over-cover the nominal coverage (90%) for eight out of twelve exchange rates.¹⁷ Note that under-coverage does not guarantee shorter intervals either in our paper, because forecast intervals of different models usually have different centers.¹⁸ In addition, we also compare the coverage of economic models and the random walk directly in an exercise not reported in this paper. There is no evidence that the coverage of economic models is systematically smaller than that of the random walk.¹⁹

As we have mentioned, comparisons across models can also be done at the distribution level. We choose interval forecasts for two reasons. First, interval forecasts have been widely used and reported by the practitioners. For instance, the Bank of England calculates forecast intervals of inflation in its inflation reports. Second, compared to evaluation metrics for density forecasts, the empirical coverage and length loss functions of interval forecasts, and the subsequent interpretations of test rejection/acceptance are more intuitive.

4. Results

We apply RS forecast intervals for each model for a given nominal coverage of $\alpha=0.9$ . There is no particular reason why we chose 0.9 as the nominal coverage. Some auxiliary results show that our qualitative findings do not depend on the choice of $\alpha$ . Due to different sample sizes across countries, we choose different sizes for the rolling window () for different countries. Our rule is very simple: for countries with $T\ge300$ , we choose , otherwise we set .²⁰ Again, from our experience, tampering with does not change the qualitative results, unless is chosen to be unusually big or small.

For time horizons and models , we construct a sequence of 90% forecast intervals $\{\widehat{I}^{0.9}_{m,\tau +h}\}_{\tau=R}^{T-h}$ for the -horizon change of the exchange rate $s_{t+h}-s_{t}$ . Then we compare economic models and the random walk by computing empirical coverages, lengths and test statistics $Ct_{m,h}^{0.9}$ and $Lt_{m,h}^{0.9}$ as described in section 3. We first report the results of our benchmark model. After that, results of alternative models are reported and discussed.

4.1 Results of Benchmark Model

Table 1 shows results of the benchmark Taylor rule model. For each time horizon and exchange rate, the first column (Cov.) reports the empirical coverage for the given nominal coverage of 90%. The second column (Leng.) reports the length of forecast intervals (the distance between upper and lower bounds). The length is multiplied by 100 and therefore expressed in terms of the percentage change of the exchange rate. For instance, the empirical coverage and length of the one-month-ahead forecast interval for the Australian dollar are and , respectively. It means that on average, with a chance of 89.5%, the one-month-ahead change of AUD/USD lies in an interval with length %. We use superscripts , , and to denote that the null hypothesis of equal empirical coverage accuracy/length is rejected in favor of the Taylor rule model at a confidence level of 10%, 5%, and 1% respectively. Superscripts , , and are used for rejections in favor of the random walk analogously.

We summarize our findings in three panels. In the first panel ((1) Coverage Test), the row of "Model Better" reports the number of exchange rates that the Taylor rule model has more accurate empirical coverages than the random walk. The row of "RW Better" reports the number of exchange rates for which the random walk outperforms the Taylor rule model under the same criterion. In the second panel ((2) Length Test Given Equal Coverage Accuracy), a better model is the one with tighter forecast intervals given equal coverage accuracy. In the last panel ((1)+(2)), a better model is the one with either more accurate coverages, or tighter forecast intervals given equal coverage accuracy.

For most exchange rates and time horizons, the Taylor rule model and the random walk model have statistically equally accurate empirical coverages. The null hypothesis of equal coverage accuracy is rejected in only six out of sixty tests (two rejections each at horizons 6, 9, and 12). Five out of six rejections are in favor of the Taylor rule model. That is, the empirical coverage of the Taylor rule model is closer to the nominal coverage than those of the random walk. However, based on the number of rejections (5) in a total of sixty tests, there is no strong evidence that the Taylor rule model can generate more accurate empirical coverages than the random walk.

In cases where the Taylor rule model and the random walk have equally accurate empirical coverages, the Taylor rule model generally has equal or significantly tighter forecast intervals than the random walk. In forty-two out of fifty-four cases, the null hypothesis of equally tight forecast intervals is rejected in favor of the Taylor rule model. In contrast, the null hypothesis is rejected in only three cases in favor of the random walk. The evidence of exchange rate predictability is more pronounced at longer horizons. At horizon twelve (), for all cases where empirical coverage accuracies between the random walk and the Taylor rule model are statistically equivalent, the Taylor rule model has significantly tighter forecast intervals than the random walk.

As for each individual exchange rate, the benchmark Taylor rule model works best for the French Franc, the Deutschmark, the Dutch Guilder, the Swedish Krona, and the British Pound: for all time horizons, the model has tighter forecast intervals than the random walk, while their empirical coverages are statistically equally accurate. The Taylor rule model performs better than the random walk in most horizons for the remaining exchange rates except the Portuguese Escudo, for which the Taylor rule model outperforms the random walk only at long horizons.

4.2 Results of Alternative Models

Five alternative economic models are also compared with the random walk: three alternative Taylor rule models that are studied in Molodtsova and Papell (2009), the PPP model, and the monetary model. Tables 2-6 report results of these alternative models.

In general, results of coverage tests do not show strong evidence that economic models can generate more accurate coverages than the random walk at either short or long horizons. However, after considering length tests, we find that economic models perform better than the random walk, especially at long horizons. Taylor rule model 4 (the benchmark model with interest rate smoothing Table 4) and the PPP model (Table 5) perform the best among alternative models. Results of these two models are very similar to that of the benchmark Taylor rule model. At horizon twelve, both models outperform the random walk for most exchange rates under our out-of-sample forecast interval evaluation criteria. The performance of Taylor rule model 2 (Table 2) and 3 (Table 3) is relatively less impressive than other models, but for more than half of the exchange rates, the economic models outperform the random walk at several horizons in out-of-sample interval forecasts.

Comparing the benchmark Taylor rule model, the PPP model and the monetary model, the performance of the PPP model (Table 5) is worse than the other two models at short horizons. Compared to the Taylor rule and PPP models, the monetary model outperforms the random walk for a smaller number of exchange rates at horizons 6, 9, and 12. Overall, the benchmark Taylor rule model seems to perform slightly better than the monetary and PPP models. Molodtsova and Papell (2009) find similar results in their point forecasts.

Table 7 shows results with heterogeneous Taylor rules.²¹ In this model, we relaxed the assumption that the Taylor rule coefficients are the same in the home and foreign countries. We replace $\pi_{t}-\pi_{t}^{\ast }$ and $y_{t}^{gap}-y_{t}^{gap\ast}$ in matrix $\mathbf{X}_{1,t}$ of the benchmark model with $\hat{\delta}_{\pi}\pi_{t}-\hat{\delta}_{\pi}^{\ast} \pi_{t}^{\ast}$ and $\hat{\delta}_{y}y_{t}^{gap}-\hat{\delta}_{y}^{\ast} y_{t}^{gap\ast}$ , where $\hat{\delta}_{\pi}$ , $\hat{\delta}_{\pi}^{\ast}$ , $\hat{\delta}_{y}$ , and $\hat{\delta}_{y}^{\ast}$ are Taylor rule coefficients estimated from the data of home and foreign countries. The main findings in the benchmark model also hold in Table 7.

4.3 Discussion

After Mark (1995) first documents exchange rate predictability at long horizons, long-horizon exchange rate predictability has become a very active area in the literature. With panel data, Engel, Mark, and West (2007) recently show that the long-horizon predictability of the exchange rate is relatively robust in the exchange rate forecasting literature. We find similar results in our interval forecasts. The evidence of long-horizon predictability seems robust across different models and currencies when both empirical coverage and length tests are used. At horizon twelve, all economic models outperform the random walk for six exchange rates: the Australian Dollar, French Franc, Italian Lira, Japanese Yen, Swedish Krona, and the British Pound in the sense that interval lengths of economic models are smaller than those of the random walk, given equivalent coverage accuracy. This is true only for the Danish Kroner and Swiss Franc at horizon one. We also notice that there is no clear evidence of long-horizon predictability based on the tests of empirical coverage accuracy only.

Molodtsova and Papell (2009) find strong out-of-sample exchange rate predictability for Taylor rule models even at the short horizon. In our paper, the evidence for exchange rate predictability at short horizons is not very strong. This finding may be a result of some assumptions we have used to simplify our computation. For instance, an $\alpha$ -coverage forecast interval in our paper is always constructed using the $(1-\alpha)/2$ and $(1+\alpha)/2$ quantiles. Alternatively, we can choose quantiles that minimize the length of intervals, given the nominal coverage.²² In addition, the development of more powerful testing methods may also be helpful. The evidence of exchange rate predictability in Molodtsova and Papell (2009) is partly driven by the testing method recently developed by Clark and West (2006, 2007). We acknowledge that whether or not short-horizon results can be improved remains an interesting question, but do not pursue this in the current paper. The purpose of this paper is to show the connection between the exchange rate and economic fundamentals from an interval forecasting perspective. Predictability either at short- or long-horizons will serve this purpose.

Though we find that economic fundamentals are helpful for forecasting exchange rates, we acknowledge that exchange rate forecasting in practice is still a difficult task. The forecast intervals from economic models are statistically tighter than those of the random walk, but they remain fairly wide. For instance, the distance between the upper and lower bound of three-month-ahead forecast intervals is usually a 20% change of the exchange rates. Figures 1-3 show the length of forecast intervals generated by the benchmark Taylor rule model and the random walk for the British Pound, the Deutschmark, and the Japanese Yen at different horizons.²³ At the horizon of 12 months, the length of forecast intervals in the Taylor rule model is usually smaller than that in the random walk. However, at shorter horizons, such as 1 month, the difference is quantitatively small.

5. Conclusion

There is a growing strand of literature that uses Taylor rules to model exchange rate movements. Our paper contributes to the literature by showing that Taylor rule fundamentals are useful in forecasting the distribution of exchange rates. We apply Robust Semiparametric forecast intervals of Wu (2009) to a group of Taylor rule models for twelve OECD exchange rates. The forecast intervals generated by the Taylor rule models are in general tighter than those of the random walk, given that these intervals cover the realized exchange rates equally well. The evidence of exchange rate predictability is more pronounced at longer horizons, a result that echoes previous long-horizon studies such as Mark (1995). The benchmark Taylor rule model is also found to perform better than the monetary and PPP models based on out-of-sample interval forecasts.

Though we find some empirical support for the connection between the exchange rate and economic fundamentals, we acknowledge that the detected connection is weak. The reductions of the lengths of forecast intervals are quantitatively small, though they are statistically significant. Forecasting exchange rates remains a difficult task in practice. Engel and West (2005) argue that as the discount factor gets closer to one, present value asset pricing models place greater weight on future fundamentals. Consequently, current fundamentals have very weak forecasting power and exchange rates appear to follow approximately a random walk. Under standard assumptions in Engel and West (2005), the Engel-West theorem does not imply that exchange rates are more predictable at longer horizons or that economic models can outperform the random walk in forecasting exchange rates based on out-of-sample interval forecasts. However, modifications to these assumptions may be able to reconcile the Engel-West explanation with empirical findings of exchange rate predictability. For instance, Engel, Wang, and Wu (2008) find that when there exist stationary, but persistent, unobservable fundamentals, for example risk premium, the Engel-West explanation predicts long-horizon exchange rate predictability in point forecasts, though the exchange rate still approximately follows a random walk at short horizons. It would also be of interest to study conditions under which our findings in interval forecasts can be reconciled with the Engel-West theorem.

We believe other issues, such as parameter instability (Rossi, 2005), nonlinearity (Kilian and Taylor, 2003), real time data (Faust, Rogers, and Wright, 2003, Molodtsova, Nikolsko-Rzhevskyy, and Papell, 2008a, 2008b), and model selection (Sarno and Valente, forthcoming) are all contributing to the Meese-Rogoff puzzle. Panel data are also found helpful in detecting exchange rate predictability, especially at long horizons. For instance, see Mark and Sul (2001), Engel, Mark, and West (2007), and Rogoff and Stavrakeva (2008). It would be interesting to incorporate these studies into interval forecasting. We leave these extensions for future research.

Table 1.-Panel 1: Results of Benchmark Taylor Rule Model

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.895 7.114 0.888 14.209^c 0.959 21.140 0.942 26.613 0.963 29.175^c

Canadian Dollar
0.814 3.480 0.794 6.440^c 0.738 8.483^c 0.675 8.669^c 0.596^x 9.707^c

Danish Kroner
0.920 8.676^c 0.939 17.415^c 0.954 26.198 0.922 28.712^c 0.968 37.123^c

French Franc
0.912 8.921^c 0.860 15.728^c 0.928^c 26.007^c 0.957 29.924^c 0.934 36.883^c

Deutschmark
0.927 8.327^c 0.879 18.634^c 0.894 27.923^c 0.960^a 33.734^c 0.969 39.618^c

Italian Lira
0.899 8.291^c 0.875 18.305 0.910 26.788^c 0.846 32.545^c 0.874 37.151^c

Japanese Yen
0.915 9.633^z 0.909 19.762 0.892 28.451^c 0.932 33.793^c 0.883 37.728^c

Dutch Guilder
0.917 8.726^c 0.907 18.615^c 0.933 27.458^c 0.941^b 30.902^c 0.959^a 40.177^c

Portuguese Escudo
0.901 8.580^z 0.928 18.758^z 0.894^c 23.552^c 0.825 27.086 0.867 32.092^c

Swedish Krona
0.839 7.360^c 0.860 15.413^c 0.874 23.930^c 0.820 28.090^c 0.834 37.432^c

Swiss Franc
0.947 9.358^c 0.916 19.655 0.963 26.553^c 0.963 30.780^c 0.899 35.008^c

British Pound
0.919 8.413^a 0.923 16.592^c 0.912 23.317^c 0.900 26.942^c 0.855 25.905^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.895	7.114	0.888	14.209^c	0.959	21.140	0.942	26.613	0.963	29.175^c
Canadian Dollar	0.814	3.480	0.794	6.440^c	0.738	8.483^c	0.675	8.669^c	0.596^x	9.707^c
Danish Kroner	0.920	8.676^c	0.939	17.415^c	0.954	26.198	0.922	28.712^c	0.968	37.123^c
French Franc	0.912	8.921^c	0.860	15.728^c	0.928^c	26.007^c	0.957	29.924^c	0.934	36.883^c
Deutschmark	0.927	8.327^c	0.879	18.634^c	0.894	27.923^c	0.960^a	33.734^c	0.969	39.618^c
Italian Lira	0.899	8.291^c	0.875	18.305	0.910	26.788^c	0.846	32.545^c	0.874	37.151^c
Japanese Yen	0.915	9.633^z	0.909	19.762	0.892	28.451^c	0.932	33.793^c	0.883	37.728^c
Dutch Guilder	0.917	8.726^c	0.907	18.615^c	0.933	27.458^c	0.941^b	30.902^c	0.959^a	40.177^c
Portuguese Escudo	0.901	8.580^z	0.928	18.758^z	0.894^c	23.552^c	0.825	27.086	0.867	32.092^c
Swedish Krona	0.839	7.360^c	0.860	15.413^c	0.874	23.930^c	0.820	28.090^c	0.834	37.432^c
Swiss Franc	0.947	9.358^c	0.916	19.655	0.963	26.553^c	0.963	30.780^c	0.899	35.008^c
British Pound	0.919	8.413^a	0.923	16.592^c	0.912	23.317^c	0.900	26.942^c	0.855	25.905^c

Note: –h denotes forecast horizons for monthly data. –For each horizon (h), the first column (Cov.) reports empirical coverages given a nominal coverage of 90%. The second column (Leng.) reports the length of forecast intervals in terms of percentage change of the exchange rate. Empirical coverages and lengths are averages across N(h) out-of-sample trials. –Superscripts a, b, c in the column of Cov. (Leng.) denote rejections of equal coverage accuracy (equal length) in favor of the economic model at a 10%, 5% and 1% confidence level respectively. Superscripts x, y, z are defined analogously for rejections in favor of the random walk

Table 1.-Panel 2: Results of Benchmark Taylor Rule Model, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 2 2 1

RW Better 0 0 0 0 1

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	2	2	1
RW Better	0	0	0	0	1

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 1.-Panel 3: Results of Benchmark Taylor Rule Model, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 8 8 8 8 10

RW Better 2 1 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	8	8	8	8	10
RW Better	2	1	0	0	0

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 1.-Panel 4: Results of Benchmark Taylor Rule Model, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 8 8 10 10 11

RW Better 2 1 0 0 1

	h=1	h=3	h=6	h=9	h=12
Model Better	8	8	10	10	11
RW Better	2	1	0	0	1

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 2.-Panel 1: Results of Benchmark Taylor Rule Model Two

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.884 7.146^y 0.899 15.086^c 0.928 21.327 0.901 27.329 0.872 30.815^b

Canadian Dollar
0.825 3.442^c 0.783 6.321^c 0.814 8.490^c 0.858 10.034^c 0.825 11.921^c

Danish Kroner
0.915 8.753^a 0.939 17.764^c 0.954 27.479^z 0.953 33.426^y 0.942 40.717

French Franc
0.951 9.042^c 0.930 18.783 0.949^c 29.161^c 0.936 34.994^c 0.868 42.081^c

Deutschmark
0.917 9.090 0.869 19.217 0.952 29.746 0.941^a 39.093^a 0.980 44.571^z

Italian Lira
0.928 9.196 0.875 18.322 0.895 26.926^c 0.869 35.883^c 0.898^a 41.235^z

Japanese Yen
0.915 9.568^x 0.914 19.734 0.912 29.344^c 0.937 36.834 0.942 44.385^c

Dutch Guilder
0.908 8.586^c 0.888 18.782^c 0.962 29.777 0.990 39.507^z 0.990 47.514^z

Portuguese Escudo
0.916 8.005 0.957 17.924^z 0.909^c 24.270^b 0.889 28.533^z 0.883^a 35.338^c

Swedish Krona
0.867 7.624 0.860 16.132 0.857 24.500^c 0.837 32.825 0.811 37.772^c

Swiss Franc
0.941 9.953^b 0.928 20.105 0.982 29.758^c 0.994 38.267^z 0.962 45.965^z

British Pound
0.919 8.627^z 0.933 17.334^c 0.922 26.227^c 0.937 31.044^c 0.957 36.397^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.884	7.146^y	0.899	15.086^c	0.928	21.327	0.901	27.329	0.872	30.815^b
Canadian Dollar	0.825	3.442^c	0.783	6.321^c	0.814	8.490^c	0.858	10.034^c	0.825	11.921^c
Danish Kroner	0.915	8.753^a	0.939	17.764^c	0.954	27.479^z	0.953	33.426^y	0.942	40.717
French Franc	0.951	9.042^c	0.930	18.783	0.949^c	29.161^c	0.936	34.994^c	0.868	42.081^c
Deutschmark	0.917	9.090	0.869	19.217	0.952	29.746	0.941^a	39.093^a	0.980	44.571^z
Italian Lira	0.928	9.196	0.875	18.322	0.895	26.926^c	0.869	35.883^c	0.898^a	41.235^z
Japanese Yen	0.915	9.568^x	0.914	19.734	0.912	29.344^c	0.937	36.834	0.942	44.385^c
Dutch Guilder	0.908	8.586^c	0.888	18.782^c	0.962	29.777	0.990	39.507^z	0.990	47.514^z
Portuguese Escudo	0.916	8.005	0.957	17.924^z	0.909^c	24.270^b	0.889	28.533^z	0.883^a	35.338^c
Swedish Krona	0.867	7.624	0.860	16.132	0.857	24.500^c	0.837	32.825	0.811	37.772^c
Swiss Franc	0.941	9.953^b	0.928	20.105	0.982	29.758^c	0.994	38.267^z	0.962	45.965^z
British Pound	0.919	8.627^z	0.933	17.334^c	0.922	26.227^c	0.937	31.044^c	0.957	36.397^c

Table 2.-Panel 2: Results of Benchmark Taylor Rule Model Two, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 2 1 2

RW Better 0 0 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	2	1	2
RW Better	0	0	0	0	0

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 2.-Panel 3: Results of Benchmark Taylor Rule Model Two, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 5 5 6 4 6

RW Better 3 1 1 4 3

	h=1	h=3	h=6	h=9	h=12
Model Better	5	5	6	4	6
RW Better	3	1	1	4	3

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 2.-Panel 4: Results of Benchmark Taylor Rule Model Two, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 5 5 8 5 8

RW Better 3 1 1 4 3

	h=1	h=3	h=6	h=9	h=12
Model Better	5	5	8	5	8
RW Better	3	1	1	4	3

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 3.-Panel 1: Results of Benchmark Taylor Rule Model Three

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.884 7.229^z 0.899 15.055^c 0.881 21.055 0.885 26.359^c 0.867 30.234^c

Canadian Dollar
0.831 3.453^b 0.789 6.408^c 0.814 8.629^c 0.864 10.220^c 0.819 11.971^c

Danish Kroner
0.920 8.753^b 0.934 17.649^c 0.949 27.523^z 0.948 33.307 0.936 40.070

French Franc
0.951 9.171 0.740 14.488^c 0.722 20.313^c 0.915 35.562^a 0.813 41.350^c

Deutschmark
0.908 9.020 0.897 19.303 0.914 29.676 0.901^c 37.291^c 0.878 44.761^z

Italian Lira
0.928 8.900^a 0.875 17.206^c 0.872 26.674^c 0.839 34.819^c 0.787 39.569^c

Japanese Yen
0.905 9.179^c 0.878 18.907^c 0.892 25.883^c 0.927 31.259^c 0.894 37.049^c

Dutch Guilder
0.927 8.910 0.907 19.204^a 0.952 29.426^a 0.951^a 36.896^c 0.959 46.321^z

Portuguese Escudo
0.930 7.961 0.942 16.883^c 0.955^a 23.786 0.905 26.620^c 0.850 33.745^c

Swedish Krona
0.867 7.316^c 0.848 15.017^c 0.840 23.241^c 0.791 29.265^c 0.757 33.751^c

Swiss Franc
0.929 9.761^b 0.922 19.517^c 0.939 28.437^b 0.926^c 37.519 0.911 45.619

British Pound
0.929 8.239^a 0.939 16.213^c 0.927 23.951^c 0.905 28.720^c 0.952 34.900^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.884	7.229^z	0.899	15.055^c	0.881	21.055	0.885	26.359^c	0.867	30.234^c
Canadian Dollar	0.831	3.453^b	0.789	6.408^c	0.814	8.629^c	0.864	10.220^c	0.819	11.971^c
Danish Kroner	0.920	8.753^b	0.934	17.649^c	0.949	27.523^z	0.948	33.307	0.936	40.070
French Franc	0.951	9.171	0.740	14.488^c	0.722	20.313^c	0.915	35.562^a	0.813	41.350^c
Deutschmark	0.908	9.020	0.897	19.303	0.914	29.676	0.901^c	37.291^c	0.878	44.761^z
Italian Lira	0.928	8.900^a	0.875	17.206^c	0.872	26.674^c	0.839	34.819^c	0.787	39.569^c
Japanese Yen	0.905	9.179^c	0.878	18.907^c	0.892	25.883^c	0.927	31.259^c	0.894	37.049^c
Dutch Guilder	0.927	8.910	0.907	19.204^a	0.952	29.426^a	0.951^a	36.896^c	0.959	46.321^z
Portuguese Escudo	0.930	7.961	0.942	16.883^c	0.955^a	23.786	0.905	26.620^c	0.850	33.745^c
Swedish Krona	0.867	7.316^c	0.848	15.017^c	0.840	23.241^c	0.791	29.265^c	0.757	33.751^c
Swiss Franc	0.929	9.761^b	0.922	19.517^c	0.939	28.437^b	0.926^c	37.519	0.911	45.619
British Pound	0.929	8.239^a	0.939	16.213^c	0.927	23.951^c	0.905	28.720^c	0.952	34.900^c

Table 3.-Panel 2: Results of Benchmark Taylor Rule Model Three, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 1 3 0

RW Better 0 0 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	1	3	0
RW Better	0	0	0	0	0

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 3.-Panel 3: Results of Benchmark Taylor Rule Model Three, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 7 11 8 8 8

RW Better 1 0 1 0 2

	h=1	h=3	h=6	h=9	h=12
Model Better	7	11	8	8	8
RW Better	1	0	1	0	2

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 3.-Panel 4: Results of Benchmark Taylor Rule Model Three, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 7 11 9 11 8

RW Better 1 0 1 0 2

	h=1	h=3	h=6	h=9	h=12
Model Better	7	11	9	11	8
RW Better	1	0	1	0	2

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 4.-Panel 1: Results of Benchmark Taylor Rule Model Four

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.895 7.119 0.888 14.424^c 0.928 20.966 0.927 25.304^c 0.872 27.492^c

Canadian Dollar
0.814 3.425^c 0.771 6.366^c 0.698 8.019^c 0.651 8.631^c 0.494y 7.693^c

Danish Kroner
0.920 8.703^c 0.929 17.536^c 0.964 26.025 0.984^x 30.891^c 0.963 36.545^c

French Franc
0.892 8.361^c 0.870 16.079^c 0.938^c 25.950^c 0.883 30.016^c 0.791 35.755^c

Deutschmark
0.927 8.314^c 0.879 18.652^c 0.894 26.803^c 0.931^c 33.350^c 0.969 36.393^c

Italian Lira
0.891 8.663^c 0.838 17.575^c 0.865 26.387^c 0.746 32.270^c 0.724 36.422^c

Japanese Yen
0.905 9.157^c 0.863 18.708^c 0.866 24.417^c 0.869 28.730^c 0.851 31.470^c

Dutch Guilder
0.936 8.815 0.897 18.368^c 0.914 26.700^c 0.931^c 30.036^c 0.796 29.462^c

Portuguese Escudo
0.901 8.525^z 0.913^a 17.110 0.939^c 23.461^c 0.889 27.096^a 0.917 28.778^c

Swedish Krona
0.861 7.289^c 0.860 15.321^c 0.869 23.340^c 0.773 27.198^c 0.728 31.843^c

Swiss Franc
0.947 9.149^c 0.940 19.782^a 0.811 22.796^c 0.808 26.148^c 0.671 26.683^c

British Pound
0.919 8.113^a 0.913 15.765^c 0.875 21.679 0.825 27.312^c 0.839 29.081^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.895	7.119	0.888	14.424^c	0.928	20.966	0.927	25.304^c	0.872	27.492^c
Canadian Dollar	0.814	3.425^c	0.771	6.366^c	0.698	8.019^c	0.651	8.631^c	0.494y	7.693^c
Danish Kroner	0.920	8.703^c	0.929	17.536^c	0.964	26.025	0.984^x	30.891^c	0.963	36.545^c
French Franc	0.892	8.361^c	0.870	16.079^c	0.938^c	25.950^c	0.883	30.016^c	0.791	35.755^c
Deutschmark	0.927	8.314^c	0.879	18.652^c	0.894	26.803^c	0.931^c	33.350^c	0.969	36.393^c
Italian Lira	0.891	8.663^c	0.838	17.575^c	0.865	26.387^c	0.746	32.270^c	0.724	36.422^c
Japanese Yen	0.905	9.157^c	0.863	18.708^c	0.866	24.417^c	0.869	28.730^c	0.851	31.470^c
Dutch Guilder	0.936	8.815	0.897	18.368^c	0.914	26.700^c	0.931^c	30.036^c	0.796	29.462^c
Portuguese Escudo	0.901	8.525^z	0.913^a	17.110	0.939^c	23.461^c	0.889	27.096^a	0.917	28.778^c
Swedish Krona	0.861	7.289^c	0.860	15.321^c	0.869	23.340^c	0.773	27.198^c	0.728	31.843^c
Swiss Franc	0.947	9.149^c	0.940	19.782^a	0.811	22.796^c	0.808	26.148^c	0.671	26.683^c
British Pound	0.919	8.113^a	0.913	15.765^c	0.875	21.679	0.825	27.312^c	0.839	29.081^c

Table 4.-Panel 2: Results of Benchmark Taylor Rule Model Four, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 1 2 2 0

RW Better 0 0 0 1 1

	h=1	h=3	h=6	h=9	h=12
Model Better	0	1	2	2	0
RW Better	0	0	0	1	1

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 4.-Panel 3: Results of Benchmark Taylor Rule Model Four, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 9 11 8 9 11

RW Better 1 0 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	9	11	8	9	11
RW Better	1	0	0	0	0

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 4.-Panel 4: Results of Benchmark Taylor Rule Model Four, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 9 12 10 11 11

RW Better 1 0 0 1 1

	h=1	h=3	h=6	h=9	h=12
Model Better	9	12	10	11	11
RW Better	1	0	0	1	1

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 5.-Panel 1: Results of Purchasing Power Parity Model

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.895 7.114^z 0.883 15.558 0.912 21.311 0.880 26.120^c 0.856 30.316^c

Canadian Dollar
0.819 3.570^z 0.806 6.872 0.767 9.615 0.728 11.078^c 0.615 12.306^c

Danish Kroner
0.925 8.697^c 0.939 18.333 0.938 25.887^c 0.937 31.673^c 0.957 37.447^c

French Franc
0.922 8.904^c 0.940 18.029^c 0.918^c 25.786^c 0.904 29.789^c 0.802 34.209^c

Deutschmark
0.936 9.079 0.935 18.797^c 0.942 27.677^c 1.000 33.585^c 0.990 40.570^c

Italian Lira
0.913 8.780^c 0.868 17.767^c 0.827 25.044^c 0.769 30.190^c 0.772 34.806^c

Japanese Yen
0.920 9.662^z 0.899 19.903 0.912 28.689^c 0.932 33.973^c 0.899 38.568^c

Dutch Guilder
0.936 8.862^y 0.935 18.904^c 0.952 27.928^c 1.000 33.468^c 0.990 41.812^c

Portuguese Escudo
0.916 8.421^y 0.928 19.027^y 0.924^c 23.918 0.857 27.450 0.867 32.467^c

Swedish Krona
0.861 7.541^c 0.876 16.089 0.886 24.345^c 0.855 31.744^b 0.799 37.943^c

Swiss Franc
0.941 9.708^c 0.946 19.694^b 0.976 27.197^c 0.950^b 31.725^c 0.880 36.235^c

British Pound
0.934 8.571^y 0.933 16.954^c 0.932 24.064^c 0.947 28.761^c 0.925^a 31.372^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.895	7.114^z	0.883	15.558	0.912	21.311	0.880	26.120^c	0.856	30.316^c
Canadian Dollar	0.819	3.570^z	0.806	6.872	0.767	9.615	0.728	11.078^c	0.615	12.306^c
Danish Kroner	0.925	8.697^c	0.939	18.333	0.938	25.887^c	0.937	31.673^c	0.957	37.447^c
French Franc	0.922	8.904^c	0.940	18.029^c	0.918^c	25.786^c	0.904	29.789^c	0.802	34.209^c
Deutschmark	0.936	9.079	0.935	18.797^c	0.942	27.677^c	1.000	33.585^c	0.990	40.570^c
Italian Lira	0.913	8.780^c	0.868	17.767^c	0.827	25.044^c	0.769	30.190^c	0.772	34.806^c
Japanese Yen	0.920	9.662^z	0.899	19.903	0.912	28.689^c	0.932	33.973^c	0.899	38.568^c
Dutch Guilder	0.936	8.862^y	0.935	18.904^c	0.952	27.928^c	1.000	33.468^c	0.990	41.812^c
Portuguese Escudo	0.916	8.421^y	0.928	19.027^y	0.924^c	23.918	0.857	27.450	0.867	32.467^c
Swedish Krona	0.861	7.541^c	0.876	16.089	0.886	24.345^c	0.855	31.744^b	0.799	37.943^c
Swiss Franc	0.941	9.708^c	0.946	19.694^b	0.976	27.197^c	0.950^b	31.725^c	0.880	36.235^c
British Pound	0.934	8.571^y	0.933	16.954^c	0.932	24.064^c	0.947	28.761^c	0.925^a	31.372^c

Table 5.-Panel 2: Results of Purchasing Power Parity Model, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 2 1 1

RW Better 0 0 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	2	1	1
RW Better	0	0	0	0	0

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 5.-Panel 3: Results of Purchasing Power Parity Model, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 5 6 8 10 11

RW Better 6 1 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	5	6	8	10	11
RW Better	6	1	0	0	0

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 5.-Panel 4: Results of Purchasing Power Parity Model, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 5 6 10 11 12

RW Better 6 1 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	5	6	10	11	12
RW Better	6	1	0	0	0

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 6.-Panel 1: Results of Monetary Model

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.879 7.108 0.848 15.151 0.830 20.090 0.770 24.642^c 0.745 30.099^b

Canadian Dollar
0.842 4.027^x 0.829 7.492 0.744 10.518 0.645 10.689^b 0.675 12.993^c

Danish Kroner
0.905 8.770^b 0.893 17.943 0.897 25.017^c 0.853 28.581^c 0.809 32.504^c

French Franc
0.922 8.791^c 0.910 18.237^c 0.949^b 26.322^c 0.957 31.032^c 0.956 35.971^c

Deutschmark
0.908 8.595 0.841 17.436^c 0.808 24.622^c 0.772 28.052^c 0.704 31.364^c

Italian Lira
0.913 8.858^c 0.882 18.439^b 0.925 26.585^c 0.931 34.857^c 0.913 40.885^c

Japanese Yen
0.930 9.556 0.919 19.374^c 0.887 28.614^c 0.864 33.401^c 0.809 36.520^c

Dutch Guilder
0.917 8.753^a 0.916 19.408 0.962 29.149^b 0.970 38.173 0.898^c 41.716^c

Portuguese Escudo
0.901 8.086 0.986 18.484 0.985 24.744 0.984 27.230 1.000 34.222

Swedish Krona
0.850 7.504^a 0.848 17.097^x 0.811 23.878^c 0.826 31.287 0.805 34.710^c

Swiss Franc
0.905 9.078^c 0.820 17.020^c 0.732 21.212^c 0.609 22.741^c 0.513^x 23.225^c

British Pound
0.909 7.811^c 0.882 14.945^c 0.787 20.788^c 0.677 24.311^c 0.656 26374^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.879	7.108	0.848	15.151	0.830	20.090	0.770	24.642^c	0.745	30.099^b
Canadian Dollar	0.842	4.027^x	0.829	7.492	0.744	10.518	0.645	10.689^b	0.675	12.993^c
Danish Kroner	0.905	8.770^b	0.893	17.943	0.897	25.017^c	0.853	28.581^c	0.809	32.504^c
French Franc	0.922	8.791^c	0.910	18.237^c	0.949^b	26.322^c	0.957	31.032^c	0.956	35.971^c
Deutschmark	0.908	8.595	0.841	17.436^c	0.808	24.622^c	0.772	28.052^c	0.704	31.364^c
Italian Lira	0.913	8.858^c	0.882	18.439^b	0.925	26.585^c	0.931	34.857^c	0.913	40.885^c
Japanese Yen	0.930	9.556	0.919	19.374^c	0.887	28.614^c	0.864	33.401^c	0.809	36.520^c
Dutch Guilder	0.917	8.753^a	0.916	19.408	0.962	29.149^b	0.970	38.173	0.898^c	41.716^c
Portuguese Escudo	0.901	8.086	0.986	18.484	0.985	24.744	0.984	27.230	1.000	34.222
Swedish Krona	0.850	7.504^a	0.848	17.097^x	0.811	23.878^c	0.826	31.287	0.805	34.710^c
Swiss Franc	0.905	9.078^c	0.820	17.020^c	0.732	21.212^c	0.609	22.741^c	0.513^x	23.225^c
British Pound	0.909	7.811^c	0.882	14.945^c	0.787	20.788^c	0.677	24.311^c	0.656	26374^c

Table 6.-Panel 2: Results of Monetary Model, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 1 0 1

RW Better 0 0 0 0 1

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	1	0	1
RW Better	0	0	0	0	1

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 6.-Panel 3: Results of Monetary Model, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 7 6 8 9 9

RW Better 1 1 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	7	6	8	9	9
RW Better	1	1	0	0	0

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 6.-Panel 4: Results of Monetary Model, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 7 6 9 9 10

RW Better 1 1 0 0 1

	h=1	h=3	h=6	h=9	h=12
Model Better	7	6	9	9	10
RW Better	1	1	0	0	1

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Table 7.-Panel 1: Results of Heterogenous Taylor Rules

Cov. h=1 Leng. h=1 Cov. h=3 Leng. h=3 Cov. h=6 Leng. h=6 Cov. h=9 Leng. h=9 Cov. h=12 Leng. h=12

Australian Dollar
0.915 7.155 0.909 14.690^c 0.959 20.547 0.963^y 26.364 0.947 29.583^c

Canadian Dollar
0.825 3.526 0.794 6.525^c 0.797 9.040^c 0.787 10.370^c 0.693 11.352^c

Danish Kroner
0.915 8.548^c 0.929 17.930^c 0.938 25.328^c 0.890 30.504^c 0.904 36.624^c

French Franc
0.912 8.864^c 0.880 15.970^c 0.845 20.693^c 0.968 30.436^c 0.714 22.789^c

Deutschmark
0.917 8.605^c 0.907 18.356^c 0.894 28.121^c 0.911^c 31.378^c 0.939 33.779^c

Italian Lira
0.913 8.659^c 0.890 18.664 0.887 25.840^c 0.831 32.037^c 0.693 32.236^c

Japanese Yen
0.920 9.637^z 0.888 19.352^b 0.871 28.018^c 0.932 33.388^c 0.878 36.859^c

Dutch Guilder
0.936 8.851 0.916 18.822^c 0.942 27.259^c 0.970 31.410^c 0.990 39.882^c

Portuguese Escudo
0.916 8.881^z 0.870 17.651 0.758 18.730^c 0.746 23.852^c 0.600 20.593^c

Swedish Krona
0.828 7.428^c 0.854 15.658^c 0.903 24.315^c 0.861 29.866^c 0.876 36.235^c

Swiss Franc
0.935 9.731^c 0.940 19.797 0.970 27.227^c 0.969 32.179^c 0.937 36.567^c

British Pound
0.919 8.350 0.908 16.774^c 0.828 20.811^c 0.783 23.105^c 0.720 23.286^c

	Cov. h=1	Leng. h=1	Cov. h=3	Leng. h=3	Cov. h=6	Leng. h=6	Cov. h=9	Leng. h=9	Cov. h=12	Leng. h=12
Australian Dollar	0.915	7.155	0.909	14.690^c	0.959	20.547	0.963^y	26.364	0.947	29.583^c
Canadian Dollar	0.825	3.526	0.794	6.525^c	0.797	9.040^c	0.787	10.370^c	0.693	11.352^c
Danish Kroner	0.915	8.548^c	0.929	17.930^c	0.938	25.328^c	0.890	30.504^c	0.904	36.624^c
French Franc	0.912	8.864^c	0.880	15.970^c	0.845	20.693^c	0.968	30.436^c	0.714	22.789^c
Deutschmark	0.917	8.605^c	0.907	18.356^c	0.894	28.121^c	0.911^c	31.378^c	0.939	33.779^c
Italian Lira	0.913	8.659^c	0.890	18.664	0.887	25.840^c	0.831	32.037^c	0.693	32.236^c
Japanese Yen	0.920	9.637^z	0.888	19.352^b	0.871	28.018^c	0.932	33.388^c	0.878	36.859^c
Dutch Guilder	0.936	8.851	0.916	18.822^c	0.942	27.259^c	0.970	31.410^c	0.990	39.882^c
Portuguese Escudo	0.916	8.881^z	0.870	17.651	0.758	18.730^c	0.746	23.852^c	0.600	20.593^c
Swedish Krona	0.828	7.428^c	0.854	15.658^c	0.903	24.315^c	0.861	29.866^c	0.876	36.235^c
Swiss Franc	0.935	9.731^c	0.940	19.797	0.970	27.227^c	0.969	32.179^c	0.937	36.567^c
British Pound	0.919	8.350	0.908	16.774^c	0.828	20.811^c	0.783	23.105^c	0.720	23.286^c

Table 7.-Panel 2: Results of Heterogenous Taylor Rules, Coverage Test

h=1 h=3 h=6 h=9 h=12

Model Better 0 0 0 1 0

RW Better 0 0 0 1 0

	h=1	h=3	h=6	h=9	h=12
Model Better	0	0	0	1	0
RW Better	0	0	0	1	0

Note: In this panel, a better model is the one with more accurate empirical coverages. RW is the abbreviation of Random Walk.

Table 7.-Panel 3: Results of Heterogenous Taylor Rules, Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 6 9 11 10 12

RW Better 2 0 0 0 0

	h=1	h=3	h=6	h=9	h=12
Model Better	6	9	11	10	12
RW Better	2	0	0	0	0

Note: In this panel, a better model is the one with tighter forecast intervals given equal coverage accuracy.

Table 7.-Panel 4: Results of Heterogenous Taylor Rules, Coverage Test and Length Test Given Equal Coverage Accuracy

h=1 h=3 h=6 h=9 h=12

Model Better 6 9 11 11 12

RW Better 2 0 0 1 0

Note: In this panel, a better model is the one with either more accurate coverages or tighter forecast intervals given equal coverage accuracy.

Figure 1a. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (British Pound), 1-Month-Ahead Forecast

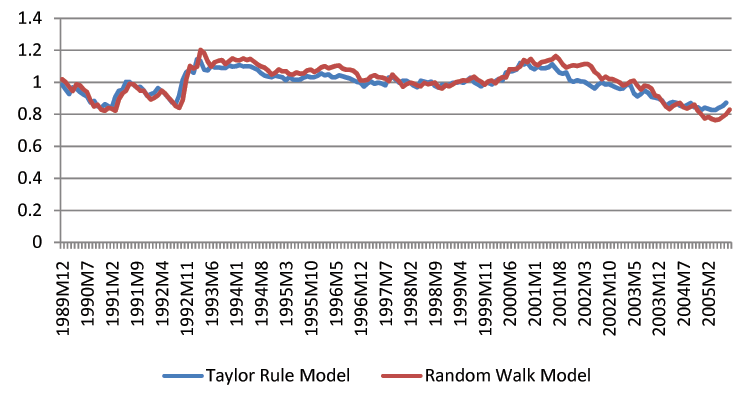
Data for Figure 1a mmediately follows

Note: To facilitate graphical comparisons, the 6- and 12-month-ahead forecast intervals of the random walk have been relocated such that they have the same center as the intervals of the Taylor rule model.

Data for Figure 1a

Date	Taylor Rule	RW
1989M12	1.0000	1.0190
1990M1	0.9848	1.0019
1990M2	0.9543	0.9714
1990M3	0.9257	0.9448
1990M4	0.9695	0.9886
1990M5	0.9600	0.9810
1990M6	0.9390	0.9562
1990M7	0.9238	0.9390
1990M8	0.9124	0.8876
1990M9	0.8743	0.8495
1990M10	0.8838	0.8610
1990M11	0.8495	0.8305
1990M12	0.8400	0.8229
1991M1	0.8629	0.8400
1991M2	0.8495	0.8362
1991M3	0.8400	0.8229
1991M4	0.9086	0.8952
1991M5	0.9467	0.9314
1991M6	0.9524	0.9467
1991M7	1.0019	0.9905
1991M8	1.0019	0.9886
1991M9	0.9848	0.9695
1991M10	0.9676	0.9467
1991M11	0.9714	0.9467
1991M12	0.9486	0.9162
1992M1	0.9143	0.8933
1992M2	0.9257	0.9029
1992M3	0.9352	0.9181
1992M4	0.9638	0.9486
1992M5	0.9467	0.9295
1992M6	0.9257	0.9029
1992M7	0.9010	0.8800
1992M8	0.8743	0.8514
1992M9	0.8648	0.8400
1992M10	0.9200	0.8895
1992M11	1.0152	1.0190
1992M12	1.0648	1.1029
1993M1	1.0800	1.0857
1993M2	1.0590	1.0971
1993M3	1.1448	1.2019
1993M4	1.1314	1.1829
1993M5	1.0781	1.1314
1993M6	1.0743	1.0971
1993M7	1.1029	1.1257
1993M8	1.0914	1.1352
1993M9	1.0933	1.1390
1993M10	1.0895	1.1143
1993M11	1.0895	1.1314
1993M12	1.1048	1.1486
1994M1	1.0971	1.1390
1994M2	1.1010	1.1371
1994M3	1.1086	1.1486
1994M4	1.0990	1.1390
1994M5	1.1010	1.1467
1994M6	1.0990	1.1295
1994M7	1.0895	1.1124
1994M8	1.0781	1.0990
1994M9	1.0571	1.0914
1994M10	1.0419	1.0743
1994M11	1.0362	1.0476
1994M12	1.0324	1.0590
1995M1	1.0419	1.0800
1995M2	1.0362	1.0686
1995M3	1.0324	1.0705
1995M4	1.0133	1.0514
1995M5	1.0324	1.0476
1995M6	1.0171	1.0610
1995M7	1.0152	1.0533
1995M8	1.0171	1.0552
1995M9	1.0305	1.0743
1995M10	1.0381	1.0781
1995M11	1.0324	1.0648
1995M12	1.0324	1.0762
1996M1	1.0400	1.0933
1996M2	1.0552	1.1010
1996M3	1.0438	1.0876
1996M4	1.0495	1.0952
1996M5	1.0324	1.1029
1996M6	1.0324	1.1048
1996M7	1.0438	1.0857
1996M8	1.0381	1.0781
1996M9	1.0305	1.0781
1996M10	1.0248	1.0724
1996M11	1.0133	1.0533
1996M12	1.0019	1.0114
1997M1	0.9981	1.0114
1997M2	0.9733	1.0152
1997M3	0.9943	1.0362
1997M4	1.0038	1.0457
1997M5	0.9905	1.0324
1997M6	0.9981	1.0305
1997M7	0.9924	1.0229
1997M8	0.9810	1.0076
1997M9	1.0305	1.0476
1997M10	1.0324	1.0248
1997M11	1.0152	1.0038
1997M12	0.9962	0.9714
1998M1	1.0095	0.9886
1998M2	1.0095	0.9981
1998M3	0.9962	0.9924
1998M4	0.9790	0.9810
1998M5	0.9695	0.9752
1998M6	1.0095	0.9962
1998M7	1.0038	0.9886
1998M8	0.9981	0.9924
1998M9	1.0038	0.9981
1998M10	0.9771	0.9695
1998M11	0.9657	0.9619
1998M12	0.9848	0.9829
1999M1	0.9771	0.9752
1999M2	0.9867	0.9867
1999M3	0.9962	1.0019
1999M4	0.9962	1.0057
1999M5	1.0038	1.0133
1999M6	0.9962	1.0095
1999M7	1.0114	1.0229
1999M8	1.0286	1.0343
1999M9	1.0000	1.0152
1999M10	0.9886	1.0038
1999M11	0.9752	0.9848
1999M12	0.9924	1.0057
2000M1	0.9962	1.0114
2000M2	0.9867	0.9943
2000M3	1.0076	1.0190
2000M4	1.0210	1.0324
2000M5	1.0114	1.0305
2000M6	1.0610	1.0819
2000M7	1.0667	1.0819
2000M8	1.0705	1.0838
2000M9	1.0781	1.0971
2000M10	1.1219	1.1390
2000M11	1.1105	1.1257
2000M12	1.1219	1.1467
2001M1	1.0914	1.1162
2001M2	1.0819	1.1067
2001M3	1.0990	1.1257
2001M4	1.0876	1.1295
2001M5	1.0876	1.1371
2001M6	1.0952	1.1429
2001M7	1.1124	1.1638
2001M8	1.0857	1.1429
2001M9	1.0610	1.1105
2001M10	1.0533	1.0914
2001M11	1.0610	1.1010
2001M12	1.0133	1.1067
2002M1	1.0019	1.1029
2002M2	1.0133	1.1086
2002M3	1.0057	1.1143
2002M4	1.0038	1.1143
2002M5	0.9905	1.0990
2002M6	0.9752	1.0648
2002M7	0.9619	1.0476
2002M8	0.9867	1.0190
2002M9	1.0000	1.0343
2002M10	0.9867	1.0210
2002M11	0.9886	1.0210
2002M12	0.9771	1.0095
2003M1	0.9676	1.0000
2003M2	0.9581	0.9810
2003M3	0.9619	0.9886
2003M4	0.9829	1.0038
2003M5	0.9829	1.0095
2003M6	0.9314	0.9790
2003M7	0.9124	0.9543
2003M8	0.9257	0.9790
2003M9	0.9486	0.9752
2003M10	0.9352	0.9600
2003M11	0.9086	0.9181
2003M12	0.9048	0.9124
2004M1	0.8990	0.8800
2004M2	0.8857	0.8495
2004M3	0.8533	0.8324
2004M4	0.8686	0.8514
2004M5	0.8762	0.8629
2004M6	0.8724	0.8705
2004M7	0.8552	0.8438
2004M8	0.8476	0.8362
2004M9	0.8590	0.8476
2004M10	0.8705	0.8610
2004M11	0.8438	0.8229
2004M12	0.8438	0.8000
2005M1	0.8267	0.7733
2005M2	0.8419	0.7848
2005M3	0.8343	0.7714
2005M4	0.8267	0.7638
2005M5	0.8267	0.7676
2005M6	0.8419	0.7848
2005M7	0.8514	0.8000
2005M8	0.8724	0.8305
2005M9	0.8438	0.8095
2005M10	0.8400	0.8057
2005M11	0.8552	0.8229
2005M12	0.8667	0.8362
2006M1	0.8419	0.8305
2006M2	0.8400	0.7943
2006M3	0.8305	0.7905
2006M4	0.8324	0.7924

Figure 1b. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (British Pound), 6-month-ahead forecast

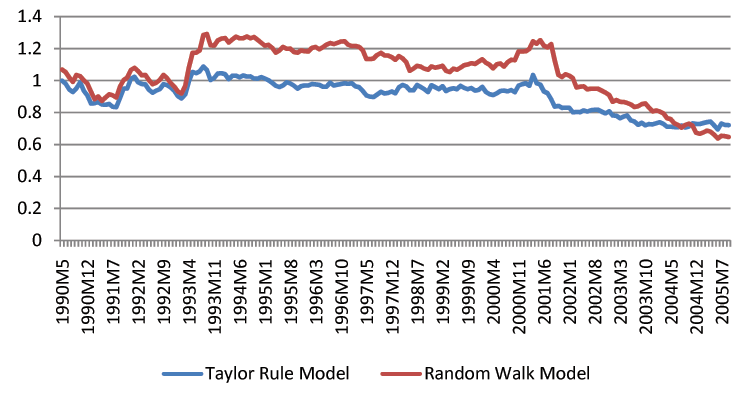
Data for Figure 1b immediately follows

Data for Figure 1b

Date	Taylor Rule	RW
1990M5	1.0000	1.0687
1990M6	0.9804	1.0528
1990M7	0.9442	1.0184
1990M8	0.9282	0.9914
1990M9	0.9515	1.0350
1990M10	0.9902	1.0270
1990M11	0.9368	1.0018
1990M12	0.9080	0.9822
1991M1	0.8564	0.9288
1991M2	0.8583	0.8840
1991M3	0.8650	0.9000
1991M4	0.8509	0.8730
1991M5	0.8479	0.8933
1991M6	0.8540	0.9135
1991M7	0.8362	0.9074
1991M8	0.8337	0.8939
1991M9	0.8920	0.9638
1991M10	0.9497	1.0031
1991M11	0.9509	1.0184
1991M12	1.0104	1.0656
1992M1	1.0227	1.0798
1992M2	0.9896	1.0595
1992M3	0.9785	1.0331
1992M4	0.9761	1.0350
1992M5	0.9429	1.0031
1992M6	0.9239	0.9767
1992M7	0.9368	0.9859
1992M8	0.9460	1.0037
1992M9	0.9779	1.0350
1992M10	0.9712	1.0153
1992M11	0.9577	0.9859
1992M12	0.9362	0.9613
1993M1	0.9025	0.9301
1993M2	0.8883	0.9178
1993M3	0.9135	0.9663
1993M4	0.9939	1.0798
1993M5	1.0546	1.1724
1993M6	1.0460	1.1736
1993M7	1.0577	1.1890
1993M8	1.0877	1.2840
1993M9	1.0656	1.2908
1993M10	1.0031	1.2209
1993M11	1.0160	1.2184
1993M12	1.0442	1.2503
1994M1	1.0460	1.2613
1994M2	1.0399	1.2650
1994M3	1.0086	1.2374
1994M4	1.0301	1.2558
1994M5	1.0313	1.2736
1994M6	1.0209	1.2644
1994M7	1.0319	1.2638
1994M8	1.0252	1.2755
1994M9	1.0270	1.2644
1994M10	1.0135	1.2724
1994M11	1.0123	1.2540
1994M12	1.0215	1.2362
1995M1	1.0129	1.2190
1995M2	1.0018	1.2233
1995M3	0.9859	1.2049
1995M4	0.9669	1.1742
1995M5	0.9595	1.1871
1995M6	0.9693	1.2098
1995M7	0.9896	1.1982
1995M8	0.9816	1.2000
1995M9	0.9687	1.1785
1995M10	0.9491	1.1736
1995M11	0.9656	1.1883
1995M12	0.9693	1.1828
1996M1	0.9693	1.1822
1996M2	0.9785	1.2037
1996M3	0.9761	1.2098
1996M4	0.9730	1.1951
1996M5	0.9613	1.2074
1996M6	0.9613	1.2245
1996M7	0.9871	1.2337
1996M8	0.9693	1.2276
1996M9	0.9736	1.2350
1996M10	0.9785	1.2442
1996M11	0.9834	1.2448
1996M12	0.9798	1.2239
1997M1	0.9834	1.2147
1997M2	0.9638	1.2166
1997M3	0.9583	1.2098
1997M4	0.9356	1.1896
1997M5	0.9067	1.1350
1997M6	0.9000	1.1337
1997M7	0.8969	1.1374
1997M8	0.9129	1.1601
1997M9	0.9294	1.1724
1997M10	0.9190	1.1577
1997M11	0.9233	1.1558
1997M12	0.9319	1.1466
1998M1	0.9209	1.1294
1998M2	0.9583	1.1528
1998M3	0.9730	1.1380
1998M4	0.9638	1.1147
1998M5	0.9393	1.0601
1998M6	0.9399	1.0748
1998M7	0.9724	1.0914
1998M8	0.9595	1.0871
1998M9	0.9460	1.0736
1998M10	0.9288	1.0669
1998M11	0.9706	1.0890
1998M12	0.9589	1.0810
1999M1	0.9460	1.0853
1999M2	0.9656	1.0920
1999M3	0.9337	1.0601
1999M4	0.9466	1.0528
1999M5	0.9521	1.0742
1999M6	0.9460	1.0675
1999M7	0.9669	1.0810
1999M8	0.9540	1.0963
1999M9	0.9466	1.1006
1999M10	0.9528	1.1086
1999M11	0.9368	1.1043
1999M12	0.9417	1.1184
2000M1	0.9607	1.1325
2000M2	0.9288	1.1110
2000M3	0.9147	1.0982
2000M4	0.9092	1.0761
2000M5	0.9209	1.1012
2000M6	0.9356	1.1061
2000M7	0.9374	1.0871
2000M8	0.9331	1.1153
2000M9	0.9411	1.1294
2000M10	0.9270	1.1276
2000M11	0.9687	1.1822
2000M12	0.9773	1.1822
2001M1	0.9828	1.1834
2001M2	0.9669	1.1982
2001M3	1.0356	1.2448
2001M4	0.9834	1.2294
2001M5	0.9748	1.2515
2001M6	0.9325	1.2190
2001M7	0.9202	1.2061
2001M8	0.8840	1.2270
2001M9	0.8368	1.1258
2001M10	0.8417	1.0356
2001M11	0.8294	1.0221
2001M12	0.8301	1.0399
2002M1	0.8294	1.0307
2002M2	0.8018	1.0147
2002M3	0.8037	0.9571
2002M4	0.8031	0.9613
2002M5	0.8141	0.9638
2002M6	0.8061	0.9454
2002M7	0.8147	0.9491
2002M8	0.8166	0.9485
2002M9	0.8172	0.9485
2002M10	0.8043	0.9356
2002M11	0.7945	0.9245
2002M12	0.8080	0.9092
2003M1	0.7810	0.8669
2003M2	0.7798	0.8779
2003M3	0.7644	0.8675
2003M4	0.7748	0.8663
2003M5	0.7816	0.8589
2003M6	0.7503	0.8503
2003M7	0.7429	0.8344
2003M8	0.7239	0.8393
2003M9	0.7362	0.8528
2003M10	0.7196	0.8571
2003M11	0.7276	0.8313
2003M12	0.7252	0.8074
2004M1	0.7319	0.8129
2004M2	0.7393	0.8055
2004M3	0.7288	0.7945
2004M4	0.7117	0.7644
2004M5	0.7110	0.7595
2004M6	0.7092	0.7325
2004M7	0.7074	0.7221
2004M8	0.7190	0.7055
2004M9	0.7067	0.7221
2004M10	0.7123	0.7307
2004M11	0.7319	0.7184
2004M12	0.7294	0.6736
2005M1	0.7282	0.6669
2005M2	0.7344	0.6761
2005M3	0.7399	0.6865
2005M4	0.7436	0.6804
2005M5	0.7190	0.6613
2005M6	0.6945	0.6380
2005M7	0.7313	0.6546
2005M8	0.7221	0.6521
2005M9	0.7215	0.6466
2005M10	0.7215	0.6491
2005M11	0.7288	0.6632
2005M12	0.7319	0.6773
2006M1	0.7632	0.7031
2006M2	0.7387	0.6521
2006M3	0.7393	0.6472
2006M4	0.6871	0.6626

Figure 1c. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (British Pound), 12-month-ahead forecast

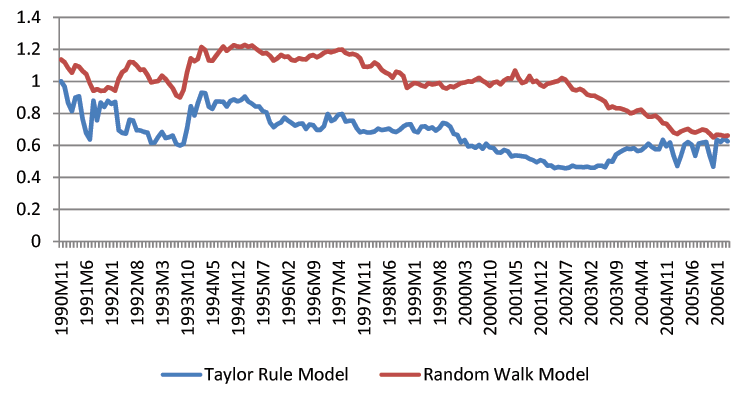
Data for Figure 1c immediately follows

Data for Figure 1c

Date	Taylor Rule	RW
1990M11	1.0000	1.1366
1990M12	0.9668	1.1196
1991M1	0.8647	1.0826
1991M2	0.8136	1.0540
1991M3	0.8987	1.1005
1991M4	0.9066	1.0917
1991M5	0.7659	1.0656
1991M6	0.6750	1.0448
1991M7	0.6364	0.9875
1991M8	0.8788	0.9402
1991M9	0.7572	0.9510
1991M10	0.8672	0.9402
1991M11	0.8406	0.9415
1991M12	0.8780	0.9622
1992M1	0.8589	0.9560
1992M2	0.8709	0.9419
1992M3	0.6945	1.0154
1992M4	0.6783	1.0569
1992M5	0.6733	1.0731
1992M6	0.7597	1.1208
1992M7	0.7547	1.1200
1992M8	0.6949	1.0984
1992M9	0.6932	1.0714
1992M10	0.6849	1.0735
1992M11	0.6795	1.0394
1992M12	0.6148	0.9938
1993M1	0.6177	0.9983
1993M2	0.6534	1.0029
1993M3	0.6833	1.0345
1993M4	0.6459	1.0149
1993M5	0.6513	0.9855
1993M6	0.6613	0.9577
1993M7	0.6081	0.9116
1993M8	0.5994	0.8991
1993M9	0.6094	0.9465
1993M10	0.7073	1.0573
1993M11	0.8447	1.1445
1993M12	0.7866	1.1266
1994M1	0.8643	1.1403
1994M2	0.9290	1.2138
1994M3	0.9261	1.1955
1994M4	0.8418	1.1312
1994M5	0.8277	1.1287
1994M6	0.8738	1.1586
1994M7	0.8738	1.1876
1994M8	0.8726	1.2171
1994M9	0.8423	1.1905
1994M10	0.8771	1.2084
1994M11	0.8871	1.2262
1994M12	0.8751	1.2171
1995M1	0.8829	1.2163
1995M2	0.9041	1.2275
1995M3	0.8734	1.2167
1995M4	0.8605	1.2246
1995M5	0.8418	1.2067
1995M6	0.8439	1.1897
1995M7	0.8149	1.1739
1995M8	0.8057	1.1773
1995M9	0.7410	1.1594
1995M10	0.7140	1.1299
1995M11	0.7323	1.1424
1995M12	0.7430	1.1648
1996M1	0.7733	1.1532
1996M2	0.7543	1.1548
1996M3	0.7401	1.1345
1996M4	0.7235	1.1295
1996M5	0.7352	1.1436
1996M6	0.7372	1.1386
1996M7	0.7020	1.1378
1996M8	0.7302	1.1590
1996M9	0.7260	1.1644
1996M10	0.6974	1.1507
1996M11	0.6966	1.1615
1996M12	0.7194	1.1781
1997M1	0.7954	1.1876
1997M2	0.7522	1.1818
1997M3	0.7630	1.1889
1997M4	0.7924	1.1972
1997M5	0.7954	1.1980
1997M6	0.7493	1.1777
1997M7	0.7530	1.1689
1997M8	0.7534	1.1714
1997M9	0.7078	1.1640
1997M10	0.6812	1.1445
1997M11	0.6878	1.0922
1997M12	0.6804	1.0909
1998M1	0.6808	1.0946
1998M2	0.6870	1.1171
1998M3	0.7049	1.1034
1998M4	0.6957	1.0722
1998M5	0.6995	1.0565
1998M6	0.7049	1.0448
1998M7	0.6895	1.0232
1998M8	0.6837	1.0589
1998M9	0.6966	1.0544
1998M10	0.7177	1.0328
1998M11	0.7302	0.9597
1998M12	0.7327	0.9751
1999M1	0.6895	0.9900
1999M2	0.6816	0.9863
1999M3	0.7165	0.9738
1999M4	0.7194	0.9676
1999M5	0.7036	0.9880
1999M6	0.7119	0.9805
1999M7	0.6920	0.9851
1999M8	0.7094	0.9905
1999M9	0.7397	0.9622
1999M10	0.7352	0.9552
1999M11	0.7169	0.9689
1999M12	0.6712	0.9635
2000M1	0.6642	0.9755
2000M2	0.6189	0.9892
2000M3	0.6330	0.9929
2000M4	0.5936	1.0004
2000M5	0.5973	0.9967
2000M6	0.5845	1.0091
2000M7	0.6027	1.0216
2000M8	0.5795	1.0025
2000M9	0.6098	0.9905
2000M10	0.5878	0.9714
2000M11	0.5832	0.9929
2000M12	0.5575	0.9975
2001M1	0.5546	0.9813
2001M2	0.5712	1.0062
2001M3	0.5637	1.0191
2001M4	0.5313	1.0170
2001M5	0.5367	1.0668
2001M6	0.5363	1.0191
2001M7	0.5330	0.9896
2001M8	0.5297	0.9988
2001M9	0.5160	1.0340
2001M10	0.5077	0.9963
2001M11	0.4948	1.0029
2001M12	0.5081	0.9780
2002M1	0.5006	0.9676
2002M2	0.4736	0.9846
2002M3	0.4745	0.9900
2002M4	0.4587	0.9971
2002M5	0.4653	1.0025
2002M6	0.4620	1.0203
2002M7	0.4570	1.0108
2002M8	0.4620	0.9809
2002M9	0.4741	0.9498
2002M10	0.4653	0.9435
2002M11	0.4662	0.9527
2002M12	0.4633	0.9411
2003M1	0.4666	0.9170
2003M2	0.4608	0.9103
2003M3	0.4608	0.9103
2003M4	0.4728	0.8979
2003M5	0.4736	0.8871
2003M6	0.4633	0.8730
2003M7	0.5035	0.8323
2003M8	0.4981	0.8427
2003M9	0.5430	0.8323
2003M10	0.5575	0.8315
2003M11	0.5687	0.8248
2003M12	0.5799	0.8165
2004M1	0.5770	0.8007
2004M2	0.5820	0.8057
2004M3	0.5645	0.8186
2004M4	0.5687	0.8227
2004M5	0.5890	0.7983
2004M6	0.6102	0.7796
2004M7	0.5907	0.7792
2004M8	0.5758	0.7862
2004M9	0.5753	0.7684
2004M10	0.6351	0.7389
2004M11	0.5953	0.7347
2004M12	0.6185	0.7082
2005M1	0.5367	0.6800
2005M2	0.4720	0.6712
2005M3	0.5330	0.6866
2005M4	0.6040	0.6953
2005M5	0.6198	0.7020
2005M6	0.6040	0.6858
2005M7	0.5351	0.6800
2005M8	0.6110	0.6887
2005M9	0.6173	0.6990
2005M10	0.6210	0.6932
2005M11	0.5372	0.6737
2005M12	0.4670	0.6501
2006M1	0.6359	0.6671
2006M2	0.6214	0.6646
2006M3	0.6430	0.6584
2006M4	0.6260	0.6613

Figure 2a. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Deutschmark), 1-month-ahead forecast

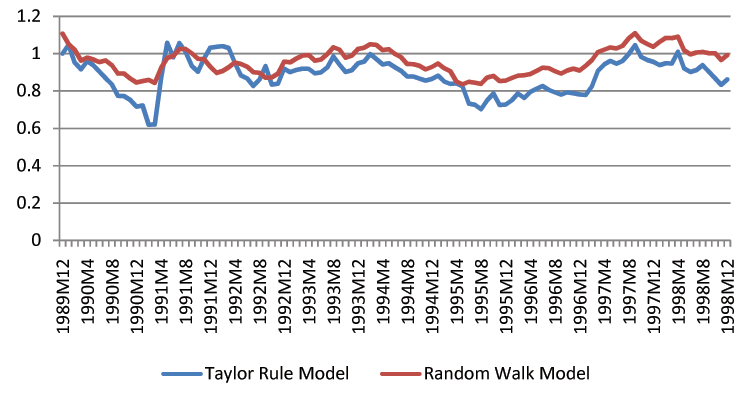
Data for Figure 2a immediately follows

Data for Figure 2a

Date	Taylor Rule	RW
1989M12	1.0000	1.1060
1990M1	1.0471	1.0497
1990M2	0.9522	1.0190
1990M3	0.9156	0.9614
1990M4	0.9594	0.9777
1990M5	0.9385	0.9673
1990M6	0.9045	0.9535
1990M7	0.8678	0.9627
1990M8	0.8344	0.9372
1990M9	0.7729	0.8920
1990M10	0.7723	0.8920
1990M11	0.7520	0.8658
1990M12	0.7160	0.8442
1991M1	0.7212	0.8514
1991M2	0.6185	0.8580
1991M3	0.6198	0.8416
1991M4	0.8691	0.9228
1991M5	1.0576	0.9771
1991M6	0.9797	0.9869
1991M7	1.0569	1.0229
1991M8	1.0098	1.0242
1991M9	0.9326	1.0000
1991M10	0.9025	0.9719
1991M11	0.9732	0.9686
1991M12	1.0308	0.9300
1992M1	1.0366	0.8966
1992M2	1.0406	0.9058
1992M3	1.0301	0.9260
1992M4	0.9509	0.9509
1992M5	0.8822	0.9437
1992M6	0.8665	0.9287
1992M7	0.8266	0.8999
1992M8	0.8606	0.8966
1992M9	0.9326	0.8698
1992M10	0.8338	0.8724
1992M11	0.8384	0.8927
1992M12	0.9195	0.9562
1993M1	0.9005	0.9529
1993M2	0.9116	0.9725
1993M3	0.9188	0.9889
1993M4	0.9182	0.9915
1993M5	0.8940	0.9620
1993M6	0.8986	0.9679
1993M7	0.9260	0.9967
1993M8	0.9849	1.0334
1993M9	0.9411	1.0203
1993M10	0.9018	0.9764
1993M11	0.9110	0.9882
1993M12	0.9483	1.0242
1994M1	0.9568	1.0308
1994M2	0.9974	1.0497
1994M3	0.9712	1.0452
1994M4	0.9424	1.0183
1994M5	0.9483	1.0236
1994M6	0.9274	0.9980
1994M7	0.9084	0.9804
1994M8	0.8783	0.9437
1994M9	0.8763	0.9424
1994M10	0.8645	0.9332
1994M11	0.8547	0.9149
1994M12	0.8639	0.9274
1995M1	0.8815	0.9470
1995M2	0.8501	0.9215
1995M3	0.8370	0.9045
1995M4	0.8403	0.8495
1995M5	0.8253	0.8344
1995M6	0.7317	0.8488
1995M7	0.7251	0.8436
1995M8	0.7016	0.8364
1995M9	0.7493	0.8711
1995M10	0.7853	0.8796
1995M11	0.7238	0.8514
1995M12	0.7264	0.8541
1996M1	0.7487	0.8678
1996M2	0.7853	0.8815
1996M3	0.7624	0.8835
1996M4	0.7945	0.8901
1996M5	0.8109	0.9064
1996M6	0.8266	0.9234
1996M7	0.8043	0.9208
1996M8	0.7919	0.9045
1996M9	0.7801	0.8927
1996M10	0.7925	0.9084
1996M11	0.7873	0.9182
1996M12	0.7808	0.9084
1997M1	0.7788	0.9332
1997M2	0.8240	0.9640
1997M3	0.9077	1.0085
1997M4	0.9424	1.0209
1997M5	0.9607	1.0314
1997M6	0.9450	1.0268
1997M7	0.9601	1.0406
1997M8	0.9974	1.0805
1997M9	1.0445	1.1086
1997M10	0.9823	1.0687
1997M11	0.9660	1.0510
1997M12	0.9562	1.0360
1998M1	0.9385	1.0615
1998M2	0.9476	1.0838
1998M3	0.9463	1.0818
1998M4	1.0092	1.0903
1998M5	0.9202	1.0164
1998M6	0.9012	0.9954
1998M7	0.9116	1.0052
1998M8	0.9378	1.0085
1998M9	0.9038	1.0020
1998M10	0.8671	1.0013
1998M11	0.8325	0.9653
1998M12	0.8613	0.9921

Figure 2b. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Deutschmark), 6-month-ahead forecast

Data for Figure 2b immediately follows

Data for Figure 2b

Date	Taylor Rule	RW
1990M5	1.0000	1.0091
1990M6	0.9614	0.9553
1990M7	0.9059	0.9300
1990M8	0.9235	0.9212
1990M9	0.9110	0.9171
1990M10	0.8822	0.9070
1990M11	0.8491	0.8944
1990M12	0.8296	0.9053
1991M1	0.8184	0.8807
1991M2	0.7747	0.8444
1991M3	0.7777	0.8446
1991M4	0.7844	0.8196
1991M5	0.7338	0.7991
1991M6	0.7651	0.8058
1991M7	0.7531	0.8116
1991M8	0.7647	0.7963
1991M9	0.7893	0.8671
1991M10	0.8610	0.9158
1991M11	0.9214	0.9457
1991M12	0.9714	1.0032
1992M1	1.0490	1.0085
1992M2	0.9406	1.0121
1992M3	0.9110	0.9830
1992M4	1.0257	0.9807
1992M5	0.9063	0.9409
1992M6	0.8749	0.9072
1992M7	0.9017	0.9165
1992M8	0.9114	0.9396
1992M9	0.9150	0.9644
1992M10	0.9354	0.9576
1992M11	0.9131	0.9419
1992M12	0.8813	0.9129
1993M1	0.8552	0.8656
1993M2	0.8082	0.8402
1993M3	0.8008	0.8425
1993M4	0.8285	0.8622
1993M5	0.9053	0.9216
1993M6	0.9034	0.9184
1993M7	0.9820	0.9371
1993M8	0.9650	0.9527
1993M9	0.9392	0.9559
1993M10	0.9252	0.9267
1993M11	0.9239	0.9328
1993M12	0.9619	0.9604
1994M1	1.0093	0.9960
1994M2	0.9521	0.9835
1994M3	0.9161	0.9415
1994M4	0.9201	0.9523
1994M5	0.9746	0.9871
1994M6	0.9866	0.9930
1994M7	1.0168	1.0115
1994M8	1.0040	1.0076
1994M9	0.9519	0.9816
1994M10	0.9585	0.9860
1994M11	0.9506	0.9616
1994M12	0.9027	0.9445
1995M1	0.8936	0.9099
1995M2	0.8856	0.9082
1995M3	0.8618	0.8993
1995M4	0.8603	0.8821
1995M5	0.8762	0.8938
1995M6	0.8917	0.9123
1995M7	0.8730	0.8883
1995M8	0.8546	0.8720
1995M9	0.7931	0.8162
1995M10	0.7827	0.8018
1995M11	0.7950	0.8183
1995M12	0.7959	0.8135
1996M1	0.7974	0.8061
1996M2	0.8192	0.8393
1996M3	0.8234	0.8476
1996M4	0.8006	0.8209
1996M5	0.8145	0.8228
1996M6	0.8326	0.8364
1996M7	0.8190	0.8497
1996M8	0.8364	0.8516
1996M9	0.8224	0.8576
1996M10	0.8351	0.8733
1996M11	0.8535	0.8896
1996M12	0.8548	0.8870
1997M1	0.8423	0.8722
1997M2	0.8243	0.8607
1997M3	0.8319	0.8754
1997M4	0.8449	0.8868
1997M5	0.8336	0.8777
1997M6	0.8614	0.9012
1997M7	0.8906	0.9315
1997M8	0.9192	0.9722
1997M9	0.9188	0.9835
1997M10	0.9300	0.9671
1997M11	0.9568	0.9593
1997M12	0.9432	0.9292
1998M1	0.9599	0.9307
1998M2	0.9417	0.9527
1998M3	0.8851	0.9220
1998M4	0.8646	0.8953
1998M5	0.8643	0.8826
1998M6	0.8896	0.9061
1998M7	0.8900	0.9254
1998M8	0.8930	0.9233
1998M9	0.8877	0.9309
1998M10	0.8904	0.9237
1998M11	0.8809	0.9044
1998M12	0.8800	0.9135

Figure 2c. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Deutschmark), 12-month-ahead forecast

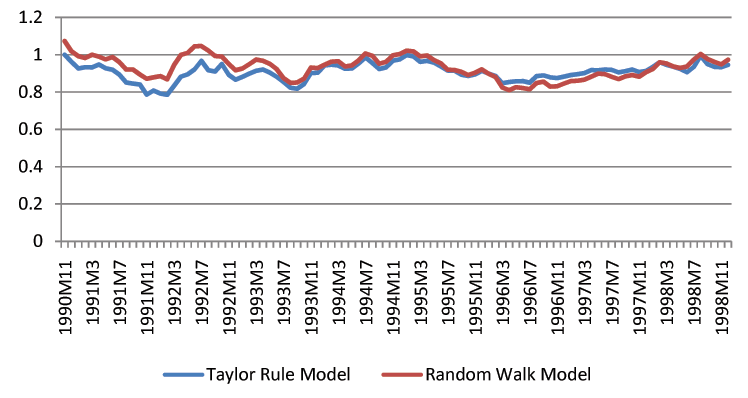
Data for Figure 2c immediately follows

Data for Figure 2c

Date	Taylor Rule	RW
1990M11	1.0000	1.0730
1990M12	0.9630	1.0191
1991M1	0.9260	0.9919
1991M2	0.9336	0.9827
1991M3	0.9319	0.9999
1991M4	0.9477	0.9887
1991M5	0.9277	0.9752
1991M6	0.9195	0.9870
1991M7	0.8944	0.9604
1991M8	0.8508	0.9207
1991M9	0.8457	0.9206
1991M10	0.8409	0.8935
1991M11	0.7862	0.8712
1991M12	0.8084	0.8786
1992M1	0.7919	0.8850
1992M2	0.7852	0.8681
1992M3	0.8335	0.9454
1992M4	0.8828	0.9985
1992M5	0.8946	1.0087
1992M6	0.9213	1.0455
1992M7	0.9676	1.0467
1992M8	0.9170	1.0223
1992M9	0.9105	0.9929
1992M10	0.9506	0.9905
1992M11	0.8925	0.9505
1992M12	0.8665	0.9166
1993M1	0.8812	0.9259
1993M2	0.8987	0.9492
1993M3	0.9136	0.9743
1993M4	0.9205	0.9672
1993M5	0.9048	0.9514
1993M6	0.8814	0.9221
1993M7	0.8546	0.8745
1993M8	0.8238	0.8487
1993M9	0.8180	0.8511
1993M10	0.8425	0.8708
1993M11	0.9015	0.9311
1993M12	0.9033	0.9277
1994M1	0.9425	0.9467
1994M2	0.9467	0.9625
1994M3	0.9424	0.9655
1994M4	0.9248	0.9362
1994M5	0.9260	0.9424
1994M6	0.9538	0.9703
1994M7	0.9853	1.0060
1994M8	0.9548	0.9936
1994M9	0.9235	0.9510
1994M10	0.9322	0.9619
1994M11	0.9680	0.9971
1994M12	0.9750	1.0031
1995M1	0.9979	1.0219
1995M2	0.9918	1.0177
1995M3	0.9619	0.9915
1995M4	0.9675	0.9960
1995M5	0.9583	0.9714
1995M6	0.9369	0.9541
1995M7	0.9152	0.9192
1995M8	0.9145	0.9174
1995M9	0.8927	0.9085
1995M10	0.8867	0.8912
1995M11	0.8951	0.9029
1995M12	0.9138	0.9216
1996M1	0.8984	0.8973
1996M2	0.8864	0.8808
1996M3	0.8469	0.8246
1996M4	0.8543	0.8099
1996M5	0.8581	0.8265
1996M6	0.8585	0.8217
1996M7	0.8501	0.8143
1996M8	0.8857	0.8476
1996M9	0.8892	0.8561
1996M10	0.8789	0.8293
1996M11	0.8752	0.8311
1996M12	0.8825	0.8448
1997M1	0.8914	0.8582
1997M2	0.8959	0.8602
1997M3	0.9019	0.8665
1997M4	0.9177	0.8821
1997M5	0.9171	0.8985
1997M6	0.9212	0.8962
1997M7	0.9188	0.8810
1997M8	0.9055	0.8694
1997M9	0.9125	0.8843
1997M10	0.9206	0.8913
1997M11	0.9076	0.8821
1997M12	0.9128	0.9058
1998M1	0.9347	0.9231
1998M2	0.9601	0.9595
1998M3	0.9460	0.9533
1998M4	0.9359	0.9365
1998M5	0.9237	0.9295
1998M6	0.9066	0.9366
1998M7	0.9347	0.9725
1998M8	0.9940	1.0035
1998M9	0.9495	0.9771
1998M10	0.9350	0.9615
1998M11	0.9332	0.9477
1998M12	0.9456	0.9731

Figure 3a. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Japanese Yen), 1-month-ahead forecast

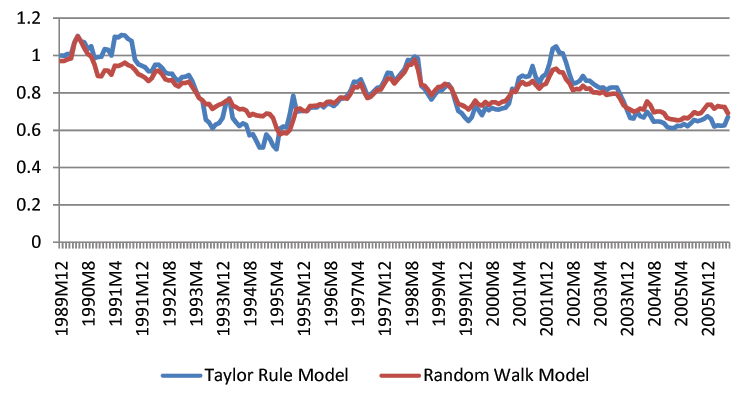
Data for Figure 3a immediately follows

Data for Figure 3a

Date	Taylor rule	RW
1989M12	1.0000	0.9695
1990M1	0.9991	0.9706
1990M2	1.0087	0.9793
1990M3	1.0061	0.9841
1990M4	1.0695	1.0666
1990M5	1.1049	1.1024
1990M6	1.0753	1.0716
1990M7	1.0710	1.0382
1990M8	1.0340	1.0067
1990M9	1.0495	0.9950
1990M10	0.9858	0.9510
1990M11	0.9925	0.8902
1990M12	0.9930	0.8877
1991M1	1.0346	0.9197
1991M2	1.0305	0.9185
1991M3	1.0002	0.8968
1991M4	1.0998	0.9448
1991M5	1.0970	0.9429
1991M6	1.1097	0.9505
1991M7	1.1078	0.9611
1991M8	1.0886	0.9478
1991M9	1.0784	0.9409
1991M10	0.9780	0.9236
1991M11	0.9529	0.8993
1991M12	0.9462	0.8915
1992M1	0.9373	0.8805
1992M2	0.9158	0.8628
1992M3	0.9161	0.8782
1992M4	0.9502	0.9137
1992M5	0.9507	0.9184
1992M6	0.9347	0.8993
1992M7	0.9094	0.8723
1992M8	0.9030	0.8657
1992M9	0.9027	0.8681
1992M10	0.8747	0.8431
1992M11	0.8661	0.8333
1992M12	0.8844	0.8519
1993M1	0.8870	0.8530
1993M2	0.8951	0.8595
1993M3	0.8640	0.8305
1993M4	0.8160	0.8047
1993M5	0.7733	0.7731
1993M6	0.7599	0.7588
1993M7	0.6571	0.7387
1993M8	0.6414	0.7406
1993M9	0.6116	0.7136
1993M10	0.6299	0.7260
1993M11	0.6388	0.7360
1993M12	0.6651	0.7419
1994M1	0.7432	0.7559
1994M2	0.7707	0.7664
1994M3	0.6653	0.7311
1994M4	0.6419	0.7228
1994M5	0.6223	0.7117
1994M6	0.6367	0.7135
1994M7	0.6287	0.7051
1994M8	0.5732	0.6770
1994M9	0.5788	0.6873
1994M10	0.5437	0.6792
1994M11	0.5076	0.6763
1994M12	0.5075	0.6742
1995M1	0.5765	0.6890
1995M2	0.5552	0.6861
1995M3	0.5173	0.6636
1995M4	0.4977	0.6115
1995M5	0.6096	0.5772
1995M6	0.6199	0.5870
1995M7	0.6166	0.5832
1995M8	0.6907	0.6022
1995M9	0.7835	0.6534
1995M10	0.7001	0.7139
1995M11	0.7031	0.7159
1995M12	0.7041	0.7031
1996M1	0.7020	0.7025
1996M2	0.7208	0.7294
1996M3	0.7221	0.7297
1996M4	0.7230	0.7307
1996M5	0.7389	0.7394
1996M6	0.7229	0.7334
1996M7	0.7409	0.7507
1996M8	0.7394	0.7523
1996M9	0.7295	0.7432
1996M10	0.7460	0.7574
1996M11	0.7686	0.7745
1996M12	0.7708	0.7738
1997M1	0.7838	0.7690
1997M2	0.8110	0.7955
1997M3	0.8599	0.8306
1997M4	0.8580	0.8293
1997M5	0.8719	0.8486
1997M6	0.8300	0.8051
1997M7	0.7843	0.7720
1997M8	0.7936	0.7793
1997M9	0.8098	0.7966
1997M10	0.8272	0.8166
1997M11	0.8304	0.8177
1997M12	0.8632	0.8469
1998M1	0.9077	0.8763
1998M2	0.9062	0.8751
1998M3	0.8611	0.8501
1998M4	0.8824	0.8719
1998M5	0.9043	0.8899
1998M6	0.9280	0.9112
1998M7	0.9761	0.9479
1998M8	0.9736	0.9510
1998M9	0.9949	0.9773
1998M10	0.9842	0.9265
1998M11	0.8384	0.8431
1998M12	0.8210	0.8378
1999M1	0.7927	0.8154
1999M2	0.7644	0.7874
1999M3	0.7904	0.8108
1999M4	0.8114	0.8303
1999M5	0.8129	0.8324
1999M6	0.8303	0.8478
1999M7	0.8464	0.8390
1999M8	0.8224	0.8204
1999M9	0.7600	0.7784
1999M10	0.7040	0.7406
1999M11	0.6917	0.7343
1999M12	0.6671	0.7251
2000M1	0.6497	0.7108
2000M2	0.6701	0.7296
2000M3	0.7260	0.7580
2000M4	0.7084	0.7367
2000M5	0.6806	0.7319
2000M6	0.7185	0.7506
2000M7	0.7078	0.7354
2000M8	0.7187	0.7498
2000M9	0.7119	0.7489
2000M10	0.7100	0.7403
2000M11	0.7171	0.7514
2000M12	0.7209	0.7553
2001M1	0.7429	0.7775
2001M2	0.8222	0.8084
2001M3	0.8069	0.8045
2001M4	0.8809	0.8420
2001M5	0.8924	0.8576
2001M6	0.8857	0.8437
2001M7	0.8906	0.8478
2001M8	0.9435	0.8627
2001M9	0.8830	0.8410
2001M10	0.8547	0.8218
2001M11	0.8877	0.8415
2001M12	0.8999	0.8482
2002M1	0.9544	0.8869
2002M2	1.0358	0.9223
2002M3	1.0490	0.9290
2002M4	1.0152	0.9111
2002M5	1.0111	0.9090
2002M6	0.9612	0.8717
2002M7	0.8995	0.8503
2002M8	0.8490	0.8132
2002M9	0.8544	0.8207
2002M10	0.8644	0.8179
2002M11	0.8908	0.8370
2002M12	0.8647	0.8214
2003M1	0.8651	0.8233
2003M2	0.8493	0.8025
2003M3	0.8372	0.8021
2003M4	0.8265	0.7977
2003M5	0.8293	0.8058
2003M6	0.8153	0.7888
2003M7	0.8273	0.7926
2003M8	0.8298	0.7951
2003M9	0.8290	0.7948
2003M10	0.7912	0.7690
2003M11	0.7533	0.7334
2003M12	0.7120	0.7194
2004M1	0.6662	0.7099
2004M2	0.6629	0.7003
2004M3	0.7001	0.7031
2004M4	0.6752	0.7150
2004M5	0.6682	0.7094
2004M6	0.6981	0.7536
2004M7	0.6776	0.7335
2004M8	0.6453	0.6950
2004M9	0.6478	0.6997
2004M10	0.6451	0.6988
2004M11	0.6382	0.6905
2004M12	0.6180	0.6646
2005M1	0.6125	0.6590
2005M2	0.6112	0.6559
2005M3	0.6232	0.6528
2005M4	0.6226	0.6547
2005M5	0.6331	0.6668
2005M6	0.6221	0.6631
2005M7	0.6373	0.6765
2005M8	0.6546	0.6964
2005M9	0.6483	0.6880
2005M10	0.6544	0.6920
2005M11	0.6616	0.7145
2005M12	0.6750	0.7368
2006M1	0.6603	0.7360
2006M2	0.6201	0.7140
2006M3	0.6267	0.7287
2006M4	0.6238	0.7252
2006M5	0.6264	0.7239
2006M6	0.6703	0.6908

Figure 3b. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Japanese Yen), 6-month-ahead forecast

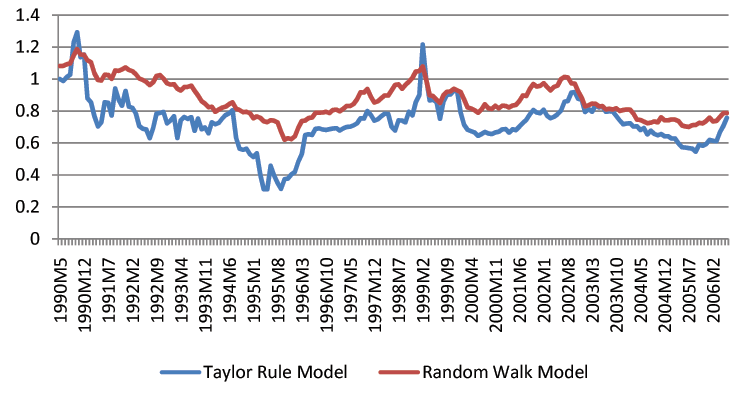
Data for Figure 3b immediately follows

Data for Figure 3b

Date	Taylor Rule	RW
1990M5	1.0000	1.0812
1990M6	0.9872	1.0825
1990M7	1.0120	1.0922
1990M8	1.0282	1.0975
1990M9	1.2311	1.1483
1990M10	1.2928	1.1869
1990M11	1.1366	1.1537
1990M12	1.1536	1.1512
1991M1	0.8790	1.1163
1991M2	0.8542	1.1045
1991M3	0.7677	1.0369
1991M4	0.7039	0.9940
1991M5	0.7292	0.9911
1991M6	0.8556	1.0269
1991M7	0.8509	1.0255
1991M8	0.7721	1.0012
1991M9	0.9407	1.0537
1991M10	0.8734	1.0516
1991M11	0.8330	1.0601
1991M12	0.9249	1.0719
1992M1	0.8268	1.0571
1992M2	0.8198	1.0494
1992M3	0.7834	1.0301
1992M4	0.7062	1.0029
1992M5	0.6896	0.9943
1992M6	0.6842	0.9820
1992M7	0.6296	0.9623
1992M8	0.6932	0.9795
1992M9	0.7836	1.0190
1992M10	0.7882	1.0242
1992M11	0.7933	1.0029
1992M12	0.7222	0.9728
1993M1	0.7394	0.9655
1993M2	0.7675	0.9682
1993M3	0.6309	0.9403
1993M4	0.7411	0.9294
1993M5	0.7627	0.9501
1993M6	0.7502	0.9514
1993M7	0.7616	0.9586
1993M8	0.6755	0.9262
1993M9	0.7527	0.8975
1993M10	0.6862	0.8622
1993M11	0.6972	0.8463
1993M12	0.6603	0.8239
1994M1	0.7295	0.8260
1994M2	0.7172	0.7959
1994M3	0.7254	0.8097
1994M4	0.7523	0.8208
1994M5	0.7751	0.8274
1994M6	0.7863	0.8430
1994M7	0.8050	0.8547
1994M8	0.6317	0.8153
1994M9	0.5649	0.8061
1994M10	0.5571	0.7937
1994M11	0.5647	0.7958
1994M12	0.5284	0.7864
1995M1	0.5120	0.7551
1995M2	0.5352	0.7665
1995M3	0.4009	0.7576
1995M4	0.3106	0.7366
1995M5	0.3105	0.7304
1995M6	0.4579	0.7431
1995M7	0.3974	0.7401
1995M8	0.3495	0.7287
1995M9	0.3129	0.6715
1995M10	0.3725	0.6208
1995M11	0.3767	0.6313
1995M12	0.4034	0.6239
1996M1	0.4188	0.6420
1996M2	0.4821	0.6954
1996M3	0.5311	0.7381
1996M4	0.6490	0.7407
1996M5	0.6547	0.7562
1996M6	0.6503	0.7599
1996M7	0.6880	0.7890
1996M8	0.6911	0.7893
1996M9	0.6845	0.7904
1996M10	0.6811	0.7952
1996M11	0.6859	0.7872
1996M12	0.6904	0.8067
1997M1	0.6921	0.8084
1997M2	0.6779	0.7986
1997M3	0.6913	0.8138
1997M4	0.6999	0.8322
1997M5	0.7018	0.8314
1997M6	0.7101	0.8438
1997M7	0.7227	0.8729
1997M8	0.7548	0.9174
1997M9	0.7529	0.9159
1997M10	0.7990	0.9374
1997M11	0.7743	0.8892
1997M12	0.7389	0.8527
1998M1	0.7481	0.8608
1998M2	0.7672	0.8799
1998M3	0.7826	0.8978
1998M4	0.7818	0.8966
1998M5	0.7019	0.9285
1998M6	0.6785	0.9634
1998M7	0.7418	0.9666
1998M8	0.7406	0.9389
1998M9	0.7297	0.9630
1998M10	0.7945	0.9829
1998M11	0.7727	1.0064
1998M12	0.8549	1.0470
1999M1	0.8992	1.0504
1999M2	1.2164	1.0794
1999M3	1.0059	0.9987
1999M4	0.8664	0.8989
1999M5	0.8722	0.8933
1999M6	0.8555	0.8694
1999M7	0.7513	0.8496
1999M8	0.8570	0.8978
1999M9	0.9023	0.9194
1999M10	0.9026	0.9217
1999M11	0.9275	0.9388
1999M12	0.9212	0.9290
2000M1	0.7895	0.9183
2000M2	0.7129	0.8713
2000M3	0.6827	0.8225
2000M4	0.6732	0.8155
2000M5	0.6660	0.8053
2000M6	0.6443	0.7894
2000M7	0.6557	0.8103
2000M8	0.6693	0.8418
2000M9	0.6586	0.8181
2000M10	0.6552	0.8128
2000M11	0.6662	0.8336
2000M12	0.6707	0.8167
2001M1	0.6845	0.8327
2001M2	0.6873	0.8317
2001M3	0.6650	0.8221
2001M4	0.6860	0.8345
2001M5	0.6802	0.8388
2001M6	0.7010	0.8635
2001M7	0.7259	0.8978
2001M8	0.7444	0.8945
2001M9	0.7790	0.9393
2001M10	0.8058	0.9692
2001M11	0.7901	0.9535
2001M12	0.7865	0.9581
2002M1	0.8084	0.9749
2002M2	0.7691	0.9504
2002M3	0.7546	0.9288
2002M4	0.7637	0.9510
2002M5	0.7795	0.9586
2002M6	0.8007	0.9991
2002M7	0.8570	1.0128
2002M8	0.8634	1.0105
2002M9	0.9152	0.9737
2002M10	0.9182	0.9709
2002M11	0.8767	0.9234
2002M12	0.8720	0.8818
2003M1	0.7943	0.8289
2003M2	0.8124	0.8363
2003M3	0.7950	0.8471
2003M4	0.8349	0.8451
2003M5	0.8219	0.8293
2003M6	0.8280	0.8312
2003M7	0.7946	0.8102
2003M8	0.7986	0.8139
2003M9	0.7961	0.8094
2003M10	0.7687	0.8177
2003M11	0.7415	0.8004
2003M12	0.7171	0.8070
2004M1	0.7217	0.8095
2004M2	0.7240	0.8093
2004M3	0.7027	0.7829
2004M4	0.7050	0.7467
2004M5	0.6797	0.7446
2004M6	0.6938	0.7347
2004M7	0.6534	0.7247
2004M8	0.6766	0.7277
2004M9	0.6571	0.7357
2004M10	0.6474	0.7299
2004M11	0.6553	0.7607
2004M12	0.6410	0.7419
2005M1	0.6428	0.7423
2005M2	0.6277	0.7474
2005M3	0.6283	0.7464
2005M4	0.5976	0.7375
2005M5	0.5734	0.7099
2005M6	0.5708	0.7039
2005M7	0.5681	0.7006
2005M8	0.5649	0.7115
2005M9	0.5456	0.7136
2005M10	0.5890	0.7267
2005M11	0.5824	0.7228
2005M12	0.5930	0.7374
2006M1	0.6185	0.7591
2006M2	0.6135	0.7349
2006M3	0.6108	0.7391
2006M4	0.6672	0.7633
2006M5	0.7075	0.7871
2006M6	0.7570	0.7871

Figure 3c. Length of Forecast Intervals for Benchmark Taylor Rule and Random Walk Models (Japanese Yen), 12-month-ahead forecast

Data for Figure 3c immediately follows

Data for Figure 3c

Date	Taylor Rule	RW
1990M11	1.0000	1.6165
1990M12	0.9901	1.6184
1991M1	1.1805	1.6329
1991M2	1.2577	1.6409
1991M3	1.4300	1.7498
1991M4	1.4912	1.8168
1991M5	1.4311	1.7661
1991M6	1.3602	1.7622
1991M7	1.1490	1.7088
1991M8	1.0786	1.6907
1991M9	0.9631	1.5872
1991M10	0.9354	1.4858
1991M11	1.0058	1.4815
1991M12	1.0488	1.5351
1992M1	0.8936	1.5329
1992M2	1.0013	1.4967
1992M3	0.9108	1.5752
1992M4	0.8965	1.5720
1992M5	0.8858	1.5847
1992M6	0.8041	1.6023
1992M7	0.7701	1.5802
1992M8	0.8993	1.5687
1992M9	0.9008	1.5398
1992M10	1.0123	1.4992
1992M11	1.0034	1.4863
1992M12	1.0202	1.4679
1993M1	0.9500	1.4384
1993M2	0.8499	1.4641
1993M3	0.9587	1.5233
1993M4	0.9606	1.5311
1993M5	1.0074	1.4992
1993M6	1.0563	1.4542
1993M7	1.0868	1.4432
1993M8	1.0865	1.4473
1993M9	1.0314	1.4056
1993M10	1.0272	1.3893
1993M11	1.0561	1.4203
1993M12	1.0505	1.4221
1994M1	1.0048	1.4330
1994M2	0.9223	1.3845
1994M3	0.9084	1.3416
1994M4	0.6862	1.2889
1994M5	0.5370	1.2651
1994M6	0.5297	1.2315
1994M7	0.5353	1.2347
1994M8	0.5219	1.1898
1994M9	0.5319	1.2104
1994M10	0.7222	1.2270
1994M11	0.7433	1.2368
1994M12	0.7589	1.2602
1995M1	0.9129	1.2777
1995M2	0.7351	1.2188
1995M3	0.7096	1.2050
1995M4	0.6967	1.1806
1995M5	0.7094	1.1607
1995M6	0.7212	1.1267
1995M7	0.6559	1.0818
1995M8	0.6451	1.0982
1995M9	0.5786	1.0853
1995M10	0.5788	1.0807
1995M11	0.5567	1.0773
1995M12	0.7131	1.1009
1996M1	0.6654	1.0964
1996M2	0.5964	1.0795
1996M3	0.2780	0.9947
1996M4	0.5406	0.9196
1996M5	0.5687	0.9352
1996M6	0.5834	0.9129
1996M7	0.3546	0.9374
1996M8	0.3770	1.0036
1996M9	0.7629	1.0609
1996M10	0.8200	1.0438
1996M11	0.8723	1.0489
1996M12	0.8593	1.0453
1997M1	0.9256	1.0854
1997M2	0.9018	1.0858
1997M3	0.8647	1.0900
1997M4	0.8324	1.1097
1997M5	0.8588	1.1219
1997M6	0.8560	1.1687
1997M7	0.8477	1.1777
1997M8	0.8487	1.1635
1997M9	0.8076	1.1857
1997M10	0.8792	1.2125
1997M11	0.8852	1.2113
1997M12	0.8906	1.2294
1998M1	0.9182	1.2718
1998M2	0.8876	1.3263
1998M3	0.8812	1.3242
1998M4	0.8928	1.3718
1998M5	0.9179	1.3014
1998M6	0.8911	1.2479
1998M7	0.8975	1.2598
1998M8	0.9038	1.2877
1998M9	0.8904	1.3200
1998M10	0.8606	1.3219
1998M11	0.8238	1.3689
1998M12	0.5344	1.4166
1999M1	0.8450	1.4146
1999M2	0.8870	1.3742
1999M3	0.8328	1.4094
1999M4	0.7842	1.4386
1999M5	0.8177	1.4729
1999M6	0.8436	1.5323
1999M7	0.8426	1.5373
1999M8	1.0542	1.5856
1999M9	0.8648	1.4738
1999M10	1.0621	1.3266
1999M11	0.8915	1.3183
1999M12	1.0623	1.2831
2000M1	1.0571	1.2417
2000M2	0.8477	1.2786
2000M3	0.8451	1.3094
2000M4	0.7853	1.3127
2000M5	0.7934	1.3370
2000M6	0.7821	1.3231
2000M7	0.7695	1.3078
2000M8	1.0103	1.2409
2000M9	0.9286	1.1713
2000M10	0.7329	1.1614
2000M11	0.7274	1.1469
2000M12	0.7153	1.1242
2001M1	0.7200	1.1540
2001M2	0.7169	1.1988
2001M3	0.7141	1.1651
2001M4	0.8048	1.1576
2001M5	0.7220	1.1871
2001M6	0.8976	1.1632
2001M7	0.8323	1.1860
2001M8	0.9516	1.1845
2001M9	0.7138	1.1709
2001M10	0.9214	1.1884
2001M11	0.9373	1.1946
2001M12	0.7969	1.2298
2002M1	0.6933	1.2786
2002M2	0.7306	1.2739
2002M3	0.6188	1.3317
2002M4	0.5480	1.3564
2002M5	0.5472	1.3345
2002M6	0.4140	1.3409
2002M7	0.3622	1.3644
2002M8	0.5346	1.3301
2002M9	0.5997	1.2998
2002M10	0.5211	1.1940
2002M11	0.3607	1.1789
2002M12	0.3331	1.2012
2003M1	0.3321	1.2379
2003M2	0.2874	1.2363
2003M3	0.8179	1.2090
2003M4	0.8381	1.1750
2003M5	0.8352	1.1125
2003M6	0.8484	1.0725
2003M7	0.8988	1.0203
2003M8	0.8980	1.0220
2003M9	0.8598	1.0378
2003M10	0.8190	1.0621
2003M11	0.8338	1.0423
2003M12	0.8399	1.0267
2004M1	0.8928	1.0008
2004M2	0.8935	1.0053
2004M3	0.8876	0.9998
2004M4	0.8756	1.0100
2004M5	0.9065	0.9886
2004M6	0.8899	0.9968
2004M7	0.8219	0.9763
2004M8	0.7525	0.9691
2004M9	0.7721	0.9371
2004M10	0.7795	0.8888
2004M11	0.7437	0.8780
2004M12	0.7726	0.8664
2005M1	0.7245	0.8546
2005M2	0.7996	0.8581
2005M3	0.7141	0.8726
2005M4	0.6893	0.8658
2005M5	0.5255	0.9023
2005M6	0.5579	0.8800
2005M7	0.5332	0.8804
2005M8	0.5097	0.8865
2005M9	0.5091	0.8853
2005M10	0.5945	0.8747
2005M11	0.6787	0.8420
2005M12	0.7025	0.8348
2006M1	0.6718	0.8310
2006M2	0.6096	0.8439
2006M3	0.5378	0.8463
2006M4	0.4247	0.8620
2006M5	0.4614	0.8573
2006M6	0.3945	0.8746

References

Berkowitz, J. and G. Lorenzo (2001) "Long-Horizon Exchange Rate Predictability?" The Review of Economics and Statistics 83(1), 81-91.

Boero, G. and E. Marrocu (2004) "The performance of SETAR models: a regime conditional evaluation of point, interval and density forecasts," International Journal of Forecasting 20(2), 305-320.

Chen, Y. and K. P. Tsang (2009) “What Does the Yield Curve Tell Us About Exchange Rate Predictability?” Manuscript, University of Washington, and Virginia Tech.

Cheung, Y., M. D. Chinn, and A. Pascual (2005) "Empirical Exchange Rate Models of the Nineties: Are Any Fit to Survive?" Journal of International Money and Finance 24, 1150-1175.

Chinn, M. D. (forthcoming) “Nonlinearities, Business Cycles and Exchange Rates,” Economics Notes.

Chinn, M. D. and R. A. Meese (1995) "Banking on Currency Forecasts: How Predictable Is Change in Money?" Journal of International Economics 38, 161-178.

Christoffersen, P. F. (1998) "Evaluating Interval Forecasts," International Economic Review 39(4), 841-862.

Christoffersen, P. F. and S. Mazzotta (2005) “The Accuracy of Density Forecasts from Foreign
Exchange Options,” Journal of Financial Econometrics 3(4), 578-605.

Clarida, R., Gali, J. and M. Gertler (1998) "Monetary Rules in Practice: Some International Evidence," European Economic Review 42, 1033-1067.

Clarida, R.H., L. Sarno, M. P. Taylor, and G. Valente (2003) "The Out-of-Sample Success of Term Structure Models as Exchange Rate Predictors: A Step Beyond," Journal of International Economics 60, 61-83.

Clark, T. and K. D. West (2006) "Using Out-of-Sample Mean Squared Prediction Errors to Test the Martingale Difference Hypothesis," Journal of Econometrics 135 (1-2), 155-186.

Clark, T. and K. D. West (2007) "Approximately Normal Tests for Equal Predictive Accuracy in Nested Models," Journal of Econometrics 138(1), 291-311.

Corradi, V. and N. Swanson (2006a) "Predictive Density and Conditional Confidence Interval Accuracy Tests," Journal of Econometrics 135, 187-228.

Corradi, V. and N. Swanson (2006b) "Predictive Density Evaluation," In Grangerm C.W.J., Elliott, G., Timmerman, A. (Eds.), Handbook of Economic Forecasting, Elsevier, Amsterdam.

Diebold, F. X., Gunther, T. A. and A. S. Tay (1998) "Evaluating Density Forecasts with Applications to Financial Risk Management," International Economic Review 39(4), 863-883.

Diebold, F. X., Hahn, J. and A .S. Tay (1999) "Multivariate Density Forecast Evaluation and Calibration in Financial Risk Management: High-Frequency Returns of Foreign Exchange," Review of Economics and Statistics 81, 661-673.

Diebold, F. X. and R. S. Mariano (1995) "Comparing Predictive Accuracy," Journal of Business and Economic Statistics 13, 253-263.

Engel, C., N. Mark, and K. West (2007) "Exchange Rate Models are Not as Bad as You Think," in NBER Macroeconomics Annual.

Engel, C. and K. West (2005) "Exchange Rates and Fundamentals," Journal of Political Economy 113, 485-517.

Engel, C. and K. D. West (2006) "Taylor Rules and the Deutschmark-Dollar Real Exchange Rate," Journal of Money, Credit and Banking 38(5), 1175-1194.

Engel, C., J. Wang, and J. J. Wu (2008) "Can Long-horizon Data Beat the Random Walk under the Engel-West Explanation?" Working Paper, University of Wisconsin-Madison, the Federal Reserve Bank of Dallas, and the Federal Reserve Board.

Faust, J., J. Rogers, and J. Wright, (2003) "Exchange Rate Forecasting: The Errors We've Really Made," Journal of International Economics 60, 35-59.

Giacomini, R. and H. White (2006) "Tests of Conditional Predictive Ability," Econometrica 74, 1545-1578.

Groen, J. J. (2000) "The Monetary Exchange Rate Model as a Long-Run Phenomenon," Journal of International Economics 52, 299-319.

Hall, P., R.C.L. Wolff, and Q. Yao (1999) "Methods for Estimating a Conditional Distribution Function," Journal of American Statistical Association 94, 154-163.

Hong, Y., H. Li, and F. Zhao (2007) "Can the Random Walk be Beaten in Out-of-Sample Density Forecasts: Evidence from Intraday Foreign Exchange Rates," Journal of Econometrics 141, 736-776.

J.P. Morgan (1996) RiskMetrics Technical Document.

Kilian, L. (1999) "Exchange Rates And Monetary Fundamentals: What Do We Learn From Long-Horizon Regressions?" Journal of Applied Econometrics 14, 491-510.

Kilian, L. and M. Taylor (2003) "Why Is It So Difficult to Beat the Random Walk Forecast of Exchange Rate?" Journal of International Economics 60, 85-107.

MacDonald, R. and M. P. Taylor (1994) "The Monetary Model of the Exchange Rate: Long-Run Relationships, Short-Run Dynamics, and How to Beat a Random Walk," Journal of International Money and Finance 13, 276-290.

Mark, N. C. (1995) "Exchange Rates and Fundamentals: Evidence on Long-Horizon Predictability,'' American Economic Review 85, 201-218.

Mark, N. C. (2007) "Changing Monetary Policy Rules, Learning, and Real Exchange Rate Dynamics," Manuscript, University of Notre Dame.

Mark, N. and D. Sul (2001) "Nominal Exchange Rates and Monetary Fundamentals Evidence from a Small Post-Bretton Woods Panel," Journal of International Economics 53, 29-52.

Meese, R. A. and K. Rogoff (1983) "Empirical Exchange Rate Models of the Seventies: Do they Fit Out-of-Sample?'' Journal of International Economics 14, 3-24.

Molodtsova, T. and D. H. Papell (2009) "Out-of-Sample Exchange Rate Predictability with Taylor Rule Fundamentals," Journal of International Economics, 77(2), 167-180.

Molodtsova, T., A. Nikolsko-Rzhevskyy, and D. H. Papell (2008a), "Taylor Rules with Real-Time Data: A Tale of Two Countries and One Exchange Rate," Journal of Monetary Economics 55, S63-S79.

Molodtsova, T., A. Nikolsko-Rzhevskyy, and D. H. Papell (2008b), “Taylor Rules and the
Euro,” Manuscript Emory University, University of Memphis, and University of Houston.

Nason, J. and J. Rogers (2008) "Exchange Rates and Fundamentals: A Generalization," International Finance Discussion Papers, Number 948, Board of Governors of the Federal Reserve System.

Newey, W. K. and K. D. West (1987) "A Simple, Positive Semi-definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix" Econometrica 55, 703-708.

Rogoff, K. S. and V. Stavrakeva (2008) “The Continuing Puzzle of Short Horizon Exchange Rate
Forecasting,” NBER Working Paper No. 14071.

Rossi, B. (2005) "Testing Long-horizon Predictive Ability with High Persistence, and the Meese-Rogoff Puzzle," International Economic Review 46(1), 61-92.

Sarno, L. and G. Valente (2005) "Empirical Exchange Rate Models and Currency Risk: Some Evidence from Density Forecasts," Journal of International, Money and Finance 24(2), 363-385.

Sarno, L. and G. Valente (forthcoming) “Exchange Rates and Fundamentals: Footloose or Evolving
Relationship?” Journal of the European Economic Association.

West, K. D. (1996) "Asymptotic Inference About Predictive Ability," Econometrica 64, 1067-1084.

Wu, J. J. (2007) "Robust Semiparametric Forecast Intervals," Manuscript, the Federal Reserve Board.

APPENDIX

A.1 Monetary and Taylor Rule Models

In this section, we describe the monetary and Taylor rule models used in the paper.

A.1.1 Monetary Model

Assume the money market clearing condition in the home country is:

$\displaystyle m_t=p_t+\gamma y_t-\alpha i_t+v_t,$

where is the log of money supply, is the log of aggregate price, is the nominal interest rate, is the log of output, and is the money demand shock. A symmetric condition holds in the foreign country and we use an asterisk in superscript to denote variables in the foreign country. Subtracting the foreign money market clearing condition from the home, we have:

$\displaystyle i_t-i_t^\ast=\frac{1}{\alpha}\left[-(m_t-m_t^\ast)+(p_t-p_t^\ast)+\gamma(y_t-y_t^\ast)+(v_t-v_t^\ast)\right].$

(A.1.1)

The nominal exchange rate is equal to its purchasing power value plus the real exchange rate:

$\displaystyle s_t=p_t-p_t^\ast+q_t.$

(A.1.2)

The uncovered interest rate parity in financial market takes the form:

$\displaystyle E_ts_{t+1}-s_t=i_t-i_t^\ast+\rho_t,$

(A.1.3)

where $\rho_t$ is the uncovered interest rate parity shock. Substituting equations (A.1.1) and (A.1.2) into (A.1.3), we have

$\displaystyle s_t=(1-b)\left[m_t-m_t^\ast-\gamma(y_t-y_t^\ast)+q_t-(v_t-v_t^\ast)\right]-b\rho_t+bE_ts_{t+1},$

(A.1.4)

where $b=\alpha/(1+\alpha)$ . Solving recursively and applying the "no-bubbles" condition, we have:

$\displaystyle s_t=E_t\left\{(1-b)\sum_{j=0}^\infty b^j\left[m_{t+j}-m_{t+1}^\ast-\gamma(y_{t+j}-y_{t+1}^\ast)+q_{t+1}-(v_{t+j}-v_{t+j}^\ast)\right]-b\sum_{j=1}^\infty b^{j}\rho_{t+j}\right\}.$

(A.1.5)

In the standard monetary model, such as Mark (1995), purchasing power parity () and uncovered interest rate parity hold ( $\rho_t=0$ ). Furthermore, it is assumed that the money demand shock is zero ( $v_t=v_t^\ast=0$ ) and $\gamma=1$ . Equation (A.1.5) reduces to:

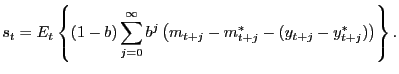$\displaystyle s_{t}=E_{t}\left\{(1-b)\sum_{j=0}^{\infty}b^{j}\left(m_{t+j}-m^{*}_{t+j}-(y_{t+j}-y^{*}_{t+j})\right)\right\}.$

A.1.2 Taylor Rule Model

We follow Engel and West (2005) to assume that both countries follow the Taylor rule and the foreign country targets the exchange rate in its Taylor rule. The interest rate differential is:

$\displaystyle i_t-i_t^\ast=\delta_s(s_t-\bar{s}_t^\ast)+\delta_y(y_t^{gap}-y_t^{gap\ast })+\delta_\pi(\pi_t-\pi_t^{\ast})+v_t-v_t^\ast,$

(A.1.6)

where $\bar{s}_t^\ast$ is the targeted exchange rate. Assume that monetary authorities target the PPP level of the exchange rate: $\bar{s}_t^\ast=p_t-p_t^\ast$ . Substituting this condition and the interest rate differential into the UIP condition, we have:

$\displaystyle s_t=(1-b)(p_t-p_t^\ast)-b\left[\delta_y(y_t^{gap}-y_t^{gap\ast })+\delta_\pi(\pi_t-\pi_t^{\ast})+v_t-v_t^\ast\right]-b\rho_t+bE_ts_{t+1},$

(A.1.7)

where $b=\frac{1}{1+\delta_s}$ . Assuming that uncovered interest rate parity holds ( $\rho_t=0$ ) and monetary shocks are zero, equation (A.1.7) reduces to the benchmark Taylor rule model in our paper:

$\displaystyle s_{t}=E_{t}\left\{(1-b)\sum_{j=0}^{\infty}b^{j}(p_{t+j}-p^{*}_{t+j})-b\sum_{j=0}^{\infty}b^{j}(\delta_{y}(y^{gap}_{t+j}-y_{t+j}^{gap*})+\delta_{\pi}(\pi_{t+j}-\pi^{*}_{t+j}))\right\}.$

A.2 Long-horizon Regressions

In this section, we derive long-horizon regressions for the monetary model and the benchmark Taylor rule model.

A.2.1 Monetary Model

In the monetary model:

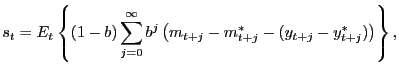$\displaystyle s_{t}=E_{t}\left\{(1-b)\sum_{j=0}^{\infty}b^{j}\left(m_{t+j}-m^{*}_{t+j}-(y_{t+j}-y^{*}_{t+j})\right)\right\},$

where $m_{t}$ and $y_{t}$ are logarithms of domestic money stock and output, respectively. The superscript denotes the foreign country. Money supplies ( and ) and total outputs ( and ) are usually I(1) variables. The general form considered in Engel, Wang, and Wu(2008) is:

$\displaystyle s_{t}$	$\displaystyle =$	$\displaystyle (1-b)\sum_{j=0}^{\infty}b^{j}E_{t}\alpha^{'}\mathbf{D}_{t}$
$\displaystyle (I_{n}-\Phi(L))\Delta\mathbf{D}_{t}$	$\displaystyle =$	$\displaystyle \varepsilon_{t}$	(A.2.1)
$\displaystyle E(\varepsilon_{t+j}\vert\varepsilon_{t},\varepsilon_{t-1},...)$	$\displaystyle \equiv$	$\displaystyle E_{t}(\varepsilon_{t+j})=0, \forall j\ge 1,$

where is the dimension of $\mathbf{D}_{t}$ and is an $n\times n$ identity matrix. is the lag operator and $\Phi(L)=\phi_{1}L+\phi_{2}L^{2}+...+\phi_{p}L^{p}$ . Assume $\Phi(1)$ is non-diagonal and the covariance matrix of $\varepsilon_t$ is given by $\Omega=E_t[\varepsilon_t\varepsilon_t']$ . We assume that the change of fundamentals follows a VAR(p) process in our setup. From proposition 1 of Engel, Wang, Wu (2008), we know that for a fixed discount factor and $p\ge 2$ ,

$\displaystyle s_{t+h}-s_{t}=\beta_{h}z_{t}+\delta^{'}_{0,h}\Delta\mathbf{D}_{t}+...+\delta^{'}_{p-2,h}\Delta\mathbf{D}_{t-p+2}+\zeta_{t+h}$

is a correctly specified regression where the regressors and errors do not correlate. In the case of , the long-horizon regressions reduces to

$\displaystyle s_{t+h}-s_{t}=\beta_{h}z_{t}+\zeta_{t+h}.$

Following the literature, for instance Mark (1995), we do not include $\Delta\mathbf{D}_{t}$ and its lags in our long-horizon regressions. The monetary model can be written in the form of (A.2.1) by setting $\mathbf{D}_{t}=[m_{t}\quad m^{*}_{t}\quad y_{t}\quad y^{*}_{t}]'$ , $\alpha=[1\quad -1\quad -1\quad 1]'$ . By definition, $z_{t}=s_{t}-(m_{t}-m^{*}_{t})+(y_{t}-y^{*}_{t})$ . This corresponds to $\beta_{m,h}=1$ , $\mathbf{X}_{m,t} =s_{t}-(m_{t}-m^{*}_{t})+(y_{t}-y^{*}_{t})$ in equation (1) of section 3.

A.2.2 Taylor Rule Model

In the Taylor rule model

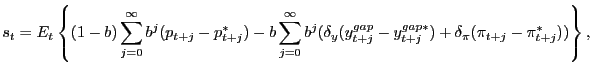$\displaystyle s_{t}=E_{t}\left\{(1-b)\sum_{j=0}^{\infty}b^{j}(p_{t+j}-p^{*}_{t+j})-b\sum_{j=0}^{\infty}b^{j}(\delta_{y}(y^{gap}_{t+j}-y_{t+j}^{gap*})+\delta_{\pi}(\pi_{t+j}-\pi^{*}_{t+j}))\right\},$

where $p_{t}$ , $y^{gap}_{t}$ and $\pi_{t}$ are domestic aggregate price, output gap and inflation rate, respectively. $\delta_{y}$ and $\delta_{\pi}$ are coefficients of the Taylor rule model. The aggregate prices and $p_t^\ast$ are usually I(1) variables. Inflation and output gap are more likely to be I(0). Engel, Wang, and Wu (2008) consider a setup which includes both stationary and non-stationary variables:

$\displaystyle s_t=(1-b)\sum_{j=0}^\infty b^jE_t\left[f_{1t+j}\right]$	$\displaystyle +b\sum_{j=0}^\infty b^jE_t\left[f_{2t+j}+u_{2t+j}\right]$
$\displaystyle f_{1t}$	$\displaystyle =\alpha_1'\mathbf{D_t}\sim I(1)$
$\displaystyle f_{2t}$	$\displaystyle =\alpha_2'\mathbf{\Delta D_t}\sim I(0)$
$\displaystyle u_{2t}$	$\displaystyle =\alpha_3'\mathbf{\Delta D_t}\sim I(0)$
$\displaystyle (I_{n}$	$\displaystyle -\Phi(L))\Delta\mathbf{X}_{t}=\varepsilon_{t},$	(A.2.2)

where $f_{1t}$ and $f_{2t}$ ( $u_{2t}$ ) are observable (unobservable) fundamentals. $\Delta\mathbf{D}_{t}$ is the first difference of $\mathbf{D}_{t}$ , which contains I(1) economic variables.²⁴From proposition 2 of Engel, Wang, and Wu (2008), we know that for a fixed discount factor and $h\ge 2$ ,

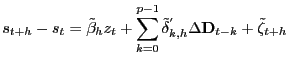$\displaystyle s_{t+h}-s_{t}=\tilde{\beta}_{h}z_{t}+\sum_{k=0}^{p-1}\tilde{\delta}^{'}_{k,h}\Delta\mathbf{D}_{t-k}+\tilde{\zeta}_{t+h}$

(A.2.3)

is a correctly specified regression, where the regressors and errors do not correlate. In the case of , the long-horizon regressions reduces to:

$\displaystyle s_{t+h}-s_{t}=\tilde{\beta}_{h}z_{t}+\tilde{\zeta}_{t+h}.$

The Taylor rule model can be written into the form of (A.2.2) by setting

$\displaystyle \mathbf{D}_{t}=\left[p_{t}\quad p^{*}_{t}\quad \sum_{s=-\infty}^t y^{gap}_{s}\quad \sum_{s=-\infty}^ty^{gap*}_s,\sum_{s=-\infty}^t\pi_{s}\quad \sum_{s=-\infty}^t\pi^{*}_{s}\right]'.$

By definition, $z_{t}=s_t-p_{t}+p^{*}_{t}+\frac{b}{1-b}(\delta_{y}(y^{gap}_{t}-y^{gap*}_{t})+\delta_{\pi}(\pi_{t}-\pi^{*}_{t}))$ . This corresponds to $\beta_{m,h}=[1\quad \frac{b}{1-b}\delta_y\quad \frac{b}{1-b}\delta_\pi]$ and $\mathbf{X}_{m,t}=[q_t\quad y_t^{gap}-y_t^{gap*}\quad \pi_t-\pi_t^*]$ , where $q_t=s_t-p_{t}+p^{*}_{t}$ is the real exchange rate. $\beta_{m,h}$ and $\mathbf{X}_{m,t}$ can be defined differently. For instance, $\beta_{m,h}=1$ and $\mathbf{X}_{m,t}=s_t-p_{t}+p^{*}_{t}+\frac{b}{1-b}(\delta_{y}(y^{gap}_{t}-y^{gap*}_{t})+\delta_{\pi}(\pi_{t}-\pi^{*}_{t}))$ . Our results do not change qualitatively under this alternative setup.

A.3 Model with Heterogeneous Taylor Rules

In the benchmark model, we assume that the Taylor rule coefficients are the same in the home and foreign countries. In this appendix, we relax the assumption of homogeneous Taylor rules in the benchmark model. It is straightforward to show in this case that the benchmark model changes to:

$\displaystyle s_{t+h}-s_t=\alpha_h+\beta_hz_t+\varepsilon_{t+h},$

(A.3.1)

where the deviation of the exchange rate from its equilibrium level is defined as:

$\displaystyle z_t=s_t-p_t+p_t^\ast+\frac{b}{1-b}\left[\delta_yy_t^{gap}-\delta_y^\ast y_t^{gap\ast}+\delta_\pi\pi_t-\delta_\pi^\ast\pi_t^\ast\right].$

(A.3.2)

According to equation (8), the matrix $\mathbf{X}_{1,t}$ in equation (1) includes economic variables $q_t\equiv s_t+p_t^\ast-p_t$ , $\delta_yy_t^{gap}-\delta_y^\ast y_t^{gap\ast}$ , and $\delta_\pi\pi_t-\delta_\pi^\ast\pi_t^\ast$ .²⁵We first estimate the Taylor rules in the home and foreign countries according to equations (2) and (3). Then $q_t\equiv s_t+p_t^\ast-p_t$ , $\hat{\delta}_yy_t^{gap}-\hat{\delta}_y^\ast y_t^{gap\ast}$ , and $\hat{\delta}_\pi\pi_t-\hat{\delta}_\pi^\ast\pi_t^\ast$ are used in the long-horizon regressions and interval forecasts. The results are very similar to the benchmark model and reported in Table 7.

Footnotes

1. We thank Menzie Chinn, Charles Engel, Bruce Hansen, Jesper Linde, Enrique Martinez-Garcia, Tanya Moldtsova, David Papell, Mark Wynne, and Ken West for invaluable discussions. We would also like to thank seminar participants at the Dallas Fed and the University of Houston for helpful comments. All views are those of the authors and do not necessarily reflect the views of the Federal Reserve Bank of Dallas, the Board of Governors or the Federal Reserve System. All GAUSS programs are available upon request. Return to text

2. Email: [email protected] Address: Research Department, Federal Reserve Bank of Dallas, 2200 N. Pearl Street, Dallas, TX 75201 Phone: (214) 922-6471. Return to text

3. Email: [email protected] Address: Board of Governors of the Federal Reserve System, 20th and C Streets, Washington, D.C. 20551 Phone: (202) 452-2556. Return to text

4. Chinn and Meese (1995) and MacDonald and Taylor (1994) find similar results. However, the long-horizon exchange rate predictability in Mark (1995) has been challenged by Kilian (1999) and Berkowitz and Giorgianni (2001) in subsequent studies. Return to text

5. For brevity, we omit RS and simply say forecast intervals when we believe that it causes no confusion. Return to text

6. The coefficients on lagged interest rates in the home and foreign countries can take different values in Molodtsova and Papell (2009). Return to text

7. We also tried the random walk with a drift. It does not change our results. Return to text

8. Clarida, Gali, and Gertler (1998) find empirical support for forward-looking Taylor rules. Forward-looking Taylor rules are ruled out because they require forecasts of predictors, which creates additional complications in out-of-sample forecasting. Return to text

9. See appendix for more detail. While the long-horizon regression format of the benchmark Taylor model is derived directly from the underlying Taylor rule model, this is not the case for the models with interest rate smoothing (models 3 and 4). Molodtsova and Papell (2009) only consider the short-horizon regression for the Taylor rule models. We include long-horizon regressions of these models only for the purpose of comparison. Return to text

10. We also tried the case of $\mathbf{X}_{1,t}=z_{t}$ . Our results do not change qualitatively. Return to text

11. We thank the authors for the data, which we downloaded from David Papell's website. For the exact line numbers and sources of the data, see the data appendix of Molodtsova and Papell (2009). Return to text

12. We choose using the method of Hall, Wolff, and Yao (1999). Return to text

13. It is consistent in the sense of convergence in probability as the estimation sample size goes to infinity. Return to text

14. While RS intervals remedy mis-specifications asymptotically, it does not guarantee such corrections in a given finite sample. Return to text

15. We use Newey and West (1987) for our empirical work, with a window width of 12. Return to text

16. Center here means the half way point between the upper and lower bound for a given interval. Return to text

17. These nine exchange rates are the Danish Kroner, the French Franc, the Deutschmark, the Japanese Yen, the Dutch Guilder, the Portuguese Escudo, the Swiss Franc, and the British pound. Similar results hold at other horizons. Return to text

18. When comparing the intervals for $S_{\tau+h} - S_{\tau}$ , the random walk model builds the forecast interval around 0, while economic model builds it around $\widehat{\beta} ^{^{\prime}}_{m,h}\mathbf{X}_{m,\tau}$ . Return to text

19. Results are available upon request. Return to text

20. The only exception is Portugal, where only 192 data points were available. In this case, we choose R = 120. Return to text

21. See Appendix A.3 for details. Return to text

22. See Wu (2009) for more discussion. Return to text

23. Figures in other countries show similar patterns. Results are available upon request. Return to text

24. To incorporate I(0) economic variables, $\mathbf{D}_{t}$ contains the levels of I(1) variables and the summation of I(0) variables from negative infinity to time . Return to text

25. Another option to incorporate heterogenous Taylor rules is to include , $y_t^{gap}$ , $y_t^{gap\ast}$ , $\pi_t$ , and $\pi_t^\ast$ in $\mathbf{X}_{1,t}$ . For instance, see Moldtsova and Papell (2009). However, increasing the number of regressors may cause the "curse of dimensionality" problem for our semiparametric method. To be comparable to our benchmark model, we define $\mathbf{X}_{1,t}$ here such that the number of regressors is the same as in the benchmark model. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

The Taylor Rule and Interval Forecast For Exchange Rates1

1. Introduction

2. Models and Data

2.1 Benchmark Taylor Rule Model

2.2 Data

3. Econometric Method

3.1 Test of Equal Empirical Coverages

3.2 Test of Equal Empirical Lengths

3.3 Discussion

4. Results

4.1 Results of Benchmark Model

4.2 Results of Alternative Models

4.3 Discussion

5. Conclusion

References

APPENDIX

A.1 Monetary and Taylor Rule Models

A.1.1 Monetary Model

A.1.2 Taylor Rule Model

A.2 Long-horizon Regressions

A.2.1 Monetary Model

A.2.2 Taylor Rule Model

A.3 Model with Heterogeneous Taylor Rules

Footnotes

The Taylor Rule and Interval Forecast For Exchange Rates¹