
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 968, March 2009 --- Screen Reader
Version*
Markup Variation and Endogenous Fluctuations
in the Price of Investment Goods1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The two sector model presented in this note suggests a simple structural decomposition of movements in the price of investment goods into exogenous and endogenous sources. The endogenous fluctuations arise in the presence of countercyclical markups which vary differently across the consumption and investment sectors. In turn, the movements in the markups are due to endogenous procyclical net business formation. The model, while being consistent with the countercyclicality of the price of investment goods, suggests that about a quarter of the movement in the price series can be attributed to this endogenous mechanism.
Keywords: Price of investment, business cycle, firm dynamics, markup
JEL classification: E32, L11, L16
1. Introduction
It is well known that the price of investment goods has been trending down over the last century in the US (see for example Greenwood, Hercowitz, and Krusell (2000) and Cummins and Violante (2002)). It has been argued that this decline accounts for a significant fraction of economic growth during that period. For instance, Greenwood and Krusell (2007) conclude that more than half of postwar growth can be attributed to investment-specific technological progress.
Recent work focuses on the cyclical properties of this price series and has emphasized that in the US (i) the price of investment goods is countercyclical, and that (ii) fluctuations in investment-specific technological progress (the inverse of the price of investment goods in many models) contribute significantly to postwar US business cycles. For example, Greenwood, Hercowitz, and Krusell (2000) suggests that this form of technological change is the source of about 30% of output fluctuations. Similarly, Fisher (2006) and Justiniano and Primiceri (2006) argue that investment-specific technological progress is the most important determinant of output variability.
Motivated by this evidence, we investigate cyclical fluctuations in the price of investment goods that can be attributed to endogenous movements. Specifically, this note studies the role of sector specific countercyclical markups in giving rise to endogenous movements in the price of investment goods. Previous work has alluded to the potential role of markup variations in generating movements in the price of investment goods. For example, Ramey (1996) suggests that a decline in markups might have partially caused the relative price of investment to fall over the postwar period. Similarly, Fisher (2006) points out that while "investment-specific technology shocks could play a key role in short-run fluctuations, the short-run correlations might be driven at least partly by factors other than technological change, such as time-varying markups."
The approach taken here is related to a literature following Hall (1986) which suggests that measured Total Factor Productivity (TFP) has important endogenous components.5 As this literature has emphasized, the presence of endogenous components can lead a researcher to overestimate the variance of TFP shocks.6 In the same spirit, we propose a mechanism that gives rise to endogenous movements in the price of investment goods, and then quantify its contribution to the cyclicality of investment good prices.
Specifically, Section 2 presents a two-sector dynamic general equilibrium model that builds upon the framework of Jaimovich and Floetotto (2008).7 There, a positive shock to the level of technology leads to changes in the number of competitors, which in turn give rise to countercyclical variations in markups. By extending this framework to a two-sector setup we can derive a simple analytical characterization of the price of investment goods. We show that this price is positively related to the ratio between the markup in the investment and consumption sector. The households' desire to smooth consumption implies, as it is common in this class of models, that investment is much more volatile than consumption. Hence, the process of firm entry and exit is more volatile in the investment good sector which in turn implies a relatively bigger movement in the markup of the investment than in the consumption sector. Countercyclical movements in the price of investment goods are thus endogenously generated by the model.
Our model suggests that a quarter of the movement in the price of investment goods can be attributed to the endogenous fluctuations as shown in Section 3. Section 4 illustrates that the model can quantitatively account for the countercyclicality of the price of investment goods. In the context of our model, endogenous fluctuations in sectoral markups are necessary to match this feature of the data.
2. Technology and Market Structure
This note proposes a simple model that represents a minimal perturbation of the prototype perfect competition two sector real business cycle (RBC) model. This greatly simplifies comparison with existing work and allows for a simple structural decomposition of the price of investment goods. The model is a two-sector version of the model in Jaimovich and Floetotto (2008). There are two sectors of production: consumption and investment. Within each period, capital and labor can be costlessly reallocated from one sector to the other. The setup of the consumption sector will be presented in some detail and the investment sector is exactly analogous.
The Consumption Sector. The sectoral good is produced with a constant-returns-to-scale production function, which aggregates a measure one continuum of industrial goods
![$\displaystyle C_{t}=\left[ \int_{0}^{1}Q_{t}^{c}(j)^{\omega}dj\right] ^{\frac{1}{\omega} },\ \omega\in(0,1)$](img3.gif) |
where
![]() denotes output of industry
denotes output of industry
![]() . The elasticity of substitution between any
two industrial goods is constant and equals
. The elasticity of substitution between any
two industrial goods is constant and equals
![]() . The consumption good
producers behave competitively. In each of the consumption
industries, there are
. The consumption good
producers behave competitively. In each of the consumption
industries, there are ![]() firms producing
differentiated intermediate goods. A
firms producing
differentiated intermediate goods. A ![]() function
aggregates those to yield the output of industry
function
aggregates those to yield the output of industry ![]()
![$\displaystyle Q_{t}^{c}(j)=\left( N_{t}^{c}\right) ^{1-\frac{1}{\tau}}\left[ \sum _{i=1}^{N_{t}^{c}}x_{t}^{c}(j,i)^{\tau}\right] ^{\frac{1}{\tau}},\ \tau \in(0,1)$](img10.gif)
|
(1) |
where
![]() is the output of firm
is the output of firm ![]() in industry
in industry ![]() .8 The elasticity of
substitution between any two goods within an industry is constant
and equals
.8 The elasticity of
substitution between any two goods within an industry is constant
and equals
![]() . The market structure of
each industry exhibits monopolistic competition; each
differentiated
. The market structure of
each industry exhibits monopolistic competition; each
differentiated
![]() is produced by one firm that
sets the price for its good to maximize profits. Finally, it is
assumed that the elasticity of substitution between any two goods
within an industry is higher than the elasticity of substitution
across industries,
is produced by one firm that
sets the price for its good to maximize profits. Finally, it is
assumed that the elasticity of substitution between any two goods
within an industry is higher than the elasticity of substitution
across industries,
![]() . Each
intermediate good,
. Each
intermediate good,
![]() , is produced using capital,
, is produced using capital,
![]() and labor,
and labor,
![]() given a level of technology
given a level of technology
![]()
| (2) |
where the parameter
![]() represents an overhead
cost. In each period, an amount
represents an overhead
cost. In each period, an amount ![]() of the
intermediate good is immediately used up, independent of how much
output is produced. As in Rotemberg and Woodford (1996) the role of this parameter
is to allow the model to reproduce the apparent absence of pure
profits despite the presence of market power. Entry into the
existing industries is costless for intermediate producers, and
hence a zero-profit condition is satisfied in each period and every
industry.
of the
intermediate good is immediately used up, independent of how much
output is produced. As in Rotemberg and Woodford (1996) the role of this parameter
is to allow the model to reproduce the apparent absence of pure
profits despite the presence of market power. Entry into the
existing industries is costless for intermediate producers, and
hence a zero-profit condition is satisfied in each period and every
industry.
We assume that the log technology shocks follow a stationary first order auto-regressive process
| (3) |
It is assumed that
![]() and
that
and
that
![]() is a normally distributed
random variable, with a mean of zero and standard deviation
is a normally distributed
random variable, with a mean of zero and standard deviation
![]() .
.
The sectoral good producer solves a static optimization problem
that results in the usual conditional demand for each industrial
good,
![]() , where
, where
![]() is the price index of industry
is the price index of industry
![]() at period
at period ![]() and
and ![]() is the price of the consumption good at period
is the price of the consumption good at period
![]() ,
,
![$\displaystyle =\left[ \frac{p_{t}^{c}(j)}{P_{t}^{c}}\right] ^{\frac {1}{\omega-1}}C_{t}$](img36.gif) |
(4) | |
![$\displaystyle =\left[ \int_{0}^{1}p_{t}^{c}(j)^{\frac{\omega}{\omega-1} }dj\right] ^{\frac{\omega-1}{\omega}}.$](img38.gif)
|
(5) |
Denoting the price of good ![]() in industry
in industry
![]() in period
in period ![]() by
by
![]() , the conditional demand
faced by the producer of each
, the conditional demand
faced by the producer of each
![]() variant is similarly defined
as
variant is similarly defined
as
![$\displaystyle =\left[ \frac{p_{t}^{c}(j,i)}{p_{t}^{c}(j)}\right] ^{\frac{1}{\tau-1}}\frac{Q_{t}^{c}(j)}{N_{t}^{c}}$](img45.gif) |
(6) | |
![$\displaystyle =\left( N_{t}^{c}\right) ^{1-\frac{1}{\tau}}\left[ \sum_{i=1}^{N_{t}^{c}}p_{t}^{c}(j,i)^{\frac{\tau}{\tau-1}}\right] ^{\frac{\tau-1}{\tau}}.$](img47.gif)
|
Using (4) and (6), the
conditional demand for good
![]() at period
at period ![]() can then be expressed in terms of the consumption good as
can then be expressed in terms of the consumption good as
![$\displaystyle x_{t}^{c}(j,i)=\left[ \frac{p_{t}^{c}(j,i)}{p_{t}^{c}(j)}\right] ^{\frac {1}{\tau-1}}\left[ \frac{p_{t}^{c}(j)}{P_{t}^{c}}\right] ^{\frac{1} {\omega-1}}\frac{C_{t}}{N_{t}^{c}}. $](img50.gif) |
The Elasticity of Demand. In the model above, there is a continuum of industries within
each sector, but within each industry the number of operating firms
is finite. While an individual firm's decisions have no effect on
the general price level ![]() , they do affect the
industrial price level
, they do affect the
industrial price level
![]() The resulting price elasticity
of demand is then a function of the number of firms within a
industry,
The resulting price elasticity
of demand is then a function of the number of firms within a
industry, ![]() . In a symmetric equilibrium,
the elasticity becomes
. In a symmetric equilibrium,
the elasticity becomes
![$\displaystyle \eta_{x^{c}(j,i)p^{c}(j,i)}(N_{t}^{c})=\frac{1}{\tau-1}+\left[ \frac {1}{\omega-1}-\frac{1}{\tau-1}\right] \frac{1}{N_{t}^{c}}$](img54.gif)
|
(7) |
implying that an increase in ![]() leads to a
more elastic demand curve. At the solution to the monopolistic
firm's problem, marginal revenue equals marginal cost
leads to a
more elastic demand curve. At the solution to the monopolistic
firm's problem, marginal revenue equals marginal cost
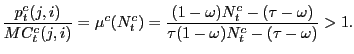
|
(8) |
Note that the markup function is monotonically decreasing in the
number of firms, i.e.
![]() . We assume that
the economy's technology is symmetric with respect to all
intermediate inputs and hence we focus on symmetric equilibria,
. We assume that
the economy's technology is symmetric with respect to all
intermediate inputs and hence we focus on symmetric equilibria,
![]() x
x![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Total capital and
hours in the consumption sector are then given by
. Total capital and
hours in the consumption sector are then given by
![]() and
and
![]() respectively.
Finally, in the symmetric equilibrium, a zero-profit condition is
imposed in every sector in every period implying that variable
profits cover the fixed cost in each period
respectively.
Finally, in the symmetric equilibrium, a zero-profit condition is
imposed in every sector in every period implying that variable
profits cover the fixed cost in each period
| (9) |
The number of firms per industry and aggregate final consumption can then be found by using (2) and the zero-profit condition (9).9
![$\displaystyle =z_{t}^{c}\left( \frac{K_{t}^{c}}{H_{t}^{c}}\right) ^{\alpha }H_{t}^{c}\left[ \frac{\mu_{t}^{c}-1}{\mu_{t}^{c}\phi^{c}}\right]$](img73.gif)
|
(10) | |
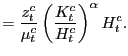
|
(11) |
We use ![]() as the numeraire and set it to
as the numeraire and set it to
![]() . This implies that the price charged by an
intermediate producer in the consumption sector is also
. This implies that the price charged by an
intermediate producer in the consumption sector is also ![]() in a symmetric equilibrium.
in a symmetric equilibrium.
The Investment Sector. The setup in the investment good sector is analogous to the
consumption sector. There is a continuum of industries, each with a
finite number ![]() of intermediate producers. The
investment good, the industrial goods, and the differentiated goods
are thus produced according to
of intermediate producers. The
investment good, the industrial goods, and the differentiated goods
are thus produced according to
![$\displaystyle =\left[ \int_{0}^{1}Q_{t}^{i}(j)^{\omega}dj\right] ^{\frac {1}{\omega}},\ \omega\in(0,1)$](img81.gif) |
|
![$\displaystyle =\left( N_{t}^{i}\right) ^{1-\frac{1}{\tau}}\left[ \sum_{i=1}^{N_{t}^{i}}x_{t}^{i}(j,i)^{\tau}\right] ^{\frac{1}{\tau}} ,\ \tau\in(0,1)$](img83.gif) |
|
The solution to the optimization problem leads to an analogous
expression for the markup charged in the investment sector
![]() . Total capital and hours in the investment sector are given by
. Total capital and hours in the investment sector are given by
![]() and
and
![]() respectively.
The zero-profit condition holds in every sector in every period,
respectively.
The zero-profit condition holds in every sector in every period,
![]() , which as
above allows us to derive the number of firms per sector and
aggregate investment
, which as
above allows us to derive the number of firms per sector and
aggregate investment
![$\displaystyle =z_{t}^{i}\left( \frac{K_{t}^{i}}{H_{t}^{i}}\right) ^{\alpha }H_{t}^{i}\left[ \frac{\mu_{t}^{i}-1}{\mu_{t}^{i}\phi^{i}}\right]$](img91.gif)
|
||
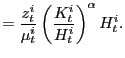 |
(12) |
The Price of Investment. In this economy capital and labor are mobile across sectors and industries. In equilibrium, factor prices have to be equalized in the consumption and investment sector.
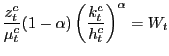 |
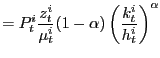 |
(13) |
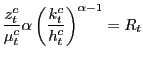 |
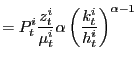 |
(14) |
This allows us to derive a simple expression for the price of
investment by solving (13) or (14) for the price
of investment goods
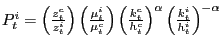 . This, however, can be simplified further by combining (13) and (14) which yields
the well known result that the capital labor ratio is the same in
both industries,
. This, however, can be simplified further by combining (13) and (14) which yields
the well known result that the capital labor ratio is the same in
both industries,
![]() . The
price of investment then becomes
. The
price of investment then becomes
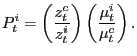
|
(15) |
The first term is standard: when productivity in the investment
sector increases relative to the consumption sector, investment
goods become cheaper in terms of consumption goods. The second
term, however, is a result of the particular sectoral structure
that we have assumed. When the investment sector becomes more
competitive relative to the consumption sector, i.e.
![]() falls, the
price of investment falls. This equation is the basis of our
quantitative exercise in the next section.
falls, the
price of investment falls. This equation is the basis of our
quantitative exercise in the next section.
3. Decomposing the Price of Investment
Using a circumflex to denote log deviations from the steady state, (15) can be expressed as
| (16) |
While the price of investment is observable, all terms on the right
hand side of the equation are latent. However, the model's
equilibrium conditions imply that we can express
![]() and
and
![]() as functions of observable
data. Taking the consumption sector as an example, one can derive
that
as functions of observable
data. Taking the consumption sector as an example, one can derive
that
![]() or
or
![]() .10
Together with the equivalent expression for the investment sector,
.10
Together with the equivalent expression for the investment sector,
![]() , we can restate (16) as
, we can restate (16) as
| (17) |
Our structural decomposition builds on equation (17) as we can express the variance in the price of investment goods as
| Var |
(18) |
Calibrating the scalars A and B. Note that four parameters - ![]()
![]() ,
, ![]() and
and ![]() - are required to assign values to
- are required to assign values to ![]() and
and
![]() . First, there is, to the best of our
knowledge, no clear evidence on the average size of markups in each
of the sectors. Similar to Jaimovich and Floetotto (2008), we calibrate the steady
state value of the value added markup to
. First, there is, to the best of our
knowledge, no clear evidence on the average size of markups in each
of the sectors. Similar to Jaimovich and Floetotto (2008), we calibrate the steady
state value of the value added markup to ![]() in
both sectors. Second, we have to choose values for
in
both sectors. Second, we have to choose values for ![]() and
and ![]() , the parameters that
determine the elasticity of substitution between differentiated
goods in the consumption and investment sector. We calibrate these
parameters as follows. Taking the consumption sector as an example,
use (8) to find
, the parameters that
determine the elasticity of substitution between differentiated
goods in the consumption and investment sector. We calibrate these
parameters as follows. Taking the consumption sector as an example,
use (8) to find
![]() . Log linearization then leads to an expression for the elasticity
of the number of firms with respect to that sector's output,
. Log linearization then leads to an expression for the elasticity
of the number of firms with respect to that sector's output,
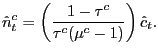
|
(19) |
Using this expression, data on
![]() and
and
![]() as well as our calibration of
as well as our calibration of
![]() , we can estimate
, we can estimate ![]() from the elasticity of the number of firms in the
consumption sector with respect to the sector's output.11
from the elasticity of the number of firms in the
consumption sector with respect to the sector's output.11
This estimation requires time series of the number of operating
firms in the consumption and investment sector. As our measure of
the number of competitors we use the number of establishments in
thirteen non-agricultural major industry groups (referred to as
"supersectors") running over 1992:3 - 2007:2 from the BLS
Business Employment Dynamics database.12 We weight each
industry group by its average share of annual payrolls as
calculated in data from the Small Business Administration
(SBA).13 We then divide the major industry
groups into consumption and investment sectors by modifying the
procedure of Harrison (2003): using BEA Input-Output Use tables, we
determine the share of each major industry group's product going
towards consumption or investment.14 This procedure
provides us with a quarterly time series of establishments in the
consumption and the investment sector, ![]() and
and
![]() ; for more details on the data
construction, please refer to the data appendix A.15
; for more details on the data
construction, please refer to the data appendix A.15
We now estimate the elasticities in (19) and the
analogous expression for the investment sector by regressing
![]() on
on
![]() and
and
![]() on
on
![]() , respectively, as shown in Table 1.16
, respectively, as shown in Table 1.16
Note there is only slight difference between the OLS and IV
estimates and so we use the former. These estimates imply that
![]() and
and
![]() . Maintaining our assumption
that
. Maintaining our assumption
that
![]() , we find that
, we find that
![]() and
and ![]() .
.
Decomposition. The price of investment goods can be decomposed easily using
(18) and the values
found for ![]() and
and ![]() . We find that
about 28% of the variation in the price of investment are due to
the endogenous time-variation in markups. Here, we use a time
series on the price of investment coming from Fisher (2006).17 It
is important to note that none of the results above require
imposing any restrictions on the model's specification of household
behavior. The simple expression for the price of investment goods
can de derived from the assumptions on technology alone.
. We find that
about 28% of the variation in the price of investment are due to
the endogenous time-variation in markups. Here, we use a time
series on the price of investment coming from Fisher (2006).17 It
is important to note that none of the results above require
imposing any restrictions on the model's specification of household
behavior. The simple expression for the price of investment goods
can de derived from the assumptions on technology alone.
4. Calibration and Simulation
In order to simulate the economy we need to close the model by specifying the household side. It is well known that the sectoral comovement of hours worked does not arise in the benchmark two sector model with separable preferences as in King, Plosser, and Rebelo (1988).18 We use the results in Jaimovich and Rebelo (forthcoming) who show that this failure can be remedied by assuming a utility function with a weak short-run wealth effect on the labor supply such as the one proposed in Greenwood, Hercowitz, and Huffman (1988).
At each point in time the economy is inhabited by a continuum of identical households. The mass of households is normalized to one. It is assumed that the representative agent has preferences over random streams of consumption and leisure. The representative agent chooses a sequence of consumption, hours and investments in capital to solve
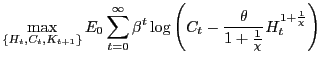
subject to the sequential budget constraint and the law of motion for capital
where the initial capital stock is given and equal to ![]() .
. ![]() and
and ![]() denote
consumption and hours worked by the household in period
denote
consumption and hours worked by the household in period ![]() .
.
![]() and
and
![]() denote the subjective time
discount factor and the depreciation rate of capital,
denote the subjective time
discount factor and the depreciation rate of capital, ![]() is the labor supply elasticity and
is the labor supply elasticity and ![]() . Households own the capital stock and take the
equilibrium rental rate,
. Households own the capital stock and take the
equilibrium rental rate, ![]() , and the equilibrium
wage,
, and the equilibrium
wage, ![]() , as given. Finally, households own the
firms and receive their profits,
, as given. Finally, households own the
firms and receive their profits, ![]() .
.
We adopt a standard calibration of the parameters in the model -
see Table 2.
In order to simulate the model we also need to specify the
parameters governing the stochastic process of ![]() and
and ![]() . We use the model's
equilibrium conditions to identify the technology shocks in the two
sectors. Log-linearizing equations (11) and (12) and employing
the exact same substitutions used to derive (17) leads to
. We use the model's
equilibrium conditions to identify the technology shocks in the two
sectors. Log-linearizing equations (11) and (12) and employing
the exact same substitutions used to derive (17) leads to
| (20) | ||
| (21) |
To construct sector specific hours, ![]() and
and
![]() , we again use the equilibrium
conditions of the model as the price of investment goods equals
, we again use the equilibrium
conditions of the model as the price of investment goods equals
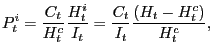
which follows from (11) and (12). Hence, using
data on
![]()
![]()
![]() and
and ![]() we can
construct a series of
we can
construct a series of ![]() and
and ![]() that together with (20) and (21) allow us to
estimate
that together with (20) and (21) allow us to
estimate
![]() and
and
![]() . For
. For
![]() we estimate the AR1
coefficient
we estimate the AR1
coefficient ![]() to equal
to equal ![]() and a standard deviation
and a standard deviation
![]() of
of ![]() . Similarly, for
. Similarly, for
![]() we estimate
we estimate
![]() and
and
![]() .
Finally, we find a correlation
.
Finally, we find a correlation
![]() of
of ![]() .19
.19
Results of Simulation. Panel I in Table 3 reports moments
for the US.20 Our benchmark model (Panel II) produces a price of investment
series that is countercyclical with a similar magnitude to the one
observed in the data. The model underperforms with respect to the
volatility of the series: the ratio of standard deviations of the
price of investment to output is ![]() in the data
while this ratio equals
in the data
while this ratio equals ![]() in the model. With
respect to other variables of interest, the performance of the
model is rather standard. Investment is more volatile than output,
consumption is less volatile than output, and the model
underestimates the volatility of hours worked. Interestingly, the
benchmark model (Panel II) generates a correlation between the
hours in the two sectors and output that resembles the estimates we
obtain in the data.
in the model. With
respect to other variables of interest, the performance of the
model is rather standard. Investment is more volatile than output,
consumption is less volatile than output, and the model
underestimates the volatility of hours worked. Interestingly, the
benchmark model (Panel II) generates a correlation between the
hours in the two sectors and output that resembles the estimates we
obtain in the data.
In order to assess the role of the endogenous markups in generating this negative correlation, Panel III reports the results of the same model with the same technology shocks where the markup is a constant. Hence, the only difference between Panels II and III is along the mechanism emphasized in this note, i.e. the endogeneity of the markup. Note from Panel III that the model generates a price of investment time series that is both (i) less volatile than in the benchmark model and, more importantly, (ii) positively correlated with output. Hence, endogenous movements in the markup are necessary for the model to generate a countercyclical process of the price of investment goods.
5. Conclusion
This note formulates a simple structural two sector model in a general equilibrium framework in which technology shocks induce the entry and exit of competitors. Endogenous variation in the number of operating firms in the two sectors leads to endogenous variation in the degree of competition over the business cycle. This model economy implies that the price of investment goods can be decomposed into an exogenous component as well as an endogenous component that results from the entry and exit of firms. Based on this decomposition, the note suggests that about a quarter of the variation in the price of investment in the US is due to this interaction. Moreover, the model, when simulated, accounts for the countercyclicality of the price of investment goods. We show that, within our model, endogenous fluctuations in the markups are necessary to match this feature of the data.
The model in this note represents a minimal perturbation of the prototype perfect competition two sector real business cycle model. This greatly simplifies comparison with existing work and allows for a simple structural decomposition of the price of investment goods. However, this simplicity is purchased at the cost of descriptive realism such as the assumption of a symmetric model with no heterogeneity in the size of competitors. Moreover, we do not consider various other elements (such as sector specific capacity utilization and labor hoarding) that could generate endogenous movements in the price of investment goods. We leave these extensions for future research.
Table 1. Estimation
| OLS: | OLS: | IV: | IV: | |
|---|---|---|---|---|
| 0.513 (0.158) | 0.535 (0.178) | |||
| 0.278 (0.035) | 0.320 (0.031) | |||
| 0.153 | 0.514 | 0.155 | 0.502 |
Note: OLS and IV
estimates; White standard errors in parentheses. Data for dependent
variables are described in the text; data for ![]() and
and ![]() are log-deviations from HP
filter (smoothing parameter 1600) for consumption series PCECC96
and investment series FPIC96, from FRED database at Federal Reserve
Bank of St. Louis. IV estimation is 2SLS using a lag of the RHS
variable. Constants (not shown) are insignificant. Data run over
1992:3-2007:2.
are log-deviations from HP
filter (smoothing parameter 1600) for consumption series PCECC96
and investment series FPIC96, from FRED database at Federal Reserve
Bank of St. Louis. IV estimation is 2SLS using a lag of the RHS
variable. Constants (not shown) are insignificant. Data run over
1992:3-2007:2.
Table 2. Calibration
| Parameter | Value | |
|---|---|---|
| Markup in steady state | 30% | |
| Elasticity within industry (consumption sector) | 0.87 | |
| Elasticity within industry (investment sector) | 0.92 | |
| Capital share | 0.30 | |
| Time spent working | 0.33 | |
| Time discount factor | 0.99 | |
| Depreciation rate | 0.025 |
Note: The calibration of ![]() ,
, ![]() and
and ![]() is explained in the main text. The
value of
is explained in the main text. The
value of
![]() and
and
![]() do not matter for the results.
The AR(1) parameter on productivity in the two sectors are
estimated to be
do not matter for the results.
The AR(1) parameter on productivity in the two sectors are
estimated to be
![]() and
and
![]() while the shocks have
standard deviations
while the shocks have
standard deviations
![]() ,
,
![]() . The
correlation between the shocks is
. The
correlation between the shocks is
![]() . The remaining parameters are standard.
. The remaining parameters are standard.
Table 3. Data and Model Moments
| I - Data: |
I - Data: |
I - Data: |
II - Benchmark: |
II - Benchmark: |
II - Benchmark: |
III - Constant Markups: |
III - Constant Markups: |
III - Constant Markups: |
|
|---|---|---|---|---|---|---|---|---|---|
| Output (y) | 0.015 | 1 | 1 | 0.018 | 1 | 1 | 0.017 | 1 | 1 |
| Consumption | 0.012 | 0.80 | 0.85 | 0.011 | 0.59 | 0.85 | 0.012 | 0.72 | 0.97 |
| Investment | 0.047 | 3.16 | 0.87 | 0.065 | 3.57 | 0.86 | 0.035 | 2.11 | 0.87 |
| Hours | 0.018 | 1.17 | 0.78 | 0.011 | 0.60 | 1.00 | 0.010 | 0.60 | 1.00 |
| Hours (C Sector) | 0.012 | 0.80 | 0.48 | 0.006 | 0.33 | 0.32 | 0.006 | 0.35 | 0.87 |
| Hours (I Sector) | 0.037 | 2.48 | 0.86 | 0.049 | 2.69 | 0.91 | 0.030 | 1.82 | 0.94 |
| Price of Investment | 0.016 | 1.07 | -0.39 | 0.014 | 0.75 | -0.32 | 0.008 | 0.48 | 0.56 |
| Markups (C Sector) | 0.001 | 0.06 | -0.85 | ||||||
| Markups (I Sector) | 0.012 | 0.65 | -0.86 |
Note: Second moments of data, benchmark model, and model with constant markups. Benchmark model has endogenous markups. Sectoral hours constructed as described in Section 4. See text for details.
References
Basu, S., and J. G. Fernald (2002): "Aggregate productivity and aggregate technology," European Economic Review, 46(6), 963-991.
Baxter, M. (1996): "Are Consumer Durables Important for Business Cycles?," The Review of Economics and Statistics, 78(1), 147-55.
Christiano, L. J., and T. J. Fitzgerald (1998): "The Business Cycle: It's Still a Puzzle,"Economic Perspectives, 22.
Cummins, J. G., and G. L. Violante (2002): "Investment-Specific Technical Change in the US (1947-2000): Measurement and Macroeconomic Consequences," Review of Economic Dynamics, 5(2), 243-284.
Evans, C. L. (1992): "Productivity shocks and real business cycles," Journal of Monetary Economics, 29(2), 191-208.
Fisher, J. D. M. (2006): "The Dynamic Effects of Neutral and Investment-Specific Technology Shocks," Journal of Political Economy, 114(3), 413-451.
Greenwood, J., Z. Hercowitz, and G. W. Huffman (1988): "Investment, Capacity Utilization, and the Real Business Cycle," American Economic Review, 78(3), 402-17.
Greenwood, J., Z. Hercowitz, and P. Krusell (2000): "The role of investment-specific technological change in the business cycle," European Economic Review, 44(1), 91-115.
Greenwood, J., and P. Krusell (2007): "Growth accounting with investment-specific technological progress: A discussion of two approaches," Journal of Monetary Economics, 54(4), 1300-1310.
Hall, R. E. (1986): "Market Structure and Macroeconomic Fluctuations," Brookings Papers on Economic Activity, 2, 285-338.
Hall, R. E. (1988): "The Relation between Price and Marginal Cost in U.S. Industry," Journal of Political Economy, 96(5), 921-47.
Hall, R. E. (1990): "The Invariance Propereties of Solow's Productivity Residual," in Growth, Productivity, and Unemployment, ed. by P. Diamond. MIT Press.
Harrison, S. G. (2003): "Returns to Scale and Externalities in the Consumption and Investment Sectors," Review of Economic Dynamics, 6(4), 963-976.
Hornstein, A., and J. Praschnik (1997): "Intermediate inputs and sectoral comovement in the business cycle," Journal of Monetary Economics, 40(3), 573-595.
Huffman, G. W., and M. A. Wynne (1999): "The role of intratemporal adjustment costs in a multisector economy," Journal of Monetary Economics, 43(2), 317-350.
Jaimovich, N., and M. Floetotto (2008): "Firm Dynamics, Markup Variations, and the Business Cycle," Journal of Monetary Economics, 55(7), 1238-1252. 14
Jaimovich, N., and S. Rebelo (forthcoming): "Can News About the Future Drive the BusinessCycle?," American Economic Review.
Justiniano, A., and G. E. Primiceri (2006): "The Time Varying Volatility of Macroeconomic Fluctuations," Nber working papers, National Bureau of Economic Research, Inc.
Kim, K. H. (2006): "Is Investment-Specific Technological Change Really Important for Business Cycles?," Discussion paper, UCSD.
King, R. G., C. I. Plosser, and S. T. Rebelo (1988): "Production, growth and business cycles: I. The basic neoclassical model," Journal of Monetary Economics, 21(2-3), 195-232.
King, R. G., and S. T. Rebelo (1999): "Resuscitating real business cycles," in Handbook of Macroeconomics, ed. by J. B. Taylor, and M. Woodford, vol. 1 of Handbook of Macroeconomics, chap. 14, pp. 927-1007. Elsevier.
Long, Jr., J. B., and C. I. Plosser (1983): "Real Business Cycles," The Journal of Political Economy, 91(1), 39-69.
Ramey, V. A. (1996): "Can Technology Improvements Cause Productivity Slowdowns? Comment," in NBER Macroeconomics Annual, vol. 11, pp. 268-274. The University of Chicago Press.
Rotemberg, J. J., and M.Woodford (1996): "Imperfect Competition and the Effects of Energy Price Increases on Economic Activity," Journal of Money, Credit and Banking, 28(4), 550-77.
A Appendix
Using the BLS data, we arrive at the total number of establishments in a supersector by adding Expansions (businesses that were already in existence and added employees) to Contractions (businesses that were already in existence and shed employees) to Openings (businesses that came into existence) and then subtract Closings (businesses that closed).
In order to weight the number of establishments according to their economic importance we use data on annual payrolls for each major industry group from the Small Business Administration (SBA), for 1988-2005. In its raw form, the SBA has data for twenty large non-agricultural industry groups. These twenty groups are a subpartition of the partition of thirteen above. We hence add these twenty sectors up to get values of the annual payroll for the thirteen BLS supersectors. The average ratio of one major industry group's payroll to the sum of all groups' payrolls is then the group weight, and we use these to calculate normalized establishment counts for the major industry groups. These weights do no vary appreciably between 1988 and 2005.
From the BEA Input-Output Use table, we are able to calculate the amount of output used for Personal Consumption Expenditure or for Fixed Private Investment for eighty-four non-agricultural industries similar to 2-digit SIC industries. Adding up the industries within each major industry group, we arrive at a value of Personal Consumption Expenditure and Fixed Private Investment for the group. We then define the group's consumption sector share as (Personal Consumption Expenditure)/(Personal Consumption Expenditure plus Fixed Private Investment), while the investment sector share is Fixed Private Investment over the same denominator.
Footnotes
1. First version: May 2008. Return to text
2. mailto:[email protected] Return to text
3. mailto:[email protected] Return to text
4. mailto:[email protected] Return to text
5. See, for example, Hall (1988), Hall (1990), as well as Basu and Fernald (2002). Return to text
6. Similarly, Kim (2006) finds that investment-specific technology shocks are Granger-caused by variables used in Evans (1992)'s analogous finding for Solow residuals. Return to text
7. Previous work on two-sector neoclassical models includes, among others, Long and Plosser (1983), Baxter (1996), Hornstein and Praschnik (1997), Huffman and Wynne (1999), and Harrison (2003). Return to text
8. The term
![]() in (1) implies that
there is no variety effect in the model. This allows us to
isolate the effect of markup varaitions on the price of investment
goods. Return to text
in (1) implies that
there is no variety effect in the model. This allows us to
isolate the effect of markup varaitions on the price of investment
goods. Return to text
9. Multiply (2) with
![]() and use the zero-profit condition
to plug in for
and use the zero-profit condition
to plug in for ![]() . In order to find
. In order to find
![]() , multiply (10) by
, multiply (10) by ![]() and use the zero-profit condition
again. Return to text
and use the zero-profit condition
again. Return to text
10. Use the equilibrium conditions of the
model to show that
![]() and log linearize. Return to
text
and log linearize. Return to
text
11. The equivalent expression in the
investment sector is
![]() Return to text
Return to text
12. Jaimovich and Floetotto (2008) argue that changes in the number of establishments might be a better measure of changes in the number of competitors in the economy. Return to text
13. The SBA has data on estimated receipts and employment as well; our results are robust to using either of these instead of payrolls. Return to text
14. These shares are virtually identical regardless of the Use table year. Return to text
15. For example, take the Transportation
& Warehousing major industry group. We see that 92% of its
output goes to consumption and 8% goes to investment, according to
the Use table. This major industry group accounts for 3.38% of
aggregate payrolls and has 76,000 establishments in 1992:3.
Therefore, it accounts for
![]() consumption sector establishments and
consumption sector establishments and
![]() investment sector establishments in that quarter. Return to text
investment sector establishments in that quarter. Return to text
16. Deviations come from the
Hodrick-Prescott (HP) filter (smoothing parameter set at 1600) on
logged data. The implied values of
![]() are robust to using growth
rates instead of the HP deviations. Consistent with our proposed
mechanism, the data show that fluctuations in the number of
investment sector firms are about 58% more volatile than the number
of consumption sector firms. Return to
text
are robust to using growth
rates instead of the HP deviations. Consistent with our proposed
mechanism, the data show that fluctuations in the number of
investment sector firms are about 58% more volatile than the number
of consumption sector firms. Return to
text
17. We thank Jonas Fisher for making these data available to us. Return to text
18. See the discussion in Christiano and Fitzgerald (1998). Return to text
19. The estimation is done as follows. We
treat
![]() and
and
![]() as first differences from
which we can build a level series of the two shocks. One approach
would then be to follow King and Rebelo (1999). They assume that
as first differences from
which we can build a level series of the two shocks. One approach
would then be to follow King and Rebelo (1999). They assume that
![]() and
and
![]() exhibit a linear trend which
they use to construct deviations. Using these approach we then
estimate
exhibit a linear trend which
they use to construct deviations. Using these approach we then
estimate
![]() and
and
![]() ,
,
![]() , and
, and
![]() and
and
![]() . When
calibrated with these parameters, the model generates a
countercyclical price of investment too. However, the resulting
series of
. When
calibrated with these parameters, the model generates a
countercyclical price of investment too. However, the resulting
series of
![]() and
and
![]() exhibit a non linear trend.
Hence, our preferred calibration is based on an estimate that uses
a more flexible specification of the trend, i.e. an HP
trend. Return to text
exhibit a non linear trend.
Hence, our preferred calibration is based on an estimate that uses
a more flexible specification of the trend, i.e. an HP
trend. Return to text
20. We use data from 1955:1-2000:4, including the Fisher (2006) price of investment series. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text