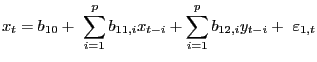Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 970, May 2009 --- Screen Reader
Version*
Pitfalls in Estimating Asymmetric Effects of Energy Price Shocks**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
A common view in the literature is that the effect of energy price shocks on macroeconomic aggregates is asymmetric in energy price increases and decreases. We show that widely used asymmetric vector autoregressive models of the transmission of energy price shocks are misspecified, resulting in inconsistent parameter estimates, and that the implied impulse responses have been routinely computed incorrectly. As a result, the quantitative importance of unanticipated energy price increases for the U.S. economy has been exaggerated. In response to this problem, we develop alternative regression models and methods of computing responses to energy price shocks that yield consistent estimates regardless of the degree of asymmetry. We also introduce improved tests of the null hypothesis of symmetry in the responses to energy price increases and decreases. An empirical study reveals little evidence against the null hypothesis of symmetry in the responses to energy price shocks. Our analysis also has direct implications for the theoretical literature on the transmission of energy price shocks and for the debate about policy responses to energy price shocks.
Keywords: Asymmetry, oil price, energy prices, net increase, shocks, propagation, transmission, vector autoregression
JEL classification: C32, E37, Q43
1. Introduction
A common view in the literature is that the effects of energy price shocks on macroeconomic aggregates such as output or employment are asymmetric. In particular, energy price increases are perceived to have larger effects than energy price decreases. This perception has been bolstered by empirical evidence that energy price increases (obtained by censoring energy price changes to exclude all energy price decreases) have seemingly large effects on the macro economy, whereas uncensored percent changes in energy prices tend to have much smaller effects. Vector autoregressive (VAR) models relating energy price increases to macroeconomic aggregates in particular have shaped the discussion of the effects of energy price shocks in recent decades. In this paper, we demonstrate that the regression models and estimation methods typically used in that literature produce inconsistent estimates of the true effects of unanticipated energy price increases and are likely to have exaggerated the impact of energy price shocks. We show that fundamental changes are needed in how these effects are estimated in practice. In addition to addressing the problem of how to estimate asymmetric responses to energy price shocks, we develop improved tests of the null hypothesis of symmetric responses to energy price increases and decreases. Our empirical evidence suggests that there is no compelling evidence against the symmetry null. Our analysis also has direct implications for the theoretical literature on the transmission of energy price shocks and for the debate about policy responses to energy price shocks.
1.1. Review of the Literature
In the view of many economists, oil price shocks are perhaps the leading alternative to monetary policy as the determinant of U.S. postwar recessions.1 Increases in the price of oil preceded the recessions of 1973-75, 1980-82, and 1990-91, for example. Given the striking coincidence of deteriorating macroeconomic outcomes and rising oil prices in the 1970s and early 1980s, it was natural at the time to suspect a strong link from oil price increases to recessions. Nevertheless, as discussed in Bernanke, Gertler and Watson (1997), it has proved surprisingly difficult to find an indicator of oil price shocks that produces the expected responses of macroeconomic and policy variables in a VAR setting. Finding a measure of oil price shocks that "works" in a VAR context in practice is not straightforward. Simple measures of energy price shocks (such as linearly unpredictable changes in energy prices) in particular sometimes imply "anomalous" effects on macroeconomic outcomes, relative to the conventional wisdom about the effects of oil price shocks on the economy. They also tend to have an unstable relationship with macroeconomic outcomes.2
Far from undermining the view that energy price shocks are important, these difficulties have led researchers to employ increasingly complicated specifications of the "true" relationship between oil prices and the economy. Today it is widely believed that the most appropriate specification of oil price shocks involves some measure of oil price increases, obtained by censoring oil price changes to exclude all oil price decreases. This consensus dates back to the work of Mork (1989). After the sharp oil price declines of 1985-86 failed to lead to an economic boom in oil importing economies, Mork (1989) pointed out that the effects of positive and negative oil price shocks on the economy need not be symmetric. He provided empirical evidence that positive changes in the real price of oil had far more important effects on U.S. real GDP than negative changes. This was widely interpreted as evidence that only oil price increases matter for the U.S. economy (see, e.g., Bernanke, Gertler and Watson 1997, p. 103). Given the a priori belief that oil price shocks have quantitatively important effects on macroeconomic aggregates and given researchers' inability to generate such responses from linear and symmetric models, VAR models of macroeconomic aggregates and oil price increases became accepted on the grounds that they produced "better looking" impulse responses (Bernanke, Gertler and Watson 1997, p. 104).3
The initial proposal to focus only on oil price increases has subsequently been refined by
Hamilton (1996, 2003), who introduced the "net oil price increase". This measure distinguishes
between oil price increases that establish new highs relative to recent experience and increases that simply reverse recent decreases. Specifically, in the context of monthly data, Hamilton's measure equals the maximum of (a) zero and (b) the difference between the log-level of the crude oil price for the current month and the maximum value of the logged crude oil price achieved in the previous 12 (or alternatively 36) months. Hooker (2002), for example, finds that the net increase measure performs "well", in the sense of having a relatively stable relationship with macroeconomic variables, and Hamilton (1996, 2003, 2009a) makes the case that this measure predicts declines in U.S. real GDP.
The most influential use of the net increase measure has been not for one-step ahead prediction from single-equation reduced form models, but in constructing estimates of the response of the economy to energy price shocks based on VAR models. Many of these VAR estimates have become accepted in academic and policy discussions of the transmission of energy price shocks (see, e.g., Dotsey and Reid 1992; Davis and Haltiwanger 2002; Lee and Ni 2002; Jones, Leiby, and Paik 2004; Jiménez-Rodriguez and Sánchez 2005; Herrera 2008). The net increase measure also plays a central role in VAR analyses of the role of monetary policy in propagating energy price shocks (see, e.g., Bernanke, Gertler and Watson 1997, 2004; Hamilton and Herrera 2004; Herrera and Pesavento 2007).4
1.2. Outline of the Paper
In this paper, we demonstrate that the estimation methods used in these VAR applications generate inconsistent estimates of the true effects of unanticipated energy price increases. We show, for example, that VAR models of the effects of energy price increases on macroeconomic outcomes will overestimate the true response to energy price increases asymptotically, when the underlying data generating process (DGP) is symmetric. Since one of the reasons that these models were adopted was precisely their ability to generate larger responses to energy price shocks than symmetric VAR models, our finding casts doubt on the results reported in this literature and, indeed, on the empirical relevance of asymmetric VAR models. Our results apply with equal force to measures of oil price increases and net oil price increases. More generally, we show that asymptotic biases in the VAR response estimates may arise whether the underlying DGP is linear and symmetric or not.
In section 2, we illustrate this point in the context of a stylized static model. We establish the inconsistency of estimators of conventional asymmetric models analytically, and we study the determinants of the asymptotic bias of the estimator by simulation. We show that static censored regressor models will be consistent only in very special and theoretically implausible cases. In section 3, we strengthen this result by showing that estimates of dynamic censored VAR models of the type frequently employed in the literature are fundamentally misspecified and produce inconsistent impulse response estimates regardless of the DGP. We demonstrate that censored VAR models will distort the quantitative importance of energy price increases asymptotically, even when energy price decreases have no effect on the economy. The reason is that such asymmetric DGPs cannot be represented as censored VAR models. We discuss how alternative, correctly specified asymmetric models may be constructed and estimated consistently using restricted maximum likelihood estimators.
An important problem in practice is that we may not know whether the DGP is symmetric or not, and whether energy price decreases should be included in the regression, if the DGP is asymmetric. In section 4, we propose a regression model that can be estimated consistently whether the true model is symmetric or not, regardless of the precise form of the asymmetry. Moreover, this model may be estimated by standard methods such as unrestricted least squares.
In section 5, we show that in addition to the misspecification of the censored VAR models used in the literature and the resulting inconsistency of the parameter estimates, the dynamic responses of macroeconomic aggregates to unanticipated energy price increases have routinely been computed incorrectly in a way that further exaggerates the quantitative importance of these shocks. We adapt existing methods of constructing nonlinear impulse responses to the structural model proposed in section 4 and demonstrate how asymmetric impulse responses may be estimated consistently. Unlike existing methods of computing nonlinear impulse responses in the econometric literature, our approach is fully structural and avoids the ambiguities of defining a shock in nonlinear reduced form models.
Both the regression model proposed in section 4 and the method of computing responses to energy price shocks developed in section 5 play a crucial role in designing tests of the symmetry of response functions in energy price increases and decreases. In section 6, we discuss the problem of testing the null hypothesis that the U.S. economy responds symmetrically to energy price increases and decreases. First, we show that traditional tests for asymmetries in the regression slopes of predictive regressions in the spirit of Mork (1989) exploit only some implications of symmetry. Based on the structural model of section 4, we propose a modified test of symmetry in the slopes with higher power. Second, we observe that statistically insignificant departures from symmetry in the slopes may cause statistically significant asymmetries in the implied impulse response functions, given the nonlinearity of these functions, while significant departures from symmetry in the slopes need not imply large asymmetries in the impulse response functions. Moreover, by construction, the extent to which responses from the linear symmetric model provide a good approximation will depend on the magnitude of the energy price shock. Thus, traditional slope-based tests, while informative about the degree of asymmetry in reduced form parameters, do not shed light on the degree of asymmetry in the impulse response functions. As an alternative, we propose a direct statistical test of the symmetry of the economy's response to unanticipated energy price increases and decreases. That test is shown to have reasonably accurate finite-sample size.
In section 7, we apply these tools in examining the evidence against the symmetry null in three prominent empirical examples. Specifically, we model the relationship between quarterly U.S. real GDP and the real price of oil, between monthly U.S. unemployment and the real price of oil, and between monthly U.S. gasoline consumption and the U.S. real retail price of gasoline. We find no compelling evidence of asymmetric responses to positive and negative energy price shocks.
In section 8, we extend the analysis to VAR models involving net energy price increases motivated by the analysis in Hamilton (1996, 2003). Despite the widespread use of the net oil price increase measure in VAR models, none of the symmetry test results in the literature provides a justification for the use of such models. In fact, notwithstanding the evidence for asymmetries in the predictive relationship between real GDP growth and oil price changes provided by Hamilton (2003), with the partial exception of Balke, Brown and Yücel (2002), no paper has adequately addressed the implications of the net increase model for impulse response analysis. In this paper, we address this question. We discuss how structural impulse responses to energy price shocks may be consistently estimated in this context, and we present two tests of symmetric impulse responses based on the net increase model, one based on the slope parameters of a modified version of the model proposed in section 4, and the other based on the impulse response functions implied by that model. Our analysis clarifies, refines, and extends the earlier analysis in Balke et al., which recognized many of the problems discussed here but had no apparent impact on the empirical practice in this literature.5
The choice of tests makes a difference. Unlike Hamilton (2003) or Balke et al. (2002), we find little, if any, evidence against the null hypothesis of symmetric responses in our three empirical examples. In fact, slope-based symmetry tests are shown to be misleading. Our results suggest that linear impulse response analysis will be adequate for many applications. This finding also has important implications for the theoretical literature on the transmission of energy price shocks and for the debate about monetary policy responses to oil price shocks. Finally, to the extent that there is evidence of asymmetries, our analysis suggests that important changes are needed in the way these asymmetries are modeled in the VAR literature. Section 9 contains the concluding remarks.
2. A Stylized Model
In this section, we illustrate the estimation biases induced by censoring regressors in the simplest possible setting. It is well known that censoring dependent variables causes OLS estimates of the coefficients of linear models to be biased (see, e.g., Amemiya 1984). Notwithstanding the existence of a large literature on the effects of censoring the dependent variable, the problems arising from censoring the explanatory variable that are the focus of our paper have rarely been analyzed. A notable recent exception is Rigobon and Stoker (2007, 2008), who make the case that researchers encounter censored regressors as often as, or perhaps more often than, censored dependent variables. Rigobon and Stoker focus on the problem of censoring regressors in static single equation models used to analyze cross-sections. Their primary interest is in double censoring, in which a regressor is top and bottom coded, as might be the case in classifying household income by range, for example.6
In contrast, our focus in this paper is on multivariate time series models with censored endogenous regressors. The type of censoring of interest in our paper occurs below zero (or, alternatively, above zero). Moreover, motivated by the literature on the transmission of energy price increases, our main interest is the effect of censoring on the impulse response estimates rather than slope parameters. Finally, whereas Rigobon and Stoker study cases in which the econometrician cannot observe the uncensored data, we study situations in which the uncensored data are observed but the researcher has chosen to estimate a regression using the censored data in order to estimate an asymmetric effect.
2.1. Asymptotic Biases from Using Censored Regressors
For expository purposes, consider the following static linear two-equation DGP:
|
|
[1] |
where
![]() ,
,
![]() ,
, ![]() are constants,
are constants,
![]() and
and
![]() are mean zero i.i.d.
Gaussian random variables with variances
are mean zero i.i.d.
Gaussian random variables with variances
![]() and
and
![]() , and t = 1,
...,T. It is straightforward to show that the OLS estimators
of
, and t = 1,
...,T. It is straightforward to show that the OLS estimators
of ![]() and
and ![]() in the regression
model
in the regression
model
|
|
[2] |
will be unbiased and consistent estimators of α and ![]() . To
illustrate the effect of replacing
. To
illustrate the effect of replacing
negative values of ![]() with zero in this
regression, define the variable
with zero in this
regression, define the variable
![]() as
as
![\begin{displaymath}{\mathrm{x}}^{\mathrm{+}}_{\mathrm{t}}=\left\{ \begin{array}[c]{c} x_{t}\ \mathrm{if}\ x_{t}>0\ 0\ \mathrm{if}\ x_{t}\le0 \end{array}\right. \end{displaymath}](img17.gif) |
[3] |
and consider estimating the censored regression model:
|
|
[4] |
rather than the unconstrained model (2). Censoring the explanatory variable renders the
estimator of b inconsistent for ![]() .
Figure 1 illustrates the problem. The values of the dependent
variable that are associated with negative values of
.
Figure 1 illustrates the problem. The values of the dependent
variable that are associated with negative values of ![]() are moved to the y-axis. Given these points, the
estimated intercept is negative and far below its true value of
zero. As a result of the negative intercept, the value of the slope
coefficient must be greater than the true value. This problem is
equivalent to the expansion bias discussed by Rigobon and Stoker
(2008) in the context of top-coding of cross-sectional data.
are moved to the y-axis. Given these points, the
estimated intercept is negative and far below its true value of
zero. As a result of the negative intercept, the value of the slope
coefficient must be greater than the true value. This problem is
equivalent to the expansion bias discussed by Rigobon and Stoker
(2008) in the context of top-coding of cross-sectional data.
The upward bias in the estimated effect of ![]() on
on ![]() is not a small-sample problem.
For the simple case where α equals zero and where
is not a small-sample problem.
For the simple case where α equals zero and where ![]() has a symmetric distribution with mean zero and
variance 1 and is uncorrelated with
has a symmetric distribution with mean zero and
variance 1 and is uncorrelated with
![]() we can derive the limits
for
we can derive the limits
for ![]() and
and ![]() .
Observe that
.
Observe that
![]() where
where
![]() . As shown in the appendix,
. As shown in the appendix, ![]() and
and
![]() converge in probability to the
following limits:
converge in probability to the
following limits:
|
|
[5] |
and
|
|
[6] |
The proof is a standard application of the Law of Large Numbers
to the OLS estimators and is described in the appendix. If the
variable ![]() has a standard normal distribution,
then
has a standard normal distribution,
then ![]() converges to about minus
0.58
converges to about minus
0.58![]() and
and ![]() converges to
roughly 1.47
converges to
roughly 1.47![]() . Therefore, in this simple example,
the effect of
. Therefore, in this simple example,
the effect of ![]() on
on ![]() is
overestimated by almost 50 percent.7
is
overestimated by almost 50 percent.7
2.2. Further Illustrations of the Asymptotic Bias from Censoring
To illustrate further the effects of censoring and its determinants, we report some simulation evidence. The first simulation illustrates that the effect of censoring negative values depends on
Figure 1: The Effect of Censoring Negative Values of the Explanatory Variable
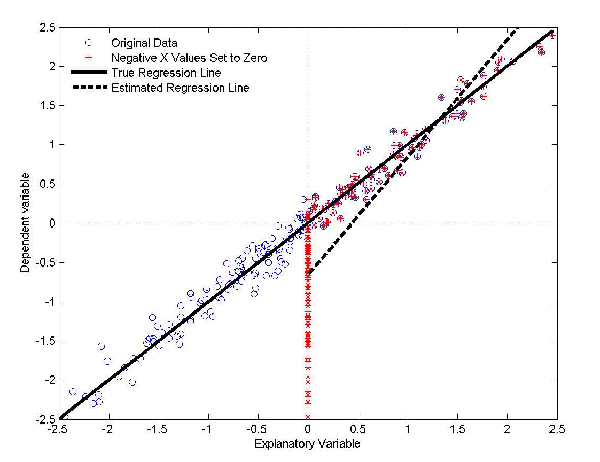
the relative frequency with which negative values occur. Table 1
reports the results of simulating data from model (1) but for
different values of
![]() . As a consequence of varying
. As a consequence of varying
![]() , the fraction of
, the fraction of ![]() 's that are positive varies. When 90 percent of the
observations are positive, the slope coefficient is still biased
upwards, although by less than 10 percent. These simulation results
approximate asymptotic results, as the number of observations per
simulated dataset is 100,000 and results are averaged across 2,000
simulated datasets.
's that are positive varies. When 90 percent of the
observations are positive, the slope coefficient is still biased
upwards, although by less than 10 percent. These simulation results
approximate asymptotic results, as the number of observations per
simulated dataset is 100,000 and results are averaged across 2,000
simulated datasets.
The analysis so far has focused on DGPs that are symmetric in
![]() , but the same problem may arise even
when the true response of
, but the same problem may arise even
when the true response of ![]() to
to ![]() is asymmetric in positive and negative values. Consider
the following DGP:
is asymmetric in positive and negative values. Consider
the following DGP:
[7] |
where ![]() captures the asymmetric response that
is of interest to many economic researchers.
captures the asymmetric response that
is of interest to many economic researchers.
This process allows for both positive and negative values of
![]() to affect
to affect ![]() ,
but with different coefficients. Equivalently, we could have
specified the second equation of model (7) as a regression
in
,
but with different coefficients. Equivalently, we could have
specified the second equation of model (7) as a regression
in ![]() and
and ![]() with
potentially different coefficients. Given this DGP, if one
estimated the equation
with
potentially different coefficients. Given this DGP, if one
estimated the equation
|
|
[8] |
one would want the value of b to equal ![]() +
+![]() in the limit.
However, as shown in Table 2, this is not the case unless
in the limit.
However, as shown in Table 2, this is not the case unless
![]() equals zero, implying that only
positive
equals zero, implying that only
positive ![]() have an effect on
have an effect on ![]() . For all other values of
. For all other values of ![]() , the value of the estimated
slope coefficient is biased upwards. Furthermore, in this example,
if the slope for negative
, the value of the estimated
slope coefficient is biased upwards. Furthermore, in this example,
if the slope for negative ![]() is at least
half of the slope for positive
is at least
half of the slope for positive ![]() then the
estimate of an increase in
then the
estimate of an increase in ![]() on
on ![]() is less biased when using the full sample than when
using the censored sample.8
is less biased when using the full sample than when
using the censored sample.8
Table 2 illustrates that, only when ![]() is known to be
zero, will the censored regression model consistently estimate the
effect of an energy price increase in the static model. This point
is important because Mork (1989) merely failed to reject the null
hypothesis that energy
is known to be
zero, will the censored regression model consistently estimate the
effect of an energy price increase in the static model. This point
is important because Mork (1989) merely failed to reject the null
hypothesis that energy
Table 1: Asymptotic Bias from Censoring in the Static Symmetric Model - Varying
the Fraction of Positive ![]() Observations
Observations
| P( | E |
|
|
|---|---|---|---|
| 0.10 | -1.28 | -1.41 | 2.70 |
| 0.20 | -0.84 | -1.08 | 2.14 |
| 0.30 | -0.52 | -0.87 | 1.83 |
| 0.40 | -0.25 | -0.72 | 1.62 |
| 0.50 | 0.00 | -0.59 | 1.47 |
| 0.60 | 0.25 | -0.47 | 1.34 |
| 0.70 | 0.52 | -0.36 | 1.24 |
| 0.80 | 0.84 | -0.26 | 1.15 |
| 0.90 | 1.28 | -0.15 | 1.08 |
Notes:
Symmetric DGP: ![]() =1,
=1,
![]() =
=
![]() ,
,
![]()
![]() 1. Average results for 2,000
samples of 100,000 observations each.
1. Average results for 2,000
samples of 100,000 observations each.
price decreases have no effect on real GDP growth. He did not
establish that ![]() =0, and indeed was careful only to suggest that
these coefficients are "perhaps zero". Nor does economic theory
predict that
=0, and indeed was careful only to suggest that
these coefficients are "perhaps zero". Nor does economic theory
predict that ![]() =0 (see, e.g., Edelstein and Kilian 2007a, Kilian
2008b). If, in fact, both energy price increases and decreases
matter for real GDP, but to a different extent, as suggested by
economic theory, then the censored regressor model is bound to
overestimate the effect of an energy price increase even in this
simplest possible model. The only way to protect from this
inconsistency is to include both energy price increases and
decreases in the regression.
=0 (see, e.g., Edelstein and Kilian 2007a, Kilian
2008b). If, in fact, both energy price increases and decreases
matter for real GDP, but to a different extent, as suggested by
economic theory, then the censored regressor model is bound to
overestimate the effect of an energy price increase even in this
simplest possible model. The only way to protect from this
inconsistency is to include both energy price increases and
decreases in the regression.
Table 2: Asymptotic Bias from Censoring in the Asymmetric Static Model
| Population Slope Parameters - | Population Slope Parameters - | Population Slope Parameters - | Average Estimated Slope | Average Estimated Slope |
|---|---|---|---|---|
| 0.00 | 1 | 1 | 0.50 | 1.00 |
| 0.25 | 0.75 | 1 | 0.62 | 1.12 |
| 0.50 | 0.50 | 1 | 0.75 | 1.23 |
| 0.60 | 0.40 | 1 | 0.80 | 1.28 |
| 0.70 | 0.30 | 1 | 0.85 | 1.32 |
| 0.80 | 0.20 | 1 | 0.90 | 1.37 |
| 1.00 | 0.00 | 1 | 1.00 | 1.47 |
| 1.25 | -0.25 | 1 | 1.12 | 1.58 |
| 1.50 | -0.50 | 1 | 1.25 | 1.70 |
Notes:
Asymmetric DGP:
![]() =
=
![]() ,
,
![]()
![]() 1. Average results for 2,000
samples of 100,000 observations each.
1. Average results for 2,000
samples of 100,000 observations each.
The static model is useful for building intuition, but extending the analysis to dynamic regression models leads to additional insights. In many cases, researchers are specifically interested in the response of the economy over time to an unexpected energy price increase:
where
![]() is the information set at the
time of the shock. In the next section, we show that the censored
VAR models routinely employed in the literature will produce
inconsistent impulse response estimates not only in the empirically
plausible case of nonzero responses to both energy price increases
and decreases but even when all coefficients on current and lagged
is the information set at the
time of the shock. In the next section, we show that the censored
VAR models routinely employed in the literature will produce
inconsistent impulse response estimates not only in the empirically
plausible case of nonzero responses to both energy price increases
and decreases but even when all coefficients on current and lagged
![]() are zero in population. In other words,
even if oil price decreases had no effect on real GDP growth in
population, as postulated in the literature, censored VAR models
would yield invalid impulse response estimates. This result is in
sharp contrast to the static model.
are zero in population. In other words,
even if oil price decreases had no effect on real GDP growth in
population, as postulated in the literature, censored VAR models
would yield invalid impulse response estimates. This result is in
sharp contrast to the static model.
3. How Empirically Relevant Is the Asymptotic Bias of VAR Models of Energy Price Increases?
It is common practice in the literature to compute responses to unanticipated energy price increases from censored VAR models. For example, Bernanke, Gertler and Watson (1997, p. 103) observe that "Knut Mork provided evidence that only positive changes in the relative price of oil have important effects on output. Accordingly, in our VARs we employ an indicator that equals the log difference of the relative price of oil when that change is positive and otherwise is zero." Similarly, Leduc and Sill (2004, p. 790) state that "to get an empirical estimate of the output response to positive oil-price shocks, we run a VAR using ...oil-price increases [...] constructed by taking the first difference of the log of oil prices, then setting negative values to zero. Thus, only oil-price increases affect the other variables in the system."
The standard approach used in the literature is based on a
recursively identified VAR model, in which the energy price
increase variable is ordered above the macroeconomic aggregate of
interest. The prototypical example is a linear bivariate
autoregression for
![]() '. Adding
additional macroeconomic variables does not affect the econometric
points of interest in this paper, and, indeed, is not required for
consistently estimating the response of
'. Adding
additional macroeconomic variables does not affect the econometric
points of interest in this paper, and, indeed, is not required for
consistently estimating the response of ![]() to an
unanticipated increase in energy prices under the maintained
assumption of predetermined (or contemporaneously exogenous) energy
prices (see Kilian 2008b). The identifying assumption of
predetermined energy prices with respect to the macroeconomic
aggregate of interest is not only standard in the literature but is
consistent with empirical evidence presented in Kilian and Vega
(2008).
to an
unanticipated increase in energy prices under the maintained
assumption of predetermined (or contemporaneously exogenous) energy
prices (see Kilian 2008b). The identifying assumption of
predetermined energy prices with respect to the macroeconomic
aggregate of interest is not only standard in the literature but is
consistent with empirical evidence presented in Kilian and Vega
(2008).
Estimates of this model have been used in constructing responses
to a one standard deviation shock in ![]() . The
construction of impulse responses from nonlinear models such as the
asymmetric models of interest in this paper is not straightforward.
Whereas impulse responses in linear models are independent of the
history of the observations, impulse responses in nonlinear models
are dependent on the history of the observations and on the
magnitude of the shock (see, e.g., Gallant Rossi and Tauchan 1993;
Koop, Pesaran and Potter 1996). Thus, the construction of impulse
responses requires Monte Carlo integration over all possible paths
of the data. This point has been routinely ignored in the
literature. In practice, researchers have presented impulse
response estimates computed exactly as in linear VAR models. For
now we follow that convention because we wish to illustrate the
asymptotic biases in the results reported in the literature.
Moreover, discussing one problem at a time will facilitate the
exposition. We will return to this point in section 5, however, and
show how impulse responses can be computed correctly.
. The
construction of impulse responses from nonlinear models such as the
asymmetric models of interest in this paper is not straightforward.
Whereas impulse responses in linear models are independent of the
history of the observations, impulse responses in nonlinear models
are dependent on the history of the observations and on the
magnitude of the shock (see, e.g., Gallant Rossi and Tauchan 1993;
Koop, Pesaran and Potter 1996). Thus, the construction of impulse
responses requires Monte Carlo integration over all possible paths
of the data. This point has been routinely ignored in the
literature. In practice, researchers have presented impulse
response estimates computed exactly as in linear VAR models. For
now we follow that convention because we wish to illustrate the
asymptotic biases in the results reported in the literature.
Moreover, discussing one problem at a time will facilitate the
exposition. We will return to this point in section 5, however, and
show how impulse responses can be computed correctly.
3.1. Linear and Symmetric VAR Data Generating Processes
The points we made in section 2 directly extend to censored VAR models. Consider a linear symmetric bivariate VAR(p) DGP of the form
[9]
|
where ![]() denotes the percent change in energy
prices,
denotes the percent change in energy
prices, ![]() denotes the percent change in the
macroeconomic aggregate of interest, and
denotes the percent change in the
macroeconomic aggregate of interest, and
![]() is
uncorrelated white noise. We focus on three illustrative examples
that are representative of models employed in the empirical
literature:
is
uncorrelated white noise. We focus on three illustrative examples
that are representative of models employed in the empirical
literature:
(1) A quarterly VAR in the percent changes in real crude oil prices and the growth rate of U.S. real GDP. The sample period is 1973.II-2007.IV. The oil price series is based on an index of U.S. refiners' acquisition cost, extrapolated as in Kilian (2008a), and deflated by the U.S. CPI. The real GDP data are from the BEA.
(2) A monthly VAR in the percent change in crude oil prices and the change in the U.S. unemployment rate. The sample period is 1973.2-2007.12. The unemployment rate data are from the BLS.
(3) A monthly VAR in the percent change in real gasoline prices and the percent change in real U.S. real gasoline consumption, as constructed by the BEA. The sample period is 1973.2-2007.12.
The lag order p is set to 6 for expository purposes. For
each data set, we construct a DGP by replacing the model parameters
by their least-squares estimates obtained from fitting this model
to the data set in question and by treating the structural errors
as Gaussian white noise. For each DGP, we generate a sample of
length T, fit a VAR(6) model for
![]() ', and
construct the cumulative response of
', and
construct the cumulative response of
![]() to a unit increase
in energy prices. We compare that response to the response of
to a unit increase
in energy prices. We compare that response to the response of
![]() to a unit increase in energy
prices in the DGP. Since we are interested in evaluating the
asymptotic bias of the responses implied by the censored VAR model,
all results in Figure 2 are based on T = 1,000,000.
to a unit increase in energy
prices in the DGP. Since we are interested in evaluating the
asymptotic bias of the responses implied by the censored VAR model,
all results in Figure 2 are based on T = 1,000,000.
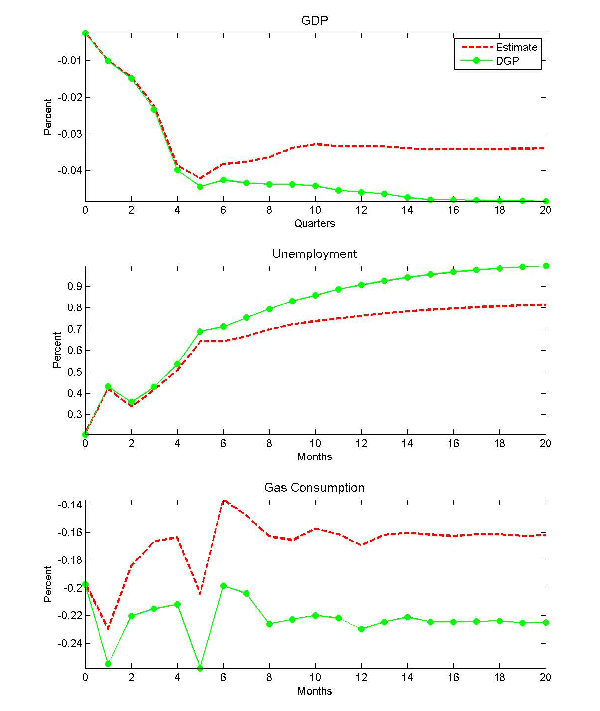
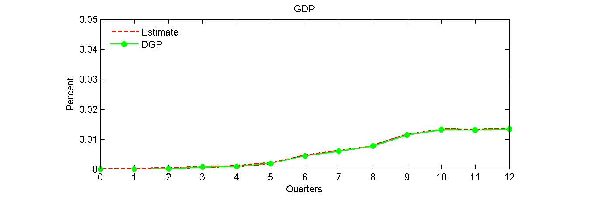
The left column of Figure 2 quantifies the asymptotic bias induced by censoring energy price decreases. The impulse response implied by the DGP is shown as the solid line. The estimated impulse response from the censored VAR model is shown as the dashed line. As shown in section 2, the censored VAR response tends to overestimate the true response in each case. For example, the response of real GDP after 6 quarters is overestimated by about one third. The right column of Figure 2 illustrates the point that our results are not driven by sampling uncertainty. It shows that the true and the estimated response lie exactly on top of one another if we fit a linear symmetric VAR model to the same data. The results in Figure 2 suggest strong caution in interpreting the results of censored VAR models.
3.2. Asymmetric Data Generating Processes
Figure 2 showed that censored VAR models will be misleading when the DGP is linear and symmetric. It is equally interesting to investigate the consistency of the censored VAR model when the DGP involves asymmetric effects of energy price increases on macroeconomic aggregates. Here we follow the bulk of the empirical literature on energy price shocks and focus on the leading example of models in which only energy price increases matter for macroeconomic aggregates. For expository purposes, first consider the simplest possible dynamic model, in which energy price decreases have no effect:
|
|
[10] |
where![]() is defined as above. Setting the
initial conditions to zero, in this system the impact
is defined as above. Setting the
initial conditions to zero, in this system the impact
Figure 2: Inconsistency of the Estimated Effect of Energy Price
Increases
Symmetric VAR DGP
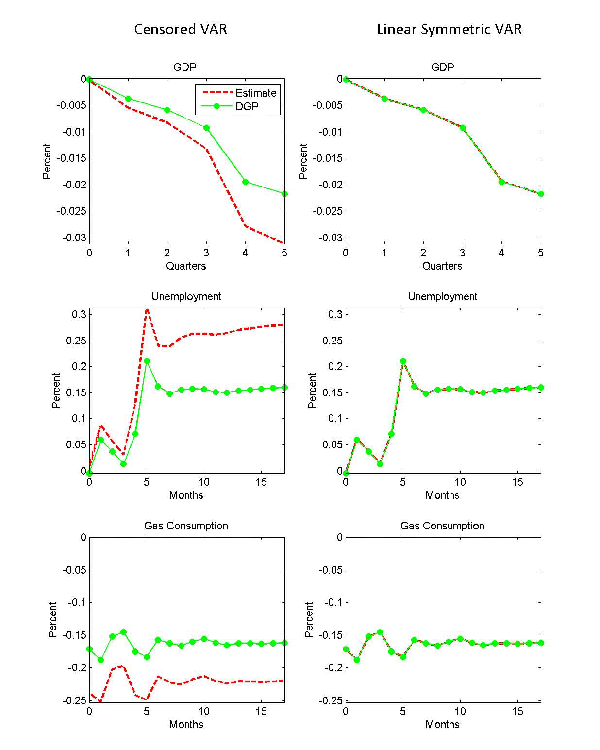
Notes: Simulations from symmetric VAR DGP based on U.S. data. T=1,000,000.
response of ![]() to a positive shock to
to a positive shock to
![]() would be
would be ![]() . In
the next period, the response would be
. In
the next period, the response would be
![]() , provided that
, provided that ![]() is positive.9 If this system is estimated, then, as
expected, estimates of both
is positive.9 If this system is estimated, then, as
expected, estimates of both ![]() and
and
![]() will be unbiased. If instead a
researcher estimated the censored system:
will be unbiased. If instead a
researcher estimated the censored system:
|
|
[11] |
the estimate of ![]() would be asymptotically
biased and so would be the impulse response estimate, even though
the estimate of
would be asymptotically
biased and so would be the impulse response estimate, even though
the estimate of ![]() is unbiased.
is unbiased.
This example illustrates that the DGP cannot be represented as a
bivariate VAR for
![]() '. In fact,
a censored VAR DGP with positive probability would generate
realizations for
'. In fact,
a censored VAR DGP with positive probability would generate
realizations for ![]() that may be negative. It
may seem that this contradiction could be avoided by censoring the
realizations much like researchers have censored percent changes in
actual energy prices, but in that case the same asymptotic biases
would arise that we already documented for the linear symmetric
model. This point is illustrated in Figure 3. Based on a censored
VAR DGP, the censored VAR run on censored realizations of
that may be negative. It
may seem that this contradiction could be avoided by censoring the
realizations much like researchers have censored percent changes in
actual energy prices, but in that case the same asymptotic biases
would arise that we already documented for the linear symmetric
model. This point is illustrated in Figure 3. Based on a censored
VAR DGP, the censored VAR run on censored realizations of
![]() generates responses to energy
price increases that are systematically higher than the pseudo-true
response even in the limit.
generates responses to energy
price increases that are systematically higher than the pseudo-true
response even in the limit.
Figure 3: Inconsistency of the Estimated Effect of Energy Price
Increases
Censored VAR DGP with Censored VAR Variable
Notes: Simulations from censored VAR DGP based on U.S. data. T=1,000,000.
The source of the problem in Figure 3 is that the censored VAR regression model is not a description of the DGP. This problem can be avoided only by fully specifying the underlying structural model:
|
|
[12] |
where the structural shocks
![]() and
and
![]() are uncorrelated and
where for expository purposes we
are uncorrelated and
where for expository purposes we
have omitted the definition of ![]() as a
function of
as a
function of
![]() Although the slope parameters
of Model
Although the slope parameters
of Model
(12) can be estimated consistently by OLS, the resulting residuals will not be uncorrelated. To impose the latter restriction requires the use of a restricted maximum likelihood estimator.
The DGP in model (12) postulates that
percent changes in energy prices evolve in an unconstrained
fashion; only the feedback from energy prices to the macroeconomic
aggregates is constrained. This model is easily recognizable as a
generalization of model (7) with
![]() to the VAR context. Note that in
this model a negative shock to
to the VAR context. Note that in
this model a negative shock to ![]() may have a
nonzero effect on
may have a
nonzero effect on ![]() if the negative shock
over time induces positive values in
if the negative shock
over time induces positive values in ![]() Also
note that model (12) is not
equivalent to the following model:
Also
note that model (12) is not
equivalent to the following model:
|
|
[13] |
The key difference between models (12) and (13) is that the impact effect of a negative value of
![]() is zero in model
(13) and is
is zero in model
(13) and is
![]() in model (12). Furthermore,
model (12) is
not equivalent to estimating the model:
in model (12). Furthermore,
model (12) is
not equivalent to estimating the model:
|
|
[14] |
where
![]() , and
applying a Cholesky decomposition to the variance covariance matrix
of the two error terms
, and
applying a Cholesky decomposition to the variance covariance matrix
of the two error terms
![]() and
and ![]() The key difference is that the Cholesky decomposition
does not discriminate between positive and negative shocks.
The key difference is that the Cholesky decomposition
does not discriminate between positive and negative shocks.
Below we confirm that even when the data are generated from
model (12),
asymptotic biases may arise when estimating the response to energy
price increases from a censored VAR model. We focus on the same
illustrative examples as in Figure 2, except that we now construct
the DGPs under the working hypothesis that the data are generated
by the asymmetric model (12) in which there
is no effect from current or lagged ![]() on
on
![]() . For each DGP example, we treat the
least-squares estimates of the slope parameters and innovation
variances obtained on the actual data as the population parameters
in the simulation and impose the zero correlation of the innovation
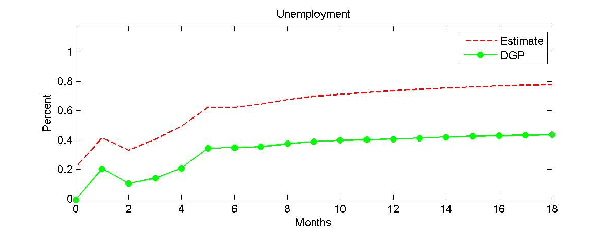
variances. All results are based on T = 1,000,000. Figure 4 shows
that even in this case the responses implied by the censored VAR
model will be asymptotically biased. The direction of the bias is
ambiguous. Especially for the unemployment rate, the bias is
substantial. After 18 months, the estimated response to an energy
price increase is only about 80 percent of the true response. By
the same reasoning as in Section 3, this result is a consequence of
inconsistently estimating the response of the price of energy to
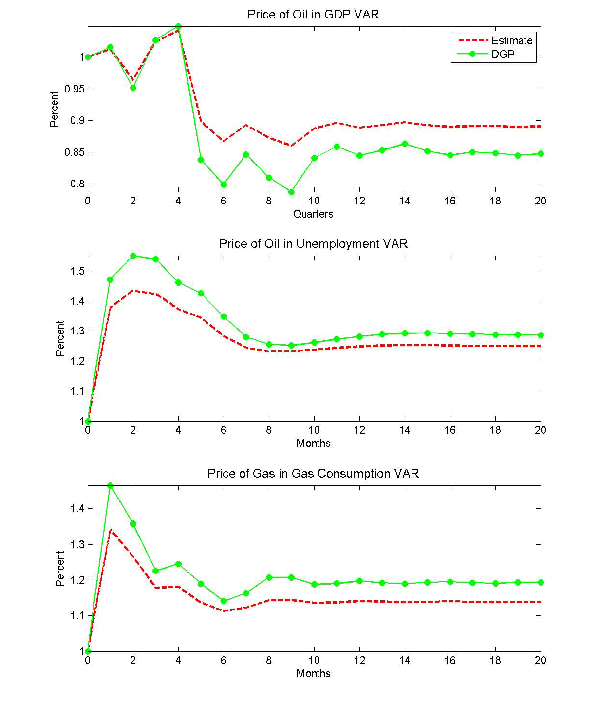
the energy price shock. Figure 5 illustrates this problem by
plotting the corresponding responses of the price of energy.
Although there is no problem in consistently estimating the second
equation of the system that includes the censored regressors (and,
indeed, the impact response of
. For each DGP example, we treat the
least-squares estimates of the slope parameters and innovation
variances obtained on the actual data as the population parameters
in the simulation and impose the zero correlation of the innovation
variances. All results are based on T = 1,000,000. Figure 4 shows
that even in this case the responses implied by the censored VAR
model will be asymptotically biased. The direction of the bias is
ambiguous. Especially for the unemployment rate, the bias is
substantial. After 18 months, the estimated response to an energy
price increase is only about 80 percent of the true response. By
the same reasoning as in Section 3, this result is a consequence of
inconsistently estimating the response of the price of energy to
the energy price shock. Figure 5 illustrates this problem by
plotting the corresponding responses of the price of energy.
Although there is no problem in consistently estimating the second
equation of the system that includes the censored regressors (and,
indeed, the impact response of ![]() is correctly
estimated in Figure 4), the fact that the censored VAR model
misspecifies the first equation of the system causes both response
estimates to be inconsistent as the energy price shock is
propagated over time. The results in Figures 4 and 5 represent the
best possible scenario in that we postulated that only energy price
increases matter in the DGP. Additional asymptotic biases would
arise if the asymmetric DGP allowed for nonzero effects from energy
price decreases, and those biases would affect even the impact
responses.10
is correctly
estimated in Figure 4), the fact that the censored VAR model
misspecifies the first equation of the system causes both response
estimates to be inconsistent as the energy price shock is
propagated over time. The results in Figures 4 and 5 represent the
best possible scenario in that we postulated that only energy price
increases matter in the DGP. Additional asymptotic biases would
arise if the asymmetric DGP allowed for nonzero effects from energy
price decreases, and those biases would affect even the impact
responses.10
4. Eliminating the Asymptotic Bias: A General Model of the Oil Price-Economy Link
Up until now, we have imposed a strong form of asymmetry in
which energy price declines have no effect on the macro aggregate
of interest. In the interest of full generality, we now relax this
assumption by allowing for both energy price increases and
decreases to have an effect, but to a different extent.11 The
first equation of the resulting model is identical to the first
equation of a standard linear VAR in ![]() and
and
![]() but the second equation now
includes both
but the second equation now
includes both
Figure 4: Inconsistency of the Estimated Effect of Energy Price Increases on Outcome Variable - Asymmetric Structural Model DGP, Fitting Censored VAR Model
Notes: Simulations based on model (12) estimated on U.S. data. T=1,000,000.
Figure 5: Inconsistency of the Estimate of Energy Price Increases on Energy Price - Asymmetric Structural Model DGP, Fitting Censored VAR Model
Notes: The responses are for the real price of oil and the real price of gasoline. Simulations based on model (12) estimated on U.S. data. T=1,000,000.
![]() and
and ![]() and, as
such, both energy price increases and decreases affect
and, as
such, both energy price increases and decreases affect ![]()
|
|
[15] |
Given estimates of these coefficients, one can calculate the dynamic responses to unanticipated positive and negative energy price changes.12 Note that the OLS residuals of model (15) are uncorrelated, whereas the OLS residuals of model (12) may be correlated. This means that model (15) may be estimated by standard regression methods.
As illustrated in Figure 6, the key advantage of model (15) is that the dynamic responses are consistently estimated regardless of whether the true DGP is symmetric or asymmetric. We focus on the real GDP data to conserve space. Similar results hold for the other data sets. The response estimates of model (15) are consistent when the DGP is the standard linear VAR (see Figure 6a). In contrast, as was shown earlier, the response estimates of model (12) and of the censored VAR model do not converge to the population response in that case. Likewise, when the DGP is the asymmetric model (12), although response estimates based on the standard VAR model are asymptotically biased, the response estimates based on model (15) are consistent (see Figure 6b). Finally, Figure 6c illustrates that model (15) allows consistent estimation of the dynamic response to a negative shock in model (12). In short, the advantage of model (15) is that it may be used without knowing the nature of the DGP. Its only limitation is that the response estimates are not efficient asymptotically and that they may be slightly biased in finite samples because of the nonlinearity of the response function.
5. Computing Reponses to Energy Price Shocks in Nonlinear Models
So far we have followed the convention in the empirical literature on energy price shocks of computing impulse responses as one would for linear and symmetric VAR models. While this
Figure 6a: Estimating the Effect of an Energy Price Increase Using the General Model Symmetric VAR DGP
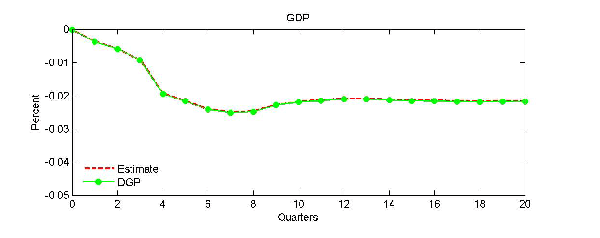
Figure 6b: Estimating the Effect of an Energy Price Increase Using the General Model Asymmetric Structural Model DGP
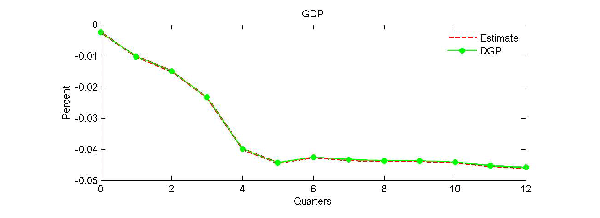
Figure 6c: Estimating the Effect of an Energy Price Decline Using the General Model Asymmetric Structural Model DGP
Notes: Simulations based on models estimated on U.S. data. T=1,000,000.
approach simplifies the computation of the responses from asymmetric models, it can be misleading in that the effect of a given shock in asymmetric models depends on the recent history of the series in question and on the magnitude of the shock. For example, the net effect of a negative innovation to energy prices on macroeconomic aggregates will depend on the extent to which the effect of this shock on energy prices is dampened or amplified by the cumulative effect of previous shocks. Thus, nonlinear impulse responses must be computed for a given shock as the average of impulse response draws obtained using alternative initial conditions. This point is well known (see, e.g., Gallant et al. 1993; Koop et al. 1996), but has been typically ignored in the literature on estimating the effects of energy price increases.
In this section we propose an adaption of methods for computing impulse responses from nonlinear models specifically designed for model (15).13Having estimated model (15), we proceed as follows:
Step 1 Take a block of p consecutive values of
![]() and
and ![]() . This defines
a history
. This defines
a history
![]() Note that the choice
of history does not affect the coefficients of the model. For all
histories, the model coefficients are fixed at their estimated
values.
Note that the choice
of history does not affect the coefficients of the model. For all
histories, the model coefficients are fixed at their estimated
values.
Step 2 Given
![]() , simulate two time
paths for
, simulate two time
paths for ![]() and
and ![]() for
i = 0, 1, ..., H. In generating the first time path,
the value of
for
i = 0, 1, ..., H. In generating the first time path,
the value of
![]() is equal to a
pre-specified value
is equal to a
pre-specified value ![]() . In generating the
other time path, the value of
. In generating the
other time path, the value of
![]() is drawn from the
marginal empirical distribution of
is drawn from the
marginal empirical distribution of
![]() . The value of
. The value of
![]() and the values of all
subsequent shocks
and the values of all
subsequent shocks
![]() and
and
![]() , i = 1, ...,
H, are drawn from their respective marginal distributions.
Since the structural errors
, i = 1, ...,
H, are drawn from their respective marginal distributions.
Since the structural errors
![]() and
and
![]() are by definition
uncorrelated, we treat the draws as independent in practice.
are by definition
uncorrelated, we treat the draws as independent in practice.
Step 3 Calculate the difference between the time paths
for ![]() i = 1, ..., H.
i = 1, ..., H.
Step 4 Average this difference across m=500 repetitions of Steps 2 and 3.
This average is the response of ![]() at
horizon i = 0,..., H, to a shock of size
at
horizon i = 0,..., H, to a shock of size ![]() conditional on
conditional on
![]() :
:
|
|
[16] |
The unconditional response
![]() is defined as
the value of
is defined as
the value of
![]() averaged
across all histories:
averaged
across all histories:
|
|
[17] |
Depending on the application, both the conditional response
![]() and the
unconditional response could be of potential interest. To determine
the general importance of oil shocks as a source of fluctuations,
the unconditional response is of most interest. Likewise, for the
evaluation of DSGE models the unconditional response is the most
appropriate object to match. In contrast, for forecasting and
policy purposes, the response conditional on current history is the
more relevant statistic. In the remainder of the paper, we will
focus on the unconditional response (17).
and the
unconditional response could be of potential interest. To determine
the general importance of oil shocks as a source of fluctuations,
the unconditional response is of most interest. Likewise, for the
evaluation of DSGE models the unconditional response is the most
appropriate object to match. In contrast, for forecasting and
policy purposes, the response conditional on current history is the
more relevant statistic. In the remainder of the paper, we will
focus on the unconditional response (17).
It is important to highlight the difference between the response in (17) and the impulse response functions typically computed in the literature on the transmission of oil price shocks. For this purpose, it is useful to introduce two alternative definitions of impulse responses to energy prices. For example,
|
|
[18] |
refers to the response obtained conditioning on a hypothetical
historical path involving
![]() for all i. Another
possible definition would be the response
for all i. Another
possible definition would be the response
|
|
[19] |
Upon integrating out across alternative histories, this expression simplifies to:
|
|
[20] |
The response most often reported in the empirical literature on energy price shocks is
![]() and may be
viewed as a combination of (18) and (20). That response
conditions neither on history nor does it allow for nonzero future
shocks.
and may be
viewed as a combination of (18) and (20). That response
conditions neither on history nor does it allow for nonzero future
shocks.
The time series literature on non-linear impulse responses has
favored
![]() over
over
![]() for at least
three reasons. First, the process of
for at least
three reasons. First, the process of
![]() may not
accurately characterize the true dynamics of a nonlinear system.
For example, Koop, Pesaran and Potter (1996, p. 125) observe that
may not
accurately characterize the true dynamics of a nonlinear system.
For example, Koop, Pesaran and Potter (1996, p. 125) observe that
![]() may not
converge to zero, even when the nonlinear stochastic DGP is
stationary. Second, Potter (2000) observes that the theoretical
treatment of nonlinear impulse responses is facilitated by treating
future shocks as random variables rather than fixed values. Third,
there is no intrinsic economic interest in any impulse response
that conditions on
may not
converge to zero, even when the nonlinear stochastic DGP is
stationary. Second, Potter (2000) observes that the theoretical
treatment of nonlinear impulse responses is facilitated by treating
future shocks as random variables rather than fixed values. Third,
there is no intrinsic economic interest in any impulse response
that conditions on
![]() .
.
One of the chief drawbacks of nonlinear impulse response analysis of the type considered by Koop et al. (1996) is that shocks cannot be defined unambiguously in the context of reduced-form models. The reason is that reduced-form regression errors are inevitably mutually correlated. In practice, researchers have resorted to presenting responses for representative draws from the joint distribution of the reduced-form errors (see, e.g., Balke et al. 2002; Herrera 2008). Such responses may be useful in characterizing the persistence of the data, but they are devoid of any economic interpretation. An attractive feature of the nonlinear impulse responses (16) and (17) that we defined above is that in the context of the structural models (12) and (15) an energy price shock is orthogonal to other shocks and uniquely defined (up to scale). This fact addresses the chief limitation of nonlinear impulse responses as discussed in Koop et al.
How the impulse response is computed directly affects the
magnitude of the estimated response. As shown in Figure 7, in the
context of our example,
![]() is much smaller
in absolute value than
is much smaller
in absolute value than
![]() . The value of
. The value of
![]() is more
comparable to the response to a very large shock in excess of ten
standard deviations. In other words, even if the regression model
were correctly specified and hence the parameter estimates were
consistent, the use of traditional impulse response functions would
greatly exaggerate the effect of a positive oil price shock. This
finding reinforces our earlier concern with the methods underlying
the existing literature. To help us understand these results, below
we provide a more in-depth analysis of the impact responses. We
show that, as
is more
comparable to the response to a very large shock in excess of ten
standard deviations. In other words, even if the regression model
were correctly specified and hence the parameter estimates were
consistent, the use of traditional impulse response functions would
greatly exaggerate the effect of a positive oil price shock. This
finding reinforces our earlier concern with the methods underlying
the existing literature. To help us understand these results, below
we provide a more in-depth analysis of the impact responses. We
show that, as ![]() increases, the importance of
accounting for the history
increases, the importance of
accounting for the history
![]() and of accounting for
the variability of
and of accounting for
the variability of
![]() declines. In other
words,
declines. In other
words,
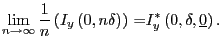
Figure 7: The Response of GDP to a Positive Energy Price Shock by Shock Size
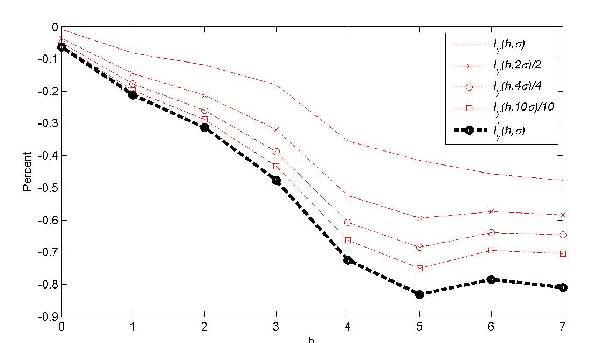
Notes:
![]() is calculated
by Monte Carlo integration over 300 histories with 10,000 paths
each. All impulse responses have been scaled (as denoted in the
legend) to ensure compatibility. h denotes the horizon.
is calculated
by Monte Carlo integration over 300 histories with 10,000 paths
each. All impulse responses have been scaled (as denoted in the
legend) to ensure compatibility. h denotes the horizon.
Impact Response of
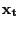
Because of the linear nature of the first equation in model
(15), the impact
effect on ![]() of a shock of size
of a shock of size ![]() will be a constant:
will be a constant:
|
|
[21] |
Impact Response of 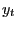
The impact effect of
![]() on
on ![]() for a given history
for a given history
![]() is
is
|
|
[22] |
The term
![]() plays a central role in the construction of nonlinear impulse
responses for
plays a central role in the construction of nonlinear impulse
responses for
![]() h = 1, ...,
H. Absent uncertainty about the value of
h = 1, ...,
H. Absent uncertainty about the value of
![]() , the value of
, the value of
![]() would be easy to calculate. In particular, consider the value
of
would be easy to calculate. In particular, consider the value
of
![]() where, for ease of notation, we define
where, for ease of notation, we define
|
|
[23] |
Here
![]() summarizes the effect of the history
summarizes the effect of the history
![]() on
on ![]() . For
. For ![]() , then
, then
|
|
[24] |
Computing the value of
![]() is more of a challenge because we need to account for uncertainty
about
is more of a challenge because we need to account for uncertainty
about
![]() . With uncertainty, we
have that
. With uncertainty, we
have that
|
|
[25] |
The value of
![]() depends on the variance of the shocks. Note that
depends on the variance of the shocks. Note that
![]() can be positive even if
can be positive even if
![]() is
negative. In fact, by Jensen's inequality,
is
negative. In fact, by Jensen's inequality,
![]() for all values of
for all values of
![]() . In
particular, if
. In
particular, if
![]() equals zero and
equals zero and
![]() has a standard normal
distribution then
has a standard normal
distribution then
![]() has a value of 0.4. Hence, when
has a value of 0.4. Hence, when
![]() and
and
![]() has a standard normal
distribution, we have that
has a standard normal
distribution, we have that
|
|
[26] |
This first result implies that the larger ![]() the smaller the effect of incorrectly treating
the smaller the effect of incorrectly treating
![]() as equal to zero under
the counterfactual path, relative to magnitude of the impulse
response. In other words, all else equal, the larger
as equal to zero under
the counterfactual path, relative to magnitude of the impulse
response. In other words, all else equal, the larger ![]() the more similar the traditional incorrectly
computed impulse response and the correctly computed unconditional
response will be. This point is important because most energy price
innovations measured at the monthly or quarterly frequency tend to
be quite small (e.g. Edelstein and Kilian 2007a). We conclude that
traditional, incorrectly computed impulse responses will tend to
exaggerate the effect of an unanticipated energy price
increase.
the more similar the traditional incorrectly
computed impulse response and the correctly computed unconditional
response will be. This point is important because most energy price
innovations measured at the monthly or quarterly frequency tend to
be quite small (e.g. Edelstein and Kilian 2007a). We conclude that
traditional, incorrectly computed impulse responses will tend to
exaggerate the effect of an unanticipated energy price
increase.
Figure 8a illustrates this point under the assumption that
![\begin{displaymath}\left( \begin{array}[c]{c} {\varepsilon}_{1,t}\ {\varepsilon}_{2,t} \end{array}\right) \sim N\left( \left( \begin{array}[c]{c} 0\ 0 \end{array}\right) ,\left( \begin{array}[c]{cc} {\sigma}^{2}_{1} & 0\ 0 & {\sigma}^{2}_{2} \end{array}\right) \right) \end{displaymath}](img229.gif)
The horizontal axis shows alternative representations of
![]() representing alternative histories. Note that the difference
between the response computed by correctly accounting for the
uncertainty of
representing alternative histories. Note that the difference
between the response computed by correctly accounting for the
uncertainty of
![]() and the incorrectly
computed response obtained from treating
and the incorrectly
computed response obtained from treating
![]() as fixed declines, as
as fixed declines, as
![]() increases, for all possible histories
increases, for all possible histories
![]()
Figure 8a:
![]()
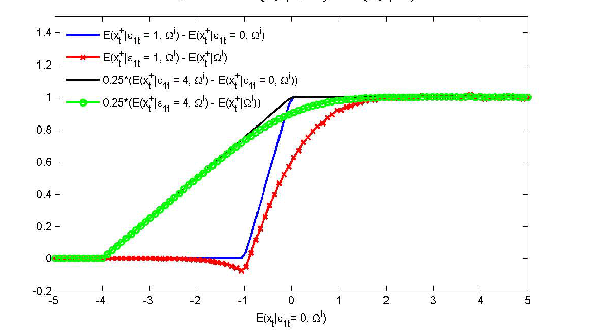
Figure 8b:
![]()
Our second point is that
![]() becomes less sensitive to
becomes less sensitive to
![]() as
as
![]() increases. Figure 8b illustrates this
relationship. As
increases. Figure 8b illustrates this
relationship. As ![]() increases, the importance of
the history
increases, the importance of
the history
![]() declines, and the magnitude of the impulse responses becomes
constant across alternative histories. The reduced importance of
the histories can be explained by the following limit argument:
declines, and the magnitude of the impulse responses becomes
constant across alternative histories. The reduced importance of
the histories can be explained by the following limit argument:
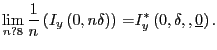
This result relies on three observations. First, note that
![]() Second,
Second,
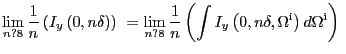
In addition, observe that
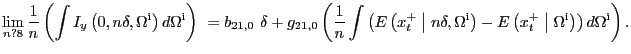
To complete the proof we need to show that
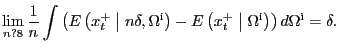
Recall that by definition
![]() Therefore,
Therefore,
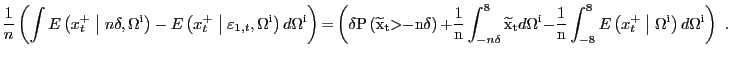
As long as
![]() does
not have too much mass in the left tail and the variance of
does
not have too much mass in the left tail and the variance of
![]() is small enough such
that
is small enough such
that
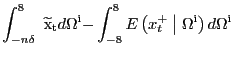
remains finite, it follows that
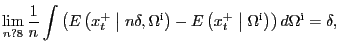
finite.
We conclude that the impulse response
![]() can be
thought of as the scaled version of the response to a very large
shock of the form
can be
thought of as the scaled version of the response to a very large
shock of the form
![]() . Hence,
for sufficiently large energy price shocks, one would expect that
the importance of
. Hence,
for sufficiently large energy price shocks, one would expect that
the importance of
![]() diminishes such that
the impulse response used in the existing VAR literature becomes a
good approximation to the correctly constructed estimate, as
illustrated in Figure 7. For smaller (and more typical) energy
price shocks, however, such as a one standard deviation increase in
diminishes such that
the impulse response used in the existing VAR literature becomes a
good approximation to the correctly constructed estimate, as
illustrated in Figure 7. For smaller (and more typical) energy
price shocks, however, such as a one standard deviation increase in
![]() , the interaction of the
innovation in the price of energy with the history
, the interaction of the
innovation in the price of energy with the history
![]() will be
quantitatively important. That is why traditional VAR impulse
responses may be quite different from the correctly computed
nonlinear responses in practice.
will be
quantitatively important. That is why traditional VAR impulse
responses may be quite different from the correctly computed
nonlinear responses in practice.
6. Testing Symmetry in Energy Price Increases and Decreases
The preceding sections have shown that the presence of asymmetries considerably complicates the econometric analysis of the transmission of positive energy price shocks. While model (15) may be used to sidestep the question of whether the model in question is asymmetric or not, this involves a cost in terms of asymptotic efficiency. Clearly, a linear symmetric VAR model would be preferable if we could convince ourselves that the DGP is symmetric. This raises the question of how to test the symmetry null hypothesis. We first discuss the case of testing for symmetry between energy price increases and decreases before adapting these tests to the problem of testing models of net energy price increases.
6.1. Slope-Based Tests
If energy price increases and decreases received exactly the
same weight in regressions of ![]() on lagged
on lagged
![]() and current and lagged
and current and lagged ![]() and
and ![]() , it would follow
immediately that the dynamic responses to energy price shocks must
be symmetric in positive and negative shocks. This line of
reasoning has motivated the development of slope-based tests of
symmetry. Such tests are attractive in that they do not require the
complete specification of the system to be estimated nor do they
require the computation of impulse responses.
, it would follow
immediately that the dynamic responses to energy price shocks must
be symmetric in positive and negative shocks. This line of
reasoning has motivated the development of slope-based tests of
symmetry. Such tests are attractive in that they do not require the
complete specification of the system to be estimated nor do they
require the computation of impulse responses.
The traditional approach to testing for symmetry in the transmission of energy price
shocks involves tests on the symmetry of the slope coefficients
in regressions of ![]() on lagged
on lagged
![]() and
and
![]() (see, e.g. Mork 1989). This is
equivalent to testing
(see, e.g. Mork 1989). This is
equivalent to testing
![]()
in model (15).
This may be accomplished by a Wald test with an asymptotic
![]() -distribution. Closer
inspection of model (15) reveals that
this test does not exploit all restrictions implied by the null
hypothesis of symmetry. Specifically, Mork's test omits the
contemporaneous regressor because he works with the reduced form. A
test of all symmetry restrictions on the slopes would involve the
null hypothesis:
-distribution. Closer
inspection of model (15) reveals that
this test does not exploit all restrictions implied by the null
hypothesis of symmetry. Specifically, Mork's test omits the
contemporaneous regressor because he works with the reduced form. A
test of all symmetry restrictions on the slopes would involve the
null hypothesis:
![]()
Hence, our proposal is that we estimate model (15) and use a Wald
Test to determine whether including
![]() improves the fit of the model. This test has an asymptotic
improves the fit of the model. This test has an asymptotic
![]() -distribution.
-distribution.
It is useful to compare the power properties of Mork's (1989) test with those of the modified slope-based test implied by the structural model (15). Tables 3 and 4 summarize the results from some Monte Carlo experiments. The size results are based on a DGP obtained by fitting the three empirical models under the assumption of symmetric responses. We simulate data under the null assumption of symmetry and report the relative frequency at which the Wald Test rejects the null hypothesis of symmetry. In assessing the power, we follow a similar strategy. We first estimate the equations
|
|
[27] |
by OLS to obtain the parameter values for the DGP. The artificial data are then generated from
|
[28] |
where
![]()
![]() {0.25,0.5,1,2,4}
controls the degree of asymmetry in the population response. The
larger is
{0.25,0.5,1,2,4}
controls the degree of asymmetry in the population response. The
larger is ![]() , the more asymmetric is the DGP
response. All simulations are based on the
, the more asymmetric is the DGP
response. All simulations are based on the
Table 3: Modified Slope Test: Rejection Rates of the 5 Percent Test for Asymmetric Coefficients
| Size | Power: |
Power: |
Power: |
Power: |
Power: |
|
|---|---|---|---|---|---|---|
| Unemployment | 0.07 |
0.08 |
0.14 |
0.43 |
0.97 |
1.00 |
| Gas Consumption | 0.07 |
0.09 |
0.18 |
0.62 |
1.00 |
1.00 |
| Real GDP | 0.11 |
0.14 |
0.19 |
0.45 |
0.96 |
1.00 |
Notes:
In all cases, the data sets are generated to have the same number
of observations as the original data. Critical Values are from the
![]() -distribution. The value of
-distribution. The value of
![]() scales
scales ![]() i = 0, ..., p, by a fixed factor and determines the
degree of asymmetry of the population response.
i = 0, ..., p, by a fixed factor and determines the
degree of asymmetry of the population response.
Table 4: Mork's (1989) Test: Rejection Rates of the 5 Percent Test for Asymmetric Coefficients
| Size | Power: | Power: | Power: | Power: | Power: | |
|---|---|---|---|---|---|---|
| Unemployment | 0.06 |
0.07 |
0.09 |
0.21 |
0.66 |
0.99 |
| Gas Consumption | 0.07 |
0.09 |
0.17 |
0.57 |
1.00 |
1.00 |
| Real GDP | 0.10 |
0.12 |
0.18 |
0.42 |
0.94 |
1.00 |
Notes:
In all cases, the data sets are generated to have the same number
of observations as the original data. Critical Values are from the
![]() -distribution. The value of
-distribution. The value of
![]() scales
scales ![]() i = 0, ..., p, by a fixed factor and determines the
degree of asymmetry of the population response.
i = 0, ..., p, by a fixed factor and determines the
degree of asymmetry of the population response.
assumption of Gaussian innovations.
Table 3 shows that, for the monthly applications, the Wald tests are quite accurate under the null. For the quarterly application, there is a modest size distortion, reflecting the smaller quarterly sample size. It is likely that one could reduce these size distortions by using bootstrap methods. Table 4 shows the corresponding results for Mork's slope-based test. A comparison of the results in Tables 3 and 4 suggests that the two tests have similar size but the fully specified symmetry test tends to have higher power than Mork's test. The power gains of the correctly specified test may be substantial. In one case the power more than doubles.
While slope based tests are useful in assessing the symmetry of the slope parameters of single-equation reduced form models, they are not obviously informative about the degree of symmetry of the impulse response function obtained from a fully specified model. There are two possible outcomes when conducting slope-based tests. If the test rejects symmetry, that is sufficient for concluding that the impulse responses are asymmetric, but it does not tell us whether the departures from symmetry are economically or statistically significant. Given that impulse response functions are highly nonlinear functions of the slope parameters and innovation variances it is quite conceivable that the degree of asymmetry in the impulse responses to positive and negative energy price shocks could be quite small, making responses based on the linear model a good approximation, despite the statistical rejection. Moreover, the quality of the linear approximation will differ depending on the magnitude of the shock. For that reason, the applied user will want to plot the point estimates of the impulse response functions and inspect them.
If the test fails to reject symmetry, on the other hand, we again learn little because statistically insignificant departures from symmetry in the slopes may cause large and statistically significant asymmetries in the implied impulse response functions, given the nonlinearity of these functions. This observation suggests that a more useful approach would be to test the symmetry of the economy's dynamic responses to unanticipated energy price increases and decreases directly based on the impulse response functions (also see Edelstein and Kilian 2007a,b). This alternative approach to testing symmetry is discussed next.
Note that what is at issue in conducting this impulse-response-based test is not the existence of asymmetries in the reduced form parameters, but the question of whether possible asymmetries in the reduced form imply significant asymmetries in the impulse response function. While any asymmetry in the reduced form representation (whether statistically significant or not) will imply some degree of asymmetry in the impulse response function, the question is whether the impulse responses constructed from linear symmetric VAR models still provide a good approximation.
6.2. Impulse-Response Based Tests
The proposal is that we estimate the unrestricted model (15) and calculate the unconditional impulse responses to both positive and negative energy price shocks. Then we construct a
Wald test of the joint null hypothesis of symmetric responses to positive and negative energy
price shocks up to a pre-specified horizon H. Symmetry means that
![]()
or equivalently
![]()
The variance covariance matrix of the vector sum of response
coefficients can be estimated by bootstrap simulation. Given the
asymptotic normality of the parameter estimators of model (15), the test has
an asymptotic
![]() -distribution.
-distribution.
Unlike the slope-based test, this test depends on the magnitude
of ![]() , so the evidence against symmetry
will depend on the magnitude of the shock considered. For small
shocks, a symmetric model will provide a better approximation than
for large shocks. How accurate and powerful the impulse-response
based test is relative to the slope-based test is an empirical
question. Table 5 reports the size properties for tests of the
symmetry of the impulse responses. Table 5 shows that, for our
examples, these tests have acceptable size properties, despite a
slight tendency for the test to overreject, as the horizon
increases.
, so the evidence against symmetry
will depend on the magnitude of the shock considered. For small
shocks, a symmetric model will provide a better approximation than
for large shocks. How accurate and powerful the impulse-response
based test is relative to the slope-based test is an empirical
question. Table 5 reports the size properties for tests of the
symmetry of the impulse responses. Table 5 shows that, for our
examples, these tests have acceptable size properties, despite a
slight tendency for the test to overreject, as the horizon
increases.
7. Empirical Tests of Symmetry in Energy Price Increases and Decreases
In this section, we use the two statistical tests discussed in section 6 to check for asymmetry in the empirical responses to energy price shocks. Table 6 shows that the evidence for asymmetry in the slope coefficients is weak. The p-values suggest no evidence against symmetry at the 10% significance level in monthly U.S. unemployment rates, in quarterly U.S. real GDP, and for U.S. gasoline. The same qualitative result, but with higher p-values, would be obtained using Mork's test. An important question is whether these empirical results are sensitive to the choice of lag order. Our baseline results rely on six lags. Table 7 shows that only for gasoline consumption are the p-values sensitive to the lag order. As the lag order of the model exceeds six lags, we find rejections of the symmetry null hypothesis at the 5% level.
In general, there is a tendency for the p-values to decline with the addition of more lags.
This reflects the fact that the
![]() distribution becomes a less
accurate approximation under the null, as illustrated in Table 8.
Table 8 shows that, in the presence of excess lags, the size
systematically increases from 6% to almost 10% for the monthly
models and from near 9% to 28% for the quarterly model. These size
distortions from overfitting help explain the general
distribution becomes a less
accurate approximation under the null, as illustrated in Table 8.
Table 8 shows that, in the presence of excess lags, the size
systematically increases from 6% to almost 10% for the monthly
models and from near 9% to 28% for the quarterly model. These size
distortions from overfitting help explain the general
Table 5: Size of the 5 Percent Test of
![]()
| Gas Consumption: 1 Std. Deviation Shock | Gas Consumption: 2 Std. Deviation Shock | GDP: 1 Std. Deviation Shock | GDP: 2 Std. Deviation Shock | Unemployment: 1 Std. Deviation Shock | Unemployment: 2 Std. Deviation Shock | |
|---|---|---|---|---|---|---|
| H | ||||||
| 1 | 0.06 |
0.05 |
0.06 |
0.05 |
0.06 |
0.05 |
| 3 | 0.07 |
0.05 |
0.07 |
0.05 |
0.07 |
0.05 |
| 5 | 0.08 |
0.05 |
0.08 |
0.06 |
0.07 |
0.05 |
| 7 | 0.09 |
0.07 |
0.10 |
0.07 |
0.09 |
0.07 |
Notes:
The data sets are generated to have the same number of observations
as the original data. All results based on 20,000 simulations from
the linear VAR DGP. Impulse responses based on an average of 90
histories. Significance levels are based on the
![]() distribution.
distribution.
Table 6: Empirical Symmetry Tests: Baseline Model
| Variable | The Modified Test of Symmetric Slope Coefficients | Marginal Significance Level | Mork's Test of Symmetric Slope Coefficients | Marginal Significance Level |
|---|---|---|---|---|
| Unemployment | 7.7224 | 0.358 | 3.1317 | 0.792 |
| Gas Consumption | 11.3755 | 0.123 | 9.2366 | 0.161 |
| Real GDP | 10.4722 | 0.163 | 9.7565 | 0.135 |
Table 7: Marginal Significance Levels for the Modified Slope-Based Symmetry Test
| Number of lags | 2 | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| Unemployment | 0.188 | 0.349 | 0.534 | 0.681 | 0.657 | 0.359 |
| Gas Consumption | 0.191 | 0.172 | 0.156 | 0.008 | 0.022 | 0.014 |
| Real GDP | 0.523 | 0.631 | 0.412 | 0.258 | 0.233 | 0.239 |
Notes:
p-values are from the
![]() distribution. Sample size
chosen so that the estimation period is the same, regardless of the
number of lags. The results may differ slightly from Table 6 given
the difference in sample periods.
distribution. Sample size
chosen so that the estimation period is the same, regardless of the
number of lags. The results may differ slightly from Table 6 given
the difference in sample periods.
decline of the p-values with increasing numbers of lags in Table 7 but do not explain the rapid drop in the p-values for gasoline consumption beyond lag 6.
Table 8: Size of the 5% Test of
![]() : DGP with 4 Lags
: DGP with 4 Lags
| Number of lags in regression model | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|
| Unemployment | 0.060 | 0.065 | 0.074 | 0.084 | 0.095 |
| Gas Consumption | 0.060 | 0.065 | 0.072 | 0.081 | 0.094 |
| Real GDP | 0.085 | 0.117 | 0.157 | 0.214 | 0.282 |
Notes: p-values are from the
![]() distribution. Sample size
chosen so that the estimation period is the same, regardless of the
number of lags.
distribution. Sample size
chosen so that the estimation period is the same, regardless of the
number of lags.
Even strong rejections of symmetry based on the slope-based
test, however, need not imply large degrees of asymmetry in the
impulse responses of ultimate interest, as discussed earlier. This
point is illustrated in Figure 9. The difference between
![]() and
and
![]() tends to
be quite small when 12 lags are included in the regression model.
This example suggests that we can never rely on slope-based
symmetry tests alone. This point holds with equal force if the
slope-based symmetry test fails to reject. Even statistically
insignificant departures from symmetry in the slope parameters may
imply highly economically and statistically significant departures
from symmetry in the impulse response functions. Thus, it makes
sense to focus on direct tests of the symmetry of these
responses.
tends to
be quite small when 12 lags are included in the regression model.
This example suggests that we can never rely on slope-based
symmetry tests alone. This point holds with equal force if the
slope-based symmetry test fails to reject. Even statistically
insignificant departures from symmetry in the slope parameters may
imply highly economically and statistically significant departures
from symmetry in the impulse response functions. Thus, it makes
sense to focus on direct tests of the symmetry of these
responses.
Table 9 reports the corresponding tests of the symmetry of the impulse response functions for the baseline model with six lags. Neither for U.S. real GDP nor for unemployment is there statistically significant evidence against the symmetry of the functions.14 For gasoline consumption, the results are mixed. Whereas there is no evidence against symmetry based on
Figure 9: The Response of Gas Consumption to a One Standard Deviation Energy Price Shock - Model with 12 Lags
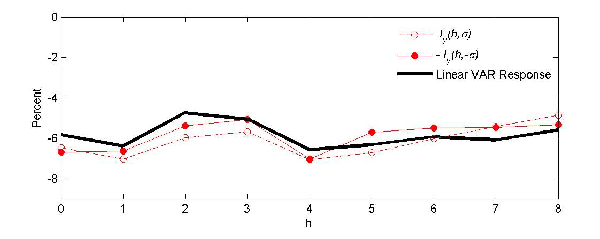
two-standard deviation shocks, based on one standard-deviation
shocks the test rejects the null hypothesis of symmetry at the 5%
level at one horizon and at the 10% level at several additional
horizons. The evidence against symmetry appears stronger than that
based on the slope-based test. However, as shown in Figure 10,
which reports
![]() and
and
![]() the
the
Table 9:
Testing the Symmetry of the Response
![]()
| Gas Consumption: 1 Std. Deviation Shock | Gas Consumption: 2 Std. Deviation Shock | GDP: 1 Std. Deviation Shock | GDP: 2 Std. Deviation Shock | Unemployment: 1 Std. Deviation Shock | Unemployment: 2 Std. Deviation Shock | |
|---|---|---|---|---|---|---|
| H | ||||||
| 0 | 0.45 | 0.47 | 0.40 | 0.47 | 0.36 | 0.43 |
| 1 | 0.13 | 0.28 | 0.44 | 0.54 | 0.65 | 0.73 |
| 2 | 0.05 | 0.15 | 0.59 | 0.69 | 0.83 | 0.88 |
| 3 | 0.09 | 0.25 | 0.56 | 0.68 | 0.92 | 0.96 |
| 4 | 0.07 | 0.21 | 0.66 | 0.78 | 0.97 | 0.98 |
| 5 | 0.04 | 0.15 | 0.78 | 0.87 | 0.99 | 1.00 |
| 6 | 0.06 | 0.18 | 0.48 | 0.59 | 1.00 | 1.00 |
| 7 | 0.09 | 0.26 | 0.58 | 0.69 | 1.00 | 1.00 |
Notes:
Based on 20,000 simulations of model (15).
p-values are based on the
![]() distribution.
distribution.
actual difference between these two responses seems fairly small, and one would be hard pressed to make the case for using the asymmetric model on economic grounds.
Figure 10: The Response of Gas Consumption to a One Standard Deviation Energy Price Shock - Baseline Model with 6 Lags
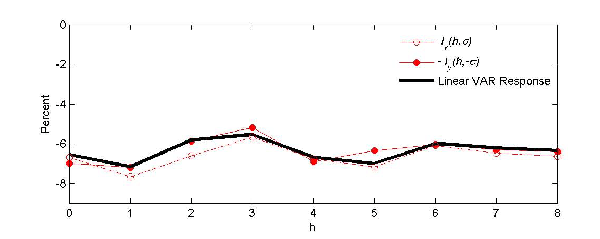
actual difference between these two responses seems fairly small, and one would be hard pressed to make the case for using the asymmetric model on economic grounds.
8. Testing Symmetry Based on Models of Net Energy Price Increases
As noted in the introduction much of the recent empirical work in the transmission of oil price shocks has focused on the net increase in the price of oil as defined in Hamilton (1996, 2003). For example, Lee and Ni (2002, p. 834) note that the "oil price variable [in their VAR] is Hamilton's (1996) 'net oil price increase', defined as the percentage change of oil price over the maximum value of the preceding year if the price of the current month exceeds the previous year's maximum, and zero otherwise." Likewise, Bernanke et al.'s (1997, p. 104) VAR analysis relies as the main measure of oil price shocks on Hamilton's measure which "equals the maximum of (a) zero and (b) the difference between the log-level of the crude oil price for the current month and the maximum value of the logged crude oil price achieved in the previous twelve months". Similar net oil price increase measures have also been used by Davis and Haltiwanger (2001), Lee and Ni (2002), and Hamilton and Herrera (2004), among others.
Given the widespread use of the net oil price increase measure in applied VAR work, it is important to assess the empirical support of that model. Hamilton (2003) proposed a formal test based on the conditional expectation function of the linear symmetric model against the alternative of a model in which only net increases matter. Rather than specifying the structural model of interest, Hamilton focused on single-equation predictive relationships in the data. His statistical evidence against the null hypothesis of linearity in the one-step-ahead predictive relationship between real GDP growth and changes in oil prices by construction implies that the underlying DGP must be asymmetric as well. Hamilton compared several nonlinear predictive models and concluded that a conditional expectations model based on the three-year net increase measure had the most predictive power one quarter ahead.
It is important to keep in mind, first, that the model Hamilton investigated differs from the VAR models estimated in the literature on estimating responses to energy price shocks such as Bernanke et al. (1997). Even if we take Hamilton's results about the existence of a nonlinear reduced-form relationship involving net oil price increases at face value, these results do not justify the use of censored VAR models of the form
|
|
where a is estimated by the Cholesky factorization of the variance covariance matrix of the reduced-form residuals. For the reasons discussed earlier, the structural models that would give rise to such asymmetries in the reduced form cannot be represented as VAR models. Using the data of the unemployment rate example, the response to a one standard deviation shock implied by the incorrectly specified net increase VAR model, as estimated in the literature, is effectively equivalent to a four standard deviation shock in the correctly specified net increase model. Similar results hold for the other two empirical examples.
Second, Hamilton's work leaves unanswered the question of how much the response of real GDP to an exogenous oil price innovation is affected by the nonlinearity of the DGP relative to the linear case. Even if there is an asymmetry in the slope parameters of the reduced form, that asymmetry need not have large effects on the implied impulse response function. We will illustrate that point below. Moreover, the extent to which responses from a linear symmetric VAR model provide a good approximation will be a function of the size of the energy price
shock. Answering that question requires a fully specified multivariate structural model.15
In closely related work, Balke, Brown and Yücel (2002) conducted an alternative test of the net increase model based on the slope parameters of regressions of real GDP growth on lagged real GDP growth, lagged oil price changes and lagged net oil price increases. Like Hamilton, they concluded that the inclusion of net oil price increases improves the predictive power of this model. Unlike Hamilton, they explicitly recognized the need for a multivariate structural model in constructing estimates of the impulse response functions and they observed, consistent with our analysis, that such models do not have a VAR representation. Balke et al. also recognized the importance of accounting for the nonlinear nature of the model in constructing impulse responses. While the description of their algorithm is terse and incomplete, their approach in many ways appears substantively identical with the procedure that we propose below. The key difference is that they simulate responses to shocks drawn from the joint distribution of reduced-form errors, as suggested by Koop et al. (1996), whereas we simulate shocks drawn from the marginal distribution of the structural errors of the model.
Moreover, with the exception of a not-for-publication appendix in Herrera (2008), no paper in the large empirical VAR literature on the asymmetric transmission of energy price shocks has adopted their proposal. Applied users have continued to employ incorrectly specified VAR models and have computed the model impulse responses incorrectly as though the model were linear. A likely reason is that Balke et al. do not elaborate on the limitations of commonly used asymmetric VAR models beyond observing that this "specification is not completely suitable for an examination of asymmetry". For that reason, we believe that it is important to restate the basic points made in Balke et al. and to do so more explicitly. Our proposal refines their approach by focusing attention on the economically more relevant structural energy price innovations. In addition, we will take their analysis a step further by proposing an explicit test of the symmetry of the impulse response functions.
As discussed below, our empirical conclusions are somewhat different from Balke et al.
(2002). Whereas Balke et al. found some evidence in favor of asymmetries in output, we do not. There are several differences between their analysis and ours. First, we focus on the more relevant measure of net increases in the real price of oil (rather than the nominal price). Second, we have the advantage of a longer time span of data from the empirically relevant post-1972 period. The key difference, however, is in the econometric analysis. Like us, Balke et al. found little evidence of asymmetries based on one standard deviation shocks, notwithstanding the rejection of symmetry in the reduced-form slopes. In the published version of their paper they concentrated exclusively on two standard deviation shocks which are much rarer in practice (and hence less precisely estimated). While increasing the shock size indeed increases the apparent degree of asymmetry in the response functions, for the reasons we discussed earlier, it also increases the uncertainty surrounding those estimates because there are fewer episodes of large oil price changes in the data. This makes it essential to conduct a formal joint test of the symmetry of the impulse response functions of the type proposed below. Based on that test, we find very little evidence against the linear symmetric model for shocks of typical magnitude in general and no evidence at all for real GDP. Moreover, our structural impulse response point estimates appear much more symmetric than their real GDP response estimates.
8.1. Slope-Based Symmetry Tests for the Net Increase Model
In this section, we outline two tests of the net increase model, building on the analysis in
section 4. Rather than testing the null hypothesis of symmetry
between net oil price decreases and net oil price increases, as in
Edelstein and Kilian (2007a), we nest the net increase model in the
standard linear symmetric VAR model. In essence, we ask whether
there is incremental explanatory power in including net oil price
increases in the baseline model. This results in a model structure
similar to model (15) with
![]() replaced by
replaced by
![]() where
where
![]() and
and
![]() is the maximum of
is the maximum of ![]() over the preceding year (or three years,
alternatively), following Hamilton (1996, 2003). We follow Kilian
(2008c) in specifying the net increase in the real price of oil
rather than the nominal price as in Hamilton (1996, 2003) because
the real price is the economically relevant measure of the price of
oil. This does affect the time path of the net increase variable,
as documented in Kilian (2008c), but is more consistent with the recent empirical literature.
over the preceding year (or three years,
alternatively), following Hamilton (1996, 2003). We follow Kilian
(2008c) in specifying the net increase in the real price of oil
rather than the nominal price as in Hamilton (1996, 2003) because
the real price is the economically relevant measure of the price of
oil. This does affect the time path of the net increase variable,
as documented in Kilian (2008c), but is more consistent with the recent empirical literature.
The problems with the use of net oil price increase measures in VAR models are fundamentally the same as with the use of oil price increase measures and can be addressed along similar lines. By analogy to the discussion in section 4 the structural model
|
|
[29] |
may be estimated consistently by least squares. Note that model
(30) also allows
us to compute impulse response functions taking account of the
magnitude and direction of the innovation
![]() as well as the history
of observations, whereas the shock in the commonly used censored
VAR model is not well defined.
as well as the history
of observations, whereas the shock in the commonly used censored
VAR model is not well defined.
In assessing the evidence for this structural net increase model, a natural starting point is the slope-based test:
![]()
based on (30].This test relates to the test conducted in Balke et al. (2002) as the slope-based test in section 6.1 relates to Mork's tests of symmetry. The only difference to the analysis in Balke et al. is the additional inclusion of contemporaneous regressors. In all cases, the null model is the linear symmetric VAR model. Table 10 suggests that there is no evidence of asymmetries using the one-year net increase measure, but using the three-year net increase measure the symmetry test rejects at the 5% level for gasoline consumption and real GDP.
Figure 11 once again illustrates that slope-based tests are of limited use in that they are not informative about the degree of asymmetry in the impulse response functions. We focus on the three-year net increase. Results for the one-year net increase are very similar. Figure 11 shows that correctly computed impulse responses from model (30) for one standard deviation shocks are almost perfectly symmetric in all three models.16 Thus, despite the partial rejection
Table 10: Slope-Based Test of the Linear Symmetric VAR Model against the Net Increase VAR - Model: Baseline Model with 6 Lags
| Variable | 1-Year Net Increase: Test of Linear Symmetric Model | 1-Year Net Increase: Marginal Significance Level | 3-Year Net Increase: Test of Linear Symmetric Model | 3-Year Net Increase: Marginal Significance Level |
|---|---|---|---|---|
| Unemployment | 10.5099 | 0.162 | 9.6332 | 0.210 |
| Gas Consumption | 9.8879 | 0.195 | 14.5307 | 0.043 |
| Real GDP | 7.2617 | 0.402 | 14.2965 | 0.046 |
of the hypothesis of symmetric slopes in Table 10, there is no compelling reason to depart from the linear symmetric model when dealing with shocks of typical magnitude.
Broadly similar results hold for two standard deviation shocks with the glaring exception of the unemployment rate model. Ironically, the unemployment rate model was the one model that passed all slope-based tests of symmetry, highlighting the importance of actually computing the impulse response functions. In contrast, the other point estimates look fairly symmetric. Although the response of real GDP to a positive two standard deviation shock is somewhat larger in absolute terms than the response to a negative shock of this magnitude, both responses are clearly negative and have a similar pattern. In the gasoline consumption model, the symmetry of the two response functions is even more pronounced.
8.2. An Impulse-Response Based Symmetry Test for the Net Increase Model
It may be tempting to decide the question of symmetry based on the estimates of the impulse response functions in Figure 11. Figure 11 underscores that there is no reason to question the symmetry assumption for shocks of typical magnitude. For two standard deviation shocks the evidence is less clear, however, especially in the unemployment example. Because the point estimates in Figure 11 are subject to considerable sampling uncertainty, especially when considering large energy price shocks, it is useful to conduct a formal test of the linear
Figure 11: Empirical Responses to One and Two Standard Deviation Positive and Negative Energy Price Shocks in Baseline Model with 6 Lags: 3-Year Net Increase

Notes: The responses to negative shocks are shown as mirror images to facilitate the comparison. Some of the responses in the left panel are nearly invisible because the responses are almost perfectly symmetric.
symmetric model based on the impulse response functions implied
by model (30).
As in section 7.1, the test is based on
![]() .17 Table 11 shows that, as expected,
the p-values decline with the magnitude of the shock. At
conventional significance levels, there is no evidence against the
symmetry null hypothesis in any of the three empirical examples in
response to a one standard deviation shock, whether we focus on the
one-year or the three-year net changes. The same results hold in
response to a two standard deviation shock when using the
three-year net changes. Similar results also hold for the one-year
net changes with the partial exception of the unemployment rate at
very short horizons. We conclude that there is
very little, if any, evidence of asymmetric responses to energy
price increases and decreases. In particular, there is no such
evidence for U.S. real GDP.
.17 Table 11 shows that, as expected,
the p-values decline with the magnitude of the shock. At
conventional significance levels, there is no evidence against the
symmetry null hypothesis in any of the three empirical examples in
response to a one standard deviation shock, whether we focus on the
one-year or the three-year net changes. The same results hold in
response to a two standard deviation shock when using the
three-year net changes. Similar results also hold for the one-year
net changes with the partial exception of the unemployment rate at
very short horizons. We conclude that there is
very little, if any, evidence of asymmetric responses to energy
price increases and decreases. In particular, there is no such
evidence for U.S. real GDP.
The evidence in Table 11 is based on a model that rules out
responses to net decreases, but there is no compelling a priori
reason that the economy is not responding to net decreases in
energy prices as well, especially since the motivation for this
model is behavioral rather than being grounded in economic theory.
We explore this possibility by augmenting model (30) with lags of
net decreases in energy prices. The corresponding results are not
shown to conserve space but can be summarized as follows: For
gasoline consumption there is no evidence against the symmetry null
hypothesis using the three-year window, whether the energy price
shock is small or large. Using the one-year window, the test fails
to reject symmetry in response to small shocks but rejects in
response to large shocks. Inspection of the point estimates,
however, suggests that this evidence, while statistically
significant, is not economically significant. The response
estimates are very similar in magnitude.
For unemployment, the evidence is mixed. There is no evidence
against symmetry using either window as long as energy price shocks
are small. For large shocks, the symmetry test rejects at one
horizon only using the three-year window, but
Table 11a: p-Values of Test of
![]() - 1-Year Net Increase
- 1-Year Net Increase
| H | Gasoline Consumption: 1 Std. Deviation Shock | Gasoline Consumption: 2 Std. Deviation Shock | GDP: 1 Std. Deviation Shock | GDP: 2 Std. Deviation Shock | Unemployment: 1 Std. Deviation Shock | Unemployment: 2 Std. Deviation Shock |
|---|---|---|---|---|---|---|
| 0 | 0.95 |
0.82 |
0.96 |
0.50 |
0.99 |
0.01 |
| 1 | 1.00 |
0.91 |
0.96 |
0.72 |
0.83 |
0.03 |
| 2 | 1.00 |
0.34 |
0.98 |
0.58 |
0.94 |
0.07 |
| 3 | 0.99 |
0.11 |
0.99 |
0.65 |
0.98 |
0.12 |
| 4 | 0.98 |
0.18 |
0.99 |
0.64 |
0.99 |
0.20 |
| 5 | 0.98 |
0.26 |
0.99 |
0.74 |
1.00 |
0.21 |
| 6 | 0.99 |
0.34 |
0.99 |
0.60 |
1.00 |
0.19 |
| 7 | 1.00 |
0.43 |
1.00 |
0.66 |
1.00 |
0.24 |
Table 11b: p-Values of Test of
![]() - 3-Year Net Increase
- 3-Year Net Increase
| H | Gasoline Consumption: 1 Std. Deviation Shock | Gasoline Consumption: 2 Std. Deviation Shock | GDP: 1 Std. Deviation Shock | GDP: 2 Std. Deviation Shock | Unemployment: 1 Std. Deviation Shock | Unemployment: 2 Std. Deviation Shock |
|---|---|---|---|---|---|---|
| 0 | 0.94 |
0.43 |
0.98 |
0.79 |
0.95 |
0.13 |
| 1 | 0.98 |
0.56 |
0.99 |
0.30 |
0.99 |
0.24 |
| 2 | 1.00 |
0.66 |
1.00 |
0.26 |
1.00 |
0.40 |
| 3 | 1.00 |
0.23 |
1.00 |
0.38 |
1.00 |
0.57 |
| 4 | 1.00 |
0.32 |
1.00 |
0.41 |
1.00 |
0.71 |
| 5 | 1.00 |
0.44 |
1.00 |
0.53 |
1.00 |
0.69 |
| 6 | 1.00 |
0.55 |
1.00 |
0.57 |
1.00 |
0.69 |
| 7 | 1.00 |
0.59 |
1.00 |
0.67 |
1.00 |
0.77 |
Notes: Based on 20,000 simulations of model (30).
p-values are based on the
![]() distribution.
distribution.
it rejects systematically using the one-year window. Indeed, the response estimates look fairly asymmetric in the latter case, suggesting caution in imposing symmetry on unemployment responses when considering large energy price shocks. In contrast, for real GDP, which is perhaps the most interesting example from the point of view of macroeconomists, there is not a single rejection of symmetry for any combination of shock size and window.
These empirical results are important in light of the consensus view, exemplified by Davis and Haltiwanger (2001, p. 509), that the evidence for asymmetric responses to oil price ups and downs is well established. Our analysis suggests that the evidence against the symmetry hypothesis has been overstated. It is of course possible that impulse-response-based tests lack the power to detect asymmetries in the data, especially if those asymmetries are relatively weak for shocks of typical size, but the rejections found in some of our empirical examples suggest that lack of power is not a concern.
We certainly would not want to rule out the existence of asymmetries in all possible applications on the basis of our empirical evidence. Part of our objective has been to provide tools for detecting asymmetries and dealing with asymmetries on a case-by-case basis. What our empirical evidence does suggest, however, is that asymmetry in the responses to energy price shocks is clearly not a pervasive and robust feature of the U.S. data. This point is important, as a large literature has developed aiming to explain the perceived asymmetry of responses to energy price shocks from a theoretical point of view (see, e.g., Bernanke 1983; Hamilton 1988; Pindyck 1991). Our evidence casts doubt on the empirical relevance of these theoretical models.
9. Conclusions
A common view in the literature on the transmission of energy price shocks is that the effect of energy price shocks on macroeconomic aggregates such as output or employment is asymmetric in energy price increases and decreases. This perception has been bolstered by empirical evidence that unanticipated percent changes in energy prices tend to have comparatively small effects on the U.S. economy, whereas similar regressions on energy price increases produce much larger effects. Measures of energy price increases in practice are obtained by censoring energy price changes to exclude all energy price decreases.
The censoring of explanatory variables is known to undermine the validity of regression estimates. This point has recently been illustrated in the context of cross-sectional models by Rigobon and Stoker (2007, 2008). As discussed in Rigobon and Stoker (2007), microeconomic data often are released in censored form, leaving the econometrician with no choice but to use these data. In contrast, in studying the effects of energy price shocks on the economy, censoring is optional. The econometrician observes both the censored and the uncensored time series data. This paper discussed various pitfalls that arise when working with censored energy price changes as regressors in dynamic time series models. The dynamic nature of the model was shown to reinforce the conclusions obtained in the static model in some cases and to overturn them in others. Allowing for dynamics also introduces econometric complications that do not arise in cross-sectional models.
We showed that standard methods for estimating the response of macroeconomic aggregates to energy price increases produce inconsistent estimates that tend to exaggerate the quantitative importance of these shocks for the U.S. economy. Although it is common to rely on censored VAR models to analyze the effects of energy price increases on macroeconomic aggregates, we established that structural models of asymmetric effects of energy price increases and decreases do not permit a VAR representation. Estimates of these models are inconsistent. We proposed an alternative structural regression model that allows consistent estimation of the responses in question whether the underlying DGP is symmetric or not. We also observed that conventional estimates of asymmetric responses to energy price shocks are computed as though the model were linear and symmetric. These response estimates are misleading in that they implicitly condition on initial conditions of zero rather than integrating over alternative paths and in that they ignore the dependence of the response on the magnitude of the energy price shock. In practice, they will overstate the importance of energy price increases, even if the underlying regression model is correctly specified and the parameter estimates are consistent. We proposed a suitable method for computing consistent impulse response estimates to positive and negative energy price shocks. We concluded that fundamental changes are required in the models and methods used by empirical researchers to quantify the asymmetric transmission of energy price shocks.
The literature has typically interpreted empirical evidence of quantitatively larger response estimates from censored VAR models of energy price shocks than from linear symmetric VAR models as persuasive evidence of asymmetries. Our analysis suggests that this interpretation is invalid, as the responses in question are inconsistent and biased upward by construction. Formal statistical evidence against the linear symmetric VAR model has been limited to tests of the symmetry of slope parameters in dynamic reduced-form regressions (see, e.g., Mork 1989, Balke et al. 2002, Hamilton 2003). We first proposed a modified slope-based test with higher power than Mork's test and showed that slope-based tests of symmetry in the reduced form parameters can be misleading when it comes to assessing the symmetry of impulse response functions. We then introduced a direct test of the symmetry of the impulse response functions, motivated by the practical limitations of slope-based tests. Finally, we considered versions of these tests designed for models involving net energy price increases.
We applied these tests to representative regression models based on actual U.S. data. We found very little, if any, evidence of asymmetries in the response of U.S. real GDP, unemployment, and gasoline consumption to energy price shocks. Even if we had found evidence of asymmetries, however, such evidence would not have justified the use of standard censored VAR models of energy price increases or the way responses to energy price shocks have been routinely computed from these VAR models. One of the central objectives of this paper has been to alert users to these pitfalls and to develop alternative models and estimation methods.
Our empirical results have important implications for studies of the transmission of energy price shocks. First, one reason that researchers had been eager to accept the apparent finding of asymmetry in the 1990s was that it seemed consistent with theoretical models of the transmission of energy price shocks that emphasized asymmetries through shifts in uncertainty or frictions to the reallocation of factors of production within and across sectors (see, e.g., Bernanke 1983; Hamilton 1988; Pindyck 1991). The latter models were required to rationalize large effects from oil price shocks that are difficult to obtain in conventional models based on cost shocks or aggregate demand shocks. Our evidence provides no support for theoretical models with built-in asymmetries. If such asymmetric effects exist, they appear to be too weak to be detected in aggregate data.
Second, in the absence of asymmetries, the responses of the U.S. economy to energy price shocks appear more modest, which is fully consistent with conventional macroeconomic models of the transmission of energy price shocks that do not predict large fluctuations in U.S. output in response to energy price shocks (see, e.g., Kilian 2008b). Thus, the absence of larger effects is not a puzzle. We conclude that oil price shocks are only one of many factors contributing to recessions, not a key determinant. Our findings also lend credence to recent linear models of how the oil demand and oil supply shocks that drive oil price shocks affect the U.S. economy (see, e.g., Kilian 2008a).
Third, our analysis calls into question several empirical findings reported in the literature about the channels of the transmission of energy price shocks. To the extent that these studies used censored VAR models and/or computed impulse responses to energy price shocks incorrectly, they are invalid. For example, much of the consensus on how monetary policy responds to oil price shocks is based on the censored VAR model introduced by Bernanke, Gertler and Watson (1997). That study and subsequent papers using the same type of model will have to be reexamined in light of our findings. Similarly, influential studies of sectoral responses to oil price shocks such as Lee and Ni (2002) or employment responses at the plant level as in Davis and Haltiwanger (2001) will have to be reexamined.
Appendix: Proof of Inconsistency
Suppose that an i.i.d. series
![]() can be expressed
as a linear combination of
can be expressed
as a linear combination of ![]() and
and
![]()
![]()
|
|
[30] |
where ![]() is a constant and
is a constant and ![]() and
and
![]() are i.i.d.
symmetrically distributed variables with mean zero and finite
fourth moments. Consider the regression model:
are i.i.d.
symmetrically distributed variables with mean zero and finite
fourth moments. Consider the regression model:
|
|
[31] |
where
![\begin{displaymath} {\mathrm{x}}^{\mathrm{+}}_{\mathrm{t}}=\left\{ \begin{array}[c]{c} x_{t}\ \mathrm{if}\ x_{t}>0\ 0\ \mathrm{if}\ x_{t}\le0 \end{array}\right. \end{displaymath}](img328.gif)
The objective is to show that censoring of the explanatory
variable renders
![]() the OLS
estimator of b, inconsistent for
the OLS
estimator of b, inconsistent for ![]() . Recall
that
and
. Recall
that
and
![]()
where
![]() ,
,
![]() ,
,
![]()
![]() and
and
![]()
Recall that
![]() where
where
![]() . Observe that
. Observe that
![]() if
if ![]() is symmetrically distributed around
zero. Because
is symmetrically distributed around
zero. Because
![]() ,
,
![]() and
and
![]() all
are i.i.d with finite variances, a standard application of the weak
law of large numbers implies that the sample averages of these
series will converge in probability to their population means. As
such we have that
all
are i.i.d with finite variances, a standard application of the weak
law of large numbers implies that the sample averages of these
series will converge in probability to their population means. As
such we have that
![]()
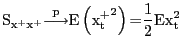
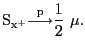
Finally, we have that
![]()
where
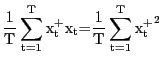
and
![]()
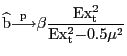
and
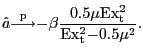
References
Amemiya (1984), "Tobit Models: A Survey" Journal of Econometrics, 2, 105-110.
Bachmeier, L.J., and J.M. Griffin (2003), "New Evidence on Asymmetric Gasoline Price Responses," Review of Economics and Statistics, 85, 772-776.
Balke, N.S., Brown, S.P.A., and M.K. Yücel (2002), "Oil Price Shocks and the U.S. Economy: Where Does the Asymmetry Originate?" Energy Journal, 23, 27-52.
Bernanke, B.S. (1983), "Irreversibility, Uncertainty, and Cyclical Investment," Quarterly Journal of Economics, 98, 85-106.
Bernanke, B.S., M. Gertler, and M. Watson (1997), "Systematic Monetary Policy and the Effects of Oil Price Shocks," Brookings Papers on Economic Activity, 1, 91-142.
Bernanke, B.S., M. Gertler, and M. Watson (2004), "Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy: A Reply," Journal of Money, Credit, and Banking, 36, 286-291.
Borenstein, S., A.C. Cameron and R. Gilbert (1997), "Do Gasoline Prices Respond Asymmetrically to Crude Oil Price Changes?" Quarterly Journal of Economics, 112, 305-339.
Davis, S.J., and J. Haltiwanger (2001), "Sectoral Job Creation and Destruction Responses to Oil Price Changes," Journal of Monetary Economics, 48, 465-512.
Dotsey, M., and M. Reid (1992), "Oil Shocks, Monetary Policy, and Economic Activity."
Economic Review, Federal Reserve Bank of Richmond 14-27.
Edelstein, P., and L. Kilian (2007a), "Retail Energy Prices and Consumer Expenditures," mimeo, Department of Economics, University of Michigan.
Edelstein, P., and L. Kilian (2007b), "The Response of Business Fixed Investment to Energy Price Changes: A Test of Some Hypotheses about the Transmission of Energy Price Shocks," B.E. Journal of Macroeconomics , 7(1) (Contributions).
Ferderer, J.P. (1996), "Oil Price Volatility and the Macroeconomy: A Solution to the Asymmetry Puzzle," Journal of Macroeconomics, 18, 1-16.
Gallant, A.R., P. Rossi, and G. Tauchen (1993). "Nonlinear dynamic structures." Econometrica, 61, 871-907.
Herrera, A.M., and E. Pesavento (2007), "Oil Price Shocks, Systematic Monetary Policy and the 'Great Moderation'", forthcoming: Macroeconomic Dynamics.
Herrera, A.M. (2008), "Oil Price Shocks, Inventories, and Macroeconomic Dynamics," mimeo, Department of Economics, Michigan State University.
Hamilton, J.D. (1983), "Oil and the Macroeconomy since World War II," Journal of Political Economy, 91, 229-248.
Hamilton, J.D. (1988) "A Neoclassical Model of Unemployment and the Business Cycle," Journal of Political Economy, 96, 593-617.
Hamilton, J.D. (1996), "This is What Happened to the Oil Price-Macroeconomy Relationship," Journal of Monetary Economics, 38, 215-220.
Hamilton, J.D. (2003), "What is an Oil Shock?" Journal of Econometrics, 113, 363-398.
Hamilton, J.D., and A.M. Herrera (2004), "Oil Shocks and Aggregate Economic Behavior: The Role of Monetary Policy: Comment," Journal of Money, Credit, and Banking, 36, 265-286.
Hamilton, J.D. (2009a), "Causes and Consequences of the Oil Shock of 2007-08," forthcoming: Brookings Papers on Economic Activity.
Hamilton, J.D. (2009b), "The Oil Shock of 2008," Presentation at the AEA Meetings, San Francisco, January 4, 2009.
Hooker, M.A. (1996a), "What Happened to the Oil Price-Macroeconomy Relationship?" Journal of Monetary Economics, 38, 195-213.
Hooker, M.A. (1996b), "This Is What Happened to the Oil Price-Macroeconomy Relationship: Reply," Journal of Monetary Economics, 38, 221-222.
Hooker, M.A. (2002), "Are Oil Shocks Inflationary? Asymmetric and Nonlinear Specifications Versus Changes in Regime," Journal of Money, Credit, and Banking, 34, 540-561.
Huntington, H.G. (1998), "Crude Oil Prices and U.S. Economic Performance: Where Does the Asymmetry Reside?" Energy Journal, 19, 107-148.
Jiménez-Rodriguez, R., and M. Sánchez (2005), "Oil Price Shocks and Real GDP Growth: Empirical Evidence for Some OECD Countries," Applied Economics, 37, 201-228.
Jones, D.W., P.N. Leiby, and I.K. Paik (2004), "Oil Price Shocks and the Macroeconomy: What Has Been Learned since 1996?"Energy Journal, 25, 1-32.
Kilian, L. (2008a), "Not All Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market," American Economic Review, forthcoming.
Kilian, L. (2008b), "The Economic Effects of Energy Price Shocks" Journal of Economic Literature,46, 871-909.
Kilian, L. (2008c), "Exogenous Oil Supply Shocks: How Big Are They and How Much Do they Matter for the U.S. Economy?" Review of Economics and Statistics, 90, 216-240.
Kilian, L., and C. Vega (2008), "Do Energy Prices Respond to U.S. Macroeconomic News? A Test of the Hypothesis of Predetermined Energy Prices," mimeo, University of Michigan.
Koop, G., Pesaran M.H., S.M. Potter (1996), "Impulse Response Analysis in Nonlinear Multivariate Models," Journal of Econometrics, 74, 119-147
Leduc, S., and K. Sill (2004), "A Quantitative Analysis of Oil Price Shocks, Systematic Monetary Policy and Downturns," Journal of Monetary Economics, 51, 781-808.
Lee, K., and S. Ni (2002), "On the Dynamic Effects of Oil Price Shocks: A Study Using Industry Level Data," Journal of Monetary Economics, 49, 823-852.
Lee, K., S. Ni, and R.A. Ratti (1995), "Oil Shocks and the Macroeconomy: The Role of Price Variability," Energy Journal, 16, 39-56.
Little, R.J.A. (1992), "Regression with Missing X's: A Review," Journal of American Statistical Association, 87, 1227-1237
Manski, C.F. and E. Tamer (2002), "Inference on Regressions with Interval Data on a Regressor or Outcome,"Econometrica, 70, 519-546.
Mork, K.A. (1989), "Oil and the Macroeconomy. When Prices Go Up and Down: An Extension of Hamilton's Results," Journal of Political Economy, 97, 740-744.
Mork, K.A., O. Olsen, and H.T. Mysen (1994), "Macroeconomic Responses to Oil Price Increases and Decreases in Seven OECD Countries." Energy Journal, 15, 19-35.
Pindyck, R.S. (1991), "Irreversibility, Uncertainty and Investment," Journal of Economic Literature, 29, 1110-1148.
Raymond, J.E., and R.W. Rich (1997), "Oil and the Macroeconomy: A Markov-Switching Approach," Journal of Money, Credit, and Banking, 29, 193-213.
Rigobon, R., and T.M. Stoker (2007), "Estimation with Censored Regressors: Basic Issues," International Economic Review, 48, 1441-1467.
Rigobon, R., and T.M. Stoker (2008), "Bias from Censored Regressors," Journal of Business Economics and Statistics, forthcoming.
Footnotes
** Acknowledgments: The corresponding author is Lutz Kilian, University of Michigan, Department of Economics, 611 Tappan Street, Ann Arbor, MI 48109-1220, USA. Email: [email protected]. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. We thank Ana-Mar�a Herrera, James Hamilton, and seminar participants at the Federal Reserve Board, the Federal Reserve Bank of New York, the University of Michigan, Michigan State University, the London School of Economics, Ente Einaudi, Frankfurt University, George Washington University, the International Monetary Fund, Texas A&M, and the University of Houston for helpful comments. Return to text
*** University of Michigan and CEPR Return to text
**** Federal Reserve Board Return to text
1. For an early exposition of this idea, see Hamilton (1983). Return to text
2. Kilian (2008a) recently has discussed some of the reasons for the apparent instability of such regressions in small samples and for the seemingly counterintuitive response estimates occasionally obtained from such regressions. Return to text
3. This finding reinforced results based on measures of oil supply disruptions such as the dummy variable constructed by Hoover and Perez (1994) and the quantitative dummy variable of Hamilton (1996, 2003). It also seemed consistent with evidence using an alternative VAR methodology provided in Davis and Haltiwanger (2001, p. 509), who considered "the evidence for asymmetric responses to oil price ups and downs as well established". Related evidence was provided by Mork, Olsen and Mysen (1994), Ferderer (1996), Hooker (1996a,b; 2002), Hamilton (1996, 2003), Raymond and Rich (1997), Huntington (1998), and Balke, Brown and Yücel (2002), among others. For a critical perspective on this literature see Edelstein and Kilian (2007a,b). Return to text
4. Similar econometric issues also arise in studying the transmission of crude oil price shocks to retail energy prices (see, e.g., Borenstein, Cameron and Gilbert 1997; Bachmeier and Griffin 2003). Return to text
5. A partial exception is Herrera (2008), who conducts a sensitivity analysis based on Balke et al.'s methodology in a not-for-publication appendix. Even Herrera, however, focuses on incorrectly computed impulse responses from censored VAR models in the body of her paper. Return to text
6. Related work also includes Manski and Tamer's (2002) work on interval data and the statistical literature on data that are missing at random (see, e.g., Little 1992). Return to text
7. Analogous results would hold if the
researcher retained only negative values of ![]() and
censored all positive values. The only change in the analysis would
be to replace
and
censored all positive values. The only change in the analysis would
be to replace ![]() with negative
with negative ![]() In
that case, the limit of the estimated intercept is positive and
equals 0.58
In
that case, the limit of the estimated intercept is positive and
equals 0.58 ![]() in magnitude, but the limit of the
slope estimator is the same as in the baseline case - roughly 50
percent larger than the true slope. Return to text
in magnitude, but the limit of the
slope estimator is the same as in the baseline case - roughly 50
percent larger than the true slope. Return to text
8. Additional simulation exercises (not shown to conserve space) confirm that the asymptotic biases reported in Tables 2 and 3 that arise from the misspecification of the regression model carry over to small samples. Relative to models with Gaussian errors, small sample biases may increase substantially when the errors are fat-tailed. Return to text
9. If ![]() were
sufficiently negative that
were
sufficiently negative that ![]() being positive
implies that
being positive
implies that ![]() would be negative, then the
response in the second period would be zero. This result is
discussed in more detail in section 5. Return to text
would be negative, then the
response in the second period would be zero. This result is
discussed in more detail in section 5. Return to text
10. Although we focused on bivariate VAR
models for
![]() ', the
same impulse response inconsistency problems would arise when
fitting trivariate VAR models for
', the
same impulse response inconsistency problems would arise when
fitting trivariate VAR models for
![]() '. Similar
problems also would arise if we were fitting a VAR model involving
'. Similar
problems also would arise if we were fitting a VAR model involving
![]() . Return to text
. Return to text
11. Theoretical models of asymmetry do not imply the strong form of asymmetry but allow for nontrivial effects of both energy price increases and decreases (see Edelstein and Kilian 2007a,b; Kilian 2008b). Return to text
12. If energy prices never declined, this model would suffer from collinearity. But in the data, we observe both energy price increases and declines. Return to text
13. The same algorithm could be applied to model (12) as well, if that model were considered appropriate for applied work. Return to text
14. These results are qualitatively consistent with the findings in Edelstein and Kilian (2007a,b) based on a somewhat different methodology. Return to text
15. Hamilton (2003, Figure 14) provides an estimate of the impulse response function eight quarters ahead based on a single-equation nonlinear reduced-form model designed for one-step-ahead prediction (see p. 392). That estimate suffers from three problems that make it unsuitable for our purposes. First, in constructing the impulse responses Hamilton imposes that the net energy price increases are strictly exogenous. That assumption is unnecessarily restrictive and has been shown to be economically and empirically implausible (see Kilian 2008b,c). Second, Hamilton's model omits the contemporaneous regressor in constructing the impulse response function. Third, Hamilton ignores the nonlinear nature of the model in computing the impulse response function. Return to text
16. By construction, a one standard deviation shock is a typical shock in that about two-thirds of energy price shocks in historical data are no larger than one standard deviation. Return to text
17. An alternative and asymptotically equivalent approach would have been to test the equality of the impulse responses obtained from the linear model on the one hand and either the response to an energy price increase or a decrease on the other. We do not pursue that approach because it is not clear how to use the bootstrap to evaluate the variance of the Wald test statistic in that case. In contrast, the symmetry test is straightforward to implement. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text